2 ))
Содержание
Как найти периметр основания правильной треугольной пирамиды
Правильная пирамида обладает следующими свойствами:
- боковые рёбра правильной пирамиды имеют равную величину;
- в правильной пирамиде каждая боковая грань — конгруэнтный равнобедренный треугольник;
- во все правильные пирамиды можно как вписать, так и описать вокруг неё сферу;
- когда центры вписанной и описанной сферы совпадают, значит, сумма плоских углов у вершины пирамиды равняется , а всякий из них соответственно , где n — число сторон многоугольника основания;
- площадь боковой поверхности правильной пирамиды равняется ½ произведения периметра основания на апофему.
Формулы для правильной пирамиды.
V — объем пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды,
Sb — площадь боковой поверхности пирамиды,
a — апофема (не путать с α) пирамиды,
P — периметр основания пирамиды,
n — число сторон основания пирамиды,
b — длина бокового ребра пирамиды,
α — плоский угол при вершине пирамиды.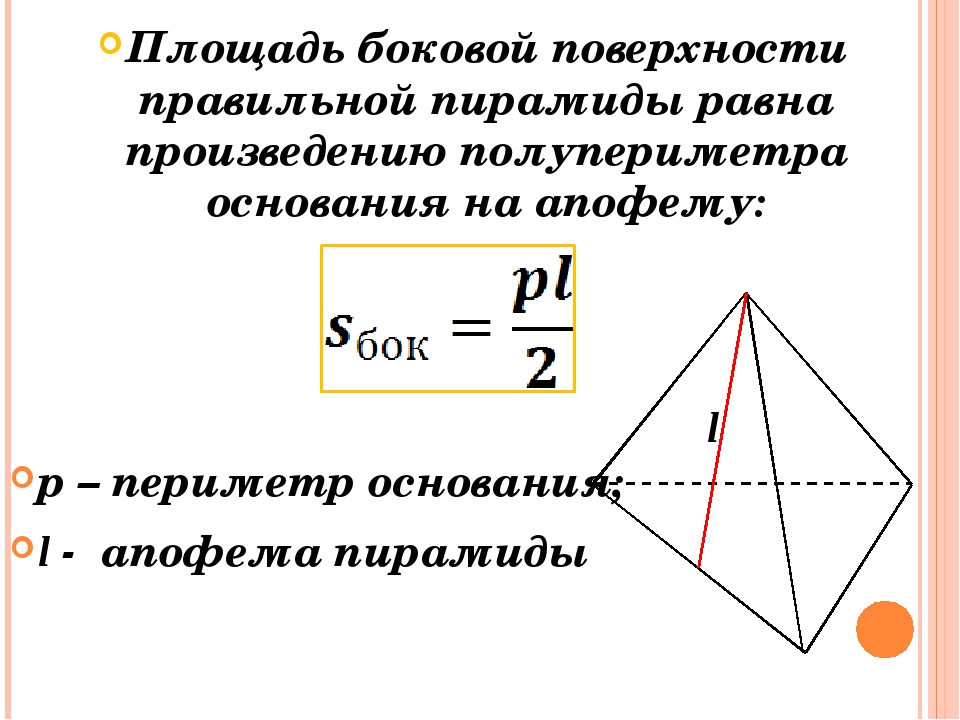
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
V — объем правильной пирамиды,
h — высота правильной пирамиды,
n — количество сторон правильного многоугольника, основания правильной пирамиды,
a — длина стороны правильного многоугольника.
Боковое ребро правильной пирамиды находят по формуле:
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) — основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида — это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
V — объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h — высота правильной пирамиды,
a — длина стороны основания правильной пирамиды.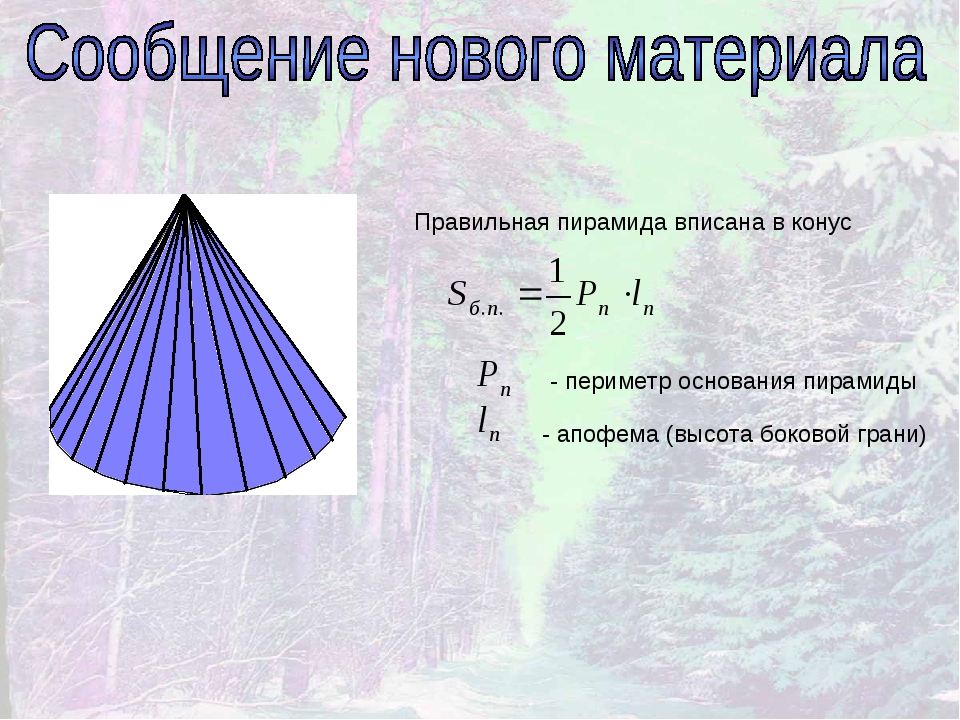
Так как правильная треугольная пирамида — это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Пирамида, основные понятия и элементы
Вспомним понятие n-угольной пирамиды. Она получается следующим образом: в плоскости
Определение.
Многогранник
Читайте также: Как записывать с помощью веб камеры
Площадь поверхности пирамиды состоит из площади боковой поверхности и площади основания:
Площадь основания пирамиды, площади основных правильных многоугольников
Рассмотрим нахождение площади основания правильной n-угольной пирамиды. Правильный n-угольник, как нам известно, имеет равные стороны и равные внутренние углы. Решим следующую задачу: для n-угольника с заданной длиной стороны () и количеством углов (n) найти площадь (рисунок 2).
Рис. 2. Нахождение площади n-угольника
Рассмотрим треугольник
Половина этого угла, угол .
Треугольник Чтобы найти площадь n-угольника, нужно сложить n площадей треугольников вида
Площадь треугольника определяется по формуле:
Теперь получим площадь всего n-угольника:
Рассмотрим наиболее распространенные частные случаи:
Площадь правильного треугольника:
Площадь правильного шестиугольника:
Чтобы нарисовать правильный шестиугольник, удобно пользоваться следующим алгоритмом (рисунок 3):
Построить окружность (зеленая пунктирная линия) Провести диаметр (синяя пунктирная линия) Отметить середины радиусов построенного диаметра Провести через середины перпендикуляры (красные пунктирные линии) Получены вершины шестиугольника – построить шестиугольник.
Рис. 3. Правильный шестиугольник
Чтобы найти площадь правильного шестиугольника действуем стандартным методом. Рассматриваем треугольник АОС, в нем находим угол ∠АОВ, таких углов шесть, имеем:
Рассматриваем треугольник АОС, в нем находим угол ∠АОВ, таких углов шесть, имеем:
Поскольку отрезки ОА и ОВ равны, то углы ∠ОАВ и ∠ОВА также составляют по . Так, рассматриваемый треугольник правильный. Его площадь нам известна:
Площадь шестиугольника состоит из шести таких площадей:
Площадь боковой поверхности пирамиды
Рассмотрим нахождение площади боковой поверхности правильной пирамиды.
Где
Рис. 4. Иллюстрация к задаче 1
Задана правильная пирамида с вершиной Р и основанием АВС. РН – высота пирамиды, РО – апофема. Сторона основания равняется По вышеприведенной формуле для того, чтобы найти площадь боковой поверхности пирамиды, необходимо найти ее апофему и полупериметр основания. Периметр основания нам известен, так как задана сторона основания. Найдем апофему из прямоугольного треугольника РНО. Один из катетов задан по условию – . Найдем второй катет ОН, он соответствует радиусу вписанной в треугольник окружности, формула нам известна:
Найдем апофему по теореме Пифагора:
Теперь можем найти площадь боковой поверхности пирамиды:
Связь площади треугольника с площадью его проекции
Площадь боковой поверхности и площадь основания пирамиды связаны через величину двугранного угла при основании.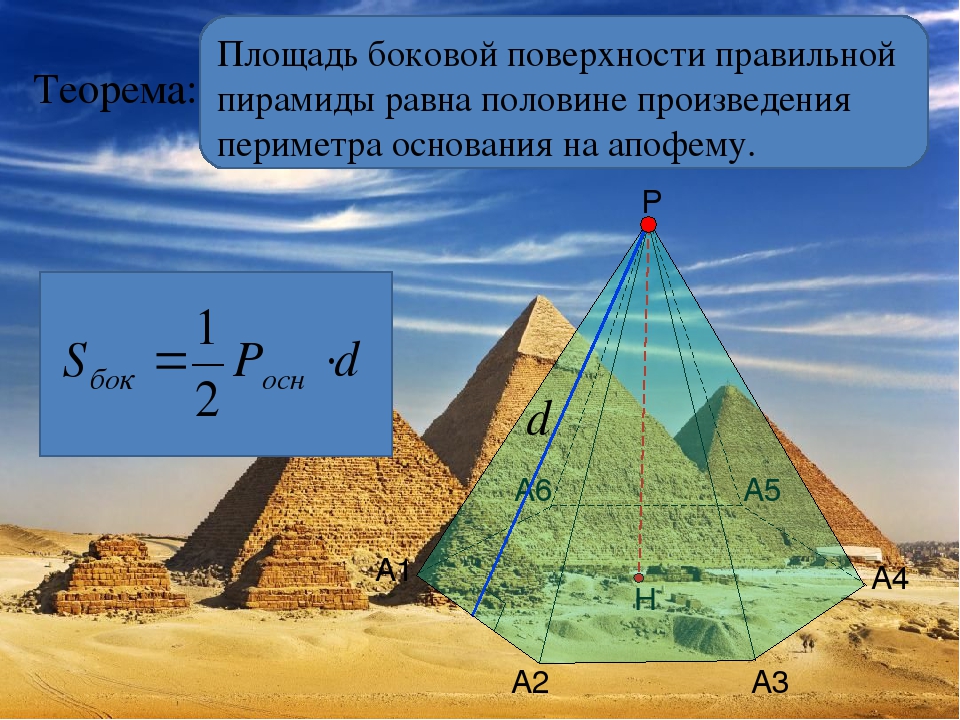
Решение задач
Задача 2
РН – перпендикуляр к плоскости треугольника АВН. Из точки Н опущен перпендикуляр НМ к прямой АВ. . Доказать:
Решение. Проиллюстрируем условие:
Рис. 5. Иллюстрация к задаче 2
Треугольник АВН – это проекция треугольника АВР. Нужно доказать, что площадь проекции есть площадь исходного треугольника на косинус двугранного угла между ними. Поскольку НМ – перпендикуляр к АВ, то и РМ – перпендикуляр к АВ по теореме о трех перпендикулярах. Значит, угол – это линейный угол двугранного угла с ребром АВ. АВР – часть боковой поверхности, АВН – часть основания.
Найдем отношение площадей интересующих нас треугольников:
Рассмотрим прямоугольный треугольник РНМ. В нем РМ – гипотенуза, НМ – катет, прилежащий к заданному углу . Отсюда заключаем:
Что и требовалось доказать.
Задача 3
Доказать для правильной треугольной пирамиды:
Рис. 6. Иллюстрация к задаче 3
6. Иллюстрация к задаче 3
Задана правильная треугольная пирамида РАВС с основанием АВС и вершиной Р. – линейный угол двугранного угла с ребром АВ, точкой Р в одной плоскости и точкой С в другой плоскости.
Очевидно, что угол наклона В задаче 2 мы доказали: .
Выполним сложение полученных выражений.
Что и требовалось доказать.
Задача 4
Боковые грани пирамиды РАВС наклонены к основанию под одним и тем же углом
Рис. 7. Иллюстрация к задаче 4
Пусть РО – высота пирамиды. Найдем место расположения точки О. Из точки О опустим перпендикуляры к сторонам треугольника АВС – .
Поскольку
Выполним сложение полученных выражений.
Что и требовалось доказать.
Итак, мы рассмотрели площадь поверхности пирамиды, в частности, площадь основания и площадь боковой поверхности, следующий урок будет посвящен задачам.
Список литературы
- И.
 М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил. - Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
- Задача 1: основанием пирамиды является квадрат, одно из боковых ребер перпендикулярно основанию. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Оценка статьи:
Загрузка…
Поделиться с друзьями:
Найдите периметр основания правильной четырехугольной пирамиды, высота которой равна 6 см и
Длина отрезка DE равна 5ми LM : DE = 5:1.
Вычисли длину отрезка LM.
Ответ: LM =
М.
Помогите пожалуйста решить задачи, с чертежами.
1)Боковое ребро прямой четырехугольной призмы равно 6 см, её основание – прямоугольник, одна из сторон
…
которого равна 12 см, а диагональ – 13 см. Найдите площадь полной поверхности призмы.
2) Сторона основания правильной треугольной пирамиды равна 6 см, а высота пирамиды — √13 см. Найдите: 1) боковое ребро пирамиды; 2) площадь боковой поверхности пирамиды.
3) Точка В находится на расстоянии 3√2 см от плоскости α. Наклонные ВА и ВС образуют с плоскостью α углы 60° и 30° соответственно. Найдите расстояние между точками А и С, если угол между проекциями наклонных равен 120°
4) Точка А равноудалена от прямых содержащих стороны правильного треугольника со стороной 30 см и находится на расстоянии 5 см от плоскости треугольника. + (y + 2)2 = 4
+ (y + 2)2 = 4
б) Определите взаимное расположение
окружности (х – 1)2 + (y+ 2)2 = 4 и прямой х=
…
3
нужна помощь!!!!!умные люди помогите!!
помогите срочно!!! задание 4 и 5
Точки А, В и С лежат на окружности. Вычисли угoл ACB, который образуют хорды AC и BC,если дуга ∪BmC= 114°, дуга ∪AnC= 145°.Ответ: ∢ ACB=
Дан треугольник АВС.Найдите сторону ВС,если АВ=3см,угол А=45° ,угол С =60°
Градусная мера дуги ACB равна 290°.Найди угол ∡AOB.Ответ: ∡AOB =
Помогите решить пожалуйста
1. Дана окружность радиусом 12 см. Чему равна длина дуги с градусной мерой 135°.А. блB 9trC. StrД.2. Три угла четырехугольника, вписанного в окружност
…
ь, взятые в порядке следования, относятся как3:7:9. Найдите углы четырехугольника.3. В окружность вписан квадрат со стороной 1,2//2см. Найдите площадь правильного треугольника,описанного около этой окружности.4. Основание АВ треугольника АВС равно 26см Медианы АК и ВМ, проведенные к боковым сторонам,равны соответственно 48 сми 45 см. Найдите площадь треугольника АВС.5. На рисунке изображен сектор круга с центром в точке О и радиусом, равным 10см (OA). OD=2см и уголDOC=45° Найдите площадь закрашенной области. (ответ округлите до целой части)РЕБЯТА ПОМОГИТЕ ПОЖАЛУЙСТА МНЕ СРОЧНО ДАМ 100 БАЛЛОВ
Найдите площадь треугольника АВС.5. На рисунке изображен сектор круга с центром в точке О и радиусом, равным 10см (OA). OD=2см и уголDOC=45° Найдите площадь закрашенной области. (ответ округлите до целой части)РЕБЯТА ПОМОГИТЕ ПОЖАЛУЙСТА МНЕ СРОЧНО ДАМ 100 БАЛЛОВ
Площадь боковой поверхности пирамиды — формула, пример расчета
Пирамида – это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.
Если в основании лежит квадрат, то пирамиду называется четырехугольной, если треугольник – то треугольной. Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:
В основном площадь пирамиды рассчитывается через периметр основания и апофему:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана пирамида с основанием ABCDE и вершиной F. AB=BC=CD=DE=EA=3 см. Апофема a = 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:
Площадь правильной треугольной пирамиды
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Площадь усеченной пирамиды
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная четырехугольная пирамида. Длины основания равны b = 5 см, c = 3 см. Апофема a = 4 см. Найдите площадь боковой поверхности фигуры.
Для начала найдем периметр оснований. В большем основании он будет равен:
В меньшем основании:
Посчитаем площадь:
Таким образом, применив несложные формулы, мы нашли площадь усеченной пирамиды.
Как найти периметр пирамиды формула. Площадь треугольной пирамиды
Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной
.
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угля пирамиды также равны между собой;
- Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P
– периметр основания, a
– длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете .Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофема равна a
= 7 см, сторона основания b
= 3 см. Рассчитайте площадь боковой поверхности многогранника.
Рассчитайте площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:
Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условия из прошлого примера.Из них мы знаем, что сторона основания b
= 3 см. Подставим данные в формулу:
Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:
Рассмотрим пример расчета площади шестиугольной пирамиды.
Пусть дана пирамида, в основании которой лежит правильный шестиугольник со стороной b
= 4 см.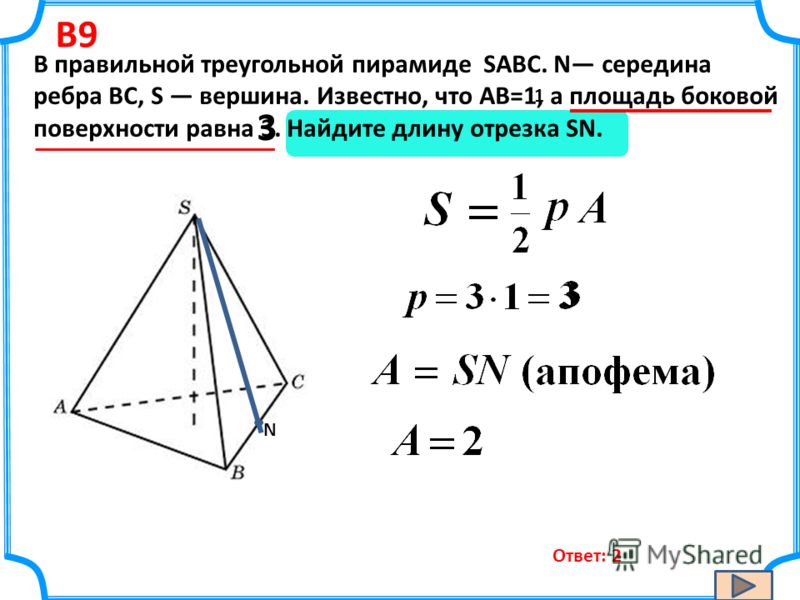 Апофема заданного многогранника равна a
Апофема заданного многогранника равна a
= 6 см. Найдите полную площадь.
Мы знаем, что полная площадь состоит из площадей основания и боковой развертки. Поэтому для начала найдем их. Рассчитаем периметр:
Теперь найдем площадь боковой поверхности:
Далее рассчитываем площадь основания, в котором лежит правильный шестиугольник:
Теперь можем сложить получившиеся результаты:
Треугольной пирамидой
называется многогранник, в основании которого лежит правильный треугольник.
В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле . А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
где p
– периметр основания, у которого все стороны равны b, a
– апофема, опущенная из вершины к этому основанию.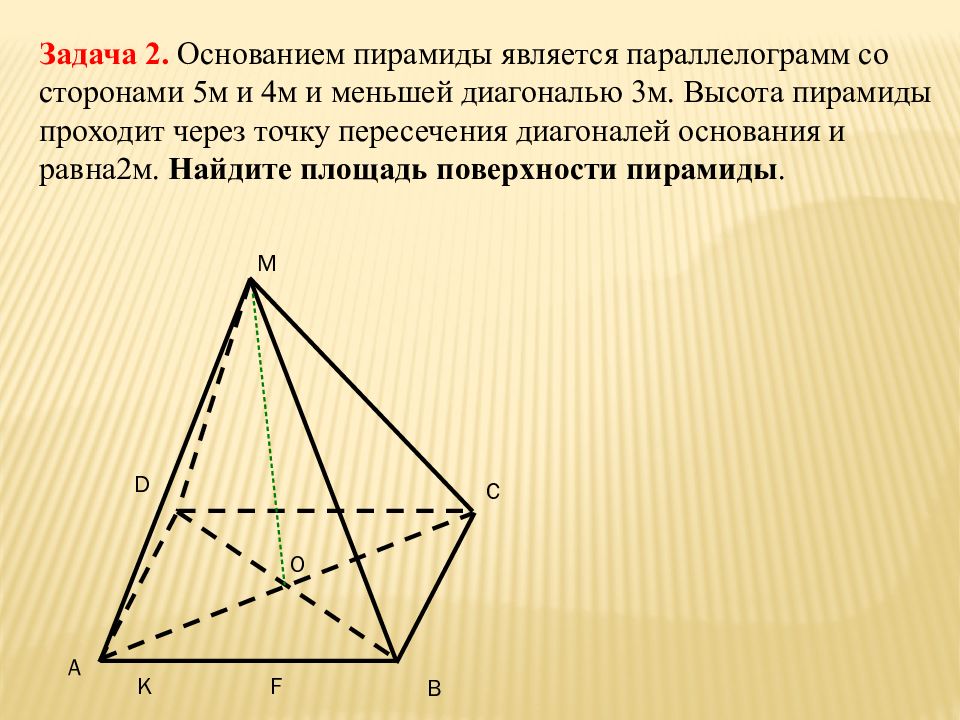 Рассмотрим пример расчета площади треугольной пирамиды.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b
= 4 см. Апофема пирамиды равна a
= 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:
Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника. Для этого используется формула :
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a
= 6 см.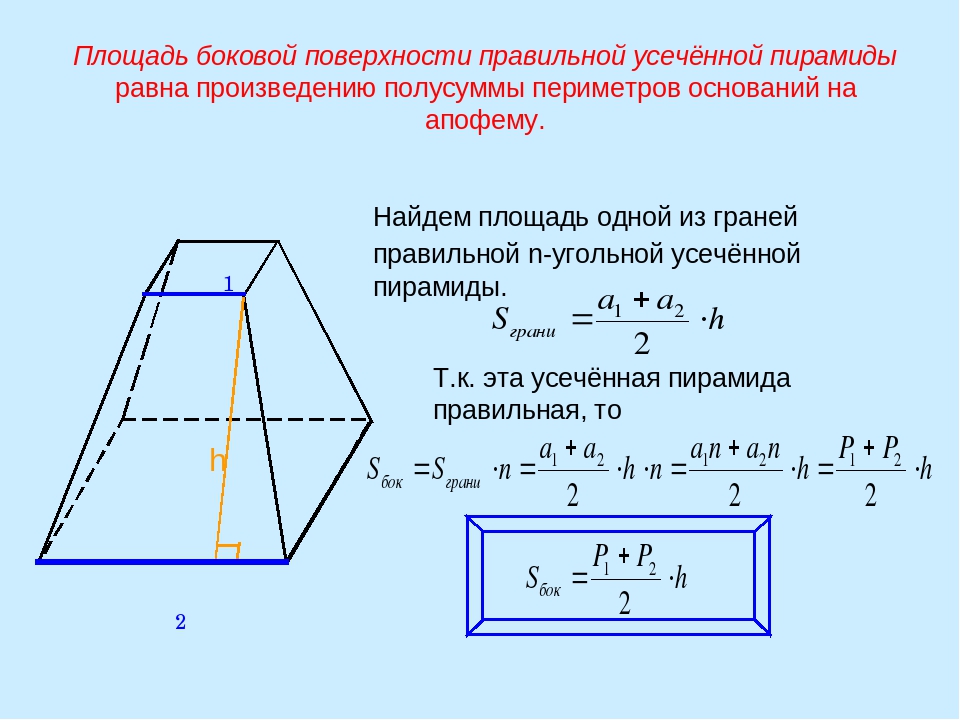 Рассчитайте площадь основания.
Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: пусть дана правильная треугольная пирамида. Сторона основания равна b
= 4 см, апофема a
= 6 см. Найдите полную площадь пирамиды.
Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:
Подставляем данные в формулу:
Теперь найдем площадь основания:
Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды:
При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.
Определение.
Боковая грань
— это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).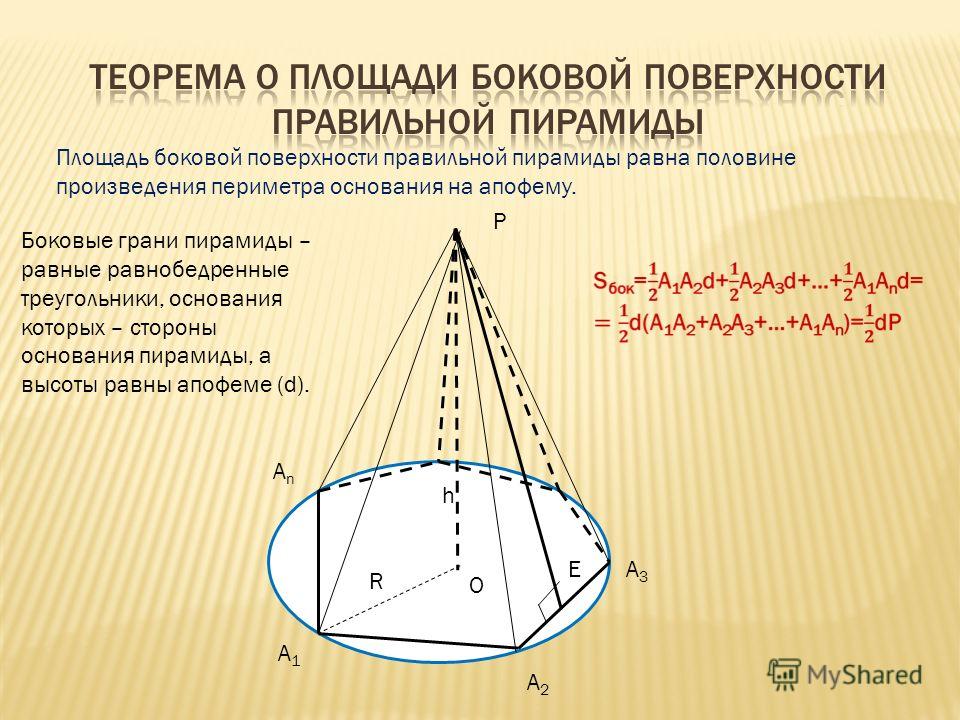
Определение.
Боковые ребра
— это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение.
Высота пирамиды
— это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение.
Апофема
— это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение.
Диагональное сечение
— это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение.
Правильная пирамида
— это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула.
Объём пирамиды
через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).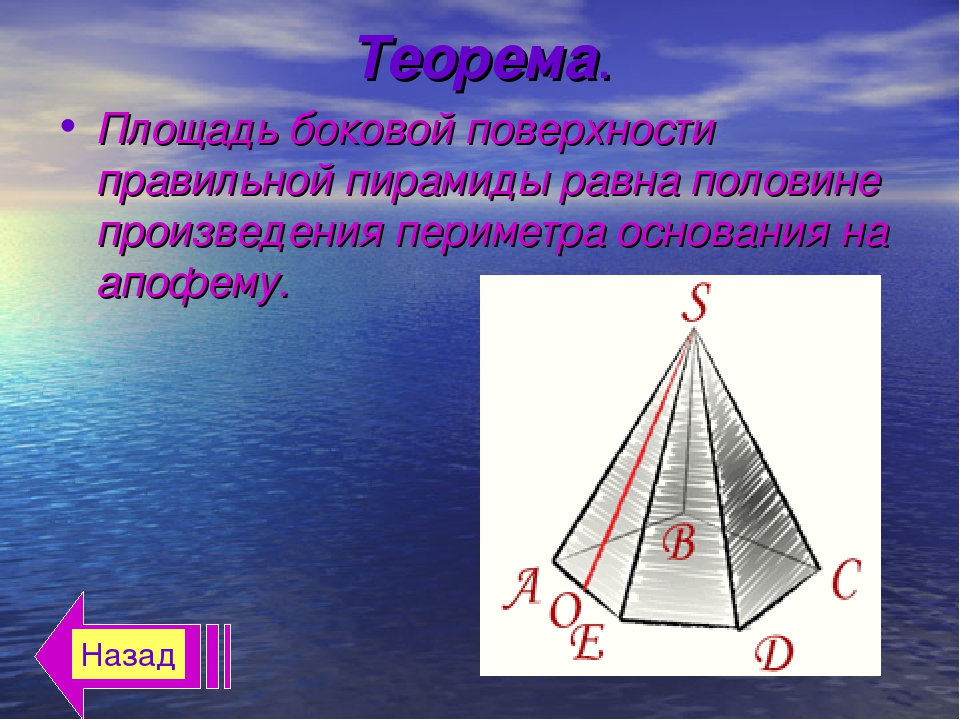
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n
, где n
— это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение.
Усеченная пирамида (пирамидальная призма)
— это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
Определение.
Треугольная пирамида (четырехгранник)
— это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол
.
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника
(GM).
Бимедианой
называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение.
Наклонная пирамида
— это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
Определение.
Прямоугольная пирамида
— это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение.
Остроугольная пирамида
— это пирамида в которой апофема больше половины длины стороны основания.
Определение.
Тупоугольная пирамида
— это пирамида в которой апофема меньше половины длины стороны основания.
Определение.
Правильный тетраэдр
— четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение.
Прямоугольный тетраэдр
называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол
и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение.
Равногранный тетраэдр
называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение.
Ортоцентричный тетраэдр
называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение.
Звездная пирамида
называется многогранник у которого основой является звезда.
Определение.
Бипирамида
— многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.
Как быть при нахождении площади основания пирамиды?
Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.
Правильный треугольник
То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:
S = (а 2 * √3) / 4.
Квадрат
Формула для вычисления его площади самая простая, здесь «а» — снова сторона:
Произвольный правильный n-угольник
У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.
S = (n * а 2) / (4 * tg (180º/n)).
Как поступить при вычислении площади боковой и полной поверхности?
Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.
Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение — «А». Общая формула для площади боковой поверхности выглядит так:
S = ½ Р*А, где Р — периметр основания пирамиды.
Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:
S = n/2 * в 2 sin α.
Задача № 1
Условие.
Найти общую площадь пирамиды, если в его основании лежит со стороной 4 см, а апофема имеет значение √3 см.
Решение.
Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см 2 .
Для треугольника в основании получится такое значение площади: (4 2 *√3) / 4 = 4√3 см 2 .
Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см 2 .
Ответ.
10√3 см 2 .
Задача № 2
Условие
. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.
Решение.
Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Первые расчеты просты и приводят к такому числу: 49 мм 2 . Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 мм 2 . Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.
Получается: 49 + 4*54,644 = 267,576 мм 2 .
Ответ
. Искомое значение 267,576 мм 2 .
Задача № 3
Условие
. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.
Решение.
Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.
Придется вспомнить теорему Пифагора и рассмотреть Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.
Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3 2 + 4 2) = 5 (см).
Теперь можно вычислять искомую величину: ½*(4*6)*5+6 2 = 96 (см 2).
Ответ.
96 см 2 .
Задача № 4
Условие.
Дана правильная Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?
Решение.
Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом вычисляется площадь основания по указанной выше формуле: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см 2 .
Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.
Расчеты по формуле Герона: √(72*(72-22)*(72-61) 2)=√435600=660 см 2 . Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см 2 . Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2 .
Ответ.
Основания — 726√3 см 2 , боковой поверхности — 3960 см 2 , вся площадь — 5217 см 2 .
Площадь треугольной пирамиды — формула, пример расчета
Треугольной пирамидой называется многогранник, в основании которого лежит правильный треугольник.
В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле площади равностороннего треугольника. А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
где p – периметр основания, у которого все стороны равны b, a – апофема, опущенная из вершины к этому основанию. Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b = 4 см. Апофема пирамиды равна a = 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:
Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника. Для этого используется формула площади правильного треугольника:
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a = 6 см. Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.
При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.
Тема 10. Стереометрия — Материалы для подготовки к вступительным экзаменам в СГГА
Если AB||A’B’ и BC||B’C’, то плоскости ABC и A’B’C’ параллельны.
Прямая BC, лежащая в плоскости ABC, перпендикулярна наклонной DB, тогда и только тогда, когда она перпендикулярна ее проекции на плоскость AB.
Площадь поверхности: S=2Sосн+Sбок, где Sбок – площадь боковой поверхности, равная сумме площадей всех граней.
Прямая призма – призма, боковое ребро которой перпендикулярно основанию.
Объем: V=Sосн∙l .
Площадь боковой поверхности: Sбок=P∙l, где P – периметр основания.
Правильная призма – прямая призма, основание которой – правильный многоугольник.
1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
2) В прямой треугольной призме основания равны 36, 29 и 25, а полная поверхность призмы 1620. Найдите высоту призмы.
3) В основании прямой призмы лежит равнобедренный прямоугольный треугольник с гипотенузой, равной . Диагональ боковой грани, соответствующей катету, равна 13. Найдите объем призмы.
4) Стороны основания прямой треугольной призмы равны 10, 17 и 21, а ее боковое ребро равно меньшей из высот основания. Найдите объем призмы.
5) Объем правильной треугольный призмы равен . Найдите высоту призмы, если радиус описанной около основания окружности равен 2. 6) Высота правильной треугольной призмы равна 8, а площадь основания . Найдите диагональ боковой грани призмы. 7) Все ребра прямой треугольной призмы равны. Найдите площадь основания призмы, если площадь ее полной поверхности равна . 8) Высота правильной четырёхугольной призмы равна , а диагональ призмы наклонена к плоскости основания под углом 300. Найти сторону основания призмы. 9) Основание прямой призмы – прямоугольный треугольник с катетами 6м и 8м, а диагональ большей по площади боковой грани равна м. Найдите объём призмы. 10) Найдите площадь поверхности куба, диагональ которого равна . 11) Площадь диагонального сечения куба равна . Найдите ребро куба.
12) Сумма длин всех ребер куба равна 48. Чему равна площадь всех его граней?
13) Если ребро куба уменьшить на 10%, на сколько процентов уменьшится его объем?
14) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Расстояние от плоскости сечения до вершины нижнего основания, не лежащей в плоскости сечения, равно 5см. Площадь сечения равна 10см2. Найти объём параллелепипеда.
15) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объём меньшего из двух многогранников, на которые параллелепипед делится плоскостью сечения, равен 40см3. Найдите объём параллелепипеда.
16) Стороны основания прямоугольного параллелепипеда 6м и 8м, а угол между диагональю параллелепипеда и плоскостью основания 300. Найдите диагональ параллелепипеда.
17) Стороны основания прямоугольного параллелепипеда равны 4м и 3м, а угол между диагональю параллелепипеда и плоскостью основания 450. Найдите длину диагонали параллелепипеда.
18) Сторона основания правильной треугольной призмы ABCDA1B1C1D1 равна 12, а боковое ребро . Найдите градусную меру угла между плоскостями A1BC и ABC. 19) ABCDA1B1C1D1 – призма, в основании которой лежит квадрат, боковые ребра которой наклонены к плоскости основания под углом 300. Диагональ AD1 перпендикулярна плоскости основания. Площадь боковой поверхности призмы равна . Найдите объем призмы. 20) В основании прямой призмы ABCDA1B1C1D1 лежит квадрат. Боковое ребро равно . Найдите длину стороны основания, если угол между плоскостью AB1C и плоскостью основания призмы равен 300.
21) Ребра треугольной пирамиды длины 4, 5 и 9 взаимно перпендикулярны. Чему равен объем пирамиды?
22) Пирамида имеет 28 ребер. Сколько у нее граней?
23) Высота правильной треугольной пирамиды равна 15, а высота ее основания 12. Найдите длину бокового ребра.
24) Высота правильной треугольной пирамиды в два раза меньше стороны основания. Найдите угол между боковой гранью пирамиды и плоскостью основания.
25) Сторона основания правильной треугольной пирамиды равна 10 см. Боковые грани наклонены к плоскости основания под углом 450. Найдите высоту пирамиды.
26) Боковое ребро правильной треугольной пирамиды равно 10, а периметр основания 36. Найдите высоту пирамиды.
27) В правильной четырёхугольной пирамиде высота равна 3см, а площадь боковой поверхности 80см2. Найти объём пирамиды.
28) Боковые грани правильной четырёхугольной пирамиды наклонены к плоскости основания под углом 600. Площадь основания равна 14м2. Найти площадь боковой поверхности пирамиды.
29) В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 600. Сторона основания пирамиды равна 6см. Найдите объём пирамиды.
30) В правильной четырёхугольной пирамиде апофема образует с плоскостью основания угол 600. Высота пирамиды равна 8см. Найдите площадь поверхности пирамиды.
31) В правильной треугольной пирамиде высота равна , а величина двугранного угла при основании 600. Найдите сторону основания пирамиды.
32) В правильной треугольной пирамиде высота равна 4, а апофема равна 5. Найдите сторону основания пирамиды.
33) Высота треугольной пирамиды SABC равна 8, а площадь треугольника ABC 12. Точки A1, B1, C1 делят ребра SA, SB и SC в отношении 1 : 1. Найдите объем усеченной пирамиды ABCA1B1C1.
34) В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами AC=4 и BC=3. Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
35) Найдите площадь боковой поверхности цилиндра, если площадь его осевого сечения равна 12.
36) Площадь основания цилиндра равна 4, а площадь его боковой поверхности равна . Найдите высоту цилиндра. 37) Высота и радиус основания цилиндра равны, соответственно, 9 и 6. Концы отрезка AB длины лежат на окружностях верхнего и нижнего оснований. Найдите расстояние от оси цилиндра до отрезка AB.
38) Радиус основания конуса равен 6, а образующая составляет с плоскостью основания угол, равный 300. Найдите расстояние от центра основания до образующей.
39) Образующая конуса равна диаметру его основания. Найдите площадь боковой поверхности конуса, если его высота равна .
40) Площадь осевого сечения конуса равна 8, а радиус основания 2. Найдите площадь боковой поверхности конуса.
41) Осевое сечение конуса – правильный треугольник со стороной . Найдите полную поверхность конуса.
42) Из точки M вне шара проведена касательная AM к его поверхности. Кратчайшее расстояние от этой точки до поверхности шара равно 6, а до центра шара 15. Найдите длину AM.
43) Если радиус сферы увеличить на 50%, на сколько процентов увеличится площадь ее поверхности?
44) Радиус шара равен . Через конец радиуса под углом 600 к нему проведена плоскость. Найти площадь сечения шара плоскостью.
45) Стороны треугольника, равные 10, 10 и 12 касаются поверхности шара Найдите радиус шара, если расстояние от центра шара до плоскости треугольника равно 4.
46) Как относятся объемы куба и описанного около него шара?
47) В шар объема вписан конус, таким образом, что основанием конуса является осевое сечение шара. Найдите площадь осевого сечения конуса.
Видео с вопросом: Определение периметра основания пирамиды с учетом ее объема и высоты
Стенограмма видеозаписи
Учитывая, что квадратная пирамида имеет
объемом 372 кубических сантиметра и высотой 31 сантиметр определяют
периметр его основания.
Итак, давайте смоделируем нашу квадратную пирамиду.
объемом 372 кубических сантиметра. Рост 31 сантиметр относится к
к высоте перпендикуляра пирамиды.Нас просят разработать
периметр основания этой квадратной пирамиды. Это расстояние полностью
вокруг снаружи.
Давайте посмотрим, что мы знаем о
объем пирамиды. Напомним, что объем
пирамида равна одной трети, умноженной на площадь основания, умноженную на
высота. Это не поможет нам напрямую в работе
по периметру. Но если бы мы могли проработать область
базы, мы могли бы продолжить работу по периметру.Итак, начнем с заполнения поля
информация, которую мы знаем в этой формуле.
Это даст нам 372 — это
объем пирамиды — равен 1/3 площади основания, умноженной на 31, что
высота пирамиды. Мы можем упростить правую часть
записав треть, умноженную на 31, как 31 на три. Затем мы хотим изолировать область
основание, поэтому мы выполняем операцию, обратную умножению на 31 на три.И это разделить на 31 больше
три, то есть умножить на три больше 31. Итак, у нас 372 раза три больше 31
равна площади основания.
Затем мы можем оценить это без
калькулятор, заметив, что 31 переходит в 372 12 раз. Это означает, что площадь основания
равно 12 умноженным на три, что составляет 36 квадратных сантиметров. Итак, теперь, когда мы разработали
площадь квадрата на основании, мы можем использовать это, чтобы определить длину сторон
и, следовательно, рассчитать периметр.
Итак, если длина наших сторон составляет 𝑥 на
𝑥, это означает, что площадь 𝑥 в квадрате будет равна 36. Следовательно, длина 𝑥 равна
к квадратному корню из 36, что составляет шесть сантиметров. Итак, периметр, который
расстояние вокруг внешней стороны этого квадрата равно шести плюс шесть плюс шесть плюс
шесть, что составляет 24 сантиметра.
Видео с вопросом: Определение периметра основания пирамиды с учетом ее объема и высоты
Стенограмма видеозаписи
Учитывая, что квадратная пирамида имеет
объемом 372 кубических сантиметра и высотой 31 сантиметр определяют
периметр его основания.
Нам не выдали схему
здесь, но иногда бывает полезно сделать набросок. Во-первых, нам говорят, что это
квадратная пирамида, поэтому мы будем знать, что длина и ширина будут одинаковыми
измерение на базе. Нам дан объем
пирамида равна 372 кубическим сантиметрам, а высота перпендикуляра равна 31
сантиметры. Напомним, что объем
пирамида равна одной трети площади основания, умноженной на перпендикуляр
высота.Мы можем использовать тот факт, что мы
учитывая объем пирамиды и ее высоту по перпендикуляру, чтобы найти площадь
база. Это позволит нам тогда
рассчитать периметр основания.
Можно подставить в значения
тогда. Объем 372, высота
31, чтобы получить 372, равно одной трети площади основания, умноженной на 31. Умножая обе стороны на три, мы
иметь 1116 равно площади основания, умноженной на 31.Затем мы разделим обе стороны на 31, чтобы
дайте нам площадь основания 36 квадратных сантиметров. Итак, как нам перейти от знания
площадь основания этой пирамиды до ее периметра? Что ж, помните, что база — это
квадратный. Итак, если мы определим длину одного
сторона как 𝑙, тогда все остальные стороны будут иметь длину 𝑙. Площадь квадрата будет
рассчитывается как 𝑙 в квадрате. В этом случае 𝑙 в квадрате должно иметь
дал нам 36.Чтобы вычислить we, мы возьмем
квадратный корень из обеих сторон, а квадратный корень из 36 равен шести. И, конечно же, единицы длины
будет в сантиметрах.
Чтобы найти периметр, это
расстояние по внешнему краю. Мы могли бы добавить шесть, шесть и шесть
а шесть или более просто сложить шесть умножить на четыре, что даст нам значение
24. И поскольку периметр по-прежнему
длина, то у нас будут сантиметры.Итак, мы обнаружили, что периметр
основания этой пирамиды составляет 24 сантиметра, и мы сделали это, используя объем
Сначала рассчитываем площадь основания.
Пирамиды
Когда мы думаем о пирамидах, мы думаем о Великих пирамидах Египта .
На самом деле это Квадратные пирамиды , потому что их основание — Квадрат.
Части пирамиды
Пирамида создается путем соединения основания с вершиной
Основание — многоугольник (плоский с прямыми краями), а все остальные грани — треугольники.Никаких кривых!
Типы пирамид
Есть много типов пирамид, и они названы в честь формы их основания.
Пролетите здесь через пирамиды.
Правая и наклонная пирамида
Это говорит нам, где находится вершина (вершина) пирамиды. Когда вершина находится прямо над центром основания, это правая пирамида , в противном случае — наклонная пирамида .
| Правая пирамида | Наклонная пирамида |
|---|
Обычная и неправильная пирамида
Это говорит нам о форме основания .Когда основание представляет собой правильный многоугольник, это правильная пирамида , в противном случае это неправильная пирамида .
| Правильная пирамида | Неправильная пирамида |
|---|---|
| Базовый стандарт | База нестандартная |
Площадь и объем
Объем пирамиды
- 1 / 3 × [Базовая площадь] × Высота
Площадь пирамиды
Если все боковые грани одинаковые:
- [Базовая область] +
1 / 2 × периметр × [наклонная длина]
Если боковые грани разные:
- [Базовая область] + [Боковая область]
Заметки о площади
Площадь поверхности состоит из двух частей: площади основания ( Базовая область ) и площади боковых граней (боковой поверхности ).
Для Базовая область :
Это зависит от формы, существуют разные формулы для треугольника, квадрата и т. Д. См. Формулы «Площадь» или наш Инструмент расчета площади
Для Боковая зона :
Когда все боковые грани одинаковые:
- Умножьте периметр на «длину наклона» и разделите на 2. Это потому, что боковые грани всегда являются треугольниками, а формула треугольника: дюймов, умноженная на высоту, деленную на 2 »
Но когда боковые грани разные (например, «неправильная» пирамида), мы должны сложить площадь каждого треугольника, чтобы найти общую боковую площадь.
Треугольная пирамида | Найдите объем и площадь поверхности (формулы)
Треугольная пирамида
Треугольная пирамида представляет собой трехмерное тело — многогранник — с треугольным основанием и тремя треугольными гранями, пересекающимися в вершине пирамиды.
Основание пирамиды может быть любой двухмерной геометрической формы:
- Треугольник
- Прямоугольник
- Квадрат
- Шестиугольник
- восьмиугольник
Есть много типов пирамид, и все пирамиды названы по форме их оснований.
Так же, как у вас может быть треугольная пирамида, у вас также может быть прямоугольная пирамида, пятиугольная пирамида и т. Д.
Великие пирамиды Египта в Гизе, например, представляют собой квадратную пирамиду, потому что ее основание (основание) — квадрат. Треугольная пирамида — это пирамида с треугольным основанием.
Грани, ребра и вершины треугольной пирамиды
В треугольной пирамиде:
- Треугольное основание
- 3 треугольных грани
- 6 граней
- 4 вершины
Правильная треугольная пирамида
Пирамида с основанием равностороннего треугольника — это правильная треугольная пирамида .Если в основе лежит разносторонний или равнобедренный треугольник, то пирамида представляет собой неправильную треугольную пирамиду .
Ни одно правило не требует, чтобы основание треугольной пирамиды было равносторонним, хотя построить разносторонние или равнобедренные треугольные пирамиды намного сложнее, чем построить равностороннюю треугольную пирамиду.
[вставить точный чертеж на основе этой ссылки на схему сети треугольной пирамиды]
Содержание
- Треугольная пирамида
- Площадь поверхности треугольной пирамиды
- Объем треугольной пирамиды
Площадь поверхности треугольной пирамиды
Для любого 3D-тела можно выполнить два различных измерения площади поверхности: площадь боковой поверхности и площадь поверхности .
Площадь боковой поверхности, LSA, не включает основание нашей пирамиды. Площадь поверхности пирамиды SA включает основание.
Площадь поверхности треугольной пирамиды с тремя конгруэнтными видимыми гранями — это площадь этих трех треугольных граней плюс площадь треугольного основания.
Формула для расчета площади поверхности включает площадь основания, периметр основания и высоту наклона любой стороны.
Площадь поверхности треугольной пирамиды по формуле
SA = площадь основания + 12 (периметр × высота наклона)
Эта формула работает, потому что вы добавляете базовую область к площади всех трех наклонных граней.Периметр дает вам сумму всех трех баз. Вы умножаете эту сумму на наклонную высоту треугольной пирамиды, как если бы у вас был один большой прямоугольник, а затем вы принимаете половину этой площади как площадь трех треугольников.
Как найти площадь поверхности треугольной пирамиды
Предположим, у вас есть треугольная пирамида:
Основание пирамиды — равносторонний треугольник, так как все три его стороны составляют 10 локтей. Чтобы найти площадь основного треугольника, используйте эту формулу для площади равностороннего треугольника со сторонами a:
Для этой конкретной треугольной пирамиды формула имеет вид:
А = 34 102 ≈ 43.3 квадратных локтя (локтей2)
Мы нашли территорию базы. Мы уже знаем, что периметр основания составляет 30 локтей (каждая из трех сторон — 10 локтей), и нам дана наклонная высота — 14 локтей.
SA = площадь основания + 12 периметров × высота наклона
SA = 43,3 локтя2 + 12 30 локтей × 14 локтей
SA = 43,3 локтя2 + 12 420 локтей2
SA = 43,3 локтя2 + 210 локтей2
SA = 253,3 локтя2
Площадь всегда измеряется в квадратных единицах, будь то см2, м2, фут2 или кубиты2.
Как рассчитать площадь боковой поверхности треугольной пирамиды
Возможно, вам нужно было потратить время на то, чтобы разобраться со всем этим, найти область базы, найти периметр, добавить все.
Чтобы найти площадь только наклонных сторон — площадь боковой поверхности (LSA) — вам нужно сделать намного меньше работы:
LSA = 12 (периметр × наклонная высота)
Эти формулы работают только для обычных пирамид.Если у вас неправильная треугольная пирамида, вычислите площадь каждой из четырех граней по отдельности (три наклонные грани и основание) и сложите их вместе.
Объем треугольной пирамиды
Объем — это объем пространства, занимаемого трехмерным телом, поэтому с помощью треугольной пирамиды мы определяем, сколько места в ней есть. Он всегда измеряется в кубических единицах. Хотя пирамида быстро уменьшается до вершины, расчет не представляет трудностей.
Формула объема треугольной пирамиды
В объеме формулы треугольной пирамиды A — это площадь основания, а h — высота от основания до вершины.
Для нашей пирамиды с основанием 10 локтей и высотой наклона 14 локтей высота h составляет 13.0767 локтей. Мы уже знаем площадь из наших предыдущих расчетов, поэтому мы можем подставить известные числа, чтобы получить объем в кубических локтях:
В = 13 Ач
V = 13 (43,3 локтя2 × 13,0767 локтя)
V = 13 (566,2211 локтей3)
V ≈ 188,75 локтей3
Обратите внимание, что с дробью как множителем при умножении у нас нет точного десятичного ответа, поэтому у нас есть приблизительное значение.
Следующий урок:
Площадь поверхности прямоугольной призмы
Как найти периметр призмы
Обновлено 22 декабря 2020 г.
Эллиот Уолш
Вы можете видеть призмы как на уроках математики, так и в повседневной жизни.Кирпич — это прямоугольная призма. Коробка апельсинового сока — это разновидность призмы. Коробка для салфеток представляет собой прямоугольную призму. Сараи представляют собой разновидность пятиугольной призмы. Пятиугольник — это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.
Призмы по определению являются твердыми объектами с одинаковыми торцевыми формами, одинаковыми поперечными сечениями и плоскими боковыми гранями (без кривых). И хотя большинство математических задач и реальных примеров, касающихся расчета призмы, связаны с формулой объема или формулой площади поверхности, есть одно вычисление, которое вам нужно понять, прежде чем вы сможете это сделать: периметр призмы .
Что такое призма?
Общее определение призмы — это трехмерная сплошная форма, которая имеет следующие характеристики:
- Это многогранник (то есть сплошная фигура).
- Поперечное сечение объекта одинаково по всей длине объекта.
- Это параллелограмм (четырехсторонняя форма, противоположные стороны которой параллельны друг другу).
- Грани объекта плоские (без изогнутых граней).
- Две формы концов идентичны .
Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольным основанием называется треугольной призмой. Призма с прямоугольным основанием называется прямоугольной призмой. Этот список можно продолжить.
Глядя на характеристики призм, можно исключить сферы, цилиндры и конусы как призмы, поскольку они имеют изогнутые грани.Это также исключает пирамиды, потому что они не имеют одинаковых базовых форм или одинаковых поперечных сечений на всем протяжении.
Периметр призмы
Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по длине призмы.
Периметр измеряет сумму длин любого многоугольника.Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.
Формула для определения периметра треугольной призмы, например, будет представлять собой сумму трех длин треугольника, составляющего основу, или:
\ text {Периметр треугольника} = a + b + c
, где a , b и c — три длины треугольника.
Это будет периметр прямоугольной призмы по формуле:
\ text {Периметр прямоугольника} = 2l + 2w
, где l — длина прямоугольника, а w — ширина.
Примените стандартные вычисления периметра к базовой форме призмы, и это даст вам периметр.
Зачем нужно рассчитывать периметр призмы?
Определение периметра призмы не кажется слишком сложным, если вы понимаете, о чем вас спрашивают. Однако периметр — важный расчет, который учитывается в формулах площади поверхности и объема для некоторых призм.
Например, это формула для определения площади поверхности правой призмы (правая призма имеет идентичные основания и стороны, все прямоугольные):
\ text {Площадь поверхности} = 2b + ph
, где b равен площади основания, p равен периметру основания и h равен высоте призмы.Вы можете видеть, что периметр необходим для определения площади поверхности.
Пример задачи: периметр прямоугольной призмы
Допустим, вам задали задачу с правой прямоугольной призмой и попросили найти периметр. Вам даны следующие значения:
Чтобы найти периметр, используйте формулу для поиска периметра прямоугольной призмы, так как название говорит вам, что основание является прямоугольником:
\ begin {align} \ text {Perimeter} & = 2l + 2w \\ & = 2 (75 \ text {cm}) + 2 (10 \ text {cm}) \\ & = 150 \ text {cm} + 20 \ text {cm} \\ & = 170 \ text {cm} \ end {align}
Затем вы можете продолжить поиск площади поверхности, потому что вам задана высота, у вас есть периметр основания и дано, что эта призма является правой призмой .2 \ end {align}
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды — это общая площадь всех сторон и граней треугольной пирамиды. По сути, треугольная пирамида имеет треугольное основание и ограничена тремя боковыми треугольными гранями, которые встречаются в одной вершине. У треугольной пирамиды все грани как треугольники. У этой пирамиды 4 грани, 6 ребер и 4 угла или вершины. Ниже приведены несколько типов треугольной пирамиды:
Правильная треугольная пирамида , все грани представляют собой равносторонние треугольники и известны как тетраэдры.
Правотреугольная пирамида , основание — равносторонний треугольник, а остальные грани — равнобедренные треугольники.
Неправильная треугольная пирамида , равнобедренный или равнобедренный треугольник образует основу.
Какова площадь прямоугольной треугольной пирамиды
Площадь поверхности любой трехмерной геометрической формы — это сумма площадей всех граней или поверхностей этого замкнутого твердого тела. У треугольной пирамиды четыре треугольных грани.Таким образом, формула для расчета площади поверхности треугольной пирамиды включает площадь основания, периметр основания и наклонную высоту любой стороны пирамиды. Площадь поверхности треугольной пирамиды равна \ (\ begin {align} \ text {Base Area} + \! \ Frac {1} {2} \ text {(Perimeter} \! \ Times \! \ Text {Slant Height} ) \ end {align} \). Площадь поверхности всегда измеряется в квадратных единицах, таких как см 2 , м 2 , фут 2 или локтей 2 .
Какова площадь поверхности формулы треугольной пирамиды?
Формула площади поверхности треугольной пирамиды вычисляется путем сложения площадей всех треугольных граней пирамиды.Площадь поверхности формулы прямоугольной призмы равна \ (\ begin {align} \ text {Base Area} + \! \ Frac {1} {2} \ text {(Perimeter} \! \ Times \! \ Text {Slant Высота}) \ end {align} \). После выставления значений получаем выражение площади поверхности треугольной пирамиды по формуле 1⁄2 (a × b) + 3⁄2 (b × s)
Где «b» — сторона треугольной пирамиды.
‘a’ — высота базового треугольника
s — наклонная высота треугольной призмы.
‘1⁄2 (a × b)’ — это базовая площадь треугольных граней.
3⁄2 (b × s) — произведение периметра и высоты наклона пирамиды.
Как рассчитать площадь поверхности треугольных пирамид?
Площадь поверхности треугольной пирамиды можно рассчитать, представив трехмерную фигуру в виде двумерной сетки, чтобы ее было легче увидеть. После расширения трехмерной фигуры на двумерную мы получим четыре треугольника.
Для расчета площади поверхности треугольной пирамиды используются следующие шаги:
- Чтобы найти площадь базовых треугольников: Площадь базовых треугольников равна (1/2 × основание треугольника × высота треугольника), которая становится основанием × высотой.
- Чтобы найти периметр треугольных граней: Периметр треугольника равен сумме всех сторон треугольника, который равен стороне 1 + стороне 2 + стороне 3 .
- Чтобы найти наклонную высоту треугольных граней: наклонная высота треугольной пирамиды обычно обозначается буквой «s».
- Сложите все области вместе.
- Таким образом, площадь поверхности формулы треугольной пирамиды равна 1⁄2 (a × b) + 3⁄2 (b × s) в квадратах.
Какова площадь боковой поверхности треугольной пирамиды?
Площадь боковой поверхности — это площадь неосновных граней, или мы можем сказать, что только площадь боковой поверхности любого объекта вычисляется путем удаления базовой площади. Боковую площадь треугольной пирамиды можно рассчитать, удалив площадь основания треугольника с произведением периметра основания и высоты наклона пирамиды. Таким образом, площадь боковой поверхности прямоугольной призмы составляет «1⁄2 (периметр основания × наклонная высота)», которая в дальнейшем становится 3⁄2 (сторона × наклонная высота)
Где «b» — сторона пирамиды, а «s» — наклонная высота основания.
Часто задаваемые вопросы о площади поверхности треугольной пирамиды по формуле
Как определить площадь поверхности треугольной пирамиды?
Формула площади поверхности пирамиды вычисляется путем сложения площадей всех треугольных граней пирамиды. что равно 1⁄2 (a × b) + 3⁄2 (b × s).
Где «b» — сторона пирамиды, «a» — это высота базового треугольника, а «s» — наклонная высота пирамиды.
Какова формула объема и площади поверхности треугольной пирамиды?
Объем треугольной пирамиды можно определить как 1/3 × Площадь основания × Высота.
Как определить площадь основания прямоугольной треугольной пирамиды?
Площадь основания прямоугольной пирамиды равна 1/2 × высота треугольника основания × нижний край треугольника основания.
Что такое боковая поверхность треугольной пирамиды?
Боковая поверхность треугольной пирамиды рассчитывается путем умножения 1/3 периметра базового треугольника и высоты наклона треугольной пирамиды.
Что представляет собой пример треугольной пирамиды?
Палатки для кемпинга, треугольные крыши и шоколадные основы Toblerone — некоторые типичные примеры треугольной пирамиды.
Сколько ребер у треугольной пирамиды?
В прямоугольной призме шесть граней.
Что такое треугольная пирамида?
Треугольная пирамида — это пирамида с треугольным основанием, ограниченная четырьмя треугольными гранями, где 3 грани пересекаются в одной вершине.
Правильные пирамиды
Правильная пирамида — это пирамида, основание которой представляет собой правильный многоугольник, а боковые стороны которой равны по длине. Пирамида названа по ее основанию.На рисунке показаны некоторые примеры правильных пирамид.
Рисунок 1 Некоторые различные типы правильных пирамид.
Боковые грани правильной пирамиды — равнобедренные равнобедренные треугольники. Высота любого из этих треугольников равна наклонной высоте правильной пирамиды. Рисунок 2 представляет собой квадратную пирамиду.
Рисунок 2 Квадратная пирамида.
Пирамиды также имеют боковую площадь, общую площадь и объем.
Теорема 93 : Боковая площадь, LA , правильной пирамиды с наклонной высотой l и периметром основания p определяется следующим уравнением.
Пример 1: Найдите боковую площадь квадратной пирамиды, показанной на рисунке 3.
Рисунок 3 Определение боковой площади, общей площади и объема квадратной пирамиды.
Поскольку пирамида имеет только одно основание, ее общая площадь складывается из площади боковой поверхности и площади основания.
Теорема 94: Общая площадь TA правильной пирамиды с боковой площадью LA и площадью основания B определяется следующим уравнением.
Пример 2: Найдите общую площадь правильной пирамиды, показанной на рисунке.
Основание правильной пирамиды — квадрат . A квадрат = (сторона) 2 . Следовательно, B = 16 2 в 2 или B = 256 в 2 .
Из предыдущего примера
Теорема 95: Объем V правильной пирамиды с площадью основания B и высотой h определяется следующим уравнением.
Пример 3: Найдите объем правильной пирамиды, показанной на рисунке.
Из предыдущего примера B = 256 из 2 . На рисунке показано, что h = 6 дюймов.
.
