Содержание
Урок 43. решение линейных уравнений с одним неизвестным — Алгебра — 7 класс
Алгебра
7 класс
Урок № 43
Решение линейных уравнений с одним неизвестным
Перечень рассматриваемых вопросов:
• Линейные уравнения.
• Корень уравнения.
• Решение линейных уравнений.
Тезаурус:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Давайте вспомним, что называется корнем уравнения?
Корнем уравнения называют, такое значение переменной, при которой уравнение преобразуется в верное числовое равенство.
А что же означает решить уравнение?
Решить уравнение означает найти все его корни или доказать, что корней нет.
Давайте попробуем сформулировать теперь, как решать линейные уравнения и подумаем, а какие у нас могут быть случаи?
Решение линейного уравнения – это приведение его путем тождественных преобразований к стандартному виду.
Давайте решим уравнение:
Следовательно, уравнение не имеет корней.
А теперь давайте решим другое уравнение:
Попробуем решить уравнение:
При любом значении переменной, уравнение принимает вид верного равенства:
0 = 0, следовательно, уравнение имеет бесконечное множество корней.
Отсюда можно сделать вывод, что возможные варианты решения уравнения, зависят от того, какие значения принимает свободный член и коэффициент при переменной.
При решении уравнения вида возможны следующие три случая:
Замечательно, а теперь узнаем, можно ли проверить, является число корнем уравнения не решая его?
Да, конечно можно. Для этого нужно подставить в уравнение вместо переменной это число, если после упрощения, мы получаем верное равенство, то данное число будет являться корнем уравнения.
Давайте проверим, так ли это. Узнаем, является ли число
Замечательно. А теперь давайте попробуем порешать линейные уравнения первой степени.
является корнем уравнения.
уравнение к стандартному виду. Слагаемые, зависящие от икс, перенесём в левую часть уравнения, числа – в правую, изменяя их знаки на противоположные.
Разбор заданий тренировочного модуля.
содержащие переменной в правую часть, меняя знак на противоположный;
слагаемые, содержащие переменную в левую часть, не содержащие переменной, в правую часть, меняя знак на противоположный;
Конспект урока по алгебре «Линейные уравнения с одним неизвестным» (7 класс)
Предмет: алгебра
Класс: 7 класс
Цели: формирование навыка пошаговой работы под руководством учителя (объяснение нового материала, первоначальное закрепление), восприятия информации на слух (карточки), формирования самооценки (рефлексия).
Задачи урока:
1) образовательная:
познакомить учащихся с видом линейного уравнения и способом его решения, добиться усвоения правила решения линейных, его понимания и умения пользоваться им при решении;
2) развивающая:
продолжить формирование математических знаний и приемов умственной деятельности (умение анализировать ситуацию и ориентироваться в действиях, научиться выполнять новое действие, довести его до автоматизации). Формировать элементы математической логики.
Формировать элементы математической логики.
3) воспитательная:
формирование навыка пошаговой работы под руководством учителя (объяснение нового материала, первоначальное закрепление), восприятия информации на слух (карточки), формирования самооценки (рефлексия).
Тип урока: комбинированный
План урока:
Организационный момент (3 мин)
Постановка целей и задач урока. Мотивация учебной деятельности (6 мин)
Актуализация (3 мин)
Первичное усвоение (10мин)
Первичная проверка понимания (5 мин)
Первичное закрепление (10 мин)
Информация о домашнем задании, инструктаж по его выполнению (3 мин)
Рефлексия (подведение итогов занятия) (5 мин)
Ход урока:
Деятельность учащихся
1
Организационный момент.
Приветствие учащихся. Проверка присутствующих. Учитель:
— Здравствуйте, ребята. Сегодня на уроке мы вспомним о чем говорили на прошлом уроке. А для начала запишем тему сегодняшнего урока «Линейные уравнения с одним неизвестным»
Ребята приветствуют учителя.
-Слушают учителя. Записывают в тетрадь тему урока.
2
Постановка целей и задач урока. Мотивация учебной деятельности.
на доске записаны уравнения:
а) (*5)+(*7)=2;
б) (*8)-(*8)=(*4)-12;
в) (*9)+(*4)=-5;
г) (-15)-(*…)=0;
д) (*8)+(*…)=-12;
е (*10)-(*…)=12.
— Вместо (*) поставить знак «+» или «-», а вместо точек – числа
— молодцы, ребята. А сейчас выполните следующее задание: Составить уравнения, равносильные уравнению:
а) х-7=5;
б) 2х-4=0;
в) х-11=х-7;
г) 2(х-12)=2х-24.
— почему?
— какую цель урока мы себе сегодня поставим?
— какие задачи мы должны решить для достижения поставленной цели?
устно выполняют задание.
а) -5+(+7)=2
б)(-8)-(+8)=(-4)-12
в)(-9)+(+4)=-5
г)(-15)-(-15)=0
д)(-8)+(-4)=-12
е)(-10)-(-22)=12
— мы не можем выполнить это задание.
— мы не знаем что такое равносильные уравнения.
ставят цель урока: узнать какие уравнения называются равносильными, составлять уравнения равносильные данным и научиться их решать.
-1.узнать определение равносильных уравнений.
2. составлять уравнения равносильные данным.
3. решать уравнения
3
актуализация
— назовите примеры уравнений первой степени с одним неизвестным х.
— напишите на доске общий вид уравнения первой степени с одним неизвестным
— что называют корнем уравнения. И что значит решить уравнение?
— приводят примеры
— пишут пример на доске
— корнем уравнения называют такое число, при подстановке которого в уравнение вместо х получается верное числовое равенство. Решить уравнение – значит найти все его корни
4
первичное усвоение
Коллективная работа с классом.
Форма коллективной работы: фронтальная
— Решим уравнение
12 — (4х-18)=(36+5х)+(28 – 6х). (1)
— какое действие нужно выполнить первым по вашему мнению?
-верно.1. Раскроем скобки. 12 — 4х+18=36+5х+28 – 6х. (2)
-можем ли мы назвать уравнеия (1) и (2) одинаковыми? Уравнения (2) и (1) равносильны.
— что можно сделать следующим шагом?
— верно. 2. Перенесём с противоположными знаками неизвестные члены так, чтобы они были только в одной части уравнения (или в левой, или в правой). Одновременно перенесём известные члены с противоположными знаками так, чтобы они были только в другой части уравнения.
Одновременно перенесём известные члены с противоположными знаками так, чтобы они были только в другой части уравнения.
Например, перенесём с противоположными знаками неизвестные члены в левую, а известные – в правую часть уравнения, тогда получим уравнение
-4х-5х+6х=36+28-18, (3)
— равносильны ли уравнения (2) и (3)
равносильное уравнению (2), а следовательно, и уравнению (1).
— что можно теперь сделать в правой и левой частях уравнения?
3. Приведём подобные слагаемые:
-3х=46. (4)
Уравнение (4) равносильно уравнению (3), а следовательно, и уравнению (1).
— и что остается сделать в последнем действии? 4. Разделим обе части уравнения (4) на коэффициент при неизвестном. Полученное уравнение х=46/-3 или -15 1/3 будет равносильно уравнению (4), а следовательно, и уравнениям (3), (2), (1).
Поэтому корнем уравнения (1) будет число -15 1/3.
— сначала нужно раскрыть скобки
один учащийся возле доски раскрывает скобки и вспоминает правило раскрытия скобок: Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобках. Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобках:
Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобках:
— можем
-перенести с х в одну сторону. Без х – в другую.
один учащийся переносит члены уравнения в разные стороны.
— да, равносильны.
— привести подобные слагаемые. (один учащийся выполняет задание на доске)
— разделить обе части уравнения на коэффициент при неизвестном. (учащийся на доске)
5
первичная проверка понимания
— давайте составим алгоритм решения уравнения
По этой схеме (алгоритму) решаем уравнения на сегодняшнем уроке.
Примечание: следует отметить, что приведённая схема не является обязательной, так как часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. При решении же других уравнений бывает проще отступить от этой схемы, как, например, в уравнении:
7(х-2)=42.
учитель раздает учащимся алгоритм решения уравнения.
учащиеся вместе с учителем составляют алгоритм решения уравнения.
1. Раскрыть скобки.
2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.
3. Привести подобные слагаемые.
4. Разделить обе части уравнения на коэффициент при неизвестном.
6
первичное закрепление
— для того, чтобы потренироваться решать уравнения по составленному нами алгоритму выполним следующие упражнения:
№ 647 (а, в, д), 645
выполняют упражнения но доске и в терадях.
7
информация о домашнем задании, инструктаж по его выполнению
запишем в дневники домашнее задание: № 646. Прочитайте вслух задание.
-как вы будете выполнять это задание?
читают задание.
— подставим все числа в это уравнения вместо х и вычислим какие из них являются корнем данного уравнения
8
рефлексия
— ребята давайте вспомним с чего начался наш урок?
— со всеми заданиями вы справились? И почему? И сможете ли вы сейчас выполнить это задание сейчас?
— мы подбирали числа и знаки в примеры, а потом нужно было составить уравнения равносильные данным.
— не смогли составить уравнения равносильные данным, потому что не знали какие уравнения называют равносильными.
— да сможем. (выполняют устно данное задание)
Урок алгебры в 7 классе по теме «Уравнение с одним неизвестным, сводящееся к линейным»
Урок алгебры 7 класс по теме «Уравнение с одним неизвестным, сводящееся к линейным»
Учебник «Алгебра -7» автор Ш.А.Алимов.
Цели:
Образовательная: отработать и систематизировать знания учащихся по решению уравнений с одним неизвестным;
Развивающая: способствовать развитию познавательного интереса к решению уравнений, развитию самостоятельности и контроля;
Воспитательная: способствовать воспитанию любознательности, пропагандировать здоровый образ жизни.
Ход урока.
1.Организация класса.
Ребята! Мы продолжаем изучать тему «Уравнения с одним неизвестным» и надеюсь многому еще научимся. Поэтому сегодня я предлагаю вам совершить пешую прогулку по всем видам решения уравнений. Я думаю, что каждый из нас любит это занятие, тем более что это один из видов спорта. А спорт делает нас сильными и здоровыми. В здоровом теле – здоровый дух.
Поэтому сегодня я предлагаю вам совершить пешую прогулку по всем видам решения уравнений. Я думаю, что каждый из нас любит это занятие, тем более что это один из видов спорта. А спорт делает нас сильными и здоровыми. В здоровом теле – здоровый дух.
Итак, вперед!
Мы находимся на первой станции – «Домашняя работа».
Поменяемся тетрадями и проверим домашнюю работу через проектор.
Поставьте напротив ответа каждого уравнения знак «+», если ответ верный, знак «-«, если ответ неверный, и поставьте оценку по количеству плюсов.
На экране демонстрируется 1 страница №86-90(2)
№86(2) -3х=2; х=; х=-
№87(2) 1,3х=-1,69; х= -1,69:1,3=-1,3; х=-1,3
№88(2) 7х+8=11; 7х=11 – 8; 7х=3; х=
№89(2) 8х – (7х+8)=7; 8х-7х-8=7; х=7 + 8; х=15
№90(2) 11(у-4) +10(5-3у)-3(4-3у) = -6
11у-44+50-30у-12+9у=-6
-10у +15=-6
-10у=-6-15
-10у=-21
У=2,1
Поменяемся тетрадями и продолжим путь.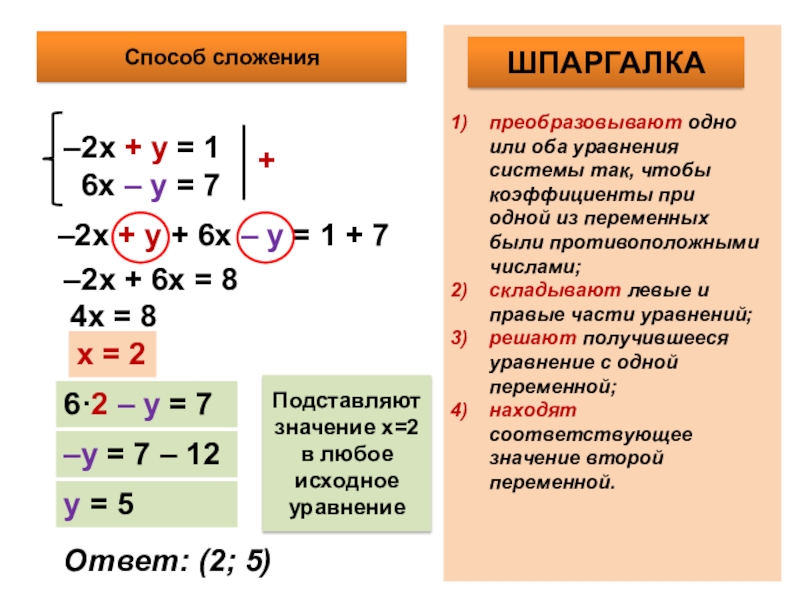
Вторая станция- Станция вопросов.
Что называется уравнением?
Что значит решить уравнения?
Что называется корнем уравнения?
Какими свойствами пользуются при решении уравнений?
Третья станция –Эстафета.
(Эстафета проводится следующим образом. Учитель предлагает ученикам комплект заданий, который надо выполнить, но не по порядку, а следующим образом: сначала всегда выполняется первое задание; число, полученное в результате его выполнения, есть номер задания, которое надо выполнить следующим; выполнив его, получаем номер следующего задания и т.д. Окончательный ответ ученик показывает учителю молча.)
Проектором проецируется лист №2
Эстафета
1.Решите уравнение х+1=5.
2.Найти корень уравнения 0,2:х=0,04
3.При каком х справедливо равенство
4.Сколько человек тянули репку в сказке «Репка»?
5.Решить уравнение 3(у+6)-5(у-1)=4-у.
(Первым трем ученикам, показавшим правильный ответ можно поставить оценку «5». Прием ответов следует прекратить сразу же, как только возникнет подозрение в «утечке информации». После этого к доске пригласить одного ученика, успешно справившихся с эстафетой, который объяснит классу, как он это сделал.)
Прием ответов следует прекратить сразу же, как только возникнет подозрение в «утечке информации». После этого к доске пригласить одного ученика, успешно справившихся с эстафетой, который объяснит классу, как он это сделал.)
Четвертая станция — Уравнения.
Разберем решения следующих уравнений. (Объясняет учитель)
Выполним решение по следующему алгоритму
Умножим обе части уравнения на общий знаменатель дробей, т.е. на 6 | |
После умножения получим | 15х-2(х-3)=6+(х-5) |
Раскроем скобки | 15х – 2х + 6 = 6 + х + 5 |
Упростим обе части уравнения | 13х + 6=х + 1 |
Перенесем с неизвестным в левую часть, а с известным в правую часть, изменив знак на противоположный. | 13х – х = 1 – 6 |
Приведем подобные слагаемые | 12х = -5 |
Ответ | Х= |
2. Решить уравнение 2(х+1) — 1=3 – (1 – 2х)
Решить уравнение 2(х+1) — 1=3 – (1 – 2х)
Выполним решение по следующему алгоритму.
Раскроем скобки | 2х + 2 – 1 = 3 – 1 + 2х |
Приведем подобные слагаемые в обеих частях уравнения | 2х + 1 = 2 + 2х |
Перенесем с неизвестным в левую часть, а с известным в правую часть, изменив знак на противоположный. | 2х – 2х = 2 — 1 |
Приведем подобные слагаемые | 0х = 1 |
ответ | Корней нет |
Пошли дальше. Ребята на нашем пути появилась калиточка, которая ведет в храм «Ума» и через неё пропускают только тех, которые могут решать уравнения.
Самостоятельная работа
Выполняем самостоятельную работу с использованием алгоритмов. Если что –то будет непонятно поднимите руку.
1вариант №93-95(1)
2вариант №93-95(3)
Самостоятельная работа проверяется с помощью откидных досок, за которые приглашаются ученики первыми выполнившие задания.
Итог урока. Вот мы и добрались до нужной станции. Укрепили своё здоровье, пройдя четыре станции, и повторили как решаются уравнения с одним неизвестным.
И запомните слова великого математика Р.Декарта «Мало иметь хороший ум, главное – хорошо его применять».
Домашнее задание: §7, №93-95(2)
Решение уравнений с одним неизвестным | Презентация к уроку (алгебра, 7 класс) по теме:
Слайд 1
Решение уравнений с одним неизвестным, сводящихся к линейным
Слайд 2
Какое равенство называется уравнением? Что такое корень уравнения? Сколько корней может иметь уравнение? Что значит –решить уравнение? Какое уравнение называют линейным? Устная работа
Слайд 3
Математический диктант Как называется уравнение -2х=17 Придумайте какое-нибудь линейное уравнение с одним неизвестным х При каком условии уравнение сх=5 имеет один корень? При каком условии уравнение ах=-3 не имеет корней? Как называется уравнение 17х=-2 Придумайте какое-нибудь линейное уравнение с одним неизвестным у При каком условии уравнение ау=3 не имеет корней? При каком условии уравнение ру=-5 имеет единственный корень?
Слайд 4
Словесная формулировка Запись в общем виде пример 1. Если к обеим частям верного равенства прибавить одно и то же число или из обеих частей верного равенства вычесть одно и то же число, то получится верное равенство Если а=в и р-любое число, то а+р=в+р а-р=в-р 7=7 7+2=7+2 7-2=7-2 2. Если обе части верного равенства умножить или разделить на одно и то же число, не равное нулю, то получится верное равенство Если а=в и р не равно 0, то ар=вр , ар:вр 27=27 27*3=27*3 27:3=27:3 Объяснение нового материала
Если к обеим частям верного равенства прибавить одно и то же число или из обеих частей верного равенства вычесть одно и то же число, то получится верное равенство Если а=в и р-любое число, то а+р=в+р а-р=в-р 7=7 7+2=7+2 7-2=7-2 2. Если обе части верного равенства умножить или разделить на одно и то же число, не равное нулю, то получится верное равенство Если а=в и р не равно 0, то ар=вр , ар:вр 27=27 27*3=27*3 27:3=27:3 Объяснение нового материала
Слайд 5
Решим уравнение 9х-23=5х-11 9х-5х=-11+23 4х=12 х =12:4 х=3 Ответ: х=3 Какие свойства использовались при решении этого уравнения? Объяснение нового материала
Слайд 6
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный. Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю. Основные свойства уравнений
Слайд 7
2(х+3)-3(х+2)=5-4(х+1) 2х+6-3х-6=5-4х-4 2х-3х+4х=5-4-6+6 3х=1 Х=1/3 Ответ: х=1/3 Решить уравнение
Слайд 8
Перенести члены, содержащие неизвестное в левую часть, не содержащие неизвестное- в правую. Привести подобные члены. Разделить обе части уравнения на коэффициент при неизвестном, если он не равен нулю. Алгоритм решения уравнений
Привести подобные члены. Разделить обе части уравнения на коэффициент при неизвестном, если он не равен нулю. Алгоритм решения уравнений
Слайд 9
Выполнить №86(1,3) Выполнить самостоятельно №87(1,3) Выполнить №88(1,3) Выполнить №89(1,3) Решение задач
Слайд 10
Сформулируйте свойства решения уравнения. Расскажите схему решения линейного уравнения одним неизвестным. Итоги урока
Слайд 11
Выучить п.7 Выполнить № 88(2,4), №89(2,4), №97(2) Принести тетрадь для контрольных работ Домашнее задание
«Линейные уравнения с одним неизвестным»
Линейные уравнения с одним неизвестным
Тест по алгебре для 7 класса
Учитель математики
Николаева Е.Н.
Содержание
Уровень 1
Уровень 2
Уровень 1
1
2
3
4
5
Заполни пропуски
равенство
Уравнение – это _______________,
содержащее переменную.
Корнем уравнения называется ________________ ,
при котором уравнение обращается в ___________________ .
значение переменной
верное равенство
Выбрать записи, являющиеся уравнениями
Выбрать уравнения, корнем которых является число 5
Выбрать пары равносильных уравнений
Выписать те уравнения, которые:
Имеют единственный корень
6х=42 0,3x=0 -3,4x=0 7x=2 2x=-0,06
- 6х=42 0,3x=0 -3,4x=0 7x=2 2x=-0,06
Не имеют корней
Имеют множество корней
4х-5=4х 0х=5
5х+2=(5х-4)+6
Уровень 2
2
1
4
3
Восстановите коэффициент
□ х = 27 x=9
□ х = -15 x=-3
□ х = 0,6 x= — 0,3
3
5
-2
Вписать пропущенные знаки и продолжить решение уравнения
4(2х-5)= -3(-5х+13)
8х … 20= …15х 39
8х … 15х=…39… 20
—
—
+
—
—
+
Решить уравнения:
6у- (у -1 ) = 2 (2у-4)
- 6у- (у -1 ) = 2 (2у-4)
3(2х-5)=7х+1
(6х-5)2=8х
-9
-16
-2,5
Завершить высказывание.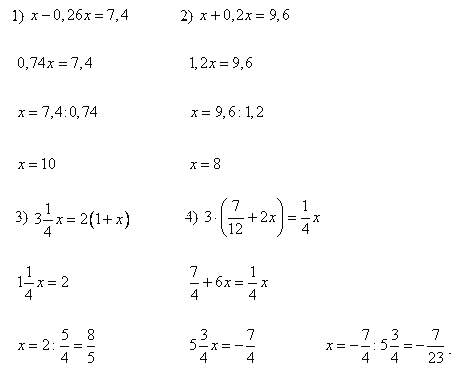
Корнем уравнения ах=26 является:
Число -2, если а= _____
Число ⅓, если а= _____
- Число -2, если а= _____ Число ⅓, если а= _____
-13
78
Линейные уравнения 7 класс | Алгебра
Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида
где a и b — числа, x — переменная.
Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).
Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.
Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:
Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: -9.
Раскрываем скобки:
Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:
(Обратите внимание: хотя сумма слагаемых с переменной равна нулю, результат записываем не как 0, а как 0x).
Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.
Ответ: x — любое число.
Раскрываем скобки:
Можно сначала привести подобные слагаемые, чтобы упростить уравнение:
а уже потом перенести: неизвестные — в одну сторону, известные — в другую:
Это уравнение не имеет корней.
Ответ: нет корней.
Раскрываем скобки:
Приводим подобные слагаемые:
Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ:
В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.
Макарычев 7. Уравнения с одной переменной
Ознакомительная версия с цитатами из учебника для принятия решения о покупке. Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — 8-е издание. М.: Просвещение (2018). ГЛАВА I учебника. § 3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ. (6. Уравнение и его корни. 7. Линейное уравнение с одной переменной. 8. Решение задач с помощью уравнений. Упражнения №№ 111 — 166. Контрольные вопросы и задания. Дополнительные упражнения №№ 233 — 252 к параграфу 3)
Контрольные вопросы и задания. Дополнительные упражнения №№ 233 — 252 к параграфу 3)
§ 3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ
6. Уравнение и его корни
Рассмотрим задачу: «На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг на полках станет поровну. Сколько книг на верхней полке?»
Обозначим буквой х число книг на верхней полке. Тогда число книг на нижней полке равно 4х. Если с нижней полки переставить на верхнюю 15 книг, то на нижней полке останется 4х – 15 книг, а на верхней будет х + 15 книг. По условию задачи после такой перестановки книг на полках окажется поровну. Значит, 4х – 15 = х + 15.
Чтобы найти неизвестное число книг, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями с одной переменной или уравнениями с одним неизвестным.
Нам надо найти число, при подстановке которого вместо х в уравнение 4х – 15 = х + 15 получается верное равенство. Такое число называют решением уравнения или корнем уравнения.
Такое число называют решением уравнения или корнем уравнения.
Из уравнения 4х – 15 = х + 15 находим, что 4х – х = 15 + 15, 3х = 30, х = 10.
Уравнение 4х – 15 = х + 15 имеет один корень – число 10.
Можно привести примеры уравнений, которые имеют два, три и более корней или не имеют корней.
Так, уравнение (х – 4)(х – 5)(х – 6) = 0 имеет три корня: 4, 5 и 6. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (х – 4) (х – 5) (х – 6), а значит, и само произведение. При любом другом значении х ни один из множителей в нуль не обращается, а значит, не обращается в нуль и произведение. Уравнение х + 2 = х не имеет корней, так как при любом значении х левая часть уравнения на 2 больше его правой части.
Уравнение х2 = 4 имеет два корня – числа 2 и –2. Уравнение (х – 2)(х + 2) = 0 также имеет корни 2 и –2. Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений используются следующие свойства:
Например, равносильны уравнения 5х = 2х + 7 и 5х – 2х = 7, равносильны также уравнения 6х = 2х + 8 и 3х = х + 4.
Указанные свойства уравнений можно доказать, опираясь на свойства числовых равенств: если к обеим частям верного равенства прибавить одно и то же число или обе части верного равенства умножить или разделить на одно и то же отличное от нуля число, то получится верное равенство.
Упражнения
7. Линейное уравнение с одной переменной
Каждое из уравнений 5х = –4, –0,2x = 0, –х = –6,5 имеет вид ах = b, где х – переменная, а и b – числа. В первом уравнении а = 5, b = –4, во втором а = –0,2, b = 0, в третьем а = –1, b = –6,5.
Такие уравнения называют линейными уравнениями с одной переменной.
Выясним, сколько корней может иметь линейное уравнение. Рассмотрим уравнение ах = b, в котором коэффициент а не равен нулю. Разделив обе части уравнения на а, получим х= b/a. Значит, линейное уравнение ах = b, в котором а ≠ 0, имеет единственный корень b/a.
Значит, линейное уравнение ах = b, в котором а ≠ 0, имеет единственный корень b/a.
Рассмотрим уравнение ах = b, у которого коэффициент а равен нулю. Если а = 0 и b ≠ 0, то уравнение ах = b же имеет корней, так как равенство 0x = b не является верным ни при каком х. Если а = 0 и b = 0, то любое значение х является корнем уравнения, так как равенство 0х = 0 верно при любом х.
Решение многих уравнений сводится к решению линейных уравнений.
Пример. Решим уравнение 4(х + 7) = 3 – х.
► Раскроем скобки: 4х + 28 = 3 – х.
Перенесём слагаемое –х в левую часть уравнения, а слагаемое 28 в правую часть, изменив при этом их знаки: 4х + х = 3 – 28.
Приведём подобные слагаемые: 5х = –25.
Разделим обе части уравнения на 5: х = –5.
Применяя свойства уравнений и выполняя тождественные преобразования, мы последовательно заменяли одно уравнение другим, равносильным ему. Значит, корнем уравнения 4(х + 7) = 3 – х является число –5.
В этом примере исходное уравнение свелось к равносильному линейному уравнению, в котором коэффициент при переменной отличен от нуля.
Если при решении уравнения мы придём к равносильному ему линейному уравнению вида 0х = b, то в этом случае либо исходное уравнение не имеет корней, либо его корнем является любое число.
Решим уравнение 2х + 5 = 2 (х + 6): 2х + 5 = 2х + 12, 2х – 2х = 12 – 5, 0х = 7.
Полученное уравнение не имеет корней. Значит, и уравнение 2х + 5 = 2 (х + 6) не имеет корней.
Уравнение 3 (х + 2) + х = 6 + 4х сводится к уравнению 0x = 0, корнем которого является любое число. Следовательно, корнем уравнения 3(х + 2) + х = 6 + 4х является любое число.
Упражнения
8. Решение задач с помощью уравнений
При решении задач с помощью уравнений поступают следующим образом:
Задача 1. В корзине было в 2 раза меньше яблок, чем в ящике. После того как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?
► Пусть в корзине было х яблок, тогда в ящике было 2х яблок. После того как из корзины переложили в ящик 10 яблок, в корзине стало х – 10 яблок, а в ящике стало 2х + 10 яблок. По условию задачи в ящике стало в 5 раз больше яблок, чем в корзине. Значит, 5(х – 10) = 2х + 10.
После того как из корзины переложили в ящик 10 яблок, в корзине стало х – 10 яблок, а в ящике стало 2х + 10 яблок. По условию задачи в ящике стало в 5 раз больше яблок, чем в корзине. Значит, 5(х – 10) = 2х + 10.
Решим составленное уравнение: 5х – 50 = 2х + 10, 5х – 2х = 10 + 50, 3х = 60, х = 20.
Следовательно, в корзине было 20 яблок. Так как 2х = 2 • 20 = 40, то в ящике было 40 яблок.
Ответ: 20 яблок и 40 яблок.
Задача 2. Предназначенные для посадки 78 саженцев смородины решили распределить между тремя бригадами так, чтобы первой бригаде досталось саженцев в 2 раза меньше, чем второй, а третьей – на 12 саженцев больше, чем первой. Сколько саженцев надо выделить первой бригаде?
► Пусть первой бригаде решили выделить х саженцев. Тогда второй следует выделить 2х саженцев, а третьей х + 12 саженцев. Общее число саженцев х + 2х + (х + 12), что по условию задачи равно 78.
Значит: х + 2х + (х + 12) = 78.
Решим полученное уравнение: х + 2х + х + 12 = 78, 4х = 78 – 12, 4х = 66, х = 16,5.
По смыслу задачи значение х должно быть натуральным числом, а корень уравнения – дробное число. Значит, распределить саженцы указанным способом нельзя.
Ответ: Такое распределение саженцев невозможно.
Упражнения
Контрольные вопросы и задания
- Сформулируйте определение корня уравнения. Является ли число 7 корнем уравнения: 6х = 42; 0х = 11; (16 – 2 • 8)х = 0?
- Что значит решить уравнение? Решите уравнение: 6х = –12; x – 2x • 6 = 0; 5х – 4х = 6 + х.
- Какие уравнения называются равносильными? Сформулируйте свойства уравнений. Приведите пример уравнения, равносильного уравнению: 5х – 1 = 3; 0,2х = 1,1; 3х – 4х + 6 = 0.
- Дайте определение линейного уравнения с одной переменной. Приведите примеры.
- В каком случае уравнение ах = b имеет единственный корень; имеет бесконечно много корней; не имеет корней? Приведите примеры.
Дополнительные упражнения к параграфу 3
Вы смотрели ознакомительную версию с цитатами из учебника: Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — 8-е издание. М.: Просвещение (2018). ГЛАВА I. § 3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ. (6. Уравнение и его корни. 7. Линейное уравнение с одной переменной. 8. Решение задач с помощью уравнений. Упражнения №№ 111 — 166. Контрольные вопросы и задания. Дополнительные упражнения №№ 233 — 252 к параграфу 3). Цитаты из учебника использованы в учебных целях.
7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — 8-е издание. М.: Просвещение (2018). ГЛАВА I. § 3. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ. (6. Уравнение и его корни. 7. Линейное уравнение с одной переменной. 8. Решение задач с помощью уравнений. Упражнения №№ 111 — 166. Контрольные вопросы и задания. Дополнительные упражнения №№ 233 — 252 к параграфу 3). Цитаты из учебника использованы в учебных целях.
вопросов и задач по алгебре для 7 класса
Представлены вопросы и задачи по алгебре 7-го класса с подробным решением. Включены вопросы по упрощению выражений, решению уравнений, факторингу выражений и т. Д.
- Оцените каждое из выражений для данного значения (значений) переменной (ей).

- 12 x 3 + 5 x 2 + 4 x — 6 для x = -1
- 2 a 2 + 3b 3 — 10 для a = 2 и b = -2
- (- 2 x — 1) / (x + 3) для x = 2
- 2 + 2 | x — 4 | для x = — 4
- Расширьте и упростите каждое из приведенных ниже выражений.

- — 2 (х — 8) + 3 (х — 7)
- 2 (а + 1) + 5b + 3 (а + b) + 3
- а (б + 3) + б (а — 2) + 2 а — 5 б + 8
- (1/2) (4x + 4) + (1/3) (6x + 12)
- 4 (- х + 2-3 (х — 2))
- Упростите каждое из приведенных ниже выражений.

- х / у + 4 / у
- (2 х / 4) (1/2)
- (3 х / 5) (х / 5)
- Упростите каждое из приведенных ниже выражений.
- 3 х 2 5 х 3
- [(2 y) 4 9 x 3 ] [4 y 4 (3 x) 2 ]
- Полностью разложите на множители каждое из приведенных ниже выражений.

- 9 х — 3
- 24 х + 18 лет
- б х + д х
- Решите каждое из приведенных ниже уравнений и проверьте свой ответ.
- 2 х + 5 = 11
- 3 х = 6/5
- 3 (2 х + 2) + 2 = 20
- Перепишем выражения 3 a a a — 5 b b с использованием экспоненты.

- Прямоугольник имеет длину 2 x + 3 единицы, где x — переменная. Ширина прямоугольника равна x + 1 единицам. Найдите значение x, если периметр прямоугольника равен 32.
- Прямоугольник имеет длину 2x — 1 единиц, где x — переменная. Ширина прямоугольника равна 3 единицам. Найдите значение x, если площадь прямоугольника равна 27.
- 45% учеников в школе — мужчины? Найдите отношение количества девочек к общему количеству учеников мужского пола в этой школе.
- Автомобиль едет со скоростью x + 30 километров за час, где x неизвестно.
 Найти x, если эта машина преодолевает 300 километров за 3 часа?
Найти x, если эта машина преодолевает 300 километров за 3 часа? - Решите пропорцию: 4/5 = a / 16
- Найдите a, если упорядоченная пара (2, a + 2) является решением уравнения 2 x + 2 y = 10?
- Найдите наибольший общий делитель чисел 25 и 45.
- Напишите число «один миллиард двести тридцать четыре миллиона семьсот пятьдесят тысяч два», используя цифры.
- Напишите прописью число 393 234 000 034.

- Найдите наименьшее общее кратное чисел 15 и 35.
- Найти x, если 2/3 x равно 30?
- Что такое 20% от 1/3?
- Заказывайте 12/5, 250%, 21/10 и 2.3 от наименьшего к наибольшему.
- Сумма 3 последовательных положительных целых чисел равна 96.Найдите наибольшее из этих чисел.
- Дэни набрал 93 балла по физике, 88 баллов по математике и результат по химии, который вдвое превышает его балл по географии.
 Средний балл по всем 4 курсам — 79. Какие у него были баллы по химии и географии?
Средний балл по всем 4 курсам — 79. Какие у него были баллы по химии и географии? - Линда набрала 265 баллов по математике, физике и английскому языку. По математике она набрала на 7 баллов больше, чем по английскому, а по физике на 5 баллов больше, чем по математике. Найдите ее баллы по всем трем предметам.
- На стоянке есть велосипеды и автомобили.Всего имеется 300 колес, в том числе 100 маленьких колес для велосипедов. Сколько машин и велосипедов?
- Разница между двумя числами равна 17, а их сумма равна 69. Найдите наибольшее из этих двух чисел.
Больше математики в средней школе (6, 7, 8, 9 классы) — бесплатные вопросы и проблемы с ответами
Больше математики в средней школе (10, 11 и 12 классы) — бесплатные вопросы и задачи с ответами
Больше начальной математики (4 и 5 классы) ) с бесплатными вопросами и проблемами с ответами
Автор —
e-mail
Домашняя страница сообщить об этом объявлении
Математика 7 класс, Раздел 6.
 7
7
Давайте посмотрим, насколько сбалансированная подвеска похожа на уравнение, а перемещение ее веса похоже на решение уравнения.
учебных целей:
- Я могу объяснить, как сбалансированная подвеска и уравнение представляют одну и ту же ситуацию.
- Я могу найти неизвестный вес на диаграмме подвески и решить уравнение, которое представляет диаграмму.
- Я могу написать уравнение, описывающее веса на сбалансированной подвеске.
7.1 Схемы подвесов
На двух диаграммах все треугольники и квадраты одинаковы.
Для каждой диаграммы придумайте. . .
- Одно, что должно быть правдой
- То, что может быть правдой
- То, что не может быть правдой
7.
 2 Соответствие подвеса и уравнения
2 Соответствие подвеса и уравнения
Фигуры с одинаковой буквой на каждой сбалансированной вешалке имеют одинаковый вес.
- 2 \ в штучной упаковке {\ phantom {3}} + 3 = 5
- 3 \ в коробке {\ phantom {3}} + 2 = 3
- 6 = 2 \ в коробке {\ phantom {3}} + 3
- 7 = 3 \ в коробке {\ phantom {3}} + 1
- Сопоставьте каждую подвеску по формуле.Завершите уравнение, написав x, y, z или w в пустом поле.
- Найдите решение каждого уравнения. Используйте вешалку, чтобы объяснить, что означает раствор.
7.3 Использование подвесок для понимания решения уравнений
Вот несколько уравновешенных вешалок, на каждой из которых указан ее вес. Для каждой диаграммы:
- Напишите уравнение.
- Объясните, как определить вес предмета, помеченного буквой, исходя из диаграммы.
- Объясните, как вычислить вес предмета, помеченного буквой, используя уравнение.
Вы готовы к большему?
Когда у вас будет время, посетите сайт https://solveme. edc.org/Mobiles.html, чтобы решить несколько более сложных головоломок, в которых используются схемы вешалок, подобные приведенным в этом уроке. Вы даже можете построить новые. (Если вы хотите сделать это во время урока, сначала посоветуйтесь со своим учителем!)
edc.org/Mobiles.html, чтобы решить несколько более сложных головоломок, в которых используются схемы вешалок, подобные приведенным в этом уроке. Вы даже можете построить новые. (Если вы хотите сделать это во время урока, сначала посоветуйтесь со своим учителем!)
Итоги урока 7
В этом уроке мы работали с двумя способами, чтобы показать, что две суммы равны: сбалансированная подвеска и уравнение.Мы можем использовать сбалансированную подвеску, чтобы подумать, как найти неизвестную сумму в соответствующем уравнении.
Подвеска показывает общий вес 7 единиц с одной стороны, который уравновешен 3 равными, неизвестными весами и 1-ю единицей веса с другой. Уравнение, которое представляет собой отношение: 7 = 3x + 1.
Мы можем снять по 1 шт. С каждой стороны, и подвеска останется в равновесии. Это то же самое, что вычесть 1 из каждой части уравнения.
Уравнение для новой сбалансированной подвески: 6 = 3x.
Таким образом, подвеска будет сбалансирована с \ frac13 веса с каждой стороны: \ frac13 \ boldcdot 6 = \ frac13 \ boldcdot 3x.
Две стороны вешалки уравновешивают следующие грузы: 6 гирь размером 1 шт. С одной стороны и 3 гири неизвестного размера с другой стороны.
Вот краткий способ записать шаги, указанные выше:
\ begin {align} 7 & = 3x + 1 & \\ 6 & = 3x & \ text {после вычитания 1 с каждой стороны} \\ 2 & = x & \ text {после умножения каждой стороны на} \ tfrac13 \\ \ end {align}
Урок 7 Практические задачи
Существует пропорциональная зависимость между объемом пробы гелия в литрах и массой этой пробы в граммах.Если масса образца 5 граммов, то его объем составляет 28 литров. (5, 28) показано на графике ниже.
- Какова константа пропорциональности в этом соотношении?
- В этой ситуации, что означает число, которое вы нашли в части а?
- Добавьте еще как минимум три точки на график выше и пометьте их координатами.

- Напишите уравнение, которое показывает взаимосвязь между массой образца гелия и его объемом. Используйте m для массы и v для объема.
Объясните, как части сбалансированной подвески сравниваются с частями уравнения.
Вот вешалка:
- Напишите уравнение подвески.
- Нарисуйте больше вешалок, чтобы показать каждый шаг, который вы предпринимаете, чтобы найти x. Объясните свои рассуждения.
- Напишите уравнение для каждой нарисованной вешалки. Опишите, как каждое уравнение соответствует своей вешалке.
Решение системных уравнений | Уравнения и неравенства
\ (- 10 х = -1 \) и
\ (- 4 х + 10 у = -9 \).
Решить относительно \ (x \):
\ begin {align *}
— 10х = -1 \\
\ поэтому x = \ frac {1} {10}
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение и решите относительно \ (y \):
\ begin {align *}
-4x + 10y & = -9 \\
-4 \ left (\ frac {1} {10} \ right) + 10y & = -9 \\
\ frac {-4} {10} + 10y & = -9 \\
100л & = -90 + 4 \\
y & = \ frac {-86} {100} \\
& = \ frac {-43} {50}
\ end {выровнять *}
Следовательно, \ (x = \ frac {1} {10} \ text {и} y = — \ frac {43} {50} \).
\ (3x — 14y = 0 \) и \ (x — 4y + 1 = 0 \)
Запишите \ (x \) через \ (y \):
\ begin {align *}
3х — 14лет & = 0 \\
3х & = 14л \\
x & = \ frac {14} {3} y
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение:
\ begin {align *}
х — 4у + 1 & = 0 \\
\ frac {14} {3} y — 4y + 1 & = 0 \\
14лет — 12лет + 3 & = 0 \\
2у & = -3 \\
y & = — \ frac {3} {2}
\ end {выровнять *}
Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *}
x & = \ frac {14 \ left (- \ frac {3} {2} \ right)} {3} \\
& = -7
\ end {выровнять *}
Следовательно, \ (x = -7 \ text {и} y = — \ frac {3} {2} \).
\ (x + y = 8 \) и \ (3x + 2y = 21 \)
Запишите \ (x \) через \ (y \):
\ begin {align *}
х + у & = 8 \\
х & = 8 — у
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение:
\ begin {align *}
3х + 2у & = 21 \\
3 (8 — у) + 2у & = 21 \\
24 — 3л + 2л & = 21 \\
y & = 3
\ end {выровнять *}
Подставить значение \ (y \) обратно в первое уравнение:
\ [x = 5 \]
Следовательно, \ (x = 5 \ text {и} y = 3 \).
\ (y = 2x + 1 \) и \ (x + 2y + 3 = 0 \)
Запишите \ (y \) через \ (x \):
\ [y = 2x + 1 \]
Подставьте значение \ (y \) во второе уравнение:
\ begin {align *}
х + 2у + 3 & = 0 \\
х + 2 (2х + 1) + 3 & = 0 \\
х + 4х + 2 + 3 & = 0 \\
5x & = -5 \\
х & = -1
\ end {выровнять *}
Подставить значение \ (x \) обратно в первое уравнение:
\ begin {align *}
у & = 2 (-1) + 1 \\
& = -1
\ end {выровнять *}
Следовательно, \ (x = -1 \ text {и} y = -1 \).
\ (5x-4y = 69 \) и \ (2x + 3y = 23 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *}
5х-4л & = 69 \\
5х & = 69 + 4у \\
x & = \ frac {69 + 4y} {5}
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение:
\ begin {align *}
2х + 3у & = 23 \\
2 \ left (\ frac {69 + 4y} {5} \ right) + 3y & = 23 \\
2 (69 + 4у) +3 (5) у & = 23 (5) \\
138 + 8л + 15л & = 115 \\
23лет & = -23 \\
\ поэтому y & = -1
\ end {выровнять *}
Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *}
x & = \ frac {69 + 4y} {5} \\
& = \ frac {69 + 4 (-1)} {5} \\
& = 13
\ end {выровнять *}
Следовательно, \ (x = 13 \ text {и} y = -1 \).
\ (x + 3y = 26 \) и \ (5x + 4y = 75 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *}
х + 3у & = 26 \\
x & = 26 — 3 года
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение:
\ begin {align *}
5х + 4у & = 75 \\
5 (26 — 3л) + 4л & = 75 \\
130 — 15л + 4л & = 75 \\
-11л & = -55 \\
\ поэтому y & = 5
\ end {выровнять *}
Подставить значение \ (y \) обратно в первое уравнение:
\ begin {align *}
х & = 26 — 3у \\
& = 26 — 3 (5) \\
& = 11
\ end {выровнять *}
Следовательно, \ (x = 11 \ text {и} y = 5 \).
\ (3x — 4y = 19 \) и \ (2x — 8y = 2 \)
Если мы умножим первое уравнение на 2, то коэффициент при \ (y \) будет одинаковым в обоих уравнениях:
\ begin {align *}
3х — 4л & = 19 \\
3 (2) х — 4 (2) у & = 19 (2) \\
6x — 8 лет & = 38
\ end {выровнять *}
Теперь мы можем вычесть второе уравнение из первого:
\ [\ begin {array} {cccc}
& 6x — 8лет & = & 38 \\
— & (2x — 8y & = & 2) \\ \ hline
& 4x + 0 & = & 36
\ конец {массив} \]
Решить относительно \ (x \):
\ begin {align *}
\ поэтому x & = \ frac {36} {4} \\
& = 9
\ end {выровнять *}
Подставьте значение \ (x \) в первое уравнение и решите относительно \ (y \):
\ begin {align *}
3х-4л & = 19 \\
3 (9) -4y & = 19 \\
\ поэтому y & = \ frac {19-3 (9)} {- 4} \\
& = 2
\ end {выровнять *}
Следовательно, \ (x = 9 \ text {и} y = 2 \).
\ (\ dfrac {a} {2} + b = 4 \) и \ (\ dfrac {a} {4} — \ dfrac {b} {4} = 1 \)
Сделайте \ (a \) предметом первого уравнения:
\ begin {align *}
\ frac {a} {2} + b & = 4 \\
а + 2b & = 8 \\
а & = 8 — 2b
\ end {выровнять *}
Подставьте значение \ (a \) во второе уравнение:
\ begin {align *}
\ frac {a} {4} — \ frac {b} {4} & = 1 \\
а — б & = 4 \\
8 — 2б — б & = 4 \\
3b & = 4 \\
b & = \ frac {4} {3}
\ end {выровнять *}
Подставить значение \ (b \) обратно в первое уравнение:
\ begin {align *}
a & = 8-2 \ left (\ frac {4} {3} \ right) \\
& = \ frac {16} {3}
\ end {выровнять *}
Следовательно, \ (a = \ frac {16} {3} \ text {и} b = \ frac {4} {3} \).
\ (- 10x + y = -1 \) и
\ (- 10x — 2y = 5 \)
Если мы вычтем второе уравнение из первого, то мы сможем решить для \ (y \):
\ [\ begin {array} {cccc}
& -10x + y & = & -1 \\
— & (-10x — 2y & = & 5) \\ \ hline
& 0 + 3г & = & -6
\ конец {массив} \]
Решить относительно \ (y \):
\ begin {align *}
3лет & = -6 \\
\ поэтому y & = -2
\ end {выровнять *}
Подставьте значение \ (y \) в первое уравнение и решите относительно \ (x \):
\ begin {align *}
-10x + y & = -1 \\
-10x — 2 & = -1 \\
-10x & = 1 \\
x & = \ frac {1} {- 10}
\ end {выровнять *}
Следовательно, \ (x = \ frac {-1} {10} \ text {и} y = -2 \).
\ (- 10 x — 10 y = -2 \) и \ (2 x + 3 y = 2 \)
Сделайте \ (x \) объектом первого уравнения:
\ begin {align *}
— 10 х — 10 у = -2 \\
5х + 5у & = 1 \\
5x & = 1 — 5л \\
\ поэтому x = -y + \ frac {1} {5}
\ end {выровнять *}
Подставьте значение \ (x \) во второе уравнение и решите относительно \ (y \):
\ begin {align *}
2х + 3у & = 2 \\
2 \ left (-y + \ frac {1} {5} \ right) + 3y & = 2 \\
-2y + \ frac {2} {5} + 3y & = 2 \\
y & = \ frac {8} {5}
\ end {выровнять *}
Подставьте значение \ (y \) в первое уравнение:
\ begin {align *}
5х + 5у & = 1 \\
5x + 5 \ влево (\ frac {8} {5} \ right) & = 1 \\
5х + 8 & = 1 \\
5x & = -7 \\
x & = \ frac {-7} {5}
\ end {выровнять *}
Следовательно, \ (x = — \ frac {7} {5} \ text {and} y = \ frac {8} {5} \).
\ (\ dfrac {1} {x} + \ dfrac {1} {y} = 3 \) и \ (\ dfrac {1} {x} — \ dfrac {1} {y} = 11 \)
Переставьте оба уравнения, умножив на \ (xy \):
\ begin {align *}
\ frac {1} {x} + \ frac {1} {y} & = 3 \\
у + х & = 3xy \\\\
\ frac {1} {x} — \ frac {1} {y} & = 11 \\
у — х & = 11xy
\ end {выровнять *}
Сложите два уравнения вместе:
\ [\ begin {array} {cccc}
& y + x & = & 3xy \\
+ & (у — х & = & 11xy) \\ \ hline
& 2y + 0 & = & 14xy
\ конец {массив} \]
Решить относительно \ (x \):
\ begin {align *}
2y & = 14xy \\
у & = 7xy \\
1 & = 7x \\
х & = \ гидроразрыв {1} {7}
\ end {выровнять *}
Подставить значение \ (x \) обратно в первое уравнение:
\ begin {align *}
y + \ frac {1} {7} & = 3 \ left (\ frac {1} {7} \ right) y \\
7у + 1 & = 3у \\
4г & = -1 \\
y & = — \ frac {1} {4}
\ end {выровнять *}
Следовательно, \ (x = \ frac {1} {7} \ text {и} y = — \ frac {1} {4} \).2 + 1 \\
0 & = 0
\ end {выровнять *}
Поскольку это верно для всех \ (x \) в действительных числах, \ (x \) может быть любым действительным числом.
Посмотрите, что происходит с \ (y \), когда \ (x \) очень маленький или очень большой:
Наименьшее значение \ (x \) может быть равно 0. Когда \ (x = 0 \), \ (y = 2- \ frac {3} {2} = \ frac {1} {2} \).2 & = 3 — ab
\ end {выровнять *}
Обратите внимание, что это то же самое, что и второе уравнение
\ (a \) и \ (b \) могут быть любыми действительными числами, кроме \ (\ text {0} \).
7 класс: Выражения и уравнения
Уровень 7: Выражения и уравнения
Рейтинг:
http: // hcpssfamilymath.weebly.com/3-expressions—equations-7ee.html
Стандарты общего ядра
Стандарты содержания
7.EE.1 — Применение свойств операций как стратегий для сложения, вычитания, разложения и расширения линейных выражений с рациональными коэффициентами.
7.EE.2 — Поймите, что переписывание выражения в различных формах в контексте проблемы может пролить свет на проблему и на то, как соотносятся количества в ней.
7.EE.3 — Решайте многоступенчатые реальные и математические задачи, поставленные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), используя инструменты стратегически.Применяйте свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить разумность ответов с помощью мысленных вычислений и стратегий оценки.
7.EE.4a — Решите задачи со словами, приводящие к уравнениям вида px + q = r и p ( x + q ) = r , где p , q и r — конкретные рациональные числа. Бегло решать уравнения этих форм.Сравните алгебраическое решение с арифметическим, определив последовательность операций, используемых в каждом подходе.
7.EE.4b — Решите проблемы со словами, приводящие к неравенствам вида пикселей + q > r или пикселей + q < r , где p , q и r — конкретные рациональные числа. Изобразите набор решений неравенства и интерпретируйте его в контексте проблемы.
7.G.5 — Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче, чтобы написать и решить простые уравнения для неизвестного угла на фигуре.
Стандарты математической практики
MP.1. Разбирайтесь в проблемах и настойчиво их решайте.
MP.2. Рассуждайте абстрактно и количественно.
MP.3. Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
MP.4. Модель с математикой.
MP.5. Используйте соответствующие инструменты.
MP.6. Обратите внимание на точность.
MP.7. Ищите и используйте структуру.
MP.8. Ищите и выражайте закономерность в повторяющихся рассуждениях.
Описание установки
В этом разделе «Выражения и уравнения» от системы государственной школы округа Ховард будут создавать выражения и уравнения с одной переменной и использовать эти уравнения для решения задач. Студенты будут использовать свойства операций для создания эквивалентных выражений.Студенты исследуют и решают реальные математические задачи, используя числовые и алгебраические выражения и уравнения. Готовясь к работе над соответствием и сходством в 8-м классе, они знакомятся со связями между углами, образованными пересекающимися линиями, и решают неизвестные на фигуре. Модуль включает в себя множество задач, которые позволяют учащимся изучить способы решения уравнений и неравенств, а также применить эти навыки в области геометрии и реальных контекстах.Это одно из пяти учебных заведений, предоставленных школьной системой округа Ховард. Хотя округ Ховард находится в штате PARCC, критерии оценки по-прежнему соответствуют SBAC .
Предупреждения
- Ограничение поддержки для учащихся, работающих ниже уровня своего класса, учащихся разного профиля и учащихся с ограниченными возможностями, а также учащихся, изучающих английский язык (ELL).
- Несмотря на то, что в каждый урок входит формативное оценивание, учителя должны будут предоставить подробные итоговые оценки.
Обоснование выбора
- Раздел предоставляет уроки, которые соответствуют строгим стандартам Общего ядра штата по математике.
- Unit предоставляет подробные и подробные ресурсы и материалы для учителей, а также дополнительную учебную поддержку. Он включает инструкции фасилитатора, а также возможные решения для учащихся и работы учащихся.
- Предоставляет студентам возможность применять математику в реальных ситуациях, а также устанавливает связи для передачи знаний между предметными областями.
Приложения линейных уравнений
Равномерное движение означает движение с неизменной скоростью или скоростью. Мы можем определить пройденное расстояние, умножив среднюю скорость на время, пройденное с этой скоростью, по формуле D = r⋅t. Приложения, связанные с равномерным движением, обычно содержат много данных, поэтому помогает сначала организовать данные в виде диаграммы, а затем создать алгебраическое уравнение, моделирующее проблему.
Пример 14: Два поезда покидают станцию одновременно, двигаясь в противоположных направлениях.Один движется со скоростью 70 миль в час, а другой — со скоростью 60 миль в час. Сколько времени нужно, чтобы расстояние между ними достигло 390 миль?
Решение: Сначала определите неизвестную величину и систематизируйте данные.
Данная информация представлена в следующей таблице. Время на каждый поезд одинаковое.
Чтобы не вводить еще две переменные, используйте формулу D = r⋅t для заполнения неизвестных расстояний, пройденных каждым поездом.
Теперь мы можем полностью заполнить график.
Алгебраическая установка определяется столбцом расстояния. Задача спрашивает, сколько времени требуется, чтобы общее расстояние достигло 390 миль.
Решить для т .
Пример 15: Поезд, идущий без остановок к месту назначения, может двигаться со средней скоростью 72 мили в час. На обратном пути поезд делает несколько остановок и может развивать скорость только 48 миль в час. Если обратный путь занимает на 2 часа дольше, чем первоначальный путь к месту назначения, то каково время в пути в каждую сторону?
Решение: Сначала определите неизвестную величину и систематизируйте данные.
Используйте формулу D = r⋅t для заполнения неизвестных расстояний.
Используйте эти выражения для заполнения диаграммы.
Алгебраическая установка снова определяется столбцом расстояния. В этом случае расстояние до пункта назначения и обратно одинаково, и уравнение равно
Решите относительно t .
Обратный путь занимает t + 2 = 4 + 2 = 6 часов.
Ответ: Прибытие в пункт назначения занимает 4 часа, а возвращение — 6 часов.
Попробуй! Мэри отправляется в школу на велосипеде со средней скоростью 6 миль в час.Ее сестра Кейт, опаздывая, уезжает через 15 минут и ездит вдвое быстрее. Сколько времени понадобится Кейт, чтобы догнать Мэри? Будь осторожен! Обратите внимание на единицы, указанные в задаче.
Ответ: Кейт наверстывает упущенное.
Тематические упражнения
Часть A: Перевести
Переведите следующее в алгебраические уравнения.
1. Сумма числа и 6 составляет 37.
2.Когда из удвоенного числа вычитается 12, получается 6.
3. Четырнадцать меньше, чем 5 умноженное на число 1.
4. Из 30 вычитается дважды какое-то число, и получается 50.
5. Пять умноженное на 6, а некоторое число равно 20.
6. 5 умноженное на некоторое число и 6 равно 20.
7. Когда сумма числа и 3 вычитается из 10, получается 5.
8.Сумма трех и пяти одинаковых чисел равна 24.
9. Десять вычитается из удвоенного числа, и в результате получается сумма числа и 2.
10. Шесть меньше некоторого числа в десять раз больше суммы этого числа и 5.
Часть B: Проблемы с номерами
Составьте алгебраическое уравнение и решите его.
11. Большее целое число на 1 больше, чем удвоенное другое целое число.Если сумма целых чисел равна 25, найдите целые числа.
12. Если большее целое число на 2 больше, чем в 4 раза больше другого целого числа, и их разница равна 32, найдите целые числа.
13. Одно целое число на 30 больше другого целого числа. Если разница между большим и удвоенным меньшим равна 8, найдите целые числа.
14. Частное числа и 4 равно 22. Найдите число.
15. Восемь раз число уменьшается в три раза на то же число, что дает разницу в 20.Какой номер?
16. Одно целое число на две единицы меньше другого. Если их сумма равна −22, найдите два целых числа.
17. Сумма двух последовательных целых чисел равна 139. Найдите целые числа.
18. Сумма трех последовательных целых чисел равна 63. Найдите целые числа.
19. Сумма трех последовательных целых чисел равна 279. Найдите целые числа.
20. Разница в два раза меньшего из двух последовательных целых чисел и большего — 39.Найдите целые числа.
21. Если меньшее из двух последовательных целых чисел вычитается из двукратного большего, получается 17. Найдите целые числа.
22. Сумма двух последовательных четных целых чисел равна 46. Найдите целые числа.
23. Сумма двух последовательных четных чисел равна 238. Найдите целые числа.
24. Сумма трех последовательных четных целых чисел равна 96. Найдите целые числа.
25. Если меньшее из двух последовательных четных целых чисел вычитается из 3-х кратного большего, результат будет 42.Найдите целые числа.
26. Сумма трех последовательных четных целых чисел равна 90. Найдите целые числа.
27. Сумма двух подряд идущих нечетных целых чисел равна 68. Найдите целые числа.
28. Сумма двух последовательных нечетных целых чисел равна 180. Найдите целые числа.
29. Сумма трех последовательных нечетных целых чисел равна 57. Найдите целые числа.
30. Если меньшее из двух последовательных нечетных целых чисел вычитается из удвоенного большего, получается 23.Найдите целые числа.
31. Дважды сумма двух последовательных нечетных целых чисел равна 32. Найдите целые числа.
32. Разница между удвоенным большим из двух подряд идущих нечетных чисел и меньшим составляет 59. Найдите целые числа.
Часть C: Проблемы геометрии
Составьте алгебраическое уравнение и решите его.
33. Если периметр квадрата 48 дюймов, найдите длину каждой стороны.
34. Длина прямоугольника на 2 дюйма больше его ширины. Если периметр 36 дюймов, найдите длину и ширину.
35. Длина прямоугольника на 2 фута меньше его ширины в два раза. Если периметр составляет 26 футов, найдите длину и ширину.
36. Ширина прямоугольника на 2 сантиметра меньше половины его длины. Если периметр 56 сантиметров, найдите длину и ширину.
37. Длина прямоугольника на 3 фута меньше двойной его ширины.Если периметр составляет 54 фута, найдите размеры прямоугольника.
38. Если длина прямоугольника вдвое больше ширины, а его периметр составляет 72 дюйма, найдите размеры прямоугольника.
39. Периметр равностороннего треугольника составляет 63 сантиметра. Найдите длину каждой стороны.
40. Равнобедренный треугольник, основание которого составляет половину длины двух других равных сторон, имеет периметр 25 сантиметров.Найдите длину каждой стороны.
41. Каждая из двух равных катетов равнобедренного треугольника в два раза длиннее основания. Если периметр составляет 105 сантиметров, то какой длины каждая ножка?
42. У треугольника есть стороны, размеры которых являются последовательными четными целыми числами. Если периметр составляет 42 дюйма, найдите размер каждой стороны.
43. У треугольника есть стороны, размеры которых — последовательные нечетные целые числа. Если периметр составляет 21 дюйм, найдите размер каждой стороны.
44. У треугольника есть стороны, размеры которых — последовательные целые числа. Если периметр составляет 102 дюйма, найдите размер каждой стороны.
45. Длина окружности составляет 50π единиц. Найдите радиус.
46. Длина окружности составляет 10π единиц. Найдите радиус.
47. Окружность круга составляет 100 сантиметров. Определите радиус с точностью до десятых долей.
48.Окружность круга составляет 20 сантиметров. Найдите диаметр, округленный до сотых.
49. Диаметр круга 5 дюймов. Определите длину окружности с точностью до десятых.
50. Диаметр круга 13 футов. Рассчитайте точное значение окружности.
Часть D: Проблемы с процентами и деньгами
Составьте алгебраическое уравнение и решите его.
51.Подсчитайте простой процент, полученный от двухлетних инвестиций в размере 1550 долларов США при годовой процентной ставке 8¾%.
52. Рассчитайте простой процент, полученный от годовой инвестиции в размере 500 долларов США при годовой процентной ставке 6%.
53. На сколько лет необходимо инвестировать 10 000 долларов под 8½% годовых, чтобы получить 4250 долларов в виде простых процентов?
54. На сколько лет необходимо инвестировать 1000 долларов под 7,75% годовых, чтобы получить 503,75 долларов в виде простых процентов?
55.По какой годовой процентной ставке нужно инвестировать 2500 долларов на 3 года, чтобы получить 412,50 долларов в виде простых процентов?
56. По какой годовой процентной ставке необходимо инвестировать 500 долларов на 2 года, чтобы получить 93,50 долларов в виде простых процентов?
57. Если простой процент, полученный за 1 год, составлял 47,25 доллара, а годовая ставка составляла 6,3%, каков был основной процент?
58. Если простые проценты, заработанные за 2 года, составляли 369,60 долларов, а годовая ставка составляла 5%, каков был основной процент?
59.Джо вложил прошлогоднюю налоговую декларацию в размере 2500 долларов в два разных счета. Он положил большую часть денег на счет денежного рынка, получая 5% простых процентов. Остальное он вложил в компакт-диск, получив 8% простых процентов. Сколько он положил на каждый счет, если общая сумма процентов за год составила 138,50 долларов?
60. Джеймс вложил 1600 долларов в два счета. Один счет приносит 4,25% простых процентов, а другой — 8,5%. Если через год процентная ставка составила 85 долларов, сколько он вложил в каждую учетную запись?
61.Джейн вложила свои сбережения в размере 5 400 долларов в два счета. Часть этих денег она хранит на компакт-диске под 3% годовых, а остальная часть — на сберегательном счете, который приносит 2% годовых. Если простые проценты, полученные с обоих счетов, составляют 140 долларов в год, то сколько у нее есть на каждом счете?
62. Марти поместил прошлогодний бонус в размере 2400 долларов на два счета. Он вложил часть в компакт-диск с годовой процентной ставкой 2,5%, а остальную часть — в фонд денежного рынка с годовой процентной ставкой 1,3%. Его общая сумма процентов за год составила 42 доллара.00. Сколько он вложил в каждый счет?
63. Алиса кладет деньги на два счета, один с 2% годовых, а другой с 3% годовых. Она инвестирует в 3 раза больше в счет с более высокой доходностью, чем в счет с более низкой доходностью. Если ее общий процент за год составляет 27,50 долларов, сколько она инвестировала в каждую учетную запись?
64. Джим вложил наследство в два отдельных банка. Один банк предложил ставку 5,5% годовых, другой — 6¼%.Он инвестировал в более доходный банковский счет вдвое больше, чем в другой. Если его общая простая процентная ставка за 1 год составляла 4860 долларов, то какова была сумма его наследства?
65. Если рекламируемый товар стоит 29,99 долларов плюс налог 9,25%, какова общая стоимость?
66. Если рекламируется товар, стоимость которого составляет 32,98 доллара США плюс 8¾% налога, какова его общая стоимость?
67. Товар, включая налог в размере 8,75%, стоил 46,49 долларов. Какова первоначальная стоимость товара до вычета налогов?
68.Товар, включая налог в размере 5,48%, стоил 17,82 доллара. Какова первоначальная стоимость товара до вычета налогов?
69. Если еда стоит 32,75 доллара, какова сумма после добавления 15% чаевых?
70. Сколько чаевых составляет 15% от счета в ресторане на сумму 33,33 доллара?
71. У Рэя есть пригоршня десятицентовиков стоимостью 3,05 доллара. У него на 5 центов больше, чем у него. Сколько у него каждой монеты?
72. У Джилл на 3 полдоллара меньше, чем у нее четвертей.Стоимость всех 27 ее монет составляет 9,75 доллара. Сколько каждой монеты у Джилл?
73. Кэти должна внести пяти- и десятидолларовые банкноты на 410 долларов. У нее 1 меньше, чем в три раза больше десятков, чем у нее пятидолларовых купюр. Сколько денег от каждого счета она должна внести?
74. У Билли есть стопка четвертаков, десятицентовиков и никелей стоимостью 3,75 доллара. У него на 3 центов больше, чем четвертей, и на 5 центов больше, чем четвертей. Сколько каждой монеты у Билли?
75.У Мэри есть банка с однодолларовыми банкнотами, полдолларовыми монетами и четвертаками стоимостью 14 долларов. У нее в два раза больше четвертаков, чем у нее полудолларовых монет, и столько же полудолларовых монет, как у однодолларовых банкнот. Сколько у нее каждого?
76. У Чада есть пачка одно-, пяти- и десятидолларовых банкнот на общую сумму 118 долларов. У него в 2 раза больше, чем в 3 раза больше, чем у него пятидолларовых банкнот, и на 1 банкнот меньше десяти, чем пяти долларов. Сколько каждой банкноты есть у Чада?
Часть D: Равномерное движение (проблемы расстояния)
Составьте алгебраическое уравнение и решите его.
77. Две машины выезжают с места, двигаясь в противоположных направлениях. Если одна машина развивает в среднем 55 миль в час, а другая — 65 миль в час, то сколько времени им потребуется, чтобы преодолеть расстояние в 300 миль?
78. Из аэропорта одновременно вылетают два самолета в противоположных направлениях. Средняя скорость самолетов составляет 450 миль в час и 395 миль в час. Сколько времени потребуется самолетам, чтобы преодолеть расстояние в 1478 единиц.75 миль друг от друга?
79. Билл и Тед мчатся по стране. Билл уезжает на час раньше, чем Тед, и едет со средней скоростью 60 миль в час. Если Тед намеревается наверстать упущенное со скоростью 70 миль в час, то сколько времени это займет?
80. Два брата уезжают из одного и того же места, один на машине, а другой на велосипеде, чтобы встретиться в доме своей бабушки за ужином. Если один из братьев в среднем проезжает 30 миль в час в машине, а другой — 12 миль в час на велосипеде, тогда у брата на велосипеде на 1 час меньше, чем в 3 раза дольше, чем у другого в машине.Сколько времени нужно каждому из них, чтобы совершить путешествие?
81. Пилот коммерческой авиакомпании летел со средней скоростью 350 миль в час, прежде чем был проинформирован о том, что аэродром его назначения может быть закрыт из-за плохих погодных условий. Пытаясь прибыть перед бурей, он увеличил скорость до 400 миль в час и летел еще 3 часа. Если общее расстояние полета составило 2950 миль, то сколько времени длилось путешествие?
82. Два брата проехали 2793 мили от Лос-Анджелеса до Нью-Йорка.Один из братьев, управляя автомобилем днем, мог развивать скорость в среднем 70 миль в час, а другой, двигаясь ночью, мог развивать скорость в среднем 53 мили в час. Если брат, ехавший ночью, ехал на 3 часа меньше, чем брат, ехавший днем, то сколько часов каждый из них ехал?
83. Джо и Эллен живут в 21 миле друг от друга. Отправляясь одновременно, они едут навстречу друг другу. Если у Джо в среднем 8 миль в час, а у Эллен — 6 миль в час, сколько времени у них уйдет на встречу?
84.Если дорога до автомастерской занимает 6 минут со средней скоростью 30 миль в час, то сколько времени потребуется, чтобы вернуться обратно со средней скоростью 4 мили в час?
85. Хайме и Алекс покидают то же место и едут в противоположных направлениях. Условия движения позволили Алексу в среднем разгоняться на 14 миль в час, чем Хайме. Через полтора часа их разделяет 159 миль. Найдите скорость, с которой каждый мог двигаться.
86. Джейн и Холли живут в 51 миле друг от друга и уезжают, путешествуя навстречу друг другу, чтобы встретиться за обедом.Джейн ехала по автостраде со скоростью вдвое большей, чем Холли. Они смогли встретиться через полчаса. С какой скоростью путешествовал каждый?
Часть F: Темы дискуссионной доски
87. Обсудите в уме идеи для расчета налогов и подсказок.
88. Изучите исторические методы представления неизвестных.
89. Изучите и сравните простые проценты и сложные проценты. В чем разница?
90.Обсудите, почему алгебра — обязательный предмет.
91. Изучите способы показать, что повторяющаяся десятичная дробь рациональна. Поделитесь своими выводами на доске обсуждений.
PDST Математика после начального образования | Новые ресурсы: преподавание математики в среде DEIS
Этот веб-сайт использует Google Analytics для сбора анонимной информации, такой как количество посетителей сайта и наиболее популярные страницы.
Включение этого файла cookie помогает нам улучшать наш веб-сайт.
Пожалуйста, сначала включите строго необходимые файлы cookie, чтобы мы могли сохранить ваши предпочтения!
Показать детали
| Имя | Провайдер | Назначение | Срок действия |
|---|---|---|---|
| _ga | Файл cookie Google Analytics, который используется для расчета данных о посетителях, сеансах и кампании, а также для отслеживания использования сайта для аналитического отчета сайта.Файлы cookie хранят информацию анонимно и присваивают случайно сгенерированный номер для идентификации уникальных посетителей. Отказаться на странице https://tools.google.com/dlpage/gaoptout | 730 дней | |
| _gat | Файл cookie Google Analytics, используемый для регулирования скорости запросов.Отказаться на странице https://tools.google.com/dlpage/gaoptout | 1 день | |
| _gid | Файл cookie Google Analytics используется для хранения информации о том, как посетители используют веб-сайт, и помогает в создании аналитического отчета о том, как работает веб-сайт.Собранные данные, включая количество посетителей, источник, откуда они пришли, и страницы, посещенные в анонимной форме. Отказаться на странице https://tools.google.com/dlpage/gaoptout | 1 день | |
| NID | Содержит уникальный идентификатор, который Google использует для запоминания ваших предпочтений и другой информации, например, предпочитаемого вами языка (например,грамм. Английский), сколько результатов поиска вы хотите отображать на странице (например, 10 или 20) и хотите ли вы, чтобы фильтр безопасного поиска Google был включен. |
Заданий по алгебре
Добро пожаловать на страницу рабочих листов по алгебре на Math-Drills.com, где неизвестные являются обычным явлением, а переменные — нормой. На этой странице вы найдете рабочие листы по алгебре в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и функции построения графиков.
Эта страница начинается с некоторых пропущенных рабочих листов для младших школьников. Затем мы сразу переходим к алгебре, помогая студентам распознавать и понимать основной язык, связанный с алгеброй. Остальная часть страницы охватывает некоторые из основных тем, с которыми вы столкнетесь в модулях алгебры. Помните, что, обучая студентов алгебре, вы помогаете создавать будущих финансовых гениев, инженеров и ученых, которые решат все проблемы нашего мира.
Алгебра намного интереснее, когда вещи более реальны.Решать линейные уравнения гораздо веселее с двумя весами, загадочными мешочками и кучей мармеладов. Многие учителя используют плитки алгебры, чтобы помочь студентам понять различные темы алгебры. И нет ничего лучше набора осей координат для решения систем линейных уравнений.
самых популярных заданий по алгебре на этой неделе
Рабочий лист свойств и законов чисел
Коммутативный закон
Коммутативный закон или коммутативное свойство гласит, что вы можете изменить порядок чисел в арифметической задаче и при этом получить те же результаты.В контексте арифметики он работает только с операциями сложения или умножения , но не со смешанными операциями сложения и умножения. Например, 3 + 5 = 5 + 3 и 9 × 5 = 5 × 9. Забавное занятие, которое вы можете использовать в классе, — это мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, затем левый, или вы можете надеть левый носок, затем правый носок, и вы получите тот же результат.Однако надевание нижнего белья и брюк не является обязательным.
Ассоциативный закон
Ассоциативный закон или ассоциативное свойство позволяет изменять группировку операций в арифметической задаче с двумя или более шагами без изменения результата. Порядок чисел остается неизменным в ассоциативном законе. Как и в случае с коммутативным законом, применяется к задачам только сложения или только умножения.Его лучше всего рассматривать в контексте порядка операций, поскольку он требует, чтобы в первую очередь работали со скобками. Пример ассоциативного закона: (9 + 5) + 6 = 9 + (5 + 6). В этом случае не имеет значения, добавляете ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, ставить предметы на поднос во время обеда. Они могут сначала положить на поднос молоко и овощи, затем бутерброд, или начать с овощей и бутерброда, а затем добавить молоко.Если их лоток выглядит одинаково оба раза, они смоделировали ассоциативный закон. Можно утверждать, что чтение книги является ассоциативным или неассоциативным, поскольку потенциально можно сначала прочитать последние главы и при этом понять книгу так же, как и тот, кто читает книгу обычным способом.
Обратные отношения с
одна заготовка
Рабочие листы
Обратные отношения охватывают навык предалгебры, призванный помочь учащимся понять взаимосвязь между умножением и делением, а также взаимосвязь между сложением и вычитанием.
Обратные отношения с
двумя пробелами
Рабочие листы с отсутствующими числами или неизвестными в уравнениях
Отсутствующие числа в таблицах уравнений трех типов: пробелы для неизвестных, символы для неизвестных и переменные для неизвестных.
Рабочие листы с пропущенными номерами с
пробелами в качестве неизвестных (Пусто Никогда в позиции ответа)
В этих таблицах неизвестное ограничено стороной вопроса в уравнении, которая может быть слева или справа от знака равенства.
Рабочие листы с пропущенными номерами с
пробелами в качестве неизвестных (пустые в любом положении)
На этих листах неизвестное может быть в любой позиции в уравнении, включая ответ.
Рабочие листы с отсутствующими номерами с
символами в качестве неизвестных (Символ никогда не находится в позиции ответа)
Рабочие листы с отсутствующими номерами с
символами в качестве неизвестных (символ в любой позиции)
Рабочие листы с отсутствующими номерами с неизвестными переменными
(переменная слева; ответ справа)
Рабочие листы с отсутствующими номерами с неизвестными переменными
(переменная никогда не находится в позиции ответа)
Рабочие листы с отсутствующими номерами с неизвестными переменными
(переменная в любом положении)
Равенства с добавлением
с обеих сторон уравнения и символов как неизвестных
Рабочие листы по алгебраическим выражениям
Использование распределительного свойства
Дистрибутивность — важный навык в алгебре.Проще говоря, это означает, что вы можете разделить один из множителей при умножении на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в мысленной математике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно ответить на вопрос, используя свойство распределенности. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70.Наконец, прибавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко сложить другой множитель перед умножением. Например, в выражении 3 (x + 5) нельзя сложить x + 5, не зная значения x. Вместо этого свойство распределения можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15.
Вычисление алгебраических выражений
Правила экспонент и свойства
Практика с
базовыми правилами экспоненты
Как сказано в названии, эти рабочие листы включают только основные вопросы по правилам экспоненты.Каждый вопрос имеет дело только с двумя экспонентами; запутанные сложные термины и вещи, которые мог бы понять более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют его как 4 2 , поэтому студенты могут сосредоточиться на изучении того, как умножать и делить показатели более или менее. в изоляции.
Линейные выражения и уравнения
Рабочие листы линейных уравнений, включая упрощение, построение графиков, оценку и решение систем линейных уравнений.
Перевод алгебраических фраз прописью в алгебраические выражения
Знание языка алгебры может помочь понять смысл словесных задач и ситуаций вне школы. В этих рабочих листах студентам предлагается преобразовать фразы в алгебраические выражения.
Упрощение линейных выражений (объединение одинаковых терминов)
Объединение одинаковых терминов — это то, что часто происходит в алгебре.Студенты могут познакомиться с темой и немного попрактиковаться с этими рабочими листами. Полоса поднимается с добавлением и вычитанием версий, которые вводят круглые скобки в выражения. Для студентов, которые хорошо разбираются в дробях, упрощение простых рабочих листов алгебраических дробей представляет собой небольшую проблему по сравнению с другими рабочими листами в этом разделе.
Переписывание линейных уравнений
Определение линейных уравнений по наклонам, пересечениям по оси Y и точкам
Линейное уравнение
Графики
Построение графиков линейных уравнений и чтение существующих графиков дает учащимся наглядное представление, которое очень полезно для понимания концепций наклона и пересечения по оси Y.
Решение линейных уравнений с мармеладом — это увлекательное занятие для студентов, впервые изучающих алгебраические понятия. В идеале вам понадобятся непрозрачные пакеты без массы, но поскольку это невозможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет студентам лучше понять уравнения. Любые мешки, которые вы используете, должны быть сбалансированы по другую сторону уравнения с пустыми мешками.
Наверное, лучший способ проиллюстрировать это на примере.Давайте используем 3 x + 2 = 14. Вы можете распознать x как неизвестное, что на самом деле является количеством мармеладов, которые мы кладем в каждый непрозрачный пакет. Число 3 в 3 x означает, что нам нужно три сумки. Лучше всего наполнить пакеты необходимым количеством мармеладов вне поля зрения учащихся, чтобы им действительно пришлось решать уравнение.
На одной стороне весов с двумя чашами поместите три пакета с мармеладом x в каждом и два рыхлых мармелада, чтобы представить + 2 часть уравнения.С другой стороны баланса поместите 14 мармеладов и три пустых мешка, которые, как вы заметите, необходимы для правильного «баланса» уравнения. А теперь самое интересное … если ученики удаляют две рыхлые мармеладки с одной стороны уравнения, все становится неуравновешенным, поэтому им нужно удалить две мармеладки с другой стороны весов, чтобы сохранить равновесие. Кушать мармелад необязательно. Цель состоит в том, чтобы изолировать мешочки с одной стороны весов без каких-либо рыхлых желейных бобов, сохраняя при этом равновесие.
Последний шаг — разделить сыпучие мармеладки с одной стороны уравнения на то же количество групп, что и мешков. Это, вероятно, даст вам хорошее представление о том, сколько мармеладов в каждом пакете. Если нет, съешьте и попробуйте еще раз. Теперь мы понимаем, что это не сработает для каждого линейного уравнения, поскольку трудно получить отрицательные желейные бобы, но это еще одна стратегия обучения, которую вы можете использовать для алгебры.
Решение линейных уравнений
Несмотря на внешность, уравнения типа a / x не являются линейными.Вместо этого они принадлежат к другому виду уравнений. Они хороши для объединения их с линейными уравнениями, поскольку они вводят понятие действительных и недействительных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений в форме a / x являются те, при которых знаменатель становится равным 0.
Линейные системы
Решение систем линейных уравнений
Решение систем линейных уравнений с помощью построения графиков
Квадратичные выражения и уравнения
Квадратные выражения и рабочие листы уравнений, включая множители, разложение на множители и решение квадратных уравнений.
Упрощение квадратных выражений (объединение одинаковых терминов)
Сложение / вычитание и упрощение квадратичных выражений
Множители квадратного выражения
Факторинг квадратичных выражений
Таблицы факторизации квадратичных выражений, представленные ниже, содержат множество практических вопросов для студентов, чтобы отточить свои стратегии разложения.Если вы предпочитаете рабочие листы с квадратными уравнениями, см. Следующий раздел. Эти рабочие листы бывают разных уровней, самые простые — в начале. Коэффициенты ‘a’, упомянутые ниже, являются коэффициентами члена x 2 , как в общем квадратичном выражении: ax 2 + bx + c.
Используете ли вы метод проб и ошибок, вычисляя квадрат или общую квадратичную формулу, эти рабочие листы включают множество практических вопросов с ответами.В первом разделе рабочие листы включают вопросы, в которых квадратичные выражения равны 0. Это делает процесс факторингом квадратичных выражений с дополнительным шагом нахождения значений для x, когда выражение равно 0. Во втором разделе выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы квадратное выражение стало равным нулю.
Решение квадратных уравнений , что равняется нулю (e.грамм. ax² + bx + c = 0)
Решение квадратного уравнения , которое равно целому числу (например, ax² + bx + c = d)
Другие полиномиальные и мономиальные выражения и уравнения
Факторизация рабочих листов неквадратичных выражений различного уровня сложности.
Упрощающие полиномы , включающие сложение и вычитание
Упрощение полиномов , включающих умножение и деление
Упрощающие полиномы , включающие сложение, вычитание, умножение и деление
Выражения факторинга, которые
не включают квадратную переменную
Факторинговые выражения
, которые всегда включают квадратную переменную
Факторинговые выражения
, которые иногда включают квадраты переменных
Умножение многочленов на два множителя
Умножение многочленов на три множителя
Неравенства с графами
Рабочие листы неравенств, включающие запись неравенства, которое соответствует графику, и отображение неравенств на числовой прямой.
