Содержание
Путь при неравномерном движении — материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Сейчас мы будем рассматривать неравномерное движение — то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.
Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент и конечный момент . Длительность рассматриваемого промежутка времени равна .
Очевидно, что за промежуток времени тело проходит путь:
(1)
Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).
Рис. 1. Путь при равномерном движении 1. Путь при равномерном движении |
Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель — его горизонтальная сторона.
Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.
Пусть скорость тела зависит от времени, и на рассматриваемом промежутке график скорости выглядит, например, так (рис. 2):
| Рис. 2. Неравномерное движение |
Дальше мы рассуждаем следующим образом.
1. Разобьём наш промежуток времени на небольшие отрезки величиной .
2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью . То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.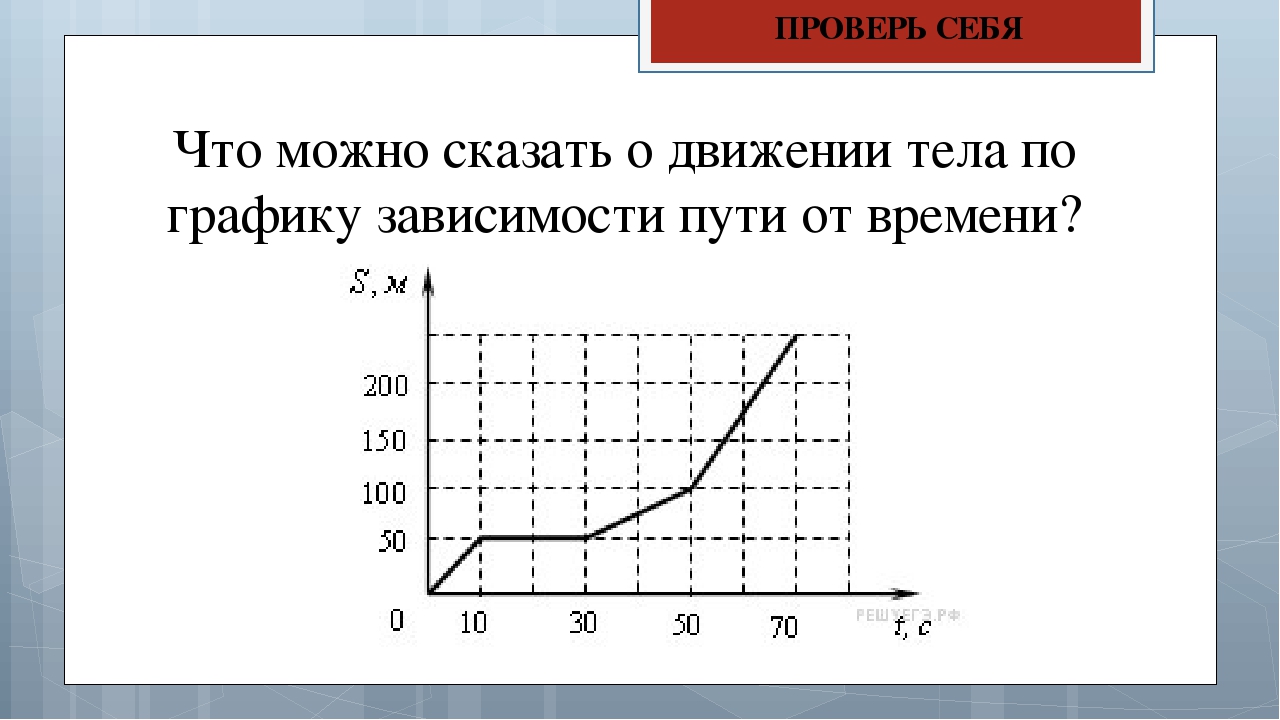
На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек на правом рисунке вдвое меньше, чем на левом.
| Рис. 3. Ступенчатая аппроксимация |
Путь, пройденный за время равномерного движения — это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого «ступенчатого» движения — это сумма площадей всех прямоугольников на графике.
3. Теперь устремляем к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от до . (рис. 4
| Рис. 4. Путь при неравномерном движении |
В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.
| Аппроксимация — это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать. |
Геометрическая интерпретация пути.Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.
Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.
Задача. Тело, имеющее скорость в начальный момент , разгоняется с постоянным ускорением . Найти путь, пройденный телом к моменту времени .
Решение. Зависимость скорости от времени в данном случае имеет вид:
(2)
График скорости — прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.
Рис.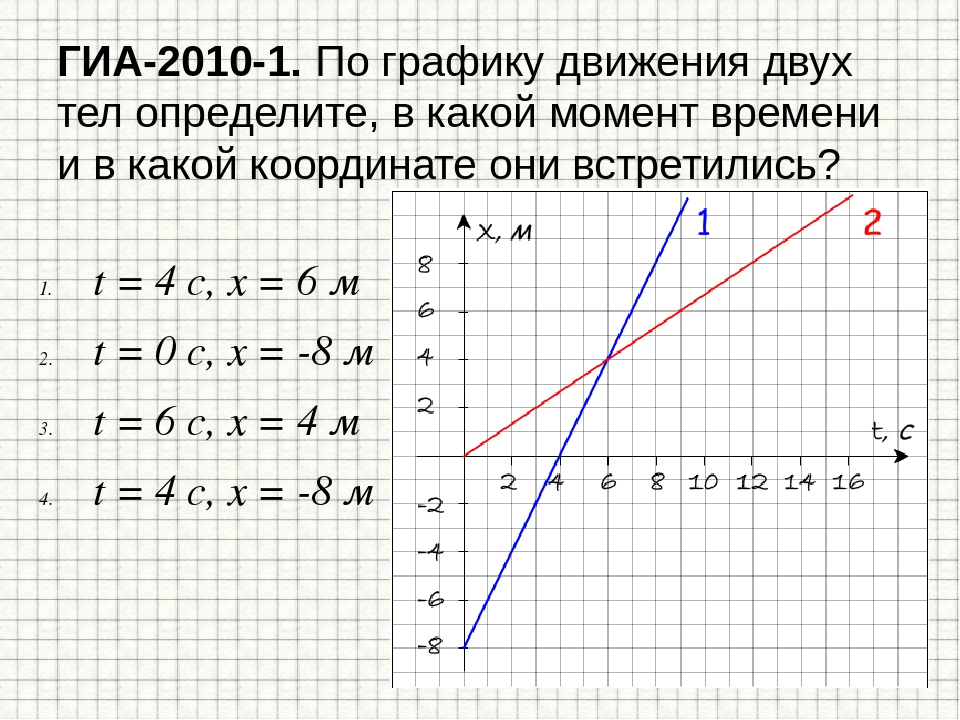 5. Путь при равноускоренном движении 5. Путь при равноускоренном движении |
Меньшее основание трапеции равно . Большее основание равно . Высота трапеции равна . Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:
Эту формулу можно переписать в более привычном виде:
Она, разумеется, вам хорошо известна из темы «Равноускоренное движение».
Задача. График скорости тела является полуокружностью диаметра (рис. 6). Максимальная скорость тела равна . Найти путь, пройденный телом за время .
Решение. Как вы знаете, площадь круга радиуса равна . Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время , а вертикальный радиус есть скорость .
Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения на горизонтальный радиус и на вертикальный радиус:
Рис.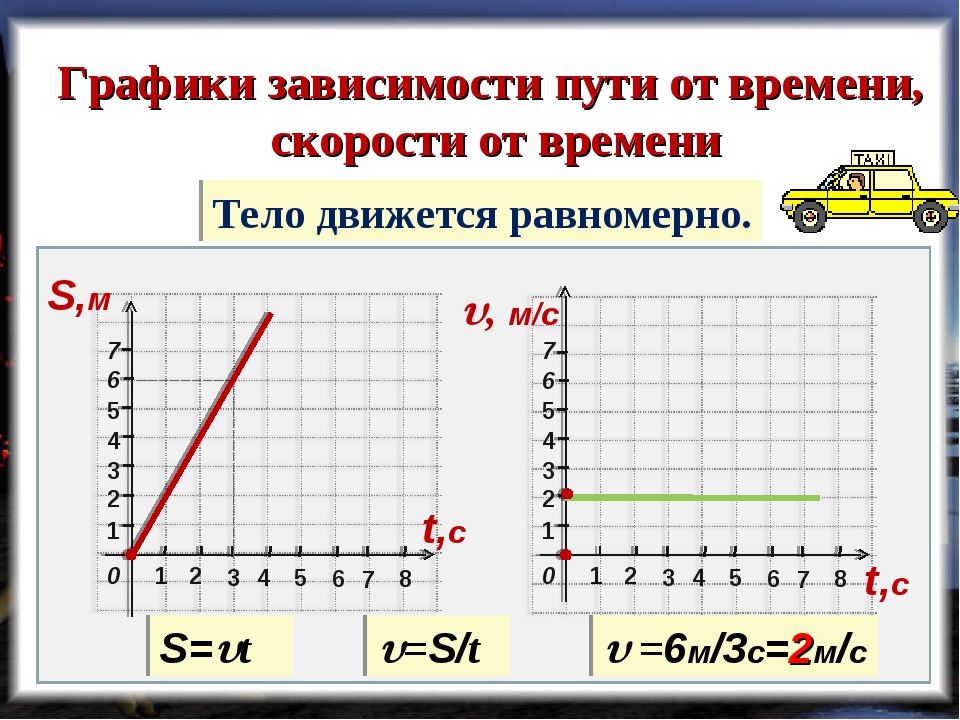 6. К задаче 6. К задаче |
Расчет пути и времени движения
Зная скорость равномерного движения тела, можно узнать путь, пройденный им за определенное время. Пусть, например, поезд равномерно движется со скоростью 20 м/с. Это значит, что за каждую секунду он проходит путь 20 м. Тогда за 5 с поезд пройдет путь в 5 раз больший, чем за 1 с, т. е. 20 м/с * 5 с = 100 м, а за 10 с – в 10 раз больший, т. е. 20 м/с * 10 с =200 м и т. д.
Чтобы определить путь, пройденный при равномерном движении, надо скорость тела умножить на время его движения:
s = vt
Зная путь и скорость равномерного движения тела, можно определить время этого движения.
Определим, за какое время пешеход, скорость движения которого 1,5 м/с, пройдет путь, равный 3 км, т. е. 3000 м.
Из формулы s=vt следует, что:
t = s/v
Подставляя в эту формулу числовое значение пути и скорости, мы найдем время: t = 3000 м/ 1,5 м/с = 2000 с.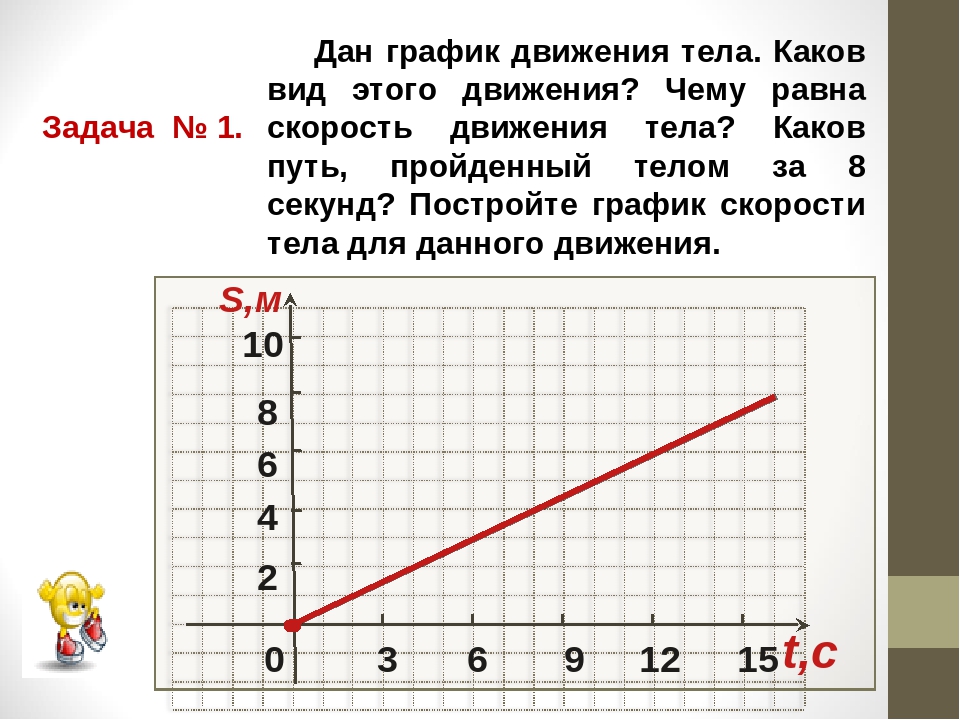
Среднюю скорость неравномерного движения вычисляют, предполагая, что движение является равномерным. Поэтому если нужно по средней скорости вычислить путь, то можно воспользоваться правилом, установленным для равномерного движения. Таким образом, путь, пройденный телом при неравномерном движении, равен произведению средней скорости на время движения, т. е.
s = vсрt.
Время, необходимое для прохождения какого-нибудь пути при неравномерном движении, равно частному от деления этого пути на среднюю скорость.
Вопросы. 1. Как определяют путь, пройденный телом при равномерном движении, если известны скорость и время движения? Как по пути и скорости определить время равномерного движения? 2. Ответьте на такие же вопросы для случая неравномерного движения.
Упражнение. 1. Найдите в таблице 1 скорости пешехода, конькобежца, поезда и определите (устно) пути, пройденные этими телами за 10 с.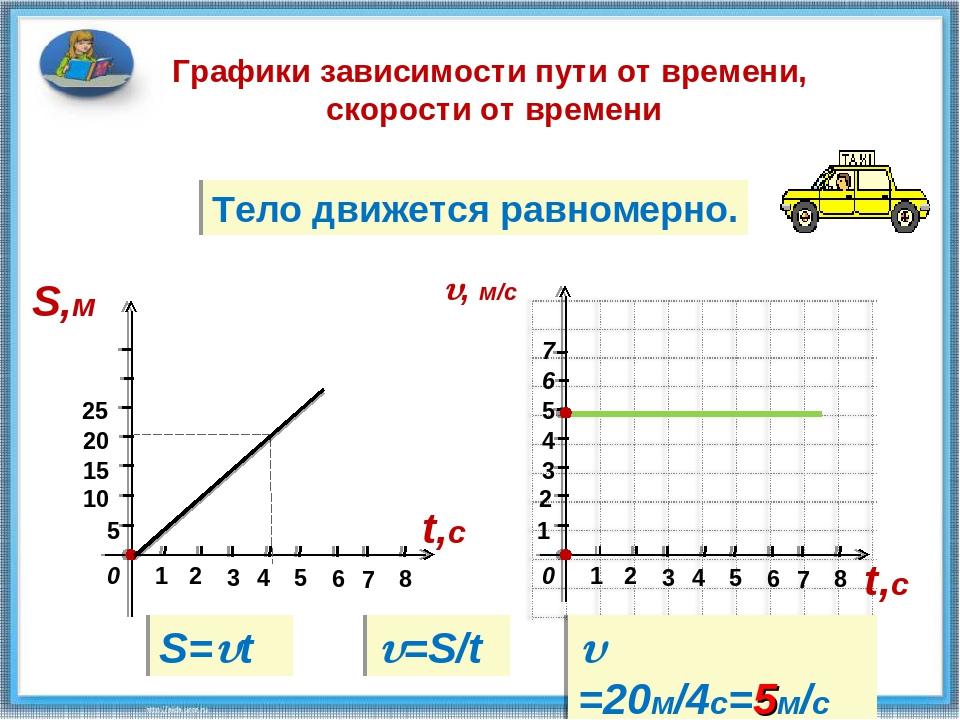 2. Самолет летит со средней скоростью 750 км/ч. Какой путь он пройдет за 6 ч полета? 3. Какое время понадобится поезду и самолету для прохождения пути 4000 м? (Скорости этих тел указаны в таблице 1.) 4. На рисунке 29 изображен график пути равномерного движения. На этом графике Os — ось пройденных путей; Ot — ось времени. Определите по этому графику путь, пройденный за 10 ч, и скорость движения. 5. На рисунке 30 изображены графики путей двух равномерных движений I и II. По графикам определите, скорость какого из этих движений больше. Ответ обоснуйте. 6. На рисунке 31 дан график скорости равномерного движения тела. Чему равна скорость движения тела? Определите путь, пройденный телом за 5 с.
2. Самолет летит со средней скоростью 750 км/ч. Какой путь он пройдет за 6 ч полета? 3. Какое время понадобится поезду и самолету для прохождения пути 4000 м? (Скорости этих тел указаны в таблице 1.) 4. На рисунке 29 изображен график пути равномерного движения. На этом графике Os — ось пройденных путей; Ot — ось времени. Определите по этому графику путь, пройденный за 10 ч, и скорость движения. 5. На рисунке 30 изображены графики путей двух равномерных движений I и II. По графикам определите, скорость какого из этих движений больше. Ответ обоснуйте. 6. На рисунке 31 дан график скорости равномерного движения тела. Чему равна скорость движения тела? Определите путь, пройденный телом за 5 с.
по графику скорости определите путь, пройденный телом за 8с
Самуилу сказали поднять рельсу, массой 200 т на высоту 50 см, надо произвести определенную работу. Какая необходима работа для того же подъема при пом
…
ощи рычага, дающего выигрыш в силе в 5 раз?
электро-велосипед массой 200 кг разогнался из состояния покоя так, что его кинетическая энергия стала 4900 Дж. До какой скорости разогнался мотоцикл?
До какой скорости разогнался мотоцикл?
…
*срочно
Построить изображение отрезка – предмета АВ, расположенного перед собирающей линзой, так что расстояние от предмета до линзы d=2F.
При измерениях из воздуха в стекло угол падения луча составил 60º, а угол преломления 30º. Сделайте пояснительный рисунок, используйте транспортир, ук
…
ажите углы, подпишите их градусную меру, вычислите показатель преломления стекла Пожалуйста помогите срочно нужноДАМ 20 БАЛЛОВ
Помогите пожалуйста срочноо очень через час впр
срочноо пожалуйста, физика, очень срочноо пж пж
Напишите сочинение-рассуждение Чудеса жизни
Камень бросили вертикально вверх сообщив ему начальную скорость 12 м/с
Пренебригая сопротивлением воздуха определи максимальную высоту h на которую по
…
дымется камень. Ускорение свободного падения 10 м/с²
примения правила равновесие рычяга к блоку,конспект
СРОЧНОО ВЫРУЧАЙТЕ !!! ЕСЛИ НАБЕРУ ПОЛНЫЙ БАЛЛ ПОМОЩНИКУ НА КАСПИЙ ГОЛД 200тг закину
Какой механизм напоминает тело, начинающее вращение под действием
…
силы? А) Наклонная плоскость
Б) Рычаг второго рода
В) Отвес
Г) Ворот 1 б
2.
а) 1 Н
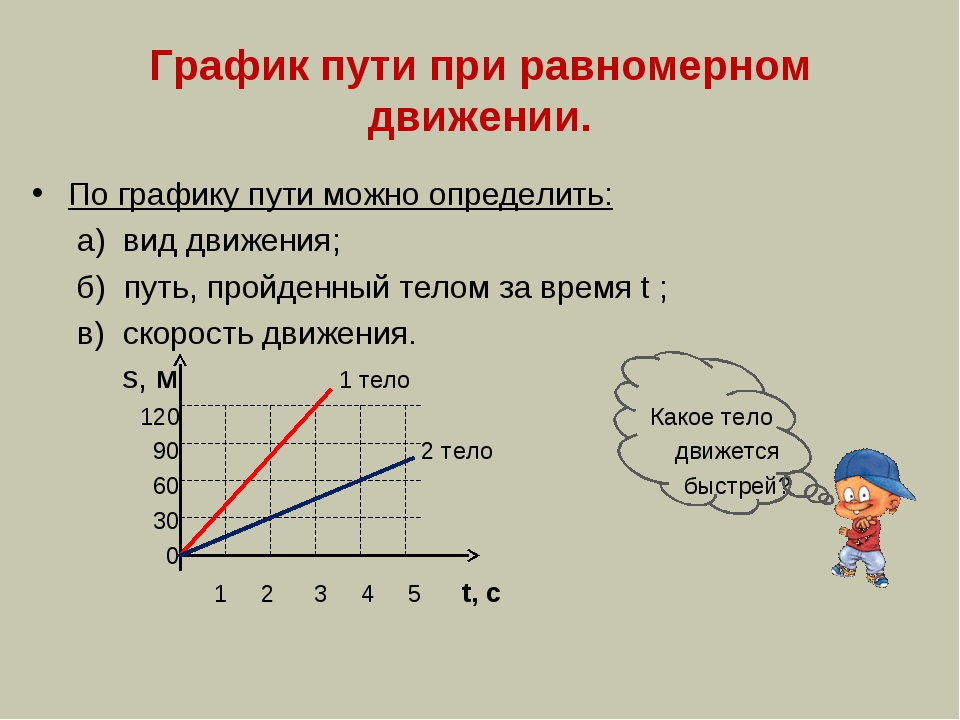
Если для поворота рычага потребовалась сила 20 Н, то взяв точку приложения силы вдвое дальше от опоры, какая сила потребуется для того же поворота?
б) 5 Н в) 10 Н г) 20 Н 1 б
3.
а) перемещение б) колебания в) вращение г) работу
Энергия — это физическая величина, показывающая что тело может совершить…?
1б
4. Кинетическая энергия Ек тела массой m, движущегося со скоростью v, равна?
1б
5. Чтобы поднять груз массой 100 кг на высоту 1 м, необходимо приложить энергию, равную:
6. Коэффициентом полезного действия называют:
1б
2б
7.
Для теплового двигателя КПД рассчитывается по формуле:
1б
Для подъема груза массы 5 кг на высоту 1 м приложили силу 100 Н. КПД механизма: б) 55% в) 80% г)100%
3б
3б
10. Под действием силы тяги 1200 Н автомобиль движется с постоянной скоростью 72 км/ч. Мощность двигателя равна:
а) 15 кВт б) 25 кВт в) 1200 кВт г) 1000 Вт 3 б
11. Рычаг находится в равновесии под действием двух сил. Первая сила 4 Н имеет плечо 15 см. Определите, чему равна вторая сила, если её плечо 10 см
а) 4 Н б) 1,6 Н в) 6 Н г) 10 Н
Физические основы механики
Если путь , пройденный материальной точкой за промежуток времени от t1 до t2, разбить на достаточно малые участки , то для каждого го участка выполняется условие
Тогда весь путь приближенно равен сумме
При стремлении всех к нулю это приближенное равенство становится точным, то есть
Подчеркнем, что здесь речь идет о модуле скорости.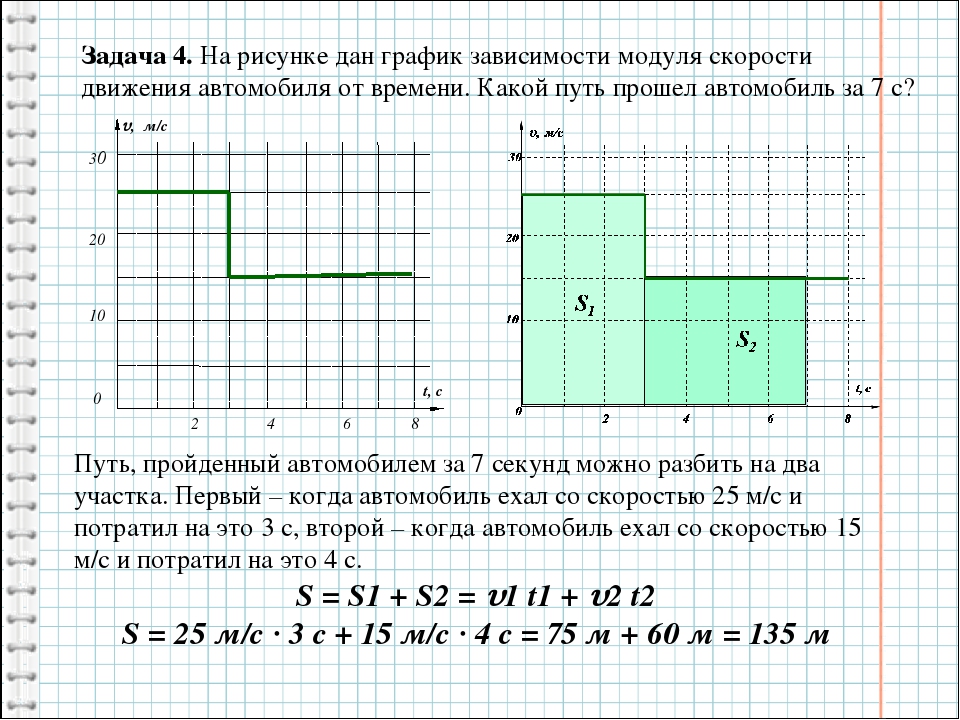 Если зависимость модуля скорости от времени выразить графически, то путь, пройденный материальной точкой за время от t2 до t1, численно равен площади фигуры, ограниченной кривой , осью времени и вертикальными прямыми, проходящими через точки с абсциссами и (рис. 2.7.).
Если зависимость модуля скорости от времени выразить графически, то путь, пройденный материальной точкой за время от t2 до t1, численно равен площади фигуры, ограниченной кривой , осью времени и вертикальными прямыми, проходящими через точки с абсциссами и (рис. 2.7.).
Рис. 2.7. Определение пройденного пути по графику зависимости скорости от времени
При равномерном движении величина скорости постоянна и может быть вынесена из-под знака интеграла:
Так как модуль скорости , то пройденный телом путь с течением времени может только возрастать (или быть постоянным, когда тело покоится).
Если нас интересует перемещение материальной точки за то же время, то мы так же разбиваем траекторию на малые участки, но суммируем теперь векторы перемещения:
Учитывая связь перемещения с вектором скорости
получаем
В отличие от выражения для пройденного пути под интегралом здесь стоит не модуль, а вектор скорости.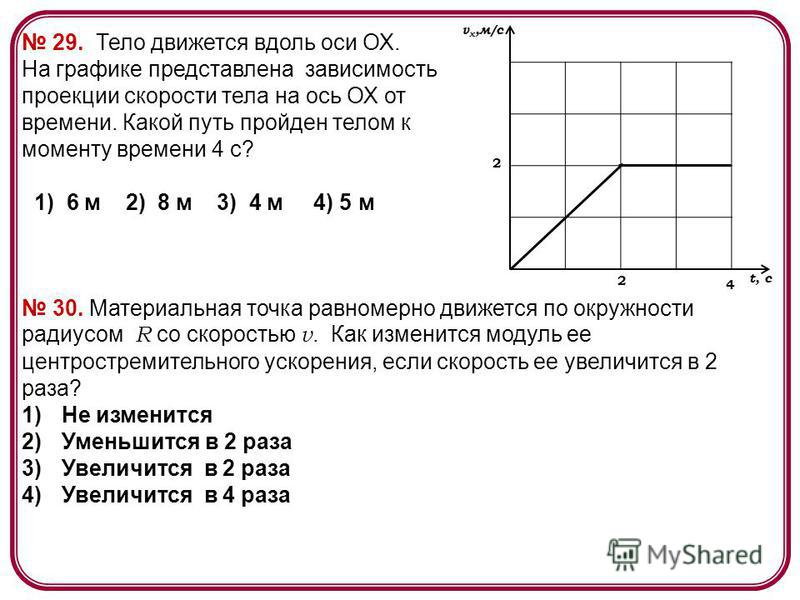 Точно так же при равномерном прямолинейном движении, когда , мы можем вынести скорость из-под знака интеграла:
Точно так же при равномерном прямолинейном движении, когда , мы можем вынести скорость из-под знака интеграла:
Чтобы практически найти перемещение, интеграл, представленный в векторной форме, необходимо записать в виде интегралов для проекций
Здесь x1, y1, z1 — координаты точки в момент времени t1, а x2, y2, z2 — координаты точки в момент времени t2, соответственно величина перемещения при этом равна
а направление вектора перемещения определяется соотношением:
Пример. Пункт A находится на бетонированном аэродроме, пункт B — на примыкающем к нему поле, на котором скорость машины в n раз меньше. Для того, чтобы за кратчайшее время добраться из в , был выбран оптимальный маршрут, показанный на рис. 2.8. Найти соотношение между синусами углов α и β.
Рис. 2.8. Оптимальный маршрут из пункта А в пункт В
2.8. Оптимальный маршрут из пункта А в пункт В
Все расстояния указаны на рисунке. Время , затрачиваемое на путь , преодолеваемый со скоростью , равно
Время t2, затрачиваемое на путь , преодолеваемый со скоростью , равно
Полное время в пути, будет
Поскольку точка 0 была выбрана так, что на путь затрачивалось минимальное время, должна быть равна нулю производная времени по координате точки перехода с бетона на траву:
Поскольку
находим, что
то есть
Сходство с известным законом преломления света на границе двух сред не случайно: природа устроена так, что свет выбирает путь, требующий минимального времени. Это так называемый принцип Ферма, который мы подробно рассмотрим в соответствующем разделе.
Физика. ЕГЭ. Текстовые задачи
Задача №1
По графику зависимости модуля скорости тела от времени, представленному на рисунке (Рис. 1), определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)
1), определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)
Рис.1
Решение
В этой задаче необходимо использовать данные, представленные на графике. Известно: чтобы по графику зависимости скорости от времени найти путь, пройденный телом за интересующий интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени. В нашем случае в интервале времени от 0 до 2 с автомобиль прошёл путь, равный сумме площадей (Рис.2):
Рис.2
S = S1 + S2
S = 0,5 х 2м/с х (1с – 0с) + 2м/с х (2с – 1с) = 3 м
Ответ: 3.
Задача №2
По графику зависимости модуля скорости тела от времени, представленному на рисунке (Рис.3), определите путь, пройденный телом от момента времени 0 с до момента времени 5 с.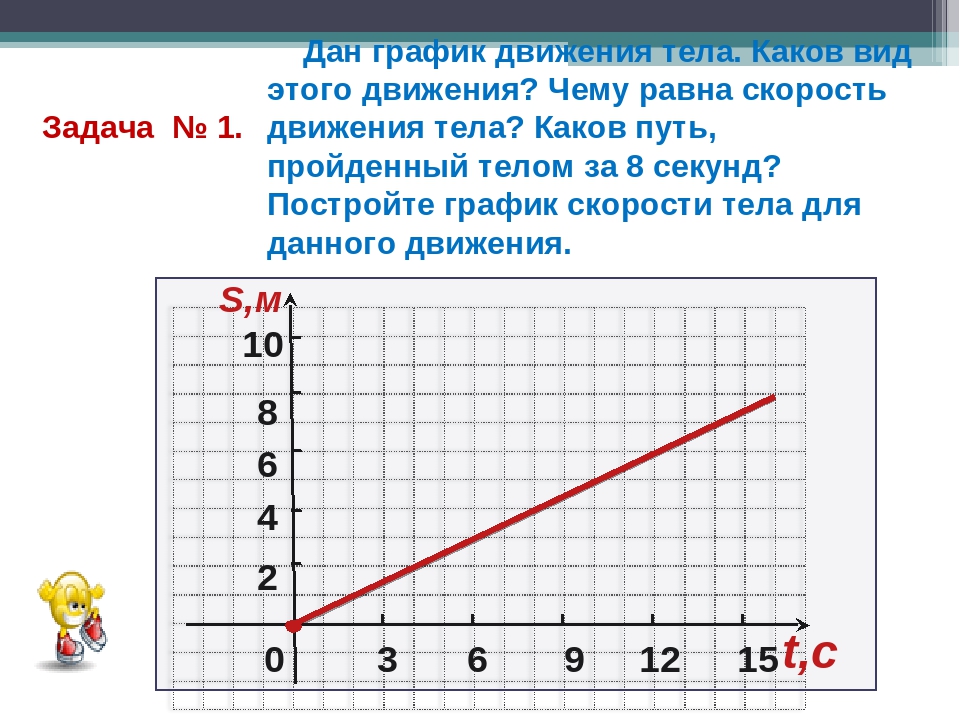 Ответ дайте в метрах.
Ответ дайте в метрах.
Рис.3
Решение
Тема этой задачи аналогична предыдущей. Повторим ход наших рассуждений. В этой задаче необходимо использовать данные, представленные на графике. Известно: чтобы по графику зависимости скорости от времени найти путь, пройденный телом за интересующий интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени. В нашем случае в интервале времени от 0 до 5 с автомобиль прошёл путь, равный сумме площадей (Рис.4):
Рис.4
S = S1 + S2 + S3 + S4
S = 0,5 х 2м/с х (1с – 0с) + 2м/с х (2с – 1с) + 0,5 х (2м/с + 6 м/с) х (4с – 2с) + 6 м/с х (5с – 4с) = 17 м
Ответ: 17.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Физика 7 класс
93 Краткие итоги главы I чиной, называемой временем . Время обозначается буквой t , единица измерения времени в СИ — секунда (с). Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути, называется равномер- ным движением . Скорость — это векторная физическая величина, характе- ризующая быстроту изменения положения тела в простран- стве. Скорость показывает, какой путь проходит тело за еди- ницу времени. Скорость численно равна отношению пути ко времени, за которое этот путь пройден. Скорость обозначается буквой v , единица скорости в СИ — метр в секунду (м/с). Движение можно представить графически. График зависи- мости пройденного телом пути от времени называется графиком пути . График зависимости скорости от времени называется гра- фиком скорости . По графику пути можно найти скорость тела. По графику скорости можно определить пройденный путь. Масса — это скалярная физическая величина, являющая- ся мерой инертных и гравитационных свойств тела. Единица массы в СИ — килограмм (кг), прибор для измерения мас- сы — рычажные весы.
Время обозначается буквой t , единица измерения времени в СИ — секунда (с). Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути, называется равномер- ным движением . Скорость — это векторная физическая величина, характе- ризующая быстроту изменения положения тела в простран- стве. Скорость показывает, какой путь проходит тело за еди- ницу времени. Скорость численно равна отношению пути ко времени, за которое этот путь пройден. Скорость обозначается буквой v , единица скорости в СИ — метр в секунду (м/с). Движение можно представить графически. График зависи- мости пройденного телом пути от времени называется графиком пути . График зависимости скорости от времени называется гра- фиком скорости . По графику пути можно найти скорость тела. По графику скорости можно определить пройденный путь. Масса — это скалярная физическая величина, являющая- ся мерой инертных и гравитационных свойств тела. Единица массы в СИ — килограмм (кг), прибор для измерения мас- сы — рычажные весы. Плотность — это скалярная физическая величина, рав- ная отношению массы тела к его объёму. Единица плотности в СИ — килограмм на кубический метр (кг/м 3 ). Плотность показывает, какую массу имеет 1 м 3 вещества. Сила — это векторная физическая величина, характеризу- ющая взаимодействие тел. Сила является причиной измене- ния скорости тела или его деформации. Результат действия силы зависит от её величины, направ- ления и точки приложения. Сила обозначается буквой F , единица силы в СИ — ньютон (Н). Силу измеряют динамометром. В механике различают силу всемирного тяготения, силу тяжести, силу упругости, вес тела и силу трения. Сила всемирного тяготения — это сила, с которой все тела во Вселенной притягиваются друг к другу. Сила тяжести — это сила, с которой Земля притягивает все тела: F т = mg .
Плотность — это скалярная физическая величина, рав- ная отношению массы тела к его объёму. Единица плотности в СИ — килограмм на кубический метр (кг/м 3 ). Плотность показывает, какую массу имеет 1 м 3 вещества. Сила — это векторная физическая величина, характеризу- ющая взаимодействие тел. Сила является причиной измене- ния скорости тела или его деформации. Результат действия силы зависит от её величины, направ- ления и точки приложения. Сила обозначается буквой F , единица силы в СИ — ньютон (Н). Силу измеряют динамометром. В механике различают силу всемирного тяготения, силу тяжести, силу упругости, вес тела и силу трения. Сила всемирного тяготения — это сила, с которой все тела во Вселенной притягиваются друг к другу. Сила тяжести — это сила, с которой Земля притягивает все тела: F т = mg .
Made with FlippingBook
RkJQdWJsaXNoZXIy NDA0NzE0
Расчет пути, скорости и времени движения: равномерное и неравномерное
Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
- Скорость = путь / время.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Нужна помощь в учебе?
Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:   Явление инерции: в чем заключается и примеры из жизни
3.
 1 Положение, смещение и средняя скорость
1 Положение, смещение и средняя скорость
Цели обучения
К концу этого раздела вы сможете:
- Определите положение, смещение и пройденное расстояние.
- Рассчитайте общее смещение для данного положения как функцию времени.
- Определите общее пройденное расстояние.
- Рассчитайте среднюю скорость с учетом смещения и затраченного времени.
Когда вы находитесь в движении, вам нужно задать следующие основные вопросы: где вы? Куда ты собираешься? Как быстро ты туда добираешься? Ответы на эти вопросы требуют, чтобы вы указали свое положение, смещение и среднюю скорость — термины, которые мы определяем в этом разделе.
Позиция
Чтобы описать движение объекта, вы должны сначала уметь описать его положение ( x ): , где он находится в любой конкретный момент времени . Точнее, нам нужно указать его положение относительно удобной системы отсчета. Система отсчета представляет собой произвольный набор осей, по которым описывается положение и движение объекта. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам на Земле.Например, запуск ракеты можно описать с точки зрения положения ракеты по отношению к Земле в целом, тогда как положение велосипедиста можно описать с точки зрения ее положения по отношению к зданиям, мимо которых он проезжает (рисунок). В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. Чтобы описать положение объекта, совершающего одномерное движение, мы часто используем переменную x .Позже в этой главе, при обсуждении свободного падения, мы будем использовать переменную y .
Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам на Земле.Например, запуск ракеты можно описать с точки зрения положения ракеты по отношению к Земле в целом, тогда как положение велосипедиста можно описать с точки зрения ее положения по отношению к зданиям, мимо которых он проезжает (рисунок). В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. Чтобы описать положение объекта, совершающего одномерное движение, мы часто используем переменную x .Позже в этой главе, при обсуждении свободного падения, мы будем использовать переменную y .
Рис. 3.2 Этих велосипедистов во Вьетнаме можно описать по их положению относительно зданий или канала. Их движение можно описать изменением положения или перемещением в системе отсчета. (кредит: Сьюзан Блэк)
(кредит: Сьюзан Блэк)
Рабочий объем
Если объект перемещается относительно системы координат — например, если профессор перемещается вправо относительно доски (рисунок), — положение объекта изменяется.Это изменение положения называется смещением . Слово смещение означает, что объект переместился или был перемещен. Хотя позиция — это числовое значение x вдоль прямой линии, где мог бы быть расположен объект, смещение дает изменение на положения вдоль этой линии. Поскольку смещение указывает направление, оно является вектором и может быть как положительным, так и отрицательным, в зависимости от выбора положительного направления. Кроме того, в анализ движения может быть встроено множество смещений.Если значение right положительно и объект перемещается на 2 м вправо, затем на 4 м влево, отдельные смещения составляют 2 м и [латекс] -4 [/ латекс] м соответственно.
Рис. 3.3 Профессор ходит влево и вправо во время лекции. Ее положение относительно Земли обозначено x. Смещение профессора на +2,0 м относительно Земли показано стрелкой, указывающей вправо.
Ее положение относительно Земли обозначено x. Смещение профессора на +2,0 м относительно Земли показано стрелкой, указывающей вправо.
Рабочий объем
Displacement [latex] \ text {Δ} x [/ latex] — изменение положения объекта:
[латекс] \ text {Δ} x = {x} _ {\ text {f}} — {x} _ {0}, [/ latex]
где [latex] \ text {Δ} x [/ latex] — это смещение, [latex] {x} _ {\ text {f}} [/ latex] — это конечное положение, а [latex] {x} _ { 0} [/ latex] — начальная позиция.
Мы используем прописную греческую букву дельта (Δ) для обозначения «изменения» любой величины, следующей за ней; таким образом, [latex] \ text {Δ} x [/ latex] означает изменение в позиции (конечная позиция минус исходная позиция). Мы всегда вычисляем смещение, вычитая начальную позицию [latex] {x} _ {0} [/ latex] из конечной позиции [latex] {x} _ {\ text {f}} [/ latex]. Обратите внимание, что единицей СИ для смещения является метр, но иногда мы используем километры или другие единицы длины. Помните, что когда в задаче используются единицы, отличные от метров, вам может потребоваться преобразовать их в метры, чтобы завершить расчет (см. Коэффициенты преобразования).
Помните, что когда в задаче используются единицы, отличные от метров, вам может потребоваться преобразовать их в метры, чтобы завершить расчет (см. Коэффициенты преобразования).
Движущиеся объекты также могут иметь серию перемещений. В предыдущем примере с профессором кардиостимулятора отдельные смещения равны 2 м и [латекс] -4 [/ латекс] м, что дает общее смещение -2 м. Мы определяем общее смещение [латекс] \ text {Δ} {x} _ {\ text {Total}} [/ latex] как сумму отдельных смещений и выражаем это математически уравнением
[латекс] \ text {Δ} {x} _ {\ text {Total}} = \ sum \ text {Δ} {x} _ {\ text {i}}, [/ latex]
где [латекс] \ text {Δ} {x} _ {i} [/ latex] — индивидуальные смещения.В предыдущем примере
[латекс] \ text {Δ} {x} _ {1} = {x} _ {1} — {x} _ {0} = 2-0 = 2 \, \ text {m.} [/ Latex]
Аналогично
[латекс] \ text {Δ} {x} _ {2} = {x} _ {2} — {x} _ {1} = — 2- (2) = — 4 \, \ text {m.} [/ латекс]
Таким образом,
[латекс] \ text {Δ} {x} _ {\ text {Total}} = \ text {Δ} {x} _ {1} + \ text {Δ} {x} _ {2} = 2-4 = -2 \, \ text {m} \ text {. } [/ Latex]
} [/ Latex]
Общее смещение составляет 2–4 = −2 м влево или в отрицательном направлении. Также полезно рассчитать величину смещения или его размер.Величина смещения всегда положительная. Это абсолютное значение смещения, потому что смещение является вектором и не может иметь отрицательного значения величины. В нашем примере величина полного смещения составляет 2 м, тогда как величина отдельных смещений составляет 2 м и 4 м.
Величину общего смещения не следует путать с пройденным расстоянием. Пройденное расстояние [латекс] {x} _ {\ text {Total}} [/ latex], это общая длина пути, пройденного между двумя позициями.В предыдущей задаче пройденное расстояние является суммой величин отдельных смещений:
[латекс] {x} _ {\ text {Total}} = | \ text {Δ} {x} _ {1} | + | \ text {Δ} {x} _ {2} | = 2 + 4 = 6 \, \ text {m} \ text {.} [/ Latex]
Средняя скорость
Чтобы вычислить другие физические величины в кинематике, мы должны ввести переменную времени. Переменная времени позволяет нам не только указывать, где находится объект (его положение) во время его движения, но и насколько быстро он движется.Скорость движения объекта определяется скоростью изменения его положения со временем.
Для каждой позиции [latex] {x} _ {\ text {i}} [/ latex] мы назначаем определенное время [latex] {t} _ {\ text {i}} [/ latex]. Если детали движения в каждый момент не важны, скорость обычно выражается как средняя скорость [латекс] \ overset {\ text {-}} {v} [/ latex]. Эта векторная величина представляет собой просто общее смещение между двумя точками, деленное на время, необходимое для путешествия между ними.Время, необходимое для перемещения между двумя точками, называется прошедшим временем [латекс] \ text {Δ} t [/ latex].
Средняя скорость
Если [латекс] {x} _ {1} [/ latex] и [latex] {x} _ {2} [/ latex] — это позиции объекта, временами [латекс] {t} _ {1} [ / latex] и [latex] {t} _ {2} [/ latex] соответственно, то
[латекс] \ begin {array} {cc} \ text {Средняя скорость} = \ overset {\ text {-}} {v} = \ frac {\ text {Смещение между двумя точками}} {\ text {Затраченное время между двумя точками}} \\ \ overset {\ text {-}} {v} = \ frac {\ text {Δ} x} {\ text {Δ} t} = \ frac {{x} _ {2} — {x} _ {1}} {{t} _ {2} — {t} _ {1}}.\ end {array} [/ latex]
Важно отметить, что средняя скорость является вектором и может быть отрицательной в зависимости от положения [латекс] {x} _ {1} [/ latex] и [latex] {x} _ {2} [/ latex] .
Пример
Доставка листовок
Джилл отправляется из своего дома, чтобы доставить листовки о распродаже во дворе, двигаясь на восток по своей улице, усеянной домами. На [latex] 0,5 [/ latex] км и через 9 минут у нее заканчиваются листовки, и ей приходится возвращаться домой, чтобы получить больше.Это займет еще 9 минут. Собрав еще листовки, она снова отправляется по тому же пути, продолжая с того места, где остановилась, и заканчивается в 1,0 км от своего дома. Этот третий этап ее путешествия занимает [латекс] 15 [/ латекс] минут. В этот момент она поворачивает обратно к своему дому, направляясь на запад. Через [латекс] 1,75 [/ латекс] км и [латекс] 25 [/ латекс] минут она останавливается, чтобы отдохнуть.
- Каково полное перемещение Джилл до точки, в которой она останавливается, чтобы отдохнуть?
- Какова величина окончательного смещения?
- Какая средняя скорость во время всего путешествия?
- Какое общее расстояние пройдено?
- Постройте график зависимости положения от времени.
Набросок движений Джилл показан на (Рисунок).
Рис. 3.4 График перемещений Джилл.
Стратегия
Задача содержит данные о различных этапах путешествия Джилл, поэтому было бы полезно составить таблицу физических величин. Нам дается позиция и время в формулировке задачи, чтобы мы могли рассчитать смещения и затраченное время. Мы принимаем восток как положительное направление. Из этой информации мы можем найти полное смещение и среднюю скорость.Дом Джилл — отправная точка [латекс] {x} _ {0} [/ latex]. В следующей таблице указаны время и позиция Джилл в первых двух столбцах, а смещения рассчитываются в третьем столбце.
| Время т i (мин) | Позиция [латекс] {x} _ {i} [/ latex] (км) | Водоизмещение [латекс] \ text {Δ} {x} _ {\ text {i}} [/ latex] (км) |
|---|---|---|
| [латекс] {t} _ {0} = 0 [/ латекс] | [латекс] {x} _ {0} = 0 [/ латекс] | [латекс] \ text {Δ} {x} _ {0} = 0 [/ латекс] |
| [латекс] {t} _ {1} = 9 [/ латекс] | [латекс] {x} _ {1} = 0.5 [/ латекс] | [латекс] \ text {Δ} {x} _ {1} = {x} _ {1} — {x} _ {0} = 0,5 [/ латекс] |
| [латекс] {t} _ {2} = 18 [/ латекс] | [латекс] {x} _ {2} = 0 [/ латекс] | [латекс] \ text {Δ} {x} _ {2} = {x} _ {2} — {x} _ {1} = — 0,5 [/ латекс] |
| [латекс] {t} _ {3} = 33 [/ латекс] | [латекс] {x} _ {3} = 1,0 [/ латекс] | [латекс] \ text {Δ} {x} _ {3} = {x} _ {3} — {x} _ {2} = 1.0 [/ latex] |
| [латекс] {t} _ {4} = 58 [/ латекс] | [латекс] {x} _ {4} = — 0,75 [/ латекс] | [латекс] \ text {Δ} {x} _ {4} = {x} _ {4} — {x} _ {3} = — 1.75 [/ латекс] |
Решение
- Покажи ответ
Из приведенной выше таблицы общее смещение равно [латекс] \ sum \ text {Δ} {x} _ {\ text {i}} = 0,5-0,5 + 1,0-1,75 \, \ text {km} = — 0,75 \ , \ text {km} \ text {.} [/ latex]
- Покажи ответ
Величина полного смещения равна [latex] | -0.75 | \, \ text {km} = 0.75 \, \ text {km} [/ latex].
- Покажи ответ
[латекс] \ text {Средняя скорость} = \ frac {\ text {Total} \, \ text {displacement}} {\ text {Elapsed} \, \ text {time}} = \ overset {\ text {-} } {v} = \ frac {-0.75 \, \ text {км}} {58 \, \ text {min}} = — 0,013 \, \ text {км / мин} [/ latex]
- Покажи ответ
Общее пройденное расстояние (сумма величин отдельных смещений) составляет [латекс] {x} _ {\ text {Total}} = \ sum | \ text {Δ} {x} _ {\ text {i}} | = 0,5 + 0,5 + 1,0 + 1,75 \, \ text {km} = 3,75 \, \ text {km} [/ latex].
- Покажи ответ
Мы можем построить график зависимости положения Джилл от времени, чтобы помочь увидеть движение; график показан на (рисунок).Рис. 3.5 На этом графике показано положение Джилл в зависимости от времени.Средняя скорость — это наклон линии, соединяющей начальную и конечную точки.
Значение
Полное перемещение Джилл составляет -0,75 км, что означает, что в конце поездки она оказывается [латексной] 0,75 \, \ text {км} [/ латексной] к западу от своего дома. Средняя скорость означает, что если кто-то будет идти прямо на запад со скоростью [латекс] 0,013 [/ латекс] км / мин, начиная с того же времени, когда Джилл вышла из дома, они оба достигнут конечной точки остановки одновременно. Обратите внимание, что если бы Джилл закончила поездку в своем доме, ее полное смещение было бы равно нулю, как и ее средняя скорость.Общее расстояние, пройденное за 58 минут времени ее поездки, составляет 3,75 км.
Проверьте свое понимание
Велосипедист едет на 3 км на запад, затем разворачивается и едет на 2 км на восток. а) Каково его смещение? б) Какое расстояние пройдено? в) Какова величина его перемещения?
Покажи ответ
(a) Перемещение всадника [латекс] \ text {Δ} x = {x} _ {\ text {f}} — {x} _ {0} = — 1 \, \ text {km} [/ latex ]. (Смещение отрицательное, потому что мы считаем восток положительным, а запад — отрицательным.) (b) Пройденное расстояние составляет 3 км + 2 км = 5 км. (c) Величина смещения составляет 1 км.
Концептуальные вопросы
Приведите пример, в котором есть четкие различия между пройденным расстоянием, смещением и величиной смещения. Определите каждое количество в вашем примере отдельно.
Показать решение
Вы едете на машине в город и возвращаетесь, чтобы проехать мимо своего дома к дому друга.
При каких обстоятельствах пройденное расстояние равно величине смещения? Каков единственный случай, когда величина смещения и смещения точно совпадают?
Бактерии перемещаются вперед и назад, используя свои жгутики (структуры, похожие на маленькие хвосты).Наблюдались скорости до 50 мкм / с (50 × 10 −6 м / с). Общее расстояние, которое проходит бактерия, велико для ее размера, тогда как перемещение невелико. Почему это?
Показать решение
Если бактерии перемещаются вперед и назад, то смещения компенсируют друг друга, и окончательное смещение невелико.
Приведите пример устройства, используемого для измерения времени, и определите, какое изменение в этом устройстве указывает на изменение времени.
Измеряет ли одометр автомобиля пройденное расстояние или перемещение?
В течение заданного промежутка времени средняя скорость объекта равна нулю.Какие выводы можно сказать о его перемещении за промежуток времени?
Проблемы
Рассмотрим систему координат, в которой положительная ось x направлена вверх вертикально. Каково положение частицы (а) на 5,0 м непосредственно над началом координат и (б) на 2,0 м ниже начала координат?
Автомобиль находится в 2,0 км к западу от светофора при t = 0 и 5,0 км к востоку от светофора при t = 6,0 мин. Предположим, что начало системы координат — это свет, а положительное направление x — на восток.(а) Каковы векторы положения автомобиля в эти два момента времени? (б) Какой рабочий объем автомобиля составляет от 0 до 6,0 мин?
Показать решение
а. [латекс] {\ overset {\ to} {x}} _ {1} = (- 2.0 \, \ text {m}) \ hat {i} [/ latex], [латекс] {\ overset {\ to} {x}} _ {2} = (5.0 \, \ text {m}) \ hat {i} [/ latex]; б. 7,0 м на восток
Шанхайский поезд на магнитной подвеске соединяет Longyang Road с международным аэропортом Пудун, расстояние до которого составляет 30 км. В среднем дорога занимает 8 минут. Какова средняя скорость поезда на магнитной подвеске?
Положение частицы, движущейся по оси x , определяется как [latex] x (t) = 4.0-2.0т [/ латекс] м. а) В какое время частица пересекает начало координат? (b) Каково смещение частицы между [latex] \ text {t} = 3.0 \, \ text {s} [/ latex] и [latex] \ text {t} = 6.0 \, \ text {s} ? [/ латекс]
Показать решение
а. [латекс] т = 2,0 [/ латекс] с; б. [латекс] x (6.0) -x (3.0) = — 8.0 — (- 2.0) = — 6.0 \, \ text {m} [/ latex]
Велосипедист едет на 8,0 км на восток в течение 20 минут, затем поворачивает и направляется на запад 8 минут и 3,2 км. Наконец, он едет на восток 16 км, что занимает 40 минут.а) Каково окончательное перемещение велосипедиста? б) Какова его средняя скорость?
15 февраля 2013 г. суперболидный метеор (ярче Солнца) вошел в атмосферу Земли над Челябинском, Россия, и взорвался на высоте 23,5 км. Очевидцы могли почувствовать сильный жар от огненного шара, а взрывная волна от взрыва выбила окна в зданиях. Взрывная волна достигла уровня земли примерно за 2 минуты 30 секунд. а) Какова была средняя скорость взрывной волны? б) Сравните это со скоростью звука, которая составляет 343 м / с на уровне моря.
Показать решение
а. 150,0 с, [латекс] \ overset {\ text {-}} {v} = 156,7 \, \ text {м / с} [/ latex]; б. 45,7% скорость звука на уровне моря
Глоссарий
- средняя скорость
- смещение, деленное на время, в течение которого происходит смещение
- рабочий объем
- изменение положения объекта
- пройденное расстояние
- общая длина пути, пройденного между двумя позициями
- истекшее время
- разница между временем окончания и временем начала
- кинематика
- описание движения с помощью таких свойств, как положение, время, скорость и ускорение
- позиция
- местоположение объекта в конкретное время
- полный рабочий объем
- сумма индивидуальных перемещений за данный период времени
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}} / 500
{{l10n_strings.TAGS}}
{{$ item}}
{{l10n_strings.ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}}
{{$ select.selected.display}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}}
{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
Инструмент
Path Of Travel в Autodesk Revit 2020
Именно то, что вам нужно для разумного планирования пространства.
Подробнее …
Инструмент «Путь перемещения» используется для определения кратчайшего расстояния между двумя точками на плане этажа.
Этот инструмент анализирует геометрию на плане и объезжает препятствия и преодолевает двери для оптимизации маршрута.
Кнопка под названием Path of Travel находится на вкладке «Анализ» ленты.
Как и обычная линия детализации, Path of Travel зависит от вида, и его свойства стиля линии можно изменить в диалоговом окне «Стили линий».
Выберите путь движения, чтобы увидеть его длину и время, необходимое для прохождения пути.
Линии Path of Travel могут быть названы, отмечены тегами и запланированы.
Линия Path of Travel может использоваться в фильтре просмотра .
На видео показан пример фильтра просмотра, который сделает любой путь путешествия непрочитанным, если он превышает 80 футов 0 дюймов.
Существует диалоговое окно настроек анализа маршрута, которое позволяет больше контролировать, какие категории считаются препятствиями, а в диалоговом окне настроек есть возможность настроить зону анализа, используемую Path of Travel для поиска препятствий в верхней и нижней части. значение смещения от уровня представления.
Если какая-либо геометрия элемента модели находится в пределах зоны анализа , это будет считаться препятствием на пути перемещения.
Путь перемещения будет создан, чтобы избежать этих препятствий, и будет рассчитан на основе геометрии только внутри обрезанной области.
Вы можете выбрать одну или несколько линий Path of Travel, и на контекстной панели ленты вы увидите кнопку обновления.
Справка по этой новой функции содержит подробную информацию о том, как создаются и обновляются пути.
Получите четкое представление о пространственных отношениях с помощью автоматического расчета времени и расстояния для интеллектуального планирования пространства.
Посмотреть все последние видео на Autodesk Revit 2020 >>
Используйте Google Maps, чтобы узнать, где вы побывали
Джош Миллер / CNET
Google Maps отслеживает всюду, где был ваш телефон, и теперь он готов поделиться этими данными с вами и только вами.Используя новую удобную функцию под названием «Ваша хронология в Интернете и Android», вы можете увидеть все места, которые вы посетили, на карте, а также подробные маршруты ваших путешествий.
Хотя перспектива того, что Google отслеживает каждое ваше движение, наверняка беспокоит некоторых людей, я обнаружил, что Your Timeline — действительно изящный инструмент для отслеживания моих поездок и отпусков или просто вспомнить случайный день из моей жизни.
Если это вас смущает, и вы не хотите, чтобы Google следил за вами, ознакомьтесь с руководством CNET, чтобы запретить Google Maps отслеживать ваше местоположение.Однако, если вас заинтриговал этот автоматически записываемый журнал посещаемых вами мест, читайте дальше, чтобы узнать, как наилучшим образом использовать вашу временную шкалу.
Начать работу
Чтобы защитить вашу конфиденциальность, вам сначала нужно дать согласие на то, чтобы Google следил за вашими путешествиями. Если в какой-то момент вы включили Историю местоположений в своей учетной записи Google, например, настроили Google Now, чтобы запоминать, где вы припарковались или ездить на работу, значит компания уже отслеживает вас.
Проверьте, включена ли для вас история местоположений, выполнив следующие действия:
- Войдите в свою учетную запись Google на компьютере.
- Перейдите на страницу Моя учетная запись .
- Щелкните Личная информация и конфиденциальность и прокрутите до «Места, которые вы посещаете».
- Если ползунок синий, История местоположений включена, и все готово.
- Щелкните Управление действием под ползунком, чтобы просмотреть свою временную шкалу.
Посмотрите на свои карты
В соответствии со своим названием, ваша шкала времени показывает ежедневные записи каждого места, где вы были, время вашего прибытия и отправления, а также примерный маршрут, который вы выбрали между местоположениями.Если вы используете Google Фото, фотографии, сделанные вами в определенном месте, дате и времени, также будут отображаться на вашей временной шкале.
Ваша шкала времени показывает места, которые вы посетили, день за днем. Нажмите, чтобы увеличить.
Скриншот Сары Митрофф / CNET
Вся эта информация отображается на странице «Хронология» на рабочем столе и в последней версии приложения «Карты Google» для Android. Однако вы получите большинство функций при просмотре на компьютере.Там вы увидите карту мира с точками на местах, где вы побывали. Вы можете увеличивать масштаб отдельных городов, чтобы получить более подробное представление, и нажимать точки, чтобы увидеть адрес или достопримечательность.
В левой части страницы вы можете просматривать различные даты, чтобы увидеть доступные временные шкалы. По моему опыту, Google, похоже, не записывает данные за каждый день, вместо этого он сосредотачивается на поездках, в которых вы покидаете свой обычный район. В моем аккаунте я могу видеть случайные поездки на работу или в магазин, но больше внимания уделяется поездкам, которые продолжаются несколько дней и уносят меня как минимум за 50 миль от дома.У меня также нет графика на каждый день, несмотря на то, что история местоположений была включена в течение последних нескольких лет. Однако ваши данные могут отличаться.
На карте отображаются все места, где вы побывали, которые были записаны Google. Нажмите, чтобы увеличить.
Скриншот Сары Митрофф / CNET
Редактирование временной шкалы
Хотя Google делает все возможное, чтобы указать точные адреса, предприятия и достопримечательности, которые вы посетили, он не всегда понимает это правильно.В этом случае вы можете отредактировать неправильные места на временной шкале и добавить места, которые он вообще пропустил.
Вы можете редактировать места в своей ежедневной шкале времени. Нажмите, чтобы увеличить.
Скриншот Сары Митрофф / CNET
- Наведите указатель мыши на название места и щелкните стрелку, чтобы выбрать другой вариант в меню или выполнить поиск определенного места.
- Чтобы добавить новое место на шкалу времени, наведите указатель мыши на крайнюю левую линию до появления знака «плюс» и щелкните его.
- Найдите место и сообщите Google о том, когда вы прибыли и уехали, затем нажмите «Сохранить», чтобы добавить его на временную шкалу.
Хотя Google столкнулся с серьезной проверкой при отслеживании вашего местоположения и отображении его на временной шкале, я думаю, что эта функция — изящный способ автоматически создавать записи о ваших путешествиях. Тем не менее, я полностью понимаю озабоченность по поводу конфиденциальности, которую вызывает Ваша Хронология, даже если данные доступны только для просмотра.
Если вам становится неудобно, просто отключите Историю местоположений, чтобы Google не отслеживал ваши местоположения.Но если вы хотите, чтобы Google оставался на вашем хвосте, ваша шкала времени может быть удобной функцией для записи ваших ежедневных поездок на работу и больших поездок.
Как рассчитать критический путь в управлении проектами
Поначалу понимание того, как рассчитать критический путь и как использовать метод критического пути в управлении проектами, может показаться сложной задачей. Но когда вы отказываетесь от концепции использования большого количества данных и алгоритмов для ее расчета, вы понимаете, что это довольно здравый смысл!
В этой статье мы окунемся в концепцию Critical Path и ее компоненты, поговорим о том, почему это полезный инструмент, и дадим вам несколько примеров методов Critical Path, решений для использования программного обеспечения для управления проектами и инструментов, которые помогут вам в этом. расчет критического пути.
Что такое критический путь
Вкратце определение критического пути выглядит следующим образом:
Критический путь — это самая длинная последовательность действий в плане проекта, которая должна быть завершена вовремя, чтобы проект завершился в установленный срок.
Большинство проектов разбиты на задачи или действия (как бы вы ни называли более мелкие части, которые необходимо выполнить для выполнения проекта). Критический путь — это серия тех задач, выполнение которых в последовательном порядке и с учетом всех вышеперечисленных переменных займет наибольшее время для завершения проекта.
Проще говоря, «Критический путь» вычисляет САМЫЙ КОРОТКИЙ срок реализации проекта, выстраивая САМОЙ ДЛИННУЮ последовательность зависимых задач, необходимых для завершения проекта.
Важность метода критического пути
Проект без критического пути подобен кораблю без руля.
Д. Мейер
Истоки использования сложных систем управления проектами, таких как метод критического пути, восходят к грандиозным проектам, таким как строительство Великой пирамиды в Гизе, Великой китайской стены, Панамского канала и Транссибирской железной дороги. , Просто назвать несколько.
Представьте, как бы выглядели эти исторические строительные проекты, если бы не системы управления проектами, такие как метод критического пути. Хаос, правда?
То же самое верно и для текущих проектов в сегодняшних организациях. Без возможности рассчитывать потенциальные препятствия в рамках графика проекта, анализировать компоненты проекта, необходимые для завершения, и разрабатывать решения, устраняющие эти препятствия, многие проекты никогда не сдвинутся с мертвой точки.
Критический путь называется «критическим», потому что это «красное предупреждение» для путей. Если ваш проект не соответствует последовательности и срокам критического пути, он не будет успешно завершен раньше установленного срока.
Обратите внимание на слово «успешно», потому что в худшем случае проект задержится. и не смогут достичь своей цели (целей).
Хотя метод критического пути, возможно, не единственный метод управления проектами, это методология, к которой обращаются многие руководители проектов.
Как рассчитать критический путь
Прежде чем мы углубимся, для тех, кто наглядно обучается среди вас, вот отличное, очень подробное видео, показывающее, как рассчитать критический путь:
Поиск критического пути для проекта основан на шести этапах, выполненных по порядку. Давайте разберем эти шаги!
ШАГ 1. Разделите проект на задачи
- Составьте список ваших задач
- Присвойте каждой задаче имя или короткий код
ШАГ 2.Упорядочить и определить зависимости
- Объедините задачи в логический ряд
- Определить зависимости
ПРИМЕЧАНИЕ РЕДАКТОРА: Обычно в проекте есть три основных типа предполагаемых зависимостей.
Обязательные зависимости — зависимости из-за физических ограничений задачи. Часто задачи в исследовательских и опытно-конструкторских проектах помечаются как обязательные.
Дискреционные зависимости — зависимости из-за решений, принимаемых командами в ходе проекта.
Внешние зависимости — зависимости, обусловленные потребностями третьей стороны, например потребности подрядчика или акционера.
Отслеживайте время именно там, где происходит
рабочих мест
Оценивайте задачи, устанавливайте бюджеты, учитывайте время и
настраивайте отчеты — все это внутри вашего инструмента управления проектами
. Простой!
ШАГ 3. Создайте сетевую диаграмму
Теперь вы можете визуализировать вашу расстановку задач. Старый добрый метод ручки и бумаги может сработать; более изощренный способ сделать это — использовать сетевую диаграмму, такую как PERT или диаграмму Ганта (подробнее об этом позже в этой статье), и соединить ваши задачи на диаграмме.
ШАГ 4. Оценка продолжительности
- Четко определите дату начала и окончания для каждой задачи.
- С учетом порядка и зависимостей установите предполагаемую продолжительность каждой задачи.
ПРИМЕЧАНИЕ РЕДАКТОРА: , чтобы рассчитать время для каждой задачи и легко расставить приоритеты, используйте приложение для отслеживания времени. Это поможет вам точно отслеживать и оценивать время, затрачиваемое на ваш проект.
ШАГ 5. Выполните выравнивание ресурсов
Основная цель выравнивания ресурсов — эффективное распределение ресурсов, чтобы завершение проекта происходило в пределах заданного времени и не возникало конфликтов ресурсов.Конфликты ресурсов могут привести к:
- Задержки в выполнении конкретных задач.
- Трудности с распределением ресурсов.
- Невозможность изменить зависимости задач.
- Удаление задач по необходимости.
- Добавление дополнительных задач по мере необходимости.
- Общие задержки и перерасход бюджета по проектам.
Приложение с функциями отслеживания времени может упростить выравнивание кадровых ресурсов, позволяя группе более точно прогнозировать будущую эффективность команды на основе времени выполнения в прошлом, особенно в ролях, требующих специализации.
ШАГ 6. Определите критический путь
Найдите на диаграмме самую длинную последовательность задач проекта. Эта последовательность — критический путь для вашего проекта!
Изображение предоставлено: Researchgate
Переменные в пределах критического пути
Давайте взглянем на некоторые термины и концепции, которые вам необходимо понять, чтобы рассчитать критический путь.
Плавающий / свободный ход
Плавающий (иногда называемый резервом времени) задачи — это продолжительность, на которую она может быть отложена без задержки выполнения следующей задачи, завершения проекта или нарушения ограничения расписания.
Ранний старт и ранний финиш
Раннее начало и раннее завершение — это именно то, что нужно: самый начальный момент, когда задача на пути может начаться, и самое раннее, когда она может закончиться.
Начало задачи при ее раннем запуске зависит от завершения задач на том же пути. Если предыдущая задача может завершиться раньше времени завершения и завершает последнюю задачу на пути, команда может начать с раннего начала следующей задачи, высвобождая больше времени для других, более непредсказуемых задач.
Метод прямого прохода для определения раннего старта :
Начиная с даты начала проекта, вы можете оценить раннюю дату начала для каждой последующей задачи на пути проекта, следуя за ней слева направо на диаграмме.
Этапы расчета даты раннего начала работы :
- Запишите время, которое потребовалось для выполнения предыдущей задачи, и добавьте его к дате начала текущей задачи.
- Добавьте любое дополнительное время, которое потребовалось для завершения проекта, или вычтите время, которое потребовалось для досрочного завершения.
- Примите во внимание ресурсы, необходимые для каждой задачи (должен быть доступный календарь ресурсов, чтобы показать это), включая оборудование, часы работы персонала или любые другие необходимые ресурсы, и добавьте любое время, которое может потребоваться для размещения этих ресурсов. (Такие вещи, как выходные, техническое обслуживание и т. Д.)
- Основываясь на трех вышеуказанных шагах, определите рассчитанную дату и используйте ее для раннего начала следующей задачи.
Поздний старт и поздний финиш
Поздний старт и поздний финиш являются неблагоприятными.Это самое последнее начало, и даты окончания задачи могут быть назначены без нарушения других задач на пути или всего проекта в целом.
Начните с даты завершения плана проекта, затем с критического пути, затем с путей в порядке убывания дат завершения. Двигайтесь вправо влево по сетевой диаграмме и вычтите время, которое займет каждая задача на каждом пути, чтобы вычислить последнюю дату, когда эта задача может начаться, при этом соблюдая дату завершения проекта.
Так же, как и в случае прямого прохода (ранний старт / финиш, слева направо), ресурсы должны быть приняты во внимание при ускорении обратного прохода.
Этапы расчета дат позднего запуска
- Назначьте общую дату завершения проекта как дату окончания задачи до ее достижения на критическом пути, а затем на всех последующих этапах от самого длинного до самого короткого.
- Вычтите любое дополнительное время, которое потребовалось для выполнения задачи, или добавьте оставшееся свободное время к предполагаемой дате позднего завершения.
- Учитывайте ресурсы, как и в случае раннего начала / завершения, и вычтите время, которое они вносят в каждую задачу.
- Укажите дату, рассчитанную на основе трех вышеуказанных шагов, как дату позднего начала для предыдущей задачи на пути.
Чтобы рассчитать поздние даты начала, начните с контрольной точки завершения проекта и назначьте ее в качестве даты окончания предшествующих операций. Выполните описанные выше шаги, чтобы оценить поздние даты начала предшествующих действий, предполагая отношения «конец-начало».
10-секундный опрос и продолжим наш рассказ! Ваш ответ поможет нам улучшить наш контент!
Инструменты и программное обеспечение для расчета критического пути
От сложного программного обеспечения до ручки и бумаги — вам и вашей команде решать, что наиболее продуктивно и полезно использовать.Ниже мы рассмотрим некоторые доступные в Интернете программы CP, шаблоны и генераторы диаграмм, которые помогут вам начать работу, оставаться организованными и добиться успеха при определении критического пути для вашего проекта.
Мы также узнаем, как использовать PERT или диаграмму Ганта для оценки критического пути, и предоставим четкую визуализированную модель для CP вашего проекта.
Инструменты для расчета критического пути
С помощью быстрого поиска в Google вы обнаружите, что существует множество инструментов для расчета CP, а также несколько шаблонов критического пути, чтобы проиллюстрировать критический путь вашего проекта.
Capterra обеспечивает сравнение функций и рейтинги наиболее популярных программ для управления проектами, доступных прямо сейчас. Многие, если не все из них, содержат настраиваемые шаблоны и генераторы диаграмм Ганта, чтобы упростить поиск критического пути для вашего проекта.
MS Project имеет довольно полный набор ресурсов для процесса критического пути, от калькуляторов до генераторов диаграмм Ганта и собственных руководств. Вы можете узнать больше о поиске критического пути в MS Project здесь.
Диаграмма
PERT для оценки критического пути
Диаграмма PERT — это визуальная схема расписания проекта, показываемая стрелкой. Он показывает последовательность задач на пути и определяет время, необходимое для выполнения каждой, и какие из них могут быть выполнены одновременно.
Как и метод критического пути, диаграмма PERT будет содержать такую информацию, как перемещение между действиями, ранние даты начала / окончания и поздние даты начала / окончания.
Обычно PERT вступает в игру на четвертом шаге процесса критического метода, определяющем время выполнения задачи.Многие менеджеры проектов используют PERT, потому что он оценивает время завершения, основываясь на наиболее вероятном сценарии, а не на нереалистичных временных рамках.
При использовании PERT вы оцените кратчайший, самый продолжительный и наиболее вероятный период времени, который может занять задача, если прогнозируется, что она займет больше времени, чем ожидалось.
Термины, которые вам необходимо знать, чтобы использовать диаграмму PERT, включают:
- Узлы: обычно кружки, которые представляют задачи и этапы проекта
- Стрелки: стрелки обозначают последовательность выполнения задачи.Стрелки на диаграмме могут расходиться, если задачи могут быть выполнены одновременно.
- PERT Событие: начало или конец задачи
- Slack: как долго задача может быть отложена без прерывания других задач или всего проекта
- Critical Path Activity: действие, при котором нет резервов
- Время выполнения: время, которое реально потребуется для выполнения задачи без задержки или вмешательства в следующую задачу.
Вот полезное видео о том, как создать диаграмму PERT:
Диаграмма Ганта для оценки критического пути
Диаграммы Ганта
лучше всего подходят для небольших проектов, связывая зависимые задачи вместо создания сетевой диаграммы, показывающей взаимосвязанные независимые задачи, как это делает диаграмма PERT для более крупных и сложных проектов.
В то время как диаграммы PERT обычно используются во время планирования проекта, чтобы определить наиболее эффективное планирование, модель диаграммы Ганта обычно используется по мере выполнения проекта. Он показывает продолжительность выполнения задачи, кто вовлечен и несет ответственность за выполнение задачи, а также выявляет конфликты планирования. На диаграмме Ганта вы можете пересматривать и редактировать даты начала и окончания вашего проекта на протяжении всего проекта.
Чтобы создать диаграмму Ганта или гистограмму, посмотрите это видео:
В чем разница между представлениями диаграммы Ганта и PERT?
Диаграммы
Ганта и PERT представляют собой визуальное изображение завершения проекта, иллюстрирующее его задачи, график выполнения этих задач и варианты, которые могут повлиять на график, например использование ресурсов и зависимости.
Основное различие между диаграммой PERT и диаграммой Ганта заключается в ее представлении на временной шкале. PERT использует сетевую диаграмму или блок-схему, тогда как диаграмма Ганта использует гистограмму как представление временной шкалы.
Метод критического пути: закрытие
Благодаря своей невероятной эффективности, критический путь является основным продуктом проектов во всех организациях. Мы надеемся, что эта статья помогла упростить изучение того, как найти критический путь. Удачного планирования!
Кредит избранного изображения: twproject
Как Google Maps рассчитывает время в пути?
Расчет предполагаемого времени прибытия или «ETA» означает учет множества переменных.Карты Google используют множество современных технологий — от GPS до мобильных приложений — но как они взаимодействуют, чтобы измерить время в пути, и как они становятся более интеллектуальными?
Как Google Maps вычисляет среднюю скорость движения
Google Maps использует GPS для отслеживания местоположения объекта, «прикрепляя» к нему устройство слежения GPS. На простейшем уровне устройство слежения оснащено приемником GPS и некоторым способом записывать свое текущее местоположение (координаты широты и долготы) через определенные промежутки времени.Затем рассчитывается средняя скорость путем деления общего пройденного расстояния на затраченное время. Приемники GPS обычно выполняют следующие задачи:
- Преобразование разницы между двумя положениями широты / долготы в единицы измерения (вы можете использовать онлайн-калькуляторы, чтобы попробовать это самостоятельно).
- Определите разницу между двумя временными метками, чтобы рассчитать, сколько времени потребовалось, чтобы добраться от точки A до точки B.
- Рассчитайте среднюю скорость на основе этих результатов.Например, если расстояние составляет три мили, а затраченное время — 2 минуты, то средняя скорость на этом расстоянии будет 90 миль в час.
Хотя этот расчет дает среднюю скорость, он не принимает во внимание все факторы, которые могут повлиять на время в пути.
Данные GPS с отдельных телефонов теперь используются Google Maps для оценки движения и скорости движения в режиме реального времени. На основе этих данных Google оценивает время в пути, уменьшая среднюю скорость в своих расчетах в периоды высокой загруженности дорог или увеличивая среднюю скорость в ясные условия.Карты Google также используют опубликованные ограничения скорости и исторические модели движения для оценки ETA. Когда вы вводите пункт назначения в Карты Google, ваша первоначальная оценка делается на основе опубликованных ограничений скорости, текущих условий движения и расстояния между начальной и конечной точкой. Ваше расчетное время прибытия будет обновлено, когда вы будете в пути, на основе обновленных данных о дорожной обстановке и вашей средней скорости движения.
Google Maps имеет хороший набор данных о предполагаемых ограничениях скорости, а также данные от GPS, показывающие, превышает ли обычно поток трафика или падает ниже среднего, и вычисляет среднее время в пути на основе их комбинации. факторы.Хотя технология GPS не является чем-то новым для Google Maps, современные приложения, смешанные с аналитикой данных, позволяют нам получать больше информации и понимания из текущих и исторических данных GPS-отслеживания.
Прогнозирование и отслеживание трафика на Картах Google
Да, Карты Google отслеживают трафик, и с течением времени это делается все чаще, используя растущий массив точек данных, как общедоступных, так и частных. Датчики трафика, такие как радар, используются как частными компаниями, так и государственными учреждениями для сбора данных о трафике на автомагистралях или основных проездах.Радар может предоставить Google и другим инструментам данные об условиях дорожного движения в реальном времени, которые затем используются для определения расчетного времени прибытия и будущих прогнозов времени в пути в заданном районе.
Пользователи GPS-слежения за автопарком сообщают о положительной рентабельности инвестиций менее чем за шесть месяцев. Получите больше интересных данных из Отчета о тенденциях развития автопарка за 2021 год. Скачать сейчас.
Краудсорсинг — еще один фактор, который помогает Google Maps и другим технологиям GPS обеспечивать точное время прибытия. Например, пользователи могут сообщать о неправильных маршрутах проезда и других проблемах, с которыми они сталкиваются при использовании Карт Google.Google использует информацию из краудсорсинга для обновления своих прогнозов и / или создания альтернативных маршрутов.
Альтернативные маршруты и ETA
На основе приведенных выше источников карты Google обновят ваше расчетное время прибытия, если вы отклонитесь от курса или иным образом отклонитесь от запланированного маршрута, но это может занять время для расчета или может быть неточным. Вы можете «переместить синюю линию» или перетащить маршрут по умолчанию, чтобы изменить свой маршрут и получить обновленное время прибытия на основе изменения. Карты Google предварительно выберут наиболее быстрый маршрут без учета других основных переменных, таких как остановки по пути или левые повороты, поэтому интеллектуальные возможности, хотя и впечатляющие, по-прежнему ограничены и не имеют многих параметров настройки.
Специализированное программное обеспечение маршрутов для владельцев автопарков
Для владельцев автопарков существует более сложное программное обеспечение для планирования маршрутов, позволяющее создавать более устойчивые и эффективные карты в зависимости от ваших потребностей. Владельцы автопарков уже используют GPS-слежение для определения скорости транспортных средств, теперь программное обеспечение GPS также можно использовать для определения альтернативных оптимизированных маршрутов. Программное обеспечение для планирования маршрутов может помочь вам найти рентабельные маршруты, позволяющие избежать больших пробок, участков с ограниченным движением, дорожных сборов и т. Д.Некоторые особенности и преимущества маршрутов, улучшенных для коммерческих автомобилей, включают:
- Возможность для карт GPS адаптировать маршруты в зависимости от задержек из-за аварии, опасной погоды или крупного строительства.
- Уникальное представление «на день вперед», которое позволяет вам в последнюю минуту вносить изменения в маршруты, такие как отсутствие водителей, вышедшие из строя автомобили и новые или измененные рабочие места.
- Автоматически назначать задание маршруту или перепланировать отдельный маршрут или выбранный набор маршрутов.
Расширенное GPS-слежение может сделать даже больше, чем просто оценить время в пути и улучшить маршруты водителя.Программное обеспечение можно использовать для воспроизведения истории маршрутов вашего автомобиля на определенные даты и отслеживания фактических маршрутов, пройденных водителями. Это помогает менеджерам автопарка понять, как произошли определенные события, такие как превышение скорости или остановки, и почему. Вы можете определить показатели и тенденции, наиболее важные для вашей команды, отдела или всего парка. Менеджеры автопарка могут создавать исторические отчеты по данным автопарка за период до двух лет, чтобы получить полезные данные, поддержать расследования и экстраполировать надежные прогнозы.
GPS-слежение — это лишь один из компонентов, позволяющих Google лучше прогнозировать время в пути и предоставлять расчетное время прибытия в рамках своего приложения «Карты».По мере того, как технология GPS становится все более интеллектуальной с использованием данных от датчиков дорожного движения, радаров, краудсорсинга и т. Д., Становится проще доставить водителей к месту назначения вовремя и по наилучшему доступному маршруту.
Verizon Connect может сделать все вышеперечисленное, используя данные двух миллионов автомобилей, использующих наше программное обеспечение сегодня. И вы по-прежнему можете получить доступ ко всему этому со своего смартфона (Apple iOS или Android) или планшета! Маршрутизация и навигация, предназначенные для тяжелых транспортных средств или транспортных средств, перевозящих опасные грузы, являются основной частью нашего предложения.Наше программное обеспечение для GPS-слежения включает информацию о том, как правильно подойти к разгрузочному доку или служебному входу, что часто отсутствует в потребительских решениях GPS. Если вы менеджер автопарка и хотите использовать GPS для улучшения маршрутов и поведения водителей, свяжитесь с Verizon Connect сегодня.
дронов | Бесплатный полнотекстовый | Исследование по планированию траектории покрытия с помощью беспилотных летательных аппаратов
Траектория покрытия обычно планируется до ее выполнения в автономной фазе, учитывая, что воздушная платформа имеет полное представление о рабочем пространстве, которое необходимо покрыть.Однако в некоторых случаях летательному аппарату приходится чередоваться между планированием и исполнением, собирая информацию с помощью своих датчиков для построения внутренней карты по мере движения по сценарию. В обоих случаях приблизительное разложение по ячейкам можно использовать для дискретизации интересующей области в сетке, в то время как решение на основе сетки может использоваться для выполнения задачи охвата. Во-первых, мы пересматриваем некоторые полные алгоритмы, предложенные для работы с областями неправильной формы, рассматривая подходы, основанные на одном (как Валенте и др.[32]) и основан на нескольких БПЛА (как Барриентос и др. [10]) с полной информацией о сценарии. Затем мы исследуем некоторые совместные биологические подходы, чтобы иметь дело со средами, содержащими только частичную информацию.
5.1. Полная информация
Схема полета вперед-назад обычно используется в таких приложениях, как сельское хозяйство, но этот тип движения создает неэффективные траектории, учитывая интересующие области неправильной формы. Подход к планированию пути покрытия для мозаики изображений в точном земледелии с полями неправильной формы предложен Валенте и др.[32]. В этом подходе, названном на основе градиента, интересующая область дискретизируется в регулярную сетку с использованием приблизительной клеточной декомпозиции, как показано на рисунке 19. Каждая ячейка представляет собой путевую точку пути, и ее размер зависит от размеров изображения на -бортовая камера. Конфигурация сетки достигается за счет требований к изображению и характеристик датчика изображения. Разложенная область преобразуется в обычный граф, численно помеченный алгоритмом волнового фронта, который представляет собой алгоритм лавинной рассылки, который отмечает соседство соседних ячеек.Глубоко ограниченный поиск (DLS) [61] применяется для обнаружения полного пути без повторного посещения ранее исследованных узлов. С помощью DLS длина исследования ограничена количеством вершин и не зацикливается на циклах или не пересматривает узел. Процедура поиска с возвратом также используется для решения таких проблем, как выбор среди соседей с равными значениями. Предлагаемый метод позволяет упростить и ускорить решение для достижения почти оптимальных результатов в сложных областях с определенными ограничениями. Другой подход, исследующий алгоритм волнового фронта и приблизительную клеточную декомпозицию для покрытия в сельскохозяйственных районах, представлен Nam et al.[62]. Путь покрытия получается по интересующей области, помеченной в соответствии с волновым фронтом, как показано на рисунке 20a, и сглаживается с помощью алгоритма кубической интерполяции, как показано на рисунке 20b. В отличие от Валенте и др. [32] авторы представляют новый критерий оптимизации времени выполнения миссии, основанный на длине пути и количестве маневров поворота. Оптимальный алгоритм CPP с квадрокоптером БПЛА представлен Bouzid et al. [63]. Интересующая область представлена в виде карты с достопримечательностями (POI).БПЛА должен пройти минимальный путь, соединяющий точки интереса и избегающий препятствий с разными форматами, чтобы гарантировать полное покрытие в зоне. Миссия планируется в два этапа. Алгоритм вычисляет стоимость поездки для исследования окрестностей, а затем определяет последовательность точек, которые следует посетить, чтобы минимизировать общее расстояние. После однократного посещения POI автомобиль должен вернуться в исходное положение. Таким образом, проблема рассматривается как задача коммивояжера (TSP), а общий кратчайший путь может быть вычислен с использованием генетического алгоритма (GA).Авторы рассматривают накопленное евклидово расстояние между точками как показатель эффективности. Кроме того, они считают потребление энергии постоянным на протяжении всей миссии, измеряя его во времени.
В реальных приложениях квадрокоптеру может потребоваться несколько раз зарядить или заменить аккумулятор при выполнении задачи, учитывая его ограниченную бортовую энергию. Таким образом, авторы исследуют другую возможность, вдохновленную проблемой маршрутизации транспортных средств (VRP). Это решение находит минимальную группу кратчайших траекторий в случаях только с одним или несколькими начальными положениями.В этом сценарии летательный аппарат выполняет обозначенную задачу и продолжает возвращаться к базовой станции каждый раз, когда ему необходимо подзарядить батарею. В то же время БПЛА также загружает полученную информацию во время каждой части миссии.
Подход к точному земледелию с участием группы разнородных квадрокоптеров обсуждается Barrientos et al. [10], включающий два основных этапа: разделение и распределение задач, а также планирование пути покрытия. На первом этапе, используя протокол согласования, разделение области и выделение результирующих субрегионов одновременно выполняются распределенным образом.На этом этапе транспортные средства должны проанализировать стоимость и окупаемость задачи, то есть охватить определенный субрегион.
С учетом своих внутренних параметров машина оценивает стоимость выполнения задачи, начальную стоимость перемещения из текущего местоположения в зону поиска, определенные ограничения, такие как NFZ, углы поворота и встроенные датчики, а также приз, связанный с выполнением миссии. Целевая функция суммирует несколько членов с разным весом, включая размер задачи и расстояние от начальной точки до местоположения миссии.Кроме того, может применяться штраф, если одна задача перекрывает другую или исследование выходит за пределы общей области.
На втором этапе область дискретизируется в регулярную сетку с использованием приблизительной клеточной декомпозиции. Каждое транспортное средство использует алгоритм волнового фронта для создания траектории покрытия для своей подобласти, минимизируя время полета, количество маневров поворота и количество повторно посещаемых ячеек. Кроме того, автомобили поддерживают постоянную высоту, чтобы гарантировать желаемое разрешение в соответствии с полем зрения бортовой камеры.Наконец, авторы представляют систему управления для улучшения стабилизации машины по высоте при маневрах на высокой скорости. Эксперименты проводились с тремя транспортными средствами на виноградном поле, характеризующемся неправильной формой и изменяющимся высотным профилем. Границы субрегионов ограничивают безопасную зону, в которую автомобили не должны заходить во избежание столкновений, как показано на рисунке 21. Сосредоточившись также на точном земледелии, Валенте и др. Предлагают метаэвристический алгоритм под названием Harmony Search (HS). al.[64], чтобы свести к минимуму количество поворотов на неровных участках. Предлагаемый алгоритм основан на импровизации джазового музыканта и его основной частью является Harmony Memory (HM). HM состоит из матрицы, где строки состоят из векторов, содержащих возможные решения, а столбцы представляют переменные решения. Результат функции стоимости помещен в последний столбец. Следуя подходу, предложенному Валенте и соавт. [64] инициализация матрицы выполняется случайным образом, и итерация, известная как импровизация, начинается после завершения первого поколения.Новые векторы создаются посредством обменов между соседними ячейками с определенной вероятностью. Если новая гармония имеет улучшение по сравнению с наихудшим решением, она заменяет старый вектор в матрице. В противном случае матрица осталась бы неизменной. Авторы сравнили подход HS с алгоритмом волнового фронта, используемым Barrientos et al. [10] с использованием того же сценария с тремя подобластями, как показано на рисунке 22. HS обеспечивает меньшее количество витков, чем волновой фронт, но более длительное время вычислений.Однако авторы не рассматривают вычислительное время как проблему, если планирование выполняется в автономном режиме. Совсем недавно Sadat et al. [65] и Sadat et al. [66] предлагают подходы к онлайн-планированию маршрутов с неоднородным покрытием. В этом контексте транспортное средство может изменять свою высоту во время покрытия в зависимости от важности каждой части области. Авторы используют древовидную структуру для работы с сетками с разным разрешением. Чем ближе узел к листьям, тем выше разрешение.Sadat et al. [65] представили три метода исследования дерева: стратегия в ширину, в глубину и эвристика быстрого доступа, в то время как Sadat et al. [66] предложили подход, основанный на Гильберте, как показано на рисунке 23, сравнив его с предыдущими стратегиями и моделью газонокосилки. При посещении интересующей зоны разрешение увеличивается за счет движения вниз по дереву. Таким образом, область, которая исследовалась родительским узлом, теперь полностью покрывается их дочерними узлами с повышенным разрешением.С другой стороны, если зона не интересна, поиск идет вверх по дереву покрытия и уменьшает разрешение. Таким образом, для выполнения миссии по территории перемещается одно транспортное средство, исследуя зоны на разных высотах. Воздушное зондирование с высоким разрешением с помощью нескольких разнородных БПЛА для невыпуклых областей обсуждается Santamaria et al. [67]. Транспортные средства имеют различный диапазон покрытия и датчики изображения, поэтому интересующая область дискретизируется в сетку с ячейками разного размера посредством приблизительного разбиения по ячейкам, как показано на рисунке 24.Первоначально приблизительная оценка определяет часть территории, которую должны исследовать БПЛА, с учетом их зоны действия бортовых датчиков. Метод лавинной рассылки выбирает начальную позицию и расширяет область соседства, пока не достигнет предполагаемого количества ячеек. Места, расположенные за пределами зоны или в пределах NFZ, являются недействительными ячейками. После первого завершенного раунда беззнаковые ячейки направляются в ближайшую область, и выполняется повторная балансировка для равномерного распределения ячеек. Следуя подходу, представленному Сантамария и др.[67], траектории полета для покрытия каждой подобласти вычисляются с использованием алгоритма для поиска удаленных сегментов свободных ячеек, называемых шагами. Алгоритм вычисляет шаги для всех неисследованных соседних ячеек фактического положения, выбирая самую длинную линию. Последняя ячейка выбранной строки превращается в текущую ячейку, повторяя процесс. Когда нет непосещенных соседних ячеек, алгоритм генерирует траектории от фактического местоположения до ближайших неисследованных ячеек, выбирает второстепенный путь и добавляет соответствующие ячейки в план покрытия.Также вычисляется кратчайшее расстояние до места посадки. Предлагаемый подход был интегрирован с AMFIS [68], которая состоит из наземной станции управления для управления и мониторинга транспортных средств в реальном времени.
