Равнодействующая двух сил, теория и примеры

Часто на тело действует одновременно не одна, а несколько сил. Рассмотрим случай, когда на тело оказывают воздействие две силы ( и ). Например, на тело, покоящееся на горизонтальной поверхности действуют сила тяжести () и реакция опоры поверхности () (рис.1).

Эти две силы можно заменить одной, которую называют равнодействующей силой (). Находят ее как векторную сумму сил и :

Определение равнодействующей двух сил

Отметим, что действие каждой силы не зависит от того, есть ли другие силы или их нет.

Второй закон Ньютона для равнодействующей двух сил

Если на тело действуют две силы, то второй закон Ньютона запишем как:

Направление равнодействующей всегда совпадает по направлению с направлением ускорения движения тела.

Это означает, что, если на тело оказывают воздействие две силы () в один и тот же момент времени, то ускорение () этого тела будет прямо пропорционально векторной сумме этих сил (или пропорционально равнодействующей сил):

m – масса, рассматриваемого тела.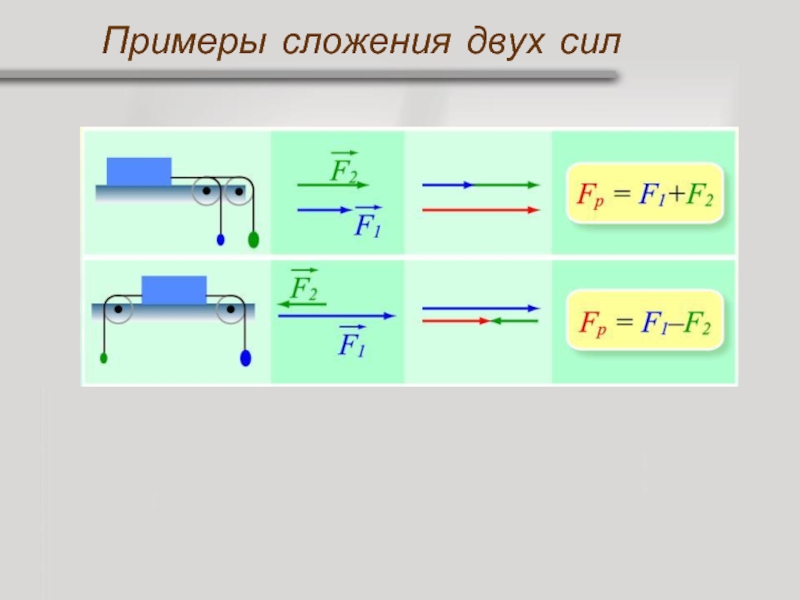 Суть второго закона Ньютона заключается в том, что силы, действующие на тело, определяют как изменяется скорость тела, а не просто величину скорости тела. Отмети, что второй закон Ньютона выполняется исключительно в инерциальных системах отсчета.

Равнодействующая двух сил может быть равна нулю, если силы, действующие на тело направлены в разные стороны и равны по модулю.

Нахождение величины равнодействующей двух сил

Для нахождения равнодействующей, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.

Допустим, что на тело действуют две силы, которые направлены по одной прямой (рис.1). Из рисунка видно, что они направлены в разные стороны.

Равнодействующая сил (), приложенных к телу, будет равна:

Для нахождения модуля равнодействующей сил выберем ось, обозначим ее X, направим вдоль направления действия сил. Тогда проектируя выражение (4) на ось X мы получим, что величина (модуль) равнодействующей (F) равен:

где – модули соответствующих сил.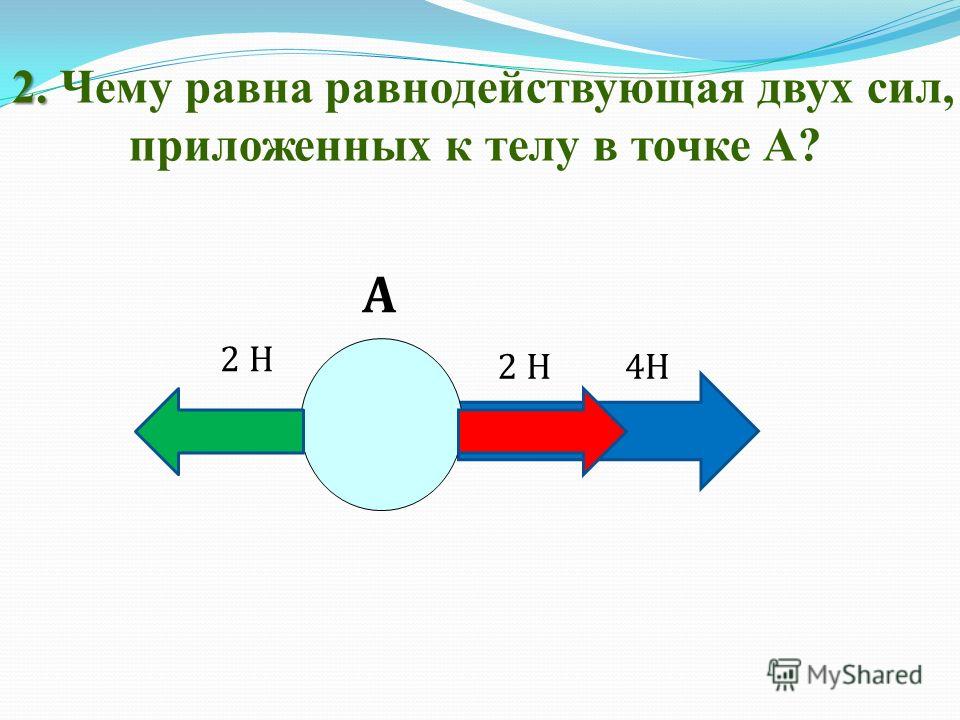

Представим, что на тело действуют две силы и , направленные под некоторым углом друг к другу (рис.2). Равнодействующую этих сил находим по правилу параллелограмма. Величина равнодействующей будет равен длине диагонали этого параллелограмма.

Примеры решения задач

Как найти равнодействующую?

☰

Когда говорят о равнодействующей, то имеют в виду силу, которая равна действию двух или более сил, одновременно приложенных к телу.

Когда на тело действует несколько сил, то их совместный эффект может быть различным, он зависит как от направления разных сил, так и от их числовых значений. В любом случае всегда можно найти одну равнодействующую им силу.

Например, на батут положили кирпич. На кирпич действуют две силы — сила тяжести и сила упругости батута. В момент, когда кирпич только положили, сила тяжести была больше, чем сила упругости, и кирпич двигался вниз. Как только силы сравнялись, кирпич остановился.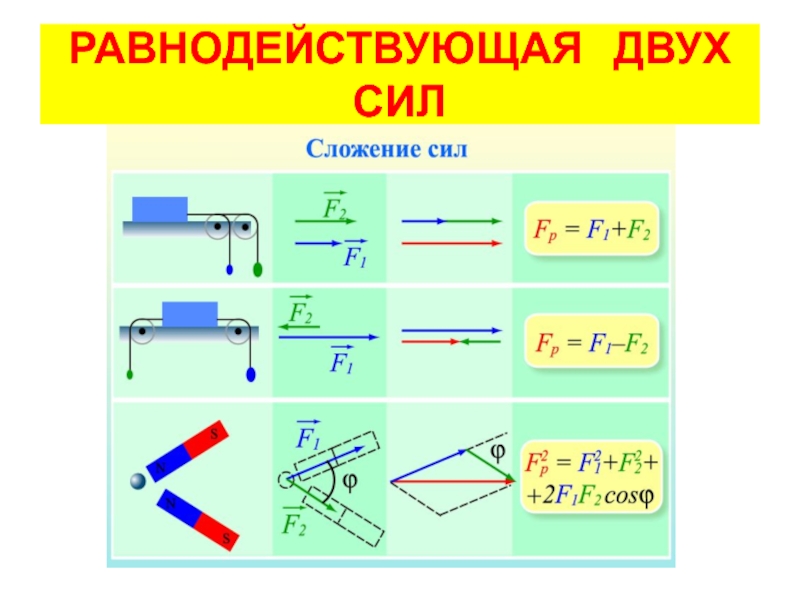

Если бы кирпич не клали на батут, а бросили со всей силы сверху, то он бы двигался вниз не только под действием силы тяжести, но и переданной ему силы броска. Под действием этих двух сил батут бы прогнулся сильнее, так как сила упругости, которая уравновесит эти силы, должна быть больше.

Когда равновесие сил будет достигнуто, и движение остановится, то равновесие снова нарушится, так как на кирпич уже не будет действовать сила броска, а только силы тяжести и упругости. Но ведь сила упругости была достигнута не только за счет веса кирпича, но за счет силы броска. Поэтому сила упругости будет больше силы тяжести, и кирпич подпрыгнет, то есть начнет двигаться вверх.

В самых простых случаях рассматривают равнодействующую сил, направленных либо в одну сторону, либо противоположно.

Если две силы, действующие на тело, направлены в одну сторону, то равнодействующая им будет равна их сумме: F₁ + F₂. Например, если тело толкают в одну сторону две силы в 10 Н и 20 Н, то равнодействующая сила этим двум будет равна 30 Н.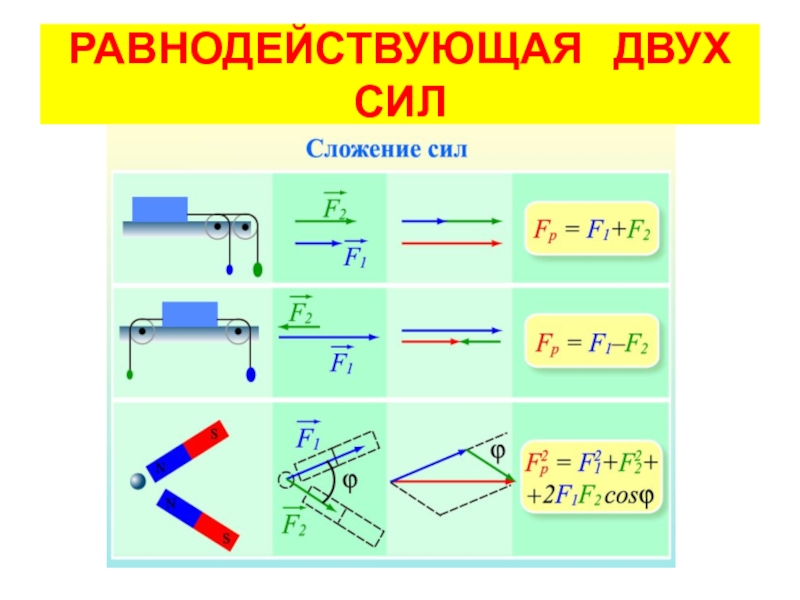

Если две силы, действующие на тело, направлены в противоположные стороны, то равнодействующая им равна модулю разности между силами и направлена в сторону большей: |F₁ – F₂|. Например, если одна сила в 10 Н толкает тело влево, а другая сила в 15 Н — вправо, то тело будет двигаться вправо под действием силы в 5 Н (|10 – 15| = 5).

Когда силы направлены противоположно, но равны по численному значению, то равнодействующая им будет равна нулю. Это значит, что равнодействующая сила не оказывает никакого влияния на тело. Если тело находилось в покое, оно в нем и останется. Если тело двигалось прямолинейно и равномерно, оно так и продолжит двигаться. Таким образом, хотя две новые силы подействовали на тело, они «взаимно уничтожились».

Допустим, на тело действуют три силы, две из которых направлены в одну сторону, а третья в другую. В этом случае сначала надо найти равнодействующую двух сил, направленных в одну сторону, сложив их. Потом сравнить ее с третьей силой, чтобы определить в какую сторону будет направлена равнодействующая трех сил.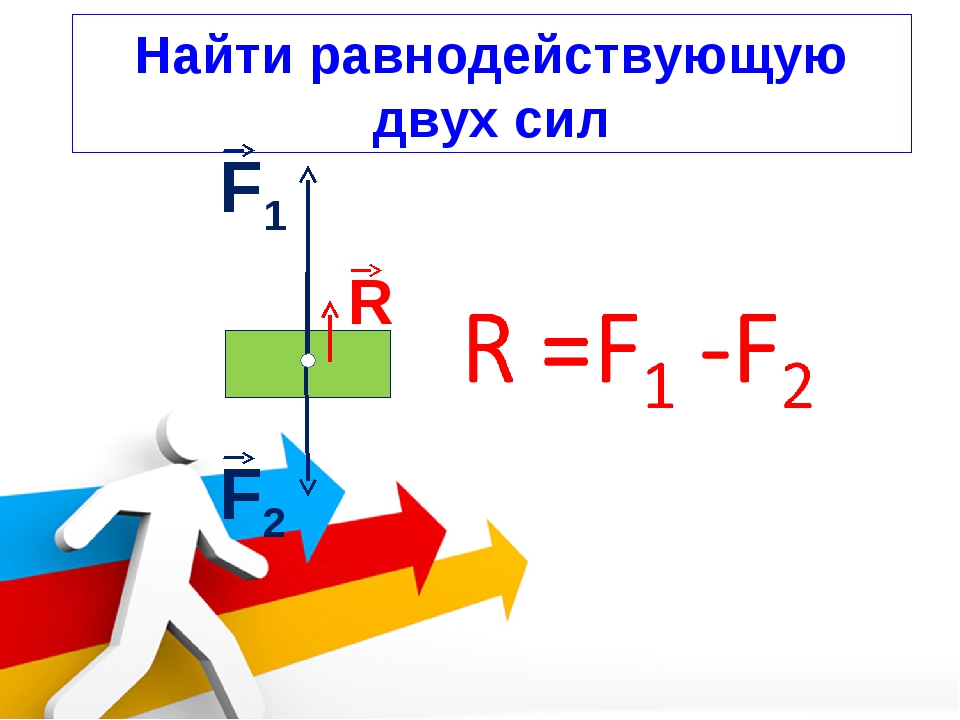 И найти модуль разности между суммой первых двух и третьей: |F₁ + F₂ – F₃|.

как найти равнодействующую двух сил, направленных по одной прямой в одну сторону?

До наших дней в некоторых арабских странах существует верблюжья кавалерия. Кавалерист
скачет на верблюде со скоростью 15 км/ч от города до оазиса, нах
…

одящегося на расстоянии
30 км. Там он останавливается на время, равное 1/2 времени движения от города до оазиса.
Затем кавалерист на уставшем верблюде отправляется обратно в город со скоростью 10 км/ч.
1) Какое время кавалерист отсутствовал в городе?
2) Определите среднюю путевую скорость кавалериста за всё время его отсутствия в городе.
Ответ: 1)
ч;
2)
км/ч.

Ю25
0
в лаборатории завода в запаянной колбе из толстого стекла хранилась ртуть. Перед
отправкой ртути в производственный цех завода лаборанту было по
…

ручено, не вскрывая
колбу, измерить массу ртути. Лаборант определил массу колбы с ртутью и внешний объём
колбы.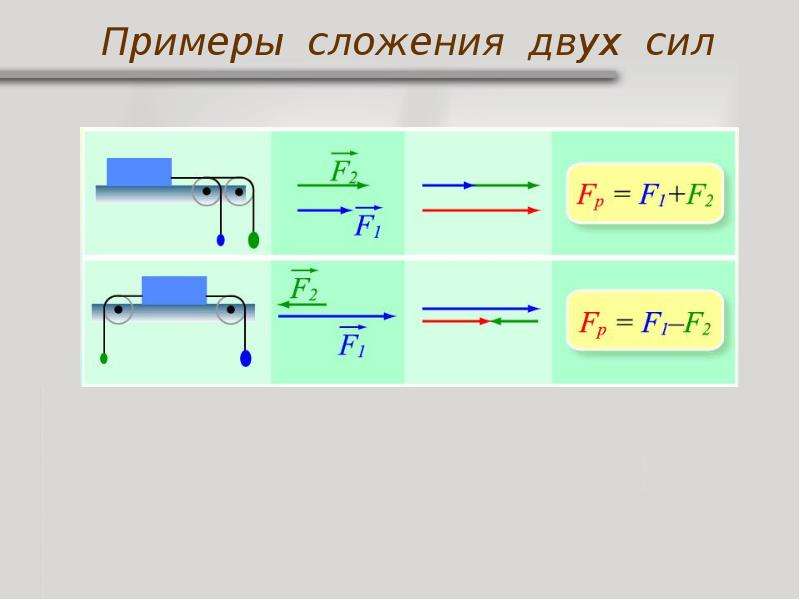 Измерения дали результат: m = 1,610 кг и V= 200 см». Используя справочные данные,
лаборант правильно вычислил массу ртути. Плотность ртути pp = 13,6 г/см», плотность стекла
Рc = 2,5 г/см.
1) Чему равна масса колбы с ртутью, если её выразить в граммах?
2) Определите массу ртути в колбе, если ртуть заполняла внутреннее пространство колбы
практически полностью.
3) Во сколько раз масса ртути больше массы пустой колбы? Округлите до сотых.
Напишите полное решение этой задачи.
Ответы на вопросы обоснуйте соответствующими рассуждениями или решением задачи.
Решение:

ВПР. Физика. 7 класс. Вариант 2
КОД 1007,6
1)
В день рождения лаборанту Григорию подарили подарок, который Григорий решил взвесить
(он всё всегда взве
…

шивал). Для этого Григорий использовал равноплечие рычажные весы. На
одну из чашек лаборант положил подарок, а на другую — поставил пустой стакан массой
175 г. Подарок перевесил. Тогда Григорий начал наливать в стакан воду порциями по 30 мл.
После пятого доливания чашка весов с подарком поднялась.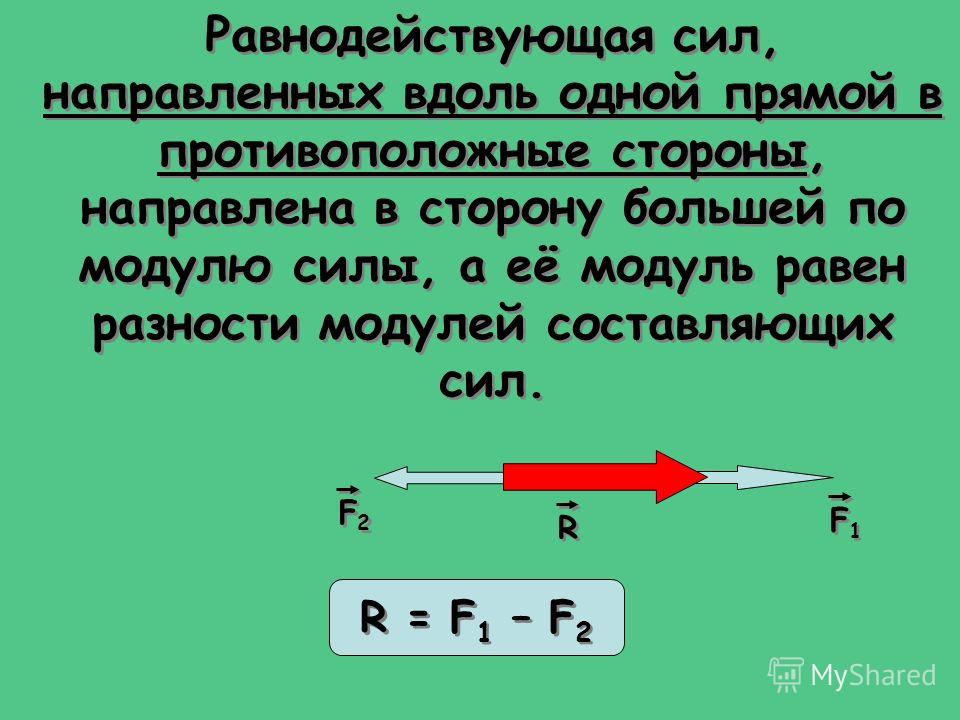 Тогда Григорий удалил из
стакана 20 мл воды, и подарок снова перевесил.
1) Какую массу имеет одна порция воды объёмом 20 мл?
2) Какая масса воды была добавлена в стакан к тому моменту, когда чаша с подарком
поднялась?
3) Оцените массу подарка
+

1 Cross out the word in each sentence which isnot correct.1 How do you like your eggs? Shall I fry / boil /grill them?2 First, chop/mix/ slice the oni
…

ons with a sharpknife.3 I think we should grate / bake / grill the fish.It’s healthier than frying.4 Fry / Boil / Roast the meat with a little oil.5 We need to spread /chop/grate the cheese allover the pizza.6 The recipe says we must boil / bake / roast it inthe oven until it’s golden brown.7 Spread / Mix / Slice the mixture with a spoon.8 Can you slice / grate / spread the carrots to putin the salad?​

Глубина озера Рыуге-Сууръярв 38 метров. Каково давление на дне озера, если давление воздуха 1000 гПа? Во сколько раз давление на дне озера будет больш
…

е давления воздуха?

чому дорівнює ккд гідравлічної машини якщо для піднімання вантажу масою 1,2 т необхідно прикласти до малого поршня силу 160 н площа поршнів 5 і 500 см
…

пожалуйста помогите СРОЧНО!!!!!!!!

Пожалуйста кто нибудь помогите надо решить лабораторную работу

Снаряд, що летів по параболі, розірвався у верхній точці траєкторії на три осколки однакової маси.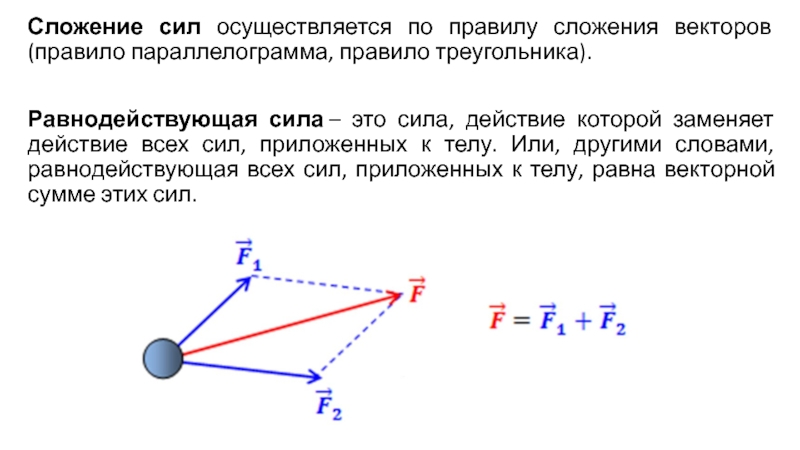 Пер- ший осколок продовжував рух по тій же параболі
…

й впав на відстані 1 км від гармати. Другий осколок рухався вертикально вниз і впав одночасно з першим. На якій відстані від гармати впав третій осколок?

постройте ход лучей в плоскомарельной пластине зделав рисунок

ДПЮ 25 БАЛОВ ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!!!!​

Равнодействующая двух сил. Равнодействующая двух сил Равны силы f1 и f2

Часто на тело действует одновременно не одна, а несколько сил. Рассмотрим случай, когда на тело оказывают воздействие две силы ( и ). Например, на тело, покоящееся на горизонтальной поверхности действуют сила тяжести () и реакция опоры поверхности () (рис.1).

Эти две силы можно заменить одной, которую называют равнодействующей силой (). Находят ее как векторную сумму сил и :

Определение равнодействующей двух сил

ОПРЕДЕЛЕНИЕ

Равнодействующей двух сил
называют силу, которая производит на тело действие аналогичное, действию двух отдельных сил.

Отметим, что действие каждой силы не зависит от того, есть ли другие силы или их нет.

Второй закон Ньютона для равнодействующей двух сил

Если на тело действуют две силы, то второй закон Ньютона запишем как:

Направление равнодействующей всегда совпадает по направлению с направлением ускорения движения тела.

Это означает, что, если на тело оказывают воздействие две силы () в один и тот же момент времени, то ускорение () этого тела будет прямо пропорционально векторной сумме этих сил (или пропорционально равнодействующей сил):

M — масса, рассматриваемого тела. Суть второго закона Ньютона заключается в том, что силы, действующие на тело, определяют как изменяется скорость тела, а не просто величину скорости тела. Отмети, что второй закон Ньютона выполняется исключительно в инерциальных системах отсчета.

Равнодействующая двух сил может быть равна нулю, если силы, действующие на тело направлены в разные стороны и равны по модулю.

Нахождение величины равнодействующей двух сил

Для нахождения равнодействующей, следует изобразить на чертеже все силы, которые необходимо учитывать в задаче, действующие на тело. Складывать силы следует по правилам сложения векторов.

Допустим, что на тело действуют две силы, которые направлены по одной прямой (рис.1). Из рисунка видно, что они направлены в разные стороны.

Равнодействующая сил (), приложенных к телу, будет равна:

Для нахождения модуля равнодействующей сил выберем ось, обозначим ее X, направим вдоль направления действия сил. Тогда проектируя выражение (4) на ось X мы получим, что величина (модуль) равнодействующей (F) равен:

где — модули соответствующих сил.

Представим, что на тело действуют две силы и , направленные под некоторым углом друг к другу (рис.2). Равнодействующую этих сил находим по правилу параллелограмма. Величина равнодействующей будет равен длине диагонали этого параллелограмма.

Примеры решения задач

ПРИМЕР 1

Задание	Тело массой 2 кг перемещают вертикально за нить вверх, при этом его ускорение равно 1 Какова величина и направление равнодействующей силы? Какие силы приложены к телу?
Решение	К телу (рис.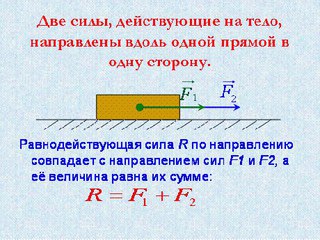 3) приложены сила тяжести () и сила реакции нити (). Равнодействующую указанных выше сил можно найти используя второй закон Ньютона: В проекции на ось X уравнение (1.1) принимает форму: Вычислим величину равнодействующей силы:
Ответ	Н, равнодействующая сила направлена так же как ускорение движения тела, то есть вертикально вверх. На тело действует две силы и .

Для ответа на этот вопрос, необходимо из условия задачи сделать некоторые выводы:

1. Направление этих сил;
2. Модульное значение сил F1 и F2;
3. Могут ли эти силы создать такую равнодействующую силу, чтобы сдвинуть тележку с места.

Направление сил

Для того, чтобы определить основные характеристики движения тележки, находящейся под воздействием двух сил, необходимо знать их направление. Например, если тележку вправо тянет сила, равная 5 Н и такая же сила тянет тележку влево, то логично предположить, что тележка будет стоять на месте.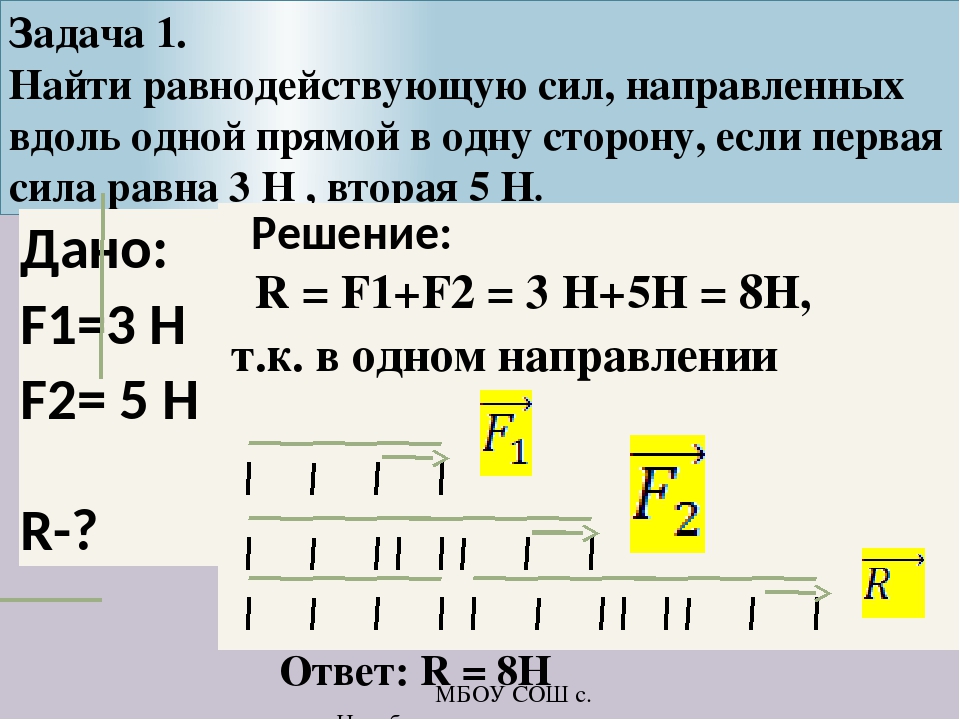 Если силы сонаправлены, для нахождения результирующей силы необходимо лишь найти их сумму. Если какая либо сила направлена под углом к плоскости движения тележки, то значение этой силы надо умножить на косинус угла между направлением действия силы и плоскостью. Математически это будет выглядеть так:

F = F1 * cosa; где

F – сила, направленная параллельно поверхности движения.

Теорема косинусов для нахождения результирующего вектора сил

Если две силы имеют свое начало в одной точке и есть определенный угол между их направлением, то тогда необходимо достроить треугольник результирующим вектором (то есть тем, который соединяет концы векторов F1 и F2). Найдем результирующую силу с помощью теоремы косинусов, которая гласит, что квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними. Запишем это в математическом виде:

F = F 1 2 + F 2 2 — 2 * F 1 * F 2 * cosa.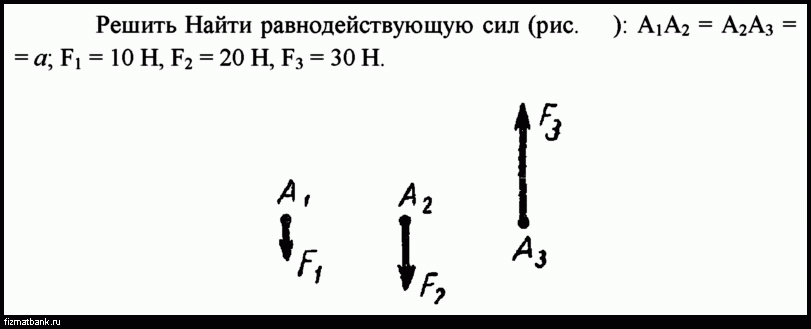

Подставив все известные величины можно определить величину результирующей силы.

Равнодействующая.
Вы уже знаете, что две силы уравновешивают друг друга, когда они равны по модулю и направлены противоположно. Таковы, например, сила тяжести и сила нормальной реакции, действующие на лежащую на столе книгу. В этом случае говорят, что равнодействующая двух сил равна нулю. В общем случае равнодействующей двух или нескольких сил называют силу, которая производит на тело такое же действие, как одновременное действие этих сил.

Рассмотрим на опыте, как найти равнодействующую двух сил, направленных вдоль одной прямой.

Поставим опыт

Положим легкий брусок на гладкую горизонтальную поверхность стола (чтобы трением между бруском и поверхностью стола можно было пренебречь). Будем тянуть брусок вправо с помощью одного динамометра, а влево — с помощью двух динамометров, как показано на рис. 16.3. Обратите внимание, что находящиеся слева динамометры прикреплены к бруску так, что силы натяжения пружин этих динамометров различны.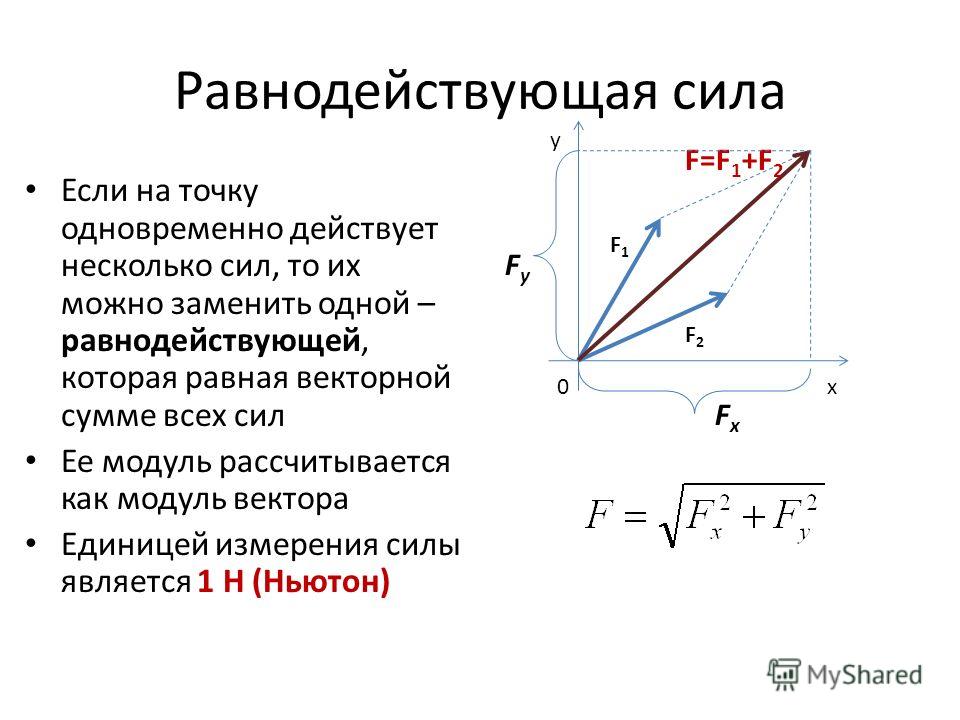

Рис. 16.3. Как можно найти равнодействующую двух сил

Мы увидим, что брусок находится в покое, если модуль силы, которая тянет его вправо, равен сумме модулей сил, тянущих брусок влево. Схема этого опыта изображена на рис. 16.4.

Рис. 16.4. Схематическое изображение сил, действующих на брусок

Сила F 3 уравновешивает равнодействующую сил F 1 и F 2 , то есть равна ей по модулю и противоположна по направлению. Значит, равнодействующая сил F 1 и F 2 направлена влево (как и эти силы), а ее модуль равен F 1 + F 2 . Таким образом, если две силы направлены одинаково, их равнодействующая направлена так же, как эти силы, а модуль равнодействующей равен сумме модулей сил-слагаемых.

Рассмотрим силу F 1 . Она уравновешивает равнодействующую сил F 2 и F 3 , направленных противоположно. Значит, равнодействующая сил F 2 и F 3 направлена вправо (то есть в сторону большей из этих сил), а ее модуль равен F 3 — F 2 . Таким образом, если две не равные по модулю силы направлены противоположно, их равнодействующая направлена как большая из этих сил, а модуль равнодействующей равен разности модулей большей и меньшей силы.

Нахождение равнодействующей нескольких сил называют сложением этих сил.

Две силы направлены вдоль одной прямой. Модуль одной силы равен 1 Н, а модуль другой силы равен 2 Н. Может ли модуль равнодействующей этих сил быть равен: а) нулю; б) 1 Н; в) 2 Н; г) 3 Н?

Содержание статьи

СТАТИКА,
раздел механики, предметом которого являются материальные тела, находящиеся в состоянии покоя при действии на них внешних сил. В широком смысле слова статика – это теория равновесия любых тел – твердых, жидких или газообразных. В более узком понимании данный термин относится к изучению равновесия твердых тел, а также нерастягивающихся гибких тел – тросов, ремней и цепей. Равновесие деформирующихся твердых тел рассматривается в теории упругости, а равновесие жидкостей и газов – в гидроаэромеханике.
См
. ГИДРОАЭРОМЕХАНИКА .

Историческая справка.

Статика – самый старый раздел механики; некоторые из ее принципов были известны уже древним египтянам и вавилонянам, о чем свидетельствуют построенные ими пирамиды и храмы. Среди первых создателей теоретической статики был Архимед (ок. 287–212 до н.э.), который разработал теорию рычага и сформулировал основной закон гидростатики. Родоначальником современной статики стал голландец С.Стевин (1548–1620), который в 1586 сформулировал закон сложения сил, или правило параллелограмма, и применил его в решении ряда задач.

Основные законы.

Законы статики вытекают из общих законов динамики как частный случай, когда скорости твердых тел стремятся к нулю, но по историческим причинам и педагогическим соображениям статику часто излагают независимо от динамики, строя ее на следующих постулируемых законах и принципах: а) законе сложения сил, б) принципе равновесия и в) принципе действия и противодействия. В случае твердых тел (точнее, идеально твердых тел, которые не деформируются под действием сил) вводится еще один принцип, основанный на определении твердого тела. Это принцип переносимости силы: состояние твердого тела не изменяется при перемещении точки приложения силы вдоль линии ее действия.

Сила как вектор.

В статике силу можно рассматривать как тянущее или толкающее усилие, имеющее определенные направление, величину и точку приложения. С математической точки зрения, это вектор, а потому ее можно представить направленным отрезком прямой, длина которого пропорциональна величине силы. (Векторные величины, в отличие от других величин, не имеющих направления, обозначаются полужирными буквами.)

Параллелограмм сил.

Рассмотрим тело (рис. 1,а
), на которое действуют силы F
1 и F
2 , приложенные в точке O и представленные на рисунке направленными отрезками OA
и OB
. Как показывает опыт, действие сил F
1 и F
2 эквивалентно одной силе R
, представленной отрезком OC
. Величина силы R
равна длине диагонали параллелограмма, построенного на векторах OA
и OB
как его сторонах; ее направление показано на рис. 1,а
. Сила R
называется равнодействующей сил F
1 и F
2 . Математически это записывается в виде R
= F
1 + F
2 , где сложение понимается в геометрическом смысле слова, указанном выше. Таков первый закон статики, называемый правилом параллелограмма сил.

Равнодействующая сила.

Вместо того чтобы строить параллелограмм OACB, для определения направления и величины равнодействующей R
можно построить треугольник OAC, перенеся вектор F
2 параллельно самому себе до совмещения его начальной точки (бывшей точки O) c концом (точкой A) вектора OA
. Замыкающая сторона треугольника OAC будет, очевидно, иметь ту же величину и то же направление, что и вектор R
(рис. 1,б
). Такой способ отыскания равнодействующей можно обобщить на систему многих сил F
1 , F
2 ,…, F
n , приложенных в одной и той же точке O рассматриваемого тела. Так, если система состоит из четырех сил (рис. 1,в
), то можно найти равнодействующую сил F
1 и F
2 , сложить ее с силой F
3 , затем сложить новую равнодействующую с силой F
4 и в результате получить полную равнодействующую R
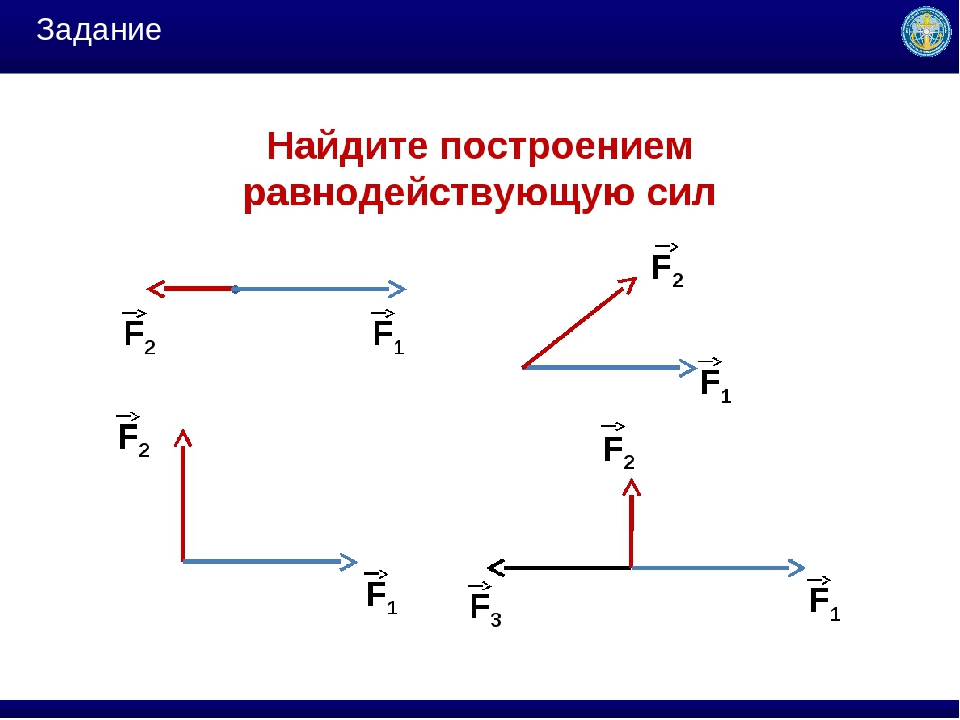. Равнодействующая R
, найденная таким графическим построением, представляется замыкающей стороной многоугольника сил OABCD (рис. 1,г
).

Данное выше определение равнодействующей можно обобщить на систему сил F
1 , F
2 ,…, F
n , приложенных в точках O 1 , O 2 ,…, O n твердого тела. Выбирается точка O, называемая точкой приведения, и в ней строится система параллельно перенесенных сил, равных по величине и направлению силам F
1 , F
2 ,…, F
n . Равнодействующая R
этих параллельно перенесенных векторов, т.е. вектор, представленный замыкающей стороной многоугольника сил, называется равнодействующей сил, действующих на тело (рис. 2). Ясно, что вектор R
не зависит от выбранной точки приведения. Если величина вектора R
(отрезок ON) не равна нулю, то тело не может находиться в покое: в соответствии с законом Ньютона всякое тело, на которое действует сила, должно двигаться с ускорением. Таким образом, тело может находиться в состоянии равновесия только при условии, что равнодействующая всех сил, приложенных к нему, равна нулю.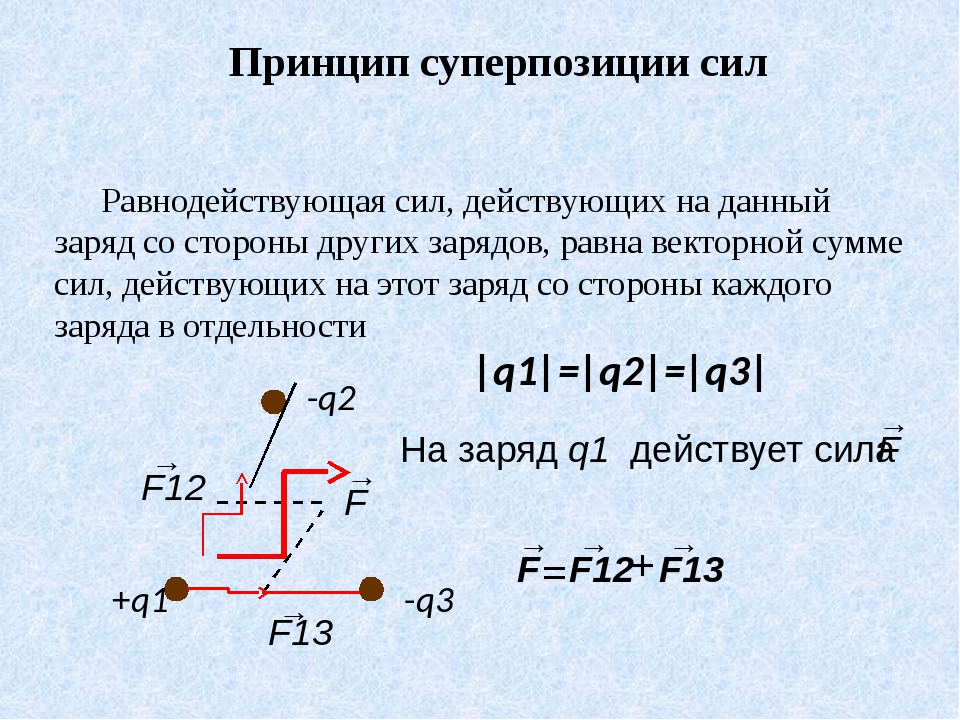 Однако это необходимое условие нельзя считать достаточным – тело может двигаться, когда равнодействующая всех приложенных к нему сил равна нулю.

В качестве простого, но важного примера, поясняющего сказанное, рассмотрим тонкий жесткий стержень длиной l
, вес которого пренебрежимо мал по сравнению с величиной приложенных к нему сил. Пусть на стержень действуют две силы F
и -F
, приложенные к его концам, равные по величине, но противоположно направленные, как показано на рис. 3,а
. В этом случае равнодействующая R
равна F
– F
= 0, но стержень не будет находиться в состоянии равновесия; очевидно, он будет вращаться вокруг своей средней точки O. Система двух равных, но противоположно направленных сил, действующих не по одной прямой, представляет собой «пару сил», которую можно характеризовать произведением величины силы F
на «плечо» l
. Значимость такого произведения можно показать путем следующих рассуждений, которые иллюстрируют правило рычага, выведенное Архимедом, и приводят к заключению об условии вращательного равновесия.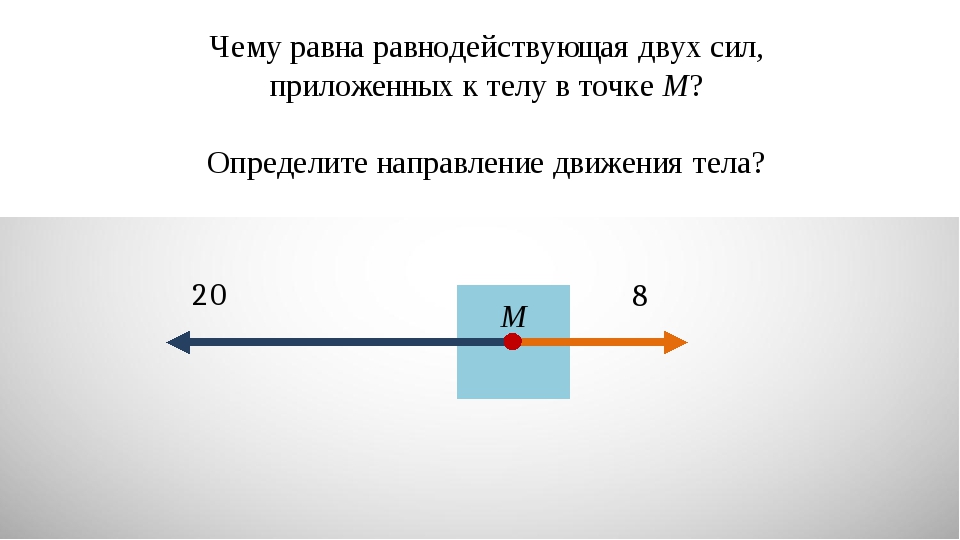 Рассмотрим легкий однородный жесткий стержень, способный поворачиваться вокруг оси в точке O, на который действует сила F
1 , приложенная на расстоянии l
1 от оси, как показано на рис. 3,б
. Под действием силы F
1 стержень будет поворачиваться вокруг точки O. Как нетрудно убедиться на опыте, вращение такого стержня можно предотвратить, приложив некоторую силу F
2 на таком расстоянии l
2 , чтобы выполнялось равенство F
2 l
2 = F
1 l
1 .

Таким образом, вращение можно предотвратить бесчисленными способами. Важно лишь выбрать силу и точку ее приложения так, чтобы произведение силы на плечо было равно F
1 l
1 . Это и есть правило рычага.

Нетрудно вывести условия равновесия системы. Действие сил F
1 и F
2 на ось вызывает противодействие в виде силы реакции R
, приложенной в точке O и направленной противоположно силам F
1 и F
2 . Согласно закону механики о действии и противодействии, величина реакции R
равна сумме сил F
1 + F
2 . Следовательно, равнодействующая всех сил, действующих на систему, равна F
1 + F
2 + R
= 0, так что отмеченное выше необходимое условие равновесия выполняется. Сила F
1 создает крутящий момент, действующий по часовой стрелке, т.е. момент силы F
1 l
1 относительно точки O, который уравновешивается действующим против часовой стрелки моментом F
2 l
2 силы F
2 . Очевидно, что условием равновесия тела является равенство нулю алгебраической суммы моментов, исключающее возможность вращения. Если сила F
действует на стержень под углом q
, как показано на рис. 4,а
, то эту силу можно представить в виде суммы двух составляющих, одна из которых (F
p), величиной F
cosq
, действует параллельно стержню и уравновешивается реакцией опоры —F
p , а другая (F
n), величиной F
sinq
, направлена под прямым углом к рычагу. В этом случае крутящий момент равен F
l
sinq
; он может быть уравновешен любой силой, которая создает равный ему момент, действующий против часовой стрелки.

Чтобы проще было учитывать знаки моментов в тех случаях, когда на тело действует много сил, момент силы F
относительно любой точки O тела (рис. 4,б
) можно рассматривать как вектор L
, равный векторному произведению r
ґ F
вектора положения r
на силу F
. Таким образом, L
= r
ґ F
. Нетрудно показать, что если на твердое тело действует система сил, приложенных в точках O 1 , O 2 ,…, O n (рис. 5), то эту систему можно заменить равнодействующей R
сил F
1 , F
2 ,…, F
n , приложенной в любой точке Oў тела, и парой сил L
, момент которых равен сумме [r
1 ґ F
1 ] + [r
2 ґ F
2 ] +… + [r
n ґ F
n ]. Чтобы убедиться в этом, достаточно мысленно приложить в точке Oў систему пар равных, но противоположно направленных сил F
1 и —F
1 ; F
2 и —F
2 ;…; F
n и —F
n , что, очевидно, не изменит состояния твердого тела.

Но сила F
1 , приложенная в точке O 1 , и сила –F
1 , приложенная в точке Oў, образуют пару сил, момент которых относительно точки Oў равен r
1 ґ F
1 . Точно так же силы F
2 и —F
2 , приложенные в точках O 2 и Oў соответственно, образуют пару с моментом r
2 ґ F
2 , и т.д. Суммарный момент L
всех таких пар относительно точки Oў дается векторным равенством L
= [r
1 ґ F
1 ] + [r
2 ґ F
2 ] +… + [r
n ґ F
n ]. Остальные силы F
1 , F
2 ,…, F
n , приложенные в точке Oў, в сумме дают равнодействующую R
. Но система не может находиться в равновесии, если величины R
и L
отличны от нуля. Следовательно, условие равенства нулю одновременно величин R
и L
является необходимым условием равновесия. Можно показать, что оно же является и достаточным, если тело первоначально покоится. Итак, задача о равновесии сводится к двум аналитическим условиям: R
= 0 и L
= 0.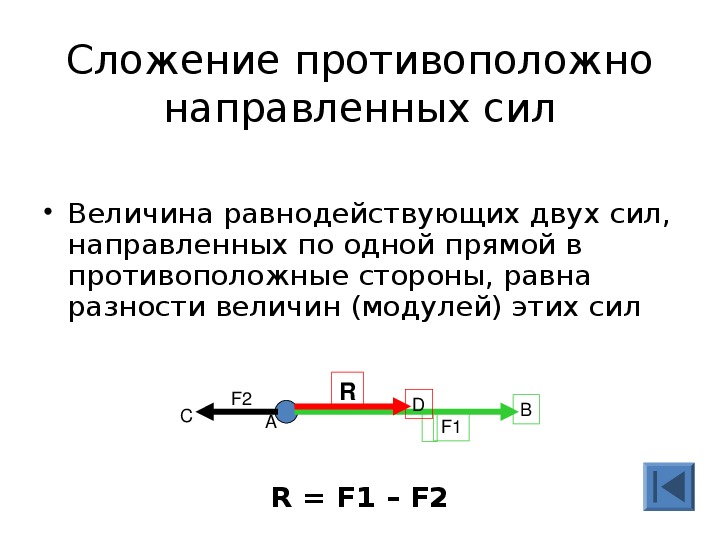 Эти два уравнения представляют собой математическую запись принципа равновесия.

Теоретические положения статики широко применяются при анализе сил, действующих на конструкции и сооружения. В случае непрерывного распределения сил суммы, которые дают результирующий момент L
и равнодействующую R
, заменяются интегралами и в соответствии с обычными методами интегрального исчисления.

Задача 3.2.1

Определить равнодействующую двух сил F 1 =50Н и F 2 =30Н, образующие между собой угол 30° (рис.3.2а).

Рисунок 3.2

Перенесем векторы сил F 1 и F 2 до точки пересечения линий действий и сложим по правилу параллелограмма (рис.2.2б). Точка приложения и направление равнодействующей показано на рисунке. Модуль полученной равнодействующей определим по формуле:

Ответ: R=77,44Н

Задача 3.2.2

Определить равнодействующую системы сходящихся сил F 1 =10Н, F 2 =15Н, F 3 =20Н, если известны углы, образованные векторами этих сил с осью Ох: α 1 =30 ° , α 2 =45 ° и α 3 =60 ° (рис. 3.3а)

Рисунок 3.3

Проецируем силы на оси Оx и Оy:

Модуль равнодействующей

На основе полученных проекций определяем направление равнодействующей (рис. 3.3б)

Ответ: R=44,04Н

Задача 3.2.3

В точке соединения двух нитей приложена вертикальная сила P=100Н (рис.3.4а). Определить усилия в нитях, если в состояния равновесия углы образованные нитями с осью OY равны α=30°, β=75°.

Рисунок 3.4

Силы натяжения нитей будут направлены вдоль нитей от узла соединения (рис.3.4б). Система сил T 1 , T 2 , P является системой сходящихся сил, т.к. линии действия сил пересекаются в точке соединения нитей. Условие равновесия данной системы:

Составляем аналитические уравнения равновесия системы сходящихся сил, проецирую векторное уравнение на оси.

Решаем систему полученных уравнений. Из первого выражаем T 2 .

Подставим полученное выражение во второе и определим T 1 и T 2 .

Н,

Проверим решение из условия, что модуль P’суммы сил T 1 и T 2 должен быть равен Р (рис.3.4в).

Ответ: T 1 =100Н, T 2 =51,76Н.

Задача 3.2.4

Определить равнодействующую системы сходящихся сил, если заданы их модули F 1 =12Н, F 2 =10Н, F 3 =15Н и угол α=60 ° (рис.3.5а).

Рисунок 3.5

Определяем проекции равнодействующей

Модуль равнодействующей:

На основе полученных проекций определяем направление равнодействующей (рис.3.5б)

Ответ: R=27,17Н

Задача 3.2.6

Три стержня АС, ВС, DC соединены шарнирно в точке C. Определить усилия в стержнях, если задана сила F=50Н, угол α=60° и угол β=75°. Сила F находится в плоскости Оyz. (рис.3.6)

Рисунок 3.6

Первоначально предполагаем, что все стержни растянуты, соответственно направляем реакции в стержнях от узла С. Полученная система N 1 , N 2 , N 3 , F является системой сходящихся сил. Условие равновесия данной системы.

Равнодействующая — Основные законы Ньютона

Равнодействующая

Как вы уже знаете из курса физики основной школы, силы – векторные величины: каждая сила характеризуется числовым значением (модулем) и направлением. Силы измеряют с помощью динамометров. Единицей силы в СИ является 1 ньютон (Н). Определение ньютона мы дадим позже.

Если на тело, которое можно считать материальной точкой, действуют несколько сил, то их можно заменить одной силой, которая является векторной суммой этих сил. Ее называют равнодействующей.

На рисунке 13.4 показано, как найти равнодействующую двух сил: а

? 2. К телу приложены две силы, равные по модулю 1 Н и 2 Н. Отвечая на следующие вопросы, сделайте пояснительные чертежи.
а) Какое наименьшее значение может принимать равнодействующая этих сил? Как направлены силы в этом случае?
б) Какое наибольшее значение может быть у равнодействующей этих сил? Как направлены силы в атом случае?
в) Может ли равнодействующая этих сил быть равной 2 Н?

? 3. К телу приложены две силы, равные по модулю 3 Н и 4 Н. Может ли их равнодействующая быть равной 5 Н? Если да, то чему в этом случае равен угол между приложенными силами?

? 4. К телу приложены три равные по модулю силы по 1 Н каждая. Как они должны быть направлены, чтобы:
а) равнодействующая была равна 1 Н?
б) равнодействующая была равна нулю?
в) равнодействующая была равна 2 Н?

Масса тела

В курсе физики основной школы рассказывалось также об опытах, которые доказывают, что под действием постоянной силы тело движется с постоянным ускорением.

Коэффициент пропорциональности между силой и ускорением характеризует инертные свойства тела и называется массой тела. Чем больше масса тела, тем большую силу надо приложить к телу, чтобы сообщить ему то же ускорение.

Единицей массы в СИ является 1 килограмм (кг). Это масса эталона, хранящегося в Международном бюро мер и весов (Франция). Приближенно можно считать, что одному килограмму равна масса 1 л воды.

Обозначают массу буквой m.

Второй закон Ньютона

Соотношение между равнодействующей всех сил, приложенных к телу, массой тела и его ускорением Ньютон сформулировал как второй из трех основных законов механики.

Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение: 

В инерциальной системе отсчета сила является причиной ускорения, поэтому второй закон Ньютона часто записывают так:

Итак, приобретаемое телом ускорение прямо пропорционально равнодействующей приложенных к телу сил, одинаково с ней направлено и обратно пропорционально массе тела.

Заметим, что второй закон Ньютона справедлив только в инерциальных системах отсчета. Напомним: в этих системах отсчета ускорение тела обусловлено только действием на него других тел.

Единицу силы в СИ определяют на основе второго закона Ньютона: сила в 1 ньютон сообщает телу массой 1 кг ускорение 1 м/с2. Поэтому 1 Н = 1 кг * м/с2.

Сила тяжести

Как вы уже знаете, под действием притяжения Земли все тела падают с одинаковым ускорением – ускорением свободного падения .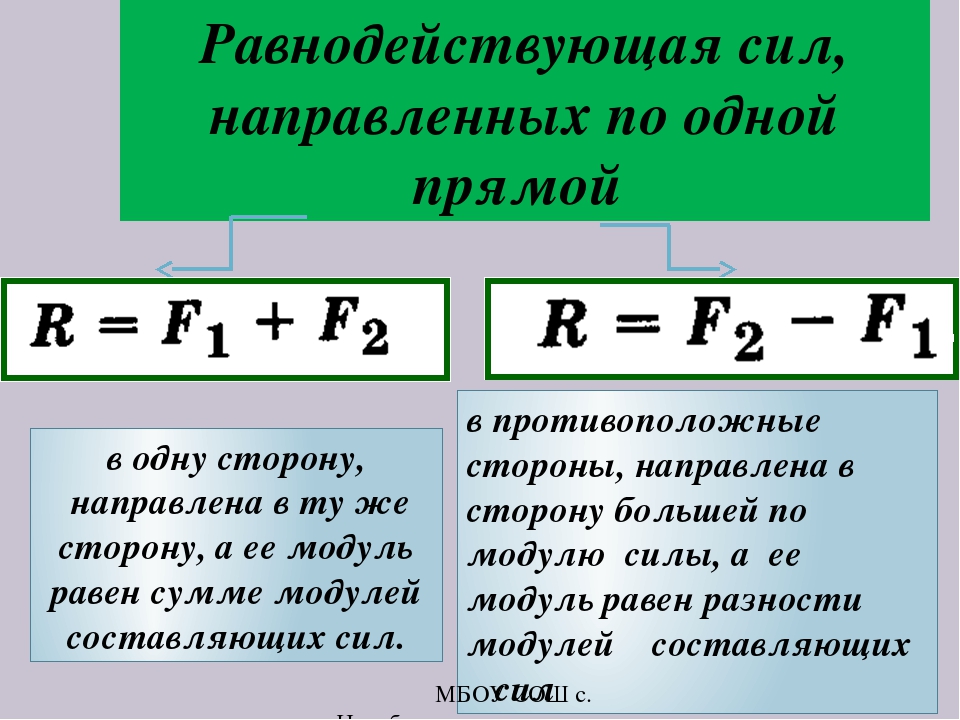 Силу притяжения, действующую на тело со стороны Земли, называют силой тяжести и обозначают т.

Когда тело свободно падает, на него действует только сила тяжести, поэтому она и является равнодействующей всех приложенных к телу сил. При атом тело движется с ускорением , поэтому из второго закона Ньютона получаем:

? 5. С какой силой Земля притягивает:
а) килограммовую гирю?
б) человека массой 60 кг?

Сила, скорость и ускорение – кто «третий лишний»?

Неочевидное следствие второго закона Ньютона состоит в том, что он утверждает: направление ускорения тела совпадает с направлением равнодействующей приложенных телу сил. Скорость же вела может быть при этом направлена как угодно!

Поставим опыт

Бросим шарик вниз, затем – вверх, а потом – под углом к горизонту (рис. 13.5)

На шарик во время всего движения действует только направленная вниз сила тяжести. Однако в первом случае (а) скорость шарика совпадает по направлению с этой силой, во втором случае (б) – скорость вначале противоположна силе тяжести, а в третьем (в) – скорость направлена под углом к силе тяжести (например, в верхней точке траектории скорость перпендикулярна силе тяжести).

? 6. Тело равномерно движется по окружности. Чему равен угол между скоростью тела и равнодействующей?

? 7. Чему равен угол между скоростью автомобиля и равнодействующей приложенных к нему сил, когда автомобиль:
а) разгоняется на прямой дороге?
б) тормозит на прямой дороге?
в) движется равномерно по дуге окружности?

Равнодействующая сила, обозначение сил, нахождение проекций на оси

Тестирование онлайн

Определение

Это векторная сумма всех сил, действующих на тело.

Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности

Взаимосвязь со вторым законом Ньютона

Вспомним закон Ньютона:

Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.

Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.

Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.

Нахождение равнодействующей силы

Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения.
Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.

Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Примеры

На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.

Обозначим силы, выберем координатные оси

Найдем проекции

Записываем уравнения

Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Блок — механическое устройство, колесо, вращающееся вокруг своей оси.
Блоки могут быть подвижными и неподвижными.

Неподвижный блок используется лишь для изменения направления силы.

Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.

Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.

Ускорение тела А в два раза меньше ускорения тела В.

Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии

Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.

Равнодействующая сила | Физика

Обычно на любое движущееся тело действует не одно, а сразу несколько окружающих его тел. Например, во время падения тела на него действует не только Земля (сила тяжести), но и воздух (сила сопротивления).

В тех случаях, когда на частицу (материальную точку) действует несколько тел, их общее действие характеризуют равнодействующей силой.

Для нахождения равнодействующей силы существуют простые правила.

1. Если к телу приложены две силы F₁ и F₂, направленные по одной прямой в одну сторону, то их равнодействующая F находится по формуле

F = F₁ + F₂.

При этом направление равнодействующей силы совпадает с направлением приложенных сил (рис. 32).

2. Если к телу приложены две силы F₁ и F₂, направленные по одной прямой в противоположные стороны, то при F₁ > F₂ их равнодействующая F находится по формуле

F = F₁ — F₂.

Направление равнодействующей силы в этом случае совпадает с направлением большей из приложенных сил (рис. 33). Если при этом F₁ = F₂, то их равнодействующая F окажется равной нулю. В этом случае покоящееся тело так и будет покоиться, а движущееся тело будет совершать равномерное и прямолинейное движение с той скоростью, которая у него была.

Про две силы, равные по величине и направленные вдоль одной прямой в противоположные стороны, говорят, что они уравновешивают или компенсируют друг друга. Равнодействующая F таких сил всегда равна нулю и потому изменить скорость тела не может.

Для изменения скорости тела относительно Земли необходимо, чтобы равнодействующая всех приложенных к телу сил была отлична от нуля. В том случае, когда тело движется в направлении равнодействующей силы, его скорость возрастает; при движении в противоположном направлении скорость тела убывает.

Так, например, во время полета парашютиста на него действуют две силы — сила тяжести и сила сопротивления воздуха. На начальной стадии спуска сила тяжести превышает силу сопротивления и их равнодействующая оказывается направленной вниз. Благодаря этому скорость падения парашютиста на данной стадии полета непрерывно увеличивается. Однако по мере увеличения скорости полета действующая на парашютиста сила сопротивления становится все больше и больше. После раскрытия парашюта сила сопротивления воздуха резко возрастает и становится больше силы тяжести. Равнодействующая этих двух сил оказывается направленной вверх, и скорость парашютиста начинает уменьшаться.

Для безопасного спуска человека площадь купола парашюта должна составлять 40—50 м². При этом минимальная скорость приземления оказывается равной 4—5 м/с.

Слово «парашют» в переводе с французского означает «предотвращающий падение». Идея его создания принадлежит Леонардо да Винчи (1452—1519). Однако первый прыжок с парашютом (с крыши высокой башни) был совершен лишь в 1617 г. венецианским инженером и механиком Ф. Веранцио. Его парашют был далек от совершенства и представлял собой раму, обтянутую полотном.

Первый ранцевый парашют, который располагался на спине человека и раскрывался при помощи вытяжного кольца, был создан в 1911 г. русским изобретателем Г. Е. Котельниковым.

1. Как находится равнодействующая двух сил, направленных по одной прямой в одну сторону? 2. Как находится равнодействующая двух сил, направленных по одной прямой в противоположные стороны? Куда она направлена? 3. Как будет двигаться тело, если к нему приложить две равные силы, которые направлены по одной прямой, но в противоположные стороны?

Результат двух сил — концепция

Я хочу поговорить об особом применении сложения векторов, и это результат двух сил. Когда две силы действуют на одну и ту же точку или объект, их сумму часто называют их равнодействующей, равнодействующей двух сил, поэтому я хочу определить равнодействующую или сумму двух сил f и g, поэтому представьте, что эти две силы f и g равны воздействуя на некоторую точку или объект, а величина f равна 500 ньютонам, это единица силы. Величина g составляет 125 ньютонов. Обе силы действуют в одном направлении, что в результате? Ой! Помните, что результат также будет вектором, поэтому вы должны описать его с точки зрения его величины и направления.
Здесь конкретики о направлении на самом деле не дается, поэтому мы можем просто сказать, находится ли результирующая в том же направлении, что и f и g, или в противоположном направлении, или что-то в этом роде. В любом случае, когда мы добавляем векторы, помните, что нам нравится сводить их лицом к лицу, или мы используем правило параллелограмма.Давайте свяжем их лицом к лицу, что я сделаю, я возьму g и переведу его так, чтобы он стоял во главе силы f, хорошо, вот так, а вот g. Теперь, когда я рисую результирующую, результирующая будет начинаться в хвосте f и заканчиваться в начале g, и это будет, этот вектор будет результирующим f + g, так что это f + g, и вы можете сказать что f + g действует в том же направлении, что и f и g. А какова величина? Величина f + g, поскольку они оба указывают в одном направлении, просто эта общая длина составляет 500 + 125 625 ньютонов.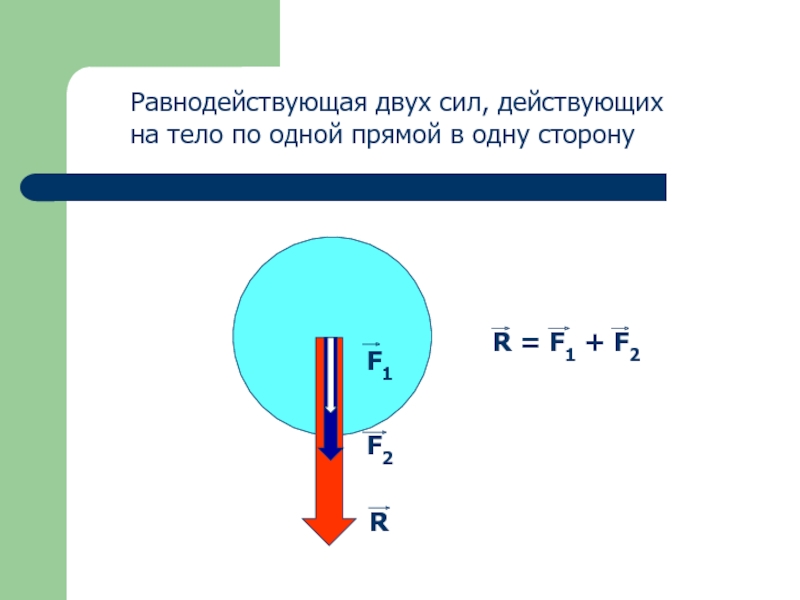
А как насчет этой ситуации в части b? f и g действуют в противоположных направлениях. Мы по-прежнему добавляем векторы таким же образом. Я возьму этот вектор и переведу его так, чтобы его хвост находился во главе вектора f, поэтому, если мы его нарисуем, вот вектор g и заметим, что результат будет начинаться в хвосте вектора f и будет заканчиваться в начале g, так что это результирующий f + g. Вы заметите, что f + g также находится в том же направлении, что и f, в том же направлении, что и f, но это направление противоположно g.И величина f + g, поскольку два вектора находятся в противоположных направлениях, у вас будет 500-125,500 ньютонов минус 125 ньютонов, то есть 375 ньютонов.
Ладно, это были слишком простые дела. Что, если векторы f и g перпендикулярны друг другу? Итак, в этом случае вы можете использовать метод «голова к хвосту», но вы часто увидите, что на уроках физики учитель будет использовать метод параллелограмма. В этом случае параллелограмм представляет собой прямоугольник. Теперь то, что вы в основном делаете, — это вы рисуете вектор, который параллелен, который в основном равен f, и другой, который равен g, и вы создаете параллелограмм.Результирующий начинается с общей конечной точки, начальной точки двух векторов, и идет к противоположному углу параллелограмма, так что это будет ваш результат, и я нарисую в голове, чтобы было ясно, так что это ваш f + г. Теперь в каком направлении? Какая величина? Что ж, величина проще всего, потому что длина этой ноги равна 500, длина — 125 ньютонов, поэтому квадрат величины равен 500 в квадрате, или пока забудьте о единицах, но, в конце концов, единицами величины будут ньютоны, 500 в квадрате плюс 125 в квадрате, поэтому давайте возьмем наши калькуляторы, 500 в квадрате плюс 125 в квадрате, а затем вы проверите квадратный корень и получите 515.4 ньютона, это примерно 515,4 ньютона, так что это величина.
А как насчет направления? Почему бы нам не найти этот угол, и мы можем сказать, что в конечном итоге направление f + g на столько градусов выше горизонтали. Давайте выясним, что это такое. Теперь вы можете видеть, что в этом трэнгле это прямоугольный треугольник, тангенс тэты равен 125, более 500 ньютонов сократятся, и вы получите одну четверть, так что тета является обратной тангенсом одной четверти. Мы снова получаем наш калькулятор. Я хочу убедиться, что я нахожусь в режиме градусов, потому что мне нужен ответ в градусах.Хорошо, арктангенс одной четверти 14 градусов приблизительно 14 градусов, это означает, что направление силы на 14 градусов выше горизонтали, величина составляет 515,4 ньютона.
Помните, когда вы описываете силу или любой вектор, задайте величину и направление.

Как вычислить результирующую силу, действующую на объект — x-engineer.org

В механике мы имеем дело с двумя типами величин (переменных): скалярными и векторными переменными. Скалярные переменные имеют только величину, например: длина, масса, температура, время. Переменные вектора имеют величину и направление, например: скорость, сила, крутящий момент. Направление вектора определяется углами действия каждой оси. Векторные переменные обычно обозначаются жирным шрифтом со стрелками вверху.

На тело или точку могут действовать несколько сил, каждая из которых имеет разное направление и величину. В инженерии основное внимание уделяется результирующей силе, действующей на тело.Результирующую параллельных сил (действующих в одной плоскости) можно найти с помощью закона параллелограмма , правила треугольника или правила многоугольника .

Две или более силы действуют одновременно — их направление пересекает общую точку. Например, две параллельные силы F ₁ и F ₂ действуют на одну и ту же точку P . Чтобы найти их результирующий R , мы можем применить либо закон параллелограмма , либо правило треугольника .

Результирующая сила — это векторная сумма между компонентами:

\ [\ overrightarrow {R} = \ overrightarrow {F_1} + \ overrightarrow {F_2} \]

Если на одну и ту же точку действует несколько сил, мы можем применить правило многоугольника , чтобы найти их равнодействующую.

\ [\ overrightarrow {R} = \ overrightarrow {F_1} + \ overrightarrow {F_2} + \ overrightarrow {F_3} + \ overrightarrow {F_4} \]

Результирующую силу можно определить также для трехмерной силы системы , используя правило многоугольника.

\ [\ overrightarrow {R} = \ overrightarrow {F_1} + \ overrightarrow {F_2} + \ overrightarrow {F_3} \]

Закон параллелограмма, правило треугольника и правило многоугольника — это геометрические методы для нахождения равнодействующей силы . Мы можем нарисовать результирующую силу, но мы не знаем точно ее величину и направление.

Чтобы вычислить величину и направление результирующей силы или вычислить значение той или иной составляющей силы, мы можем использовать закон синусов и закон косинусов.{\ circ} — \ alpha — \ beta)} \ tag {3} \]

Результирующую силу также можно вычислить аналитический , используя проекции силы. Используя метод проецирования силы , мы можем вычислить величину и углы направления результирующей силы.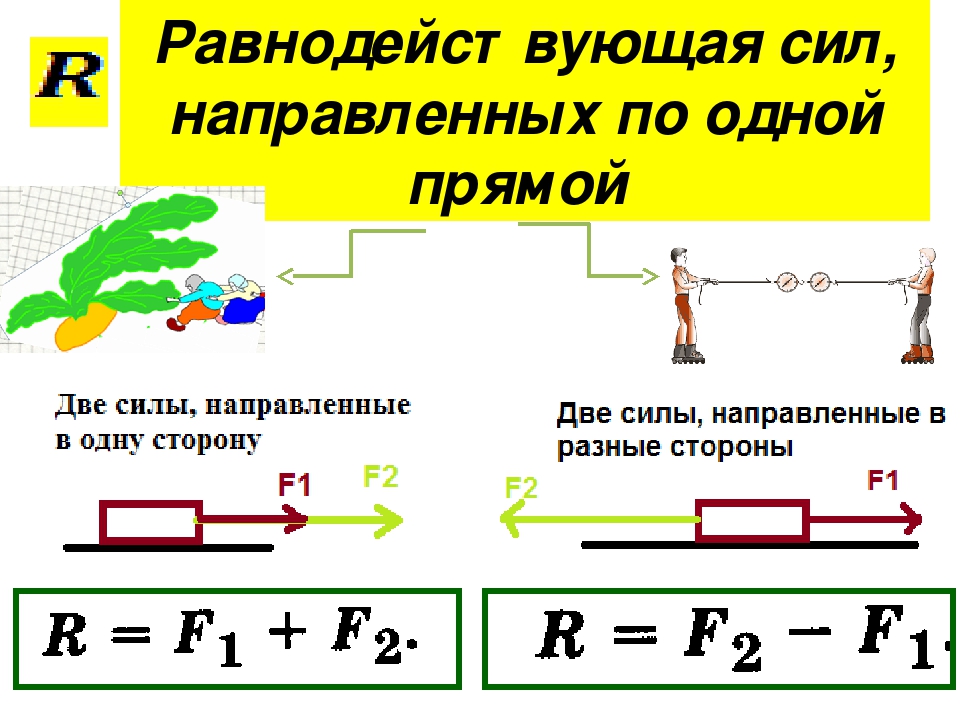 {n} F_ {iz}
\ end {split} \]

, где n — количество действующих сил, а F _x , F _{y 900 33} и F _z — равнодействующие силы на каждой оси.2}}
\ end {split} \]

Метод проецирования силы также можно использовать для вычисления результирующей силы в копланарной (оси x, оси y).

Пример 1 . Учитывая силы F ₁ = 2,91 Н , F ₂ = 2,67 Н , F ₃ = 2,47 Н и F ₄ = 2,23 Н и углы α = 60 ° и β = 30 ° , вычислить равнодействующую силу R и ее угол γ с осью абсцисс.

Шаг 1 . Чтобы получить представление о том, как может выглядеть результирующая сила, мы можем применить правило многоугольника.

Как видите, величина равнодействующей почти равна величине силы F ₃ . Кроме того, угол γ должен быть около значения α .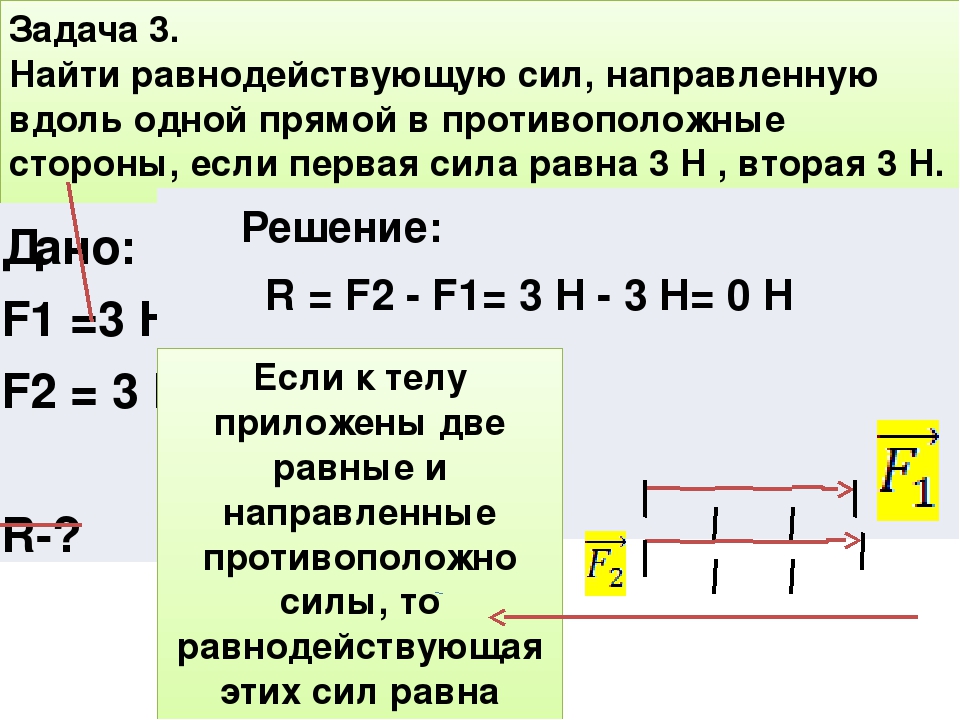 Это геометрическое решение полезно, потому что мы знаем, каких результатов следует ожидать от аналитического решения.

Шаг 2 .{\ circ} \]

Как и ожидалось, аналитическое решение (проекция сил) дает те же результаты, что и геометрическое решение (правило многоугольника).

Пример 2 . Учитывая силы F ₁ = 6,12 Н , F ₂ = 4,32 Н , F ₃ = 1,84 Н и их углы α = 16 ° , β = 22 ° , γ = 36 ° , вычислить равнодействующую силы R и ее углы α _R , β _R , γ _R с осями x, y и z.Силы — это диагонали с каждой стороны прямоугольного параллелепипеда.

Шаг 1 . Рассчитайте проекции силы на каждую ось.

\ [\ begin {split}
F_x & = F_1 \ cdot \ text {cos} (\ alpha) + F_2 \ cdot \ text {cos} (\ beta) & = 9.89 \ text {N} \\
F_y & = F_1 \ cdot \ text {cos} \ left (\ frac {\ pi} {2} — \ alpha \ right) + F_3 \ cdot \ text {cos} \ left (\ frac {\ pi} {2} — \ gamma \ right) & = 2,77 \ text {N} \\
F_z & = F_3 \ cdot \ text {cos} (\ gamma) + F_2 \ cdot \ text {cos} \ left (\ frac {\ pi} {2 } — \ beta \ right) & = 3. \ circ} {\ pi}, \ text {if} F_ {x}
\ end {matrix} \ right. \]

Пример 3 . В качестве примера возьмем систему сил из упражнения , упражнение 1, и вычислим результирующую силу и ее угол с горизонтальной осью ( O-x ).

Чтобы этот метод работал, все углы должны быть привязаны к горизонтальной оси, O-x .

Силы и углы следующие:

• F ₁ = 2,91 Н, α ₁ = 0 °
• F ₂ = 2.67 Н, α ₂ = 60 °
• F ₃ = 2,47 Н, α ₃ = 150 °
• F ₄ = 2,23 Н, α ₄ = 270 °

Шаг 1 . Вычислите горизонтальную составляющую результирующего

\ [F_ {x} = 2,91 \ cdot \ cos (0) + 2,67 \ cdot \ cos (60) + 2,47 \ cdot \ cos (150) + 2,23 \ cdot \ cos (270). = 2.106 \ text {N} \]

Наблюдение: если расчет выполняется на портативном калькуляторе программного приложения, аргумент функции cos () должен быть указан в радианах, например:

\ [\ cos \ left (60 \ cdot \ frac {\ pi} {180} \ right) \]

Шаг 2 .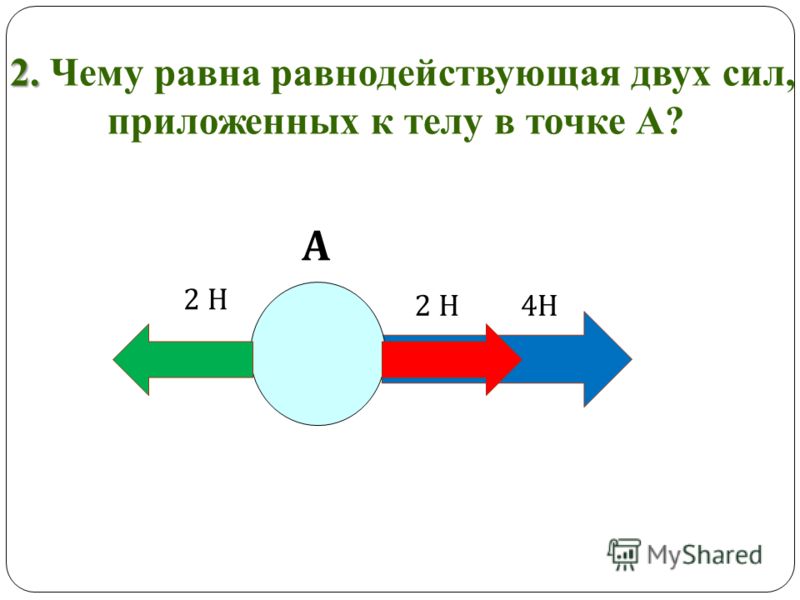 {2} + 1.{\ circ} \]

Этот метод можно распространить на любое количество сил, если известны значения сил и углы.

Вы также можете проверить свои результаты, используя калькулятор ниже.

Калькулятор результирующей силы

Используйте калькулятор выше, чтобы вычислить и оценить различное распределение сил. Наведя указатель мыши на линейные силы, вы можете увидеть их координаты, которые представляют компоненты F _x [N] и F _y [N].

Не забывайте ставить лайки, делиться и подписываться!

Результирующий вектор — объяснение и примеры

В векторной геометрии результирующий вектор определяется как:

«Результирующий вектор представляет собой комбинацию или, проще говоря, может быть определен как сумма двух или более векторов, которые имеют свою величину и направление.”

В этом разделе мы рассмотрим следующие концепции:

• Что такое результирующий вектор?
• Как найти результирующий вектор?
• Как найти равнодействующую более трех векторов?
• Как нарисовать получившийся вектор?
• Какова формула и метод вычисления результирующего вектора?
• Примеры
• Практические вопросы.

Что такое результирующий вектор?

Результирующий вектор — это вектор, который дает комбинированный эффект всех векторов.Когда мы складываем два или более векторов, результатом является результирующий вектор.

Давайте рассмотрим эту концепцию на простом практическом примере. Предположим, есть балка с двумя лежащими на ней коробками, как показано на рисунке ниже:

Сможете ли вы рассчитать вес балки и вес двух коробок? Да! Вы можете это сделать, поскольку вы познакомитесь с концепцией результирующего вектора.

В этом случае результирующий вектор будет суммой сил, действующих на два блока, т.е.е., вес ящиков, который будет равен и противоположен весу балки. В этом случае результирующий вектор будет суммой двух сил, поскольку они параллельны и направлены в одном направлении.

Предположим, что есть три вектора на плоскости: вектор A, B и C. Результирующий R может быть вычислен путем сложения всех трех векторов.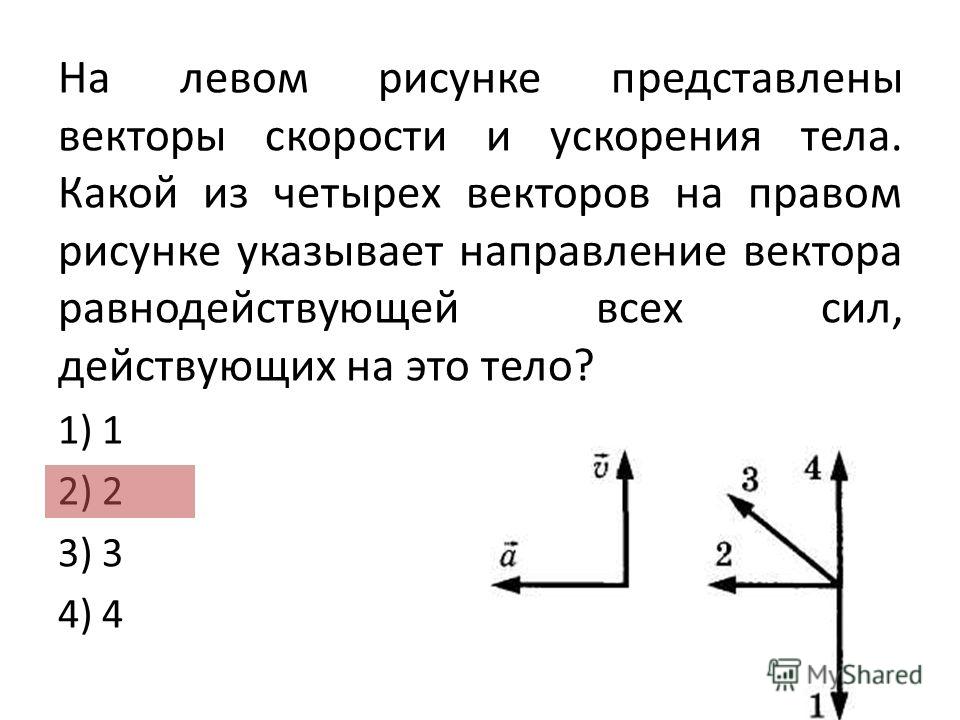 Результирующий R можно точно определить, нарисовав правильно масштабированную и точную диаграмму сложения векторов, как показано на рисунке ниже:

A + B + C = R

Давайте лучше поймем концепцию с помощью примера.

Пример 1

Рассчитайте результирующий вектор трех параллельных сил, направленных вверх. OA = 5N, OB = 10N и OC = 15N.

Решение

Как известно, результирующий вектор имеет вид:

R = OA + OB + OC

R = 5 + 10 + 15

R = 30N

Пример 2

Найти результирующий вектор данных векторов OA = (3,4) и OB = (5,7).

Решение

Добавление x-компонентов для нахождения Rx и y-компонентов для вычисления RY.

RX = 3 + 5

RX = 8

Ry = 4 + 7

Ry = 11

Итак, результирующий вектор R = (8,11)

Как найти результирующие векторы

Векторов можно добавить геометрически, нарисовав их с использованием общего масштаба в соответствии с соглашением «голова к хвосту», которое определяется как

“ Соедините хвост первого вектора с головой второго вектора, который даст другой вектор, голова которого соединена с головой второго вектора и хвостом первого вектора… »

… это называется результирующим вектором.

Шаги для определения результирующего вектора с использованием правила «голова к хвосту»

Ниже приведены шаги, которые необходимо выполнить, чтобы сложить два вектора и найти результирующий вектор:

1. Нарисуйте первый вектор в соответствии с выбранным масштабом в данном направлении.
2. Теперь соедините хвост второго вектора с головой первого вектора, нарисованного в соответствии с заданным масштабом и в заданном направлении.
3. Чтобы нарисовать результирующий вектор, соедините хвост первого вектора с головой второго вектора и поместите стрелку.
4. Чтобы определить величину, измерьте длину результирующей величины R, и, чтобы узнать направление, измерьте угол результирующей величины с осью x.

Пример 3

Рассмотрим корабль, идущий под углом 45 ° к северо-востоку. Затем он меняет свой курс на 165o на север. Нарисуйте получившийся вектор.

Решение

Результирующий вектор из более чем двух векторов

Правила нахождения результирующего вектора или сложения более двух векторов могут быть продлены на любое количество векторов.

R = A + B + C + ………………………….

Предположим, что имеется три вектора A, B, и C , как показано на рисунках ниже. Чтобы сложить эти векторы, нарисуйте их в соответствии с правилом «голова к хвосту» так, чтобы голова одного вектора совпадала с другим вектором. Итак, результирующий вектор имеет следующий вид:

R = A + B + C

Примечание: Сложение вектора является коммутативным по своей природе; сумма не зависит от порядка добавления.

R = A + B + C = C + B + C

Расчет результирующего вектора с использованием прямоугольных компонентов

Нахождение компонентов результирующего вектора известен как аналитический метод; этот метод более математический, чем геометрический, и его можно рассматривать как более точный и точный, чем геометрический метод, то есть конфигурирование с использованием правила «голова к хвосту».

Предположим, что есть два вектора A, и B, , образующие углы θA и θB соответственно с положительной осью x.Эти векторы будут разделены на их составляющие. Они будут использоваться для вычисления результирующих компонентов x и y результирующего вектора R, , который будет суммой двух компонентов x и y по отдельности.

R = A + B

R X = A X + B X экв. Y + B Y eq 2

Так как прямоугольными компонентами

R = R X + R X eq 3

eq Теперь подставим значения 1 и уравнение 2 в уравнении 3

R = (A X + B X ) + (A Y + B 0 Y 8) 9 По прямоугольной составляющей величина результирующего вектора задается как

| R | = √ ((Rx) 2+ (Ry) 2)

| R | = √ ((Ax + BX) 2+ (Ay + BY) 2)

По прямоугольным компонентам направление результирующего вектора определяется как:

θ = tan-1 (RY / Rx)

. применимо для любого количества векторов A, B, C, D …… , чтобы найти результирующий вектор R.

R = A + B + C + ……

R X = A X + B 904 24 904 X + … ..

R Y = A Y + B Y + C Y + ……

R904 904 X + R X

θ = tan-1 (RY / Rx)

Нахождение результирующего вектора с помощью метода параллелограмма

Согласно закону сложения векторов параллелограмма:

5 “If424 два вектора, действующих одновременно в точке, могут быть представлены смежными сторонами параллелограмма, проведенного из точки, тогда результирующий вектор представлен диагональю прохода параллелограмма проходя через эту точку.”

Рассмотрим два вектора A, и B , действующих в точке и представленные двумя сторонами параллелограмма, как показано на рисунке.

θ — угол между векторами A, и B, и R называется результирующим вектором. Тогда, согласно закону сложения векторов параллелограмма, диагональ параллелограмма представляет собой результат векторов A и B .

Математические производные на

Ниже приведены математические выводы:

R = A + B

Теперь разверните S до T и нарисуйте QT перпендикулярно OT.

Из треугольника OTQ,

SQ2 = OT2 + TQ2 экв 1,4

SQ2 = (OS + ST) 2 + TQ2

В треугольнике STQ,

cosθ = ST / SQ

SQcosθ = ST

Также,

sinθ = TQ / SQ

TQ = SQsinθ

Ввод в уравнение 1.4 дает

| SQ | = √ ((A + SQsinθ) 2+ (SQcosθ) 2)

Пусть, SQ = OP = D

| SQ || = √ ((A + Dsinθ) 2+ (Dcosθ) 2)

Решение приведенного выше уравнения дает

| SQ | = √ (A2 + 2ADcosθ + D2)

Итак, | SQ | дает величину результирующего вектора.

Теперь выясняем направление результирующего вектора,

tanφ = TQ / SQ

φ = tan-1 (TQ / OT)

tanφ = TQ / (OS + ST)

tanφ = Dsinθ / A + Dcosθ

φ = tan –1 (Dsinθ / A + Dcosθ)

Давайте лучше разберемся на примере.

Пример 4

Сила 12 Н составляет угол 45o с положительной осью x, а вторая сила 24N составляет угол 120o с положительной осью x.Рассчитайте величину равнодействующей силы.

Решение

Разложив вектор на его прямоугольные компоненты, мы знаем, что

R X = F 1X + F 2X

R Y 1-летние + Ф. 2-летние

| R | = √ ((Rx) 2+ (Ry) 2) eq 1.1

Расчет значений | RX | и | RY |,

| Rx | = | F1X | + | F2X | уравнение 1.2

| F1X | = F1cosθ1

| F1X | = 12cos45

| F1X | = 8,48N

| F2X | = F2cosθ2

| F2X | = 24cos120

| F2x | = -120002 Положим

значений в уравнении 1.2 дает:

| Rx | = 8,48 + (- 12)

| Rx | = -3.52N

Теперь, нахождение y-компоненты результирующего вектора

| RY | = | F1Y | + | F2Y | уравнение 1.3

| F1Y | = F1sinθ1

| F1Y | = 12sin45

| F1Y | = 8.48N

| F2Y | = F2 sinθ2

| F2Y | = 24sin120

| F2Y | = 20.78N

Подставляя значения в уравнение 1.2, получаем

| Ry | = 8,48 + 20,78

| Ry | = 29.26N

Теперь, подставив значения в уравнение 1.1 для вычисления величины результирующего вектора R ,

| R | = √ ((-3,52) 2+ (29,26) 2)

| R | = √ (12,4 + 856,14)

| R | = 29,5 N

Итак, величина результирующего вектора R равна 29,5N.

Пример 5

Две силы величиной 5Н и 10Н наклонены под углом 30o.Вычислите величину и направление результирующего вектора, используя закон параллелограмма.

Решение

При наличии двух сил F 1 = 5 Н и F 2 = 10 Н и угла θ = 30o.

Используя формулу,

| R | = √ (F12 + 2F1F2cosθ + F22)

| R | = √ ((5) 2 + 2 (5) (10) cos30 + (10) 2)

| R | = 14,54N

φ = tan –1 (F2sinθ / F1 + F2cosθ)

φ = tan-1 (10sin30 / (5 + 10cos30))

φ = 20,1o

Итак, величина результирующего вектора R составляет 14.54N, а направление — 20,1o.

Практические задачи

1. Найдите результирующий вектор следующего вектора, параллельный друг другу, указывающий в том же направлении

1. OA = 12N, OB = 24N ( Ans: 36N)
2. OA = 7N, OB = 10N ( Ans: 17N)
3. PQ = (3,8) RQ = (2,4) ( Ans: (5, 12)

1. Сила 15 Н составляет угол 70o ​​с положительной осью x, а вторая сила 25N составляет угол 220o с положительной осью x.Рассчитайте величину равнодействующей силы. (Ответ : 37N)
2. Вычислите направление результирующего вектора, определенного в задаче № 3. (Ответ : 21.80)
3. Сила 30N действует под углом 25o к северо-востоку. Еще одна сила 45Н, действующая под углом 60o. Вычислите и нарисуйте получившийся вектор. (Ответ : 22N)
4. Две силы величиной 12,7N и 35N наклонены под углом 345o. Вычислите величину и направление результирующего вектора, используя закон параллелограмма.( Ответ: 38.3N)

Предыдущий урок | Главная страница | Следующий урок

Расчеты с участием сил — Сила и законы Ньютона — CCEA — Редакция GCSE Physics (Single Science) — CCEA

Результирующая сила — это единственная сила, которая имеет тот же эффект, что и две или более сил, действующих вместе.

Две силы в одном направлении

Две силы, действующие в одном направлении, создают результирующую силу, превышающую любую отдельную силу.

Вы можете легко вычислить результирующую силу двух сил, действующих по прямой линии в одном направлении, сложив их размеры.

Пример

Две силы, 3 Н и 2 Н, действуют вправо. Рассчитайте результирующую силу.

Две силы, действующие в одном направлении

Результирующая сила F = 3 Н + 2 Н = 5 Н вправо.

Результирующая сила справа 5 Н.

Две силы в противоположных направлениях

Две силы, действующие в противоположных направлениях, создают результирующую силу, которая меньше любой отдельной силы.

Чтобы найти результирующую силу, вычтите величину меньшей силы из величины большей силы.

Направление результирующей силы совпадает с направлением большей силы.

Пример

Сила 5 Н действует вправо, а сила 3 ​​Н — влево.

Рассчитайте результирующую силу.

Две силы, действующие в противоположных направлениях

Результирующая сила F

Результирующая сила F = 5 Н — 3 Н = 2 Н вправо.

Результирующая сила составляет 2 Н. вправо.

Что такое результат?

Результат — это векторная сумма двух или более векторов. Это результат сложения двух или более векторов вместе. Если векторы смещения A, B и C складываются вместе, результатом будет вектор R. Как показано на диаграмме, вектор R может быть определен с помощью точно нарисованной, масштабированной диаграммы сложения векторов.

Сказать, что вектор R представляет собой результирующее смещение векторов смещения A, B и C, значит сказать, что человек, который шел со смещениями A, затем B и затем C, сместится на ту же величину, что и человек, который ходил со смещением R.Вектор смещения R дает тот же результат , что и векторы смещения A + B + C. Поэтому можно сказать, что

А + В + С = рэнд

Вышеупомянутое обсуждение относится к результату добавления векторов смещения. Когда векторы смещения добавлены, результатом будет результирующее смещение . Но любые два вектора могут быть добавлены, если они являются одной и той же векторной величиной. Если добавлены два или более вектора скорости, результатом будет результирующая скорость .Если добавляются два или более вектора силы, то результатом является равнодействующая сила . Если сложить два или более вектора импульса, то результат будет …

Во всех таких случаях результирующий вектор (вектор смещения, вектор силы, вектор скорости и т. Д.) Является результатом сложения отдельных векторов. Это то же самое, что добавить A + B + C + …. «Выполнить A + B + C — это то же самое, что сделать R.» В качестве примера рассмотрим футболиста, которого одновременно ударили три игрока противоположной команды (игроки A, B и C).Футболист испытывает три различных приложенных силы. Каждая приложенная сила вносит свой вклад в общую или результирующую силу. Если эти три силы складываются вместе с использованием методов сложения векторов (обсужденных ранее), то можно определить результирующий вектор R. В этом случае испытать три силы A, B и C — это то же самое, что испытать силу R. Попадание по игрокам A, B и C приведет к той же силе, что и удар одного игрока, применяющего силу R. » Выполнить A + B + C — это то же самое, что сделать R.»Вектор R — это тот же результат, что и векторы A + B + C !!

Таким образом, результат — это векторная сумма всех отдельных векторов. Результирующий результат является результатом объединения отдельных векторов вместе. Результирующая может быть определена путем сложения отдельных сил вместе с использованием методов сложения векторов.

Хотим предложить…

Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или интерактивной игры «Угадывание векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте и обеспечить интерактивный опыт с навыком добавления векторов.

Графические методы разрешения копланарной силы

Графические методы разрешения копланарной силы

Графические методы разрешения копланарной силы