Как называется треугольник у которого две стороны равны ответ: треугольник, у которого две стороны равны?

alexxlab

Содержание

ПНШ 3 класс. Математика. Учебник № 1, с. 133

Разносторонние и равнобедренные треугольники

Ответы к с. 133

439. Может ли равнобедренный треугольник быть остроугольным? Попробуй начертить такой треугольник.


Да, может. На рисунке у равнобедренного треугольника все углы острые.

440. Начерти равнобедренный прямоугольный треугольник.

441. Начерти равнобедренный тупоугольный треугольник.

442. Начерти равнобедренный треугольник, у которого две стороны имеют длину 5 см.

443. Начерти равнобедренный треугольник, у которого только одна сторона – 5 см.

444. Является ли равнобедренный треугольник симметричной фигурой? Проверь этот факт с помощью модели равнобедренного треугольника, сделанной из бумаги.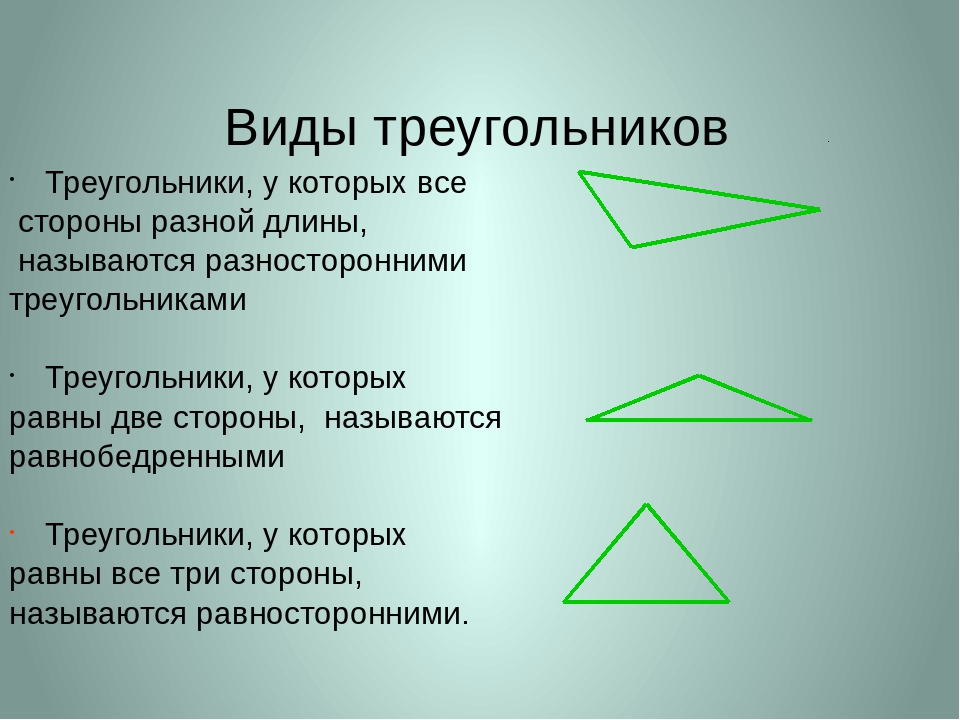

Треугольник АВС является равнобедренным. В нём проведён отрезок ВD, проходящий через середину треугольника и перпендикулярный основанию треугольника АС, делящий основание треугольника на два равных отрезка. Поскольку сторона АВ равна стороне ВС, а отрезки АD и DС равны между собой, то треугольник АВD равен треугольнику DВС. Получается, что равнобедренный треугольник – симметричная фигура и осью симметрии в нём является отрезок (или прямая) ВD. Бумажную модель треугольника нужно сложить пополам (линия сгиба – отрезок ВD) и убедиться, что половины равны.

445. Можно ли равнобедренный треугольник разбить на два равных прямоугольных треугольника? Покажи на чертеже, как это можно сделать.

На рисунке из предыдущего задания 444 видно, что нужно провести перпендикуляр из вершины треугольника на основание. Получаются два равных прямоугольных треугольника: АВD и ВDC.

446. Может ли разносторонний треугольник быть равнобедренным? Почему?

Не может, потому что у равнобедренного треугольника две стороны равны между собой, а у разностороннего треугольника все стороны разные по длине.

Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

4.9
/
5
(
69

голосов
)

Треугольники /qualihelpy

Треугольником называют многоугольник, имеющий три вершины (рис. 8.27 – 8.29).

Классификация треугольников по сторонам

1. Если все три стороны треугольника равны, то треугольник равносторонний. Все внутренние углы равностороннего треугольника равны. 

Например, на рисунке 8.27 изображен равносторонний треугольник : ; .

2. Если две стороны треугольника равны, то треугольник равнобедренный. Стороны, имеющие одинаковую длину, называют боковыми сторонами, а третью сторону – основанием этого треугольника. Углы при основании равнобедренного треугольника равны.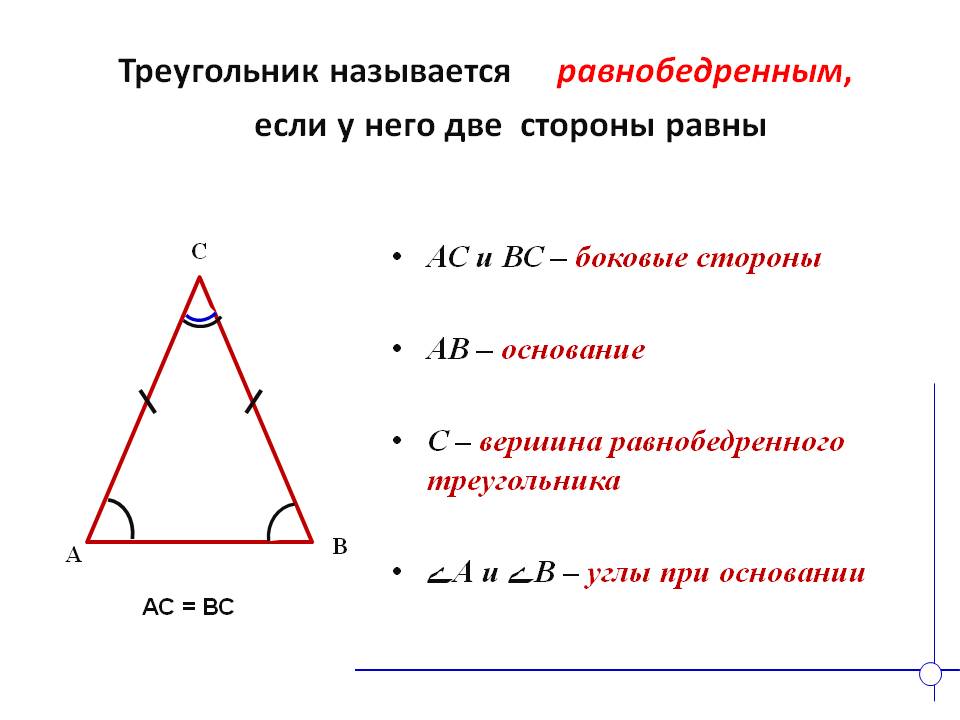  

Например, на рисунке 8.28 изображен равнобедренный треугольник  с боковыми сторонами  и основанием , а .

3. Если все стороны треугольника имеют различную длину, то треугольник разносторонний (произвольный). 

Например, на рисунке 8.29 изображен разносторонний треугольник . 

Длина стороны треугольника меньше суммы длин двух других его сторон, причем, большая сторона треугольника лежит против большего его угла. 

Например: 1) если на рисунке 8.27 , то ; 2) если на рисунке 8.28 , то длина стороны  меньше 8, но больше 4. 

Классификация треугольников по углам

1. Если все углы треугольника острые, то треугольник остроугольный (на рисунке 8.27 треугольник ).2. Если один из углов треугольника тупой, то треугольник тупоугольный (на рисунке 8.28 треугольник ).3. Если один из углов треугольника прямой, то треугольник прямоугольный. Сторону прямоугольного треугольника, лежащую против прямого угла, называют гипотенузой, две другие стороны – катетами. Например, на рисунке 8.29 треугольник  – прямоугольный, отрезок  – гипотенуза этого треугольника, а отрезки  и  – его катеты.Рассмотрим прямоугольный треугольник, у которого  и  – катеты,  – гипотенуза,  – острый угол (рис. 8.30).

Теорема Пифагора: квадрат гипотенузы треугольника равен сумме квадратов его катетов:

, (8.3)где  – гипотенуза,  и  – катеты.

Например, если катеты треугольника соответственно равны 3 и 4, то гипотенуза этого треугольника равна 5. Такой треугольник называют египетским.  

Соотношения между сторонами и углами в прямоугольном треугольнике

1. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

2. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему катету.

Например, на рисунке 8. 30: ; ; . Катет, лежащий против угла , равен половине гипотенузы. Рассмотрим произвольный треугольник, у которого  – стороны,  – соответственно противолежащие им углы (рис. 8.31).

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих же сторон на косинус угла между ними:

, (8.4)

или 

, (8.4.1)

или 

. (8.4.2)

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих им углов: 

 (8.5)

или 

, (8.5.1)где  – радиус окружности, описанной около этого треугольника.

Линии в треугольнике

Среди всех линий, которые можно провести в треугольнике выделяют среднюю линию треугольника, биссектрису треугольника, его медиану и высоту. 

Средней линией треугольника называют отрезок, соединяющий середины двух его сторон. 

Свойства средней линии треугольника

1. Средняя линия треугольника равна половине длины его третьей стороны.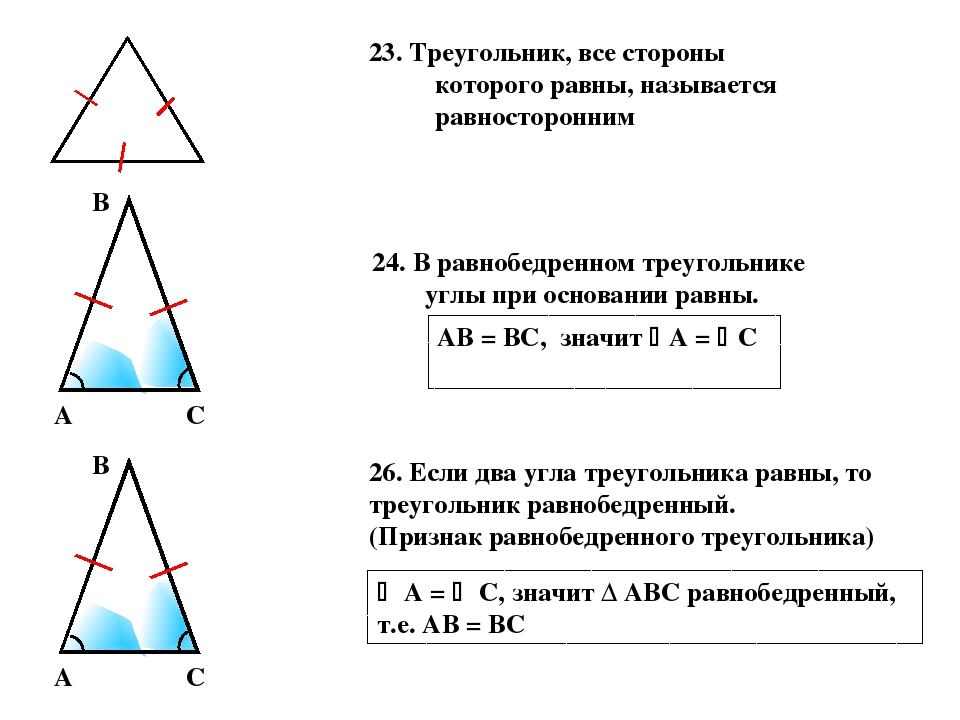

2. Средняя линия треугольника параллельна одной из сторон треугольника.

Высотой треугольника называют перпендикуляр, проведенный из вершины треугольника на прямую, содержащую противолежащую сторону. 

Например, на рисунке 8.33 изображены высоты остроугольного треугольника : отрезки  и .На рисунке 8.34 изображена одна из высот тупоугольного треугольника : высота .На рисунке 8.35 изображены три высоты прямоугольного треугольника : высоты  и .

Свойства высоты треугольника

1. В остроугольном и прямоугольном треугольнике три высоты треугольника пересекаются в одной точке (точка  на рисунке 8.33 и точка  на рисунке 8.35). 

2. Если высота треугольника проведена из вершины прямого угла к гипотенузе, то она является средним геометрическим проекций катетов на гипотенузу (рис. 8.5):

, (8.6)где  и  – проекции катетов на гипотенузу.3. Для всякого треугольника зависимость между его высотами , ,  и радиусом вписанной окружности r выражается формулой: .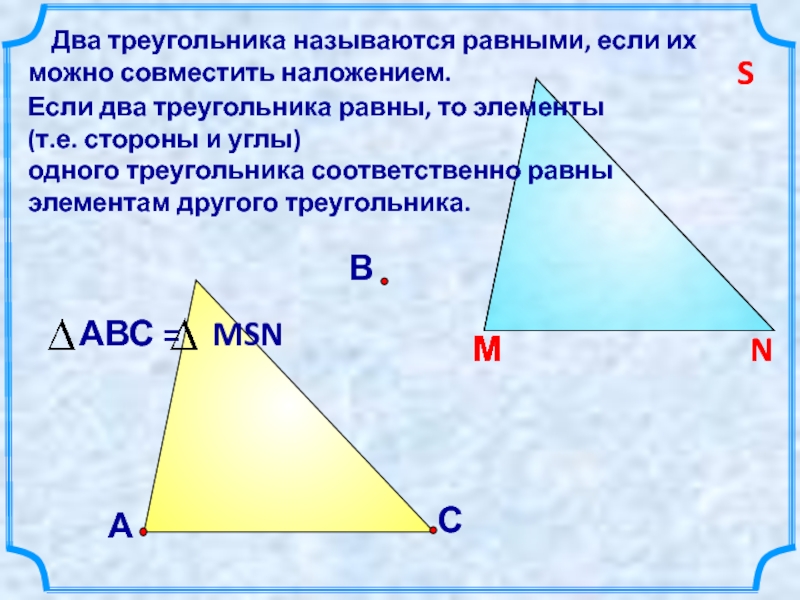 (8.7)

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. 

Например, на рисунке 8.36 изображены медианы треугольника : отрезки  и .

Свойства медианы треугольника

1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении , считая от вершины. Например, на рисунке 8.36 .

2. Медиана делит треугольник на два равновеликих треугольника (треугольники, имеющие равные площади, называют равновеликими). 

Например, на рисунке 8.36 треугольники  и  равновеликие. 

3. Если медиана проведена к гипотенузе прямоугольного треугольника, то она равна половине гипотенузы. 

Например, на рисунке 8.37 . 

Биссектрисой треугольника называют отрезок биссектрисы внутреннего угла треугольника, заключенный между вершиной треугольника и точкой пересечения биссектрисы угла и стороны треугольника. 

Например, на рисунке 8.38 отрезки  и  – биссектрисы внутренних углов треугольника .

Свойства биссектрисы треугольника

1. Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник. 

Например, точка  на рисунке 8.38.

2. В равностороннем треугольнике все биссектрисы равны и являются высотами и медианами этого треугольника. 

Например, на рисунке 8.39 биссектрисы  – высоты и медианы правильного треугольника  и .

3. Если биссектриса проведена из вершины равнобедренного треугольника к его основанию, то она является высотой и медианой этого треугольника. 

Например, на рисунке 8.40 биссектриса  – высота и медиана равнобедренного треугольника .

4. Биссектриса треугольника делит сторону этого треугольника на отрезки, пропорциональные прилежащим к ним сторонам. 

Например, если  – биссектриса треугольника , изображенного на рисунке 8.41, то .

Формулы для вычисления площади треугольника

Для вычисления площади треугольника можно применять одну из следующих формул: 

, (8.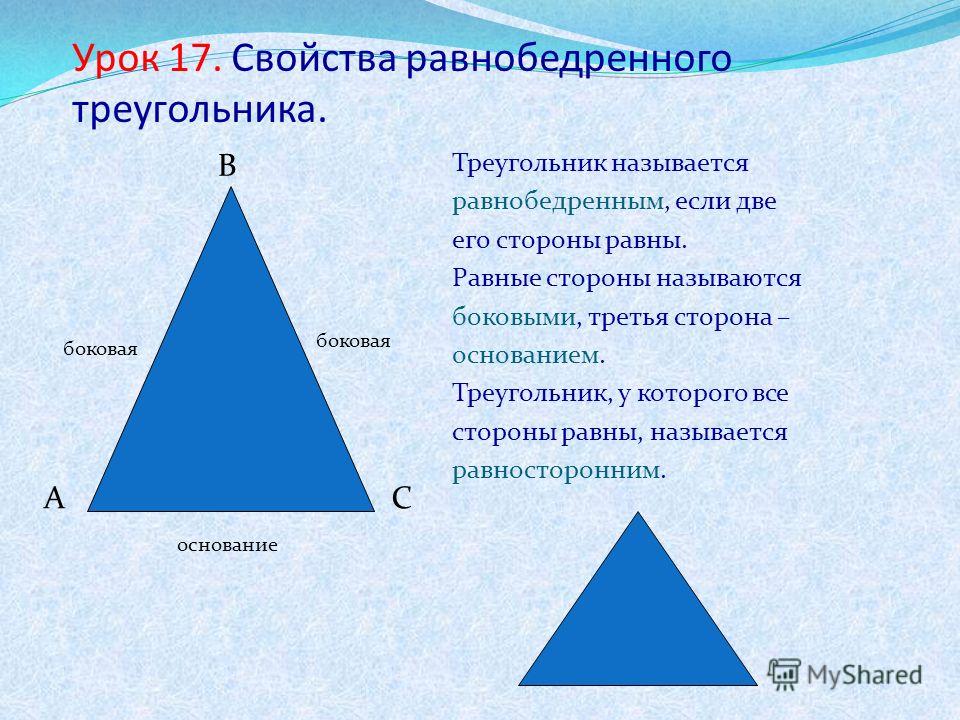 8)где  – сторона равностороннего треугольника; , (8.9)где  – сторона,  – высота, проведенная к стороне  произвольного треугольника; , (8.10)где  и  – катеты прямоугольного треугольника; , (8.11)где  и  – стороны,  – величина угла между ними произвольного треугольника;

Формула Герона: 

, (8.12)где  – стороны,  – полупериметр треугольника;, (8.13)где  — полупериметр треугольника,  — радиус окружности, вписанной в треугольник;, (8.14)где  – стороны,  – радиус окружности, описанной около треугольника.

Два треугольника равны, если все их соответственные стороны и углы равны. 

Признаки равенства треугольников

1. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника. 

Например, на рисунке 8.42 треугольники  и  равны по двум сторонам и углу между ними.

2. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.  

Например, на рисунке 8.43 треугольники  и  равны по стороне и прилежащим к ней углам.

3. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого треугольника. 

Например, на рисунке 8.44 треугольники  и  равны по трем сторонам.

Признаки равенства прямоугольных треугольников

1. Прямоугольные треугольники равны, если катеты одного треугольника соответственно равны катетам другого треугольника. 

Например, на рисунке 8.45 треугольники  и  равны по двум катетам.

2. Прямоугольные треугольники равны, если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника. 

Например, на рисунке 8,46 треугольники  и  равны по катету и прилежащему острому углу.

3. Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника.  

Например, на рисунке 8.47 треугольники  и  равны по гипотенузе и острому углу.

4. Прямоугольные треугольники равны, если гипотенуза и катет одного треугольника соответствравны гипотенузе и катету другого треугольника. 

Например, на рисунке 8.48 треугольники  и  равны по гипотенузе и катету.

Два треугольника подобны, если все углы одного треугольника соответственно равны углам другого, а все стороны одного пропорциональны соответствующим (сходственным) сторонам другого треугольника.

Признаки подобия треугольников

1. Два треугольника подобны, если два угла одного треугольника равны двум углам другого. 

2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, заключенные между ними, равны. 

3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого. 

Например, на рисунке 8. 51 изображены подобные треугольники, так как длины сторон одного из них в два раза больше длин сторон другого. 

Отношение сходственных сторон подобных треугольников называют коэффициентом подобия . Отношение периметров подобных треугольников равно коэффициенту подобия . Отношение площадей подобных треугольников равно квадрату коэффициента подобия .

Равнобедренный треугольник

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона – основанием равнобедренного треугольника.

 

 

Треугольник, все стороны которого равны, называется равносторонним.

 

Теорема. В равнобедренном треугольнике углы при оcновании равны.

Доказательство.

Рассмотрим равнобедренный треугольник АВС с основанием ВС и докажем, что В =С. Пусть АD — биссектриса треугольника АВС.

 

 

Треугольники АВD и АСD равны по первому признаку равенства треугольников (АВ = АС по условию, АD — общая сторона, 1 =2, так как AD — биссектриса).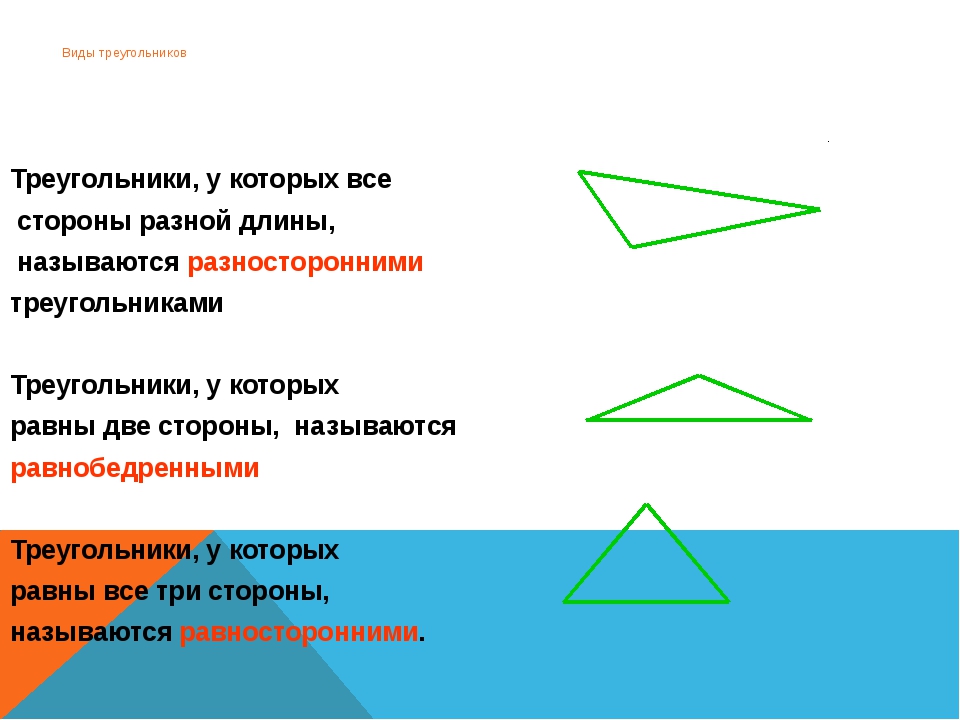 В равных треугольниках против равных сторон лежат равные углы, поэтомуВ =С. Теорема доказана.

 

Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Доказательство.

Обратимся снова к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.

Из равенства треугольников АВD и АСD следует, что ВD = DC и 3 =4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана.

 

Биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:

  1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
  2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

 

Теорема. Признак равнобедренного треугольника.

Если два угла треугольника равны, то треугольник равнобедренный.

Доказательство.

Докажем этот признак. Пусть в треугольнике два угла равны. Тогда равны и стороны, лежащие против этих углов. Действительно, если предположить, что одна из указанных сторон больше другой, то угол, лежащий против нее, будет больше угла, лежащего против другой стороны, а это противоречит условию (тому, что данные углы равны). Итак, в треугольнике две стороны равны, т.е. треугольник – равнобедренный.

Проверочная работа по теме «Равнобедренный треугольник», ФГОС

Проверочная работа  по теме  «Равнобедренный треугольник»

Вариант 1

В заданиях 1 – 3 выберите один правильный ответ из трех предложенных.

 

Результаты внесите в бланк ответов.

 

1.     Равнобедренным называется треугольник, у которого

1)     все стороны равны;

2)     все стороны разной длины;

3)     две стороны равны.

 

2.     Равносторонний треугольник изображен на рисунке

 

3.     В равнобедренном треугольнике боковая сторона равна 7 см, а основание – 4 см. Найдите периметр треугольника.

1)  15 см;  2) 18 см;  3) 22 см.

 

В задании 4 заполните таблицу и перенесите результаты в бланк ответов.

4.     Заполните таблицу, отметив знаком « + » верные утверждения, а знаком « — »  ошибочные.

А) равные стороны равнобедренного треугольника называются  боковыми;

Б) в равнобедренном треугольнике одна боковая сторона и два основания;

В) равнобедренный треугольник не является равносторонним;

Г) в равнобедренном треугольнике все углы равны.

 

 

 

В заданиях 5 и 6 необходимо получить ответ, оформление решения не учитывается.

В задании  7 сделайте чертеж и запишите подробное решение в бланке ответов.

 

5.     Найдите основание  равнобедренного треугольника, если боковая сторона на 6 см больше основания, а периметр равен 42 см.

6.     Найдите боковую сторону равнобедренного треугольника, если его периметр равен 3 дм, а основание – 13 см.

7.     Боковая сторона равнобедренного треугольника ABC служит стороной  равностороннего треугольника ABK. Периметр треугольника ABC равен  60 см, а его основание равно 18 см. Найдите периметр  треугольника ABK.

 

Проверочная работа по теме  «Равнобедренный треугольник»

Вариант 2

 

В заданиях 1 – 3 выберите один правильный ответ из трех предложенных.

 

Результаты внесите в бланк ответов.

1.     Равносторонним называется треугольник, у которого

1)     все стороны равны;

2)     все стороны разной длины;

3)     две стороны равны.

2.     Равнобедренный треугольник изображен на рисунке

3.     В равнобедренном треугольнике боковая сторона равна 5 см, а основание – 8 см. Найдите периметр треугольника.

1)     18 см;  2) 21 см;  3) 26 см

 

В задании 4 заполните таблицу и перенесите результаты в бланк ответов.

4.     Заполните таблицу, отметив знаком « + » верные утверждения, а знаком « — »  ошибочные.

А) равные стороны равнобедренного треугольника называются  основаниями;

Б) в равнобедренном треугольнике две боковые стороны и одно основание;

В) любой равносторонний треугольник является равнобедренным;

Г) в равнобедренном треугольнике два угла имеют равные градусные меры.

 

 

В заданиях 5 и 6 необходимо получить ответ, оформление решения не учитывается.

 

В задании  7 сделайте чертеж и запишите подробное решение в бланке ответов.

 

5.     Найдите боковую сторону  равнобедренного треугольника, если основание в 3 раза  меньше боковой стороны, а периметр равен 56 см.

6.     Найдите основание равнобедренного треугольника, если его периметр равен 1 м, а боковая сторона – 31,2 см.

7.     Основание равнобедренного треугольника ABC служит стороной  равностороннего треугольника ABN. Периметр треугольника ABC равен  52 см, а его боковая сторона равна   20 см. Найдите периметр  треугольника ABN.

 

 

Инструкция

Работа состоит из 7 заданий: задания с выбором ответа (№ 1 – 3), задание  на установление истинности  утверждений (№ 4), задания с кратким ответом (№ 5,6), задание с развернутым ответом (№ 7).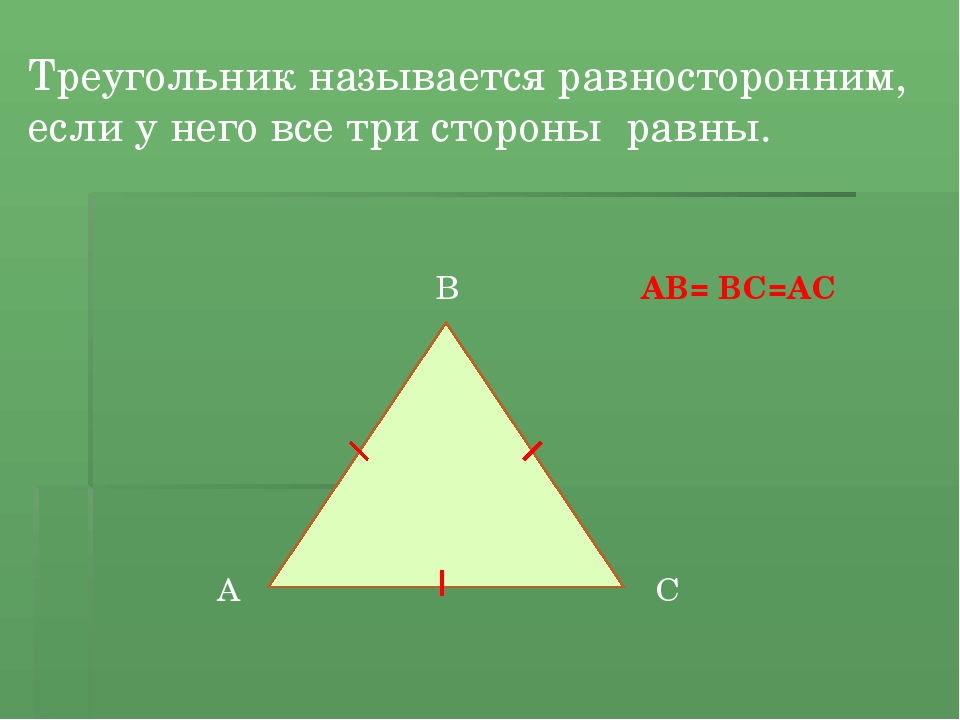 Задания 1 — 4 оцениваются в 1 балл, задания 5,6 – 2 балла, задание 7 – 3 балла. Общее число баллов – 11. Продолжительность выполнения работы – 15 – 20 минут.  

Критерии оценивания задания 7:

1 балл – верно сделан чертеж, решение отсутствует;

2 балла – верно сделан чертеж, решение недостаточно обосновано или допущена вычислительная ошибка;

3 балла – верно сделан чертеж и приведено обоснованное решение.

 

Система оценивания:

«5» —  набрано 10 – 11 баллов

«4» — набрано 7 – 9 баллов

«3» — 4 – 6 баллов

«2» — 0 – 3 балла

 

Примерная форма бланка ответов

 

 

Фамилия, имя учащегося ____________________________________   

Вариант   _________

 

Номер

задания

1

2

3

4

5

6

7

Ответ

 

 

 

 

 

 

 

 

Задание 5                                                                             

 

 Задание 6

 

Задание 7

 

 

 

 

 

 

Ответы

Вариант 1

 

Номер

задания

1

2

3

4

5

6

7

Ответ

3

1

2

А

Б

В

Г

+

 

  —

+

 

  —

 

10

8,5

63

 

Решение задания 7

     

Вариант 2

 

Номер

задания

1

2

3

4

5

6

7

Ответ

1

3

1

А

Б

В

Г

 

  —

+

+

+

 

24

37,6

36

 

Решение задания 7

 

Тест 7 класс.

Свойства равнобедренного треугольника

Свойства
равнобедренного треугольника

Задание 1Треугольник, у которого две
стороны равны, называется …

Запишите
ответ:__________________________________________

Задание 2Как называются равные стороны
равнобедренного треугольника?

Запишите
ответ:__________________________________________

Задание 3На рисунке изображён
равнобедренный треугольник АВС. Какая из его сторон называется
основанием?

Выберите
один из 3 вариантов ответа: 1) АВ  2) ВС   3) АС

Задание 4В равнобедренном треугольнике АВС
сторона АВ равна стороне ВС. Чему равна градусная мера угла АСВ,
если угол ВАС равен 50°?

Выберите
один из 4 вариантов ответа:

1)
50°

2)
80°

3)
30°

4)
25°

Задание 5

Отрезок
ВD — медиана,
проведенная из вершины равнобедренного треугольника ABC. Чему равен
угол ABD, если градусная мера угла CBD равна 33°?

 

 

Выберите
один из 4 вариантов ответа:

1)
66°

2)
33°

3)
99°

4)
90°

 

Задание 6

Является
ли любой равнобедренный треугольник равносторонним?

Выберите
один из 2 вариантов ответа:

1)
Является

2)
Не является

 

Задание 7

Является
ли любой равносторонний треугольник равнобедренным?

 

Выберите
один из 2 вариантов ответа:

1)
Является

2)
Не является

 

Задание 8

Вопрос:

Верно
ли утверждение: «Высота равнобедренного треугольника, проведённая к
основанию, является медианой и биссектрисой»?

 

Запишите
ответ:

__________________________________________

 

Задание 9

Вопрос:

Периметр
равнобедренного треугольника АВС равен 17 см. Найдите длину основания
АС, если АВ = 5 см.

 

Выберите
один из 4 вариантов ответа:

1)
14 см

2)
10 см

3)
5 см

4)
7 см

 

Задание 10

В
равнобедренном треугольнике длина основания равна 6 см. Чему равен периметр
треугольника, если боковая сторона на 4 см больше основания?

 

Выберите
один из 4 вариантов ответа:

1)
10 см

2)
16 см

3)
26 см

4)
32 см

 

 

 

 

 

Ответы:

1)
(1 б.) Верный ответ: «равнобедренным».

2)
(1 б.) Верный ответ: «боковые стороны».

3)
(1 б.) Верные ответы: 3;

4)
(1 б.) Верные ответы: 1;

5)
(1 б.) Верные ответы: 2;

6)
(1 б.) Верные ответы: 2;

7)
(1 б.) Верные ответы: 1;

8)
(1 б.) Верный ответ: «Верно».

9)
(1 б.) Верные ответы: 4;

10)
(1 б.) Верные ответы: 3;

Конец


§14.

Треугольник и его виды

ПОВТОРЯЕМ ТЕОРИЮ

146. Заполните пропуски.

1) Из всех многоугольников наименьшее количество углов и сторон имеют треугольники.
2) Треугольники можно классифицировать по виду их углов и по количеству равных сторон.
3) По виду углов треугольники бывают остроугольными, прямоугольными, тупоугольными.
4) Остроугольным называют треугольник, у которого все углы острые.
5) Прямоугольным называют треугольник, у которого один угол прямой, т.е. равен 90 градусам.
6) Тупоугольным называют треугольник, у которого один из углов тупой.
7) По количеству равных сторон треугольники делятся на разносторонние, равнобедренные, равносторнние.
8) Равнобедренным называют треугольник, у которого две стороны равны.
9) Равные стороны равнобедренного треугольника называют боковыми сторонами, а его третью сторону называют основанием.
10) Равносторонним называют треугольник, у которого все стороны равны.
11) Периметр равностороннего треугольника со стороной а вычисляют по формуле Р=3-а.
12) Разносторонним называют треугольник, у которого все стороны треугольника разные.


РЕШАЕМ ЗАДАЧИ

147. Определите вид треугольника.

148. Периметр треугольника со сторонами 12 см, 18 см, 24 см равен 54 см.

149. Периметр равностороннего треугольника сто стороной 7 см равен 21 см.

150. Одна сторона треугольника равна 17 см, вторая сторона — на 7 см больше первой, а третья — в 3 раза меньше второй. Вычислите периметр треугольника.

Решение:
1) 17+7=24 (см) длина второй стороны треугольника
2) 24:3=8 (см) третья сторона
3) 17+24+8=49 (см) периметр треугольника

Ответ: периметр треугольника равен 49 см.

151. Найдите периметр равнобедренного треугольника, основание которого равно 9 см, а боковая сторона — 6 см.

Решение:
Р=9+6*2=9+12=21 (см)

Ответ: периметр треугольника равен 21 см.

152. С помощью линейки и транспортира постройте треугольник и укажите его вид, если:

1) две стороны равны 2 см и 3 см, а угол между ними 50 градусов.
2) две стороны равны 4 см и 2 см 5 мм, а угол между ними — 100 градусов.

3) две стороны равны 1 см и 3 см, а угол между ними — 90 градусов.
4) две стороны равны по 2 см 5 мм, а угол между ними — 70 градусов.

5) две стороны равны по 2 см, а угол между ними — 60 градусов.
6) одна сторона равна 4 см 5 мм, а углы, прилежащие к этой стороне — 20 и 80 градусов.

7) одна сторона равна 1 см, а углы, прилежащие к этой стороне, — 110 и 50 градусов.
8) одна сторона равна 2 см, а углы, прилежащие к этой стороне, — 90 и 45 градусов.

9) одна сторона равна 3 см, а углы, прилежащие к этой стороне, — по 30 градусов.
10) одна сторона равна 4 см, а углы, прилежащие к этой стороне, — по 45 градусов.

153. Из скольких одинаковых палочек нельзя сложить треугольник (палочки ломать нельзя): 1) 7, 2) 6, 3) 5, 4) 4?

1) можно: 2, 2, 3.
2) можно: 2, 2, 2.
3) моно: 2, 2, 1.
4) нельзя.

1 Билет.

  1.   I.
    Если две параллельные прямые пересечены
    третьей прямой, то внутренние накрест
    лежащие углы равны.

        

        
    II. Если две параллельные прямые пересечены
    секущей, то сумма внутренних односторонних
    углов равна 180°.

        

        
    III. Если две параллельные прямые
    пересечены секущей, то соответственные
    углы равны.

  2. Треуго́льник —
    это геометрическая фигура,
    которая состоит из трёх точек, не лежащих
    на одной прямой,
    и трёх отрезков,
    соединяющих эти три точки. 

Если
все углы треугольника острые, то
треугольник называется остроугольным;

Если
один из углов треугольника тупой (больше
90°), то треугольник называется тупоугольным;

Если
один из углов треугольника прямой (равен
90°), то треугольник называется
прямоугольным.
Две стороны, образующие прямой угол,
называются катетами,
а сторона, противолежащая прямому углу,
называется гипотенузой.

Если
сумма углов треугольника равна 180о,
то такой треугольник называется
развернутым.

  • Равнобедренным называется
    треугольник, у которого две стороны
    равны. Эти стороны называются боковыми,
    третья сторона называется основанием.
    В равнобедренном треугольнике углы
    при основании равны. Высота, медиана и биссектриса
    равнобедренного треугольника, опущенные
    на основание, совпадают.

  • Равносторонним называется
    треугольник, у которого все три стороны
    равны. В равностороннем треугольнике
    все углы равны 60°, а центры вписанной и описанной
    окружностей совпадают.

  • Формулировка
    теоремы косинусов    :

  • Для
    плоского треугольника со сторонами
    a,b,c и углом α, противолежащим стороне
    a, справедливо соотношение: 

  • квадрат
    одной стороны треугольника равен сумме
    квадратов двух других сторон за вычетом
    удвоенного их произведения, умноженного
    на косинус угла между ними.  

  • Доказательство
    теоремы косинусов    :

  • Рассмотрим
    треугольник ABC. 

    Из
    вершины C на сторону AB опустим высоту
    CD.   

  • Исходя
    из того, что треугольник ADC является
    прямоугольным, то величину стороны AD
    можно найти из соотношения тригонометрических
    функций :   

    AD
    / AC =   cos α 

    AD
    = AC  cos α 

    AD
    = b cos α 

  • Длину
    стороны BD найдем как разность AB и AD: 

    BD
    = AB — AD 

    BD
    = c − b cosα     

    Теперь
    запишем теорему Пифагора для двух
    прямоугольных треугольников ADC и BDC:
      

    CD2 +
    BD2 =
    BC2 

    CD2 +
    AD2 =
    AC2 

    откуда 

    CD2 =
    BC2  — BD2 

    CD2 =
    AC2 — 
    AD2

  • Поскольку
    левые части уравнений равны, то приравняем
    правые части уравнений: 

    BC2  — BD2 = 
    AC2 — 
    AD2 

  • подставим
    значения сторон (a,b,c) 

     a2  —
    (  c − b cos α  )2 
    =  b2 — 
    ( b cos α  )2  a2  =
    (  c − b cos α  )2 
    +  b2 — 
    ( b cos α  )2 

     a2  =
      b2 +
    c 2 
    — 2bc cos α +  ( b cos α  )2  
    —  ( b cos α  )2 

    a2  =
      b    2 +
    c     2 
    — 2bc cos α     

     
         

    Случай,
    когда один из углов при основании тупой
    (и высота падает на продолжение
    основания), полностью аналогичен
    рассмотренному.   

Второй способ решения задачи. Координатный метод.

1.
Введём прямоугольную систему координат
с началом в точке А так, чтобы точка
В лежала на положительной полуоси
AX, а точка С имела положительную
ординату.

Решение
записывают все учащиеся.

2.
Запишем координаты точек: B(c; 0) ;
C(bcosA; bsinA).

3.
Найдём квадрат стороны BC:

BC2 =
a2 =
(bcosA — c)2 +
(bsinA)2 =

=
b2cos2A
– 2bccosA + c2 +
b2sin2A
=

= b2(cos2A
+ sin2A)
+ c2 –
2bccosA =

= b2 +
c2 –
2bccosA.

a2 =
b2 +
c2 –
2bccosA – теорема
косинусов 

b2 =
a2 +
c2 –
2accosB

c2 =
b2 +
a2 –
2abcosC

Рис.
5

Вывод:
Таким образом, квадрат стороны треугольника
равен сумме квадратов двух других его
сторон без удвоенного произведения
этих сторон на косинус угла между ними.

Что такое скаленовый треугольник? [Определение, факты и пример]

Что такое скаленовый треугольник?

Треугольник — это многоугольник, состоящий из трех сторон и трех углов.

Мы можем классифицировать треугольники по длине их сторон.

(i) Равносторонний треугольник : Если все стороны треугольника равны, то он называется равносторонним треугольником.

(ii) Равнобедренный треугольник : Если две стороны треугольника равны, то он называется равнобедренным треугольником.

(iii) Масштабный треугольник : если ни одна из трех сторон треугольника не равны друг другу, он называется разносторонним треугольником.

Свойства разностороннего треугольника:

Все углы разностороннего треугольника неравны. Разносторонний треугольник не имеет линии симметрии. Угол, противоположный самой длинной стороне, будет наибольшим углом, и наоборот.

У данного разностороннего треугольника все стороны не равны.

Данный треугольник нельзя разделить на две одинаковые половины. Нет линии симметрии.

В этом треугольнике угол E будет наибольшим углом, поскольку он противоположен наибольшей стороне GO, а угол O будет наименьшим углом, поскольку он противоположен наименьшей стороне GE.

Разносторонний треугольник может быть остроугольным, тупоугольным или прямоугольным.

Тупой разносторонний треугольник Острый разносторонний треугольник Правый разносторонний треугольник

Примеры из жизни

Интересные факты

  • Термин «разносторонний треугольник» происходит от латинского «scalēnus» и древнегреческого слова «σκᾰληνός», что означает неравный или неравномерный.

Классификация треугольника | Типы треугольников | Равнобедренные | Равносторонние

По сторонам

Классификация треугольников по их сторонам. Треугольник в
у которого все стороны равны, называется равносторонним треугольником. Треугольник в
у которого любые две стороны равны, называется равнобедренным треугольником. Если ни одна из его сторон
равны он называется разносторонним треугольником. Теперь давайте классифицируем треугольники на основе
по их углам.

1. Скаленовый треугольник:

Треугольник, у которого все три стороны не равны по длине, называется разносторонним треугольником .

AC> BC> AB

6 см> 5 см> 4,5 см.

2. Равнобедренный треугольник:

Треугольник, в котором две стороны равны, называется равнобедренным треугольником .

PQ = ПР = 6 см.

3. Равносторонний треугольник:

Треугольник, у которого все три стороны равны по длине, называется равносторонним треугольником .

LM = MN = NL = 5,5 см

По углам

1. Острый треугольник:

Треугольник, у которого все три острых угла меньше 90 °, называется остроугольным треугольником или острым треугольником .

Другими словами, треугольник, все три угла которого являются острыми, называется остроугольным треугольником.

На данном рисунке ∠A, ∠B и ∠C — острые углы. Таким образом,
∆ABC — остроугольный треугольник.

2. Тупой треугольник:

Треугольник, один угол которого тупой или больше 90 °, но меньше 180 °, называется тупоугольным треугольником или тупым треугольником .

Треугольник, угол одного из углов которого превышает 90 °.
известен как тупоугольный треугольник.

На рисунке выше ∠STU = 120 °. Таким образом, ∆STU — это тупоугольный треугольник.

3. Правый треугольник:

Треугольник, один из углов которого является прямым углом (то есть 90 °), называется прямоугольным треугольником или прямым углом .

Другими словами, треугольник, в котором любой из трех углов равен точно 90 °, называется прямоугольным треугольником.

На рисунке выше ∠PQR = 90 °. Таким образом, ∆PQR — прямоугольный треугольник.

Вопросы и ответы по классификации треугольника:

I. Заполните пропуски:

(i) Треугольник с равными сторонами …………………….

(ii) А ……………………. У треугольника все стороны разной длины.

(iii) Каждый угол равностороннего треугольника равен …………………….

(iv) ……………………. треугольник имеет две равные стороны.

(v) В тупоугольном треугольнике один угол равен ……………………. 90 °.

(vi) Каждый угол острого треугольника равен ……………………. чем 90 °.

Ответы:

(i) Равносторонний

(ii) Скален

(iii) Равно

(iv) Равнобедренный

(v) Больше

(vi) Менее

II. Классифицируйте следующий треугольник:

(i) Стороны треугольника равны 4 см, 4 см и 7 см

(ii) Углы треугольника равны 90 °, 60 ° и 30 °

(iii) Углы треугольника равны 110 °, 40 ° и 30 °

(iv) Стороны треугольника 5 см, 13 см и 12 см

(v) Углы треугольника 60 °, 60 ° и 60 °

Ответы:

(i) Равнобедренный треугольник

(ii) Прямоугольный треугольник

(iii) Тупоугольный треугольник

(iv) Масштабный треугольник

(v) Равносторонний треугольник

Введение в типы треугольников [Видео]

Типы of Triangles

Привет, и добро пожаловать в этот обзор различных типов треугольников! Прежде чем мы начнем, рассмотрим основы: у треугольника есть три соединяющиеся прямые стороны.Длина сторон может быть разной, но длина самой большой стороны не может быть равна или больше суммы двух других сторон. Кроме того, треугольник имеет три внутренних угла, и сумма этих трех углов всегда равна 180 градусам. Это верно для всех треугольников, включая шесть типов, которые мы рассматриваем сегодня.

Мы собираемся разбить наши шесть типов треугольников на две группы по три.

Начнем с трех типов треугольников, которые классифицируются по величине наибольшего угла.Это острый, правильный и тупой треугольники.

Но как узнать, что есть что? Взгляните на самый большой угол каждого треугольника и обратите внимание, больше ли он, меньше или равен 90 градусам. Мы видим, что наибольший угол в треугольнике слева составляет 70 градусов. 70 меньше 90, поэтому это острый треугольник . Только помните, что острые углы меньше 90 градусов. Это легко запомнить, так как «милые» вещи часто бывают маленькими, например, щенками и котятами.

Мы видим, что в среднем треугольнике наибольший угол составляет ровно 90 градусов. Возможно, вы помните, что угол в 90 градусов — это прямой угол, поэтому этот треугольник прямоугольный .

Наконец, в треугольнике справа наибольший угол составляет 117 градусов. Поскольку это более 90 градусов, это тупой угол, поэтому мы называем этот треугольник тупым треугольником .

Вот и все, что касается этих трех типов. Мы просто находим наибольший угол, и название треугольника будет соответствовать названию этого угла.

Наш второй набор треугольников классифицируется по тому, сколько сторон имеют одинаковую длину. Вот три треугольника с длинами сторон:

В треугольнике слева мы видим, что все три стороны имеют одинаковую длину и имеют размер 9 сантиметров. Такой треугольник, как этот, у которого все стороны равны, называется равносторонним треугольником . Это имя не так уж сложно запомнить, так как начало равностороннего слова звучит как слово равный, а слово латеральное означает «сторона».”

В среднем треугольнике мы видим, что две стороны имеют одинаковую длину и составляют 8 см, а третья — 9 см. Когда две стороны треугольника совпадают, он называется равнобедренным треугольником . Его сложно написать по буквам, но легко распознать!

В нашем последнем треугольнике ни одна из сторон не имеет одинаковой длины, поэтому он называется разносторонним треугольником .

Хотя вы часто видите эти три типа треугольников, идентифицируемых по длине их сторон, их также можно разделить на категории по их углам.Это работает точно так же:

Когда все углы равны 60 градусам, получается равносторонний треугольник . Технически это называется равносторонним треугольником, но это одно и то же, потому что все равносторонние треугольники также являются равноугольными треугольниками. Когда два угла совпадают, получается равнобедренный треугольник. А когда ни один из углов не совпадает, получается разносторонний треугольник.

На данный момент мы рассмотрели шесть типов треугольников, которые технически являются всеми типами, но мы еще не закончили.Если мы хотим быть действительно конкретными при именовании треугольников, мы можем комбинировать имена из каждой группы; один из первой группы и один из второй группы.

Например, этот треугольник является остроугольным треугольником . Его наибольший угол меньше 90 градусов, поэтому он острый, и ни один из его углов не совпадает, поэтому он разносторонний.

Прежде чем мы продолжим, как насчет того, чтобы вы попробовали. Остановите видео и определите эти два треугольника, выбрав острый, правый или тупой, а затем выбрав равносторонний, равнобедренный или разносторонний.

Думаете, вы поняли? Треугольник слева — тупой разносторонний треугольник, а справа — равнобедренный прямоугольный треугольник.

Надеюсь, этот обзор был полезен! Спасибо за просмотр и удачной учебы!

Открытые учебники | Сиявула

Математика

Наука

    • Читать онлайн

    • Учебники

      • Английский

        • Класс 7A

        • Марка 7Б

        • 7 класс (A и B вместе)

      • Африкаанс

        • Граад 7А

        • Граад 7Б

        • Граад 7 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 8A

        • Марка 8Б

        • Оценка 8 (вместе A и B)

      • Африкаанс

        • Граад 8А

        • Граад 8Б

        • Граад 8 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 9А

        • Марка 9Б

        • 9 класс (A и B вместе)

      • Африкаанс

        • Граад 9А

        • Граад 9Б

        • Граад 9 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Класс 4A

        • Класс 4Б

        • Класс 4 (вместе A и B)

      • Африкаанс

        • Граад 4А

        • Граад 4Б

        • Граад 4 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 5A

        • Марка 5Б

        • Оценка 5 (вместе A и B)

      • Африкаанс

        • Граад 5А

        • Граад 5Б

        • Граад 5 (A en B saam)

    • Пособия для учителя

    • Читать онлайн

    • Учебники

      • Английский

        • Марка 6A

        • Марка 6Б

        • 6 класс (A и B вместе)

      • Африкаанс

        • Граад 6А

        • Граад 6Б

        • Граад 6 (A en B saam)

    • Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без марочного знака)

Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

математики: треугольники

математика: треугольники

Введение

Есть много разных форм.Там
может показаться, что это сотни разных форм, и вы можете попытаться выучить их
все, кроме:

  1. Это сбивает с толку

  2. Это пустая трата времени

  3. Это бессмысленно. Нам нужно увидеть, что
    у них есть общее и чем они отличаются.

Намного лучше сосредоточиться на
свойства форм. Таким образом вы сможете запомнить несколько фактов и использовать их для
узнайте больше о различных формах.

3
свойства форм, которые мы собираемся рассмотреть:

  1. Количество сторон

  2. Уголки внутренние (углы
    внутри).

  3. Длина сторон.

Эти свойства помогают запоминать
какие формы какие и почему они так называются (в некоторых случаях).

Начнем с фигуры, у которой 3
стороны: ТРЕУГОЛЬНИКИ (три-
означает 3) .

Треугольники ВСЕГДА
иметь 3 стороны.
Сумма внутренних углов треугольника составляет 180 градусов.

Вот треугольники, которые вы ожидаете
знать о:

  1. Равносторонний треугольник

  2. Равнобедренный треугольник

  3. Прямоугольный треугольник

  4. Чешуйчатый треугольник

Кажется, не так уж много, не так ли? Давайте
посмотрите на свойства треугольников.

Равносторонний
Треугольник

Равносторонний треугольник имеет 3 стороны равной длины и 3
углы равны .
Так как ВСЕ углы в треугольнике в сумме дают 180, то 180, разделенное на 3, должно быть
60.

Подсказка в названии EQUILateral.
Итак, если длина одной из сторон 8 см, какова общая длина
две другие стороны?

Ответ

Ответ
16 см, потому что 8 см — это длина одной стороны равностороннего треугольника, тогда
каждая другая сторона должна быть 8 см.Итак, 8 см + 8 см = 16 см.

Это простой треугольник. Давайте посмотрим на
Еще один.

Равнобедренный
Треугольник

Равнобедренный треугольник имеет две стороны равной длины и 2
углы равны .

Какое значение имеет угол при
вершина этого равнобедренного треугольника?
Ответ

ответ 80˚.Сумма всех углов в треугольнике составляет 180˚, поэтому 180 —
(50 + 50) = 80˚

Итак, равнобедренный треугольник имеет только
две стороны равной длины и два одинаковых угла.

А как насчет еще одного треугольника?

Правый
Угловой треугольник

Прямоугольный треугольник содержит
угол прямой (угол 90˚)

Что должно быть в прямоугольном треугольнике?
другие два угла в сумме составляют?

Ответ

90˚.Ты знаешь
Зачем?

Поскольку все углы в треугольнике складываются
до 180˚, а у прямоугольного треугольника один угол составляет 90˚.

Ну, остался только один треугольник, чтобы
идти

Скален
Треугольник

Разносторонний треугольник — самый простой из
торговый центр. Разносторонний треугольник имеет NO, стороны равной длины и NO .
углы такие же.

Но это треугольник. Ты можешь думать о
две причины почему?

Ответ

Это
треугольник:

  1. Потому что его внутренние (внутренние) углы
    сложить до 180.

  2. Потому что у него 3 стороны.

Ладно, это было не так уж плохо, правда? Давайте
просмотрите то, что вы отредактировали сегодня.

Есть 4 типа треугольника. Каждый из
они имеют разные свойства в количестве сторон одинаковой длины и
количество равных углов.

Посмотрите на имена ниже и убедитесь, что вы
могут вспомнить, какими свойствами они обладают. Когда вы подумали обо всем
четыре нажмите «Проверить ответы» и посмотрите, были ли вы правы.

Равносторонний треугольник

Равнобедренный треугольник

Прямоугольный треугольник

Скален
Треугольник

Проверить
ваши ответы

Здесь
что нужно помнить

Равносторонний треугольник имеет 3 стороны равной длины и 3
углы равны .

Равнобедренный треугольник имеет две стороны равной длины и 2
углы равны .

Прямоугольный треугольник содержит
угол прямой (угол 90˚)

У разностороннего треугольника НЕТ сторон
равная длина и НИКАКИЕ углы одинаковые.

Вернуться в
верх

Gr7 Математика

В этой главе вы
узнает о различных видах 2D-форм. Вы узнаете имена, данные
разные формы. Вы также узнаете о различных свойствах, которые
разные типы форм имеют по отношению к их сторонам и углам.

Треугольники, четырехугольники, окружности и прочие

Решите, что есть что, и нарисуйте несколько фигур

Треугольник — замкнутая фигура с тремя прямыми сторонами и тремя углами.

Четырехугольник имеет четыре прямые стороны и четыре угла.

Окружность круглая, а край всегда находится на одинаковом расстоянии от центра.

  1. Какие фигуры на противоположной странице
    круги?

  2. Какие фигуры на противоположной странице
    треугольники?

  3. Какие фигуры на противоположной странице
    четырехугольники?

    Используйте линейку для следующих действий:

  4. Сделать
    рисование одного треугольника с тремя острыми углами, а другого треугольника с одним
    тупой угол.

    1. Нарисуйте четырехугольник
      с двумя тупыми углами.

    2. Можете ли вы
      нарисовать треугольник с двумя тупыми углами?

    1. Нарисуйте треугольник с одним прямым углом и
      треугольник без прямых углов.

    2. Можете ли вы нарисовать треугольник?
      с двумя прямыми углами?

    3. Можете ли вы нарисовать
      четырехугольник с четырьмя прямыми углами?

  7. Эти четыре строки образуют
    четырехугольник ABCD.

    Две красные стороны, BC и AD, называются противоположными сторонами четырехугольника ABCD.

    Какие две другие стороны ABCD также являются противоположными сторонами?

  8. Линии DA и AB на рисунке в
    вопрос 7 называются соседними сторонами . Они встречаются в месте, которое является одним из
    вершины (угловые точки) четырехугольника.

    1. Назовите еще два
      смежные стороны в ABCD.

    2. AB примыкает к DA в четырехугольнике ABCD.Какая другая сторона ABCD также примыкает к DA?

  9. Уильям говорит:

    «Каждая сторона четырехугольника имеет две смежные стороны.

    Каждая сторона четырехугольника также имеет две противоположные стороны ».

    Уильям прав? Обоснуйте свой ответ.

  10. Уильям также говорит:

    «В треугольнике каждая сторона примыкает ко всем остальным сторонам.»

    Это правда? Обоснуйте свой ответ.

  11. В каждом случае укажите,
    две стороны являются противоположными сторонами или смежными сторонами четырехугольника
    PQRS.

    1. КП и ПС

    2. QP и SR

    3. PQ и RQ

    4. PS и QR

    5. SR и QR

Треугольники разных типов

Треугольники равносторонние, равнобедренные, разносторонние и прямоугольные

Треугольник с двумя равными сторонами называется равнобедренным треугольником .

Треугольник с тремя равными сторонами называется равносторонним треугольником .

Треугольник с прямым углом называется прямоугольным треугольником .

Треугольник с тремя сторонами разной длины и без прямого угла называется разносторонним треугольником .

  1. Измерьте каждый угол в каждом из равнобедренных треугольников , указанных выше. Делать
    вы заметили что-нибудь особенное? Если вы не уверены, нарисуйте больше равнобедренных треугольников.
    в тетради.

  2. Измерьте углы и стороны
    следующие треугольники. Что особенного в этих треугольниках? Другими словами, что
    отличает эти треугольники от других треугольников?

    Эти треугольники называются равносторонними треугольниками .

    1. Измерьте каждый угол в каждом из следующих треугольников.
      Вы замечаете что-нибудь особенное в этих углах?

    2. Определите самый длинный
      стороны в каждом из треугольников.Если вы не уверены, какой из них самый длинный
      сторона, измерьте стороны. Что вы заметили в самой длинной стороне каждого из
      эти треугольники?

Эти треугольники называются прямоугольными треугольниками .

Сравнение и описание треугольников

Если две или более сторон фигуры равны по длине, мы показываем это короткими линиями на одинаковых сторонах.

  1. Используйте
    следующие треугольники, чтобы ответить на следующие вопросы:

    1. Какой
      треугольник имеет только две стороны, которые равны?

      Как называется этот тип треугольника?

    2. В каком треугольнике есть все три
      стороны равны?

      Как называется этот тип треугольника?

    3. Какой треугольник имеет угол?
      равно 90 °?

      Как называется этот тип треугольника?

  2. Запишите тип каждого из следующих треугольников в поле.
    предоставлено:

Нахождение неизвестных сторон в треугольниках

    1. Назовите каждый тип
      треугольника ниже.

    2. Используйте данную информацию, чтобы
      определить длину сторон:

      AB:

      до н.э .:

      EF:

    3. Можете ли вы определить длину GH и HI?
      Поясните свой ответ.

  2. Площадь в углу ул.
    \ (\ треугольник \) JKL показывает, что это прямой угол. Назовите причину для каждого из ваших
    ответы ниже.

    1. Это треугольник
      разносторонний, равнобедренный или равносторонний?

    2. Назовите две стороны треугольника, которые
      равный.

    3. Какая длина JK?

    4. Назовите два равных угла в этом треугольнике.

    5. Какой размер
      \ (\ hat {J} \) и
      \ (\ hat {L} \)?

Различные типы четырехугольников

Исследование четырехугольника

  1. Два
    на следующих страницах показаны различные группы четырехугольников.

    1. В котором
      группы обе пары противоположных сторон параллельны?

    2. В каких группах всего несколько
      смежные стороны равны?

    3. В каких группах все четыре
      углы равны?

    4. В какие группы входят все
      стороны в каждом четырехугольнике равны?

    5. В каких группах все четыре
      стороны равны?

    6. В каких группах находится каждая сторона
      перпендикулярно прилегающим к нему сторонам?

    7. В каких группах противоположные
      стороны равны?

    8. В каких группах есть хотя бы одна
      пара соседних сторон равны?

    9. В каких группах есть хотя бы одна
      пара противоположных сторон параллельна?

    10. В какие группы входят все
      углы прямые углы?

  2. Фигуры группы 1 называются
    параллелограммов .

    1. Что вы наблюдаете
      о противоположных сторонах параллелограммов?

    2. Что вы наблюдаете относительно углов
      параллелограммы?

  3. Фигуры группы 2 называются
    воздушных змеев .

    1. Что вы наблюдаете
      о сторонах воздушных змеев?

    2. Что еще вы заметили в воздушных змеях?

    Группа 1

    Группа 2

    Группа 3

    Группа 4

    Группа 5

    Группа 6

  4. Цифры в
    группа 3 называется ромбов .

    1. Что вы наблюдаете
      о сторонах ромбов?

    2. Что еще вы заметили в ромбах?

    Примечание: один
    ромб ; два или более ромбов .

  5. Фигуры группы 4 называются
    прямоугольников .

    1. Что вы наблюдаете
      про противоположные стороны прямоугольников?

    2. Что вы наблюдаете относительно углов
      прямоугольники?

    3. Что вы заметили на соседних сторонах
      прямоугольники?

  6. Фигуры группы 5 называются
    трапеции .Что вы наблюдаете по поводу противоположных сторон
    трапеции?

    Стрелками показано, какие стороны параллельны друг другу.

  7. Фигуры группы 6 называются
    квадратов .

    1. Что вы наблюдаете
      о сторонах квадратов?

    2. Что вы наблюдаете относительно углов
      квадраты?

Сравнение и описание форм

  1. Имя
    каждую фигуру в каждой группе.

    Группа A

    Группа B

  2. Каким образом
    одинаковы ли цифры в каждой группе?

    Группа A:

    Группа B:

  3. Каким образом одна из фигур
    в каждой группе отличаются от двух других фигур в группе?

    Группа A:

    Группа B:

Нахождение неизвестных сторон четырехугольника

Используйте свои знания о сторонах и углах четырехугольника, чтобы ответить на следующие вопросы. Обоснуйте свои ответы.

    1. Какой четырехугольник у ABCD?

    2. Назовите сторону, равную AB.

    3. Какова длина BC?

    1. Какой четырехугольник у EFGH?

    2. Какова длина следующих сторон?

      EF:

      GH:

    1. Какой четырехугольник у JKLM?

    2. Какая длина JK?

  4. Рисунок PQRS — воздушный змей с PQ = 4 см и QR = 10 см.Завершите следующий рисунок:

    1. разметка вершин кайта

    2. с указанием на чертеже равных сторон

    3. маркировка длины каждой стороны.

Круги

    1. Нарисуйте точку в середине круга справа. Напишите букву M рядом с точкой. Если ваша точка находится в середине круга, она называется средней точкой или центром .

    2. Проведите линии MA, MB и MC от M до красных точек A, B и C.

    три красные точки находятся на окружности со средней точкой M.

    Прямая линия, например AC, проведенная через
    окружность, проходящая через ее среднюю точку, называется диаметром
    круг.

  2. Измерьте MA, MB и MC.

    Если MA, MB и MC равны по длине, вы правильно выбрали среднюю точку.Если они не равны, вы можете улучшить свой набросок круга и его частей.

Прямая линия от середины круга до
точка на окружности называется радиусом окружности.

Синяя линия MA — это
радиус . Любая прямая линия от центра до круга — это
радиус.

Черная линия AB
соединяет две точки на окружности. Мы называем это аккордом
круг.

В
На следующих двух диаграммах цветные секции представляют собой сегментов
круг.Сегмент — это область между хордой и дугой.

В круге справа красный участок называется сектором круга. Как видите, сектор — это область между двумя радиусами и дугой.

Подобные и совпадающие формы

На этой и следующей страницах показаны три группы четырехугольников.

Чем каждая группа отличается от других, кроме цвета?

  1. Группа
    А:

  2. Группа B:

  3. Группа C:

    Группа A

    Группа B

    Группа C

    Фигуры одинаковой формы, такие как синие фигуры на предыдущей странице, называются похожими друг на друга.Подобные формы могут отличаться по размеру, но всегда будут иметь одинаковую форму.

    Пример аналогичной формы

    Пример конгруэнтных форм

    Фигуры одинаковой формы и размера, такие как красные фигуры на предыдущей странице, называются конгруэнтными друг другу. Эти формы всегда имеют одинаковый размер и форму.

  4. Красные фигуры на предыдущей странице
    похожи друг на друга?

  5. Посмотрите на группы D, E, F и G на этом
    страницу и следующую.В каждом случае скажите, похожи ли формы и
    конгруэнтный, подобный, но не конгруэнтный, или ни подобный, ни конгруэнтный.

    1. Группа D:

    2. Группа E:

    3. Группа F:

    4. Группа G:

    Группа D

    Группа E

    Группа F

    Группа G

Использование свойств треугольников для решения задач

Результаты обучения

  • Найдите площадь, основание и высоту треугольника
  • Найдите длину одной стороны треугольника по периметру и двух других длин

Теперь мы знаем, как найти площадь прямоугольника.Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике ниже мы обозначили длину [латекс] b [/ латекс] и ширину [латекс] h [/ латекс], поэтому его площадь равна [латекс] bh [/ латекс].

Площадь прямоугольника равна основанию [латекс] b [/ латекс], умноженному на высоту [латекс] h [/ латекс].

Мы можем разделить этот прямоугольник на два равных треугольника (см. Изображение ниже). Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны.Площадь каждого треугольника составляет половину площади прямоугольника или [латекс] \ frac {1} {2} bh [/ latex]. Этот пример помогает нам понять, почему формула площади треугольника [латекс] A = \ frac {1} {2} bh [/ latex].

Прямоугольник можно разделить на два треугольника равной площади. Площадь каждого треугольника составляет половину площади прямоугольника.

Формула площади треугольника: [латекс] A = \ frac {1} {2} bh [/ latex], где [latex] b [/ latex] — основа, а [latex] h [/ latex ] — высота.\ circ [/ latex]
Периметр треугольника равен сумме длин сторон.

[латекс] P = a + b + c [/ latex]
Площадь треугольника равна половине основания [латекс] b [/ латекс], умноженной на высоту [латекс] h [/ латекс].

[латекс] A = \ frac {1} {2} bh [/ латекс]

пример

Найдите площадь треугольника, основание которого составляет [латекс] 11 [/ латекс] дюймов, а высота — [латекс] 8 [/ латекс] дюймов.

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите , что вы ищете. площадь треугольника
Шаг 3. Имя. Выберите переменную для ее представления. let A = площадь треугольника
Шаг 4. Translate.

Напишите соответствующую формулу.

Запасной.

Шаг 5. Решите уравнение. [латекс] A = 44 [/ латекс] квадратных дюйма.
Шаг 6. Проверка:

[латекс] A = \ frac {1} {2} bh [/ латекс]

[латекс] 44 \ stackrel {?} {=} \ Frac {1} {2} (11) 8 [/ латекс]

[латекс] 44 = 44 \ галочка [/ латекс]

Шаг 7. Ответьте на вопрос. Площадь [латекс] 44 [/ латекс] квадратных дюймов.

пример

Периметр треугольного сада составляет [латекс] 24 [/ латекс] фута.Длина двух сторон составляет [латекс] 4 [/ латекс] ножки и [латекс] 9 [/ латекс] ножек. Какова длина третьей стороны?

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите , что вы ищете. длина третьей стороны треугольника
Шаг 3. Имя. Выберите переменную для ее представления. Пусть c = третья сторона
Шаг 4. Translate.

Напишите соответствующую формулу.

Заменить в данной информации.

Шаг 5. Решите уравнение. [латекс] 24 = 13 + c [/ латекс]

[латекс] 11 = c [/ латекс]

Шаг 6. Проверка:

[латекс] P = a + b + c [/ латекс]

[латекс] 24 \ stackrel {?} {=} 4 + 9 + 11 [/ латекс]

[латекс] 24 = 24 \ галочка [/ латекс]

Шаг 7. Ответьте на вопрос. Третья сторона [латекс] длиной 11 [/ латекс] футов.

пример

Площадь треугольного церковного окна [латекс] 90 [латекс] квадратных метров. Основание окна [латекс] 15 [/ латекс] метров. Какая высота окна?

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.
Шаг 2. Определите , что вы ищете. высота треугольника
Шаг 3. Имя. Выберите переменную для ее представления. Пусть h = высота
Шаг 4. Translate.

Напишите соответствующую формулу.

Заменить в данной информации.

Шаг 5. Решите уравнение. [латекс] 90 = \ frac {15} {2} ч [/ латекс]

[латекс] 12 = h [/ латекс]

Шаг 6. Проверка:

[латекс] A = \ frac {1} {2} bh [/ латекс]

[латекс] 90 \ stackrel {?} {=} \ Frac {1} {2} \ cdot 15 \ cdot 12 [/ латекс]

[латекс] 90 = 90 \ галочка [/ латекс]

Шаг 7. Ответьте на вопрос. Высота треугольника [латекс] 12 [/ латекс] метров.

Равнобедренные и равносторонние треугольники

Помимо прямоугольного треугольника, некоторые другие треугольники имеют особые имена.Треугольник с двумя сторонами равной длины называется равнобедренным треугольником. Треугольник с тремя сторонами равной длины называется равносторонним треугольником. На изображении ниже показаны оба типа треугольников.

В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.

Равнобедренные и равносторонние треугольники

Равнобедренный треугольник имеет две стороны одинаковой длины.
Равносторонний треугольник имеет три стороны равной длины.

пример

Периметр равностороннего треугольника составляет [латекс] 93 [/ латекс] дюйма. Найдите длину каждой стороны.

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.

Периметр = [латекс] 93 [/ латекс] дюйм

Шаг 2. Определите , что вы ищете. длина сторон равностороннего треугольника
Шаг 3. Имя. Выберите переменную для ее представления. Пусть s = длина каждой стороны
Шаг 4. Translate.

Напишите соответствующую формулу.

Запасной.

Шаг 5. Решите уравнение. [латекс] 93 = 3с [/ латекс]

[латекс] 31 = s [/ латекс]

Шаг 6. Чек:

[латекс] 93 \ stackrel {?} {=} 31 + 31 + 31 [/ латекс]

[латекс] 93 = 93 \ галочка [/ латекс]

Шаг 7. Ответьте на вопрос. Каждая сторона [латекс] 31 [/ латекс] дюйм.

пример

У Арианны [латекс] 156 [латексных] дюймов бусинок, которые можно использовать в качестве отделки вокруг шарфа. Платок будет представлять собой равнобедренный треугольник с основанием

.

[латекс] 60 [латекс] дюймов.Как долго она сможет сделать две равные стороны?

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию.

P = [латекс] 156 [/ латекс] дюйм

Шаг 2. Определите , что вы ищете. длины двух равных сторон
Шаг 3. Имя. Выберите переменную для ее представления. Пусть s = длина каждой стороны
Шаг 4.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

2024 © Все права защищены.