виды, свойства, определение простым языком

Определение кристаллической решетки

Определение кристаллической решетки

Как мы знаем, все материальные вещества могут пребывать в трех базовых состояниях: жидком, твердом, и газообразном. Правда есть еще состояние плазмы, которое ученые считают ни много ни мало четвертым состоянием вещества, но наша статья не о плазме. Твердое состояние вещества потому твердое, так как имеет особую кристаллическую структуру, частицы которой находятся в определенном и четко заданном порядке, создавая, таким образом, кристаллическую решетку. Строение кристаллической решетки состоит из повторяющихся одинаковых элементарных ячеек: атомов, молекул, ионов, других элементарных частиц, связанных между собой различными узлами.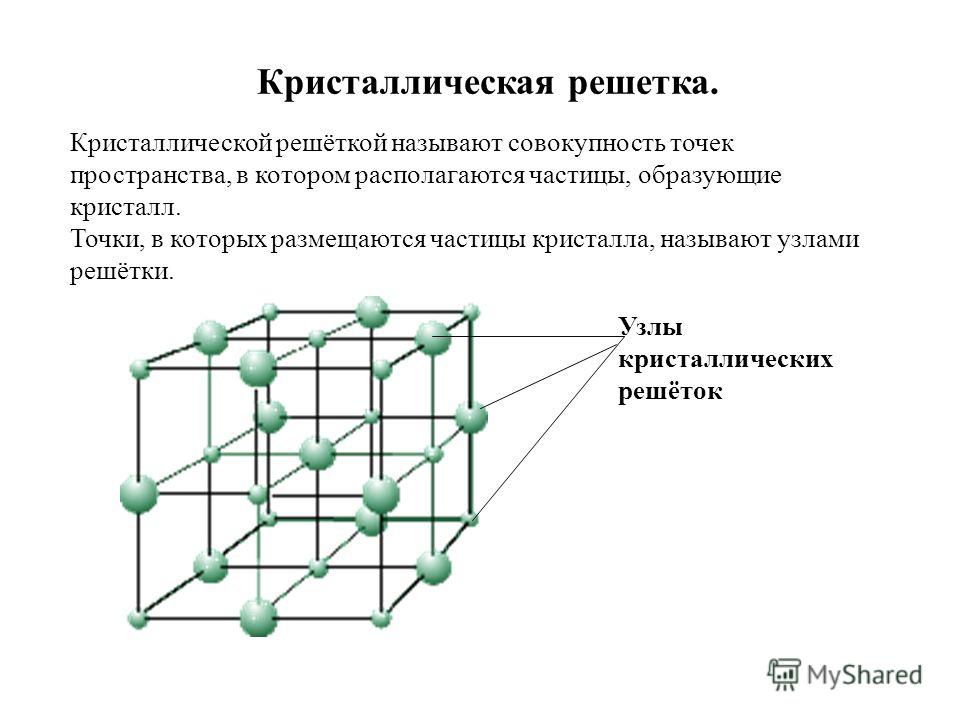

Виды кристаллических решеток

В зависимости от частиц кристаллической решетки существует четырнадцать типов оной, приведем наиболее популярные из них:

• Ионная кристаллическая решетка.
• Атомная кристаллическая решетка.
• Молекулярная кристаллическая решетка.
• Металлическая кристаллическая решетка.

Далее более подробно опишем все типы кристаллической решетки.

Ионная кристаллическая решетка

Главной особенностью строения кристаллической решетки ионов являются противоположные электрические заряды, собственно, ионов, вследствие чего образуется электромагнитное поле, определяющее свойства веществ, имеющих ионную кристаллическую решетку. А это тугоплавкость, твердость, плотность и возможность проводить электрический ток. Характерным примером ионной кристаллической решетки может быть поваренная соль.

Атомная кристаллическая решетка

Вещества с атомной кристаллической решеткой, как правило, имеют в своих узлах, состоящих собственно из атомов сильные ковалентные связи. Ковалентная связь происходит, когда два одинаковых атома делятся друг с другом по-братски электронами, образуя, таким образом, общую пару электронов для соседних атомов. Из-за этого ковалентные связи сильно и равномерно связывают атомы в строгом порядке – пожалуй, это самая характерная черта строения атомной кристаллической решетки. Химические элементы с подобными связями могут похвастаться своей твердостью, высокой температурой плавления. Атомную кристаллическую решетку имеют такие химические элементы как алмаз, кремний, германий, бор.

Молекулярная кристаллическая решетка

Молекулярный тип кристаллической решетки характеризуется наличием устойчивых и плотноупакованных молекул. Они располагаются в узлах кристаллической решетки. В этих узлах они удерживаются такими себе вандервальсовыми силами, которые в десять раз слабее сил ионного взаимодействия. Ярким примером молекулярной кристаллической решетки является лед – твердое вещество, имеющее однако свойство переходить в жидкое – связи между молекулами кристаллической решетки совсем слабенькие.

Металлическая кристаллическая решетка

Тип связи металлической кристаллической решетки гибче и пластичнее ионной, хотя внешне они весьма похожи. Отличительной особенностью ее является наличие положительно заряженных катионов (ионов метала) в узлах решетки. Между узлами живут электроны, участвующие в создании электрического поля, эти электроны еще называются электрическим газом. Наличие такой структуры металлической кристаллической решетки объясняет ее свойства: механическую прочность, тепло и электропроводность, плавкость.

Кристаллические решетки, видео

И в завершение подробное видео пояснения о свойствах кристаллических решеток.

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

Эта статья доступна на английском – Crystal Lattice in Chemistry.

Определение кристаллической структуры | Рентгеновская кристаллография

Древние греки считали, что «Krystallos» (кристалл) заморожен до состояния льда, и он настолько твердый, что его невозможно расплавить. Впоследствии кристаллография первоначально изучала внешнюю симметрию кристаллов, чтобы объяснить их внутреннюю структуру. Отец и сын Брэгги были первыми учеными, которые использовали метод рентгеновской дифракции (XRD) для изучения внутреннего строения кристаллов и показали регулярное расположение атомов в кристалле.

В настоящее время рентгеновская кристаллография используется во многих областях химии, минералогии и физики. Исследования затрагивают не только так называемое кристаллическое состояние (строго фиксированное положение ионов, атомов или молекул), но и аморфные вещества и жидкости, которые не обладают дальним порядком.   

Кристаллография — это наука, лежащая в основе определения новых структур, количественного анализа с использованием метода Ритвельда, полного рассеивания, анализа текстур и др.

Программное решение XRD от Malvern Panalytical

Необходимые шаги для кристаллографического анализа данных порошковой рентгеновской дифракции включены в программное обеспечение HighScore Plus:

• Пиковый поиск и приближения пиков с различными (a)симметричными функциями профиля
• Методы реального и обратного пространства для индексирования
• Уточнение элементарной ячейки, включая нулевое смещение или смещение образца
• Определение пространственных групп с помощью индексированных пиков, полных профилей пиков или с помощью систематического анализа ослабления
• Приближения ЛеБэйла и Паули для уточнения параметров решетки
• Инструмент Symmetry Explorer, охватывающий все стандартные и нестандартные установки пространственных групп
• Встроенный метод переворота зарядов для обнаружения позиций атома
• Расчет разности Фурье для поиска отсутствующих атомов
• Преобразование между пространственными группами с одновременным изменением данных ячейки и структуры
• Автоматическая стандартизация нестандартных параметров пространственной группы
• Уменьшение ячейки (ячейка Ниггли) и поиск традиционной ячейки
• Уточнение структуры, включая расчеты угла и расстояния
• Построение графика для визуализации структуры

Решения XRD от компании Malvern Panalytical

Кристаллографический анализ использует дифракционные данные высокого качества. Прибор Empyrean Alpha-1 от Malvern Panalytical, оснащенный монохроматором Ge (тип Иогансона), позволяет получать для Cu или Co точные данные о пиках Kα₁ на основе геометрии отражения Брэгга — Брентано и определять структуру. С помощью гибридного монохроматора PreFIX на Empyrean создается геометрия пропускания параллельного луча при α₁ для режимов пропускания или работы капилляров.

Машинное обучение помогло кристаллографам распознать решетки Браве

Изображения дифракции отраженных электронов, на которых обучалась нейросеть

Kevin Kaufmann et al. / Science, 2020

Американские ученые разработали и протестировали модель машинного обучения для распознавания характеристик кристаллической структуры образцов (тип решетки Браве и кристаллографическую группу) по изображениям дифракционных картин, полученных методом дифракции отраженных электронов. Обе из использованных нейросетей оказались способны точно (более 90 процентов) определять эти параметры. Результаты исследования опубликованы в журнале Science.

Кристаллическая структура материала сильно влияет на его свойства, поэтому определение структуры белков, микро- и макромолекул, фармацевтических препаратов, новых материалов и геологических объектов очень важно. Наиболее часто для решения сложных задач определения параметров решетки, симметрии кристаллов и фаз используют либо метод дифракции рентгеновского излучения, либо дифракции электронов конвергентного пучка.

Одним из более удобных методов определения структуры кристаллических материалов и геологических объектов становится метод дифракции отраженных электронов, совмещенный со сканирующим электронным микроскопом. Он не требует такой сложной подготовки проб, как методы, использующие просвечивающий электронный микроскоп, и позволяет анализировать большие области образца за меньшее время. Это делает его удобным для изучения ориентаций с высокой точностью (до двух градусов), разрешением углов до двух десятых градуса и пространственным разрешением около 40 нанометров.

Разработка методов автоматизации обработки изображений в девяностых годах ускорила анализ и позволила использовать метод для более сложных и трудоемких задач, однако все равно обработка данных требует временных затрат. Часто метод применяется для определения фаз и ориентаций в образцах с несколькими фазами. Исследователь выбирает фазы, которые предположительно есть в образце, и программа ищет наиболее подходящие на экспериментально полученной дифракционной картине. В отличие от просвечивающей микроскопии или метода рентгеновской дифракции, дифракция отраженных электронов позволяет увидеть несколько фаз в пространственном разрешении, однако метод ограничен необходимостью задавать фазы, которые присутствуют в образце, а они не всегда известны заранее.

Кевин Кауфманн (Kevin Kaufmann) с коллегами из Калифорнийского университета в Сан-Диего разработали алгоритм машинного обучения, способный определять параметры кристаллической структуры образца (решетку Браве или кристаллографическую группу) по дифракционным картинам, полученным методом дифракции отраженных электронов. Авторы обучили и протестировали две сверточные нейронные сети. Слои обучались по мере нахождения алгоритмом мотивов, которые отвечали той или иной кристаллографической симметрии на дифракционной картине.

Схема распознования кристаллографической группы и решетки Браве с помощью сверточной нейронной сети

Kevin Kaufmann et al. / Science, 2020

Обученную модель применили на различных сериях образцов, на которых она не обучалась, но которые обладали той же симметрией, и она с высокой точностью определяла их решетку Браве и кристаллографическую группу. Каждая из двух нейросетей примерно одинаково хорошо (более 90 процентов) классифицировала около 300 тысяч дифракционных картин. Алгоритму без помощи пользователя удалось определить, к какой из 14 решеток Браве принадлежала дифракционная картина.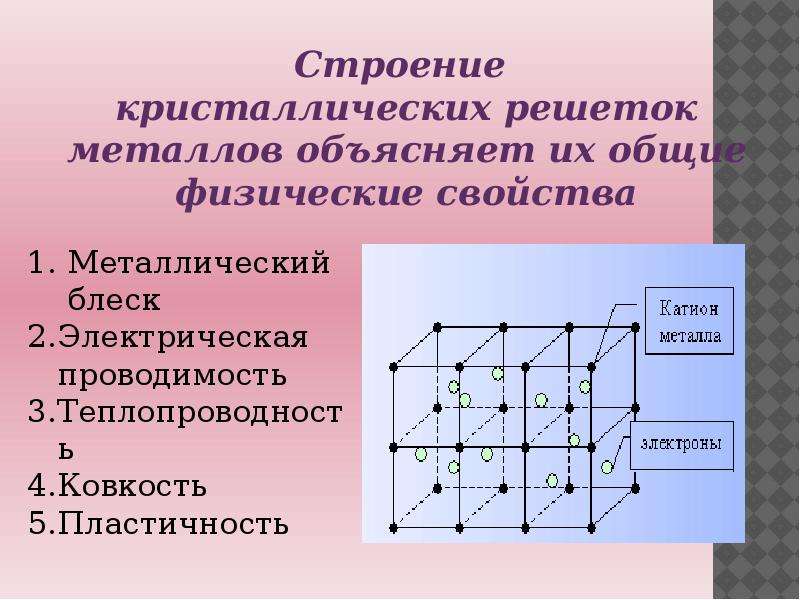

Для слепого тестирования определения симметрии кристаллов алгоритмами авторы собрали 50 тысяч изображений дифракции отраженных электронов девяти совершенно разных материалов. Каждая из нейросетей правильно определила решетки в 93 и 91 процентов случаев. Базоцентрированная моноклинная кристаллическая решетка оказалась самой трудной для определения. Нейросети ее часто путали с примитивной орторомбической или ромбоэдрической, которые отличаются на один элемент симметрии.

Распознование нейросетью типа решетки Браве образцов, на которых сеть не обучалась. Синим закрашены клетки, которые соответствуют верно определеным решеткам

Kevin Kaufmann et al. / Science, 2020

Авторы продемонстрировали возможности алгоритма определять фазы в мультифазном образце на примере кварца с включениями рутила — фазы, которой не было в обучающей выборке. Из семи допущенных моделью ошибок пять было в местах, в которых стандартным методом определить симметрию было невозможно.

По словам авторов, метод можно развить до возможности определять полную кристаллическую структуру, разрабатывая нейросети под каждый мультифазный образец или добавив в него больше данных.

В последнее время машинное обучение часто применяют в фундаментальных исследованиях. Прошлой осенью физики разработали модель, которая могла предсказывать температуру Кюри ферромагнетиков на основе данных о его химическом составе. А другой группе ученых удалось с помощью нейросети скорректировать параметры синхротрона так, что амплитуда колебаний пучка снизилась на порядок.

Больше о системах машинного обучения можно почитать в нашем материале «Азбука ИИ: „Машинное обучение“».

Алина Кротова

Таблица типов кристаллических решёток: йода, алмаза, графита, натрия

Химия — удивительная наука. Столько невероятного можно обнаружить в, казалось бы, обычных вещах.

Всё материальное, что окружают нас повсюду, существует в нескольких агрегатных состояниях: газы, жидкости и твёрдые тела. Учёные выделили ещё и 4-е — плазму. При определённой температуре какое-либо вещество может переходить из одного состояние в другое. Например, вода: при нагревании свыше 100, из жидкой формы, превращается в пар. При температуре ниже 0 переходит в следующее агрегатную структуру — лёд.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Весь материальный мир имеет в своём составе массу одинаковых частиц, которые между собой связаны. Эти мельчайшие элементы строго выстраиваются в пространстве и образуют так называемый пространственный каркас.

Это интересно: анионы и катионы в химии, таблица растворимости.

Определение

Кристаллическая решётка — особая структура твёрдого вещества, при которой частицы стоят в геометрически строгом порядке в пространстве. В ней можно обнаружить узлы — места, где расположены элементы: атомы, ионы и молекулы и межузловое пространство.

Твёрдые вещества, в зависимости от диапазона высоких и низких температур, являются кристаллическими или аморфными — они характеризуются отсутствием определённой температуры плавления. При воздействии повышенных температур они размягчаются и постепенно переходят в жидкую форму. К такого рода веществам относятся: смола, пластилин.

Это интересно: водородная связь — примеры, механизм образования.

В связи с этим можно поделить на несколько видов:

• атомную;
• ионную;
• молекулярную;
• металлическую.

Но при различных температурах одно вещество может иметь различные формы и проявлять многообразные свойства. Это явление называется аллотропной модификацией.

Это интересно: металлы и неметаллы в периодической таблице Менделеева.

Атомный тип

В этом типе в узлах расположены атомы того или иного вещества, которые связаны ковалентными связями. Этот вид связи образован парой электронов двух соседних атомов. Благодаря этому они связываются равномерно и в строгом порядке.

Вещества с атомной кристаллической решёткой характеризуются следующими свойствами: прочность и большая температура плавления. Такой тип связи представлен у алмаза, кремния и бора.

Ионный тип

Противоположно заряженные ионы находятся на узлах, которые создают электромагнитное поле, характеризующее физические свойства вещества. К таковым будут относиться: электропроводность, тугоплавкость, плотность и твёрдость. Поваренная соль и нитрат калия характеризуются наличием ионной кристаллической решётки.

Не пропустите: механизм образования металлической связи, конкретные примеры.

Молекулярный тип

В узлах такого типа находятся ионы, связанные между собой ван-дер-ваальсовыми силами. Благодаря слабым межмолекулярным связям такие вещества, например, лёд, двуокись углерода и парафин, характеризуются пластичностью, электро- и теплопроводностью.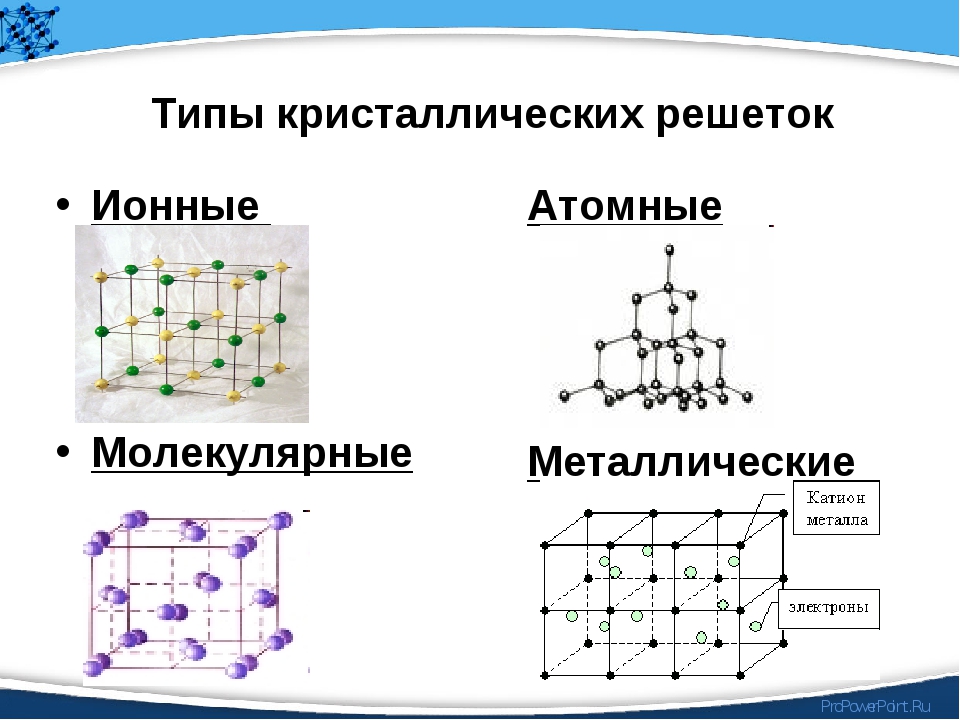

Металлический тип

В своём строении напоминает молекулярную, но имеет всё же более прочные связи. Отличие данного типа в том, что на её узлах находятся положительно заряженные катионы. Электроны, которые находятся в межузловом пространстве, участвуют в образовании электрического поля. Они ещё носят название электрического газа.

Простые металлы и сплавы, характеризуются металлическим типом решётки. Для них характерно наличие металлического блеска, пластичность, тепло- и электропроводность. Они могут плавиться при различных температурах.

Виды	Вещества	Свойства
Атомная	Алмаз, графит, кремний, бор	Твёрдые, тугоплавкие, не растворяются в воде
Молекулярная	Йод, сера, белый фосфор, органические вещества	Нетвёрдые, легко плавятся, летучие
Ионная	Соли, оксиды и гидроксиды тяжёлых металлов	Твёрдые, хрупкие, легкоплавкие, электропроводны
Металлическая	Металлы и сплавы	Блестящие, ковкие, тепло- и электропроводны.

Различные вещества

• Алмаз. Минерал обладает высокой ценностью и после огранки используется в ювелирных украшениях. Так в чём же заключается секрет популярности этого камня? Атомы углерода составляют основу всей решётки. Между атомами минерала существует прочная ковалентная связь. Для кристаллической решётки алмаза характерно плотное содержание атомов в виде куба. Другими словами, узлами считаются атомы углерода, а своеобразными гранями куба являются прочные ковалентные связи. Такой минерал считается самым прочным на планете, и неизвестно, сколько таких своеобразных кубов включает в себя цельный алмаз.
• Графит. Углерод также может быть и в другой кристаллической модификации. Атомная решётка данного элемента включает в себя только атомы углерода, ей присуща слоистая структура. В графите каждый атом связан тремя атомами углерода. Из-за этого он обладает металлическим блеском, высокой теплопроводностью.
• Кристаллическая решётка йода имеет молекулярный тип. 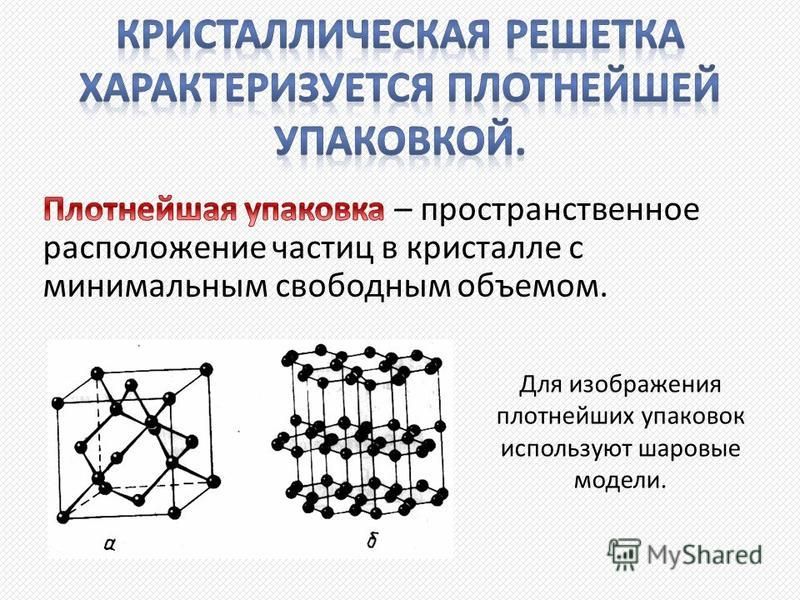Атомы молекул соединяются ковалентными связями, но молекулы химического элемента имеют слабые силы притяжения. Это характеризует йод тем, что он имеет малую твёрдость, низкую температуру плавления.
• Натрий. Представитель металлической кристаллической решётки. Между катионами, расположенными в узлах решётки, двигаются электроны. Они, присоединяясь к катионам, нейтрализуют их заряд, в свою очередь, нейтральные атомы отпускают часть электронов, преобразуясь в катионы. Такой тип кристаллической решётки наделяет металл пластичностью, электро- и теплопроводностью.
• Сухой лёд. Или оксид углерода в затвердевшем виде. Имеет молекулярную кристаллическую решётку в форме куба. Молекулы удерживаются между собой слабыми связями. Диффузия читайте в нашей статье.

Это интересно: как определить валентность по таблице Менделеева?

Типы кристаллических решёток

Для определения
типа кристаллической решётки поступают следующим образом. Если связь в
соединении ионная, то кристаллическая решётка всегда ионного типа:
хлорид калия, нитрат калия, нитрид кальция, карбид кальция, оксид алюминия.

Если связь
металлическая, то и кристаллическая решётка всегда металлическая: латунь, железо,
медь, натрий.

Если связь
ковалентная, то решётка может быть, как атомной, так и молекулярной. Веществами с
атомной кристаллической решёткой являются: карборунд, оксид кремния четыре,
бор, кремний, алмаз, графит, чёрный и красный фосфор.

У веществ с молекулярной
кристаллической решёткой в узлах кристаллической решётки расположены
молекулы, прочность данной связи слабая.

Для веществ с молекулярной
кристаллической решёткой характерны низкие температуры плавления,
то есть они легкоплавки и летучи, значительная сжимаемость, иногда запах, а
также явление сублимации, или возгонки, как для йода и твёрдого углекислого
газа.

Для веществ с молекулярной
кристаллической решёткой характерна небольшая твёрдость,
большинство этих веществ хорошо растворимы в воде. Молекулярную кристаллическую
решётку имеют газы и жидкости в твёрдом агрегатном состоянии. Например,
кристаллический йод, сера, белый фосфор, углекислый газ, большинство
органических соединений.

У веществ с атомной
кристаллической решёткой в узлах расположены атомы. Связь между атомами в
кристаллические решётки – ковалентная, очень прочная. Для
этих веществ характерны высокие температуры кипения и плавления, то есть они
тугоплавки и нелетучий, очень твёрдые, практически не растворимы в воде и не
имеют запаха.

Примером веществ с
таким типом кристаллических решёток являются алмаз и графит.

Как известно,
твёрдость алмаза оценивается по шкале Мооса самым высоким значением –
10. Благодаря высокой твёрдости алмаз используют для изготовления буров, свёрл,
шлифовальных инструментов, стеклорезов. Алмаз является камнем ювелиров, они
используют отшлифованные алмазы – бриллианты.

Графит также является
веществом с атомной кристаллической решёткой, но несмотря на это, он мягкий,
так как имеет слоистую структуру. В кристаллической решётке графита атомы
углерода, лежащие в одной плоскости, связаны в правильные шестиугольники. Связи
между слоями непрочные, за счёт этого графит мягкий. Графит, как и алмаз,
тугоплавкий. Из него изготавливают электроды, твёрдые смазки, стержни для
карандашей, замедлители нейтронов в ядерных реакторах.

Атомные
кристаллические решётки имеют не только простые, но и сложные вещества. Например,
все разновидности оксида алюминия. Такие, как наждак, корунд, рубин, сапфир.

Наиболее
распространённое соединение кремния – это оксид кремния четыре, который
также имеет атомную кристаллическую решётку. Почти чистым оксидом кремния
четыре является минерал кварц.

У веществ с ионным
типом связи в узлах кристаллической решётки расположены ионы, связь между
частицами – ионная, она прочная.

Для веществ с
ионным типом связи характерны следующие свойства: высокие температуры
плавления и кипения, они тугоплавки и нелетучи, они твёрдые, хрупкие,
многие растворимы в воде. Их хрупкость объясняется тем, что если попробовать
деформировать такую кристаллическую решётку, то один из её слоёв будет
двигаться относительно другого слоя до тех пор, пока одинаково заряженные ионы
не будут друг против друга. Эти ионы начнут отталкиваться друг от друга, и
кристаллическая решётка разрушиться.

Вещества с ионным
типом связи плохо проводят электрический ток и тепло. Но их растворы и расплавы
проводят электрический ток. Вещества с ионным типом связи не имеют запаха.

Ионное соединение
представляет собой гигантскую ассоциацию ионов, расположенных в пространстве
благодаря равновесию сил притяжения и отталкивания.

Например, кристалл
хлорида натрия состоит из катионов натрия и анионов хлора. Каждый катион натрия
окружён шестью анионами хлора, а каждый анион хлора – шестью катионами натрия.
Наименьшей структурной единицей кристалла является элементарная ячейка.
Строение элементарной ячейки зависит от соотношения размеров катиона и аниона.

У веществ с
металлическим типом связи в узлах кристаллической решётки расположены
атом-ионы, связь между ними металлическая. Связь может быть различной по
прочности.

Металлическая
кристаллическая решётка определяет свойства металлов: ковкость,
пластичность, электро-и теплопроводность, металлический блеск, способность
образовывать сплавы.

Пластичность выражается в
способности металлов деформироваться под действием механической нагрузки. Это
свойство лежит в основе ковки, прокатки металлов, их способности вытягиваться в
проволоку. Пластичность объясняется тем, что под воздействием силы слои
перемещаются относительно друг друга без разрыва связи между ними.

Например, если
двумя плоскими стеклянными пластинками поместить несколько капель воды, то
пластинки будут свободно скользить относительно друг друга, но вот разъединить
их будет достаточно сложно. Таким образом, в данном опыте вода играла роль
свободных электронов, которые находятся в металлической кристаллической
решётке.

Наиболее
пластичными металлами являются золото, серебро и медь. Именно из золота можно
сделать самую тонкую фольгу толщиной три тысячных миллиметра. Такую тонкую
фольгу использую для золочения. Примером может служить Янтарная комната в
Большом Екатерининском дворце.

Высокая
электропроводность металлов обусловлена наличием свободных электронов, которые
под действием электрического тока приобретают направленное движение.

Лучшими
проводниками
электрического ока являются серебро и медь, немного худшим
– алюминий. Однако в большинстве случаев в качестве электропроводов используют
алюминий, а не медь.

Теплопроводность
металлов
также объясняется движением свободных электронов, которые
сталкиваются с атом-ионами в узлах кристаллической решётки и обмениваются с
ними энергией. Благодаря этому свойству металлическая посуда равномерно
нагревается.

Вещества с
металлическим типом кристаллической решётки имеют металлический блеск из-за
отражения световых лучей.

Высокой
светоотражающей способностью обладают ртуть, серебро, палладий и алюминий. Из
серебра, палладия и алюминия изготавливают зеркала, прожектора и фары. В
порошкообразном состоянии металлы теряют свой блеск, только магний и алюминий
сохраняют его.

Большинство
металлов имеет серебристо-белый цвет. Только золото окрашено в жёлтый цвет, а
медь в красный.

Металлическая
кристаллическая решётка характерна не только для металлов, но и для сплавов.
Это отличает металлические сплавы от других сплавов: стекла, фарфора, керамики,
базальтов, гранитов, гнейсов.

Типы кристаллических решёток — урок. Химия, 8 класс.

Большинство твёрдых веществ имеет кристаллическое строение, которое характеризуется строго определённым расположением частиц. Если соединить частицы условными линиями, то получится пространственный каркас, называемый кристаллической решёткой. Точки, в которых размещены частицы кристалла, называют узлами решётки. В узлах воображаемой решётки могут находиться атомы, ионы или молекулы.

В зависимости от природы частиц, расположенных в узлах, и характера связи между ними различают четыре типа кристаллических решёток: ионную, металлическую, атомную и молекулярную.

Ионными  называют решётки, в узлах которых находятся ионы.

Их образуют вещества с ионной связью. В узлах такой решётки располагаются положительные и отрицательные ионы, связанные между собой электростатическим взаимодействием.

Ионные кристаллические решётки имеют соли, щелочи, оксиды активных металлов. Ионы могут быть простые или сложные. Например, в узлах кристаллической решётки хлорида натрия находятся простые ионы натрия Na+ и хлора Cl−, а в узлах решётки сульфата калия чередуются простые ионы калия  K+ и сложные сульфат-ионы SO42−. 

Связи между ионами в таких кристаллах прочные. Поэтому ионные вещества твёрдые, тугоплавкие, нелетучие. Такие вещества хорошо растворяются в воде.  

Кристаллическая решётка хлорида натрия

Кристалл хлорида натрия

Металлическими называют решётки, которые состоят из положительных ионов и атомов  металла и свободных электронов.

Их образуют вещества с металлической связью. В узлах металлической решётки находятся атомы и ионы (то атомы, то ионы, в которые легко превращаются атомы, отдавая свои внешние электроны в общее пользование).

Такие кристаллические решётки характерны для простых веществ металлов и сплавов.

Температуры плавления металлов могут быть разными (от \(-37°С\)  у ртути до двух- трёх тысяч градусов). Но все металлы имеют характерный металлический блеск, ковкость, пластичность, хорошо проводят электрический ток и тепло.

Металлическая кристаллическая решётка

Металлические изделия

Атомными называют кристаллические решётки, в узлах которых находятся отдельные атомы, соединённые ковалентными связями.

Такой тип решётки имеет алмаз — одно из аллотропных видоизменений углерода. К веществам с атомной кристаллической решёткой относятся графит, кремний, бор и германий, а также сложные вещества, например карборунд  SiC и кремнезём, кварц, горный хрусталь, песок, в состав которых входит оксид кремния (IV) SiO2.

Таким веществам характерны высокая прочность и твёрдость. Так, алмаз является самым твёрдым природным веществом. У веществ с атомной кристаллической решёткой очень высокие температуры плавления и кипения. Например, температура плавления кремнезёма \(1728°С\), а у графита она выше \(4000°С\). Атомные кристаллы практически нерастворимы.

Кристаллическая решётка алмаза

Алмаз

Молекулярными  называют решётки, в узлах которых находятся молекулы, связанные слабым межмолекулярным взаимодействием.

Несмотря на то, что внутри молекул атомы соединены очень прочными ковалентными связями, между самими молекулами действуют слабые силы межмолекулярного притяжения. Поэтому молекулярные кристаллы имеют небольшую прочность и твёрдость, низкие температуры плавления и кипения. Многие молекулярные вещества при комнатной температуре представляют собой жидкости и газы. Такие вещества летучи. Например, кристаллические иод и твёрдый оксид углерода(IV) («сухой лёд») испаряются, не переходя в жидкое состояние. Некоторые молекулярные вещества имеют запах. 

Такой тип решётки имеют простые вещества в твёрдом агрегатном состоянии: благородные газы с одноатомными молекулами  (He,Ne,Ar,Kr,Xe,Rn), а также неметаллы с двух- и многоатомными молекулами (h3,O2,N2,Cl2,I2,O3,P4,S8). 

Молекулярную кристаллическую решётку имеют также вещества с ковалентными полярными связями: вода — лёд, твёрдые аммиак, кислоты, оксиды неметаллов. Большинство органических соединений тоже представляют собой молекулярные кристаллы (нафталин, сахар, глюкоза).

Кристаллическая решётка углекислого газа

«Сухой лёд»

Кристаллики иода

Если известно строение вещества, то можно предсказать его свойства.

Попробуем определить, каковы примерно температуры плавления у фторида натрия, фтороводорода и фтора.

 У фторида натрия ионная кристаллическая решётка. Значит, его температура плавления будет высокой. Фтороводород и фтор имеют молекулярные кристаллические решётки. Поэтому их температуры плавления будут невысокими. Молекулы фтороводорода полярные, а фтора — неполярные. Значит, межмолекулярное взаимодействие у фтороводорода будет сильнее и его температура плавления будет выше по сравнению со фтором.

Экспериментальные данные подтверждают эти предположения: температуры плавления NaF, HF и F2 составляют соответственно  \(995°С\), \(-83°С\),  \(-220°С\).

Источники:

Габриелян О.С. Химия  8 класс. Учебник для общеобразовательных учреждений. М.:Дрофа, 2013. 133с  

Рудзитис Г.Е., Фельдман Ф.Г. Химия 8 класс. М.:Просвещение, 2011. 147 с.

Анализ текстур и определение типа кристаллической решётки на наномасштабных изображениях Текст научной статьи по специальности «Компьютерные и информационные науки»

АНАЛИЗ ТЕКСТУР И ОПРЕДЕЛЕНИЕ ТИПА КРИСТАЛЛИЧЕСКОИ РЕШЕТКИ НА НАНОМАСШТАБНЫХ ИЗОБРАЖЕНИЯХ

Куприянов А.В.

Самарский государственный аэрокосмический университет имени академика С.П. Королёва (национальный исследовательский университет), Учреждение Российской академии наук Институт систем обработки изображений РАН

Аннотация

Современные приборы регистрации изображений микро- и наноструктур и методы компьютерной обработки изображений позволяют решать различные задачи анализа текстуры поверхности. Особенности обработки и анализа наномасштабных изображений, получаемых в электронной микроскопии высокого разрешения, показаны на примере решения задачи определения типа кристаллических решёток.

Ключевые слова: наномасштабные изображения, текстура, кристаллическая решётка.

Введение

Понятие текстура обычно относят к объединению признаков, характеризующих расположение составных частей материала в пространстве и относительно друг друга.

Так, геологический словарь даёт следующее определение: Текстура (горных пород) [textura — ткань, сплетение, сложение] — совокупность признаков строения обусловленных ориентировкой и относительным расположением и распределением составных частей породы [1].

Словарь иностранных слов определяет текстуру как особенности строения твёрдого вещества, обусловленные характером расположения его составных частей (кристаллов, зёрен и т.д.) [2].

В своём основном значении структура есть внутреннее устройство чего-либо. По аналогии можно заключить, что понятие «структура» характеризует признаки строения, описывающие величину и форму составных частей, из которых состоит материал.

В случае кристаллических материалов наличие текстуры показывает, что зёрна в них ориентированы не хаотично, а располагаются вдоль некоторых внешних направлений или плоскостей, т.е. структура материала является упорядоченной.

Знание текстуры позволяет рассчитать свойства поликристаллического материала на основе свойств монокристаллов. В ряде случаев наличие определённой текстуры благоприятно влияет на эксплуатационные и технологические свойства материалов. Иногда текстуру, наоборот, стараются устранить, определённым образом воздействуя на структуру расположения зёрен монокристаллов, чтобы получить изотропный материал [3].

На рис. 1 и 2 приведено сравнение структуры базальта и текстуры доломита. Визуально на изображении базальта (рис. 1) можно наблюдать разнообразные включения, имеющие различную ориентацию. На изображениях доломита (рис. 2) ориентация структур выстраивается вдоль опредёленных направлений, что характеризует собой наличие текстуры. Для сравнения на рис. 2 представлены две

различные текстуры, при этом структура материала остаётся одной и той же.

Рис. 2. Текстуры доломита

Харалик отмечал в [4], что, несмотря на повсеместное присутствие в изображениях текстуры, формального подхода к её описанию и определению не существует и методы различения текстур, как правило, разрабатываются отдельно для каждого конкретного случая. Можно выделить два основных подхода к определению термина «текстура».

Во-первых, это интерпретация текстуры как повторения базовых примитивов, имеющих различную ориентацию в пространстве. Примерами в этом слу-

чае могут служить текстуры ткани, кирпичной стены и т.д. Сторонники такого определения ориентировали себя на спектральный анализ и представление текстуры [5].

Во-вторых, текстура рассматривается как некий анархичный и однородный аспект, не обладающий ярко выраженными краями. Для сторонников этого метода не существует заметных образцов или доминирующей частоты в текстуре (например, дёрн, кора, земля и так далее, рассматриваемые с большого расстояния), т.е. они ориентировали себя на вероятностный метод решения проблемы текстуры [6].

Текстурные методы анализа изображений формируют основание для распознавания и классификации объектов на основе выделения текстурных признаков. В работе [7] оценивается пять различных методов формирования признаков: метод автокорреляции, метод предельной частоты, метод длины примитива, а также методы, основанные на матрицах вероятностного распределения [8 — 10] и мерах текстурной энергии [11, 12].

Как показано в статье [13], наномасштабные изображения позволяют изучать свойства наноматериалов на основе анализа их атомарной структуры. Текстура на таких изображениях определяется характером расположения составных элементов и их ориентацией в пространстве. Проблема сегментации текстур на изображениях электронной микроскопии заключается в том, чтобы различить типы материалов, представленных на изображении, для этого необходимо отыскать зоны, однородные по какому-либо признаку. В настоящей работе предлагается подход к распознаванию текстур на изображениях электронной микроскопии высокого разрешения, основанный на классификации и определении типов фундаментальных составных элементов кристаллических структур — решёток Бравэ.

1. Типы кристаллических решёток

Классическое определение кристалла как однородного твёрдого анизотропного тела, способного самоограняться, сформулированное ещё тогда, когда о внутреннем строении кристаллов строились лишь гипотезы, подразумевает и главную особенность, отличающую кристалл от некристаллических (аморфных) тел, — трёхмерную периодичность в расположении слагающих его структуру эквивалентных материальных частиц: атомов, ионов, молекул [14].

Расположением атомов в кристалле управляет кристаллическая решётка, являющаяся тем главным элементом симметрии, без которого нельзя представить строение ни одного кристалла [15]. Материальные частицы (атомы, ионы, молекулы), образующие кристаллическую структуру, располагаются в пространстве закономерно, периодически повторяясь в строго определённых направлениях, через строго определённые промежутки. Геометрической схемой, описывающей расположение материальных частиц в кристалле, является пространственная решётка. Для полной характеристики пространственной решётки необходимо вы-

явить все возможные случаи расположения узлов в ячейке. Характеристическая ячейка, наиболее полно отражающая все особенности трёхмерной решётки, имеет минимальную площадь и называется элементарной ячейкой (или ячейкой Бравэ) [15].

Исходя из идеи о периодическом расположении центров масс сферических материальных частиц в кристаллическом веществе, Огюст Бравэ в 1848 году математическим путём доказал, что всё многообразие кристаллических структур можно описать с помощью 14 типов решёток, отличающихся формами элементарных ячеек и симметрией и подразделяющихся на 7 кристаллографических сингоний [15]. Эти решётки были названы решётками Бравэ. Каждая решётка Бравэ — это группа трансляций, характеризующих расположение материальных частиц в пространстве. Все типы решёток Бравэ приведены в табл. 1.

Решётка Бравэ строится на трёх основных некомпланарных трансляциях, или параметрах решётки: а, Ь, с. В зависимости от величин и взаимной ориентировки трансляций а, Ь, с пространственные решётки имеют различную симметрию. Три элементарные трансляции решётки определяют элементарную ячейку. В зависимости от соотношения между длинами этих трансляций и углами между ними а, в, у выделяют семь различных сингоний, которые распадаются на три категории в зависимости от числа равных длин трансляций [15]:

• низшая категория (все трансляции не равны друг другу):

о триклинная: а Ф Ь Ф с, а Ф в Ф у Ф 90°; о моноклинная: а Ф Ь Ф с, а = в = 90°,

У Ф 90° Ф 120°; о ромбическая: а Ф Ь Ф с, а = в = у = 90°;

• средняя категория (две трансляции из трёх равны между собой):

о тетрагональная: а = Ь Ф с, а = в = у = 90°; о гексагональная: а = ЬФ с, а = в = 90°, у = 120°;

• высшая категория (все трансляции равны между собой):

о тригональная: а = Ь = с, а = в = у < 120°, Ф90; о кубическая: а = Ь = с, а = в = у = 90°.

Если рёбра ячейки Бравэ соответствуют трём последовательным минимальным трансляциям, т.е. узлы рёшетки располагаются только в вершинах параллелепипеда, то такая «пустая» ячейка (и, соответственно, решётка) называется примитивной.

Если же координатные трансляции ячейки Бравэ не соответствуют трём последовательным минимальным трансляциям, т. е. в ячейке есть более короткие (не координатные) векторы, то в ней, кроме вершинных, окажутся дополнительные узлы. Указанная ячейка (а следовательно, и решётка) будет не примитивной. Ячейки с дополнительными узлами принято называть центрированными. При этом наличие дополнительных узлов не нарушает симметрию решётки и не уменьшает объём ячейки.

Таблица 1. Типы решёток Бравэ

Сингония

Триклинная

Моноклинная

Ромбическая

Тетрагональная

Кубическая

Тригональная

Гексагональная

Примитивная

д

ъ \

А

ч

а \

А

г-4

Базо-центрированная

ы

д

Л

Объёмно-центрированная

А

X ‘ / \

л

ь Ч

А

X ‘ / \

л

га

‘л

ш

Гране-центрированная

Если зацентрирована пара противоположных граней, перпендикулярных оси Ъ ячейки, то такую решётку называют базоцентрированной. Ячейку с дополнительным узлом в центре её объёма называют объёмноцентрированной. Ячейки, в которых центрированы все грани, называются гранецентри-рованными [15].

2. Анализ изображений кристаллических решёток

На изображениях проекции кристаллических решёток, сделанных с помощью электронного микроскопа высокого разрешения, видны только материальные частицы (атомы, ионы, молекулы). На рис. 3 приведены примеры изображений кристаллов, сделанные с помощью электронного микроскопа при увеличении в 1,5 миллиона раз.

По изображениям электронной микроскопии очень трудно невооружённым глазом определить, какую структуру имеет кристалл. Для того, чтобы определить структуру кристалла, нужно определить зависимость расположения материальных частиц

(атомов, ионов, молекул) в кристаллической решётке, т.ЩяЁЩШ 6′) !

Рис. 3. Изображения кристаллических структур, полученных на электронном микроскопе высокого разрешения: кремний (а), гальваническая медь (б)

Для восстановления проекции расположения атомов в кристалле необходимо определить центры частиц, наблюдаемых на изображении. На рис. 4 показано изображение с выделенными центрами частиц.

Будем предполагать уже решёнными задачи предварительной обработки изображения проекции и определения центров материальных частиц. Следует отметить, что задача определения центров час-

тиц на изображениях проекций является нетривиальной и КР-полной.

Таким образом, исходными данными для обработки являются координаты центров материальных частиц. Для удобства визуального анализа исходные данные могут быть представлены в виде изображений проекций центров. На рис. 5 показаны такие проекции примитивных кристаллических решёток при различных углах поворота.

Для классификации кристаллической решётки Бравэ по изображению её проекции можно использовать распределение зависимости количества одинаковых расстояний от расстояния между материальными частицами.

г,

Рис. 4. Изображение кристалла Ва2МаМЬ5015, сделанное с помощью электронного микроскопа, с выделением структуры материальных частиц

Угол наблюдения

Тип решётки -30° 0° 45°

Триклинная щ. \ \ :

Моноклинная ‘Ш- \ \ щ.

Ромбическая \ :У//<

Тетрагональная ш мм ММ»/

Гексагональная мм хММ

Кубическая Ш- ММ ‘■.’ММ

Рис. 5. Обрабатываемые данные (в виде изображений проекций кристаллических решёток)

Было установлено, что у решёток разных типов в зависимости от угла поворота будет различным характер распределения количества одинаковых расстояний между частицами. Поэтому для того, чтобы определить тип решётки на обрабатываемом изображении, сформируем выборку, состоящую из расстояния между каждой парой частиц, как показано на рис. 6.

Рис. 6. Определение расстояний между частицами

В качестве признаков классификации были выбраны отсчёты гистограммы распределения расстояний между центрами материальных частиц на изображении. На рис. 7 показаны примеры построенных гистограмм для двух различных решёток. ичество

-82-84-

801- ‘

70 60 50 40

30^22—24~ 20 10 О.

и

_26_

30

28

~2Г

и=д

а)

8,64 28,64 48,64 68,64 88,64 18,64 38,64 58,64 78,64 98,64 Расстояние между точками

Количество 140-

120 100 80 60 40 20 О

-116-

46

~28~

—74-

61

~27~

-13-

10,75 30,75 50,75 70,75 90,75

20,75 40,75 60,75 80,75 100,75 б) Расстояние между точками

Рис. 7. Пример гистограммы распределения расстояний для триклинной (а) и кубической (б) решёток Бравэ

3. Определение типа кристаллических решёток

В результате проведённых исследований и анализа методов классификации был выбран метод нейронных сетей [16] для классификации решёток

Бравэ как наиболее подходящий конкретно для нашей задачи. Проекции тригональной и кубической решёток при угле поворота, отличном от 0 и 90 градусов, невозможно отличить, основываясь лишь на информации о центрах частиц. Для разделения три-гональных и кубических решёток необходима информация об угле наблюдения решётки.

Таким образом, было предложено использовать классификатор, состоящий из 15 нейронных сетей, которые охватывают все возможные попарные перестановки 6 типов примитивных решёток Бравэ. Каждая сеть различает два класса. Результатом классификации является класс, получивший наибольшее число голосов при попарном сравнении. Для каждой нейронной сети была выбрана архитектура с двумя скрытыми слоями и сигмоидальной функцией активации.

Был проведён вычислительный эксперимент для определения ошибки классификации решётки Бравэ в зависимости от угла поворота, задающего ориентацию решётки в пространстве. Эксперименты проводились для всех типов примитивных решёток Бравэ. Было использовано 48 тестовых выборок, т.е для каждого типа решётки с разными углами поворота от 10 до 90 градусов. Результаты классификации представлены в табл. 2 и 3, значение в таблице показывает, сколько классификаторов при определении типа решётки, указанной в строке, отнесли её к типу, указанному в столбце.

Таблица 2. Результаты классификации решёток при угле

поворота 10 градусов (выделены ячейки, набравшие наибольшее количество голосов)

Тип решётки Количество голосов |

Трик-линная Моноклинная Ромбическая Тетрагональная Гексагональная Кубическая

Триклин-ная 3 2 2 2 3 3

Моноклинная 3 1 3 2 5 1

Ромбическая 3 0 5 4 2 1

Тетрагональная 5 1 2 4 1 2

Гексагональная 5 4 1 3 2 0

Кубическая 2 4 1 1 2 5

Таблица 3. Результаты классификации решёток при угле поворота 70 градусов (выделены ячейки, набравшие наибольшее количество голосов)

Тип решётки Количество голосов |

Трик-линная Моноклинная Ромбическая Тетрагональная Гексагональная Кубическая

Триклин-ная 5 4 1 2 3 0

Моноклинная 3 5 1 1 3 2

Ромбическая 2 2 5 4 2 0

Тетрагональная 3 2 2 5 3 0

Гексагональная 4 1 2 2 5 1

Кубическая 2 2 1 2 3 5

Больше всего ошибок классификации приходится на угол поворота 10 градусов. Только ромбическая и кубическая решётки были определены правильно. Также было много ошибок классификации при углах 30 и 60 градусов. Классификатор ни разу не ошибся при угле поворота, равном 70 градусам.

В итоге можно сделать вывод, что лучше всего проходят классификацию изображения проекций кубических, тетрагональных и ромбических решёток. Гексагональные и моноклинные решётки Бравэ предложенным способом классифицируются хуже всего. Наибольшее количество ошибок встречается при угле поворота решётки от 10 до 30 градусов.

Для подтверждения возможности использования данного метода на практике был проведён эксперимент с реальным изображением. При проведении этого эксперимента использовалось изображение кристаллической решётки родонита СаМщ (а = 7,68 А, Ь = 11,82 А, с = 6,71 А, а = 92,4, Р = 93,9, у = 105,7), относящейся к типу примитивной трик-линной решётки Бравэ [17]. На изображении родонита, полученном на просвечивающем электронном микроскопе [18], были вручную выделены центры материальных частиц (рис. 8).

Рис. 8. Изображение решётки родонита с выделенными центрами материальных частиц

В табл. 4 приведён результат классификации родонита с использованием построенного классификатора.

Таким образом, можно считать, что классификация прошла успешно, тип решётки был определён правильно. Триклинная решётка получила больше всего голосов.

Таблица 4. Результаты классификации решётки родонита при попарном сравнении (выделена ячейка, набравшая наибольшее количество голосов)

Заключение

Предложенный метод классификации, основанный на анализе гистограммы распределения расстояний между материальными частицами на изо-

бражении, можно использовать для классификации решёток Бравэ по изображениям их проекции.

Дополнительные экспериментальные исследования, проведённые в рамках данной работы, также подтвердили работоспособность метода при небольших величинах интенсивности импульсного шума или сдвига частиц. Это показал и эксперимент с реальным изображением.

Метод классификации будет использован в качестве основы для сегментации текстур на изображениях, полученных с использованием электронных микроскопов с высоким разрешением.

Благодарности

Автор выражает благодарность В.С. Лысову и А.И. Пластинину за помощь, оказанную при проведении исследований и подготовке материала для статьи.

Работа выполнялась при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 02.740.11.0841), при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов РФФИ 10-07-00341-а, 10-01-90708-моб_ст, программы РАН «Фундаментальные науки — медицине».

Литература

1. Геологический словарь: в 2-х томах / под ред. К.Н. Паффенгольца [и др.]. — М.: Недра, 1978.

2. Толковый словарь иностранных слов / под ред. Л.П. Крысина.- М.: Русский язык, 1998.

3. Уманский, Я. С. Кристаллография, рентгенография и электронная микроскопия / Я.С. Уманский, Ю.А. Ска-ков, А.Н. Иванов, Л.Н. Расторгуев. — М.: Металлургия, 1982. — 632 с.

4. Haralick, R.M. Statistical and structural approaches to textures / R.M. Haralick // Proc. IEEE. — 1979. — Vol. 67.

— P. 786-804.

5. D’Astous, F. Texture discrimination based on detailed measures of the power spectrum / F. D’Astous and M.E. Jernigan // Proc. Of 7th International Conference on Pattern Recognition, Montreal, July 1984. — P. 83-86.

6. Chen, P.C. Segmentation by Texture Using Correlation / P.C. Chen, T. Pavlidis // PAMI (5). — 1983. — N 1. — P. 64-69.

7. Singh, M. Spatial texture analysis: a comparative study / M. Singh, S. Singh // Int. Conf. Pattern Recognition, 2002.

— Vol. 1. — P. 676-679.

8. Haralick, R.M. Textural features for image classification / R.M. Haralick, K. Shanmugam, I. Dinstein // IEEE Trans. on Systems, Man and Cybernetics. — 1973. — V. 3. -P. 610-621.

9. Ильясова, Н.Ю. Классификация кристаллограмм с использованием методов статистического анализа текстурных изображений / Н.Ю. Ильясова, А.В. Куприянов, А.Г. Храмов // Компьютерная оптика. — 2000. -№ 20. — С. 122-127.

10. Kupriyanov, A.V. Statistical Features of Image Texture for Crystallogram Classification / A.V. Kupriyanov, A.G. Khramov, N.Yu. Ilyasova // Pattern Recognition and Image Analysis. — 2001. — Vol. 11, N 1. — P. 180-183.

11. Laws, K.I. Rapid Texture Identification / K.I. Laws // SPIE. — 1980. — Vol. 238. — P. 376-380.

12. Куприянов, А.В. Сегментация текстурных изображений на основе оценивания локальных статистических

Тип решётки

Трик- Моно- Ромби- Тетра- Гекса- Куби-

линная клинная ческая гональ- гональ- ческая

ная ная

Количество голосов 5 4 1 2 0 3

признаков / А.В. Куприянов // Вестник Самарского государственного аэрокосмического университета им. академика С .П. Королёва. — 2008. — № 2. — C. 245-251.

13. Сойфер, В.А Анализ и распознавание наномасштаб-ных изображений: Традиционные подходы и новые постановки задач / В.А. Сойфер, А.В. Куприянов // Компьютерная оптика — 2011. — Т. 35, № 2. — C. 136-144.

14. Егоров-Тисменко, Ю.К. Кристаллография и кристаллохимия / Ю.К. Егоров-Тисменко. — М.: КДУ, 2005. -592 с.

15. Брандон, Д. Микроструктура материалов. Методы исследования и контроля / Д. Брандон, У. Каплан. — М.: Техносфера, 204. — 384 с.

16. Хайкин, С. Нейронные сети: полный курс / С. Хай-кин. — М.: Вильямс, 2006. — 1104 с.

17. Конспект лекций по дисциплине «Кристаллография, минералогия» /Кафедра геологии, минералогии и петрографии Сибирского федерального университета // Красноярск, 2007. — 355 с. [http ://btn. sfu-kras.ru/eb ibl/ umkd/81/u lectures.pdf]

18. Veblen, D.R. TEM study of a pyroxene-to-pyroxenoid reaction / David R. Veblen // American Mineralogist. -1985. — Vol. 70. — P. 885-901.

References

1. Geological dictionary in 2 volumes / edited by К.М Puf-fengoldz [et al.]. — Moscow: «Nedra» Publisher, 1978. -(in Russian).

2. Glossary of foreign words / edited by L.P. Krysin. — Moscow: «Russkiy Yazyk» Publisher, 1998. — (in Russian).

3. Umansky, Ya.C. Krisltallographiya, rentgenographiya I electronnaya microskopiya / Ya.C. Umanskiy [et al.] // Moscow: «Metallurgiya» Publisher, 1982. — 632 p. — (in Russian).

4. Haralick, R.M. Statistical and structural approaches to textures / R.M. Haralick // Proc. IEEE . — 1979.- Vol. 67. — P. 786-804.

5. D’Astous, F. Texture discrimination based on detailed measures of the power spectrum / F. D’Astous and M.E. Jernigan // Proc. Of 7th International Conference on Pattern Recognition, Montreal, July 1984. — P. 83-86.

6. Chen, P.C. Segmentation by Texture Using Correlation / P.C. Chen, T. Pavlidis // PAMI (5). — 1983. — N 1. — P. 64-69.

7. Singh, M. Spatial texture analysis: a comparative study / M. Singh, S. Singh // Int. Conf. Pattern Recognition. -2002. — Vol. 1. — P. 676-679.

8. Haralick, R.M. Textural features for image classification / R.M. Haralick, K. Shanmugam, I. Dinstein // IEEE Trans. on Systems, Man and Cybernetics. — 1973. — V. 3. -P. 610-621.

9. Ilyasova, N.Yu. Crystallogramm classification with statistical analysis of textural images / N.Yu. Ilyasova, A.V. Ku-priyanov, A.G. Khramov // Computer Optics. — 2000. -N 20. — P. 122-127. — (in Russian).

10. Kupriyanov, A.V. Statistical Features of Image Texture for Crystallogram Classification / A.V. Kupriyanov, A.G. Khramov, N.Yu. Ilyasova // Pattern Recognition and Image Analysis. — 2001. — Vol. 11, N 1. — P. 180-183.

11. Laws, K.I. Rapid Texture Identification / K.I. Laws // SPIE. — 1980. — Vol. 238. — P. 376-380.

12. Kupriyanov, A.V. Segmentation of the textural images based on the estimation of local statistical features / A.V. Kupriyanov // Vestnik of the Samara state aerospace university. — 2008. — N 2. — P. 245-251. — (in Russian).

13. Soifer, V.A. Analysis and recognition of the nanoscale images: conventional approach and novel problem statement / V.A. Soifer, A.V. Kupriyanov // Computer Optics. — 2011. — V. 35, N 2. — P. 136-144. — (in Russian).

14. Egorov-Tismenko, Yu.K Kristallographiya i kristal-lokhimiya / Yu.K. Egorov-Ticmenko. — Moscow: «KDU» Publisher, 2005. — 592 p. — (in Russian).

15. Brandon, D. Microstructural Characterization of Materials / D. Branon, W. Kaplan. — Moscow: «Technosfera» Publisher, 2004. — 384 p. — (in Russian).

16. Khaykin, S. Neural networks: complete course / S. Khay-kin // Moscow: «Williams» Publisher, 2006. — 1104 p. -(in Russian)

17. Lecture course «Kristallographiya i mineralogiya» / Department of the geology, mineralogy and petrography of Siberian federal university // Krasnoyarsk, 2007. — 355 p. [http://btn.sfu-kras.ru/ebibl/umkd/81/u lectures.pdf]. — (in Russian).

18. Veblen, D.R. TEM study of a pyroxene-to-pyroxenoid reaction / David R. Veblen // American Mineralogist. -1985. — Vol. 70. — P. 885-901.

TEXTURE ANALYSIS AND IDENTIFICATION OF THE CRYSTAL LATTICE TYPE

UPON THE NANOSCALE IMAGES

A. V. Kupriyanov

S.P. Korolyov Samara State Aerospace University (National Research University), Image Processing Systems Institute of the RAS

Abstract

The high end equipment intended for image acquisition of the micro- and nanostructures and various methods of the image processing allows one to solve the problems of surface texture analysis. The specifics of processing and analysis of the nanoscale images obtained via high resolution electronic microscopy are presented as an example solution of the task of crystal lattice type identification.

Key words: nanoscale images, texture, crystal lattice.

Сведения об авторе — см. стр. 144 этого номера.

Поступила в редакцию 4 февраля 2011 г.

10.6 Структуры решеток в кристаллических твердых телах — химия

Цели обучения

К концу этого раздела вы сможете:

• Опишите расположение атомов и ионов в кристаллических структурах
• Вычислить ионные радиусы, используя размеры элементарной ячейки
• Объяснить использование измерений дифракции рентгеновских лучей для определения кристаллических структур

Более 90% твердых веществ природного и антропогенного происхождения являются кристаллическими.Большинство твердых веществ образуются с регулярным расположением своих частиц, потому что общее притягивающее взаимодействие между частицами максимизируется, а общая межмолекулярная энергия сводится к минимуму, когда частицы упаковываются наиболее эффективным образом. Регулярное расположение на атомном уровне часто отражается на макроскопическом уровне. В этом модуле мы исследуем некоторые детали структур металлических и ионных кристаллических твердых тел и узнаем, как эти структуры определяются экспериментально.

Мы начнем обсуждение кристаллических твердых тел с рассмотрения элементарных металлов, которые относительно просты, поскольку каждый содержит только один тип атомов. Чистый металл — это кристаллическое твердое тело, атомы которого плотно упакованы в повторяющийся узор. Некоторые свойства металлов в целом, такие как их пластичность и пластичность, во многом обусловлены наличием одинаковых атомов, расположенных в правильном порядке. Различные свойства одного металла по сравнению с другим частично зависят от размеров их атомов и особенностей их пространственного расположения.В следующих разделах мы исследуем сходства и различия четырех наиболее распространенных геометрических форм металлических кристаллов.

Структуру кристаллического твердого вещества, будь то металл или нет, лучше всего описать, рассматривая его простейшую повторяющуюся единицу, которая упоминается как ее элементарная ячейка . Элементарная ячейка состоит из узлов решетки, которые представляют расположение атомов или ионов. Вся структура состоит из этой элементарной ячейки, повторяющейся в трех измерениях, как показано на рисунке 1.

Рис. 1. Элементарная ячейка показывает расположение точек решетки, повторяющихся во всех направлениях.

Давайте начнем наше исследование структуры кристаллической решетки и элементарных ячеек с самой простой структуры и самой простой элементарной ячейки. Чтобы визуализировать это, представьте, что вы берете большое количество одинаковых сфер, таких как теннисные мячи, и равномерно размещаете их в контейнере. Самый простой способ сделать это — создать слои, в которых сферы в одном слое находятся прямо над сферами в слое ниже, как показано на рисунке 2.Эта конструкция называется простой кубической структурой , а элементарная ячейка называется простой кубической элементарной ячейкой или примитивной кубической элементарной ячейкой.

Рис. 2. Когда атомы металла расположены сферами в одном слое непосредственно над или под сферами в другом слое, структура решетки называется простой кубической. Обратите внимание, что сферы соприкасаются.

В простой кубической структуре сферы не упакованы так плотно, как могли бы, и они «заполняют» только около 52% объема контейнера.Это относительно неэффективное устройство, и только один металл (полоний, Po) кристаллизуется в простой кубической структуре. Как показано на рисунке 3, твердое тело с таким расположением состоит из плоскостей (или слоев), в которых каждый атом контактирует только с четырьмя ближайшими соседями в своем слое; один атом прямо над ним в верхнем слое; и один атом прямо под ним в слое ниже. Число других частиц, с которыми контактирует каждая частица в кристаллическом твердом теле, известно как его координационное число .Следовательно, для атома полония в простом кубическом массиве координационное число равно шести.

Рис. 3. Атом в простой структуре кубической решетки контактирует с шестью другими атомами, поэтому его координационное число равно шести.

В простой кубической решетке элементарная ячейка, повторяющаяся во всех направлениях, представляет собой куб, определяемый центрами восьми атомов, как показано на рисунке 4. Атомы в соседних углах этой элементарной ячейки контактируют друг с другом, поэтому длина ребра этой ячейки ячейка равна двум атомным радиусам или одному атомному диаметру.Кубическая элементарная ячейка содержит только те части этих атомов, которые находятся в ней. Поскольку атом в углу простой кубической элементарной ячейки состоит в общей сложности из восьми элементарных ячеек, только одна восьмая этого атома находится в конкретной элементарной ячейке. А поскольку каждая простая кубическая элементарная ячейка имеет по одному атому в каждом из восьми «углов», в одной простой кубической ячейке находится [латекс] 8 \; \ times \; \ frac {1} {8} = 1 [/ latex] атом. ячейка.

Рис. 4. Простая элементарная ячейка кубической решетки содержит одну восьмую атома в каждом из восьми углов, поэтому она содержит всего один атом.

Пример 1

Расчет атомного радиуса и плотности металлов, часть 1
Длина края элементарной ячейки альфа-полония составляет 336 мкм.

(а) Определите радиус атома полония.

(b) Определите плотность альфа-полония.

Раствор
Альфа-полоний кристаллизуется в простой кубической элементарной ячейке:

(а) Два соседних атома По контактируют друг с другом, поэтому длина края этой ячейки равна двум атомным радиусам По: l = 2 r .Следовательно, радиус Po равен [latex] r = \ frac {\ text {l}} {2} = \ frac {336 \; \ text {pm}} {2} = 168 \; \ text {pm} [ /латекс].

(b) Плотность определяется как [латекс] \ text {density} = \ frac {\ text {mass}} {\ text {volume}} [/ latex]. Плотность полония можно определить, определив плотность его элементарной ячейки (масса, содержащаяся в элементарной ячейке, деленная на объем элементарной ячейки). Поскольку элементарная ячейка По содержит одну восьмую атома По в каждом из восьми углов, элементарная ячейка содержит один атом По.

Массу элементарной ячейки По можно найти по формуле:

[латекс] 1 \; \ text {Po \; unit \; cell} \; \ times \; \ frac {1 \; \ text {Po \; atom}} {1 \; \ text {Po \; unit \; cell}} \; \ times \; \ frac {1 \; \ text {mol \; Po}} {6.3 [/ латекс]

Поскольку фактическая плотность Ni не близка к этой, Ni не образует простой кубической структуры.

Большинство металлических кристаллов являются одним из четырех основных типов элементарных ячеек. А пока мы сосредоточимся на трех кубических элементарных ячейках: простая кубическая (которую мы уже видели), объемноцентрированная кубическая элементарная ячейка и гранецентрированная кубическая элементарная ячейка , все из которых показаны на рисунке 5. (Обратите внимание, что на самом деле существует семь различных систем решеток, некоторые из которых имеют более одного типа решетки, всего 14 различных типов элементарных ячеек.Мы оставляем более сложные геометрические формы на потом в этом модуле.)

Рисунок 5. Кубические элементарные ячейки металлов показывают (на верхних рисунках) расположение узлов решетки и (на нижних рисунках) атомов металла, расположенных в элементарной ячейке.

Некоторые металлы кристаллизуются в структуре, которая имеет кубическую элементарную ячейку с атомами во всех углах и атомом в центре, как показано на рисунке 6. Это называется объемно-центрированным кубическим (ОЦК) твердым телом . Атомы в углах элементарной ячейки ОЦК не контактируют друг с другом, а контактируют с атомом в центре.Элементарная ячейка BCC содержит два атома: по одной восьмой атома в каждом из восьми углов ([latex] 8 \; \ times \; \ frac {1} {8} = 1 [/ latex] атом от углов) плюс один атом от центра. Любой атом в этой структуре касается четырех атомов в слое над ним и четырех атомов в слое под ним. Таким образом, атом в структуре ОЦК имеет координационное число восемь.

Рис. 6. В объемно-центрированной кубической структуре атомы в определенном слое не соприкасаются друг с другом. Каждый атом касается четырех атомов в слое выше и четырех атомов в слое ниже.

Атомы в структурах ОЦК упакованы гораздо эффективнее, чем в простой кубической структуре, занимая около 68% от общего объема. Изоморфные металлы со структурой BCC включают K, Ba, Cr, Mo, W и Fe при комнатной температуре. (Элементы или соединения, которые кристаллизуются с одинаковой структурой, называются изоморфными .)

Многие другие металлы, такие как алюминий, медь и свинец, кристаллизуются в структуре, которая имеет кубическую элементарную ячейку с атомами во всех углах и в центре каждой грани, как показано на рисунке 7.Такое расположение называется гранецентрированным кубическим телом (ГЦК) . Элементарная ячейка FCC содержит четыре атома: по одной восьмой атома в каждом из восьми углов ([latex] 8 \; \ times \; \ frac {1} {8} = 1 [/ latex] атом от углов) и по половине атома на каждой из шести граней ([latex] 6 \; \ times \; \ frac {1} {2} = 3 [/ latex] атома от граней). Атомы в углах касаются атомов в центрах смежных граней по диагоналям граней куба. Поскольку атомы находятся в идентичных узлах решетки, они имеют идентичное окружение.

Рис. 7. Гранецентрированное кубическое твердое тело имеет атомы в углах и, как следует из названия, в центрах граней его элементарных ячеек.

Атомы в системе ГЦК упакованы как можно ближе друг к другу, причем атомы занимают 74% объема. Эта структура также называется кубической плотнейшей упаковки (CCP) . В CCP есть три повторяющихся слоя гексагонально расположенных атомов. Каждый атом контактирует с шестью атомами в своем собственном слое, с тремя в слое выше и с тремя в слое ниже.В этом расположении каждый атом касается 12 ближайших соседей и, следовательно, имеет координационное число 12. Тот факт, что устройства FCC и CCP эквивалентны, может быть не сразу очевиден, но почему они на самом деле являются одной и той же структурой, показано на рисунке 8.

Рис. 8. Компоновка CCP состоит из трех повторяющихся слоев (ABCABC…) гексагонально расположенных атомов. Атомы в структуре CCP имеют координационное число 12, потому что они контактируют с шестью атомами в своем слое, плюс три атома в слое выше и три атома в слое ниже.Поворачивая перспективу, мы видим, что структура CCP имеет элементарную ячейку с гранью, содержащей атом из слоя A в одном углу, атомы из слоя B по диагонали (в двух углах и в середине лица) и атом из слоя C в оставшемся углу. Это то же самое, что и гранецентрированное кубическое расположение.

Поскольку более тесная упаковка максимизирует общее притяжение между атомами и минимизирует общую межмолекулярную энергию, атомы в большинстве металлов упаковываются таким образом. Мы находим два типа плотнейшей упаковки в простых металлических кристаллических структурах: CCP, с которой мы уже сталкивались, и гексагональной плотнейшей упаковки (HCP) , показанной на рисунке 9.Оба состоят из повторяющихся слоев гексагонально расположенных атомов. В обоих типах второй слой (B) размещается на первом слое (A), так что каждый атом во втором слое контактирует с тремя атомами в первом слое. Третий слой размещается одним из двух способов. В HCP атомы в третьем слое находятся непосредственно над атомами в первом слое (т. Е. Третий слой также относится к типу A), а наложение состоит из чередующихся плотноупакованных слоев типа A и типа B (то есть ABABAB ⋯). В CCP атомы в третьем слое не находятся над атомами ни в одном из первых двух слоев (т.е.е., третий слой относится к типу C), а наложение состоит из чередующихся плотно упакованных слоев типа A, типа B и типа C (то есть ABCABCABC). Около двух третей всех металлов кристаллизуются в плотноупакованных массивах с координационным числом 12. Металлы, которые кристаллизуются в структуре HCP, включают Cd, Co, Li, Mg, Na и Zn, а металлы, которые кристаллизуются в структуре CCP, включают Ag , Al, Ca, Cu, Ni, Pb и Pt.

Рис. 9. В обоих типах плотнейшей упаковки атомы упакованы максимально компактно.Гексагональная плотнейшая упаковка состоит из двух чередующихся слоев (ABABAB…). Плотнейшая кубическая упаковка состоит из трех чередующихся слоев (ABCABCABC…).

Пример 2

Расчет атомного радиуса и плотности металлов, часть 2
Кальций кристаллизуется в гранецентрированной кубической структуре. Длина ребра его элементарной ячейки составляет 558,8 мкм.

(а) Каков атомный радиус Са в этой структуре?

(b) Рассчитайте плотность Ca.

Решение

(a) В структуре ГЦК атомы Са контактируют друг с другом по диагонали грани, поэтому длина диагонали равна четырем атомным радиусам Са (d = 4 r ).2} {16}} = 197,6 \; \ text {pmg \; для \; a \; Ca \; radius} [/ latex].

(b) Плотность определяется как [латекс] \ text {density} = \ frac {\ text {mass}} {\ text {volume}} [/ latex]. Плотность кальция можно определить, определив плотность его элементарной ячейки: например, массу, содержащуюся в элементарной ячейке, деленную на объем элементарной ячейки. Гранецентрированная элементарная ячейка Са имеет по одной восьмой атома в каждом из восьми углов ([латекс] 8 \; \ times \; \ frac {1} {8} = 1 [/ латекс] атом) и один — половина атома на каждой из шести граней [латекс] 6 \; \ times \; \ frac {1} {2} = 3 [/ latex]), всего четыре атома в элементарной ячейке.3 [/ латекс]

Проверьте свои знания
Серебро кристаллизуется в структуре FCC. Длина ребра его элементарной ячейки 409 мкм.

(а) Каков атомный радиус Ag в этой структуре?

(б) Рассчитайте плотность Ag.

Ответ:

(а) 144 вечера; (б) 10,5 г / см ³

В общем, элементарная ячейка определяется длиной трех осей ( a , b и c ) и углами ( α , β и γ ) между ними, как проиллюстрировано на рисунке 10.Оси определяются как длины между точками пространственной решетки. Следовательно, оси элементарной ячейки соединяют точки с идентичной средой.

Рис. 10. Элементарная ячейка определяется длиной трех ее осей ( a , b и c ) и углами ( α , β и γ ) между топоры.

Существует семь различных систем решеток, некоторые из которых имеют более одного типа решетки, всего четырнадцать различных элементарных ячеек, которые имеют форму, показанную на рисунке 11.

Рис. 11. Существует семь различных систем решеток и 14 различных элементарных ячеек.

Ионные кристаллы состоят из двух или более различных типов ионов, которые обычно имеют разные размеры. Упаковка этих ионов в кристаллическую структуру более сложна, чем упаковка атомов металла того же размера.

Большинство одноатомных ионов ведут себя как заряженные сферы, и их притяжение для ионов противоположного заряда одинаково во всех направлениях. Следовательно, стабильные структуры для ионных соединений возникают (1), когда ионы одного заряда окружены как можно большим количеством ионов противоположного заряда, и (2) когда катионы и анионы контактируют друг с другом.Структуры определяются двумя основными факторами: относительными размерами ионов и соотношением количества положительных и отрицательных ионов в соединении.

В простых ионных структурах мы обычно находим анионы, которые обычно больше, чем катионы, расположенные в виде плотноупакованного массива. (Как было замечено ранее, дополнительные электроны, притянутые к одному и тому же ядру, делают анионы больше, а меньшее количество электронов, притягиваемых к тому же ядру, делает катионы меньше по сравнению с атомами, из которых они образованы.Катионы меньшего размера обычно занимают один из двух типов лунок, (или пустот), оставшихся между анионами. Меньшее из отверстий находится между тремя анионами в одной плоскости и одним анионом в соседней плоскости. Четыре аниона, окружающие это отверстие, расположены по углам тетраэдра, поэтому отверстие называется тетраэдрическим отверстием . Дыра большего размера находится в центре шести анионов (три в одном слое и три в соседнем слое), расположенных в углах октаэдра; это называется октаэдрическим отверстием .На рисунке 12 показаны оба этих типа отверстий.

Рис. 12. Катионы могут занимать два типа дырок между анионами: октаэдрические дырки или тетраэдрические дырки.

В зависимости от относительных размеров катионов и анионов, катионы ионного соединения могут занимать тетраэдрические или октаэдрические дырки, как показано на рисунке 13. Относительно небольшие катионы занимают тетраэдрические дырки, а более крупные катионы занимают октаэдрические дырки. Если катионы слишком велики, чтобы поместиться в октаэдрические отверстия, анионы могут принять более открытую структуру, такую ​​как простой кубический массив.Тогда более крупные катионы могут занять большие кубические отверстия, что стало возможным благодаря более открытому пространству.

Рис. 13. Размер катиона и форма отверстия, занимаемого соединением, напрямую связаны.

Есть две тетраэдрические дырки для каждого аниона в массиве анионов HCP или CCP. Соединение, которое кристаллизуется в виде плотноупакованного массива анионов с катионами в тетраэдрических отверстиях, может иметь максимальное соотношение катион: анион 2: 1; все тетраэдрические отверстия заполнены при этом соотношении.Примеры включают Li ₂ O, Na ₂ O, Li ₂ S и Na ₂ S. Соединения с соотношением менее 2: 1 также могут кристаллизоваться в виде плотноупакованного массива анионов с катионами. в тетраэдрических отверстиях, если подходят размеры ионов. Однако в этих соединениях часть тетраэдрических дырок остается вакантной.

Пример 3

Заполнение четырехгранных отверстий
Сульфид цинка является важным промышленным источником цинка, а также используется в качестве белого пигмента в красках.Сульфид цинка кристаллизуется с ионами цинка, занимающими половину тетраэдрических отверстий в плотноупакованном массиве сульфид-ионов. Какая формула сульфида цинка?

Раствор
Поскольку на каждый анион (сульфид-ион) приходится две тетраэдрических дырки и половина этих дырок занята ионами цинка, должен быть [латекс] \ frac {1} {2} \; \ times \; 2 [/ латекс], или 1 ион цинка на ион сульфида. Таким образом, формула ZnS.

Проверьте свои знания
Селенид лития можно описать как плотнейшую упаковку селенид-ионов с ионами лития во всех тетраэдрических отверстиях.Какая у него формула селенида лития?

Отношение октаэдрических дырок к анионам в структуре HCP или CCP составляет 1: 1. Таким образом, соединения с катионами в октаэдрических дырках в плотноупакованном массиве анионов могут иметь максимальное соотношение катион: анион 1: 1. Например, в NiO, MnS, NaCl и KH все октаэдрические отверстия заполнены. Отношения менее 1: 1 наблюдаются, когда некоторые из октаэдрических отверстий остаются пустыми.

Пример 4

Стехиометрия ионных соединений
Сапфир — оксид алюминия.Оксид алюминия кристаллизуется с ионами алюминия в двух третях октаэдрических дырок в плотноупакованном массиве оксидных ионов. Какая формула оксида алюминия?

Раствор
Поскольку на каждый анион (оксидный ион) приходится одна октаэдрическая дырка и только две трети этих дырок заняты, отношение алюминия к кислороду должно быть [латекс] \ frac {2} {3}: 1 [ / latex], что даст [латекс] \ text {Al} _ {2/3} \ text {O} [/ latex]. Простейшее целочисленное отношение 2: 3, поэтому формула Al ₂ O ₃ .

Проверьте свои знания
Белый пигмент оксида титана кристаллизуется с ионами титана в половине октаэдрических отверстий в плотноупакованном массиве оксидных ионов. Какая формула оксида титана?

В простом кубическом массиве анионов есть одно кубическое отверстие, которое может быть занято катионом для каждого аниона в массиве. В CsCl и других соединениях с такой же структурой все кубические дырки заняты. Половина кубических дырок занята в SrH ₂ , UO ₂ , SrCl ₂ и CaF ₂ .

Различные типы ионных соединений часто кристаллизуются в одной и той же структуре, если относительные размеры их ионов и их стехиометрия (две основные характеристики, определяющие структуру) схожи.

Многие ионные соединения кристаллизуются с кубическими элементарными ячейками, и мы будем использовать эти соединения, чтобы описать общие особенности ионных структур.

Когда ионное соединение состоит из катионов и анионов одинакового размера в соотношении 1: 1, оно обычно образует простую кубическую структуру.Примером этого является хлорид цезия, CsCl (проиллюстрированный на Фигуре 14), при этом Cs ⁺ и Cl ^— имеют радиусы 174 и 181 мкм соответственно. Мы можем представить это как ионы хлорида, образующие простую кубическую элементарную ячейку с ионом цезия в центре; или в виде ионов цезия, образующих элементарную ячейку с ионом хлорида в центре; или как простые кубические элементарные ячейки, образованные ионами Cs ⁺ , перекрывающими элементарные ячейки, образованные ионами Cl ^— . Ионы цезия и ионы хлора соприкасаются по диагоналям тела элементарных ячеек.Один ион цезия и один ион хлорида присутствуют в элементарной ячейке, что дает стехиометрию 1: 1, требуемую формулой для хлорида цезия. Обратите внимание, что в центре ячейки нет точки решетки, и CsCl не является структурой BCC, потому что ион цезия не идентичен иону хлорида.

Рис. 14. Ионные соединения с катионами и анионами аналогичного размера, такие как CsCl, обычно образуют простую кубическую структуру. Их можно описать элементарными ячейками с катионами по углам или анионами по углам.

Мы сказали, что расположение точек решетки произвольно. Это иллюстрируется альтернативным описанием структуры CsCl, в которой узлы решетки расположены в центрах ионов цезия. В этом описании ионы цезия расположены в точках решетки в углах ячейки, а ион хлора расположен в центре ячейки. Две элементарные ячейки разные, но они описывают идентичные структуры.

Когда ионное соединение состоит из катионов и анионов в соотношении 1: 1, которые значительно различаются по размеру, оно обычно кристаллизуется с помощью элементарной ячейки FCC, как показано на рисунке 15.Примером этого является хлорид натрия, NaCl, причем Na ⁺ и Cl ^— имеют радиусы 102 и 181 мкм соответственно. Мы можем представить это как ионы хлора, образующие ячейку FCC, причем ионы натрия расположены в октаэдрических отверстиях в середине краев ячейки и в центре ячейки. Ионы натрия и хлора соприкасаются друг с другом по краям ячейки. Элементарная ячейка содержит четыре иона натрия и четыре иона хлорида, что дает стехиометрию 1: 1, требуемую формулой NaCl.

Рис. 15. Ионные соединения с анионами, которые намного больше, чем катионы, такие как NaCl, обычно образуют структуру ГЦК. Их можно описать элементарными ячейками ГЦК с катионами в октаэдрических дырках.

Кубическая форма сульфида цинка, цинковая обманка, также кристаллизуется в элементарной ячейке FCC, как показано на рисунке 16. Эта структура содержит ионы сульфида в узлах решетки решетки FCC. (Расположение сульфид-ионов идентично расположению хлорид-ионов в хлориде натрия.) Радиус иона цинка составляет всего около 40% от радиуса сульфид-иона, поэтому эти маленькие ионы Zn ²⁺ расположены в чередующихся тетраэдрических дырках, то есть в одной половине тетраэдрических дырок. В элементарной ячейке четыре иона цинка и четыре иона сульфида, что дает эмпирическую формулу ZnS.

Рис. 16. ZnS, сульфид цинка (или цинковая обманка) образует элементарную ячейку FCC с ионами сульфида в узлах решетки и ионами цинка гораздо меньшего размера, занимающими половину тетраэдрических отверстий в структуре.

Элементарная ячейка с фторидом кальция, подобная той, что показана на рисунке 17, также является элементарной ячейкой FCC, но в этом случае катионы расположены в точках решетки; эквивалентные ионы кальция расположены в узлах решетки ГЦК-решетки. Все тетраэдрические позиции в массиве ГЦК ионов кальция заняты ионами фтора. В элементарной ячейке четыре иона кальция и восемь ионов фтора, что дает соотношение кальций: фтор 1: 2 в соответствии с химической формулой CaF ₂ . Внимательное изучение рисунка 17 покажет простой кубический массив ионов фтора с ионами кальция в одной половине кубических дырок.Структура не может быть описана в терминах пространственной решетки и точек на фторид-ионах, потому что не все фторид-ионы имеют одинаковое окружение. Ориентация четырех ионов кальция относительно ионов фтора различается.

Рис. 17. Фторид кальция, CaF ₂ , образует элементарную ячейку FCC с ионами кальция (зеленый) в узлах решетки и ионами фтора (красный), занимающими все тетраэдрические узлы между ними.

Если мы знаем длину края элементарной ячейки ионного соединения и положение ионов в ячейке, мы можем вычислить ионные радиусы для ионов в соединении, если мы сделаем предположения об индивидуальных формах ионов и контактах.

Пример 5

Расчет ионных радиусов
Длина края элементарной ячейки LiCl (NaCl-подобная структура, FCC) составляет 0,514 нм или 5,14 Å. Предполагая, что ион лития достаточно мал, чтобы ионы хлора контактировали, как на рисунке 15, рассчитайте ионный радиус для иона хлорида.

Примечание. Единица измерения длины, Å, часто используется для представления размеров в атомном масштабе и эквивалентна 10 ⁻¹⁰ м.

Раствор
На лицевой стороне элементарной ячейки LiCl ионы хлорида контактируют друг с другом по диагонали грани:

Рисуя прямоугольный треугольник на лицевой стороне элементарной ячейки, мы видим, что длина диагонали равна четырем радиусам хлорида (один радиус от каждого углового хлорида и один диаметр, равный двум радиусам, от иона хлорида в центре). грани), поэтому d = 4 r .{-} \; \ text {радиус} [/ латекс].

Проверьте свои знания
Длина края элементарной ячейки KCl (NaCl-подобная структура, FCC) составляет 6,28 Å. Предполагая, что анион-катионный контакт проходит по краю ячейки, рассчитайте радиус иона калия. Радиус иона хлорида составляет 1,82 Å.

Ответ:

Радиус иона калия 1,33 Å.

Важно понимать, что значения ионных радиусов, рассчитанные на основе длин краев элементарных ячеек, зависят от множества предположений, таких как идеальная сферическая форма для ионов, которые в лучшем случае являются приблизительными.Следовательно, такие расчетные значения сами по себе являются приблизительными, и сравнения нельзя зайти слишком далеко. Тем не менее, этот метод оказался полезным для расчета ионных радиусов на основе экспериментальных измерений, таких как рентгеновские кристаллографические определения.

Размер элементарной ячейки и расположение атомов в кристалле могут быть определены из измерений дифракции рентгеновских лучей на кристалле, называемой рентгеновской кристаллографией . Дифракция — это изменение направления движения, которое испытывает электромагнитная волна, когда она встречает физический барьер, размеры которого сопоставимы с размерами длины волны света.Рентгеновские лучи — это электромагнитное излучение с длиной волны, равной расстоянию между соседними атомами в кристаллах (порядка нескольких Å).

Когда пучок монохроматических рентгеновских лучей попадает на кристалл, его лучи рассеиваются во всех направлениях атомами внутри кристалла. Когда рассеянные волны, распространяющиеся в одном направлении, сталкиваются друг с другом, они подвергаются интерференции , процессу, при котором волны объединяются, приводя к увеличению или уменьшению амплитуды (интенсивности) в зависимости от степени, в которой максимумы объединяющихся волн находятся разделены (см. рисунок 18).

Рис. 18. Световые волны, занимающие одно и то же пространство, испытывают интерференцию, объединяясь, давая волны большей (а) или меньшей (б) интенсивности, в зависимости от разделения их максимумов и минимумов.

Когда рентгеновские лучи определенной длины волны, λ , рассеиваются атомами в соседних кристаллических плоскостях, разделенных расстоянием d , они могут подвергаться конструктивной интерференции, когда разница между расстояниями, пройденными двумя волнами до их комбинация представляет собой целочисленный множитель длины волны n .Это условие выполняется, когда угол дифрагированного луча θ связан с длиной волны и межатомным расстоянием уравнением:

[латекс] n {\ lambda} = 2d \; \ text {sin} \; {\ theta} [/ latex]

Это соотношение известно как уравнение Брэгга в честь У. Х. Брэгга , английского физика, который первым объяснил это явление. На рисунке 19 показаны два примера дифрагированных волн от одних и тех же двух плоскостей кристалла. На рисунке слева изображены волны, дифрагированные под углом Брэгга, приводящие к конструктивной интерференции, а на рисунке справа показаны дифракция и другой угол, который не удовлетворяет условию Брэгга, что приводит к деструктивной интерференции.

Рис. 19. Дифракция рентгеновских лучей, рассеянных атомами внутри кристалла, позволяет определить расстояние между атомами. Верхнее изображение показывает конструктивную интерференцию между двумя рассеянными волнами и результирующей дифрагированной волной высокой интенсивности. На нижнем изображении показаны деструктивная интерференция и дифрагированная волна низкой интенсивности.

Посетите этот сайт, чтобы получить более подробную информацию об уравнении Брэгга и симуляторе, который позволяет исследовать влияние каждой переменной на интенсивность дифрагированной волны.

Рентгеновский дифрактометр, такой как показанный на рисунке 20, можно использовать для измерения углов, под которыми рентгеновские лучи дифрагируют при взаимодействии с кристаллом, как описано ранее. Из таких измерений можно использовать уравнение Брэгга для вычисления расстояний между атомами, как показано в следующем примере упражнения.

Рис. 20. (a) В дифрактометре луч рентгеновских лучей попадает на кристаллический материал, создавая (b) картину дифракции рентгеновских лучей, которая может быть проанализирована для определения кристаллической структуры.

Пример 6

Использование уравнения Брэгга
В дифрактометре рентгеновские лучи с длиной волны 0,1315 нм использовались для создания дифракционной картины для меди. Дифракция первого порядка ( n = 1) происходила под углом θ = 25,25 °. Определите расстояние между дифрагирующими плоскостями в меди.

Решение
Расстояние между плоскостями находится путем решения уравнения Брэгга: nλ = 2 d sin θ для d .{\ circ})} = 0,154 \; \ text {нм} [/ латекс]

Проверьте свои знания
Кристалл с расстоянием между плоскостями, равным 0,394 нм, дифрагирует рентгеновские лучи с длиной волны 0,147 нм. Каков угол дифракции первого порядка?

Рентгеновский кристаллограф Розалинд Франклин

Открытие структуры ДНК в 1953 году Фрэнсисом Криком и Джеймсом Уотсоном является одним из величайших достижений в истории науки. Они были удостоены Нобелевской премии по физиологии и медицине 1962 года вместе с Морисом Уилкинсом , предоставившим экспериментальное доказательство структуры ДНК.Британский химик Розалинд Франклин внес неоценимый вклад в это грандиозное достижение благодаря своей работе по измерению рентгеновских дифракционных изображений ДНК. В начале своей карьеры исследования Франклин структуры углей оказались полезными для британских военных действий. В начале 1950-х годов Франклин и докторант Реймонд Гослинг переключили свое внимание на биологические системы и обнаружили, что ДНК состоит из двух форм: длинного тонкого волокна, образующегося при намокании (тип «B»), и короткого широкого волокна, образующегося при сушке ( наберите «А»).Ее рентгеновские дифракционные изображения ДНК (рис. 21) предоставили важную информацию, которая позволила Уотсону и Крику подтвердить, что ДНК образует двойную спираль, и определить детали ее размера и структуры. Франклин также провел новаторское исследование вирусов и РНК, содержащей их генетическую информацию, обнаружив новую информацию, которая радикально изменила совокупность знаний в этой области. После развития рака яичников Франклин продолжала работать до своей смерти в 1958 году в возрасте 37 лет. Среди множества посмертных признаний ее работы, Чикагская медицинская школа Финчского университета медицинских наук изменила свое название на Университет медицины и науки Розалинды Франклин в 2004 году. и приняла изображение ее знаменитого рентгеновского дифракционного изображения ДНК в качестве официального логотипа университета.

Рис. 21. На этой иллюстрации показано изображение дифракции рентгеновских лучей, подобное тому, которое Франклин нашла в своем исследовании. (Источник: Национальные институты здравоохранения)

Структуры кристаллических металлов и простых ионных соединений можно описать в терминах упаковки сфер. Атомы металла могут упаковываться в гексагональные структуры с плотнейшей упаковкой, кубические структуры с плотнейшей упаковкой, объемно-центрированные структуры и простые кубические структуры. Анионы в простых ионных структурах обычно принимают одну из этих структур, а катионы занимают пространство, остающееся между анионами.Маленькие катионы обычно занимают тетраэдрические дырки в плотноупакованном массиве анионов. Катионы большего размера обычно занимают октаэдрические отверстия. Катионы еще большего размера могут занимать кубические дырки в простом кубическом массиве анионов. Структуру твердого тела можно описать, указав размер и форму элементарной ячейки и ее содержимое. Тип структуры и размеры элементарной ячейки могут быть определены путем измерения дифракции рентгеновских лучей.

• [латекс] n {\ lambda} = 2d \; \ text {sin} \; {\ theta} [/ latex]

Химия: упражнения в конце главы

1. Опишите кристаллическую структуру железа, которое кристаллизуется с двумя эквивалентными атомами металла в кубической элементарной ячейке.
2. Опишите кристаллическую структуру Pt, которая кристаллизуется с четырьмя эквивалентными атомами металла в кубической элементарной ячейке.
3. Какое координационное число атома хрома в объемноцентрированной кубической структуре хрома?
4. Какое координационное число атома алюминия в гранецентрированной кубической структуре алюминия?
5. Металлический кобальт кристаллизуется в гексагональной плотноупакованной структуре. Какое координационное число атома кобальта?
6. Металлический никель кристаллизуется в кубической плотноупакованной структуре.Какое координационное число атома никеля?
7. Вольфрам кристаллизуется в объемно-центрированной кубической элементарной ячейке с длиной ребра 3,165 Å.

   (а) Каков атомный радиус вольфрама в этой структуре?

   (б) Рассчитайте плотность вольфрама.

8. Платина (атомный радиус = 1,38 Å) кристаллизуется в кубической плотноупакованной структуре. Рассчитайте длину кромки гранецентрированной кубической элементарной ячейки и плотность платины.
9. Барий кристаллизуется в объемноцентрированной кубической элементарной ячейке с длиной ребра 5.025 Å

   (а) Каков атомный радиус бария в этой структуре?

   (б) Рассчитайте плотность бария.

10. Алюминий (атомный радиус 1,43 Å) кристаллизуется в кубической плотноупакованной структуре. Рассчитайте длину ребра гранецентрированной кубической элементарной ячейки и плотность алюминия.
11. Плотность алюминия 2,7 г / см ³ ; кремния 2,3 г / см ³ . Объясните, почему Si имеет более низкую плотность, хотя в нем более тяжелые атомы.
12. Свободное пространство в металле может быть найдено путем вычитания объема атомов в элементарной ячейке из объема ячейки. Вычислите процент свободного пространства в каждой из трех кубических решеток, если все атомы в каждой имеют одинаковый размер и касаются своих ближайших соседей. Какая из этих структур представляет собой наиболее эффективную упаковку? То есть в каких упаковках меньше всего неиспользуемого места?
13. Сульфид кадмия, иногда используемый художниками в качестве желтого пигмента, кристаллизуется с кадмием, занимая половину тетраэдрических отверстий в плотно упакованном массиве сульфид-ионов.Какая формула сульфида кадмия? Поясните свой ответ.
14. Соединение кадмия, олова и фосфора используется в производстве некоторых полупроводников. Он кристаллизуется с кадмием, занимающим одну четверть тетраэдрических дырок, и оловом, занимающим одну четверть тетраэдрических дырок в плотно упакованном массиве фосфид-ионов. Какая формула соединения? Поясните свой ответ.
15. Какова формула магнитного оксида кобальта, используемого в записывающих лентах, который кристаллизуется с атомами кобальта, занимающими одну восьмую тетраэдрических дырок и половину октаэдрических дырок в плотно упакованном массиве оксидных ионов?
16. Соединение, содержащее цинк, алюминий и серу, кристаллизуется с плотнейшей упаковкой сульфид-ионов.Ионы цинка находятся в одной восьмой тетраэдрических дырок, а ионы алюминия — в половине октаэдрических дырок. Какова эмпирическая формула соединения?
17. Соединение таллия и йода кристаллизуется в виде простого кубического массива иодид-ионов с ионами таллия во всех кубических дырках. Какая формула этого йодида? Поясните свой ответ.
18. Какой из следующих элементов реагирует с серой с образованием твердого тела, в котором атомы серы образуют плотно упакованный массив со всеми занятыми октаэдрическими отверстиями: Li, Na, Be, Ca или Al?
19. Каков массовый процент титана в рутиле, минерале, содержащем титан и кислород, если структуру можно описать как плотнейшую упаковку оксидных ионов с ионами титана в половине октаэдрических отверстий? Какова степень окисления титана?
20. Объясните, почему химически похожие хлориды щелочных металлов NaCl и CsCl имеют разную структуру, тогда как химически разные NaCl и MnS имеют одинаковую структуру.
21. Поскольку минералы образовались из расплавленной магмы, разные ионы занимали одни и те же участки в кристаллах. Литий часто встречается вместе с магнием в минералах, несмотря на разницу в заряде их ионов. Предложите объяснение.
22. Иодид рубидия кристаллизуется с кубической элементарной ячейкой, содержащей иодид-ионы по углам и ион рубидия в центре. Какая формула соединения?
23. Один из различных оксидов марганца кристаллизуется с кубической элементарной ячейкой, содержащей ионы марганца по углам и в центре.Ионы оксида расположены в центре каждого края элементарной ячейки. Какая формула соединения?
24. NaH кристаллизуется с той же кристаллической структурой, что и NaCl. Длина ребра кубической элементарной ячейки NaH составляет 4,880 Å.

    (a) Рассчитайте ионный радиус H ^— . (Ионный радиус Li ⁺ составляет 0,0,95 Å.)

    (b) Рассчитайте плотность NaH.

25. Иодид таллия (I) кристаллизуется с той же структурой, что и CsCl. Длина ребра элементарной ячейки TlI равна 4.20 Å. Вычислите ионный радиус TI ⁺ . (Ионный радиус I ^— составляет 2,16 Å.)
26. Кубическая элементарная ячейка содержит ионы марганца по углам и ионы фтора в центре каждого края.

    (а) Какова эмпирическая формула этого соединения? Поясните свой ответ.

    (б) Каково координационное число иона Mn ³⁺ ?

    (c) Рассчитайте длину края элементарной ячейки, если радиус иона Mn ³⁺ составляет 0,65 А.

    (d) Рассчитайте плотность соединения.

27. Каково расстояние между плоскостями кристалла, которые дифрагируют рентгеновские лучи с длиной волны 1,541 нм под углом θ 15,55 ° (отражение первого порядка)?
28. Дифрактометр, использующий рентгеновские лучи с длиной волны 0,2287 нм, дает пик дифракции первого порядка для угла кристалла θ = 16,21 °. Определите расстояние между дифрагирующими плоскостями в этом кристалле.
29. Металл с расстоянием между плоскостями 0,4164 нм дифрагирует рентгеновские лучи с длиной волны 0.2879 нм. Каков угол дифракции для дифракционного пика первого порядка?
30. Золото кристаллизуется в кубической гранецентрированной элементарной ячейке. Отражение второго порядка (n = 2) рентгеновских лучей для плоскостей, составляющих вершину и основание элементарных ячеек, находится при θ = 22,20 °. Длина волны рентгеновского излучения составляет 1,54 Å. Какова плотность металлического золота?
31. Когда электрон в возбужденном атоме молибдена падает с L на K-оболочку, испускается рентгеновское излучение. Эти рентгеновские лучи дифрагируют под углом 7.75 ° плоскостями с расстоянием 2,64 Å. Какова разница в энергии между K-оболочкой и L-оболочкой в ​​молибдене в предположении дифракции первого порядка?

Глоссарий

объемно-центрированная кубическая (ОЦК) сплошная

Кристаллическая структура, которая имеет кубическую элементарную ячейку с точками решетки по углам и в центре ячейки

объемно-центрированная кубическая элементарная ячейка

простейший повторяющийся элемент объемно-центрированного кубического кристалла; это куб, содержащий точки решетки в каждом углу и в центре куба

Уравнение Брэгга

Уравнение, связывающее углы, под которыми рентгеновские лучи дифрагируют атомами внутри кристалла

координационный номер

Число атомов, ближайших к любому данному атому в кристалле или к центральному атому металла в комплексе

плотнейшая кубическая упаковка (ПГУ)

Кристаллическая структура, в которой плоскости плотно упакованных атомов или ионов уложены в виде серии из трех чередующихся слоев с различной относительной ориентацией (ABC)

дифракция

Перенаправление электромагнитного излучения, возникающее при встрече с физическим барьером соответствующих размеров

гранецентрированная кубическая (FCC) сплошная

Кристаллическая структура, состоящая из кубической элементарной ячейки с точками решетки по углам и в центре каждой грани

гранецентрированная кубическая элементарная ячейка

простейший повторяющийся элемент гранецентрированного кубического кристалла; это куб, содержащий точки решетки в каждом углу и в центре каждой грани

Гексагональная плотная набивка (HCP)

Кристаллическая структура, в которой плотно упакованные слои атомов или ионов уложены в виде серии из двух чередующихся слоев с разной относительной ориентацией (AB)

отверстие

(также междоузлия) пространство между атомами внутри кристалла

изоморфный

с такой же кристаллической структурой

октаэдрическое отверстие

открытое пространство в кристалле в центре из шести частиц, расположенных по углам октаэдра

простая кубическая элементарная ячейка

(также примитивная кубическая элементарная ячейка) элементарная ячейка в простой кубической структуре

простая кубическая структура

Кристаллическая структура с кубической элементарной ячейкой с узлами решетки только по углам

пространственная решетка

все точки в кристалле, которые имеют идентичное окружение

четырехгранное отверстие

тетраэдрическое пространство, образованное четырьмя атомами или ионами в кристалле

элементарная ячейка

Наименьшая часть пространственной решетки, которая повторяется в трех измерениях, образуя всю решетку

Рентгеновская кристаллография

Экспериментальный метод определения расстояний между атомами в кристалле путем измерения углов, под которыми рентгеновские лучи дифрагируют при прохождении через кристалл

Решения

Ответы на упражнения в конце главы по химии

1.Структура этой низкотемпературной формы железа (ниже 910 ° C) является объемно-центрированной кубической. В каждом из восьми углов куба находится по 1/8 атома, а в центре куба — по одному атому.

3. восемь

5. 12

7. (а) 1,370 Å; (б) 19,26 г / см

9. (а) 2,176 Å; (б) 3,595 г / см ³

11. Кристаллическая структура Si показывает, что он менее плотно упакован (координационное число 4) в твердом теле, чем Al (координационное число 12).

13.В наиболее плотно упакованном массиве для каждого аниона существуют две тетраэдрические дырки. Если занята только половина тетраэдрических дырок, количество анионов и катионов равно. Формула сульфида кадмия — CdS.

15. Co ₃ O ₄

17. В простом кубическом массиве только одно кубическое отверстие может быть занято катионом для каждого аниона в массиве. Соотношение таллия и йодида должно быть 1: 1; следовательно, формула таллия — TlI.

19 59,95%; Степень окисления титана +4.

21. Оба иона близки по размеру: Mg 0,65; Ли 0,60. Это сходство позволяет им довольно легко поменяться местами. Разница в заряде обычно компенсируется переключателем Si ⁴⁺ на Al ³⁺ .

23. Mn ₂ O ₃

25. 1,48 Å

27. 2,874 Å

29. 20.2 °

31. 1,74 × 10 ⁴ эВ

структур кристаллической решетки металлов

структура кристаллической решетки металлов

ПРОСТОЙ КУБИЧЕСКИЙ МЕТАЛЛ

В металле все атомы идентичны, и большинство из них имеют сферическую форму (
склеивание не зависит от направления).Таким образом, металлы имеют тенденцию принимать относительно
простые конструкции. Самый простой:

Простой кубик (sc)

Вот два способа нарисовать элементарную ячейку для простой кубической структуры.
В элементарной ячейке слева атомы в углах обрезаны, потому что
только часть (в данном случае 1/8) принадлежит этой ячейке. Остаток от
атом принадлежит соседним ячейкам, как показано на рисунке ниже.

Нажмите на левую элементарную ячейку вверху, чтобы просмотреть фильм о ее вращении.

Здесь мы видим две элементарные ячейки, уложенные стопкой в ​​решетку.

Обратите внимание, что в каждом случае обнаруживается одна и та же общая структура.

Фильм, представленный ниже, даст вам почувствовать общую решетку
шаблон.

Щелкните изображение, чтобы просмотреть его.

Мы можем думать об этой решетке как о слоях квадратных упакованных сфер.В
слои уложены так, чтобы каждая сфера находилась прямо над сферой в
слой ниже.

Хотя мы показали пространство между сферами, это только для
«открыть» структуру для просмотра. В настоящем кристалле сферы соприкасаются
как показано в элементарной ячейке и решетке ниже.

Таким образом, длина края ячейки в 2 раза больше радиуса сферы.

Щелкните элементарную ячейку и решетку выше, чтобы увидеть, как они вращаются.

В 3-D эффективность упаковки определяется по формуле:

P.E. = (объем сфер) / (объем ячейки)

Для простой кубической решетки это:
P.E. = (1 / 8×8) (4/3 pi r ³ ) / (2r) ³ =
пи / 6 = 52,35%.

Это низкое значение неудивительно. Помните, что двумерная квадратная решетка
неэффективно использует пространство. Простая кубическая решетка является ее трехмерным аналогом, а
также содержит много пустого места.

Обратим внимание на пустоты в решетке. Каждый
В центре элементарной ячейки находится одно крупное междоузлие (47,65%
громкость). К этому пространству прикасаются 8 атомов, поэтому
межузельное координационное число равно 8, а его геометрия
кубический (у куба 8 углов).

Поскольку каждая элементарная ячейка содержит (8 x 1/8 =) 1 атом и 1 междоузлие
сайта, количество атомов и междоузлий одинаковое.

Изучите структуру ниже, которая показывает расположение любого
одиночный атом в простой кубической решетке; обратите внимание, что каждый атом имеет
6 соседей, поэтому координация атомов
число равно 6. Координационная геометрия
октаэдр (у октаэдра 6 углов).

Октаэдрическая координация атома. An
октаэдр.

Поскольку и координационное число, и эффективность упаковки низкие,
простая кубическая решетка неэффективно использует пространство. Очень мало примеров простых
кубические решетки известны (альфа-полоний — один из немногих известных простых
кубические решетки).

Ниже мы снова видим сечение простой кубической решетки в виде
«на самом деле» — с атомами, соприкасающимися друг с другом. Обратите внимание на каналов
формируется путем совмещения межстраничных объявлений.Эти пустые места могут позволить
другие маленькие атомы входят в кристалл.

Щелкните изображение ниже, чтобы увидеть решетку.

Нажмите здесь, чтобы перейти к
следующая страница.

Структура кристаллов

Кристаллические решетки

Единичные ячейки

От элементарной ячейки к решетке

От решетки к элементарной ячейке

Стехиометрия

Упаковка и геометрия

Простой
Кубические металлы

Плотно упакованные конструкции

Телоцентрированный кубик

Хлорид цезия

хлорид натрия

Оксид рения

Оксид ниобия

Если не указано иное, все изображения, фильмы
и VRML являются собственностью и авторским правом
по

Др.Барбара Л. Саулс и доктор Фредерик С. Саулс
1998.

Свяжитесь с владельцами для получения индивидуального разрешения
использовать. [email protected]

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.
  Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г.,
  браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
  Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Кристаллическая решетка: определение и структура — научный класс [видео 2021 года]

Структура кристаллической решетки

Когда мы смотрим на структуру кристаллической решетки, помните о схемах расположения каждой точки, а также об их симметрии.Участки кристаллической решетки просматриваются только под микроскопом и невидимы невооруженным глазом. Чтобы увидеть эти структуры, мы должны взять кристалл (твердый объект), поместить его под микроскоп и рассмотреть узлы кристаллической решетки.

Здесь показана структура кристаллической решетки. Вспомните, что кристаллическая решетка — это расположение атомов в кристалле (черные и белые точки на изображении — это ваши атомы). Это расположение можно определить как пересечение трех параллельных плоскостей.Итак, если мы разрежем эту диаграмму на три части, вы увидите три разных плоскости. Когда эти плоскости пересекаются друг с другом, в результате получается трехмерная сеть с гранями. Думайте о каждом лице как о параллельном прямоугольнике.

Симметрия

Вы не думаете, что я забуду о симметрии нашего друга, не так ли? Конечно, нет; Фактически, эти коробки (или грани) вносят вклад в симметрию структуры кристаллической решетки.Каждый блок содержит информацию о симметрии, необходимую для обеспечения трансляционной кристаллической структуры.

Трансляционная симметрия возникает, когда объект перемещается (или перемещается) на определенное расстояние в определенном месте. Например, вы хотите построить деревянный пол с рисунком. Вы кладете один кусок дерева по диагонали через каждые 20 дюймов. Этот стиль дерева с определенным рисунком имеет определенное расстояние (20 дюймов) и направление (диагональ).

Классификация

Кристаллические решетки можно разделить на одноатомные и многоатомные.Эта классификация основана на типе атомов, присутствующих на поверхности в решетчатой ​​структуре. Если для создания грани (или прямоугольника) используется только один тип атома, это одноатомный . Многоатомная кристаллическая решетка содержит более одного типа атомов, используемых для создания грани.

Если мы посмотрим на структуру кристаллической решетки поваренной соли (NaCl) — решетки (а) и алмаза — решетки (б), мы увидим, что обе они имеют разные структуры решетки. Одно лицо в поваренной соли состоит из красных и зеленых точек.Это означает, что существует более одного типа атомов. Следовательно, эта структура многоатомна. В структуре алмазной решетки есть только одна цветная точка (синяя). Эта структура одноатомна.

Типы структур кристаллической решетки

Существует 14 различных типов кристаллических решеток. Каждый тип уникально описывает геометрическую симметрию кристалла.В частности, эти типы кристаллических решеток называются решетками Браве . Решетка Браве просто описывает разные типы трех разных решеток, которые могут быть созданы для данного кристалла.

Каждый из 14 типов решеток подразделяется на 7 кристаллических систем. Думайте о каждой системе как о группе структур кристаллической решетки (решетки Браве), которые однозначно описывают геометрическую симметрию кристалла. Приведены таблицы, в которых перечислены семь систем и их структуры.Если мы вернемся к нашему примеру с поваренной солью, как вы думаете, к какому типу кристаллической системы она принадлежит? Верно! Поваренная соль (NaCl) относится к системе кубической решетки.

Кристаллические решетки являются основой структуры твердого объекта.В следующий раз, когда вы будете поливать пищу солью или чистить этот сверкающий алмаз, вспомните об упорядоченной структуре кристаллической решетки, использованной для создания этого объекта.

Краткое содержание урока

Большинство твердых объектов содержат крошечные переплетенные кристаллы. Кристалл представляет собой твердый материал, который содержит атомы или группы атомов, расположенные в высокоупорядоченной структуре. Эта структурная схема является трехмерной. Кристаллическая решетка описывает расположение этих атомов в кристалле и характеризуется трансляционной симметрией.Если на поверхности кристаллической решетки присутствует один тип атома, он называется одноатомным . Наличие более одного типа атомов означает, что структура решетки состоит из многоатомных атомов и . Существует 14 различных типов кристаллических решеток, которые называются решетками Браве . Каждая из этих решетчатых структур подразделяется на семь кристаллических систем.

Ключевые термины для кристаллической решетки

• Кристалл : твердое вещество, содержащее атомы или группы атомов, расположенные в упорядоченной структуре
• Кристаллическая решетка : расположение атомов в кристаллических формах с трансляционной симметрией
• Одноатомный : только один тип атомов в решетке
• Многоатомный : более одного типа атомов в решетке
• Bravais Lattices : 7 кристаллических систем, состоящих из 14 различных типов кристаллических решеток

Результаты обучения

Завершите этот урок, чтобы успешно выполнить следующие задачи:

• Опишите кристаллическую решетку
• Покажите, как формируются кристаллические решетки
• Деталь различных типов кристаллических решеток

Единичных Ячеек

Единичные ячейки

Единичные ячейки:
Простейший повторяющийся блок в кристалле

Строение твердых тел можно описать так, как если бы они
объемные аналоги куска обоев.Обои имеют
регулярный повторяющийся дизайн, который простирается от одного края до
Другие. Кристаллы имеют похожий повторяющийся дизайн, но в этом случае
конструкция простирается в трех измерениях от одного края твердого тела
к другому.

Однозначно можно описать кусок обоев по
указание размера, формы и содержимого простейшего
повторяющийся блок в дизайне. Мы можем описать трехмерный
кристалл, указав размер, форму и содержимое
простейший повторяющийся блок и способ, которым эти повторяющиеся блоки складываются
сформировать кристалл.

Простейшая повторяющаяся единица в кристалле называется единицей .
ячейка . Каждая элементарная ячейка определяется с помощью узлов решетки
точки в пространстве, вокруг которых частицы могут свободно колебаться в
кристалл.

Структуры элементарной ячейки для различных солей являются
показано ниже.

В 1850 году Огюст Браве показал, что кристаллы можно разделить.
на 14 элементарных ячеек, которые соответствуют следующим критериям.

• Элементарная ячейка — простейшая повторяющаяся единица в
  кристалл.
• Противоположные грани элементарной ячейки параллельны.
• Край элементарной ячейки соединяет эквивалентные точки.

14 элементарных ячеек Браве показаны на рисунке ниже.

Эти элементарные ячейки делятся на семь категорий, которые различаются
три длины кромки элементарной ячейки ( a , b и c )
и три внутренних угла (a, � и g), как показано в таблице
ниже.

Семь категорий элементарных ячеек Браве

Мы остановимся на категории кубических, в которую входят три
типы элементарных ячеек простые
кубический, объемно-центрированный кубический и гранецентрированный кубический показаны
на рисунке ниже.

Эти элементарные ячейки важны по двум причинам. Первый
количество металлов, ионных твердых частиц и интерметаллических соединений
кристаллизуются в кубических элементарных ячейках. Во-вторых, относительно легко
делать расчеты с этими элементарными ячейками, потому что край ячейки
все длины одинаковы, а углы ячеек равны 90.

Простая кубическая элементарная ячейка — простейшая повторяющаяся
агрегат в простой кубической конструкции. Каждый угол элементарной ячейки равен
определяется точкой решетки, в которой атом, ион или молекула могут
можно найти в кристалле. По соглашению край элементарной ячейки
всегда соединяет равнозначные точки. Каждый из восьми углов
поэтому элементарная ячейка должна содержать идентичную частицу. Другой
частицы могут присутствовать на краях или гранях элементарной ячейки,
или внутри тела элементарной ячейки.Но минимум, который должен быть
для того, чтобы элементарная ячейка была классифицирована как простая кубическая,
восемь эквивалентных частиц на восьми углах.

Объемно-центрированная кубическая элементарная ячейка является самой простой
повторяющийся блок в объемно-центрированной кубической структуре. Снова,
есть восемь одинаковых частиц на восьми углах
ячейка. Однако на этот раз есть девятая идентичная частица
в центре тела элементарной ячейки.

Гранецентрированная кубическая элементарная ячейка также начинается с
одинаковые частицы на восьми углах куба.Но это
структура также содержит такие же частицы в центрах
шесть граней элементарной ячейки, всего 14 одинаковых решеток
точки.

Гранецентрированная кубическая элементарная ячейка — простейшая повторяющаяся
агрегат в кубической плотноупакованной структуре. Фактически наличие
гранецентрированных кубических элементарных ячеек в этой структуре объясняет, почему
структура известна как кубических наиболее плотно упакованных.

Единичные ячейки: A
Трехмерный график

Точки решетки в кубической элементарной ячейке могут быть описаны в
условия трехмерного графа.Потому что все три ячейки-края
длины одинаковые в кубической элементарной ячейке, неважно, какие
ориентация используется для a , b и c
топоры. В качестве аргумента мы определим ось и как
вертикальная ось нашей системы координат, как показано на
рисунок ниже.

Затем ось b будет описывать движение поперек фронта.
элементарной ячейки, а ось c будет представлять движение
к задней части элементарной ячейки.Кроме того, мы произвольно
определить нижний левый угол элементарной ячейки как начало координат
(0,0,0). Координаты 1,0,0 указывают точку решетки, которая
на одну длину края ячейки от начала координат по a
ось. Точно так же 0,1,0 и 0,0,1 представляют точки решетки, которые
смещены на одну длину края ячейки от начала координат по оси b
и c осей соответственно.

Представление об элементарной ячейке как о трехмерном графике
позволяет описать структуру кристалла с
на удивление мало информации.Мы можем указать
структура хлорида цезия, например, всего из четырех частей
информации.

• CsCl кристаллизуется в элементарной кубической ячейке.
• Длина края элементарной ячейки 0,4123 нм.
• В координатах 0,0,0 находится ион Cl ^— .
• В координатах
  1 / 2,1 / 2,1 / 2.

Поскольку край ячейки должен соединять эквивалентные точки решетки,
наличие иона Cl ^— в одном углу установки
ячейка (0,0,0) подразумевает присутствие иона Cl ^— в
каждый уголок клетки.Координаты 1 / 2,1 / 2,1 / 2 описывают
точка решетки в центре ячейки. Потому что нет
другая точка в элементарной ячейке на расстоянии одного края ячейки
по этим координатам это единственный ион Cs ⁺ в
сотовый. Таким образом, CsCl представляет собой простую кубическую элементарную ячейку Cl ^— .
ионы с Cs ⁺ в центре тела клетки.

Элементарные ячейки: NaCl и ZnS

NaCl должен кристаллизоваться в кубическом массиве плотнейшей упаковки Cl ^— .
ионов с ионами Na ⁺ в октаэдрических дырках между
плоскости ионов Cl ^— .Мы можем перевести эту информацию
в модель элементарной ячейки для NaCl, помня, что
гранецентрированная кубическая элементарная ячейка — простейшая повторяющаяся единица в
кубическая структура плотнейшей упаковки.

В гранецентрированной кубической единице есть четыре уникальных положения.
клетка. Эти позиции определяются координатами: 0,0,0;
0,1 / 2,1 / 2; 1 / 2,0,1 / 2; и 1 / 2,1 / 2,0. Наличие частицы
в одном углу элементарной ячейки (0,0,0) требуется наличие
эквивалентная частица на каждом из восьми углов устройства
клетка.Поскольку край элементарной ячейки соединяет эквивалентные точки,
наличие частицы в центре нижней грани
(0,1 / 2,1 / 2) подразумевает наличие эквивалентной частицы в
центр верхней грани (1,1 / 2,1 / 2). Точно так же наличие
частицы в центре граней 1 / 2,0,1 / 2 и 1 / 2,1 / 2,0
элементарная ячейка подразумевает эквивалентные частицы в центрах
1 / 2,1,1 / 2 и 1 / 2,1 / 2,1 грани.

На рисунке ниже показано, что в корпусе есть октаэдрическое отверстие.
центр гранецентрированной кубической элементарной ячейки, в координатах
1 / 2,1 / 2,1 / 2.Любая частица в этот момент касается частиц в
центры шести граней элементарной ячейки.

Другие октаэдрические дырки в гранецентрированной кубической элементарной ячейке
находятся на краях ячейки, как показано на рисунке ниже.

Если ионы Cl ^— занимают узлы решетки
гранецентрированная кубическая элементарная ячейка и все октаэдрические дырки
заполненная ионами Na ⁺ , мы получаем элементарную ячейку, показанную на
рисунок ниже.

Таким образом, мы можем описать структуру NaCl в терминах
Следующая информация.

• NaCl кристаллизуется в кубической элементарной ячейке.
• Длина края ячейки 0,5641 нм.
• На позициях 0,0,0 находятся ионы Cl ^— ;
  1 / 2,1 / 2,0; 1 / 2,0,1 / 2; и 0,1 / 2,1 / 2.
• На позициях находятся ионы Na ⁺ .
  1 / 2,1 / 2,1 / 2; 1 / 2,0,0; 0,1 / 2,0; и 0,0,1 / 2.

Размещение иона Cl ^— в этих четырех положениях подразумевает
наличие иона Cl ^— на каждой из 14 решеток
точки, которые определяют гранецентрированную кубическую единицу. Размещение Na ⁺
ион в центре элементарной ячейки (1 / 2,1 / 2,1 / 2) и на трех
уникальные края элементарной ячейки (1 / 2,0,0; 0,1 / 2,0; и 0,0,1 / 2)
требуется эквивалентный ион Na ⁺ в каждом октаэдре
отверстие в элементарной ячейке.

ZnS кристаллизуется как кубическая плотноупакованная матрица S ^2-
ионы с ионами Zn ²⁺ в тетраэдрических дырках.Модель S ^2-
ионы в этом кристалле занимают те же позиции, что и Cl ^—
ионы в NaCl. Единственная разница между этими кристаллами — это
расположение положительных ионов. На рисунке ниже показано, что
тетраэдрические дырки в гранецентрированной кубической элементарной ячейке находятся в
углы элементарной ячейки с такими координатами, как 1 / 4,1 / 4,1 / 4. An
атом с этими координатами коснется атома в этом углу
а также атомы в центрах трех граней, которые образуют
этот угол.Хотя без
трехмерная модель, четыре атома, окружающие эту дыру
расположены к углам тетраэдра.

Поскольку углы элементарной кубической ячейки идентичны,
должно быть четырехгранным отверстием в каждом из восьми углов
гранецентрированная кубическая элементарная ячейка. Если ионы S ^2- занимают
решетки гранецентрированной кубической элементарной ячейки и Zn ²⁺
ионы упакованы во все остальные тетраэдрические отверстия, мы получаем
Элементарная ячейка ZnS показана на рисунке ниже.

Таким образом, структуру ZnS можно описать следующим образом.

• ZnS кристаллизуется в элементарной кубической ячейке.
• Длина края ячейки 0,5411 нм.
• На позициях 0,0,0 находятся ионы S ^2-;
  1 / 2,1 / 2,0; 1 / 2,0,1 / 2; и 0,1 / 2,1 / 2.
• Имеются ионы Zn ²⁺ на позициях
  1 / 4,1 / 4,1 / 4; 1 / 4,3 / 4,3 / 4; 3 / 4,1 / 4,3 / 4; и 3 / 4,3 / 4,1 / 4.

Обратите внимание, что только половина тетраэдрических отверстий занята в
этот кристалл, потому что есть два тетраэдрических отверстия на каждые S ^2-
ион в наиболее плотно упакованном массиве этих ионов.

Единичные ячейки: измерение
Расстояние между частицами

Никель — один из металлов, кристаллизующихся в кубической форме.
плотноупакованная структура. Если учесть, что атом никеля
имеет массу всего 9,75 x 10 ^-23 г и ионный радиус
всего 1,24 x 10 ^-10 м, это замечательное достижение
уметь описать структуру этого металла. Очевидное
вопрос: откуда мы знаем, что никель упаковывается в кубический
плотноупакованная структура?

Единственный способ определить структуру вещества на атомной
масштаб — использовать зонд еще меньшего размера.Один из многих
полезные зонды для изучения материи в этом масштабе
электромагнитное излучение.

В 1912 году Макс ван Лауэ обнаружил, что рентгеновские лучи, попавшие в
поверхность кристалла дифрагировала на узоры, похожие на
узоры, возникающие при прохождении света через очень узкую
щель. Вскоре после этого Уильям Лоуренс Брэгг, который только что
получил степень бакалавра физики в Кембридже,
объяснил результаты ван Лауэ с помощью уравнения, известного как Брэгга.
уравнение , которое позволяет рассчитать расстояние между
плоскости атомов в кристалле от картины дифракции
рентгеновские лучи известной длины волны.

n
= 2 d sin T

Диаграмма дифрагирования рентгеновских лучей на металлическом никеле
предполагает, что этот металл упаковывается в кубическую элементарную ячейку с
расстояние между плоскостями атомов 0,3524 нм. Таким образом
длина края ячейки в этом кристалле должна составлять 0,3524 нм. Знаю это
никель кристаллизуется в кубической элементарной ячейке недостаточно. Мы все еще
нужно решить, простая ли это кубическая, объемно-центрированная кубическая,
или кубическая гранецентрированная элементарная ячейка.Это можно сделать, измерив
плотность металла.

Единичные клетки: определение
Элементарная ячейка кристалла

Атомы на углах, краях и гранях элементарной ячейки
совместно используется более чем одной элементарной ячейкой, как показано на рисунке ниже.
Атом на грани делится на две элементарные ячейки, поэтому только половина
атом принадлежит каждой из этих ячеек. Атом на ребре — это
разделяют четыре элементарные ячейки, а атом в углу разделяет
восемь элементарных ячеек.Таким образом, только четверть атома на ребре
и одна восьмая часть атома в углу может быть назначена каждому из
элементарные ячейки, которые разделяют эти атомы.

Если никель кристаллизовался в простой кубической элементарной ячейке, то
будет атом никеля на каждом из восьми углов ячейки.
Поскольку только одна восьмая из этих атомов может быть отнесена к данному
элементарной ячейке, каждая элементарная ячейка в простой кубической структуре будет иметь
один чистый атом никеля.

Простая кубическая структура:

8 углов x 1/8 = 1 атом

Если бы никель образовывал объемно-центрированную кубическую структуру,
быть двумя атомами на элементарную ячейку, потому что атом никеля в центре
тела не будет делиться ни с какими другими элементарными ячейками.

Телоцентрированная кубическая структура:

(8 углов x 1/8) + 1 тело = 2 атома

Если никель кристаллизовался с гранецентрированной кубической структурой,
шесть атомов на гранях элементарной ячейки дадут три
чистые атомы никеля, всего четыре атома на элементарную ячейку.

Гранецентрированная кубическая структура:

(8 углов x 1/8) + (6 граней x 1/2) = 4 атома

Поскольку они имеют разное количество атомов в элементарной ячейке,
каждая из этих структур будет иметь разную плотность. Давайте
поэтому рассчитайте плотность никеля на основе каждого из этих
структуры и длина кромки элементарной ячейки для никеля, приведенная в
предыдущий раздел: 0,3524 нм. Для этого нам нужно знать
объем элементарной ячейки в кубических сантиметрах и масса
одиночный атом никеля.

Объем ( V ) элементарной ячейки равен
длина края ячейки ( a ) в кубе.

V = a ³ = (0,3524
нм) ³ = 0,04376 нм ³

Так как в метре 10 ⁹ нм, а в метре 100 см
метр, в сантиметре должно быть 10 ⁷ нм.

Таким образом, мы можем преобразовать объем элементарной ячейки в см ³
следующим образом.

Массу атома никеля можно рассчитать по атомной
вес этого металла и число Авогадро.

Плотность никеля, если он кристаллизовался в простой кубической форме.
структура, следовательно, будет 2,23 г / см ³ , до трех
значимые фигуры.

Простая кубическая структура:

Потому что в элементарной ячейке было бы вдвое больше атомов, если бы
никель кристаллизовался в объемноцентрированной кубической структуре,
плотность никеля в этой структуре была бы вдвое больше.

Телоцентрированная кубическая структура:

В гранецентрированной ячейке будет четыре атома на элементарную ячейку.
кубическая структура и плотность никеля в этой структуре будет
быть в четыре раза больше.

Гранецентрированная кубическая структура:

Экспериментальное значение плотности никеля 8,90 г / см ³ .
Напрашивается очевидный вывод, что никель кристаллизуется в
гранецентрированная кубическая элементарная ячейка и, следовательно, имеет кубическую
плотноупакованная структура.

Элементарные ячейки: расчет
Металлический или ионный радиус

Можно найти оценки радиусов большинства атомов металлов. Где
откуда эти данные? Откуда мы знаем, например, что
радиус атома никеля 0,1246 нм?

Никель кристаллизуется в гранецентрированной кубической элементарной ячейке с
длина края ячейки 0,3524 нм для расчета радиуса никеля
атом.

Показана одна из граней гранецентрированной кубической элементарной ячейки.
на рисунке ниже.

Согласно этому рисунку, диагональ на лицевой стороне
элементарная ячейка в четыре раза больше радиуса атома никеля.

Теорема Пифагора утверждает, что диагональ через
прямоугольный треугольник равен сумме квадратов другого
стороны. Таким образом, диагональ на поверхности элементарной ячейки равна
связаны с длиной края элементарной ячейки следующим уравнением.

Извлечение квадратного корня из обеих частей дает следующее
результат.

Теперь подставим в это уравнение соотношение между
диагональ на грани этой элементарной ячейки и радиус
атом никеля:

Решение для радиуса атома никеля дает значение
0,1246 нм:

Аналогичный подход можно использовать для оценки размера
ион. Начнем с того, что длина края ячейки в
хлорид цезия составляет 0,4123 нм для расчета расстояния между
центры ионов Cs ⁺ и Cl ^— в
CsCl.

CsCl кристаллизуется в простой кубической элементарной ячейке Cl ^—
ионов с ионом Cs ⁺ в центре тела
ячейку, как показано на рисунке ниже.

Прежде чем мы сможем вычислить расстояние между центрами
ионы Cs ⁺ и Cl ^— в этом кристалле,
однако мы должны признать справедливость одного из простейших
предположения об ионных твердых телах: положительные и отрицательные ионы
эти кристаллы соприкасаются.

Таким образом, мы можем предположить, что диагональ через тело
элементарная ячейка CsCl эквивалентна сумме радиусов двух
Ионы Cl ^— и два иона Cs ⁺ .

Трехмерный эквивалент теоремы Пифагора
предполагает, что квадрат диагонали на теле
куб — это сумма квадратов трех сторон.

Извлечение квадратного корня из обеих частей этого уравнения дает
следующий результат.

Если длина края ячейки в CsCl составляет 0,4123 нм, диагональ
поперек тела в этой элементарной ячейке составляет 0,7141 нм.

Сумма ионных радиусов Cs ⁺ и Cl ^—
ионов составляет половину этого расстояния, или 0,3571 нм.

Если бы у нас была оценка размера либо Cs ⁺
или ион Cl ^— , мы могли бы использовать результаты для расчета
радиус другого иона. Ионный радиус Cl ^—
ion равен 0.181 нм. Подставляя это значение в последнее уравнение
дает значение 0,176 нм для радиуса Cs ⁺
ион.

Результаты этого расчета находятся в разумном согласии.
со значением 0,169 нм, известным для радиуса Cs ⁺
ион. Расхождение между этими значениями отражает тот факт, что
ионные радиусы варьируются от кристалла к кристаллу. Табличные
значения являются средними результатами ряда расчетов
этот тип.

Задачи к упражнениям 3: Кристаллическая структура

В кристалле атомы расположены прямыми рядами в трехмерной периодической структуре.
Небольшая часть кристалла, которая может повторяться для образования всего кристалла, называется элементарной ячейкой.

Кристалл можно указать несколькими способами.Один из способов — повторить примитивную элементарную ячейку в каждом векторе трансляции,

$$ \ vec {T} = h \ vec {a} _1 + k \ vec {a} _2 + l \ vec {a} _3 $$

Здесь $ \ vec {a} _1 $, $ \ vec {a} _2 $, $ \ vec {a} _3 $ — это примитивные векторы решетки, а $ h $, $ k $ и $ l $ — целые числа. Примитивные векторы решетки не уникальны; возможны различные варианты выбора примитивных векторов решетки.

Другой распространенный способ задания кристалла — задать параметры решетки $ (a, b, c, \ alpha, \ beta, \ gamma) $, пространственную группу и асимметричную единицу.Параметры решетки $ a $, $ b $ и $ c $ — длины сторон параллелепипеда; $ \ alpha $ — угол между $ b $ и $ c $; $ \ beta $ — угол между $ a $ и $ c $; а $ \ gamma $ — угол между $ a $ и $ b $. Этот параллелепипед может иметь больший объем, чем примитивная элементарная ячейка. Если возможно использовать кубическую элементарную ячейку, кристаллографы используют наименьший возможный куб в качестве обычной элементарной ячейки. Для простой кубической элементарной ячейки обычная элементарная ячейка является примитивной элементарной ячейкой, но для ОЦК объемная элементарная ячейка в два раза превышает объем примитивной элементарной ячейки, а для ГЦК-ячейки обычная элементарная ячейка имеет объем в четыре раза больше примитивной элементарной ячейки.Асимметричная единица — это минимальное количество атомов, которое необходимо указать для создания основы путем применения симметрии пространственной группы к асимметричной единице.

Параметры решетки, обычные элементарные ячейки и примитивные элементарные ячейки некоторых обычных кристаллических структур связаны ниже.

3.1 Объясните, что такое решетка Браве и что такое базис. Как можно построить основу из асимметричного блока?

3.2 Фторид кальция, CaF ₂ , имеет ГЦК решетку Браве и основу с Ca в 000 и F в дробных координатах ¼ ¼ ¼ и ¾ ¾ ¾ обычной (кубической) элементарной ячейки.Нарисуйте одну условную (кубическую) элементарную ячейку структуры. Нарисуйте примитивную элементарную ячейку. Постоянная решетки составляет $ a = $ 5,451 Å. Каково расстояние от атома Са до атома F в Ангстремах?

3.3 Графен представляет собой двумерную решетку, которая построена путем непрерывного расположения правильных шестиугольников sp²-гибридизованных атомов углерода (см. Ниже). Расстояние между ближайшими соседними атомами 0,14 нм.

(а) Что такое решетка Браве графена?

(b) Изобразите примитивную элементарную ячейку Вигнера-Зейтца.

(c) Сколько атомов в примитивной элементарной ячейке?

(d) Определите базисные векторы, которые описывают положения атомов в элементарной ячейке. Сначала запишите эти базисные векторы в терминах абсолютных положений (с компонентами x и y и расстояниями в Ангстремах), а затем в дробных координатах. Для дробных координат задайте позиции в терминах обычных векторов решетки. В этом случае обычные векторы решетки такие же, как и векторы примитивной решетки.

3.4 Пространственная группа кристалла — 227. Как определить точечную группу и решетку Браве этого кристалла?

3.5 Ниже показаны стандартные параметры элементарной ячейки и решетки графита.

Что такое решетка Браве, базис, примитивные векторы решетки и объем примитивной элементарной ячейки?

3,6 Обычная (кубическая) элементарная ячейка из цинковой обманки, ZnS, показана ниже. Обратите внимание на сходство со структурой алмаза.

(а) Сколько атомов каждого типа содержится в обычной элементарной ячейке?

(б) Что такое решетка Браве?

(c) Дайте набор фундаментальных векторов трансляции $ (\ vec {a} _1, \ vec {a} _2, \ vec {a} _3) $, который можно использовать для определения примитивной элементарной ячейки. Сколько атомов в примитивной ячейке?

3.7 Двумерный кристалл показан ниже.

(a) Изобразите элементарную ячейку, показывающую два примитивных вектора решетки в этой плоскости.{\ circ} $. Вычислите объем примитивной элементарной ячейки в $ a $.

3.10 Покажите для идеальной структуры ГПУ, что соотношение $ c / a $ равно

\ [\ begin {уравнение}
\ frac {c} {a} = \ sqrt {\ frac {8} {3}} = 1,633.
\ конец {уравнение} \]

3.11 Имеется четыре ромбических решетки Браве, но только две тетрагональные решетки Браве.

(a) Покажите, что тетрагональная решетка с центром в основании (C) эквивалентна примитивной (P) тетрагональной решетке.

(b) Покажите, что гранецентрированная (F) тетрагональная решетка эквивалентна объемно-центрированной (I) тетрагональной решетке.

Четырнадцать решеток Браве

3.12 Изобразите следующие кристаллические структуры: простую кубическую, ГЦК, ОЦК, NaCl, CsCl, гексагональную, тетрагональную и ромбическую.

3.13 Покажите, что максимальная доля доступного объема, который может быть заполнен твердыми сферами, расположенными на различных решетках, составляет: простая кубическая, 0,52; объемно-центрированный кубический, 0,68; гранецентрированный кубический, 0,74.

Индексы Миллера
Каждая точка решетки Браве может быть достигнута из начала координат вектором трансляции вида

\ [\ begin {уравнение}
\ vec {T} _ {hkl} = h \ vec {a} _1 + k \ vec {a} _2 + l \ vec {a} _3,
\ конец {уравнение} \]

, где $ \ vec {a} _1 $, $ \ vec {a} _2 $, $ \ vec {a} _3 $ — это примитивные векторы решетки, а $ h $, $ k $ и $ l $ — целые числа, называемые Индексы Миллера.Направление, которое указывает вектор $ \ vec {T} _ {hkl} $, обозначено квадратными скобками, $ [hkl] $. Если есть направления, эквивалентные по симметрии, любое из эквивалентных направлений указывается угловыми скобками <$ hkl $>.

Например, в кубической системе:
= [100], [010], [001], [-100], [0-10], [00-1]
= [110], [-1-10] ], [1-10], [-110], [101], [-10-1], [-101], [10-1], [011], [0-1-1], [0- 11], [01-1].

Часто знаки минус рисуются как надстрочные линии [-10-1] = $ \ left [\ overline {1} 0 \ overline {1} \ right] $.Это произносится как one-bar zero one-bar.

Плоскости
С помощью индексов Миллера плоскости обозначаются изогнутыми скобками $ (hkl) $. Плоскость $ (hkl) $ пересекает ось в направлении $ \ vec {a} _1 $ в $ \ frac {| \ vec {a} _1 |} {h} $, ось в направлении $ \ vec {a} _2 $ в точке $ \ frac {| \ vec {a} _2 |} {k} $, а ось в направлении $ \ vec {a} _3 $ в точке $ \ frac {| \ vec {a} _3 |} {l} $.

Эквивалентные плоскости обозначены фигурными скобками $ \ {hkl \} $. Три точки, которые можно использовать для определения плоскости $ (hkl) $: $ \ left (\ frac {a_ {1x}} {h}, \ frac {a_ {1y}} {h}, \ frac {a_ {1z) }} {h} \ right) $, $ \ left (\ frac {a_ {2x}} {k}, \ frac {a_ {2y}} {k}, \ frac {a_ {2z}} {k} \ right) $ и $ \ left (\ frac {a_ {3x}} {l}, \ frac {a_ {3y}} {l}, \ frac {a_ {3z}} {l} \ right) $.Вектор нормали к этой плоскости может быть определен как произведение двух векторов в плоскости. Если $ (h, k, l \ ne 0) $, два подходящих вектора: $ \ vec {v} _1 = \ frac {\ vec {a} _1} {h} — \ frac {\ vec {a} _3} {l} $ и $ \ vec {v} _2 = \ frac {\ vec {a} _2} {k} — \ frac {\ vec {a} _3} {l} $. {\ circ} $.Из этой информации определяют примитивные векторы решетки. Какова длина вектора сдвига при $ h = 4 $, $ k = 3 $ и $ l = 1 $?

3.16 Изобразите плоскости (111) и (222) в простой кубической элементарной ячейке с постоянной решетки $ a $. Определите нормальное расстояние между двумя плоскостями.

3.17 Изобразите кристаллическую структуру NaCl. Что такое решетка Браве? Какую форму имеет ячейка Вигнера-Зейтца? Каково положение атомов базиса в дробных координатах условной (кубической) элементарной ячейки? Нарисуйте плоскость (111).

3.18 Рассчитайте угол между направлением [110] и направлением [111] для моноклинной решетки с a = 0,3 нм, b = 0,4 нм, c = 0,5 нм и β = 107 °.

3,19 Металл имеет кристаллическую структуру с ГЦК-решеткой. Постоянная решетки составляет 0,38 нм, а атомный вес атомов — 85. Постоянная решетки — это длина обычной (кубической) элементарной ячейки. Масса атома равна атомному весу, умноженному на атомную постоянную массы $ u $ = 1.6605402 × 10 ^-27 кг.

а) Какова плотность этого металла?

б) Какое расстояние между соседними атомами?

c) Металл разрезается так, чтобы выступ (111) выступал на поверхности. Нарисуйте расположение атомов, которое вы бы увидели, если бы посмотрели на эту поверхность. Обозначьте два направления в плоскости (111).

3.20 ОЦК кристалл разрезают так, чтобы плоскость (011) выходила на поверхность. Изобразите расположение атомов на поверхности кристалла.Как можно экспериментально определить структуру атомов на поверхности металла?

Набор плоскостей, перпендикулярных вектору \ (A_x \ hat {x} + A_y \ hat {y} + A_z \ hat {z} \) равен,

$$ A_xx + A_yy + A_zz = C, $$

где \ (C \) — любая постоянная. Если точка \ ((x_0, y_0, z_0) \) на плоскости известна, \ (C \) можно вычислить,

$$ C = A_xx_0 + A_yy_0 + A_zz_0. $$

Приложение ниже решит 3 линейных уравнения для трех неизвестных. (Он определяет точку пересечения трех плоскостей.)

3.21 Грани ячейки Вигнера-Зейтца определяются плоскостями, которые перпендикулярно делят векторы пополам от начала координат к точкам решетки Браве. Чтобы определить, где находятся углы ячейки Вигнера-Зейтца, необходимо найти точки пересечения трех плоскостей. Для ОЦК-решетки примитивные векторы решетки равны,

$ \ vec {a} _1 = \ frac {a} {2} (\ hat {x} + \ hat {y} — \ hat {z}), \ quad \ vec {a} _2 = \ frac {a } {2} (- \ hat {x} + \ hat {y} + \ hat {z}), \ quad \ vec {a} _3 = \ frac {a} {2} (\ hat {x} — \ шляпа {y} + \ hat {z}) $.

Здесь $ a $ — длина стороны условной кубической элементарной ячейки. В какой точке пересекаются плоскости, разделяющие векторы $ \ vec {a} _1 $, $ \ vec {a} _2 $ и $ \ vec {a} _3 $?

3.22 Индексы Миллера $ hkl $ обозначают конкретную плоскость в решетке Браве, в качестве обозначения плоскости индексы Миллера даны в круглых скобках. Обратите внимание, что три индекса Миллера взаимно просты (teilerfremd). Это означает, что плоскость пересекает точки решетки Браве. Пример плоскости (623) показан ниже.

(a) Нарисуйте плоскость (313).

(b) Нарисуйте плоскость (340).

3.23. Плоскость разрезает кристаллографические оси кристалла в точках $ 3 \ vec {a} $, $ 4 \ vec {b} $ и $ 6 \ vec {c} $, где $ \ vec {a} $, $ \ vec {b} $ , а $ \ vec {c} $ — примитивные векторы решетки. Какие у этого самолета индексы Миллера?

3.24 Изобразите ячейки Вигнера-Зейтца следующих решеток:

1. Решетка наклонная в 2-D
2. Центрированная прямоугольная решетка в 2-D
3. ОЦК решетка в 3-D

В двух измерениях решетка Браве имеет два примитивных вектора решетки \ (\ vec {a} \) и \ (\ vec {b} \).Длины этих векторов являются постоянными решетки \ (a \) и \ (b \). Угол между примитивными векторами решетки равен \ (\ gamma \). Имеется пять двумерных решеток Браве,

• кубический: \ (a = b \), \ (\ gamma \) = 90 °.
• шестиугольник: \ (a = b \), \ (\ gamma \) = 120 °.
• прямоугольный: \ (a \ neq b \), \ (\ gamma \) = 90 °.
• прямоугольных с центром: \ (a \ neq b \), \ (\ gamma \) = 90 ° и две точки решетки на элементарную ячейку.
• наклон: \ (a \ neq b \), \ (\ gamma \ neq \) 90 °.

Если для описания периодической структуры можно использовать более одной решетки Браве, существуют правила приоритета для определения двумерных решеток Браве.

1. Используйте решетку Браве с высшей симметрией (кубическая> шестиугольная> прямоугольная> наклонная).
2. Используйте решетку Браве с наименьшей площадью элементарной ячейки.
3. Используйте Bravais с наименьшими постоянными решетки a и b.
4. Используйте \ (a \ leq b \), \ (\ gamma \ geq \) 90 °.

3.25 В мозаике Каира двумерная плоскость полностью заполнена пятиугольниками. Геометрия единого пятиугольника образована четырьмя сторонами одинаковой длины (синий) и одной стороной с разной длиной (красный) и углами 90 ° и 120 °. ВНИМАНИЕ !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

(a) Определите двумерную решетку Браве мозаичного покрытия Каира.

(b) Изобразите векторы элементарной ячейки \ (\ vec {a} \) и \ (\ vec {b} \) и заключенный в них угол \ (\ gamma \).

(c) Определить \ (\ gamma \).

(d) Сколько плиток находится в одной элементарной ячейке?

3.26 Плитка треугольник-шестиугольник покрывает двумерную плоскость с равносторонними треугольниками и шестиугольниками. Используются две разные длины (нарисованные синим и красным) с соотношением 3: 2. Расположение плиток показано на рисунке ниже.

(a) Определите двумерную решетку Браве мозаики.

(b) Нарисуйте точки решетки Браве.

(c) Изобразите векторы элементарной ячейки \ (\ vec {a} \) и \ (\ vec {b} \) и заключенный в них угол \ (\ gamma \).

(d) Сколько треугольников и шестиугольников в элементарной ячейке?

(e) Сколько треугольников и шестиугольников связано с одной точкой решетки Браве?

3.{\ circ}) $ четыре индекса Миллера $ (hkil) $ используются для обозначения кристаллографической плоскости. Индекс Миллера $ i $ определяется как $ i = -h-k $. Использование индекса $ i $ упрощает идентификацию эквивалентных плоскостей (эквивалентные плоскости — это плоскости с одинаковым межплоскостным расстоянием $ d_ {hkl} $ гексагональной решетки, поскольку циклическая перестановка индексов $ hki $ внутри $ (hkil) $ дает эквивалентные самолеты.

Показать графически все плоскости, эквивалентные (11-20).

3,28 Полюса — это направления, перпендикулярные кристаллографической плоскости

Рассмотрим ромбическую решетку с постоянными $ a = 3 $ Å, $ b = 4 $ Å, $ c = 5 $ Å.Укажите (приблизительное) полюсное направление плоскости (210), которое является кристаллографическим направлением [uvw], ориентированным перпендикулярно плоскости (210).

Комментарий:
Эта проблема может быть решена графически, графическое решение более сложно для общей плоскости, такой как (213).

3.29 Рассмотрим кубическую решетку. Задайте монокристаллографическое направление [uvw], которое находится в плоскости (111). Обратите внимание, что в плоскости (111) много направлений.

Более сложная проблема: рассмотрим триклинную решетку.Укажите все кристаллографические направления [uvw], которые находятся в плоскости (111).

Базы данных по кристаллической структуре

Следующие онлайн-ресурсы содержат файлы, которые можно загрузить для интерактивного просмотра либо из автономного программного обеспечения для визуализации, либо просмотреть с веб-сайта в виде Java-апплета.

• База данных по кристаллической структуре американских минералогов. Этот сайт представляет собой интерфейс к базе данных кристаллических структур, которая включает все структуры, опубликованные в American Mineralogist, Canadian Mineralogist и European Journal of Mineralogy.База данных поддерживается Минералогическим обществом Америки и Минералогической ассоциацией Канады и финансируется Национальным научным фондом. Сайт доступен для поиска по минералу, автору, химическому составу или параметрам ячейки и симметрии. (подробнее)
• Структуры кристаллической решетки. Эта страница, поддерживаемая Лабораторией военно-морских исследований США, предлагает краткий указатель общих структур кристаллической решетки, в том числе из минералов и неминералов.Несколько различных графических представлений, интерактивный Java-апплет структуры и полезную информацию о решетках можно получить, щелкнув изображения кристаллических структур. (подробнее)
• Кристаллические структуры. На этом веб-сайте представлены интерактивные Java-апплеты различных кристаллических структур минералов и неминералов. Аплет Java позволяет пользователю вращать и изменять размер кристалла. На сайте также есть ссылки на другие веб-страницы о кристаллических структурах.(подробнее)
• Кристаллографическая база данных минералов и их структурных аналогов. Эта доступная для поиска база данных, которую ведет Российский фонд фундаментальных исследований, включает 4785 записей (2365 уникальных названий минералов). Каждый минерал можно искать по названию, спецификации, кристаллохимической формуле или характеристикам кристаллической структуры. Информация о кристаллической структуре включает в себя название минерала, спецификацию, кристаллохимическую формулу, пространственную группу, параметры элементарной ячейки, координаты, тепловые факторы и расположение атомов, а также ссылки на литературу по определению кристаллической структуры.(подробнее)
• Открытая база данных кристаллографии. Эта база данных является сестрой Базы данных по кристаллической структуре американских минералогов (AMCSD) и содержит все данные, которые есть в AMCSD, а также данные, депонированные отдельными лицами и лабораториями. База данных доступна для поиска по тексту, словам, элементам, объему или количеству элементов. Данные о кристаллической структуре можно загрузить в формате CIF, и пользователи могут загружать данные о кристаллах в виде файлов CIF или REF. (подробнее)
• ICSD Web: База данных неорганических кристаллов. Этот сайт содержит бесплатную демонстрационную версию базы данных неорганических кристаллов. Эта база данных содержит 3325 структурных подмножеств из 76480 неорганических структур по состоянию на 2004 год. Демонстрационная версия может быть запрошена и доступна через веб-интерфейс, который позволяет использовать несколько методов поиска, а полученные кристаллические структуры затем можно просмотреть в Интернете (с помощью CHIME плагин) или загружены для просмотра с помощью другого программного обеспечения для визуализации. На сайте также представлены обновления с исправлениями ошибок, условия использования и цены, советы по отображению структур, галерея изображений, флэш-ролик и инструкции по установке сервера ICSD.