Содержание
Масштаб. Измерение расстояний по планам, картам и глобусу
Чтобы измерить расстояние по плану, карте или глобусу, нужно знать, что такое масштаб и уметь им пользоваться. Масштаб – одна из основных математических составляющих любой географической модели Земли, он показывает, во сколько раз уменьшены все расстояния на карте по сравнению с теми же расстояниями на местности.
Если масштабирование не произвести, то никакой бумаги не хватит, чтобы изобразить на ней даже небольшой участок поверхности. На старинных картах размеры и расстояния уменьшены в неодинаковое количество раз, поэтому по ним можно узнать очертания объектов, но не их величину.
Как обозначается масштаб?
Масштаб плана или карты всегда один, но указываться он может тремя разными способами. Способы обозначения масштаба следующие:
- численные;
- именованные;
- графические (линейные и поперечные).
Численный масштаб имеет вид дроби, например 1:1000, числитель которой показывает единицу измерения на карте, а знаменатель – во сколько раз она уменьшена по сравнению с действительным расстоянием, второе число называется величиной масштаба. Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб топографическтй карты
Но, зная математику, мы легко можем перевести сантиметры в метры или километры. Чтобы делать это быстрее, переводя в метры, просто зачёркиваем 2 нуля, так как в 1м – 100 см, а в километры – убираем 5 нулей. Пример: 1:1000 – убираем 2 нуля и получаем 10 метров. Если масштаб один к ста тысячам, например, тогда уже можно перевести знаменатель и в километры – 1:100 000, для этого уберём 5 нулей, потому что в 1 км 100 000 см. Получим, что в 1 см на карте 10 км на местности, а это будет уже другой вид масштаба – именованный.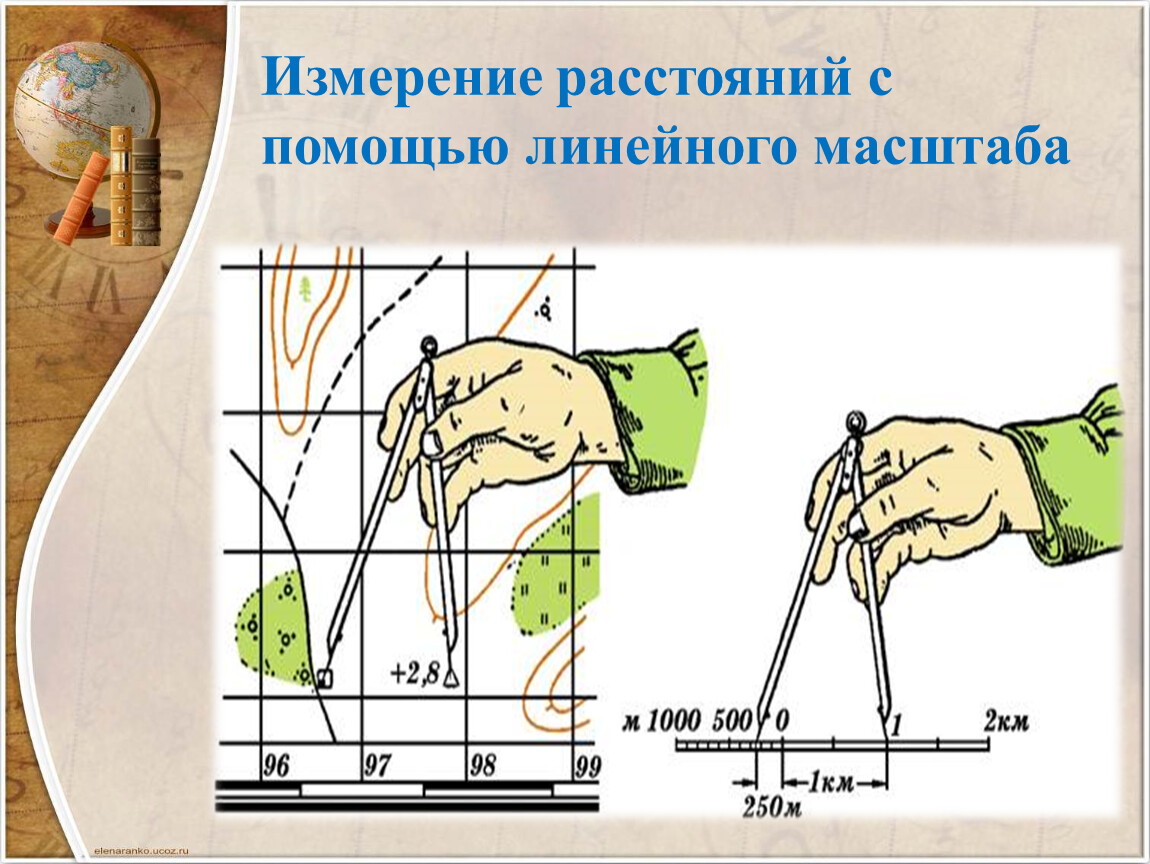
Именованный масштаб указывается на всех картах, он дополняется словами. В 1 см – 10 м, 10 м – это величина масштаба. Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
- 1:25 000 000 – 1см-250 км;
- 1:10 000 000 – 1см-100 км;
- 1:20 000 – 1см-200 м.
При необходимости обратного перевода добавляем те же нули, при переводе километров в сантиметры добавим 5 нулей, метров в сантиметры – 2 нуля. Например:
- 1 см-300 м – это 1:30 000;
- 1см-250 км – это 1:25 000 000.
Для непосредственного определения расстояния по картам и планам служит линейный масштаб. Это график, помещаемый внизу карты в виде линейки (масштабная линейка), в России она разделёна на сантиметры. Справа от нуля у каждого деления линейки подписано истинное расстояние на местности, равное одному, двум или нескольким величинам масштаба. Слева от нуля сантиметр линейки разбивают на меньшие деления, например на миллиметры, для получения более точных результатов.
Как измерять расстояние по карте, плану или глобусу?
Измерять расстояния можно при помощи масштаба или градусной сетки (на плане её нет). Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Измерения нужно производить очень точно, учитывая миллиметры. Затем полученные данные умножить на величину масштаба. Например, если при измерении мы получили расстояние 1,4 см, а масштаб карты в 1см 10 000 км, нужно умножить 1,4 на 10 000, получится 14 000 км – это и есть расстояние на местности. Нужно знать, что мы узнаём не действительное расстояние, а его проекцию. Линия на карте может иметь разные неточности в связи с углом наклона земной поверхности.
При помощи линейного масштаба измеряют расстояние линейкой или циркулем, переносят это расстояние на масштабную линейку и без дополнительных расчетов получают искомое расстояние. При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Глобус – объёмная модель Земли. Он показывает шарообразную форму нашей планеты. На нём все объекты изображены в неискажённом виде. В отличие от карты, они сохраняют свою форму, площадь, длину. Направления на глобусе совпадают с направлениями на Земле. У глобуса всюду один и тот же масштаб, который обычно надписывается в южной части Тихого океана. Масштабы школьных глобусов очень мелкие: 1:50 000 000, т. е. в 1 см – 500 км, истинное расстояние на нём уменьшается в 50 миллионов раз.
Для определения расстояний по глобусу надо ниткой или полоской бумаги измерить расстояние между заданными пунктами и, зная масштаб глобуса, вычислить истинное расстояние с помощью пропорции, как по обычной карте.
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
- мелкомасштабные (обзорные) — с масштабом менее 1: 1 000 000;
- среднемасштабные (обзорно-топографические) – в пределах 1: 200 000 до 1: 1 000 000;
- крупномасштабные (топографические) – от 1: 200 000 до 1: 10 000.
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.
Вам будет интересно
Как рассчитать расстояние по параллели.
 Определение расстояний на карте
Определение расстояний на карте
Масштабом
называется отношение длины линии на чертеже, плане или карте к длине соответствующей линии в действительности. Масштаб показывает, во сколько раз расстояние на карте уменьшено относительно реального расстояния на местности. Если, например, масштаб географической карты 1: 1 000 000, это значит, что 1 см на карте соответствует 1 000 000 см на местности, или 10 км. Различают численный, линейный и именованный масштабы.
Численный масштаб
изображается в виде дроби, у которой числитель равен единице, а знаменатель – число, показывающее, во сколько раз уменьшены линии на карте (плане) относительно линий на местности. Например, масштаб 1:100 000 показывает, что все линейные размеры на карте уменьшены в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем масштаб мельче, при меньшем знаменателе масштаб крупнее. Численный масштаб – это дробь, поэтому числитель и знаменатель даются в одинаковых измерениях (сантиметрах). Линейный масштаб
Линейный масштаб
представляет собой прямую линию, разделенную на равные отрезки. Эти отрезки соответствуют определенному расстоянию на изображаемой местности; деления обозначаются цифрами. Мера длины, по которой нанесены деления на масштабной линейке, называются основанием масштаба. В нашей стране основание масштаба принято равным 1 см. Количество метров или километров, соответствующее основанию масштаба, называют величиной масштаба. При построении линейного масштаба цифру 0, от которой начинается отсчет делений, обычно ставят не у самого конца масштабной линии, а отступив на одно деление (основание) вправо; на первом же отрезке налево от 0 наносят наименьшие деления линейного масштаба – миллиметры. Расстояние на местности, соответствующее одному наименьшему делению линейного масштаба, отвечает точности масштаба, а 0,1 мм – предельной точности масштаба. Линейный масштаб по сравнению с численным имеет то преимущество, что дает возможность без дополнительных вычислений определять действительное расстояние на плане и карте.
Именованный масштаб
– масштаб, выраженный словами, например, в 1 см 75 км. (рис. 5).
Измерение расстояний на карте и плане
. Измерение расстояний с помощью масштаба.. Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1: 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е. на местности это расстояние составляет 1ж5 = 5 (км). Измерять расстояние по карте можно и с помощью циркуля-измерителя. В этом случае удобно пользоваться линейным масштабом.
Измерение расстояний с помощью градусной сети.
Для расчета расстояний по карте или глобусу можно использовать следующие величины: длина дуги 1° меридиана и 1° экватора равна приблизительно 111 км. Для меридианов это верно всегда, а длина дуги 1° по параллелям уменьшается к полюсам. На экваторе его можно тоже принять равному 111 км. А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.
А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.
ü Частный масштаб площади (р).
ü Искажение площади (vp).
ü Наибольший масштаб (а).
ü Наименьший масштаб (b).
ü Максимальный угол искажений (w).
ü Коэффициент искажения форм (k).
В ходе курсовой работы использованы следующие обозначения:
n – масштаб по параллели;
m – масштаб по меридиану;
e – уклонение угла t от 90°;
t – угол между меридианом и касательной к параллели;
l1 – длина меридиана в выделенной трапеции на карте;
L1 – длина меридиана в выделенной трапеции на местности;
l2 – длина параллели в выделенной трапеции на карте;
L2 – длина параллели в выделенной трапеции на местности.
Частный масштаб площади определяется по формуле:
где ;
;
Искажение площади
.
Наибольший и наименьший масштабы определяются из системы:
;
где а – наибольший масштаб;
b – наименьший масштаб.
Максимальный угол искажений:
Коэффициент искажения форм:
1.
Выберем на карте т. А. Ограничим относительно т. А площадь по долготе от 34° до 36°, по широте от 58° до 60°.
Определение длин меридиана и параллели
2.
Определили масштаб по меридиану. Масштаб вдоль меридиана вычислили по формуле:
где l1 – длина меридиана в мм;
m – знаменатель масштаба карты;
L1 – длина дуги соответствующего меридиана по поверхности эллипсоида.
где Li – длины дуг меридианов в 1° по широте
L1 = 222794 м = 222794 ´103 мм
m === 1,000925.
3.
Определили масштаб по параллели
где l2 – длина параллели в мм;
L2 – длина соответствующей параллели на поверхности эллипсоида (L2 = LjА´Dl)
LjА – длина параллели в м соответствует 1° на широте jА
Dl – длина параллели в градусной мере равна разности долгот между восточным и западным меридианом.
L2 = 57476 м ´ 2 = 114952 м = 114952 ´103 мм
n === 0,991718.
4.
На карте транспортиром измерили угол t (угол между меридианом и параллелью), определили уклонения угла t от 90° по формуле:
e = 90° – t (3)
e = 90° – 89°59¢ = 0°01¢
5.
Вычислили масштаб площади:
p = m ´ n ´ cose (4)
где m – масштаб по меридиану (1)
n – масштаб по параллели (2)
e – уклонение угла t от 90° (3)
p = 1,000925 ´ 0,991718 ´ cos 0°01¢ = 0,992635
6.
Определили наибольшее искажение углов в точке А по формуле:
где a – b =
a + b =
a – b = = 0,009207
a + b = = 1,992643
7.
Вычислили коэффициент искажения форм по формуле
Для нормальной конической проекции с одной главной параллелью значение m, n частных масштабов и масштаб площади р вычислены по следующей формуле:
где mо= 1000000 (знаменатель масштаба карты),
r – радиусы параллелей.
результаты вычислений представлены в таблице по форме 6.
Вычисление масштабов длин и площадей для нормальной конической проекции с одной главной параллелью
На основании найденных масштабов длин и площадей построены кривые изменения масштабов m=n, p.
График масштабов длин и площадей в нормальной равноугольной конической проекции
2.4
Содержание и назначение карты
Для составления карты масштаба 1:1000000 привлекаются топографические карты разных масштабов. Наиболее удобно использовать листы географической карты масштаба 1:1000000.
При выполнении данной курсовой работы в качестве картографического источника используется карта Вологодской области масштаба 1:1000000.
Картографическое изображение включает физико-географические и социально-экономические объекты содержания карты.
К физико-географическим объектам относятся:
ü гидрография;
ü рельеф;
ü растительность;
КАРТА 2014
1.Понятие
.
КАРТА — Это уменьшенное обобщенное изображение большого участка земли построенное в картографической проекции в мелком и среднем с помощью условных знаков.
2. признаки карты
.
Учитывается кривизна земли,-есть искажение,-есть градусная сеть — изображены большие участки земли
Условные знаки даны обобщенно (генерализация), не похожи на реальные объекты,-средний и мелкий масштаб
3. картографические проекции
-это математические способы изображения шарообразной Поверхности на плоскость
Виды проекции по вспомогательной поверхности
ВИДЫ КАРТ
ОПРЕДЕЛЕНИЕ ПО КАРТАМ РАССТОЯНИЙ, ВЫСОТЫ, ГЛУБИНЫ,НАПРАВЛЕНИЙ
ГРАДУСНАЯ СЕТЬ
1.Понятие
—
система меридианов, параллелей на картах и глобусах, служащая для определения географических координат объекта
2. причина существования-
вращение шарообразной земли вокруг своей оси, в результате чего образуется две неподвижные точки- полюса, через которые проведена система меридианов и параллелей.
3. характеристика полюсов-
это математически высчитаны точки пересечения воображаемой оси с земной поверхностью.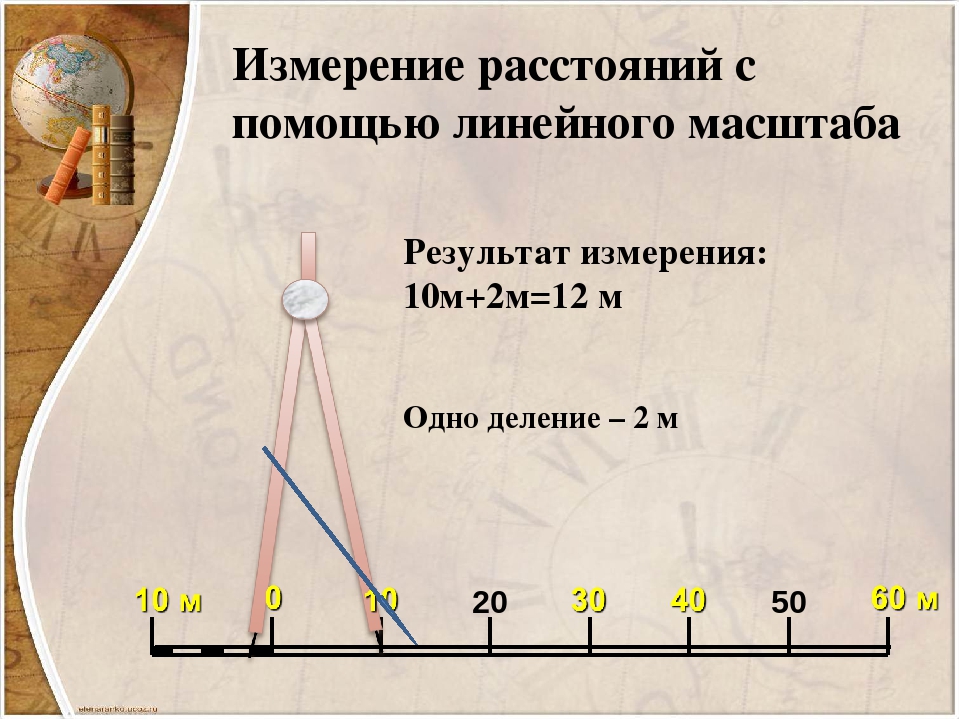 Бывает северный и южный полюс.
Бывает северный и южный полюс.
4. характеристика меридианов
— это воображаемая кратчайшая линия проведенная между северным и южным полюсам.
5 Характеристика параллелей-
это воображаемая линия проведенная на одинаковом расстоянии параллельно экватору
6. характеристика широты
—
это расстояние от экватора до заданного объекта выраженное в градусах
7. характеристика долготы
—
это расстояние от нулевого меридиана до заданного объекта выраженного в градусах.
8. значение
—
определения координат и расстояний.
ЗАДАНИЯ
ЗАДАНИЯ НА ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ПО ГРАДУСНОЙ СЕТКЕ
| По меридианам | |
| (Через 10°,20…..) | |
| 111 км. | |
| По параллелям | |
(Через 10°,20…. .) .) | |
| 3.Находят в километрах длину дуги в 1° по данной параллели 0° – 111,3 км 10° – 109,6 км 20° – 104,6 км 30° – 96,5 км 40° – 85,3 км | 50° – 71,1 км 60° – 55,8 км 70° – 38,2 км 80° – 19,8 км 90° – 0 км |
| По меридианам между точками 1-2 | |
| 1. Сначала определяют, через сколько градусов проведены меридианы на данной карте | Через20 |
| 2. Вычисляют расстояние в градусах между объектами, считая, градусные клетки или разницу по долготе | 1 клетка=20 градусов Т1 лежит на 40 з.д. Т2 лежит на 20 з.д. 40-20=20 градусов |
| 3.Вспоминают, чему равна в километрах длина дуги в 1° по меридиану | 111 км. |
| 4.Умножают данное расстояние в градусах между объектами на 111 км | 20 умножить на 111км=2220км |
| По параллелям между точками 1-3 | |
1. Сначала определяют, через сколько градусов проведены параллели на картах полушарий Сначала определяют, через сколько градусов проведены параллели на картах полушарий | Через 20 Широта 40 с.ш. |
| 2. Вычисляют расстояние в градусах считая, градусные клетки или разницу по широте | 2 клетка=40 градусов |
| 3.Находят в километрах длину дуги в 1° по данной параллели | 20° – 104,6 км |
| 4. Умножают данное расстояние в градусах между объектами на длину дуги в 1° по данной параллели | 40 умножить на 104,6 км= |
| | | следующая лекция ==> | |
как определить расстояние по параллелям? как определить расстояние по параллелям в атласе? и получил лучший ответ
Ответ от Nat f[новичек]
С помощью линейки — измеряется расстояние от точки «А» до точки «Б» , полученное расстояние умножается на масштаб и получается расстояние на местности,
С помощью циркуля — между ножками циркуля-измерителя установить небольшой раствор, затем перемещать циркуль вдоль измеряемой линии. Число перестановок циркуля умножить на взятое между иглами расстояние. После чего это число умножить на масштаб.
Число перестановок циркуля умножить на взятое между иглами расстояние. После чего это число умножить на масштаб.
Например, расстояние между Киевом и Санкт-Петербургом, расположенными примерно на меридиане 30°, составляет 111 км *9,5° = 1054 км; расстояние между Киевом и Харьковом (примерно параллель 50°) – 71 км*6° = 426 км.
Источник:
Ответ от Марина Черенцева
[активный]
до чего докатились отличники!
Ответ от Бейкут Балгышева
[активный]
Меридианы Земли это полуокружности или дуги, которые содержат в себе 180 градусов, (вся окружность 360) или 20 000 км. (длина окружности Земли равна 40 000 км.) , тогда 1 градус меридиана это примерно 111 км. (40 000 км. поделить на 360 градусов) — зная расстояние в градусах меридиана можно вычислить расстояние в километрах, умножив это расстояние на 111 км.
Параллели — это окружности, радиусы которых уменьшаются к полюсам, на разных параллелях величина 1 градуса в километрах неодинакова. Чтобы определить расстояние в километрах на карте или глобусе между двумя пунктами, расположенными на одном меридиане, число градусов между пунктами умножают на 111 км. Для определения расстояния в километрах между пунктами, лежащими на одной параллели, число градусов умножают на длину дуги 1° параллели, обозначенную на карте или определенную по таблицам.
Для определения расстояния в километрах между пунктами, лежащими на одной параллели, число градусов умножают на длину дуги 1° параллели, обозначенную на карте или определенную по таблицам.
Длина дуг параллелей и меридианов на эллипсоиде Красовского
Ответ от Александр Силин
[новичек]
а
Ответ от 3 ответа
[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: как определить расстояние по параллелям? как определить расстояние по параллелям в атласе?
Главный масштаб
. Со странами мира вы впервые познакомились в начальной школе по карте полушарий. В географическом атласе, где помещена, эта карта, указан ее масштаб: в 1 см 900 км. Проверим его. На одном из полушарий измерим расстояние по экватору или по среднему меридиану. Оно составляет 20 см. Это же расстояние в действительности равно 20 000 км. Значит, масштаб карты будет: в 1 см 1000 км. Чем же объяснить такое расхождение?
Для удобства работы картографа ввели понятие «главный масштаб», который относится к определенным местам проекции. Такими местами могут быть точки или линии касания поверхностей, на которые проектируется градусная сетка с глобуса на карту. Для проекции полушария точка касания, называемая точкой нулевых искажений, находится в центре окружности. Непосредственно в точке определить масштаб нам не удастся, но мы можем это сделать на небольшом протяжении в районе этой точки. Для этого измерим здесь длину дуги экватора в 20°. Она получилась равной 2,5 см. В натуре эта дуга составляет 2220 км (20° Х 111 км). Поделим это расстояние на 2,5 см, и мы получим величину масштаба, равную примерно подписанной на карте (в 1 см 900 км).
Такими местами могут быть точки или линии касания поверхностей, на которые проектируется градусная сетка с глобуса на карту. Для проекции полушария точка касания, называемая точкой нулевых искажений, находится в центре окружности. Непосредственно в точке определить масштаб нам не удастся, но мы можем это сделать на небольшом протяжении в районе этой точки. Для этого измерим здесь длину дуги экватора в 20°. Она получилась равной 2,5 см. В натуре эта дуга составляет 2220 км (20° Х 111 км). Поделим это расстояние на 2,5 см, и мы получим величину масштаба, равную примерно подписанной на карте (в 1 см 900 км).
Вопрос о масштабах очень важный и интересный, и мы рассмотрим его более подробно, используя уже знакомый нам . Все три карты, показанные на нем, составлены в цилиндрических проекциях, а для них характерно касание цилиндра по линии экватора. Следовательно, по экватору и будут считаться главные масштабы для наших карт. Нетрудно догадаться, что в данном случае все карты имеют один и тот же главный масштаб, так как промежутки между 10-градусными меридианами везде равны и составляют 4 мм. Нетрудно также определить и величину главного масштаба. Нам известно, что дуга экватора в 10° на земном шаре равна 1110 км. Этому расстоянию соответствует на карте отрезок, равный 0,4 см. Значит, в 1 см карты содержится 2780 км (1110: 0,4) и численный масштаб будет выражен отношением 1:278 000 000.
Нетрудно также определить и величину главного масштаба. Нам известно, что дуга экватора в 10° на земном шаре равна 1110 км. Этому расстоянию соответствует на карте отрезок, равный 0,4 см. Значит, в 1 см карты содержится 2780 км (1110: 0,4) и численный масштаб будет выражен отношением 1:278 000 000.
Кроме главного масштаба, на каждой карте имеются частные масштабы. На карте в квадратной проекции (рис. 27, б) частный масштаб по всем меридианам на всем протяжении одинаковый. На карте в равноугольной проекции (рис. 27, в) он будет постепенно увеличиваться от экватора к полюсу, а на карте в равновеликой проекции (рис. 27, а), наоборот, уменьшаться. Частный масштаб по параллелям на всех трех картах по мере приближения их к полюсу резко возрастает, а на самом полюсе им бессмысленно пользоваться, ибо точка, обозначающая полюс, «растянулась» на всю ширину земной поверхности.
Определим частные масштабы для наших карт по 60-й параллели. Чтобы решить такую задачу, нужно знать длины дуг параллелей на разных широтах.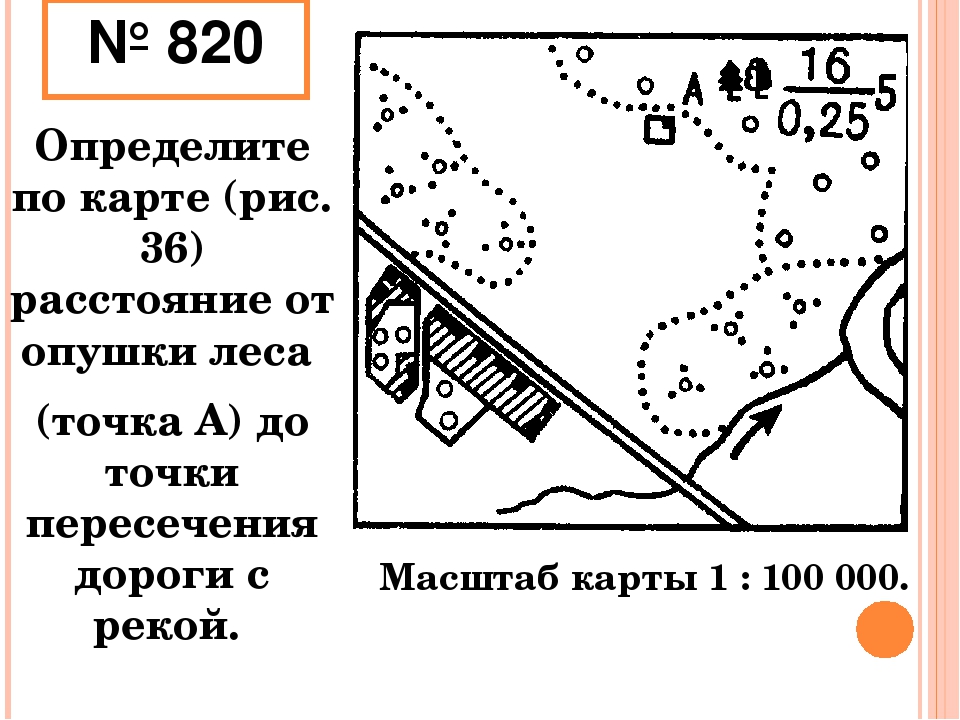 Значения их в 1° возьмем из . Протяженность дуги в 10° будет в 10 раз больше и на широте 60° составит 558 км.
Значения их в 1° возьмем из . Протяженность дуги в 10° будет в 10 раз больше и на широте 60° составит 558 км.
Частный масштаб по 60-й параллели на всех трех картах будет один и тот же, ибо отрезки параллелей, заключенных между меридианами, равны и соответствуют так же, как и по экватору, 0,4 см. Поделим действительное расстояние на этот отрезок и получим величину масштаба, равную примерно 1390 км в 1 см (558:0,4), т. е. масштаб будет в 2 раза крупнее главного. Так можно определить частный масштаб, когда он остается постоянным по всей линии. Если же масштаб непрерывно меняется, то мы получим лишь среднюю его величину. Например, на карте в равноугольной проекции (рис. 27, в) отрезок между 60-й и 70-й параллелями в 2 раза больше, чем у экватора. Значит, на этом отрезке средний масштаб крупнее главного в 2 раза.
Рис. 30. Карты полушария с одним и тем же главным масштабом
Две карты одного масштаба
. В картографической практике не принят термин «средний масштаб» и на всех картах подписывают только главный.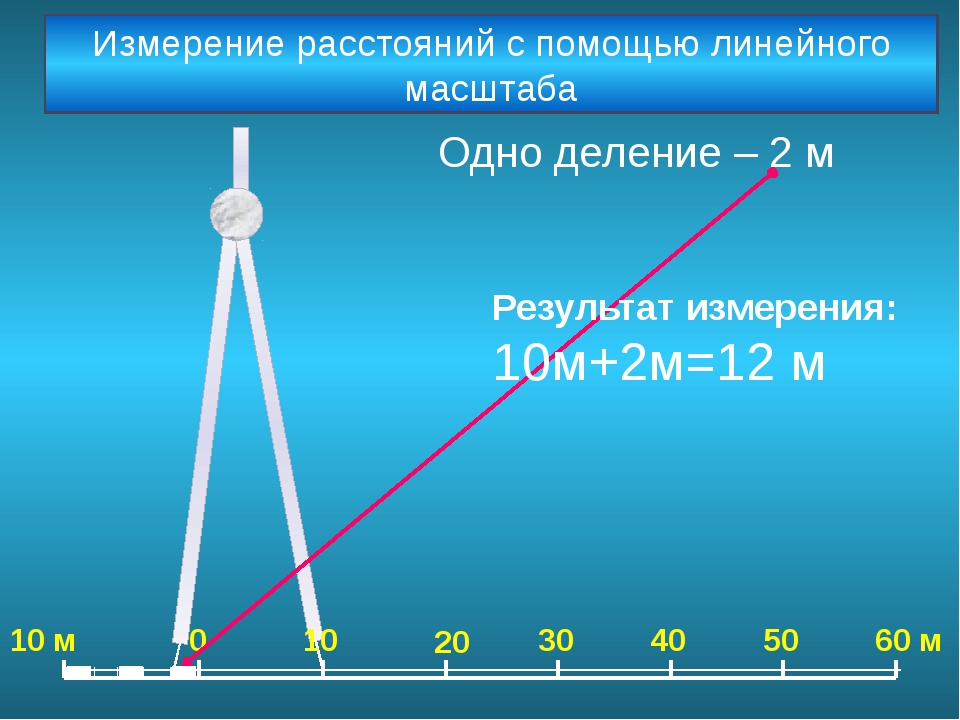 Для тех, кто пользуется картой, главный масштаб не всегда понятен, так как он часто не выражает общей масштабности изображения. Обратимся к рисунку 30, на котором показано полушарие в двух проекциях. По виду геометрической поверхности, на которую проектируется сетка глобуса, обе проекции поперечные азимутальные, а по виду искажений одна из них равноугольная, а вторая произвольная. Диаметр полушария в первой проекции вдвое больше, чем во второй. И тем не менее их главный масштаб одинаков. В это трудно поверить, но это так. Приведем доказательства.
Для тех, кто пользуется картой, главный масштаб не всегда понятен, так как он часто не выражает общей масштабности изображения. Обратимся к рисунку 30, на котором показано полушарие в двух проекциях. По виду геометрической поверхности, на которую проектируется сетка глобуса, обе проекции поперечные азимутальные, а по виду искажений одна из них равноугольная, а вторая произвольная. Диаметр полушария в первой проекции вдвое больше, чем во второй. И тем не менее их главный масштаб одинаков. В это трудно поверить, но это так. Приведем доказательства.
В азимутальных поперечных проекциях картографическую сетку переносят на плоскость, касательную в определенной точке экватора, которая является точкой нулевых искажений. Для нее-то и подписывают на карте главный масштаб. Его величину можно определить следующим образом.
Возьмем клетку картографической сетки, расположенную в районе точки нулевых искажений. В первом приближении она имеет форму квадрата и размеры его в обоих проекциях примерно одинаковы.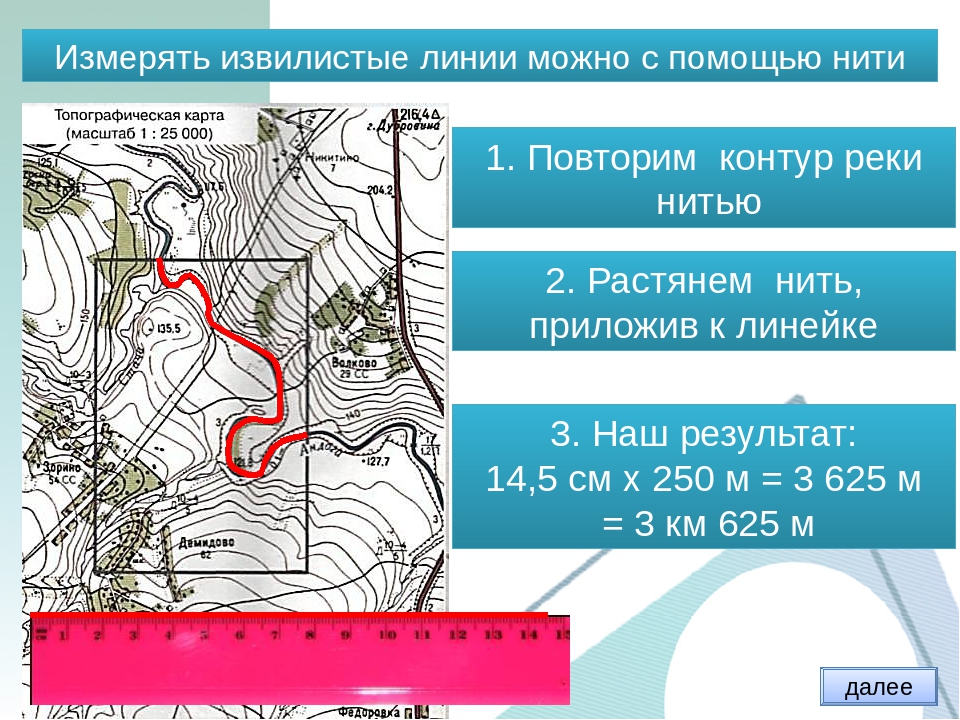 Измерим какую-нибудь сторону квадрата, например ту, которая составляет дуга экватора с разностью долгот в 20°. Она получилась в обеих проекциях равной 0,5 см. Действительное ее расстояние по экватору составляет 2220 км. Значит, масштаб в центральной части той и другой проекции будет равен 1:444 000 000, или в 1 см 4440 км (2220:0,5).
Измерим какую-нибудь сторону квадрата, например ту, которая составляет дуга экватора с разностью долгот в 20°. Она получилась в обеих проекциях равной 0,5 см. Действительное ее расстояние по экватору составляет 2220 км. Значит, масштаб в центральной части той и другой проекции будет равен 1:444 000 000, или в 1 см 4440 км (2220:0,5).
Как неудивительно, но. масштаб, подписанный на этих картах (главный масштаб), будет одинаков, несмотря на разные размеры полушарий.
Универсальный масштаб
. На картах обычно дается не только численный, но и линейный масштаб в виде графической шкалы. Понятно, что для карты определенного масштаба строят соответствующую шкалу. А нельзя ли построить один график, который можно использовать для карт разных масштабов? Попытаемся это сделать.
Рис. 31. Универсальный масштаб
Проведем две взаимно перпендикулярные оси и отложим по вертикальной оси вверх отрезок ВС, равный 10 см, а по горизонтальной оси влево отрезок ВА, равный 2,5 см (рис. 31). (Этот последний отрезок будем считать основанием линейного масштаба для карты 1:20 000 000. В этом масштабе он будет соответствовать 500 км. Чтобы найти расстояние СЕ, от которого нужно отложить основание следующего масштаба (1:25 000 000), нужно воспользоваться соотношением. полученным из подобия треугольников АВС и DEC: CB/AB = CE/DE; СЕ = (СВ x DE)/АВ.
31). (Этот последний отрезок будем считать основанием линейного масштаба для карты 1:20 000 000. В этом масштабе он будет соответствовать 500 км. Чтобы найти расстояние СЕ, от которого нужно отложить основание следующего масштаба (1:25 000 000), нужно воспользоваться соотношением. полученным из подобия треугольников АВС и DEC: CB/AB = CE/DE; СЕ = (СВ x DE)/АВ.
Величина DE — основание линейного масштаба — для масштаба карты 1:25 000 000 будет равна 2 см (500 км:25 000 000), а СЕ — 8 см. Таким же путем рассчитываются расстояния от точки С до линий, где будут строиться основания линейных масштабов других карт.
Построенный нами график можно использовать не только для измерения расстояний по картам разных масштабов, но и для определения частного или среднего масштаба карты по любому меридиану и любой параллели. Масштаб карты по меридиану определяется так. Возьмем с карты циркулем-измерителем отрезок меридиана с разностью широт 10°, что будет соответствовать расстоянию 1110 км. Этот раствор циркуля ведем по нашему графику вдоль параллельных линий до тех пор, пока он не уложится в расстояние 1110 км. В нашем случае взятый отрезок MN уложился в расстояние 1110 км между линиями масштабов 1:25 000 000 и 1:30 000 000 (ближе к 1:30 000 000). Значит, частный масштаб карты по данному меридиану получился равным 1:28 000 000.
Этот раствор циркуля ведем по нашему графику вдоль параллельных линий до тех пор, пока он не уложится в расстояние 1110 км. В нашем случае взятый отрезок MN уложился в расстояние 1110 км между линиями масштабов 1:25 000 000 и 1:30 000 000 (ближе к 1:30 000 000). Значит, частный масштаб карты по данному меридиану получился равным 1:28 000 000.
Чтобы определить масштаб карты по параллели, нужно вначале найти по таблице 1 длину дуги параллели в 10° на определенной широте, а затем порядок действий будет тот же, что и при определении масштаба карты по меридиану.
Наилучший вариант. Когда задача имеет слишком много решений, всегда возникает вопрос, нельзя ли выбрать из нее лучшее. В 1856 году русский математик П. Л. Чебышев поставил и решил следующую теорему для географических карт: найти наиболее подобное изображение данной страны, чтобы искажение масштаба оказалось минимальным. Без доказательства он сообщил, что для этого нужно, чтобы масштаб во всех точках границы страны был одним и тем же. П. Л. Чебышев умер, не опубликовав своей теоремы.
П. Л. Чебышев умер, не опубликовав своей теоремы.
Долгие годы математики всего мира искали это доказательство и, в конце концов, стали сомневаться в правильности утверждения. Лишь в 1896 году русский ученый Д. А. Граве сумел восстановить доказательство Чебышева.
Картографическую проекцию, удовлетворяющую поставленному условию, можно создать только в том случае, когда северная и южная границы страны проходят по параллелям, а западная и восточная — по меридианам. Практически так не бывает. Границы стран обычно проходят по кривым, или ломаным, линиям, не совпадающим с параллелями и меридианами. Тем не менее для каждой страны можно составить проекцию, которая довольно близко подходит к нашему условию.
Идея П. Л. Чебышева нашла практическое воплощение при составлении карт СССР. Такие карты обычно составляют в конической проекции с условием сохранения масштаба по всем меридианам и двум параллелям, одна из которых пересекает южную границу страны, а вторая проходит на несколько градусов южнее побережья Северного Ледовитого океана. Получается так, что конус не касается глобуса, а сечет его по двум заданным параллелям: 47 и 62°.
Получается так, что конус не касается глобуса, а сечет его по двум заданным параллелям: 47 и 62°.
Возможно, у вас возник вопрос: почему северная параллель сечения, так же как и южная, не пересекает границу страны, а находится южнее ее? Нетрудно догадаться, в чем тут дело. Перенос параллели касания к югу вызван тем, что северные окраины нашей страны слабо обжиты, и поэтому предпочтение в точности картографического изображения отдается местам, более населенным.
Измерение расстояний на местности
Расстояние между близко расположенными предметами можно измерить с помощью рулетки. Но узнать пройденный путь в походе с её помощью уже не получится. В таком случае необходимо сначала посчитать шаги, а потом умножить их на среднюю длину вашего шага.
Напомним, что для определения средней длины шага нужно отмерить на местности с помощью рулетки расстояние, например в 100 м. Затем обычным шагом пройти этот путь, подсчитывая шаги. Скажем, 100 м вы прошли, сделав 150 шагов. Значит, средняя длина шага равна приблизительно 66 см (10 000 см : 150 « 66 см).
Значит, средняя длина шага равна приблизительно 66 см (10 000 см : 150 « 66 см).
При измерении больших расстояний шаги удобнее подсчитывать парами (например, только под левую ногу). Длина одной пары шагов в два раза больше средней длины шага. Используют также и специальный прибор — шагомер.
Кроме того, расстояние определяется ещё и по времени, затраченному на ходьбу. Правда, этот способ менее точный. Так, если 1 км вы проходите за 15 минут, то за час пройдёте 4 км.
Определяют расстояние на глаз или с помощью дальномера.
Лазерный дальномер — прибор для измерения расстояний с применением лазерного луча. Часто его называют лазерной рулеткой, так как он заменил обычную рулетку во многих отраслях производства и строительства. Лазерные дальномеры широко применяются при топографической съёмке местности, в навигации. Они позволяют с большой точностью определить расстояние до объекта.
Простейший дальномер легко изготовить самим из куска картона. Чтобы с помощью такого дальномера определить расстояние, скажем, от вас до стоящего вдали человека, прибор необходимо держать на вытянутой руке перед глазами и, двигая вправо или влево, добиться того, чтобы фигура человека целиком попала в прорезь прибора.
Цифра на шкале внизу будет соответствовать величине расстояния от наблюдателя до человека.
Изображение расстояний на чертеже
Предположим, расстояние от школы до библиотеки равно 620 м. Показать натуральную длину на бумаге невозможно, поэтому придётся вычертить его в масштабе. Если на бумаге расстояние изображать в 10 000 раз меньшим, чем в действительности, тогда 1 см будет соответствовать 10 000 см (или 100 м) на местности. В таком масштабе расстояние от школы до библиотеки будет равно 6 см 2 мм.
Определение расстояний на карте
При помощи линейного масштаба расстояние определить удобнее, чем с помощью численного. Для этого достаточно лишь померить циркулем или полоской бумаги расстояние между нужными точками на карте и приложить это расстояние к линейному масштабу. По надписям на нём сразу видно, чему равняется расстояние на местности.
Если требуется определить расстояние по ломаной линии, например по дороге, то определяется отдельно каждое расстояние между поворотами дороги и затем берётся сумма этих расстояний.
Измерительные приемы при работе с картой. Координатомер. Курвиметр. Хордоугломер. численный и линейный масштаб, точки местности. Поперечный масштаб. Азимут. Дирекционный угол
В практической работе с топографической картой часто приходится измерять расстояния как по прямой линии (определение дальности до целей, расстояний между местными предметами, координат точек), так и по извилистой линии (определение длины маршрута), а также измерять, вычислять различные углы.
Чтобы измерить расстояние по карте, нужно знать ее масштаб. Масштаб карты указывается под нижней рамкой карты и выражается численно — численный масштаб и графически — линейный масштаб (рис. 5).
Рис. 5. Численный и линейный масштабы карты
Чтобы определить по карте расстояние между местными предметами (точками местности) пользуясь численным масштабом, измеряют линейкой или циркулем расстояние между этими предметами (точками местности) в сантиметрах и умножают полученное число на величину масштаба. Например, по карте масштаба 1 : 25 000 расстояние между наблюдательными пунктами равно 5,5 см, а расстояние между этими пунктами на местности будет равно 5,5 X 250 = 1375 м.
Например, по карте масштаба 1 : 25 000 расстояние между наблюдательными пунктами равно 5,5 см, а расстояние между этими пунктами на местности будет равно 5,5 X 250 = 1375 м.
При определении небольших расстояний между двумя точками проще пользоваться линейным масштабом. Для этого циркулем или линейкой измеряют на карте расстояние между этими точками и прикладывают его к линейному масштабу карты, по которому определяют искомое расстояние (в километрах и метрах) на местности.
При отсутствии циркуля и линейки расстояние между точками по карте можно определить по линейному масштабу, пользуясь ровной полоской бумаги. Для этого полоску бумаги прикладывают к точкам на карте, между которыми определяют расстояние, и против этих точек на бумаге делают отметки в виде штрихов. Приложив отмеченный штрихами отрезок бумаги к линейному масштабу, определяют расстояние между этими точками на местности.
На крупномасштабных картах часто приходится определять координаты точек (целей, ориентиров, элементов боевого порядка своих войск и войск противника).
Координатами точки называют угловые или линейные величины, характеризующие ее положение на поверхности или в пространстве.
Поскольку определение координат по карте очень распространено, подробно этот вопрос будет изложен в разделе 9.
При измерении расстояний для определения координат точек пользуются так называемой координатной меркой (рис. 6) или координатомером (рис. 7), которые несколько упрощают работу, заменяя при этом масштаб, циркуль и линейку.
Рис. 6. Координатная мерка
Рис. 7. Координатомер и пользование им для определения координат точки на карте
Координатная мерка представляет собой прозрачную целлулоидную пластинку с координатной сеткой. Две взаимно перпендикулярные линии делят координатную сетку на четыре равных квадрата; эти линии оканчиваются стрелками, имеющими обозначения: С (север), Ю (юг), В (восток) и 3 (запад). Расстояние между линиями сетки равно 2 мм; цена делений сетки для карт масштабов 1 : 25 000 и 1 : 50 000 соответственно равна 50 и 100 м. В северо-восточной части сетки выделен жирными линиями квадрат со сторонами в 2 см. На углах пластинки имеются шкалы, служащие для определения координат точек карты при разных ее масштабах. Шкалы для масштабов 1 : 25 000 и 1 : 50 000 имеют миллиметровые деления и оцифрованы в сотнях метров: шкала для масштаба 1 : 42 000, оцифрованная через 0,2 дюйма, предназначается для старых карт, разграфленных на дюймовые и двухдюймовые квадраты. В центре пластинки имеется отверстие для накола точек при нанесении их на карту.
В северо-восточной части сетки выделен жирными линиями квадрат со сторонами в 2 см. На углах пластинки имеются шкалы, служащие для определения координат точек карты при разных ее масштабах. Шкалы для масштабов 1 : 25 000 и 1 : 50 000 имеют миллиметровые деления и оцифрованы в сотнях метров: шкала для масштаба 1 : 42 000, оцифрованная через 0,2 дюйма, предназначается для старых карт, разграфленных на дюймовые и двухдюймовые квадраты. В центре пластинки имеется отверстие для накола точек при нанесении их на карту.
Координатомер имеет вид угольника, на внутренних сторонах которого нанесены миллиметровые деления, оцифрованные в сотнях метров.
Если расстояния между штрихами делений равны 2 мм, то цена деления для карт масштабов 1 : 25 000 и 1 : 50 000 соответственно равна 50 и 100 м.
Координатомеры любого масштаба легко изготовить из картона, пластика или целлулоида.
Большие расстояния по прямым линиям измеряют на карте по частям. Для этого по масштабу устанавливают раствор циркуля, соответствующий целому числу километров, и этим раствором измеряют на карте заданное расстояние.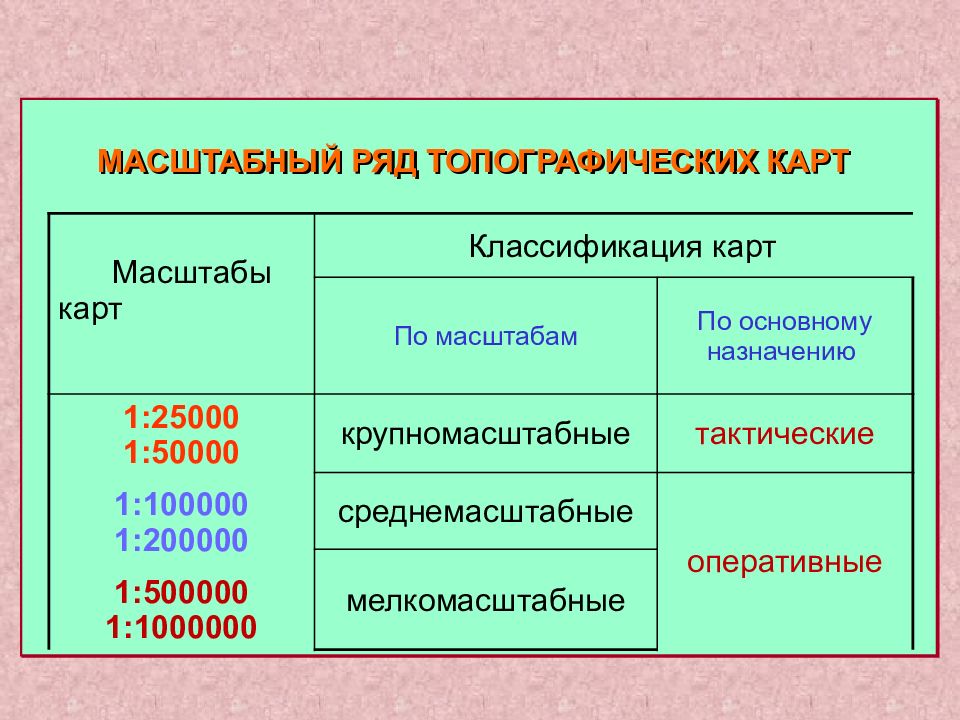 При этом отрезок на конце измеряемого расстояния, не укладывающийся в растворе циркуля, определяют с помощью линейного масштаба и полученное значение прибавляют к отсчитанному числу километров.
При этом отрезок на конце измеряемого расстояния, не укладывающийся в растворе циркуля, определяют с помощью линейного масштаба и полученное значение прибавляют к отсчитанному числу километров.
Таким же способом измеряют расстояния по кривым и извилистым линиям. В этом случае раствор циркуля делают небольшим в зависимости от степени извилистости измеряемого расстояния.
Для удобства определения длины маршрута, особенно по длинным и извилистым линиям, пользуются специальным прибором- курвиметром (рис. 8).
Рис. 8. Курвиметр
Прибор представляет собой круглую коробочку с держателем. В центре прибора находится циферблат со стрелкой, внизу имеется колесико, при помощи которого обводится маршрут. Колесико соединено системой передач со стрелкой на циферблате, которая ведет отсчет величины пройденного расстояния по карте.
Деления на шкале циферблата бывают различные: на одних курвиметрах они обозначают путь, проходимый колесиком по карте, в сантиметрах, на других — показывают непосредственно расстояние на местности в километрах в зависимости от масштаба карты.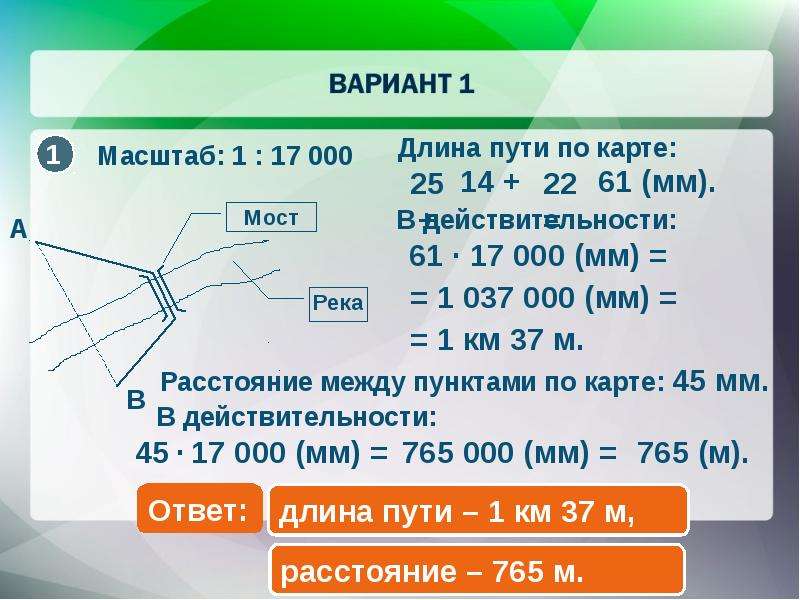 На рисунке показан курвиметр с тремя шкалами различных масштабов (1 : 100 000, 1 : 50 000, 1 : 25 000). Деления на шкалах показывают расстояния на местности в километрах.
На рисунке показан курвиметр с тремя шкалами различных масштабов (1 : 100 000, 1 : 50 000, 1 : 25 000). Деления на шкалах показывают расстояния на местности в километрах.
Для определения длины маршрута с помощью курвиметра стрелку прибора устанавливают на нулевое положение циферблата. Затем курвиметр ставят вертикально колесиком на начальную точку маршрута и с равномерным нажимом прокатывают его вдоль маршрута так, чтобы показания стрелки возрастали. В конечной точке маршрута снимают отсчет по нужной шкале циферблата. Длина маршрута равна отсчету, умноженному на цену деления шкалы. Если курвиметр дает показания в сантиметрах, то для получения соответствующего им расстояния на местности умножают отсчет по шкале на величину масштаба карты.
По карте можно определять расстояния и приближенно. Для этого обычно используют километровую сетку.
Однако точность определения расстояний этим способом небольшая.
Точность определения расстояний по карте зависит от многих причин: от масштаба карты и ее качества, от характера измеряемых расстояний и точности их измерения, от рельефа местности.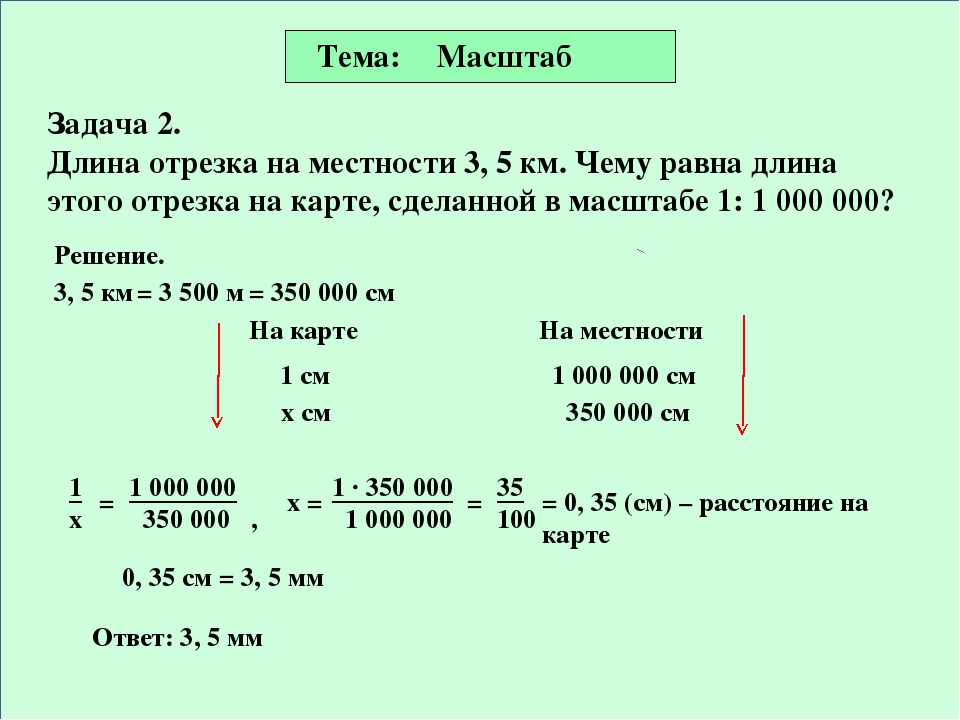
Точность измерения расстояний по линейному масштабу ограничивается тем, что делить его основание на очень мелкие части нельзя, так как это затруднит отсчет. Для повышения точности измерений применяют так называемый поперечный масштаб.
Поперечный масштаб представляет собой прямоугольник (рис. 9), горизонтальная сторона которого разделена на несколько равных частей, обычно, по 2 см каждая.
Рис. 9. Поперечный масштаб
Каждая такая часть называется основанием масштаба. Крайнее левое основание в верхней и нижней частях поперечного масштаба делится на десять равных частей. Концы этих десятых долей основания соединяются между собой прямыми, отсекающими на горизонтальных линиях сотые доли основания.
Таким образом, на поперечном масштабе измеряемое расстояние может быть выражено в целых, десятых и сотых долях основания масштаба. А поскольку известна величина основания масштаба (2 см), то можно легко определить «цену» основания в метрах. Так, для масштаба 1 : 25 000 «цена» основания поперечного масштаба составит 500 м, его десятая доля — 50 м, а одна сотая часть — 5 м. Кроме того, на глаз можно взять еще и половину «сотни» — 2,5 м.
Кроме того, на глаз можно взять еще и половину «сотни» — 2,5 м.
На рис. 9 показано, как надо пользоваться поперечным масштабом. Циркулем измеряют расстояние между двумя предметами на карте. Затем прикладывают циркуль к нижней линии поперечного масштаба и отсчитывают расстояние, которое получается — 2200 м с излишком. Для определения величины этого излишка циркуль передвигают параллельно нижней линии вверх До пересечения с диагональю и считывают окончательную величину расстояния — 2220 м.
Ориентирование на местности, а также решение многих специальных задач осуществляется посредством азимутов и дирекциониых углов направлений.
Поясним, что такое азимут и дирекционный угол.
Существует два вида азимутов: азимут истинный (А) и азимут магнитный (Ам).
Истинным азимутом называется угол между северным направлением географического (истинного) меридиана и направлением на местный предмет, отсчитанный по ходу часовой стрелки.
Магнитным азимутом называется угол, отсчитанный по ходу часовой стрелки от северного направления магнитного меридиана до направления на местный предмет; магнитный азимут всегда определяется с помощью магнитной стрелки.
Дирекционный угол (а) — это угол между северным направлением вертикальной линии координатной (километровой) сетки и направлением на местный предмет, отсчитанный по ходу часовой стрелки.
Определение азимутов и дирекционных углов направлений, а также углов между местными предметами связано с измерением этих углов на карте и местности.
Углы на карте и местности измеряют в градусной системе, а также в делениях угломера.
Одно деление угломера — это величина центрального угла, который соответствует дуге в 1/6000 окружности. Длина дуги, соответствующая углу в одно деление угломера, равна
С достаточным для практики округлением принимают, что длина этой дуги равна 1/1000 радиуса данной окружности. Этим и объясняется другое, часто употребляемое наименование деления угломера — тысячная.
На практике иногда применяют термины «малое деление угломера» и «большое деление угломера». «Малым делением угломера» называют одно деление угломера (одну «тысячную дальности»), «большим делением-100 делений угломера (100 «тысячных дальности»).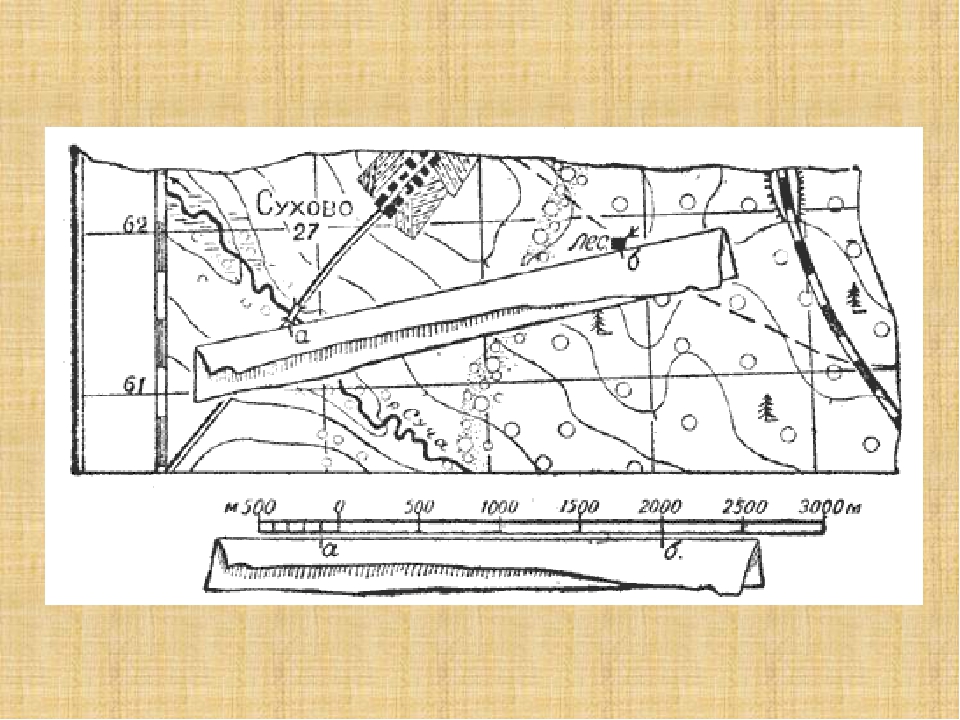
Так как окружность содержит 360″ или 360*60 = 21 600′, то одно деление угломера равно 21600/6000= 3′,6, а 100 делений (одно большое деление угломера) равны 3′,6*100 = 360′ = 6°.
Для системы измерения углов в тысячных существует простая зависимость между угловыми и линейными величинами, а именно: угловое расстояние между двумя равноудаленными от наблюдателя местными предметами равно линейному расстоянию между ними, умноженному на 1000 и деленному на величину дальности. Эта зависимость выражается формулой
где а — угловое расстояние между местными предметами в делениях угломера;
l — линейное расстояние между местными предметами в метрах;
Д- расстояние от наблюдателя до местных предметов в метрах.
Пример. Расстояние от наблюдателя до линии электропередачи Д = 500 м; линейное расстояние между столбами l = 50 м. Определить угловое расстояние а между этими столбами.
Решение:
Пользуясь приведенной формулой, можно определить линейное расстояние между предметами, если известны дальность до них и измерен угол
Если определено линейное и угловое расстояние между двумя предметами, то дальность до них
Величины углов, измеренных в тысячных, произносят, разделяя число сотен и число единиц. Например, величину угла в 1235 делений угломера записывают 12-35, а произносят «двенадцать тридцать пять». Угол в 38 делений угломера записывают 0-38, а произносят «ноль тридцать восемь», угол в 300 тысячных записывают 3-00, а произносят «три ноль» и т. д.
Например, величину угла в 1235 делений угломера записывают 12-35, а произносят «двенадцать тридцать пять». Угол в 38 делений угломера записывают 0-38, а произносят «ноль тридцать восемь», угол в 300 тысячных записывают 3-00, а произносят «три ноль» и т. д.
Для измерения и построения углов на карте пользуются транспортирами и целлулоидными кругами. Для более точных измерений и построений углов применяют специальные хордоугломеры.
Хордоугломер представляет собой латунную хромированную пластинку, на одной стороне которой нанесен собственно хордоугломер, а на другой — два поперечных масштаба.
Собственно хордоугломер (рис. 10)-это график хорд для углов, выраженных в делениях угломера, построенный по принципу поперечного масштаба.
Рис.10. Хордоугломер
Способ измерения и построения углов по хордам основан на том, что каждому острому углу (до 15-00) соответствует определенной величины хорда окружности, проведенной из вершины угла.
По верхней горизонтальной линии графика от начальной точки отложены хорды, соответствующие углам через 0-20. У концов хорд, соответствующих углам от 1-00 до 15-00, написаны числа от «1» до «15».
У концов хорд, соответствующих углам от 1-00 до 15-00, написаны числа от «1» до «15».
Каждое большое деление на верхней горизонтальной линии графика разделено на пять малых делений ценой 0-20, обозначенных цифрами «2». «4», «6», «8», что соответствует 0-20, 0-40, 0-60, 0-80. Слева на вертикальной линии графика на концах четных горизонтальных линий проставлены числа «2», «4», «6»… до «18», соответствующие 0-02, 0-04, 0-06 и т. д.
Тупые углы (от 15-00 до 30-00) находят путем измерения соответствующего дополнительного до 30-00 угла.
Для отыскания хорд острых углов, дополнительных до 30-00, большие деления нижней горизонтальной линии оцифрованы справа налево числами «15», «16», «17»… до «30», а деления правой вертикальной линии графика — снизу вверх числами «2», «4», «6»… до «18».
Порядок измерения углов на карте с помощью хордо-угломера следующий (рис. 11).
Рис.11. Измерение углов на карте с помощью хордоугломера
Из вершины измеряемого угла А при помощи циркуля проводят дугу радиусом, равным хорде угла 10-00 на хордоугломере. Циркулем берут величину хорды БВ измеряемого угла и переносят его на хордоугломер.
Циркулем берут величину хорды БВ измеряемого угла и переносят его на хордоугломер.
Расположив левую ножку циркуля в нулевой точке левой вертикальной линии графика хордоугломера, а правую ножку на верхней горизонтальной линии, передвигают обе ножки по вертикали вниз. Передвижение происходит до тех пор, пока правая ножка циркуля не совпадет с пересечением одной из наклонных линий с одной из горизонтальных линий графика; при этом обе ножки циркуля должны быть на одной горизонтальной линии (точки а и б на рис. 10).
Читают величину угла по верхнему ряду цифр графика против наклонной линии, на которой расположилась правая ножка циркуля, и прибавляют к ней количество делений по левому ряду цифр против горизонтальной линии, на которой находятся обе ножки циркуля. Измеренный угол равен 5-17
Связанные статьи:
1. Что такое местность?
2. Назначение и содержание топографических карт
3. Классификация топографических карт
4. Подготовка карты к работе
5.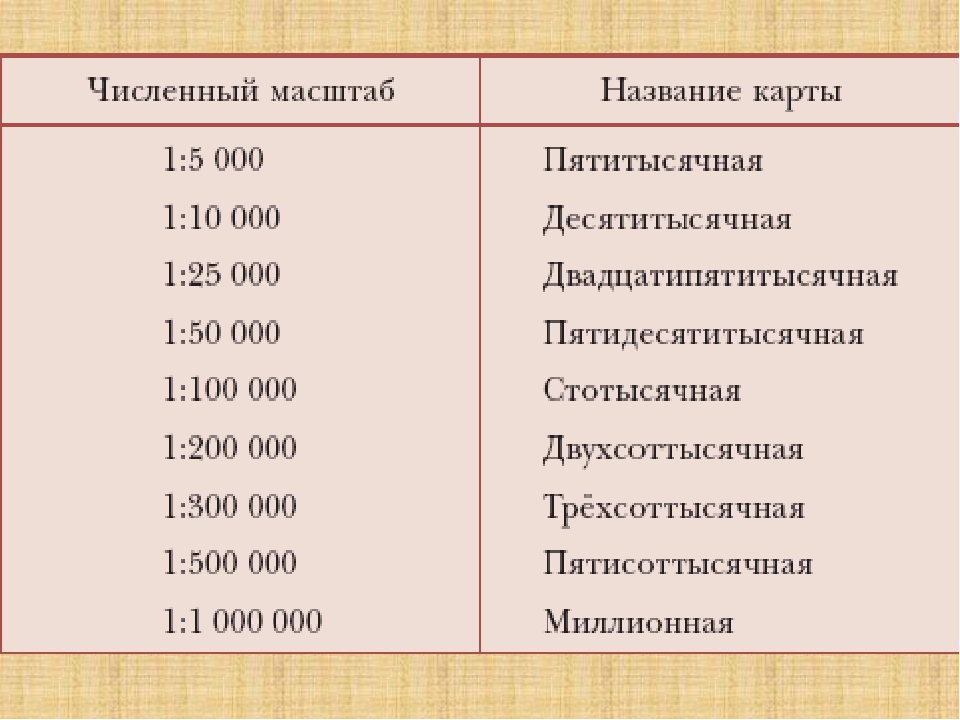 Измерительные приемы, применяемые при работе с картой
Измерительные приемы, применяемые при работе с картой
6. Топографическое ориентирование по карте
7. Изучение местности по карте
8. Оценка маршрута движения, выбранного или назначенного по карте
9. Определение координат точек по карте
10. Целеуказание по карте
11. Топографическая привязка с помощью карты
12. Хранение и сбережение карт
Для удобства работы в полевых условиях жидкостный компас размещен на прозрачной пластине, оборудован угловой шкалой, миллиметровой и масштабной линейками, иногда лупой для чтения мелких деталей карты. Как найти азимут на местности?С помощью такого компаса удобно определять азимут на любой местный предмет. Для этого нужно направить пластину компаса на предмет, азимут на которыймы хотим измерить. Затем, не сбивая положение пластины, вращать колбу компаса, пока нулевая отметка шкалы не совпадетс северным концом стрелки. Измерение азимута по карте производится еще проще. Нужно расположить пластину на карте так, чтобы край пластины расположился по направлению измеряемого азимута. Затем, не сдвигая пластины, необходимо повернуть колбу компаса так, чтобы линии, нанесенные на ее нижнюю сторону, были параллельны северным линиям карты, а нулевая отметка шкалы была направлена в сторону севера. Осевая линия пластины компаса будет показывать на шкале значение искомого азимута. Помните! При измерении азимута на картене нужно обращать внимания на магнитную стрелку. Дело в том, что при измерении азимута по карте достаточно иметь только транспортир, компас не нужен.Ведь необходимо измерить угол между двумя линиями — направлением на предмети севернойлинией карты. Другое дело на местности, где никто не нарисовал для нас северных линий, и нам необходимо воспользоваться помощью магнитной стрелки. Как использовать азимут в спортивном ориентировании и спортивной радиопеленгации, вы узнаете немного позже. Но несколько примеров мы все же рассмотрим. Например, нам необходимо нанести на карту заводскую трубу, расположенную на другом берегу реки. Стоя на развилке,мы измерим азимут на трубу. Затем возьмем карту, положим на нее компас так, чтобы край пластины проходил через нашу развилку. И не сбивая положения капсулы, повернем компас так, чтобы линии на дне колбы стали параллельны северным линиям стрелки, а 0° был направлен в сторону севера. Затем тонким карандашом проведем по пластине компаса линию за реку. Теперь пройдем по дороге полкилометра до домика лесника. Стоя около угла дома, повторим наши действия. Наши линии пересекутся в некоторой точке на другом берегу реки. И мы смело можем нарисовать там условный знак заводской трубы. Рассмотрим теперь другой пример. В сосновом бору, расположенном неподалеку от нас, есть лесное озеро изумительной красоты. Задания для самостоятельной работы.
|
Как работает инструмент Пошаговая пространственная автокорреляция—ArcGIS Pro
При большом объеме анализируемых пространственных данных очень важен масштаб анализа. По умолчанию Определение пространственных взаимоотношений для, например, инструмента Анализ горячих точек, это Полоса фиксированных расстояний, при этом требуется указать значение расстояния. Многие инструменты обработки плотностей требуют значения радиуса. Выбранное расстояние должно быть связано с масштабом вопроса, на который вы пытаетесь ответить, или масштабом устранения последствий. Предположим, что вы хотите проанализировать степень ожирения среди детей. Каков масштаб вашего анализа? Это отдельные семьи или целые районы? В этом случае расстояние, используемое для определения масштаба анализа, будет небольшим, чтобы охватить дома в одном или двух кварталах друг от друга. Или же, каким будет масштаб устранения последствий? Возможно, рассматриваемый вопрос учитывает наличие фитнес-программ после школы для сокращения ожирения детей. В этом случае расстояние должно отражать школьные зоны. Иногда определить нужный масштаб довольно легко. Если вы изучаете закономерности ежедневных поездок в город из пригородов и знаете, что среднее расстояние поездки составляет 15 км, вы можете использовать для анализа фиксированное расстояние в 15 км. В других ситуациях обосновать расстояние анализа сложнее. В этом случае инструмент Пошаговая пространственная автокорреляция очень полезен.
В этом случае расстояние должно отражать школьные зоны. Иногда определить нужный масштаб довольно легко. Если вы изучаете закономерности ежедневных поездок в город из пригородов и знаете, что среднее расстояние поездки составляет 15 км, вы можете использовать для анализа фиксированное расстояние в 15 км. В других ситуациях обосновать расстояние анализа сложнее. В этом случае инструмент Пошаговая пространственная автокорреляция очень полезен.
Когда вы видите пространственную кластеризацию в ландшафте, вы видите доказательства работы внутренних пространственных процессов. Знание о пространственном масштабе, в котором будут работать базовые процессы, может помочь вам выбрать необходимое расстояние анализа. Инструмент Пошаговая пространственная автокорреляция запускает инструмент Пространственная автокорреляция (Глобальный индекс Морана I) с последовательностью увеличивающимися расстояниями для измерения интенсивности пространственной кластеризации для каждого расстояния. Интенсивность кластеризации определяется z-оценкой. Обычно при увеличении расстояния растет и z-оценка, что указывает на повышенную интенсивность кластеризации. Однако на определенном расстоянии возникает пик z-оценки. Иногда пиков несколько.
Обычно при увеличении расстояния растет и z-оценка, что указывает на повышенную интенсивность кластеризации. Однако на определенном расстоянии возникает пик z-оценки. Иногда пиков несколько.
Пиковые z-оценки соответствует расстояниям, при которых пространственные процессы, обеспечивающие пространственную кластеризацию, наиболее выражены. Цвет каждой точки на графике соответствует статистической значимости значений z-оценок.
Одна из стратегий для определения необходимого масштаба анализа – выбор расстояния, связанного со статистически значимым пиком, которое лучше всего отражает масштаб анализа. Зачастую это первый статистически значимый пик.
Как выбрать начальное расстояние и приращение расстояния?
Все измерения расстояния основываются на центроидах объектов, а значение параметра Начальное расстояние по умолчанию является наименьшим расстоянием, которое гарантирует, что у каждого объекта есть хотя бы один соседний объект. Обычно это хороший вариант, если набор данных не содержит выбросы по местоположению. Определите, есть ли у вас выбросы по местоположению, а затем выберите все объекты, кроме объектов с выбросами, и запустите инструмент Пошаговая пространственная автокорреляция. Если вы нашли пиковое расстояние для выбранного набора объектов, используйте это расстояние для создания файла матрицы пространственных весов на основе всех ваших объектов (даже выбросов). При запуске инструмента Построить матрицу пространственных весов для создания файла матрицы пространственных весов установите для параметра Количество соседей определенное значение, чтобы у всех объектов было такое число соседних объектов.
Значение параметра Приращение расстояния – это среднее расстояние от каждого объекта до ближайшего к нему соседнего объекта. Если вы определили нужное начальное расстояние, используя стратегии, описанные выше, но не нашли пиковое расстояние, можно поэкспериментировать с меньшими или большими приращениями расстояния.
Что если на графике совсем нет пиков?
В некоторых случаях вы используете инструмент Пошаговая пространственная автокорреляция и получаете график с z-оценкой, которая постоянно растет при увеличении расстояний; пикового значения нет. Это чаще всего происходит, когда данные были объединены, а масштаб процессов, влияющих на переменную Входное поле, меньше схемы агрегации. Вы можете попробовать уменьшить приращение расстояние и посмотреть, появятся ли более выраженные пики. Иногда пики не возникают из-за наличия в области изучения нескольких пространственных процессов, каждый из которых работает на разном расстоянии. Это часто происходит при работе с большими точечными наборами данных с множеством помех (без четкого пространственного шаблона для анализируемых данных). В этом случае нужно обосновать масштаб анализа с помощью других критериев.
Интерпретация результатов
При запуске инструмента Пошаговая пространственная автокорреляция результаты z-оценки для каждого расстояния записываются как сообщения внизу панелиГеообработка. Вы можете получить доступ к сообщениям, переместив курсор мыши на индикатор выполнения, щелкнув на всплывшую кнопку или развернув раздел сообщений в панели Геообработка. Вы можете получить доступ к сообщениям для выполненного ранее инструмента из панели История геообработки. Если вы указываете путь для дополнительного параметра Выходная таблица, создается таблица с полями Distance, Morans I, Expected I, variance, z_score и p_value.
Изучив значения z-оценок, сохраненных как сообщения, или открыв эти значения в Выходной таблице, можно определить наличие пиковых расстояний.Однако чаще пиковые расстояния определяются по графику в дополнительном файле Выходного отчета. Этот отчет состоит из трех страниц. Пример первой страницы отчета приведен ниже. Учтите, что на этом графике три пиковые z-оценки, связанные с расстояниями 5000, 9000 и 13000 футов. Гало отображается для выделения первого пикового расстояния и максимального пикового расстояния, но все пики представляют расстояния, где процессы, обеспечивающие пространственную кластеризацию, наиболее очевидны. Можно выбрать пик, который лучше всего отражает масштаб анализа. В некоторых случаях показывается только одно гало, так как первый и максимальный пики находятся на одном расстоянии. Если ни один из пиков z-оценок не является статистически значимым, то ни для одного из них не будет отображаться светло-синее гало. Учтите, что цвет нарисованной z-оценки соответствует критическим значениям статистической значимости.
На второй странице отчета расстояния и z-оценки представлены в формате таблицы. На последней странице отчета показаны все настройки параметров, использованные при запуске инструмента. Чтобы получить файл отчета, укажите путь в параметре Выходной отчет (Output Report).
Дополнительные ресурсы
Отзыв по этому разделу?
Определение расстояний по карте различными способами » Блог о самостоятельном туризме
При создании топографических карт, спроецированные на уровенную поверхность линейные размеры всех объектов местности уменьшают в определенное количество раз. Степень такого уменьшения называется масштабом карты. Масштаб карты может быть выражен в численной форме (численный масштаб) или в графической (линейный, поперечный масштабы), в виде графика.
Расстояния по карте измеряют, пользуясь обычно численным или линейным масштабом. Более точные измерения выполняются с помощью поперечного масштаба.
На шкале линейного масштаба оцифрованы отрезки, соответствующие расстояниям на местности в метрах или километрах. Это облегчает процесс измерения расстояний, так как не требуется производить вычисления.
Определение по карте расстояний и площадей.Измерение расстояний.
При пользовании численным масштабом расстояние, измеренное на карте в сантиметрах, умножают на знаменатель численного масштаба в метрах.
Например, расстояние от пункта ГГС отм. 174,3 (кв. 3909 ) до развилки дорог (кв. 4314) на карте составляет 13,96 см, на местности оно будет: 13,96 х 500 = 6980 м. (карта масштаба 1: 50 000 У-34-85-А).
Если расстояние, измеренное на местности надо отложить на карте, то его надо разделить на знаменатель численного масштаба. Например, расстояние, измеренное на местности, равно 1550 м., на карте масштаба 1: 50 000 оно будет 3,1 см.
Измерения по линейному масштабу выполняют с помощью циркуля-измерителя. Раствором циркуля соединяют две контурные точки на карте, между которым надо определить расстояние, затем прикладывают к линейному масштабу и получают расстояние на местности. Криволинейные участки определяют по частям или при помощи курвиметра.
Площадь участка местности определяют по карте чаще всего подсчетом квадратов координатной сетки, покрывающих этот участок. Величину долей квадратов определяют на глаз или с помощью специальной палетки. Каждый квадрат, образуемый линиями координатной сетки, соответствует : 1: 25 000 и 1: 50 000 – 1 км.кв., 1: 100 000 – 4 км.кв., 1: 200 000 – 16 км.кв.
Полезно помнить, следующие соотношение 2 х 2 мм., соответсвуют для масштабов:
1: 25 000 – 0,25 га = 0,0025 км.кв.
1: 50 000 – 1 га = 0, 01 км.кв.
1: 100 000 – 4 га = 0, 04 км.кв.
1: 200 000 – 16 га = 0, 16 км.кв.
Определение площадей отдельных участков проводится при отчуждении земельных участков для Министерства обороны.
Точность определения расстояний по карте. Поправка в длину маршрута.
Точность измерения линий, площадей по топографической карте. Приобрести седельные тягачи и грузовики по самым лучшим ценам, вы сможете на сайте auto-holland.ru. Все грузовые автомобили прошли предпродажную подготовку и инспекционный контроль (инструментальный, компьютерный и визуальный).
Точность измерения линий и площадей, в первую очередь, зависит от масштаба карты. Чем крупнее масштаб карты, тем точнее определяются по ней длины линий и площади. При этом точность зависит не только от точности измерений, но и от погрешности самой карты, неизбежно при ее составлении и печати. Ошибки могут достигать для равнинных районов 0, 5, а в горах до 0, 7 мм. Источником ошибок измерений также является деформация карты и сами измерения.
Абсолютно с такой же погрешностью определяются плоские прямоугольные координаты по топографическим картам вышеперечисленных масштабов.
Например, расстояние между двумя пунктами, измеренное по карте, на местности с углом наклона 12 градусов равно 9270 м. Действительное же расстояние между этими пунктами будет 9270 х 1.02 = 9455 м. Таким образом, при измерении расстояний по карте, необходимо вводить поправки за наклон линий (рельеф).
Прямолинейные расстояния большой протяженности в одной шестиградусной зоне могут быть рассчитаны по формуле:
Этот способ определения расстояния используется в основном при подготовке стрельбы артиллерии и при пуске ракет по наземным целям.
Расчет расстояния на карте (неделя 3)
Мы можем определить по карте много информации, например расстояния, направления и площади. Мы можем измерить расстояние от Йоханнесбурга до Претории, определить, что Претория находится к северу от Йоханнесбурга, или вычислить размер провинции Гуатенг. При определении расстояний и площадей необходимо учитывать масштаб карты ВСЕГДА .
Для объяснения расстояния по прямой будет использован пример:
Шаг 1
- Расстояние
на карте рассчитывается между двумя точками, например между школой и музеем.
Сначала необходимо измерить длину линейкой с четкими единицами измерения в сантиметрах или миллиметрах от школы до музея.
Шаг 2
например 4см
Шаг 3
например 1:50 000
например 4 см x 50 000
= 200 000 см
Шаг 4
км | ч | плотина | м | дм | см | мм |
1 | 0 | 0 | 0 | 0 | 0 |
Мы использовали сантиметры для измерения расстояния между школой и музеем, поэтому мы должны переводить сантиметры в километры.
Этого можно достичь, поместив 1 под квадратом километров на шкале и выставив нули по мере движения вправо, пока не достигнете сантиметров. Согласно приведенной выше шкале пересчета, 1 км равен 100 000 см.
Затем, чтобы преобразовать ваши сантиметры в километры, вам нужно будет разделить 200 000 см на 100 000.
= 200 000
100 000
= 2 км
Для расчета расстояния на карте необходимо сделать следующее:
Измерьте расстояние между двумя точками на карте в см или мм.
Умножьте это на масштаб карты и разделите на 100 000, если вы использовали сантиметры, или на 1000 000, если вы использовали миллиметры, чтобы получить километры.
Если требуется расстояние в метрах, разделите сантиметры на 100 или миллиметры на 1000 в соответствии со следующей таблицей.
км | ч | плотина | м | дм | см | мм |
|
|
| 1 | 0 | 0 |
|
1 м = 100 см
4.Иногда расстояние можно рассчитать по извилистой реке или тропинке, это
сделать, используя кусок веревки, размещенный вдоль объекта намотки, а затем
растяните его вдоль единиц линейки, чтобы определить длину, а затем
рассчитайте, как показано в предыдущих шагах.
Измерьте расстояние на карте (ArmyStudyGuide.com)
УСЛОВИЯ
Дана стандартная военная карта масштаба 1: 50 000, полоска бумаги или линейка и карандаш.
СТАНДАРТЫ
1. Определите расстояние по прямой в метрах между двумя точками с погрешностью не более 5 процентов.
2. Определите расстояние дороги (по кривой) в метрах между двумя точками с погрешностью не более 10 процентов.
ОБУЧЕНИЕ И ОЦЕНКА
Информация об обучении Описание
Примечание: солдаты могут использовать свои карты для измерения расстояния между двумя местами. Карты нарисованы в масштабе. Это означает, что определенное расстояние на карте равно определенному расстоянию на Земле.Масштаб указан внизу и вверху каждой карты (масштаб 1:50 000). Это означает, что 1 дюйм на карте равен 50 000 дюймов на земле. Чтобы изменить расстояние на карте в милях, метрах или ярдах, используйте шкалу шкалы внизу карты (рис. 5-29).
Рисунок 5-29. Барные весы.
Рисунок 5-30. Измерение расстояния.
а. Возьмите линейку или край листа бумаги и отметьте на нем расстояние по прямой между двумя вашими точками (рис. 5-30).
г. Затем поместите линейку или бумагу под одну из линейных шкал и прочтите расстояние до земли в милях, метрах или ярдах. Гистограмма на Рисунке 5-31 показывает расстояние до земли 1500 метров.
Рисунок 5-31. Определение расстояния.
г. Предположим, вы хотите найти расстояние между точками A и B на повороте дороги. Возьмите полоску бумаги, сделайте на ней небольшую отметку и совместите отметку с точкой А. Совместите бумагу с краем дороги, пока не дойдете до изгиба, сделайте еще одну отметку на бумаге и на карте и затем поверните бумагу так, чтобы она продолжала следовать по краю дороги.Продолжайте повторять это, пока не дойдете до B. Всегда держите бумагу по краю дороги. Сделайте отметку на бумаге в том месте, где она попадает в точку B, а затем перейдите к шкале шкалы, чтобы определить расстояние (рис. 5-32).
2. Обычно вам необходимо измерять расстояние в метрах, и вы можете столкнуться с проблемой, которая выходит за пределы линейной шкалы. Шкала метровой линейки позволяет измерять расстояния до 5000 метров. Если вам необходимо измерить расстояния более 5000 метров, выполните следующую процедуру:
a.Поместите начальную точку на листе под нулем шкалы. Отмерьте 4 000 метров и поставьте новую отметку на бумаге.
Рисунок 5-32. Карта расстояния 1800 метров.
б. Поместите эту вторую отметку также под нулем на шкале столбцов и определите, находится ли теперь расстояние на бумаге в пределах шкалы столбцов. Если это так, добавьте это значение к 4000, чтобы получить общее расстояние. Если этого не произошло, повторите последний шаг (а) до тех пор, пока расстояние на бумаге не попадет в полосу шкалы.Не забудьте добавить это последнее значение к общему количеству метров, которое вы уже измерили.
Руководство по оценке:
Измерение расстояния на карте
Показатели эффективности
1. Измерьте расстояние по прямой на карте с помощью линейки.
2. Поместите бумагу под шкалу шкалы метра.
3. Определите расстояние с погрешностью не более 5 процентов.
4. Измерьте расстояние по изогнутой линии с помощью полоски бумаги.
5.Положите бумагу под шкалу шкалы метра.
6. Определите расстояние с погрешностью не более 10 процентов.
Измерение расстояний на карте
1. Предложите учащимся отгадать загадку.
Спросите: Где можно найти два целых города на площади в дюйм? (На карте!)
2. Продемонстрируйте использование масштаба на карте штата.
Спроецируйте карту своего штата с помощью одностраничных карт MapMaker и предоставьте каждому учащемуся печатную версию карты, на которой показаны города.Попросите их использовать линейку для измерения расстояния на карте между городами. Спросите: Видите ли вы два города в пределах дюйма друг от друга?
Продемонстрируйте, как измерять расстояние с помощью масштаба карты. Выровняйте лист обычной бумаги так, чтобы его край совпадал с масштабом проецируемой карты. Отметьте карандашом начало и конец шкалы. Напишите количество миль (или километров), которое представляет это расстояние. Объясните, что измерение на бумаге работает в любом месте этой карты, но масштаб, вероятно, будет другим на другой карте.Найдите на карте два места, которые примерно равны масштабу скопированной вами карты, и покажите их учащимся. Попросите учащихся выполнить то же задание с бумагой, карандашом и своими картами состояний. Спросите: Почему длина вашей статьи намного короче моей, если мы смотрим на одну и ту же карту? (Проектор делает карту намного больше, поэтому масштабная полоса карты тоже больше.)
3. Практикуйтесь в измерении расстояний, которые короче и длиннее шкалы.
Объясните, что расстояние между двумя городами не всегда соответствует длине шкалы.Иногда он оказывается между началом и концом шкалы, и тогда вы оцениваете расстояние. Найдите расстояние, которое составляет примерно половину длины шкалы, и попросите учащихся оценить его.
Для расстояний, превышающих масштаб, продемонстрируйте, как можно увеличить длину шкалы, добавляя сегменты к листу бумаги. Для второго сегмента увеличьте длину вдвое. Снова добавьте длину третьего и так далее. При необходимости направьте учащихся к предоставленной фотогалерее «Как увеличить масштаб карты».
4. Покажите учащимся, как измерять с помощью интерактивной карты.
Спросите учащихся, использовали ли они когда-нибудь или видели, как взрослый использует компьютер, смартфон или GPS для нанесения на карту маршрута и расстояния до пункта назначения. Объясните, что интерактивные онлайн-карты имеют возможности измерения, которые позволяют легко определять расстояние от одного места до другого.
Спроецируйте интерактивный картограф National Geographic и увеличьте масштаб своего штата. Выберите инструмент линии на панели инструментов рисования.Затем щелкните начальную точку, например свой родной город, а затем перетащите и дважды щелкните другую точку. Инструмент проведет линию с обозначенным расстоянием. Вы также можете щелкнуть и переместить курсор несколько раз, чтобы измерить искривленное расстояние.
5. Предложите учащимся составить контрольные измерения.
Попросите учащихся поработать в парах или по отдельности, чтобы создать тест по измерениям карты, используя свою карту состояния. Попросите их написать десять вопросов для измерения. Затем они могут использовать свои бумажные весы, чтобы найти ответы и создать отдельный ключ для ответа.Перед тем, как обмениваться тестами, попросите учащихся подойти к компьютерам и проверить свои ответы с помощью интерактивной карты и инструмента измерения. После того, как они обменяются и пройдут свои викторины, попросите их вернуть их и проверить ответы. Обсудите, насколько ответ «правильный» — иными словами, насколько близко он должен быть?
Руководство для начинающих по измерению расстояния на карте
Измерение расстояния — это ключевой инструмент при чтении карт, который особенно полезен для туристов и велосипедистов, которые хотят измерить, как далеко они проехали или как далеко они хотят пройти.Узнайте, как легко измерить расстояние, с помощью нашего простого и быстрого руководства.
Шаг 1. Найдите свои весы
Прежде всего, вы должны знать свой масштаб. Если вы понимаете масштаб карты, это здорово, но если вам это сложно, вы все равно можете точно измерить расстояния.
Внизу каждой карты есть шкала, которая показывает расстояние на карте. Когда вы измеряете расстояние на карте, просто сравните его с масштабом, и он мгновенно покажет вам расстояние в реальном мире.
Пример масштаба из карты OS Explorer 1:25 000
Шаг 2: Измерение расстояния
Вы можете измерить расстояния по прямой линии на карте с помощью линейки — она часто находится сбоку от компаса. Однако, если вы воспользуетесь описанной выше техникой, вы сможете использовать практически что угодно — карандаш, пальцы или веточку — чтобы определить расстояние и сравнить его с масштабом карты. Математика не требуется!
У этого есть один большой недостаток — вы можете измерять только прямые линии, что не так часто встречается за пределами городов.Хотя вы можете провести множество небольших измерений и сложить их, есть более простой способ, используя лишь небольшую часть простой старой строки. Попробуйте использовать шнурок от компаса или запасной шнурок, если у вас нет удобной веревки в кармане.
Разложите веревку вдоль трассы. Возможно, вам придется использовать дополнительные пальцы, чтобы закрепить его на месте. После того, как вы пройдете маршрут, внимательно отметьте веревку (или просто держите ее в нужном месте) и сравните ее с масштабом вашей карты.
Поместите веревку на карту и затем измерьте ее по шкале
Шаг 3: Расчет расстояния по шкале
Иногда нельзя просто сравнить масштаб карты с распечатанной картой.Возможно, вы используете карту без напечатанного масштаба или сложили карту в футляр для карт и не можете легко добраться до нее. Если у вас есть удобная линейка, вы все равно можете рассчитать расстояние.
Измерьте расстояние, используя линейку или веревку, как указано выше. Если вы использовали отрезок веревки, измерьте веревку, чтобы получить расстояние в сантиметрах.
Теперь вам нужно умножить это расстояние на масштаб карты и преобразовать его в метры или километры.
Примеры:
1: 8.5 см на карте OS Explorer в масштабе 1:25 000
| Умножить расстояние на масштаб 8,5 см x 25 000 = | 212 500 см |
| Преобразовать в метры 212,500 / 100 = | 2,125 м |
| Преобразовать в км: 2,125 / 1,000 = | 2.125 км |
2: 12,8 см, измерено на карте Landranger для ОС 1:50 000
| Умножить расстояние на масштаб 12.8 см x 50 000 = | 640 000 см |
| Преобразовать в метры 640,000 / 100 = | 6 400 м |
| Преобразовать в км: 6,400 / 1,000 = | 6.4 км |
Поскольку вы умножаете, а затем делите, чтобы преобразовать в км, вы можете упростить свои математические вычисления одним меньшим вычислением:
1: 25 000 — четверть сантиметра для расчета км give km
Поскольку сделать это без калькулятора иногда может быть сложно, неплохо иметь возможность сделать приблизительное значение.
Для карты 1:25 000 масштаб также показывает «от 4 см до 1 км». Так что мои 8,5 см — это 2 км плюс 1/8 км или 0,125, но даже если бы я округлил это до 2 км и «чуть-чуть», этого, вероятно, было бы достаточно для большинства целей.
Для карты 1: 50 000 масштаб составляет от 2 см до 1 км. Мои 12,8 см — это 6 км плюс чуть меньше половины.
ВАЖНО: Если вы путешествуете в условиях плохой видимости или на открытой местности с небольшим количеством ориентиров, вы можете быть более точными и точно рассчитать расстояния.
Совет!
Помните, что линии сетки на карте масштаба 1:25 000 находятся на расстоянии 1 км друг от друга. Быстрый способ оценить расстояние — это подсчитать каждый квадрат, который вы пересекаете по прямой. Если идти по диагонали, то расстояние по квадрату сетки составляет около 1½ км.
Бонус: другие способы измерения расстояния по карте
Вы также можете рассчитать расстояния на карте с помощью измерителя или измерителя карты.
Ромер — это линейка, масштабируемая в соответствии с определенным масштабом карты.Вместо того, чтобы читать в сантиметрах и преобразовывать, вы можете читать расстояние напрямую. Просто убедитесь, что вы используете romer с тем же масштабом, что и карта, которую вы используете — линейка компасов OS имеет правильный масштаб для наших самых популярных карт 1:25 000 OS Explorer и 1:50 000 OS Landranger.
Измеритель карты — это механический или электронный инструмент с маленьким колесиком, которым вы управляете по карте. Затем вы можете считать преобразованное расстояние. Опять же, проверьте руководство, чтобы убедиться, что вы используете правильные преобразования масштаба.
Дополнительная литература: Расширенное руководство по измерению расстояний
Ознакомьтесь с нашим путеводителем Pathfinder под названием Навыки навигации для пешеходов, включая чтение карты, компас и GPS.
Измерение расстояния на карте
Инструмент измерения расстояния — это простой способ найти расстояние между двумя или более точками на карте.
Выберите скорость …
Или выберите вид транспорта …
Как использовать инструмент измерения расстояния
Просто щелкните один раз на одной точке, затем щелкните еще раз на второй точке.Затем должно отображаться расстояние. Вы можете щелкнуть более двух точек, чтобы построить непрерывный маршрут.
Используйте переключатель миль / км / морских миль / ярдов для измерения расстояний в км, милях или морских милях. Параметр Автопанорамирование перемещает карту по мере того, как вы щелкаете по точкам.
Текстовое поле «Поиск местоположения» позволяет быстро добраться до нужной области, не тратя время на масштабирование и панорамирование, чтобы найти ее. Например, если вы хотите найти город Рим в Италии, введите «Рим, Италия», а затем нажмите «Поиск».Затем карта переместится прямо в Рим. Обратите внимание на формат «[город] [запятая] [пробел] [округ]».
Переключить маркеры, чтобы показать или скрыть маркеры, если они мешают.
Очистить последнюю удаляет последнюю точку с карты
Увеличить по размеру — масштабирование и панорамирование карты для получения наилучшего соответствия всех ваших точек при максимально возможном увеличении.
Очистить карту — это кнопка сброса, которая очищает все точки и позволяет снова начать измерение расстояния.
Вы можете редактировать положение любых существующих точек, перетаскивая маркер (когда они отображаются) и бросая маркер в его новом положении
Вы также можете настроить высоту карты, чтобы она была большой, средней или маленькой.
Вы можете удалить точку, щелкнув узел правой кнопкой мыши.
Будущие идеи и улучшения
- Автоматическое изменение маршрута для оптимального расстояния (задача коммивояжера)
- Есть другие скорости, такие как оптоволоконный кабель (~ .6 c) и Mach
- Возможность добавления заголовка к маркеру, который затем появляется при наведении курсора мыши и экспорте данных
- Добавить байдарку в список видов транспорта
История версий
- 21 февраля 2021 г. — выбранные единицы измерения расстояния сохраняются и вызываются при следующем посещении
- 6 июля 2020 г. — Новая опция для экспорта ссылки на маршрут.Находится в разделе «Параметры экспорта»
- 2 июня 2019 — Исправлена ошибка, из-за которой не работал вывод счетчиков
- 29 мая 2019 — Реализованы листовки-карты
- 20 мая 2019 г. — Исправлена ошибка в браузере IE
- 9 мая 2019 г. — Исправлена ошибка, из-за которой расстояние не сбрасывалось до нуля при нажатии кнопки «Очистить карту».
- 14 сентября 2017 — Расстояние теперь отображается на карте в полноэкранном режиме
- , 4 августа 2017 г. — Переключатель единиц измерения обновлен. Футов добавлено
- 24 июля 2017 г. — Полноэкранный режим перенесен на карту.Теперь находится в правом верхнем углу
- , 4 июля 2017 г. — Исправлена проблема с экспортом CSV и XLSX
- 29 января 2017 г. — Возможность отображения карты высот и экспорта файла CSV с данными о высоте вдоль маршрута
- 25 ноября 2016 г. — экспорт KML для отображения контактов на каждом узле маршрута
- 23 ноября 2016 г. — добавлена опция загрузки KML, CSV и XLSX
- 19 июля 2016 г. — Исправлены ошибки, связанные с изменением вида транспорта и расчетного времени в пути при изменении единиц измерения
- 5 июля 2016 — Добавлены метры как единицы расстояния
- 25 июня 2016 — Единицы скорости движения меняются в зависимости от единиц расстояния
- , 20 июня 2016 г. — Исправлена ошибка, из-за которой количество дней отображалось в два раза больше фактического значения
- 24 марта 2016 — Точки маршрута теперь можно добавлять в середине пути.Очки также можно удалить, щелкнув правой кнопкой мыши
- 25 января 2016 г. — Скорость теперь можно вводить вручную
- 28 декабря 2015 г. — Добавлена возможность переключения между минутами, часами и днями для оценки времени в пути
- 24 июня 2014 — Добавлена опция привязки к дорогам
- 24 марта 2014 г. — Добавлена опция «Панорама до моего местоположения»
- 11 января 2012 г. — Реализован Google Maps API V3. Добавлен полноэкранный режим
- 12 октября 2010 г. — маркеры теперь показывают их широту и долготу при наведении на них курсора
- 15 октября 2009 г. — Добавлен вывод времени в пути
- 12 октября 2009 г. — Добавлен вариант карты местности
- 20 февраля 2008 г. — Обновленный дизайн теперь с перетаскиваемыми маркерами
- 1 ноября 2007 г. — Добавлено текстовое поле быстрого поиска
- 19 октября 2007 г. — Ярды добавлены в качестве единицы измерения
- 9 октября 2007 г. — добавлены морские мили в качестве единицы измерения
- 5 сентября 2007 г. — обновлен описательный текст
- 28 июня 2007 г. — Страница создана
Соответствующие ссылки
Если вы пытаетесь измерить расстояние между двумя городами, то инструмент «Как далеко между ними», вероятно, больше подходит для ваших нужд.
Использование шкалы для измерения расстояния
Программа CSEC требует от учащихся уметь использовать масштаб карты для определения фактических расстояний между точками на земле. Масштаб карты, в которой вы будете представлены, может иметь форму отношения, например 1: 25 000 . Это означает, что одна единица на карте представляет 25000 из этих одинаковых единиц на земле. Следовательно, на карте с таким масштабом на один сантиметр на карте представляет 25000 сантиметров на земле. Один дюйм на этой карте представляет 25000 дюймов на земле.
Ваша карта также должна иметь линейный или графический масштаб. Это черно-белая полоса, показывающая расстояния в километрах или милях (или обоих).
Эта линейная или графическая шкала показывает расстояния на карте как в километрах, так и в милях.
Измерение расстояния по прямой
Вам может потребоваться измерить расстояние по прямой между двумя объектами на вашей карте.Назовем их объектами A и B. Это относительно простой процесс. Все, что вам нужно сделать, это измерить расстояние от объекта A до объекта B на вашей карте и использовать масштаб, чтобы определить фактическое расстояние.
Метод 1
Предположим, что расстояние между объектами на карте при измерении с помощью линейки составляет 10 см , а масштаб карты составляет 1: 25 000 . Фактическое расстояние можно определить, умножив расстояние на карте на 25 000, как показано ниже.
10 см X 25000 = 250000 см = 2500 метров = 2,5 км
Метод 2
Используйте лист бумаги, чтобы отметить расстояние между объектами A и B на карте. Затем поднесите лист бумаги к графической шкале, чтобы определить фактическое расстояние. Убедитесь, что вы начинаете измерение с точки шкалы, отмеченной нулем. Видео ниже демонстрирует этот процесс.
Как измерить расстояние между точками на картах Google
Google Maps может помочь вам ориентироваться в реальном мире, но он также может помочь вам определить расстояние между точками на любой карте.
Но не волнуйтесь — это не требует от вас оценки с помощью эталонной шкалы, которая отображается в нижней части настольной версии, чтобы помочь вам получить представление о расстояниях.
Вместо этого есть функция измерения, которую можно использовать для получения определенного измерения между двумя или более точками. Вот как им пользоваться, независимо от того, используете ли вы настольную или мобильную версию Google Maps.
Идет загрузка.
Обратите внимание на продукты, упомянутые в этой статье:
iPhone XS (от 999,99 долларов США в Best Buy)
Google Pixel 3 (от 449,99 долларов США в Best Buy)
Как выполнить измерения на Google Maps на вашем компьютере
Выполнение этой задачи — относительно простая задача, и ее выполнение займет у вас около минуты, если вы знаете все местоположения, которые хотите использовать:
1. Перейдите на maps.google.com.
2. Щелкните правой кнопкой мыши начальную точку и выберите «Измерить расстояние».
Выберите Измерение расстояния в нижней части меню.Девон Дельфино / Business Insider
3. Щелкните конечную точку (или вторую точку), чтобы создать прямую линию от исходной точки и получить расстояние между ними.
Щелкните конечную точку, чтобы измерить расстояние.Девон Дельфино / Business Insider
4. Если вы хотите измерить расстояние между несколькими точками, просто щелкните следующую точку на карте.
Выберите другую точку для измерения нескольких расстояний.Девон Дельфино / Business Insider
Общее расстояние будет отображаться как на черной линии, соединяющей каждую точку, так и во всплывающем окне в нижней части экрана.
Как измерить расстояние на Google Maps на вашем телефоне
Шаги для измерения расстояния в мобильном приложении одинаковы для пользователей Android и iPhone:
1. Откройте приложение Google Maps.
2. Коснитесь карты, с которой вы хотите начать (вы можете найти местоположение, если оно не рядом с вами или вашим сохраненным «домашним» местоположением).
3 . Коснитесь названия места, расположенного внизу экрана.
4. Прокрутите вниз и выберите «Измерить расстояние».
5. Переместите карту так, чтобы черный кружок или перекрестие оказались в следующей точке.
6. Нажмите «Добавить» (символ плюса) в правом нижнем углу экрана.
7. При необходимости повторите шаги пятый и шестой.
Вы увидите, что в нижней части страницы отображается общее расстояние, указанное как в милях, так и в километрах.
.

 Осевая линия пластины компаса будет показывать на шкале значение искомого азимута.
Осевая линия пластины компаса будет показывать на шкале значение искомого азимута.
 Но, к сожалению,к заповедному озеру нет дорог. Только старожилы да лесник могут его отыскать. Но у нас есть карта. Измерим азимут от домика лесника на озеро по карте. Затем возьмем компас в руки(не сбивая положения капсулы) и, направив пластину вперед, повернемся вместе с компасом так, чтобы стрелка показала на 0°. Нам остается двигаться по направлению пластины, следя, чтобы стрелка все время показывала на 0°. Тогда мы дойдемдо заповедного озера.
Но, к сожалению,к заповедному озеру нет дорог. Только старожилы да лесник могут его отыскать. Но у нас есть карта. Измерим азимут от домика лесника на озеро по карте. Затем возьмем компас в руки(не сбивая положения капсулы) и, направив пластину вперед, повернемся вместе с компасом так, чтобы стрелка показала на 0°. Нам остается двигаться по направлению пластины, следя, чтобы стрелка все время показывала на 0°. Тогда мы дойдемдо заповедного озера.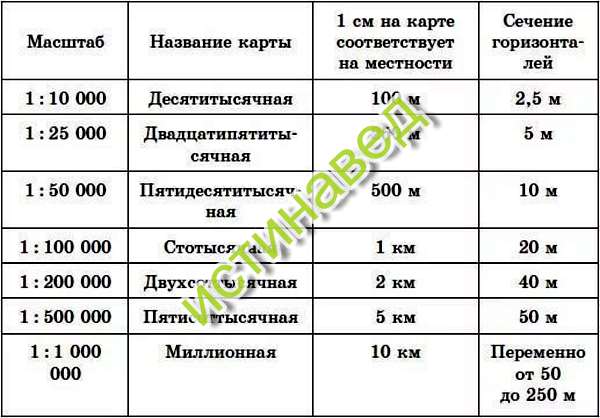
 Знание масштаба позволяет нам измерять расстояния по карте и переводить их в расстоянияна местности.В примере,рассмотренномв предыдущем параграфе, мы, двигаясь к лесному озеру, не знали, сколько нам до него идти. Вдруг мы отклонилисьот азимутаи озеро давно уже позади? Такого вопроса не возникло,если бы мы, измерив расстояние от домика лесника до озера по карте, рассчитали это расстояние на местности.
Знание масштаба позволяет нам измерять расстояния по карте и переводить их в расстоянияна местности.В примере,рассмотренномв предыдущем параграфе, мы, двигаясь к лесному озеру, не знали, сколько нам до него идти. Вдруг мы отклонилисьот азимутаи озеро давно уже позади? Такого вопроса не возникло,если бы мы, измерив расстояние от домика лесника до озера по карте, рассчитали это расстояние на местности.

