Содержание
Линейные уравнения с двумя переменными тест с ответами
Сложность: знаток.Последний раз тест пройден 1 час назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Выберите линейное уравнение с двумя переменными:
- Правильный ответ
- Неправильный ответ
- Вы и еще 64% ответили правильно
- 64% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Найдите решение уравнения: 2х + 3у = 2
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Выразите переменную х через переменную у из уравнения: 5у — 2х = -15
- Правильный ответ
- Неправильный ответ
- Вы и еще 67% ответили правильно
- 67% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Абсцисса точки, принадлежащей графику уравнения 2х — 3у = -7, равна 4.
 Найдите ординату этой точки.
Найдите ординату этой точки.- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Пара чисел (-4; -1) является решением уравнения ах + 3у — 5 = 0, если а равно:
- Правильный ответ
- Неправильный ответ
- Вы и еще 56% ответили правильно
- 56% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Подберите к данному уравнению 2х + 3у = -11 такое уравнение, чтобы решением получившейся системы была пара (2; -5)
- Правильный ответ
- Неправильный ответ
- Вы и еще 52% ответили правильно
- 52% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Найдите решение уравнения: 4х — 3у = 5
- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Выразите переменную х через переменную у из уравнения -6у +3х = 24
- Правильный ответ
- Неправильный ответ
- Вы и еще 63% ответили правильно
- 63% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Ордината точки, принадлежащей графику уравнения 6х + 2у = 2, равна 4.
 Найдите абсциссу этой точки.
Найдите абсциссу этой точки.- Правильный ответ
- Неправильный ответ
- Вы и еще 58% ответили правильно
- 58% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Пара чисел (-4; -1) является решением уравнения 4х + ау + 5 = 0, если а равно:
- Правильный ответ
- Неправильный ответ
- Вы и еще 52% ответили правильно
- 52% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Елена Тимофеева
9/10
Валентина Бизюкина
10/10
Павел Селивёрстов
10/10
Niyaz Gavrilov
9/10
Сикорская Анна
10/10
Максим Акманов
8/10
Аня Алексеева
9/10
Екатерина Лебедева
3/10
Валерий Цыганков
9/10
Константин Никитич
10/10
ТОП-3 тестакоторые проходят вместе с этим
Тест «Линейные уравнения с двумя переменными» соответствует министерской программе. Он предназначен для семиклассников, которые хотят проверить и закрепить материал. Вопросы охватывают все правила раздела, требует умения применять их на практике (решать уравнения, изображать графики).
Он предназначен для семиклассников, которые хотят проверить и закрепить материал. Вопросы охватывают все правила раздела, требует умения применять их на практике (решать уравнения, изображать графики).
Данная подборка заданий – отличный помощник в процессе домашней подготовки к уроку. Правильные ответы к заданиям уже даны, поэтому не придется тратить время на их поиск, тем не менее, желательно дополнить их информацией из учебника. Представленные вопросы разного уровня сложности, что позволяет объективно оценить свои знания. Тесты можно просматривать в электронном виде с любого устройства. Подборка подойдет и для учеников 8-9 классов, которые хотят «освежить» в памяти материал по теме.
Тест по линейным уравнениям с ответами – один из самых эффективных методов самооценивания и самоподготовки.
Рейтинг теста
Средняя оценка: 3.6. Всего получено оценок: 1140.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
ГДЗ по алгебре 7 класс контрольно-измерительные материалы Мартышова Решебник
Итак, мы разобрались в том, что алгебра действительно, сложный предмет. Но ее изучение просто необходимо для освоения школьного курса. Ее знание потребуется и для сдачи ОГЭ и ЕГЭ, и для поступления в вуз, и для дальнейшей учебы и работы. Эта дисциплина занимает главенствующее место наравне с русским и иностранным языками. Если не разобраться в каждой математической теме по отдельности, то в скором времени возникнут проблемы с учебой. И чтобы такого не было, не игнорируйте наше подспорье, которое станет вашим верным другом и соратником.
Но ее изучение просто необходимо для освоения школьного курса. Ее знание потребуется и для сдачи ОГЭ и ЕГЭ, и для поступления в вуз, и для дальнейшей учебы и работы. Эта дисциплина занимает главенствующее место наравне с русским и иностранным языками. Если не разобраться в каждой математической теме по отдельности, то в скором времени возникнут проблемы с учебой. И чтобы такого не было, не игнорируйте наше подспорье, которое станет вашим верным другом и соратником.
Кому можно использовать решебник по алгебре 7 класс контрольно-измерительные материалы Мартышовой
Наш учебно-методический комплекс можно и нужно использовать всем без исключения, кто только пожелает овладеть «царицей наук». А именно его могут применять:
- семиклассники для изучения предмета в учебном году;
- выпускники 9 и 11 классов, которых ждет сдача выпускных экзаменов;
- абитуриенты для подготовки к вступительным испытаниям и поступлению в профессиональное учебное заведение;
- школьники других классов для подготовки к участию в олимпиадах и конференциях;
- преподаватели для доступного изложения материала на уроках;
- репетиторы для более качественных занятий со студентами, которые вообще не разбираются в математике;
- родители, которые контролируют учебный процесс для проверки выполненных упражнений.

Какие темы есть в онлайн-ГДЗ по алгебре 7 класс контрольно-измерительные материалы автора: Мартышова, Л. И.
Ваш подросток изучит и подробно раскроет следующие темы, представленные на страницах подспорья:
- Тождества, выражения и уравнения.
- Функции.
- Степень с натуральным показателем.
- Многочлены.
- Формулы сокращенного умножения.
- Системы линейного уравнения.
С нашей подмогой, обучающийся освоит такие сложные алгебраические понятия и их решения: числовые выражения, переменные и их сравнения, натуральные показатели степени и ее свойства, решение задач через уравнение, статические характеристики (среднее арифметическое, медиана, мода, размах).
Главное, чтобы взрослые не забывали осуществлять контроль за тем, как выполняются задания: семиклассник ни в коме случае не должен списывать готовые д/з. Такой способ обучения не принесет положительных результатов, а только усугубит ситуацию. И тогда подросток ничего не поймет, а получит только больше пробелов в данной науке. ГДЗ необходимо для того чтобы применять его как образец, а не как готовую «домашку». И школьник должен это понимать и осознавать. А если он этого не делает, то вы должны сами ему это разъяснить, чтобы в дальнейшем не возникло проблем.
И тогда подросток ничего не поймет, а получит только больше пробелов в данной науке. ГДЗ необходимо для того чтобы применять его как образец, а не как готовую «домашку». И школьник должен это понимать и осознавать. А если он этого не делает, то вы должны сами ему это разъяснить, чтобы в дальнейшем не возникло проблем.
Тест по теме: «Системы линейных уравнений» | Тест по алгебре (7 класс) на тему:
Тест 7
«Системы линейных уравнений»
Вариант 1
А1. Какая из пар чисел является решением линейного уравнения .
1) 2) 3) 4)
А2. Для какого уравнения пара чисел является решением?
1) 2) 3) 4)
А3. Решите систему уравнений
1) 2) 3) 4)
А4. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А5. Пусть — решение системы линейных уравнений
Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А6. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А7. На каком из рисунков изображено графическое решение системы линейных уравнений
1) | 2) | 3) | 4) | |||
А8. Найдите координаты точки пересечения графиков уравнений и .
1) 2) 3) 4)
А9. Сколько точек пересечения имеют графики уравнений и ?
Сколько точек пересечения имеют графики уравнений и ?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
А10. Сколько решений имеет система уравнений
1) 1 2) 2 3) бесчисленное количество 4) ни одного
Тест 7
«Системы линейных уравнений»
Вариант 2
А1. Какая из пар чисел является решением линейного уравнения ?
1) 2) 3) 4)
А2. Для какого уравнения пара чисел является решением?
1) 2) 3) 4)
А3. Решите систему уравнений
1) 2) 3) 4)
А4. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А5. Пусть — решение системы линейных уравнений
Найдите .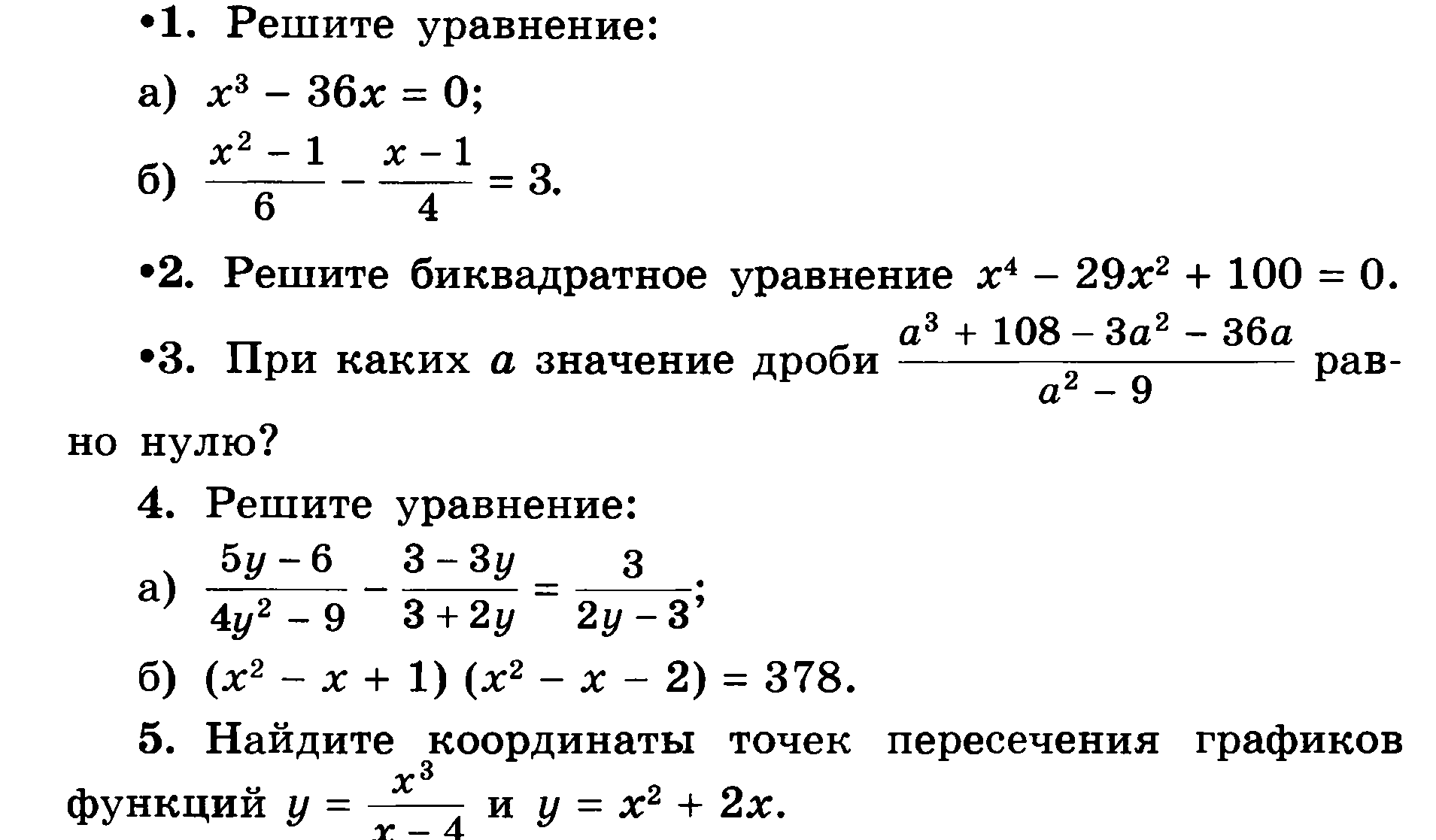 1) 2) 3) 4)
1) 2) 3) 4)
А6. Пусть — решение системы линейных уравнений
Найдите . 1) 2) 3) 4)
А7. На каком из рисунков изображено графическое решение системы линейных уравнений
1) | 2) | 3) | 4) | |||
А8. Найдите координаты точки пересечения графиков уравнений и .
1) 2) 3) 4)
А9. Сколько точек пересечения имеют графики уравнений и ?
1) 1 2) 2 3) бесчисленное количество 4) ни одной
А10. Сколько решений имеет система уравнений
Сколько решений имеет система уравнений
1) 1 2) 2 3) бесчисленное количество 4) ни одного
Ответы:
Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
1 | 1 | 4 | 2 | 2 | 1 | 3 | 2 | 4 | 3 | 4 |
2 | 4 | 4 | 3 | 3 | 4 | 2 | 1 | 2 | 4 | 3 |
Тесты по алгебре для 7 класса
Тест 3
Уравнения
Вариант 1
ЧАСТЬ А
А1. Корнем какого уравнения является число 2,25 ?
Корнем какого уравнения является число 2,25 ?
3)
2) 2, 25
1)
4 2
3
3
5
5
х
х
х
х
3
А2. При каком значении х выполняется равенство
2
х
1
9
2
9
х 4)
4
2
х
4
3,5
?
х
3
1) 14 2) 12 3) 42 4) 28
А3. Найдите корень уравнения
х
1,5
3, 2
3
.
1) 1,8 2) 2,4 3) 0,8 4) 1,6
А4. Решите уравнение
25
х
4
2
х
5 4
х
3
3
х
1) х – любое число 2) 0 3) нет корней 4) 2,5
8х ?
А5. При каком значении а уравнение 4
а имеет корень
9
х
1) 21 2) 23 3) 31 4) 28
А6. В магазине было 850 тетрадей. Продали m упаковок, в каждой из которых
было по 50 тетрадей. Составьте уравнение по условию задачи, если в магазине
350
осталось 350 тетрадей. 1) 850 50
350
3) 50
х
А7. Какое из чисел является корнем уравнения:
Какое из чисел является корнем уравнения:
1) 3,5 2) 9,5 3) 9,5 4) 5,5
А8. Решите уравнение:
1) 4,1; 2) 5,4; 3) 4,1; 4) 5,4.
А9. На доске было записано решение линейного уравнения:
2)
4)
х
4
350
350 850
5
50 850
850 50
m
m
m
m
1,3 0,1
?
11
2,1
4
3
3
.
х
х
6
х
х
…..
2,5.
Правую часть уравнения стерли. Что было записано в правой части уравнения?
1) 15 2) 2,5х 3) 2,5 4) 15
А10. Решите уравнение:
14
х
15
1)
5
8
2)
8
5
; 3)
4)
8
3
3
8
5
8
х
.
ЧАСТЬ B
найдите значения а, при которых корнем
1
В1. Для уравнения
этого уравнения является число 6.
11 3
ах
х В2. Решите уравнение:
ответе укажите их сумму.
х
1
7,5
. Если корней уравнения несколько, то в
Тест 3
Уравнения
Вариант 2
ЧАСТЬ А
А1. Корнем какого уравнения является число 36 ?
1)
2) 2,25
3)
4
2
5
3
5
3
х
х
х
х
3
А2. При каком значении х выполняется равенство
2
х
1
9
2
9
х 4)
4
2
х
7
0, 2
?
х
5
1) 1,4 2) 2,8 3) 3,5 4) 7
А3. Найдите корень уравнения
1,8
2,5
9
.
х
1) 12,5 2) 12,4 3) 1,25 4) 15
А4. Решите уравнение
17
х
12 2 9
х
5
х
2
.
1) х – любое число 2) 0 3) нет корней 4) 2,5
х ?
6
А5. При каком значении а уравнение 3
имеет корень
4
а
х
1) 12 2) 14 3) 8 4) 22
256 12
n
112
А6. В магазине было 256 книг. Продали n пачек книг, в каждой из которых было
по 12 книг. Составьте уравнение по условию задачи, если в магазине осталось 112
книг. 1)
1)
112
3) 12
А7. Какое из чисел является корнем уравнения:
1) 3,5 2) 5,5 3) 9,5 4) 5,5
А8. Решите уравнение:
1) 3,72; 2) 2,42; 3) 2,42; 4) 3,4.
А9. На доске было записано решение линейного уравнения:
12 256
n
4) 256 12
2)
7,2 2 0,3
2,35 4
112
256
n
?
3,25
n
112
10
5
3
3
4
х
х
х
х
.
х
…..
х
5
1, 4.
Правую часть уравнения стерли. Что было записано в правой части уравнения?
1) 1,4x 2) 7 3) 6,4 4) 1,4
А10. Решите уравнение:
19
х
20
1)
9
14
2)
9
14
5
9
х
.
; 3)
ЧАСТЬ B
4)
5
9
5
9
найдите значения а, при которых корнем
8
В1. Для уравнения
Для уравнения
этого уравнения является число 8.
12 5
ах
х х
1
9,5
. Если корней уравнения несколько, то в
В2. Решите уравнение:
ответе укажите их сумму.
Ответы:
Вариант А1
1
2
1
2
А2
3
3
А3
4
1
А4
3
1
А5
2
2
А6
1
4
А7
2
4
А8 А9 А10
1
3
4
2
3
2
В1
5
5,5
В2
2
2
|
1. |
Будет ли корнем уравнения данное число?
|
1 |
|
2. 
|
Решение уравнения с переносом слагаемых
|
1 |
|
3. |
Выбирать правильный вариант ответа
|
1 |
|
4. 
|
Решить уравнение (целые коэффициенты)
|
2 |
|
5. |
Решить уравнение (коэффициенты — десятичные дроби)
|
2 |
|
6. 
|
Определить корень уравнения с дробными коэффициентами
|
2 |
|
7. |
Решение уравнения с раскрытием скобок
|
2 |
|
8. 
|
Решить уравнение
|
3 |
|
9. |
Определить значение выражения
|
3 |
|
10. 
|
Решение уравнения, содержащего дроби с разными знаменателями
|
4 |
Сценарий урока алгебры в 7 классе по теме «Решение линейных уравнений»
Вынесение множителя из-под знака корня
ГБОУ ГИМНАЗИЯ 190 Технологическая карта урока алгебры, 8 класс Вынесение множителя из-под знака корня Фролова Любовь Алексеевна, учитель математики 01. 02.2016 Урок алгебры в 8классе Тема «Вынесение множителя
02.2016 Урок алгебры в 8классе Тема «Вынесение множителя
Подробнее
y 12 = 2y 7,5 y 2y = 12 7,5 -y = 4,5 y = — 4,5
Муниципальное бюджетное общеобразовательное учреждениесредняя общеобразовательная школа 7г. Белгорода Разработка урока по теме «Решение уравнений» (6 класс) Подготовила учитель математики Гриценко Т.Г.
Подробнее
Тема урока «Теорема Виета» 8 класс
Тема урока «Теорема Виета» 8 класс Учитель: Демина Т.В. Цели урока: 1. Познакомить учащихся с теоремой Виета; 2. Научить применять теорему Виета для составления квадратных уравнений; 3. Сформулировать
Подробнее
Ход урока: 1 Организационный момент.
Цель: Организовать деятельность учащихся по закреплению графического метода решения уравнений с параметром, проводить исследование на наличие корней уравнения для каждого значения параметра. Задачи: 1.
Задачи: 1.
Подробнее
Занятие 1 (2 часа) Ход занятия.
Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие
Подробнее
( урок математики в 5 классе)
МУНИЦИПАЛЬНОЕ КАЗЁННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 3» ул.чугунова,д.4,г.людиново Калужской области, 249400 Телефон:(48444) 6-19-43, 6-18-79, 6-62-99 Факс:(48444) 6-19-43
Подробнее
Оборудование: проектор, ноутбуки, рабочие листы, тетради, учебники, раздаточный материал
Достаточно часто в школах мы встречаем ситуацию, когда учитель прекрасно объясняет материал, учащиеся его внимательно слушают, но через несколько минут, выходя из кабинета, забывают, о чем шла речь на
Подробнее
Методическая разработка открытого урока
Довлатбегян Виктория Александровна, учитель математики МБОУ «Лицей» г. протвино, МО Методическая разработка открытого урока «Разложение многочлена на множители с помощью комбинации различных приемов» Алгебра.
протвино, МО Методическая разработка открытого урока «Разложение многочлена на множители с помощью комбинации различных приемов» Алгебра.
Подробнее
Учебник: Алгебра (Дорофеев Г.В.) гг.
Класс 9.3.1, 9.3.2 (база) Учебник: Алгебра (Дорофеев Г.В.) 2018-2019 гг. Тема модуля: «Уравнения и системы уравнений» Основные теоретические сведения, необходимые для успешного выполнения теста: 1. Понятие
Подробнее
ОТКРЫТЫЙ УРОК АЛГЕБРЫ В 9-А КЛАССЕ.
113 Учитель математики Кузнецова Г. Ю. ОТКРЫТЫЙ УРОК АЛГЕБРЫ В 9-А КЛАССЕ. Тип урока Тема: Объяснения нового материала и первичного закрепления полученных знаний. «Целое уравнение и его корни». Цели урока:
Подробнее
Конспект урока, 7 класс.
Конспект урока алгебры в 7 классе. Взаимное расположение графиков линейных функций Автор: Дмитриева Наталья Анатольевна, Московская область, город Подольск, МОУ «Лицей 26». Описание материала: Предлагаю
Описание материала: Предлагаю
Подробнее
Тема: Решение систем уравнений
Цель урока: МОУ гимназия 11 г. Елец Липецкой области Разработчик: учитель информатики Губина Т.Н. Методическая разработка системы интегрированных уроков по информатике и математике в 10 классе Урок 7 Тема:
Подробнее
ПЛАН УРОКА. ЮКО, Отырарский район, с. Шаульдер, ШГ им. Ш. Калдаякова, 8 класс Уравнения, приводящие к квадратным уравнениям
ПЛАН УРОКА Предмет Алгебра Учитель Тəшімбет З. М. Школа, класс Тема урока ЮКО, Отырарский район, с. Шаульдер, ШГ им. Ш. Калдаякова, 8 класс Уравнения, приводящие к квадратным м Цель обучения: изучив данную
Подробнее
IV. Актуализация опорных знаний
КАЛЕЙДОСКОП КОП УРОКОВ ОВ УРАВНЕНИЯ И НЕРАВЕНСТВА Подготовка к государственной итоговой аттестации 9 класс Т В Желтуха Цель: обобщить и систематизировать знания учащихся об уравнениях и неравенствах; закрепить
Подробнее
ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ
Методическая разработка по алгебре (8 класс) ФОРМУЛА КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ Амосова Галина Владимировна, учитель математики и информатики ГБОУ СОШ 2 Василеостровского района Санкт-Петербурга «Метод
Подробнее
Бутыгина Татьяна Федоровна Аннотация
Бутыгина Татьяна Федоровна, учитель математики высшей квалификационной категории МОУ «СОШ 11 с углубленным изучением иностранных языков» г. Ноябрьска ЯНАО Тюменской области. Аннотация Все знают: «Повторение
Ноябрьска ЯНАО Тюменской области. Аннотация Все знают: «Повторение
Подробнее
ГДЗ Алгебра 7 класс Мартышова
Алгебра 7 класс
Контрольно-измерительные материалы
Мартышова
ВАКО
С введением в курс программы данного предмета учащимся предстоит окунуться в сложные математические вычисления. Дети, которые не обладают соответствующим складом ума порой испытываю серьезные проблемы с выполнением упражнений. Нечего и говорить о том, что любых проверочных испытаний они бояться, как огня. Дополнительные тренировки должны помочь школьникам лучше понять подоплеку изучаемого материала. Лучше всего осуществлять их, имея под рукой решебник к учебнику «Алгебра. Контрольно-измерительные материалы 7 класс» Мартышова, в котором приведены расширенные разъяснения по всем темам.
Что содержится в издании
В пособии имеется двадцать три тестовых работы, которые предусмотрены задания для двух вариантов. Девятнадцать самостоятельных и десять контрольных охватывают весь учебный курс этого года. Подробно изложенные в ГДЗ по алгебре 7 класс Мартышова решения по всем упражнениям помогут ребятам подготовиться к всевозможным проверочным испытаниям.
Девятнадцать самостоятельных и десять контрольных охватывают весь учебный курс этого года. Подробно изложенные в ГДЗ по алгебре 7 класс Мартышова решения по всем упражнениям помогут ребятам подготовиться к всевозможным проверочным испытаниям.
Зачем им надо пользоваться
Школьники уже давно привыкли к всевозможным испытаниям, которые призваны выявить уровень их познаний. Некоторые из них серьезно подходят к ним и заранее готовятся, а другие надеяться на авось. Как бы то ни было, основополагающим фактором все же является наличие твердой базы знаний. А получить ее возможно только при внимательном отношении школьников к изучаемой дисциплине. Если же ученик относится к предмету поверхностно и не особо стремится к его познанию, то даже шпаргалки ему могут не помочь. Решебник к учебнику «Алгебра. Контрольно-измерительные материалы 7 класс» Мартышова содержит детальные сведения по всем нюансам программы, поэтому можно не только подготовиться к проверочным работам, но и подробнее разобрать непонятные темы. «ВАКО», 2017 г.
«ВАКО», 2017 г.
Название
Условие
Решение
4.1. Решение систем линейных уравнений с двумя переменными — промежуточная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Решите систему уравнений заменой
- Решите систему уравнений методом исключения
- Выбрать наиболее удобный метод решения системы линейных уравнений
Будьте готовы 4.1
Перед тем, как начать, пройдите тест на готовность.
Для уравнения y = 23x − 4, y = 23x − 4,
Ⓐ Является ли (6,0) (6,0) решением? Ⓑ Является ли (−3, −2) (- 3, −2) решением?
Если вы пропустили эту проблему, просмотрите Пример 3.2.
Будьте готовы 4,2
Найдите наклон и пересечение y прямой 3x − y = 12,3x − y = 12.
Если вы пропустили эту проблему, просмотрите Пример 3.16.
Будьте готовы 4.3
Найдите точки пересечения x- и y прямой 2x − 3y = 12.2х − 3у = 12.
Если вы пропустили эту проблему, просмотрите Пример 3.8.
Определить, является ли упорядоченная пара решением системы уравнений
В разделе «Решение линейных уравнений» мы научились решать линейные уравнения с одной переменной. Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений.
Система линейных уравнений
Когда два или более линейных уравнения сгруппированы вместе, они образуют систему линейных уравнений .
В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Позже в этой главе мы решим более крупные системы уравнений.
Ниже показан пример системы двух линейных уравнений. Мы используем скобку, чтобы показать, что два уравнения сгруппированы вместе и образуют систему уравнений.
{2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Линейное уравнение с двумя переменными, например 2x + y = 7,2x + y = 7, имеет бесконечное количество решений. Его график представляет собой линию. Помните, что каждая точка на линии — это решение уравнения, а каждое решение уравнения — это точка на линии.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары (x, y) (x, y), которые делают оба уравнения истинными. Они называются решениями системы уравнений.
Решения системы уравнений
Решения системы уравнений — это значения переменных, которые делают все истинными.Решение системы двух линейных уравнений представляется упорядоченной парой (x, y). (X, y).
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения истинными, это решение системы.
Пример 4.1
Определите, является ли упорядоченная пара решением системы {x − y = −12x − y = −5. {X − y = −12x − y = −5.
ⓐ (−2, −1) (- 2, −1) ⓑ (−4, −3) (- 4, −3)
Решение
ⓐ
ⓑ
Попробуй 4.1
Определите, является ли упорядоченная пара решением системы {3x + y = 0x + 2y = −5. {3x + y = 0x + 2y = −5.
ⓐ (1, −3) (1, −3)
Ⓑ (0,0) (0,0)
Попробуйте 4.2
Определите, является ли упорядоченная пара решением системы {x − 3y = −8−3x − y = 4. {X − 3y = −8−3x − y = 4.
ⓐ (2, −2) (2, −2)
Ⓑ (−2,2) (- 2,2)
Решение системы линейных уравнений с помощью построения графиков
В этом разделе мы будем использовать три метода для решения системы линейных уравнений. Первый метод, который мы будем использовать, — это построение графиков.
График линейного уравнения представляет собой линию. Каждая точка на линии — это решение уравнения. Для системы двух уравнений мы построим график двумя линиями. Затем мы можем увидеть все точки, которые являются решениями каждого уравнения. И, обнаружив, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, все числа являются решениями.
Точно так же, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий в одной плоскости, есть три возможных случая, как показано.
Рисунок 4.2
Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его в той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.
Пример 4.2
Как решить систему уравнений с помощью построения графиков
Решите систему, построив график {2x + y = 7x − 2y = 6.{2x + y = 7x − 2y = 6.
Попробуйте 4.3
Решите систему, построив график: {x − 3y = −3x + y = 5. {X − 3y = −3x + y = 5.
Попробуйте 4.4
Решите систему, построив график: {−x + y = 13x + 2y = 12. {- x + y = 13x + 2y = 12.
Здесь показаны шаги, которые нужно использовать для решения системы линейных уравнений с помощью построения графиков.
How To
Решите систему линейных уравнений с помощью построения графиков.
- Шаг 1. Постройте первое уравнение.
- Шаг 2. Постройте второе уравнение в той же прямоугольной системе координат.
- Шаг 3. Определите, пересекаются ли линии, параллельны или совпадают.
- Шаг 4. Определите решение системы.
- Если линии пересекаются, укажите точку пересечения. Это решение системы.
- Если линии параллельны, у системы нет решения.
- Если строки совпадают, система имеет бесконечное количество решений.
- Шаг 5. Проверьте решение в обоих уравнениях.
В следующем примере мы сначала перепишем уравнения в форме углового пересечения, так как это упростит нам быстрое построение графиков линий.
Пример 4.3
Решите систему, построив график: {3x + y = −12x + y = 0. {3x + y = −12x + y = 0.
Решение
Мы решим оба этих уравнения относительно yy, чтобы мы могли легко построить их график, используя их наклоны и точки пересечения y .
Попробуй 4.5
Решите систему, построив график: {−x + y = 12x + y = 10. {- x + y = 12x + y = 10.
Попробовать 4.6
Решите систему, построив график: {2x + y = 6x + y = 1. {2x + y = 6x + y = 1.
До сих пор во всех системах линейных уравнений линии пересекались и решение было одной точкой.В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, которая имеет бесконечное число решений.
Пример 4.4
Решите систему, построив график: {y = 12x − 3x − 2y = 4. {Y = 12x − 3x − 2y = 4.
Попробуйте 4.7
Решите систему, построив график: {y = −14x + 2x + 4y = −8. {Y = −14x + 2x + 4y = −8.
Попробуйте 4.8
Решите систему, построив график: {y = 3x − 16x − 2y = 6. {Y = 3x − 16x − 2y = 6.
Иногда уравнения в системе представляют собой одну и ту же линию.Поскольку каждая точка на прямой делает оба уравнения истинными, существует бесконечно много упорядоченных пар, которые делают оба уравнения истинными. У системы бесконечно много решений.
Пример 4.5
Решите систему, построив график: {y = 2x − 3−6x + 3y = −9. {Y = 2x − 3−6x + 3y = −9.
Решение
Если вы напишете второе уравнение в форме пересечения наклона, вы можете заметить, что уравнения имеют одинаковый наклон и одинаковое пересечение y .
Попробуй 4.9
Решите систему, построив график: {y = −3x − 66x + 2y = −12. {Y = −3x − 66x + 2y = −12.
Попробовать 4.10
Решите систему, построив график: {y = 12x − 42x − 4y = 16. {Y = 12x − 42x − 4y = 16.
Когда мы нарисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две линии совпадают. Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y — .
Совпадающие линии
Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y- .
Каждая система уравнений в Примере 4.2 и Примере 4.3 имела две пересекающиеся линии. У каждой системы было одно решение.
В примере 4.5 уравнения давали совпадающие линии, поэтому система имела бесконечно много решений.
Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая по крайней мере одно решение, называется согласованной системой .
Система с параллельными линиями, подобная примеру 4.4, не имеет решения.Мы называем такую систему уравнений несогласованной. Нет решения.
Согласованные и несовместимые системы
Непротиворечивая система уравнений — это система уравнений, имеющая по крайней мере одно решение.
Несогласованная система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, каждое из них имеет собственный набор решений.Пересекающиеся линии и параллельные линии независимы.
Если два уравнения зависимы, все решения одного уравнения также являются решениями другого уравнения. Когда мы строим график двух зависимых уравнений, мы получаем совпадающие линии.
Давайте подведем итог, посмотрев на графики трех типов систем. См. Ниже и Таблицу 4.1.
| линий | Пересечение | Параллельный | Совпадение |
|---|---|---|---|
| Количество решений | 1 балл | Нет решения | Бесконечно много |
| Согласованный / непоследовательный | Согласованный | Несоответствие | Согласованный |
| Зависимые / независимые | Независимая | Независимая | Иждивенец |
Таблица 4.1
Пример 4.6
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y = 3x − 16x − 2y = 12 {y = 3x − 16x − 2y = 12 ⓑ {2x + y = −3x − 5y = 5 {2x + y = −3x − 5y = 5
Решение
ⓐ Сравним наклоны и пересечения двух линий.
| Первое уравнение уже имеет форму пересечения наклона. | {y = 3x − 16x − 2y = 12y = 3x − 1 {y = 3x − 16x − 2y = 12y = 3x − 1 |
| Запишите второе уравнение в форме углового пересечения. | 6x − 2y = 12−2y = −6x + 12−2y − 2 = −6x + 12−2y = 3x − 66x − 2y = 12−2y = −6x + 12−2y − 2 = −6x + 12−2y = 3х − 6 |
| Найдите наклон и точку пересечения каждой прямой. | y = 3x − 1y = 3x − 6m = 3m = 3b = −1b = −6y = 3x − 1y = 3x − 6m = 3m = 3b = −1b = −6 |
| Поскольку наклоны одинаковые, а точки пересечения y разные, линии параллельны. |
Система уравнений, графики которой представляют собой параллельные прямые, не имеет решения, непоследовательна и независима.
ⓑ Мы сравним наклон и пересечения двух линий.
| {2x + y = −3x − 5y = 5 {2x + y = −3x − 5y = 5 | |
| Запишите оба уравнения в форме углового пересечения. | 2x + y = −3x − 5y = 5y = −2x − 3−5y = −x + 5−5y − 5 = −x + 5−5y = 15x − 12x + y = −3x − 5y = 5y = −2x −3−5y = −x + 5−5y − 5 = −x + 5−5y = 15x − 1 |
| Найдите наклон и точку пересечения каждой прямой. | y = −2x − 3y = 15x − 1m = −2m = 15b = −3b = −1y = −2x − 3y = 15x − 1m = −2m = 15b = −3b = −1 |
| Поскольку уклоны разные, линии пересекаются. |
Система уравнений, графики которой пересекаются, имеет одно решение, непротиворечива и независима.
Попробовать 4.11
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y = −2x − 44x + 2y = 9 {y = −2x − 44x + 2y = 9 ⓑ {3x + 2y = 22x + y = 1 {3x + 2y = 22x + y = 1
Попробовать 4.12
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y = 13x − 5x − 3y = 6 {y = 13x − 5x − 3y = 6 ⓑ {x + 4y = 12 − x + y = 3 {x + 4y = 12 − x + y = 3
Решение систем линейных уравнений с помощью графиков — хороший способ визуализировать типы решений, которые могут возникнуть.Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы маленькой сетки с x и y , оба между -10-10 и 10, построение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.
Решите систему уравнений подстановкой
Теперь решим системы линейных уравнений методом подстановки.
Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.
{2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Сначала мы решим одно из уравнений для x или y . Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной.Наконец, мы проверяем наше решение и убеждаемся, что оно выполняет оба уравнения.
Пример 4.7
Как решить систему уравнений подстановкой
Решите систему с помощью замены: {2x + y = 7x − 2y = 6. {2x + y = 7x − 2y = 6.
Попробовать 4.13
Решите систему с помощью замены: {−2x + y = −11x + 3y = 9. {- 2x + y = −11x + 3y = 9.
Попробуй 4.14
Решите систему заменой: {2x + y = −14x + 3y = 3. {2x + y = −14x + 3y = 3.
How To
Решите систему уравнений путем подстановки.
- Шаг 1. Решите одно из уравнений для любой переменной.
- Шаг 2. Подставьте выражение из шага 1 в другое уравнение.
- Шаг 3. Решите полученное уравнение.
- Шаг 4. Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Шаг 5. Запишите решение в виде упорядоченной пары.
- Шаг 6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Будьте очень осторожны со знаками в следующем примере.
Пример 4.8
Решите систему заменой: {4x + 2y = 46x − y = 8. {4x + 2y = 46x − y = 8.
Решение
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно y .
Попробуй 4.15
Решите систему с помощью замены: {x − 4y = −4−3x + 4y = 0. {X − 4y = −4−3x + 4y = 0.
Попробуйте 4.16
Решите систему с помощью замены: {4x − y = 02x − 3y = 5.{4x − y = 02x − 3y = 5.
Решите систему уравнений методом исключения
Мы решили системы линейных уравнений с помощью построения графиков и подстановки. Построение графиков хорошо работает, когда переменные коэффициенты малы, а решение имеет целочисленные значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения.Когда мы решали систему с помощью подстановки, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добиться этого.
Метод исключения основан на добавочном свойстве равенства. Свойство сложения равенства говорит, что когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство. Мы расширим свойство сложения равенства, чтобы сказать, что когда вы добавляете равные количества к обеим сторонам уравнения, результаты равны.
Для любых выражений a, b, c, и d .
ifa = bandc = dthena + c = b + d. ifa = bandc = dthena + c = b + d.
Чтобы решить систему уравнений методом исключения, мы начнем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет легче всего устранить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
{3x + y = 52x − y = 0 ————— 5x = 5 {3x + y = 52x − y = 0 ————— 5x = 5
Добавляем y к нулю, и мы получаем единицу уравнение с одной переменной.
Давайте попробуем еще один:
{x + 4y = 22x + 5y = −2 {x + 4y = 22x + 5y = −2
На этот раз мы не видим переменную, которую можно было бы немедленно исключить, если мы добавим уравнения.
Но если мы умножим первое уравнение на −2, −2, мы сделаем коэффициенты при x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2. − 2.
Затем перепишите систему уравнений.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому значение x будет исключено, когда мы сложим эти два уравнения.
Как только мы получаем уравнение с одной переменной, мы его решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы увидим, как использовать исключение для решения той же системы уравнений, которую мы решили с помощью построения графиков и подстановки.
Пример 4.9
Как решить систему уравнений методом исключения
Решите систему методом исключения: {2x + y = 7x − 2y = 6.{2x + y = 7x − 2y = 6.
Попробуйте 4.17
Решите систему методом исключения: {3x + y = 52x − 3y = 7. {3x + y = 52x − 3y = 7.
Попробуй 4.18
Решите систему методом исключения: {4x + y = −5−2x − 2y = −2. {4x + y = −5−2x − 2y = −2.
Шаги перечислены здесь для удобства.
How To
Решите систему уравнений методом исключения.
- Шаг 1. Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Шаг 2.Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную исключить.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
- Шаг 3. Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Шаг 4. Найдите оставшуюся переменную.
- Шаг 5. Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Шаг 6.Запишите решение в виде упорядоченной пары.
- Шаг 7. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Теперь мы рассмотрим пример, в котором нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Пример 4.10
Решите систему методом исключения: {4x − 3y = 97x + 2y = −6. {4x − 3y = 97x + 2y = −6.
Решение
В этом примере мы не можем умножить одно уравнение на любую константу, чтобы получить противоположные коэффициенты.Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположности.
Попробуй 4.19
Решите систему методом исключения: {3x − 4y = −95x + 3y = 14. {3x − 4y = −95x + 3y = 14.
Попробовать 4.20
Решите каждую систему методом исключения: {7x + 8y = 43x − 5y = 27. {7x + 8y = 43x − 5y = 27.
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.
Пример 4.11
Решите систему методом исключения: {x + 12y = 632x + 23y = 172. {X + 12y = 632x + 23y = 172.
Решение
В этом примере в обоих уравнениях есть дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
Попробуйте 4.21
Решите каждую систему методом исключения: {13x − 12y = 134x − y = 52. {13x − 12y = 134x − y = 52.
Попробуйте 4.22
Решите каждую систему методом исключения: {x + 35y = −15−12x − 23y = 56.{x + 35y = −15−12x − 23y = 56.
Когда мы решили систему с помощью построения графиков, мы увидели, что не все системы линейных уравнений имеют единственную упорядоченную пару в качестве решения. Когда два уравнения действительно представляли собой одну и ту же линию, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные линии, решения не было. Мы назвали это несовместимой системой.
То же самое и с заменой или исключением. Если уравнение в конце замены или исключения является истинным утверждением, у нас есть непротиворечивая, но зависимая система, а система уравнений имеет бесконечно много решений.Если уравнение в конце замены или исключения является ложным утверждением, мы имеем несовместимую систему и система уравнений не имеет решения.
Пример 4.12
Решите систему методом исключения: {3x + 4y = 12y = 3−34x. {3x + 4y = 12y = 3−34x.
Решение
| {3x + 4y = 12y = 3−34x {3x + 4y = 12y = 3−34x | |
| Запишите второе уравнение в стандартной форме. | {3x + 4y = 1234x + y = 3 {3x + 4y = 1234x + y = 3 |
| Очистите дроби, умножив второе уравнение на 4. | {3x + 4y = 124 (34x + y) = 4 (3) {3x + 4y = 124 (34x + y) = 4 (3) |
| Упростить. | {3x + 4y = 123x + 4y = 12 {3x + 4y = 123x + 4y = 12 |
| Чтобы исключить переменную, мы умножаем второе уравнение на -1. Упростите и добавьте. | {3x + 4y = 12−3x − 4y = −12 ______________ 0 = 0 {3x + 4y = 12−3x − 4y = −12 ______________ 0 = 0 |
Это верное заявление. Уравнения непротиворечивы, но зависимы. Их графики будут одной линией. У системы бесконечно много решений.
Заметили ли вы, что после того, как мы очистили дроби во втором уравнении, эти два уравнения совпадают? Это означает, что у нас есть совпадающие линии.
Попробуйте 4.23
Решите систему методом исключения: {5x − 3y = 15y = −5 + 53x. {5x − 3y = 15y = −5 + 53x.
Попробуйте 4.24
Решите систему методом исключения: {x + 2y = 6y = −12x + 3. {X + 2y = 6y = −12x + 3.
Выберите наиболее удобный метод решения системы линейных уравнений
Когда вы решаете систему линейных уравнений в приложении, вам не сообщат, какой метод использовать.Вам нужно будет принять это решение самостоятельно. Так что вы захотите выбрать самый простой метод, который сводит к минимуму ваши шансы на ошибку.
Выберите наиболее удобный метод для решения системы линейных уравнений Графическое отображение ———— Замена ————— Исключение ————— Используйте, когда вам нужно использовать, когда одно уравнение является стандартная форма. легко решается для одной переменной. Выберите наиболее удобный метод для решения системы линейных уравнений. Графическое отображение ———— Замена ————— Исключение ————— Используется, когда вам нужно Использовать, когда одно уравнение используется, когда уравнения представляют собой ситуация.уже решена или может быть в стандартной форме. легко решается для одной переменной.
Пример 4.13
Решите для каждой системы линейных уравнений, что удобнее решить: заменой или исключением. Поясните свой ответ.
ⓐ {3x + 8y = 407x − 4y = −32 {3x + 8y = 407x − 4y = −32 ⓑ {5x + 6y = 12y = 23x − 1 {5x + 6y = 12y = 23x − 1
Решение
ⓐ
{3x + 8y = 407x − 4y = −32 {3x + 8y = 407x − 4y = −32
Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
ⓑ
{5x + 6y = 12y = 23x − 1 {5x + 6y = 12y = 23x − 1
Так как одно уравнение уже решено для y , использование подстановки будет наиболее удобным.
Попробуйте 4.25
Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.
ⓐ {4x − 5y = −323x + 2y = −1 {4x − 5y = −323x + 2y = −1 ⓑ {x = 2y − 13x − 5y = −7 {x = 2y − 13x − 5y = −7
Попробуйте 4.26
Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением.Поясните свой ответ.
ⓐ {y = 2x − 13x − 4y = −6 {y = 2x − 13x − 4y = −6 ⓑ {6x − 2y = 123x + 7y = −13 {6x − 2y = 123x + 7y = −13
Раздел 4.1. Упражнения
Практика ведет к совершенству
Определить, является ли упорядоченная пара решением системы уравнений
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
1.
{2x − 6y = 03x − 4y = 5 {2x − 6y = 03x − 4y = 5
ⓐ (3,1) (3,1) ⓑ (−3,4) (- 3,4)
2.
{−3x + y = 8 − x + 2y = −9 {−3x + y = 8 − x + 2y = −9
ⓐ (−5, −7) (- 5, −7) ⓑ (−5,7) (- 5,7)
3.
{x + y = 2y = 34x {x + y = 2y = 34x
ⓐ (87,67) (87,67) ⓑ (1,34) (1,34)
4.
{2x + 3y = 6y = 23x + 2 {2x + 3y = 6y = 23x + 2
ⓐ (−6,2) (- 6,2) ⓑ (−3,4) (- 3,4)
Решение системы линейных уравнений с помощью построения графиков
В следующих упражнениях решите следующие системы уравнений с помощью построения графиков.
5.
{3x + y = −32x + 3y = 5 {3x + y = −32x + 3y = 5
6.
{−x + y = 22x + y = −4 {−x + y = 22x + y = −4
7.
{y = x + 2y = −2x + 2 {y = x + 2y = −2x + 2
8.
{y = x − 2y = −3x + 2 {y = x − 2y = −3x + 2
9.
{y = 32x + 1y = −12x + 5 {y = 32x + 1y = −12x + 5
10.
{y = 23x − 2y = −13x − 5 {y = 23x − 2y = −13x − 5
11.
{x + y = −4 − x + 2y = −2 {x + y = −4 − x + 2y = −2
12.
{−x + 3y = 3x + 3y = 3 {−x + 3y = 3x + 3y = 3
13.
{−2x + 3y = 3x + 3y = 12 {−2x + 3y = 3x + 3y = 12
14.
{2x − y = 42x + 3y = 12 {2x − y = 42x + 3y = 12
15.
{x + 3y = −6y = −43x + 4 {x + 3y = −6y = −43x + 4
16.
{−x + 2y = −6y = −12x − 1 {−x + 2y = −6y = −12x − 1
17.
{−2x + 4y = 4y = 12x {−2x + 4y = 4y = 12x
18.
{3x + 5y = 10y = −35x + 1 {3x + 5y = 10y = −35x + 1
19.
{4x − 3y = 88x − 6y = 14 {4x − 3y = 88x − 6y = 14
20.
{x + 3y = 4−2x − 6y = 3 {x + 3y = 4−2x − 6y = 3
21.
{x = −3y + 42x + 6y = 8 {x = −3y + 42x + 6y = 8
22.
{4x = 3y + 78x − 6y = 14 {4x = 3y + 78x − 6y = 14
23.
{2x + y = 6−8x − 4y = −24 {2x + y = 6−8x − 4y = −24
24.
{5x + 2y = 7−10x − 4y = −14 {5x + 2y = 7−10x − 4y = −14
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
25.
{y = 23x + 1−2x + 3y = 5 {y = 23x + 1−2x + 3y = 5
26.
{y = 32x + 12x − 3y = 7 {y = 32x + 12x − 3y = 7
27.
{5x + 3y = 42x − 3y = 5 {5x + 3y = 42x − 3y = 5
28.
{y = −12x + 5x + 2y = 10 {y = −12x + 5x + 2y = 10
29.
{5x − 2y = 10y = 52x − 5 {5x − 2y = 10y = 52x − 5
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
30.
{2x + y = −43x − 2y = −6 {2x + y = −43x − 2y = −6
31.
{2x + y = −23x − y = 7 {2x + y = −23x − y = 7
32.
{x − 2y = −52x − 3y = −4 {x − 2y = −52x − 3y = −4
33.
{x − 3y = −92x + 5y = 4 {x − 3y = −92x + 5y = 4
34.
{5x − 2y = −6y = 3x + 3 {5x − 2y = −6y = 3x + 3
35.
{−2x + 2y = 6y = −3x + 1 {−2x + 2y = 6y = −3x + 1
36.
{2x + 5y = 1y = 13x − 2 {2x + 5y = 1y = 13x − 2
37.
{3x + 4y = 1y = −25x + 2 {3x + 4y = 1y = −25x + 2
38.
{2x + y = 5x − 2y = −15 {2x + y = 5x − 2y = −15
39.
{4x + y = 10x − 2y = −20 {4x + y = 10x − 2y = −20
40.
{y = −2x − 1y = −13x + 4 {y = −2x − 1y = −13x + 4
41.
{y = x − 6y = −32x + 4 {y = x − 6y = −32x + 4
42.
{x = 2y4x − 8y = 0 {x = 2y4x − 8y = 0
43.
{2x − 16y = 8 − x − 8y = −4 {2x − 16y = 8 − x − 8y = −4
44.
{y = 78x + 4−7x + 8y = 6 {y = 78x + 4−7x + 8y = 6
45.
{y = −23x + 52x + 3y = 11 {y = −23x + 52x + 3y = 11
Решите систему уравнений методом исключения
В следующих упражнениях решите системы уравнений методом исключения.
46.
{5x + 2y = 2−3x − y = 0 {5x + 2y = 2−3x − y = 0
47.
{6x − 5y = −12x + y = 13 {6x − 5y = −12x + y = 13
48.
{2x − 5y = 73x − y = 17 {2x − 5y = 73x − y = 17
49.
{5x − 3y = −12x − y = 2 {5x − 3y = −12x − y = 2
50.
{3x − 5y = −95x + 2y = 16 {3x − 5y = −95x + 2y = 16
51.
{4x − 3y = 32x + 5y = −31 {4x − 3y = 32x + 5y = −31
52.
{3x + 8y = −32x + 5y = −3 {3x + 8y = −32x + 5y = −3
53.
{11x + 9y = −57x + 5y = −1 {11x + 9y = −57x + 5y = −1
54.
{3x + 8y = 675x + 3y = 60 {3x + 8y = 675x + 3y = 60
55.
{2x + 9y = −43x + 13y = −7 {2x + 9y = −43x + 13y = −7
56.
{13x − y = −3x + 52y = 2 {13x − y = −3x + 52y = 2
57.
{x + 12y = 3215x − 15y = 3 {x + 12y = 3215x − 15y = 3
58.
{x + 13y = −113x + 12y = 1 {x + 13y = −113x + 12y = 1
59.
{13x − y = −323x + 52y = 3 {13x − y = −323x + 52y = 3
60.
{2x + y = 36x + 3y = 9 {2x + y = 36x + 3y = 9
61.
{x − 4y = −1−3x + 12y = 3 {x − 4y = −1−3x + 12y = 3
62.
{−3x − y = 86x + 2y = −16 {−3x − y = 86x + 2y = −16
63.
{4x + 3y = 220x + 15y = 10 {4x + 3y = 220x + 15y = 10
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что было бы удобнее решить систему уравнений путем замены или исключения.
64.
ⓐ {8x − 15y = −326x + 3y = −5 {8x − 15y = −326x + 3y = −5
ⓑ {x = 4y − 34x − 2y = −6 {x = 4y − 34x − 2y = — 6
65.
ⓐ {y = 7x − 53x − 2y = 16 {y = 7x − 53x − 2y = 16
ⓑ {12x − 5y = −423x + 7y = −15 {12x − 5y = −423x + 7y = −15
66.
ⓐ {y = 4x + 95x − 2y = −21 {y = 4x + 95x − 2y = −21
ⓑ {9x − 4y = 243x + 5y = −14 {9x − 4y = 243x + 5y = −14
67.
ⓐ {14x − 15y = −307x + 2y = 10 {14x − 15y = −307x + 2y = 10
ⓑ {x = 9y − 112x − 7y = −27 {x = 9y − 112x − 7y = −27
Письменные упражнения
68.
В системе линейных уравнений два уравнения имеют одинаковые точки пересечения.Опишите возможные решения системы.
69.
Решите систему уравнений путем подстановки и объясните все шаги словами: {3x + y = 12x = y − 8. {3x + y = 12x = y − 8.
70.
Решите систему уравнений методом исключения и объясните все шаги словами: {5x + 4y = 102x = 3y + 27. {5x + 4y = 102x = 3y + 27.
71.
Решите систему уравнений {x + y = 10x − y = 6 {x + y = 10x − y = 6
ⓐ построением графика ⓑ заменой
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
Если большая часть ваших чеков была:
… уверенно. Поздравляю! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.
… с некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не осваиваете, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому вы можете обратиться за помощью? Ваши одноклассники и инструктор — хорошие помощники. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, не понимаю! Это предупреждающий знак, игнорировать его нельзя. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
College Algebra Цели обучения
Введение
Учебник
Практические задачи
|
Практические вопросы по бесплатной алгебре — Практика с видео ответами
5.D
Цена увеличилась с 20 до 25 долларов (5 долларов), поэтому вопрос в том, какой процент от 20. Или 5/20 = x / 100; 500/20 = 25%
6. C
7. D
В первый раз Брайан ответил правильно на 150 вопросов, а во второй раз он ответил на 30% правильнее, так что
150 + (30/100 * 150); 30% от 150 = 45, или (30 * 150) / 100
, поэтому 150 + 45 = 195
8. B
Позвольте нам называть этот номер по x:
Это число увеличивается на 2: x + 2
Затем умножается на 3: 3 (x + 2)
Результат 24: 3 (x + 2) = 24… Решая это линейное уравнение, получаем значение числа:
х + 2 = 24/3
х + 2 = 8
х = 8–2
х = 6
9.В
Мой возраст: x
Мой брат старше меня на 3 года: x + 3
Моему отцу на 3 года меньше моего возраста, чем в 2 раза: 2x — 3
Возраст моего отца, разделенный на 5, равен возрасту моего брата, разделенному на 3: (2x — 3) / 5 = (x + 3) / 3
Крестным умножением:
5 (x + 3) = 3 (2x — 3)
5x + 15 = 6x — 9
х = 24
Возраст моего отца: 2 . 24-3 = 48-3 = 45
10. C
Есть две дроби, содержащие x, и знаменатели разные.Во-первых, давайте найдем общий знаменатель, чтобы упростить выражение. Наименьший общий множитель 4 и 7 равен 28. Тогда
7 (x — 2) / 28 — 4 (3x + 5) / 28 = — 3 . 28/28… Так как теперь в знаменателе 28 записаны обе части, мы можем их исключить:
7 (x — 2) — 4 (3x + 5) = — 84
7x — 14 — 12x — 20 = — 84
— 5x = — 84 + 14 + 20
— 5x = — 50
х = 50/5
х = 10
11. B
Мы можем следовать методу изнутри внутрь, чтобы решить этот тип проблем.x находится во внутренней части этой дроби; затем нам нужно сузить круг, чтобы достичь x:
1 / (1 + 1 / (1 — 1 / x)) = 4
Это означает, что (1 + 1 / (1 — 1 / x)) равно 1/4. Затем
1 + 1 / (1 — 1 / x) = 1/4
1 / (1 — 1 / х) = 1/4 — 1
1 / (1 — 1 / х) = — 3/4
Это означает, что 1 — 1 / x = — 4/3. Затем
1 — 1 / x = — 4/3
1 + 4/3 = 1 / х
1 / х = 7/3
Итак, x = 3/7.
Система линейных уравнений | Нет уникального решения | GMAT Math Practice Questions
Образец вопроса GMAT в количественном выражении, приведенный ниже, представляет собой вопрос о линейных уравнениях и проверяет концепции, связанные с типами решений для системы линейных уравнений.Эта концепция обычно проверяется в GMAT как вопрос о достаточности данных, а не как вопрос для решения проблемы. Практический вопрос GMAT уровня ниже 600 в системе линейных уравнений.
Вопрос 3 : Для каких значений ‘k’ пара уравнений 3x + 4y = 12 и kx + 12y = 30 НЕ будет иметь единственное решение?
- 9
- 12
- 3
- 7,5
- 2,5
Достичь Q51 в GMAT Quant
Онлайн-курс GMAT
@ индийских рупий 3500
Видео Объяснение
Онлайн-классы GMAT
Начало вт, 25 мая 2021 г.
Пояснительный ответ
Условие однозначного решения линейных уравнений
Система линейных уравнений ax + by + c = 0 и dx + ey + g = 0 будет иметь уникальное решение, если две линии, представленные уравнениями ax + by + c = 0 и dx + ey + g = 0 пересекаются в точке.
то есть, если две линии не параллельны и не совпадают.
По сути, наклон двух линий должен быть разным.
Что это означает?
ax + by + c = 0 и dx + ey + g = 0 будут пересекаться в одной точке, если их наклоны различны.
Выразите оба уравнения в стандартизированном формате y = mx + c, где m — наклон линии, а c — точка пересечения с y.
ax + by + c = 0 можно записать как y = \ — \ frac {a} {b} x — \ frac {c} {a} \\)
И dx + ey + g = 0 можно записать как y = \ — \ frac {d} {e} x — \ frac {g} {e} \\)
Наклон первой линии равен \ — \ frac {a} {b} \\), а наклон вторая строка — \ — \ frac {d} {e} \\)
Для уникального решения наклон линий должен быть другим.
∴ \ — \ frac {a} {b} \ neq — \ frac {d} {e} \\)
Или \\ frac {a} {d} \ neq \ frac {b} {e} \\)
Условие, чтобы уравнения НЕ имели единственного решения
Наклоны должны быть равны
Или \\ frac {a} {d} = \ frac {b} {e} \\)
Примените условие в данном уравнения для нахождения k
В приведенном выше вопросе a = 3, b = 4, d = k и e = 12.
Следовательно, \\ frac {3} {k} = \ frac {4} {12} \ \)
Или «k» должно быть равно 9, чтобы система линейных уравнений НЕ имела единственного решения.
Вопрос: «Каково значение k?»
Когда k = 9, система уравнений будет представлять собой пару параллельных линий (их пересечения по оси Y разные). Таким образом, этого НЕТ решения. система линейных уравнений с двумя переменными.
Вариант А — правильный ответ.
Mathematics_part_ _i_ (решения) для Class 10 Math Chapter 1
Страница № 4:
Вопрос 1:
Выполните следующее действие, чтобы решить одновременные уравнения.
5 x + 3 y = 9 —— (I)
2 x + 3 y = 12 —— (II)
Ответ:
Отказ от ответственности: в Q есть ошибка. В (II) должно было быть 2 x — 3 y = 12
5 x + 3 y = 9 —— (I)
2 x — 3 y = 12 —— (II)
Сложить (I) и (II)
7 x = 21
x = 3
Положить значение x = 3 в (I) получаем
53 + 3y = 9⇒15 + 3y = 9⇒3y = 9-15 = -6⇒y = -2
Таким образом, ( x , y ) = (3, — 6).
Страница № 5:
Вопрос 2:
Решите следующие одновременные уравнения.
(1) 3 a + 5 b = 26; a + 5b = 22
(2) x + 7 y = 10; 3 x — 2 y = 7
(3) 2 x — 3 y = 9; 2 x + y = 13
(4) 5 м — 3 n = 19; м — 6 n = –7
(5) 5 x + 2 y = –3; x + 5 y = 4
(6) 13x + y = 103; 2x + 14y = 114
(7) 99 x + 101 y = 499; 101 x + 99 y = 501
(8) 49 x — 57 y = 172; 57 x — 49 y = 252
Ответ:
(1) 3 a + 5 b = 26; ….. (I)
a + 5b = 22 ….. (II)
Вычитание (II) из (I)
2 a = 4
⇒ a = 2
Подстановка значения из a = 2 дюйма (II)
5b = 22 — 2 = 20
⇒ b = 205 = 4
Таким образом, a = 2 и b = 4.
(2) x + 7 y = 10; ….. (I)
3 x -2 y = 7….. (II)
Умножение (I) на 3
3 x + 21 y = 30; ….. (III)
3 x -2 y = 7 ….. (IV)
Вычитая (IV) из (III), получаем
23 y = 23
⇒ y = 1
Подставляя значение y в (IV), получаем
3 x — 2 = 7
⇒3 x = 7 + 2 = 9
⇒3 x = 9
⇒ x = 3
Таким образом, ( x, y ) = (3, 1)
(3) 2 x — 3 y = 9….. (I)
2 x + y = 13 ….. (II)
Вычитая (II) из (I), получаем
-3 y — y = 9-13
⇒-4y = -4⇒y = 1
Подставляя это значение в (I), получаем
2x-31 = 9⇒2x = 9 + 3 = 12⇒x = 122 = 6
Таким образом, ( x, y ) = (6, 1)
(4) 5 м — 3 n = 19 ….. (I)
м — 6 n = –7 ….. (II)
Умножая (I) на 2, получаем
10 m — 6 n = 38….. (III)
m — 6 n = –7 ….. (IV)
Вычитая (IV) из (III), получаем
10m-m-6n — 6n = 38- -7⇒9m = 45⇒m = 459 = 5
Подставляя значение m = 5 в (II), получаем
5-6n = -7⇒-6n = -7-5⇒-6n = -12⇒n = -12-6 = 2
Таким образом, (m, n) = (5, 2).
(5) 5 x + 2 y = –3 ….. (I)
x + 5 y = 4 ….. (II)
Умножить (II) на 5 получаем
5 x + 25 y = 20….. (III)
Вычитая (III) из (I), получаем
5x-5x + 2y-25y = -3-20⇒-23y = -23⇒y = -23-23 = 1
Подставляем значение из y = 1 в (II) получаем
x + 51 = 4⇒x + 5 = 4⇒x = 4-5 = -1
Таким образом, ( x, y ) = (−1, 1)
(6)
13x + y = 103 ….. I2x + 14y = 114 ….. (II)
Умножить (I) на 3 и (II) на 4
x + 3y = 10 .. … III8x + y = 11 ….. IV
Умножаем (IV) на 3
24 x + 3 y = 33….. (V)
Вычитание (V) из (III)
x-24x + 3y-3y = 10-33⇒-23x = -23⇒x = 1
Подставляем значение x = 1 дюйм ( III)
1 + 3y = 10⇒3y = 10-1 = 9⇒y = 93 = 3
Таким образом, ( x, y ) = (1, 3)
(7) 99 x + 101 y = 499 ….. (I)
101 x + 99 y = 501 ….. (II)
Сложение (I) и (II)
200x + 200y = 1000⇒x + y = 5 ….. (III)
Вычитание (II) из (I)
99x-101x + 101y-99y = 499-501⇒-2x + 2y = -2⇒-x + y = -1….. IV
Складываем (III) и (IV)
x + y = 5-x + y = -1⇒2y = 4⇒y = 2
Подставляя значение y = 2 в (III), мы получаем
x + 2 = 5⇒x = 5-2 = 3
Таким образом, ( x, y ) = (3, 2)
(8) 49 x — 57 y = 172 … .. (I)
57 x — 49 y = 252 ….. (II)
Сложение (I) и (II)
49x + 57x-57y-49y = 172 + 252⇒106x-106y = 424⇒xy = 4 ….. III
Вычитая (II) из (I), получаем
49x-57y-57y — 49y = 252-172⇒-8x-8y = -80⇒-xy = -10 ⇒x + y = 10….. IV
Складывая (III) и (IV)
xy = 4x + y = 10⇒2x = 14⇒x = 7
Подставляя значение x = 7 в (IV), получаем
7+ y = 10⇒y = 10-7⇒y = 3
Таким образом, ( x, y ) = (7, 3).
Страница № 8:
Вопрос 1:
Заполните следующую таблицу, чтобы нарисовать график уравнений —
(I) x + y = 3 (II) x — y = 4
|
|
Ответ:
| x | 3 | -2 | 0 |
| y | 0 | 5 | 3 |
| ( x , y ) | (3, 0) | -2, 5 | (0, 3) |
| x | 4 | –1 | 0 |
| y | 0 | -5 | –4 |
| ( x , y ) | 4,0 | -1, -5 | (0, –4) |
Страница № 8:
Вопрос 2:
Решите следующие одновременные уравнения графически.
(1) x + y = 6; x — y = 4
(2) x + y = 5; x — y = 3
(3) x + y = 0; 2 x — y = 9
(4) 3 x — y = 2; 2 x — y = 3
(5) 3 x — 4 y = –7; 5 x — 2 y = 0
(6) 2 x — 3 y = 4; 3 y — x = 4
Ответ:
(1) x + y = 6;
x — y = 4
Точка пересечения двух линий — (5, 1).
(2) x + y = 5
x — y = 3
Точка пересечения двух линий — (4, 1)
(3) x + y = 0
2 x — y = 9
Точка пересечения двух прямых — (3, −3).
(4) 3 x — y = 2
2 x — y = 3
Точка пересечения двух прямых — (−1, −5).
(5) 3 x — 4 y = –7
| x | 1 | 0 | −2,3 |
| y | 2,5 | 1,75 | 0 |
5 x -2 y = 0
Точка пересечения двух прямых — (1, 2.5).
(6) 2 x — 3 y = 4
3 y — x = 4
Точка пересечения двух прямых — (8, 4).
Страница № 16:
Вопрос 1:
Заполните пропуски правильным номером
3 24 5 = 3 × — × 4 = –8 =
Ответ:
3 24 5 = 35-24 = 15-8 = 7
Таким образом, имеем
3 24 5 = 3 × 5 — 2 × 4 = 15 –8 = 7
Страница № 16:
Вопрос 2:
Найдите значения следующих определителей.
(1) -1 7 2 4
(2) 5 3-7 0
(3) 73533212
Ответ:
(1) -1 7 2 4
= -14-72 = -4-14 = -18
(2) 5 3-7 0 = 5 × 0-3 × -7 = 0 + 21 = 21
(3) 73533212 = 73 × 12-53 × 32 = 76-52 = 7-156 = -86 = -43
Страница № 16:
Вопрос 3:
Решите следующие одновременные уравнения, используя правило Крамера.
(1) 3 x — 4 y = 10; 4 x + 3 y = 5
(2) 4 x + 3 y — 4 = 0; 6 x = 8 — 5 y
(3) x + 2 y = –1; 2 x — 3 y = 12
(4) 6 x — 4 y = –12; 8 x — 3 y = –2
(5) 4 м + 6 n = 54; 3 м + 2 n = 28
(6) 2x + 3y = 2; х-у2 = 12
Ответ:
(1) 3 x — 4 y = 10
4 x + 3 y = 5
D = 3-443 = 3 × 3—4 × 4 = 9 + 16 = 25Dx = 10 -453 = 10 × 3—4 × 5 = 30 + 20 = 50Dy = 31045 = 3 × 5-10 × 4 = 15-40 = -25
x = DxD = 5025 = 2y = DyD = -2525 = -1x , y = 2, -1
(2) 4 x + 3 y — 4 = 0; 6 x = 8-5 y
D = 4365 = 4 × 5-6 × 3 = 20-18 = 2Dx = 4385 = 4 × 5-3 × 8 = 20-24 = -4Dy = 4468 = 4 × 8-6 × 4 = 32-24 = 8
x = DxD = -42 = -2y = DyD = 82 = 4x, y = -2,4
(3) x + 2 y = — 1; 2 x — 3 y = 12
D = 122-3 = 1 × -3-2 × 2 = -3-4 = -7Dx = -1212-3 = -1 × -3-2 × 12 = 3-24 = -21Dy = 1-1212 = 1 × 12—1 × 2 = 12 + 2 = 14
x = DxD = -21-7 = 3y = DyD = 14-7 = -2x, y = 3, -2
(4) 6 x — 4 y = –12; 8 x — 3 y = –2
D = 6-48-3 = 6 × -3-4 × 8 = -18 + 32 = 14Dx = -12-4-2-3 = — 12 × -3—4 × -2 = 36-8 = 28Dy = 6-128-2 = 6 × -2—12 × 8 = -12 + 96 = 84
x = DxD = 2814 = 2y = DyD = 8414 = 6x, y = 2,6
(5) 4 м + 6 n = 54; 3 м + 2 n = 28
D = 4632 = 4 × 2-6 × 3 = 8-18 = -10Dx = 546282 = 54 × 2-6 × 28 = 108-168 = -60Dy = 454328 = 4 × 28-54 × 3 = 112-162 = -50
x = DxD = -60-10 = 6y = DyD = -50-10 = 5x, y = 6,5
(6) 2x + 3y = 2; x-y2 = 12
D = 231-12 = 2 × -12-3 × 1 = -1-3 = -4Dx = 2312-12 = 2 × -12-3 × 12 = -1-32 = -52Dy = 22112 = 2 × 12-2 × 1 = 1-2 = -1
x = DxD = -52-4 = 58y = DyD = -1-4 = 14x, y = 58,14
Страница № 19:
Вопрос 1:
Решите следующие одновременные уравнения.
1 2x-3y = 15; 8x + 5y = 772 · 10x + y + 2x-y = 4; 15x + y-5x-y = -23 27x-2 + 31y + 3 = 85; 31x-2 + 27y + 3 = 894 13x + y + 23x-y = 34; 123x + y-123x-y = -18
Ответ:
1 2x-3y = 15; 8x + 5y = 77
Пусть 1x = u и 1y = v
Итак, уравнение принимает вид
2u-3v = 15 ….. I8u + 5v = 77 ….. II
Умножьте (I) на 4 we получаем
8u-12v = 60 ….. III
(II) — (III)
8u-8u + 5v — 12v = 77-60⇒17v = 17⇒v = 1 Вставляем значение v в I2u-31 = 15⇒2u = 15 + 3 = 18⇒u = 9
Таким образом,
1x = u = 9⇒x = 191y = v = 1⇒y = 1x, y = 19,1
2 10x + y + 2x- у = 4; 15x + y-5x-y = -2
Пусть 1x + y = u и 1x-y = v
Итак, уравнение принимает вид
10u + 2v = 4….. I15u-5v = -2 ….. II
Умножая (I) на 5 и (II) на 2, получаем
50u + 10v = 20 ….. III30u-10v = -4 .. … IV
Складывая (III) и (IV), получаем
u = 1680 = 15
Подставляя это значение в (I)
10 × 15 + 2v = 4⇒2 + 2v = 4⇒v = 1
1x + y = 15 и 1x-y = 1⇒x + y = 5 и xy = 1 Решая эти уравнения, мы получаем x = 3 и y = 2
3 27x-2 + 31y + 3 = 85; 31x-2 + 27y + 3 = 89
Пусть 1x-2 = u и 1y + 3 = v
27u + 31v = 85 ….. I31u + 27v = 89….. IIСложив I и II58u + 58v = 174u + v = 3 ….. III Вычтя II из I4u-4v = 4⇒uv = 1 ….. IV
Складывая (III) и (IV), получаем
2u = 4⇒u = 2
Подставляем значение u в III
2 + v = 3⇒v = 1
1x-2 = u = 2⇒x-2 = 12⇒x = 52
1y + 3 = 1⇒y + 3 = 1⇒y = -2
x, y = 52, -2
4 13x + y + 23x-y = 34; 123x + y-123x-y = -18
Пусть 13x + y = u и 13x-y = v
u + 2v = 34 и 12u-12v = -18
Итак, уравнения становятся
4u + 4v = 3 .. … I4u-4v = 1….. II
Складываем (I) и (II)
8u = 4⇒u = 12
Подставляем значение u в (I)
12 + 2v = 34⇒v = 14
13x + y = u и 13x-y = v⇒13x + y = 123x + y = 2 ….. III Также, 13x-y = 14⇒3x-y = 4 ….. IV
(III) + (IV) получаем
6x = 6⇒x = 1y = -1
Страница № 26:
Вопрос 1:
Два числа отличаются на 3. Сумма удвоенного меньшего числа и троекратного большего числа равна 19.Найдите числа.
Ответ:
Пусть меньшее число будет x , а большее число будет y .
Учитывая, что два числа отличаются на 3, поэтому
yx = 3 ….. (I)
Кроме того, сумма удвоенного меньшего числа и троекратного большего числа равна 19
Итак, 2x + 3y = 19 … … (II)
Два полученных уравнения:
yx = 3
2x + 3y = 19
Умножая (I) на 3, получаем
3y-3x = 9….. (III)
Складывая (III) и (II), получаем
4 y = 28
⇒y = 284 = 7
Подставляя значение y = 7 дюймов (I), получаем
7 -x = 3⇒-x = 3-7⇒-x = -4⇒x = 4
Таким образом, два числа — 4 и 7.
Страница № 26:
Вопрос 2:
Выполните следующее.
Ответ:
Длина данного прямоугольника равна 2x + y + 8 и 4x-y
2x + y + 8 = 4x-y⇒y + y + 8 = 4x-2x⇒8 + 2y = 2x⇒2x-2y = 8 Делим на 2х-у = 4….. I
Ширина прямоугольника 2 y и x + 4.
2y = x + 4⇒x-2y = -4 ….. II
Вычитание (II) из (I)
xxy — 2y = 4—4⇒-y + 2y = 8⇒y = 8 Подставляя значение y = 8 в (I), получаем x-8 = 4⇒x = 4 + 8 = 12
Length = 4x- y = 412-8 = 40
Ширина = 2 × 8 = 16
Периметр = 2 длина + ширина = 240 + 16 = 112 единиц
Площадь = длина × ширина = 40 × 16 = 640 единиц2
Страница № 26:
Вопрос 3:
Сумма возраста отца и возраста его сына составляет 70 лет.Если мы удвоим возраст отца и прибавим его к возрасту его сына, получится 95. Найдите их нынешний возраст.
Ответ:
Пусть возраст отца будет x лет, а возраст сына y лет.
Сумма возраста отца и удвоенного возраста его сына равна 70, так что
x + 2y = 70 …… (I)
Удвоенный возраст отца, прибавленный к возрасту его сына, получится 95
2х + у = 95….. (II)
Складывая (I) и (II), получаем
3x + 3y = 165 Делим на 3x + y = 55 ….. III
Вычитая (I) из (II)
2x-x + y-2y = 95-70⇒xy = 25 ….. IV
Складывая (III) и (IV), получаем
2x = 80⇒x = 40 Подставляя значение x = 40 в III40 + y = 55⇒y = 55-40⇒y = 15
Таким образом, возраст отца — 40 лет, а возраст сына — 15 лет.
Страница № 26:
Вопрос 4:
Знаменатель дроби на 4 больше, чем ее числитель.Знаменатель становится в 12 раз больше числителя, если и числитель, и знаменатель уменьшаются на 6. Найдите дробь.
Ответ:
Пусть дробь будет xy.
Знаменатель дроби на 4 раза больше ее числителя.
Итак,
y = 4 + 2x⇒2x-y = -4 ….. I
Кроме того, знаменатель становится в 12 раз больше числителя, если и числитель, и знаменатель уменьшаются на 6.
Итак,
y-6 = 12x-6⇒y-6 = 12x-72⇒12x-y = 72-6 = 66⇒12x-y = 66 ….. II
Вычитание (I) из (II)
12x-2x-y — y = 66—4⇒10x = 70⇒x = 7010 = 7⇒x = 7
Подставляем значение x = 7 в (I)
27-y = -4⇒ 14-y = -4⇒y = 14 + 4 = 18
Таким образом, полученная дробь равна 718.
Страница № 26:
Вопрос 5:
Два типа ящиков A, B должны быть помещены в грузовик грузоподъемностью 10 тонн.Когда в грузовик загружается 150 ящиков типа А и 100 ящиков типа В, он весит 10 тонн. Но когда в грузовик загружено 260 ящиков типа A, он все еще может вместить 40 ящиков типа B, так что он полностью загружен. Найдите вес каждого типа коробки.
Ответ:
Пусть вес коробки A составляет x , а вес коробки B — y .
Когда 150 ящиков типа A и 100 ящиков типа B загружены в грузовик, он весит 10 тонн i.е 10000 кг.
Итак,
150x + 100y = 10000⇒15x + 10y = 1000⇒3x + 2y = 200 ….. I
Когда 260 ящиков типа A загружены в грузовик, он все еще может вместить 40 ящиков типа B, чтобы он был полностью загружен.
260x + 40y = 10000⇒26x + 4y = 1000⇒13x + 2y = 500 ….. II
Вычитая (I) из (II), получаем
13x-3x + 2y-2y = 500-200⇒10x = 300⇒x = 30 Подставляем значение x = 30 в I330 + 2y = 200⇒90 + 2y = 200⇒2y = 200-90 = 110⇒y = 1102 = 55
Таким образом, вес коробки A = 30 кг, а вес коробки ящик Б = 55 кг.
Страница № 26:
Вопрос 6:
Из 1900 км Вишал проехал некоторое расстояние на автобусе, а часть на самолете. Автобус движется со средней скоростью 60 км / час, а средняя скорость самолета составляет 700 км / час. Путешествие занимает 5 часов. Определив расстояние, Вишал ехал на автобусе.
Ответ:
Мы знаем скорость = расстояние и время
Средняя скорость автобуса = 60 км / ч.
Пусть время в автобусе составит x часов.
Средняя скорость автобуса = 700 км / ч.
Пусть в автобусе будет y часов.
Общее пройденное расстояние = 1900 км
60x + 700y = 1900⇒6x + 70y = 190⇒3x + 35y = 95 ….. I
Путешествие занимает 5 часов, поэтому
x + y = 5 .. … II
Умножая (II) на 3
3x + 3y = 15 ….. III
Вычитая (III) из (I), получаем
3x-3x + 35y-3y = 95-15⇒32y = 80 ⇒y = 2,5
Положив значение y = 2.5 в (II) получаем
x + 2,5 = 5⇒x = 2,5
Расстояние, пройденное Vishal на автобусе = скорость × время = 60 × 2,5 = 150 км.
Страница № 27:
Вопрос 1:
Выберите правильный вариант для каждого из следующих вопросов
(1) Чтобы нарисовать график 4 x +5 y = 19, найдите y , когда x = 1.
| А) 4 | (В) 3 | (К) 2 | (Д) –3 |
(2) Для одновременных уравнений в переменных x и y , D x = 49, D y = –63, D = 7, тогда что будет x ?
| А) 7 | (В) –7 | (К) 17 | (Д) -17 |
(3) Найдите значение 53-7-4
| A) –1 | (В) –41 | (К) 41 | (Г) 1 |
(4) Решить x + y = 3; 3 x — 2 y — 4 = 0 методом определителя найти D.
| А) 5 | (В) 1 | (К) –5 | (Д) –1 |
(5) ax + на = c и mx + ny = d и на ≠ bm , тогда эти одновременные уравнения имеют —
| (А) | Только одно общее решение. | (А) | Нет решения. |
| (К) | Бесконечное количество решений. | (Г) | Всего два решения. |
Ответ:
(1) 4 x +5 y = 19
Когда x = 1, тогда y будет
41 + 5y = 19⇒4 + 5y = 19⇒5y = 19-4 = 15⇒ 5y = 15⇒y = 155 = 3
Следовательно, правильный ответ — вариант (B).
(2) x = DxD = 497 = 7
Следовательно, правильный ответ — вариант (A).
(3) 53-7-4 = 5 × -4-3 × -7 = -20 + 21 = 1
Следовательно, правильный ответ — вариант (D).
(4) x + y = 3; 3 x — 2 y — 4 = 0
D = 113-2 = 1 × -2-1 × 3 = -2-3 = -5
Следовательно, правильный ответ — вариант (C).
(5) ax + на = c и mx + ny = d
D = abmn = an-bm
an ≠ bm
So, D ≠ 0.
Итак, данные уравнения имеют единственное решение или только одно общее решение.
Следовательно, правильный ответ — вариант А.
Страница № 27:
Вопрос 2:
Заполните следующую таблицу, чтобы построить график 2 x — 6 y = 3
| x | –5 | х |
| y | х | 0 |
| ( x, y ) | х | х |
Ответ:
2 x — 6 y = 3
| x | –5 | 32 |
| y | -136 | 0 |
| ( x, y ) | -5, -136 | 32,0 |
Страница № 27:
Вопрос 3:
Решите следующие одновременные уравнения графически.
(1) 2 x + 3 y = 12; x — y = 1
(2) x — 3 y = 1; 3 x — 2 y + 4 = 0
(3) 5 x — 6 y + 30 = 0; 5 x + 4 y — 20 = 0
(4) 3 x — y — 2 = 0; 2 x + y = 8
(5) 3 x + y = 10; x — y = 2
Ответ:
(1) 2 x + 3 y = 12
x — y = 1
Решением данных уравнений является точка пересечения двух прямых i.е (3, 2).
(2) x — 3 y = 1
3 x -2 y + 4 = 0
Решением данных уравнений является точка пересечения двух прямых, т.е. (-2, -1).
(3) 5 x — 6 y + 30 = 0
5 x + 4 y -20 = 0
Решением данных уравнений является точка пересечения двух прямых, т.е. (0, 5).
(4) 3 x — y — 2 = 0
2 x + y = 8
Решением данных уравнений является точка пересечения двух прямых, т.е. (2, 4).
(5) 3 x + y = 10
x — y = 2
Решением данных уравнений является точка пересечения двух прямых, т.е. (3, 1).
Страница № 27:
Вопрос 4:
Найдите значения каждого из следующих определителей.
| (1) 4327 | (2) 5-2-31 | (3) 3-114 |
Ответ:
(1) 4327 = 4 × 7-3 × 2 = 28-6 = 22
(2) 5-2-31 = 5 × 1-2 × -3 = 5-6 = -1
(3 ) 3-114 = 3 × 4—1 × 1 = 12 + 1 = 13
Страница № 28:
Вопрос 5:
Решите следующие уравнения методом Крамера.
(1) 6 x — 3 y = –10; 3 x + 5 y — 8 = 0
(2) 4 м — 2 n = –4; 4 м + 3 n = 16
(3) 3 x — 2 y = 52; 13x + 3y = -43
(4) 7 x + 3 y = 15; 12 y -5 x = 39
(5) x + y-82 = x + 2y-143 = 3x-y4
Ответ:
(1) 6 x — 3 y = –10; 3 x + 5 y — 8 = 0
D = 6-335 = 6 × 5—3 × 3 = 30 + 9 = 39Dx = -10-385 = -10 × 5—3 × 8 = -50 + 24 = -26Dy = 6-1038 = 6 × 8—10 × 3 = 48 + 30 = 78x = DxD = -2639 = -23y = DyD = 7839 = 2x, y = -23,2
( 2) 4 м — 2 n = –4; 4 м + 3 n = 16
D = 4-243 = 4 × 3—2 × 4 = 12 + 8 = 20Dx = -4-2163 = -4 × 3—2 × 16 = -12 + 32 = 20Dy = 4-4416 = 4 × 16—4 × 4 = 64 + 16 = 80x = DxD = 2020 = 1y = DyD = 8020 = 4x, y = 1,4
(3) 3 x — 2 y = 52; 13x + 3y = -43
D = 3-2133 = 9 + 23 = 293Dx = 52-2-433 = 152-83 = 296Dy = 35213-43 = -4-56 = -296x = DxD = 296293 = 12y = DyD = -296293 = -12x, y = 12, -12
(4) 7 x + 3 y = 15; 12 y — 5 x = 39
D = 73-512 = 7 × 12-5 × 3 = 84 + 15 = 99Dx = 1533912 = 15 × 12-39 × 3 = 180-117 = 63Dy = 715 -539 = 7 × 39—5 × 15 = 273 + 75 = 348x = DxD = 6399 = 711y = DyD = 34899 = 11633x, y = 711,11633
(5) x + y-82 = x + 2y- 143 = 3x-y4
x + y-82 = x + 2y-143⇒3x + 3y-24 = 2x + 4y-28⇒xy = -4….. Iи x + 2y-143 = 3x-y4⇒4x + 8y-56 = 9x-3y⇒5x-11y = -56 ….. II
Из (I) и (II)
D = 1-15-11 = -11 × 1—1 × 5 = -11 + 5 = -6Dx = -4-1-56-11 = -11 × -4—1 × -56 = 44-56 = — 12Dy = 1-45-56 = -56 × 1-4 × 5 = -56 + 20 = -36x = DxD = -12-6 = 2y = DyD = -36-6 = 6x, y = 2,6
Страница № 28:
Вопрос 6:
Решите следующие одновременные уравнения.
(1) 2х + 23у = 16; 3x + 2y = 0
(2) 72x + 1 + 13y + 2 = 27; 132x + 1 + 7y + 2 = 33
(3) 148x + 231y = 527xy; 231x + 148y = 610xy
(4) 7x-2yxy = 5; 8x + 7yxy = 15
(5) 123x + 4y + 152x-3y = 14; 53x + 4y-22x-3y = -32
Ответ:
(1) 2х + 23у = 16; 3x + 2y = 0
Пусть 1x = u и 1y = v
2u + 23v = 16 12u + 4v = 1….. I3u + 2v = 0 ….. II
Умножьте (II) на 2
6u + 4v = 0 ….. III
I-III
6u = 1⇒u = 16
Ввод значения из и во II.
3 × 16 + 2v = 0⇒12 + 2v = 0⇒v = -14
1x = u⇒x = 61y = v⇒y = -4x, y = 6, -4
(2) 72x + 1 + 13лет + 2 = 27; 132x + 1 + 7y + 2 = 33
Пусть 12x + 1 = u и 1y + 2 = v
7u + 13v = 27 ….. I13u + 7v = 33 ….. II
(I) + ( II)
20u + 20v = 60u + v = 3 ….. III
(II) — (I)
6u-6v = 6 uv = 1….. IV
(III) + (IV)
2u = 4⇒u = 2 Подставляем значение u в (IV) 2-v = 1⇒v = 1
12x + 1 = u = 2 ⇒2x + 1 = 12⇒x = -14 и 1y + 2 = v = 1⇒y + 2 = 1⇒y = -1x, y = -14, -1
(3) 148x + 231y = 527xy; 231x + 148y = 610xy
Умножаем на xy
148y + 231x = 527 ….. I 231y + 148x = 610 ….. II Добавляем I и II 379y + 379x = 1137⇒x + y = 3 … ..IIIII-I83y-83x = 83⇒yx = 1 ….. IVIII + IV2y = 4⇒y = 2
Подставляем значение y в (IV)
2-x = 1⇒x = 1x , y = 1,2
(4) 7x-2yxy = 5; 8x + 7yxy = 15
⇒ 7y-2x = 5 и 8y + 7x = 15
Пусть 1x = u, 1y = v
7v-2u = 5….. I8v + 7u = 15 ….. II
Умножьте (I) на 7 и (II) на 2
49v-14u = 35 ….. III16v + 14u = 30 ….. IV
Складываем (III) и (IV)
65v = 65⇒v = 1 и 1y = v = 1⇒y = 1
Подставляем значение v в (I)
71-2u = 5⇒u = 11x = u = 1⇒x = 1x, y = 1,1
(5) 123x + 4y + 152x-3y = 14; 53x + 4y-22x-3y = -32
13x + 4y = u, 12x-3y = v12u + 15v = 14 ⇒10u + 4v = 5 ….. I5u-2v = -32⇒10u-4v = -3 ….. II
(I) + (II)
20u = 2⇒u = 110
Подставляем значение u в (II)
10 × 110-4v = -3⇒1 + 3 = 4v⇒ v = 1
13x + 4y = u = 110⇒3x + 4y = 10….. III12x-3y = v = 1⇒2x-3y = 1 ….. IV
Умножаем (III) на 2 и (IV) на 3
6x + 8y = 20 ….. V6x-9y = 3 ….. VI
(V) — (VI)
17y = 17⇒y = 1
Подставляем значение y в (VI)
6x-9 = 3⇒6x = 12⇒x = 2x , у = 2,1
Страница № 28:
Вопрос 7:
Решите следующие задачи со словами.
(1) Двухзначное число и число с замененными цифрами в сумме дают 143.В данном номере цифра в разряде единиц на 3 больше, чем цифра в разряде десятков. Найдите исходный номер.
(2) Кантабай купил в магазине 112 кг чая и 5 кг сахара. Она заплатила 50 рупий в качестве обратного проезда на рикше. Общие расходы составили 700 рупий. Затем она поняла, что, заказывая товары в Интернете, товары можно купить с бесплатной доставкой на дом по той же цене. Поэтому в следующем месяце она разместила онлайн-заказ на 2 кг чая и 7 кг сахара. Она заплатила за это 880 рупий. Найдите норму сахара и чая на кг.
(3) Чтобы узнать количество записок, которые были у Анушки, выполните следующее задание.
(4) Сумма нынешнего возраста Маниша и Савиты составляет 31 год. Возраст Маниша 3 года назад был в 4 раза старше возраста Савиты. Найдите их нынешний возраст.
(5) На фабрике соотношение заработной платы квалифицированных и неквалифицированных рабочих составляет 5: 3. Общая заработная плата за один день для обоих составляет 720 рупий. Найдите дневную заработную плату квалифицированных и неквалифицированных рабочих.
(6) Пункты A и B находятся на расстоянии 30 км друг от друга и находятся на прямой дороге. Хамид едет из пункта А в пункт Б. на велосипеде. В то же время Джозеф стартует из точки B на велосипеде и едет в сторону A.Они встречаются через 20 минут. Если бы Джозеф стартовал из B в то же время, но в противоположном направлении (а не в направлении A), Хамид догнал бы его через 3 часа. Найдите скорость Хамида и Джозефа.
Ответ:
(1) Пусть число на месте единицы будет x , а цифра на месте десяти будет y.
Таким образом, число будет 10 y + x
После перестановки цифр число станет 10 x + y.
Учитывая, что двузначное число и число с замененными цифрами дают в сумме 143.
Итак, 10 y + x + 10 x + y = 143
⇒11x + 11y = 143⇒x + y = 13. …. I
Также в данном номере цифра в месте единицы на 3 больше, чем цифра в разряде десятков.
Итак, xy = 3 ….. II
Складывая (I) и (II), получаем
2x = 16⇒x = 8
Подставляя значение x в (I), получаем
8 + y = 13⇒y = 13-8 = 5
Таким образом, число 58.
(2) Пусть цена чая будет x рупий за кг, а цена сахара — y рупий за кг.
Когда Кантабай покупал товары в магазине,
32x + 5y + 50 = 700⇒3x + 10y = 1300 ….. I
Когда Кантабай покупал товары в Интернете, тогда
2x + 7y = 880 …. .II
Умножая (I) на 2 и (II) на 3, получаем
6x + 20y = 2600 ….. III6x + 21y = 2640 ….. IV
(IV) — (III)
y = 40
Положив значение y = 40 в (II)
2x + 740 = 880⇒2x = 880-280 = 600⇒x = 300
Таким образом, чай стоит 300 рупий за кг, а сахар — 40 рупий за кг. .
(3) Заявление об отказе от ответственности: В данном вопросе есть ошибка. Вместо банкнот по 10 рупий должны быть банкноты по 100 рупий.
Пусть количество банкнот в 100 рупий составляет x , а количество банкнот в размере 50 составляет y .
100x + 50y = 2500⇒2x + y = 50 ….. I
Когда количество нот меняется местами,
50x + 100y = 2000⇒x + 2y = 40 ….. II
Умножение (I) с 2
4x + 2y = 100 ….. III
Вычитая (III) из (II), получаем
3x = 60⇒x = 203x = 60⇒x = 20
Подставляя значение x в (I ) получаем
y = 10
Таким образом, получается 20 банкнот по 100 рупий и 10 банкнот по 50 рупий.
(4) Пусть нынешний возраст Маниша будет x лет, а возраст Савиты — y лет.
Сумма их нынешнего возраста = 31
x + y = 31 ….. I
Их возраст 3 года назад был
Возраст Маниша = x-3
Возраст Савиты = y-3
Возраст Маниша 3 года назад был в 4 раза возраст Савиты.
x-3 = 4y-3⇒x-3 = 4y-12⇒x-4y = -9 ….. II
(I) — (II) получаем
5y = 40⇒y = 8
Положив значение y в (I) получаем
x + 8 = 31⇒x = 23
Таким образом, возраст Маниша составляет 23 года, а возраст Савиты — 8 лет.
(5) Отношение заработной платы квалифицированного к неквалифицированному рабочему = 5: 3
Пусть дневная заработная плата квалифицированного специалиста составляет x , а неквалифицированного человека — лет.
Их общая дневная заработная плата 720
x + y = 720 ….. I
Кроме того,
xy = 53⇒3x = 5y⇒3x-5y = 0 ….. II
Умножение (I) на 3 получаем
3x + 3y = 2160 ….. III
(III) — (II)
8y = 2160⇒y = 270
Подставляя значение y в (I), получаем
x = 450
One дневная заработная плата квалифицированного специалиста 450 рупий, неквалифицированного человека 270 рупий.
(6) Пусть скорость Хамида составляет x км / ч, а скорость Джозефа — y км / ч.
Когда оба едут в одном направлении, расстояние, которое они преодолевают вместе, составит 30 км.
Мы знаем Скорость = Расстояние Время
Они встречаются через 20 минут = 2060 = 13 часов
x3 + y3 = 30⇒x + y = 90 ….. I
Когда Джозеф стартовал из точки B, но двигался в противоположном направлении.
Расстояние, пройденное Хамидом — Расстояние, пройденное Джозефом = 30
⇒3x-3y = 30⇒x-y = 10….. II
Складывая (I) и (II), получаем
2x = 100⇒x = 50
Подставляя значение x в (II), получаем
50-y = 10⇒y = 40
Таким образом скорость Хамида — 50 км / ч, Иосифа — 40 км / ч.
Просмотреть решения NCERT для всех глав класса 10
Форма линейного уравнения с пересечением наклона (Алгебра 1, Визуализация линейных функций) — Mathplanet
Ранее в этой главе мы выражали линейные уравнения в стандартной форме Ax + By = C.Теперь мы собираемся показать другой способ выражения линейных уравнений, используя форму углового пересечения y = mx + b.
В форме пересечения наклона вы используете наклон линии и точку пересечения оси Y для выражения линейной функции.
$$ y = mx + b $$
Где m — наклон, а b — точка пересечения с y.
Пример
Постройте уравнение
$$ y-2x = 1 $$
переписать в форме пересечения наклона
$$ y = 2x + 1 $$
Определите наклон и точку пересечения оси Y
m = 2 и b = 1
Постройте точку, соответствующую точке пересечения оси y, (0,1)
Значение m, наклон, говорит нам, что для каждого шага вправо по оси x мы перемещаемся на 2 шага вверх по оси y (поскольку m = 2)
И как только у вас будет вторая точка, вы можете просто провести линию через две точки и продлить ее в обоих направлениях.
Вы можете проверить правильность нарисованной линии, подставив координаты второй точки в исходное уравнение. Если уравнение верно, значит, верен второй пункт.
Наша вторая точка = (1, 3)
$$ y-2x = 1 $$
$$ 3-2 \ cdot 1 = 3-2 = 1 $$
Наш второй пункт — это решение уравнения, т. Е. Линия, которую мы нарисовали, верна.
Линия, проходящая через начало координат, имеет Y-пересечение нуля, b = 0, и представляет собой прямое изменение.
$$ y = mx $$
В прямой вариации ненулевое число m называется постоянной вариации.
Вы можете назвать функцию f, используя понятие функции
$$ f \ влево (x \ вправо) = mx + b $$
f (x) — другое имя для y и читается как «значение f в x» или «f of x». Для именования функций можно использовать буквы, отличные от f.
Группа функций со схожими характеристиками называется семейством функций. Все функции, которые можно записать в виде f (x) = mx + b, принадлежат семейству линейных функций.
