Содержание
Линейные уравнения для 5 класса
Одним из самых важных навыков при поступлении в 5 класс является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу.
1 тип: «луковичные»
Это уравнения, которые почти со вероятностью встретятся Вам при поступлении в любую школу или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз. Например, или .
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:
Сложение
- слагаемое1 + слагаемое2 = сумма
- слагаемое1 = сумма — слагаемое2
- слагаемое2 = сумма — слагаемое1
Вычитание
- уменьшаемое — вычитаемое = разность
- уменьшаемое = вычитаемое + разность
- вычитаемое = уменьшаемое — разность
Умножение
- множитель1 * множитель2 = произведение
- множитель1 = произведение : множитель2
- множитель2 = произведение : множитель1
Деление
- делимое : делитель = частное
- делимое = делитель * частное
- делитель = делимое : частное
Разберём на примере, как применять данные правила.
Заметим, что мы делим на и получаем . В этой ситуации мы знаем делитель и частное. Чтобы найти делимое, нужно делитель умножить на частное:
Мы стали немного ближе к самому . Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:
И ещё один «слой» снят с неизвестной! Теперь мы видим ситуацию с известным значением произведения () и одним известным множителем ().
Теперь ситуация «уменьшаемое — вычитаемое = разность»
И последний шаг — известное произведение () и один из множителей ()
2 тип: уравнения со скобками
Уравнения данного типа чаще всего встречаются в задачах — именно к ним сводится 90% всех задач для поступления в 5 класс. В отличие от «луковичных уравнений» переменная здесь может встретиться несколько раз, поэтому решить её методами из предыдущего пункта невозможно. Типичные уравнения: или
Основная трудность — это правильно раскрыть скобки. После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение», которое умеем решать. Но обо всём по-порядку.
После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение», которое умеем решать. Но обо всём по-порядку.
Раскрытие скобок. Мы приведём несколько правил, которыми следует пользоваться в данном случае. Но, как показывает практика, верно раскрывать скобки ученик начинает только после 70-80 прорешанных задач. Основное правило таково: любой множитель, стоящий за скобками необходимо умножить на каждое слагаемое внутри скобок. А минус, стоящий перед скобкой, меняет знак всех выражений, что стоят внутри. Итак, основные правила раскрытия:
Приведение подобных. Здесь всё гораздо легче: Вам необходимо путём переноса слагаемых через знак равенства добиться того, чтобы с одной стороны стояли только слагаемые с неизвестной, а с другой — только числа. Основное правило таково: каждое слагаемое, переносимое через , меняет свой знак — если оно было с ,то станет с , и наоборот. После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение».
После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение».
Приведём пример:
(раскроем скобки. Обратите внимание на смену знаков!)
(выполним умножения)
(перенесём , и через знак равенства — они «превратятся» в , и )
(посчитаем итоговое количество справа и число слева)
(ситуация «известный множитель и произведение»)
Освоив эти два типа уравнений, Вы можете быть уверенны, что сможете решить добрую половину всех заданий во вступительной олимпиаде в 5 класс.
Решение сложных уравнений в 5-6 классах способом подстановки
Решение сложных уравнений в 5-6 классах способом подстановки.
В 5-6 классах учащиеся затрудняются решать уравнения такого типа, как
(х + 39) – 43 =27.
Традиционное объяснение в должной мере воспринимают только сильные ученики, а для слабых – это тайна за семью печатями. Каково же традиционное объяснение решения такого уравнения? Чтобы найти уменьшаемое х + 39, надо к вычитаемому 43 прибавить разность 27:
Каково же традиционное объяснение решения такого уравнения? Чтобы найти уменьшаемое х + 39, надо к вычитаемому 43 прибавить разность 27:
х + 39 = 43 + 27;
х + 39 = 70.
Далее рассуждают так: чтобы найти неизвестное слагаемое Х, надо из суммы 70 вычесть другое слагаемое 39:
х = 70 – 39;
х = 31.
В большинстве случаев ученики не видят в этом уравнении вычитаемого 43 и уменьшаемого Х + 39. Поэтому я разработала алгоритм решения таких уравнений. Суть этого приёма состоит в том, чтобы любое сложное уравнение свести к простейшему. Главное, иметь хороший навык решения простейших уравнений. Рассмотрим применение этого алгоритма на конкретных примерах.
1) ( х+ 121) + 38 = 269.
Обозначим выражение, стоящее в скобках через a: х + 121 = а.
Тогда получим такое уравнение:
а + 38 = 269;
а = 269 – 38;
а = 231.
Теперь возвращаемся к выражению, стоящему в скобках:
х + 121 = а;
х + 121 = 231;
х = 231 – 121;
х = 110.
Ответ: 110.
2) ( m – 379) + 125 = 3000
Подстановка m – 379 = а;
а + 125 = 3000;
а = 3000 – 125;
а = 2875;
m – 379 = 2875;
m = 2875 + 379;
m = 3254.
3) ( 127 + р ) – 89 = 1009.
Подстановка 127 + р = а;
а – 89 = 1009;
а = 1009 + 89;
а = 1098;
127 + р = 1098;
р = 1098 – 127;
р = 971.
4) ( х – 315 ) – 27 = 36.
Подстановка х – 315 = а;
а – 27 = 36;
а = 36 + 27;
а = 63;
х – 315 = 63;
х = 315 + 63;
х = 378.
5) 872 – ( 407 + с ) = 122
Подстановка 407 + с = а;
872 – а = 122;
а = 872 – 122;
а = 750;
407 + с = 750;
с = 750 – 407;
с = 343.
6) (7001+ х).42 = 441000
Подстановка 7001 + х = а;
а . 42 = 441000;
а = 441000 : 42;
а = 10500;
7001 + х = 10500;
х = 10500 – 7001;
х = 3499.
Таким образом, очень хорошо видно, что с помощью данного приёма очень легко решаются такие сложные уравнения.
Для тех учащихся, кто так и не усвоил правил нахождения неизвестных: слагаемого, вычитаемого, множителя и т.д., я использую при решении простейших уравнений приём «по аналогии».
Например, нужно решить уравнение: х – 128 = 312.
В стороне от этого уравнения слабый ученик записывает простейший арифметический пример 5 — 3 = 2.
Ученик смотрит, где в этом примере должен стоять х (на месте 5). Как из этого простого примера найти 5. Надо к 3 прибавить 2. Значит, и в уравнении, чтобы найти Х надо 128 сложить с 312.
Данный алгоритм решения уравнений служит пропедевтикой для решения в старших классах уравнений способом подстановки.
Как решать уравнения со скобками?
Не все уравнения, содержащие скобки, решаются одинаково. Конечно, чаще всего в них требуется раскрыть скобки и привести подобные слагаемые (при этом способы раскрытия скобок разняться).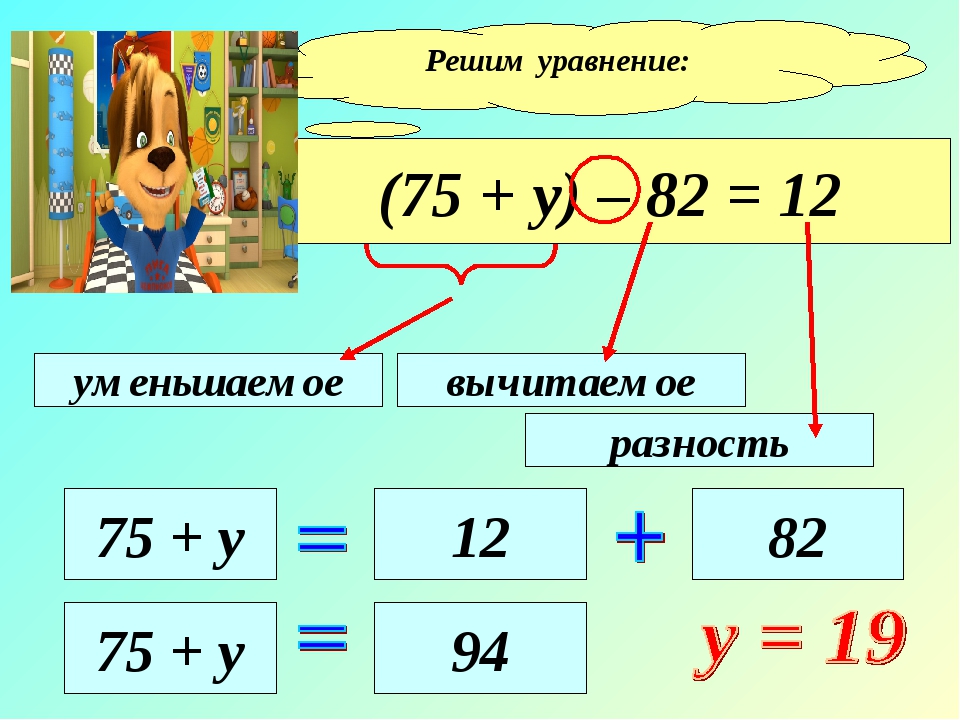 Но иногда скобки раскрывать не нужно. Рассмотрим все эти случаи на конкретных примерах:
Но иногда скобки раскрывать не нужно. Рассмотрим все эти случаи на конкретных примерах:
- 5х — (3х — 7) = 9 + (-4х + 16).
- 2х — 3(х + 5) = -12.
- (х + 1)(7х — 21) = 0.
Решение уравнений через раскрытие скобок
Данный метод решения уравнений встречается наиболее часто, но и он при всей своей кажущейся универсальности, делится на подвиды в зависимости от способа раскрытия скобок.
1) Решение уравнения 5х — (3х — 7) = 9 + (-4х + 16).
В данном уравнении перед скобками стоят знаки минус и плюс. Чтобы раскрыть скобки в первом случае, где перед ними стоит знак минус, следует все знаки внутри скобок поменять на противоположные. Перед второй парой скобок стоит знак плюс, который на знаки в скобках никах не повлияет, значит их можно просто опустить. Получаем:
5х — 3х + 7 = 9 — 4х + 16.
Слагаемые с х перенесем в левую часть уравнения, а остальные в правую (знаки переносимых слагаемых будут меняться на противоположные):
5х — 3х + 4х = 9 + 16 — 7.
Приведем подобные слагаемые:
6х = 18.
Чтобы найти неизвестный множитель х, разделим произведение 18 на известный множитель 6:
х = 18 / 6 = 3.
2) Решение уравнения 2х — 3(х + 5) = -12.
В этом уравнении также сначала нужно раскрыть скобки, но применив распределительное свойство: чтобы -3 умножить на сумму (х + 5) следует -3 умножить на каждое слагаемое в скобках и сложить полученные произведения:
2х — 3х — 15 = -12
-х = -12 + 15
-х = 3
х = 3 / (-1) = 3.
Решение уравнений без раскрытия скобок
Третье уравнение (х + 1)(7х — 21) = 0 тоже можно решить раскрыв скобки, но гораздо проще в таких случаях воспользоваться свойством умножения: произведение равно нулю тогда, когда один из множителей равен нулю. Значит:
х + 1 = 0 или 7х — 21 = 0.
а) х + 1 = 0
х1 = -1.
б) 7х — 21 = 0
7х = 21
х = 21 / 7
х2 = 3.
Нахождение неизвестного слагаемого, множителя, и т.
 п.: правила, примеры, решения
п.: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Допустим, у нас есть некоторое количество шариков в двух вазах, например, 9. Мы знаем, что во второй вазе 4 шарика. Как найти количество во второй? Запишем эту задачу в математическом виде, обозначив число, которое нужно найти, как x. Согласно первоначальному условию, это число вместе с 4 образуют 9, значит, можно записать уравнение 4+x=9. Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x? Для этого надо использовать правило:
Согласно первоначальному условию, это число вместе с 4 образуют 9, значит, можно записать уравнение 4+x=9. Слева у нас получилась сумма с одним неизвестным слагаемым, справа – значение этой суммы. Как найти x? Для этого надо использовать правило:
Определение 1
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения. Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если a+b=c, то c−a=b и c−b=a, и наоборот, из выражений c−a=b и c−b=a можно вывести, что a+b=c.
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Пример 1
Возьмем то уравнение, что у нас получилось выше: 4+x=9. Согласно правилу, нам нужно вычесть из известной суммы, равной 9, известное слагаемое, равное 4.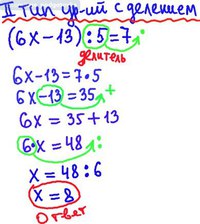 Вычтем одно натуральное число из другого: 9-4=5. Мы получили нужное нам слагаемое, равное 5.
Вычтем одно натуральное число из другого: 9-4=5. Мы получили нужное нам слагаемое, равное 5.
Обычно решения подобных уравнений записывают следующим образом:
- Первым пишется исходное уравнение.
- Далее мы записываем уравнение, которое получилось после того, как мы применили правило вычисления неизвестного слагаемого.
- После этого пишем уравнение, которое получилось после всех действий с числами.
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
4+x=9,x=9−4,x=5.
Мы можем проверить правильность полученного ответа. Подставим то, что у нас получилось, в исходное уравнение и посмотрим, выйдет ли из него верное числовое равенство. Подставим 5 в 4+x=9 и получим: 4+5=9. Равенство 9=9 верное, значит, неизвестное слагаемое было найдено правильно. Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки. Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.
Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Определение 2
Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Пример 2
Например, у нас есть уравнение x-6=10. Неизвестно уменьшаемое. Согласно правилу, нам надо прибавить к разности 10 вычитаемое 6, получим 16. То есть исходное уменьшаемое равно шестнадцати. Запишем все решение целиком:
x−6=10,x=10+6,x=16.
Проверим получившийся результат, добавив получившееся число в исходное уравнение: 16-6=10. Равенство 16-16 будет верным, значит, мы все подсчитали правильно.
Переходим к следующему правилу.
Определение 3
Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Пример 3
Воспользуемся правилом для решения уравнения 10-x=8. Мы не знаем вычитаемого, поэтому нам надо из 10 вычесть разность, т.е. 10-8=2. Значит, искомое вычитаемое равно двум. Вот вся запись решения:
10-x=8,x=10-8,x=2.
Сделаем проверку на правильность, подставив двойку в исходное уравнение. Получим верное равенство 10-2=8 и убедимся, что найденное нами значение будет правильным.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Определение 4
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных 0, c: a=b, c: b=c и наоборот.
Пример 4
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·0=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на 0, а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от 0. Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Определение 5
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Пример 5
Решим с его помощью уравнение x:3=5. Перемножаем между собой известное частное и известный делитель и получаем 15, которое и будет нужным нам делимым.
Вот краткая запись всего решения:
x:3=5,x=3·5,x=15.
Проверка показывает, что мы все подсчитали верно, ведь при делении 15 на 3 действительно получается 5. Верное числовое равенство – свидетельство правильного решения.
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Определение 6
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Пример 6
Возьмем простой пример – уравнение 21:x=3. Для его решения разделим известное делимое 21 на частное 3 и получим 7. Это и будет искомый делитель. Теперь оформляем решение правильно:
21:x=3,x=21:3,x=7.
Удостоверимся в верности результата, подставив семерку в исходное уравнение. 21:7=3, так что корень уравнения был вычислен верно.
Важно отметить, что это правило применимо только для случаев, когда частное не равно нулю, ведь в противном случае нам опять же придется делить на 0. Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0:x=0, то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0, с делимым, отличным от 0, решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5:x=0, которое не имеет ни одного корня.
Если же частным будет нуль, возможны два варианта. Если делимое также равно нулю и уравнение выглядит как 0:x=0, то значение переменной будет любым, то есть данное уравнение имеет бесконечное число корней. А вот уравнение с частным, равным 0, с делимым, отличным от 0, решений иметь не будет, поскольку таких значений делителя не существует. Примером может быть уравнение 5:x=0, которое не имеет ни одного корня.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
Пример 7
У нас есть уравнение вида 3·x+1=7. Вычисляем неизвестное слагаемое 3·x, отняв от 7 единицу. Получим в итоге 3·x=7−1, потом 3·x=6. Это уравнение решить очень просто: делим 6 на 3 и получаем корень исходного уравнения.
Вот краткая запись решения еще одного уравнения (2·x−7):3−5=2:
(2·x−7):3−5=2,(2·x−7):3=2+5,(2·x−7):3=7,2·x−7=7·3,2·x−7=21,2·x=21+7,2·x=28,x=28:2,x=14.
Уравнения и примеры с отрицательными числами и модул…
Все рациональные числа, которые мы можем себе представить, можно разделить на положительные и отрицательные. Изучается данная тема в 5-6 классах. Начиная с этих классов, учащиеся решают примеры, уравнения и задачи, в которых могут быть как положительные, так и отрицательные числа.
Решение примеров с отрицательными числами без ошибок — очень важный математический навык. То же самое касается и решения уравнений с отрицательными числами. В этом контексте в школьном курсе рассматривается и понятие модуля числа.
Давайте сегодня разберем эти вопросы.
Чтобы отличить положительное число от отрицательного, перед отрицательным числом ставят знак минус.
Например:
«5» – положительное число
«-5» — отрицательное число Если рассматривать числа на координатной прямой, то все числа, находящиеся слева от нуля, будут называться отрицательными, а числа, находящиеся справа от нуля – будут, соответственно, положительными.
Правила сложения, вычитания, умножения и деления отрицательных чисел имеют свои особенности.
Например, если нам необходимо выполнить действие:
«7 + 5»
Т.е. сложить два положительных числа, мы механически складываем их величины и получаем результат:
7 + 5 = 12
Если даже у нас будет длинный и трудоемкий пример, принцип его решения будет точно такой же, если числа положительные, то мы механически складываем их:
7 + 5 + 21 + 17 + 19 + 25 = 94
Операция вычитания может быть уже не такой простой.
Если выражение:
7 – 5 = 2
Мы вычисляем легко, то выражение:
5 – 7 = — 2
Это уже серьезная проверка наших знаний в области отрицательных чисел. Здесь важно в ответе правильно поставить знаки «плюс» и «минус».
Здесь перед числом «7» стоит знак «минус». Получается из меньшего числа «5» нужно вычесть большее число «7».
Как не запутаться?
Есть несколько способов. Один из которых вот какой:
Необходимо вспомнить понятие модуля числа.
Модуль числа – это число, записанное в вертикальных скобках:
|5| или |-7|
Когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем:
|5| = 5
|-7| = 7
Записываем наше выражение для модулей этих чисел:
|5| – |7|
Такая запись позволяет нам определить, какое число большее «по модулю», т.е. по своему абсолютному значению, без учета знака «минус» перед числом и стоит правее на числовой оси.
В нашем случае, это число «7».
Поэтому мы из большего «по модулю» числа вычитаем меньшее «по модулю» число и в ответе ставим тот знак (плюс или минус), который стоял в выражении перед большим «по модулю» числом:
|5| – |7| = — |7 — 5| = — |2| = -2
Второй способ вот какой:
Запишем:
5 + (– 7)
Представим каждое слагаемое как выражение двух чисел, с умножением на «-1», получим:
5 = — 1 · (- 5)
— 7 = — 1 · 7
Теперь сложим эти выражения, как в нашем примере, получим:
5 + (– 7) = (- 1 · (- 5)) + (- 1 · 7)
Вынесем за скобки «-1»:
-1·(- 5 + 7) = -1·(7 – 5) = -1· 2 = — 2
Когда мы выносим за скобку «-1», мы получаем возможность вычитать из большего числа меньшее, что гораздо удобнее.
Теперь мы знаем, как решать примеры с отрицательными числами.
Умножение на «-1» помогает нам вспомнить правила умножения и деления, в выражениях с положительными и отрицательными числами. Вот эти правила:
«Если умножать «минус» на «плюс», то получается в ответе «минус».»
«А если умножать «минус» на «минус», то получается в ответе «плюс».»
Проиллюстрируем все возможные варианты применения этих правил:
5 · 7 = 35
5 · (– 7) = — 35
(- 5) · 7 = — 35
(- 5) · (– 7) = 35
Возьмем более сложный случай, вычислим:
7 · (- 5) · 21 · (- 17)
Чтобы было проще, выполним вычисления по действиям:
1) 7 · (- 5) = — 35
2) 21 · (- 17) = — 357
3) (- 35) · (-357) = 12495
Таким образом:
7· (- 5) · 21 · (- 17) = 12495
Теперь рассмотрим, как решать уравнения с отрицательными числами и переменными.
Возьмем пример с уравнением:
3 + 4(5 – х) = 15
Сначала раскроем скобки:
3 + 4 · 5 + 4 · (- х) = 15
Обязательно обращаем внимание на минусы, стоящие перед числами и переменной «х», помним о приведенном выше правиле, получаем:
3 + 20 – 4х = 15
Приведем подобные (3 + 20 = 23) и запишем:
23 – 4х = 15
Переносим слагаемое без переменной «х» из левой части в правую, меняя при этом перед ним знак на противоположный
— 4х = 15 – 23
После приведения подобных в правой части уравнения (15 – 23 = — 8), получим:
— 4х = — 8
Деление отрицательных чисел проводим по тем же правилам, что и умножение:
х = — 8 : (- 4)
«Минус» делим на «минус», получаем «плюс»:
х = 2
Давайте теперь разберем примеры с модулем числа.

Напомню, что, когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем.
Например:
|5| + |-7| = 5 + 7 = 12
|5| — |-7| = 5 — 7 = — 2
|5| · |-7| = 5 · 7 = 35
|-35| : |-7| = 35 : 7 = 5
Как видите, в примерах, где числа стоят под знаком модуля, необходимо следовать правилу:
«Сначала раскрываем скобки модуля, а потом проводим операции сложения, вычитания, умножения или деления».
Конечно, существуют и более сложные примеры с отрицательными числами и модулями. Чтобы познакомиться с правилами их решения, а также вспомнить все, что необходимо, связанное с модулями — следите за нашими уроками или обратитесь к репетитору на нашем сайте.
Основные принципы решения уравнений в 4-5 классе
В этом уроке мы рассмотрим, что такое уравнения, для чего они нужны, основные методы решения уравнений в 4 и 5 классе.
Простейшие уравнения
Ранее вы могли проходить в школе такого рода примеры:
Впишите в кружок подходящее число:
5+ ⃝ = 11
Как вы знаете, такие выражения называются уравнениями, а вместо кружка используется буква x или любая другая.
5 + x = 11 – это уравнение. Уравнением оно называется потому что в нём левая часть равняется правой. Если условие равенства не выполняется, значит уравнение записано неверно. Буква x называется неизвестным, или корнем уравнения. Целью решения уравнения является нахождение неизвестного.
Как вы уже знаете, для того, чтобы решить уравнение, надо x оставить в одной части, а все числа перенести в другую часть с противоположным знаком.
Правило:
Мы можем переносить числа и неизвестные из одной части равенства в другую, поменяв при этом знак на противоположный.
То есть если у нас
5 + x =11
то
x = 11 – 5
x = 6
Другой пример:
y + 21 = 37
y = 37 — 21
y = 16
Обратите внимание, что я специально здесь использовал вместо x букву y – для того, чтобы подчеркнуть, что в уравнении неизвестное может обозначаться не только x, но и любой другой буквой или даже комбинацией букв.
Если же мы имеем уравнение вот такого вида:
26 – x = 18
то мы можем записать, что
26 – 18 = x – здесь, как вы видите, мы 18 перенесли в левую часть со знаком минус, а x – в правую со знаком плюс.
При этом мы можем поменять левую и правую часть местами, от этого суть уравнения не поменяется. То есть мы можем записать, что
x = 26 — 18
x = 8
Для проверки решения уравнения надо найденное неизвестное подставить в исходное уравнение. Т.е. в нашем случае это
26 – 8 = 18
18 = 18 – решение верное.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Пример:
z – 7 = 14
z = 14 + 7
z = 21
Проверка:
21 – 7 = 14
14 = 14 – решение верное
Уравнения с делением и умножением
Запишем равенство
6 = 6
Если мы умножим обе части равенства на одно и то же число, то оно останется верным
6∙3 = 6∙3
Если мы разделим обе части равенства на одно и то же число, то оно тоже останется верным
6:2 = 6:2
Важно: эти принципы часто используются при решении уравнений
Уравнение c множителями
5∙x = 15
Как уже говорилось ранее, мы можем разделить правую и левую часть на одно и то же число, и равенство сохранится. Чтобы найти x, это уравнение нужно разделить на 5.
Чтобы найти x, это уравнение нужно разделить на 5.
Для того, чтобы разделить на 5 выражение 5∙x мы можем записать
5x:5
или
(5:5)x = 1∙x = x
Таким образом, из начального уравнения 5∙x = 15 получим:
5x:5 = 15:5
x = 3
Можно сказать по другому:
Здесь 5 и x – это множители, а 15 – произведение.
Для того, чтобы найти неизвестный множитель, надо произведение разделить на другой множитель, который нам известен.
То есть x = 15:5 = 3
Проверка:
5∙3 = 15
15 = 15
Пример:
x∙4 = 32 (x∙4 – это то же самое, что 4∙x)
x = 32:4
x = 8
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Уравнение с делителями
z:4 = 16
Здесь z – делимое, 4 – делитель, 16 – частное. Для того, чтобы найти делимое, надо частное умножить на делитель. Ещё раз обращаю ваше внимание, что неизвестное может обозначаться любой буквой, не обязательно только x.
Ещё раз обращаю ваше внимание, что неизвестное может обозначаться любой буквой, не обязательно только x.
z = 16∙4
z = 64
В правой части у нас остался один z, потому что ранее это был z в 4 раза меньший, и раз мы его умножили на 4, то он стал в 4 раза больше, т.е. полным z.
Проверка
64:4 = 16
16 = 16
Пример
120:x = 30
120 = 30∙x – мы умножили на x левую и правую часть, в результате чего в левой части он исчез, а в правой части он появился. Левая часть – это было число 120, уменьшенное в x раз (так как деление – это уменьшение числа в заданное число раз). Соответственно, раз мы левую часть умножаем на тот же x, то она перестаёт быть числом 120, уменьшенным в x раз, и станет просто числом 120.
Таким образом, мы перешли к уже известным нам уравнениям с множителями
Мы можем переписать равенство как
30∙x = 120
x = 120:30
x = 4
Про это же уравнение можно сказать следующее:
Для того, чтобы найти неизвестный делитель x надо делимое разделить на частное.
120:x = 30
120 – делимое, x – делитель, 30 — частное
Пример:
96:x = 6
96 = 6x
x = 96:6 – тут мы пропустили шаг перестановки частей равенства 6x = 96 – его записывать необязательно
x = 16
Усложнённые уравнения
Неизвестные можно складывать и вычитать, как и числа
Пример:
3x + x = 24
4x = 24
x = 24:4
x = 6
Проверка:
3x + x = 24
3∙6 + 6 = 24
18 + 6 = 24
24 = 24
11x – 3x + 5x = 65
13x = 65
x = 65:13
x = 5
Проверка:
11∙5 – 3∙5 + 5∙5 = 65
55 – 15 + 25 = 65
65 = 65
Раскрытие скобок
Предположим, у нас есть выражение
9∙(10 — 4)
Мы можем записать его как
9∙6
так как выражение в скобках 10-4 равно 6. 9∙6 = 54
Или же мы можем раскрыть скобки.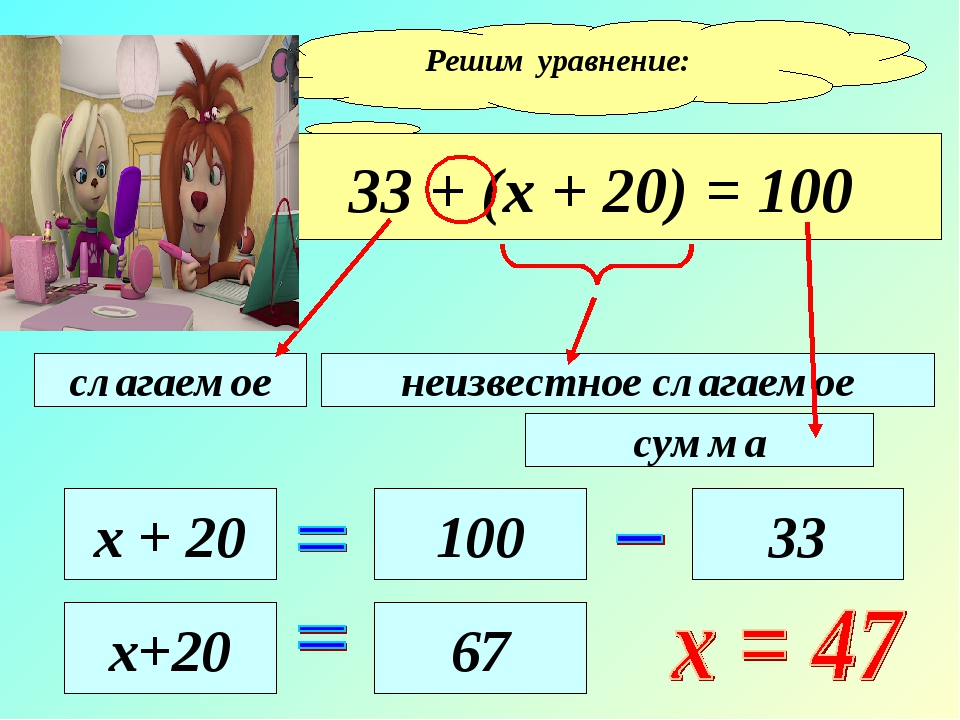
При раскрытии скобок множитель, стоящий перед скобками (или после них), умножается на каждое число в скобках, при этом знаки сохраняются.
Т.е
9∙(10 — 4) = 9∙10 – 9∙4 = 90 – 36 = 54
Аналогично, если в скобках будет больше членов и с разными знаками.
Например:
(11 + 2 – 5)∙4 = 4∙8 = 32
или
(11 + 2 – 5)∙4 = 4∙11 + 4∙2 – 4∙5 = 44 + 8 – 20 = 32 —
как мы уже говорили, множитель может стоять и после скобок, от этого правила раскрытия скобок не меняются.
Если в скобках вместо числа будет стоять неизвестное, то скобки раскрываются аналогично.
12∙(8x + 2x – 5) = 12∙8x + 12∙2x – 12∙5 = 96x + 24x – 60 = 120x — 60
Пример:
16∙(x – 4) = 4∙(x+2)
У правой части мы видим множитель 4. В левой части множитель 16. Т.е. мы смело можем разделить обе части на 4, избавишись таким образом от множителя в правой части
4∙(x – 4) = x +2
4x – 16 = x + 2
далее переносим x в левую часть, а числа – в правую
4x – x = 16+2
3x = 18
x = 6
Проверка:
16∙(6 – 4) = 4∙(6+2)
16∙2 = 4∙8
32 = 32
Пример:
5∙(15 – x) = 25∙(x-3)
Разделим обе части уравнения на 5
15 – x = 5∙(x-3)
15 – x = 5x – 15
15 + 15 = 5x + x
30 = 6x
x = 5
Проверка:
5∙(15 – 5) = 25∙(5 – 3)
5∙10 = 25∙2
50 = 50
ВИДЕОКУРС 2plus2. online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример:
100:(x – 25) = 20
Точно так же, как мы решали ранее уравнение 120:x = 30 путём умножения обеих частей на делитель, т.е. на x, и получая 120 = 30x, это уравнение мы тоже решим, умножив обе части на делитель, т.е. на x-25
100 = 20(x-25)
100 = 20x – 500
100 + 500 = 20x
600 = 20x
x = 30
Проверка
100:(30-25) = 20
100:5 = 20
20 = 20
Пример
(x – 4):6 = 16
x – 4 = 16∙6
x – 4 = 96
x = 96+4
x = 100
Проверка:
(100-4):6 = 16
96:6 = 16
16 = 16
Конспект урока + презентация «Обобщение и систематизация знаний по теме «Решение уравнений»
Тема: «Обобщение и систематизация знаний по теме «Решение уравнений».
Цели урока
Образовательные:
— систематизировать и обобщить знания учащихся по теме «Решение уравнений»;
— совершенствовать вычислительные навыки;
— активизировать познавательную деятельность.
Развивающие:
-расширять кругозор учащихся;
-формировать целостное отношение учащихся к предмету, к процессу познания путём разнообразных методов и приёмов;
— развивать логическое мышление;
—развивать навыки рефлексии
— развивать навык самооценки.
Воспитательные:
— развивать коммуникативные компетенции;
— формировать умения мыслить системно, находить творческий подход в своей работе;
— формировать умение действовать в нестандартных ситуациях;
— прививать любовь к предмету, мотивировать на его дальнейшее изучение.
-воспитывать умение работать в парах ,выслушивать точку зрения партнера и принимать общее решение;
-врспитывать умение доводить дело до конца
Оборудование:
мультимедийный проектор, компьютер, маршрутные карты, задания, медали
Организация пространства: фронтальная работа ,парная работа, самостоятельная индивидуальная работа.
Планируемые образовательные результаты.
Предметные: знать правила раскрытия скобок, правила выполнения действий с рациональными числами, алгоритм решения уравнений,
Метапредметные: уметь соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией, уметь осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей.
Личностные: оценивать ситуацию на уроке с точки зрения важности образования; положительно относиться к учению, к познавательной деятельности, желать приобретать новые знания, умения, совершенствовать имеющиеся.
Технологическая карта урока
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, я ответила на вопрос, как использовать игровые технологии обучения, адекватные содержанию и учебным целям в предложенном проекте урока по математике с использованием игры.
Задача учителя состоит не только в передаче знаний, но и в удовлетворении интересов учащихся . Школа не должна быть для детей «скучным» местом, поэтому, я считаю, что в преподавание необходимо внедрять игровые технологии в разумных пределах и в нужный момент. Ведь именно в игре ребёнок возвращается в свою сущность, в свой мир и полностью раскрывает свои способности, при этом забывая чувства скованности, страха и нерешительности. Во время игры присутствует момент социального взаимодействия, формируются установки профессиональной деятельности и самооценки.
Использованная литература:
-
Педагогические технологии: учеб. пособие / Под ред. В.С. Кукушина. – М.: ИКЦ «МарТ», 2004. – 336 с.
пособие / Под ред. В.С. Кукушина. – М.: ИКЦ «МарТ», 2004. – 336 с.
-
Сазонова О. Ю. Использование игровых технологий на уроках математики и во внеклассной работе [Электронный ресурс] / О. Ю. Сазонова. – Режим доступа к статье : http://www.26206s014.edusite.ru /188aal.html. -
Сафенкова Е. Н. Игровые технологии на уроках математики [Электронный ресурс] / Е. Н. Сафенкова. – Режим доступа к статье : http://nsportal.ru/shola/algebra/library/igrovye—tehnologii—na—urokax—matematiki. -
. Синквейн –это https://www.kakprosto.ru/kak-914060-chto-takoe-sinkveyn-i-kak-ego-sostavlyat -
Титаренко Т. Л. Игровые технологии обучения математики в старших классах [Электронный ресурс] / Т. Л. Титаренко. – Режим доступа к статье : http://festival.1september.ru/articles.
Л. Титаренко. – Режим доступа к статье : http://festival.1september.ru/articles.
Учитель математики МБОУ / Н.В.Марковская/
Нижневартовского района
«Покурская общеобразовательная средняя школа»
Приложение 1
1. «Прогноз погоды»
2. «Умники и умницы»
А) -2,36+ 0,49 =
Б) -17+ (-45)=
В)
Г)
Д)
3. « В гостях у сказки»
« В гостях у сказки»
У Василисы Прекрасной 2 ведерка живой воды. В первом ведерке в 3 раза больше живой воды, чем во втором. Если из первого ведерка перелить 20л во второе ,то живой воды в ведерках станет поровну. Сколько живой воды было в каждом ведерке первоначально?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. « Спортивное обозрение» Раскройте скобки и упростите:
« Спортивное обозрение» Раскройте скобки и упростите:
х-(2х-7)
12-(8-5а)
3у-(5+2у)
15-(2п+5)
4+(2-у)
5. «Слабое звено» Найди ошибки и исправь их:
-18*(-5)-10=80
-78: (-13)+ (-6)=-22
-54:9+ (-14)=20
14*(-5) +33=37
-25*4+1000:10=0
96:16-15*4=-55
6. «Фигурное катание» Решите уравнения
6x – 12 = 5x + 4 7а = – 310 + 3а
– 4· ( – z + 7) = z + 17 (30-7а)*8=352
Приложение 2
Карта успеха _______________(фамилия имя ученика)
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
Порядок операций — PEDMAS
Порядок операций можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. Без согласованного порядка работы можно совершить большие ошибки во время вычислений.
Без согласованного порядка работы можно совершить большие ошибки во время вычислений.
Например, выражение, которое влечет за собой больше, чем операцию, такую как вычитание, сложение, умножение или деление, требует стандартного метода определения того, какую операцию выполнить первой.
Например, если вы хотите решить такую проблему, как; 5 + 2 x 3, возникает проблема, какая операция запускается первой?
Поскольку у этой проблемы есть два варианта решения, какой ответ правильный?
Если мы сначала выполняем сложение, а затем умножение, результат будет:
5 + 2 x 3 = (5 + 2) x 3 = 10 x 3 = 30
Если мы сначала выполним умножение, а затем сложение, результат:
5 + 2 x 3 = 5 + (2 x 3) = 5 + 6 = 11
Чтобы узнать, какой из них является правильным, есть мнемоническое слово «PEMDAS», которое полезно, поскольку оно напоминает нам правильного порядка действий.
PEMDAS
PEMDAS — это аббревиатура, обозначающая скобки, экспоненты, умножение, сложение и вычитание. Порядок действий:
Порядок действий:
- P для круглых скобок: (), скобок [], фигурных скобок {} и дробных черт.
- E — экспонента, включая корни.
- M для отдела.
- D для умножения.
- A — для дополнения.
- S — вычитание.
Правила PEMDAS
- Всегда начинайте с вычисления всех выражений в скобках
- Упростите все экспоненты, такие как квадратные корни, квадраты, кубы и корни куба
- Выполните умножение и деление, начиная слева направо
- Наконец, проделайте сложение и вычитание аналогично, начиная слева направо.
Один из способов освоить этот порядок работы — вспомнить любую из следующих трех фраз; Выберите тот, который вам легче запомнить.
- «P аренда E xcuse M y D ухо A Unt S »
- «Большие слоны уничтожают мышей и улиток».
- «Розовые слоны уничтожают мышей и улиток».
Пример 1
Решить
30 ÷ 5 x 2 + 1
Решение
Поскольку скобок и экспонент нет, начните с умножения, а затем деления слева направо.Завершите операцию сложением.
30 ÷ 5 = 6
6 x 2 = 12
12 + 1 = 13
ПРИМЕЧАНИЕ: Следует отметить, что, хотя умножение в PEMDAS предшествует делению, однако операция двух всегда слева направо.
Выполнение умножения перед делением приводит к неправильному ответу:
5 x 2 = 10
30 ÷ 10 = 3
3 + 1 = 4
Пример 2
Решите следующее выражение: 5 + (4 — 2) 2 x 3 ÷ 6 — 1
Решение
- Начните со скобок;
(4-2) = 2
- Перейти к экспоненциальной операции.
2 2 = 4
- Теперь у нас осталось; 5 + 4 x 3 ÷ 6 — 1 =?
- Выполните умножение и деление, начиная слева направо.
4 x 3 = 12
5 + 12 ÷ 6 — 1
Начиная справа;
12 ÷ 6 = 2
5 + 2 — 1 =?
5 + 2 = 7
7 — 1 =?
7 — 1 = 6
Пример 3
Упростить 3 2 + [6 (11 + 1 — 4)] ÷ 8 x 2
Решение
Для решения этой проблемы используется PEMDAS. применяется следующим образом;
- Начните операцию с скобок.
- Начните внутри скобок, пока все группировки не будут устранены. Добавление сделано;
11 + 1 = 12
- Выполните вычитание; 12 — 4 = 8
- Проработать кронштейны как; 6 x 8 = 48
- Выполните экспоненты как; 3 2 = 9
9 + 48 ÷ 8 x 2 =?
- Выполните умножение и деление слева направо;
48 ÷ 8 = 6
6 x 2 = 12
Пример 4
Вычислить выражение; 10 ÷ 2 + 12 ÷ 2 × 3
Решение
При применении правила PEMDAS умножение и деление оцениваются слева направо.Желательно вставить круглые скобки, чтобы напомнить себе о порядке работы
10 ÷ 2 + 12 ÷ 2 × 3
= (10 ÷ 2) + (12 ÷ 2 × 3)
= 23
Пример 5
Вычислить 20 — [3 x (2 + 4)]
Решение
Сначала определите выражения в скобках.
= 20 — [3 x 6]
Найдите оставшиеся скобки.
= 20 — 18
Наконец, выполните вычитание, чтобы получить 2 в качестве ответа.
Пример 6
Тренировка (6 — 3) 2 — 2 x 4
Решение
- Начните с раскрытия скобок
= (3) 2 — 2 x 4
= 9 — 2 x 4
- Теперь произведите умножение
= 9 — 8
- Завершите операцию вычитанием, чтобы получить 1 как правильный ответ.
Пример 7
Решите уравнение 2 2 — 3 × (10 — 6)
Решение
- Вычислить в скобках.
= 2 2 — 3 × 4 - Определите показатель степени.
= 4 — 3 x 4 - Произвести умножение.
= 4 — 12 - Завершите операцию вычитанием.
= -8
Пример 8
Упростите выражение 9-5 ÷ (8-3) x 2 + 6, используя порядок операций.
Решение
- Тренировка в скобках
= 9-5 ÷ 5 x 2 + 6
= 9 — 1 x 2 + 6
- Произвести умножение
= 9 — 2 + 3
- Сложение, а затем вычитание
= 7 + 6 = 13
Заключение
В заключение, иногда выражение может содержать две операции на одном уровне.
Например, если выражение содержит и квадрат, и куб, сначала можно обработать любой из них. Всегда выполняйте операцию слева направо, следуя правилу PEMDAS. Если вы встретите выражение без символов группировки, таких как фигурные скобки, скобки и круглые скобки, вы можете упростить операцию, добавив свои собственные символы группировки.
Работа с выражениями, содержащими дроби, решается путем упрощения сначала числителя, а затем знаменателя. Следующий шаг — по возможности упростить числитель и знаменатель.
Практические вопросы
1) Упростите выражение;
2 + 3 2 (5-1)
2) Решите
4-3 [4-2 (6-3)] ÷ 2
3) Упростите следующее выражение с помощью PEMDAS:
16 — 3 (8 — 3) 2 ÷ 5
4) Используя PEMDAS, упростите следующее алгебраическое выражение:
14 z + 5 [6 — (2 z + 3)]
5) Упростите алгебраическое выражение ниже;
— {2 y — [3 — (4 — 3 y)] + 6 y
6) Вычислите следующее выражение, используя порядок операций:
3 + 6 x (4 + 5) ÷ 3 — 7
7) Оцените приведенное ниже выражение с помощью PEMDAS.
150 ÷ (6 + 3 x 8) — 5
8) Упростите следующее выражение;
45 ÷ (8 {5 — 4} — 3)
Предыдущий урок | Главная страница | Следующий урок
Круглые скобки — математика для 3-го класса
Узнайте о скобках () в уравнениях
Во 2-м классе вы научились решать многоступенчатые уравнения, подобные этим:
15 + 20 + 10 =?
30 — 12 — 6 =?
Но иногда вы можете увидеть такие уравнения:
13 + ( 12 + 8 ) =?
Это уравнение содержит пару круглых скобок (), , называемых скобками.
Что такое круглые скобки?
Круглые скобки — это пара скобок () , которые говорят вам, что решить в первую очередь.
Всегда сначала решайте вопросы в скобках . 👍
👉 Скобки очень важны, потому что они могут изменить ответ на ваше уравнение!
Посмотрим как. 🙇
Посмотрите на это уравнение.
27-10 + 7 = ?
Если мы заключим в скобки первые два числа , какой ответ мы получим?
(27-10) + 7 = ?
Сначала мы решаем выражение внутри скобок .
Совет: переписывайте уравнение после каждого шага.
17 + 7 = 24
Отличная работа!
Теперь давайте попробуем заключить в круглые скобки последние два числа , вместо первых двух.
27 — (10 + 7) = ?
Получим ли мы такое же значение при решении этого уравнения?
27 — 17 = 10
Ответ изменился с 24 на 10! 🤓
Добавление скобок изменило ответ.Это степень скобок . 💪
Решение уравнений в круглых скобках
Попробуем решить некоторые уравнения со скобками.
Пример 1
14 + (19-13) = ?
🤔 Какую операцию вы решите сначала в этом уравнении — сложение или вычитание?
Верно! 👍
✅ Поскольку вычитание заключено в круглые скобки, мы должны сначала решить его.
Давайте теперь решим уравнение.🤗
Как вы теперь знаете, мы должны сначала решить скобки .
14 + (19–13) = 14 + 6
Теперь давайте сложим два числа , которые у нас есть.
14 + 6 = 20
Отличная работа! 👏
__
Попробуем еще один пример.
Пример 2
(30-20) + (9 + 6) — 3 = ?
Какие части уравнения вы решите в первую очередь? 🤔
Очень хорошо! 👌
✅ Сначала необходимо решить детали в скобках .
Во-первых, давайте решим первые скобки .
😺 Совет: переписывайте уравнение после каждого шага.
Теперь давайте решим другие скобки.
Давайте теперь решим оставшуюся часть уравнения.
10 + 15 — 3 = 25 — 3
25-3 = 22
Отлично! 😎
Смотри и учись
Вы отлично справились на уроке! 👏 Теперь попробуйте самостоятельно освоить круглые скобки.
Сначала умножить или сложить? Порядок обучения правилам операций
Когда ученики 3-х классов и выше учатся складывать, вычитать, умножать, делить и работать с основными числовыми выражениями, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Например, вы сначала складываете или умножаете? А как насчет умножения или деления? В этой статье объясняется, в каком порядке выполняются операции, и приводятся примеры, которые вы также можете использовать со студентами.Он также содержит два урока, которые помогут вам представить и развить концепцию.
Стандарт ключа:
- Выполнять арифметические операции, включающие сложение, вычитание, умножение и деление в обычном порядке, независимо от того, присутствуют ли скобки или нет. (3 класс)
Порядок операций — это пример очень процедурной математики. Легко ошибиться, потому что это не столько концепция, которую вы усвоили, а скорее список правил, которые вам нужно запомнить.Но не обманывайтесь, думая, что процедурные навыки не могут быть глубокими! Он может представлять сложные проблемы, подходящие для старших школьников и созревшие для обсуждения в классе:
- Меняется ли правило слева направо, когда умножение подразумевается, а не прописано? (Например, \ (3g \) или \ (8 (12) \) вместо \ (3 \ times g \) или \ (8 \ cdot 12 \).)
- Где факториал попадает в порядок операции?
- Что произойдет, если вы возведете показатель степени в другой показатель, но скобок нет? (Обратите внимание, что этот урок не включает экспоненты, хотя, если учащиеся готовы, вы можете расширить свой урок, включив их.)
Что первично в порядке работы?
Со временем математики согласовали набор правил, называемый порядком операций , чтобы определить, какую операцию выполнить в первую очередь. Когда выражение включает только четыре основных операции, вот правила:
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
При упрощении выражения, такого как \ (12 \ div 4 + 5 \ times 3-6 \), сначала вычислите \ (12 \ div 4 \), поскольку порядок операций требует сначала оценки любого умножения и деления (в зависимости от того, что первый) слева направо перед вычислением сложения или вычитания.В данном случае это означает сначала вычисление \ (12 \ div 4 \), а затем \ (5 \ times 3 \). После того, как все умножение и деление будут завершены, продолжайте, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
| \ (12 \ div 4 + 5 \ times 3-6 \) | |
| \ (3 + 5 \ times 3-6 \) | Потому что \ (12 \ div 4 = 3 \) |
| \ (3 + 15-6 \) | Потому что \ (5 \ times 3 = 15 \) |
| \ (18-6 \) | Потому что \ (3 + 15 = 18 \) |
| \ (12 \) | Потому что \ (18-6 = 12 \) |
Рассмотрим в качестве примера другое выражение:
| \ (6 + 4 \ times 7-3 \) | |
| \ (6 + 28-3 \) | Потому что \ (4 \ times 7 = 28 \), что выполняется первым, потому что умножение и деление оцениваются в первую очередь. |
| \ (34-3 \) | Потому что \ (6 + 28 = 34 \) |
| \ (31 \) | Потому что \ (34-3 = 1 \) |
Иногда мы можем захотеть убедиться, что сначала выполняется сложение или вычитание. Группировка символов , таких как скобки \ (() \), скобки \ ([] \) или фигурные скобки \ (\ {\} \), позволяет нам определять порядок, в котором выполняются определенные операции. выполнено.
Порядок операций требует, чтобы операции внутри символов группировки выполнялись перед операциями вне их.Например, предположим, что выражение 6 + 4 заключено в круглые скобки:
| \ ((6 + 4) \ times 7-3 \) | |
| \ (10 \ times 7-3 \) | Потому что \ (6 + 4 = 10 \), что и сделано во-первых, потому что он заключен в круглые скобки. |
| \ (70-3 \) | Потому что \ (10 \ times 7 = 70 \), и скобок больше нет. |
| \ (67 \) | Потому что \ (70 — 3 = 67 \) |
Обратите внимание, что выражение имеет совершенно другое значение! Что, если вместо этого мы заключим \ (7 — 3 \) в круглые скобки?
| \ (6 + 4 \ times (7-3) \) | |
| \ (6 + 4 \ times 4 \) | На этот раз \ (7-3 \) находится в скобках, так что мы делаем это в первую очередь. |
| \ (6 + 16 \) | Поскольку \ (4 \ times 4 = 16 \) и когда скобок не осталось, мы продолжаем умножение перед сложением. |
| \ (22 \) | Потому что \ (6 + 16 = 22 \) |
Этот набор скобок дает еще один ответ. Итак, когда используются круглые скобки, правила порядка операций следующие:
- Операции в скобках или групповые символы.
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
Порядок операций — BODMAS
Операции
«Операции» означают такие вещи, как сложение, вычитание, умножение, деление, возведение в квадрат и т. Д. Если это не число, это, вероятно, операция.
Но, когда вы видите что-то вроде …
7 + (6 × 5 2 + 3)
… какую часть нужно рассчитать в первую очередь?
Начать слева и пойти направо?
Или идти справа налево?
Предупреждение: вычислите их в неправильном порядке, и вы можете получить неправильный ответ!
Итак, давным-давно люди согласились соблюдать правила при расчетах, а это:
Порядок действий
Сначала делайте что-то в скобках
| 4 × (5 + 3) | = | 4 × 8 | = | 32 | |||
| 4 × (5 + 3) | = | 20 + 3 | = | 23 | (неверно) |
Показатели (степени, корни) перед умножением, делением, сложением или вычитанием
| 5 × 2 2 | = | 5 × 4 | = | 20 | |||
| 5 × 2 2 | = | 10 2 | = | 100 | (неверно) |
Умножьте или разделите перед сложением или вычитанием
| 2 + 5 × 3 | = | 2 + 15 | = | 17 | |||
| 2 + 5 × 3 | = | 7 × 3 | = | 21 | (неправильно) |
В противном случае просто идите слева направо
| 30 ÷ 5 × 3 | = | 6 × 3 | = | 18 | |||
| 30 ÷ 5 × 3 | = | 30 ÷ 15 | = | 2 | (неверно) |
Как я все это помню…? БОДМЫ!
Б | B ракетки первые |
О | O rders (т. Е. Степени, квадратные корни и т. Д.) |
DM | D ivision и M ultiplication (слева направо) |
AS | A ddition и S ubtraction (слева направо) |
Разделение и умножение ранжируются одинаково (и идут слева направо).
Сложение и вычитание ранжируют одинаково (и идут слева направо)
Так сделай так:
После того, как вы сделали «B» и «O», просто идите слева направо, выполняя любую «D» или «M», как вы их найдете.
Затем идите слева направо, выполняя любую букву «A» или «S», если найдете их.
Примечание: единственное странное название — «Заказы». «Экспоненты» используется в Канаде, поэтому вы можете предпочесть «БЕДМЫ».Также есть «Индексы», что делает его «БИДМАС». В США вместо скобок пишут «круглые скобки», поэтому это «PEMDAS»
.
Примеры
Пример: как вычислить
3 + 6 × 2 ?
M ultiplication до A ddition:
Сначала 6 × 2 = 12 , затем 3 + 12 = 15
Пример: как вычислить
(3 + 6) × 2 ?
B первая ракетка:
Сначала (3 + 6) = 9 , затем 9 × 2 = 18
Пример: Как вы работаете с
12/6 × 3/2 ?
M ultiplication и D ivision ранжируются одинаково, поэтому просто идите слева направо:
Сначала 12/6 = 2 , затем 2 × 3 = 6 , затем 6/2 = 3
Практический пример:
Пример: Сэм бросил мяч прямо вверх со скоростью 20 метров в секунду, как далеко он улетел за 2 секунды?
Сэм использует эту особую формулу, которая включает гравитацию:
высота = скорость × время — (1/2) × 9.8 × время 2
Сэм устанавливает скорость 20 метров в секунду и время 2 секунды:
высота = 20 × 2 — (1/2) × 9,8 × 2 2
Теперь о расчетах!
Начать с: 20 × 2 — (1/2) × 9,8 × 2 2
Кронштейны сначала: 20 × 2 — 0,5 × 9,8 × 2 2
Тогда Заказы (2 2 = 4): 20 × 2 — 0,5 × 9,8 × 4
Затем умножается: 40 — 19,6
Вычесть и СДЕЛАНО! 20.4
Мяч достигает 20,4 метра за 2 секунды
Показатели степени …
А как насчет этого примера?
4 3 2
Показатели — особые: идут сверху вниз, (сначала экспонента сверху). Итак, вычисляем так:
| Начать с: | 4 3 2 | |
| 3 2 = 3 × 3: | 4 9 | |
| 4 9 = 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4: | 262144 |
Так 4 3 2 = 4 (3 2 ) , а не (4 3 ) 2
И, наконец, как насчет примера с самого начала?
Начать с: 7 + (6 × 5 2 + 3)
Сначала скобки , а затем «Заказы» : 7 + (6 × 25 + 3)
Затем Умножить : 7 + (150 + 3)
Затем Добавьте : 7 + (153)
Кронштейны завершено: 7 + 153
Последняя операция: Добавить : 160
Порядок операций — Бесплатная математическая справка
Введение
Порядок операций — очень простая концепция, жизненно важная для правильного понимания математики.В отличие от чтения, где мы всегда работаем слева направо, иногда с математикой нам нужно проработать одну часть задачи перед другой, иначе окончательный ответ может быть неверным! Мы используем термин «порядок операций», чтобы описать, с какой частью проблемы нужно работать в первую очередь. Возьмем, к примеру, это уравнение:
$$ 4 + 6 \ div 2 * 11 =? $$
Если бы вы просто решали слева направо, ответ был бы неверным. Давайте сделаем это сейчас: 4 + 6 = 10. Разделите это на 2, чтобы получить 5. Умножьте 5 на 11, чтобы получить 55.К сожалению, хотя это казалось нормальным, этот ответ неверен.
Правильный порядок действий
Порядок действий позволит вам решить эту проблему правильно. Порядок следующий: Круглая скобка , Показатели , Умножение и деление и, наконец, Сложение и вычитание . Всегда сначала выполняйте операции внутри круглых скобок, а затем выполняйте операции с показателями. После этого выполняйте все умножение и деление слева направо и, наконец, все операции сложения и вычитания слева направо.
Популярным способом запоминания порядка является аббревиатура PEMDAS. Круглые скобки, экспоненты, умножение и деление, сложение и вычитание. Вы также можете создать небольшую фразу, например « P lease E xcuse M y D ear A Unt S ally». Что бы вы ни выбрали, убедитесь, что вы хорошо знаете все шесть этапов порядка действий.
Давайте попробуем решить это уравнение еще раз, на этот раз с помощью PEMDAS.
$$ 4 + 6 \ div 2 * 11 =? $$
Шаг 1) Круглые скобки.Нет ни одного. Двигаться дальше.
Шаг 2) Показатели. Никто. Продолжай …
Шаг 3) Умножение и деление. Идите слева направо, выполняя все операции умножения и деления по мере того, как вы сталкиваетесь с этим, поэтому разделите 6 на 2, чтобы получить 3, и умножьте это на 11, чтобы получить 33.
Шаг 4) Сложение и вычитание. Слева направо 4 + 33 = 37.
$$ 4 + 6 \ div 2 * 11 $$
$$ 4 + 3 * 11 $$
$$ 4 + 33 $$
$ 37 $
Вся идея состоит в том, чтобы просто следовать правилу: PEMDAS. Теперь мы можем попытаться решить одну с помощью скобок и показателей.2 \ div 5 $$
$$ 5 + 144 \ div 5 $$
$$ 5 + 28,8 $$
33,8 $ $
К настоящему времени вы должны иметь базовое представление о порядке операций. Чтобы продолжить изучение этой темы, вы можете продолжать просматривать наш сайт или попробовать поискать в Интернете на Yahoo или Google. MathGoodies.com также предлагает отличный урок о порядке операций.
Определение порядка действий | Помощь с математикой
Урок «Использование групповых символов» показывает, когда использовать круглые, квадратные и фигурные скобки в выражениях.Эти группирующие символы — первый шаг в правилах, давно разработанных математиками.
Наличие стандартного порядка решения математических задач позволяет всем получить одинаковый результат. На этом уроке вы будете изучать и практиковать остальные правила порядка работы.
Результаты обучения
К концу этого урока ваши дети будут в состоянии следовать правилам порядка действий, чтобы правильно оценивать математические выражения и уравнения.
Если вы еще этого не сделали, просмотрите вместе с детьми урок «Использование групповых символов в выражениях».Он охватывает символы группировки: круглые, квадратные и фигурные скобки, которые используются в выражениях и уравнениях.
Разминка
Когда нет специальных группирующих символов, математические задачи решаются слева направо. Правила порядка операций сообщают вам порядок, в котором вы должны выполнять операции (сложение / вычитание / умножение / деление) в математическом выражении (математические предложения, в которых не , включают знак равенства) или уравнение (математическое предложения, которые от до включают знак равенства).В уроке «Использование символов группировки в выражениях» были рассмотрены символы группировки: круглые скобки, квадратные скобки и фигурные скобки. Вы знаете, что математика, заключенная в один из этих символов группировки, выполняется перед математикой, которая не находится внутри пары символов группировки. Вы также знаете, что скобки — это наиболее часто используемые символы группировки.
По мере того, как вы начинаете изучать и практиковать применение правил порядка операций, вам необходимо уметь быстро определять символы группировки и знаки операций. Пройдите следующий предварительный тест, чтобы узнать, готовы ли вы к этому уроку.
Рабочий лист предварительной оценки
Попросите ваших детей пройти предварительный тест, чтобы проверить, готовы ли они к этому уроку. Если они наберут 5 или меньше правильных ответов, просмотрите введение вместе с ними или вернитесь к уроку о группировке символов, прежде чем продолжить урок.
— Порядок операций в выражениях — предварительная оценка
Основной урок: порядок действий
Некоторые люди используют PEMDAS или « P lease E xcuse M y D ear A U S ally », чтобы запомнить порядок операций.
P = скобки (и другие символы группировки)
E = показатели (введены в 6-м классе)
M = умножить
D = разделить
A = сложить
S = вычесть
Когда математики со всего мира давно встретились, чтобы решить стандартный порядок выполнения математических операций, они договорились о следующем порядке:
- Сначала выполните любые вычисления внутри символов группировки: круглые, квадратные и фигурные скобки.
- Оценивайте числа с показателями: Показатели целых чисел будут объяснены на уроках 6-го класса. Они не включены в этот урок, кроме как знать правильный порядок.
- Умножение или деление: Умножение и деление имеют одинаковый приоритет. Когда вы читаете слева направо, делайте то, к чему вы пришли раньше. Пропустите сложение и вычитание, пока не будут выполнены все умножение и деление.
- Сложение или вычитание: сложение и вычитание имеют одинаковый приоритет.Когда вы читаете слева направо, делайте то, к чему вы пришли раньше.
Попросите детей поработать над этими задачами, чтобы попрактиковаться в применении правил порядка выполнения операций. После этих модельных задач ваши дети могут попробовать еще несколько практических задач.
Практика использования порядка операций
| 14 — (7 + 6) |
Сначала идут круглые скобки, поэтому 7 + 6 = 13. Вставьте 13, где было (7 + 6), так: 14 — 13 В этом уроке нет показателей, так что переходите к операциям. Эта задача содержит только вычитание, поэтому вычитайте. |
| (8-4) + 5 x 8 |
Сначала идут круглые скобки, поэтому 8-4 = 4. Вставьте 4, где было (8-4), так: 4 + 5 x 8. В этом уроке нет показателей, так что переходите к операциям. Эта задача содержит сложение и умножение. Умножение предшествует сложению, поэтому 5 x 8 = 40. Остается 4 + 40.Наконец, прибавляем 4 + 40 = 44. |
Дети часто не справляются со сложными математическими выражениями или уравнениями. Напомните им, чтобы они сосредотачивались только на одном шаге за раз. Если разбить большие задачи на мелкие, их легче решать и решать.
Попробуйте оценить эти выражения, следуя правилам порядка операций, а затем проверьте свои ответы, щелкнув ссылку «Показать / скрыть ответ».
| 4 + (3 — 1) x 6 |
| Нажмите, чтобы показать / скрыть ответ Сначала идут круглые скобки, поэтому 3-1 = 2. 4 + 2 х 6 Умножение предшествует сложению, поэтому 2 x 6 = 12 4 + 12 Сложение — это все, что осталось, поэтому 4 + 12 = 16. |
| (11 + 9) — 5 x 2 |
| Нажмите, чтобы показать / скрыть ответ Сначала идут круглые скобки, поэтому 11 + 9 = 20 20-5 х 2 Умножение предшествует вычитанию, поэтому 5 x 2 = 10 20–10 Вычитание — это все, что осталось, поэтому 20-10 = 10 |
| [17 — (2 + 8) + 2] ÷ 3 |
| Нажмите, чтобы показать / скрыть ответ Сначала идут символы группировки, а перед скобками — скобки, поэтому 2 + 8 = 10. Остается: [17-10 + 2] в скобках. 17-10 = 7, 7 + 2 = 9. Итоговое значение в скобках — 9. Остается только деление: 9 ÷ 3 = 3 |
Резюме
- Математики согласовали определенные правила решения математических задач, называемые порядком операций.
- Сначала идут символы группировки. Если имеется более одного символа группировки, они идут в следующем порядке: круглые скобки, квадратные скобки, фигурные скобки.
- экспонентов.Вы будете использовать их в будущих уроках. Для этого урока вам просто нужно знать, что они идут после группировки символов по порядку.
- Далее идет умножение или деление. У них одинаковый приоритет, поэтому то, что идет первым, слева направо, идет первым.
- Далее идет Сложение или Вычитание. У них одинаковый приоритет, поэтому то, что идет первым, слева направо, идет первым.
- Не перегружайте себя сложными проблемами. Выполняйте их шаг за шагом, по одному, и вы сможете их решить!
Далее следуют
Контрольные вопросы
Просмотрите приведенные выше пункты резюме со своими детьми, а затем распечатайте Таблицу оценки, приведенную ниже.
Как минимум 7 из 10 правильных ответов покажут, что ваши дети готовы перейти к следующему уроку: «Написание простых выражений».
Заданий по алгебре
Добро пожаловать на страницу рабочих листов по алгебре на Math-Drills.com, где неизвестные являются обычным явлением, а переменные — нормой. На этой странице вы найдете рабочие листы по алгебре в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и функции построения графиков.
Эта страница начинается с некоторых пропущенных рабочих листов для младших школьников.Затем мы сразу переходим к алгебре, помогая студентам распознавать и понимать основной язык, связанный с алгеброй. Остальная часть страницы охватывает некоторые из основных тем, с которыми вы столкнетесь в модулях алгебры. Помните, что, обучая студентов алгебре, вы помогаете создавать будущих финансовых гениев, инженеров и ученых, которые решат все проблемы нашего мира.
Алгебра намного интереснее, когда вещи более реальны. Решать линейные уравнения гораздо веселее с двумя весами, загадочными мешочками и кучей мармеладов.Многие учителя используют плитки алгебры, чтобы помочь студентам понять различные темы алгебры. И нет ничего лучше набора осей координат для решения систем линейных уравнений.
Самые популярные задания по алгебре на этой неделе
Листы свойств и законов чисел
Коммутативный закон
Коммутативный закон или свойство коммутативности гласит, что вы можете изменить порядок чисел в арифметической задаче и при этом получить те же результаты.В контексте арифметики он работает только с операциями сложения или умножения , но не с смешанными операциями сложения и умножения. Например, 3 + 5 = 5 + 3 и 9 × 5 = 5 × 9. Забавное занятие, которое вы можете использовать в классе, — это мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, затем левый, или вы можете надеть левый носок, затем правый носок, и вы получите тот же результат.Однако надевание нижнего белья и брюк не является обязательным.
Ассоциативный закон
Ассоциативный закон или ассоциативное свойство позволяет изменять группировку операций в арифметической задаче с двумя или более шагами без изменения результата. Порядок чисел остается неизменным в ассоциативном законе. Как и в случае с коммутативным законом, применяется к задачам только сложения или только умножения.Его лучше всего рассматривать в контексте порядка операций, поскольку он требует, чтобы в первую очередь работали со скобками. Пример ассоциативного закона: (9 + 5) + 6 = 9 + (5 + 6). В этом случае не имеет значения, добавляете ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, ставить предметы на поднос во время обеда. Они могут сначала положить на поднос молоко и овощи, затем бутерброд, или начать с овощей и бутерброда, а затем добавить молоко.Если их лоток выглядит одинаково оба раза, они смоделировали ассоциативный закон. Можно утверждать, что чтение книги является ассоциативным или неассоциативным, поскольку потенциально можно сначала прочитать последние главы и при этом понять книгу так же, как и тот, кто читает книгу обычным способом.
Обратные отношения с
одна заготовка
Рабочие листы по обратным отношениям охватывают навыки предварительной алгебры, призванные помочь учащимся понять взаимосвязь между умножением и делением, а также взаимосвязь между сложением и вычитанием.
Обратные отношения с
двумя пробелами
Пропущенные числа или неизвестные в таблицах уравнений
Отсутствующие числа в таблицах уравнений трех типов: пробелы для неизвестных, символы для неизвестных и переменные для неизвестных.
Рабочие листы с пропущенными номерами с
пробелами в качестве неизвестных (Пусто никогда в позиции ответа)
В этих таблицах неизвестное ограничено стороной вопроса в уравнении, которая может быть слева или справа от знака равенства.
Рабочие листы с пропущенными номерами с
пробелами в качестве неизвестных (пустые в любом положении)
В этих таблицах неизвестное может быть в любой позиции в уравнении, включая ответ.
Рабочие листы с пропущенными номерами с неизвестными символами
(Символ никогда не находится в позиции ответа)
Рабочие листы с пропущенными номерами с
неизвестными символами (символ в любой позиции)
Рабочие листы с отсутствующими номерами с неизвестными переменными
(переменная слева; ответ справа)
Рабочие листы с пропущенными номерами с неизвестными переменными
(переменная никогда не находится в позиции ответа)
Рабочие листы с отсутствующими номерами с неизвестными переменными
(переменная в любом положении)
Равенства с добавлением
с обеих сторон уравнения и символов как неизвестных
Рабочие листы по алгебраическим выражениям
Использование распределительного свойства
Дистрибутивность — важный навык в алгебре.Проще говоря, это означает, что вы можете разделить один из множителей при умножении на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в мысленной математике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно ответить на вопрос, используя свойство распределенности. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70.Наконец, прибавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко сложить другой множитель перед умножением. Например, в выражении 3 (x + 5) нельзя сложить x + 5, не зная значения x. Вместо этого свойство распределения можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15.
Вычисление алгебраических выражений
Правила экспонент и свойства
Практика с
базовыми правилами экспоненты
Как сказано в названии, эти рабочие листы включают только основные вопросы по правилам экспоненты.Каждый вопрос имеет дело только с двумя экспонентами; запутанные сложные термины и вещи, которые мог бы понять более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют его как 4 2 , поэтому студенты могут сосредоточиться на изучении того, как умножать и делить показатели более или менее. в изоляции.
Линейные выражения и уравнения
Рабочие листы линейных уравнений, включая упрощение, построение графиков, оценку и решение систем линейных уравнений.
Перевод алгебраических фраз прописью в алгебраические выражения
Знание языка алгебры может помочь понять смысл словесных задач и ситуаций за пределами школы. В этих рабочих листах студентам предлагается преобразовать фразы в алгебраические выражения.
Упрощение линейных выражений (объединение одинаковых терминов)
Комбинирование одинаковых терминов — это то, что часто случается в алгебре.Студенты могут познакомиться с темой и немного попрактиковаться с этими рабочими листами. Полоса поднимается с добавлением и вычитанием версий, которые вводят круглые скобки в выражения. Для студентов, которые хорошо разбираются в дробях, упрощение простых рабочих листов алгебраических дробей представляет собой небольшую проблему по сравнению с другими рабочими листами в этом разделе.
Переписывание линейных уравнений
Определение линейных уравнений по наклонам, пересечениям по оси Y и точкам
Линейное уравнение
Графики
Построение графиков линейных уравнений и чтение существующих графиков дают учащимся наглядное представление, которое очень полезно для понимания концепций наклона и пересечения по оси Y.
Решение линейных уравнений с мармеладом — это увлекательное занятие для студентов, впервые изучающих алгебраические понятия. В идеале вам понадобятся непрозрачные пакеты без массы, но поскольку это невозможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет студентам лучше понять уравнения. Любые мешки, которые вы используете, должны быть сбалансированы по другую сторону уравнения с пустыми мешками.
Наверное, лучший способ проиллюстрировать это на примере.Давайте используем 3 x + 2 = 14. Вы можете распознать x как неизвестное, что на самом деле является количеством мармеладов, которые мы кладем в каждый непрозрачный пакет. Число 3 в 3 x означает, что нам нужно три сумки. Лучше всего наполнить пакеты необходимым количеством мармеладов вне поля зрения учащихся, чтобы им действительно пришлось решать уравнение.
На одной стороне весов с двумя чашами поместите три пакета с мармеладом x в каждом и два рыхлых мармелада, чтобы представить + 2 часть уравнения.С другой стороны баланса поместите 14 мармеладов и три пустых мешка, которые, как вы заметите, необходимы для правильного «баланса» уравнения. А теперь самое интересное … если ученики удаляют две рыхлые мармеладки с одной стороны уравнения, все становится неуравновешенным, поэтому им нужно удалить две мармеладки с другой стороны весов, чтобы сохранить равновесие. Кушать мармелад необязательно. Цель состоит в том, чтобы изолировать мешочки с одной стороны весов без каких-либо рыхлых желейных бобов, при этом сохраняя баланс.
Последний шаг — разделить сыпучие мармеладки с одной стороны уравнения на то же количество групп, что и мешков. Это, вероятно, даст вам хорошее представление о том, сколько мармеладов в каждом пакете. Если нет, съешьте и попробуйте еще раз. Теперь мы понимаем, что это не сработает для каждого линейного уравнения, поскольку трудно получить отрицательные желе-бобы, но это еще одна обучающая стратегия, которую вы можете использовать для алгебры.
Решение линейных уравнений
Несмотря на внешность, уравнения типа a / x не являются линейными.Вместо этого они принадлежат к другому виду уравнений. Они хороши для объединения их с линейными уравнениями, поскольку они вводят понятие действительных и недействительных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений в форме a / x являются те, при которых знаменатель становится равным 0.
Линейные системы
Решение систем линейных уравнений
Решение систем линейных уравнений с помощью построения графиков
Квадратичные выражения и уравнения
Квадратные выражения и рабочие листы уравнений, включая множители, факторизацию и решение квадратных уравнений.
Упрощение квадратичных выражений (объединение одинаковых терминов)
Сложение / вычитание и упрощение квадратичных выражений
Множители из квадратичных выражений
Факторизация квадратичных выражений
Таблицы факторизации квадратичных выражений, представленные ниже, содержат множество практических вопросов для студентов, чтобы отточить свои стратегии разложения.Если вы предпочитаете рабочие листы с квадратными уравнениями, см. Следующий раздел. Эти рабочие листы бывают разных уровней, самые простые — в начале. Коэффициенты ‘a’, упомянутые ниже, являются коэффициентами члена x 2 , как в общем квадратичном выражении: ax 2 + bx + c.
Независимо от того, используете ли вы метод проб и ошибок, вычисляя квадрат или общую квадратную формулу, эти рабочие листы включают множество практических вопросов с ответами.В первом разделе рабочие листы включают вопросы, в которых квадратичные выражения равны 0. Это делает процесс факторингом квадратичных выражений с дополнительным шагом нахождения значений для x, когда выражение равно 0. Во втором разделе параметр выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы квадратное выражение стало равным нулю.
Решение квадратных уравнений , что Equal Zero (e.грамм. ax² + bx + c = 0)
Решение квадратных уравнений , что равно целому числу (например, ax² + bx + c = d)
Другие полиномиальные и мономиальные выражения и уравнения
Таблицы факторинга неквадратичных выражений разного уровня сложности.
Упрощающие полиномы , которые включают сложение и вычитание
Упрощение полиномов , включающих умножение и деление
Упрощающие полиномы , включающие сложение, вычитание, умножение и деление
Факторинговые выражения, которые
не включают квадратную переменную
Факторинговые выражения
, которые всегда включают квадратную переменную
Факторинговые выражения
, которые иногда включают квадраты переменных
Умножение многочленов на два множителя
Умножение многочленов на три множителя
Неравенства с графами
Рабочие листы неравенств, включающие запись неравенства, которое соответствует графику, и отображение неравенств на числовой прямой.

 Организа ционный
Организа ционный
 Право главного режиссёра я оставляю за собой. Только я буду строгим начальником: буду наказывать за любую провинность работе -шум, крики, подсказки, неверные ответы.
Право главного режиссёра я оставляю за собой. Только я буду строгим начальником: буду наказывать за любую провинность работе -шум, крики, подсказки, неверные ответы.
 Актуализация знаний
Актуализация знаний
 Организация активной мыслительной деятельности.
Организация активной мыслительной деятельности.

 (15 мин.)
(15 мин.)
 В программе «Слабое звено» найдите ошибки в вычислениях, исправьте их. (слайд 10)
В программе «Слабое звено» найдите ошибки в вычислениях, исправьте их. (слайд 10)

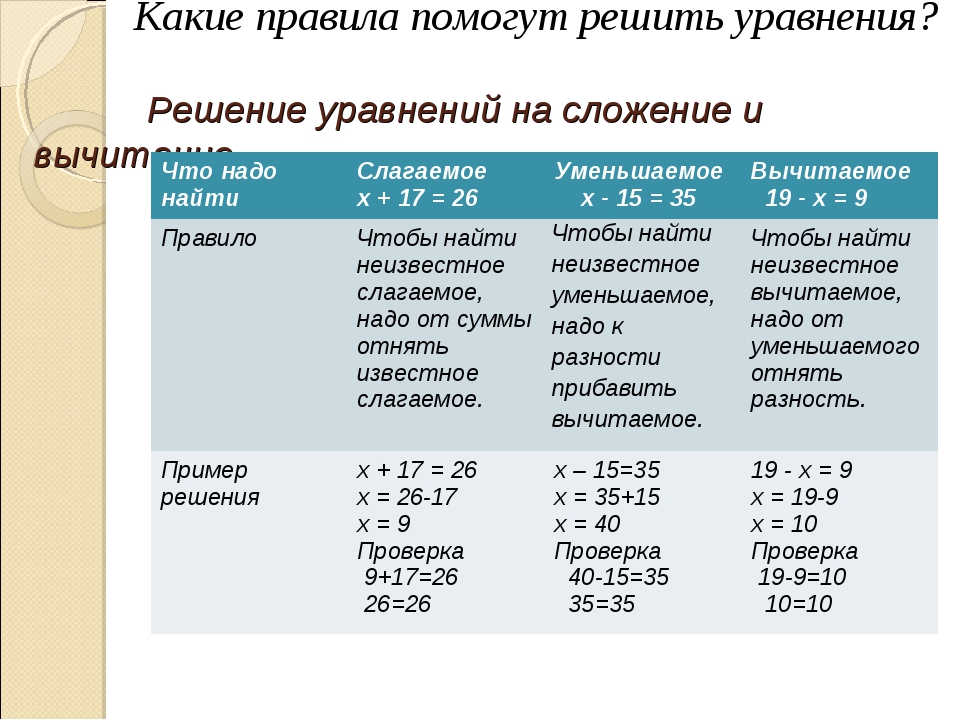 Одно неловкое движение и можете получить травму. Найдите корни уравнений. (слайд 14) (Самопроверка, выставление оценок).
Одно неловкое движение и можете получить травму. Найдите корни уравнений. (слайд 14) (Самопроверка, выставление оценок).
 В программе «Вести недели» это научное открытие было широко освещено. (слайд 16)
В программе «Вести недели» это научное открытие было широко освещено. (слайд 16)



 работа
работа