Содержание
Пошаговое построение сечения шестиугольной призмы
В этой статье приведено несколько примеров пошагового построения сечения правильной шестиугольной призмы методом следов. Иногда к методу следов был взят в помощь аксиоматический метод. Я старалась избегать пользоваться методом внутреннего проецирования намеренно, чтобы показать построение именно методом следов.
Задача 1. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .
Задача 1. Дано.
Шаг 1. Проведем прямую , принадлежащую плоскости сечения. Благодаря тому, что точки и лежат в основании призмы, прямая также принадлежит плоскости основания, а значит, будет пересекаться с другими прямыми, также лежащими в этой плоскости. Тогда можно провести прямую , и определить точку пересечения и – . Точка принадлежит плоскости грани , поскольку прямая принадлежит ей.
Задача 1. Шаг 1.
Шаг 2. Точки и можно соединить прямой. Прямая пересечет ребро в точке . Проводим прямую в плоскости основания и находим ее пересечение с прямой – точку .
Проводим прямую в плоскости основания и находим ее пересечение с прямой – точку .
Задача 1. Шаг 2.
Шаг 3. Через точки и проводим прямую. Она принадлежит плоскости грани , поэтому обязательно пересечется с прямой этой плоскости – в точке . Точка лежит “под” призмой, ниже ее основания. Точка , благодаря принадлежности прямой , также принадлежит и плоскости грани , а в этой плоскости у нас имеется точка – точка .
Задача 1. Шаг 3.
Шаг 4. Следовательно, можно соединить точки и прямой. Эта прямая пересечет ребро в точке .
Задача 1. Шаг 4.
Шаг 5. Точка принадлежит прямой , а следовательно, лежит в плоскости грани , таким образом, ее можно соединить с точкой этой же плоскости прямой . Эта прямая пересечет ребро в точке . Для дальнейшего построения нам нужны точки в плоскости верхней грани призмы. Добудем их. Продлим прямую до пересечения с прямой . Отметим точку .
Задача 1. Шаг 5.
Шаг 6. Проведем прямую , принадлежащую грани , и найдем точку ее пересечения с прямой – точку .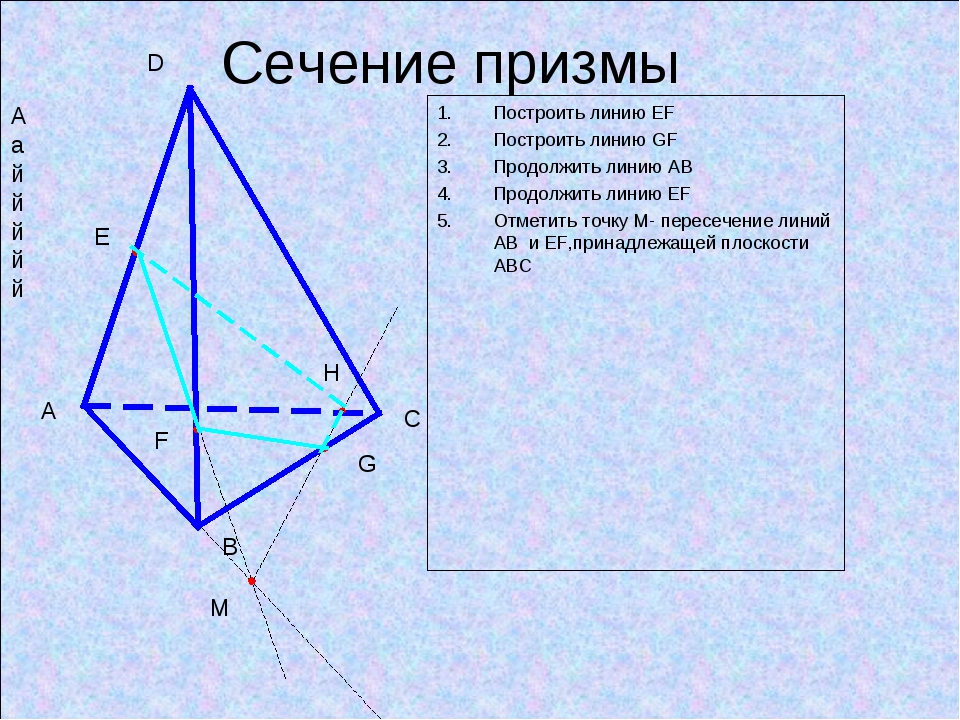 Тогда точки и принадлежат плоскости верхней грани (за счет принадлежности прямым этой плоскости) и их можно соединять прямой.
Тогда точки и принадлежат плоскости верхней грани (за счет принадлежности прямым этой плоскости) и их можно соединять прямой.
Задача 1. Шаг 6.
Шаг 7. Находим точки пересечения прямой с ребрами и – точки и .
Задача 1. Шаг 7.
Шаг 8. Соединяем все полученные точки отрезками.
Задача 1. Шаг 8.
Окончательный вид сечения:
Окончание построения
Задача 2. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .
Задача 2. Дано
Шаг 1. Проведем прямую . Она принадлежит секущей плоскости. Также проведем проекцию этой прямой на плоскость нижнего основания призмы – прямую . Точка их пересечения одновременно принадлежит секущей плоскости и плоскости нижнего основания призмы. Обозначим ее .
Задача 2. Шаг 1.
Шаг 2. Аналогично поступим с точками и : проводим прямую и ее проекцию в плоскости нижнего основания. Их пересечение – точка секущей плоскости , одновременно лежащая в нижнем основании.
Задача 2. Шаг 2.
Шаг 3. Имея две точки в плоскости нижнего основания, проведем через них прямую , точки которой принадлежат секущей плоскости.
Проведем прямую . Она лежит в плоскости основания, но одновременно – в плоскости боковой грани, поэтому ее точки принадлежат этой боковой грани. Точка пересечения прямых и , таким образом, принадлежит плоскости боковой грани призмы и плоскости сечения.
Задача 2. Шаг 3.
Шаг 4. Проводим прямую в плоскости боковой грани и отыскиваем точку пересечения ею ребра – точку .
Осталось немного: найти точку плоскости сечения на ребре , и пару точек в плоскости основания.
Задача 2. Шаг 4.
Шаг 5. Проведем прямые и в плоскости основания. Они пересекут прямую секущей плоскости в точках и .
Задача 2. Шаг 5.
Шаг 6. Точки и принадлежат плоскости грани , проведем через них прямую. Найдем точку, где эта прямая пересечет ребро – точку . Точки и лежат в плоскости грани . Проводим через них прямую и находим точку пересечения этой прямой с ребром – .
Задача 2. Шаг 6.
Шаг 7. Соединяем точки отрезками.
Задача 2. Шаг 7.
Окончательный вид построенного сечения:
Окончательный вид построенного сечения
Задача 3. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .
Задача 3. Дано
Шаг 1. Проводим прямую секущей плоскости, а также ее проекцию в плоскости основания . Прямая принадлежит плоскости основания и пересечет прямую в точке . Заметим, что точка не является точкой секущей плоскости.
Задача 3. Шаг 1.
Шаг 2. Из точки проводим перпендикуляр к плоскости основания (к прямой ), его пересечение с прямой – точка – принадлежит секущей плоскости, а также плоскости грани .
Задача 3. Шаг 2.
Шаг 3. Соединим точки и . Прямая пересечет ребро призмы в точке .
Задача 3. Шаг 3.
Шаг 4. Заполучив точку , можем провести отрезок . Вот тут-то нам и понадобится аксиоматический метод. Так как грань параллельна грани , то плоскость рассечет ее по прямой, которая будет параллельна . Вот и проведем через такую параллельную прямой прямую. Она пересечет ребро в точке .
Так как грань параллельна грани , то плоскость рассечет ее по прямой, которая будет параллельна . Вот и проведем через такую параллельную прямой прямую. Она пересечет ребро в точке .
Задача 3. Шаг 4.
Шаг 5. Проведем также через точку прямую, параллельную прямой . Это можно сделать, так как грань параллельна грани . Прямая эта пересечет ребро в точке .
Задача 3. Шаг 5.
Шаг 6. Соединяем точки отрезками.
Задача 3. Шаг 6.
Окончательный вид:
Задача 3. Окончательный вид
Задача 4. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .
Задача 4. Дано
Шаг 1. Через точки и проводим прямую секущей плоскости. Также проведем проекции этой прямой на верхнее и нижнее основание – на верхнее, и – на нижнее. Точки пересечения прямой с проекциями – это точки прокола данной прямой оснований призмы. Верхнее основание прямая прошьет в точке , а нижнее – в точке . Таким образом, мы заполучили точки секущей плоскости в плоскостях верхнего и нижнего оснований.
Таким образом, мы заполучили точки секущей плоскости в плоскостях верхнего и нижнего оснований.
Задача 4. Шаг 1.
Шаг 2. Точки и принадлежат одной плоскости, проводим через них прямую. Эта прямая даст нам две точки: точку , в которой она пересечет ребро , и точку , в которой она пересечет ребро .
Шаг 3. Приобретя точку в грани , проведем прямую . Она пересечет ребро в точке .
Задача 4. Шаги 2-3.
Шаг 4. Проведем через точку в плоскости основания призмы прямую, параллельную прямой (или можно провести через точки и ). Эта прямая пересечет ребро в точке .
Задача 4. Шаг 4.
Шаг 5. Соединяем точки отрезками.
Задача 4. Шаг 5.
Окончательный вид:
Окончательный вид сечения
Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника. Чтобы построить след, достаточно знать две его точки, т. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани. е. точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой грани.Основные правила построения сечений методом следа:
То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Рассмотрим задачи: Пример 1 Постройте сечение призмы A1B1C1D1ABCD плоскостью, проходящей через три точки M, N, K. Рассмотрите все случаи расположения точек M, N, K на поверхности призмы Рассмотрим случай M ϵ BB1 , N ϵ CC1D1D, K ϵ AA1E . В данном случае очевидно, что М1 = Построение 1. MN ∩ M1N1 2. MK M1K1 3. XY =s – след секущей плоскости 4. A1K1 5. A1K∩ AA1 6. D1N1 7. D0N ∩ DD1 AMCDE — искомое сечение Постройте сечение пирамиды SABCDE плоскостью, проходящей через точку M, принадлежащую грани SBC и прямую l, лежащую в грани SED Построение 1. 2. 3. 4. 5. 6. При объяснении шагов построения можно использовать факты стереометрии, опираясь на наглядное представление о данных в условии задачи фигурах.
Пример 3 Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R Построение
|
Построение сечений многогранника на примере призмы
Слайд 1
Построение сечений многогранников на примере пр измы ® Создатели : Антон Дмитриев, Киреев Александр. При содействии: Гудковой Ольги Викторовны
Слайд 2
План урока Алгоритмы построения сечений Самопроверка Демонстрационные задачи Задачи для закрепления материала
Слайд 3
Алгоритмы построения сечений следов параллельных прямых параллельного переноса секущей плоскости внутреннего проектирования комбинированный метод дополнения n -угольной призмы до треугольной призмы Построение сечения методом :
Слайд 4
Построение сечения методом следов Основные понятия и умения Построение следа прямой на плоскости Построение следа секущей плоскости Построение сечения
Слайд 5
Алгоритм построения сечения методом следов Выяснить имеются ли в одной грани две точки сечения (если да, то через них можно провести сторону сечения). Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом). Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани. Выполнить п.1.
Построить след сечения на плоскости основания многогранника. Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом). Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани. Выполнить п.1.
Слайд 6
Построение сечения призмы Двух точек принадлежащих одной грани нет. Точка R лежит в плоскости основания. Найдем след прямой KQ на плоскости основания: — KQ ∩K1Q1=T1, T1R- след сечения. 3. T1R ∩CD=E. 4. Проведем EQ. EQ∩DD1=N. 5. Проведем NK. NK ∩AA1=M. 6. Соединяем M и R . Построить сечение плоскостью α , проходящей через точки K,Q,R; K є ADD1, Q є CDD1, R є AB.
Слайд 7
Метод параллельных прямых В основу метода положено свойство параллельных плоскостей: «Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Основные умения и понятия Построение плоскости параллельной данной Построение линии пересечения плоскостей Построение сечения
Слайд 8
Алгоритм построения сечения методом параллельных прямых. Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q ) и их проекции проводим плоскость. Через третью точку (например R) строим параллельную ей плоскость α . Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q . Через точку R проводим прямую а параллельную PQ . Находим точки пересечения прямой а с прямыми m и n. Находим точки пересечения с ребрами соответствующей грани.
Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q ) и их проекции проводим плоскость. Через третью точку (например R) строим параллельную ей плоскость α . Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q . Через точку R проводим прямую а параллельную PQ . Находим точки пересечения прямой а с прямыми m и n. Находим точки пересечения с ребрами соответствующей грани.
Слайд 9
(ПРИЗМА) Строим проекции точек P и Q на плоскости верхнего и нижнего оснований. Проводим плоскость P1Q1Q2P2. Через ребро, содержащее точку R, проводим плоскость α параллельную P1Q1Q2. Находим линии пересечения плоскостей ABB1 и CDD1 с плоскость α . Через точку R проводим прямую a||PQ . a∩n=X, a∩m=Y. XP∩AA1=K, XP∩BB1=L; YQ∩CC1=M, YQ∩DD1=N. KLMNR – искомое сечение. Построить сечение плоскостью α , проходящей через точки P,Q,R; P є ABB1, Q є CDD1, R є EE1.
Слайд 10
Метод параллельного переноса секущей плоскости Строим вспомогательное сечение данного многогранника, которое удовлетворяет следующим требованиям: оно параллельно секущей плоскости; в пересечении с поверхностью данного многогранника образует треугольник. Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани. Соединяем вершину треугольника с этими точками. Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.
Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани. Соединяем вершину треугольника с этими точками. Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.
Слайд 11
ПРИЗМА R є AA1, P є EDD1, Q є CDD1. Построим вспомогательное сечение AMQ1 ||RPQ. Проведем AM||RP, MQ1||PQ, AMQ1∩ABC=AQ1. P1- проекция точек Р и М на АВС. Проведем Р1В и Р1С. Р1В∩ AQ1=O1, P1C ∩ AQ1=O2. Через точку Р проведем прямые m и n соответственно параллельные МО1 и МО2. m∩BB1=K, n∩CC1=L. LQ∩DD1=T, TP∩EE1=S. RKLTS – искомое сечение Построить сечение призмы плоскостью α , проходящей через точки P,Q,R; P є EDD1, Q є CDD1, R є AA1 .
Слайд 12
Алгоритм построения сечения методом внутреннего проектирования. Построить вспомогательные сечения и найти линию их пересечения. Построить след сечения на ребре многогранника. Если точек сечения не хватает для построения самого сечения повторить пп.1-2.
Построить след сечения на ребре многогранника. Если точек сечения не хватает для построения самого сечения повторить пп.1-2.
Слайд 13
Построение вспомогательных сечений. ПРИЗМА Параллельное проектирование .
Слайд 14
Построение следа сечения на ребре
Слайд 15
Комбинированный метод. Через вторую прямую q и какую-нибудь точку W первой прямой р провести плоскость β . В плоскости β через точку W провести прямую q‘ параллельную q . Пересекающимися прямыми p и q‘ определяется плоскость α . Непосредственное построение сечения многогранника плоскостью α Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом. Применяется для построения сечения многогранника с условием параллельности. 1. Построение сечения многогранника плоскостью α , проходящей через заданную прямую p параллельно другой заданной прямой q .
Слайд 16
ПРИЗМА Построить сечение призмы плоскостью α , проходящей через прямую PQ параллельно AE1; P є BE, Q є E1C1. 1. Проведем плоскость через прямую AE1 и точку P. 2. В плоскости AE1P через точку P проведем прямую q’ параллельную AE1. q’∩E1S’=K. 3. Пересекающимися прямыми PQ и PK определяется искомая плоскость α. 4. P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V. TVMNL-искомое сечение.
1. Проведем плоскость через прямую AE1 и точку P. 2. В плоскости AE1P через точку P проведем прямую q’ параллельную AE1. q’∩E1S’=K. 3. Пересекающимися прямыми PQ и PK определяется искомая плоскость α. 4. P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V. TVMNL-искомое сечение.
Слайд 17
Метод дополнения n -угольной призмы(пирамиды) до треугольной призмы(пирамиды). Данная призма(пирамида) достраивается до треугольной призмы(пирамиды) из тех граней на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение. Строится сечение полученной треугольной призмы(пирамиды). Искомое сечение получается как часть сечения треугольной призмы(пирамиды).
Слайд 18
Основные понятия и умения Построение вспомогатель- ных сечений Построение следа сечения на ребре Построение сечения Центральное проектирование Параллельное проектирование
Слайд 19
ПРИЗМА Q є BB1C1C, P є AA1, R є EDD1E1. Достраиваем призму до треугольной. Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A 1 E 1 , B 1 C 1 , E 1 D 1. AE ∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1. Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR , используя метод внутреннего проектирования. Это сечение является частью искомого. Строим искомое сечение.
Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A 1 E 1 , B 1 C 1 , E 1 D 1. AE ∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1. Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR , используя метод внутреннего проектирования. Это сечение является частью искомого. Строим искомое сечение.
Слайд 20
Правило для самоконтроля Если многогранник выпуклый, то сечение выпуклый многоугольник. Вершины многоугольника всегда лежат на ребрах многогранника. Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении. Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении. Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника. Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.
Слайд 21
Базовые задачи на построение сечений многогранников Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей. M є AD, N є DCC1, D1 ; ABCDA1B1C1D1- куб M є ADD1, D1 є ADD1, MD1. D1 є D1DC, N є D1DC, D1N ∩ DC=Q. M є ABC, Q є ABC, MQ. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. M є CC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC. M є DCC1, D1 є DCC1, MD1. A є ABC, K є ABC, AK.
M є AD, N є DCC1, D1 ; ABCDA1B1C1D1- куб M є ADD1, D1 є ADD1, MD1. D1 є D1DC, N є D1DC, D1N ∩ DC=Q. M є ABC, Q є ABC, MQ. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. M є CC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC. M є DCC1, D1 є DCC1, MD1. A є ABC, K є ABC, AK.
Слайд 22
III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла). M є AB, N є AA1, K є A1D1; ABCDA1B1C1D1- куб. NK∩AD=F1 — вершина трехгранного угла образованного плоскостями α , ABC, ADD1. F1M∩CD=F2 — вершина трехгранного угла образованного плоскостями α , ABC, CDD1. F1M ∩BC=P. NK∩DD1=F3 — вершина трехгранного угла образованного плоскостями α , D1DC, ADD1. F3F2∩D1C1=Q, F3F2∩CC1=L. IV. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает ее, то линия пересечения параллельна данной прямой. A1, C, α ||BC1; ABCA1B1C1- призма. α∩ BCC1=n, n||BC1, n∩BB1=S. SA1∩AB=P. Соединяем A1,P и C.
Соединяем A1,P и C.
Слайд 23
V. Если прямая лежит в плоскости сечения, то точка ее пересечения с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую. M є A1B1C1, K є BCC1, N є ABC; ABCDA1B1C1- параллелепипед. 1 . Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями : α , ABC, MKK1. 2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.
Слайд 24
Задачи . На каком рисунке изображено сечение куба плоскостью ABC ? Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? Давайте вспомним этапы построения сечений тетраэдра (параллелепипеда, куба). Какие многоугольники могут при этом получиться?
Построить сечение онлайн. Учимся строить сечения
Само же задание обычно звучит так: «построить натуральный вид фигуры сечения»
. Конечно же, мы решили не оставлять этот вопрос в стороне и постараться по возможности объяснить, как происходит построение наклонного сечения.
Конечно же, мы решили не оставлять этот вопрос в стороне и постараться по возможности объяснить, как происходит построение наклонного сечения.
Для того, чтобы объяснить, как строится наклонное сечение, я приведу несколько примеров. Начну конечно же с элементарного, постепенно наращивая сложность примеров. Надеюсь, что проанализировав эти примеры чертежей сечений, вы разберетесь в том, как это делается, и сможете сами выполнить свое учебное задание.
Рассмотрим «кирпичика» с размерами 40х60х80 мм произвольной наклонной плоскостью. Секущая плоскость разрезает его по точкам 1-2-3-4. Думаю, тут все понятно.
Перейдем к построению натурального вида фигуры сечения.
1. Первым делом проведем ось сечения. Ось следует чертить параллельно плоскости сечения — параллельно линии, в которую проецируется плоскость на главном виде — обычно именно на главном виде задают задание на построение наклонного сечения
(Далее я всегда буду упоминать про главный вид, имея в виду что так бывает почти всегда в учебных чертежах).
2. На оси откладываем длину сечения. На моем чертеже она обозначена как L. Размер L определяется на главном виде и равен расстоянию от точки вхождения сечения в деталь до точки выхода из нее.
3. Из получившихся двух точек на оси перпендикулярно ей откладываем ширины сечения в этих точках. Ширину сечения в точке вхождения в деталь и в точке выхода из детали можно определить на виде сверху. В данном случае оба отрезка 1-4 и 2-3 равны 60 мм. Как видно из рисунка выше, края сечения прямые, поэтому просто соединяем два наших получившихся отрезка, получив прямоугольник 1-2-3-4. Это и есть — натуральный вид фигуры сечения нашего кирпичика наклонной плоскостью.
Теперь давайте усложним нашу деталь. Поставим кирпичик на основание 120х80х20 мм и дополним фигуру ребрами жесткости. Проведем секущую плоскость так, чтобы она проходила через все четыре элемента фигуры (через основание, кирпичик и два ребра жесткости). На рисунке ниже вы можете увидеть три вида и реалистичое изображение этой детали
Попробуем построить натуральный вид этого наклонного сечения. Начнем опять с оси сечения: проведем ее параллельно плоскости сечения обозначенного на главном виде. На ней отложим длину сечения равную А-Е. Точка А является точкой входа сечения в деталь, а в частном случае — точкой входа сечения в основание. Точкой выхода из основания является точка В. Отметим точку В на оси сечения. Аналогичным образом отметим и точки входа-выхода в ребро, в «кирпичик» и во второе ребро. Из точек А и В перпендикулярно оси отложим отрезки равные ширине основания (в каждую сторону от оси по 40, всего 80мм). Соединим крайние точки — получим прямоугольник, являющийся натуральным видом сечения основания детали.
Начнем опять с оси сечения: проведем ее параллельно плоскости сечения обозначенного на главном виде. На ней отложим длину сечения равную А-Е. Точка А является точкой входа сечения в деталь, а в частном случае — точкой входа сечения в основание. Точкой выхода из основания является точка В. Отметим точку В на оси сечения. Аналогичным образом отметим и точки входа-выхода в ребро, в «кирпичик» и во второе ребро. Из точек А и В перпендикулярно оси отложим отрезки равные ширине основания (в каждую сторону от оси по 40, всего 80мм). Соединим крайние точки — получим прямоугольник, являющийся натуральным видом сечения основания детали.
Теперь настал черед построить кусочек сечения, являющийся сечением ребра детали. Из точек В и С отложим перпендикуляры по 5 мм в каждую сторону — получатся отрезки по 10 мм. Соединим крайние точки и получим сечение ребра.
Из точек С и D откладывем перпендикулярные отрезки равные ширине «кирпичика» — полностью аналогично первому примеру этого урока.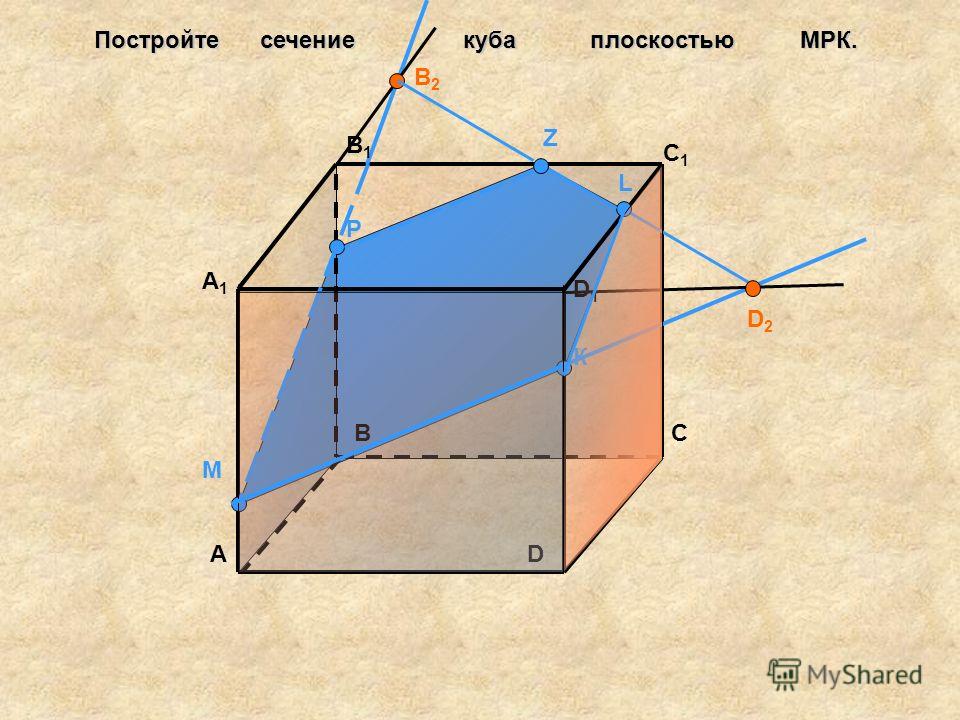
Отложив перпендикуляры из точек D и Е равные ширине второго ребра и соединив крайние точки получим натуральный вид его сечения.
Остается стереть перемычки между отдельными элементами получившегося сечения и нанести штриховку. Должно получиться что-то вроде этого:
Если же по заданному сечению произвести разделение фигуры, то мы увидим следующий вид:
Я надеюсь, что вас не запугали нудные абзацы описания алгоритма. Если вы прочли все вышенаписанное и еще не до конца поняли, как начертить наклонное сечение
, я очень советую вам взять в руки лист бумаги и карандаш и попытаться повторить все шаги за мной — это почти 100% поможет вам усвоить материал.
Когда-то я пообещал продолжение данной статьи. Наконец-то я готов представить вам пошагового построения наклонного сечения детали, более приближенной к уровню домашних заданий. Более того, наклонное сечение задано на третьем виде (наклонное сечение задано на виде слева)
или
запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи
или
создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое на более сложной детали, с фасками и конусовидным отверстием например.
Спасибо. А разве на разрезах ребра жесткости не штрихуются?
Именно. Именно они и не штрихуются. Потому что таковы общие правила выполнения разрезов. Однако их обычно штрихуют при выполнении разрезов в аксонометрических проекциях — изометрии, диметрии и т.д. При выполнении наклонных сечений, область относящаяся к ребру жесткости так же заштриховывается.
Спасибо,очень доступно.Скажите,а наклонное сечение можно выполнить на виде с верху,или на виде слева?Если да,то хотелось бы увидеть простейший пример.Пожалуйста.
Выполнить такие сечения можно. Но к сожалению у меня сейчас нет под рукой примера. И есть еще один интересный момент: с одной стороны, там ничего нового, а с другой стороны на практике такие сечения чертить реально сложнее. Почему-то в голове все начинает путаться и у большинства студентов возникают сложности. Но вы не сдавайтесь!
Но вы не сдавайтесь!
Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое, но с отверстиями (сквозными и несквозными), а то в элипс они в голове так и не превращаются
помогите мне по комплексной задаче
Жаль, что вы именно тут написали. Написали бы в почту — может мы смогли бы успеть все обсудить.
Хорошо объясняете.
Как быть если одна из сторон детали полукруглая? А также в детали есть отверстия.
Илья, используйте урок из раздела по начертательной геометрии «Сечение цилиндра наклонной плоскостью». С его помощью сможете разобраться, что делать с отверстиями (они же по сути тоже цилиндры) и с полукруглой стороной.
благодарю автора за статью!кратко и доступно пониманию.лет 20 назад сам грыз гранит науки,теперь сыну помогаю.
многое забыл,но Ваша статья вернула фундаментальное понимание темы.Пойду с наклонным сечением цилиндра разбираться)
Добавьте свой комментарий.
Цели урока:
рассмотреть решение задач на построение сечений, если две точки сечения принадлежат одной грани.
Ход урока
Изучение новых понятий
Определение 1.
Секущая плоскость многогранника — любая плоскость, по обе стороны от которой имеются точки данного многогранника.
Определение 2.
Сечение многогранника — это многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани многогранника.
Задание. Назовите отрезки, по которым секущая плоскость пересекает грани параллелепипеда (рис. 1). Назовите сечение параллелепипеда.
Основные действия при построении сечений
Теоретическая основа | Ответ | |
| 1. Как проверить: построено сечение или нет | Определение сечения | Это должен быть многоугольник, стороны которого принадлежат граням многогранника |
| 2. До начала работы определить: можно ли по данным задачи построить сечение | Способы задания плоскости | Можно, если данные элементы задают однозначно плоскость, то есть даны три точки, не лежащие на одной прямой, точка и прямая и т.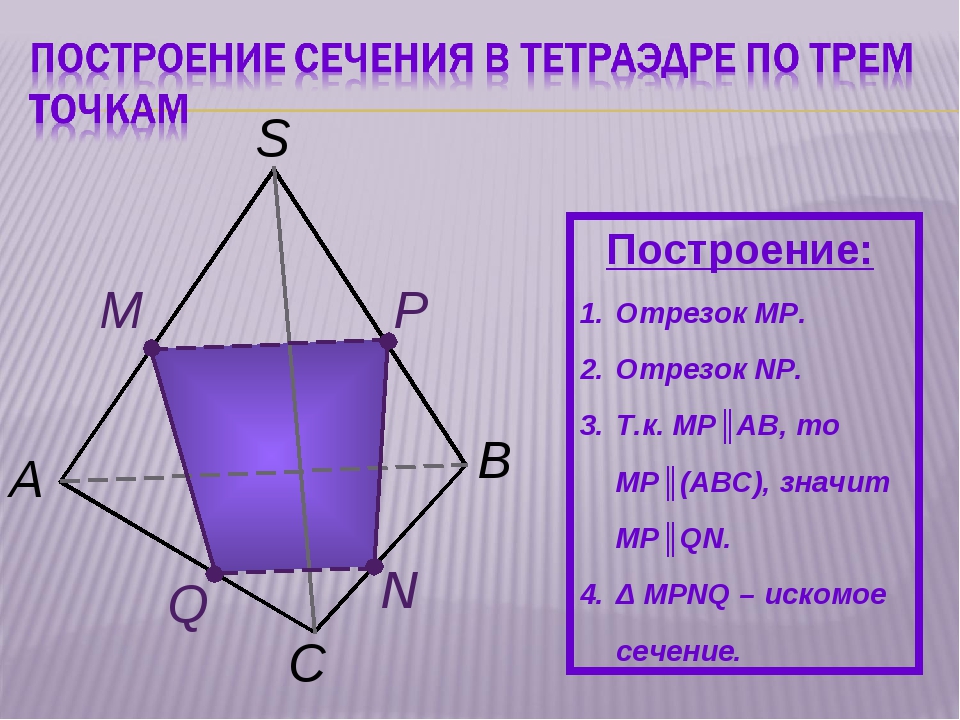 д. д. |
| 3. В плоскости какой-то грани есть две точки секущей плоскости | Если две точки принадлежат плоскости, то вся прямая принадлежит плоскости | Через эти точки провести прямую |
| 4. В одной из параллельных граней есть сторона сечения, а в другой — точка сечения | Свойство параллельных плоскостей | Через эту точку провести прямую, параллельную данной |
| 5. В одной грани есть точка сечения и известно, что секущая плоскость проходит через прямую, параллельную этой грани | Признак параллельности прямой и плоскости. Свойство параллельных плоскостей | Построить прямую пересечения плоскостей, параллельную данной прямой |
| 6. Две точки сечения принадлежат одной грани, а третья точка лежит в смежной | Аксиомы стереометрии | Секущая плоскость пересекает грани по отрезкам OC и AB, которые называются следом секущей плоскости на гранях |
Решение задач
Задача 1.
Какой из четырехугольников, EFKM или EFKL, может быть сечением данного многогранника (рис. 2)? Почему?
Задача 2.
Ученик изобразил сечение тетраэдра (рис. 3). Возможно ли такое сечение?
Решение
. Нужно доказать, что N, M и H, L лежат в одной плоскости. Пусть точки N и M принадлежат задней грани, H и L — нижней грани, то есть точка пересечения NM и HL должна лежать на прямой, принадлежащей обеим граням, то есть AC. Продлим прямые NM и HL и найдем точку их пересечения. Эта точка не будет принадлежать прямой AC. Значит, точки N, M, L, H не образуют плоский многоугольник. Невозможно.
Задача 3.
Построить сечение тетраэдра ABCS плоскостью, проходящей через точки K, L, N, где K и N — середины ребер SA и SB соответственно (рис. 4).
1. В какой грани можно построить стороны сечения?
2. Выбираем одну из точек, на которой оборвалось сечение.
Решение. Способ I.
Выбираем точку L.
Определяем грань, в которой лежит выбранная точка и в которой надо построить сечение.
Определяем грань, в которой лежит прямая KN, не проходящая через выбранную точку L.
Находим линию пересечения граней ABC и ASB.
Каково взаимное расположения прямых KN и AB (рис. 5)?
[Параллельны.]
Что нужно построить, если секущая плоскость проходит через прямую, параллельную линии пересечения плоскостей?
[Через точку L провести прямую,
параллельную AB. Эта прямая
пересекает ребро CB в точке P.]
Соединяем точки, принадлежащие одной грани. KLPN — искомое сечение.
Способ II
. Выбираем точку N (рис. 6).
Определяем грани, в которых лежат точка N и прямая KL.
Линией пересечения этих плоскостей будет прямая SC. Находим точку пересечения прямых KL и SC. Обозначим ее Y.
Соединяем точки N и Y. Прямая NY пересекает ребро CB в точке P.
Соединяем точки, принадлежащие одной
грани.
KLNP — искомое сечение.
Объясните данное решение.
Один учащийся работает у доски, остальные в тетрадях.
Задача 4
. Построить сечение параллелепипеда, проходящее через точки M, P и H, H ` (A1B1C1) (рис. 7).
Решение.
1. Соедините точки, принадлежащие одной грани.
2. Какую прямую и точку выбираем для построения сечения?
3. Что определяем дальше?
4. Каково взаимное расположение выбранной прямой и линии пересечения граней (рис. 8)?
5. Как построить след секущей плоскости на грани B1C1D1A1, проходящий через точку H?
6. Соедините точки, принадлежащие одной грани.
7. Какую прямую и точку нужно выбрать для построения следа секущей плоскости на грани AA1D1D?
8. Каково взаимное расположение граней BB1C1C и AA1D1D?
9. Каким свойством необходимо воспользоваться для построения следа секущей плоскости на грани AA1D1D?
10. Назовите искомое сечение.
Задача 5.
Построить сечение пирамиды SABCD, проходящее через точки M, P и H,
H` (ABC) (рис. 9).
Ответ: см. рисунок 10.
Задание на дом
Задача
. Как изменятся построения, если точ-
Как изменятся построения, если точ-
ка H изменит свое положение? Построить сечения, используя разные варианты (рис. 11).
В этом методе мы
первым действием (после нахождения
вторичных проекций данных точек) строим
след секущей плоскости на плоскости
верхнего или нижнего основания призмы
или усечённой пирамиды или на основании
пирамиды
Зад
2.
Дано
изображение треугольной призмы
ABCA
1 B
1 C
1
и трёх точек
M
,
N
,
P
,
которые лежат
соответственно на ребре СС
1
и гранях
ABB
1 A
1 ,
BCC
1 B
1 .
Построить
сечение призмы плоскостью
,
проходящей
через
M
,
N
,
P
.
Решение.
Мы уже имеем одну точку на верхнем
основании призмы, поэтому и след мы
будем строить на верхнем основании.
Строим вторичные проекции точек N
и P
на верхнее
основание.Затем: 1
.N
P
N
3 P
3 =X
;
2
. M
M
X
=p
–след; 3
.p
B
1 C
1 =D
.
Дальнейшие действия
уже были показаны выше на чертеже.
Зад
3.
Реш.
Мы будем
строить след секущей плоскости на нижнем
основании призмы.
Строим:1.
M
N
E
D
=X
,
M
P
EP
3 =Y
;
2. p
=XY
– след;3.
p
B
C
=G
,
p
D
C
=H
.
Нам нужно найти
точку
на ребре
BB
1
или на ребре AA
1 .
ВграниABB
1 A
1
мы уже
имеем одну точку P
.
Поэтому нижнее ребро этой грани, т.е.
AB
,
мы продолжаем до пересечения со следом.
4. A
B
p
=Z
.
5. P
Z
AA
1 =F
;
P
Z
BB
1 =K
.Дальнейшие
действия уже показаны выше.
Если окажется, что
линия AB
не пересекается
со следом, то искомая FK
тоже будет
параллельна следу.
Зад
4.
Реш.
1.
P
N
P
o N
o =X
;
2. M
N
CN
o =Y
;3.
p
=XY
– след;
3.
C
B
p
=Z
;4.
Z
M
S
B
=E
;
5. E
N
S
A
=G
6.
GEMF
– иск
сечение.
17. Построение сечения цилиндра.
Если секущая
плоскость задана тремя точками, то мы
всегда можем найти её след на плоскости
основания цилиндра или конуса и точку
(P
,
O
)
на его оси. Поэтому считаем, что секущая
плоскость задана именно этими элементами.
Сначала
рас-им случай, когда плоскость пересекает
только боковую поверхность цилиндра.
Тогда сечением цилиндра будет эллипс
(;¯ и его изображение – тоже эллипс.
Мы знаем способ построения эллипса,
если известны два его сопряжённых
диаметра. Мы сейчас покажем, как можно
найти изображение главных диаметров
эллипса (;¯.
Пусть
и 1
– эллипсы,
изображающие нижнее и верхнее основания
цилиндра, O
и O
1
– их центры.
Проведём диаметр A
3 B
3
нижнего основания, параллельный следу
и сопряжённый ему диаметр C
3 D
3 .
Для построения C
3 D
3
мы используем
хорду K
3 L
3 ,
один конец которой принадлежит контурной
образующей. Напомним, что
A
3 B
3
и C
3 D
3
изображают
перпендикулярные диаметры. Продолжим
C
3 D
3
до пересечения
со следом. Получим точ X
.
Прям.PX
наз-ём осью
сечения.
Поднимем точки
C
3
и D
3
до оси
сечения. Получим C
и D
.
Отрезок
CD
является изображением большогодиаметра
сечения. Поднимем отрезок
A
3 B
3 на
высоту OP
.
Получим отрезок AB
,
который является изображением малого
диаметра сечения. Отр-и AB
и CD
–сопряж-ые
диам. эллипса .
Найти
ещё точки, в которых эллипс переходит
с видимой стороны цилиндра на невидимую,
а значит, сплошная линия переходит в
пунктир. Это точки пересечения секущей
Это точки пересечения секущей
плоскости с контурными образующими.
ПустьY
3 =K
3 L
3 C
3 D
3 .
Поднимем Y
3
до оси
сечения. Получим точку Y
.
Поднимем хорду K
3 L
3
на высоту
YY
3 .
Получим отрезок KL
.
Мы нашли требуемую точку K
,
а попутно, ещё одну дополнительную точку
L
.
Точка M
,
изобр-щая пересечение секущей плоск-и
со второй контурной образующей симметрична
точкеK
относительно точкиP
.Допол-но
построим точN
,
симметричнуюL
относ-нточки
P
Покажем способ,
как можно найти любое кол-во точек на
сечении без испол-ия этих диаметров.
выбираем люб.
точкуV
3
на эллипсе .
Проводим диаметрV
3 T
3
и продолжаем его до пересечения со
следом.Получим точкуU
.
Поднимаем точки V
3
и T
3
до прямой
UP
.
Получаем две точки V
и T
на сечении. Выбирая вместо V
3
другую
точку, получим др. 2 точки на сеч.Если
2 точки на сеч.Если
выбрать точку K
3 ,
лежащую на контурно образующей, мы
найдём точки K
и M
,
в которых сплошная линия на сечении
должна перейти в пунктирную.
А вы знаете, что называется сечением многогранников плоскостью? Если вы пока сомневаетесь в правильности своего ответа на этот вопрос, то можете довольно просто себя проверить. Предлагаем пройти небольшой тест, представленный ниже.
Вопрос. Назовите номер рисунка, на котором изображено сечение параллелепипеда плоскостью?
Итак, правильный ответ – на рисунке 3.
Если вы ответите правильно, это подтверждает то, что вы понимаете, с чем имеете дело. Но, к сожалению, даже правильный ответ на вопрос-тест не гарантирует вам наивысших отметок на уроках по теме «Сечения многогранников». Ведь самым сложным является не распознавание сечений на готовых чертежах, хотя это тоже очень важно, а их построении.
Для начала сформулируем определение сечения многогранника. Итак, сечением многогранника называют многоугольник, вершины которого лежат на ребрах многогранника, а стороны – на его гранях.
Теперь потренируемся быстро и безошибочно строить точки пересечения данной прямой с заданной плоскостью. Для этого решим следующую задачу.
Построить точки пересечения прямой MN с плоскостями нижнего и верхнего оснований треугольной призмы ABCA 1 B 1 C 1 , при условии, что точка M принадлежит боковому ребру CC 1 , а точка N – ребру BB 1 .
Начнем с того, что продлим на чертеже прямую MN в обе стороны (рис. 1). Затем, чтобы получить необходимые по уловию задачи точки пересечения, продлеваем и прямые, лежащие в верхнем и нижнем основаниях. И вот наступает самый сложный момент в решении задачи: какие именно прямые в обоих основаниях необходимо продлить, так как в каждом из них имеется по три прямые.
Чтобы правильно сделать заключительный шаг построения, необходимо определить, какие из прямых оснований находятся в той же плоскости, что и интересующая нас прямая MN. В нашем случае – это прямая CB в нижнем и C 1 B 1 в верхнем основаниях. И именно их и продлеваем до пересечения с прямой NM (рис. 2).
2).
Полученные точки P и P 1 и есть точки пересечения прямой MN с плоскостями верхнего и нижнего оснований треугольной призмы ABCA 1 B 1 C 1 .
После разбора представленной задачи можно перейти непосредственно к построению сечений многогранников. Ключевым моментом здесь будут рассуждения, которые и помогут прийти к нужному результату. В итоге постараемся в итоге составить шаблон, который будет отражать последовательность действий при решении задач данного типа.
Итак, рассмотрим следующую задачу. Построить сечение треугольной призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки X, Y, Z, принадлежащие ребрам AA 1 , AC и BB 1 соответственно.
Решение: Выполним чертеж и определим, какие пары точек лежат в одной плоскости.
Пары точек X и Y, X и Z можно соединить, т.к. они лежат в одной плоскости.
Построим дополнительную точку, которая будет лежать в той же грани, что и точка Z. Для этого продлим прямые XY и СС 1 , т.к. они лежат в плоскости грани AA 1 C 1 C. Назовем полученную точку P.
Назовем полученную точку P.
Точки P и Z лежат в одной плоскости – в плоскости грани CC 1 B 1 B. Поэтому можем их соединить. Прямая PZ пересекает ребро CB в некоторой точке, назовем ее T. Точки Y и T лежат в нижней плоскости призмы, соединяем их. Таким образом, образовался четырехугольник YXZT, а это и есть искомое сечение.
Подведем итог. Чтобы построить сечение многогранника плоскостью, необходимо:
1) провести прямые через пары точек, лежащих в одной плоскости.
2) найти прямые, по которым пересекаются плоскости сечения и грани многогранника. Для этого нужно найти точки пересечения прямой, принадлежащей плоскости сечения, с прямой, лежащей в одной из граней.
Процесс построения сечений многогранников сложен тем, что в каждом конкретном случае он различен. И никакая теория не описывает его от начала и до конца. На самом деле есть только один верный способ научиться быстро и безошибочно строить сечения любых многогранников – это постоянная практика. Чем больше сечений вы построите, тем легче в дальнейшем вам будет это делать.
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Практическое занятие: «Параллелепипед. Построение сечений параллелепипеда ».
1.
Цель практической работы
: .
Закрепить знания теоретического материала о многогранниках,
навыки решения задач на построение сечений,
умения анализировать чертеж.
2.Дидактическое оснащение практической работы
: АРМ, модели и развёртки многогранников, измерительные инструменты, ножницы, клей, плотная бумага.
Время:2 часа
Задания к работе:
Задание 1
Построить сечение параллелепипеда ABCDA
1
B
1
C
1
D
1
плоскостью, проходящей через точки M, N, P, лежащие, на прямых, соответственно, A
1
B
1,
А
D
,
DC
Образец
и последовательность решения задачи:
1.Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
2.Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
3.Так как точка M также принадлежит плоскости сечения и пересекает прямую АА
1
в некоторой точке Х.
4.Точки X и N лежат в одной плоскости грани АА
1
D
1
D, соединим их и получим прямую XN.
5.Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A
1
B
1
C
1
D
1
, параллельную прямой NP. Эта прямая пересечет сторону В
1
С
1
в точке Y.
6.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
Задание 2
Вариант1.
Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, заданной следующими точками
M
,
N
и
P
1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныА
2 Уровень.
M
лежит в грани AA1D1D,
N
лежит в грани АА1В1В,
P
лежит в грани СС1D1D.
3 Уровень.
M
лежит на диагонали B1D,
N
лежит на диагонали АС1,
P
лежит на ребре С1D1.
Вариант2.
Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через прямую DQ, где точка Q лежит на ребре СС1 и точку Р, заданную следующим образом
1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныС
2 Уровень: М лежит на продолжении ребра А1В1, причем точка А1 находится между точками В1 и Р.
3 Уровень: Р лежит на диагонали В1D
Порядок выполнения работы:
1.Изучите теоретический материал по темам:
Параллелепипед.
Прямой параллелепипед.
Наклонный параллелепипед.
Противолежащие грани параллелепипеда.
Свойства диагоналей параллелепипеда.
П
онятие секущей плоскости и правила её построения.
Какие виды многоугольников получаются в сечении куба и параллелепипеда.
2. Постройте
параллелепипед
ABCDA
1
B
1
C
1
D
1
3. Разберите решение задачи № 1
Разберите решение задачи № 1
4.Последовательно постройте сечение
параллелепипеда
ABCDA
1
B
1
C
1
D
1
плоскостью, проходящей через точки P, Q, R задачи № 1.
5.Постройте ещё три параллелепипеда и выделите на них сечения к задачам 1, 2, и 3 уровней
Критерии оценивания
:
Литература: Атанасян Л.С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. — М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. — М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. — М.: Просвещение, 2010г
Дидактический материал к заданию практического занятия
К задаче № 1:
Некоторые возможные сечения:
Построить сечения параллелепипеда плоскостью, проходящей через данные точки
Сечение куба плоскостью
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Обучение построению сечений как средство развития пространственного представления на уроках стереометрии Текст научной статьи по специальности «Математика»
ОБУЧЕНИЕ ПОСТРОЕНИЮ СЕЧЕНИЙ КАК СРЕДСТВО
развития пространственного представления
НА УРОКАХ СТЕРЕОМЕТРИИ
TEACHING SECTIONS PLOTTING AS A TOOL FOR DEVELOPMENT OF SPATIAL REPRESENTATION IN SOLID GEOMETRY CLASSES
В. И. Бутырина
Рассматривается проблема формирования и развития пространственных представлений у учащихся 10-х и 11-х классов. В качестве одного из средств решения данной проблемы предложено и подробно рассмотрено обучение построению сечений.
В качестве одного из средств решения данной проблемы предложено и подробно рассмотрено обучение построению сечений.
Ключевые слова: пространственное тело, плоскость, сечение, многогранник, пространственное восприятие.
V. I. Butyrina
We consider the problem of the formation and development of spatial representations of tenth and eleventh grades students. Teaching sections plotting is considered in detail as a means of solving this problem.
Keywords: spatial body, plane, section, polyhedron, spatial perception.
Одной из важнейших задач преподавания стереометрии в школе является формирование и развитие у учащихся пространственного воображения, а также умения работать с пространственными объектами. Знание и понимание стереометрии опирается не столько на теоретические основы, представленные в учебной литературе, сколько на способность учащегося видеть и правильно представлять пространственную фигуру.
Проблема данного исследования заключается в нахождении способов формирования и развития пространственных представлений у учащихся. Трудно сомневаться, что процесс формирования пространственного воображения у школьников является самым главным и самым первым основным этапом в изучении стереометрии.
Правильное восприятие пространственных фигур не всем легко дается. Научиться можно только через упражнения. Многократные упражнения в построении изображений фигур и операции с ними постепенно уберут барьер в восприятии пространства и плоскости.
На наш взгляд, одним из наиболее продуктивных упражнений такого характера являются задачи на построение сечений многогранников и тел вращения плоскостью. Наличие секущей плоскости во внутренней области изображения пространственной фигуры визуально придает данному изображению объем, к тому же видно, на какие части построенное сечение разбивает фигуру. Пример построения сечения пространственной фигуры плоскостью на первых шагах изучения будет более понятным, если реализовать это построение практически, используя модель многогранника или тела вращения.
Пример построения сечения пространственной фигуры плоскостью на первых шагах изучения будет более понятным, если реализовать это построение практически, используя модель многогранника или тела вращения.
Проблема, выдвинутая нами, не нова. Во второй половине XX в. ею занимались А. Б. Василевский, Н. Ф. Четве-рухин, И. Г. Польский, П. Г. Казаков. Изданные ими пособия нами изучены и проанализированы, в частности, подробно изучены методы построения сечений пространствен-
ных тел как одного из способов развития пространственного восприятия у школьников.
Каждый из авторов по-разному подходил к подбору и изложению материала по теме «Построение сечений».
Н. Ф. Четверухин большое внимание уделил методам внутреннего и центрального проектирования, подобрав ряд задач, в которых необходимо построить сечение многогранников и тел вращения. Задачи классифицированы с соблюдением принципа «от простого к сложному». Группировка задач по такому принципу очень удобна, так как позволяет при переходе к следующей задаче ссылаться на предыдущую как вспомогательную.
Задачи классифицированы с соблюдением принципа «от простого к сложному». Группировка задач по такому принципу очень удобна, так как позволяет при переходе к следующей задаче ссылаться на предыдущую как вспомогательную.
И. Г. Польский считал эффективным и использовал метод внутреннего проектирования. Задачи, приведенные им в пособии, более разнообразны, однако они ограничиваются только задачами на построение сечений многогранников.
П. Г. Казаков достаточно подробно и доступно изложил материал по данной теме. В отличие от предыдущих авторов, он большое внимание уделил методу следов, когда след и точка заданы в различных комбинациях.
А. Б. Василевский помимо знакомого всем метода следов рассмотрел еще несколько методов построения сечений: метод деления п-угольной пирамиды (призмы) на треугольные пирамиды (призмы), метод дополнения п-угольной пирамиды (призмы) до треугольной пирамиды (призмы), метод параллельных прямых, метод переноса секущей плоскости.
Но, следует заметить, что только в пособии П. Г. Казакова дано определение сечения. «Сечением многогранника называется фигура, образованная линиями пересечения секущей плоскости с гранями многогранника». Однако, на наш взгляд, данное определение является недостаточно полным, так как не охватывает сечения всех тел пространства.
Нами предложено следующее определение сечения тела: сечением тела называется плоская фигура, ко-
а)
б)
в)
г)
Рис. 1. Фигуры, образующиеся в результате пересечения многогранника плоскостью
С
С1
Рис. 2. Построение сечения многогранника плоскостью,
2. Построение сечения многогранника плоскостью,
проходящей через три заданные точки, лежащие на соседних ребрах
В
Р
торая образуется при пересечении секущей плоскости с боковой поверхностью тела.
Также хочется отметить, что при всем многообразии грамотно и доступно изложенного материала нет предложения того, как подвести учеников к методу построения сечений, что должны знать учащиеся, прежде чем приступить к изучению данного материала, нет определенной схемы изложения материала.
В данном исследовании мы постараемся восполнить отмеченные пробелы.
Не стоит забывать, что основным источником информации для учащихся является учебник. К сожалению, в учебной программе за 10-й класс отводится недостаточно времени на изучение задач на построение сечений. В подтверждение к сказанному, в учебнике Л. С. Атанасяна на тему «Построение сечений многогранников» отводится два часа, причем сопровождающих данную тему задач всего восемь. В учебнике А. В. Погорелова на построение сечений отведено около трех часов и десять задач, причем сначала рассматривается построение изображения призмы, а после — построение ее сечений, затем построение изображения пирамиды и ее сечений. Корректнее было бы поместить тему «Построение сечений многогранников» после изложения темы «Многогранники». Классифицировать материал по тематике задач с соблюдением принципа «от простого к сложному» можно следующим образом:
— определение сечения многогранников;
— построение сечений призмы, параллелепипеда, пирамиды методом следов.
В упомянутых учебниках также нет определения сечения тела.
Перейдем непосредственно к примерной разработке подхода к изучению материала по теме «Построение сечений».
Так как различные сложные виды сечений тел вращения не входят в программу средней школы, то мы подробнее рассмотрим метод построения сечений многогранников.
Поскольку построение плоскости сечения проходит в зависимости от способа задания плоскости, ученик, приступив к изучению темы «Построение сечений многогранников», должен к этому моменту хорошо усвоить для себя, что плоскость определяется:
— тремя точками;
— прямой и точкой;
— двумя параллельными прямыми;
— двумя пересекающимися прямыми.
Это необходимо знать, чтобы понимать, почему именно можно построить сечение тела, если даны три точки на поверхности тела, точка и след, прямая на боковой поверхности тела и след.
Прежде чем ввести учащихся в суть методов построения сечений, следует обратить внимание на вопрос: что может получиться при пересечении многогранника плоскостью? Это могут быть (см. рис. 1): пустая фигура (а), точка (б), отрезок (в), многоугольник (г).
Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.
в с
А И М’
Заметим, что отрезок и точка ни у одного из вышеупомянутых авторов не являются сечениями, хотя они имеют место.
Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.
Теперь перейдем к вопросу, как сгруппировать материал так, чтобы его изучение было как можно более доступным.
В самом начале уместно рассматривать задачи наиболее простые, усложняя их, переходя от одной к другой.
Так как плоскость определяется тремя точками, то предложим задачу на построение сечения многогранника плоскостью, проходящей через три заданные точки, лежащие на соседних ребрах многогранника.
В
с
А Ао
А,
М ч
Б
П- Г с^ Е
* у Р
\/
°1\/7 ¿3
1 1Ьч \Е1
г,
X Рис. 5. Построение сечения призмы по трем точ кам, лежащим не на соседних ребрах
5. Построение сечения призмы по трем точ кам, лежащим не на соседних ребрах
Рис. 4. Построение сечения призмы по трем точкам, одна из которых лежит не на соседних ребрах
Если мы имеем треугольную призму с точками на ребрах, то сечение данной призмы мы можем получить, последовательно соединив данные точки (рис. 2).
Если же мы имеем призму (рис. 3), в основании которой выпуклый п-угольник, где п > 3, то построение сечения призмы проводится с помощью метода следов.
Сначала последовательно соединяем данные точки на соседних ребрах призмы, а затем проведем рассуждения:
1) Рассмотрим грань призмы ААДР. В этой грани лежат точки сечения М и Р, заданные по условию, значит, секущая плоскость будет проходить через эти точки, поэтому можно провести прямую МР.
2) Точки А1 и й1 являются проекциями точек М и Р на основание АДСД. Пересекая прямую МР с ее проекцией А1В1, находим точку пересечения X этой прямой с основной плоскостью. Точка X будет принадлежать следу.
3) Проводя аналогичные рассуждения, получаем точку У пересечением прямой ИР и ее проекции С1й1. Точка У также будет принадлежать следу.
4) Проведем прямую ХУ, которая и является следом секущей плоскости на плоскость нижнего основания призмы.
5) Точка N лежит в плоскости грани ВВ1С1С. Точка С1 является проекцией точки N на основную плоскость. Через точки С1 и В1, принадлежащие плоскости ВВ1С1С, проводим прямую В1С1 до пересечения прямой В1С1 со следом. Через данную точку и через точку N проведем прямую Данная прямая пересекает грань призмы по отрезку РИ. Остальные отрезки, принадлежащие сечению призмы, находятся аналогично.
Остальные отрезки, принадлежащие сечению призмы, находятся аналогично.
Далее задачу можно усложнить, расположив две точки на соседних ребрах, а одну на отдаленном ребре.
Задача решается аналогично. Единственное, на что нужно обратить внимание, как строится след в этом случае (рис. 4).
После можно рассмотреть случай, когда все три точки лежат не на соседних ребрах. Построение сечения призмы в этой задаче сводится к предыдущей (рис. 5).
Задачу можно усложнить, если одну из трех точек поместить на поверхности грани призмы (рис. 6). В этом случае
следует обратить внимание на то, что нужно построить проекцию этой точки на основание призмы, полученная проекция не будет совпадать с вершинами призмы. Далее процесс построения сечений сводится к предыдущим задачам.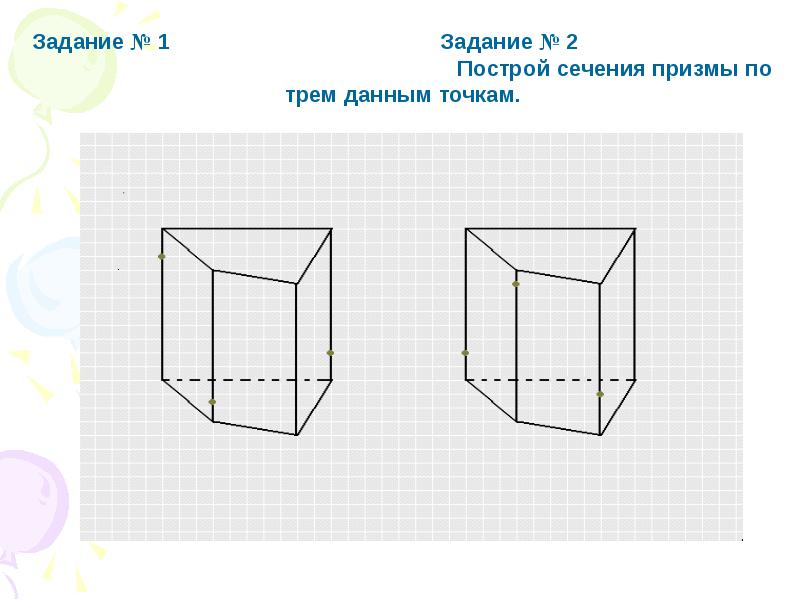
Далее уместно будет рассмотреть задачи на построение сечения при заданной точке на поверхности фигуры и при заданном следе (так как плоскость определяется точкой и прямой) в разных положениях. Порядок задач также следует задать, придерживаясь принципа «от простого к сложному».
Завершить данный этап изучения темы «Построение сечений» следует задачами при заданном следе и заданной прямой на поверхности фигуры (так как плоскость определяется двумя параллельными или пересекающимися прямыми).
Комбинируя задачи таким образом, мы делаем каждую предыдущую задачу опорной для каждой последующей, более сложной.
список источников и ЛИТЕРАТУРЫ
1. Четверухин Н. Ф. Стереометрические задачи на проекционном чертеже. М.: УЧПЕДГИЗ, 1952. С. 24-39.
24-39.
2. Польский И. Г. Сборник задач на построение на проекционном чертеже. М.: УЧПЕДГИЗ, 1958. С. 15-28.
B C
Рис. 6. Построение сечения призмы по двум точкам, лежащим на ребрах, и одной точке, находящейся грани
3. Казаков П. Г. Параллельные проекции и методы решения конструктивных задач. М.: УЧПЕДГИЗ, 1960. С. 54-79.
4. Василевский А. Б. Параллельные проекции и решение задач по стереометрии. Минск: Народная асвета, 1978. С. 29-33.
5. Атанасян Л. С. Геометрия 10-11. М.: Просвещение, 2009. С. 27-28.
6. Погорелов А. В. Геометрия 7-11. М.: Просвещение, 1998. С. 298-307.
РОЛЬ СИСТЕМ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ НА ПРАКТИЧЕСКИХ зАНЯТИЯХ ПО ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
THE ROLE OF SYSTEMS OF COMPUTER MATHEMATICS FOR PRACTICAL EXERCISES ON DIFFERENTIAL EQUATIONS
Р. М. Асланов, А. С. Безручко
М. Асланов, А. С. Безручко
В статье говорится о роли системы компьютерной математики в курсе дифференциальных уравнений. Сообщается, что они могут в значительной степени расширить класс задач, изучаемых в данной дисциплине, увеличить наглядность курса, его прикладное и практическое значения и тем самым помочь будущим учителям в понимании сущности изучаемого предмета.
Ключевые слова: системы компьютерной математики, дифференциальные уравнения, прикладная направленность, моделирование, наглядность.
R. M. Aslanov, A. S. Bezruchko
In given paper, it is SPK about what role is played by systems of computer mathematics in the course of the differential equations. It is informed that they can dilate substantially a class of tasks studied in the given discipline, to increment visualisation of course, its applied and practical values and by that to help to realise the future teacher essence of mathematics.
Keywords: systems of computer mathematics, the differential equations, an applied trend, modeling, visualization.
Сегодня мы являемся свидетелями скачка в компьютеризации общества, который произошел с началом массового производства и внедрения персональных компьютеров. По мере развития компьютерной
техники интенсивно развивается программное обеспечение, автоматизирующее математическую деятельность.
Сегодняшняя компьютерная математика обладает универсальными программными средствами символьных
Построение сечения многогранников
Урок обобщения и систематизации знаний учащихся по геометрии в 10 классе.
Что изучает стереометрия ?
Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления.
Стереометрия дает метод научного познания, способствует развитию логического мышления.
Стереометрия – сама по себе очень интересна. Она имеет яркую историю, связанную с именами знаменитых ученых
«Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет».
Леонардо да Винчи
http://blogs.nnm.ru/page6/
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 1.
В
С
А
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Аксиома 2:
В
А
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Аксиома 3:
М
m
В таком случае говорят, что плоскости пересекаются по прямой
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
М
m
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
b
а
Две прямые лежат в одной плоскости
2. Прямые
пересекаются
1. Прямые
параллельны
Одна общая точка
Нет общих точек
Не лежат в одной плоскости:
являются скрещивающимися
m
М
a
1. Прямая лежит в плоскости
Бесконечно много общих точек
2. Прямая пересекает плоскость
Одна общая точка
3. Прямая параллельна плоскости.
Нет общих точек
Признак параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
По прямой и не лежащей
на ней точке (следствие 1)
По трем точкам
(аксиома 1)
По двум параллельным прямым (по определению параллельных прямых)
По двум пересекающимся
прямым (следствие 2)
А
Одна точка пересечения
Нет точек пересечения
В
А
А
С
В
Пересечением
является плоскость
Пересечением
является отрезок
Многоугольник, полученный при пересечении многогранника и плоскости, называется сечением многогранника указанной плоскостью
Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому можно лишь подражая избранным образцам и постоянно тренируясь..
Д. Пойа
№ 1.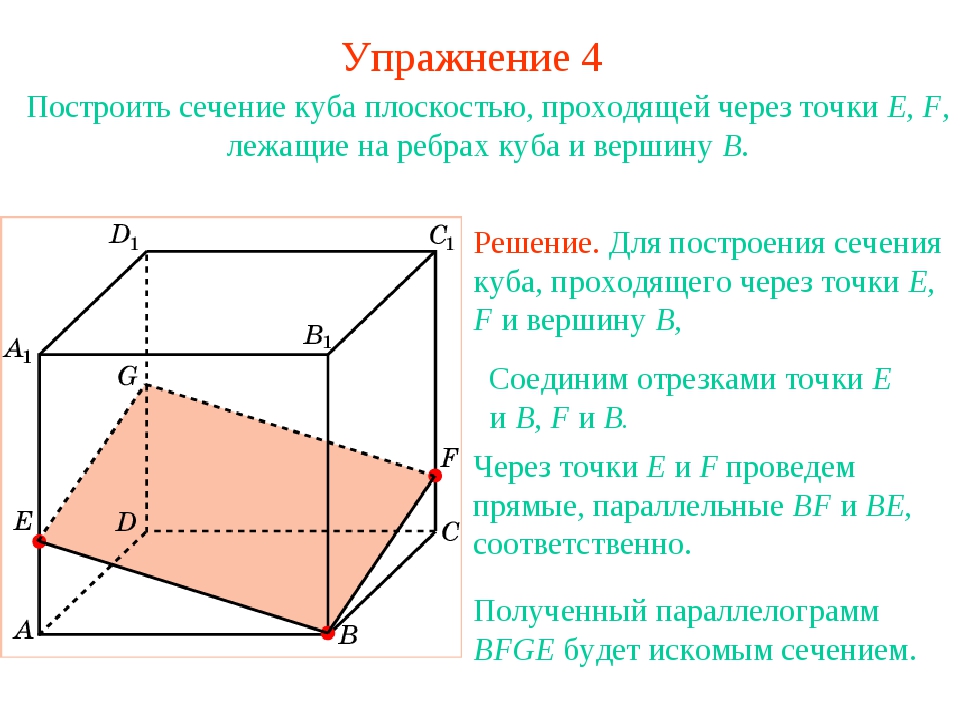 Построить сечение, определенное точками K, L, M.
Построить сечение, определенное точками K, L, M.
Р
K
2. Прямая МL
L
3. Прямая КL
В
КМL –сечение
?
А
(аксиома 1)
M
N2. Построить сечение, определяемое параллельными прямыми АА 1 и CC 1 .
С 1
В 1
1. Прямая А 1 С 1
2. Прямая АС
D 1
А 1
АА 1 С 1 С — сечение
В
С
?
D
А
N3. Построить сечение, определяемое пересекающимися прямыми АС 1 и А 1 С.
В 1
С 1
1. Прямые А 1 С 1 и АС
2. Прямые АА 1 и СС 1
А 1
D 1
АА 1 С 1 С — сечение
В
С
?
D
А
(следствие 2)
N4. Построить сечение по прямой BC и
точке М .
Р
1. Прямая ВС
2. Прямая СМ
М
3. Прямая ВМ
ВСМ — сечение
В
?
А
(следствие 1)
С
N5. Определите вид сечения куба АВСДА 1 В 1 С 1 Д 1 плоскостью, проходящей через ребро А 1 Д 1 и середину ребра ВВ 1 .
1. Прямая А 1 М
D 1
С 1
A 1 D 1
2. Прямая МК
3. Прямая D 1 K
К
А 1
В 1
A 1 D 1 KM — сечение
D
С
М
А
В
N6 . Постройте сечение куба плоскостью, проходящей через точку М и прямую АС .
1. Прямая СМ
М
В 1
С 1
К
2. Прямая МК II AC
А 1
3. Прямая AK
D 1
AKМС — сечение
С
В
D
А
N7. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ и точку М середину ребра В 1 С 1 .
К
А 1
С 1
М
1. Прямая ВМ
В 1
2. Прямая МК параллельно АВ
3. Прямая АК
С
А
АКМВ — сечение
В
N8. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.
S
1. Прямая КМ II AD
2. Прямая КN II DC
3. Прямая МP II AB
N
P
4. Прямая PN II BC
M
К
В
С
KMPN — сечение
А
D
МЕТОД СЛЕДОВ
Суть метода: построение вспомогательной прямой, являющейся линией пересечения секущей плоскости с плоскостью грани фигуры.
Эту линию называют следом секущей плоскости.
Просмотр учебного видеофильма.
Постройте сечение куба, проходящее через точки P, М, К.
М
А
К
О
С
В
1. Прямая МК
Т
2. Прямая КР
Р
3. Прямая ОТ
МАВРС — сечение
M
M
P
N
P
M
N
N
P
N
M
N
M
P
P
P
M
N
Решения варианта 1.
M
M
P
N
P
M
N
N
P
Решения варианта 2.
N
M
N
M
P
P
P
M
N
Составить две задачи на построение сечений многогранников с использованием полученных знаний.
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их
(Д. Пойа)
ЛИТЕРАТУРА
1. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»
2. Электронное издание « Решебник по геометрии. Пособие для абитуриентов . Полный курс за 7-11 классы»
3. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений
Изображение с сайта: http://www.cdvseti.ru/id3700.html
Портреты математиков взяты с диска «Математика 5-11».
Изображение с сайта: http://www.thg.ru/education/20050714/images/arhimed_cut.jpg
Анимация с сайта: http://badbad-girl.narod.ru/zelenie.html
сечений прямоугольной призмы
Пересечение — это точка или набор точек, общих для двух или более геометрических фигур. Плоскость — это плоская поверхность, которая простирается во всех направлениях.
Плоскость — это плоская поверхность, которая простирается во всех направлениях.
Поперечное сечение — это пересечение трехмерной фигуры и плоскости. Представьте себе плоскость, пересекающую показанную пирамиду, конус или призму.
На приведенном ниже рисунке показано пересечение конуса и плоскости. Поперечное сечение — круг.
На приведенном ниже рисунке показано пересечение треугольной призмы и плоскости. Поперечное сечение — треугольник.
Трехмерная фигура может иметь несколько различных поперечных сечений в зависимости от положения и направления среза.
Например, если бы пересечение плоскости и конуса было вертикальным, поперечное сечение образовало бы треугольник.
Практические вопросы
Вопрос 1:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше треугольное.
Вопрос 2:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.
Вопрос 3:
Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой параллелограмм.
Вопрос 4:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.
Вопрос 5:
Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.
Ответ:
Поперечное сечение указанной выше правой прямоугольной призмы представляет собой треугольник или равносторонний треугольник.
Вопрос 6:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.
Вопрос 7:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше треугольное.
Вопрос 8:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы вверху представляет собой кривую в форме радуги.
Вопрос 9:
Возможно ли круглое сечение в правой прямоугольной призме?
Ответ:
Нет, в правой прямоугольной призме нет кривых.
Вопрос 10:
Показана правая прямоугольная пирамида с неквадратным основанием.
(В правой пирамиде точка, где встречаются треугольные стороны, центрирована над основанием. )
)
Какова форма основания и каждой стороны пирамиды?
Ответ:
Форма основания — прямоугольник, а форма каждой стороны — треугольник.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебраные задачи на 4 слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариации
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
Word по типам ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Разметка и разметка задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы с линейными неравенствами
Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с помощью long di видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Что такое призма? — Определение, факты и пример
Prism Games
Объем твердых тел
Найдите объем твердых тел, умножив площадь основания на высоту твердого тела. Помните, что эта объемная область может быть добавлена.
Помните, что эта объемная область может быть добавлена.
охватывает Common Core Curriculum 5.MD.5.cИграть сейчасПосмотреть все игры по геометрии >>
Учитесь с полной программой обучения математике K-5
Что такое Prism
Призма — это трехмерная форма с двумя одинаковыми формами, обращенными друг к другу. Эти идентичные формы называются «основаниями».
Основание может быть треугольником, квадратом, прямоугольником или любым другим многоугольником.
Остальные грани призмы — параллелограммы или прямоугольники.
Поперечное сечение призм
Поперечное сечение геометрической формы или объекта — это форма, полученная прямым разрезом. Это также называется пересечением плоскости с трехмерным объектом. Поперечное сечение призмы, параллельное основанию призмы, такое же, как и ее основание.
Обычная и неправильная призма
Основание призмы может быть правильным или неправильным многоугольником. В зависимости от формы основания призмы бывают правильными или неправильными.
В зависимости от формы основания призмы бывают правильными или неправильными.
Площадь поверхности и объем призмы
Площадь поверхности призмы — это сумма площадей всех ее граней.
Объем призмы — это объем пространства внутри призмы.
Давайте посмотрим, как найти площадь поверхности и объем треугольной призмы.
Площадь поверхности = Площадь базовых треугольников + Площадь боковых параллелограммов
= 2 × (1 2 x шир x в) + 2 × (l x s) + (l x b)
= bh + 2ls + фунт
Объем = Площадь базового треугольника × длина
= (1 2 ш x в) × l
= 1 2 бхл
Пример: Рассчитайте площадь поверхности и объем следующей призмы.
Длина (l) = 12 см, высота (h) = 4 см, основание (b) = 6 см, стороны = 5 см
Площадь поверхности = bh + 2ls + lb = 6 × 4 + 2 × 12 × 5 + 12 × 6 = 24 + 120 + 72 = 216 см 2 | Объем = 1 2 мл = 1 2 × 6 × 4 × 12 = 144 см 3 |
Правая призма и наклонная призма
Когда два основания призмы идеально выровнены, а ее грани являются прямоугольниками (перпендикулярными основанию), это правая призма, в противном случае — наклонная.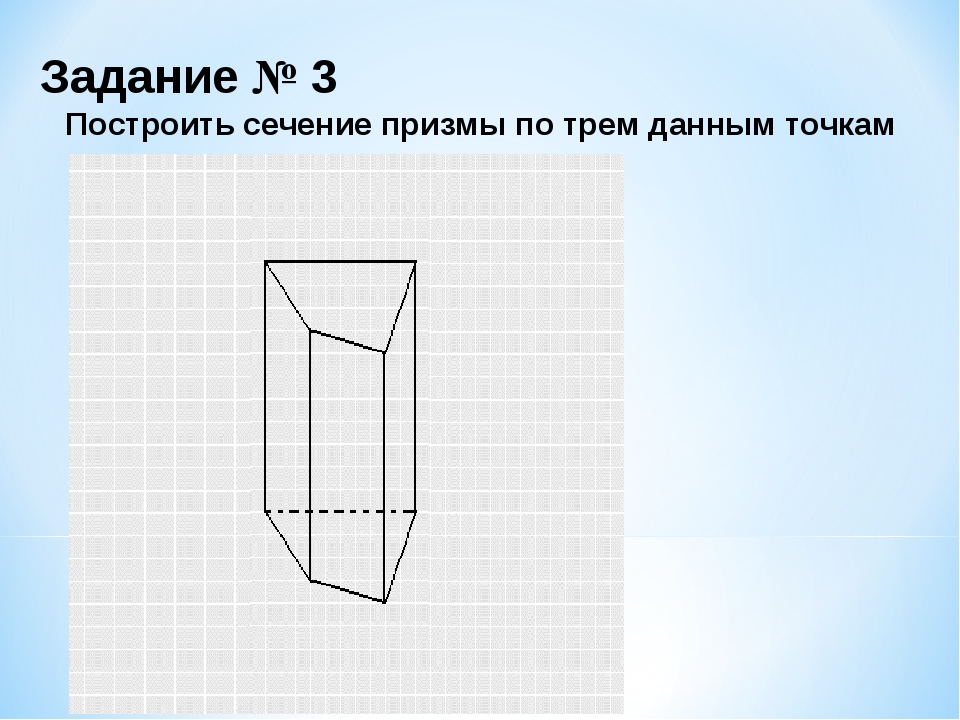 Они характеризуются следующим образом:
Они характеризуются следующим образом:
Правая призма | Косая призма | |
| Высота | Высота по боковой кромке. | Высота — это высота за пределами призмы. |
Боковые поверхности | Боковые грани — прямоугольники. | Боковые грани — параллелограммы. |
Площадь | bh + 2ls + lb | bh + 2ls + lb |
| Объем | 1 2 бхл | 1 2 бхл |
Интересные факты |
Треугольная призма
Треугольная призма — это призма с треугольным основанием. На рисунке ниже представлены три типа треугольных призм.
На рисунке ниже представлены три типа треугольных призм.
Свойства треугольной призмы
Треугольная призма — это многогранник, состоящий из двух параллельных и совпадающих треугольников, называемых основаниями. Боковые грани (стороны, не являющиеся основанием) представляют собой параллелограммы, прямоугольники или квадраты. У треугольной призмы три боковые грани. Ребро — это отрезок прямой, образованный пересечением двух смежных граней. Вершина — это точка пересечения трех ребер.
Треугольные призмы, подобные приведенной выше, имеют в общей сложности 5 граней, 2 основания и 3 боковые грани.У него также 9 ребер и 6 вершин.
Любое поперечное сечение треугольной призмы, параллельное основаниям, образует треугольник, конгруэнтный основаниям.
Два треугольных сечения треугольной призмы показаны выше зеленым цветом. Они соответствуют двум треугольным основаниям треугольной призмы, поскольку они образованы поперечными сечениями, расположенными в плоскостях, параллельных основаниям. Это верно для любого параллельного сечения треугольной призмы.
Классификация треугольных призм по их пересекающимся граням
Треугольные призмы можно классифицировать по тому, как их основания и боковые грани пересекаются или встречаются.Если основания перпендикулярны боковым граням, то есть встречаются под прямым углом, это прямоугольная призма. В противном случае это наклонная треугольная призма.
| Прямоугольная призма | Косая треугольная призма |
|---|---|
Правильная и неправильная треугольная призма
Треугольные призмы также можно классифицировать по типу треугольника, образующего его основу. Правильная призма определяется призмой, основания которой являются правильными многоугольниками.Следовательно, если основания треугольной призмы представляют собой равносторонние треугольники, это правильная треугольная призма. В противном случае это нерегулярно. Часто под правильной треугольной призмой подразумевают прямоугольную призму.
| Правильная треугольная призма | Неправильная треугольная призма |
|---|---|
Объем треугольной призмы
Объем V треугольной призмы равен площади одного из ее оснований, умноженной на ее высоту:
S = B · ч
, где B — площадь треугольного основания, а h — высота (расстояние между двумя параллельными основаниями) треугольной призмы.
Геометрия
— Построение поперечного сечения куба плоскостью, проходящей через три заданные точки
Мне кажется, что в этом случае пересечение будет шестиугольником. Плоскость, конечно же, будет пересекать куб в ДРУГИХ точках, кроме этих трех. Но вы можете получить довольно хорошее представление о вещах, нарисовав треугольник, содержащий три точки; плоскость — единственная плоскость, содержащая этот треугольник.
Обозначим четыре верхних края A, B, C, D, где A будет точкой с точкой, а остальные будут читаться по часовой стрелке, так что B начинается с правого конца A.Затем следующие четыре ребра — вертикальные — назовите их P, Q, R и S, снова считывая по часовой стрелке с точки с точкой. И затем четыре нижних края: назовите их W, X, Y, Z, причем W находится непосредственно под A, так что точка находится на краю C.
Затем, чтобы заполнить картинку, я бы поместил точку посередине вдоль края B (или, возможно, немного ближе к задней части), еще одну четверть пути вверх по краю 3, еще 2/5 пути вверх по краю 4. Имея Сделав это, я бы соединил любую пару точек, находящихся на одной грани, прямой линией, получив в результате шестиугольное пересечение.
Вот некоторые подробности (первая попытка, а затем полное решение)
(1) Проведите диагональную линию на задней стороне.
(2) Нарисуйте параллельную диагональ на передней поверхности, чтобы определить, где плоскость пересекает эту переднюю поверхность. Отметьте вершину вдоль вертикального ребра.
(3) Теперь мы подошли к той части, где я не могу дать точного рецепта: нарисуйте точку пересечения (я использовал фиолетовый) на правом верхнем крае, а другую — на левом нижнем. Края, соединяющие их с двумя ближайшими пересечениями (я нарисовал оранжевым), должны быть параллельны.
(4) И теперь, когда вы добавляете два последних ребра (я использовал цвет морской волны), они тоже должны быть параллельны:
С другой стороны, они также должны замкнуть петлю, чего у меня нет. Если вы переместите одну пурпурную точку немного назад, другая тоже должна будет сдвинуться немного вперед (чтобы оранжевые линии оставались параллельными), и аква-линия внизу не закроет шестиугольник в той точке, на которую вы надеетесь. Таким образом, вы вынуждены перемещать эту фиолетовую точку взад и вперед, пока не достигнете оптимальной точки. Вот пример со смещенными фиолетовыми точками, который почти работает:
Я нарисовал еще один пример (где начальная точка на лицевой стороне слева), который лучше демонстрирует, что идет не так, когда ваше предположение о местоположении фиолетовой точки неверно:
Я считаю, что идеальное место для пурпурной точки, вероятно, можно определить с помощью чего-то вроде теоремы Паскаля, но я не понимаю, как это сделать.Однако я надеюсь, что эти размышления будут вам полезны.
Вот полное решение:
- Проведите линию через две точки на задней стороне; расширяйте его, пока он не встретится с продолжением правой вертикальной стороны задней грани, и поместите там зеленую точку.
- Сделайте параллельную копию этой линии, проходящую через переднюю точку; отметьте пересечение с правым вертикальным краем красной точкой; затем вытяните линию, пока она не встретится с продолжением левого вертикального края передней грани.Поставьте синюю точку.
- Зеленая точка и крайняя правая красная точка лежат на плоскости разреза И плоскости правой грани; следовательно, и граница между ними тоже; нарисуйте это оранжевым. Проделайте то же самое с правым лицом.
- Пересечения этих оранжевых сегментов и сегментов спереди назад, отмеченные пурпурными точками, являются двумя последними вершинами шестиугольника.
- Нарисуйте шестиугольник.
Спасибо, что задали этот вопрос — он заставил меня немного подумать и узнать что-то новое!
Как рассчитать площадь поперечного сечения
Обновлено 7 февраля 2020 г.
Кевин Бек
Проверено: Lana Bandoim, B.S.
Вы можете столкнуться с ситуациями, в которых у вас есть трехмерное твердое тело и вам нужно определить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.
Например, если под вашим домом проходит цилиндрическая труба размером 20 метров (м) в длину и 0,15 м в поперечнике, вы можете узнать площадь поперечного сечения трубы.
Поперечные сечения могут быть перпендикулярны ориентации осей твердого тела, если таковые существуют.В случае сферы любая плоскость, пересекающая сферу, независимо от ориентации, приведет к получению диска определенного размера.
Площадь поперечного сечения зависит от формы твердого тела, определяющего границы поперечного сечения, и угла между осью симметрии твердого тела (если есть) и плоскостью, которая создает поперечное сечение.
Площадь поперечного сечения прямоугольного твердого тела
Объем любого прямоугольного твердого тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.
Следовательно, если поперечное сечение параллельно верху или низу твердого тела, площадь поперечного сечения составляет l × w. Если плоскость сечения параллельна одной из двух сторон, площадь поперечного сечения задается как l × h или w × h.
Если поперечное сечение не перпендикулярно какой-либо оси симметрии, создаваемая форма может быть треугольником (если поместить его через угол твердого тела) или даже шестиугольником.
Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м 3 .
Так как l = w = h для куба, любое одно ребро куба должно быть 3 м в длину (так как 3
× 3
× 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м 2 .
Площадь поперечного сечения цилиндра
Цилиндр — это твердое тело, образованное протяжением круга через пространство, перпендикулярное его диаметру. Площадь круга определяется формулой πr 2 , где r — радиус.Следовательно, имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг с площадью πr 2 . Если секущая плоскость вставлена под другим углом, создается форма эллипса. Для определения площади используется соответствующая формула: πab (где a — наибольшее расстояние от центра эллипса до края, а b — самое короткое).
Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?
Площадь поперечного сечения сферы
Любая теоретическая плоскость, проходящая через сферу, приведет к образованию круга (подумайте об этом на несколько минут). Если вам известен диаметр или длина окружности, образующей поперечное сечение, вы можете использовать соотношения C = 2πr и A = πr 2 для получения решения.
Пример : Плоскость грубо проходит через Землю очень близко к Северному полюсу, удаляя часть планеты 10 м вокруг.Какова площадь поперечного сечения этого холодного кусочка Земли?
- Поскольку C = 2πr = 10 м, r = 10 / 2π = 1,59 м; A = πr 2 = π (1,59) 2 = 7,96 м 2 .
Трехмерные формы | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью.Все физические предметы, к которым можно прикоснуться, трехмерны.
Эта страница охватывает как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) — это твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.
См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые кромки .
- Плоские стороны называются гранями .
- Углы, называемые вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые у них есть, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках).Многогранники также могут быть вогнутыми или выпуклыми.
Куб — один из самых простых и известных многогранников. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных тел — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник. Платоновы тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
См. Диаграмму выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы. Стороны призмы равны параллелограммам — четырехгранным формам с двумя парами сторон равной длины.
Антипризмы похожи на обычные призмы, их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре ее основания, правая пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Есть еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. 6 граней — правильные восьмиугольники, а остальные 8 — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с закругленными или закругленными краями не являются многогранниками. Многогранники могут иметь только прямые стороны.
Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца в форме круга или овала.Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или земного шара, представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Обычный кольцевой тор в форме кольца, шины или бублика образуется путем вращения меньшего круга вокруг большего круга. Существуют также более сложные формы торов. |
Площадь поверхности
На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы, чтобы рассчитать площадь поверхности трехмерных фигур.
Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двумерных форм для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы прорабатываете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба 10 × 10 см = 100 см 2 .Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба равна 600 см 2 .
Другие правильные многогранники
Аналогично, площадь поверхности других правильных многогранников (платоновых тел) может быть вычислена, если найти площадь одной стороны и затем умножить ответ на общее количество сторон — см. Диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Затем вы можете либо разделить полученный ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножить на 4, чтобы получить площадь поверхности всех четырех сторон, либо просто умножьте площадь поверхности одного треугольника на 2.
Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы вычислить площадь поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (боковая площадь), вам может потребоваться измерить стороны по отдельности.
Диаграммы сети
Геометрическая сеть — это двухмерный «узор» для трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о сетевых диаграммах см. Нашу страницу 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два конца одинаковые и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа (концы × стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и приплюснуть, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.
Сначала проработайте область одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
Предполагая радиус 5 см, площадь одной из окружностей равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как есть два круга 157см 2
Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314 см 2 .
Общую площадь поверхности можно найти, сложив вместе площади кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «склона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга у основания конуса равна π (пи) × радиус 2 .
В этом примере сумма равна 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь боковой части, наклонного участка, может быть найдена по следующей формуле:
π (пи) × радиус × длина уклона.
В нашем примере сумма равна 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к боковой области, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто легче измерить диаметр — расстояние по сфере. Затем вы можете найти радиус, равный половине диаметра.
Диаметр стандартного теннисного мяча — 2.6 дюймов. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам понадобится радиус в квадрате. 1,3 × 1,3 = 1,69.
Таким образом, площадь теннисного мяча составляет:
.
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаковый для каждой детали.
Формула: площадь поверхности = (2πR) (2πr)
Для определения площади поверхности примера тора.
(2 × π × R) = (2 × 3.14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Умножьте два ответа вместе, чтобы найти общую площадь поверхности примера тора.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь своим детям в учебе, эта книга для вас.
Заполнение твердого тела: Том
Для трехмерных форм вам также может потребоваться знать, какой объем у них есть.
Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
12 упражнений для отработки поперечных сечений трехмерных фигур, как ниндзя
Поиск формы, полученной в результате вырезания трехмерной формы, — это забавная тема. Студентам очень нравится эта тема. Когда вы будете искать идеи для преподавания этой темы, вы неизбежно найдете вводное упражнение с использованием play-doh. Ученики делают трехмерные фигуры из пластилина, а затем вырезают их какой-нибудь веревкой. Но есть и другие способы помочь учащимся увидеть и понять эту тему, поэтому сегодня я поделюсь с вами 12 других заданий (но вы можете увидеть несколько разных версий этого упражнения здесь и здесь).
В преподавании этой темы мне интересно то, что речь идет о трех измерениях, но учащиеся должны понимать ее в двухмерном пространстве на бумаге или экранах компьютеров. Это то, что делает эту тему уникальной.
В моем классе мы много тренируемся как с бумажными, так и с онлайн-играми и заданиями. В этом посте я хотел бы поделиться с вами некоторыми из этих идей. У студентов много практических занятий, и они действительно этим занимаются.Вы увидите, что этот список занятий предлагает широкий спектр занятий.
Вот список:
Крестики-нолики
Карты задач
Онлайн-модели Geogebra
Игра в куб
Игра на совпадение
Графический органайзер поперечных сечений БЕСПЛАТНО
Рабочий лист с фигурами
Листовка сечений
Задача производительности
PBS Video
Рабочий лист с множественным выбором
Kahoot
Людям действительно нравится эта игра в крестики-нолики.Он включает в себя четыре различных карты крестики-нолики. У трех карт просто старые формы, а на последней — настоящие объекты. Вы можете использовать это задание в качестве упреждающего набора. Кроме того, это очень хорошо работает для быстрой партнерской активности. Особенно мне нравятся примеры из реального мира. Студенты играют в партнеры и в конечном итоге много говорят о формах, которые они изучают, и их поперечных сечениях. В целом, эта игра дает студентам некоторую практику визуализации трехмерных фигур на бумаге и размышлений о том, как выглядят поперечные сечения.
Мне нравится универсальность карточек задач. Вы можете выполнять множество различных мероприятий, таких как скутер, работа с партнерами, весь класс с досками или выходные билеты. В этот набор карточек заданий входит 27 карточек. Первые 9 карточек содержат обзор названий трехмерных фигур, а остальные 18 карточек обозначают форму, полученную в результате трехмерного среза. Эти карточки с заданиями идеально подходят для легкой и быстрой практики.
У
Geogebra есть несколько замечательных онлайн-инструментов. Без сомнения, мой любимый инструмент для этой темы — их поперечные сечения и твердые тела.Это дает детям такой классный интерактивный взгляд на то, что мы подразумеваем под поперечными сечениями трехмерных фигур. В этом инструменте есть множество форм, и вы можете управлять нарезкой по-разному. Вы можете соединить это с нашим графическим органайзером ниже, и тогда учащимся не нужно будет просто снимать в темноте при работе с этими формами. Вы обязательно захотите смоделировать, как его использовать, и показать учащимся различные функции. Им нравится работать с такими инструментами на компьютере.
Если вам нужно задание, чтобы вывести учащихся из режима рабочего листа, вы можете попробовать эту игру в куб.Он включает в себя два разных способа игры и дает учащимся много повторений с определением поперечных сечений. В одной из версий этого кубического упражнения используется графический органайзер, и в него играют со всем классом. Вы катите куб, а затем определяете различные характеристики трехмерных фигур. Другая версия игры предназначена для партнеров или небольших групп и использует карты и кубики. Учащиеся выбирают карточку, а затем катят куб, на котором написано множество вопросов. Они должны ответить на вопросы.Мои дети любят играть в эту игру, потому что она социальная, а мне она нравится, потому что они повторяют так много раз за такой короткий промежуток времени.
Соответствующие задания дают учащимся другой взгляд на концепции. В этом задании по сопоставлению учащимся дается форма, и они должны найти поперечные сечения, параллельные основанию, перпендикулярные основанию и диагональные к основанию. Они используют рабочий коврик и кладут маленькие кусочки бумаги. Мои студенты сказали, что им нравится вырезать и перемещать бумагу.Вы можете повторно использовать набор (в качестве центра и т. Д.) Или попросить учащихся склеить его и положить в свои интерактивные записные книжки.
Хотите больше идей и ресурсов для забавных игр для средней школы, в том числе БЕСПЛАТНОЕ задание в математическом лабиринте, которое отправляется вам каждый месяц прямо на ваш почтовый ящик? Присоединяйтесь к клубу «Лабиринт месяца», и вы ВХОДИТЕ!
Да! Запишитесь в Клуб Математического Лабиринта месяца!
Не могу дождаться встречи с вами там.
Обожаю графические органайзеры. Когда я был первым учителем, у меня был 4-часовой блок-класс со студентами ELL.Мы работали над изучением английского языка большую часть дня. Я использовал множество графических органайзеров, подобных этому, и с тех пор я как бы одержим ими. В этом графическом органайзере учащиеся несколько раз отвечают на один и тот же вопрос, используя разные формы. Это отличный инструмент, который помогает учащимся говорить о поперечных сечениях в академической манере. Все, что им нужно сделать, это взять свой ответ и превратить его в предложение. Это особенно хорошо работает с ELL и учащимися со специальным образованием. Скачать бесплатно здесь.
Этот рабочий лист содержит отличные наглядные пособия, которые помогают учащимся увидеть срез в поперечных сечениях. Вы можете попросить учащихся поработать над этим заданием с партнером и поговорить с ними по математике. Кроме того, вы можете использовать его для всего класса и показывать студентам по одному из примеров за раз. Затем я предлагал студентам отвечать на вопросы на своих досках или SmartPals. Вот несколько вопросов, которые вы могли бы использовать:
- Какая двухмерная форма получается в результате среза, показанного на рисунке?
- Как он изменится, если разрезать его в другом направлении?
- Какова основа этой формы и сколько у нее граней?
Есть много вещей, которые вы можете сделать, чтобы рабочие листы были больше, чем рабочие листы.Как вы можете видеть выше, один из простых способов улучшить его — это просто пойти немного дальше с вопросами и иллюстрациями из рабочего листа.
Мне нравится, когда дети могут манипулировать математикой на своих терминах и пытаться во всем разобраться. Это делает математику более реальной, а не просто список шагов. Этот флаер великолепен тем, что делает именно это. Студенты могут видеть различные формы, такие как конус, цилиндр, пирамида и призмы. Также они могут менять основание и перемещать поперечное сечение. Прежде чем я предлагаю им опробовать конкретные вещи с помощью этого инструмента, я даю студентам несколько минут и просто поиграю с ним.Вам понравится слушать, как говорят ваши ученики, используя этот онлайн-инструмент.
Это практическое задание из «Иллюстративной математики» — это практическое задание, в котором учащиеся должны взять то, что они узнали о поперечных сечениях, и применить это на практике. Название задания — «Кубические ниндзя», и мне это нравится, потому что я думаю, что детям нравится все, что содержит слово «ниндзя». Если вам нравится заниматься этим, вы можете выполнять целую рутину ниндзя, когда знакомите с этим занятием. Я мог бы это сделать, если буду в хорошем настроении!
Само задание предлагает учащимся проанализировать различные срезы куба.Они должны нарисовать диаграмму и использовать точный математический язык для описания происходящего. Если у вас мало времени (как и я в большинстве случаев), вы можете раздать разные фрагменты разным группам и выполнить своего рода задачу по составлению мозаики. В конце концов позвольте каждой группе быстро представить свои выводы.
Это видео с PBS Video очень забавное и отлично работает в качестве упреждающего набора во время этого блока. У них есть группа детей, которые разыгрывают рекламный ролик, в котором продаются кусочки разных продуктов.Мне это нравится, потому что он дает всем примеры из реальной жизни. К тому же это незабываемо. Когда мы все смотрим что-то запоминающееся, например это видео, это дает нам то, на что мы можем ссылаться через устройство. После того, как студенты посмотрят видео, убедитесь, что они поговорили об этом с партнером. Дайте им возможность переварить увиденное в видео.
Этот рабочий лист даст вам немного практики для ваших учеников в форме теста с множественным выбором.Мне нравится использовать игры с таблицами. Игра, которую я использовал с этим листом, называется «Выбор 4 карты». Учитель помещает задачу на документ-камеру, а ученики решают ее на своей доске. Когда все заканчивают, учитель задает вопросы о проблеме, и тот, кто отвечает, берет карту из колоды. После того, как каждый из четырех учеников выберет карту, остальные ученики запишут одно из имен учеников, которое, по их мнению, будет иметь самую высокую карту. Студент с самой высокой картой получает 4 балла, следующая по величине — 3 балла, следующая по величине — 2 балла, а самая низкая карта — 1 балл.Остальной класс получает количество баллов, которое набрал выбранный ими ученик. Эта простая игра добавляет немного удовольствия, отвечая на некоторые вопросы.
Рабочие листы по этой ссылке содержат подробные изображения некоторых поперечных сечений и спрашивают, какое сечение получается из них. Кроме того, вы можете спросить о основании, названии формы или количестве граней. Эти рабочие листы помогают закрепить некоторые основы этой концепции.
Kahoot — это компьютерная игра, в которой весь класс тренируется в поперечных сечениях трехмерных фигур.В этом Kahoot есть 27 вопросов, которые заставят детей задуматься. Если 27 вопросов звучат слишком много, помните, что вы можете загрузить игру в свою учетную запись и отредактировать ее. Вы можете удалить некоторые вопросы и ускорить игру. Иногда дети слишком увлекаются Kahoot, и вы должны напоминать им, что мы тренируемся, а не просто играем в игры.
Вопросы в этом Kahoot касаются либо того, какая форма получается из определенного поперечного сечения, либо какая форма может иметь определенное поперечное сечение.Здесь не так много вопросов, но для этого достаточно быстро получить много практики. Также помните, что результаты игр Kahoot можно загрузить на свой Google Диск, что делает их хорошей формирующей оценкой.
Попробуй одно
Мы рассмотрели множество занятий, но у вас, вероятно, нет времени на все. Моя задача — попробовать что-то новое и посмотреть, как все пойдет. Если все пройдет хорошо, вы можете добавить это упражнение или инструмент в свой набор приемов учителя.
Большое спасибо за чтение! До скорого.
Связанные
.

 Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры.
Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. 
 Например, в последнем примере комментарии учителя могут быть следующими:
Например, в последнем примере комментарии учителя могут быть следующими:  Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.