Как построить сечение: Учимся строить сечения многогранников. Часть 2. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Учимся строить сечения многогранников. Часть 2.

Эта статья для тех, кто хочет научиться строить сечения. Она содержит 11 заданий для построения сечений, подсказки и ответы к каждому заданию. Рекомендую сначала прочитать эту статью и посмотреть это видео.

Вспомним, что сечение многогранника плоскостью представляет собой плоский многоугольник, вершины которого принадлежат сторонам, а ребра — граням многогранника. Две соседние вершины принадлежат одной грани многогранника.

Чтобы найти точку, лежащую одновременно в двух плоскостях, нужно найти точку пересечения прямой, лежащей в первой плоскости, с прямой, лежащей во второй плоскости.

В подсказках и ответах изображение дополнительных прямых, используемых при построении сечения, сплошными линиями или пунктирными, не зависит от того, видимы эти прямые или нет.

Рядом с каждой дополнительной прямой указан ее порядковый номер при построении сечения. Все прямые проведены через две точки, принадлежащие определенной плоскости. Прямые пронумерованы в порядке их построения. Рекомендуется при использовании подсказки и воспроизведении построения сечения проговаривать, какой плоскости принадлежит данная прямая, каким плоскостям принадлежит точка их пересечения.

Постройте сечения, проходящие через точки .

Задание 1:

Подсказка. показать

Ответ. показать

Задание 2:

Подсказка: показать

Ответ: показать

Задание 3:

Подсказка: показать

Ответ: показать

Задание 4:

Подсказка: показать

Ответ: показать

Задание 5:

Подсказка: показать

Ответ: показать

Задание 6:

Подсказка: показать

Ответ: показать

Задание 7:

Подсказка: показать

Ответ: показать

Задание 8:

Подсказка: показать

Ответ: показать

Задание 9:

Подсказка: показать

Ответ: показать

Задание 10:

Подсказка: показать

Ответ: показать

Задание 11:

Подсказка: показать

Ответ: показать

И. В. Фельдман, репетитор по математике.

построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

Пример.

Построить сечение плоскостью (MNP)

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.

Треугольник MNP — искомое сечение.

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

Получим след MT.

T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).

Стереометрия. Задачи на построение сечений

В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.

Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.

Как вы думаете — может ли восьмиугольник быть сечением куба?

И может ли правильный пятиугольник быть сечением куба?

Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.

А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.

Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.

При построении сечений мы часто используем следующие теоремы:

1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2. Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник — искомое сечение.

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

3. Постройте сечение куба проходящее через вершину и середины ребер и

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем

Проведем — в плоскости задней грани и — в плоскости левой грани куба;

Пятиугольник — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

4. Постройте сечение куба проходящее через вершину В и середины ребер и

Пусть М — середина ребра , N — середина ребра

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ.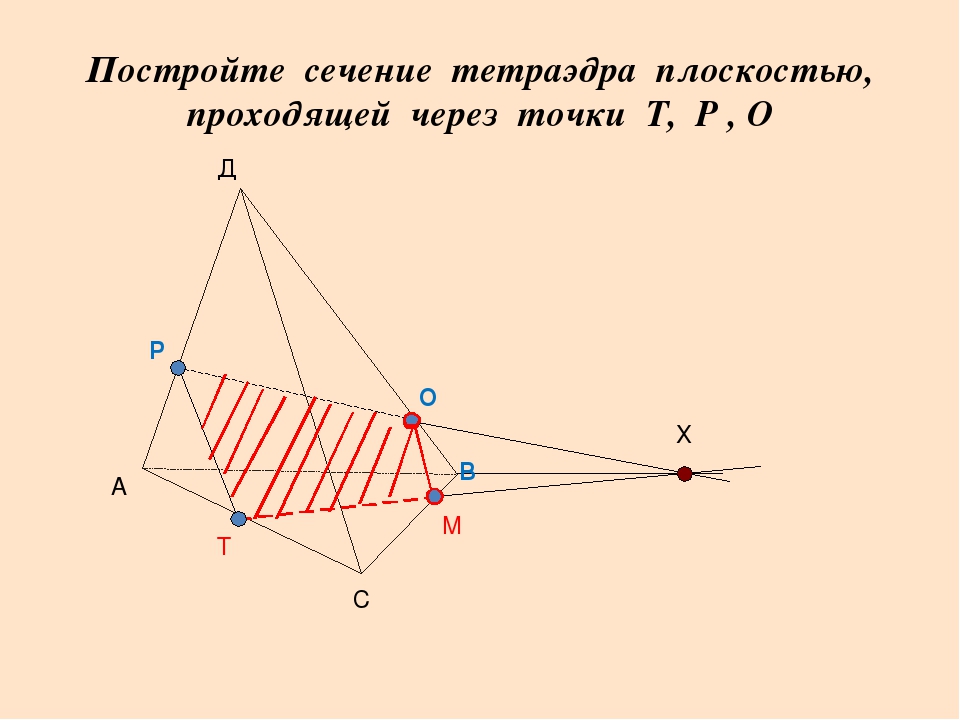 Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

где — середина ;

— искомое сечение.

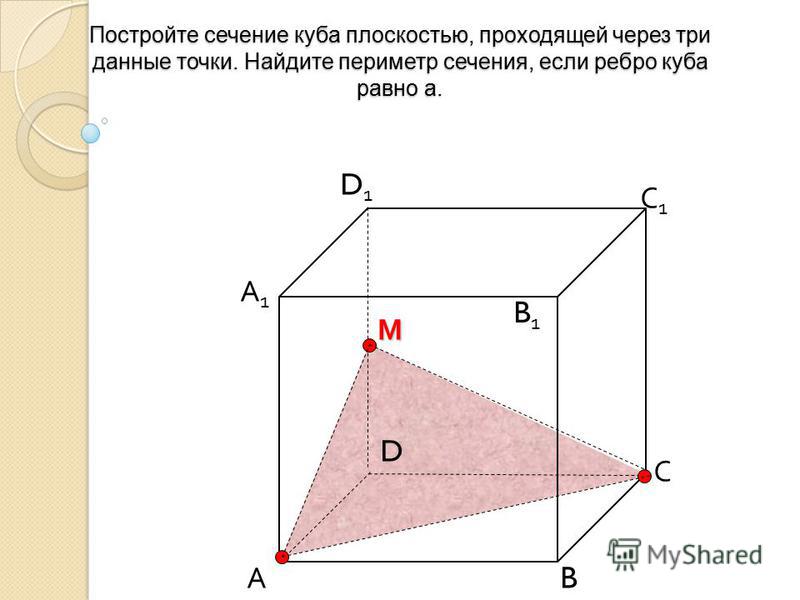
7. Постройте сечение куба , проходящее через точку М, лежащую на ребре и точки Т и К, принадлежащие граням АВС и .

Точки М и К лежат в плоскости задней грани . Соединив М и К, получим, что

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

Пусть точки и — проекции точек M и N на плоскость нижней грани

Плоскость проходит через параллельные прямые и .

Проведем в этой плоскости MN и

Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.

Сечение параллелепипеда по трем точкам примеры.

Задачи на построение сечений

Цели урока:
рассмотреть решение задач на построение сечений, если две точки сечения принадлежат одной грани.

Ход урока

Изучение новых понятий
Определение 1.

Секущая плоскость многогранника — любая плоскость, по обе стороны от которой имеются точки данного многогранника.
Определение 2.

Сечение многогранника — это многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани многогранника.
Задание. Назовите отрезки, по которым секущая плоскость пересекает грани параллелепипеда (рис. 1). Назовите сечение параллелепипеда.

Основные действия при построении сечений

	Теоретическая основа	Ответ
1. Как проверить: построено сечение или нет	Определение сечения	Это должен быть многоугольник, стороны которого принадлежат граням многогранника
2. До начала работы определить: можно ли по данным задачи построить сечение	Способы задания плоскости	Можно, если данные элементы задают однозначно плоскость, то есть даны три точки, не лежащие на одной прямой, точка и прямая и т.д.
3. В плоскости какой-то грани есть две точки секущей плоскости	Если две точки принадлежат плоскости, то вся прямая принадлежит плоскости	Через эти точки провести прямую
4. В одной из параллельных граней есть сторона сечения, а в другой — точка сечения	Свойство параллельных плоскостей	Через эту точку провести прямую, параллельную данной
5. В одной грани есть точка сечения и известно, что секущая плоскость проходит через прямую, параллельную этой грани	Признак параллельности прямой и плоскости. Свойство параллельных плоскостей	Построить прямую пересечения плоскостей, параллельную данной прямой
6.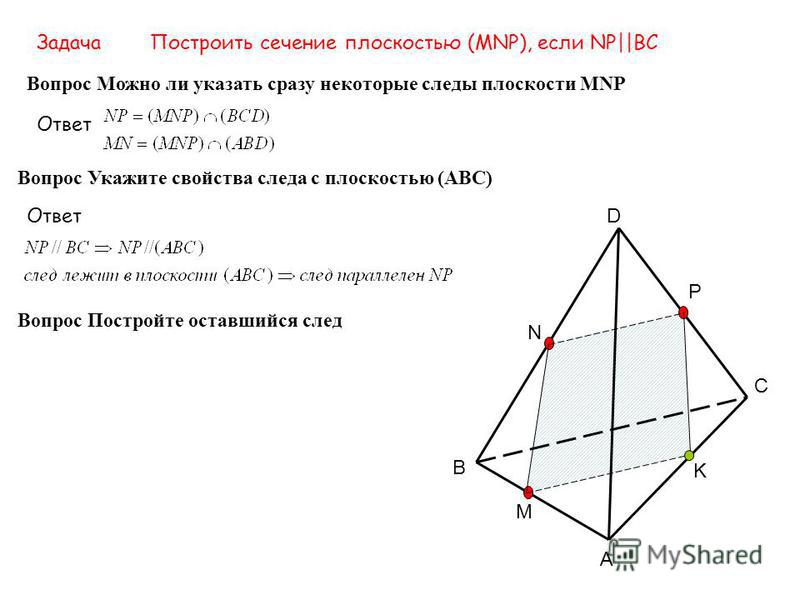 Две точки сечения принадлежат одной грани, а третья точка лежит в смежной	Аксиомы стереометрии	Секущая плоскость пересекает грани по отрезкам OC и AB, которые называются следом секущей плоскости на гранях

Решение задач

Задача 1.
Какой из четырехугольников, EFKM или EFKL, может быть сечением данного многогранника (рис. 2)? Почему?

Задача 2.
Ученик изобразил сечение тетраэдра (рис. 3). Возможно ли такое сечение?

Решение
. Нужно доказать, что N, M и H, L лежат в одной плоскости. Пусть точки N и M принадлежат задней грани, H и L — нижней грани, то есть точка пересечения NM и HL должна лежать на прямой, принадлежащей обеим граням, то есть AC. Продлим прямые NM и HL и найдем точку их пересечения. Эта точка не будет принадлежать прямой AC. Значит, точки N, M, L, H не образуют плоский многоугольник. Невозможно.

Задача 3.
Построить сечение тетраэдра ABCS плоскостью, проходящей через точки K, L, N, где K и N — середины ребер SA и SB соответственно (рис.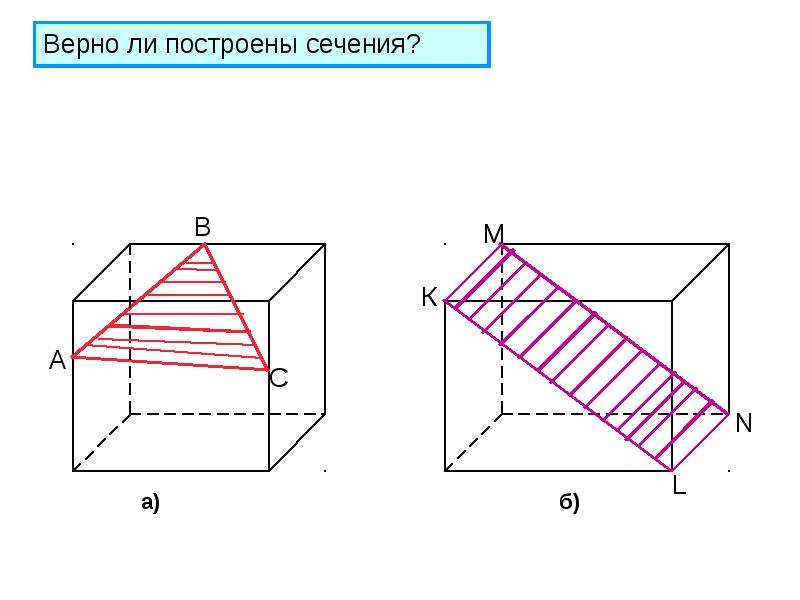 4).

1. В какой грани можно построить стороны сечения?

2. Выбираем одну из точек, на которой оборвалось сечение.
Решение. Способ I.
Выбираем точку L.
Определяем грань, в которой лежит выбранная точка и в которой надо построить сечение.

Определяем грань, в которой лежит прямая KN, не проходящая через выбранную точку L.

Находим линию пересечения граней ABC и ASB.

Каково взаимное расположения прямых KN и AB (рис. 5)?
[Параллельны.]

Что нужно построить, если секущая плоскость проходит через прямую, параллельную линии пересечения плоскостей?
[Через точку L провести прямую,
параллельную AB. Эта прямая
пересекает ребро CB в точке P.]

Соединяем точки, принадлежащие одной грани. KLPN — искомое сечение.
Способ II
. Выбираем точку N (рис. 6).

Определяем грани, в которых лежат точка N и прямая KL.

Линией пересечения этих плоскостей будет прямая SC. Находим точку пересечения прямых KL и SC. Обозначим ее Y.
Соединяем точки N и Y. Прямая NY пересекает ребро CB в точке P.
Соединяем точки, принадлежащие одной
грани.
KLNP — искомое сечение.
Объясните данное решение.
Один учащийся работает у доски, остальные в тетрадях.

Задача 4
. Построить сечение параллелепипеда, проходящее через точки M, P и H, H ` (A1B1C1) (рис. 7).

Решение.
1. Соедините точки, принадлежащие одной грани.
2. Какую прямую и точку выбираем для построения сечения?
3. Что определяем дальше?
4. Каково взаимное расположение выбранной прямой и линии пересечения граней (рис. 8)?

5. Как построить след секущей плоскости на грани B1C1D1A1, проходящий через точку H?
6. Соедините точки, принадлежащие одной грани.
7. Какую прямую и точку нужно выбрать для построения следа секущей плоскости на грани AA1D1D?
8. Каково взаимное расположение граней BB1C1C и AA1D1D?
9. Каким свойством необходимо воспользоваться для построения следа секущей плоскости на грани AA1D1D?
10. Назовите искомое сечение.

Задача 5.
Построить сечение пирамиды SABCD, проходящее через точки M, P и H,
H` (ABC) (рис. 9).

Ответ: см. рисунок 10.

Задание на дом

Задача
. Как изменятся построения, если точ-
ка H изменит свое положение? Построить сечения, используя разные варианты (рис. 11).

Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.

С самого раннего детства мы сталкиваемся с сечениями. Режем хлеб, колбасу и другие продукты, обстругиваем палочку или карандаш ножом. Секущей плоскостью во всех этих случаях является плоскость ножа. Сечения (срезы кусочков) оказываются различными.

Сечение выпуклого многогранника есть выпуклый многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многоугольника, а стороны- линиями пересечения секущей плоскости с гранями.

Для построения прямой пересечения двух плоскостей достаточно найти две общие точки этих плоскостей и провести через них прямую. Это основано на следующих утверждениях:

1.если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости;

2.если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Как я уже сказал ппостроение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей. Вместе с тем, существуют определенные методы построения плоских сечений многогранников. Наиболее эффективными являются следующие три метода:

Метод следов

Метод внутреннего проектирования

Комбинированный метод.

В изучении геометрии и, в особенности, тех её разделов, где рассматриваются изображения геометрических фигур, изображения геометрических фигур помогают использования компьютерных презентаций. С помощью компьютера многие уроки геометрии становятся более наглядной и динамичной. Аксиомы, теоремы, доказательства, задачи на построения, задачи на построения сечений можно сопровождать последовательными построениями на экране монитора. Сделанные с помощью компьютера чертежи можно сохранять и вставлять их в другие документы.

Хочу показать несколько слайдов по теме: «Построения сечений в геометрических телах»

Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную прямую. Тогда искомая точка является точкой пересечения найденной прямой с данной. Проследим это на следующих слайдах.

Задача 1.

На ребрах тетраэдра DABC отмечены две точки М и N; М GAD, N б DC. Укажите точку пересечения прямой MN с плоскостью основания.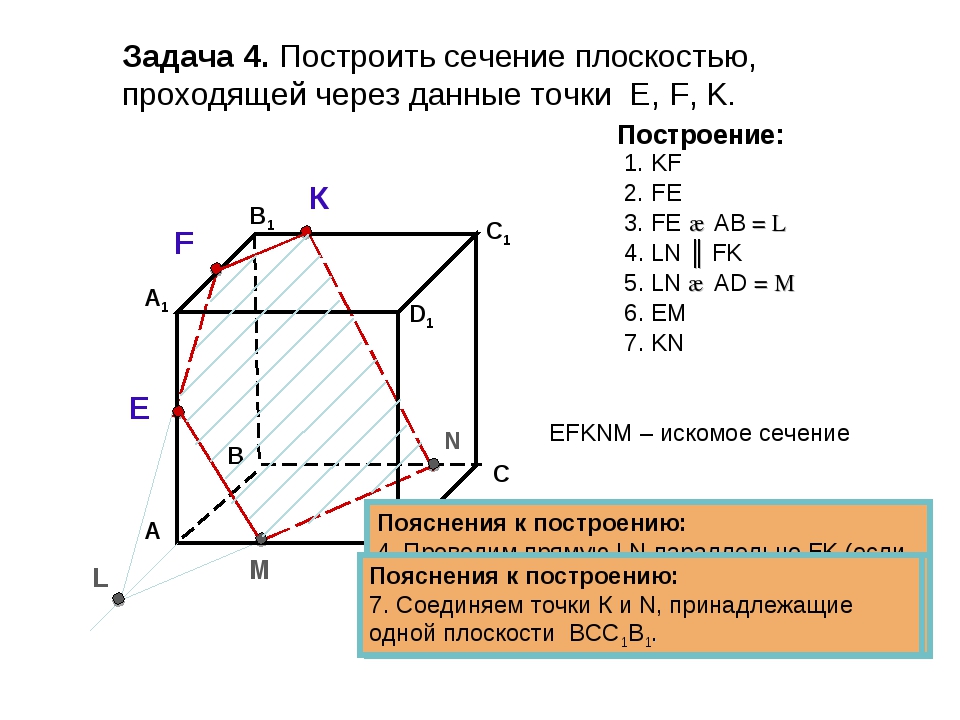

Решение: для того, чтобы найти точку пересечения прямой MN с плоскостью

основания мы продолжим АС и отрезок MN. Отметим точку пересечения этих прямых через X. Точка X принадлежит прямой MN и грани АС, а АС лежит в плоскости основания, значит точка X тоже лежит в плоскости основания. Следовательно, точка X есть точка пересечения прямой MN с плоскостью основания.

Рассмотрим вторую задачу. Немного усложним его.

Задача 2.

Дан тетраэдр DABC точки М и N, где М € DA, N С (DBC). Найти точку пересечения прямой MN с плоскостью ABC .

Решение: точка пересечения прямой MN с плоскостью ABC должна лежать в плоскости, которая содержит прямую MN и в плоскости основания. Продолжим отрезок DN до точки пересечения с ребром DC. Точку пересечения отметим через Е. Продолжим прямую АЕ и MN до точки их пересечения. Отметим X. Точка X принадлежит MN, значит она лежит на плоскости которая содержит прямую MN и X принадлежит АЕ, а АЕ лежит на плоскости ABC. Значит X тоже лежит в плоскости ABC.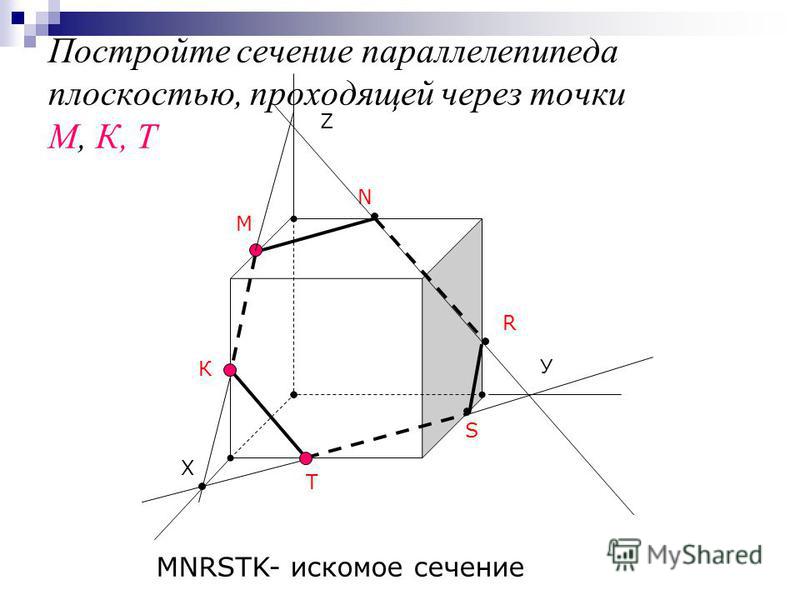 Следовательно X и есть точка пересечения прямой MN и плоскости ABC.

Усложним задачу. Рассмотрим сечение геометрических фигур плоскостями, проходящими через три данные точки.

Задача 3

На ребрах AC, AD и DB тетраэдра DABC отмечены точки М, N и Р. Построить сечение тетраэдра плоскостью MNP.

Решение: построим прямую, по которой плоскость MNP. Пересекается с плоскостью грани ABC. Точка М является общей точкой этих плоскостей. Для построения ещё одной общей точки продолжим отрезок АВ и NP. Точку пересечения отметим через X, которая и будет второй общей точкой плоскости MNP и ABC. Значит эти плоскости пересекаются по прямой MX . MX пересекает ребро ВС в некоторой точке Е. Так как Е лежит на MX, а MX прямая принадлежащей плоскости MNP, значит РЕ принадлежит MNP. Четырёхугольник MNPE искомое сечение.

Задача 4

Построим сечение прямой призмы АВСА1В1С1 плоскостью проходящей через точки P,
Q
,R, где R принадлежит (AA
1C
1C
), Р
принадлежит В
1С1,

Q принадлежит АВ

Решение:
Все три точки P,Q,R лежат в разных гранях, поэтому построить линию пересечения секущей плоскости с какой- либо гранью призмы мы пока не можем. Найдем точку пересечения PR с ABC. Найдем проекции точек Р и R на плоскость основания PP1 перпендикулярно ВС и RR1 перпендикулярна АС. Прямая P1R1 пересекается с прямой PR в точке X. X точка пересечения прямой PR с плоскостью ABC. Она лежит в искомой плоскости К ив плоскости основания, как и точка Q. XQ- прямая пересекающая К с плоскостью основания. XQ пересекает АС в точке К. Следовательно, KQ отрезок пересечения плоскости Х с гранью ABC. К и R лежат в плоскости Х и в плоскости грани АА1С1С. Проведем прямую KR и точку пересечения с A1Q отметим Е. КЕ является линией пересечения плоскости Х с этой гранью. Найдем линию пересечения плоскости Х с плоскостью граней BB1A1A. КЕ пересекается с А1А в точке У. Прямая QY есть линия пересечения секущей плоскости с плоскостью AA1B1B. FPEKQ- искомое сечение.

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый).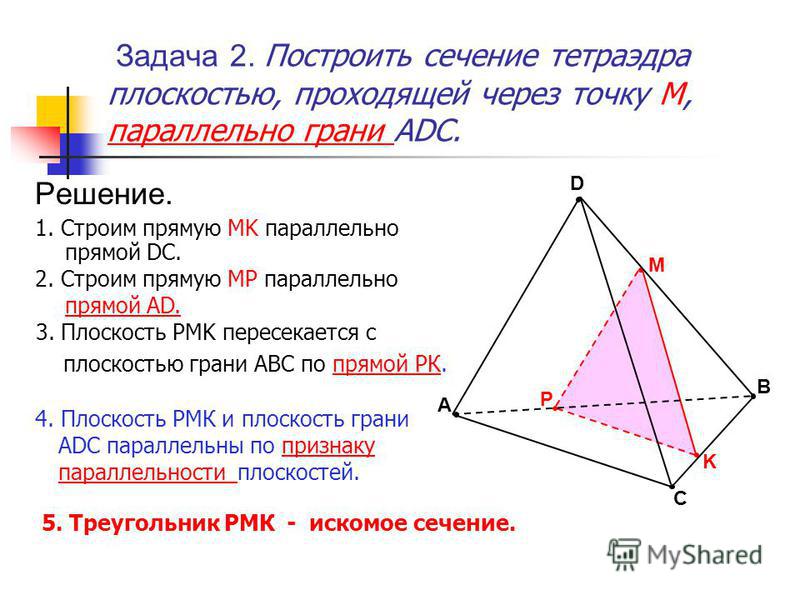 Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости (ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Пример.

Построить сечение плоскостью (MNP)

Треугольник MNP — сечение пирамиды

Треугольник MNP — искомое сечение.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

Получим след MT.

T — точка пересечения прямых MH и AC.

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

В этом методе мы
первым действием (после нахождения
вторичных проекций данных точек) строим
след секущей плоскости на плоскости
верхнего или нижнего основания призмы
или усечённой пирамиды или на основании
пирамиды

Зад

2.
Дано
изображение треугольной призмы

ABCA
1 B
1 C
1
и трёх точек
M
,
N
,
P
,
которые лежат
соответственно на ребре СС
1
и гранях

ABB
1 A
1 ,
BCC
1 B
1 .
Построить
сечение призмы плоскостью
,
проходящей
через
M
,
N
,
P
.

Решение.

Мы уже имеем одну точку на верхнем
основании призмы, поэтому и след мы
будем строить на верхнем основании.
Строим вторичные проекции точек N

и P

на верхнее
основание.Затем: 1
.N
P
N
3 P
3 =X
;
2
.M
X
=p

–след; 3
.p
B
1 C
1 =D
.

Дальнейшие действия
уже были показаны выше на чертеже.

Зад

3.
Реш.

Мы будем
строить след секущей плоскости на нижнем
основании призмы.

Строим:1.
M
N
E
D
=X
,
M
P
EP
3 =Y
;

2. p
=XY

– след;3.
p
B
C
=G
,
p
D
C
=H
.

Нам нужно найти
точку
на ребре
BB
1
или на ребре AA
1 .

ВграниABB
1 A
1
мы уже
имеем одну точку P
.
Поэтому нижнее ребро этой грани, т.е.
AB
,
мы продолжаем до пересечения со следом.

4. A
B
p
=Z
.

5. P
Z
AA
1 =F
;
P
Z
BB
1 =K
.Дальнейшие
действия уже показаны выше.

Если окажется, что
линия AB

не пересекается
со следом, то искомая FK

тоже будет
параллельна следу.
Зад

4.
Реш.

1.
P
N
P
o N
o =X
;

2. M
N
CN
o =Y
;3.
p
=XY

– след;

3.
C
B
p
=Z
;4.
Z
M
S
B
=E
;

5. E
N
S
A
=G
6.

GEMF
– иск
сечение.

17. Построение сечения цилиндра.

Если секущая
плоскость задана тремя точками, то мы
всегда можем найти её след на плоскости
основания цилиндра или конуса и точку
(P
,
O
)
на его оси. Поэтому считаем, что секущая
плоскость задана именно этими элементами.

Сначала
рас-им случай, когда плоскость пересекает
только боковую поверхность цилиндра.
Тогда сечением цилиндра будет эллипс
(;¯ и его изображение – тоже эллипс.
Мы знаем способ построения эллипса,
если известны два его сопряжённых
диаметра. Мы сейчас покажем, как можно
найти изображение главных диаметров
эллипса (;¯.

Пусть 
и  1
– эллипсы,
изображающие нижнее и верхнее основания
цилиндра, O

и O
1
– их центры.
Проведём диаметр A
3 B
3
нижнего основания, параллельный следу
и сопряжённый ему диаметр C
3 D
3 .
Для построения C
3 D
3
мы используем
хорду K
3 L
3 ,
один конец которой принадлежит контурной
образующей. Напомним, что
A
3 B
3
и C
3 D
3
изображают
перпендикулярные диаметры. Продолжим
C
3 D
3
до пересечения
со следом. Получим точ X
.
Прям.PX

наз-ём осью
сечения.

Поднимем точки
C
3
и D
3
до оси
сечения. Получим C

и D
.
Отрезок
CD

является изображением большогодиаметра
сечения. Поднимем отрезок
A
3 B
3 на
высоту OP
.
Получим отрезок AB
,
который является изображением малого
диаметра сечения. Отр-и AB

и CD

–сопряж-ые
диам. эллипса .

Найти
ещё точки, в которых эллипс переходит
с видимой стороны цилиндра на невидимую,
а значит, сплошная линия переходит в
пунктир. Это точки пересечения секущей
плоскости с контурными образующими.
ПустьY
3 =K
3 L
3 C
3 D
3 .
Поднимем Y
3
до оси
сечения. Получим точку Y
.
Поднимем хорду K
3 L
3
на высоту
YY
3 .
Получим отрезок KL
.
Мы нашли требуемую точку K
,
а попутно, ещё одну дополнительную точку
L
.
Точка M
,
изобр-щая пересечение секущей плоск-и
со второй контурной образующей симметрична
точкеK

относительно точкиP
.Допол-но
построим точN
,
симметричнуюL

относ-нточки
P

Покажем способ,
как можно найти любое кол-во точек на
сечении без испол-ия этих диаметров.

выбираем люб.
точкуV
3
на эллипсе .
Проводим диаметрV
3 T
3
и продолжаем его до пересечения со
следом.Получим точкуU
.
Поднимаем точки V
3
и T
3
до прямой
UP
.
Получаем две точки V

и T

на сечении. Выбирая вместо V
3
другую
точку, получим др. 2 точки на сеч.Если
выбрать точку K
3 ,
лежащую на контурно образующей, мы
найдём точки K

и M
,
в которых сплошная линия на сечении
должна перейти в пунктирную.

Обучение с МК

Пример: модели МК в электронном учебнике

Сечения многогранников

ТЕОРИЯ

В этом разделе мы рассмотрим методы построения сечений многогранников. Плоскость сечения, как правило, будет задаваться тремя точками – K, L, M. Сложность такой задачи во многом определяется расположением точек, задающих плоскость сечения.

Пример 1

Самый простой случай – когда точки лежат на трёх смежных рёбрах пирамиды – не нуждается в разборе.

Модель 1

Основной метод, который используется при построении сечений, называется методом следов.

Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника. Если такой след найден, то точки его пересечения с соответствующими рёбрами многогранника и будут вершинами искомого сечения.

Пример 2

Пусть теперь точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания.

Модель 2

Проведём в плоскости SAC прямую KL – след сечения в этой плоскости.
Отметим точку P пересечения KL с SC.
Проведём прямую PM – след сечения в плоскости SBC, – и отметим точку пересечения PM и BC.
Все четыре вершины сечения получены – строим сечение.

Пример 3

Несколько труднее случай, когда одна из точек лежит на ребре, а две другие — на гранях пирамиды.

Модель 3

Теперь сразу построить след плоскости сечения в какой-то из граней нельзя.

Рассмотрим вспомогательную плоскость SKM, которая пересекает рёбра AC и BC в точках E и F соответственно.
Построим в этой плоскости прямую KM – след плоскости сечения – и отметим точку P пересечения KM с EF.
Точка P лежит в плоскости сечения и в плоскости ABC. Но в этой же плоскости лежит и точка L. Проведём прямую PL – след сечения в плоскости ABC – и отметим точку пересечения PL с BC.
Строим след сечения в плоскости SBC и отмечаем точку его пересечения с SC.
Строим след сечения в плоскости SAC и отмечаем точку его пересечения с SA.
Все четыре вершины сечения получены – строим сечение.

Использованный на первом шаге построения приём часто называют методом вспомогательных плоскостей. Рассмотрим ещё один пример, где он используется.

Пример 4

Рассмотрим теперь самый общий случай, когда все три точки K, L и M лежат на гранях пирамиды.

Модель 4

Как и в предыдущем случае проведём вспомогательную плоскость CKM, которая пересекает рёбра SA и SB в точках E и F соответственно.
Построим в этой плоскости прямую KM — след плоскости сечения – и отметим точку P пересечения KM с EF.
Точка P, как и L, лежит в плоскости SAB, поэтому прямая PL будет следом сечения в плоскости SAB, а её точки пересечения с SA и SB – вершинами сечения.
Теперь можно построить следы сечения в плоскостях SAC и SBC и отметить их точки пересечения с рёбрами AC и BC.
Все четыре вершины сечения получены – строим сечение.

С помощью метода вспомогательных плоскостей можно строить сечения, «не выходя» за пределы многогранника. Вернёмся в связи с этим к примеру 2.

Пример 2’

Точки K и M лежат на боковых рёбрах пирамиды, а точка L – на стороне основания. Построим сечение, «не выходя» за пределы многогранника.

Модель 5

Проведём вспомогательную плоскость SLB и в ней отрезок LM, который принадлежит плоскости сечения.
Проведём ещё одну вспомогательную плоскость BCK и построим точку пересечения SL и CK – точку E. Эта точка принадлежит обеим вспомогательным плоскостям.
Отметим точку пересечения отрезков LM и EB – точку F. Точка F лежит в плоскости сечения и в плоскости BCK.
Проведём прямую KF и отметим точку пересечения этой прямой c BC – точку N. Эта точка будет недостающей четвёртой вершиной сечения.
Все четыре вершины сечения получены – построим сечение.

Можно использовать ту же самую идею иначе. Проведём в начале анализ построенного сечения – т.е. начнём с конца. Допустим, что по точкам K, L и M построено сечение KLMN.

Модель 6

Анализ

Обозначим через F точку пересечения диагоналей четырёхугольника KLMN. Проведём прямую CF и обозначим через F₁ точку её пересечения с гранью SAB. С другой стороны, точка F₁ совпадает с точкой пересечения прямых KB и MA, исходя из чего её и можно построить.

Построение

Проведём прямые KB и MA и отметим точку их пересечения F₁.
Проведём прямые CF₁ и LM и отметим точку их пересечения F.
Проведём прямую KF и отметим точку её пересечения с ребром CB – точку N. Эта точка будет недостающей четвёртой вершиной сечения.
Все четыре вершины сечения получены – построим сечение.

Использованный в этом решении приём называют методом внутреннего проектирования. Построим с его помощью сечение из примера 4, когда все три точки лежат на гранях пирамиды.

Пример 3’

Точки K, L и M лежат на гранях пирамиды. Построим сечение, «не выходя» за пределы многогранника.

Допустим, что сечение уже построено.

Модель 7

Анализ

Пусть плоскость сечения пересекает ребро CB в точке P. Обозначим через F точку пересечения KM и LP. Построим центральные проекции точек K, F и M из точки C на плоскость SAB и обозначим их K₁, F₁ и M₁. Точки K₁ и M₁ легко находятся, а точку F₁ можно получить как точку пересечения K₁M₁ и LB.

Построение

Построим центральные проекции точек K и M из точки C на плоскость SAB и обозначим их K₁ и M₁.
Проведём прямые K₁M₁ и LB и отметим точку их пересечения F₁.
Проведём прямые CF₁ и KM и отметим точку их пересечения F.
Проведём прямую LF и отметим точку её пересечения с ребром CB – точку P. Это первая вершина искомого сечения.
Проведём прямую PM и отметим точку её пересечения с ребром SB. Это вторая вершина сечения.
Из второй вершины проведём прямую через точку L и найдём третью вершину сечения.
Из третьей вершины проведём прямую через точку K и найдём четвёртую вершину сечения.
Все четыре вершины сечения получены – построим сечение.

УПРАЖНЕНИЯ

Более сложные упражнения помечены звёздочкой.

1. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M (см. модели).

2. Постройте сечение куба плоскостью, проходящей через точки K, L и M (см. модели).

3. На рёбрах пирамиды SABC отмечены точки K, L и M. Постройте:

4*. На рёбрах пирамиды SABC отмечены точки K, L, M, P, N и Q. Постройте:

5*. На ребре AB треугольной пирамиды SABC отмечена точка K. Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной BC и SA.

Модель

6*. На рёбрах AB и CS треугольной пирамиды SABC отмечены точки K и M. Постройте сечение пирамиды плоскостью, проходящей через точки K и M и параллельной AS.

Модель

7*. Постройте сечение треугольной пирамиды плоскостью, проходящей через точки K, L и M, лежащих в плоскостях её боковых граней (но не на самих гранях!).

Модель

8*. На плоскости проведены три луча с общим началом – a, b и с – и отмечены три точки – A, B и C. Постройте треугольник, вершины которого лежат на этих лучах, а стороны проходят через точки A, B и C.

Модель

‎App Store: iCrosss

iCrosss является уникальным образовательным приложением, которое поможет вам легко изучить стереометрию. Оно позволяет строить сечения каждого из имеющихся многогранников заданной вами плоскостью. Плоскость может быть построена по трем точкам, установленным на поверхности многогранника. Приложение поддерживает такие виды многогранников: правильные многогранники, пирамиды, призмы, антипризмы и Архимедовы тела и двойственные многогранники. Многогранники отображаются в 3D, что позволяет вращать их в любом направлении. Использованный для отображения стиль школьной доски, мела и специально подобранные шрифты служат лучшему восприятию информации. Для построения сечения вам нужно поставить три точки на поверхности многогранника, которые зададут плоскость сечения.

Существует несколько режимов просмотра, которые можно использовать при построении сечения: 3D-режим, режим эпюра (3 проекции), 3D-режим разреза. 3D-режим разреза доступен только когда вы уже построили сечение. В этом режиме вы можете выбрать одну из двух частей исходного многогранника продолжать работу с ней. Доступна возможность печати и отправки по почте многогранника или его сечения. Также вы можете просмотреть информацию о выбранном многограннике, которая включает в себя краткое описание, число граней, вершин, ребер, веб-ссылку для получения дополнительной информации и полезные формулы. Многогранники организованы в виде простого списка сгруппированного по категориям. Более того, вы можете выбрать многогранники, которые вас интересуют и добавить их в список избранного. Избранные многогранники отмечены звездочкой в списке. Также получить доступ к ним можно при помощи списка избранного.

Чтобы быстро разобраться с приложением, используйте режим обучения, он продемонстрирует вам все основные возможности приложения.
Существует несколько режимов просмотра, которые можно использовать при построении сечения: 3D-режим, режим эпюра (3 проекции), 3D-режим разреза. 3D-режим разреза доступен только когда вы уже построили сечение. В этом режиме вы можете выбрать одну из двух частей исходного многогранника продолжать работу с ней. Доступна возможность печати и отправки по почте многогранника или его сечения. Также вы можете просмотреть информацию о выбранном многограннике, которая включает в себя краткое описание, число граней, вершин, ребер, веб-ссылку для получения дополнительной информации и полезные формулы. Многогранники организованы в виде простого списка сгруппированного по категориям. Более того, вы можете выбрать многогранники, которые вас интересуют и добавить их в список избранного. Избранные многогранники отмечены звездочкой в списке. Также получить доступ к ним можно при помощи списка избранного.

Чтобы быстро разобраться с приложением, используйте режим обучения, он продемонстрирует вам все основные возможности приложения.

Примеры построения сечений многогранников

Как известно, любой экзамен по математике содержит в качестве основной части решение задач. Умение решать задачи – основной показатель уровня математического развития.

Достаточно часто на школьных экзаменах, а так же на экзаменах, проводимых в ВУЗах и техникумах, встречаются случаи, когда ученики, показывающие хорошие результаты в области теории, знающие все необходимые определения и теоремы, запутываются при решении весьма простых задач.

За годы обучения в школе каждый ученик решает большое число задач, но при этом для всех учеников задачи предлагаются одни и те же. И если некоторые ученики усваивают общие правила и методы решения задач, то другие, встретившись с задачей незнакомого вида, даже не знают, как к ней подступиться.

Одной из причин такого положения является то, что если одни ученики вникают в ход решения задачи и стараются осознать и понять общие приёмы и методы их решения, то другие не задумываются над этим, стараются как можно быстрее решить предложенные задачи.

Многие учащиеся не анализируют решаемые задачи, не выделяют для себя общие приёмы и способы решения. В таких случаях задачи решаются только ради получения нужного ответа.

Так, например, многие учащиеся даже не знают, в чём суть решения задач на построение. А ведь задачи на построение являются обязательными задачами в курсе стереометрии. Эти задачи не только красивы и оригинальны в методах своего решения, но и имеют большую практическую ценность.

Благодаря задачам на построение развивается способность мысленно представлять себе ту или иную геометрическую фигуру, развивается пространственное мышление, логическое мышление, а так же геометрическая интуиция. Задачи на построение развивают навыки решения проблем практического характера.

Задачи на построения не являются простыми, так как единого правила или алгоритма для их решения не существует. Каждая новая задача уникальна и требует индивидуального подхода к решению.

Процесс решения любой задачи на построение – это последовательность некоторых промежуточных построений, приводящих к цели.

Построение сечений многогранников базируется на следующих аксиомах:

1) Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в данной плоскости;

2) Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Теорема: если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.

Примеры построения сечений многогранников

Построить сечение многогранника плоскостью, проходящей через точки А, В и С. Рассмотрим следующие примеры.

Метод следов

I. Построить сечение призмы плоскостью, проходящей через данную прямую g (след) на плоскости одного из оснований призмы и точку А.

Случай 1.

Точка А принадлежит другому основанию призмы (или грани, параллельной прямой g) – секущая плоскость пересекает это основание (грань) по отрезку ВС, параллельному следу g.

Случай 2.

Точка А принадлежит боковой грани призмы:

1) строится точка D, в которой плоскость грани пересекает данный след g;

2) проводится прямая через точки А и D.

Отрезок ВС прямой AD и есть пересечение данной грани с секущей плоскостью.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. И т. д.

Случай 3.

Построение сечения четырехугольной призмы плоскостью, проходящей через прямую g в плоскости нижнего основания призмы и точку А на одном из боковых ребер.

II. Построить сечение пирамиды плоскостью, проходящей через данную прямую g (след) на плоскости основания пирамиды и точку А.

Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.

Случай 1.

Если точка А принадлежит грани, параллельной прямой g, то секущая плоскость пересекает эту грань по отрезку ВС, параллельному следу g.

Случай 2.

Если точка А, принадлежащая сечению, расположена на грани, не параллельной грани следу g, то:

1) строится точка D, в которой плоскость грани пересекает данный след g;

2) проводится прямая через точки А и D.

Отрезок ВС прямой АD и есть пересечение данной грани с секущей плоскостью.

Случай 3.

Построение сечения четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из боковых ребер.

Задачи на построение сечений через точку на грани

1. Построить сечение тетраэдра АВСD плоскостью, проходящей через вершину С и точки М и N на гранях АСD и АВС соответственно.

Точки С и М лежат на грани АСD, значит, и прямая СМ лежит в плоскости этой грани (рис. 1).

Пусть Р – точка пересечения прямых СМ и АD. Аналогично, точки С и N лежат в грани АСВ, значит прямая СN лежит в плоскости этой грани. Пусть Q – точка пересечения прямых СN и АВ. Точки Р и Q принадлежат и плоскости сечения, и грани АВD. Поэтому отрезок РQ – сторона сечения. Итак, треугольник СРQ – искомое сечение.

2. Построить сечение тетраэдра АВСD плоскостью MPN, где точки M, N, P лежат соответственно на ребре АD, в грани ВСD и в грани АВС, причем MN не параллельно плоскости грани АВС (рис. 2).

Остались вопросы? Не знаете, как построить сечение многогранника?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

Чертеж в разрезе — Designing Buildings Wiki

«Чертеж в разрезе», «разрез» или «чертеж в разрезе» показывает вид конструкции, как если бы она была разрезана пополам или разрезана по другой воображаемой плоскости.

Для зданий это может быть полезно, поскольку дает вид через пространства и окружающие конструкции (обычно в вертикальной плоскости), который может выявить взаимосвязи между различными частями зданий, которые могут быть не видны на чертежах плана. Чертежи плана на самом деле являются разновидностью разреза, но они прорезают здание в горизонтальной, а не вертикальной плоскости.

Направление плоскости, через которую разрезается разрез, часто отображается на чертежах плана и фасадах линией из длинных и коротких штрихов, называемой плоскостью разреза. Если есть несколько секций, линия может иметь буквы на каждом конце, указывающие имя чертежа разреза, и стрелку, показывающую направление, в котором принимает вид.

Линия разреза может проходить через здание косвенным путем, если это помогает показать наиболее важные элементы или перекрестки в здании, как показано на рисунке ниже.

В этом случае чертеж сечения будет называться «Разрез B-B».

Затенение, перекрестная штриховка или другие стили заливки и / или более толстые линии могут использоваться для обозначения прорезанных частей конструкции, таких как стены, крыши и полы.

Масштаб чертежа в разрезе будет зависеть от размера нарисованного здания и уровня детализации, который необходимо показать. Разделы могут отображать все здание или могут быть сосредоточены на конкретном компоненте, соединении или сборке.В этом случае они могут быть похожи на сборочные чертежи, но отличаться тем, что обычно не содержат деталей фактического процесса сборки.

Различные типы перекрестной штриховки могут использоваться для различения различных типов компонентов на подробных чертежах в разрезе. Существуют стандарты штриховки, которую следует использовать на некоторых распространенных материалах, например, двойные диагональные линии указывают на кирпичную кладку, волна указывает на изоляцию и так далее.

Перспективные разрезы включают трехмерную проекцию пространств за плоскостью сечения и могут использоваться для графической иллюстрации взаимосвязи между пространствами и компонентами здания, а также их глубины, что может быть очень полезно при попытке интерпретировать сложный дизайн.

Все чаще чертежи разрезов могут создаваться автоматически с помощью программного обеспечения для трехмерного моделирования, включая перспективные разрезы, где это необходимо.

[править] Статьи по теме «Проектирование зданий» Wiki

[править] Внешние ссылки

«Справочник по строительству» (6-е изд.), ЧАДЛИ, Р. и ГРИНО, Р., Баттерворт-Хайнеманн (2007)

Архитектура 101: Что такое чертеж сечения?

Architizer Journal поддерживается читателем.Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Узнать больше

Мы представили удивительную новую книгу архитекторов LTL Manual of Section с чертовски сложной (или невероятно простой?) Викториной. Если вы еще не проверяли свои архитектурные знания, сделайте это сейчас.

Руководство раздела предлагает исчерпывающую галерею орфографических срезов известных зданий, но оно идет дальше: на первых страницах сборника этот раздел анализируется как инструмент архитектурного представления и выкристаллизовывается определение этого элементарного типа чертежа.

В следующем отрывке архитекторы Пол Льюис, Марк Цурумаки и Дэвид Дж. Льюис возвращаются к основам и задают фундаментальный вопрос, который должен оказаться информативным как для студентов-архитекторов, так и для опытных профессионалов: что такое секция? Читайте окончательное определение.

Архитектура 101: Что такое чертеж сечения?

«Мы начинаем с, казалось бы, очевидного вопроса:« Что такое секция? »В отношении архитектурного чертежа термин секция обычно описывает разрез в корпусе здания перпендикулярно линии горизонта.Чертеж разреза — это чертеж, на котором показан вертикальный разрез, обычно вдоль первичной оси, объекта или здания.

В разрезе одновременно видны его внутренний и внешний профили, внутреннее пространство и материал, мембрана или стена, отделяющая интерьер от внешнего, обеспечивая вид объекта, который обычно не виден. Эта изобразительная техника принимает различные формы и графические замыслы, каждая из которых разработана для иллюстрации различных форм архитектурных знаний, от строительных секций, в которых используется сплошная заливка или поче, чтобы подчеркнуть профиль формы, до деталей конструкции, которые изображают материалы через линии и графические условные обозначения.

Пантеон, Рим, Италия; через Scribblelive

Comédie-Française, Charles de Wailly, 1770

В ортогональном разрезе интерьер также описывается через внутренние фасады основных архитектурных поверхностей, в то время как комбинация разреза с перспективой подробно описывает интерьер как пространство с использованием методов перспективной проекции.

Поскольку раздел начинается с визуализации того, что нельзя увидеть напрямую, он остается абстрагированным от доминирующего способа понимания архитектуры через фотографии и визуализации.Разделы предоставляют уникальную форму знания, которая по необходимости смещает акцент с изображения на исполнение, с поверхности на пересечение структуры и материальности, составляющее тектоническую логику архитектуры.

Предложение по скоростной автомагистрали Нижнего Манхэттена от Пола Рудольфа , 1972; любезно предоставлено Библиотекой Конгресса

Барбакан, Лондон, Англия; через mbds

В то же время раздел демонстрирует обмен между множеством аспектов воплощенного опыта и архитектурного пространства, делая явным пересечение масштаба и пропорции, зрения и обзора, прикосновения и досягаемости, которые визуализируются в вертикальном измерении (в отличие от сверху. вниз).В разрезе показаны внутренние фасады стен и поверхностей, сочетающие — для изучения и исследования — структуру и орнамент, оболочку и интерьер.

Планы и разрезы аналогичны условным обозначениям и служат важной точкой сравнения. Оба изображают отношения, не воспринимаемые человеческим глазом напрямую, между массой здания и пространством. Оба описывают разрезы — один горизонтальный, другой вертикальный. Горизонтальное деление плана в первую очередь прорезает стены, а не полы.С другой стороны, секции могут показывать прорези как в стенах, так и в полу и организовывать пространство в соответствии с размером и масштабом стоящей человеческой фигуры.

Слева: Природный город от WORKac, 2012; любезно предоставлено WORKac. Справа: Park Tower от LTL Architects, 2004 г .; любезно предоставлено LTL Architects

Часть секции Park Tower от LTL Architects; через LTL Architects

Обычно утверждается, что планы являются средоточием проектного агентства, а разделы понимаются как средство для проявления эффектов плана через структуру и ограждение.По сравнению с типами планов, которые различаются своими пространственными последствиями, типы разрезов обычно идентифицируются по масштабу их разреза: разрезы участка, разрезы здания, разрезы стен, разделы деталей.

Секции стен и деталей передают технические проблемы с использованием графических условных обозначений линий, штриховок и тонов, а также изображают системы материалов и тектонику. Разделы сайта подчеркивают массивность построенной формы и ее взаимосвязь с окружающей средой и уменьшают роль внутреннего пространства.Но именно в строительной части возникает ряд важных вопросов, включая формальные, социальные, организационные, политические, пространственные, структурные, тепловые и технические ».

Хотите узнать больше? Чтобы заказать копию «Руководства по разделу», , нажмите здесь .

Типы чертежей разрезов — Строительные чертежи

Можно нарисовать сечения всего здания, внутреннего пространства или объекта. Они называются полными разделами. Однако, если нужно проиллюстрировать только изолированную область, можно нарисовать и частичный разрез.Разделы можно разрезать разными способами, чтобы отображалась более подробная информация. Секция может быть прорезана на всем протяжении здания (так называемая секция здания) или только через стену (секция стены).

Могут понадобиться и то, и другое, потому что небольшой масштаб и сложность строительной секции обычно означает, что материалы и детали, относящиеся к стенам, не могут быть там нарисованы. Символ на секции здания, показанной на Рисунке 8-4, отмечает площадь стены, которую необходимо увеличить. Сечение стены (рис. 8-5) нарисовано, чтобы точно показать многие детали и материалы, необходимые для сборки.

фин. напольный плавник. жалюзи пол

ДЕРЕВЯННЫЕ ДОМА

1/16 ‘НАБ. ХОРОШАЯ ОБОЛОЧКА

р-40 изоляция

ДЕРЕВЯННЫЕ ДОМА

1/16 ‘НАБ. ХОРОШАЯ ОБОЛОЧКА

р-40 ребро изоляционное. напольный плавник. Louer floor

/2 «ceiuns chase

Рис. 8-6. В увеличенном виде может быть просто показана часть сборки здания, чтобы изобразить определенные детали, такие как конструкция встроенного шкафа.

/2 «ceiuns chase

ОТДЕЛЕНИЕ СТЕНЫ

Рисунок 8-5 Это увеличенная часть стены, обозначенная на разрезе здания на Рисунке 8-4.

НАБОР ВЫШЕ

раскрыть — покрасить в черный цвет дверцы шкафа —

2 регулируемые полки ■ Блокировка из МДФ 3/4 дюйма, законченная отделка drtujall

РАЗДЕЛ ШКАФА

НАБОР ВЫШЕ

раскрыть — покрасить в черный цвет дверцы шкафа —

2 регулируемые полки ■ 3/4 дюйма МДФ с блокировкой из бетона с отделкой «drtujall» отделка нижней стороны шкафа «для соответствия вертикальным поверхностям в полную высоту обратная заслонка

МДФ 3/4 дюйма с выдвижным ящиком на кромке 1-1 / 2 ‘с Accuride (OR equal / glides

Тяги для проволоки 3 фута из нержавеющей стали — тип.• нижний ящик «шкафы регулируемая полка f3 / 4 ‘мдф; на системе отверстий под штифт — с шагом 1/4 дюйма с хромированными опорами для полок дверцы шкафа — МДФ 3/4 дюйма и основание

В дополнение к секциям здания и стен может также потребоваться провести секцию через встроенные или нестандартные компоненты в пространстве, такие как стеллажи, стойки регистрации, стойки регистрации, стойки, витрины, шкафы и прилавки. На Рис. 8-6 показана секция встроенного шкафа. Эти типы разделов более подробно обсуждаются в главе 9.

СЕКЦИЯ ШКАФА

На чертежах внутренних конструкций иногда термины «раздел» и «деталь» меняются местами, что вызывает некоторую путаницу. Например, разрезы небольших участков конструкции или объектов часто называют деталями. Но детали не всегда прорисовываются в разрезе. Они также могут включать увеличенные части плана этажа или фасада.

Масштаб чертежей в разрезе может варьироваться от y% «до 3» (от 3,17 мм до 76 мм), в зависимости от размера бумаги для рисования, размера здания (или компонента) и желаемых характеристик, которые необходимо показать.Конкретная информация, отображаемая в разделе, может варьироваться в зависимости от того, является ли это проектным или строительным чертежом. На строительных чертежах показаны только те элементы или компоненты пространства, которые встроены в конструкцию или прикреплены к ней. Подвижная мебель на этом типе чертежа не показана.

Прочтите здесь: Стандарты разработки

Была ли эта статья полезной?

Как создать свой первый раздел темы Shopify — Разработка темы Shopify

Предоставление вашим клиентам творческого контроля является ключевым моментом, особенно когда они хотят иметь возможность настраивать свой магазин.Параметры раздела Shopify — мощные инструменты для персонализации сайта.

Клиенты ожидают, что пользовательский интерфейс будет удобным и интуитивно понятным, а это означает, что правильный раздел или блок в нужном месте может иметь огромное влияние на конверсию.

Если вы создаете тему Shopify с нуля или настраиваете тему для клиента, вам нужно будет создать несколько разных типов разделов, которые будут различаться в зависимости от контекста. С помощью блоков вы можете перейти в роль куратора и предоставить своим продавцам выбор решать, какой контент они размещают и где он появляется.

В этой статье мы рассмотрим, как начать создавать различные типы тематических разделов, чтобы вы могли помочь своим клиентам настроить свой магазин. Мы также рассмотрим два функциональных примера блоков и изучим различные способы раскрытия их потенциала.

Узнайте больше о разработке тем Shopify, работе с Shopify Theme Kit или метаполях Shopify.

Развивайте свой бизнес с помощью партнерской программы Shopify

Предлагаете ли вы услуги по маркетингу, настройке или веб-дизайну и разработке, партнерская программа Shopify настроит вас на успех.Присоединяйтесь бесплатно и получите доступ к возможностям распределения доходов, инструментам для развития вашего бизнеса и увлеченному коммерческому сообществу.

Зарегистрироваться

Что такое тематические разделы?

Разделы — это модульные настраиваемые элементы страницы, которые могут иметь определенные функции. Представленные на Unite 2016 разделы могут быть статически, включены в шаблоны темы (например, верхний и нижний колонтитулы), или они могут быть динамически добавлены на домашнюю страницу темы из редактора тем.

Найдите свой новый любимый редактор Markdown в нашем обзоре.

Создание статического раздела в вашей теме Shopify

Статический раздел звучит так же, как и его название — это фиксированный компонент, который можно настроить с помощью редактора тем. Положение этого раздела на странице заблокировано в зависимости от того, где он был назначен в шаблоне страницы. В каком-то смысле это как отрывок, но со сверхспособностями! Разделы добавляются в шаблоны Liquid с переменной {% section 'header'%} вместо {% include 'my-snippet-file'%} .

Например, вы можете захотеть создать раздел, который позволяет клиентам добавлять произвольный текст на свою страницу корзины. Это особенно полезно для продавцов, время доставки которых меняется в зависимости от сезона, поскольку позволяет добавлять информацию о доставке.

Создание раздела, позволяющего клиентам добавлять собственный текст на страницу корзины, может быть очень полезным для всех, чье время доставки меняется в зависимости от сезона.

Когда вы создаете новый раздел в редакторе файлов темы, автоматически создается шаблон с тегами схемы, CSS и Javascript.В теги схемы мы добавим JSON, который определит, как редактор тем «читает» наш контент. Теги CSS и Javascript можно использовать для добавления стиля или функций, специфичных для этого раздела, но по умолчанию этот раздел будет извлекать свои стили из основной таблицы стилей темы.

Чтобы добавить контент в раздел, вам нужно добавить теги HTML и Liquid в самый верх файла. Затем ваши теги Liquid могут быть определены в схеме, поэтому раздел можно настроить в редакторе тем.Вы можете увидеть различные значения, которые можно добавить в настройки схемы, в нашей документации.

В приведенном выше примере я создал раздел под названием text.liquid , в котором есть настраиваемый заголовок, а также настраиваемое поле для расширенного текста. Вы можете видеть, что теги Liquid в HTML соответствуют настройкам в разделе схемы. В этом примере я создал простое поле текст и поле richtext , но вы можете добавить широкий диапазон типов вывода, в зависимости от требований вашего клиента.Другие допустимые типы ввода включают image_picker , radio , video_url и font .

В настройках схемы id относится к определяемому тегу Liquid, тип назначает тип создаваемого нами вывода, ярлык определяет имя для этого вывода, а по умолчанию назначает заполнитель .

Я хочу, чтобы этот раздел текстового поля отображался на странице корзины, поэтому мне нужно добавить {% section 'text'%} в корзину .Файл шаблона liquid . Это работает аналогично тому, как вы добавляете фрагмент в шаблон страницы.

Теперь, когда мы переходим в редактор тем и переходим на страницу корзины, мы видим, что этот раздел появляется под основным содержимым страницы корзины и над нижним колонтитулом. Вот как выглядит результат:

Суть ниже представляет собой весь код этого раздела, и я бы посоветовал вам поэкспериментировать с различными стилями и типами разделов, чтобы увидеть, что лучше всего подходит для магазинов ваших клиентов.

Вам также может понравиться: Как использовать Liquid для создания пользовательских шаблонов целевых страниц.

В отличие от статических разделов, динамические разделы можно перемещать в разные позиции на главной странице. Эта функция перетаскивания означает, что при создании настраиваемых динамических разделов будет разблокирован широкий спектр параметров для персонализации магазинов. Вы можете создавать подвижные разделы для видео, продуктов или галерей изображений.

Чтобы сделать динамический раздел, нам просто нужно добавить пресеты в файл раздела.Предустановки определяют способ отображения раздела в редакторе тем, и предустановки должны иметь имя и категорию .

После добавления этих предустановок разделы будут автоматически доступны для добавления на страницу индекса. Предустановки не включаются в базовый файл, когда вы щелкаете Добавить новый раздел в редакторе тем, но добавить их вручную очень просто.

Например, я создал раздел для кнопки призыва к действию с тегами Liquid, чтобы определить имя (заголовок), URL и текст кнопки в разделе схемы.

Здесь отличаются предустановки в конце массива схемы . Shopify теперь автоматически распознает, что это динамический раздел, который можно добавить на страницу индекса. Это означает, что когда мы переходим в редактор тем и добавляем раздел на домашнюю страницу, мы видим следующее:

Этот раздел теперь можно перемещать по странице в разные позиции.

Теперь вы можете создавать другие динамические разделы, которые можно перемещать по странице индекса, используя разные типы вывода, и ваши клиенты будут иметь полную свободу действий над тем, как выглядит их домашняя страница.

`Что такое секционные блоки?`

Мы можем думать о блоках как о секциях внутри секций. Как мы видели выше, разделы можно перемещать по главной странице. Что отличает блоки от разделов, так это то, что элементы можно перемещать внутри раздела.

В разделы могут быть добавлены различные типы блоков, и положение этих блоков может быть изменено в Редакторе тем. Блок может быть изображением, видео, настраиваемым текстом или любым из параметров типов настроек ввода, показанных ниже.

Теперь ваши клиенты могут перемещать элементы по разделу, а не ограничиваться определенным макетом. Они могут добавлять элементы в соответствии с установленными вами правилами. Это добавляет еще один уровень персонализации, который позволит вашим клиентам создать идеальный магазин.

Блоки

можно использовать в динамических и статических разделах, и важно подумать, какие типы блоков будут лучше всего работать в определенных областях. Возможность добавления блока информационного бюллетеня может не подходить, например, в динамическом разделе, но возможность добавления настраиваемого текстового блока может быть полезна в этом контексте.

Поскольку блоки могут быть повторяемыми, очень важно установить ограничения там, где это необходимо, чтобы вы могли избежать любых ошибок пользовательского интерфейса. Например, вы можете создать блок с видеоконтентом. Хотя может возникнуть соблазн разрешить добавление большого количества видеоблоков в этот раздел, это повлияет на время загрузки сайта, а также приведет к загромождению страницы. Вместо этого было бы разумнее ограничиться одним видео. С большой властью приходит большая ответственность!

`Добавление блоков в динамический раздел`

Первый раздел, который мы рассмотрим, - это динамический раздел с блоками кнопок призыва к действию, которые можно перемещать.Это может быть полезно, если вашим клиентам нужно предоставить клиентам разные варианты, например, загрузить подкаст или электронную книгу.

В приведенном ниже примере вы можете увидеть элементы, которые нужно вывести: заголовок для всего раздела с блокировочными переменными для ссылки и текст ссылки.

Как мы видели с разделами, настройки блоков добавляются в файлы темы, а затем определяются в тегах схемы. С блоками синтаксис этих настроек (или переменных Liquid) выглядит как {{block.settings.id}} , где ID указан в разделе схемы.

Итак, для нашего блока, в котором есть ссылка и текст ссылки, мы увидим:

Что также очень важно, контейнер заключен в цикл for , который выполняет итерацию по каждому блоку в section.blocks . Это позволит правильно отображать блоки в редакторе тем. Вы можете увидеть это ниже:

Схема Область файла раздела использует JSON для определения различных значений каждого параметра и блока.Это работает так же, как мы видели ранее, когда рассматривали создание раздела, но с несколькими новыми дополнениями.

В настройках основной схемы мы можем назначить максимальное количество блоков в разделе. Я установил это значение на три, но это может быть любое число. В зависимости от типа вывода вы можете по-разному ограничить или «ограничить» возможное количество блоков, чтобы страница не была загромождена.

Ниже этого, поскольку это динамический раздел, у нас есть предустановок , которые позволят добавить этот раздел на страницу индекса.Мы можем определить, сколько блоков будет отображаться по умолчанию, добавив блоки из предустановок . Это означает, что появятся две кнопки призыва к действию, и, если вы помните, я установил максимум на три, поэтому можно добавить дополнительный блок.

Итак, давайте взглянем на редактор тем и посмотрим, как он будет выглядеть, когда мы попробуем его:

`Добавление блоков в статический раздел`

Добавляя различные параметры к блокам, веб-дизайнеры действительно могут вывести настройку на новый уровень. Это означает, что клиенты могут выбирать различные типы блоков в разделе и изменять расположение этих блоков.

Такая гибкость может быть особенно полезна при настройке фиксированного или статического раздела, например нижнего колонтитула. Теперь ваши клиенты могут добавлять видео, текст, изображения и многое другое в одном разделе, а также изменять последовательность этих элементов. Перед блоками, если вашему клиенту нужно было внести такие изменения, это потребовало бы покопаться в коде. Но теперь мы можем добиться всего этого из редактора тем.

Используя теги case / when управления потоком, мы можем настроить различные параметры для включения типов вывода.Например, если мы хотим, чтобы в нижнем колонтитуле были параметры блокировки для настраиваемого текста, значков социальных сетей или формы подписки на информационный бюллетень, код для этих параметров блокировки будет выглядеть следующим образом:

Как вы можете видеть выше, мы снова оборачиваем блоки в теги логики Liquid, чтобы обеспечить их отображение в редакторе тем, но мы также извлекаем контент из-за пределов файла нижнего колонтитула. В случае с новостной рассылкой и социальными ссылками мы включаем код из фрагментов в файлы темы. Это означает, что вы можете добавлять функциональные возможности к блокам, которые существуют в папке ваших фрагментов.

Мы также можем создать условия для макета с помощью тегов потока управления, чтобы вы могли точно определить, как блоки будут отображаться при их добавлении. В этом примере я устанавливаю максимальное количество блоков равным шести, и я назначаю определенную ширину столбца для каждого возможного количества блоков.

В разделе схемы мы можем установить ограничения на уровне отдельного блока. Если ваш клиент добавил несколько версий своих социальных иконок в нижний колонтитул, это может сбить с толку клиентов, поэтому этого можно избежать, добавив ограничение в один для этого конкретного блока.Продавец по-прежнему сможет настроить, где будет отображаться социальный блок в разделе, но можно добавить только одну версию блока. Вот как будет выглядеть добавление этого конкретного лимита:

Полный файл раздела для этого нижнего колонтитула будет выглядеть так:

После того, как этот раздел будет включен в theme.liquid , вывод в редакторе тем будет выглядеть следующим образом:

Вам также могут понравиться: 4 основных совета по созданию вашей первой темы Shopify.

`Расширение возможностей для творчества`

Теперь, когда вы увидели, как легко добавлять разделы и блоки в свои темы, вы можете добавлять бесконечные возможности в магазины своих клиентов. Использование предустановок означает, что разделы освобождаются от застревания на одной позиции на главной странице, что позволит продавцам строить свой магазин именно так, как они хотят, - с определенным указанием от вас.

Вы экспериментировали со статическими и динамическими разделами для разработки тем? Мы хотели бы услышать о вашем опыте в комментариях ниже.

`Семь советов, которые помогут вам выбрать идеальную секцию для построения на`

Есть несколько шагов к строительству нового дома, и выбор секции - одно из первых, что вам нужно сделать. Это также одно из самых важных.

Выбор правильной секции может упростить сборку и обеспечить комфортное и безопасное место в вашем новом доме. С другой стороны, неправильный выбор - верный способ превратить простую сборку в кошмар.

1.Подумайте о доступе

Строительство дома требует определенного уровня доступа к сайту, который может быть заблокирован или затруднен деревьями, линиями электропередач, общими подъездными путями и другими препятствиями. Перед покупкой раздела позвоните нам, чтобы еще раз проверить доступность вашего сайта.

2. Проверьте аспект и форму

Секции, затененные высокими зданиями или выходящие на юг, могут затруднить попадание естественного света в новый дом. Поищите участок на северной стороне, залитый светом весь день, если можете.

Также следует учитывать форму секции. Вообще говоря, широкая квадратная земля проще и лучше и обеспечивает большую гибкость при проектировании дома, тогда как длинные узкие участки менее идеальны.

Перед покупкой раздела узнайте расположение инженерных коммуникаций

3. Учесть расположение инженерных коммуникаций

Подключение таких коммуникаций, как вода и электричество, к новому дому стоит денег, и чем дальше эти коммуникации находятся от дома, тем дороже это будет.Прежде чем покупать какой-либо раздел, проверьте, как далеко находятся инженерные сети, и получите представление о том, сколько будет стоить их подключение.

4. Получить геотехнический отчет

Секция - это больше, чем верхний дюйм травы и почвы. Вы также покупаете и строите землю под травой, поэтому важно знать, что там происходит. Геотехнический отчет расскажет вам все, что вам нужно знать об устойчивости участка и обычно требуется при подаче заявки на разрешение на строительство.

5. Еще раз проверьте заголовок

Всегда проверяйте право собственности на землю со своим юристом перед покупкой участка. Особенно важно отметить любые сервитуты на земле и наличие сервитутов, чтобы облегчить подключение услуг к участку.

Выбор правильной секции - один из самых важных шагов в любой сборке.

6. Исследование зонирования и ковенантов

Зонирование и / или соглашения могут ограничивать тип, размер или стиль дома, который вы можете построить на участке, поэтому вам необходимо знать о них перед покупкой.Ваш юрист может проверить их в офисе совета перед покупкой, чтобы убедиться, что вы не столкнетесь с неприятными сюрпризами после покупки.

7. Изучите риски и проблемы

Если ваш участок расположен на утесе или на берегу моря, вам необходимо знать, является ли край обрыва и сам участок устойчивым. Если поблизости есть ручей или источник воды, вам нужно узнать больше о том, есть ли это риск наводнения. Существует еще много возможных рисков, из-за которых ваш раздел может быть сложно построить и поддерживать, поэтому вам нужно убедиться, что вы понимаете их, прежде чем покупать.

Поговорите со своим местным советом и своим строителем, поскольку они могут предоставить вам информацию о факторах риска на вашем участке или поблизости от него. Хороший отчет по геотехнике также должен помочь ответить на ваши вопросы. Но если это не так, убедитесь, что вы продолжили расследование, чтобы избежать покупки проблемного раздела.

Выбор раздела может быть непростым, и многое зависит от вашего решения. Если вам нужна помощь или совет на любом этапе, не стесняйтесь обращаться к команде Golstruct Homes для разговора.Мы готовы помочь на каждом этапе вашего строительства, от выбора пустого раздела до передачи ключей от вашего нового дома.

`Как создать раздел заголовка вашего веб-сайта с помощью CSS (Раздел 1)`

Часть серии: Как создать сайт с помощью CSS

Это руководство является частью серии по созданию и настройке этого веб-сайта с помощью CSS, языка таблиц стилей, используемого для управления представлением веб-сайтов.Вы можете следить за всей серией, чтобы воссоздать демонстрационный веб-сайт и познакомиться с CSS, или использовать описанные здесь методы для других проектов веб-сайтов CSS.

Прежде чем продолжить, мы рекомендуем вам иметь некоторые знания HTML, стандартного языка разметки, используемого для отображения документов в веб-браузере. Если вы не знакомы с HTML, вы можете изучить первые десять руководств нашей серии "Как создать веб-сайт с помощью HTML", прежде чем начинать эту серию.

`Введение`

В этом руководстве вы воссоздадите верхний заголовок демонстрационного веб-сайта с помощью HTML и CSS.Вы можете заменить информацию Сэмми своей собственной, если хотите поэкспериментировать или изменить размер. Методы, которые вы здесь используете, могут быть применены к другим проектам веб-сайтов CSS / HTML.

`Предварительные требования`

Чтобы следовать этому руководству, убедитесь, что вы настроили необходимые файлы и папки, как описано в предыдущем руководстве из этой серии «Как настроить проект CSS и HTML».

`Добавление заголовка и подзаголовка к заголовку веб-страницы`

Заголовок нашего веб-сайта включает заголовок («Акула Сэмми»), подзаголовок («СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN») и небольшое изображение профиля.Эти элементы заключены в контейнер

, который стилизован с классом, определенным в таблице стилей CSS. Вы воссоздадите этот раздел, добавив текст и содержимое изображения, создав класс для контейнера , а затем обернув содержимое текста и изображения в контейнер , которому назначен вновь созданный класс. Чтобы добавить заголовок и подзаголовок на свой сайт, добавьте следующий выделенный фрагмент кода между открывающим и закрывающим тегами в индексе .html файл. Замените информацию Сэмми своей собственной, если вы хотите персонализировать свой сайт: index.html . . . Акула Сэмми СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN В этом фрагменте кода вы добавили заголовок Sammy the Shark и присвоили ему тег заголовка , поскольку это самый важный заголовок этой веб-страницы.Вы также добавили подзаголовок SENIOR SELACHIMORPHA AT DIGITALOCEAN и присвоили ему тег заголовка , поскольку это менее важный заголовок. Обратите внимание, что вы также добавили комментарий непосредственно перед заголовком. Комментарий используется для сохранения пояснительных примечаний к вашему коду для дальнейшего использования и не отображается браузером для посетителей сайта (если они не просматривают исходный код веб-страницы). В HTML комментарии записываются между и -> , как показано во фрагменте кода выше.Обязательно закройте свой комментарий закрывающим тегом комментария ( -> ), иначе весь ваш контент будет закомментирован. Добавление и стилизация небольшого изображения профиля в заголовок веб-страницы Затем вы добавите небольшое изображение профиля в раздел заголовка. Выберите фото профиля, которое хотите разместить на своем сайте. Если у вас нет фотографии профиля, вы можете использовать любое альтернативное изображение (например, изображение профиля Сэмми) или создать аватар на таком сайте, как Getavataaars.com. Выбрав изображение, сохраните его в папке изображений как small-profile.jpeg . Теперь добавьте изображение профиля на веб-страницу с помощью тега и атрибута src , назначенного пути к файлу изображения вашего профиля. Добавьте следующий выделенный фрагмент кода в файл index.html сразу после строки и перед строкой Sammy the Shark : Индекс .html . . . Акула Сэмми СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN Сохраните файл и загрузите его в браузере. Теперь ваша веб-страница должна иметь заголовок, подзаголовок, изображение профиля и фоновое изображение: Обратите внимание, что изображение имеет другой стиль, чем изображение профиля на демонстрационном сайте.Чтобы воссоздать форму, размер и границу изображения профиля на демонстрационном сайте, добавьте следующий набор правил в свой файл styles.css : styles.css . . . / * Изображение профиля верхнего заголовка * / .profile-small { высота: 150 пикселей; радиус границы: 50%; граница: сплошная 10px # FEDE00; } Прежде чем двигаться дальше, давайте рассмотрим каждую строку кода, которую вы только что добавили: / * Изображение профиля верхнего заголовка * / - это комментарий CSS для маркировки кода. Текст .profile-small относится к имени класса, который мы определяем с помощью набора правил. Этот класс будет применен к изображению профиля на следующем шаге. Декларация высота: 150 пикселей; устанавливает высоту изображения на 150 пикселей и автоматически регулирует ширину для сохранения пропорций размера изображения. Объявление border-radius: 50%; закругляет края изображения в круглую форму. Граница объявления : твердое тело 10px # FEDE00; дает изображению сплошную границу шириной 10 пикселей и имеет цветовой код HTML # FEDE00 . Сохраните файл и вернитесь к файлу index.html , чтобы добавить класс profile-small в свой тег , например: index.html . . . . . . Сохраните файл и перезагрузите его в браузере. Изображение вашего профиля теперь должно иметь высоту 150 пикселей, круглую форму и желтую рамку: На следующем шаге вы примените дополнительный стиль к заголовку, подзаголовку и изображению профиля в целом. Стилизация и позиционирование содержимого заголовка с помощью CSS Теперь вы определите класс с помощью CSS для стилизации и размещения содержимого заголовка. Вернитесь к файлу styles.css и создайте класс заголовка , добавив следующий набор правил CSS: styles.css . . . / * Заголовок * / .header { отступ: 40 пикселей; выравнивание текста: центр; фон: # f9f7f7; маржа: 30 пикселей; размер шрифта: 20 пикселей; } Давайте сделаем короткую паузу, чтобы понять каждую строку кода, который вы только что добавили: / * Заголовок заголовка * / - это комментарий, который не отображается в браузере. Текст .header - это имя селектора класса, который мы создаем и определяем с помощью этого набора правил. Поле : 40 пикселей; Объявление создает 40 пикселей заполнения между содержимым и границей элемента. выравнивание текста: по центру; Объявление перемещает содержимое в центр элемента. Вы также можете изменить значение на слева или справа , чтобы выровнять текст соответствующим образом. Фон : # f9f7f7; Объявление устанавливает цвет в соответствии с конкретным цветовым кодом HTML, используемым на демонстрационном веб-сайте.В этом руководстве не рассматриваются цветовые коды HTML в этой серии руководств, но вы также можете использовать названия цветов HTML ( черный , белый , серый , серебристый , фиолетовый , красный , фуксия , салатовый , оливковый , зеленый , желтый , бирюзовый , темно-синий , синий , бордовый и аква ), чтобы изменить значение цвета этого свойства. Поле : 30 пикселей; Объявление создает поле в 30 пикселей между периметром элемента и периметром области просмотра или любых окружающих элементов. Размер шрифта : 20 пикселей; Объявление увеличивает размер как заголовка, так и подзаголовка. Сохраните файл styles.css . Затем вы примените этот класс заголовка к содержимому вашего заголовка. Вернитесь на страницу index.html и оберните содержимое заголовка (которое вы уже добавили в свой файл) в тег , которому назначен заголовок класс : . . . Акула Сэмми СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN Сохраните файл index.html и перезагрузите его в браузере. Теперь ваш заголовок, подзаголовок и изображение профиля должны быть стилизованы внутри контейнера в соответствии с правилами, которые вы объявили в заголовке . class: Заключение Вы воссоздали раздел заголовка демонстрационного веб-сайта на своей веб-странице с помощью HTML и CSS.Вы добавили и стилизовали заголовок, подзаголовок и изображение профиля, используя контейнеры и классы CSS. Если вам интересно, вы можете продолжить изучение возможностей дизайна, изменив правила CSS для содержимого заголовка. Когда вы будете готовы, вы можете перейти к следующему руководству, где вы воссоздадите второй раздел демонстрационного сайта. Справочник по командам rpmbuild Когда RPM вызывается с опцией -b , процесс сборки пакета начато.Остальная часть команды будет точно определить, что должно быть построено и как далеко должна быть построена продолжить. В этой главе мы исследуем каждый аспект об / мин. -b . Команда сборки RPM должна содержать две дополнительные части информации, сверх " rpmbuild ": Имена одного или нескольких файлов спецификаций, представляющих программное обеспечение, которое будет в упаковке. Желаемый этап, на котором необходимо остановить сборку. Как мы обсуждали в главе 10, файл спецификации является одним входов в процесс сборки RPM. Он содержит информацию необходимо RPM для выполнения сборки и упаковки программного обеспечения. RPM проходит несколько этапов во время сборки. От указав, что процесс сборки должен остановиться на определенном этапе, конструктор пакетов может отслеживать прогресс сборки, вносить любые изменения необходимо, и перезапустите сборку.Начнем с рассмотрения различных этапы, которые можно указать в команде сборки. Команда rpmbuild -bp указывает RPM на выполнение самого первый шаг в процессе сборки. В файле спецификации этот шаг с маркировкой % преп . Каждая команда в % prepare Раздел будет выполнен, когда -bp вариант. Вот простой раздел % prepare из файла спецификации, который мы используется в главе 11: Эта секция подготовки % состоит из одного % настройка макрос.При использовании об / мин -bp относительно этого файла спецификации, мы можем точно увидеть, что % setup : # rpmbuild -bp cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + cd / usr / src / redhat / СТРОИТЬ + rm -rf cdplayer-1.0 + gzip -dc /usr/src/redhat/SOURCES/cdplayer-1.0.tgz + tar -xvvf - drwxrwxr-x root / пользователи 0 4 августа 22:30 1996 cdplayer-1.0 / -rw-r - r-- root / users 17982 10 ноября 01:10 1995 cdplayer-1.0 / КОПИРОВАНИЕ -rw-r - r-- root / users 627 10 ноября 01:10 1995 cdplayer-1.0 / ChangeLog … -rw-r - r-- root / users 2806 10 ноября 01:10 1995 cdplayer-1.0 / volume.c -rw-r - r-- root / users 1515 10 ноября 01:10 1995 cdplayer-1.0 / volume.h + [0 -ne 0] + компакт-диск cdplayer-1.0 + компакт-диск /usr/src/redhat/BUILD/cdplayer-1.0 + chown -R root.root. + chmod -R a + rX, g-w, o-w. + выход 0 # Во-первых, RPM подтверждает, что пакет cdplayer предмет этой сборки.Затем он устанавливает маску и запускает выполнение раздела % Prep . На данный момент % setup Макрос делает свое дело. Меняется каталог в область сборки и удаляет все старые копии дерево сборки cdplayer. Далее, установка % распаковывает исходники и использует tar для создания дерева сборки. Мы удалили полный список файлов, но будьте готовы увидеть лота вывода, если упаковываемое программное обеспечение большой. Наконец, % setup изменяет каталог на дерево сборки cdplayer меняет владельца и права доступа к файлам. Выход 0 означает конец подготовки % раздел, и, следовательно, конец настройки % макрос. Поскольку мы использовали опцию -bp , обороты остановились. с этой точки зрения. Посмотрим, какой RPM остался в области сборки: # cd / usr / src / redhat / BUILD # ls -l всего 1 drwxr-xr-x 2 root root 1024 4 августа 22:30 cdplayer-1.0 # Есть каталог верхнего уровня. Смена каталога на cdplayer-1.0, мы обнаруживаем, что исходники готовы к работе построено: # cd cdplayer-1.0 # ls -lF всего 216 -rw-r - r-- 1 root root 17982 10 ноября 1995 г. КОПИРОВАНИЕ -rw-r - r-- 1 root root 627 10 ноября 1995 г. Изменения … -rw-r - r-- 1 root root 2806 10 ноября 1995 г., том.c -rw-r - r-- 1 root root 1515 10 ноя 1995 том.ч # Мы видим, что настройка % chown и chmod команды сделали то, что должны были - файлы принадлежат root, с установленными разрешениями соответственно. Если не остановлен опцией -bp , следующий шаг в Процесс сборки RPM будет заключаться в создании программного обеспечения.RPM также может быть остановился в конце раздела сборки % в spec файл. Это делается с помощью опции -bc : Когда параметр -bc используется во время сборки, RPM останавливается после создания программного обеспечения. Что касается файла спецификации, каждая команда в разделе % build будет выполнен. В следующем примере мы удалили вывод из % Prep Секция для сокращения избыточного выхода, но имейте в виду, что он тем не менее выполняется: # rpmbuild -bc cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (% build): + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + сделать gcc -Wall -O2 -c -I / usr / include / ncurses cdp.c gcc -Wall -O2 -c -I / usr / include / ncurses color.c gcc -Wall -O2 -c -I / usr / include / ncurses display.c gcc -Wall -O2 -c -I / usr / include / ncurses misc.c gcc -Wall -O2 -c -I / usr / include / ncurses volume.c volume.c: В функции `mix_set_volume ': volume.c: 67: предупреждение: неявное объявление функции `ioctl ' gcc -Wall -O2 -c -I / usr / include / ncurses оборудование.c gcc -Wall -O2 -c -I / usr / include / ncurses database.c gcc -Wall -O2 -c -I / usr / include / ncurses getline.c gcc -o cdp cdp.o color.o display.o misc.o volume.o hardware.o database.o getline.o -I / usr / include / ncurses -L / usr / lib -lncurses groff -Tascii -man cdp.1 | сжать> cdp.1.Z + выход 0 # После команды мы видим, что RPM выполняет подготовку % раздел (который мы почти полностью удалили). Далее начинается RPM выполнение содержимого раздела % build .В в нашем примере файла спецификации, раздел % build выглядит как это: Мы видим, что до команды make обороты менялись. в каталог верхнего уровня cdplayer. Затем RPM запускает make , который заканчивается groff команда. На этом этапе выполнение % build раздел завершен. Поскольку Использовалась опция -bc , обороты останавливаются в этот момент. Следующим шагом в процессе сборки будет установка недавно созданного программное обеспечение. Это делается в % install (и % проверьте ) в разделе спецификации. RPM может быть остановлен после завершения установки с помощью -bi опция: При использовании опции -bi частота вращения останавливается. после того, как программное обеспечение будет полностью построено и установлено, и набор тестов был запущен в системе сборки.Вот что вывод сборки с использованием опции -bi выглядит так: # rpmbuild -bi cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (% build): … + выход 0 Выполнение (% install): + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + сделать установку chmod 755 cdp chmod 644 cdp.1.Z cp cdp / usr / local / bin ln -s / usr / local / bin / cdp / usr / local / bin / cdplay cp cdp.1 / usr / местные / человек / человек1 + выход 0 Выполнение (% check): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + cd cdplayer-1.0 + сделать тест Все тесты проходят успешно. + выход 0 Выполняется (% doc): + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + DOCDIR = // usr / doc / cdplayer-1.0-1 + rm -rf //usr/doc/cdplayer-1.0-1 + mkdir -p //usr/doc/cdplayer-1.0-1 + cp -ar README //usr/doc/cdplayer-1.0-1 + выход 0 # Как и раньше, мы удалили большую часть ранее описанных разделов. В этом примере раздел % install выглядит так: После % подготовки и % сборки разделов, выполняется раздел % install .Глядя на результат, мы видим, что RPM меняет каталог на каталог верхнего уровня cdplayer и выдает make install Команда , единственная команда в % установить раздел. Выход с этой точки до первый выход 0 , это с сделать установку . Следующая часть вывода - это проверка % раздел, т.е. единственная команда делает тест . Остальные команды связаны с содержимым файла спецификации. % файлов список. Вот как это выглядит: % файлов % doc README / USR / местные / bin / cdp / USR / местные / bin / cdplay /usr/local/man/man1/cdp.1 Ответственная линия - % doc README . В % тег doc идентифицирует файл как документация.RPM обрабатывает файлы документации, создавая каталог в / usr / doc и поместив все документация в нем. Выход 0 на конец означает конец раздела % install . Обороты останавливаются из-за опции -bi . Следующий шаг, на котором процесс сборки RPM может быть остановлен, происходит после файл двоичного пакета программного обеспечения был создан. Это делается с помощью опция -bb : # rpmbuild -bb cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (% build): … + выход 0 Выполнение (% install): … + выход 0 Выполнение (% check): … + выход 0 Выполняется (% doc): … + выход 0 Бинарная упаковка: cdplayer-1.0-1 Поиск зависимостей ... Требуется (2): libc.so.5 libncurses.so.2.0 usr / doc / cdplayer-1.0-1 usr / doc / cdplayer-1.0-1 / README USR / местные / бен / cdp USR / местные / бен / cdplay usr / местные / человек / человек1 / cdp.1 93 блока Генерация подписи: 0 Написал: /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm Выполнение (% clean): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + cd cdplayer-1.0 + выход 0 # После выполнения подготовки % , % сборка , % установка и % проверяют разделов и обрабатывают любые специальные файлов документации, RPM затем создает двоичный файл пакета. В выходных данных примера мы видим, что первый об / мин выполняет автоматическую проверку зависимостей. Это достигается путем определения какие разделяемые библиотеки требуются исполняемым программам содержится в упаковке.Затем RPM архивирует файлы для packaged, необязательно подписывает файл пакета и выводит готовый продукт. Последняя часть вывода RPM подозрительно похожа на раздел в spec-файл выполняется. В нашем примере нет % чистый раздел. Если бы, однако, RPM выполнили любые команды в разделе. В отсутствие % чистая секция , RPM просто выдает обычную cd команды и нормально завершается. Опция -ba указывает RPM на выполнение все этапы сборки пакета. С этим одна команда, об / мин: Распаковывает первоисточники. Применяет исправления (при желании). Создает программное обеспечение. Устанавливает программное обеспечение. Запускает набор тестов для программного обеспечения. Создает файл двоичного пакета. Создает файл исходного пакета. Это довольно много работы для одной команды! Вот он в действии: # rpmbuild -ba cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (% build): … + выход 0 Выполнение (% install): … + выход 0 Выполнение (% check): … + выход 0 Выполняется (% doc): … + выход 0 Бинарная упаковка: cdplayer-1.0-1 … Выполнение (% clean): … + выход 0 Исходный код: cdplayer-1.0-1 cdplayer-1.0.spec cdplayer-1.0.tgz 80 блоков Генерация подписи: 0 Написал: /usr/src/redhat/SRPMS/cdplayer-1.0-1.src.rpm # Как и в предыдущих примерах, RPM выполняет подготовку % , % сборка , % установка и % проверяет секций, обрабатывает любые специальные файлы документации, создает двоичный файл пакета и очищает после себя. Последним шагом в процессе сборки является создание пакета с исходным кодом. файл. Как видно из выходных данных, он состоит из файла спецификации и первоисточники. Пакет с исходным кодом может дополнительно включать один или несколько патч-файлы, хотя в нашем примере cdplayer не требует. В конце сборки с использованием опции -ba программное обеспечение было успешно создано и упаковано как в двоичном, так и в исходная форма.Но есть еще несколько вариантов сборки, которые мы можем использовать. Один из них - вариант -bl : Есть одна последняя буква, которая может быть указана при об / мин. -b , но в отличие от других, которые указывают стадию, на которой процесс сборки должен быть остановлен, эта опция выполняет множество проверок в списке % файлов в названном файле спецификации. Когда l добавлен в сборку rpmbuild , выполняются следующие проверки: Расширяет список % файлов спецификации и проверяет, действительно ли существует каждый указанный файл. Определяет, какие разделяемые библиотеки требуются программному обеспечению. проверка каждого исполняемого файла в списке. Определяет, какие разделяемые библиотеки предоставляются пакетом. Зачем нужно делать все эти проверки? Когда это будет полезно? Имейте в виду, что должен быть сгенерирован список % файлов вручную.При использовании опции -bl следующие шаги - это все, что необходимо для создания % файлов список: Для выполнения этих шагов может потребоваться более одной итерации, но в конечном итоге проверка списка пройдет. Использование -bl возможность проверить % файлов список конечно лучше чем начать двухчасовую сборку пакета, только чтобы узнать конец, что список содержит имя файла с ошибкой. Вот пример действия опции -bl : # rpmbuild -bl cdplayer-1.0.spec * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 Поиск зависимостей ... Требуется (2): libc.so.5 libncurses.so.2.0 # Трудно точно понять, что делает RPM на выходе, но если мы добавьте -vv , мы можем получить немного больше информации: # rpmbuild -bl -vv cdplayer-1.0.spec D: Перешел на пакет BASE D: Источник (0) = sunsite.unc.edu:/pub/Linux/apps/sound/cds/cdplayer-1.0.tgz D: Переход к партии: 12 D: fileFile = D: переключено на пакет: (null) D: Переход к части: 2 D: fileFile = D: Переход к партии: 3 D: fileFile = D: Переход к партии: 4 D: fileFile = D: Переход к партии: 10 D: fileFile = D: переключено на пакет: (null) * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 D: ДОБАВЛЕНИЕ: /usr/doc/cdplayer-1.0-1 D: ДОБАВЛЕНИЕ: /usr/doc/cdplayer-1.0-1/README D: ДОБАВЛЕНИЕ: / usr / local / bin / cdp D: ДОБАВЛЕНИЕ: / usr / local / bin / cdplay D: ДОБАВЛЕНИЕ: / usr / local / man / man1 / cdp.1 D: md5 (/usr/doc/cdplayer-1.0-1/README) = 2c149b2fb1a4d65418131a19b242601c D: md5 (/ usr / local / bin / cdp) = 0f2a7a2f81812c75fd01c52f456798d6 D: md5 (/ usr / local / bin / cdplay) = d41d8cd98f00b204e9800998ecf8427e D: md5 (/usr/local/man/man1/cdp.1) = b32cc867ae50e2bdfa4d6780b084adfa Поиск зависимостей ... D: Добавление требует: libncurses.so.2.0 D: Добавление require: libc.so.5 Требуется (2): libc.so.5 libncurses.so.2.0 # Глядя на этот более подробный вывод, легко увидеть, что есть отличный сделка продолжается.Некоторые из них не имеют прямого отношения к проверке Однако % файлов список. Например, вывод от первой строки до строки со значением * Пакет: cdplayer , отражает обработку, которая требует место во время сборки пакета, и его можно игнорировать. После этого раздела находится фактический список % файлов проверять. В этом разделе каждый файл, названный в % файлов Список проверяется на наличие.В фраза, ДОБАВЛЕНИЕ: , снова отражает число оборотов в минуту корни здания пакета. При использовании опции -bl , однако RPM просто проверяет наличие файлов в сборке. система. Если опция --timecheck (немного описана позже в разделе под названием --timecheck - Распечатать предупреждение, если файлы для упаковки закончились старый ) есть присутствует, здесь выполняются проверки, требуемые этой опцией, так как хорошо. После проверки списка вычисляются контрольные суммы MD5 каждого файла. и отображается. Хотя эта информация жизненно важна во время фактического пакета здания, он не используется при использовании опции -bl . Наконец, RPM определяет, в каких разделяемых библиотеках перечислены файлы. требовать. В данном случае их всего два - libc.so.5 и libncurses.so.2.0. Хотя это не совсем часть процесс проверки списка, отображение зависимостей разделяемых библиотек может быть весьма полезным на этом этапе.Он может указать на возможные проблемы, например, предположение, что целевые системы имеют определенную библиотеку установлены, хотя на самом деле их нет. До сих пор мы видели только то, что происходит, когда % файлов список правильный. Давай посмотрим что происходит где в списке есть проблемы. В этом примере мы добавили фиктивный в список % файлов пакета: # rpmbuild -bl cdplayer-1.0.spec * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 Файл не найден: / usr / local / bin / bogus Сборка не удалась. # Отражая больше своих корней сборки, об / мин -bl говорит, что «сборка не удалась». Но суть в том, что что нет такого файла, как / usr / bin / bogus. В в этом примере мы сделали имя явно неправильным, но в более в реальных условиях, имя, скорее всего, будет написано с ошибкой в % файлов список.ОК, давайте исправим Список % файлов и повторите попытку: # rpmbuild -bl cdplayer-1.0.spec * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 Файл не найден: / usr / local / bin / cdplay Сборка не удалась. # Еще одна ошибка! В этом случае файл написан правильно, но он не в системе сборки, хотя она должна быть. Возможно это было удалил случайно.В любом случае давайте пересобираем софт и пробуем очередной раз: # rpmbuild -bi cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (% build): … + выход 0 Выполнение (% install): … ln -s / usr / local / bin / cdp / usr / local / bin / cdplay … + выход 0 Выполнение (% check): … + выход 0 Выполняется (% doc): … + выход 0 # # rpmbuild -bl cdplayer-1.0.spec * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 Поиск зависимостей ... Требуется (2): libc.so.5 libncurses.so.2.0 # Готово! Мораль этой истории заключается в том, что при об / мин -bl и исправление отмеченной ошибки не обязательно означает ваш список % файлов готов к работе в прайм-тайм: всегда запустите его еще раз, чтобы убедиться! Хотя это звучит опасно, - короткое замыкание вариант может быть вашим другом.Эта опция используется во время начального разработка пакета. Ранее в этой главе мы исследовали остановка процесса сборки RPM на разных этапах. С использованием - короткое замыкание , можем запустить процесс сборки на разных этапах. Один раз, когда - короткое замыкание пригодится, это когда вы пытаетесь создать программное обеспечение правильно. Подумай, что это было бы похоже на то, что вы взламываете источники, пытаетесь построить, получить сообщение об ошибке и еще немного взломать, чтобы исправить эту ошибку.Без - короткозамыкающего вам пришлось бы: Внесите изменения в источники. Используйте tar для создания нового исходного архива. Начните сборку примерно с rpmbuild -bc . Смотрите еще одну ошибку. Вернитесь к шагу 1. Довольно громоздко! Поскольку процесс сборки RPM предназначен для запуска с исходниками в исходном файле tar , если только ваши модификации попадают в этот файл tar , они не будет использоваться в следующей сборке. Но есть другой способ. Просто выполните следующие действия: Поместите исходный файл tar в пакеты RPM Каталог ИСТОЧНИКИ. Создайте частичный файл спецификации в SPECS RPM каталог (обязательно включите действительный Source линия). Выполните сборку rpmbuild -bp для правильного создания сборки среда. Теперь используйте --short-circuit для попытки компиляции. Вот пример: # rpmbuild -bc --short-circuit cdplayer-1.0.spec * Пакет: cdplayer Выполнение (% build): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + сделать gcc -Wall -O2 -c -I / usr / include / ncurses cdp.c gcc -Wall -O2 -c -I / usr / include / ncurses color.c gcc -Wall -O2 -c -I / usr / include / ncurses display.c gcc -Wall -O2 -c -I / usr / include / ncurses misc.c gcc -Wall -O2 -c -I / usr / include / ncurses volume.c volume.c: В функции `mix_set_volume ': volume.c: 67: предупреждение: неявное объявление функции `ioctl ' gcc -Wall -O2 -c -I / usr / include / ncurses оборудование.c gcc -Wall -O2 -c -I / usr / include / ncurses database.c gcc -Wall -O2 -c -I / usr / include / ncurses getline.c gcc -o cdp cdp.o color.o display.o misc.o volume.o hardware.o database.o getline.o -I / usr / include / ncurses -L / usr / lib -lncurses groff -Tascii -man cdp.1 | сжать> cdp.1.Z + выход 0 # Обычно опция -bc указывает об / мин на остановить сборку после % build раздел spec-файла выполнен.Однако, добавив - короткозамыкание , об / мин запускает сборку, выполнив % build section и останавливается, когда все в % Сборка выполнена. Есть только один другой этап сборки, который может быть - короткое замыкание 'ed, и это этап установки. Причина этого ограничения - затруднить обход RPM использует чистые исходные коды.Если бы можно было - короткое замыкание на -bb или -ba , сборщик пакетов может пойти по "легкому" пути и просто взламывайте дерево сборки, пока программное обеспечение успешно, затем упакуйте взломанные исходники. Таким образом, RPM будет только - короткое замыкание на -bc или -bi . Больше ничего не поделаешь. Что именно делает rpmbuild -bi --short-circuit , в любом случае? Как и rpmbuild -bc --short-circuit , запускается выполняется на указанном этапе, который в данном случае % установить .Обратите внимание, что среда сборки должна быть готов к установке, прежде чем пытаться - короткое замыкание на % установить сцена. Если программное обеспечение устанавливается через , выполните установку , make автоматически скомпилирует программное обеспечение в любом случае. А что будет, если среда сборки не готова и - попытка короткого замыкания ? Посмотрим: # rpmbuild -bi --short-circuit cdplayer-1.0.spec * Пакет: cdplayer Выполнение (% install): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 / var / tmp / rpmbu01157aaa: cdplayer-1.0: нет такого файла или каталога Плохой статус выхода # RPM вслепую начал выполнение этапа % install , но внезапно остановился, когда попытался сменить каталог на cdplayer-1.0, которого не существовало. После предоставления описательное сообщение об ошибке, RPM завершился со статусом сбоя.Кроме для некоторых незначительных отличий rpmbuild -bc будет иметь потерпели неудачу точно так же. Параметр --buildarch используется для переопределения числа оборотов в минуту. логика определения архитектуры. За опцией следует желаемый название архитектуры. Вот пример: # rpmbuild -ba --buildarch i486 cdplayer-1.0.spec * Пакет: cdplayer … Бинарная упаковка: cdplayer-1.0-1 … Написал: /usr/src/redhat/RPMS/i486/cdplayer-1.0-1.i486.rpm … Написал: /usr/src/redhat/SRPMS/cdplayer-1.0-1.src.rpm # Мы удалили большую часть вывода RPM из этого примера, но основной из этого примера видно, что пакет был создан для архитектура i486, за счет включения параметр --buildarch в командной строке. Мы можем также обратите внимание, что RPM написал бинарный пакет в директория по архитектуре, / USR / SRC / Redhat / RPMS / i486.Использование RPM --queryformat опция подтверждает пакет архитектура: # rpmquery -qp --queryformat '% {arch} \ n' /usr/src/redhat/RPMS/i486/cdplayer-1.0-1.i486.rpm i486 # Для получения дополнительной информации о пакетах сборки для нескольких архитектур, см. главу 19. Параметр --buildos используется для отмены числа оборотов в минуту. логика обнаружения операционной системы.За опцией следует желаемое имя операционной системы. Вот пример: # rpmbuild -ba --buildos osf1 cdplayer-1.0.spec … Бинарная упаковка: cdplayer-1.0-1 … Написал: /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm Исходный код: cdplayer-1.0-1 … Написал: /usr/src/redhat/SRPMS/cdplayer-1.0-1.src.rpm # В выходных данных сборки нет ничего, что явно указывало бы на сборку Операционная система установлена на osf1 .Посмотрим, если --queryformat сообщит нам: # rpmquery -qp --queryformat '% {os} \ n' /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm osf1 # Пакет действительно был создан для указанной операционной системы. Для больше информации о создании пакетов для нескольких операционных систем, см. главу 19. Параметр --sign указывает RPM на добавление цифрового подпись создаваемого пакета.В настоящее время это делается с помощью PGP. Вот пример действия --sign : # rpmbuild -ba --sign cdplayer-1.0.spec Введите парольную фразу: парольную фразу (не отображается эхом) Фраза-пароль хороша. * Пакет: cdplayer … Бинарная упаковка: cdplayer-1.0-1 … Генерация подписи: 1002 Написал: /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm … Исходный код: cdplayer-1.0-1 … Генерация подписи: 1002 Написал: / usr / src / redhat / SRPMS / cdplayer-1.0-1 об / мин # Наиболее очевидный эффект от добавления опции --sign к команде сборки - RPM затем запрашивает ваш закрытый ключ кодовая фраза. После ввода ключевой фразы (которая не отображается эхом) сборка продолжается как обычно. Единственная другая разница между этим и не подписанная сборка - это то, что Generating подпись: строк имеют ненулевое значение. Давайте проверим только что созданные исходные и двоичные пакеты и посмотрим. если они действительно подписаны: # rpmsign --checksig / usr / src / redhat / SRPMS / cdplayer-1.0-1 об / мин /usr/src/redhat/SRPMS/cdplayer-1.0-1.src.rpm: размер pgp md5 OK # rpmsign --checksig /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm: размер pgp md5 OK # Дело в том, что в --checksig показывает, что пакеты были подписаны. Дополнительную информацию о подписании пакетов см. В главе 17.Также Приложение G содержит информацию о получении и установке PGP. Бывают случаи, когда может потребоваться более подробное представление конкретной сборки. Используя опцию --test , это просто. Когда --test добавляется в сборку , сценарии, которые RPM обычно использует для фактического выполнения build, создаются и сохраняются для просмотра. Посмотрим как это работает: # rpmbuild -ba --test cdplayer-1.0.spec * Пакет: cdplayer # В отличие от обычной сборки, вывода не так много. Но - test опция вызвала набор скриптов, написано и сохранено для вас. Возникает вопрос: где они? Если вы используете настроенный файл rpmrc, скрипты будут записаны в каталог, указанный в rpmrc запись tmppath . если ты не меняли этот параметр, RPM по умолчанию записывает скрипты в / var / tmp.Вот они: # ls -l / var / tmp всего 4 -rw-rw-r-- 1 root root 670 17 сен 20:35 rpmbu00236aaa -rw-rw-r-- 1 root root 449 17 сентября 20:35 rpmbu00236baa -rw-rw-r-- 1 root root 482 17 сентября 20:35 rpmbu00236caa -rw-rw-r-- 1 root root 552 17 сентября 20:35 rpmbu00236daa # Каждый файл содержит сценарий, который выполняет заданную часть сборки.Вот первый файл: #! / Bin / sh -e # Скрипт сгенерирован rpm RPM_SOURCE_DIR = "/ usr / src / redhat / ИСТОЧНИКИ" RPM_BUILD_DIR = "/ usr / src / redhat / BUILD" RPM_DOC_DIR = "/ usr / doc" RPM_OPT_FLAGS = "- O2 -m486 -fno-force-reduce" RPM_ARCH = "i386" RPM_OS = "Linux" RPM_ROOT_DIR = "/ tmp / cdplayer" RPM_BUILD_ROOT = "/ tmp / cdplayer" RPM_PACKAGE_NAME = "cdplayer" RPM_PACKAGE_VERSION = "1.0" RPM_PACKAGE_RELEASE = "1" установить -x маска 022 echo Executing (% преп) cd / usr / src / redhat / BUILD cd / usr / src / redhat / BUILD rm -rf cdplayer-1.0 gzip -dc /usr/src/redhat/SOURCES/cdplayer-1.0.tgz | tar -xvvf - если [$? -ne 0]; тогда выход $? фи компакт-диск cdplayer-1.0 компакт-диск /usr/src/redhat/BUILD/cdplayer-1.0 chown -R root.root. chmod -R a + rX, g-w, o-w. Как мы видим, этот скрипт содержит % prepare раздел из файла спецификации. Сценарий начинается с определения количество переменных среды, а затем приводит к % преп секция.В файле спецификации, используемом в этом сборка, секция подготовки % состоит из одного % настройка макрос. В этом файле мы можем увидеть, как именно RPM расширяет этот макрос. Остальные файлы следуют тому же основному layout - раздел, определяющий переменные среды, за которым следует команды, которые нужно выполнить. Обратите внимание, что опция --test создаст только сценарий файлы для каждого этапа сборки, как указано в командной строке.Для Например, если указанная выше команда была изменена на: # rpmbuild -bp --test cdplayer-1.0.spec # только один файл сценария, содержащий % подготовительных команды, были бы написаны. В любом случае независимо от того, какой RPM билд используется команда, опция --test может позволить вам увидеть что именно будет происходить во время сборки. Опция --clean может использоваться для проверки того, что дерево каталогов сборки пакета удаляется в конце сборки.Хотя его можно использовать на любом этапе сборки, он не всегда есть смысл сделать так: # rpmbuild -bp --clean cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): … + выход 0 Выполнение (- чистое): + cd / usr / src / redhat / СТРОИТЬ + rm -rf cdplayer-1.0 + выход 0 # В этом примере мы видим типичный участок подготовки на %. выполняется.Линия « Executing (- clean): » означает начало активности --clean . После смены каталога на каталог сборки, RPM затем выполняет рекурсивное удаление на каталог верхнего уровня пакета. Как мы отметили выше, этот конкретный пример не имеет особого смысла. Мы выполняем только раздел подготовки % , который создает дерево сборки пакета и с помощью - очистить , который его удаляет! С использованием --clean с опцией -bc тоже не очень продуктивен, так как недавно созданное программное обеспечение остается в дерево сборки.Опять же, после --clean сделал свое дело. Обычно опция --clean используется после того, как программное обеспечение строится и может быть успешно упаковано. Это особенно полезно, когда нужно собрать более одного пакета, так как --clean гарантирует, что файловая система, содержащая область сборки не будет заполняться деревьями сборки из каждого пакета. Обратите внимание, что опция --clean удаляет только файлы, которые находятся в дереве сборки программного обеспечения.Если есть файлы, которые сборка создает вне этой иерархии, будут необходимо написать сценарий для файла спецификации % чистый раздел. Параметр --buildroot может усложнить два ситуации намного проще: Давайте подробнее рассмотрим первую ситуацию. Скажем, для Например, этот sendmail должен быть упакован. В процессе создания sendmail пакет, программное обеспечение должно быть установлено.Это означало бы, что критические файлы sendmail, такие как sendmail.cf и псевдонимы, будет перезаписан. Обработка почты в системе сборки почти конечно будет сорвано. Во втором случае, конечно, можно установить такие разрешения, как что пользователи без полномочий root могут устанавливать программное обеспечение, но маловероятно, что системный администратор, стоящий их соли, сделает это. Что может быть сделано чтобы сделать эти ситуации более разумными? Параметр --buildroot используется для указания RPM используйте каталог, отличный от /, в качестве "корня сборки".Эта фраза немного вводит в заблуждение, поскольку корень сборки , а не корневой каталог, в котором программное обеспечение построено. Скорее, это корневой каталог для фазы установки сборка. Если корень сборки не указан, программное обеспечение packaged устанавливается относительно корневого каталога системы сборки "/". Однако недостаточно просто указать корень сборки в команде линия.Файл спецификации для пакета должен быть настроен для поддержки сборки корень. Если вы не внесете необходимые изменения, это то, что вы видеть: # rpmbuild -ba --buildroot / tmp / foo cdplayer-1.0.spec Пакет не может выполнять префиксы сборки Сборка не удалась. # Глава 16 содержит полные инструкции по модификации, необходимые для настройки пакета для использования альтернативного build root, а также методы, позволяющие пользователям создавать пакеты без рут-доступа.Предполагая, что необходимые модификации имеют Сделано, вот как будет выглядеть сборка: # rpmbuild -ba --buildroot / tmp / foonly cdplayer-1.0.spec * Пакет: cdplayer Выполняется (% преп): + cd / usr / src / redhat / СТРОИТЬ … + выход 0 Выполнение (% build): + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 … + выход 0 Выполнение (% install): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + сделать ROOT = / tmp / только для установки установить -m 755 -o 0 -g 0 -d / tmp / foonly / usr / local / bin / установить -m 755 -o 0 -g 0 cdp / tmp / foonly / usr / local / bin / cdp rm -f / tmp / foonly / usr / local / bin / cdplay ln -s / tmp / foonly / usr / local / bin / cdp / tmp / foonly / usr / local / bin / cdplay установить -m 755 -o 0 -g 0 -d / tmp / foonly / usr / local / man / man1 / установить -m 755 -o 0 -g 0 cdp.1 /tmp/foonly/usr/local/man/man1/cdp.1 + выход 0 Выполнение (% check): + umask 022 … + выход 0 Выполняется (% doc): + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + DOCDIR = / tmp / foonly // usr / doc / cdplayer-1.0-1 + rm -rf /tmp/foonly//usr/doc/cdplayer-1.0-1 + mkdir -p /tmp/foonly//usr/doc/cdplayer-1.0-1 + cp -ar README /tmp/foonly//usr/doc/cdplayer-1.0-1 + выход 0 Бинарная упаковка: cdplayer-1.0-1 Поиск зависимостей ... Требуется (2): libc.so.5 libncurses.so.2.0 usr / doc / cdplayer-1.0-1 usr / doc / cdplayer-1.0-1 / README USR / местные / бен / cdp USR / местные / бен / cdplay usr / местные / человек / man1 / cdp.1 93 блока Генерация подписи: 0 Написал: /usr/src/redhat/RPMS/i386/cdplayer-1.0-1.i386.rpm Выполнение (% clean): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + компакт-диск cdplayer-1.0 + выход 0 Исходный код: cdplayer-1.0-1 cdplayer-1.0.spec cdplayer-1.0.tgz 82 блока Генерация подписи: 0 Написал: /usr/src/redhat/SRPMS/cdplayer-1.0-1.src.rpm # Как видно из отредактированного вывода, % prepare , % построить и % установить разделов выполняются в обычном каталоге сборки RPM.Тем не менее --buildroot опция вступает в игру, когда make install завершено. Как видим, ROOT Переменная установлена на / tmp / foonly - значение, следующее за --buildroot в командной строке. С этого момента на, мы видим, что make заменил новую сборку корневое значение на этапе установки. Корень сборки также используется при установке файлов документации.Каталог документации cdplayer-1.0-1: создан в / tmp / foonly / usr / doc, а В него помещается файл README. Единственная оставшаяся разница, возникающая в результате использования --buildroot , это то, что файлы, которые будут включены в бинарный пакет не расположен относительно корня системы сборки каталог. Вместо этого они расположены относительно корня сборки / tmp / foonly. Результирующий двоичный файл и исходный код файлы пакетов функционально эквивалентны пакетам, созданным без использование --buildroot . Использование --buildroot может вас укусить! Хотя опция --buildroot может решить некоторые проблемы, использование корня сборки может быть опасным. Как? Рассмотрим следующую ситуацию: В файле спецификации настроен корень сборки Например, / tmp / blather. В секции подготовки % , есть rm -rf $ RPM_BUILD_ROOT команда для очистки любого старого установленного программного обеспечения. Вы решили собрать программное обеспечение так, чтобы оно устанавливало относительную в корневой каталог вашей системы, поэтому вы вводите следующий команда: « rpmbuild -ba --buildroot / foo.spec ». Конечный результат? Поскольку указание "/" в качестве корень сборки устанавливает $ RPM_BUILD_ROOT в "/", эта безобидная маленькая rm -rf $ RPM_BUILD_ROOT превращается в rm -rf / ! Рекурсивное удаление, начиная с корня вашей системы каталог, может не быть полной катастрофой, если вы его быстро поймаете, но в любом случае вы будете проверять свою способность восстанавливать из резервное копирование ... У вас или есть резервные копии, не надо Вы? Мораль этой истории - быть очень осторожно при использовании --buildroot .Хорошее практическое правило: чтобы всегда указывать уникальный корень сборки. Например, вместо указание / tmp в качестве корня сборки (и, возможно, потеряв системный каталог для хранения временных файлов), используйте путь / tmp / mypackage, где каталог mypackage используется только пакетом, который вы строительство. Хотя можно обнаружить много ошибок в % files list using rpmbuild -bl , there - это еще один тип проблемы, которую невозможно обнаружить.Рассмотрим следующий сценарий: Пакет, который вы создаете, создает файл / usr / bin / foo. Из-за проблемы с make-файлом пакета, foo никогда не копируется в / usr / bin. Старая несовместимая версия foo, создан несколько месяцев назад, уже существует в / usr / bin. RPM создает файл двоичного пакета. Несовместимый / usr / bin / foo включен в упаковка? Вы держите пари, что это так! Если бы только был способ RPM поймать такого рода проблемы ... Ну, есть! Добавив --timecheck , а затем число, RPM проверит каждый упаковываемый файл, чтобы убедиться, что файл старше указанного количества секунд.Если это так, предупреждение отображается сообщение. Опция --timecheck работает с -ba или -bl параметры. Вот пример использования -bl : # rpmbuild -bl --timecheck 3600 cdplayer-1.0.spec * Пакет: cdplayer Проверка списка файлов: cdplayer-1.0-1 предупреждение: сбой TIMECHECK: /usr/doc/cdplayer-1.0-1/README Поиск зависимостей ... Требуется (2): libc.так.5 libncurses.so.2.0 # В этом примере файл /usr/doc/cdplayer-1.0-1/README больше 3600 секунды или один час назад. Если мы посмотрим на файл, мы найдем что это: # ls -al /usr/doc/cdplayer-1.0-1/README -rw-r - r-- 1 root root 1085 10 ноября 1995 г. README # В данном случае предупреждение от --timecheck не является поводом для тревоги.Поскольку README файл был просто скопирован с оригинала источник, который был создан 10 ноября 1995 года, его дата не изменилась. Если бы файл был исполняемым файлом или библиотекой, предположительно построено недавно, предупреждение --timecheck должно быть воспринимается более серьезно. Если вы хотите установить значение проверки времени по умолчанию на один час, вы можете включите следующую строку в свой файл rpmrc: Это значение может быть заменено значением в командной строке, если желанный.Для получения дополнительной информации об использовании rpmrc, см. Приложение B. В отличие от большинства других команд RPM, здесь нет -v вариант для rpmbuild . Это потому, что команда по умолчанию должен быть подробным. Однако можно получить еще больше информации. получается добавлением -vv . Вот пример: # rpmbuild -bp -vv cdplayer-1.0.spec D: Перешел на пакет BASE D: Источник (0) = солнце.unc.edu:/pub/Linux/apps/sound/cds/cdplayer-1.0.tgz D: Переход к партии: 12 D: fileFile = D: переключено на пакет: (null) D: Переход к части: 2 D: fileFile = D: Переход к партии: 3 D: fileFile = D: Переход к партии: 4 D: fileFile = D: Переход к партии: 10 D: fileFile = D: переключено на пакет: (null) * Пакет: cdplayer D: РАБОТАЕТ:% преп. Выполняется (% преп): + umask 022 + cd / usr / src / redhat / СТРОИТЬ + cd / usr / src / redhat / СТРОИТЬ + rm -rf cdplayer-1.0 + gzip -dc /usr/src/redhat/SOURCES/cdplayer-1.0.тгз + tar -xvvf - drwxrwxr-x root / пользователи 0 4 августа 22:30 1996 cdplayer-1.0 / -rw-r - r-- root / users 17982 10 ноября 01:10 1995 cdplayer-1.0 / КОПИРОВАНИЕ … -rw-r - r-- root / users 1515 10 ноября 01:10 1995 cdplayer-1.0 / volume.h + [0 -ne 0] + компакт-диск cdplayer-1.0 + компакт-диск /usr/src/redhat/BUILD/cdplayer-1.0 + chown -R root.root. + chmod -R a + rX, g-w, o-w. + выход 0 # Большая часть вывода, генерируемого параметром -vv , является предшествует D: .В этом примере дополнительный вывод представляет внутреннюю обработку RPM во время начало процесса сборки. Использование опции -vv с другими командами сборки будет производить другой результат. Как мы упоминали выше, команда сборки обычно многословна. В - опция может использоваться для сокращения вывод команды: # rpmbuild -ba --quiet cdplayer-1.0.spec * Пакет: cdplayer volume.c: В функции `mix_set_volume ': volume.c: 67: предупреждение: неявное объявление функции `ioctl ' 90 блоков 82 блока # Это полный вывод сборки пакета CD-плеер. Обратите внимание, что предупреждающие сообщения (на самом деле, все, что отправлено на стандартный вывод), все еще печатаются. Параметр --rcfile используется для указания файла содержащий настройки по умолчанию для RPM.Обычно этот вариант не нужный. По умолчанию RPM использует / etc / rpmrc и файл с именем .rpmrc, расположенный в вашем логине каталог. Эта опция использовалась бы при необходимости переключения между несколько наборов значений RPM по умолчанию. Posted in Разное

Учимся строить сечения многогранников. Часть 2.

построить сечение пирамиды

Стереометрия. Задачи на построение сечений

Сечение параллелепипеда по трем точкам примеры.

17. Построение сечения цилиндра.

Обучение с МК

Сечения многогранников

ТЕОРИЯ

Пример 1

Пример 2

Пример 3

Пример 4

Пример 2’

Пример 3’

УПРАЖНЕНИЯ

‎App Store: iCrosss

Примеры построения сечений многогранников

Чертеж в разрезе — Designing Buildings Wiki

[править] Статьи по теме «Проектирование зданий» Wiki

[править] Внешние ссылки

Архитектура 101: Что такое чертеж сечения?

Архитектура 101: Что такое чертеж сечения?

Типы чертежей разрезов — Строительные чертежи

СЕКЦИЯ ШКАФА

Как создать свой первый раздел темы Shopify — Разработка темы Shopify

Что такое тематические разделы?

Создание статического раздела в вашей теме Shopify

Что такое секционные блоки?

Добавление блоков в динамический раздел

Добавление блоков в статический раздел

Расширение возможностей для творчества

Семь советов, которые помогут вам выбрать идеальную секцию для построения на

Как создать раздел заголовка вашего веб-сайта с помощью CSS (Раздел 1)

Введение

Предварительные требования

Добавление заголовка и подзаголовка к заголовку веб-страницы

Акула Сэмми

СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN

Добавление и стилизация небольшого изображения профиля в заголовок веб-страницы

Sammy the Shark

Акула Сэмми

СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN

Стилизация и позиционирование содержимого заголовка с помощью CSS

Акула Сэмми

СТАРШИЙ СЕЛАХИМОРФА В DIGITALOCEAN

Заключение

Справочник по командам rpmbuild

Использование

Добавить комментарий Отменить ответ

`Что такое секционные блоки?`

`Добавление блоков в динамический раздел`

`Добавление блоков в статический раздел`

`Расширение возможностей для творчества`

`Семь советов, которые помогут вам выбрать идеальную секцию для построения на`

`Как создать раздел заголовка вашего веб-сайта с помощью CSS (Раздел 1)`

`Введение`

`Предварительные требования`

`Добавление заголовка и подзаголовка к заголовку веб-страницы`

`Добавление и стилизация небольшого изображения профиля в заголовок веб-страницы`

`Sammy the Shark`

`Добавить комментарий Отменить ответ`