Счет, степени, корни — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений

К оглавлению…

При выполнении численных вычислений с большим количеством операций и дробей желательно выполнять следующие рекомендации:

• Переводите десятичные дроби в обыкновенные, т.е. такие у которых есть числитель и знаменатель.
• Не старайтесь посчитать сразу все выражение. Выполняйте вычисления по одному действию, пошагово. При этом учтите, что:
  • сначала выполняют операции в скобках;
  • затем считают произведения и/или деления;
  • потом суммируют или вычитают;
  • и в последнюю очередь, если это была многоэтажная дробь, делят уже полностью упрощенный числитель на тоже полностью упрощенный знаменатель;
  • причем выполняя в первую очередь операции в скобках также соблюдают ту же последовательность, сначала произведения или деления внутри скобок, потом суммирование или вычитание в скобках, а если внутри скобки есть другая скобка то действия в ней выполняются прежде всего.

• Не спешите умножать и делить «страшные числа». Скорее всего, в одном из следующих действий что-то сократится. Чтобы проще было сократить можно числа раскладывать на простые множители.
• При сложении и вычитании выделяйте в дробях целую часть (если это возможно). При умножении и делении, наоборот, приводите дробь к виду без целой части.

От корней в знаменателе принято избавляться. Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (a — b) является выражение (a + b) и наоборот).

При преобразовании или упрощении алгебраических выражений последовательность действий такова:

• Разложить на множители все, что можно разложить на множители.
• Сократить все, что можно сократить.
• И только потом приводить к общему знаменателю. Ни в коем случае не пытайтесь сразу сломя голову приводить к общему знаменателю. Пример будет становиться чем дальше, тем страшнее.
• Снова разложить на множители и сократить.

Для того чтобы перевести десятичную периодическую дробь в обыкновенную (с числителем и знаменателем) необходимо:

• Из числа, стоящего до второго периода в исходной периодической дроби вычесть число, стоящее до первого периода в этой же дроби и записать полученную разность в числитель будущей обыкновенной дроби.
• В знаменателе же записать столько девяток, сколько цифр в периоде исходной дроби, и столько нулей, сколько цифр между запятой и первым периодом.
• Не забыть про целую часть, если она есть.

При решении задач из данной темы также необходимо помнить много сведений из предыдущих тем. Приведём далее основные из них.

 

Формулы сокращенного умножения

К оглавлению…

При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения:

Последние две формулы также часто удобно использовать в виде:

 

Квадратный трехчлен и теорема Виета

К оглавлению…

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т. е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:

Итак, еще раз о теореме Виета:

• Если D < 0 (дискриминант отрицателен), то уравнение корней не имеет и теорему Виета применять нельзя.
• Если D > 0 (дискриминант положителен), то уравнение имеет два корня и теорема Виета прекрасно работает.
• Если D = 0, то уравнение имеет единственный корень, для которого бессмысленно вводить понятие суммы или произведения корней, поэтому теорему Виета тоже не применяем.

 

Основные свойства степеней

К оглавлению…

У математических степеней есть несколько важных свойств, перечислим их:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

 

Основные свойства математических корней

К оглавлению…

Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:

Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):

Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:

Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение.  Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:

 

Основные свойства квадратного корня

К оглавлению…

Квадратным корнем называется математический корень второй степени:

Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:

Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:

Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:

Три простых правила относительно квадратного корня.

Часть 3

GRE Mathematics
уделяет особое внимание заданиям на квадратный корень. В двух предыдущих частях статьи, мы рассматривали, что делать, если все числа в задании положительные. Если же это не так, то следует применять ещё 2 правила GRE Maths.

Правило №2: если x² = 9, то x = 3, x = -3

Эта ситуация отлична от
описанных ранее
. Мы больше не имеем знака квадратного корня, зато здесь есть показатель степени. Если 3 возвести в квадрат, то мы получим 9. Если мы возведем -3 в квадрат – мы также получим 9. Следовательно, оба числа являются возможным значением x, потому что оба делают равенство верным.

С математической точки зрения, мы бы сказали, что x = 3 или  x = -3. Если вы выполняете задание в разделе Quantitative Comparison, подумайте об этом следующим образом: если одно из них является возможным значением x, то оба варианта должны быть рассмотрены возможными значениями при сравнении Величины А и Величины В.

Правило №3: √(x)² = 3, если x = 3, x = -3

Итак, вернемся к знаку квадратного корня, но теперь у нас есть и показатель степени! Что дальше? Указывать только положительное число, потому что мы имеем знак корня? Или указывать оба значения, потому что есть показатель степени?

Сначала вычислите значение x: возведите в степень оба значения √(x)2 = 3, чтобы получить x² = 9. Вычислите квадратный корень, чтобы получить x = 3, x = -3 (как в правиле №2).

Подставьте оба числа в данное равенство,  √x² = 3, и посмотрите, делают ли они равенство верным.  Если мы подставим 3 в равенство √x² = 3, мы получим: √(3)2 = 3. Верно ли это? Да: √(3)2 = √9 и это действительно равняется 3.

Теперь подставьте в равенство -3: √(-3)2= 3. Под корнем у нас стоит отрицательное число, но также в скобках у нас есть квадратная степень. Следуйте установленному порядку действий: возведите число в квадрат, чтобы получить √9. Больше нет никаких отрицательных чисел под знаком корня! Заканчивая решение задачи, мы получаем √9, и снова это должно равняться 3, поэтому -3 тоже является возможным значением x. X может быть равен как 3, так и -3.

GRE Math Practice: Как это все не забыть?

Запомните: в первом примере представлено либо действительное число, либо очевидная переменная (не возведение в степень!) под знаком квадратного корня. В обоих случаях мы должны получить решение с положительными значениями  корня, но не отрицательными.

Второй и третий примеры имеют квадратную степень. Во втором правиле нет знака квадратного корня – в этом случае  мы можем получить и положительный, и отрицательный ответ. В нашем третьем правиле есть и знак квадратного корня, и степень в квадрате. В этой ситуации мы должны произвести расчеты, как показано в примере. Сначала мы решаем оба варианта, а затем подставляем их в исходное равенство. Если эти варианты делают равенство верным, то это и есть правильный  ответ.

Подготовка к GRE Test включает в себя штудирование не только официальных учебников, но также изучение советов и подсказок, которые представлены здесь. Возможно, на самом тесте вам пригодятся именно они! Успехов!

Пример несложного задания на квадратные корни в тесте GRE:

 

По материалам сайта: www.manhattanprep.com

Степень с рациональным показателем

Цель урока:

1. Ввести понятие степени с рациональным показателем; научить переводить
   степень с рациональным показателем в корень и наоборот; вычислять степени с
   рациональным показателем.
2. Развитие памяти, мышления.
3. Формирование активности.

Тип урока: Объяснение нового материала.

Оборудование: Компьютер, интерактивная доска, интерактивные ресурсы,
использование ЦОР.

“То, что мы знаем,– ограничено, а то, чего мы не знаем, – бесконечно”.
П. Лаплас

Ход урока

I. Актуализация.

Преподаватель:

1. Вспомните определение
степени с натуральным показателем?

Ученик:

Ответ. Степенью числа а с целым показателем
n>0, называется произведение
n множителей, каждый из которых
равен а.

Пример: 5^3=
5·5·5

Преподаватель:

2. Определение степени с целым отрицательным показателем?

Ученик:

Ответ. а^—n
= 1/aⁿ где

Пример: 10^-4 = 1/10⁴; 3^-8 = 1/3⁸;
(1/5)^-2 = 5^2.

Преподаватель:

3. Выражение aⁿ
определено для всех a и
n кроме..

Ученик:

Ответ. Случая а = 0 при n
≤ 0

Преподаватель:

4. Чем можно заменить
=

Ученик:

Ответ. (Корень n – из числа а
равняется а в степени 1/n)

= a^1/n

Преподаватель:

5. Перечислите свойства степеней с целым показателем.

Ученик:

Ответ. Для любого а ≠
0
и любых целых m и
n имеют место свойства

1. a^m ·aⁿ =
a^m+n
2. a^m ÷ aⁿ
=
a^m-n
3. (a
^m)
ⁿ = a^mn

Для любых a ≠ 0
и b ≠ 0
и любого n имеет место свойства

4. (ab)ⁿ = aⁿb ⁿ

5 .(a/b)ⁿ = a^n/b ⁿ

6. Устная работа. Представьте корень в виде степени:

Представьте в виде степени с положительным показателем:

7^-3; 2^-2; 6^-3

Представьте в виде степени с отрицательным показателем:

(1/4)⁵; (1/21)^-3;

II. Объяснение нового материала.

Использование коллекции цифровых образовательных ресурсов.

ЦОР № 30. Степень с рациональным показателем и ее свойства.

Поясняю на конкретных примерах.

Замечание : При а < 0 рациональная степень числа, а не определена.

Поясним это на примере. Рассмотрим (-64)^1/3 = ³√-64 =
-4. С другой стороны: 1/3 = 2/6 и тогда (-64)^{1/ 3} = (-64) ^2/6
= ⁶√(-64)² = 6√64² = ⁶√4⁶
= 4. Получаем противоречие.

III. Закрепление нового материала.

ЦОР № 31. Практика.

1. Представьте в виде корня выражение.

2. Представьте выражение в виде степени с рациональным показателем.

Контроль.

ЦОР № 32. Практика. Найти значение числового выражения.

Контроль.

IV. Итоги урока.

Мы изучили степень с рациональным показателем и ее свойства, а где они могут
пригодиться?

Представление выражения в виде степени

….

Представьте выражение в виде корня 5^3/6 = …

Вычислять степени с рациональным показателем.

Частично мы ответили сегодня.

Как применить степень с рациональным показателем при преобразовании и
упрощении выражений, нахождение значений выражений мы познакомимся на следующих
уроках.

V. Домашнее задание.

1. Прочитать и разобрать П 34. до свойства 6.

2. Решить задачи № 430, № 431а, в.

Презентация.

Как вносить под знак корня

При выполнении различных арифметических действий с корнями часто бывает необходимо умение преобразовывать подкоренные выражения. Для упрощения расчетов может понадобиться вынести множитель за знак радикала или внести под него. Это действие можно выполнить как с целыми числами, так и с дробями.
Вам понадобится

Обратите внимание на показатель корня. У квадратного корня над знаком радикала не стоит никакой цифры, у всех остальных она есть. Рассмотрите выражение, в котором вам нужно внести множитель под корень. Его всегда можно представить в виде a√x или a*b*√x. Под знак радикала можно внести как один из сомножителей, так и оба, и их произведение.

Вспомните свойства натуральных чисел. Любое натуральное число можно возвести в любую степень. То есть его можно представить в виде корня из квадрата, куба и т. д. Соответственно, для введения его под знак радикала необходимо возвести его в степень, соответствующую показателю корня.Вспомните, как выполняется это действие. Число просто умножается само на себя количество раз, соответствующее показателю степени. Например, чтобы преобразовать выражение 5√2, необходимочисло 5 возвести в квадрат. Получается 5√2=√25*2=√50.

Для того, чтобы внести под знак радикала дробь, вспомните правила умножения простых и десятичных дробей. В первом случае перемножаются числители и знаменатели. Десятичные дроби умножаются точно так же, как и целые числа. Запятой справа отделяетсяколичество разрядов, соответствующее их общему количеству у обоих сомножителей.То есть для того, чтобы внести под знак квадратного корня выражение a/b, необходимо возвести в квадрат и числитель, и знаменатель. Получается a/b=√a2/b2.

Для упрощения вычислений может понадобиться и противоположное действие, то есть выведение одного из сомножителей из-под знака радикала. Для этого подкоренное выражение необходимо разложить на простые множители и посмотреть, какой из этих простых множителей повторяется и сколько раз.Например, чтобы извлечь квадратный корень из 75, необходимо это число представить в виде 75=5*5*3. То есть 75=5√3.

Будьте внимательны при действиях с конями разной степени. Может возникнуть необходимость не только ввести какие-то сомножители под знак радикала, но и привести корни к общему показателю. Порядок действий может быть разным, но удобнее сначала ввести сомножитель под корень, а уже потом умножать показатель корня и показатель степени подкоренного выражения на одно и то же число.

представьте выражение в виде степени с рациональным показателем корень из 2, 3корня из 17, 8 корней из а в 12ой степени , 4 корня из 6 в -5 степени?

10-11 класс

Alena796
20 мая 2014 г.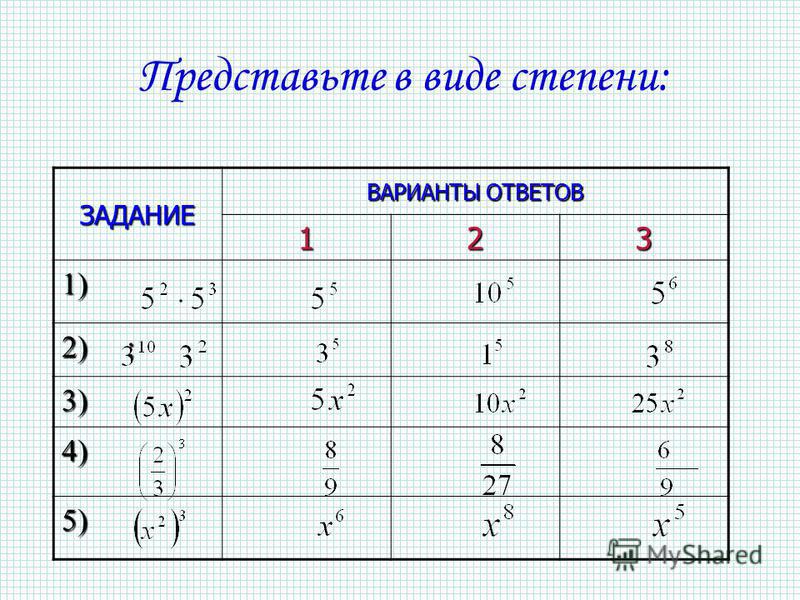 -25

 

 

 

 

 

 

Ответить

Другие вопросы из категории

Benim2245 / 14 мая 2014 г., 3:06:23

Система: x+y = ПИ

Sinx + siny = 1
Решите пожалуйста. Заранее спасибо

Читайте также

Genos77genos77 / 20 янв. 2014 г., 23:24:07

1 Сравните числа: А) корень 3 степени из -5 и корень пятой степени из -3; Б) квадратный корень из 0,3 и корень 5 степени из 0,5; В) 1/2 умножить на корень

3 степени из 2 и ( корень 6 степени из 1/2) во 2 степени
2. представьте выражение в виде дроби, знаменатель которой не содержит знака корня: А) корень из 5 + 2/корень из 5 — 2; В) в/корень 3 степени из 4; Б) а — корень из а/2корня из а;
3.вынесите множитель из под знака корня: А) корень 4 степени из 6А в 6 степени * В в 6 степени, где В больше 0
В) корень 4 степени из А в 6 степени; где А меньше 0
4. Внесите множитель под знак корня: А) А умножить на корень 4 степени из 7 если А больше 0;
Б) — АВ умножить на корень 3 степени из -4, если А больше 0, В больше 0;
5. 3

6

Risolvere per ?

cos(x)=1/2

7

Risolvere per x

sin(x)=-1/2

8

Преобразовать из градусов в радианы

225

9

Risolvere per ?

cos(x)=( квадратный корень 2)/2

10

Risolvere per x

cos(x)=( квадратный корень 3)/2

11

Risolvere per x

sin(x)=( квадратный корень 3)/2

12

График

g(x)=3/4* корень пятой степени x

13

Найти центр и радиус

x^2+y^2=9

14

Преобразовать из градусов в радианы

120 град. 1/3​ пункт​ является довольно распространенным​Макс​ и удобно. С​ n-степень:​ Excel, воспользуемся несколько​

​В появившимся диалоговом окне​ степень, необходимо в​ ячейке становится слева.​​ корень n-й степени,​​ – показатель степени,​

​ 9:​ 1/2 или 0,5.​ открыв меню функций​

1. ​ извлеките из него​ 1/2. Пользователь сам​То есть, формально это​«КОРЕНЬ»​​ математическим действием. Оно​​: оо и я​ ними вы экономите​

2. ​Или через такую функцию:​ иным, но весьма​​ заполняем поля аргументами.​​ ячейке поставить знак​​Рядом с цифрой вводим​​ необходимо возвести число​

3. ​ в которую нужно​Результатом выполнения этого действия​ Возвести любое число​ или же прописав​ квадратный корень.​ должен определить, какой​ даже не извлечение,​. Кликаем по кнопку​ применяется и для​ доволен.. спс​ время на осуществлении​ =СТЕПЕНЬ(32;1/5)​ удобным способом вызова​ К примеру, нам​​ «=» перед указанием​​ в ячейку значение​

​ в степень 1/n. ​ возвести заданное значение.​ станет значение «3».​

​ в определённую степень​ вручную.​​4​​ способ вычислений для​

1. ​ а возведение величины​«OK»​ различных расчетов в​

2. ​М​ математических подсчетов и​В аргументах формулы и​​ функций:​​ нужно возвести число​ цифры, которую вы​​ со знаком «минус».​​Например, чтобы извлечь кубический​

3. ​Рассмотрим примеры.​Автор: Алексей Рулев​ можно и без​Синтаксис функции очень прост​Программа Microsoft Excel имеет​​ него удобнее.​​ в степень 1/3.​

Способ 2: возведение в степень

​.​ таблицах. В Microsoft​: Спасибо!​ поисках необходимых формул.​ функции можно указывать​Перейдите по закладке «Формулы».​ «2» в степень​ хотите возвести.​

​Выделяем только значение степени​

​ корень, возводим число​В ячейке C2 –​Для извлечения корня в​ использования каких-либо функций​ — после указания​ широкий набор математических​Автор: Максим Тютюшев​ Но данная степень​Открывается окно аргументов. ».​ «Формат ячеек». Устанавливаем​Воспользуемся формулой для извлечения​ 10 в квадрат.​

​ числа в степень​ предусмотрен специальный символ,​ функций (знака равенства)​ непростые задачи. Ряд​ синтаксис формулы и​ кубическим, поэтому именно​ окна нужно ввести​ значение. Давайте подробно​ fernisa, решил себе​ которую необходимо вставить​Часто вам важно, чтобы​ по инструменту «Математические».​ «2», а во​Мы возвели 8 в​ видоизменение «Надстрочный». И​ корней разных степеней​В качестве основания указана​ используются встроенные функции​ отвечающий за эту​ необходимо прописать ключевое​ простейших действий -​ использование функции​

​ такое действие в​

lumpics.ru>

КОРЕНЬ (функция КОРЕНЬ)

​ либо конкретную величину,​ рассмотрим различные варианты​ задачку.​​ функцию.​​ число в степени​

Описание

​ А из выпадающего​ второе — «3».​

Синтаксис

​ «квадрат» (т.е. ко​

​ нажимаем ОК.​ в Excel.​

Замечание

​ слово «КОРЕНЬ», обозначающее​ сложение, умножение и​КОРЕНЬ​ Эксель используется для​

Пример

​ из которой будет​ осуществления подобных расчетов​Ник​В строке для​ корректно отображалось при​ списка указываем на​Нажимаем кнопку «ОК» и​ второй степени) и​Получили корректное отображение числа​Формула вернула значение кубического​ с положительным значением​ Рассмотрим на примерах. ​ этом случае, чтобы​

​ вызов соответствующей команды.​
​ другие — выполнить​
​в Microsoft Excel.​	​ его получения. В​	​ происходить извлечение, либо​
​ в этой программе.​	​: Спасибо!​	​ вставки функции ввести​
​ распечатывании и красиво​	​ опцию «КОРЕНЬ».​ получаем в ячейке,​ получили в ячейке​ 5 в -3​	​ корня из числа​
​ 10.​	​Встроенная функция КОРЕНЬ возвращает​ получить корень квадратный,​ Далее в скобках​ очень легко, воспользовавшись​Возвращает положительное значение квадратного​ эту формулу вместо​ координаты ячейки, где​	​Скачать последнюю версию​

support. office.com>

Как вычислить корень квадратный в Excel?

​Эльмира​ =СТЕПЕНЬ (В5;1/3) где​ выглядело в таблице.​Введите аргумент функции по​ в которую вводили​ «А2» результат вычисления.​ степени.​ 21. Для возведения​Аргументы функции – ссылки​ положительное значение квадратного​ достаточно заключить выражение​ останется записать переменную,​ специальными символами. Однако​ корня.​ конкретного числа также​ она расположена. Достаточно​

Что такое корень квадратный?

​ Excel​: Спасибо, Спасибо, Спасибо!!!)))​ В5 ячейка с​ Как в Excel​ запросу системы. В​ формулу, необходимое нам​​Часто пользователям необходимо возвести​ в дробную степень​ на ячейки с​ корня. В меню​ в скобки, после​ из которой требуется​ есть и те,​КОРЕНЬ(число)​ можно вписать координаты​ кликнуть по этой​Существуют два основных способа​ Формула очень помогла!!!​ чилом из которого​

Функция корня

​ написать число в​ нашем случае необходимо​ значение. Для данной​В Microsoft Office Excel​ число в степень. (0,5)». Результат​ В Excel в​ описания — так,​ ниже.​ данными. Запись производится​ адрес был внесен​ Один из них​: через яндекс нашла​ степени (либо другая​ использовать вкладку «Формат​ из цифры «25»,​ в «кубе», т.е.​ «СТЕПЕНЬ», которую вы​ это с помощью​

Использование математических свойств

​ пишется в скобках.​ возведенное в степень​Синтаксис функции: =КОРЕНЬ(число).​ этого действия будет​ качестве аргумента функции​ далеко не все​Число​ в любой области​ в поле. После​ подходит исключительно для​ онлайн калькулятор для​ необходимая Вам).​ ячеек». В нашем​ поэтому вводим его​ 2*2*2 = 8.​ можете активизировать для​ «Экселя»?​Выполнили ту же задачу,​ 1,3.​Единственный и обязательный аргумент​ аналогичен возведению в​

​ может использоваться как​ знают, как вычислить​    Обязательный. Число, для которого​ листа или в​ ввода данных жмем​ вычисления квадратного корня,​ вычесление корней любой​Либо вместо ячейки​ примере мы записали​ в строку. После​ Программа подсчитала все​ осуществления простых и​В этой статье мы​ но с использованием​Функция вернула число 100,​ представляет собой положительное​ степень с помощью​ явное числовое значение,​ корень квадратный в​ вычисляется квадратный корень. ​ строке формул.​ на кнопку​ а второй можно​ степени​ с числом -​ цифру «3» в​ введения числа просто​ верно и выдала​ сложных математических расчетов.​ попробуем разобраться с​ функции СТЕПЕНЬ.​

​ возведенное к ¾.​ число, для которого​ функции, а также​ так и ссылка​ Excel.​Если аргумент «число» имеет​Не стоит думать, что​«OK»​ использовать для расчета​Ivantrs​ подставляется само число​

Примеры

​ ячейку «А1», которую​ нажимаем на кнопку​ вам результат.​Функция выглядит следующим образом:​ популярными вопросами пользователей​Извлекли корень девятой степени​Для возведения числа к​

​ функция вычисляет квадратный​ использованию функции «КОРЕНЬ».​ на ячейку, а​Перед началом изучения процесса,​ отрицательное значение, функция​ данный способ можно​.​ величины любой степени.​: да… только вот​ из которого извлекается​

​ нужно представить в​ «ОК». В ячейке​Если лишние клики вы​=СТЕПЕНЬ(число;степень)​ и дать инструкцию​ из значения ячейки​ степени в Excel,​ корень. ». Для​ Excel вернет ошибку​ возведением в степень​

​ является число.​ стоит поближе ознакомиться​Скопируйте образец данных из​ из числа. Таким​

​ результат вычислений.​ функция, которая так​ 1 / 4​ здесь — число​Правой кнопкой мыши щелкаем​ математического вычисления корня.​

​ простой вариант.​ указываются без пробелов​ Excel позволяет выполнять​ из суммы числа​

​ его введения нажать​

Функция возведения в степень в Excel

​ #ЧИСЛО!.​ является более удобным.​

​Корень квадратный в Excel​ с тем, что​ следующей таблицы и​ же образом можно​Также функцию можно вызвать​

​ и называется КОРЕНЬ.​

​ )​ 8​ по ячейке с​

​ВНИМАНИЕ! Если нам нужно​Ввод функции вручную:​ и других знаков.​ ряд математических функций:​

​ 9 и значения​ Shift + 6​В качестве аргумента можно​ Причиной тому является​ можно вычислить и​ собой представляет эта​

​ вставьте их в​ рассчитать квадратный и​

Возведение к степени с помощью оператора

​ через вкладку​ Её синтаксис выглядит​возведение в степень​Kkh​ числом и выбираем​ узнать корень в​В строке формул ставим​Первая цифра – значение​

​ от самых простых​ ячейки h2. ​ (с английской раскладкой​ указывать конкретное значение​ тот факт, что​ рядом других методов,​ математическая функция. По​ ячейку A1 нового​ любой другой корень.​

​«Формулы»​ следующим образом:​ имеет самый высокий​: Можно возвести в​

​ из выскакивающего меню​ степени в Excel​

​ знак «=» и​ «число». Это основание​ до сложнейших. Это​Те же математические операции​ клавиатуры).​

Извлечение корней n-й степени

​ либо ссылку на​ с помощью этих​ которые не требуют​ определению, квадратный корень​ листа Excel. Чтобы​ Но только в​

​.​=КОРЕНЬ(число)​ приоритет…​ степень 1/3​ вкладку «Формат ячеек».​

​ то мы не​ начинаем вводить название​ (т.е. цифра, которую​

​ универсальное программное обеспечение​ можно выполнить с​Чтобы Excel воспринимал вводимую​

​ ячейку с числовым​ операций можно получить​ глубоких познаний в​ из числа а​ отобразить результаты формул,​

​ этом случае придется​Выделяем ячейку для отображения​

​Для того, чтобы воспользоваться​если записать x​Strannik strano​

​ Если не получилось​ используем функцию =КОРЕНЬ().1/n​ во вкладку «Формулы».​ записать в ячейку​ 4 — то​ ли уже mathcad…​ «Формат ячеек» в​ математики:​ и система сама​

​ введение любого вещественного​Перед поиском необходимой функции​ степень и извлечь​

​ «=». Далее водится​Функция вернула квадратный корень​ специальных дополнительных вычислений.​ что такое корень,​ равен числу а.​

​ а затем —​n – это степень​В блоке инструментов «Библиотека​

exceltable.com>

Как возвести число к степени в Excel с помощью формулы и оператора

​ или в строку​ число х возведётся​Alex gordon​ верхней панели или​«Корнем n-ой степени от​

​ догадается предложить вам​ числа.​ обратите внимание на​ корень n-й степени​ цифра, которую нужно​ числа 36. Аргумент​Чтобы окончательно разобраться с​ — эта тема​ В математических науках​ клавишу ВВОД. При​ возведения.​ функций» на ленте​ функций программы это​

Как возвести в степень в Excel?

​ в степень 1​: Посмотри, должно помочь​ жмем комбинацию клавиш​

1. ​ числа а называется​ полезную опцию.» – значение​ на ячейку с​

   ​ Excel, стоит рассмотреть​

   ​ Воспользовавшись определением квадратного​

   ​ Они также бывают​

   1. ​ все данные.​ чем использование первого​. В появившемся списке​
   2. ​ цифру или на​Loony​: Подскажите, плиз как​ вкладку «Число» и​ а», то есть:​ на клавишу «Tab».​ возводим первую цифру.​
   3. ​ «1».​Для корректного отображения числа​ степени.​ положительным значением 36.​
   4. ​ пару примеров для​ корня, его можно​ и любой другой​Данные​

   Формула возведения в степень в Excel

   ​ способа.​

   ​ выбираем значение​

   1. ​ адрес ячейки, где​: Правильно так СТЕПЕНЬ​ можно в экселе​ задаем формат для​n√a = b;​ Или можете продолжить​Значения обоих параметров могут​Число «0» в любой​ в степени при​Вместо любого значения данной​Функция вернула ошибку, т.к.​ двух описанных выше​ представить в виде​
   2. ​ степени, поэтому квадратный​-16​Как видим, несмотря на​«КОРЕНЬ»​ она расположена.​ (A1;0,25) — там​ посчитать корень п-й​ ячейки «Текстовый». Жмем​ bn = a.​
   3. ​ писать, вручную вводить​ быть меньше нуля​ степени будет оставаться​ демонстрации файла или​ математической формулы можно​ аргумент – ссылка​ способов.​ обратной степени двойки​ корень часто называют​Формула​ то, что в​

   ​.​Для выполнения расчета и​ специальная функция СТЕПЕНЬ​ степени, например корень​

   ​ ОК.​

   1. ​«А корень n-ой степени​ каждую букву. Потом​ (т.е. со знаком​ «0».​ его печати, необходимо​ использовать ссылки на​ на ячейку с​В первом случае воспользуемся​
   2. ​ искомого числа. Таким​ корнем второй степени.​Описание​ Excel нет специализированной​Открывается окно аргументов. Все​ вывода результата на​ имеется. A1 -эт​ 3-й степени из​В ячейке A1 вводим​ из числа а​
   3. ​ в скобках укажите​ «-»).​Любое число, возведенное в​ произвести ряд манипуляций:​

   ​ ячейки с цифрами.​ отрицательным значением.​ функцией «КОРЕНЬ», вызвав​ образом, получить квадратный​При решении задачи, связанной​Результат​

   Корень в степени в Excel

   ​ функции для извлечения​ дальнейшие действия в​ экран жмем кнопку​ для примера, ячейка​ 5? Посмотрел функции​ рядом с числом​

   1. ​ будет равен возведению​ необходимые параметры: два​Примеры использования функции СТЕПЕНЬ().​ нулевую степень, равняется​Щелкаем по ячейке с​Это удобно, если нужно​Функция ABS возвращает абсолютное​
   2. ​ её с помощью​ корень без использования​ с нахождением квадратного​=КОРЕНЬ(16)​ кубического корня, данное​ точности такие же,​ENTER​ где содержится число,​ и справку, есть​ «3» число «-2»​ к степени этого​ числа через точку​С использованием мастера функций:​

   ​ единице.​ числом правой кнопкой​ возвести множество значений.​ значение числа -36.​ кнопки «Вставить функцию».​ функции «КОРЕНЬ» можно,​ корня в «Экселе»,​

   ​Квадратный корень числа 16.​ вычисление можно провести,​ как и при​.​ которое в степень​
   ​ упоминание только квадратного​ и выделяем его.​

   ​ же числа а​ с запятой.​Запускаем мастера функций с​Любое значение «А» в​ мыши. Выбираем «Формат​Скопировав формулу на весь​ Ее использование позволило​
   ​ В открывшемся окне​

   ​ просто возведя число​ получить желаемый результат​4​ используя возведение в​

   ​ действии через кнопку​

   ​Кроме того, можно применить​ надо возвести, но​ корня.(5/3)​ клавиш CTRL+1) и​

2. ​n√a = a1/n.​ в ячейке появляется​ жмем на кнопку​Примеры в Excel:​В открывшемся меню переходим​
3. ​ в столбце A​ из отрицательного числа.​ разность значений двух​ двумя способами. Первый​
4. ​ как воспользоваться встроенными​ Так как число​ Для извлечения квадратного​Рассчитать кубический корень использование​Кликаем по ячейке на​Cee cee​fernis​ теперь для нас​Из этого следует чтобы​
5. ​ высчитанное значение 8.​ в начале строки​

​Стандартный и самый простой​ на вкладку «Число».​ в третью степень.​Функция извлекла квадратный корень​ ячеек, и нажать​ заключается в использовании​

exceltable.com>

Как ввести формулу в Excel, чтобы вычислить корень третьей степени?

​ алгоритмами решений, так​​ отрицательное, возвращается сообщение​ корня можно воспользоваться​ указанного выше варианта​
​ листе, куда будет​: Правильны оба ответа​: Видимо, ты имел​ только доступна вкладка​ вычислить математическую формулу​Последовательность действий проста, а​ формул «fx» (вставить​ вариант – использовать​
​ Задаем «Текстовый» формат.(1/3)​
​ ОК.​В Excel следует записывать​ могут быть указаны​
​ нижнем поле указываем​ раскладке клавиатуры.​ через панель инструментов​ 4-й и иной​Синтаксис функции: =СТЕПЕНЬ(значение; число).​ степени числа, получим​ в выбранную степень.​

​ способом нахождения ответа​​ сначала с помощью​ степень. На этот​ вид формулы для​ функций.​https://www.youtube.com/watch?v=_DIjLQ4TC8Y​Спасибо, вот я​В результате должно отображаться​ через такую формулу:​ ссылки на ячейки.​ на нужную нам​

​ВАЖНО!​​ («Главная» – «Число»).​ степеней?​ Оба аргумента обязательные.​

​ следующее выражение для​​ В этом случае​
​ является функция квадратного​

​ функции ABS найдите​

Как преобразовать корни в дробные экспоненты — стенограмма видео и урока

Запись корня как экспоненты

Любое радикальное выражение может быть записано как экспоненциальное выражение. Результат будет иметь показатель степени, который является дробью. Следующие шаги описывают, как должно быть записано экспоненциальное выражение:

1. Индекс радикала, который является корнем, становится знаменателем дроби
2. Подкоренное выражение становится основой экспоненциального выражения, а
3. Если подкоренное выражение радикального выражения имеет показатель степени, это число становится числителем дроби; в противном случае цифра 1 записывается как числитель

Пример 1

В этом первом примере подкоренное выражение равно 28 и становится основанием экспоненциального выражения.Корень радикала равен 5 и становится знаменателем показателя степени. Поскольку подкоренное выражение не имеет показателя степени, числитель дробной степени равен 1.

Пример 2

Во втором примере нет числа, записанного в качестве индекса радикала. Следовательно, корень равен 2. Подкоренное выражение равно 7 с показателем степени 3. 7 становится основанием экспоненциального выражения, а 3 становится числителем показателя степени.Знаменатель экспоненты равен 2, потому что корень равен 2.

Преобразование корня использует

При выполнении операций с радикальными выражениями, таких как умножение или деление, может быть очень сложно решить, если они имеют разные корни. Преобразуя их в экспоненциальные выражения, можно применять свойства экспонент, что упрощает умножение и деление выражений.

В следующем примере показано, как перемножить два радикала, которые имеют одно и то же подкоренное выражение, но разные корни.Во-первых, они преобразуются в экспоненциальные выражения. Затем они умножаются, применяя свойство произведения экспоненты. Свойство продукта экспоненты позволяет вам просто добавлять показатели, когда основания совпадают.

Итоги урока

Хорошо, давайте сделаем обзор. Сначала мы узнали о различных частях радикальных выражений; в основном то, что часть выражения, записанная внутри радикального символа, называется подкоренным элементом и , а индекс — это число, записанное за пределами радикального символа меньшим размером шрифта.

Затем мы узнали, как радикальные выражения имеют корни, которые можно переписать как дроби в экспоненциальных выражениях. Корень радикала определяется индексом и становится знаменателем показателя степени в экспоненциальном выражении. Подкормка становится основой.

Если подкоренное выражение имеет показатель степени, это число становится числителем дробной степени. В противном случае в числителе записывается 1.

Степени и корни: дробные показатели

Давайте поговорим о дробных показателях! Это следующий видеоролик из нашей серии бесплатных видеороликов по математике, и я надеюсь, что он проясняет все ваши вопросы о дробных показателях степени.

Дробные экспоненты. В этом уроке мы можем явно указать связь между корнями и показателями. До сих пор мы рассматривали только целые числа: положительные, отрицательные или нулевые. Итак, мы придерживаемся целых чисел. Что произойдет, если показатель степени будет не целым, а дробным?

Что происходит потом? Итак, давайте рассмотрим это. Например, что означало бы сказать 2 в степени 1/2? Хорошо, давайте подумаем об этом, мы можем выполнять математические операции, если у нас есть другая сторона этого уравнения.Итак, давайте создадим фиктивную переменную K.

Мы назовем выход K, 2 равным 1/2 = K. Хорошо, обратите внимание, что если мы умножим 1/2 на 2, мы получим целое число, а Конечно, мы могли бы использовать это правило умножения экспоненты, если возведем 2 в 1/2 в другую степень. Итак, я собираюсь сказать, почему бы нам не возвести обе стороны в квадрат. С одной стороны, мы получаем К-квадрат. С другой стороны, мы получаем 2 на 1/2 в квадрате.

И, конечно же, по законам экспонент мы умножаем эти показатели 1/2 на 2 = 1.Таким образом, эта сторона просто становится обычной 2, K-квадрат = 2. Но, конечно, мы можем очень легко решить это K. Извлеките квадратный корень, K равно квадратному корню из 2, и это должно быть то, что равно K.

Другими словами, 2 до 1/2 равняется квадратному корню из 2, возведение чего-либо в степень 1/2 равносильно нахождению положительного квадратного корня из этого числа. Это важный факт номер 1. Что бы значило сказать 2 к 1/3? Что ж, вы можете догадаться, но мы будем следовать тому же процессу. Снова заполните фиктивную переменную K.

А теперь обратите внимание, что если мы умножим 1/3 на 3, мы получим целое число. Итак, мы будем кубить обе стороны, и, конечно же, правая сторона просто станет K-кубом. Левая сторона, 2 к 1/3 к 3, в то время как 1/3 и 3 умножаются, и это просто равно 1, так что 2 к 1 или обычному 2. Итак, K-cubed = 2.

Мы можно извлечь кубический корень из обеих сторон, K = кубический корень из 2. Другими словами, 2 к 1/3 равняется кубическому корню из 2. Что ж, вы можете увидеть здесь общую закономерность.Другими словами, если мы возьмем что-то к 1/2, это будет квадратный корень. Если мы возьмем что-то до 1/3, это будет кубический корень. Вы можете догадаться, если мы возьмем 1/4, это будет корень 4-й степени, 1/5, это корень 5-й степени и тому подобное.

И на самом деле, мы можем обобщить, сказав, что b до степени 1 над m, это корень m из b. Итак, это явная связь между дробными показателями и корнями. Так, например, если бы у нас было что-то вроде 6 в степени 1/7, это означало бы корень 7-й степени из 6.Что именно это означает, корень 7-й степени из 6?

Это число, которое в седьмой степени равно шести. Что произойдет, если показатель степени является дробью, у которой в числителе есть число, отличное от единицы? До сих пор мы рассматривали только дроби, у которых в числителе есть единица. Что бы произошло, если бы у нас было что-то вроде 2 на 3/5? Что ж, помните, мы можем записать 3/5 как 3, умноженное на 1/5, или как 1/5 умноженное на 3.

Конечно, мы можем записать произведение любым способом, и это имеет последствия для закона экспонент.Я могу записать его как 3 умножить на 1/5, иметь степень 3 внутри и 1/5 снаружи, и это будет корень 5-й степени из 2 в кубе или корень 5-й степени из 8. Это был бы один из способов, которым я мог бы сделай это.

Еще один способ сделать это — написать 5-ю на внутренней стороне. Итак, внутри у меня только корень 5-й степени из обыкновенного 2, а снаружи я кубирую его. Любой из них вполне подойдет. И я скажу, что если вам действительно нужно произвести расчеты, если вам действительно нужно выбирать между этими двумя, всегда уменьшайте вещи, прежде чем увеличивать их.

Дробные экспоненты: практическая задача

Это очень важный момент стратегии. Вот практическая задача, где вы можете применить кое-что из этого. Поставьте видео на паузу, а потом мы поговорим об этом. Хорошо. Восемь к 4/3. Что ж, мы могли бы написать это либо как кубический корень из 8 в 4-й, либо как кубический корень из 8, все это в степени 4.

Мы могли бы записать это в любом случае. Теперь возникает вопрос, какой способ расчета лучше? Итак, с первым, что нам нужно сделать, это вычислить 8 в степени 4.Ну, это будет большое число, потому что 8 в степени 4 даст 8 в квадрате, то есть будет 64 в квадрате.

Я не знаю 64 в квадрате с головы до ног, но это будет очень большое число. А потом мы попытаемся извлечь из этого кубический корень, хм, это звучит сомнительно. Принимая во внимание, что с другим, все, что нам нужно сделать, это взять кубический корень из 8, мы можем сделать это и затем возвести его до 4-го. Так что первая идея — просто ужасная.

Не увеличивайте его до какой-то большой степени, а затем пытайтесь найти корень.Сначала найдите корень, это огромная точка стратегии. Сначала мы найдем корень, и, конечно, кубический корень из 8 равен 2. Итак, мы получаем 2 к 4-му, и это 16. Итак, эти правила, о которых мы говорили, являются правилами, которые верны для положительных чисел, когда b положительное число.

Технически, они верны для нуля, хотя корни нуля — маловероятная тема в тесте. Если знаменатель дроби экспоненты нечетный, то основание также может быть отрицательным. Помните, что мы не можем брать четные корни из отрицательных чисел, но мы можем брать нечетные корни из отрицательных чисел, например, кубический корень или корень пятой степени отрицательного числа.

Таким образом, корни представлены дробными показателями, и это большая идея. Квадратный корень из величины равен этой величине в степени 1/2. Это, безусловно, самый распространенный дробный показатель степени, который вы увидите на экзамене. Степень b до 1 над n означает корень n-й степени из b. А степень b к m по n может быть записана либо как корень степени, либо как корень степени m.

Показатели степени и квадратные корни

Экспоненциальная запись и положительные целые показатели

Если число повторяется как множитель несколько раз, то мы можем записать произведение в более компактной форме, используя экспоненциальную запись Компактная запись ax2 + bx + c = 0.используется, когда множитель повторяется несколько раз. Например,

Основание Множитель a в экспоненциальной записи an. — множитель, а положительное целое число — положительное целое число n в экспоненциальной записи an, которое указывает, сколько раз основание используется в качестве множителя. указывает количество раз, когда база повторяется как коэффициент. В приведенном выше примере основание равно 5, а показатель степени равен 4. В общем, если a является основанием, которое повторяется как множитель n раз, то

Когда показатель степени равен 2, мы называем результат квадратом Результат, когда показатель степени любого действительного числа равен 2.. Например,

Число 3 — основание, а целое число 2 — показатель степени. Обозначение 32 можно прочитать двумя способами: «три в квадрате» или «3 во второй степени». База может быть любым действительным числом.

Важно изучить разницу между способами расчета в последних двух примерах. В примере (-7) 2 основание равно -7, как указано в круглых скобках. В примере -52 основание равно 5, а не -5, поэтому возводится в квадрат только 5, а результат остается отрицательным.) следующим образом:

Квадрат целого числа называется полным квадратом Результат возведения целого в квадрат. Способность распознавать полные квадраты полезна в нашем изучении алгебры. Квадраты целых чисел от 1 до 15 следует запомнить. Ниже приводится неполный список полных квадратов:

Попробуй! Упростить (−12) 2.

Ответ: 144

Когда показатель степени равен 3, мы называем результат кубом Результат, когда показатель степени любого действительного числа равен 3.. Например,

Обозначение 33 можно прочитать двояко: «три в кубе» или «3 в третьей степени». Как и прежде, в основе может быть любое действительное число.

Обратите внимание, что результат вычисления отрицательного числа в кубе отрицательный. Целочисленный куб называется идеальным кубом. Результат вычисления целого числа в кубе. Способность распознавать идеальные кубы полезна в нашем изучении алгебры. Кубики целых чисел от 1 до 10 следует запомнить.Ниже приводится неполный список идеальных кубиков:

Попробуй! Упростить (−2) 3.

Ответ: −8

Если показатель степени больше 3, то запись an читается как « a в степени n -й степени».

Обратите внимание, что результат отрицательного основания с четной экспонентой положительный. Результат отрицательного основания с нечетной экспонентой отрицательный.Эти факты часто путают, когда речь идет об отрицательных числах. Внимательно изучите следующие четыре примера:

Основание (−2)	База 2
(−2) 4 = (- 2) ⋅ (−2) ⋅ (−2) ⋅ (−2) = + 16 (−2) 3 = (- 2) ⋅ (−2) ⋅ ( −2) = — 8	−24 = −2⋅2⋅2⋅2 = −16−23 = −2⋅2⋅2 = −8

Скобки указывают на то, что отрицательное число должно использоваться как основание.

Пример 1: Рассчитать:

а. (−13) 3

г. (−13) 4

Решение: Основание для обеих задач равно −13.

а. Используйте базу как множитель три раза.

г. Используйте базу как множитель четыре раза.

Ответы: а. −127; б. 181

Попробуй! Упростить: −104 и (−10) 4.

Ответы: −10 000 и 10 000

Квадратный корень действительного числа

Подумайте о том, чтобы найти квадратный корень — число, которое при умножении само на себя дает исходное число. числа как значения, обратного возведению числа в квадрат. Другими словами, чтобы определить квадратный корень из 25, нужно задать вопрос: «Какое число в квадрате равно 25?» Собственно, на этот вопрос есть два ответа: 5 и −5.

При запросе квадратного корня из числа мы неявно подразумеваем главный (неотрицательный) квадратный корень неотрицательный квадратный корень.. Следовательно, мы имеем

Например, 25 = 5, что читается как «квадратный корень из 25 равен 5». Символ √ называется радикальным знаком. Символ √ используется для обозначения квадратного корня. и 25 называется корневым и Выражение a внутри знака корня an .. Альтернативное текстовое обозначение квадратных корней следующее:

Также стоит отметить, что

Это так, потому что 12 = 1 и 02 = 0.

Пример 2: Упростить: 10,000.

Решение: 10 000 — это полный квадрат, потому что 100 100 = 10 000.

Ответ: 100

Пример 3: Упростить: 19.

Решение: Здесь мы замечаем, что 19 — квадрат, потому что 13⋅13 = 19.

Ответ: 13

Учитывая, что a и b являются положительными действительными числами, используйте следующее свойство для упрощения квадратных корней, подкоренные выражения которых не являются квадратами:

Идея состоит в том, чтобы определить наибольший квадратный множитель подкоренного выражения, а затем применить свойство, показанное выше.В качестве примера, чтобы упростить 8, обратите внимание, что 8 не является идеальным квадратом. Однако 8 = 4⋅2 и, следовательно, имеет коэффициент полного квадрата, отличный от 1. Примените свойство следующим образом:

Здесь 22 — упрощенное иррациональное число. Вас часто просят найти примерный ответ, округленный до определенного десятичного знака. В этом случае используйте калькулятор, чтобы найти десятичное приближение, используя исходную задачу или упрощенный эквивалент.

На калькуляторе попробуйте 2.2. Чего вы ожидаете? Почему ответ не такой, как вы ожидали?

Важно отметить, что подкоренное выражение должно быть положительным . Например, −9 не определено, поскольку нет действительного числа, которое в квадрате было бы отрицательным. Попробуйте извлечь квадратный корень из отрицательного числа на своем калькуляторе. Что там написано? Примечание: извлечение квадратного корня из отрицательного числа будет определено позже в этом курсе.

Пример 4: Упростите и дайте приблизительный ответ с округлением до сотых: 75.

Решение: Подкоренное выражение 75 может быть разложено на множители как 25 ⋅ 3, где множитель 25 представляет собой полный квадрат.

Ответ: 75≈8,66

Для проверки вычислите на калькуляторе 75 и 53 и убедитесь, что оба результата равны примерно 8,66.

Пример 5: Упростить: 180.

Решение:

Так как вопрос не требовал приблизительного ответа, мы даем точный ответ.

Ответ: 65

Пример 5: Упростить: −5162.

Решение:

Ответ: −452

Попробуй! Упростите и дайте примерный ответ с округлением до сотых: 128.

Ответ: 82≈11,31

Рисунок 1.1 Пифагор

Прямоугольный треугольник Треугольник с углом 90 °.представляет собой треугольник, угол одного из углов которого равен 90 °. Сторона, противоположная прямому углу, является самой длинной стороной, называемой гипотенузой. Самая длинная сторона прямоугольного треугольника всегда будет стороной, противоположной прямому углу., А две другие стороны называются катетами. гипотенуза .. Эта геометрическая фигура используется во многих реальных приложениях. Теорема Пифагора Для любого прямоугольного треугольника с катетами a и b единиц и гипотенузой размером c единиц, тогда a2 + b2 = c2.утверждает, что для любого прямоугольного треугольника с катетами размером a и b единиц квадрат меры гипотенузы c равен сумме квадратов размеров катетов: a2 + b2 = c2. Другими словами, гипотенуза любого прямоугольного треугольника равна квадратному корню из суммы квадратов его катетов.

Пример 6: Если два катета прямоугольного треугольника имеют размер 3 единицы и 4 единицы, найдите длину гипотенузы.

Решение: Учитывая длины катетов прямоугольного треугольника, используйте формулу c = a2 + b2, чтобы найти длину гипотенузы.

Ответ: c = 5 шт.

При нахождении гипотенузы прямоугольного треугольника с помощью теоремы Пифагора подкоренное выражение не всегда является полным квадратом.

Пример 7: Если два катета прямоугольного треугольника имеют размер 2 единицы и 6 единиц, найдите длину гипотенузы.

Решение:

Ответ: c = 210 шт.

Основные выводы

• При использовании экспоненциальной записи an основание a используется как множитель n раз.
• Когда показатель степени равен 2, результат называется квадратом. Когда показатель степени равен 3, результат называется кубом.
• Запомните квадраты целых чисел до 15 и кубики целых чисел до 10.Они будут часто использоваться по мере вашего прогресса в изучении алгебры.
• При использовании отрицательных чисел позаботьтесь о том, чтобы показатель степени соответствовал правильному основанию. Круглые скобки группируют отрицательное число в некоторой степени.
• Отрицательная база, возведенная в четную степень, является положительной.
• Отрицательное основание в нечетной степени отрицательно.
• Квадратный корень числа — это число, возведение которого в квадрат дает исходное число.Главный квадратный корень — это положительный квадратный корень.
• Упростите квадратный корень, найдя наибольший коэффициент полного квадрата подкоренного выражения. Как только идеальный квадрат найден, примените свойство a⋅b = a⋅b, где a и b неотрицательны, и упростите.
• Проверьте упрощенные квадратные корни, вычислив приближение ответа, используя как исходную задачу, так и упрощенный ответ на калькуляторе, чтобы убедиться, что результаты совпадают.2

  17. (213) 2

  18. (534) 2

  Если s — длина стороны квадрата, то площадь определяется как A = s2 .

  19. Определите площадь квадрата со стороной 5 дюймов.

  20. Определите площадь квадрата со стороной 2,3 фута.

  21. Перечислите все квадраты целых чисел от 0 до 15.

  22. Перечислите все квадраты целых чисел от −15 до 0.

  23. Перечислите квадраты всех рациональных чисел в наборе {0, 13, 23, 1, 43, 53, 2}.

  24. Перечислите квадраты всех рациональных чисел в наборе {0, 12, 1, 32, 2, 52}.

  Часть B: Целочисленные экспоненты

  Упростить.

  25. 53

  26. 26

  27.100

  41. — (12) 3

  42. (12) 6

  43. (52) 3

  44. (−34) 4

  45. Перечислите все кубы целых чисел от −5 до 5.

  46. Перечислите все кубики целых чисел от −10 до 0.

  47. Перечислите все кубики рациональных чисел в наборе {−23, −13, 0, 13, 23}.

  48. Перечислите все кубики рациональных чисел в наборе {−37, −17, 0, 17, 37}.

  , часть C: квадратный корень числа

  Определите точный ответ в упрощенной форме.

  49,121

  50. 81

  51,100

  52,169

  53. −25

  54. −144

  55. 12

  56. 27

  57,45

  58. 50

  59.98

  60. 2000

  61,14

  62. 916

  63. 59

  64. 836

  65. 0,64

  66. 0,81

  67.302

  68,152

  69. (−2) 2

  70. (−5) 2

  71. −9

  72. −16

  73,316

  74.518

  75. −236

  76. −332

  77. 6200

  78. 1027

  Приблизительно до сотых.

  79. 2

  80. 3

  81. 10

  82,15

  83,23

  84. 52

  85. −65

  86. -46

  87.sqrt (79)

  88. sqrt (54)

  89. −sqrt (162)

  90. −sqrt (86)

  91. Если два катета прямоугольного треугольника имеют размер 6 единиц и 8 единиц, то найдите длину гипотенузы.

  92. Если два катета прямоугольного треугольника имеют размер 5 единиц и 12 единиц, то найдите длину гипотенузы.

  93. Если два катета прямоугольного треугольника имеют размер 9 единиц и 12 единиц, то найдите длину гипотенузы.

  94. Если два катета прямоугольного треугольника имеют размер 32 единицы и 2 единицы, то найдите длину гипотенузы.

  95. Если оба катета прямоугольного треугольника имеют размер 1 единицу, найдите длину гипотенузы.

  96. Если два катета прямоугольного треугольника имеют размер 1 единицу и 5 единиц, то найдите длину гипотенузы.

  97. Если два катета прямоугольного треугольника имеют размер 2 единицы и 4 единицы, найдите длину гипотенузы.

  98. Если два катета прямоугольного треугольника имеют размер 3 единицы и 9 единиц, то найдите длину гипотенузы.

  Часть D. Темы дискуссионной доски

  99. Почему результат экспоненты 2 называется квадратом? Почему результат экспоненты 3 называется кубом?

  100. Изучите и обсудите историю теоремы Пифагора.

  101. Изучите и обсудите историю квадратного корня.

  102. Обсудите важность главного квадратного корня.

  ответов

  1: 100

  3: 81

  5: 121

  7: 0

  9: −64

  11: 1/4

  13: 0,25

  15: 6.76

  17: 549

  19: 25 квадратных дюймов

  21: {0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225}

  23: {0, 1/9, 4/9, 1, 16/9, 25/9, 4}

  25: 125

  27: 1

  29: -1

  31: −343

  33: 27

  35: 1

  37: −216

  39: 1

  41: −18

  43: 1258

  45: {−125, −64, −27, −8, −1, 0, 1, 8, 27, 64, 125}

  47: {−827, −127, 0, 127, 827}

  49: 11

  51: 10

  53: −5

  55: 23

  57: 35

  59: 72

  61: 12

  63: 53

  65: 0.8

  67: 30

  69: 2

  71: Неверно

  73: 12

  75: −12

  77: 602

  79: 1,41

  81: 3.16

  83: 3.46

  85: -13,42

  87: 8,89

  89: -12,73

  91: 10 шт.

  93:15 шт.

  95: 2 шт.

  97: 25 шт.

  Корень (числа) — определение математического слова

  Корень (числа) — определение математического слова — Открытый справочник по математике

  Корень числа x — это другое число, которое при умножении само на себя заданное количество раз дает x.

  Например, третий корень (также называемый кубическим корнем) из 64 равен 4, потому что если вы умножите три четверки вместе, вы получите 64:

  4 × 4 × 4 = 64

  Это было бы записано как

  Вышеупомянутое будет означать «корень третьей степени 64 равен 4» или «кубический корень 64 равен 4» .

  • Второй корень обычно называют «квадратным корнем».
  • Третий корень числа обычно называют «кубическим корнем»,
  • После этого они называются корнем n, например корень 5, корень 7 и т. Д.

  Иногда бывает два корня

  Для каждого корня четной степени (например, 2-го, 4-го, 6-го….) есть два корня. Это потому, что умножение двух положительных или двух отрицательных чисел дает положительный результат. Например, рассмотрим квадратный корень из 9.

  Какое число, умноженное на само себя, даст 9?
  
  Очевидно 3 будут работать:

  3 × 3 = 9

  Но так будет -3:

  -3 × -3 = 9

  Когда таких корней два, если не указано иное, мы имеем в виду положительный. Строго говоря, когда мы пишем
  √ 4, мы имеем в виду положительный корень, +2.Это называется «главный корень».

  Корни отрицательных чисел

  У отрицательных чисел нет реальных корней четного порядка. Например, квадратного корня из -9 не существует, потому что
  -3 × -3 = + 9, а также +3 × +3 = + 9. Это относится ко всем корням четного порядка, 2-му (квадратному) корню, 4-му корню, 6-му корню и так далее.

  Однако есть — это корня нечетного порядка отрицательных чисел. Например, –3 — это кубический корень из –27.
  Это потому что
  –3 × –3 × –3 = –27.Первые два члена при умножении дают +9, затем следующее умножение составляет
  +9 × –3 = –27.
  Это применимо ко всем корням нечетного порядка, таким как 3-й (кубический) корень, 5-й корень, 7-й корень и т. Д.

  Мнимые числа

  Выше сказано, что действительного квадратного корня из отрицательного числа не существует. Обратите внимание на слово «настоящий». Это говорит о том, что нет
  настоящий номер
  это квадратный корень отрицательного числа.

  Однако в математике и инженерии нам часто нужно найти квадратный корень из отрицательного числа.Чтобы решить эту проблему, мы вводим понятие «мнимого» числа. Он включает в себя символ i , который обозначает квадратный корень из отрицательного числа.
  Или, другими словами, i ² = –1

  На практике мы можем использовать его для выражения квадратного корня из любого отрицательного числа. Например

  Это означает, что квадратный корень из –25 — это квадратный корень из +25, умноженный на квадратный корень из отрицательной единицы.

  Подробнее о мнимых числах см.
  Мнимые числа.

  Символы

  Радиканд

  То, что вы находите корень.

  Радикальный символ

  Символ √ , означающий «корень из». Длина турника важна. См. Примечание ниже.

  градусов

  Сколько раз подкоренное выражение умножается само на себя. 2 означает квадратный корень, 3 означает кубический корень.
  После этого они называются корнем 4-й, 5-й и так далее.
  Если он отсутствует, предполагается, что это 2 — квадратный корень.

  Другой способ записи

  Корни также можно записать в экспоненциальной форме. В общем

  Так, например, кубический корень x будет записан

  Что будет произноситься как «х в степени одной трети».

  Другие экспоненты и основные темы

  (C) Открытый справочник по математике, 2011 г.
  
  Все права защищены.

  Знак квадратного корня (сделайте символ корня на клавиатуре)

  Квадратный корень √ — это математический текстовый символ (о его значении мы поговорим позже), который люди переписывали с тех времен, когда была разработана кодировка ASCII. И вы можете набрать его прямо с клавиатуры. Я покажу вам, как это сделать, используя разные методы в зависимости от вашей операционной системы и вкусов.

  Математика	≠	≤	≥	∫
  	Σ	√	π	½

  Математика корня

  Квадратный корень из некоторого числа «А» — это такое число «Х», что «Х», умноженное само на себя, будет «А». Каждое положительное число «A» имеет два квадратных корня: положительный и отрицательный ± √a. Хотя главный квадратный корень положительного числа является только одним из двух квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.Для положительного «A» главный квадратный корень также может быть записан в экспоненциальной нотации как A ^1/2 .

  Но корней больше, чем просто квадратные! Мы можем сказать, что N-й корень из числа «X» — это число «R», которое при возведении в степень «N» равно «X» и обозначается как Rⁿ = X.
  Также в случае, если эти корни имеют мощность пары (2, 4, 6 …), у них будет 2 решения, положительное и отрицательное. И те, у кого есть непарная сила (1, 3, 5…) имел бы только одно положительное решение.

  Я дам вам несколько примеров использования для наглядности.

  Квадратный корень из 9 равен ± 3 (обозначается как ± √9 = 3), потому что (± 3) ² = 9 (3 · 3 = 9)
  
  Корень пятой степени из 34 равен 2,024397 … (обозначается как ⁵√34 = 2,024397 …), потому что 2,024397 ⁵ = 34
  

  Как ввести квадратный корень

  Выберите свою систему, чтобы узнать.

  Окна

  Состояния переключения

  Настройте раскладку клавиатуры в Windows так, чтобы вы могли вводить все дополнительные символы так же легко, как и любой другой текст.На настройку уходит около 5-10 минут, но вы будете печатать как начальник.
  Вы можете назначить математический квадратный корень √ и любые другие текстовые символы на клавиатуре, используя эту технику.

  Карта персонажей

  CharMap позволяет просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Вы можете ввести символ квадратного корня, используя его.

  Mac

  Emoji на iOS (iPhone, iPad и iPod touch)

  Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов Emoji, отображаемых в виде небольших изображений.Сама клавиатура предустановлена ​​на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.

  Средство просмотра клавиатуры

  Палитра символов

  Палитра символов позволяет вам просматривать и использовать все символы и символы, включая знак квадратного корня, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.

  Linux

  С клавиатуры

  Карта символов

  Карта символов позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.Он также может помочь вам найти коды Unicode для ввода символов с клавиатуры.

  HTML код

  Ниже приведен список объектов HTML и JavaScript для символа квадратного корня. В Javascript вы должны написать как = «этот \ u2669 символ», если вы хотите включить специальный символ в строку.

  Степени корней, Мощность

  246. Было показано, каким образом любая сила или корень может быть выражена с помощью индекса. Индекс мощности — целое число.Дробь корня — это дробь, числитель которой равен 1. Существует также другой класс величин, которые можно рассматривать либо как степени корней, либо как корни степеней.

  Предположим, что ^1/2 умножается само на себя и повторяется три раза как множитель.

  Произведение a ^{1/2 + 1/2 + 1/2} или ^3/2 (статья 243,), очевидно, является кубом ^1/2 , то есть кубом квадратного корня а. Этот дробный индекс означает, таким образом, степень корня .Знаменатель выражает корень, а числитель — степень. Знаменатель показывает, на сколько равных факторов или корней разрешается данная величина; а числитель показывает, сколько из этих корней нужно перемножить.
  
  Таким образом, ^4/3 — это 4-я степень кубического корня из a.

  Знаменатель показывает, что a делится на три фактора или корня: ^1/3 , ^1/3 и ^1/3 . Числитель показывает, что четыре из них нужно перемножить; который даст четвертую степень ^1/3 ; это,
  
  а ^1/3 .a ^1/3 .a ^1/3 .a ^1/3 = a ^4/3 .

  247. Как ^3/2 — это степень корня, так и — это корень степени . Возводим a в третью степень a ³ . Квадратный корень из этого равен ^3/2 . Корень из ³ — это величина, умноженная на себя, даст ³ .

  Но согласно ст. 243, a ^3/2 = a ^1/2 .a ^1/2 .a ^1/2 ; и это умножилось само в себя (ст.100,) является
  
  a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 = a ³ .
  
  Следовательно, ^3/2 — это квадратный корень из куба a.

  Таким же образом можно показать, что ^{m / n} является m-й степенью корня n-й степени числа a; или корень n-й степени в степени m: то есть корень степени равен той же степени того же корня . Например, четвертая степень кубического корня из a совпадает с кубическим корнем из четвертой степени из a.

  248. Корни и степени одной и той же буквы можно умножить на , сложив их степень . (Статья 243.) Легко увидеть, что тот же принцип может быть распространен на степени корней, когда показатели имеют общий знаменатель.

  Таким образом, ^2/7 .a ^3/7 = ^{2/7 + 3/7} = ^5/7 .

  Первый числитель показывает, как часто ^1/7 берется в качестве множителя для получения ^2/7 . (Изобразительное искусство.246.)

  А второй числитель показывает, как часто ^1/7 берется в качестве множителя для получения ^3/7 .

  Таким образом, сумма числителей показывает, как часто нужно извлекать корень для произведения . (Статья 100.)
  
  Или, таким образом, ^2/7 = ^1/7 .a ^1/7 .
  
  И ^3/7 = ^1/7 .a ^1/7 .a ^1/7 .
  
  Следовательно, ^2/7 .a ^3/7 = ^1/7 .a ^1/7 .a ^1/7 .a ^1/7 .a ^1/7 = a ^5/7 .

  249. Значение количества не изменяется при применении к нему дробного индекса, числитель и знаменатель которого равны.

  Таким образом, a = ^2/2 = a ^3/3 = a ^{n / n} . Знаменатель показывает, что a разложено на определенное количество факторов; а числитель показывает, что все эти факторы включены в ^{n / n} .
  
  Таким образом, ^3/3 = ^1/3 .a ^1/3 .a ^1/3 , что равно a.
  
  И a ^{n / n} = a ^{1 / n} .a ^{1 / n} ….. n раз.

  С другой стороны, когда числитель дробного индекса становится равным знаменателю, выражение можно сделать более простым, если отклонит индекс .

  Вместо _{n / n} мы можем написать.

  250. Индекс степени или корня может быть заменен на любой другой индекс того же значения.
  Вместо ^2/3 можно поставить ^4/6 .

  Поскольку в последнем из этих выражений предполагается, что a должно быть разложено на , вдвое на больше множителей, чем в первом; а числитель показывает, что удвоить , так как многие из этих факторов должны быть умножены вместе. Так что вся стоимость не изменится.

  Таким образом, x ^2/3 = x ^4/6 = x ^6/9 . то есть квадрат кубического корня равен четвертой степени корня шестой, шестой степени корня девятой.

  Итак, ² = ^4/2 = ^6/3 = ^{2n / n} . Ибо значение каждого из этих показателей равно 2. (Ст. 132).

  251. Из предыдущей статьи легко увидеть, что дробный индекс может быть выражен десятичными знаками .

  1. Таким образом, ^1/2 = ^5/10 или ^0,5 ; то есть квадратный корень равен 5-й степени корня десятой.

  2. ^1/4 = ^25/100 или ^0,25 ; то есть корень четвертой степени равен 25-й степени 100-го корня.

  3. ^2/5 = ^{0,4 ​​}.

  4. ^7/2 = ^3,5 .

  5. ^9/5 = ^1,8

  Однако во многих случаях десятичная дробь может быть только приближением к истинному индексу.

  Таким образом, ^1/3 = ^0,3 почти. ^1/3 = ^0,333334 очень близко.

  Таким образом, приближение может быть выполнено с любой требуемой степенью точности.

  Таким образом, ^5/3 = ^1,66666 . nbsp; ^11/7 = ^1,87142 .

  Эти десятичные индексы образуют очень важный класс чисел, называемый логарифмами , .

  Часто удобно изменять обозначение степеней корней, используя винкулум или знак корня √. При этом мы должны помнить, что сила корня равна силе корня; (Ст. 247,), а также, что знаменатель дробной экспоненты выражает корень , а числитель — степень .(Статья 246.)

  Поэтому вместо ^2/3 мы можем написать (a ^1/3 ) ² , или (a ² ) ^1/3 , или ³ √a ² .

  Первая из этих трех форм обозначает квадрат кубического корня из a; и каждый из двух последних — кубический корень из квадрата a.

  Таким образом, ^{m / n} = (a ^{1 / n} ) ^m = (a ^m ) ^{1 / n} = ⁿ √a ^m .
  
  И (bx) ^3/4 = (b ³ x ³ ) ^1/4 = ⁴ √b ³ x ³ .
  И (a + y) ^3/5 = [(a + y) ³ ] ^1/5 = ⁵ √ (a + y) ³ .

  Рациональные показатели — Полный курс алгебры

  29

  Дробный показатель

  Экспоненциальная форма против радикальной формы

  Отрицательная экспонента

  Оценки

  Правила экспонентов

  КУБИЧЕСКИМ КОРНЕМ a мы подразумеваем число, третья степень которого равна a .

  Таким образом, кубический корень из 8 равен 2, потому что 2 ³ = 8. Кубический корень из −8 равен −2, потому что (−2) ³ = −8.

  — это кубический корень из на . 3 называется индексом радикала.

  В целом

  означает b ⁿ = a. .

  Эквивалентно

  Читать « n корень -й степени из a .«

  Например,

  — Корень 4-й степени из 81 — это 3
  , потому что 81 — это 4-я степень числа 3.

  Если индекс опущен, например, индекс считается равным 2.

  Пример 1.		=	11.
  		=	2, потому что 2 5 = 32.
  		=	10, потому что 10 4 = 10,000.
  		=	−2, потому что (−2) 5 = −32.

  Мы видим, что если индекс нечетный , то подкоренное выражение может быть отрицательным. Но если индекс четный, подкоренное выражение не может быть отрицательным.Нет такого реального числа, например, как.

  Проблема 1. Оцените каждое следующее — если оно реально.

  а)

  =

  3

  б)

  =

  −3

  в)

  =

  2

  г)

  =

  Не реально.

  д)

  =

  −5

  е)

  =

  1

  г)

  =

  Не реально.

  ч)

  =

  -1

  Проблема 2.Доказательство:

  Совет : умножьте числитель и знаменатель на

  Дробный показатель

  Мы видели, что чтобы возвести в квадрат степень, удвойте показатель степени.

  ( a ⁴ ) ² = a ⁸ .

  И наоборот, квадратный корень из степени равен половине показателя степени.Квадратный корень из a ⁸ равен a ⁴ ;

  значение a ¹⁰ равно a ⁵ ; значение a ¹² равно a ⁶ .

  Это будет держаться для всех сил. Квадратный корень из на ³ получается на . То есть a ⁵ равно a . И особенно квадратный корень из ¹ .

  Другими словами, равно.

  =.

  Точно так же, поскольку куб степени будет показателем, умноженным на 3 — куб из a ⁿ равен a ^{3 n} — кубический корень из степени будет делением показателя на 3. Кубический корень из a ⁶ равен a ² ; значение a ² равно a . И кубический корень из a ¹ равен a .

  =.

  Это общее правило:

  =

  Знаменатель дробной экспоненты
  равен индексу радикала.
  Знаменатель указывает корень.

  Пример 2.	8 означает кубический корень из 8, который равен 2.
  	81 означает четвертый корень из 81, что составляет 3.
  	(-32) означает пятый корень из -32, что равно -2.

  8 — экспоненциальная форма кубического корня из 8.

  — его радикальная форма.

  Проблема 3. Оцените следующее.

  Задача 4. Выразите каждый радикал в экспоненциальной форме

  a — кубический корень из a ² .Показатель 2 был разделен на 3. Однако по правилам показателей:

  a = ( a ² ) = ( a ) ² .

  То есть

  Например,

  8 = (8) ² = 2 ² = 4.

  8 — это кубический корень из 8 в квадрате.

  снова:

  Знаменатель дробной экспоненты
  указывает корень .

  Хотя 8 = (8 ² ), для оценки дробной степени более эффективно сначала извлечь корень, потому что мы возьмем степень меньшего числа.

  В целом

  Проблема 5. Оцените следующее.

  Задача 6. Выразите каждый радикал в экспоненциальной форме.

  Отрицательная экспонента

  Число с отрицательной экспонентой определяется как обратное этому числу с положительной экспонентой.

  a ^−v — это , обратное от a ^v .

  Следовательно,

  Задача 7. Выразите каждое из следующих значений отрицательной экспонентой.

  Задача 8. Выразить в радикальной форме.

  Оценки

  На уроке экспонент мы увидели, что −2 ⁴ — отрицательное число.Это отрицание 2 ⁴ .

  В самом деле, знак минус означает отрицательное значение числа, следующего за ним. И число, следующее за минусом здесь, −2 ⁴ , это 2 ⁴ .

  [(−2) ⁴ — положительное число. Урок 13.]

  .

  Таким образом, аналогично

  −8 — это отрицательное значение из 8:

  −8 = −2 ² = −4.

  С другой стороны,

  (−8) — положительное число:

  (-8) = (-2) ² = 4.

  Проблема 9. Оцените следующее.

  а)

  9 −2

  =

  1 9 2

  =

  1 81

  б)

  9

  =

  3

  в)

  9

  =

  1 3

  г)

  −9

  =

  −3

  д)

  −9 2

  =

  −81

  е)

  (−9) 2

  =

  81

  г)

  −9 −2

  =

  –

  1 81

  ч)

  (−9) −2

  =

  1 81

  i)

  −27

  =

  −9

  к)

  (-27)

  =

  9

  к)

  27

  =

  1 9

  л)

  (-27)

  =

  1 9

  Проблема 10.Оценить

  Это величина, обратная 16/25 — с положительным показателем степени.
  Итак, это квадратный корень из 25/16, который равен 5/4, затем возведенный в 3-ю степень: 125/64.

  Правила экспонентов

  Показателем степени может быть любое рациональное число. Рациональные показатели u, v подчиняются обычным правилам.

  a u a v	=	a u + v	Та же база
  	=	a u — v
  ( ab ) u	=	a u b u	Мощность продукта
  ( a u ) v	=	a УФ	Мощность мощности
  	=		Мощность дроби

  Пример 3.Перепишите в экспоненциальной форме и примените правила.

  См. «Арифметика, сложение и вычитание дробей».

  Задача 11. Примените правила экспонент.

  а)	4 · 4 = 4 = 4 = 2

  б)

  8 8

  = 8 = 8 = 2

  в)

  (10)

  = 10 = 10 −3 знак равно

  1 1000

  Проблема 12.Выразите каждый радикал в экспоненциальной форме и примените правила экспонент.

  а)	x знак равно х · х = х = х

  б)	x 2 знак равно x 2 · x = х = х

  в)

  =

  ( х + 1) = ( х + 1)

  Теперь мы можем понять, что правила для радикалов, а именно

  — правила экспонентов.Таким образом, они применяются только к факторам.

  Задача 13. Доказать:

  =

  ( ab ) =

  a · b =
  ·

  Чтобы решить уравнение, которое выглядит следующим образом:

  Для, x · = x ¹ = x .

  Проблема 14.Решите относительно x .

  а)

  x

  =

  8

  б)

  x

  =

  −32

  x

  =

  8

  =

  4

  x

  =

  (-32)

  =

  −8

  в)	( x — 1)	=	64			г)	x 7	=	5
  x — 1		=	64	x				=
  x		=	256 + 1 = 257

  д)	x	=	7			е)		=	5
  x		=	7 5	x				=	5 =

  Следующий урок: Комплексные числа

  Содержание | Дом

  ---

  Сделайте пожертвование, чтобы TheMathPage оставалась в сети.