6 = 9³ : (2³ * 2³) = 4,5³ : 2³ = 2,25³ = 11,390625.

Решение показательных уравнений и неравенств

ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ

Показательным называется уравнение, в котором неизвестная Х
содержится в показателе степени.
_{Примеры:}

Методы решения показательных уравнений

1. Метод приведения к одному основанию

   если в уравнении имеется два слагаемых в виде степеней, которые можно привести к одному основанию, то надо:
   1- перенести слагаемые в разные стороны
   2- привести степени к одному основанию т.е. получить уравнение вида

   3- приравнять показатели степеней т.е.
   4- решить получившееся уравнение

Пример 1:

Решение:

Ответ:

1. Метод вынесения общего множителя за скобки

   если в уравнении несколько слагаемых в виде степеней с одинаковым основанием и коэффициенты перед переменной Х одинаковые, то надо:
   1- слагаемое без Х перенести в другую часть уравнения
   2- найти наименьший показатель степени
   3- выделить у каждой степени наименьший показатель ( если его там нет)
   4- раскрыть сумму в показателе степени по формуле

   5- выделить у каждого слагаемого степень с наименьшим показателем и вынести этот общий
   множитель за скобки
   6- упростить получившееся уравнение и привести его к виду

   7- приравнять показатели степеней т. е. и решить получившееся уравнение

Пример 2:

Решение:

Ответ:

1. Метод приведения к квадратному уравнению

   если в уравнении три слагаемых, два из которых это степени с одинаковым основанием и коэффициенты перед Х в два раза больше ( или противоположные по знаку), то надо:
   1- найти степень с наименьшим показателем и заменить её на новую переменную
   2- записать получившееся квадратное уравнение относительно новой переменной
   3- решить квадратное уравнение (относительно новой переменной)
   4- вернуться к замене и решить получившиеся простые уравнения вида

   Пример 3:

_{Решение:}

Вернемся к замене

Ответ: х=2, х=1

ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА

Показательным называется неравенство, в котором неизвестная Х
содержится в показателе степени

Примеры:

План решения показательных неравенств:

1. Перенести слагаемые в разные стороны неравенства

2. Привести степени к одному основанию т. е. к виду

3. Выписать основание _{« »
   — если , то функция возрастает и знак неравенства сохраняем между показателями степеней т.е.
   если , то функция убывает и знак неравенства меняем между показателями степеней т.е.}
   

4. Решить получившееся неравенство, отметить штриховку на прямой

5. Записать ответ

Пример 4:

Решение:

_Ответ:

Пример 5:
Решение:

_Ответ:

Задания для самостоятельного решения

Показатеьные уравнения. Алгебра, 11 класс: уроки, тесты, задания.

1.	Определение показательного уравнения Сложность: лёгкое	1
2.	Показательное уравнение с отрицательным показателем степени Сложность: лёгкое	2
3.	Определение показательного уравнения (корень n-ой степени) Сложность: лёгкое	1
4.	Определение корня n — ой степени Сложность: лёгкое	1
5.	Показательное уравнение с корнем Сложность: среднее	1
6.	Показательное уравнение (приведение к одному основанию) Сложность: среднее	2
7.	Показательное уравнение с приведением к одному основанию Сложность: среднее	2
8.	Показательное уравнение (приведение к общему основанию) Сложность: среднее	2
9.	Показательное уравнение (дробные показатели) Сложность: среднее	2
10.	Показательное уравнение (общий множитель) Сложность: среднее	2
11.	Показательное уравнение с общим множителем Сложность: среднее	2
12.	Показательное уравнение (умножение степеней) Сложность: среднее	2
13.	Показательное уравнение (деление степеней) Сложность: среднее	2
14.	Решение показательного уравнения (умножение степеней) Сложность: среднее	2
15.	Количество корней показательного уравнения, графический метод Сложность: среднее	1
16.	Показательное уравнение и неравенство, графический метод Сложность: среднее	3
17.	Показательное уравнение (новая переменная) Сложность: среднее	4
18.	Показательное уравнение с обратной дробью Сложность: среднее	4
19.	Показательное уравнение, сводимое к одному основанию Сложность: сложное	3
20.	Свойства степени в показательном уравнении Сложность: сложное	3
21.	Однородное уравнение Сложность: сложное	7

Логарифм и его свойства – Сайт Александра Бабаева

Понятие о логарифме.

{p}}} =$

По пятому свойству, получим:

$= \frac{\log_{a}{x}}{p \cdot \log_{a}{a}} = $

По второму свойству, будем иметь:

$= \frac{\log\limits_{a}{x}}{p}.$

Информация о записи:

01 февраля 2015 в 14:04:28

31 декабря 2015 в 15:03:20

Логарифм и его свойства

Свойства оснований логарифмов

Для снятия логарифма в обеих частях уравнения должны находиться логарифмы с одинаковым основанием. Если основания различны, тогда нужно привести все логарифмы к одному основанию. Обычно общим основанием становится одно из оснований логарифмов, присутствующих в уравнении. Желательно, чтобы это было самое простое основание. Например, из оснований 3 и нужно выбирать “3”; из оснований , x² + 4 x + 2 и x желательно выбрать основание “x”; но в случае оснований и x² + 2 желательно переходить к основанию “2”. Т.е. желательно упрощать основания логарифмов, используя свойство №7, при этом из них должны исчезнуть степени и корни.

Заметьте, что замена основания в логарифмах приводит к появлению логарифмов в знаменателе. Если эти логарифмы не рассчитываются и не сокращаются, тогда с ними можно бороться заменой переменных или переносом в другую часть уравнения. Например, уравнение:

Приводится заменой основания к виду:А затем преобразуется в:

Внимание. При решении неравенств нужно помнить о смене знака неравенства при домножении на отрицательное число. Так например, в последнем примере, если бы это было неравенство, при умножении обеих частей неравенства на log₃ x знак неравенства поменяется на интервале x О ( 0 ; 1) и не поменяется на интервале x О [ 1 ; + Ґ ). Эти два интервала нужно рассматривать по отдельности, а затем объединять ответы.

–

Перед заменой оснований в логарифмах, в том числе для упрощения перехода к единому основанию, можно проверить, нельзя ли упростить логарифмы. Имеется в виду использование свойств №3 и №2. Т.е. нужно представить наиболее сложные аргументы логарифмических функций в виде произведения, затем использовать свойство логарифма произведения, и наконец, сократить, по возможности, те логарифмы, где основание и аргумент совпадают с точностью до степени, т.е. использовать свойство №2. Например, выражение:

Желательно представить в виде: log_{x + 3} x + 2.

При переходе от более сложного основания к более простому иногда можно произвести упрощение аргумента логарифмической функции и после замены основания.

Заметьте, что наличие в уравнении каких-либо чисел-слагаемых, и наличие многочленов второй и более высоких степеней в качестве аргументов и оснований логарифмов должно натолкнуть Вас на мысль о возможности преобразований.

–

Замена оснований возможна и в показательных уравнениях, но там она происходит при переходе от переменного основания к фиксированному и выражается в умножении показателя на логарифм старого основания по новому основанию, т. е. используется свойство №6. Например, в уравнении:

Производится переход к основанию 2, т.е. показатель степени в правой части умножается на log₂ x:

Решение показательных неравенств

3 января 2017

Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое. И что научиться их решать — чуть ли не великое искусство, постичь которое способны лишь Избранные…

Полная брехня! Показательные неравенства — это просто. И решаются они всегда просто. Ну, почти всегда.:)

Сегодня мы разберём эту тему вдоль и поперёк. Этот урок будет очень полезен тем, кто только начинает разбираться в данном разделе школьной математики. Начнём с простых задач и будем двигаться к более сложным вопросам. Никакой жести сегодня не будет, но того, что вы сейчас прочитаете, будет достаточно, чтобы решить большинство неравенств на всяких контрольных и самостоятельных работах. {n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.

Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:

\[\begin{align} & -\frac{8x}{3} \lt 4-4x; \\ & 4x-\frac{8x}{3} \lt 4; \\ & \frac{4x}{3} \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end{align}\]

Вот и всё. Окончательный ответ: $x\in \left( -\infty ;3 \right)$.

Выделение устойчивого выражения и замена переменной

В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. {5}}=3125. \\\end{align}\]

Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.

Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)

Смотрите также:

1. Простейшие показательные уравнения
2. Преобразование показательных уравнений
3. Десятичные дроби
4. Решение задач B12: №448—455
5. Метод интервалов: случай нестрогих неравенств
6. ЕГЭ-2014 по математике и открытый банк задач

11 класс. Алгебра. Показательная и логарифмическая функции. Понятие логарифма. Функция y=logₐx, ее свойства и график.

— Переход к новому основанию логарифма. Решение задач.

Комментарии преподавателя

Пе­ре­ход к но­во­му ос­но­ва­нию ло­га­риф­ма

На­пом­ним цен­траль­ное опре­де­ле­ние – опре­де­ле­ние ло­га­риф­ма. Оно свя­за­но с ре­ше­ни­ем по­ка­за­тель­но­го урав­не­ния . По­ка­за­тель­ная функ­ция  мо­но­тон­на, каж­дое по­ло­жи­тель­ное зна­че­ние b она до­сти­га­ет при един­ствен­ном зна­че­нии ар­гу­мен­та, то есть при кон­крет­ном зна­че­нии b урав­не­ние имеет един­ствен­ный ко­рень. Этот ко­рень на­зы­ва­ют ло­га­риф­мом b по ос­но­ва­нию а: 

Опре­де­ле­ние:

Ло­га­риф­мом числа b по ос­но­ва­нию а на­зы­ва­ет­ся такой по­ка­за­тель сте­пе­ни, в ко­то­рую нужно воз­ве­сти ос­но­ва­ние а, чтобы по­лу­чить число b.

На­пом­ним ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство.

Вы­ра­же­ние  (вы­ра­же­ние 1) яв­ля­ет­ся кор­нем урав­не­ния  (вы­ра­же­ние 2). Под­ста­вим зна­че­ние х из вы­ра­же­ния 1 вме­сто х в вы­ра­же­ние 2 и по­лу­чим ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство:

При­ме­ры:

 при любом а;

 при любом а;

По­вто­рим из­вест­ные нам свой­ства ло­га­риф­мов. Здесь :

1. Ло­га­рифм про­из­ве­де­ния:

 (про­из­ве­де­ние  может быть по­ло­жи­тель­ным, если  оба – от­ри­ца­тель­ные числа, но, ис­хо­дя из пра­вой части,  стро­го по­ло­жи­тель­ны)

2. Ло­га­рифм част­но­го:

3. Ло­га­рифм сте­пе­ни:

Ино­гда в за­да­чах не ука­за­но, что  и  – по­ло­жи­тель­ные числа, тогда необ­хо­ди­мо при рас­кры­тии ло­га­риф­ма ста­вить мо­дуль:

 ( – это любые числа кроме нуля, но их про­из­ве­де­ние долж­но быть по­ло­жи­тель­ным)

Пе­рей­дем к ос­нов­ной фор­му­ле дан­но­го урока.

Дано:

До­ка­зать:

До­ка­за­тель­ство:

При­ме­ним рав­но­силь­ные пре­об­ра­зо­ва­ния. По­сколь­ку в зна­ме­на­те­ле стоит ло­га­рифм, а он не может быть равен нулю, т. к. , имеем право до­мно­жить обе части на дан­ный ло­га­рифм:

Со­глас­но свой­ству ло­га­риф­ма, вне­сем со­мно­жи­тель под знак ло­га­риф­ма как по­ка­за­тель сте­пе­ни:

При­ме­ним ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство:

Что и тре­бо­ва­лось до­ка­зать.

При­мер 1 – вы­чис­лить:

Чтобы вос­поль­зо­вать­ся свой­ством ло­га­риф­ма, нужно при­ве­сти за­дан­ные ло­га­риф­мы к од­но­му ос­но­ва­нию. При­ве­дем вто­рой ло­га­рифм к ос­но­ва­нию 2:

По­лу­чим вы­ра­же­ние:

Имеем сумму ло­га­риф­мов с оди­на­ко­вым ос­но­ва­ни­ем. При­ме­ним свой­ство:

При­мер 2 – ре­шить урав­не­ние:

Оче­вид­но, что необ­хо­ди­мо вы­брать новое ос­но­ва­ние и при­ве­сти к нему все ло­га­риф­мы, чтобы вос­поль­зо­вать­ся свой­ства­ми и ре­шить урав­не­ние. Вы­бе­рем ос­но­ва­ние 2:

В ре­зуль­та­те пре­об­ра­зо­ва­ний по­лу­чи­ли урав­не­ние:

При­ве­дем по­доб­ные:

Раз­де­лим обе части на :

По опре­де­ле­нию ло­га­рим­фа:

Итак, мы вы­ве­ли и рас­смот­ре­ли новую важ­ную фор­му­лу – пе­ре­хо­да к но­во­му ос­но­ва­нию ло­га­риф­ма.  

Пе­ре­ход к но­во­му ос­но­ва­нию ло­га­риф­ма, ре­ше­ние задач

На­пом­ним цен­траль­ное опре­де­ле­ние – опре­де­ле­ние ло­га­риф­ма. Оно свя­за­но с ре­ше­ни­ем по­ка­за­тель­но­го урав­не­ния . По­ка­за­тель­ная функ­ция  при­ни­ма­ет все по­ло­жи­тель­ные зна­че­ния. Она мо­но­тон­на, каж­дое по­ло­жи­тель­ное зна­че­ние b она до­сти­га­ет при един­ствен­ном зна­че­нии ар­гу­мен­та, то есть при кон­крет­ном зна­че­нии b урав­не­ние имеет един­ствен­ный ко­рень. Этот ко­рень на­зы­ва­ют ло­га­риф­мом b по ос­но­ва­нию а: 

Опре­де­ле­ние:

Ло­га­риф­мом числа b по ос­но­ва­нию а на­зы­ва­ет­ся такой по­ка­за­тель сте­пе­ни, в ко­то­рую нужно воз­ве­сти ос­но­ва­ние а, чтобы по­лу­чить число b.

На­пом­ним ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство.

Вы­ра­же­ние  (вы­ра­же­ние 1) яв­ля­ет­ся кор­нем урав­не­ния  (вы­ра­же­ние 2). Под­ста­вим зна­че­ние х из вы­ра­же­ния 1 вме­сто х в вы­ра­же­ние 2 и по­лу­чим ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство:

По­вто­рим из­вест­ные нам свой­ства ло­га­риф­мов.  Здесь :

1. Ло­га­рифм про­из­ве­де­ния:

 (про­из­ве­де­ние  может быть по­ло­жи­тель­ным, если  – оба от­ри­ца­тель­ные числа, но, ис­хо­дя из пра­вой части,  стро­го по­ло­жи­тель­ны)

2. Ло­га­рифм част­но­го:

3. Ло­га­рифм сте­пе­ни:

На­пом­ним важ­ную фор­му­лу – пе­ре­хо­да к но­во­му ос­но­ва­нию ло­га­риф­ма:

Здесь 

На­при­мер, вы­чис­лить:

Неслож­но за­ме­тить, что ло­га­риф­мы в чис­ли­те­ле и зна­ме­на­те­ле имеют одно и то же ос­но­ва­ние, по фор­му­ле пе­ре­хо­да по­лу­ча­ем:

Пе­ре­хо­дим к след­стви­ям из фор­му­лы пе­ре­хо­да.

След­ствие 1:

Здесь 

Рас­пи­шем по фор­му­ле пе­ре­хо­да к но­во­му ос­но­ва­нию:

Что и тре­бо­ва­лось до­ка­зать.

Ино­гда дан­ное свой­ство ис­поль­зу­ют в сле­ду­ю­щем виде:

След­ствие 2:

Здесь 

При­ме­ним фор­му­лу пе­ре­хо­да к но­во­му ос­но­ва­нию, а имен­но, от ос­но­ва­ния к ос­но­ва­нию а:

Что и тре­бо­ва­лось до­ка­зать

Рас­смот­рим важ­ное уточ­не­ние для чет­ных сте­пе­ней:

Здесь 

По­яс­не­ние:

По­сколь­ку  – чет­ное число, до­пус­ка­ют­ся как по­ло­жи­тель­ные, так и от­ри­ца­тель­ные зна­че­ния b. Ана­ло­гич­но до­пус­ка­ют­ся как по­ло­жи­тель­ные, так и от­ри­ца­тель­ные зна­че­ния а, за ис­клю­че­ни­ем . Если мы не по­ста­вим в пра­вой части мо­ду­ли, то а и b будут толь­ко по­ло­жи­тель­ны­ми чис­ла­ми, об­ласть опре­де­ле­ния сузит­ся.

До­ка­за­тель­ство:

Пе­ре­хо­дим к но­во­му ос­но­ва­нию:

Важно, что с по­мо­щью мо­ду­ля мы со­хра­ни­ли неиз­мен­ной об­ласть опре­де­ле­ния, не сузи­ли ее. Так мы можем предо­хра­нить себя от мно­го­чис­лен­ных ти­по­вых оши­бок.

Фор­му­ла пе­ре­хо­да к но­во­му ос­но­ва­нию и след­ствия из нее ши­ро­ко ис­поль­зу­ют­ся при ре­ше­нии раз­лич­ных ти­по­вых задач.

При­мер 1 – вы­чис­лить:

Пре­об­ра­зу­ем по­ка­за­те­ли сте­пе­ни со­глас­но фор­му­лам пе­ре­хо­да к но­во­му ос­но­ва­нию:

По­лу­ча­ем:

Пре­об­ра­зу­ем ос­но­ва­ния сте­пе­ней:

При­ме­ним свой­ство сте­пе­ни:

В по­ка­за­те­лях сте­пе­ней вне­сем мно­жи­те­ли под знак ло­га­риф­ма со­глас­но свой­ству:

При­ме­ним ос­нов­ное ло­га­риф­ми­че­ское тож­де­ство:

При­мер 2 – ре­шить урав­не­ние:

При­ве­дем все три ло­га­риф­ма к од­но­му ос­но­ва­нию, на­при­мер к ос­но­ва­нию 4:

Ис­поль­зу­ем фор­му­лу 

В ре­зуль­та­те пре­об­ра­зо­ва­ний по­лу­чи­ли урав­не­ние:

Со­кра­тим трой­ку:

Вы­ра­зим х, ис­хо­дя из опре­де­ле­ния ло­га­риф­ма:

со­глас­но ос­нов­но­му ло­га­риф­ми­че­ско­му тож­де­ству:

Итак, мы рас­смот­ре­ли неко­то­рые ти­по­вые за­да­чи на фор­му­лу пе­ре­хо­да к но­во­му ос­но­ва­нию ло­га­риф­ма и след­ствия из нее.  

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/perehod-k-novomu-osnovaniyu-logarifma

http://interneturok.ru/ru/school/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/perehod-k-novomu-osnovaniyu-logarifma-reshenie-zadach

http://mathematics-tests.com/11-klass-uroki-presentatsii/algebra-11-klass-urok-perehod-k-novomu-osnovaniu-logarifma

https://downloader.disk.yandex.ru/disk/197fa925c280a3c019e8f0b97c7065779aec80a75626f3c3c7877370509af9a4/56a1139b/gl1wdmatkHwr1IvHwfPzjlCbLxx51K2AXTrKx-khOfQ1WIGwVJDIxTfxWZJp9W23tYCJlb2c61QroEWHqjfeTQ%3D%3D?uid=0&filename=%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1. pdf&disposition=attachment&hash=Ev/JAxs9FONy74%2BMIKGz214ILPNlyMZo/xnQbixz5Z8%3D%3A/%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&limit=0&content_type=application%2Fpdf&fsize=18366111&hid=c9e0cd334be9f7c6de02c1f2d04edf87&media_type=document&tknv=v2

http://www.mathematics-repetition.com/11-klass-algebra/11-4-9-1-logarifm-obshtaya-formula-perehoda-k-novomu-osnovaniyu.html

Переход к новому основанию логарифма

http://www.berdov.com/docs/logarithm/what_test_hard/

http://www.berdov.com/docs/logarithm/basic_properties/

http://vseuchebniki.net/uploads/posts/2015-01/1422313744_algebra_10-11_mordkovich_p2_2009.jpg

http://cdndl.zaycev.net/117190/12852/didyulya_-_put_domoy_(zaycev. net).mp3

Как преобразовать градусы в дюймы или миллиметры

Преобразование угла (ø) в расстояние (d) имеет смысл только тогда, когда рассматриваемое расстояние находится на окружности круга или на поверхности сферы. В этом случае используйте уравнение ø = d / r — где r — радиус круга или сферы. Это дает значение в радианах, которое легко преобразовать в градусы. Если вы знаете угол в градусах и хотите найти длину дуги, преобразуйте угол в радианы, а затем используйте обратное выражение: d = ø • r.Чтобы получить расстояние в английских единицах, вы должны выразить радиус в английских единицах. Точно так же вы должны выразить радиус в метрических единицах, чтобы получить расстояние в километрах, метрах, сантиметрах или миллиметрах.

Измерение углов в радианах

Радиан — это угловое измерение, основанное на длине радиуса круга или сферы. Радиус — это линия, проведенная от центра круга до точки A на его окружности или по периметру, если это сфера. Когда радиальная линия перемещается из точки A в другую точку B на окружности, она очерчивает дугу длиной d, в то же время очерчивая угол ø в центральной точке окружности.

По определению, один радиан — это угол, который вы записываете, когда длина дуги от точки A до точки B равна длине радиуса. В общем, вы определяете величину любого угла ø в радианах, разделив длину дуги, проведенную линиями в радианах между двумя точками, на радиус. Это математическое выражение: ø (радианы) = d / r. Чтобы это выражение работало, вы должны выразить длину и радиус дуги в одних и тех же единицах.

Например, предположим, что вы хотите определить угол дуги, очерченной радиальными линиями, идущими от центра Земли до Сан-Франциско и Нью-Йорка.Эти два города находятся на расстоянии 2572 миль (4139 километров) друг от друга, а экваториальный радиус Земли составляет 3963 мили (6378 километров). Мы можем найти угол, используя метрические или английские единицы, если мы используем их последовательно: 2572 мили / 3963 мили = 4139 км / 6378 км = 0,649 радиана.

Радианы в градусы

Мы можем получить простой коэффициент для преобразования радианов в градусы, заметив, что круг имеет 360 градусов, а длина окружности равна 2πr единицам.Когда радиальная линия проходит по всей окружности, длина дуги составляет 2πr / r = 2π, а поскольку линия проходит под углом в 360 градусов, мы знаем, что 360 градусов = 2π радиан. Разделив обе части этого уравнения на 2, мы получим:

Это означает, что 1 градус = π / 180 радиан и 1 радиан = 180 / π градусов.

Преобразование градусов в длину дуги

Нам нужна одна ключевая информация, прежде чем мы сможем преобразовать градусы в длину дуги, а именно радиус круга или сферы, на которой мы измеряем дугу.Как только мы это узнаем, преобразование будет простым. Вот двухэтапная процедура:

1. Преобразуйте градусы в радианы.
2. Умножьте на радиус, чтобы получить длину дуги в тех же единицах.

Если вам известен радиус в дюймах и вам нужна длина дуги в миллиметрах, вы должны сначала преобразовать радиус в миллиметры.

Пример 50-дюймовой окружности

В этом примере вы хотите определить длину дуги — в миллиметрах — на окружности окружности диаметром 50 дюймов, проведенной парой линий, образующих угол 30 градусов.

1. Начните с преобразования угла в радианы. 30 градусов = 30π / 180 радиан. Поскольку π приблизительно равно 3,14, получаем 0,523 радиана.
2. Помните, что радиус круга равен половине его диаметра. В данном случае r = 25 дюймов.
3. Преобразуйте радиус в целевые единицы — миллиметры — используя преобразование 1 дюйм = 25,4 миллиметра. Получаем 25 дюймов = 635 миллиметров.
4. Умножьте радиус на угол в радианах, чтобы получить длину дуги.635 мм • 0,523 радиана = 332,1 мм.

Как переводить градусы в радианы

Что такое радиан?

Радиан — это единица измерения углов. Другая единица измерения углов, с которой вы, вероятно, более знакомы, — это градусы. Хотя существует более двух единиц измерения угла, радиан и градусы — это те две единицы, с которыми вам придется иметь дело больше всего.

Вы, наверное, задаетесь вопросом, почему мы должны использовать радианы, когда у нас уже есть градусы.Это потому, что градусы на самом деле не числа. Чтобы вычислить математику, нам нужно работать с числами. Хороший пример, похожий на эту концепцию, — использование десятичных дробей, когда у нас есть проценты. Хотя процентное соотношение может быть показано с помощью числа, за которым следует знак%, когда мы выполняем математические вычисления, мы преобразуем его в десятичное число (или дробь).

В этом уроке мы узнаем, как преобразовать радианы в градусы, а также наоборот: преобразовать градусы в радианы.

Преобразование радианов в градусы

Для начала давайте сначала преобразуем радианы в единицы, с которыми мы больше знакомы: градусы. \ circ}} {{\ pi \; rad}} πrad180∘.\ circ}} 180∘πрадиан. При необходимости используйте калькулятор для умножения. Тогда мы получим окончательный ответ.

В качестве онлайн-ресурса, если вы хотите быстро преобразовать радианы в десятичные дроби, используйте этот онлайн-конвертер, чтобы помочь вам или дважды проверить свою работу.

градусов и радианов — объяснения и примеры

Как и любая другая величина, у углов также есть единицы измерения. Радианы и Градусы — две основные единицы измерения углов .Существуют и другие единицы измерения углов (например, градуса и MRAD), но в средней школе вы увидите только эти две единицы.

Что такое градусы и радианы?

Самая популярная единица измерения углов, с которой знакомо большинство людей, — это градус ( ° ). Единицы градуса — минуты и секунды. Есть 360 градусов, 180 градусов для полукруга (полукруга) и 90 градусов для четверти круга (прямоугольный треугольник) в полном круге или одном полном вращении.

Градусы в основном указывают направление и размер угла . Лицом к северу означает, что вы смотрите в направлении 0 градусов. Если вы повернете на юг, вы окажетесь лицом к лицу в 90 градусов. Если вы вернетесь на север после полного поворота, вы повернетесь на 360 градусов. Обычно положительным считается направление против часовой стрелки. Если повернуть на запад с севера, угол будет либо -90 градусов, либо +270 градусов.

В геометрии есть еще одна единица измерения углов, известная как радиан ( рад, ).

Итак, зачем нам радианы, когда мы уже привыкли к углам?

Большинство математических вычислений связаны с числами. Поскольку градусы на самом деле не являются числами, предпочтительнее использовать радианы, которые часто требуются для решения проблем.

Хороший пример , который похож на эту концепцию, использует десятичные дроби, когда у нас есть проценты . Хотя процент может быть показан с помощью числа, за которым следует знак%, мы преобразуем его в десятичную дробь (или дробь).

Концепция нахождения угла по длине дуги использовалась давно. Радиан был введен намного позже. Роджер Котес дал понятие радиан в 1714 году, но он не дал ему такого названия, а просто назвал его круговой мерой угла.

Термин « радиан, » впервые был использован в 1873 году. Позднее это название привлекло всеобщее внимание и получило разрешение.

Из этой статьи вы узнаете, как преобразовать градусы в радианы и наоборот (радианы в градусы).Давайте взглянем.

Как перевести градусы в радианы?

Чтобы преобразовать градусы в радианы, мы умножаем заданный угол (в градусах) на π / 180.

Угол в градусах (°) x π / 180 = Угол в радианах (рад)

Где π = 22/7 или 3,14

Пример 1

Преобразование следующих углов из градусов в радианы

1. 0 °
2. 30 °
3. 45 °
4. 60 °
5. 90 °
6. 120 °
7. 150 °
8. 180 °
9. 210 °
10. 240 °
11. 360 °

Решение

Угол в градусах (°) x π / 180 = Угол в радианах (рад)

1. 0 ° x π / 180

= 0 Rad

2. 30 ° x π / 180

= π / 6

= 0,5 Rad

3. 45 ° x π / 180

= π / 4

= 0,785 рад

4. 60 ° x π / 180

= π / 3

= 1,047 рад

5. 90 ° x π / 180

= π / 2

= 1,571рад

6. 120 ° x π / 180

= 2π / 3

= 2,094 Rad

7. 150 ° x π / 180

= 5π / 6

= 2,618 Rad

8. 180 ° x π / 180

= π

= 3.14 Rad

9. 210 ° x π / 180

= 7π / 6

= 3.665 Rad

10. 240 ° x π / 180

= 3π / 2

= 4.189 Rad

11. 360 ° x π / 180

= 2π

= 6,283 Rad

Пример 2

Преобразование 700 градусов в радианы.

Решение

Угол в градусах (°) x π / 180 = Угол в радианах (Rad)

Путем замены,

Угол в радианах (Rad) = 700 x π / 180.

= 35 π / 9

= 12,21 рад.

Пример 3

Преобразовать — 300 ° в радианы.

Раствор

Угол в радианах = -300 ° x π / 180.

= — 5π / 3

= — 5,23 Rad

Пример 4

Преобразовать — 270 ° в радианы.

Решение

Угол в радианах = -270 ° x π / 180.

= — 3π / 2

= -4,71 Рад.

Пример 5

Преобразуйте 43 градуса, 6 минут и 9 секунд в радианы.

Solution

Первый экспресс 43 градуса, 6 минут и 9 секунд только до градусов.

43 ° 6 ′ 9 ″ = 43,1025 °

43,1025 ° x π / 180 = угол в радианах

= 0,752 рад.

Пример 6

Преобразовать 102 ° 45 ’54 ″ в радианы.

Решение

102 ° 45 ′ 54 ″ равно 102,765 °

Угол в радианах = 102,765 ° x π / 180.

= 1,793 Рад.

Как преобразовать радианы в градусы?

Чтобы преобразовать радианы в градусы, умножьте радиан на 180 / π. Таким образом, формула имеет вид,

Угол в радианах x 180 / π = Угол в градусах.

Пример 7

Преобразуйте каждый из следующих углов в радианах в градусы.

1. 1,46
2. 11π / 6
3. π / 12
4. 3,491
5. 7,854
6. -8,14
7. π / 180

Решение

Угол в радианах x 180 / π = Угол в градусах.

1. 46 x 180 / π

= 83.69 градусов.

1. 11π / 6 x 180 / π

= 330 градусов.

1. π / 12 x 180 / π

= 15 градусов.

3. 491 x 180 / π

= 200,1 градуса

7. 854 x 180 / π

= 450,2 градуса.

8. -8,14 x 180 / π

= — 466,6 градуса.

1. π / 180 x 180 / π

= 1 градус.

Пример 8

Преобразуйте угол π /5 радиан в градусы.

Решение

Угол в радианах x 180 / π = Угол в градусах.

Путем замены

π /5 x 180 / π = 36 градусов.

Пример 9

Преобразование угла — π /8 радиан в градусы

Решение

-π /8 x 180 / π = — 22,5 градусов.

Пример 10

Радиус куска пиццы составляет 9 см.Если периметр куска составляет 36,850 см, найдите угол куска пиццы в радианах и градусах.

Решение

Пусть длина дуги детали = x

Периметр = 9 + 9 + x

36,850 см = 18 + x

Вычтите 18 с обеих сторон.

18,85 = x

Итак, длина дуги детали составляет 18,85 см.

Но, длина дуги = θr

Где θ = угол в радианах, а r = радиус.

18,85 см = 9 θ

Разделите обе стороны на 9

θ = 2.09 Rad

θ в градусах:

Угол в радианах x 180 / π = Угол в градусах.

= 2,09 x 180 / π

= 120 градусов.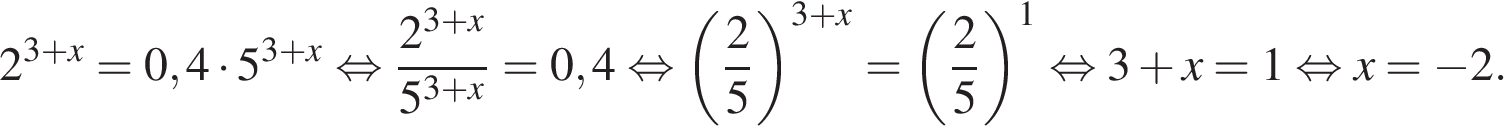

Пример 11

Радиус сектора 3 м, а его площадь 3π / 4 м ² . Найдите центральный угол сектора в градусах и радианах.

Решение

Учитывая, что

Площадь сектора = (r ² θ) / 2

Где θ = центральный угол в радианах.

Заменитель.

3π / 4 = (3 ² θ) / 2

3π / 4 = 9θ / 2

Перекрестное умножение.

6 π = 36 θ

Разделим обе части на 36, чтобы получить

θ = 0,52 рад.

Преобразует угол в градусы.

= 0,52 x 180 / π

= 29,8 градуса.

Пример 12

Найдите центральный угол сектора с радиусом 56 см и площадью 144 см ² .

Раствор

A = (θ / 360) πr ²

144 = (θ / 360) x 3.14 x 56 x 56.

144 = 27,353 θ

Разделите обе стороны на θ.

θ = 5,26

Таким образом, центральный угол составляет 5,26 градуса.

Пример 13

Площадь сектора 625 мм ² . Если радиус сектора равен 18 мм, найдите центральный угол сектора в радианах.

Решение

Площадь сектора = (θ r ² ) / 2

625 = 18 x 18 x θ / 2

625 = 162 θ

Разделите обе стороны на 162.

θ = 3,86 радиан.

Практические вопросы

1. Преобразование 330 ° в радианы.
2. Преобразовать -750 ° в радианы
3. Преобразовать каждый из следующих углов в радианах в градусы:

a. 21π / 5

б. -15π / 2

Предыдущий урок | Главная страница | Следующий урок

Тригонометрия: преобразование градусов и минут

Обычно угол в окружности составляет 360 градусов. Хотя угол обычно измеряется в градусах, дробные части градусов измеряются в минутах и ​​секундах, и их представление выглядит следующим образом.

1 степень = 1 ⁰

1 минута = 1 ’

1 секунда = 1 ’’ .

и

1 ⁰ = 60 минут => 1 ‘= 1/60 ⁰

1 ‘= 60‘ ’=> 1‘ ’= 1/60‘

Таким образом, вместе 1 ‘’ = 1/60 * 1/60 градусов = 1/3600 ’’ .

Вот несколько примеров, которые проиллюстрируют процесс преобразования градусов в минуты, минут в градусы, секунд в градусы и т. Д.

Пример-1:

Преобразование 45,3 ⁰ в градусы и минуты.

Решение:

45,3 ⁰ = 45 + 0,3 ⁰

У нас 1 ‘= 60‘ ’

Итак, 45,3 ⁰ = 45 + 0,3 ⁰ = 45 ⁰ + (0. 3 * 60) ‘= 45 ⁰ + 18‘ = 45 ⁰ 18 ’.

Пример-2:

Преобразуйте угол 25 ⁰ 12 ’ в градусы.

Решение:

25 ⁰ 12 ’= 25 ⁰ +12’

У нас 1 ‘= 1/60 ⁰

Итак, 25 ⁰ 12 ’= 25 ⁰ +12’ = 25 ⁰ + (12/60) ⁰ = 25 ⁰ +0.2 ⁰ = 25,2 ⁰

Пример-3:

Преобразование 42 ⁰ 15’45 ’’ в градусы.

Решение:

У нас

1 ‘= 1/60 ⁰

1 ‘’ = 1/3600 ’’

Итак, 42 ⁰ 15’45 ’’ = 42 ⁰ + (15/60) ⁰ + (45/3600) ⁰

= 42 ⁰ +0,25 ⁰ +0. 0125 ⁰ = 42,2625 ⁰

SchoolTutoring Academy — ведущая компания в сфере образовательных услуг для школьников и школьников. Мы предлагаем учебные программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Orangeville, посетите: Репетиторство в Orangeville.

Как преобразовать направление ветра в градусах в направления по компасу

Вы чувствуете себя потерянным при просмотре данных о направлении ветра, которые указаны в градусах? Например, можете ли вы представить себе, в каком направлении находится 195 градусов? Было бы проще, если бы ваш регистратор данных мог вместо этого записывать ваши данные в направлениях компаса? В этой статье я поделюсь с вами простым методом преобразования данных о направлении ветра из градусов в направления по компасу с помощью языка программирования CRBasic.

Направление по компасу и градусы

Если вы похожи на меня, направления по компасу (север, юг, восток и запад) легче понять, чем градусы. Например, если кто-то спрашивает меня, как проехать, я не говорю: «Пройдите пять кварталов по курсу 270 градусов». Мне и потерявшемуся водителю будет легче, если я скажу: «Иди на запад пять кварталов».

Точно так же, когда дело доходит до описания направления ветра, точки компаса легче понять, чем градусы. Метеорологи используют точки компаса в своих прогнозах погоды, потому что их легче визуализировать и запомнить.Например, метеоролог может сказать: «Шторм надвигается с запада».

Что касается направления ветра, то и к счастью, и к несчастью, регистраторы данных не «думают», как мы, люди.

• К счастью, наши регистраторы данных сканируют наши датчики, преобразуют измерения в электрические сигналы и сохраняют данные в градусах, которые более точны, чем направления компаса.
• К сожалению, нам трудно разобраться в данных о направлении ветра в градусах.

Использование индексированного массива

Чтобы разобраться в данных о направлении ветра в градусах, давайте приступим к процессу преобразования. Чтобы преобразовать градусы в направления по компасу, я сначала разделил компас на 16 секторов по 22,5 градуса каждый. Секторы похожи на кусочки пирога, центрированные по стрелкам компаса.

Совет: Если вы хотите использовать восемь секторов вместо 16, с более короткой таблицей поиска, разделите на 45 градусов вместо 22,5 градусов.

Для преобразования я использую индексированный массив в качестве таблицы поиска вместо инструкции Case . Я предпочитаю индексированный массив, потому что код быстрее и компактнее, чем код инструкции Case . Кроме того, индексированный массив хорошо подходит для равномерно распределенных бункеров данных, например для заданного числа градусов. (Бункеры данных — это категории для диапазонов чисел.) Напротив, команда Case является лучшим выбором для приложений, в которых ваши бункеры данных не расположены равномерно, например для определения диапазонов температур, в которых вода описывается как горячая, теплая или холодная . («Горячие» и «холодные» значения будут иметь больший размер, а «теплый» — меньший размер.)

Поскольку север на компасе можно описать как 0 градусов или 360 градусов, мы должны использовать для него две ячейки данных. Это означает, что для наших 16 секторов компаса нам действительно нужно 17 значений в нашей таблице поиска. И первое, и последнее значение — север. В таблице ниже показаны 17 значений для 16 различных секторов компаса:

Вы можете использовать массив в программе регистратора данных в качестве таблицы поиска. Простой способ заполнить массив — присвоить начальные значения. Убедитесь, что вы используете тип String и заключите каждое значение в кавычки. Строка кода длинновата, но довольно проста:

   Тусклый сектор (17) в виде строки * 3 = {"N", "NNE", "NE", "ENE", "E", "ESE", "SE", "SSE", "S", "SSW", "SW", "WSW", "W", "WNW", "NW", "NNW", "N"}
   

Отделение по модулю

Теперь нам нужно преобразовать направление ветра в целые числа, которые соответствуют 17 значениям индекса в нашем массиве.

Чтобы ограничить направление ветра до 360 градусов, нам нужно выполнить операцию по модулю, чтобы найти остаток после деления общего количества градусов на 360.

Примечание: Хотя этот шаг необязателен для большинства датчиков, он не вызовет никаких проблем, если вы включите его в свои программы.

Согласование с массивом

Если мы разделим направление ветра на 22,5 (градуса для каждого сектора) и округлим, мы получим числа от 0 до 16. Поскольку метки, хранящиеся в массиве, имеют индекс от 1 до 17, мы должны добавить 1, чтобы соответствовать диапазону:

   Индекс = WindDir MOD 360
Индекс = Круглый (Индекс / 22.5,0) +1
CompassDir = сектор (индекс)
   

Мы можем поместить всю математическую функцию в индексный параметр массива.Скобки определяют порядок действий изнутри:

   CompassDir = Sector (Round ((WindDir MOD 360) / 22.5,0) +1)
   

Объединяя программу

Соединив все части вместе, мы получим следующую программу регистратора данных. Просто добавьте свои измерения и таблицы данных.

   'Объявление общедоступных переменных
Public WindDir As Float
Единицы WindDir = градусы
Тусклый сектор (17) в виде строки * 3 = {"N", "NNE", "NE", "ENE", "E", "ESE", "SE", "SSE", "S", "SSW" , "SW", "WSW", "W", "WNW", "NW", "NNW", "N"}
Public CompassDir как строка * 3
 
'Основная программа
BeginProg
Сканирование (1, сек, 0,0)
'Добавьте сюда измерения датчика ветра
CompassDir = Sector (Round ((WindDir MOD 360) / 22.5,0) +1) 'Округляет направление ветра на 17 секторов.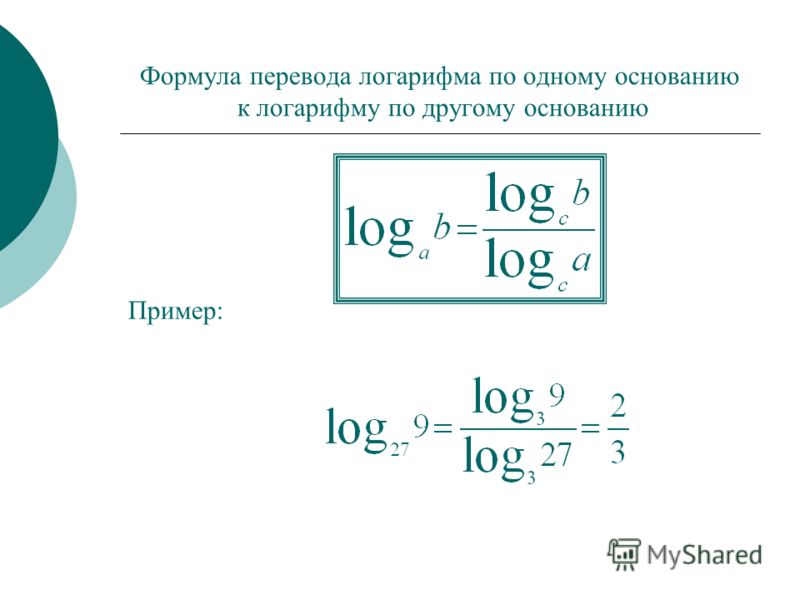  Секторы 1 и 17 оба являются N.
NextScan
EndProg
   

Идеи приложений

В этой статье я надеюсь, что помог вам найти способ лучше понять, использовать и поделиться своими данными о направлении ветра с помощью некоторого программного кода CRBasic. Если у вас есть какой-либо из наших программных продуктов RTMC, это программное обеспечение может принимать данные о направлении ветра и напрямую преобразовывать градусы в отображение компаса.

Не стесняйтесь рассказывать о ситуациях, когда вы хотите сообщить направление ветра с помощью точек компаса.Можете ли вы представить себе подобные случаи с равномерно распределенными бункерами данных, в которых вы могли бы использовать этот метод? Разместите свои идеи ниже.

Преобразование углов градусы / минуты / секунды в десятичные и обратно — Office

• 650Z» data-article-date-source=»git»> 08.04.2021
• Читать 3 минуты

• Применимо к:

  Excel 2010, Microsoft Office Excel 2007, Microsoft Office Excel 2003

В этой статье

Примечание

Office 365 профессиональный плюс переименовывается в Microsoft 365 Apps для предприятий .Дополнительные сведения об этом изменении см. В этом сообщении в блоге.

Сводка

Угловые измерения обычно выражаются в градусах, минутах и ​​секундах (DMS). 1 градус равен 60 минутам, а одна минута — 60 секундам. Чтобы упростить некоторые математические вычисления, вы можете выразить угловые измерения в градусах и десятичных долях градусов.

В этой статье содержится образец настраиваемой функции, которую вы можете использовать для преобразования значения градуса, хранящегося в десятичном формате, в DMS, сохраненного в текстовом формате, и пример функции, которая преобразует DMS в значение градуса, сохраненное в десятичном формате.

Дополнительная информация

Microsoft предоставляет примеры программирования только для иллюстрации, без явных или подразумеваемых гарантий, включая, но не ограничиваясь, подразумеваемые гарантии товарной пригодности и / или пригодности для определенной цели. В этой статье предполагается, что вы знакомы с демонстрируемым языком программирования и инструментами, используемыми для создания и отладки процедур. Специалисты службы поддержки Майкрософт могут помочь объяснить функциональность конкретной процедуры, но они не будут изменять эти примеры для предоставления дополнительных функций или построения процедур для удовлетворения ваших конкретных потребностей.

Если у вас ограниченный опыт программирования, вы можете обратиться в консультационную службу Microsoft. Для получения дополнительной информации посетите веб-сайт Microsoft:

Консультационные услуги Microsoft — https://support.microsoft.com/gp/advisoryservice

Для получения дополнительных сведений о доступных вариантах поддержки и о том, как связаться с Microsoft, см. Https://support.microsoft.com.

Преобразование десятичных градусов в градусы / минуты / секунды

Следующая пользовательская функция Microsoft Visual Basic для приложений принимает угол, отформатированный как десятичное значение, и преобразует его в текстовое значение, отображаемое в градусах, минутах и ​​секундах.

  Функция Convert_Degree (Decimal_Deg) как вариант
    С приложением
        'Установить степень в целое число пройденного аргумента
        Градусы = Целое (Десятичное_Десятичное число)
        'Установите минуты так, чтобы в 60 раз больше числа справа
        'десятичной дроби для переменной Decimal_Deg
        Минуты = (Decimal_Deg - Градусы) * 60
        'Установите в секундах значение, в 60 раз превышающее число справа от
        'десятичная дробь для переменной Минуты
        Секунды = Формат (((Минуты - Целые (Минуты)) * 60), «0»)
        'Возвращает результат преобразования степени.
        '(например, 10.46 = 10 ~ 27 '36 дюймов)
        Convert_Degree = "" & Градусы & "°" & Int (Минуты) & "'" & Секунды + Chr (34)
    Конец с
Конечная функция
  

Чтобы использовать эту функцию, создайте формулу преобразования, как в следующем примере:

1. Запустите Excel и нажмите ALT + F11, чтобы запустить редактор Visual Basic.

2. В меню «Вставка» выберите «Модуль».

3. Введите пример кода для пользовательской функции Convert_Degree, описанной выше, в лист модуля.

4. Нажмите ALT + F11, чтобы вернуться в Excel.

5. В ячейке A1 введите 10.46.

6. В ячейке A2 введите формулу: = Convert_Degree (A1)

   Формула возвращает 10 ° 27’36 «

Преобразование градусов / минут / секунд в десятичные градусы

Следующая пользовательская функция Microsoft Visual Basic для приложений принимает текстовую строку с градусами, минутами и секундами, отформатированными в том же формате, что и функция Convert_Degree (например, 10 ° 27 ’36 дюймов), и преобразует ее в форматированный угол. как десятичное значение.Это в точности обратное пользовательской функции Convert_Degree.

Предупреждение

Эта пользовательская функция не работает, если аргумент Degree_Deg не имеет формат <градусы> ° <минуты> ‘<секунды> «, даже если значение секунд равно 0.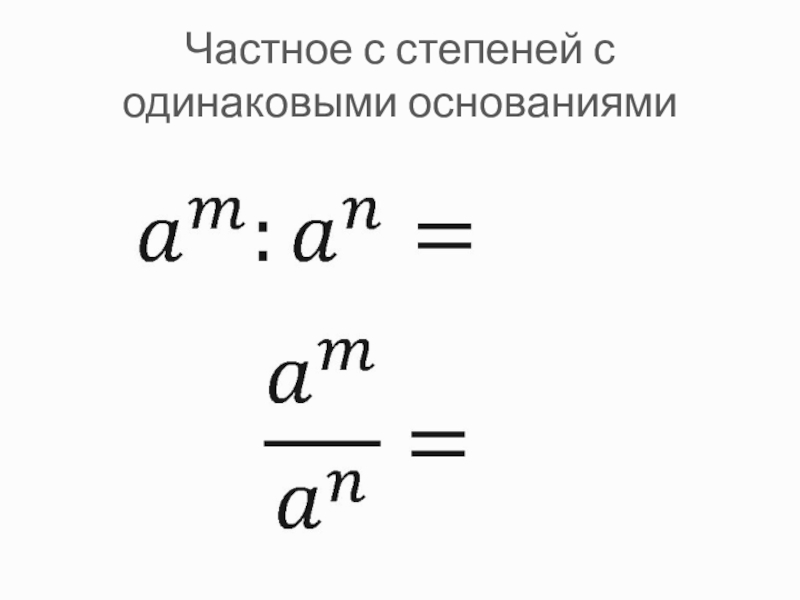

  Функция Convert_Decimal (Degree_Deg As String) As Double
    'Объявить переменные с плавающей запятой двойной точности.
    Тусклые градусы как двойные
    Тусклые минуты как двойные
    Тусклые секунды как двойные
    'Установить градус на значение до «°» переданного аргумента.градусы = Val (Left (Degree_Deg, InStr (1, Degree_Deg, "°") - 1))
    'Установите минуты на значение между "°" и "'"
    'текстовой строки для переменной Degree_Deg, разделенной на
    60. Функция Val преобразует текстовую строку в число.
    минут = Val (Mid (Degree_Deg, InStr (1, Degree_Deg, "°") + 2, _
    InStr (1, Degree_Deg, "'") - InStr (1, Degree_Deg, _
    "°") - 2)) / 60
    'Установите секунды на число справа от "" ", то есть
    'конвертируется в значение, а затем делится на 3600.секунды = Val (Mid (Degree_Deg, InStr (1, Degree_Deg, '") + _
    2, Len (Degree_Deg) - InStr (1, Degree_Deg, '") - 2)) _
    / 3600
    Convert_Decimal = градусы + минуты + секунды
Конечная функция
  

Чтобы использовать эту функцию, создайте формулу преобразования, как в следующем примере:

1. Запустите Excel и нажмите ALT + F11, чтобы запустить редактор Visual Basic.

2. В меню «Вставка» выберите «Модуль».

3. Введите образец кода для пользовательской функции Convert_Decimal, описанной выше, в лист модуля.

4. Нажмите ALT + F11, чтобы вернуться в Excel.

5. В ячейке A1 введите следующую формулу:

   = Convert_Decimal («10 ° 27 ’36» «»)

   Примечание

   Вам необходимо ввести три кавычки («» «) в конце аргумента этой формулы, чтобы сбалансировать кавычки для секунд и кавычки для текстовой строки. Для ссылки на ячейку кавычки не требуются.

6. Формула возвращает 10., круглая, потолочная, напольная

   по модулю, остаток, частное от

   sin, cos, tan, asin, acos, atan

   преобразовать радианы в градусы, преобразовать градусы в радианы

   Блок базовых номеров

   Может использоваться как любое положительное или отрицательное число. Нажатие на «0» в блоке позволит вам изменить число.

   Блок поддерживает обычные числа с основанием 10 (например: 2, 12 и 2.12), а также C-подобные префиксы для других числовых баз. Поддерживает:

   • Base-2 (двоичные) числа, например 0b10 (2 в десятичной системе)
   • Base-8 (восьмеричные) числа, например 0o14 (12 в десятичной системе)
   • Base-16 (шестнадцатеричные) числа, например 0xd4 (212 в десятичной системе)

   Блок счисления системы счисления

   Представляет десятичное число. Щелчок по «0» позволит вам изменить число.

   Щелчок по раскрывающемуся списку позволит вам ввести число в другой системе счисления (также известной как основание системы счисления).Затем число будет «переведено» в десятичное (также известное как основание 10).

   Например, эти три блока эквивалентны:

   Выпадающий список поддерживает: десятичный (base-10), двоичный (base-2), восьмеричный (base-8) и шестнадцатеричный (base-16) форматы ввода.

   Десятичный режим позволяет вводить любое положительное или отрицательное число (например, 2, -12, 2,12). В других режимах можно вводить только целое число (то есть любое положительное число или ноль).

   = {# =}

   Проверяет, равны ли два числа, и возвращает истину или ложь.

   ≠ {# not =}

   Проверяет, не равны ли два числа, и возвращает истину или ложь.

   >

   Проверяет, больше ли первое число второго и возвращает истину или ложь.

   ≥

   Проверяет, больше ли первое число второму или равно ему, и возвращает истину или ложь.

   <

   Проверяет, меньше ли первое число второго и возвращает истину или ложь.

   ≤

   Проверяет, меньше ли первое число второму или равно ему, и возвращает истину или ложь.

   +

   Возвращает результат сложения любого количества блоков, имеющих числовое значение. Блоки с числовым значением включают в себя базовый числовой блок, длину списка или текста, переменные с числовым значением и т. Д. Этот блок является мутатором и может быть расширен, чтобы добавить больше чисел в сумму.

   –

   *

   Возвращает результат умножения любого количества блоков, имеющих числовое значение.

   Возвращает результат первого числа в степени второго.

   случайное целое число

   Возвращает случайное целое число между заданными значениями включительно. Порядок аргументов не имеет значения.

   случайная дробь

   Возвращает случайное значение от 0 до 1.

   случайное начальное число для

   Используйте этот блок для генерации повторяющихся последовательностей случайных чисел.Вы можете сгенерировать ту же последовательность случайных чисел, сначала вызвав random set seed с тем же значением. Это полезно для тестирования программ, использующих случайные значения.

   мин.

   Возвращает наименьшее значение набора чисел. Если в блоке есть отключенные сокеты, min также будет считать 0 в своем наборе чисел. Этот блок представляет собой мутатор и раскрывающийся список.

   макс.

   Возвращает наибольшее значение набора чисел. Если в блоке есть отключенные сокеты, max также будет считать 0 в своем наборе чисел.

   Возвращает e (2,71828…) в степени данного числа.

   раунд

   Возвращает заданное число, округленное до ближайшего целого. Если дробная часть <0,5, она будет округлена в меньшую сторону. Если оно> 0,5, оно будет округлено в большую сторону. Если он точно равен 0,5, числа с четной целой частью будут округлены в меньшую сторону, а числа с нечетной целой частью будут округлены в большую сторону. (Этот метод называется округлением до четного.)

   потолок

   Возвращает наименьшее целое число, которое больше или равно заданному числу.

   этаж

   Возвращает наибольшее целое число, меньшее или равное заданному числу.

   по модулю

   По модулю (a, b) то же самое, что и остаток (a, b), когда a и b положительны. В более общем смысле, модуль (a, b) определяется для любых a и b так, что (floor (a / b) × b) + modulo (a, b) = a. Например, по модулю (11, 5) = 1, по модулю (-11, 5) = 4, по модулю (11, -5) = -4, по модулю (-11, -5) = -1. По модулю (a, b) всегда имеет тот же знак, что и b, в то время как остаток (a, b) всегда имеет тот же знак, что и a.

   остаток

   Remainder (a, b) возвращает результат деления a на b и взятия остатка. Остаток — это дробная часть результата, умноженная на b.

   Например, остаток (11,5) = 1, потому что

   11/5 = 2 ¹ ⁄ ₅

   В данном случае ¹ ⁄ ₅ — дробная часть. Мы умножаем это на b, в данном случае на 5, и получаем 1, наш остаток.

   Другие примеры: остаток (-11, 5) = -1, остаток (11, -5) = 1 и остаток (-11, -5) = -1.

   частное

   Возвращает результат деления первого числа на второе и отбрасывания любой дробной части результата.

   грех

   Возвращает синус заданного числа в градусах.

   cos

   Возвращает косинус заданного числа в градусах.

   загар

   Возвращает тангенс заданного числа в градусах.

   asin

   Возвращает арксинус заданного числа в градусах.

   acos

   Возвращает арккосинус заданного числа в градусах.

   атан

   Возвращает арктангенс заданного числа в градусах.

   atan2

   Возвращает арктангенс y / x для заданных y и x.

   преобразовать радианы в градусы

   Возвращает значение заданного числа в градусах в радианах. Результатом будет угол в диапазоне [0, 360)

   .

   преобразовать градусы в радианы

   Возвращает значение заданного числа в градусах в радианах.Результатом будет угол в диапазоне [-π, + π)

   .

   десятичный формат

   Форматирует число как десятичное с заданным количеством знаков после запятой. Количество мест должно быть целым неотрицательным числом. Результат получается округлением числа (если мест слишком много) или добавлением нулей справа (если их слишком мало).

   — это номер?

   Возвращает истину, если данный объект является числом, и ложь в противном случае.

   преобразовать число

   Принимает текстовую строку, представляющую положительное целое число с одной базой, и возвращает строку, которая представляет то же самое число с другой базой. Например, если входная строка равна 10, то преобразование из базы 10 в двоичное даст строку 1010; в то время как, если входная строка — это то же самое 10, тогда преобразование из двоичного в базовый 10 даст строку 2. Если входная строка такая же 10, то преобразование из базы 10 в шестнадцатеричное приведет к строке A.

   побитовое и

   Принимает два числа и сравнивает каждую пару битов. Каждый бит результата равен 1, только если соответствующие биты обоих операндов равны 1.

   Пример:

   	Десятичное	Двоичное (внутреннее представление)
   	6	0 1 1 0
   	3	0 0 1 1
   Результат:	2	0 0 1 0

   Побитовое ИЛИ (включительно)

   Принимает два числа и сравнивает каждую пару битов.Каждый бит результата равен 1, если любой из соответствующих битов в каждом операнде равен 1.

   Пример:

   	Десятичное	Двоичное (внутреннее представление)
   	6	0 1 1 0
   	3	0 0 1 1
   Результат:	7	0 1 1 1

   побитовое ИЛИ (Исключительно)

   Принимает два числа и сравнивает каждую пару битов.