Содержание
Урок 14. числовые выражения. порядок действий в числовых выражениях. скобки. сравнение числовых выражений — Математика — 2 класс
Математика, 2 класс
Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений
Перечень вопросов, рассматриваемых в теме:
— Что такое числовые выражения?
— Как правильно читать и записывать числовые выражения?
— Как выполнять порядок действий, если есть скобки?
— Как сравнить два выражения?
Глоссарий по теме:
Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.
Значение выражения – это результат выполненных действий.
Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.
Скобки — парные знаки ( )
Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.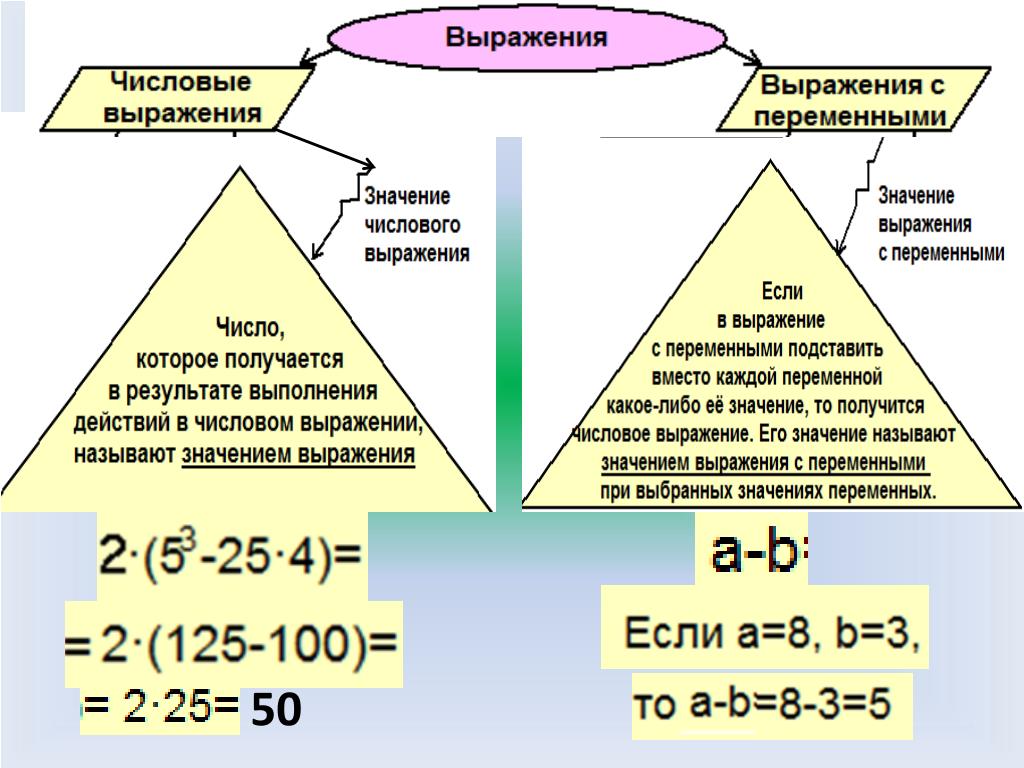
Основная и дополнительная литература по теме:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40
2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27
3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16
Теоретический материал для самостоятельного изучения
Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.
Маша: 12 – 7 + 3 = 8
Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.
Миша: 12 — 7 + 3 = 2
Кто из них вычислил верно? Решил верно, Миша.
В математике для обозначения действий, которые должны выполняться первыми используют специальный знак ( ) — скобки.
Запишем пример, который решали дети правильно:
12 — (7 + 3) =2
Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.
Посмотрим на запись.
9 – (6 + 2) = 1
Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».
Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.
Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.
9 – (6 + 2) = 1
числовое значение
выражение числового
выражения
Прочитаем выражение: 10 + (8 — 3) =
К числу 10 прибавить разность чисел 8 и 3.
Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.
10+(8-3)=15
Давайте сравним значения двух выражений:
11 — 4 и 16 — 7.
Сначала найдем значение каждого из выражений и их сравним.
11 — 4 = 7
16 — 7 = 9
7 < 9, значит, 11-4 < 16-7
Выводы: Итак, оказывается, порядок должен быть и в действиях, он так и называется «Порядок выполнения действий». Если в числовом выражении стоят скобки, это означает, что действие, которое в них записано, должно быть выполнено первым, а все остальные действия выполняют по порядку.
Тренировочные задания.
1.Выберите правильный ответ. Как правильно прочитать данное числовое выражение: 13 – (7 + 3)?
Вариант ответов:
1. К 13 прибавить сумму чисел 7 и 3
2. Из 13 вычесть 7 плюс 3
3. Из 13 вычесть сумму чисел 7 и 3
Из 13 вычесть сумму чисел 7 и 3
4. Разность чисел 13 и 7 плюс 3
Правильный ответ:
3. Из 13 вычесть сумму чисел 7 и 3
2. Соотнесите числовые выражения с их значениями
3+ (16-6) 15
10-4+9 16
13-(6+4) 13
9+ (13-6) 3
Правильный ответ:
3+ (16 – 6) 13
10 – 4 + 9 15
13 – (6 + 4) 3
9 + (13 – 6) 16
примеры, значение, числовое равенство, правила
Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением.
Например, следующие записи:
- (100-32)/17,
- 2*4+7,
- 13,
- 4*0.7 -3/5,
- 1/3 +5/7
будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13.
В нашем примере, это число 13.
А, например, следующие записи
не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков.
Значение числового выражения
Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.
Например,
(100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4.
2*4+7=15, число 15 будет являться значением числового выражения 2*4+7.
Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто «значение выражения», опуская при этом слово «числового».
Числовое равенство
Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например, выражение 2*4+7=15 является числовым равенством.
Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий.
Вообще, все действия разделены на несколько ступеней.
- Действия первой ступени: сложение и вычитание.
- Действия второй ступени: умножение и деление.
- Действия третей ступени – возведение в квадрат и возведение в куб.
Правила при вычислении значений числовых выражений
При вычислении значений числовых выражений следуют руководствоваться следующими правилами.
- 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень. Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право.
- 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
- 3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель.

- 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок.
Нужна помощь в учебе?
Предыдущая тема: Наименьшее общее кратное (НОК): определение, как найти, общая схема
Следующая тема:   Выражения с переменными: разбираем пример с фокусом
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Значение переменной x подставляется в выражение x + 10
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомните второй урок «Основные операции». Чтобы понять, что такое сложение, мы привели пример 5 + 2 = 7, и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.
И вот, имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа мы подставим вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия. В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения 5 + x при x = 4
Задание 2. Найдите значение выражения a + 3 при a = 7
Задание 3. Найдите значение выражения a + a + a при a = 10
Задание 4. Найдите значение выражения a + b при a = 10 и b = 20
Задание 5. Найдите значение выражения b + b + b при b = 5
Найдите значение выражения b + b + b при b = 5
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Числовые и буквенные выражения — что такое математическое выражение
Автор Ольга Андрющенко На чтение 3 мин. Просмотров 944 Опубликовано
При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.
Правила математики о числовых и буквенных выражениях
Числовое выражение — это такое выражение, которое составлено из чисел и имеет знаки «+», «-», а также знаки умножения или деления. В числовом выражении могут также быть и скобки.
В числовом выражении могут также быть и скобки.
Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.
Буквенные выражения — это выражения, содержащие латинские буквы, а также знаки математических операций сложения, вычитания, умножения и деления или скобки (при необходимости).
Числа, которые заменяют букву, называются значениями этой буквы.
Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.
Посмотрите видео:
Примеры числовых выражений
— в левой части этого равенства стоит числовое выражение, а в правой части — значение числового выражения.
— в левой части равенства — числовое выражение, а в правой части — значение числового выражения.
Посмотрите еще примеры числовых выражений:
Примеры буквенных выражений
Примеры буквенных выражений:
Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.
Когда применяются буквенные выражения
Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:
, где — ширина прямоугольника, а — его длина.
В правой части вы увидели буквенное выражение, значениями букв и — будут числа — значения ширины и длины прямоугольника.
Математические выражения
Математическое выражение — это выражение, содержащее и числовое и буквенное выражение, а также их произведение, сумму, разность или деление.
То есть, например
— это математическое выражение.
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.
Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.
Если вам все понятно — выполните тест «Числовые и буквенные выражения».
Числовые и буквенные выражения. Формула
Числовые и буквенные выражения.
Формула
Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:
+ (читаем «плюс«) — знак операции сложения,
— (читаем «минус«) — знак операции вычитания,
∙ (читаем «умножить«) — знак операции умножения,
: (читаем «разделить«) — знак операции деления.
Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.
По аналогии заполните таблицу полностью.
Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное b : 0 не определено.
Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны a, b, c, d, e, f, g, то формула (буквенное выражение) для вычисления его периметра p имеет вид:
p = a + b + c + d + e + f + g
При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.
При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.
Блок 1. Словарь
Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.
- Операции: сложение, вычитание, умножение, деление.
2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «:» (разделить).
3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.
4.Результат выполнения действий над числами в числовом выражении.
5. Знак, стоящий перед значением числового выражения.
Знак, стоящий перед значением числового выражения.
6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).
7. Общее название букв в буквенном выражении.
8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.
9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.
10. Числовое выражение, значение которого для натуральных чисел может быть найдено.
11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.
12. Алфавит, малые буквы которого используются для записи буквенных выражений.
Блок 2. Установите соответствие
Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…
Ответ запишите в виде: 1а, 2г, 3б…
Блок 3. Фасетный тест. Числовые и буквенные выражения
Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.
- Дан треугольник со сторонами c, d, m, выраженными в см
- Дан четырехугольник со сторонами b, c, d, m, выраженными в м
- Скорость автомобиля в км/ч равна b, время движения в часах равно d
- Расстояние, которое преодолел турист за m часов, составляет с км
- Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
- Сумма двух чисел больше второго числа на 15
- Разность меньше уменьшаемого на 7
- Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест.
 В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду - Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
- m = 8, n = 10, k = 5
- m = 6, n = 8, k = 15
- t = 121, x = 1458
ТО:
- Значение данного выражения
- Буквенное выражение для периметра имеет вид
- Периметр, выраженный в сантиметрах
- Формула пути s, пройденного автомобилем
- Формула скорости v, движения туриста
- Формула времени t, движения туриста
- Путь, пройденный автомобилем в километрах
- Скорость туриста в километрах в час
- Время движения туриста в часах
- Первое число равно…
- Вычитаемое равно….
- Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
- Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
- Буквенное выражение для возраста Кати
- Возраст Кати
- Координата точки В, если координата точки С равна t
- Координата точки D, если координата точки С равна t
- Координата точки А, если координата точки С равна t
- Длина отрезка BD на числовом луче
- Длина отрезка CА на числовом луче
- Длина отрезка DА на числовом луче
Ответы (равно, имеет вид, не определено):
а)1; б) s=b ∙d; в) 9; г) 40; д) b + c + d + m; е) 7; ж) выражение не имеет смысла (некорректно) для натуральных чисел; з) 2 ∙ m (m + n) ∙ k; и) (m + n) – k; к) 6; л) 15; м) 3760; н) t – 3; о) фигура не может быть треугольником; п) 22; р) t – 3 ∙ 7; с) 0; т) 32; у) 59600; ф) 6019; х) 2880; ц) 10378; ч)1440; ш) на ноль делить нельзя; щ) 13; ы) 1800; э) 496; ю) 2; я) 12; аа) 14; бб) 5; вв) 35; дд) 79200; ее) 1900; жж) 118; зз) 18; ии) 12800; кк) 98; лл) 1458; мм) v = c : m; нн) 100; оо) 19900; пп) t = b : m; рр) 2520; сс) c + d + m; тт) x; уу) 1579; фф) t + 2; хх) 10206; цц) 135; чч) t + 2 ∙ 7; шш) 7 ∙ x; щщ) x – 2; ыы) 7 ∙ x – 2 ∙ 7; ээ) t + x ∙ 7; юю) 10192; яя) t + x; ааа) 123; ббб) 1456; ввв) 10327.
ПОКАЗАТЕЛИ ТЕСТА. Число задач 70, время выполнения 2 – 3 часа, сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать следующую шкалу оценок.
Блок 4. Давайте поиграем
Блок 5. Обучающая игра «Уроки кота Леопольда»
Для учителя приводим ответы к блокам параграфа 6
Ответы к игре «Уроки Леопольда»
Западня 1 : 1/2, 1/3, 2/3, 7/8. Западня 2. 12, 2, 13 5. Западня 3. 6
Западня 4. 15. Западня 5. 396
Блок 1. Словарь
Блок 2. Установите соответствие.
Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п
Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в
Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Ответы к игре «Сокровища»
Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.
Числовые выражения, преобразование числовых выражений
Числовые выражения, преобразование числовых выражений (рациональных и иррациональных). Друзья! В этой статье для вас представлено решение числовых рациональных и иррациональных выражений. Это несложные задания на ЕГЭ по математике, достаточно знать свойства степеней и корней. Ещё необходимо уметь работать с дробями (находить их сумму, разность, произведение, частное). Процесс решения такого задания занимает минуты две, не более. Не много теории:
Говоря простым (не математическим) языком рациональные выражения — это целые и дробные выражения. Ниже рассматриваются дробные выражения.
Алгебраическое выражение называется иррациональным, если в выражении, наряду с операциями сложения, вычитания, умножения и деления производится операция возведения в рациональную (не целую) степень.
Обыкновенная дробь – это отношение, вида:
*ОТНОШЕНИЕ это есть действие — ДЕЛЕНИЕ (в данном случае «a» делим на «b»).
Также может быть записано в виде: a/b или a:b (косая черта и знак «:» означает — деление). Примеры обыкновенных дробей:
Как видно, число 4 можно записать в виде дроби 4/1. Есть дроби которые можно сократить, например, 48/8 = 6. Некоторые можно представить как конечные десятичные дроби: ½ = 0,5 ¼ = 0,25.
Если имеем целое число с дробной частью (смешанная дробь) и нам необходимо выполнить действие, то её нужно представить в виде простой дроби. Как?
Имеем число вида:
Чтобы получить дробное равное ему число, целую часть умножаем на знаменатель и прибавляем числитель, результат записываем в числитель, знаменатель остаётся прежний:
Например:
Если нужно вычислить сумму (разность) двух дробей с разными знаменателями, необходимо дроби привести к такому виду, чтобы их знаменатели были равны:
*То есть мы получили общий знаменатель путём умножения числителя и знаменателя первой дроби на знаменатель второй и умножением числителя и знаменателя второй дроби на знаменатель первой. Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.
Я намеренно не упоминаю здесь наименьшее общее кратное, так как для некоторых, закончивших школу «давно», возможна перегрузка информацией.
Весь смысл действия в том, чтобы привести дроби к общему знаменателю, так как с разными знаменателями дроби складывать нельзя. Если же дроби имеют общий знаменатель, то результатом суммы дробей будет дробь с тем же знаменателем, а числители складывают.
Если нужно вычислить произведение двух дробей, то результатом будет дробь, числитель которой равен произведению числителей этих дробей, а знаменатель равен произведению знаменателей:
Если одну дробь необходимо разделить на другую, то данное действие сводится к произведению делимого и дроби обратной делителю:
*То есть, говоря простым языком, мы «переворачиваем» ту дробь на которую делим и деление заменяем умножением.
Свойства степени и корня можно посмотреть здесь.
Рассмотрим задания:
77387. Найдите значение выражения
Ответ: 8
77389. Найдите значение выражения
Найдите значение выражения
Ответ: 5
77391. Найдите значение выражения
Ответ: 10
77392. Найдите значение выражения
*В данной задаче не нужно вычислять произведения и затем отношение. Глядя на числа видно, что они прекрасно сокращаются. Достаточно произвести несложные преобразования и пример вычисляется устно.
Ответ: 10
86983. Найдите значение выражения
Упрощаем, используя формулу разности квадратов
и вычисляем:
Ответ: 702
61513. Найдите значение выражения
Ответ: 24
62385. Найдите значение выражения
Ответ: 2
62647. Найдите значение выражения
Ответ: 2
68141. Найдите
Определим числитель и знаменатель:
Числитель равен знаменателю. Это означает, что отношение равно единице:
Ответ: 1
26745. Найдите значение выражения
*Если корни имеют разные степени, то преобразования с внесением выражений под один корень выполнять нельзя. Требуется привести все корни к равной степени. Используем свойство:
Ответ: 1
77405. Найдите значение выражения
*На заключительном этапе использовали:
Ответ: 7
Полезным будет посмотреть статью с показательными выражениями.
26900. Найдите значение выражения
Посмотреть решение
77390. Найдите значение выражения
Посмотреть решение
26735. Найдите значение выражения
Посмотреть решение
26736. Найдите значение выражения
Посмотреть решение
26737. Найдите значение выражения
Посмотреть решение
26743. Найдите значение выражения
Посмотреть решение
26744. Найдите значение выражения
Посмотреть решение
26746. Найдите значение выражения
Посмотреть решение
26750. Найдите значение выражения
Посмотреть решение
26752. Найдите значение выражения
Посмотреть решение
На этом всё. Посмотрите, какие чудеса можно нарисовать простым карандашом.
Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Числовые и буквенные выражения. Значение выражения
Числовые выражения
Числовое выражение — это запись, составленная со смыслом, в которой числа обозначены цифрами (в неё также могут входить знаки арифметических действий и скобки). Числовые выражения так же называются арифметическими выражениями.
7 — числовое выражение,
2 + 2 — 1 — числовое выражение,
7 — 2 · + : 1 — бессмысленный набор символов.
Вычислить значение выражения — это значит выполнить все арифметические действия, указанные в выражении. Действия выполняются в определённом порядке, в зависимости от самих действий и присутствия в выражении скобок. Про порядок выполнения действий можно прочитать в теме Порядок действий
.
Значение числового выражения — это число, получившееся после выполнения всех вычислений. Например, в выражении
6 + 2 = 8,
число 8 — это значение числового выражения 6 + 2.
Пример 1. Найдите значение числового выражения 4 + 3.
Решение:
4 + 3 = 7.
Ответ: 7.
Пример 2. Вычислите значение числового выражения 4 · 3.
Решение:
4 · 3 = 12.
Ответ: 12.
Пример 3. Запишите числовые выражения и найдите их значения.
1) Из числа 60 вычесть сумму чисел 23 и 7.
2) К частному чисел 30 и 6 прибавить 18.
3) Число 93 уменьшить на произведение 5 и 6.
4) Из разности чисел 57 и 7 вычесть число 8.
Решение:
1) 60 — (23 + 7) = 60 — 30 = 30.
2) 30 : 6 + 18 = 5 + 18 = 23.
3) 93 — 5 · 6 = 93 — 30 = 63.
4) (57 — 7) — 8 = 50 — 8 = 42.
С помощью числовых выражений можно записывать решение задач.
Задача. Из куска шёлка длиной 18 метров сшили 4 платья, расходуя на каждое по 3 метра. Сколько метров шёлка осталось в куске?
Решение: Задача решается в два действия: сначала узнаём сколько шёлка было израсходовано на платья, а затем сколько шёлка осталось. Решение по действиям можно записать так:
1) 3 · 4 = 12 (м) — израсходовали на платья.
2) 18 — 12 = 6 (м) — осталось в куске.
Объединив эти два действия, получим числовое выражение
18 — 3 · 4 = 6 (м).
Значение этого выражения является ответом на вопрос данной задачи.
Буквенные выражения
Буквенное выражение — это числовое выражение, в котором числа могут быть обозначены и цифрами, и буквами. Буквенные выражения так же называются алгебраическими выражениями.
При обозначении чисел буквами обычно используют строчные (маленькие) буквы латинского алфавита:
7 · a — буквенное выражение,
a – (b + c) — буквенное выражение.
Чаще всего в буквенных выражениях разные числа обозначены разными буквами, но, например, в выражении:
a = b
подразумевается, что a и b являются одним и тем же числом.
Значение буквенного выражения — это число, получившееся после выполнения всех вычислений. Действия в буквенных выражениях выполняются после подстановки вместо букв их численных значений.
Пример. Найдите значение буквенного выражения 2 · a + 3 при a = 7.
Решение:
2 · 7 + 3 = 14 + 3 = 17.
Ответ: 17.
Если в записи выражения одна и та же буква, например a, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны иметь ввиду одно и тоже число.
Пример. Найдите значение буквенного выражения 5x — 2x при x = 4.
Решение:
5 · 4 — 2 · 4 = 20 — 8 = 12.
Ответ: 12.
В арифметике буквенные обозначения употребляют, когда необходимо выразить, что свойство (или правило) относится не к каким-нибудь отдельным числам, а является общим для любых чисел. Например:
a + b = b + a.
Данное равенство показывает нам, что, как бы мы не переставляли слагаемые, сумма от этого не изменится. Подставив вместо букв любые числа, мы можем убедиться в этом сами:
1 + 2 = 2 + 1.
Запись буквенных выражений
При записи буквенных выражений, знак умножения пишется только:
- между буквой и числом:
a · 3;
- между закрывающей скобкой и следующей за ней буквой или числом:
(3 + 5) · 4,
(3 + 5) · a.
Знак умножения между числом и буквой, между буквами и перед открывающей скобкой не пишут:
7a вместо 7 · a;
xy вместо x · y;
a(b + c) вместо a · (b + c).
В буквенных выражениях числовой множитель записывается перед буквенными множителями:
5x вместо x · 5;
3bc вместо b · c · 3;
2(x + y) вместо (x + y) · 2.
Частное двух чисел, обозначенных буквами, обычно записывается с помощью дробной черты, например:
Оценка числовых выражений
Правило
PEMDAS можно использовать для упрощения или оценки сложных числовых выражений с помощью более чем одной бинарной операции.
Очень простой способ запомнить правило PEMDAS:
P ——>
Скобки (или скобки)
E ——> Показатели
M ——> Умножение
D ——> Раздел
A ——> Сложение
S ——> Вычитание
Важные примечания:
1.В конкретном упрощении, если у вас есть и умножение, и деление, выполняйте операции одну за другой в порядке слева направо.
2. Умножение не всегда предшествует делению. Мы должны делать это по очереди слева направо.
Примеры:
16 ÷ 4 x 3 = 4 x 3 = 12
В приведенном выше упрощении мы имеем как деление, так и умножение.
Слева направо сначала деление, затем умножение.
Итак, сначала делим, а потом умножаем.
Практические задачи
Задача 1:
Вычислите следующее числовое выражение.
29-5 x 3
Решение:
Выражение 29 — 5 x 3 | Оценка = 29 — 5 x 3 = 29-15 = 14 | Операция Умножение Вычитание Результат |
Задача 2:
Вычислите следующее числовое выражение.
(14 + 12) x 3
Решение:
Выражение (14 + 12) x 3 | Оценка = (14 + 12) x 3 = 26 x 3 = 78 | Операция Скобки Умножение Результат |
Задача 3:
Вычислите следующее числовое выражение.
9 2 -15 ÷ 3
Решение:
Выражение 9 2 — 15 ÷ 3 | Оценка = 9 2 — 15 ÷ 3 = 81 — 15 ÷ 3 = 81 — 5 = 81 — 5 9007 = 81 — 5
| Операция Мощность Раздел Вычитание Результат |
Задача 4:
Вычислите следующее числовое выражение.
5 + 5 x (5 + 7) ÷ 4-6
Решение:
Выражение 5 + 5 x (5 + 7) ÷ 4-6 | Оценка = 5 + 5 x (5 + 7) ÷ 4-6 = 5 + 5 x 12 ÷ 3-6 = 5 + 60 ÷ 3 -6 = 5 + 20 -6 = 25-6 = 19 | Операция Круглые скобки Умножение Деление Сложение Вычитание Результат |
Задача 5:
Вычислите следующее числовое выражение.
36-2 (20 + 12 ÷ 4 x 3-2 x 2) + 10
Решение:
Задача 6:
Вычислите следующее числовое выражение.
6 + [(16-4) ÷ (2 2 + 2)] — 2
Решение:
Выражение 6 + [(16-4) ÷ (2² + 2)] — 2 | Оценка = 6+ [(16-4) ÷ (2 2 +2)] -2 = 6+ [12 ÷ ( 2 2 +2)] — 2 = 6+ [12 ÷ (4 + 2) ] -2 = 6+ [12 ÷ 6] -2 = 6 + 2 -2 = 8-2 = 6 | Операция Круглые скобки Степень Круглые скобки Круглые скобки Добавление Вычитание Результат |
Задача 7:
Вычислите следующее числовое выражение.
(96 ÷ 12) + 14 x (12 + 8) ÷ 2
Решение:
Выражение (96 ÷ 12) + 14x (12 + 8) ÷ 2 | Оценка = (96 ÷ 12) + 14x (12 + 8) ÷ 2 = 8 + 14x 20 ÷ 2 = 8 + 280 ÷ 9000 2 = 8 + 140 = 148 | Операция Скобки Умножение Деление Сложение Результат |
Задача 8:
Вычислите следующее числовое выражение.
(93 + 15) ÷ (3 x 4) — 24 + 8
Решение:
Выражение (93 + 15) ÷ (3×4) -24 + 8 | Оценка = (93 + 15) ÷ (3×4) -24 + 8 = 108 ÷ 12 -24 + 8 = 9-24 + 8 = -15 + 8 = -7 | Операция Круглые скобки Раздел Вычитание Вычитание Результат |
Задача 9:
Вычислите следующее числовое выражение.
55 ÷ 11 + (18-6) x 9
Решение:
Выражение 55 ÷ 11 + (18-6) x9 | Оценка = 55 ÷ 11 + (18-6) x9 = 55 ÷ 11 + 12×9 = 5 + 12×9 = 5 + 108 = 113 | Операция Круглые скобки Деление Умножение Сложение Результат |
Задача 10:
Вычислите следующее числовое выражение.
(7 + 18) x 3 ÷ (2 + 13) — 28
Решение:
Выражение (7 + 18) x3 ÷ (2 + 13) — 28 | Оценка = (7 + 18) x3 ÷ (2 + 13) -28 = 25 x 3 ÷ 15-28 = 75 ÷ 15 — 28 = 5 — 28 = -23 | Операция Круглые скобки Умножение Деление Вычитание Результат |
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Задачи со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по скорости единицы
Задачи по сравнению ставок
Преобразование обычных единиц Word задачи
Преобразование метрических единиц Word задачи
Word задачи по простому проценту
Word задачи по сложным процентам
Word задачи по типам ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами
и прибылью и убытками
Задачи
Задачи с десятичными словами
Задачи со словами на дроби
Задачи со словами на смешанных фракциях
Одношаговые задачи со словами с уравнениями
Проблемы со словами с линейным неравенством
Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами на постоянной скорости
Проблемы со словами на средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон
рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л.Метод CM для решения временных и рабочих задач
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Как написать числовое выражение? — Определение и примеры — Видео и стенограмма урока
Примеры числовых выражений
Единственными требованиями к числовому выражению являются то, что они должны содержать только числа и символы операций.Некоторые числовые выражения имеют только один символ операции. У других их два и более. Вот несколько примеров числовых выражений:
4 + 5
134 — 75
56 * 4 + 6
68/8 * 7-2 + 1
Примеры нечисловых выражений
Поскольку числовые выражения могут содержать только числа , выражения, содержащие переменных (например, x или y ), не могут считаться числовыми выражениями. Вместо этого они называются алгебраическими выражениями .Вот два примера алгебраических выражений:
4 x + 5
134 — x
Написание числовых выражений
Когда дана устная или записанная задача слов , важно уметь переводить преобразовать слова в числовое выражение, чтобы вы могли решить проблему. Вот несколько примеров.
Пример 1:
У Аманды было 12 мармеладных мишек, и 2 она отдала своему брату. Затем она съела 4 мармеладных мишек. Сколько мармеладных мишек осталось у Аманды?
Аманда начала с 12, отдала два (-2) и съела 4 (-4).В этом примере нужно было использовать только операцию вычитания. Числовое выражение можно записать как:
12-2-4
Пример 2:
Джордж хочет выяснить, сколько он будет зарабатывать за год на работе с частичной занятостью. Он зарабатывает 500 долларов в месяц.
Числовое выражение можно записать как:
500 * 12
Пример 3:
У Джоди есть неделя, чтобы прочитать всю книгу для школы. В книге 455 страниц. Она хочет равномерно распределить свои чтения в течение следующих семи дней.
Числовое выражение может быть записано как:
455/7
Пример 4:
Аарон пробегает 5 миль на этой неделе, 6 на следующей неделе и 7 на следующей неделе. Он хочет знать, сколько миль он пробежал за три недели.
Числовое выражение может быть записано как:
5 + 6 + 7
Сводка урока
Числовое выражение — это математическое предложение, состоящее только из чисел и одного или нескольких символов операций. Поскольку числовые выражения могут содержать только числа, выражения, содержащие переменные (например, x или y ), не могут считаться числовыми выражениями.При наличии устной или письменной проблемы со словом важно уметь перевести слова в числовое выражение, чтобы вы могли решить проблему.
Составление обзора числовых выражений
| Условия | Определения |
|---|---|
| Переменные | (например, x или y ) не могут считаться числовыми выражениями |
| Алгебраические выражения | выражения, содержащие переменные |
| Проблема со словом | устная или письменная математическая задача |
Результаты обучения
По окончании урока подтвердите свою способность:
- Определить числовое выражение
- Определение переменных в алгебраическом уравнении
- Запишите числовые выражения
Запись и интерпретация числовых выражений Видео от NUMBEROCK
Узнайте все о написании и интерпретации числовых выражений в этом футуристическом музыкальном видео о планете, вращающейся вокруг Альфы Центури.После просмотра числовых выражений видео затем вводит ключевые слова, которые могут помочь нам интерпретировать выражения, задачи со словами и многое другое!
Числовые выражения Текст:
Verse 1
Операции и шаги
числового выражения находятся в его словах, которые подробно описывают процесс.
Посмотрите на символы группировки, чтобы определить
, какие вычисления должны быть выполнены перед другими.
Давайте посмотрим, что я имею в виду, на нескольких примерах —
— на нескольких примерах числовых выражений.
Но сначала соло на Бонго… поехали!
Что такое «четырехкратное частное двадцати и десяти»?
Прежде чем умножить, нам нужно найти частное;
заключаем в скобки «двадцать, разделенные на десять» —
получаем «четыре умножить на два» — «восемь» отвечает на вопрос.
Припев
Чтобы писать и интерпретировать числовые выражения
, мы внимательно их читаем и задаем следующие вопросы:
Какие операции описаны в этой задаче?
И в каком порядке будем их решать?
Verse 2
Что такое «девяносто, разделенное на разницу в четырнадцать и пять»?
«Четырнадцать минус пять» попадает в скобки — их разница составляет «девять».
Следующий шаг обозначен знаком деления.
Разделим «девяносто на девять» и «десять», чтобы получить частное.
Давайте посмотрим на пример — еще раз —
с лучшими рифмами, которые вы когда-либо когда-либо находили.
Но сначала соло на Бонго… поехали!
Что такое «в десять раз больше суммы сорока пятидесяти трех»?
Сначала заключите «сорок плюс пятьдесят три» в круглые скобки;
слова говорят нам сначала сложить и получить «девяносто три» —
затем «умножить на десять», чтобы закончить стих.
Мост
Когда математический класс находится в сеансе
и мы читаем числовое выражение,
слов подсказки могут помочь нам выбрать операции,
, чтобы мы могли делать правильные вычисления.
Плюс, все, вместе, всего, всего и сумма…
это все ключевые слова для сложения.
Сколько еще, минус, осталось, меньше, разница…
— все ключевые слова для вычитания.
На, умножить, умножить, произведение, на…
— все это ключевые слова для умножения.
Сколько раз, разделить, перейти, частное…
— все это ключевые слова для деления.
Узнать больше
Эта песня ориентирована на стандарты обучения Common Core для 5-х классов. Ознакомьтесь с соответствующими стандартами здесь.
Если вы заинтересованы в том, чтобы получить идеи о том, как спланировать надежный и согласованный со стандартами урок по написанию и интерпретации выражений, мы рекомендуем ознакомиться с рекомендациями Instructure для общих основных стандартов 5.OA.2 Эта страница помогает разобрать стандартный язык и выставить оценку -соответствующий уровень строгости для каждой концепции и предлагает различные предложения по занятиям (семена урока), которые помогают учащимся достичь своих учебных целей.
Чтобы продолжить просмотр библиотеки материалов по математике Numberock, щелкните здесь. Чтобы получить доступ к растущей библиотеке премиум-контента Numberock, щелкните здесь.
Понимание числовых выражений Факты и рабочие листы
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатную пробную версию Загрузить образец
Скачать этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже участник? Авторизуйтесь, чтобы скачать.
В этом уроке мы попытаемся написать и интерпретировать числовых выражений , используя круглые, квадратные или фигурные скобки. Мы также напишем простые выражения, которые записывают вычисления с числами и интерпретируют такие выражения, не оценивая их.
См. Файл фактов ниже для получения дополнительной информации о понимании числовых выражений или, в качестве альтернативы, вы можете загрузить нашу 29-страничную рабочую таблицу «Общие сведения о числовых выражениях» для использования в классе или дома.
Основные факты и информация
СЛОВАРЬ
- Подтяжки
- Символы, используемые для группировки определенных частей математического выражения, {}.
- Кронштейны
- Символы, используемые для группировки определенных частей математического выражения, [].
- Круглые скобки
- Символы, используемые для группировки определенных частей математического выражения, ().
- Числовое выражение
- Математическая комбинация чисел, операций и символов группировки.Это математическая фраза, представляющая одно значение. Эти операции включают сложение, вычитание, умножение и деление.
- Всегда помните, что в числовом выражении НЕ ДОЛЖНО быть знака равенства «=». В противном случае это было бы уравнение.
- Уравнение — это числовое предложение, описывающее связь между двумя выражениями.
- Что из следующего является числовым выражением?
- х + у + 3
- 1 + 3 = 2 + 2
- (4 года + 5) / 3
- 24 х (8-1)
НАПИСАНИЕ ЧИСЛОВЫХ ВЫРАЖЕНИЙ
- При работе с числовыми выражениями из словесных утверждений вам необходимо ознакомиться с ключевыми терминами, представляющими четыре операции: сложение, вычитание, умножение, деление.
- Используйте круглые скобки () или квадратные скобки, чтобы сгруппировать вычисления, чтобы быть уверенным, что некоторые вычисления выполняются в особом порядке.
- Когда вы используете круглые скобки, вы подразумеваете, что ученики «сделайте это в первую очередь».
- Напишите числовое выражение, используя приведенную ниже словесную фразу:
- Сумма восьми и четырех, умноженная на пять
- Глядя на этот пример, вы должны понимать, что вам нужно получить сумму восемь и четыре, а затем умножить полученный ответ на пять.
- Это должно быть сделано в первую очередь — сумма восьми и четырех
- Тогда, какой бы ни был ответ — умножьте его на пять
- Операция, которая должна быть выполнена первой, должна быть заключена в круглые скобки.
- Итак, числовое выражение, которое мы можем получить: (8 + 4) x 5
- Напишите числовое выражение, используя приведенную ниже словесную фразу:
- Сумма восьми и произведение четырех и пяти
- Сравнивая его с первым примером, оба используют одинаковые числа и одинаковые операции.Более того, оба примера включают числа восемь, четыре и пять, а также операции сложения и умножения. Но действительно ли они означают одно и то же? №
- В примере 2 операция, которая должна быть выполнена в первую очередь, — это умножить четыре на пять, а затем прибавить восемь к полученному произведению.
- Это нужно сделать в первую очередь — произведение четырех и пяти
- Тогда, какой бы ни был ответ — прибавьте к восьми
- Итак, числовое выражение, которое мы можем получить: 8 + (4 x 5)
- Давайте сравним две словесные фразы.
- Сумма восьми и четырех, умноженная на пять: (8 + 4) x 5
- Сумма восьми и произведение четырех и пяти: 8 + (4 x 5)
- Мы можем сказать, что оба словесных утверждения могут иметь одни и те же числа и могут включать одни и те же операции; однако они означают разные вещи. При оценке они дадут разные ответы.
- Обратите внимание на данную фразу и сгруппируйте числа с операциями, которые необходимо выполнить в первую очередь.
ПОРЯДОК РАБОТЫ
- В выражении с несколькими операциями используйте правила, называемые Порядком операций.
- Некоторые выражения выглядят сложно, потому что они содержат круглые и квадратные скобки. Вы можете думать о скобках как о «внешних» скобках. Сначала вы выполняете оценку в круглых скобках.
- ПОРЯДОК РАБОТЫ
- Сначала выполните все операции, указанные в скобках.
- Выполняйте умножение и деление слева направо.
- Все операции сложения и умножения выполняются слева направо.
- Помимо круглых скобок (), квадратные скобки [] и фигурные скобки {} — это другие виды символов группировки, используемые в выражениях.Чтобы оценить выражение с разными символами группировки, сначала выполните операцию в самом внутреннем наборе символов группировки, а затем оцените выражение изнутри.
- 2 x [(9 x 4) — (17–6)]
- Сначала выполните операции, указанные в скобках (). Умножать, вычитать и переписывать. Выполните операции в скобках []. Вычтите и перепишите. Умножьте 2 на 25, чтобы получить 50.
- 2 x {5 + {(10–2)] + (4–1)]}
- Сначала выполните операции, указанные в скобках.Вычтите, затем перепишите. Далее проделываем операции в скобках []. Добавить и переписать. Затем решайте операции в фигурных скобках {}, складывайте и переписывайте. Умножьте 2 и 6, чтобы получить 32.
Рабочие листы с пониманием числовых выражений
Это фантастический комплект, который включает в себя все, что вам нужно знать о понимании числовых выражений на 29 страницах с подробным описанием. Это готовые к использованию рабочие листы «Понимание числовых выражений», которые идеально подходят для обучения студентов числовым выражениям с помощью скобок, скобок или фигурных скобок.Мы также напишем простые выражения, которые записывают вычисления с числами и интерпретируют такие выражения, не оценивая их.
Полный список включенных рабочих листов
- План урока
- Понимание числовых выражений
- Положить в банку
- Произнесите числовое выражение
- Облечь в слова
- Время совпадения
- Что приходит первым?
- Порядок действий
- Собственные выражения
- Создайте свою проблему
- Анализ ошибок
- Математический лабиринт
Ссылка / процитирование этой страницы
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.
Понимание числовых выражений. Факты и рабочие листы: https://kidskonnect.com — KidsKonnect, 2 июля 2020 г.
Ссылка будет отображаться в виде фактов и рабочих листов «Понимание числовых выражений»: https://kidskonnect.com — KidsKonnect, 2 июля 2020 г.,
Использование с любой учебной программой
Эти рабочие листы были специально разработаны для использования в любой международной учебной программе.Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
Обработайте числовое выражение, которое может включать переменные
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Математика для 6-х классов — Раздел 5: Числовые и алгебраические выражения
Краткое описание агрегата
В Модуле 5 шестиклассники впервые углубляются в область Выражений и Уравнений, расширяя свое понимание арифметики, чтобы увидеть, как она применяется к алгебраическим выражениям.Они начинают с числовых выражений с показателями степени, переписывая выражения в более простые формы, пока не будет определено окончательное значение. Затем учащиеся используют переменные в выражениях для представления неизвестных или изменяющихся величин. Используя свойства операций, учащиеся будут исследовать, что делает выражения эквивалентными другим, концепция, которая пронизывает всю область выражений и уравнений средней школы. На протяжении этого раздела студенты уделяют пристальное внимание структуре выражений, понимают роль скобок, порядок операций и способ словесного описания выражений (MP.7). Примечание о беглости: оценка выражений дает учащимся хорошую возможность продолжить развитие и продемонстрировать свободное владение десятичными операциями. Некоторые проблемы в устройстве включают десятичные значения; включать дополнительные задачи в практику для студентов по мере необходимости.
В начальной школе ученики использовали переменные для представления неизвестных величин, и они оценивали и описывали числовые выражения без показателей. Они использовали свойство коммутативности, чтобы улучшить свое понимание умножения и сложения, а также свойство распределения при моделировании частичных областей.Все эти концепции объединяются и помогают учащимся понять в этом модуле шестого класса.
Сразу после этого урока шестиклассники начнут урок по уравнениям и неравенствам, где они будут использовать алгебру для моделирования и решения реальных проблем. Они также пересмотрят проценты, используя новые навыки работы с выражениями и уравнениями, чтобы эффективно решать процентные задачи. В седьмом и восьмом классах учащиеся продолжают упрощать и решать более сложные выражения и уравнения, используя те же инструменты, что и в этом разделе.
Темп: 16 учебных дней (12 уроков, 3 гибких дня, 1 оценочный день)
Инструкции по корректировке темпа обучения на 2020-2021 учебный год из-за закрытия школ см. В нашем разделе «Рекомендуемые корректировки объема и очередности занятий для 6-го класса».
Написать числовое выражение | Планы уроков
Этот урок операций и алгебраического мышления учит студентов писать числовые выражения.Урок включает стратегии, основанные на исследованиях, и стратегические вопросы, которые готовят учащихся к оцениванию. На этом уроке студенты переведут простые английские описания чисел и операций в числовые выражения. Этот урок — отличное введение в расшифровку словесных задач, и этот урок включает в себя несколько примеров, которые студенты должны выполнить.
Войдите, чтобы просмотреть этот урок.Если у вас нет учетной записи, подпишитесь сейчас и начните бесплатную 30-дневную пробную версию.
- Оценок:
5
- Тем:
Математика
Войдите, чтобы просмотреть этот урок.
