Содержание
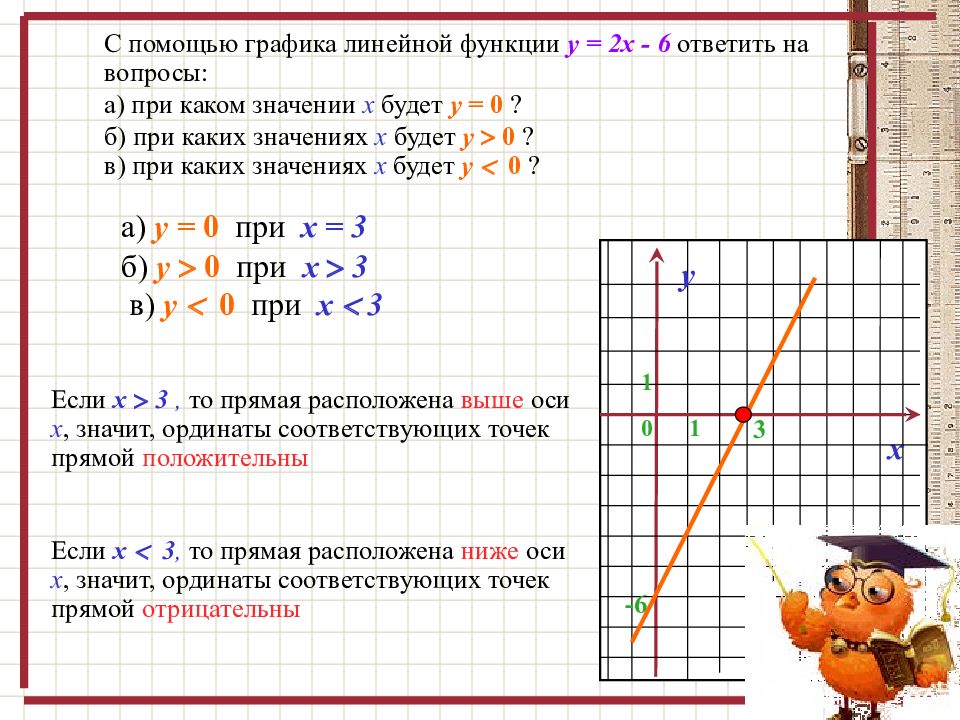
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
Если a>0, прямая будет проходить через I и III координатные четверти.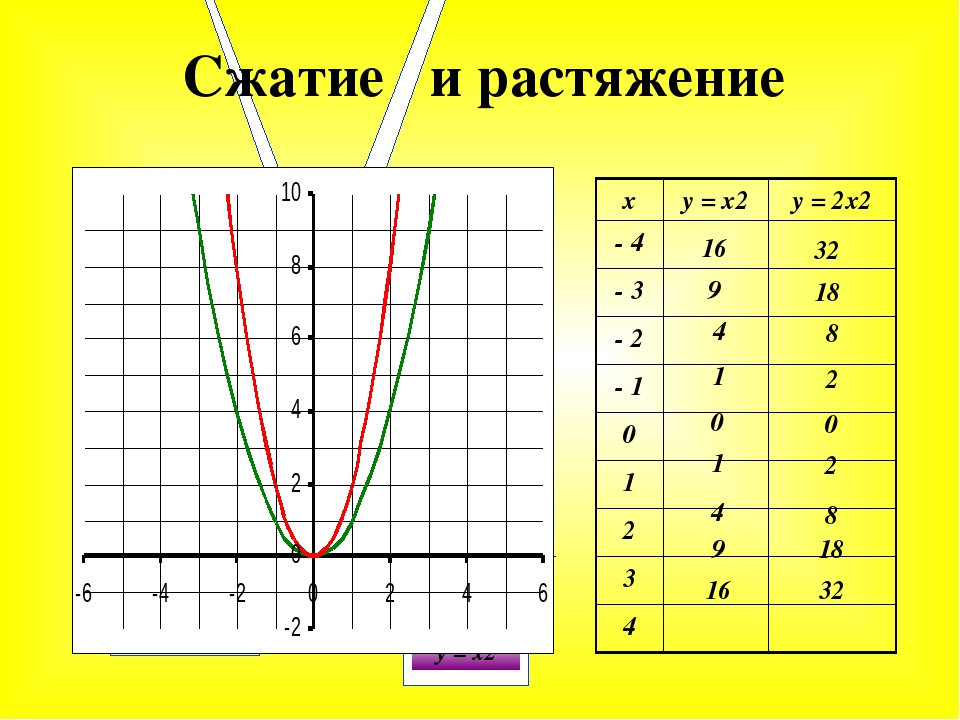
b – точка пересечения прямой с осью y.
Если a<0, прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y.
Если a=0, функция принимает вид y=b.
Отдельно выделим график уравнения x=a.
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
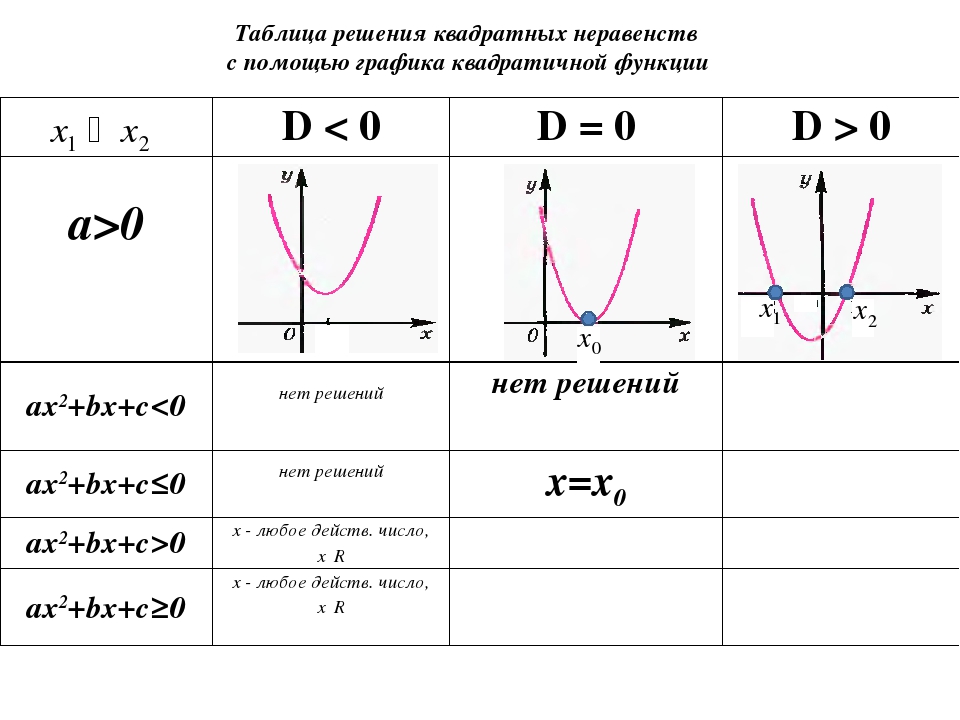
Графиком функции y=ax2+bx+c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a>0 , ветки параболы направлены вверх.
- Если a<0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти xв – координату вершины параболы.
xв=−b2a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D>0 – две точки пересечения.
- Если D=0 – одна точка пересечения.
- Если D<0 – нет точек пересечения.
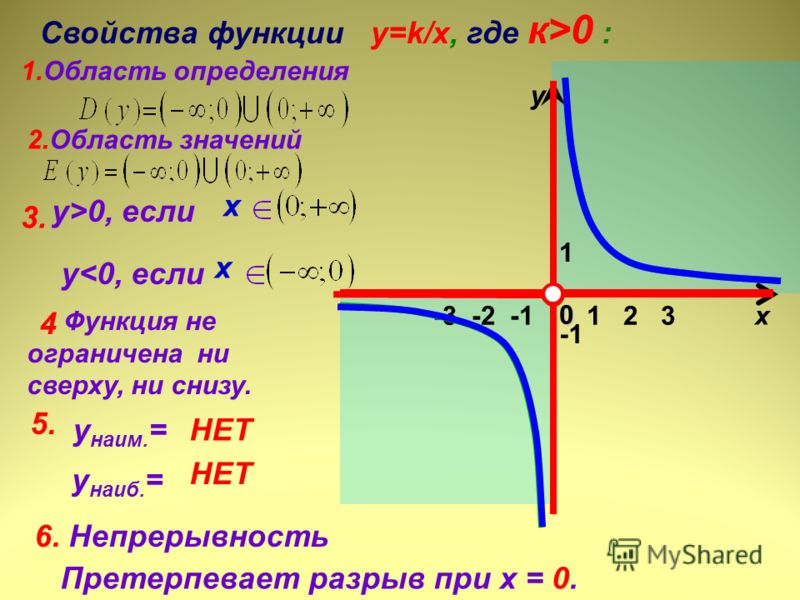
Графиком функции y=kx является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.
Если k < 0, ветви гиперболы проходят через II и IV четверти.
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:
Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y).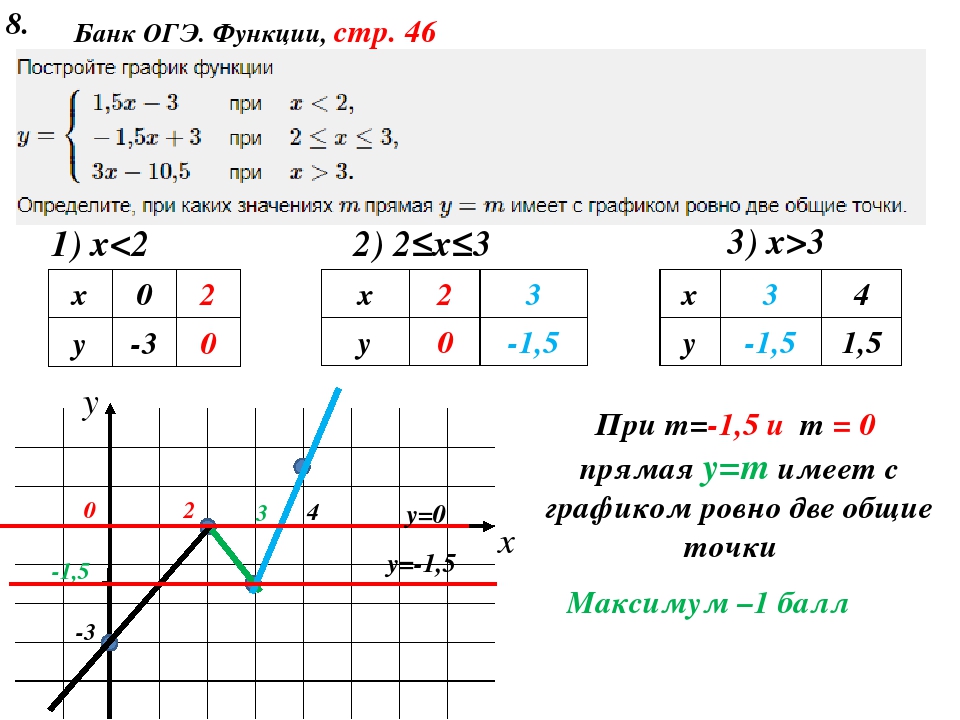 Это значение и будет являться наибольшим значением функции.
Это значение и будет являться наибольшим значением функции.
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.
Скачать домашнее задание к уроку 5.
«Как построить график функции F(x)+m»
Дата публикации: .
Презентация и урок на тему: «Как построить график функции f(x)+m»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Как построить график функции f(x)+m (PPTX)
Ребята, сегодня мы научимся еще одному методу построения графиков функций!
Поступим как на прошлом уроке, построим в одной системе координат три параболы: $y=x^2$,
$y=x^2+3$, $y=x^2-3$. 2-4, -1<x≤2. \end {cases}$
2-4, -1<x≤2. \end {cases}$
найти область определения функции онлайн | калькулятор предназначен для определения четности и нечетности функции |
определения точек пересечения графика функции с осями координат | нахождение асимптот графика функции онлайн |
методом неопределенных коэффициентов | онлайн калькулятор для определения периодичности |
и интервалы его выпуклости и вогнутости онлайн | кусочно-непрерывных функций |
u=f(x,y,z) | и построение графика |
найти интервалы знакопостоянства | они же точки пересечения |
и интервалы монотонности | обратное преобразования Лапласа онлайн |
интегральное преобразование Лапласа онлайн | по формуле общего члена ряда |
вычислить угол наклона | рассчитать угловой коэффициент |
онлайн калькулятор | достаточно задать функцию, чтобы получить значения максимума |
одно из необходимых условий наличия минимума | функция в этих точках не является непрерывной |
провести исследование графика функции | решать пределы любых функций онлайн |
составить и решить уравнение касательно | найти как косинусы и синусы угла, так и решить выражения |
функции относятся к простейшим | график функции |
раскладывается в степенной ряд по степеням | любое число раз и в некоторой окрестности |
абсолютно любую четную функцию можно разложить в ряды Фурье | нахождение формулы |
найти прямую перпендикулярной прямой | в полярных координатах на плоскости |
найти прямую перпендикулярной прямой | в полярных координатах на плоскости |
в полярных координатах | построить полином по точкам |
переменной | на отрезке в заданном интервале |
на отрезке в заданном интервале | найти точки экстремума функции |
найти область значений фукции | найти нули производной |
значение функции на отрезке | производная функции равна 0 или не существует |
| Найти угловые точки графика функции |
Что такое алгебра?! Функция и аргумент в алгебре.

В данной статье разберемся, что такое алгебра. Узнаем о таких понятиях, как функция и аргумент в алгебре и дадим простые и понятные определения.
Один из разделов математики это алгебра, которая подразумевает выполнение различных операций с числами, так как сложение, умножение и т.д. Можно сказать, что алгебра это нечто вроде расширения арифметики до более высокого уровня. Понять, что такое алгебра и откуда она взялась, помогут исторические факты. Первые предпосылки алгебры появились в разных уголках мира, людям нужна была алгебра для того, чтобы решить определенные уравнения. Например, в Древней Греции впервые об уравнениях заговорил Диофант, это был 2-3 век нашей эры.
В Китае примерно 2 тысячи лет до нашей времени уже было умение решать квадратные уравнения и уравнения первой степени. Также некоторые предпосылки алгебры встречались у индийского народа и жителей арабских стран. Согласно историческому прошлому, также отличилось издание «Алгебра» аль-Хваризми, которое стало популярным в 12-ом веке благо переводу на латинском языке. Человечество нуждалось в проведение расчетов, так появилась алгебра. Что такое алгебра для вас и нужна или нет, каждый решает сам. Потребность в алгебре появилась, как необходимость решать однотипные задачи. В школе алгебра всегда была и остается обязательным предметом.
Человечество нуждалось в проведение расчетов, так появилась алгебра. Что такое алгебра для вас и нужна или нет, каждый решает сам. Потребность в алгебре появилась, как необходимость решать однотипные задачи. В школе алгебра всегда была и остается обязательным предметом.
Когда начинают учить алгебру в школе?
Разделение математики на несколько областях определило для алгебры решение определенных уравнений, под названием алгебраические уравнения. Что такое алгебра как предмет можно узнать только в 7-ом классе. Именно тогда вместе привычной математики появляется два отдельных предмета: алгебра и геометрия. Изучение начинается с простых понятий, также как и в случае других учебных процессов, все строится от простого материала к сложному.
7 класс оптимальное время для того, чтобы узнать, что такое алгебра. Вместо обычных операций с числами осуществляется переход на переменные. Так проще понять общие законы арифметики, научиться работать с неизвестными и функциями.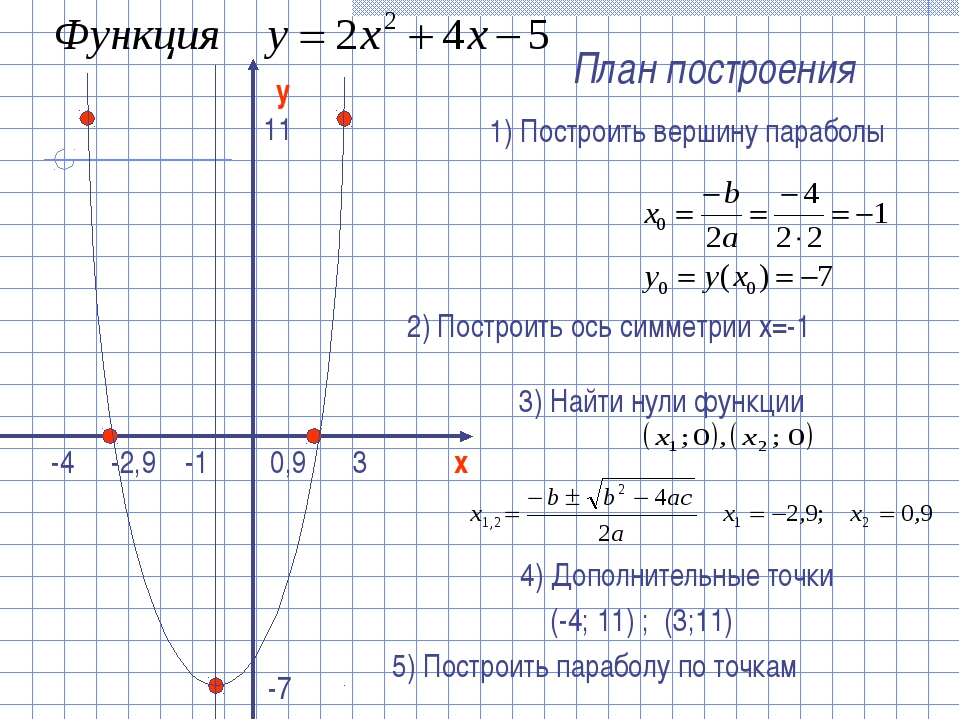 Алгебру можно разделить на 5 отдельных категорий:
Алгебру можно разделить на 5 отдельных категорий:
— общая алгебра
— элементарная алгебра
— линейная алгебра
— универсальная алгебра
— алгебраическая комбинаторика.
Школьная программа подразумевает изучение исключительно элементарной категории. Элементарная алгебра занимается изучением операций с вещественными числами. Перемененные и постоянные обозначены в алгебре символами в виде букв. С их помощью происходит преображение уравнений и математических выражений на основе четких правил.
Функция в алгебре
Понимание алгебры как предмет требует знание определенных элементов, так как функция, аргумент и определение. Что такое функция в алгебре и чем она определена? Функция является одним из основных понятий и определяет зависимость между переменными с неодинаковой величиной.
Что такое функция?:
Функция в алгебре представляет собой сопоставимость между двумя множествами. Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.
Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.
Функция задается различным образом:
— таблицей
— графиками
— согласно словесной формулировке (описание словами)
— аналитическим образом (используя формулу).
Школьная алгебра всецело сосредоточена над изучением числовых функций. Функция и аргумент указаны в виде чисел. Пример: y=f(x), где x перемена независимого типа, а y функция наоборот зависимая. У функции есть еще такие параметры как: область определения (D) и область значения (E). Первый параметр представляет собой совокупность значений для переменной «х», в то время как второй обозначает множество значений для «у».
Аргумент в алгебре
Что такое аргумент в алгебре? Это не что иное, как перемена х, от которой зависит у, то есть функция. Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции.
Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением. Остается только решить уравнение относительно x для того, чтобы значение стало известным. Существует возможность определения данного параметра и по графику функции.
Определение алгебры и ее практическая польза
Определение, что такое алгебра, позволяет понять какая от нее практическая польза. Только понимая область деятельности этой части математики, появляется стремление ее изучать. Благодаря алгебре, можно шагать на более высокий уровень познания математики. Алгебра это та простая ступень, которая позволяет делать прогресс в процессе изучения современной математики. Благодаря ней, появилась возможность взглянуть иначе на множества.
Постепенно элементарные значения алгебры перешли в более сложные понятия. Так появилась универсальная алгебра, которая стала основой для развития топологии. Алгебра это ступень, которая позволяет ступать дальше, и без нее не быть некоторым явлений прогресса.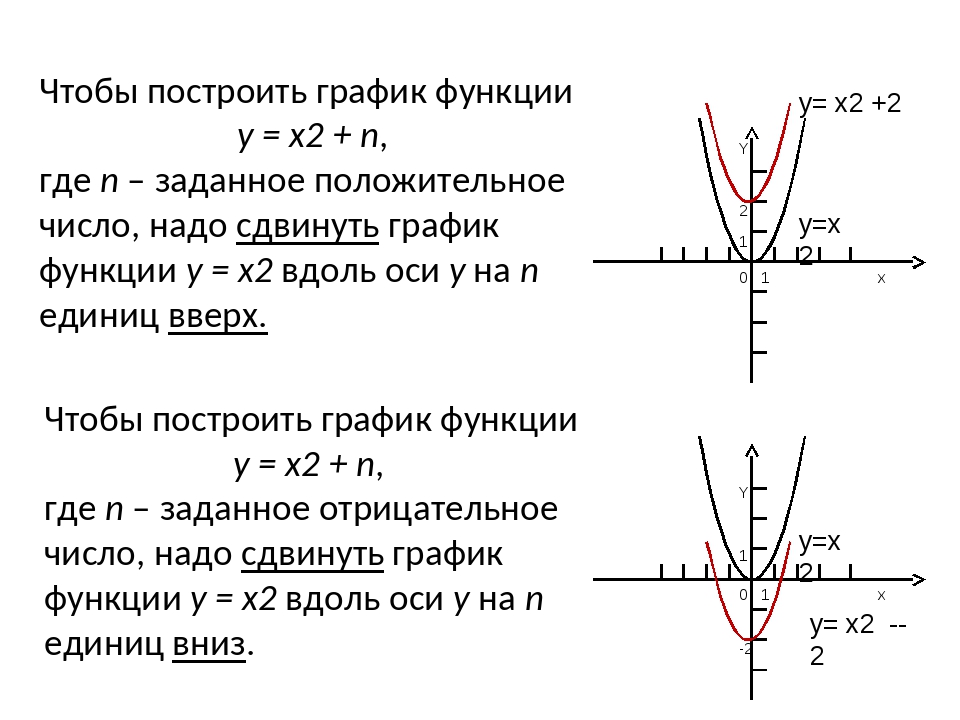 Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.
Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Креативный урок алгебры в 9-м классе по теме «Графики уравнений, содержащих символ модуля»
Тема урока: Графики уравнений, содержащих символ модуля.
Предмет: алгебра.
Тип урока: комбинированный.
Рис. 1. Блок-схема урока
Продолжительность занятия: 90 минут.
Главная дидактическая цель урока: выявление области приложения темы «График уравнения» в алгебре и в её связи с геометрией, формирование знаний по данной теме при решении стандартных и нестандартных алгебраических задач. Развитие у учащихся навыков исследовательской работы.
Цели урока:
- Формирование умений распознавать стандартные задачи в различных формулировках.
- Формирование способности к интеграции знаний из различных тем курса математики.
- Содействовать развитию логического мышления учащихся, умение выделять главное, обобщать.
- Формирование исследовательской, креативной работы учащихся.
- Воспитание графической культуры учащихся.
- Совершенствование коммуникативной культуры учащихся.
Оборудование: доска, мультимедийное оборудование, раздаточный дидактический материал для учащихся.
План урока
1. Блок мотивации. Изучая темы «Графики функций» и «Векторы», мы обнаруживаем тесную связь геометрии и алгебры, и, естественно, возникает вопрос – нельзя ли геометрические фигуры такие как квадрат, прямоугольник, ромб, треугольник задавать алгебраическими уравнениями и иследовать свойства этих фигур алгебраическими методами. Выявлению этой связи между геометрией и алгеброй и будет посвящён урок. Мы введём новое понятие «График уравнения» и рассмотрим графики уравнений в алгебраических и графических задачах. (3 мин.)
Выявлению этой связи между геометрией и алгеброй и будет посвящён урок. Мы введём новое понятие «График уравнения» и рассмотрим графики уравнений в алгебраических и графических задачах. (3 мин.)
2. Блок творческого разогрева. Повторение определения функции и графика функции. Обсуждение необходимости введения понятия «График уравнения».
Устная работа (20 мин.)
Актуализация знаний учащихся: повторение, анализ, обобщение.
Работа учащихся в следующих режимах: диалог, обсуждение, самостоятельная деятельность.
Материалы для проведения устной работы оформлены на доске.
Повторение определения функции и графика функции.
На доске представлены следующие чертежи (Рис. 2).
Каждый ученик получает раздаточный материал с этими чертежами.
Обсуждение:
1) На каких чертежах представлены графики функций? Почему?
2) Графики каких функций представлены на этих чертежах?
3) На каких чертежах графики не задают функции? Почему?
Обсуждается необходимость введения понятия графика уравнения.
Определение: Графиком уравнения называют множество точек координатной плоскости, координаты которых удовлетворяют заданному уравнению.
Рис. 2.
3. Теоретический блок 1. Изображение множества точек, координаты которых удовлетворяют заданным условиям. Ведущие идеи: симметрия, сдвиг графика уравнения (Рис. 3).
Рис. 3.
Обсуждается наилучший способ построения графика этого уравнения.
Варианты:
1. Решить задачу “в лоб”: раскрыть модули в четырёх случаях:
3. Замечаем, что переменные
входят в уравнение симметрично.
Так как, то график уравнения должен быть симметричным как относительно оси , так и относительно оси
Рис. 4
Рис. 5
4. Блок экспериментов.
Эксперимент. Преобразовать уравнение которое описывает квадрат так, чтобы уравнение задавало ромб.
Гипотеза: уравнение должно иметь вид:
После обсуждения учащиеся получают задание на два варианта:
Построить графики уравнений:
Рис. 6 Рис. 7
Рис. 8.
Гипотеза: график уравнения получается из графика уравнения в результате сдвига на две единицы вправо вдоль оси и на две единицы в отрицательном направлении вдоль оси График уравнения будет представлять собой квадрат, центр симметрии которого находится в точке Осями симметрии квадрата будут прямые
Рис. 9.
Выполняется непосредственная проверка гипотезы. Раскрываются модули в четырёх случаях:
6. Блок экспериментов 2.
Блок экспериментов 2.
Эксперимент 1. Построить график уравнения:
Рассматриваем четыре случая:
График уравнения представляет собой квадрат центром симметрии которого является точка сторона Рис. 10.
которого а площадь .
Рис. 11.
Рис. 12
7. Теоретический блок 3. Методика применения полученных знаний и навыков при решении уравнений некоторых типов с модулем и параметром.
Задание: Решить уравнение
При решении уравнений и неравенств с одним неизвестным, содержащих параметр, удобно проводить исследование на координатно-параметрической плоскости (Значение параметра будем откладывать по вертикальной оси, а значение неизвестного по горизонтальной оси).
Построим на плоскости график данного уравнения. Для этого построим прямые и , которые разобьют плоскость на 4 части.
Рис. 13
8. Блок постановки творческих задач.
Обсуждение и комментарии к домашнему заданию (7 мин.).
Домашнее задание к следующему уроку будет содержать:
1) Обязательная часть (индивидуальная работа) (Рис. 14).
Рис. 14.
При решении задания 4 допускается совместное творчество.
2) Творческая часть (допускается совместное творчество) (Рис. 15).
Рис. 15.
Учащиеся должны построить графики этих уравнений и убедиться в том, что одно уравнение описывает параллелограмм, а второе – треугольник. Учащимся предлагается поэкспериментировать с этими уравнениями, меняя коэффициенты при неизвестных, и понаблюдать как это влияет на геометрию получаемых геометрических фигур. Результаты этой самостоятельной работы учащиеся смогут продемонстрировать на следующем уроке.
Результаты этой самостоятельной работы учащиеся смогут продемонстрировать на следующем уроке.
Блок резюме.
1. Учащиеся формулируют главные выводы урока:
— Дано определение графика уравнения в сравнении с определением графика функции.
— Научились строить графики уравнений, содержащих символ модуля.
— Установили связь геометрии с алгеброй: различные геометрические фигуры могут быть заданы алгебраическими уравнениями. В частности, были построены квадрат, ромб и прямоугольник.
— Познакомились графическим методом решения уравнений с модулем и параметром, с использованием навыков полученных при построении графиков уравнений.
2. Оценивание работы учащихся: самооценка, взаимооценка, оценка работы учащихся учителем.
3. Выяснение мнения учащихся об уроке.
Ссылки на источники
- А. Г. Мордкович, Н. П. Николаев Алгебра 9. Учебник для учащихся общеобразовательных учреждений.
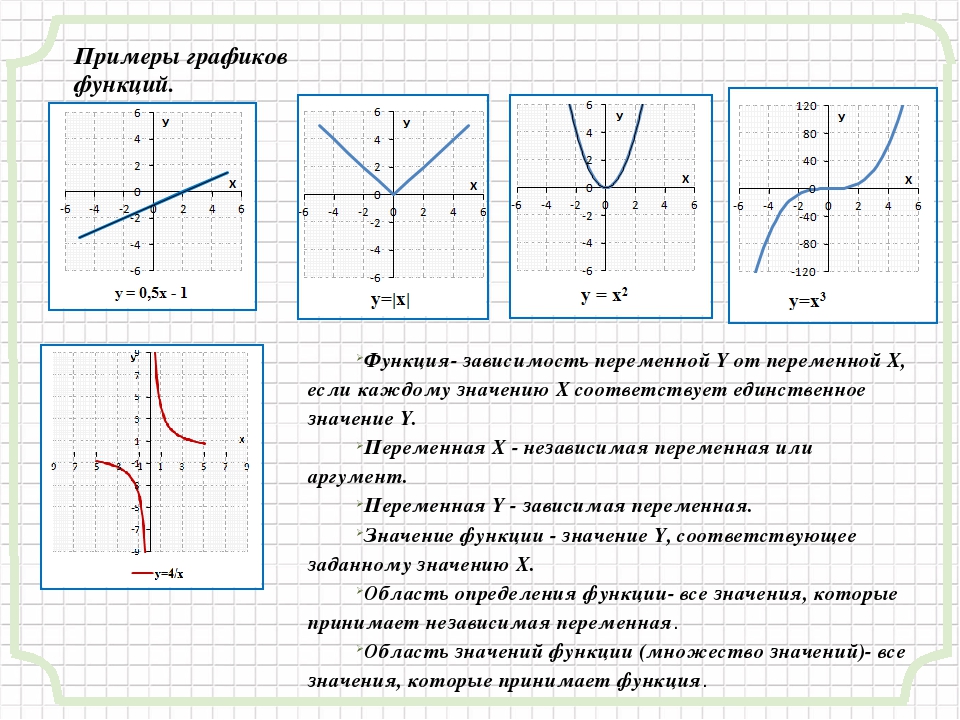 2+q $$
2+q $$Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.
В качестве переменной может выступать любая латинсая буква.
Например: \( x, y, z, a, b, c, o, p, q \) и т.д.Числа можно вводить целые или дробные.
 2 \)
2 \)При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)Сдвиги графиков функций
☰
Изменение значения k влияет на вид графика (степень крутизны в случае параболы), расположение ветвей в координатных четвертях и др. Однако точкой, через которую можно провести ось симметрии графиков, является точка O с координатами (0; 0).
Если же рассматривать функций, подобные перечисленным выше, у которых к переменной x или ко всей исходной функции прибавляется (или вычитается) какое-либо число, то графики этих функций остаются такими же как у исходных, однако смещаются относительно точки (0; 0).
Если обозначить исходные функции как y = f(x), то прибавление к x числа дает функции вида y = f(x+l), а прибавление ко всей исходной функции значения дает вид y = f(x) + m.
Например, если исходная функция y = 2x2, то примером первого типа будет функция y = 2(x+5)2, а второго — y = 2x2 + 5.

Для функций вида y = f(x+l) график смещается влево на l единиц, если l прибавляется. Если же l вычитается, то график смещается вправо. Действительно, представим параболу функции y = x2 и сравним ее с функцией y = (x+1)2. Когда x = 1, то для первой функции y = 1, а для второй — y = 4. Когда x = 0, для первой y = 0, для второй y = 1. Когда x = –1, для первой y = 1, для второй y = 0.
То есть график второй функции касается оси x в точке (–1; 0). Это значит, что график смещен влево по сравнению с исходным на 1.
Для функций вида y = f(x) + m график соответствующей функции y = f(x) смещается на m единиц, но уже по вертикальной оси (ось y). Здесь если m прибавляется, то график сдвигается вверх. Если m вычитается, то график сдвигается вниз.
Рассмотрим ту же параболу y = x2 и функцию y = x2 + 1. Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно.
 {2} + 2p [/ latex], решите относительно [латекс] h \ left (p \ right) = 3 [/ latex].{2} + 2p — 3 = 0 && \ text {Вычтите по 3 с каждой стороны}. \\ & \ left (p + 3 \ text {) (} p — 1 \ right) = 0 && \ text {Factor}. \ end {align} [/ latex]
{2} + 2p [/ latex], решите относительно [латекс] h \ left (p \ right) = 3 [/ latex].{2} + 2p — 3 = 0 && \ text {Вычтите по 3 с каждой стороны}. \\ & \ left (p + 3 \ text {) (} p — 1 \ right) = 0 && \ text {Factor}. \ end {align} [/ latex]Если [латекс] \ left (p + 3 \ right) \ left (p — 1 \ right) = 0 [/ latex], либо [latex] \ left (p + 3 \ right) = 0 [/ latex] или [латекс] \ left (p — 1 \ right) = 0 [/ latex] (или оба они равны 0). Мы установим каждый коэффициент равным 0 и решим для каждого случая [латекс] p [/ латекс].
[латекс] \ begin {align} & p + 3 = 0, && p = -3 \\ & p — 1 = 0, && p = 1 \ hfill \ end {align} [/ latex]
Это дает нам два решения.Выход [латекс] h \ left (p \ right) = 3 [/ latex], когда вход либо [latex] p = 1 [/ latex], либо [latex] p = -3 [/ latex].
Мы также можем проверить, построив график, как на рисунке 5. График проверяет, что [latex] h \ left (1 \ right) = h \ left (-3 \ right) = 3 [/ latex] и [latex] h \ left (4 \ справа) = 24 [/ латекс].

Попробуйте
Учитывая функцию [латекс] g \ left (m \ right) = \ sqrt {m — 4} [/ latex], решите [latex] g \ left (m \ right) = 2 [/ latex].
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения .Если возможно выразить выход функции с помощью формулы , включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс] 2n + 6p = 12 [/ латекс] выражает функциональную взаимосвязь между [латексом] n [/ латексом] и [латексом] p [/ латексом]. Мы можем переписать его, чтобы решить, является ли [latex] p [/ latex] функцией [latex] n [/ latex].
Практическое руководство. Для данной функции в форме уравнения напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства с другой стороной как выражение, которое включает только входную переменную.
- Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.
Пример: поиск уравнения функции
Выразите отношение [латекс] 2n + 6p = 12 [/ latex] как функцию [latex] p = f \ left (n \ right) [/ latex], если это возможно.
Показать решение
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где [latex] p [/ latex] является функцией [latex] n [/ latex], что означает запись его как [latex] p = [/ latex] выражение, включающее [latex] n [/ latex].
[латекс] \ begin {align} & 2n + 6p = 12 \\ [1mm] & 6p = 12 — 2n && \ text {Subtract} 2n \ text {с обеих сторон}. \\ [1mm] & p = \ frac {12 — 2n} {6} && \ text {Разделите обе стороны на 6 и упростите}. \\ [1 мм] & p = \ frac {12} {6} — \ frac {2n} {6} \\ [1 мм] & p = 2- \ frac {1} {3} n \ end {align} [/ latex ]
Следовательно, [латекс] p [/ latex] как функция [latex] n [/ latex] записывается как
[латекс] p = f \ left (n \ right) = 2- \ frac {1} {3} n [/ latex]
Анализ решения
Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой.
 {y} [/ latex], если мы хотим выразить [latex] y [/ latex] как функцию [latex] x [/ latex], не существует простой алгебраической формулы, включающей только [latex] x [/ latex] что равно [латекс] y [/ латекс]. Однако каждый [latex] x [/ latex] действительно определяет уникальное значение для [latex] y [/ latex], и существуют математические процедуры, с помощью которых [latex] y [/ latex] может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex] y [/ latex] как функции [latex] x [/ latex], даже если формулу нельзя записать явно.
{y} [/ latex], если мы хотим выразить [latex] y [/ latex] как функцию [latex] x [/ latex], не существует простой алгебраической формулы, включающей только [latex] x [/ latex] что равно [латекс] y [/ латекс]. Однако каждый [latex] x [/ latex] действительно определяет уникальное значение для [latex] y [/ latex], и существуют математические процедуры, с помощью которых [latex] y [/ latex] может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex] y [/ latex] как функции [latex] x [/ latex], даже если формулу нельзя записать явно.Оценка функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф.
 Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев.И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.
Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев.И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.Функция, которая связывает тип домашнего животного с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу ниже.
Домашнее животное Объем памяти в часах Щенок 0,008 Взрослая собака 0.083 Кот 16 Золотая рыбка 2160 Бета рыба 3600 Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию [латекс] П [/ латекс].
Домен функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память домашнего животного.Мы можем оценить функцию [latex] P [/ latex] при входном значении «золотая рыбка». Мы бы написали [латекс] P \ left (\ text {goldfish} \ right) = 2160 [/ latex]. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex] P [/ latex] кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.
Практическое руководство. Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите данный вход в строке (или столбце) входных значений.
- Определите соответствующее выходное значение в паре с этим входным значением.
- Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
- Определите входные значения, соответствующие заданному выходному значению.
Пример: оценка и решение табличной функции
Используя приведенную ниже таблицу,
- Вычислить [латекс] g \ left (3 \ right) [/ latex].
- Решите [латекс] g \ left (n \ right) = 6 [/ latex].
[латекс] n [/ латекс] 1 2 3 4 5 [латекс] г (п) [/ латекс] 8 6 7 6 8 Показать решение
- Оценка [latex] g \ left (3 \ right) [/ latex] означает определение выходного значения функции [latex] g [/ latex] для входного значения [latex] n = 3 [/ latex].Выходное значение таблицы, соответствующее [latex] n = 3 [/ latex], равно 7, поэтому [latex] g \ left (3 \ right) = 7 [/ latex].

- Решение [latex] g \ left (n \ right) = 6 [/ latex] означает определение входных значений, [latex] n [/ latex], которые дают выходное значение 6. В таблице ниже показаны два решения: [ латекс] n = 2 [/ латекс] и [латекс] n = 4 [/ латекс].
[латекс] n [/ латекс] 1 2 3 4 5 [латекс] г (п) [/ латекс] 8 6 7 6 8 Когда мы вводим 2 в функцию [latex] g [/ latex], мы получаем 6.Когда мы вводим 4 в функцию [latex] g [/ latex], наш результат также равен 6.
Попробуйте
Используя таблицу из предыдущего примера, оцените [латекс] g \ left (1 \ right) [/ latex].
Показать решение
[латекс] г \ влево (1 \ вправо) = 8 [/ латекс]
Поиск значений функций из графика
Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.
 Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.
Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.Пример: чтение значений функций из графика
Учитывая график ниже,
- Вычислить [латекс] f \ left (2 \ right) [/ latex].
- Решите [латекс] f \ left (x \ right) = 4 [/ latex].
Показать решение
- Чтобы оценить [латекс] f \ left (2 \ right) [/ latex], найдите точку на кривой, где [latex] x = 2 [/ latex], затем прочтите [latex] y [/ latex] — координата этой точки.Точка имеет координаты [latex] \ left (2,1 \ right) [/ latex], поэтому [latex] f \ left (2 \ right) = 1 [/ latex].
- Чтобы решить [латекс] f \ left (x \ right) = 4 [/ latex], мы находим выходное значение [latex] 4 [/ latex] по вертикальной оси. Двигаясь горизонтально по линии [latex] y = 4 [/ latex], мы обнаруживаем две точки кривой с выходным значением [latex] 4: [/ latex] [latex] \ left (-1,4 \ right) [/ латекс] и [латекс] \ влево (3,4 \ вправо) [/ латекс].
 Эти точки представляют два решения [латекса] f \ left (x \ right) = 4: [/ latex] [latex] x = -1 [/ latex] или [latex] x = 3 [/ latex].Это означает [латекс] f \ left (-1 \ right) = 4 [/ latex] и [latex] f \ left (3 \ right) = 4 [/ latex], или когда ввод [латекс] -1 [ / latex] или [latex] \ text {3,} [/ latex] вывод будет [latex] \ text {4} \ text {.} [/ latex] См. график ниже.
Эти точки представляют два решения [латекса] f \ left (x \ right) = 4: [/ latex] [latex] x = -1 [/ latex] или [latex] x = 3 [/ latex].Это означает [латекс] f \ left (-1 \ right) = 4 [/ latex] и [latex] f \ left (3 \ right) = 4 [/ latex], или когда ввод [латекс] -1 [ / latex] или [latex] \ text {3,} [/ latex] вывод будет [latex] \ text {4} \ text {.} [/ latex] См. график ниже.
Попробуйте
Используя график, решите [латекс] f \ left (x \ right) = 1 [/ latex].
Показать решение
[латекс] x = 0 [/ латекс] или [латекс] x = 2 [/ латекс]
Попробуйте
Вы можете использовать онлайн-инструмент построения графиков для построения графиков функций, поиска значений функций и оценки функций.2 + x + 4 [/ latex] с использованием обозначения функций.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства с другой стороной как выражение, которое включает только входную переменную.
- Вычислить функцию при [latex] x = 1 [/ latex]
- Составьте таблицу значений, которая ссылается на функцию. Включите хотя бы интервал [latex] [- 5,5] [/ latex] для значений [latex] x [/ latex].

- Решите функцию для [latex] f (0) [/ latex]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить страницуПодробнее
Обозначение функций
: Определения и оценка по номеру
Purplemath
Вы уже некоторое время играете с уравнениями типа « y =».И вы видели, что «красивые» уравнения (например, прямые линии, а не эллипсы) — это те уравнения, которые вы можете решить для « y =», а затем подключить к графическому калькулятору. Эти уравнения « y =» являются функциями. Но в данный момент вы сталкиваетесь с вопросом: «Зачем мне нужна эта нотация функции, особенно когда у меня есть очень хорошее ‘ y =’, и как эта нотация работает?»
Вспомните, когда вы учились в начальной школе. Ваш учитель дал вам рабочие листы, содержащие такие утверждения, как «[] + 2 = 4», и сказал вам заполнить поле. Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4», и предлагал вам «решить для x ».
Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие утверждения, как « x + 2 = 4», и предлагал вам «решить для x ».
MathHelp.com
Почему ваши учителя перешли от ящиков к переменным? Что ж, подумайте: сколько форм вы бы использовали для формул, подобных той, которая используется для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? Формула выглядит следующим образом:
Если вы попытаетесь выразить вышеупомянутое или что-то более сложное, используя прямоугольники различной формы, вы быстро потеряете формы. Кроме того, по опыту вы знаете, что « A » обозначает «площадь», « h » обозначает «высоту», а « a » и « b » обозначают длину параллельной вершины и нижние стороны. Только небо знает, что может означать квадратная или треугольная коробка!
Кроме того, по опыту вы знаете, что « A » обозначает «площадь», « h » обозначает «высоту», а « a » и « b » обозначают длину параллельной вершины и нижние стороны. Только небо знает, что может означать квадратная или треугольная коробка!
Другими словами, они переключились с ящиков на переменные, потому что, хотя прямоугольники и буквы означают одно и то же (а именно, слот, ожидающий заполнения значения), переменные лучше.Переменные более гибкие, их легче читать, и они могут дать вам больше информации.
То же самое верно для « y » и « f ( x )» (произносится как «эфф-оф-экс»). Для функций два обозначения означают одно и то же, но « f ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « y = 2 x + 3; найти y , когда x = –1». Теперь вы говорите: « f ( x ) = 2 x + 3; найдите f (–1)» (произносится как « f -of- x равно 2 x плюс три; найти f -of-negative-one «).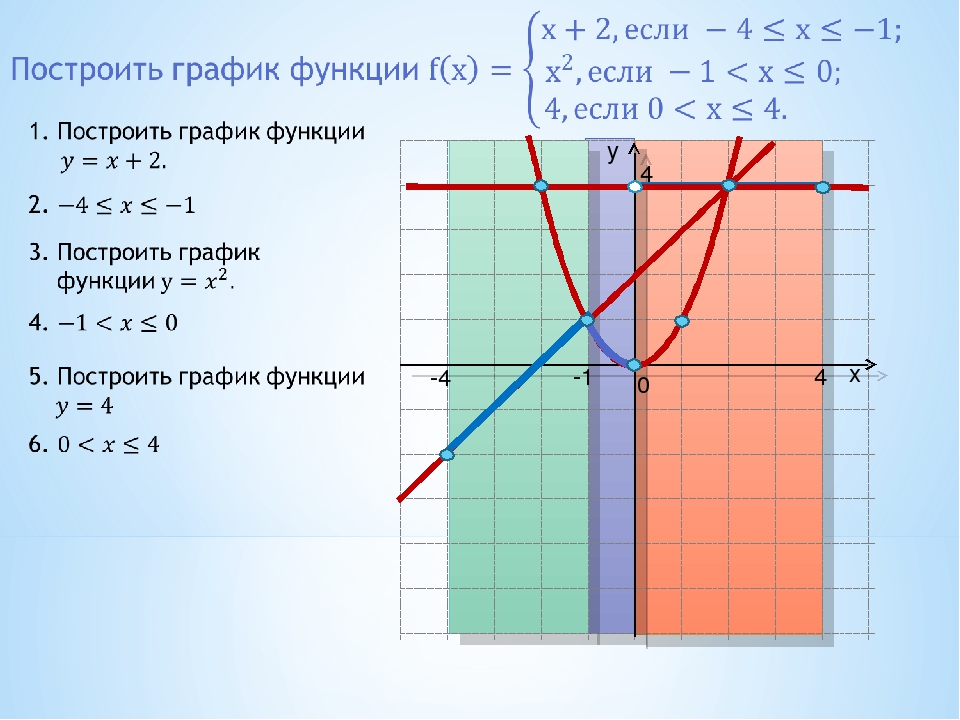 В любой форме вы делаете одно и то же: подставляете –1 для x , умножаете на 2, а затем складываете 3, упрощая, чтобы получить окончательное значение +1.
В любой форме вы делаете одно и то же: подставляете –1 для x , умножаете на 2, а затем складываете 3, упрощая, чтобы получить окончательное значение +1.
Но обозначение функций дает вам большую гибкость, чем использование просто « y » для каждой формулы. Например, ваш графический калькулятор будет перечислять различные функции как y1, y2 и т. Д., Поэтому вы можете различать уравнения, когда, скажем, просматриваете их значения в «ТАБЛИЦЕ».
Точно так же в учебниках и при написании вещей мы используем разные имена функций, такие как f ( x ), g ( x ), h ( x ), s ( t ) и т. Д., Чтобы отслеживать и работать с более чем одной формулой в любом контексте.С обозначением функций теперь мы можем использовать более одной функции одновременно, не запутываясь и не путая формулы, заставляя себя задаться вопросом: «Хорошо, что ‘ y ‘ — это , это ?» И обозначения могут быть полезными для пояснения.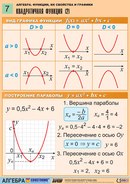
Из геометрии вы знаете, что « A ( r ) = π r 2 » обозначает площадь круга, выраженную через значение радиуса r , а « C ( r ) = 2π r «указывает длину окружности, выраженную в виде радиуса r .Обе функции имеют одинаковую переменную плагина (« r »), но « A » напоминает вам, что первая функция является формулой для «площади», а « C » напоминает вам, что вторая функция формула для «окружности».
Помните: обозначение « f ( x )» в точности то же, что и « y ». Вы даже можете пометить ось y на своих графиках как « f ( x )», если хотите.
Позвольте мне прояснить еще один момент. В то время как круглые скобки до сих пор всегда указывали на умножение, это не относится к обозначениям функций. Вопреки всему предыдущему опыту, круглые скобки для обозначения функции не , а не указывают на умножение.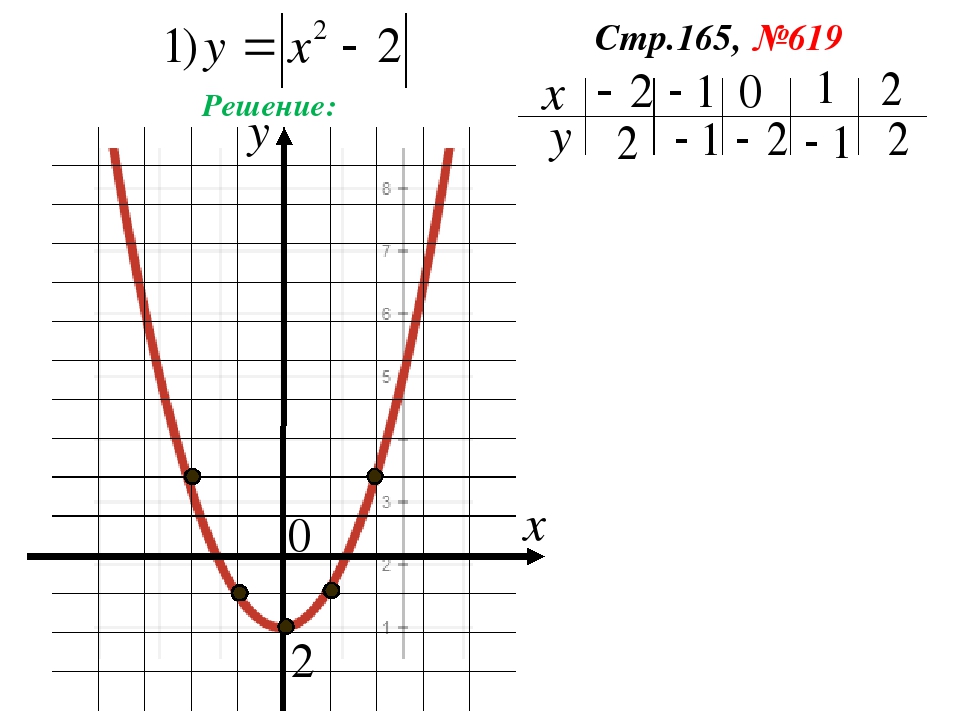
Выражение « f ( x )» означает «формула с именем f , имеет x в качестве входной переменной».Это означает, что , а не , означает «умножить на и x »!
Не смущайтесь, произнося (или думая) « f ( x )» как « f умножить на x », а никогда не пытайтесь «умножить» имя функции, заключенное в скобки. Вход.
В обозначении функции « x » в « f ( x )» называется «аргументом функции» или просто «аргументом».Поэтому, если они дадут вам выражение « f (2)» и попросят «аргумент», ответ будет просто «2».
В сторону: Почему ввод называется «аргументом»? Термин «аргумент» имеет давнюю историю. Первоначально это был логический термин, относящийся к утверждению, содержащему доказательство или, в менее формальном смысле, утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить.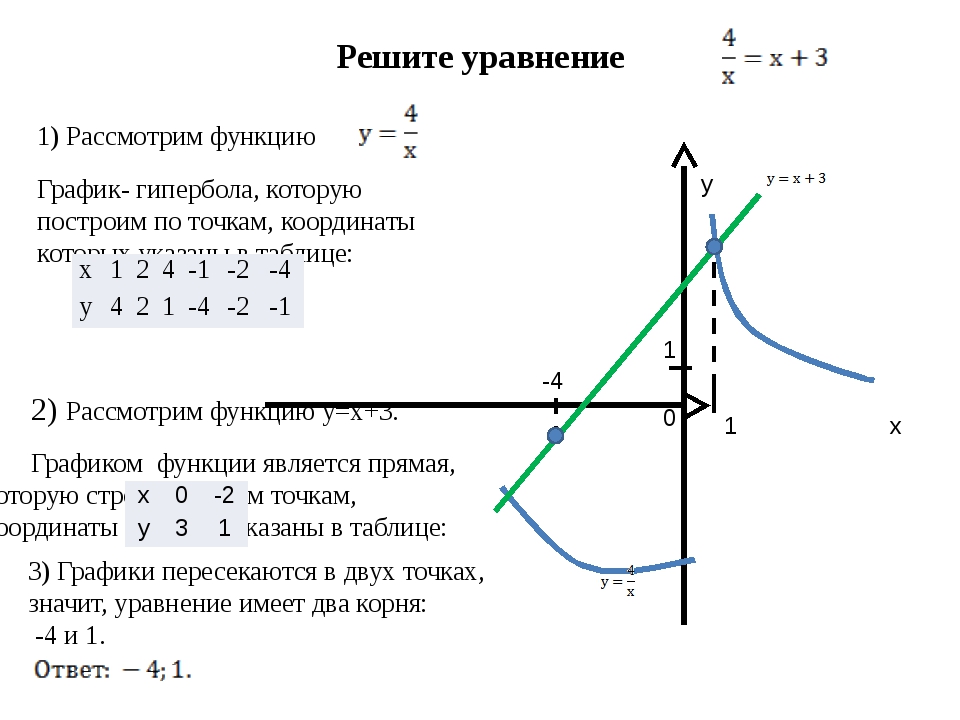 В конце концов, этот термин стал обозначать в раннем научном контексте любое математическое значение, которое требовалось в качестве входных данных для других вычислений, или любое значение, от которого зависели последующие результаты.
В конце концов, этот термин стал обозначать в раннем научном контексте любое математическое значение, которое требовалось в качестве входных данных для других вычислений, или любое значение, от которого зависели последующие результаты.
В двадцатом веке, когда компьютерное кодирование стало обычным явлением, кодировщики приняли математическое значение для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» — это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а вывод функции — это зависимая переменная (та, значение которой зависит от того, что было подключено. in, обычно это значение y ).
Учитывая
h ( s ), каково имя функции и какой аргумент?
Сначала сделаю вторую часть.Аргумент — это то, что находится в круглых скобках, поэтому здесь аргумент s .
Имя функции — это переменная, которая стоит перед круглыми скобками. В этом случае имя функции — h .
имя функции: h
аргумент: s
Каков аргумент
f ( y )?
Аргумент — это то, что подключено.В этом частном (необычном) случае подключаемая переменная — « y ». (В конце концов, не существует правила, согласно которому y не может быть независимой переменной.) Итак:
Учитывая
г ( t ) = t 2 + t , как называется функция? В г (–1), какой аргумент?
Имя функции — это то, что стоит перед круглыми скобками, поэтому имя функции здесь — g .
Во второй части вопроса меня просят аргументировать. В первой части, где они дали мне имя функции и аргумент (часть « g ( t )») и формулу (часть « t 2 + t »), аргумент был т . Но во второй части ввели конкретное значение для т . Итак, во второй части аргументом является число –1.
название функции: г
аргумент г (–1): –1
Оценка по номеру
Вы оцениваете « f ( x )» точно так же, как вы всегда оценивали « y ».А именно, вы берете число, которое они дают вам, в качестве входной переменной, вы подключаете его к переменной, и вы упрощаете получение ответа. Например:
Дано
f ( x ) = x 2 + 2 x — 1, найдите f (2).
Чтобы оценить f ( x ) при x = 2, я вставлю 2 для каждого экземпляра x в правило функции:
f (2) = (2) 2 +2 (2) — 1
Чтобы держать все в голове (и яснее в своей работе), я заключил в круглые скобки каждый экземпляр аргумента 2 в формуле для f .Теперь я могу упростить:
Тогда мой ответ:
Дано
f ( x ) = x 2 + 2 x — 1, найдите f (–3).
Для оценки делаю то, что делал всегда. Я подставлю данное значение (–3) для указанной переменной ( x ) в данную формулу:
f (–3) = (–3) 2 + 2 (–3) — 1
Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу. В данном случае круглые скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:
В данном случае круглые скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:
Тогда мой ответ:
Если вы испытываете трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как то, стоит ли показатель степени у знака «минус». И это просто хорошая привычка.
Важный тип функции называется «кусочной» функцией, потому что, ну, она разбита на части.Например, это кусочная функция:
Как видите, эта функция разделена на две половины: половину, которая идет перед x = 1, и половину, которая идет от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:
Учитывая функцию
f ( x ), как определено выше, оцените функцию при следующих значениях: x = –1, x = 3 и x = 1.
Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожен, чтобы вставить аргумент в правильную часть функции.
Они сначала хотят, чтобы я оценил как x = –1. Поскольку это меньше 1, этот аргумент переходит в первую часть функции. Чтобы обновить, функция следующая:
Затем я вставлю –1 в правило 2 x 2 — 1:
f (–1) = 2 (–1) 2 — 1
= 2 (1) — 1
= 2 — 1 = 1
Затем они хотят, чтобы я нашел значение f (3).Поскольку 3 больше 1, мне нужно будет подключить вторую часть функции, поэтому:
Наконец, они хотят, чтобы я оценил f ( x ) как x = 1. Это единственное значение x , которое немного сложно. Какую половину использовать?
Это единственное значение x , которое немного сложно. Какую половину использовать?
Внимательно глядя на правила для функций, я вижу, что первая часть — это правило для значений x , которые строго меньше единицы; правило не применяется, если x равно 1.С другой стороны, вторая часть применяется, когда x больше или равно 1. Поскольку здесь я имею дело с x = 1, то применяется правило второй части.
Тогда мой ответ:
f (–1) = 1
f (3) = 7
f (1) = 5
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций по заданному числовому значению.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.
Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/fcnnot.htm
Определение функции (практические задачи)
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-4: Определение функции
Для задач 1–3 определите, является ли данное отношение функцией.
- \ (\ left \ {{\ left ({2,4} \ right), \ left ({3, — 7} \ right), \ left ({6,10} \ right)} \ right \} \) Решение
- \ (\ left \ {{\ left ({- 1,8} \ right), \ left ({4, — 7} \ right), \ left ({- 1,6} \ right), \ left ( {0,0} \ right)} \ right \} \) Решение
- \ (\ left \ {{\ left ({2,1} \ right), \ left ({9,10} \ right), \ left ({- 4,10} \ right), \ left ({- 8,1} \ right)} \ right \} \) Решение
Для задач 4–6 определите, является ли данное уравнение функцией. 2} + 6 \), определите каждое из следующих значений.
2} + 6 \), определите каждое из следующих значений.
- \ (h \ влево (0 \ вправо) \)
- \ (h \ left ({- 2} \ right) \)
- \ (в \ влево (2 \ вправо) \)
- \ (h \ left ({\ sqrt x} \ right) \)
- \ (h \ left ({3 — t} \ right) \)
Решение
Решение
Решение
Для задач 12 и 13 вычислите коэффициент разности для данной функции. 2} — 8x + 15}}} \) Решение
2} — 8x + 15}}} \) Решение
Обозначение функций — пояснения и примеры
Концепция функций была разработана в семнадцатом веке, когда Рене Декарт использовал эту идею для моделирования математических отношений в своей книге Geometry . Термин «функция» был затем введен Готфридом Вильгельмом Лейбницем через пятьдесят лет после публикации Geometry.
Позже Леонард Эйлер формализовал использование функций, когда ввел понятие обозначения функций; у = f (х).Так продолжалось до 1837 года, когда немецкий математик Петер Дирихле дал современное определение функции.
Что такое функция?
В математике функция — это набор входных данных с одним выходом в каждом случае. У каждой функции есть домен и диапазон. Область — это набор независимых значений переменной x для определенного отношения или функции. Проще говоря, домен — это набор значений x, которые генерируют реальные значения y при подстановке в функцию.
С другой стороны, диапазон — это набор всех возможных значений, которые может выдать функция. Диапазон функции может быть выражен в виде интервалов или содержать информацию о неравенствах.
Что такое обозначение функций?
Обозначение можно определить как систему символов или знаков, которые обозначают такие элементы, как фразы, числа, слова и т. Д.
Следовательно, обозначение функций — это способ, которым функция может быть представлена с помощью символов и знаков.Нотация функций — это более простой метод описания функции без подробного письменного объяснения.
Наиболее часто используется обозначение функции f (x), которое читается как «f» или «x». В этом случае буква x, помещенная в круглые скобки, и весь символ f (x) обозначают набор доменов и набор диапазонов соответственно.
Хотя f — самая популярная буква, используемая при написании обозначений функций, любая другая буква алфавита также может использоваться как в верхнем, так и в нижнем регистре.
Преимущества использования обозначения функций
- Так как большинство функций представлены различными переменными, такими как; a, f, g, h, k и т. д., мы используем f (x), чтобы избежать путаницы относительно того, какая функция оценивается.
- Обозначение функций позволяет легко идентифицировать независимую переменную.
- Обозначение функции также помогает нам идентифицировать элемент функции, который необходимо исследовать.
Рассмотрим линейную функцию y = 3x + 7. Чтобы записать такую функцию в обозначении функции, мы просто заменяем переменную y фразой f (x), чтобы получить;
f (x) = 3x + 7.Эта функция f (x) = 3x + 7 читается как значение f для x или как f для x.
Типы функций
В алгебре есть несколько типов функций.
К наиболее распространенным типам функций относятся:
Линейная функция — это полином первой степени. Линейная функция имеет общий вид f (x) = ax + b, где a и b — числовые значения и a ≠ 0.
Полиномиальная функция второй степени известна как квадратичная функция. Общая форма квадратичной функции: f (x) = ax 2 + bx + c, где a, b и c — целые числа и a 0.
Это полиномиальная функция от 3 rd градусов, которая имеет форму f (x) = ax 3 + bx 2 + cx + d
Логарифмическая функция — это уравнение, в котором переменная отображается как аргумент логарифма. Общая функция функции f (x) = log a (x), где a — основание, а x — аргумент.
Экспоненциальная функция — это уравнение, в котором переменная отображается как показатель степени. Экспоненциальная функция представлена как f (x) = a x .
f (x) = sin x, f (x) = cos x и т. Д. Являются примерами тригонометрических функций
Identity Function:
Идентификационная функция такова, что f: A → B и f (x ) = x, ∀ x ∈ A
Рациональная функция:
Функция называется рациональной, если R (x) = P (x) / Q (x), где Q (x) ≠ 0.
Как оценивать функции?
Оценка функции — это процесс определения выходных значений функции. Это делается путем подстановки входных значений в обозначение данной функции.
Пример 1
Запишите y = x 2 + 4x + 1, используя обозначение функции, и оцените функцию при x = 3.
Решение
Учитывая, y = x 2 + 4x + 1
Применяя обозначение функции, мы получаем
f (x) = x 2 + 4x + 1
Оценка:
Заменить x на 3
f (3) = 3 2 + 4 × 3 + 1 = 9 + 12 + 1 = 22
Пример 2
Вычислите функцию f (x) = 3 (2x + 1), когда x = 4.
Решение
Подставьте x = 4 в функцию f (x).
f (4) = 3 [2 (4) + 1]
f (4) = 3 [8 + 1]
f (4) = 3 x 9
f (4) = 27
Пример 3
Запишите функцию y = 2x 2 + 4x — 3 в обозначении функции и найдите f (2a + 3).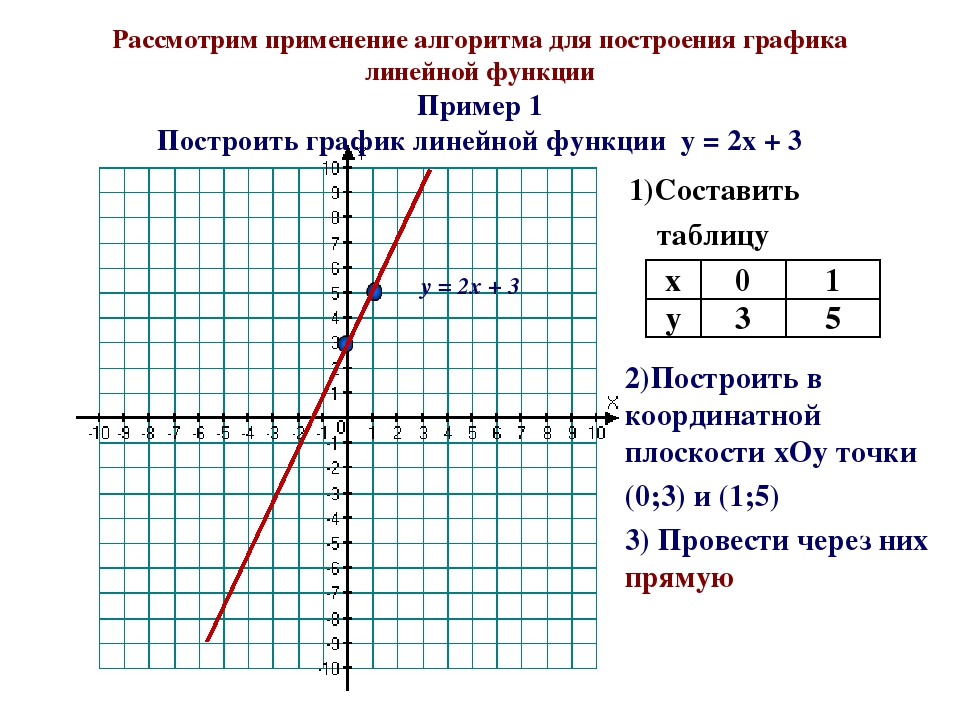
Решение
y = 2x 2 + 4x — 3 ⟹ f (x) = 2x 2 + 4x — 3
Заменить x на (2a + 3).
f (2a + 3) = 2 (2a + 3) 2 + 4 (2a + 3) — 3
= 2 (4a 2 + 12a + 9) + 8a + 12 — 3
= 8a 2 + 24a + 18 + 8a + 12-3
= 8a 2 + 32a + 27
Пример 4
Представьте y = x 3 — 4x, используя обозначение функции и решите для y при x = 2.
Решение
Учитывая функцию y = x 3 — 4x, замените y на f (x), чтобы получить;
f (x) = x 3 — 4x
Теперь оцените f (x), когда x = 2
⟹ f (2) = 2 3 — 4 × 2 = 8-8 = 0
Следовательно , значение y при x = 2 равно 0
Пример 5
Найдите f (k + 2) при условии, что f (x) = x² + 3x + 5.
Решение
Чтобы оценить f (k + 2), замените x на (k + 2) в функции.
⟹ f (k + 2) = (k + 2) ² + 3 (k + 2) + 5
⟹ k² + 2² + 2k (2) + 3k + 6 + 5
k² + 4 + 4k + 3k + 6 + 5
= k² + 7k + 15
Пример 6
Учитывая обозначение функции f (x) = x 2 — x — 4. Найдите значение x, когда f ( x) = 8
Решение
f (x) = x 2 — x — 4
Заменить f (x) на 8.
8 = x 2 — x — 4
x 2 — x — 12 = 0
Решите квадратное уравнение путем разложения на множители, чтобы получить;
⟹ (x — 4) (x + 3) = 0
⟹ x — 4 = 0; x + 3 = 0
Следовательно, значения x при f (x) = 8 равны;
х = 4; x = -3
Пример 7
Вычислите функцию g (x) = x 2 + 2 при x = −3
Решение
Замените x на -3.
г (−3) = (−3) 2 + 2 = 9 + 2 = 11
Примеры обозначения функций из реальной жизни
Обозначение функций можно применять в реальной жизни для оценки математических задач, как показано ниже Примеры:
Пример 8
Для производства определенного продукта компания тратит x долларов на сырье и y долларов на рабочую силу. Если себестоимость продукции описывается функцией f (x, y) = 36000 + 40x + 30y + xy / 100.Рассчитайте стоимость производства, если фирма тратит 10 000 и 1 000 долларов на сырье и рабочую силу соответственно.
Если себестоимость продукции описывается функцией f (x, y) = 36000 + 40x + 30y + xy / 100.Рассчитайте стоимость производства, если фирма тратит 10 000 и 1 000 долларов на сырье и рабочую силу соответственно.
Решение
Дано x = 10000 долларов США и y = 1000 долларов США
Подставьте значения x и y в функцию производственных затрат
⟹f (10000, 1000) = 36000 + 40 (10000) + 30 (1000) + (10000) (1000) / 100.
⟹ f (10000, 1000) = 36000 + 4000000 + 30000 + 100000
⟹ 4136000 долларов.
Пример 9
Мэри экономит 100 долларов в неделю на предстоящем праздновании дня рождения.Если у нее уже есть 1000 долларов, сколько у нее будет через 22 недели.
Решение
Пусть x = количество недель, а f (x) = общая сумма. Мы можем записать эту проблему в обозначении функции как;
f (x) = 100x + 1000
Теперь оцените функцию, когда x = 22
f (22) = 100 (22) +1000
f (22) = 3200
Таким образом, общая сумма составит 3200 долларов.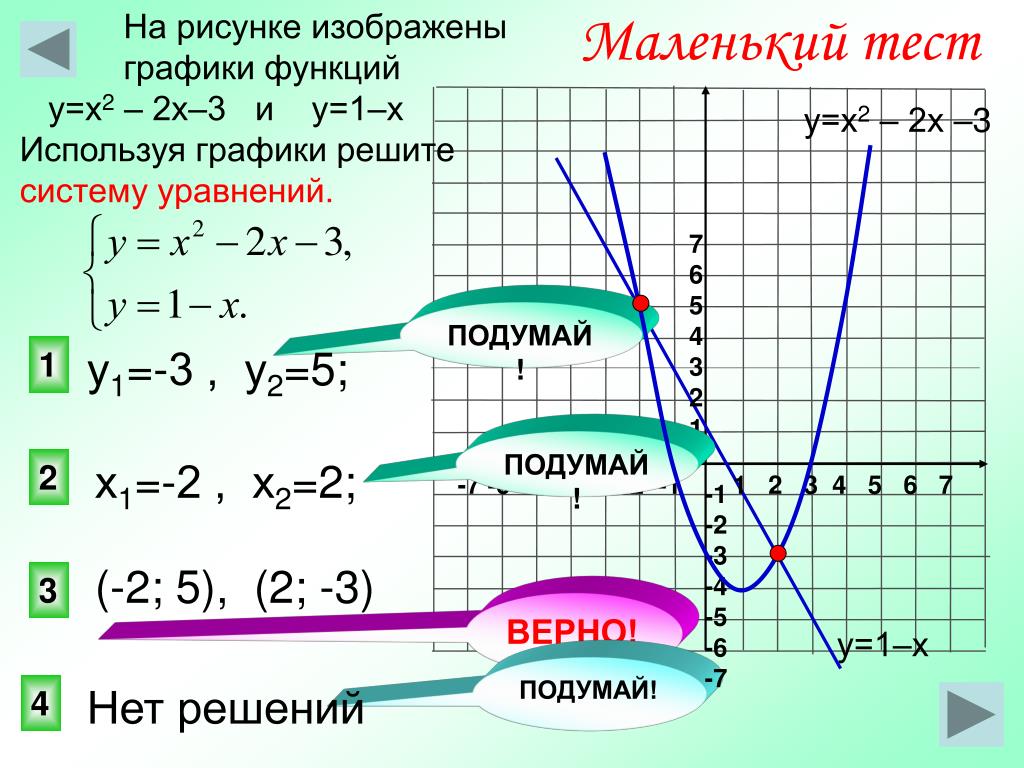
Пример 10
Стоимость разговора в двух мобильных сетях A и B составляет 34 доллара плюс 0.05 / мин и 40 долларов плюс 0,04 / мин соответственно.
- Представьте эту проблему в обозначении функций.
- Какая мобильная сеть является доступной с учетом того, что в среднем каждый месяц используется 1 160 минут.
- Когда будут равны ежемесячные счета двух сетей?
Решение
- Пусть x будет количеством минут, используемых в каждой сети.
Следовательно, функция сети A равна f (x) = 0,05x + 34, а функция сети B — f (x) = 0.04x + 40 долларов.
- Чтобы определить, какая сеть доступна, подставьте x = 1160 в каждую функцию
A ⟹ f (1160) = 0,05 (1160) + 34
= 58 + 34 = 92 доллара США
B f (1160) = 0,04 (1160) + 40
= 46,4 + 40
= 86,4 долл. США
Следовательно, сеть B является доступной, поскольку ее общая стоимость времени разговора меньше, чем у A.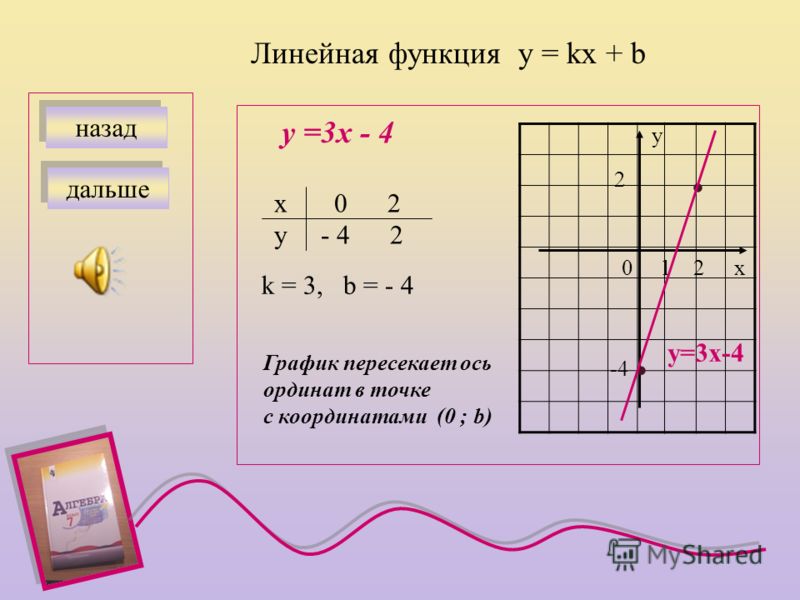
- Приравняйте две функции и решите x
⟹ 0,05x +34 = 0,04x + 40
⟹ 0,01x = 6
x = 600
Ежемесячный счет для A и B будет равен, когда среднее количество минут составляет 600.
Доказательство:
A ⟹ 0,05 (600) +34 = 64 доллара США
B ⟹ 0,04 (600) + 40 = 64 доллара США
Пример 11
Определенное число такое, что при добавлении его к 142, результат на 64 раза больше исходного числа. Найдите номер.
Решение
Пусть x = исходное число, а f (x) будет результатом добавления 142.
f (x) = 142 + x = 3x + 64
2x = 78
x = 39
Пример 12
Если произведение двух последовательных положительных целых чисел равно 1122, найдите два целых числа.
Решение
Пусть x будет первым целым числом;
второе целое число = x + 1
Теперь сформируйте функцию как;
f (x) = x (x + 1)
найти значение x, если f (x) = 1122
Заменить функцию f (x) на 1122
1122 = x (x + 1)
1122 = x 2 + 1
x 2 = 1121
Найдите квадрат обеих сторон функции
x = 33
x + 1 = 34
Целые числа 33 и 34.
Предыдущий урок | Главная страница | Следующий урок
Функции и обозначение функций — College Algebra
Цели обучения
В этом разделе вы:
- Определите, представляет ли отношение функцию.
- Найдите значение функции.
- Определите, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- Изобразите функции, перечисленные в библиотеке функций.
Реактивный лайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.
Определение того, представляет ли отношение функцию
Отношение — это набор упорядоченных пар. Набор, состоящий из первых компонентов каждой упорядоченной пары, называется областью , а набор, состоящий из вторых компонентов каждой упорядоченной пары, называется диапазоном .Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
Домен — Диапазон
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и является часто обозначается строчной буквой
Функция — это отношение, которое назначает один элемент в диапазоне каждому элементу в домене . Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене сопряжен ровно с одним элементом в диапазоне,
Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как
Обратите внимание, что каждый элемент в домене — это , а не , спаренный ровно с одним элементом в диапазоне. Например, термин «нечетный» соответствует трем значениям из домена, а термин «четный» соответствует двум значениям из range, Это нарушает определение функции, поэтому это отношение не является функцией.
(рисунок) сравнивает отношения, которые являются функциями, а не функциями.
Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».
Входные значения составляют область, а выходные значения составляют диапазон.
Учитывая взаимосвязь между двумя величинами, определите, является ли взаимосвязь функцией.
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Определение того, являются ли прайс-листы меню функциями
Меню кофейни, показанное на (Рисунок), состоит из позиций и их цен.
- Цена зависит от товара?
- Товар зависит от цены?
- Начнем с рассмотрения ввода как пунктов меню.Выходные значения — это цены.
Каждый элемент в меню имеет только одну цену, поэтому цена зависит от элемента.
- Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. (Рисунок).
Следовательно, товар не зависит от цены.
Определение того, являются ли правила оценки класса функциями
В конкретном математическом классе общая оценка в процентах соответствует средней оценке.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? (Рисунок) показывает возможное правило присвоения баллов.
| Процентное содержание | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Средний балл | 0,0 | 1,0 | 1.5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Для любой процентной оценки существует соответствующий средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.
В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3.0 может иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
(Рисунок) 1 перечисляет пять величайших бейсболистов всех времен в порядке рангов.
| Игрок | Рейтинг |
|---|---|
| Бэйб Рут | 1 |
| Уилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
- Является ли ранг функцией имени игрока?
- Имя игрока зависит от ранга?
а.да; б. да. (Примечание: если бы два игрока были разделены, скажем, на 4-м месте, то имя не зависело бы от ранга.)
Представление функций с помощью таблиц
Обычный метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.
(рисунок) перечисляет входное число каждого месяца (январь = 1, февраль = 2 и т. Д.) И выходное значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце, где месяцы идентифицируются целым числом, а не именем.
| Номер месяца, (ввод) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Количество дней в месяце (вывод) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
(рисунок) определяет функцию Помните, это обозначение говорит нам, что это имя функции, которая принимает входные данные и выдает выходные данные.
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
(Рисунок) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.
| Возраст в годах, (ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах (на выходе) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Учитывая таблицу входных и выходных значений, определите, представляет ли таблица функцию.
- Определите входные и выходные значения.
- Проверьте, сопряжено ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет функцию.
Идентификационные таблицы, представляющие функции
Какая таблица (рисунок), (рисунок) или (рисунок) представляет функцию (если есть)?
| Вход | Выход |
|---|---|
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
(рисунок) и (рисунок) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. (Рисунок) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.
Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.
Функция, представленная (Рисунок), может быть представлена записью
Аналогично заявления
представляют функцию на (Рисунок).
(рисунок) не может быть выражен аналогичным образом, потому что он не представляет функцию.
Представляет ли (рисунок) функцию?
| Ввод | Выход |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, обычно вычислить функцию несложно.Например, функция может быть вычислена путем возведения входного значения в квадрат, умножения на 3 и последующего вычитания произведения из 5.
Учитывая формулу функции, оцените.
- Замените входную переменную в формуле указанным значением.
- Рассчитайте результат.
Учитывая функцию оценки
Решающие функции
Учитывая функцииolve для
Оценка функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.
Функция, которая связывает тип домашнего животного с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. (Рисунок).
| Домашнее животное | Объем памяти в часах |
|---|---|
| Щенок | 0,008 |
| Взрослая собака | 0,083 |
| Кот | 16 |
| Золотая рыбка | 2160 |
| Бета рыба | 3600 |
Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений.Здесь позвольте нам вызвать функцию. Домен функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца. Мы можем оценить функцию по входному значению «золотая рыбка». Мы бы написали Заметьте, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функций кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.
Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите данный вход в строке (или столбце) входных значений.
- Определите соответствующее выходное значение в паре с этим входным значением.
- Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
- Определите входные значения, соответствующие заданному выходному значению.
Оценка и решение табличной функции
Использование (рисунок),
- Оценить
- Решить
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной в начале этой главы, цена акции составляла 1000 фунтов стерлингов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 фунтов стерлингов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как показано на (Рисунок).
| Буквенный класс | Средний балл |
|---|---|
| А | 4,0 |
| В | 3,0 |
| С | 2,0 |
| D | 1,0 |
Эта система оценок представляет собой функцию «один к одному», потому что каждая введенная буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной входной букве.
Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, схематически изображенные на (Рисунок) (a) и (Рисунок) (b) . Функция в части (a) показывает взаимосвязь, которая не является взаимно-однозначной функцией, потому что входы и оба выдают выходные данные Функция в части (b) показывает взаимосвязь, которая является взаимно-однозначной функцией, потому что каждый вход связан с одним выход.
Индивидуальный подход
Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.Нет повторяющихся значений x или y .
Определение, является ли отношение однозначной функцией
Площадь круга зависит от его радиуса? Если да, то функция взаимно однозначная?
- Является ли остаток функцией номера банковского счета?
- Является ли номер банковского счета функцией баланса?
- Является ли баланс однозначной функцией номера банковского счета?
а. да, потому что на каждом банковском счете в любой момент времени имеется единый баланс; б.нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс; c. нет, потому что один и тот же выход может соответствовать более чем одному входу.
- Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
- Если да, то функция взаимно однозначная?
- Да, буквенная оценка является функцией процентной оценки;
- Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.
Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают большое количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение и выходное значение, и мы говорим, что это функция или когда функция называется График функции — это набор всех точек на плоскости, которые удовлетворяют уравнению Если функция определена только для нескольких входных значений, то График функции состоит только из нескольких точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на (Рисунок) говорят нам об этом, и тем не менее, набор всех удовлетворяющих точек представляет собой кривую. Показанная кривая включает и потому, что кривая проходит через эти точки.
Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. (Рисунок).
Для графика используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
- Если такая линия есть, определите, что график не представляет функцию.
Применение теста вертикальной линии
Какой из графиков на (Рисунок) представляет функцию
Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) (Рисунок). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекала бы график более чем в одной точке, как показано на (Рисунок).
Представляет ли график на (Рисунок) функцию?
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии.Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.
Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию.
- Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
- Если такая линия есть, определите, что функция не взаимно однозначна.
Применение теста горизонтальной линии
Рассмотрим функции, показанные на (Рисунок) (a) и (Рисунок) (b) . Являются ли какие-либо функции взаимно однозначными?
Функция на (Рисунок) (a) не является взаимно однозначной. Горизонтальная линия, показанная на (Рисунок), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках).
Функция на (Рисунок) (b) взаимно однозначна.Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.
Соответствует ли график (рисунок) один к одному?
Нет, потому что он не проходит тест горизонтальной линии.
Определение основных функций набора инструментов
В этом тексте мы будем исследовать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем. Когда учимся читать, мы начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел.При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать как входную, так и выходную переменную.
Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги.Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную на (Рисунок).
Ключевые концепции
- Отношение — это набор упорядоченных пар. Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу. См. (Рисунок) и (Рисунок).
- Функциональная нотация — это сокращенный метод соотнесения ввода и вывода в форме (см. (Рисунок) и (рисунок)).
- В табличной форме функция может быть представлена строками или столбцами, относящимися к входным и выходным значениям. См. (Рисунок).
- Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением. См. (Рисунок) и (Рисунок).
- Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение. См. (Рисунок).
- Алгебраическая форма функции может быть записана из уравнения.См. (Рисунок) и (Рисунок).
- Входные и выходные значения функции можно определить по таблице. См. (Рисунок).
- Связь входных значений с выходными значениями на графике — еще один способ оценить функцию. См. (Рисунок).
- Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению. См. (Рисунок).
- График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке. См. (Рисунок).
- График функции «один к одному» проходит проверку горизонтальной линии.См. (Рисунок).
Упражнения по разделам
Устный
В чем разница между отношением и функцией?
Отношение — это набор упорядоченных пар. Функция — это особый вид отношения, в котором никакие две упорядоченные пары не имеют одинаковой первой координаты.
В чем разница между вводом и выводом функции?
Почему тест с вертикальной линией сообщает нам, представляет ли график отношения функцию?
Когда вертикальная линия пересекает график отношения более одного раза, это означает, что для этого входа существует более одного выхода.При любом конкретном входном значении может быть только один выход, если отношение должно быть функцией.
Как определить, является ли отношение однозначной функцией?
Почему тест горизонтальной линии показывает, является ли график функции взаимно однозначным?
Когда горизонтальная линия пересекает график функции более одного раза, это указывает на то, что для этого вывода существует более одного ввода. Функция взаимно однозначна, если каждый выход соответствует только одному входу.
Технологии
Для следующих упражнений создайте график в данном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
Для следующих упражнений создайте график в данном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
Для следующих упражнений создайте график в данном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра.Покажите каждый график.
Для следующих упражнений создайте график в данном окне просмотра. Определите соответствующий диапазон для каждого окна просмотра. Покажите каждый график.
Сноски
- 1 http://www.baseball-almanac.com/legendary/lisn100.shtml. Дата обращения 24.03.2014.
Глоссарий
- зависимая переменная
- выходная переменная
- домен
- набор всех возможных входных значений для отношения
- функция
- отношение, в котором каждое входное значение дает уникальное выходное значение
- тест горизонтальной линии
- метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
- независимая переменная
- входная переменная
- вход
- каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция
- индивидуальная функция
- функция, для которой каждое значение вывода связано с уникальным значением ввода
- выход
- каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию
- диапазон
- набор выходных значений, которые являются результатом входных значений в отношении
- отношение
- комплект заказанных пар
- тест вертикальной линии
- метод проверки того, представляет ли график функцию путем определения того, пересекает ли вертикальная линия график не более одного раза
3.1 Функции и обозначение функций — College Algebra
Реактивный лайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.
Определение того, представляет ли отношение функцию
Отношение — это набор упорядоченных пар.Набор первых компонентов каждой упорядоченной пары называется доменом , а набор вторых компонентов каждой упорядоченной пары называется диапазоном . Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
{(1,2), (2,4), (3,6), (4,8), (5,10)} {(1,2), (2,4), (3,6), (4,8), (5,10)}
Домен: {1,2,3,4,5}. {1,2,3,4,5}.
Диапазон составляет {2,4,6,8,10}. {2,4,6,8,10}.
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой x.x. Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой y.y.
Функция ff — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, {1,2,3,4,5}, {1,2,3,4,5 }, сочетается ровно с одним элементом в диапазоне, {2,4,6,8,10}.{2,4,6,8,10}.
Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Это выглядело бы как
{(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5)} {(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5)}
Обратите внимание, что каждый элемент в домене, {четный, нечетный} {четный, нечетный}
, а не в паре с ровно одним элементом в диапазоне, {1,2,3,4,5}. {1,2,3,4,5}.
Например, термин «нечетный» соответствует трем значениям из диапазона, {1,3,5} {1,3,5}
а термин «даже» соответствует двум значениям из диапазона {2,4}.{2,4}.
Это нарушает определение функции, поэтому это отношение не является функцией.
На рисунке 1 сравниваются отношения, которые являются функциями, а не функциями.
Рис. 1 (a) Это отношение является функцией, потому что каждый вход связан с одним выходом. Обратите внимание, что входные qq и rr дают выход n.n. (б) Эта связь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход qq связан с двумя разными выходами.
Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».
Входные значения составляют область, а выходные значения составляют диапазон.
Как записаться
Учитывая взаимосвязь между двумя величинами, определите, является ли взаимосвязь функцией.
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию.Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Пример 1
Определение того, являются ли прайс-листы меню функциями
Меню кофейни, показанное ниже, состоит из позиций и их цен.
Ⓐ Цена зависит от товара?
Ⓑ Товар зависит от цены?
Решение
ⓐ Начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены.
У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.
ⓑ Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Изображение ниже.
Следовательно, товар не зависит от цены.
Пример 2
Определение, являются ли правила оценки класса функциями
В конкретном математическом классе общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице 1 показано возможное правило присвоения баллов.
| Процентное содержание | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Средний балл | 0,0 | 1,0 | 1.5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Таблица 1
Решение
Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.
В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу.Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
Попробуй # 1
Таблица 2 перечисляет пять величайших бейсболистов всех времен в порядке рангов.
| Игрок | Рейтинг |
|---|---|
| Бэйб Рут | 1 |
| Уилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
Таблица 2
- ⓐРанг зависит от имени игрока?
- ⓑИмя игрока зависит от ранга?
Использование обозначения функций
Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли их понять и использовать, а иногда и чтобы мы могли программировать их в компьютерах.Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.
Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных hh
на рост и аа
для возраста. Буквы f, g, f, g и hh часто используются для обозначения функций точно так же, как мы используем x, y, x, y и zz для обозначения чисел и A, B, A, B,
и CC для представления множеств.
Его fof a Мы называем функцию f; рост является функцией возраста.h = f (a) Мы используем круглые скобки для обозначения ввода функции. f (a) Мы называем функцию f; выражение читается как «fof a». his fof a Мы называем функцию f; высота является функцией возраста. h = f (a) Мы используем круглые скобки для обозначения ввода функции. f (a) Назовем функцию f; выражение читается как «fof a».
Помните, мы можем использовать любую букву для названия функции; обозначение h (a) h (a) показывает нам, что hh зависит от a.a. Чтобы получить результат, необходимо передать значение aa в функцию hh. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.
Мы также можем дать алгебраическое выражение в качестве входных данных для функции. Например, f (a + b) f (a + b) означает «сначала сложите a и b , и результат будет входом для функции f ». Для получения правильного результата операции необходимо выполнять именно в таком порядке.
Обозначение функций
Обозначение y = f (x) y = f (x) определяет функцию с именем f.f. Это читается как «y» y является функцией x. X «. Буква xx представляет входное значение или независимую переменную.Буква y, y или f (x), f (x) представляет выходное значение или зависимую переменную.
Пример 3
Использование обозначения функций для дней в месяце
Используйте обозначение функции для представления функции, входом которой является название месяца, а выходом — количество дней в этом месяце. Предположим, что домен не включает високосные годы.
Решение
Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию f, f, мы запишем дни = f (месяц) дни = f (месяц)
или d = f (m).d = f (м). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.
Рисунок 2
Например, f (март) = 31, f (март) = 31, потому что в марте 31 день. Обозначение d = f (m) d = f (m) напоминает нам, что количество дней, dd (выход), зависит от названия месяца, мм (вход).
Анализ
Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.
Пример 4
Интерпретация обозначений функций
Функция N = f (y) N = f (y) дает количество полицейских, N, N, в городе в год y.y. Что означает f (2005) = 300f (2005) = 300?
Решение
Когда мы читаем f (2005) = 300, f (2005) = 300, мы видим, что входным годом является 2005. Значение выходных данных, количество полицейских (N), (N), равно 300.Помните, N = f (y). N = f (y). Выражение f (2005) = 300f (2005) = 300 говорит нам, что в 2005 году в городе было 300 полицейских.
Попробуй # 2
Используйте обозначение функции, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях d.d.
Вопросы и ответы
Вместо обозначений, таких как y = f (x), y = f (x), могли бы мы использовать тот же символ для вывода, что и для функции, например y = y (x), y = y (x ), что означает: « y является функцией x ?»
Да, это часто делается, особенно в прикладных предметах, использующих высшую математику, таких как физика и инженерия.Однако при изучении самой математики нам нравится различать такие функции, как f, f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретному входу x.x. Вот почему мы обычно используем такие обозначения, как y = f (x), P = W (d), y = f (x), P = W (d) и т. Д.
Представление функций с помощью таблиц
Распространенным методом представления функций является таблица. Строки или столбцы таблицы отображают соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.
Таблица 3 перечисляет входное число каждого месяца (январь = 1, февраль = 2 и т. Д.) И выходное значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце ff, где D = f (m) D = f (m) определяет месяцы целым числом, а не именем.
| Номер месяца, мм (ввод) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Дни в месяце, DD (выход) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Таблица 3
Таблица 4 определяет функцию Q = g (n).Q = g (n). Помните, что эта запись говорит нам, что gg — это имя функции, которая принимает вход nn и выдает на выходе Q .Q.
| nn | 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 7 | 6 | 8 |
Таблица 4
В таблице 5 показан возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.
| Возраст в годах, а.о. (ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах, hh (на выходе) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Таблица 5
Как сделать
Учитывая таблицу входных и выходных значений, определите, представляет ли таблица функцию.
- Определите входные и выходные значения.
- Проверьте, сопряжено ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет функцию.
Пример 5
Идентификация таблиц, представляющих функции
Какая таблица, таблица 6, таблица 7 или таблица 8, представляет функцию (если есть)?
| Ввод | Выход |
|---|---|
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
Таблица 7
Решение
Таблица 6 и Таблица 7 определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.
Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.
Функция, представленная в Таблице 6, может быть представлена записью
f (2) = 1, f (5) = 3 и f (8) = 6f (2) = 1, f (5) = 3 и f (8) = 6
.
g (−3) = 5, g (0) = 1 и g (4) = 5g (−3) = 5, g (0) = 1 и g (4) = 5
представляют функцию в таблице 7. .
Таблица 8 не может быть выражена подобным образом, потому что она не представляет функцию.
Попробуй # 3
Представляет ли таблица 9 функцию?
| Ввод | Выход |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
Таблица 9
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, обычно вычислить функцию несложно.Например, функция f (x) = 5−3x2f (x) = 5−3×2 может быть вычислена путем возведения входного значения в квадрат, умножения на 3 и последующего вычитания произведения из 5.
Как записаться
Учитывая формулу функции, оцените.
- Замените входную переменную в формуле на указанное значение.
- Рассчитайте результат.
Пример 6
Оценка функций при определенных значениях
Вычислить f (x) = x2 + 3x − 4f (x) = x2 + 3x − 4 в:
- ⓐ 22
- ⓑ aa
- ⓒ а + га + ч
- ⓓ Теперь оцените f (a + h) −f (a) hf (a + h) −f (a) h
Решение
Заменить xx
в функции с каждым указанным значением.
- ⓐ Поскольку входное значение представляет собой число 2, мы можем использовать простую алгебру для упрощения.
f (2) = 22 + 3 (2) −4 = 4 + 6−4 = 6 f (2) = 22 + 3 (2) −4 = 4 + 6−4 = 6
- ⓑ В данном случае вводимое значение представляет собой букву, поэтому мы не можем дальше упрощать ответ.
f (a) = a2 + 3a − 4f (a) = a2 + 3a − 4
- При входном значении a + h, a + h мы должны использовать свойство распределения.
f (a + h) = (a + h) 2 + 3 (a + h) −4 = a2 + 2ah + h3 + 3a + 3h − 4f (a + h) = (a + h) 2 + 3 (a + h) −4 = a2 + 2ah + h3 + 3a + 3h − 4 - ⓒ В этом случае мы применяем входные значения к функции более одного раза, а затем выполняем алгебраические операции над результатом.Мы уже обнаружили, что
f (a + h) = a2 + 2ah + h3 + 3a + 3h − 4f (a + h) = a2 + 2ah + h3 + 3a + 3h − 4, и мы знаем, что
f (a) = a2 + 3a − 4f (a) = a2 + 3a − 4
Теперь объединим результаты и упростим.
f (a + h) −f (a) h = (a2 + 2ah + h3 + 3a + 3h − 4) — (a2 + 3a − 4) h = 2ah + h3 + 3hh = h (2a + h + 3) hФактор h. = 2a + h + 3 Упростить. F (a + h) −f (a) h = (a2 + 2ah + h3 + 3a + 3h − 4) — (a2 + 3a − 4) h = 2ah + h3 + 3hh = h (2a + h + 3) hФактор h. = 2a + h + 3 Упростить.
Пример 7
Оценка функций
Учитывая функцию h (p) = p2 + 2p, h (p) = p2 + 2p, вычислить h (4) .h (4).
Решение
Чтобы оценить h (4), h (4), мы подставляем значение 4 для входной переменной pp в данной функции.
h (p) = p2 + 2ph (4) = (4) 2 + 2 (4) = 16 + 8 = 24 h (p) = p2 + 2ph (4) = (4) 2 + 2 (4) = 16 + 8 = 24
Следовательно, для входа 4 у нас есть выход 24.
Попробуй # 4
Учитывая функцию g (m) = m − 4, g (m) = m − 4, вычислите g (5).г (5).
Пример 8
Решающие функции
Учитывая функцию h (p) = p2 + 2p, h (p) = p2 + 2p, решить относительно h (p) = 3. h (p) = 3.
Решение
h (p) = 3 p2 + 2p = 3 Подставим исходную функцию h (p) = p2 + 2p.p2 + 2p − 3 = 0 Вычтем по 3 с каждой стороны. (p + 3) (p − 1) = 0Factor. h (p) = 3 p2 + 2p = 3 Подставим исходную функцию h (p) = p2 + 2p.p2 + 2p − 3 = 0 Вычтем по 3 с каждой стороны. (p + 3) (p − 1) = 0Factor.
Если (p + 3) (p − 1) = 0, (p + 3) (p − 1) = 0, либо (p + 3) = 0 (p + 3) = 0, либо (p − 1) = 0 (p − 1) = 0 (или оба равны 0).Мы установим каждый коэффициент равным 0 и решим для каждого случая pp.
(p + 3) = 0, p = −3 (p − 1) = 0, p = 1 (p + 3) = 0, p = −3 (p − 1) = 0, p = 1
Это дает нам два решения. Выходной сигнал h (p) = 3h (p) = 3, когда на входе либо p = 1p = 1, либо p = −3.p = −3. Мы также можем проверить, построив график, как на рисунке 3. График проверяет, что h (1) = h (−3) = 3h (1) = h (−3) = 3 и h (4) = 24.h (4) = 24.
Рисунок 3
Попробуй # 5
Дана функция g (m) = m − 4, g (m) = m − 4, решить g (m) = 2.g (m) = 2.
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнений.Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение 2n + 6p = 122n + 6p = 12 выражает функциональную связь между nn
и п.п. Мы можем переписать его, чтобы решить, является ли pp функцией n.n.
Как записаться
Для функции в форме уравнения напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства с другой стороной как выражение, которое включает только входную переменную.
- Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.
Пример 9
Нахождение уравнения функции
Выразите соотношение 2n + 6p = 122n + 6p = 12 как функцию p = f (n), p = f (n), если это возможно.
Решение
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где pp является функцией n, n, что означает запись его как p = [expressioninvolvingn].p = [выражениеinvolvingn].
2n + 6p = 126p = 12−2n Вычтите 2n с обеих сторон. P = 12−2n6 Разделите обе стороны на 6 и упростите. P = 126−2n6p = 2−13n2n + 6p = 126p = 12−2n Вычтите 2n с обеих сторон. P = 12− 2n6 Разделите обе части на 6 и упростите. P = 126−2n6p = 2−13n
Следовательно, pp как функция от nn записывается как
p = f (n) = 2−13np = f (n) = 2−13n
Анализ
Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой.
Пример 10
Выражение уравнения круга как функции
Представляет ли уравнение x2 + y2 = 1×2 + y2 = 1 функцию с xx на входе и yy на выходе? Если это так, выразите взаимосвязь как функцию y = f (x).у = f (х).
Решение
Сначала мы вычитаем x2x2 с обеих сторон.
Теперь мы пытаемся найти yy в этом уравнении.
y = ± 1 − x2 = + 1 − x2and −1 − x2y = ± 1 − x2 = + 1 − x2and −1 − x2
Мы получаем два выхода, соответствующие одному и тому же входу, поэтому это соотношение не может быть представлено как одна функция у = е (х). у = е (х).
Попробуй # 6
Если x − 8y3 = 0, x − 8y3 = 0, выразите yy как функцию от x.x.
Вопросы и ответы
Существуют ли отношения, выраженные уравнением, которое действительно представляет функцию, но по-прежнему не может быть представлено алгебраической формулой?
Да, такое бывает.Например, учитывая уравнение x = y + 2y, x = y + 2y, если мы хотим выразить yy как функцию от x, x, не существует простой алгебраической формулы, включающей только xx, равную y.y. Однако каждый xx определяет уникальное значение для y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции от x, x, даже если формулу нельзя записать явно.
Оценка функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.
Функция, которая связывает тип домашнего животного с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу 10.
| Домашнее животное | Объем памяти в часах |
|---|---|
| Щенок | 0,008 |
| Взрослая собака | 0,083 |
| Кот | 16 |
| Золотая рыбка | 2160 |
| Бета-рыба | 3600 |
Таблица 10
Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений.Здесь вызовем функцию P.P.
Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца. Мы можем оценить функцию PP при входном значении «золотая рыбка». Мы бы написали P (золотая рыбка) = 2160.P (золотая рыбка) = 2160. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.
Как записаться
Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.
- Найдите данный вход в строке (или столбце) входных значений.
- Определите соответствующее выходное значение в паре с этим входным значением.
- Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
- Определите входные значения, соответствующие заданному выходному значению.
Пример 11
Вычисление и решение табличной функции
Используя таблицу 11,
Ⓐ Оцените g (3) .g (3).
Ⓑ Решите g (n) = 6.g (n) = 6.
| nn | 1 | 2 | 3 | 4 | 5 |
| г (н) г (н) | 8 | 6 | 7 | 6 | 8 |
Таблица 11
Решение
ⓐ Вычисление g (3) g (3) означает определение выходного значения функции gg для входного значения n = 3.п = 3. Выходное значение таблицы, соответствующее n = 3n = 3, равно 7, поэтому g (3) = 7.g (3) = 7.
Ⓑ Решение g (n) = 6g (n) = 6 означает определение входных значений n, n, которые производят выходное значение 6. Таблица 11 показывает два решения: 22 и 4.4.
| nn | 1 | 2 | 3 | 4 | 5 |
| г (н) г (н) | 8 | 6 | 7 | 6 | 8 |
Когда мы вводим 2 в функцию g, g, на выходе получаем 6.Когда мы вводим 4 в функцию g, g, наш результат также равен 6.
Поиск значений функций из графика
Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.
Пример 12
Чтение значений функций из графика
Учитывая график на рисунке 4,
ⓐ Оцените f (2).f (2).
Ⓑ Решите f (x) = 4. f (x) = 4.
Рисунок 4
Решение
ⓐ Чтобы оценить f (2), f (2), найдите точку на кривой, где x = 2, x = 2, затем прочтите координату y этой точки. Точка имеет координаты (2,1), (2,1), поэтому f (2) = 1. f (2) = 1. См. Рисунок 5.
Рисунок 5
Ⓑ Чтобы решить f (x) = 4, f (x) = 4, мы находим выходное значение 44 на вертикальной оси. Двигаясь горизонтально по линии y = 4, y = 4, мы обнаруживаем две точки кривой с выходным значением 4: 4: (−1,4) (- 1,4) и (3,4).(3,4). Эти точки представляют два решения f (x) = 4: f (x) = 4: −1−1 или 3.3. Это означает, что f (−1) = 4f (−1) = 4 и f (3) = 4, f (3) = 4, или когда на входе −1−1 или 3,3, на выходе будет 4,4. См. Рисунок 6.
Рисунок 6
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям. Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице 12.
| Буквенный класс | Средний балл |
|---|---|
| А | 4,0 |
| В | 3.0 |
| С | 2,0 |
| D | 1,0 |
Таблица 12
Эта система оценок представляет собой функцию «один к одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.
Чтобы наглядно представить эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рис. 1 (a), и рис. 1, (b), .Функция в части (a) показывает взаимосвязь, которая не является взаимно-однозначной, потому что оба входа qq и rr дают выход n.n. Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.
Индивидуальные встречи
Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.
Пример 13
Определение того, является ли отношение однозначной функцией
Площадь круга зависит от его радиуса? Если да, то функция взаимно однозначная?
Решение
Окружность радиуса rr имеет уникальную меру площади, равную A = πr2, A = πr2, поэтому для любого входа r, r существует только один выход A.A. Площадь является функцией радиуса r.r.
Если функция является взаимно однозначной, выходное значение, площадь, должно соответствовать уникальному входному значению, радиусу. Любая мера площади AA задается формулой A = πr2.A = πr2. Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: Aπ.Aπ. Таким образом, площадь круга однозначно зависит от радиуса круга.
Попробуй # 9
- ⓐ Является ли остаток функцией номера банковского счета?
- ⓑ Является ли номер банковского счета функцией баланса?
- ⓒ Является ли баланс однозначной функцией номера банковского счета?
Попробуй # 10
Оцените следующее:
- ⓐ Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
- ⓑ Если да, то функция взаимно однозначная?
Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика.Графики отображают большое количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение xx и выходное значение y, y, и мы говорим, что yy является функцией от x, x или y = f (x) y = f (x), когда функция называется f.f. График функции — это совокупность всех точек (x, y) (x, y) на плоскости, которая удовлетворяет уравнению y = f (x).у = f (х). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на рисунке 7 говорят нам, что f (0) = 2f (0) = 2 и f (6) = 1.f (6) = 1. Однако набор всех точек (x, y) (x, y), удовлетворяющих y = f (x) y = f (x), является кривой. Показанная кривая включает (0,2) (0,2) и (6,1) (6,1), потому что кривая проходит через эти точки.
Рисунок 7
Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. Рисунок 8.
Рисунок 8
Как записаться
Для графика используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
- Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
- Если такая линия есть, определите, что график не представляет функцию.
Пример 14
Применение теста вертикальной линии
Какой из графиков на рисунке 9 представляет функцию y = f (x)? Y = f (x)?
Рисунок 9
Решение
Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку из двух графиков, показанных в частях (a) и (b) рисунка 9. Из этого мы можем сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке 10.
Рисунок 10
Попробуй # 11
Представляет ли график на рисунке 11 функцию?
Рисунок 11
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли она взаимно однозначной функцией, — это использовать тест горизонтальной линии.Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.
Как записаться
Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию.
- Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
- Если такая линия есть, определите, что функция не взаимно однозначна.
Пример 15
Применение теста горизонтальной линии
Рассмотрим функции, показанные на рисунке 9 (a) и рисунке 9 (b) . Являются ли какие-либо функции взаимно однозначными?
Решение
Функция на рисунке 9 (a) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)
Рисунок 12
Функция на рисунке 9 (b) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.
Попробуй # 12
График, показанный на Рисунке 9, взаимно однозначен?
Определение базовых функций набора инструментов
В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем. Когда учимся читать, мы начинаем с алфавита.Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y = f (x) y = f (x) в качестве выходной переменной.
Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги.Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную в Таблице 13.
3.1 Раздел Упражнения
Устный
1.
В чем разница между отношением и функцией?
2.
В чем разница между вводом и выводом функции?
3.
Почему тест с вертикальной линией сообщает нам, представляет ли график отношения функцию?
4.
Как определить, является ли отношение однозначной функцией?
5.
Почему тест горизонтальной линии показывает, является ли график функции взаимно однозначным?
Алгебраический
В следующих упражнениях определите, представляет ли отношение функцию.
6.
{(a, b), (c, d), (a, c)} {(a, b), (c, d), (a, c)}
7.
{(a, b), (b, c), (c, c)} {(a, b), (b, c), (c, c)}
Для следующих упражнений определите, представляет ли отношение yy как функцию от x.Икс.
Для следующих упражнений оцените функцию ff при указанных значениях f (−3), f (2), f (−a), — f (a), f (a + h) .f (−3), f (2), f (−a), — f (a), f (a + h).
28.
f (x) = — 5×2 + 2x − 1f (x) = — 5×2 + 2x − 1
30.
f (x) = 6x − 15x + 2f (x) = 6x − 15x + 2
31.
f (x) = | x − 1 | — | x + 1 | f (x) = | x − 1 | — | x + 1 |
32.
Учитывая функцию g (x) = 5 − x2, g (x) = 5 − x2, вычислим g (x + h) −g (x) h, h ≠ 0. G (x + h) −g (x ) h, h ≠ 0.
33.
Учитывая функцию g (x) = x2 + 2x, g (x) = x2 + 2x, вычислим g (x) −g (a) x − a, x ≠ a.g (x) −g (a) x − a, x ≠ a.
34.
Для функции k (t) = 2t − 1: k (t) = 2t − 1:
- ⓐ Вычислить k (2) .k (2).
- ⓑ Решить k (t) = 7. k (t) = 7.
35.
Для функции f (x) = 8−3x: f (x) = 8−3x:
- ⓐ Вычислить f (−2) .f (−2).
- ⓑ Решить f (x) = — 1.f (x) = — 1.
36.
Для функции p (c) = c2 + c: p (c) = c2 + c:
- ⓐ Вычислите p (−3) .p (−3).
- ⓑ Решить p (c) = 2.p (c) = 2.
37.
Дана функция f (x) = x2−3x: f (x) = x2−3x:
- ⓐ Оцените f (5).f (5).
- ⓑ Решить f (x) = 4. f (x) = 4.
38.
Для функции f (x) = x + 2: f (x) = x + 2:
- ⓐ Оцените f (7) .f (7).
- ⓑ Решить f (x) = 4. f (x) = 4.
39.
Рассмотрим соотношение 3r + 2t = 18,3r + 2t = 18.
- ⓐ Запишите отношение как функцию r = f (t) .r = f (t).
- ⓑ Вычислите f (−3) .f (−3).
- ⓒ Решить f (t) = 2.f (t) = 2.
Графический
В следующих упражнениях используйте тест вертикальной линии, чтобы определить, какие графики показывают отношения, являющиеся функциями.
40.
42.
44.
46.
48.
50.
52.
Учитывая следующий график,
- ⓐ Вычислить f (−1) .f (−1).
- ⓑ Решить относительно f (x) = 3. f (x) = 3.
53.
Учитывая следующий график,
- ⓐ Вычислить f (0) .f (0).
- ⓑ Решить относительно f (x) = — 3.f (x) = — 3.
54.
Учитывая следующий график,
- ⓐ Оцените f (4) .f (4).
- ⓑ Решить относительно f (x) = 1. f (x) = 1.
Для следующих упражнений определите, является ли данный график взаимно однозначной функцией.
56.
58.
Числовой
В следующих упражнениях определите, представляет ли отношение функцию.
60.
{(−1, −1), (- 2, −2), (- 3, −3)} {(- 1, −1), (- 2, −2), (- 3, −3) }
61.
{(3,4), (4,5), (5,6)} {(3,4), (4,5), (5,6)}
62.
{(2,5), (7,11), (15,8), (7,9)} {(2,5), (7,11), (15,8), (7,9) }
Для следующих упражнений определите, представляет ли отношение, представленное в виде таблицы, yy как функцию от x.x.
Для следующих упражнений используйте функцию ff, представленную в таблице ниже.
| xx | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| f (x) f (x) | 74 | 28 | 1 | 53 | 56 | 3 | 36 | 45 | 14 | 47 |
Таблица 14
Для следующих упражнений оцените функцию ff при значениях f (−2), f (−1), f (0), f (1), f (−2), f (−1), f (0 ), f (1) и f (2).f (2).
70.
f (x) = 8×2−7x + 3f (x) = 8×2−7x + 3
72.
f (x) = x − 2x + 3f (x) = x − 2x + 3.
Для следующих упражнений оцените выражения с учетом функций f, g, f, g и h: h:
f (x) = 3x − 2f (x) = 3x − 2
g (x) = 5 − x2g (x) = 5 − x2
h (x) = — 2×2 + 3x − 1h (x) = — 2×2 + 3x − 1
74.
3f (1) −4g (−2) 3f (1) −4g (−2)
75.
f (73) −h (−2) f (73) −h (−2)
Технологии
Для следующих упражнений построим график y = x2y = x2 в заданной области.Определите соответствующий диапазон. Покажите каждый график.
Для следующих упражнений построим график y = x3y = x3 в заданной области. Определите соответствующий диапазон. Покажите каждый график.
Для следующих упражнений нарисуйте график y = xy = x в заданной области. Определите соответствующий диапазон. Покажите каждый график.
Для следующих упражнений построим график y = x3y = x3 в заданной области. Определите соответствующий диапазон. Покажите каждый график.
85.
[-0,001,0,001] [- 0,001,0,001]
86.
[-1000,1000] [- 1000,1000]
87.
[-1,000,000,1,000,000] [- 1,000,000,1,000,000]
Реальные приложения
88.
Количество мусора G, G, производимого городом с населением pp, определяется выражением G = f (p) .G = f (p). GG измеряется в тоннах в неделю, а pp — в тысячах человек.
- ⓐ Город Тола с населением 40 000 человек производит 13 тонн мусора каждую неделю. Выразите эту информацию в терминах функции f.f.
- ⓑ Объясните значение утверждения f (5) = 2.f (5) = 2.
89.
Количество кубических ярдов земли, D, D, необходимое для покрытия сада площадью aa квадратный фут, определяется как D = g (a) .D = g (a).
- ⓐ Для сада площадью 5000 футов 2 требуется 50 ярдов 3 земли. Выразите эту информацию в терминах функции g.g.
- ⓑ Объясните значение утверждения g (100) = 1. g (100) = 1.
90.
Пусть f (t) f (t) будет количеством уток в озере через tt годы после 1990 года. Объясните значение каждого утверждения:
- ⓐ f (5) = 30f (5) = 30
- ⓑ f (10) = 40f (10) = 40
91.
Пусть h (t) h (t) будет высотой над землей в футах ракеты через tt секунд после запуска. Объясните значение каждого утверждения:
- ⓐ ч (1) = 200 ч (1) = 200
- ⓑ ч (2) = 350 ч (2) = 350
92.
Покажите, что функция f (x) = 3 (x − 5) 2 + 7f (x) = 3 (x − 5) 2 + 7 равна , а не взаимно однозначно.
Оценка функции — ChiliMath
Обычное обозначение функции обычно записывается как
Не думайте об этом слишком буквально, то есть f умножается на x.Вместо этого рассмотрите это как математическое выражение, которое читается как
ИЛИ
Функции также могут быть записаны по-разному с использованием других переменных, например
Кроме того, функции могут принимать другие входные значения, кроме x.
Основная идея состоит в том, чтобы всегда помнить, что переменная вне скобок — это « имя » функции, а переменная внутри скобок — это входное значение функции.
Например, следующая функция называется функцией k с входным значением m.
Основные примеры оценивающих функций
Пример 1: Оцените функцию.
Это обычное обозначение функции, где функция — это f, а входное значение — x. Чтобы оценить функцию, мы хотим заменить каждый экземпляр x в выражении, а затем упростить.
Поскольку x = — 1, мы подставляем это значение в функцию и упрощаем.При этом мы получаем решение, которое выглядит так.
Пример 2: Оцените функцию.
Обратите внимание, что здесь функция h, а входное значение — k. Как и в нашем предыдущем примере, мы хотим заменить любое числовое значение, присвоенное k, в данную функцию и упростить.
Поскольку k = 3, ваше решение должно выглядеть примерно так:
Пример 3: Оцените каждое значение x в таблице ниже, используя функцию ниже.Постройте точки на оси xy и соедините точки, чтобы отобразить график функции.
Поскольку имеется семь x-входов, это означает, что мы также оценим функцию семь раз. Попробуйте решить это самостоятельно, а затем вернитесь, чтобы проверить свои ответы.
Если вы все сделали правильно, это значения:
Теперь мы можем поместить эти выходные значения в таблицу.
Считайте выходные значения функции f \ left (x \ right) значениями y. Вот так график выглядит на оси xy.2} — 3x + 1, найдите g \ left ({2x — 1} \ right).
В предыдущих примерах мы оценивали функцию по числу. На этот раз входное значение больше не является фиксированным числовым значением, а является выражением. Это может показаться сложным, но процедура остается той же.
Мы заменим каждый экземпляр x в g \ left (x \ right) входным значением, равным 2x — 1. Упростим, возведя в квадрат бином, применив свойство распределения и комбинируя похожие термины.
Пример 5: Учитывая, что p \ left (x \ right) = {{4x — 1} \ over x}, вычисляем p \ left (1 \ right) — p \ left ({- 1} \ right) .
Поначалу проблема может показаться пугающей, но как только мы проанализируем ее и применим то, что уже знаем, как оценивать функции, это уже не так уж плохо!
Здесь нам нужно оценить функцию при x = 1, затем вычесть на значение функции при оценке при x = — \, 1.
Будьте очень осторожны при замене значений и в процессе упрощения. Если вы не будете осторожны на каждом этапе, очень легко совершить ошибку, когда вы складываете, вычитаете, умножаете или делите положительные и отрицательные числа.
Расширенный пример применения концепции оценивания функций
Пример 6: Если f \ left (2 \ right) = 9, найдите значение a в функции ниже.
В уравнении f \ left (2 \ right) = 9, нам говорят, что если вход функции равен 2; вывод функции будет 9.
