Содержание
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2
Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Определение 4
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0.
 Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1
Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2
Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3
Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5
Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4
Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5
Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6
Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 6
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком.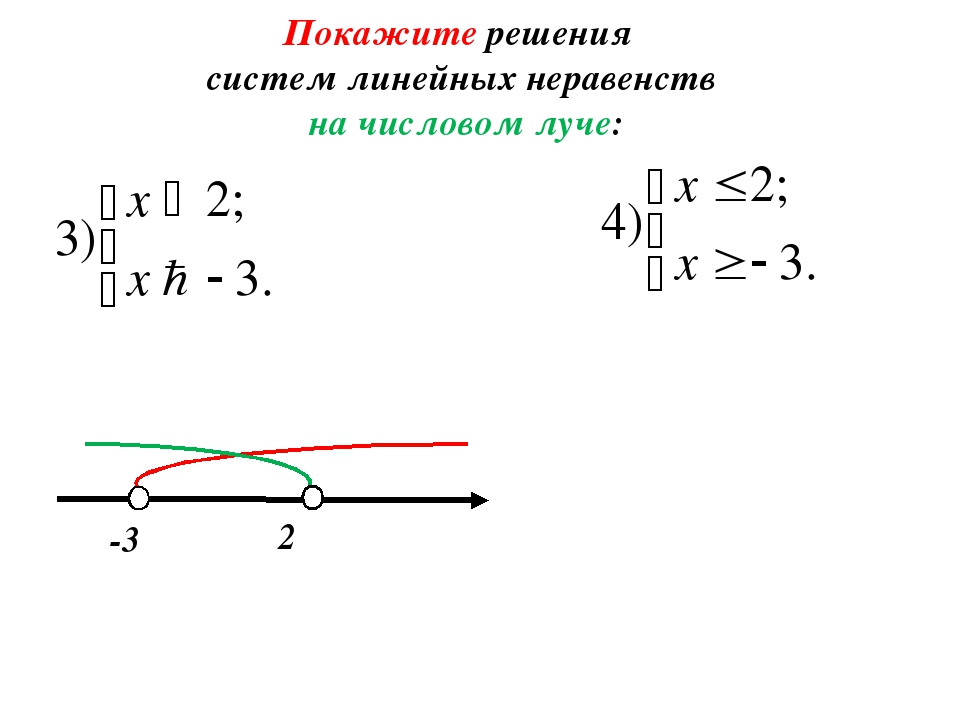 Рассмотрим чертеж, приведенный ниже.
Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7
- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8
Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Пример 7
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35.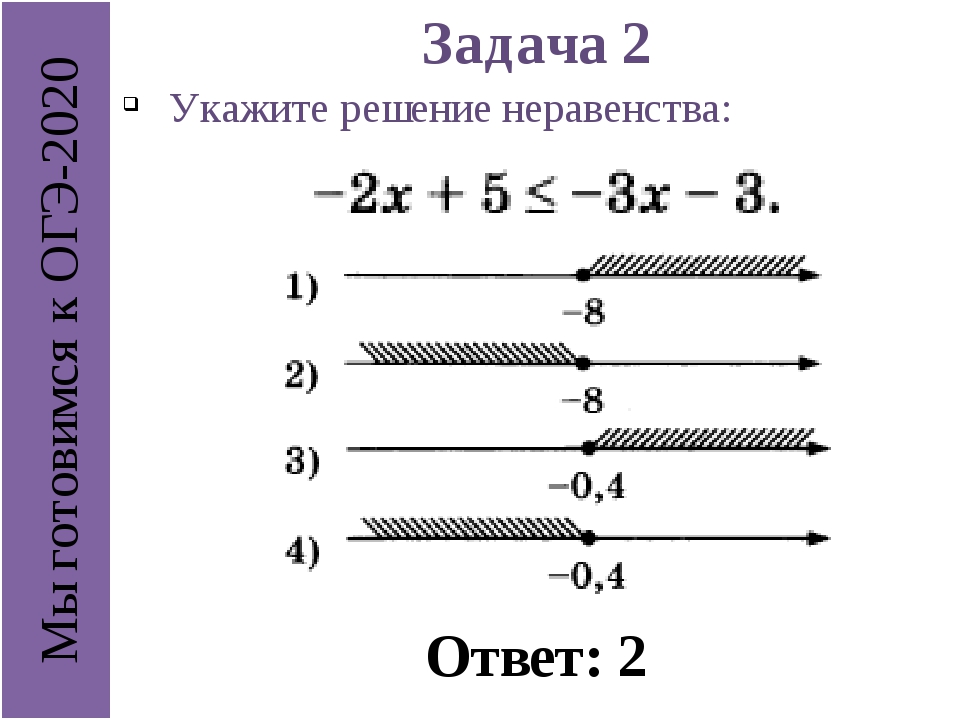 Изобразим графически.
Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8
Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Пример 9
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2
Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.

Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Определение 4
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1
Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2
Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3
Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5
Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4
Решить неравенство 0·x+7>0.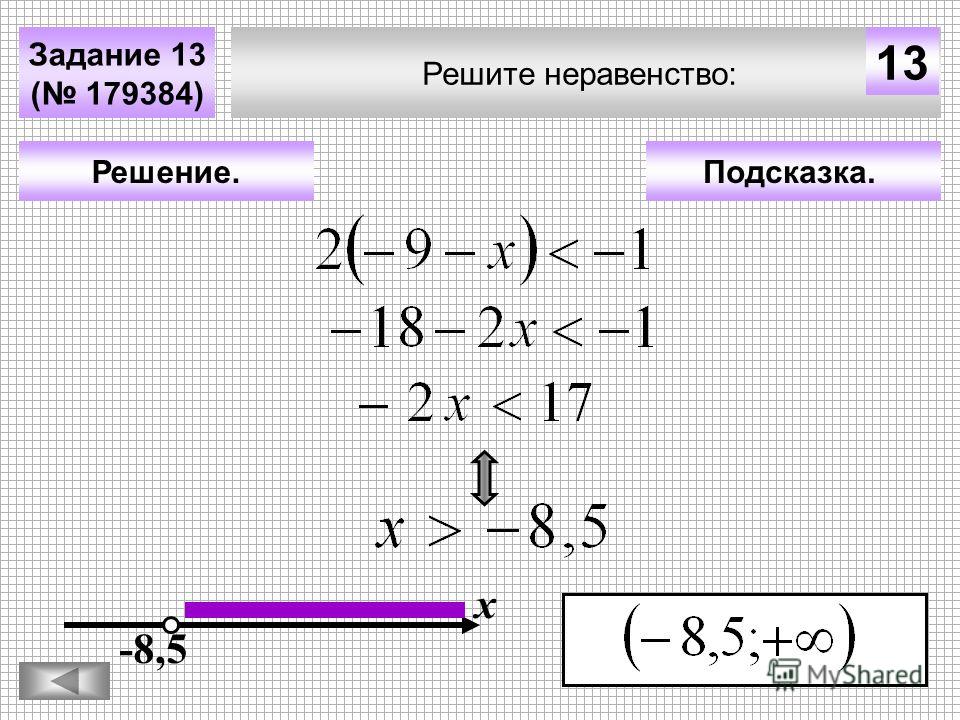
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5
Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6
Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 6
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7
- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике.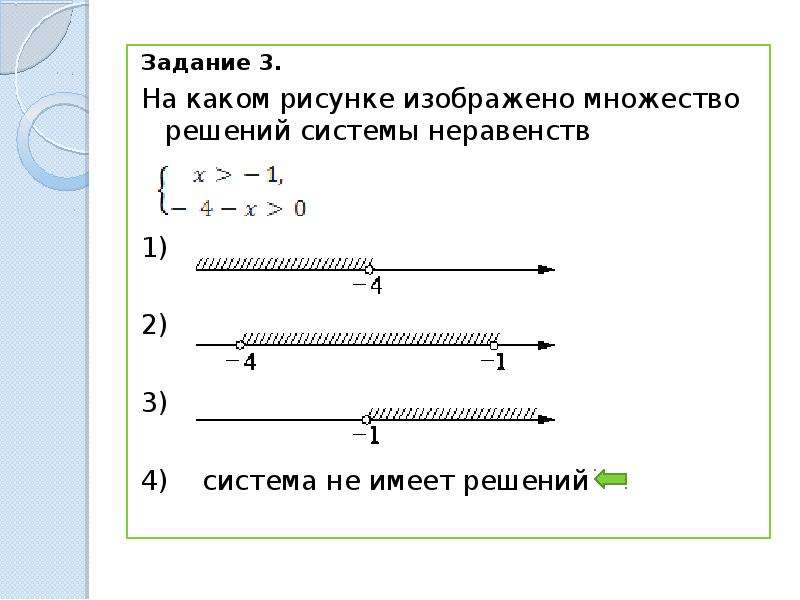 В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8
Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Пример 7
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8
Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Пример 9
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2
Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Определение 4
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1
Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2
Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3
Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5
Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4
Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5
Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6
Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 6
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7
- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8
Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Пример 7
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8
Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Пример 9
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
|
1. |
Решение строгого линейного неравенства
|
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
Решение неравенства
|
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
Положительные или отрицательные значения двучлена
|
3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
Неотрицательные или неположительные значения двучлена
|
3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. |
Дробное неравенство, сводимое к линейному (числитель — одночлен)
|
4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
6. |
Значения двучлена, большие или меньшие 2
|
4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
7. |
Решение линейного неравенства
|
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. |
Решение строгого, дробного линейного неравенства
|
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. |
Тест по решению нестрогого неравенства
|
1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10. |
Решение линейного неравенства
|
2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11. |
Значение, которое является решением неравенства
|
5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
12. |
Значения двучлена, не меньшие или не большие значений другого двучлена
|
5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
13. |
Сумма дробей
|
5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
14. |
Линейное неравенство (распределительный закон умножения)
|
5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
15. |
Линейное неравенство (минус перед скобками)
|
6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
16. |
Наименьшее целое решение неравенства
|
5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
17. |
Решение линейного неравенства
|
3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
18. |
Выбор интервала как решения строгого неравенства
|
3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
19. |
Решение двойного неравенства
|
3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
20. |
Область допустимых значений выражения, линейное уравнение
|
4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
21. |
Область допустимых значений выражения, дробь
|
4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
22.{2}}<3\) \( \displaystyle -2x+11<3\) \( \displaystyle -2x<3-11\) \( \displaystyle -2x<-8\) Делим обе части на отрицательное число \( \displaystyle \left( -2 \right)\), не забывая поменять знак неравенства на противоположный: \( \displaystyle -2x<-8\) \( \displaystyle x>\frac{8}{2}\) \( \displaystyle x>4\) Неравенство нестрогое, поэтому \( \displaystyle 4\) — не включается в промежуток: Линейные неравенства. Решение линейных неравенствЛинейные неравенства – такие неравенства, которые можно привести к одному из видов:
Решение линейных неравенств
Решением неравенства будет любое число, подстановка которого вместо переменной сделает неравенство верным. Решить неравенство – значит найти все такие числа.
При умножении или делении неравенства на любое отрицательное число (или выражение) нужно менять знак сравнения на противоположный (почему так – смотри здесь).
Особый случай №1: решение неравенства – любое число
Особый случай №2: неравенство не имеет решений
Скачать статью Линейные неравенства с одной переменной
Как решать линейные неравенства с одной переменной вида ax+b>cx+d? Для этого используем всего два правила. 1) Слагаемые можно переносить из одной части неравенства в другую с противоположным знаком. Знак неравенства при этом не меняется. 2) Обе части неравенства можно разделить на число, стоящее перед иксом (или другой переменной). При делении на положительное число знак неравенства не меняется. При делении на отрицательное число знак неравенства изменяется на противоположный. В общем виде решение линейного неравенства с одной переменной
можно изобразить так: 1) Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:
2) Если число перед иксом не равно нулю (a-c≠0), обе части неравенства делим на a-c. Если a-c>0, знак неравенства не изменяется:
Если a-c<0, знак неравенства изменяется на противоположный:
Если a-c=0, то это — частный случай. Частные случаи решения линейных неравенств рассмотрим отдельно. Примеры.
Это — линейное неравенство. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -2<0, знак неравенства изменяется на противоположный:
Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой. Штриховка от 10 влево, на минус бесконечность. Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой. Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как 10>0, знак неравенства при этом не изменяется:
Так как неравенство нестрогое, -2,3 на числовой прямой отмечаем закрашенной точкой. Штриховка от -2,3 идёт вправо, на плюс бесконечность. Так как неравенство строгое и точка закрашенная, -2,3 в ответ записываем с квадратной скобкой. Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположным знаком.
Обе части неравенства делим на число, стоящее перед иксом. Поскольку 3>0, знак неравенства при этом не изменяется:
Так как неравенство строгое, x=2/3 на числовой прямой изображаем выколотой точкой. Так как неравенство строгое и точка выколотая, в ответ 2/3 записываем с круглой скобкой. Ответ:
Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Так как -4 — отрицательное число, знак неравенства при этом изменяется на противоположный:
Поскольку неравенство нестрогое, -2,25 на числовой прямой отмечаем закрашенной точкой. Так как неравенство нестрогое и точка закрашенная, -2,25 включаем в ответ, то есть записываем с квадратной скобкой. Ответ:
Решать линейные неравенства с одной переменной в алгебре приходится не только в виде отдельных примеров, но также при нахождении области определения функций, области допустимых значений выражений, решении уравнений и более сложных неравенств. Вот почему важно вовремя понять эту тему и научиться применять её. Алгебра — линейные неравенстваПоказать мобильное уведомление Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 2-11: Линейные неравенстваДо этого момента в этой главе мы сосредоточились на решении уравнений. Пришло время немного переключиться и начать думать о решении проблемы неравенства.Прежде чем мы перейдем к решению неравенств, мы должны сначала рассмотреть пару основных моментов. На данном этапе вашей математической карьеры предполагается, что вы знаете, что \ [a означает, что \ (a \) — некоторое число, которое строго меньше \ (b \). Также предполагается, что вы знаете, что \ [а \ ге б \] означает, что \ (a \) — это некоторое число, которое либо строго больше, чем \ (b \), либо точно равно \ (b \). Точно так же предполагается, что вы знаете, что делать с двумя оставшимися неравенствами.> (больше) и \ (\ le \) (меньше или равно). Мы хотим обсудить некоторые проблемы с обозначениями и некоторые тонкости, которые иногда возникают у студентов, когда они действительно начинают работать с неравенством. Во-первых, помните, что когда мы говорим, что \ (a \) меньше \ (b \), мы имеем в виду, что \ (a \) находится слева от \ (b \) на числовой строке. Итак, \ [- 1000 — истинное неравенство. Затем не забывайте, как правильно интерпретировать \ (\ le \) и \ (\ ge \).Оба следующих утверждения являются истинными неравенствами. \ [4 \ le 4 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} — 6 \ le 4 \] В первом случае 4 равно 4 и, следовательно, «меньше или равно» 4. Во втором случае -6 строго меньше 4 и, таким образом, «меньше или равно» 4. Наиболее часто встречается ошибка состоит в том, чтобы решить, что первое неравенство не является истинным неравенством. Также будьте осторожны, чтобы не принять эту интерпретацию и не перевести ее на <и / или>. Например, \ [4 не является истинным неравенством, поскольку 4 равно 4, а не строго меньше 4. Наконец, в этом и последующих разделах мы увидим множество двойных неравенств , поэтому о них нельзя забывать. Следующее — двойное неравенство. \ [- 9 В двойном неравенстве мы говорим, что оба неравенства должны выполняться одновременно. В этом случае 5 определенно больше -9 и в то же время меньше или равно 6. Следовательно, это двойное неравенство является истинным неравенством. С другой стороны, \ [10 \ le 5 не является истинным неравенством.Хотя верно, что 5 меньше 20 (так что второе неравенство верно), неверно, что 5 больше или равно 10 (поэтому первое неравенство неверно). Если хотя бы одно из неравенств в двойном неравенстве неверно, то все неравенство неверно. Этот момент более важен, чем вы можете себе представить. В следующем разделе мы встретимся с ситуациями, когда многие студенты пытаются объединить два неравенства в двойное неравенство, которое просто невозможно объединить, так что будьте осторожны. Следующая тема, которую нам нужно обсудить, — это идея обозначения интервала . Обозначение интервалов — это очень хорошее обозначение неравенств, которое будет широко использоваться в следующих нескольких разделах этой главы. Наилучшим способом определения обозначения интервалов является следующая таблица. В таблице три столбца. Каждая строка содержит неравенство, график, представляющий неравенство, и, наконец, обозначение интервала для данного неравенства. Помните, что квадратные скобки «[» или «]» означают, что мы включаем конечную точку, а круглые скобки «(» или «)» означают, что мы не включаем конечную точку. Итак, с первыми четырьмя неравенствами в таблице обозначение интервалов на самом деле представляет собой не что иное, как график без числовой прямой. С последними четырьмя неравенствами обозначение интервала — это почти график, за исключением того, что нам нужно добавить соответствующую бесконечность, чтобы убедиться, что мы получаем правильную часть числовой прямой.Также обратите внимание, что бесконечности НИКОГДА не получают скобки. У них есть только круглые скобки. Прежде чем переходить к решению неравенств, необходимо сделать последнее замечание об обозначении интервалов. Всегда помните, что когда мы записываем интервальное обозначение для неравенства, число слева должно быть меньшим из двух. Пришло время подумать о решении линейных неравенств. При решении неравенств мы будем использовать следующий набор фактов.Обратите внимание, что факты приведены для <. Однако мы можем записать эквивалентный набор фактов для остальных трех неравенств.
Это почти те же факты, которые мы использовали для решения линейных уравнений. Единственное реальное исключение — третий факт. Это важный факт, поскольку он часто используется неправильно и / или часто забывается при решении проблемы неравенства. Если вы не уверены, что полагаете, что знак \ (c \) имеет значение для второго и третьего фактов, рассмотрите следующий пример числа. \ [- 3 Я надеюсь, что мы все согласимся, что это истинное неравенство. Теперь умножьте обе стороны на 2 и -2. \ [\ begin {align *} — 3 и 5 \ left ({- 2} \ right) \\ — 6 & — 10 \ end {align *} \] Конечно, при умножении на положительное число направление неравенства остается неизменным, однако при умножении на отрицательное число направление неравенства меняется. Хорошо, давайте устраним некоторые неравенства. Мы начнем с неравенств, в которых есть только одно неравенство. Другими словами, мы отложим решение двойных неравенств для следующего набора примеров. Здесь мы должны помнить, что мы просим определить все значения переменной, которые мы можем подставить в неравенство и получить истинное неравенство. Это означает, что наши решения в большинстве случаев сами по себе будут неравенствами. Пример 1 Решение следующих неравенств. Приведите как неравенство, так и интервальную форму записи решения.
Показать все решения Скрыть все решения Показать обсуждение Решение отдельных линейных неравенств во многом повторяет процесс решения линейных уравнений.Мы упростим обе стороны, получим все члены с переменной с одной стороны и числа с другой стороны, а затем умножим / разделим обе стороны на коэффициент переменной, чтобы получить решение. Вы должны помнить одну вещь: если вы умножаете / делите на отрицательное число, то меняете направление неравенства. a \ (- 2 \ left ({m — 3} \ right) Показать решение Здесь действительно особо нечего делать, кроме как следовать описанному выше процессу. \ [\ begin {align *} — 2 \ left ({m — 3} \ right) & \ frac {{13}} {7} \ end {align *} \] Вы уловили тот факт, что направление неравенства здесь изменилось, не так ли? Мы разделились на «-7» и нам пришлось менять направление. Неравенство решения имеет вид \ (m> \ frac {{13}} {7} \). Обозначение интервала для этого решения: \ (\ left ({\ frac {{13}} {7}, \ infty} \ right) \). b \ (2 \ left ({1 — x} \ right) + 5 \ le 3 \ left ({2x — 1} \ right) \) Показать решение Опять же, здесь особо нечего делать. \ [\ begin {align *} 2 \ left ({1 — x} \ right) + 5 & \ le 3 \ left ({2x — 1} \ right) \\ 2 — 2x + 5 & \ le 6x — 3 \\ 10 & \ le 8x \\ \ frac {{10}} {8} & \ le x \\ \ frac {5} {4} & \ le x \ end {align *} \] Теперь, с этим неравенством, мы закончили с переменной с правой стороны, когда это более традиционно с левой стороны. Итак, давайте поменяем местами, чтобы переменная оказалась слева. Обратите внимание, однако, что нам нужно будет также изменить направление неравенства, чтобы убедиться, что мы не изменим ответ.Итак, вот обозначение неравенства для неравенства. \ [x \ ge \ frac {5} {4} \] Обозначение интервала для решения: \ (\ left [{\ frac {5} {4}, \ infty} \ right) \). А теперь давайте решим несколько двойных неравенств. Этот процесс в некотором смысле похож на решение отдельных неравенств, но в остальном сильно отличается. Поскольку существует два неравенства, невозможно получить переменные с «одной стороны» неравенства и числа с другой.Легче увидеть, как это работает, если мы рассмотрим пару примеров, так что давайте сделаем это. Пример 2 Решите каждое из следующих неравенств. Приведите для решения формы обозначений неравенства и интервалов.
Показать все решения Скрыть все решения a \ (- 6 \ le 2 \ left ({x — 5} \ right) Показать решение Процесс здесь довольно похож на процесс для одиночных неравенств, но сначала нам нужно быть осторожными в нескольких местах.Нашим первым шагом в этом случае будет удаление скобок в среднем члене. \ [- 6 \ le 2x — 10 Теперь мы хотим, чтобы \ (x \) был сам по себе в среднем члене и только числа в двух внешних членах. Для этого мы будем добавлять / вычитать / умножать / делить по мере необходимости. Единственное, что нам нужно здесь помнить, это то, что если мы делаем что-то для среднего срока, мы должны делать то же самое с ОБЕИМ из исходящих терминов. Одна из наиболее распространенных ошибок на этом этапе — добавить что-то, например, в середину, и добавить это только к одной из двух сторон. Хорошо, мы прибавим 10 ко всем трем частям, а затем разделим все три части на две. \ [\ begin {array} {c} 4 \ le 2x Это неравенство формы ответа. Ответ в виде интервальной записи \ (\ left [{2, \ frac {{17}} {2}} \ right) \). b \ (- 3 Показать решение В этом случае первое, что нам нужно сделать, это очистить дроби, умножив все три части на 2. Затем мы продолжим, как и в первой части. \ [\ begin {array} {c} — 6 На этом мы еще не закончили, но нам нужно быть очень осторожными на следующем шаге. На этом этапе нам нужно разделить все три части на -3. Однако напомним, что всякий раз, когда мы делим обе стороны неравенства на отрицательное число, нам нужно изменить направление неравенства. Для нас это означает, что оба неравенства должны изменить направление здесь. \ [4> х \ ge — \ frac {4} {3} \] Итак, существует форма неравенства решения.Нам нужно будет быть осторожным с обозначением интервалов для решения. Во-первых, обозначение интервала НЕ \ (\ left ({4, — \ frac {4} {3}} \ right] \). Помните, что в обозначении интервала меньшее число всегда должно располагаться слева! правильное обозначение интервала для решения: \ (\ left [{- \ frac {4} {3}, 4} \ right) \). Также обратите внимание, что это также соответствует форме неравенства решения. Неравенство говорит нам, что \ (x \) — это любое число от 4 до \ (- \ frac {4} {3} \) или, возможно, само \ (- \ frac {4} {3} \), и это в точности что нам говорят обозначения интервалов. Кроме того, неравенство можно перевернуть, чтобы получить меньшее число слева, если мы захотим. Вот та форма, \ [- \ frac {4} {3} \ le x При этом не забудьте также правильно обработать неравенства. c \ (- 14 Показать решение Ничего особенного для этого. Мы продолжим так же, как и в предыдущих двух. \ [\ begin {array} {c} — 14 Не волнуйтесь, что одна из сторон теперь равна нулю.Это не проблема. Опять же, как и в предыдущей части, мы будем делить на отрицательное число, поэтому не забудьте изменить направление неравенств. \ [\ begin {array} {c} \ displaystyle 0> x> — \ frac {{15}} {{21}} \\ \ displaystyle 0> x> — \ frac {5} {7} \ hspace {0,25 in} {\ mbox {OR}} \ hspace {0,25in} — \ frac {5} {7} Для решения подойдет любое из неравенств во второй строке. Интервальное обозначение решения — \ (\ left ({- \ frac {5} {7}, 0} \ right) \). При решении двойных неравенств обязательно обратите внимание на неравенства, которые есть в исходной задаче. Одна из наиболее распространенных ошибок здесь — начать с задачи, в которой одно из неравенств имеет вид <или>, а другое — \ (\ le \) или \ (\ ge \), как мы делали в первых двух частях в предыдущем примере, а затем в окончательном ответе они оба являются <или>, либо они оба являются \ (\ le \) или \ (\ ge \). Другими словами, легко сделать оба неравенства одинаковыми.Будьте осторожны с этим. Есть еще один последний пример, над которым мы хотим работать. Пример 3 Если \ (- 1 Это проще, чем может показаться на первый взгляд. Все, что мы действительно собираемся сделать, это начать с данного неравенства, а затем изменить средний член, чтобы он выглядел как второе неравенство. Опять же, нам нужно помнить, что все, что мы делаем со средним термином, нам также необходимо сделать с двумя внешними членами. Итак, сначала умножим все на 2. \ [- 2 Теперь прибавьте 3 ко всему. \ [1 Теперь у нас есть средний член, идентичный второму неравенству в формулировке задачи, поэтому все, что нам нужно сделать, это выбрать \ (a \) и \ (b \). Из этого неравенства видно, что \ (a = 1 \) и \ (b = 11 \). Решение линейных неравенств — ChiliMathБольшинство правил или методов, используемых при решении многоэтапных уравнений, должно быть легко преобразовано в решение неравенств. Единственная большая разница заключается в том, как символ неравенства переключает направление , когда отрицательное число умножается или делится на обе стороны уравнения. В этом уроке я рассмотрю семь (7) рабочих примеров с разным уровнем сложности, чтобы обеспечить достаточную практику. Символы неравенства с примерами и иллюстрациями на числовых линияхБОЛЬШЕ, ЧЕМ больше или равно МЕНЬШЕ МЕНЬШЕ ИЛИ РОВНО Примеры решения и построения графика линейных неравенствПример 1: Решите и изобразите решение неравенства . Чтобы решить это неравенство, мы хотим найти всех значений x, которые могут ему удовлетворить.Это означает, что существует почти бесконечное количество значений x, которые при подстановке дают истинные утверждения. Проверьте значения x = 0, x = 1, x = 2, x = 3, x = 5, x = 6 и x = 7. Какое из этих значений x является верным? После выполнения некоторых обратных замен вы должны согласиться, что работают только 5, 6 и 7; а остальные терпят неудачу. Но вопрос в том, есть ли больше значений x, кроме упомянутых? Ответ положительный! Теперь давайте решим неравенство, чтобы выяснить весь набор значений, которые могут сделать его истинным.
Пример 2: Решите и изобразите решение неравенства . Этот пример показывает, что происходит с символом неравенства при делении на отрицательное число.
ВСЕГДА меняет направление неравенства всякий раз, когда вы делите или умножаете отрицательное число на обе стороны неравенства. Используйте закрытое или закрашенное отверстие , чтобы указать, что 7 является частью решения. Решение неравенства x \ le 7 включает 7 и все, что находится слева от него. Пример 3: Решите и изобразите решение неравенства . В этой задаче у меня есть переменные по обе стороны неравенства.Хотя не имеет значения, где мы храним переменную, слева или справа, имеет смысл всегда быть последовательным, изолировав ее слева. Думаю, это просто «стандартный» способ. Однако, если вы попытаетесь сохранить переменную справа, убедитесь, что вы знаете об их тонкостях. Например, ответ на эту проблему: x <- \, 6, что совпадает с - \, 6> x. Они эквивалентны, потому что начало неравенства также указывает на — \, 6. Следовательно, это означает, что если я переключаю переменную и константу в своем окончательном ответе, я также должен изменить направление символа, чтобы значение оставалось неизменным.
Обратите внимание, что I не изменил направление неравенства, потому что I разделил обе стороны на положительное число.
Пример 4: Решите и изобразите решение неравенства . Я построил эту задачу, чтобы подчеркнуть шаг, необходимый при работе с символом скобки . Я знаю, что это вас не смутит, потому что вы уже видели это раньше, когда решали линейные уравнения, верно? Чтобы избавиться от скобок, необходимо применить свойство распределения умножения над сложением.Однако я должен предостеречь вас, чтобы вы были осторожны со знаками в процессе умножения. Помните, что произведение двух членов с одинаковыми знаками является положительным, а если знаки не совпадают, произведение отрицательное.
Пример 5: Решите и изобразите решение неравенства . Мой общий подход здесь состоит в том, чтобы немедленно удалить круглые скобки, используя свойство распределения, объединить одинаковые термины с обеих сторон и, наконец, оставить x слева, а константу — с противоположной стороны.
Что касается правой стороны, это похожие термины, поэтому я просто объединю их.
Пример 6: Решите и изобразите решение неравенства . «Сложность» этой проблемы не должна вас беспокоить. Ключом к успешному решению этой проблемы является применение всех техник, которые вы уже усвоили из наших предыдущих примеров. Если вам нужен обзор, пожалуйста, оглядывайтесь назад. Попробуйте решить эту проблему, не просматривая подробное решение. Каждый раз, когда вы думаете, что закончили, сравните то, что у вас есть на бумаге, с ответом ниже.
Пример 7: Решите и изобразите решение неравенства . Давайте закончим, сделав последний пример мастерства! Опять же, сначала сделайте это самостоятельно на бумаге, а затем сравните свое решение с ответом ниже.
Затем упростите правую часть, объединив похожие термины, появившиеся после распространения.
Практика с рабочими листамиВозможно, вас заинтересует: Шаги по построению графика линейных неравенств Примеры построения графиков линейных неравенств Графические системы линейных неравенств Решение сложных неравенств
Решение линейных неравенствНеравенства — это математические предложения, сравнивающие две величины, которые не равны (или, возможно, не равны). Есть пять символов неравенства:
Часто для последних четырех типов неравенств нам нужно решить неравенство, чтобы переменная находилась только на одной стороне.Это делается с помощью аналогов свойства равенства : сложение или вычитание одинаковой величины с обеих сторон, либо умножение или деление обеих сторон на одинаковую величину. Единственный
Чтобы понять почему, рассмотрим простое неравенство вроде 1 < 2 .Если умножить обе части на - 1 не меняя знака, получаем — 1 < - 2 , что явно неверно! Решить для Икс . — 3 Икс + 2 ≤ 14 Сначала вычтите 2 с обеих сторон. — 3 Икс ≤ 12 Теперь разделите обе стороны на — 3 . Икс ≥ — 4 Когда у вас будет решение, вас могут попросить изобразить это . 2.7 Решение линейных неравенств — элементарная алгебра 2eЗадачи обученияК концу этого раздела вы сможете:
Будьте готовы 2.18 Прежде чем начать, пройдите тест на готовность. Перевести с алгебры на английский: 15> x15> x. Будьте готовы 2.19 Решите: n − 9 = −42.n − 9 = −42. Будьте готовы 2.20 Решите: −5p = −23. − 5p = −23. Будьте готовы 2.21 Решите: 3a − 12 = 7a − 20.3a − 12 = 7a − 20. Неравенства в графике на числовой прямойВы помните, что означает число, являющееся решением уравнения? Решение уравнения — это значение переменной, которое делает истинное утверждение при подстановке в уравнение. А как насчет решения неравенства? Какое число сделало бы неравенство x> 3x> 3 истинным? Вы думаете, « x может быть 4»? Это правильно, но x тоже может быть 5, 20 или даже 3.001. Любое число больше 3 является решением неравенства x> 3x> 3. Мы показываем решения неравенства x> 3x> 3 на числовой прямой, закрашивая все числа справа от 3, чтобы показать, что все числа больше 3 являются решениями. Поскольку число 3 само по себе не является решением, мы помещаем открывающую скобку в 3. График x> 3x> 3 показан на рисунке 2.7. Обратите внимание, что используется следующее соглашение: голубые стрелки указывают в положительном направлении, а синие стрелки указывают в отрицательном направлении. Рисунок 2.7 На этой числовой прямой изображено неравенство x> 3x> 3. График неравенства x≥3x≥3 очень похож на график x> 3x> 3, но теперь нам нужно показать, что 3 также является решением. Мы делаем это, помещая скобку в положение x = 3x = 3, как показано на рисунке 2.8. Рис. 2.8 На этой числовой прямой изображено неравенство x≥3x≥3. Обратите внимание, что символ открытых скобок (, показывает, что конечная точка неравенства не включена. Символ открытой скобки, [, показывает, что конечная точка включена. Пример 2.66График на числовой прямой: ⓐ x≤1x≤1 ⓑ x <5x <5 ⓒ x> −1x> −1 Решение
Попробуйте 2.131 График на числовой прямой: ⓐ x≤ − 1x≤ − 1 ⓑ x> 2x> 2 ⓒ x <3x <3 Попробуйте 2.132 График на числовой прямой: ⓐ x> −2x> −2 ⓑ x <−3x <−3 ⓒ x≥ − 1x≥ − 1 Мы также можем представить неравенства, используя интервальную нотацию . Как мы видели выше, неравенство x> 3x> 3 означает все числа больше 3. У решения этого неравенства нет верхнего предела. В обозначениях интервалов мы выразим x> 3x> 3 как (3, ∞). (3, ∞). Символ ∞∞ читается как «бесконечность». Это не настоящее число. На рис. 2.9 показаны числовая линия и обозначение интервалов. Рис. 2.9 Неравенство x> 3x> 3 изображено на этой числовой прямой и записано в интервальной записи. Неравенство x≤1x≤1 означает все числа, меньшие или равные 1.У этих цифр нет нижнего предела. Мы пишем x≤1x≤1 в обозначении интервалов как (−∞, 1] (- ∞, 1]. Символ −∞ − ∞ читается как «отрицательная бесконечность». На рисунке 2.10 показаны как числовая строка, так и обозначение интервала. Рис. 2.10 На этой числовой прямой изображено неравенство x≤1x≤1 и записано в интервальной записи. Неравенства, числовые линии и обозначение интерваловВы заметили, как скобка или квадратная скобка в обозначении интервала соответствует символу в конце стрелки? Эти отношения показаны на рисунке 2.11. Рисунок 2.11 Для обозначения неравенств на числовой прямой и в обозначении интервалов используются аналогичные символы для обозначения конечных точек интервалов. Пример 2.67График в числовой строке и запись в интервальной записи. ⓐ x≥ − 3x≥ − 3 ⓑ x <2,5x <2,5 ⓒ x≤ − 35x≤ − 35 Попробуйте 2.133 График на числовой строке и запись в интервале записи: ⓐ x> 2x> 2 ⓑ x≤ − 1,5x≤ − 1,5 ⓒ x≥34x≥34 Попробуй 2.134 График на числовой строке и запись в интервале записи: ⓐ x≤ − 4x≤ − 4 ⓑ x≥0,5x≥0,5 ⓒ x <−23x <−23 Решите неравенства, используя свойства неравенства вычитания и сложенияСвойства равенства вычитания и сложения утверждают, что если две величины равны, когда мы прибавляем или вычитаем одинаковую сумму из обеих величин, результаты будут равными. Свойства равенстваСвойство вычитания равенства Сложение Свойство равенства Для любых чисел a, b и c, для любых чисел a, b и c, если a = b, то a − c = b − c.если a = b, то a + c = b + c. Свойство вычитания равенства Сложение Свойство равенства Для любых чисел a, b и c, для любых чисел a, b и c, если a = b, то a − c = b − c. ifa = b, тогда a + c = b + c. Аналогичные свойства сохраняются и для неравенств.
Аналогичным образом мы могли бы показать, что неравенство остается неизменным и для сложения. Это приводит нас к свойствам неравенства на вычитание и сложение. Свойства неравенстваСвойство вычитания неравенстваСвойство неравенства сложения Для любых чисел a, b и c, для любых чисел a, b и c, если a Мы используем эти свойства для решения неравенств, выполняя те же действия, что и при решении уравнений. Решая неравенство x + 5> 9x + 5> 9, шаги будут выглядеть так:
Таблица 2.6 Любое число больше 4 является решением этого неравенства. Пример 2.68Решите неравенство n − 12≤58n − 12≤58, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.135 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. p − 34≥16p − 34≥16 Попробуйте 2.136 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. r − 13≤712r − 13≤712 Решайте неравенства, используя свойства неравенства деления и умноженияСвойства равенства деления и умножения утверждают, что если две величины равны, когда мы делим или умножаем обе величины на одинаковую величину, результаты также будут равны (при условии, что мы не не делить на 0). Свойства равенстваСвойство деления в равенстве Свойство умножения равенства Для любых чисел a, b, c и c ≠ 0, для любых действительных чисел a, b, c, ifa = b, thenac = bc.ifa = b, thenac = bc.Свойство деления в свойстве EqualityMultiplication в EqualityFor любые числа a, b, c и c ≠ 0, для любых действительных чисел a, b, c, если a = b, то ac = bc. ifa = b, thenac = bc. Существуют ли аналогичные свойства для неравенств? Что происходит с неравенством, когда мы делим или умножаем обе части на константу? Рассмотрим числовые примеры. Знаки неравенства остались прежними, знаки неравенства остались прежними. Неравенство сохраняется, когда мы делим или умножаем на отрицательное число? Знаки неравенства поменяли свое направление. Знаки неравенства изменили свое направление. Когда мы делим или умножаем неравенство на положительное число, знак неравенства остается прежним. Когда мы делим или умножаем неравенство на отрицательное число, знак неравенства меняется на противоположный. Вот свойства неравенства деления и умножения для удобства. Свойства неравенства деления и умноженияДля любых действительных чисел a, b, cifa
Пример 2.69Решите неравенство 7y <427y <42, нанесите решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.137 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. (с 8) (с 8) Попробуйте 2.138 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. 12d≤ 6012d≤ 60 Пример 2.70Решите неравенство −10a≥50−10a≥50, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.139 Решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. −8q <32−8q <32 Попробуйте 2.140 Решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. −7r≤ −70−7r≤ −70 Устранение неравенствИногда при решении неравенства переменная оказывается справа. Мы можем переписать неравенство в обратном порядке, чтобы переменная оказалась слева. x> a имеет то же значение, что и a Пример 2.71Решите неравенство −20 <45u − 20 <45u, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.141 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. 24≤38м24≤38м Попробуйте 2.142 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. −24 <43n − 24 <43n Пример 2.72Решите неравенство t − 2≥8t − 2≥8, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.143 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. к − 12≤15 к − 12≤15 Попробуйте 2.144 Решите неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. u − 4≥ − 16u − 4≥ − 16 Устранение неравенств, требующих упрощенияДля устранения большинства неравенств потребуется более одного шага. Мы следуем тем же шагам, что и в общей стратегии решения линейных уравнений, но обязательно обращаем особое внимание во время умножения или деления. Пример 2.73Решите неравенство 4m≤9m + 174m≤9m + 17, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.145 Решите неравенство 3q ≥ 7q — 233q ≥ 7q — 23, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.146 Решите неравенство 6x <10x + 196x <10x + 19, нанесите решение на числовой прямой и запишите решение в интервальной записи. Пример 2.74Решите неравенство 8p + 3 (p − 12)> 7p − 288p + 3 (p − 12)> 7p − 28, нанесите решение на числовой прямой и запишите решение в интервальной записи. Решение
Попробуйте 2.147 Решите неравенство 9y + 2 (y + 6)> 5y − 249y + 2 (y + 6)> 5y − 24, нанесите решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.148 Решите неравенство 6u + 8 (u − 1)> 10u + 326u + 8 (u − 1)> 10u + 32, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Подобно тому, как некоторые уравнения являются тождествами, а некоторые — противоречиями, неравенства могут быть тождествами или противоречиями. Мы узнаем эти формы, когда у нас остаются только константы при решении неравенства. Если результатом является истинное утверждение, у нас есть личность. Если результатом является ложное утверждение, мы приходим к противоречию. Пример 2.75Решите неравенство 8x − 2 (5 − x) <4 (x + 9) + 6x8x − 2 (5 − x) <4 (x + 9) + 6x, отобразите решение на числовой прямой и запишите решение. в интервальной записи. Решение
Попробуйте 2.149 Решите неравенство 4b − 3 (3 − b)> 5 (b − 6) + 2b4b − 3 (3 − b)> 5 (b − 6) + 2b, отобразите решение на числовой прямой и запишите решение. в интервальной записи. Попробуйте 2.150 Решите неравенство 9h − 7 (2 − h) <8 (h + 11) + 8h9h − 7 (2 − h) <8 (h + 11) + 8h, отобразите решение на числовой прямой и запишите решение. в интервальной записи. Пример 2.76Решите неравенство 13a − 18a> 524a + 3413a − 18a> 524a +34, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуйте 2.151 Решите неравенство 14x − 112x> 16x + 7814x − 112x> 16x + 78, обозначьте решение на числовой прямой и запишите решение в интервальной записи. Попробуй 2.152 Решите неравенство 25z − 13z <115z −3525z − 13z <115z −35, нанесите решение на числовой прямой и запишите решение в интервальной записи. Переведите на неравенство и решитеЧтобы перевести английские предложения в неравенства, нам нужно распознавать фразы, указывающие на неравенство. Некоторые слова просты, например «больше чем» и «меньше чем». Но другие не так очевидны. Подумайте о фразе «по крайней мере» — что значит быть «не моложе 21 года»? Значит 21 или больше. Фраза «по крайней мере» означает «больше или равно». В таблице 2.7 приведены некоторые общие фразы, указывающие на неравенство.
Таблица 2.7 Пример 2.77Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. Двенадцать раз c не более 96. Попробуйте 2.153 Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. Двадцать раз y не более 100 Попробуйте 2.154 Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. Девять раз z не меньше 135 Пример 2.78Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. Тридцать меньше x не меньше 45. Попробуйте 2.155 Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. Девятнадцать менее p не менее 47 Попробуй 2.156 Переведите и решите. Затем запишите решение в интервальной записи и нанесите график на числовой прямой. На четыре больше a не больше 15. Раздел 2.7 УпражненияПрактика ведет к совершенствуНеравенства графика на числовой прямой В следующих упражнениях нарисуйте каждое неравенство на числовой прямой. 430. x≤ − 2x≤ − 2 431. x> 1x> 1ⓑ x <−2x <−2 432. x≥ − 3x≥ − 3ⓑ x <4x <4ⓒ x≤ − 2x≤ − 2 433. ⓐ x≤0x≤0ⓑ x> −4x> −4ⓒ x≥ − 1x≥ − 1 В следующих упражнениях нарисуйте каждое неравенство на числовой прямой и запишите в интервальной нотации. 434. ⓐ х <−2x <−2ⓑ x≥ − 3,5x≥ − 3,5ⓒ x≤23x≤23 435. ⓐ x> 3x> 3ⓑ x≤ − 0,5x≤ − 0,5ⓒ x≥13x≥13 436. x≥ − 4x≥ − 4ⓑ x <2,5x <2,5ⓒ x> −32x> −32 437. ⓐ x≤5x≤5ⓑ x≥ − 1,5x≥ − 1,5ⓒ x <−73x <−73 Решите неравенства, используя свойства неравенства вычитания и сложения В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. 444. f − 1320 <−512f − 1320 <−512 445. г − 1112 <−518 г − 1112 <−518 Решение неравенств с использованием свойств неравенства деления и умножения В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. Устранение неравенств, требующих упрощения В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. 470. 12x + 3 (x + 7)> 10x − 24 12x + 3 (x + 7)> 10x − 24 471. 9y + 5 (y + 3) <4y − 359y + 5 (y + 3) <4y − 35 472. 6ч − 4 (час − 1) ≤7ч − 116ч − 4 (час − 1) ≤7ч − 11 473. 4k− (k − 2) ≥7k − 264k- (k − 2) ≥7k − 26 474. 8 м − 2 (14 − м) ≥ 7 (м − 4) + 3 м 8 м − 2 (14 − м) ≥ 7 (м − 4) + 3 м 475. 6n − 12 (3 − n) ≤9 (n − 4) + 9n6n − 12 (3 − n) ≤9 (n − 4) + 9n 476. 34b-13b <512b-1234b-13b <512b-12 477. 9u + 5 (2u − 5) ≥12 (u − 1) + 7u9u + 5 (2u − 5) ≥12 (u − 1) + 7u 478. 23 г-12 (г-14) ≤16 (г + 42) 23 г-12 (г-14) ≤16 (г + 42) 479. 56a − 14a> 712a + 2356a − 14a> 712a + 23 480. 45h − 23 (h − 9) ≥115 (2h + 90) 45h − 23 (h − 9) ≥115 (2h + 90) 481. 12v + 3 (4v − 1) ≤19 (v − 2) + 5v12v + 3 (4v − 1) ≤19 (v − 2) + 5v Смешанная практика В следующих упражнениях решите каждое неравенство, нанесите решение на числовой прямой и запишите решение в интервальной записи. 484. 23p − 2 (6−5p)> 3 (11p − 4) 23p − 2 (6−5p)> 3 (11p − 4) 485. 18q − 4 (10−3q) <5 (6q − 8) 18q − 4 (10−3q) <5 (6q − 8) 486. −94x≥ − 512−94x≥ − 512 487. −218y≤ − 1528−218y≤ − 1528 Перевести на неравенство и разрешить В следующих упражнениях переведите и решите. Затем запишите решение в интервальной нотации и нанесите график на числовой прямой. 492. Четырнадцать раз d больше 56. 493. Девяносто раз c меньше 450. 494. В восемь раз z меньше -40-40. 495. Десять раз y не больше −110−110. 496. Три более ч не менее 25. 497. Шесть больше k больше 25. 498. Десять меньше w не меньше 39. 499. Двенадцать меньше x не меньше 21. 500. Отрицательное пять раз r не более 95. 501. Дважды отрицательное значение с меньше 56. 502. Девятнадцать меньше b не больше −22−22. 503. Пятнадцать меньше, чем , а не меньше −7−7. Повседневная математика504. Безопасность Рост ребенка h должен быть не менее 57 дюймов, чтобы ребенок мог безопасно ездить на переднем сиденье автомобиля. Запишите это как неравенство. 505. Летчики-истребители Максимальная высота летчика-истребителя h составляет 77 дюймов. Запишите это как неравенство. 506. Лифты Общий вес пассажиров лифта w не может превышать 1 200 фунтов. Запишите это как неравенство. 507. Покупки Количество товаров, n , которые покупатель может иметь в полосе экспресс-оформления, не превышает 8. Запишите это как неравенство. Письменные упражнения508. Приведите пример из своей жизни, используя фразу «хотя бы». 509. Приведите пример из своей жизни, используя фразу «максимум». 510. Объясните, почему необходимо обратить неравенство при решении −5x> 10−5x> 10. 511. Объясните, почему необходимо обратить неравенство при решении n − 3 <12n − 3 <12. Самопроверкаⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела. ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения? Линейные неравенства (одна переменная)Некоторые ключевые слова и фразы, указывающие на неравенство, приведены ниже: Как и во всех приложениях, внимательно прочтите проблему несколько раз и найдите ключевые слова и фразы.Определите неизвестные и назначьте переменные. Далее переведем формулировку в математическое неравенство. Наконец, используйте изученные свойства, чтобы решить неравенство и выразить решение графически или в интервальной нотации. Пример 9: Перевести: Пять меньше двух, число не больше 25. Решение: Сначала выберите переменную для неизвестного числа и определите ключевые слова и фразы. Ответ: 2n − 5≤25. Ключевая фраза «не больше» указывает на то, что максимальное значение количества составляет 25 или меньше. Пример 10: Температура в пустыне может колебаться от 10 ° C до 45 ° C за один 24-часовой период. Найдите эквивалентный диапазон в градусах Фаренгейта, F , учитывая, что C = 59 (F − 32). Решение: Установите составное неравенство, при котором температура в градусах Цельсия находится в диапазоне от 10 ° C до 45 ° C. Затем подставьте в неравенство выражение, эквивалентное температуре Цельсия, и решите для F . Ответ: Эквивалентный диапазон по Фаренгейту составляет от 50 ° F до 113 ° F. Пример 11: В первых четырех видах соревнований гимнастка получает 7,5, 8,2, 8,5 и 9,0 баллов. Какой результат она должна набрать в пятом соревновании, чтобы в среднем не менее 8,5? Решение: Среднее значение должно быть не менее 8,5; это означает, что среднее значение должно быть больше или равно 8,5. Ответ: Она должна набрать не менее 9,3 балла в пятом соревновании. Тематические упражненияЧасть A: Поиск решений Определите, является ли данное число решением заданного неравенства. 1. 2x − 3 <6; х = -1 2. −3x + 1≤0; х = −2 3. 5x − 20> 0; х = 3 4. 12x + 1> −34; х = −14 5. −5 <7x + 1 <9; х = 0 6. −20≤ − 3x − 5≤ − 10; х = 5 7. x <−3 или x> 3; х = -10 8. x <0 или x≥1; х = 12 9. 2x + 1 <−3 или 2x + 1≥5; х = 2 10. 4x − 1 <−17 или 3x + 2≥6; х = 1 Часть B: Решение линейных неравенств Решите и изобразите набор решений.Кроме того, представьте набор решений в интервальной записи. 11. x + 5> 1 12. x − 3 <−4 13. 6x≤24 14. 4x> −8 15. −7x≤14 16. −2x + 5> 9 17. 7x − 3≤25 18. 12x + 7> −53 19. −2x + 5 <−7 20. −2x + 4≤4 21. −15x + 10> 20 22.−8x + 1≤29 23. 17x − 3 <1 24. 12x − 13> 23 25. 53x + 12≤13 26. −34x − 12≥52 27. −15x + 34 <−15 28. −23x + 1 <−3 29,2 (−3x + 1) <14 30. −7 (x − 2) +1 <15 31. 9x − 3 (3x + 4)> — 12 32. 12x − 4 (3x + 5) ≤ − 2 33. 5−3 (2x − 6) ≥ − 1 34.9x− (10x − 12) <22 35. 2 (x − 7) −3 (x + 3) ≤ − 3 36. 5x − 3> 3x + 7 37,4 (3x − 2) ≤ − 2 (x + 3) +12 38,5 (x − 3) ≥15x− (10x + 4) 39. 12x + 1> 2 (6x − 3) −5 40. 3 (x − 2) +5> 2 (3x + 5) +2 41. −4 (3x − 1) + 2x≤2 (4x − 1) −3 42. −2 (x − 2) + 14x <7 (2x + 1) Задайте алгебраическое неравенство и решите его. 43.Сумма троекратного числа и 4 больше отрицательного 8. 44. Сумма семи и трехкратного числа меньше или равна 1. 45. Когда число вычитается из 10, результат не превышает 12. 46. Если 5 раз вычесть число из 6, получится не менее 26. 47. Если пять прибавить к тройному числу, результат будет меньше двадцати. 48. Если из числа, умноженного на два, вычесть три, результат будет больше или равен девяти. 49. Билл зарабатывает 12 долларов в день плюс 0,25 доллара за каждого человека, которого он регистрирует для голосования. Сколько человек он должен зарегистрироваться, чтобы заработать не менее 50 долларов в день? 50. Если членство в гольф-клубе стоит 100 долларов в месяц, каждый раунд игры в гольф стоит всего 25 долларов. Сколько раундов в гольф может сыграть участник, если он хочет, чтобы его расходы не превышали 250 долларов в месяц? 51. Джо набрал 72, 85 и 75 баллов на первых трех экзаменах по алгебре.Что он должен набрать на четвертом экзамене, чтобы в среднем не менее 80? 52. Морис заработал 4, 7 и 9 баллов из 10 в первых трех тестах. Что он должен набрать в четвертой викторине, чтобы получить в среднем не менее 7 баллов? 53. Компьютер выключается, если температура превышает 40 ° C. Приведите эквивалентное утверждение в градусах Фаренгейта. (Подсказка: C = 59 (F − 32).) 54. Гарантия того, что определенная марка макияжа не будет работать, если температура ниже 35 ° C.Приведите эквивалентное утверждение в градусах Фаренгейта. Часть C: Сложные неравенства Решите и изобразите набор решений. Кроме того, представьте набор решений в интервальной записи. 55. -1 <х + 3 <5 56. −10≤5x <20 57. −2≤4x + 6 <10 58. −10≤3x − 1≤ − 4 59. −15 <3x − 6≤6 60. −22 <5x + 3≤3 61.−1≤12x − 5≤1 62. 1 <8x + 5 <5 63. −15≤23x − 15 <45 64. −12 <34x − 23≤12 65. −3≤3 (x − 1) ≤3 66. −12 <6 (x − 3) ≤0 67,4 <−2 (x + 3) <6 68. −5≤5 (−x + 1) <15 69. −32≤14 (12x − 1) +34 <32 70. −4≤ − 13 (3x + 12) <4 71. −2≤12−2 (x − 3) ≤20 72.−5 <2 (x − 1) −3 (x + 2) <5 73. 3x≤ − 15 или 2x> 6 74. 4x − 1 <−17 или 3x + 2≥8 75. −2x + 1 <−1 или −2x + 1> 1 76. 7x + 4≤4 или 6x − 5≥1 77. 3x − 7 <14 или 2x + 3> 7 78. −3x + 1 <−5 или −4x − 3> −23 79. 12x − 2 <−1 или 12x − 2> 1 80. 13x + 3≥ − 2 или 13x + 3≤2 81.3x + 7≤7 или −5x + 6> 6 82. −10x − 3≤17 или 20x − 6> −26 83. 2x − 10 <−2 или −3x + 4> −5 84. 5x + 3 <4 или 5−10x> 4 85. 3x <18 и 5x> −20 86. x + 7≤5 и x − 3≥ − 10 87. 2x − 1 <5 и 3x − 1 <10 88. 5x + 2 <−13 и 3x + 4> 13 Установите составное неравенство для следующего и решите. 89. Пятикратное превышение некоторого числа от 15 до 25. 90. Четыре, вычтенные из троекратного некоторого числа, составляет от −4 до 14. 91. Клинт желает получить оценку B, которая составляет не менее 80, но менее 90. Какой диапазон он должен набрать на четвертом экзамене, если первые три были 65, 75 и 90? 92. Некоторые антифризы эффективны в диапазоне температур от –35 ° C до 120 ° C. Найдите эквивалентный диапазон в градусах Фаренгейта. 93. Средняя температура в Лондоне колеблется от 23 ° C летом до 14 ° C зимой. Найдите эквивалентный диапазон в градусах Фаренгейта. 94. Если основание треугольника составляет 5 дюймов, то в каком диапазоне должна быть высота, чтобы площадь составляла от 10 квадратных дюймов до 20 квадратных дюймов? 95. Прямоугольник имеет длину 7 дюймов. Найдите все возможные значения ширины, если площадь должна составлять от 14 до 28 квадратных дюймов. 96. Ширина прямоугольника 3 сантиметра. Найдите все возможные длины, если периметр должен быть не менее 12 сантиметров и не более 26 сантиметров. 97. Периметр квадрата должен составлять от 40 до 200 футов. Найдите длины всех возможных сторон, удовлетворяющих этому условию. 98. Если дважды угол составляет от 180 до 270 градусов, то каковы границы исходного угла? 99.Если угол в три раза составляет от 270 до 360 градусов, то каковы границы исходного угла? Часть D. Темы дискуссионной доски 100. Изучите и обсудите использование нотации построителя множеств с пересечениями и объединениями. 101. Можем ли мы объединить логическое «или» в одно утверждение, как мы это делаем для логического «и»? ответов1: Есть 3: № 5: Есть 7: Есть 9: Есть 11: х> −4; (−4, ∞) 13: x≤4; (−∞, 4] 15: x≥ − 2; [−2, ∞) 17: x≤4; (−∞, 4] 19: х> 6; (6, ∞) 21: х <-23; (−∞, −23) 23: х <28; (−∞, 28) 25: x≤ − 110; (−∞, −110] 27: х> 194; (194, ∞) 29: х> -2; (−2, ∞) 31: ∅ 33: x≤4; (−∞, 4] 35: x≥ − 20; [-20, ∞) 37: x≤1; (−∞, 1] 39: рэнд 41: x≥12; [12, ∞) 43: n> −4 45: n≥ − 2 47: n <5 49: Билла необходимо зарегистрировать не менее 152 человек. 51: Джо должен набрать не менее 88 баллов на четвертом экзамене. 53: компьютер выключится, когда температура превысит 104 ° F. 55: -4 <х <2; (−4, 2) 57: −2≤x <1; [−2, 1) 59: −3 61: 8≤x≤12; [8, 12] 63: 0≤x <32; [0, 32) 65: 0≤x≤2; [0, 2] 67: −6 69: -16≤x <8; [−16, 8) 71: −1≤x≤10; [-1, 10] 73: x≤ − 5 или x> 3; (−∞, −5] ∪ (3, ∞) 75: x> 1 или x <0; (−∞, 0) ∪ (1, ∞) 77: рэнд 79: x <2 или x> 6; (−∞, 2) ∪ (6, ∞) 81: x≤0; (−∞, 0] 83: х <4; (−∞, 4) 85: -4 <х <6; (−4, 6) 87: х <3; (−∞, 3) 89: 5 <п <20 91: Клинт должен набрать балл в диапазоне от 90 до 100. 93: Средняя температура в Лондоне колеблется от 57,2 ° F до 73,4 ° F. 95: ширина должна быть от 2 до 4 дюймов. 97: Стороны должны быть от 10 футов до 50 футов. 99: угол между 90 и 120 градусами. Линейных неравенств В этом разделе мы узнаем , как решить линейное неравенство .Это неравенств с неизвестным \ (x \), которые выглядят следующим образом: Чтобы решить линейное равенство вида \ (ax \ leq b \) или даже \ (ax + b> cx + d \), мы выполняем те же шаги, что и для решения Другими словами, когда мы умножаем или делим обе части неравенства на отрицательное число: \ (> \) становится \ ( \ (\ geq \) становится \ (\ leq \) \ (\) \ (\ leq \) становится \ (\ geq \) Это дополнительно объясняется, и некоторые примеры рассматриваются в учебнике 1 . Если вы еще этого не сделали, посмотрите его сейчас. Теперь, когда мы узнали правила решения линейных неравенств , мы можем применить полученные знания на практике. Решите каждое из следующих неравенств и проиллюстрируйте свой ответ числовой прямой: Ответы без работы Ответы с рабочими Ответы с рабочими |
