Содержание
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1. Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
где a , b , c – заданные числа.
Определение 2. Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1. Найти решение уравнения
Решение. Выразим из равенства (2) переменную y через переменную x :
| (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание. Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3. Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
| (4) |
где a1 , b1 , c1 , a2 , b2 , c2 – заданные числа.
Определение 4. В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных, а числа c1 , c2 – свободными членами.
Определение 5. Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6. Две системы уравнений называют равносильными (эквивалентными), если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «»
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных, который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
Решить систему уравнений
| (5) |
Решение. Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х.
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
| (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Ответ. (–2 ; 3) .
Пример 3. Найти все значения параметра p , при которых система уравнений
| (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение. Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
| (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если , то уравнение (9) имеет единственное решение
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда , система (7) имеет единственное решение
Если p = – 2 , то уравнение (9) принимает вид
,
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел
,
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.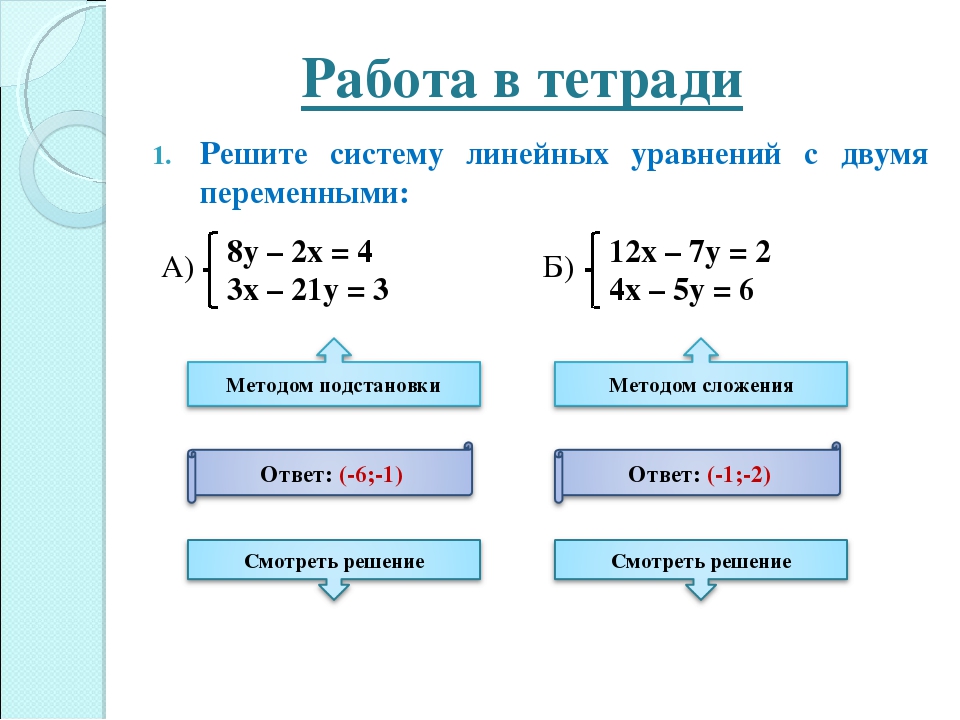
Системы из трех линейных уравнений с тремя неизвестными
Определение 7. Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
| (10) |
где a1 , b1 , c1 , d1 , a2 , b2 , c2 , d2 , a3 , b3 , c3 , d3 – заданные числа.
Определение 8. В системе уравнений (10) числа a1 , b1 , c1 , a2 , b2 , c2 , a3 , b3 , c3 называют коэффициентами при неизвестных, а числа d1 , d2 , d3 – свободными членами.
Определение 9. Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
| (11) |
Решение. Будем решать систему (11) при помощи метода последовательного исключения неизвестных.
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
| (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему
| (13) |
Из системы (13) последовательно находим
z = – 2 ; x = 1 ; y = 2 .
Ответ. (1 ; 2 ; –2) .
Пример 5. Решить систему уравнений
| (14) |
Решение. Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Ответ: (3 ; 0 ; –1) .
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Внеклассный урок — Система уравнений с двумя переменными. Системы уравнений с двумя переменными. Способы решения.
Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
Уравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1
Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
↓
│2x = 6
│2y = 4
↓
│x = 6 : 2
│y = 4 : 2
↓
│x = 3
│y = 2
Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
↓
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + у
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 1
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
↓
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
Системы уравнений. Простейшие системы уравнений с двумя неизвестными
Напомним,
что любое конечное множество уравнений называется системой уравнений.
Систему
уравнений принято записывать с помощью фигурной скобки.
Общий
вид системы двух уравнений с двумя переменными:
Решением
системы двух уравнений с двумя переменными называется пара
чисел ,
при подстановке которых вместо соответствующих переменных оба
уравнения системы обращаются в верные числовые равенства.
Решить
систему уравнений – значит найти все её решения или
доказать, что решений нет.
Две
системы уравнений называются равносильными, если они имеют одно и то же
множество решений. Если обе системы не имеют решений, то они также считаются равносильными.
Теоремы
о равносильности систем уравнений.
1.
Пусть дана система двух уравнений с двумя переменными. Если одно уравнение
системы оставить без изменения, а второе уравнение заменить равносильным, то
полученная система будет равносильна заданной.
2.
Пусть дана система двух уравнений с двумя переменными. Если одно уравнение
системы оставить без изменения, а второе заменить суммой или разностью обоих
уравнений системы, то полученная система будет равносильна заданной.
3.
Если обе части уравнения ни
при каких ,
одновременно
не обращаются в нуль, то следующие системы равносильны:
Вспомним
основные методы решения систем уравнений. Итак, основными методами решения
систем уравнений являются метод алгебраического сложения, метод подстановки и
метод введения новых переменных.
Метод
алгебраического сложения. Сущность этого метода заключается в
следующем:
1.
обе части первого уравнения умножают на некоторый множитель, обе части второго
уравнения умножают на другой множитель (если это требуется). Эти множители
Эти множители
подбираются так, чтобы коэффициенты при одной из переменных в обоих уравнениях
стали противоположными числами;
2.
уравнения почленно складывают и решают полученное уравнение с одной переменной;
3.
вторую переменную находят подстановкой найденного значения первой переменной в
одно из уравнений системы.
Решите
систему уравнений .
Решение.
Решите
систему уравнений .
Решение.
Метод
подстановки. Сущность этого метода заключается в
следующем:
1)
выражают из какого-либо уравнения системы одну переменную через другую;
2)
подставляют в другое уравнение системы вместо этой переменной полученное
выражение;
3)
решают получившееся уравнение с одной переменной;
4)
находят соответствующие значения второй переменной.
Решите
систему уравнений .
Решение.
Решите
систему уравнений .
Решение.
Метод
введения новых переменных. При сопутствующем выборе
вспомогательных переменных иногда решение исходной системы можно свести к
решению более простой системы уравнений, чем исходная.
Решите
систему уравнений .
Решение.
Решите
систему уравнений .
Решение.
Рассмотренные
методы решения систем уравнений применяются и к решению систем, содержащих показательную
и логарифмическую функции.
Решите
систему уравнений .
Решение.
Решите
систему уравнений .
Решение.
Решение систем уравнений с примерами решения
Содержание:
- Графический метод решения систем уравнений
- Начнём с графического метода
- Решение систем уравнений методом подстановки
- Симметричные системы уравнений с двумя неизвестными
Графический метод решения систем уравнений
Вспоминаем то, что знаем
Что такое график уравнения с двумя неизвестными?
Что представляет собой график линейного уравнения с двумя неизвестными?
Решите графическим методом систему линейных уравнений:
Открываем новые знания
Решите графическим методом систему уравнений:
Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту
В курсе алгебры 7-го класса вы изучали системы линейных уравнений.
Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Начнём с графического метода
Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.
Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.
Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.
Возможно вам будут полезны данные страницы:
Примеры с решением
Пример 1:
Решим систему уравнений:
Построим графики уравнений
Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).
Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).
Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.
Ответ: (2; 5) и (-1; 2).
Пример 2:
Выясним количество решений системы уравнений:
Построим графики уравнений
Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.
Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.
Ответ: Два решения.
Решение систем уравнений методом подстановки
Вспоминаем то, что знаем
Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.
Решите систему линейных уравнений методом подстановки:
Открываем новые знания
Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?
Решите систему уравнений методом подстановки:
Как решить систему двух уравнений с двумя неизвестными методом подстановки?
Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?
Ранее вы решали системы уравнений первой степени.
Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.
Пример 3:
Решим систему:
Пусть (х; у) — решение системы.
Выразим х из уравнения
Подставим найденное выражение в первое уравнение:
Решим полученное уравнение:
Найдём х:
Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.
Ответ: (5; 1), (-2;-2,5).
Чуть сложнее дело обстоит в следующем примере.
Пример 4:
Решим систему уравнений:
Пусть (х; у) — решение системы.
Выразим у из линейного уравнения:
Подставим найденное выражение в первое уравнение системы:
После преобразований получим:
Найдём у:
Ответ: (-0,5; 0,5), (4; 5).
Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».
Пример 5:
Решим систему:
Подставим во второе уравнение тогда его можно переписать в виде:
Теперь выразим х через у из первого уравнения системы:
Подставим в полученное ранее уравнение ху = 2:
Корни этого уравнения:
Найдём х:
.
Ответ: (2; 1), (-1;-2).
Иногда решить систему можно, используя метод алгебраического сложения.
Пример 6:
Решим систему:
Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:
.
Корни этого уравнения:
Подставим найденные значения в первое уравнение. Рассмотрим два случая:
1)
2) , получим уравнение корней нет.
Ответ: (0; 1), (1; 1).
Иногда упростить решение удаётся, используя различные варианты замены неизвестных.
Пример 7:
Решим систему уравнений:
Обозначим
Второе уравнение системы примет вид:
Решим полученное уравнение. Получим, умножая обе части на 2а:
Таким образом:
Осталось решить методом подстановки линейные системы:
Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями
Напомним, что при решении задач обычно действуют следующим образом:
1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;
2) решают полученную систему;
3) отвечают на вопрос задачи.
Пример 8:
Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.
Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.
Воспользуемся теоремой Пифагора:
Получим систему:
Решим систему. Выразим из первого уравнения у:
Подставим во второе уравнение:
Корни уравнения:
Найдём
С учётом условия получим ответ: длина — 12 см, ширина — 5 см.
Пример 9:
Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.
Введём обозначения.
Пусть х — первое число, у — второе число.
Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.
Получим систему:
Вычтем из второго уравнения первое. Получим:
Дальше будем решать методом подстановки:
Подставим в первое уравнение выражение для у:
Корни уравнения: (не подходит по смыслу задачи).
Найдём у из уравнения:
Получим ответ: 16 и 7.
Симметричные системы уравнений с двумя неизвестными
Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.
Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.
ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.
Например, если в системе уравнений
переставить местами неизвестные х и у, то получим систему:
Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.
Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.
Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:
Сначала научитесь выражать через неизвестные выражения:
Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными»
Библиографическое описание:
Бородина, М. Ю. Разработка урока по алгебре в 7 классе по теме «Нестандартный способ решения систем линейных уравнений с двумя переменными» / М. Ю. Бородина. — Текст : непосредственный // Молодой ученый. — 2017. — № 33 (167). — С. 1-4. — URL: https://moluch.ru/archive/167/45372/ (дата обращения: 05.06.2021).
В данной статье предлагается разработка урока алгебры в 7 классе по учебнику А. Г. Мордковича. Школьникам скоро предстоит сдавать экзамены, и многие из них хотят, как можно хорошо и быстро научиться решать задачи. И в таких случаях можно применять нестандартные решения. Задания: «Решить систему уравнений» входят в задания экзамена как после 9 класса, так и после 11 класса. Данное изучение лучше применить на втором уроке в теме «Решение систем уравнений способ сложения».
Г. Мордковича. Школьникам скоро предстоит сдавать экзамены, и многие из них хотят, как можно хорошо и быстро научиться решать задачи. И в таких случаях можно применять нестандартные решения. Задания: «Решить систему уравнений» входят в задания экзамена как после 9 класса, так и после 11 класса. Данное изучение лучше применить на втором уроке в теме «Решение систем уравнений способ сложения».
Цель: Познакомиться с нестандартным решением систем линейных уравнений.
Задача: Научиться решать системы линейных уравнений методом Крамера и сравнить с другими методами решения.
Ход урока
- Сегодня на уроке мы рассмотрим нестандартный способ решения систем уранений с двумя переменными и сравним данный способ решения с другими решенями. Но сначала повторим темы прошлых уроков:
– Что значит «решить систему линейных уравнений»? (Найти все его корни, или показать, что их нет.)
– Что является решением системы с двумя переменными? (Пара значений переменных, обращающая каждое уравнение системы в верное равенство. )
)
– Какие способы решения систем уравнений мы применяли? (способ сравнения; графический способ; способ подстановки; способ сложения)
К доске вызываются четыре ученика и решают систему различными способами, а остальные по вариантам. После решения ученики рассказывают алгоритм решения, в случае затруднения помогает класс.
- При решении систем уравнений с двумя переменными можно применить еще один способ, применяя метод Крамера. Габриэль Крамер (Gabriel Cramer) (31.07.1704 — 04.01.1752). Швейцарский математик, один из создателей линейной алгебры.
Данный метод значительно ускоряет процесс решения систем линейных уравнений и очень удобно применять его для систем с громоздкими вычислениями.
Метод Крамера применяется в Высшей математике при решении системы линейных уравнений с тремя неизвестными или решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Вам будет интересно научиться применять решение, не просто школьного курса, а решение, которые применяют студенты первых курсов высших заведений.
В данном методе при решении используют понятие определителя системы:
Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается Δ(дельта) и вычисляется по формуле.
где, , — заданные числа; х и у- неизвестные, числа — называются коэффициентами, а числа — свободными членами.
Δ = = а11 · а22 — а12 · а21.
Для нахождения неизвестных н6ам нужно найти еще два определителя и , путём замены коэффициентов при соответствующих неизвестных свободными членами:
= = в1 · а22 — а12 · в2.
= а11 · в2 — в1 · а21.
Формула Крамера для нахождения неизвестных: х = ; у = .
Найти значения неизвестных можно только при условии, когда определитель не равен нулю (Δ≠0).
Замечание: если определитель системы равен нулю, то система может иметь бесконечно много решений или не имеет решений.
Пример:
Δ = = 3·4–2·5 = 12–10=2≠0
Найдем еще два определителя и , путём замены коэффициентов при соответствующих неизвестных свободными членами:
= 2;
Формула Крамера для нахождения неизвестных: х = ; у = . Ответ: (1;-2).
- Решите систему уравнений способ сложения и методом Крамера:
а) ; б) ; в)
Решив системы, сделаем вывод: какой способ решается быстрее и легче?
– способ сравнения: выразим переменную у через х, решим уравнение через х, приравняв правые части уравнения, и найдем переменную у;
– графический способ: выразим переменную у через х, построим график. Но на графике не всегда можно увидеть точное решение;
– способ подстановки: выразим одну переменную через другую, подставим и решим уравнение, найдем другую переменную;
– способ сложения: умножим уравнения системы на такие множители, чтобы коэффициенты при одной из переменных стали противоположными; сложим левые и правые части уравнений системы; решим получившееся уравнение с одной переменной и найдем другую переменную;
– методом Крамера: по формулам найдем три определителя и переменные.
При рассмотрении решений несколькими способами ученики убеждаются, что метод Крамера упрощает время и трудности вычисления для нахождения неизвестных в решении систем уравнений.
- Итоги урока:
— Сегодня на уроке мы обобщили все методы решения систем линейных уравнений с двумя переменными.
— Какие способы решения вы знаете?
— Каким бы способом вы решали системы уравнений и почему?
— А какой способ решения вы бы применили на экзамене?
- Домашнее задание: 1225(а, б), 1226.
Литература:
1. Ю. Н. Макарычев, Н. Г. Миндюк, К.И. и др. Алгебра 7 класс. Учебник. –М.: Просвещение 3-е изд. — М.: 2014. — 256 с.
- Письменный Д. Т. Конспект лекций по высшее математике. 1 часть.- второе издание, испр.- М: Айрис-пресс, 2003.-288с.: ил.
- Лисичкин В. Т., Соловейчик И. Л. математика: учебное пособие для техникумов.
 -М.: Высшая школа, 1991 480 с: ил.
-М.: Высшая школа, 1991 480 с: ил. - Пичурин Л. Ф. За страницами учебника алгебры. — М: Просвещение, 1990–224с., ил.
Основные термины (генерируются автоматически): нахождение неизвестных, переменная, определитель системы, решение систем уравнений, решение системы, способ сложения, уравнение, графический способ, замена коэффициентов, какой способ решения.
Метод подстановки при решении системы линейных уравнений
☰
При решении системы линейных уравнений с двумя переменными можно использовать графический метод. Однако алгебраический является более надежным. Одним из алгебраических методов является метод подстановки.
Суть метода подстановки заключается в следующем. В одном уравнении (не важно каком) системы одна переменная выражается через другую. После этого во второе уравнение системы вместо соответствующей переменной подставляется выражение, которому равна эта переменная, полученное ранее. Приведем пример; допустим, дана система уравнений:
Приведем пример; допустим, дана система уравнений:
| 10x + 10y + 10 = 0
| –2x – 4y – 8 = 0
Выразим во втором уравнении y через x:
–4y = 2x + 8
y = (2x + 8) / –4
y = –0.5x – 2
Теперь подставим в первое уравнение вместо y выражение –0.5x – 2. Это допустимо, так как y равен этому выражению, то есть y и это выражение эквивалентны. Получим:
10x + 10(–0.5x – 2) + 10 = 0
Теперь решим полученное уравнение с одной переменной, то есть найдем значение x.
10x – 5x – 20 + 10 = 0
5x – 10 = 0
5x = 10
x = 2
Для того, чтобы найти y надо подставить значение x в любое линейное уравнение из системы, но проще в то, где y уже выражен через x:
y = –0.5x – 2 = y = –0.5 * 2 – 2 = –1 – 2 = –3
Таким образом решением заданной системы уравнений являются значения x = 2, y = –3.
Проверим это, подставив соответствующие значения в одно или оба линейных уравнения системы:
10x + 10y + 10 = 10 * 2 + 10 * (–3) + 10 = 20 – 30 + 10 = 0 — верное равенство
–2x – 4y – 8 = –2 * 2 – 4 * (–3) – 8 = –4 + 12 – 8 = 0 — верное равенство
При использовании метода подстановки не важно выражать ли x через y или как в приведенном примере y через x. При выборе исходить надо из удобства: что проще из чего выразить. Например, в уравнении 4.35x + y – 1.5 проще выразить y через x: y = 1.5 – 4.35x. А вот в уравнении 2x – 4y = 0 лучше выразить x через y: x = 2y.
При выборе исходить надо из удобства: что проще из чего выразить. Например, в уравнении 4.35x + y – 1.5 проще выразить y через x: y = 1.5 – 4.35x. А вот в уравнении 2x – 4y = 0 лучше выразить x через y: x = 2y.
Как отмечалось выше уравнение, которое подвергается преобразованию, также можно выбрать произвольно, исходя из принципа удобства.
Abitur
Системы уравнений первой степени с двумя неизвестными
Способы решения систем уравнений.
1. Метод сложения:
Данный метод решения систем уравнений первой степени с двумя неизвестными состоит в том, что путем сложения двух уравнений мы получаем третье, в котором отсутствует одна из переменных.
2. Метод подстановки:
Данный метод решения систем уравнений первой степени с двумя неизвестными состоит в том, что из одного из уравнений выражаем любую переменную и подставляем это выражение во второе уравнение. Решаем его. Найденное значение подставляем в любое уравнение и находим другую переменную.
Решение примеров.
1. Решите систему уравнения методом сложения:
| a). |
| 1). |
| 2). | Сложим 2 уравнения и получим: 6y=12 |
| 4). | Подставим это число в первое уравнение и найдем х: x=7-4.2=-1 |
2. Решите систему уравнения методом подстановки:
| a). |
| 1). | Из второго уравнения выражаем х: x=3y-6 |
2). | Подставляем полученное выражение в первое уравнение: 2(3y-6)+y=-5 |
| 5). | Подставим это число во второе уравнение и найдем х: x-3.1=-6 |
Задания.
1. Решите систему уравнений:
| a). | b). |
| c). | d). |
| e). |
Решение системы уравнений с двумя неизвестными — видео и стенограмма урока
Системы уравнений
Системы уравнений могут показаться столь же сложными. Система уравнений — это группа из двух или более уравнений с одинаковыми переменными. Множественные уравнения? Несколько переменных? Этого достаточно, чтобы вы захотели сбежать. К счастью, решение систем уравнений намного проще, чем кажется.
Множественные уравнения? Несколько переменных? Этого достаточно, чтобы вы захотели сбежать. К счастью, решение систем уравнений намного проще, чем кажется.
В этом уроке мы попрактикуемся в двух наиболее распространенных методах решения систем уравнений.Во-первых, это метод подстановки. Метод замены — это когда вы решаете одно уравнение для любой переменной, а затем подставляете решение в другое уравнение.
Тогда есть метод исключения. Метод исключения — это когда мы складываем или вычитаем уравнения, чтобы найти переменную. Давайте попробуем каждый метод при решении некоторых уравнений.
Практика замены
Начнем с метода замены. Вот два уравнения:
y — 2 x = 1 и 5 x — 2 y = 3
Давайте возьмем первое и решим относительно y .Складываем 2 x , чтобы получить y = 1 + 2 x . Затем мы заменяем 1 + 2 x на y во втором уравнении. Итак, получаем 5 x — 2 (1 + 2 x ) = 3. Решаем для x . Сначала мы распределяем -2 и получаем -2-4 x . Тогда 5 x — 4 x — это всего лишь x . Мы прибавляем 2 к обеим сторонам, чтобы получить x = 5.
Решаем для x . Сначала мы распределяем -2 и получаем -2-4 x . Тогда 5 x — 4 x — это всего лишь x . Мы прибавляем 2 к обеим сторонам, чтобы получить x = 5.
Теперь у нас есть значение x . Давайте подключим это к любому уравнению и получим значение y .Просто выберите тот, который, по вашему мнению, будет проще. Воспользуемся первым. y — 2 (5) = 1. y — 10 = 1. Складываем 10, и получаем y = 11.
Хорошая проверка — вернуть обе переменные обратно в оба уравнения. Если они не работают, вы знаете, что где-то ошиблись. Давайте попробуем это здесь.
y — 2 x = 1 становится 11 — 2 (5) = 1. Это 11 — 10 = 1. И да, 1 = 1. И 5 x — 2 y = 3 становится 5 (5) — 2 (11) = 3.Это 25 — 22 = 3. И снова да! 3 = 3. У нас все хорошо! И ни один будущий родственник не был оскорблен при решении этой проблемы.
Попробуем еще. Вот два уравнения:
y = 3 x — 4 и 2 y — 5 x = 2
В этом уравнении мы уже решили одно для y , поэтому давайте просто подставим 3 x — 4 дюйма для y во втором уравнении. Получаем 2 (3 x — 4) — 5 x = 2. 2 * 3 x равно 6 x , а 2 * 4 равно 8.6 x — 5 x — это всего лишь x . Затем мы прибавляем 8 к обеим сторонам, и получаем x = 10.
Получаем 2 (3 x — 4) — 5 x = 2. 2 * 3 x равно 6 x , а 2 * 4 равно 8.6 x — 5 x — это всего лишь x . Затем мы прибавляем 8 к обеим сторонам, и получаем x = 10.
Теперь подставим 10, чтобы получить x в первом уравнении. y = 3 (10) — 4. y = 30 — 4, или 26.
Хорошо, давайте проверим нашу работу. У нас есть y = 3 x — 4, мы получаем 26 = 3 (10) — 4. Это 30 — 4, что составляет 26! И 2 y — 5 x = 2 становится 2 (26) — 5 (10) = 2. Это 52 — 50 = 2. Успех!
Практика на выбывание
Давайте попробуем применить практику на выбывание.Вот два уравнения:
x + y = 5 и 5 y — 1 = 2 x
Думайте об этом, как о приготовлении бутерброда. Вам нужно, чтобы ингредиенты выстроились в одну линию. Если ваш помидор зайдет слишком далеко, он выскользнет. Итак, давайте все выровняем.
x + y = 5
5 y — 1 = 2 x
Отлично! Теперь нам нужно сбалансировать коэффициенты для одной из переменных, чтобы они уравнялись. Это все равно, что следить за балансом количества майонеза и горчицы. Здесь мы можем умножить верхнее уравнение на 2, чтобы получить 2 x сверху, чтобы соответствовать 2 x снизу.
Это все равно, что следить за балансом количества майонеза и горчицы. Здесь мы можем умножить верхнее уравнение на 2, чтобы получить 2 x сверху, чтобы соответствовать 2 x снизу.
А теперь вычтем. 2 x сокращаются. У нас осталось -3 y = 9. Разделим на -3 и y = -3. Теперь подставьте -3 для y в первом уравнении. x — 3 = 5. Итак, x = 8. Вот и наш бутерброд! Но ждать. Давайте проверим нашу работу, прежде чем съесть ее.
В x + y = 5, мы получаем 8 — 3 = 5. Это работает. В 2 x + 5 y = 1 мы получаем 2 (8) + 5 (-3) = 1. Это 16-15 = 1. Успех!
Давайте попробуем другой:
2 x — y = 3
-4 x + 3 y = 1
Эй, смотрите — наши термины аккуратно сложены. Спасибо, боги сэндвичей! И мы можем умножить верхнее уравнение на 2, чтобы избавиться от членов размером x . Таким образом, получается 4 x — 2 y = 6.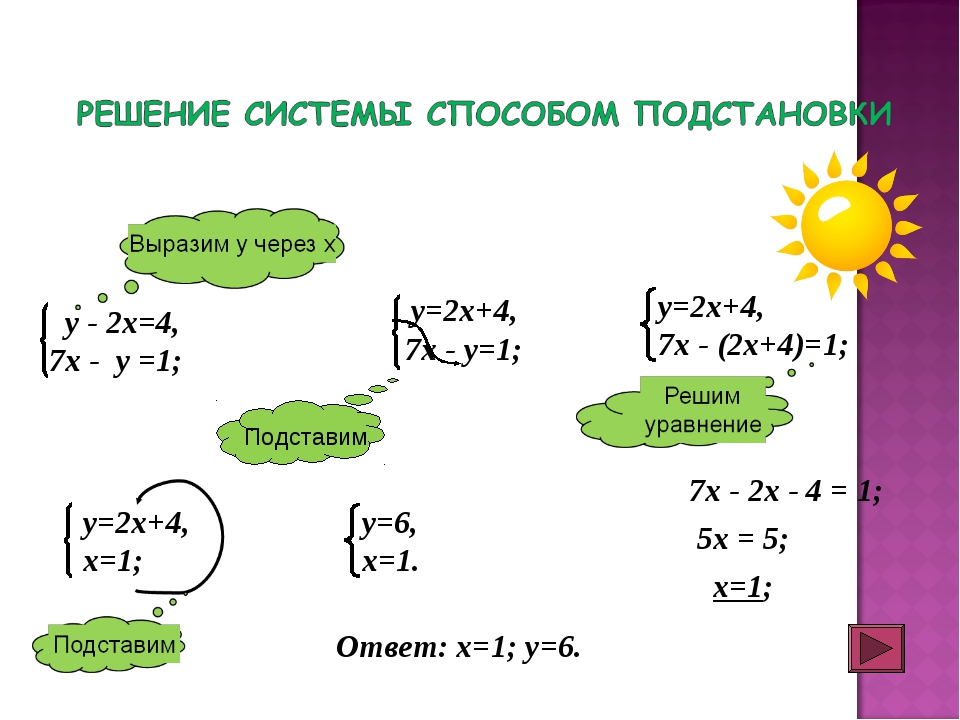 Здесь мы хотим добавить. -2 y + 3 y — это всего лишь y . И 6 + 1 равно 7. Итак, y = 7.
Здесь мы хотим добавить. -2 y + 3 y — это всего лишь y . И 6 + 1 равно 7. Итак, y = 7.
Теперь подставьте 7, чтобы получить y в одном из уравнений. 2 x — 7 = 3. 2 x = 10. x = 5.
Давайте проверим наши ответы. 2 x — y = 3 становится 2 (5) — 7 = 3. Это 10 — 7 = 3, так что это работает. И -4 x + 3 y = 1 становится -4 (5) + 3 (7) = 1. Это -20 + 21 = 1, так что это тоже работает.Мы сделали это!
Краткое содержание урока
В общем, свадьбы — это сложно. Также мы практиковались в решении систем уравнений . Есть два распространенных метода решения систем уравнений. Первый — это метод замены . Это включает в себя решение одного из уравнений для одной из переменных, а затем замену результата для этой переменной в другое уравнение. Другой метод — это метод исключения . Этот метод включает в себя сложение уравнений и умножение членов в одно так, чтобы при сложении или вычитании уравнений одна из переменных исчезла.
Результат обучения
После просмотра этого видеоурока вы должны уметь решать системы уравнений с двумя неизвестными переменными как методом подстановки, так и методом исключения.
предварительное вычисление алгебры — Как решить систему двух линейных уравнений с двумя неизвестными?
предварительное вычисление алгебры — Как решить систему двух линейных уравнений с двумя неизвестными? — Обмен математическими стеками
Сеть обмена стеком
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.
Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
744 раза
$ \ begingroup $
Как решить эту систему уравнений?
$$ \ begin {case} 7 (a + b) = b-a \\ 4 (3a + 2b) = b-8 \ end {cases} $$
Прогресс
Я пробовал и замену, и исключение, но когда я освобождаю $ a $ или $ b $ с одной стороны, я продолжаю получать $ a $ или $ b $ также и с другой стороны.
Создан 06 сен.
$ \ endgroup $
3
$ \ begingroup $
$$ 7 \ cdot (a + b) = b — a \ Rightarrow a = — \ dfrac {6} {8} b $$
Заменить a во втором уравнении
$$ 4 \ cdot (3a + 2b) = b-8 \ Rightarrow 12a + 7b = -8 $$
$$ 7b + 12 \ cdot \ left (- \ dfrac {6} {8} b \ right) = -8 $$
В этом уравнении есть только $ b $ неизвестных, поэтому решите для $ b $, а затем используйте $ b $, чтобы найти $ a $
Создан 06 сен.
Уоррен ХиллУоррен Хилл
2,9141212 серебряных знаков2424 бронзовых знака
$ \ endgroup $
$ \ begingroup $
Подсказка:
Попробуйте выполнить алгебру над обоими уравнениями, пока не получите символы $ a $ и $ b $ с одной стороны и число с другой.Затем посмотрите, сможете ли вы «объединить» их вместе.
Создан 06 сен.
$ \ endgroup $
$ \ begingroup $
$$ 7 (a + b) = ba \ Rightarrow 7a + 7b = ba \ Rightarrow 7a + a = b-7b \ Rightarrow 8a = -6b \ Rightarrow a = — \ frac {6} {8} b \\ \ Rightarrow a = — \ frac {3} {4} b \\ 4 (3a + 2b) = b-8 \ Rightarrow 12a + 8b = b-8 \ Rightarrow 12a = b-8b-8 \ Rightarrow 12a = -7b-8 \ overset {a = — \ frac {3} {4} b} {\ Rightarrow} 12 \ left (- \ frac {3} {4} b \ right) = -7b-8 \ Rightarrow -9b = -7b- 8 \ Rightarrow -9b + 7b = -8 \ Rightarrow -2b = -8 \\ \ Rightarrow b = 4 $$
Заменяя на $ a = — \ frac {3} {4} b $, получаем $ a = — \ frac {3} {4} 4 \ Rightarrow a = -3 $
Создан 06 сен.
Мэри СтарМэри Стар
11.7k99 золотых знаков3636 серебряных знаков119119 бронзовых знаков
$ \ endgroup $
$ \ begingroup $
ВНИМАНИЕ: это нестандартный подход.
В обоих уравнениях выделите переменную $ a $ в LHS:
Из $$ 7 (a + b) = b-a \ следует 8a = -6b \ следует 4a = -3b, $$
$$ 4 (3a + 2b) = b-8 \ подразумевает12a = -7b-8. $$
Теперь приравняем два:
$$ (12a =) — 9b = -7b-8.$$
Это уравнение с одной неизвестной ($ b $).
$$ — 2b = -8 \ подразумевает b = 4, $$
а также
$$ 4a = -3b \ подразумевает a = -3. $$
Создан 06 сен.
Ив ДаустИв Дауст
1k1414 золотых знаков120120 серебряных знаков306306 бронзовых знаков
$ \ endgroup $
$ \ begingroup $
Подсказка: из первого уравнения имеем $$ a = — \ frac {3} {4} b.
$
Теперь подставьте это во второе уравнение, и вы получите уравнение в $ b $. Решите это (для $ b $), затем найдите $ a $ (снова), используя тот факт, что $$ a = — \ frac {3} {4} b. $$
Создан 06 сен.
бип-буп
11k88 золотых знаков4040 серебряных знаков6868 бронзовых знаков
$ \ endgroup $
$ \ begingroup $
Вот другой подход:
$ \ begin {cases} 7 (a + b) = ba \\ 4 (3a + 2b) = b-8 \ end {ases} $ $ \ Leftrightarrow $ $ \ begin {cases} 8a + 6b = 0 \\ 12a + 7b = -8 \ end {cases}
долларов США
Затем
$ \ begin {bmatrix} 8 & 6 & 0 \\ 12 & 7 & -8 \ end {bmatrix} $ $ \ Leftrightarrow $ $ \ begin {bmatrix} 1 & 3/4 & 0 \\ 12 & 7 & -8 \ end {bmatrix} $ $ \ Leftrightarrow $ $ \ begin {bmatrix} 1 & 3/4 & 0 \\ 0 & -2 & -8 \ end {bmatrix} $ $ \ Leftrightarrow $ $ \ begin {bmatrix} 1 & 3/4 & 0 \\ 0 & 1 & 4 \ end {bmatrix} $ $ \ Leftrightarrow $ $ \ begin {bmatrix } 1 & 0 & -3 \\ 0 & 1 & 4 \ end {bmatrix}
долларов США
Результат: $ a = -3 $ a и $ b = 4 $.
Создан 06 сен.
Аарон Мароя
16.8k55 золотых знаков2020 серебряных знаков5353 бронзовых знака
$ \ endgroup $
Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
Решение линейных уравнений с двумя неизвестными
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Задачи о смеси (системы уравнений с двумя переменными)
Задачи о смеси (системы уравнений с двумя переменными)
Проблемы со смесью
Сколько унций 20% раствора соляной кислоты и
70% раствор соляной кислоты необходимо смешать, чтобы получить 20 унций 50% раствора.
раствор соляной кислоты?
Что мы пытаемся найти в этой проблеме?
Мы хотим знать необходимое количество 20% раствора кислоты, и мы хотим знать
необходимое количество 70% раствора кислоты.Нам понадобится переменная для
представляют каждое из этих неизвестных:
x = необходимо 20% раствора
г = необходимо унции 70% раствора
Поскольку у нас есть два неизвестных, нам придется написать систему
двух переменных для поиска неизвестных.
Чтобы помочь нам организовать информацию в задаче, давайте
представьте, что мы в лаборатории, глядя на две бутылки с кислотой, которые мы
собирается смешаться вместе. На одной из бутылок написано «20%», и на ней
в нем x унций жидкости.Другая бутылка помечена надписью «70%», и
в нем y унций жидкости. Вот как выглядят две бутылки
нравиться; количество кислоты в каждой бутылке указано под бутылками:
Если мы объединим две бутылки с кислотой, мы получим 20
унций 50% раствора кислоты. Объединение (сложение) двух
бутылки с кислотой можно показать, добавив к нашему рисунку:
х унций | + | y унций | = | 20 унций |
Первое из наших уравнений будет происходить от суммы
жидкость в бутылках — добавление жидкости в две бутылки приведет к
дайте нам 20 унций раствора:
х + у = 20
Второе из двух наших уравнений будет происходить от суммы
чистой кислоты в каждой бутылке.
В первой бутылке 20% x унций жидкости
чистая кислота, поэтому количество чистой кислоты в первой бутылке составляет 0,20x.
Во второй бутылке 70% годовых
жидкость — это чистая кислота, поэтому количество чистой кислоты во второй бутылке равно
.70г.
В комбинированной смеси 50% от 20 унций
жидкости — это чистая кислота, поэтому количество чистой кислоты в комбинированной смеси
составляет 0,50 (20).
| чистая кислота в первой бутылке | + | чистая кислота во втором баллоне | = | кислота чистая в смеси |
Так
.20x + 0,70y = 0,50 (20)
или же
.20x + .70y = 10
Умножьте обе части этого уравнения на 10, чтобы
очистить десятичные дроби:
2x + 7y = 100
Это второе уравнение, которое мы будем использовать.
Теперь решите систему уравнений.
2х + 7у = 100
х + у = 20
Умножьте второе уравнение на -2, затем сложите два уравнения.
все вместе:
2х + 7у = 100
-2x — 2y = -40
5лет = 60
у = 12
Нам понадобится 12 унций 70% раствора кислоты.
Чтобы найти необходимое количество 20% раствора кислоты, замените
12 для y в любом уравнении; мы воспользуемся более простым уравнением:
х + у = 20
х + 12 = 20
х = 8
Итак, потребуется 8 унций 20% раствора кислоты.
Решение системы линейных уравнений с двумя переменными — концепция
Система линейных уравнений — это два или более уравнений, содержащих одинаковые переменные.Решения системы уравнений — это точка пересечения линий. Существует четыре метода решения систем линейных уравнений : построение графиков, подстановка, исключение и матрицы. Решение систем уравнений впервые появляется в алгебре I, но более сложные приложения встречаются в алгебре II.
Решение системы линейных уравнений с двумя переменными, поэтому, если вы помните, линейное уравнение — это в основном просто уравнение для линии, и когда мы решаем систему, мы смотрим на два уравнения, поэтому у нас есть две линии, и мы пытаемся выяснить, где пересекаются эти две линии, и если они вообще пересекаются, хорошо, значит, это может произойти тремя способами, хорошо? У нас есть две линии, которые могут пересекаться в одной точке, что означает, что у нас будет один ответ, который будет координатной точкой xy, скажем, 2, -4, что-то в этом роде.
Другая ситуация, которая может возникнуть, эти линии могут быть параллельны, что означает, что у них не будет никакого пересечения этих линий, у них не будет никакого решения, где эти две линии равны друг другу и, наконец, эти два уравнения может быть для одной и той же точной линии, что означает, что у нас будет бесконечное количество точек, лежащих на любой из этих линий, которые дадут нам решение, хорошо, и поэтому мы собираемся поговорить о каждой из этих .
Существует несколько различных способов решения этих проблем, вы можете решить их графически, и в Алгебре 2 мы обычно не делаем слишком много этого решения графически. это, и вы увидите, где они пересекаются, хорошо, поэтому мы знаем, как это сделать, но на самом деле это не даст нам математического ответа, мы не сможем найти эту точку, если наши графики не будут полностью точными, что является своего рода трата времени, поэтому мы можем сделать это алгебраически, и в нашем распоряжении есть два способа: подстановка, когда мы решаем переменную и вставляем ее, или исключение, когда мы складываем или вычитаем два уравнения в надежде избавиться от одной из переменных so.
Системы линейных уравнений, в основном касающиеся того, как линии пересекаются или не пересекаются, и у нас есть несколько способов сделать это, а именно замена или исключение.
Систем уравнений с более чем двумя переменными
Чтобы решить любую систему линейных уравнений, вам необходимо иметь, по крайней мере, такое же количество независимых уравнений, как количество переменных. Затем это может быть решено с помощью алгебраического метода или метода алгебраического исключения.Вы можете применить любой метод достаточно раз, чтобы свести каждое отношение из системы трех или более уравнений с 3 или более переменными к системе из 2 уравнений и двух переменных.
Пример
Решите относительно x, y и z:
$$ 2x — y + 6z = 1 \ text {(уравнение 1)} $$
$$ x — y + z = 2 \ text {(уравнение 2)} $$
$$ x + y + z = 1 \ text {(уравнение 3)} $$
Шагов для решения:
1) Решите уравнение 1 относительно y. После применения базовых навыков алгебры уравнение 1 превращается в \ (y = 2x + 6z — 1 \).
2) Подставьте значение y, равное \ ((2x + 6z -1) \), в уравнения 2 и 3. Уравнение 2 принимает следующий вид:
$$ x — y + z = 2 $$
$$ x — (2x + 6z -1) + z = 2 $$
$$ x -2x — 6z + 1 = 2 $$
$$ -x — 6z = 2-1 $$
$$ -x -6z = 1 $$
… и уравнение 3 становится:
$$ x + y + z = 1 $$
$$ x + 2x + 6z -1 + z = 1 $$
$$ 3x + 7z -1 = 1 $$
$$ 3x + 7z = -1 + 1 $$
$$ 3x + 7z = 0 $$
Теперь мы подошли к системе двух уравнений и двух переменных. Вот два уравнения и две переменные:
$$ -x — 6z = 1 \ text {(новое уравнение A)} $$
$$ 3x + 7z = 0 \ text {(новое уравнение B)} $$
3) Решите уравнение A относительно x:
$$ -x — 6z = 1 $$
$$ -x = 6z + 1 $$
$$ x = -6z — 1 $$
4) Подставьте значение x в уравнение B, чтобы найти z:
$$ 3x + 7z = 0 $$
$$ 3 (-6z — 1) + 7z = 0 $$
$$ -18z — 3 + 7z = 0 $$
$$ -11z — 3 = 0 $$
$$ -11z = 3 $$
$$ z = \ frac {-11} {3} $$
5) Теперь подставьте значение z в уравнение A, чтобы найти x:
$$ -x — 6z = 1 $$
$$ -x -6 \ frac {-11} {3} = 1 $$
$$ -x + 22 = 1 $$
$$ -x = -22 + 1 $$
$$ -x = -21 $$
$$ x = 21 $$
6) Наконец, вернитесь к ЛЮБОМУ из исходных 3 уравнений, чтобы найти значение y, подставив найденные вами значения на x и z.Я выберу уравнение 3.
$$ x + y + z = 1 $$
$$ 21 + y — \ frac {11} {3} = 1 $$
$$ \ frac {52} {3} + y = 1 $$
$$ y = \ frac {-52} {3} + 1 $$
$$ y = \ frac {-49} {3} $$
Окончательный ответ:
$$ x = 21, y = \ frac {-49} {3}, z = \ frac {-11} {3} $$
Бывают случаи, когда НИКАКОЕ решение системы невозможно. Решение системы происходит там, где графики уравнений пересекаются или встречаются. Из-за этого мы можем сказать, что параллельные линии (которые имеют одинаковый наклон) НЕ имеют решения, потому что параллельные линии никогда не пересекаются, не касаются и не встречаются.
Эти две линии никогда не пересекаются и, следовательно, не имеют пересечения:
Также можно столкнуться с вопросом, где ОБА уравнения разделяют ОДНУ ЛИНИЮ на плоскости xy. Например, \ (2r -s = 5 \) и \ (4r — 2s = 10 \) могут быть сокращены до \ (s = 2r — 5 \). Эти два уравнения разделяют ОДНУ ЛИНИЮ на плоскости xy. Они не являются независимыми, и единственного решения для системы не существует.
Первоначально принадлежит г-ну Фелизу, © 2005
Два уравнения с двумя неизвестными
У нас есть два ответа для вас
Привет Мэри.
Два уравнения могут находиться в одном из трех соотношений друг с другом:
- Это разные выражения одной и той же строки. Например, y = 2x и 2y = 4x на самом деле одна и та же линия. В этом случае существует «бесконечно много решений», потому что существует бесконечное количество значений x, которые дают значение для y, совпадающее в обоих уравнениях. Также обратите внимание, что в этом случае наклоны и точки пересечения по оси Y двух уравнений будут совпадать.
- Это параллельные прямые.Например, y = 2x и y = 2x + 1 параллельны. Параллельные линии имеют одинаковый наклон, но разные точки пересечения по оси y. Поскольку нет точек (x, y), которые одновременно находятся на обеих линиях, мы говорим, что «нет решения».
- Они пересекаются в одной точке. Единственный момент — это «уникальное решение». Это может быть только в том случае, если два уравнения имеют
разные склоны. Перехват y не имеет значения.
Чтобы определить, какой из этих случаев у вас есть для данной пары уравнений, часто проще всего написать оба уравнения в форме y = mx + b и сравнить наклоны, а затем, при необходимости, сравнить точки пересечения y.Однако это не скажет вам, что на самом деле представляет собой уникальное решение (если они пересекаются в одной точке, а не являются идентичными или параллельными линиями).
Вот как обстоят дела, когда вы используете метод подстановки для «решения» двух уравнений:
Пример 1:
2x + y = 1
-3x + 2y = 0Решите одно уравнение для одной переменной (какую? Просто выберите то, что выглядит проще всего!)
2x + y = 1
y = 1-2xЗатем подставьте это выражение (которое равно y) вместо y в другом уравнении.Таким образом,
-3x + 2y = 0
становится
-3x + 2 (1-2x) = 0И решите относительно x:
-3x + 2 — 4x = 0
-7x = -2
x = 2/7.Поскольку он дал нам единственное значение x, я знаю, что мы получим уникальное решение. Я использую это значение x, чтобы найти значение y. Просто выберите одно из исходных уравнений (неважно какое) и замените x на 2/7.
2x + y = 1
становится
2 (2/7) + y = 1
y = 3/7.Итак, единственное решение этой пары уравнений — (2/7, 3/7).
Давайте посмотрим на две другие ситуации, чтобы увидеть, что могло бы произойти.
Пример 2:
2x + y = 1
-2x — y = 2Решите первое относительно y:
y = 1-2xПодставляем во второе уравнение:
-2x — (1 — 2x) = 2
-2x — 1 + 2x = 2
-1 = 2.Очевидно, противоречие! Значит, решения нет. Эти два уравнения представляют собой параллельные линии.
Пример 3:
2x + y = 1
6x + 3y = 3Решите первое относительно y:
y = 1-2xПодставляем во второе уравнение:
6x + 3 (1 — 2x) = 3
6x + 3 — 6x = 3
3 = 3.Это трюизм: это верно независимо от значения x, поэтому существует бесконечное количество решений. Эти два уравнения на самом деле являются всего лишь двумя способами выражения одного и того же уравнения (умножьте первое уравнение на 3 с обеих сторон, и вы убедитесь в этом).
Я надеюсь, что это объяснение и набор примеров помогут вам решить любые ваши проблемы с двумя линейными уравнениями.
Cheers,
Стивен Ла Рок.
Привет Мэри,
Фактически не решая эту систему уравнений, мы можем определить, что на самом деле будет ТОЛЬКО ОДНО решение. Первое уравнение имеет наклон -4 (мы можем изменить его, чтобы читать y = -4x + 4), а второе уравнение имеет наклон -1/4 (мы можем изменить его, чтобы читать y = -1 / 4x).Когда две линии имеют разные уклоны, они гарантированно пересекаются в одной точке, что дает нам одно решение.
Если бы у этой системы не было решений или было бы бесконечно много решений, уравнения должны были бы иметь одинаковый наклон. Кроме того, они должны были бы иметь разные точки пересечения по оси Y, чтобы не было решения, и одну точку пересечения по оси Y, чтобы иметь бесконечно много решений.
