{\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).
Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).
И по условию, эта степень равна \( 2\): \( \displaystyle {{x}^{2}}=x+2\). {2}}-x-2=0\).
{2}}-x-2=0\).
Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.
\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)
Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\). Если корней несколько, в ответе укажите меньший из них.
Решение:
\( \displaystyle {{\log }_{x+1}}\left( 2x+5 \right)=2\).
В первую очередь напишем ОДЗ:
\( \displaystyle \left\{ \begin{array}{l}x+1>0\\x+1\ne 1\\2x+5>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0\\x>-\frac{5}{2}\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>-1\\x\ne 0.\end{array} \right.\)
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание \( \displaystyle x+1\), чтобы получить аргумент \( \displaystyle 2x+5\)?
Хотите читать учебник без ограничений? Зарегистрируйтесь:
Во вторую. То есть:
\( \displaystyle {{\left( x+1 \right)}^{2}}=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}+2x+1=2x+5\text{ }\Leftrightarrow \text{ }{{x}^{2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2. \end{array} \right.\)
\end{array} \right.\)
Казалось бы, меньший корень равен \( \displaystyle -2\). Но это не так: согласно ОДЗ корень \( \displaystyle x=-2\) – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: \( \displaystyle x=2\).
Ответ: \( \displaystyle x=2\).
Содержание
Калькулятор онлайн — Решение логарифмических уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Логарифмическая функция. Логарифмы
Задача 1. Найти положительный корень уравнения x4 = 81
По определению арифметического корня имеем \( x = \sqrt[4]{81} = 3 \)
Задача 2. Решить уравнение 3x = 81
Запишем данное уравнение так: 3x = 34, откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. {-2} = \frac{1}{25}$$
{-2} = \frac{1}{25}$$
Решить уравнение log3(1-x) = 2
По определению логарифма 32 = 1 — x, откуда x = -8
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются
различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
1) loga(bc) = logab + logac
2) \( \log_a \frac{b}{c} = \log_a b — \log_a c \)
3) logabr = r logab
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора.
И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение. {\infty} \frac{1}{n!} $$
{\infty} \frac{1}{n!} $$
$$ e \approx 2,7182818284 $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.
Для этого используется формула замены основания логарифма:
$$ \log_a b = \frac{\log_c b}{\log_c a} $$
где b > 0, a > 0, \( a \neq 1 \), c > 0, \( c \neq 1 \)
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$
Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, \( a \neq 1 \)
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0
5) Если a > 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0
Если 0 ax принимает положительные значения при 0
отрицательные при х > 1.
Ось Oy является вертикальной асимптотой графика функции y = logax
Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Теорема. Если logax1 = logax2 где a > 0, \( a \neq 1 \),
x1 > 0, x2 > 0, то x1 = x2
Логарифмическая функция y = logax и показательная функция y = ax, где a > 0, \( a \neq 1 \), взаимно обратны.
Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х2 + 4х + 3 = 8, т.е. х2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т. е. х = -5 не является корнем этого
е. х = -5 не является корнем этого
уравнения.
Ответ x = 1
Решить уравнение lg(2x2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x2 — 4x + 12) = lg(x2 + 3x)
откуда
2x2 — 4x + 12 = x2 + 3x
x2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Как решить логарифмическое уравнение: подробное объяснение
Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.
Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.
Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.
- Как решать уравнения с логарифмами: 2 способа с примерами
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Как сделать проверку – это важно
Как решать уравнения с логарифмами: 2 способа с примерами
Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.
Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.
При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!
Давайте посмотрим, как это работает на примере:
Воспользуемся определением логарифма и получим:
2х + 3 = 32
Теперь перед нами простейшее уравнение, решить которое не составит труда:
2х + 3 = 9
2х = 6
х = 3
Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 32 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Ответ: х = 3
Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
Поэтому мы покажем еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:
Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.
Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Для этого вспоминаем еще одно свойство логарифма:
Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
2х + 3 = 32
2х + 3 = 9
2х = 6
х = 3
Ответ: х = 3
Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:
3х – 5 = 4
3х = 9
х = 3
Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Следовательно, х = 3 является корнем уравнения.
Ответ: х = 3
Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:
Решим данное квадратное уравнение, найдем дискриминант:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:Верно, следовательно, х1 = 1 является корнем уравнения.
Теперь подставим х2 = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Ответ: х = 1
Пример решения логарифмического уравнения с разными основаниями
Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,
А что же делать, если основания у логарифмов разные? Например,
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:
Мы знаем, что 1/3 = 3-1. Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.
Ответ: х = 4.
Пример решения логарифмического уравнения с переменными основаниями
Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т. е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х2+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х2+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
1. Аргумент логарифма должен быть больше ноля, следовательно:
2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:
Сведем все требования в систему:
Данную систему требований мы можем упростить. Смотрите х2+5х-5 больше ноля, при этом оно приравнивается к (х + 1)2, которую в свою очередь так же больше ноля. Следовательно, требование х2+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Смотрите х2+5х-5 больше ноля, при этом оно приравнивается к (х + 1)2, которую в свою очередь так же больше ноля. Следовательно, требование х2+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:
Т.к. 32=9, то последнее выражение верно.
Ответ: х = 2
Как сделать проверку
Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т. е. больше ноля.
е. больше ноля.
Если наше уравнение имеет вид loga (f(x)) = loga (g(x)), то должны выполняться следующие ограничения:
После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!
Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.
Простейшие логарифмические уравнения
Сегодня мы научимся решать самые простые логарифмические уравнения, где не требуются предварительные преобразования и отбор корней. Но если научиться решать такие уравнения, дальше будет намного проще.
Простейшее логарифмическое уравнение — это уравнение вида logaf (x) = b, где a, b — числа (a > 0, a ≠ 1), f (x) — некоторая функция.
Отличительная особенность всех логарифмических уравнений — наличие переменной x под знаком логарифма. Если изначально в задаче дано именно такое уравнение, оно называется простейшим. Любые другие логарифмические уравнения сводятся к простейшим путем специальных преобразований (см. «Основные свойства логарифмов»). Однако при этом надо учитывать многочисленные тонкости: могут возникнуть лишние корни, поэтому сложные логарифмические уравнения будут рассмотрены отдельно.
Как решать такие уравнения? Достаточно заменить число, стоящее справа от знака равенства, логарифмом по тому же основанию, что и слева. Затем можно избавиться от знака логарифма. Получим:
Затем можно избавиться от знака логарифма. Получим:
logaf (x) = b ⇒ logaf (x) = logaab ⇒ f (x) = ab
Получили обычное уравнение. Его корни являются корнями исходного уравнения.
Вынесение степеней
Зачастую логарифмические уравнения, которые внешне выглядят сложно и угрожающе, решаются буквально в пару строчек без привлечения сложных формул. Сегодня мы рассмотрим именно такие задачи, где все, что от вас потребуется — аккуратно свести формулу к канонической форме и не растеряться при поиске области определения логарифмов.
Сегодня, как вы уже наверняка догадались из названия, мы будем решать логарифмические уравнения по формулам перехода к канонической форме. Основной «фишкой» данного видеоурока будет работа со степенями, а точнее, вынесение степени из основания и аргумента. Давайте рассмотрим правило:
Давайте рассмотрим правило:
Аналогичным образом можно вынести степень и из основания:
Как видим, если при вынесении степени из аргумента логарифма у нас просто появляется дополнительный множитель спереди, то при вынесении степени из основания — не просто множитель, а перевернутый множитель. Это нужно помнить.
Наконец, самое интересное. Данные формулы можно объединить, тогда мы получим:
Разумеется, при выполнении данных переходов существуют определенные подводные камни, связанные с возможным расширением области определения или, наоборот, сужением области определения. Судите сами:
log3x2 = 2 ∙ log3x
Если в первом случае в качестве x могло стоять любое число, отличное от 0, т. е. требование x ≠ 0, то во втором случае нас устроят лишь x, которые не только не равны, а строго больше 0, потому что область определения логарифма состоит в том, чтобы аргумент был строго больше 0. Поэтому напомню вам замечательную формулу из курса алгебры 8—9 класса:
То есть, мы должны записать нашу формулу следующим образом:
log3x2 = 2 ∙ log3 |x|
Тогда никакого сужения области определения не произойдет.
Однако в сегодняшнем видеоуроке никаких квадратов не будет. Если вы посмотрите на наши задачи, то увидите только корни. Следовательно, применять данное правило мы не будем, однако его все равно необходимо держать в голове, чтобы в нужный момент, когда вы увидите квадратичную функцию в аргументе или основании логарифма, вы вспомните это правило и все преобразования выполните верно.
Итак, первое уравнение:
Для решения такой задачи предлагаю внимательно посмотреть на каждое из слагаемых, присутствующих в формуле.
Давайте перепишем первое слагаемое в виде степени с рациональным показателем:
Смотрим на второе слагаемое: log3 (1 − x). Здесь делать ничего не нужно, здесь все уже преобразовании.
Наконец, 0, 5. Как я уже говорил в предыдущих уроках, при решении логарифмических уравнений и формул очень рекомендую переходить от десятичных дробей к обычным. Давайте так и сделаем:
0,5 = 5/10 = 1/2
Перепишем наше исходную формулу с учетом полученных слагаемых:
log3 (1 − x) = 1
Теперь переходим к канонической форме:
log3 (1 − x) = log3 3
Избавляемся от знака логарифма, приравнивая аргументы:
1 − x = 3
−x = 2
x = −2
Все, мы решили уравнение. Однако давайте все-таки подстрахуемся и найдем область определения. Для этого вернемся к исходной формуле и посмотрим:
Однако давайте все-таки подстрахуемся и найдем область определения. Для этого вернемся к исходной формуле и посмотрим:
1 − x > 0
−x > −1
x < 1
Наш корень x = −2 удовлетворяет это требование, следовательно, x = −2 является решением исходного уравнения. Вот теперь мы получили строгое четкое обоснование. Все, задача решена.
Переходим ко второй задаче:
Давайте разбираться с каждым слагаемым отдельно.
Выписываем первое:
Первое слагаемое мы преобразовали. Работаем со вторым слагаемым:
Наконец, последнее слагаемое, которое стоит справа от знака равенства:
Подставляем полученные выражения вместо слагаемых в полученной формуле:
log3x = 1
Переходим к канонической форме:
log3x = log3 3
Избавляемся от знака логарифма, приравнивая аргументы, и получаем:
x = 3
Опять же, давайте на всякий случай подстрахуемся, вернемся к исходному уравнению и посмотрим. В исходной формуле переменная x присутствует только в аргументе, следовательно,
В исходной формуле переменная x присутствует только в аргументе, следовательно,
x > 0
Во втором логарифме x стоит под корнем, но опять же в аргументе, следовательно, корень должен быть больше 0, т. е. подкоренное выражение должно быть больше 0. Смотрим на наш корень x = 3. Очевидно, что он удовлетворяет это требование. Следовательно, x = 3 является решением исходного логарифмического уравнения. Все, задача решена.
Ключевых моментов в сегодняшнем видеоуроке два:
1) не бойтесь преобразовывать логарифмы и, в частности, не бойтесь выносить степени за знак логарифма, при этом помните нашу основную формулу: при вынесении степени из аргумента она выносится просто без изменений как множитель, а при вынесении степени из основания эта степень переворачивается.
2) второй момент связан с само канонической формой. Переход к канонической форме мы выполняли в самом конце преобразования формулы логарифмического уравнения. Напомню следующую формулу:
a = logbba
Разумеется, под выражением «любое число b», я подразумеваю такие числа, которые удовлетворяют требования, накладываемые на основание логарифма, т. е.
е.
1 ≠ b > 0
Вот при таких b, а поскольку основание у нас уже известно, то это требование будет выполняться автоматически. Но при таких b — любых, которые удовлетворяют данное требование — данный переход может быть выполнен, и у нас получится каноническая форма, в которой можно избавиться от знака логарифма.
Расширение области определения и лишние корни
В процессе преобразования логарифмических уравнений может произойти неявное расширение области определения. Зачастую ученики этого даже не замечают, что приводит к ошибкам и неправильным ответам.
Начнем с простейших конструкций. Простейшим логарифмическим уравнением называется следующее:
logaf(x) = b
Обратите внимание: x присутствует лишь в одном аргументе одного логарифма. Как мы решаем такие уравнения? Используем каноническую форму. Для этого представляем число b = logaab, и наше уравнение перепишется в следующем виде:
logaf(x) = logaab
Данная запись называется канонической формой. Именно к ней следует сводить любое логарифмическое уравнение, которое вы встретите не только в сегодняшнем уроке, но и в любой самостоятельной и контрольной работе.
Именно к ней следует сводить любое логарифмическое уравнение, которое вы встретите не только в сегодняшнем уроке, но и в любой самостоятельной и контрольной работе.
Как прийти к канонической форме, какие приемы использовать — это уже вопрос практики. Главное понимать: как только вы получите такую запись, можно считать, что задача решена. Потому что следующим шагом будет запись:
f(x) = ab
Другими словами, мы избавляемся от знака логарифма и просто приравниваем аргументы.
К чему весь этот разговор? Дело в том, что каноническая форма применима не только к простейшим задачам, но и к любым другим. В частности и к тем, которые мы будем решать сегодня. Давайте посмотрим.
Первая задача:
В чем проблема данного уравнения? В том, что функция стоит сразу в двух логарифмах. Задачу можно свести к простейшей, просто вычтя один логарифм из другого. Но возникают проблемы с областью определения: могут появиться лишние корни. Поэтому давайте просто перенесем один из логарифмов вправо:
Вот такая запись уже гораздо больше похожа на каноническую форму.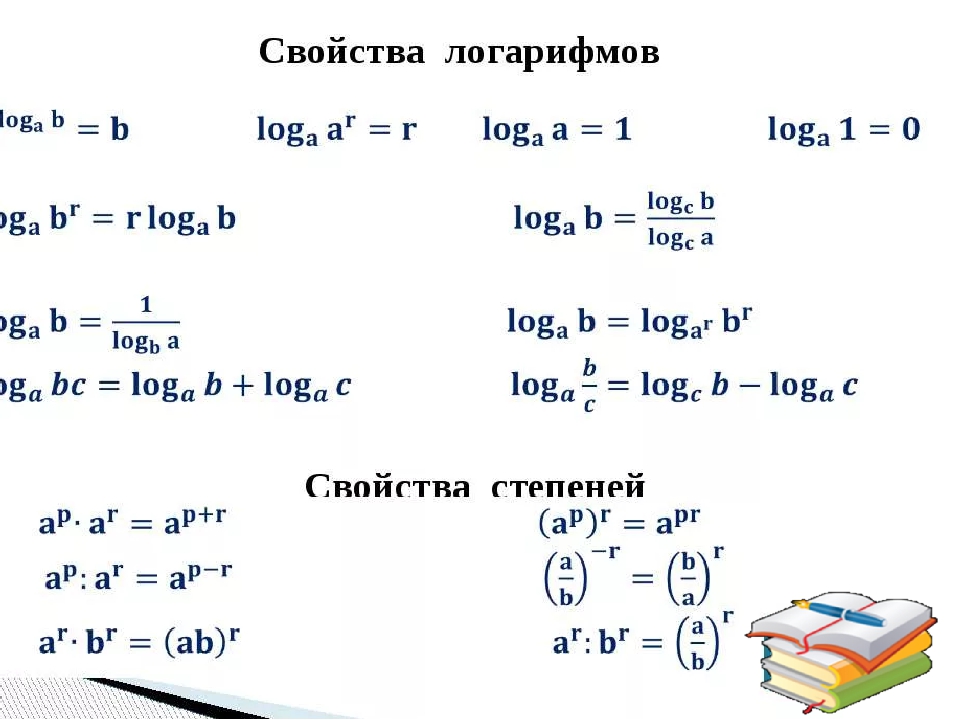 Но есть еще один нюанс: в канонической форме аргументы должны быть одинаковы. А у нас слева стоит логарифм по основанию 3, а справа — по основанию 1/3. Знаит, нужно привести эти основания к одному и тому же числу. Например, вспомним, что такое отрицательные степени:
Но есть еще один нюанс: в канонической форме аргументы должны быть одинаковы. А у нас слева стоит логарифм по основанию 3, а справа — по основанию 1/3. Знаит, нужно привести эти основания к одному и тому же числу. Например, вспомним, что такое отрицательные степени:
1/3 = 3−1
А затем воспользуемся вынесем показатель «−1» за пределы log в качестве множителя:
Обратите внимание: степень, которая стояла в основании, переворачивается и превращается в дробь. Мы получили почти каноническую запись, избавившись от разных оснований, но взамен получили множитель «−1» справа. Давайте внесем этот множитель в аргумент, превратив его в степень:
Разумеется, получив каноническую форму, мы смело зачеркиваем знак логарифма и приравниваем аргументы. При этом напомню, что при возведении в степень «−1» дробь просто переворачивается — получается пропорция.
Воспользуемся основным свойством пропорции и перемножим ее крест-накрест:
(x− 4) (2x− 1) = (x− 5) (3x− 4)
2x2 − x− 8x + 4 = 3x2 − 4x− 15x + 20
2x2 − 9x + 4 = 3x2 − 19x + 20
x2 − 10x + 16 = 0
Перед нами приведенное квадратное уравнение, поэтому решаем его с помощью формул Виета:
(x − 8)(x − 2) = 0
x1 = 8; x2 = 2
Вот и все. Думаете, уравнение решено? Нет! За такое решение мы получим 0 баллов, потому что в исходном уравнении присутствуют сразу два логарифма с переменной x. Поэтому требуется учесть область определения.
Думаете, уравнение решено? Нет! За такое решение мы получим 0 баллов, потому что в исходном уравнении присутствуют сразу два логарифма с переменной x. Поэтому требуется учесть область определения.
И здесь начинается самое веселое. Большинство учеников путаются: в чем состоит область определения логарифма? Разумеется, все аргументы (у нас их два) должны быть больше нуля:
(x− 4)/(3x− 4) > 0
(x− 5)/(2x− 1) > 0
Каждое из этих неравенств нужно решить, отметить на прямой, пересечь — и только потом посмотреть, какие корни лежат на пересечении.
Скажу честно: такой прием имеет право на существование, он надежный, и вы получите правильный ответ, однако в нем слишком много лишних действий. Поэтому давайте еще раз пройдемся по нашему решению и посмотрим: где именно требуется применить область определения? Другими словами, нужно четно понимать, когда именно возникают лишние корни.
- Изначально у нас было два логарифма. Потом мы перенесли один из них вправо, но на область определения это не повлияло.
- Затем мы выносим степень из основания, но логарифмов все равно остается два, и в каждом из них присутствует переменная x.
- Наконец, мы зачеркиваем знаки log и получаем классическое дробно-рациональное уравнение.
Именно на последнем шаге происходит расширение области определения! Как только мы перешли к дробно-рациональному уравнению, избавившись от знаков log, требования к переменной xрезко поменялись!
Следовательно, область определения можно считать не в самом начале решения, а только на упомянутом шаге — перед непосредственным приравниваем аргументов.
Здесь-то и кроется возможность для оптимизации. С одной стороны, от нас требуется, чтобы оба аргумента были больше нуля. С другой — далее мы приравниваем эти аргументы. Следовательно, если хотя бы один и них будет положителен, то и второй тоже окажется положительным!
Вот и получается, что требовать выполнение сразу двух неравенств — это излишество. Достаточно рассмотреть лишь одну из этих дробей. Какую именно? Та, которая проще. Например, давайте разберемся с правой дробью:
(x− 5)/(2x− 1) > 0
Это типичное дробно-рациональное неравенство, решаем его методом интервалов:
Как расставить знаки? Возьмем число, заведомо большее всех наших корней. Например 1 млрд. И подставляем его дробь. Получим положительное число, т.е. справа от корня x = 5 будет стоять знак «плюс».
Затем знаки чередуются, потому что корней четной кратности нигде нет. Нас интересуют интервалы, где функция положительна. Следовательно, x∈ (−∞; −1/2)∪(5; +∞).
Теперь вспоминаем про ответы: x = 8 и x = 2. Строго говоря, это еще не ответы, а лишь кандидаты на ответ. Какой из них принадлежит указанному множеству? Конечно, x = 8. А вот x = 2 нас не устраивает по области определения.
Итого ответом к первому логарифмическому уравнению будет x = 8. Вот теперь мы получили грамотное, обоснованное решение с учетом области определения.
Переходим ко второму уравнению:
log5 (x − 9) = log0,5 4 − log5 (x − 5) + 3
Напоминаю, что если в уравнении присутствует десятичная дробь, то от нее следует избавиться. Другими словами, перепишем 0,5 в виде обычной дроби. Сразу замечаем, что логарифм, содержащий это основание, легко считается:
Это очень важны момент! Когда у нас и в основании, и в аргументе стоят степени, мы можем вынести показатели этих степеней по формуле:
Возвращаемся к нашему исходному логарифмическому уравнению и переписываем его:
log5 (x− 9) = 1 − log5 (x− 5)
Получили конструкцию, довольно близкую к канонической форме. Однако нас смущают слагаемые и знак «минус» справа от знака равенства. Давайте представим единицу как логарифм по основанию 5:
log5 (x − 9) = log5 51 − log5 (x − 5)
Вычтем логарифмы справа (при этом их аргументы делятся):
log5(x − 9) = log5 5/(x− 5)
Прекрасно. Вот мы и получили каноническую форму! Зачеркиваем знаки logи приравниваем аргументы:
(x − 9)/1 = 5/(x − 5)
Это пропорция, которая легко решается умножением крест-накрест:
(x − 9)(x − 5) = 51
x2 − 9x − 5x + 45 = 5
x2 − 14x + 40 = 0
Очевидно, перед нами приведенное квадратное уравнение. Оно легко решается с помощью формул Виета:
(x − 10)(x − 4) = 0
x1 = 10
x2 = 4
Мы получили два корня. Но это не окончательные ответы, а лишь кандидаты, потому что логарифмическое уравнение требует еще и проверки области определения.
Напоминаю: не надо искать, когда каждый из аргументов будет больше нуля. Достаточно потребовать, чтобы один аргумент — либо x − 9, либо 5/(x − 5) — был больше нуля. Рассмотрим первый аргумент:
x − 9 > 0
x > 9
Очевидно, что этому требованию удовлетворяет лишь x = 10. Это и есть окончательный ответ. Все задача решена.
Еще раз ключевые мысли сегодняшнего урока:
- Как только переменная x появляется в нескольких логарифмах, уравнение перестает быть элементарным, и для него придется считать область определения. Иначе можно запросто записать в ответ лишние корни.
- Работу с самой областью определения можно существенно упростить, если выписывать неравенство не сразу, а ровно в тот момент, когда мы избавляемся от знаков log. Ведь когда аргументы приравниваются друг к другу, достаточно потребовать, чтобы больше нуля был лишь один из них.
Разумеется, мы сами выбираем, из какого аргумента составлять неравенство, поэтому логично выбирать самый простой. Например, во втором уравнении мы выбрали аргумент (x − 9) —линейную функцию, в противовес дробно-рациональному второму аргументу. Согласитесь, решать неравенство x − 9 > 0 значительно проще, чем 5/(x − 5) > 0. Хотя результат получается один и тот же.
Данное замечание существенно упрощает поиск ОДЗ, но будьте внимательны: использовать одно неравенство вместо двух можно только том случае, когда аргументы именно приравниваются друг к другу!
Конечно, кто-то сейчас спросит: а что, бывает по-другому? Да, бывает. Например, в самом шаге, когда мы перемножаем два аргумента, содержащие переменную, заложена опасность возникновения лишних корней.
Судите сами: сначала требуется, чтобы каждый из аргументов был больше нуля, но после перемножения достаточно, чтобы их произведение было больше нуля. В результате упускается случай, когда каждая из этих дробей отрицательна.
Поэтому если вы только начинаете разбираться со сложными логарифмическими уравнениями, ни в коем случае не перемножайте логарифмы, содержащие переменную x — уж слишком часто это приведет к возникновению лишних корней. Лучше сделайте один лишний шаг, перенесите одно слагаемое в другую сторону составьте каноническую форму.
Ну, а как поступать в том случае, если без перемножения таких логарифмов не обойтись, мы обсудим в следующем видеоуроке.:)
Еще раз о степенях в уравнении
Сегодня мы разберем довольно скользкую тему, касающуюся логарифмических уравнений, а точнее — вынесение степеней из аргументов и оснований логарифмов.
Я бы даже сказал, речь пойдет о вынесении четных степеней, потому что именно с четными степенями возникает большинство затруднений и при решении реальных логарифмических уравнений.
Начнем с канонической формы. Допустим, у нас есть уравнение вида logaf(x) = b. В этом случае мы переписываем число b по формуле b = logaab. Получается следующее:
logaf(x) = logaab
Затем мы приравниваем аргументы:
f(x) = ab
Канонической формой называется предпоследняя формула. Именно к ней стараются свести любое логарифмическое уравнение, каким бы сложным и страшным оно не казалось на первый взгляд.
Вот давайте и попробуем. Начнем с первой задачи:
Предварительное замечание: как я уже говорил, все десятичные дроби в логарифмическом уравнении лучше перевести ее в обычные:
0,001 = 1/1000
0,5 = 5/10 = 1/2
Перепишем наше уравнение с учетом этого факта. Заметим, что и 1/1000, и 100 являются степенью десятки, а затем вынесем степени отовсюду, где они есть: из аргументов и даже из основания логарифмов:
И вот здесь у многих учеников возникает вопрос: «Откуда справа взялся модуль?» Действительно, почему бы не написать просто (х − 1)? Безусловно, сейчас мы напишем (х − 1), но право на такую запись нам дает учет области определения. Ведь в другом логарифме уже стоит (х − 1), и это выражение должно быть больше нуля.
Но когда мы выносим квадрат из основания логарифма, мы обязаны оставить в основании именно модуль. Поясню почему.
Дело в том, что с точки зрения математики вынесение степени равносильно извлечению корня. В частности, когда из выражения (x− 1)2 выносится квадрат, мы по сути извлекаем корень второй степени. Но корень из квадрата — это не что иное как модуль. Именно модуль, потому что даже если выражение х − 1 будет отрицательным, при возведении в квадрат «минус» все равно сгорит. Дальнейшее извлечение корня даст нам положительное число — уже без всяких минусов.
В общем, чтобы не допускать обидных ошибок, запомните раз и навсегда:
Корень четной степени из любой функции, которая возведена в эту же степень, равен не самой функции, а ее модулю:
Возвращаемся к нашему логарифмическому уравнению. Говоря про модуль, я утверждал, что мы можем безболезненно снять его. Это правда. Сейчас объясню почему. Строго говоря, мы обязаны были рассмотреть два варианта:
- x− 1 > 0 ⇒ |х − 1| = х − 1
- x − 1 < 0 ⇒ |х − 1| = −х + 1
Каждый из этих вариантов нужно было бы решить. Но есть одна загвоздка: в исходной формуле уже присутствует функция (х − 1) без всякого модуля. И следуя области определения логарифмов, мы вправе сразу записать, что х − 1 > 0.
Это требование должно выполняться независимо от всяких модулей и других преобразований, которые мы выполняем в процессе решения. Следовательно, второй вариант рассматривать бессмысленно — он никогда не возникнет. Даже если при решении этой ветки неравенства мы получим какие-то числа, они все равно не войдут в окончательный ответ.
В общем, можно считать, что |х − 1| = х − 1. Тогда наше уравнение перепишется в следующем виде:
Теперь мы буквально в одном шаге от канонической формы логарифмического уравнения. Давайте представим единицу в следующем виде:
1 = logx − 1 (x− 1)1
Кроме того, внесем множитель −4, стоящий справа, в аргумент:
logx − 1 10−4 = logx − 1 (x− 1)
Перед нами каноническая форма логарифмического уравнения. Избавляемся от знака логарифма:
10−4 = x− 1
Но поскольку в основании стояла функция (а не простое число), дополнительно потребуем, чтобы эта функция была больше нуля и не равна единице. Получится система:
Поскольку требование х − 1 > 0 выполняется автоматически (ведь х − 1 = 10−4), одно из неравенств можно вычеркнуть из нашей системы. Второе условие также можно вычеркнуть, потому что х − 1 = 0,0001 < 1. Итого получаем:
х = 1 + 0,0001 = 1,0001
Это единственный корень, который автоматически удовлетворяет всем требованиям области определения логарифма (впрочем, все требования были отсеяны как заведомо выполненные в условиях нашей задачи).
Итак, второе уравнение:
3 log3xx = 2 log9xx2
Чем это уравнение принципиально отличается от предыдущего? Уже хотя бы тем, что основания логарифмов — 3х и 9х — не являются натуральными степенями друг друга. Следовательно, переход, который мы использовали в предыдущем решении, невозможен.
Давайте хотя бы избавимся от степеней. В нашем случае единственная степень стоит во втором аргументе:
3 log3xx = 2 ∙ 2 log9x|x|
Впрочем, знак модуля можно убрать, ведь переменная х стоит еще и в основании, т.е. х > 0 ⇒ |х| = х. Перепишем наше логарифмическое уравнение:
3 log3xx = 4 log9xx
Получили логарифмы, в которых одинаковые аргументы, но разные основания. Как поступить дальше? Вариантов тут множество, но мы рассмотрим лишь два из них, которые наиболее логичны, а самое главное — это быстрые и понятные приемы для большинства учеников.
Первый вариант мы уже рассматривали: в любой непонятной ситуации переводите логарифмы с переменным основанием к какому-нибудь постоянному основанию. Например, к двойке. Формула перехода проста:
Разумеется, в роли переменной с должно выступать нормальное число: 1 ≠ c > 0. Пусть в нашем случае с = 2. Теперь перед нами обычное дробно-рациональное уравнение. Собираем все элементы слева:
Очевидно, что множитель log2x лучше вынести, поскольку он присутствует и в первой, и во второй дроби.
Дальше все просто. Произведение равно нулю, когда хотя бы один из множителей равен нулю:
log2x = 0;
х = 1;
3 log2 9х = 4 log2 3x
Разбиваем каждый log на два слагаемых:
log2 9х = log2 9 + log2x = 2 log2 3 + log2 x;
log2 3x = log2 3 + log2x
Перепишем обе части равенства с учетом этих фактов:
3 (2 log2 3 + log2x) = 4 (log2 3 + log2x)
6 log2 3 + 3 log2x = 4 log2 3 + 4 log2x
2 log2 3 = log2x
Теперь осталось внести двойку под знак логарифма (она превратится в степень: 32 = 9):
log2 9 = log2x
Перед нами классическая каноническая форма, избавляемся от знака логарифма и получаем:
х = 9
Как и предполагалось, этот корень оказался больше нуля. Осталось проверить область определения. Посмотрим на основания:
3х ≠ 1
9х ≠ 1
Но корень x = 9 удовлетворяет этим требованиям. Следовательно, он является окончательным решением.
Вывод из данного решения просто: не пугайтесь длинных выкладок! Просто в самом начале мы выбрали новое основание наугад — и это существенно усложнило процесс.
Но тогда возникает вопрос: какое же основание является оптимальным? Об этом я расскажу во втором способе.
Давайте вернемся к нашему исходному уравнению:
3 log3xx = 2 log9xx2
3 log3xx = 2 ∙ 2 log9x |x|
х > 0 ⇒ |х| = х
3 log3xx = 4 log9xx
Теперь немного подумаем: какое число или функция будет оптимальным основанием? Очевидно, что лучшим вариантом будет с = х — то, что уже стоит в аргументах. В этом случае формула logab = logcb/logca примет вид:
Другими словами, выражение просто переворачивается. При этом аргумент и основание меняется местами.
Эта формула очень полезна и очень часто применяется при решении сложных логарифмических уравнений. Однако при использовании этой формулы возникает один очень серьезный подводный камень. Если вместо основания мы подставляем переменную х, то на нее накладываются ограничения, которых ранее не наблюдалось:
0 < х ≠ 1
Такого ограничения в исходном уравнении не было. Поэтому следует отдельно проверить случай, когда х = 1. Подставим это значение в наше уравнение:
3 log3 1 = 4 log9 1
0 = 0
Получаем верное числовое равенство. Следовательно, х = 1 является корнем. Точно такой же корень мы нашли в предыдущем методе в самом начале решения.
А вот теперь, когда мы отдельно рассмотрели этот частный случай, смело полагаем, что х ≠ 1. Тогда наше логарифмическое уравнение перепишется в следующем виде:
3 logx 9x = 4 logx 3x
Раскладываем оба логарифма по той же формуле, что и раньше. При этом заметим, что logxx = 1:
3 (logx 9 + logxx) = 4 (logx 3 + logxx)
3 logx 9 + 3 = 4 logx 3 + 4
3 logx 32 − 4 logx 3 = 4 − 3
2 logx 3 = 1
Вот мы и пришли к канонической форме:
logx 9 = logxx1
x = 9
Получили второй корень. Он удовлетворяет требованию х ≠ 1. Следовательно, х = 9 наравне с х = 1 является окончательным ответом.
Как видим, объем выкладок немножко сократился. Но при решении реального логарифмического уравнения количество действий будет намного меньше еще и потому, что от вас не требуется столь подробно расписывать каждый шаг.
Ключевое правило сегодняшнего урока состоит в следующем: если в задаче присутствует четная степень, из которой извлекают корень такой же степени, то на выходе мы получи модуль. Однако этот модуль можно убрать, если обратить внимание на область определения логарифмов.
Но будьте внимательны: большинство учеников после этого урока считают, что им все понятно. Но при решении реальных задач они не могут воспроизвести всю логическую цепочку. В результате уравнение обрастает лишними корнями, а ответ получается неправильным.
Поэтому обязательно практикуйтесь: скачивайте задачи для самостоятельной работы, решайте их и сравнивайте с ответами. А у меня на сегодня все.:)
Смотрите также:
- Логарифмические уравнения: несколько видеоуроков по теме
- Квадратные уравнения относительно логарифма
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Пробный ЕГЭ-2011 по математике, вариант №2
- Пробный ЕГЭ по математике 2015: 4 вариант
- Задачи на проценты: считаем проценты с помощью пропорции
Логарифмические уравнения — подготовка к ЕГЭ по Математике
Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.
Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.
.
При этом .
Обратим внимание на область допустимых значений логарифма:
.
Основное логарифмическое тождество:
,
.
Основные формулы для логарифмов:
(Логарифм произведения равен сумме логарифмов)
(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)
Формула перехода к новому основанию:
.
Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.
Все это пригодится нам в решении логарифмических уравнений.
Простейшие логарифмические уравнения
1.Решите уравнение:
Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.
Получаем:
Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .
Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.
2. Решите уравнение:
В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.
Ответ: -124
3. Решите уравнение:
Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.
;
;
;
4. Решите уравнение:
Область допустимых значений: Значит,
Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .
.
Ответ: 21.
5. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:
Ответ: –4.
Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.
6.Решите уравнение: .
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Запишем решение как цепочку равносильных переходов.
Ответ: 19.
7.Решите уравнение: .
Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.
ОДЗ:
Теперь можно «убрать» логарифмы.
— посторонний корень, поскольку должно выполняться условие .
Ответ:
8. Решите уравнение .
ОДЗ уравнения:
Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.
Вернемся к переменной х:
9.Решите уравнение:
Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.
Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.
«Отбрасываем» логарифмы.
Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену
Вернемся к переменной х. Получим:
. Мы нашли все корни исходного уравнения.
Ответ: .
Логарифмические уравнения могут встретиться вам и в задании №5 Профильного ЕГЭ по математике, и в задании №13. И если в задании №5 нужно решить простейшее уравнение, то в задаче 13 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.
Раскрытие логарифмических уравнений
На предыдущем уроке из курса ВНО подготовки Вы познакомились с формулой раскрытия логарифмов
logaf(x)=c⇔f(x)=ac.
{x>0, x≠1, f(x)>0}
и ее частичными случаями:
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Мы настолько часто пользуемся этими свойствами логарифмов, что после прочтения всех примеров Вы точно будете знать, где и для чего нужны эти формулы.
Примеры раскрытия логарифмических уравнений
Курс подготовки ВНО состоит из 40 примеров от простых до сложных, так что по номеру примера Вы можете следить, какой класс задач решается. По мере углубления Вы будете знакомиться с новыми формулами и свойствами логарифмов, без которых уравнение невозможно решить.
Пример 16.7 Решить уравнение log2(x+1)-log2(x-1)=1 и указать промежуток, которому принадлежит его корень.
Решение: Выписываем ОДЗ:
По правилу, разницу логарифмов выражений заменяем логарифмом частки + логарифм основания равен единице, в результате опускаем логарифмы и приравниваем выражения:
x=3 – корень заданного уравнения, принадлежащий промежутку (2,9;3,1).
Ответ: (2,9;3,1) – В.
Пример 16.8 Решить уравнение log2(x+1)+log(x+2)=3-log24 и указать промежуток, которому принадлежит его корень.
Решение: Составим систему неравенств для ОДЗ:
Используя ряд свойств логарифма, сводим уравнение к одному основанию, и раскрываем его.
Далее раскладываем неполное квадратное уравнение на простые множители
x1=0
x2=-3<-1 (не принадлежит ОДЗ).
x=0 – единственный корень заданного уравнения с интервала (-0,1;0,1).
Ответ: (-0,1;0,1) – Б.
Пример 16.10 Указать уравнение, равносильное уравнению
log3x-log9x+log81x=7.
Решение: ОДЗ: x>0
Вынесем степени из основания логарифмов и сгруппируем
Уравнение log3x=4 и есть равносильное заданному.2 в результате логарифмирования обеих его частей.
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части уравнения по основанию 10.
При этом помните, что десятичный логарифм 10 равен 1
таким образом нашли уравнение, которое равносильно начальному.
(x1=1000 или x2=0,1).
Ответ: lg2(x)-2•lg(x)-3=0 – Д.
Пример 16.13 Указать уравнение, равносильное уравнению 2lgx2-lg2(-x)=4.
Решение: ОДЗ: -x>0, x<0.
Вынесем из под логарифма степень =2 и перегруппируем слагаемые
Это и есть все манипуляции, чтобы найти уравнение, которое равносильно заданному
2lgx2-lg2(-x)=4.
С помощью других преобразований Вы бы его не получили.
(x=-100).
Ответ: lg2(-x)-4•lg(-x)+4=0 – Г.
Пример 16.14 Решить уравнения
logalogblogcx=0.
Решение: ОДЗ: x>0.
Имеем три вложенные логарифмы, поэтому по свойствам добиваемся равных основ логарифмов справа и слева от знака равенства, и раскрываем уравнение за схемой
Такого плана задания в свое время были популярны на олимпиадах.
Ответ: cb – А.
Пример 16.15 Указать количество корней уравнения
А | Б | В | Г | Д |
Четыре | три | два | один | ни одного |
Решение: ОДЗ: x≠0.
Путем введения замены переменных уравнение сводим к квадратному, после вычисления которого решаем 2 простых логарифмических уравнения.
Подробные объяснения хода преобразований приведены в таблице
Все найденные значения (-8; -4; 4; 8) принадлежат ОДЗ, уравнение имеет четыре решения.
Ответ: Четыре – А.
Пример 16.24 Установить соответствие между уравнениями (1-4) и произведениями их корней (А–Д).
Решение: Все 4 варианта логарифмических уравнений сводим путем замены переменных к квадратным, после нахождения корней последних возвращаемся к замене и вычисляем простые уравнения с логарифмами. Так как в ответе нужно найти произведение корней, то условие ОДЗ допускает все значения.
Решение уравнений с логарифмами невозможно без знания их свойств. Обращайте внимание на подчеркивания в формулах, они даются не просто так, эти две формулы к концу занятий Вы должны выучить на память и поверьте, что у Вас это получится.
А сейчас переходите к новым готовым ответам с ВНО подготовки на логарифмические уравнения.
Вычисление логарифмов: способы, примеры, решения
Вычисление логарифмов по определению
В простейших случаях возможно достаточно быстро и легко выполнить нахождение логарифма по определению. Давайте подробно рассмотрим, как происходит этот процесс.
Его суть состоит в представлении числа b в виде ac, откуда по определению логарифма число c является значением логарифма. То есть, нахождению логарифма по определению отвечает следующая цепочка равенств: logab=logaac=c.
Итак, вычисление логарифма по определению сводится к нахождению такого числа c, что ac=b, а само число c есть искомое значение логарифма.
Учитывая информацию предыдущих абзацев, когда число под знаком логарифма задано некоторой степенью основания логарифма, то можно сразу указать, чему равен логарифм – он равен показателю степени. Покажем решения примеров.
Найдите log22−3, а также вычислите натуральный логарифм числа e5,3.
Определение логарифма позволяет нам сразу сказать, что log22−3=−3. Действительно, число под знаком логарифма равно основанию 2 в −3 степени.
Аналогично находим второй логарифм: lne5,3=5,3.
log22−3=−3 и lne5,3=5,3.
Если же число b под знаком логарифма не задано как степень основания логарифма, то нужно внимательно посмотреть, нельзя ли прийти к представлению числа b в виде ac. Часто такое представление бывает достаточно очевидно, особенно когда число под знаком логарифма равно основанию в степени 1, или 2, или 3, …
Вычислите логарифмы log525, и .
log525=2, и .
Когда под знаком логарифма находится достаточно большое натуральное число, то его не помешает разложить на простые множители. Это часто помогает представить такое число в виде некоторой степени основания логарифма, а значит, вычислить этот логарифм по определению.
В заключение этого пункта отметим, что мы не ставили целью рассмотреть все способы представления числа под знаком логарифма в виде некоторой степени основания. Наша цель заключалась в том, чтобы дать самые часто используемые варианты действий, приводящие к результату при вычислении логарифмов по определению.
Как решать «вложенные» логарифмические уравнения
Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого. Оба уравнения мы будем решать с помощью канонической формы. Напомню, если у нас есть простейшее логарифмическое уравнение вида logaf(x) = b, то для решения такого уравнения мы выполняем следующие шаги. В первую очередь, нам нужно заменить число b:
b = logaab
Заметьте: ab— это аргумент. Точно так же в исходном уравнении аргументом является функция f(x). Затем мы переписываем уравнение и получаем вот такую конструкцию:
logaf(x) = logaab
Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:
f(x) = ab
В результате мы получим новое уравнение. При этом никаких ограничений на функцию f(x) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.
Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:
log2 (1 + 3 log2x) = 2
Как видим, перед нами простейшее логарифмическое уравнение. В роли f(x) выступает конструкция 1 + 3 log2x, а в роли числа b выступает число 2 (в роли aтакже выступает двойка). Давайте перепишем эту двойку следующим образом:
2 = log2 22
Важно понимать, что первые две двойки пришли к нам из основания логарифма, т. е. если бы в исходном уравнении стояла 5, то мы бы получили, что 2 = log5 52. В общем, основание зависит исключительно от логарифма, который изначально дан в задаче. И в нашем случае это число 2.
Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:
log2 (1 + 3 log2x) = log2 4
Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:
1 + 3 log2x = 4
Отсюда легко находится 3 log2x:
3 log2x = 3
log2x = 1
Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:
1 = log2 21 = log2 2
Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:
log2x = log2 2
Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:
х = 2
Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.
Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.
Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.
Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.
Давайте перейдем ко второму уравнению, оно чуть интересней:
log2 (log1/2 (2x− 1) + log2 4) = 1
Если обозначить выражение внутри большого логарифма функцией f(x), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log2 21 = log2 2.
Переписываем наше большое уравнение:
log2 (log1/2 (2x − 1) + log2 4) = log2 2
Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log2 4 = 2:
log1/2 (2x− 1) + 2 = 2
log1/2 (2x− 1) = 0
Перед нами снова простейшее логарифмическое уравнение вида logaf(x) = b. Переходим к канонической форме, т. е. представляем ноль в виде log1/2 (1/2)0 = log1/2 1.
Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:
log1/2 (2x− 1) = log1/2 1
2x − 1 = 1
2х = 2
х = 1
Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.
Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.
А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.
Откуда возникают такие лишние корни? Этот момент нужно очень четко понимать. Взгляните на исходные уравнения: везде функция х стоит под знаком логарифма. Следовательно, поскольку мы записали log2x, то автоматически выставляем требование х > 0. Иначе данная запись просто не имеет смысла.
Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.
Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.
Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.
Тонкости и хитрости решения
Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.
И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.
Логарифмические уравнения. Методы решения
На самом деле существует целая масса подходов: это и разложение на множители, и потенцирование, и замена, и работа с основаниями…
Но все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду::
| Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение. |
Однако, тут есть один подводный камень: поскольку логарифм определен только тогда, когда
то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку!!! Я не поленюсь и повторю еще раз:
В ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЯХ МЫ ВСЕГДА ДЕЛАЕМ ПРОВЕРКУ ПОЛУЧЕННЫХ КОРНЕЙ!!
Те учащиеся, которые игнорируют это требование, как правило допускают глупейшие и непростительные ошибки!
Согласись, обидно решить правильно уравнение, а потом не сделать самую малость: проверку, и записать лишние корни, и записать из-за этого неправильный ответ!
Формулы логарифмов. Логарифмы примеры решения
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.
Примеры решения логарифмов на основании формул
Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.
Логарифмы, примеры:
log28 = 3, т.к. 23 = 8
log749 = 2, т.к. 72 = 49
log51/5 = -1, т.к. 5-1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
lg100 = 2
log10100 = 2, т.к. 102 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
Основное логарифмическое тождество
a logab = b
Пример.
82log83 = (82log83)2 = 32 = 9
Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4
Логарифм частного равен разности логарифмов
loga (b/c) = logab — logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81
Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа logab m = mlogab
Показатель степени основания логарифма loganb =1/n*logab
loganb m = m/n*logab,
если m = n, получим loganb n = logab
Пример.
log49 = log223 2 = log23
Переход к новому основанию
logab = logcb/logca,
если c = b, получим logbb = 1
тогда logab = 1/logba
Пример.
log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям.
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться .
Почему так?
Начнем с простого: допустим, что . Тогда, например, число не существует, так как в какую бы степень мы не возводили , всегда получается . Более того, не существует ни для какого . Но при этом может равняться чему угодно (по той же причине – в любой степени равно ). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае : в любой положительной степени – это , а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что ).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть ), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение .
Вспомним определение: логарифм – это степень, в которую надо возвести основание , чтобы получить аргумент . И по условию, эта степень равна : .
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна , а произведение . Легко подобрать, это числа и .
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
– верно.
– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и , сразу отбросим корень , и напишем правильный ответ.
Использование свойств логарифмов при вычислении
Мощным инструментом вычисления логарифмов является использование свойств логарифмов.
Некоторые свойства логарифмов позволяют сразу указать значение логарифмов. К таким свойствам относятся свойство логарифма единицы и свойство логарифма числа, равного основанию: log11=logaa0=0 и logaa=logaa1=1. То есть, когда под знаком логарифма находится число 1 или число a, равное основанию логарифма, то в этих случаях логарифмы равны 0 и 1 соответственно.
Чему равны логарифмы и lg10?
Так как , то из определения логарифма следует .
Во втором примере число 10 под знаком логарифма совпадает с его основанием, поэтому десятичный логарифм десяти равен единице, то есть, lg10=lg101=1.
и lg10=1.
Отметим, что вычисление логарифмов по определению (которое мы разобрали в предыдущем пункте) подразумевает использование равенства logaap=p, которое является одним из свойств логарифмов.
На практике, когда число под знаком логарифма и основание логарифма легко представляются в виде степени некоторого числа, очень удобно использовать формулу , которая соответствует одному из свойств логарифмов. Рассмотрим пример нахождения логарифма, иллюстрирующий использование этой формулы.
Вычислите логарифм .
.
Не упомянутые выше свойства логарифмов также используются при вычислении, но об этом поговорим в следующих пунктах.
Зачем в жизни нужны логарифмы?
Я уже говорил, что математики СУПЕРленивые люди? Это правда.
Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!
Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!
То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.
Круто, да?
Пример Найдите корень уравнения.
Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:
То есть внесем число 3 справа под знак логарифма.
или
Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим
Делаем проверку:
Получаем:
Ответ:
Степень можно выносить за знак логарифма
log a b p =p log a b (a>0,a≠1,b>0) (7)
И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
log a (f (x) 2 =2 log a f(x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Формула перехода к новому основанию
log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)
Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .
Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)
Несколько простых примеров с логарифмами
Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b =b (a>0,a≠1) |
| log a a=1 (a>0,a≠1) |
| log a 1=0 (a>0,a≠1) |
| log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) |
| log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) |
| log a b p =p log a b (a>0,a≠1,b>0) |
| log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) |
| log a b= 1 log b a (a>0,a≠1,b>0,b≠1) |
Сложные задачи
Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:
- Возникновение лишних корней из-за расширения области определения логарифмов. Чтобы не допускать такие обидные ошибки, просто внимательно следите за каждым преобразованием;
- Потери корней из-за того, что ученик забыл рассмотреть некоторые «тонкие» случаи — именно на таких ситуациях мы сегодня и сосредоточимся.
Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.
Первое уравнение выглядит вполне стандартно:
logx + 1 (x − 0,5) = logx − 0,5 (x + 1)
Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:
logab = 1/logba
Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:
b > 0
1 ≠ a > 0
Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма ( следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но logb 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.
Итак, ограничения на переменную a сохраняется. Но что происходит с переменной b? С одной стороны, из основания следует b> 0, с другой — переменная b≠ 1, потому что основание логарифма должно быть отлично от 1. Итого из правой части формулы следует, что 1 ≠ b > 0.
Но вот беда: второе требование (b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить, что аргумент bотличен от единицы!
Вот давайте и проверим. Применим нашу формулу:
[Подпись к рисунку]
А теперь, прежде чем идти дальше, выпишем все требования области определения, накладываемые на исходную задачу:
1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0
Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:
Предлагаю ввести новую переменную:
logx + 1 (x − 0,5) = t
В этом случае наша конструкция перепишется следующим образом:
(t2− 1)/t = 0
Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:
(t − 1)(t + 1)/t = 0
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:
t1 = 1;
t2 = −1;
t ≠ 0.
Как видим, оба значения переменной tнас устраивают. Однако на этом решение не заканчивается, ведь нам требуется найти не t, а значение x. Возвращаемся к логарифму и получаем:
logx + 1 (x − 0,5) = 1;
logx + 1 (x − 0,5) = −1.
Давайте приведем каждое из этих уравнений к канонической форме:
logx + 1 (x − 0,5) = logx + 1 (x + 1)1
logx + 1 (x − 0,5) = logx + 1 (x + 1)−1
Избавляемся от знака логарифма в первом случае и приравниваем аргументы:
х − 0,5 = х + 1;
х − х = 1 + 0,5;
0 = 1,5.
Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:
(х − 0,5)/1 = 1/(х + 1)
Решаем пропорцию — получим:
(х − 0,5)(х + 1) = 1
Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:
(х − 1/2)(х + 1) = 1;
x2 + x− 1/2x− 1/2 − 1 = 0;
x2 + 1/2x− 3/2 = 0.
Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:
(х + 3/2) (х − 1) = 0;
x1 = −1,5;
x2 = 1.
Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:
1,5 ≠ х > 0,5; 0 ≠ х > −1.
Эти требования равносильны двойному неравенству:
1 ≠ х > 0,5
Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.
Переходим ко второй задаче:
logx 25 + log125x 5 = log25x 625
На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:
25 = 52>;>4
А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:
logabn = n ∙ logab
На данное преобразование также накладываются ограничения в том случае, когда на месте bстоит функция. Но у нас b— это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:
2 ∙ logx 5 + log125x 5 = 4 ∙ log25x 5
Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.
Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:
Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:
log5x = t
В этом случае наше уравнение будет переписано следующим образом:
Выпишем числитель и раскроем скобки:
2 (t + 3) (t + 2) + t (t + 2) − 4t (t + 3) = 2 (t2 + 5t + 6) + t2 + 2t − 4t2 − 12t = 2t2 + 10t + 12 + t2 + 2t − 4t2 − 12t = −t2 + 12
Возвращаемся к нашей дроби. Числитель должен быть равен нулю:
А знаменатель — отличен от нуля:
t ≠ 0; t ≠ −3; t ≠ −2
Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.
Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t:
Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:
У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:
1 ≠ х > 0;
С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.
Итого мы получили четыре ограничения:
1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25
А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.
С другой стороны, 1 = 50, 1/25 = 5−2, 1/125 = 5−3, а это значит, что данные ограничения для наших корней (у которых, напомню, в показателе стоит иррациональное число) также выполнены, и оба ответа являются решениями задачи.
Итак, мы получили окончательный ответ. Ключевых моментов в данной задаче два:
- Будьте внимательны при перевороте логарифма, когда аргумент и основание меняются местами. Подобные преобразования накладывают лишние ограничения на область определения.
- Не бойтесь преобразовывать логарифмы: их можно не только переворачивать, но и раскрывать по формуле суммы и вообще менять по любым формулам, которые вы изучали при решении логарифмических выражений. Однако при этом всегда помните: некоторые преобразования расширяют область определения, а некоторые — сужают.
Логарифм: что это? Все формулы. Простейшие уравнения и неравенства
Сейчас речь пойдет о трех страшных буквах: l o g.Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).
Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.
Тогда, если дело касается логарифма:
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?
На самом деле в этом и заключается основная формула (определение логарифма):
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.
У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?
Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).
А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).
Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.
Всегда, когда существует логарифм, должно быть:
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.
А теперь разберем теорию на практике:
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).
Два нужно четыре раза умножить само на себя, чтобы получить 16.
Ответ: 4.
Нахождение логарифмов через другие известные логарифмы
Информация этого пункта продолжает тему использования свойств логарифмов при их вычислении. Но здесь основное отличие состоит в том, что свойства логарифмов используются для того, чтобы выразить исходный логарифм через другой логарифм, значение которого известно. Приведем пример для пояснения. Допустим, мы знаем, что log23≈1,584963, тогда мы можем найти, например, log26, выполнив небольшое преобразование с помощью свойств логарифма: log26=log2(2·3)=log22+log23≈
В приведенном примере нам было достаточно использовать свойство логарифма произведения. Однако намного чаще приходится применять более широкий арсенал свойств логарифмов, чтобы вычислить исходный логарифм через заданные.
Вычислите логарифм 27 по основанию 60, если известно, что log602=a и log605=b.
Итак, нам нужно найти log6027. Несложно заметить, что 27=33, и исходный логарифм в силу свойства логарифма степени можно переписать как 3·log603.
Теперь посмотрим, как log603 выразить через известные логарифмы. Свойство логарифма числа, равного основанию, позволяет записать равенство log6060=1. С другой стороны log6060=log60(22·3·5)=
Наконец, вычисляем исходный логарифм: log6027=3·log603=
log6027=3·(1−2·a−b)=3−6·a−3·b.
Отдельно стоит сказать о значении формулы перехода к новому основанию логарифма вида . Она позволяет от логарифмов с любыми основаниями переходить к логарифмам с конкретным основанием, значения которых известны или есть возможность их отыскать. Обычно от исходного логарифма по формуле перехода переходят к логарифмам по одному из оснований 2, e или 10, так как по этим основаниям существуют таблицы логарифмов, позволяющие с определенной степенью точности вычислять их значения. В следующем пункте мы покажем, как это делается.
Источники
- http://www.cleverstudents.ru/logarithms/computation_of_logarithms.html
- https://www.berdov.com/docs/logarithm/reshenie-logarifmicheskih-uravneniy/
- https://youclever.org/book/logarifmicheskie-uravneniya-1
- https://rgiufa.ru/matematika-fizika-himiya/kakie-sushhestvuyut-formuly-logarifmov.html
- https://youclever.org/book/logarifmy-1
- https://repetitor-mathematics.ru/kak-reshat-logarifmicheskie-uravneniya-podrobnyiy-razbor/
Решение логарифмических уравнений — ChiliMath
Обычно существует два типа логарифмических уравнений. Внимательно изучите каждый случай, прежде чем приступить к рассмотрению приведенных ниже примеров.
Типы логарифмических уравнений
- Первый тип выглядит так.
Если у вас есть один логарифм на каждой стороне уравнения с одинаковым основанием, вы можете установить аргументы, равные друг другу, и решить. Аргументами здесь являются алгебраические выражения, представленные \ color {blue} M и \ color {red} N.
- Второй тип выглядит так.
Если у вас есть один логарифм на одной стороне уравнения, вы можете выразить его в виде экспоненциального уравнения и решить.
Давайте научимся решать логарифмические уравнения на нескольких примерах.
Примеры решения логарифмических уравнений
Пример 1: Решите логарифмическое уравнение.
Поскольку мы хотим преобразовать левую часть в одно логарифмическое уравнение, мы должны использовать правило произведения в обратном порядке, чтобы сжать его.Вот правило на всякий случай, если вы забыли.
- Распределить: \ left ({x + 2} \ right) \ left (3 \ right) = 3x + 6
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу.
- Затем решите линейное уравнение. Я знаю, что у тебя есть эта часть!
Просто большое предостережение. ВСЕГДА проверяйте решенные значения с помощью исходного логарифмического уравнения.
Помните :
- Хорошо, иметь значения x, такие как положительные, 0 и отрицательные числа.
- Однако НЕ ДОПУСКАЕТСЯ иметь логарифм отрицательного числа или логарифм нуля, 0, при замене или вычислении в исходное уравнение логарифма.
⚠︎ ВНИМАНИЕ: логарифм отрицательного числа и логарифм нуля не определены.
{\ log _b} \ left ({{\ rm {negative \, \, number}}} \ right) = {\ rm {undefined}}
{\ log _b} \ left (0 \ right) = {\ rm {undefined}}
Теперь давайте проверим наш ответ, является ли x = 7 допустимым решением.Подставьте его обратно в исходное логарифмическое уравнение и проверьте, верно ли оно.
Да! Поскольку x = 7 проверок, у нас есть решение в \ color {blue} x = 7.
Пример 2: Решите логарифмическое уравнение.
Начните с сжатия логарифмических выражений слева в один логарифм с помощью правила произведения. Мы хотим иметь по одному логарифмическому выражению для каждой стороны уравнения. Будьте готовы решить квадратное уравнение, так как x будет иметь степень 2.2} — 2x
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу
- Решите квадратное уравнение, используя метод факторизации. Но вам нужно переместить все на одну сторону, заставив противоположную сторону равной 0.
- Установите каждый коэффициент равным нулю, затем решите относительно x.
x — 5 = 0 означает, что x = 5
x + 2 = 0 означает, что x = — 2
Итак, возможные решения: x = 5 и x = — 2.Не забывайте всегда подставлять возможные решения обратно в исходное логарифмическое уравнение.
Давайте проверим наши возможные ответы x = 5 и x = — 2, если они будут действительными решениями. Подставьте его обратно в исходное логарифмическое уравнение и проверьте, верно ли оно.
После проверки наших значений x мы обнаружили, что x = 5 определенно является решением. Однако x = -2 генерирует некоторые отрицательные числа внутри скобок (логарифм нуля и отрицательные числа не определены), что заставляет нас исключить x = -2 как часть нашего решения.
Следовательно, окончательное решение будет просто \ color {blue} x = 5. Мы не принимаем во внимание x = -2, потому что это постороннее решение.
Пример 3: Решите логарифмическое уравнение.
Это интересная проблема. Здесь мы имеем различие логарифмических выражений по обе стороны уравнения. Упростите или сожмите журналы с обеих сторон, используя правило Quotient Rule, которое выглядит следующим образом.
- Разница в журналах говорит нам о том, что нужно использовать правило частного.Преобразуйте операцию вычитания снаружи в операцию деления внутри скобок. Сделайте это с обеими сторонами уравнений.
- Я думаю, что мы готовы установить каждый аргумент равным друг другу, так как мы можем уменьшить проблему до одного логарифмического выражения для каждой стороны уравнения.
- Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу. Обратите внимание, что это рациональное уравнение. Один из способов решить эту проблему — получить Cross Product .
- Это выглядит так после получения перекрестного продукта.
- Упростите обе стороны с помощью свойства распределения. На этом этапе мы понимаем, что это всего лишь квадратное уравнение. Тогда ничего страшного. Сдвиньте все в одну сторону, и это заставит одну сторону уравнения равняться нулю.
- Это легко факультативно. Теперь установите каждый коэффициент равным нулю и решите относительно x.
- Итак, это наши возможные ответы.
Я предоставлю вам проверить наши возможные ответы обратно в исходное логарифмическое уравнение.Вы должны убедиться, что \ color {blue} x = 8 — единственное решение, а x = -3 — нет, поскольку он генерирует сценарий, в котором мы пытаемся получить логарифм отрицательного числа. Нехорошо!
Пример 4: Решите логарифмическое уравнение.
Если вы видите «журнал» без явного или письменного основания, предполагается, что он имеет основание 10. Фактически, логарифм с основанием 10 известен как десятичный логарифм .
Нам нужно сжать обе части уравнения в одно логарифмическое выражение.С левой стороны мы видим разницу журналов, что означает, что мы применяем правило Quotient Rule, в то время как с правой стороны требуется правило продукта, потому что они представляют собой сумму журналов.
Есть только одна вещь, на которую вы должны обратить внимание на левую сторону. Вы видите этот коэффициент \ Large {1 \ over 2} \ ,?
Что ж, мы должны представить это как экспоненту, используя правило мощности в обратном порядке.
- Выведите этот коэффициент \ large {1 \ over 2} как показатель степени (см. Крайний левый член)
- Упростите показатель степени (все еще относится к крайнему левому члену)
- Затем сократите бревна с обеих сторон уравнения.Используйте правило частного слева и правило продукта справа.
- Здесь я использовал разные цвета, чтобы показать, что, поскольку у нас одна и та же база (если явно не показано, предполагается, что это база 10), можно установить их равными друг другу.
- Удаление журналов и просто приравнивание аргументов внутри скобок.
- На этом этапе вы можете решить рациональное уравнение, выполнив перекрестное произведение. Переместите все члены в одну сторону уравнения, затем вычтите их.
- Установите каждый коэффициент равным нулю и решите относительно x.
Пора проверить свои потенциальные ответы. Когда вы проверите x = 0 обратно в исходное логарифмическое уравнение, вы получите выражение, которое включает в себя получение логарифма нуля, который не определен, что означает — нехорошо! Итак, мы должны игнорировать или отбросить \ color {red} x = 0 как решение.
Проверка \ Large {x = {3 \ over 4}} подтверждает, что действительно \ Large {\ color {blue} {x = {3 \ over 4}}} является единственным решением.
Пример 5: Решите логарифмическое уравнение.
Эта проблема связана с использованием символа \ ln вместо \ log для обозначения логарифма.
Думайте о \ ln как о особом логарифме с основанием e, где e \ приблизительно 2,71828.
- Используйте правило продукта с правой стороны
- Сначала запишите переменную, а затем константу, чтобы быть готовым к использованию метода FOIL.
- Упростите два бинома, умножив их вместе.
- На этом этапе я просто закодировал выражение в круглых скобках цветом, чтобы показать, что мы готовы установить их равными друг другу.
- Ага! Здесь мы говорим, что содержимое в левой скобке равно содержимому в правой скобке.
Не забудьте символ \ pm.
- Далее, упрощая, мы должны получить следующие возможные ответы.
Проверьте, являются ли найденные выше потенциальные ответы возможными, подставив их обратно в исходные логарифмические уравнения.
Вы должны убедиться, что ЕДИНСТВЕННЫМ допустимым решением является \ large {\ color {blue} x = {1 \ over 2}}, что делает \ large {\ color {red} x = — {1 \ over 2}} лишним. отвечать.
Пример 6: Решите логарифмическое уравнение.
В этом уравнении есть только одно логарифмическое выражение. Мы рассматриваем это как второй случай, когда у нас
Мы преобразуем уравнение из логарифмической формы в экспоненциальную, а затем решим его.
- Я закодировал части логарифмического уравнения цветом, чтобы показать, куда они идут при преобразовании в экспоненциальную форму.4} = 81.
Вы должны убедиться, что значение \ color {blue} x = 12 действительно является решением логарифмического уравнения.
Пример 7: Решите логарифмическое уравнение.
Соберите все логарифмические выражения на одной стороне уравнения (оставьте его слева) и переместите константу в правую часть. Используйте правило частного, чтобы выразить разницу журналов в виде дробей в скобках логарифма.
- Переместите все логарифмические выражения в левую часть уравнения, а константу — вправо.{\ color {красный} 1} = 5.
- Это рациональное уравнение из-за наличия переменных в числителе и знаменателе.
Я бы решил это уравнение, используя правило перекрестного произведения. Но сначала я должен выразить правую часть уравнения с явным знаменателем, равным 1. То есть 5 = {\ large {{5 \ over 1}}}
- Выполните перекрестное умножение, а затем решите полученное линейное уравнение.
Когда вы проверяете x = 1 обратно в исходное уравнение, вы должны согласиться с тем, что \ large {\ color {blue} x = 1} является решением логарифмического уравнения.
Пример 8: Решите логарифмическое уравнение.
Эта проблема очень похожа на №7. Давайте соберем все логарифмические выражения слева, оставив константу справа. Поскольку у нас есть разница журналов, мы будем использовать правило Quotient Rule.
- Переместите выражения журнала в левую часть, а константу оставьте вправо.
- Примените правило Quotient Rule, поскольку они представляют собой разность журналов.
- Здесь я использовал разные цвета, чтобы показать, куда они уходят после перезаписи в экспоненциальной форме.
- Обратите внимание, что выражение внутри круглых скобок остается на своем текущем месте, а \ color {red} 5 становится показателем степени основания.
- Чтобы решить это рациональное уравнение, примените правило перекрестного произведения.
- Упростите правую часть с помощью свойства распределения. Похоже, мы имеем дело с квадратным уравнением.
- Переместите все в левую сторону и сделайте правую сторону равной нулю.
Выносим трехчлен за скобки.Установите каждый коэффициент равным нулю, затем решите относительно x.
- Когда вы решаете для x, вы должны получить эти значения x как потенциальные решения.
Убедитесь, что вы проверили возможные ответы из исходного логарифмического уравнения.
Согласитесь, что \ color {blue} x = -32 — единственное решение. Это делает \ color {red} x = 4 лишним решением, так что не обращайте на него внимания.
Пример 9: Решите логарифмическое уравнение
Я надеюсь, что теперь вы получили основное представление о том, как подходить к этому типу проблемы.Здесь мы видим три логических выражения и константу. Давайте разделим логарифмические выражения и константу на противоположных сторонах уравнения.
- Давайте оставим логарифмические выражения слева, а константу — справа.
- Начните с сжатия выражений журнала с помощью правила продукта для обработки суммы журналов.
- Затем сожмите выражения журнала, используя правило Quotient Rule, чтобы учесть разницу в журналах.
- На этом этапе я использовал разные цвета, чтобы проиллюстрировать, что я готов выразить логарифмическое уравнение в его экспоненциальной форме.
- Сохраните выражение внутри символа группировки ( синий ) в том же месте, сделав константу \ color {red} 1 с правой стороны как показатель степени основания 7.
- Решите это рациональное уравнение, используя перекрестное произведение. Выразите 7 как \ large {7 \ over 1}.
- Переместите все члены в левую часть уравнения. Выносим за скобки трехчлен. Затем установите каждый коэффициент равным нулю и решите относительно x.
- Это ваши потенциальные ответы.Всегда проверяйте свои ценности.
Очевидно, что когда мы подставляем x = -8 обратно в исходное уравнение, получается логарифм с отрицательным числом. Следовательно, вы исключаете \ color {red} x = -8 как часть вашего решения.
Таким образом, единственное решение — \ color {blue} x = 11.
Пример 10: Решите логарифмическое уравнение.
- Сохраните логарифмическое выражение слева и переместите все константы в правую сторону.
- Думаю, мы готовы преобразовать это логарифмическое уравнение в экспоненциальное уравнение.3} = 27. Перед нами простое радикальное уравнение.
Отметьте этот отдельный урок, если вам нужно напомнить, как решать различные типы радикальных уравнений.
- Чтобы избавиться от радикального символа в левой части, возведите обе части уравнения в квадрат.
- После возведения в квадрат обеих сторон, похоже, у нас есть линейное уравнение. Просто решите это как обычно.
Верните свой потенциальный ответ в исходное уравнение.
После этого вы должны убедиться, что действительно \ color {blue} x = -104 — верное решение.
Практика с рабочими листами
Возможно, вас заинтересует:
Уплотняющие логарифмы
Расширяющиеся логарифмы
Объяснение логарифма
Правила логарифмирования
Решение логарифмических уравнений с экспонентами
Purplemath
Второй тип логарифмического уравнения требует использования отношения:
—Взаимосвязь—
y = b x
……….. эквивалентно …………
(означает то же самое, что и)
журнал b ( y ) = x
В анимированной форме два уравнения связаны, как показано ниже:
MathHelp.com
Обратите внимание, что основание как в экспоненциальной форме уравнения, так и в логарифмической форме уравнения — «b», но x и y меняют сторону при переключении между двумя уравнениями.Если вы помните это — что бы ни было , было аргументом журнала, становится «равным», а все, что было было «равно», становится экспонентой в экспоненте, и наоборот — тогда у вас не должно быть слишком много проблемы с решением уравнений журнала.
Поскольку это уравнение имеет форму «журнал (чего-то) равен числу», а не «журнал (чего-то) равен журналу (чего-то еще)»), я могу решить уравнение, используя Соотношение:
журнал 2 ( x ) = 4
2 4 = x
16 = х
Я могу решить эту проблему, преобразовав логарифмический оператор в его эквивалентную экспоненциальную форму, используя The Relationship:
Но 8 = 2 3 , поэтому я могу приравнять степени двойки:
Обратите внимание, что это также можно было решить, работая непосредственно с определением логарифма.
Какая сила при установке на «2» даст вам 8? Конечно же, сила 3!
Если вы хотите много работать, вы также можете сделать это в своем калькуляторе, используя формулу замены базы:
Подключите это к своему калькулятору, и вы получите «3» в качестве ответа. Хотя этот метод смены базы не особенно полезен в данном случае, вы можете видеть, что он действительно работает. (Попробуйте это сделать на своем калькуляторе, если вы еще этого не сделали, чтобы быть уверенным, что вы знаете, какие клавиши нажимать и в каком порядке.Эта техника понадобится вам в последующих задачах.
Я не говорю, что вы обязательно захотите, чтобы решал уравнения, используя формулу замены базы, или всегда используя определение журналов, или какой-либо другой конкретный метод. Но я предлагаю вам убедиться, что вы знакомы с различными методами, и что вы не должны паниковать, если вы и ваш друг использовали полностью разных методов для решения одного и того же уравнения.
Журнал решения
2 ( x ) + журнал 2 ( x — 2) = 3
Я пока ничего не могу сделать с этим уравнением, потому что у меня его еще нет в форме «журнал (чего-то) равно числу». Поэтому мне нужно использовать правила журнала, чтобы объединить два члена в левой части уравнения:
журнал 2 ( x ) + журнал 2 ( x — 2) = 3
журнал 2 [( x ) ( x — 2)] = 3
журнал 2 ( x 2 -2 x ) = 3
Теперь уравнение устроено в удобной форме.На этом этапе я могу использовать Отношение, чтобы преобразовать логарифмическую форму уравнения в соответствующую экспоненциальную форму, а затем я могу решить результат:
журнал 2 ( x 2 -2 x ) = 3
2 3 = x 2 -2 x
8 = x 2 -2 x
0 = x 2 — 2 x — 8
0 = ( x -4) ( x + 2)
x = 4, –2
Но если x = –2, то «log 2 ( x )» из исходного логарифмического уравнения будет иметь отрицательное число в качестве аргумента (как и термин «log 2 ( x — 2) «).Поскольку журналы не могут иметь нулевых или отрицательных аргументов, решение исходного уравнения не может быть x = –2.
Тогда мое решение:
Имейте в виду, что вы всегда можете проверить свои ответы на любое упражнение «решение», вставив эти ответы обратно в исходное уравнение и проверив, что решение «работает». В этом случае я вставлю свое значение решения в любую сторону исходного уравнения и проверю, что каждая сторона оценивает одно и то же число:
левая сторона:
журнал 2 ( x ) + журнал 2 ( x — 2)
= журнал 2 (4) + журнал 2 (4-2) 3
= журнал 2 (4) + журнал 2 (2)
= журнал 2 (2 2 ) + журнал 2 (2 1 )
= 2 + 1 = 3
Правая часть исходного уравнения уже была упрощена до «3», поэтому это решение проверяется.
Это уравнение может показаться слишком сложным, но это всего лишь еще одно логарифмическое уравнение. Чтобы решить эту проблему, мне нужно дважды применить The Relationship. Я начинаю с исходного уравнения и работаю с «внешним» журналом:
Отношение преобразует вышеуказанное в:
Теперь я применю Отношение во второй раз:
Тогда решение:
Журнал решения
2 ( x 2 ) = (лог 2 ( x )) 2
Во-первых, я расширю квадрат справа, чтобы он был явным произведением двух журналов:
журнал 2 ( x 2 ) = [лог 2 ( x )] 2
журнал 2 ( x 2 ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я применяю правило журнала, чтобы переместить «квадрат» изнутри журнала в левой части уравнения, вынимая его перед этим журналом в качестве множителя:
2 · журнал 2 ( x ) = [журнал 2 ( x )] [журнал 2 ( x )]
Затем я перенесу этот член из левой части уравнения в правую:
0 = [журнал 2 ( x )] [журнал 2 ( x )] — 2 · журнал 2 ( x )
Это уравнение может показаться плохим, но внимательно присмотритесь.На данный момент это не более чем упражнение по факторингу. Итак, я фактор, а затем я решу факторы, используя The Relationship:
.
0 = [журнал 2 ( x )] [журнал 2 ( x ) — 2]
журнал 2 ( x ) = 0 или журнал 2 ( x ) — 2 = 0
2 0 = x или лог 2 ( x ) = 2
1 = x или 2 2 = x
1 = x или 4 = x
Тогда мое решение:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении логарифмических уравнений (или пропустите виджет и продолжите урок).Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvelog2.htm
Как решать логарифмические уравнения
Решение логарифмических уравнений
Правила или законы логарифмов:
Как вы знаете, логарифм — это математическая операция, обратная возведению в степень.Это выражается сокращением «журнал». Прежде чем приступить к решению логарифмических уравнений, есть несколько стратегий и «правил», с которыми мы должны сначала ознакомиться.
Во-первых, чтобы решать логарифмические уравнения, как и в случае с многочленами, вы должны уметь строить графики логарифмических функций. Посмотрите наше видео о построении графиков логарифмических функций для обзора, если это необходимо. Кроме того, прежде чем мы перейдем к правилам логарифмирования, важно, чтобы вы также понимали одну из простейших стратегий логарифмирования — изменение базовой формулы.Опять же, посмотрите наше видео об изменении базовой формулы, если вам нужно напомнить. Теперь, когда вы все это освоили, давайте взглянем на некоторые из наиболее важных правил логарифмирования:
1) Правило логарифмического произведения
В целом правило произведения логарифмов определяется следующим образом:
logA + logB = log (A × B) \ log A + \ log B = \ log (A \ times B) logA + logB = журнал (A × B)
То есть, добавляя два журнала из с одной и той же базой , вы можете переписать выражение как один журнал, умножив члены в логарифмическом выражении.
2) Правило логарифмического частного
Как правило, правило частного логарифмов определяется следующим образом:
logA − logB = log (AB) \ log A — \ log B = \ log (\ frac {A} {B}) logA − logB = log (BA)
То есть при вычитании двух журналов из из одной и той же базы вы можете переписать выражение как один журнал, разделив члены в логарифмическом выражении. {B} = B \ times \ log Alog (A) B = B × logA
То есть, когда есть показатель степени в члене в логарифмическом выражении, вы можете уменьшить этот показатель и умножить его на журнал.{\ log_ {A} (B)} = BAlogA (B) = B
То есть увеличение логарифма числа по основанию равняется этому числу.
6) Правило идентификации журнала
В целом правило идентичности логарифмов определяется следующим образом:
logAA = 1 \ log_ {A} A = 1 logA A = 1
То есть, когда логарифм чего-то берется за основу того же самого, логарифмическое выражение просто равно 1.
7) Особые журналы
Хотя это не обязательно правила, есть пара журналов, которые вы должны знать наизусть, чтобы упростить задачу.Их:
журнал1 = 0 \ журнал 1 = 0 журнал1 = 0
log0 = undefined \ log 0 = undefined log0 = undefined
Оба этих случая всегда верны, независимо от основания. Кроме того, первый особый случай иногда называют правилом логарифмического нуля.
Все эти правила, вместе взятые, представляют собой чрезвычайно мощные инструменты, которые мы можем использовать для решения любой логарифмической задачи. Чтобы посмотреть видеообзор этих концепций, посмотрите наши видеоролики о свойствах логарифмов и правиле частного для логарифмов.Теперь, когда мы рассмотрели основы, давайте приступим к решению проблем с журналом!
Как решать проблемы с журналом:
Как и все в математике, лучший способ научиться решать задачи журнала — это выполнять некоторые практические задачи! Мы будем использовать правила, которые мы только что обсудили, для решения некоторых примеров.
Пример 1:
Решите логарифмическое уравнение:
log (3 − x) + log (4−3x) −log (x) = log7 \ log (3 — x) + \ log (4 — 3x) — \ log (x) = \ log 7log (3 − x) + журнал (4−3x) −log (x) = log7
Шаг 1. Используйте известные правила журнала
В любой задаче, связанной с решением логарифмических уравнений, первым делом всегда старайтесь упростить использование правил журнала.{2} — 20x + 12 = 03×2−20x + 12 = 0
(3x − 2) (x − 6) = 0 (3x — 2) (x — 6) = 0 (3x − 2) (x − 6) = 0
3x − 2 = 0 или x − 6 = 03x — 2 = 0 или x — 6 = 03x − 2 = 0 или x − 6 = 0
x = 23 или x = 6x = \ frac {2} {3} или x = 6x = 32 или x = 6
Шаг 3. Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
log (3−23) + log (4−3 (23)) — log (23) = log7 \ log (3 — \ frac {2} {3}) + \ log (4 — 3 ( \ frac {2} {3})) — \ log (\ frac {2} {3}) = \ log 7log (3−32) + log (4−3 (32)) — log (32) = log7
Решение x = 23x = \ frac {2} {3} x = 32 является правильным.
log (3−6) + log (4−3 (6)) — log (6) = log7 \ log (3-6) + \ log (4-3 (6)) — \ log ( 6) = \ log 7log (3−6) + log (4−3 (6)) — log (6) = log7
Решение x = 6x = 6x = 6 отклоняется, поскольку логарифм отрицательного числа не определен.
Пример 2:
Шаг 1. Используйте известные правила журнала
В этом случае мы будем использовать правила журнала мощности и частного. Мы делаем это, чтобы попытаться составить полиномиальное / алгебраическое уравнение, которое было бы легче решить. Это показано ниже:
2log3 (x + 4) −log3 (−x) = 22 \ log_ {3} (x + 4) — \ log_ {3} (-x) = 22log3 (x + 4) −log3 ( −x) = 2
log3 (x + 4) 2 − log3 (−x) = 2 \ log_ {3} (x + 4) ^ {2} — \ log_ {3} (-x) = 2log3 (x + 4 ) 2 − log3 (−x) = 2
log3 (x2 + 8x + 16 − x) = 2 \ log_ {3} (\ frac {x ^ {2} + 8x + 16} {- x}) = 2log3 (−xx2 + 8x + 16) = 2
Шаг 2. Упростите
Мы можем преобразовать в экспоненциальную форму, потому что одна сторона имеет лог, а другая — нет.{2} + 17x + 16 = 0x2 + 17x + 16 = 0
(х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0
x = −16orx = −1x = -16 или x = -1x = −16orx = −1
Шаг 4. Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
2log3 ((- 16) +4) −log3 (- (- 16)) = 22 \ log_ {3} ((-16) + 4) — \ log_ {3} (- (- 16)) = 22log3 ((−16) +4) −log3 (- (- 16)) = 2
Решение x = -16 отклоняется.
2log3 ((- 1) +4) −log3 (- (- 1)) = 22 \ log_ {3} ((-1) + 4) — \ log_ {3} (- (- 1)) = 22log3 ((−1) +4) −log3 (- (- 1)) = 2
Решение x = -1 правильное.
Пример 3:
Шаг 1. Упростить
Умножьте обе части уравнения на 2, чтобы избавиться от дроби.
log2x = 2 + 12log2 (x − 3) \ log_ {2} x = 2 + \ frac {1} {2} \ log_ {2} (x — 3) log2 x = 2 + 21 log2 (Х − 3)
2log2x = 4 + log2 (x − 3) 2 \ log_ {2} x = 4 + \ log_ {2} (x — 3) 2log2 x = 4 + log2 (x − 3)
Шаг 2. Используйте известные правила журнала
В этом случае мы будем использовать правила журнала и частного журнала. Затем мы можем упростить, как в предыдущем примере, чтобы получить экспоненциальную форму.{2} — 16x + 48 = 0x2−16x + 48 = 0
(x − 4) (x − 12) = 0 (x — 4) (x — 12) = 0 (x − 4) (x − 12) = 0
х = 4 или х = 12 х = 4 или х = 12 х = 4 или х = 12
Шаг 4. Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
log24 = 2 + 12log2 (4−3) \ log_ {2} 4 = 2 + \ frac {1} {2} \ log_ {2} (4–3) log2 4 = 2 + 21 log2 (4−3)
Решение x = 4 подтверждается.
log212 = 2 + 12log2 (12−3) \ log_ {2} 12 = 2 + \ frac {1} {2} \ log_ {2} (12–3) log2 12 = 2 + 21 log2 (12−3)
То же самое и x = 12.{-2} x = 10−2 неверно.
И это тоже все! Чтобы проверить свою работу с будущими практическими задачами, обязательно воспользуйтесь этим отличным калькулятором. Наконец, для видеообзора всего, что мы только что рассмотрели, посмотрите наше видео о том, как решать уравнения журнала.
Алгебра — логарифмические функции
Показать уведомление для мобильных устройств
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6-2: Логарифмические функции
В этом разделе нам нужно перейти к функциям логарифмирования.Это может быть непростой момент для построения графика. Будет несколько других обозначений, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивно понятными. Однако не расстраивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж и плохи, и обычно требуется немного поработать с ними, чтобы разобраться в них.
Вот определение логарифмической функции.
Если \ (b \) — любое число такое, что \ (b> 0 \) и \ (b \ ne 1 \) и \ (x> 0 \), то
\ [y = {\ log _b} x \ hspace {0.y} = x \) называется экспоненциальной формой .
Обратите внимание, что требование \ (x> 0 \) на самом деле является результатом того факта, что мы также требуем \ (b> 0 \). Если подумать, это будет иметь смысл. Мы возводим положительное число в степень, и поэтому результат не может быть чем-то другим, кроме другого положительного числа. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Теперь давайте обратимся к используемым здесь обозначениям, поскольку это обычно самое большое препятствие, которое ученики должны преодолеть, прежде чем начать понимать логарифмы.Во-первых, «журнал» функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не переменные и не означают умножения. Они просто говорят нам, что мы имеем дело с логарифмом.
Далее, \ (b \), стоящий в нижнем индексе в части «журнала», указывает нам, что такое основание, поскольку это важная часть информации. Кроме того, несмотря на то, как это может выглядеть, в приведенной выше форме логарифма нет возведения в степень.x} \) в этой форме, но это не так. Похоже, что это могло быть именно так.
Важно, чтобы запись с логарифмами была прямой, в противном случае вам будет очень трудно понять их и работать с ними.
Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.
Пример 1 Вычислите каждый из следующих логарифмов.
- \ ({\ log _4} 16 \)
- \ ({\ log _2} 16 \)
- \ ({\ log _6} 216 \)
- \ (\ displaystyle {\ log _5} \ frac {1} {{125}} \)
- \ ({\ log _ {\ frac {1} {3}}} 81 \)
- \ ({\ log _ {\ frac {3} {2}}} \ displaystyle \ frac {{27}} {8} \)
Показать все решения Скрыть все решения
Показать обсуждение
Теперь реальность такова, что непосредственное вычисление логарифмов может быть очень сложным процессом даже для тех, кто действительно их понимает.Обычно гораздо проще сначала преобразовать форму логарифма в экспоненциальную форму. В такой форме мы обычно можем получить ответ довольно быстро.
a \ ({\ log _4} 16 \) Показать решение
Хорошо, мы действительно спрашиваем вот о чем.
\ [{\ log _4} 16 =? \]
Как было предложено выше, давайте преобразуем это в экспоненциальную форму.
\ [{\ log _4} 16 =? \ hspace {0,25 дюйма} \ Rightarrow {\ mbox {}} \ hspace {0.4} \), и т. Д. , пока вы не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно
.
\ [{\ log _2} 16 = 4 \]
Прежде чем перейти к следующей части, обратите внимание, что их основа является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
c \ ({\ log _6} 216 \) Показать решение
Мы сделаем это без каких-либо реальных объяснений, чтобы увидеть, насколько хорошо вы вычислили логарифмы.3}}} = \ frac {{27}} {8} \]
Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете понимать систему обозначений. Однако есть еще несколько вычислений, которые мы хотим сделать, нам нужно ввести некоторые специальные логарифмы, которые появляются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.
\ [\ begin {align *} & {\ mbox {десятичный логарифм:}} \ hspace {0.25 дюймов} \ log x = {\ log _ {10}} x \\ & {\ mbox {натуральный логарифм:}} \ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ конец {выравнивание *} \]
Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы отбрасываем часть записи с основанием 10. Точно так же натуральный логарифм — это просто логарифм \ (\ bf {e} \) с другим обозначением, и где \ (\ bf {e} \) — это то же число, которое мы видели в предыдущем разделе, и определяется как \ ({\ bf {e}} = 2,718281828 \ ldots \).
Давайте взглянем на еще пару оценок.
Пример 2 Вычислите каждый из следующих логарифмов.
- \ (\ лог 1000 \)
- \ (\ log \ displaystyle \ frac {1} {{100}} \)
- \ (\ ln \ displaystyle \ frac {1} {{\ bf {e}}} \)
- \ (\ ln \ sqrt {\ bf {e}} \)
- \ ({\ log _ {34}} 34 \)
- \ ({\ log _8} 1 \)
Показать все решения Скрыть все решения
Показать обсуждение
Для проведения первых четырех оценок нам просто нужно запомнить, каковы их обозначения и какое основание подразумевается в них.0} = 1 \). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
Итак, при вычислении логарифмов все, что мы действительно спрашиваем, — это какой показатель степени мы положили на основание, чтобы получить число в логарифме.
Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала сделаем пару быстрых графиков.
Пример 3 Нарисуйте график десятичного и натурального логарифма на одной и той же системе координат.Показать решение
В этом примере есть две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам возможность попрактиковаться в использовании нашего калькулятора для вычисления этих логарифмов, потому что на самом деле именно так нам нужно будет проводить большинство этих вычислений.
Вот таблица значений двух логарифмов.
| \ (х \) | \ (\ журнал x \) | \ (\ ln x \) |
|---|---|---|
| \ (\ frac {1} {2} \) | -0.3010 | -0,6931 |
| 1 | 0 | 0 |
| 2 | 0,3010 | 0,6931 |
| 3 | 0,4771 | 1.0986 |
| 4 | 0.r}} \ right) = r {\ log _b} x \) Мы не будем ничего делать с последним свойством в этом разделе; это здесь только для полноты картины. Мы подробно рассмотрим это свойство в нескольких разделах. Первые два свойства, перечисленные здесь, могут поначалу немного сбивать с толку, поскольку с одной стороны у нас есть произведение или частное внутри логарифма, а с другой стороны — сумма или разность двух логарифмов.Нам просто нужно быть осторожными с этими свойствами и обязательно использовать их правильно. Также обратите внимание, что нет никаких правил, как разбить логарифм суммы или разности двух членов. Чтобы прояснить это, отметим следующее: \ [\ begin {align *} {\ log _b} \ left ({x + y} \ right) & \ ne {\ log _b} x + {\ log _b} y \\ {\ log _b} \ left ( {x — y} \ right) & \ ne {\ log _b} x — {\ log _b} y \ end {align *} \] Будьте осторожны с ними и не пытайтесь использовать их, поскольку они просто не соответствуют действительности.5}} \ right) \) Показать решение Обратите внимание, что на данном этапе мы не можем использовать свойство 7 для приведения 3 и 5 вниз перед логарифмом. Чтобы использовать свойство 7, весь член логарифма должен быть возведен в степень. В этом случае два показателя степени относятся только к отдельным членам логарифма, поэтому свойство 7 здесь использовать нельзя. Однако у нас есть произведение внутри логарифма, поэтому мы можем использовать свойство 5 для этого логарифма. 5}} \ right) \] Теперь, когда мы это сделали, мы можем использовать свойство 7 для каждого из этих отдельных логарифмов, чтобы получить окончательный упрощенный ответ.{\ frac {1} {2}}} \] Написано в этой форме, мы видим, что есть один показатель степени для всего члена, и поэтому мы позаботимся об этом в первую очередь. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ ln \ left ({xy} \ right) \] Теперь займемся продуктом. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ left ({\ ln x + \ ln y} \ right) \] Обратите внимание на круглые скобки в этом ответе. \ (\ Frac {1} {2} \) умножает исходный логарифм, поэтому ему также потребуется умножить весь «упрощенный» логарифм.2}} \ справа) \] Теперь мы подошли к сути этой проблемы. Второй логарифм настолько упрощен, насколько это возможно. Помните, что мы не можем разбить журнал суммы или разницы, и поэтому он не может быть разбит дальше. Кроме того, мы можем иметь дело с показателями, только если весь член возведен в степень. Тот факт, что обе части этого члена возведены в квадрат, не имеет значения. Это должен быть квадрат всего члена, как в первом логарифме. Итак, мы можем еще больше упростить первый логарифм, но второй логарифм упростить уже нельзя.2}} \ справа) \] Теперь нам нужно проработать несколько других примеров. Следующий набор примеров, вероятно, более важен, чем предыдущий. Мы будем выполнять такую логарифмическую работу в нескольких разделах. Пример 5 Запишите каждое из следующих значений в виде одного логарифма с коэффициентом 1.
Показать все решения Скрыть все решения Показать обсуждение Инструкция, требующая коэффициента 1, означает, что когда мы переходим к окончательному логарифму, перед логарифмом не должно быть числа. Также обратите внимание, что в этих примерах будут использоваться свойства 5–7, только мы будем использовать их в обратном порядке. У нас будут выражения, которые выглядят как правая часть свойства, и мы будем использовать свойство для записи, чтобы оно выглядело как левая часть свойства. a \ (7 {\ log _ {12}} x + 2 {\ log _ {12}} y \) Показать решение Первый шаг здесь — избавиться от коэффициентов при логарифмах. Это будет использовать свойство 7 в обратном порядке.6}}}} \ справа) \] c \ (5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x \) Показать решение В этом случае у нас есть три термина, и ни одно из свойств не содержит трех терминов. Это не проблема. Давайте сначала позаботимся о коэффициентах, а заодно вычтем минус из двух последних членов. Причина этого станет очевидной на следующем шаге. \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ left ({\ ln {y ^ 2} + \ ln {x ^ 8}} \ right) \] Теперь обратите внимание, что величина в скобках представляет собой сумму двух логарифмов и поэтому может быть объединена в один логарифм с произведением следующим образом: \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ ln \ left ( {{y ^ 2} {x ^ 8}} \ right) \] Теперь у нас осталось два логарифма, и они представляют собой разность логарифмов, поэтому мы можем записать это как единственный логарифм с частным.8}}}} \ справа) \] Последняя тема, которую нам нужно обсудить в этом разделе, — это изменение формулы базы . Большинство современных калькуляторов могут вычислять десятичные и натуральные логарифмы. Однако это все, так что же нам делать, если нам нужно вычислить еще один логарифм, что не может быть сделано легко, как мы это сделали в первом наборе примеров, которые мы рассмотрели? Для этого у нас есть изменение базовой формулы.Вот изменение базовой формулы. \ [{\ log _a} x = \ frac {{{{\ log} _b} x}} {{{{\ log} _b} a}} \] , где мы можем выбрать \ (b \) как угодно. Чтобы использовать это, чтобы помочь нам вычислить логарифмы, это обычно обычный или натуральный логарифм. Вот изменение базовой формулы с использованием как десятичного, так и натурального логарифма. \ [{\ log _a} x = \ frac {{\ log x}} {{\ log a}} \ hspace {0,25 дюйма} {\ log _a} x = \ frac {{\ ln x}} {{\ ln a}} \] Давайте посмотрим, как это работает, на примере.?} = 7 \] , и это не то, на что кто-то может ответить сразу. Если бы 7 была 5, или 25, или 125, и т. Д. . мы могли бы это сделать, но это не так. Следовательно, мы должны использовать замену базовой формулы. Теперь мы можем использовать любой из них, и мы получим тот же ответ. Итак, давайте воспользуемся обоими и проверим это. Начнем с десятичного логарифма изменения основания. \ [{\ log _5} 7 = \ frac {{\ log 7}} {{\ log 5}} = \ frac {{0.845098040014}} {{0,698970004336}} = 1.205512 \] Теперь давайте попробуем натуральный логарифм изменения основной формулы. \ [{\ log _5} 7 = \ frac {{\ ln 7}} {{\ ln 5}} = \ frac {{1.945 906}} {{1.609437 }} = 1.205512 \] Итак, мы получили один и тот же ответ, несмотря на то, что дроби содержали разные ответы. Алгебра — решение логарифмических уравненийРешите каждое из следующих уравнений. 2} = 25 \] Обратите внимание, что это уравнение, которое мы можем легко решить. \ [2x = 21 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = \ frac {{21}} {2} \] Теперь, как и в случае с первым набором примеров, нам нужно снова вставить это в исходное уравнение и посмотреть, будет ли оно давать отрицательные числа или нули в логарифмах. Если да, то это не может быть решением, а если нет, то это решение. \ [\ begin {align *} {\ log _5} \ left ({2 \ left ({\ frac {{21}} {2}} \ right) + 4} \ right) & = 2 \\ {\ log _5} \ left ({25} \ right) & = 2 \ end {align *} \] Только положительные числа в логарифме, поэтому \ (x = \ frac {{21}} {2} \) на самом деле является решением. b \ (\ log x = 1 — \ log \ left ({x — 3} \ right) \) Показать решение В этом случае у нас есть два логарифма в задаче, поэтому нам придется объединить их в один логарифм, как мы это сделали в первом наборе примеров. Выполнение этого для этого уравнения дает \ [\ begin {align *} \ log x + \ log \ left ({x — 3} \ right) & = 1 \\ \ log \ left ({x \ left ({x — 3} \ right)} \ вправо) & = 1 \ end {выровнять *} \] Теперь, когда мы получили уравнение в правильной форме, мы преобразуем его в экспоненциальную форму.2} — 3x — 10 & = 0 \\ \ left ({x — 5} \ right) \ left ({x + 2} \ right) & = 0 \ hspace {0,25in} \ Rightarrow \ hspace {0,25in} x = — 2, \, \, x = 5 \ end {align *} \] Итак, у нас есть два возможных решения. Давайте проверим их обоих. \ (* х = — 2: \) \ [\ log \ left ({- 2} \ right) = 1 — \ log \ left ({- 2 — 3} \ right) \] У нас есть отрицательные числа в логарифмах, поэтому это не может быть решением. \ (х = 5: \) \ [\ begin {align *} \ log 5 & = 1 — \ log \ left ({5 — 3} \ right) \\ \ log 5 & = 1 — \ log 2 \ end {align *} \] Нет отрицательных чисел или нулей в логарифмах, поэтому это решение. 2} — 6 \ left (2 \ right)} \ right) & = 3 + {\ log _2} \ left ({1 — 2} \ right) \\ {\ log _2} \ left ({4 — 12} \ right) & = 3 + {\ log _2} \ left ({- 1} \ right) \ end {align *} \] В этом случае, несмотря на то, что потенциальное решение положительно, мы получаем отрицательные числа в логарифмах, и поэтому оно не может быть решением. Следовательно, мы получаем единственное решение этого уравнения, \ (x = — 4 \). OpenAlgebra.com: решение логарифмических уравненийИспользуйте однозначное свойство логарифмов для решения логарифмических уравнений. Шаг 1 : Используйте правила экспонент, чтобы изолировать логарифмическое выражение (с одинаковым основанием) с обеих сторон уравнения. Обязательно проверьте, решают ли полученные решения исходное логарифмическое уравнение. В этом учебном пособии мы поставим галочку рядом с решением после того, как определим, что оно действительно решает уравнение. Этот процесс иногда приводит к посторонним решениям, поэтому мы должны проверить свои ответы.
Конечно, подобные уравнения очень особенные. Большинство проблем, с которыми мы столкнемся, не имеют логарифма с обеих сторон. Шаги по их решению приведены ниже. Шаг 1 : Используйте свойства логарифма, чтобы изолировать журнал с одной стороны. Если ответ на логарифмическое уравнение делает аргумент отрицательным, то он не имеет значения. Это не исключает отрицательных ответов. Мы должны обязательно проверить все наши решения. Обучающее видео : Решение логарифмических уравнений Решить . Совет : Не все отрицательные решения являются посторонними! Посмотрите на предыдущий набор проблем и убедитесь, что на некоторые из них есть отрицательные ответы.Галочка означает, что мы действительно вставили ответы, чтобы убедиться, что они действительно решают исходный текст. Пожалуйста, не пропускайте этот шаг, часто встречаются посторонние решения. Чтений: Использование определения логарифма для решения логарифмических уравнений Мы уже видели, что каждое логарифмическое уравнение | |
| Рассчитать 2 3 | [латекс] \ displaystyle {8} = {6} {x} — {10} [/ latex] | |
| Добавьте 10 к обеим сторонам | [латекс] \ displaystyle {18} = {6} {x} [/ latex] | |
| Разделить на 6 | [латекс] \ displaystyle {x} = {3} [/ latex] |
Использование определения логарифма для решения логарифмических уравнений
Для любого алгебраического выражения
S и вещественных чисел b и c , где b > 0, b ≠ 1,
log
b ( S ) = c c тогда и только тогда, когда b c = S
Пример 1
Использование алгебры для решения логарифмического уравнения
- Решить [латекс] \ displaystyle {2} {ln {{x}}} + {3} = {7} [/ latex]
- Вычесть 3:
[латекс] \ displaystyle {2} {ln {{x}}} = {4} [/ latex] - Разделить на 2:
[латекс] \ displaystyle {ln {{x}}} = {2} [/ latex] - Записываем в экспоненциальной форме:
[latex] \ displaystyle {x} = {e} ^ {{2}} [/ latex]
- Вычесть 3:
- Решить [латекс] \ displaystyle {6} + {ln {{x}}} = {10} [/ latex]
Использование алгебры до и после использования определения натурального логарифма
- Решить [латекс] \ displaystyle {2} {ln {{({6} {x})}}} = {7} [/ latex]
- Разделить на 2:
[латекс] \ displaystyle {ln {{({6} {x})}}} = \ frac {{7}} {{2}} [/ latex] - Используйте определение ln:
[латекс] \ displaystyle {6} {x} = {e} ^ {{{(\ frac {{7}} {{2}})}}} [/ latex] - Разделить на 6:
[латекс] \ displaystyle {x} = \ frac {{1}} {{6}} {e} ^ {{{(\ frac {{7}} {{2}})}} } [/ латекс]
- Разделить на 2:
- Решите [латекс] \ displaystyle {2} {ln {{({x} + {1})}}} = {10} [/ latex]
- Используя график, чтобы понять решение логарифмического уравнения, решите [latex] \ displaystyle {ln {{x}}} = {3} [/ latex] Графики y = ln x и y = 3 крестик в точке ( e 3 , 3), что приблизительно равно (20.0855, 3).
- Используйте графический калькулятор, чтобы оценить приближенное решение логарифмического уравнения 2 x = 1000, решите с точностью до 2 десятичных знаков.
x ≈ 9,97
Как и в случае с экспоненциальными уравнениями, мы можем использовать свойство однозначности для решения логарифмических уравнений. Однозначное свойство логарифмических функций говорит нам, что для любых действительных чисел
x > 0, S > 0, T > 0 и любого положительного действительного числа b , где b ≠ 1,
журнал b S = журнал b T тогда и только тогда, когда S = T
Например,
Если журнал 2 ( x — 1) = log 2 (8), то x — 1 = 8.
Итак, если
x — 1 = 8,
, то мы можем решить для
x , и мы получим x = 9. Чтобы проверить, мы можем заменить x = 9 в исходное уравнение: log 2 (9 — 1) = log 2 (8) = 3. Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны. Это также применимо, когда аргументы являются алгебраическими выражениями. Следовательно, когда дано уравнение с журналами с одинаковым основанием на каждой стороне, мы можем использовать правила логарифмов, чтобы переписать каждую сторону как единый логарифм.Затем мы используем тот факт, что логарифмические функции взаимно однозначны, чтобы установить аргументы, равные друг другу, и найти неизвестное.
Например, рассмотрим уравнение
[латекс] \ displaystyle {log {{({3} {x} — {2})}}} — {log {{({2})}}} = {log {{ ({x} + {4})}}} [/ латекс]. Чтобы решить это уравнение, мы можем использовать правила логарифмов, чтобы переписать левую часть как единый логарифм, а затем применить свойство «один к одному», чтобы найти
[латекс] \ displaystyle {log {{({3} { x} — {2})}}} — {log {{({2})}}} = {log {{({x} + {4})}}} [/ latex]
| Применить правило частного логарифмов | [латекс] \ displaystyle {журнал {{(\ frac {{{3} {x} — {2}}} {{2}})}}} = {журнал {{({x} + {4}) }}} [/ latex] |
| Примените свойство логарифма один к одному. | [латекс] \ displaystyle \ frac {{{3} {x} — {2}}} {{2}} = {x} + {4} [/ latex] |
| Умножьте обе части уравнения на 2 | [латекс] \ displaystyle {3} {x} — {2} = {3} {x} + {8} [/ latex] |
| Вычтем 2 x и прибавим 2 | [латекс] \ displaystyle {x} = {10} [/ latex] |
Чтобы проверить результат, замените
на
[латекс] \ displaystyle {журнал {{({3} {({10})} — {2})}}} — {журнал {{({2})}}} = {журнал {{({( {10})} + {4})}}} [/ латекс]
[латекс] \ displaystyle {log {{({28})}}} — {log {{({2})}}} = {log {{({14})}}} [/ latex]
[латекс] \ Displaystyle {журнал {{(\ frac {{28}} {{2}})}}} = {журнал {{({14})}}} [/ латекс]
Решение проверяет.
Использование однозначного свойства логарифмов для решения логарифмических уравнений
Для любых алгебраических выражений
S и T и любого положительного действительного числа b , где b ≠ 1, log b S = log b T тогда и только тогда, когда S = т
Обратите внимание: при решении уравнения, включающего логарифмы, всегда проверяйте, правильный ли ответ или является ли это посторонним решением. {{2}} — {2} {x} — {3} = {0} [/ latex] Фактор с использованием FOIL: [latex] \ displaystyle {({x} — {3})} {({x} + {1})} = {0} [/ латекс]
Если продукт равен нулю, один из факторов должен быть равен нулю: [latex] \ displaystyle {x} — {3} = {0} {\ text {или}} {x} + {1} = {0} [ / латекс]
Решите относительно x : [latex] \ displaystyle {x} = {3} {\ text {or}} {x} = — {1} [/ latex]
Анализ
Есть два решения:
x = 3 или x = –1.{{2}})}}} = {ln {{1}}} [/ latex]
OpenStax, Precalculus, «Экспоненциальные и логарифмические уравнения», под лицензией CC BY 3.0.
.
