Интересные задания по математике 5 класс

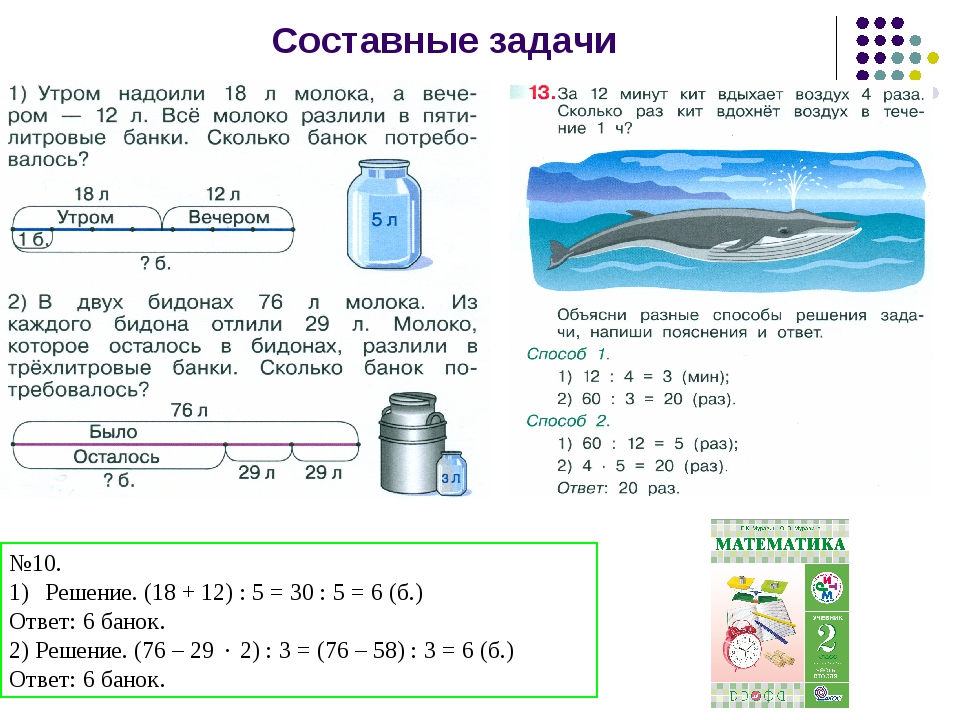
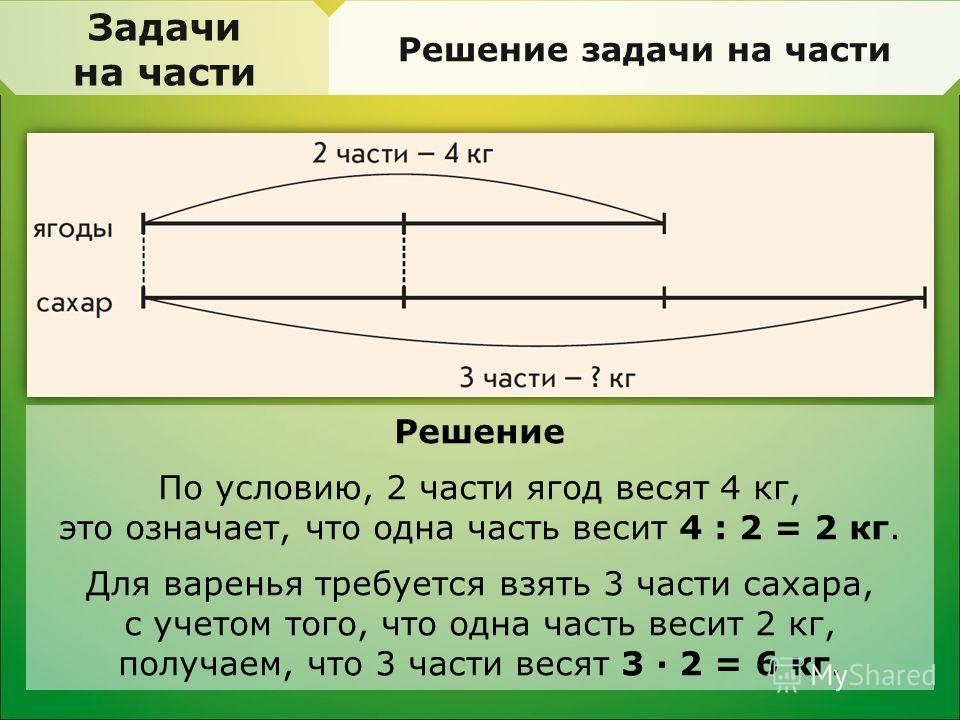
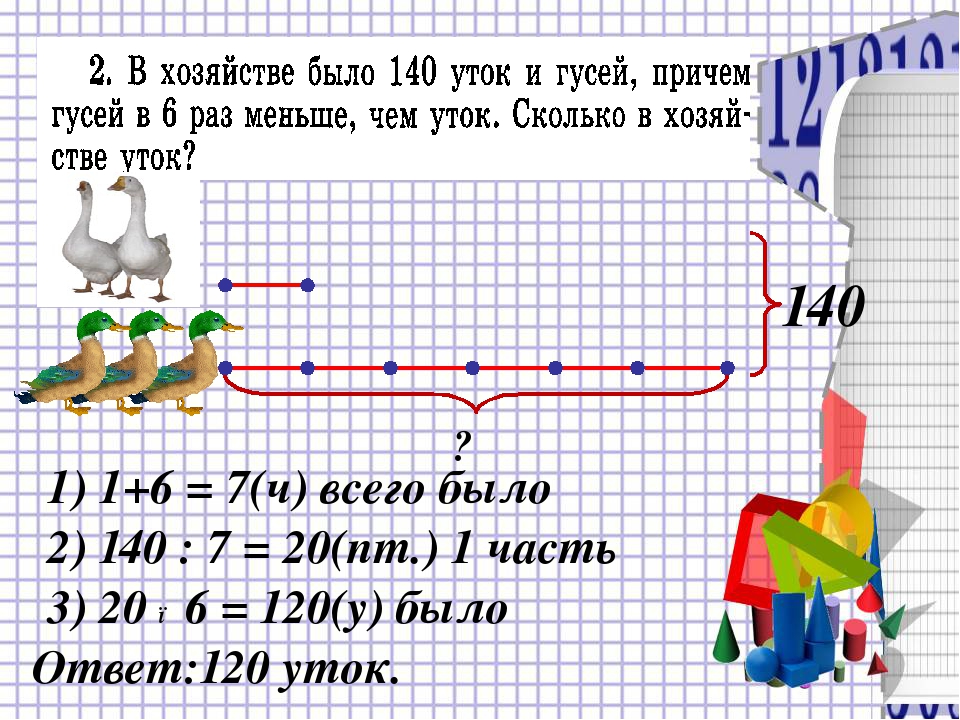
Каждому учителю по математике непременно следует не только владеть навыком быстро решать математические задания любого уровня сложности, но и уметь грамотно и понятно «донести» это до своего ученика. Опять же следует помнить, что все дети совершенно разные: кто-то улавливает все на лету, а до кого-то «доходит» всё очень медленно. Каждому маленькому человечку нужен индивидуальный подход! Чтобы пятиклассникам было понятно и у них проявился интерес к предмету, все задачи, по возможности, желательно показывать визуально. Для этого можно использовать либо предметы, либо рисунки. Все математические задачи для школьников имеют разные направления. Некоторые из них установлены на внимание, другие на логическое мышление, третьи на вычислительные способности. В большинстве случаев, все интересные задания для школьников 5-го класса являются комбинированными, то есть включают в себя все три вышеуказанные направления. Итак, для начала рассмотрим несколько интересных заданий на логическое. .. В четырёхугольной комнате, в каждом углу сидит кошка. Каждая кошка наблюдает за тремя, сидящими напротив, кошками. Сколько в комнате кошек? Нарисовав прямоугольник(квадрат) на доске, учителю нужно попросить ребят представить, что это комната. В каждом углу квадрата, преподавателю следует нарисовать кружок, объяснив, что это кошка. Нарисовав на доске такую картину и при этом стрелочками показать, как смотрит каждая кошка, ученикам станет сразу понятно, что в комнате 4 кошки. Также есть и такая задача: У отца и матери пятеро сыновей; у каждого сына имеется по две сестры. Какое количество детей имеется в этой семье? У швеи в наличии 300 метров ткани. Ежедневно, начиная с 20 января она отрезала от этого куска по 30 метров. Какого числа будет отрезан последний кусок. На сколько дней хватит материала? Эти задачи решаются и объясняются на подобии первой…. В саду цветут пять яблонь. На каждой яблоне по 5 больших веток, каждая из которых имеет по пять маленьких веток. На каждой маленькой веточке растут по пять яблок. Сколько на дереве всего яблок? Сколько яблок всего в саду? Подобные задачи решаются при помощи умножения. Для начала следует посчитать сколько маленьких веток на одной яблоне. Итак, на одной яблоне 25 маленьких веток; значит яблок на одной яблоне будет 125 штук. Значит в саду на пяти яблонях будут расти 725 яблок. Чтобы такие задачи запоминались лучше, школьникам 5-го класса желательно задавать их в качестве домашнего задания, с обязательным выполнением рисунка. Но, конечно же, не обязательно рисовать все 5 яблонь с 725 яблоками, в данном случае достаточно будет одной яблони. Таким образом у ребёнка будут развиваться не только математические способности, но и фантазия. Логических задач много, ниже приведены ещё несколько примеров данного типа задач. На дереве сидело 50 ворон. Проходя, охотник выстрелил из ружья и убил 2 вороны, сколько птиц осталось на этом дереве?  Два отца и два сына, взяв три яблока и три апельсина, разделили их между собой так, что каждому досталось по одному яблоку и одному апельсину. Как это у них получилось?… У человека в наличии два ведра – 4-х и 9-ти литровые. Как из речки принести ровно 6 литров воды, используя только эти вёдра? А теперь непременно стоит разобрать каждую из этих задач. В задаче с воронами, половина пятиклассников непременно стали бы заниматься вычислениями, и дали бы ответ : «на дереве осталось 48 ворон». Но подвох этой задачи в том, что птицы сидят именно на дереве, а не в клетке. При издающемся шуме (особенно в их сторону) они всегда улетают. Поэтому ответ будет таков: «на дереве нет ворон». Что же касается второй задачи: мальчик (сын) , отец мальчика (сын дедушки мальчика) , дедушка мальчика (папа отца мальчика) = 2 отца и 2 сына. В итоге всего трое людей, поэтому и фрукты не пришлось разрезать…. Задачка про вёдра интересна по своему, но она немного сложнее предыдущих. По статистике, каждый седьмой пятиклассник удачно справляется с данным видом задачи. Итак, человеку нужно полностью заполнить водой девятилитровое ведро. Пользуясь 4-х литровым ведром, из большого ведра нужно слить 8 литров воды. Один литр, который остался в большом ведре, сливается в пустое 4-х литровое ведро( но не выливается) . В девятилитровое ведро следует залить полностью воду, после чего из него нужно отлить в воду в маленькое ведро, а это и есть 3 литра. В итоге, в большом ведре останется 6 литров воды. Все задачи по математике 5-го класса идентичные. Если школьник научится решать лёгкие задачи, то он справится и со сложными заданиями. В статье описаны интересные задания для школьника 5 класса, а также решение к ним. Ученикам 5 класса следует не менее часа в день уделять математики, при этом нужно стараться решать задачи повышенной сложности…. взято с http://veselajashkola.ru/klass/zadachi/interesnye-zadaniya-dlya-shkolnikov-po-matematike-5-j-klass/

Технологическая карта по математике 5 класс по теме «Деление с остатком»

Технологическая карта урока математики в 5 классе

по теме «Деление с остатком»

Цели урока: обобщение и закрепление материала по теме «Деление с остатком».

Задачи, направленные на развитие:

• в личностном направлении (воспитательные): развивать умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;

• в метапредметном направлении (развивающие): развивать внимание, логическое мышление, математическую речь

• в предметном направлении (общеобразовательные): повторить деление с остатком, формировать навыки деления с остатком.

Тип урока: комбинированный урок (изучения нового материала и первичного закрепления изученного).

Формы работы учащихся: фронтальная, индивидуальная, работа в парах.

Необходимое техническое оборудование: компьютер, проектор, экран.

ХОД УРОКА

Приветствие учителя.

— Здравствуйте, садитесь!

Посмотрите все ль в порядке

Ручки, книжки и тетрадки

Все ль готовы вычитать,

И делить, и умножать?

Все готовы?

Делаем заявку на урок, какую отметку вы сегодня получите .

Ученики стоя приветствуют учителя.

Настраиваются на работу.

Ученику делают заявку.

Разделить примеры на две группы

Оцените работу друг друга (взаимооценка).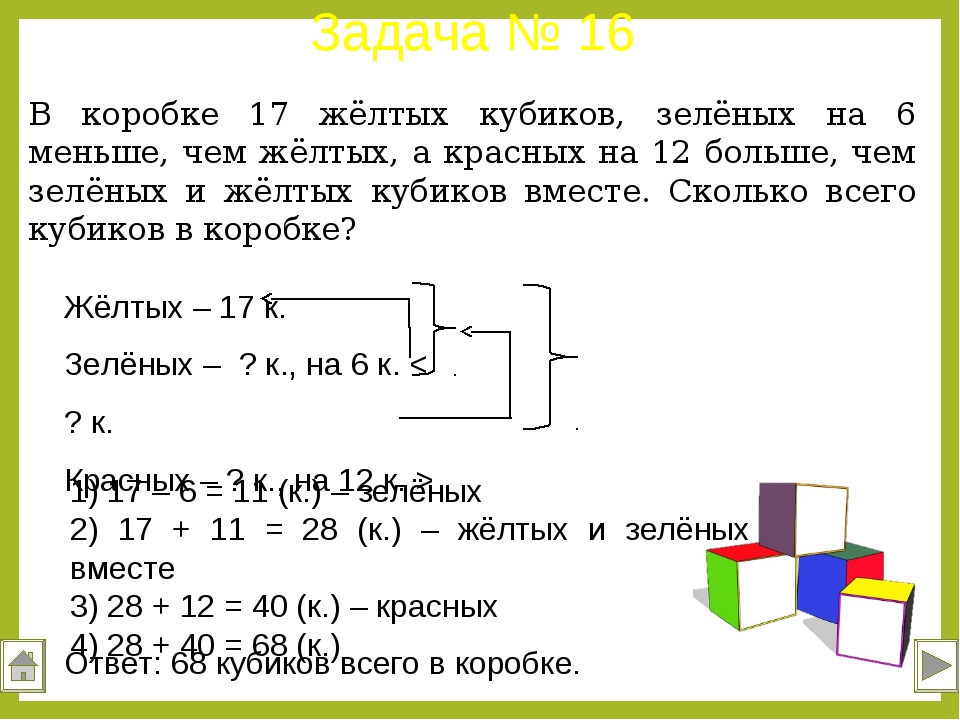

Дети решают примеры в паре.

Дети отвечают – деление нацело и деление с остатком. Деление с остатком

13:2 = 6 (ост.1)

24:5=4 (ост.4)

26:7= 3 (ост.5)

III. Этап сообщения темы (3 минуты)

1. А теперь, ребята, мы с вами попробуем решить такую задачу : У нас есть 22 сливы. Как нам разделить их поровну между 4 детьми?

2. Как называются элементы деления с остатком? Найдите правильные соответствия.

— Как вы думаете, какая тема нашего урока сегодня?

Запишите в тетрадях решение задачи в столбик

22 4

20 5

2

23 остаток

4 неполное частное

5 делимое

3 делитель

Дети отвечают деление с остатком.

IV Систематизация материала (10 минут)

Вычислите устно:

17:3 = 5 (ост.2)

25 : 4 = 6 (ост.1)

28 : 5 = 5 (ост.3)

— Какой вывод можно сделать из этого?

— Ребята, подумайте и решите как найти неизвестное делимое, зная делитель, неполное частное и остаток. Проверяем!

— Молодцы! Давайте сформулируем правило как найти делимое, если известен делитель, неполное частное и остаток.

— Давайте напишем формулу для нахождения делимого, если обозначим:

а – делимое

b – делитель

c – неполное частное

d — остаток

Оценивает учитель

— Остаток не может быть больше делителя.

Х : 6 = 5 (ост.3)

Х = 5*6 + 3

Х =33

— Чтобы найти делимое, надо неполное частное умножить на делитель и прибавить остаток.

Записывают в тетради

а= b*с +d

V. Физкультминутка. (3 минуты)

Быстро встали, улыбнулись,

Выше-выше подтянулись.

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали, сели, встали,

И на месте побежали.

VI этап. Проверка понимания усвоения (3 минуты)

Заполним таблицу, решая устно:

Самопроверка и самооценка.

Устное решение.

ГДЗ тетрадь-экзаменатор по математике 5 класс Сафонова Просвещение

Изучение математики не будет казаться скучным и трудным, если подойти к реализации этой задачи творчески. Главное – суметь все организовать и относиться к такой работе предельно ответственно, выделяя на нее достаточное количество времени ежедневно. Помочь на начальном этапе пятиклассникам могут родители, а в качестве основы для подготовки взять полезный и интересный справочник и гдз тетрадь экзаменатор по математике за 5 класс Сафонова Выполняя в день минимум по одному варианту заданий, представленных в сборнике (на каждую тему автор предлагает по 4 варианта – два зачетных и два тестовых), уже через несколько недель можно отметить существенное улучшение результатов, более глубокие знания по дисциплине.

Для кого будут полезны готовые решения для тетради экзаменатора по математике за 5 класс Сафоновой

Наиболее полезными готовые домашние задания будут:

• пятиклассникам, переведенным на домашнюю, дистанционную, семейную формы обучения. Здесь они найдут все те пояснения по выполнению практических работ и использованию теоретических знаний, которые могли бы получить от учителя, если бы учились в классе очно;
• подросткам, которые пропускают большое количество учебных классных уроков из-за болезни или поездок на конкурсы, соревнования, спортивные сборы. Регулярно применяя онлайн-решебники, эти ребята смогут хорошо понять тему, ответить на вопросы учителя, выполнить задания контрольных и проверочных работ, ВПР без проблем;
• заинтересованным в математике детям, планирующим в дальнейшем принимать участие в предметных математических олимпиадах и заранее начавшим такую подготовку;
• родителям, стремящимся быстро и с гарантией высокого качества проверить уровень знаний своего ребенка, не вникая глубоко в саму суть задания, темы;
• школьным учителям, проверяющим тетради, чтобы сократить время на такую проверку, поскольку сегодня у педагогов много других, неотложных рабочих задач.

Вред или польза?

Хотя есть преподаватели, критикующие использование еуроки ГДЗ, считающие, что эти ресурсы не позволяют школьникам думать самостоятельно, многие их коллеги, а также родители и сами учащиеся, напротив, считают эти материалы крайне полезными, поскольку:

• они доступны всем пользователям, круглосуточно и каждый день;
• на их основе можно овладеть навыком самоподготовки и самоконтроля, которые считаются сегодня одними из самых полезных и важных, приобретаемых в школе;
• поиск на ресурсах максимально удобен и позволяет найти нужное решение оперативно, в сжатые сроки.

Знания и умения, приобретаемые пятиклассниками с помощью онлайн справочника к тетради экзаменатору по математике за 5 класс Сафоновой Н. В., пригодятся не только в школе, но и в будущем. Быстро находить и применять на практике важную информацию — вот главный навык, определяющий критерий качества сегодняшнего образования в условиях доступа к огромному количеству данных сейчас во всем мире.

«Олимпиадные задания по математике (5 класс)»

Школьный этап Всероссийской олимпиады по математике

5 класс

(Время – 60 минут)

1. (1 балл)  Найдите значение выражения:

                      2012  ‒  2011 + 2010  ‒  2009 + 2008 ‒   … + 2 – 1.

2. (2 балла)  Как разложить 9 гирь массой 1, 2, 3, 4, 5, 6, 7, 8, 9 граммов на 3 части, равных по массе?

3. (3 балла)  В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

4. (4 балла) Король хочет построить 6 крепостей и соединить каждые две из них дорогой. Начертите такую схему расположения крепостей и дорог, чтобы на ней было только три перекрестка, и на каждом из них пересекались только две дороги.

5.  (5 баллов) Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

   Методические рекомендации

Критерии оценивания работы в 5 классе.

Максимальное количество баллов – 15 баллов.

1).

2).

3).

4).

5).

Ответы и указания к решению

5 класс

1. 
    Найдите значение выражения:

                             2012  ‒  2011 + 2010  ‒  2009 + 2008  ‒ … + 2 ‒ 1.

Решение.

Заметим, что разность чисел 2012 и 2011 равна 1, аналогично разность чисел 2010 и 2009 равна 1 и т. д. Всего таких разностей будет 2012:2=1006. В результате получается, что значение выражения равно 1006.

2.  Как разложить 9 гирь массой 1, 2, 3, 4, 5, 6, 7, 8, 9 граммов на 3 части, равных по массе?

Решение.

1. 
            1+2+3+4+5+6+7+8+9=45 (г) общая масса гирь.
2. 
            45:3=15 (г) – в одной части.

Гири разложили так:(2+9+4) г; (1+8+6) г; (3+5+7) г.

3. 
            В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

Решение.

   5 лет — возраст ребёнка детского сада. Самый младший ребёнок — девочка в возрасте 5 лет.

    Зная, что Аня старше Бори, получаем, что Ане либо 13, либо 15 лет.

    Так как сумма лет Ани и Веры делится на 3, то получаем три случая:

1. 
            Ане 15 лет, Вере 5 лет.  15+5=20, не делится на 3.
2. 
            Ане 15 лет, Вере 8 лет.   15+8=23, не делится на 3.
3. 
            Ане 13 лет, Вере 5 лет.  13+5=18, делится на 3.

Значит, Боре-8 лет, Гале-15 лет.

Ответ: Вере-5 лет, Боре-8 лет, Ане-13 лет, Гале-15 лет.

4. Король хочет построить 6 крепостей и соединить каждые две из них дорогой. Начертите такую схему расположения крепостей и дорог, чтобы на ней было только три перекрестка, и на каждом из них пересекались только две дороги.

Решение 1.

Рисуем 6 крепостей (на каждой надписываем цифру 1,2,3,4 и т.д.) От крепости номер 1 проводим дорогу к номеру 3, от 2 к 4, от 3 крепости проводим дорогу к 5 и от четвертой к шестой. При таком соединении образуется 3 перекреста и на каждом из них пересекутся 2 дороги.

Решение 2.

0-крепость
—  -дорога
0—0
0—0
0—0

5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

Решение.

 Кошка = 6 мышек;  жучка = 5 кошек = 30 мышек;  внучка = 4 жучки = 120 мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек. Все вместе дедка+бабка+внучка+жучка+кошка+мышка= 720+360+120+30+6+1=1237 мышек.

Есть идея все выражать в мышках, но не доведено до конца или неправильно доведено (например, посчитано, что дедка —  это 720 мышек и в ответ записано 720 ) – 2 балла. Вычислительная ошибка – минус 1 балл (если вычислительных ошибок несколько, соответственно вычитается больше).

Разработка урока по математике 5 класс «Решение текстовых задач с помощью сложения и вычитания»

Автор: Трушина Н.В.

МБОУ «Краснопоймовская СОШ»

Учитель: Трушина Наталья Вячеславовна

Класс: 5 класс

Предмет: математика

Конспект урока на тему: «Решение текстовых задач с помощью сложения и вычитания»

Продолжительность: 45 минут

Тип урока: комбинированный

Форма урока: урок-сказка

Цели урока:

Образовательные цели: создать условия для углубления навыков решения текстовых задач арифметическим способом.

Развивающие цели: создать условия для развития логического мышления, поисково-познавательной активности обучающихся, смекалки, настойчивости и математической речи.

Воспитательные цели: создать условия для воспитания трудолюбия, чувства ответственности за свои знания, за успехи своего коллектива.

План урока:

Организационный момент (1 мин)

Актуализация знаний и умений (устный счет – 10 мин)

Формирование умений и навыков (25 мин)

Физкультминутка (4 мин)

Итоги урока (3 мин)

Постановка домашнего задания (2 мин)

1. Организационный момент (1 мин)

Приветствие, постановка темы и цели урока.

-Здравствуйте, ребята! Сегодня 19 сентября и тема нашего урока «Решение текстовых задач»

Как вы думаете, чему мы должны с вами сегодня научиться?

А кто мне скажет, какую задачу мы называем текстовой?

Открываем свои тетради, записываем число, классная работа и тема урока. Как вы правильно сказали, целью нашего сегодняшнего урока будет углубление навыков решения текстовых задач. А помогут нам в этом сказочные герои. Ну, что ж, начнем!

— В мире много сказок

Грустных и смешных.

И прожить на свете

Нам нельзя без них!

Пусть герои сказок

Дарят нам тепло,

Пусть добро навеки

Побеждает зло!

2. Актуализация знаний и умений (10 мин)

Устный счет

Помогите Золушке вовремя вернуться домой. Вычислите устно:

а) 23+8+11-12=31+11-12=32-12-8=12

б) 59-56+29-14=3+29-14=32-14-6=12

в) 90-16/2+23/5=12

г) 60-22/2+46/5=12

Помогите Иа найти ошибку и исправить ее:

а) 90+81+9=180

б) 18*4+28*3=156

в) 223+3*9=252

г) 20+16+42=77

3. Формирование умений и навыков (25мин)

А теперь давайте попробуем решить такую задачу:

Задача №1

В окрестностях пруда четыре болота. В каждом болоте по 58 кочек, а на каждой кочке живет по шесть лягушек. Каждая лягушка мечтает стать лягушкой – путешественницей.

Сколько нужно уток, чтобы осуществилась их мечта?

Надеюсь, вы не забыли способ передвижения лягушки – путешественницы по воздуху!?

Решение:

4*58*6*2=2784 (ут)

Ответ: нужно 2784 утки

Задача №2

Узнав о дне рождения ослика Иа, Винни – Пух решил подарить ему несколько горшочков меда. Придя домой, он обнаружил, что у него есть 25 горшочков. Мед из 15 горшочков он тут же съел, а остальные захватил с собой. По дороге он съел мед еще из 3 горшочков. Сколько горшочков с медом все – таки получил в подарок ослик Иа?

Решение:

25-15-3=7 (г)

Ответ: Иа получил 7 горшочков с медом.

4. Физкультминутка

Раз – подняться, потянуться.

Два – нагнуться, разогнуться.

Три – в ладоши три хлопка.

Головою три кивка.

На четыре – руки шире,

Пять – руками помахать,

Шесть – на место тихо сесть.

Семь и восемь – лень отбросим!

Пока мы с вами отдыхали, наши герои тоже решили попить чай. И вот, что у них произошло…

Задача №3

Белоснежка, Золушка и Спящая Красавица решили попить чай. Белоснежка и Золушка выпили вдвоем 11 чашек, Белоснежка и Спящая Красавица выпили вдвоем 15 чашек, а Золушка и Спящая Красавица выпили вдвоем 14 чашек. Вопрос: сколько чашек чая выпили все три девушки вместе?

Решение:

(11+15+14)/2=20 (ч)

Ответ: вместе они выпили 20 чашек чая.

Решите задачу из учебника:

С. 20 № 74

Первая бригада собрала за смену 52 прибора, вторая – на 9 приборов меньше, чем первая, а третья – на 12 приборов больше, чем вторая. Сколько всего приборов собрали три бригады за смену?

1 бригада – 52 прибора

2 бригада — ? приборов, на 9 приборов меньше, чем первая

3 бригада — ? приборов, на 12 приборов больше, чем вторая

Решение:

1. 52-9=43 (пр) – собрала 2 бригада;

2. 43+12=55 (пр) – собрала 3 бригада;

3. 52+43+55=150 (пр) – собрали три бригады вместе.

Ответ: всего три бригады собрали 150 приборов за смену.

5. Итоги урока (3 мин)

Итак, ребята, сегодня на уроке мы с вами вспомнили, что такое текстовая задача; повторили методы решения текстовых задач, которые вы уже знали и научились новым методам.

6. Постановка домашнего задания:

№68 – на оценку «3»

№72 – на оценку «4»

№75 – на оценку «5»

«Взмах» — частная школа — Санкт-Петербург

Давайте знакомиться! Мы, в БШ — настоящая команда!

Живем весело! Кутузов и компания. Открытие школы 2012

Учимся – с удовольствием

Любим мы это дело!

Умеем решать трудные задачки

Английским занимаемся за круглым столом. У нас в гостях
ребята из Америки

Изучаем робототехнику

И даже проводим битвы роботов

Готовимся к ЕГЭ, участвуем в олимпиадах!

Весной, каждый год — Конференция по Античной истории

А иногда – конференции посвящены специальным датам.
например, годовщине войны 1812 года

Научный день посвященный дню рождения школы. Он тоже
проводится ежегодно

Свои доклады защищают слушатели, подготовившие лучшие
исследовательские работы

Победитель — выигрывает грант на бесплатное обучение

Уважаем мы и естесственные науки

Очень любим ставить опыты и проводить эксперименты. ..

Проводим литературные суды. в этот раз — над д’Артаньяном

В сентябре — традиционный гуманитарный интенсив

И конкурс оформления классов!Чтобы облик каждого кабинета
отражал характеры тех, кто в нем учится

Вот кабинет оформленный в романтическом стиле

А здесь — попадаем в сказочную страну

Самая любимая традиция БШ…

…Представление классов

«Серебряный век» от 11го класса, выпуск 2009 года

Влад Подкохо в роли сказочника

И знаменитый «Красный танец»

На сцене и взрослые…

…и самые юные

А еще у нас есть театр

Совершенно настоящий!

В театре играют и слушатели школы…

…и преподаватели!

День рождения школы, 2017 год. Спектакль»Тиль»

День рождения школы – всегда грандиозный праздник!

Юбилей школы 25 лет

На сцене – почти каждый!

Вручение номинаций – долгожданный момент на праздновании Дня
Рождения школы!

Учимся быть предпринимателями!

Издаем газету «Газета»! Историческая редакция — все в
сборе!..

Зимой — выезды на природу

Учимся преодолевать препятствия

Часто побеждаем в командных соревнованиях по фризби и
лазертагу!

. ..и получаем заслуженные награды

О, деловые игры! Каждый бизнес-школьник опытный игрок!

Какие только команды не попробовали силы на Чемпионате
России по деловым играм, который уже 15 лет проводят во “Взмахе”!

Денежный дождь – фееричная кульминация Открытия Чемпионата

Чемпионат России по деловым играм. Посвящение новых команд…

Наши цели ясны, задачи определены, за работу, товарищи!

Проводим мы и ролевые игры. «Рыцарский турнир» 2007 год

Главный праздник года. Конечно… Выпускной! 2014 год

Учителя говорят напутственные слова, которые потом
вспоминаются всю жизнь!

Девятиклассники получают первый в своей жизни аттестат

Многие наши выпускники — теперь успешные ученые!!!

. .. И предприниматели

А рулит всем — классная команда БШ! Вместе – мы сила!

Всем сердцем любим мы нашу школу!

Когда и как работодатель может уволить сотрудника без его желания? — Право на vc.ru

5 базовых оснований для увольнения со стороны компании и еще одно, которое использовать крайне непросто

Увольнение по собственному желанию – одна из простых норм трудового законодательства. Работник решил уйти и написал заявление об уходе. По сути лишь одно правило – предупредить компанию за 2 недели. Хотя и это не всегда обязательно. А вот как работодатель может расторгнуть договор с сотрудником и какие на это есть основания? Разберем базовые ситуации.

Сокращение штата

Юридически сокращение – законная процедура, и никто не может запретить работодателю ее проводить по необходимости. Но есть нюансы, на которые часто акцентируют внимание и сотрудники, и судьи в трудовых спорах. Например, нередко вместо сокращения штата компания применяет условие ст. 74 и ст. 77 ТК РФ – увольнение из-за несогласия сотрудника работать в связи с изменением определенных условий трудового договора. Такую подмену компании иногда делают, чтобы платить меньше компенсации. И чаще всего это происходит в случае конфликта с сотрудником. В таких ситуациях дело обычно доходит до суда, решение которого будет основано на доказательствах сторон. Второй нюанс при сокращении – оценка преимущественного права. Сотрудники обращают внимание на то, что компания не оценивала, кого оставить на работе, а кого можно сократить. Но надо помнить, что преимущество оценивается, если сокращается несколько из одинаковых должностей. Если, скажем, сокращают всех менеджеров по продажам или это уникальная должность – оценивать ничего не нужно.

Следующий момент – предложение вакансий. Закон не уточняет, сколько раз предлагать вакансии сокращаемому и какие именно. А если речь идет о вакансиях в другом регионе, закон ссылается на коллективный договор, обязывая предлагать лишь то, что есть в данной местности. Именно эти нюансы часто являются предметом спора. Кроме того, надо уведомлять о сокращении профсоюз и центр занятости. И мнение профсоюза будет играть важную роль. Поэтому, если сотрудник не согласен с сокращением, он имеет полное право жаловаться. Но в интересах работодателя не допускать такого сценария (хотя если есть все доказательства и компания уверена, то выбор за вами), и лучше – детально все разъяснить сотруднику.

Несколько дисциплинарных взысканий

Эта процедура подробно описана в ТК РФ, нюанс в том – чтобы правильно ее применять. Есть немало кейсов, когда суд вставал на сторону сотрудника, т.к. компания что-то сделала неправильно. Применять дисциплинарные взыскания за проступки или неисполнение обязанностей можно не позднее 6 месяцев с даты проступка и 1 месяца со дня, когда он обнаружен. Иначе у суда все права отменить наказание из-за срока давности. Взысканий бывает 3 – замечание, выговор и увольнение. Для рядовых проступков лучше применять замечания, т.к. выговор сложнее обосновать. Второй момент – работодатель обязан потребовать объяснение о причине проступка. Работник не обязан давать его, хотя это не запрещает в итоге применять взыскание.

Важно, что на объяснение дается два рабочих дня, и компания должна это зафиксировать в требовании. Еще важнее оценить отношение работника к труду, уважительность причины проступка. Без этого взыскание так же могут отменить. Другими словами, работодатель должен следовать всей процедуре, а работник может обжаловать любой просчет в действиях компании.

Однократное грубое нарушение

С однократным грубым нарушением или грубым проступком все тоже не так просто. Про них говорит п.6 ст. 81 ТК РФ, и речь не столько о дисциплине, а именно о проступках: появление в состоянии опьянения, прогул, хищение, утрата доверия.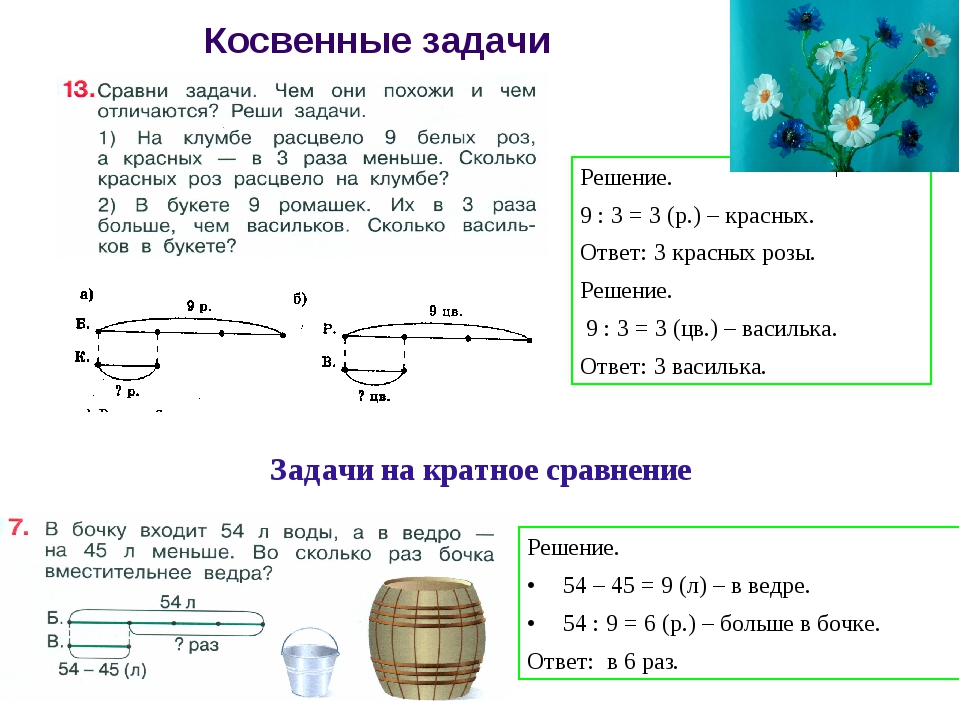 Но, как и любой проступок, грубое нарушение надо тоже доказать, оценить причину, влияние на задачи компании и т.д.

Каждая из причин скрывает нюансы. Скажем, есть практика отпускать раньше сотрудников в день рождения, и прогулом это не признает даже суд. Даже при грубом проступке работодатель обязан собрать доказательства и обосновать, что сотрудник относился к труду плохо, что его действия привели к серьезным последствиям и что увольнение оправдано и обосновано. Человек же может зацепиться за любой небольшой промах в действиях компании.

Несоответствие должности

Несоответствие должности из-за низкой квалификации – определить непросто. Конечно, формально компания может уволить его на этом основании, но именно формально. Сотрудник может пожаловаться в суд и с 95% вероятностью его восстановят. Дело в том, что если сотрудника взяли и он прошел испытательный срок, просто так его не уволить. А несоответствие должности надо четко определить, зафиксировать, подтвердить и обосновать.

Это трудоемкая и затратная процедура, к ней прибегают отнюдь не все. Для этого нужно созвать и легализовать внутреннюю или внешнюю комиссию, которая будет проводить аттестацию сотрудников. Только на основании ее работы и выводов можно будет признать несоответствие.

Ликвидация

С юридической точки зрения у сокращения и ликвидации одно общее – это увольнение по инициативе работодателя. Основное правило при ликвидации – компания должна уведомить об этом за 2 месяца до события. Увольняют всех сотрудников, в т.ч. льготных категорий. При этом ст. 180 ТК РФ позволяет с письменного согласия работника расторгнуть договор раньше 2 месяцев, выплатив допкомпенсацию за то время, которое осталось до увольнения. Т.е. если работник захочет уйти раньше, может написать об этом, и компания может пойти навстречу, хотя и не обязана. Кроме того, об увольнениях надо сообщить в Центр занятости и профсоюз. И в такой ситуации у сотрудников нет вариантов для действий. Ликвидация – законная процедура.

Есть, конечно, еще одно основание – которое нередко применяют, считая его подходящим во многих случаях. И когда других вариантов нет. Речь об изменении условий трудового договора, в соответствии со ст. 74 ТК РФ. Компания планирует изменить условия договора, и, если сотрудник не соглашается, расстается с ним. Но кроме всех прочих правил такого сценария, есть еще 2 серьезных препятствия. Во-первых, увольнение по этой статье в 100% случаев заканчивается спором в суде. Во-вторых, для такого увольнения судьи всегда требуют обосновать необходимость организационных или технологических изменений. То есть – почему вы решили изменить условия договора и можно ли обойтись без этого. И судебная практика крайне неоднозначна, т.к. компании далеко не всегда могут обосновать свои действия.

Так или иначе, в случае конфликта лучше разобраться с ситуацией внутри – поговорить с начальником, пригласить на встречу HR, обсудить с профсоюзом. Только если выход не найден – идти дальше: обращаться в ГИТ, прокуратуру. Если же обращаться к юристам – надо проверить их экспертизу в трудовом праве. У нас немало кейсов, когда такие горе-юристы не только проигрывали дело подзащитных – работников, но и портили репутацию компании и самого сотрудника. В конце концов, даже при конфликте и увольнении – имидж и репутация важны обеим сторонам – и работодателю, и сотруднику.

Задачи по математике для 5 класса с помощью Smartick

Задачи по математике со словами — действительно важная часть Smartick. В этой статье мы специально рассмотрим некоторые из задач для пятого класса, которые вы можете найти в Smartick.

Математические задачи со словами с одной операцией

Дополнение

Вчера многие из нас ходили завтракать в школьную столовую и выпили весь сок. Если бы они подали на 470 литров меньше сока, они бы подали то же количество литров, что и сегодня.Сегодня они подали 910 литров сока. Сколько литров сока подали вчера?

Вчера подали неизвестное количество литров. Если мы отнимем 470 литров от этого количества, мы получим количество литров, которое они обслужили сегодня. Чтобы вычислить, сколько литров они подали вчера, мы должны добавить:

910 + 470 = 1380

Вчера подали 1380 литров.

Вычитание

Чарли пригласил нас к себе домой попробовать клубнично-малиновый торт.Когда он начал делать это, он понял, что ему нужно на 400 больше клубники, чтобы получить столько же клубники, сколько 680 ягод малины, которые у него были. Посчитайте, сколько у него было клубники.

У Чарли было на 400 ягод меньше клубники, чем малины. Так как малины у него было 680, нам нужно вычесть:

680–400 = 280

У Чарли было 280 ягод клубники.

Умножение

Сейчас сезон распродаж, и в магазине Сесилии 15 пакетов картофельных чипсов.Альфред сказал мне, что в магазине Сесилии в 5 раз меньше пакетов картофельных чипсов, чем в его. Посчитайте, сколько пакетов картофельных чипсов есть в магазине Альфреда.

В магазине Сесилии в 5 раз меньше пакетов картофельных чипсов, чем в магазине Альфреда. Это означает, что у Альфреда в 5 раз больше сумок, чем у Сесилии. Чтобы вычислить, сколько сумок в магазине Альфреда, нам нужно умножить:

15 х 5 = 75

В магазине Альфреда 75 пакетов картофельных чипсов.

Отдел

Всего в понедельник в супермаркете было продано 1000 кг продуктов, включая овощи, фрукты, мясо, рыбу и хлеб. Во вторник они продали намного меньше, ровно в 5 раз меньше, чем продали в понедельник. Сколько килограммов еды они продали во вторник?

Они продали еды во вторник в 5 раз меньше, чем в понедельник. Поскольку мы знаем, что они продали 1000 килограммов в понедельник, нам нужно разделить, чтобы вычислить, сколько килограммов они продали во вторник:

1000 ÷ 5 = 200

Во вторник продали 200 кг еды.

Математические задачи с двумя операциями

Сложение и вычитание

Так как я люблю рыбу, я поставил в своей комнате аквариум, в котором есть 8 оранжевых и 5 зеленых рыбок. Я также добавил кое-что, чтобы украсить аквариум, например, песок, ракушки и улиток. Энтони тоже любит рыбу, но в аквариуме у него всего шесть штук. Сколько рыбы нужно было бы купить Энтони, чтобы у меня было столько же рыбы?

Прежде чем мы сможем вычесть рыбу, которая у меня есть, из рыбы Энтони, мы должны знать, сколько рыбы у меня есть.Для этого нам нужно добавить:

8 + 5 = 13

13 — количество рыб, которые у меня есть. Теперь нам нужно найти разницу между количеством рыб, которые у меня есть, и количеством рыбок, которые есть у Энтони. Для этого нам нужно вычесть.

13–6 = 7

Энтони пришлось бы купить 7 рыбок, чтобы у меня было столько же рыбок.

Дроби

Валентина — фотограф природы, и все фотографии в ее альбомах — это сельская местность и животные.1/9 альбома, который она только что начала, составляют фотографии сельской местности, а 1/6 — фотографии животных. Какую часть альбома она заполнила?

Она заполнила одну часть альбома фотографиями сельской местности, а другую — фотографиями животных. Итак, чтобы вычислить общий объем альбома, который она заполнила, нам нужно добавить:

1/9 + 1/6 = 15/54

Она заполнила 15/54 альбома.

Таблицы

Завтра премьера фильма «Алан vs.Пришельцы », и он будет показан на всех экранах Space Cinema. Осталось 14 билетов на 17:00. просмотр, что составляет половину количества билетов, оставшихся до 15:00. скрининг. Заполните таблицу имеющихся билетов.

Мы должны посмотреть данные в таблице и заполнить пробелы.

Осталось 14 билетов на 17:00. скрининг. Если осталось 5 билетов для экрана 1 и 4 осталось для экрана 3, сколько осталось билетов для экрана 2?

14–5–4 = 5

Осталось 5 билетов по 5 р.м. отображение на Экране 2.

Осталось 28 билетов на 15:00. просмотр (удвоить количество билетов, оставшихся на просмотр в 17:00). Если осталось 11 билетов на Экран 2 и 4 осталось на Экран 3, сколько билетов осталось на Экран 1?

28–11–4 = 13

Осталось 13 билетов на 15:00. отображение на Экране 1.

Заполненная таблица будет выглядеть так:

Это несколько примеров математических задач со словами, которые вы можете найти в Smartick.Если вы хотите увидеть больше задач по математике, зарегистрируйтесь в Smartick и попробуйте бесплатно.

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Математика / Решение задач в общем ядре

«> Обзор

Использование моделей — важный шаг, помогающий учащимся перейти от конкретной манипулятивной работы с текстовыми задачами к абстрактному этапу создания уравнения для решения контекстных задач.Научившись использовать простые модели для представления ключевых математических соотношений в словесной задаче, учащиеся могут легче разбираться в словесных задачах, распознавать как числовые отношения в данной задаче, так и связи между типами задач, и успешно решать задачи с уверенностью в том, что их решения разумны.

Важность

Почему моделирование текстовых задач важно?

У студентов часто возникают проблемы со словами.Многие студенты просто ищут какие-то числа и что-то с ними делают, надеясь, что они решат проблему.

Учащиеся должны выработать привычку сначала разбираться в проблеме. Диаграмма или модель часто фокусируются на понимании проблемы, а не просто на получении ответа. Затем модель можно использовать для создания продуманного уравнения. Модель и уравнение можно использовать в качестве проверки рассуждений после того, как учащийся получит решение.

Решение проблем не заканчивается на ответе.Процесс должен продолжаться после «получения ответа» на рассуждение о том, имеет ли ответ смысл.

Что такое моделирование текстовых задач?

Модели на любом уровне могут варьироваться от простых до сложных, от реалистичных до представительных. Молодые студенты часто решают начальные словесные задачи, разыгрывая их и моделируя их с реальными объектами проблемной ситуации, например плюшевых мишек или игрушечных машинок. Со временем они расширяются до использования репрезентативных рисунков, сначала рисуя рисунки, которые реалистично изображают элементы проблемы, а затем переходят к многоцелевым представлениям, таким как круги или отметки.После множества конкретных опытов с реальными задачами со словами, включающими соединение и разделение, или умножение и разделение объектов, учителя могут переводить учащихся на рисунки модели с перевернутой буквой V и гистограммы, которые являются многоцелевыми графическими организаторами, привязанными к определенным типам задач со словами.

Моделирование основных числовых отношений

Простые диаграммы, иногда известные как числовые связи, треугольники фактов, ситуационные диаграммы или графические изображения, все чаще появляются в учебных материалах.Но способности учащихся решать проблемы и относительное мышление выиграют, если будут более рутинно использовать эти диаграммы и модели.

Маленькие дети могут начать видеть числовые отношения, существующие в семье фактов, благодаря использованию модели, из которой они выводят уравнения. Связь чисел и перевернутая буква V — это одна простая модель, которая помогает учащимся увидеть отношения сложения / вычитания в семействе фактов и может использоваться с задачами со словами, требующими простого соединения и разделения.Связь чисел, а затем модель перевернутой буквы V могут быть адаптированы для семейств фактов умножения и деления. Кроме того, учащиеся могут подумать об отношениях между числами в перевернутой букве V в формальных терминах, , добавление и , сумма , или, проще, , часть , и , всего , как показано на схемах ниже.

Конкретный пример для данной суммы 10 будет следующим, в зависимости от того, какой элемент проблемы неизвестен.

6 + 4 =? 6+? = 10? + 4 = 1

4 + 6 =? 10-6 =? 10 — 4 =?

Несмотря на то, что они часто используются с семействами фактов и изучением основных фактов, диаграммы связи чисел и перевернутые V-диаграммы также могут хорошо работать при решении текстовых задач. Студентам необходимо подумать о том, что они знают и чего не знают в словесной задаче — известны ли обе части или только одна из них? Правильно разместив известные величины на перевернутой V-диаграмме, учащиеся с большей вероятностью определят полезное уравнение для решения проблемы и увидят результат как разумный для ситуации.Например, рассмотрим следующую задачу:

Захари имел 10 вагонов. Захари подарил своему брату 3 вагона. Сколько вагонов сейчас у Закари?

Студенты должны определить, со сколькими суммами Захари начал (всего или всего ), и сколько он отдал ( часть от общего числа ). Итак, им нужно узнать, сколько осталось (другая часть от общего числа ). Следующая перевернутая V-диаграмма представляет отношения между номерами этой проблемы:

3 +? = 10 или 10 — 3 =?, Значит, у Закари осталось 7 вагонов.

По мере того, как учащиеся переходят к умножению и делению, модель перевернутой буквы V все еще может использоваться либо в режиме повторного сложения, либо в режиме умножения. Ситуации разделения не требуют новой модели; деление рассматривается как обратное умножению или ситуация, когда один из факторов неизвестен.

Опять же, перевернутая V-диаграмма может быть полезна при решении задач умножения и деления слов. Например, рассмотрим следующую задачу:

Фонг посадил 18 растений томатов в 3 ряда.Если в каждом ряду было одинаковое количество растений, сколько растений было в каждом ряду?

Студенты могут видеть, что они знают продукт и количество строк. Число В строке неизвестно. Любая из приведенных ниже диаграмм может помочь решить эту проблему, убедив учащихся, что шесть раз подряд — разумный ответ.

Хотя перевернутая V-диаграмма может быть расширена до многозначных чисел, она обычно используется с проблемами, связанными с базовыми семействами фактов. Расширение использования модельной диаграммы с перевернутой буквой V должно усилить взаимосвязь между числами в семействе фактов, что сделает его полезным и быстрым визуальным средством для решения простых задач со словами с дополнительным преимуществом использования и увеличения удержания основных фактов.

Модели и типы задач для вычислений

По мере того, как дети переходят к работе с многозначными числами, учителя могут переводить учащихся на чертежи ленточных диаграмм / гистограмм, быстрые наброски, которые помогают учащимся увидеть взаимосвязь между важными числами в словесной задаче и определить, что известно и неизвестно в ситуации.

Знакомя учащихся с грифельными моделями, учитель получает важные наглядные пособия, помогающие учащимся думать о математических отношениях между числами в заданной задаче со словом.

С ленточной диаграммой / гистограммой отношения между числами во всех этих типах задач становятся более прозрачными и помогают студенту перебросить мышление от работы с манипуляторами и рисования картинок к символической стадии написания уравнения для ситуации. При рутинном использовании диаграмм и хорошо организованных обсуждениях учителями ученик начнет понимать части словесной задачи и то, как эти части соотносятся друг с другом.

Проблемы частично-частично-целиком.Задачи Part-Part-Whole полезны со словесными задачами, которые относятся к совокупности вещей, например коллекции. Обычно это более статичные ситуации, включающие два или более подмножества целого набора. Рассмотрим проблему,

Коул имеет 11 красных блоков и 16 синих блоков. Сколько всего блоков у Коула?

Учащиеся могут построить простой прямоугольник из двух частей, чтобы обозначить два известных набора блоков (части / дополнения). Неважно, чтобы части прямоугольника были точно пропорциональны числам в задаче, но некоторое внимание к их относительному размеру может помочь в решении проблемы.Неизвестным в этой задаче является то, сколько их всего (всего / всего / суммы), что обозначается скобкой (или перевернутой буквой V) над полосой, обозначающей общее количество двух наборов блоков. Первая барная модель ниже отражает информацию в задаче о блоках Коула.

11 + 16 =? Итак, у Коула всего 27 блоков.

Аналогичная модель будет работать для задачи, когда известна вся сумма, но одна из частей (недостающее слагаемое) неизвестна. Например:

У Коула было 238 блоков.100 из них были желтыми. Если все блоки Коула синие или желтые, сколько их было синими?

Следующая модель стержня может быть полезна в решении этой проблемы.

100 +? = 238 или 238 — 100 =? Итак, у Коула 138 синих блоков.

Ответ должен быть немного больше 100, потому что 100 + 100 равно 200, но здесь всего 238, поэтому синих блоков должно быть чуть больше 100.

Модель стержня «часть-часть-целая» легко может быть расширяется до больших чисел и других числовых типов, таких как дроби и десятичные дроби.Рассмотрим задачу:

Летисия прочитала 7 ½ книг для читателей. Всего она хочет прочитать 12 книг. Сколько еще книг ей нужно прочитать?

Первая диаграмма ниже отражает эту проблему. Любая словесная проблема, которую можно рассматривать как части и целое, реагирует на диаграммы моделирования стержней. Если у задачи есть несколько слагаемых, учащиеся просто рисуют на полосе достаточно частей, чтобы отразить количество слагаемых или частей, и указывают, является ли одна из частей или целое / сумма неизвестными, как показано на втором рисунке ниже.

12 — 7 ½ =? или 7 ½ +? = 12, поэтому Летиции нужно прочитать еще 4 ½ книги.

Задачи соединения (сложения) и разделения (вычитания).

Студенты, которые не могут решить, нужно ли им прибавлять или вычитать, а затем умножать или делить, находят организационный потенциал гистограммы невероятно полезным.

У Марии было 20 долларов. Она получила еще 11 долларов за присмотр за детьми. Сколько у нее сейчас денег? Рассмотрим эту задачу объединения:

Студенты могут определить, что начальная сумма в 20 долларов является одной из частей, 11 долларов — другая часть (добавочная сумма), а неизвестным является сумма / вся сумма или сколько денег она есть сейчас.Первая диаграмма ниже помогает представить эту проблему.

Рассмотрим соответствующую ситуацию с вычитанием:

У Марии был 31 доллар. Часть денег она потратила на новый компакт-диск. У Марии осталось 16 долларов.

Вторая диаграмма выше представляет эту ситуацию. Студенты могут использовать модель, чтобы помочь им определить, что общая сумма сейчас составляет 31 доллар, одна из частей (вычитающее изменение) неизвестна, поэтому другая часть — это те 16 долларов, которые у нее остались.

Проблемы сравнения. Проблемы со сравнением обычно считались трудными для детей. Частично это может быть связано с акцентом на вычитание, который используется в задачах со словами, которые включают ситуации «убрать», а не нахождение «разницы» между двумя числами. Интересно, что исследования в странах, которые часто используют гистограммы, показали, что учащиеся не находят задачи сравнения намного более сложными, чем задачи «часть-часть-целое» (Yeap, 2010, стр. 88-89).

Модель с двойным стержнем может помочь сделать задачи сравнения менее загадочными.В основном, задачи сравнения включают две величины (либо одна величина больше другой, либо они равны), а также разницу между величинами. Можно нарисовать две полосы, по одной для каждой величины, причем разница будет представлена ​​пунктирной областью, добавленной к меньшему количеству. Например, учитывая задачу:

Тамека ездил на 26 окружных ярмарочных аттракционах. Ее друг, Джексон, проехал 19 поездок. На сколько аттракционов ездил Тамека больше, чем Джексон?

Учащиеся могут создать диаграмму сравнения столбцов, показанную ниже, где большее количество, 26, является более длинным столбцом.Пунктирная часть показывает разницу между количеством поездок Джексона и Тамеки, или насколько больше у Тамека, чем у Джексона, или на сколько дополнительных поездок Джексон должен был бы проехать, чтобы иметь такое же количество поездок, как и Тамека.

26-19 =? или 19+? = 26; разница в 7, так что Тамека проехал еще 7 аттракционов.

Задачи сравнения выражают несколько различных формулировок отношений. Если Тамека проехал на 7 аттракционов больше, чем Джексон, то Джексон проехал на 7 аттракционов меньше, чем Тамека.Варианты схемы модели с двойной полосой могут сделать для учащихся более наглядными отношения, сформулированные по-разному. Студентам часто бывает полезно осознать, что в какой-то момент обе величины имеют одинаковое количество, как показано на модели ниже пунктирной линией, проведенной от конца прямоугольника, представляющего меньшее количество. Но у одной из величин больше, на что указывает область справа от пунктирной линии на более длинной полосе. Разницу между количествами можно определить путем вычитания 19 из 26 или сложения от 19 до 26 и получения 7, что означает, что 26 на 7 больше, чем 19, или 19 означает, что на 7 меньше 26.

Проблемы со сравнительными словами особенно проблематичны для изучающих английский язык, поскольку вопрос можно задать несколькими способами. Изменение полос сравнения может сделать вопросы более прозрачными. Вот несколько вариантов ответов на вопросы о двух количествах поездок, на которых ездили Тамека и Джексон:

• На сколько аттракционов проехал Тамека больше, чем Джексон?
• На сколько поездок Джексон совершил меньше поездок, чем Тамека?
• Сколько еще поездок пришлось бы проехать Джексону, чтобы проехать столько же поездок, что и Тамека?
• На сколько меньше поездок пришлось бы проехать Тамеке, чтобы проехать столько же поездок, что и Джексон?

Сравнения также могут быть мультипликативными.Рассмотрим проблему:

В коллекции Хуана 36 компакт-дисков. Это в 3 раза больше дисков, чем у его брата Маркоса. Сколько компакт-дисков у Маркоса?

В этой ситуации ученики должны построить модель стержня, показанную ниже слева, из 3 частей. Студенты могут разделить 36 на 3 равные группы, чтобы показать количество, которое нужно взять 3 раза, чтобы создать в 3 раза больше компакт-дисков для Хуана.

36 ¸ 3 =? или 3 раза? = 36 12 + 12 + 12 =? (или 3 x 12 =?)

, так что у Маркоса 12 компакт-дисков.Итак, у Хуана 36 компакт-дисков.

Аналогичную модель можно использовать, если большее количество неизвестно, но меньшее количество и мультипликативное отношение известны. Если проблема была:

У Хуана есть компакт-диски. У него в 3 раза больше компакт-дисков, чем у Маркоса, у которого 12 компакт-дисков. Сколько компакт-дисков у Хуана?

Как видно на диаграмме вверху справа, ученики могут положить 12 в коробку, чтобы показать количество компакт-дисков, которые есть у Маркоса; затем продублируйте это 3 раза, чтобы увидеть, что у Хуана в 3 раза больше компакт-дисков.Тогда общее количество, которое есть у Хуана, будет суммой этих трех частей.

Задачи умножения и деления. Та же модель, что и для мультипликативных сравнений, также будет работать для основных задач умножения слов, начиная с однозначных множителей. Рассмотрим проблему:

У Аланы было 6 пакетов жевательной резинки. В каждой упаковке 12 штук жевательной резинки. Сколько всего жевательных резинок у Аланы?

В следующей гистограмме используется повторное сложение умножения для визуализации проблемы.

12 + 12 + 12 + 12 + 12 + 12 = 72 (или 6 x 12 = 72)

, так что у Аланы 72 кусочка жевательной резинки.

По мере того, как учащиеся переходят к многозначным множителям, они могут использовать модель с многоточием, чтобы упростить гистограмму. Например:

Сэм в апреле пробегает 32 км в день, чтобы подготовиться к гонке. Если Сэм бегает каждый день месяца, сколько всего километров он пробежал в апреле?

30 x 32 км = 30 x 30 км + 30 x 2 км = 960 км

Сэм пробежал 960 км за 30 дней апреля.

Поскольку деление — это обратное умножение, в задачах деления слов будет использоваться модель мультипликативного столбца, в которой произведение (делимое) известно, но один из факторов (делитель или частное) неизвестен.

Задачи, связанные со ставками, дробями, процентами и несколькими шагами. По мере того, как учащиеся переходят в старшие классы, они могут применять новые концепции и многоступенчатые задачи со словами к чертежам моделей стержней. Скемп (1993) определил, что реляционное мышление имеет решающее значение для развития математики.Учащийся должен уметь расширять свое мышление на основе моделей, которые они использовали ранее, связывая и адаптируя свои знания к новым ситуациям.

Рассмотрим задачу о скорости и расстоянии:

Фонг проехала 261 милю, чтобы увидеться с бабушкой. В среднем она разгонялась до 58 миль в час. Сколько времени ей понадобилось, чтобы добраться до дома бабушки?

Следующая модель строится на основе модели «часть-часть-целое» с использованием формата повторяющегося сложения для умножения и деления. Предполагается, что учащиеся имеют опыт использования модели для задач деления, частные которых являются не просто целыми числами.По мере того, как они увеличивают (или делят) 261 милю, они вычисляют, что пять 58-х будут соответствовать 5 часам путешествия, а оставшиеся 29 миль будут представлены половинным квадратом, поэтому решение состоит в том, что Фонг займет 5½ часов. времени в пути, чтобы добраться до дома бабушки.

Даже более сложную проблему скорости можно решить с помощью комбинации подобных моделей. Рассмотрим эту задачу:

Сью и ее подруга Энн вместе отправились в путешествие. Сью проехала первые 2/5 поездки, а Энн проехала 210 миль за последние 3/5 поездки.Средняя скорость Сью составляла 60 миль в час, а Энн — 70 миль в час. Как долго у них была поездка?

Есть несколько способов, которыми учащиеся могут комбинировать или изменять базовую модель стержня. Одно из решений может заключаться в следующем, где первое неизвестное — сколько миль проехала Сью. Полоса, разделенная на пятые части, показывает, как рассчитать километры, которые проехала Сью. Поскольку мы знаем, что 210 миль, которые проехала Энн, составляют 3/5 всего пути, каждая из ящиков Анны, каждая из которых представляет 1/5 пути, составляет 70 миль. Таким образом, Сью проехала две части по 70 миль, или 140 миль, что составляет 2/5 от общего пути.

Теперь диаграмму необходимо расширить, чтобы показать, как рассчитать количество часов. Участок 210 миль Анны, разделенный на ее скорость 70 миль в час, займет 3 часа, как указано в следующем расширении диаграммы. Расстояние Сью в 140 миль теперь необходимо разделить на сегменты со скоростью 60 миль в час, чтобы определить время ее вождения, равное 2 1/3 часа. Таким образом, общая поездка в 350 миль займет 5 1/3 часа времени вождения, учитывая две нормы вождения.

Рассмотрим более простую многоступенчатую задачу:

Роберто купил 5 спортивных напитков по 1 доллару.25 каждый. Роберто дал кассиру 20 долларов. Сколько сдачи он получил обратно?

Опять же, у учащихся могут быть вариации, когда они начнут расширять использование диаграмм в многоэтапных или более сложных задачах. Некоторые ученики могут использовать сразу две диаграммы, как показано ниже слева. Другие могут указывать вычисления на одной диаграмме, как показано на диаграмме справа.

Имея рутинный опыт моделирования стержней, учащиеся могут расширить использование моделей для решения задач, связанных с отношениями, которые могут быть выражены с помощью переменных.Рассмотрим эту простую задачу, которую можно представить алгебраически:

Каллан и Авриэль собрали в общей сложности 190 ошибок для научного проекта. Каллан собрал на 10 ошибок больше, чем Авриель. Сколько жуков собрал Каллан?

Пусть n равно количеству ошибок, собранных Авриель, а n + 10 равно количеству ошибок, собранных Калланом. Студенты могут создать следующую модель:

Поскольку n + n = 180 (или 2 n = 180), n = 90.Таким образом, Каллан собрал 90 + 10 или 100 ошибок, а Авриэль собрала 90 ошибок, всего 190 ошибок, собранных вместе.

При использовании модельного метода учащиеся должны переводить информацию и отношения в словах в визуальные представления, которые являются моделями. Они также должны манипулировать и преобразовывать визуальные представления, чтобы генерировать информацию, полезную для решения данных проблем.

Понимание структуры словесной задачи включает в себя знание того, как связана математическая информация в данной текстовой задаче и как выделить компоненты, необходимые для решения проблемы.Чертежи ленточной диаграммы / гистограммы могут помочь учащимся лучше определять переменные, участвующие в проблеме, а также отношения между ними. Эта способность сосредотачиваться на отношениях между числами в данной задаче и распознавать математическую структуру как особый тип проблемы является частью реляционного мышления — критически важным навыком для успеха в алгебре. Использование перевернутой буквы V и гистограммы в предалгебраическую работу в классах K-7 может сделать учащихся более подготовленными к формальному изучению алгебры.

Это отличный сайт для практики решения задач — моделирования задач с помощью ленточной диаграммы / гистограммы

Как обучать задачам на сложение и вычитание слов

Мои ученики изо всех сил пытались решить , как решать задачи на сложение и вычитание слов для того, что казалось вечностью. Они могли бы подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа, не понимая сути проблемы.

Тьфу.

Можете рассказать?

Я большой сторонник того, чтобы НЕ учить спискам ключевых слов. Просто он не работает последовательно со всеми проблемами. Это ярлык, ведущий к сбоям в математическом мышлении. Я подробно расскажу о том, почему это не работает, в книге «Проблема с использованием ключевых слов для решения проблем со словами».

Вы можете узнать больше о ресурсе «Проблемы со сложением и вычитанием слов», который я использую в своем классе, в этом сообщении блога.

Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении задачам со словами с использованием любых ресурсов.

Итак, как мне научить решать задачи со словами? Это довольно сложно, но очень весело, когда вы в него входите.

Основные компоненты обучения задачам на сложение и вычитание слов включают:

1. Обучение соотношению чисел s — Как учитель, знайте тип задачи и помогайте ученикам решать действия в задаче. Числа — дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязнув в вычислениях.
2. Используйте академический словарь — и будьте последовательны в том, что вы используете.
3. Прекратить поиск «ответа» — дело не в ответе; речь идет о процессе
4. Различия между моделями и стратегиями — одна связана с соотношением чисел, а другая — с тем, как учащиеся «решают» или вычисляют задачу.

Учите соотношению чисел в задачах со словами

Я учу задачи со словами, удаляя числа. Звучит странно, правда? Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на ситуации, в которой возникла проблема, и понять действие или взаимосвязь чисел.Это также мешает студентам решить задачу до того, как мы поговорим о соотношении чисел.

Когда я преподаю задачи со словами, я даю студентам задачи с пробелами и без чисел. Сначала мы поговорим о действии в проблеме. Мы определяем, добавляется ли что-то к чему-то или берется из чего-то еще. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.

___ + ___ = unknown

Хотите бесплатный образец словесных задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже.БЕСПЛАТНЫЙ образец задач Word по типу задачи

Дифференцируйте числа в словах Задачи

Только после того, как мы обсудим задачу, я даю учащимся номера. Я разделяю числа в зависимости от потребностей студентов. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что студенты понимают процесс.

После того, как студенты ознакомятся с процессом, я начинаю давать разным студентам разные числа в зависимости от их уровня математического мышления.Я также меняю числа в течение года, с однозначных на двузначные числа. Прелесть пустых мест в том, что я могу поставить в задачу любые числа, какие захочу, чтобы практиковать стратегии, над которыми мы работали в классе.

В какой-то момент мы действительно создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, объединяют ли эти действия что-то или разделяют. Сколько вы можете придумать? Вот несколько идей:

Присоединиться: положил, получил, взял, купил, сделал
Отдельно: съел, потерял, отложил, уронил, использовал

Не бойтесь использовать академический словарный запас

Я учу своих учеников определять начало проблемы, заменяет в проблеме и приводит к проблеме.Учу их искать неизвестный . Это все слова, которые мы используем при решении задач, и мы узнаем структуру проблемы со словом через словарь и соотношение чисел.

Фактически, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.

Возьмите эти примеры, можете ли вы определить начало , изменить и результат в каждой проблеме?

Подсказка: посмотрите на код, используемый для типа проблемы, в правом нижнем углу.

Для задач сравнения мы используем следующие термины: больше , меньше , больше и меньше . Попробуйте эти задачи и посмотрите, сможете ли вы определить компоненты словесных проблем.

Перестаньте искать «ответ»

Это самое сложное заблуждение, чтобы разрушить его. Студенты не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.

Ладно, они первоклассники и второклассники. Я знаю.

Мои ученики все еще могут объяснить после инструктажа, что они начинают ed с одного числа. Проблема , результат ред в другом другом номере. Затем учащиеся знают, что они ищут изменение между этими двумя числами.

Все дело в отношениях.

Различия между моделями и стратегиями

Пару лет назад я наткнулся на эту статью о необходимости помочь студентам разработать адекватные модели для понимания взаимосвязи чисел в задаче.

В голове перегорела лампочка. Мне нужно было провести различие между моделями, которые используют ученики, чтобы понять взаимосвязь чисел в задаче, и стратегиями для решения вычислений в задаче. Эти две вещи работают в тандеме, но очень разные.

Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми ученик решает проблему, складывая и разбирая числа.

Самое главное в моделях — отойти от них.Я знаю, это звучит странно.

Вы так долго учите студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. На самом деле, вы хотите, чтобы студенты двигались к повышению эффективности.

Младшие ученики будут разыгрывать задачи, рисовать задачи с помощью репрезентаций и рисовать задачи с помощью кругов или линий. Двигайте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять взаимосвязь чисел

. Это яркий пример перехода от модели с перевернутой буквой v к модели стержней.

Вот ученик, переходящий от рисования кругов к использованию перевернутой буквы v.

Студенты должны твердо использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока они выясняют сходство между моделями.

Студенты также должны уметь создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли наклеить в свои тетради, а иногда студенты рисовали свои собственные модели. Они должны нести ответственность за выбор того, что им лучше всего подходит.Начните свое обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них. Всегда подталкивайте студентов к более эффективным моделям.

То же самое и со стратегиями вычислений. Изучите стратегии сначала на практике математических фактов, прежде чем применять их к задачам со словами, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них. При обучении сосредоточьтесь на одной или двух стратегиях. Когда учащиеся овладеют некоторыми стратегиями, предложите им выбрать стратегии, которые подходят для решения различных задач.

Будьте целенаправленны в числах, которые вы выбираете для своих задач со словами. Различные наборы чисел поддаются разным стратегиям и разным моделям. Используйте числовые наборы, которые студенты уже отработали на вычислительной технике. Если вы научили делать 10, используйте числа, которые дают 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислением и решением проблемы, тем лучше.

Приведенные выше примеры в основном предназначены для задач объединения и разделения.Неудивительно, что нашим ученикам так сложно сравнивать задачи, поскольку мы не учим их в той же степени, что и объединять и разделять задачи. Нашим ученикам нужно еще больше практики с такими типами задач, потому что соотношение чисел более абстрактное. Но я оставлю это для другого сообщения в блоге.

Вы хотите БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения Задачи на сложение и вычитание слов по типу задачи ? Щелкните эту ссылку или изображение ниже.

Полный ресурс также доступен в моем магазине для покупки и на сайте Teachers Pay Teachers
.

Возможно, вас заинтересует. . .

% PDF-1.4
%
448 0 объект
>
эндобдж

xref
448 82
0000000016 00000 н.
0000002775 00000 н.
0000002922 00000 н.
0000003419 00000 п.
0000003751 00000 н.
0000004062 00000 н.
0000004260 00000 н.
0000004374 00000 н.
0000004486 00000 н.
0000004599 00000 н.
0000004708 00000 п.
0000005172 00000 п.
0000005199 00000 п.
0000005635 00000 п.
0000005662 00000 н.
0000006228 00000 п.
0000006624 00000 н.
0000006651 00000 п.
0000006678 00000 н.
0000007142 00000 п.
0000007282 00000 н.
0000007415 00000 н.
0000007550 00000 н.
0000007687 00000 н.
0000008233 00000 н.
0000008771 00000 п.
0000009330 00000 н.
0000009891 00000 н.
0000010435 00000 п.
0000010462 00000 п.
0000010856 00000 п.
0000010994 00000 п.
0000011520 00000 п.
0000011783 00000 п.
0000012286 00000 п.
0000012575 00000 п.
0000012846 00000 п.
0000014112 00000 п.
0000025731 00000 п.
0000025844 00000 п.
0000027008 00000 н.
0000027316 00000 н.
0000027431 00000 н.
0000030282 00000 п.
0000030600 00000 п.
0000030719 00000 п.
0000031960 00000 п.
0000032273 00000 п.
0000032400 00000 п.
0000034380 00000 п.
0000034704 00000 п.
0000034774 00000 п.
0000034854 00000 п.
0000038726 00000 п.
0000039000 00000 н.
0000039288 00000 п.
0000039358 00000 п.
0000039438 00000 п.
0000044340 00000 п.
0000044609 00000 п.
0000044923 00000 п.
0000044993 00000 п.
0000045073 00000 п.
0000069237 00000 п.
0000069502 00000 п.
0000069902 00000 н.
0000069972 00000 н.
0000070052 00000 п.
00000

00000 п.
00000

00000 п.
0000091413 00000 п.
0000091483 00000 п.
0000091563 00000 п.
0000091772 00000 п.
0000091987 00000 п.
0000092208 00000 п.
0000092447 00000 п.
0000112047 00000 н.
0000153155 00000 н.
0000214671 00000 н.
0000002590 00000 н.
0000001936 00000 н.
трейлер
] / Назад 1142289 / XRefStm 2590 >>
startxref
0
%% EOF

529 0 объект
> поток
hb«b`TA ؀, `׍ $ 009 | _9 GSXDqqE’KfZjM] Mg 斬` ᑮ M | JIS, * ygt2t,
ptYoyD, & pIp8 ɯpDZ) DVmzFbSidv} | ¡v! -FgF6K9p13i5 ݘ ​​b> Lsw϶D # W7 *
N4
sirY9yEʨoH: 9mE / o _? @ 3NJ

Важные математические навыки для пятиклассников

Хотите помочь своему пятикласснику осваивать математику? Вот некоторые из навыков, которые ваш пятиклассник будет изучать в классе.

Сложение, вычитание, умножение и деление

Многозначные целые числа

Быстро и точно умножайте многозначные целые числа. Разделите целые числа (до четырех цифр) на двузначные числа.

Пример:

Решить 4,824 ÷ 12 =?

Объясните или проиллюстрируйте, как вы решили эту проблему.

Совет: выделите практическое применение математики.

По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога.Важно, чтобы ваш ребенок занимался математикой и помогал ему понять, как в реальной жизни применяются концепции, которые ребенок изучает в школе. Составление бюджета на школьные принадлежности или на их ежемесячное пособие — это один из способов практиковать сложение и вычитание. Если вы попросите их помочь вам с приготовлением или выпечкой, это покажет им, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.

Связанные

Понимание разряда

Расширьте понимание разряда: в многозначном числе цифра в одном месте представляет 1⁄10 того, что она представляет в месте слева от него, и в 10 раз больше как он изображен справа от него.

Сравнение десятичных знаков

Чтение, запись и сравнение десятичных знаков с разрядами тысячных, используя символы> (больше чем) и <(меньше чем). Например:

• Прочтите это десятичное число: 23,002.
• Запишите две и шестьдесят две тысячные в виде десятичного числа.
• Какой знак подтверждает это утверждение: 5,389 _? _ 5,420
• Исследователь измеряет количество бактерий, выросших на образцах неохлажденных продуктов. Ваш ребенок насчитывает 73.343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий до наименьшего. Объясните или проиллюстрируйте, как вы приводите эти образцы в порядок.

Связанные

Десятичные доли до сотых

Сложение, вычитание, умножение и деление десятичных долей до сотых.

Совет: потренируйтесь в вычислениях с использованием десятичных знаков.

Свяжите работу с десятичными знаками, которую ваш ребенок делает в классе, с реальным миром, поощряя их делать покупки по выгодным ценам.Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы определить стоимость каждого товара. Итак, сколько вы платите за рулон бумажного полотенца или за банку газировки при покупке оптом? Или попросите ребенка подсчитать, сколько вы сэкономите на каждом товаре, если цены со скидкой предполагают оптовые скидки.

Что такое показатель степени

Понять, что такое показатель степени. Например, «2» в 10² указывает, сколько раз нужно умножить число само на себя. 10² можно читать как «10 в степени 2», «10 в степени 2» или «10 в квадрате» и означает 10 x 10 или 100.10³ (или «10 в третьей степени» или «10 в кубе») означает 10 x 10 x 10 или 1000.

Дроби

Решение задач со словами

Решение задач со словами, включающих сложение и вычитание дробей.

Пример:

Пятый класс собирает пазл из 600 деталей. Они начали вчера и собрали 100 частей — всего одну шестую (1⁄6) головоломки. Сегодня их собрано 400 штук. Какая часть головоломки завершена? Нарисуйте картинку И запишите математику, чтобы показать, как вы решили задачу.

Совет: выделите практическое применение математики.

По мере того, как математика, которую они изучают, становится более сложной и менее очевидно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревога. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять практическое применение концепций, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — один из способов для нее практиковать сложение и вычитание.Если вы попросите ее помочь вам с приготовлением или выпечкой, это покажет ей, как работают дроби. Помогать рассчитывать цены при покупке продуктов — тоже хорошая практика.

Нахождение общего знаменателя

Решите задачи со словами, включающие сложение и вычитание дробей с разными знаменателями (нижние числа), преобразовывая их в дроби с одинаковым знаменателем, называемые общим знаменателем.

Пример:

Самая высокая девочка в пятом классе имеет рост 51 7⁄8 дюйма.Самый высокий мальчик в пятом классе имеет рост 49 сантиметров. Какая разница в их росте?

После вечеринки остались две чашки лимонада. В одной миске 1⁄3 галлона. В другом — 1⁄2 галлона лимонада. Друг говорит, что не стоит пытаться объединить их в 1-галлонный контейнер, потому что лимонад вытечет наверх. Вы согласны? Почему или почему нет?

Умножение дробей

Решайте задачи со словами, включающие умножение дробей на другие дроби и умножение дробей на смешанные числа (целое число и дробь, например 11⁄4 или 21⁄2).

Пример:

• В оркестре средней школы 1⁄3 учащихся-музыкантов играют на струнных инструментах. Из учеников, играющих на струнных инструментах, 3⁄4 играют на скрипке. Какая часть оркестра играет на скрипке?
• Утром во время экскурсии в яблоневый сад пятиклассники собрали 4⁄5 бушеля яблок. После обеда в полдень они собрали в 2,5 раза больше яблок. Уместятся ли все яблоки, собранные ими днем, в ящик на 2 бушеля? Откуда вы знаете?

Совет: потренируйтесь использовать дроби.

Помогите своему ребенку познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Пусть они начнут с того, что уменьшат рецепт вдвое или вдвое. Когда они почувствуют себя комфортно, попросите их преобразовать его на 1 1/2, чтобы рецепт, который должен был накормить семью из четырех человек, работал на семью из шести человек.

Дроби единицы деления

Разделите дроби единицы (дроби с 1 в числителе или верхним числом) на целые числа. Разделите целые числа на единичные дроби.

Пример:

Если три человека разделят ½ фунта шоколада поровну, сколько шоколада получит каждый? Объясните или проиллюстрируйте, как вы решили эту проблему.

Умножение на дроби

Помните, что умножение числа на дробь меньше 1 приведет к ответу меньше числа — например: 12 x ¾ = 9. Умножение числа на дробь больше 1 даст результат в ответе больше числа — например: 12 x 2 ½ = 30.

Измерения и данные

Преобразование единиц и дробей

Преобразование единиц и долей единиц в одной системе измерения.

Пример:

Сколько минут составляет 1⁄5 часа? Объясните или проиллюстрируйте, как вы решили эту проблему.

Проблемы многоступенчатого преобразования единиц измерения

Решайте многоступенчатые задачи преобразования слов, используя преобразование стандартных единиц измерения разного размера.

Пример:

У меня 75 см ленты.Для выполнения проекта мне нужно в семь раз больше ленты. Сколько еще метров ленты мне нужно?

Объясните или проиллюстрируйте, как вы решили эту проблему.

Использование линейного графика

Решайте проблемы, используя информацию (в единицах дроби), представленную на линейном графике.

Геометрия

Что такое объем

Под объемом понимается измерение пространства внутри трехмерной или твердой фигуры. Используйте формулы длина x ширина x высота или основание x высота , чтобы измерить объем трехмерного или твердого объекта с прямоугольными сторонами, например куба.Измеряйте объем для решения реальных проблем.

Пример:

Прямоугольный контейнер для мороженого имеет длину 8 дюймов и высоту 4 дюйма. Каков объем контейнера, выраженный в кубических дюймах?

Советы, которые помогут вашему пятикласснику в уроке математики, можно найти на нашей странице с советами по математике для пятого класса.

Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.

Оценка: 5 — Алгебраическое мышление 3

Особенности специального образования

Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.

Проблемы со словами | Уравнения и неравенства

г.{2} & = 4 \\
b & = \ pm 2
\ end {выровнять *}

Следовательно, ширина равна \ (\ text {2} \) \ (\ text {m} \), а длина вдвое больше, \ (\ text {4} \) \ (\ text {m} \). Обратите внимание, что ширина не может быть отрицательным числом, поэтому мы не рассматриваем это решение.

Кевин сыграл несколько партий в боулинг с десятью кеглями. В третьей игре Кевин забил на \ (\ text {80} \) больше, чем во второй игре. В первой игре Кевин набрал \ (\ text {110} \) меньше, чем в третьей.Его общий счет в первых двух играх был \ (\ text {208} \). Если он хочет набрать в среднем \ (\ text {146} \), что он должен набрать в четвертой игре?

Допустим, что счет в первой игре будет \ (a \), счет во второй игре будет \ (b \), счет в третьей игре будет \ (c \), а счет в четвертой игре будет \ (г \).

Теперь отметим следующее:

\ begin {align *}
c & = 80 + b \\
а & = с — 110 \\
а + б & = 208 \\
\ frac {a + b + c + d} {4} & = 146
\ end {выровнять *}

Мы делаем \ (c \) предметом первых двух уравнений:

\ begin {align *}
c & = 80 + b \\
c & = a + 110
\ end {выровнять *}

Затем мы используем \ (a = 208 — b \), чтобы найти \ (b \):

\ begin {align *}
80 + b & = 208 — b + 110 \\
2b & = 208 + 110 — 80 \\
2b & = 238 \\
b & = 119
\ end {выровнять *}

Теперь мы можем найти \ (a \):

\ begin {align *}
а + б & = 208 \\
а + 119 & = 208 \\
а & = 89
\ end {выровнять *}

И мы можем найти \ (c \):

\ begin {align *}
c & = 80 + b \\
с & = 80 + 208 \\
c & = 288
\ end {выровнять *}

Наконец, мы можем найти \ (d \):

\ begin {align *}
\ frac {a + b + c + d} {4} & = 164 \\
496 + d & = 656 \\
d & = 187
\ end {выровнять *}

Кевин должен забить \ (\ text {187} \) в четвертой игре.{2} — 4 (1) (100)}} {2 (1)} \\
& = \ dfrac {1 \ pm \ sqrt {1 + 400}} {2} \\
& = \ dfrac {1 \ pm \ sqrt {401}} {2}
\ end {выровнять *}

Поскольку время не может быть отрицательным, единственное решение — \ (t = \ dfrac {1 + \ sqrt {401}} {2} \ приблизительно \ text {10,5} \ text {s} \).

В таблице ниже указано время, которое Шейла тратит на пройденное расстояние.

Нанесите точки.

Найдите уравнение, описывающее связь между временем и расстоянием. Затем используйте уравнение, чтобы ответить на следующие вопросы:

1. Сколько времени потребуется Шейле, чтобы идти \ (\ text {21} \) \ (\ text {km} \)?

2. Как далеко пройдет Шейла за \ (\ text {7} \) минут?

Если бы Шейла шла вдвое медленнее, чем сейчас, как бы выглядел график ее расстояния и времени?

Уравнение \ (t = 5d \).

Шейла займет \ (t = 5 (21) = 105 \) минут пешком \ (\ text {21} \) \ (\ text {km} \).

Шейла пройдет \ (d = \ frac {7} {5} = \ text {1,4} \) километров за \ (\ text {7} \) минут.

Градиент графика будет в два раза больше градиента первого графика. График будет круче и будет лежать ближе к оси \ (y \).

Мощность \ (P \) (в ваттах), подаваемая в цепь от батареи с напряжением \ (\ text {12} \) вольт, определяется по формуле \ (P = 12I — \ text {0,5} I ^ 2 \) где \ (I \) — ток в амперах.