Содержание
Линейные уравнения для 5 класса
Одним из самых важных навыков при поступлении в 5 класс является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу.
1 тип: «луковичные»
Это уравнения, которые почти со вероятностью встретятся Вам при поступлении в любую школу или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз. Например, или .
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:
Сложение
- слагаемое1 + слагаемое2 = сумма
- слагаемое1 = сумма — слагаемое2
- слагаемое2 = сумма — слагаемое1
Вычитание
- уменьшаемое — вычитаемое = разность
- уменьшаемое = вычитаемое + разность
- вычитаемое = уменьшаемое — разность
Умножение
- множитель1 * множитель2 = произведение
- множитель1 = произведение : множитель2
- множитель2 = произведение : множитель1
Деление
- делимое : делитель = частное
- делимое = делитель * частное
- делитель = делимое : частное
Разберём на примере, как применять данные правила.
Заметим, что мы делим на и получаем . В этой ситуации мы знаем делитель и частное. Чтобы найти делимое, нужно делитель умножить на частное:
Мы стали немного ближе к самому . Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:
И ещё один «слой» снят с неизвестной! Теперь мы видим ситуацию с известным значением произведения () и одним известным множителем ().
Теперь ситуация «уменьшаемое — вычитаемое = разность»
И последний шаг — известное произведение () и один из множителей ()
2 тип: уравнения со скобками
Уравнения данного типа чаще всего встречаются в задачах — именно к ним сводится 90% всех задач для поступления в 5 класс. В отличие от «луковичных уравнений» переменная здесь может встретиться несколько раз, поэтому решить её методами из предыдущего пункта невозможно. Типичные уравнения: или
Основная трудность — это правильно раскрыть скобки. После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение», которое умеем решать. Но обо всём по-порядку.
После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение», которое умеем решать. Но обо всём по-порядку.
Раскрытие скобок. Мы приведём несколько правил, которыми следует пользоваться в данном случае. Но, как показывает практика, верно раскрывать скобки ученик начинает только после 70-80 прорешанных задач. Основное правило таково: любой множитель, стоящий за скобками необходимо умножить на каждое слагаемое внутри скобок. А минус, стоящий перед скобкой, меняет знак всех выражений, что стоят внутри. Итак, основные правила раскрытия:
Приведение подобных. Здесь всё гораздо легче: Вам необходимо путём переноса слагаемых через знак равенства добиться того, чтобы с одной стороны стояли только слагаемые с неизвестной, а с другой — только числа. Основное правило таково: каждое слагаемое, переносимое через , меняет свой знак — если оно было с ,то станет с , и наоборот. После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение».
После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение».
Приведём пример:
(раскроем скобки. Обратите внимание на смену знаков!)
(выполним умножения)
(перенесём , и через знак равенства — они «превратятся» в , и )
(посчитаем итоговое количество справа и число слева)
(ситуация «известный множитель и произведение»)
Освоив эти два типа уравнений, Вы можете быть уверенны, что сможете решить добрую половину всех заданий во вступительной олимпиаде в 5 класс.
ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: —>> Математика 5 класс Тарасенкова.
Задание: —>> 553 — 569 570 — 586
наверх
|
|
Задание 553.

Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 — y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х — 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0;
2) Не имеет решений;
3) x = 1;
4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
2) (у — 25) + 18 = 40;
3) (70 — х) — 35 = 12;
4) 60 -(y + 34) = 5;
5) 52 — (19 + х) = 17;
6) 9y — 18 = 72;
7) 20 + 5х = 100;
8) 90 — y * 12 = 78;
9) 10х — 44 = 56;
10) 84 — 7у = 28;
| 11) 121 : (х — 45) = 11;
12) 77 : (у + 10) = 7;
13) (х — 12) : 10 = 4;
14) 55 — y * 10 = 15;
15) х : 12 + 48 = 91;
16) 5y + 4y = 99;
17) 54х — 27х = 81;
18) 36y — 16y + 5y = 0;
19) 14х + х — 9х + 2 = 56;
20) 20y — 14у + 7у — 13 = 13.
|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
2) (у — 34) — 10 = 32;
3) (48 — х) + 35 = 82;
4) 77 — (28 + y) = 27;
5) 90 + y * 8 = 154; | 6) 9х + 50 = 86;
7) 120 : (х — 19) = 6;
8)(y + 50) : 14 = 4;
9) 48 + у : 6 = 95;
10) 8х + 7х — х = 42.
|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число — x.
- x + 67 = 109;
- x = 109 — 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 — 38;
- x = 207.

- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Некоторое число уменьшили на 22 и получили число 105. Найдите это число.
Решение:
- x — 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 — x = 79;
- x = 128 — 79;
- x = 49.
- Ответ: 49.

Задание 566.
Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 — 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 — y) * 2 = 64
- 32 — y = 64 : 2;
- 32 — y = 32;
- y = 32 — 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 — 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 — 12;
- x = 33;
- 5) (y — 12) : 6 = 18
- y — 12 = 18 * 6;
- y — 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y — 17) * 3 = 63
- y — 17 = 63 : 3;
- y — 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.

Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y — 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 — 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 — 10;
- y = 54;
- 4) 3x — 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили. В результате получили число 22. Найдите неизвестное число.
В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 — 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x — 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: —>> 553 — 569 570 — 586
Решение сложных уравнений в 5-6 классах способом подстановки
Решение сложных уравнений в 5-6 классах способом подстановки.
В 5-6 классах учащиеся затрудняются решать уравнения такого типа, как
(х + 39) – 43 =27.
Традиционное объяснение в должной мере воспринимают только сильные ученики, а для слабых – это тайна за семью печатями. Каково же традиционное объяснение решения такого уравнения? Чтобы найти уменьшаемое х + 39, надо к вычитаемому 43 прибавить разность 27:
Каково же традиционное объяснение решения такого уравнения? Чтобы найти уменьшаемое х + 39, надо к вычитаемому 43 прибавить разность 27:
х + 39 = 43 + 27;
х + 39 = 70.
Далее рассуждают так: чтобы найти неизвестное слагаемое Х, надо из суммы 70 вычесть другое слагаемое 39:
х = 70 – 39;
х = 31.
В большинстве случаев ученики не видят в этом уравнении вычитаемого 43 и уменьшаемого Х + 39. Поэтому я разработала алгоритм решения таких уравнений. Суть этого приёма состоит в том, чтобы любое сложное уравнение свести к простейшему. Главное, иметь хороший навык решения простейших уравнений. Рассмотрим применение этого алгоритма на конкретных примерах.
1) ( х+ 121) + 38 = 269.
Обозначим выражение, стоящее в скобках через a: х + 121 = а.
Тогда получим такое уравнение:
а + 38 = 269;
а = 269 – 38;
а = 231.
Теперь возвращаемся к выражению, стоящему в скобках:
х + 121 = а;
х + 121 = 231;
х = 231 – 121;
х = 110.
Ответ: 110.
2) ( m – 379) + 125 = 3000
Подстановка m – 379 = а;
а + 125 = 3000;
а = 3000 – 125;
а = 2875;
m – 379 = 2875;
m = 2875 + 379;
m = 3254.
3) ( 127 + р ) – 89 = 1009.
Подстановка 127 + р = а;
а – 89 = 1009;
а = 1009 + 89;
а = 1098;
127 + р = 1098;
р = 1098 – 127;
р = 971.
4) ( х – 315 ) – 27 = 36.
Подстановка х – 315 = а;
а – 27 = 36;
а = 36 + 27;
а = 63;
х – 315 = 63;
х = 315 + 63;
х = 378.
5) 872 – ( 407 + с ) = 122
Подстановка 407 + с = а;
872 – а = 122;
а = 872 – 122;
а = 750;
407 + с = 750;
с = 750 – 407;
с = 343.
6) (7001+ х).42 = 441000
Подстановка 7001 + х = а;
а . 42 = 441000;
а = 441000 : 42;
а = 10500;
7001 + х = 10500;
х = 10500 – 7001;
х = 3499.
Таким образом, очень хорошо видно, что с помощью данного приёма очень легко решаются такие сложные уравнения.
Для тех учащихся, кто так и не усвоил правил нахождения неизвестных: слагаемого, вычитаемого, множителя и т.д., я использую при решении простейших уравнений приём «по аналогии».
Например, нужно решить уравнение: х – 128 = 312.
В стороне от этого уравнения слабый ученик записывает простейший арифметический пример 5 — 3 = 2.
Ученик смотрит, где в этом примере должен стоять х (на месте 5). Как из этого простого примера найти 5. Надо к 3 прибавить 2. Значит, и в уравнении, чтобы найти Х надо 128 сложить с 312.
Данный алгоритм решения уравнений служит пропедевтикой для решения в старших классах уравнений способом подстановки.
Решение линейных уравнений с примерами. Уравнения онлайн Примеры уравнений 5
Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид
aх + b = 0
, где a и b произвольные числа, называется линейным уравнением
с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.
Cегодня разберёмся, как эти линейные уравнения решать.
Например, все уравнения:
2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.
Значение неизвестного, обращающее уравнение в верное равенство называется решением
или корнем уравнения
.
Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.
А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.
Решение любых линейных уравнений сводится к решению уравнений вида
aх + b = 0.
Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим
Если a ≠ 0, то х = ‒ b/a
.
Пример 1.
Решите уравнение 3х + 2 =11.
Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.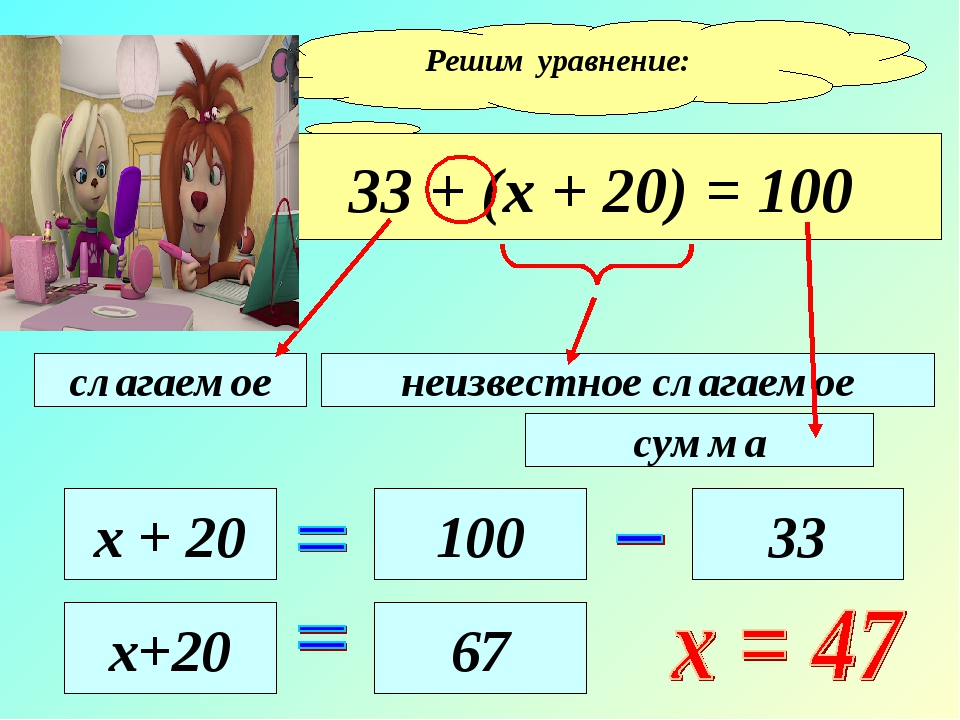
Выполним вычитание, тогда
3х = 9.
Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9: 3.
Значит, значение х = 3 является решением или корнем уравнения.
Ответ: х = 3
.
Если а = 0 и b = 0
, то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.
Пример 2.
Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.
Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.
5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.
Приведем подобные члены:
0х = 0.
Ответ: х — любое число
.
Если а = 0 и b ≠ 0
, то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .
Пример 3.
Решите уравнение х + 8 = х + 5.
Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.
Приведем подобные члены:
0х = ‒ 3.
Ответ: нет решений.
На рисунке 1
изображена схема решения линейного уравнения
Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.
Пример 4.
Пусть надо решить уравнение
1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.
2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)
3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .
4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.
5) Приведем подобные члены:
‒ 22х = ‒ 154.
6) Разделим на – 22 , Получим
х = 7.
Как видим, корень уравнения равен семи.
Вообще такие уравнения можно решать по следующей схеме
:
а) привести уравнение к целому виду;
б) раскрыть скобки;
в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;
г) привести подобные члены;
д) решить уравнение вида aх = b,которое получили после приведения подобных членов.
Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2
), третьего (Пример. 1, 3
) и даже с пятого этапа, как в примере 5.
Пример 5.
Решите уравнение 2х = 1/4.
Находим неизвестное х = 1/4: 2,
х = 1/8
.
Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.
Пример 6.
Решите уравнение 2 (х + 3) = 5 – 6х.
2х + 6 = 5 – 6х
2х + 6х = 5 – 6
Ответ: ‒ 0, 125
Пример 7.
Решите уравнение – 6 (5 – 3х) = 8х – 7.
– 30 + 18х = 8х – 7
18х – 8х = – 7 +30
Ответ: 2,3
Пример 8. Решите уравнение
3(3х – 4) = 4 · 7х + 24
9х – 12 = 28х + 24
9х – 28х = 24 + 12
Пример 9.
Найдите f(6), если f (x + 2) = 3 7-х
Решение
Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.
Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.
Если х = 4, тогда
f(6) = 3 7-4 = 3 3 = 27
Ответ: 27.
Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ . Буду рада Вам помочь!
Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решаем дробно-рациональное уравнение 5/х = 100. Данное уравнение можно решить двумя способами. Давайте рассмотрим каждый из них.
План решения уравнения 5/x = 100
- найдем область допустимых значений для заданного уравнения;
- первый способ решения уравнения рассмотрев его как на пропорцию;
- второй способ решения уравнения, находя неизвестный делитель.
Находим неизвестный член пропорции
Сначала найдем ОДЗ уравнения. В левой части уравнения присутствует знак дроби и он равносилен знаку деления. Известно, что на ноль делить нельзя. Значит из ОДЗ мы должны исключить значения обращающие знаменатель в ноль.
В левой части уравнения присутствует знак дроби и он равносилен знаку деления. Известно, что на ноль делить нельзя. Значит из ОДЗ мы должны исключить значения обращающие знаменатель в ноль.
ОДЗ: x принадлежит R \ {0}.
Теперь посмотрим на наше уравнение как на пропорцию.
Основное свойство пропорции.
Произведение крайних членов пропорции равно произведению ее средних членов.
Для пропорции a: b = c: d
или a/b = c/d
основное свойство записывается так: a · d = b · c.
Применим его и получим линейное уравнение:
100 * x = 5 * 1;
Разделим на 100 обе части уравнения, тем самым избавимся от коэффициента перед переменной х:
Находим неизвестный делитель
Посмотрим на уравнение как на частное. Где делимое равно 5, делитель x, а результат деления — частное равно 100.
Вспомним правило как найти неизвестный делитель — нужно делимое разделить на частное.
Найденный корень принадлежит ОДЗ уравнения.
Проверим найденное решение уравнения. Для этого подставим найденные корень в исходное уравнение и произведем вычисления:
Решение найдено верно.
Одним из самых важных навыков при поступлении в 5 класс
является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу
.
1 тип: «луковичные»
Это уравнения, которые почти со вероятностью встретятся Вам при поступлении в любую школу
или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз. Например, или .
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:
Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:
Сложение
- слагаемое1 + слагаемое2 = сумма
- слагаемое1 = сумма — слагаемое2
- слагаемое2 = сумма — слагаемое1
Вычитание
- уменьшаемое — вычитаемое = разность
- уменьшаемое = вычитаемое + разность
- вычитаемое = уменьшаемое — разность
Умножение
- множитель1 * множитель2 = произведение
- множитель1 = произведение: множитель2
- множитель2 = произведение: множитель1
Деление
- делимое: делитель = частное
- делимое = делитель * частное
- делитель = делимое: частное
Разберём на примере, как применять данные правила.
Заметим, что мы делим на и получаем . В этой ситуации мы знаем делитель и частное. Чтобы найти делимое, нужно делитель умножить на частное:
Мы стали немного ближе к самому . Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:
Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:
И ещё один «слой» снят с неизвестной! Теперь мы видим ситуацию с известным значением произведения () и одним известным множителем ().
Теперь ситуация «уменьшаемое — вычитаемое = разность»
И последний шаг — известное произведение () и один из множителей ()
2 тип: уравнения со скобками
Уравнения данного типа чаще всего встречаются в задачах — именно к ним сводится 90% всех задач для поступления в 5 класс
. В отличие от «луковичных уравнений»
переменная здесь может встретиться несколько раз, поэтому решить её методами из предыдущего пункта невозможно. Типичные уравнения: или
Основная трудность — это правильно раскрыть скобки. После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение»
, которое умеем решать. Но обо всём по-порядку.
Но обо всём по-порядку.
Раскрытие скобок
. Мы приведём несколько правил, которыми следует пользоваться в данном случае. Но, как показывает практика, верно раскрывать скобки ученик начинает только после 70-80 прорешанных задач. Основное правило таково: любой множитель, стоящий за скобками необходимо умножить на каждое слагаемое внутри скобок. А минус, стоящий перед скобкой, меняет знак всех выражений, что стоят внутри. Итак, основные правила раскрытия:
Приведение подобных
. Здесь всё гораздо легче: Вам необходимо путём переноса слагаемых через знак равенства добиться того, чтобы с одной стороны стояли только слагаемые с неизвестной, а с другой — только числа. Основное правило таково: каждое слагаемое, переносимое через , меняет свой знак — если оно было с ,то станет с , и наоборот. После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение»
.
Приложение
Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему.
д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения.
Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее.
Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
=
Урок 42. уравнения первой степени с одним неизвестным. линейные уравнения с одним неизвестным — Алгебра — 7 класс
Алгебра
7 класс
Урок № 42
Уравнения первой степени с одним неизвестным. Линейные уравнения с одним неизвестным
Перечень рассматриваемых вопросов:
Линейные уравнения.
Корень уравнения.
Решение линейных уравнений.
Тезаурус:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Линейное уравнение – уравнение вида ax = b, где x – переменная, a, b – некоторые числа.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Давайте посмотрим на 2 уравнения: 10x = 36 и 3x2 = 2
Можем ли мы сказать, что оба уравнения являются линейными уравнениями первой степени?
Конечно, нет. Хотя, по определению линейных уравнений, оба уравнения подходят, у второго уравнения переменная входит в него во второй степени, а это противоречит отличительной особенности линейного уравнения первой степени.
Определение: Уравнение вида ax = b, где – x переменная, a, b – некоторые числа, называется линейным уравнением с одной переменной.
А что означает решить уравнение?
Решить уравнение – означает найти все его корни или доказать, что корней нет.
Линейными уравнениями называются не только уравнения вида ax + b = 0, но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду.
Давайте подумаем, является ли уравнение 2(5x + 4) = 2x – 16 – линейным уравнением первой степени? Нет, так как оно не записано в виде ax = b. Можно ли привести его к такому виду?
Попробуем это сделать. Переменная x входит в это уравнение первой степени. Все такие уравнения можно преобразовать в вид ax + b = 0 с помощью тождественных преобразований. Для этого раскроем скобки в левой части уравнения, воспользовавшись распределительным законом умножения.
10x + 8 = 2x + 16
Вычтем из правой и левой частей уравнения 2x и 8.
Затем приведём подобные слагаемые в левой и правой частях уравнения и получим уравнение стандартного вида.
8x = 8
А как же проверить, является ли число корнем уравнения, не решая его?
В таком случае, нам достаточно подставить значение переменной в уравнение и проверить, выполняется равенство или нет.
Чтобы узнать, является ли число корнем уравнения, нужно:
— Подставить вместо переменной числовое значение.
— Упростить.
— Посмотреть, получилось верное равенство или нет.
Если верное, то число является корнем уравнения, в противном случае – нет.
Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнения, в которых есть только неизвестные в первой степени и числа.
2(3x – 5) = x – 3
Приведём это уравнение к стандартному виду. В левой части раскроем скобки:
6x – 10 = x – 3
6x – x = 10 – 3
5x = 7
Линейное уравнение имеет вид:
ax = b, где a = 5 и b = 7.
Тренировочные задания.
Задание 1. Какое значение переменной удовлетворяет уравнению 4x – 2 = 14?
Варианты ответа:
x = 0
x = 2,5
x = 4
x = 0,1
Решение:
Для того чтобы определить, какое из значений удовлетворяет уравнению, нужно подставить вместо переменной соответствующее значение и проверить, получается ли истинное равенство. Соответственно, при истинности, значение переменной будет удовлетворять условию.
При x = 0 получаем: 4 · 0 – 2 = 14
–2 = 14 – ложь. Следовательно, x = 0 не удовлетворяет решению уравнения.
При x = 2,5 получаем: 4 · 2,5 – 2 = 14
3 = 14 – ложь. Следовательно, x = 2,5 не удовлетворяет решению уравнения.
При x = 4 получаем: 4 · 4 – 2 = 14
14 = 14 – истина. Следовательно, x = 4 удовлетворяет решению уравнения.
При x = 0,1 получаем: 4 · 0,1 – 2 = 14
–1,6 = 14 – ложь. Следовательно, x = 0,1 не удовлетворяет решению уравнения.
Ответ: x = 4
Задание 2. Уравнение 2(2x – 3) = 2x + 16 надо привести к стандартному виду.
Варианты ответа:
4x + 3 = 2x + 16
2x – 19 = 3x
4x = 22
2x = 22
Решение:
Для того чтобы определить, какое из значений является верным приведением уравнения к стандартному виду, нужно просто привести уравнение к стандартному виду.
2(2x – 3) = 2x + 16 – раскроем скобки, умножив число на разность;
4x – 6 = 2x + 16 – преобразуем уравнение, перенеся слагаемые, содержащие переменные в левую часть уравнения, а числа в правую, меняя при этом знак на противоположный;
4x – 2x = 16 – 6 – упростим выражение, приведя подобные слагаемые;
2x = 22 – полученное уравнение приведено к стандартному виду ax = b, где a = 1, b = 22
Ответ: 2x = 22
Решение уравнений с дробями — как решать дробные уравнения
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
| Основные свойства дробей |
|---|
|
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Приходите решать увлекательные задачки по математике в детскую школу Skysmart. Поможем разобраться в сложной теме, подтянем оценки и покажем, что математика может быть захватывающим приключением.
Запишите ребенка на бесплатный вводный урок: познакомим с форматом, выявим пробелы и наметим индивидуальную программу обучения.
Ты можешь записаться на онлайн-уроки по математике для учеников 1-11 классов!
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
| Универсальный алгоритм решения |
|---|
|
А теперь еще несколько способов, которые пригодятся ребенку на уроках математики.
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
Как решаем:
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
| Что еще важно учитывать при решении |
|---|
|
А вот и полезные видео для закрепления материала:
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
Как решаем:
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
1 + 2x = 5х
- Решим обычное уравнение.
5x — 2х = 1
3x = 1
х = 1/3
Ответ: х = 1/3.
Пример 2. Найти корень уравнения
Как решаем:
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
- Переведем новый множитель в числитель..
- Сократим левую часть на (х+2), а правую на 2.
4 = х + 2
х = 4 — 2 = 2
Ответ: х = 2.
Пример 3. Решить дробное уравнение:
Как решаем:
- Найти общий знаменатель:
3(x-3)(x+3)
- Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
3(x+3)(x+3)+3(x-3)(x-3)=10(x-3)(x+3)+3*36
- Выполним возможные преобразования. Получилось квадратное уравнение:
x2-9=0
- Решим полученное квадратное уравнение:
x2=9
- Получили два возможных корня:
x1=−3, x2=3
х = 4 — 2 = 2
- Если x = −3, то знаменатель равен нулю:
3(x-3)(x+3)=0
Если x = 3 — знаменатель тоже равен нулю.
- Вывод: числа −3 и 3 не являются корнями уравнения, значит у данного уравнения нет решения.
Ответ: нет решения.
Если нужно решить уравнение с дробями быстро — поможет онлайн-калькулятор дробей. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Онлайн урок: Решение уравнений по предмету Математика 6 класс
Решить линейное уравнение с одним неизвестным вида a ∙ x = b — это значит найти все его корни или доказать, что корней нет.
Наличие и количество корней линейного уравнения зависит от значений коэффициента а и значения свободного члена уравнения b.
1. Линейное уравнение при a ≠ 0 и b — любое число, будет иметь один единственный корень; это значит, что неизвестная имеет единственное верное решение, при котором уравнение обращается в верное равенство.
Известно, что деление — это обратное действие умножению (т.е. по известному множителю и произведению можно определить неизвестный множитель).
Следовательно, решение уравнения a ∙ x = b, где a ≠ 0 выглядит так:
x = b ÷ a
или \(\mathbf{x = \frac{b}{a}}\) (это корень линейного уравнения).
2. Линейное уравнение при a = 0 и b ≠ 0 не имеет корней.
Если коэффициент а равен нулю, линейное уравнение запишется, как
0 ∙ x = b
Свойство умножения числа на нуль дает право утверждать, что при любом значении неизвестной х уравнение обращается в неверное равенство 0 = b.
Равенство 0 = b при b ≠ 0 неверно, а это значит, что в таком случае решения уравнения нет, т.е. уравнение не имеет корней.
3. Линейное уравнение при а = 0 и b = 0 имеет бесконечное множество корней, т.е. при любом значении неизвестной х уравнение обращается в верное равенство.
0 ∙ x = 0
0 = 0 (верное равенство)
Чтобы решить линейное уравнение необходимо выполнить ряд математических преобразований.
У меня есть дополнительная информация к этой части урока!
Закрыть
Некоторые математические преобразования позволяют перейти от решаемого уравнения к равносильному (эквивалентному), что порой упрощает решение первоначального уравнения.
Два уравнения равносильны, если у них одинаковые корни или оба не имеют корней, т.е. если определенное число является решением первого уравнения, то оно подойдет в качестве решения второму.
Например, равносильными можно считать уравнения:
Уравнение 1 | Уравнение 2 |
16 ∙ x= 32 \(\mathbf{x = \frac{32}{16}}\) х = 2 Ответ: х = 2
| х + 3 = 5 х = 5 — 3 х = 2 Ответ: х = 2 |
Так как каждое из уравнений имеет только один корень, и он равен двум.
Равносильными, например, будут уравнения x ∙ 0 = 0 и х + 13 = 13 + х, так как решением этих уравнений может быть любое число, следовательно, решения их совпадают
Линейные уравнения обладают свойствами, которые позволяют совершать равносильные преобразования с различными уравнениями и сводить их к линейному уравнению с одной неизвестной стандартного вида, решать которое мы уже умеем.
Известно, что уравнение — это математическое равенство.
Если это равенство верно при определенных значениях неизвестной, то уравнение имеет верное решение.
Попробуем провести аналогию между уравновешенными весами и уравнением ax = b.
Как нам известно, уравновешенные весы нам показывают, что на каждой чаше весов находятся грузы равной массы.
Если весы были уравновешены, то добавив груз на одну чашу весов, необходимо добавить такой же по массе груз на вторую чашу, чтобы равновесие весов не было нарушено.
Аналогично, если убрать часть груза с одной чаши весов, то такую же часть груза нужно убрать со второй чаши, чтобы весы оставались уравновешенными.
А сейчас представим, что левая чаша весов — это левая часть линейного уравнения (ах), правая чаша весов — свободный член этого уравнения (b).
В таком случае получается, что если к левой и правой части уравнения прибавим (отнимем) одно и тоже число, то верное равенство не нарушится — получается уравнение равносильное исходному.
Добавлять к исходному можно любые числа, но необходимо выбирать то, которое упростит уравнение.
Рассмотрим пример:
Дано линейное уравнение 5х + 12 = 37
Для того, чтобы привести данное уравнение к стандартному виду: ax = b, прибавим к левой и правой части равенства —12 (противоположное числу 12, которое находится в правой части равенства, чтобы избавится в правой части от свободного члена уравнения),
5х + 12 + (-12) = 37 + (-12)
5х + 12 — 12 = 37 — 12
5х = 37 — 12
Если посмотреть внимательно на решение, то можно заметить, что число +12 исчезло из левой части исходного уравнения и появилось в правой части полученного после преобразований, при этом сменило знак и стало равным —12.
5х = 25 получили уравнение вида ax = b, так как a ≠ 0 и b ≠ 0 уравнение имеет единственный корень, найдем его:
х = 25/5
х = 5
Ответ: х = 5
Первое свойство равносильного преобразования уравнения
Любое слагаемое можно перенести из одно части уравнения в другую, при этом сменив знак этого слагаемого на противоположный, в результате получится новое уравнение, равносильное исходному.
Обычно слагаемые с неизвестным переносят в левую часть уравнения, а все остальные слагаемые в правую часть.
У меня есть дополнительная информация к этой части урока!
Закрыть
Чтобы лучше усвоить первое свойство равносильного преобразования уравнения, можно запомнить такое интересное сравнение.
Представьте ситуацию.
К хозяину дома приходит долгожданный гость.
Так как гость пришел с улицы, ему нужно уличную обувь переодеть на гостевые домашние тапочки.
Попробуем провести аналогию между рассмотренной ситуацией и первым свойством равносильного преобразования уравнения.
Например, возьмем уравнение 8х — 3 = 2х + 4.
Итак, в левой части уравнения слагаемое 8х является «хозяином» — он у себя «дома», «обувь» ему переодевать не нужно, значит, 8х знак свой не меняет.
Из правой части уравнения идет его «гость», слагаемое 2х. Ему как «гостю» приходится менять «обувь», т.е. менять свой знак на противоположный.
В правой части 2х был со знаком «+», при переходе меняет свой знак на противоположный и в левой части в «гостях» появляется со знаком «-».
Аналогично число 4 является «хозяином» в правой части уравнения, его знак остается неизменным, он у себя «дома».
Из левой части уравнения в «гости» идет слагаемое -3. Ему как «гостю» приходится менять «обувь», т.е. менять свой знак на противоположный.
В правой части слагаемое -3 было со знаком «-», при переходе знак меняется на противоположный и в левой части, в «гостях», становится знаком «+».
Получилось эквивалентное уравнение исходному, оно выглядит так:
8х — 2х =4 + 3
Приведем подобные, получим простейшее линейное уравнение.
6х = 7
\(\mathbf{x = \frac{7}{6}}\)
\(\mathbf{x =1 \frac{1}{6}}\)
Ответ: \(\mathbf{x =1 \frac{1}{6}}\)
Рассмотрим второе свойство равносильного преобразования уравнения.
Снова обратимся к аналогии с весами.
Для того, чтобы весы оставались в равновесии, увеличивая массу груза в 1,5 раза в одной из чаш, необходимо увеличить массу груза в 1,5 раза в другой чаше весов.
Увеличивая или уменьшая массу грузов на каждой чаше весов в одинаковое количество раз, равновесие весов будет сохраняться.
Так же происходит и с уравнением. Сформулируем второе свойство равносильного преобразования уравнения:
Разделив (или умножив) обе части на одно и тоже ненулевое число, равенство остается верным, получится уравнение равносильное исходному.
Рассмотрим пример
Дано уравнение 4 ∙ (2х — 1) = 16
Приведем данное уравнение к стандартному виду: ax =b
Раскрытие скобок только усложнит исходное уравнение.
Заметим, что левую и правую часть можем разделить на 4 (это наименьшее общее кратное чисел 4 и 16).
4 ∙ (2х — 1) = 16 |÷4
\(\mathbf{\frac{4 \cdot (2x — 1)}{4} = 16 \div 4}\)
2х — 1 = 4
Слагаемые с неизвестным оставляем в левой часть уравнения, а слагаемое -1 переносим в правую часть уравнения, сменив знак числа на противоположный, т.е. на «+».
2x = 4 + 1
2x = 5 получили уравнение вида ax = b
х = 5/2
x = 2,5
Ответ: х = 2,5
Решение линейных уравнений происходит с помощью нескольких преобразований, которые могут быть выполнены в любом порядке.
1. Освобождение от дробных членов уравнения (если такие есть) с помощью умножения левой и правой части уравнения на одно и тоже ненулевое число
2. Деление левой и правой части уравнения на одно и тоже ненулевое число
3. Раскрытие скобок (если они есть и это необходимо)
4. Перенос членов уравнения из одной части в другую со сменой их знаков на противоположные
5. Приведение подобных слагаемых
Завершая решение уравнения, стоит выполнить проверку, подставив в исходное уравнение найденное значение неизвестного. Если уравнение обратилось в верное равенство, значит, корень уравнения найден верно.
Итогом решения уравнения является ответ, в котором перечисляются все найденные корни уравнения.
Решение линейных уравнений с одним неизвестным
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
словарных задач с одним неизвестным
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Уравнений с переменными (предалгебра, введение в алгебру) — Mathplanet
В этом разделе вы узнаете, как решать уравнения, содержащие неизвестные переменные.Вы узнаете, как решать уравнения мысленно, используя таблицу умножения, и вы также узнаете, как найти решение уравнения с заданными числами, а также с помощью обратных операций.
Вы можете решить простое уравнение в уме с помощью таблицы умножения.
Пример
$$ \ begin {array} {lcl} 8x = 64 \ end {array} $$
$$ \ begin {array} {lcl} 8 \ cdot x = 64 \ end {array} $$
На какое число нужно умножить 8, чтобы получить произведение 64? Используя таблицу умножения, мы знаем, что число равно 8.
$$ 8 \ cdot 8 = 64 $$
Когда мы решаем уравнение, мы выясняем, какое значение x (или любой другой переменной) делает утверждение истинным (удовлетворяет уравнению).
Пример
Какое из следующих чисел является решением уравнения? х = 2, 7 или 8?
$$ 14-x = 7 $$
Здесь вам даны числа 2, 7 и 8. Одно из этих чисел будет удовлетворять уравнению. Если вы не знаете решение сразу, вы можете исследовать, какое из приведенных чисел дает правильный ответ, подставляя различные значения x.
$$ \ begin {matrix} x = 2 \ Rightarrow & 14-2 = 12 & {\ color {red} {Wrong}} \: \: \\ x = 7 \ Rightarrow & 14-7 = 7 \: & { \ color {green} {Correct}} \\ x = 8 \ Rightarrow & 14-8 = 6 \: & {\ color {red} {Wrong}} \: \: \ end {matrix} $$
Ответ: x = 7
Вы уже решили уравнения, решения которых довольно легко увидеть, с помощью мысленной математики или шаблонов. Большинство уравнений труднее решить, и вам нужно упростить уравнение, прежде чем вы сможете увидеть решение.Один из способов сделать это — использовать обратные операции.
Операция — это, например, сложение, умножение, деление и вычитание. Обратная операция — это операция, которая обращает эффект другой операции. Сложение и вычитание противоположны друг другу, как и деление и умножение.
Пример
С номерами
$$ 18 + 4 = 22 $$
$$ 18 + 4 {\ color {blue} \, — \, 4} = 22 {\ color {blue} \, — \, 4} $$
$$ 18 = 18 $$
С переменными и числами
$$ x + 4 = 22 $$
$$ x + 4 {\ color {blue} \, — \, 4} = 22 {\ color {blue} \, — \, 4} $$
$$ x = 18 $$
Отнимаем 4 с обеих сторон.
Пример
С переменными и числами
$$ x \ cdot 2 = 10 $$
$$ \ frac {x \ cdot 2} {{\ color {blue} 2}} = \ frac {10} {{\ color {blue} 2}} $$
$$ x = 5 $$
Делим обе стороны на 2
Видеоуроки
Решите следующее уравнение
$$ 8 \ cdot x-x = 21 $$
Решите следующее уравнение, используя обратные операции
$$ 6x + 4 = 28 $$
Решение одностадийных линейных уравнений: сложение и вычитание
Purplemath
«Линейные» уравнения — это уравнения с простой старой переменной, такой как « x », а не с чем-то более сложным, например, x 2 или x / y , или квадратными корнями, или другими более сложные выражения.Линейные уравнения — это самые простые уравнения, с которыми вам придется столкнуться.
Вы, наверное, уже решили линейные уравнения; ты просто не знал этого. Еще в ранние годы, когда вы учились сложению, ваш учитель, вероятно, дал вам рабочие листы для выполнения, в которых были упражнения вроде следующих:
Заполните поле: & квадрат; + 3 = 5
Заполните поле: & квадрат; + 3 = 5
Как только вы достаточно хорошо усвоили факты сложения, вы знали, что вам нужно поставить цифру «2» внутри квадрата.
MathHelp.com
Решение уравнений работает примерно так же, но теперь мы должны выяснить, что входит в x , а не то, что входит в коробку.Однако, поскольку сейчас мы старше, чем когда заполняли поля, уравнения также могут быть намного сложнее, и поэтому методы, которые мы будем использовать для решения уравнений, будут немного более продвинутыми.
В общем, чтобы решить уравнение для данной переменной, нам нужно «отменить» все, что было сделано с переменной. Мы делаем это для того, чтобы получить переменную сама по себе; технически мы «изолируем» переменную. Это приводит к тому, что уравнение изменяется так, чтобы говорить «(переменная) равно (некоторому числу)», где (некоторое число) — это ответ, который они ищут.Например:
Переменная — это буква x . Чтобы решить это уравнение, мне нужно получить x отдельно; то есть мне нужно получить x с одной стороны от знака «равно» и какое-то число с другой стороны.
Поскольку я хочу только x с одной стороны, это означает, что мне не нравится «плюс шесть», который в настоящее время находится на той же стороне, что и x . Поскольку 6 — это , добавленное к x , мне нужно вычесть из этого 6, чтобы избавиться от него.То есть мне нужно будет вычесть 6 из x , чтобы «отменить» их добавление к нему 6.
Это вызывает наиболее важное соображение с уравнениями:
Неважно, с каким уравнением мы имеем дело — линейным или каким-либо другим — что бы мы ни делали с одной стороной уравнения, мы должны сделать то же самое, что и , с другой стороной уравнения. В этом отношении уравнения похожи на малышей:
Мы должны быть полностью, полностью справедливыми по отношению к обеим сторонам, иначе последует несчастье!
Что бы вы ни делали с уравнением, проделайте ТОЧНО ТАК ЖЕ с ОБЕИМИ сторонами этого уравнения!
Вероятно, лучший способ отследить это вычитание 6 с обеих сторон — это отформатировать свою работу следующим образом:
Изображение выше анимировано на «живой» странице.
Здесь вы видите, что я вычел 6 с обеих сторон, нарисовал горизонтальную полосу «равно» под всем уравнением, а затем сложил. В левой части (LHS) уравнения это дает мне:
x плюс ничего равно x , а 6 минус 6 равно нулю
В правой части (RHS) уравнения у меня:
Решение — последнее направление моей работы; а именно:
Та же процедура «отмены» работает для уравнений, в которых переменная была объединена в пару с вычитанием.
Переменная находится в левой части (LHS) уравнения в паре с оператором «вычесть три». Поскольку я хочу получить x отдельно, мне не нравится «3», которое в настоящее время вычитается из него. Противоположность вычитанию — это сложение, поэтому я отменю «вычитание 3», добавив 3 к обеим сторонам уравнения, а затем добавлю вниз, чтобы упростить, чтобы получить свой ответ:
Тогда мой ответ:
Вас могут попросить «проверить свои решения», по крайней мере, на ранних этапах обучения решению уравнений.Чтобы выполнить эту «проверку», вам нужно только подставить свой ответ в исходное уравнение и убедиться, что в итоге вы получили верное утверждение. (Это, в конце концов, определение решения уравнения; а именно, решение — это любое значение или набор значений [для более сложных уравнений, позже], что делает исходное уравнение истинным.)
Итак, чтобы проверить мое решение вышеприведенного уравнения, вы должны вставить «–2» вместо x в левой части (LHS) исходного уравнения и проверить, что это упрощает, чтобы получить исходное значение. для правой части (RHS) уравнения:
Проверок:
LHS: (–2) — 3 = –5
RHS: –5
Поскольку каждая сторона исходного уравнения теперь дает одно и то же значение, это подтверждает, что решение действительно правильное.
Решите 4 =
x — 3 и проверьте свое решение.
На этот раз переменная находится в правой части (RHS) уравнения. Это нормально; не имеет значения, где находится переменная, пока я могу изолировать ее (то есть, пока я могу получить ее отдельно от знака «равно»).
В этом уравнении у меня вычитается тройка из переменной.Чтобы отменить вычитание, я добавлю по три с каждой стороны уравнения.
4 = х — 3
+3 + 3
———-
7 = х
(Я мог бы записать правую часть после добавления как « x + 0», но «плюс ноль» обычно игнорируется. Поэтому я перенес только x с правой стороны .)
Теперь, в рамках моей практической работы, мне нужно показать, что я проверил это решение, вставив его обратно в правую часть исходного уравнения и подтвердив, что я получил левую часть исходного уравнения; то есть я получаю 4:
«Проверка» — это то, что я сделал выше.Я постарался четко обозначить вещи, чтобы оценщик смог найти мой «чек» (так что я получу полную оценку за упражнение). Мой окончательный ответ:
Когда я решил последнее упражнение выше, переменная оказалась справа от знака «равно». Но в своем решении я написал ответ с помощью переменной слева от знака «равно». Это довольно стандартно. Когда вы решаете, переменная окажется там, где она окажется.Когда вы записываете решение, переменная идет слева. Почему? Так как.
Это уравнение почти решено. Но не совсем так. У меня нет старого доброго x с правой стороны; вместо этого у меня — x . Что делать?
Я могу представить — x как 0- x . Итак, что произойдет, если я добавлю x к каждой стороне уравнения?
2 = –x
+ х + х
——-
х + 2 = 0
Хорошо; это помогло.Взяв переменную и «добавив ее на другую сторону», я получил переменную в том формате, который мне нравится. И это также преобразовало исходное уравнение в простое одношаговое уравнение. Я избавлюсь от двойки в левой части, «вычтя ее» в правой части:
х + 2 = 0
-2 = -2
———-
х = -2
Этот ответ имеет смысл.Если отрицательное значение переменной равняется положительным двум, то положительное значение переменной должно равняться отрицательным двум. Итак, мой ответ:
Технически последний пример представлял собой двухэтапное уравнение, потому что для его решения требовалось прибавить одну вещь к обеим сторонам уравнения, а затем вычесть другую к обеим сторонам. Важно отметить, что вы можете добавлять и вычитать переменные к другой стороне уравнения, точно так же, как вы можете складывать и вычитать числа с другой стороны.Точно такие же методы работают как с переменными, так и с числами.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейного уравнения путем сложения или вычитания. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvelin.htm
Как решать алгебру
y = 24 — 4x
Пояснение:
Как показано в приведенном выше примере, мы вычисляем значение переменной из одного уравнения и подставляем его в другое.
Нам дано, что
у = 24 — 4x —— (1)
2x + y / 2 = 12 —— (2)
Здесь мы выбираем уравнение (1) для вычисления значения x. Поскольку уравнение (1) уже находится в
самая упрощенная форма:
(Подставляя это значение y в уравнение (2), а затем решая для x
дает)
2x + (24-4x) / 2 = 12 —— (2) (∵ y = 24 — 4x)
2x + 24 / 2- 4x / 2 = 12
2x + 12 — 2x = 12
12 = 12
Вы можете подумать, что это тот же сценарий, что обсуждался выше (24 = 24).Но
ждать! Вы слишком рано пытаетесь сделать вывод. В предыдущем сценарии
результат 24 = 24 был получен потому, что мы поместили значение переменной в то же уравнение, что и
используется для его вычисления. Здесь мы этого не сделали.
Результат 12 = 12 имеет какое-то отношение к природе системы уравнений, которую мы
дано.Независимо от того, какой метод решения вы можете использовать, решение системы линейных
уравнения лежат в единственной точке, где их линии пересекаются. В этом сценарии две строки
в основном одинаковы (одна линия над другой. На следующем рисунке показан этот сценарий.
Такая система называется зависимой системой
уравнения.И решение такой системы — это вся линия (каждая точка на линии — это точка
пересечения двух линий)
Следовательно, решением данной системы уравнений является вся
строка: y = 24 — 4x
Другой возможный сценарий:
Подобно этому примеру, существует другой сценарий, в котором замена одной переменной
в уравнение 2 nd приводит к результату, аналогичному показанному ниже:
23 = –46
или
5 = 34
Такой сценарий возникает, когда не существует решения данной системы уравнений.Т.е.,
когда две линии вообще не пересекаются ни в одной точке.
Следовательно, в случае такого результата, когда кажется, что ваши основные математические правила не работают, простой вывод
заключается в том, что решения данной системы не существует. Такая система уравнений называется Несогласованная система .
Решение простых уравнений
Решая простое уравнение, думайте об уравнении как о балансе, где знак равенства (=) является точкой опоры или центром. Таким образом, если вы делаете что-то с одной стороной уравнения, вы должны сделать то же самое с другой стороной. Выполнение одного и того же действия с обеими сторонами уравнения (скажем, добавление 3 к каждой стороне) сохраняет уравнение сбалансированным.
Решение уравнения — это процесс получения того, что вы ищете, или решения относительно с одной стороны от знака равенства и всего остального с другой стороны.Вы действительно сортируете информацию. Если вы решаете для x , вы должны получить x с одной стороны.
Уравнения сложения и вычитания
Некоторые уравнения включают только сложение и / или вычитание.
Пример 1
Решите относительно x .
х + 8 = 12
Чтобы решить уравнение x + 8 = 12, вы должны получить x на одной стороне. Поэтому вычтите 8 с обеих сторон.
Чтобы проверить свой ответ, просто подставьте свой ответ в уравнение:
Пример 2
Решите относительно и .
y — 9 = 25
Чтобы решить это уравнение, вы должны получить y отдельно с одной стороны. Поэтому прибавьте 9 к обеим сторонам.
Для проверки просто замените y на 34:
Пример 3
Решите относительно x .
х + 15 = 6
Чтобы решить, отнимите 15 с обеих сторон.
Для проверки просто замените x на –9:
.
Обратите внимание, что в каждом из приведенных выше случаев используются противоположных операций ; то есть, если в уравнении есть сложение, вы вычитаете с каждой стороны.
Уравнения умножения и деления
Некоторые уравнения включают только умножение или деление. Обычно это происходит, когда переменная уже находится на одной стороне уравнения, но существует либо несколько переменных, например 2 x , либо часть переменной, например
.
или
Таким же образом, как при сложении или вычитании, вы можете умножить или разделить обе части уравнения на одно и то же число, , если оно не равно нулю , и уравнение не изменится.
Пример 4
Решите относительно x .
3 x = 9
Разделите каждую часть уравнения на 3.
Для проверки замените x на 3:
Пример 5
Решите относительно и .
Чтобы решить, умножьте каждую сторону на 5.
Для проверки замените y на 35:
Пример 6
Решите относительно x .
Чтобы решить, умножьте каждую сторону на.
Или, без отмены,
Обратите внимание, что слева вы обычно не пишете, потому что это всегда отменяется до 1 x или x .
Комбинации операций
Иногда для решения уравнения требуется более одного шага. В большинстве случаев сначала выполните этап сложения или вычитания. Затем, после того, как вы отсортировали переменные в одну сторону, а числа в другую, умножьте или разделите, чтобы получить только одну из переменных (то есть переменную без номера или 1 перед ней: x , а не 2 x ).
Пример 7
Решите относительно x .
2 x + 4 = 10
Вычтите 4 с обеих сторон, чтобы получить 2 x на одной стороне.
Затем разделите обе стороны на 2, чтобы получить x .
Чтобы проверить, подставьте свой ответ в исходное уравнение:
Пример 8
Решите относительно x .
5x — 11 = 29
Добавьте 11 с обеих сторон.
Разделите каждую сторону на 5.
Для проверки замените x на 8:
Пример 9
Решите относительно x .
Вычтем по 6 с каждой стороны.
Умножаем каждую сторону на.
Для проверки замените x на 9:
Пример 10
Решите относительно и .
Добавьте 8 с обеих сторон.
Умножаем каждую сторону на.
Для проверки замените y на –25:
Пример 11
Решите относительно x .
3 x + 2 = x + 4
Вычтем 2 с обеих сторон (то же самое, что прибавить –2).
Вычтите x с обеих сторон.
Обратите внимание, что 3 x — x совпадает с 3 x — 1 x .
Разделите обе стороны на 2.
Для проверки замените x на 1:
Пример 12
Решите относительно и .
5 y + 3 = 2 y + 9
Вычтем 3 с обеих сторон.
Вычтем 2 y с обеих сторон.
Разделите обе стороны на 3.
Для проверки замените y на 2:
Иногда вам нужно упростить каждую сторону (объединить одинаковые термины) перед фактическим запуском процесса сортировки.
Пример 13
Решите относительно x .
3 х + 4 + 2 = 12 + 3
Во-первых, упростите каждую сторону.
Вычтем 6 с обеих сторон.
Разделите обе стороны на 3.
Для проверки замените x на 3:
Пример 14
Решите относительно x .
4 x + 2 x + 4 = 5 x + 3 + 11
Упростите каждую сторону.
6 x + 4 = 5 x + 14
Вычтем 4 с обеих сторон.
Вычтите 5 x с обеих сторон.
Для проверки замените x на 10:
Бесплатные рабочие листы по линейным уравнениям (6-9 классы, предалгебра, алгебра 1)
Вы здесь: На главную → Рабочие таблицы → Линейные уравнения
Здесь вы найдете неограниченное количество распечатываемых рабочих листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html.Вы можете настроить рабочие листы, включив в них одношаговые, двухэтапные или многоступенчатые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Рабочие листы подходят для курсов предварительной алгебры и алгебры 1 (6-9 классы).
Вы можете выбрать из СЕМЬ основных типов уравнений, от простых до сложных, описанных ниже (например, одношаговые уравнения, переменные с обеих сторон или необходимость использования свойства распределения). Настройте рабочие листы с помощью генератора ниже.
Основные инструкции для рабочих листов
Каждый рабочий лист генерируется случайным образом и поэтому уникален.Ключ ответа создается автоматически и помещается на вторую страницу файла.
Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — оба легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать рабочий лист html ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Иногда сгенерированный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
- Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.
- Формат Html: просто обновите страницу рабочего листа в окне браузера.
Рабочие листы готовые
См. Также
Рабочие листы для упрощения выражений
Рабочие листы для вычисления выражений с переменными
Рабочие листы для написания выражений с переменными из словесных выражений
Рабочие листы для линейных неравенств
Ключ к учебным пособиям по алгебре
Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения.


