Как складывать числа со степенями: Сложение и вычитание степеней ⬅️ — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Сложение и вычитание степеней ⬅️

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

где

a — основание степени

n — показатель степени

Соответственно, aⁿ= a·a·a·a…·a

Читается такое выражение, как a в степени n.

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то решается она довольно просто:

2 — основание степени

3 — показатель степени

Действия, конечно, можно выполнять и в онлайн калькуляторе — вот несколько подходящих:

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Число	Вторая степень	Третья степень
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	729
10	100	1000

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — давайте их рассмотрим.

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

a — основание степени

m, n — показатели степени, любые натуральные числа.

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Свойство 3: возведение степени в квадрат

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

a — основание степени (не равное нулю)

m, n — показатели степени, натуральное число

Свойство 4: степень возведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

a, b — основание степени (не равное нулю)

n — показатели степени, натуральное число

Записывайся на онлайн курсы по математике для учеников с 1 по 11 классы!

Свойство 5: степень частного

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,

n — показатель степени, натуральное число

Сложение и вычитание степеней

Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания. Примеры:

2³+ 3⁴= 8 + 81= 89
6³— 3³= 216 — 27 = 189

И еще несколько правил:

при наличии скобок — начинать вычисления нужно внутри них
только потом возведение производим в степень
затем выполняем остальные действия: сначала умножение и деление
после — сложение и вычитание

Сложение степеней с разными показателями

В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.

Сложение степеней с разными основаниями

В целом, это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.

3⁴+ 5⁴=81 + 625 = 706
1⁴+ 7²= 1+ 49 = 50

Как складывать числа с одинаковыми степенями

Точно также, как и в предыдущем примере. Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень.
Сначала возводим каждое число в степень и затем выполняем сложение.

В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a², например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a².

2, 3, 5 — коэффициенты

a² — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Вычитание степеней с одинаковым основанием

Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.

Вычитание степеней с разными основаниями

Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.

5⁴— 4⁴= 625 — 256 = 369
7⁴— 3²= 2401 — 9 = 2392

Вычитание чисел с одинаковыми степенями

Все точно также, как и со сложением. Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.

И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a²) — их коэффициенты можно вычитать. Коэффициент — это число перед переменной a².

6, 3, 2 — коэффициенты

a² — переменная

Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.

Подготовиться к сложной контрольной ребенку помогут в детской онлайн-школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Запишите вашего ребенка на бесплатный вводный урок математики и начните заниматься ей с удовольствием уже завтра.

Сложение чисел с разными показателями степени. Действия с одночленами

Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?

В алгебре найти произведение степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:

При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

Рассмотрим, как умножать степени, на конкретных примерах.

Единицу в показателе степени не пишут, но при умножении степеней — учитывают:

При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:

В выражениях возведение в степень выполняется в первую очередь.

Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:

www.algebraclass.ru

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками
.

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных
могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.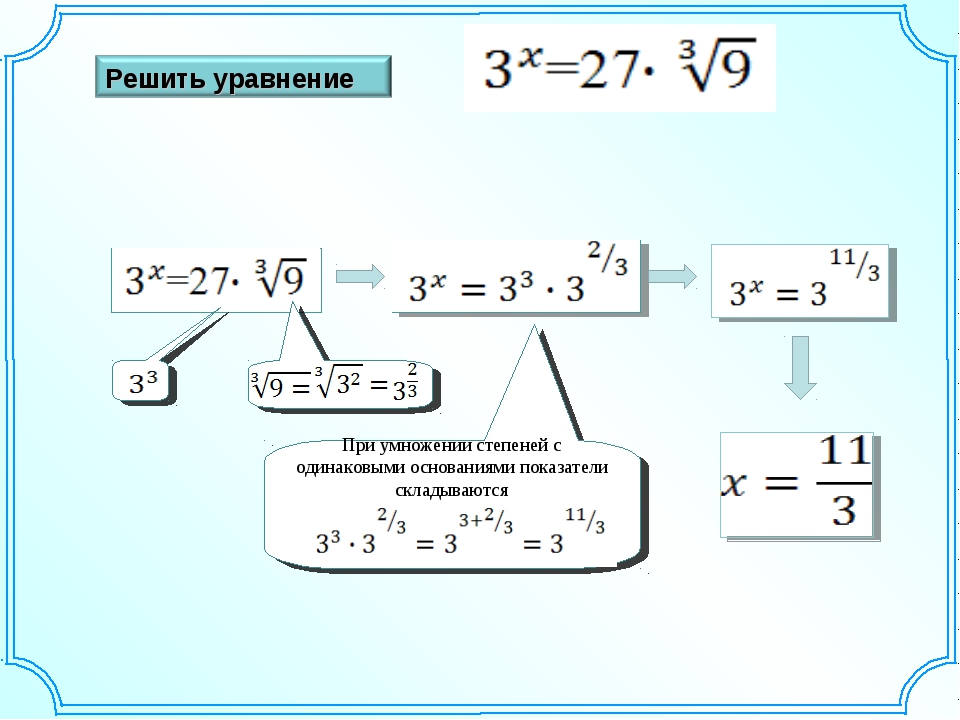

Но степени различных переменных
и различные степени
одинаковых переменных
, должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание
степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:

2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:

x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме
степеней слагаемых.

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:

4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные
.

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат
, результат будет равен сумме или разнице этих чисел в четвёртой
степени.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.

Таким образом a 3 b 2 делённое на b 2 , равно a 3 .

Запись a 5 , делённого на a 3 , выглядит как $\frac $. 3$

Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.

2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней
с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1

Произведение степеней

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17

Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями
. Оно не относится к их сложению.

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2

Частное степеней

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Вычислить.

11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Найти значение выражения, используя свойства степени.

2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3

Возведение степени в степень

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

(a n · b n)= (a · b) n

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000

Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5

Степень частного (дроби)

(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

Степени и корни

Операции со степенями и корнями. Степень с отрицательным
,

нулевым и дробным
показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются:

a m
· a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели
вычитаются
.

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

(a / b
) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² =
2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

Операции с корнями.

Во всех нижеприведенных формулах символ означает арифметический корень
(подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень
подкоренное число:

4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:

5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени.

До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным
, нулевым
и дробным
показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем.

Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:

Т еперь формула a m
: a n
= a m — n
может быть использована не только при m
, большем, чем n
, но и при m
, меньшем, чем n
.

П р и м е р. a
4: a
7 = a
4 — 7 = a
— 3 .

Если мы хотим, чтобы формула a m
: a n
= a m
— n
была справедлива при m = n
, нам необходимо определение нулевой степени.

Степень с нулевым показателем.

Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (–
5) 0 = 1, (–
3 / 5) 0 = 1.

Степень с дробным показателем.

Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:

О выражениях, не имеющих смысла.

Есть несколько таких выражений.

где a
≠ 0 , не существует.

В самом деле, если предположить, что x
– некоторое число, то в соответствии с определением операции деления имеем: a
= 0· x
, т.e. a
= 0, что противоречит условию: a
≠ 0

— любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x
, то согласно определению операции деления имеем: 0 = 0 · x
. Но это равенство имеет место при любом числе x
, что и требовалось доказать.

0 0 — любое число.

Р е ш е н и е. Рассмотрим три основных случая:

1) x
= 0 –
это значение не удовлетворяет данному уравнению

2) при x
> 0 получаем: x / x
= 1, т.e. 1 = 1, откуда следует,

что x
– любое число; но принимая во внимание, что в

нашем случае x
> 0 , ответом является x
> 0 ;

Правила умножения степеней с разным основанием

СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ IV

§ 69. Умножение и деление степеней с одинаковыми основаниями

Теорема 1.
Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним
, то есть

Доказательство.
По определению степени

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.

Теорема 2.
Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить
прежним, то есть при
т > п

(a

=/= 0)

Доказательство.
Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a

=/= 0, это все равно, что доказать формулу

Если т > п

, то число т — п

будет натуральным; следовательно, по теореме 1

Теорема 2 доказана.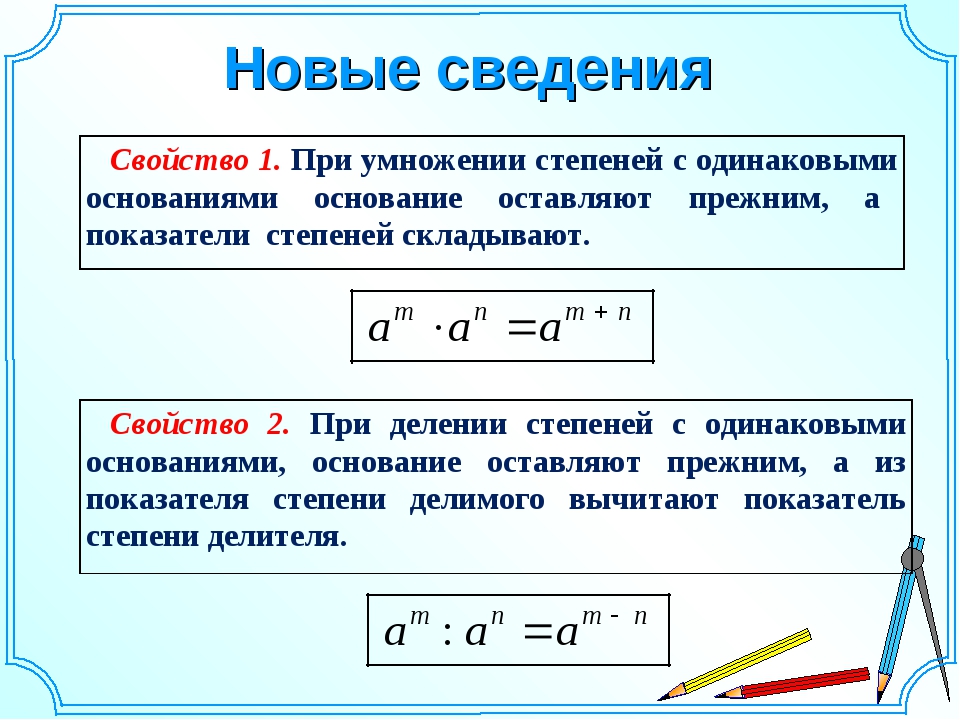

Следует обратить внимание на то, что формула

доказана нами лишь в предположении, что т > п

. Поэтому из доказанного пока нельзя делать, например, таких выводов:

К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 —

2 .

Теорема 3.
Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним
, то есть

Доказательство.
Используя определение степени и теорему 1 этого параграфа, получаем:

что и требовалось доказать.

Например, (2 3) 2 = 2 6 = 64;

518 (Устно.) Определить х

из уравнений:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x

; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x

;

2) 3 3 3 3 5 3 7 3 9 = 3 x

; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x

.

519. (У с т н о. ) Упростить:

520. (У с т н о.) Упростить:

521. Данные выражения представить в виде степеней с одинаковыми основаниями:

1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;

2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .

Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени

Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.

1-е свойство.

Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.

2-е свойство.

3-е свойство.

Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.

4-е свойство.

Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.

Свойство работает только при делении, при вычитании не применяется!

5-е свойство.

6-е свойство.

Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.

7-е свойство.

Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.

8-е свойство.

9-е свойство.

Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.

Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.

10-е свойство.

Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.

11-е свойство.

Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.

12-е свойство.

Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Показательные уравнения и неравенства

Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Онлайн-калькулятор возведения в степень

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом:

a n = a * a * a * …a n .

Например:

2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
4 2 = 4 в степ. два = 4 * 4 = 16;
5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

a n * a m = (a) (n+m) ;
a n: a m = (a) (n-m) ;
(a b) m =(a) (b*m) .

Проверим на примерах:

2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.

(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием
? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

3 3 + 2 4 = 27 + 16 = 43;
5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.

А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.

Как производить вычисления в более сложных случаях
? Порядок тот же:

при наличии скобок – начинать нужно с них;
затем возведение в степень;
потом выполнять действия умножения, деления;
после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5
(смотри пункт выше), получается
:

A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.

И наоборот:

1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.

А если дробь?

(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.

Степень с натуральным показателем

Под ней понимают степень с показателями, равными целым числам.

Что нужно запомнить:

A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.

A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.

Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.

Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.

Дробная степень

Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.

С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.

Степень с иррациональным показателем

Пусть α – иррациональное число, а А ˃ 0.

Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:

А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;

А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;

В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.

Например, показатель степени число π.
Оно рациональное.

r 1 – в этом случае равно 3;

r 2 – будет равно 4.

Тогда, при А = 1, 1 π = 1.

А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.

А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.

Для таких степеней характерны все математические операции и специфические свойства, описанные выше.

Заключение

Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.

Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.

Так, сумма a 3 и b 2 есть a 3 + b 2 .

Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных
могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Или:

2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:

x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.

Выражение примет вид: a 5 b 5 y 3 .

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:

4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .

Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные
.

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.5}$. Ответ: $\frac{2x}{1}$ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.

a 2 .a -4 есть a -2 первый числитель.

a 3 .a -3 есть a 0 = 1, второй числитель.

a 3 .a -4 есть a -1 , общий числитель.

После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.

Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.

Если вам нужно возвести какое-то конкретное число в степень, можете воспользоваться . А сейчас мы более подробно остановимся на свойствах степеней
.

Экспоненциальные числа
открывают большие возможности, они позволяют нам преобразовать умножение в сложение, а складывать гораздо легче, чем умножать.

Например, нам надо умножить 16 на 64. Произведение от умножения этих двух чисел равно 1024. Но 16 – это 4×4, а 64 – это 4х4х4. То есть 16 на 64=4x4x4x4x4, что также равно 1024.

Число 16 можно представить также в виде 2х2х2х2, а 64 как 2х2х2х2х2х2, и если произвести умножение, мы опять получим 1024.

А теперь используем правило . 16=4 2 , или 2 4 , 64=4 3 , или 2 6 , в то же время 1024=6 4 =4 5 , или 2 10 .

Следовательно, нашу задачу можно записать по-другому: 4 2 х4 3 =4 5 или 2 4 х2 6 =2 10 , и каждый раз мы получаем 1024.

Мы можем решить ряд аналогичных примеров и увидим, что умножение чисел со степенями сводится к сложению показателей степени
, или экспонент, разумеется, при том условии, что основания сомножителей равны.

Таким образом, мы можем, не производя умножения, сразу сказать, что 2 4 х2 2 х2 14 =2 20 .

Это правило справедливо также и при делении чисел со степенями, но в этом случае экспонента делителя вычитается из экспоненты делимого
. Таким образом, 2 5:2 3 =2 2 , что в обычных числах равно 32:8=4, то есть 2 2 . Подведем итоги:

a m х a n =a m+n , a m: a n =a m-n , где m и n — целые числа.

С первого взгляда может показаться, что такое умножение и деление чисел со степенями
не очень удобно, ведь сначала надо представить число в экспоненциальной форме. Нетрудно представить в такой форме числа 8 и 16, то есть 2 3 и 2 4 , но как это сделать с числами 7 и 17? Или как поступать в тех случаях, когда число можно представить в экспоненциальной форме, но основания экспоненциальных выражений чисел сильно различаются. Например, 8×9 – это 2 3 х3 2 , и в этом случае мы не можем суммировать экспоненты. Ни 2 5 и ни 3 5 не являются ответом, ответ также не лежит в интервале между этими двумя числами.

Тогда стоит ли вообще возиться с этим методом? Безусловно стоит. Он дает огромные преимущества, особенно при сложных и трудоемких вычислениях.

Свойства степеней при сложении. Основные свойства степеней. Примеры на умножение степеней с одинаковыми показателями

Каждая арифметическая операция порою становится слишком громоздкой для записи и её стараются упростить. Когда-то так было и с операцией сложения. Людям было необходимо проводить многократное однотипное сложение, например, посчитать стоимость ста персидских ковров, стоимость которого составляет 3 золотые монеты за каждый. 3+3+3+…+3 = 300. Из-за громоздкости было придумано сократить запись до 3 * 100 = 300. Фактически, запись «три умножить на сто» означает, что нужно взять сто троек и сложить между собой. Умножение прижилось, обрело общую популярность. Но мир не стоит на месте, и в средних веках возникла необходимость проводить многократное однотипное умножение. Вспоминается старая индийская загадка о мудреце, попросившем в награду за выполненную работу пшеничные зёрна в следующем количестве: за первую клетку шахматной доски он просил одно зерно, за вторую – два, третью – четыре, пятую – восемь и так далее.3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.

Формулы степеней
используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c
является n
-ной степенью числа a
когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m
·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например
. (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4
.

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n
раз и в тоже время возвести в n
-ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n
раз и в тоже время извлечь корень n
-ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем.
Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m
:a n =a m — n
можно использовать не только при m
> n
, но и при m
n
.

Например
. a
4:a 7 = a 4 — 7 = a -3
.

Чтобы формула a m
:a n =a m — n
стала справедливой при m=n
, нужно присутствие нулевой степени.

Степень с нулевым показателем.
Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например
. 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем.
Чтобы возвести действительное число а
в степень m/n
, необходимо извлечь корень n
-ой степени из m
-ой степени этого числа а
.

Операции со степенями и корнями.
Степень с отрицательным

нулевым и дробным

показателем. О выражениях, не имеющих смысла.

Операции со
степенями.

1. При умножении степеней с
одинаковым основанием их показатели складываются
:

a m

·

a n = a m + n .

2. При делении степеней с
одинаковым основанием их показатели

вычитаются

.

3. Степень
произведения двух или нескольких сомножителей равна произведению
степеней этих сомножителей.

(
abc

…
)
n

a
n

·
b

·
c

…

4. Степень отношения (дроби) равна
отношению степеней делимого (числителя) и делителя (знаменателя):

(
a

/
b

)
n

=
a

/
b

5. При возведении степени в
степень их показатели перемножаются:

)

n

=
a

m
n

Все вышеприведенные формулы читаются и выполняются в обоих
направлениях слева направо и наоборот.

П р и
м е р. (2

·

3

·

5 / 15)

²

=

·

5

/ 15

= 900 / 225 = 4 .

Операции с корнями.

Во всех нижеприведенных формулах символ

означает арифметический корень
(подкоренное выражение
положительно).

Корень из произведения
нескольких сомножителей равен произведению

корней из этих сомножителей:

Корень
из отношения равен отношению корней делимого и делителя:

3.
При
возведении корня в степень достаточно возвести в эту степень

подкоренное число:

4.
Если
увеличить степень корня в
m

раз и одновременно возвести в

m
-ую
степень подкоренное число, то значение корня не изменится:

Если уменьшить степень корня
в
m

раз и одновременно извлечь корень

m
-ой
степени из подкоренного числа, то значение корня не
изменится:

Расширение понятия
степени.

До
сих пор мы рассматривали степени только с натуральным показателем;
но
действия
со
степенями и корнями
могут приводить также к отрицательным
, нулевым
и
дробным
показателям. Все эти показатели степеней требуют
дополнительного определения.

Степень с отрицательным
показателем.

Степень
некоторого числа с

отрицательным (целым) показателем
определяется как единица, делённая

на степень того же числа с
показателем, равным абсолютной велечине

отрицательного показателя:

еперь
формула
a
m

:

a

=
a

—

может быть использована не
только при
m

, большем, чем

, но и при
m

, меньшем, чем
n

П р и м е р

.
a

4
: a

7
= a

4
—
7 = a

—
3
.

Если
мы хотим, чтобы формула
a

m

:

a
n
=
a
m

—
n
была
справедлива при
m

=
n

,
нам необходимо
определение нулевой степени.

Степень
с нулевым показателем.

Степень любого ненулевого числа с
нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1,
(–
5) 0 = 1, (–
3 / 5) 0 = 1.

Степень с дробным показателем.

Для того, чтобы возвести действительное число

в степень

, нужно извлечь корень

n
–ой
степени из

m
-ой
степени этого числа

О выражениях, не имеющих смысла.

Есть несколько таких выражений.
любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x
, то согласно
определению операции деления имеем: 0 = 0 · x
. Но это равенство имеет место при любом числе x
, что и требовалось доказать.

Случай 3.

0
0

— любое число.

Действительно,

Р е ш е н и е.
Рассмотрим три основных случая:

= 0 –
это значение не удовлетворяет данному уравнению

(Почему?).

2) при
x

> 0 получаем:
x

/
x

= 1, т.e. 1 = 1, откуда следует,

что

x

– любое число; но принимая во внимание, что в

Нашем
случае
x

> 0 , ответом является
x

> 0 ;

3) при
x

/
x

= 1, т.
e
.
–1 = 1, следовательно,

В этом
случае нет решения.

Таким образом,

x

> 0.

Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?

В алгебре найти произведение степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:

При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

Рассмотрим, как умножать степени, на конкретных примерах.

Единицу в показателе степени не пишут, но при умножении степеней — учитывают:

В выражениях возведение в степень выполняется в первую очередь.

www.algebraclass.ru

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных
могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Или:

2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:

x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:

4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные
.

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.3$

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.

2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

Свойства степени

Свойство № 1

Произведение степеней

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17

Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2

Частное степеней

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Вычислить.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000

Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5

Степень частного (дроби)

(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12

Степени и корни

Операции со степенями и корнями. Степень с отрицательным
,

нулевым и дробным
показателем. О выражениях, не имеющих смысла.

Операции со степенями.

1. При умножении степеней с одинаковым основанием их показатели складываются:

a m
· a n = a m + n .

2. При делении степеней с одинаковым основанием их показатели
вычитаются
.

3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):

(a / b
) n = a n / b n .

5. При возведении степени в степень их показатели перемножаются:

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² =
2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

2. Корень из отношения равен отношению корней делимого и делителя:

3. При возведении корня в степень достаточно возвести в эту степень
подкоренное число:

П р и м е р. a
4: a
7 = a
4 — 7 = a
— 3 .

Степень с нулевым показателем.

Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы. 2 0 = 1, (–
5) 0 = 1, (–
3 / 5) 0 = 1.

О выражениях, не имеющих смысла.

Есть несколько таких выражений.

где a
≠ 0 , не существует.

— любое число.

0 0 — любое число.

Р е ш е н и е. Рассмотрим три основных случая:

1) x
= 0 –
это значение не удовлетворяет данному уравнению

2) при x
> 0 получаем: x / x
= 1, т.e. 1 = 1, откуда следует,

что x
– любое число; но принимая во внимание, что в

нашем случае x
> 0 , ответом является x
> 0 ;

Правила умножения степеней с разным основанием

СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,

СТЕПЕННАЯ ФУНКЦИЯ IV

§ 69. Умножение и деление степеней с одинаковыми основаниями

Доказательство.
По определению степени

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

(a

=/= 0)

Если т > п

, то число т — п

будет натуральным; следовательно, по теореме 1

Теорема 2 доказана.

Следует обратить внимание на то, что формула

Доказательство.
Используя определение степени и теорему 1 этого параграфа, получаем:

что и требовалось доказать.

Например, (2 3) 2 = 2 6 = 64;

518 (Устно.) Определить х

из уравнений:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x

; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x

;

2) 3 3 3 3 5 3 7 3 9 = 3 x

; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x

.

519. (У с т н о.) Упростить:

520. (У с т н о.) Упростить:

521. Данные выражения представить в виде степеней с одинаковыми основаниями:

1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;

2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .

Свойства степеней с одинаковыми основаниями

☰

Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это

Произведение двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть сумма показателей исходных множителей.
Частное двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность показателей исходных множителей.
Возведение степени числа в степень равно выражению, в котором основание — это то же самое число, а показатель — это произведение двух степеней.

Будьте внимательны! Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует.

Запишем эти свойства-правила в виде формул:

a^m × aⁿ = a^m+n
a^m ÷ aⁿ = a^m–n
(a^m)ⁿ = a^mn

Теперь рассмотрим их на конкретных примерах и попробуем доказать.

5² × 5³ = 5⁵ — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:

5² × 5³ = 5 × 5 × 5 × 5 × 5 = 5⁵ — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5⁵.

3⁹ ÷ 3⁵ = 3^9–5 = 3⁴. Запишем деление в виде дроби:

Ее можно сократить:

В результате получим:

Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.

Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку мы рассматриваем степени только с натуральными показателями, то не можем в результате вычитания показателей получить число меньше, чем 1. Поэтому на формулу a^m ÷ aⁿ = a^m–n накладываются ограничения: a ≠ 0 и m > n.

Перейдем к третьему свойству:
(2²)⁴ = 2^2×4 = 2⁸

Запишем в развернутом виде:
(2²)⁴ = (2 × 2)⁴ = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁸

Можно прийти к такому выводу и логически рассуждая. Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.

Складывание чисел с разными степенями. Правила вычитания и сложения степеней

Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов! Получаем:

Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.

Но важно запомнить: меняются все знаки одновременно
!

Вернемся к примеру:

И снова формула:

Целыми
мы называем натуральные числа, противоположные им (то есть взятые со знаком « ») и число.

целое положительное число
, а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.

А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного.

Любое число в нулевой степени равно единице
:

Как всегда, зададимся вопросом: почему это так?

Рассмотрим какую-нибудь степень с основанием. Возьмем, например, и домножим на:

Итак, мы умножили число на, и получили то же, что и было — . А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на. Значит.

Можем проделать то же самое уже с произвольным числом:

Повторим правило:

Любое число в нулевой степени равно единице.

Но из многих правил есть исключения. И здесь оно тоже есть — это число (в качестве основания).

С одной стороны, в любой степени должен равняться — сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, как и любое число в нулевой степени, должен равняться. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.

Поехали дальше. Кроме натуральных чисел и числа к целым относятся отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:

Отсюда уже несложно выразить искомое:

Теперь распространим полученное правило на произвольную степень:

Итак, сформулируем правило:

Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым:
(т.к. на делить нельзя).

Подведем итоги:

I. Выражение не определено в случае. Если, то.

II. Любое число в нулевой степени равно единице: .

III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: .

Задачи для самостоятельного решения:

Ну и, как обычно, примеры для самостоятельного решения:

Разбор задач для самостоятельного решения:

Знаю-знаю, числа страшные, но на ЕГЭ надо быть готовым ко всему! Реши эти примеры или разбери их решение, если не смог решить и ты научишься легко справляться с ними на экзамене!

Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.

Теперь рассмотрим рациональные числа.
Какие числа называются рациональными?

Ответ: все, которые можно представить в виде дроби, где и — целые числа, причем.

Чтобы понять, что такое «дробная степень»
, рассмотрим дробь:

Возведем обе части уравнения в степень:

Теперь вспомним правило про «степень в степени»
:

Какое число надо возвести в степень, чтобы получить?

Эта формулировка — определение корня -ой степени.

Напомню: корнем -ой степени числа () называется число, которое при возведении в степень равно.

То есть, корень -ой степени — это операция, обратная возведению в степень: .

Получается, что. Очевидно, этот частный случай можно расширить: .

Теперь добавляем числитель: что такое? Ответ легко получить с помощью правила «степень в степени»:

Но может ли основание быть любым числом? Ведь корень можно извлекать не из всех чисел.

Никакое!

Вспоминаем правило: любое число, возведенное в четную степень — число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!

А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.

А что насчет выражения?

Но тут возникает проблема.

Число можно представить в виде дргих, сократимых дробей, например, или.

И получается, что существует, но не существует, а ведь это просто две разные записи одного и того же числа.

Или другой пример: раз, то можно записать. Но стоит нам по-другому записать показатель, и снова получим неприятность: (то есть, получили совсем другой результат!).

Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем
.

Итак, если:

— натуральное число;
— целое число;

Примеры:

Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:

5 примеров для тренировки

Разбор 5 примеров для тренировки

1. Не забываем об обычных свойствах степеней:

2. . Здесь вспоминаем, что забыли выучить таблицу степеней:

ведь — это или. Решение находится автоматически: .

Ну а теперь — самое сложное. Сейчас мы разберем степень с иррациональным показателем
.
Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением
Ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя;
…число в нулевой степени
— это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число;
…степень с целым отрицательным показателем
— это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число.
Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
КУДА МЫ УВЕРЕНЫ ТЫ ПОСТУПИШЬ! (если научишься решать такие примеры:))
Например:
Реши самостоятельно:

Разбор решений:

1. Начнем с уже обычного для нас правила возведения степени в степень:

Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:

В данном случае,

Получается, что:

Ответ:
.

2. Приводим дроби в показателях степеней к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например:

Ответ:
16

3. Ничего особенного, применяем обычные свойства степеней:

ПРОДВИНУТЫЙ УРОВЕНЬ

Определение степени

Степенью называется выражение вида: , где:

—
основание степени;
— показатель степени.

Степень с натуральным показателем {n = 1, 2, 3,…}

Возвести число в натуральную степень n — значит умножить число само на себя раз:

Степень с целым показателем {0, ±1, ±2,…}

Если показателем степени является целое положительное
число:

Возведение в нулевую степень
:

Выражение неопределенное, т.к., с одной стороны, в любой степени — это, а с другой — любое число в -ой степени — это.

Если показателем степени является целое отрицательное
число:

(т.к. на делить нельзя).

Еще раз о нулях: выражение не определено в случае. Если, то.

Примеры:

Степень с рациональным показателем

— натуральное число;
— целое число;

Примеры:

Свойства степеней

Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.

Посмотрим: что такое и?

По определению:

Итак, в правой части этого выражения получается такое произведение:

Но по определению это степень числа с показателем, то есть:

Что и требовалось доказать.

Пример

: Упростите выражение.

Решение

: .

Пример

: Упростите выражение.

Решение

: Важно заметить, что в нашем правиле обязательно
должны быть одинаковые основания. Поэтому степени с основанием мы объединяем, а остается отдельным множителем:

Еще одно важное замечание: это правило — только для произведения степеней
!

Ни в коем случае нелья написать, что.

Так же, как и с предыдущим свойством, обратимся к определению степени:

Перегруппируем это произведение так:

Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -я степень числа:

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: !

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать? Но это неверно, ведь.

Степень с отрицательным основанием.

До этого момента мы обсуждали только то, каким должен быть показатель
степени. Но каким должно быть основание? В степенях с натуральным

показателем

основание может быть любым числом

.

И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?

Например, положительным или отрицательным будет число? А? ?

С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.

Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на (), получится — .

И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:

четную
степень, — число положительное
.
Отрицательное число, возведенное в нечетную
степень, — число отрицательное
.
Положительное число в любой степени — число положительное.
Ноль в любой степени равен нулю.

Определи самостоятельно, какой знак будут иметь следующие выражения:

Справился? Вот ответы:

1)
; 2)
; 3)
; 4)
; 5)
; 6)
.

В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.

В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание — степень четная, а значит, результат всегда будет положительным. Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).

Пример 6) уже не так прост. Тут нужно узнать, что меньше: или? Если вспомнить, что, становится ясно, что, а значит, основание меньше нуля. То есть, применяем правило 2: результат будет отрицательным.

И снова используем определение степени:

Все как обычно — записываем определение степеней и, делим их друг на друга, разбиваем на пары и получаем:

Прежде чем разобрать последнее правило, решим несколько примеров.

Вычисли значения выражений:

Решения

:

Получаем:

Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило 3. Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Если домножить его на, ничего не поменяется, верно? Но теперь получается следующее:

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках. Но важно запомнить: меняются все знаки одновременно!
Нельзя заменить на, изменив только один неугодный нам минус!

Вернемся к примеру:

И снова формула:

Итак, теперь последнее правило:

Как будем доказывать? Конечно, как обычно: раскроем понятие степени и упростим:

Ну а теперь раскроем скобки. Сколько всего получится букв? раз по множителей — что это напоминает? Это не что иное, как определение операции умножения
: всего там оказалось множителей. То есть, это, по определению, степень числа с показателем:

Пример:

Степень с иррациональным показателем

В дополнение к информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением — ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа, кроме рациональных).

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах. Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя; число в нулевой степени — это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число; степень с целым отрицательным показателем — это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)

Например:

Реши самостоятельно:

Ответы:

Вспоминаем формулу разность квадратов. Ответ: .
Приводим дроби к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например: .
Ничего особенного, применяем обычные свойства степеней:

КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ

Степенью
называется выражение вида: , где:

Степень с целым показателем

степень, показатель которой — натуральное число (т.е. целое и положительное).

Степень с рациональным показателем

степень, показатель которой — отрицательные и дробные числа.

Степень с иррациональным показателем

степень, показатель которой — бесконечная десятичная дробь или корень.

Свойства степеней

Особенности степеней.

Отрицательное число, возведенное в четную
степень, — число положительное
.
Отрицательное число, возведенное в нечетную
степень, — число отрицательное
.
Положительное число в любой степени — число положительное.
Ноль в любой степени равен.
Любое число в нулевой степени равно.

ТЕПЕРЬ ТЕБЕ СЛОВО…

Как тебе статья? Напиши внизу в комментариях понравилась или нет.

Расскажи о своем опыте использования свойств степеней.

Возможно у тебя есть вопросы. Или предложения.

Напиши в комментариях.

И удачи на экзаменах!

Напоминаем, что в данном уроке разбираются свойства степеней

с натуральными показателями и нулём.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках
для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют
упрощать вычисления в примерах со степенями.

Свойство № 1

Произведение степеней

Запомните!

При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.

a m · a n = a m + n
, где
«a
» — любое
число, а «m
», «n
» — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.

b · b 2 · b 3 · b 4 · b 5 =
b 1 + 2 + 3 + 4 + 5 = b 15
Представить в виде степени.

6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 =
6 17
Представить в виде степени.

(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Важно!

Обратите внимание, что в указанном свойстве речь шла только об умножении
степеней с одинаковыми основаниями

. Оно не относится к их сложению.

Нельзя
заменять сумму
(3 3 + 3 2)
на 3 5
. Это понятно, если
посчитать
(3 3 + 3 2) = (27 + 9) = 36
, а
3 5 = 243

Свойство № 2

Частное степеней

Запомните!

При делении степеней с одинаковыми основаниями основание остаётся без изменений,
а из показателя степени делимого вычитают показатель степени делителя.

=
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44

Пример. Решить уравнение. Используем свойство частного степеней.

3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение.

4 5m + 6 · 4 m + 2: 4 4m + 3 =
4 5m + 6 + m + 2: 4 4m + 3 =
4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
=
=
=
=
=
2 11 − 5 = 2 6 = 64
Важно!
Обратите внимание, что в свойстве 2 речь шла только
о делении степеней с одинаковыми основаниями.

Нельзя
заменять разность
(4 3 −4 2)
на 4 1
. Это понятно, если посчитать
(4 3 −4 2) = (64 − 16) = 48
, а
4 1 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степень
Запомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней
перемножаются.
(a n) m = a n · m
, где
«a
» — любое
число, а «m
», «n
» — любые натуральные числа.
Свойства 4
Степень произведения
Запомните!
При возведении в степень произведения каждый из множителей
возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n
, где
«a
», «b
» — любые рациональные
числа; «n
» — любое натуральное число.
Пример 1.
(6 · a 2 · b 3 · c) 2 =
6 2 · a 2 · 2 · b 3 · 2
· с 1 · 2 = 36 a 4 · b 6
· с 2
Пример 2.
(−x 2 · y) 6 =
((−1) 6 · x 2 · 6 · y 1 · 6) =
x 12 · y 6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней,
применяют и в обратном порядке.
(a n · b n)=
(a · b) n
То есть, чтобы перемножить степени с одинаковыми
показателями можно перемножить основания, а показатель степени оставить неизменным.
Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 =
10 4 = 10 000
Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 =
1
В более сложных примерах могут встретиться случаи, когда умножение и деление
надо выполнить над степенями с разными основаниями и разными показателями.
В этом случае советуем поступать следующим образом.
Например,
4 5 · 3 2 = 4 3 ·
4 2 · 3 2 = 4 3 · (4 · 3) 2 =
64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 ·
(−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 =
4 · 1 = 4
Свойства 5
Степень частного (дроби)
Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель,
и первый результат разделить на второй.
(a: b) n = a n: b n
, где
«a
», «b
» — любые рациональные
числа, b ≠ 0, n
— любое натуральное число.3=8$.
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1
Степенное выражение
– это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , (2 + 1) 5 , (− 0 , 1) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , (a 2) 3 . А также степени с нулевым показателем: 5 0 , (a + 1) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: (0 , 5) 2 + (0 , 5) — 2 2 .
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .
В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x
.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1
Вычислите значение степенного выражения 2 3 · (4 2 − 12)
.
Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · (4 2 − 12) = 2 3 · (16 − 12) = 2 3 · 4
.
Нам остается заменить степень 2 3
ее значением 8
и вычислить произведение 8 · 4 = 32
. Вот наш ответ.
Ответ:
2 3 · (4 2 − 12) = 32 .
Пример 2
Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7
.
Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1
.
Ответ:
3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .
Пример 3
Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.
Решение

Представим число 9 как степень 3 2
и применим формулу сокращенного умножения:
9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1
Ответ:
9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2 + 0 , 3 · 7) 5 − 3 , 7
и . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2 + 0 , 3 · 7) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3
. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a · (a + 1) − a 2) 2 · (x + 1)
и получить степенное выражение более простого вида a 2 · (x + 1)
.
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a
и b
– это любые положительные числа, а r
и s
— произвольные действительные числа:
Определение 2
a r · a s = a r + s ;
a r: a s = a r − s ;
(a · b) r = a r · b r ;
(a: b) r = a r: b r ;
(a r) s = a r · s .
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n
, где m
и n
– натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0
.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Пример 4
Представьте выражение a 2 , 5 · (a 2) − 3: a − 5 , 5
в виде степени с основанием a
.
Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a 2) − 3
. Затем используем свойства умножения и деления степеней с одинаковым основанием:
a 2 , 5 · a − 6: a − 5 , 5 = a 2 , 5 − 6: a − 5 , 5 = a − 3 , 5: a − 5 , 5 = a − 3 , 5 − (− 5 , 5) = a 2 .
Ответ:
a 2 , 5 · (a 2) − 3: a − 5 , 5 = a 2 .
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5
Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .
Решение

Если мы применим равенство (a · b) r = a r · b r
, справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .
Есть еще один способ провести преобразования:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · (3 · 7) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21
Ответ:
3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21
Пример 6
Дано степенное выражение a 1 , 5 − a 0 , 5 − 6
, введите новую переменную t = a 0 , 5
.
Решение

Представим степень a 1 , 5
как a 0 , 5 · 3
. Используем свойство степени в степени (a r) s = a r · s
справа налево и получим (a 0 , 5) 3: a 1 , 5 − a 0 , 5 − 6 = (a 0 , 5) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5
: получаем t 3 − t − 6
.
Ответ:
t 3 − t − 6 .
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7
Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .
Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2
Ответ:
3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Пример 8
Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a
, б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .
Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a ,
следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3
. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3
не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a 0 , 3
:
a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a
б) Обратим внимание на знаменатель:
x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2
Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x
и y
выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2
Ответ:
а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .
Пример 9
Сократите дробь: а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .
Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1
и на x + 2 · x 1 1 3 — 5 3 .
Получаем:
30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1)
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4
Ответ:
а) 30 · x 3 · (x 0 , 5 + 1) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · (x 0 , 5 + 1) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10
Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .
Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x 1 2 — 1 · x 1 2 + 1
Вычтем числители:
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2
Теперь умножаем дроби:
4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2
Произведем сокращение на степень x 1 2
, получим 4 x 1 2 — 1 · x 1 2 + 1 .
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .
Ответ:
x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1
Пример 11
Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на (x 2 , 7 + 1) 2
. Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .
Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .
Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .
Ответ:
x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x + 1) — 0 , 2 3 · x — 1 можно заменить на x 3 · (x + 1) 0 , 2 .
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12
Представьте выражение x 1 9 · x · x 3 6 в виде степени.
Решение

Область допустимых значений переменной x
определяется двумя неравенствами x ≥ 0
и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞)
.
На этом множестве мы имеем право перейти от корней к степеням:
x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6
Используя свойства степеней, упростим полученное степенное выражение.
x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3
Ответ:
x 1 9 · x · x 3 6 = x 1 3 .
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0
.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .
Теперь поделим обе части равенства на 7 2 · x
. Это выражение на ОДЗ переменной x принимает только положительные значения:
5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0
Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .
Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 (1 — log 3 5) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Статьи по естественным наукам и математике
Свойства степеней с одинаковыми основаниями
Существует три свойства степеней с одинаковыми основаниями и натуральными показателями. Это
Произведение
сумма

Частное
двух степеней с одинаковыми основаниями равно выражению, где основание то же самое, а показатель есть разность
показателей исходных множителей.
Возведение степени числа в степень
равно выражению, в котором основание — это то же самое число, а показатель — это произведение
двух степеней.
Будьте внимательны! Правил относительно сложения и вычитания
степеней с одинаковыми основаниями не существует
.
Запишем эти свойства-правила в виде формул:
a m ? a n = a m+n
a m ? a n = a m–n
(a m) n = a mn
Теперь рассмотрим их на конкретных примерах и попробуем доказать.
5 2 ? 5 3 = 5 5 — здесь мы применили правило; а теперь представим как бы мы решали этот пример, если бы не знали правила:
5 2 ? 5 3 = 5 ? 5 ? 5 ? 5 ? 5 = 5 5 — пять в квадрате — это пять умноженное на пять, а в кубе — произведение трех пятерок. В результате получилось произведение пяти пятерок, но это нечто иное как пять в пятой степени: 5 5 .
3 9 ? 3 5 = 3 9–5 = 3 4 . Запишем деление в виде дроби:
Ее можно сократить:
В результате получим:
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать.
Однако при делении нельзя, чтобы делитель был равен нулю (так как на ноль делить нельзя). Кроме того, поскольку мы рассматриваем степени только с натуральными показателями, то не можем в результате вычитания показателей получить число меньше, чем 1. Поэтому на формулу a m ? a n = a m–n накладываются ограничения: a ? 0 и m > n.
Перейдем к третьему свойству:
(2 2) 4 = 2 2?4 = 2 8
Запишем в развернутом виде:
(2 2) 4 = (2 ? 2) 4 = (2 ? 2) ? (2 ? 2) ? (2 ? 2) ? (2 ? 2) = 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 ? 2 = 2 8
Можно прийти к такому выводу и логически рассуждая. Нужно перемножить два в квадрате четыре раза. Но в каждом квадрате две двойки, значит всего двоек будет восемь.
scienceland.info
Правила сложения и вычитания.
1. От перемены мест слагаемых сумма не изменится (коммутативное свойство сложения)

13+25=38, можно записать как: 25+13=38
2.
Результат сложения не изменится, если соседние слагаемые заменить их суммой (ассоциативное свойство сложения).
10+13+3+5=31 можно записать как: 23+3+5=31; 26+5=31; 23+8=31 и т.д.
3.
Единицы складываются с единицами, десятки с десятками и т.д.

34+11=45 (3 десяка плюс еще 1 десяток; 4 единицы плюс 1 единица).
4. Единицы вычитаются из единиц, десятки из десятков и т.д.

53-12=41 (3 единицы минус 2 единицы; 5 десятков минус 1 десяток)
примечание: 10 единиц составляют один десяток. Это надо помнить при вычитании, т.к. если количество единиц у вычитаемого больше, чем у уменьшаемого, то мы можем «занять» один десяток у уменьшаемого.

41-12=29 (Для того чтобы и 1 вычесть 2, мы сначала должны «занять» единицу у десятков, получаем 11-2=9; помним, что у уменьшаемого остается на 1 десяток меньше, следовательно, остается 3 десятка и от него отнимается 1 десяток. Ответ 29).

5. Если из суммы двух слагаемых вычесть одно из них, то получится второе слагаемое.

Это значит, что сложение можно проверить с помощью вычитания.
Для проверки из суммы вычитают одно из слагаемых: 49-7=42 или 49-42=7
Если в результате вычитания вы не получили одно из слагаемых, значит в вашем сложении была допущена ошибка.

6. Если к разности прибавить вычитаемое, то получится уменьшаемое.

Это значит, что вычитание можно проверить сложением.
Для проверки к разности прибавим вычитаемое: 19+50=69.
Если в результате описанной выше процедуры вы не получили уменшьшаемое, значит в вашем вычитании была допущена ошибка.

Сложение и вычитание рациональных чисел
В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.
Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби, где a –
это числитель дроби, b
– знаменатель дроби. Причем b
не должно быть нулём.
В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа
.
Навигация по уроку:

Пример 1.
Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении является знаком операции и не относится к дроби. У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше.
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:
Модуль рационального числа больше, чем модуль рационального числа. Поэтому мы из вычли . Получили ответ. Затем сократив эту дробь на 2, получили окончательный ответ .
При желании некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:
Пример 2.
Найти значение выражения
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который дан в выражении является знаком операции и не относится к дроби.
Дробь в данном случае является положительным рациональным числом, имеющим знак плюса, который невидим. Но мы запишем его для наглядности:
Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число противоположное вычитаемому:
Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Пример 3.
Найти значение выражения
В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к одинаковому (общему) знаменателю. Не будем подробно останавливаться на этом. Если испытываете трудности, обязательно вернитесь к уроку действия с дробями и повторите его.
После приведения дробей к общему знаменателю выражение примет следующий вид:
Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший и перед полученным ответом ставим тот знак, модуль которого больше:
Пример 4.
Найти значение выражения
Получили сумму из трёх слагаемых. Сначала найдём значение выражения, затем к полученному ответу прибавим
Первое действие:

Второе действие:

Таким образом, значение выражения равно.
Решение для данного примера можно записать покороче
Пример 5
. Найти значение выражения
Заключим каждое число в скобки вместе со своими знаками. Для этого смешанное число временно развернём
Вычислим целые части:
В главном выражении вместо запишем полученную единицу:
Полученное выражение свернём. Для этого опустим скобки и запишем единицу и дробь вместе
Решение для данного примера можно записать покороче:
Пример 6.
Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальную часть перепишем как есть:
Заключим каждое рациональное число в скобки вместе со своими знаками:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Сложим модули этих чисел и перед полученным ответом поставим минус:
Таким образом, значение выражения равно .
Решение для данного примера можно записать покороче:
Пример 7.
Найти значение выражение
Запишем смешанное число в развёрнутом виде. Остальное перепишем как есть:
Заключим каждое рациональное число в скобки вместе своими знаками
Заменим вычитание сложением там, где это можно:
Вычислим целые части:
В главном выражении вместо запишем полученное число?7
Выражение является развёрнутой формой записи смешанного числа . Можно сразу записать ответ, записав вместе числа?7 и дробь (спрятав минус этой дроби)
Таким образом, значение выражения равно
Решение для данного примера можно записать значительно короче. Если пропустить некоторые подробности, то его можно записать следующим образом:
Пример 8.
Найти значение выражения
Данное выражение можно вычислить двумя способами. Рассмотрим каждый из них.
Первый способ.
Целые и дробные части выражения вычисляются по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Заключим каждое число в скобки вместе со своими знаками:
Заменим вычитание сложением там, где это можно:
Получили сумму из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение содержит несколько слагаемых, то сумма не будет зависеть от порядка действий. Это позволит нам сгруппировать целые и дробные части по отдельности:
Вычислим целые части:
В главном выражении вместо запишем полученное число?3
Вычислим дробные части:
В главном выражении вместо запишем полученное смешанное число
Чтобы вычислить получившееся выражение, смешанное число нужно временно развернуть, затем заключить в скобки каждое число и заменить вычитание сложением. Делать это нужно очень аккуратно, чтобы не перепутать знаки слагаемых.
После преобразования выражения мы получили новое выражение , которое легко вычисляется. Похожее выражение было в примере 7. Напомним, что мы отдельно сложили целые части, а дробную оставили как есть:
Значит значение выражения равно
Решение для данного примера можно записать покороче
В коротком решении пропускаются этапы заключения чисел в скобки, замена вычитания сложением, проставление модулей. Если вы учитесь в школе или в другом учебном заведении, то от вас будут требовать пропускать эти примитивные действия, чтобы сэкономить время и место. Приведённое выше короткое решение можно записать ещё короче. Выглядеть оно будет так:
Поэтому, находясь в школе или в ином учебном заведении, будьте готовы к тому, что некоторые действия придётся выполнять в уме.
Второй способ.
Смешанные числа выражения переводят в неправильные дроби и вычисляют, как обычные дроби.
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением:
Теперь смешанные числа и переведём в неправильные дроби:
Получили сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим минус:
Получили ответ как и в прошлый раз.
Подробное решение вторым способом выглядит следующим образом:
Пример 9.
Найти выражения выражения
Первый способ.
Сложим целые и дробные части по отдельности.
В этот раз попробуем пропустить некоторые примитивные действия, такие как запись выражения в развёрнутом виде, заключение чисел в скобки, замена вычитания сложением, проставление модулей:
Обратите внимание, что дробные части были приведены к общему знаменателю.
Второй способ.
Переведём смешанные числа в неправильные дроби и вычислим, как обычные дроби.
Пример 10.
Найти значение выражения
Заменим вычитание сложением:
В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки. Тогда получим простейшее выражение, которое вычисляется легко:
В данном примере целые и дробные части были вычислены по отдельности.
Пример 11.
Найти значение выражения
Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед полученными числом поставим тот знак, модуль которого больше:
Пример 12.
Найти значение выражения
Выражение состоит из нескольких параметров. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.
Сначала вычислим выражение , затем выражение Полученные ответы сложим.
Первое действие:

Второе действие:

Третье действие:

Ответ:
значение выражения равно
Пример 13.
Найти значение выражения
Заменим вычитание сложением:
Получили сложением рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше. Но мы имеем дело со смешанными числами. Чтобы понять какой модуль больше, а какой меньше, нужно сравнить модули этих смешанных чисел. А чтобы сравнить модули смешанных чисел, нужно перевести их в неправильные дроби и сравнить, как обычные дроби.
На следующем рисунке показаны все этапы сравнения модулей смешанных чисел
Узнав какой модуль больше, а какой меньше, мы можем продолжить вычисление нашего примера:
Таким образом, значение выражения равно
Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть, как положительными, так и отрицательными.
Пример 14.
Найти значение выражения?3,2 + 4,3
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:
Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше.
А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:
Модуль числа 4,3 больше, чем модуль числа?3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку в ответе должен стоять знак большего модуля, то есть модуля |+4,3|.
Таким образом, значение выражения?3,2 + (+4,3) равно 1,1
Пример 15.
Найти значение выражения 3,5 + (?8,3)
Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим тот знак, модуль которого больше
3,5 + (?8,3) = ?(|?8,3| ? |3,5|) = ?(8,3 ? 3,5) = ?(4,8) = ?4,8
Таким образом, значение выражения 3,5 + (?8,3) равно?4,8
Этот пример можно записать покороче:
Пример 16.
Найти значение выражения?7,2 + (?3,11)
Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
7,2 + (?3,11) = ?7,20 + (?3,11) = ?(7,20 + 3,11) = ?(10,31) = ?10,31
Таким образом, значение выражения?7,2 + (?3,11) равно?10,31
Этот пример можно записать покороче:
Пример 17.
Найти значение выражения?0,48 + (?2,7)
Это сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим знак минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
0,48 + (?2,7) = (?0,48) + (?2,70) = ?(0,48 + 2,70) = ?(3,18) = ?3,18
Пример 18.
Найти значение выражения?4,9 ? 5,9
Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который дан в выражении, является знаком операции и не относится к десятичной дроби 5,9. У этой десятичной дроби свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:
Заменим вычитание сложением:
Получили сложение отрицательных рациональных чисел. Сложить их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
(?4,9) + (?5,9) = ?(4,9 + 5,9) = ?(10,8) = ?10,8
Таким образом, значение выражения?4,9 ? 5,9 равно?10,8
= ?(4,9 + 5,9) = ?(10,8) = ?10,8
Пример 19.
Найти значение выражения 7 ? 9,3
Заключим в скобки каждое число вместе со своим знаками
Заменим вычитание сложением
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше. Запись с модулями можно пропустить, чтобы не загромождать выражение:
(+7) + (?9,3) = ?(9,3 ? 7) = ?(2,3) = ?2,3
Таким образом, значение выражения 7 ? 9,3 равно?2,3
Подробное решение данного примера записывается следующим образом:
7 ? 9,3 = (+7) ? (+9,3) = (+7) + (?9,3) = ?(|?9,3| ? |+7|) =
Короткое решение будет выглядеть так:
Пример 20.
Найти значение выражения?0,25 ? (?1,2)
Заменим вычитание сложением:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед ответом поставим тот знак, модуль которого больше:
0,25 + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
Подробное решение данного примера записывается следующим образом:
0,25 ? (?1,2) = (?0,25) + (+1,2) = |+1,2| ? |?0,25| = 1,2 ? 0,25 = 0,95
Короткое решение будет выглядеть так:
Пример 21.
Найти значение выражения?3,5 + (4,1 ? 7,1)
В первую очередь выполним действия в скобках, затем сложим полученный ответ с числом?3,5. Запись с модулями пропустим, чтобы не загромождать выражения.
Первое действие:

4,1 ? 7,1 = (+4,1) ? (+7,1) = (+4,1) + (?7,1) = ?(7,1 ? 4,1) = ?(3,0) = ?3,0
Второе действие:

3,5 + (?3,0) = ?(3,5 + 3,0) = ?(6,5) = ?6,5
Ответ:
значение выражения?3,5 + (4,1 ? 7,1) равно?6,5.
3,5 + (4,1 ? 7,1) = ?3,5 + (?3,0) = ?6,5
Пример 22.
Найти значение выражения (3,5 ? 2,9) ? (3,7 ? 9,1)
Выполним действия в скобках, затем из числа которое получилось в результате выполнения первых скобок вычтем число, которое получилось в результате выполнения вторых скобок. Запись с модулями пропустим, чтобы не загромождать выражения.
Первое действие:

3,5 ? 2,9 = (+3,5) ? (+2,9) = (+3,5) + (?2,9) = 3,5 ? 2,9 = 0,6
Второе действие:

3,7 ? 9,1 = (+3,7) ? (+9,1) = (+3,7) + (?9,1) = ?(9,1 ? 3,7) = ?(5,4) = ?5,4
Третье действие

0,6 ? (?5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6
Ответ:
значение выражения (3,5 ? 2,9) ? (3,7 ? 9,1) равно 6.
Короткое решение данного примера можно записать следующим образом:
(3,5 ? 2,9) ? (3,7 ? 9,1) = 0,6 ? (?5,4) = 6,0 = 6
Пример 23.
Найти значение выражения?3,8 + 17,15 ? 6,2 ? 6,15
Заключим в скобки каждое рациональное число вместе со своими знаками
Заменим вычитание сложением там, где это можно
Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.
Не будем изобретать велосипед, а сложим все слагаемые слева направо в порядке их следования:
Первое действие:

(?3,8) + (+17,15) = 17,15 ? 3,80 = 13,35
Второе действие:

13,35 + (?6,2) = 13,35 ? ?6,20 = 7,15
Третье действие:

7,15 + (?6,15) = 7,15 ? 6,15 = 1,00 = 1
Ответ:
значение выражения?3,8 + 17,15 ? 6,2 ? 6,15 равно 1.
Короткое решение данного примера можно записать следующим образом:
3,8 + 17,15 ? 6,2 ? 6,15 = 13,35 + (?6,2) ? 6,15 = 7,15 ? 6,15 = 1,00 = 1
Короткие решения создают меньше проблем и путаниц, поэтому желательно привыкнуть к ним.
Пример 24.
Найти значение выражения
Переведём десятичную дробь?1,8 в смешанное число. Остальное перепишем, как есть. Если испытываете затруднения с переводом десятичной дроби в смешанное число, обязательно повторите урок десятичные дроби.
Пример 25.
Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь (?4,4) в неправильную дробь
В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и опустить скобки. Тогда получим простое выражение на сложение, которое решается легко
Пример 26.
Найти значение выражения
Переведём смешанное число в неправильную дробь, а десятичную дробь?0,85 в обыкновенную дробь. Получим следующее выражение:
Получили сложение отрицательных рациональных чисел. Сложим их модули и перед полученным ответом поставим знак минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 27.
Найти значение выражения
Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:
После перевода обеих дробей в неправильные дроби, получим следующее выражение:
Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший и перед полученным ответом поставим тот знак, модуль которого больше:
Пример 28.
Найти значение выражения
Заменим вычитание сложением. Попутно переведём десятичную дробь в обыкновенную дробь
Пример 29.
Найти значение выражения
Переведём десятичные дроби?0,25 и?1,25 в обыкновенные дроби, остальное оставим как есть. Получим следующее выражение:
Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим. Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного числа вычесть рациональное число . Этим вариантом и воспользуемся.
Первое действие:

Второе действие:

Ответ:
значение выражения равно?2.
Пример 30.
Найти значение выражения
Переведём десятичные дроби в обыкновенные. Остальное оставим как есть
Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.
Первое действие:

Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас
Второе действие:

Ну и сложим полученное число?7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, то есть их сумма будет равна нулю, поскольку сумма противоположных чисел равна нулю
Третье действие:

Ответ:
значение выражения равно
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Сложение и вычитание целых чисел
В этом уроке мы изучим сложение и вычитание целых чисел
, а также правила для их сложения и вычитания.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, а где положительные.
Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате, мы окажемся в точке, где располагается число 4. На рисунке можно увидеть как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 2.
Найдём значение выражения 1 ? 3.
Значение данного выражения равно?2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число?2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 ? 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3.
Найти значение выражения?2 + 4
Значение данного выражения равно 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.
Видно, что мы сдвинулись из точки где располагается отрицательное число?2 в правую сторону на четыре шага и оказались в точке, где располагается положительное число 2.
Знак плюса в выражении?2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Пример 4.
Найти значение выражения?1 ? 3
Значение данного выражения равно?4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число?4
Видно, что мы сдвинулись из точки где располагается отрицательное число?1 в левую сторону на три шага и оказались в точке, где располагается отрицательное число?4.
Знак минуса в выражении?1 ? 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.
Пример 5.
Найти значение выражения?2 + 2
Значение данного выражения равно 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число?2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число?2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Знак плюса в выражении?2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.
Правила сложения и вычитания целых чисел
Чтобы вычислить то или иное выражение, необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1.
Найти значение выражения?2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. ?2 это отрицательное число, а 5 — положительное. Для таких случаев предусмотрено следующее правило:
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа?2. Правило требует из большего модуля вычесть меньший. Поэтому, мы должны из 5 вычесть 2, и перед полученным ответом поставить тот знак, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть, ответ будет положительным:
Обычно записывают покороче?2 + 5 = 3
Пример 2.
Найти значение выражения 3 + (?2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 — это положительное число, а?2 — отрицательное. Обратите внимание, что число?2 заключено в скобки, чтобы сделать выражение понятнее и красивее. Это выражение намного проще для восприятия, чем выражение 3+?2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим тот знак, модуль которого больше:
3 + (?2) = |3| ? |?2| = 3 ? 2 = 1
Модуль числа 3 больше, чем модуль числа?2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили тот знак модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.
Обычно записывают покороче 3 + (?2) = 1
Пример 3.
Найти значение выражения 3 ? 7
В этом выражении из меньшего числа вычитается большее. Для такого случая предусмотрено следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 ? 7 как мы узнали равно?4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны?4
Но мы видим, что на втором этапе располагается выражение 7 ? 3, которое не равно?4.
Чтобы исправить эту ситуацию, выражение 7 ? 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 ? 7 = ? (7 ? 3) = ? (4) = ?4
В этом случае равенство будет соблюдаться на каждом этапе:
После того как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 ? 7 = ? (7 ? 3) = ? (4) = ? 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a ? b = ? (b ? a)

Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 ? 7 = ? 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Что это означает? Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 ? 3. На начальных этапах изучения математики мы просто ставили знак равенства и записывали ответ:
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5?3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число?3. Записываем новое выражение:
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели выше. Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший, и перед полученным ответом поставить тот знак, модуль которого больше:
5 + (?3) = |5| ? |?3| = 5 ? 3 = 2
Модуль числа 5 больше, чем модуль числа?3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без своего знака плюс.
Например, в выражении 3 ? 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами по традиции не записывают.
А стало быть для наглядности данное выражение можно записать следующим образом:
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще. Вычитаемое в данном случае это число (+1), а противоположное ему число (?1). Заменим операцию вычитания сложением и вместо вычитаемого (+1) записываем противоположное ему число (?1)
(+3) ? (+1) = (+3) + (?1) = |+3| ? |?1| = 3 ? 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 ? 7, используя правило вычитания. Сначала приведём выражение к нормальному виду, расставив каждому числу свои знаки. У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она также является положительным числом:
Заменим вычитание сложением:
Дальнейшее вычисление не составляет труда:
Пример 7.
Найти значение выражения?4 ? 5
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (?4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (?5).
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев предусмотрено следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.

Итак, сложим модули чисел, как от нас требует правило и поставим перед полученным ответом минус:
(?4) ? (+5) = (?4) + (?5) = |?4| + |?5| = 4 + 5 = ?9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(?4) ? (+5) = (?4) + (?5) = ?(|?4| + |?5|) = ?(4 + 5) = ?(9) = ?9
Решение для данного примера можно записать покороче:
Пример 8.
Найти значение выражения?3 ? 5 ? 7 ? 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа?3 являются положительными, поэтому у них будут знаки плюса:
Заменим операции вычитания операциями сложения. Все минусы (кроме минуса, который перед тройкой) поменяются на плюсы и все положительные числа поменяются на противоположные:
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
= ?(|?3| + |?5| + |?7| + |?9|) = ?(3 + 5 + 7 + 9) = ?(24) = ?24
Решение для данного примера можно записать покороче:
3 ? 5 ? 7 ? 9 = ?(3 + 5 + 7 + 9) = ?24
Пример 9.
Найти значение выражения?10 + 6 ? 15 + 11 ? 7
Приведём выражение к понятному виду:
Здесь сразу две операции: сложение и вычитание. Сложение оставляем как есть, а вычитание заменяем сложением:
(?10) + (+6) ? (+15) + (+11) ? (+7) = (?10) + (+6) + (?15) + (+11) + (?7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:

(?10) + (+6) = ? (10 ? 6) = ? (4) = ? 4
Второе действие:

(?4) + (?15) = ? (4 + 15) = ? (19) = ? 19
Третье действие:

(?19) + (+11) = ? (19 ? 11) = ? (8) = ?8
Четвёртое действие:

(?8) + (?7) = ? (8 + 7) = ? (15) = ? 15
Таким образом, значение выражения?10 + 6 ? 15 + 11 ? 7 равно?15
Примечание
. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить тот знак, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить знак минуса.
Вычесть одно число из другого означает, прибавить к уменьшаемому число противоположное вычитаемому.

Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить знак минус.
Хоккей без правил В Контакте
Игра была выпущена в сентябре 2012 года, и набрала уже почти 700 000 пользователей. Предусмотрено два режима игры и множество возможностей для комплектования команды.
Течение матча в Хоккее без правил В Контакте напоминает ранние игры серии NHL от Electronic Arts. 3 игрока на […]
Правила покера Омаха Холдем
Омаха Хай-Лоу и пятикарточная Омаха
Омаха Холдем (Omaha Hold»Em) является небольшим видоизменением Техасского Холдема. Если вы плохо знакомы с этой самой популярной разновидностью покера, изучайте правила Техасского Холдема по ссылке; их знание необходимо для понимания правил Омахи.
Все […]
Решение задач по генетике с использованием 1 и 2 законов Менделя Лекция 8 Julia Kjahrenova 1. — презентация
Презентация была опубликована 3 года назад пользователемАлина Артемьева
Похожие презентации
Презентация на тему: » Решение задач по генетике с использованием 1 и 2 законов Менделя Лекция 8 Julia Kjahrenova 1.» […]
5-7 алгебра правила
Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом d, называют арифметической прогрессией. Число d называют разностью арифметической прогрессии. В арифметической прогрессии, т. е. в […]
Определяем ставку транспортного налога для фургонов и других нетипичных автомобилей с категорией «B»
Вылавливаем нужную информацию из ПТС
Сразу скажем, что данные, указанные в строке 4 «Категория ТС (A, B, C, D, прицеп)» паспорта транспортного средства (ПТС), учитывать не нужно. Ведь категория «B» вовсе не означает, […]
Рейтинг страховых компаний ОСАГО
ОСАГО относится к обязательному страхованию, оно действует не только на территории России, но и в других странах ближнего зарубежья. Оформлением данных полисов занимаются многие страховые компании, которые получили соответствующую лицензию на ведение подобной деятельности. Однако, […]
Проживание гостиница уфа
Мини-отель в Уфе 5 Five Rooms
Приглашаем гостей столицы в уютный комфортабельный отель, расположенный в центре города Уфа по улице Комсомольская 159/1. В непосредственной близости от отеля расположены кинокомплекс «Искра IMAX», цирк, ресторан-клуб А кафе, ресторан Beer Berry, ТРЦ […]
Правила использования Present Simple Tense в английском языке
Present Simple Tense – это грамматическое время, которое считается одним из самых простых в понимании, поскольку, настоящее простое время существует во всех языках.
В славянских языках так точно.
Если вы читаете эту статью, это значит, что вы только […]
Смысл степени с натуральным,отрицательным,дробным показателем,Правила действия над степенями: — МегаЛекции

1)Степени с натуральным показателем:
В стране чисел возникли проблемы. Астрономы собрались посчитать размеры видимой части Вселенной. Они утверждали, что для этого необходимо умножить 25 раз число 10 само на себя. Поскольку для этого требовалось очень много места, они требовали снести Дворец алгоритма Евкида, выставку чисел-близнецов и многие другие объекты. Хотя всем хотелось узнать, какая же наша Вселенная, но никому не хотелось жертвовать столь прекласными и ценными сооружениями. Была создана комиссия, которая занялась поисками требуемой свободной площади, но вскоре зашла в тупик.
Неожиданно положение Таблица умножения. Она рассказла свою историю: — Меня придумали для того, чтобы не складывать большое количество одинаковых слагаемых. Ведь теперь никто не пишет 3 + 3 + 3 + 3 + 3 + 3 + 3, теперь записывают 3 х 7. Это очень экономит место. Давайте придумаем что-нибудь похожее для умножения.
И сразу придумали. Число множителей стали записываь маленькой цифрой сзади числа:
Все выражение стали на зывать степенью, количество множителей (маленькую цифру сверху) – показателем степени, а сам множитель – основание степени.
Не прошло и получаса, как торжественно ввели новое действие – возведение в степень, как по стране чисел стали бегать 5⁶, 17⁴ и многие другие. Но только бегать неинтересно, хочется выполнять сложение, умножение, вычитание, то есть вести себя как все порядочные числа. и ту возникли следующие проблемы. После введения действий надо установить правила действий, так, чтобы никому не мешать и никакие законы не нарушать.
Сначала попробовали выполнять сложение, открыли свод законов и ничего не нашли. О вычитании даже думать не стали, а умножение пошло очень легко, ведь всякая степень получается из множителей, значит, если взять одинаковые основания степени, то
Сразу записали в свод законов новое правило:
При умножении степеней с одинаковым основание основание остается неизменным, а показатели складывают

С делением возникли проблемы. Всем казалось, что если деление действие обратное уиножению, то приделении надо показатели вычитать, но если , а если .Тогда постановили (под влиянием консервативного меньшинства), что
При делении степеней с одинаковыми основаниями , если m>n, и , если n>m.
Провести проверку нового правил предложили 6⁵ и 6³: , а
При делении степеней с одинаковыми основаниями показатели вычитаются. а полностью правило сформулировать трудно.

Разобралися также со степенями с разными основаниями и одинаковыми показателями. На помощь пришли переместительный и сочетательный законы: , потому, что ;
Чтобы умножить степени с одинаковыми показателями надо перемножить основания, а показатель оставить без изменения.
Чтобы разделить степени содинаковыми основаниями надо разделит основания, а показатель оставить без изменения.
;
Оказалось, что можно даже возводить степени в степень.
Наступил всеобщий праздник. Особенно понравилось сокращать дроби, раскладывая их на множители:
Подарок преподнес распределительный закон. Он предложил как складывать одинаковые степени, например, , ,т.е. можно складывать коэффициенты.
А если степени с одинаковыми основаниями, но с разными коэффициентами, то можно общий множитель вынести за скобку:
2)степени с отрицательным показателем:
Все уже привыкли к действиям со степенями с натуральными показателями (их так называют, потомучто показатели – натуральные числа).
И нашлись недовольные, те кто не принял участие в создании новых чисел.Революционно настроенные представители отрицательных чисел выступили с заявлением, что их притесняют, не дают развиваться науке,
— Всем известно, что при вычитании может получаться 0, а также отрицательные числа, — говорили они и организовали движение в поддержку степеней с отрицательным показателе.
— Как же может быть отрицательное количество сомножителей?- удивились натуральные числа.
— Надо определить , это как раз подходит под ваше правило:.
-А степени с отрицательным показателем определить, как ( Z_— — отрицательнын целые числа).
Например,
Тогда формула для деления степеней станет просто
— Хорошо, — сказали хранители Свода законов, — тогда докажите, что все правила действий со степенями сохранятся и при введении степеней с отрицательным показателями.

Больше того, отрицательные числа предложили план доказательства всех теорем, о действиях со степенями.
1.В выражении по определению заменить степень с отрицательным показателем на степень с натуральным показателем.
2.Выполнить действия по правилам действий со степенями с натуральными показателями
3.По определению перейти от степеней с натуральными показателя к степеням с отрицательными показателями.
А также привели поясняющие примеры: , записывать можно короче:
Итак, оказалось, что все правила действий сохранились для степеней с отрицательными показателями.
3)степени с дробным показателем:
при извлечении корня из степени делят показатель степени на показатель корня, если такое деление выполнется нацело; например: √a⁴= a², ³√x⁹ = x³ и т. п. Условимся теперь распространить это правило и на те случаи, когда показатель степени не делится нацело на показатель корня. Например, мы условимся принимать, что
Вообще мы условимся, что выражение означает корень, показатель которого есть знаменатель, а показатель подкоренного числа — числитель дробного показателя (т. е.ⁿ√a^m).
Условимся еще допускать и отрицательные дробные показатели в том же смысле, в каком мы допустили отрицательные целые показатели; например, условимся, что
Замечание. Дробные показатели были введены в алгебру главным образом голландским инженером Симоном Стевином в начале XVII столетия Позднее, в конце XVII столетия, Оксфордский профессор Джон Валлис ввел в употребление отрицательные показатели.
259. Основное свойство дробного показателя. Величина степени с дробным показателем не изменится, если мы умножим или разделим на одно и то же число (отличное от нуля) числитель и знаменатель дробного показателя. Так:
Действительно, знаменатель дробного показателя означает показатель корня, а числитель его означает показатель подкоренного выражения, а такие показатели, как мы видели можно умножать и делить на одно и то же число.
Основываясь на этом свойстве, мы можем преобразовывать дробный показатель совершенно так же, как и обыкновенную дробь: например, мы можем сокращать дробный показатель, или приводить несколько дробных показателей к одному знаменателю.

Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Калькулятор степеней онлайн: формула, примеры с решением
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 13⁴ — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 13⁴ на 13², то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 13⁶. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
a^m × aⁿ = a^(m+n).
Если разделить 13⁴ на 13², то нам потребуется вычислить дробь вида:
(13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 13². Очевидно, деление чисел, возведенных в степень, соответствует вычитанию их показателей. Второе правило действий со степенями математически выглядит так:
a^m / aⁿ = a^(m – n).
Теперь давайте возведем 11⁴ в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:
(a^m)ⁿ = a^(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 15⁰? Давайте воспользуемся вторым правилом действий степенями и попробуем разделить 15⁴ на 15⁴, что запишется как дробь:
15⁴ / 15⁴.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 15⁰. Следовательно:
15⁴ / 15⁴ = 15⁰ = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:
a⁰ = 1.
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 8² на 8⁴ и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8^-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
a^-m = 1 / a^m
При этом для значения -1 правило трансформируется в элегантную формулу:
a^-1 = 1 / a.
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7^(1/2). Очевидно, что возвести его в квадрат, и тогда по третьему правилу в результате у нас останется только семерка. Степень 1/2 — это извлечение квадратного корня, так как при возведении его в квадрат мы получаем целое число. Степень 1/3 соответствует извлечению кубического корня, но как быть с показателем 2/3? Логично, что это кубический корень из числа, возведенного в квадрат. Последнее правило гласит, что знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически это выглядит как:
a^(m/n) есть корень n-ной степени из a^m.
Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e^(kt),
где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x^2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Заключение
Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.
Добавление экспонентов — методы и примеры
Алгебра — один из основных курсов математики. Чтобы понять алгебру, важно знать, как использовать показатели и радикалы. Добавление показателей является частью учебной программы по алгебре, и по этой причине для учащихся важно иметь более прочную основу в математике.
Многие студенты часто путают сложение показателей степени со сложением чисел и, следовательно, в конечном итоге совершают ошибки. Эти недоразумения обычно влекут за собой различие в значении таких терминов, как возведение в степень и экспоненты.
Прежде чем углубляться в советы о том, как добавлять показатели, давайте начнем с определения терминов для показателей. Начнем с того, что показатель степени — это просто многократное умножение числа на само себя. В математике эта операция называется возведением в степень. Следовательно, возведение в степень — это операция, включающая числа в форме b ⁿ, где b называется основанием, а число n является показателем степени или индексом или степенью . Например, x ⁴ содержит 4 как показатель степени, а x называется основанием.
Показатели иногда называют степенями чисел. Показатель показывает, сколько раз число должно быть умножено само на себя. Например, x ⁴ = x × x × x × x.
Как складывать экспоненты?
Для сложения показателей степени и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и полномочиями. Это правило согласуется также с умножением и делением экспонент.
Ниже приведены шаги для сложения показателей степени:
Проверьте термины, если они имеют одинаковое основание и показатель степени
Например, 4 ² +4 ², эти термины имеют одинаковое основание 4 и показатель степени 2.
Вычислить каждый член отдельно, если у них разное основание или показатель степени.
Например, 3 ² + 4 ³, эти члены имеют разные показатели степени и основания.
Сложите результаты.
Сложение показателей с разными показателями и основаниями
Сложение показателей выполняется путем вычисления сначала каждого показателя, а затем добавления: Общая форма таких показателей: a ⁿ + b ^m .
Пример 1
4 ² + 2 ⁵ = 4⋅4 + 2⋅2⋅2⋅2 = 16 + 32 = 48
8 ³ + 9 ² = (8) (8) (8) + (9) (9) = 512 + 81 = 593
3 ² + 5 ³ = (3) (3) + (5) (5) ) (5) = 9 + 125 = 134
6 ² + 6 ³ = 252.
3 ⁴ + 3 ⁶ = 81 + 729 = 810.
Сложение показателей с одинаковыми основаниями и показателями
Общая формула имеет следующий вид:
b ⁿ + b ⁿ = 2b ⁿ
Пример 2
4 ² + 4 ² = 2⋅4 ² = 2⋅4⋅4 = 32
8 ³ + 8 ³ + 8 ³ = 3 (8 ³) = 3 * 512 = 1536
3 ² + 3 ² = 2 (3 ²) = 2 * 9 = 18
5 ² + 5 ² = 2 (5 ²) = 2 * 25 = 50.
Как складывать отрицательные экспоненты с разными основаниями?
Добавление отрицательных показателей выполняется путем вычисления каждого показателя отдельно и последующего добавления:
a ^-n + b ^-m = 1 / a ⁿ + 1 / b ^m
Пример 3
4 ^-2 + 2 ^-5 = 1/4 ² + 1/2 ⁵ = 1 / (4⋅4) + 1 / (2⋅2⋅2⋅2⋅2) = 1/16 + 1/32 = 0,09375
Как сложить дробную с разными основаниями и показателями?
Добавление дробных показателей выполняется путем вычисления каждого показателя отдельно и последующего добавления:
a ^{n / m} + b ^{k / j} .
Пример 4
3 ^3/2 + 2 ^5/2 = √ (3 ³) + √ (2 ⁵) = √ (27) + √ (32 ) = 5,196 + 5,657 = 10,853
Как сложить дробные показатели с одинаковыми основаниями и одинаковыми дробными показателями?
b ^{н / м} + b ^{н / м} = 2b ^{н / м}
Пример 5
4 ^2/3 + 4 ^2/3 = 2⋅4 ^2/3 = 2 ⋅ ³ √ (4 ²) = 5.04
Как складывать переменные с разными показателями степени?
Сложение показателей осуществляется путем вычисления каждого показателя по отдельности и последующего сложения:
x ⁿ + x ^m
Как складывать переменные с одинаковыми показателями?
x ⁿ + x ⁿ = 2x ⁿ
Пример 6
x ² + x ² = 2 x ²
Пример 7
(4 ^-1 + 8 ^-1) ÷ (2/3) ^-1
= (1/4 + 1/8) ÷ (3/2)
= ( 2 + 1) / 8 ÷ 3/2
= (3/8 ÷ 3/2)
= (3/8 ÷ 2/3)
= ¼
Пример 8
Упростить: (1 / 2) ^-2 + (1/3) ^-2 + (1/4) ^-2
Решение:
(1/2) ^-2 + (1/3) ^-2 + (1/4) ^-2
= (2/1) ² + (3/1) ² + (4/1) ²
= (2 ² + 3 ² + 4 ²)
= (4 + 9 + 16)
= 29
Практические вопросы
Сэм может красить стену за t ² Майк может рисовать та же стена в т ^3/2 часов.Если t = 1,5, насколько быстро Майк от Сэма красит стену? Дайте свой ответ в считанные минуты.
Какое из следующих значений равно члену (5) ^-1/3. (1/5) ^-2/3
а. (5) ^-2/9
б. (5) ^-1/3
с. 1
г. (5) ^1/3
Ответы
25 минут
d
Предыдущий урок | Главная страница | Следующий урок
Показатели: основные правила — сложение, вычитание, деление и умножение
Обновлено 14 декабря 2020 г.
Ли Джонсон
Выполнение вычислений и работа с показателями является важной частью математики более высокого уровня.Хотя выражения, включающие несколько показателей степени, отрицательные показатели степени и т. Д., Могут показаться очень запутанными, все то, что вам нужно сделать для работы с ними, можно свести к нескольким простым правилам. Узнайте, как складывать, вычитать, умножать и делить числа с помощью показателей степени и как упростить любые выражения, включающие их, и вы почувствуете себя более комфортно, решая проблемы с показателями.
TL; DR (слишком долго; не читал)
Умножьте два числа на показатели, сложив показатели вместе: x ^m x x ⁿ = x ^m ^{+ n}
Разделите два числа с показателями, вычтя одну экспоненту из другой: x ^m ÷ x ⁿ = x ^m ^{^— ⁿ}
Когда показатель степени возводится в степень, умножьте показатели вместе: ( x ^y ) ^z = x ^y ^× ^z
Любое число, возведенное в степень нуля, равно единице: x ⁰ = 1
Что такое экспонента?
Показатель степени относится к числу, в степень которого что-то возводится.4 = x × x × x × x
Показатели также могут быть переменными; например, 4 ^x представляет четыре, умноженные на себя x раз.
Правила для экспонент
Выполнение вычислений с показателями степени требует понимания основных правил, регулирующих их использование. Вам нужно подумать о четырех основных вещах: сложении, вычитании, умножении и делении.
Сложение и вычитание показателей
Сложение показателей и вычитание показателей на самом деле не требует применения правила.Если число возведено в степень, добавьте его к другому числу, возведенному в степень (либо с другим основанием, либо с другим показателем), вычислив результат члена показателя степени и затем напрямую добавив его к другому. Когда вы вычитаете экспоненты, применяется тот же вывод: просто вычислите результат, если можете, а затем выполните вычитание как обычно. Если показатели степени и основания совпадают, вы можете складывать и вычитать их, как любые другие совпадающие символы в алгебре. Например:
x ^ y + x ^ y = 2x ^ y \ text {и} 3x ^ y — 2x ^ y = x ^ y
Умножение показателей
Показатели умножения зависят от простого правила: просто сложите показатели вместе, чтобы завершить умножение.{10} \ end {align}
Основы алгебры — Показатели — Углубленно
Показатели
используются во многих задачах алгебры, поэтому важно понимать
правила работы с экспонентами. Давайте подробно рассмотрим каждое правило и посмотрим
несколько примеров.
Правила
из 1
Есть два
запомнить простые «правила 1».
Во-первых, любое число
возведенный в степень «один», равняется самому себе.Это имеет смысл, потому что
степень показывает, во сколько раз основание умножается само на себя. Если это только
умножается один раз, то логично, что он равен самому себе.
Во-вторых, один
возведен в любую власть — один. Это тоже логично, потому что один раз один раз
один, сколько бы раз вы его умножали, всегда равен единице.
Товар
Правило
Показатель степени
«правило произведения» говорит нам, что при умножении двух степеней, которые имеют
на той же базе можно складывать экспоненты.В этом примере вы можете увидеть, как
оно работает. Добавление экспонентов — это всего лишь короткий путь!
Мощность
Правило
«Власть»
правило «говорит нам, что чтобы возвести степень в степень, просто умножьте степень.
Здесь вы видите, что 5 ² в 3-й степени равно 5 ⁶.
Частное
Правило
Частное
Правило говорит нам, что мы можем разделить две степени с одинаковым основанием, вычитая
экспоненты.Вы поймете, почему это работает, если изучите показанный пример.
Правило нуля
Согласно
«правило нуля», любое ненулевое число, возведенное в степень нуля
равно 1.
Отрицательный
Показатели
Последнее правило
в этом уроке говорится, что любое ненулевое число в отрицательной степени
равно его обратному возведению в противоположную положительную силу.
назад
наверх
Сложение и вычитание с экспонентами — видео и стенограмма урока
Основы экспоненты
Как и супергерои, экспоненты обладают особыми способностями. Они могут упростить многократное умножение, чтобы мы могли сэкономить место! Хорошо, может быть, их способности не так уж интересны, но они, безусловно, полезны в математике и естественных науках. Мы можем выполнять все виды различных математических вычислений с показателями, но в этом уроке мы сосредоточимся только на двух: сложении и вычитании с показателями.5
Это выражение имеет коэффициент 8, основание x и показатель степени 5.
Кстати, если перед переменной или символом нет числа, то коэффициент будет 1. То же верно, если вы не видите экспоненту. Следовательно, член y будет иметь коэффициент 1 и показатель степени 1; их просто не нужно писать, что немного упрощает ситуацию. Вот еще один пример: 2 x будет означать коэффициент 2, основание x и показатель степени 1.
Понял? Теперь мы можем перейти к некоторым простым правилам, чтобы, наконец, начать складывать и вычитать члены с показателями.
Сложение, вычитание, умножение и деление степеней
Сложение и вычитание полномочий
Очевидно, что степени можно складывать, как и другие величины, , объединяя их одну за другой со своими знаками.
Таким образом, сумма a ³ и b ² составляет ³ + b.

И сумма a ³ — b ⁿ и h ⁵ -d ⁴ составляет a ³ — b ⁿ + h ⁵ — d ⁴.
одинаковых степеней одних и тех же букв подобны величинам , и их коэффициенты могут быть добавлены или вычтены.
Таким образом, сумма 2a ² и 3a ² составляет 5a ².
Столь же очевидно, что удвоенный квадрат a и троекратный квадрат a в пять раз больше квадрата a, как и дважды a и трижды a равны пятикратному a.
Но степени разных букв и разных степеней той же буквы , должны быть добавлены, записывая их вместе с их знаками.
Сумма ² и ³ дает ² + ³.
Очевидно, что квадрат a и куб a не в два раза больше квадрата a и не в два раза больше куба a.
Сумма a ³ b ⁿ и 3a ⁵ b ⁶ составляет a ³ b ⁿ + 3a ⁵ b ⁶.
Вычитание степеней должно выполняться таким же образом, как и сложение, за исключением того, что знаки вычитаемого числа должны быть изменены.
из 2a ⁴ 3ч ²б ⁶ 5 (а — в) ⁶
Под. -6a ⁴ 4ч ²б ⁶ 2 (а — в) ⁶
Разн. 8a ⁴ -h ² b ⁶ 3 (а — в) ⁶
ИЛИ:
2a ⁴ — (-6a ⁴) = 8a ⁴
3h ² b ⁶ — 4h ² b ⁶ = -h ² b ⁶
5 (a — з) ⁶-2 (а — ч) ⁶ = 3 (а — ч) ⁶
Умножение степеней
Силы можно умножать, как и другие величины, записывая множители один за другим со знаком умножения или без знака умножения между ними.
Таким образом, произведение ³ на b ² дает ³ b ² или aaabb.
Разн. х ^-3 3a ⁶ y ² a ² b ³ y ²
В а ^м -2x а ³ б ² л
Прод. a ^м x ^-3 -6a ⁶ xy ² a ² b ³ y ² a ³ b ² y
OR:
x ^-3 × a ^m = a ^m x ^-3
3a ⁶ y ² × (-2x) = -6a ⁶ xy ²
a ² b ³ y ² × a ³ b ² y = a ² b ³ y ² a ³ b ² y
Продукт в последнем примере можно сократить, объединив повторяющиеся буквы.
Тогда он станет ⁵ b ⁵ y ³.
Причина этого будет очевидна, если вернуться к ряду полномочий в Ст. 204, а именно.
Сравнивая несколько членов друг с другом, можно увидеть, что если любые два или более из них будут умножены вместе, их произведение будет степенью, показатель степени которой равен сумме и показателей степени факторов.
Таким образом, a ² ⋅a ³ = aa⋅aaa = aaaaa = a ⁵.
Здесь 5, показатель степени произведения, равен 2 + 3, сумме показателей степени факторов.
Итак, ⁿ ⋅a ^m = a ^{m + n}.
Для ⁿ — множитель, равный количеству единиц в n;
А ^м — множитель, равный количеству единиц в м;
Следовательно, произведение должно быть равно множителю, равному количеству единиц в m и n.Следовательно,
Степени одного и того же основания можно умножить, сложив их показатели.
Это ² ⋅a ⁶ = a ^{2 + 6} = a ⁸. И x ³ ⋅x ² ⋅x = x ^{3 + 2 + 1} = x ⁶.
Умножить 4a ⁿ б ² л ³ (б + в — у) ^н
В 2a ⁿ б ⁴ л (б + в — у)
Товар 8a ²ⁿ б ⁶ л ⁴ (б + в — у) ^{п + 1}
OR:
4a ⁿ × 2a ⁿ = 8a ²ⁿ
b ² y ³ × b ⁴ y = b ⁶ y ⁴
(b + h — y ) ⁿ × (b + h — y) = (b + h — y) ^{n + 1}
Mult.x ³ + x ² y + xy ² + y ³ в x — y.
Ответ: x ⁴ — y ⁴.

Мульт. x ³ + x — 5 на 2x ³ + x + 1.
Правило в равной степени применимо к степеням, показатель степени которых равен отрицательным .
1. Таким образом, ^-2 .a ^-3 = ^-5. Это $ \ frac {1} {aa} \ cdot \ frac {1} {aaa} = \ frac {1} {aaaaa} $.
2. y ^-n ⋅y ^-m = y ^-n-m.
3. a ^-n ⋅a ^m = a ^m-n.
Если a + b умножить на a — b, произведение будет a ² — b ²: то есть
Произведение суммы и разности двух величин равно разности их квадратов.
Если умножить сумму и разность квадратов , произведение будет равно разности четвертых степеней.
Таким образом, (a — y) ⋅ (a + y) = a ² — y ².
(a ² — y ²) ⋅ (a ² + y ²) = a ⁴ — y ⁴.

(a ⁴ — y ⁴) ⋅ (a ⁴ + y ⁴) = a ⁸ — y ⁸.
Разделение властей
Полномочия могут быть разделены, как и другие величины, путем исключения из делимого множителя, равного делителю; или поместив делитель под делимым в виде дроби.
Таким образом, частное от деления ³ b ² на b ² дает ³.
Разделить 9a ³ y ⁴ a ² by + 3a ² y ² d⋅ (а — в + у) ³
По -3a ³ а ² л (а — в + у) ³
Частное -3 года ⁴ б + 3г д
Частное от деления ⁵ на ³ дает ⁵/³.Но это равно ². Ибо в сериале

a ⁺⁴, a ⁺³, a ⁺², a ⁺¹, a ⁰, a ^-1, a ^-2, a ^-3, a ^-4.

, если один член делится на другой, показатель степени частного будет равен разнице между показателем делимого и показателем делителя.
Степень может быть разделена на другую степень того же основания путем вычитания показателя делителя из показателя делимого .
Таким образом, y ³: y ² = y ^3-2 = y ¹. То есть yyy / yy = y.
И ^{n + 1}: a = a ^{n + 1-1} = a ⁿ. То есть aa ⁿ / a = a ⁿ.
Разделить л ^{2 м} 8a ^{n + m} 12 (б + у) ^н
По л ^м 4a ^м 3 (б + у) ³
Quot. л ^м 2a ⁿ 4 (б + у) ^п-3
Правило в равной степени применимо к степеням, показатель степени которых равен отрицательным .

Частное ^-5 на ^-3, составляет ^-2.

Это $ \ frac {1} {aaaaa}: \ frac {1} {aaa} = \ frac {1} {aaaaa} \ cdot \ frac {aaa} {1} = \ frac {aaa} {aaaaa} = \ frac {1} {aa} $.
3. h ²: h ^-1 = h ^{2 + 1} = h ³.То есть h ²: (1 / h) = h ² ⋅ (h / 1) = h ³
Умножение и разделение полномочий путем сложения и вычитания их индексов должно быть хорошо знакомо; поскольку они имеют многочисленные и важные приложения в высших разделах алгебры.
Примеры дробей, содержащих силы
В разделе о дробях следующие примеры были опущены, чтобы избежать предвкушения субъекта полномочий.
1.Уменьшите 5a ⁴ / 3a ² до более низких сроков. Ответ: 5а ²/3.
2. Уменьшите 6x ⁶ / 3x ⁵ до более низких значений. Ответ: 2x / 1 или 2x.
3. Приведите ² / a ³ и ^-3 / a ^-4 к общему знаменателю.

a ² ⋅a ^-4 — это ^-2 первый числитель. (Статья 146.)

a ³ ⋅a ^-3 — это ⁰ = 1, второй числитель.

a ³ ⋅a ^-4 — это ^-1, общий знаменатель.
Таким образом, уменьшенные дроби равны ^-2 / a ^-1 и 1 / a ^-1.
4. Приведите 2a ⁴ / 5a ³ и ² / a ⁴ к общему знаменателю.

Ответ: 2a ³ / 5a ⁷ и 5a ⁵ / 5a ⁷ или 2a ³ / 5a ² и 5 / 5a ². (Статья 142.)
5. Умножьте (a ³ + b) / b ⁴ на (a — b) / 3.
6.Умножьте (a ⁵ + 1) / x ² на (b ² — 1) / (x + a).
7. Умножьте b ⁴ / a ^-2 на h ^-3 / x и ⁿ / y ^-3.
8. Разделите ⁴ / y ³ на ³ / y ². Ответ: в / у.
9. Разделите (h ³ — 1) / d ⁴ на (d ⁿ + 1) / час.
Правила экспоненты
Термины «показатель степени» и «степень» обычно используются взаимозаменяемо для обозначения верхнего индекса «n» в b ⁿ.Для простоты на этой странице термин «экспонента» будет использоваться для обозначения чисел в форме b ⁿ, а степень будет использоваться для обозначения верхнего индекса «n». «b» — основание.
сложение или вычитание показателей
Для сложения или вычитания показателей степени должны иметь одинаковое основание и одинаковую степень.
Пример
3 (3 ²) + 3 ² = (3 + 1) (3 ²) = 4 (3 ²)
3x ⁵ — 6x ⁵ = (3-6) x ⁵ = -3x ⁵
Если показатели степени не имеют одинакового основания и одинаковой степени, вы не можете складывать или вычитать их (даже их коэффициенты!).
степень умножения
Для умножения показателей степени должны иметь одинаковое основание и / или одинаковую степень. Чтобы умножить экспоненты с одинаковым основанием, оставьте одно и то же основание и сложите степени вместе. Если у экспонентов разные базы, вы не можете складывать их силы.
Если у показателей степени есть коэффициенты, прикрепленные к их основаниям, умножьте коэффициенты вместе. Коэффициенты можно перемножать, даже если показатели имеют разное основание.
Пример
3 ² × 3 ³ = 3 ^{2 + 3} = 3 ⁵
4x ⁶ × 5y ⁴ = (4 × 5) x ⁶ y ⁴ = 20x ⁶ y ⁴
Если экспоненты имеют одинаковую мощность, но разные основания, вы можете сначала перемножить основания, прежде чем брать степень их произведения.
Пример
4 ² × 6 ² = (4 × 6) ² = 24 ² = 576
Если показатели степени имеют одинаковую мощность и одинаковое основание, вы можете выбрать любой метод для упрощения.
Пример
5 ² × 5 ² = 5 ^{2 + 2} = 5 ⁴ = 625
5 ² × 5 ² = (5 * 5) ² = 25 ² = 625
показатели деления
Для деления показателей степени должны иметь одинаковое основание и / или одинаковую степень.Чтобы разделить показатели с одинаковым основанием, оставьте такое же основание и вычтите степень знаменателя из мощности числителя. Если у экспонентов разные основания, вы не можете вычесть их силы.
Если у показателей степени есть коэффициенты, прикрепленные к их основаниям, разделите коэффициенты. Коэффициенты можно разделить, даже если у показателей есть разные основания.
Пример
Если показатель степени имеет отрицательную степень, вам все равно нужно сохранить тот же знак и вычесть степень.
Пример
Если показатели имеют одинаковую мощность, но разные основания, вы можете сначала разделить основания, прежде чем брать степень частного.
Пример
Если экспоненты имеют одинаковую мощность и одинаковую базу, они уравняются до 1.
Пример
Превращая власть в силу, остерегайтесь скобок (если они есть). Следуйте порядку операций, так как они также применимы к показателям степени.
Если основание и первая степень указаны в скобках, вы можете умножить первую и вторую степень вместе. Вы также можете сначала возвести основание в степень первой степени, а затем возвести это значение в степень второй степени.
Пример
(4 ³) ² = 4 ^{3 × 2} = 4 ⁶ = 4096
(4 ³) ² = 64 ² = 4096
Если основание и первая степень не указаны в скобках, возьмите степень первой степени до второй, а затем упростите.
Пример
4 ^{3 ²} = 4 ^{(3 ²)} = 4 ⁹ = 262144
Число 3 в степени 2 имеет приоритет перед числом 4 в степени 3, потому что оно не заключено в круглые скобки. Мелкие детали могут существенно повлиять на ответ!
В показателях степени можно также использовать круглые скобки для обозначения коэффициента и его переменной. В этом случае распределите показатель степени как на коэффициент, так и на переменную.
Пример
(5x) ³ = 5 ³ x ³ = 125x ³
Это также может быть применено к разделу:
Пример
См. Также объединение подобных терминов, отрицательные показатели, порядок операций.
4 простых способа умножения показателей [+ действия]
Что общего у землетрясений, фондового рынка, информатики и ядерной физики?
Все они включают экспонентов умножения .
Показатели являются неотъемлемой частью алгебры, полиномиальных уравнений и математических курсов более высокого уровня, но многим студентам сложно понять, как с ними работать. Вы ознакомились с правилами экспонента со своим классом, и теперь пора применить их.
Давайте рассмотрим: правила экспонент
Прежде чем вы начнете учить своих учеников умножению экспонентов, вы можете сделать с ними быстрый обзор основ работы экспонентов.
Показатели (также называемые степени ) регулируются правилами, как и все остальное в математическом классе. Вот краткое резюме:
Показатель степени — это способ выражения повторного умножения . Например, 35 представляет собой три, умноженные на себя пять раз:
35 = 3 × 3 × 3 × 3 × 3 = 243
35 = 243
Первое число называется основанием . Представляет собой число, которое умножается.
Второе меньшее число — это показатель степени . Он представляет собой количество раз, когда основание умножается само на себя.
Существует семь правил экспоненты :
Правило произведения степеней : сложение степеней при умножении подобных оснований
Правило соотношения степеней : вычитание степеней при делении подобных оснований
Правило силы полномочий : Умножение степеней вместе при увеличении степени на другой показатель
Степень произведения rul e: Распределение мощности на каждую базу при возведении нескольких переменных в степень
Степень правила частного : Распределение мощности на все значения в частное
Правило нулевой степени : Любое основание, возведенное в степень нуля, становится единицей
Правило отрицательной экспоненты : Чтобы изменить отрицательную экспоненту на положительную, переверните ее на обратную
Понятно? Тогда давай продолжим.
Как умножить экспоненты 4 способами
Помните, что все эти стратегии — просто ярлыки, помогающие упростить более сложные уравнения. Чтобы найти фактическое значение показателя степени, учащиеся должны сначала понять, что это означает: повторное умножение .
Познакомьте студентов с основами, такими как выражение показателей в виде произведений, прежде чем переходить к умножению показателей.
Когда они освоятся с концепцией, пора начинать.
1. Умножение степеней с одним и тем же основанием
При умножении степеней используйте первое правило: складывайте степени при умножении одинаковых оснований.
52 × 56 =?
Основания уравнения остаются неизменными, а значения показателей складываются.
52 × 56 = 58
Но почему это работает? Давайте посмотрим немного внимательнее:
Сложение экспонент — это всего лишь быстрый путь к ответу. Когда мы складываем экспоненты, мы увеличиваем количество раз, когда основание умножается само на себя.
Это правило остается неизменным, независимо от сложности вопроса. Вот более сложный пример с переменными:
(2𝒙8) (3𝒙5) =?
Сначала умножьте числа (2 и 3) вместе, поскольку они представляют собой коэффициентов , а не основание. (Коэффициент — это число, умноженное на переменную, например 𝒙.)
Затем сложите показатели степени.
(2𝒙8) (3𝒙5) = 6𝒙13
2. Умножение степеней с разными основаниями
Можно умножать экспоненты с разными основаниями, но есть одна важная загвоздка: экспоненты должны быть одинаковыми.
Вот как это сделать:
54 × 24 =?
Сначала умножьте основания вместе. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте то же самое.
54 × 24 = 104
Вот почему это работает:
Это из-за правила четвертой степени: распределяет мощность на каждую базу при возведении нескольких переменных в степень . Это уравнение также можно записать как (5 × 2) 4, что означает, что показатель степени распределяется между 5 и 2.
А теперь попробуем умножить переменные на показатели.
(3y3) (4y3) =?
Помните, что правило остается в силе до тех пор, пока , поскольку показатели степени и переменные равны (потому что переменные 𝒙 и y не могут быть объединены).
(3y3) (4y3) = 12y3
3. Умножение показателей степени с разными основаниями и показателями
Что происходит, когда вы хотите умножить разные показатели степени с разными основаниями?
Короткий ответ: вы не можете. В отличие от приведенных выше примеров, здесь нет ярлыка.
Например:
Поскольку 24 и 32 не имеют ничего общего, чтобы их можно было объединить, ответ не может быть упрощен до одного показателя степени и должен быть выражен как обычное число.
4. Умножение отрицательных показателей
Это может показаться сложным, но умножение показателей степени на отрицательные числа в точности совпадает с умножением показателей степени на неотрицательные числа.
Начните с рассмотрения свойств отрицательных чисел. В частности, просмотрите, как их складывать и умножать.Ваши ученики должны чувствовать себя комфортно, работая с отрицательными числами, прежде чем они перейдут к отрицательным показателям.
Затем запомните правило седьмого показателя степени: , чтобы изменить отрицательный показатель степени на положительный, переверните его на обратное значение .
То же основание, разные степени:
4-3 × 42 =?
Помните — складывайте экспоненты с одинаковыми основаниями.
4-3 × 42 = 4-1
Чтобы решить эту экспоненту, переверните отрицательную экспоненту в обратную.
4-1 = ¼ = 0.25
Разное основание, но одинаковые показатели:
2-5 × 3-5 =?
Как и выше, умножьте основания и оставьте степень без изменений.
2-5 × 3-5 = 6-5
Чтобы решить, переверните отрицательный показатель степени в обратную величину.
6-5 = ⅙5
Если показатели степени не имеют ничего общего, решите уравнение напрямую:
2-3 × 32
Сначала преобразуйте отрицательные показатели степени в обратные, затем вычислите.
Когда вы умножаете показатели, напомните учащимся:
Сложите показатели , если основания одинаковые
Умножьте основания , если показатели одинаковые
Если ничего не одинаково , просто решите это
Упражнения для практики умножения на экспоненты
1.Prodigy
Повышение беглости математики — важная часть уверенности учащихся в курсах математики в средней школе и колледже. Студенты могут практиковать умножение показателей и другие математические концепции с Prodigy, в то время как вы задаете индивидуальные внутриигровые вопросы, основанные на содержании урока.
Ваш класс будет исследовать мир, наполненный увлекательными заданиями, экзотическими домашними животными и изучением математики. Вы сможете выбрать, на какие вопросы они будут отвечать, и в режиме реального времени получать данные о том, что они усвоили, над чем работают и где им может потребоваться дополнительная помощь.
Обладая 1400 навыками и большим количеством навыков, вы сможете предоставить материалов, соответствующих учебной программе, по любой теме, которую вы изучаете, включая умножение показателей.
2. Exponent War
Education.com
Классическая карточная игра, но с невероятно интересным поворотом!
Ученики работают в группах по двое и соревнуются друг с другом. Раздайте каждой команде колоду карт (с вынутыми дамами, валетами и королями) и попросите каждого игрока вытащить по две карты.Первая карта — это база, а вторая карта — экспонента.
Каждой паре предстоит соревноваться, чтобы решить свое уравнение и найти продукт. Побеждает команда с наибольшим ответом. Установите таймер для класса и посмотрите, кто наберет больше очков.
Пока ученики играют, пройдитесь по классу и убедитесь, что они не пропустили ни одной ступеньки. Если вы видите много ошибок или затруднений у учащихся, примите это как знак того, что вам, возможно, придется пересмотреть.
3. Exponent Scavenger Hunt
Дайте вашим ученикам возможность искать сокровища и исследовать класс с помощью экспоненциальной охоты на мусорщиков.
Разделите ваш класс на группы по три или четыре человека. В зависимости от количества групп, сделайте несколько разных наборов карточек. Начинайте каждый набор с карточки, на которой есть проблема. Напишите ответ на проблему на следующей карточке, а другую задачу на обратной стороне. Продолжайте, пока не получите три или четыре набора задач (или больше).
Начиная с первой карточки, каждая группа должна решить задачу и найти правильный ответ где-нибудь еще в классе .Найдя правильную карточку с ответами, они могут перевернуть ее и решить следующую задачу. Раздайте учащимся записки для решения и позвольте им начать поиск ответов. Какая бы команда ни финишировала первой, становится победителем!
4. Exponent Jeopardy
Каждый ученик любит классическую игру Jeopardy. Используя настраиваемый шаблон, замените мелочи вопросами, которые дают студентам возможность попрактиковаться в умножении показателей, и разделите класс на две команды.
Вот несколько советов, которые помогут обеспечить бесперебойную работу игры:
Если у вас большой класс, подумайте о том, чтобы разделить класс на несколько игр, чтобы у каждого ученика была возможность участвовать.
Чтобы объединить математические и компьютерные навыки, Предложите учащимся сделать игру самостоятельно.Дайте им шаблон (или пусть более продвинутые ученики начнут с нуля) и попросите их сделать небольшую игру.
Используйте его в качестве конечного упражнения перед тестом и комбинируйте более важные вопросы с более сложными ответами.
5. Рабочие листы для умножения показателей
Рабочие листы — это проверенный метод развития математики свободное владение определенным набором навыков. Они также могут быть индикатором понимания учащимся, когда используются как часть стратегии формирующего оценивания.Вот некоторые из наших фаворитов:
Если вы ищете рабочий лист, который охватывает больше, чем просто умножение экспонент, ознакомьтесь с нашей таблицей правил экспонент (с ключом ответа).
Для чего-то более уникального, попробуйте это упражнение с умножением полиномов. Как и в обычном рабочем листе, в нем есть вопросы, на которые студенты должны ответить, но он также содержит «банк ответов» для студентов. Вырежьте сопутствующие полоски и перемешайте их. Попросите учащихся сопоставить ответы с правильным разделом на своем листе после решения уравнения и демонстрации своей работы.
Умножение степеней: давайте рассмотрим
Если ваши ученики помнят только три вещи, убедитесь, что это следующие концепции: произведение многократного умножения

Если они запомнят эти три правила, у них будет прочный фундамент, построенный еще до их первого урока алгебры в средней школе.

Как всегда, делайте это медленно и убедитесь, что учащиеся понимают основы, прежде чем все усложняется. Это может показаться сложной идеей для преподавания, но придерживайтесь шагов и продвигайтесь в логическом порядке, чтобы увидеть, как знания ваших учеников растут.

из	2a ⁴	3ч ²б ⁶	5 (а — в) ⁶
Под.	-6a ⁴	4ч ²б ⁶	2 (а — в) ⁶
Разн.	8a ⁴	-h ² b ⁶	3 (а — в) ⁶

Разн.	х ^-3	3a ⁶ y ²	a ² b ³ y ²
В	а ^м	-2x	а ³ б ² л
Прод.	a ^м x ^-3	-6a ⁶ xy ²	a ² b ³ y ² a ³ b ² y

Умножить	4a ⁿ	б ² л ³	(б + в — у) ^н
В	2a ⁿ	б ⁴ л	(б + в — у)
Товар	8a ²ⁿ	б ⁶ л ⁴	(б + в — у) ^{п + 1}

Разделить	9a ³ y ⁴	a ² by + 3a ² y ²	d⋅ (а — в + у) ³
По	-3a ³	а ² л	(а — в + у) ³
Частное	-3 года ⁴	б + 3г	д

Разделить	л ^{2 м}	8a ^{n + m}	12 (б + у) ^н
По	л ^м	4a ^м	3 (б + у) ³
Quot.	л ^м	2a ⁿ	4 (б + у) ^п-3

Сложение и вычитание степеней ⬅️

Что такое степень числа

Таблица степеней

Свойства степеней: когда складывать, а когда вычитать

Свойство 1: произведение степеней

Свойство 2: частное степеней

Свойство 3: возведение степени в квадрат

Свойство 4: степень возведения

Свойство 5: степень частного

Сложение и вычитание степеней

Сложение степеней с разными показателями

Сложение степеней с разными основаниями

Как складывать числа с одинаковыми степенями

Вычитание степеней с одинаковым основанием

Вычитание степеней с разными основаниями

Вычитание чисел с одинаковыми степенями

Сложение чисел с разными показателями степени. Действия с одночленами

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Умножение степеней

Деление степеней

Примеры решения примеров с дробями, содержащими числа со степенями

Свойства степени

Свойство № 1

Свойство № 2

Свойство № 3

Свойства 5

Степени и корни

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

Правила умножения степеней с разным основанием

Свойства степени

Применение степеней и их свойств

Показательные уравнения и неравенства

Онлайн-калькулятор возведения в степень

Что такое степень числа

Таблица степеней от 1 до 10

Свойства степеней

Степень с отрицательным показателем

Степень с натуральным показателем

Дробная степень

Степень с иррациональным показателем

Заключение

Умножение степеней

Свойства степеней при сложении. Основные свойства степеней. Примеры на умножение степеней с одинаковыми показателями

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Умножение степеней

Деление степеней

Примеры решения примеров с дробями, содержащими числа со степенями

Свойства степени

Свойство № 1

Свойство № 2

Свойство № 3

Свойства 5

Степени и корни

Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

Правила умножения степеней с разным основанием

Свойства степеней с одинаковыми основаниями

Складывание чисел с разными степенями. Правила вычитания и сложения степеней

Разбор 5 примеров для тренировки

ПРОДВИНУТЫЙ УРОВЕНЬ

Определение степени

Степень с натуральным показателем {n = 1, 2, 3,…}

Степень с целым показателем {0, ±1, ±2,…}

Степень с рациональным показателем

Свойства степеней

Степень с иррациональным показателем

КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ

ТЕПЕРЬ ТЕБЕ СЛОВО…

Свойство № 1

Свойство № 2

Свойство № 3

Свойства 4

Свойства 5

Что представляют собой степенные выражения?

Основные виды преобразований степенных выражений

Работа с основанием и показателем степени

Использование свойств степеней

Преобразование дробей, содержащих степени

Все вышеприведенные формулы читаются и выполняются в обоих
направлениях слева направо и наоборот.