Содержание
Формулы для решения задач по химии
от 01.01.2017 года
Настоящее пользовательское (лицензионное) соглашение (далее – «Соглашение»)
заключается между Обществом с ограниченной ответственностью «АЛЕКТА» (далее –
«Лицензиар»), и Пользователем (физическим лицом, выступающем в роли конечного
потребителя Продукта) совместно именуемые «Стороны».
Пожалуйста, внимательно ознакомьтесь с текстом настоящего Соглашения. Оно
представляет собой публичную оферту и, после его принятия Вами, образует соглашение
между Вами (Пользователем) и Лицензиаром о предмете и на условиях, изложенных в
тексте Соглашения.
Принимая настоящее Соглашение, Вы соглашаетесь с положениями, принципами, а
также соответствующими условиями лицензионного соглашения, изложенными ниже.
1. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
1.1. Программный продукт — экземпляры программы для ЭВМ «ХиШник», состоящей
из Серверной части (свидетельство о государственной регистрации базы данных
№2014621526) и Клиентского приложения (свидетельство о государственной
регистрации программы для ЭВМ № 2014661592), права на использование которой
предоставляются в соответствии с настоящим Соглашением.
1.2. Серверная часть — часть Программного продукта, размещенная в сети Интернет и
используемая для хранения данных в базе данных Лицензиара под наименованием
«ХиШник» (далее также – «база данных»), а также для хранения, обработки,
передачи данных Пользователя между базой данных и клиентским приложением.
1.3. Клиентское приложение — часть Программного продукта, устанавливаемая на
компьютер Пользователя или на мобильное устройство Пользователя и
позволяющая получить доступ к базе данных Лицензиара, а также данным
Пользователя, хранящимся в памяти сервера Лицензиара.
1.4. Пользовательское (лицензионное) соглашение – текст настоящего Соглашения со
всеми дополнениями, изменениями, приложениями к нему, размещенный на сайте
Лицензиара и доступный в сети интернет по адресу: http://www.hishnik-school.ru
1.5. Заключение Пользовательского (лицензионного) соглашения (акцепт
публичной оферты) — полное и безоговорочное принятие условий настоящего
Соглашения Пользователем путем совершения Пользователем одного (или
нескольких) из следующих действий:
прохождение регистрации и (или) авторизации на Сайте Лицензиара в
установленном им порядке;
внесение платежа за предоставление права на использование Программного
продукта;
начало использования Пользователем Программного продукта в любой иной
форме.
1.6. Лицензиар — сторона в настоящем Соглашении, обладающая исключительным
правом на Программный продукт и предоставляющая по настоящему Соглашению
Пользователю право использования Программного продукта, в пределах и
способами, указанными в настоящем Соглашении.
1.7. Пользователь — физическое лицо, которое устанавливает на компьютер или
мобильное устройство Клиентское приложение и использует его.
1.8. Неисключительная лицензия — лицензионный договор, предусматривающий
предоставление права использования Программного продукта с сохранением за
Лицензиаром права заключения лицензионного договора с другими лицами.
1.9. Роль – набор функций, которые доступны в Программном продукте Пользователю.
Настоящим Соглашением предусмотрены следующие роли:
1.9.1. Администратор — сотрудник образовательного учреждения,
осуществляющий регистрацию и предоставление доступа к Программному
продукту Пользователям – участникам образовательного процесса в
образовательном учреждении.
1.9.2. Преподаватель – сотрудник образовательного учреждения, организующий
и осуществляющий образовательный процесс посредством использования
функций Программного продукта.
1.9.3. Репетитор – преподаватель, дающий частные уроки, может проводить как
индивидуальные, так и групповые занятия посредством использования
функций Системы вне рамок Образовательного учреждения.
1.9.4. Учащийся – обучающийся в Образовательном учреждении и (или) вне его,
получающий и проверяющий свои знания посредством Системы.
1.10. Профиль — запись в базе данных, содержащая идентифицирующие сведения о
Пользователе и его роли.
1.11. Демонстрационный режим – режим использования Программного продукта для
целей ознакомления с его функциональными возможностями.
1.12. Продуктивный режим – режим использования Программного продукта для целей
применения в образовательном процессе.
1.13. Регистрационный ключ — набор цифр и букв, посредством которого Пользователь
получает право использования Программного продукта в Продуктивном режиме с
полным доступом к Серверной части.
1.14. Логин – уникальный идентификатор Пользователя в базе данных.
1.15. Пароль – набор цифр и букв, посредством которого и совместно с Логином
Пользователь получает доступ в Клиентское приложение Программного продукта.
1.16. Интернет сайт Лицензиара — http://www.hishnik-school.ru.
1.17. Контент — все объекты, размещенные на Сайте и в Программном продукте, в том
числе элементы дизайна, текст, графические изображения, иллюстрации, видео,
скрипты, программы, музыка, звуки и другие объекты и их подборки.
2. ПРЕДМЕТ СОГЛАШЕНИЯ
2.1. Лицензиар предоставляет Пользователю право использования Программного
продукта «ХиШник» на условиях простой (неисключительной) лицензии в пределах
и способами, указанными в настоящем Соглашении, а Пользователь обязуется
уплатить Лицензиару вознаграждение за предоставление права использования
Программного продукта в соответствии с условиями настоящего Соглашения.
2.2. Лицензиар гарантирует, что он является правообладателем исключительных прав на
Программный продукт и имеет права на заключение Соглашения. Лицензиару в
настоящий момент в соответствии с тем знанием, которым он обладает, не известны
права третьих лиц, нарушаемые данным Соглашением.
2.3. Пользователь не вправе полностью или частично предоставлять (передавать) права
третьим лицам, полученные им по Соглашению, в том числе продавать,
тиражировать, копировать Программный продукт, предоставлять доступ третьим
лицам, отчуждать иным образом, в т.ч. безвозмездно, без получения на все
вышеперечисленные действия предварительного письменного согласия Лицензиара.
2.4. Соглашение предоставляет Пользователю право использования Программного
продукта с сохранением за Лицензиаром права выдачи лицензий другим лицам.
Пользователь может использовать экземпляр Программного продукта только в
пределах тех прав и теми способами, которые предусмотрены Соглашением.
Предоставляемое Пользователю Лицензиаром право на использование
Программного продукта действует в течение срока действия Соглашения.
2.5. Программный продукт «ХиШник», состоящий из Серверной части и Клиентского
приложения, представляет собой программу для ЭВМ, предназначенную для
осуществления образовательного процесса.
2.6. Право использования Программного продукта (неисключительная лицензия),
предоставляемое Пользователю в соответствии с настоящим Соглашением,
включает право на использование Программного продукта в двух режимах:
2.6.1. Демонстрационный режим, ограниченный правом установки на компьютер
или мобильное устройство, запуска, настройки Клиентского приложения и
ограниченного доступа к Серверной части, для целей ознакомления с
функциональными возможностями Программного продукта.
2.6.2. Продуктивный режим, ограниченный правом установки на компьютер или
мобильное устройство, запуска, настройки Клиентского приложения и
полного доступа к Серверной части, для целей применения Программного
продукта в образовательном процессе.
2.7. Право использования Программного продукта предоставляется:
2.7.1. В демонстрационном режиме — с момента установки Клиентского приложения
на компьютер или мобильное устройство.
2.7.2. В продуктивном режиме — с момента поступления денежных средств на счет
Лицензиара.
2.8. Права на использование Программного продукта считаются предоставленными
Пользователю:
2.8.1. В демонстрационном режиме — в момент установки Клиентского приложения
на компьютер или мобильное устройство.
2.8.2. В продуктивном режиме — в момент направления Пользователю на
электронную почту письма с регистрационным ключом.
2.9. Право использования Программного продукта предоставляется как на территории
Российской Федерации, так и на территории всех иных стран мира, если не
противоречит национальному законодательству этих стран.
2.10. Требования к компьютерам (оборудованию), необходимому для функционирования
Клиентского приложения размещены в сети Интернет на сайте Лицензиара.
3. СТОИМОСТЬ И ПОРЯДОК ОПЛАТЫ
3.1. Размер вознаграждения Лицензиара за предоставление Пользователю прав на
продуктивное использование Программного продукта размещен на Сайте
Лицензиара.
3.2. Вознаграждение Лицензиара за предоставление прав продуктивного использования
Программного продукта не облагаются НДС на основании подпункта 26 пункта 2
статьи 149 Налогового кодекса РФ.
3.3. Оплата предоставленных прав за продуктивное использование Программного
продукта по настоящему Соглашению производится Пользователем в форме
ежегодных платежей.
3.4. Способ оплаты по Соглашению: безналичное перечисление Пользователем
денежных средств в валюте Российской Федерации (рубль) на расчетный счет
Лицензиара способами, обозначенными на Сайте Лицензиара. При этом обязанность
Пользователя в части оплаты вознаграждения по Соглашению считается
исполненной со дня зачисления денежных средств банком на счет Лицензиара.
3.5. Лицензиар имеет право на одностороннее изменение условий и размера
вознаграждения по настоящему Соглашению. Актуальный размер вознаграждения
публикуется на Сайте Лицензиара.
4. СРОК ДЕЙСТВИЯ СОГЛАШЕНИЯ
4.1. Настоящее Соглашение вступает в силу с момента его заключения в соответствии с
п.2.7.
4.2. Срок предоставления права продуктивного использования Программного продукта в
соответствии с Соглашением составляет 1 (Один) год с момента авторизации
Пользователя посредством Регистрационного ключа. Соглашение считается
Соглашение считается
заключенным на тех же условиях на новый срок, равный 1 (Одному) году, при
условии осуществления Пользователем полной оплаты за продление права
продуктивного использования Программного продукта. Количество пролонгаций не
ограничивается.
4.3. Предоставление права демонстрационного использования Программного продукта
не ограничен по сроку.
4.4. Расторжение настоящего Соглашения возможно в соответствии с условиями,
указанным в действующем законодательстве РФ.
5. ПРАВА И ОБЯЗАННОСТИ СТОРОН
5.1. Пользователь обязуется:
5.1.1. Соблюдать права Лицензиара на Программный продукт и не использовать
Программный продукт иными способами кроме тех, что предусмотрены
настоящим Соглашением.
5.1.2. Не предпринимать попыток получения исходного кода Программного
продукта для дальнейшего его использования, а также не извлекать материалы
базы данных.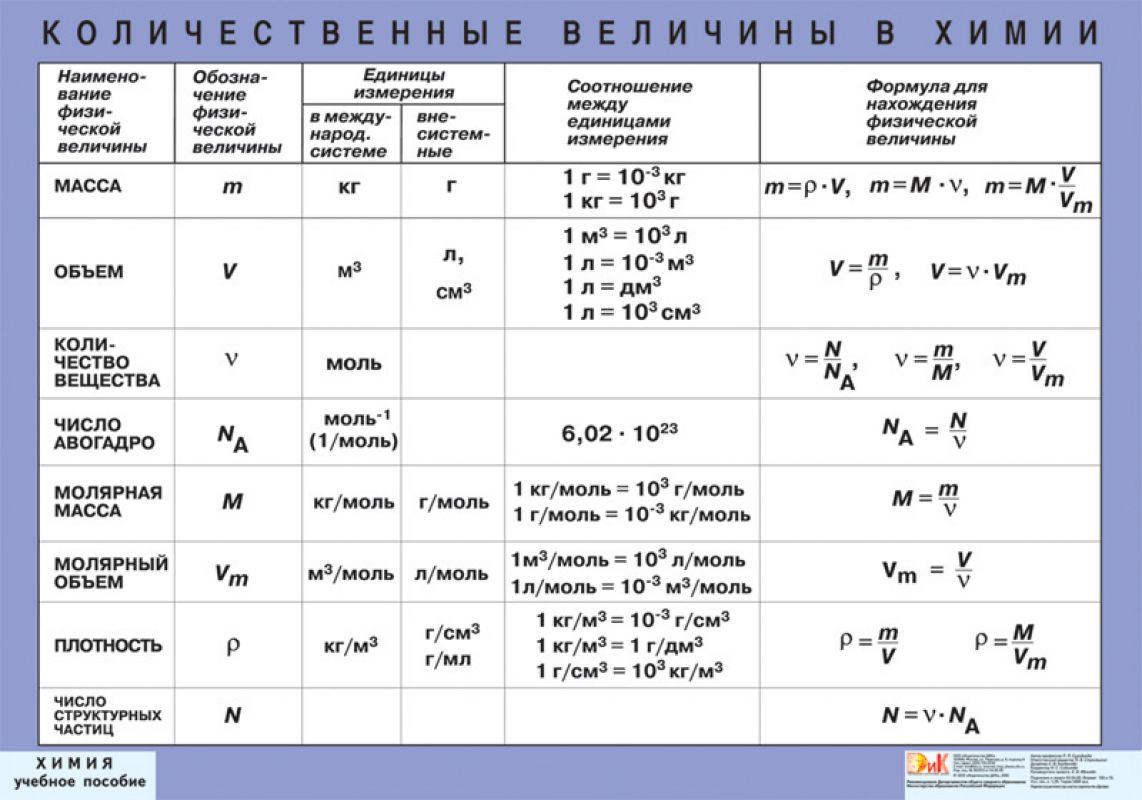
5.1.3. Своевременно уплачивать Лицензиару вознаграждение за предоставление
Пользователю права продуктивного использования Программного продукта в
порядке и сроки, установленные настоящим Соглашением.
5.1.4. Указывать достоверную информацию, в том числе свой адрес электронной
почты и иные данные, запрашиваемые Лицензиаром. При этом в случае
указания Пользователем недостоверной информации, все возможные риски,
которые могут возникнуть в связи с выполнением настоящего Соглашения,
Пользователь принимает на себя.
5.1.5. Строго придерживаться и не нарушать условий Соглашения, а также
обеспечить конфиденциальность коммерческой и технической информации
Лицензиара.
5.1.6. Не устанавливать Программный продукт на компьютерах (оборудованиях), не
соответствующих техническим требованиям для функционирования
Программного продукта.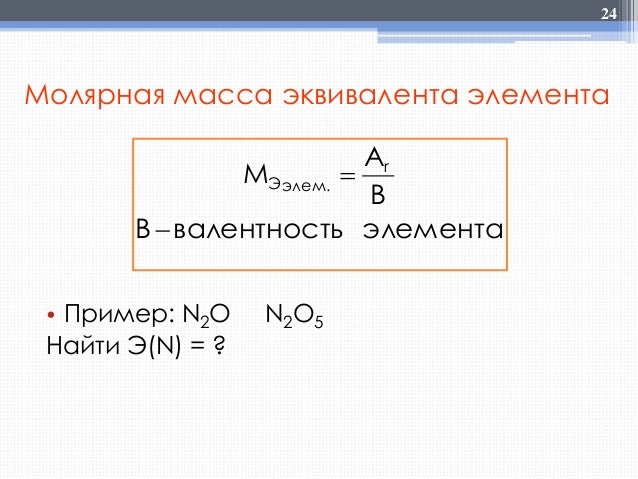
5.1.7. Заботиться о том, чтобы права Лицензиара на Программный продукт не были
нарушены третьими лицами на территории действия настоящего Соглашения,
и обязан сообщить Лицензиару обо всех ставших ему известными
нарушениях.
5.2. Пользователь вправе:
5.2.1. Использовать Программный продукт только посредством установки (записи)
Клиентского приложения Программного продукта на компьютер или
мобильное устройство и его настройки для осуществления ознакомительного
или образовательного процесса с помощью базы данных.
5.2.2. Использовать Программный продукт для любых целей Пользователя, за
исключением ограничений, определенных Соглашением.
5.3. Лицензиар обязуется:
5.3.1. Обеспечить технические условия функционирования Серверной части и
Клиентского приложения для использования Программного продукта
Пользователем, в том числе обеспечить возможность получения и/или
предоставить дистрибутив (установочные файлы) Клиентского приложения, с
помощью которого осуществляется использование Программного продукта.
5.3.2. Защищать данные Пользователя, которые стали известны Лицензиару в связи
с исполнением Сторонами своих обязательств в соответствии с настоящим
Соглашением.
5.3.3. Уведомлять Пользователя о невозможности использования Программного
продукта в связи с выполнением сервисных работ не менее чем за 48 (Сорок
восемь) часов путем отправки сообщения на электронную почту, указанную
при регистрации.
5.3.4. Воздерживаться от каких-либо действий, способных затруднить
осуществление Пользователя предоставленного ему права использования
Программного продукта в установленных Соглашением пределах.
5.3.5. Предоставлять новые версии (обновления) Программного продукта путем их
размещения в сети Интернет на сайте Лицензиара либо в системе Google Play
с возможностью скачивания.
5. 3.6. Информировать Пользователя о новых версиях (обновлениях) Программного
3.6. Информировать Пользователя о новых версиях (обновлениях) Программного
продукта, посредством направления уведомления на адрес электронной почты
Пользователя, указанный при регистрации и (или) авторизации на Сайте
Лицензиара.
5.3.7. Обеспечивать круглосуточный прием обращений в Службу поддержки по
адресу электронной почты: [email protected].
5.3.8. Осуществлять обработку поступивших обращений и консультации через
Службу поддержки, в период с 5:00 до 14:00 по московскому времени с
понедельника по пятницу, за исключением выходных и праздничных дней.
5.4. Лицензиар вправе:
5.4.1. Производить сервисные работы, которые могут повлечь перерывы в работе
Клиентского приложения.
5.4.2. В случае нарушения Пользователем условий (способов) использования прав
на Программный продукт в соответствии с настоящим Соглашением, лишить
Пользователя лицензии на использование прав на Программный продукт
путем закрытия доступа к Программному продукту.
5.4.3. Изменять в одностороннем порядке условия настоящего Соглашения в
установленном порядке.
5.4.4. Отказаться в одностороннем порядке от исполнения Соглашения в порядке,
предусмотренном применимым правом и/или настоящим Соглашением;
5.4.5. Осуществлять иные права, предусмотренные применимым правом, а также
настоящим Соглашением.
6. ПОРЯДОК ИСПОЛЬЗОВАНИЯ ПРОГРАММНОГО ПРОДУКТА
6.1. Пользователю для использования Программного продукта предлагается установить
(записать в память ЭВМ) и запустить Клиентское приложение Лицензиара,
экземпляр которого скачивается Пользователем самостоятельно одним из
следующих способов:
в сети Интернет на сайте Лицензиара;
в системе Google Play;
с флэш-накопителя, предоставленного Лицензиаром (опция).
6.2. После установки (записи в память ЭВМ) и запуска Клиентского приложения
Лицензиара Пользователю предоставляется право использования Программного
продукта в Демонстрационном режиме.
6.3. Для использования Программного продукта в Продуктивном режиме Пользователю
необходимо в Клиентском приложении ввести Регистрационный ключ, который
Лицензиар направляет Пользователю на адрес электронной почты, указанный на
Сайте Лицензиара в запросе на предоставление доступа. Пользователь
самостоятельно осуществляет использование Программного продукта путем запуска
и настройки Клиентского приложения.
6.4. Программный продукт предоставляется Пользователю по принципу «as is» («как
есть»), что подразумевает: Пользователю известны важнейшие функциональные
свойства продукта, в отношении которого предоставляются права на использование,
Пользователь несет риск соответствия Программного продукта его желаниям и
потребностям, а также риск соответствия условий и объема предоставляемых прав
своим желаниям и потребностям. Лицензиар не несет ответственность за какие-либо
Лицензиар не несет ответственность за какие-либо
убытки или ущерб, независимо от причин их возникновения (включая особый,
случайный или косвенный ущерб; убытки, связанные с недополученной прибылью,
прерыванием коммерческой или производственной деятельности, утратой деловой
информации, небрежностью, или какие-либо иные убытки), возникшие вследствие
использования или невозможности использования Программного продукта.
6.5. Программный продукт предназначен для личных, образовательных и иных не
связанных с осуществлением предпринимательской деятельности нужд физических
лиц. Использование Программного продукта в коммерческих целях не допускается.
7. ОТВЕТСТВЕННОСТЬ СТОРОН
7.1. За невыполнение или ненадлежащее выполнение обязательств по настоящему
Соглашению Стороны несут ответственность в соответствии с действующим
законодательством, если иное не установлено Соглашением.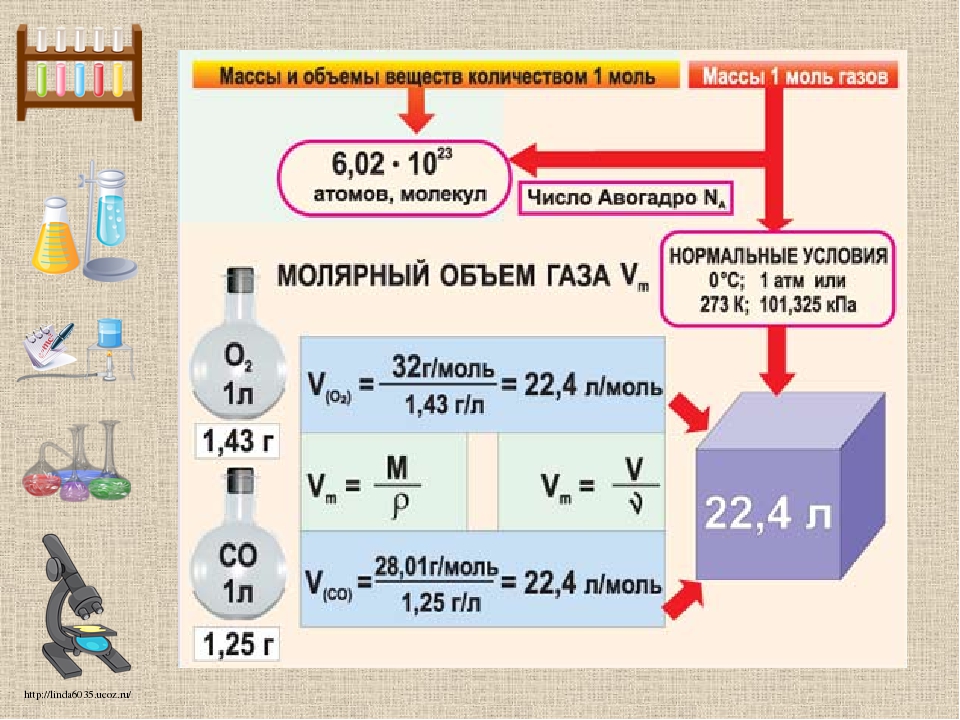
7.2. Стороны освобождаются от ответственности за неисполнение (ненадлежащее
исполнение) Соглашения, если такое неисполнение (ненадлежащее исполнение)
явилось следствием действий обстоятельств непреодолимой силы, наступление
которых Стороны не могли предвидеть и предотвратить. Сторона, для которой
надлежащее исполнение обязательства стало невозможным ввиду действия
обстоятельств непреодолимой силы, обязана незамедлительно уведомить об этом
другую Сторону. Стороны вправе ссылаться на действия обстоятельств
непреодолимой силы лишь при условии, что они сделали все возможное в целях
предотвращения и/или минимизации негативных последствий действия указанных
обстоятельств.
7.3. Лицензиар не гарантирует абсолютную бесперебойность использования
Программного продукта и не дает гарантию того, что произведенные третьими
лицами программы для ЭВМ или любые другие средства, используемые при работе
Программного продукта, абсолютно защищены от компьютерных вирусов и других
вредоносных компонентов. Лицензиар обязуется осуществить все разумные меры
Лицензиар обязуется осуществить все разумные меры
для защиты информации Пользователя и обеспечения бесперебойного
использования Программного продукта.
7.4. Пользователь самостоятельно отвечает за содержание информации, передаваемой им
или иным лицом по сети Интернет и хранимой в памяти сервера Лицензиара, в том
числе за ее достоверность и правомерность ее хранения и распространения.
7.5. В случае привлечения Лицензиара к ответственности или наложения на него
взыскания в связи с допущенными Пользователем нарушениями прав третьих лиц, а
равно установленных законодательством запретов или ограничений, Пользователь
обязан в полном объеме возместить убытки Лицензиара.
7.6. В случае нарушения Пользователем условий и ограничений настоящего
Соглашения, он является нарушителем исключительного права на Программный
продукт.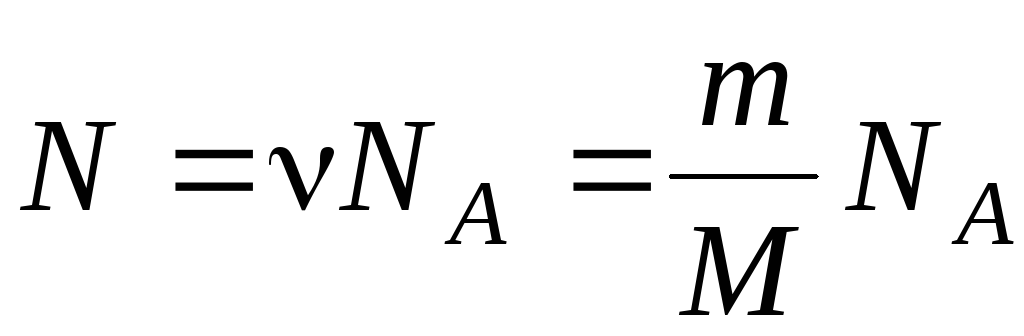 За нарушение авторских прав на Программный продукт Пользователь несет
За нарушение авторских прав на Программный продукт Пользователь несет
ответственность в соответствии с законодательством Российской Федерации.
7.7. Совокупная кумулятивная ответственность Лицензиара перед Пользователем в
отношении требований любого рода, возникающих из настоящего Соглашения, не
будет превышать сумму вознаграждения по данному Соглашению, фактически
выплаченного Пользователем за Программный продукт, в отношении которого
возникло требование, в течение 12 (двенадцати) месяцев, предшествующих
возникновению требования. Вышеуказанные ограничения ответственности
применяются даже в том случае, если с помощью вышеуказанного способа защиты
права не удается добиться его основной цели.
8. ПЕРСОНАЛЬНЫЕ ДАННЫЕ
8.1. Информация, предоставленная Пользователем является конфиденциальной.
8. 2. Предоставляя свои персональные данные Лицензиару, Пользователь соглашается на
2. Предоставляя свои персональные данные Лицензиару, Пользователь соглашается на
их обработку, как с использованием средств автоматизации, так и без использования
средств автоматизации, в частности сбор, хранение, передачу третьим лицам и
использование информации Лицензиаром в целях исполнения обязательств перед
Пользователем в соответствии с настоящим Соглашением; получения
Пользователем персонализированной рекламы; проверки, исследования и анализа
данных, позволяющих поддерживать и улучшать Программный продукт.
8.3. Лицензиар обязуется не разглашать полученную от Пользователя информацию. Не
считается нарушением предоставление Лицензиаром информации, в том числе
персональные данные Пользователя третьим лицам, действующим на основании
договора с Лицензиаром, в целях исполнения настоящего Соглашения.
8.4. Не считается нарушением обязательств по неразглашению информации
Не считается нарушением обязательств по неразглашению информации
предоставленной Пользователем, в том числе персональные данные Пользователя, в
целях обеспечения соблюдения требований действующего законодательства
Российской Федерации (в том числе в целях предупреждения и/или пресечения
незаконных и/или противоправных действий Пользователей).
8.5. Пользователь не имеет права передавать свои Логин и Пароль третьим лицам.
8.6. Пользователь обязуется обеспечивать конфиденциальность своего Логина и Пароля
и несет ответственность за использование Логина и Пароля третьими лицами. Ни
при каких обстоятельствах Лицензиар не несет ответственность за использование
третьими лицами Логина и пароля Пользователя.
8.7. В случае несанкционированного доступа к логину и паролю и/или персональной
странице Пользователя, или распространения логина и пароля Пользователь обязан
незамедлительно сообщить об этом Лицензиару посредством заполнения формы
обратной связи, представленной на Сайте.
8.8. Лицензиар не несет ответственности за использование кем бы то ни было
общедоступных персональных данных Пользователей.
9. ИСКЛЮЧИТЕЛЬНЫЕ ПРАВА НА КОНТЕНТ
9.1. Все объекты, размещенные на Сайте и в Программном продукте, в том числе
элементы дизайна, текст, графические изображения, иллюстрации, видео, скрипты,
программы, музыка, звуки и другие объекты и их подборки (далее — Контент),
являются объектами исключительных прав Лицензиара, все права на эти объекты
защищены.
9.2. Кроме случаев, установленных настоящим Соглашением, а также действующим
законодательством Российской Федерации, Контент не может быть скопирован
(воспроизведен), переработан, распространен, отображен во фрейме, опубликован,
скачан, передан, продан или иным способом использован целиком или по частям без
предварительного разрешения правообладателя, кроме случаев, когда
правообладатель явным образом выразил свое согласие на свободное использование
Контента любым лицом.
9.3. Использование Пользователем Контента, доступ к которому получен исключительно
для личного некоммерческого использования, допускается при условии сохранения
всех знаков авторства или других уведомлений об авторстве, сохранения имени
автора в неизменном виде, сохранении произведения в неизменном виде.
9.4. Любое использование Контента, кроме разрешенного в настоящем Соглашении или
в случае явно выраженного согласия правообладателя на такое использование, без
предварительного письменного разрешения правообладателя, категорически
запрещено.
10. ПРОЧИЕ УСЛОВИЯ
10.1. Все споры и разногласия, возникающие в связи с исполнением и (или) толкованием
настоящего Соглашения, разрешаются Сторонами путем переговоров. При
невозможности урегулирования Сторонами возникших разногласий путем
переговоров, спор подлежит разрешению в арбитражном суде по месту нахождения
ответчика с обязательным соблюдением претензионного порядка урегулирования
споров и разногласий. Срок ответа на претензию 30 (тридцать) календарных дней с
момента ее поступления в письменной форме или в электронном виде.
10.2. Ни одно из положений настоящего Соглашения не является и не может
рассматриваться как передача (отчуждение) исключительных прав на
интеллектуальную собственность Лицензиара.
10.3. В случае поступления от Пользователя замечаний к Программному продукту,
предоставляемому в рамках настоящего Соглашения, такие замечания подлежат
рассмотрению Лицензиаром по его желанию и необязательны для учета.
10.4. Условия настоящего Соглашения распространяются на последующие версии
Программного продукта, которые являются его обновлениями. Заключения иных
соглашений в отношении обновлений Программного продукта не требуется.
10.5. Во всем ином, что не предусмотрено настоящим Соглашением, Стороны
руководствуются действующим законодательством РФ.
11. АДРЕС, РЕКВИЗИТЫ ЛИЦЕНЗИАРА
ООО «АЛЕКТА»
Юридический адрес: 630090, г. Новосибирск, Проспект академика Лаврентьева 2/2.
Почтовый адрес: 630090, г. Новосибирск, Проспект академика Лаврентьева 2/2.
ОГРН 1025403657135
ИНН 5408128408
КПП 540801001
ОКВЭД 72.19, 62.01, 62.02, 68.20.2;
ОКПО 26335100;
ОКАТО 50401384000;
ОКФС 16;
ОКОПФ 65.
E-mail: [email protected]
Урок 8. количество вещества. молярная масса. молярный объём газазакон авогадро — Химия — 8 класс
Количество вещества. Молярная масса. Молярный объем газа. Закон Авогадро
Из курса физики мы знаем о таких физических величинах, как масса, объём и плотность. При помощи этих величин легко характеризовать вещества. Например, мы идём в магазин и покупаем 1 кг сахара или литровую бутылку минеральной воды. Но оказывается, что этих величин недостаточно, если необходимо рассмотреть вещество с точки зрения числа частиц. Сколько молекул сахара содержится в 1 кг сахара? А сколько молекул воды в литровой бутылке? А в одной капле? Ответ на этот вопрос можно получить, если знать ещё об одной физической величине, которая называется количество вещества. Точное число молекул посчитать сложно, но если считать не штуками, а порциями, то задача упрощается. Например, мы никогда не покупаем в магазине спички поштучно, но купив одну порцию спичек – коробок, знаем, что там 100 штук. И салфетки мы тоже поштучно не покупаем, но купив пачку салфеток, то есть порцию, мы точно будем знать, сколько штук салфеток мы купили.
Количество вещества – это порция вещества с определённым числом структурных частиц. Количество вещества принято обозначать греческой буквой ν [ню]. В системе СИ единица измерения количества вещества называется моль. Один моль вещества содержит столько же структурных частиц, сколько атомов содержится в 12 г углерода, а именно 6*1023 частиц. Это количество является постоянной величиной и называется «постоянная Авогадро». Количество вещества можно определить как отношение числа структурных частиц к числу частиц в одном моле вещества.
Например, количество вещества, которое соответствует 3*1023 атомов железа можно легко рассчитать по этой формуле.
Преобразовав исходную формулу легко определить число структурных частиц по известному количеству вещества: N = v * NA
Своё имя эта постоянная получила в честь Амедео Авогадро, который в 1811 году сделал предположение, которое затем подтвердилось экспериментально и теперь носит имя Закона Авогадро. Закон Авогадро: «в равных объёмах различных газов при одинаковых условиях (температура и давление) содержится одинаковое количество молекул».
Из закона Авогадро следует, что при одинаковых условиях массы газов, содержащие одинаковое число структурных частиц, будут занимать одинаковый объём. При давлении 1 атмосфера и температуре 0 градусов Цельсия 1 моль любого газа занимает объём равный 22, 4 л. Этот объём называется молярный объём. А условия – нормальные условия. Молярный объём обозначается Vm, показывает объём газа количеством 1 моль. При нормальных условиях является постоянной величиной.
При нормальных условиях количество вещества это отношение объёма к молярному объему.
По этой формуле можно определить объём вещества, если известно его количество: V = ν * Vm
Массу вещества количеством 1 моль называют молярной массой, обозначают буквой M. Молярная масса численно равна относительной молекулярной массе. Единица измерения молярной массы г/моль.
Зная массу вещества, легко определить количество вещества.
Найдём количество вещества 5,6 г железа.
Чтобы найти массу вещества по известному количеству преобразуем формулу: m = ν * M
Справочный материал
• Количество вещества ν [ню] – это физическая величина, характеризующая количество однотипных структурных единиц (любые частицы, из которых состоит вещество – атомы, молекулы, ионы и т.д), содержащихся в веществе. Единица измерения количества вещества в Международной системе единиц (СИ) – моль.
• Моль – это единица измерения количества вещества. Один моль вещества содержит столько же структурных частиц, сколько атомов содержится в 12 г углерода.
• Молярная масса (M) – масса вещества количеством один моль. Единица измерения г/моль.
• Нормальные условия (н.у.) – физические условия, определяемые давлением 101325 Па (нормальная атмосфера) и температурой 273,15 К (0 °С).
• Молярный объём (Vm) – объём вещества количеством один моль. Единица измерения л/моль; при н.у. Vm = 22,4 л/моль
• Закон Авогадро – в равных объёмах различных газов при одинаковых условиях (температура и давление) содержится одинаковое количество молекул.
• Постоянная Авогадро (NA) показывает число структурных частиц в веществе количеством один моль.
Основные Химические формулы для решения задач.
| № | Количественные характеристики вещества | Обозначение | Единицы измерения | Формула для расчета |
|---|---|---|---|---|
| 1 | Плотность вещества | ρ | кг/м³ | ρ = m / V(Массу делим на объем вещества) |
| 2 | Относительная атомная масса элемента | Аr | — | Ar = ma / u см. в периодической система химических элементов |
| 3 | Атомная единица массы | u а.е.м. | кг | u = 1/12 * ma (12C) const = 1.66*10-27 |
| 4 | Масса атома (абсолютная) | ma | кг | ma = Ar * u |
| 5 | Относительная молекулярная (формульная) масса вещества | Mr | — | Mr (AxBy)=m(AB) / u Mr(AxBy)=x*Ar(A) + y*Ar(B) |
| 6 | Масса молекулы (формульной единицы) | m M | кг | mM = Mr*u |
| 7 | Количество вещества | n | моль | n=m/M n=N/NA n=V/VM |
| 8 | Молярная масса (масса 1 моль вещества) | M | г/моль | M=m/n M=Mr M=Ar (для простых веществ) |
| 9 | Масса вещества | m | г (кг) | m=M*n m=ρ*V |
| 10 | Число структурных единиц | N | атомов, молекул, ионов, частиц, формульных единиц (Ф.Е.) | N=NA*n |
| 11 | Молярный объем — число 1 моль ГАЗООБРАЗНОГО вещества в нормальных условиях (н.у.) | VM | л/моль | const=22,4 |
| 12 | Объем газа при н.у. | V | л | V=VM*n V=m/ρ |
| 13 | Постоянная Авогадро | NA | частиц/моль | const=6,02*1023 |
| 14 | Массовая доля вещества (омега) | ωЭ/В | % | ωЭ/В = (Ar(э) * k) / Mr(В) |
| Формула | Название кислоты | Формула кислотного остатка | Название кислотного остатка |
|---|---|---|---|
| HF | Фтороводород, плавиковая | F— | Фторид |
| HCl | Хлороводород, соляная | Cl— | Хлорид |
| HBr | Бромоводород | Br— | Бромид |
| HI | Йодоводород | I— | Йодид |
| h3S | Сероводород | S2- | Сульфид |
| HCN | Циановодородная | CN— | Цианид |
| HNO2 | Азотистая | NO2— | Нитрит |
| HNO3 | Азотная | NO3— | Нитрат |
| h4PO4 | Ортофосфорная | PO43- | Фосфат |
| h4AsO4 | Мышьяковая | AsO43- | Арсенат |
| h3SO3 | Сернистая | SO32- | Сульфит |
| h3SO4 | Серная | SO42- | Сульфат |
| h3CO3 | Угольная | CO32- | Карбонат |
| h3SiO3 | Кремниевая | SiO32- | Силикат |
| h3CrO4 | Хромовая | CrO42- | Хромат |
| h3Cr2O7 | Дихромовая | Cr2O72- | Дихромат |
| HMnO4 | Марганцовая | MnO4— | Перманганат |
| HClO | Хлорноватистая | ClO— | Гипохлорит |
| HClO2 | Хлористая | ClO2— | Хлорит |
| HClO3 | Хлорноватая | ClO3— | Хлорат |
| HClO4 | Хлорная | ClO4— | Перхлорат |
| HCOOH | Метановая, муравьиная | HCOO— | Формиат |
| Ch4COOH | Этановая, уксусная | Ch4COO— | Ацетат |
| h4C2O4 | Этандиовая, щавелевая | C2O42- | Оксалат |
Нажмите на картинку для увеличения
ХИМИЧЕСКИЙ ЭКВИВАЛЕНТ
Эквивалент – это реальная или условная
частица, которая в кислотно-основных реакциях присоединяет
(или отдает) один ион Н+ или ОН–, в
окислительно-восстановительных реакциях принимает (или отдает) один
электрон, реагирует с одним атомом водорода или с одним эквивалентом
другого вещества. Например, рассмотрим следующую
реакцию:
H3PO4 + 2KOH
®
K2HPO4 + 2H2O.
В
ходе этой реакции только два атома водорода замещаются на атомы
калия, иначе, в реакцию вступают два иона Н+ (кислота
проявляет основность 2). Тогда по определению эквивалентом
H3PO4
будет являться условная частица 1/2H3PO4,
т.к. если одна молекула H3PO4
предоставляет два иона Н+, то один ион Н+ дает
половина молекулы H3PO4.
С
другой стороны, на реакцию с одной молекулой ортофосфорной кислотой
щелочь отдает два иона ОН–, следовательно, один ион ОН–
потребуется на взаимодействие с 1/2 молекулы кислоты. Эквивалентом
кислоты является условная частица 1/2Н3РО4, а
эквивалентом щелочи частица КОН.
Число, показывающее, какая часть молекулы
или другой частицы вещества соответствует эквиваленту, называется
фактором эквивалентности (fЭ).
Фактор эквивалентности – это безразмерная величина, которая меньше,
либо равна 1. Формулы расчета фактора эквивалентности приведены в
таблице 1.1.
Таким образом, сочетая фактор эквивалентности и формульную единицу
вещества, можно составить формулу эквивалента какой-либо частицы,
где фактор эквивалентности записывается как химический коэффициент
перед формулой частицы:
|
|
В примере, рассмотренном выше, фактор эквивалентности для кислоты,
соответственно, равен 1/2, а для щелочи КОН равен 1.
Между H3PO4
и КОН также могут происходить и другие реакции. При этом кислота
будет иметь разные значения фактора эквивалентности:
H3PO4 + 3KOH
®
K3PO4 + 3H2O fЭ(H3PO4)
= 1/3
H3PO4 + KOH
®
KН2PO4
+ H2O fЭ(H3PO4)
= 1.
Следует учитывать, что эквивалент одного
и того же вещества может меняться в зависимости от того, в какую
реакцию оно вступает. Эквивалент элемента также может быть
различным в зависимости от вида соединения, в состав которого он
входит. Эквивалентом может являться как сама молекула или
какая-либо другая формульная единица вещества, так и ее часть.
Таблица 1.1 –
Расчет фактора эквивалентности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример.
Определите фактор эквивалентности и эквивалент у солей: а)
ZnCl2, б) КНСО3, в)
(MgOH)2SO4.
Решение: Для расчетов воспользуемся формулами, приведенными в
таблице 1.1.
а)
ZnCl2 (средняя соль):
.
fЭ(ZnCl2)
= 1/2, поэтому эквивалентом ZnCl2
является частица 1/2ZnCl2.
б) КНСО3
(кислая соль):
.
fЭ(КНСО3) = 1,
поэтому эквивалентом КНСО3 является частица КНСО3.
в) (MgOH)2SO4
(основная соль):
.
fЭ(
(MgOH)2SO4
) = 1/2, поэтому эквивалентом
(MgOH)2SO4
является частица 1/2(MgOH)2SO4.
Эквивалент, как частица, может быть охарактеризован молярной массой
(молярным объемом) и определенным
количеством вещества
nэ.
Молярная масса эквивалента (МЭ)
– это масса одного моль эквивалента. Она равна
произведению молярной массы вещества на фактор эквивалентности:
Молярная масса
эквивалента имеет размерность «г/моль».
Молярная масса эквивалента сложного
вещества равна сумме молярных масс эквивалентов образующих его
составных частей, например:
|
|
Газообразные вещества помимо молярной массы эквивалента имеют
молярный объем эквивалента (
или VЭ)
– объем, занимаемый молярной массой эквивалента или объем одного
моль эквивалента. Размерность «л/моль».
При н.у. получаем:
Закон
эквивалентов был открыт в 1792 г. И. Рихтером.
Современная формулировка закона:
вещества реагируют и образуются согласно их эквивалентам.
Все вещества в уравнении реакции связаны законом эквивалентов,
поэтому:
|
|
Из закона эквивалентов следует, что массы (или объемы)
реагирующих и образующихся веществ пропорциональны молярным массам
(молярным объемам) их эквивалентов. Для любых двух веществ,
связанных законом эквивалентов, можно записать:
где m1 и
m2 – массы реагентов и
(или) продуктов реакции, г;
, –
молярные массы эквивалентов реагентов и (или) продуктов реакции,
г/моль;
V1, V2
– объемы реагентов и (или) продуктов реакции, л;
,–
молярные объемы эквивалентов реагентов и (или) продуктов реакции,
л/моль.
Л.А. Яковишин
|
Космическая химия
Современным астрономам известно около трех с половиной тысяч экзопланет, которые находятся от нас на расстоянии от четырех до двадцати восьми тысяч световых лет. Некоторые из них очень похожи на Землю. Попасть на какую-нибудь из них в обозримом будущем будет сложно — разве что человечество совершит огромный технологический скачок. Тем не менее, экзопланеты уже сегодня представляют собой огромный интерес с точки зрения астрохимии. Об этом — наш новый материал, написанный в партнерстве с Уральским федеральным университетом.
Основную часть вещества Вселенной (если говорить о барионном веществе) составляет водород — около 75 процентов. На втором месте идет гелий (около 23 процентов). Однако в космосе можно найти самые разнообразные химические элементы и даже сложные молекулярные соединения, включая органические. Изучением процессов образования и взаимодействия химических соединений в космосе занимается астрохимия. Представителям этой специальности очень интересно исследовать экзопланеты, потому что на них могут реализоваться самые разные сценарии, которые приведут к появлению необычных соединений.
Радуга на службе у астрономов
Основным инструментом получения информации о химическом составе отдаленных объектов является спектроскопия. Она использует тот факт, что атомы химических элементов (или молекулы соединений) могут излучать или поглощать свет только на определенных частотах, отвечающих переходам системы между различными уровнями энергии. В результате формируется спектр излучения (или поглощения), по которому можно однозначно определить вещество. Это как отпечатки пальцев, только для атомов.
Наглядным примером разложения света в спектр является радуга. Нам переходы от одного цвета к другому кажутся плавными и непрерывными, а на самом деле некоторых цветов в радуге нет, потому что определенные длины волн поглощаются содержащимися в Солнце водородом и гелием. Кстати, гелий впервые открыли именно по наблюдению за спектром Солнца (поэтому он и называется «гелий», от др.-греч. ἥλιος — «солнце»), а в лаборатории его выделили только через 27 лет. Это был первый успешный пример использования спектроскопии для изучения звезд.
Фраунгоферовы линии поглощения на фоне непрерывного спектра фотосферы Солнца.
Wikimedia commons
В простейшем случае атома водорода спектр излучения представляет собой серию линий, отвечающих переходам между уровнями с различными значениями главного квантового числа n (эта картина хорошо описывается формулой Ридберга). Самой известной и удобной для наблюдений является линия Бальмера Hα, имеющая длину волны 656 нанометров и лежащая в области видимого спектра. Например, на этой линии астрономы наблюдают за далекими галактиками и распознают облака молекулярного газа, которые в большинстве своем как раз состоят из водорода. Следующие серии линий (Пашена, Брэкета, Пфунда и так далее) целиком лежат в инфракрасном диапазоне, а серия Лаймана расположена в области ультрафиолетового излучения. Это несколько усложняет наблюдения.
В то же время у молекул сложных соединений есть другой способ излучать кванты света, в каком-то смысле даже более простой. Связан он с тем, что вращательная энергия молекулы квантуется, что также позволяет им излучать в линиях (кроме того, они могут излучать и непрерывный спектр). Энергия таких квантов света не очень большая, поэтому их частота лежит уже в радиодиапазоне. Один из самых простых вращательных спектров принадлежит молекуле угарного газа CO, по ней астрономы тоже часто распознают облака холодного газа, когда не могут разглядеть в них водород. Методы радиоастрономии позволили найти в молекулярных облаках также метанол, этанол, формальдегид, синильную и муравьиную кислоту, а также другие элементы. Например, именно с помощью радиотелескопа ученые обнаружили алкоголь в хвосте кометы Лавджоя.
Что можно найти в космосе
Проще всего методы спектроскопии применять для изучения химического состава звезд. В этом случае астрономы исследуют спектры поглощения, а не излучения элементов. В самом деле, свет от них легко наблюдать, особенно в видимом диапазоне. Правда, химический состав звезд сам по себе обычно не очень интересен: по большей части они состоят из водорода и гелия с небольшой примесью тяжелых элементов.
Более тяжелые элементы образуются во вспышках сверхновых, и их тоже можно наблюдать. Например, некоторые ученые утверждают, что после недавно зарегистрированного слияния двух нейтронных звезд должны были образоваться огромные количества золота, платины и других элементов из последних строк таблицы Менделеева. Но так или иначе, очень сложные или органические соединения в звездах существовать не могут, поскольку они обязательно распадаются из-за больших температур.
Другое дело — облака холодного межзвездного газа. Они очень сильно разрежены и излучают гораздо слабее, чем звезды, зато сами по себе гораздо больше. И состав у них более интересный. В них можно найти огромное число самых разных молекул — начиная от простых двухатомных и заканчивая относительно сложными многоатомными органическими соединениями. Среди сложных молекул особенно стоит выделить «пребиотические» соединения, например, аминоацетонитрил, который может участвовать в образовании глицина, простейшей аминокислоты. Некоторые ученые предполагают, что в молекулярных облаках может образоваться и рибоза, один из основных кирпичиков органической жизни. Если такие соединения попадут в благоприятные условия, это уже будет ступенькой для возникновения жизни.
Изображение туманности Ориона M42, полученное Коуровской астрономической обсерваторией УрФУ. Красный цвет — это результат рекомбинации в линии излучения Hα на длине волны 656,3 нанометра.
УрФУ
Чуть ближе к планетам
К сожалению, для определения химического состава экзопланет метод спектроскопии применить сложно. Все-таки для этого нужно зарегистрировать свет от них, а звезда, вокруг которой вращается планета, мешает это сделать, поскольку она светит намного ярче. Пытаться наблюдать за такой системой — все равно что смотреть на свет спички на фоне прожектора.
Тем не менее, некоторую информацию об экзопланете можно получить, не измеряя спектр ее излучения напрямую. Хитрость заключается в следующем. Если у планеты есть атмосфера, она должна поглощать часть излучения звезды, причем в разных спектральных диапазонах по-разному. Грубо говоря, на одной длине волны планета будет казаться чуть меньше, а на другой длине — чуть больше. Это позволяет строить предположения о свойствах атмосферы, в частности, о ее химическом составе. Такой способ наблюдений особенно хорошо работает на горячих, близко расположенных к звездам планетах, потому что их радиус проще измерять.
Кроме того, химический состав планеты должен быть связан с составом газопылевого облака, из которого она образовалась. Например, в облаках с большим отношением концентраций атомов углерода к атомам кислорода образующиеся планеты будут состоять преимущественно из карбонатов. С другой стороны, химический состав звезды, образовавшейся из такого облака, также должен отражать его состав. Это позволяет строить некоторые предположения, основываясь на изучении спектра одной только звезды. Так, астрономы из Йельского университета проанализировали данные о химическом составе 850 звезд и обнаружили, что в 60 процентах систем концентрации магния и кремния в звезде указывают на то, что рядом с ней могут находиться каменистые планеты, похожие на Землю. В оставшихся 40 процентах химический состав звезд говорит нам о том, что состав планет вокруг них должен существенно отличаться от земного.
Вообще говоря, в последнее время прямая спектроскопия особенно горячих планет на фоне тусклых звезд все-таки стала возможна благодаря возросшей точности измерительных приборов. В этом случае уже можно искать в их свете следы различных химических элементов и сложных соединений. Например, с помощью ИК-спектрографа CONICA, установленного на телескопе VLT и объединенного с системой адаптивной оптики NAOS, ученым удалось измерить спектр экзопланеты HR 8799 c, которая вращается вокруг белого карлика и разогрета так сильно, что сама излучает свет. В частности, из анализа ее спектра следовало, что в атмосфере планеты содержится меньше, чем ожидалось, метана и угарного газа. Также совсем недавно астрономы измерили спектр другого «горячего юпитера», обнаружив в его атмосфере оксид титана. Тем не менее, непосредственные измерения спектра менее горячих каменистых планет (на которых существование жизни более вероятно) до сих пор представляет большую сложность.
Изображение системы HR 8799. Планета HR 8799 c находится в правом верхнем углу
Jason Wang et al / NASA NExSS, W. M. Keck Observatory
Состав планеты можно также определить косвенно, рассчитав ее плотность. Для этого нужно знать радиус и массу планеты. Массу можно найти, наблюдая за гравитационным взаимодействием планеты со звездой или другими планетами, а радиус оценить по изменению блеска звезды при прохождении планеты по ее диску. Очевидно, газовые планеты должны иметь меньшую плотность по сравнению с каменистыми. Например, средняя плотность Земли равна примерно 5,5 грамма на кубический сантиметр, и для поиска обитаемых планет астрономы ориентируются именно на это значение. В то же время плотность «самого рыхлого горячего юпитера» составляет 0,1 грамма на кубический сантиметр.
«Невозможные» соединения
С другой стороны, экзопланеты можно изучать и вовсе не выходя из лаборатории, как бы странно это ни звучало. Речь идет о моделировании (в основном численном) химических и физических процессов, которые должны на них происходить. Из-за того что условия на экзопланетах могут быть самые экзотические (простите за каламбур), вещества на них могут образоваться тоже самые необычные, «невозможные» в привычных для нас условиях.
Большинство открытых экзопланет относится к «горячим юпитерам» — сильно разогретым из-за небольшого расстояния до звезды газовым гигантам. Конечно, это не обязательно означает, что такие планеты преобладают в звездных системах, просто их легко найти. Температура атмосферы таких гигантов может превышать тысячу градусов по Цельсию, и состоит она в основном из паров силикатов и железа (при такой температуре оно начинает испаряться, но еще не кипит). В то же время, давление внутри этих планет должно достигать огромных значений, при которых водород и другие привычные для нас газы переходят в твердые агрегатные состояния. Эксперименты по моделированию подобных экстремальных условий проводятся давно, однако впервые металлический водород удалось получить только в январе этого года.
С другой стороны, в недрах каменистых планет также могут достигаться большие давления и температуры, а «зоопарк» химических элементов там может быть даже больше. Например, по некоторым оценкам, давление внутри каменистых планет с массами в несколько земных масс может достигать значений до 30 миллионов атмосфер (внутри Земли давление не превышает четырех миллионов атмосфер). С помощью компьютерного моделирования удалось выяснить, что в таких условиях начинают образовываться экзотические соединения магния, кремния и кислорода (которых в составе каменистых планет должно быть много). Например, при давлениях более 20 миллионов атмосфер стабильными становится не только привычный для нас оксид кремния SiO2, но и «невозможные» SiO и SiO3. Также интересно, что в недрах особенно массивных планет (до 20 масс Земли) может образоваться MgSi3O12 — оксид, обладающий свойствами электрического проводника.
Нестандартные условия можно моделировать не только на компьютере, но и в лаборатории, пусть и не для такого большого диапазона давлений и температур. С помощью алмазной наковальни можно получить давления до 10 миллионов атмосфер, как раз соответствующие условиям в недрах планет, а разогреть образец до высоких температур можно лазером. Эксперименты по моделированию таких условий действительно активно проводятся в последнее время. Например, в 2015 году группа ученых, в состав которой входили российские исследователи, экспериментально наблюдали образование пероксида магния MgO2 уже при давлениях около 1,6 тысяч атмосфер и температурах больше двух тысяч градусов Цельсия. Подробно об исследованиях поведения вещества при больших давлениях вы можете прочитать в другом нашем материале.
Рентгеновская спектроскопия образца, состоящего из атомов магния и кислорода, при давлении около десяти тысяч атмосфер и температуре около двух тысяч Кельвин. Пунктиром выделена область с повышенным содержанием кислорода.
S. Lobanov et al / Scientific Reports
***
В УрФУ есть группа ученых, которые занимаются изучением протопланетного вещества в дальнем космосе и Солнечной системе. Мы попросили ведущего специалиста Коуровской астрономической обсерватории УрФУ Вадима Крушинского более подробно рассказать об изучении экзопланет.
N +1: Зачем мы изучаем экзопланеты?
Вадим Крушинский: Еще 25 лет назад нам было известно о существовании единственной планетной системы — Солнечной. Теперь же мы уверены в том, что планеты есть у огромного числа звезд, возможно, почти у каждой звезды во Вселенной. Прогресс технологий получения и обработки данных привел к тому, что найти свою экзопланету может даже продвинутый любитель астрономии. Открытие очередного «горячего юпитера» — это открытие целой планетной системы, просто мы видим только самую заметную ее часть. Планеты меньшего размера или находящиеся дальше от родительской звезды открываются гораздо реже, это эффект наблюдательной селекции.
Вадим Крушинский в составе группы ученых Уральского федерального университета работает над проектом по исследованию протопланетного вещества в дальнем космосе, Солнечной системе и на Земле.
Это один из шести прорывных научных проектов университета, им занимается стратегическая академическая единица (САЕ) — Институт естественных наук и математики УрФУ — вместе с академическими и индустриальными партнерами из России и других стран. От успеха исследователей зависят позиции университета в российских и международных рейтингах, прежде всего в предметных.
Единичный эксперимент не позволяет делать выводы о наблюдаемом явлении. Эксперимент должен быть повторен многократно и независимо. Каждая открытая экзопланетная система — это отдельный независимый эксперимент. И чем больше их известно, тем надежнее прослеживаются общие законы происхождения и эволюции планетных систем. Нам необходимо набирать статистику!
Что же можно узнать об экзопланетах, наблюдая за ними с таких больших расстояний?
Прежде всего нужно определить свойства родительской звезды. Это позволяет вычислить размеры планет, их массу и радиусы орбит. Зная светимость родительской звезды и радиус орбиты, можно оценить температуру поверхности экзопланеты. Кроме того, атмосферы планет имеют разную прозрачность в разных спектральных диапазонах (об этом писал еще Ломоносов). Для наблюдателя это выглядит как разный диаметр планеты при наблюдении в разных фильтрах. Это позволяет обнаружить атмосферу и оценить ее толщину и плотность. Свет родительской звезды, прошедший через атмосферу планеты во время транзита, несет информацию о составе ее атмосферы. А во время вторичного затмения, когда планета прячется за свою звезду, мы можем наблюдать изменения спектра, связанные с отражением от атмосферы и поверхности планеты. Так же, как и у Луны, у экзопланет можно наблюдать фазы. Если изменения блеска системы, вызванные этим эффектом, не постоянны, то это говорит о том, что альбедо планеты (способность отражать свет) меняется. Например, вследствие движения облаков в ее атмосфере.
Свойства экзопланет должны быть связаны со свойствами родительских облаков. Изучая материю на стадии звездообразования, мы вносим вклад в понимание эволюции планетных систем. К сожалению, Земля претерпела значительные изменения в ходе истории, и уже мало напоминает то протопланетное вещество, из которого когда-то родилась. Но совсем рядом с нами летают метеориты и кометы. Некоторые из них даже падают на Землю и попадают в лаборатории. До каких-то из них могут долететь космические аппараты. Прямо перед нами отличный объект исследования! Остается только доказать, что и другие планетные системы эволюционировали так же, как наша.
Можно ли найти жизнь на других планетах?
Для этого нужно обнаружить биомаркеры — проявления жизнедеятельности организмов. Лучшим биомаркером были бы передачи условного «Первого канала», но сойдет и наличие кислорода. Без жизни кислород на Земле был бы связан и исчез из атмосферы за десяток тысяч лет. Обнаружив кислород в атмосферах экзопланет, мы сможем утверждать, что не одиноки во Вселенной. Как его найти, было рассказано выше. Но вот только приборов с достаточной чувствительностью пока нет. Прорыв в этом направлении ожидается после запуска космического телескопа им. Джеймса Вебба (JWST).
Что могут сделать в этой области ученые из России и, в частности, из УрФУ?
Несмотря на то, что в плане изучения экзопланет Россия отстает от остального научного сообщества, у нас есть возможность сократить это отставание. Относительно малобюджетные программы по поиску экзопланетных систем (пилотный проект KPS Коуровской обсерватории УрФУ) позволят сделать первый шаг и помогут в наборе данных для статистического анализа. Высокоточные фотометрические измерения можно проводить и на имеющемся оборудовании, это позволяет искать атмосферы у некоторых экзопланет. Спектральные наблюдения во время транзитов и вторичных затмений относительно доступны для крупнейших телескопов России. Что нужно сделать для старта этих программ — найти заинтересованных людей и оплатить их работу. Немного вложиться в оборудование.
Второе направление — моделирование и интерпретация наблюдаемых эффектов. Это может быть как теоретическая работа, так и экспериментальная — исследование поведения и свойств образцов в условиях космоса и сравнение с наблюдаемыми эффектами. Для этого необходимо создание установки, имитирующей условия космического пространства. В качестве образцов можно использовать метеориты из коллекции УрФУ.
Дмитрий Трунин
Расчет количества продукта по данным раствора другого вещества.
Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:
1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:
* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:
* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:
После чего следует рассчитать массу растворенного вещества по формуле 1.
2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:
3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.
4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:
Если в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.
5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:
Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:
Рассмотрим пару примеров расчетных задач по этой теме.
Пример 1
Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.
Решение:
1) Рассчитаем массу чистой серной кислоты:
m(H2SO4) = w(H2SO4) ∙ m(р-ра H2SO4)/100% = 147 г ∙ 20% /100% = 29,4 г
2) Рассчитаем количество вещества (моль) серной кислоты:
n(H2SO4) = m(H2SO4) / M(H2SO4) = 29,4 г/98 г/моль = 0,3 моль.
3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:
H2SO4 + Ba(NO3)2 = BaSO4↓ + 2HNO3
4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:
n(BaSO4)/n(H2SO4) = k(BaSO4)/k(H2SO4), где n — количество вещества, а k — коэффициент в уравнении реакции,
можем записать:
n(BaSO4) = n(H2SO4) ∙ k(H2SO4)/k(BaSO4) = 0,3 моль ∙ 1/1 = 0,3 моль
5) Тогда масса осадка, т.е. сульфата бария, может быть рассчитана следующим образом:
m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г
Пример 2
Какой объем газа (н.у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.
Решение:
1) Рассчитаем массу раствора соляной кислоты:
m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г
Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:
m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г
2) Рассчитаем количество вещества хлороводорода:
n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;
3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:
FeS + 2HCl = FeCl2 + H2S↑
4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:
n(HCl)/n(H2S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и H2S соответственно
Следовательно:
n(H2S) = n(HCl)/2 = 0,5/2 = 0,25 моль
5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = Vm ∙ n(газа), тогда:
V(H2S) = Vm ∙ n(H2S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л
Расчет молей и числа частиц Учебное пособие по химии
Ключевые концепции
- 1 моль любого вещества содержит 6.022 × 10 23 частиц.
- 6,022 × 10 23 известно как число Авогадро или константа Авогадро и обозначается символом N A (1)
- N = n × N A
N = количество частиц в веществе
n = количество вещества в молях (моль)
N A = Число Авогардро = 6.022 × 10 23 частиц моль -1
N = n × (6.022 × 10 23 )
- Чтобы найти количество частиц N в веществе:
N = n × N A
N = n × (6.022 × 10 23 )
- Чтобы найти количество вещества в молях, n:
n = N ÷ N A
n = N ÷ (6.022 × 10 23 )
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Вывод и применение уравнения N = n × N
A
1 моль чистого вещества содержит N A частиц, или 6,022 × 10 23 частиц.
| Представьте себе ящик, содержащий 1 моль газообразного гелия, He (г), представленный на диаграмме справа как X Эта коробка содержит:
|
|
| Представьте, что теперь мы добавляем еще один моль газообразного гелия, He (g), также представленный на диаграмме справа как X Эта коробка теперь содержит:
|
Число атомов гелия (N) в коробке равно числу молей атомов гелия (n), умноженному на число Авогадро (N A ):
N = n × N A
Мы можем использовать это математическое уравнение (математическую формулу или математическое выражение), чтобы найти количество частиц (N) в любом количестве вещества (n), просто умножив количество в молях (n) на число Авогадро (N A ), как показано в таблице ниже:
| n (количество вещества в молях) | × | N A (номер Авогадро) | = | N (количество частиц) |
|---|---|---|---|---|
| 1 моль | × | 6.022 × 10 23 | = | 6.022 × 10 23 частиц |
| 2 моль | × | 6.022 × 10 23 | = | 1,204 × 10 24 частиц |
| 10 моль | × | 6.022 × 10 23 | = | 6.022 × 10 24 частиц |
| 0,5 моль | × | 6.022 × 10 23 | = | 3,011 × 10 23 частиц |
Математическое уравнение N = n × N A может использоваться для определения количества атомов, ионов или молекул в любом количестве (в молях) атомов, ионов или молекул:
- 10 молей из атомов гелия = 10 × (6.022 × 10 23 ) = 6.022 × 10 24 атомов гелия
- 10 моль ионов натрия = 10 × (6.022 × 10 23 ) = 6.022 × 10 24 ионов натрия
- 10 моль молекул воды = 10 × (6.022 × 10 23 ) = 6.022 × 10 24 молекул воды
Математическое уравнение N = n × N A также можно использовать для определения количества атомов каждого элемента в известном количестве (в молях) соединения.
Для соединения с молекулярной формулой X a Y b :
- 1 молекула соединения X a Y b содержит
a атомов элемента X
b атомов элемента Y
- 1 моль соединения X a Y b содержит
a молей атомов элемента X
b молей атомов элемента Y
- н-моль соединения X a Y b содержит
(n × a ) молей атомов элемента X
(n × b ) молей атомов элемента Y
- н-моль соединения X a Y b содержит
(n × a ) × N A атомов элемента X
(n × b ) × N A атомов элемента Y
- н-моль соединения X a Y b содержит
(n × a ) × 6.022 × 10 23 атомов элемента X
(n × b ) × 6.022 × 10 23 атомов элемента Y
Рассмотрим n моль каждого из этих соединений с общей формулой XY 2 .
В таблице ниже указано количество молей каждого элемента, присутствующего в соединении, а также показано, как рассчитать количество атомов каждого присутствующего элемента:
| XY 2 формула | n (XY 2 ) моль XY 2 | n (X) моль атомов элемента X | N (X) Число атомов X | n (Y) моль атомов элемента Y | N (Y) Число атомов Y |
|---|---|---|---|---|---|
| CO 2 | n | n × 1 = n моль атомов C | n × N A атомов C | n × 2 = 2n моль атомов O | 2n × N A атомов O |
| НЕТ 2 | n | n × 1 = n моль атомов азота | n × N A атомов N | n × 2 = 2n моль атомов O | 2n × N A атомов O |
| SCl 2 | n | n × 1 = n моль атомов S | n × N A атомов S | n × 2 = 2n моль атомов Cl | 2n × N A атомов Cl |
Если у нас есть, например, 5 моль каждого соединения, указанного выше, то мы можем вычислить моль каждого элемента и количество атомов каждого элемента, как показано в таблице ниже:
| XY 2 формула | n (XY 2 ) моль XY 2 | n (X) моль атомов элемента X | N (X) Число атомов X | n (Y) моль атомов элемента Y | N (Y) Число атомов Y |
|---|---|---|---|---|---|
| CO 2 | 5 | 5 × 1 = 5 моль C | 5 × N A Атомы углерода | 5 × 2 = 10 моль O | 10 × N A Атомов O |
| НЕТ 2 | 5 | 5 × 1 = 5 моль N | 5 × N A N атомов | 5 × 2 = 10 моль O | 10 × N A Атомов O |
| SCl 2 | 5 | 5 × 1 = 5 моль S | 5 × N A Атомы S | 5 × 2 = 10 моль Cl | 10 × N A Атомы Cl |
Получение и применение уравнения n = N ÷ N
A (n = N / N A )
В предыдущем разделе мы вывели математическое уравнение:
N = n × N A
где:
N = количество частиц, присутствующих в веществе
n = количество частиц в веществе в молях (моль)
N A = число Авогадро = 6.022 × 10 23 частиц моль -1
Если мы разделим обе части этого уравнения на N A , как показано ниже:
Мы приходим к уравнению, показанному ниже:
, который мы можем использовать для нахождения молей вещества, если мы знаем, сколько частиц вещества присутствует.
Уравнение n = N / N A можно использовать для расчета:
- моль атомов (n), если вы знаете количество присутствующих атомов (N)
- моль ионов (n), если вы знаете количество присутствующих ионов (N)
- моль молекул (n), если вы знаете количество присутствующих молекул (N)
В таблице ниже показано вычисление молей (n) с учетом количества частиц (N):
| N (количество частиц) | ÷ | N A (номер Авогадро) | = | n (моль частиц) |
|---|---|---|---|---|
| (3.011 × 10 23 ) | ÷ | (6,022 × 10 23 ) | = | 0,5 моль |
| (1,204 × 10 24 ) | ÷ | (6,022 × 10 23 ) | = | 2 моль |
| (6,022 × 10 24 ) | ÷ | (6.022 × 10 23 ) | = | 10 моль |
Если известно, что вещество содержит 3,011 × 10 23 частиц вещества, то количество молей вещества будет (3,011 × 10 23 ) ÷ (6,022 × 10 23 ) = 0,5 моль.
3,011 × 10 23 атома гелия = 0,5 моль из атомов гелия
3,011 × 10 23 ионы натрия = 0.5 моль ионов натрия
3,011 × 10 23 молекулы воды = 0,5 моль молекул воды
Уравнение n = N ÷ N A также можно использовать для определения количества в молях атомов или ионов в соединении, если вы знаете как молекулярную формулу соединения, так и количество присутствующих молекул соединения.
Для молекул N соединения общей формулы X a Y b :
Рассмотрим следующие примеры, в которых 1.927 × 10 24 молекул соединения общей формулы X 2 Y присутствуют
| X 2 Y формула | Н (X 2 Y) (количество X 2 молекул Y) | N (X) (число атомов элемента X) | n (X) (моль атомов X) | N (Y) (число атомов элемента Y) | n (Y) (моль атомов Y) |
|---|---|---|---|---|---|
| H 2 S | 1.927 × 10 24 | 2 × (1.927 × 10 24 ) атомов H = 3.854 × 10 24 атомов H | (3.854 × 10 24 ) ÷ (6.022 × 10 23 ) = 6.4 моль атомов H | 1 × (1.927 × 10 24 ) атомов S = 1.927 × 10 24 атомов S | (1,927 × 10 24 ) ÷ (6,022 × 10 23 ) = 3,2 моль атомов S |
| H 2 O | 1.927 × 10 24 | 2 × (1.927 × 10 24 ) атомов H = 3.854 × 10 24 атомов H | (3.854 × 10 24 ) ÷ (6.022 × 10 23 ) = 6.4 моль атомов H | 1 × (1.927 × 10 24 ) атомов O = 1.927 × 10 24 атомов O | (1,927 × 10 24 ) ÷ (6,022 × 10 23 ) = 3,2 моль атомов O |
Рабочие примеры расчета числа Крота-Авогадро
Расчет количества частиц (N = n × N
A )
Вопрос 1: Вычислите количество молекул аммиака, NH 3 , в 3.5 моль аммиака.
Решение:
- Что вас просят сделать?
Рассчитайте количество молекул аммиака.
N (аммиак) = количество молекул аммиака =?
- Какая информация (данные) дана в вопросе?
Молекулярная формуладля аммиака: NH 3
n = количество молекул аммиака в молях = 3.5 моль
- Какая связь между молями частиц и количеством частиц?
N = n × N A где N = количество частиц n = моль частиц N A = Число Авогадро = 6,022 × 10 23 - Напишите уравнение связи между молями молекул аммиака и числом молекул аммиака:
N (NH 3 ) = n (NH 3 ) × N A
= n (NH 3 ) × (6.022 х 10 23 )
- Заменить в значениях и решить для N:
Н (NH 3 ) = 3,5 × (6,022 × 10 23 )
= 2,1 × 10 24 молекул аммиака (NH 3 )
Вопрос 2. Определите количество атомов водорода в 1,5 молях воды, H 2 O, молекул.
Решение:
- Что вас просят сделать?
Рассчитайте количество атомов водорода.
N (атомов H) = количество атомов водорода =?
- Какая информация (данные) дана в вопросе?
Молекулярная формула воды: H 2 O
n (H 2 молекул O) = моль молекул воды = 1,5 моль
- Какая связь между молями частиц и числом частиц?
N = n × N A где N = количество частиц n = моль частиц N A = Число Авогадро = 6.022 × 10 23 - Какая связь между молями молекул воды и числом атомов водорода?
(i) соотношение между молями молекул воды и числом молекул воды:
N (H 2 молекул O) = n (H 2 молекул O) × N A где N (H 2 молекул O) ) = количество молекул воды n (H 2 молекул O) = моль молекул воды = 1.5 моль N A = число Авогадро = 6,022 × 10 23 N (H 2 молекул O) = 1,5 × (6,022 × 10 23 ) = 9,033 × 10 23 (ii) соотношение между числом атомов водорода и числом молекул воды:
Из молекулярной формулы мы видим, что 1 молекула воды состоит из 2 атомов водорода и 1 атома кислорода.
N (атомы H) = 2 × N (H 2 молекул O)
- Подставьте значения и решите уравнение:
N (атомы H) = 2 × N (H 2 молекул O)
= 2 × (9,033 × 10 23 )
= 1,8 × 10 24 атомов водорода
Расчет количества молей вещества (n = N / N
A )
Вопрос 1. Проба газа содержит 4,4 × 10 24 молекул углекислого газа.
Сколько молей молекул углекислого газа присутствует в образце?
Решение:
- Что вас просят сделать?
Вычислить моль молекул углекислого газа.
n (молекулы углекислого газа) = моль молекул углекислого газа =?
- Какая информация (данные) дана в вопросе?
N (молекулы углекислого газа) = количество молекул углекислого газа = 4.4 × 10 24 молекул углекислого газа - Какова связь между молями (n) частиц и числом (N) частиц?
n = N
N Aгде N A = число Авогадро = 6,022 × 10 23 - Какова взаимосвязь между молями (n) молекул диоксида углерода и количеством (N) молекул диоксида углерода?
n (молекулы углекислого газа) = N (молекулы углекислого газа)
N A= N (молекулы углекислого газа)
6.022 × 10 23 - Подставьте значения в уравнение и решите:
n (молекулы углекислого газа) = N (молекулы углекислого газа)
6.022 × 10 23= 4.4 × 10 24
6.022 × 10 23= 7,3 молекулы углекислого газа
Вопрос 2. Образец содержит 2,4 × 10 22 молекул газообразного кислорода (O 2 ).
Сколько молей атомов кислорода присутствует в образце?
Решение:
- Что вас просят сделать?
Вычислить моль атомов кислорода.
n (атомы O) = моль атомов кислорода =?
- Какая информация (данные) дана в вопросе?
Молекулярная формула газообразного кислорода: O 2
N (O 2 молекул) = количество молекул кислорода (O 2 ) = 2,4 × 10 22
- Какова связь между молями (n) частиц и числом (N) частиц?
n = N
N A, где N A = число Авогадро = 6.022 × 10 23 - Какова взаимосвязь между молями атомов кислорода n (атомы O) и числом молекул кислорода N (O 2 молекул)?
(i) соотношение между молями атомов кислорода n (атомы O) и числом атомов кислорода N (атомы O)
n (атомы O) = N (атомы O)
N Aгде N A = Число Авогадро = 6.022 × 10 23 (ii) соотношение между числом молекул кислорода N (O 2 молекул) и числом атомов кислорода N (атомов O):
Одна молекула O 2 состоит из 2 атомов кислорода
количество атомов кислорода = 2 × количество молекул кислорода
N (атомов O) = 2 × N (O 2 молекул)
(iii) соотношение между молями атомов кислорода n (атомы O) и числом молекул кислорода N (O 2 молекул):
n (атомы O) = N (атомы O)
N A= 2 × N (O 2 молекул)
N A= 2 × N (O 2 молекул)
6.022 × 10 23 - Подставьте значения и решите уравнение:
n (атомы O) = 2 × N (O 2 молекул)
6.022 × 10 23= 2 × (2.4 × 10 22 )
6.022 × 10 23= 0,080 моль атомов кислорода
Решение проблем с использованием родинок, количества частиц и числа Авогадро
Проблема: Биолог изучал действие хлорид-ионов, Cl — , на клетки растений.Бо попросил химика Криса приготовить 1 литр раствора, содержащего 0,50 моль хлорид-ионов, Cl —, растворенных в воде.
Раствор также должен содержать равное количество ионов натрия Na + и ионов калия K + .
Крис делает раствор, растворяя немного хлорида натрия, NaCl, и хлорида калия, KCl, в 1 литре деионизированной воды.
Сколько ионов натрия присутствует в растворе?
Решение проблемы с использованием модели StoPGoPS для решения проблем:
| СТОП! | Сформулируйте вопрос. | Что вас просят сделать? Определите количество ионов натрия в растворе. N (ионы натрия) = количество ионов натрия =? | ||||||
| ПАУЗА! | План. | Какой химический принцип вам нужно будет применить? Применить стехоиметрию (N = n × N A ) Какую информацию (данные) вам предоставили? Шаг 1: Рассчитайте количество ионов Cl — в растворе.
Шаг 2: Напишите уравнение для взаимосвязи между количеством ионов хлорида, ионов натрия и ионов калия.
Шаг 3: Решите уравнение, чтобы определить количество ионов натрия. | ||||||
| Вперед! | Следуйте плану. | Шаг 1: Рассчитайте количество ионов Cl — в растворе.
Шаг 2: Напишите уравнение для взаимосвязи между количеством ионов хлорида, ионов натрия и ионов калия.
Шаг 3: Решите уравнение, чтобы определить количество ионов натрия.
| ||||||
| ПАУЗА! | Поразмышляйте над правдоподобием. | Вы ответили на заданный вопрос? Да, мы определили количество ионов натрия в растворе. Разумно ли ваше решение вопроса?
| ||||||
| СТОП! | Назовите решение. | Какое количество ионов натрия в растворе? 1,5 × 10 23 ионов натрия в растворе |
Сноски:
(1) Число Авогадро иногда называют числом Лошмидта и обозначают символом L.
Массово-мольные вычисления Учебное пособие по химии
Ключевые концепции
- 1 моль чистого вещества имеет массу, равную его молекулярной массе (1) , выраженной в граммах.
Это известно как молярная масса M и измеряется в г моль -1 (граммы на моль вещества).
- Связь между молярной массой, массой и молями может быть выражена математическим уравнением, как показано ниже:
г моль -1 = г ÷ моль
молярная масса = масса ÷ моль
M = m ÷ n
где:
M = молярная масса чистого вещества (измеряется в г · моль -1 )
m = масса чистого вещества (измеряется в граммах, г)
n = количество чистого вещества (измеряется в молях, моль) - Это математическое уравнение можно преобразовать в следующее:
п = м ÷ М
моль = масса ÷ молярная массам = n × M
масса = моль × молярная масса - Для расчета молей чистого вещества: n = m ÷ M
- Для расчета массы чистого вещества: m = n × M
- Для расчета молярной массы чистого вещества: M = m ÷ n
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Расчет массы чистого вещества (m = нМ)
1 моль чистого вещества определяется как имеющий массу в граммах, равную его относительной молекулярной массе.
Эта величина известна как молярная масса (символ M).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах.
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г-моль -1 )
Или, масса 1 моля = M (г-моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| название | молекулярная формула | относительная молекулярная масса | молярная масса (г моль -1 ) | масса 1 моль (г) |
|---|---|---|---|---|
| газообразный гелий | He | 4.003 | 4,003 г моль -1 | 4,003 г |
| газообразный кислород | O 2 | 2 × 16,00 = 32,00 | 32,00 г моль -1 | 32,00 г |
| углекислый газ | CO 2 | 12,01 + (2 × 16,00) = 44,01 | 44,01 г моль -1 | 44,01 г |
| жидкая вода | H 2 O | (2 × 1,008) + 16.00 = 18,016 | 18,016 г моль -1 | 18,016 г |
Из таблицы видно, что 1 моль воды имеет массу 18,016 грамма, что не очень много (о массе воды в паре маленьких кубиков льда, которые вы бы сделали в своей семейной морозильной камере).
Но что, если бы у вас было 10 молей воды? Какой будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 моль воды = 10 × масса 1 моля воды
масса 10 молей воды = 10 × 18.016 = 180,16 г (примерно масса воды, которую можно налить в небольшой стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем вычислить массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, поскольку масса 1 моля воды в граммах называется его молярной массой, мы можем записать:
масса воды = моль воды × молярная масса воды
В таблице ниже сравнивается масса различных количеств воды в молях, и данные представлены в виде графика справа:
| |||||||||||||||||||||||||||||||||||
| Из данных в таблице мы можем обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна количеству молей вещества, умноженных на массу 1 моля вещества: масса = моль × масса 1 моля и поскольку масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль) масса (г) = моль × молярная масса (г моль -1 ) м = n × M | На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для прямой выглядит следующим образом: y = наклон × x где y — масса воды (г) и x — моль воды (моль) и наклон (уклон) линии = вертикальный подъем ÷ горизонтальный ход = 270.24 г ÷ 15 моль = 18,016 г моль -1 = молярная масса воды (г моль -1 ) Итак, уравнение для этой строки: масса (H 2 O) = молярная масса (H 2 O) × моль (H 2 O) В целом: масса (г) = молярная масса (г-моль -1 ) × моль (моль) |
Выполните следующие действия, чтобы рассчитать массу чистого вещества с учетом количества вещества в молях:
- Извлеките данные из вопроса:
масса = m =? (единицы — граммы)
родинок = n = запишите, что вам говорят в вопросе
молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) - Проверить единицы на соответствие и при необходимости преобразовать:
Количество вещества должно быть в молях (моль)!
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в километрах (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль). - Напишите математическое уравнение (математическую формулу):
масса = моль × молярная масса
или
м = n × M - Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Расчет молей чистого вещества (n = m / M)
В приведенном выше обсуждении мы обнаружили, что можем рассчитать массу чистого вещества, используя моль и молярную массу вещества:
масса (г) = моль (моль) × молярная масса (г-моль -1 )
Как бы мы вычислили количество молей чистого вещества, если бы мы знали массу вещества?
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на молярную массу:
| масса | = | моль × |
| молярная масса | |
моль = масса ÷ молярная масса
п = м ÷ М
(b) Мы могли бы использовать некоторую логику:
| мы знаем массу в единицах | граммов (г) |
| мы знаем молярную массу в единицах | граммов на моль (г моль -1 ) |
| нам нужно найти моль в единицах | моль (моль) |
При рассмотрении единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 ».
молярная масса / масса = г моль -1 / г = моль -1
Если мы перевернем это вверх дном (с математической точки зрения, возьмем обратную величину), мы получим величину с единицами измерения «моль», что нам и нужно:
масса / молярная масса = г / г моль -1 = моль
так
моль = масса ÷ молярная масса
п = м ÷ М
Выполните следующие действия, чтобы рассчитать количество чистого вещества в молях с учетом массы вещества:
- Извлеките данные из вопроса:
масса = m = запишите, что вам говорят в вопросе
молей = n =? (единицы моль)
молярная масса = M = запишите, что вам говорят в вопросе (единицы измерения: г моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) - Проверить единицы на соответствие и при необходимости преобразовать:
Масса должна быть в граммах!
Если масса указана в миллиграммах (мг), разделите ее на 1000, чтобы получить массу в граммах (г).
Если масса дана в микрограммах (мкг), разделите ее на 1000000, чтобы получить массу в граммах (г).
Если масса указана в килограммах (кг), умножьте ее на 1000, чтобы получить массу в граммах (г). - Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
п = м ÷ М - Подставьте значения и решите уравнение, чтобы найти количество молей веществ (моль).
Расчет молярной массы чистого вещества (M = m / n)
Что, если бы вы знали количество чистого вещества в молях и его массу?
Не могли бы вы вычислить его молярную массу?
Напомним, что масса = моль × молярная масса или m = n × M
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на моли:
| масса | = | |
| моль | |
молярная масса = масса ÷ моль
M = m ÷ n
(b) Мы могли бы использовать некоторую логику:
Изучая единицы измерения, мы видим, что, разделив массу в граммах на количество в молях, мы приходим к количеству единиц в граммах на моль (г · моль -1 ), которые являются единицами измерения молярной массы.
Следовательно, молярная масса (г · моль -1 ) = масса (г) ÷ моль (моль)
или вы можете написать
M = m × n
Выполните следующие действия, чтобы рассчитать молярную массу чистого вещества с учетом количества вещества в молях и массы вещества:
- Извлеките данные из вопроса:
масса = m = запишите, что вам говорят в вопросе
родинок = n = запишите, что вам говорят в вопросе
молярная масса = M =? (ед.гмоль -1 ) - Проверить единицы на соответствие и при необходимости преобразовать:
Масса должна быть в граммах (г)!
Количество, моль, должно быть в молях (моль)! - Напишите математическое уравнение (математическую формулу):
молярная масса = масса ÷ моль
или
M = m ÷ n - Подставьте значения и решите уравнение, чтобы найти молярную массу вещества в граммах на моль.
Рабочие примеры расчета массы, молей, молярной массы
Рабочий пример: масса = моль × молярная масса (m = n × M)
Рассчитайте массу 0,25 моля воды, H 2 O.
- Извлеките данные из вопроса:
моль = n = 0,25 моль
молярная масса = M = (2 × 1,008) + 16,00 = 18,016 г моль -1 (рассчитано с использованием периодической таблицы)
масса = m =? грамм - Проверить данные на соответствие:
Количество воды в молях (моль)? Да.
Преобразовывать это не нужно. - Напишите математическое уравнение (математическую формулу):
масса = моль × молярная масса
или
м = n × M - Подставьте значения в уравнение и решите для массы (г):
масса = m = 0,25 × 18,016 = 4,504 г
Работает Пример: моль = масса & разделить молярную массу (n = m / M)
Вычислите количество кислородного газа, O 2 , в молях, присутствующее в 124.5 г газообразного кислорода.
- Извлеките данные из вопроса:
масса = m = 124,5 г
молярная масса = M = 2 × 16,00 = 32,00 г моль -1 (рассчитано с использованием периодической таблицы)
молей = n =? моль - Проверить данные на соответствие:
Масса газообразного кислорода выражена в граммах (г)? Да.
Преобразовывать это не нужно. - Напишите математическое уравнение (математическую формулу):
моль = масса ÷ молярная масса
или
п = м ÷ М - Подставьте значения в уравнение и решите, чтобы найти количество молей газообразного кислорода:
моль = n = 124.5 ÷ 32,00 = 3,89 моль
Работает Пример: молярная масса = масса ÷ моль (M = m / n)
Вычислите молярную массу чистого вещества, если масса 1,75 моль вещества составляет 29,79 г.
- Извлеките данные из вопроса:
масса = m = 29,79 г
моль = n = 1,75 моль - Проверить данные на соответствие:
Масса в граммах (г)? Да.Нам не нужно это преобразовывать.
Количество вещества в молях (моль)? Да. Нам не нужно это преобразовывать. - Напишите уравнение:
молярная масса = масса ÷ моль
или
M = m ÷ n - Подставьте значения в уравнение и решите для молярной массы:
молярная масса = M = 29,79 ÷ 1,75 = 17,02 г моль -1
Решение задач с использованием молей, массы и молярной массы
Проблема: Карбонат кальция, CaCO 3 , является важным промышленным химическим веществом.У химика Криса есть нечистый образец карбоната кальция.
Масса загрязненного образца составляет 0,1250 кг, и он состоит из 87,00% (по массе) карбоната кальция.
Прежде чем Крис сможет использовать этот карбонат кальция в химической реакции, Крису необходимо знать количество в молях карбоната кальция, присутствующего в этом образце.
Рассчитайте количество карбоната кальция в молях, присутствующее в этом загрязненном образце карбоната кальция.
Решение проблемы с использованием модели StoPGoPS для решения проблем:
| СТОП! | Сформулируйте вопрос. | Что вас просят сделать? Рассчитать количество карбоната кальция в молях n (CaCO 3 ) = моль карбоната кальция =? моль |
| ПАУЗА! | План. | Какой химический принцип вам нужно будет применить? Применить стехоиметрию (n = m ÷ M) Какую информацию (данные) вам предоставили? Шаг 1: Напишите математическое уравнение для расчета молей карбоната кальция:
Шаг 2: Рассчитайте массу карбоната кальция в образце в килограммах (кг).
Шаг 3: Преобразовать массу карбоната кальция в килограммах (кг) в массу в граммах (г).
Шаг 4: Рассчитайте молярную массу карбоната кальция (используйте Периодическую таблицу, чтобы найти молярную массу каждого элемента):
Шаг 5: Подставьте значения m (CaCO 3 ) в граммах и M (CaCO 3 ) в г · моль -1 в математическое уравнение и решите для n (моль)
|
| Вперед! | Следуйте плану. | Шаг 1: Напишите математическое уравнение для расчета молей карбоната кальция:
Шаг 2: Рассчитайте массу карбоната кальция в образце в килограммах (кг).
Шаг 3: Преобразовать массу карбоната кальция в килограммах (кг) в массу в граммах (г).
Шаг 4: Рассчитайте молярную массу карбоната кальция (используйте Периодическую таблицу, чтобы найти молярную массу каждого элемента):
Шаг 5: Подставьте значения m (CaCO 3 ) в граммах и M (CaCO 3 ) в г · моль -1 в математическое уравнение и решите для n (моль)
|
| ПАУЗА! | Поразмышляйте над правдоподобием. | Вы ответили на заданный вопрос? Да, мы рассчитали количество молей карбоната кальция в образце. Разумно ли ваше решение вопроса?
|
| СТОП! | Назовите решение. | Сколько молей карбоната кальция присутствует в образце? n (CaCO 3 ) = 1,087 моль |
Сноски:
(1) Молекулярная масса также известна как молекулярная масса, формульная масса или формульная масса.
6.9. Расчет молекулярных формул для соединений
.
Цели обучения
- Поймите разницу между эмпирическими формулами и молекулярными формулами.
- Определите молекулярную формулу по процентному составу и молярной массе соединения.
Ниже мы видим два углевода: глюкозу и сахарозу. Сахароза почти в два раза больше глюкозы, хотя их эмпирические формулы очень похожи. Некоторые люди могут различать их по вкусу, но пробовать химические вещества — не лучший вариант.Лучший способ отличить глюкозу от сахарозы — это определить молярные массы — этот подход позволяет легко определить, какое соединение является каким.
Рисунок \ (\ PageIndex {1} \): (A) молекулярная структура глюкозы и (B) молекулярная структура сахарозы.
Молекулярные формулы
Молекулярные формулы определяют вид и количество атомов каждого элемента, присутствующего в молекулярном соединении. Во многих случаях молекулярная формула совпадает с эмпирической формулой. Химическая формула всегда будет некоторым целым числом, кратным (\ (n \)) эмпирической формулы (т.е. целые кратные индексов эмпирической формулы).
\ [\ text {Молекулярная формула} = n (\ text {Эмпирическая формула}) \]
следовательно
\ [n = \ dfrac {\ text {Молекулярная формула}} {\ text {Эмпирическая формула}} \]
Целочисленное кратное n также может быть получено делением молярной массы \ (MM \) соединения на эмпирическую формулу массы \ (EFM \) (молярная масса, представленная эмпирической формулой).
\ [n = \ dfrac {MM (молярная масса)} {EFM (молярная масса по эмпирической формуле)} \]
Таблица \ (\ PageIndex {1} \) показывает сравнение между эмпирической и молекулярной формулами метана, уксусной кислоты и глюкозы, а также различными значениями n.Молекулярная формула метана \ (\ ce {CH_4} \), и поскольку он содержит только один атом углерода, это также его эмпирическая формула. Однако иногда молекулярная формула представляет собой простое целое число, кратное эмпирической формуле. Уксусная кислота — это органическая кислота, которая является основным компонентом уксуса. Его молекулярная формула \ (\ ce {C_2H_4O_2} \). Глюкоза — это простой сахар, который клетки используют в качестве основного источника энергии. Его молекулярная формула \ (\ ce {C_6H_ {12} O_6} \). Структуры обеих молекул показаны на рисунке \ (\ PageIndex {2} \).Это очень разные соединения, но оба имеют одну и ту же эмпирическую формулу \ (\ ce {CH_2O} \).
| Название соединения | Молекулярная формула | Эмпирическая формула | n |
|---|---|---|---|
| Метан | \ (\ ce {CH_4} \) | \ (\ ce {CH_4} \) | 1 |
| Уксусная кислота | \ (\ ce {C_2H_4O_2} \) | \ (\ ce {CH_2O} \) | 2 |
| Глюкоза | \ (\ ce {C_6H_ {12} O_6} \) | \ (\ ce {CH_2O} \) | 6 |
Рисунок \ (\ PageIndex {2} \): уксусная кислота (слева) имеет молекулярную формулу \ (\ ce {C_2H_4O_2} \), а глюкоза (справа) имеет молекулярную формулу \ (\ ce {C_6H_ {12} О_6} \).Оба имеют эмпирическую формулу \ (\ ce {CH_2O} \).
Эмпирические формулы могут быть определены на основе процентного содержания соединения, как описано в разделе 6.8. Чтобы определить его молекулярную формулу, необходимо знать молярную массу соединения. Химики используют инструмент, называемый масс-спектрометром, для определения молярной массы соединений. Чтобы перейти от эмпирической формулы к молекулярной формуле, выполните следующие действия:
- Рассчитайте по эмпирической формуле молярной массы (EFM) .
- Разделите молярную массу соединения на молярную массу, полученную по эмпирической формуле. Результат должен быть целым числом или очень близким к целому числу.
- Умножьте все индексы в эмпирической формуле на целое число, полученное на шаге 2. Результатом является молекулярная формула.
Пример \ (\ PageIndex {1} \)
Эмпирическая формула соединения бора и водорода: \ (\ ce {BH_3} \). Его молярная масса равна \ (27,7 \: \ text {г / моль} \). Определите молекулярную формулу соединения.
Решение
| Шаги для решения проблем | Определите молекулярную формулу \ (\ ce {BH_3} \). |
|---|---|
| Определите «данную» информацию и то, что проблема просит вас «найти». | Дано: Эмпирическая формула \ (= \ ce {BH_3} \) Молярная масса \ (= 27,7 \: \ text {g / mol} \) Находка: химическая формула \ (=? \) |
| Рассчитайте массу по эмпирической формуле (EFM). | \ [\ text {Молярная масса по эмпирической формуле (EFM)} = 13,84 \: \ text {г / моль} \ nonumber \] |
| Разделите молярную массу соединения на массу, полученную по эмпирической формуле. Результат должен быть целым числом или очень близким к целому числу. | \ [\ frac {\ text {молярная масса}} {\ text {EFM}} = \ frac {27,7 г / моль} {13,84 г / моль} = 2 \ nonumber \] |
| Умножьте все нижние индексы в эмпирической формуле на целое число, полученное на шаге 2.Результатом является молекулярная формула. | \ [\ ce {BH_3} \ times 2 = \ ce {B_2H_6} \ nonumber \] |
| Напишите молекулярную формулу. | Молекулярная формула соединения \ (\ ce {B_2H_6} \). |
| Подумайте о своем результате. | Молярная масса молекулярной формулы соответствует молярной массе соединения. |
Упражнение \ (\ PageIndex {1} \)
Витамин С (аскорбиновая кислота) содержит 40.92% C, 4,58% H и 54,50% O по массе. Экспериментально определенная молекулярная масса составляет 176 а.е.м. Каковы эмпирические и химические формулы аскорбиновой кислоты?
- Ответ Эмпирическая формула
- C 3 H 4 O 3
- Ответ Молекулярная формула
- С 6 В 8 О 6
Сводка
- Описана процедура, позволяющая вычислить точную молекулярную формулу соединения.
Материалы и авторство
Эта страница была создана на основе содержимого следующими участниками и отредактирована (тематически или широко) командой разработчиков LibreTexts в соответствии со стилем, представлением и качеством платформы:
электрохимия — Как определить значение n в уравнении свободной энергии Гиббса и окислительно-восстановительного потенциала?
Принятый ответ неверен, число $ n $ не равно 2 просто потому, что 2 является наименьшим общим кратным 2 и 1.Кроме того, $ n $ — это не «количество молей электронов», которое могло бы иметь единицы $ \ pu {mol} $; $ n $ на самом деле безразмерный .
На самом деле число $ n $ может быть любым, и это зависит от того, как вы скомбинируете два полууравнения.
Чтобы использовать другой (не очень реалистичный, но мне все равно) пример, рассмотрим полуреакции (данные из Википедии)
$$ \ begin {align}
\ ce {Na + (aq) + e- & -> Na (s)} & E_1 & = \ pu {-2,71 V} \ tag {1} \\
\ ce {Br2 (l) + 2e- & -> 2Br- (aq)} & E_2 & = \ pu {+1.07 V} \ tag {2} \ end {align} $$
У нас есть $ E_ \ mathrm {cell} = E_2 — E_1 = \ pu {+3,78 V} $. Чтобы построить полную реакцию для этой клетки, «обычная» процедура состоит в том, чтобы взять (1), умножить его на 2 и вычесть из (2).
$$ \ ce {Br2 (l) + 2Na (s) -> 2Na + (водн.) + 2Br- (водн.)} \ Tag {3} $$
В этом случае мы имеем $ n = 2 $, поскольку в этой реакции передаются два электрона от брома к натрию. Точно так же вы можете думать о (3) как о сумме двух полуреакций, каждая из которых показывает усиление или потерю двух электронов:
$$ \ begin {align}
\ ce {2Na (s) & -> 2Na + (aq) + 2e-} \ tag {4} \\
\ ce {Br2 (l) + 2e- & -> 2Br- (aq)} \ tag {5}
\ end {align} $$
Обратите внимание, что стехиометрический коэффициент $ \ ce {e -} $ — числа перед электронами — равен 2 для обоих полууравнений.
Однако вы легко можете построить другую полную реакцию, просто отличаясь от (3) мультипликативным множителем. Нет причин, по которым вы не можете, например, разделить (2) на 2, а затем вычесть (1), чтобы получить:
$$ \ ce {1/2 Br2 (l) + Na (s) -> Na + (водн.) + Br- (водн.)} \ Tag {3 *} $$
и здесь у вас должно быть только $ n = 1 $, потому что здесь переносится только один электрон, от брома к натрию. Опять же, вы можете разложить это на полуреакции:
$$ \ begin {align}
\ ce {Na (s) & -> Na + (aq) + e-} \ tag {4 *} \\
\ ce {1 / 2Br2 (l) + e- & -> Br- (aq)} \ tag {5 *}
\ end {align} $$
и стехиометрический коэффициент при $ \ ce {e -} $ здесь просто 1.
Суть в том, что
- $ E_ \ mathrm {cell} $ не меняется со стехиометрическими коэффициентами.
- $ n $ делает, и, следовательно, $ \ Delta G = -nFE_ \ mathrm {cell} $ делает. Ваш выбор реакции полной ячейки определяет значение $ n $, с которым вы работаете.
- Лучшее определение $ n $ — это стехиометрический коэффициент для электронов в полуреакциях, на которые может быть разделена клеточная реакция (Atkins & de Paula, Physical Chemistry ).
Концентрационные установки | Безграничная химия
Молярность
Молярность определяется как количество молей растворенного вещества на объем всего раствора.
Цели обучения
Расчет концентрации раствора с использованием молярности.
Основные выводы
Ключевые моменты
- Молярность (M) указывает количество молей растворенного вещества на литр раствора (моль / литр) и является одной из наиболее распространенных единиц, используемых для измерения концентрации раствора.
- Молярность может использоваться для расчета объема растворителя или количества растворенного вещества.
- Связь между двумя растворами с одинаковым количеством молей растворенного вещества может быть представлена формулой c 1 V 1 = c 2 V 2 , где c — концентрация, а V — объем.
Ключевые термины
- разбавление : Процесс, при котором раствор становится менее концентрированным путем добавления большего количества растворителя.
- Единица СИ : Современная форма метрической системы, широко используемой в науке (сокращенно СИ от французского: Système International d’Unités).
- молярность : Концентрация вещества в растворе, выраженная в количестве молей растворенного вещества на литр раствора.
- концентрация : относительное количество растворенного вещества в растворе.
В химии концентрацию раствора часто измеряют в молярности (М), которая представляет собой количество молей растворенного вещества на литр раствора. Эта молярная концентрация (c i ) рассчитывается путем деления молей растворенного вещества (n i ) на общий объем (V):
[латекс] \ text {c} _ \ text {i} = \ frac {\ text {n} _ \ text {i}} {\ text {V}} [/ latex]
Единица СИ для молярной концентрации — моль / м 3 .Однако моль / л является более распространенной единицей измерения молярности. Раствор, который содержит 1 моль растворенного вещества на 1 литр раствора (1 моль / л), называется «один молярный» или 1 М. Единицу моль / л можно преобразовать в моль / м 3 , используя следующее уравнение:
1 моль / л = 1 моль / дм 3 = 1 моль дм −3 = 1 M = 1000 моль / м 3
Расчет молярности
Для расчета молярности раствора количество молей растворенного вещества необходимо разделить на общее количество литров полученного раствора.Если количество растворенного вещества указано в граммах, мы должны сначала рассчитать количество молей растворенного вещества, используя молярную массу растворенного вещества, а затем рассчитать молярность, используя количество молей и общий объем.
Расчет молярности с учетом молей и объема
Если в воде (растворителе) растворено 10,0 граммов NaCl (растворенного вещества) для получения 2,0 л раствора, какова молярность этого раствора?
Во-первых, мы должны перевести массу NaCl в граммах в моль. Делаем это делением на молекулярную массу NaCl (58.4 г / моль).
[латекс] 10,0 \ text {граммы NaCl} \ times \ frac {\ text {1 моль}} {58,4 \ text {г / моль}} = 0,17 \ text {моль NaCl} [/ латекс]
Затем мы делим количество молей на общий объем раствора, чтобы получить концентрацию.
[латекс] \ text {c} _ \ text {i} = \ frac {\ text {n} _ \ text {i}} {\ text {V}} [/ latex]
[латекс] \ text {c} _ \ text {i} = \ frac {0,17 \ text {моль NaCl}} {2 \ text {литры раствора}} [/ латекс]
[латекс] \ text {c} _ \ text {i} = 0,1 \ text {M} [/ latex]
Раствор NaCl — 0.1 М раствор.
Расчет молей с учетом молярности
Чтобы вычислить количество молей в растворе с учетом молярности, мы умножаем молярность на общий объем раствора в литрах.
Сколько молей хлорида калия (KCl) содержится в 4,0 л 0,65 М раствора?
[латекс] \ text {c} _ {\ text {i}} = \ frac {\ text {n} _ {\ text {i}}} {\ text {V}} [/ latex]
[латекс] 0,65 \ text {M} = \ frac {\ text {n} _ \ text {i}} {4,0 \ text {L}} [/ латекс]
[латекс] \ text {n} _ \ text {i} = (0.65 \ text {M}) (4.0 \ text {L}) = 2.6 \ text {моль KCl} [/ латекс]
В 0,65 М растворе, занимающем 4,0 л, содержится 2,6 моль KCl.
Расчет объема с учетом молярности и молей
Мы также можем рассчитать объем, необходимый для достижения определенной массы в граммах с учетом молярности раствора. Это полезно для определенных растворенных веществ, которые не могут быть легко собраны с помощью весов. Например, диборан (B 2 H 6 ) является полезным реагентом в органическом синтезе, но также очень токсичен и легковоспламеняем.Диборан безопаснее использовать и транспортировать, если растворен в тетрагидрофуране (ТГФ).
Сколько миллилитров 3,0 М раствора Bh4-THF необходимо для получения 4,0 г Bh4?
Сначала мы должны преобразовать граммы BH 3 в моль, разделив массу на молекулярную массу.
[латекс] \ frac {4.0 \ text {g} \ text {BH} _3} {13.84 \ text {g / mol} \ text {BH} _3} = 0.29 \ text {moles} \ text {BH} _3 [ / латекс]
Как только мы узнаем, что нам нужно получить 0,29 моль BH 3, , мы можем использовать это и заданную молярность (3.0 M) для расчета объема, необходимого для достижения 4,0 г.
[латекс] \ text {c} _ {\ text {i}} = \ frac {\ text {n} _ {\ text {i}}} {\ text {V}} [/ latex]
[латекс] 3.0 \ text {M} = \ frac {0.29 \ text {moles BH} _3} {\ text {V}} [/ latex]
[латекс] \ text {V} = 0,1 \ text {L} [/ латекс]
Теперь, когда мы знаем, что в 0,1 л содержится 4,0 г BH 3 , мы знаем, что нам нужно 100 мл раствора для получения 4,0 г BH 3 .
Разведение
Разбавление — это процесс снижения концентрации растворенного вещества в растворе, обычно путем добавления большего количества растворителя.Это соотношение представлено уравнением c 1 V 1 = c 2 V 2 , где c 1 и c 2 — начальная и конечная концентрации, а V 1 и V 2 — начальный и конечный объемы раствора.
Пример 1
У ученого есть 5,0 М раствор соляной кислоты (HCl), и для его нового эксперимента требуется 150,0 мл 2,0 М HCl. Сколько воды и 5,0 M HCl должен использовать ученый, чтобы получить 150.0 мл 2,0 М HCl?
c 1 V 1 = c 2 V 2
c 1 и V 1 — концентрация и объем исходного раствора, который представляет собой 5,0 М HCl. c 2 и V 2 — концентрация и объем желаемого раствора или 150,0 мл 2,0 М раствора HCl. Объем пока не нужно переводить в литры, потому что обе части уравнения используют мл. Следовательно:
[латекс] (5.0 \ text {M HCl}) (\ text {V} _1) = (2.0 \ text {M HCl}) (150.0 \ text {mL}) [/ latex]
V 1 = 60,0 мл 5,0 M HCl
Если для приготовления желаемого раствора используется 60,0 мл 5,0 М HCl, можно рассчитать количество воды, необходимое для правильного разбавления раствора до нужной молярности и объема:
150,0 мл — 60,0 мл = 90,0 мл
Для того, чтобы ученый приготовил 150,0 мл 2,0 М HCl, ему потребуется 60,0 мл 5,0 М HCl и 90,0 мл воды.
Пример 2
Воду добавляли к 25 мл исходного раствора 5.0 M HBr, пока общий объем раствора не достиг 2,5 л. Какова молярность нового раствора?
Нам дано следующее: c 1 = 5 ° M, V 1 = 0,025 л, V 2 = 2,50 л. Нам предлагается найти c 2 , что является молярностью разбавленного раствора. решение.
(5,0 м) (0,025 л) = c 2 (2,50 л)
[латекс] \ text {c} _2 = \ frac {(5.0 \ text {M}) (0.025 \ text {L})} {2.50 \ text {L}} = 0,05 \ text {M} [/ latex]
Обратите внимание, что все единицы объема были преобразованы в литры.Мы рассчитали, что у нас будет 0,05 М раствор, что соответствует нашим ожиданиям, учитывая, что мы разбавили 25 мл концентрированного раствора до 2500 мл.
Моляльность
Моляльность — это свойство раствора, которое указывает количество молей растворенного вещества на килограмм растворителя.
Цели обучения
Рассчитайте молярность раствора и объясните, почему это коллигативное свойство
Основные выводы
Ключевые моменты
- Моляльность — это свойство раствора, определяемое как количество молей растворенного вещества на килограмм растворителя.
- Единица измерения моляльности в системе СИ — моль / кг. Раствор с моляльностью 3 моль / кг часто описывается как «3 моль» или «3 моль». Однако, следуя системе единиц СИ, теперь предпочтительнее моль / кг или связанная с ней единица СИ.
- Поскольку объем раствора зависит от температуры и давления окружающей среды, масса может иметь большее значение для измерения растворов. В этих случаях подходящим измерением является молярность (а не молярность).
Ключевые термины
- моляльность : Концентрация вещества в растворе, выраженная как количество молей растворенного вещества на килограмм растворителя.
- коллигативное свойство : свойство растворов, которое зависит от отношения количества частиц растворенного вещества к количеству молекул растворителя в растворе, а не от типа присутствующих химических соединений.
- интенсивное свойство : свойство вещества, не зависящее от количества вещества.
Измерения массы (молярности) в зависимости от объема (молярности)
Моляльность — это интенсивное свойство растворов, и она рассчитывается как количество молей растворенного вещества, деленное на килограммы растворителя.В отличие от молярности, которая зависит от объема раствора, молярность зависит только от массы растворителя. Поскольку объем может изменяться из-за температуры и давления, молярность также зависит от температуры и давления. В некоторых случаях использование веса является преимуществом, поскольку масса не зависит от условий окружающей среды. Например, моляльность используется при работе с диапазоном температур.
Определение моляльности
Моляльность, b (или m), раствора определяется как количество вещества растворенного вещества в молях, n растворенного вещества , деленное на массу в кг растворителя, м растворитель :
[латекс] \ text {bM} _ {\ text {solute}} = \ frac {\ text {n} _ {\ text {solute}}} {\ text {m} _ {\ text {растворитель}}} [/ латекс]
Моляльность основана на массе, поэтому ее можно легко преобразовать в массовое отношение, обозначенное w:
[латекс] \ text {bM} _ {\ text {solute}} = \ frac {\ text {n} _ {\ text {solute}}} {\ text {m} _ {\ text {растворитель}}} = \ frac {\ text {w} _ {\ text {solute}}} {\ text {w} _ {\ text {Solute}}} [/ latex]
По сравнению с молярной концентрацией или массовой концентрацией приготовление раствора заданной моляльности проще, поскольку для этого требуется только хороший масштаб; и растворитель, и растворенное вещество являются массами, а не измеряются по объему.Во многих слабых водных растворах молярность и моляльность аналогичны, поскольку один килограмм воды (растворителя) занимает один литр объема при комнатной температуре, а небольшое количество растворенного вещества мало влияет на объем растворителя.
Водный раствор соли : Поваренная соль легко растворяется в воде с образованием раствора. Если массы соли и воды известны, можно определить моляльность.
шт.
Единица измерения моляльности в системе СИ — моль / кг, или моль растворенного вещества на кг растворителя.Раствор с моляльностью 1 моль / кг часто описывается как «1 моль» или «1 моль». Однако, следуя системе единиц СИ, Национальный институт стандартов и технологий, являющийся органом США по измерениям, считает термин «моляль» и символ единицы измерения «м» устаревшими и предлагает использовать моль / кг. или другая связанная единица СИ.
Расчет моляльности
Моляльность легко вычислить, если мы знаем массу растворенного вещества и растворителя в растворе. Моляльность — это интенсивное свойство, поэтому оно не зависит от измеряемого количества.Это верно для всех концентраций гомогенного раствора, независимо от того, исследуем ли мы образец одного и того же раствора объемом 1,0 л или 10,0 л. Концентрация или моляльность остается постоянной.
Расчет молярности с учетом массы
Если мы массируем 5,36 г KCl и растворяем это твердое вещество в 56 мл воды, какова моляльность раствора? Помните, что моляльность составляет моль растворенного вещества / кг на растворитель. KCl — это наше растворенное вещество, а вода — наш растворитель. Сначала нам нужно рассчитать количество родинок в 5.36 г KCl:
[латекс] \ text {моль KCl} = 5,36 \ text {g} \ times (\ frac {1 \ text {moles}} {74,5 \ text {g}}) = 0,0719 \ text {моль KCl} [/ латекс ]
Нам также необходимо преобразовать 56,0 мл воды в эквивалентную массу в граммах, используя известную плотность воды (1,0 г / мл):
[латекс] 56,0 \ \ text {mL} \ times (\ frac {1.0 \ text {g}} {\ text {mL}}) = 56,0 \ \ text {g} [/ latex]
56,0 г воды эквивалентно 0,056 кг воды. Имея эту информацию, мы можем разделить моли растворенного вещества на кг растворителя, чтобы найти моляльность раствора:
[латекс] \ text {molality} = (\ frac {\ text {moles}} {\ text {кг растворителя}}) = (\ frac {0.0719 \ text {моль KCl}} {0,056 \ text {кг воды}}) = 1,3 \ \ text {m} [/ latex]
Моляльность нашего раствора KCl и воды составляет 1,3 м. Поскольку раствор очень разбавленный, молярность почти идентична молярности раствора, которая составляет 1,3 М.
Расчет массы с учетом моляльности
Мы также можем использовать моляльность, чтобы найти количество вещества в растворе. Например, сколько уксусной кислоты в мл необходимо для приготовления 3,0 м раствора, содержащего 25,0 г KCN?
Во-первых, мы должны преобразовать образец KCN из граммов в моль:
[латекс] \ text {моль KCN} = 25.0 \ text {g} \ times (\ frac {1 \ text {moles}} {65.1 \ text {g}}) = 0,38 \ text {moles} [/ latex]
Затем можно использовать моль KCN для определения килограмма уксусной кислоты. Мы умножаем количество молей на величину, обратную данной моляльности (3,0 моль / кг), чтобы наши единицы соответственно сокращались. В результате получаем желаемую массу уксусной кислоты, которая нам нужна для приготовления нашего 3-миллиметрового раствора:
[латекс] 0,38 \ text {моль KCl} \ times (\ frac {\ text {кг уксусной кислоты}} {3,0 \ text {моль KCl}}) = 0,12 \ text {кг уксусной кислоты} [/ латекс]
Получив массу уксусной кислоты в кг, переводим из кг в граммы: 0.12 кг равняется 120 г. Затем мы используем плотность уксусной кислоты (1,05 г / мл при 20 o ° C) для преобразования в требуемый объем в мл. Чтобы добиться этого, мы должны умножить на обратную величину плотности:
[латекс] 120,0 \ text {g уксусная кислота} \ times (\ frac {\ text {mL}} {1.05 \ text {g}}) = 114,0 \ text {мл уксусной кислоты} [/ латекс]
Следовательно, нам требуется 114 мл уксусной кислоты для приготовления 3,0 м раствора, содержащего 25,0 г KCN.
Молярность vs.молярность : В этом уроке вы узнаете, чем отличаются молярность и молярность.
Молярная доля и молярный процент
Мольная доля — это количество молекул данного компонента в смеси, деленное на общее количество молей в смеси.
Цели обучения
Рассчитайте мольную долю и мольный процент для данной концентрации смеси
Основные выводы
Ключевые моменты
- Мольная доля описывает количество молекул (или молей) одного компонента, деленное на общее количество молекул (или молей) в смеси.
- Молярная доля полезна, когда два реакционноспособных компонента смешиваются вместе, так как соотношение двух компонентов известно, если известна мольная доля каждого.
- Умножение мольной доли на 100 дает мольный процент, который описывает то же самое, что и мольная доля, только в другой форме. Мольные доли могут быть получены из различных концентраций, включая составы молярности, молярности и массовых процентов.
Ключевые термины
- моль : основная единица СИ для количества вещества; количество вещества, которое содержит столько элементарных объектов, сколько атомов в 0.012 кг углерода-12.
- мольная доля : отношение количества молей одного компонента в смеси к общему количеству молей.
Молярная доля
В химии мольная доля, x i , определяется как количество молей компонента, n i , деленное на общее количество молей всех компонентов в смеси, n тот :
[латекс] \ text {x} _ {\ text {i}} = \ frac {\ text {n} _ {\ text {i}}} {\ text {n} _ {\ text {tot}}} [/ латекс]
Мольные доли безразмерны, а сумма всех мольных долей в данной смеси всегда равна 1.
Свойства мольной доли
Мольная доля очень часто используется при построении фазовых диаграмм. Имеет ряд преимуществ:
- Он не зависит от температуры, в отличие от молярной концентрации, и не требует знания плотности фазы (фаз).
- Смесь с известными мольными долями может быть приготовлена путем взвешивания соответствующих масс компонентов.
- Мера симметричная; в мольных долях x = 0.1 и x = 0,9, роли «растворителя» и «растворенного вещества» обратимы.
- В смеси идеальных газов мольную долю можно выразить как отношение парциального давления к общему давлению смеси.
Мольная доля в растворе хлорида натрия : Мольная доля увеличивается пропорционально массовой доле в растворе хлорида натрия.
Молярный процент
Умножение мольной доли на 100 дает молярный процент, также называемый процентом количество / количество (сокращенно n / n%).Для общей химии все мольные проценты смеси составляют в сумме 100 мольных процентов. Мы можем легко преобразовать молярный процент обратно в мольную долю, разделив на 100. Таким образом, мольная доля 0,60 равна 60,0% молярного процента.
Расчеты с молярной долей и мольным процентом
Молярная доля в смесях
Смесь газов была образована путем объединения 6,3 моль O 2 и 5,6 моль N 2 . Какая мольная доля азота в смеси?
Сначала мы должны найти общее количество молей с n всего = n N2 + n O2 .
[латекс] \ text {n} _ {\ text {total}} = 6.3 \ \ text {moles} +5.6 \ \ text {moles} = 11.9 \ \ text {moles} [/ latex].
Далее мы должны разделить моли N 2 на общее количество молей:
[латекс] x (\ text {мольная доля}) = (\ frac {\ text {моль} \ text {N} _2} {\ text {моль} \ text {N} _2 + \ text {моль} O_2} ) = (\ frac {5.6 \ text {moles}} {11.9 \ text {moles}}) = 0.47 [/ latex]
Мольная доля азота в смеси составляет 0,47.
Молярная доля в растворах
Молярная доля также может применяться в случае растворов.Например, 0,100 моль NaCl растворяют в 100,0 мл воды. Какая мольная доля NaCl?
Нам дано количество молей NaCl, но не объем воды. Сначала мы преобразуем этот объем в массу, используя плотность воды (1,00 г / мл), а затем преобразуем эту массу в моль воды:
[латекс] 100 \ \ text {mL} \ H_2O \ times (\ frac {1.0 \ text {g}} {1 \ text {mL}}) = 100.0 \ \ text {g} \ \ text {H} _2 \ text {O} \ times (\ frac {1 \ text {moles}} {18.0 г}) = 5.55 \ text {moles} \ text {H} _2 \ text {O} [/ latex]
С помощью этой информации мы можем найти общее количество присутствующих родинок: 5.55 + 0,100 = 5,65 моль. Если разделить моли NaCl на общее количество молей, мы найдем мольную долю этого компонента:
[латекс] \ text {x} = (\ frac {0.100 \ text {moles}} {5.65 \ text {moles}}) = 0,0176 [/ латекс]
Мы находим, что мольная доля NaCl составляет 0,0176.
Молярная доля с многокомпонентными смесями
Молярные доли также могут быть найдены для смесей, состоящих из нескольких компонентов. К ним относятся не иначе, чем раньше; опять же, общая мольная доля смеси должна быть равна 1.
Например, раствор образуется при смешивании 10,0 г пентана (C 5 H 12 ), 10,0 г гексана (C 6 H 14 ) и 10,0 г бензола (C 6 H 6 ). Какая мольная доля гексана в этой смеси?
Сначала мы должны определить количество молей, присутствующих в 10,0 г каждого компонента, с учетом их химической формулы и молекулярной массы. Количество молей каждого находится путем деления его массы на соответствующую молекулярную массу.Мы обнаружили, что имеется 0,138 моль пентана, 0,116 моль гексана и 0,128 моль бензола.
Мы можем найти общее количество молей, взяв сумму всех молей: 0,138 + 0,116 + 0,128 = 0,382 общих молей. Если разделить моли гексана на общее количество молей, мы вычислим мольную долю:
[латекс] \ text {x} = (\ frac {0,116 \ text {moles}} {0,382 \ text {moles}}) = 0,303 [/ латекс]
Мольная доля гексана составляет 0,303.
Молярная доля от моляльности
Мольную долю можно также рассчитать по моляльности.Если у нас есть 1,62 м раствор столового сахара (C 6 H 12 O 6 ) в воде, какова мольная доля столового сахара?
Поскольку нам дана моляльность, мы можем преобразовать ее в эквивалентную мольную долю, которая уже является массовым соотношением; помните, что моляльность = моль растворенного вещества / кг растворителя. Учитывая определение моляльности, мы знаем, что у нас есть раствор, содержащий 1,62 моля сахара и 1,00 кг (1000 г) воды. Поскольку мы знаем количество молей сахара, нам нужно найти количество молей воды, используя его молекулярную массу:
[латекс] 1000 \ \ text {g} \ \ text {H} _2 \ text {O} \ times (\ frac {1 \ \ text {мол}} {18.0 \ \ text {g}}) = 55,5 \ text {moles} \ text {H} _2 \ text {O} [/ latex]
Общее количество молей — это сумма молей воды и сахара, или 57,1 молей всего раствора. Теперь мы можем найти мольную долю сахара:
[латекс] \ text {x} = (\ frac {1,62 \ text {молей сахара}} {57,1 \ text {молей раствор}}) = 0,0284 [/ латекс]
При мольной доле 0,0284 мы видим, что имеем 2,84% раствор сахара в воде.
Молярная доля от массового процента
Мольную долю можно также рассчитать из массовых процентов.Какова мольная доля коричной кислоты, которая имеет массовый процент 50,00% мочевины в коричной кислоте? Молекулярная масса мочевины составляет 60,16 г / моль, а молекулярная масса коричной кислоты составляет 148,16 г / моль.
Во-первых, мы предполагаем общую массу 100,0 г, хотя можно принять любую массу. Это означает, что у нас есть 50,0 г мочевины и 50,0 г коричной кислоты. Затем мы можем вычислить количество присутствующих молей, разделив каждый на его молекулярный вес. У нас 0,833 моль мочевины и 0,388 моль коричной кислоты, так что у нас 1.Всего 22 моля.
Чтобы найти мольную долю, разделим количество молей коричной кислоты на общее количество молей:
[латекс] \ text {x} = (\ frac {.388 \ text {моль коричной кислоты}} {1,22 \ text {моль раствор}}) = 0,318 [/ латекс]
Мольная доля коричной кислоты составляет 0,318.
ДОМ Главы курса Основы калькулятора Обзор математики Основные понятия Advanced Concepts Раздел Тесты Предварительное испытание Пост-тест Полезные материалы Глоссарий Онлайн-калькуляторы Калькулятор окислительно-восстановительного потенциала Калькулятор кинетики Аррениуса Калькулятор термодинамики Калькулятор ядерного распада Регрессия методом наименьших квадратов Решатель уравнений метода Ньютона Калькулятор сжимаемости Калькулятор перевода единиц Калькулятор номенклатуры Ссылки по теме Калькуляторы Texas Instruments Калькуляторы Casio Калькуляторы Sharp Калькуляторы Hewlett Packard Кредиты Связаться с веб-мастером | В стехиометрических расчетах мы предполагаем, что реакции завершаются.Однако, когда химическая реакция проводится в закрытом сосуде, система достигает равновесия. Можно написать выражение равновесия для реакции. jA + kB -> lC + mD выражение равновесия: Где: K — константа равновесия Для каждой реакции при определенной температуре существует только одно значение Для реакций в газовой фазе положения равновесия также можно выразить через давление. K p , константа равновесия по давлению, связана с K уравнением: K p = K (RT) delta n Где: дельта n — сумма коэффициентов газообразных продуктов минус Коэффициент реакции Q — это выражение, которое имеет дело с начальными значениями, а не с равновесным значением, с которым имеет дело K. Мы сравниваем Q и K, чтобы определить, в каком направлении пойдет реакция до достижения равновесия. Если Q больше, чем K, s Чтобы найти концентрации, которые характеризуют равновесие, лучше всего пройти через процесс «запуск, изменение, равновесие». Это подразумевает, что следует начинать с начальных концентраций, определять изменение и использовать K для нахождения равновесной концентрации. Пример задачи «Старт, изменение, равновесие»: C 2 H 6 (г) + Cl 2 (г) C 2 H 5 Cl (s) + HCl (г) Принцип Ле Шателье позволяет нам предсказать влияние изменений температуры, давления и концентрации на систему, находящуюся в состоянии равновесия. В нем говорится, что если система в состоянии равновесия испытывает изменение, система сместит свое равновесие на t
Растворимость — это количество растворенного вещества в растворе, обычно указывается в г / л. Ksp — это равновесное выражение, связанное с концентрацией ионов в растворе. Например, в уравнение: AgBr (s) -> Ag + (водн.) + Br — (водн.) K sp = [Ag + ] [Br –] Добавление обычных ионов, кислот или оснований влияет на растворимость вещества. Если взять приведенную выше реакцию в качестве примера, если вы добавите AgNO 3 , [Ag + ] увеличится, что приведет к смещению системы влево и, следовательно, к солюбилизации способность уменьшаться.Если вы добавите Pb (NO 3 ) 2 , Pb и Br будут образовывать осадок, который уменьшит [Br — ] и приведет к смещению системы вправо и, следовательно, к увеличению растворимости. Посмотрите на следующий ответ BaCO 3 (s) -> Ba ++ (водн.) + CO 3 — (водн.) Если вы добавите HNO 3 , образуется слабая кислота HF, которая снижает Пример проблемы Ksp: Задача практического равновесия: Рассчитайте равновесные концентрации трех молекул и Практика Ksp Задача: формы тейт? [Расширенный указатель] |
Молевые отношения в примерных задачах сбалансированных уравнений
Это решенные химические задачи, показывающие, как рассчитать количество молей реагентов или продуктов в сбалансированном химическом уравнении.
Проблема родственных отношений № 1
Определите количество молей N 2 O 4 , необходимое для полной реакции с 3.62 моль N 2 H 4 для реакции 2 N 2 H 4 (л) + N 2 O 4 (л) → 3 N 2 (г) + 4 H 2 О (л).
Как решить проблему
Первый шаг — убедиться, что химическое уравнение сбалансировано. Убедитесь, что количество атомов каждого элемента одинаково с обеих сторон уравнения. Не забудьте умножить коэффициент на все следующие за ним атомы. Коэффициент — это число перед химической формулой.Умножайте каждый нижний индекс только на атом прямо перед ним. Индексы — это нижние числа, следующие сразу за атомом. Убедившись, что уравнение сбалансировано, вы можете установить взаимосвязь между количеством молей реагентов и продуктов.
Найдите связь между молями N 2 H 4 и N 2 O 4 , используя коэффициенты сбалансированного уравнения:
2 моль N 2 H 4 пропорционально 1 моль N 2 O 4
Следовательно, коэффициент пересчета составляет 1 моль N 2 O 4 /2 моль N 2 H 4 :
моль N 2 O 4 = 3.62 моль N 2 H 4 x 1 моль N 2 O 4 /2 моль N 2 H 4
моль N 2 O 4 = 1,81 моль N 2 O 4
Ответ
1.81 моль N 2 O 4
Проблема взаимоотношений между родителями № 2
Определите количество молей N 2 , образовавшихся в реакции 2 N 2 H 4 (л) + N 2 O 4 (л) → 3 N 2 (г) + 4 H 2 O (l), когда реакция начинается с 1.24 моля N 2 H 4 .
Решение
Это химическое уравнение сбалансировано, поэтому можно использовать молярное соотношение реагентов и продуктов. Найдите связь между молями N 2 H 4 и N 2 , используя коэффициенты сбалансированного уравнения:
2 моль N 2 H 4 пропорционально 3 моль N 2
В этом случае мы хотим перейти от молей N 2 H 4 к молям N 2 , поэтому коэффициент пересчета составляет 3 моль N 2 /2 моль N 2 H 4 :
моль N 2 = 1.24 моль N 2 H 4 x 3 моль N 2 /2 моль N 2 H 4
моль N 2 = 1,86 моль N 2 O 4
Ответ
1,86 моль N 2
Советы для успеха
Ключи к правильному ответу:
- Убедитесь, что химическое уравнение сбалансировано.
- Используйте коэффициенты перед соединениями, чтобы получить молярные отношения.
- Убедитесь, что вы используете соответствующее количество значащих цифр для атомных масс и указываете массу, используя правильное количество цифр.
.
