Решение линейных уравнений и систем линейных уравнений, содержащих параметры (4 урока)

Цели урока: формировать умение решать системы линейных уравнений, содержащих параметры; осуществить оперативный контроль и самоконтроль учащихся; развивать исследовательскую и познавательную деятельность школьников.

Тип урока: введение нового материала.

Ход урока

1. Проверка домашнего задания.

2. Введение нового материала.

Говорят, что дана система двух уравнений первой степени с двумя неизвестными x и y, если требуется найти пары чисел (x₀; y₀), являющиеся решениями одновременно и первого, и второго уравнения.

Если

то система имеет единственное решение.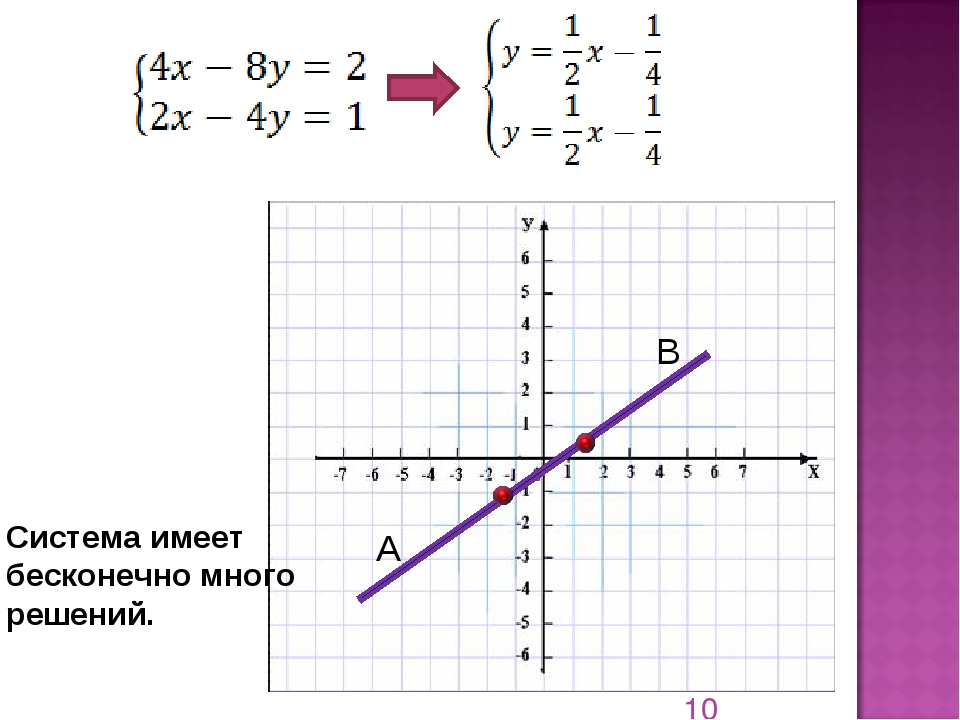
Если 

то система не имеет решений.
Если 

то система имеет бесконечно много решений.

Пример 1. При каких значениях параметра a система

а) имеет бесконечное множество решений;
б) имеет единственное решение?

Решение.

Ответ: а) если a=4, то система имеет бесконечное множество решений; б) если

то решение единственное.

Пример 2. Решите систему уравнений

Решение.

система имеет единственное решение.

1–ym–y=n–2y   , –ym+y=n–1;

исходная система решений не имеет.

система имеет бесконечно много решений.

Ответ: если m=1 и n1, то решений нет; если m = 1 и n = 1, то решений бесконечное множество,

если m  1 и n – любое, то

Пример 3. (Предложите ученикам выполнить это задание самостоятельно с последующей проверкой.) Решите систему уравнений

Решение.

Пример 4. Определите, при каком условии уравнение

а) имеет единственное решение;
б) имеет бесконечно много корней;
в) не имеет корней.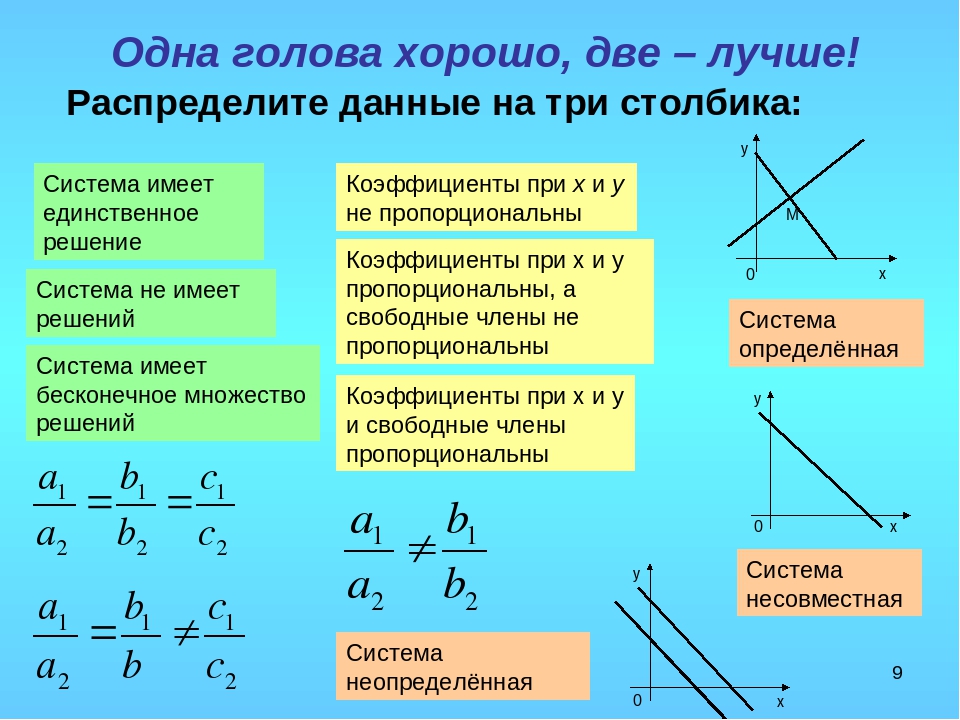

Решение.

– при этом условии уравнение корней не имеет.

– при этом условии решение исходного уравнения есть любое число из R.

Ответ:

б) если a = 0 или b = 0, то x – любое число;
в) если 2b = a, a  0, b  0, то корней нет.

Самостоятельная работа

Вариант 1

1. При каком значении k система

имеет бесконечное множество решений?

2. Решите систему уравнений

Вариант 2

1.  При каком значении d система

не имеет решений?

2. Решите систему уравнений

Ответы

В-1.  1. k = 2,5.  2. Если b = 0, c = 0, то решений нет; если b = c, d  0, a – любое число, то решений нет; если a = 0, b, c, d – любые числа, то решений нет; если c  0, b  0, a  0, b  c, d – любое число, то

если b = c, d = 0, то

В-2.  1. d = – 20.  2. Если b = 0, c = 0, то решений нет; если c = – b, то решений нет; если b  0 и c  0, c  – b, то

если c = – b и dbc = ac, то

Задание на дом

1. При каких значениях параметра b система уравнений

а) имеет бесконечное множество решений;
б) не имеет решений?

2.  Графики функций y = ax + 3 и y = (2 – a)x + a пересекаются в точке с абсциссой – 1. Найдите ординату точки пересечения графиков.

3. Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.

а) Найдите b и k.
б) найдите координаты точки пересечения этих графиков.

4. Решите систему уравнений

Ответы:  1. а) b = 10; б) b  10.  2.

 
3. а) b = 6, k = – 4; б) (0; 6).  4. Если mn = – 1 и m ­ 1, n ­ – 1, то решений нет; если m = 1 и n = – 1, то x – любое число, y = 1 + mx; если mn  1 и n  – 1, m  1, то

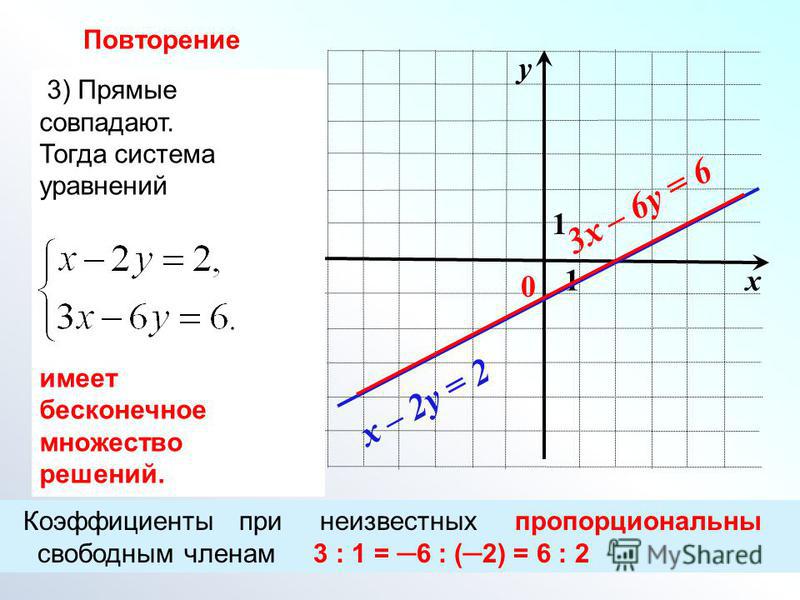
3. Если , то система имеет бесконечно много решений.

Пример
4. Решить
систему линейных уравнений
_.

Решение.
Составим определитель из коэффициентов
при неизвестных и вычислим его:

,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители
и значения неизвестных.

Ответ:

.

Рассмотрим пример,
в котором СЛУ
имеет бесконечное множество решений,
и они будут найдены с применением формул
Крамера.

Пример
5.
Решить СЛУ.

Решение.

Вычислим
определитель системы:

Заметим,
что третье уравнение системы равно
сумме первых двух уравнений, т.е. зависит
от первых двух уравнений. Отбросив
третье уравнение, получим равносильную
систему двух уравнений с тремя
неизвестными:

Оставим
в левой части системы те неизвестные,
коэффициенты при которых образуют
определитель, не равный нулю, например,

.
Неизвестное
является
свободным,
а неизвестные

и
— базисными
неизвестными.
Запишем систему в виде
и применим
к ней правило Крамера:

;

—
общее
решение
неопределенной СЛУ, где

— любое действительное число.

Из
общего решения можно получить частные
решения,
если придать свободной неизвестной
какое-то конкретное значение. Например,
пусть

,
тогда

;
частное решение

.

3. Матричный метод решения слу

3.1. Матричная запись системы линейных уравнений

Пусть

— матрица коэффициентов при неизвестных,

— матрица-столбец неизвестных,

— матрица-столбец свободных членов.
Система

уравнений с

неизвестными в матричном виде запишется
как

(матричное уравнение системы):

.

3.2. Решение системы уравнений с помощью обратной матрицы

Умножив
обе части уравнения

системы на обратную матрицу
слева и
используя свойство

,
получим выражение для матрицы неизвестных

.
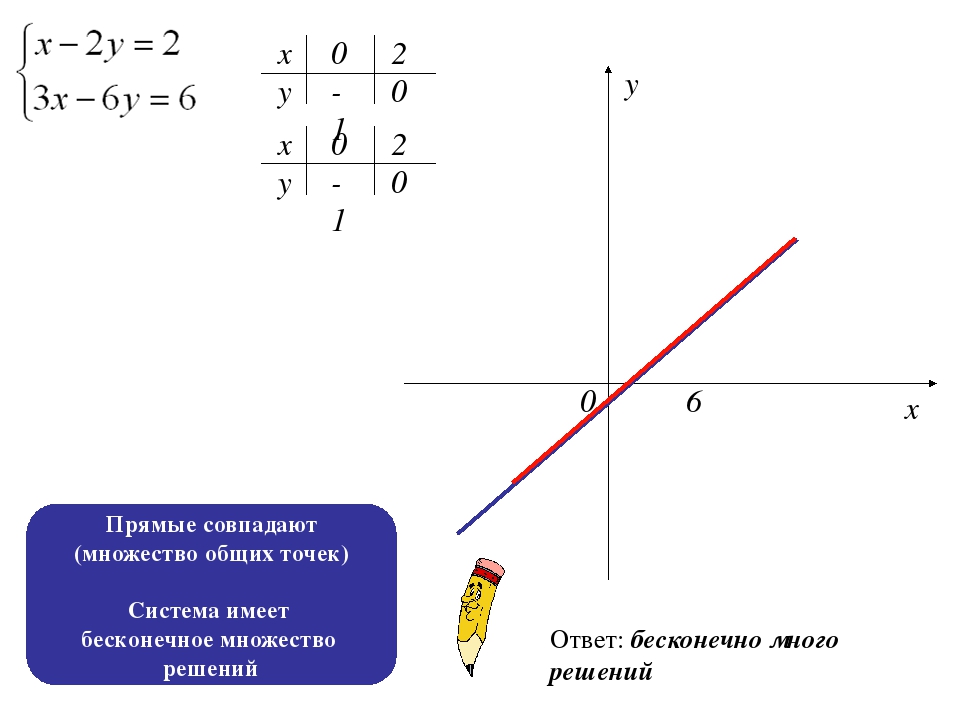
Оно показывает, как найти решение
системы

линейных уравнений с

неизвестными с помощью обратной матрицы.

Пример
6. Решить с
помощью обратной матрицы систему
уравнений

.

Решение.
Вычислим определитель:

.
Так как

,
то система уравнений имеет единственное
решение

.

2)
Составим обратную матрицу. Матрица

существует, т.к. определитель

.
Найдем алгебраические дополнения

.

,

,

,

,

,

,

,

,

.

Составим
матрицу из алгебраических дополнений

и транспонируем ее.

.

Разделим
каждый элемент этой матрицы на определитель

,
получим искомую обратную матрицу:

.

3)
Матрица неизвестных

равна произведению матрицы

на матрицу свободных членов

:

.

Вычислим
значения неизвестных:

,

,

.

Ответ.
Система имеет единственное решение

.

4. Сущность метода исключения неизвестных (метода Гаусса). Элементарные преобразования

Сущность
метода Гаусса
состоит в том, что система линейных
уравнений с помощью элементарных
преобразований приводится к равносильной
системе треугольного или трапецеидального
вида, из которой легко находится решение
системы или делается вывод о несовместности
системы. Метод Гаусса применяется к
любой СЛУ,
в которой число уравнений равно числу
неизвестных, или больше числа неизвестных,
или меньше числа неизвестных.

К элементарным преобразованиям над
уравнениями системы относятся:

1. Перестановка
   уравнений местами.

2. Умножение уравнения
   на число, не равное нулю.

3. Прибавление одного
   уравнения к другому уравнению, умноженному
   на какое-либо число.

4. Отбрасывание
   одинаковых уравнений (кроме одного), а
   также уравнения вида

   .

Решение систем линейных уравнений с параметрами

Решение систем линейных уравнений с параметрами — страница №1/1

Занятие 3.

Тема: Решение систем линейных уравнений с параметрами.

Объяснение теоретического материала.

Определение. Системой линейных уравнений с двумя переменными называется два линейных уравнения, рассматриваемых совместно:

Решениями системы линейных уравнений называются такие пары чисел , которые являются решениями одновременно и первого, и второго уравнения системы.

Пусть числа a,b,сотличны от нуля.

Если , то система имеет единственное решение.

Если , то система не имеет решений.

Если , то система имеет бесконечно много решений.

Если с_1, с₂ равны нулю, то система называется однородной и всегда имеет решение (0 ; 0). Если однородная система имеет нулевое решение (x₀; y₀), значит, она имеет бесконечное множество решений (kx₀; ky₀).

Пример 1. При каких значениях параметра a система

_{а) имеет бесконечное множество решений;}

б) имеет единственное решение?

Решение. Данная система уравнений является линейной, причем коэффициенты первого уравнения отличны от нуля.

а) Система имеет бесконечное множество решений, если а = 4.

б) Система имеет единственное решение, если а4

Обратить внимание на то, что уравнения поменяли местами, так как число а неопределенно. В нашем случае а=0 является решением в случае б), чтобы не было недоумений с делением на нуль, лучше вторым считать то уравнение, в котором все коэффициенты определены и не равны нулю.

Ответ: а) если а = 4, то система имеет бесконечное множество решений; б) если а4, то решение единственное.

Пример 2. Решите систему уравнений:

Решение. Данная система уравнений является линейной.

а) Система имеет единственное решение, если , то есть m.

Решим систему при m:

1-(m+1) y = n-2y;

2y-(m+1) y = n-1;

y (1-m) = n-1;

, где m1.

Найдем х, воспользовавшись любым уравнением системы:

Итак, при m 1 решением системы является пара .

б) Система не имеет решений, если , то есть при m =1, n1.

в) Система имеет бесконечно много решений, если , то есть m =1, n =1.

Пары вида , где x₀ – любое число, являются решением системы в этом случае.

Ответ: если m =1, n1 то решений нет; если m =1, n =1, то решений бесконечное множество ;

если mи n – любое число, то решение единственное: .

Решить самостоятельно.

1. 
   При каких значениях параметра b система уравнений

а) имеет бесконечное множество решений

б) не имеет решений?

2.Графики функций y = ax+3 и y=(2-a)x+a пересекаются в точке с абсциссой -1. Найдите ординату точки пересечения графиков.

3. Решите систему уравнений:

Глава А5.

Система трех уравнений с тремя
неизвестными

Глава П5. Решение и исследование системы трех
уравнений первой степени с тремя неизвестными

Рассмотрим систему уравнений

,
,
(1)

с неизвестными x, y, z
(коэффициенты
,
, …,
и свободные
члены
,
,
предположим
данными). Введем обозначения

,
,
,
.

Определитель
, составленный из
коэффициентов при неизвестных системы (1),
называется определителем данной системы.

Полезно заметить, что определители
,
,
получаются из определителя

при помощи замены соответственно его первого,
второго и, наконец, третьего столбца столбцом
свободных членов данной системы. Если
,
то система (1) имеет единственное решение; оно
определяется формулами

,
,
.

Предположим теперь, что определитель
системы равен нулю:
. Если в случае

хотя бы один из определителей
,
,

отличен от нуля, то система (1) совсем не имеет
решений.

В случае, когда
и одновременно
,
,
, система (1) также может совсем не
иметь решений; но если система (1) при этих
условиях имеет хотя бы одно решение, то она имеет
бесконечно много различных решений. Однородной
системой трех уравнений первой степени с тремя
неизвестными называется система вида

,
,
(2)

то есть система уравнений, свободные
члены которых равны нулю. Очевидно, что такая
система всегда имеет решение: x=0,
y=0, z=0; оно называется нулевым. Если
,
то это решение является единственным. Если же
,
то однородная система (2) имеет бесконечно много
ненулевых решений.

«Решение задач с параметрами» (стр. 2 из 4)

Если 3а-1=0, т.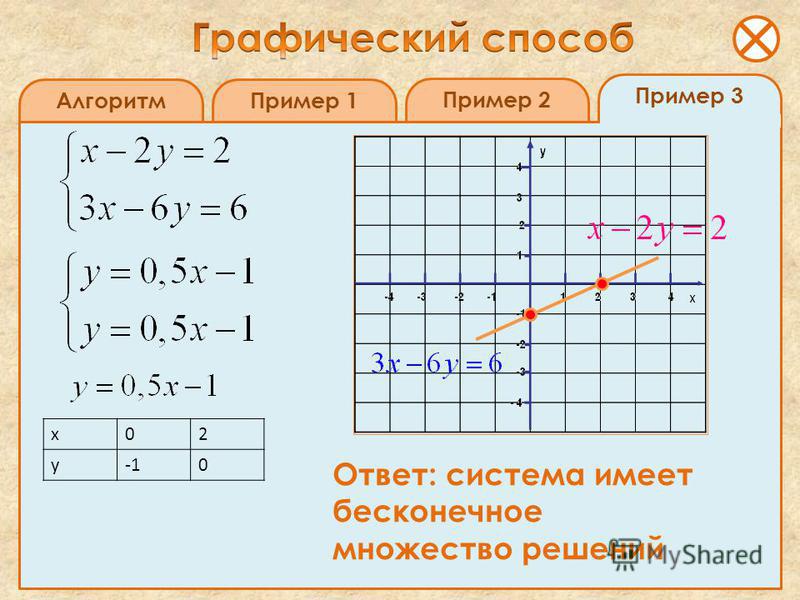 е. а=

, то уравнение примет вид 2х 0=0, его решением является любое число.

Ответ: уравнение имеет бесконечное множество решений при а=

.

Пример 4. При каких значениях параметра а уравнение не имеет решений?

=2а.

Приведем данное уравнение к виду х(5+2а)=4а-8.

Если 5+2а

0,т.е. а — , то х= .

Если 5+2а =0,т.е. а =-

, то уравнение примет вид х 0=-18, это уравнение не имеет решений.

Ответ. уравнение не имеет решений при а =-

.

1.2. Квадратные уравнения, содержащие параметр.

Уравнение вида ах²+вх+с=0, где а,в,с –некоторые числа (а

0), х-переменная, называется квадратным уравнением.

Для решения квадратного уравнения следует вычислить дискриминант

D= b²-4ac.

Если D=0, то квадратное уравнение имеет единственный корень:

х=-

(или два, но сливающихся корня х₁=х₂).

Если D>0, то квадратное уравнение имеет два корня:

х₁ =

; х₂ = .

Если D<0, то квадратное уравнение не имеет корней.

Если один из коэффициентов в или с равен нулю, то квадратное уравнение можно решать, не вычисляя дискриминанта:

1. в=0, с

0; _1,2= .

2. в

0, с=0, то х₁=0, х₂=- .

Следующие теоремы также помогают при решении квадратных уравнений с параметрами.

Теорема Виета (прямая) утверждает: если х₁ и х₂ являются корнями квадратного уравнения ах²+вх+с=0, то выполняются соотношения:

х₁+х₂=-

и х₁ х₂= .

Обратная теорема утверждает: если для некоторых постоянных а, в, с существуют числа х₁ и х₂, удовлетворяющие соотношениям

х₁+х₂=-

и х₁ х₂= , то эти числа х₁ и х₂ являются корнями уравнения ах²+вх+с=0.

Пример 5. Решить относительно х:

ах²-2х+4=0

Если а=0, тогда уравнение примет вид -2х+4=0, отсюда х=2.

Если а

0, то D=4-16а.

Если 4-16а≥0, т.е а≤

, х_1,2=

Если 4-16а<0, т.е. а>

, то уравнение не имеет решений.

Ответ: если а=0, то х=2;

если а

0 и а≤ , то уравнение имеет два решения х_1,2=

если а

0 и а> , то уравнение не имеет решений.

Пример 6. При каких значениях а уравнение ах²-х+3=0 имеет единственное решение?

Если а=0, тогда уравнение примет вид –х+3=0, отсюда х=3.

Если а

0, то D=1-12а.

Уравнение будет иметь единственное решение при D=0.

1-12а=0, отсюда а=

.

Ответ: уравнение имеет единственное решение при а=0 или а=

.

Пример 7. При каких значениях а уравнение ах²+4х+а+3=0 имеет более одного корня?

Если а=0, то уравнение примет вид 4х+3=0, которое имеет единственный корень, что не удовлетворяет условию задачи.

Если а

0, то D=16-4а²-12а.

Уравнение имеет более одного корня при D>0.

16-4а²-12а>0.

Рассмотрим функцию у=16-4а²-12а.

Найдем нули этой функции, решая уравнение 16-4а²-12а=0.

а₁=-4; а₂=1.

Функция принимает положительные значения, если -4<а<1.

Ответ: уравнение имеет более одного корня, если -4<а<0 и 0<а<1.

Пример 8. Найти коэффициент а, если корни уравнения х²-2х+а=0.

связаны соотношением 2х₁+х₂=3.

х²-2х+а=0.

По теореме Виета х₁+х₂=а и х₁

х₂=2.

Составляю систему:

Решая эту систему, получаю, что х₁=1, х₂=1.

Тогда а=1.

Ответ: а=1.

1.3. Системы линейных уравнений с параметром.

Системы линейных уравнений вида

1) имеют единственное решение, если

;

2) не имеют решений, если

= ;

3) имеют бесконечное множество решений, если

= = .

Пример 9. Найти все значения параметра а, при котором система имеет бесконечное множество решений:

Система имеет бесконечное множество решений, если выполняется условие:

= = .

1)

= ;

ОДЗ: а

0, а -3.

Как доказать что система имеет единственное решение

Решение. A = . Найдем r(А). Так как матрица А имеет порядок 3х4, то наивысший порядок миноров равен 3. При этом все миноры третьего порядка равны нулю (проверить самостоятельно). Значит, r(А) Пример 2. Определить совместность системы уравнений

Решить эту систему, если она окажется совместной.

Решение.

A = , C = . Oчевидно, что r(А) ≤ 3, r(C) ≤ 4. Так как detC = 0, то r(C) матричным методом по формуле X = A -1 B (при Δ ≠ 0 ), которая получается из (2) умножением обоих частей на А -1 .

Пример 1. Решить систему уравнений

матричным методом ( в параграфе 2.2 эта система была решена по формулам Крамера)

Решение. Δ = 10 ≠ 0 А = – невырожденная матрица.

= (убедитесь в этом самостоятельно, произведя необходимые вычисления).

A -1 = (1/Δ)х= .

Х = A -1 В = х= .

Ответ: .

С практической точки зрения матричный метод и формулы Крамера связаны с большим объемом вычислений, поэтому предпочтение отдается методу Гаусса , который заключается в последовательном исключении неизвестных. Для этого систему уравнений приводят к эквивалентной ей системе с треугольной расширенной матрицей (все элементы ниже главной диагонали равны нулю). Эти действия называют прямым ходом . Из полученной треугольной системы переменные находят с помощью последовательных подстановок ( обратный ход ).

Пример 2 . Методом Гаусса решить систему

(Выше эта система была решена по формуле Крамера и матричным методом).

Решение.

Прямой ход . Запишем расширенную матрицу и с помощью элементарных преобразований приведем ее к треугольному виду:

.

Получим систему

Обратный ход.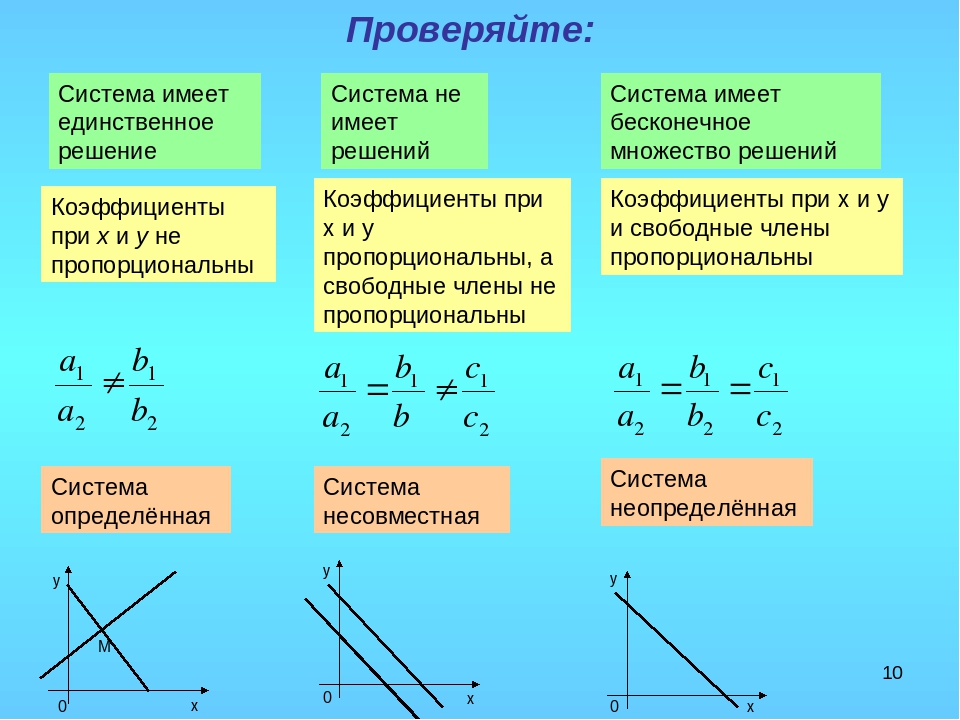 Из последнего уравнения находим х₃ = -6 и подставим это значение во второе уравнение:

Подставляя далее х₂ = -4, х₃ = -6 в первое уравнение системы, получим:

Ответ: .

2.5. Общее решение системы линейных уравнений

Пусть дана система линейных уравнений = b_i(i =). Пусть r(A) = r(C) = r, т.е. система совместна. Любой минор порядка r, отличный от нуля, является базисным минором. Не ограничивая общности, будем считать, что базисный минор располагается в первых r (1 ≤ r ≤ min(m,n)) строках и столбцах матрицы А. Отбросив последние m-r уравнений системы, запишем укороченную систему:

которая эквивалентна исходной. Назовем неизвестные х₁,….х_r базисными , а х_r+1,…, х_r свободными и перенесем слагаемые, содержащие свободные неизвестные, в правую часть уравнений укороченной системы. Получаем систему относительно базисных неизвестных:

koтоторая для каждого набора значений свободных неизвестных х_r+1 = С₁,…, х_n = С_n-rимеет единственное рeшение х₁( С₁,…, С_n-r),…, х_r(С₁,…, С_n-r), находимое по правилу Крамера.

Соответствующее решение укороченной, а следовательно, и исходной системы имеет вид:

Х(С₁,…, С_n-r) = – общее решение системы.

Если в общем решении свободным неизвестным придать какие-нибудь числовые значения, то получим решение линейной системы, называемое частным .

Пример. Установить совместность и найти общее решение системы

Решение. А = , С = .

Так как r(A) = r(C) = 2 (убедитесь в этом самостоятельно), то исходная система совместна и имеет бесчисленное множество решений (так как r

Следовательно, общее решение исходной системы имеет вид:

Х(С₁;С₂) =

2.

6. Системы однородных уравнений

Система однородных уравнений = 0 (i =) всегда является совместной, так как r(A) = r(C).

Одним из решений системы однородных уравнений является тривиальное решение х₁ = х₂ = … = х_n = 0.

Для однородной системы важно установить, имеет ли она ненулевые решения. Из теоремы Кронекера – Капелли следует, что система однородных уравнений имеет ненулевое (нетривиальное) решение тогда и только тогда, когда r(A)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – | 7538 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: . Поскольку A -1 A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A -1 B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.

Решите матричное уравнение: XA+B=C, где

Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А -1 .

Решите матричное уравнение AX+B=C, где

Из уравнения получаем .

Следовательно,

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .

1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y,y Î R.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь

Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.

Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $
ang A=
angwidetilde$.

Следствие из теоремы Кронекера-Капелли

Если $
ang A
eq
angw >Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.

Исследовать СЛАУ $ left <egin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. end
ight.$ на совместность. Если СЛАУ совместна, указать количество решений.

Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:

Способ №1. Вычисление рангов по определению.

Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:

$$ Delta A=left| egin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end
ight|=-21. $$

Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца.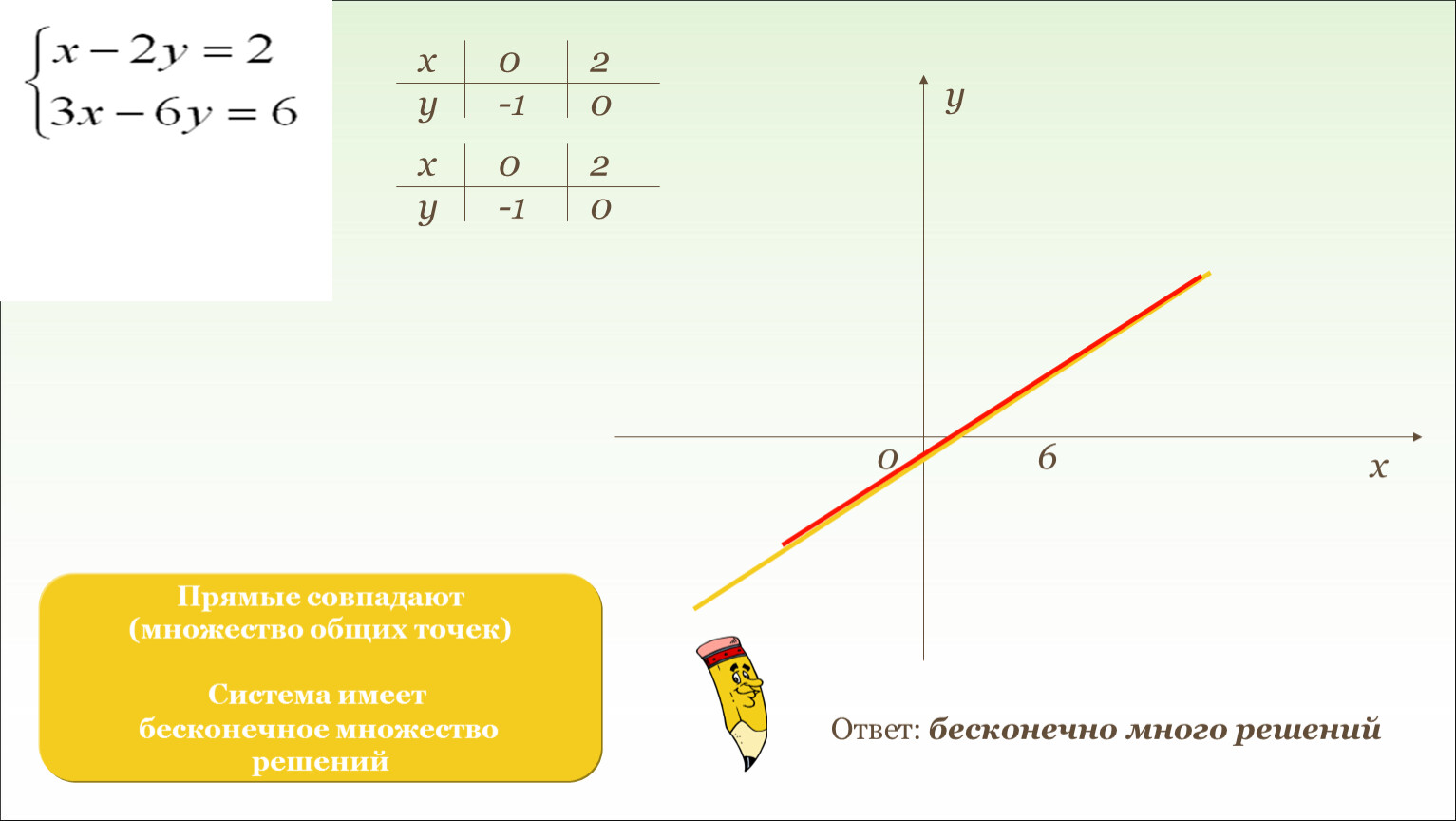 Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $
ang A=3$.

Нам требуется найти также и $
angw >

Так как $
ang A=
angw >

Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.

Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.

Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.

Способ №2. Вычисление ранга методом элементарных преобразований.

egin &w >Мы привели матрицу $w >

Так как $
ang A=
angw >

Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.

Ответ: Заданная СЛАУ совместна и определена.

Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований. Расширенная матрица системы: $w > $$ left( egin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end
ight) eginphantom<0>\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1end
ightarrow left( egin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end
ight) eginphantom<0>\phantom<0>\r_3-r_2\ r_4-r_2\r_5+r_2end
ightarrow\ $$ $$
ightarrowleft( egin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end
ight) eginphantom<0>\phantom<0>\phantom<0>\ r_4-r_3\phantom<0>end
ightarrow left( egin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end
ight) $$

Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $
angw >

Ответ: система несовместна.

Приводим расширенную матрицу системы к ступенчатому виду:

$$ left( egin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end
ight) overset> <
ightarrow>$$ $$
ightarrowleft( egin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end
ight) eginphantom<0>\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end
ightarrow left( egin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end
ight) eginphantom<0>\ phantom<0>\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end
ightarrow $$ $$
ightarrowleft( egin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end
ight) eginphantom<0>\ phantom<0>\phantom <0>\ r_4-r_3 \ r_5+r_2 end
ightarrow left( egin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end
ight) $$

Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $
angw >

Ответ: система является неопределённой.

Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.

Конспект учебного занятия по теме: «Система линейных уравнений с параметром» | План-конспект занятия по алгебре (8, 9, 10 класс) на тему:

Конспект учебного  занятия по теме: «Система линейных уравнений с параметром»

Попченко Светлана Николаевна, учитель математики 

Параметр ( от греческого слова parametron – отмеривающий) – величина, значения которой служат для различения элементов некоторого множества между собой.

 Исследование многих систем, процессов в жизни осуществляется с использованием параметров. Если для движущегося тела указан закон движения, то его положение в пространстве полностью определяется параметром времени. В качестве параметра для оценки состояния спортсмена тренером используется частота сердечных сокращений. Состояние больного врач- терапевт определяет с помощью параметров температуры, давления. Для функции Y=K/X  в качестве параметра выступает коэффициент K обратной пропорциональности. Общим для всех примеров является выделение некоторых характеристик систем, по изменениям которых оценивается состояние всей системы.

В учебном пособии Г.А. Ястребинецкого « Уравнения и неравенства, содержащие параметры» параметр рассматривается как переменная, которая при решении уравнений и неравенств считается постоянной величиной. В сборнике «514 задач с параметрами»под редакцией С.А.Тынянкина параметры- величины, численные значения которых не заданы конкретно, но должны считаться известными, причем параметры могут принимать произвольные значения. Аналогичный взгляд на параметры изложен в  книге П.И. Горнштейна и др. «Задачи с параметрами»: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет общаться с параметром как с числом, а во-вторых, степень свободы ограничивается его неизвестностью. В учебном пособии «Элементы теории и общие методы решения уравнений и неравенств с параметрами» В.И. Горбачева уравнения и неравенства с параметрами рассматриваются как уравнения и неравенства с несколькими переменными, при этом в качестве параметра может быть выбрана любая из переменных.

Главная особенность задач с параметрами — ветвление решения в зависимости от значения параметров. Другими словами, процесс решения осуществляется классификацией частных уравнений (неравенств) по типам с последующим поиском общих решений каждого типа. Построение «картины» граничных значений параметров и выделяемых ими областей однотипности – составная часть выделения и исследования каждого типа частных уравнений и неравенств.

Поставим задачу:  

Решение и исследование систем линейных уравнений. Правило Крамера.

1. Если ставится задача найти множество общих решений двух или нескольких уравнений с двумя переменными, то говорят, что надо решить систему уравнений.
2. Решить систему уравнений – значит найти все её решения
3. Систему называют  определенной, если она имеет конечное число решений

                                     неопределенной, если она имеет бесконечное множество решений

                                     совместной, если она имеет хотя бы одно решение

                                     несовместной, если она не имеет ни одного решения

Пусть дана система двух линейных уравнений с двумя переменными

Главным определителем системы называется число, которое равно

Первым вспомогательным определителем называется число, которое вычисляется по формуле:

причем, он получается из главного определителя, если столбец коэффициентов при x  заменить столбцом свободных членов .

Вторым вспомогательным определителем называется число, которое вычисляется по формуле:

причем, он получается из главного определителя, если столбец коэффициентов при y  заменить столбцом свободных членов .

Правило Крамера

1. Если главный определитель системы отличен от нуля , то система совместна и имеет единственное решение, причем   

2. Если главный определитель системы равен нулю , а хотя бы один из вспомогательных отличен от нуля  то система несовместна.

3. Если главный определитель системы и оба вспомогательных равны нулю, то система совместна и имеет бесконечное множество решений (является неопределенной), причем, если  тогда  где

С помощью правила Крамера легко проводить исследование систем уравнений с параметрами.

Исследовать систему уравнений — это значит решить вопрос о ее совместности или несовместности, и если она совместна, то найти все ее решения.

1. Исследовать систему уравнений

Решение

Найдем главный и оба вспомогательных определителя системы:

1. Главный определитель системы не равен нулю, если  тогда система совместна и имеет единственное решение:

2. Если a — 1= 0, a = 1, тогда  значит система совместна и имеет бесконечное множество решений, т. е. является неопределенной.

Пусть  тогда из первого или второго уравнения  где

Ответ: 1. Если  тогда система совместна и имеет единственное решение

            2. Если a = 1, тогда система совместна и имеет бесконечное множество решений,   где

2. Исследовать систему уравнений:

Решение

Найдем главный и оба вспомогательных определителя системы:

1. Если  тогда система совместна и имеет единственное решение  

2. Если a = 2, тогда  значит система несовместна.

3. Если a = 0, тогда  значит система имеет бесконечное множество решений, т. е. является неопределенной. Положим x = t, тогда из первого или второго уравнения находим  где

Ответ:

1. Если  тогда система совместна и имеет единственное решение

2. Если a = 2, тогда система несовместна.

3. Если a = 0, тогда система совместна и имеет бесконечное множество решений:

 где

3. Исследовать систему уравнений

Решение

Найдем главный и оба вспомогательных определителя системы:

1. Если   тогда система совместна и имеет единственное решение  

2. Если a = -b, тогда  система имеет бесконечное множество решений, т. е. является неопределенной. Положим  тогда  где

Ответ:

1. Если  тогда система совместна и имеет единственное решение

2. Если  тогда система совместна и имеет бесконечное множество решений  где

4. Найти все значения а, при которых система уравнений  имеет единственное решение.

Решение

Найдем главный и оба вспомогательных определителя системы:

Если , то система имеет единственное решение.

Ответ:

5. Найти все значения , при которых система уравнений

 имеет бесконечное множество решений.

Решение

Найдем главный и оба вспомогательных определителя системы:

,

.

Если m = 5, тогда все три определителя равны нулю , а значит система совместна и имеет бесконечное множество решений.

Ответ: m = 5.

6. Найти все значения а, при которых система уравнений  не имеет решений.

Решение

Найдем главный и оба вспомогательных определителя системы:

.

.

При a = -2 главный определитель равен нулю , а оба вспомогательных не равны нулю .

Ответ: a = -2.

Задачи для самостоятельного решения

Исследовать системы уравнений:

1.

                                                                                Ответ:

1. Если , то система совместна и имеет единственное решение .

2. Если a = 0, то система совместна и имеет бесконечное множество решений.

2.

                                                                                Ответ:

1. Если , то система совместна и имеет единственное решение:

.

2. Если a = -1, то система совместна и имеет бесконечное множество решений.

3. Если , то система несовместна.

3.

Ответ:

1. Если , то система совместна и имеет единственное решение:

.

2. Если a = -1 или a = 2, то система имеет бесконечное множество решений.

3. Если a = 1 или a = 0, то система несовместна.

4.

Ответ:

1. Если , то система совместна и имеет единственное решение (a; b).

2. Если a = b, то система  совместна и имеет б/м решений.

5. Найти все значения a, при которых система уравнений  имеет единственное решение.

                                                                                Ответ: .

6. Найти все значения m, при которых система уравнений  имеет бесконечное множество решений.

                                                                                Ответ: m = -7.

7. Найти все значения a, при которых система уравнений  не имеет решений.

                                                                                Ответ:  .

Литература

1. Сборник задач по математике для поступающих во втузы: учебное пособие / Под редакцией МИ. Сканави. — М.: Высшая школа, 1992.
2. Задачи с параметрами и методы их решения В.С.Крамор. -М. Мир и образование, 2007.
3. Элементы теории и общие методы решения уравнений и неравенств с параметрами   В.И. Горбачев. –  Брянск, 1998.

         4.    Материалы для подготовки к ЕГЭ и централизованному тестированию для выпускников школ и абитуриентов  В.И.Тишин. – Комаричи, 2008 г.

системы, зависящие от алгебры колледжа

определитель — Система линейного уравнения не имеет решения, единственного решения или бесконечного решения?

Вероятно, самый простой метод (чтобы полностью различить различные возможности), который я видел, — это преобразование соответствующей расширенной матрицы в эшелонированную форму с сокращенными строками.В этом случае вы должны начать с: $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & -4 \\ 4 & -1 & 2 & 3 \\ 2 & -1 & -3 & 1 \ end {array} \ right] $$ Вычитая $ 4 $ первую строку из второй и $ 2 $, умноженную на первую строку из третьей, мы получаем: $$ \ left [\ begin {array} { ccc | c} 1 & 3 & -1 & -4 \\ 0 & -13 & 6 & 19 \\ 0 & -7 & -1 & 9 \ end {array} \ right] $$ Вычитание 2 $, умноженное на треть в строке со второго мы имеем: $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & -4 \\ 0 & 1 & 8 & 1 \\ 0 & -7 & -1 & 9 \ end {array} \ right] $$ Добавив $ 7 $ из второй строки к третьей, мы получим: $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & -4 \\ 0 & 1 & 12 & 1 \\ 0 & 0 & 55 & 16 \ end {array} \ right] $$

На данный момент у нас есть только нули ниже главной диагонали, но нет нулей на диагонали, поэтому существует единственное решение. Продолжая уменьшать, пока часть расширенной матрицы $ 3 \ times 3 $ не станет просто единичной матрицей $ 3 \ times 3 $, мы получим $$ \ left [\ begin {array} {ccc | c} 1 & 0 & 0 & 3 / 11 \\ 0 & 1 & 0 & -73/55 \\ 0 & 0 & 1 & 16/55 \ end {array} \ right] $$ Это говорит нам, что $ x = 3/11, $ $ y = -73 / 55, $ z = 16/55 $ — единственное решение системы.

Давайте рассмотрим другую систему: $$ \ begin {ases} x + 3y-z = 4 \\ 4x-y + 2z = 8 \\ 2x-7y + 4z = -3, \ end {ases} $$, которая имеет соответствующая матрица $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & 4 \\ 4 & -1 & 2 & 8 \\ 2 & -7 & 4 & -3 \ end {array }\верно].$$ Начав таким же образом, мы получим $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & 4 \\ 0 & -13 & 6 & -8 \\ 0 & -13 & 6 & -11 \ end {array} \ right], $$ и вычитание второй строки из третьей дает нам $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & 4 \\ 0 & -13 & 6 & -8 \\ 0 & 0 & 0 & -3 \ end {array} \ right]. $$ Теперь у нас есть только нули ниже главной диагонали, но у нас есть ноль на главной диагонали, тоже. Это говорит нам о том, что решений либо нет, либо их бесконечно много.В обратном переводе на $ x, y, z $ это эквивалентная система $$ \ begin {cases} x + 3y + -z = 4 \\ 0x-13y + 6z = -8 \\ 0x + 0y + 0z = — 3, \ end {ases} $$ или, альтернативно, $$ \ begin {ases} x = — \ frac5 {13} z + \ frac {28} {13} \\ y = \ frac6 {13} z + \ frac8 {13} \\ 0 = 3, \ end {ases} $$, но нет решения последнего уравнения, поэтому нет решения системы.

Upshot : У нас не будет решений, когда мы закончим с одной или несколькими строками всех $ 0 $ s , за исключением последнего столбца , когда мы уменьшаем расширенную матрицу.

Напротив, если бы мы начали с системы $$ \ begin {cases} x + 3y-z = 4 \\ 4x-y + 2z = 8 \\ 2x-7y + 4z = 0, \ end {cases } $$, которому соответствует матрица $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & 4 \\ 4 & -1 & 2 & 8 \\ 2 & -7 & 4 & 0 \ end {array} \ right], $$ тогда наш процесс сокращения даст нам $$ \ left [\ begin {array} {ccc | c} 1 & 3 & -1 & 4 \\ 0 & -13 & 6 & -8 \\ 0 & 0 & 0 & 0 \ end {array} \ right]. $$ Опять же, у нас не должно быть решения или должно быть бесконечно много.Продолжая максимально сокращать количество строк, мы получаем $$ \ left [\ begin {array} {ccc | c} 1 & 0 & 5/13 & 28/13 \\ 0 & 1 & -6/13 & 8 / 13 \\ 0 & 0 & 0 & 0 \ end {array} \ right]. $$ В обратном переводе на $ x, y, z $ это эквивалентная система $$ \ begin {cases} x + 0y + \ frac5 {13} z = \ frac {28} {13} \\ 0x + y- \ frac6 {13} z = \ frac8 {13} \\ 0 = 0. \ end {ases} $$ Одно из этих уравнений всегда истинно, поэтому одна из наших переменных может принимать любое значение. Мы могли бы также позволить $ z $ принимать любое значение, после чего два других уравнения сообщат нам значения, которые должны принимать $ x $ и $ y $.Следовательно, у нас есть бесконечно много решений.

Upshot : У нас будет бесконечно много решений всякий раз, когда мы заканчиваем с одной или несколькими строками всех $ 0 $ s по мере уменьшения расширенной матрицы, пока у нас нет строк со всеми $ 0 $ s, кроме последний столбец.

Добавлено : просто берется определитель нерасширенной матрицы системы — значение $$ \ begin {bmatrix} 1 & 3 & -1 \\ 4 & -1 & 2 \\ 2 & -1 & — 3 \ end {bmatrix} $$ в первом примере и $$ \ begin {bmatrix} 1 & 3 & -1 \\ 4 & -1 & 2 \\ 2 & -7 & 4 \ end {bmatrix} $$ в двух других примерах — даст нам часть ответа.Если определитель равен $ 0 $ (как во втором и третьем примерах), то система либо не имеет решения, либо бесконечно много, но мы не можем (только этим методом) сказать какое. В противном случае система имеет уникальное решение, но мы не можем (только этим методом) сказать, каким оно могло бы быть. Вот почему я предпочитаю первый предложенный мной метод, по крайней мере, когда имею дело только с несколькими уравнениями и несколькими переменными: он рассказывает нам всю историю.

предварительное вычисление алгебры — Как алгебраически определить, имеет ли уравнение бесконечное решение или нет?

Чтобы однозначно решить четыре неизвестных с помощью линейных уравнений,
четыре уравнения требуются , но в целом недостаточно. 2 + Q’x + R ‘, $
ты получаешь
$$ P + Q + R = P ‘+ Q’ + R ‘.$$
Вот что мы получаем, взяв $ P = P ‘, $ $ Q = Q’, $ и $ R = R ‘$.
(три уравнения, которые у вас уже были), сложив три левых части,
сложение трех правых частей и приравнивание этих сумм.
Это очень простой пример использования линейной комбинации трех уравнений для получения четвертого уравнения.

Если вы сделаете это с вашими тремя уравнениями в их исходной записи (используя $ A, B, C, $ и $ D $ вместо $ P, $ Q, $ и т. Д.), Вы можете подтвердить, что ваше четвертое уравнение — это именно то, что вам нужно. вы получите, сложив остальные три вместе.

Поскольку ваше четвертое уравнение было просто линейной комбинацией трех других,
не является линейно независимым, он совершенно бесполезен для того, чтобы сделать решение уникальным.
У вас еще есть бесконечно много решений.
Однако, поскольку остальные три уравнения были линейно независимыми,
их достаточно для определения трех переменных; так
как только вы произвольно присваиваете значение одному из четырех значений $ A, B, C, $ или $ D, $ определяются остальные три.

Добавление других значений $ x $ только даст вам более линейные комбинации первых трех уравнений.2 + Q’x + R ‘$ для всех $ x $ подразумевает, что
$ P = P ‘, $ $ Q = Q’, $ и $ R = R ‘, $ вы можете доказать этот факт, подставив различные значения $ x $ в уравнение.
Трех значений $ x $ должно быть достаточно.

Некоторые связанные примечания по разложению на частичную дробь:

«Частичное дробное разложение» обычно представляет собой особый алгоритм, которому вы должны следовать определенным образом.

Как вы это делаете, вы можете закончить (в конце разложения)
с такими терминами, как $ \ frac {Ax + B} {x + 5}.2} $
… не в вашей проблеме, конечно, поскольку у вас нет квадратов множителей в знаменателе, но в целом квадраты множителей могут иметь место, и это один из способов их решения.
Но я не знаю ни одного стандартного метода, который позволял бы поместить $ Ax + B $ в числитель с одним множителем, например, $ x + 5 $ в знаменателе.
Поскольку у вас есть только один множитель $ x + 5 $, обычные методы позволяют записать в числитель только константу со знаменателем $ x + 5, $ то есть $ \ frac {A} {x + 5}. $

И, как уже указывалось в другом ответе, ограничение, которое вы должны начать с правильной дроби, на самом деле не является препятствием для использования метода,
потому что, если вы начнете с неправильной дроби, вы можете использовать полиномиальное деление в столбик, чтобы превратить его в сумму простого полинома (не дроби!) и правильной дроби.Если вы последуете этому методу на своем примере, у вас будет только два неизвестных, а не четыре.

Системы уравнений с тремя переменными

Решение систем уравнений с тремя переменными

Система уравнений с тремя переменными включает два или более уравнений, каждое из которых содержит от одной до трех переменных.

Цели обучения

Решите систему уравнений с тремя переменными графически, используя замену или исключение

Основные выводы

Ключевые моменты

• В системе из уравнений с тремя переменными у вас может быть одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z . Введение переменной z означает, что функции на графике теперь представляют плоскости, а не линии.
• Метод подстановки включает решение одной из переменных в одном из уравнений и включение этого в остальные уравнения для сокращения системы. Повторяйте, пока не останется одно уравнение, а затем, используя это уравнение, вернитесь назад, чтобы решить предыдущие уравнения.
• Графический метод включает построение системы в виде графика и нахождение единственной точки пересечения плоскостей.
• Метод исключения включает добавление или вычитание кратных значений одного уравнения из других уравнений, удаление переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется одна переменная.

Ключевые термины

• Система уравнений с тремя переменными : Набор из одного или нескольких уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x, y и z.
• Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.

Системы уравнений с тремя переменными

В математике одновременные уравнения — это система уравнений, содержащая несколько переменных. Этот набор часто упоминается как система уравнений . Решение системы уравнений — это конкретная спецификация значений всех переменных, которая одновременно удовлетворяет всем уравнениям. Графически решение находится там, где функции пересекаются.

В системе уравнений с тремя переменными вы можете иметь одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z .Введение переменной z означает, что функции на графике теперь представляют плоскости, а не линии.

Простой пример

Это набор линейных уравнений, также известный как линейная система уравнений, с тремя переменными:

[латекс] \ left \ {\ begin {matrix} 3x + 2y-z = 6 \\ -2x + 2y + z = 3 \\ x + y + z = 4 \\ \ end {matrix} \ right. [ / латекс]

Решение этой системы уравнений:

[латекс] \ left \ {\ begin {matrix} x = 1 \\ y = 2 \\ z = 1 \\ \ end {matrix} \ right.[/ латекс]

Подставьте эти значения в каждое из уравнений, чтобы убедиться, что решение удовлетворяет всем трем уравнениям.

Решение систем уравнений с тремя переменными

Графический метод

Графический метод решения системы уравнений с тремя переменными включает построение плоскостей, которые образуются при построении графика каждого уравнения в системе, а затем нахождение точки пересечения всех трех плоскостей. Единственная точка пересечения всех трех плоскостей — это единственное решение системы.

Система линейных уравнений: На этом изображении показана система трех уравнений с тремя переменными. Точка пересечения (белая точка) — единственное решение этой системы.

Метод замещения

Метод подстановки для решения системы уравнений с тремя переменными включает определение уравнения, которое может быть легко записано с одной переменной в качестве предмета (путем решения уравнения для этой переменной). Затем замените это выражение, где эта переменная появляется в двух других уравнениях, тем самым получив меньшую систему с меньшим количеством переменных.После того, как эта меньшая система решена, будь то дальнейшее применение метода подстановки или другими методами, подставьте найденные решения для переменных обратно в первое выражение в правой части.

Например, рассмотрим эту систему уравнений:

[латекс] \ left \ {\ begin {matrix} 3x + 2y-z = 6 \\ -2x + 2y + z = 3 \\ x + y + z = 4 \\ \ end {matrix} \ right. [ / латекс]

Поскольку коэффициент z уже равен 1 в первом уравнении, решите относительно z , чтобы получить:

[латекс] z = 3x + 2y-6 [/ латекс]

Подставьте это выражение для z в два других уравнения:

[латекс] \ left \ {\ begin {matrix} -2x + 2y + (3x + 2y-6) = 3 \\ x + y + (3x + 2y-6) = 4 \\ \ end {matrix} \ right.[/ латекс]

Эта новая система упрощается до:

[латекс] \ left \ {\ begin {matrix} x + 4y = 9 \\ 4x + 3y = 10 \\ \ end {matrix} \ right. [/ Latex]

Теперь, решая относительно x в первом уравнении, получаем:

[латекс] х = 9-4лет [/ латекс].

Подставьте это выражение для x в последнее уравнение системы и решите относительно y :

[латекс] \ displaystyle \ begin {align} 4 (9-4y) + 3y & = 10 \\ 36-16y + 3y & = 10 \\ 13y & = 26 \\ y & = 2 \ end {align} [/ latex]

Теперь, когда у вас есть значение и , восстановите уравнение.Подставьте [латекс] y = 2 [/ latex] в уравнение [latex] x = 9-4y [/ latex], чтобы получить [latex] x = 1 [/ latex].

Работая снова, подставьте [latex] (1,2) [/ latex] в первое подставленное уравнение и решите относительно z :

[латекс] \ begin {align} z & = 3x + 2y-6 \\ z & = (3 \ cdot 1) + (2 \ cdot 2) -6 \\ z & = 1 \ end {align} [/ latex]

Следовательно, решение системы уравнений — [латекс] (1,2,1) [/ латекс].

Метод исключения

Устранение разумным умножением — еще один широко используемый метод решения одновременных линейных уравнений. Он использует общие принципы, согласно которым каждая сторона уравнения по-прежнему равна другой, когда обе стороны умножаются (или делятся) на одну и ту же величину, или когда одна и та же величина добавляется (или вычитается) с обеих сторон.

По мере того, как уравнения становятся проще за счет исключения некоторых переменных, переменная в конечном итоге появляется в полностью решаемой форме, и это значение затем может быть «подставлено обратно» в ранее выведенные уравнения, подставив это значение в качестве переменной. Обычно каждая «обратная подстановка» может позволить решить другую переменную в системе.

Давайте посмотрим на следующую систему:

[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ x-y + 3z = 4 \\ 2x + 2y + z = 3 \\ \ end {matrix} \ right. [/ латекс]

Используя метод исключения, начните с вычитания первого уравнения из второго и упрощения:

[латекс] \ displaystyle \ begin {align} x-y + 3z- (x + y + z) & = 4-2 \\ — 2y + 2z & = 2 \ end {align} [/ latex]

Теперь у нас есть следующая система уравнений:

[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ -2y + 2z = 2 \\ 2x + 2y + z = 3 \\ \ end {matrix} \ right. [/ латекс]

Теперь вычтите дважды первое уравнение из третьего, чтобы получить

.

[латекс] \ begin {align} 2x + 2y + z-2 (x + y + z) & = 3-2 (2) \\ 2x + 2y + z-2x-2y-2z & = — 1 \\ z & = 1 \ end {align} [/ latex]

При этом отображается новая система:

[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ -2y + 2z = 2 \\ z = 1 \\ \ end {matrix} \ right. [/ Latex]

Затем вычтите дважды третье уравнение из второго уравнения и упростите:

[латекс] \ begin {align} -2y + 2z-2z & = 2-2 \\ y & = 0 \ end {align} [/ latex]

При этом отображается новая система:

[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ y = 0 \\ z = 1 \\ \ end {matrix} \ right.[/ латекс]

Наконец, вычтите третье и второе уравнение из первого уравнения, чтобы получить

[латекс] \ begin {align} x + y + z-y-z & = 2-0-1 \\ x & = 1 \ end {align} [/ latex]

Таким образом, окончательная решенная система:

[латекс] \ left \ {\ begin {matrix} x = 1 \\ y = 0 \\ z = 1 \\ \ end {matrix} \ right. [/ Latex]

Несогласованные и зависимые системы с тремя переменными

Системы уравнений с тремя переменными могут быть независимыми, зависимыми или несовместимыми; каждый случай можно установить алгебраически и представить графически.

Цели обучения

Объясните графически, что это значит, что системы уравнений с тремя переменными непоследовательны или зависимы, а также как распознать алгебраически, когда это имеет место

Основные выводы

Ключевые моменты

• Зависимые системы имеют бесконечное количество решений. Графически бесконечное количество решений находится на линии или плоскости, которая служит пересечением трех плоскостей в пространстве.
• Решение зависимой системы путем исключения приводит к выражению, которое всегда истинно, например [latex] 0 = 0 [/ latex].
• Несогласованные системы не имеют решения. Графически система без решения представлена ​​тремя плоскостями, не имеющими общей точки.
• Решение противоречивой системы путем исключения приводит к утверждению, которое является противоречием, например [латекс] 3 = 0 [/ латекс].

Ключевые термины

• Независимая система : Система уравнений с одним решением. Для систем уравнений с тремя переменными это решение представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex], которая представляет собой единственную точку пересечения трех плоскостей.
• Зависимая система : Система уравнений с бесконечным числом решений. Для систем уравнений с тремя переменными существует бесконечное количество решений на прямой или плоскости, которая является пересечением трех плоскостей в пространстве.
• Несогласованная система : Система уравнений без решения. Система уравнений с тремя переменными, не имеющая решений, представлена ​​тремя плоскостями, не имеющими общей точки.

Определение зависимых и несовместимых систем

Напомним, что решение линейной системы — это присвоение чисел переменным таким образом, чтобы все уравнения выполнялись одновременно. Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex] и описывает точку пересечения трех плоскостей в пространстве.

Существует три возможных сценария решения систем трех уравнений с тремя переменными:

• Независимые системы имеют единое решение. Решение системы путем исключения приводит к единственной упорядоченной тройке [латекс] (x, y, z) [/ latex]. Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
• Зависимые системы имеют бесконечное количество решений. Графически решения попадают на линию или плоскость, которая является пересечением трех плоскостей в пространстве.
• Несогласованные системы не имеют решения. Графически система без решения представлена ​​тремя плоскостями, не имеющими общей точки.

Зависимые системы уравнений с тремя переменными

Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений. То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может возникнуть из нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на линии, имеющей бесконечное количество решений (см. Ниже графическое представление). Или два уравнения могут быть одинаковыми и пересекать третье по линии (см. Пример задачи для графического представления).

Зависимые системы: Пример трех различных уравнений, пересекающихся на линии.

Например, рассмотрим эту систему уравнений:

[латекс] \ left \ {\ begin {matrix} \ begin {align} 2x + y — 3z & = 0 \\ 4x + 2y — 6z & = 0 \\ x — y + z & = 0 \ end {align } \ end {matrix} \ right. [/ latex]

Сначала умножьте первое уравнение на [латекс] -2 [/ латекс] и добавьте его ко второму уравнению:

[латекс] \ begin {align} -2 (2x + y — 3z) + (4x + 2y — 6z) & = 0 + 0 \\ (-4x + 4x) + (-2y + 2y) + (6z — 6z) & = 0 \\ 0 & = 0 \ end {align} [/ latex]

Нам больше не нужно идти. В результате мы получаем тождество [latex] 0 = 0 [/ latex], которое говорит нам, что эта система имеет бесконечное количество решений. Есть и другие способы начать решать эту систему, например, умножив третье уравнение на [латекс] -2 [/ латекс] и прибавив его к первому уравнению. Затем мы выполняем те же шаги, что и выше, и получаем тот же результат, [latex] 0 = 0 [/ latex].

Если бы мы изобразили график каждого из трех уравнений, у нас были бы три плоскости, изображенные ниже. Обратите внимание, что две плоскости одинаковы, и они пересекают третью плоскость по прямой.Множество решений бесконечно, так как все точки на линии пересечения будут удовлетворять всем трем уравнениям.

Зависимая система : два уравнения представляют одну и ту же плоскость, и они пересекают третью плоскость на прямой.

Несогласованные системы уравнений с тремя переменными

Как и в случае с системами уравнений с двумя переменными, мы можем встретить несовместимую систему уравнений с тремя переменными, что означает, что у нее нет решения, которое удовлетворяет всем трем уравнениям. Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном месте. Процесс исключения приведет к ложному утверждению, например [латекс] 3 = 7 [/ латекс], или другому противоречию.

Несогласованные системы : Все три цифры представляют системы три на три без решения. (а) Три плоскости пересекаются друг с другом по трем различным параллельным линиям, которые не пересекаются в общей точке.(b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. (c) Все три плоскости параллельны, поэтому точки пересечения нет.

Например, рассмотрим систему уравнений

[латекс] \ left \ {\ begin {matrix} \ begin {align} x — 3y + z & = 4 \\ -x + 2y — 5z & = 3 \\ 5x — 13y + 13z & = 8 \ end { align} \ end {matrix} \ right. [/ latex]

Используя метод исключения для решения системы уравнений с тремя переменными, обратите внимание, что мы можем добавить первое и второе уравнения, чтобы сократить [latex] x [/ latex]:

[латекс] \ begin {align} (x — 3y + z) + (-x + 2y — 5z) & = 4 + 3 \\ (x — x) + (-3y + 2y) + (z-5z) & = 7 \\ -y — 4z & = 7 \ end {align} [/ latex]

Затем умножьте первое уравнение на [латекс] -5 [/ латекс] и добавьте его к третьему уравнению:

[латекс] \ begin {align} -5 (x — 3y + z) + (5x — 13y + 13z) & = -5 (4) + 8 \\ (-5x + 5x) + (15y — 13y) + (-5z + 13z) & = -20 + 8 \\ 2y + 8z & = -12 \ end {align} [/ latex]

Теперь обратите внимание, что у нас есть система уравнений с двумя переменными:

[латекс] \ left \ {\ begin {matrix} \ begin {align} -y — 4z & = 7 \\ 2y + 8z & = -12 \ end {align} \ end {matrix} \ right. [/ латекс]

Мы можем решить эту проблему, умножив верхнее уравнение на 2 и прибавив его к нижнему уравнению:

[латекс] \ begin {align} 2 (-y-4z) + (2y + 8z) & = 2 (7) -12 \\ (-2y + 2y) + (-8z + 8z) & = 14 — 12 \\ 0 & = 2 \ end {align} [/ latex]

Окончательное уравнение [латекс] 0 = 2 [/ латекс] является противоречием, поэтому мы заключаем, что система уравнений несовместима и, следовательно, не имеет решения.

Бесконечные решения — определение, условия и примеры

Все мы хорошо знакомы с уравнениями и выражениями.Мы почти ежедневно решаем ее по математике. Давайте просто быстро освежим значения терминов еще раз, прежде чем мы углубимся. Уравнение — это выражение, между которым стоит знак равенства (=). Например, 4 + 3 = 7. А выражение состоит из переменных, таких как x или y, и постоянных членов, которые соединяются вместе с помощью алгебраических операторов. Например, 2x + 4y — 9, где x и y — переменные, а 9 — постоянная. Насколько мы можем судить, обычно существует одно решение уравнения. Но не исключено, что уравнение не может иметь более одного решения, бесконечного числа решений или вообще не иметь решений.Отсутствие решения означает, что уравнение не имеет ответа, тогда как бесконечные решения уравнения означают, что любое значение переменной сделает уравнение истинным.

Что такое бесконечные решения?

Общее количество переменных в уравнении определяет количество решений, которые оно даст. Исходя из этого, решения можно сгруппировать в три типа:

1. Уникальное решение (имеющее только 1 решение).

2. Нет решений (без решений)

3. Бесконечные решения (с множеством решений)

Но как вы узнаете, является ли решение вашего решенного уравнения бесконечным решением? Что ж, есть простой способ узнать, является ли ваше решение бесконечным. У бесконечного решения обе стороны равны. Например, 6x + 2y — 8 = 12x + 4y — 16. Если вы упростите уравнение, используя формулу или метод бесконечных решений, вы получите равные обе части, следовательно, это будет бесконечное решение. Бесконечность представляет собой безграничность или безграничность. Обычно обозначается символом «∞».

Условия для бесконечного решения

Уравнение дает бесконечное решение, если оно удовлетворяет некоторым условиям для бесконечных решений. Бесконечное решение может быть получено, если линии совпадают и у них должно быть одинаковое пересечение по оси y.Две линии, имеющие одинаковую точку пересечения по оси Y и наклон, на самом деле являются одной и той же линией. Проще говоря, мы можем сказать, что если две линии делят одну и ту же линию, тогда система приведет к бесконечному решению. Следовательно, система будет непротиворечивой, если система уравнений имеет бесконечное число решений.

Например, рассмотрим следующие уравнения.

y = x + 3

5y = 5x + 15

Если мы умножим 5 на уравнение 1, мы получим уравнение 2, а разделив уравнение 2 на 5, мы получим точное первое уравнение.

Пример бесконечного решения

Какой пример бесконечного решения? Это вопрос, которого мы так долго ждали. Но для решения системы уравнений с двумя или тремя переменными важно понимать, является ли уравнение зависимым или независимым, является ли это непротиворечивым уравнением или несовместимым уравнением. Непротиворечивая пара линейных уравнений всегда будет иметь уникальные или бесконечные решения.

Пример 1) Вот два уравнения с двумя переменными.

a1x + b1y = c1 ——- (1)

a2x + b2y = c2 ——- (2)

Если (a1 / a2) = (b1 / b2) = (c1 / c2)

Тогда Уравнение — это непротиворечивое и зависимое уравнение, которое имеет бесконечно много решений.

Пример 2) Вот несколько уравнений с бесконечными решениями -6x + 4y = 2

3x — 2y = -1

Теперь, если мы умножим второе уравнение на -2, мы получим первое уравнение.

-2 (3x-2y) = -2 (-1)

-6x + 4y = 2

Следовательно, уравнения эквивалентны и будут иметь один и тот же график.Таким образом, решение, которое будет работать для одного уравнения, будет работать и для других уравнений. Следовательно, они являются бесконечными решениями системы.

Пример 3) x-10 + x = 8 + 2x-18

Итак, как мы поступаем

x-10 + x = 8 + 2x-18

2x-10 = 2x-10

-2x = -2x

__________________

-10 = -10

Поскольку -10 = -10, остается истинное утверждение, и мы можем сказать, что это бесконечное решение.

Пример 4) Возьмем другой пример: x + 2x + 3 + 3 = 3 (x + 2)

x + 2x + 3 + 3 = 3 (x + 2)

3x + 6 = 3x + 6

-3x = -3x

6 = 6

Коэффициенты и константы совпадают после объединения одинаковых членов.Это дает нам верное утверждение. Поэтому их можно назвать бесконечными решениями.

Пример 5) Рассмотрим 4 (x + 1) = 4x + 4 как уравнение.

4 (x + 1) = 4x + 4

4x + 4 = 4x + 4

Мы видим, что в окончательном уравнении обе части равны. Следовательно, это бесконечное решение.

1.9: Упражнения — математика LibreTexts

Графически найдите точку \ (\ left (x_ {1}, y_ {1} \ right) \), которая лежит на обеих прямых, \ (x + 3y = 1 \) и \ (4x-y = 3.\) То есть нанесите на график каждую линию и посмотрите, где они пересекаются.

\ (\ begin {array} {c} x + 3y = 1 \\ 4x-y = 3 \ end {array} \). Решение: \ (\ left [x = \ frac {10} {13}, y = \ frac {1} {13} \ right] \).

Графически найдите точку пересечения двух прямых \ (3x + y = 3 \) и \ (x + 2y = 1. \), То есть нанесите на график каждую линию и посмотрите, где они пересекаются.

\ (\ begin {array} {c} 3x + y = 3 \\ x + 2y = 1 \ end {array} \). Решение: \ (\ left [x = 1, y = 0 \ right] \ )

У вас есть система \ (k \) уравнений с двумя переменными, \ (k \ geq 2 \).Объясните геометрическое значение числа

.

1. Нет решения.

2. Уникальное решение.

3. Бесконечное количество решений.

[Chapter1Q8] Рассмотрим следующую расширенную матрицу, в которой \ (\ ast \) обозначает произвольное число, а \ (\ blacksquare \) обозначает ненулевое число. Определите, согласована ли данная расширенная матрица. Если согласовано, является ли решение уникальным? \ [\ left [\ begin {array} {ccccc | c} \ blacksquare & \ ast & \ ast & \ ast & \ ast & \ ast \\ 0 & \ blacksquare & \ ast & \ ast & 0 & \ ast \ \ 0 & 0 & \ blacksquare & \ ast & \ ast & \ ast \\ 0 & 0 & 0 & 0 & \ blacksquare & \ ast \ end {array} \ right] \]

Решение существует, но не уникальное.

Рассмотрим следующую расширенную матрицу, в которой \ (\ ast \) обозначает произвольное число, а \ (\ blacksquare \) обозначает ненулевое число. Определите, согласована ли данная расширенная матрица. Если согласовано, является ли решение уникальным? \ [\ left [\ begin {array} {ccc | c} \ blacksquare & \ ast & \ ast & \ ast \\ 0 & \ blacksquare & \ ast & \ ast \\ 0 & 0 & \ blacksquare & \ ast \ конец {массив} \ right] \]

Решение существует и уникально.

Рассмотрим следующую расширенную матрицу, в которой \ (\ ast \) обозначает произвольное число, а \ (\ blacksquare \) обозначает ненулевое число.Определите, согласована ли данная расширенная матрица. Если согласовано, является ли решение уникальным? \ [\ left [\ begin {array} {ccccc | c} \ blacksquare & \ ast & \ ast & \ ast & \ ast & \ ast \\ 0 & \ blacksquare & 0 & \ ast & 0 & \ ast \\ 0 & 0 & 0 & \ blacksquare & \ ast & \ ast \\ 0 & 0 & 0 & 0 & \ blacksquare & \ ast \ end {array} \ right] \]

Рассмотрим следующую расширенную матрицу, в которой \ (\ ast \) обозначает произвольное число, а \ (\ blacksquare \) обозначает ненулевое число.Определите, согласована ли данная расширенная матрица. Если согласовано, является ли решение уникальным? \ [\ left [\ begin {array} {ccccc | c} \ blacksquare & \ ast & \ ast & \ ast & \ ast & \ ast \\ 0 & \ blacksquare & \ ast & \ ast & 0 & \ ast \ \ 0 & 0 & 0 & 0 & \ blacksquare & 0 \\ 0 & 0 & 0 & 0 & \ ast & \ blacksquare \ end {array} \ right] \]

Может быть решение. Если так, то их бесконечно много.

Предположим, что в системе уравнений меньше уравнений, чем переменных.Обязательно ли такая система будет последовательной? Если да, объясните, почему, а если нет, приведите пример, который не соответствует действительности.

Нет. Рассмотрим \ (x + y + z = 2 \) и \ (x + y + z = 1. \)

Если в системе уравнений больше уравнений, чем переменных, может ли она иметь решение? Если да, то приведите пример, а если нет, скажите, почему бы и нет.

У них есть решение. Например, \ (x + y = 1,2x + 2y = 2,3x + 3y = 3 \) даже имеет бесконечное множество решений.

Найдите \ (h \) такое, что \ [\ left [\ begin {array} {rr | r} 2 & h & 4 \\ 3 & 6 & 7 \ end {array} \ right] \] является расширенной матрицей из несовместимой системы .

\ (h = 4 \)

Найдите \ (h \) такое, что \ [\ left [\ begin {array} {rr | r} 1 & h & 3 \\ 2 & 4 & 6 \ end {array} \ right] \] является расширенной матрицей согласованной системы .

Any \ (h \) будет работать.

Найдите \ (h \) такое, что \ [\ left [\ begin {array} {rr | r} 1 & 1 & 4 \\ 3 & h & 12 \ end {array} \ right] \] является расширенной матрицей согласованной системы .

Any \ (h \) будет работать.

Выберите \ (h \) и \ (k \) так, чтобы показанная расширенная матрица имела каждое из следующих значений:

1. одно решение

2. нет решения

3. бесконечно много решений

\ [\ left [\ begin {array} {rr | r} 1 & h & 2 \\ 2 & 4 & k \ end {array} \ right] \]

Если \ (h \ neq 2 \) будет единственное решение для любого \ (k \).Если \ (h = 2 \) и \ (% k \ neq 4, \), решений нет. Если \ (h = 2 \) и \ (k = 4, \), то решений бесконечно много.

Выберите \ (h \) и \ (k \) так, чтобы показанная расширенная матрица имела каждое из следующих значений:

1. одно решение

2. нет решения

3. бесконечно много решений

\ [\ left [\ begin {array} {rr | r} 1 & 2 & 2 \\ 2 & h & k \ end {array} \ right] \]

Если \ (h \ neq 4, \), то существует ровно одно решение.Если \ (h = 4 \) и \ (k \ neq 4, \), то решений нет. Если \ (h = 4 \) и \ (k = 4, \), то решений бесконечно много.

Определите, согласована ли система. Если да, то является ли решение уникальным? \ [\ begin {array} {c} x + 2y + zw = 2 \\ x-y + z + w = ​​1 \\ 2x + yz = 1 \\ 4x + 2y + z = 5 \ end {array} \ ]

Нет решения. Система непоследовательна. Вы можете видеть это из расширенной матрицы. \ (\ left [\ begin {array} {rrrrr} 1 & 2 & 1 & -1 & 2 \\ 1 & -1 & 1 & 1 & 1 \\ 2 & 1 & -1 & 0 & 1 \\ 4 & 2 & 1 & 0 & 5 \ end {array} \ right] \),: \ (\ left [\ begin {array} {rrrrr} 1 & 0 & 0 & \ vspace {0.05in} \ frac {1} {3} & 0 \\ 0 & 1 & 0 & — \ vspace {0,05 дюйма} \ frac {2} {3} & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \ end {array} \ right]. \)

Определите, согласована ли система. Если да, то является ли решение уникальным? \ [\ begin {array} {c} x + 2y + zw = 2 \\ x-y + z + w = ​​0 \\ 2x + yz = 1 \\ 4x + 2y + z = 3 \ end {array} \ ]

Решение: \ (\ left [w = \ frac {3} {2} y-1, x = \ frac {2} {3} — \ frac {1} {2} y, z = \ frac {1 } {3} \ right] \)

Определите, какие матрицы находятся в.

1. \ (\ left [\ begin {array} {rrr} 1 & 2 & 0 \\ 0 & 1 & 7 \ end {array} \ right] \)

2. \ (\ left [\ begin {array} {rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 & 0 \ end {array} \ right] \)

3. \ (\ left [\ begin {array} {rrrrrr} 1 & 1 & 0 & 0 & 0 & 5 \\ 0 & 0 & 1 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 & 1 & 3 \ end {array} \ right] \)

1. Это не так.

2. Вот это.

3. Вот это.

Строку уменьшите следующую матрицу, чтобы получить. Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 2 & -1 & 3 & -1 \\ 1 & 0 & 2 & 1 \\ 1 & -1 & 1 & -2 \ end {array} \ right] \]

Строку уменьшите следующую матрицу, чтобы получить. Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 0 & 0 & -1 & -1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & -1 \ end {array} \ right] \ ]

Строку уменьшите следующую матрицу, чтобы получить.Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 3 & -6 & -7 & -8 \\ 1 & -2 & -2 & -2 \\ 1 & -2 & -3 & -4 \ end { массив} \ справа] \]

Строку уменьшите следующую матрицу, чтобы получить. Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 2 & 4 & 5 & 15 \\ 1 & 2 & 3 & 9 \\ 1 & 2 & 2 & 6 \ end {array} \ right] \]

Строку уменьшите следующую матрицу, чтобы получить. Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 4 & -1 & 7 & 10 \\ 1 & 0 & 3 & 3 \\ 1 & -1 & -2 & 1 \ end {array} \ right] \ ]

Строку уменьшите следующую матрицу, чтобы получить.Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} 3 & 5 & -4 & 2 \\ 1 & 2 & -1 & 1 \\ 1 & 1 & -2 & 0 \ end {array} \ right] \ ]

Строку уменьшите следующую матрицу, чтобы получить. Затем продолжайте получать. \ [\ left [\ begin {array} {rrrr} -2 & 3 & -8 & 7 \\ 1 & -2 & 5 & -5 \\ 1 & -3 & 7 & -8 \ end {array} \ справа] \]

Найдите решение системы с расширенной матрицей \ [\ left [\ begin {array} {rrr | r} 1 & 2 & 0 & 2 \\ 1 & 3 & 4 & 2 \\ 1 & 0 & 2 & 1 \ end {array} \ right] \]

Найдите решение системы с расширенной матрицей \ [\ left [\ begin {array} {rrr | r} 1 & 2 & 0 & 2 \\ 2 & 0 & 1 & 1 \\ 3 & 2 & 1 & 3 \ end {array} \ right] \]

Это \ (\ left [\ begin {array} {rrr | r} 1 & 0 & \ vspace {0.05in} \ frac {1} {2} & \ vspace {0.05in} \ frac {1} {2} \\ 0 & 1 & — \ vspace {0.05in} \ frac {1} {4} & \ vspace { 0,05 дюйма} \ frac {3} {4} \\ 0 & 0 & 0 & 0 \ end {array} \ right]. \) Следовательно, решение имеет вид \ (z = t, y = \ frac { 3} {4} + t \ left (\ frac {1} {4} \ right), x = \ frac {1} {2} — \ frac {1} {2} t \), где \ (t \ in \ mathbb {R} \).

Найдите решение системы, у которой расширенная матрица равна \ [\ left [\ begin {array} {rrr | r} 1 & 1 & 0 & 1 \\ 1 & 0 & 4 & 2 \ end {array} \ right] \]

Это \ (\ left [\ begin {array} {rrr | r} 1 & 0 & 4 & 2 \\ 0 & 1 & -4 & -1 \ end {array} \ right] \) и поэтому решение равно \ (z = t, y = 4t, x = 2-4t.\)

Найдите решение системы, расширенная матрица которой равна \ [\ left [\ begin {array} {rrrrr | r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 1 & 2 & 0 & 0 & 1 & 3 \\ 1 & 0 & 1 & 0 & 2 & 2 \ end {array} \ right] \]

Это \ (\ left [\ begin {array} {rrrrr | r} 1 & 0 & 0 & 0 & 9 & 3 \\ 0 & 1 & 0 & 0 & -4 & 0 \\ 0 & 0 & 1 & 0 & -7 & -1 \\ 0 & 0 & 0 & 1 & 6 & 1 \ end {array} \ right] \) и поэтому \ (x_ {5} = t, x_ {4} = 1-6t , x_ {3} = — 1 + 7t, x_ {2} = 4t, x_ {1} = 3-9t \).

Найдите решение системы, расширенная матрица которой равна \ [\ left [\ begin {array} {rrrrr | r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 0 & 2 & 0 & 0 & 1 & 3 \\ 1 & -1 & 2 & 2 & 2 & 0 \ end {array} \ right] \]

Это \ (\ left [\ begin {array} {rrrrr | r} 1 & 0 & 2 & 0 & — \ vspace {0,05 дюйма} \ frac {1} {2} & \ vspace {0,05 дюйма} \ frac {5} {2} \\ 0 & 1 & 0 & 0 & \ vspace {0,05 дюйма} \ frac {1} {2} & \ vspace {0.05in} \ frac {3} {2} \\ 0 & 0 & 0 & 1 & \ vspace {0,05 дюйма} \ frac {3} {2} & — \ vspace {0,05 дюйма} \ frac {1} {2} \\ 0 & 0 & 0 & 0 & 0 & 0 \ end {array} \ right] \). Следовательно, пусть \ (x_ {5} = t, x_ {3} = s. \), Тогда другие переменные задаются как \ (x_ {4} = — \ frac {1} {2} — \ frac {3} {2} t, x_ {2} = \ frac {3} {2} -t \ frac {1} {2} ,, x_ {1} = \ frac {5} {2} + \ frac {1} { 2} т-2с. \)

Найдите решение системы уравнений: \ (7x + 14y + 15z = 22, \) \ (2x + 4y + 3z = 5, \) и \ (3x + 6y + 10z = 13. \)

Решение: \ (\ left [x = 1-2t, z = 1, y = t \ right] \)

Найдите решение системы уравнений, \ (3x-y + 4z = 6, \) \ (y + 8z = 0, \) и \ (- 2x + y = -4.\)

Решение: \ (\ left [x = 2-4t, y = -8t, z = t \ right] \)

Найдите решение системы уравнений: \ (9x-2y + 4z = -17, \) \ (13x-3y + 6z = -25, \) и \ (- 2x-z = 3. \)

Решение: \ (\ left [x = -1, y = 2, z = -1 \ right] \)

Найдите решение системы уравнений: \ (65x + 84y + 16z = 546, \) \ (81x + 105y + 20z = 682, \) и \ (84x + 110y + 21z = 713. \)

Решение: \ (\ left [x = 2, y = 4, z = 5 \ right] \)

Найдите решение системы уравнений: \ (8x + 2y + 3z = -3,8x + 3y + 3z = -1, \) и \ (4x + y + 3z = -9.\)

Решение: \ (\ left [x = 1, y = 2, z = -5 \ right] \)

Найдите решение системы уравнений: \ (- 8x + 2y + 5z = 18, -8x + 3y + 5z = 13, \) и \ (- 4x + y + 5z = 19. \)

Решение: \ (\ left [x = -1, y = -5, z = 4 \ right] \)

Найдите решение системы уравнений, \ (3x-y-2z = 3, \) \ (y-4z = 0, \) и \ (- 2x + y = -2. \)

Решение: \ (\ left [x = 2t + 1, y = 4t, z = t \ right] \)

Найдите решение системы уравнений: \ (- 9x + 15y = 66, -11x + 18y = 79 \), \ (- x + y = 4 \) и \ (z = 3 \).

Решение: \ (\ left [x = 1, y = 5, z = 3 \ right] \)

Найдите решение системы уравнений: \ (- 19x + 8y = -108, \) \ (- 71x + 30y = -404, \) \ (- 2x + y = -12, \) \ (4x + г = 14. \)

Решение: \ (\ left [x = 4, y = -4, z = -2 \ right] \)

Предположим, что в системе уравнений меньше уравнений, чем переменных, и вы нашли решение этой системы уравнений. Возможно ли, что ваше решение единственное? Объяснять.

Нет. Рассмотрим \ (x + y + z = 2 \) и \ (x + y + z = 1. \)

Предположим, что система линейных уравнений имеет расширенную матрицу \ (2 \ times 4 \), а последний столбец является сводным.Может ли система линейных уравнений быть непротиворечивой? Объяснять.

Нет. Это приведет к \ (0 = 1. \)

Предположим, что матрица коэффициентов системы \ (n \) уравнений с \ (n \) переменными обладает тем свойством, что каждый столбец является сводным столбцом. Следует ли из этого, что система уравнений должна иметь решение? Если да, должно ли решение быть уникальным? Объяснять.

Да. Имеет уникальное решение.

Предположим, существует единственное решение системы линейных уравнений. Что должно быть правдой в отношении сводных столбцов в расширенной матрице?

Последний столбец не должен быть сводным.Остальные столбцы должны быть сводными столбцами.

Установившаяся температура \ (u \) пластины решает уравнение Лапласа \ (\ Delta u = 0. \) Один из способов аппроксимации решения — разделить пластину на квадратную сетку и потребовать температуру в каждой точке. узел, равный среднему значению температуры в четырех соседних узлах. На следующем рисунке числа представляют наблюдаемую температуру в указанных узлах. Найдите температуру во внутренних узлах, обозначенных \ (x, y, z, \) и \ (w \).Одно из уравнений: \ (z = \ vspace {0.05in} \ frac {1} {4} \ left (10 + 0 + w + x \ right) \).

(1,60) (100,0)

(1,1) (0,30) (1,0) 90 (0,60) (1,0) 90 (30,0) (0,1) 90 (60,0) (0,1) 90 (60,0) (30,0) (0,60) (0,30) (30,30) (30,60) (60,30) (60,60) (60,90) (30,90) (90,30) (90,60) (63, -4) \ (10 ​​\) (33, -4) \ (10 ​​\) (-10,60) \ (20 \) (-10,30) \ (20 \) (34,34) \ (х \) (34,64) \ (у \) (64,34) \ (z \) (64,64) \ (w \) (64,90) \ (30 \) (34,90) \ (30 \) (94,30) \ (0 \) (94,60) \ (0 \)

Вам понадобится \ (\ begin {array} {c} \ frac {1} {4} \ left (20 + 30 + w + x \ right) -y = 0 \\ \ frac {1} {4} \ left (y + 30 + 0 + z \ right) -w = 0 \\ \ frac {1} {4} \ left (20 + y + z + 10 \ right) -x = 0 \\ \ frac {1} { 4} \ left (x + w + 0 + 10 \ right) -z = 0 \ end {array} \). Решение: \ (\ left [w = 15, x = 15, y = 20, z = 10 \верно] .\)

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrr} 4 & -16 & -1 & -5 \\ 1 & -4 & 0 & -1 \\ 1 & -4 & -1 & -2 \ end {массив } \ right] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrr} 3 & 6 & 5 & 12 \\ 1 & 2 & 2 & 5 \\ 1 & 2 & 1 & 2 \ end {array} \ right] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrrr} 0 & 0 & -1 & 0 & 3 \\ 1 & 4 & 1 & 0 & -8 \\ 1 & 4 & 0 & 1 & 2 \\ -1 & -4 & 0 & -1 & -2 \ end {array} \ right] \]

Найдите ранг следующей матрицы.\ [\ left [\ begin {array} {rrrr} 4 & -4 & 3 & -9 \\ 1 & -1 & 1 & -2 \\ 1 & -1 & 0 & -3 \ end {array} \ справа] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrrr} 2 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 7 \\ 1 & 0 & 0 & 1 & 7 \ end {array} \ right] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrr} 4 & 15 & 29 \\ 1 & 4 & 8 \\ 1 & 3 & 5 \\ 3 & 9 & 15 \ end {array} \ right] \]

Найдите ранг следующей матрицы.\ [\ left [\ begin {array} {rrrrr} 0 & 0 & -1 & 0 & 1 \\ 1 & 2 & 3 & -2 & -18 \\ 1 & 2 & 2 & -1 & -11 \ \ -1 & -2 & -2 & 1 & 11 \ end {array} \ right] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrrr} 1 & -2 & 0 & 3 & 11 \\ 1 & -2 & 0 & 4 & 15 \\ 1 & -2 & 0 & 3 & 11 \\ 0 & 0 & 0 & 0 & 0 \ end {array} \ right] \]

Найдите ранг следующей матрицы.\ [\ left [\ begin {array} {rrr} -2 & -3 & -2 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ -3 & 0 & -3 \ end {array} \ справа] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrrr} 4 & 4 & 20 & -1 & 17 \\ 1 & 1 & 5 & 0 & 5 \\ 1 & 1 & 5 & -1 & 2 \\ 3 & 3 и 15 и -3 и 6 \ end {array} \ right] \]

Найдите ранг следующей матрицы. \ [\ left [\ begin {array} {rrrrr} -1 & 3 & 4 & -3 & 8 \\ 1 & -3 & -4 & 2 & -5 \\ 1 & -3 & -4 & 1 & -2 \\ -2 & 6 & 8 & -2 & 4 \ end {array} \ right] \]

Предположим, что \ (A \) — это матрица \ (m \ times n \).Объясните, почему ранг \ (A \) всегда не превышает \ (\ min \ left (m, n \ right). \)

Это потому, что у вас не может быть больше чем \ (\ min \ left (m, n \ right) \) ненулевых строк в. Напомним, что количество сводных столбцов совпадает с количеством ненулевых строк из описания этого.

Укажите, возможен ли каждый из следующих наборов данных для матричного уравнения \ (AX = B \). Если возможно, опишите набор решений. То есть сказать, существует ли единственное решение, нет решения или бесконечно много решений.Здесь \ (\ left [A | B \ right] \) обозначает расширенную матрицу.

1. \ (A \) — матрица \ (5 \ times 6 \), \ (\ limfunc {rank} \ left (A \ right) = 4 \) и \ (\ limfunc {rank} \ left [A | B \ right] = 4. \)

2. \ (A \) — матрица \ (3 \ times 4 \), \ (\ limfunc {rank} \ left (A \ right) = 3 \) и \ (\ limfunc {rank} \ left [A | B \ right] = 2. \)

3. \ (A \) — матрица \ (4 \ times 2 \), \ (\ limfunc {rank} \ left (A \ right) = 4 \) и \ (\ limfunc {rank} \ left [A | B \ right] = 4.\)

4. \ (A \) — матрица \ (5 \ times 5 \), \ (\ limfunc {rank} \ left (A \ right) = 4 \) и \ (\ limfunc {rank} \ left [A | B \ right] = 5. \)

5. \ (A \) — матрица \ (4 \ times 2 \), \ (\ limfunc {rank} \ left (A \ right) = 2 \) и \ (\ limfunc {rank} \ left [A | B \ right] = 2 \).

1. Это говорит о том, что \ (B \) находится в промежутке между четырьмя столбцами. Таким образом, столбцы не являются независимыми. Бесконечное множество решений.

2. Этого точно не может быть.Если добавить в другой столбец, ранг не станет меньше.

3. Это говорит о том, что \ (B \) находится в диапазоне столбцов, и столбцы должны быть независимыми. У вас не может быть ранга 4, если у вас только два столбца.

4. Это говорит о том, что \ (B \) не находится в диапазоне столбцов. В этом случае нет решения системы уравнений, представленной расширенной матрицей.

5. В этом случае существует единственное решение, поскольку столбцы \ (A \) независимы.

Рассмотрим систему \ (- 5x + 2y-z = 0 \) и \ (- 5x-2y-z = 0. \) Оба уравнения равны нулю, поэтому \ (- 5x + 2y-z = -5x-2y -z \), что эквивалентно \ (y = 0. \) Следует ли, что \ (x \) и \ (z \) могут равняться чему-либо? Обратите внимание, что когда \ (x = 1 \), \ (z = -4, \) и \ (y = 0 \) подключены к уравнениям, уравнения не равны \ (0 \). Почему?

Это недопустимые операции со строками. Они не сохраняют набор решений системы.

Уравновесить следующие химические реакции.{2} AB \) имеет единицы силы. Опишите систематический способ получения таких комбинаций переменных, которые приведут к чему-то, что имеет единицы силы.

Рассмотрим следующую схему из четырех цепей.

Ток в амперах в четырех цепях обозначается как \ (I_ {1}, I_ {2}, I_ {3}, I_ {4} \), и подразумевается, что движение происходит против часовой стрелки. Если \ (I_ {k} \) оказывается отрицательным, это означает, что ток течет по часовой стрелке.

На приведенной выше диаграмме верхний левый контур должен давать уравнение \ [2I_ {2} -2I_ {1} + 5I_ {2} -5I_ {3} + 3I_ {2} = 5 \] Для схемы нижнего слева, у вас должно быть \ [4I_ {1} + I_ {1} -I_ {4} + 2I_ {1} -2I_ {2} = — 10 \] Напишите уравнения для каждой из двух других схем, а затем дайте решение к полученной системе уравнений.

Два других уравнения: \ [\ begin {align} 6I_ {3} -6I_ {4} + I_ {3} + I_ {3} + 5I_ {3} -5I_ {2} & = & — 20 \\ 2I_ {4} + 3I_ {4} + 6I_ {4} -6I_ {3} + I_ {4} -I_ {1} & = & 0 \ end {align} \] Тогда система \ [\ begin {array} { c} 2I_ {2} -2I_ {1} + 5I_ {2} -5I_ {3} + 3I_ {2} = 5 \\ 4I_ {1} + I_ {1} -I_ {4} + 2I_ {1} — 2I_ {2} = — 10 \\ 6I_ {3} -6I_ {4} + I_ {3} + I_ {3} + 5I_ {3} -5I_ {2} = — 20 \\ 2I_ {4} + 3I_ { 4} + 6I_ {4} -6I_ {3} + I_ {4} -I_ {1} = 0 \ end {array} \] Решение: \ [\ begin {align} I_ {1} & = & — \ frac {750} {373} \\ I_ {2} & = & — \ frac {1421} {1119} \\ I_ {3} & = & — \ frac {3061} {1119} \\ I_ {4} & = & — \ frac {1718} {1119} \ end {align} \]

Рассмотрим следующую схему трех цепей.

Ток в амперах в четырех цепях обозначен \ (I_ {1}, I_ {2}, I_ {3} \), и понятно, что движение происходит против часовой стрелки. Если \ (I_ {k} \) оказывается отрицательным, это означает, что ток течет по часовой стрелке.

Найдите \ (I_ {1}, I_ {2}, I_ {3} \).

У вас есть \ [\ begin {align} 2I_ {1} + 5I_ {1} + 3I_ {1} -5I_ {2} & = & 10 \\ I_ {2} — I_ {3} + 3I_ {2} + 7I_ {2} + 5I_ {2} -5I_ {1} & = & — 12 \\ 2I_ {3} + 4I_ {3} + 4I_ {3} + I_ {3} -I_ {2} & = & 0 \ конец {выровнено} \] Упрощение этого дает \ [\ begin {выравнивание} 10I_ {1} -5I_ {2} & = & 10 \\ -5I_ {1} + 16I_ {2} — I_ {3} & = & — 12 \\ -I_ {2} + 11I_ {3} & = & 0 \ end {выровнено} \] Решение дается выражением \ [I_ {1} = \ frac {218} {295}, I_ {2} = — \ frac {154} {295}, I_ {3} = — \ frac {14} {295} \]

Метод исключения бесконечного решения | Sciencing

Когда вы начинаете с трех уравнений и трех неизвестных (переменных), вы можете подумать, что у вас достаточно информации для решения всех переменных.Однако при решении системы линейных уравнений с использованием метода исключения вы можете обнаружить, что система недостаточно определена, чтобы найти один единственный ответ, и вместо этого возможно бесконечное количество решений. Это происходит, когда информация в одном из уравнений в системе избыточна для информации, содержащейся в других уравнениях.

A 2×2 Пример

3x + 2y = 5 6x + 4y = 10 Эта система уравнений явно избыточна. Вы можете создать одно уравнение из другого, просто умножив его на константу.Другими словами, они передают одну и ту же информацию. Несмотря на наличие двух уравнений для двух неизвестных, x и y, решение этой системы нельзя сузить до одного значения для x и одного значения для y. (x, y) = (1,1) и (5 / 3,0) оба решают его, как и многие другие решения. Это своего рода «проблема», эта нехватка информации, которая также приводит к бесконечному количеству решений в более крупных системах уравнений.

A 3×3 Пример

x + y + z = 10 x-y + z = 0 x _ + _ z = 5 [Подчеркивание используется только для сохранения интервала.] Методом исключения удалите x из второй строки, вычтя вторую строку из первой, получив x + y + z = 10 _2y = 10 x_ + z = 5 Удалите x из третьей строки, вычитая третью строку с самого начала. x + y + z = 10 _2y = 10 y = 5 Очевидно, что последние два уравнения эквивалентны. y равно 5, и первое уравнение можно упростить, исключив y. x + 5 + z = 10 y __ = 5 или x + z = 5 y = 5 Обратите внимание, что метод исключения не дает здесь красивой треугольной формы, как это происходит при наличии одного уникального решения.Вместо этого последнее уравнение (если не большее) само будет поглощено другими уравнениями. Теперь система состоит из трех неизвестных и только двух уравнений. Система называется «недоопределенной», потому что не хватает уравнений для определения значений всех переменных. Возможны бесконечное количество решений.

Как написать бесконечное решение

Бесконечное решение для вышеупомянутой системы может быть записано в терминах одной переменной.