Содержание
Перевод корней в степени и обратно: объяснение, примеры
Часто преобразование и упрощение математических выражений требует перехода от корней к степеням и наоборот. Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.
Переход от степеней с дробными показателями к корням
Допустим, мы имеем число с показателем степени в виде обыкновенной дроби — amn. Как записать такое выражение в виде корня?
Ответ вытекает из самого определения степени!
Определение
Положительное число a в степени mn — это корень степени n из числа am.
amn=amn.
При этом, обязательно должно выполнятся условие:
a>0; m∈ℤ; n∈ℕ.
Дробная степень числа нуль определяется аналогично, однако в этом случае число m принимается не целым, а натуральным, чтобы не возникло деления на 0:
0mn=0mn=0.
В соответствии с определением, степень amn можно представить в виде корня amn.
Например: 325=325, 123-34=123-34.
Однако, как уже было сказано, не следует забывать про условия: a > 0 ; m ∈ ℤ ; n ∈ ℕ .
Так, выражение -813 нельзя представить в виде -813, так как запись -813 попросту не имеет смысла — степень отрицательных чисел на определена.При этом, сам корень -813 имеет смысл.
Переход от степеней с выражениями в основании и дробными показателями осуществляется аналогично на всей области допустимых значений (далее — ОДЗ) исходных выражений в основании степени.
Например, выражение x2+2x+1-412 можно представить в виде квадратного корня x2+2x+1-4.Выражение в степени x2+x·y·z-z3-73 переходит в выражение x2+x·y·z-z3-73 для всех x, y, z из ОДЗ данного выражения.
Как представить корень в виде степени?
Обратная замена корней степенями, когда вместо выражения с корнем записывается выражения со степенью, также возможна. Просто перевернем равенство из предыдущего пункта и получим:
amn=amn
Опять же, переход очевиден для положительных чисел a. Например, 764=764, или27-53=27-53.
Например, 764=764, или27-53=27-53.
Для отрицательных a корни имеют смысл. Например -426, -23. Однако, представить эти корни в виде степеней -426 и -213 нельзя.
Можно ли вообще преобразовать такие выражения со степенями? Да, если произвести некоторые предварительные преобразования. Рассмотрим, какие.
Используя свойства степеней, можно выполнить преобразования выражения -426.
-426=-12·426=426.
Так как 4>0, можно записать:
426=426.
В случае с корнем нечетной степени из отрицательного числа, можно записать:
-a2m+1=-a2m+1.
Тогда выражение -23 примет вид:
-23=-23=-213.
Разберемся теперь, как корни, под которыми содержатся выражения, заменяются на степени, содержащие эти выражения в основании.
Обозначим буквой A некоторое выражение. Однако не будем спешить с представлением Amn в виде Amn. Поясним, что здесь имеется в виду. Например, выражение х-323, основываясь на равенстве из первого пункта, хочется представить в виде x-323. Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.
Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.
Таким образом, в рассмотренном примере преобразование вида Amn=Amn является преобразованием, сужающим ОДЗ, а из-за неаккуратного применения формулы Amn=Amn нередко возникают ошибки.
Чтобы правильно перейти от корня Amn к степени Amn, необходимо соблюдать несколько пунктов:
- В случае, если число m — целое и нечетное, а n — натуральное и четное, то формула Amn=Amn справедлива на всей ОДЗ переменных.
- Если m — целое и нечетное, а n — натуральное и нечетное,то выражение Amn можно заменить:
— на Amn для всех значений переменных, при которых A≥0;
— на —Amn для для всех значений переменных, при которых A<0; - Если m — целое и четное, а n — любое натуральное число, то Amn можно заменить на Amn.
Сведем все эти правила в таблицу и приведем несколько примеров их использования.
Вернемся к выражению х-323. Здесь m=2 — целое и четное число, а n=3 — натуральное число. Значит, выражение х-323 правильно будет записать в виде:
х-323=x-323.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Приведем еще один пример с корнями и степенями.
Пример. Перевод корня в степень
x+5-35=x+5-35, x>-5—x-5-35, x<-5
Обоснуем результаты, приведенные в таблице. Если число m — целое и нечетное, а n — натуральное и четное, для всех переменных из ОДЗ в выражении Amn значение A положительно или неотрицательно (при m>0). Именно поэтому Amn=Amn.
Во втором варианте, когда m — целое, положительное и нечетное, а n — натуральное и нечетное, значения Amn разделяются. Для переменных из ОДЗ, при которых A неотрицательно, Amn=Amn=Amn. Для переменных, при которых A отрицательно, получаем Amn=-Amn=-1m·Amn=-Amn=-Amn=-Amn.
Аналогично рассмотрим и следующий случай, когда m — целое и четное, а n — любое натуральное число. Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.
Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.
Таким образом, в третьем случае для всех переменных из ОДЗ можно записать Amn=Amn.
Корень степени N
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)
У вас тоже так? Читайте дальше — и всё поймёте
Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. {2}}=1$.
{2}}=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
\[\begin{align} & \sqrt[3]{27}=3; \\ & \sqrt[3]{-64}=-4; \\ & \sqrt[3]{343}=7. \\ \end{align}\]
Ну, и парочка «экзотических примеров»:
\[\begin{align} & \sqrt[4]{81}=3; \\ & \sqrt[5]{-32}=-2. \\ \end{align}\]
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. {n}}=a\]
{n}}=a\]
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
\[\sqrt{2}=1,414213562…\]
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
Пример.
\[\begin{align} & \sqrt{2+\sqrt[3]{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt[3]{\sqrt[5]{-32}}=\sqrt[3]{-2}\approx -1,2599… \\ \end{align}\]
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}=4\]
{2}}=4\]
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
\[\sqrt{4}=2\]
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
- Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
- Из отрицательных чисел корень с чётным $n$ вообще не извлекается.
 {3}}$:
{3}}$:Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке.
 Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок.
 {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
\[\sqrt[2n+1]{-a}=-\sqrt[2n+1]{a}\]
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
\[\begin{align} & \sqrt[3]{-8}=-\sqrt[3]{8}=-2; \\ & \sqrt[3]{-27}\cdot \sqrt[5]{-32}=-\sqrt[3]{27}\cdot \left( -\sqrt[5]{32} \right)= \\ & =\sqrt[3]{27}\cdot \sqrt[5]{32}= \\ & =3\cdot 2=6. \end{align}\]
\end{align}\]
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.
{n}}=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
Область поиска арифметического корня — неотрицательные числа
Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
{2}}}=\sqrt[6]{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]
{n}}=a \right. \right\}\]
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt[3]{-27}};\quad \overline{\sqrt[4]{-16}}.
\]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt[3]{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt[4]{-16}}=\varnothing \]
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt[4]{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются.
Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
На этом всё. В следующем уроке мы рассмотрим все ключевые свойства корней и научимся, наконец, упрощать иррациональные выражения.:)
Смотрите также:
- Умножение корней n-й степени
- Свойства арифметического квадратного корня
- Тест к уроку «Округление с избытком и недостатком» (1 вариант)
- Пробный ЕГЭ 2012 от 7 декабря. Вариант 5 (без производной)
- Задача B4: случай с неизвестным количеством товара
- Задача B2 про комиссию в терминале
Возведение в степень и извлечение корня в Excel
Для извлечения корня в Excel и возведения числа в степень используются встроенные функции и математические операторы. Рассмотрим на примерах.
Примеры функции КОРЕНЬ в Excel
Встроенная функция КОРЕНЬ возвращает положительное значение квадратного корня. В меню «Функции» она находится в категории «Математические».
Синтаксис функции: =КОРЕНЬ(число).
Единственный и обязательный аргумент представляет собой положительное число, для которого функция вычисляет квадратный корень. Если аргумент имеет отрицательное значение, Excel вернет ошибку #ЧИСЛО!.
В качестве аргумента можно указывать конкретное значение либо ссылку на ячейку с числовым значением.
Рассмотрим примеры.
Функция вернула квадратный корень числа 36. Аргумент – определенное значение.
Аргумент функции – ссылка на ячейку с положительным значением 36.
Функция вернула ошибку, т.к. аргумент – ссылка на ячейку с отрицательным значением.
Функция ABS возвращает абсолютное значение числа -36. Ее использование позволило избежать ошибки при извлечении квадратного корня из отрицательного числа.
Функция извлекла квадратный корень от суммы 13 и значения ячейки C1.
Функция возведения в степень в Excel
Синтаксис функции: =СТЕПЕНЬ(значение; число). Оба аргумента обязательные.
Значение – любое вещественное числовое значение. ».
».
Обратите внимание! Дробная степень пишется в скобках.
Выполнили ту же задачу, но с использованием функции СТЕПЕНЬ.
Извлекли корень девятой степени из значения ячейки h2.
Извлекли корень пятой степени из суммы числа 9 и значения ячейки h2.
Те же математические операции можно выполнить с помощью функции СТЕПЕНЬ:
Таким образом, возвести в степень и извлечь корень n-й степени в Excel можно с помощью одной функции.
Как написать число в степени
Для корректного отображения числа в степени при демонстрации файла или его печати, необходимо произвести ряд манипуляций:
- Щелкаем по ячейке с числом правой кнопкой мыши. Выбираем «Формат ячеек» (или нажмите CTRL+1).
- В открывшемся меню переходим на вкладку «Число». Задаем «Текстовый» формат. Текстовый формат для значения в ячейке можно также задать через панель инструментов («Главная» – «Число»). После установки текстового формата цифра в ячейке становится слева.
- Рядом с цифрой вводим в ячейку значение со знаком «минус».

- Выделяем только значение степени («-3»). Вызываем меню «Формат ячеек». Устанавливаем видоизменение «Надстрочный». И нажимаем ОК.
Получили корректное отображение числа 5 в -3 степени.
Калькулятор извлечения корня n-ой степени онлайн
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица 4-ой и 5-ой степени чисел от 1 до 100. Поделиться:
Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
%d0%ba%d0%be%d1%80%d0%b5%d0%bd%d1%8c%20n-%d0%b9%20%d1%81%d1%82%d0%b5%d0%bf%d0%b5%d0%bd%d0%b8 — со всех языков на все языки
1
delatoriusdēlātōrius, a, um (delator), zum Angeber gehörig, eines Angebers, curiositas, Ulp.
 dig. 22, 6, 6: libelli, Denunziationschriften, Cod. Theod. 10, 10, 7: calices perlucidi sine delatoria nota, Fronto de fer. Als. 3. p. 224, 20N.
dig. 22, 6, 6: libelli, Denunziationschriften, Cod. Theod. 10, 10, 7: calices perlucidi sine delatoria nota, Fronto de fer. Als. 3. p. 224, 20N.lateinisch-deutsches > delatorius
2
delatoriusdēlātōrius, a, um (delator), zum Angeber gehörig, eines Angebers, curiositas, Ulp. dig. 22, 6, 6: libelli, Denunziationschriften, Cod. Theod. 10, 10, 7: calices perlucidi sine delatoria nota, Fronto de fer. Als. 3. p. 224, 20N.
Ausführliches Lateinisch-deutsches Handwörterbuch > delatorius
См. также в других словарях:
20N — may refer to : * New York State Route 20N * 20 N, an abbreviation for two well known dates in Spanish historyee also* N20 … Wikipedia
20N — Este artículo trata sobre la conmemoración del aniversario de los fallecimientos de Francisco Franco y José Antonio Primo de Rivera.
 Para otros acontecimientos relacionados con la fecha, véase 20 de noviembre. Para las elecciones previstas para… … Wikipedia Español
Para otros acontecimientos relacionados con la fecha, véase 20 de noviembre. Para las elecciones previstas para… … Wikipedia EspañolNew York State Route 20N — NYS Route 20N Map of the Syracuse area with NY 20N highlighted in red Route information … Wikipedia
List of highways numbered 20N — The following highways are numbered 20N:* (Former) … Wikipedia
New York State Route 20SY — NYS Route 20SY Map of the Syracuse area with NY 20SY highlighted in red Route information … Wikipedia
List of numbered roads in Durham Region — The numbered roads in the Regional Municipality of Durham account for about 832 kilometres (517 mi) of the county road system in the Canadian province of Ontario. The Durham Region Works Department owns and maintains the regional roads and… … Wikipedia
New York State Route 92 — NYS Route 92 Map of the Syracuse area with NY 92 highlighted in red Route information … Wikipedia
New York State Route 173 — NYS Route 173 Map of the Syracuse area with NY 173 highlighted in red Route information … Wikipedia
Doomsday argument — World population from 10,000 BC to AD 2000 The Doomsday argument (DA) is a probabilistic argument that claims to predict the number of future members of the human species given only an estimate of the total number of humans born so far.
 Simply… … Wikipedia
Simply… … WikipediaNew York State Route 174 — NYS Route 174 Map of the Syracuse area with NY … Wikipedia
New York State Route 175 — NYS Route 175 Map of the Syracuse area with NY 175 highlighted in red … Wikipedia
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Степень с целочисленным показателем
Понятие степени с целочисленным показателем включает в себя три определения.
Определение. Пусть n – произвольное натуральное число, а a – произвольное действительное число. Тогда n – ой степенью числа a называют произведение n сомножителей, равных a :
Число a называют основанием степени, а число n – показателем степени.
Определение. Пусть a – произвольное действительное число, отличное от 0 . Тогда, по определению:
a0 = 1 .
Число a называют основанием степени, а число 0 – показателем степени.
Определение. Пусть n – произвольное натуральное число, а a – произвольное действительное число, отличное от 0 . Тогда, по определению:
Число a называют основанием степени, а число (– n) – показателем степени.
Таким образом, степень с целочисленным показателем определена.
Пример 1.
Замечание 1. Число нуль нельзя возвести в нулевую степень и нельзя возвести в отрицательную степень.
Арифметический корень
Пусть n – произвольное натуральное число, а a – произвольное положительное число.
Определение. Число x называют арифметическим корнем n – ой степени из числа a , если, во-первых, число x положительное, а, во-вторых, является решением уравнения
xn = a .
В этом случае при для арифметического корня используется обозначение:
или эквивалентное обозначение:
Если же n = 2, то для арифметического квадратного корня используется обозначение:
или эквивалентное обозначение:
Замечание 2. В курсах математики, выходящих за рамки средней школы, доказывается, что арифметический корень всегда существует, причем только один.
Замечание 3. Очень важно помнить о том, что в формуле
содержится ошибка, за которую мгновенно следует безжалостная кара на экзаменах.
Пример 2. Решить уравнение
x2 = 25 .
Решение. Это уравнение имеет два корня:
x1 = 5 и x2 = – 5 .
Корень уравнения x1 = 5 является арифметическим квадратным корнем из числа 25, а корень уравнения x2 = – 5 является числом, противоположным к арифметическому квадратному корню из числа 25.
Пример 3. Решить уравнение
x3 = – 27 .
Решение. Это уравнение имеет единственный вещественный корень x = – 3, но это число не является арифметическим кубическим корнем из числа (– 27), так как у отрицательных чисел не бывает арифметических корней. Число x = – 3 является числом, противоположным к арифметическому кубическому корню из числа 27. Поэтому
Число x = – 3 является числом, противоположным к арифметическому кубическому корню из числа 27. Поэтому
Замечание 4. Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.
Избавление от иррациональностей в знаменателе дроби
В некоторых задачах требуется перейти от дроби к равной ей дроби, но такой, у которой в знаменателе нет корней (иррациональностей). Эта операция носит название «избавление от иррациональностей в знаменателе дроби» и осуществляется при помощи умножения числителя и знаменателя дроби на подходящее число. Часто это число находится с помощью формул сокращенного умножения. Покажем это на примере.
Пример 4. Преобразовать дробь
к такому виду, чтобы в знаменателе не было иррациональностей.
Решение. Воспользовавшись формулой сокращенного умножения «Разность квадратов», совершим следующие эквивалентные преобразования:
Мы получили дробь, у которой в знаменателе иррациональностей нет, что и требовалось.
С понятием степени с рациональным показателем и свойствами степеней можно ознакомиться в разделе «Степень с рациональным показателем» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
На сайте можно также ознакомиться с нашимиучебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Уловка пятого корня | Найдите 5-й корень в своей голове
У Numberphile есть хорошее видео о трюке с корнем пятой степени: кто-то возводит двузначное число в пятую степень, читает его вслух, и вы сразу же сообщаете им, какое это было число.
Вот вкратце трюк. Для любого числа n , n 5 оканчивается той же последней цифрой, что и n . Вы можете доказать это грубой силой или теоремой Эйлера. Поэтому, когда кто-то говорит вам n 5 , вы сразу узнаете последнюю цифру.Теперь вам нужно найти первую цифру, и вы можете сделать это, приблизительно изучив степени (10k) 5 для i = 1, 2, 3,…, 9. Затем вы можете определить первую цифру с помощью диапазон.
Вот где видео немного расплывчато. В нем говорится, что вам не нужно очень точно знать степень 10 k . Это правда, но насколько точно и вам нужно знать диапазоны?
Если двузначное число кратно 10, вы узнаете нули в конце, а последняя ненулевая цифра — это первая цифра n .5 |
| — + ————— + ————— |
| 1 | 59 049 | 161,051 |
| 2 | 2,476,099 | 4,084,101 |
| 3 | 20,511,149 | 28 629 151 |
| 4 | 90,224,199 | 115,856,201 |
| 5 | 282 475 249 | 345 025 251 |
| 6 | 714,924,299 | 844,596,301 |
| 7 | 1,564,031,349 | 1 804 229 351 |
| 8 | 3,077,056,399 | 3 486 784 401 |
| 9 | 5,584,059,449 | 6,240,321,451 |
| — + ————— + ————— |
Таким образом, любая пятая степень меньше миллиона имеет однозначный корень пятой степени. Любое число от 1 до 3 миллионов имеет первую цифру 1. И т. Д.
Любое число от 1 до 3 миллионов имеет первую цифру 1. И т. Д.
Если хотите, можете выбрать следующие границы.
| --- + ---------------- | | k | верхняя граница | | --- + ---------------- | | 1 | 1,000,000 | | 2 | 3,000,000 | | 3 | 25,000,000 | | 4 | 100,000,000 | | 5 | 300,000,000 | | 6 | 800,000,000 | | 7 | 1,700,000,000 | | 8 | 3,200,000,000 | | 9 | 6,000,000,000 | | --- + ---------------- |
В видеоролике Numberphile говорится, что вам нужно попросить кого-нибудь произнести номер вслух, словами.Итак, как только вы слышите «шесть миллиардов…», вы знаете, что первая цифра n — 9. Если вы слышите «пять миллиардов» или «четыре миллиарда», вы знаете, что первая цифра — 8. Если вы слышите «три миллиарда» », Тогда вы должны обратить внимание на следующее число, чтобы решить, будет ли первая цифра 7 или 8. Когда вы услышите первые несколько слогов числа, вы можете перестать обращать внимание, пока не услышите последний или два слога.
Таблица пятого корня и 5-го показателя
Интерактивная таблица чисел корня и экспоненты.
| Найдите корень 5 -го из … | Корень 5 -го |
|---|---|
| 1 | 1.0000 |
| 2 | 1.1487 |
| 3 | 1.2457 |
| 4 | 1,3195 |
| 5 | 1,3797 |
| 6 | 1,4310 |
| 7 | 1,4758 |
| 8 | 1.5157 |
| 9 | 1,5518 |
| 10 | 1,5849 |
| 11 | 1,6154 |
| 12 | 1,6438 |
| 13 | 1,6703 |
| 15 | 1,7188 |
| 16 | 1,7411 |
| 17 | 1,7623 |
| 18 | 1,7826 |
| 19 | 1.8020 |
| 20 | 1.8206 |
| 21 | 1. 8384 8384 |
| 22 | 1.8556 |
| 23 | 1.8722 |
| 24 | 1.8882 |
| 25 | 1.8882 |
| 25 | |
| 26 | 1,9186 |
| 27 | 1,9332 |
| 28 | 1,9473 |
| 29 | 1,9610 |
| 30 | 1.9744 |
| 31 | 1.9873 |
| 32 | 2.0000 |
| 33 | 2.0123 |
| 34 | 2.0244 |
| 35 | 2.0362 |
| 36 | |
| 37 | 2,0589 |
| 38 | 2,0699 |
| 39 | 2,0807 |
| 40 | 2,0913 |
| 41 | 2.1016 |
| 42 | 2,1118 |
| 43 | 2,1217 |
| 44 | 2,1315 |
| 45 | 2,1411 |
| 46 | 2,1506 |
| 47 | |
| 48 | 2,1689 |
| 49 | 2,1779 |
| 50 | 2,1867 |
| 51 | 2,1954 |
| 52 | 2. 2039 2039 |
| 53 | 2,2124 |
| 54 | 2,2206 |
| 55 | 2,2288 |
| 56 | 2,2369 |
| 57 | 2,2448 |
| 58 | 2,2448 |
| 58 | |
| 59 | 2,2603 |
| 60 | 2,2679 |
| 61 | 2,2754 |
| 62 | 2,2829 |
| 63 | 2.2902 |
| 64 | 2.2974 |
| 65 | 2.3045 |
| 66 | 2.3116 |
| 67 | 2.3185 |
| 68 | 2.3254 |
| 2 | |
| 70 | 2,3389 |
| 71 | 2,3456 |
| 72 | 2,3522 |
| 73 | 2,3587 |
| 74 | 2.3651 |
| 75 | 2. 3714 3714 |
| 76 | 2.3777 |
| 77 | 2.3840 |
| 78 | 2.3901 |
| 79 | 2.3962 |
| 80 | 2. 962 |
| 80 | |
| 81 | 2.4082 |
| 82 | 2,4141 |
| 83 | 2.4200 |
| 84 | 2,4258 |
| 85 | 2.4316 |
| 86 | 2.4372 |
| 87 | 2.4429 |
| 88 | 2.4485 |
| 89 | 2.4540 |
| 90 | 2.4595 |
| 91 | 2.4595 |
| 91 | |
| 92 | 2,4703 |
| 93 | 2,4757 |
| 94 | 2.4810 |
| 95 | 2.4862 |
| 96 | 2.4915 |
| 97 | 2.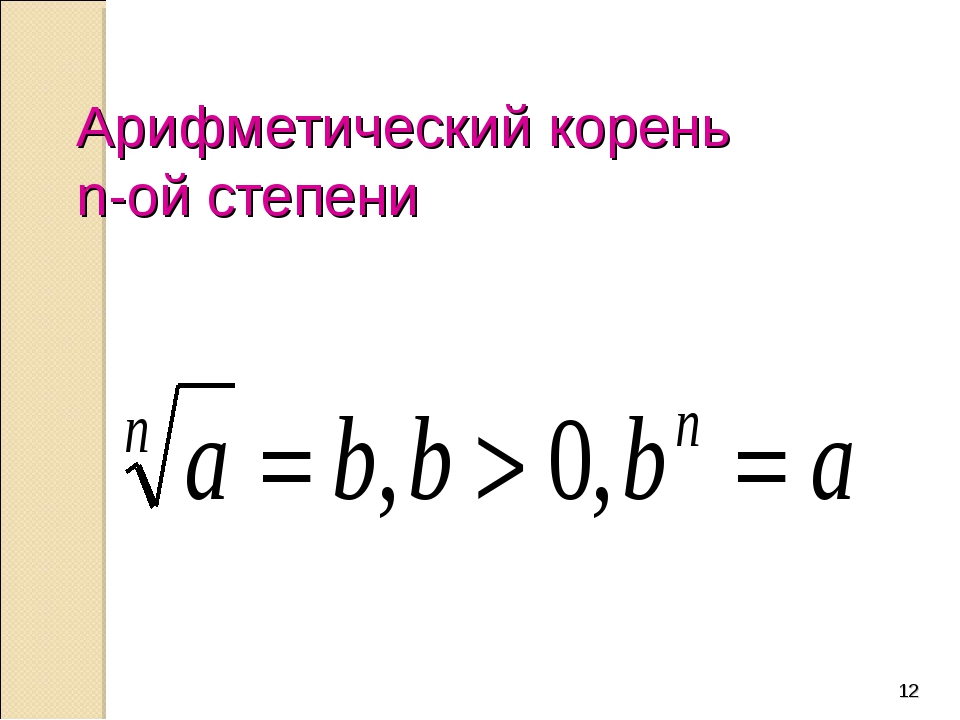 4966 4966 |
| 98 | 2,5018 |
| 99 | 2,5068 |
| 100 | 2,5119 |
| Найти показатель степени 5 … | Показатель степени 5 | ||
|---|---|---|---|
| 1 | 1 | ||
| 2 | 32 | ||
| 3 | 243 | ||
| 4 | 1024 | ||
| 5 | 3125 | ||
| 6 | 7776 | ||
| 7 | 16807 | ||
| 8 | 32768 | ||
| 9 | 59049 | ||
| 10 | 100000 | ||
| 11 | 161051 | ||
| 11 | 161051 | ||
| 248832 | |||
| 13 | 371293 | ||
| 14 | 5 37824 | ||
| 15 | 759375 | ||
| 16 | 1048576 | ||
| 17 | 1419857 | ||
| 18 | 1889568 | ||
| 19 | 2476099 | ||
| 20 | 2476099 | ||
| 20 | 2476099 | ||
| 20 | |||
| 21 | 4084101 | ||
| 22 | 5153632 | ||
| 23 | 6436343 | ||
| 24 | 7962624 | ||
| 25 | 9765625 | ||
| 26 | 26 | 27 | 14348907 |
| 28 | 17210368 | ||
| 29 | 20511149 | ||
| 30 | 24300000 | ||
| 31 | 28629151 | ||
| 32 | 3355 | 3 93 | 34 | 45435424 |
| 35 | 52521875 | ||
| 36 | 60466176 | ||
| 37 | 69343957 | ||
| 38 | 79235168 | 2 87| 40 | 102400000 | 41 | 115856201 | 42 | 1306 | 43 | 147008443 | 44 | 164 | 4 4512 | 184528 | 205962976 | 47 | 229345007 | 48 | 254803968 | 49 | 282475249 | 50 | 312500000 | 51 | 345025251 | 900 73 53 | 418195493 | 54 | 45 | 24 55 | 503284375 | 56 | 550731776 | 57 | 6016 | 58 | 6016 | 59 | 714924299 | 60 | 777600000 | 61 | 844596301 | 62 | 2832 63 | 992436543 | 64 | 24 11602 | 66 | 1252332576 | 67 | 1350125107 | 68 | 1453933568 | 69 | 9004 1564031349 70 | 1564031349 | 70 | 9008 90 087 72 | 1934 | 73 | 2073071593 | 74 | 221 | 24 75 | 2373046875 | 76 | 253558225376 | 270777 |
| 78 | 2887174368 | ||
| 79 | 3077056399 | ||
| 80 | 3276800000 | ||
| 81 | 3486784401 | ||
| 82 | 3707398432 | ||
| 4182119424 | |||
| 85 | 4437053125 | ||
| 86 | 4704270176 | ||
| 87 | 4984209207 | ||
| 88 | 527731987168 | 557731987 | 89558 | 59040 |
| 91 | 6240321451 | ||
| 92 | 65 | 232 | |
| 93 | 6956883693 | ||
| 94 | 733 | ||
| 9587 | |||
| 97 | 8587340257 | ||
| 98 | 07968 | ||
| 99 | 95099 | ||
| 100 | 10000000000 |
Генератор корня и экспонент
Что такое корень 5
th ?
Корень 5-й степени числа — это число, которое нужно умножить само на себя 5 раз, чтобы получить исходное число.
Что такое показатель степени 5?
Показатель 5 числа находится путем умножения этого числа на само себя 5 раз.
дробных (рациональных) экспонентов | Purplemath
Purplemath
Вам уже известна одна взаимосвязь между экспонентами и радикалами: соответствующий радикал «отменяет» показатель степени, а правая сила «отменяет» корень.Например:
Но есть еще одно соотношение, которое, кстати, может значительно упростить вычисления, подобные приведенным выше.
MathHelp.com
Для квадратного (или «второго») корня мы можем записать его как половинную степень, например:
. ..или:
..или:
Кубический (или «третий») корень — это степень одной трети:
Корень четвертой степени равен четвертой степени:
Корень пятой степени равен одной пятой степени; и так далее.
Глядя на первые примеры выше, мы можем переписать их так:
Вы можете ввести дробные показатели на вашем калькуляторе для оценки, но не забудьте использовать круглые скобки.Если вы пытаетесь вычислить, скажем, 15 (4/5) , вы должны заключить в круглые скобки «4/5», потому что иначе ваш калькулятор будет думать, что вы имеете в виду «(15 4 ) ÷ 5».
Дробные показатели обеспечивают большую гибкость (вы часто это увидите в исчислении), их часто проще написать, чем эквивалентный радикальный формат, и они позволяют выполнять вычисления, которые вы не могли раньше. Например:
Например:
Всякий раз, когда вы видите дробную экспоненту, помните, что верхнее число — это степень, а нижнее число — это корень (если вы конвертируете обратно в радикальный формат).Например:
Кстати, некоторые десятичные степени могут быть записаны и в виде дробных показателей. Если вы получили что-то вроде «3 5.5 «, вспомните, что 5.5 = 11/2, поэтому:
Однако, как правило, когда вы получаете десятичную степень (что-то другое, кроме дроби или целого числа), вы должны просто оставить ее как есть или, если необходимо, вычислить ее в своем калькуляторе. Например, 3 π , где π — это число, которое вы узнали в геометрии, и примерно равно 3.14159, нельзя упростить или преобразовать в радикал.
Технический момент: когда вы имеете дело с этими показателями с переменными, вам, возможно, придется принимать во внимание тот факт, что вы иногда получаете ровные корни. Подумайте об этом: предположим, вы начали с числа –2. Тогда:
Подумайте об этом: предположим, вы начали с числа –2. Тогда:
Другими словами, вы вводите отрицательное число и получаете положительное число! Это официальное определение абсолютной величины:
.
Да, я знаю: они никогда не говорили вам этого, но они ожидают, что вы каким-то образом узнаете, поэтому я говорю вам сейчас.
Итак, если они дадут вам, скажем, x 3/6 , тогда x лучше не быть отрицательным, потому что x 3 все равно будет отрицательным, и вы попытаетесь извлечь шестой корень отрицательного числа. Если они дадут вам x 4/6 , тогда отрицательное значение x станет положительным (из-за четвертой степени) и затем будет корнем шестой степени, поэтому оно станет | x | 2/3 (за счет уменьшения дробной мощности). С другой стороны, если они дадут вам что-то вроде x 4/5 , тогда вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)
С другой стороны, если они дадут вам что-то вроде x 4/5 , тогда вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)
Технологический момент: калькуляторы и другое программное обеспечение не вычисляют вещи так, как это делают люди; они используют заранее запрограммированные алгоритмы.Иногда конкретный метод, используемый калькулятором, может создать трудности в контексте дробных показателей.
Например, вы знаете, что кубический корень из –8 равен –2, а квадрат –2 равен 4, поэтому (–8) (2/3) = 4. Но некоторые калькуляторы возвращают комплексное значение или сообщение об ошибке, как в случае с одним из моих графических калькуляторов:
Ясно, что это не ожидаемый результат, особенно если вы еще не изучали комплексные числа. (2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.
(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.
Некоторые калькуляторы и программы будут выполнять вычисления, как ожидалось, как показано справа от моего другого графического калькулятора:
Разница связана с заранее запрограммированными вычислительными алгоритмами. Эти алгоритмы обычно пытаются выполнять вычисления способами, требующими наименьшего количества «операций», чтобы обработать введенные вами данные как можно быстрее.
Но иногда самый быстрый метод не всегда самый полезный, и ваш калькулятор «давится».
К счастью, проблему можно обойти. Разделив числитель и знаменатель дробной степени, вы можете ввести выражение, чтобы ваш калькулятор получил правильное значение. Получив бесполезный ответ в моем первом калькуляторе, я повторно ввел число с разбитой на части степенью:
Как вы можете видеть выше, не имело значения, возьму ли я сначала кубический корень из отрицательной восьмерки, а затем возведу в квадрат или сначала возведу в квадрат, а затем получу кубический корень; в любом случае, подавая числитель и знаменатель в калькулятор по отдельности, я смог заставить калькулятор возвращать правильное значение «4».
URL: https://www.purplemath.com/modules/exponent5.htm
N-й корень и рациональные экспоненты
Результаты обучения
- Упростите корни N-й степени.
- Запишите радикалы как рациональные экспоненты.
Использование рациональных корней
Хотя квадратные корни являются наиболее распространенными рациональными корнями, мы также можем найти кубические корни, корни четвертой степени, корни пятой степени и многое другое.{5} = — 243 [/ латекс]. Если [latex] a [/ latex] является действительным числом с хотя бы одним n -м корнем, то основной n -й корень [latex] a [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], который при увеличении до n в -й степени равен [latex] a [/ latex].
Главный n -й корень [латекса] a [/ latex] записывается как [latex] \ sqrt [n] {a} [/ latex], где [latex] n [/ latex] является положительным целым числом больше чем или равно 2. В выражении радикала [латекс] n [/ латекс] называется индексом радикала.
A Общее примечание: основной
n -й корень
Если [latex] a [/ latex] является действительным числом с хотя бы одним n -м корнем, то основной n -й корень [latex] a [/ latex], записанный как [latex] \ sqrt [n] {a} [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], которое при увеличении до n в -й степени равно [latex] a [/ latex]. Индекс радикала — [латекс] n [/ латекс].
Пример: упрощение
n корней -й степени
Упростите каждое из следующего:
- [латекс] \ sqrt [5] {- 32} [/ латекс]
- [латекс] \ sqrt [4] {4} \ cdot \ sqrt [4] {1,024} [/ латекс]
- [латекс] — \ sqrt [3] {\ dfrac {8 {x} ^ {6}} {125}} [/ латекс]
- [латекс] 8 \ sqrt [4] {3} — \ sqrt [4] {48} [/ латекс]
Показать решение
- [латекс] \ sqrt [5] {- 32} = — 2 [/ латекс], потому что [латекс] {\ left (-2 \ right)} ^ {5} = — 32 \\ \ text {} [/ латекс]
- Во-первых, выразите произведение как одно радикальное выражение.{2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex]
- [латекс] \ begin {align} \\ & 8 \ sqrt [4] {3} -2 \ sqrt [4] {3} && \ text {Упростите, чтобы получить одинаковые подкоренные выражения}. \\ & 6 \ sqrt [4] {3} && \ text {Добавить}. \ end {align} [/ latex]
Попробуйте
Упростить.
- [латекс] \ sqrt [3] {- 216} [/ латекс]
- [латекс] \ dfrac {3 \ sqrt [4] {80}} {\ sqrt [4] {5}} [/ латекс]
- [латекс] 6 \ sqrt [3] {9,000} +7 \ sqrt [3] {576} [/ латекс]
Показать решение
- [латекс] -6 [/ латекс]
- [латекс] 6 [/ латекс]
- [латекс] 88 \ sqrt [3] {9} [/ латекс]
Использование рациональных экспонентов
Радикальные выражения также можно записывать без использования радикального символа.{m}} \ end {align} [/ latex]
Как: дано выражение с рациональной экспонентой, запишите выражение как радикал.
- Определите степень, посмотрев на числитель экспоненты. {\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Калькулятор пятого корня — впечатляющий калькулятор пятого корня
Онлайн калькулятор пятого корня:
Воспользуйтесь нашим онлайн-калькулятором пятого корня.
Пример 5-го корня из x
- 5-й корень из 2 составляет ± 1,148.
- Корень 5-й степени из 10 составляет ± 1,584.
- Корень 5-й степени из 16 равен ± 1.741.
- 5-й корень из 32 равен ± 2.
- 5-й корень из 64 составляет ± 2,297.
- 5-й корень из 243 равен ± 3.
- 5-й корень из 1024 равен ± 4.
- 5-й корень из 3125 равен ± 5.
Формула вычисления пятого корня:
a 5 = x.
5 √x
Формула пятого корня
Определение пятого корня:
Определение пятого корня :
В математике пятый корень x a числа число r , которое при возведении в степень 5 дает x:
r 5 = x.
Определение пятого корня
Идеальные пятые корни
Пятый корень из 5 √x Пятый корень из 1 из 32 2 Пятый корень из 243 3 Пятый корень из 1024 4 Пятый корень из 3125 5 Пятый корень из 7776 6776 Пятый корень из 16807 7 Пятый корень из 32768 8 Пятый корень из 59049 9 Пятый корень из 100000 10 87 9 161051 11 Пятый корень из 248832 12 Идеальные пятые корни
Таблица o f Пятый корень:
Пятый корень x 5 √x Пятый корень x 5 √x F-1 1 Пятый корень из 26 1,9186 Пятый корень из 2 1,1487 Пятый корень из 27 1,9332 Пятый корень из 3 1,2457 Корень пятый из 28 1,9473 Корень пятый из 4 1,3195 Корень пятый из 29 1,961 Корень пятый из 5 1,3797 Пятый корень из 30 1,9744 Корень пятой степени из 6 1,431 Корень пятой степени из 31 1,9873 Корень пятой степени из 7 1,4758 Корень пятой степени из 32 2 90 087 Пятый корень из 8 1,5157 Пятый корень из 33 2,0123 Пятый корень из 9 1,5518 Пятый корень из 34 2,0244 Корень пятый из 10 1,5849 Корень пятый из 35 2,0362 Корень пятый из 11 1,6154 Корень пятый из 36 2,0477 Пятый корень из 12 1,6438 Пятый корень из 37 2,0589 Пятый корень из 13 1,6703 Пятый корень из 38 2,0699 Пятый корень из 14 1,6952 Пятый корень из 39 2,0807 Пятый корень из 15 1,7188 Пятый корень из 40 2,0913 Пятый корень из 16 1,7411 Корень пятой степени из 4 1 2,1016 Пятый корень из 17 1,7623 Пятый корень из 42 2,1118 Пятый корень из 18 1,7826 Пятый корень из 43 2,1217 Корень пятый из 19 1,802 Корень пятый из 44 2,1315 Корень пятый из 20 1,8206 Корень пятый из 45 2,1411 Пятый корень из 21 1,8384 Пятый корень из 46 21506 Пятый корень из 22 1,8556 Пятый корень из 47 2,1598 Корень пятый из 23 1,8722 Корень пятый из 48 2,1689 Корень пятый из 24 1,8882 Корень пятый из 49 2,1779 Корень пятый из 25 1,9037 900 87 Пятый корень из 50 2,1867 Пятая корневая диаграмма
Подробнее Калькулятор корня
ссылка: n -й корень из Википедии
Полномочия и корни чисел — Видео и стенограмма урока
Корней чисел
Давайте посмотрим на следующий телевизор на полке, у которого тоже квадратный экран.Учитывая, что этот экран имеет площадь 400 квадратных дюймов, давайте вычислим s :
Обратите внимание, что s — это число, которое мы умножили бы само на себя два раза, чтобы получить 400, что составляет 20, потому что 20 ⋅ 20 = 400. В математике мы называем это квадратным корнем из s . Квадратный корень из числа x , обозначенный как √ x , представляет собой число, умноженное на себя два раза, чтобы получить x .
В общем, n -й корень из x — это число, умноженное на само себя n раз, чтобы получить x .Обозначение, которое мы используем для n -го корня из x , такое же, как квадратный корень, но мы пишем маленькое n в верхнем левом углу от символа корня. Мы также можем записать n -й корень x как x 1/ n .
Например, рассмотрим третий корень, также называемый кубическим корнем , из 125. Это число равно числу, которое мы бы умножили само на себя три раза, чтобы получить 125, или 5.
Поскольку корни чисел могут быть записаны как число в степени, они удовлетворяют всем тем же свойствам степеней.Например, предположим, что мы хотим упростить кубический корень x 5 x 4. Мы можем использовать наши свойства для упрощения.
Кубический корень из x 5 ⋅ x 4 можно упростить до x 3.
Вот еще один пример: предположим, мы хотим упростить √8. Еще раз, мы можем использовать наши свойства для упрощения.
Получаем √8 = 2√2.
Квадратных корней отрицательных чисел
А теперь представьте, что нас попросили найти квадратный корень из -4. Логическое предположение будет 2 или -2. Однако:
- 2 ⋅ 2 = 4
- -2 ⋅ -2 = 4
Ни одно из этих уравнений не дает -4, потому что умножение двух отрицательных чисел или двух положительных чисел всегда дает положительное число. Чтобы компенсировать это, мы используем мнимое число , i , комплексное число, которое может быть выражено как действительное число, где i = √ (-1).
Мы видим, что √ (-4) = 2 i . Мнимые числа позволяют нам работать с квадратными корнями из отрицательных чисел, что в противном случае было бы невозможно.
Итоги урока
Давайте рассмотрим. Степень числа — это число, возведенное в другое число, которое принимает форму a b . Чтобы вычислить степени чисел, умножьте основание или на на себя, или на показатель степени или степень , обозначенную как b .
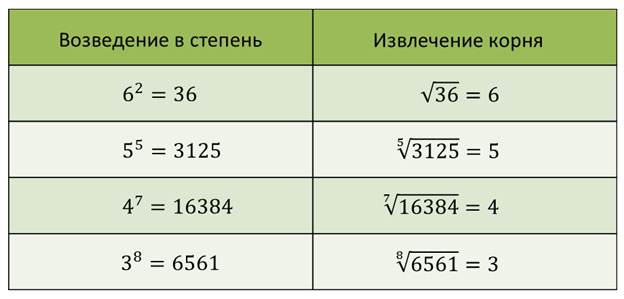
Квадратный корень из числа x (обозначается √ x ) — это число, умноженное на само себя два раза, чтобы получить x , а кубический корень — это число, умноженное на само себя в три раза. . n -й корень из x — это число, умноженное на себя n раз, чтобы получить x . Мнимое число ( i ) — это комплексное число, которое может быть выражено как действительное число и позволяет нам работать с квадратными корнями из отрицательных чисел.
Существуют основные свойства степеней, которые позволяют нам работать и упрощать как степени, так и корни чисел.
Задачи, связанные со степенями и корнями чисел, часто возникают в мире вокруг нас, поэтому так полезно знать их определения и свойства!
Видео-вопрос: поиск пятых корней единства
Стенограмма видеозаписи
Найдите пятый корень единства.
Итак, это пять значений для, которые удовлетворяют уравнению 𝑧 в том, что пятое значение равно единице. И мы можем использовать теорему де Муавра, чтобы решить это уравнение относительно. Теперь это означает, что для комплексного числа, которое равно 𝑟, умноженному на cos 𝜃 плюс sin 𝜃, тогда корень-й степени из задается формулой 𝑧 в степени единицы над, равной 𝑟 в степени единицы. более 𝑛, умноженное на cos 𝜃 плюс два 𝜋𝑘 сверх 𝑛 плюс 𝑖 sin 𝜃 плюс два 𝜋𝑘 сверх 𝑛 для значений 𝑘 от нуля, единицы, двух, до 𝑛 минус один.
Итак, оглядываясь назад на наше уравнение, мы получили к пяти равняется единице. И мы можем записать единицу в полярной форме как один умноженный на cos нуля плюс sin нуля. Другими словами, 𝑟 равно единице, а 𝜃 равно нулю. Тогда, когда 𝑟 равно единице, 𝑟 до единицы над 𝑛 просто будет равняться единице. И с 𝜃 равным нулю, мы можем сказать, что к единице над equal равно cos двух 𝜋𝑘 над плюс 𝑖 sin two 𝜋𝑘 над 𝑛, где 𝑘 принимает целые значения от нуля до 𝑛 минус один. И мы могли бы записать это в экспоненциальной форме как 𝑒 в степени двойки 𝜋𝑘 над 𝑖.
Итак, теперь у нас есть общая формула для нахождения корней-й степени из единицы. Вернемся назад и ответим на наш конкретный вопрос. Чтобы найти корни пятой степени из единицы, мы собираемся установить 𝑛 равным пяти, а 𝑘 примет целочисленные значения от нуля до пяти минус один. Итак, четыре. Когда 𝑘 равно нулю, до единицы больше пяти равно cos двух 𝜋 умножить на ноль над пятью плюс sin двойки умножить на ноль над пятью. Ну, два 𝜋 умножить на ноль — это ноль. Таким образом, получается cos, равный нулю, плюс sin нуля, или, в экспоненциальной форме, в степени нуля 𝑖, что, конечно, равно 𝑒 в степени нуля или единицы.Итак, наш первый корень — это один.
Давайте подключим 𝑘 к следующему корневому каталогу, равному единице. Это дает нам cos, умноженный на два, умноженный на пять, плюс sin, умноженный на два 𝜋, умноженный на пять. И, конечно, два 𝜋 умножить на пять — это всего два 𝜋 больше пяти. Тогда в экспоненциальной форме наш следующий корень равен is в степени два 𝜋 над пятью 𝑖. Итак, продолжаем. Когда 𝑘 равно двум, мы получаем cos, равный двум 𝜋, умноженным на два, на пять плюс sin два 𝜋, умноженным на два, на пять, что упрощается до cos из четырех four на пять плюс sin четыре 𝜋 на пять, и, в экспоненциальной форме, это 𝑒 в степени четырех 𝜋 больше пяти 𝑖.Затем мы подставляем 𝑘, равное трем, и обнаруживаем, что наш следующий корень равен cos из шести 𝜋 по пяти плюс 𝑖 sin шесть 𝜋 по пяти.
Но мы обычно стараемся давать наши ответы так, чтобы этот главный аргумент здесь был больше отрицательного 𝜋, но меньше или равнялся положительному. Итак, давайте найдем эквивалентный угол в этом интервале. Из-за периодического характера этой функции мы можем просто вычесть два 𝜋 и посмотреть, даст ли это ответ в правильном интервале. Ну, шесть 𝜋 больше пяти минус два 𝜋 эквивалентно шести больше пяти минус 10𝜋 больше пяти, что отрицательно четыре 𝜋 больше пяти.И это в требуемом интервале, поэтому мы можем использовать это значение. И эквивалентная экспоненциальная форма равна отрицательным четырем 𝜋 более пяти 𝑖.
Теперь, для нашего последнего корня, мы можем вставить 𝑘, равное четырем. И это дает нам cos восьми больше пяти плюс sin восьми 𝜋 больше пяти. И снова значение нашего основного аргумента больше. Итак, если мы вычтем два, мы получим отрицательные два из пяти. Тогда наш окончательный корень в экспоненциальной форме равен с отрицательными двумя 𝜋 над пятью.Итак, наши пятые корни единства равны единице, 𝑒 к двум пятым 𝜋𝑖, 𝑒 к четырем пятым 𝜋𝑖, 𝑒 к отрицательным четырем пятым 𝜋𝑖 и 𝑒 к отрицательным двум пятым 𝜋𝑖.
.

 Введите свой запрос:
Введите свой запрос: