Содержание
ХИ2.ОБР.ПХ (функция ХИ2.ОБР.ПХ) — Служба поддержки Office
Возвращает значение, обратное правосторонней вероятности распределения хи-квадрат.
Если вероятность = ХИ2.РАСП.ПХ(x;…), то ХИ2.ОБР.ПХ(вероятность;…) = x. Эта функция позволяет сравнить наблюдаемые результаты с ожидаемыми, чтобы определить, верна ли исходная гипотеза.
Синтаксис
ХИ2.ОБР.ПХ(вероятность;степени_свободы)
Аргументы функции ХИ2.ОБР.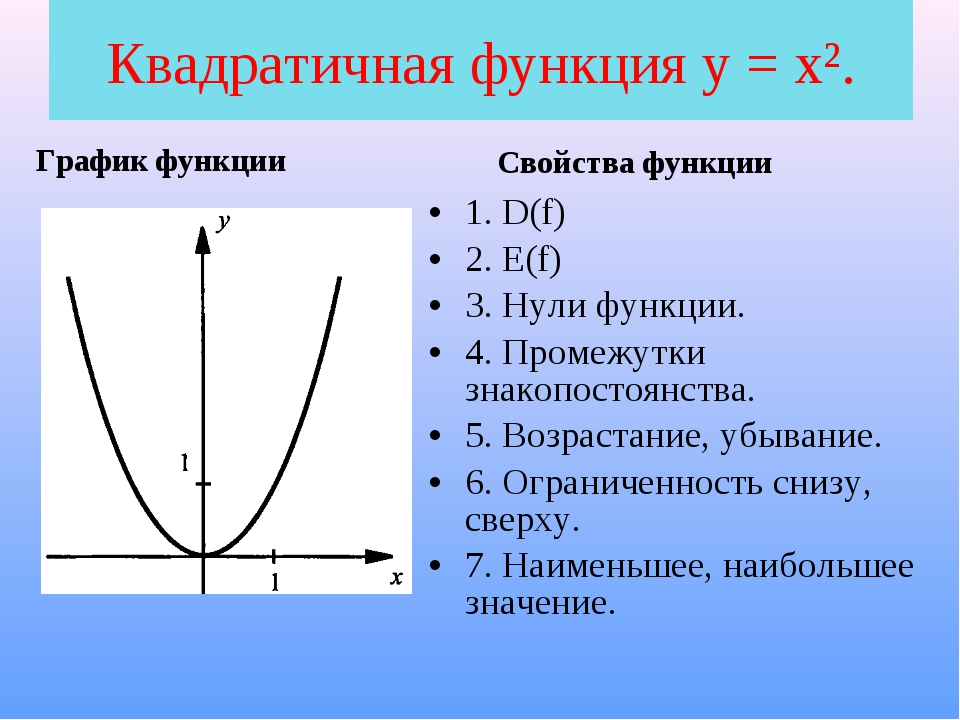 ПХ описаны ниже.
ПХ описаны ниже.
-
Вероятность — обязательный аргумент. Вероятность, связанная с распределением хи-квадрат. -
Степени_свободы — обязательный аргумент. Число степеней свободы.
Замечания
-
Если любой из аргументов не является числом, ХИ2. ОПС. RT возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если вероятность < 0 или вероятность > 1, ХИ2. INV. RT возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значение степени_свободы не целое, оно усекается.
-
Если deg_freedom < 1, ХИ2. ОПС. RT возвращает #NUM! значение ошибки #ЗНАЧ!.
По значению вероятности функция ХИ2.ОБР.ПХ ищет значение x, для которого ХИ2.РАСП.ПХ(x;степень_свободы) = вероятность. Таким образом, точность функции ХИ2.ОБР.ПХ зависит от точности ХИ2.РАСП.ПХ. В функции ХИ2.ОБР.ПХ для поиска применяется метод итераций. Если поиск не заканчивается после 64 итераций, функция возвращает значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.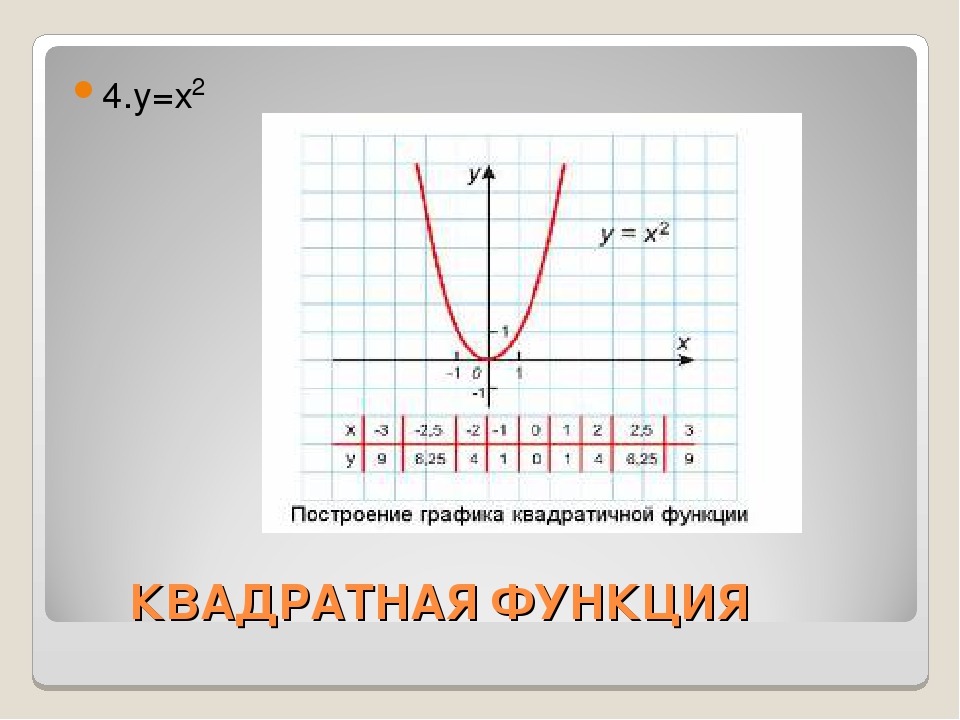
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
0,050001
|
Вероятность, связанная с распределением хи-квадрат
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
10
|
Степени свободы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
=ХИ2. Предупреждение |
Ф- | ХЭ- | Р- | П- | СК- |
ХЭ- | Р- | П- | СК- | Ф- |
Р- | П- | СК- | Ф- | ХЭ- |
П- | СК- | Ф- | ХЭ- | Р- |
СК- | Ф- | ХЭ- | Р- | П- |
Ф- | ХЭ- | Р- | П- | СК- |
ХЭ- | Р- | П- | СК- | Ф- |
Р- | П- | СК- | Ф- | ХЭ- |
П- | СК- | Ф- | ХЭ- | Р- |
СК- | Ф- | ХЭ- | Р- | П- |
Ф- | ХЭ- | Р- | П- | СК- |
ХЭ- | Р- | П- | СК- | Ф- |
Р- | П- | СК- | Ф- | ХЭ- |
П- | СК- | Ф- | ХЭ- | Р- |
СК- | Ф- | ХЭ- | Р- | П- |
Итоговая таблица по результатам обработки методики
«Квадрат функций»
Функции | СК | П | Р | ХЭ | Ф | Сумма баллов |
Кол-во баллов | =150 | |||||
Место по значению |
Итоговая таблица по результатам обработки методики
«Квадрат функций»
Функции | СК | П | Р | ХЭ | Ф | Сумма баллов |
Кол-во баллов | =150 | |||||
Место по значению |
Возведение в степень в Python, квадрат числа на примерах
В этом руководстве разберем процесс возведения в степень в Python. ) — это оператор возведения числа в степень, ведь именно он обозначает эту операцию в математике. Однако в большинстве языков программирования этот знак выступает в качестве побитового
) — это оператор возведения числа в степень, ведь именно он обозначает эту операцию в математике. Однако в большинстве языков программирования этот знак выступает в качестве побитового xor.
В Python оператор возведения в степень обозначается двумя символами звездочки ** между основанием и числом степени.
Функциональность этого оператора дополняет возможности оператора умножения *: разница лишь в том, что второй оператор указывает на то, сколько раз первые операнд будет умножен сам на себя.
print(5**6)Чтобы умножить число 5 само на себя 6 раз, используется ** между основанием 5 и операндом степени 6. Вывод:
15625Проверим оператор с другими значениями.
Инициализируем целое число, отрицательное целое, ноль, два числа с плавающей точкой float, одно больше нуля, а второе — меньше. Степеням же присвоим случайные значения.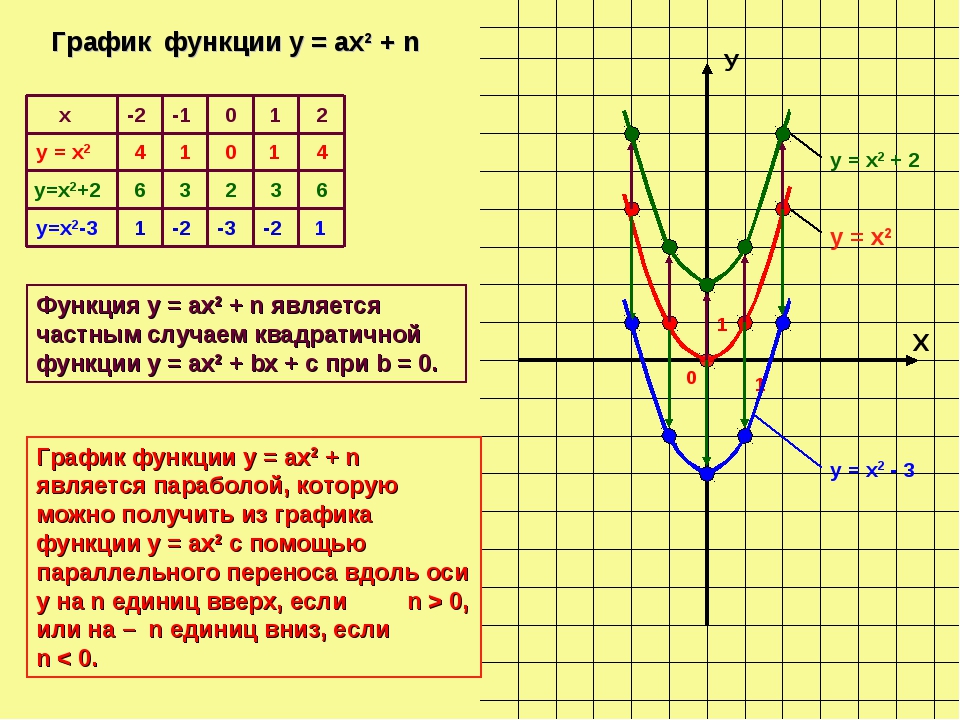 8 = 0.00390625
8 = 0.00390625
pow() или math.power() для возведения в степень
Также возводить в степень в Python можно с помощью функции pow() или модуля math, в котором есть своя реализация этого же модуля.
В обе функции нужно передать два аргумента: основание и саму степень. Попробуем вызвать обе функции и посмотрим на результат.
Вывод:
-2097152 -2097152.0 2.8284271247461903 2.8284271247461903 64 64.0 32.0 32.0Отличие лишь в том, что
math.pow()всегда возвращает значение числа с плавающей точкой, даже если передать целые числа. А вотpow()вернет число с плавающей точкой, если таким же был хотя бы один из аргументов.numpy.np() для возведения в степень
В модуле numpy есть своя функция
power()для возведения в степень. Она принимает те же аргументы, что иpow(), где первый — это основание, а второй — значение степени.Выведем те же результаты.
-2097152 2.8284271247461903 64 32.0Как получить квадрат числа в Python?
Для возведения числа в квадрат, нужно указать2в качестве степени. Встроенной функции для получения квадрата в Python нет.
Например, квадрат числа 6 —6**2—> 36.Сравнение времени работы разных решений
Теперь сравним, сколько занимает выполнение каждой из трех функций и оператора
**. Для этого используем модульtimeit.Основанием будет 2, а значением степени — 9999999.
import numpy as np import math import time start = time.process_time() val = 2**9999999 print('** за', time.process_time() - start, 'ms') start = time.process_time() val = pow(2, 9999999) print('pow() за', time.process_time() - start, 'ms') start = time.process_time() val = np.power(2, 9999999) print('np.power() за', time.process_time() - start, 'ms') start = time.process_time() val = math.pow(2, 9999999) print('math.pow() за', time.process_time() - start, 'ms')** за 0.078125 ms pow() за 0.0625 ms np.power() за 0.0 ms Traceback (most recent call last): File "C:\Programs\Python\Python38\test.py", line 18, in <module> val = math.pow(2, 9999999) OverflowError: math range errorВ первую очередь можно обратить внимание на то, что
math.pow()вернула ошибкуOverflowError.Это значит, что функция не поддерживает крупные значения степени.
Различия между остальными достаточно простые, но можно увидеть, что
np.power()— самая быстрая.
Семинар 4. Уравнение Шредингера Аналог классического волнового уравнения был предложен
4.1. Уравнение Шредингера В квантовой физике изменение
где
в которой заменены y, z и , : х → =
Так как уравнение Шредингера Уравнение Шредингера для стационарного состояния, когда потенциальная энергия Это уравнение называют стационарным уравнением Шредингера. Так как в стационарном состоянии
и вероятность найти частицу в момент t в точке 4.2. Частица в одномерной |
| (4.5) |
|
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x)
= 0.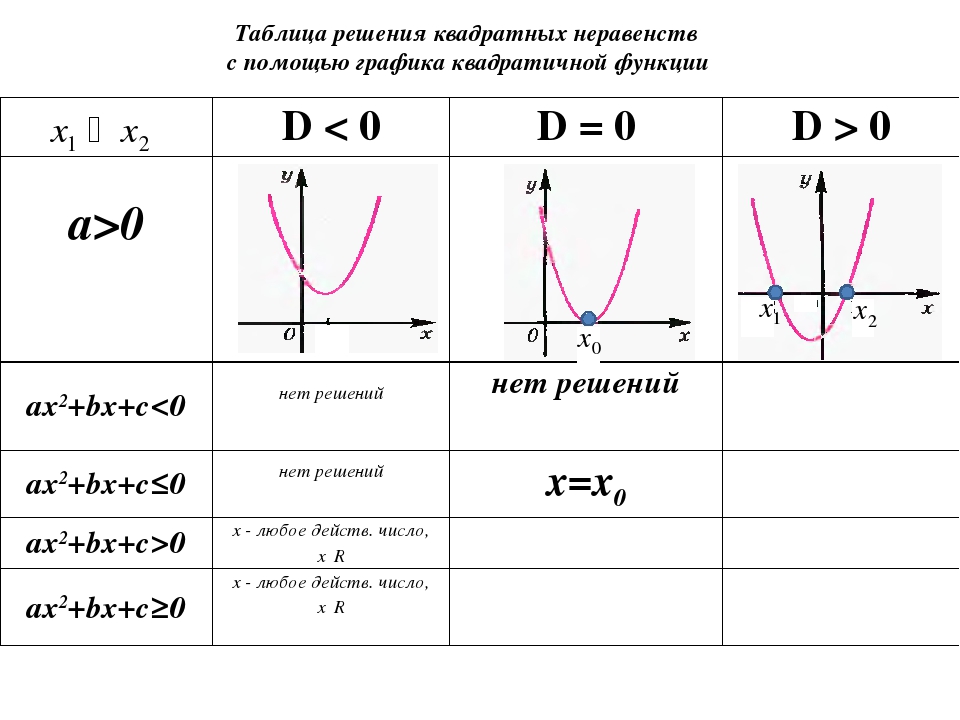 Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
| (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ2)1/2.
Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой
функции следует
kL = nπ,
n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими
стенками устанавливаются стоячие волны, а энергия состояния частиц имеет
дискретный спектр значений En
| n = 1, 2, 3, … | (4.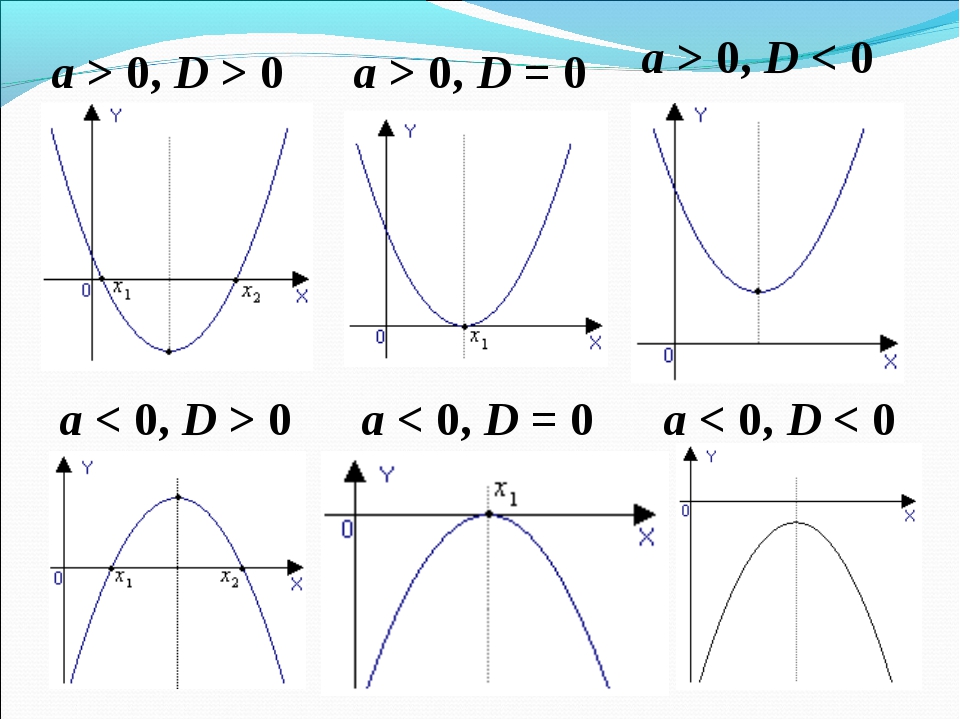 9) 9) |
Частица может находиться в
каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует
волновая функция ψn(x), которая с учетом
условия нормировки
имеет вид
| (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может
иметь энергию
E < ћ2π2/(2mL2).
Состояния частицы ψn в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы
Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции
|Ψ|2 определяет
вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной
ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная
энергия имеет вид
| (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
| (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического
осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое
описание частицы переходит в классическое.
Частица в одномерной потенциальной ямеОдномерная прямоугольная яма шириной L:
n = 1, 2, … Одномерный гармонический осциллятор: En = ћω0(n |
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в
центральном потенциале U(r)
имеет вид
| (4.14) |
Решение уравнения (4.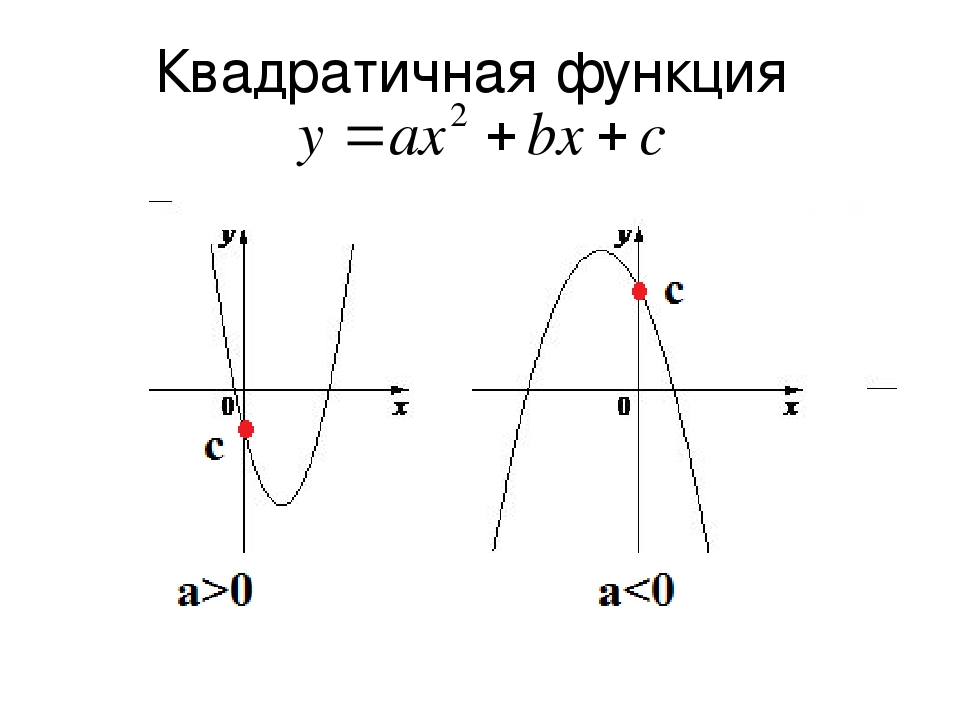 14) записываются в виде произведения радиальной и
14) записываются в виде произведения радиальной и
угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и
угловая функция Ylm(θ,φ),
называемая сферической, удовлетворяют уравнениям
| 2Ylm(θ,φ) = ћ2l(l +1)Ylm(θ,φ) | (4.16) |
или
| Ylm(θ,φ) = ћ2l(l +1)Ylm(θ,φ) | (4.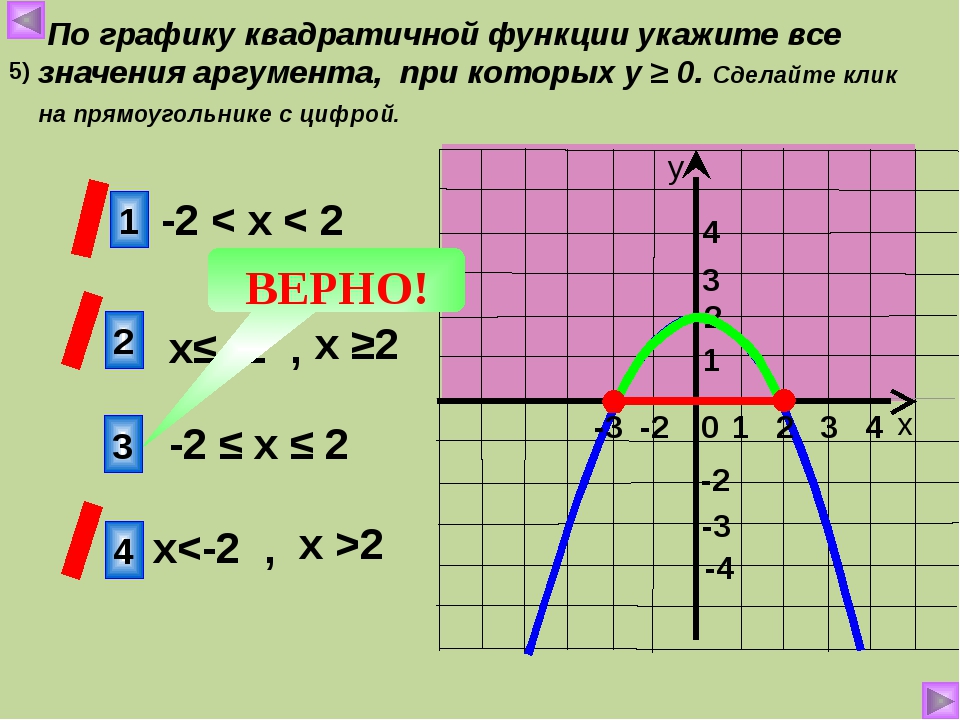 17) 17) |
Уравнение (4.16) определяет возможные собственные значения
l и собственные функции Ylm(θ,φ) оператора
квадрата момента 2.
Уравнение (4.17) определяет собственные значения энергии Е и радиальные
собственные функции Rnl(r),
от которых зависит энергия системы (рис. 4.3).
Схема уровней (последовательность и абсолютные значения энергий) зависит от
радиальной функции Rnl(r),
которая в свою очередь определяется потенциалом U(r),
в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в
кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ2/mee2 ≈
0.529·108 cм.
| Решения уравнения существуют лишь при |
4.5. Орбитальный момент количества движения
Собственные значения
L2 и
Lz являются
решением уравнений
2Ylm(θ,φ) =
L2Ylm(θ,φ) и zYlm(θ,φ) =
LzYlm(θ,φ).
Они имеют следующие дискретные значения
L2 =
ћ2l(l
+ 1), где l = 0, 1, 2, 3, …,
Lz =
ћm,
где m = 0, ± 1,
± 2, ± 3,…,
± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
и.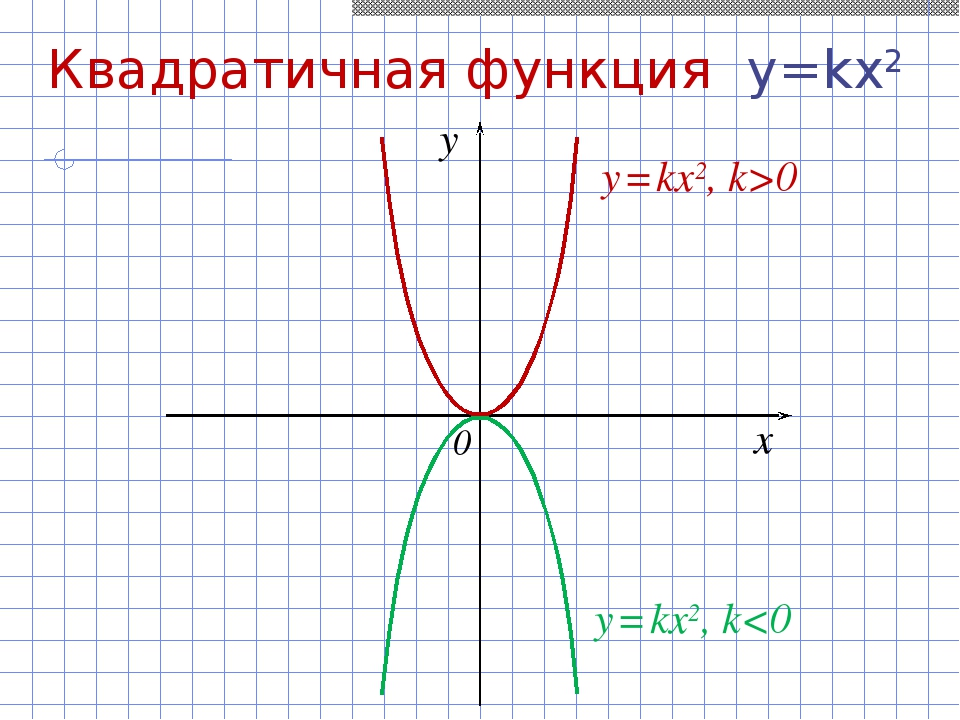 т. д. т. д. |
Состоянию с l = 0 отвечает сферически симметричная
волновая функция. В тех случаях, когда l ≠ 0
волновая функция не имеет сферической симметрии. Симметрия волновой функции
определяется симметрией сферических функций Ylm(θ,φ).
Имеет место интересное квантовое явление, когда решение сферически симметричной
задачи (потенциал описывает сферически симметричную систему) приводит к
состояниям, не обладающим сферической симметрией. Таким образом, симметрия
уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого
решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина
орбитального момента количества движения L:
| (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента
количества движения, называют этой величиной квантовое число
l, имея в виду, что между l и
L имеется однозначная связь (4. 18).
18).
Рис. 4.4 Возможные ориентации вектора |
Так как величина l может принимать только
целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения
L квантуется.
Например, для частицы с l = 2 момент
количества движения
=
= 6.58·10-22√6
МэВ·сек ≈ 2.6·10—34
Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является
векторной величиной. Так как величина орбитального момента количества движения
квантуется, то и направление
по
отношению к выделенному направлению z, например, к
внешнему магнитному полю, также квантуется и принимает дискретные значения
Lz =
ћm,
где m изменяется от +l до –l,
т. е. имеет 2l + 1 значений. Например, при
l = 2 величина m принимает
значения +2, +1, 0, -1, -2 (см.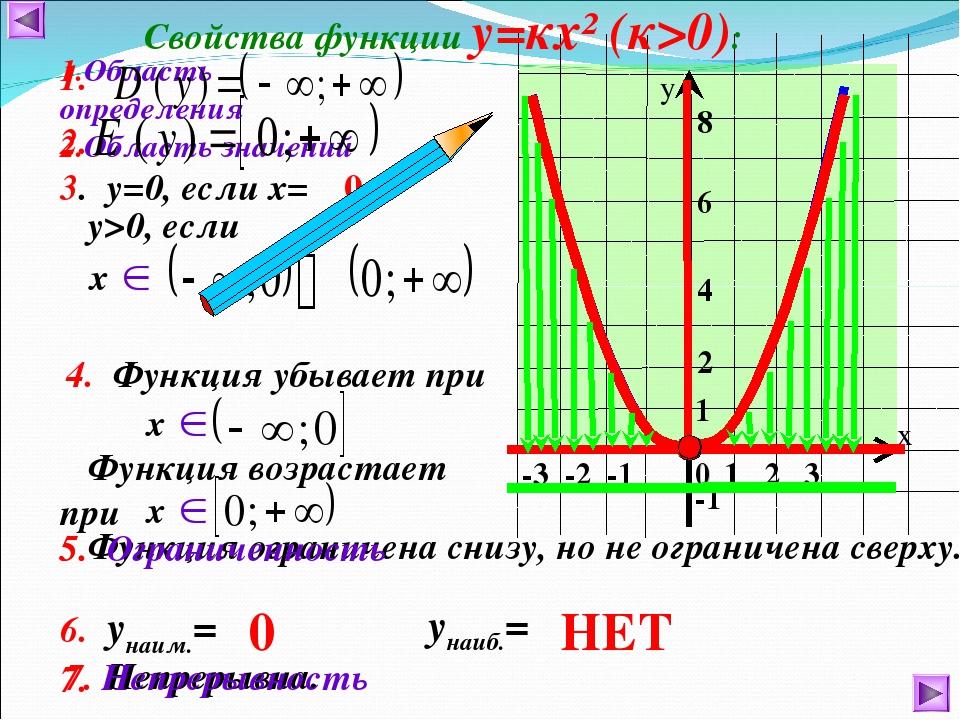 рис. 4.4). Вместе с тем энергия системы не
рис. 4.4). Вместе с тем энергия системы не
зависит от m, т. е. от направления вектора
,
что является очевидным следствием сферической симметрии системы.
Состояние частицы, находящейся в сферически симметричном поле, полностью
описывается тремя квантовыми числами: n,
l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер
этой симметрии определяет возможные значения квантовых чисел. Очевидно, что
система, описываемая функцией eimφ, примет прежнее
значение только тогда, когда азимутальный угол φ в результате поворота вокруг
оси z примет прежнее значение φ. Этому условию функция
eimφ удовлетворяет только в случае, когда величина
mφ кратна 2π. Т.е. величина m
должна иметь целые значения. Так как необходимо учитывать вращение в двух
противоположных направлениях и отсутствие вращения, единственно возможными
значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы.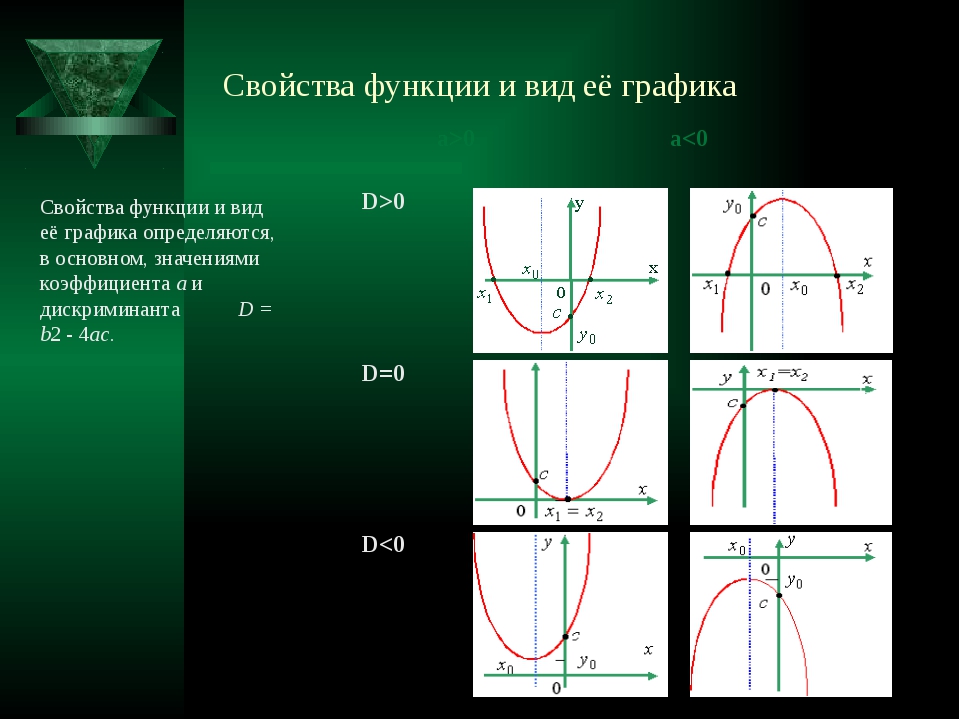 Между значением
Между значением
вектора спина
и
квантовым числом спина s выполняется такое же
соотношение, как между величиной значением вектора орбитального момента
и
орбитальным квантовым числом l:
| 2 = ћ2s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l,
которое может быть лишь целым числом или нулем, спиновое квантовое число
s (в дальнейшем просто спин) может быть как целым
(включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2,
… , но при этом для каждой элементарной частицы спин может принимать
единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов
равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2.
Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина,
спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также
Спин частицы невозможно изменить, также
как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина
на
любое фиксированное направление в пространстве (например, на ось
z) может принимать 2s + 1
значение:
szћ =
±sћ, ±(s
− 1)ћ, ±(s
− 2)ћ,…,
±1/2ћ или 0.
Число sz −
это квантовое число проекции спина. Максимальная величина sz совпадает
с s. Так как спин электрона равен 1/2, то проекция
этого спина может принимать лишь два значения sz
=
±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если
проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц
является
векторной суммой орбитального
и
спинового моментов
количества движения.
=
+
.
Квадрат полного момента имеет значение:
2
= ћ2j(j + 1).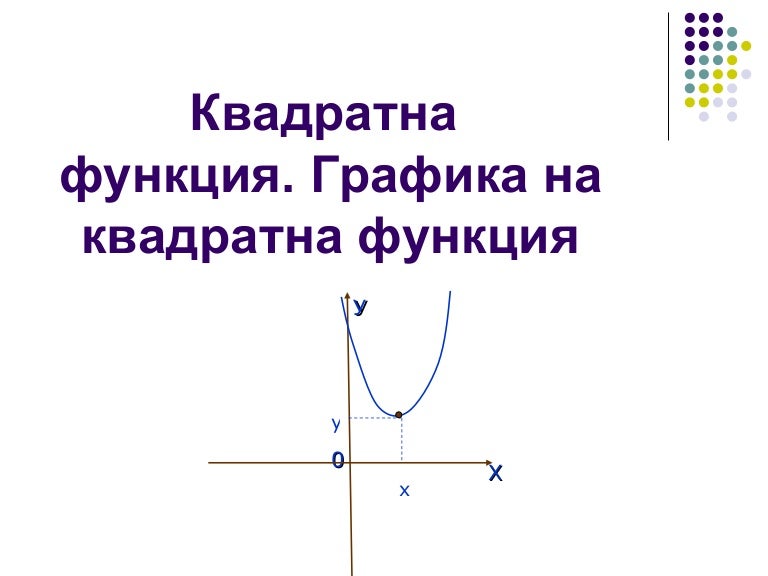
Квантовое число полного момента j, соответствующее
сумме двух векторов
и
,
может принимать ряд дискретных значений, отличающихся на 1:
j = l + s, l + s −1,…,
|l − s|
Проекция на
выделенную ось Jz также принимает дискретные значения:
Jz = ћjz;
= -j, -j + 1,…, j − 1, j.
Число значений проекции Jz равно 2j + 1.
Если для и
определены
единственные значения проекций на ось z lz и
sz, то jz также определена
однозначно: jz = lz + sz.
4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все
возможные значения физической величины, характеризующей различные квантовые
системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и Определяет число узлов волновой функции иэнергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы. 2 = ћ2j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L2 = ћ2l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s.  Оно может быть либо положительным Оно может быть либо положительнымцелым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S2 = ћ2s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии → — (зеркальном отражении). Полная четность частицы Р = π(-1)l , где π – её внутренняя четность, а (-1)l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.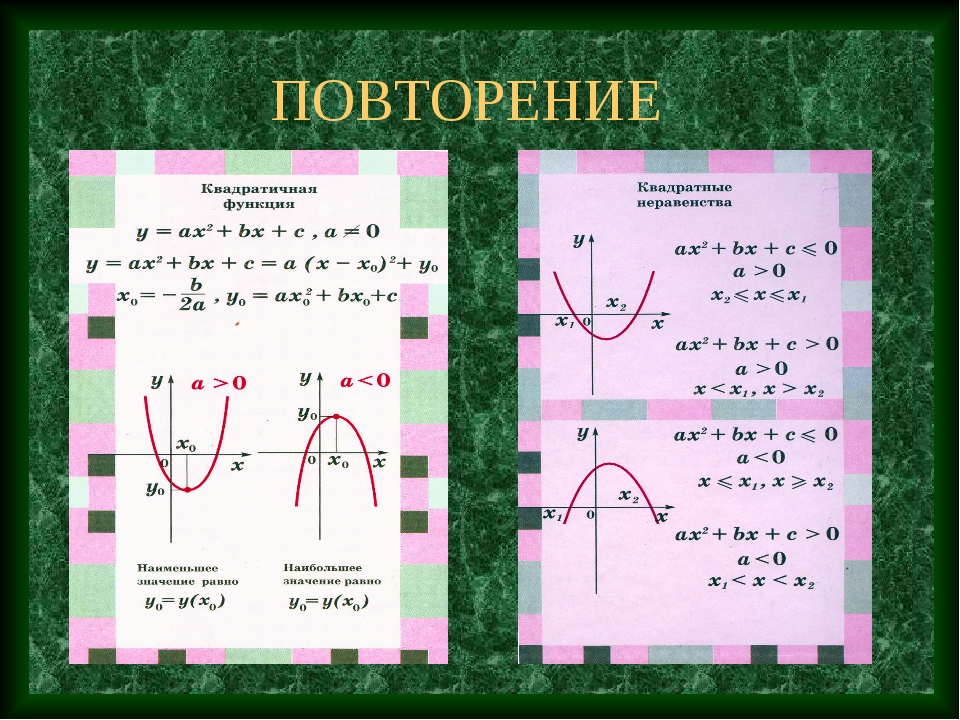
Все состояния, в которых может находиться квантовая система, описываются с
помощью полного набора квантовых чисел. Так в случае протона в ядре состояние
протона описывается с помощью четырех квантовых чисел, соответствующих четырем
степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …,
∞), - Орбитальное квантовое число l (0, 1, 2,
…), - Проекция орбитального момента m (± l,
± (l-1), …, ±1, 0), - Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются
различные сферически симметричные потенциалы с различной радиальной
зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U
= kr2, - Потенциал Вудса-Саксона (с его помощью описываются внутриядерные
взаимодействия):
где U0,
а и R – положительные константы (R
– радиус ядра). Во всех случаях сферически симметричные системы можно
Во всех случаях сферически симметричные системы можно
описать с помощью набора квантовых чисел n,
l, j,
jz,
однако, в зависимости от радиального вида потенциала энергетический спектр
состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со
свойствами симметрии гамильтониана системы. Например, в случае, если квантовая
система обладает центральной симметрией U = U(r),
то этой системе соответствует сохранение орбитального момента количества
движения l и одной из его проекций
m. При этом из-за сферической симметрии задачи энергия состояний не будет
зависеть от величины m, т. е. состояния будут
вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными
преобразованиями, в квантовой физике существуют и другие симметрии –
дискретные. Одной из них является зеркальная симметрия волновой функции
относительно инверсии координат (→
-).
Оператору инверсии соответствует квантовое число четность, которое может
принимать два значения +1 и -1 в зависимости от того, сохраняется ли знак
волновой функции при инверсии или меняется на противоположный.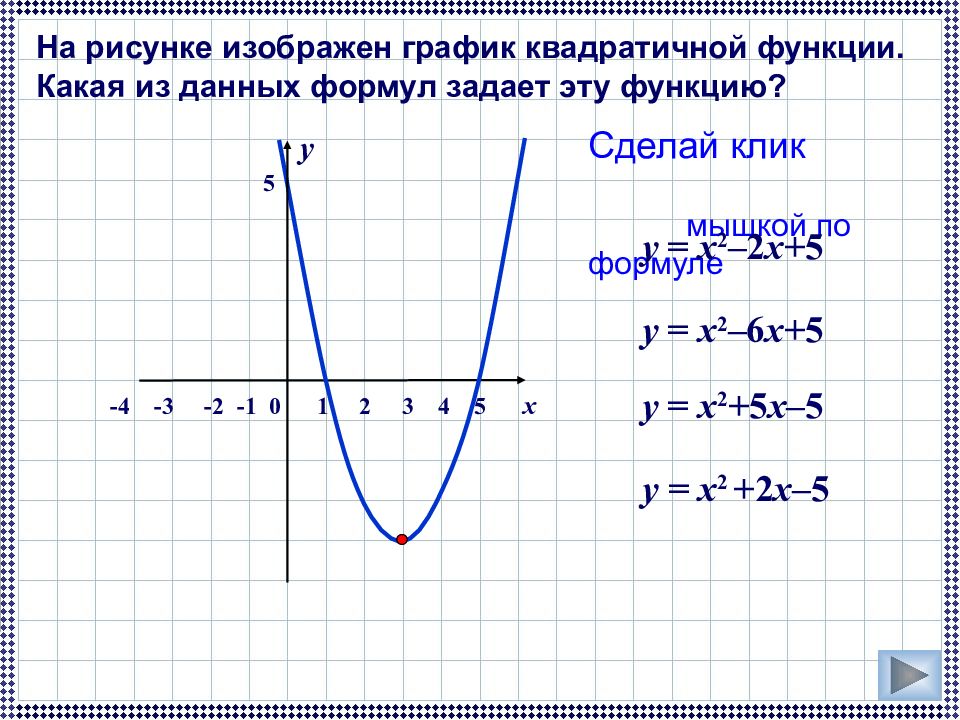
Система тождественных частиц характеризуется еще одной симметрией –
симметрией относительно перестановок тождественных частиц. Эта симметрия
определяется свойствами частиц, образующих систему. Системы частиц с целым
спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым
спином (фермионов) − антисимметричными волновыми функциями.
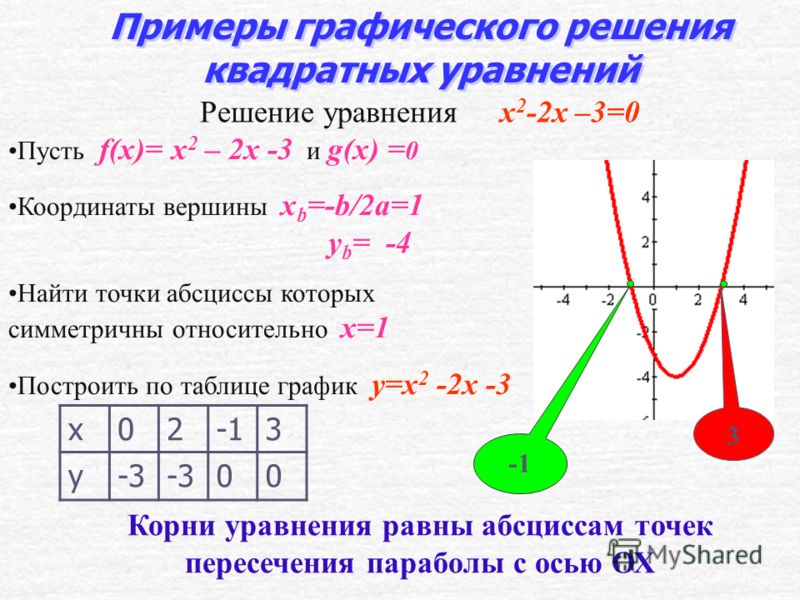
§ 08. Линейные и квадратичные функции
Линейная функция . Функция определена на всей числовой прямой, . Множество ее изменения – также множество всех действительных чисел, . Функция не ограничена. Она не имеет точек экстремума. При функция является возрастающей, при – убывающей. При функция является постоянной. Графиком линейной функции является прямая. Угловой коэффициент K прямой равен тангенсу угла между прямой и положительным направлением оси абсцисс, (рис. 31). Из аксиом геометрии известно, что если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.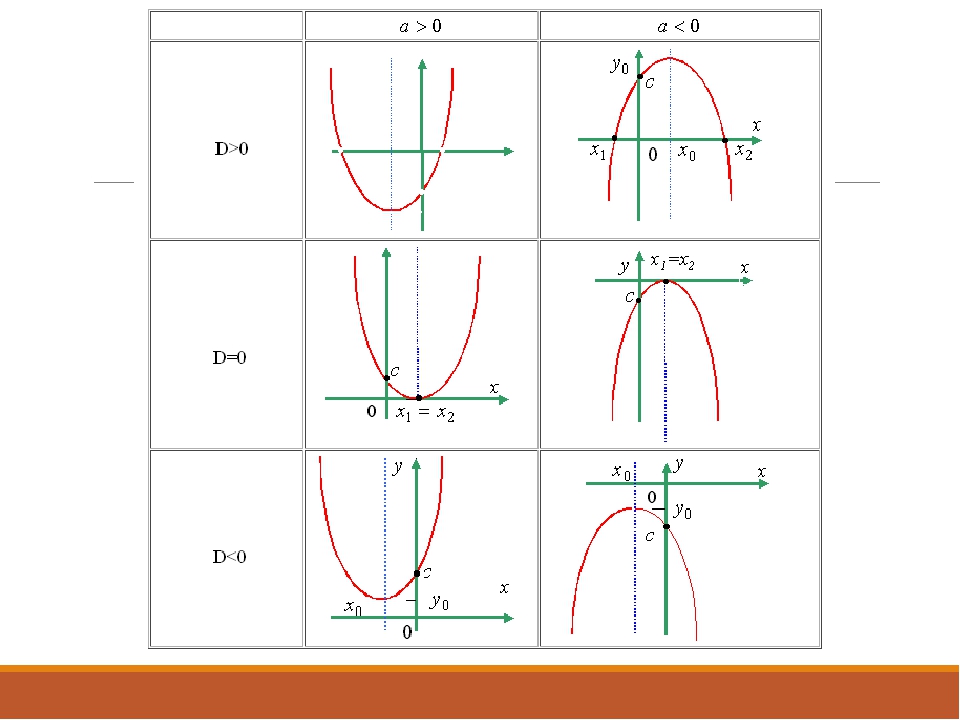 Поэтому для построения графика линейной функции достаточно задать две точки.
Поэтому для построения графика линейной функции достаточно задать две точки.
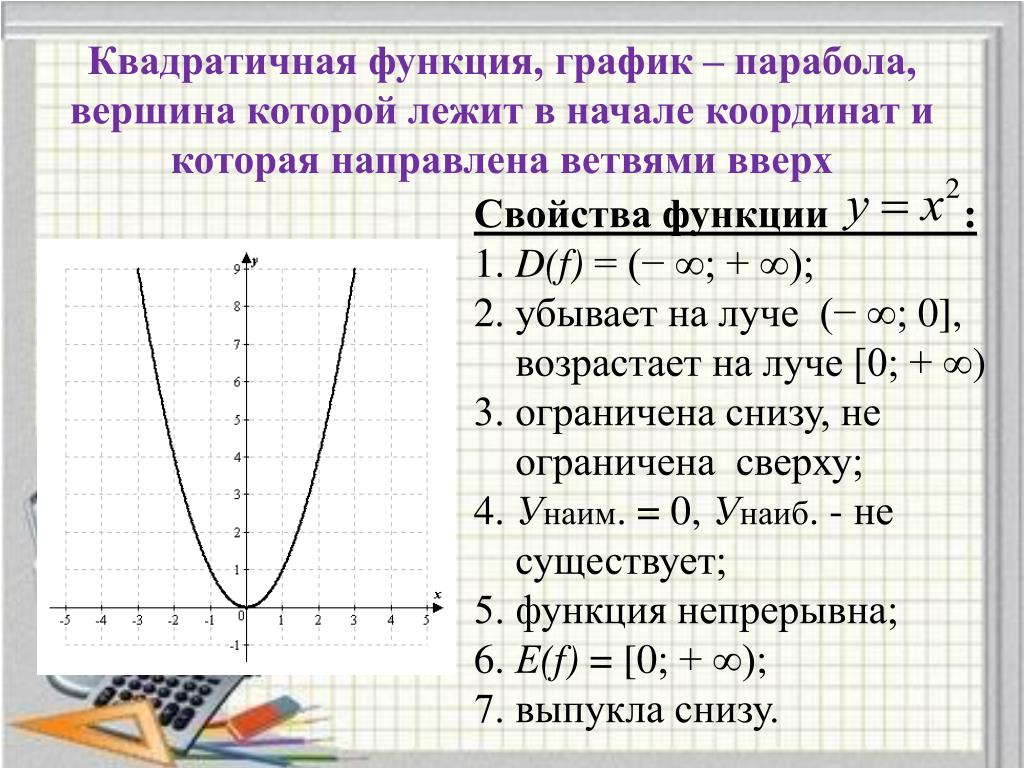
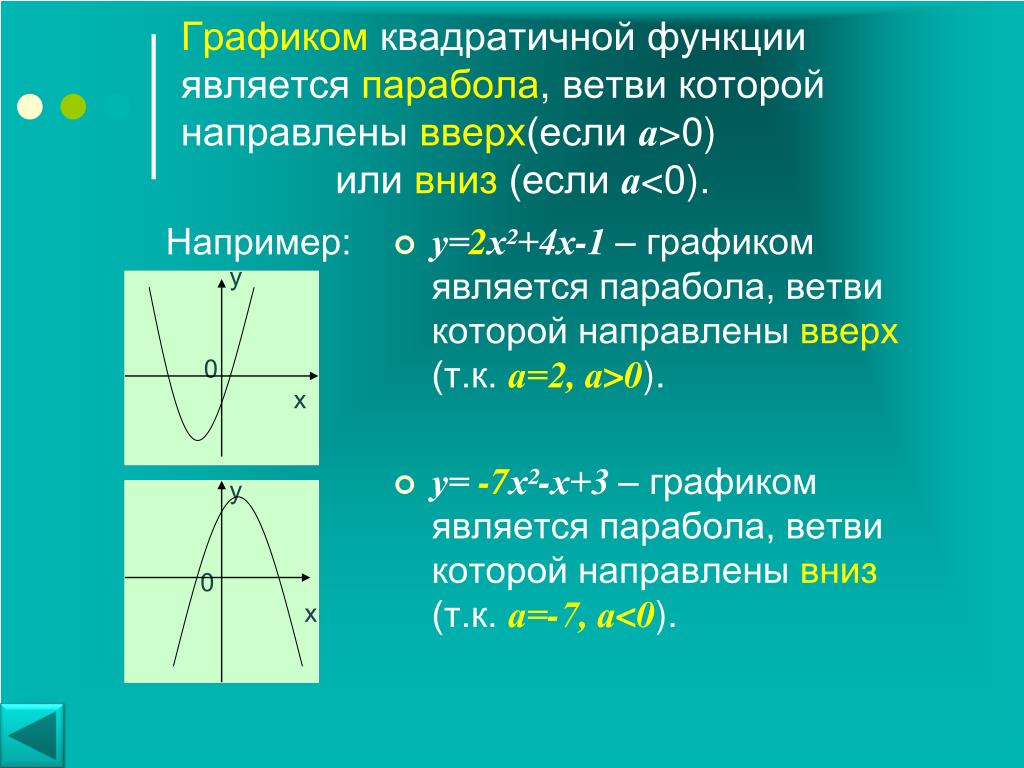
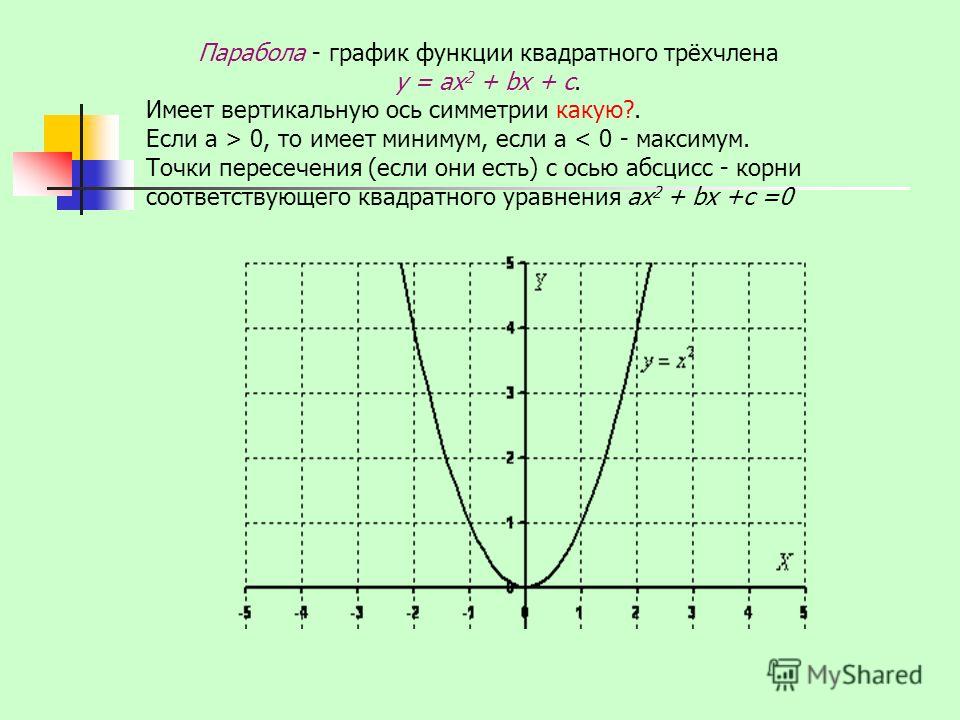
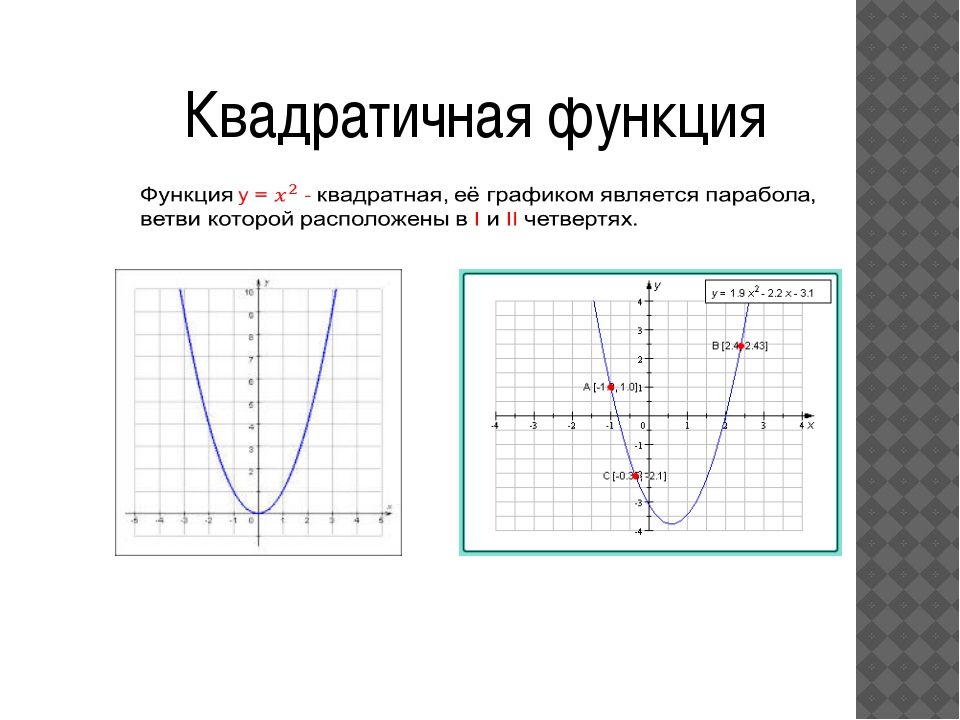
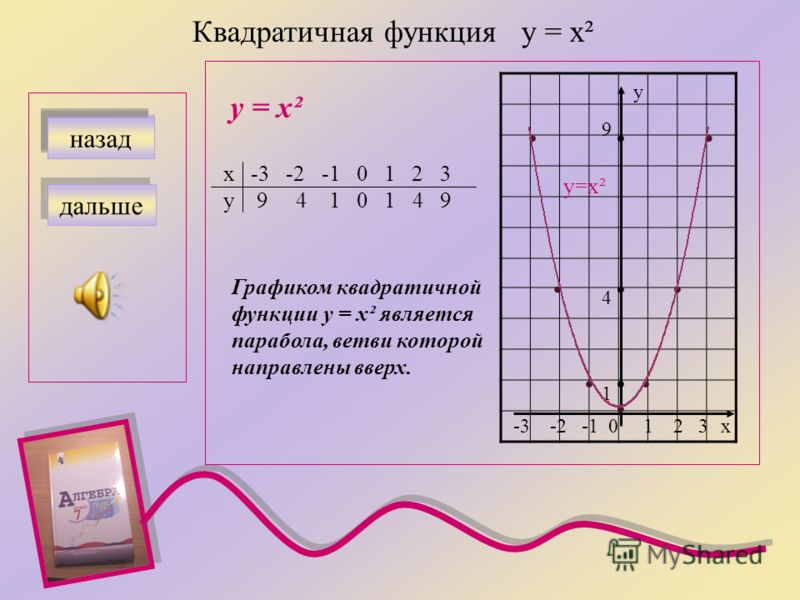
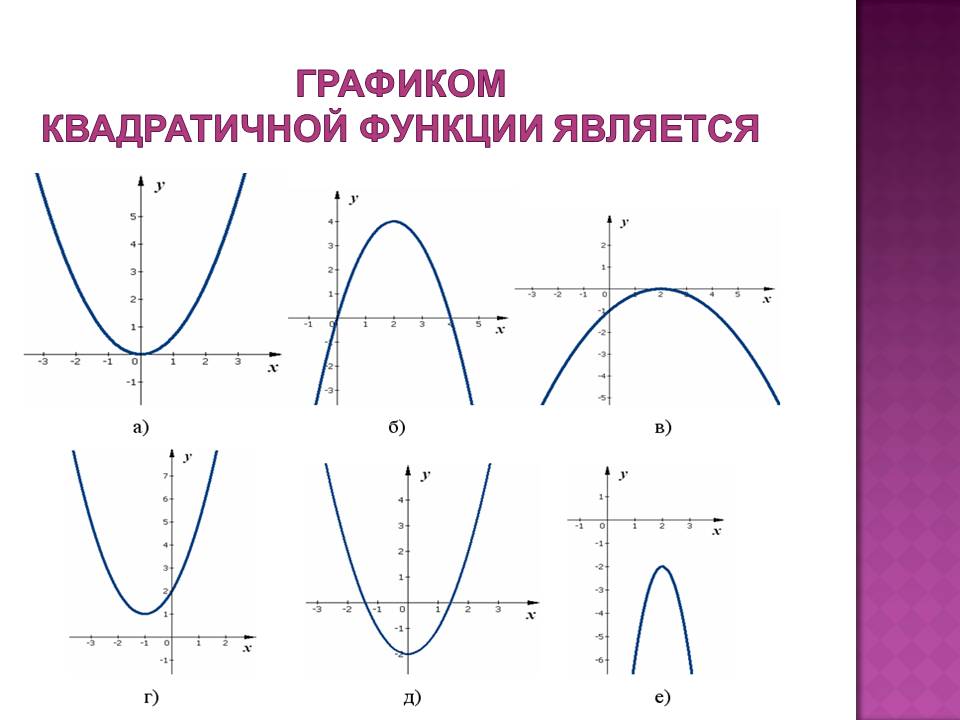
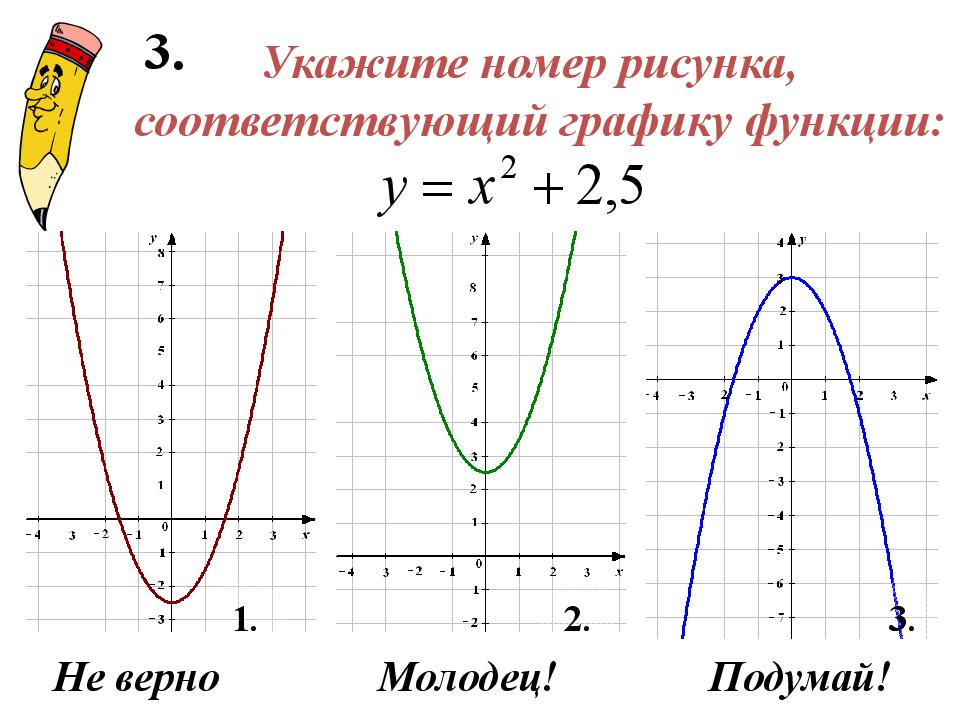
Квадратичная функция (). Функция определена на всей числовой прямой. Графиком квадратичной функции является парабола.
Для построения графика квадратичной функции целесообразно преобразовать формулу, выделив полный квадрат: , где . Таким образом, получаем, что вершина параболы находится в точке с координатами . График квадратичной функции симметричен относительно прямой .
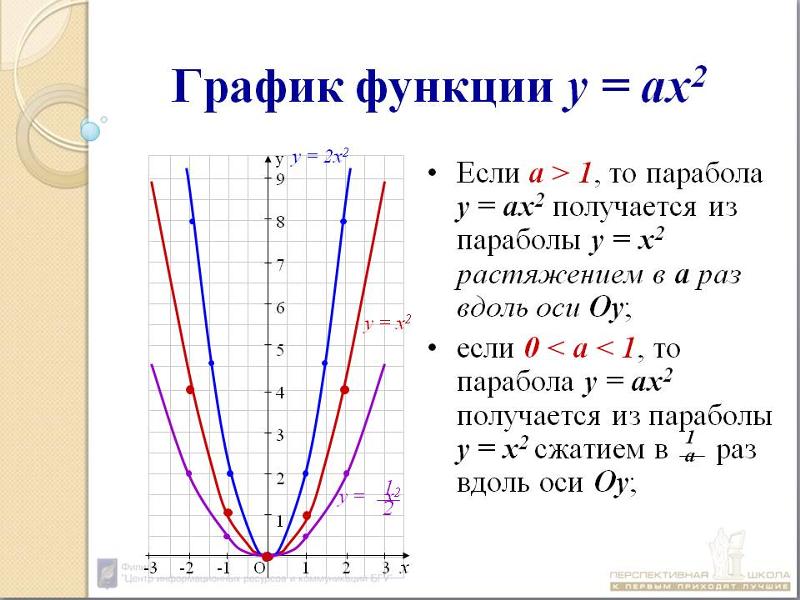
При ветви параболы направлены вверх. В точке функция имеет минимум и принимает в этой точке наименьшее значение. При функция возрастает, при функция убывает. В этом случае квадратичная функция ограничена снизу и не ограничена сверху.
При ветви параболы направлены вниз. В точке функция имеет максимум и принимает в этой точке наибольшее значение. При функция убывает, при функция возрастает. В этом случае квадратичная функция ограничена сверху и не ограничена снизу.
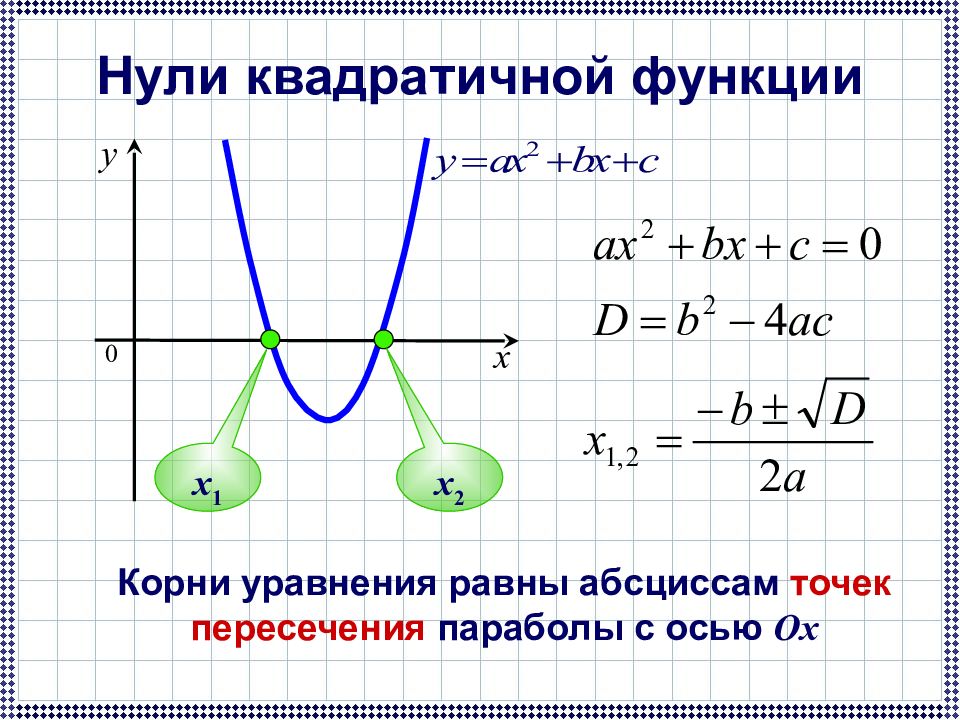
Если дискриминант соответствующего квадратного уравнения положителен, то парабола пересекает ось абсцисс в двух точках. Если дискриминант равен нулю, то парабола касается оси абсцисс. Если дискриминант отрицателен, то парабола расположена выше оси абсцисс, если , и ниже оси абсцисс, если .
Если дискриминант равен нулю, то парабола касается оси абсцисс. Если дискриминант отрицателен, то парабола расположена выше оси абсцисс, если , и ниже оси абсцисс, если .
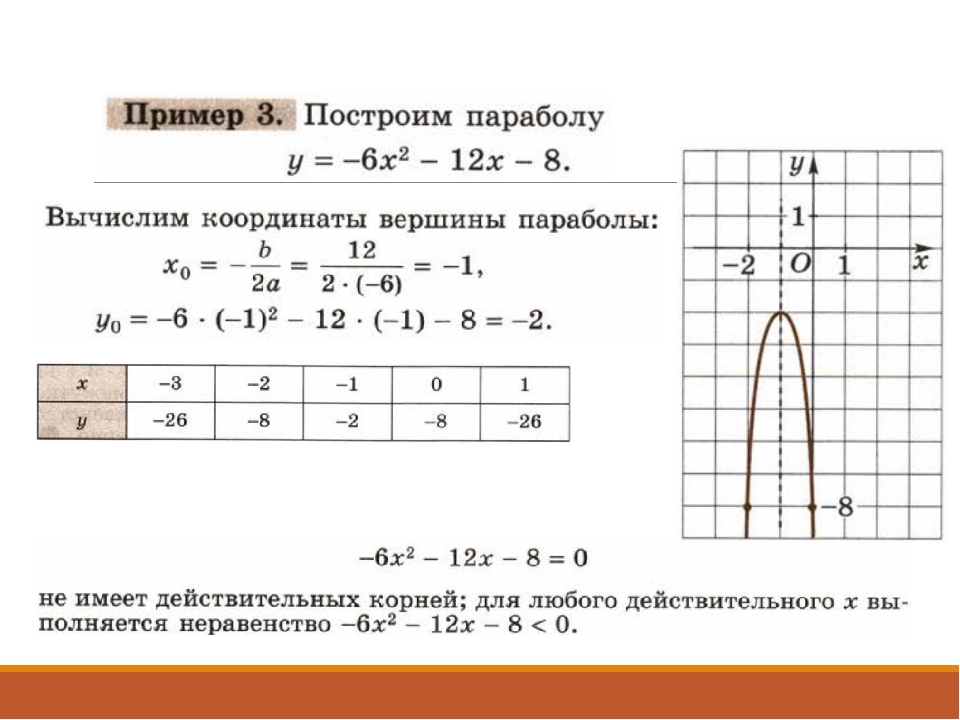
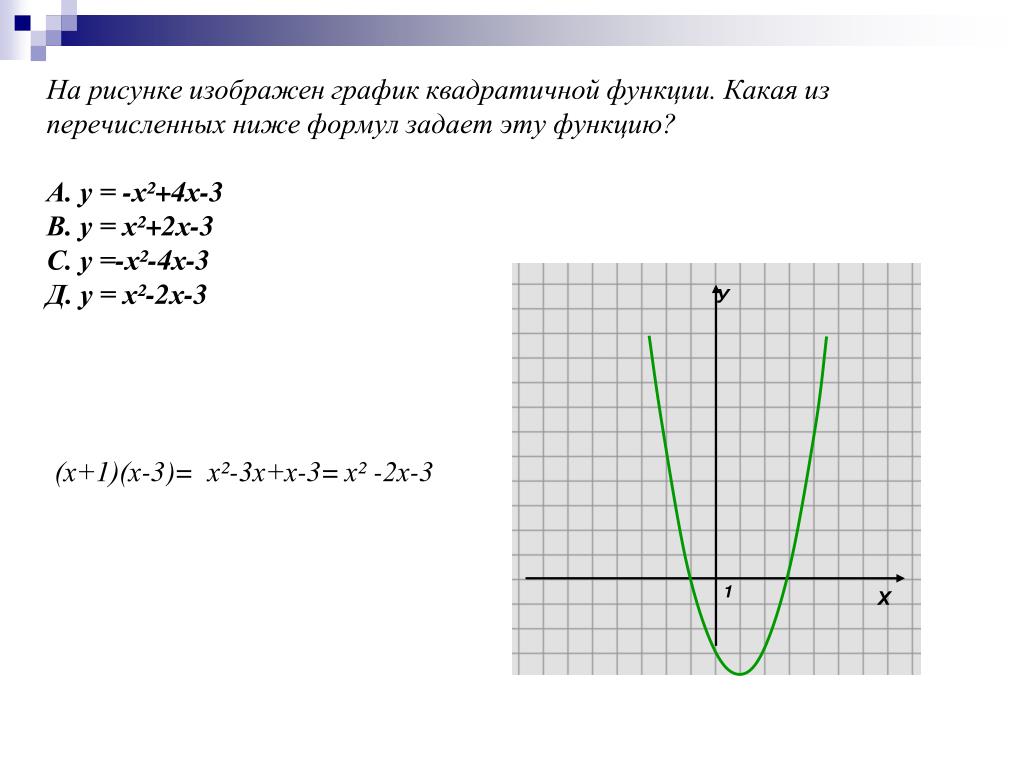
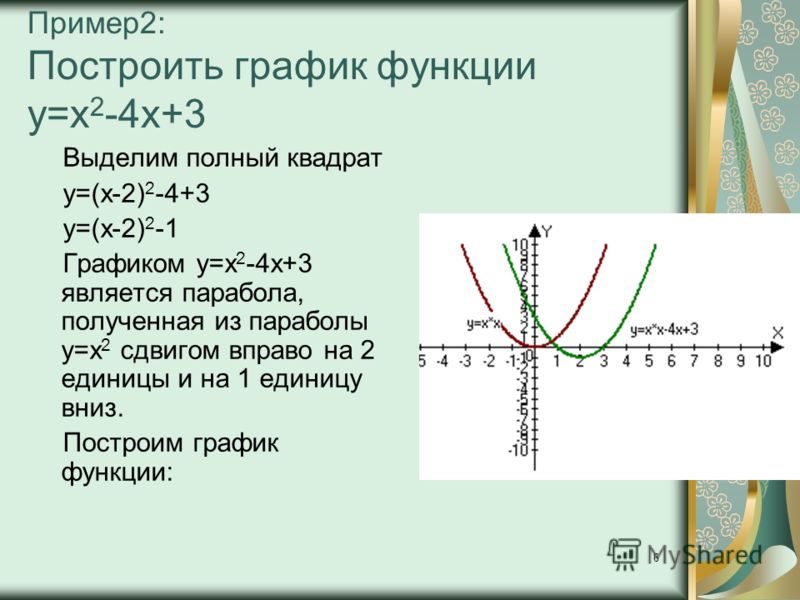
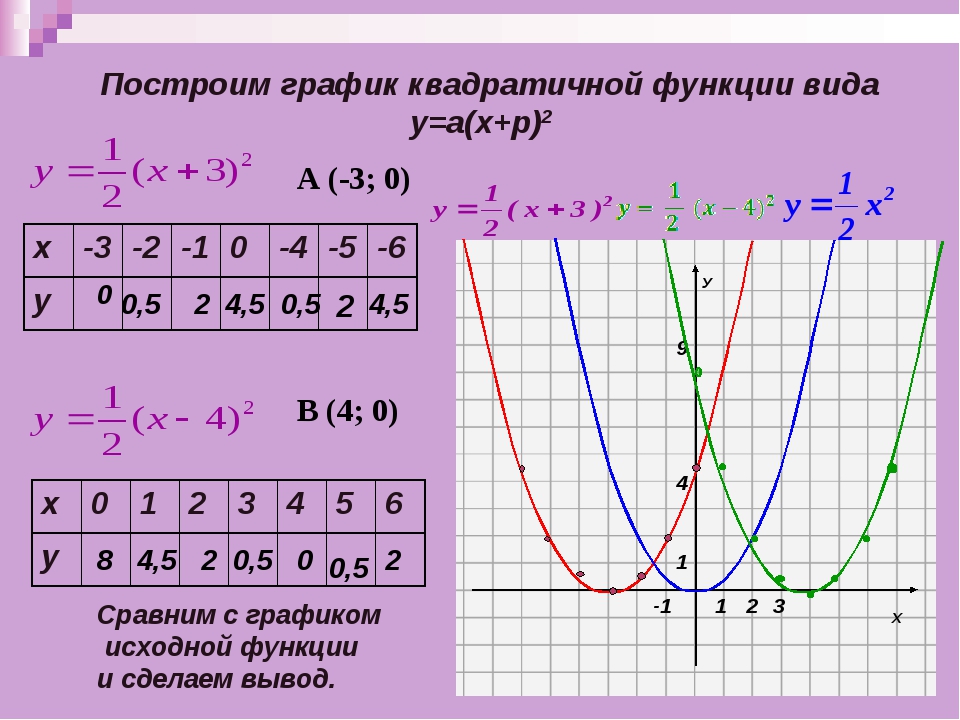
Пример 10. Постройте графики функций и .
Решение. Вершина параболы имеет координаты и . Так как старший коэффициент положителен, то ветви параболы направлены вверх. Также, решив уравнение , можно найти точки пересечения с осью абсцисс: и (рис. 32).
Для параболы аналогично получаем, что и , и ветви ее направлены вниз. Данная парабола не имеет точек пересечения с осью абсцисс, так как дискриминант соответствующего квадратного уравнения отрицателен (рис. 33).
| < Предыдущая | Следующая > |
|---|
9.1: Функция квадратного корня
В этом разделе мы обратим наше внимание на функцию квадратного корня, функцию, определяемую уравнением
\ [\ begin {массив} {c} {f (x) = \ sqrt {x}} \\ \ end {array} \]
Мы начинаем раздел с рисования графика функции, затем обращаемся к домену и диапазону. После этого мы исследуем ряд различных преобразований функции.
После этого мы исследуем ряд различных преобразований функции.
График функции квадратного корня
Давайте создадим таблицу точек, которая удовлетворяет уравнению функции, а затем нанесем точки из таблицы в декартовой системе координат на миллиметровую бумагу.Мы продолжим создавать и наносить точки, пока не убедимся в окончательной форме графика.
Мы знаем, что нельзя извлечь квадратный корень из отрицательного числа. Поэтому мы не хотим помещать в нашу таблицу отрицательные значения x . Чтобы еще больше упростить наши вычисления, давайте использовать числа, квадратный корень которых легко вычисляется. Это напоминает идеальные квадраты, такие как 0, 1, 4, 9 и так далее. Мы поместили эти числа как значения x в таблицу на , рис. 1, (b), а затем вычислили квадратный корень из каждого.На рис. 1 (рис. 1) (a) каждая точка из таблицы изображена сплошной точкой. Если мы продолжим добавлять точки в таблицу, строить их, график в конечном итоге заполнится и примет форму сплошной кривой, показанной на рис.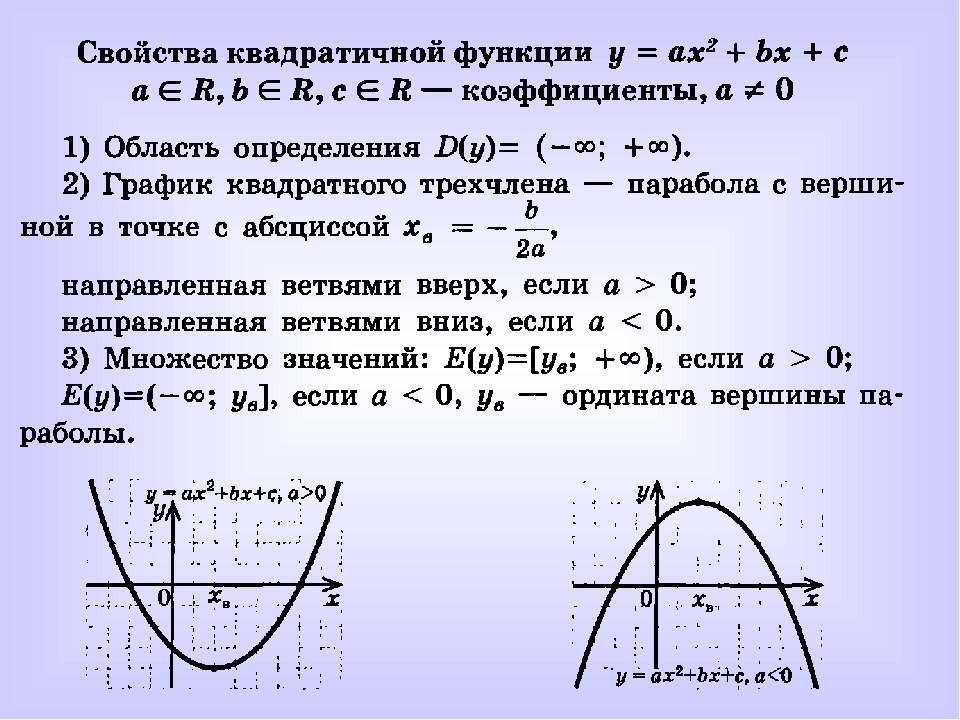 1 (c).
1 (c).
Рис. 1.} \ text {Создание графика} f (x) = \ sqrt {x}} \\ \ nonumber \ end {array} \]
Подход точечного построения, используемый для построения графика \ (f (x ) = \ sqrt {x} \) в Рисунок 1 — это проверенная и знакомая процедура. Однако более сложный подход включает теорию инверсий, развитую в предыдущей главе.2 \), \ (x \ ge 0 \), что изображено на Рисунок 2 (c). Обратите внимание на точное совпадение с графиком функции квадратного корня на рис. 1 (c).
Последовательность графиков в Рисунок 2 также помогает нам определить область и диапазон функции квадратного корня.
- В рис. 2 (a) парабола неограниченно раскрывается наружу, как влево, так и вправо. Следовательно, доменом является \ (D_ {f} = (- \ infty, \ infty) \) или все действительные числа. Кроме того, граф имеет вершину в начале координат и неограниченно открывается вверх, поэтому диапазон равен \ (R_ {f} = [0, \ infty) \).
 {−1}} = [0, \ infty) \).
{−1}} = [0, \ infty) \).
Конечно, мы также можем определить область и диапазон функции квадратного корня, спроецировав все точки на графике на оси x и y , как показано на рисунках 3 (a) и ( б) соответственно.
Рис. 3.} \ text {Спроецируйте на оси, чтобы найти домен и диапазон}} \\ \ nonumber \ end {array} \]
Кто-то может возразить против диапазона, спросив: «Откуда мы знаем, что график изображение функции квадратного корня в Рис. 3 (b) растет бесконечно? » Опять же, ответ кроется в последовательности графиков на рис. , рис. 2, .2 \), \ (x \ ge 0 \), открывается бесконечно вправо по мере того, как график уходит в бесконечность. Следовательно, после отражения этого графика через линию y = x результирующий график должен бесконечно подниматься вверх при движении вправо. Таким образом, диапазон функции квадратного корня равен \ ([0, \ infty) \).
Переводы
Если мы сдвинем график \ (y = \ sqrt {x} \) вправо и влево или вверх и вниз, это затронет домен и / или диапазон.
Пример \ (\ PageIndex {4} \)
Нарисуйте график \ (f (x) = \ sqrt {x − 2} \).Используйте свой график, чтобы определить домен и диапазон.
Мы знаем, что основное уравнение \ (y = \ sqrt {x} \) имеет график, показанный на Рисунках 1 (c). Если мы заменим x на x — 2, основное уравнение \ (y = \ sqrt {x} \) станет \ (f (x) = \ sqrt {x − 2} \). Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сместит график на две единицы вправо, как показано на рис. 4 (а) и (б).
Рисунок 4. Чтобы нарисовать график \ (f (x) = \ sqrt {x − 2} \), сдвиньте график \ (y = \ sqrt {x} \) на две единицы вправо.
Чтобы найти область, мы проецируем каждую точку графика f на ось x, как показано на рис. 4 (a). Обратите внимание, что все точки справа от 2 или включая 2 заштрихованы на оси абсцисс. Следовательно, область определения f равна
Домен = \ ([2, \ infty) \) = {x: \ (x \ ge 0 \)}
Поскольку сдвига в вертикальном направлении не произошло, диапазон остается прежним.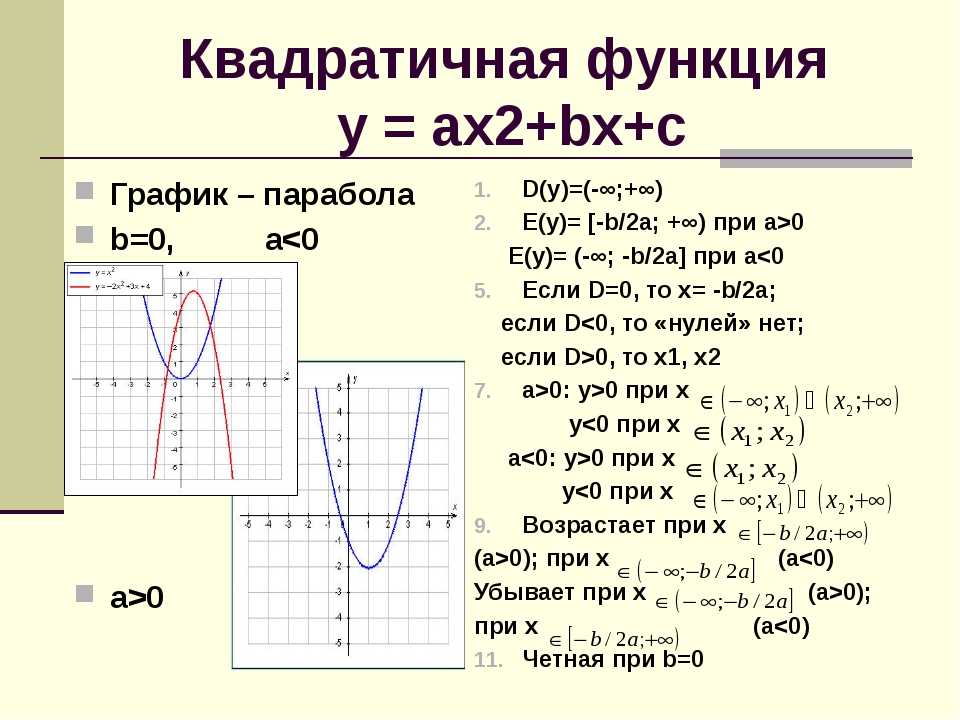 Чтобы найти диапазон, мы проецируем каждую точку на графике на ось Y, как показано на Рис. 4 (b).Обратите внимание, что все точки, равные нулю и выше, заштрихованы на оси ординат. Таким образом, диапазон f равен
Чтобы найти диапазон, мы проецируем каждую точку на графике на ось Y, как показано на Рис. 4 (b).Обратите внимание, что все точки, равные нулю и выше, заштрихованы на оси ординат. Таким образом, диапазон f равен
.
Диапазон = \ ([0, \ infty) \) = {y: \ (y \ ge 0 \)}.
Мы можем найти область определения этой функции алгебраически, исследуя ее определяющее уравнение \ (f (x) = \ sqrt {x − 2} \). Мы понимаем, что нельзя извлекать квадратный корень из отрицательного числа. Следовательно, выражение под радикалом должно быть неотрицательным (положительным или нулевым). То есть
\ (х — 2 \ ge 0 \).
Решение этого неравенства для x ,
\ (х \ ge 2 \).
Таким образом, область определения f — это Domain = \ ([2, \ infty) \), что соответствует графическому решению, приведенному выше.
Давайте посмотрим на другой пример.
Пример \ (\ PageIndex {5} \)
Нарисуйте график \ (f (x) = \ sqrt {x + 4} + 2 \). Используйте свой график, чтобы определить домен и диапазон f.
Используйте свой график, чтобы определить домен и диапазон f.
Опять же, мы знаем, что основное уравнение \ (y = \ sqrt {x} \) имеет график, показанный на рис. 1 (рис. 1) (c). Если мы заменим x на x +4, основное уравнение \ (y = \ sqrt {x} \) станет \ (y = \ sqrt {x + 4} \).Из нашей предыдущей работы с геометрическими преобразованиями мы знаем, что это сдвинет график \ (y = \ sqrt {x} \) на четыре единицы влево, как показано на рис. 5 (a).
Если мы знаем, что прибавляем 2 к уравнению \ (y = \ sqrt {x + 4} \), чтобы получить уравнение \ (y = \ sqrt {x + 4} + 2 \), это сдвинет график \ ( y = \ sqrt {x + 4} \) на две единицы вверх, как показано на рис. 5 (b).
Рис. 5. Перевод исходного уравнения \ (y = \ sqrt {x} \) для получения графика \ (y = \ sqrt {x + 4} + 2 \)
. Идентификация области \ (f (x ) = \ sqrt {x + 4} + 2 \), мы проецируем все точки на графике f на ось x, как показано на рис. 6 (a).Обратите внимание, что все точки справа от — 4 или включая его заштрихованы на оси x . Таким образом, область определения \ (f (x) = \ sqrt {x + 4} + 2 \) равна
6 (a).Обратите внимание, что все точки справа от — 4 или включая его заштрихованы на оси x . Таким образом, область определения \ (f (x) = \ sqrt {x + 4} + 2 \) равна
Домен = \ ([- 4, \ infty) \) = {x: \ (x \ ge −4 \)}
Рисунок 6. Спроецируйте точки f на оси, чтобы определить область и диапазон
. Аналогичным образом, чтобы найти диапазон f , спроецируйте все точки на графике f на ось y , как показано в Рисунок 6 (б). Обратите внимание, что все точки на оси y больше или включая 2 затенены.Следовательно, диапазон f составляет
Диапазон = \ ([2, \ infty) \) = {y: \ (y \ ge 2 \)}
Мы также можем найти область определения f алгебраически, исследуя уравнение \ (f (x) = \ sqrt {x + 4} + 2 \). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулевым или положительным). Следовательно,
\ (х + 4 \ ge 0 \).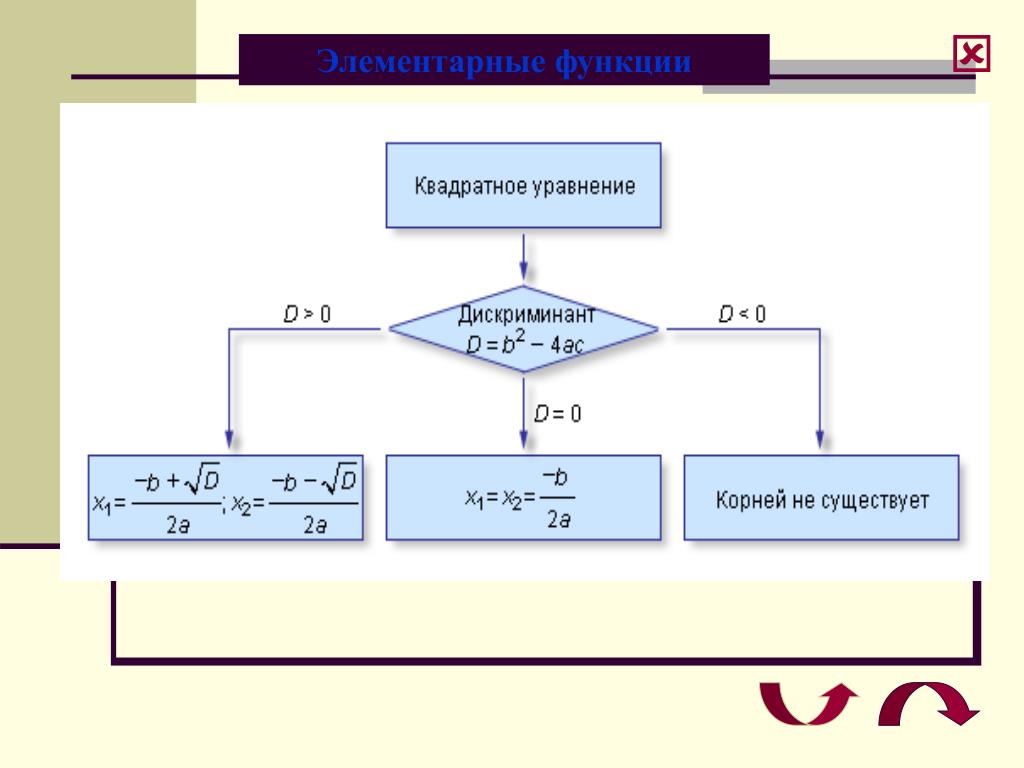
Решение этого неравенства для x ,
\ (х \ ge −4 \).
Таким образом, область определения f — это Domain = \ ([- 4, \ infty) \), что соответствует графическому решению, представленному выше.
Отражения
Если мы начнем с основного уравнения \ (y = \ sqrt {x} \), а затем заменим x на −x, тогда график полученного уравнения \ (y = \ sqrt {−x} \) будет захвачен путем отражения график \ (y = \ sqrt {x} \) (см. Рис. 1 (c)) по горизонтали поперек оси y. График \ (y = \ sqrt {−x} \) показан на рис. , , , 7, (a).
Точно так же график \ (y = — \ sqrt {x} \) будет вертикальным отражением графика \ (y = \ sqrt {x} \) поперек оси x, как показано на рис. (б).
Рис. 7. Отражение графика \ (y = \ sqrt {x} \) по осям x и y.
Чаще всего вам будет предложено выполнить рефлексию и перевод.
Пример \ (\ PageIndex {6} \)
Нарисуйте график \ (f (x) = \ sqrt {4− x} \).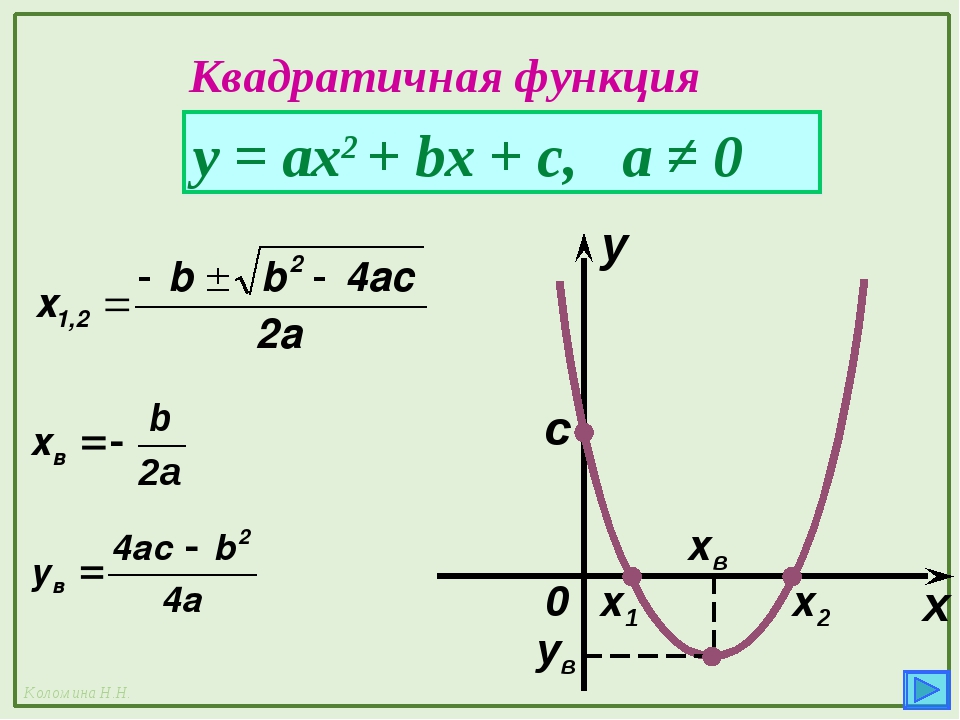 Используйте полученный график, чтобы определить домен и диапазон f.
Используйте полученный график, чтобы определить домен и диапазон f.
Сначала перепишите уравнение \ (f (x) = \ sqrt {4− x} \) следующим образом:
\ (f (x) = \ sqrt {- (x − 4)} \)
Определение
Первые размышления .Обычно более интуитивно понятно выполнять размышления перед переводом.
Помня об этом, мы сначала нарисуем график \ (f (x) = \ sqrt {−x} \), который является отражением графика \ (f (x) = \ sqrt {x} \ ) по оси y . Это показано на Рис. 8 (a).
Теперь в \ (f (x) = \ sqrt {−x} \) замените x на x — 4, чтобы получить \ (f (x) = \ sqrt {- (x − 4)} \). Это сдвигает график \ (f (x) = \ sqrt {−x} \) на четыре единицы вправо, как показано на , рис. 8, (b).
Рисунок 8. Отражение с последующим переводом.
Чтобы найти область определения функции \ (f (x) = \ sqrt {- (x − 4)} \) или, что эквивалентно, \ (f (x) = \ sqrt {4 − x} \), спроецируйте каждый точка на графике f на оси x , как показано на рис.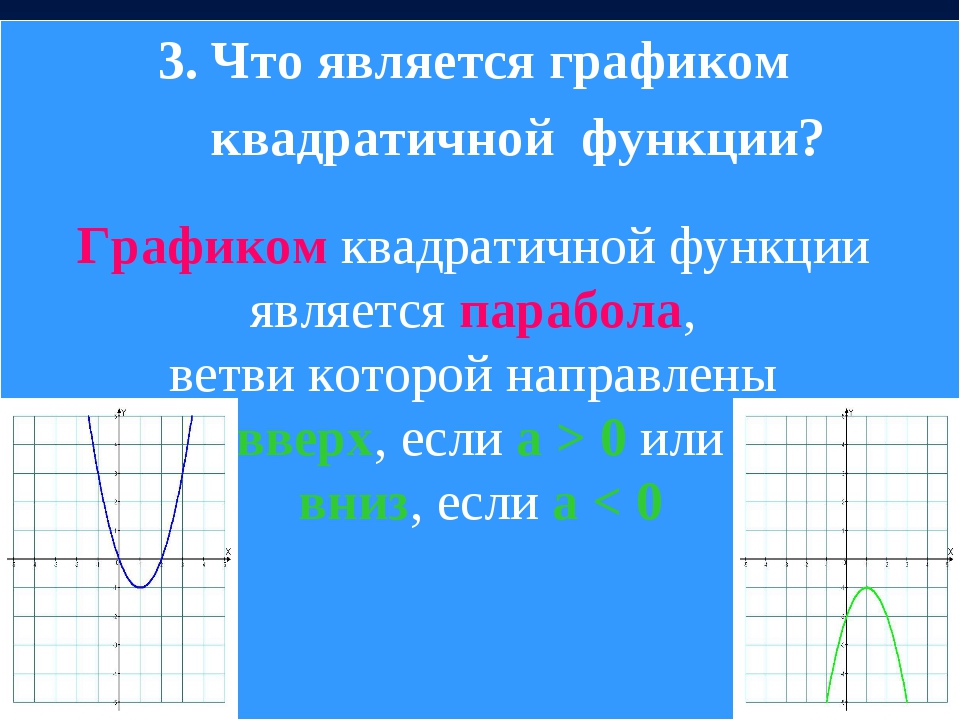 9 (a). Обратите внимание, что все действительные числа, меньшие или равные 4, заштрихованы на оси x . Следовательно, домен f —
9 (a). Обратите внимание, что все действительные числа, меньшие или равные 4, заштрихованы на оси x . Следовательно, домен f —
Домен = \ ((- \ infty, 4] \) = {x: \ (x \ le 4 \)}.
Аналогичным образом, чтобы получить диапазон f, спроецируйте каждую точку на графике f на их ось, как показано на рис. 9 (b).Обратите внимание, что все действительные числа, большие или равные нулю, заштрихованы на оси ординат. Следовательно, диапазон f равен
.
Диапазон = \ ([0, \ infty) \) = {x: \ (x \ ge 0 \)}.
Мы также можем найти область определения функции f , исследуя уравнение \ (f (x) = \ sqrt {4 − x} \). Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под корнем должно быть неотрицательным (нулевым или положительным). Следовательно,
\ (4 — х \ ge 0 \).
Рисунок 9. Определение области и диапазона \ (f (x) = \ sqrt {4 − x} \)
Решите это последнее неравенство для x . Сначала вычтите 4 из обеих частей неравенства, затем умножьте обе части полученного неравенства на — 1. Конечно, умножение на отрицательное число меняет знак неравенства на противоположное.
Сначала вычтите 4 из обеих частей неравенства, затем умножьте обе части полученного неравенства на — 1. Конечно, умножение на отрицательное число меняет знак неравенства на противоположное.
\ (- х \ ge −4 \)
\ (х \ ле 4 \)
Таким образом, область определения f равна {x: \ (x \ le 4 \)}. В обозначении интервалов Domain = \ ((- \ infty, 4] \). Это хорошо согласуется с приведенным выше графическим результатом.
Чаще всего требуется сочетание вашего графического калькулятора и небольших алгебраических манипуляций, чтобы определить область определения функции квадратного корня.
Пример \ (\ PageIndex {7} \)
Нарисуйте график \ (f (x) = \ sqrt {5−2x} \). Используйте график и алгебраическую технику, чтобы определить область определения функции.
Загрузите функцию в Y1 в меню Y = вашего калькулятора, как показано на рис. 10 (a). Выберите 6: ZStandard из меню ZOOM, чтобы построить график, показанный на рис. 10 (b).
10 (b).
Рисунок 10. Построение графика f (x) = \ sqrt {5−2x} на графическом калькуляторе.
Внимательно посмотрите на график , рис. 10, (b) и обратите внимание, что трудно сказать, идет ли график полностью вниз, чтобы «коснуться» оси x около \ (x \ приблизительно 2.5 \). Однако наш предыдущий опыт использования функции извлечения квадратного корня заставляет нас думать, что это всего лишь артефакт недостаточного разрешения калькулятора, который не позволяет графику «касаться» оси x в точке \ (x \ приблизительно 2,5 \).
Алгебраический подход разрешит проблему. Мы можем определить область определения f, исследуя уравнение \ (f (x) = \ sqrt {5 — 2x} \). Следовательно, Мы не можем извлечь квадратный корень из отрицательного числа, поэтому выражение под радикалом должно быть неотрицательным (нулевым или положительным).
\ (5 — 2x \ ge 0 \).
Решите это последнее неравенство для x . Сначала вычтем 5 из обеих частей неравенства.
\ (- 2x \ ge −5 \).
Затем разделите обе части этого последнего неравенства на −2. Помните, что мы должны обратить неравенство в тот момент, когда делим на отрицательное число.
\ (\ frac {−2x} {- 2} \ le \ frac {−5} {- 2} \).
\ (х \ le \ frac {5} {2} \).
Таким образом, область определения f равна {x: \ (x \ le \ frac {5} {2} \)}. В интервальной записи Домен = \ ((- \ infty, \ frac {5} {2}] \).Это хорошо согласуется с приведенным выше графическим результатом.
Дальнейшее самоанализ показывает, что этот аргумент также решает вопрос о том, касается ли граф оси x в точке \ (x = \ frac {5} {2} \). Если вас это не убедило, замените \ (x = \ frac {5} {2} \) на \ (f (x) = \ sqrt {5−2x} \) , чтобы увидеть
\ (f (\ frac {5} {2}) = \ sqrt {5-2 (\ frac {5} {2})} = \ sqrt {0} = 0 \).
Таким образом, график f «касается» оси x в точке \ ((\ frac {5} {2}, 0) \).
В упражнении Exercise 1-10 выполните все следующие задачи:
- Установите систему координат на миллиметровой бумаге.
 Обозначьте и масштабируйте каждую ось.
Обозначьте и масштабируйте каждую ось. - Заполните таблицу баллов по данной функции. Постройте каждую точку в своей системе координат, а затем используйте их, чтобы нарисовать график данной функции.
- Используйте карандаши разных цветов, чтобы спроецировать все точки на оси x и y , чтобы определить область и диапазон.Используйте интервальную нотацию для описания области данной функции.
Упражнение \ (\ PageIndex {1} \)
\ (f (x) = — \ sqrt {x} \)
- Ответ
х
0
1
4
9
ф (х)
0
– 1
– 2
– 3
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 0] \).
Упражнение \ (\ PageIndex {2} \)
\ (f (x) = \ sqrt {−x} \)
Упражнение \ (\ PageIndex {3} \)
\ (f (x) = \ sqrt {x + 2} \)
- Ответ
х
– 2
– 1
2
7
f ( x )
0
1
2
3
Отметьте точки в таблице и используйте их для построения графика.
Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([ — 2, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {4} \)
\ (f (x) = \ sqrt {5 − x} \)
Упражнение \ (\ PageIndex {5} \)
\ (f (x) = \ sqrt {x} +2 \)
- Ответ
Нанесите точки в таблицу и используйте их для построения графика f .
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([2, \ infty) \).
Упражнение \ (\ PageIndex {6} \)
\ (f (x) = \ sqrt {x} −1 \)
Упражнение \ (\ PageIndex {7} \)
\ (f (x) = \ sqrt {x + 3} +2 \)
- Ответ
х
– 3
– 2
1
6
ф (х)
2
3
4
5
Постройте точки в таблице и используйте их для построения графика f .
- Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([ — 3, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([2, \ infty) \).
Упражнение \ (\ PageIndex {8} \)
\ (f (x) = \ sqrt {x − 1} +3 \)
Упражнение \ (\ PageIndex {9} \)
\ (f (x) = \ sqrt {3 − x} \)
- Ответ
х
– 6
– 1
2
3
f ( x )
3
2
1
0
Постройте точки в таблице и используйте их для построения графика f .
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ (( — \ infty, 3] \). Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Диапазон = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {10} \)
\ (f (x) = — \ sqrt {x + 3} \)
В упражнениях 11 — 20 выполните каждую из следующих задач.
- Установите систему координат на миллиметровой бумаге.Обозначьте и масштабируйте каждую ось. Не забудьте нарисовать все линии линейкой.
- Используйте геометрические преобразования, чтобы нарисовать график данной функции в вашей системе координат без использования графического калькулятора. Примечание. Вы можете проверить свое решение с помощью калькулятора, но вы сможете построить график без использования калькулятора.
- Используйте карандаши разных цветов, чтобы спроецировать точки на графике функции на оси x и y .
 Используйте обозначение интервала для описания области и диапазона функции.
Используйте обозначение интервала для описания области и диапазона функции.
Упражнение \ (\ PageIndex {11} \)
\ (f (x) = \ sqrt {x} +3 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a). Затем добавьте 3, чтобы получить уравнение \ (y = \ sqrt {x} + 3 \). Это сдвинет график \ (y = \ sqrt {x} \) вверх на 3 единицы, как показано в (b).
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \).Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([3, \ infty) \).
Упражнение \ (\ PageIndex {12} \)
\ (f (x) = \ sqrt {x + 3} \)
Упражнение \ (\ PageIndex {13} \)
\ (f (x) = \ sqrt {x − 2} \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).
 Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).
Затем замените x на x — 2, чтобы получить уравнение \ (y = \ sqrt {x − 2} \). Это сдвинет график \ (y = \ sqrt {x} \) вправо на 2 единицы, как показано в (b).Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([2, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {14} \)
\ (f (x) = \ sqrt {x} −2 \)
Упражнение \ (\ PageIndex {15} \)
\ (f (x) = \ sqrt {x + 5} +1 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на x + 5, чтобы получить уравнение \ (y = \ sqrt {x + 5} \). Затем добавьте 1, чтобы получить уравнение \ (f (x) = \ sqrt {x + 5} +1 \). Это сдвинет график \ (y = \ sqrt {x} \) влево на 5 единиц, а затем вверх на 1 единицу, как показано в (b).
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([- 5, \ infty) \).
 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([1, \ infty) \).
Упражнение \ (\ PageIndex {16} \)
\ (f (x) = \ sqrt {x − 2} −1 \)
Упражнение \ (\ PageIndex {17} \)
\ (y = — \ sqrt {x + 4} \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, замените x на x + 4, чтобы получить уравнение \ (y = — \ sqrt {x + 4} \). Это сдвинет график \ (y = — \ sqrt {x} \) на четыре единицы влево, как показано в (c).
Спроецируйте все точки графика на ось x, чтобы определить домен: Domain = \ ([- 4, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 0] \).
Упражнение \ (\ PageIndex {18} \)
\ (f (x) = — \ sqrt {x} +4 \)
Упражнение \ (\ PageIndex {19} \)
\ (f (x) = — \ sqrt {x} +3 \)
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).
 Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).
Затем инвертируйте, чтобы получить \ (y = — \ sqrt {x} \). Это отразит график \ (y = \ sqrt {x} \) по оси x, как показано в (b). Наконец, добавьте 3, чтобы получить уравнение \ (y = — \ sqrt {x} +3 \).Это сдвинет график \ (y = — \ sqrt {x} \) на три единицы вверх, как показано в (c).Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ([0, \ infty) \). Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ((- \ infty, 3] \).
Упражнение \ (\ PageIndex {20} \)
\ (f (x) = — \ sqrt {x + 3} \)
Упражнение \ (\ PageIndex {21} \)
Чтобы построить график функции \ (f (x) = \ sqrt {3 − x} \), выполните последовательно каждый из следующих шагов без помощи калькулятора.
- Установите систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \).
 Обозначьте график соответствующим уравнением.
Обозначьте график соответствующим уравнением. - Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x — 3)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {3 − x} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на — x , чтобы получить уравнение \ (y = \ sqrt {−x} \). Это будет отражать график \ (y = \ sqrt {x} \) по оси y , как показано на (b). Наконец, замените x на x — 3, чтобы получить уравнение \ ( y = \ sqrt { — ( x — 3)} \). Это сдвинет график \ (y = \ sqrt {−x} \) на три единицы вправо, как показано в (c).
Спроецируйте все точки на графике на ось x, чтобы определить домен: Domain = \ ((- \ infty, 3] \).
 Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось Y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {22} \)
Чтобы построить график функции \ (f (x) = \ sqrt {−x − 3} \), последовательно выполните каждый из следующих шагов.
- Установите систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \).Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x + 3)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {−x − 3} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
Упражнение \ (\ PageIndex {23} \)
Чтобы построить график функции \ (f (x) = \ sqrt {−x − 3} \), выполните последовательно каждый из следующих шагов без помощи калькулятора.
- Установите систему координат и нарисуйте график \ (y = \ sqrt {x} \).Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \). Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x + 1)} \). Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {−x − 1} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
- Ответ
Сначала постройте график \ (y = \ sqrt {x} \), как показано на (a).Затем замените x на −x, чтобы получить уравнение \ (y = \ sqrt {−x} \). Это будет отражать график \ (y = \ sqrt {x} \) по оси y, как показано в (b). Наконец, замените x на x + 1, чтобы получить уравнение \ (y = \ sqrt {- (x + 1)} \). Это сдвинет график \ (y = \ sqrt {−x} \) на одну единицу влево, как показано в (c).
Спроецируйте все точки на графике на ось x, чтобы определить область: Domain = \ ((- \ infty, −1] \).
 Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Спроецируйте все точки на графике на ось y, чтобы определить диапазон: Range = \ ([0, \ infty) \).
Упражнение \ (\ PageIndex {24} \)
Чтобы построить график функции \ (f (x) = \ sqrt {1 − x} \), последовательно выполните каждый из следующих шагов.
- Установите систему координат и нарисуйте график \ (y = \ sqrt {x} \). Обозначьте график соответствующим уравнением.
- Установите вторую систему координат и нарисуйте график \ (y = \ sqrt {−x} \). Обозначьте график соответствующим уравнением.
- Установите третью систему координат и нарисуйте график \ (y = \ sqrt {- (x − 1)} \).Обозначьте график соответствующим уравнением. Это график \ (y = \ sqrt {1 − x} \). Используйте обозначение интервала, чтобы указать домен и диапазон этой функции.
В упражнениях 25 — 28 выполните каждую из следующих задач.
- Нарисуйте график данной функции с помощью графического калькулятора.
 Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график соответствующим уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи.
Скопируйте изображение из окна просмотра на свою домашнюю работу. Обозначьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. Обозначьте свой график соответствующим уравнением.Используйте график, чтобы определить область определения функции и описать область с помощью интервальной записи. - Используйте чисто алгебраический подход, чтобы определить область определения данной функции. Для описания результата используйте обозначение интервалов. Согласуется ли он с графическим результатом из части 1?
Упражнение \ (\ PageIndex {25} \)
\ (f (x) = \ sqrt {2x + 7} \)
- Ответ
Мы используем графический калькулятор для построения следующего графика \ (f (x) = \ sqrt {2x + 7} \)
По нашим оценкам, домен будет состоять из всех действительных чисел справа примерно — 3 . 5. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа.
 Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.
Следовательно, выражение под корнем в \ (f (x) = \ sqrt {2x + 7} \) должно быть больше или равно нулю.\ (2x + 7 \ ge 0 \)
\ (2x \ ge −7 \)
\ (x \ ge — \ frac {7} {2} \)
Следовательно, домен равен \ ([- \ frac {7} {2}, \ infty) \).
Упражнение \ (\ PageIndex {26} \)
\ (f (x) = \ sqrt {7−2x} \)
Упражнение \ (\ PageIndex {27} \)
\ (f (x) = \ sqrt {12−4x} \)
- Ответ
Мы используем графический калькулятор, чтобы построить следующий график \ (f (x) = \ sqrt {12−4x} \).
По нашим оценкам, область будет состоять из всех действительных чисел справа от приблизительно 3. Чтобы найти алгебраическое решение, обратите внимание, что вы не можете извлечь квадратный корень из отрицательного числа. Следовательно, выражение под корнем в \ (f (x) = \ sqrt {12−4x} \) должно быть больше или равно нулю.

\ (12−4x \ ge 0 \)
\ (- 4x \ ge −12 \)
\ (х \ ле 3 \)
Следовательно, домен равен \ ((- \ infty, 3] \).
Упражнение \ (\ PageIndex {28} \)
\ (f (x) = \ sqrt {12 + 2x} \)
В упражнениях 29 — 40 найдите область определения заданной функции алгебраически.
Упражнение \ (\ PageIndex {29} \)
\ (f (x) = \ sqrt {2x + 9} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, 2x + 9 должно быть больше или равно нулю. Поскольку \ (2x + 9 \ ge 0 \) означает, что \ (x \ ge — \ frac {9} {2} \), область представляет собой интервал \ ([- \ frac {9} {2}, \ infty ) \).
Упражнение \ (\ PageIndex {30} \)
\ (f (x) = \ sqrt {−3x + 3} \)
Упражнение \ (\ PageIndex {31} \)
\ (f (x) = \ sqrt {−8x − 3} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом.
 Таким образом, −8x − 3 должно быть больше или равно нулю. Поскольку \ (- 8x − 3 \ ge 0 \) означает, что \ (x \ le — \ frac {3} {8} \), область представляет собой интервал \ ((- \ infty, — \ frac {3} { 8}] \).
Таким образом, −8x − 3 должно быть больше или равно нулю. Поскольку \ (- 8x − 3 \ ge 0 \) означает, что \ (x \ le — \ frac {3} {8} \), область представляет собой интервал \ ((- \ infty, — \ frac {3} { 8}] \).
Упражнение \ (\ PageIndex {32} \)
\ (f (x) = \ sqrt {−3x + 6} \)
Упражнение \ (\ PageIndex {33} \)
\ (f (x) = \ sqrt {−6x − 8} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, −6x − 8 должно быть больше или равно нулю.Поскольку \ (- 6x − 8 \ ge 0 \) влечет, что \ (x \ le — \ frac {4} {3} \), область представляет собой интервал \ ((- \ infty, \ frac {4} {3 }] \).
Упражнение \ (\ PageIndex {34} \)
\ (f (x) = \ sqrt {8x − 6} \)
Упражнение \ (\ PageIndex {35} \)
\ (f (x) = \ sqrt {−7x + 2} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом.
 Таким образом, −7x + 2 должно быть больше или равно нулю. Поскольку \ (- 7x + 2 \ ge 0 \) означает, что \ (x \ le \ frac {2} {7} \), область представляет собой интервал \ ((- \ infty, \ frac {2} {7} ] \).
Таким образом, −7x + 2 должно быть больше или равно нулю. Поскольку \ (- 7x + 2 \ ge 0 \) означает, что \ (x \ le \ frac {2} {7} \), область представляет собой интервал \ ((- \ infty, \ frac {2} {7} ] \).
Упражнение \ (\ PageIndex {36} \)
\ (f (x) = \ sqrt {8x − 3} \)
Упражнение \ (\ PageIndex {37} \)
\ (f (x) = \ sqrt {6x + 3} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом. Таким образом, 6x + 3 должно быть больше или равно нулю. Поскольку \ (6x + 3 \ ge 0 \) означает, что \ (x \ ge — \ frac {1} {2} \), область представляет собой интервал \ ([- \ frac {1} {2}, \ infty ) \).
Упражнение \ (\ PageIndex {38} \)
\ (f (x) = \ sqrt {x − 5} \)
Упражнение \ (\ PageIndex {39} \)
\ (f (x) = \ sqrt {−7x − 8} \)
- Ответ
Четный корень отрицательного числа не считается действительным числом.
 Таким образом, −7x − 8 должно быть больше или равно нулю. Поскольку \ (- 7x − 8 \ ge 0 \) влечет, что \ (x \ le — \ frac {8} {7} \), область представляет собой интервал \ ((- \ infty, — \ frac {8} { 7}] \)
Таким образом, −7x − 8 должно быть больше или равно нулю. Поскольку \ (- 7x − 8 \ ge 0 \) влечет, что \ (x \ le — \ frac {8} {7} \), область представляет собой интервал \ ((- \ infty, — \ frac {8} { 7}] \)
Упражнение \ (\ PageIndex {40} \)
\ (f (x) = \ sqrt {7x + 8} \)
Как найти домен функции квадратного корня
Обновлено 5 декабря 2020 г.
Джек Джерард
В математике домен функции сообщает вам, для каких значений x функция действительна.Это означает, что любое значение в этом домене будет работать в функции, в то время как любое значение, выходящее за пределы домена, не будет. У некоторых функций (например, линейных) есть домены, которые включают все возможные значения x . Другие (например, уравнения, в которых в знаменателе фигурирует x ) исключают определенные значения x , чтобы избежать деления на ноль. Функции квадратного корня имеют более ограниченные области, чем некоторые другие функции, поскольку значение внутри квадратного корня (известное как подкоренное выражение) должно быть положительным числом, чтобы результат был «действительным». «
«
TL; DR (слишком долго; не читал)
Область определения функции извлечения квадратного корня — это все значения x , которые приводят к корню, равному нулю или превышающему его.
Функции квадратного корня
Функция квадратного корня — это функция, которая содержит радикал, который чаще называется квадратным корнем. Если вы не уверены, как это выглядит,
f (x) = \ sqrt {x}
считается основной функцией извлечения квадратного корня.В этом случае x не может быть отрицательным числом; все радикалы должны быть равны или больше нуля, чтобы результат был реальным. Если вы можете включить «мнимые» числа (с и , определенными как квадратный корень из −1), тогда все усложняется, но в большинстве случаев вам нужно рассматривать только действительные числа.
Это не означает, что все функции извлечения квадратного корня так же просты, как извлечение квадратного корня из одного числа.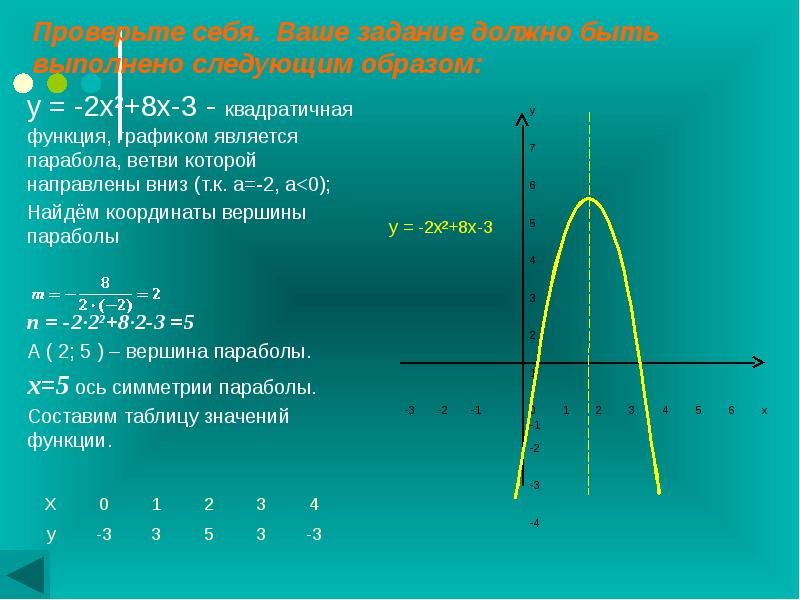 Более сложные функции извлечения квадратного корня могут иметь вычисления внутри радикала, вычисления, которые изменяют результат радикала, или даже радикал как часть более крупной функции (например, в числителе или знаменателе уравнения).Примеры этих более сложных функций выглядят так:
Более сложные функции извлечения квадратного корня могут иметь вычисления внутри радикала, вычисления, которые изменяют результат радикала, или даже радикал как часть более крупной функции (например, в числителе или знаменателе уравнения).Примеры этих более сложных функций выглядят так:
f (x) = 2 \ sqrt {x + 3} \ text {или} g (x) = \ sqrt {x — 4}
Домены функций квадратного корня
Чтобы вычислить область определения функции квадратного корня, решите неравенство x ≥ 0 с заменой x на подкоренное выражение. Используя один из приведенных выше примеров, вы можете найти домен
f (x) = 2 \ sqrt {x + 3}
, установив подкоренное выражение ( x + 3) равным x в неравенстве.Это дает вам неравенство
x + 3 ≥ 0
, которое вы можете решить, вычитая 3 с обеих сторон. Это дает вам решение x ≥ −3, что означает, что в вашем домене все значения x больше или равны −3. Вы также можете записать это как [−3, ∞), где скобка слева показывает, что −3 — это конкретный предел, а скобка справа показывает, что ∞ — нет. Поскольку подкоренное выражение не может быть отрицательным, вам нужно вычислить только положительные или нулевые значения.
Вы также можете записать это как [−3, ∞), где скобка слева показывает, что −3 — это конкретный предел, а скобка справа показывает, что ∞ — нет. Поскольку подкоренное выражение не может быть отрицательным, вам нужно вычислить только положительные или нулевые значения.
Диапазон функций квадратного корня
Понятие, связанное с областью определения функции, — это ее диапазон. В то время как домен функции — это все значения x , которые допустимы в функции, его диапазон — это все значения y , в которых функция действительна. Это означает, что диапазон функции равен всем допустимым выходным данным этой функции. Вы можете рассчитать это, установив y равными самой функции, а затем решив, чтобы найти любые значения, которые не являются допустимыми.
Для функций извлечения квадратного корня это означает, что диапазон функции — это все значения, полученные, когда x дает подкоренное выражение, равное или большее нуля.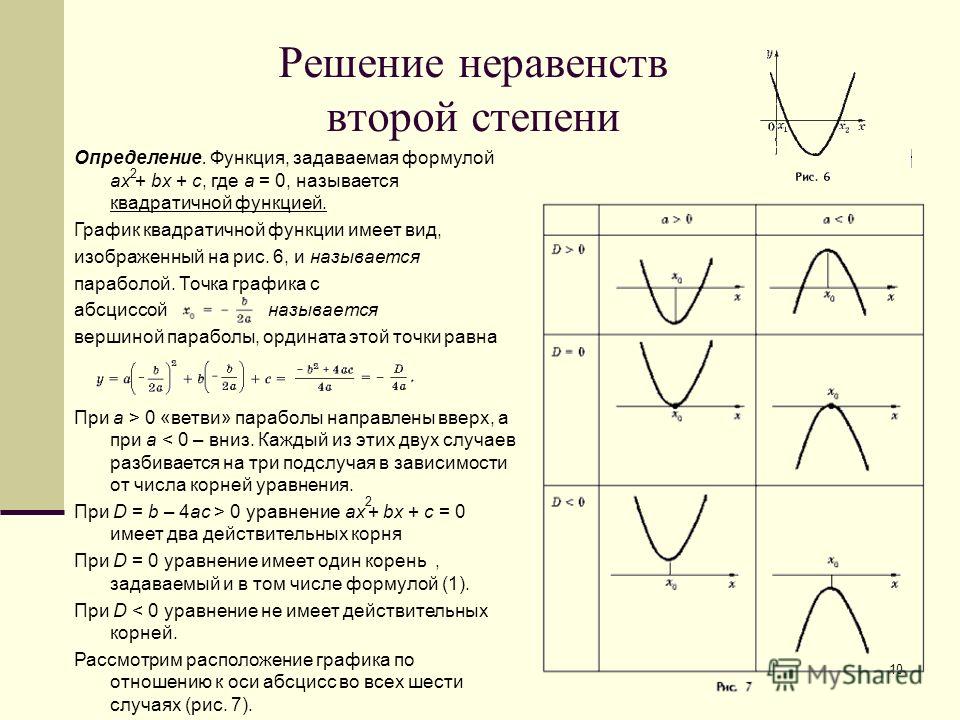 Вычислите область определения функции квадратного корня, а затем введите значение области в функцию, чтобы определить диапазон. Если ваша функция —
Вычислите область определения функции квадратного корня, а затем введите значение области в функцию, чтобы определить диапазон. Если ваша функция —
f (x) = \ sqrt {x — 2}
и вы вычисляете домен как все значения x , большие или равные 2, то любое допустимое значение, которое вы вводите в
y = \ sqrt {x — 2}
даст вам результат, который больше или равен нулю.Следовательно, ваш диапазон составляет y ≥ 0 или [0, ∞).
КОРЕНЬ (функция КОРЕНЬ) — служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции КОРЕНЬ в Microsoft Excel.
Описание
Возвращает положительный квадратный корень.
Синтаксис
SQRT (номер)
Аргументы функции КОРЕНЬ имеют следующие аргументы:
Замечание
Если число отрицательное, SQRT возвращает # ЧИСЛО! значение ошибки.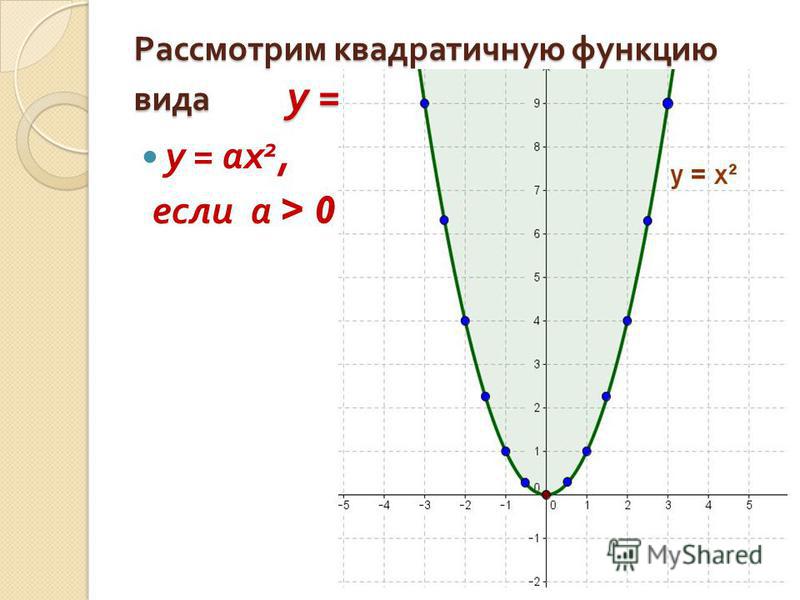
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Данные | ||
|---|---|---|
-16 | ||
Формула | Описание | результат |
= КОРЕНЬ (16) | Корень квадратный из 16. | 4 |
= КОРЕНЬ (A2) | Корень квадратный из -16. Поскольку число отрицательное, # ЧИСЛО! сообщение об ошибке возвращается. | # ЧИСЛО! |
= КОРЕНЬ (АБС (A2)) | Как избежать #NUM! сообщение об ошибке, сначала используя функцию ABS, чтобы найти абсолютное значение -16, а затем найти квадратный корень. | 4 |
Функция квадрата — ArcGIS Pro | Документация
Доступно с лицензией Image Analyst.
Доступно с лицензией Spatial Analyst.
Обзор
Вычисляет квадрат значений пикселей в растре.
Примечания
Если входное значение является целым числом, выходной растр будет целочисленного типа.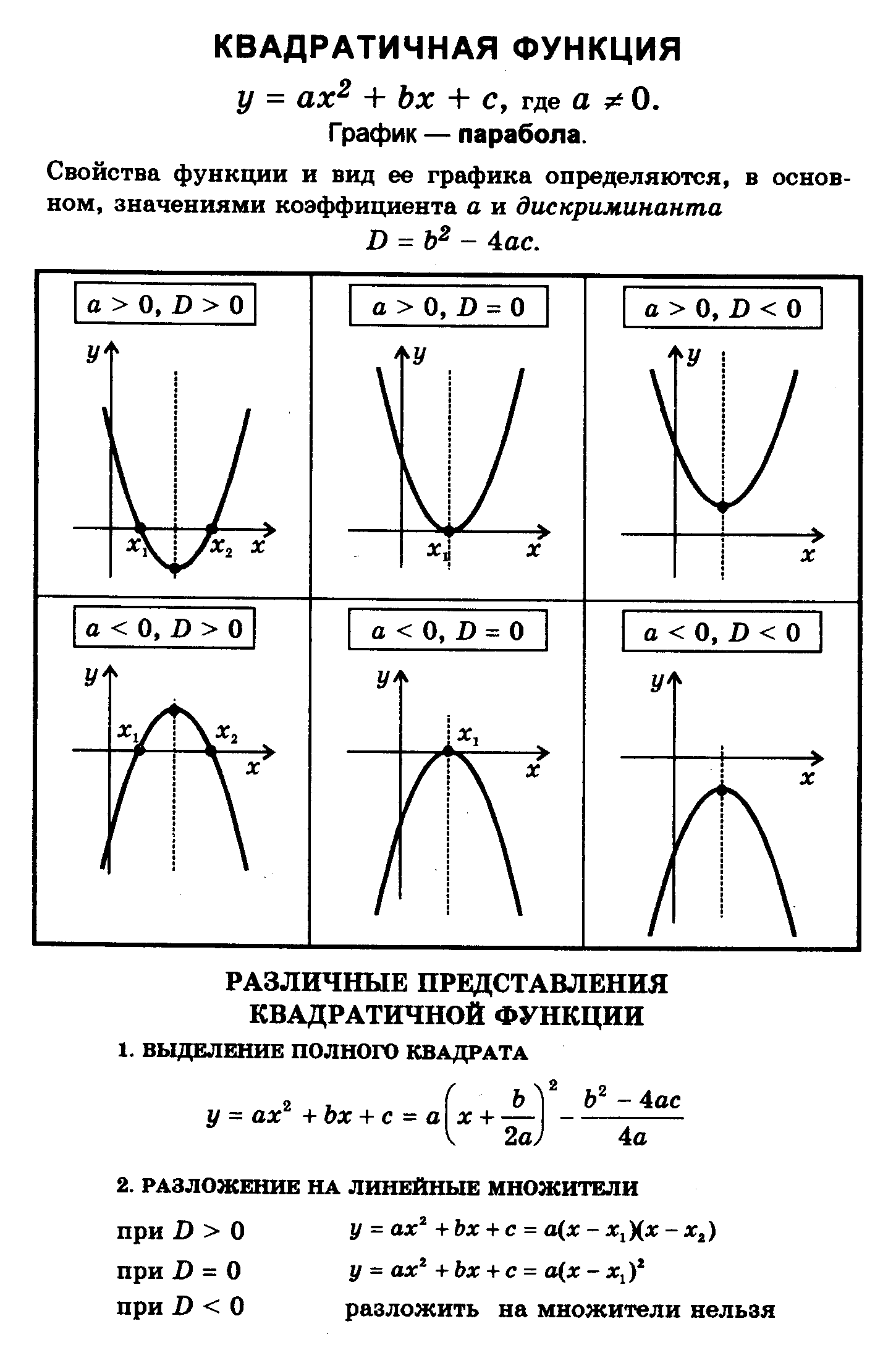 Если ввод с плавающей запятой, выходной растр будет с плавающей запятой.
Если ввод с плавающей запятой, выходной растр будет с плавающей запятой.
Если на входе многополосный растр, на выходе будет многополосный растр. Функция выполнит операцию для каждого диапазона на входе.
Если входные данные — многомерный растр, все срезы всех переменных будут обработаны, а на выходе будет многомерный растр.
Параметры
| Имя параметра | Описание |
|---|---|
Растр | Входные значения возвести в квадрат. |
Тип экстента | Выберите, какой экстент будет использоваться в выходном растре: |
Тип размера ячеек | Выберите размер ячейки для использования в выходном растре.
|
Связанные темы
Отзыв по этой теме?
создание квадратной функции в Python
Вам необходимо проверить, как функции и их параметры работают в Python, поскольку сейчас вы не используете их должным образом, поэтому код не работает.Однако вы находитесь на правильном пути решения проблемы, поэтому не расстраивайтесь.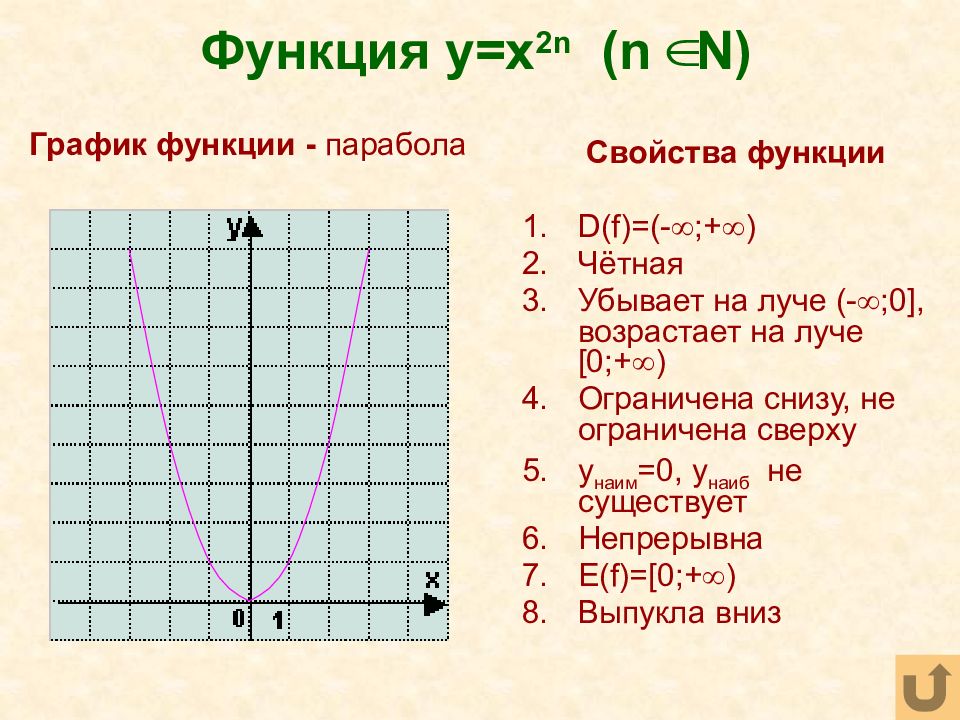
Чтобы помочь вам решить эту проблему самостоятельно, я сначала попытаюсь дать несколько советов, в конце вы найдете решение, если вы все еще не можете решить это самостоятельно.
Попытайтесь запомнить точку параметра в функции. Параметры — это данные, которые вы передаете функции для использования. Посмотрите на свой параметр функции, правильно ли вы его используете? Помните, что параметром должно быть число, которое вы собираетесь возвести в квадрат.
Помните, что в области видимости переменной в настоящее время вы используете переменную, которая еще не была определена в функции, так что это не сработает для вас. Кроме того, спросите себя, почему вы вообще используете эти переменные, если вы передаете данные в функцию в качестве параметра.
Зачем создавать дополнительную переменную в функции, все, что вам действительно нужно, это вернуть значение параметра в квадрате вправо?
Почему вы печатаете данные и запрашиваете ввод? Проблема не в том, чтобы вас просить об этом.
 В общем, вы не должны делать лишних вещей, которых не требует задача. Это потому, что даже если вы получите правильное решение, оно может сбить с толку тесты утверждения и привести к сбою задачи. Кроме того, это хорошая практика для реального мира, потому что вы не будете делать лишних вещей, которые вам не велят делать на работе.
В общем, вы не должны делать лишних вещей, которых не требует задача. Это потому, что даже если вы получите правильное решение, оно может сбить с толку тесты утверждения и привести к сбою задачи. Кроме того, это хорошая практика для реального мира, потому что вы не будете делать лишних вещей, которые вам не велят делать на работе.
Попробуйте использовать приведенные выше данные, чтобы исправить свое решение. Однако, если вам все еще нужна помощь, вот решение:
импорт математики
def квадрат (число):
номер возврата * номер
Обратите внимание, что если вам нужно прочитать предложенное мной решение, я советую вам вернуться и еще раз просмотреть предыдущие видео, чтобы закрепить ваше обучение.Потому что вы не запоминаете необходимые концепции.
fa. Функциональный анализ — где-то определен квадрат дельта-функции?
Когда Л. Шварц «изобрел» распределения (на самом деле, он только изобрел математическую теорию как часть функционального анализа, потому что распределения уже использовались физиками), он случайно доказал, что невозможно определить продукт таким образом, чтобы распределения образуют алгебру с приемлемыми топологическими свойствами. 2 $,
2 $,
$$ (1) \ qquad \ delta_ {x = 0} = \ delta_ {x_1 = 0} \ delta_ {x_2 = 0}. $$
Ж.-Ф. Коломбо изобрел в 70-х годах алгебру обобщенных функций, которая имеет какое-то отношение к распределениям. Но каждое распределение имеет бесконечно много представителей в алгебре, и вам придется играть с равенством и «слабым равенством» (или «ассоциацией»). Я не знаю примера, когда этот инструмент решал бы открытую проблему. В алгебре Коломбо квадрат $ \ delta_0 $ имеет смысл, но не уникален.d} $, который приближается к Дираку в начале координат. Аналогичное тождество происходит при замене ортогональных осей произвольным списком осей $ d $; то правая часть равна $ C \ delta $, где константа $ C $ вычисляется путем решения случая задачи Минковского.
График радикальной функции (Алгебра 1, Радикальные выражения) — Mathplanet
Как вы помните, радикал — это то, что находится под знаком радикала, например квадратный корень. Радикальная функция содержит радикальное выражение с независимой переменной (обычно x) в подкоренном выражении. Обычно радикальные уравнения, в которых радикал является квадратным корнем, называют функциями квадратного корня.
Обычно радикальные уравнения, в которых радикал является квадратным корнем, называют функциями квадратного корня.
Пример радикальной функции:
$$ y = \ sqrt {x} $$
Это родительская функция извлечения квадратного корня, и ее график выглядит как
Если мы сравним это с функцией извлечения квадратного корня
$$ y = a \ sqrt {x} $$
Мы заметим, что график растягивается или сжимается по вертикали, когда мы изменяем
$$ \ begin {matrix} \ left | а \ право | > 0 \: \: \: \: \: \: \: & & \ Rightarrow vertical \: stretch \\ 0 <\ left | a \ right | <1 & & \ Rightarrow vertical \: shrink \: \: \: \\ \ end {matrix} $$
На графике ниже представлены радикальные функции с разными значениями
Если a <0 график
$$ y = a \ sqrt {x} $$
Отражение по оси абсцисс графика
$$ y = \ left | a \ right | \ sqrt {x} $$
Другое уравнение квадратного корня было бы
$$ y = a \ sqrt {x-b} + c $$
Если вы посмотрите на графики, все выше которых имеют c = 0, вы увидите, что все они имеют диапазон ≥ 0 (все графики начинаются с x = 0, поскольку нет реальных решений квадратного корня из отрицательного числа) .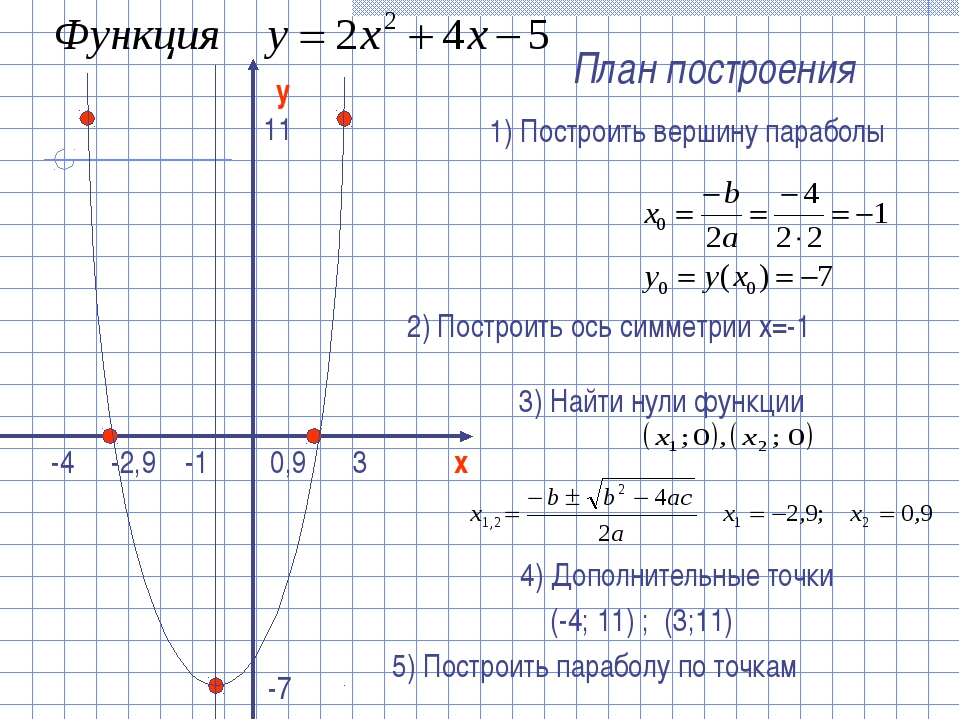 Если у вас c ≠ 0, у вас будет радикальная функция, которая начинается с (0, c). Пример этого можно увидеть на графике ниже
Если у вас c ≠ 0, у вас будет радикальная функция, которая начинается с (0, c). Пример этого можно увидеть на графике ниже
.
Значение b говорит нам, где начинается область определения радикальной функции. Опять же, если вы посмотрите на родительскую функцию, она имеет b = 0 и, следовательно, начинается с (0, 0). Если у вас b ≠ 0, то радикальная функция начинается с (b, 0).
Если и b ≠ 0, и c ≠ 0, то радикальная функция начинается в (b, c)
Видеоурок
Сравните радикальные функции
$$ y_ {1} = \ sqrt {x} $$
$$ y_ {2} = 3 \ sqrt {x} $$
$$ y_ {3} = \ sqrt {x} + 2 $$
$$ y_ {4} = \ sqrt {x- 1} $$
$$ y_ {5} = \ sqrt {x (x-2)} + 1 $$
.

 2
2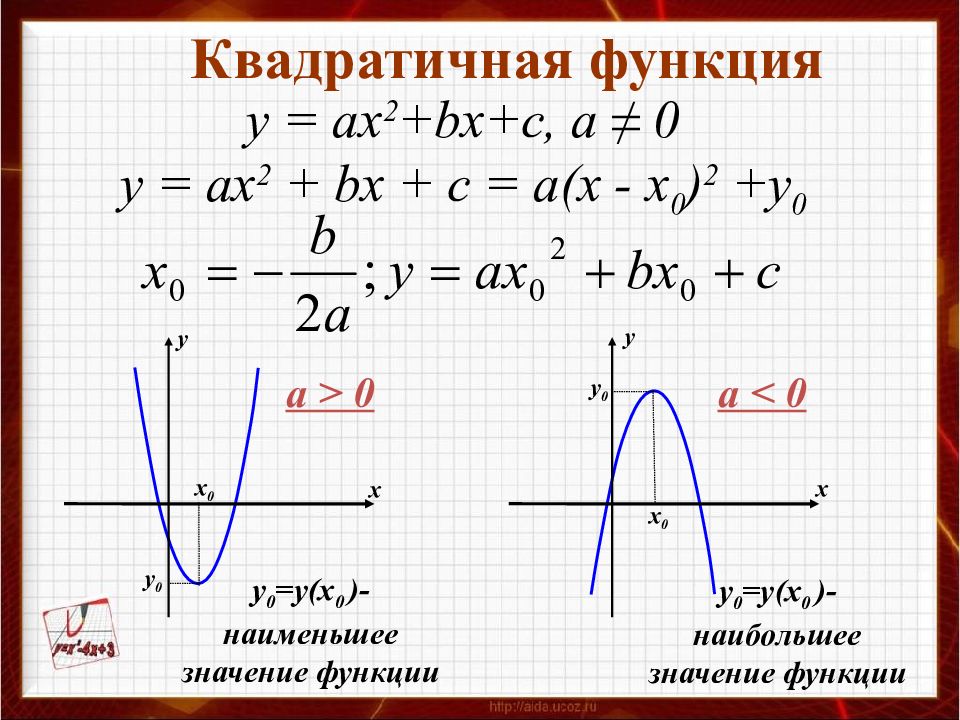 Некоторые люди так поступали, но я с этим не согласен.
Некоторые люди так поступали, но я с этим не согласен. 2) ## total sum of squares
rsq <- 1 - rss/tss
#[1] -2.375
2) ## total sum of squares
rsq <- 1 - rss/tss
#[1] -2.375
 » на необходимую.
» на необходимую.
 Выбрать из списка «Математические», нажать на функцию «СТЕПЕНЬ».
Выбрать из списка «Математические», нажать на функцию «СТЕПЕНЬ».


 Так появилась основная матрица данной методики, с которой и начинается работа.
Так появилась основная матрица данной методики, с которой и начинается работа.
 Возможны два варианта. Первый предусматривает исправление наиболее «слабых» функций, т. е. получивших наименьшее значение. В этом случае совместно с педагогом может быть выбрана соответствующая тема для самообразования (индивидуальная методическая тема) на ближайший период. Второй вариант предусматривает дальнейшую работу с функцией, показавшей наивысший результат, т. е. это образовательная область, в которой у данного педагога накоплен наибольший положительный опыт.
Возможны два варианта. Первый предусматривает исправление наиболее «слабых» функций, т. е. получивших наименьшее значение. В этом случае совместно с педагогом может быть выбрана соответствующая тема для самообразования (индивидуальная методическая тема) на ближайший период. Второй вариант предусматривает дальнейшую работу с функцией, показавшей наивысший результат, т. е. это образовательная область, в которой у данного педагога накоплен наибольший положительный опыт.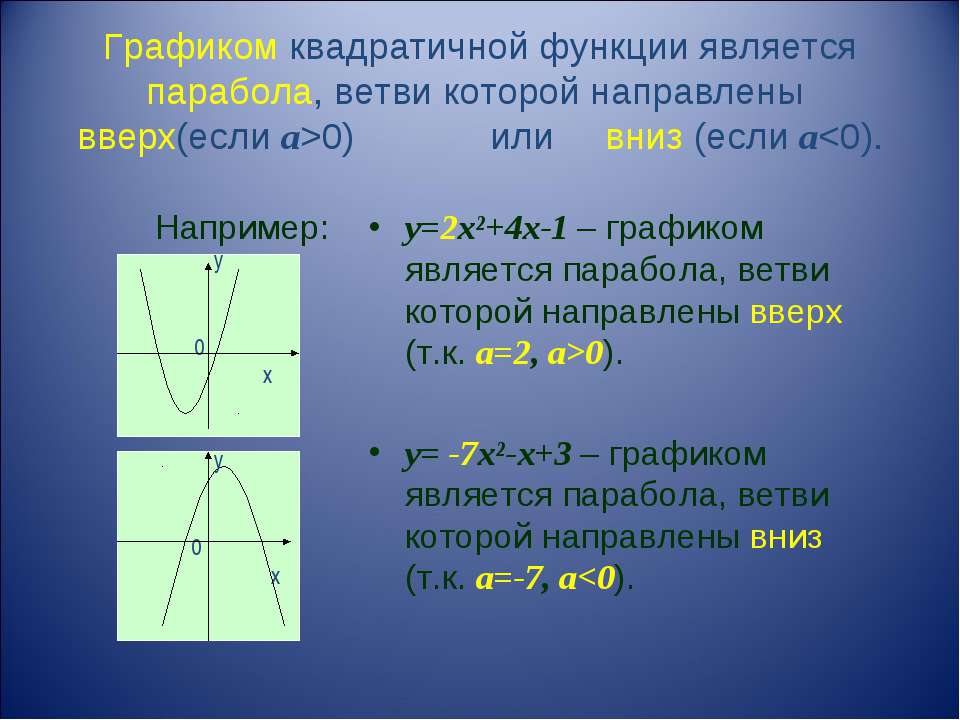

 Гармонический
Гармонический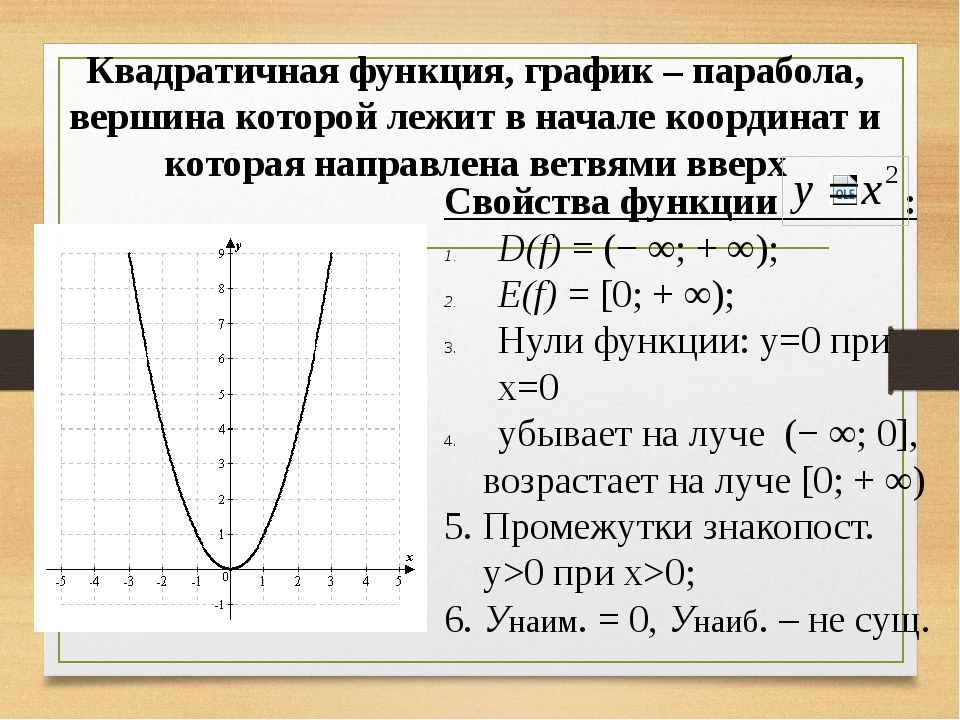 2)
2)
 4)
4)

 Если все размеры входных ячеек одинаковы, все параметры дадут одинаковые результаты.
Если все размеры входных ячеек одинаковы, все параметры дадут одинаковые результаты.