Содержание
Квадратные уравнения. Полное квадратное уравнение. Неполное квадратное уравнение. Дискриминант.
Как решить квадратное уравнение?
Как выглядит формула квадратного уравнения?
Какие бывают квадратные уравнения?
Что такое полное квадратное уравнение?
Что такое неполное квадратное уравнение?
Что такое дискриминант?
Сколько корней имеет квадратное уравнение?
Эти вопросы вас больше не будут мучить, после изучения материала.
Формула квадратного уравнения:
ax2+bx+c=0,где a≠0
где x — переменная,
a,b,c — числовые коэффициенты.
Виды квадратного уравнения
Пример полного квадратного уравнения:
3x2-3x+2=0
x2-16x+64=0
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта:
D=b2-4aс
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
Корни квадратного уравнения
Если D=0, уравнение имеет один корень
корень уравнения
Если D<0, уравнение не имеет вещественных корней.
Рассмотрим пример №1:
x2-x-6=0
Записываем сначала, чему равны числовые коэффициенты a, b и c.
Коэффициент a всегда стоит перед x2, коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6
Находим дискриминант:
D=b2-4ac=(-1)2-4∙1∙(-6)=1+24=25
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
Нахождения корней по дискриминанту
Ответ: x1=3; x2=-2
Пример №2:
x2+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
Далее находи дискриминант.
D=b2-4ac=(2)2-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1
Ответ: x=-1
Пример №3:
7x2-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
Далее находи дискриминант.
D=b2-4ac=(-1)2-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.
Рассмотрим неполное квадратное уравнение:
ax2+bx=0, где числовой коэффициент c=0.
Пример как выглядят такие уравнения:
x2-8x=0
5x2+4x=0
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax2+bx=0
x(ax+b)=0
x1=0 x2=-b/a
Пример №1:
3x2+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0
3x+6=0
3x=-6
Делим все уравнение на 3, чтобы получить у переменной x коэффициент равный 1.
x=(-6)/3
x2=-2
Ответ: x1=0; x2=-2
Пример №2:
x2-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x1=0
x-1=0
x2=1
Ответ: x1=0; x2=1
Рассмотрим неполное квадратное уравнение:
ax2+c=0, где числовой коэффициент b=0.
Чтобы решить это уравнение, нужно записать так:
x2=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом:
корень квадратного уравнения
Пример №1:
x2+5=0
x2=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения
Пример №2:
3x2-12=0
3x2=12
x2=12/3
x2=4
4>0 следовательно, есть решение,
x1=√4
x1=2
x2=-√4
x2=-2
Ответ: x1=2; x2=-2
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Неполные квадратные уравнения | Алгебра
Как решать неполные квадратные уравнения? Решение и количество корней зависят от вида уравнения.
Неполные квадратные уравнения бывают трёх видов.
Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.
I. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
Общий множитель x выносим за скобки:
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Второе уравнение — линейное. Решаем его:
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
Общий множитель x выносим за скобки:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; -18.
Общий множитель 5x выносим за скобки:
Приравниваем к нулю каждый множитель:
Ответ: 0; 3.
II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).
Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.
1. Если знаки a и c — разные, уравнение имеет два корня.
В курсе алгебры 7 класса такие уравнения решают разложением левой части на множители по формуле разности квадратов (поскольку квадратные корни начинают учить только в курсе 8 класса, коэффициенты a и c в 7 классе обычно являются квадратами некоторых рациональных чисел):
Уравнение типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Раскладываем левую часть уравнения по формуле разности квадратов:
Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:
приравниваем к нулю каждый множитель:
Ответ: 7; -7.
Ответ: 2,25; -2,25.
2. Если знаки a и c — одинаковые, уравнение не имеет корней.
Корней нет, так как сумма положительных чисел не может равняться нулю.
Ответ: нет корней.
Корней нет, так как сумма отрицательных чисел не может равняться нулю.
Ответ: нет корней.
В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:
Примеры.
Ответ:±2.
Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:
Ответ:
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Нет корней, так как квадратный корень не может быть равным отрицательному числу.
Ответ: нет корней.
III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.
Уравнение такого рода имеет единственный корень x=0
В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:
Примеры.
Ответ: 0.
Ответ: 0.
Ответ: 0.
В следующий раз рассмотрим примеры решения полных квадратных уравнений.
Составьте квадратное уравнение.
Неполные квадратные уравнения
Учитель математики и физики: Балакина Е.Н.
ЦЕЛИ УРОКА:
- Познакомиться с понятием квадратного уравнения;
- Научиться определять является ли уравнение квадратным;
Научиться определять коэффициенты квадратного уравнения;
Составлять по заданным коэффициентам квадратное уравнение;
Научиться определять вид квадратного уравнения: полное или неполное;
Научиться выбирать алгоритм решения неполного квадратного уравнения.
- Научиться определять является ли уравнение квадратным;
- Научиться определять коэффициенты квадратного уравнения;
- Составлять по заданным коэффициентам квадратное уравнение;
- Научиться определять вид квадратного уравнения: полное или неполное;
- Научиться выбирать алгоритм решения неполного квадратного уравнения.
ВОПРОСЫ:
- Что такое уравнение?
- Что значит решить уравнение?
- Что называется корнем уравнения?
- Какие уравнения мы знаем?
Выберите квадратные уравнения:
5х + 26 = 8х – 3,
— 13х = 0,
9х + 2 — 17 = 0,
34 + 5 — 22х = 11
9х + 7 — 13 = 0,
— 42х – 29 = 0,
-3 — 35х + 14 = 0,
+22 – 5х = 0,
-7 — 46х + 17 = 0,
8х – 6 = 0,
25 — 4х – 9 = 0.
КВАДРАТНЫМ УРАВНЕНИЕМ НАЗЫВАЕТСЯ
УРАВНЕНИЕ ВИДА
a
+
bx+c=0,
где
х —
переменная,
a,b,c —
некоторые числа,
причем
a
=
0.
а – первый коэффициент,
b – второй коэффициент,
c – свободный член.
Составьте квадратное уравнение
-9 + 23x – 11 = 0
-4 + x + 5 = 0
4 + 9x = 0
+ 7x + 1 = 0
-3 + 15 = 0
-3 — x + 7 = 0
4 + 3 = 0
a = 3, b = -7, c = 12
a = -9, b = 23, c = -11
a = 8, b = 0, c = 0
a = 5, b = -22, c = -3
a = -4, b = 1, c = 5
a = 4, b = 9, c = 0
a = 1, b = 7, c = 1
a = -3, b = 0, c =15
a = -3, b = -1, c =7
a = 4, b = 0, c = 3
Если в квадратном уравнении a
+
bx+c=0
хотя бы один из коэффициентов b
или с
равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трех видов:
- a
= 0 - a
+ b
x
= 0 - a
+ c
= 0
1 вариант
— ; У
0;3 И
0;-2 П
н. р. В
р. В
-3;3 Р
0;2 Е
0 Н
0;4 А
-2,5;2,5 О
— ; Д
2 вариант
- + 2х = 0
- 2 — 18 = 0
- 4 — 11= — 11+ 9х
- 9 + 1 = 0
- 2 = 4х
- 7 — 14 = 0
- 9 – 2 + 16х = 6 + 9
- — 4 = 0
- 9 + 1 = 1
- 4 — 25 = 0
- -2 + 4х = 0
- — 3х = 0
- 7 = 0
- 12х = 6
- 2 = 7 + 2
- 6 + 24 = 0
- 3 + 7 = 12х + 7
- + 2х – 3 = 2х + 6
- 9 — 4 = 0
- 7х = 2 + 3х
На доске выписаны числа 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1
Ученики выписывают буквы соответствующие корням данных уравнений; варианты работают навстречу друг другу.
ПРИВЕДЕННЫМ
КВАДРАТНЫМ УРАВНЕНИЕМ
Называют квадратное
уравнение, в котором коэффициент
при равен 1:
+
bx+c=0
ДОМАШНЕЕ ЗАДАНИЕ
№
24. 11 (УСТНО),
11 (УСТНО),
№
24.16 (б, в, г),
№
24.18 (б, в, г).
Историческая справка
Квадратные уравнения решали в Вавилоне около 2000 лет до нашей эры.
В Европе в 2002 году праздновали 800-летие квадратных уравнений, т.к. именно в 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения.
Только в 17 веке, благодаря Ньютону, Декарту и другим ученым эти формулы приняли современный вид.
В Древней Индии
уже в 499 году
были распространены публичные соревнования по решению задач на составление квадратных уравнений. Одной из таких задач является задача знаменитого индийского математика Бхаскары
:
Обезьянок резвых стая
Всласть поевши, развлекаясь,
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам
Стали прыгать, повисая.
Сколько было обезьянок
Ты скажи мне в этой стае?
Слайд 2
«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».
А. Эйнштейн.
Слайд 3
Здравствуйте, ребята!
Повторим:
Я — ваш помощник, я проведу
вас по всей большой теме
» Квадратные уравнения».
В 7 и 8 классе вы уже рассматривали и даже решали квадратные уравнения.
Слайд 4
Сегодня вы узнаете:
1. Какие уравнения называют квадратными?
2. Что в определении квадратного уравнения основное, что следует запомнить и учитывать?
3. Какие частные случаи квадратных уравнений бывают?
4. Каковы способы решения квадратных уравнений в каждом частном случае?
А теперь давайте вместе искать ответы на эти вопросы.
Желаю удачи!
Слайд 5
Что общего у этих уравнений?
Слайд 6
Квадратным уравнением
называют уравнение вида …
ax² + bx + c = 0, где а ≠ 0,
х — переменная,
а, в, с — некоторые числа.
а–старший (первый) коэффициент,
b-второй коэффициент,
с-свободный член.
а–старший (первый) коэффициент,
b-второй коэффициент,
с-свободный член.
а – старший (первый) коэффициент,
в — второй коэффициент,
с — свободный член.
Слайд 7
Если a = 1,
то квадратное уравнение
x² + bx + c= 0
называют приведенным.
Решим № 513 (устно).
Слайд 8
Попробуем решить:
5
5
-3
3
2
-4
1
4
3
-2
1
-1
4
-4
1
Слайд 9
Интересно,
а что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а)
превратятся в нули.
Давайте проведём исследование.
Слайд 10
Неполные квадратные уравнения
10.01.2017
10
Если с=0,
ax2+ bх= 0
ax2
ax2
Если b,с=0,
ax2= 0
Если b =0,
ax2+ c = 0
Слайд 11
Рассмотрим все возможные случаи
Слайд 12
Слайд 13
Неполные квадратные уравнения вида:
нет корней.
Слайд 14
Неполные квадратные уравнения вида:
Слайд 15
Ответ:
х=0.
нет корней.
Выпишите неполные квадратные уравнения:
Слайд 16
Запишите квадратные уравнения с указанными коэффициентами:
а=1, b=0, c=16;
a=-1, b=5, c=0;
b=0, a=-3, c=0;
c=-8, a=1, b=0;
a=1,5, c=0,b=-3;
b= , a= , c
Установите соответствие между уравнениями и следующими
а) уравнение имеет два корня,
б) уравнение имеет один корень,
в) уравнение не имеет корней.
(в)
(а)
(б)
(а)
(а)
(а)
Установите соответствие между уравнениями и следующими утверждениями:
Слайд 17
17
Проверьте решение № 515 (а, в, г).
а).4х2-9=0 в). -0,1х2+10=0 г). 6v2+24=0
4х2 =9 -0,1х2 =-10 6v2 =-24
х2 =9/4х2 =-10/(-0,1)v2 =-24/6
х1=-3/2=-1,5; х2=100 v2 =-4
х2 =3/2=1,5; х1=-10 Ответ: нет решения.
Ответ:-1,5;1,5;Ответ:-10;10;
Слайд 18
10.01.2017
18
Рассмотрим решение
неполных квадратных уравнений
№517 (б, г, д)
б). -5х2+ 6х=0 г). 4а2 — 3а=0д). 6z2– z =0
х(-5х+6)=0 а(4а-3)=0 z(6z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z=0 или 6z –1 =0
-5х= -6 4а=36z=1
х = -6/(-5) =1,2 а=3/4=0,75 z=1/6
Ответ: 0; 1,2. Ответ: 0; 0,75. Ответ: 0; 1/6..
.
Презентация урока алгебры в 8 классе по теме «Квадратные уравнения. Решение неполных квадратных уравнений». Введение понятия полного и неполного квадратных уравнений. Первичное закрепление способов решения неполных квадратных уравнений.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
Презентация урока алгебры в 8 классе « Квадратные уравнения. Решение непо л н ых квадратн ых у равнений »
Загадочное, но нам знакомое, В нем есть что-то неизвестное Его корень – вот искомое Найти его – интересно всем Каждый скажет без сомнения Перед вами (уравнение)
Решите уравнения а) у – 7 = 0; б) х + 0,5 = 0; в) а х = 0; г) 2 х – 1/3 = 0; д) а (а – 1) = 0; е) х 2 + 4 = 0.
Задача В кинозале количество зрительскихх мест в каждом ряду на 8 больше количества рядов. Всего на сеанс пришло 884 зрителя и все места были заняты. Сколько рядов в кинозале?
x – рядов; x +8 – мест в каждом ряду C оставим уравнение: x (х+8)=884; x 2 +8х-884=0.
« Квадратные уравнения. Решение непо л н ых квадратн ых у равнений » Тема урок а: эпиграф: уравнение – это ключ, которым можн о открыть т ы сячу дверей в не известное.
цель: ввести понятие квадратного уравнения; Научиться решать непо лные квадратн ые у равнения.
О пр е деление квадратного у равнения Квадратн ы м у равнением наз ы ва е тся у равнение вид а ax²+bx+c=0 , де х – переменная, а, b , с – параметры, а≠0. Число а называ е тся пер вым ко э ф фи ц ие нтом, число b – вторым ко эф ф ицие нтом и с – свободным членом. Квадратное у равнение наз ы вают также у равнением второй степен и, так как е го л е вая част ь является многочлен ом второй степен и.
Число а называ е тся пер вым ко э ф фи ц ие нтом, число b – вторым ко эф ф ицие нтом и с – свободным членом. Квадратное у равнение наз ы вают также у равнением второй степен и, так как е го л е вая част ь является многочлен ом второй степен и.
При меры квадратн ы х у равнений: a b c -2x²+x-1,4=0 -2 1 -1,4 5x²-4x=0 5 -4 0 3X²+10,3=0 3 0 10,3
За дание 1 Являются ли данные уравнения квадратными? 4x²-5x+2=0 -5,6x²-2x- 0,5 =0 13-7x²=0 16x²-x³-5=0 1-16x=0 -x²=0
За дание 2 Наз овите ко э ффиц ие нт ы в квадратном у равнении. 3x²-6x+2=0 -x²+5x+10=0 x²-8x+1,5=0 -4x²+5=0 -36x²-3x=0 12x²=0
Непо лные квадратн ые у равнения Если в квадратном уравнении ax²+bx+c=0 хотя бы один и з ко э ф фи ц ие нт о в b или c р а вен нулю, то так ое уравнение наз ы вают непо л н ы м квадратн ы м у равнением. a b c -3x²+5=0 -3 0 5 2x²-10x=0 2 -10 0 16x²=0 16 0 0
Классификация квадратных уравнений полные неполные Аль-Хорезми, где a ≠ 0 b=0 b=0, c=0 c=0 или или или
Ре ши м уравнение если b=0. -4x²+25=0 — 4x² =- 25 4x² = 25 или I
-4x²+25=0 — 4x² =- 25 4x² = 25 или I
Решим уравнение если b=0 ,c=0. III
Решим уравнение если C=0 . (35 + у) y = 0 35 + у = 0 или II y = 0 y=-35
Тестирование
1 . 2. 3. 4. 5 0; -5 -5; 5 0 За дание №1. Укажите корни уравнения помощь
За дание №2. Укажите корни уравнения 1. 2. 3. 4. -4 ; 4 — 4 ; 0 16 0 ; 4
За дание №3. Укажите корни уравнения 1 . 2. 3. 4. 3 -3 ; 0 -3 0 ; 3
За дание №4. Укажите корни уравнения 1. 2. 3. 4. 0; 4 16 -4; 4 -4; 0
05/01/17 За дание №5. Укажите корни уравнения 1. 2. 3. 4. -2; 2 4 2 2; 0
Итоги урока: Сегодня на уроке я узнал… понял… научился… мои успехи – это… трудности я почувствовал… я не умел, а теперь умею… на следующем уроке я хочу…
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Урок по теме «Неполные квадратные уравнения». Подготовили учителя математики МОУ «Успенская ООШ МО «Ахтубинский район» Зенина Н. Г., Крамаренко Т.Н.
Г., Крамаренко Т.Н.
«Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно». А. Эйнштейн.
Здравствуйте, ребята! Повторим: Я — ваш помощник, я проведу вас по всей большой теме » Квадратные уравнения». В 7 и 8 классе вы уже рассматривали и даже решали квадратные уравнения.
Сегодня вы узнаете: 1. Какие уравнения называют квадратными? 2. Что в определении квадратного уравнения основное, что следует запомнить и учитывать? 3. Какие частные случаи квадратных уравнений бывают? 4. Каковы способы решения квадратных уравнений в каждом частном случае? А теперь давайте вместе искать ответы на эти вопросы. Желаю удачи!
Что общего у этих уравнений?
Квадратным уравнением называют уравнение вида … ax ² + bx + c = 0, где а ≠ 0, х — переменная, а, в, с — некоторые числа. а–старший (первый) коэффициент, b -второй коэффициент, с-свободный член. а–старший (первый) коэффициент, b -второй коэффициент, с-свободный член. а – старший (первый) коэффициент, в — второй коэффициент, с — свободный член.
а–старший (первый) коэффициент, b -второй коэффициент, с-свободный член. а – старший (первый) коэффициент, в — второй коэффициент, с — свободный член.
Если a = 1 , то квадратное уравнение x ² + bx + c = 0 называют приведенным. Решим № 513 (устно) .
а в с 5x² + 5х – 3 = 0 3 x² + 2 х – 4 = 0 х² + 4х + 3 = 0 -2 x² + х – 1 = 0 4 х ²- 4 х + 1 = 0 5 5 -3 3 2 -4 1 4 3 -2 1 — 1 4 — 4 1 Попробуем решить:
Интересно, а что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а) превратятся в нули. Давайте проведём исследование.
Неполные квадратные уравнения 28.04.17 Если с = 0 , ax 2 + b х = 0 ax 2 ax 2 Если b, с = 0 , ax 2 = 0 Если b = 0 , ax 2 + c = 0
Рассмотрим все возможные случаи
Неполные квадратные уравнения вида: нет корней.
Неполные квадратные уравнения вида:
Ответ: х= 0. нет корней. Выпишите неполные квадратные уравнения:
Запишите квадратные уравнения с указанными коэффициентами: а=1, b=0, c=16; a=-1, b=5, c=0; b=0, a=-3, c=0; c=-8, a=1, b=0; a=1,5, c=0,b=-3; b= , a= , c Установите соответствие между уравнениями и следующими а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней. (в) (а) (б) (а) (а) (а) Установите соответствие между уравнениями и следующими утверждениями:
(в) (а) (б) (а) (а) (а) Установите соответствие между уравнениями и следующими утверждениями:
Проверьте решение № 515 (а, в, г). а).4х 2 -9=0 в). -0,1х 2 +10=0 г). 6 v 2 +24=0 4х 2 = 9 -0,1х 2 =- 10 6 v 2 =-24 х 2 = 9 /4 х 2 =- 10 /(-0,1) v 2 =-24/6 х 1 = -3/2=-1,5; х 2 =100 v 2 =-4 х 2 =3/2=1,5; х 1 = -10 Ответ: нет решения. Ответ:-1,5;1,5; Ответ:-10;10 ;
28.04.17 Рассмотрим решение неполных квадратных уравнений № 517 (б, г, д) б). -5х 2 + 6х=0 г). 4а 2 — 3а=0 д). 6 z 2 – z =0 х(-5х+6)=0 а(4а-3)= 0 z (6 z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z =0 или 6 z –1 =0 -5х= -6 4а=3 6 z =1 х = -6/(-5) =1,2 а=3/4=0,75 z =1/6 Ответ: 0; 1 ,2. Ответ: 0; 0,75. Ответ: 0; 1/6.. .
1) При каких значениях а уравнение является квадратным уравнением? Нет решений 2) При каких значениях a уравнение является неполным квадратным уравнением?
3) Решите уравнение при полученных значениях а. Ответ: а = − 2, х= − 15, х= 0; а = 0,
Подведем итоги Какое же уравнение называется квадратным? Почему а≠ 0 ? Как называются числа а, в и с? Сколько видов неполных квадратных уравнений мы узнали? Как решают уравнения I вида? II вида? III вида?
Вот и завершается наш урок. Ребята! Вы получили ответы на интересующие вас вопросы? Поняли, что нас впереди ждут интересные, а самое главное – важные темы? Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.
Ребята! Вы получили ответы на интересующие вас вопросы? Поняли, что нас впереди ждут интересные, а самое главное – важные темы? Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.
Домашнее задание: П. 21 учебника; №№ 318, 321 а,в, 323 а. Дополнительно: 520, 532. П. 21 (определения), №518, 520 (а,в) 511 Дополнительно (для учащихся с повышенным интересом) №520, №531.
Тренировочные задания на решение квадратных уравнений 8 класс
Квадратные уравнения 8 класс алгебра
Учитель: Федулкина Т.А.
- Что такое квадратные уравнения. Виды уравнений.
Формула квадратного уравнения: ax2+bx+c=0,где a≠0, где x — переменная, a,b,c — числовые коэффициенты.
Пример полного квадратного уравнения:
3x2-3x+2=0
x2-16x+64=0
Решение полных квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта: D=b2-4aс
Если D>0, то уравнение имеет два корня и находим эти корни по формуле:
Если D=0, уравнение имеет один корень
Если D<0, уравнение не имеет вещественных корней.
№1 x2-x-6=0
Записываем сначала, чему равны числовые коэффициенты a, b и c.
Коэффициент a всегда стоит перед x2, коэффициент b всегда перед переменной x, а коэффициент c – это свободный член.
a=1,b=-1,c=-6
D=b2-4ac=(-1)2-4∙1∙(-6)=1+24=25
Дискриминант больше нуля, следовательно, у нас два корня, найдем их:
Ответ: x1=3; x2=-2
№2 x2+2x+1=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=1,b=2,c=1
D=b2-4ac=(2)2-4∙1∙1=4-4=0
Дискриминант равен нулю, следовательно, один корень:
x=-b/2a=-2/(2∙1)=-1
Ответ: x=-1
№3 7x2-x+2=0
Записываем, чему равны числовые коэффициенты a,b и c.
a=7,b=-1,c=2
D=b2-4ac=(-1)2-4∙7∙2=1-56=-55
Дискриминант меньше нуля, следовательно, корней нет.
Рассмотрим неполное квадратное уравнение:
ax2+bx=0, где числовой коэффициент c=0.
Пример как выглядят такие уравнения: x2-8x=0, 5x2+4x=0.
Чтобы решить такое уравнение необходимо переменную x вынести за скобки. А потом каждый множитель приравнять к нулю и решить уже простые уравнения.
ax2+bx=0 x(ax+b)=0 x1=0 x2=-b/a
№1 3x2+6x=0
Выносим переменную x за скобку,
x(3x+6)=0
Приравниваем каждый множитель к нулю,
x1=0 3x+6=0 3x=-6 x2=-2
Ответ: x1=0; x2=-2
№2 x2-x=0
Выносим переменную x за скобку,
x(x-1)=0
Приравниваем каждый множитель к нулю,
x1=0
x2=1
Ответ: x1=0; x2=1
Рассмотрим неполное квадратное уравнение:
ax2+c=0, где числовой коэффициент b=0.
Чтобы решить это уравнение, нужно записать так:
x2=c/a , если число c/a будет отрицательным числом, то уравнение не имеет решения.
А если c/a положительное число, то решение выглядит таким образом: корень квадратного уравнения
№1 x2+5=0
x2=-5, видно, что -5<0, значит нет решения.
Ответ: нет решения
№2 3x2-12=0
3x2=12
x2=12/3
x2=4
x1=2
x2=-2
Ответ: x1=2; x2=-2
2) Тренировочные задания на решение квадратных уравнений 8 класс алгебра.
Задания для устного решения:
- Решите неполное квадратное уравнение:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Решите квадратное уравнение, используя теорему Виета:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Решите квадратное уравнение, используя формулу :
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Найдите дискриминант квадратного уравнения по формуле D= :
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
- Сколько корней имеет квадратное уравнение, если D= равно:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
3)Решить квадратные уравнения:
- Решите квадратное уравнение:
1) | 6) | 11) | 16) |
2) | 7) | 12) | 17) |
3) | 8) | 13) | 18) |
4) | 9) | 14) | 19) |
5) | 10) | 15) | 20) |
скачать файл
Дата публикации — 03. 12.2017
12.2017
Квадратные уравнения (способы решения)
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.
Определение
Уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.
Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.
| Корни уравнения ax2 + bx + c = 0 находят по формуле |
Выражение D = b2— 4ac называют дискриминантом квадратного уравнения.
- если D < 0, то уравнение не имеет действительных корней;
- если D = 0, то уравнение имеет один действительный корень;
- если D > 0, то уравнение имеет два действительных корня.
В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Формулы
Полное квадратное уравнение
Неполные квадратные уравнения
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Способы решения неполных квадратных уравнений:
- c = 0, то уравнение примет вид
ax2 + bx = 0.
x(ax + b) = 0 ,
x = 0 или ax + b = 0, x = —b : a. - b = 0, то уравнение примет вид
ax2 + c = 0,
x2 = —c / a,
x1, 2 = ±√(-c / a). - b = 0 и c = 0 , то уравнение примет вид
ax2 = 0,
x = 0
Решение неполного квадратного уравнения
Квадратные уравнения с комплексными переменными
Сначала рассмотрим простейшее квадратное уравнение z2 = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:
На множестве действительных чисел это уравнение:
- имеет один корень z = 0, если а = 0;
- имеет два действительных корня z1, 2 = ±√a
- Не имеет действительных корней, если a < 0
Решение квадратных уравнений с помощью графиков
Не используя формул квадратное уравнение можно решить графическим способом. Например x2 + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x2; y = x + 1.
y = x2, квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.
Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.
Решение задач с помощью квадратных уравнений
| Процессы | Скорость км/ч | Время ч. | Расстояние км. |
|---|---|---|---|
| Вверх по реке | 10 — x | 35 / (10 — x) | 35 |
| Вверх по протоку | 10 — x + 1 | 18 / (10 — x + 1) | 18 |
| V течения | x | ||
| V притока | x + 1 |
Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.
ОДЗ: ∀ x ≠ 9, 10.
Практикум
т.к. D1
Ответ: корней нет.
Ответ: x = 2,5.
Заключение
Ещё в древности люди пользовались ими не зная, что это – квадратные уравнения.
В наше время невозможно представить себе решение как простейших, так и сложных задач не только в математике, но и в других точных науках, без применения решения квадратных уравнений.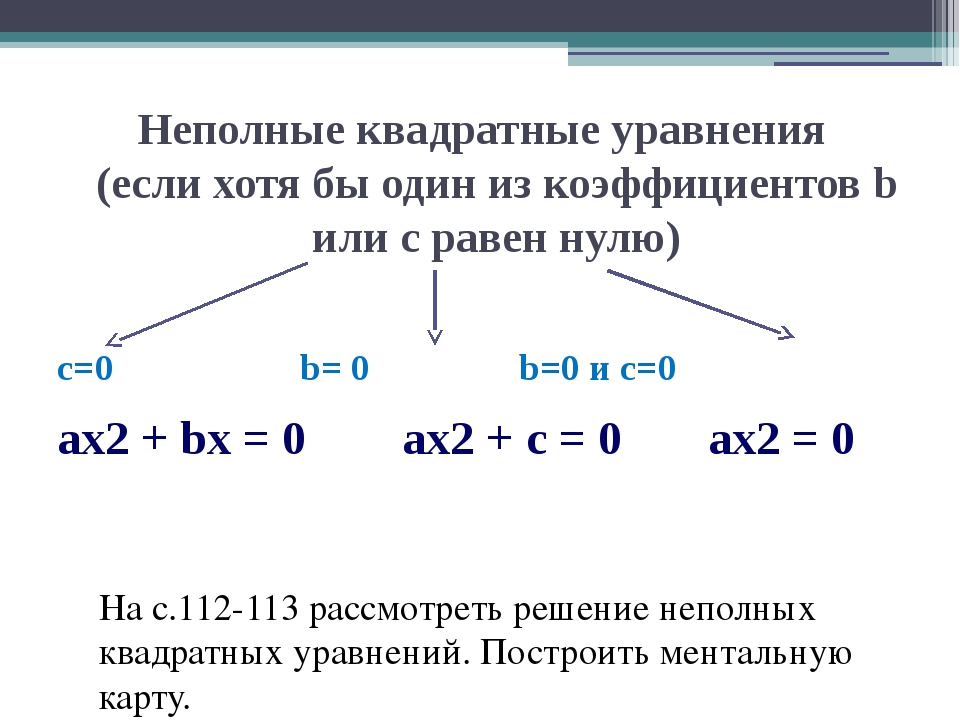 2-4ac\),
2-4ac\),
где D – дискриминант, а a, b, c – коэффициенты квадратного уравнения.
Чем конкретно нам может помочь дискриминант?
- Если D < 0 – то квадратное уравнение не имеет решений;
- Если D = 0 – то уравнение будет иметь только один корень;
- Если D > 0 – то уравнение имеет два решения.
То есть благодаря дискриминанту мы будем знать о результате и количестве решений квадратного уравнения.
Итак, мы посчитали, чему равен наш дискриминант, потом определили количество решений уравнения, что дальше? А дальше определяем корни квадратного уравнения по формулам.
- В первом случае, когда D < 0, считать ничего не нужно, т.к. уравнение не имеет решений. Это значит, что корней квадратного уравнения на множестве действительных чисел нет.
- Во втором варианте, когда D = 0, решение будет одно и единственный корень квадратного уравнения будет равен: \(x=\frac{-b}{2a}\)
- Третий случай, при D > 0, наиболее сложный из всех трех возможных: в ответе должно получиться два корня квадратного уравнения.

\(x_1=\frac{-b+\sqrt D}{2a}\)– первый корень квадратного уравнения;
\(x_1=\frac{-b-\sqrt D}{2a}\)– второй корень квадратного уравнения.
Решение квадратных уравнений на самом деле не настолько сложное, как кажется на первый взгляд. Всего-то нужно запомнить несколько формул и алгоритм действий. Главное — не бояться вида квадратных уравнений, мы уверены: все у тебя получится! Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Тест: Квадратные уравнения — Математика 8 класс
Квадратные уравнения
Тест содержит 12 вопросов.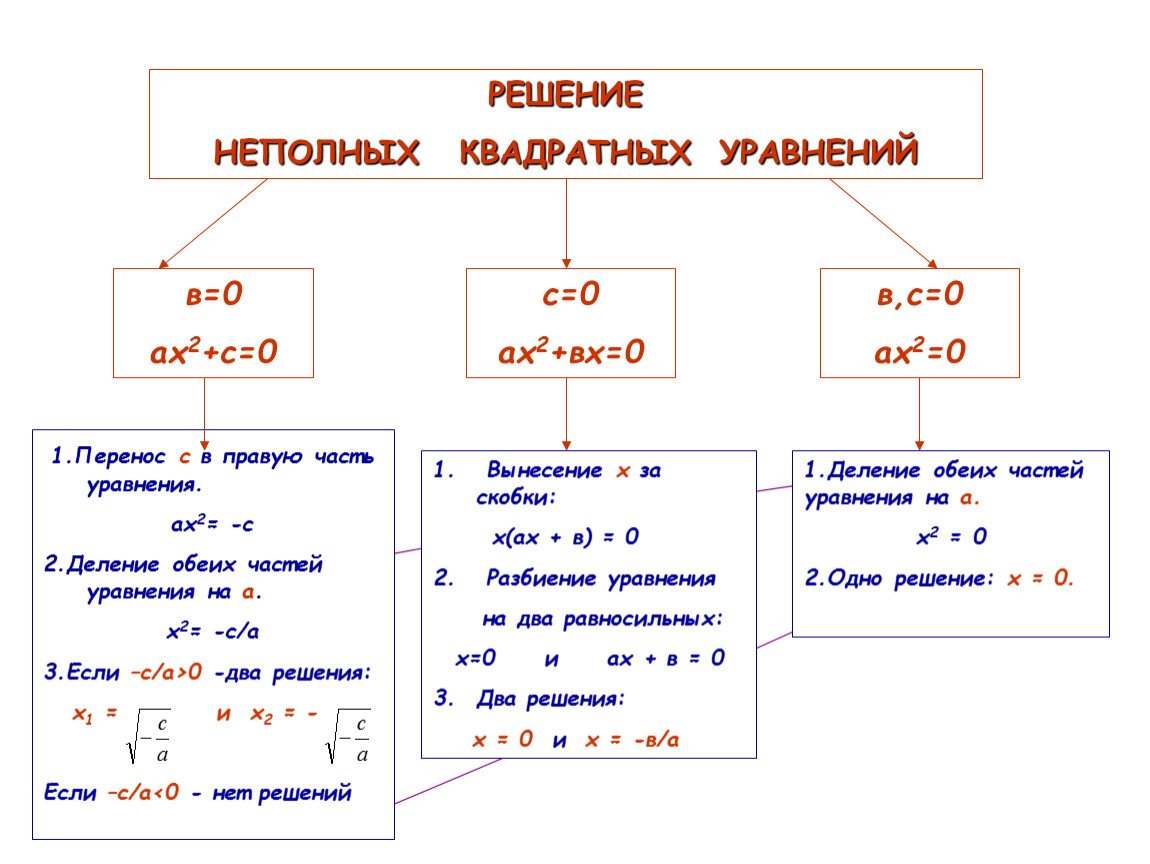 Рассматриваются неполные, полные и приведенные квадратные уравнения. Применение теоремы Виета, решение задачи с помощью квадратного уравнения. Задание с параметром.
Рассматриваются неполные, полные и приведенные квадратные уравнения. Применение теоремы Виета, решение задачи с помощью квадратного уравнения. Задание с параметром.
Математика 8 класс | Автор: Бурякова Вера Николаевна | ID: 1085 | Дата: 17.1.2014
«;} else {document.getElementById(«torf1″).innerHTML=»»;};
if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;};
if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;};
if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ. charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
if (answ.charAt(10)==»1″) {document.getElementById(«torf11″).innerHTML=»»;} else {document.getElementById(«torf11″).innerHTML=»»;};
if (answ.charAt(11)==»1″) {document.getElementById(«torf12″).innerHTML=»»;} else {document.getElementById(«torf12″).innerHTML=»»;};
}
}
Получение сертификата
о прохождении теста
Квадратное уравнение
Квадратное уравнение
Введение
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a, b и c — константы, а a 0.
Слово «квадратичный» происходит от латинского. В латинском языке «квадратичный» используется вместо «квадрат» .
Поскольку наибольшая степень неизвестной переменной, которая появляется в уравнении, равна квадрату,
поэтому подобные уравнения стали известны как квадратные уравнения.
Стандартная форма квадратного уравнения
Стандартная форма квадратного уравнения — ax 2 + bx + c = 0, где
◾ a, b и c — постоянные, а
◾ a не равно 0 (нулю).
Вот несколько примеров стандартной формы квадратного уравнения:
| Уравнение | Коэффициент |
|---|---|
| x 2 + 2x + 1 = 0 | , где a = 1, b = 2 и c = 1 |
| x 2 + 5x + 11 = 0 | , где a = 1, b = 5 и c = 11 |
Полное квадратное уравнение
◾ Когда b не равно нулю
| Некоторые примеры полной формы квадратного уравнения |
|---|
| ◾ x 2 + 2x + 1 = 0, где a = 1, b = 2 и c = 1 |
| ◾ x 2 + 5x + 11 = 0, где a = 1, b = 5 и c = 11 |
Чистое или неполное квадратное уравнение
◾ Когда b равно нулю, уравнение известно как чистое или неполное квадратное уравнение относительно x.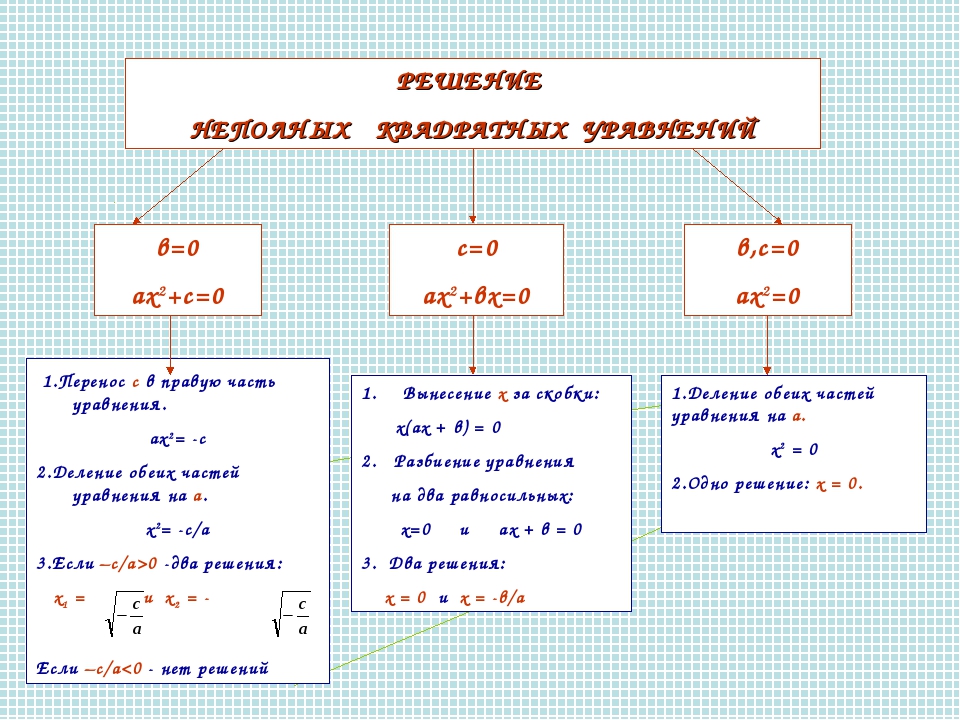
| Некоторые примеры чистой или неполной формы квадратного уравнения |
|---|
| ◾ 6x 2 -24 = 0, где b = 0 |
| ◾ 6x 2 -11 = 0, где b = 0 |
Корни квадратного уравнения
Корни или решение квадратного уравнения ax 2 + bx + c = 0 — это значения переменной ‘x’, которые удовлетворяют квадратному уравнению i.е. сделать топор 2 + bx + c равным нулю.
Например:
x 2 + 5x — 50 = 0
x 2 — 5x + 10x -50 = 0
х (х — 5) + 10 (х — 5) = 0
(х — 5) (х + 10) = 0
х = 5 и х = -10
Как видите, если поставить 5 или -10 вместо x, квадратное уравнение x 2 + 5x — 10 будет равно нулю. Следовательно, 5 и -10 являются корнями квадратного уравнения x 2 + 5x — 50 = 0.
Решение квадратного уравнения
Есть три метода решения квадратного уравнения:
◾ Факторизация
◾ Заполнив квадрат
◾ Используя формулу корней квадратного уравнения
Решение по факторизации
Пошаговый процесс решения квадратного уравнения методом факторизации:
Шаг 1: Преобразуйте уравнение в стандартную форму: ax 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую и сделайте правую часть равной нулю.
Если правая часть не равна нулю, перенесите ее в левую и сделайте правую часть равной нулю.
Шаг 2: Полностью разложите левую часть на множители.
Шаг 3: Используйте закон нулевого фактора: если ab = 0, то a = 0 или b = 0.
Шаг 4: Решите полученные линейные уравнения, приравняв каждый линейный коэффициент к нулю. Эти значения x будут решением квадратного уравнения.
Пример: Решить 3x 2 + 5x — 5 = -3
Шаг 1: Преобразование в стандартную форму
3x 2 + 5x -5 + 3 = 0
3x 2 + 5x — 2 = 0
Шаг 2: Разложите левую часть на множители
3x 2 + 6x — x — 2 = 0
3x (x + 2) -1 (x + 2) = 0
(3x — 1) (x + 2) = 0
Шаг 3: Приравнять каждый линейный коэффициент к нулю.
3x — 1 = 0 или x + 2 = 0
3x = 1 или x = -2
x = 1/3, x = — 2 являются корнями уравнения.
Ловушка:
У вас может возникнуть соблазн разделить обе части выражением, содержащим x. Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень от x) и можете потерять другое решение (значение x).
Например: рассмотрим x 2 = 7x
Правильное решение:
x 2 = 7x
x 2 -7x = 0
х (х-7) = 0
x = 0 и X = 7
Неправильное решение:
x 2 = 7x
Разделив обе стороны на x, получим
Х = 7
выше — неправильный способ решения уравнения, поскольку мы не смогли найти другое значение x, равное нулю.
Решение Завершив квадрат
Как вы уже знаете, все квадраты не могут быть легко разложены на множители. Например, x 2 + 4x + 1 нельзя разложить на множители простой факторизацией. Это означает, что мы не можем записать x 2 + 4x + 1 в форме (x — a) (x — b), где a, b — рациональные числа.
Существует альтернативный способ решения уравнений, например x 2 + 4x + 1 = 0, то есть путем до завершения квадрата .
Уравнения вида ax 2 + bx + c = 0 можно преобразовать в форму (x + p) 2 = q. Так легко найти решения.
Пошаговый процесс решения квадратного уравнения путем заполнения квадрата:
Шаг I: Составьте квадратное уравнение в стандартной форме ax 2 + bx + c = 0.
Шаг II: теперь разделите обе части уравнения на коэффициент x 2 , если он еще не равен 1.
Шаг III: Сдвиньте постоянный член вправо.
Шаг IV: Добавьте квадрат половины коэффициента x к L.H.S. и R.H.S.
Шаг V: Запишите L.H.S в виде полного квадрата и упростите R.H.S.
Шаг VI: Найдите x, извлекая квадратный корень из L. H.S. и R.H.S.
H.S. и R.H.S.
Решим квадратное уравнение -3x 2 + 12x + 5 = 0 по «завершая квадрат»
-3x 2 + 12x + 5 = 0
x 2 — 4x — (5/3) = 0
x 2 — 4x = (5/3)
x 2 — 4x + 2 2 = (5/3) + 2 2
(х — 2) 2 = (17/3)
x — 2 = & pm; & Sqrt; (17/3)
x = 2 & pm; & Sqrt; (17/3)
x 1 = 2 + & Sqrt; (17/3)
x 2 = 2 — & Sqrt; (17/3)
Итак, Здесь x 1 и x 2 — корни уравнения.
Используя формулу корней квадратного уравнения
Квадратичная формула, которая также может использоваться для решения любого квадратного уравнения, получается в результате решения квадратного уравнения ax 2 + bx + c = 0, a ≠ 0 для x путем заполнения квадрата.
Бывают случаи, когда решение квадратного уравнения факторизацией или завершение квадрата требует много времени, длительно или сложно. В таких случаях мы используем квадратную формулу для решения квадратного уравнения.
В таких случаях мы используем квадратную формулу для решения квадратного уравнения.
Пошаговый процесс решения квадратного уравнения по формуле корней квадратного уравнения:
Шаг I: Составьте квадратное уравнение в стандартной форме ax 2 + b x + c = 0.
Шаг II: Сравните решаемое квадратное уравнение со стандартным квадратным уравнением и найдите значения коэффициентов a, b, c.
Шаг III: Поместите эти значения a, b, c в формулу квадратного уравнения.
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
Как вы можете заметить в формуле. Квадратичная формула вычисляет два значения x: x 1 и x 2 , где
| x 1 = | −b + & Sqrt; b2 — 4ac |
| 2a |
| x 2 = | −b — & Sqrt; b2 — 4ac |
| 2a |
Эти два значения x, для которых выполняется ax 2 + bx + c = 0, называются решениями квадратного уравнения, также называемыми корнями квадратного уравнения.
Шаг I: — Преобразуйте квадратное уравнение, которое вы хотите решить, в стандартную форму квадратного уравнения, ax 2 + bx + c = 0
Например, если у вас есть квадратное уравнение в форме x 2 — 10x = -24, преобразуйте его в стандартную форму квадратного уравнения.
x 2 -10x = -24 преобразуется в x 2 — 10x + 24 = 0
Шаг II: — Найдите значение коэффициентов a, b и c, сравнив его со стандартной формой квадратного уравнения ax 2 + bx + c = 0
Например, сравнивая x 2 — 10x + 24 = 0 с ax 2 + bx + c = 0, получаем
a = 1,
b = -10,
c = 24
Шаг III:
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
| x 1 = | −b + & Sqrt; b2 — 4ac |
| 2a |
| = | — (- 10) + & Sqrt; (-10) 2-4 (1) (24) | = 6 |
| 2 (1) |
| x 2 = | −b — & Sqrt; b2 — 4ac |
| 2a |
| = | — (- 10) — & Sqrt; (-10) 2-4 (1) (24) | = 4 |
| 2 (1) |
Дискриминант
Мы узнали, что квадратная формула —
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
В приведенной выше квадратной формуле величина «b 2 — 4ac» , которая находится под знаком квадратного корня, называется дискриминантом квадратного уравнения.
Дискриминант = b 2 — 4ac
Выражение «b 2 — 4ac» говорит о природе корней квадратного уравнения. Корни могут быть реальными, равными или мнимыми.
Возможны три случая:
◾ Если b 2 — 4ac мнимый и неравный.
◾ Если b 2 — 4ac = 0, то корни будут действительными, равными и рациональными .(Это означает, что левая часть уравнения представляет собой полный квадрат).
◾ Если b 2 — 4ac> 0, то корни действительные и неравные.
Если b 2 — 4ac> 0, то корни действительны и неравны, и есть две возможности — здесь корни могут быть рациональными или иррациональными
◾ b 2 — 4ac — это полный квадрат, корни действительные, рациональные и неравные . (Это означает, что уравнение может быть решено путем факторизации).
◾ b 2 — 4ac несовершенный, тогда корни действительные, иррациональные и неравные.
Сводка
| Дискриминантное значение Случаи | Корни квадратичной | Факторизация квадратичной |
|---|---|---|
| Дискриминантное значение> 0 | два настоящих отдельных корня | два различных линейных фактора |
| Дискриминантное значение = 0 | два одинаковых настоящих корня | два одинаковых линейных фактора |
| Дискриминантное значение | Настоящих корней нет | Невозможно разложить на множители |
Случай I — Когда Дискриминант> 0
Для квадратного уравнения x 2 + 7x + 4 = 0, определить природу корней по его определителю
Ответ
х 2 + 7x + 4 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 7, c = 4
Дискриминант = 7 2 — 4 x 1 x 4 = 49 — 16 = 33
Дискриминант> 0, следовательно, есть два настоящих корня
Случай II — Когда Дискриминант = 0
Для квадратного уравнения x 2 + 6x + 9 = 0, определить природу корней по его определителю
Ответ
x 2 + 6x + 9 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 6, c = 9
Дискриминант = 6 2 — 4 x 1 x 9 = 36 — 36 = 0
Дискриминант = 0, следовательно, есть два одинаковых реальных корня
Случай III- Когда Дискриминант
Для квадратного уравнения x 2 + 4x + 4 = 0, определить природу корней по его определителю
Ответ
х 2 + 4х + 5 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 4, c = 5
Дискриминант = 4 2 — 4 x 1 x 5 = 16-20 = -4
Дискриминант
Yahoo Answers закрылся | Справка Yahoo
Yahoo Answers прекратил работу с 4 мая 2021 года. Yahoo Answers когда-то был ключевой частью продуктов и услуг Yahoo, но с годами его популярность снизилась по мере изменения потребностей наших участников. Мы решили переместить наши ресурсы с Yahoo Answers, чтобы сосредоточиться на продуктах, которые лучше обслуживают наших участников и выполняют обещание Yahoo по предоставлению высококачественного надежного контента.
Yahoo Answers когда-то был ключевой частью продуктов и услуг Yahoo, но с годами его популярность снизилась по мере изменения потребностей наших участников. Мы решили переместить наши ресурсы с Yahoo Answers, чтобы сосредоточиться на продуктах, которые лучше обслуживают наших участников и выполняют обещание Yahoo по предоставлению высококачественного надежного контента.
С 4 мая 2021 года вы больше не можете получить доступ к сайту, но вы все равно можете запросить загрузку ваших данных Yahoo Answers до 30 июня 2021 года. Чтобы помочь вам с этим переходом, мы составили список вопросов, которые могут возникают во время этого процесса.
Повлияет ли это на мою учетную запись Yahoo или другие службы Yahoo?
Нет, эти изменения относятся к Yahoo Answers. Они не повлияют на вашу учетную запись Yahoo или другие службы Yahoo.
Куда мне обратиться, если у меня возникнут вопросы в будущем?
Yahoo Search можно использовать для поиска ответов и информации в Интернете. Наша страница Yahoo COVID предоставляет информацию и ресурсы о пандемии коронавируса.
Наша страница Yahoo COVID предоставляет информацию и ресурсы о пандемии коронавируса.
Могу ли я загрузить свой контент Yahoo Answers?
Какой контент мне доступен?
При загрузке данных Yahoo Answers будет возвращен весь пользовательский контент, включая ваши вопросы, ответы и изображения. Вы не сможете загружать контент, вопросы или ответы других пользователей.
Нужно ли мне скачивать мой контент?
Нет, загрузка содержимого не обязательна. Однако, если вы решите загрузить свой контент, вы должны сделать это до 30 июня 2021 года.
Когда я получу контент Yahoo Answers?
Наша команда работает как можно быстрее, чтобы сделать данные доступными, но загрузка вашего контента может занять до 30 дней.
Я загрузил свой контент Yahoo Answers, как мне его просмотреть?
Ваш контент будет отформатирован в JSON (объектная нотация JavaScript), и его будет сложно просмотреть с первого взгляда. У нас есть ресурсы по просмотру и управлению данными вашей учетной записи, которые помогут вам понять, как загружаются ваши данные.
Как я могу поделиться своими комментариями / отзывами об этом изменении?
Присылайте любые комментарии или отзывы относительно этого решения по адресу [email protected]. Спасибо, что нашли время поделиться с нами своими мыслями.
квадратных уравнений | Superprof
В этой статье вы узнаете, что такое квадратные уравнения, свойства их корней, как представить их графически и как решить их с помощью трех методов с примерами.Итак, приступим.
Здесь a — старший коэффициент уравнения, и он не должен быть равен нулю. Значения x, которые делают уравнение истинным, известны как нулей или корней квадратного уравнения. Вы можете видеть, что квадратное уравнение представляет собой полином второй степени , что означает, что наивысшая степень этого уравнения равна 2.
Это самый простой способ найти корни квадратичных функций. Все, что нам нужно сделать, это расширить средний член, чтобы получить четыре члена, сгруппировать похожие термины и разложить их на множители. В этот процесс обычно входят следующие шаги:
В этот процесс обычно входят следующие шаги:
Пример
Решите
с помощью факторинга.
Решение
Вы можете видеть, что константа находится в правой части уравнения. Следовательно, мы перенесем его в левую часть уравнения и положим уравнение равным нулю.
Теперь мы разложим средний член на два члена таким образом, чтобы произведение было равно
, а сумма или разность равнялась
Мы получили два новых уравнения, установив каждый коэффициент равным до нуля.Мы решим два уравнения отдельно для x:
и
и
Следовательно, -10 и -8 являются корнями уравнения. Чтобы проверить наш ответ, мы подставим эти значения в исходное уравнение:
на
на
Следовательно, наш ответ правильный, т. Е. -10 и -8 — решения уравнения.
ii.Квадратичная формула
В большинстве случаев мы не можем найти множители квадратного уравнения. В этих задачах использование формулы корней квадратного уравнения помогает нам определить корни или нули уравнения. Мы особенно используем квадратную формулу, когда корни или нули квадратных уравнений не являются рациональными числами. Следующая формула используется для квадратного уравнения
В этих задачах использование формулы корней квадратного уравнения помогает нам определить корни или нули уравнения. Мы особенно используем квадратную формулу, когда корни или нули квадратных уравнений не являются рациональными числами. Следующая формула используется для квадратного уравнения
,
Элемент формулы, представленный под радикальным знаком
, называется дискриминантом.Дискриминант квадратной формулы определяет следующие три возможности:
Пример
Найти корни уравнения
Решение
Мы не можем разложить уравнение на множители в этом примере, поэтому мы перейдем к использованию квадратной формулы для нахождения корней уравнения:
Здесь a = 7, b = -2 и c = -8.
Мы заменим значения a, b и c в формуле:
Упростите приведенное выше выражение, чтобы получить следующие решения:
и
. Здесь вы можете найти репетитора по математике. .
iii. Завершение квадрата
Третий метод решения квадратных уравнений — завершение квадратного метода. Если корни уравнения являются действительными из мнимых чисел, то этот метод является наиболее подходящим. Для решения квадратных уравнений с помощью этого метода используются следующие шаги:
Если корни уравнения являются действительными из мнимых чисел, то этот метод является наиболее подходящим. Для решения квадратных уравнений с помощью этого метода используются следующие шаги:
- Возьмите константу в правой части уравнения, чтобы преобразовать уравнение в форму
- Старший коэффициент «a» должен быть равен 1.Если это не так, вы должны сделать его равным 1, разделив все уравнение на старший коэффициент a.
- Используйте значение b, чтобы сделать правильный квадрат в левой части уравнения. Добавьте к обеим сторонам уравнения.
- На последнем этапе извлеките квадратный корень из обеих частей уравнения и решите полученное уравнение относительно неизвестного значения x.
Пример
Решите уравнение
, заполнив квадратный метод.
Решение
Возьмите константу в правой части уравнения:
Вычислите значение
и добавьте его к обеим частям уравнения:
Извлеките квадратный корень из обеих частей уравнения и решить полученное уравнение относительно x:
или
или
или
▷ КВАДРАТИЧЕСКОЕ УРАВНЕНИЕ | Как решать квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0 , где a не равно нулю. В зависимости от значений, которые имеют b и c , мы будем говорить о полных или неполных уравнениях.
В зависимости от значений, которые имеют b и c , мы будем говорить о полных или неполных уравнениях.
Полное квадратное уравнение
Полные квадратные уравнения являются конкретными, в которых b и c отличны от нуля, и решаются по следующей формуле:
Пример полного квадратного уравнения:
Дискриминантное уравнение
Дискриминант уравнения используется для определения количества решений уравнения.
Неполное квадратное уравнение
Неполное квадратное уравнение — это уравнение, в котором b = 0 или c = 0 , и его можно решить очень просто, без необходимости применять какие-либо формулы.
Факторинговые квадраты
Квадраты факторизации — это квадратики, у которых есть факторные произведения в форме паралича, при котором появляется неизвестная переменная. Для ее решения устраняются факторы, и она решается по формуле полных уравнений.
Пример квадратичного разложения:
Помните : для решения квадратных уравнений, то есть «произведения нескольких множителей, равных нулю», мы приравниваем каждый множитель к нулю и решаем соответствующие уравнения.
Радикальные уравнения
Радикальные уравнения — это уравнения, содержащие корни. например:
Как решить уравнения радикалов:
- Мы изолируем радикал в одном элементе, передавая другой в другой:
- Мы возводим два элемента в квадрат:
- Мы передаем все элементу и заказываем его:
- Решаем полученное уравнение: ( a = –3, b = 8, c = 3 )
- В этом типе радикального уравнения при возведении в квадрат (2-й шаг ) могут появиться ложные решения.Следовательно, необходимо проверить решения, полученные путем их подстановки в исходное уравнение.
 В этом случае x = –1 / 3 не является решением, а x = 3 является. Уравнение имеет решение: x = 3
В этом случае x = –1 / 3 не является решением, а x = 3 является. Уравнение имеет решение: x = 3
Упражнения с квадратными уравнениями
1. Рассчитайте значения неизвестных и индикаторов от наименьшего к наибольшему:
Информация
Вы уже проходили викторину раньше.Следовательно, вы не можете запустить его снова.
Вы должны войти или зарегистрироваться, чтобы начать викторину.
Вы должны пройти следующую викторину, чтобы начать эту викторину:
Ваше время:
Истекло время
Вы набрали 0 из 0 баллов, (0)
| Средний балл | |
| Ваша оценка |
2.Рассчитайте и укажите минимально возможные решения:
Информация
Вы уже проходили викторину раньше. Следовательно, вы не можете запустить его снова.
Вы должны войти или зарегистрироваться, чтобы начать викторину.
Вы должны пройти следующую викторину, чтобы начать эту викторину:
Ваше время:
Истекло время
Вы набрали 0 из 0 баллов, (0)
| Средний балл | |
| Ваша оценка |
Уравнение квадратного корня.Решение неполных квадратных уравнений. Квадратные уравнения. Коротко о главном
Библиографическое описание: Гасанов А.Р., Курамшин А.А., Елков А.А., Ширенков Н.В., Уланов Д.Д., Смелева О.В. Способы решения квадратных уравнений // Молодой ученый. — 2016. — №6.1. — С. 17-20..02.2019).
Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не включенными в школьную программу.Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самостоятельно, а также познакомить одноклассников с этими способами.
Что такое «квадратные уравнения»?
Квадратное уравнение — уравнение типа aX. 2
+ BX + C = 0 , где a. , г. , г. — Некоторые числа ( a ≠ 0 ), x. — Неизвестно.
Числа a, b, C называются коэффициентами квадратного уравнения.
- a называется первым коэффициентом;
- b называется вторым коэффициентом;
- c — член свободный.
А кто первый «изобрел» квадратные уравнения?
Некоторые алгебраические методы решения линейных и квадратных уравнений были известны 4000 лет назад в древнем Вавилоне. Древние вавилонские глиняные плиты, найденные где-то между 1800 и 1600 годами до нашей эры, являются самым ранним свидетельством изучения квадратных уравнений. На этих же знаках представлены методы решения некоторых типов квадратных уравнений.
Необходимость решения уравнений не только первой, но и второй степени в древности была вызвана необходимостью решения задач, связанных с расположением земельных участков и с земляными работами военного характера, а также с развитием астрономии. и сама математика.
Правило решения этих уравнений, изложенное в вавилонских текстах, по существу совпадает с современным, но неизвестно, как вавилоняне достигли этого правила. Практически все тексты клинбоу, найденные до сих пор, только задачи с решениями, изложенными в форме рецептов, без указания того, как они были найдены.Несмотря на высокий уровень развития алгебры в Вавилоне, в текстах клинокса нет понятия отрицательного числа и общих методов решения квадратных уравнений.
Вавилонская математика примерно с IV века до нашей эры. Использовал метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 г. до н. Э. Евклид предложил более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII век нашей эры).
Брахмагупта изложил общее правило решения квадратных уравнений, представленных в единой канонической форме:
aX2 + BX = C, A> 0
В этом уравнении коэффициенты могут быть отрицательными. Правило брахмагупты по сути совпадает с нашим.
В Индии раздавались публичные соревнования по решению сложных задач. В одной из старинных индийских книг о таких состязаниях сказано следующее: «Как солнце светит своими тенями, так и ученого омрачают народные сборники, предлагающие и решающие алгебраические задачи.«Задачи часто имеют поэтическую форму.
В алгебраическом трактате Аль-Хорезми Дана классификация линейных и квадратных уравнений. Автор включает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т.е. Ah3 = BX.
2) «Квадраты равны числу», т.е. Ah3 = s.
3) «Корни равны числу», то есть Ах3 = р.
4) «Квадраты и числа равны корням», т.е. Ah3 + C = BX.
5) «Квадраты и корни равны числу», то есть Ah3 + BX = p.
6) «Корни и числа равны квадратам», то есть BX + C = = Ah3.
Для аль-Хорезми, избегая использования отрицательных чисел, члены каждого из этих уравнений находят, а не вычитают. При этом явно не учитываются уравнения, не имеющие положительных решений. Автор предлагает способы решения этих уравнений, используя методы аль-Джабра и аль-Мукабалы.Его решение, конечно, не совпадает с нашим. Уже не говоря о том, что это чисто риторический характер, следует отметить, например, что при решении неполного квадратного уравнения первого вида аль-Корезми, как и вся математика до XVII века, не учитывает нулевое решение , видимо потому, что в конкретных практических задачах практического значения не имеет. Решая полные квадратные уравнения, всегда на частных числовых примерах излагаются правила решения, а затем их геометрические доказательства.
Формы решения квадратных уравнений для образца аль-Хорезми в Европе впервые были изложены в «Книге Абака», написанной в 1202г. Итальянский математик Леонард Фибоначчи . Автор самостоятельно разработал несколько новых алгебраических примеров решения задач и первым в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но также в Германии, Франции и других странах Европы.Многие задания из этой книги вошли практически во все европейские учебники XIV-XVII веков. Общее правило решения квадратных уравнений, приведенных к единой канонической форме X2 + BX = C со всевозможными комбинациями знаков и коэффициентов B, C, было сформулировано в Европе в 1544 г. г. М. Штиффелем.
Вывод формулы решения квадратного уравнения в целом доступен в Vieta, но Viet распознавал только положительные корни. Итальянские математики Тарталия, Кардано, Бомбелли Среди первых в XVI веке.Даны, помимо положительных, и отрицательные корни. Только в XVII в. Благодаря труду Жирара, Декарта, Ньютона и других ученых метод решения квадратных уравнений принимает современный вид.
Рассмотрим несколько способов решения квадратных уравнений.
Стандартные способы решения квадратных уравнений из школьной программы:
- Разложение левой части фабричного уравнения.
- Метод выделения полной площади.
- Решение квадратных уравнений по формуле.
- Графическое решение квадратного уравнения.
- Решение уравнений с помощью теоремы Виета.
Остановимся на решении вышеуказанных и не перечисленных квадратных уравнений теоремы Виета.
Напомним, что для решения вышеуказанных квадратных уравнений достаточно найти два таких числа, произведение которых равно свободному члену, а величина — второму коэффициенту с противоположным знаком.
Пример. х. 2
-5х + 6 = 0
Необходимо найти числа, у которых работа 6, а сумма 5. Такими числами будут 3 и 2.
Ответ: X. 1
= 2, х 2
= 3.
Но этот метод можно использовать для уравнений, у которых первый коэффициент не равен единице.
Пример. 3X. 2
+ 2х-5 = 0
Возьмите первый коэффициент и умножьте его на свободный член: x 2 + 2x-15 = 0
Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2.Это числа 5 и 3. Чтобы найти корни исходного уравнения, полученные корни нужно разделить на первый коэффициент.
Ответ: X. 1
= -5 / 3, х 2
= 1
6. Решение уравнений методом «транзита».
Рассмотрим квадратное уравнение ah 2 + BX + C = 0, где a ≠ 0.
Умножая обе части на A, получаем уравнение a 2 x 2 + ABH + AC = 0.
Пусть oh = y, где x = y / A; Тогда приходим к уравнению в 2 + BY + AC = 0, эквивалентному этому. Его корни в 1 и 2 найдем с помощью теоремы Виета.
Окончательно получаем x 1 = in 1 / a и x 2 = y 2 / a.
В этом методе коэффициент A умножается на свободный член, независимо от того, как «передается» ему, поэтому он называется «транзитным» методом. Этот метод используется, когда вы можете легко найти корни уравнения с помощью теоремы Виета и, что наиболее важно, когда дискриминант представляет собой точный квадрат.
Пример. 2x 2
— 11х + 15 = 0.
«Перенесем коэффициент 2 на свободный член и произведем замену, чтобы получилось уравнение в 2 — 11U + 30 = 0.
Согласно обратной теореме Виета
в 1 = 5, х 1 = 5/2, х 1 = 2,5; в 2 = 6, х 2 = 6/2, х 2 = 3.
Ответ: H. 1
= 2,5; H. 2
= 3.
7. Свойства коэффициентов квадратного уравнения.
Пусть квадратное уравнение ah 2 + BX + C = 0, а ≠ 0.
1. Если A + B + C = 0 (т.е. сумма коэффициентов уравнения равна нулю), то x 1 = 1.
2. Если a — b + c = 0, или b = a + s, то x 1 = — 1.
Пример. 345x 2
— 137х — 208 = 0.
Поскольку a + b + c = 0 (345 — 137 — 208 = 0), то x 1 = 1, x 2 = -208/345.
Ответ: H. 1
= 1; H. 2
= -208/345
.
Пример. 132x 2
+ 247x + 115 = 0
Поскольку A-B + C = 0 (132 — 247 + 115 = 0), то x 1 = — 1, x 2 = — 115/132
Ответ: H. 1
= — 1; H. 2
= — 115/132
Есть и другие свойства коэффициентов квадратного уравнения.Но ледяное использование сложнее.
8. Решение квадратных уравнений с номограммой.
Рис. 1. Номограмма
Это старый и сейчас забытый способ решения квадратных уравнений, размещенный на S.83 Сборник: Brandis V.M. Четырехзначные математические таблицы. — М., Просвещение, 1990.
.
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейный масштаб номограммы строится по формулам (рис. 1):
Считается OS = P, ED = Q, OE = A (все в см), из фиг.1 подобия треугольников San и CDF. Получаем пропорцию
, где после замен и упрощений следует уравнение z 2 + pz + q = 0, , кроме того, буква z. означает метку любой точки криволинейной шкалы.
Фиг.2 Решение квадратных уравнений с использованием номограммы
Примеры.
1) для уравнения z. 2
— 9z + 8 = 0 Номограмма дает корни z 1 = 8,0 и z 2 = 1,0
Ответ: 8,0; 1.0.
2) решения с уравнением номограммы
2z. 2
— 9z + 2 = 0.
Делим коэффициенты этого уравнения на 2, получаем уравнение z 2 — 4.5z + 1 = 0,
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
Ответ: 4; 0,5.
9. Геометрический метод решения квадратных уравнений.
Пример. ч. 2
+ 10x = 39
В оригинале эта задача сформулирована так: «Квадрат и десять корней равны 39».
Рассмотрим квадрат со стороны X, прямоугольники построены по его сторонам так, чтобы другая сторона каждого из них была равна 2.5, поэтому каждая площадь в 2,5 раза больше. Полученная фигура дополняется затем до нового Квадрата ABSD, завершая четыре равных квадрата в углах, сторона каждого из них равна 2,5, а площадь равна 6,25
Рис. 3 графический метод решения уравнения x 2 + 10x = 39
Квадрат ABCD S можно представить как количество пространства: исходный квадрат X 2, четыре прямоугольника (4 ∙ 2,5x = 10x) и четыре прикрепленных квадрата (6,25 ∙ 4 = 25), т.е. S = x 2 + 10х = 25.Заменяя x 2 + 10x на число 39, получаем, что S = 39+ 25 = 64, откуда следует, что сторона квадрата AVD, т.е. Cut AB = 8. Для искомой стороны x исходного квадрата мы получить
10. Решение уравнений с помощью теоремы mouture.
Теорема косить. Вычет от деления многочлена P (x) на скручивание x — α равен p (α) (то есть значение p (x) при x = α).
Если число α является корнем многочлена P (x), то этот многочлен делится на X -α без остатка.
Пример. x²-4x + 3 = 0
P (x) = x²-4x + 3, α: ± 1, ± 3, α = 1, 1-4 + 3 = 0. Делим p (x) на (x — 1): (x² -4x + 3) / (x — 1) = x-3
x²-4x + 3 = (x — 1) (x — 3), (x — 1) (x — 3) = 0
х — 1 = 0; х = 1, или х-3 = 0, х = 3; Ответ: H. 1
= 2, х 2
= 3.
Вывод: Способность быстро и рационально решать квадратные уравнения просто необходима для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, уравнений двухкомпонентного режима, а также в старшей школе тригонометрических, ориентировочных и логарифмические уравнения.Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных методов, решение метода преобразования (6) и решение уравнений для коэффициента свойства (7), так как они более доступны для понимания.
Литература:
- Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
- Алгебра 8 класс: Учебник для 8 кл. общее образование. Учреждения Макарычев Ю. Н., Миндюк Н. Г., Нешков К.И., Суворов С.Б. Под ред. С. А. Теликовский 15 изд., Дорабы. — М .: Просвещение, 2015
- https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE% D0. % B5_% D1% 83% D1% 80% D0% B0% D0% B2% D0% BD% D0% B5% D0% BD% D0% B8% D0% B5
- Глейзер Г.И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодой. — М .: Просвещение, 1964.
.
.
Эта тема изначально может показаться сложной из-за набора не самой простой формулы. Мало того, что сами квадратные уравнения имеют длинные записи, также корни проходят через дискриминант.Итого три новых формулы. Не очень легко запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы запомнятся сами собой.
Общий вид квадратного уравнения
Предлагает их явную запись, когда сначала записывается наибольшая степень, а далее — по убыванию. Нередко бывают ситуации, когда комплектующие стоят болото. Тогда лучше переписать уравнение в порядке убывания от переменной.
Введем обозначения.Они представлены в таблице ниже.
Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.
Причем коэффициент A ≠ 0. Обозначим эту формулу цифрой один.
Когда уравнение указано, неясно, сколько корней будет в ответе. Поскольку всегда возможен один из трех вариантов:
- , решение будет двумя корнями;
- ответ будет одним числом;
- корней уравнения не будет полностью.
И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в том или ином случае.
Типы записей квадратных уравнений
В задачах могут быть разные записи. Они не всегда будут выглядеть как общая формула квадратного уравнения. Иногда этого бывает недостаточно для некоторых сроков. Выше было написано полное уравнение. Если убрать в нем второй или третий срок, то достанется что-то другое.Эти записи также называются квадратными уравнениями, только неполные.
И только термы, в которых коэффициенты «В» и «С» могут исчезнуть. Число «А» не может быть равно нулю ни при каких обстоятельствах. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполных видов уравнений будут такими:
Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет номер два, а вторая — три.
Дискриминант и зависимость количества корней от его значения
Это число необходимо знать для вычисления корней уравнения.Его всегда можно рассмотреть, какой бы ни была формула квадратного уравнения. Чтобы вычислить дискриминант, вам нужно воспользоваться записанным ниже равенством, которое будет иметь номер четыре.
После подстановки в эту формулу значений коэффициентов можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два разных корня. При отрицательном числе корней квадратное уравнение будет отсутствовать.В случае его равенства нулевой ответ будет один.
Как решить квадратное уравнение полного обзора?
Фактически рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того, как будет установлено, что есть корни квадратного уравнения, и известно их количество, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.
Поскольку стоит знак «±», то будет два значения.Выражение под знаком квадратного корня является дискриминантом. Поэтому формулу можно переписать по-разному.
Формула номер пять. Из той же записи ясно, что если дискриминант равен нулю, оба корня будут принимать одинаковые значения.
Если решение квадратных уравнений еще не выработано, лучше перед применением формул дискриминанта и переменной записать значения всех коэффициентов. В дальнейшем этот момент не вызовет затруднений.Но в самом начале возникает путаница.
Как решить квадратное уравнение неполных видов?
Здесь все намного проще. В дополнительных формулах нет необходимости. И те, что уже записаны на дискриминант и неизвестны, вам не понадобятся.
Сначала рассмотрим неполное уравнение под номером два. В этом равенстве предполагается сделать неизвестную величину за скобкой и решить линейное уравнение, которое останется в скобках.Ответ будет два корня. Первый обязательно равен нулю, потому что есть множитель, состоящий из самой переменной. Второй приведет к решению линейного уравнения.
Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Затем нужно разделить коэффициент на неизвестное. Остается только извлечь квадратный корень и не забыть дважды записать его с противоположными знаками.
Далее записываются некоторые действия, помогающие научиться решать все виды равенств, которые преобразуются в квадратные уравнения.Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недостатки являются причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет выполнять постоянно. Потому что будет устойчивый навык.
- Сначала необходимо записать уравнение в стандартной форме. То есть сначала член с наибольшей степенью переменной, а затем — без степени и последний — просто число.
- Если коэффициент «А» окажется минусом, то это может усложнить работу новичку по изучению квадратных уравнений. Лучше избавиться от него. Для этого все равенство необходимо умножить на «-1». Это означает, что все компоненты поменяют знак на противоположный.
- Таким же образом рекомендуется избавиться от фракций. Просто умножьте уравнение на соответствующий множитель, чтобы знаменатели уменьшились.
Примеры
Требуются следующие квадратные уравнения:
x 2 — 7x = 0;
15 — 2х — х 2 = 0;
х 2 + 8 + 3х = 0;
12х + х 2 + 36 = 0;
(х + 1) 2 + х + 1 = (х + 1) (х + 2).
Первое уравнение: x 2 — 7x = 0. Оно неполное, поэтому решается, как описано для формулы номер два.
После изготовления скобки получается: x (x — 7) = 0.
Первый корень принимает значение: x 1 = 0. Второй будет найден из линейного уравнения: x — 7 \ u003d 0. Легко заметить, что x 2 = 7.
Второе уравнение: 5x 2 + 30 = 0. Опять неполное. Он решается только так, как описано для третьей формулы.
После перенесения 30 в правую часть равенства: 5х 2 = 30.Теперь нужно сделать деление на 5. Получается: x 2 = 6. Ответами будут числа: x 1 = √6, x 2 = — √6.
Третье уравнение: 15 — 2x — x 2 = 0. Здесь и далее решение квадратных уравнений начнем с их переписывания к стандартному виду: — x 2 — 2x + 15 = 0. Теперь пора воспользоваться вторым полезный совет и умножьте все на минус один. Получается x 2 + 2x — 15 = 0. По четвертой формуле необходимо вычислить дискриминант: d = 2 2 — 4 * (- 15) = 4 + 60 = 64.Это положительное число. Из сказанного выше получается, что уравнение имеет два корня. Их нужно рассчитывать по пятой формуле. Получается, что x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда x 1 = 3, x 2 = — 5.
Четвертое уравнение x 2 + 8 + 3x = 0 преобразуется в такое: x 2 + 3x + 8 = 0. Его дискриминант равен этому значению: -23. Поскольку это отрицательное число, ответом на эту задачу будет следующая запись: «Корней нет».
Пятое уравнение 12x + x 2 + 36 = 0 нужно переписать так: x 2 + 12x + 36 = 0.После применения формулы дискриминанта получается число ноль. Это значит, что у него будет один корень, а именно: x = -12 / (2 * 1) = -6.
Шестое уравнение (x + 1) 2 + x + 1 = (x + 1) (x + 2) требует преобразований, которым должны быть даны такие компоненты, до разрыва скобки. На сайте есть такое выражение: x 2 + 2x + 1. После равенства появится запись: x 2 + 3x + 2. После подсчета таких слагаемых уравнение примет вид: x 2 — x = 0.2 + b * x + c = 0, где x — переменная, a, b, c — константы; А.0. Задача — найти корни уравнения.
Геометрический смысл квадратного уравнения
График функции, представленной квадратным уравнением, представляет собой параболу. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (x). Из этого следует, что возможны три случая:
1) Парабола не имеет точек пересечения с осью абсцисс.Это означает, что он находится в верхней плоскости ветвями вверх или внизу ветвями вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
2) Парабола имеет одну точку пересечения с осью oh. Такая точка называется вершиной парабола, и квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3) Последний случай на практике интереснее — есть две точки пересечения параболы с осью абсцисс.Это означает, что существует два действительных корня уравнения.
На основе анализа коэффициентов степеней переменных можно сделать интересные выводы о размещении параболы.
1) Если коэффициент больше нуля, парабола направлена вверх, если отрицательный — ветви параболы направлены вниз.
2) Если коэффициент b больше нуля, то вершина параболы лежит в левой полуплоскости, если принимает отрицательное значение — то в правой.2 и реализовать преобразование
Отсюда найти
Формула дискриминанта и корни квадратного уравнения
Дискриминант называется значением условного выражения, он положительный, уравнение имеет два действительные корни, вычисляемые по формуле При нулевом дискриминанте квадратное уравнение имеет одно решение (два совпадающих корня), которое легко получить из приведенной выше формулы при d = 0 с отрицательным дискриминантом уравнения действительных корней.Однако, чтобы сохранить решения квадратного уравнения в комплексной плоскости, и их значение вычисляется по формуле
Теорема Виета
Рассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение. Сама запись легко сопровождается самой теоремой Виета: если у нас есть квадратное уравнение типа, сумма его корней равна коэффициенту P, взятому с обратным знаком, а произведение корней уравнения равно свободному срок Q.Формулы, приведенные выше, можно увидеть в классическом уравнении константы A, отличной от нуля, тогда все уравнение следует разделить на нее, а затем применить теорему Виета.
График квадратного уравнения для множителей
Пусть задача: разложить квадратное уравнение на множители. Для его выполнения сначала решаем уравнение (находим корни). Далее найденные корни подставляются в формулу разложения квадратного уравнения в этой задаче.2-26x + 120 = 0.
Решение: Пишем коэффициенты и подставляем в формулу дискриминанта
Корень этого значения равен 14, его легко найти с помощью калькулятора или запомнить при частом использовании Однако для удобства в конце статьи я приведу список квадратов с цифрами, которые часто могут встретиться с подобными задачами.
Подставляем фундамент в формулу корня
И получаем
Задача 2. Решаем уравнение
2x 2 + x-3 = 0.
Решение: имеем полное квадратное уравнение, выписываем коэффициенты и находим дискриминант
По известным формулам находим корни квадратного уравнения
Задача 3. Решаем уравнение
9x 2 -12x + 4 = 0.
Решение: У нас есть полное квадратное уравнение. Определить дискриминант
Мы получили случай, когда корни совпадают. Найдите значения корней по формуле
Задание 4.2 + x-6 = 0.
Решение: В случаях, когда есть небольшие коэффициенты при x, целесообразно применить теорему Виета. По ее словам, получаем два уравнения
Из второго условия получаем, что работа должна быть равна -6. Это означает, что один из корней отрицательный. У нас есть следующая возможная пара решений (-3; 2), (3; -2). Принимая во внимание первое условие, вторая пара решений отклоняется.
Корневые уравнения равны
Задача 5.Найдите длину стороны прямоугольника, если его периметр равен 18 см, а площадь равна 77 см. 2.
Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим x — наибольшую сторону, тогда 18-x — меньшая сторона. Площадь прямоугольника равна произведению этих длин:
х (18-х) = 77;
или
x 2 -18x + 77 = 0.
Находим дискриминант уравнения
Вычисляем корни уравнения
Если ax = 11, то 18h = 7, наоборот, тоже истина (если х = 7, то 21-х = 9).
Задание 6. Квадратный квадрат 10x 2 -11x + 3 = 0 Уравнения для множителей.
Решение: вычислить корни уравнения, для этого находим дискриминант
Подставляем найденное значение в формулу корня и вычисляем
Применяем формулу разложения квадратного уравнения по корням
Расположение скобок будет получить личность.
Квадратное уравнение с параметром
Пример 1. При каких значениях параметра но уравнение (A-3) x 2 + (3-A) x-1/4 = 0 имеет один корень?
Решение: прямой подстановкой значения A = 3 видим, что у него нет решения.Далее мы используем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Дискриминант напитка
упростим его и приравняем к нулю
Получено квадратное уравнение для параметра A, решение которого легко получить на методе Виета. теорема. Количество корней равно 7, а их работа 12. Простая переборка, установив, что числа 3.4 будут корневыми уравнениями. Поскольку решение А = 3 мы уже отвергли в начале расчетов, единственно правильным будет — а = 4.2 + (2a + 6) x-3a-9 = 0 имеет более одного корня?
Решение: Рассмотрим первые особые точки, они будут значениями = 0 и a = -3. При A = 0 уравнение упростится до вида 6x-9 = 0; х = 3/2 и будет один корень. При A = -3 получаем тождество 0 = 0.
Вычисляем дискриминант
и находим значения, в которых он положительный
Из первого условия получим> 3. Для второго находим дискриминант и корни уравнения
Определим промежутки, в которых функция принимает положительные значения.Цифра точка а = 0 Получить 3> 0
.
Итак, за интервалом (-3; 1/3) функция отрицательная. Не забываем про точку а = 0, это следует исключить, потому что исходное уравнение в ней имеет один корень.
В результате получаем два интервала, удовлетворяющих условию задачи
На практике будет много похожих задач, попробуйте разобраться с задачами самостоятельно и не забывайте учитывать взаимоисключающие условия. Хорошо прочтите формулы решения квадратных уравнений, они часто нужны при расчетах в разных задачах и науках.
Некоторые задачи по математике требуют умения вычислять значение квадратного корня. К таким задачам относится решение уравнений второго порядка. В этой статье мы даем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят о том, что его начали использовать впервые в первой половине XVI века в Германии (первая немецкая работа по алгебре Кристофера Рудольфа).Ученые считают, что указанный символ представляет собой преобразованную латинскую букву R (Radix в переводе с латыни означает «корень»).
Этому значению равен корень из любого числа, квадрат которого соответствует управляемому выражению. На языке математики это определение будет выглядеть так: √x = y, если y 2 = x.
Корень положительного числа (X> 0) тоже положительное число (Y> 0), но если они пустят корень из отрицательного числа (x
Приведем два простых примера:
√9 \ u003d 3, так как 3 2 = 9; √ (-9) = 3i, так как i 2 = -1.
Итерационная формула Герона для нахождения значений квадратных корней
Приведенные выше примеры очень просты, и вычисление корней в них не представляет никаких затруднений. Трудности начинают появляться уже при нахождении значений корня для любого значения, которое невозможно представить в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что что на практике необходимо найти корни для простых чисел: например √ (12.15), √ (8.5) и так далее.
Во всех вышеперечисленных случаях следует применять специальный метод вычисления корня из квадрата. В настоящее время существует несколько таких методов: например, разложение по ряду Тейлора, разделение на столбец и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский метод определения квадратных корней (есть свидетельства того, что древние вавилоняне использовали ее в своих практических вычислениях). ).
Пусть нужно определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
a n + 1 = 1/2 (a n + x / a n), где Lim n-> ∞ (a n) => x.
Определите эту математическую запись. Для вычисления √x нужно взять некоторое число A 0 (оно может быть произвольным, однако для быстрого получения результата следует выбрать его так, чтобы (A 0) 2 было как можно ближе к x. Затем подставить его в по указанной формуле вычисления квадратного корня и получите новое число A 1, которое уже будет ближе к желаемому значению.После этого уже необходимо подставить выражение и получить 2. Эту процедуру следует повторить до получения необходимой точности.
Пример применения итерационной формулы Gerona
Приведенный выше алгоритм получения квадратного корня из некоторого заданного числа может показаться для многих довольно сложным, на самом деле все оказывается намного проще, так как эта формула очень сходится быстро (особенно если выбрано удачное число A 0).
Приведем простой пример: необходимо вычислить √11. Выбираем 0 = 3, так как 3 2 = 9, что ближе к 11, чем 4 2 = 16. Подставляя в формулу, получаем:
a 1 = 1/2 (3 + 11/3) = 3,333333;
а 2 = 1/2 (3,33333 + 11 / 3,33333) = 3,316668;
a 3 = 1/2 (3,316668 + 11 / 3,316668) = 3,31662.
Нет смысла продолжать вычисления, так как мы получили, что A 2 и A 3 начинают различаться только пятым знаком после запятой.Таким образом, достаточно было всего 2 раза применить формулу, чтобы вычислить √11 с точностью 0,0001.
В настоящее время калькуляторы и компьютеры широко используются, тем не менее, отмеченная формула полезна, чтобы иметь возможность вручную рассчитать их точное значение.
Уравнения второго порядка
Понимание того, что такое квадратный корень, и способность его вычислять, используется при решении квадратных уравнений. Эти уравнения называются равенствами с одной неизвестной, общий вид которых показан на рисунке ниже.
Здесь C, B и A — некоторые числа, причем A не должно быть равным нулю, а значения C и B могут быть совершенно произвольными, включая ноль.
Любые значения ICA, удовлетворяющие равенству, указанному на рисунке, называются его корнями (не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x 2), корней не может быть больше двух чисел. Как найти эти корни, рассмотрим далее в статье.
Нахождение корней квадратного уравнения (формулы)
Этот метод решения рассматриваемого типа равенства еще называют универсальным, или методом через дискриминант. Его можно использовать для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
Она показывает, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление X 1 отличается от вычисления X 2 только знаком перед квадратным корнем.Выражение кормления, равное B 2 — 4AC, есть не что иное, как дискриминант рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, так как он определяет количество и тип решений. Итак, если он равен нулю, решение будет только одно, если оно положительное, уравнение имеет два действительных корня, наконец, отрицательный дискриминант приводит к двум комплексным корням x 1 и x 2.
Теорема Виета или некоторые свойства корней уравнения уравнения второго порядка
В конце XVI века один из основоположников современной французской алгебры, изучая уравнения второго порядка, смог получить свойства его корней.Математически их можно записать как:
x 1 + x 2 = -b / a и x 1 * x 2 = c / a.
Оба равенства легко могут получить каждое, для этого необходимо только произвести соответствующие математические операции с корнями, полученными по формуле с дискриминантом.
Комбинация этих двух выражений по праву может быть названа второй формулой корней квадратного уравнения, которая дает возможность угадывать его решения без использования дискриминанта.Здесь следует отметить, что, хотя оба выражения всегда действительны, их удобно применять для решения уравнения, только если оно может быть разложено на множители.
Задание на закрепление полученных знаний
Решаем математическое задание, в котором продемонстрируем все рассмотренные в статье приемы. Условия задания следующие: необходимо найти два числа, для которых произведение равно -13, а сумма равна 4.
Это условие сразу напоминает теорему Виета, использующую формулы суммы квадратов. корни и их работа, напишите:
x 1 + x 2 = -b / a = 4;
х 1 * х 2 = с / у = -13.
Если считать, что a = 1, то b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x 2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получаем следующие корни:
x 1,2 = (4 ± √ d) / 2, d = 16-4 * 1 * (-13) = 68.
То есть задача сводится к нахождению числа √68. Обратите внимание, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получаем: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a 0 = 4, затем:
a 1 = 1/2 (4 + 17/4) = 4,125;
а 2 = 1/2 (4,125 + 17 / 4,125) = 4,1231.
В Расчет А 3 нет необходимости, потому что найденные значения в сумме различаются на 0,02. Таким образом, √68 = 8246. Подставив его в формулу для x 1,2, получим:
x 1 = (4 + 8,246) / 2 = 6,123 и x 2 = (4-8,246) / 2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если они найдут свою работу, она будет -12,999, что с точностью до 0 удовлетворяет задаче задачи.001.
Я надеюсь, что изучая эту статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения квадратных уравнений используются другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».
Какие квадратные уравнения называются полными? Это уравнений вида ah 2 + b x + c = 0 где коэффициенты a, b и не равны нулю. Итак, чтобы решить полное квадратное уравнение, необходимо вычислить дискриминант D.
D = b 2 — 4As.
В зависимости от того, какой степени важности является дискриминант, мы напишем ответ.
Если дискриминант является отрицательным числом (D
Если дискриминант равен нулю, x = (-b) / 2a. Когда дискриминант — положительное число (D> 0),
, то x 1 = (-b — √d) / 2a, а x 2 = (-b + √d) / 2a.
Например. Решите уравнение x 2 — 4x + 4 = 0.
D = 4 2 — 4 · 4 = 0
х = (- (-4)) / 2 = 2
Ответ: 2
Решите уравнение 2. х 2
+ х + 3 = 0.
Д = 1 2 — 4 · 2 · 3 = — 23
Ответ: Нет корней .
Решите уравнение 2. x 2
+ 5х — 7 = 0 .
Д = 5 2 — 4 · 2 · (-7) = 81
х 1 = (-5 — √81) / (2 · 2) = (-5 — 9) / 4 = — 3,5
х 2 = (-5 + √81) / (2 · 2) = (-5 + 9) / 4 = 1
Ответ: — 3,5; один .
Итак, представим себе решение полных квадратных уравнений по схеме на Рисунке 1.
По этим формулам можно решить любое полное квадратное уравнение. Нужно только внимательно следить за , чтобы уравнение было записано полиномом стандартного типа.
но x 2
+ BX + C, Иначе можно ошибиться. Например, в записи уравнения x + 3 + 2x 2 = 0 ошибочно можно решить, что
а = 1, b = 3 и c = 2.затем
D = 3 2 — 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (См. Решение примера 2 выше).
Следовательно, если уравнение записано не в многочлен стандартного вида, то сначала следует записать полное квадратное уравнение полиномом стандартного вида (в первую очередь следует снять отметку с наибольшим показателем, то есть ). но x 2
затем с меньшим —
bX., а затем свободный член от.
При решении данного квадратного уравнения и квадратного уравнения с четным коэффициентом со вторым членом можно использовать другие формулы. Познакомимся с этими формулами. Если в полном квадратном уравнении во втором члене коэффициент будет четным (b = 2k), то уравнение по формулам на рисунке 2 можно решить.
Полное квадратное уравнение называется приведенным выше, если коэффициент равен x 2
равно единице и уравнение примет вид x 2 + px + q = 0 .Такое уравнение можно задать для решения или получить путем деления всех коэффициентов на уравнение коэффициентов , но означает x 2
.
На рисунке 3 показана схема решения приведенных выше квадратных
уравнений. Рассмотрим на примере применение формул, рассмотренных в этой статье.
Пример. Решите уравнение
3 x 2
+ 6х — 6 = 0.
Давайте решим это уравнение, используя формулы, показанные на схеме на Рисунке 1.
D = 6 2 — 4 · 3 · (- 6) = 36 + 72 = 108
√D = √108 = √ (36 · 3) = 6√3
х 1 = (-6 — 6√3) / (2 · 3) = (6 (-1- √ (3))) / 6 = -1 — √3
х 2 = (-6 + 6√3) / (2 · 3) = (6 (-1+ √ (3))) / 6 = -1 + √3
Ответ: -1 — √3; -1 + √3
Видно, что коэффициент при x в этом уравнении — четное число, то есть b = 6 или b = 2k, откуда k = 3.Затем пытаемся решить уравнение по формулам, приведенным на схеме D 1 = 3 2 — 3 · (- 6) = 9 + 18 = 27
√ (D 1) = √27 = √ (9 · 3) = 3√3
х 1 = (-3 — 3√3) / 3 = (3 (-1 — √ (3))) / 3 = — 1 — √3
х 2 = (-3 + 3√3) / 3 = (3 (-1 + √ (3))) / 3 = — 1 + √3
Ответ: -1 — √3; -1 + √3 . Заметили, что все коэффициенты в этом квадратном уравнении делятся на 3 и, выполняя деление, мы получаем сокращенное квадратное уравнение x 2 + 2x — 2 = 0, решая это уравнение с использованием формул для указанного квадрата
уравнения Рис.3.
D 2 = 2 2 — 4 · (- 2) = 4 + 8 = 12
√ (D 2) = √12 = √ (4 · 3) = 2√3
х 1 = (-2 — 2√3) / 2 = (2 (-1 — √ (3))) / 2 = — 1 — √3
х 2 = (-2 + 2√3) / 2 = (2 (-1+ √ (3))) / 2 = — 1 + √3
Ответ: -1 — √3; -1 + √3.
Как видим, решая это уравнение по разным формулам, мы получили один и тот же ответ. Поэтому, хорошо зная формулы, показанные на схеме на Рисунке 1, всегда можно решить любое полное квадратное уравнение.
blog.set, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Solver: Калькулятор квадратного уравнения
Чтобы найти корни (нули) функции второй степени, начните с преобразования этой функции в каноническую форму (максимально упрощая) и приравняйте ее к нулю. После этого шага у вас будет уравнение второй степени, в котором второй член равен нулю. Чтобы решить это уравнение, начните с попытки определить, является ли оно полным или неполным уравнением второй степени.2 + bx + c = 0`. В то время как в неполном `b` или` c` отсутствует или оба. Затем введите коэффициенты членов уравнения в соответствующие поля калькулятора. Таким образом, вы можете не только узнать нули, но и шаг за шагом просмотреть разрешение. Если это полное уравнение, используется общая формула полных уравнений второй степени. Если он неполный, первым шагом в решении этого типа уравнений является построение общего множителя, поскольку в обоих членах повторяется «x».Наконец, у нас есть два фактора, результат которых равен нулю, поэтому один из двух должен быть 0.
×
ПРИМЕЧАНИЕ
Если вы хотите выполнить вычисления, в которых коэффициент является дробью, вы должны ввести число в десятичной форме. Например, вместо «1/4» вы должны ввести «0,25».
Решить (полное) квадратное уравнение
Пошаговое разрешение (полного) квадратного уравнения
Решите неполное уравнение второй степени (независимый член отсутствует)
Пошаговое разрешение (неполного) квадратного уравнения
Решите неполное уравнение второй степени (член первой степени отсутствует)
Пошаговое разрешение (неполного) квадратного уравнения
Любое квадратное уравнение может иметь: 2 решения , если дискриминант (число внутри корня) больше нуля; одно решение , если дискриминант равен нулю; нет решения , если дискриминант отрицательный.Если мы работаем во вселенной комплексных чисел, то уравнение второй степени всегда имеет хотя бы одно решение.
Урок закрепления неполных квадратных уравнений. Неполные квадратные уравнения
Неполные квадратные уравнения
Учитель математики и физики: Балакина Е.Н.
ЦЕЛИ ЗАНЯТИЯ:
- Познакомиться с понятием квадратного уравнения;
- Научитесь определять, является ли уравнение квадратичным; Научитесь определять коэффициенты квадратного уравнения; Составьте квадратное уравнение для заданных коэффициентов; Научитесь определять вид квадратного уравнения: полное или неполное; Научитесь выбирать алгоритм решения неполного квадратного уравнения.
- Научитесь определять, является ли уравнение квадратичным;
- Научитесь определять коэффициенты квадратного уравнения;
- Составьте квадратное уравнение для заданных коэффициентов;
- Научитесь определять форму квадратного уравнения: полное или неполное;
- Научитесь выбирать алгоритм решения неполного квадратного уравнения.
ВОПРОСЫ:
- Что такое уравнение?
- Что значит решить уравнение?
- Что называется корнем уравнения?
- Какие уравнения мы знаем?
Выберите квадратные уравнения:
5x + 26 = 8x — 3,
— 13x = 0,
9x + 2-17 = 0,
34 + 5 — 22x = 11
9x + 7-13 = 0,
— 42x — 29 = 0,
-3 — 35x + 14 = 0,
+ 22 — 5х = 0,
-7 — 46х + 17 = 0,
8х — 6 = 0,
25 — 4х — 9 = 0.
НАЗЫВАЕТСЯ КВАДРАТНОЕ УРАВНЕНИЕ
ПРОСМОТР УРАВНЕНИЯ
a
+
bx + c = 0,
где x —
переменная,
a, b, c —
некоторые номера
кроме того a
=
0.
a — первый коэффициент,
b — второй коэффициент,
c является бесплатным участником.
Квадратное уравнение
-9 + 23x — 11 = 0
-4 + x + 5 = 0
4 + 9x = 0
+ 7x + 1 \ u003d 0
-3 + 15 = 0
-3 — х + 7 = 0
4 + 3 = 0
a = 3, b = -7, c = 12
a = -9, b = 23, c = -11
a = 8, b \ u003d 0, c = 0
a = 5, b = -22, c = -3
a = -4, b = 1, c = 5
a = 4, b = 9, c = 0
a = 1, b = 7, c = 1
a = -3, b = 0, c = 15
a = -3, b = -1, c = 7
a = 4, b = 0, c = 3
Если в квадратном уравнении a
+
bx + c = 0
хотя бы один из коэффициентов b
или из
равно нулю, то такое уравнение называется неполным квадратным уравнением.
Неполные квадратные уравнения бывают трех типов:
- a
= 0 - a
+ б
x = 0 - a
+ c
= 0
1 вариант
-; At 0; 3 AND 0; -2 P n.a. IN -3; 3 R 0; 2 E 0 N 0; 4 A -2,5; 2,5 ПРО -; D
Вариант 2
- + 2x = 0
- 2 — 18 = 0
- 4-11 = — 11+ 9x
- 9 + 1 = 0
- 2 = 4х
- 7-14 = 0
- 9-2 + 16x = 6 + 9
- -4 = 0
- 9 + 1 = 1
- 4-25 = 0
- -2 + 4x = 0
- — 3x = 0
- 7 = 0
- 12x = 6
- 2 = 7 + 2
- 6 + 24 = 0
- 3 + 7 = 12x + 7
- + 2x — 3 = 2x + 6
- 9-4 = 0
- 7х = 2 + 3х
На доске написаны числа 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1
Ученики пишут буквы, соответствующие корням этих уравнений; варианты работают навстречу друг другу.
LED КВАДРАТНОЕ УРАВНЕНИЕ
Вызывается квадрат
уравнение, в котором коэффициент
при равенстве 1:
+
bx + c = 0
ДОМАШНИЕ РАБОТЫ
№
24.11 (ОТВЕТ),
№
24,16 (б, в, г),
№
24,18 (б, в, г).
Историческая справка
Квадратные уравнения были решены в Вавилоне примерно в 2000 году до нашей эры.
В Европе в 2002 году праздновали 800-летие квадратных уравнений, поскольку именно в 1202 году итальянский ученый Леонард Фибоначчи сформулировал формулы квадратных уравнений.
Только в 17 веке, благодаря Ньютону, Декарту и другим ученым, эти формулы приобрели современный вид.
IN Древняя Индия Уже в 499 году проводились публичные соревнования по решению задач по составлению квадратных уравнений.Одна из таких задач принадлежит известному индийскому математику. Бхаскара :
Обезьянья резвая стая
Полностью поев, развлекаясь,
Их квадратная часть восемь
На лугу она развлекалась.
И двенадцать по виноградным лозам
Начали прыгать, висеть.
Сколько было обезьян
Подскажите в этой пачке?
Проведение урока алгебры в 8 классе по теме «Квадратные уравнения.Решение неполных квадратных уравнений ». Введение в понятия полных и неполных квадратных уравнений. Первичная фиксация методов решения неполных квадратных уравнений.
Скачать:
Предварительный просмотр:
Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (учетную запись) Google и войдите в нее: https://accounts.google.com
Подписи к слайдам:
Презентация урока алгебры в классе 8 «Квадратные уравнения. Решение неполных квадратных уравнений »
Загадочное, но знакомое нам, У него есть что-то неизвестное Его корень — вот то, что ищут Найти — интересно всем Каждый скажет без сомнения Перед вами (уравнение)
Решите уравнения a) y — 7 = 0; б) х + 0.5 = 0; в) а х = 0; г) 2 х — 1/3 = 0; д) а (а — 1) = 0; е) х 2 + 4 = 0.
Задача В кинотеатре количество мест в каждом ряду на 8 больше, чем количество рядов. Всего на сеанс пришло 884 зрителя и все места были заняты. Сколько рядов в кинотеатре?
х — ряды; x +8 — места в каждой строке C оставляем уравнение: x (x + 8) = 884; x 2 + 8x-884 = 0.
«Квадратные уравнения. Решение неполных квадратных уравнений» Тематический урок: эпиграф: уравнение — это ключ, с помощью которого можно открыть двери в неизведанное.
цель: ввести понятие квадратного уравнения; Узнайте, как решать неполные квадратные уравнения.
Определение квадратного уравнения Квадратное уравнение — это уравнение вида a ax² + bx + c = 0, de x — переменная, a, b, c — параметры, а ≠ 0. Число a называется величиной первый коэффициент, число b — второй коэффициент, а c — свободный член. Квадратное уравнение также называют уравнением второй степени и, поскольку правая часть является многочленом второй степени и.
Пример квадратных уравнений: abc -2x² + x-1,4 = 0-2 1 -1,4 5x²-4x = 0 5-4 0 3X² + 10,3 = 0 3 0 10,3
Упражнение 1 Are эти уравнения квадратные? 4x²-5x + 2 = 0 -5,6x²-2x- 0,5 = 0 13-7x² = 0 16x²-x³-5 = 0 1-16x = 0 -x² = 0
Задача 2 Назовите эффективность в квадратном уравнении. 3x²-6x + 2 = 0 -x² + 5x + 10 = 0 x²-8x + 1,5 = 0 -4x² + 5 = 0 -36x²-3x = 0 12x² = 0
Неполные квадратные уравнения Если в квадратном уравнении ax² + bx + c = 0 хотя бы один из них равен b или равен нулю, то это уравнение называется неполными квадратными метрами.abc -3x² + 5 = 0-3 0 5 2x²-10x = 0 2-10 0 16x² = 0 16 0 0
Классификация квадратных уравнений полная неполная Аль-Хорезми, где a ≠ 0 b = 0 b = 0, c = 0 c = 0 или либо, либо
Решаем уравнение, если b = 0. -4x² + 25 = 0 — 4x² = — 25 4x² = 25 или I
We решите уравнение, если b = 0, c = 0. III
Решите уравнение, если C = 0. (35 + y) y = 0 35 + y = 0 или II y = 0 y = -35
Тестирование
ед.2. 3. 4. 5 0; -5-5; 5 0 Для задачи № 1. Укажите корни уравнения help
Для задачи № 2. Укажите корни уравнения 1. 2. 3. 4. -4; От 4 до 4; 0 16 0; 4
Для задания № 3. Укажите корни уравнения 1. 2. 3. 4. 3 -3; 0-3 0; 3
Для задания № 4. Укажите корни уравнения 1. 2. 3. 4. 0; 4 16-4; 4-4; 0
01.05.17 Для задания № 5. Укажите корни уравнения 1. 2. 3. 4. -2; 2 4 2 2; 0
Краткое содержание урока: Сегодня я усвоил урок… Я понял … узнал … мои успехи … Я почувствовал трудности … не знал как, но теперь могу … на следующем уроке хочу …
Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (учетную запись) Google и войдите в нее: https://accounts.google.com
Подписи к слайдам:
Урок по неполным квадратным уравнениям. Подготовлено учителем математики МОУ «Успенская ООШ МО» Ахтубинского района »Зенина Н.Г., Крамаренко Т.Н.
« Мне приходится делить свое время между политикой и уравнениями.Однако уравнения, на мой взгляд, гораздо важнее, потому что политика существует только на данный момент, а уравнения будут существовать вечно ». А. Эйнштейн.
Привет, ребята! Мы повторяем: я ваш помощник, я буду направлять вас через всю большую тему «Квадратные уравнения». В 7 и 8 классах вы уже рассматривали и даже решали квадратные уравнения.
Сегодня вы узнаете: 1. Какие уравнения называются квадратными? 2. Что главное в определении квадратного уравнения, которое следует запомнить и учтено? 3.Какие частные случаи квадратных уравнений? 4. Как можно решать квадратные уравнения в каждом конкретном случае? А теперь давайте вместе поищем ответы на эти вопросы. Удачи!
Что общего у этих уравнений?
Квадратное уравнение — это уравнение вида … ax ² + bx + c = 0, где a ≠ 0, x — переменная, а a, b, c — некоторые числа. а — старший (первый) коэффициент, б — второй коэффициент, в — свободный член. а — старший (первый) коэффициент, б — второй коэффициент, в — свободный член.а — старший (первый) коэффициент, в — второй коэффициент, с — свободный срок.
Если a = 1, то квадратное уравнение x ² + bx + c = 0 называется приведенным. Решите № 513 (устно).
и при 5x² + 5x — 3 = 0 3 x² + 2 x — 4 = 0 x² + 4x + 3 = 0 -2 x² + x — 1 = 0 4 x ²- 4 x + 1 = 0 5 5 -3 3 2 -4 1 4 3 -2 1 — 1 4 — 4 1 Попробуем решить:
Интересно, что будет, если коэффициенты квадратного уравнения меняются по очереди или все сразу (кроме а) превращаются в нули.Давайте проведем небольшое исследование.
Неполные квадратные уравнения 28.04.17 Если c = 0, ax 2 + bx = 0 ax 2 ax 2 Если b, c = 0, ax 2 = 0 Если b = 0, ax 2 + c = 0
Рассмотрим все возможные случаи.
Неполные квадратные уравнения вида: без корней.
Неполные квадратные уравнения вида:
Ответ: x = 0. корней нет. Запишите неполные квадратные уравнения:
Запишите квадратные уравнения с указанными коэффициентами: a = 1, b = 0, c = 16; а = -1, б = 5, с = 0; б = 0, а = -3, с = 0; c = -8, a = 1, b = 0; а = 1.5, c = 0, b = -3; b =, a =, c Установите соответствие между уравнениями и следующими: а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней. (c) (a) (b) (a) (a) (a) Установите соответствие между уравнениями и следующими утверждениями:
Проверьте решение № 515 (a, c, d). а). 4х 2-9 = 0 в). -0,1 х 2 + 10 = 0 г). 6 v 2 + 24 = 0 4x 2 = 9-0,1x 2 = — 10 6 v 2 = -24 x 2 = 9/4 x 2 = — 10 / (- 0,1) v 2 = -24 / 6 х 1 = -3 / 2 = -1.5; х 2 = 100 в 2 = -4 х 2 = 3/2 = 1,5; х 1 = -10 Ответ: решения нет. Ответ: -1,5; 1,5; Ответ: -10; 10;
28.04.17 Рассмотрим решение неполных квадратных уравнений № 517 (б, г, д) б). -5х 2 + 6х = 0 г). 4а 2 — 3а = 0 г). 6 z 2 — z = 0 x (-5x + 6) = 0 a (4a-3) = 0 z (6 z –1) = 0 x = 0 или -5x + 6 = 0 a = 0 или 4a-3 = 0 z = 0 или 6 z –1 = 0 -5x = -6 4a = 3 6 z = 1 x = -6 / (- 5) = 1 .2 а = 3/4 = 0,75 z = 1/6 Ответ: 0; 12. Ответ: 0; 0,75. Ответ: 0; 1/6 …
1) Для каких значений a есть квадратное уравнение? Нет решений 2) При каких значениях a уравнение является неполным квадратным уравнением?
3) Решите уравнение с полученными значениями а. Ответ: а = — 2, х = — 15, х = 0; а = 0,
Подведем итог. Какое уравнение называется квадратным? Почему ≠ 0? Как называются числа a, b и c? Сколько видов неполных квадратных уравнений мы узнали? Как решаются уравнения типа I? II вид? III род?
Итак, наш урок подошел к концу.Ребята! Вы получили ответы на свои вопросы? Вы поняли, что впереди нас ждут интересные, а главное важные темы? Просто хочу напомнить, что при решении задач, примеров нужно искать рациональные подходы и применять самые разные способы.
Домашнее задание: Учебник с. 21; № 318, 321 а, с, 323 а. Дополнительно: 520, 532. P. 21 (определения), № 518, 520 (а, в) 511 Дополнительно (для учащихся с повышенным интересом) № 520, № 531.
Slide 2
«У меня есть делить свое время между политикой и уравнениями.Однако уравнения, на мой взгляд, гораздо важнее, потому что политика существует только на данный момент, а уравнения будут существовать вечно ». А. Эйнштейн.
Slide 3
Привет, ребята!
Мы повторяем: я ваш помощник, я проведу вас по всей большой теме «Квадратные уравнения». В 7 и 8 классах вы уже рассматривали и даже решали квадратные уравнения.
Slide 4
Сегодня вы узнаете: 1. Какие уравнения называются квадратными? 2.Что главное в определении квадратного уравнения, которое следует запомнить и учесть? 3. Каковы некоторые частные случаи квадратных уравнений? 4. Как можно решать квадратные уравнения в каждом конкретном случае? А теперь давайте вместе поищем ответы на эти вопросы. Удачи!
Slide 5
Что общего у этих уравнений?
Slide 6
Квадратное уравнение — это уравнение вида … ax² + bx + c = 0, где a ≠ 0, x — переменная, а a, b, c — некоторые числа.а — старший (первый) коэффициент, б — второй коэффициент, в — свободный срок. а — старший (первый) коэффициент, б — второй коэффициент, в — свободный срок. а — старший (первый) коэффициент, в — второй коэффициент, с — свободный срок.
Slide 7
Если a = 1, то квадратное уравнение x² + bx + c = 0 называется приведенным. Решите № 513 (устно).
Слайд 8
Попробуем решить:
5
5
-3
3
2
-4
1
4
3
-2
1
-1
4
-4
1
Slide 9
Интересно, что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме a) превратятся в нули.Давайте проведем небольшое исследование.
Слайд 10
Неполные квадратные уравнения
10.01.2017 10 Если c = 0, ax2 + bx = 0 ax2 ax2 Если b, c = 0, ax2 = 0 Если b = 0, ax2 + c = 0
Slide 11
Рассмотрим все возможные случаи.
Слайд 12
Slide 13
Неполные квадратные уравнения вида: без корней.
Слайд 14
Неполные квадратные уравнения вида:
Слайд 15
Ответ: x = 0.без корней. Запишите неполные квадратные уравнения:
Slide 16
Запишите квадратные уравнения с указанными коэффициентами: a = 1, b = 0, c = 16; а = -1, б = 5, с = 0; б = 0, а = -3, с = 0; c = -8, a = 1, b = 0; а = 1,5, с = 0, b = -3; b =, a =, c Установите соответствие между уравнениями и следующими: а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней.(c) (a) (b) (a) (a) (a) Установите соответствие между уравнениями и следующими утверждениями:
Слайд 17
17 Проверьте решение № 515 (a, c, d). а). 4х2-9 = 0 в). -0,1х2 + 10 = 0 г). 6v2 + 24 = 0 4×2 = 9 -0,1×2 = -10 6v2 = -24 x2 = 9 / 4×2 = -10 / (- 0,1) v2 = -24 / 6 x1 = -3 / 2 = -1, 5; х2 = 100 v2 = -4 х2 = 3/2 = 1,5; x1 = -10 Ответ: решения нет. Ответ: -1,5; 1,5; Ответ: -10; 10;
Slide 18
10.01.2017 18 Рассмотрим решение неполных квадратных уравнений No.517 (б, г, д) б). -5х2 + 6х = 0 г). 4a2 — 3a = 0d). 6z2– z = 0 x (-5x + 6) = 0 a (4a-3) = 0 z (6z –1) = 0 x = 0 или -5x + 6 = 0 a = 0 или 4a-3 = 0 z = 0 или 6z –1 = 0 -5x = -6 4a = 36z = 1 x = -6 / (- 5) = 1,2 a = 3/4 = 0,75 z = 1/6 Ответ: 0; 1,2. Ответ: 0; 0,75. Ответ: 0; 1/6 …
.
