Содержание
Алгебра 7-9 классы. 19. Квадратные уравнения. Разложение квадратного трехчлена на множители
Алгебра 7-9 классы. 19. Квадратные уравнения. Разложение квадратного трехчлена на множители
- Подробности
- Категория: Алгебра 7-9 классы
ОСНОВНЫЕ ПОНЯТИЯ
Определение 1. Квадратным уравнением называют уравнение вида
где коэффициенты а, b, с — любые действительные числа, причем а ≠ 0.
Коэффициенты а, b, с различают по названиям: а — первый, или старший, коэффициент; b — второй коэффициент, или коэффициент при х; с — свободный член.
Определение 2. Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.
Так, уравнение
— неприведенное квадратное уравнение (старший коэффициент равен 2), а уравнение
— приведенное квадратное уравнение.
Кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.
Определение 3. Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля. Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b, с равен нулю.
Обратите внимание: об ах2 речи нет, этот член всегда присутствует в квадратном уравнении.
Опрелеление 4. Корнем квадратного уравнения
называют всякое значение переменной х, при котором квадратный трехчлен
обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.
Можно сказать и так: корень квадратного уравнения
— это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0 = 0.
Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.
Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Рассмотрим несколько таких уравнений.
Пример 1. Решить неполные квадратные уравнения:
Решение.
а) Имеем
Поэтому либо х = 0, либо 2х — 7 = 0, откуда находим х = 3,5. Итак, уравнение имеет два корня: х1 = 0, х2 = 3,5.
Итак, уравнение имеет два корня: х1 = 0, х2 = 3,5.
б) Имеем
Уравнение имеет два корня: х1 = 0, х2 = 5.
в) Имеем
Ранее, мы уже говорили о том, что уравнение вида х2 = а, где а > О, имеет два корня: и . Значит, для уравнения х2 = 16 получаем х1 = 4, x2 = — 4 (мы учли, что ).
Допускается более экономная запись:
г) Имеем
Уравнение имеет два корня: И в этом случае можно записать короче
д) Имеем
Так как выражение Зx2неотрицательно при любых значениях х, то уравнение Зx2 = — 10 не имеет корней. Иными словами, нет ни одного числа, подстановка которого вместо переменной х обратила бы это уравнение в верное числовое равенство.
Иногда в таких случаях уточняют: нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; мнимые корни у этого уравнения есть.
е) Если 5x2 = 0, то x2 = 0, откуда x = 0 единственный корень уравнения.
Этот пример показывает, как решаются неполные квадратные уравнения:
1. Если уравнение имеет вид ах2 = 0, то оно имеет один корень х = 0.
2. Если уравнение имеет вид , то используется метод разложения на множители: ; значит, либо x = 0, либо ах + b = 0. В итоге получаем два корня:
3. Если уравнение имеет вид , то его преобразуют к виду и далее . В случае, когда — отрицательное число, уравнение не имеет корней (значит, не имеет корней и исходное уравнение ). В случае, когда
— положительное число, т. е., где m > 0, уравнение х2 = m имеет два корня: (в этом случае, как мы условились выше, допускается более короткая запись:
е., где m > 0, уравнение х2 = m имеет два корня: (в этом случае, как мы условились выше, допускается более короткая запись:
).
Неполное квадратное уравнение, как мы только что видели, может иметь два корня, один корень, ни одного корня. То же можно сказать и о полном квадратном уравнении. Почему?
Мы с вами знаем, что графиком функции является парабола. Корнями квадратного уравнения служат абсциссы точек пересечения параболы с осью х. Парабола может пересекать ось х в двух точках, может касаться оси х, т. е. иметь с ней лишь одну общую точку, может вообще не пересекаться с осью х (рис. 92, а, б, в). Это значит, что квадратное уравнение может иметь либо два корня, либо один корень, либо вообще не иметь корней.
Конечно, неплохо знать, сколько корней имеет квадратное уравнение, но еще лучше уметь находить эти корни. Если уравнение неполное, то, как мы видели выше, особых проблем не возникает. А если мы имеем полное квадратное уравнение? Ниже на примере одного такого уравнения напомним, какими способами мы пользовались до сих пор, когда приходилось встречаться с квадратным уравнением.
Если уравнение неполное, то, как мы видели выше, особых проблем не возникает. А если мы имеем полное квадратное уравнение? Ниже на примере одного такого уравнения напомним, какими способами мы пользовались до сих пор, когда приходилось встречаться с квадратным уравнением.
Пример 2. Решить уравнение х2 — 4х + 3 = 0.
Решение.
I способ. Рассмотрим квадратный трехчлен х2 — 4х + 3 и разложим его на множители, используя способ группировки; предварительно представим слагаемое — 4х в виде — х — Зх. Имеем
Значит, заданное уравнение можно переписать в виде (х — 1) (х — 3) = 0, откуда ясно, что уравнение имеет два корня; х1 = 1, х2 = 3; при х = 1 обращается в нуль множитель х — 1, а при х = 3 обращается в нуль множитель х — 3.
II способ. Рассмотрим квадратный трехчлен х2 — 4х + 3 и разложим его на множители, используя метод выделения полного квадрата; предварительно представим слагаемое 3 в виде 4-1. Имеем
Воспользовавшись формулой разности квадратов, получим
Рассуждая, как и в I способе, находим, что .
III способ. Построим график функции :
1) Имеем Значит, вершиной параболы является точка (2; -1), а осью параболы — прямая х = 2.
2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 1 и х = 3. Имеем ; построим на координатной плоскости точки (1; 0) и (3; 0).
3) Через точки (1; 0), (2; -1), (3;0) проводим параболу (рис. 93).
93).
Корнями уравнения х2 — 4х + 3 = 0 служат абсциссы точек пересечения параболы с осью х. Таких точек две: (1; 0) и (3; 0). Итак, х1 = 1, х2 = 3.
IV способ. Преобразуем уравнение к виду х2 — 4х — 3. Построим в одной системе координат графики функций у = х2 и у = 4х — 3 (рис. 94). Они пересекаются в точках А( 1; 1) и B(3; 9). Корнями уравнения служат абсциссы точек А и B, поэтому х1 = 1, х2 = 3.
V способ. Преобразуем уравнение к виду x2 + 3 = 4х. Построим в одной системе координат графики функций у = х2 + 3 и у = 4х (рис. 95). Они пересекаются в точках А (1; 4) и B (3; 12). Корнями уравнения служат абсциссы точек А и B, таким образом,
95). Они пересекаются в точках А (1; 4) и B (3; 12). Корнями уравнения служат абсциссы точек А и B, таким образом,
VI способ. Преобразуем уравнение к виду и далее , т. е. . Построим в одной системе координат параболу у = (х — 2)2 и прямую у = 1 (рис. 96). Они пересекаются в точках А (1; 1) и B(3; 1). Корнями уравнения служат абсциссы точек А и B, следовательно, .
VII способ. Разделив почленно обе части уравнения на х, получим
и далее
Построим в одной системе координат гиперболу прямую у = х — 4. Они пересекаются в точках А (1; -3) и (3; — 1) (рис. 97). Корнями уравнения служат абсциссы точек А и B, значит,
Итак, мы решили уравнение х2 — 4х + 3 = 0 семью способами. Тем не менее знание этих способов не есть, как говорится, панацея от всех бед. Ведь наши успехи в решении квадратных уравнений зависели до сих пор от наличия одного из двух благоприятных обстоятельств:
Тем не менее знание этих способов не есть, как говорится, панацея от всех бед. Ведь наши успехи в решении квадратных уравнений зависели до сих пор от наличия одного из двух благоприятных обстоятельств:
1) квадратный трехчлен удавалось разложить на множители;
2) графики, которые мы использовали для графического решения уравнения, пересекались в «хороших» точках.
Надеяться на такие подарки судьбы математики, естественно, не могли. Они искали универсальный способ, пригодный для решения любых квадратных уравнений, и нашли его.
10 способов решения уравнений 8-9 классы
10 способов решения уравнений
Содержание.
I. История развития квадратных уравнений ……………………….2
1. Квадратные уравнения в Древнем Вавилоне………………………..2
2. Как составлял и решал Диофант квадратные уравнения……………2
3. Квадратные уравнения в Индии……………………………………. ..3
..3
4. Квадратные уравнения у ал- Хорезми ………………………………4
5. Квадратные уравнения в Европе XIII — XVII вв……………………….5
6. О теореме Виета ………………………………………………………6
II. Способы решения квадратных уравнений ……………………….7
Способ…………………………………………………………………7
Способ…………………………………………………………………7
Способ…………………………………………………………………7
Способ………………………………………………………………….9
Способ………………………………………………………………….9
Способ…………………………………………………………………10
Способ…………………………………………………………………12
Способ…………………………………………………………………13
Способ…………………………………………………………………15
Способ…………………………………………………………………16
III. Заключение……………………………………………………………..18
Литература……………………………………………………………….19
История развития квадратных уравнений.
1. Квадратные уравнения в Древнем Вавилоне.
Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X2 + X = ¾; X2 — X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
2. Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х.
Разность между ними 2х.
Отсюда уравнение:
(10 + х)(10 — х) = 96
или же:
100 — х2 = 96
х2 — 4 = 0 (1)
Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 — у) = 96,
у2 — 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
3. Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x/8)2 + 12 = x
Бхаскара пишет под видом:
х2 — 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
х2 — 64х + 322 = -768 + 1024,
(х — 32)2 = 256,
х — 32 = ± 16,
х1 = 16, х2 = 48.
4. Квадратные уравнения у ал — Хорезми.
В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах2 + с = bх.
2) «Квадраты равны числу», т.е. ах2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т.е. ах2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида
Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида
ал — Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Приведем пример:
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
5. Квадратные уравнения в Европе XIII — XVII вв.
Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.
и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
х2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
6. О теореме Виета.
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A — A2, равно BD, то A равно В и равно D».
Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b)х — х2 = ab,
т.е.
х2 — (а + b)х + аb = 0,
то
х1 = а, х2 = b.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
Итак: Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ: Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х — 24 = 0. Разложим левую часть на множители:
х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х2 + 6х — 7 = 0. Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2• х • 3 + 32 = (х + 3)2.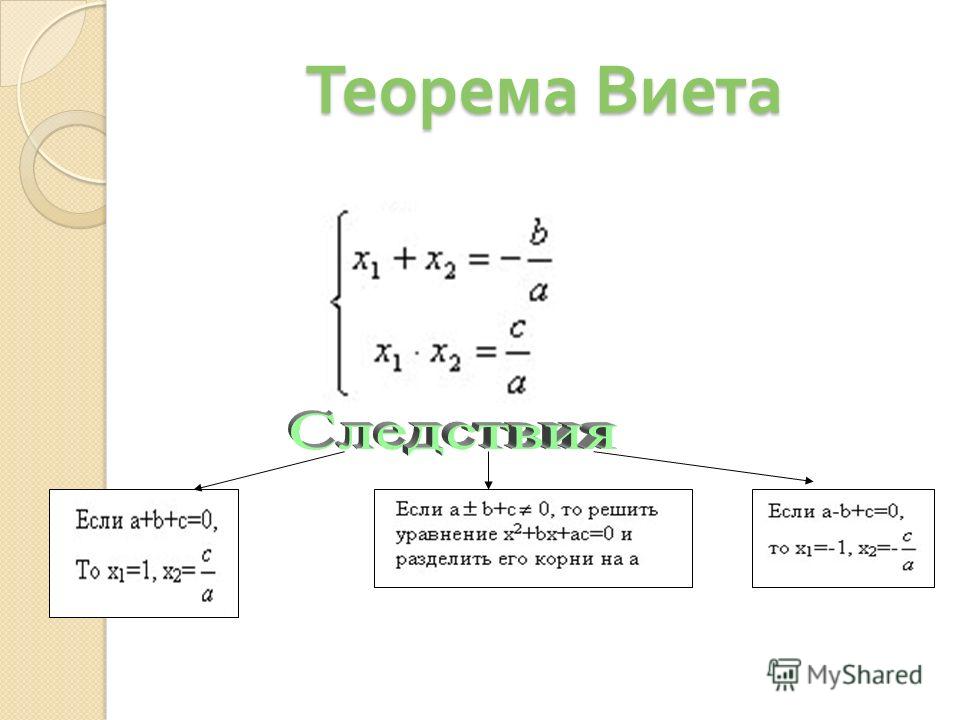
Преобразуем теперь левую часть уравнения
х2 + 6х — 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 — 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,
(2ax + b)2 = b2 — 4ac,
2ax + b = ± √ b2 — 4ac,
2ax = — b ± √ b2 — 4ac,
• Примеры.
а) Решим уравнение: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 — 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 — 4ac < 0, уравнение
ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
(1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = — 3 < 0;
x2 + 8x + 7 = 0; x1 = — 7 и x2 = — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x2 + 4x – 5 = 0; x1 = — 5 и x2 = 1, так как q= — 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = — 1, так как q = — 9 < 0 и p = — 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х1 = у2/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
• Пример.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
Согласно теореме Виета
x1 + x2 = — b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = — а + b/a= -1 – c/a,
x1x2 = — 1• ( — c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
• Примеры.
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
• Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение
х2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
принимает вид:
Формулу (3) особенно удобно использовать, когда р — четное число.
•Пример. Решим уравнение х2 – 14х – 15 = 0.
Решение. Имеем: х1,2 =7±
Ответ: х1 = 15; х2 = -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении
х2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х2 = — px — q.
Построим графики зависимости у = х2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —
прямая (рис.1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках,
абсциссы точек пересечения являются корнями квад- ратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
• Примеры.
1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = — 1 и х2 = 4. Ответ: х1 = — 1;
х2 = 4.
2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х — 1.
Построим параболу у = х2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и
линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
Итак:
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
• Пример.
Решим уравнение х2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = — 1; х2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью
номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений,
помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-
там определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
пропорцию
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
• Примеры.
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2,
получим уравнение
z2 — 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения
z2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t,
получим уравнение
t2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
10. СПОСОБ: Геометрический способ решения квадратных
уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
• Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т.е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.
Решение представлено на рис. 16, где
у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис.16).
3) Решить геометрически уравнение у2 — 6у — 16 = 0.
Преобразуя уравнение, получаем
у2 — 6у = 16.
На рис. 17 находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
получаем: (у — 3)2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у1 = 8 и у2 = — 2.
Заключение
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.
Здесь я остановилась на вопросе решения квадратных уравнений, а что,
если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.
Литература:
1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. — М., Просвещение, 1981.
2. Брадис В.М. Четырехзначные математические таблицы для средней школы.
Изд. 57-е. — М., Просвещение, 1990. С. 83.
3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. — М., высшая школа, 1969.
4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М., Просвещение, 1972.
5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.
6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.
7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение, 1970.
Урок по алгебре «Биквадратные уравнения» (9 класс)
Урок по математике в 9 классе.
Учебник Алгебра 9 (Макарычев Ю. Н.)
Тема: «Биквадратное уравнение»
Тип урока: изучение новых знаний.
Цели урока:
познакомить учащихся с новым видом уравнения с одной переменной;
изучить и закрепить способ решения биквадратных уравнений;
развивать умения работать с книгой, самостоятельно добывать знания;
развивать логическое мышление, математическую речь;
воспитывать аккуратность, самостоятельность, интерес к предмету.
Ход урока:
I. Организационный момент
Приветствие учащихся, мобилизация внимания.
II. Актуализация опорных знаний.
Учитель: (открывает первый слайд презентации )
— Сегодня на уроке мы закрепим ваши знания по решению квадратных уравнений; познакомимся с новым видом уравнения, приводимого к квадратному, поэтому повторим изученное, вспомнив основные определения, формулы и теоремы.
— Итак, ребята, скажите, какое уравнение называется квадратным?
(Ответ: Квадратным уравнением называется уравнение вида ,
где ).
— Что называется дискриминантом квадратного уравнения?
(Ответ: Число ).
— Какие виды квадратных уравнений вы знаете?
(Ответ: неполные квадратные уравнения; приведенные квадратные уравнения).
— Какое квадратное уравнение называется неполным?
(Ответ: Квадратное уравнение называется неполным, если у него хотя бы один из коэффициентов (кроме старшего) равен 0:
).
-Какое уравнение называется приведенным? Какой формулой оно задается?
(Ответ: Квадратное уравнение называется приведенным, если старший коэффициент равен 1:).
— Ребята, давайте вспомним, по каким же формулам находятся корни квадратных уравнений различных видов.
— По каким формулам находятся корни уравнения квадратного уравнения стандартного вида: ?
(Ответ: ; при D>0; при D=0; действительных корней нет при D<0).
— Ребята, кто из вас может сказать, как звучит теорема Виета?
(Ответ: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).
— Как же будет звучать обратная теорема ? Сформулируйте.
(Ответ: Если числа m и n таковы, что их сумма равна – p, а произведение равно q, то эти числа являются корнями уравнения х2 + pх +q=0).
Вопросы к учащимся:
Устно решите уравнения, назовите корни этих уравнений, если они есть:
(Демонстрирует карточки с условиями уравнений).
Учитель акцентирует внимание учащихся на том, что они должны уметь решать неполные и полные квадратные уравнения на “ отлично” для успешного усвоения новой темы.
III. Мотивация обучения. (3 мин, кроссворды лежат на партах у всех учащихся)
Учитель: Нам предстоит работа по разгадыванию кроссворда. Разгадав его, мы узнаем название нового вида уравнений, который научимся решать на уроке. Работаем по цепочке. Учащиеся читают вопрос вслух по цепочке, допускаются хоровые ответы. Записывает ответ учащийся I варианта, учащиеся II варианта — читают вопрос вслух.
Разгадав кроссворд, ребята прочитают слово “ биквадратные”. ( смотри приложение 1)
IV. Изучение темы «Биквадратные уравнения».
Запишем тему урока в тетрадях. ( Учитель пишет тему на доске и открывает второй слайд презентации, учащиеся пишут тему в тетрадях).
— Ребята, мы с вами повторили квадратные уравнения. Это нам понадобится при изучении алгебраических уравнений высших порядков. Биквадратные уравнения являются представителем класса алгебраических уравнений высших порядков.
— Определение: Биквадратным уравнением называется уравнение вида . Биквадратное уравнение решается с помощью замены переменной z = x2. Если вместо х2 подставляем z, то вместо х4 будет z2. Тогда мы получаем квадратное уравнение: az2+bz+c=0. Запишите определение биквадратного уравнения в тетрадь.
— Сейчас мы с вами разберем примеры решения таких уравнений.
Давайте посмотрим ролик с объяснением решения биквадратного уравнения.
(учащиеся смотрят видеоклип с сайта http://egetrener.ru/view_rolik.php?id=378).
Решим биквадратное уравнение: .
Решение.
Произведем замену переменной z = x2. При подстановке новой переменной в уравнение, мы получим квадратное уравнение: z2-13z+36=0. Решаем данное квадратное уравнение по известным нам формулам: D=b2-4c= =169-144=25, D>0, 2 корня:. Мы с вами получили два корня квадратного уравнения z1 и z2. Нам нужно найти х. Теперь мы возвратимся к замене: z = x2.
Так как z1=9, то х2=9, следовательно, х1,2=, х1=3 и х2= -3. Так и z2=4, то х2=4, x3,4=, x3=2 и х4= -2.
Итак, мы получили корни биквадратного уравнения. Это х1=3; х2= -3; x3=2 и х4= -2.
Ответ: х1=3; х2= -3; x3=2 и х4= -2.
(третий слайд презентации)
— Я хочу обратить ваше внимание на то обстоятельство, что мы получили 4 корня – это максимальное число корней биквадратного уравнения. Но возможно и так, что корней может быть меньше или вообще биквадратное уравнение не имеет решений. Дальше мы рассмотрим такой пример.
— Теперь запишите решение рассмотренного биквадратного уравнения. У кого какие вопросы есть по данному решению?
(четвёртый и пятый слайды презентации)
V. Формирование навыков решения биквадратного уравнения.
Во время самостоятельной работы учитель помогает в случае необходимости учащемуся индивидуально, контролирует ход работы, оценивает отдельных учащихся за работу на уроке по новой теме.
По мере решения уравнений, после проверки учителем работы ученика, ученики записывают результат, заполняя таблицу. 15 минут класс работает самостоятельно (смотри приложение 2).
После окончания работы появляется шестой слайд презентации и обучающиеся проверяют свои работы.
Учитель: Подведем итоги самостоятельной работы над новыми уравнениями.
Ученики: (анализируют данные таблицы) — фронтальный метод.
VI. Итог урока.
Учитель: Оцените, достигли ли вы намеченных целей и задач урока?
Ученики читают вопросы на слайде и отвечают на них.
Учитель:
Какие же уравнения называются биквадратными? (Определение)
Алгоритм решения биквадратного уравнения?
От чего зависит число решений биквадратного уравнения?
VII. Домашнее задания.
Запишите домашнее задание к следующему уроку: п.12, стр. 75, № 278 (б, д), № 282 (б ),
Вы должны знать алгоритм и уметь применять прием решения биквадратного уравнения.
Дополнительно 281*(а).
Приложение 1
Кроссворд. Если вписать верные слова, то получится название одного из видов уравнений.
Кроссворд.
Третья степень числа. (Куб)
Подкоренное выражение в формуле корней квадратного уравнения. (Дискриминант)
Значение переменной, обращающее уравнение в верное равенство. (Корень)
Уравнения, имеющие одинаковые корни. (Равносильные)
Равенство с переменной. (Уравнение)
Квадратное уравнение, с первым коэффициентом равным нулю. (Приведенное)
Многочлен в правой части квадратного уравнения. (Трехчлен)
Равенство, содержащее числа и переменные. (Формула)
Французский математик. (Виет)
Числовой множитель — в произведении. (Коэффициент)
Один из видов квадратного уравнения. (Неполное)
Множество корней уравнения. (Решения)
Приложение 2
Алгоритм решения биквадратного уравнения. Метод решения — замены переменной.
Ввести замену переменной: пусть х2 = t,
2. Составить квадратное уравнение с новой переменной: аt2 + bt + с = 0 (2)
3. Решить новое квадратное уравнение (2).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного уравнения.
7. Записать ответ.
Таблица для исследования числа решения биквадратных уравнений
№
Уравнение
Знак дискриминананта (D)
Корни промежуточного (нового) уравнения t1 и t2
Знаки корней нового уравнения
Корни исходного уравнения
Количество решений биквадрат. уравнения
1
х4 — 10х2 + 9 = 0
2
2х4 — х2 — 1 = 0
3
х4 + 5х2 + 4 = 0
4
х4 — 4х2 = 0
5
х4 — 8х2 + 16 = 0
6
х4 + 8х2 + 16 = 0
Решение квадратных уравнений с параметром в 9 классе | Методическая разработка по алгебре (9 класс) на тему:
Слайд 1
Решение квадратных уравнений содержащих параметры в 9 классе.
Слайд 2
При решении задач с параметрами приходится всё время производить несложные, но последовательные рассуждения, составлять для себя логическую схему решаемой задачи. Поэтому такие задачи – незаменимое средство для тренировки логического мышления. Их решение позволяет намного лучше понять обычные, без параметров, задачи. А привычка к математическим рассуждениям очень полезна при изучении высшей математики и использовании полученных знаний впоследствии.
Слайд 3
Для квадратного уравнения a в ыделяем три случая: 1. Если D= — 4 ac
Слайд 4
1. Важную роль при решении задач с параметром для квадратных уравнений играет теорема Виета . Для квадратного уравнения a , а — корни уравнения (случай D ≥0), выполнено равенство a )(х — ). Отсюда вывод теоремы Виета: + = — = .
Слайд 5
2. Второе важное замечание состоит в том, что при решении задач, сводящихся к исследованию квадратных уравнений, нужно помнить о геометрической интерпретации квадратного уравнения a , где ( ; ) – координаты вершины параболы. При а >0 ветви параболы направлены вверх, причем абсцисса вершины параболы является точкой минимума. При а
Слайд 6
Пример 1 . ( ЕГЭ, 2005, ). При каких значениях а функция у = имеет максимум при х = 4? Решение . Исходную функцию представим в виде у = . Поскольку 2>1, то данная функция монотонно возрастает и максимум данная функция достигает в той точке, что и у квадратичной функции f(x) = — + ax + 7. У этой параболы ветви направлены вниз, следовательно, максимум достигается в вершине параболы, т.е. в точке = . Согласно условию = 4, следовательно a = 8. Ответ: а = 8.
Слайд 7
Пример 2 . Решите уравнение (а – 1 ) + 2(2a + 1)x +(4a + 3) = 0. Решение . По виду это уравнение представляется квадратным. Но (внимание!) значение параметра а нам неизвестно, и оно вполне может оказаться равным 1; в этом случае коэффициент перед обращается в нуль и уравнение становится линейным. Квадратные и линейные уравнения решаются по разным алгоритмам. Итак нам надо рассмотреть два случая: а = 1 и а ≠ 1.
Слайд 8
Пусть а =1, тогда уравнение принимает вид: 0· Решив это уравнение , получаем: х = — . Частичный ответ : если а = 1, то х = — .
Слайд 9
Пусть а ≠ 1. Мы имеем квадратное уравнение (а – 1 ) + 2(2a + 1)x +(4a + 3) = 0 . Найдем его дискриминант: D =( — Итак, D = . Дальнейшие рассуждения зависят от знака дискриминанта. Если D 0 , то уравнение имеет два корня. Дискриминант обращается в нуль при а = — , положителен при а > — , отрицателен при а
Слайд 10
Пусть а — (но, напомним а ≠ 1). В этом случае дискриминант больше нуля и квадратное уравнение имеет два корня, которые мы найдем по формуле корней квадратного уравнения: = Частичный ответ : при а > — ( а ≠1) =
Слайд 11
Осталось рассмотреть случай, когда а = — . Используя формулу корней квадратного уравнения, получаем = = — . Частичный ответ : при а = — , х = — . Ответ: если а =1, то х = — если а = — , то х =- если а > — ( а ≠1 ), то = если а
Слайд 12
Пример 3. При каких значениях параметра а корни уравнения — Решение. Если а = 0, то уравнение примет вид 2 х – 2 = 0. Корень этого уравнения будет х = -1. Этот корень удовлетворяет условию x
Слайд 13
Если а ≠0, то заданное уравнение является квадратным. График функции у= f(x) , где f(x)= — 2x-3a-2 является парабола с ветвями вверх, если 2 а > 0, и ветвями вниз, если 2а 0) или на рис. 2 (для 2а
Слайд 15
Дадим аналитическое описание геометрической модели, представленной на рис.1. Во-первых, напомним, при 2 а > 0 ветви параболы направлены вверх. Во-вторых, парабола обязательно пересекается с осью Ох ( в крайнем случае касается её), иначе у квадратного уравнения не будет корней. Корни есть, значит дискриминант не отрицателен. В-третьих, в точке х =1 имеем f(1)>0. В четвертых,
Слайд 16
Итак получаем систему неравенств – аналитическую модель, дающую описание геометрической модели, представленной на рис.1.
Слайд 17
Аналогичные рассуждения позволяют составить вторую систему неравенств – аналитическую модель, дающую описание геометрической модели, представленной на рис. 2:
Слайд 18
Решим первую систему неравенств. Найдем дискриминант. D =4-4·2 а ·(-3а-2)=24 +16 a +4. Найдем f(1). f (1)=2 a · -2·1-3 a -2=- a -4. Найдем = . Так как , получаем: a Таким образом, первая система неравенств имеет следующий вид :
Слайд 19
Эта система не имеет решений, поскольку из первого её неравенства получаем а >0, а из третьего получаем а
Слайд 20
Сразу обратим внимание на то, что квадратный трехчлен имеет отрицательный дискриминант ( D= — 4·4 24 0 , а потому квадратное неравенство в данной системе неравенств можно отбросить. Далее имеем: Решением данной системы является -4
Слайд 21
Итак, мы нашли все интересующие нас значения параметра а: а=0; -4
Слайд 22
Пример 4 . Какие значения может принимать сумма квадратов действительных, различных корней уравнения +2 ax +2 — 2 – 12 =0? Решение. Квадратное уравнение имеет два различных действительных корня, когда дискриминант больше нуля. Решим неравенство D >0. -4 -2-12)>0, п олучаем а (-3;4). По теореме Виета + = -2a ; · =2 — a -12. Следовательно, + = ( -2 = 2 a +24. Т.к. a О твет :
Слайд 23
Вывод: основой для усвоения материала является здравый смысл ученика, а не только и не столько его предварительные знания. Спасибо за внимание .
Тест Решение уравнений (9 класс) по алгебре
Сложность: эксперт.Последний раз тест пройден более 24 часов назад.
Вопрос 1 из 10
Решить уравнение методом неопределенных коэффициентов: x4-6x3+6x2+10x-3=0
- Правильный ответ
- Неправильный ответ
- Вы и еще 58% ответили правильно
- 58% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Решите уравнение и укажите его корни: -2x2+3√3x-2x+3=√3
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 65% участников
- 35% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Решить систему уравнений:
- Правильный ответ
- Неправильный ответ
- Вы и еще 55% ответили правильно
- 55% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Укажите корни уравнения (x-2)2-(2x+1)(1-2x)=4x2
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 62% участников
- 38% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Решить систему уравнений:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 75% участников
- 25% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Укажите корни уравнения 2x(x-1)=x2-3x+2
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 57% участников
- 43% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Найти значение параметра а, при котором будет иметь единственное решение система уравнений:
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 77% участников
- 23% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Укажите корни уравнения x2-5x-6=0
- Правильный ответ
- Неправильный ответ
- Вы и еще 59% ответили правильно
- 59% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Какое квадратное уравнение является неполным?
- Правильный ответ
- Неправильный ответ
- Вы и еще 52% ответили правильно
- 52% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Решите уавнение и укажите его корни: x2-3√2x+4=0
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 59% участников
- 41% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
ТОП-3 тестакоторые проходят вместе с этим
Рейтинг теста
Средняя оценка: 3.4. Всего получено оценок: 127.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Линейные и квадратные уравнения
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). \[f(x)=g(x) \qquad \qquad (1)\]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой \(x\).
Замечание
Заметим, что \(x\) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида \((1)\) будем называть множество значений переменной \(x\), при которых определены (то есть не теряют смысла) функции \(f(x)\) и \(g(x)\).
Пример
Уравнение \(\dfrac {10}{x-1}=5\) определено при всех значениях переменной \(x\), кроме \(x=1\), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения \(x\in
(-\infty;1)\cup(1;+\infty)\).
Определение
Корнем уравнения называется то числовое значение \(x\), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число \(x=3\), потому как тогда уравнение принимает вид \(\dfrac{10}{3-1}=5\) или, что то же самое, \(5=5\), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение \(\dfrac 1x=0\) ни при каких значениях \(x\) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла.3=64\) является \(x=4\).
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Трехчленные уравнения
Трёхчленными уравнениями называют уравнения вида
| a f 2(x)+ b f (x) + c = 0, | (1) |
а также уравнения вида
| (2) |
где a, b, c – заданные числа, а f (x) – некоторая функция.
Для того, чтобы решить трехчленное уравнения вида (1), обозначим
тогда уравнение (1) станет квадратным уравнением относительно переменной y :
Затем найдем корни уравнения (4), а после этого, подставив каждый из найденных корней в равенство (3), решим полученное уравнение относительно x .
Для того, чтобы решить трехчленное уравнение вида (2), сначала введем обозначение (3), а затем умножим полученное уравнение на знаменатель. В результате уравнение (2) примет вид (4), а схема решения уравнения (4) уже описана выше.
Покажем, как это осуществляется на примерах.
Пример 1. Решить уравнение
| (x2 – 2x)2 – – 2(x2 – 2x) – 3 = 0 . | (5) |
Решение. Если обозначить
то уравнение (5) превратится в квадратное уравнение
Решим уравнение (7):
В первом случае из равенства (6) получаем:
Во втором случае из равенства (6) получаем:
Ответ: – 1, 1, 3.
Пример 2. Решить уравнение
| (8) |
Решение. Если обозначить
| , | (9) |
то уравнение (8) превратится в квадратное уравнение
которое эквивалентно уравнению
| 2y2 – 3 y – 2 = 0 . | (10) |
Решим уравнение (10):
В первом случае из равенства (9) получаем уравнение:
которое, в силу неотрицательности арифметического корня, решений не имеет.
Во втором случае из равенства (9) получаем:
Ответ:
Пример 3. Решить уравнение
| (11) |
Решение. Если обозначить
| (12) |
то уравнение (11) превратится в квадратное уравнение
y2 – 9 + 3 – 5y = 0 ,
которое эквивалентно уравнению
| y2 – 5y – 6 = 0 . | (13) |
Решим уравнение (13):
y1 = – 1, y2 = 6 .
В первом случае из равенства (12) получаем уравнение:
которое, в силу неотрицательности арифметического корня, решений не имеет.
Во втором случае из равенства (12) получаем:
Ответ:
Пример 4. Решить биквадратное уравнение
| x4 – x2 – 12 = 0 . | (14) |
Решение. Если обозначить
то уравнение (14) превратится в квадратное уравнение
| y2 – y – 12 = 0 . | (16) |
Решим уравнение (16):
y1 = – 3, y2 = 4 .
В первом случае из равенства (15) получаем уравнение:
x2 = – 3,
которое решений не имеет.
Во втором случае из равенства (15) получаем:
Ответ: – 2, 2 .
Пример 5. Решить уравнение
| (17) |
Решение. Если обозначить
уравнение (17) превращается в уравнение
которое при умножении на y принимает вид
Решим уравнение (19):
y1 = – 4, y2 = 2 .
В первом случае из равенства (18) получаем квадратное уравнение:
которое решений не имеет.
Во втором случае из равенства (18) получаем:
Ответ:
Пример 6. Решить уравнение
| (20) |
Решение. Если обозначить
| , | (21) |
уравнение (20) превращается в уравнение
которое при умножении на y принимает вид
| 3y2 – 2y – 1 = 0 . | (22) |
Решим уравнение (22):
В первом случае из равенства (21) получаем уравнение
которое, в силу неотрицательности арифметического корня, решений не имеет.
Во втором случае из равенства (21) получаем:
Ответ: – 2 .
Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии
Рассмотрим уравнение
| (ax + b)(ax + b + + c)(ax + + b + 2c)(ax + + b + 3c) = d , | (23) |
где a, b, c, d – заданные числа, и заметим, что левая часть этого уравнения представляет собой произведение четырёх последовательных членов арифметической прогрессии, первый член которой равен ax+b, а разность равна c.
Схема решения уравнений вида (23) заключается в следующем.
Сначала обозначим
Тогда уравнение (23) примет вид:
| y (y + c)(y + + 2c)(y + 3c) = d . | (25) |
Перегруппируем сомножители в левой части уравнения (25) следующим образом:
| [y (y + 3c)][(y + + c)(y + 2c)] = d . | (26) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (26), то получим:
| [y2 + 3cy][y2 + + 3cy + 2c2] = d . | (27) |
Если теперь в уравнении (27) обозначить
то уравнение (27) станеи квадратным уравнением
| z2 + 2c2 z – d = 0 . | (29) |
Для того, чтобы найти корни уравнения (23), остаётся решить уравнение (29), затем для каждого корня уравнения (29) решить уравнение (28) относительно y , а затем в каждом из полученных случаев решить уравнение (24) относительно x .
Пример 7 . Решить уравнение
| (2x + 3)(2x + 5)(2x + + 7)(2x + 9) = 384 . | (30) |
Решение.Если обозначить
уравнение (30) превращается в уравнение
| y (y + 2)(y + + 4)(y + 6) = 384 . | (32) |
Перегруппируем сомножители в левой части уравнения (32):
| [y (y + 6)][(y + + 2)(y + 4)] = 384 . | (33) |
Если раскрыть круглые скобки внутри каждой квадратной скобки из левой части уравнения (33), то уравнение (33) примет вид:
| [y2 + 6y][y2 + + 6y + 8] = 384 . | (34) |
Если теперь обозначить
то уравнение (34) станет квадратным уравнением
| z2 + 8 z – 384 = 0 . | (36) |
Решим уравнение (36):
z1 = – 24, z2 = 16 .
В первом случае из равенства (35) получаем уравнение:
которое корней не имеет.
Во втором случае из равенства (35) получаем:
В первом из этих случаев, из равенства (31) получаем:
Во втором случае из равенства (31) получаем:
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Примеры квадратного уравнения
Квадратное уравнение — это уравнение второй степени, то есть оно содержит по крайней мере один член, возведенный в квадрат. Стандартная форма — ax² + bx + c = 0, где a, b и c являются константами или числовыми коэффициентами, а x — неизвестной переменной. Одно абсолютное правило состоит в том, что первая константа «а» не может быть нулем.
Уравнения стандартной формы
Вот примеры квадратных уравнений в стандартной форме (ax² + bx + c = 0):
- 6x² + 11x — 35 = 0
- 2x² — 4x — 2 = 0
- -4x² — 7x +12 = 0
- 20x² -15x — 10 = 0
- x² -x — 3 = 0
- 5x² — 2x — 9 = 0
- 3x² + 4x + 2 = 0
- -x² + 6x + 18 = 0
Вот примеры квадратных уравнений без линейного коэффициента или «bx»:
- 2x² — 64 = 0
- x² — 16 = 0
- 9x² + 49 = 0
- -2x² — 4 = 0
- 4x² + 81 = 0
- -x² — 9 = 0
- 3x² — 36 = 0
- 6x² + 144 = 0
Вот примеры квадратных уравнений без постоянного члена или «c»:
- x² — 7x = 0
- 2x² + 8x = 0
- -x² — 9x = 0
- x² + 2x = 0
- -6x² — 3x = 0
- -5x² + x = 0
- -12x² + 13x = 0
- 1 1x² — 27x = 0
Вот примеры квадратного уравнения в факторизованной форме:
- (x + 2) (x — 3) = 0 [после вычисления становится x² -1x — 6 = 0]
- (x + 1) (x + 6) = 0 [при вычислении становится x² + 7x + 6 = 0]
- (x — 6) (x + 1) = 0 [при вычислении становится x² — 5x — 6 = 0
- -3 (x — 4) (2x + 3) = 0 [при вычислении становится -6x² + 15x + 36 = 0]
- (x — 5) (x + 3) = 0 [при вычислении становится x² — 2x — 15 = 0 ]
- (x — 5) (x + 2) = 0 [при вычислении становится x² — 3x — 10 = 0]
- (x — 4) (x + 2) = 0 [при вычислении становится x² — 2x — 8 = 0]
(2x + 3) (3x — 2) = 0 [после вычисления становится 6x² + 5x — 6]
Вот примеры других форм квадратных уравнений:
- x (x — 2) = 4 [при умножении и перемещении 4 становится x² — 2x — 4 = 0]
- x (2x + 3) = 12 [при умножении и перемещении 12 становится 2x² — 3x — 12 = 0]
- 3x (x + 8 ) = -2 [при умножении и mo значение -2 становится 3x² + 24x + 2 = 0]
- 5x² = 9 — x [перемещение 9 и -x в другую сторону становится 5x² + x — 9]
- -6x² = -2 + x [перемещение -2 и x в другую сторону становится -6x² — x + 2]
- x² = 27x -14 [перемещение -14 и 27x на другую сторону становится x² — 27x + 14]
- x² + 2x = 1 [перемещение «1» на другой стороне становится x² + 2x — 1 = 0]
- 4x² — 7x = 15 [перемещение 15 на другую сторону становится 4x² + 7x — 15 = 0]
- -8x² + 3x = -100 [перемещение -100 в другую сторону становится -8x² + 3x + 100 = 0]
- 25x + 6 = 99 x² [перемещение 99 x2 на другую сторону становится -99 x² + 25x + 6 = 0]
Есть много разных типы квадратных уравнений, как показывают эти примеры. {2} — 6a & = 0 \\
3а (3а — 2) & = 0 \\
3а & = 0 \\
а & = 0 \\
\ text {или} & \\
3а — 2 & = 0 \\
a & = \ frac {2} {3} \\
\ поэтому a = 0 & \ text {или} a = \ frac {2} {3}
\ end {выровнять *}Квадратное уравнение | Примечания, видео, контроль качества и тесты | 9 класс> Обязательная математика> Алгебра
Квадратное уравнение
Уравнение, подобное ax 2 + bx + c = 0, где a 0, которое содержит только одну переменную и «2» в качестве его наибольшей степени, называется квадратным уравнением.2 -4ac}} {2a} $$
Квадратные уравнения бывают двух типов
и. Чистое квадратное уравнение:
Квадратичное уравнение вида ax 2 + c = 0, в котором пропущен средний член, содержащий степень 1, известно как чистое квадратное уравнение.
например x 2 = 9 или, x 2 — 9 = 0
, т.е. ax 2 + c = 0 (a ≠ o, c = 0)ii. Адфицированное квадратное уравнение:
Стандартная форма квадратного уравнения известна как присоединенное квадратное уравнение.
ax 2 + bx + c = 0 — это квадратное уравнение.
например x 2 — 9x — 15 = 0
, т.е. ax 2 + bx + c = 0 (a ≠ o, b o)Решение квадратного уравнения
Квадратное уравнение — это уравнение второй степени с одной переменной. Таким образом, мы получаем два решения переменной, содержащейся в этом уравнении. Решение квадратного уравнения называется корнями. Следовательно, квадратное уравнение имеет два корня.Решение корней, полученных из квадратного уравнения, должно удовлетворять уравнению. Существует три основных метода решения квадратного уравнения:
- Метод факторизации
- Комплектация квадратным методом
- По формуле
a) Решение квадратного уравнения методом факторизации:
В этом методе квадратное уравнение ax 2 + bx + c = 0 разлагается на множители и выражается как произведение двух линейных множителей. 2-4ac}} {2a} \)
‘a’ — коэффициент x 2
‘b’ — коэффициент перед x и
«c» — постоянный член.2-4ac}} {2a} \) и найти два корня данного квадратного уравнения.
вопросов по алгебре с ответами для 9 класса
Представлены вопросы по пропорциональной алгебре 9-го класса с ответами. Включены вопросы по решению линейных и квадратных уравнений, упрощению выражений, включая выражения с дробями, нахождению наклонов прямых. Также включены решения и подробные объяснения.
Вопросы
- Упростите следующие алгебраические выражения.
- — 6x + 5 + 12x -6
- 2 (х — 9) + 6 (-x + 2) + 4x
- 3x 2 + 12 + 9x — 20 + 6x 2 — x
- (х + 2) (х + 4) + (х + 5) (- х — 1)
- 1,2 (х — 9) — 2,3 (х + 4)
- (x 2 y) (xy 2 )
- (-x 2 y 2 ) (xy 2 )
- Упростите выражения.
- (a b 2 ) (a 3 b) / (a 2 b 3 )
- (21 x 5 ) / (3 x 4 )
- (6 x 4 ) (4 y 2 ) / [(3 x 2 ) (16 y)]
- (4х — 12) / 4
- (-5x — 10) / (x + 2)
- (x 2 — 4x — 12) / (x 2 2x 24)
- Решите относительно x следующие линейные уравнения.
- 2x = 6
- 6х — 8 = 4х + 4
- 4 (х — 2) = 2 (х + 3) + 7
- 0,1 х — 1,6 = 0,2 х + 2,3
- — х / 5 = 2
- (х — 4) / (- 6) = 3
- (-3x + 1) / (x — 2) = -3
- х / 5 + (х — 1) / 3 = 1/5
- Найдите реальные решения следующих квадратных уравнений.
- 2 х 2 — 8 = 0
- х 2 = -5
- 2x 2 + 5x — 7 = 0
- (х — 2) (х + 3) = 0
- (х + 7) (х — 1) = 9
- х (х — 6) = -9
- Найдите любые реальные решения для следующих уравнений.
- х 3 — 1728 = 0
- х 3 = — 64
- sqrt (x) = -1
- sqrt (x) = 5
- sqrt (x / 100) = 4
- sqrt (200 / x) = 2
- Оцените для данных значений a и b .
- a 2 + b 2 , для a = 2 и b = 2
- | 2a — 3b | , для a = -3 и b = 5
- 3a 3 — 4b 4 , для a = -1 и b = -2
- Решите следующие неравенства.
- х + 3 <0
- х + 1> -x + 5
- 2 (х — 2) <- (х + 7)
- При каком значении константы k квадратное уравнение x 2 + 2x = — 2k имеет два различных действительных решения?
- При каком значении константы b линейное уравнение 2x + by = 2 имеет наклон, равный 2?
- Каков отрезок оси y линии -4x + 6y = -12 ?
- Каков отрезок оси x линии -3x + y = 3 ?
- Какая точка пересечения линий x — y = 3 и -5x — 2y = -22 ?
- При каком значении константы k прямая -4x + ky = 2 проходит через точку (2, -3) ?
- Каков наклон прямой с уравнением y — 4 = 10 ?
- Каков наклон прямой с уравнением 2x = -8 ?
- Найдите точки пересечения x и y прямой с помощью уравнения x = — 3 ?
- Найдите точки пересечения x и y прямой с помощью уравнения 3y — 6 = 3 ?
- Каков наклон прямой, параллельной оси x?
- Каков наклон прямой, перпендикулярной оси x?
Решения и подробные пояснения к вышеуказанным вопросам.
Ответы на вышеуказанные вопросы
- 6x — 1
- — 6
- 9x 2 + 8 x — 8
- 3
- -1,1x — 20
- х 3 у 3
- — х 3 у 4
- а 2
- 7x
- (1/2) x 2 y
- х — 3
- -5
- (х + 2) / (х + 4)
- х = 3
- х = 6
- х = 21/2
- х = -39
- х = -10
- х = -14
- нет решения
- х = 1
- набор растворов {-2,2}
- нет реальных решений
- {1, -7 / 2}
- {2, -3}
- {2, -8}
- {3}
Набор растворов
Набор растворов
Набор растворов
Набор растворов
- х = 12
- х = -4
- нет решений
- х = 25
- х = 1600
- х = 50
- х = 12
- Оцените для данных значений a и b .
- 8
- 21
- -67
- 8
- х <-3
- х> 2
- х <-1
- k <1/2
- б = -1
- (0, -2)
- (-1, 0)
- (4, 1)
- к = -10/3
- наклон = 0
- Наклон не определен
- x — перехват: (-3,0), no y — перехват.
- нет x — точка пересечения, y — точка пересечения: (0, 3)
- наклон = 0
- Наклон не определен.
Дополнительные ссылки и ссылки
Математика средней школы (6, 7, 8, 9 классы) — Бесплатные вопросы и задачи с ответами
Математика средней школы (10, 11 и 12 классы) — Бесплатные вопросы и проблемы с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и задачами с ответами Домашняя страницаОбзор различных методов решения квадратного уравнения — Концепция
Решение квадратных уравнений может быть трудным, но, к счастью, есть несколько различных методов, которые мы можем использовать в зависимости от того, какой тип квадратичного уравнения мы пытаемся решить.Четыре метода решения квадратного уравнения — это факторизация с использованием квадратных корней, завершение квадрата и квадратной формулы.
Итак, сейчас я хочу поговорить об обзоре всех различных способов решения квадратного уравнения. Под этим я подразумеваю что-нибудь в форме: ax² плюс bx плюс c. Итак, у нас есть четыре различных способа, которые нам удобнее.У нас есть факторизация, свойство извлечения квадратного корня, завершение квадрата и квадратная формула. Мы можем использовать эти методы в разное время, и я просто хочу поговорить о том, когда мы можем их использовать, почему они хороши и почему плохие. Так что я просто спущусь вниз по ряду и расскажу о каждом из них. «Чек» означает «за», а «минус» — «против». Факторинг обычно является самым быстрым и простым способом решения чего-либо, когда это возможно. Часто мы имеем дело с квадратичным коэффициентом, который нельзя факторизовать, поэтому факторинг нам не поможет.Так что это быстро и просто, когда его можно использовать, но также не всегда можно использовать. Так быстро и просто, но не всегда применимо.
Следующее, о чем мы поговорим, — это свойство квадратного корня. Это когда у нас есть что-то квадратное. Итак, профи: это здорово, когда вы решаете что-то квадратное. Единственная проблема в том, что мы не всегда имеем дело с ситуацией. Каждый раз, когда у вас есть X-термин или что-то в этом роде, мы не сможем его использовать. Так что это не всегда квадратный термин.Когда это применимо, это здорово, но не всегда. На самом деле это не так часто бывает.
Завершение кв. Самое замечательное в завершении квадрата — это то, что мы всегда можем это сделать. Никогда не будет времени, когда вы не сможете завершить квадрат. Но недостаток в том, что это может стать некрасивым. Если вы имеете дело с коэффициентом или нечетным средним членом или чем-то в этом роде, вы собираетесь ввести дроби. Это не всегда лучшая ситуация.
Наконец, квадратная формула.Опять же, это здорово, потому что им всегда можно воспользоваться. И минусы, это зависит от человека. Если вы используете квадратные корни, что не всегда нравится некоторым людям, вам всегда нужно использовать квадратные корни. Обычно это не так просто, как некоторые из этих других методов, я бы сказал, что завершение квадрата немного проще, но это то, что вы должны запомнить. Поэтому вам нужно запомнить формулу, и она может стать некрасивой.
Итак, это четыре разных способа, плюсы и минусы, а также некоторые вещи, о которых следует подумать при решении проблемы.На самом деле я не собираюсь ничего решать за вас. Я только что сделал небольшую диаграмму, чтобы вы знали, какие ресурсы у вас есть, а также плюсы и минусы каждого из них.Решение квадратных уравнений с квадратичной формулой
Purplemath
Кто-то (возможно, в Индии седьмого века) решал множество квадратных уравнений, завершая квадрат.В какой-то момент он (и, да, тогда это был бы парень) заметил, что он всегда делал одни и те же шаги в одном и том же порядке для каждого уравнения.
Великая сила алгебры заключается в том, что она дает нам возможность иметь дело с абстракциями, такими как формулы, которые всегда работают. Это может избавить нас от бремени и беспорядка, связанного с необходимостью возиться с числами каждый раз, когда мы делаем одно и то же. Используя эту способность по отношению к решению квадратичных квадратов путем завершения квадрата, он составил формулу из того, что он делал; а именно квадратичная формула, которая гласит:
MathHelp.com
Квадратичная формула: Дано квадратное уравнение в следующей форме:
… где a , b и c — числовые коэффициенты членов квадратичного уравнения, значение переменной x определяется следующим уравнением:
Квадратичная формула хороша тем, что она всегда работает.Есть некоторые квадраты (на самом деле большинство из них), которые мы не можем решить с помощью факторинга. Но квадратная формула всегда даст ответ, независимо от того, было ли квадратное выражение факторизованным.
Давайте попробуем еще раз эту первую задачу с предыдущей страницы, но на этот раз мы будем использовать квадратичную формулу вместо трудоемкого процесса завершения квадрата:
Используйте квадратичную формулу для решения
x 2 — 4 x — 8 = 0
Квадратичная формула требует, чтобы у меня было квадратичное выражение с одной стороны от знака «равно» и «ноль» с другой стороны.Они уже дали мне уравнение в такой форме. Кроме того, Формула выражается в виде числовых коэффициентов при квадратичном выражении. Глядя на коэффициенты в этом уравнении, я вижу, что a = 1, b = –4 и c = –8. Я вставлю эти числа в формулу и упрощу. (Я должен получить тот же ответ, что и раньше.)
Это тот же ответ, который я получил ранее, который подтверждает, что квадратичная формула работает так, как задумано.Еще раз, мой окончательный ответ:
Самое приятное в квадратичной формуле (по сравнению с завершением квадрата) состоит в том, что мы просто подставляем формулу. Нет никаких «шагов», которые нужно запомнить, и, следовательно, меньше возможностей для ошибок. При этом сказано:
Следите за тем, чтобы не пропустить знак «±» перед радикалом.
Не проводите дробную линию только под квадратным корнем, потому что она также находится под начальной частью «- b ».
Не забывайте, что знаменатель формулы — «2 a », а не просто «2». То есть, когда ведущий член представляет собой что-то вроде «5 x 2 », вам нужно не забыть поместить в знаменатель значение « a = 5».
Используйте круглые скобки вокруг коэффициентов, когда вы впервые вводите их в формулу, особенно когда любой из этих коэффициентов отрицательный, чтобы не потерять знаки «минус».
Решите 4
x 2 + 3 x — 2 = 0, используя квадратичную формулу.
Сначала я зачитаю значения коэффициентов, которые я буду подставлять в формулу:
Теперь все, что мне нужно сделать, это вставить эти значения в формулу и упростить, чтобы получить ответ:
x = [- (3) ± sqrt {(3) 2 — 4 (4) (- 2}] / [2 (4)]
= [–3 ± sqrt {9 + 32}] / [8]
= [–3 ± sqrt {41}] / [8]
Абсолютно ничего не упростит, так что я закончил.Мой ответ:
x = [–3 ± sqrt {41}] / [8]
Вы должны обязательно запомнить квадратную формулу. Меня не волнует, скажет ли ваш учитель, что даст вам его на следующем тесте; все равно запомните его, потому что он вам понадобится позже. Это не так уж и долго, и есть даже песня, которая поможет вам ее запомнить, на мелодию «Pop Goes the Weasel»:
X равно отрицательному B
Плюс или минус квадратный корень
Из B-квадрата минус четыре A C
Всего два A(Вышеупомянутая песня для меня не оригинальна.Я узнал это в другом месте.)
При использовании формулы будьте осторожны, потому что, пока вы делаете свою работу аккуратно, квадратичная формула каждый раз будет давать вам правильный ответ.
У меня есть урок по квадратичной формуле, который предоставляет рабочие примеры и показывает связь между дискриминантом (часть « b 2 — 4 ac » внутри квадратного корня), количеством и типом решений квадратное уравнение и график соответствующей параболы.Если вам нужна дополнительная помощь с формулой, изучите урок по указанной выше гиперссылке.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений с помощью квадратной формулы. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить с помощью квадратичной формулы», чтобы сравнить свой ответ с ответом Матвея. (Или пропустите виджет и перейдите на следующую страницу.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvquad4.htm
Решение квадратных уравнений
Решение квадратных уравнений
Квадратичное уравнение — это уравнение, которое можно записать как
топор 2 + bx + c = 0
, когда a 0.
Существует три основных метода решения квадратных уравнений: факторинг, использование формулы квадратиков и завершение квадрата.
Факторинг
Чтобы решить квадратное уравнение путем факторизации,
Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
- Коэффициент
.
Установите каждый коэффициент равным нулю.
Решите каждое из этих уравнений.
Проверьте, подставив свой ответ в исходное уравнение.
Пример 1
Решить x 2 — 6 x = 16.
Следуя инструкциям,
x 2 — 6 x = 16 становится x 2 — 6 x — 16 = 0
Коэффициент
.
( x -8) ( x + 2) = 0
Установка каждого коэффициента на ноль,
Затем проверить,
Оба значения, 8 и –2, являются решениями исходного уравнения.
Пример 2
Решить y 2 = — 6 y — 5.
Устанавливая все члены равными нулю,
y 2 + 6 y + 5 = 0
Коэффициент
.
( y + 5) ( y + 1) = 0
Установка каждого коэффициента на 0,
Для проверки, y 2 = –6 y — 5
Квадратичный с отсутствующим членом называется неполным квадратичным элементом (при условии, что член ax 2 не пропущен).
Пример 3
Решить x 2 — 16 = 0.
Коэффициент
.
Для проверки, x 2 — 16 = 0
Пример 4
Решить x 2 + 6 x = 0.
Коэффициент
.
Для проверки, x 2 + 6 x = 0
Пример 5
Решить 2 x 2 + 2 x — 1 = x 2 + 6 x — 5.
Во-первых, упростите, поместив все термины в одну сторону и комбинируя одинаковые термины.
Теперь фактор.
Для проверки, 2 x 2 + 2 x — 1 = x 2 + 6 x — 5
Квадратичная формула
Многие квадратные уравнения не могут быть решены факторизацией. Обычно это верно, когда корни или ответы не являются рациональными числами. Второй метод решения квадратных уравнений включает использование следующей формулы:
a, b, и c взяты из квадратного уравнения, записанного в его общем виде
топор 2 + bx + c = 0
, где a — это число перед x 2 , b — это число перед x , а c — это число без переменной рядом с ним (a .k.a., «постоянная»).
При использовании формулы корней квадратного уравнения вы должны знать о трех возможностях. Эти три возможности различаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком корня, b 2 — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее:
Два разных действительных корня, если дискриминант b 2 -4 ac является положительным числом.
Один действительный корень, если дискриминант b 2 — 4 ac равен 0.
Нет действительного корня, если дискриминант b 2 -4 ac является отрицательным числом.
Пример 6
Решить относительно x : x 2 — 5 x = –6.
Установка всех членов равными 0,
x 2 -5 x + 6 = 0
Затем замените 1 (который, как предполагается, стоит перед x 2 ), –5 и 6 вместо a , b и c, соответственно в формуле квадратного уравнения и упростите.
Поскольку дискриминант b 2 — 4 ac положительный, вы получаете два разных действительных корня.
Пример
производит рациональные корни. В примере
, квадратная формула используется для решения уравнения, корни которого нерациональны.Пример 7
Решить относительно y : y 2 = –2y + 2.
Установка всех членов равными 0,
y 2 + 2 y — 2 = 0
Затем замените 1, 2 и –2 на a , b и c, соответственно в формуле корней квадратного уравнения и упростите.
Обратите внимание, что два корня иррациональны.
Пример 8
Решить относительно x : x 2 + 2 x + 1 = 0.
Подставляя в формулу корней квадратного уравнения,
Поскольку дискриминант b 2 -4 ac равен 0, уравнение имеет один корень.
Квадратичная формула также может использоваться для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в действительной системе счисления.
Пример 9
Найдите x : x ( x + 2) + 2 = 0 или x 2 + 2 x + 2 = 0.
Подставляя в формулу корней квадратного уравнения,
Поскольку дискриминант b 2 — 4 ac отрицателен, это уравнение не имеет решения в действительной системе счисления.
Но если бы вы выразили решение с помощью мнимых чисел, решения были бы такими.
Завершение квадрата
Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.
Запишите уравнение в виде ax 2 + bx = — c .
Убедитесь, что a = 1 (если a ≠ 1, умножьте уравнение на, прежде чем продолжить).
Используя значение b из этого нового уравнения, добавьте к обеим сторонам уравнения, чтобы получить полный квадрат в левой части уравнения.
Найдите квадратный корень из обеих частей уравнения.
Решите полученное уравнение.
Пример 10
Решить относительно x : x 2 — 6 x + 5 = 0.
Оформить в виде
Поскольку a = 1, добавьте или 9 к обеим сторонам, чтобы завершить квадрат.
Извлеките квадратный корень из обеих частей.
x — 3 = ± 2
Решить.
Пример 11
Решить относительно y : y 2 + 2 y — 4 = 0.
Оформить в виде
Поскольку a = 1, прибавьте или 1 к обеим сторонам, чтобы завершить квадрат.
Извлеките квадратный корень из обеих частей.
Решить.
Пример 12
Решить относительно x : 2 x 2 + 3 x + 2 = 0.
Оформить в виде
Поскольку a ≠ 1, умножаем уравнение на.
