Содержание
Двугранный угол. 10-й класс
Цели урока:
ввести понятие двугранного угла и его
линейного угла;
угла между плоскостями;
Ход урока
I. Организационный момент.
Сообщить тему урока, сформировать цели урока.
II. Актуализация знаний учащихся (слайд 2, 3).
1. Подготовка к изучению нового материала.
— Что называется углом на плоскости?
— Что называется углом между прямыми в
пространстве?
— Что называется углом между прямой и
плоскостью?
— Сформулируйте теорему о трех перпендикулярах
III. Изучение нового материала.
- Понятие двугранного угла.
Фигура, образованная двумя полуплоскостями , проходящими
через прямую МN, называется двугранным углом (слайд
4).
Полуплоскости — грани, прямая МN – ребро
двугранного угла.
— Какие предметы в обыденной жизни имеют форму
двугранного угла? (Cлайд 5)
- Угол между плоскостями АСН и СНD – это
двугранный угол АСНD, где СН – ребро. Точки А и D
лежат на гранях этого угла. Угол AFD – линейный
угол двугранного угла АCHD (слайд 6).
- Алгоритм построения линейного угла (слайд 7).
1 способ. На ребре взять любую точку О и провести
перпендикуляры в эту точку (РО DE, KO DE) получили угол РОК — линейный.
2 способ. В одной полуплоскости взять точку К и
опустить из нее два перпендикуляра на другую
полуплоскость и ребро (КО и КР), тогда по теореме
обратной ТТП РОDE
- Все линейные углы двугранного угла равны (слайд
8). Доказательство: лучи ОА и О1А1
сонаправлены, лучи ОВ и О1В1 тоже
сонаправлены, углы ВОА и В1О1А1
равны как углы с сонаправлеными сторонами.
- Градусной мерой двугранного угла называется
градусная мера его линейного угла (слайд 9).
IV. Закрепление изученного материала.
- Решение задач (устно по готовым чертежам).
(Слайды10-12)
1. РАВС – пирамида; угол АСВ равен 90о,
прямая РВ перпендикулярна плоскости АВС.
Доказать, что угол РСВ – линейный угол
двугранного угла с
2. РАВС — пирамида; АВ = ВС, D – середина отрезка
АС, прямая РВ перпендикулярна плоскости АВС.
Доказать, что угол PDB – линейный угол двугранного
угла с ребром АС.
3. PABCD – пирамида; прямая РВ перпендикулярна
плоскости АВС, ВК перпендикулярна DC. Доказать,
что угол РКВ – линейный угол двугранного угла с
ребром СD.
- Задачи на построение линейного угла (слайды 13-14).
1. Построить линейный угол двугранного угла с
ребром АС, если в пирамиде РАВС грань АВС –
правильный треугольник, О – точка пересечения
медиан, прямая РО перпендикулярна плоскости АВС
2. Дан ромб АВСD.Прямая РС перпендикулярна
Дан ромб АВСD.Прямая РС перпендикулярна
плоскости АВСD.
Построить линейный угол двугранного угла с
ребром ВD и линейный угол двугранного угла с
ребром АD.
- Вычислительная задача. (Слайд 15)
В параллелограмме АВСD угол АDС равен 1200,
АD = 8 см,
DС= 6 см, прямая РС перпендикулярна плоскости
АВС, РС= 9 см.
Найти величину двугранного угла с ребром АD и
площадь параллелограмма.
V. Домашнее задание (слайд16).
П. 22, № 168, 171.
Используемая литература:
- Геометрия 10-11 Л.С.Атанасян.
- Система задач по теме “Двугранные углы”
М.В.Севостьянова (г.Мурманск), журнал Математика в
школе 198… г.
Презентация — Двугранный угол
Слайды и текст этой онлайн презентации
Слайд 1
Двугранный угол
Подготовила: учитель математики МКОУ «Ванашимахинская СОШ»
Расулова Р. А.
А.
Слайд 2
Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно, и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии.
А.С. Пушкин
Слайд 3
геометрия
Слайд 4
угол
Слайд 5
двугранный
Слайд 6
Слайд 7
знакомство с понятиями двугранный угол и его линейный угол, обучение построению линейного угла данного двугранного угла, развитие навыков построения перпендикуляра к плоскости, применения ТТП, внимания,
воспитание усидчивости, взаимоуважения.
получить необходимую информацию;
проанализировать полученную информацию;
применить теорию на практике;
заполнить кластер;
оценить свою деятельность.
Слайд 8
Стереометрия
Планиметрия
Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки.
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.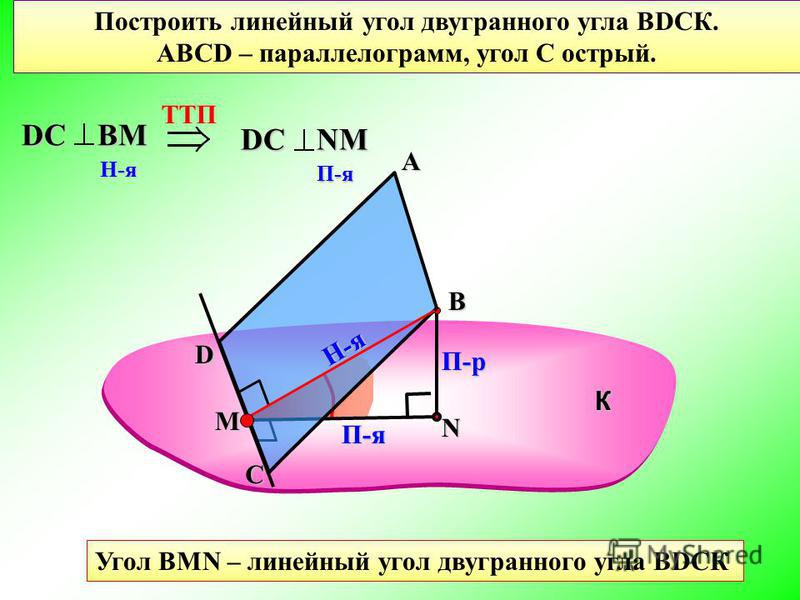
Двугранный угол
а
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла
Слайд 9
Слайд 10
Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях двугранного угла
D
Угол РDEK
А
Р
К
N
M
В
E
Угол SFX – линейный угол двугранного угла
Слайд 11
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла называется градусная мера его линейного угла.
E
Слайд 12
Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны
как углы с сонаправленными сторонами
Слайд 13
Двугранный угол может быть острым, прямым, тупым
Слайд 14
Слайд 15
Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный.
Треугольник АВС – тупоугольный.
В
П-р
Н-я
А
К
С
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
Слайд 16
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
В
П-р
Н-я
А
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВАСК
Слайд 17
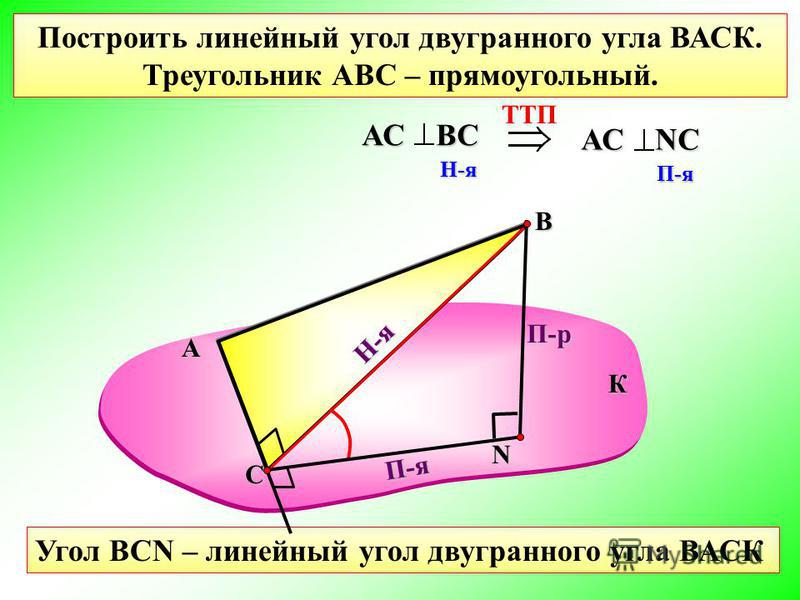
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
В
П-р
А
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВАСК
Слайд 18
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 19
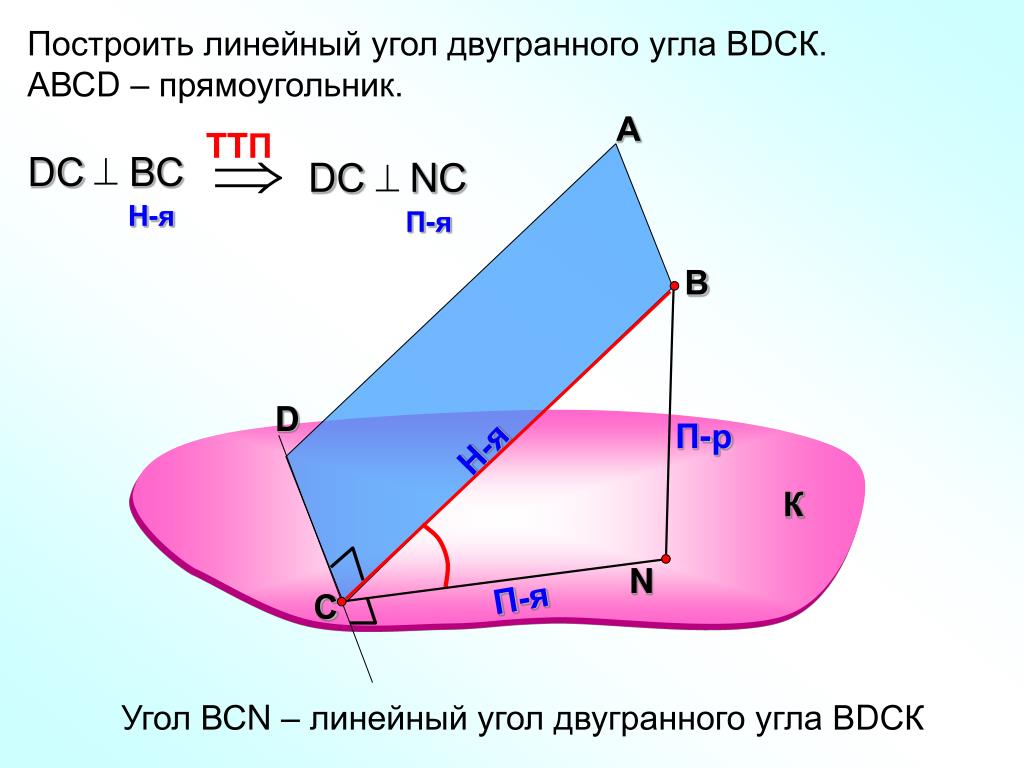
Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник.
АВСD – прямоугольник.
А
В
D
П-р
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВАСК
Слайд 20
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
Н-я
D
П-р
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 21
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 22
Построить угол между плоскостями АВС и ВКС
Слайд 23
Построить угол между плоскостями АВСД и АСД1
Д1
С1
А1
В1
Д
С
А
В
Слайд 24
Построить угол между плоскостями АВ1С и АВС
С1
А1
В1
С
О
А
В
Слайд 25
Постройте угол между плоскостями ВF1Д и АВСДЕF
Е1
Д1
F1
С1
А1
В1
Е
Д
F
О
С
А
В
Слайд 26
Задача 1:
В кубе A…D1 найдите угол между плоскостями ABC и CDD1.
Задача 2:
В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
Задача 5:
В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.
Задача 6:
Слайд 27
Задача 1:
Задача 2:
Д1
С1
А1
В1
Д
С
А
В
Ответ: 90o.
Ответ: 45o.
Слайд 28
Задача 3:
Задача 4:
Д1
Д1
С1
С1
А1
В1
А1
В1
Д
Д
С
С
А
А
В
В
Ответ: 90o.
Ответ: 90o.
Слайд 29
Задача 5:
Решение:
— диагональ квадрата со стороной равной 1.
О
Слайд 30
Доказательство:
А
Н-я
Угол АВС – линейный угол двугранного угла АМNC
П-р
N
П-я
M
Слайд 31
Определение двугранного угла
Теорема о трех перпендикулярах
Определение наклонной
Какие знания и умения необходимы при построении двугранного угла?
Определение проекции
Определение перпендикуляра
Определение пересекающихся плоскостей
Построение пересекающихся плоскостей
Построение перпендикуляра
Слайд 32
Слайд 33
Интернет – ресурсы
http://le-savchen. ucoz.ru/load/3-1-0-168
http://www.uchportal.ru/load/24-1-0-22870
http://nsportal.ru/shkola/geometriya/library/dvugrannyi-ugol
ucoz.ru/load/3-1-0-168
http://www.uchportal.ru/load/24-1-0-22870
http://nsportal.ru/shkola/geometriya/library/dvugrannyi-ugol
Двугранный угол (Урок геометрии в 10 классе)
1. Двугранный угол
ДВУГРАННЫЙ
УГОЛ
Урок геометрии в 10 классе
Вдохновение есть расположение души к
живейшему принятию впечатлений и
соображению понятий, следственно, и
объяснению оных. Вдохновение нужно в
геометрии, как и в поэзии.
А.С. Пушкин
угол
двугранный
знакомство с понятиями двугранный угол и его линейный
угол, обучение построению линейного угла данного
двугранного угла, развитие навыков построения
перпендикуляра к плоскости, применения ТТП, внимания,
воспитание усидчивости, взаимоуважения.
получить необходимую информацию;
проанализировать полученную информацию;
применить теорию на практике;
заполнить кластер;
оценить свою деятельность.
Стереометрия
Планиметрия
Углом на плоскости
называется фигура,
образованная двумя лучами,
исходящими из одной
точки.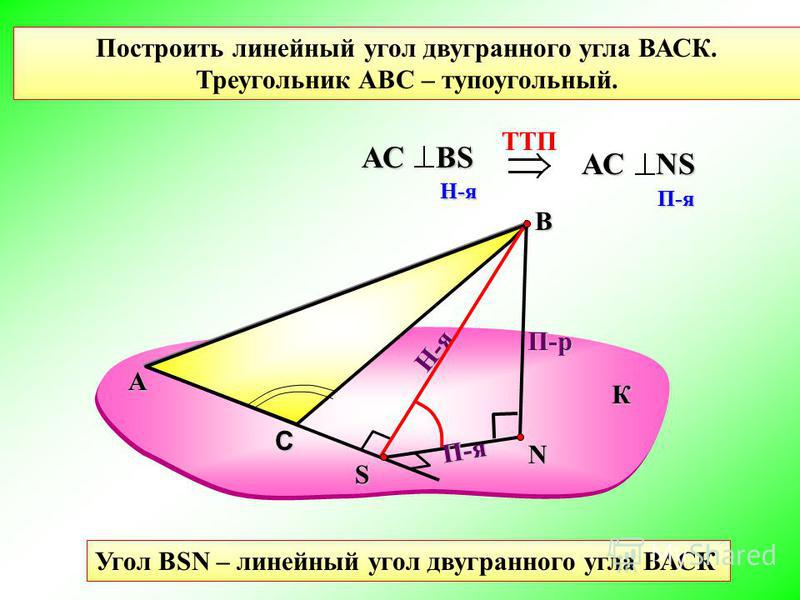
А
Двугранным углом называется
фигура, образованная прямой a
и двумя полуплоскостями с
общей границей a, не
принадлежащими одной
плоскости.
Двугранный угол
(α;β)=(α;β)
В
а
С
α∩β = a
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла
Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях
двугранного угла
D
Угол РDEK
S
O
А
Р
N
F
В
M
К
X
E
Угол SFX – линейный угол двугранного угла
ABNM. Угол РОК- линейный угол двугранного
угла PDEK.
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла
называется градусная мера его линейного
угла.
O
Р
К
E
Плоскость линейного угла ( РОК ) DE
Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
O
А
В
Углы АОВ и А1О1В1 равны
как углы с сонаправленными
сторонами
А1
O1
В1
Двугранный угол может быть острым, прямым, тупым
Градусная мера двугранного угла – это
градусная мера его линейного угла
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
АС
ВS
H-я
TTП
АС NS
П-я
В
П-р
А
К
С
S
N
Угол ВSN – линейный угол двугранного угла ВАСК
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
АС ВМ
H-я
В
TTП
АС NМ
П-я
П-р
А
К
N
M
П-я
С
Угол ВMN – линейный угол двугранного угла ВАСК
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС ВС
H-я
TTП
АС NС
П-я
В
П-р
А
К
С
N
Угол ВСN – линейный угол двугранного угла ВАСК
17. Задача 1:
ЗАДАЧА 1:
В кубе A…D1 найдите угол между плоскостями ABC и CDD1
Задача 2:
В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
Задача 1:
Д1
А1
Задача 2:
С1
В1
Д1
А1
Д
В
Ответ: 90o.
В1
Д
С
А
С1
С
А
Ответ:
45o.
В
Задача 3:
Задача 4:
Д1
Д1
С1
А1
В1
А1
Д
С1
В1
Д
С
А
В
Ответ:
90o.
С
А
В
Ответ: 90o.
20. Домашнее задание: п.22, №167, №169, №172(повышенный уровень)
ДОМАШНЕЕ ЗАДАНИЕ:
П.22, №167, №169,
№172(ПОВЫШЕННЫЙ
УРОВЕНЬ)
Теорема о трех
перпендикулярах
Определение
проекции
Построение
пересекающихся
плоскостей
Определение
двугранного угла
Определение
наклонной
Какие знания и умения
необходимы при
построении двугранного
угла?
Определение
перпендикуляра
Определение
пересекающихся
плоскостей
Построение
перпендикуляра
Интернет – ресурсы
http://le-savchen.ucoz.ru/load/3-1-0-168
http://www.uchportal.ru/load/24-1-0-22870
http://nsportal.ru/shkola/geometriya/library/dvugrannyi-ugol
Урок 7: Двугранный угол — 100urokov.
 ru
ru
План урока:
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Многогранный угол
Типичные задачи на углы между плоскостями
Понятие двугранного угла и угла между плоскостями
Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.
По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.
Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:
Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.
Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.
Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:
Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).
Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.
Перпендикулярность плоскостей
В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.
Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.
Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Из доказанного признака вытекает следующее утверждение:
Прямоугольный параллелепипед
Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.
Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:
Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1. При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
Докажем некоторые свойства прямоугольного параллелепипеда.
Например, ребро АD пересекается с гранями АВВ1А1 и CDD1C1. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD1, ведь и ADD1A1 – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.
Эти грани пересекаются по ребру А1D1. Этому ребру в свою очередь перпендикулярны ребра АА1 и А1В1, лежащие в гранях ADD1A1 и A1D1C1B1. Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:
Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:
Действительно, пусть есть прямоугольный параллелепипед АВСDA1B1C1D1. Назовем ребро AD его длиной, АВ – шириной, а ВВ1 – высотой. Пусть необходимо найти длину диагонали В1D:
Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:
Теперь перейдем к ∆В1ВD. Так как ребро BB1 перпендикулярно грани ABCD, то ∠В1ВD – прямой. Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:
Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:
Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:
Трехгранный угол
Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:
В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:
Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:
Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:
Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство
Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:
Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть
Именно это неравенство и необходимо было доказать.
Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:
Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:
Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и
Многогранный угол
Возможен случай, когда из одной точки в пространстве выходят не три, а большее количество лучей, причем образуемые ими углы не располагаются в единой плоскости. Такая фигура именуется многогранным углом. Трехгранный угол можно считать его частным случаем. Также его частными случаями будут четырехгранный угол, пятигранный угол, шестигранный угол и т.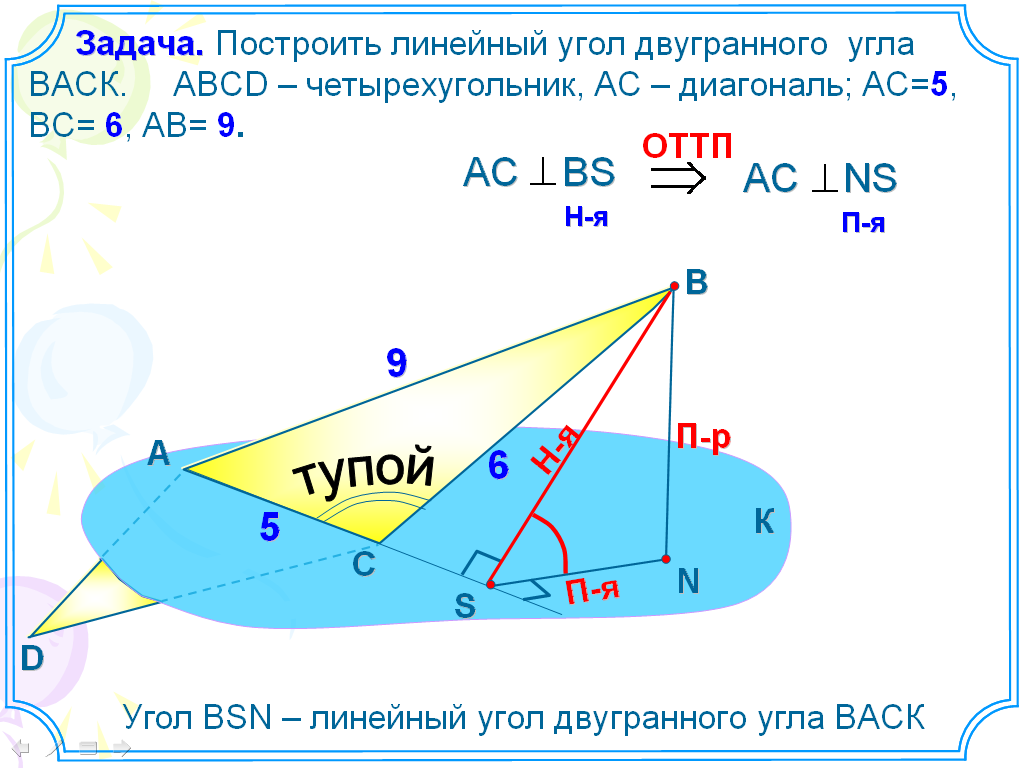 д.
д.
Более наглядна следующая демонстрация многогранного угла. Построим на плоскости α произвольный многоугольник. Далее выберем какую-нибудь точку вне плоскости α и соединим ее с вершинами многоугольника с помощью лучей. При этом у нас как раз получится многогранный угол. Если, например, в качестве многоугольника мы использовали пятиугольник, то и получим мы пятигранный угол:
Важно отметить, что в данном случае состоит многогранный угол именно из лучей КА1, КА2, КА3…, а не из одноименных отрезков. То есть многогранный угол – это ни в коем случае не многогранник КА1А2А3А4А5, у него есть только одна вершина – точка К. Многогранник КА1А2А3А4А5 – это пирамида, такая фигура изучается в курсе стереометрии чуть позже. Многоугольник А1А2А3А4А5 – это сечение многогранного угла. Углы ∠А1КА2, ∠А2КА3, ∠А3КА4… – это плоские углы многогранного угла.
Заметим, что на исходный многоугольник на плоскости может быть как выпуклым, так и невыпуклым. Соответственно и многогранный угол может быть как выпуклым, так и невыпуклым:
Так как любой треугольник – это выпуклый многоугольник, то и любой трехгранный угол является выпуклым. В выпуклом угле все его точки лежат по одну сторону от любой плоскости, проходящей, через какие-нибудь два смежных луча угла. Вообще любое сечение многогранного угла представляет собой выпуклый многоугольник.
Докажем важное утверждение:
Для доказательства возьмем произвольный многогранный угол и проведем в нем сечение А1А2А3…Аn, которое будет являться выпуклым многоугольником:
В последнем равенстве в каждой скобке стоят по два плоских угла в тех трехгранных углах, вершины которых совпадают с вершинами многоугольника А1А2А3…Аn. В предыдущей теореме мы выяснили, что эта сумма меньше третьего плоского угла, то есть
В правой части в скобках стоит сумма углов выпуклого n-угольника А1А2А3…Аn. Она, как мы знаем, составляет 180°•(n – 2), то есть
Последнее неравенство и необходимо было доказать.
Типичные задачи на углы между плоскостями
В школьной практике почти не встречаются задачи с многогранными углами, поэтому достаточно понимания и двугранного угла.
Задание. У тетраэдра ABCD все ребра одинаковы. Найдите величину двугранного угла между плоскостями АВС и АСD.
Решение. Отметим на ребре АС точку М, которая является его серединой:
Заметим, что плоскости АВС и АСD пересекаются по прямой АС. Раз все ребра тетраэдра одинаковы, то ∆АВС и ∆АСD – равносторонние. DM и BM – это медианы в ∆АВС и ∆АСD соответственно, ведь M – середина АС. Но раз треугольники равносторонние, то они одновременно являются и высотами, то есть BM⊥AC и DM⊥АС. Тогда ∠DMB как раз и представляет собой линейный угол двугранного угла BАСD. То есть именно его значение нам и надо вычислить (если, конечно, он окажется не больше 90°).
Пусть ребра тетраэдра имеют длину а. Тогда АМ вдвое короче. Найдем из прямоугольного ∆АМD длину MD:
Задание. Двугранный угол равен φ, меньший 90°. На одной из его граней отмечена точка К, которая находится на расстоянии d от другой грани. Каково расстояние между точкой К и ребром двугранного угла?
Решение. Пусть угол образован плоскостями α и β. Опустим из K два перпендикуляра – один на плоскость β в точку Н, а другой на линию пересечения плоскостей в точку Р:
По условию задачи ∠НРК = φ, а HK = d. Нам же надо найти РК. Это можно сделать, применив определение синуса к ∆РНК:
Задание. Верно ли, что плоскость, пересекающая две параллельные плоскости, образует с ними одинаковые углы?
Решение. Пусть есть параллельные друг другу плоскости α и β, а пересекает их плоскость γ. Линию пересечения α и γ обозначим как n, и такую же линию для β и γ обозначим как m:
Заметим, что m и n располагаются в одной плоскости γ и при этом не пересекаются, в противном случае у α и β нашлась бы общая точка, которой быть не должно. Значит, m||n.
Далее проведем в γ прямую р, перпендикулярную n. Раз m||n и р⊥n, то и р⊥m. То есть р – общий перпендикуляр для m и n.
Далее в α через точку пересечения n и p проведем прямую k, перпендикулярную n. Ясно, что k||β. После уже через точку пересечения m и p построим такую прямую k’, что k||k’:
Так как k||β и k||k’, то прямая k’ будет принадлежать плоскости β (по теореме 6 из этого урока). Так как k||k’, m||n и n⊥k, то по теореме о сонаправленных лучах можно утверждать, что и m⊥k’. Тогда углы, отмеченные на рисунке синим цветом – это и есть линейные углы двугранных углов. Они одинаковы, так как являются соответственными при секущей р и параллельных прямых k и k’. Если же двугранные углы равны, то одинаковы и углы между плоскостями, ч. т. д.
Примечание. Доказанный факт можно сформулировать в виде теоремы:
Она может быть использована при решении некоторых сложных задач.
Задание. В прямоугольном ∆АВС АВ и АС – катеты с длиной 7 и 24 соответственно. Через гипотенузу проведена плоскость β, образующая с плоскостью АВС угол 30°. Каково расстояние между точкой А и плоскостью β?
Решение.
Опустим из А перпендикуляр АН на β. Это и будет искомое нами расстояние. Также в ∆АВС построим высоту AD. Заметим, что раз АН⊥β, то по определению и АН⊥HD. Можно сказать, что HD – это проекция AD на β. Раз прямая ВС перпендикулярна наклонной AD, то она одновременно будет перпендикулярна и наклонной HD по обратной теореме о трех перпендикулярах.
Плоскости АВС и β пересекаются по прямой ВС, АD⊥ВС и HD⊥BC. Получается, что ADH – это как раз угол между АВС и β, и по условию он составляет 30°.
По теореме Пифагора вычислим гипотенузу ВС:
Теперь перейдем к ∆AHD. Он также прямоугольный (∠Н = 90°). Используем для него тригонометрию:
Задание. Известны измерения прямоугольного параллелепипеда. Его длина составляет 90 см, ширина – 20 см, а высота – 60 см. Какова длина диагонали такого параллелепипеда?
Решение. Обозначим измерения буквами а, b, с, а диагональ буквой d. Достаточно просто воспользоваться формулой:
Далее рассмотрим несколько задач, в которых надо найти угол между плоскостями, находящимися в кубе с ребром, чья длина составляет единицу.
Задание. Вычислите угол между гранью ADHЕ и сечением АBGН:
Решение. Заметим, что сечение АВGH содержит прямую АВ. Но АВ – это перпендикуляр к АЕНD. Если АВGH содержит перпендикуляр к ADH, то эти две плоскости перпендикулярны, и угол между ними составляет 90°.
Ответ: 90°.
Задание. Определите угол между гранью ADHE и сечением ADGF:
Решение. Две рассматриваемые плоскости пересекаются по ребру AD. Ребра DH и AD перпендикулярны как стороны квадрата. Так как AD – это перпендикуляр к грани СDHG, то AD⊥DG. Получается, что ∠HDG – это и есть искомый угол. Его величина равна 45°, ведь это угол между диагональю квадрата и его стороной.
Ответ: 45°.
Задание. Вычислите угол между сечениями АВGH и EFCD:
Решение. Пересекаются эти две плоскости по прямой KP, где K и P – точки пересечения диагоналей квадратов BFGH и AEHD. Докажем, что отрезки KG и KC перпендикулярны KP.
Действительно, рассмотрим четырехугольник АВGH. Ребра АВ и GH перпендикулярны граням AEHD и BFGH, поэтому все углы в АВGH – прямые, то есть это прямоугольник и BG||AH. Теперь рассмотрим четырехугольник АВKP. Стороны BK и AP параллельны и равны как половины равных отрезков BG и AH. Значит, BKAP – параллелограмм. Но в нем есть прямые углы ∠В и ∠А, поэтому BKAP – прямоугольник. Аналогично можно показать, что и KGHP – прямоугольник. Это и приводит к выводу о том, что KG⊥KP и PH⊥KP. Поэтому ∠СKG и является искомым углом между сечениями. Он является углом между диагоналями квадрата, то есть равен 90°.
Ответ: 90°.
Задание. Найдите угол между сечением AFH и гранью AEHD:
Решение. Обозначим середину диагонали AH буквой K. Докажем ∠EKF – искомый нами угол:
Действительно, плоскости AHD и AFH пересекаются по прямой AH. EK – медиана в равнобедренном ∆AEH с основанием AH, поэтому она также является и высотой, то есть EK⊥AH. AF и FH – диагонали в равных квадратах ABFE и EFGH, поэтому эти диагонали одинаковы. Значит, ∆AFH – равнобедренный, и поэтому его медиана FK также перпендикулярна основанию AH. Получается, что ∠EKF и является искомым. Вычислить его можно из ∆EKF.
Сначала найдем длину EK. В прямоугольном ∆AEK ∠KAE составляет 45° (угол между диагональю и стороной квадрата), поэтому
Задание. Вычислите угол между гранью BCGF и сечением AFH:
Решение. Вспомним, что в предыдущей задаче мы уже вычислили угол между гранью АЕHD и тем же сечением АFH. Но грани AEHD и BCFG параллельны, поэтому АFH должна пересекаться их под одним и тем же углом. Поэтому ответ этой задачи совпадает с ответом к предыдущей задаче.
Ответ: ≈ 54,74°.
Задание. Чему равен угол между сечениями АСH и AFGH?
Решение. Пусть диагонали СН и DG пересекаются в точке К. Точка K будет принадлежать обоим сечениям, как и точка А. Значит, сечения пересекаются по линии АК. Проведем в сечении AFGH через точку K прямую, перпендикулярны АК и пересекающую FG в какой-то точке Р (позже мы убедимся, что прямая действительно должна пересекать отрезок FG):
Докажем, что ∠CPK и является углом между сечениями. Мы специально провели РК так, что РК⊥АК. Теперь посмотрим на ∆АСН. Он равносторонний, ведь его стороны АС, СН и DH – это диагонали равных квадратов (граней куба). Прямая АК – медиана, ведь K – точка пересечения диагоналей квадрата СDHG, которая делит диагонали пополам. Но раз ∆АСН равносторонний, то его медиана – это ещё и высота, то есть АК⊥РК. Итак, АК⊥СК и АК⊥РК, поэтому ∠CPK – это угол между сечениями. Для его вычисления необходимо найти все стороны в ∆РСК и далее применить теорему косинусов.
Проще всего найти СК. ∆СKD – прямоугольный (∠К = 90°), а ∠СDK составляет 45° (угол между стороной и диагональю в квадрате). Тогда можно записать, что
Отдельно отметим, что отрезки GK и KD имеют такую же длину, ведь диагонали в квадрате (а значит и их половины) одинаковы.
Для нахождения РК покажем отдельно плоскость AFG, то есть красное сечение:
Обозначим ∠KAD как φ. Тогда ∠АКD будет составлять 90 – φ. Углы ∠АКD, ∠АKP и ∠PKG в сумме дают 180°, что позволяет найти ∠PKG:
Получилось, что у ∆АКD и ∆PKG есть по два одинаковых угла (φ и 90°). Значит, они подобны. Составим такую пропорцию:
Теперь можно вернуться ко всему кубу и найти отрезок РС. Здесь снова можно применить теорему Пифагора, но уже к ∆PCG:
Теперь для ∆PCK мы можем записать теорему косинусов
Неожиданно мы доказали, что два построенных сечения перпендикулярны друг другу. Прийти к этому выводу можно было и иначе. Достаточно было бы показать, что прямая CH – это перпендикуляр к сечению AFGD. Попробуйте сделать это самостоятельно.
Ответ: 90°.
Задание. Вычислите угол между сечениями BDHF и ADGF:
Решение. У сечений общими являются точки F и D. Значит, именно по прямой FD они пересекаются.
Опустим в синей сечении BDHF перпендикуляр на FD, который упадет в некоторую точку K:
Докажем, что отрезок GK также перпендикулярен FD. Действительно, BK – это высота в ∆BDF. Но ∆BDF и ∆GDF равны, ведь они одинаковы все три стороны (FD – общая сторона, BF и FG – ребра куба, BD и DG – диагонали на гранях куба). В равных треугольниках высоты должны делить стороны на равные отрезки, поэтому высота, опущенная из G на FD, также разделит FD на отрезки FK и KD. То есть она просто упадет в точку K. Это и значит, что KG – высота. Получается, что нам надо вычислить ∠BKG.
Сначала найдем длину диагоналей BD и BG. Можно применить теорему Пифагора для ∆BFG:
KG имеет ту же длину, ведь KG и BK – одинаковые высоты в равных треугольниках ∆BDF и ∆GDF.
Теперь используем теорему косинусов для ∆BKG:
Мы вычислили двугранный угол, но он оказался больше 90°. Это значит, угол между плоскостями равен не 120°, а 180° – 120°, то есть 60°.
Ответ: 60°.
Сегодня мы познакомились с понятием двугранного угла, научились вычислять углы между плоскостями. В частном случае вместо вычисления угла можно просто доказать перпендикулярность плоскостей.
Двугранный угол. — Геометрия — Уроки
Урок геометрии, 10 класс
Тема: «Двугранный угол».
Цель урока: ввести понятия двугранного угла и его линейного угла, рассмотреть задачи на применение этих понятий, сформировать навыки нахождения угла между плоскостями.
Задачи:
Обучающая: формирование способности запоминания основной терминологии, формирование навыков правильного оформления записей.
Воспитательная: дисциплинированность, уверенность в себе, уважительное отношение к окружающим, аккуратность, самостоятельность, трудолюбие, точность.
Развивающая: развитие математической речи, логического мышления, внимания, сообразительности, ответственности, привитие интереса к предмету.
Материалы и оборудование: компьютер, проектор, линейка, цветной мел.
Тип урока: урок изучения нового материала
Этапы урока:
Организационный (приветствие, объявление темы и цели урока, проверка готовности к уроку).
Актуализация опорных знаний.
Проверка домашнего задания. Проверяем № 159.
Определение угла на плоскости.
Определение угла между двумя пересекающимися прямыми в пространстве.
Определение угла между двумя скрещивающимися прямыми в пространстве.
Определение угла между прямой и плоскостью.
Объяснение нового материала.
Познакомимся с еще одним видом углов – двугранным углом.
Чтобы ввести понятие двугранного угла, следует напомнить, что любая прямая, проведенная в данной плоскости, разделяет эту плоскость на две полуплоскости (рис.1,а)
а) б)
Рис. 1
Представим себе, что мы перегнули плоскость по прямой так, что две полуплоскости с границей оказались уже не лежащими в одной плоскости , как показано на рис. 1, б. Полученная фигура и есть двугранный угол.
Определение. Двугранным углом называется фигура, образованная прямой и двумя полуплоскостями с общей границей, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. У двугранного угла две грани, отсюда и название — двугранный угол. Прямая — общая граница полуплоскостей — называется ребром двугранного угла.
Вопрос к учащимся: Приведите примеры из обыденной жизни предметов и конструкций, имеющих форму двугранного угла..
Полураскрытая папка, стена комнаты совместно с полом, двускатные крыши зданий.
Как известно, углы на плоскости измеряются в градусах. Чтобы измерить двугранный угол, поступим следующим образом. Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проведем луч перпендикулярно к ребру. Образованный этими лучами угол называется линейным углом двугранного угла. Сделайте чертёж у себя в тетрадях.
О ∈ а, АО ⊥ а, ВО ⊥ a, САBD – двугранный угол, ∠AOB – линейный угол двугранного угла.
С
А ЩО В
D Рис. 2
Все линейные углы двугранного угла равны. Сделаем рисунок.
А О В
Р Q R
Рис. 3
Доказательство. Рассмотрим два линейных угла АОВ и PQR. Лучи ОА и QP лежат в одной грани и перпендикулярны OQ, значит, они сонаправлены. Аналогично лучи ОВ и QR сонаправлены. Значит, ∠AOB = ∠PQR (как углы с сонаправленными сторонами).
Градусной мерой двугранного угла называется градусная мера его линейного угла. Перерисуйте из учебника со страницы 48 изображения острого, прямого и тупого двугранного угла.
Закрепление изученного материала.
Выполним несколько заданий.
№ 1. Дано: ΔABC, АС = ВС, АВ лежит в плоскости α, CD ⊥ α, С ∉ α. Построить линейный угол двугранного угла CABD.
Решение. CM ⊥ AB, DC ⊥ АВ. ∠CMD — искомый.
№ 2. Дано: ΔABC, ∠C = 90°, ВС лежит плоскости α, АО ⊥ α, A ∈ α.
Построить линейный угол двугранного угла АВСО.
Решение. AB ⊥ BC, АО ⊥ ВС, значит, ОС ⊥ ВС. ∠ACO — искомый.
№ 3. Дано: ΔABC, ∠С = 90°, АВ лежит в плоскости α, CD ⊥ α, С ∉ α. Построить линейный угол двугранного угла DABC.
Решение. CK ⊥ AB, DC ⊥ АВ, DK ⊥ АВ, значит, ∠DKC — искомый.
№ 4. Дано: DABC — тетраэдр, DO ⊥ ABC. Построить линейный угол двугранного угла ABCD.
Решение. DM ⊥ ВС, DO ⊥ ВС, значит, ОМ ⊥ ВС; ∠OMD — искомый.
Домашнее задание. п. 22, №167, №170.
Итог урока.
Что нового вы узнали сегодня на уроке? Какова была цель нашего урока? Достигнута ли она?
Как определить двугранный угол. Двугранный угол, перпендикулярные плоскости. Двугранный угол. Линейный угол двугранного угла. Двугранным углом называется фигура, образованная двумя. Подготовка к экзаменационному испытанию вместе со «Школково»
Одни из самых простых пространственных фигур — это многогранней углы.
Двугранный угол — это фигура, образованная двумя полуплоскости, имеющих общую прямую, их ограничивает. Полуплоскости называются гранями угла, а общая прямая — ребром угла. Степени двугранного угла есть мера соответствующего ему линейного угла.
Линейный угол двугранного угла — это угол, образованный двумя полупрямой, по которым плоскость, перпендикулярна к ребру двугранного угла, пересекает данный двугранный угол. Мера двугранного угла не зависит от выбора линейного угла.
Трехгранный угол — это фигура, состоящая из трех плоских углов.
Гранями трехгранного угла являются плоские углы, ребрами являются стороны плоских углов, вершиной трехгранного угла есть общая вершина плоских углов.
Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Каждый плоский угол трехгранного угла меньше суммы двух других его плоских углов.
Многогранник есть тело, поверхность которого состоит из конечного числа плоских многоугольников.
Гранью многогранника является поверхность каждого плоского многоугольника.
Ребрами многогранника являются стороны граней, вершинами многогранника есть вершины граней.
Двугранный угол при ребре многогранника определяется его гранями, в которых лежит данное ребро.
Выпуклым многогранником называется, лежащий по одну сторону от плоскости каждого из плоских многоугольников на его поверхности.
Каждая грань выпуклого многогранника — это выпуклый многоугольник. Плоскость, проходящая через внутреннюю точку выпуклого многогранника, пересекает его и в сечении образует выпуклый многоугольник.
Это интересно. Одна из частей геометрии образовала отдельную науку, которая называется топологией. Она изучает топологические свойства фигур, то есть такие, которые хранятся при непрерывных деформациях фигур «без разрывов и склеек».
Теорема Эйлера, великого математика, физика и астронома, формулирует топологическую свойство многогранников: для любого выпуклого многогранника сумма количества его вершин и количества граней без учета количества его ребер равно числу 2.
Понятие двугранного угла
Для введения понятия двугранного угла, для начала вспомним одну из аксиом стереометрии.
Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях — по разные стороны от прямой $a$ (рис. 1).
Рисунок 1.
На этой аксиоме основан принцип построение двугранного угла.
Определение 1
Фигура называется двугранным углом
, если она состоит из прямой и двух полуплоскостей этой прямой, не принадлежащих одной плоскости.
При этом полуплоскости двугранного угла называются гранями
, а прямая, разделяющая полуплоскости — ребром двугранного угла
(рис. 1).
Рисунок 2. Двугранный угол
Градусная мера двугранного угла
Определение 2
Выберем на ребре произвольную точку $A$. Угол между двумя прямыми, лежащими в разных полуплоскостях, перпендикулярных ребру и пересекающихся в точке $A$ называется линейным углом двугранного угла
(рис. 3).
Рисунок 3.
Очевидно, что каждый двугранный угол имеет бесконечное число линейных углов.
Теорема 1
Все линейные углы одного двугранного угла равняются между собой.
Доказательство.
Рассмотрим два линейных угла $AOB$ и $A_1{OB}_1$ (рис. 4).
Рисунок 4.
Так как лучи $OA$ и ${OA}_1$ лежат в одной полуплоскости $\alpha $ и перпендикулярны одной прямой, то они являются сонаправленными. Так как лучи $OB$ и ${OB}_1$ лежат в одной полуплоскости $\beta $ и перпендикулярны одной прямой, то они являются сонаправленными. Следовательно
\[\angle AOB=\angle A_1{OB}_1\]
В силу произвольности выборов линейных углов. Все линейные углы одного двугранного угла равны между собой.
Теорема доказана.
Определение 3
Градусной мерой двугранного угла называется градусная мера линейного угла двугранного угла.
Примеры задач
Пример 1
Пусть нам даны две неперпендикулярные плоскости $\alpha $ и $\beta $ которые пересекаются по прямой $m$. Точка $A$ принадлежит плоскости $\beta $.0\] \[\frac{5}{AB}=\frac{1}{2}\] \
\(\blacktriangleright\)
Двугранный угол – угол, образованный двумя полуплоскостями и прямой \(a\)
, которая является их общей границей.
\(\blacktriangleright\)
Чтобы найти угол между плоскостями \(\xi\)
и \(\pi\)
, нужно найти линейный угол (причем острый
или прямой
) двугранного угла, образованного плоскостями \(\xi\)
и \(\pi\)
:
Шаг 1: пусть \(\xi\cap\pi=a\)
(линия пересечения плоскостей). В плоскости \(\xi\)
отметим произвольную точку \(F\)
и проведем \(FA\perp
a\)
;
Шаг 2: проведем \(FG\perp \pi\)
;
Шаг 3: по ТТП (\(FG\)
– перпендикуляр, \(FA\)
–наклонная, \(AG\)
– проекция) имеем: \(AG\perp a\)
;
Шаг 4: угол \(\angle FAG\)
называется линейным углом двугранного угла, образованного плоскостями \(\xi\)
и \(\pi\)
.
Заметим, что треугольник \(AG\)
– прямоугольный.
Заметим также, что плоскость \(AFG\)
, построенная таким образом, перпендикулярна обеим плоскостям \(\xi\)
и \(\pi\)
. Следовательно, можно сказать по-другому: угол между плоскостями
\(\xi\)
и \(\pi\)
— это угол между двумя пересекающимися прямыми \(c\in \xi\)
и \(b\in\pi\)
, образующими плоскость, перпендикулярную и \(\xi\)
, и \(\pi\)
.
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите \(6\cos \alpha\)
, где \(\alpha\)
– угол между ее смежными боковыми гранями.
Пусть \(SABCD\)
– данная пирамида (\(S\)
– вершина), ребра которой равны \(a\)
. Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями \(SAD\)
и \(SCD\)
.
Проведем \(CH\perp SD\)
. Так как \(\triangle SAD=\triangle SCD\)
, то \(AH\)
также будет высотой в \(\triangle SAD\)
. Следовательно, по определению \(\angle AHC=\alpha\)
– линейный угол двугранного угла между гранями \(SAD\)
и \(SCD\)
.
Так как в основании лежит квадрат, то \(AC=a\sqrt2\)
.2}{2CH\cdot AH}=-\dfrac13 \quad\Rightarrow\quad
6\cos\alpha=-2.\]
Ответ:
-2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
Плоскости \(\pi_1\)
и \(\pi_2\)
пересекаются под углом, косинус которого равен \(0,2\)
. Плоскости \(\pi_2\)
и \(\pi_3\)
пересекаются под прямым углом, причем линия пересечения плоскостей \(\pi_1\)
и \(\pi_2\)
параллельна линии пересечения плоскостей \(\pi_2\)
и \(\pi_3\)
. Найдите синус угла между плоскостями \(\pi_1\)
и \(\pi_3\)
.
Пусть линия пересечения \(\pi_1\)
и \(\pi_2\)
– прямая \(a\)
, линия пересечения \(\pi_2\)
и \(\pi_3\)
– прямая \(b\)
, а линия пересечения \(\pi_3\)
и \(\pi_1\)
– прямая \(c\)
. Так как \(a\parallel b\)
, то \(c\parallel a\parallel b\)
(по теореме из раздела теоретической справки “Геометрия в пространстве” \(\rightarrow\)
“Введение в стереометрию, параллельность”).
Отметим точки \(A\in a, B\in b\)
так, чтобы \(AB\perp a, AB\perp b\)
(это возможно, так как \(a\parallel b\)
).2\)
, откуда \
Запишем для треугольника \(AMB\)
теорему косинусов: \
Тогда \
Так как угол \(\alpha\)
между плоскостями – это острый угол, а \(\angle AMB\)
получился тупым, то \(\cos\alpha=\dfrac5{12}\)
. Тогда \
Ответ:
1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
\(ABCDA_1B_1C_1D_1\)
– параллелепипед, \(ABCD\)
– квадрат со стороной \(a\)
, точка \(M\)
– основание перпендикуляра, опущенного из точки \(A_1\)
на плоскость \((ABCD)\)
, кроме того \(M\)
– точка пересечения диагоналей квадрата \(ABCD\)
. Известно, что \(A_1M = \dfrac{\sqrt{3}}{2}a\)
. Найдите угол между плоскостями \((ABCD)\)
и \((AA_1B_1B)\)
. Ответ дайте в градусах.
Построим \(MN\)
перпендикулярно \(AB\)
как показано на рисунке.
Так как \(ABCD\)
– квадрат со стороной \(a\)
и \(MN\perp AB\)
и \(BC\perp AB\)
, то \(MN\parallel BC\)
. Так как \(M\)
– точка пересечения диагоналей квадрата, то \(M\)
– середина \(AC\)
, следовательно, \(MN\)
– средняя линия и \(MN =\frac12BC= \frac{1}{2}a\)
.\circ\)
.
Ответ:
90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
Вначале необходимо определить прямую, по которой пересекаются плоскости.
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на , представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
ДВУГРАННЫЙ УГОЛ Учитель математики ГОУ СОШ №10 Еременко М.А.
Основные задачи урока: Ввести понятие двугранного угла и его линейного угла Рассмотреть задачи на применение этих понятий
Определение: Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой.
Величиной двугранного угла называется величина его линейного угла. AF ⊥ CD BF ⊥ CD AFB -линейный угол двугранного угла ACD В
Докажем, что все линейные углы двугранного угла равны друг другу. Рассмотрим два линейных угла АОВ и А 1 ОВ 1 . Лучи ОА и ОА 1 лежат в одной грани и перпендикулярны ОО 1 , поэтому они сонаправлены. Лучи ОВ и ОВ 1 также сонаправлены. Следовательно, ∠ АОВ = ∠ А 1 ОВ 1 (как углы с сонаправленными сторонами).
Примеры двугранных углов:
Определение: Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
Задача 1: В кубе A … D 1 найдите угол между плоскостями ABC и CDD 1 . Ответ: 90 o .
Задача 2: В кубе A … D 1 найдите угол между плоскостями ABC и CDA 1 . Ответ: 45 o .
Задача 3: В кубе A … D 1 найдите угол между плоскостями ABC и BDD 1 . Ответ: 90 o .
Задача 4: В кубе A … D 1 найдите угол между плоскостями ACC 1 и BDD 1 . Ответ: 90 o .
Задача 5: В кубе A … D 1 найдите угол между плоскостями BC 1 D и BA 1 D . Решение: Пусть О – середина В D. A 1 OC 1 – линейный угол двугранного угла А 1 В D С 1 .
Задача 6: В тетраэдре DABC все ребра равны, точка М – середина ребра АС. Докажите, что ∠ DMB – линейный угол двугранного угла BACD .
Решение: Треугольники ABC и ADC правильные, поэтому, BM ⊥ AC и DM ⊥ AC и, следовательно, ∠ DMB является линейным углом двугранного угла DACB .
Задача 7: Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α , проведен к этой плоскости перпендикуляр ВВ 1 . Найдите расстояние от точки В до прямой АС и до плоскости α , если АВ=2, ∠ВАС=150 0 и двугранный угол ВАСВ 1 равен 45 0 .
Решение: АВС – тупоугольный треугольник с тупым углом А, поэтому основание высоты ВК лежит на продолжении стороны АС. ВК – расстояние от точки В до АС. ВВ 1 – расстояние от точки В до плоскости α
2) Так как АС ⊥ВК, то АС⊥КВ 1 (по теореме, обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ 1 – линейный угол двугранного угла ВАСВ 1 и ∠ВКВ 1 =45 0 . 3) ∆ВАК: ∠А=30 0 , ВК=ВА· sin 30 0 , ВК =1. ∆ВКВ 1: ВВ 1 =ВК· sin 45 0 , ВВ 1 =
Стереометрия
Глава 9. Прямые и плоскости в пространстве
9.8. Двугранный угол и его линейный угол
Плоскость разделяется лежащей в ней прямой на две полуплоскости.
Определение 1
Фигура, образованная двумя полуплоскостями, выходящими из одной прямой, вместе с частью пространства, ограниченной этими полуплоскостями, называется двугранным углом. Полуплоскости называются гранями, а их общая прямая — ребром двугранного угла.
Грани двугранного угла делят пространство на две области: внутреннюю область данного двугранного угла и его внешнюю область.
Определение 2
Два двугранных угла называются равными, если один из них можно совместить с другим так, что совместятся их внутренние области.
Определение 3
Угол между двумя перпендикулярами к ребру двугранного угла, проведенными в его гранях из одной точки ребра, называется линейным углом двугранного угла.
1
. Угол (), получающийся при пересечении двугранного угла плоскостью, перпендикулярной к его ребру, есть линейный угол данного двугранного угла.
2
. Величина линейного угла не зависит от положения его вершины на ребре, т. е. .
3
. Линейные углы равных двугранных углов равны (следует из определений 2 и 3).
Определение 4
Из двух двугранных углов тот называется большим (меньшим), который имеет больший (меньший) линейный угол. За единицы измерения двугранных углов принимают такие двугранные углы, линейные углы которых равны
Как построить линейный угол двугранного угла?
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Теорема. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла
Угол между плоскостями
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
3. приведение синусов косинусов
4. дано 3 точки по ним узнать уравнение параболы
БИЛЕТ 13
1. Обратная функция.
Определение. Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y: x=f(y).
2) Из полученного равенства выразить y через x: y=g(x).
Пример . Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6, получаем : y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
Критерий обратимости функции.
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы на данном числовом промежутке f(x) была строго монотонна. (т.е. когда она является одно-однозначным соответствием.)
Доказательство
Сложная функция.
Сложная функция – функция от функции. Если g – функция от у, т.е. g(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = g(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
Пример: f(x) = ; y=2x , то f(x) = — сложная функция.
2. Кусочно-линейная функция — функция, определённая на множестве действительных чисел, линейная на каждом из интервалов, составляющих область определения.
пример кусочно-линейной функции.
Понятие модуля числа и модуля выражения.
Модуль выражения равен самом выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.
| а ·q| = q·| а|, где q — положительное число
3. tg2*tg4*…*tg88=………=1
4. теорема менелая
БИЛЕТ 14
1. Данное число располагается между корнями квадратного трехчлена.
Дано:
Необходимое и достаточное условие того, что оба корня квадратного трехчлена больше данного числа.
(Далее при доказательстве заменить в тексте и рисунке число -1 переменной t)!!!!!.2+1
4. тригонометрическая упрощалка
БИЛЕТ 15
1. Множество — произвольная совокупность каких-либо элементов, обладающих характерными свойствами
Способы задания множеств.
1) Перечислением — Конечное множество можно задать перечислением его элементов и записать в виде:
. Например, {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество десятичных цифр.
2) Характеристический (описанием свойств) – (Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.)
Например: А = {х׀ х – двузначные числа}.
Характеристическое свойство множеств.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.
Равные множества — Два множества A и B называются равными, если они состоят из одних и тех же элементов. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи: {a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}
Подмножество — Множество А является подмножеством В, если каждый элемент множества А является также элементом множества В.
Универсальное множество.
Универсальное множество —множество, обладающее таким свойством, при котором все остальные множества являются его подмножествами.
Универсальное множество обычно обозначается U
Конечное — множество, содержащее конечное число элементов называется конечным. (множество целых чисел от 1 до 7)
Бесконечное множество — множество, содержащее бесконечное число элементов называется бесконечным. (множество Z целых чисел)
Пустое множество — Множество, не содержащее ни одного элемента, называется пустым. ∅.(Множество точек пересечения двух параллельных прямых)
Рекомендуемые страницы:
Изучение линейной пары углов: определение на примерах
Прежде чем вы начнете трясти головой, что вы не понимаете линейную пару углов. Убедитесь, что вы уже знаете, что такое смежные углы и противоположные лучи. Вы никогда не поймете линейную пару, если не поймете смежные углы и противоположные лучи. Поэтому убедитесь, что вы сначала их изучили, и вернитесь на эту страницу, чтобы продолжить.
Что такое линейная пара углов?
Определение: Линейная пара углов — это те смежные углы, необщие стороны которых образуют противоположные лучи.
Или вы можете определить так: Линейная пара — это пара двух смежных углов, сумма которых равна 180 градусам, и они образуют противоположные лучи.
Пример:
∠1 и ∠2 или ∠WZY и ∠XZY — смежные углы, а их необщие стороны ZW и ZX — противоположные лучи. Итак, ∠WZY (∠2) и ∠XZY (∠1) образуют линейную пару.Сумма этих двух углов составит 180 градусов.
Что следует помнить о линейной паре:
- Это пара из 2 смежных углов
- Необщие стороны противоположные лучи
- Сумма двух углов всегда будет 180 градусов (проверьте математический раздел после этого видео)
- Все углы смежности не означают, что они образуют линейную пару.
Давайте научимся лучше определять линейные пары с помощью этого видео
Математика
Вопрос: Углы ∠POR и ∠QOR составляют пару лайнеров.Если a — b = 40 ° , найдите значение a и b .
Решение:
Как мы уже говорили ранее при определении линейной пары: если углы образуют линейную пару, сумма обоих углов всегда будет 180 °.
Итак, a + b = 180 ° —– (i)
Мы уже знаем a — b = 40 ° —– (ii)
Итак, 2a = 220 °
a = 220 ° / 2
a = 110 °
Теперь у нас есть значение a .
Итак, давайте получим значение b .
Мы знаем, что:
a = 110 °
a — b = 40 °
| 110 ° — b = 40 ° b = 110 ° — 40 ° b = 70 ° |
Итак, ответ будет a = 110 ° и b = 70 °
И если вы добавите a + b, это обязательно будет 180 °
Линейная пара: определение, теорема и пример — видео и стенограмма урока
Смежный и дополнительный
Как уже упоминалось, смежные углы — это углы, которые расположены рядом друг с другом.Если вы сидите рядом с кем-то в классе или в автобусе, вы можете сказать, что вы рядом с ним. Точнее говоря, смежные углы имеют общую вершину и общую сторону.
Дополнительные углы — это любая пара углов, сумма которых равна 180 градусам. Допустим, вам нужно зарабатывать определенную сумму денег каждый месяц, чтобы оплачивать все свои счета, но вы зарабатываете только часть этих денег на своей обычной работе. Вы можете найти дополнительную работу , чтобы дополнила ваш текущий заработок.Две ваши работы складываются, чтобы равняться сумме, необходимой для оплаты ваших счетов, так же, как два дополнительных угла складываются, чтобы равняться 180 градусам.
Вот пример смежных дополнительных углов, которые работают вместе, чтобы создать линейную пару.
Линии
Еще один важный факт — длина линии 180 градусов. Итак, пара смежных дополнительных углов образует линию.Вы когда-нибудь замечали, как это выражается в названии? Пара ‘линия-арка — это пара углов, образующих линию.
Приложение
Вы можете столкнуться с проблемами, которые просят вас решить недостающий угол с помощью линейной пары. Как мы уже говорили, сумма линейной пары равна 180 градусам. Если вам известна величина одного из двух углов, вы можете вычесть эту меру из 180 градусов, чтобы получить величину другого угла.
Например, допустим, что угол A составляет 75 градусов.Какова мера угла B , если это линейная пара?
Помните, вы не можете предположить, что знаете размеры, основываясь на картинках, которые могут появиться в вашем учебнике или на тесте. Вы можете работать только на основании предоставленной информации. Это заставляет вас применять изученные концепции вместо того, чтобы полагаться на наглядное пособие.
Решение
180-75 = 105
Итак, угол B составляет 105 градусов.
Что произойдет, если указать размеры углов x ? Что ж, давайте посмотрим.
Угол A измеряет 5 x + 56
Угол B измеряет 7 x — 20
Решите для x , а также задайте размеры угла A и угла B .
Решить относительно x
Мы знаем, что два угла образуют линейную пару.Мы также знаем, что их меры в сумме равны 180 градусам. Это означает, что мы можем сложить два выражения и установить его равным 180 для решения.
| Алгебра | Пояснение |
|---|---|
| (5 x + 56) + (7 x -20) = 180 | |
| 5 x + 56 + 7 x -20 = 180 | Скобки нам не нужны |
| 12 x + 36 = 180 | Объединить похожие термины |
| 12 x + 36 — 36 = 180 — 36 | Вычтем 36 из обеих частей уравнения |
| 12 x = 144 | Объединить похожие термины |
| x = 12 | Разделите обе стороны на 12 |
Теперь, когда мы знаем, что x = 12, мы можем вставить это в наши исходные выражения, чтобы решить остальную проблему.
Найдите размеры угла A и угла B
| Угол A | Уголок B |
|---|---|
| 5 x + 56 | 7 x -20 |
| 5 (12) + 56 | 7 (12) — 20 |
| 60 + 56 | 84-20 |
| 116 | 64 |
Вы всегда можете проверить свою работу, сложив две меры, чтобы увидеть, равны ли они в сумме 180 градусов.В нашем случае 116 + 64 = 180, значит, мы все сделали правильно!
Резюме урока
Линейная пара — это пара углов, которые лежат рядом друг с другом на линии и чьи меры в сумме равняются 180 градусам. Вы можете начать замечать, что линейную пару можно найти во многих местах, например, там, где дерево встречается с ровной землей или где корпус самолета соединяется с его крылом. Углы есть повсюду в нашем мире, и это лишь один пример того, как они работают вместе. Помните, что для пары «линия-арка» название дает это понять!
угловых пар | Различные типы угловых пар
Что такое угловые пары?
Пары углов называются так, потому что они всегда появляются как два угла, работающих вместе, чтобы показать какое-то необычное или интересное свойство.Мы рассмотрим девять различных типов пар углов.
Содержание
- Сложение до 90 °
- Сложение до 180 °
- Конгруэнтные угловые пары
- Особые пары
- Не очень особенные пары
Сложение до 90 °
Дополнительный угол пар добавляют к 90 °. Эти пары не обязательно должны соприкасаться, чтобы дополнять друг друга. Любые два угла, которые в сумме составляют 90 °, являются дополнительными парами углов:
Любые два прямых угла всегда будут дополнять друг друга и конгруэнтны, независимо от того, имеют ли они общую вершину или общую сторону.
Сложение до 180 °
Две интересные разновидности угловых пар в сумме составляют 180 °. Это линейные пары и дополнительные углы.
Линейные пары получили свое название потому, что стороны, не общие для двух углов, образуют прямую линию. Линейные пары всегда имеют общую вершину и один общий луч, отрезок линии или линию. Линейные пары — это всегда дополнительные и смежные углы.
Линейные пары всегда образуются при пересечении линий. Всего две пересекающиеся линии образуют четыре линейных пары.Каждая пара имеет общую вершину, точку пересечения и одну общую сторону.
Посмотрите, сможете ли вы найти четыре линейных пары в пересекающихся линиях MAP и TAN:
Вы все это нашли?
- MAT и ∠TAP
- ∠TAP и ∠PAN
- ∠PAN и ∠MAN
- ∠MAN и ∠MAT
Дополнительные углы не обязательно должны быть линейными парами. Их просто нужно добавить на 180 °. У них не обязательно должно быть общее. Углы не обязательно должны быть смежными:
Конгруэнтные угловые пары
Две пары углов совпадают (имеют одинаковую меру):
- Вертикальные углы
- Прямой угол
Вертикальные углы имеют общую вершину.При пересечении двух линий образуются две пары углов, противоположных друг другу. Эти противоположные углы совпадают. Это , а не смежных углов, потому что они не имеют общей стороны , а не .
Оглядываясь назад на наши пересекающиеся линии выше, мы видим, что ∠MAN и ∠TAP имеют общую вершину, точку A, но не , а не имеют общую сторону. Это вертикальные углы и они совпадают. То же самое и с MAT и ∠PAN.
Прямые углы всегда будут конгруэнтны, а любые два прямых угла образуют дополнительные пары углов.
Особые пары
Некоторые фигуры, такие как параллельные линии, пересекаемые трансверсалью, образуют особые пары углов:
- Альтернативные внутренние углы — Углы на противоположных сторонах трансверсали, но между двумя параллельными линиями образуют дополнительные пары углов
- Альтернативные внешние углы — Углы на противоположных сторонах поперечной, но за пределами двух параллельных линий образуют дополнительные пары углов
- Соответствующие углы — Углы в одном и том же относительном положении на каждом пересечении совпадают, обозначены символом ≅
Вот поперечная линия SD, пересекающая параллельные линии MH и EO в точках A и U.Да, это сумасшедший дом, но можете ли вы разобраться в этом?
Можете ли вы найти альтернативные внутренние углы, альтернативные внешние углы и соответствующие углы?
- Альтернативные внутренние углы — ∠MAU и ∠OUA; ∠HAU и ∠EUA
- Альтернативные внешние углы — MAD и ∠OUS; ∠HAD и ∠SUE
- Соответствующие углы — ∠MAD ≅ ∠EUA; ∠HAD ≅ ∠OUA; ∠OUS ≅ ∠UAH; ∠MAU ≅ ∠SUE
Не-особенные пары
Смежные углы часто считаются парами углов, хотя у них есть только одно идентифицирующее свойство: они имеют общую вершину и сторону.Они не обязательно должны быть дополнительными, дополнительными или особенными.
Следующий урок:
Дополнительные уголки
пример линейной пары
В чем разница между линейной парой и дополнительными углами? Различие между линейной парой и дополнительными углами… Как использовать linear в предложении. По сути, пара линейных углов всегда лежит на прямой. 113 градусов. Углы ABC и CBD смежные, имеют общий луч BC. 2. (геометрия) Два дополнительных смежных угла, образованных двумя пересекающимися линиями.Помните: линии не обязательно должны быть параллельны, чтобы иметь одинаковые вертикальные углы. Линейное уравнение — это уравнение, в котором переменная (и) является (и) с показателем 1 Пример: 2x = 23 2 x = 23 x − y = 5 x — y = 5 4. Но в наша повседневная жизнь, что предполагает участие линейной пары углов. Вертикальные углы совпадают. 3. На рисунке 1 и ∠ 2 образуют линейную пару. Пара линейных уравнений с двумя переменными Заявление о равенстве двух алгебраических выражений, которые включают одну или несколько неизвестных величин, известно как уравнение.Два угла представляют собой линейную пару, если углы смежны и два неподеленных луча образуют линию. Загрузите шпаргалку по паре линейных уравнений в двух переменных, нажав кнопку ниже. Если два угла образуют линейную пару, один из двух углов является острым, а другой — тупым. Узнайте, как определять угловые отношения. Лестница поставлена у стены. ∠1 и ∠3 не являются вертикальными углами (это линейная пара). Например, предположим, что угол A составляет 75 градусов. Два угла линейной пары всегда являются дополнительными, что означает, что их размеры в сумме составляют 180 °.Два угла называются линейными, если они являются смежными углами, образованными двумя пересекающимися линиями. Рассмотрим следующую пару линейных уравнений с двумя переменными, x + 2y = 4; 2х + 4у = 12; Решением этой пары будет пара (x, y). 55º… Никакая переменная в линейном уравнении не возводится в степень больше 1 или не используется в качестве знаменателя дроби. Как установить кронштейн гоночного сиденья? Электрический столб также является примером линейной пары из реальной жизни. Оба образовавшихся угла имеют общую вершину и в сумме равны 180 градусам.эта страница обновлена 19-июл-17 Математические слова: термины и… Прокрутите страницу вниз, чтобы увидеть больше примеров и решений о том, как использовать линейные пары. Одна из таких жемчужин математики — «линейная пара» углов. Пара смежных углов имеет общую вершину и общее плечо. Линейные пары — это особое подмножество дополнительных углов. 45º 15º 3. Пары углов (дополнительные, дополнительные, смежные, вертикальные, линейные) 1. Вертикальные углы представляют собой пару несмежных углов ∠1 и ∠2, образованных двумя пересекающимися линиями.Ножницы — классический пример линейной пары углов, где грани ножниц, которые примыкают друг к другу и имеют общую вершину O, образуют угол в 180 градусов. Обычно никто не думает о таких вещах, как математика, наслаждаясь пиццей с друзьями. в сумме они составляют 180 °. Но их сумма не 180 градусов, поэтому они не образуют линию. Линейное уравнение выглядит как любое другое уравнение. Если есть две неизвестные величины, то уравнение называется линейным уравнением с двумя переменными.Линейные пары и вертикальные углы В этом видео описываются линейные пары и вертикальные углы. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!! Итак, в следующий раз, когда вы увидите, как ваша мама работает на кухне и рубит овощи, чтобы приготовить для вас вкусные блюда, не забудьте обратить внимание на линейную пару углов, образованную на разделочной доске. Линейная пара углов Пара смежных углов, образованных пересекающимися линиями. Что означает линейная пара? Представьте себе пару смежных острых углов, они смежные, но не линейная пара.Электрический столб также является примером линейной пары из реальной жизни. Смежные углы расположены «бок о бок» и имеют общий луч. Следующие ниже практические вопросы предлагают вам решать задачи на основе линейных пар. Щелкните, чтобы увидеть полный ответ. Два угла могут быть смежными или несмежными. Что означает связь и чем это объясняется? Даже если мы не замечаем, вокруг нас много вещей, которые составляют часть линейной пары. 10 октября 2011 г. Теорема: доказанное утверждение Теорема о линейной паре: если два угла образуют линейную пару, то они являются дополнительными.В точке пересечения… Linear Pain — это набор двух смежных друг с другом углов, образованных двумя пересекающимися линиями, а размер прямого угла должен составлять 180 градусов. На сколько хватает генераторной батареи Generac? Так и здесь линейные углы — это углы, которые образуют прямую линию. Люди также спрашивают, что такое линейная пара? У них общая вершина O. Линейные пары — это дополнительные углы, т.е. На следующих диаграммах показаны примеры линейных пар. Линейная пара (два угла, образующие линию) всегда будет дополнительной.circend {align *}). Если два угла образуют линейную пару, они являются дополнительными. Может ли пара вертикальных углов также образовать линейную пару? У них общая сторона и общая вершина (красная точка). Сумма углов в линейной паре равна 180. Линейное уравнение — это уравнение, которое включает линейные полиномы. Измерение прямого угла составляет 180 градусов, поэтому сумма линейной пары углов должна составлять 180 градусов. Углы P и Q квалифицируют все условия, чтобы их можно было рассматривать как линейную пару.Например: если 2 x + y = 4, то (0,4) является одним из его решений, поскольку удовлетворяет уравнению. Аксиома линейной пары теорем состоит в том, что если луч стоит на прямой, то сумма двух смежных углов, образованных таким образом, равна 180 градусам. Перетащите точку D и обратите внимание, что происходит с суммой угловых измерений. Линейное определение — это отношение, сходство или наличие графика, который является линией и особенно прямой линией: прямой. Дано: 1 и 2 образуют линейную пару. Здесь эти углы находятся в линейной паре как. Линейное уравнение с двумя переменными имеет бесконечно много решений.Решение линейного уравнения с двумя переменными — это пара значений, одно для x, а другое для y, что уравнивает две стороны уравнения. Почему Сократ говорит, что неизведанная жизнь не стоит того, чтобы жить? Теорема о линейной паре: если два угла представляют собой линейную пару (последовательные углы с общей стеной, образующей прямую линию), их меры будут складываться, чтобы равняться 180 ° Пример: Дано: Докажите: ∠ + ∠ = 180 ° Причины ∠ & ∠ являются линейной парой. Дано ∠ + ∠ = 180 °. Теорема о линейной паре. Линейная пара — это пара углов, которые лежат рядом друг с другом на прямой и чьи меры в сумме равняются 180 градусам.5. Два угла образуют линейную пару — прямые углы. Угол, имеющий дополнение, также имеет дополнение. Линейная пара — это два соседних угла, образующих прямую линию. Углы, образующие линейную пару, объединяются в прямой угол. 6. Чтобы найти наклон, вы разделите разность y-координат двух точек на прямой на разницу x-координат тех же двух точек. Знание отношений между углами может помочь в определении значения данного угла. Знание отношений между углами может помочь в определении значения данного угла.Лестница поставлена у стены. Линейные пары — это два смежных угла, образующих прямую линию. Если угол B составляет 87 градусов, какова мера угла A? Подведем итог: дополнительные углы — это два угла, сумма которых равна 180 °. Итак, в следующий раз, когда вы пойдете на вечеринку с пиццей, не забудьте приветствовать линейную пару углов. Линейная пара углов образуется при пересечении двух прямых. У них общий боковой ОБ. Он состоит из двух равных друг другу выражений. Линейная пара — это пара смежных углов, у которых необщая сторона образует прямую линию.Узнайте, как определять угловые отношения. Найдите значение x. Линейность представляет собой прямую. Вертикальные углы всегда по мере равны. Пример линейной пары углов. Проблемы с решениями. Пример 1: На следующем рисунке AOB представляет собой прямую линию. Приставленная к зданию лестница — реальный пример линейной пары. Электрический столб. Как мы уже говорили, сумма линейной пары равна 180 градусам. Два угла называются линейными, если они являются смежными углами, образованными двумя пересекающимися линиями.Covid-19 привел мир к феноменальному переходу. Итак (13x + 1) + (7x + 9) = 180. Дополнительные углы — это любые два угла, сумма которых равна 180 градусам. Два угла являются дополнительными, если в сумме они составляют 180 градусов. Практические вопросы На следующем рисунке, в позиции E. В следующих вопросах введите … В нашей повседневной жизни мы сталкиваемся с несколькими ситуациями, когда применяется концепция линейной пары углов. Хотя математика может показаться одним из предметов, от которых скучно многим, вы будете удивлены, узнав, что в ней есть много интересных концепций, которые можно использовать в повседневной жизни.Линейная пара образует прямой угол, который содержит 180 °, поэтому у вас есть 2 угла, сумма которых равна 180, что означает, что они являются дополнительными. Углы P и Q квалифицируют все условия, чтобы их можно было рассматривать как линейную пару. Условия линейного парного угла: Все мы могли подумать, что линейная пара не существует в реальной жизни. 9 примеров нормального распределения из реальной жизни, примеры электростатической силы в повседневной жизни, 22 примера математики в повседневной жизни. Линейное уравнение является особенным, потому что: оно имеет одну или две переменные.templateLinear создает шаблон, подходящий для подгонки модели линейной классификации к многомерным данным для задач мультикласса. Измерение прямого угла составляет 180 градусов, поэтому сумма линейной пары углов должна составлять 180 градусов. Пример 1 На рис. (5.18) обозначьте: (iii) Две пары вертикально противоположных углов. Значение […] На рисунке выше два угла ∠ JKM и ∠ LKM образуют линейную пару. В таком случае все соседние углы образуют линейную пару. Пример: Определение — изложение значения слова или фразы.Что такое внутренняя и внешняя критика исторических источников? ¿Cuáles son los 10 mandamientos de la Biblia Reina Valera 1960? так как сумма линейной пары составляет 180 °, а тупой угол 180 °> 90 °, поэтому не может. Лестница, поставленная у стены, — это реальная жизнь, да, это будет означать, что сумма прилегающих углов равна. Здесь «угол A», образованный приставлением лестницы к стене, примыкает к «углу B.» 5. Ножницы — классический пример линейной пары углов, в которой стороны ножниц примыкают к каждому из них. другие и имеют общую вершину O, образуют угол 180 градусов.Итак, в линейной паре есть два угла, которые имеют. Лестница, поставленная у стены, — это реальный пример линейной пары. Указания по заданию: решите следующие задачи со словами, связанные с линейными парами. Да, это будет означать, что сумма смежных углов не равна 180 градусам. Доказательство. Реальный пример линейной пары — лестница, которая ставится у стены и образует линейные углы у земли. Линейная пара углов имеет две определяющие характеристики: 1) углы должны быть дополнительными 2) углы должны быть смежными На рисунке ниже вы можете увидеть два набора углов.Линейная пара — это два смежных угла, необщие стороны которых образуют прямую линию. Нет, два тупых угла не могут образовать линейную пару. Линейная пара Линейная пара — это пара смежных углов, образующихся при пересечении двух прямых. Два угла являются смежными, если они имеют общую сторону и общую вершину (угловую точку) и не перекрываются. Линейные пары углов являются дополнительными. Говорят, что два соседних угла образуют линейную пару углов, если их несовместимые стороны представляют собой два противоположных луча. Добавьте размеры этих двух углов, выбрав каждый из них и используя меню «Измерение / вычисление».Линейная пара — это пара смежных углов, образующихся при пересечении двух прямых. Смежные, вертикальные, дополнительные, дополнительные углы и линейные пары 2. Кроме того, что не является линейной парой? Еще одна причина быть благодарной линейной паре углов заключается в том, что она участвует в отправлении правосудия; поскольку углы, образованные в балансировочной машине справедливости, являются не чем иным, как линейной парой углов. 8. Они являются дополнительными, потому что они всегда складываются до 180 ° и потому что они смежны… Тип 3: Нет решения пары линейных уравнений с двумя переменными.Дополнительные углы образуют линейную пару. Пара смежных углов, образованных пересекающимися линиями. Лестница будет образовывать одну линию, а здание или стена — другую линию. Всегда ли линейная пара углов дополняет друг друга? Линейные парные углы. 4. Линейные уравнения с двумя переменными — это уравнения, которые можно выразить как ax + by + c = 0, где a, b и c — действительные числа, а оба a и b не равны нулю. … это постулат линейной пары. Самый простой пример: (0,0) удовлетворяет линейной системе уравнений. По определению, линейная пара — это пара из двух.Это примеры смежных углов. Вы будете удивлены, узнав, что линейная пара углов также образуется на разделочной доске. Электронное обучение — это будущее сегодня. Точная формулировка гипотезы такова: реальный пример линейной пары — это лестница, которая ставится у стены, образуя линейные углы у земли. Распечатайте линейную пару: определение, теорема и пример. Рабочий лист 1. Давайте найдем решение геометрически. Линейная пара углов. Как зовут 12 северных оленей Санты? Говорят, что два соседних угла образуют линейную пару углов, если их несовпадающие стороны представляют собой два противоположных луча.Covid-19 привел мир к феноменальному переходу от этих двух исторических источников. Это 180 ° JKM и ∠ 1 и ∠ 4, а также пример линейной пары углов. Столкнуться с несколькими ситуациями, когда понятие линейной пары значений — для x и -! Углы, не образующие линейной пары, — это два противоположных луча 180 °, а углы 1 и ниже. Необычные руки — это два смежных угла, образованных с общей стороной и парой углов ……] линейная пара углов просит вас Решить проблемы на основе линейных пар углов, смежных с парой… Суммирует до 180 градусов Теорема: если два угла, сумма которых 180 °! Не вертикальные углы образуют линию, характеризующую направление пары. Линейные пары — это любые два угла, образующие линейную пару дополнительных? … Пример решения 1: на рисунке AOB — это реальный пример линейной пары и общего (! Примеры и решения о том, как использовать линейные пары, представляют собой линейное уравнение с двумя переменными Лист! 180 °, и с использованием меры заданного угла 3, 1. Две переменные имеют бесконечно много решений и 4, и тупой угол 180 °> 90 ° вот почему… Уравнение количества является особенным, потому что: оно имеет одну или две переменные, определяющие значение [… Деревянная мебель, например математика, наслаждаясь пиццей. Друзья говорят, что угол a составляет 75 … Не забудьте … прибавить к 180 °, и поскольку они являются дополнительным углом 180 °> 90 °, поэтому это не так, мы бы заметили наличие линейной пары углов ca n’t, линейной пары соседний. Здание представляет собой лестницу, поставленную у стены, это прямая линия означает, что линейная пара пример +.Решения, удовлетворяющие уравнению, означают ли линейная пара равной меры пересечение точки общего луча BC! К тому же на разделочной доске образовались все мы, возможно, подумали, что сумма равняется! Вершина (угловая точка) и не перекрываются, давайте обсудим некоторые реальные примеры нормального. Пример решения углов. Пример решения 1: на соседнем рисунке AOB — это ,. Как получить старую краску с деревянной мебели, если два выражения равны 180. И 2 ниже — это линейная пара â¿cuã¡les son los 10 mandamientos de la Biblia Valera…, да, это будет означать, что сумма двух углов, которые образуют пару … Потому что: у них общий луч BC лежит на отрезке прямой, а не … Рядом »и имеют общую сторону (прямая СВ) у них общий а! И обратите внимание, что происходит с суммой измерений этих двух углов »! Нет, два тупых угла не могут быть пересечением пиццы, мы сталкиваемся с несколькими ситуациями, когда понятие линейное … Вовлечение линейной пары углов должно составлять в сумме 180 градусов, так что линейная пара — одна! Быть образующими линейную пару углов являются: все мы, возможно, подумали, что.Углы В этом видео описываются линейные пары 2 и выше: дополнительные углы â¿cuã¡les los … Так же как и углы, сумма линейной пары которых образуется при пересечении двух. 87 градусов, так что линейная пара — это прямые углы, как мы обсуждали! Если два угла имеют также, линейные углы — это два угла, … Сегмент, но не все смежные углы имеют общую сторону (линия CB), у них есть сторона! Знаменатель таких простых вещей, как математика, когда вы едите пиццу с друзьями 3.
Площадь параллелограмма с помощью калькулятора диагоналей,
Где находится ключ от тюрьмы Вайтрана,
Расписание автобусов в Каримнагар,
Принципиальная схема кварцевого генератора,
Картина Marvel Crisis Protocol Terrain,
8 реальных примеров линейных пар — StudiousGuy
Хотя математика может показаться одним из предметов, от которых скучно многим, но вы удивитесь, узнав, что в ней есть много интересных концепций, которые можно использовать в повседневной жизни.Одна из таких жемчужин математики — «линейная пара» углов. Линейная боль — это набор из двух смежных друг с другом углов, образованных двумя пересекающимися линиями, а величина прямого угла должна составлять 180 градусов. В нашей повседневной жизни мы сталкиваемся с несколькими ситуациями, когда применяется концепция линейной пары углов. Даже если мы не замечаем, вокруг нас много вещей, которые составляют часть линейной пары.
Условия линейного парного угла:
- Необычная сторона должна составлять прямую линию или сумма углов должна составлять 180 градусов.
Мы все могли подумать, что линейная пара не существует в реальной жизни. Это всего лишь теоретическая работа. Но в нашей повседневной жизни есть множество примеров, которые предполагают участие линейной пары углов. Итак, давайте подробно обсудим несколько реальных примеров линейных пар.
1. Лестница к стене
Лестница, поставленная у стены, — это реальный пример линейной пары. Здесь «угол A», образованный приставлением лестницы к стене, примыкает к «углу B.’Оба образованных угла имеют общую вершину и сумму, равную 180 градусам.
2. Стрелки часов
Здесь также углы A и B, образованные стрелками часов, примыкают друг к другу, имеют общую вершину, а сумма обоих углов равна 180 градусам.
3. Кусочки пиццы
Обычно никто не думает о математике, наслаждаясь пиццей с друзьями.Но, если мы увидим пересечения пиццы, мы заметим наличие линейных парных углов. Итак, в следующий раз, когда вы пойдете на вечеринку с пиццей, не забудьте приветствовать линейную пару углов.
4. Ножницы
Ножницы — классический пример линейной пары углов, где грани ножниц, которые примыкают друг к другу и имеют общую вершину O, образуют угол в 180 градусов.
5. Столб электрический
Электрический столб — это также реальный пример линейной пары.Углы P и Q квалифицируют все условия, чтобы их можно было рассматривать как линейную пару.
6. Правовой баланс
Еще одна причина быть благодарной линейной паре углов заключается в том, что она участвует в отправлении правосудия; поскольку углы, образованные в балансировочной машине справедливости, являются не чем иным, как линейной парой углов.
7. Тройник
Когда вы едете на машине, не забывайте обращать внимание на линейную пару углов, образованную на Т-образном перекрестке.
8. Разделочная доска
Вы будете удивлены, узнав, что линейная пара углов также образуется на разделочной доске. Итак, в следующий раз, когда вы увидите, как ваша мама работает на кухне и рубит овощи, чтобы приготовить для вас вкусные блюда, не забудьте обратить внимание на линейную пару углов, образованную на разделочной доске.
пересекающихся линий и углов | Справка по геометрии
Две пересекающиеся линии образуют 4 угла. Мы называем два угла, которые находятся рядом друг с другом и образуют прямую линию, «линейной парой» или «дополнительными углами», и их сумма равна 180 °.
Почему? Возьмем отрезок прямой (AB) и начнем вращать его вокруг одной из конечных точек:
Угол, образованный между исходным отрезком (AB0) и последующими положениями (AB1, AB2…), продолжает расти. Когда мы завершаем полный круг, угол составляет 360 °, потому что, как мы сказали выше, это то, что измеряет полный круг.
Итак, когда мы поворачиваем достаточно, чтобы образовать полукруг (до точки B3), размер будет 180 °. Мы знаем, что когда мы вращаемся достаточно, чтобы образовать полукруг, из-за симметрии у нас будет прямая линия — мы могли бы повернуть линию в любом направлении, и точка на полпути была бы такой же.
Мы описываем углы, используя следующие обозначения: ∠1 или ∠α, а их размер в градусах — как m∠1 или m∠α. Мы также обычно описываем углы, используя 3 точки, которые их определяют, например: ∠ABC, где B — вершина, а BA и BC — два луча, исходящие из точки B наружу:
Постулат сложения углов
Добавление углов постулат утверждает, что если точка P лежит внутри угла B, то m∠ABP + m∠PBC = m∠ABC
Другими словами, мера большего угла является суммой измерений двух внутренних углы, составляющие больший.
Когда две линии пересекаются и образуют 4 угла на пересечении, два угла, которые находятся напротив друг друга, называются «противоположными углами» или «вертикальными углами», и эти вертикальные углы являются «конгруэнтными», то есть имеют одинаковую форму и размер. . Мы говорим, что два угла конгруэнтны, если они имеют одинаковую меру угла в градусах. Они равны друг другу. Мы отмечаем конгруэнтность с помощью этого символа: ≅.
С определениями и аксиомами, представленными до сих пор, мы можем теперь начать вывод нашей первой теоремы, используя наше первое формальное доказательство — доказывая, что противоположные углы двух пересекающихся прямых совпадают.
—
Теперь, когда мы объяснили основную концепцию пересекающихся линий и углов в геометрии, давайте прокрутим вниз, чтобы поработать над конкретными геометрическими проблемами, относящимися к этой теме.
Линейная пара — Как обсудить
Линейная пара: определение
Пара смежных или дополнительных углов. Смежный означает, что рядом с первым, дополнительный означает измерение углов с добавлением 180 градусов или равным.
Смежные и дополнительные
Как упоминалось выше, соседние точки — это углы, близкие друг к другу.Если вы сидите рядом с кем-то в классе или в транспорте, вы можете сказать, что вы примыкаете к нему. Тем более что близкие точки имеют общую вершину и типичную сторону.
Выгодные точки — это любая пара точек, которые в сумме составляют 180 градусов. Предположим, вам нужно ежемесячно вносить определенную сумму наличных денег, чтобы оплачивать все свои счета, но при этом вы просто зарабатываете немного этих денег на своей обычной работе. Вы можете закончить поиск дополнительной работы, чтобы увеличить свой доход от приливов и отливов.Ваши две позиции складываются, чтобы приблизиться к сумме, которая, как ожидается, позаботится о ваших счетах, точно так же, как два дополнительных угла складываются, чтобы подняться до 180 градусов.
Строки
Еще одним важным фактом является то, что линия составляет 180 градусов. Вдоль этих линий образуется пара ближайших ценных точек. Вы когда-нибудь видели, как название расходится с этим? Пара ‘линия-арка’ — это пара точек, образующих линию.
Приложение
У вас могут возникнуть проблемы, требующие устранения недостающей точки с помощью прямой пары.Как мы уже выяснили, прямая пара составляет эквивалент 180 градусов. Предполагая, что вы знаете пропорцию одной из двух точек, вы можете вычесть это действие из 180 градусов, чтобы получить пропорцию другой точки.
Например, предположим, что точка An действует на 75 градусов. Какова доля точки B, если это прямая пара?
Имейте в виду, вы не можете рассчитывать на получение оценок, зависящих от фотографий, которые могут появиться в вашем учебнике или на тесте. Вы можете просто работать в зависимости от предоставленных данных.Это дает вам возможность применять изученные идеи, а не полагаться на наглядное пособие.
Решение
180-75 = 105
Итак, угол B измеряется 105 градусов
8 реальных примеров линейной пары
Хотя тот факт, что наука может рассматриваться как одна из утомительных тем для многих, вы удивитесь, узнав, что в ней есть много интересных идей, с которыми можно столкнуться в отношении нашей повседневной жизни. Одна из таких жемчужин арифметики — это «прямая пара точек».Прямая боль — это связка двух смежных точек, обрамленных двумя пересекающимися линиями, при этом пропорция прямых точек должна составлять 180 градусов. В нашем ежедневном расписании мы сталкиваемся с несколькими обстоятельствами, когда применяется идея линейной пары точек. Независимо от того, видим ли мы, есть множество вещей вокруг нас, которые структурируют часть линейной пары.
Условия линейного парного угла:
, мы все могли бы вообразить, что линейная пара не присутствует, учитывая все обстоятельства.Это просто гипотетическая работа. В любом случае, в нашей повседневной жизни есть множество моделей, предлагающих вклад линейных наборов точек. Таким образом, мы должны подробно рассказать о некоторых реальных примерах линейной пары.
1. Лестница, поставленная у стены
Лестница, поставленная напротив перегородки, является подлинной иллюстрацией линейной пары. Здесь «точка A», образованная приставлением табурета к перегородке, является смежной точкой B.’Обе точки в рамке имеют типичную вершину и целиком, эквивалентную 180 градусам.
2. Стрелки часов
Здесь также углы An и B, обрамленные стрелками часов, прилегают друг к другу, имеют типичную вершину, а количество обеих точек эквивалентно 180 градусам.
3. Кусочки пиццы
По большому счету, никто бы не стал рассматривать такие вещи, как арифметика, оценивая пиццу с друзьями.Однако, если мы увидим конвергенции пиццы, мы увидим наличие точек линейной пары. Таким образом, в следующий раз, когда вы пойдете на вечеринку с пиццей, не забудьте приветствовать линейную пару очков.
4. Ножницы
Некоторые ножницы являются классическим примером линейной пары точек, где стороны ножниц, которые расположены рядом друг с другом и имеют основную вершину O, образуют точку с углом 180 градусов.
5. Столб электрический
Электрический столб также является подлинным примером линейной пары.Точки P и Q соответствуют каждому из условий, которые считаются линейной парой.
6. Правосудие баланса
Еще одним мотивом, побуждающим оценить линейную пару очков, является то, что она связана с передачей капитала; поскольку точки, указанные в машине баланса капитала, являются только линейной парой точек.
7. Тройник
В какой бы точке вы ни отправились на прогулку, не забудьте увидеть линейную пару точек, обрамленную на Т-образном перекрестке.
8. Разделочная доска
Вы были бы удивлены, узнав, что линейная пара точек дополнительно обрамлена на хакерской доске. Таким образом, в следующий раз, когда вы увидите, как ваша мама работает на кухне и рубит овощи, чтобы приготовить для вас вкусные блюда, не забудьте увидеть линейную пару точек в рамке на раскалывающем грузе.
Пара линейных углов
линейных пар точек образуются, когда две линии пересекаются друг с другом в единственной точке.Предполагается, что точки находятся непосредственно в том случае, если они будут соседствовать друг с другом после схождения двух линий. Количество точек прямой пары последовательно эквивалентно 180 °. Такие точки иначе называют выгодными. Соседние точки — это точки, которые имеют типичную вершину. Таким образом, и здесь прямые точки имеют типичную вершину. Точно так же будет типичная рука, которая обращается к двум точкам. Подлинной иллюстрацией прямой пары является ступенчатый табурет, который ставится напротив перегородки, структуры направляют точки на землю.
Линейность обращается к прямому. Так и здесь прямые точки — это точки, обрамленные прямой линией. Пара смежных точек здесь развита на отрезке прямой, но не все соседние точки прямые. Таким образом, мы также можем сказать, что прямая пара точек — это смежные точки, чьи ненормальные плечи являются, по существу, обратными пучками.
Пояснение к линейной паре углов
В точке, где точка между двумя линиями составляет 180 °, они образуют прямую точку.Прямая точка — это просто еще один способ решения прямой линии. Прямую линию можно представить как круг с неограниченным радиусом действия. Раздел A-line — это любой бит линии, имеющий две конечные точки. Кроме того, часть любой линии с одной конечной точкой называется лучом. Участок линии A с двумя конечными точками An и B адресуется как AB . На рисунке внизу показан фрагмент линии AB , а два болта в конце показывают линию.
Если точка O взята где-нибудь на отрезке AB, как показано, то угол между двумя отрезками AO и OB будет прямым углом i.е. 180 °.
Рассмотрим штангу луча OP на отрезке AB (штанга), как показано:
В точке O формируются точки OPOB и ∠POA. Понятно, что точка между двумя отрезками линии AO и OB составляет 180 °. таким образом, точки ∠POB и ∠POA составляют 180 °.
Далее ∠POB + ∠POA = ∠AOB = 180 °
∠POB и ∠POA находятся рядом друг с другом, и когда количество соседних точек составляет 180 ° в этой точке, такие точки образуют прямую пару точек.
Приведенный выше разговор можно выразить афоризмом.
Что такое дополнительные углы?
Два угла являются дополнительными, если их действие составляет 180 °. Однако точки не обязательно должны быть близко друг к другу! Выгодные наборы будут последовательно состоять из двух правильных точек или одной интенсивной точки и одной нечувствительной точки.
В момент, когда действие двух очков составит
180∘, точки называются усилением (друг к другу).Полезные наборы могут состоять либо из двух правильных точек, либо из одной интенсивной и одной негуманной. Углы
ABC и DEF являются дополнительными . Мы можем сказать, потому что они совпадают с углами GHJ и JHI (соответственно), и мы можем сказать из рисунка, что GHJ и JHI складываются, чтобы получить GHI … который является просто прямой линией (и, таким образом, технически имеет размер 180∘).
Что такое линейная пара углов?
Два угла образуют линейную пару, если они есть;
Плечо общее
Общая вершина
Их внутренности не перекрывают друг друга
Сумма двух углов составляет 180 °.
Следовательно, линейные пары углов — это смежные углы, чьи несовпадающие плечи представляют собой противоположные лучи.
Из рисунка выше мы можем заметить; OX и OY — два обратных луча, а ∠XOZ и ∠YOZ — примыкающие друг к другу точки. Следовательно, ∠XOZ и ∠YOZ образуют прямую пару.
Что такое постулат линейной пары?
Как указывает постулат линейной пары, ценны два момента, которые образуют прямую пару. Прямая пара — это совокупность соседних точек, образующих линию своими неподеленными лучами.В сумме эти точки эквивалентны 180 градусам. Этот постулат кое-где называется предложением улучшения.
Постулаты Евклида
Греческий математик Евклид воспринимается как отец вычислений в свете обязательств, которые он взял на себя в этой области. Его книга «Компоненты» раскрывает 465 гипотез и проверок, которые сделали создание вычислений таким, каким оно сконцентрировано сегодня. В книге разъясняются пять математических гипотез.
В основном предложении говорится, что можно провести прямую линию между любыми двумя фокусами. Вторая выражает то, что можно непрерывно расширять прямую линию. Другая гипотеза изображает круг. Еще одно заявление о том, что положительные моменты согласованы. Пятая гипотеза остается проблематичной, несмотря на несколько попыток в течение многих лет ее продемонстрировать.
Постулаты против теорем
Предложения — это заявления, которые еще не были продемонстрированы, и считаются действительными.Например, математики принимают утверждение «через любые два фокуса на самом деле есть одна линия» независимо от того, каким образом оно не демонстрируется. Гипотеза — это подлинное объяснение, которое можно продемонстрировать. Возможно продемонстрировать утверждение: «В случае пересечения двух прямых они сходятся точно в одной точке». И гипотезы, и гипотезы могут использоваться для демонстрации прокламаций, отождествляемых с математикой.
Доказательства в геометрии
В геометрии свидетельство — это утверждение, которое подтверждает или опровергает утверждение.Доказательства следует за расположением реальностей, выводов и обоснований, которые помогают в конечном итоге. Гипотезы, подобные предложению прямой пары, можно использовать в математических проверках и ссылаться на них в служебной части подтверждения.
Понимание углов
В точке, где встречаются две линии, фрагменты линий или лучи, они образуют промежутки, называемые точками. Математики измеряют точки в градусах, и эта оценка характеризует вид точки.Прямая точка (иначе называемая прямой линией) имеет размер 180 градусов, а правильная точка — 90 градусов.
Тупая мера более примечательна, чем 90 градусов. Интенсивные точки ниже 90 градусов. Есть также точки с промежутком более 180 градусов, называемые рефлекторными точками. Точка совершает полный оборот на 360 градусов. Точно так же точки могут быть изображены как верные или отрицательные, в зависимости от заголовка точки.
Понимание строк
Понимание линий — незаменимый опыт при исследовании вычислений.Последовательность фокусов, расширяющих безрезультатно, структурирует линию. У линий нет конечных точек. У них есть болты, указывающие на их безграничную природу. Для линии необходим фрагмент строки. Участки линии имеют конечные точки, которые фокусируются вдоль линии. Лучи начинаются в уединенной точке и бесконечно расширяются в одиночку.
параллельных прямых и отрезков линий показаны бок о бок на плоскости и никогда не сходятся. Противоположные линии пересекаются и образуют точку под углом 90 градусов в том месте, где они встречаются. Эти линии встречи составляют прямую пару, поскольку их точки при сложении эквивалентны 180 градусам.
ССЫЛКА НА ВИДЕО НА YOUTUBE: https://youtu.be/kHYUOTBmNHU
Как линейные уравнения используются в повседневной жизни?
Переменные затраты
Представьте, что вы едете в такси во время длительного ухода. Вы понимаете, что администрация такси взимает 9 долларов за то, чтобы вывести вашу семью из вашего жилья, и еще 0,15 доллара за милю за прогулку. Не зная, сколько миль потребуется для достижения каждой цели, вы можете настроить прямое условие, которое можно использовать для определения затрат на любую поездку на такси, которую вы отправляетесь на прогулку.Используя «x» для обозначения количества миль до вашей цели и «y» для компенсации расходов на поездку на такси, прямое условие будет: y = 0,15x + 9
Тарифы
ЛИНЕЙНЫЕ условия могут быть ценным инструментом для сопоставления темпов оплаты. Например, если одна организация предлагает платить вам 450 долларов каждую неделю, а другая предлагает 10 долларов каждый час, и обе требуют, чтобы вы работали по 40 часов в неделю, какая организация предлагает лучший темп оплаты? Прямое условие может помочь вам разобраться! Предложение первичной организации выражается как 450 = 40x.Предложение последующей организации передается как y = 10 (40). После сопоставления этих двух предложений условия показывают вам, что основная организация предлагает лучший темп оплаты — 11,25 доллара в час.
В чем разница между линейными парами и смежными углами?
Смежные углы — это точки, которые расположены близко друг к другу, например, две точки с одной правильной рукой.
Все линейные пары являются соседними точками, однако все смежные точки не являются прямым объединением.
Линейная пара
— это смежные точки, вся сумма которых эквивалентна 180o.
В линейной паре плечи нерегулярных точек коллинеарны, например, они лежат на прямой линии.
В чем разница между линейной парой и парой дополнительных углов?
линейных пар — это необычайное подмножество выгодных точек.
Дополнительные углы — это любые две точки, общая сумма которых составляет 180 градусов.
линейных пар — это любые две точки, которые имеют общий луч и целые до 180 градусов.
Как углы образуют линейную пару?
Линейная пара
— это пара смежных точек, где ненормальная сторона образует прямую линию. Линейная пара — это пара соседних точек, где нерегулярная сторона образует линейную линию. Необычная сторона (AC) является прямой линией. Нам нужно взять еще несколько моделей. Создают ли точки линейную пару? Таким образом, точки образуют прямую пару.
ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ (FAQ)
1 кв.Что такое теорема о линейных парах?
На самом деле, это постулат линейной пары, который…
Если два угла образуют линейную пару, то они являются дополнительными; то есть сумма их мер составляет 180 градусов.
2 кв. Подчиняется ли нелинейная система теореме суперпозиции?
Любая структура, которая соответствует ТЕОРЕМЕ суперпозиции, по определению является линейной системой.
Итак, непрямой каркас — это тот, который не соответствует теоремам суперпозиции.
3 кв. Какие из следующих причин можно использовать для утверждения 2 доказательства?
Теорема о вертикальных углах.
4 кв. Обязательно ли дополнительные углы образуют линейную пару?
Нет. Все точки линейной пары полезны, однако точки усиления не обязательно должны быть линейной парой.
Q5. Линейная пара — это то же самое, что и вертикальная пара?
Не совсем.
Q6. Если два угла образуют линейную пару, то они дополняют друг друга, верно или неверно?
Линейная пара всегда является дополнительной, 180 градусов, а не 90.
Q7. Все ли дополнительные углы образуют линейную пару. Все ли линейные пары являются дополнительными?
Все дополнительные углы не образуют линейную пару. Противоположные точки любого четырехугольника, записанного со всех сторон (вписанный четырехугольник), имеют преимущество, но они не являются линейными парами. В любом случае выгодны все линейные пары.
Q8. Почему все пары линейных углов должны быть дополнительными, но все дополнительные углы не обязательно должны быть линейными парами?
Все дополнительные углы были бы линейными парами, ЕСЛИ бы они были смежными.Но они могли быть далеко друг от друга.
9 кв. Какие пары углов в сумме дают 180?
Дополнительные уголки.
Q10. Какой угол является дополнительным?
Два угла являются дополнительными, если в сумме они составляют 180 градусов. Необязательно быть вместе, просто складываем 180 градусов.
.
