{2 n}}{n}+\ldots, |x| \lt 1$
Читать дальше: десятичный логарифм.
Содержание
Логарифм. Свойства логарифмов
Логарифм. Свойства логарифмов
Рассмотрим равенство . Пусть нам известны значения и и мы хотим найти значение .
То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .
Пусть переменная может принимать любое действительное значение, тогда на переменные и накладываются такие ограничения: , ,
Если нам известны значения и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое действие, которое называется логарифмирование.
Чтобы найти значение , мы берем логарифм числа по основанию :
Итак,
Логарифмом числа по основанию называется показатель степени, в которую надо возвести , чтобы получить .
То есть основное логарифмическое тождество:
, ,
является по сути математической записью определения логарифма.
Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.
Перечислим основные свойства логарифмов:
(, , , ,
1.
2.
3.
4.
5.
Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:
6.
7.
8.
9.
Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию:
10.
11.
12. (следствие из свойства 11)
Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:
13.
14.
15.
Частные случаи:
— десятичный логарифм
— натуральный логарифм
При упрощении выражений, содержащих логарифмы применяется общий подход:
1. Представляем десятичные дроби в виде обыкновенных.
2. Смешанные числа представляем в виде неправильных дробей.
3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.
4. Стараемся привести все логарифмы к одному основанию.
5. Применяем свойства логарифмов.
Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.
Пример 1.
Вычислить:
Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.
==(по свойству 7)=(по свойству 6) =
Подставим показатели, которые у нас получились в исходное выражение. Получим:
Получим:
Ответ: 5,25
Пример 2. Вычислить:
Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):
Разложим числа, стоящие под знаком логарифма на простые множители:
Применим свойства 4 и 6:
Введем замену
Получим:
Ответ: 1
Скачать таблицу логарифм и его свойства
И.В. Фельдман, репетитор по математике.
Как решить логарифмическое уравнение: подробное объяснение
Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.
Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.
Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.
- Как решать уравнения с логарифмами: 2 способа с примерами
- Пример решения логарифмического уравнения с разными основаниями
- Пример решения логарифмического уравнения с переменными основаниями
- Как сделать проверку – это важно
Как решать уравнения с логарифмами: 2 способа с примерами
Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.
При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!
Давайте посмотрим, как это работает на примере:
Воспользуемся определением логарифма и получим:
2х + 3 = 32
Теперь перед нами простейшее уравнение, решить которое не составит труда:
2х + 3 = 9
2х = 6
х = 3
Сделаем проверку.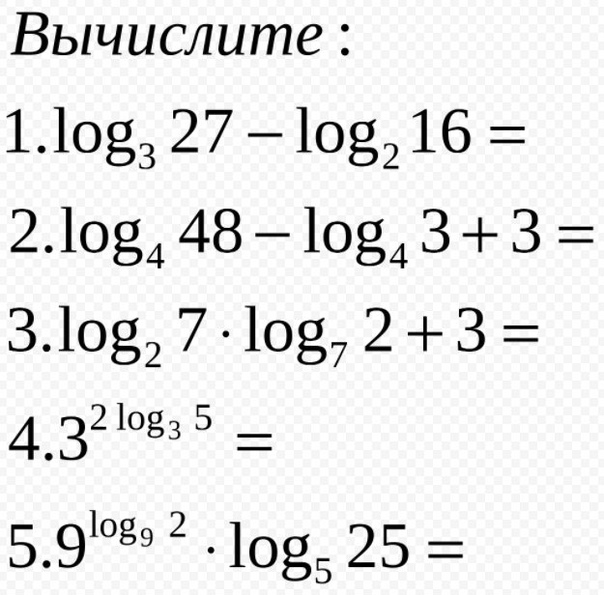 Подставим найденный Х в исходное уравнение:Так как 32 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Подставим найденный Х в исходное уравнение:Так как 32 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Ответ: х = 3
Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании logaf(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.
Поэтому мы покажем еще один способ решения логарифмических уравнений.
Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:
Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.
Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.
Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:
Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:
2х + 3 = 32
2х + 3 = 9
2х = 6
х = 3
Ответ: х = 3
Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.
Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:
3х – 5 = 4
3х = 9
х = 3
Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.
Ответ: х = 3
Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:
Решим данное квадратное уравнение, найдем дискриминант:
Сделаем проверку, подставим х1 = 1 в исходное уравнение:Верно, следовательно, х1 = 1 является корнем уравнения.
Теперь подставим х2 = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х2 = -5 – посторонний корень.
Ответ: х = 1
Пример решения логарифмического уравнения с разными основаниями
Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,
Правильно, нужно привести логарифмы в правой и левой части к одному основанию!
Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:
Мы знаем, что 1/3 = 3-1. Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:
Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.
Ответ: х = 4.
Пример решения логарифмического уравнения с переменными основаниями
Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, logx+1(х2+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:
1. Аргумент логарифма должен быть больше ноля, следовательно:
Аргумент логарифма должен быть больше ноля, следовательно:
2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:
Сведем все требования в систему:
Данную систему требований мы можем упростить. Смотрите х2+5х-5 больше ноля, при этом оно приравнивается к (х + 1)2, которую в свою очередь так же больше ноля. Следовательно, требование х2+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.
Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:
Т.к. 32=9, то последнее выражение верно.
Ответ: х = 2
Как сделать проверку
Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.
Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.
Если наше уравнение имеет вид loga (f(x)) = loga (g(x)), то должны выполняться следующие ограничения:
После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!
Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.
Действия с логарифмами.
 Набиваем руку!
Набиваем руку!
В данном уроке мы будем учиться работать с логарифмом на уже весьма и весьма приличном уровне. Поэтому для успешного решения примеров этого урока рекомендую погулять по ссылкам:
Что такое логарифм?
Действия с логарифмами. Постигаем азы!
Почитайте, пока не поздно.) Почитали? Всё понятно! Отлично! Тогда движемся дальше.)
Теперь настал черёд завязывания более крепкой дружбы с логарифмами и, соответственно, решения серьёзных (в том числе сложных и нестандартных) примеров.
Чтобы не скакать из темы в тему, прежде всего я ещё разочек выпишу все основные свойства и формулы логарифмов. Вот они:
Это основной набор формул, необходимых для успешной работы с логарифмами практически на любом уровне сложности. Иногда в школе (и в некоторых продвинутых учебниках) дают больше формул, но в целом приведённого перечня для решения большей части примеров оказывается вполне достаточно. Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Эти формулы надо помнить! Но, ещё раз повторяю, не просто помнить, а уметь применять! Причём в обоих направлениях — как слева направо, так и справа налево. Вроде бы это всё и так понятно и очевидно, но… дальше всё поймёте.) Как надо помнить формулы, я вам вряд ли смогу подсказать, а вот как уметь применять — подробно расскажу и покажу в этом уроке.
Итак, продолжаем наши игры!
Все формулы. Все степени. Много дробей! Двоюродные и троюродные братья.
Ну что ж, теперь приступаем к работе со всеми формулами (кроме последней формулы перехода к новому основанию). Используем все свойства степеней и активно включаем в работу степени с отрицательными и дробными показателями. Поди сообрази, что, например,
0,04 = 5-2.
Или
Это уже не родные, а двоюродные и троюродные братья по степени получаются…)
Посему, если есть пробелы в степенях, то для начала милости прошу сюда:
Что такое степень. Свойства степеней.
Свойства степеней.
Ну, а для тех, кто со степенями давно на «ты» — продолжаем.)
Пример 1
За что зацепиться? Хорошо, если сразу догадались, а если нет? Если нет, значит, перечитываем первый практический совет прошлого урока — переходим к обыкновенным дробям!
У нас в одну кучу намешаны десятичная дробь и смешанное число. Вот и перейдём к единообразию — к обычным дробям. А там, глядишь, и забрезжит свет в конце тоннеля…
Пишем:
Так, уже кое-чего проясняется: 49 с семёркой родня, а 100 — с десяткой:
49 = 72
100 = 102
Стало быть, по свойствам степеней можно записать:
Ну, вот и спасительный лучик света! Выносим двойку за логарифм и получаем:
Уже всё стало выглядеть гораздо симпатичнее. Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
Всё бы ничего, только основание 7/10 и аргумент 10/7 у нас записаны кверху ногами. Что делать? Да свойства степеней вспомнить! На этот раз — с отрицательным показателем:
И снова выносим показатель степени (минус единицу) за знак логарифма, переворачиваем аргумент и получаем:
Ответ: -2
Готово дело.) Теперь пробуем самостоятельно:
Ответ: -1
А теперь вовлекаем в наш увлекательный процесс корни. То есть, не что иное, как… степени с дробными показателями. Да-да!
Пример 2
Надеюсь, вы не забыли, что lg — это просто логарифм по основанию 10? Или десятичный логарифм? Пример достаточно простой, без заморочек. Надо всего лишь вспомнить, что корень кубический из 7000 — это 70001/3. С семёркой — аналогично. А дальше по формуле разности логарифмов да по формуле деления степеней. Получим:
Получим:
Ответ: 1
Вот так вот. Здесь мы снова перешли к обычным дробям. Но не от десятичных дробей или смешанных чисел, а от корней. В этом безобидном примере вполне можно было бы и без дробей обойтись, работать напрямую с корнями, но в более сложных примерах корни могут вконец запутать. Как, например, вот в таком примерчике:
Пример 3
С чего начать? И тройка есть, и девятка. Правда, три в квадрате — это и будет девятка… Но в примере ещё и корни разных степеней смешались в кучу — квадратный и кубический! Ужас… Но паниковать и сдаваться рано. Перейдём-ка от корней к степеням с дробными показателями! Распишем девятку как 32. А там, того гляди, всё и наладится.)
Верные мысли! Итак, по свойствам степеней для основания и для аргумента мы можем записать:
Вот всё и прояснилось.) Оба числа — и основание, и аргумент — оказались… родственниками! По тройке. ) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
) Только совсем уж дальними. Даже не троюродными, а десятиюродными братьями: основание — это три в степени 3/2, а аргумент — та же тройка, но в степени 7/3… Тем не менее факт остаётся фактом — родство по степени (хоть и очень дальнее) установлено. Вот и все формулы и свойства заработали! Выносим наши дробные показатели из за знак логарифма и аккуратно считаем:
Вот так. Здесь уже, конечно, немножко повозиться со степенями пришлось. А что делать… Так что не стесняемся переходить от корней к дробям! И всё получится. Обязательно.)
Вот вам и очередные практические советы:
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями.
При наличии корней переходим от корней к степеням с дробными показателями.
Что ж, пришла пора разгрызть и какой-нибудь особо крепкий орешек. Как, например, вот такой примерчик:
Пример 4
Вычислить:
Опять же, с чего начинать? Если имеете хоть малейшее представление — флаг вам в руки. Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
Вперёд и с песнями, как говорится.) Если понятия не имеете — подключаем зелёные практические советы и размышляем синим цветом. Примерно так:
«Ух, наворотили… Кошмар! Напролом явно не решается, надо сначала как-то преобразовывать пример. Но — как? Будем вспоминать практические советы.
1. Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.
Где здесь дроби? Дробей не видно. Ладно, этот пункт пока пропустим. Что там у нас ещё есть? Вот это:
2. Степени популярных чисел надо знать. В лицо! При наличии в примере разных чисел пытаемся найти «братьев по степени».
Так, кое-какая зацепочка уже появилась… 121 — это 11 в квадрате. Ещё можно расписать 125 как 5 в кубе и 9 как 3 в квадрате, но 5 и 3 — никакие не братья и не сёстры по степени. Пригодится или нет — пока непонятно, но к сведению примем. Поехали дальше.)
3. Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.
Коэффициентов в нашем примере нет, логарифмы и так чистые. Отметаем этот совет. Что у нас там ещё припасено?
4. Всегда прикидываем, нельзя исходное выражение преобразовать под какую-нибудь готовую формулу?
Вот и прикидываем: на что похож внешний вид нашего примера? Ну же? Ну, конечно! На самую первую формулу — основное логарифмическое тождество! Единственная формула, где логарифм тусуется в показателе степени.
С ним мы пока что ни разу не работали. Что ж, поработаем! Попробуем преобразовать наш пример под эту формулу: других вариантов как-то выкрутиться у нас просто нет!
Но в формуле в показателе стоит один логарифм! А у нас — сумма. Что нам мешает сложить логарифмы по соответствующей формуле суммы? Основания мешают! Они… они — разные! Ну-ка, может, ещё не все практические советы у нас использованы? Вспоминаем:
5. При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
При наличии дробей в примере, переходим от дробей к степеням с отрицательными показателями. При наличии корней переходим от корней к степеням с дробными показателями.
Так, ну дробей в нашем примере нету, это видно. А вот корень в основании — преобразуем. Вот так:
А во втором логарифме в основании тоже стоит 11, только в квадрате… Уже кое-какие проблески! Выпишу-ка я показатель отдельно, дабы не запутаться… С учётом наших размышлений.)
Уже лучше. Теперь выносим показатели степеней из оснований перед логарифмами (не забыть бы перевернуть…):
Великолепно! Основания логарифмов выровнялись! Только вот новая беда… Коэффициенты появились… Хотелось бы сложить логарифмы, ан нет, не канает… Так стоп! Чего же я туплю-то! Можно же их по другой формуле спрятать вовнутрь!
Ну вот. Уже идеально для формулы сложения! Только внутри логарифмов что-то несусветное стало твориться. Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Не беда, перейдём к маленьким числам: зря, что ли, мы 125 и 9 в виде степеней пятёрки и тройки расписывали?
Пока всё чин-чинарём. Теперь, по правилам действий со степенями, можно записать:
Вот, практически, и всё. Досчитываем наш показатель по формуле сложения логарифмов:
Пример становится всё лучше и лучше! Возвращаемся к нашему исходному примеру, вставляем в него наш преобразованный показатель и получаем ответ!
Йес!!! Ничего себе, примерчик, однако ж…»
Ответ: 75
Вот такой пример. Запутанный, да, я не спорю. И зачем я так детально его разобрал? С практическими советами, мыслями… Мог бы и в пару строк уложиться… Дело в том, что разбор одного конкретного примера — занятие бесполезное. Не попадётся он. А вот разъяснить на конкретном примере, как именно надо выкручиваться в любом (да-да, любом!) задании — совсем другое дело!
Главное в этом разборе — подход. Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Мы применяем весь наш арсенал инструментов к конкретному примеру. Пробуем поочерёдно все инструменты, как ключики к замку. Что-то срабатывает, а что-то нет. Это не страшно и не смертельно. Не подошло — пробуем что-то другое! Что-то обязательно подойдёт! Сложные и запутанные задания именно так и решаются. И никак иначе.)
Конечно, с опытом всё будет делаться гораздо короче и какие-то шаги будут в уме делаться и вообще пропускаться. За ненадобностью. Тут практика рулит. Тренироваться и решать надо. Используя изложенный здесь подход. И тогда всё получится. Обязательно!
Формула перехода к новому основанию. Немного приколов… И немного формул сокращённого умножения.
Поднимаемся ещё на ступень повыше. Запускаем теперь в дело самую последнюю формулу из нашего списка — это формула перехода к новому основанию. Вот она:
В чём суть этой формулы, когда она применяется и как именно она работает? Объясняю по пунктам.
Формула эта применяется, когда основания логарифмов — разные. Но не просто разные, а ещё и не родственные по степени! Которые друг в друга через простую степень не превращаются. Скажем, 2 и 3. Или 5 и 7. Заметьте, что нам уже встречались разные основания у логарифмов в одном и том же примере, но там или всё и так славненько срасталось, или переход был через степени. Например, если основания логарифмов 1/125 и 25, то можно догадаться, что это родня! По пятёрке. Ибо 1/125 = 5-3, а 25 = 52. Не так очевидно, конечно, но и мы уже всё-таки на серьёзном уровне с вами. А дальше дело техники: выносим показатели за логарифмы и — вперёд.
Но если основания не родственные, а без выравнивания оснований в примере никак, то выход только один — работать по этой формуле.
Запомнить её очень легко. По шагам:
1) Слева пишем логарифм, основание которого нам не нравится. Справа рисуем черту дроби.
2) В числитель пишем логарифм числа b, но уже по новому основанию k. Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
Какому именно основанию? А какому угодно! В том-то весь и фокус! Естественно, тому, которое нам удобнее. Кроме единицы, разумеется.)
3) В знаменатель пишем логарифм старого основания a по тому же новому основанию k.
Обратите внимание на саму структуру формулы: слева в основании буквы k вообще нет! В этом-то и вся фишка! Это означает, что новому логарифму мы можем выбрать какое угодно основание. Обычно выбирают то, которое нам удобно в конкретном примере. Если, скажем, в примере куча логарифмов по основанию 3 и затесался один по основанию 7, то его и менять будем. На тройку.
А в знаменатель пишем логарифм старого основания. Так уже математика требует. В результате логарифм со старым основанием исчезает из примера. Вот и всё. Вот и вся суть формулы перехода. Ну что, посмотрим на формулу перехода в действии?
Пример 5
Вычислить:
Что тут можно увидеть? Ну, во-первых, разные основания. Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Причём не родственные: из четвёрки пятёрку простым возведением в степень никак не получить. Во-вторых, наблюдаем произведение логарифмов. Такой формулы в наших свойствах нету. Не путаем с логарифмом произведения! Или с суммой логарифмов… Что же делать? Первым делом перейдём к одному основанию. Что-то же делать всё равно надо! К какому основанию пойдём? Ну, ясное дело, что не к 30 или 1,234. У нас на выбор два варианта — либо к четвёрке, либо к пятёрке. В данном примере абсолютно без разницы, к чему переходить. Давайте к четвёрке пойдём: всё-таки число поменьше.) Итак, первый логарифм не трогаем (у него и так основание четыре), а вот второй логарифм превращаем по формуле перехода в дробь:
Всё. Логарифм по основанию 5 из примера благополучно исчез, и в основаниях остались только четвёрки. Вставляем полученную дробь в наш пример, упрощаем и считаем:
Ответ: 2
Вот так. Откуда же я узнал, что надо переходить к другому основанию? Ведь я мог и что-то ещё замутить. Скажем, log516 расписать как
Скажем, log516 расписать как
log516 = log524 = 4log52
и дальше как-то ещё выкручиваться. Да. Можно. Но с богатым опытом приходит уже так называемое математическое чутьё на формулы и преобразования.) Когда в уме наперёд уже умеешь просчитывать, к чему может привести тот или иной манёвр и не идёшь по заведомо негодному пути.
Вот вам очередной практический совет на данную тему.
Если перед вами сложное логарифмическое выражение, в котором основания логарифмов разные, то первым делом пробуем сделать их одинаковыми. Или через степени или по формуле перехода. Очень часто этот манёвр срабатывает проясняет дальнейшую ситуацию.
А теперь рассмотрим один фокус на формулу перехода, который частенько любят проделывать составители примеров. По-другому эту фишку даже и не назовёшь. Настолько элементарна, а в тупик может поставить даже отличника!
Настолько элементарна, а в тупик может поставить даже отличника!
Пример 6
Вычислить:
Основания уже одинаковые, но формулы деления логарифмов не существует, да… Можно, конечно, сообразить, что 125 = 53 и старым добрым способом, но что делать, если внутри логарифмов сидит что-нибудь более навороченное? Вот и впадают в ступор…
Здесь же достаточно всего лишь разглядеть формулу перехода к новому основанию. Вернее, не просто формулу, а её правую часть! И, если запустить эту формулу справа налево, то сразу получим:
И все дела! Да-да! Это ответ.)
Ответ: 3
Частенько эту фишку применяют с какими-нибудь совершенно дикими основаниями. На испуг берут, типа.) Как, например, вот такое задание:
Пример 7
Вычислить:
В основании число «пи», как тут не испугаться… Однако, если догадаться, что наша ужасная дробь — всего лишь правая часть формулы перехода к новому основанию и сработать справа налево, то получим всего-навсего:
Вот и всё. И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
И нету больше никакого «пи».) А уж сложить парочку логарифмов с одинаковыми основаниями — пустяшное дело. Не пример, а одно удовольствие:
log1236 + log124 = log12144 = 2
Ответ: 2
Вот такой вот приёмчик. Теперь, надеюсь, не растеряетесь, в случае чего.)
Рассмотрим ещё одну распространённую фишку с формулой перехода. Вернее, её частный случай.
Что произойдёт, если за новое основание мы возьмём аргумент логарифма? Давайте посмотрим!
Во как! Оказывается, если поменять местами a и b, то наш новый логарифм станет всего лишь обратным к старому! Весьма и весьма полезная формулка. Имеет смысл запомнить.) Решим примерчик и на эту тему:
Пример 8
Вычислить:
Что делать будем? Скобки раскрывать? Можно, конечно, но пример явно намекает на более элегантное преобразование. Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Перейдём в логарифме по основанию 40 к основанию 2. Двойка чем-то привлекательнее, чем сорок, не находите?) Поскольку в аргументе логарифма стоит также двойка, то при переходе к основанию 2 достаточно просто перевернуть этот логарифм. И все дела.)
Получим:
И что дальше? Куда пристегнуть тройку? А дальше новый фокус! Дело всё в том, что мы не можем напрямую сложить логарифм и число. Но зато логарифмы между собой — запросто! Как выкрутимся? А сделаем-ка из тройки… логарифм! Да-да! Для этого сначала выберем ему основание. Вариантов выбора много, но я предлагаю выбрать 2. Думаю, возражений не будет?)
А дальше пишем вот такое простое равенство:
3 = log223
Всё легко и просто: тройка уходит показателем в степень нашего выбранного основания. Сама цепочка превращений выглядит вот так:
По этапам:
1) Вместо тройки пишем степень с выбранным основанием 2 и показателем, равным этой самой тройке.
2) Берём логарифм от этой степени по тому же самому основанию 2.
3) Всё!
Конечно, можно было бы и сразу тройку на логарифм заменить, благо здесь числа совсем простые, но лучше запомнить эту простую цепочку. А то придётся где-нибудь, к примеру, превращать в логарифм по основанию 11 число 1/7… А по цепочке всё совсем элементарно:
Просекли фишку? Тогда возвращаемся к нашим баранам и дорешиваем:
Ответ: 1
Да… Кто бы мог подумать.)
Конечно, в числовых выражениях этот приёмчик с превращением числа в логарифм достаточно экзотичен. Но вот в логарифмических уравнениях и неравенствах он применяется на полную катушку! Имейте его в виду.)
Заметьте, что обычно мы стараемся поступать наоборот — упрощать всякие ужасы типа дробей, корней, синусов да логарифмов. Доводить их, по возможности, до конечного числа. А тут — наоборот, из числа делаем логарифм. Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Что хотим, то и творим! Так что математика — на самом деле весьма и весьма творческая наука! Во многом даже искусство.)
Запоминаем:
При необходимости любое число можно превратить в логарифм по любому основанию (кроме единицы, конечно).
Осталось разобраться с совсем уж хардкорными примерами. Где и так пробуешь и сяк, но не упрощается он никак! На такие примеры есть своё особое секретное оружие.) Срабатывает безотказно. Если уметь грамотно им пользоваться, конечно. Как вам такой примерчик!
Пример 9
Вычислить:
За что зацепиться? Все основания уже одинаковые (семёрка), но это особо не спасает. Кстати, обращаю ваше внимание на весьма и весьма частый косяк. В числителе стоят квадраты логарифмов. Именно самих логарифмов, а не их аргументов! Это означает, что вынести двойки из логарифмов наружу мы не имеем права! Не там двойки стоят… Стало быть, уже привычных нам логарифмических формул, готовых к употреблению, нету. Что же делать?
Что же делать?
Спокойно! Без паники! Никто и никогда не может гарантировать, что сразу влёт всё решится.) К сожалению…
Чтобы расправиться с этим злым примером, забудем на минутку про логарифмы и плавненько переместимся в седьмой класс. Формулы сокращённого умножения не забыли, надеюсь? А теперь внимательно присматриваемся к нашему примеру. Что ещё, кроме логарифмов, в нём можно увидеть? Разность… Разность ква… Ну, конечно! Разность квадратов! Такая родная и до боли знакомая формула:
a2–b2 = (a—b)(a+b)
Правда, в применении к логарифмам. Ну и что из этого? Ведь в формуле под буковками a и b может скрываться всё что угодно — и логарифмы, и синусы, и степени — любые выражения! Формула всё равно сработает!
Итак, заменяем наш числитель на произведение скобок по формуле разности квадратов:
Вот и всё встало на свои места! И все формулы заработали! Решать пример стало одно удовольствие. )
)
В первых скобках (разность) получается:
Во вторых скобках (сумма) будет:
Вставляем в пример наши промежуточные результаты, сокращаем и получаем:
Ответ: 1
Простенько и со вкусом.) Здесь-то всё ясно. Но в тревожной боевой обстановке ЕГЭ подобный пример может и в ступор вогнать. Дело всё в том, что большинство учеников подсознательно пытаются решить пример в том формате, в котором он задан. Например, если задан пример на логарифмы, то мы с головой погружены в логарифмы и варимся только в них, а вынырнуть на поверхность да оглядеться вокруг — не можем. С тригонометрией аналогично — решаем пример только в рамках тригонометрии. И, в случае чего, не можем напрячься и выскочить из этих жёстких рамок… А надо уметь! Хотя бы иногда.)
Посему очередной по счёту практический совет:
Замороченные примеры проверяем на алгебру седьмого класса — разложение на множители, формулы сокращённого умножения и т. п.
п.
Ещё из той же оперы для самостоятельного решения:
lg24 + lg16·lg25 + lg225 =
Ответ: 4
Ну что, поздравляю! Вот мы и набрались достаточного количества знаний для уверенной работы с логарифмами практически на любом уровне сложности! Дальше путь только один — решать примеры! Как можно больше.) И особо рекомендую не пренебрегать зелёными советами. Они не зря даются в материале.) Их надо помнить и им надо следовать.) И тогда не логарифмы будут командовать вами, а вы — логарифмами.)
До встречи!
11.4.4. Натуральный логарифм.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 264 Опубликовано
Логарифм по основанию е (Неперово число е≈2,7) называют натуральным логарифмом.
ln7=loge7, ln7 – натуральный логарифм числа 7.
Примеры.
Вычислить, используя определение логарифма.
1) lne². По определению натуральный логарифм числа e² — это показатель степени, в которую нужно возвести число е, чтобы получить число е². Очевидно, что это число 2.
lne²=2.
2) ln (1/e). По определению натуральный логарифм числа 1/е — это показатель степени, в которую нужно возвести число е, чтобы получить 1/е. Очевидно, что это число -1, так как е-1=1/е.
ln (1/e)=-1.
3) lne3+lne4=3+4=7.
4) lne-ln (1/e2)=1- (-2)=1+2=3.
Вычислить, применив основное логарифмическое тождество:
и формулу возведения степени в степень: (am)n=amn=(an)m.
1) eln24=24.
2) e2ln11=(eln11)2=112=121.
3) e-ln20=(eln20)-1=20-1=1/20=0,05.
4) (e4)ln5=(eln5)4=54=625.
Упростить, применив основное логарифмическое тождество:
формулу возведения степени в степень: (am)n=amn=(an)m ;
формулу произведения степеней с одинаковыми основаниями: am∙an=am+n и
формулу возведения в степень произведения: (a∙b)n=an∙bn.
1) eln4+2=eln4∙e2=4∙e2=4e2.
2) e1+ln3=e1∙eln3=e∙3=3e.
3) (e4+ln5)2=(e4∙eln5)2=(e4∙5)2=e4∙2∙52=e8∙25=25e8.
4) (eln2+3)4=(eln2∙e3)4=(2∙e3)4=24∙e3∙4=16e12.
Упростить, применив основное логарифмическое тождество:
формулу возведения степени в степень: (am)n=amn=(an)m ;
формулу частного степеней с одинаковыми основаниями: am:an=am-n и
формулу возведения в степень произведения: (a∙b)n=an∙bn.
1) e2-ln3=e2:eln3=e2:3=e2/3.
2) e1-ln5=e1:eln5=e:5=e/5=0,2e.
3) (e5-ln10)3=(e5:eln10)3=(e5:10)3=(0,1e5)3=0,13∙e5∙3=0,001e15.
4) (e3-ln2)4=(e3:eln2)4=(e3:2)4=(0,5e3)4=(0,5)4∙(e3)4=0,0625e12.
Раскрытие логарифмических уравнений
На предыдущем уроке из курса ВНО подготовки Вы познакомились с формулой раскрытия логарифмов
logaf(x)=c⇔f(x)=ac.
{x>0, x≠1, f(x)>0}
и ее частичными случаями:
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Мы настолько часто пользуемся этими свойствами логарифмов, что после прочтения всех примеров Вы точно будете знать, где и для чего нужны эти формулы.
Примеры раскрытия логарифмических уравнений
Курс подготовки ВНО состоит из 40 примеров от простых до сложных, так что по номеру примера Вы можете следить, какой класс задач решается. По мере углубления Вы будете знакомиться с новыми формулами и свойствами логарифмов, без которых уравнение невозможно решить.
Пример 16.7 Решить уравнение log2(x+1)-log2(x-1)=1 и указать промежуток, которому принадлежит его корень.
Решение: Выписываем ОДЗ:
По правилу, разницу логарифмов выражений заменяем логарифмом частки + логарифм основания равен единице, в результате опускаем логарифмы и приравниваем выражения:
x=3 – корень заданного уравнения, принадлежащий промежутку (2,9;3,1).
Ответ: (2,9;3,1) – В.
Пример 16. 2 в результате логарифмирования обеих его частей.
2 в результате логарифмирования обеих его частей.
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части уравнения по основанию 10.
При этом помните, что десятичный логарифм 10 равен 1
таким образом нашли уравнение, которое равносильно начальному.
(x1=1000 или x2=0,1).
Ответ: lg2(x)-2•lg(x)-3=0 – Д.
Пример 16.13 Указать уравнение, равносильное уравнению 2lgx2-lg2(-x)=4.
Решение: ОДЗ: -x>0, x<0.
Вынесем из под логарифма степень =2 и перегруппируем слагаемые
Это и есть все манипуляции, чтобы найти уравнение, которое равносильно заданному
2lgx2-lg2(-x)=4.
С помощью других преобразований Вы бы его не получили.
(x=-100).
Ответ: lg2(-x)-4•lg(-x)+4=0 – Г.
Пример 16.14 Решить уравнения
logalogblogcx=0.
Решение: ОДЗ: x>0.
Имеем три вложенные логарифмы, поэтому по свойствам добиваемся равных основ логарифмов справа и слева от знака равенства, и раскрываем уравнение за схемой
Такого плана задания в свое время были популярны на олимпиадах.
Ответ: cb – А.
Пример 16.15 Указать количество корней уравнения
А | Б | В | Г | Д |
Четыре | три | два | один | ни одного |
Решение: ОДЗ: x≠0.
Путем введения замены переменных уравнение сводим к квадратному, после вычисления которого решаем 2 простых логарифмических уравнения.
Подробные объяснения хода преобразований приведены в таблице
Все найденные значения (-8; -4; 4; 8) принадлежат ОДЗ, уравнение имеет четыре решения.
Ответ: Четыре – А.
Пример 16.24 Установить соответствие между уравнениями (1-4) и произведениями их корней (А–Д).
Решение: Все 4 варианта логарифмических уравнений сводим путем замены переменных к квадратным, после нахождения корней последних возвращаемся к замене и вычисляем простые уравнения с логарифмами. Так как в ответе нужно найти произведение корней, то условие ОДЗ допускает все значения.
Решение уравнений с логарифмами невозможно без знания их свойств. Обращайте внимание на подчеркивания в формулах, они даются не просто так, эти две формулы к концу занятий Вы должны выучить на память и поверьте, что у Вас это получится.
А сейчас переходите к новым готовым ответам с ВНО подготовки на логарифмические уравнения.
Натуральный логарифм. Что такое логарифм? Решение логарифмов
Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.
Определение
Натуральный логарифм
— это функция y = ln
x
,
обратная к экспоненте , x = e y
,
и являющаяся логарифмом по основанию числа е
:
ln
x = log
e x
.
Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln
x)′ = 1/
x
.
Исходя из определения
, основанием натурального логарифма является число е
:
е
≅ 2,718281828459045…
;
.
График функции y = ln
x
.
График натурального логарифма (функции y = ln
x
) получается из графика экспоненты зеркальным отражением относительно прямой y = x
.
Натуральный логарифм определен при положительных значениях переменной x
.
Он монотонно возрастает на своей области определения.
При x → 0
пределом натурального логарифма является минус бесконечность ( — ∞
).
При x → + ∞
пределом натурального логарифма является плюс бесконечность ( + ∞
). При больших x
логарифм возрастает довольно медленно. Любая степенная функция x a
с положительным показателем степени a
растет быстрее логарифма.
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.
Основные свойства натурального логарифма представлены в таблице.
Значения ln x
ln 1 = 0
Основные формулы натуральных логарифмов
Формулы, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:
Доказательства этих формул представлены в разделе «Логарифм» .
Обратная функция
Обратной для натурального логарифма является экспонента .
Если , то
Если , то .
Производная ln x
Производная натурального логарифма:
.
Производная натурального логарифма от модуля x
:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Интеграл вычисляется интегрированием по частям :
.
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексной переменной z
:
.
Выразим комплексную переменную z
через модуль r
и аргумент φ
:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ
определен не однозначно. Если положить
,
где n — целое,
то будет одним и тем же числом при различных n
.
Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Рис. 16. Поведение функции f(x) = x4
4×3
При переходе через точку x = 0 производная не меняет знака: функция убывает как на промежутке (1; 0], так и на промежутке . Поэтому точка x = 0 является седловой точкой функции.
А вот при переходе через точку x = 3 производная меняет знак с () на (+). На промежутке )
Описание аргументов:
- число
– обязательный для заполнения аргумент, характеризующий числовое значение показателя логарифма, то есть число, полученное в результате возведения основания логарифма в некоторую степень, которая и будет вычислена функцией LOG; - [основание] – необязательный для заполнения аргумент, характеризующий числовое значение основания логарифма.
 Если аргумент явно не указан, логарифм считается десятичным (то есть основание равно 10).
Если аргумент явно не указан, логарифм считается десятичным (то есть основание равно 10).
Примечания:
- Несмотря на то, что результат вычисления функции LOG может являться отрицательным числом (например, функция =LOG(2;0,25) вернет значение -0,5), аргументы данной функции должны быть взяты из диапазона положительных значений. Если хотя бы один из аргументов является отрицательным числом, функция LOG вернет код ошибки #ЧИСЛО!.
- Если в качестве аргумента [основание] было передано значение 1, функция LOG вернет код ошибки #ДЕЛ/0!, поскольку результат возведения 1 в любую степень будет всегда одинаковым и равным 1.
Функция LOG10 имеет следующую синтаксическую запись:
LOG10(число
)
- число
– единственный и обязательный для заполнения аргумент, смысл которого тождественен одноименному аргументу функций LN и LOG.
Примечание:
если в качестве аргумента число было передано отрицательное число или 0, функция LOG10 вернет код ошибки #ЧИСЛО!.
Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.
Определение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2.
 Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать. - Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой. x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:
x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные:
Свойства функции $y=\ln{x}$
1. $D(f)=(0;+∞)$.
2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.
В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции
.
Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.
Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять. 6=1$.
6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:
Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $}
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ
1. Чтобы решить логарифмическое уравнение, перепишите уравнение в экспоненциальной форме и решите относительно переменной.
Пример 1: Решите относительно x в уравнении Ln ( x ) = 8.
Решение:
- Шаг 1: Пусть обе стороны являются показателями основания e. Уравнение Ln ( x ) = 8 можно переписать.
- Шаг 2: К настоящему моменту вы должны знать, что, когда основание экспоненты и основание логарифма одинаковы, в левой части можно записать x.
 Теперь уравнение можно записать
Теперь уравнение можно записать
. - Шаг 3: Точный ответ:
и приблизительный ответ
Чек: Вы можете проверить свой ответ двумя способами. Вы можете построить график функции Ln ( x ) -8 и посмотреть, где она пересекает ось x.Если вы правы, график должен пересекать ось x в ответе, который вы получили алгебраически.
Вы также можете проверить свой ответ, подставив значение x в начальное
уравнение и определите, равна ли левая часть правой. Для
Например, если Ln (2,980.95798704) = 8, вы правы. Это так, и вы правы.
Пример 2: Найдите x в уравнении 7 Log (3 x ) = 15.
Решение:
- Шаг 1: Выделите логарифмический член перед преобразованием логарифмического уравнения в экспоненциальное уравнение.Разделите обе части исходного уравнения на 7:
- Шаг 2: Преобразуйте логарифмическое уравнение в экспоненциальное уравнение: если основание не указано, это означает, что основание логарифма равно 10.
 Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен
. Уравнениетеперь можно написать
- Шаг 3: Разделите обе части приведенного выше уравнения на 3:
это точный ответ и приблизительный ответ.
Чек: Вы можете проверить свой ответ двумя способами: построив график функции
или подставив значение x в исходное уравнение. Если вы выберете построение графика, точка пересечения по оси x должна быть такой же, как и ответ, который вы
полученный ( ).
Если вы выберете замену, значение левой части оригинала
уравнение должно равняться значению правой части уравнения после того, как вы
вычислили значение каждой стороны на основе вашего ответа на x.
Пример 3: Решите относительно x в уравнении
Решение:
- Шаг 1: Обратите внимание, что первый член Ln ( x -3) действителен только тогда, когда x > 3; термин Ln ( x -2) действителен только тогда, когда x > 2; и термин Ln (2 x +24) действителен только тогда, когда x > -12.
 Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными.Если все три члена верны, то уравнение действительно.
Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными.Если все три члена верны, то уравнение действительно. - Шаг 2: Упростим левую часть приведенного выше уравнения: по свойствам логарифмов мы знаем, что
- Шаг 3: Теперь уравнение можно записать
- Шаг 4: Пусть каждая сторона приведенного выше уравнения будет показателем степени основания e:
- Шаг 5: Упростите приведенное выше уравнение:
Другой способ взглянуть на уравнение на шаге 3 — понять, что если Ln ( a )
= Ln ( b ), тогда a должно быть равно b.В случае этой проблемы, тогда - Шаг 6: Упростите левую часть приведенного выше уравнения:
- Шаг 7: Вычтем 2x + 24 с каждой стороны:
- Шаг 8: Разложите на множители левую часть приведенного выше уравнения:
- Шаг 9: Если произведение двух множителей равно нулю, по крайней мере один из множителей должен быть равен нулю.
 Если . Если
Если . Если
. x = 9 — наше единственное решение. Почему 9 — единственное решение? Мы определили наш домен как все действительные числа больше 3.
Чек: Вы можете проверить свой ответ, построив график функции
и определение того, равен ли отрезок оси x также 9. Если это так, вы
правильно сработали проблему.
Вы также можете проверить свой ответ, заменив 9 слева x и
правые части исходного уравнения. Если после подстановки левый
сторона уравнения имеет то же значение, что и правая часть уравнения,
вы правильно решили проблему.
Если вы хотите просмотреть другой пример, щелкните «Пример».
Решите следующие задачи. Если вы хотите просмотреть ответ и
решение, нажмите «Ответить».
Задача 1: Решите относительно x в уравнении
Ответ
Задача 2: Решите относительно x в уравнении
Ответ
Задача 3: Решите относительно x в уравнении
Ответ
Задача 4: Решите относительно x в уравнении
Ответ
Задача 5: Решите относительно x в уравнении
Ответ
Задача 6: Решите относительно x в уравнении
Ответ
[Назад к правилам логарифмов]
[Назад к экспоненциальным функциям]
[Алгебра]
[Тригонометрия]
[Сложный
Переменные] S. Домашняя страница O.S MATHematics
Домашняя страница O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
Автор: Нэнси
Маркус
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час
Как решать логарифмические уравнения
Решение логарифмических уравнений
Правила или законы логарифмов:
Как вы знаете, логарифм — это математическая операция, обратная возведению в степень.Это выражается сокращением «журнал». Прежде чем приступить к решению логарифмических уравнений, есть несколько стратегий и «правил», с которыми мы должны сначала ознакомиться.
Во-первых, чтобы решать логарифмические уравнения, как и в случае с многочленами, вы должны уметь строить графики логарифмических функций. Посмотрите наше видео о построении графиков логарифмических функций для обзора, если это необходимо. Кроме того, прежде чем мы перейдем к правилам логарифмирования, важно, чтобы вы также поняли одну из простейших стратегий логарифмирования — изменение базовой формулы.Опять же, посмотрите наше видео об изменении базовой формулы, если вам нужно напомнить. Теперь, когда вы все это освоили, давайте взглянем на некоторые из наиболее важных правил логарифмирования:
Кроме того, прежде чем мы перейдем к правилам логарифмирования, важно, чтобы вы также поняли одну из простейших стратегий логарифмирования — изменение базовой формулы.Опять же, посмотрите наше видео об изменении базовой формулы, если вам нужно напомнить. Теперь, когда вы все это освоили, давайте взглянем на некоторые из наиболее важных правил логарифмирования:
1) Правило логарифмического произведения
В целом правило произведения логарифмов определяется следующим образом:
logA + logB = log (A × B) \ log A + \ log B = \ log (A \ times B) logA + logB = журнал (A × B)
То есть, добавляя два журнала по с одной и той же базой , вы можете переписать выражение как один журнал, умножив члены в логарифмическом выражении.
2) Правило логарифмического частного
Как правило, правило частного логарифмов определяется следующим образом:
logA − logB = log (AB) \ log A — \ log B = \ log (\ frac {A} {B}) logA − logB = log (BA)
То есть, при вычитании двух журналов из из одной и той же базы , вы можете переписать выражение как один журнал, разделив члены в логарифмическом выражении. {B} = B \ times \ log Alog (A) B = B × logA
{B} = B \ times \ log Alog (A) B = B × logA
То есть, когда есть показатель степени в члене в логарифмическом выражении, вы можете уменьшить этот показатель и умножить его на журнал.{\ log_ {A} (B)} = BAlogA (B) = B
То есть увеличение логарифма числа по основанию равняется этому числу.
6) Правило идентификации журнала
В целом правило идентичности логарифмов определяется следующим образом:
logAA = 1 \ log_ {A} A = 1 logA A = 1
То есть, если взять логарифм чего-то на основе того же самого, логарифмическое выражение будет просто равно 1.
7) Особые журналы
Хотя это не обязательно правила, есть пара журналов, которые вы должны знать наизусть, чтобы упростить задачу.Их:
журнал1 = 0 \ журнал 1 = 0 журнал1 = 0
log0 = undefined \ log 0 = undefined log0 = undefined
Оба этих случая всегда верны, независимо от основания. Кроме того, первый особый случай иногда называют правилом логарифмического нуля.
Все эти правила, вместе взятые, представляют собой чрезвычайно мощные инструменты, которые мы можем использовать для решения любой логарифмической задачи. Чтобы посмотреть видеообзор этих концепций, посмотрите наши видеоролики о свойствах логарифмов и правиле частного для логарифмов.Теперь, когда мы рассмотрели основы, давайте приступим к решению проблем с журналом!
Чтобы посмотреть видеообзор этих концепций, посмотрите наши видеоролики о свойствах логарифмов и правиле частного для логарифмов.Теперь, когда мы рассмотрели основы, давайте приступим к решению проблем с журналом!
Как решать проблемы с журналом:
Как и все в математике, лучший способ научиться решать задачи журнала — это выполнять некоторые практические задачи! Мы будем использовать правила, которые мы только что обсудили, для решения некоторых примеров.
Пример 1:
Решите логарифмическое уравнение:
log (3 − x) + log (4−3x) −log (x) = log7 \ log (3 — x) + \ log (4 — 3x) — \ log (x) = \ log 7log (3 − x) + журнал (4−3x) −log (x) = log7
Шаг 1. Используйте известные правила журнала
В любой проблеме, связанной с решением логарифмических уравнений, первым делом всегда старайтесь упростить, используя правила журнала.{2} — 20x + 12 = 03×2−20x + 12 = 0
(3x − 2) (x − 6) = 0 (3x — 2) (x — 6) = 0 (3x − 2) (x − 6) = 0
3x − 2 = 0 или x − 6 = 03x — 2 = 0 или x — 6 = 03x − 2 = 0 или x − 6 = 0
x = 23 или x = 6x = \ frac {2} {3} или x = 6x = 32 или x = 6
Шаг 3. Проверьте решения
Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
log (3−23) + log (4−3 (23)) — log (23) = log7 \ log (3 — \ frac {2} {3}) + \ log (4 — 3 ( \ frac {2} {3})) — \ log (\ frac {2} {3}) = \ log 7log (3−32) + log (4−3 (32)) — log (32) = log7
Решение x = 23x = \ frac {2} {3} x = 32 является правильным.
log (3−6) + log (4−3 (6)) — log (6) = log7 \ log (3-6) + \ log (4-3 (6)) — \ log ( 6) = \ log 7log (3−6) + log (4−3 (6)) — log (6) = log7
Решение x = 6x = 6x = 6 отклоняется, поскольку логарифм отрицательного числа не определен.
Пример 2:
Шаг 1. Используйте известные правила журнала
В этом случае мы будем использовать правила журнала мощности и частного. Мы делаем это, чтобы попытаться составить полиномиальное / алгебраическое уравнение, которое было бы легче решить. Это показано ниже:
2log3 (x + 4) −log3 (−x) = 22 \ log_ {3} (x + 4) — \ log_ {3} (-x) = 22log3 (x + 4) −log3 ( −x) = 2
log3 (x + 4) 2 − log3 (−x) = 2 \ log_ {3} (x + 4) ^ {2} — \ log_ {3} (-x) = 2log3 (x + 4 ) 2 − log3 (−x) = 2
log3 (x2 + 8x + 16 − x) = 2 \ log_ {3} (\ frac {x ^ {2} + 8x + 16} {- x}) = 2log3 (−xx2 + 8x + 16) = 2
Шаг 2. Упростите
Упростите
Мы можем преобразовать в экспоненциальную форму, потому что одна сторона имеет лог, а другая — нет.{2} + 17x + 16 = 0x2 + 17x + 16 = 0
(х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0
x = −16orx = −1x = -16 или x = -1x = −16orx = −1
Шаг 4. Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
2log3 ((- 16) +4) −log3 (- (- 16)) = 22 \ log_ {3} ((-16) + 4) — \ log_ {3} (- (- 16)) = 22log3 ((−16) +4) −log3 (- (- 16)) = 2
Решение x = -16 отклоняется.
2log3 ((- 1) +4) −log3 (- (- 1)) = 22 \ log_ {3} ((-1) + 4) — \ log_ {3} (- (- 1)) = 22log3 ((−1) +4) −log3 (- (- 1)) = 2
Решение x = -1 правильное.
Пример 3:
Шаг 1. Упростите
Умножьте обе части уравнения на 2, чтобы избавиться от дроби.
log2x = 2 + 12log2 (x − 3) \ log_ {2} x = 2 + \ frac {1} {2} \ log_ {2} (x — 3) log2 x = 2 + 21 log2 (Х − 3)
2log2x = 4 + log2 (x − 3) 2 \ log_ {2} x = 4 + \ log_ {2} (x — 3) 2log2 x = 4 + log2 (x − 3)
Шаг 2. Используйте известные правила журнала
Используйте известные правила журнала
В этом случае мы будем использовать правила журнала и частного журнала. Затем мы можем упростить, как в предыдущем примере, чтобы получить экспоненциальную форму.{2} — 16x + 48 = 0x2−16x + 48 = 0
(x − 4) (x − 12) = 0 (x — 4) (x — 12) = 0 (x − 4) (x − 12) = 0
х = 4 или х = 12 х = 4 или х = 12 х = 4 или х = 12
Шаг 4. Проверьте решения
Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.
log24 = 2 + 12log2 (4−3) \ log_ {2} 4 = 2 + \ frac {1} {2} \ log_ {2} (4–3) log2 4 = 2 + 21 log2 (4−3)
Решение x = 4 подтверждается.
log212 = 2 + 12log2 (12−3) \ log_ {2} 12 = 2 + \ frac {1} {2} \ log_ {2} (12–3) log2 12 = 2 + 21 log2 (12−3)
То же самое и x = 12.{-2} x = 10−2 неверно.
И это тоже все! Чтобы проверить свою работу с будущими практическими задачами, обязательно воспользуйтесь этим отличным калькулятором. Наконец, для видеообзора всего, что мы только что рассмотрели, посмотрите наше видео о том, как решать уравнения журнала. {y} = x [/ латекс].Мы можем использовать этот факт вместе с правилами логарифмов для решения логарифмических уравнений, в которых аргумент является алгебраическим выражением.
{y} = x [/ латекс].Мы можем использовать этот факт вместе с правилами логарифмов для решения логарифмических уравнений, в которых аргумент является алгебраическим выражением.
Например, рассмотрим уравнение [латекс] {\ mathrm {log}} _ {2} \ left (2 \ right) + {\ mathrm {log}} _ {2} \ left (3x — 5 \ right) = 3 [/ латекс]. Чтобы решить это уравнение, мы можем использовать правила логарифмов, чтобы переписать левую часть в компактной форме, а затем применить определение журналов для решения x :
[латекс] \ begin {case} {\ mathrm {log}} _ {2} \ left (2 \ right) + {\ mathrm {log}} _ {2} \ left (3x — 5 \ right) = 3 \ hfill & \ hfill \\ \ text {} {\ mathrm {log}} _ {2} \ left (2 \ left (3x — 5 \ right) \ right) = 3 \ hfill & \ text {Применить правило продукта логарифмов}.{2} \ hfill & \ text {Перепишите в экспоненциальной форме}. \ Hfill \ end {cases} [/ latex]
Попробуй 9
Решите [латекс] 6+ \ mathrm {ln} x = 10 [/ latex].
Решение
Пример 10: Использование алгебры до и после использования определения натурального логарифма
Решите [латекс] 2 \ mathrm {ln} \ left (6x \ right) = 7 [/ latex].
Решение
[латекс] \ begin {case} 2 \ mathrm {ln} \ left (6x \ right) = 7 \ hfill & \ hfill \\ \ text {} \ mathrm {ln} \ left (6x \ right) = \ frac {7} {2} \ hfill & \ text {Разделить на 2}.{x} = 1000 [/ latex] с точностью до 2 десятичных знаков.
Решение
BioMath: логарифмические функции
В этом разделе мы научимся решать уравнения, содержащие экспоненту или
логарифмическая функция. Мы начнем с рассмотрения двух простых уравнений:
(1) 5 e x = 11,
(2) журнал (2 x ) = 3.
Чтобы решить (1) и (2), нам нужно найти значение (я) x , для которого уравнения
верное заявление.Важно понимать, что (1) и (2) НЕ верны для всех
значения x . Начнем с уравнения (1).
Решение уравнения 1:
5 e x = 11
Как и при решении любого другого уравнения, наша цель — выделить член, включающий x . Здесь мы начнем с деления обеих частей уравнения на 5,
Здесь мы начнем с деления обеих частей уравнения на 5,
.
Теперь, когда член e x находится сам по себе с одной стороны, мы должны «отменить» экспоненту
освободить x .Поскольку наша экспонента имеет основание e , мы берем логарифм с основанием e
обе стороны (т.е. натуральный логарифм обеих сторон),
Таким образом, решение уравнения (1) равно
Решение уравнения 2:
журнал (2 x ) = 3
В этом уравнении член, включающий x , уже выделен в одну сторону уравнения.Поэтому мы начинаем с «отмены» логарифмической функции по основанию 10, возведя в степень оба
стороны уравнения с основанием 10,
10 журнал (2 x ) = 2 x = 10 3 = 1000.
Следовательно, мы находим решение уравнения (2) равным
Сейчас попробуем
решение некоторых более сложных уравнений.
Хотя эти уравнения могут показаться более сложными, наша цель остается прежней:
решите для значений x , которые делают утверждения истинными.
Решение экспоненциальных уравнений, использующих базы, которых нет в вашем калькуляторе
Решение уравнения 3 :
6 · 2 9+ x = 30
Начнем с выделения термина, включающего x ,
Чтобы найти x , мы должны отменить экспоненту. Хотя экспонента
основание 2, мы будем использовать общий логарифм (основание 10), так как будет легче получить
примерный ответ на нашем калькуляторе,
Используя свойства логарифмов, мы упрощаем приведенное выше уравнение как,
(9 + x ) журнал (2) = журнал (5).
Решение относительно x дает,
Вы всегда можете проверить свой ответ, подставив точный ответ, который вы нашли
обратно в исходное уравнение.
Решение уравнения 4:
3 журнала 6 (4 + 3 x ) — 2 = 6
Начнем с выделения термина, включающего x ,
Чтобы найти x , нам нужно освободить x изнутри логарифма с основанием 6.Для этого возведем в степень обе стороны с основанием 6,
Решая для x имеем,
Решение уравнений с экспонентами с разным основанием
Решение уравнения 5:
3 7−2 x = 4 3+ x
В этом уравнении экспоненты имеют разное основание.Мы возьмем
общий (с основанием 10) логарифм обеих сторон, чтобы отменить эти экспоненты, и
использовать свойства логарифмов,
Приведение терминов x в одну сторону и всех остальных терминов в другую,
Вынос x урожайности,
Теперь мы можем решить уравнение
Решение уравнений с кратным логарифмом
Решение уравнения 6:
2 журнал 3 (2x) = журнал 3 (4) + журнал 3 (3 + 2x)
В этом уравнении следует обратить внимание на две вещи: обе части имеют логарифмы, и
одна сторона имеет несколько логарифмов.При работе с несколькими логарифмами на
с одной стороны, проще всего объединить их в один логарифм, используя
то
свойства логарифмов. Однако при этом вам необходимо проверить свои решения.
когда вы закончите решение проблемы, потому что объединение логарифмов может привести к посторонним решениям.
Начнем с упрощения обеих сторон, используя свойства
логарифмы,
Возведение в степень обе стороны с основанием 3 дает,
Чтобы найти x , мы должны решить квадратное уравнение,
4 x 2 — 8 x — 12 = 0.
Используя формулу корней квадратного уравнения, решения даются как,
Таким образом, мы находим решения равными x = 3 и x = −1. Поскольку мы объединили
логарифмы, мы должны проверить эти решения в исходном уравнении. Проверка
x = 3 дает,
2 log 3 (2 · 3) = 2 log 3 (6) ≈ 3.26,
слева и
лог 3 (4) + лог 3 (3 + 2 · 3) = лог 3 (4) + лог 3 (9) ≈ 3,26,
с правой стороны. Эти решения проверяют.
Решение x = −1, однако,
не проверяет. Если мы попытаемся подставить
x = −1 в исходное уравнение,
у нас было бы,
2 лог 3 (2 · -1),
с левой стороны.Конечно, логарифм отрицательного числа не определен.
на действительной прямой, и мы заключаем, что x = −1 является посторонним решением.
Следовательно,
заключаем, что решение уравнения (6) составляет x = 3.
*****
Теперь попробуйте несколько практических задач с использованием логарифмов и решения логарифмических уравнений.
Проблемы
Свойства логарифмов
Свойства логарифмов
Содержание: Эта страница соответствует § 4.3
(стр. 341) текста.
Предлагаемые задачи из текста:
с. 345 № 3, 7, 9, 11, 13, 25, 27, 33, 35, 45, 49, 53, 91
Изменение базы
Свойства логарифмов
Изменение базы
В то время как большинство научных калькуляторов имеют кнопки только для десятичного и натурального логарифмов, другие
логарифмы могут быть вычислены с помощью следующей формулы замены основания.
Формула смены базы
Пример 1 .
Журнал вычислений 5 3. Формула изменения базы позволяет нам вычислить это выражение, используя любое другое
логарифм, поэтому мы решим эту проблему двумя способами, используя сначала натуральный логарифм, а затем десятичный.Натуральный логарифм:
десятичный логарифм:
Упражнение 1 :
Из логарифмического тождества 1 следует, что log 2 8 = 3.
(a) Используйте калькулятор и формулу замены основания с натуральным логарифмом, чтобы убедиться, что логарифм 2
8 = 3.(b) Используйте калькулятор и формулу замены основания с десятичным логарифмом, чтобы убедиться, что журнал 2
8 = 3.Ответ
Упражнение 2 :
Из логарифмического тождества 2 следует, что. Убедитесь в этом, оценив log 4 7, а затем возведя 4 в эту степень.
Ответ
Вернуться к содержанию
Свойства логарифмов
| 1. log a (uv) = log a u + log a v | 1. ln (uv) = ln u + ln v |
| 2. log a (u / v) = log a u — log a v | 2. ln (u / v) = ln u — ln v |
| 3.журнал a u n = n журнал a u | 3. ln u n = n ln u |
Свойства слева относятся к любому основанию a.
Свойства справа являются повторением общих свойств натурального логарифма.
Многие логарифмические выражения можно переписать, развернуть или сжать, используя три указанных выше свойства.
Расширение — это разбиение сложного выражения на более простые компоненты.Конденсация — обратное этому
процесс.
Пример 2 .
Раскрытие выражения.
перепишите в экспоненциальной записи недвижимость 3 недвижимость 1
Пример 3 .
Раскрытие выражения.
недвижимость 2 недвижимость 1 недвижимость 3
Пример 4 .
Уплотнение выражения.
недвижимость 3 недвижимость 1 недвижимость 2
Общие ошибки
- Логарифмы разбивают произведения на суммы по свойству 1, но логарифм суммы не может быть переписан как .Для
Например, мы ничего не можем сделать с выражением ln (x 2 + 1). - log u — log v равен log (u / v) по свойству 2, не равен log u / log v.
Упражнение 3 :
(a) Разверните выражение. Ответ
(b) Уплотните выражение 3 log x + 2 log y — (1/2) log z. Ответ
Вернуться к содержанию
Решение логарифмических уравнений — предварительное вычисление
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
10.5 Решение экспоненциальных и логарифмических уравнений — Промежуточная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решите логарифмические уравнения, используя свойства логарифмов
- Решите экспоненциальные уравнения с помощью логарифмов
- Использование экспоненциальных моделей в приложениях
Будьте готовы 10.13
Прежде чем начать, пройдите тест на готовность.
Решите: x2 = 16. x2 = 16.
Если вы пропустили эту проблему, просмотрите Пример 6.46.
Будьте готовы 10.14
Решите: x2−5x + 6 = 0.x2−5x + 6 = 0.
Если вы пропустили эту проблему, просмотрите Пример 6.45.
Будьте готовы 10,15
Решите: x (x + 6) = 2x + 5.x (x + 6) = 2x + 5.
Если вы пропустили эту проблему, просмотрите Пример 6.47.
Решите логарифмические уравнения, используя свойства логарифмов
В разделе, посвященном логарифмическим функциям, мы решили некоторые уравнения, переписав уравнение в экспоненциальной форме.Теперь, когда у нас есть свойства логарифмов, у нас есть дополнительные методы, которые мы можем использовать для решения логарифмических уравнений.
Если в нашем уравнении есть два логарифма, мы можем использовать свойство, которое говорит, что если logaM = logaNlogaM = logaN, то верно, что M = N.M = N. Это однозначное свойство логарифмических уравнений.
Однозначное свойство логарифмических уравнений
Для M> 0, N> 0, a> 0, M> 0, N> 0, a> 0 и a ≠ 1a ≠ 1 — любое действительное число:
Если logaM = logaN, то M = N. Если logaM = logaN, то M = N.
Чтобы использовать это свойство, мы должны быть уверены, что обе части уравнения записаны с одинаковым основанием.
Помните, что логарифмы определены только для положительных действительных чисел. Проверьте свои результаты в исходном уравнении. Возможно, вы получили результат, который дает логарифм нуля или отрицательное число.
Пример 10.38
Решить: 2log5x = log581.2log5x = log581.
Решение
| 2log5x = log5812log5x = log581 | |
| Используйте свойство Power. | журнал5×2 = журнал581log5x2 = журнал581 |
| Используйте свойство «один к одному», если logaM = logaNlogaM = logaN, то M = NM = N | х2 = 81х2 = 81. |
| Решите, используя свойство квадратного корня. | х = ± 9х = ± 9 |
| Мы исключаем x = −9x = −9, так как мы не можем логарифмировать отрицательное число. | х = 9, х = -9х = 9, х = -9 |
| Чек. | |
| x = 92log5x = log5812log59 =? Log581log592 =? Log581log581 = log581 ✓x = 92log5x = log5812log59 =? Log581log592 =? Log581log581 = log581 ✓ |
Попробуй 10.75
Решить: 2log3x = log3362log3x = log336
Попробовать 10.76
Решить: 3logx = log643logx = log64
Еще одна стратегия решения логарифмических уравнений — это сжатие сумм или разностей в один логарифм.
Пример 10.39
Решите: log3x + log3 (x − 8) = 2. log3x + log3 (x − 8) = 2.
Решение
| log3x + log3 (x − 8) = 2log3x + log3 (x − 8) = 2 | |
| Используйте свойство продукта, logaM + logaN = logaM⋅NlogaM + logaN = logaM⋅N. | log3x (x − 8) = 2log3x (x − 8) = 2 |
| Записываем в экспоненциальной форме. | 32 = х (х-8) 32 = х (х-8) |
| Упростить. | 9 = x2−8×9 = x2−8x |
| Вычтите 9 с каждой стороны. | 0 = x2−8x − 90 = x2−8x − 9 |
| Коэффициент. | 0 = (x − 9) (x + 1) 0 = (x − 9) (x + 1) |
| Используйте свойство нулевого произведения. | х-9 = 0, х + 1 = 0х-9 = 0, х + 1 = 0 |
| Решите каждое уравнение. | х = 9, х = -1 х = 9, х = -1 |
| Чек. | |
| x = −1log3x + log3 (x − 8) = 2log3 (−1) + log3 (−1−8) =? 2x = −1log3x + log3 (x − 8) = 2log3 (−1) + log3 (−1−8) =? 2 | |
| Журнал отрицательного числа взять нельзя. | |
| x = 9log3x + log3 (x − 8) = 2log39 + log3 (9−8) =? 22 + 0 =? 22 = 2 ✓x = 9log3x + log3 (x − 8) = 2log39 + log3 (9 −8) =? 22 + 0 =? 22 = 2 ✓ |
Попробовать 10.77
Решите: log2x + log2 (x − 2) = 3log2x + log2 (x − 2) = 3
Попробуй 10.78
Решите: log2x + log2 (x − 6) = 4log2x + log2 (x − 6) = 4
Если на обеих сторонах есть логарифмы, мы конденсируем каждую сторону в один логарифм. Не забудьте использовать свойство Power по мере необходимости.
Пример 10,40
Решите: log4 (x + 6) −log4 (2x + 5) = — log4x.log4 (x + 6) −log4 (2x + 5) = — log4x.
Решение
| log4 (x + 6) −log4 (2x + 5) = — log4xlog4 (x + 6) −log4 (2x + 5) = — log4x | |
| Используйте свойство Quotient слева и свойство Power справа. | log4 (x + 62x + 5) = log4x − 1 log4 (x + 62x + 5) = log4x − 1 |
| Записываем x − 1 = 1xx − 1 = 1x. | log4 (x + 62x + 5) = log41xlog4 (x + 62x + 5) = log41x |
| Используйте свойство «один к одному», если logaM = logaNlogaM = logaN, то M = NM = N. | х + 62x + 5 = 1xx + 62x + 5 = 1x |
| Решите рациональное уравнение. | х (х + 6) = 2х + 5х (х + 6) = 2х + 5 |
| Распространить. | х2 + 6х = 2х + 5х2 + 6х = 2х + 5 |
| Запишите в стандартной форме. | x2 + 4x − 5 = 0x2 + 4x − 5 = 0 |
| Коэффициент. | (x + 5) (x − 1) = 0 (x + 5) (x − 1) = 0 |
| Используйте свойство нулевого произведения. | х + 5 = 0, х-1 = 0х + 5 = 0, х-1 = 0 |
| Решите каждое уравнение. | х = -5, х = 1x = -5, х = 1 |
| Чек. | |
| Оставляем вам чек. |
Попробовать 10.79
Решить: log (x + 2) −log (4x + 3) = — logx.журнал (x + 2) −log (4x + 3) = — журналx.
Попробуйте 10.80
Решите: log (x − 2) −log (4x + 16) = log1x.log (x − 2) −log (4x + 16) = log1x.
Решите экспоненциальные уравнения с помощью логарифмов
В разделе, посвященном показательным функциям, мы решили некоторые уравнения, записав обе части уравнения с одинаковым основанием. Затем мы написали новое уравнение, установив равные степени.
Не всегда возможно или удобно писать выражения с одной и той же базой. В этом случае мы часто используем десятичный или натуральный логарифм обеих сторон, если экспонента изолирована.
Пример 10.41
Решите 5x = 11,5x = 11. Найдите точный ответ и округлите его до трех десятичных знаков.
Решение
| 5x = 115x = 11 | |
| Поскольку экспонента изолирована, возьмите обе части логарифма. Используйте свойство Power, чтобы получить xx как множитель, а не как показатель степени. Решить относительно x.x. Найдите точный ответ. Примерный ответ. | log5x = log11xlog5 = log11x = log11log5x≈1.490log5x = log11xlog5 = log11x = log11log5x≈1,490 |
| Поскольку 51 = 551 = 5 и 52 = 25,52 = 25, имеет ли смысл, что 51,490≈11? 51,490≈11? | |
Попробуйте 10.81
Решите 7x = 43,7x = 43. Найдите точный ответ и округлите его до трех десятичных знаков.
Попробуйте 10,82
Решите 8x = 98,8x = 98. Найдите точный ответ и округлите его до трех десятичных знаков.
Когда мы возьмем логарифм обеих сторон, мы получим один и тот же результат независимо от того, используем ли мы общий или натуральный логарифм (попробуйте использовать натуральный логарифм в последнем примере.Вы получили тот же результат?) Когда экспонента имеет основание e , мы используем натуральный логарифм.
Пример 10.42
Решите 3ex + 2 = 24,3ex + 2 = 24. Найдите точный ответ и округлите его до трех десятичных знаков.
Решение
| 3ex + 2 = 243ex + 2 = 24 | |
| Выделите экспоненту, разделив обе части на 3. | пр. + 2 = 8 пр. + 2 = 8 |
| Возьмите натуральный логарифм от обеих сторон. | lnex + 2 = ln8lnex + 2 = ln8 |
| Используйте свойство Power, чтобы получить xx как множитель, а не как показатель степени. | (x + 2) lne = ln8 (x + 2) lne = ln8 |
| Используйте свойство lne = 1lne = 1 для упрощения. | х + 2 = ln8x + 2 = ln8 |
| Решите уравнение. Найдите точный ответ. | х = ln8−2x = ln8−2 |
| Примерный ответ. | x≈0,079x≈0,079 |
Попробовать 10,83
Решите 2ex − 2 = 18.2ex − 2 = 18. Найдите точный ответ и округлите его до трех десятичных знаков.
Попробовать 10,84
Решите 5e2x = 25,5e2x = 25. Найдите точный ответ и округлите его до трех десятичных знаков.
Использование экспоненциальных моделей в приложениях
В предыдущих разделах мы смогли решить некоторые приложения, которые были смоделированы с помощью экспоненциальных уравнений. Теперь, когда у нас есть намного больше вариантов решения этих уравнений, мы можем решать больше приложений.
Мы снова будем использовать формулы сложного процента, поэтому мы перечисляем их здесь для справки.
Сложные проценты
Для основного долга P , инвестированного под процентную ставку, r , на t лет, новый баланс A составляет:
A = P (1 + rn) n, когда компаундируется раз в год. A = Pert, когда компаундируется непрерывно. A = P (1 + rn) nt, когда складывается раз в год. A = Pert, когда компаундируется непрерывно.
Пример 10,43
Родители Джермаэля вложили 10 000 долларов в его колледж в его первый день рождения.Они надеются, что инвестиции будут стоить 50 000 долларов, когда ему исполнится 18 лет. Если проценты будут постоянно расти, какие приблизительно темпы роста им понадобятся для достижения своей цели?
Решение
| A = 50 000 долларов США A = 50 000 долларов США | |
| P = 10 000 долларов P = 10 000 долларов | |
| Определите переменные в формуле | г =? Г =? |
| t = 17лет = 17лет | |
| A = PertA = Pert | |
| Подставьте значения в формулу. | 50,000 = 10,000er · 1750,000 = 10,000er · 17 |
| Решить для р.р. Разделите каждую сторону на 10 000. | 5 = e17r5 = e17r |
| Возьмите натуральное бревно с каждой стороны. | ln5 = lne17rln5 = lne17r |
| Используйте свойство Power. | ln5 = 17rlneln5 = 17rlne |
| Упростить. | ln5 = 17rln5 = 17r |
| Разделите каждую сторону на 17. | ln517 = rln517 = r |
| Примерный ответ. | r≈0,095r≈0,095 |
| Преобразовать в проценты. | r≈9,5% r≈9,5% |
| Им нужен темп роста примерно 9,5% 9,5%. |
Попробовать 10,85
Гектор инвестирует 10 000 долларов 10 000 долларов в возрасте 21 года. Он надеется, что инвестиции будут стоить 150 000 долларов США, когда ему исполнится 50 лет. Если процентные ставки будут постоянно увеличиваться, какие приблизительно темпы роста ему потребуются для достижения своей цели?
Попробуй 10.86
Рэйчел инвестирует 15 000 долларов 15 000 долларов в возрасте 25 лет. Она надеется, что вложения будут стоить 90 000 долларов 90 000 долларов, когда ей исполнится 40 лет. Если проценты будут постоянно увеличиваться, какие приблизительно темпы роста ей потребуются для достижения своей цели?
Мы видели, что рост и распад моделируются экспоненциальными функциями. Для роста и распада мы используем формулу A = A0ekt.A = A0ekt. Экспоненциальный рост имеет положительную скорость роста или константу роста, kk, а экспоненциальный спад имеет отрицательную скорость роста или константу спада, k .
Экспоненциальный рост и спад
Для исходной суммы, A0, A0, которая увеличивается или уменьшается со скоростью k , за определенное время, t , окончательная сумма, A , составляет:
Теперь мы можем решать приложения, которые дают нам достаточно информации, чтобы определить скорость роста. Затем мы можем использовать эту скорость роста для прогнозирования других ситуаций.
Пример 10,44
Исследователи зафиксировали, что определенная популяция бактерий выросла со 100 до 300 за 3 часа.При такой скорости роста сколько бактерий будет через 24 часа после начала эксперимента?
Решение
Эта проблема требует двух основных шагов. Сначала мы должны найти неизвестную скорость, k . Затем мы используем это значение k , чтобы помочь нам найти неизвестное количество бактерий.
| Определите переменные в формуле. | A = 300A0 = 100k =? T = 3 часаA = A0ektA = 300A0 = 100k =? T = 3 часаA = A0ekt |
| Подставьте значения в формулу. | 300 = 100эк · 3300 = 100эк · 3 |
| Решите для kk. Разделите каждую сторону на 100. | 3 = e3k3 = e3k |
| Возьмите натуральное бревно с каждой стороны. | ln3 = lne3kln3 = lne3k |
| Используйте свойство Power. | лн3 = 3клнн3 = 3клнэ |
| Упростить. | ln3 = 3kln3 = 3k |
| Разделите каждую сторону на 3. | ln33 = kln33 = k |
| Примерный ответ. | k≈0,366k≈0,366 |
| Мы используем эту скорость роста, чтобы предсказать количество бактерий, которые появятся в течение 24 часов. | A =? A0 = 100k = ln33t = 24 часа A = A0ektA =? A0 = 100k = ln33t = 24 часа A = A0ekt |
| Подставить значения. | A = 100eln33 · 24A = 100eln33 · 24 |
| Оценить. | A≈656,100A≈656,100 |
| При такой скорости роста они могут ожидать 656 100 бактерий. |
Попробуй 10.87
Исследователи зафиксировали, что определенная популяция бактерий выросла со 100 до 500 за 6 часов. При такой скорости роста сколько бактерий будет через 24 часа после начала эксперимента?
Попробовать 10,88
Исследователи зафиксировали, что определенная популяция бактерий сократилась с 700 000 до 400 000 за 5 часов после приема лекарств. При такой скорости разложения сколько бактерий будет через 24 часа после начала эксперимента?
Радиоактивные вещества распадаются или разлагаются по формуле экспоненциального распада.Время, необходимое для того, чтобы вещество распалось до половины своего первоначального количества, называется периодом полураспада вещества.
Как и в предыдущем примере, мы можем использовать данную информацию для определения константы распада, а затем использовать эту константу для ответа на другие вопросы.
Пример 10,45
Период полураспада радия-226 составляет 1590 лет. Сколько образца 100 мг останется через 500 лет?
Решение
Эта проблема требует двух основных шагов.Сначала мы должны найти постоянную распада k . Если мы начнем со 100 мг, в период полувыведения останется 50 мг. Мы будем использовать эту информацию, чтобы найти k . Затем мы используем это значение k , чтобы помочь нам найти количество образца, которое останется через 500 лет.
| Определите переменные в формуле. | A = 50A0 = 100k =? T = 1590 лет A = A0ektA = 50A0 = 100k =? T = 1590 лет A = A0ekt |
| Подставьте значения в формулу. | 50 = 100эк · 159050 = 100эк · 1590 |
| Решите для kk. Разделите каждую сторону на 100. | 0,5 = e1590k0,5 = e1590k |
| Возьмите натуральное бревно с каждой стороны. | ln0.5 = lne1590kln0.5 = lne1590k |
| Используйте свойство Power. | лн0,5 = 1590клн0,5 = 1590клн |
| Упростить. | ln0.5 = 1590kln0.5 = 1590k |
| Разделите каждую сторону на 1590. | ln0.51590 = kexact answerln0.51590 = ответ kexact |
| Мы используем этот темп роста, чтобы спрогнозировать, сколько останется через 500 лет. | A =? A0 = 100k = ln0,51590t = 500 лет A = A0ektA =? A0 = 100k = ln0,51590t = 500 лет A = A0ekt |
| Подставить значения. | A = 100eln0,51590 · 500A = 100eln0,51590 · 500 |
| Оценить. | A≈80,4 мгA≈80,4 мг |
| Через 500 лет останется примерно 80,4 мг. |
Попробуй 10.89
Период полураспада магния-27 составляет 9,45 минут. Сколько образца 10 мг останется через 6 минут?
Попробовать 10.90
Период полураспада радиоактивного йода составляет 60 дней. Сколько образца 50 мг останется через 40 дней?
Раздел 10.5 Упражнения
Практика ведет к совершенству
Решение логарифмических уравнений с использованием свойств логарифмов
В следующих упражнениях решите для x .
288.
log464 = 2log4xlog464 = 2log4x
290.
3log3x = log3273log3x = log327
291.
3log6x = log6643log6x = log664
292.
log5 (4x − 2) = log510log5 (4x − 2) = log510
293.
log3 (x2 + 3) = log34xlog3 (x2 + 3) = log34x
294.
log3x + log3x = 2log3x + log3x = 2
295.
log4x + log4x = 3log4x + log4x = 3
296.
log2x + log2 (x − 3) = 2log2x + log2 (x − 3) = 2
297.
log3x + log3 (x + 6) = 3log3x + log3 (x + 6) = 3
298.
журналx + журнал (x + 3) = 1logx + журнал (x + 3) = 1
299.
журналx + журнал (x − 15) = 2logx + журнал (x − 15) = 2
300.
журнал (x + 4) −log (5x + 12) = — logxlog (x + 4) −log (5x + 12) = — logx
301.
журнал (x − 1) −log (x + 3) = log1xlog (x − 1) −log (x + 3) = log1x
302.
log5 (x + 3) + log5 (x − 6) = log510log5 (x + 3) + log5 (x − 6) = log510
.
303.
log5 (x + 1) + log5 (x − 5) = log57 log5 (x + 1) + log5 (x − 5) = log57
.
304.
log3 (2x − 1) = log3 (x + 3) + log33log3 (2x − 1) = log3 (x + 3) + log33
.
305.
журнал (5x + 1) = журнал (x + 3) + log2log (5x + 1) = журнал (x + 3) + log2
Решите экспоненциальные уравнения с помощью логарифмов
В следующих упражнениях решите каждое экспоненциальное уравнение.Найдите точный ответ и округлите его до трех десятичных знаков.
В следующих упражнениях решите каждое уравнение.
330.
log5 (3x − 8) = 2log5 (3x − 8) = 2
331.
log4 (7x + 15) = 3log4 (7x + 15) = 3
335.
7log3x = log31287log3x = log3128
336.
log6x + log6 (x − 5) = log624log6x + log6 (x − 5) = log624
337.
log9x + log9 (x − 4) = log912log9x + log9 (x − 4) = log912
338.
log2 (x + 2) −log2 (2x + 9) = — log2xlog2 (x + 2) −log2 (2x + 9) = — log2x
.
339.
log6 (x + 1) −log6 (4x + 10) = log61xlog6 (x + 1) −log6 (4x + 10) = log61x
В следующих упражнениях найдите x , получив точный ответ, а также приближение к трем десятичным знакам.
Использование экспоненциальных моделей в приложениях
В следующих упражнениях решите.
344.
Сунг Ли инвестирует 5 000 долларов 5 000 долларов в 18 лет. Он надеется, что вложения будут стоить 10 000 долларов 10 000 долларов, когда ему исполнится 25 лет. Если проценты будут постоянно увеличиваться, какие приблизительно темпы роста ему понадобятся для достижения своей цели? Это разумное ожидание?
345.
Алиса инвестирует 15000 долларов в возрасте 30 лет из подписного бонуса своей новой работы. Она надеется, что вложения будут стоить 30 000 долларов 30 000 долларов, когда ей исполнится 40 лет. Если проценты будут постоянно расти, какие приблизительно темпы роста ей потребуются для достижения своей цели?
346.
Coralee инвестирует 5000 долларов в счет, на котором ежемесячно начисляются проценты и который приносит 7% 0,7%. Сколько времени потребуется, чтобы ее деньги удвоились?
347.
Simone инвестирует 8000 долларов в счет, на котором ежеквартально начисляются проценты и доход составляет 5%.5%. Сколько времени потребуется, чтобы его деньги удвоились?
348.
Исследователи зафиксировали, что определенная популяция бактерий сократилась со 100 000 до 100 за 24 часа. При такой скорости разложения сколько бактерий будет за 16 часов?
349.
Исследователи зафиксировали, что определенная популяция бактерий сократилась с 800 000 до 500 000 за 6 часов после приема лекарств. При такой скорости разложения сколько бактерий будет за 24 часа?
350.
Вирусу требуется 6 дней, чтобы удвоить свою первоначальную популяцию (A = 2A0).(А = 2А0). Сколько времени потребуется, чтобы утроить его население?
351.
Бактерия удваивает свою первоначальную популяцию за 24 часа (A = 2A0) (A = 2A0). Насколько большим будет его население через 72 часа?
352.
Углерод-14 используется для археологического датирования углерода. Его период полураспада составляет 5730 лет. Сколько 100-граммового образца углерода-14 останется через 1000 лет?
353.
Радиоактивный технеций-99m часто используется в диагностической медицине, поскольку он имеет относительно короткий период полураспада, но длится достаточно долго, чтобы провести необходимое тестирование на пациенте.Если его период полураспада составляет 6 часов, какое количество радиоактивного материала из 0,5 мл инъекции будет в организме за 24 часа?
Письменные упражнения
354.
Объясните метод, который вы использовали бы для решения этих уравнений: 3x + 1 = 81,3x + 1 = 81,
3x + 1 = 75,3x + 1 = 75. Требует ли ваш метод логарифмов для обоих уравнений? Почему или почему нет?
355.
В чем разница между уравнением экспоненциального роста и уравнением экспоненциального убывания?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
