Содержание
Решение задач. Движение тела по окружности
Цель: научить решать задачи на движение тела по окружности.
Ход урока
I. Повторение. Беседа
1. Точка движется равномерно по окружности. Постоянна ли ее скорость?
2. Есть ли ускорения у точки, которая движется по окружности?
3. Куда направлено ускорение?
4. Что такое период? Частота?
5. Как связаны между собой ускорение, скорость и радиус при равномерном движении тела по окружности.
6. Что называется осью вращения твердого тела?
7. Что такое угловая скорость?
8. Как связаны между собой угловая и линейная скорости? Угловая скорость и центростремительное ускорение?
II. Решение задач
I группа
1. Скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 м/с. Допустима ли посадка круга на вал электродвигателя, совершающего 1400 об/мин, 2800 об/мин? (Да, нет.)
2. Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч? (45 000)
Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч? (45 000)
3. Период вращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м. (3,14 м/с)
4. Скорость точек экватора Солнца при его вращении вокруг своей оси 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек экватора. (253 сут., 5,7 мм/с?)
II группа
1. Минутная стрелка в 1,5 раза длиннее часовой. Определите, во сколько раз скорость конца часовой стрелки меньше скорости конца минутной стрелки. (В 18 раз)
2. Определите центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 36 км/ч и при этом частота вращения колеса равна 4е-1. (251,2 м/с?)
3. Две материальные точки движутся по окружности радиусами R1 и R2 причем R1 = 2R2. Сравните их центростремительные ускорения, если равны их периоды обращения. (2:1)
(2:1)
4. Минутная стрелка часов в 2 раза длиннее секундной. Найдите отношение скоростей концов стрелок. (1:30)
III группа
1. Чему равен радиус вращающегося колеса, если известно, что скорость точки, лежащей на ободе, в 2,5 раза больше скорости точки, лежащей на расстоянии 5 см ближе к оси колеса? (8,5 см)
2. Найдите линейную скорость и центростремительное ускорение точек на широте 60°. Радиус Земли равен 6400 км. (233 м/с, 1,7410-2 м/с?)
3. Небольшое тело движется по окружности радиуса R со скоростью, которая линейно увеличивается со временем по закону v = kt. Найдите зависимость полного ускорения тела от времени.
4. Какое расстояние пройдет велосипедист при 60 оборотах педалей, если диаметр колеса 70 см, ведущая зубчатка имеет 48 зубцов, а ведомая -18 зубцов? (352 м)
Домашнее задание
П. 20,21, задачи на стр. 51.
Решения задач по теме: «Движение тела по окружности»
Урок №________ Дата_________ Класс_9______ Учитель Физики Османова Л. М.
М.
Тема урока: Решения задач по теме: «Движение тела по окружности»
Цели урока: закрепить представление о криволинейном движении, основных характеристик частоты, периода, центростремительного ускорения и центростремительной силы.
Задачи урока :
Образовательные:
Повторить виды механического движения. Закрепить понятия: движение по окружности, центростремительное ускорение, период, частота.
Развивающие:
Развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.
Воспитательные:
Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность.
Воспитание коммуникативной и информационной культуры учащихся.
Оборудование: компьютер, проектор, экран, презентация к уроку « Решение задач на тему «Движение тела по окружности», распечатка карточек с заданиями. .
.
Форма работы: фронтальная, индивидуальная, групповая.
Тип урока: повторение и обобщение знаний, умений решать задачи по теме.
Вид урока: комбинированный с элементами исследования
Ход урока
Организационный момент.
Мотивация к учебной деятельности
Учитель.
«Незнающие пусть научатся, знающие – вспомнят еще раз
II. Актуализация опорных знаний.
Физический диктант:
Изменение положения тела в пространстве с течением времени. (Движение)
Физическая векторная величина, измеряемая в метрах. (Перемещение)
Физическая векторная величина, характеризующая быстроту движения. (Скорость)
Основная единица измерения длины в физике. (Метр)
Физическая величина, единицами измерения которой служат год, сутки, час.
 (Время)
(Время)Длина траектории. (Путь)
Единицы измерения ускорения (м/с2)
(Проведение диктанта с последующей проверкой, самооценка работ учениками) Работа в паре.
Тема урока : Решения задач по теме: «Движение тела по окружности»
Учитель. Что характеризует движение тела по окружности
Опрос детей устно
Решение у доски задачи с подробным объяснением
Колесо делает 120 оборотов за 2 минуты. Какова частота вращения колеса и период вращения?
Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч?
Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту?
Период обращения первого космического корабля — спутника Земли «Восток» равнялось 90 минут.
 Средняя высота спутника над Землей была равна 320 км. Радиус Земли 6400 км. Вычислить скорость корабля.
Средняя высота спутника над Землей была равна 320 км. Радиус Земли 6400 км. Вычислить скорость корабля.
физкультминутка
Домашнее задание
Подведение итогов урока. Выставление оценок.
Рефлексия.
Вариант №1
З адача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?
Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.
Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?
Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?
Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиус ом 50 см при частоте вращения 5 оборотов в секунду?
Вариант 2
задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.
Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.
Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.
Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?
Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?
Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.
9кл.Самостоятельная работа по теме : «Движение тела по окружности»
Вариант№1
Задача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?
Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.
Найти скорость точек на ободе колеса.
Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?
Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?
Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?
9 кл. Самостоятельная работа по теме : «Движение тела по окружности»
Вариант№2
задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.
Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.
Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.
Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?
Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?
Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.
Разработка урока на тему «Движение по окружности. Движение на поворотах»
Ключевые слова:
физика,
Движение по окружности
Учащиеся должны знать: зависимость устойчивости автомобиля на повороте от скорости движения, радиуса кривизны дороги и коэффициент трения.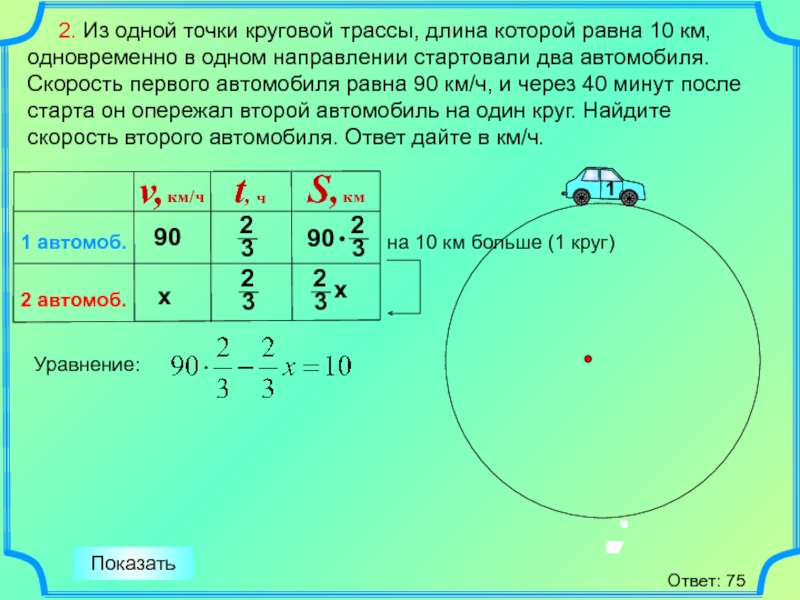
Мотивирующий прием: актуальность, яркое пятно.
Картинка: авария лесовоза на дороге.
Технологическая карта урока
Задача на следующий урок: вывести правило – алгоритм решения задач по теме «Динамика движения тел по окружности» (с помощью подводящего диалога) и использовать этот алгоритм при решения задач разного типа (движение конькобежца, велосипедиста на треке, самолета входящего в «мертвую петлю», автомобиля на мосту и т.д).
Угловой скоростью называют величину, равную отношению угла поворота радиуса-вектора точки, движущейся по окружности к промежутку времени t, в течение которого произошел этот поворот.
Мгновенная скорость тела в каждой точке криволинейной траектории направлена по касательной к траектории. Следовательно, в криволинейном движении направление скорости тела непрерывно изменяется, т.е. движение по окружности со скоростью, постоянной по модулю является ускоренным.
Исходя из данной информации, какой вопрос у вас возникает?
Движение по окружности
| № | Период, | Частота, | Линейная скорость, м/с | Циклическая частота, рад/с | Радиус окружности, м | Нормальное ускорение, м/с² |
1 | 4 |
|
|
| 10 |
|
2 |
| 0,2 | 16 |
|
|
|
3 |
|
| 20 |
| 800 |
|
4 | 0,2 |
| 30 |
|
|
|
5 |
|
|
| 15,7 |
| 60 |
6 |
| 2,5 |
|
| 1,25 |
|
7 | 0,04 |
|
|
| 0,6 |
|
8 |
|
|
|
| 40 | 10 |
9 | 0,05 |
| 12 |
|
|
|
10 | 0,1 |
|
|
| 0,2 |
|
ОТВЕТЫ
| № | Период, | Частота, | Линейная скорость, | Циклическая частота, рад/с | Радиус окружности, м | Нормальное ускорение, м/с² |
1 |
| 0,25 | 15,7 | 1,57 |
| 24,65 |
2 | 5 |
|
| 1,26 | 13 | 20 |
3 | 250 | 4 10-3 |
| 0,025 |
| 0,5 |
4 |
| 5 |
| 31,4 | 100 | 900 |
5 | 0,4 | 2,5 | 3,8 |
| 0,24 |
|
6 | 0,4 |
| 20 | 16 |
| 320 |
7 |
| 25 | 94 | 157 |
| 5,3 103 |
8 | 12,56 | 0,08 | 20 | 0,5 |
|
|
9 |
| 20 |
| 127 | 0,1 | 1440 |
10 |
| 10 | 12,56 | 63 |
| 790 |
Задача. Круг радиусом R катится по кругу радиусом 4R. Сколько оборотов совершит малый круг по возвращении в первоначальное положение?
Круг радиусом R катится по кругу радиусом 4R. Сколько оборотов совершит малый круг по возвращении в первоначальное положение?
Вопросы
- При каком условии возникает криволинейное движение?
- Как направлена скорость тела в любой точке криволинейной траектории?
- Почему движение по окружности является равноускоренным?
- Как направлено ускорение тела, движущегося по окружности?
- Что называется периодом обращения?
- Что называется частотой?
- От чего зависит центростремительное ускорение?
- Как связаны между собой период и частота?
- Какой угол между векторами скорости и ускорения?
- Какие параметры описывают движение точки по окружности?
- Чему равно перемещение точки за время равное периоду?
- Почему ускорение считается переменным?
- Что называется угловой скоростью?
- Какое движение называется вращательным?
- Если при движении по окружности модуль скорости точки меняется, будет ли ускорение направлено к центру? Почему?
- Как зависит линейная скорость движения точки по окружности от расстояния до оси вращения?
- В каком месте Земли центростремительное ускорение наибольшее?
- Во сколько раз угловая скорость минутной стрелки часов больше часовой?
- Когда скорость иглы проигрывателя относительно пластинки больше, в начале проигрывания или в конце?
- Почему верхние спицы катящегося колеса иногда сливаются для глаз, в то время как нижние видны раздельно?
Тест
A1.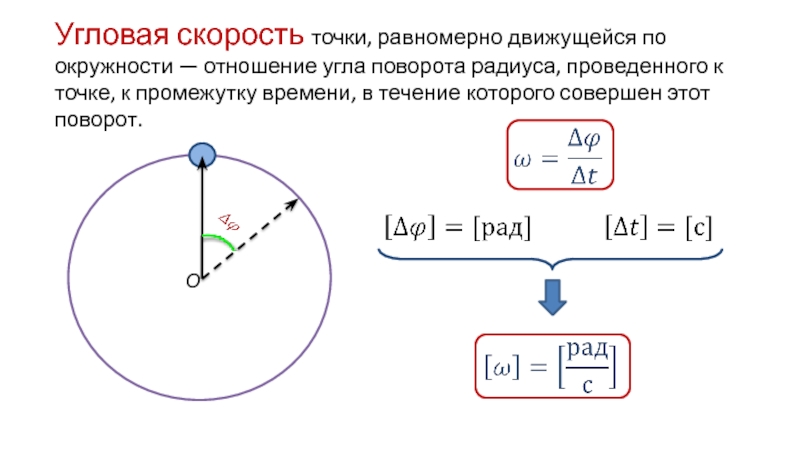 Шарик движется по окружности радиусом r со скоростью v. Как изменится центростремительное ускорение шарика, если его скорость уменьшить в 2 раза?
Шарик движется по окружности радиусом r со скоростью v. Как изменится центростремительное ускорение шарика, если его скорость уменьшить в 2 раза?
1) уменьшится в 2 раза;
2) увеличится в 2 раза;
3) уменьшится в 4 раза;
4) увеличится в 4 раза.
A2. Тело движется равномерно по окружности против часовой стрелки. Как направлен вектор ускорения при таком движении
1) 1;
2) 2;
3) 3;
4) 4.
A3. Тело равномерно движется по окружности радиуса 40 см со скоростью 4,5 м/с. Какое расстояние будет пройдено телом за время равное периоду?
1) 180 см;
2) 4,5 м;
3) 0,125 м;
4) 2,5 м.
A4. Автомобиль движется по закруглению дороги радиусом 20м с центростремительным ускорением 5м/с². Скорость автомобиля равна
1) 12,5 м/с;
2) 10 м/с;
3) 5 м/с;
4) 4 м/с.
A5. Вектор ускорения при равномерном движении точки по окружности
1) постоянен по модулю и по направлению;
2) равен нулю;
3) постоянен по модулю, но непрерывно меняется по направлению;
4) постоянен по направлению но непрерывно изменяется по модулю.
Приложение 1
- Какова должна быть предельная (максимальная) масса груза лесовоза, массой 6 тонн, движущегося по скользкому закруглению радиусом 50 м со скоростью 36 км/ч, если коэффициент трения колес об асфальт 0,5?
- Лесовоз движется по закруглению дороги радиусом 30м и не опрокидывается. Какой радиус кривизны должна иметь дорога, по которой движется лесовоз массой 10 т со скоростью 36 км/ч, чтобы он не опрокидывался, если коэффициент трения колес об асфальт 0,5?
- Какова максимальная допустимая скорость лесовоза массой 10 т, который движется по закруглению дороги радиусом 30 м если коэффициент трения колес об асфальт 0,5?
- Какой должен быть минимальный коэффициент трения колес о мокрый асфальт, при котором может произойти переворот лесовоза, если масса лесовоза 10 т, скорость 36 км/ч, радиус кривизны дороги 28,5 м.
Презентация по теме «Равномерное движение по окружности» | Презентация к уроку по физике (10 класс) на тему:
Слайд 1
1 2 Равномерное движение по окружности — это такое движение при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности. Равномерное движение по окружности Решение зАдач 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Равномерное движение по окружности Решение зАдач 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Слайд 2
Период обращения 2 1 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Время одного оборота по окружности называется периодом вращения T N — число оборотов, совершаемых за время t . Единица частоты обращения — 1 оборот в секунду (1 с -1 ) Частота обращения
Слайд 3
3 2 10 1 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Угловая скорость
Слайд 4
4 2 10 3 1 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Модуль вектора линейной скорости равен:
Слайд 5
5 2 10 3 4 1 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Модуль вектора центростремительного ускорения равен:
Слайд 6
6 2 10 3 4 5 1 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Какова линейная скорость точек на ободе колеса паровой турбины с диаметром колеса 1 м и частотой вращения 300 об/мин? Показать решение
Слайд 7
7 2 10 3 4 5 6 1 8 9 Ляхович Е. Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться равномерно по окружности вдвое большего радиуса с той же угловой скоростью? Показать решение
Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Во сколько раз изменится центростремительное ускорение тела, если оно будет двигаться равномерно по окружности вдвое большего радиуса с той же угловой скоростью? Показать решение
Слайд 8
8 2 10 3 4 5 6 7 1 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Задача. Угловая скорость лопастей вентилятора 20π рад/с. Найти число оборотов за 30 мин. Показать решение
Слайд 9
1 Вариант 2 Вариант 1. Угловая скорость лопастей вентилятора 20π рад/с. Найти число оборотов за 30 мин. 2 . Частота вращения воздушного винта самолета 1500 об/мин. Сколько оборотов сделает винт на пути 90 км при скорости полета 180 км/ч 2 . Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его колеса, если их радиус 50 см? 1 . На повороте вагон трамвая движется с постоянной по модулю скоростью 5 м/с. Чему равно его центростремительное ускорение, если радиус закругления пути 50 м. 9 2 10 3 4 5 6 7 8 1 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Слайд 10
ОТВЕТЫ 1 Вариант 2 Вариант 1 . 18000. 2 . 45000 2 . 5,31 [1/с] 1 . 0,5 м/с 2 . 1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
18000. 2 . 45000 2 . 5,31 [1/с] 1 . 0,5 м/с 2 . 1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск
Слайд 11
1 2 10 3 4 5 6 7 8 9 Ляхович Е.Ю., МБВСОУ «ВСОШ №3», г. Нижнекамск Показать решение
Конспект урока «Движение тела по окружности»
Конспект урока
«Движение тела по окружности. Период и частота»
(9 класс)
Подготовила
учитель физики
ГУЛНР «ЛОУСОШ №18»
Шляханова С.Д.
Цель урока: повторить виды механического движения, познакомить учащихся с новыми понятиями: движение по окружности, центростремительное ускорение, период, частота; выявить на практике связь периода, частоты и центростремительного ускорения с радиусом обращения; развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента; формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность; воспитывать коммуникативную и информационную культуру учащихся.
Тип урока: урок изучения нового материала
Ход урока:
І. Организационный момент
ІІ. Проверка домашнего задания
№212 (Р.)
Дано: Решение:
Ответ:
ІІІ. Актуализация опорных знаний
Физический диктант:
Изменение положения тела в пространстве с течением времени. (Движение)
Физическая векторная величина, измеряемая в метрах. (Перемещение)
Физическая векторная величина, характеризующая быстроту движения. (Скорость)
Основная единица измерения длины в физике. (Метр)
Физическая величина, единицами измерения которой служат год, сутки, час.
 (Время)
(Время)Длина траектории. (Путь)
Единицы измерения ускорения (м/с2)
(Проведение диктанта с последующей проверкой, самооценка работ учениками)
ІV. Изложение нового материала
В природе и в технике очень часто встречаются движения, траектории, которых представляют собой не прямые, а кривые линии. Это криволинейное движение. По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли, а на Земле — всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т. д.
Если прижать к вращающемуся точильному камню конец стального прутика, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной движутся брызги от колес буксующего автомобиля.
Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной движутся брызги от колес буксующего автомобиля.
Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различное направление. По модулю же скорость может быть всюду одинакова или изменяться от точки к точке.
Но даже, если модуль скорости не изменяется, ее нельзя считать постоянной. Скорость — векторная величина. Для векторной величины модуль и направление одинаково важны. Криволинейное движение — это всегда движение с ускорением, даже если по модулю скорость постоянная.
Запись в тетрадь: мгновенная скорость в данной точке траектории направлена по касательной к траектории в этой точке, то есть перпендикулярно радиусу проведённому из центра окружности в данную точку.
Итак, пусть у нас есть некоторая сложная криволинейная траектория.
Из рисунка видно, что отдельные части криволинейной траектории представляют собой приблизительно дуги окружностей. Выходит, что движение по любой криволинейной траектории можно представить как движение по дугам некоторых окружностей.
Запись в тетрадь: Равномерным движением по окружности называется движение по окружности с постоянной по модулю скоростью.
Ускорение тела, равномерно движущегося по окружности, в любой, точке центростремительное, т. е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости.
Запись в тетрадь: при равномерном движении по окружности ускорение в каждый момент времени направлено по радиусу к центру окружности.
Модуль центростремительного ускорения , где — линейная скорость тела, a — радиус окружности.
Движение по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот. Эта величина называется периодом обращения и обозначается буквой Т.
Эта величина называется периодом обращения и обозначается буквой Т.
Запись в тетрадь:
Характеристики равномерного движения по окружности:
Найдем связь между периодом обращения Т и модулем скорости при равномерном движении по окружности радиуса R. Т. к. , а путь S равен длине окружности: , то
Линейная скорость связана с угловой скоростью соотношением:
V. Закрепление нового материала
Фронтальная работа
Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 3 раза?
В центрифуге стиральной машины белье при отжиме движется по окружности с постоянной по модулю скоростью в горизонтальной плоскости. Как при этом направлен вектор его ускорения?
Конькобежец движется со скоростью 10 м/с по окружности радиусом 20 м.
 Определите его центростремительное ускорение.
Определите его центростремительное ускорение.Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью?
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить втрое?
Колесо машины делает 20 оборотов за 10 с. Определите период обращения колеса?
VI. Домашнее задание
Выучить §4,5, №105 (Р.)
Государственное учреждение образования «Средняя школа №27 г. Гомеля» — Официальный веб-сайт государственного учреждения образования
Международный день защиты детей отмечается ежегодно более чем в 30 странах мира и является одним из наиболее старых международных праздников. Решение о его проведении было принято в 1925 году на Всемирной конференции в Женеве, посвященной вопросам благополучия детей. Впервые день Читать дальше …
Впервые день Читать дальше …
24 мая в актовом зале государственного учреждения образования «Средняя школа N 27 г.Гомеля» прошло ежегодное чествование лучших учащихся «Лучший ученик года 2021». В девяти номинациях были определены победители. Лауреаты и победители конкурса были отмечены памятными дипломами. Наградой для победителей конкурса Читать дальше …
«Внимание — дети!» В связи с окончанием учебного года и началом летних каникул в целях предупреждения дорожных происшествий с участием детей с 25 мая по 5 июня в Республике Беларусь будет проведено республиканское профилактическое специальное комплексное мероприятие «Внимание — дети!», в период проведения которого в соответствии с Читать дальше …
УТВЕРЖДЕНО Приказ директора 12.05.2021 № 217-од Расписание консультаций к выпускным экзаменам по завершении обучения и воспитания на II ступени общего среднего образования в 2020/2021 учебном году Класс Предмет Ф. И.О. учителя Дата Время Кабинет 9а математика Судас Е.С. 01.06 15.00 3-3 Читать дальше …
И.О. учителя Дата Время Кабинет 9а математика Судас Е.С. 01.06 15.00 3-3 Читать дальше …
УТВЕРЖДЕНО Приказ директора 12.05.2021 № 217од Расписание консультаций к выпускным экзаменам по завершении обучения и воспитания на III ступени общего среднего образования в 2020/2021 учебном году Класс Предмет Ф.И.О. учителя Дата Время Кабинет 11а математика Судас Е.С. 31.05 14.30 Читать дальше …
УТВЕРЖДАЮ Директор государственного учреждения образования «Средняя школа № 27 г. Гомеля» _____________________ С.В.Кубышкина «______» ___________________________________ Примерный план работы летней спортивной оздоровительной площадки «Здоровый я – здоровая страна!» на базе гимназии № 56 г. Гомеля, средней школы № 27 г.Гомеля Читать дальше …
Гомеля, средней школы № 27 г.Гомеля Читать дальше …
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Математика кругового движения
Есть три математические величины, которые будут для нас в первую очередь интересны, когда мы будем анализировать движение объектов по кругу. Эти три величины — скорость, ускорение и сила. Скорость объекта, движущегося по кругу, определяется следующим уравнением.
Скорость объекта, движущегося по кругу, определяется следующим уравнением.
Ускорение объекта, движущегося по кругу, можно определить с помощью одного из двух следующих уравнений.
Уравнение справа (вверху) получено из уравнения слева путем подстановки выражения для скорости.
Чистая сила ( F net ), действующая на объект, движущийся по кругу, направлена внутрь. Хотя на объект может действовать более одной силы, их векторная сумма должна составлять результирующую силу. В общем, внутренняя сила больше, чем внешняя сила (если таковая имеется), так что внешняя сила компенсируется, и неуравновешенная сила направлена в направлении центра круга. Чистая сила связана с ускорением объекта (как всегда бывает) и, таким образом, определяется следующими тремя уравнениями:
Уравнения в середине (вверху) и справа (вверху) получены из уравнения слева путем подстановки выражений для ускорения.
Этот набор уравнений кругового движения можно использовать двумя способами:
Эти два способа показаны ниже.
Уравнения как руководство к мышлению
Уравнение выражает математическую связь между величинами, присутствующими в этом уравнении. Например, уравнение второго закона Ньютона определяет, как ускорение связано с чистой силой и массой объекта.
Взаимосвязь, выражаемая уравнением, заключается в том, что ускорение объекта прямо пропорционально действующей на него чистой силе. Другими словами, чем больше значение чистой силы, тем больше будет значение ускорения. По мере увеличения чистой силы ускорение увеличивается. Фактически, если бы чистая сила была увеличена в 2 раза, уравнение предсказало бы, что ускорение увеличится в 2 раза. Точно так же, если бы чистая сила была уменьшена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза.
Уравнение второго закона Ньютона также показывает связь между ускорением и массой. Согласно уравнению, ускорение объекта обратно пропорционально массе объекта.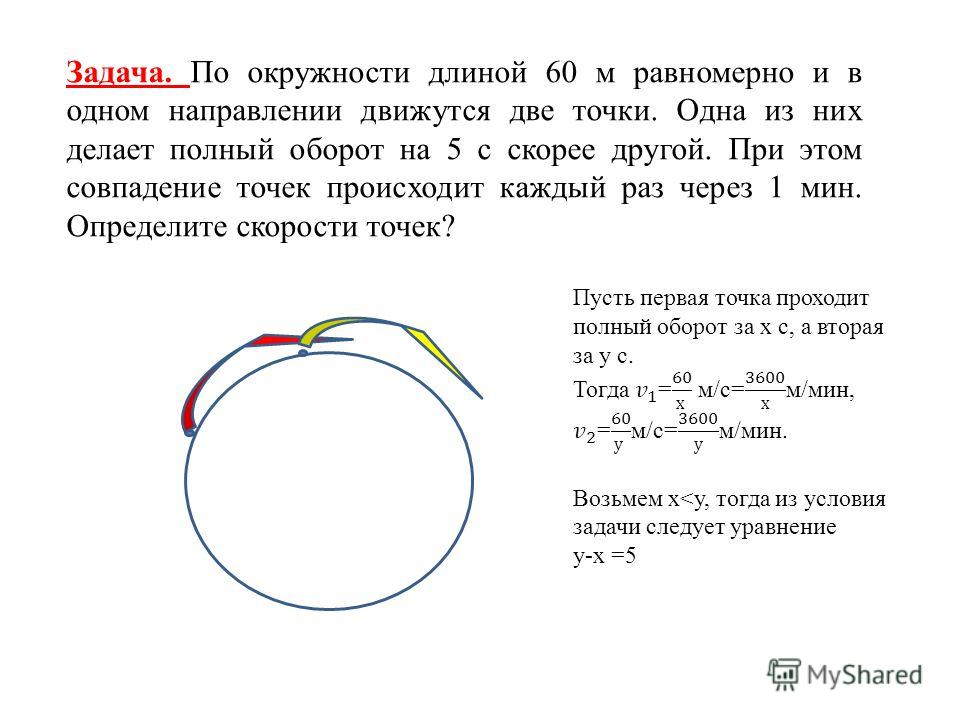 Другими словами, чем больше значение массы, тем меньше будет значение ускорения. По мере увеличения массы ускорение уменьшается. Фактически, если бы масса была увеличена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса была уменьшена в 2 раза, уравнение предсказало бы, что ускорение будет увеличиваются в 2 раза.
Другими словами, чем больше значение массы, тем меньше будет значение ускорения. По мере увеличения массы ускорение уменьшается. Фактически, если бы масса была увеличена в 2 раза, уравнение предсказало бы, что ускорение уменьшится в 2 раза. Точно так же, если бы масса была уменьшена в 2 раза, уравнение предсказало бы, что ускорение будет увеличиваются в 2 раза.
Как упоминалось ранее, уравнения позволяют делать прогнозы о влиянии изменения одной величины на вторую величину. Поскольку уравнение второго закона Ньютона показывает три величины, каждая из которых возведена в первую степень, предсказательная способность уравнения довольно проста. Прогностическая способность уравнения усложняется, когда одна из величин, включенных в уравнение, возводится в степень. Например, рассмотрим следующее уравнение, связывающее чистую силу ( F net ) со скоростью ( v ) объекта, движущегося равномерно по кругу.
Это уравнение показывает, что чистая сила, необходимая для движения объекта по кругу, прямо пропорциональна квадрату скорости объекта. При постоянной массе и радиусе сеть F пропорциональна скорости 2 .
При постоянной массе и радиусе сеть F пропорциональна скорости 2 .
Коэффициент, на который изменяется чистая сила, является квадратом коэффициента, на который изменяется скорость. Впоследствии, если скорость объекта удваивается, чистая сила, необходимая для кругового движения этого объекта, увеличивается в четыре раза.И если скорость объекта уменьшается вдвое (уменьшается в 2 раза), требуемая полезная сила уменьшается в 4 раза.
Уравнения как рецепт решения проблем
Математические уравнения, представленные выше для движения объектов по кругу, могут использоваться для решения задач кругового движения, в которых необходимо определить неизвестную величину. Процесс решения задачи кругового движения очень похож на любую другую задачу в классе физики.Процесс включает в себя внимательное прочтение проблемы, идентификацию известной и необходимой информации в переменной форме, выбор соответствующего уравнения (й), замену известных значений в уравнение и, наконец, алгебраическое манипулирование уравнением для определения отвечать. Рассмотрим применение этого процесса к следующим двум задачам кругового движения.
Рассмотрим применение этого процесса к следующим двум задачам кругового движения.
| Пример задачи № 1 Автомобиль массой 900 кг, движущийся со скоростью 10 м / с, совершает разворот по окружности с радиусом 25.0 мин. Определите ускорение и чистую силу, действующую на автомобиль. |
Решение этой проблемы начинается с выявления известной и запрашиваемой информации.
Известная информация:
| Запрошенная информация:
|
Чтобы определить ускорение автомобиля, используйте уравнение a = v 2 / R. Решение следующее:
Решение следующее:
а = v 2 / R
a = (10,0 м / с) 2 / (25,0 м)
a = (100 м 2 / с 2 ) / (25,0 м)
a = 4 м / с 2
Чтобы определить чистую силу, действующую на автомобиль, используйте уравнение F net = m • a. Решение следующее.
F net = m • a
F нетто = (900 кг) • (4 м / с 2 )
F нетто = 3600 N
| Пример задачи № 2 Полузащитник весом 95 кг делает разворот на футбольном поле.Полузащитник прокладывает путь, который представляет собой часть круга радиусом 12 метров. Полузащитник делает четверть оборота по кругу за 2,1 секунды. Определите скорость, ускорение и чистую силу, действующую на полузащитника. |
Решение этой проблемы начинается с выявления известной и запрашиваемой информации.
Известная информация:
| Запрошенная информация:
|
Чтобы определить скорость полузащитника, используйте уравнение v = d / t, где d составляет одну четвертую окружности, а время равно 2.1 с. Решение следующее:
v = d / t
v = (0,25 • 2 • pi • R) / т
v = (0,25 • 2 • 3,14 • 12,0 м) / (2,1 с)
v = 8,97 м / с
Чтобы определить ускорение полузащитника, используйте уравнение a = v 2 / R. Решение следующее:
а = v 2 / R
a = (8,97 м / с) 2 / (12,0 м)
а = (80. 5 м 2 / с 2 ) / (12,0 м)
5 м 2 / с 2 ) / (12,0 м)
a = 6,71 м / с 2
Чтобы определить чистую силу, действующую на полузащитника, используйте уравнение F net = m • a. Решение следующее.
F нетто = m * a
F нетто = (95,0 кг) * (6,71 м / с 2 )
F нетто = 637 N
В Уроке 2 этого модуля принципы кругового движения и приведенные выше математические уравнения будут объединены для объяснения и анализа различных сценариев реального движения, включая аттракционы в парке развлечений и круговые движения в легкой атлетике.
Хотим предложить …
Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства однородного кругового движения. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу.
Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать взаимосвязь между скоростью, ускорением и силой для объекта, движущегося по кругу.
Проверьте свое понимание
1. Анна Литикал практикует демонстрацию центростремительной силы дома. Она наполняет ведро водой, привязывает его к прочной веревке и крутит по кругу. Анна вращает ведро, когда оно наполовину наполнено водой, а когда оно на четверть. В каком случае для вращения ведра по кругу требуется больше силы? Объясните, используя уравнение как «руководство к размышлениям».
2.Линкольн Континенталь и Юго делают поворот. Линкольн в четыре раза массивнее Юго. Если они совершают поворот с одинаковой скоростью, то как сравнить центростремительные силы, действующие на две машины? Объяснять.
3. Cajun Cliffhanger в Great America — это аттракцион, в котором пассажиры выстраиваются по периметру цилиндра и вращаются по кругу с высокой скоростью поворота. Когда цилиндр начинает очень быстро вращаться, пол убирается из-под ног гонщиков.Какое влияние удвоение скорости оказывает на центростремительную силу? Объяснять.
Cajun Cliffhanger в Great America — это аттракцион, в котором пассажиры выстраиваются по периметру цилиндра и вращаются по кругу с высокой скоростью поворота. Когда цилиндр начинает очень быстро вращаться, пол убирается из-под ног гонщиков.Какое влияние удвоение скорости оказывает на центростремительную силу? Объяснять.
4. Определите центростремительную силу, действующую на ребенка весом 40 кг, который совершает 10 оборотов вокруг клиффхэнгера за 29,3 секунды. Радиус ствола — 2,90 метра.
Анализ круговых движений в легкой атлетике
Круговое движение характерно почти для всех спортивных мероприятий.Будь то гонки на спортивных автомобилях или легкая атлетика, бег по бейсболу или катание на коньках, движение объектов по кругу является обычным явлением для спортивных телезрителей во всем мире. Как и любой объект, движущийся по кругу, движение этих объектов, которые мы наблюдаем с трибуны стадиона или наблюдаем на телевизионном мониторе, регулируется законами движения Ньютона. Их круговое движение — каким бы коротким или продолжительным оно ни было — характеризуется внутренним ускорением и вызвано внутренней чистой силой.Математический анализ таких движений может быть проведен способом, представленным ранее в Уроке 2. В этой части Урока 2 мы исследуем различные применения принципов кругового движения в мире спорта и будем использовать законы Ньютона для математического анализа таких движений. Акцент будет сделан не на изучении деталей каждого возможного вида спорта, а скорее на изучении того, как применять некоторые общие принципы, чтобы впоследствии их можно было применить ко всем видам спорта.
Их круговое движение — каким бы коротким или продолжительным оно ни было — характеризуется внутренним ускорением и вызвано внутренней чистой силой.Математический анализ таких движений может быть проведен способом, представленным ранее в Уроке 2. В этой части Урока 2 мы исследуем различные применения принципов кругового движения в мире спорта и будем использовать законы Ньютона для математического анализа таких движений. Акцент будет сделан не на изучении деталей каждого возможного вида спорта, а скорее на изучении того, как применять некоторые общие принципы, чтобы впоследствии их можно было применить ко всем видам спорта.
Поворот
Самый распространенный пример физики кругового движения в спорте связан с поворотом.Это может быть полузащитник в футболе, завернувший за угол линии. Или это может быть игрок в софтбол, который управляет базами и делает поворот вокруг второй базы. Или это может быть бобслей на Олимпийских играх, который делает поворот на трассе. Каким бы ни было поворотное движение, вы можете быть уверены, что поворот основан на принципах кругового движения. Теперь наверняка не все повороты включают полный круг; и не все повороты имеют идеально круглую форму. Некоторые повороты составляют лишь четверть оборота, например, защитник, огибающий угол линии в футболе.А некоторые повороты вообще не могут быть круговыми. Тем не менее, любой поворот можно представить как часть большего круга или как часть нескольких кругов разного размера. Крутой поворот можно считать частью небольшого круга. Более постепенный поворот — это часть большего круга. Некоторые повороты могут начинаться резко и постепенно менять резкость, или наоборот. Во всех случаях движение вокруг поворота можно аппроксимировать как часть круга или как набор кругов. На схеме ниже показаны различные пути, по которым может пройти поворот.
Каким бы ни было поворотное движение, вы можете быть уверены, что поворот основан на принципах кругового движения. Теперь наверняка не все повороты включают полный круг; и не все повороты имеют идеально круглую форму. Некоторые повороты составляют лишь четверть оборота, например, защитник, огибающий угол линии в футболе.А некоторые повороты вообще не могут быть круговыми. Тем не менее, любой поворот можно представить как часть большего круга или как часть нескольких кругов разного размера. Крутой поворот можно считать частью небольшого круга. Более постепенный поворот — это часть большего круга. Некоторые повороты могут начинаться резко и постепенно менять резкость, или наоборот. Во всех случаях движение вокруг поворота можно аппроксимировать как часть круга или как набор кругов. На схеме ниже показаны различные пути, по которым может пройти поворот.
Поскольку поворот за угол включает в себя движение объекта, который на мгновение движется по траектории круга, к такому движению могут применяться как концепции, так и математика кругового движения. Концептуально такой объект движется с внутренним ускорением — внутреннее направление — к центру любого круга , по которому движется объект. Для такого движения также потребуется центростремительная сила.То есть должен быть какой-то объект, доставляющий внутреннюю силу или внутренний компонент силы. Когда человек делает поворот на горизонтальной поверхности, он часто наклоняется в поворот . При наклоне поверхность толкает вверх под углом к вертикали . Таким образом, существует как горизонтальный, так и вертикальный компонент, возникающий в результате контакта с поверхностью ниже. Это контактное усилие . выполняет две функции: оно уравновешивает направленную вниз силу тяжести и отвечает требованиям центростремительной силы для объекта, находящегося в равномерном круговом движении.Восходящий компонент контактной силы достаточен для уравновешивания нисходящей силы тяжести, а горизонтальный компонент контактной силы толкает человека к центру круга.
Концептуально такой объект движется с внутренним ускорением — внутреннее направление — к центру любого круга , по которому движется объект. Для такого движения также потребуется центростремительная сила.То есть должен быть какой-то объект, доставляющий внутреннюю силу или внутренний компонент силы. Когда человек делает поворот на горизонтальной поверхности, он часто наклоняется в поворот . При наклоне поверхность толкает вверх под углом к вертикали . Таким образом, существует как горизонтальный, так и вертикальный компонент, возникающий в результате контакта с поверхностью ниже. Это контактное усилие . выполняет две функции: оно уравновешивает направленную вниз силу тяжести и отвечает требованиям центростремительной силы для объекта, находящегося в равномерном круговом движении.Восходящий компонент контактной силы достаточен для уравновешивания нисходящей силы тяжести, а горизонтальный компонент контактной силы толкает человека к центру круга.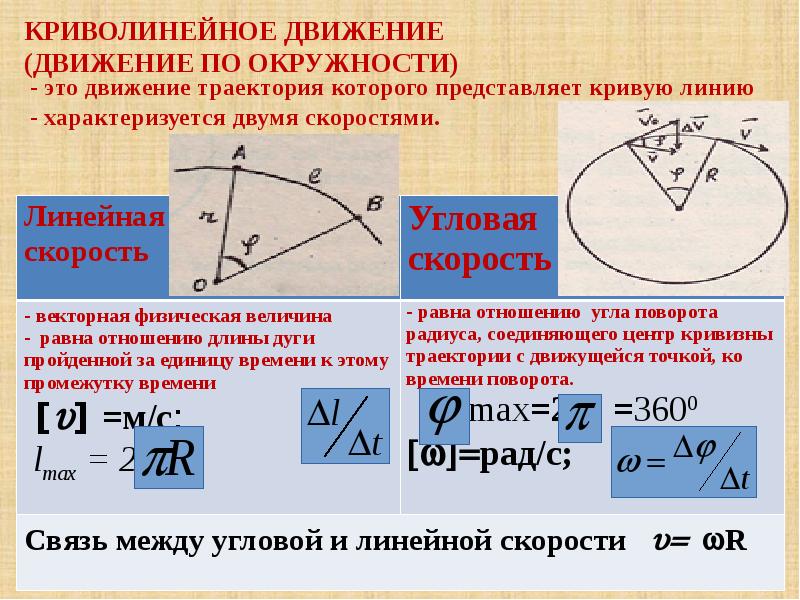 Это контактное усилие показано на диаграмме ниже для конькобежца, совершающего поворот на льду.
Это контактное усилие показано на диаграмме ниже для конькобежца, совершающего поворот на льду.
В случае с конькобежцем, указанным выше, сила, возникающая в результате контакта коньков со льдом, имеет две составляющие. Сила представляет собой векторную комбинацию нормальной силы и силы трения.Нормальная сила — это результат того, что устойчивая поверхность обеспечивает опору для любого объекта, толкающего ее вниз. Сила трения является результатом силы статического трения, возникающей в результате взаимодействия коньков и коньков. Когда фигуристка наклоняется в повороте, она толкает лед вниз и наружу, . Из-за высокого давления и температуры лезвия на льду образуется неглубокая канавка , в которой на мгновение остается лезвие. Лезвие продвигается наружу по вертикальной стенке этой канавки и вниз по дну этой канавки.Как и следовало ожидать из третьего закона движения Ньютона, существует сила реакции , равная , когда лед толкает коньки вверх и внутрь. Если этого движения лезвия со льдом не происходит, фигурист все равно может наклониться и попытаться оттолкнуться от льда. Тем не менее, лезвие не сможет захватить лед на льду, и фигурист будет рисковать не сделать поворот. В результате коньки у фигуристки выскочили из-под нее, она упала на лед, и она пошла по прямолинейной инерционной траектории.Без внутренней силы фигурист не может пройти поворот.
Если этого движения лезвия со льдом не происходит, фигурист все равно может наклониться и попытаться оттолкнуться от льда. Тем не менее, лезвие не сможет захватить лед на льду, и фигурист будет рисковать не сделать поворот. В результате коньки у фигуристки выскочили из-под нее, она упала на лед, и она пошла по прямолинейной инерционной траектории.Без внутренней силы фигурист не может пройти поворот.
Тот же принцип наклона, который позволяет конькобежцу совершать поворот вокруг части круга, применим и к множеству других спортивных соревнований, где участники наклоняются в повороте, чтобы на мгновение двигаться по кругу. Горнолыжник делает поворот, прислонившись к снегу. Снег отталкивается как внутрь, так и вверх, уравновешивая силу тяжести и обеспечивая центростремительную силу.Футболист делает свой ход, опираясь на землю. Земля отталкивается как внутрь, так и вверх, уравновешивая силу тяжести и обеспечивая центростремительную силу. Велосипедист делает поворот точно так же, как и наклоняется под углом к горизонтали. Поверхность дороги толкает с восходящей составляющей силы, чтобы уравновесить нисходящую силу тяжести. Дорожное покрытие также толкает с горизонтальной составляющей силы к центру круга, по которому велосипедист поворачивает.Аналогичным образом совершает поворот бобслейная команда, поднимаясь на наклонный участок трассы. При наклоне они естественно наклоняются, и нормальная сила действует под углом к вертикали; эта нормальная сила обеспечивает как восходящую силу, чтобы уравновесить силу тяжести, так и центростремительную силу, позволяющую совершать круговое движение.
| Поворот возможен только тогда, когда есть составляющая силы, направленная к центру круга, по которому движется человек. | ||
Анализ силы поворотов в легкой атлетике
Те же математические уравнения, которые описывают движение объектов по кругу, применимы к движениям спортсменов, совершающих повороты на спортивном поле. Использование этих уравнений кругового движения было введено в первом разделе Урока 1, а затем впоследствии применено к анализу движения автомобилей американских горок.Было подчеркнуто, что любую данную физическую ситуацию можно проанализировать с точки зрения индивидуальных сил, действующих на объект; эти отдельные силы должны складываться в результирующую силу. Кроме того, результирующая сила должна быть равна массе, умноженной на ускорение. Процесс проведения силового анализа физической ситуации был впервые представлен в Блоке 2 Физического Класса. Теперь мы исследуем использование этих фундаментальных принципов при анализе ситуаций, связанных с движением спортсменов по кругу.Мы будем использовать базовый подход к решению проблем, который был представлен ранее в Уроке 2. Этот подход можно резюмировать следующим образом.
Предлагаемый метод решения задач кругового движения
|
Объедините анализ сил с вышеуказанным методом, чтобы решить следующую задачу кругового движения.
Пример задачи конькобежца Бонни катается на коньках на Олимпийских играх.Она делает крутой разворот радиусом 22,6 м и скоростью 16,1 м / с. Используйте второй закон Ньютона, чтобы определить ускорение и угол наклона тела Бонни весом 55,0 кг. |
Шаги 1 и 2 включают построение диаграммы свободного тела и идентификацию известных и неизвестных величин. Это показано ниже.
Информация: м = 55.0 кг v = 16,1 м / с r = 22,6 м Найдите: а = ??? Угол наклона = ??? |
Шаг 3 предлагаемого метода включает разделение любых сил, действующих под углом, на горизонтальные и вертикальные составляющие. Это показано на диаграмме справа. Контактное усилие можно разбить на две составляющие — F горизонт и F vert .Вертикальная составляющая силы уравновешивает силу тяжести; и как таковая вертикальная составляющая будет равна по величине силе тяжести. Горизонтальная составляющая силы остается неуравновешенной. Как упоминалось в вышеупомянутом обсуждении, эта горизонтальная составляющая представляет собой чистую внутреннюю силу; и поэтому F горизонт равен м * . Наконец, два компонента связаны с углом наклона с помощью функции касательной. Простая алгебраическая манипуляция даст соотношение, показанное на рисунке справа.Таким образом, угол наклона можно определить, если известны вертикальная и горизонтальная составляющие силы.
Шаг 4 предлагаемого метода включает определение любых известных сил. В этом случае силу тяжести можно определить из уравнения F grav = m • g . o сила тяжести, действующая на тело Бонни массой 55,0 кг, составляет примерно 539 Н. И поскольку эта сила уравновешивается вертикальной составляющей контактной силы, F vert также составляет 539 Н.Шаг 5 включает определение ускорения Бонни при повороте. Этого можно добиться, используя уравнение ускорения для кругового движения.
а = v 2 / R
a = (16,1 м / с) 2 / (22,6 м) = 11,5 м / с 2
Теперь, когда ускорение найдено, можно определить угол наклона. Как упомянуто в приведенном выше уравнении, угол наклона («тета») можно определить, зная горизонтальную и вертикальную составляющие контактной силы.Вертикальная составляющая уже была рассчитана и составляет 539 Н (равняется гравитации F ). И, как упоминалось ранее, горизонтальная составляющая будет равна F net ; это показано ниже.
F горизонт = F net = m • a
F горизонт = (55,0 кг) • (11,5 м / с / с) = 631 Н
Теперь, наконец, можно определить угол наклона.
Вышеупомянутая задача иллюстрирует процедуру объединения второго закона движения Ньютона с векторными принципами и уравнениями кругового движения для анализа поворотных движений спортсменов.Теперь используйте ту же общую процедуру, описанную выше, для решения следующей практической задачи. По завершении нажмите кнопку, чтобы просмотреть ответы.
| Круговое движение в футболе 90-килограммовый защитник GBS обходит левую часть финиша. Путь защитника, как видно сверху, показан на схеме. Во время поворота он на мгновение совершает круговое движение, образуя четверть круга с радиусом 4.0 метров. Защитник делает разворот со скоростью 5,0 м / с. Используйте диаграмму свободного тела и ваше понимание кругового движения и второго закона Ньютона, чтобы определить . а. разгон |
Повороты — не единственные ситуации в спорте, в которых люди или предметы движутся по кругу.Хотя повороты, вероятно, являются наиболее распространенными примерами кругового движения, они не единственные. Есть определенные соревнования по легкой атлетике — метание молота и метание диска, — в которых спортсмены набирают обороты в предмете, который впоследствии должен быть брошен. Импульс перед броском передается снаряду путем вращения внутри круга. Как только импульс накоплен, молот или диск запускаются в воздух под оптимальным углом, чтобы максимально увеличить пройденное расстояние.Независимо от спортивного вида анализ круговых движений остается прежним. Законы Ньютона описывают взаимосвязь силы-массы-ускорения; векторные принципы описывают взаимосвязь между отдельными силами и любыми угловыми силами; а уравнения кругового движения описывают соотношение скорость-радиус-ускорение.
Проверьте свое понимание
1.Игрок в софтбол весом 55,0 кг бежит со скоростью 7,0 м / с по кривой с радиусом 15,0 м. Контактная сила (векторная комбинация силы трения и нормальной силы), действующая между землей и ногами игрока, обеспечивает центростремительную силу для поворота и восходящую силу для уравновешивания веса игрока. Используйте диаграмму свободного тела и свое понимание кругового движения и второго закона Ньютона, чтобы определить:
а. ускорение
г. F грав
г.F норма
г. F фрикт
e. Угол наклона
2. При броске молота сфера вращается по круговой траектории на конце цепи. После пяти оборотов метатель отпускает цепь, и «молот» запускается под углом к горизонтали. Справа показана схема спортсмена и молота.Предположим, что молот движется по кругу в горизонтальной плоскости со скоростью 27,0 м / с. Предположим, что молот имеет массу 7,30 кг и движется по кругу с радиусом 1,25 м. Поскольку молот движется в горизонтальной плоскости, центростремительная сила направлена горизонтально. Вертикальная составляющая натяжения цепи (направленная вверх) уравновешивается весом молотка (направленным вниз). Используйте диаграмму и понимание компонентов вектора, чтобы определить натяжение цепи.
Круговое движение — Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
6.1 Угол поворота и угловая скорость
Угловая скорость
Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости.Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота. В форме уравнения угловая скорость равна
.
6.2 ω = ΔθΔt, ω = ΔθΔt,
, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Теперь давайте рассмотрим направление угловой скорости, что означает, что теперь мы должны называть ее угловой скоростью.Направление угловой скорости — вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма перемещается по длине дуги (Δs) (Δs) за короткое время (Δt) (Δt), поэтому его тангенциальная скорость равна
Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs = rΔθ. Подставляя это в выражение для v , получаем
v = rΔθΔt = rω. v = rΔθΔt = rω.
Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшим r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрывать большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Рисунок 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. Рисунок 6.5). Чем быстрее вращается шина, тем быстрее движется машина — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать большую линейную (тангенциальную) скорость, v, для автомобиля. Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω.Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шины, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление.Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.
Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу.Направление угловой скорости в данном случае указано на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью. Здесь также показано, как преобразовать число оборотов в радианы.
Проверка захвата
Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?
- Да, потому что тангенциальная скорость не зависит от радиуса.
- Да, потому что тангенциальная скорость зависит от радиуса.
- Нет, поскольку тангенциальная скорость не зависит от радиуса.
- Нет, потому что тангенциальная скорость зависит от радиуса.
4 мая 2015 г.
Мы считаем самоочевидной истину о том, что детям необходимо передвигаться, и создание возможностей для передвижения во время урока математики может окупиться с лихвой.
Таким образом, у нас есть коллекция некоторых из наших любимых быстрых заданий по математике / движению, которыми мы можем поделиться. Они особенно хороши для K-4, хотя их можно адаптировать и к старшим, и к младшим классам. Они обеспечивают дозу движения, веселья и математических упражнений в сокращенном временном интервале — идеально подходят для остановок и переходов.
Если нам не хватает ваших фаворитов, дайте нам знать!
PDF-файл с тегами Common Core доступен на нашей странице «Уроки».
Игры под руководством учителя
- Группы (2-5 минут)
Учитель называет номер (3), и у учеников есть 10 секунд, чтобы разбиться на группы такого размера.Каждый раз может оказаться невозможным попасть в группу каждый раз, но каждый новый номер дает каждому еще один шанс. В основной игре просто набирайте отдельные номера. Как только учащиеся поймут суть, вы можете называть задачи на сложение или вычитание (например, «разбиться на группы по 7–4»). Не забудьте назвать группу из 1 человека и группу, сколько студентов в целом класс в какой-то момент игры. - Встань / сядь (2-5 минут)
Правила просты: если учитель называет число 10, ученики встают.Любой другой номер, они садятся. Хитрость в том, что учитель будет говорить такие вещи, как «7 + 3» и «14-5» (выберите подходящие суммы и разности, чтобы ваши ученики решили мысленно). Это отличная игра, в которой можно попытаться «обмануть» студентов, вставая или садясь, когда они должны делать противоположное. Существует бесконечное количество вариантов. Например:
— стойте, когда число больше 5; сядьте, если он 5 или ниже
— стойте, если номер четный; сидеть, когда оно нечетное
— стоять, если на номере появляется цифра 1; сидеть иначе. - Больше / Меньше / Равно (2-5 минут)
Если учитель говорит число больше 10, ученики расширяют свое тело, чтобы занять как можно больше места (при этом ноги твердо стоят на земле — нет бегать). Если учитель говорит число меньше 10, ученики сжимаются, чтобы занять как можно меньше места. Если учитель дает точное число 10, ученики держат свое тело нейтрально и показывают руками знак равенства. Как и раньше, учитель переходит к суммам и разницам, как только ученики усвоят правила. - Ритмичные хлопки / счет (2-5 минут)
Учитель хлопает в ладоши / отсчитывает ритм. Студенты имитируют ритм хлопка и счета. - Подсчет пропусков с движением (2-5 минут)
Составьте движение, состоящее из 2, 3 или более частей. Прошепчите первые части и громко произнесите последний ход. Пример: Ветряные мельницы. Шепните «1» и коснитесь правой рукой левой ноги. Шепните «2» и коснитесь левой рукой правой ноги. Назови «3» и сделай прыжок! Продолжайте так считать до 30, называя числа, кратные 3, и прошептав числа между ними.Пример: http://mathandmovement.com/pdfs/skipcountingguide.pdf - Круговой счет (2-5 минут)
Встаньте в круг и постарайтесь отсчитывать как можно быстрее на всем протяжении круга. Начните с 1, затем ученик справа говорит «2», а ученик справа говорит «3» и так далее, пока счет не вернется к вам. Призовите детей учиться как можно быстрее и плавнее. Когда каждый сможет делать это умело, считайте по двойкам, пятеркам, десяткам или тройкам. Вы также можете начать с чисел больше 1 или попробовать обратный отсчет.
Студенческие парные игры
- Finger Speed-Sums (1-5 минут)
Учащиеся встречаются парами с одной рукой за спиной. На счет до трех каждый из них выдвинул некоторое количество пальцев. Выигрывает тот, кто первым назовет сумму. Затем пара распадается, и каждый находит нового человека, с которым можно поиграть. Опытные игроки могут использовать две руки вместо одной. - Разница в скорости пальцев (1-5 минут)
То же, что и для суммирования скорости, за исключением того, кто первым обнаружит разницу между двумя числами. - Five High Fives (1-2 минуты или дольше с исследованием)
Учащиеся пытаются дать пять пять разным одноклассникам. Когда они сделали пять «дай пять», они садятся. Эта игра — отчасти загадка: иногда каждый может получить пять; иногда нет. Разница (которую учитель знает, а ученики — нет) в том, что это возможно только в том случае, если четное количество людей дает пять. Попробуйте эту игру в разное время и позвольте учащимся угадать, думают ли они, что все получат пять или нет.Почему это срабатывает только иногда, а не всегда? Если вы сделаете четыре или шесть «дай пять» вместо пяти, то каждый сможет получать «дай пять» каждый раз.
Почему мы любим эти игры
Заставить детей двигаться — беспроигрышный вариант. Движение освежает ваших учеников, давая им новый взгляд на математические концепции. Эти игры очень быстрые и очень увлекательные для всех.
Советы для занятий
- Убедитесь, что детям никогда не будет стыдно, если они еще не знают правильный ответ.Вы также можете настроить соревновательные игры, чтобы сделать их совместными.
- Ваш энтузиазм имеет решающее значение в этих играх. Определите свои любимые и расширьте их, или попросите учащихся придумать свои собственные варианты. Если вы увлечены ими и хорошо проводите время, дети тоже будут хорошо проводить время.
Объекты, движущиеся по вертикальным кругам: проблемы анализа и практики — стенограмма видео и урока
Уравнения
Чтобы проанализировать движение по вертикальному кругу и составить некоторые уравнения, мы можем использовать комбинацию энергии и сил.Уравнение энергии движения, вероятно, является самым простым. Вверху у нас есть гравитационная потенциальная энергия и кинетическая энергия, а внизу — просто кинетическая энергия. Таким образом, половина mv-квадрата вверху плюс mgh вверху равна половине mv-квадрата внизу. Где v-top — скорость вверху в метрах в секунду, v-bottom — скорость внизу, также в метрах в секунду, m — масса объекта, движущегося по кругу, в килограммах, g — ускорение гравитации, которая равна 9.8 на Земле, а h — высота круга, которую можно заменить на 2-кратный радиус круга, 2r.
Что касается сил, мы знаем, что сила в круге равна центростремительной силе, возведенной в квадрат mv над r. Итак, наверху у нас есть натяжение и гравитация, которые вносят вклад в эту силу, а это означает, что натяжение наверху (Т-образная вершина, измеренная в ньютонах) плюс mg (сила тяжести) равняется mv-квадрату над r.
Но внизу гравитация уменьшает центростремительную силу. Итак, здесь сила натяжения за вычетом mg будет равна mv в квадрате над r. Итак, теперь у нас есть уравнение для сил вверху и внизу. Если вы подставите одно уравнение в другое, вы обнаружите, что натяжение внизу равно натяжению вверху плюс 6 мг.
Мы можем использовать эти уравнения в совокупности для описания движения по вертикальному кругу и решения проблем.
Практические задачи
Практическая задача 1: мяч на веревке вращается по вертикальному кругу. Если натяжение струны в верхней части круга составляет 15 ньютонов, а мяч весит 0,1 килограмма, каково натяжение струны в нижней части круга?
Прежде всего, мы должны записать то, что мы знаем. Натяжение вверху (Т-образный верх) составляет 15 ньютонов, а масса шара (м) составляет 0,1 килограмма, и мы хотим найти натяжение внизу (Т-образное основание). Чтобы решить эту проблему, мы можем использовать это уравнение натяжения:
Подставьте числа и решите Т-образное дно, и мы получим 20.9 ньютонов. И это наш ответ.
Практическая задача 2: С сумкой для покупок обращаться проще. Если сумка для покупок весит 1 килограмм и она вращается по вертикальному кругу радиусом 0,1 метра, а сумка для покупок движется со скоростью 2,5 м / с в нижней части круга, как быстро она движется в верхней части круга? ?
Записывая то, что мы знаем, мы видим, что масса (m) равна 1 килограмму, а радиус (r) равен 0,1 метру. Мы также знаем, что скорость внизу (v-bottom) равна 2.5 м / с. Нас просят найти скорость вверху (v-top).
Здесь нам понадобится уравнение энергии. Мы знаем все в этом уравнении, кроме v-top. Итак, сделайте v-образную вершину, подставьте числа и решите, и мы получим 1,53 м / с.
Резюме урока
Движение по вертикальному кругу сильно отличается от горизонтального. Это потому, что сила тяжести направлена к центру круга вверху и от центра круга внизу. Это приводит к изменению скорости (самая медленная вверху, самая быстрая внизу) и означает, что натяжение также должно изменяться во время движения.
Вот несколько уравнений, которые мы вывели для описания этого движения:
Уравнение энергии говорит, что половина mv-квадрата вверху (кинетическая энергия) плюс mg2r вверху (гравитационная потенциальная энергия) равна половине mv-квадрата внизу (кинетическая энергия на Нижний). Где v-top — скорость вверху, измеренная в метрах в секунду, v-bottom — скорость внизу, также измеряемая в метрах в секунду, m — масса объекта, движущегося по кругу, в килограммах, g — ускорение свободного падения, равное 9.8 на Земле, а r — радиус круга, измеряемый в метрах.
У нас также есть уравнения для описания сил вверху и внизу, и общее уравнение, которое говорит нам, как натяжение вверху соотносится с натяжением внизу: что натяжение внизу равно натяжению вверху плюс 6мг. Мы можем использовать эти уравнения в совокупности для описания движения по вертикальному кругу и решения проблем.
Результаты обучения
После этого урока вы сможете:
- Объяснять, почему скорость и напряжение меняются во время движения по вертикальному кругу
- Определите уравнения, описывающие движение по вертикальному кругу
Движение по кругу — Математика A-Level, редакция
Эта страница описывает движение по кругу.
Угловая скорость
Представьте, что объект движется по круговой траектории.
Угловая скорость — это скорость изменения угла (который я обозначил буквой «а»). Таким образом, он измеряет, насколько быстро объект движется по кругу.
Угловая скорость обычно измеряется в радианах в секунду (рад / с -1 ), то есть на сколько радиан проходит частица за секунду. Кроме того, его можно измерить в оборотах в секунду, т.е. сколько полных кругов объект проходит за секунду.
Существует формула, соединяющая «нормальную» скорость (обычно называемую «линейной скоростью») и угловую скорость:
где v — линейная скорость, r — радиус окружности, а w — угловая скорость.
Пример
Частица движется по окружности радиусом 10 см. Угловая скорость 2 рад / с -1 . Найдите (линейную) скорость.
Нам нужен радиус в метрах, то есть 0,1 м. Используя формулу выше, получаем:
v = 0,1 × 2 = 0,2
Значит скорость 0,2 мс -1 .
Обратите внимание, что если вам дана угловая скорость в оборотах в секунду, вам нужно сначала преобразовать в радианы в секунду.Для этого помните, что 1 оборот в секунду равен 2p радианам в секунду, потому что в круге 2p радиана.
Радиальное ускорение
Если тело движется по окружности, даже если оно движется с постоянной скоростью, оно ускоряется. Это потому, что он меняет направление (не движется по прямой).
Направление этого ускорения — к центру круга, а его величина определяется выражением:
где v — скорость, а r — радиус окружности.
Используя нашу формулу выше, это также можно записать как:
Какие из них вы будете использовать, будет зависеть от того, имеете ли вы дело со скоростью или угловой скоростью.
Ускорение происходит из-за действующей силы:
Представьте, что вы едете в машине, которая быстро свернет за поворот налево. Вы почувствуете, как сила тянет вас в сторону (левую сторону). Это сила, вызывающая ускорение. Сила действует по направлению к центру круга.
Конический маятник
Конический маятник выглядит примерно так:
P — частица.AP — это строка. P движется по синему кругу с угловой скоростью w.
Пример
Предположим, что у нас есть конический маятник, как указано выше, где частица имеет массу 2 кг, радиус круга, по которому частица движется, составляет 0,5 м, а угол при A равен 45 градусам. Найдите угловую скорость P.
Вес 2 г (W = мг), где g — ускорение свободного падения.
Вертикальное разрешение: Tcos45 = 2g
Следовательно (√2T) / 2 = 2g, поэтому T = 2√2 g (1)
Теперь используйте 2-й закон Ньютона, чтобы найти уравнение движения в радиальном направлении:
(«F = m r w 2 «)
Tsin45 = 2 × 5 × w 2
Используйте (1), чтобы исключить T:
2√2 g × (√2) / 2 = 10w 2
g / 5 = w 2
Итак, w = √ (g / 5)
Принимая g = 9.8, мы находим, что угловая скорость равна 1,4 рад с -1
Движение на береговой поверхности
Теперь рассмотрим движение частицы по «наклонной поверхности». Под этим я, например, имею в виду кольцевую гоночную трассу, которая наклонена вверх от центра, чтобы помочь автомобилям / мотоциклам оставаться на трассе на высоких скоростях.
Так вот, если машина едет очень быстро, она будет скользить по склону, двигаясь по кругу. Если он будет двигаться медленно, он поскользнется.
Если автомобиль не имеет тенденции к скольжению, силы и ускорение, действующие на кузов, будут такими, как на этой диаграмме (сила трения отсутствует):
Однако, если бы машина двигалась быстрее, она бы соскользнула по склону при движении по трассе. Поэтому сила трения будет действовать, пытаясь предотвратить это:
.
