Содержание
Упражнения в нахождении однородных членов предложения и их графическом обозначении
Русский язык
ПРЕДЛОЖЕНИЯС ОДНОРОДНЫМИ ЧЛЕНАМИ
Тема: Упражнения в нахождении однородных членов предложения и их графическом обозначении
Цель: совершенствование умений в составлении графических схем предложений
Задачи:
Образовательные:
Развивающие:
Развитие умений находить однородные члены предложения и составлять их графические схемы.
Развитие умений обосновывать постановку запятой или её отсутствие между однородными членами.
Учиться применять полученные знания и умения на практике;
Развивать устную и письменную речь;
Воспитательные:
Ι. Актуализация знаний.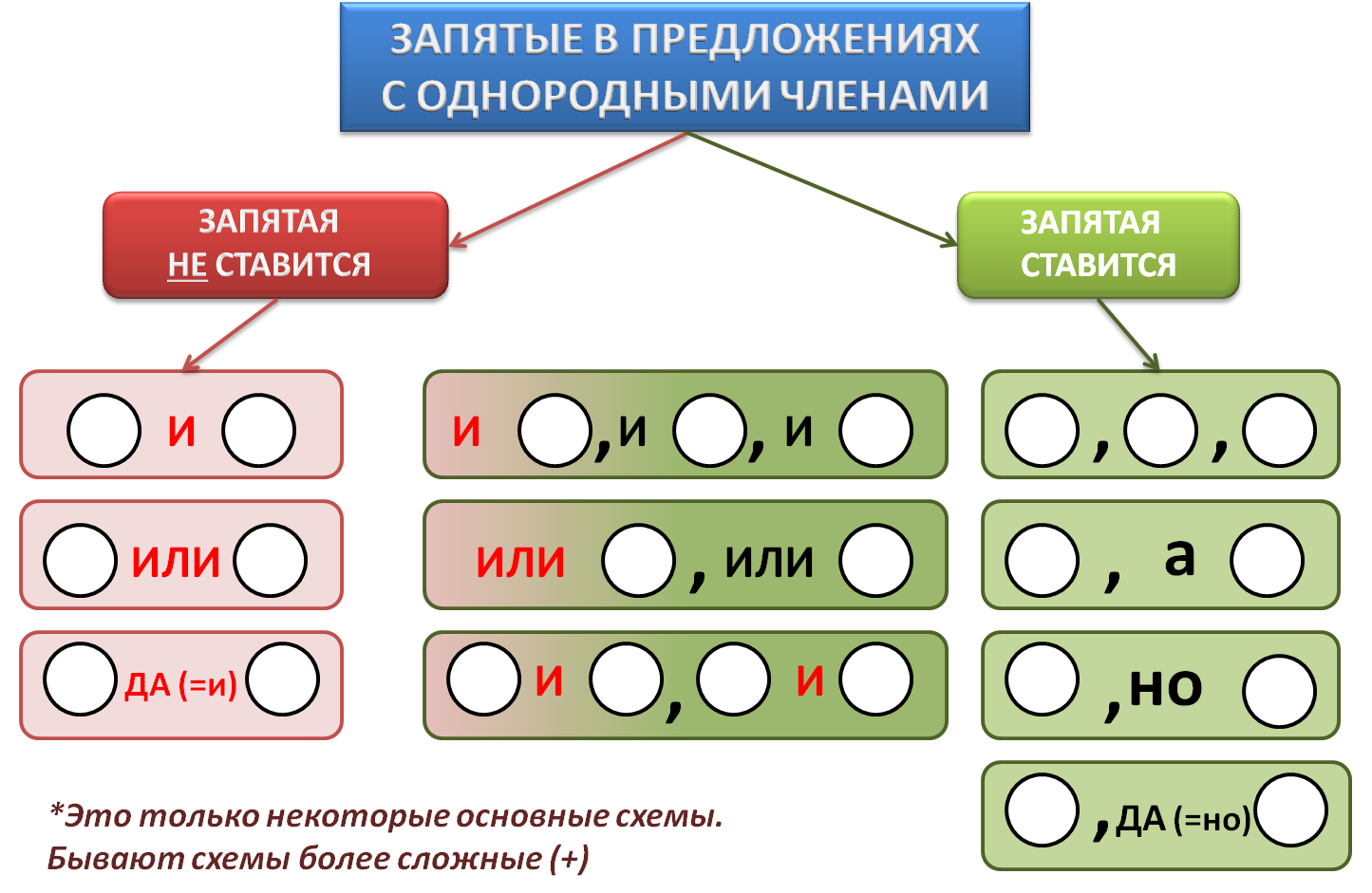
– Откройте тетрадь.
– Что надо записать? (Дату.)
Комментированная запись числа.
– Напишите «Классная работа».
Языковая разминка с элементами проверки домашнего задания.
1. – Дополните предложения словарными словами. Запишите, обозначьте орфограммы.
В полях расцвели ______, _____ ,_____. (Ромашки, васильки, колокольчики.)
В корзине лежали спелые ____, ____и ____. (Яблоки, абрикосы и мандарины.)
– Составим схемы этих предложений.
– Прочитайте грамматическую основу первого предложения.
– Какие члены здесь однородные? Как они обозначаются графически?
– Какая схема получилась? ( – , – , – . )
Схема второго предложения: ( – , – – . )
)
– Сравните схемы предложений.
2. – Прочитайте предложения из домашней работы.
– Составьте схему одного из прослушанных предложений (это может быть последнее предложение).
Познавательные УУД
1. Развиваем умения извлекать информацию из схем, иллюстраций, текстов.
2. Представлять информацию в виде схемы.
3. Выявлять сущность, особенности объектов.
4. На основе анализа объектов делать выводы.
5. Обобщать и классифицировать по признакам.
6. Ориентироваться на развороте учебника.
7. Находить ответы на вопросы в иллюстрации.
II. Формулирование проблемы.
– На основе выполненных заданий сформулируйте цель урока. (Научиться составлять схемы предложений с однородными членами.)
(Научиться составлять схемы предложений с однородными членами.)
III. Развитие умений.
1. Актуализация изученного.
Беседа-опрос.
– Что такое главные члены предложения?
– Что такое однородные члены предложения?
– Как называется предложение, если в нём только главные члены?
– Если в предложении есть только одно сказуемое и при нём три подлежащих, то какое это предложение: распространённое или нераспространённое? (Нераспространённое.)
– Как ещё называется такое предложение? (С однородными членами.)
– Какие члены предложения могут быть однородными?
2. Работа в учебнике.
Упр. 427 – развивается умение находить однородные подлежащие и сказуемые, составлять графические схемы.
После самостоятельного выполнения на доске три ученика выполняют графические схемы предложений.
3. Наблюдение над постановкой запятой между однородными членами.
а) Упр. 428 – совершенствуются умения находить однородные сказуемые, составлять графические схемы предложений с однородными
сказуемыми и выявлять закономерности в постановке знаков препинания между однородными членами.
Выполняется самостоятельно в группах (один человек из группы – капитан – выполняет на листочке, который затем передаётся в другую группу).
Взаимопроверка.
– Когда между однородными сказуемыми ставится запятая? Прочитайте такие предложения.
– Когда между однородными членами не ставится запятая? Есть ли такое предложение в тексте? (Да. Второе предложение.)
б) – Проверьте свои наблюдения по тексту правила в рамке на с. 163.
163.
Чтение правила про себя.
– Что разделяет однородные члены в письменной речи? (Запятая.)
– А что соединяет? (Союз и.)
– Какой основной знак между однородными членами? (Запятая.)
– Что «мешает» его постановке? (Союз и.)
4. Выборочное письмо.
– Прочитайте предложения, представленные на слайде (доске).
– Выпишите предложения:
I вариант: с однородными сказуемыми;
II вариант: с однородными подлежащими.
– Покажите графически, какие члены предложения однородные.
Дым быстро поднимается кверху столбами.
Проснулись рыбаки в шалаше и сняли с шестов сети.
Мелькают в тумане леса и луга.
Личностные результаты
1. Развиваем умения выказывать своё отношение к героям, выражать свои эмоции.
Развиваем умения выказывать своё отношение к героям, выражать свои эмоции.
2. Оценивать поступки в соответствии
с определённой ситуацией.
3. Формируем мотивацию к обучению
и целенаправленной познавательной деятельности.
Коммуникативные УУД
1. Развиваем умение слушать и понимать других.
2. Строить речевое высказывание в соответствии с поставленными задачами.
3. Оформлять свои мысли в устной форме.
4. Умение работать в паре.
IV. Итог урока.
– Проверьте понимание темы, выполнив задание № 1, тема 12 в рабочей тетради.
– Что помогло вам в нахождении предложения с однородными членами? (Союз и.)
– Какие однородные члены он соединяет? (Однородные сказуемые. )
)
V. Домашнее задание.
1. Упр. 1, с. 170–171.
2. Подготовить рассказ о знаках препинания между однородными членами.
Синтаксический разбор простого предложения
Строение и значение простого предложения изучается начиная с 5 класса. Полный набор признаков простого предложения обозначается в 8 классе, а в 9 классе основное внимание уделяется сложным предложениям.
В этом виде разбора соотносятся уровни морфологии и синтаксиса: ученик должен уметь определять части речи, узнавать их формы, находить союзы, понимать способы связи слов в словосочетании, знать признаки главных и второстепенных членов предложения.
Начнём с самого простого: поможем ребятам подготовиться к выполнению синтаксического разбора в 5 классе. В начальной школе ученик запоминает последовательность разбора и выполняет его на элементарном уровне, указывая грамматическую основу, синтаксические связи между словами, вид предложения по составу и цели высказывания, учится составлять схемы и находить однородные члены.
В начальной школе используются разные программы по русскому языку, поэтому уровень требований и подготовка учащихся разные. В пятом классе я принимала детей, обучавшихся в начальной школе по программам образовательной системы «Школа 2100», «Школа России» и «Начальная школа XXI века». Отличия есть и большие. Учителя начальной школы проделывают колоссальную работу, чтобы компенсировать недостатки своих учебников, и сами «прокладывают» преемственные связи между начальной и средней школой.
В 5 классе материал по разбору предложения обобщается, расширяется и выстраивается в более полную форму, в 6-7 классах совершенствуется с учётом вновь изученных морфологических единиц (глагольные формы: причастие и деепричастие; наречие и категория состояния; служебные слова: предлоги, союзы и частицы).
Покажем на примерах отличия между уровнем требований в формате синтаксического разбора.
|
В 4 классе
|
В 5 классе
|
|
В простом предложении выделяется грамматическая основа, над словами обозначаются знакомые части речи, подчёркиваются однородные члены, выписываются словосочетания или рисуются синтаксические связи между словами.
Сущ.(главное слово)+прил.,
Гл.(главное слово)+сущ.
Гл.(главное слово)+мест.
Нареч.+гл.(главное слово)
|
Синтаксические связи не рисуются, словосочетания не выписываются, схема и основные обозначения такие же, но характеристика иная: повествовательное, невосклицательное, простое, двусоставное, распространённое, осложнено однородными сказуемыми.
Разбор постоянно отрабатывается на уроках и участвует в грамматических заданиях контрольных диктантов.
|
|
В сложном предложении подчёркиваются грамматические основы, нумеруются части, над словами подписываются знакомые части речи, указывается вид по цели высказывания и эмоциональной окраске, по составу и наличию второстепенных членов. Схема разбора: [О и О]1, [ ]2, и [ ]3.
|
Схема остаётся той же, но характеристика иная: повествовательное, невосклицательное, сложное, состоит из 3 частей, которые связаны бессоюзной и союзной связью, в 1 части есть однородные члены, все части двусоставные и распространённые.
Разбор сложного предложения в 5 классе носит обучающий характер и не является средством контроля.
|
|
Схемы предложения с прямой речью: А: «П!» или «П,» — а. Вводится понятие цитаты, совпадающее по оформлению с прямой речью.
|
Схемы дополняются разрывом прямой речи словами автора: «П, — а. — П.» и «П, — а, — п». Вводится понятие диалога и способы его оформления.
Схемы составляют, но характеристика предложений с прямой речью не производится.
|
План разбора простого предложения
1. Определить вид предложения по цели высказывания (повествовательное, вопросительное, побудительное).
Определить вид предложения по цели высказывания (повествовательное, вопросительное, побудительное).
2. Выяснить тип предложения по эмоциональной окраске (невосклицательное или восклицательное).
3. Найти грамматическую основу предложения, подчеркнуть её и обозначить способы выражения, указать, что предложение простое.
4. Определить состав главных членов предложения (двусоставное или односоставное).
5. Определить наличие второстепенных членов (распространённое или нераспространённое).
6. Подчеркнуть второстепенные члены предложения, указать способы их выражения (части речи): из состава подлежащего и состава сказуемого.
7. Определить наличие пропущенных членов предложения (полное или неполное).
8. Определить наличие осложнения (осложнено или не осложнено).
9. Записать характеристику предложения.
10. Составить схему предложения.
Для анализа мы использовали предложения из прекрасных сказок Сергея Козлова про Ёжика и Медвежонка.
1) Это был необыкновенный осенний день!
2) Обязанность каждого — трудиться.
3) Тридцать комариков выбежали на поляну и заиграли на своих писклявых скрипках.
4) У него нет ни папы, ни мамы, ни Ёжика, ни Медвежонка.
5) И Белка взяла орешков и чашку и поспешила следом.
6) И они сложили в корзину вещи: грибы, мёд, чайник, чашки — и пошли к реке.
7) И сосновые иголки, и еловые шишки, и даже паутина — все распрямились, заулыбались и затянули изо всех сил последнюю осеннюю песню травы.
8) Ёжик лежал, по самый нос укрытый одеялом, и глядел на Медвежонка тихими глазами.
9) Ёжик сидел на горке под сосной и смотрел на освещённую лунным светом долину, затопленную туманом.
10) За рекой, полыхая осинами, темнел лес.
11) Так до самого вечера они бегали, прыгали, сигали с обрыва и орали во всё горло, оттеняя неподвижность и тишину осеннего леса.
12) И он прыгнул, как настоящий кенгуру.
13) Вода, куда ты бежишь?
14) Может, он с ума сошёл?
15) Мне кажется, он вообразил себя. .. ветром.
.. ветром.
Образцы разбора простых предложений
Скачать образцы разборов в формате .doc 75,5 КБ
Урок 9 ОДНОРОДНЫЕ ЧЛЕНЫ ПРЕДЛОЖЕНИЯ | Поурочные планы по русскому языку 4 класс
Урок 9 ОДНОРОДНЫЕ ЧЛЕНЫ ПРЕДЛОЖЕНИЯ
24.07.2013
12141
0
Ц
е л ь: ознакомить с особенностями однородных членов
предложения.
Х
о д у р о к а
I. Орфографическая минутка.
Учащиеся
под диктовку записывают слова:
Буфет,
берет, акробат, вопрос, гладкий, глазки, лопатка, лодка, монетка, косьба,
комнатка, краска, крепко, мягкий, узкий.
Подчеркните
«ошибкоопасные» места, проанализируйте их написание.
–
Что объединяет эти слова? (Парные согласные.)
Устно
выполняется к о л л е к т и в н а я п р о в е р к а.
II. Актуализация опорных знаний.
И
г р а «Найди пару».
О
п и с а н и е. На доске записаны предложения и даны их схемы, но порядок
расположения предложений и схем не соответствует правильному выбору.
Учащиеся
должны соединить стрелкой схему с соответствующим предложением, то есть «найти
пару»: предложение и его схему.
1. Ребята поставили в классе 2. Там плавают маленькие рыбки. 3. Ребята ухаживают за аквариумом. | 1. 2. 3. |
III. Наблюдения над особенностями
однородных членов и употреблением в речи предложений с однородными членами.
1.
П о с т а н о в к а у ч е б н о й з а д а ч и.
–
Прочитайте в учебнике название темы, которую мы начинаем изучать.
–
Какова ваша задача сегодня на уроке? (Нам нужно узнать, какие члены
предложения называются однородными и с какой целью мы их употребляем в речи. )
)
Н
а д о с к е записаны три предложения.
1)
В саду 2)
В саду 3)
В саду
–
Подумайте, нельзя ли сказать о том же самом, но кратко. Можно ли из трех
предложений составить одно?
–
Запишите получившееся предложение и подчеркните грамматическую основу.
Учащиеся
записывают в тетрадях предложение:
–
Какое предложение получилось? Для чего в речи нужны такие предложения? (У
нас получилось предложение, в котором три подлежащих и одно сказуемое. Нужны
нам в речи такие предложения для того, чтобы сделать нашу речь более краткой,
более четкой.)
IV. Формирование новых знаний.
1.
В ы п о л н е н и е упражнения 24 устно.
На
доске составляют схемы двух первых предложений.
1-е предложение | 2-е |
Учащиеся
анализируют схемы и отвечают на вопросы:
–
Чем отличаются предложения по составу?
–
Является ли первое предложение распространенным? А второе?
З
а д а н и е. Прочитайте сведения о языке на с. 14.
Прочитайте сведения о языке на с. 14.
–
Посмотрите на схемы, составленные к упражнению 24. В каком предложении есть
однородные подлежащие?
2.
В ы п о л н е н и е упражнения 25.
–
Выпишите предложения, в которых при одном сказуемом два подлежащих. Разберите
эти предложения по составу.
–
Как вы думаете, однородными членами предложения могут быть только подлежащие?
3.
В ы п о л н е н и е упражнения 26 по заданию учебника.
–
Прочитайте сведения о языке на с. 15. Верно ли вы рассуждали?
V. Распознавание однородных подлежащих и
сказуемых в предложении.
1.
В ы п о л н е н и е упражнения 28.
Р
а б о т а проводится по вариантам.
В
а р и а н т I – выписывают предложения с однородными подлежащими, разбирают
их по составу.
В
а р и а н т II – выписывают предложения с однородными сказуемыми и разбирают
их по составу.
–
Обменяйтесь тетрадями с соседом по парте и проверьте работу товарища.
Коллективно
проводится лексическая работа и разбираются слова по составу.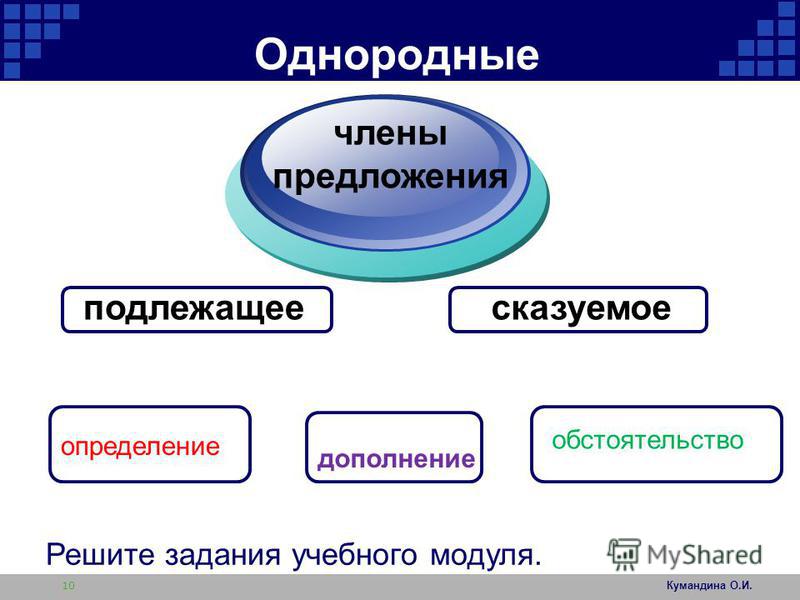
VI. Итог урока.
–
Что нового узнали на уроке?
–
Какие однородные члены предложения вы знаете?
–
Предположите, могут ли быть однородными членами дополнения, обстоятельства и
определения. А вот верно ли вы предполагаете, мы узнаем на следующем уроке.
Домашнее задание: упражнение
27.
Однородные члены предложения
Арасланова Светлана Викторовна, учитель русского языка и литературы МОУ «Увинская СОШ № 4» п.Ува Увинского района Удмуртской Республики
Однородные члены предложения. Обобщение изученного материала
Цель урока: повторить и систематизировать сведения об однородных членах
Задачи:– образовательная: способствовать выработке умений и навыков по применению знаний об однородных членах предложения на письме, различать однородные и неоднородные определения, строить структурные схемы предложения, развитие умения составлять предложения по схемам
– развивающая: формировать умения лаконично, полно и содержательно отвечать, делать обобщающие выводы, развивать наглядно-образное мышление, память и умение сравнивать и анализировать
–воспитательная: содействовать воспитанию рационального распределения времени и ответственному отношению к предмету, воспитывать интерес к книге, чтению
Тип урока: обобщение материала
УМК:Русский язык 8 класс под редакцией М.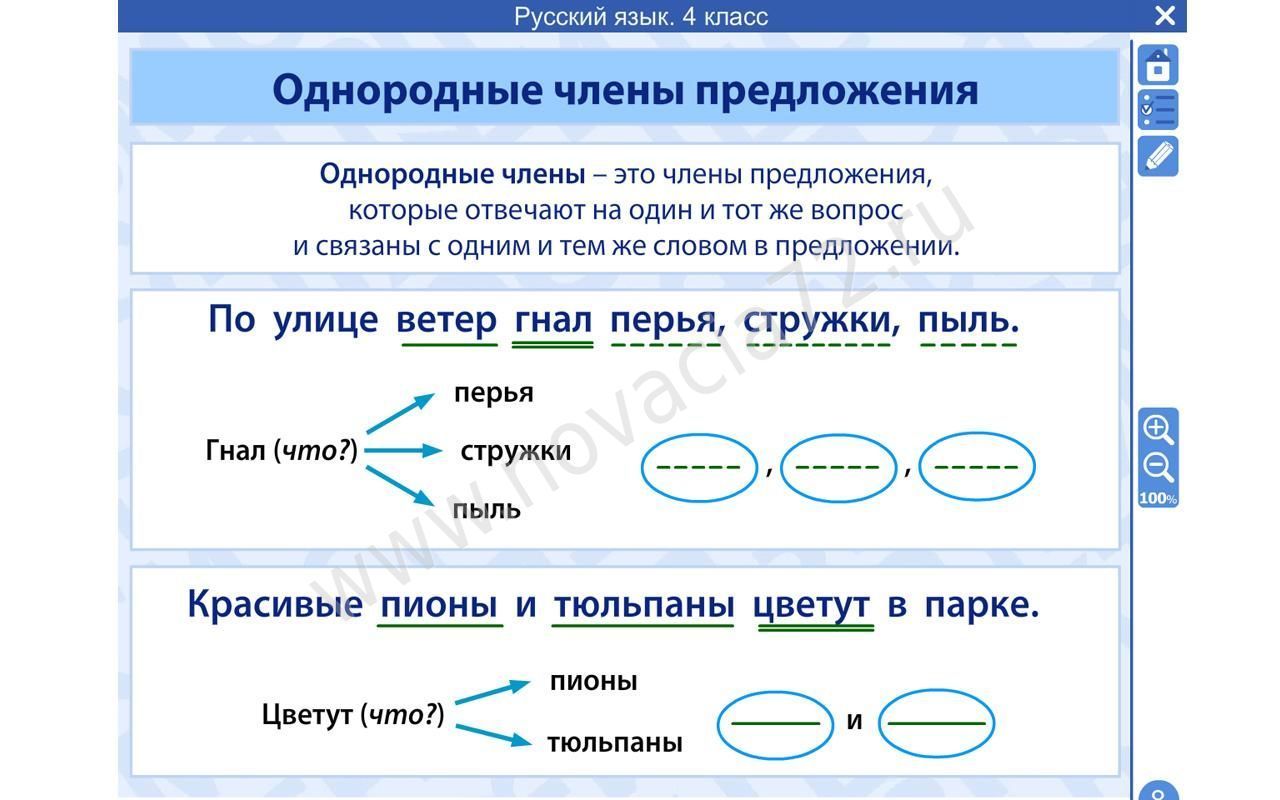 М.Разумовской, П.А.Леканта
М.Разумовской, П.А.Леканта
Методы организации учебной деятельности:
фронтальная
индивидуальная
ученик – учитель
ученик – схема
Оборудование: опорные таблицы, индивидуальные карточки с текстом, толковый словарь, индивидуальные карточки с тестовыми вопросами
Ход урока
Мотивационно – целевой и ориентировочный этап
— Тема сегодняшнего урока «Повторение и обобщение изученного об однородных членах предложения». Мы должны с вами обобщить материал по теме и подготовиться к контрольной работе.
— Как вы думаете, на какие вопросы мы будем сегодня искать вопросы?
Какие члены предложения называются однородными?
Какие союзы могут связывать однородные члены?
В каких случаях при однородных членах предложения ставим запятые?
В каких случаях запятые не ставятся?
Что можете сказать о знаках препинания при обобщающих словах при однородных членах?
Какие слова могут употребляться как обобщающие слова?
— А какие источники информации могут помочь нам в случае затруднения?
(учебники, справочники, карточки – схемы)
На этом уроке мы продолжим изучение и закрепление знаний об однородных членах и обобщающих словах при них, а также будем работать над закреплением навыков постановки запятых, тире и двоеточия в предложениях с однородными членами и обобщающими словами
Практический этап
Работа над повторением и закреплением материала
1) ответить на вопросы:
Какие члены предложения называются однородными?
Какие союзы могут связывать однородные члены?
В каких случаях при однородных членах предложения ставим запятые?
В каких случаях запятые не ставятся?
Что можете сказать о знаках препинания при обобщающих словах при однородных членах?
Какие слова могут употребляться как обобщающие слова?
2) построить схемы данных предложений (предложения не писать):
В лесу и на полях всё было занесено снегом.
На земле как-то тихо и голо без пшеницы, и ржи, и овса.
Май леса наряжает и лето в гости приглашает.
Со всех сторон: из-за заборов, из калитки и изо всех углов – посыпались выстрелы.
2)Синтаксический разбор предложения.
Составьте предложение, выполнив следующие действия:
— возьмите подлежащее предложения Хорошая книга позволяет за несколько часов прожить чужую жизнь. (Книга)
— из предложения Добрая книга добру учит возьмите определение, поставьте его в форму мужского рода, единственного числа, именительного падежа. (Добрый)
— из предложения За вину умный винит себя выпишите подлежащее, выраженное прилагательным.(Умный)
— из предложения Старый друг лучше новых двух выпишите подлежащее. (Друг)
б) Сделайте синтаксический разбор полученного предложения (Книга-добрый, умный и честный друг), составьте его схему.
в) Согласны ли вы с этим утверждением? Составьте небольшое рассуждение (работа в тетрадях).
3)работа с текстом «Чудодейственное средство»
Я летал над бе..конечными просторами тайги (одно)образным безмолвием тундры над ледя..ыми торосами Заполярья и над ра..калёнными барханами (средне)азиатских пустынь. (На)чём только (н..)летал на истребителях бомбардировщиках на т..жёлых транспортных машинах и штурмовиках на самолётах (винто)моторных и реактивных. Мне довелось спасать людей потерпевших бе..ствие во льдах Чуко..ского моря. Три года командуя авиацио..ым корпусом штурмовиков я провёл в боях с фашис..кими захватчиками.
Но всего этого могло (со)мной и (н..)быть, (н..)найди я в своё время (чудо)действенного лекарства. (Н..)было(бы) в моей судьбе н.. т..жёлых и героических фронтовых лет н.. космодрома Байконур, н.. тридцати правительстве..ых наград во главе со Звездой Героя. И жизнь моя была(бы) куда бедней событиями, куда менее интересной и содержательной.
(Не)обыкнове..ое лекарство, которое позволило мне забыть о болезнях и сохранить высокую (работо)способность на десятки лет, это (физ)культура. Лекарство очень даже простое и доступное.
Лекарство очень даже простое и доступное.
(По Н.П.Каманину)
Выполнение заданий по данному тексту:
1.Прочитайте текст.
2. Встретились ли вам в тексте незнакомые слова? Объясните значение этих слов
(Торосы – ледяные глыбы, образующиеся при сжатии льдов.
Барханы – песчаные холмы в пустыне). Сверьтесь со словарем.
О чём идёт речь в данном тексте?
Объясните, какие буквы пропущены в отдельных словах и почему вы выбрали именно эти буквы.
Найдите в тексте предложение с обособленным определением. Расскажите, какие знаки ставятся при обособленных определениях.
Найдите в тексте предложение с обособленным обстоятельством.
Найдите предложения с однородными членами. Объясните знаки препинания при однородных членах.
Выпишите предложение с обобщающим словом при однородных членах и составьте его схему.
Рефлексивно – оценочный этап
— Ребята, как вы думаете, мы достигли поставленной цели?
— А что мы для этого сделали?
— Как вы думаете, справитесь с тестовыми вопросами по теме?
Тест с выбором ответа
Вариант 1.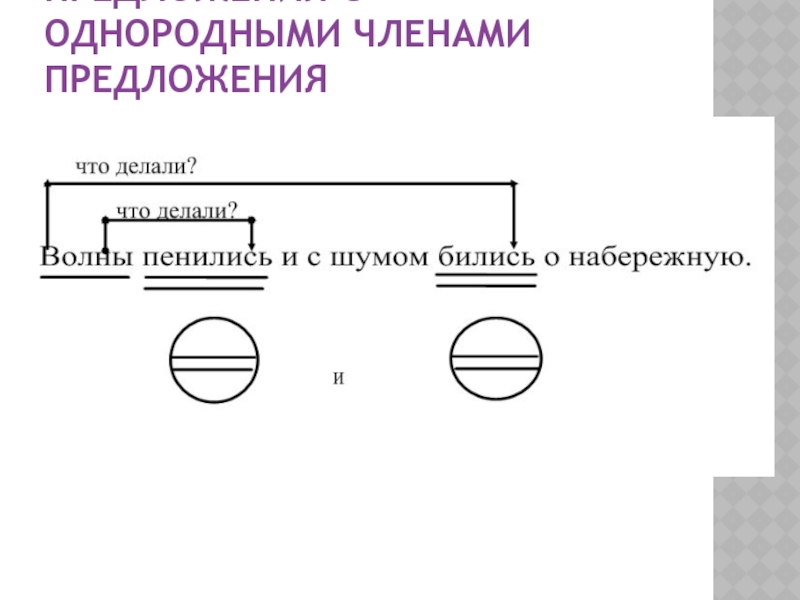
1.Укажите, как нужно расставить знаки препинания в предложении:
Всё в облике матроса (1) русые волосы, белые глаза, тонкие губы (2) всё напоминало скорее Финляндию, нежели Кострому, его родину.
1- тире, 2- двоеточие
1- тире, 2- тире
1- двоеточие, 2- запятая
1- двоеточие, 2- тире
2.Укажите предложение с однородными членами.
Ты сер, а я, приятель, сед.
На одном месте и камень мохом обрастает.
Не делайте упражнение, не вспомнив правило.
Мы ехали по отлогостям гор, то взбираясь вверх, то опускаясь.
3.Какие однородные члены и какие союзы используются в предложении:
Финский залив и вдали от берега весь усеян мелями, зато превосходно обставлен маяками.
однородные сказуемые; противительный союз
однородные сказуемые; соединительный и разделительный союзы
однородные сказуемые и дополнения; противительный союз
однородные сказуемые и дополнения; соединительный и противительный союзы
4. Найдите предложения, в которых допущены пунктуационные ошибки.
Найдите предложения, в которых допущены пунктуационные ошибки.
А звёзды нежданно в тумане блеснули и свет свой холодный под липами льют.
Синицы, скворцы, живущие в наших лесах — истребители вредных насекомых.
И дубы на холмах, и барашки кустов, и даже лошадь с маленьким жеребёнком кажутся синими.
Странный свет приближался и двигался над зарослями кустов и стволами спиленных осин, и берёз.
5.Укажите предложение с однородными определениями (знаки препинания не проставлены).
Он легко справлялся с трудными математическими задачами.
Приятный нежный голосок птички звенел не умолкая.
Незатейливая деревянная резьба наличников привлекла его внимание.
Окна в бревенчатом доме под железной ржавой крышей были темны.
6.Укажите предложение, в котором перед союзом да (да и) нужна запятая.
Учился читать да писать, а выучился петь да плясать.
Тишина нарушалась только однообразным всплеском волн да жужжанием насекомых.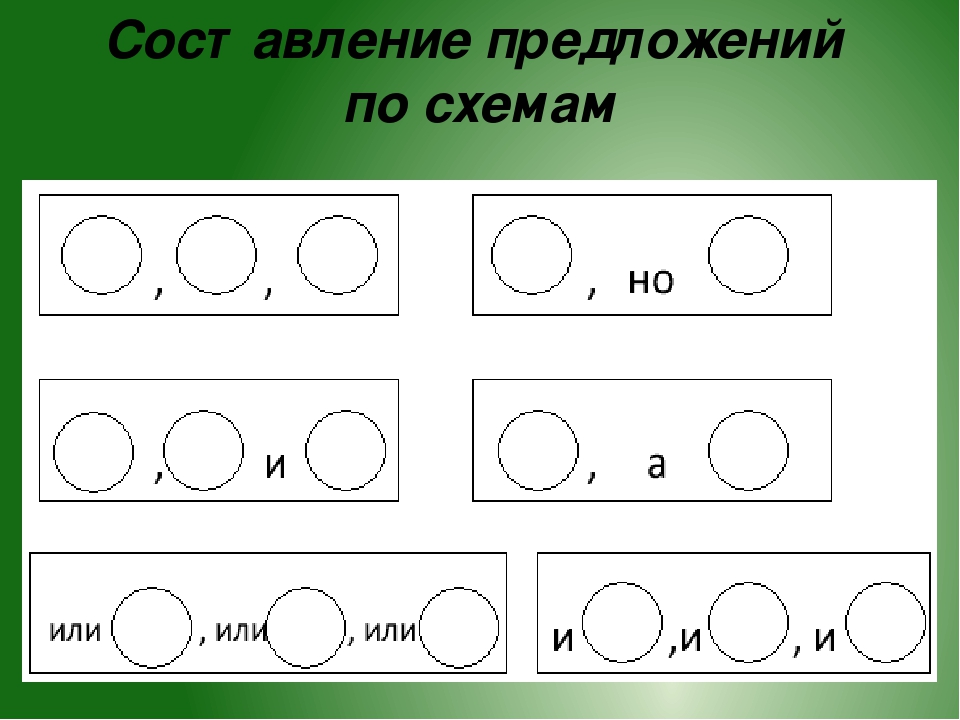
Ум имей хоть маленький да свой.
Богатырским сном угостил их Калина да ещё каких-то особо звонких птиц припас на пробуждение.
7.Какая пунктуационная ошибка допущена в одном из предложений:
Гость и недолго гостит да много видит.
В тайге растут как хвойные, так и лиственные деревья.
Небо было всё время облачно, и нельзя было видеть ни восхода, ни заката.
а) недостаёт запятой перед ДА в предложении 1.
б) недостаёт запятой перед КАК в предложении 2.
в) недостаёт запятой после слова “видеть” в предложении 3.
г) поставлена лишняя запятая перед И в предложении 3.
8. Укажите, как нужно расставить знаки препинания в предложении:
Во всех языках мира (1) арабском, китайском, эскимосском и прочих (2) есть глаголы и существительные.
а)1- двоеточие, 2- тире
б)1- двоеточие, 2- запятая
в)1- тире, 2- запятая
г)1- запятая
9.Укажите предложение с однородными членами.
1)Согласному стаду и волк не нужен.
2)Саша неплохо закончил школу, но вступительный экзамен в институте не сдал.
3)Не было бы счастья, да несчастье помогло.
4)Море колыхалось целой массой, как густой расплавленный металл.
10. Найдите предложение, соответствующее схеме: [О, и О, и О, и О]
а) Учёные и инженеры конструкторы и техники участвуют в создании этого проекта.
б) На картинах Сурикова вы увидите Петра 1 и стрельцов и царевну Софью и покорителей Сибири.
в) Но работник был далеко и ничего не слыхал и не видел.
г) Лоси и медведи и волки и лисы и многие другие звери водятся здесь.
Проверка: 1 — 4; 2 – 4; 3 – 1; 4 – 4; 5 – 2; 6 – 3; 7 – а; 8 – 1; 9 – 2; 10 – б
Домашнее задание: подготовиться к контрольному диктанту по теме “Однородные члены предложения”, выполнить упр.219 (стр.149)
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/207166-odnorodnye-chleny-predlozhenija
Однородные члены предложения | Коллекции учебных материалов
Однородные члены предложения
Однородные члены – это члены предложения, связанные с одним и тем же словом и отвечающие на один и тот же вопрос. Они равноправны, не зависят друг от друга и являются одним и тем же членом предложения. Между собой они соединены сочинительной или бессоюзной синтаксической связью.
Сочинительная связь выражена интонационно и с помощью сочинительных союзов: одиночных или повторяющихся. Бессоюзная связь выражена интонационно.
Я люблю мороженое. (простое двусоставное распространённое предложение)
Я люблю мороженое, шоколад, печенье и торты. (простое двусоставное распространённое предложение, осложнённое однородными членами)
Любой член предложения может быть выражен рядом однородных членов. Однородными могут быть подлежащие, сказуемые, дополнения, определения и обстоятельства.
В зале были мальчишки, девчонки и их родители. (мальчишки, девчонки и их родители – однородные подлежащие)
Девочка воспитанна и прекрасно образованна. (воспитанна и образованна – однородные сказуемые)
Я любил книжки , конструкторы и мультфильмы. (книжки, конструкторы, мультфильмы – однородные дополнения)
Все дни мы проводили в лесу или на речке. (в лесу, на речке – однородные обстоятельства)
Был ясный, жаркий, по-настоящему летний день. (ясный, жаркий, летний – однородные определения)
Чаще всего однородные члены предложения выражаются словами одной части речи, но возможны и такие однородные члены, которые выражены словами разных частей речи, словосочетаниями и фразеологизмами. То есть однородные члены могут быть по-разному оформлены грамматически. Девочка отвечала на экзамене бойко, толково, прекрасным языком.
(однородные обстоятельства, выраженные наречиями бойко, толково и именным словосочетанием прекрасным языком)
Осложнение однородными членами может быть по-разному введено в предложение и быть по- разному оформлено пунктуационно. Однородные члены предложения, как было сказано выше, образуют сочетание слов на основе сочинительной и/или бессоюзной связи. Если это второстепенные члены предложения, то связь со словами, от которых они зависят, подчинительная. Однородные члены в устной речи оформлены интонационно, а в письменной речи пунктуационно.
В одном предложении может быть несколько рядов однородных членов.
Маша, Серёжа и Петя сидели вокруг стола в столовой и рисовали.
(Маша, Серёжа и Петя – однородные подлежащие – 1-й ряд однородных членов)
(сидели и рисовали – однородные сказуемые – 2-й ряд однородных членов)
Знаки препинания при однородных членах без обобщающего слова
Главным знаком при оформлении однородных членов без обобщающего слова является запятая.
Запятая ставится:
1) между однородными членами, не связанными союзами, например:
Сотрудники музея тщательно хранили коллекции, систематизировали, изучали их, организовывали выставки, публиковали научные статьи.
Схема: о, о, о, о, о (здесь и далее: о – однородный член)
2) между однородными членами, связанными противительными союзами а, но, да (в значении но), однако, зато, например:
Сотрудники музея тщательно хранили коллекции, систематизировали, изучали их, но организовать выставку в то время они не могли.
Схема: о, о, о, но о
3) между однородными членами, связанными повторяющимися союзами:
сочинительными и, да (в значении и), ни… ни и разделительными или, либо, то… то, то ли… то ли, не то… не то) , например:
Сотрудники музея и хранили коллекции, и систематизировали, и изучали их, и организовывали выставки, и публиковали научные статьи.
Схема: и о, и о, и о, и о, и о
4) перед второй частью двойных союзов не только…, но и…; как…, так и…; не столько…, сколько; хотя и…, но…; если не…, то и др., например:
Сотрудники музея не только хранили коллекции, но и систематизировали, изучали их, организовывали выставки, публиковали научные статьи.
Схема: не только о, но и о, о, о, о
5) между парными однородными членами, связанными союзами и и или, например:
Сотрудники музея тщательно хранили коллекции и изучали их, организовывали выставки и публиковали научные статьи.
Схема: о и о, о и о
Запятая не нужна:
1) между двумя однородными членами, если они связаны одиночным союзом, например:
Сотрудники музея тщательно хранили коллекции, изучали и систематизировали их.
Схема: о, о и о
2) между двумя однородными членами, если они связаны одиночным союзом в пару, например:
Сотрудники музея тщательно хранили коллекции и изучали их.
Схема: о и о
2) в устойчивых сочетаниях, например:
ни пуха ни пера, и смех и грех, ни свет ни заря
Запятые не ставятся, если несколько определений не являются однородными членами, например:
Андрюшка играл новой жёлтой маленькой машинкой.
Знаки препинания при однородных членах с обобщающим словом
Предложения с однородными членами с обобщающим словом имеют особенности в пунктуационном оформлении:
1) если обобщающее слово стоит перед однородными членами, то после него нужно двоеточие, например:
Сотрудники музея делали всё возможное: тщательно хранили коллекции, изучали, систематизировали их, организовывали выставки и публиковали научные статьи.
Схема: обоб.сл.: о, о ,о, о и о (здесь и далее: обоб.сл. – обобщающее слово, о – однородный член)
2) если обобщающее слово стоит после однородных членов, то перед ним нужно тире, например:
Сотрудники музея тщательно хранили коллекции, изучали, систематизировали их, организовывали выставки и публиковали научные статьи – делали всё возможное.
Схема: о, о, о, о и о – обоб.сл.
Примечание:
1. Если обобщающее слово стоит перед однородными членами, но после них предложение продолжается, то ряд однородных членов и продолжение предложения разделяются тире, например:
В центре Москвы повсюду: на бульварах, у станций метро, на больших улицах — появился прокат велосипедов.
Сотрудники музея делали всё возможное: тщательно хранили коллекции, изучали, систематизировали их, организовывали выставки и публиковали научные статьи – никто не смог бы в те годы сделать больше.
Схема: обоб.сл.: о, о, о, о и о — …
2. Если после обобщающего слова стоят слова: например, то есть, а именно, как то и др. под., то их разграничивает запятая, а данные слова и однородные члены – двоеточие.
Сотрудники музея делали всё возможное, а именно: тщательно хранили коллекции, изучали, систематизировали их, организовывали выставки и публиковали научные статьи.
Схема: обоб.сл., то есть: о, о, о, о и о
3. Если после однородных членов перед обобщающим словом стоят вводные слова: короче говоря, иначе говоря, одним словом, словом, другими словами и др. под., то перед вводными словами ставится тире, а после них – запятая, например:
Сотрудники музея тщательно хранили коллекции, изучали, систематизировали их, организовывали выставки, публиковали статьи – другими словами, делали всё возможное для сохранения культурного наследия края.
Схема: о, о, о, о и о – другими словами, …
Задание. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не расставлены.)
1) По сторонам тропы высокими и крутыми стенами стоял шиповник и цвел алым и влажным огнем.
2) Видны были только верхушки деревьев да извилистый край противоположного берега. 3) Рука его и лицо и синяя спецовка лоснились от сажи и машинного масла.
4) В атмосфере тайных обществ проходила жизнь Пушкина как в Петербурге так и в дальнейшем на юге.
Вариант ответа №1. Прочитай еще раз Ловушку №1. Находим однородные члены предложения. Здесь их три ряда: высокими и крутыми (какими?, зависят от слова «стенами»), стоял и цвел (что делал?), алым и влажным (каким?, зависят от слова «огнем). Три ряда однородных членов предложения, каждый из которых внутри связан одиночным союзом И, поэтому запятых не требуется. Вариант ответа №2. В предложении один ряд однородных членов: верхушки да край (что?, зависят от слова «были видны»). Они соединены одиночным союзом да в значении и, поэтому запятой не требуется. Вариант ответа №3. В предложении два ряда однородных членов. Во-первых, рука и лицо и спецовка (что?, являются подлежащими), которые соединены повторяющимся союзом и. Расставляем запятые после каждого однородного члена предложения: Рука его, и лицо, и синяя спецовка. Во-вторых, от сажи и масла (от чего?, зависят от «лоснились»), они соединены одиночным союзом и, поэтому запятой не требуется. Вариант ответа №4. Один ряд однородных членов предложения: как в Петербурге так и на юге (где?, зависят от слова «проходила»). Они связаны двойным союзом как… так и, поэтому запятую поставим только перед второй частью союза, то есть: как в Петербурге, так и на юге. Таким образом, правильный вариант – ответ №4.
Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не расставлены.)
1) Официальная медицина выступает против самолечения и лечения непроверенными средствами.
2) Северные районы оказались неравноценны как по численности жителей так и по возможностям экономического развития.
3) Иногда лекарственные растения полностью теряют свои лечебные свойства или сохраняют их в незначительной степени.
4) Лебеди величаво плыли по реке либо кружили над водой либо отдыхали у своего домика.
Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не расставлены.)
1) На одном и том же кусте сирени я увидел желтые листья и начавшие набухать почки.
2) Гусак разговаривал сам с собой сипловатым басом и подбирал просыпанные семечки. 3) Культура наша сильна не только и не столько столичными деятелями сколько жителями глубинки.
4) Очевидны факты изменения животных и растений под влиянием селекции.
Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не расставлены.)
1) Разговор перескакивал с предмета на предмет и становился бессмысленным и ненужным.
2) Тут были старинный сундучок и часы в футляре и комод со множеством отделений.
3) Дом невелик да лежать не велит.
4) Репин писал Пушкина то с вдохновленным лицом то улыбающимся то смотрящим куда-то вдаль.
Ответы: 2, 3, 3.
При письме части сложного предложения разделяются запятой. Если части сложного предложения соединяют союзы (и, а, но), запятая ставится перед союзом.
Сравниваем схемы предложений и запоминаем правила постановки запятой
Предложения нашего языка очень разнообразны. Иногда при одном подлежащем может быть несколько сказуемых или при одном сказуемом может быть несколько подлежащих. Такие члены предложения называются однородными. Однородные члены отвечают на один и тот же вопрос и относятся к одному и тому же члену предложения. В схеме каждый однородный член мы будем обводить в кружок.
Какой вывод можно сделать из сравнения этих схем?
В первой строке даны схемы сложных предложений, а во второй строке — схемы простых предложений с однородными сказуемыми (они показаны в кружке).
В простых предложениях с однородными членами и в сложных предложениях между их частями используются одни и те же союзы: и, а, но.
Помни!
1. Перед союзами а, но всегда ставится запятая.
2. Союз и требует особого внимания: соединяет однородные члены – запятая чаще всего не ставится; употреблён между частями сложного предложения — запятая обычно нужна.
Вставляем пропущенные запятые в предложениях
Потренируемся. Поставим пропущенные запятые.
1) Ночью собака подкралась к даче и улеглась под террасой.
2) Люди спали и собака ревниво сторожила их. (По Л. Андрееву)
3) Пеликан бродил вокруг нас шипел кричал но в руки не давался. (По К. Паустовскому)
4) Весна сияет на небе но лес ещё по-зимнему засыпан снегом. (М. Пришвин)
1) Ночью собака подкралась к даче и улеглась под террасой.
Предложение простое, так как одна основа, одно подлежащее и два сказуемых — собака подкралась и улеглась. Союз и соединяет однородные сказуемые, поэтому запятая не ставится.
2) Люди спали, и собака ревниво сторожила их.
Предложение сложное, так как две основы – люди спали, собака сторожила. Союз и соединяет части сложного предложения, поэтому перед союзом нужна запятая.
3) Пеликан бродил вокруг нас, шипел, кричал, но в руки не давался.
Предложение простое, так как одна основа, одно подлежащее и 4 сказуемых – пеликан бродил, шипел, кричал, не давался. Перед союзом но всегда ставится запятая. Запятые ставим между однородными сказуемыми.
4) Весна сияет на небе, но лес ещё по-зимнему засыпан снегом.
Предложение сложное, так как две основы – весна сияет, лес засыпан. Перед союзом но всегда ставится запятая.
Вставляем пропущенные запятые в схемах предложений
Рассмотрите схемы и решите, за какими схемами скрываются сложные предложения, а за какими – простые с однородными членами; в каких их них нужно поставить знаки препинания.
Первые три схемы отражают строение простого предложения с однородными главными членами. Они обведены в кружок. В 1 схеме запятая не нужна, так как однородные подлежащие соединяет союз и. Во 2 и 3 схемах должны быть поставлены запятые. 4 схема соответствует сложному предложению. В ней тоже должна быть поставлена запятая между частями сложного предложения.
С каких слов обычно начинается новая часть сложного предложения?
Предложения, в которые входят слова что, чтобы, поэтому, потому что, — чаще всего сложные. С этих слов обычно начинается новая часть сложного предложения. В таких случаях перед ними всегда ставится запятая.
Приведём примеры.
Мы увидели, что волчица пролезла вместе с волчатами в нору.
Это сложное предложение, перед словом что ставится запятая.
Всю ночь зима вязала кружевные узоры, чтобы принарядились деревья. (К. Паустовский)
Это сложное предложение, перед словом чтобы ставится запятая.
Птицы умеют сообщать обо всём голосом, поэтому они поют.
Это сложное предложение, перед словом поэтому ставится запятая.
Я люблю сказки, потому что в них добро всегда побеждает зло.
Это сложное предложение, перед словом потому что ставится запятая.
Подбираем к каждому предложению свою схему
1. Как-то днём Винни — Пух прогуливался по лесу и ворчал себе под нос новую песенку.
2. Винни – Пух вставал рано, по утрам он старательно занимался гимнастикой.
3. Винни незаметно дошёл до песчаного откоса.
(Б. Заходер)
1.
2.
3.
1 предложению соответствует 3 схема, так как это простое предложение с одним подлежащим (Винни-Пух) и двумя сказуемыми (прогуливался и ворчал).
2 предложению соответствует схема 1, так как это сложное предложение имеет две основы (Винни-Пух вставал, он занимался). Запятая разделяет части предложения.
3 предложению соответствует 2 схема, так как это простое предложение с одной основой (Винни дошёл).
Заключение
На уроке вы узнали, что предложение, в котором две и больше грамматических основ,- сложное предложение. Части сложных предложений соединяются при помощи интонации и союзов а, и, но. При письме части сложного предложения разделяются запятой.
ПУНКТУАЦИЯ — это собрание правил расстановки знаков препинания, а также сама система знаков препинания.
4 класс. Однородные члены предложения. Проверочная работа с. 15 – 17
Ответы по русскому языку. 4 класс. Проверочные и контрольные работы. Максимова Т.Н.
ОДНОРОДНЫЕ ЧЛЕНЫ ПРЕДЛОЖЕНИЯ
Проверочная работа
Ответы к стр. 9 – 12
В а р и а н т 1
1. Рассмотри схемы. Поставь пропущенные запятые.
а) Ο, О и О б) О, а О и О в) О, О, но О
2. Поставь, где надо запятые.
Дети увидели в лесу ёжика, но не пошли к нему.
Птичка примчалась из-за моря, села и запела.
Пронеслись с шумом дрозды и скрылись вдали.
3. Поставь нужные знаки в конце предложений. Подчеркни повествовательное предложение, в котором есть однородные подлежащие.
Как там оказались собака и кот?
Как уютно устроились под елью боровик и нарядный мухомор!
На юг потянулись журавли и крикливые гуси.
Утро было сырое и прохладное.
4. Вставь пропущенные буквы, расставь знаки препинания. Найди предложение с однородными сказуемыми и подчеркни его.
Только осенью можно оценить красоту ясеня, осины, рябины, клёна. Листья осины жёлтые, малиновые, пурпурные. Хорошо смотреть на осенние деревья при закате. Лес весь лучится, сверкает, светится.
5. Раздели текст на предложения. Расставь необходимые знаки препинания.
У кумушки лисы зубки острые, рыльце тоненькое, ушки на макушке, хвостик на отлёте, шубка тёпленькая. Хорошо кума принаряжена: шерсть пушистая, мягкая. На груди жилет, а на шее белый галстучек.
В а р и а н т 2
1. Рассмотри схемы. Поставь пропущенные запятые.
а) Ο, О, а О б) О, но О и О в) О, О и О
2. Поставь, где надо запятые.
Через разрывы облаков можно видеть поля, леса, дороги, селения.
В городе много парков, аллей и площадей.
День был сырой, пасмурный, но тёплый.
3. Поставь нужные знаки в конце предложений. Подчеркни повествовательное предложение, в котором есть однородные подлежащие.
Куда направились сороки и галки?
На улице было морозно и свежо.
Как здорово в осеннем лесу!
Мамы и папы приехали к своим детям.
4. Вставь пропущенные буквы, расставь знаки препинания. Найди предложение с однородными сказуемыми и подчеркни его.
Мачеха поглядит, покряхтит, спрячет холст в сундук и сидит тихо. Золотой луг накрыли густой туман и дымка. Частые капли дождя повисли на траве, на кустах, на деревьях. На поляне высыхают трава, листья, хвоя, мох.
5. Раздели текст на предложения. Расставь необходимые знаки препинания.
Солнце уже довольно высоко стояло на чистом небе, но поля и луга ещё блестели росой. К полуночи тучи ушли, и над вершинами сосен и берёз начало переливаться холодными огнями небо. Над полем свистели злые ветры, и мороз студил землю.
Ответы по русскому языку. 4 класс. Проверочные и контрольные работы. Максимова Т.Н.
Ответы по русскому языку. 4 класс
4.4
/
5
(
91
голос
)
CSE 341 — Основы схемы
CSE 341 — Основы схемы
Схема профиля
- функциональный (но не чистый)
- динамическая, строгая типизация
- Хранилище исключительно на основе кучи с GC
- пройти по значению
- лексическая область видимости (слава богу, но не оригинальный Лисп)
- первоклассные функции
- анонимных функций
- синтаксически простой, обычный (но с множеством скобок)
- все списками!
- программных данных (Это делает
легко писать программы Scheme, которые обрабатывают / производят другие
программы, e.грамм. компиляторы, редакторы структур, отладчики и т. д.)
Эквивалентность
- Диалект Лиспа
- обычно интерпретируется (но существуют хорошие компиляторы)
Области применения Лиспа:
- AI (экспертные системы, планирование и т. Д.)
- Симуляторы, Моделирование
- Программирование приложений (emacs, CAD, Mathematica)
- Быстрое прототипирование
(Lisp был разработан в конце 50-х годов Джоном Маккарти. Диалект Scheme был
разработан Гаем Стилом и Джерри Сассманом в середине 70-х годов.В 80-е годы
Был разработан стандарт Common Lisp. Common Lisp — это язык кухонной раковины:
много-много функций.)
Типы данных и операции примитивной схемы
Некоторые примитивные ( атомарные ) типы данных:
- номеров
- целых чисел (примеры: 1, 4, -3, 0)
- реалов (примеры: 0,0, 3,5, 1,23E + 10)
- рациональных чисел (например, 2/3, 5/2)
- символов (например, fred, x, a12, set!)
- boolean: Схема использует специальные символы #f и #t для обозначения false и
правда. - строк (например, «привет, моряк»)
- символов (например, # \ c)
Регистр обычно не имеет значения (кроме символов или строк). Примечание
что у вас могут быть забавные символы, такие как +, — или! в центре
символы. (Однако скобок использовать нельзя.) Вот некоторые из основных
операторы, которые схема предусматривает для вышеуказанных типов данных.
- Арифметические операторы (+, -, *, /,
абс, sqrt) - Относительный (=, <,>,
<=,> =) (для чисел) - Relational (eqv ?, equal?) Для произвольных данных
(подробнее об этом позже) - Логический (и, или, не): и и
или являются логическими операторами короткого замыкания.
Некоторые операторы являются предикатами , то есть являются проверками истинности.
В Scheme они возвращают #f или #t. Особенность: в схеме MIT
пустой список эквивалентен #f, а #f печатается как (). Но хорошо
стиль — писать #t или #f всякий раз, когда вы имеете в виду истину или ложь, и
write (), когда вы действительно имеете в виду пустой список. Также см. «Boolean
Особенности »ниже.
- номер? целое число? пара? символ? логическое? нить?
- экв? равный?
- = <>
<=> =
Применяющие операторы, функции
Итак, мы знаем названия группы операторов.Как мы их используем?
Схема предоставляет нам единый синтаксис для вызова функций:
(функция arg1 arg2 ... argN)
Это означает, что все операторы, включая арифметические, имеют
Префикс Синтаксис . Аргументы передаются по значению (кроме
специальные формы , обсуждаемые позже, чтобы учесть такие приятные вещи, как
короткое замыкание).
Примеры:
(+ 2 3) (абс -4) (+ (* 2 3) 8) (+ 3 4 5 1) ;; обратите внимание, что + и * могут принимать произвольное количество аргументов ;; на самом деле так может - и / но у вас заболит голова, пытаясь вспомнить ;; что это значит ;; ;; точка с запятой означает, что оставшаяся часть строки является комментарием
Тип данных списка
Возможно, самый важный встроенный тип данных в Scheme — это
список.В схеме списки неограниченны, возможно, неоднородны.
коллекции данных. Примеры:
(Икс) (Элмер Фадд) (2 3 5 7 11) (2 3 x y "зоопарк" 2.9) ()
Представление списков в виде прямоугольников и стрелок:
_______________ ________________
| | | | | |
| о | ---- | -----> | о | о |
| ___ | ___ | _______ | | ____ | ___ | ___ | ___ |
| | |
| | |
Элмер Фадд ()
Или же
_______________ _____________
| | | | | / |
| о | ---- | -----> | о | / |
| ___ | ___ | _______ | | ____ | ___ | / ___ |
| |
| |
Элмер Фадд
Заметки:
- (x) не то же самое, что x
- () — пустой список
- Списки списков: ((a b) (c d)) или ((fred) ((x)))
- Списки схем могут содержать элементы разных типов:
(1 1.5 х (а) ((7)))
Вот некоторые важные функции, которые работают со списками:
- length — длина списка
- равно? — проверить, равны ли два списка (рекурсивно)
- вагон — первый элемент списка
- cdr — остальная часть списка
- cons — создать новую ячейку списка (также известную как cons-ячейка )
- список — составить список
(Для вашего удобства Scheme также предопределяет составы
вагон и цдр , эл.г., (кадр с)
определить d как (автомобиль (cdr s)) .)
Предикаты для списков:
- null? — список пуст?
- пара? — это непустой список?
Вычисление выражений
Пользователи обычно взаимодействуют со схемой через чтение-оценку-печать .
петля ( REPL ). Схема ожидает, пока пользователь наберет
выражение, читает его, оценивает и печатает возвращаемое значение.
Выражения схемы (часто называемые S-выражениями , для
Символьные выражения ) либо списки, либо атомы.Списки
состоит из других S-выражений (обратите внимание на рекурсивное определение).
Списки часто используются для представления вызовов функций, где список
состоит из имени функции, за которым следуют ее аргументы. Однако списки
также может использоваться для представления произвольных наборов данных.
В этих заметках мы обычно пишем:
=>
когда мы хотим показать S-выражение и оценка этого
S-выражение. Например:
(+ 2 3) => 5 (минусы 1 ()) => (1)
Правила оценки:
- Числа, строки, #f и #t являются литералами, то есть они
оцените для себя. - Символы рассматриваются как переменные, и для их оценки
их привязки ищутся в текущей среде. - Для списков первый элемент определяет функцию. Остальные
элементы списка указывают аргументы. Оцените первый элемент
в нынешних условиях
найти функцию и
оценить каждый из
аргументы в текущей среде и вызывают функцию для этих значений.
Например:(+ 2 3) => 5 (+ (* 3 3) 10) => 19 (= 10 (+ 4 6)) => #t
Использование символов (атомов) и списков в качестве данных
Если мы попробуем оценить
(список elmer fudd) мы получим ошибку.Почему? Так как
Схема будет рассматривать атом elmer как имя переменной и пытаться искать
за его привязку, которую он не найдет. Поэтому нам нужно «процитировать»
имена Элмер и Фадд, что означает, что мы
хочу схему относиться к ним буквально. Схема предоставляет для этого синтаксис.
Оценка цитируемых объектов заключается в том, что цитируемый объект оценивает сам себя.
'х => х (список elmer fudd) => ошибка! Элмер - это несвязанный символ (список 'elmer' fudd) => (elmer fudd) (элмер фадд) => ошибка! Элмер - неизвестная функция '(элмер фадд) => (элмер фадд) (равно? (x) (x)) => ошибка! x - неизвестная функция (равно? '(x)' (x)) => #t (cons 'x' (y z)) => (x y z) (cons 'x ()) => (x) (автомобиль '(1 2 3)) => 1 (cdr (cons 1 '(2 3))) => (2 3)
Обратите внимание, что есть 3 способа составить список:
- ‘(x y z) => (x y z)
- (cons ‘x (cons’ y (cons ‘z ()))) => (x y z)
- (список ‘x’ y ‘z) => (x y z)
Внутри кавычки символы и списки представлены с помощью специальных
цитата по функции.Когда читатель прочитает «(а б), это
переводит это в (quote (a b)), который затем передается в
оценщик. Когда оценщик видит выражение формы (цитата
s-expr) он просто возвращает s-expr. цитата иногда
называется «специальной формой», потому что в отличие от большинства других операций схемы, она
не оценивает свой аргумент. Кавычка — это пример того, что
называется «синтаксическим сахаром».
'х => х (цитата x) => x
(Алан Перлис: «синтаксический сахар вызывает рак точки с запятой».)
Переменные
Схема имеет как локальные, так и глобальные переменные. В схеме переменная
имя, привязанное к некоторому объекту данных (с помощью указателя). Там
не являются объявлениями типов для переменных. Правило оценки
символы: символ оценивает значение переменной, которую он называет. Мы
может связывать переменные с помощью специальной формы , определяющей :
(определить символьное выражение)
Использование определяет связывает символ (ваша переменная
name) к результату вычисления выражения . define — это особая форма, потому что первый параметр,
символ , не оценивается.
В строке ниже объявляется переменная с именем clam (если она не
существует) и относит его к 17:
(определить моллюск 17) моллюск => 17 (определите моллюск 23); это восстанавливает моллюска до 23 (+ моллюск 1) => 24
(определите bert '(a b c)) (определите Эрни Берта)
Схема использует указатели: теперь bert и ernie указывают на один и тот же список.
В 341 мы будем использовать определение только для привязки глобальных переменных, и мы
не будет повторно связывать их после связывания, за исключением случаев отладки.
Переменные с лексической областью видимости с let и let *
Мы используем специальную форму для объявления и привязки локальных,
временные переменные. Пример:
;; общая форма let
(пусть ((имя1 значение1)
(имя2 значение2)
...
(имяN значениеN))
выражение1
выражение2
...
выражениеQ)
;; переверните список и удвойте его
;; менее эффективная версия:
(определить (r2 x)
(добавить (обратный х) (обратный х)))
;; более эффективная версия:
(определить (r2 x)
(пусть ((r (обратный x)))
(добавить r r)))
Одна проблема с Let заключается в том, что пока создаются привязки,
выражения не могут ссылаться на привязки, которые были сделаны ранее.Например, это не работает, поскольку x неизвестен вне тела:
(пусть ((x 3)
(у (+ х 1)))
(+ х у))
Чтобы обойти эту проблему, Scheme предоставляет нам let *:
(пусть * ((x 3)
(у (+ х 1)))
(+ х у))
Определение собственных функций
Лямбды: анонимные функции
Вы можете использовать специальную форму лямбда для создания
анонимные функции. Эта специальная форма занимает
(лямбда (param1 param2... парамк); список официальных лиц
expr); тело
лямбда-выражение вычисляет анонимную функцию
который при применении (выполнении) принимает k аргументов и возвращает
результат вычисления expr . Как и следовало ожидать,
параметры имеют лексическую область видимости и могут использоваться только в
выражение .
Пример:
(лямбда (x1 x2)
(* (- x1 x2) (- x1 x2)))
Оценка приведенного выше примера приводит только к анонимной функции,
но мы пока ничего не делаем.Результат
лямбда-выражение можно напрямую применить, предоставив
аргументы, как в этом примере, который оценивается как 49:
((лямбда (x1 x2)
(* (- x1 x2) (- x1 x2)))
2-5);
Определение именованных функций
Если вы столкнетесь с проблемой определения функции, вы часто захотите
сохраните его для дальнейшего использования. Вы добиваетесь этого, привязывая результат
лямбда в переменную, используя , определить , так же, как
вы бы с любым другим значением.(Это показывает, как функции
первоклассный по схеме. Это использование определяет не
отличается от привязки переменных к другим видам значений.)
(определить квадратную разницу
(лямбда (x1 x2)
(* (- x1 x2) (- x1 x2))))
Поскольку определение функций - очень распространенная задача, Scheme предоставляет
специальная версия ярлыка определяет , который не использует
лямбда явно:
(определить (имя-функции param1 param2... парамк)
выражение)
Вот еще несколько примеров использования , определение в этом
путь:
(определить (двойной x)
(* 2 х))
(двойной 4) => 8
(определить (по шкале Цельсия по Фаренгейту c)
(+ (* 1,8 с) 32,0))
(Цельсия к Фаренгейту 100,0) => 212,0
x в функции double является формальной
параметр. Он имеет область видимости только внутри функции. Рассмотрим три
разные x вот здесь ...
(определить x 10)
(определить (добавить1 x)
(+ х 1))
(определить (дважды добавить x)
(двойной (добавить1 х)))
(дважды добавить x) => 22
Функции могут принимать 0 аргументов:
(определить (тест) 3)
(тест) => 3
Обратите внимание, что это не то же самое, что , как привязка переменной к
значение:
(определите не-функцию 3)
не-функция => 3
(not-a-function) =>; Объект 3 не применим.
Равенство и идентичность: равно ?, eqv ?, eq?
Схема предоставляет три примитива для проверки равенства и идентичности:
- экв? сравнение указателей. Он возвращает #t, если и только если его аргументы
буквально относятся к одним и тем же объектам в памяти. Символы
уникальны ('Фред всегда оценивает один и тот же объект).
Два символа, которые выглядят одинаково, называются ур. Две переменные
которые относятся к одному и тому же объекту, являются ур. - экв? как эк? но поступает правильно при сравнении
числа.экв? возвращает #t, если и только если его
аргументы - это или , если его аргументы - числа, которые имеют
такое же значение. экв? не
преобразовать целые числа в числа с плавающей запятой при сравнении целых чисел и чисел с плавающей запятой. - равно? возвращает истину, если его аргументы имеют одинаковую структуру.
Формально можно определить
равный? рекурсивно.
равный? возвращает #t, если его аргументы равны eqv, или если
его аргументы - списки, соответствующие элементы которых равны
(обратите внимание на рекурсию).Два объекта, которые являются эквалайзером, являются как eqv, так и
равный.Два объекта
которые равны,
но не обязательно эк. Два объекта, которые
равны не обязательно равны или
экв. эквалайзер иногда
называется личность
сравнение и равенство называется сравнением на равенство.
Примеры:
(определить моллюск '(1 2 3))
(определение моллюска-осьминога); моллюск и осьминог относятся к одному и тому же списку
(eq? 'clam' clam) => #t
(eq? clam clam) => #t
(eq? моллюск осьминог) => #t
(eq? clam '(1 2 3)) => #f; (или () в схеме MIT)
(eq? '(1 2 3)' (1 2 3)) => #f
(уравнение? 10 10) => #t; (обычно, но зависит от реализации)
(уравнение? 10.0 10.0) => #f; (обычно, но зависит от реализации)
(eqv? 10 10) => #t; всегда
(eqv? 10.0 10.0) => #t; всегда
(eqv? 10.0 10) => #f; нет преобразования между типами
(равно? clam '(1 2 3)) => #t
(равно? '(1 2 3)' (1 2 3)) => #t
Схема дает = для сравнения
два числа, и будет принуждать один тип к другому.
Например, (равно? 0 0,0) возвращает #f , но
(= 0 0.0) возвращает #t .
Логические операторы
Схема предоставляет нам несколько полезных логических операторов, в том числе
и, или, и не. Операторы и
и / или имеют особую форму и делают не обязательно
оцените все аргументы. Они просто оценивают столько аргументов, сколько необходимо
чтобы решить, возвращать ли #t или #f (например,
символы && и || операторы в C ++). Однако можно было
легко написать версию, которая оценивает все ее аргументы.
(и expr1 expr2 ... expr-n)
; вернуть истину, если все выражения верны
; ... или, точнее, вернуть expr-n, если все expr оцениваются как
; что-то кроме #f. В противном случае верните #f
(и (равно? 2 3) (равно? 2 2) #t) => #f
(или expr1 expr2 ... expr-n)
; вернуть истину, если хотя бы одно из выражений истинно
; ... или, точнее, вернуть expr-j, если expr-j - первое выражение, которое
; оценивается не как #f. В противном случае верните #f.
(или (равно? 2 3) (равно? 2 2) #t) => #t
(или (равно? 2 3) 'fred (equal? 3 (/ 1 0))) =>' фред
(определить (однозначный x)
(и (> x 0) (#t
Логические особенности
В R4 схемы пустой список эквивалентен #f, а все остальное -
эквивалент #t.Однако в R5 пустой
list также эквивалентен #t! Мораль: используйте только #f и #t для логических значений
константы.
Условные
для специальной формы
(если условие true_expression false_expression)
Если условие истинно, то результат
оценка true_expression возвращается; в противном случае
результат вычисления false_expression возвращается.
if - это специальная форма, например, цитата , потому что она
, а не , автоматически оценивает все свои аргументы.
(если (= 5 (+ 2 3)) 10 20) => 10
(если (= 0 1) (/ 1 0) (+ 2 3)) => 5
; обратите внимание, что (/ 1 0) не оценивается
(определить (my-max x y)
(если (> x y) x y))
(мой-макс 10 20) => 20
(определить (my-max3 x y z)
(если (и (> x y) (> x z))
Икс
(если (> y z)
y
з)))
cond - более общий условный
Общая форма специальной формы cond:
(cond (test1 expr1)
(test2 expr2)
....
(иначе выражение))
Как только мы находим тест, который соответствует действительности, мы оцениваем
соответствующее выражение и вернуть его значение. Остальные тесты не
оценивается, а все остальные выражения не оцениваются.
Если ни один из тестов не дает истинного значения, мы оцениваем выражение exprn ("else"
part) и верните его значение. (Вы можете оставить остальную часть, но это не так
хороший стиль.)
(определить (погода f)
(cond ((> f 80) 'слишком жарко)
((> f 60) 'красиво)
((
Стиль комментирования
Если Scheme находит строку текста с точкой с запятой, остальная часть строки
(после точки с запятой) рассматривается как пробел.Однако часто используемый
соглашение заключается в том, что одна точка с запятой используется для короткого комментария в строке
код, две точки с запятой используются для комментария внутри самой функции
строка, а три точки с запятой используются для вводного или глобального комментария
(вне определения функции).
Схема | Datomic
Применимы составные кортежи:
- , когда объект домена имеет ключ с несколькими атрибутами
- для оптимизации запроса, объединяющего более одного высокопопуляренного
атрибуты одного объекта
Например, рассмотрим домен конечно регистраций, смоделированный
со следующими типами сущностей:
- курсов представляют собой курс, e.грамм. Алгебра II
- семестров представляют собой период времени, когда курс проводится,
например «Осень 2019» - студентов могут посещать курсы в отдельных семестрах
[{: db / identify: student / first
: db / valueType: db.type / строка
: db / cardinality: db.cardinality / one}
{: db / identify: student / last
: db / valueType: db.type / строка
: db / cardinality: db.cardinality / one}
{: db / identify: student / email
: db / valueType: db.type / строка
: db / cardinality: db.cardinality / one
: db / unique: db.unique / identity}
{: db / идент: семестр / год
: db / valueType: db.тип / длинный
: db / cardinality: db.cardinality / one}
{: db / идент: семестр / сезон
: db / valueType: db.type / ключевое слово
: db / cardinality: db.cardinality / one}
{: db / identify: семестр / год + сезон
: db / valueType: db.type / кортеж
: db / tupleAttrs [: семестр / год: семестр / сезон]
: db / cardinality: db.cardinality / one
: db / unique: db.unique / identity}
{: db / ident: course / id
: db / valueType: db.type / строка
: db / уникальный: db.unique / identity
: db / cardinality: db.cardinality / one}
{: db / идент: курс / имя
: db / valueType: db.тип / строка
: db / cardinality: db.cardinality / one}]
Регистрационный номер — это уникальное сочетание студента, семестра,
и конечно. В Datomic схеме:
{: db / идент: рег / курс
: db / valueType: db.type / ref
: db / cardinality: db.cardinality / one}
{: db / identify: reg / semester
: db / valueType: db.type / ref
: db / cardinality: db.cardinality / one}
{: db / identify: reg / student
: db / valueType: db.type / ref
: db / cardinality: db.cardinality / one}
Данная комбинация курс / семестр / студент уникальна в
база данных.Чтобы смоделировать это, вы можете создать составной кортеж,
: атрибуты db / tupleAttrs являются
{: db / идент: рег / семестр + курс + студент
: db / valueType: db.type / кортеж
: db / tupleAttrs [: reg / course: reg / semester: reg / student]
: db / cardinality: db.cardinality / one
: db / unique: db.unique / identity}
После установки этого композита уникальная идентичность Datomic обеспечит
что все утверждения о комбинации семестр / курс / студент разрешаются
к тому же объекту.
Составные атрибуты полностью управляются Datomic — вы никогда не утверждаете
или уберите их сами.Каждый раз, когда вы утверждаете или отменяете какой-либо атрибут
который является частью композита, Datomic автоматически заполнит
составное значение.
Учитывая базу данных со схемой курсов и семестров, добавьте некоторые исходные данные:
[{: семестр / год 2018
: семестр / сезон: осень}
{: курс / идентификатор "БИО-101"}
{: студент / первый "Джон"
: студентка / последняя "Лань"
: студент / электронная почта "[email protected]"}]
Теперь, если вы зарегистрируете Джона для участия в программе Bio 101 осенью 2018 года, совершив транзакцию:
[{: reg / course [: course / id "BIO-101"]
: reg / semester [: семестр / год + сезон [2018: осень]]
: reg / student [: student / email "johndoe @ university.edu "]}]
Datomic также добавит данные составного кортежа:
#datom [20736789299855447 83 [63243967637 44112406506373204 641103239
094] 13194139533320 true]]
Обратите внимание, что идентификаторы ваших объектов будут отличаться от приведенных в примере выше.
Если текущее значение объекта не включает все атрибуты составного элемента, отсутствующие атрибуты будут нулевыми.
Например, для составного кортежа из 4 кортежей: рег / семестр + курс + студент + оценка, которая также включает оценку студента,
приведенные выше утверждения приведут к заполнению Datomic:
#datom [20736789299855447 83 [63243967637 44112406506373204 641103239
094 nil] 13194139533320 true]]
Обратите внимание, что nil сортируется ниже, чем все другие значения, поэтому кортежи с завершающими nil могут быть полезны для запросов диапазона.
Если вы уберете все составляющие композита, Datomic уберет композит. Например, транзакция:
[[: db / retract 20736789299855447: reg / course [: course / id "BIO-101"]] [: db / retract 20736789299855447: reg / semester [: семестр / год + сезон [2018: осень]]] [: db / retract 20736789299855447: reg / student [: student / email "[email protected]"]]]
заставит Datomic отозвать композит:
#datom [20736789299855447 83 [63243967637 44112406506373204 641103239
094] 13194139533321 ложь]]
Опять же, обратите внимание, что вам нужно будет заменить идентификаторы сущностей из исходной транзакции, чтобы воспроизвести этот пример в вашей системе.
Примечания к схеме
Примечания к схеме
ПРИМЕЧАНИЯ
ПО СХЕМЕ
[A
резюме первых четырех глав
Essentials
языков программирования ]
(последняя
обновлено: 6 января 1999 г.)
Если вы найдете
какие-либо ОШИБКИ или КОММЕНТАРИИ,
напишите мне
Спасибо всем, кто отправлял такие письма в прошлом.
Заявление
это конструкция языка программирования, которая оценивается только по ее результату.
Пример:
операторы присваивания, операторы ввода / вывода, операторы управления,
… и т. д.
Выражение
это конструкция, которая оценивается для получения значения.
Пример:
арифметические выражения.
ВЫРАЖЕНИЯ
литерал
(или постоянная )
всегда возвращает указанное значение.
Пример:
строки, логические значения, символы.
A переменная
ссылка
это значение, связанное в настоящее время с, или привязано
на номер ,
Переменная. Говорят, что переменная обозначает
значение его привязки. Данные, которые можно привязать к переменным
составляют обозначенный
значения .
Идентификаторы
представляют собой переменные.
Процедуры
то есть значения стандартных привязок называются стандартными
процедуры .
Функции
возвращают значения, в то время как выражения и процедуры не возвращают значения.
Функция
вызовы — это выражения, а вызовы процедур — это инструкции, но схема
не содержит утверждений, поэтому не делает различий.
Тем не менее, функции Scheme обычно называются процедурами, поэтому их
вызовы функций обычно называют вызовами процедур.
Процедура
(или функции) вызовы иногда называют приложений
или комбинаций .
В
общий синтаксис вызовов процедур (оператор
операнд_1 операнд_2. . . operand_n ).
Оператор
и каждый операнд
компоненты, которые сами по себе являются выражениями, называемыми подвыражениями .
Подвыражение оператора вычисляется для получения процедуры, в то время как
операнд
подвыражения оцениваются для получения аргументов вызова перед
вызывая процедуру .Аргументы также упоминаются в как
фактические параметры ,
или просто параметры .
В схеме порядок, в котором оператор и операнд
подвыражения оцениваются не указано. Процедуры, которые возвращаются
процедуры звоните вышестоящего
процедуры ,
и выражения, возвращающие процедуры, называются более высокого порядка
Выражения .
Специальный
идентификаторы формы
позвонил ключевые слова
выражать операции, которые нельзя выразить как вызовы процедур.Каждый
особая форма имеет собственную последовательность
Правило .
Условные выражения — это вторая ситуация, в которой особое
форма обязательна.
В
типичный программирование
окружающая среда
в котором используется язык схемы — это интерактивная программа .
режим ,
во время которого чтение-оценка-печать
петля есть
неоднократно казнен. Проводя четкое различие между
язык программирования и среды программирования, которые его поддерживают, мы
рассматривать сам язык как абстракцию, допускающую то же
язык для использования во многих различных средах.
«>
«- приглашение схемы», ;
«- маркер комментария, а» #
«означает, что процедура была возвращена. Символы, которые
видны при печати, представлены как литералы, предшествующие
их с помощью # \ .
Непечатаемые символы также имеют представление, например # \ space .
и # \ newline .
Индексирование
отсчитывается от нуля.
Когда
идентификаторы обрабатываются как значения, они называются символов .
Единственный
литералы, которые «цитируются сами», — это числа, логические значения,
строки и символы.
Списки
Список A
это упорядоченная последовательность из элементов ,
которые могут быть произвольного типа. Списки позволяют комбинировать
несколько значений в один составной объект. Списки представлены
заключая представления его элементов в круглые скобки.
конструкторов :
список , минусы
минусы
всегда принимает два аргумента. Первое может быть любым значением схемы, и
второй должен быть списком. Название минусы
стоит минусов трут,
потому что минусы
создает новый составной объект. Если первый аргумент — v
а его второй аргумент — это список ( v 0 v 1
… в н-1 ),
то минусы
возвращает список ( v
v 0 v 1
… v н-1 ).
(Собственно минусов х
второй аргумент может быть любым, но если это не список, то
возвращаемое значение также не будет перечислено).
(минусы
‘(c d))
=> (a c d)
Списки
производное
тип данных, потому что они построены с использованием примитива
типы данных: cons-ячейка и пустой список.Самый простой способ
разделить список между первым элементом и остальной частью списка.
селекторов :
легковой , cdr
Первое
элемент списка известен как его вагон
а остальная часть списка известна как его cdr .
Автомобиль
и cdr
отменить что минусы
делает.Можно взять составы вагон
и cdr
путем создания таких процедур, как cadr или caddar.
Примите к сведению
что звонить в машину — ошибка
или cdr
с пустым списком .
Ты можешь
тест на пустой
список по
с использованием предиката null .
Пар
Непустой
Списки представлены в виде пар .Пара — это структура с двумя полями, которая называется car и cdr .
Процедура минусы
создает новую пару с вагоном
и cdr
поля инициализированы значениями его первого и второго аргументов,
соответственно. Фактически, эти клетки могут быть использованы для создания клеток
произвольная длина. Обратите внимание, что пару иногда называют пунктирной
пара или минусы
сотовый .
Коробка
диаграммы могут использоваться для иллюстрации структур значений, построенных из
пары. Таким образом, список представлен либо пустым списком, либо цепочкой
пар, связанных их полями cdr, с пустым списком в cdr
поле последней пары цепочки.
А
Связанная cdr цепочка cons-ячеек, которая не заканчивается в пустом списке,
назвал неправильным
список ,
хотя это вовсе не список.
Мы можем
обозначать такие структуры данных в линейном формате записью (a.г) для
пара, чья машина
это , а
cdr — это d . точка
обозначение
могут смешиваться с обычными списковыми обозначениями. Точечная запись
требуется только при написании неправильных списков.
Пары могут
быть общий ,
поскольку разные привязки переменных и парные поля могут относиться к
та же пара. Стандартные печатные обозначения не означают обмен, но
коробки диаграммы делаю. Обратите внимание, что совместное использование литералов не указано.
Векторы
Гетерогенный
означает, что элементы ADT могут различаться по своему типу.
Однородный
означает, что элементы ADT должны быть одного типа.
ADT
обеспечивает произвольный доступ к своим компонентам, если каждый из его элементов
доступ за такое же количество времени.
Списки делают
не указывать имена для всех своих элементов или произвольный доступ к ним,
в то время как векторы обеспечивают произвольный доступ через номера индексов и могут быть
неоднородный.Стандартная процедура вектор
принимает произвольное количество аргументов и строит вектор,
элементы содержат значения аргументов. Векторы пишутся списками,
но с решёткой (#) непосредственно перед левой круглой скобкой. Векторы
должны быть заключены в кавычки, когда они появляются в программах как литералы.
селектор :
вектор-ссылка
принимает вектор и индекс, отсчитываемый от нуля, и возвращает значение
элемент, обозначенный индексом.
Ячейки
Ячейка
«одноэлементная» структура данных, состоящая из одноэлементной
вектор. Процедура make-cell ,
конструирует клетку, ссылка на ячейку
ссылается на ячейку, а ячейку?
определяет, является ли его аргумент ячейкой.
Процедуры
это
возможно создать новую процедуру, которая не может быть привязана к
переменные.Именование может быть выполнено с помощью другого выражения, например, , определить .
Специальная форма для создания новой процедуры — лямбда .
Его наиболее распространенный синтаксис: ( лямбда
формальный кузов ).
Здесь формальных
— (возможно, пустой) список переменных, а тело
любое выражение. Перечисленные переменные считаются формальными.
параметры ,
или связанных переменных ,
процедуры.Схема автоматически отслеживает типы при запуске
время, поэтому декларации не требуются. Когда процедура вызывается,
формальные параметры (если есть): первые граница
на номер
(связанных с) аргументами, а затем оценивается тело.
В теле значения аргументов могут быть получены с помощью переменных
соответствующие формальным параметрам. Привязки лямбда не
доступны вне тела процедуры: они называются
локально по отношению к телу процедуры.
Процедуры
без имен, которые не являются привязкой переменной, называются
быть аноним ,
и часто используются в качестве аргументов. Процедуры карта
и и карта
оба анонимны.
Значение
Говорят, что первый
класс если
он может быть передан и возвращен из процедур и сохранен в данных
конструкции. В схеме все значения являются первоклассными, включая процедуры.
Имея
функции более чем одного аргумента, безусловно, удобны, но это
не совсем необходимо. Любая процедура p из n ³ 2 аргументов
всегда можно преобразовать в процедуру p ‘одного аргумента, который
возвращает процедуру из n-1 аргументов, такую что ((p ‘x 1 )
х 2
… x n )
= (p x 1 x 2
… x n ).
Повторяя это преобразование n-1 раз, мы получаем процедуру
p «такой, что (… ((п «x 1 )
х 2 )
… x n )
= (p x 1 x 2
… x n ).
Это преобразование известно как каррирование .
A каррированный
версия процедуры принимает только один аргумент. Если существующий
заменяется каррированной версией, все вызовы
процедура должна быть изменена.
Артикул
процедуры — это количество аргументов, которые она принимает.Самая лямбда
выражения имеют фиксированную арность, хотя можно определить новые
процедуры переменной арности с лямбда-выражением вида ( лямбда формальный
корпус ) где формальный
это единственная переменная. Когда вызывается результирующая процедура, это
переменная привязана к списку значений аргументов.
индуктивно
Указанные данные
Данные
Тип состоит из набора значений и набора операций над
эти ценности. Индуктивный
спецификация
это мощный метод определения набора значений.
Для
Например, числовой список типа данных является наименьшим набором значений
удовлетворяющие двум свойствам:
Пустой
list — это список номеров, и- Если l
это список чисел и n
— число, то пара ( n
. l ) — это список чисел.
Обозначение
по телефону Бакус-Наур
Форма или BNF
был разработан, чтобы выразить идею индуктивной спецификации.
BNF можно использовать для индуктивного определения сразу нескольких наборов. Эти
наборы называются синтаксическими
категории ,
или иногда нетерминалов ,
и обычно заключаются в угловые скобки вокруг имени
набор: <список-номеров>.
Таким образом
В определении списка номеров BNF есть два правила, которые соответствуют
два объекта недвижимости:
<список-номеров>
:: = ()
<список-номеров>
:: = (<номер>. <список-номеров>)
Каждое правило
начинается с названия определяемой синтаксической категории, за которым следует
:: = (читать равно ).
Правая часть каждого правила определяет метод построения
члены синтаксической категории с точки зрения других синтаксических
категорий и терминал
символы ,
такие как левая и правая круглые скобки, а точка в
предыдущий пример.
BNF может быть
упрощается за счет объединения двух правил в одно с использованием специального символа
| (читать или ):
<список-номеров>
:: = () | (<номер>. <список-номеров>)
Другой
упрощением до BNF является Kleene
звезда ,
выражается обозначением {.
. .} * . Когда
это появляется в правой части правила, это означает последовательность
из ноль или более
экземпляры из
все, что появляется между скобками.Если экземпляров нет, мы
получить пустой список.
С использованием
Звезда Клини, определение
обозначение просто:
<список-номеров>
:: = ({<число>} *)
К
указать последовательность
из один или несколько экземпляров ,
мы используем вариант звездной записи: Kleene
плюс
{. . .} + .
Синтаксис
вывод
может использоваться, чтобы доказать, что данное значение данных является членом типа.Такой вывод начинается с нетерминала, соответствующего
тип. На каждом шаге, обозначенном стрелкой =>, нетерминал
заменяется правой частью соответствующего правила или
известный член своего синтаксического класса, если класс оставлен неопределенным.
Следующий
является синтаксическим производным, демонстрирующим, что (14. ()) представляет собой список чисел:
<список-номеров>
=> (<номер>. <список-номеров>)
=> (<14>.<список-номеров>)
=> (<14>. ())
Термин датум
относится к любому буквальному представлению данных. BNF может использоваться для указания
кратко синтаксическая категория данных в схеме. Следующее
набор правил BNF, также называемый грамматикой :
<список>
:: = ({
:: = ({
.<дата>)
<вектор>
:: = # ({
<дата>
:: = <число> | <символ> |
<строка> | <список> |
Правила BNF
считаются контекстно-свободными, потому что правило, определяющее данную синтаксическую
категория может применяться в любом контексте, который ссылается на
синтаксическая категория.
Специфический
типы данных могут иметь контекст
чувствительный
ограничений, но для простоты мы обычно указываем только
контекстно-свободная грамматика с использованием BNF.
Следующий
являются определениями общих типов данных BNF:
Многие
процедуры манипулирования символами предназначены для работы со списками
которые содержат только символы
и другие списки с ограниченным доступом:
:: = ({<символ-выражение>} *)
<символ-выражение>
:: = <символ> |
Бинарный файл
дерево с
числовые листы и внутренние узлы, помеченные символами:
<дерево>
:: = <число> | (<символ> <дерево> <дерево>)
Узел в
бинарное дерево поиска
либо пусто, либо содержит ключ и два поддерева:
:: = () | (<ключ>
Рекурсивный
процедуры
определены так, что
то
структура программы отражает структуру ее данных и- рекурсивных
вызовы используются в точках, где рекурсия используется в данных
индуктивное определение типа.
Два или
больше процедур взаимно
рекурсивный
когда они рекурсивно обращаются друг к другу.
Это может быть
полезно или необходимо ввести вспомогательный
процедуры
решить проблему.
Статический
Свойства переменных
Те
свойства программы, которые можно определить, анализируя текст
программы называются статическими ,
в отличие от динамический
свойства, которые определяются входными данными времени выполнения.
Статический
свойства могут быть проанализированы компилятором для обнаружения ошибок перед запуском
время и повысить эффективность объектного кода.
В схеме
связь между ссылкой на переменную и формальным параметром к
на которое он ссылается, является статическим свойством.
Лямбда
Исчисление
Чтобы
для изучения связывания переменных в абстрактном контексте мы вводим новый
язык называется Лямбда
Исчисление .В этом языке всего переменных.
ссылки , лямбда
выражение с одним формальным параметром ,
и вызовов процедур :
:: =
|
(лямбда ()
|
(
Переменная
ссылка называется привязана
в выражении, если оно относится к формальному параметру, введенному в
выражение. Ссылка на переменную, не привязанная к формальному
параметр в выражении называется бесплатно .
Переменная
говорит к
происходит связанный
в выражении, если выражение содержит связанную ссылку на
Переменная. Говорят, что переменная происходит
бесплатно в
выражение, если выражение содержит свободную ссылку на переменную.
Все
ссылки на переменные должны иметь некоторое связанное значение, когда они
оцениваются во время выполнения, если они привязаны к формальному параметру, они
лексически называются
Связанный .В противном случае они должны быть либо связаны определениями на верхнем уровне, либо
поставляться системой. В этом случае их называют во всем мире.
Связанный . Это
является ошибкой ссылки на переменную, которая не является ни лексической, ни
глобально связанный.
Значение
выражения зависит только от значений, связанных с
переменные, которые встречаются в выражении бесплатно.
Значение
off выражение не зависит от привязок переменных, которые
не встречается в выражении свободно.
Лямбда
выражения без свободных переменных называются комбинаторами .
Переменная
x происходит бесплатно
в выражении E iff
E — это
ссылка на переменную и E то же самое, что и x; или- E — это
формы (E 1 E 2 )
и x встречается бесплатно в E 1
или E 2 ;
или - E — это
формы (lambda (y) E ‘), где y отличается от x, а x встречается
бесплатно в E ‘.
Переменная
x встречается в выражении E тогда и только тогда, когда
E имеет
от (E 1 E 2 )
и x встречается в E 1
или E 2 ;
или- E — это
off the from (lambda (y) E ‘), где x встречается в E’ или x и y
— одна и та же переменная, а y свободно входит в E ‘.
Нет
переменная встречается в выражении, состоящем только из одной переменной.
Область применения
и лексический адрес
Площадь
программы, в которой действует объявление переменной, — это область .
На схеме областью формального параметра является тело лямбда-выражения.
выражение, а область вне определения верхнего уровня — это весь
программа. Прицел
объявления переменной — это текст, в котором ссылки на
переменная относится к объявлению.Регион и область действия переменной
может быть одинаковым, но охват не включает весь регион.
Объявления имеют ограниченную область видимости, поэтому одно и то же имя переменной может
преследовать разные цели в разных частях программы. В большинстве
языки, включая Scheme, регион и область объявления могут быть
определяется статически. Таких языков называют лексически
или статически
область действия .
Большинство современных языков позволяют регионам быть вложенными
друг в друге, как когда в теле появляется одно лямбда-выражение
другого.Регионы иногда называют блоками ,
и такие языки называются блочными
структурированный .
В
объявление переменной v
имеет область действия, которая включает в себя все упоминания о том, что встречаются
бесплатно в
регион, связанный с объявлением. Эти ссылки на v
что происходят связанные
в области, связанной с его объявлением, затенены внутренними объявлениями.
Пансионеры
областей называются контурами. Можно пересечь ряд контуров
прежде чем прийти к соответствующему объявлению. Количество контуров
скрещенный называется лексический
(или статический )
глубина
ссылки на переменную.
В
объявления, связанные с регионом, могут быть пронумерованы в порядке
их появление в тексте. Тогда каждая ссылка на переменную может быть
связаны с двумя числами: его лексической глубиной и положением
свое объявление в декларирующем контуре (его декларация
позиция ).
Взятый
вместе эти два числа составляют лексический
адрес
ссылки на переменную. Таким образом, ссылка на переменную v
в выражении можно заменить на ( v
: д п ),
где d
это его лексическая глубина и с,
— позиция его объявления (с использованием индексации с нулевой базой для d и p).
Мы желаем
получаем общее правило преобразования программы, но мы сталкиваемся с двумя
трудности.Во-первых, новое имя переменной не должно конфликтовать с
любые другие имена переменных, используемые в этой части программы. Второй
трудности возникают, если объявление внутреннего формального параметра создает
дыра в области внешнего формального параметра: ссылки на
внутреннее объявление не должно изменяться.
Результат подстановки выражения y для всех свободных вхождений
переменной x в выражении exp записывается exp [y / x], читаем
«выражение с y для x.»Общее переименование переменных
правило для лямбда-выражений с одним формальным параметром может быть
выражается как (lambda (var) exp) = (lambda (var ‘) exp [var’ / var]), где
var ‘- это любая переменная, которая не встречается в exp. В лямбде
исчисление это называется а-преобразованием (альфа-преобразованием).
Если ты собираешься
чтобы получить что-нибудь от всей этой страницы, обратите внимание на эти удивительные
таблицы, которые разделяют многие формы синтаксиса, используемые в Scheme.
ПРОЦЕДУРЫ | СИНТАКСИС | НАЗНАЧЕНИЕ |
ноль? | проверяет, равен ли его аргумент нулю | |
добавить | ( приложение list_1 list_2 ) | Добавить все элементы списка_1 в начало списка_2 |
легковой | Автомобиль ( список ) | Извлекает первый элемент списка |
кдр | Cdr ( список ) | Извлекает все, что следует за первым элементом списка |
длина | ( длина список) | Определяет количество элементов в списке |
список-исх. | ( список-исх. список-индекс ) | Возвращает элемент, обозначенный индексом |
вектор-ссылка | ( vector-ref vector index ) | Возвращает значение элемента, указанного индексом |
длина вектора | ( длина вектора вектор ) | Возвращает количество элементов в векторе |
вектор-> список | Преобразует составной тип данных vector в список | |
список-> вектор | Преобразует составной тип данных списка в вектор | |
применить | Принимает процедуру и список и возвращает результат вызова | |
карта | ( карта список процедур ) | Процедура должна принимать один аргумент, и список может быть любой длины. Он строит новый список, элементы которого получаются путем вызова |
и карта | ( и карта список процедур ) | Процедура должна принимать один аргумент, и список может быть любой длины. Он применяет процедуру к каждому элементу списка и возвращает истину. |
ошибка | ( error « message to std output «) | Сигнализирует об ошибке y при печати своих аргументов, в данном случае одного |
СПЕЦИАЛЬНЫЕ ФОРМЫ | СИНТАКСИС | НАЗНАЧЕНИЕ |
определить | ( определить переменное выражение ) | связывает переменную со значением выражения |
если | ( если test-exp, затем-exp else-exp ) | если test-exp истинно, то вычисляется then-exp, иначе оценивается else-exp |
Цитируемый литерал | (указать данные) или ‘датум | Символьные литералы специально помечаются, иначе они были бы |
лямбда | ( лямбда корпус ) | Создает процедуру |
и | ( и test1 test2… test_n ) | Формирует логическое выражение, которое истинно, если все его |
или | ( или test1 test2 … test_n ) | Образует логическое выражение, которое истинно, если любое его |
ПРЕДИКАТЫ ТИПА | НАЗНАЧЕНИЕ | |
символ? | Предикат типа | Проверяет произвольное значение, чтобы узнать, является ли оно символом |
номер ? | Предикат типа | Принимает произвольное значение, чтобы узнать, является ли это числом |
логическое? | Предикат типа | Проверяет произвольное значение на логическое значение |
список? | Предикат типа | Проверяет произвольное значение, чтобы убедиться, что это список |
пара? | Предикат типа | Проверяет произвольное значение, чтобы узнать, является ли оно парой |
вектор? | Предикат типа | Проверяет произвольное значение, чтобы узнать, является ли оно вектором |
null? | Предикат | Проверяет свой аргумент, чтобы убедиться, что это пустой список |
процедура? | Предикат типа | Проверяет свой аргумент, чтобы убедиться, что это процедура |
экв? | Проверяет, являются ли любые два объекта одним и тем же объектом | |
не | Выполняет логическое отрицание |
ПРЕДИКАТЫ ДЛЯ ХАРАКТЕРА | НАЗНАЧЕНИЕ | |
симв.? | Предикат типа | Принимает произвольное значение и возвращает истину, если его аргумент — |
char =? | Процедура | Сравнивает два символа на равенство |
char | Процедура | Определяет порядок знаков |
char —> целое | Процедура | Принимает символ и возвращает целочисленное представление символа |
буквенно-символьный? | Процедура | Определяет класс персонажа |
символьно-числовой? | Процедура | Определяет класс персонажа |
символ-пробел? | Процедура | Определяет класс символа, возвращая истину, когда его |
СТРОЧНЫЕ ПРОГНОЗЫ | НАЗНАЧЕНИЕ | |
строка? | Предикат типа | Принимает произвольное значение и возвращает истину, если его аргумент является строкой. |
длина жала | Процедура | Принимает строку и возвращает целое число, указывающее количество |
присоединение строки | Процедура | Объединяет свои аргументы в новую строку |
строка -> символ | Процедура | Преобразует строку в символ |
строка -> номер | Процедура | Преобразует строку в число |
строка -> список | Процедура | Преобразует строку в список символов |
строка | Процедура | Преобразует символы в строку |
ссылка на строку | Процедура | Принимает строку и неотрицательное целое число меньше, чем длина |
Составитель Алексей Батько
<абатко АТ cs.mcgill.ca> в мае и июне 1998 г.
Все ошибки, дополнения и комментарии присылайте мне.
Спасибо всем, кто раньше отправлял такую почту.
Краткое изложение Essentials
языков программирования
(8-е издание)
Даниил
П. Фридман, Митчелл
Палочка и Кристофер
Т. Хейнс.
Посетите EOPL
ftp-сайт.
© 1992
посредством
MIT Press
% PDF-1.4
%
5 0 obj
>
эндобдж
8 0 объект
(Абстрактный)
эндобдж
9 0 объект
>
эндобдж
12 0 объект
(Благодарности)
эндобдж
13 0 объект
>
эндобдж
16 0 объект
(Содержание)
эндобдж
17 0 объект
>
эндобдж
20 0 объект
(Список рисунков)
эндобдж
21 0 объект
>
эндобдж
24 0 объект
(От скриптов к программам)
эндобдж
25 0 объект
>
эндобдж
28 0 объект
(Типизированная схема через примеры)
эндобдж
29 0 объект
>
эндобдж
32 0 объект
(Простая типизированная схема)
эндобдж
33 0 объект
>
эндобдж
36 0 объект
(Полиморфизм и вывод локального типа)
эндобдж
37 0 объект
>
эндобдж
40 0 объект
(Интеграция с нетипизированной схемой)
эндобдж
41 0 объект
>
эндобдж
44 0 объект
(Ввод вхождения)
эндобдж
45 0 объект
>
эндобдж
48 0 объект
(Функции переменной арности)
эндобдж
49 0 объект
>
эндобдж
52 0 объект
(Типы уточнения)
эндобдж
53 0 объект
>
эндобдж
56 0 объект
(Как проверить примеры)
эндобдж
57 0 объект
>
эндобдж
60 0 объект
(Выбор дизайна)
эндобдж
61 0 объект
>
эндобдж
64 0 объект
(Отклонение программ с неверным набором текста)
эндобдж
65 0 объект
>
эндобдж
68 0 объект
(Явный ввод)
эндобдж
69 0 объект
>
эндобдж
72 0 объект
(Детализация на уровне модуля)
эндобдж
73 0 объект
>
эндобдж
76 0 объект
(Предварительно раскрывающиеся макросы)
эндобдж
77 0 объект
>
эндобдж
80 0 объект
(Нет новых идиом)
эндобдж
81 0 объект
>
эндобдж
84 0 объект
(Предыдущая работа)
эндобдж
85 0 объект
>
эндобдж
88 0 объект
(Статическая проверка схемы и LISP)
эндобдж
89 0 объект
>
эндобдж
92 0 объект
(Межъязыковая совместимость)
эндобдж
93 0 объект
>
эндобдж
96 0 объект
(Реализация типов в схеме)
эндобдж
97 0 объект
>
эндобдж
100 0 объект
(Контракты и модули)
эндобдж
101 0 объект
>
эндобдж
104 0 объект
(Интеграция типизированного и нетипизированного кода)
эндобдж
105 0 объект
>
эндобдж
108 0 объект
(Отношение к типизированной схеме)
эндобдж
109 0 объект
>
эндобдж
112 0 объект
(Неформальный тур)
эндобдж
113 0 объект
>
эндобдж
116 0 объект
(Формальная основа)
эндобдж
117 0 объект
>
эндобдж
120 0 объект
(Разумность)
эндобдж
121 0 объект
>
эндобдж
124 0 объект
(Ввод вхождения)
эндобдж
125 0 объект
>
эндобдж
128 0 объект
(Синтаксис и операционная семантика)
эндобдж
129 0 объект
>
эндобдж
132 0 объект
(Правила набора)
эндобдж
133 0 объект
>
эндобдж
136 0 объект
(Небольшой пример)
эндобдж
137 0 объект
>
эндобдж
140 0 объект
(Управление фильтрами)
эндобдж
141 0 объект
>
эндобдж
144 0 объект
(Расширения для ввода вхождения)
эндобдж
145 0 объект
>
эндобдж
148 0 объект
(Добавление путей)
эндобдж
149 0 объект
>
эндобдж
152 0 объект
(Используя логику)
эндобдж
153 0 объект
>
эндобдж
156 0 объект
(Доказательство правильности)
эндобдж
157 0 объект
>
эндобдж
160 0 объект
(Типы уточнения)
эндобдж
161 0 объект
>
эндобдж
164 0 объект
(Формализация уточнений)
эндобдж
165 0 объект
>
эндобдж
168 0 объект
(Разумность)
эндобдж
169 0 объект
>
эндобдж
172 0 объект
(Расширенный пример)
эндобдж
173 0 объект
>
эндобдж
176 0 объект
(Полиморфизм переменной арности)
эндобдж
177 0 объект
>
эндобдж
180 0 объект
(Синтаксис)
эндобдж
181 0 объект
>
эндобдж
184 0 объект
(Система типов)
эндобдж
185 0 объект
>
эндобдж
188 0 объект
(Выполнение)
эндобдж
189 0 объект
>
эндобдж
192 0 объект
(Макросы)
эндобдж
193 0 объект
>
эндобдж
196 0 объект
(Модули, или вы хотите, когда и снова?)
эндобдж
197 0 объект
>
эндобдж
200 0 объект
(Макро-протоколы)
эндобдж
201 0 объект
>
эндобдж
204 0 объект
(Условия ввода)
эндобдж
205 0 объект
>
эндобдж
208 0 объект
(Модули набора текста)
эндобдж
209 0 объект
>
эндобдж
212 0 объект
(Оценка)
эндобдж
213 0 объект
>
эндобдж
216 0 объект
(Портированные программы)
эндобдж
217 0 объект
>
эндобдж
220 0 объект
(Изменения в программе)
эндобдж
221 0 объект
>
эндобдж
224 0 объект
(Статистика и результаты)
эндобдж
225 0 объект
>
эндобдж
228 0 объект
(Связанных с работой)
эндобдж
229 0 объект
>
эндобдж
232 0 объект
(Постепенный набор)
эндобдж
233 0 объект
>
эндобдж
236 0 объект
(Типовые особенности системы)
эндобдж
237 0 объект
>
эндобдж
240 0 объект
(Типы уточнения)
эндобдж
241 0 объект
>
эндобдж
244 0 объект
(Типы и логика)
эндобдж
245 0 объект
>
эндобдж
248 0 объект
(Ввод вхождения)
эндобдж
249 0 объект
>
эндобдж
252 0 объект
(Полиморфизм переменной арности)
эндобдж
253 0 объект
>
эндобдж
256 0 объект
(Типы и анализ потока)
эндобдж
257 0 объект
>
эндобдж
260 0 объект
(Заключение)
эндобдж
261 0 объект
>
эндобдж
264 0 объект
(Вклады)
эндобдж
265 0 объект
>
эндобдж
268 0 объект
(Будущая работа)
эндобдж
269 0 объект
>
эндобдж
272 0 объект
(Библиография)
эндобдж
273 0 объект
>
эндобдж
276 0 obj>
поток
x ڍ Rn WkNH «j 63FpNdF ꊇ yso w? ϛj ~ @ bD
% PDF-1.2
%
1349 0 объект
>
эндобдж
xref
1349 148
0000000016 00000 н.
0000003316 00000 н.
0000076617 00000 п.
0000076779 00000 п.
0000076945 00000 п.
0000077197 00000 п.
0000077408 00000 п.
0000077734 00000 п.
0000078121 00000 п.
0000078424 00000 п.
0000078742 00000 п.
0000078990 00000 н.
0000079298 00000 п.
0000079488 00000 п.
0000079746 00000 п.
0000079990 00000 н.
0000080296 00000 п.
0000080614 00000 п.
0000080858 00000 п.
0000081157 00000 п.
0000081394 00000 п.
0000081714 00000 п.
0000082040 00000 п.
0000082426 00000 п.
0000082771 00000 п.
0000083192 00000 п.
0000083371 00000 п.
0000083751 00000 п.
0000083967 00000 п.
0000084188 00000 п.
0000084612 00000 п.
0000084918 00000 п.
0000085324 00000 п.
0000085828 00000 п.
0000086156 00000 п.
0000086531 00000 п.
0000086749 00000 п.
0000086941 00000 п.
0000087312 00000 п.
0000087590 00000 п.
0000087643 00000 п.
0000087779 00000 п.
0000088123 00000 п.
0000088759 00000 п.
0000089009 00000 п.
0000089363 00000 п.
0000089446 00000 п.
0000089571 00000 п.
0000089740 00000 п.
00000
00000 п.
0000000000 п.
00000 00000 п.
00000 00000 п.
0000000000 п.
0000000000 п.
0000000000 п.
0000092706 00000 п.
0000093279 00000 п.
0000093765 00000 п.
0000094259 00000 п.
0000094733 00000 п.
0000095163 00000 п.
0000095533 00000 п.
0000096016 00000 п.
0000096069 00000 п.
0000096527 00000 п.
0000096657 00000 п.
0000096953 00000 п.
0000097142 00000 п.
0000097437 00000 п.
0000097728 00000 п.
0000098128 00000 п.
0000098522 00000 п.
0000098826 00000 п.
0000099507 00000 п.
0000099907 00000 н.
0000100315 00000 н.
0000100654 00000 н.
0000101020 00000 н.
0000101374 00000 н.
0000101750 00000 н.
0000102107 00000 н.
0000102447 00000 н.
0000102742 00000 н.
0000103053 00000 п.
0000103337 00000 н.
0000103550 00000 н.
0000103876 00000 н.
0000104198 00000 п.
0000104418 00000 н.
0000104717 00000 н.
0000105002 00000 п.
0000105305 00000 н.
0000105551 00000 н.
0000105939 00000 н.
0000106285 00000 н.
0000106635 00000 н.
0000106992 00000 п.
0000107045 00000 н.
0000107485 00000 н.
0000107798 00000 н.
0000108165 00000 н.
0000108467 00000 н.
0000108836 00000 н.
0000109208 00000 н.
0000109520 00000 н.
0000109927 00000 н.
0000110313 00000 н.
0000110586 00000 п.
0000110971 00000 п.
0000111193 00000 н.
0000111499 00000 н.
0000111619 00000 н.
0000111799 00000 н.
0000112082 00000 н.
0000112135 00000 н.
0000112477 00000 н.
0000113198 00000 п.
0000113709 00000 н.
0000114099 00000 н.
0000114513 00000 н.
0000114656 00000 н.
0000115050 00000 н.
0000115395 00000 н.
0000115845 00000 н.
0000116175 00000 н.
0000116534 00000 н.
0000116753 00000 н.
0000117049 00000 п.
0000117399 00000 н.
0000117710 00000 н.
0000118044 00000 н.
0000118285 00000 н.
0000118570 00000 н.
0000118876 00000 н.
0000119219 00000 н.
0000119505 00000 н.
0000119799 00000 н.
0000120136 00000 н.
0000120457 00000 н.
0000120755 00000 н.
0000121024 00000 н.
0000121337 00000 н.
0000121596 00000 н.
0000121894 00000 н.
0000122322 00000 н.
0000003375 00000 н.
0000076592 00000 п.
трейлер
]
>>
startxref
0
%% EOF1350 0 объект
>
эндобдж
1495 0 объект
>
поток
HԔ [g @
(
58TR% $.JEPEȪ-l "E" (; $ a {DQL !! lbd ~ R + O4 @ ` @ Qg`5b2 (T2ĨaǼBkb۱U) V!) RAAHtTfk} LT㎦> & s 놦 hc; 1h "/ 3 $ Fxr j} u q
sR? 4 ڏ7_` Htnxd # B? DDa? 0Xbu⮞ @ `m CC [2%! PS-Adobe-2.0
%% Создатель: dvipsk 5.58f Авторские права 1986, 1994 Radical Eye Software
%% Заголовок: sahsh.dvi
%% Страниц: 21
%% PageOrder: Ascend
%% BoundingBox: 0 0 612 792
%% EndComments
% DVIPSCommandLine: dvips sahsh.dvi -o
% DVIPSParameters: dpi = 600, сжато, комментарии удалены
% DVIPS Источник: вывод TeX 2000.10.07: 1849
%% BeginProcSet: texc.pro
/ TeXDict 250 dict def Начало TeXDict / N {def} def / B {привязка def} N / S {exch} N
/ X {S N} B / TR {translate} N / isls false N / vsize 11 72 mul N / hsize 8.5 72
mul N / landplus90 {false} def / @ rigin {isls {[0 landplus90 {1 -1} {- 1 1}
ifelse 0 0 0] concat} if 72 Разрешение div 72 VR Разрешение div neg масштаб
isls {landplus90 {VResolution 72 div vsize mul 0 exch} {Разрешение -72 div
hsize mul 0} ifelse TR}, если разрешение VResolution vsize -72 div 1 add mul
TR [матрица currentmatrix {dup dup round sub abs 0.00001 lt {round} if}
forall round exch round exch] setmatrix} N / @ landscape {/ isls true N} B
/ @ manualfeed {statusdict / manualfeed true put} B / @ копий {/ # копий X} B
/ FMat [1 0 0 -1 0 0] N / FBB [0 0 0 0] N / nn 0 N / IE 0 N / ctr 0 N / df-tail {
/ nn 8 dict N nn begin / FontType 3 N / FontMatrix fntrx N / FontBBox FBB N
строка / базовый массив X / BitMaps X / BuildChar {CharBuilder} N / кодирование IE N
end dup {/ foo setfont} 2 array copy cvx N load 0 nn put / ctr 0 N [} B / df {
/ sf 1 N / fntrx FMat N df-tail} B / dfs {div / sf X / fntrx [sf 0 0 sf neg 0 0]
N df-tail} B / E {pop nn dup definefont setfont} B / ch-width {ch-data dup
длина 5 sub get} B / ch-height {ch-data dup length 4 sub get} B / ch-xoff {
128 ch-data dup length 3 sub get sub} B / ch-yoff {ch-data dup length 2 sub
получить 127 sub} B / ch-dx {ch-data dup length 1 sub get} B / ch-image {ch-data
dup type / stringtype ne {ctr get / ctr ctr 1 add N} if} B / id 0 N / rw 0 N
/ rc 0 N / gp 0 N / cp 0 N / G 0 N / sf 0 N / CharBuilder {save 3 1 roll S dup
/ base get 2 index get S / BitMaps get S get / ch-data X pop / ctr 0 N ch-dx
0 ch-xoff ch-yoff ch-height sub ch-xoff ch-width добавить ch-yoff
setcachedevice ch-width ch-height true [1 0 0 -1 -.1 ч-хофф суб ч-йофф
.1 sub] / id ch-image N / rw ch-width 7 добавить 8 idiv строка N / rc 0 N / gp 0 N
/ cp 0 N {rc 0 ne {rc 1 sub / rc X rw} {G} ifelse} восстановление маски изображения} B / G {{id
gp get / gp gp 1 add N dup 18 mod S 18 idiv pl S get exec} loop} B / adv {cp
add / cp X} B / chg {rw cp id gp 4 index getinterval putinterval dup gp add
/ gp X adv} B / nd {/ cp 0 N rw exit} B / lsh {rw cp 2 copy get dup 0 eq {pop 1} {
dup 255 eq {pop 254} {dup dup add 255 и S 1 и или} ifelse} ifelse положить 1
adv} B / rsh {rw cp 2 copy get dup 0 eq {pop 128} {dup 255 eq {pop 127} {dup 2
idiv S 128 и or} ifelse} ifelse помещает 1 adv} B / clr {rw cp 2 index string
putinterval adv} B / set {rw cp fillstr 0 4 index getinterval putinterval
adv} B / fillstr 18 string 0 1 17 {2 copy 255 put pop} для N / pl [{adv 1 chg}
{adv 1 chg nd} {1 add chg} {1 add chg nd} {adv lsh} {adv lsh nd} {adv rsh} {
adv rsh nd} {1 add adv} {/ rc X nd} {1 add set} {1 add clr} {adv 2 chg} {adv 2
chg nd} {pop nd}] dup {bind pop} forall N / D {/ cc X dup type / stringtype ne {]
} if nn / base get cc ctr put nn / BitMaps get S ctr S sf 1 ne {dup dup
length 1 sub dup 2 index S get sf div put} if put / ctr ctr 1 add N} B / I {
cc 1 add D} B / bop {userdict / bop-hook known {bop-hook} if / SI save N @rigin
0 0 moveto / V matrix currentmatrix dup 1 get dup mul exch 0 get dup mul
Добавлять .99 lt {/ QV} {/ RV} ifelse load def pop pop} N / eop {SI restore userdict
/ eop-hook известно {eop-hook} if showpage} N / @ start {userdict / start-hook
известное {start-hook} if pop / VResolution X / Resolution X 1000 div / DVImag X
/ IE 256 array N 0 1 255 {IE S 1 string dup 0 3 index put cvn put} для
65781,76 дел / размер X 65781,76 дел / размер X} N / p {show} N / RMat [1 0 0 -1 0
0] N / BDot 260 string N / rulex 0 N / ruley 0 N / v {/ ruley X / rulex X V} B / V
{} B / RV statusdict begin / product where {pop product dup length 7 ge {0 7
getinterval dup (Display) eq exch 0 4 getinterval (NeXT) eq или} {pop false}
ifelse} {false} ifelse end {{gsave TR -.1 .1 TR 1 1 шкала rulex ruley false
RMat {BDot} imagemask grestore}} {{gsave TR -.1 .1 TR rulex ruley scale 1 1
false RMat {BDot} imagemask grestore}} ifelse B / QV {gsave newpath transform
round exch round exch itransform moveto rulex 0 rlineto 0 ruley neg
rlineto rulex neg 0 rlinto fill grestore} B / a {moveto} B / delta 0 N / tail
{dup / delta X 0 rmoveto} B / M {S p delta add tail} B / b {S p tail} B / c {-4 M}
B / d {-3 M} B / e {-2 M} B / f {-1 M} B / g {0 M} B / h {1 M} B / i {2 M} B / j {3 M} B / k {
4 M} ч / б {0 rmoveto} B / l {p -4 w} B / m {p -3 w} B / n {p -2 w} B / o {p -1 w} B / q {
p 1 w} B / r {p 2 w} B / s {p 3 w} B / t {p 4 w} B / x {0 S rmoveto} B / y {3 2 рулона p
a} B / bos {/ SS сохранить N} B / eos {SS restore} B конец
%% EndProcSet
Начало TeXDict 40258437 52099154 1200600600 (sahsh.dvi)
@start / Fa 34123 df12 D44
DI65
D73 D77
DIII82 D87
D90 D97
DIIIIIIII108 DIIII114 DIIIII121
DI E / Fb 2 49 df0 D48
D E / Fc 5110 df58 D105 DII109 D E / Fd 48
123 df12 DI34
D40 DI44 DII49 DII59 D69
DI73 D76 D80
D
82 D84
D86 DI92 D97
DIIIIIIIIIIIIIIIIIIIIIIIII E / Fe 6 53 df43
D48 DIIII E / Ff 28 126 df0 DI14
D16 D
III26 D [51
298 104 131 79 32 D [51298 125 131 79 I48 DI56 D58 D60 D62
D64 DI77
D80 DI83 D88 DI122 DIII E / Fg 26117 df40 DI43 D48
DIIIIIIIII61
D97
D100 DI103 D105 D108 DIII114 DII E / Fh 14104 df0 D15
D20
DI33
D48 DII54
D65
D100
DIII E / Fi 35120 df11 D15 D27
DI30
D32
D58 DI61
D65 DII69 D72
DI77 DI80
D83 D97 DII101 DI105 DIIIII114 DII118 DI E / Fj 54123 df11 DI15 D27
DI30 D
32 DI58 D
IIII65
DII69 D71 DII75 DIIIII82
DI
85 DI88
D97 DIIIII105 DIIIIIII114 DIII
я
II
II E / Fk 80124 df6 D11
DIII22 D32 D34 D39
DII43 DIII48 DIIIIIIIIIII61 D63
D65 DIIIII
III75 DII
III82
DII86 DI91
DIII97 DIIIIIIIIIIIIIIIIIIIIIIIIII E
/ Fl 6 123 df0 D102
DI106
D121 DI E / Fm 7 113 df58 DI71 D105 DI110 D112 D E
/ Fn 76124 df11
DI19 D32 D34 D
38 DIII44
DII48
DIIIIIIIII61 D65 DIIIIIIIIIIIII80 D82 DIIIIIII91
DII
97 DIIIIIIIIIIIIIIIIIIIIIIIIII
E / Fo 17 117 df46 D48 DI51
DIIIIII65
D97 DII114 DII E / Fp 30123 df0 D8
D14
D
18 D20 DI33
D49
DI54
D56
D58 D65 D71 DI85 D91 DI94 D98 D
IIIII106
D110 D112 D
121 DI E / Fq 43122 df32 D46 D49 DIIIIIIII65 D67 DIII72 D75 DIIII82
DIII90 D97
D99 DIII104 DI108 DIIII114 D
116 D120
DI E / Fr 48124 df45
D
I49 DIIIIII65 D67 DIIIIII76 DIIII82 DI85
DI90 D97
DIII
III
105 DНеоднородные пуассоновские процессы - GeeksforGeeks
Модель неоднородного пуассоновского процесса ( NHPP ) представляет количество отказов, имевших место до момента времени t - неоднородный пуассоновский процесс {N (t), t ≥ 0 }.
Основная проблема модели NHPP состоит в том, чтобы определить подходящую функцию среднего значения для обозначения ожидаемого числа отказов, возникших до определенного времени.
При разных допущениях модель будет иметь разные функциональные формы функции среднего значения. Обратите внимание, что в процессе обновления экспоненциальное предположение для времени между прибытиями между отказами ослаблено, а в NHPP ослаблено предположение о стационарности.Неоднородная модель пуассоновского процесса основана на следующих предположениях:
-> Процесс отказа имеет независимое приращение, т.е.е. количество отказов в течение временного интервала (t, t + s) зависит от текущего времени t и продолжительности временного интервала s и не зависит от прошлой истории процесса.
-> Интенсивность отказов процесса определяется как P {ровно один отказ в (t, t + ∆t)} = P {N (t, t + ∆t) - N (t) = 1} = (t) ∆t + o (∆t) где (t) - функция интенсивности.

 Схема: [О -, О]. Повествовательное, невосклицательное, простое, распространённое, с однородными сказуемыми.
Схема: [О -, О]. Повествовательное, невосклицательное, простое, распространённое, с однородными сказуемыми.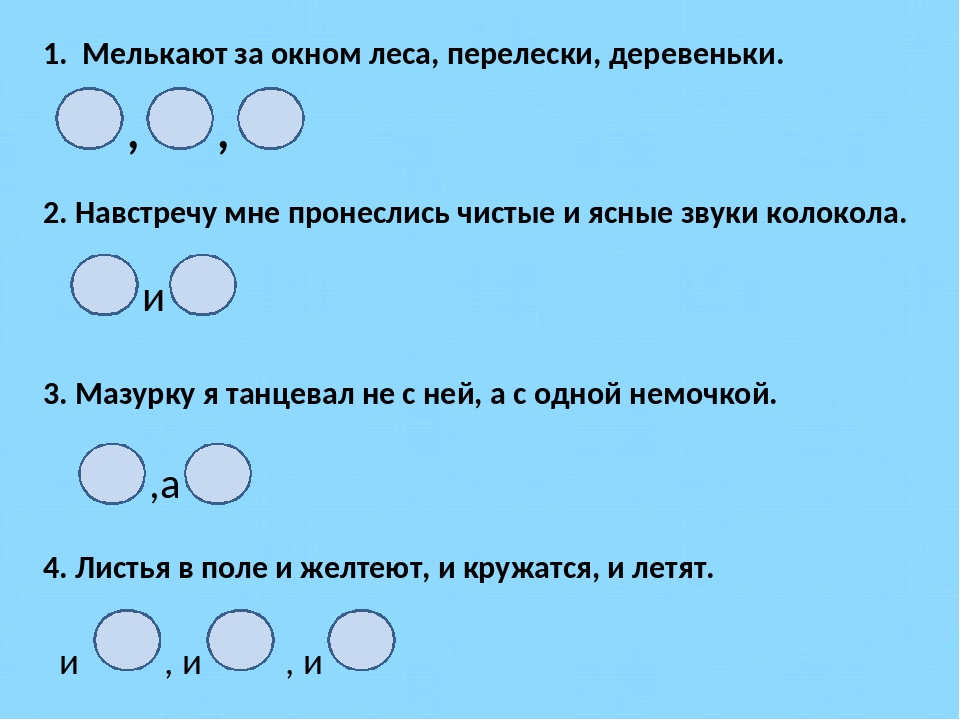 Повествовательное, невосклицательное, сложное, распространённое.
Повествовательное, невосклицательное, сложное, распространённое.