Содержание
Масштабы на чертежах
Масштаб является отношением размеров предмета, изображенного на чертеже, к его настоящим размерам. Масштабом пользуются для изображения слишком больших или слишком мелких деталей.
Если изображение на чертеже и размеры предмета в реальности совпадают, то считается, что чертеж выполнен в натуральную величину, другими словами имеет масштаб 1:1 (один к одному).
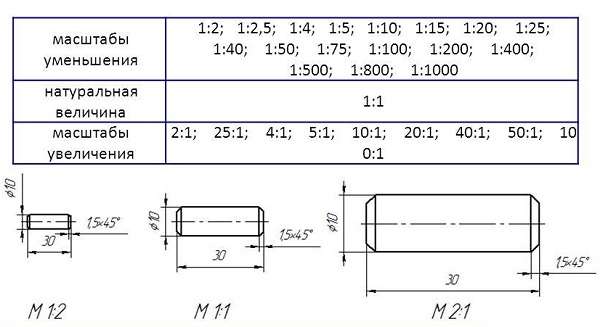
Когда размеры изображения больше действительных размеров предмета, то используется масштаб увеличения. По стандарту может иметь вид: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1
Чертеж детали в разных масштабах
Если же изображение на чертеже наоборот меньше, чем действительные размеры предмета, то тогда используется масштаб уменьшения, имеющий вид: 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000.
Если проектируются генеральные планы крупных объектов, то применяют масштабы типа 1:2000; 1:5000; 1:10 000; 1:20 000; 1:25 000; 1:50 000
Надо иметь ввиду, что какой бы масштаб не использовался на чертеже указывают действительные размеры, а масштаб записывается в графе основной надписи, например: 1:2; 1:4 .
А на изображении может быть указан масштаб только для тех деталей, которые имеют уменьшение или увеличение не совпадающие с масштабом, заявленным в основной надписи. При этом над изображением делают запись такого вида: М 1:2; М 2:1 и т. д.
Если детали чертежа строятся в масштабе 2:1, то линейные размеры изображения увеличивают в два раза. А при выполнении чертежа изображения в масштабе 1:2 — линейные размеры уменьшают в два раза.
Отличная возможность обустроить свой дом или дачу септиком Танк производителя самых лучших септиков в России. Уникальный дизайн и высокое качество, сэкономят ваши средства и прослужат долго, радуя своей надежностью.
масштаб чертежа 2:1 как это
Порой не всегда удается изобразить деталь на чертежном документе в натуральную величину. Наибольшие трудности вызывает построение объемных деталей с большими габаритами, выходящими за рамки форматов А1 и А0. Специалисты используют в работе чаще масштаб 2 к 1. Это как? Все очень просто — нужно пропорционально увеличить все размеры детали или какого-либо механизма в 2 раза для того, чтобы их лучше было видно на листе. Что такое масштабирование? Для построения любых чертежей используют в качестве основы Единую систему конструкторской документации, где описаны не только принципы масштабирования, но и правила расположения деталей на чертеже, нанесения размеров, штриховки, заполнения основной надписи. Само слово «масштабирование» взято из немецкого языка и означает в оригинальном переводе «размер, измерение». Применяют масштабы для изображения габаритных изделий — деталей самолетов, конструктивных элементов жилых и общественных зданий и др., а также для увеличения малогабаритных деталей — механизма наручных часов. М 1:1 — это реальная величина начерченной детали, а 1:2 — это уменьшение величины детали в 2 раза, чтобы она поместилась на листе определенного формата. Масштаб 2 к 1 — это как бы зрительное увеличение натуральных размеров изделия в 2 раза, чтобы конструктору на производстве было понятнее, как должна выглядеть готовая деталь.
Это как? Все очень просто — нужно пропорционально увеличить все размеры детали или какого-либо механизма в 2 раза для того, чтобы их лучше было видно на листе. Что такое масштабирование? Для построения любых чертежей используют в качестве основы Единую систему конструкторской документации, где описаны не только принципы масштабирования, но и правила расположения деталей на чертеже, нанесения размеров, штриховки, заполнения основной надписи. Само слово «масштабирование» взято из немецкого языка и означает в оригинальном переводе «размер, измерение». Применяют масштабы для изображения габаритных изделий — деталей самолетов, конструктивных элементов жилых и общественных зданий и др., а также для увеличения малогабаритных деталей — механизма наручных часов. М 1:1 — это реальная величина начерченной детали, а 1:2 — это уменьшение величины детали в 2 раза, чтобы она поместилась на листе определенного формата. Масштаб 2 к 1 — это как бы зрительное увеличение натуральных размеров изделия в 2 раза, чтобы конструктору на производстве было понятнее, как должна выглядеть готовая деталь. Чертежный стандарт от 1968 г. дает представление о существующих масштабах и способах их построения: 1:1; 1:75; 1:500; 1:1000; 100:1; 4:1; 2:1. Масштаб 2 к 1 это как бы самый мелкий из всех масштабов увеличения. Как построить деталь? Для изображения элементов на чертеже необходимо знать или измерить их линейные размеры, затем умножить их все на два и уже по удвоенным размерам делать чертеж. Важно помнить, что размеры углов при этом и радиусы скруглений увеличивать или уменьшать не нужно! При нанесении размеров после построения чертежа указываются натуральные линейные размеры деталей. Для того чтобы конструктор мог понять, что деталь увеличена намеренно в 2 раза, необходимо указать «масштаб 2 к 1» на чертеже. Это прописывается в таблице «Основная надпись» в разделе «Масштаб». Если же на чертеже были увеличены в 2 раза только отдельные элементы, то над изображением этих элементов прописывают «масштаб 2 к 1» — это как бы увеличение выделенного объекта (см. на рисунке выше).
Чертежный стандарт от 1968 г. дает представление о существующих масштабах и способах их построения: 1:1; 1:75; 1:500; 1:1000; 100:1; 4:1; 2:1. Масштаб 2 к 1 это как бы самый мелкий из всех масштабов увеличения. Как построить деталь? Для изображения элементов на чертеже необходимо знать или измерить их линейные размеры, затем умножить их все на два и уже по удвоенным размерам делать чертеж. Важно помнить, что размеры углов при этом и радиусы скруглений увеличивать или уменьшать не нужно! При нанесении размеров после построения чертежа указываются натуральные линейные размеры деталей. Для того чтобы конструктор мог понять, что деталь увеличена намеренно в 2 раза, необходимо указать «масштаб 2 к 1» на чертеже. Это прописывается в таблице «Основная надпись» в разделе «Масштаб». Если же на чертеже были увеличены в 2 раза только отдельные элементы, то над изображением этих элементов прописывают «масштаб 2 к 1» — это как бы увеличение выделенного объекта (см. на рисунке выше).
«Масштаб 1:2, 1:5, 1:10, 1:100.
 Построение отрезков». 5-й класс
Построение отрезков». 5-й класс
Задачи:
- Ознакомить с понятием масштаба;
- закрепить умение переводить из одной меры в другую; расширить знания о масштабе, придать им практическую направленность;
- корригировать и развивать устную и письменную речи;
- воспитывать интерес к предмету, бережное отношение к окружающему миру.
Ход урока
I
. Организация учащихся на урок.
II. Устный счет.
1. Задание 1 Слайд 2 Приложение 1
- Однажды проводился конкурс красоты среди насекомых.
- Хотите узнать, какое из насекомых стало победителем?
- Оно спряталось под листочком, на котором ответ – четное число.
| 6 × 6 | 72 : 8 |
| + 24 | + 11 |
| — 20 | : 4 |
| : 8 | × 8 |
| 5 | 40 |
– Какое число является четным?
– Королева красоты – божья коровка.
– Что украшает красную спинку божьей коровки?
– Сколько точек у нее на спинке?
Задание 2
Закончить запись: Слайд 3
- 70 см = … дм;
- 47 м = … дм;
- 120 дм = … м.
2. Игра “Задачи от королевы красоты” Слайд 4
- Одна божья коровка 5 точечная, а другая – 15 точечная. Во сколько раз больше точек у одной коровки, чем у другой?
- На 8 листочках по 3 божьи коровки. Сколько всего божьих коровок?
- Красных божьих коровок 32, а желтых в 4 раза меньше. Сколько жёлтых божьих коровок?
- У одной божьей коровки на спинке 6 точек, а у другой на 8 точек больше. Сколько точек у второй божьей коровки?
Потрудились с божьей коровкой, а теперь отгадайте самое большое наземное животное.
Слайд 5
В зоопарке можно встретить,
Его не можешь не заметить,
Он огромен и силен
С хоботом, конечно … (слон)
3. Подготовка к новому материалу. Слайд 6
Подготовка к новому материалу. Слайд 6
Рост слона к 30 годам составляет
350 см = … м … дм (300 см + 50 см = 3 м 5 дм)
Уши слона, если измерить, то длина и ширина одинаковая и составляет:
7 дм 6 см= … см (70 см + 6 см = 76 см)
Если бы у слона не стирались и не обламывались бивни, они могли бы вырасти до таких размеров:
6 м = … дм (60 дм)
Из-за бивней слонов уничтожают и Африканские слоны занесены в Красную книгу. (Подчеркнуть на экране красным пером это выражение).
III. Физическая минутка.
Слайд 7
IV. Работа с новым материалом.
Слайд 8
Мы потрудились и с божьей коровкой, и со слоном. Посмотрите на них внимательно.
Такого ли размера они в природе?
Что использовал художник для изображения каждого из них?
ПЕЙЗАЖ
МАСШТАБ
ОРНАМЕНТ
Почему? Докажи.
Найдем это понятие в учебнике (с. 193, № 935). Слайд 9
193, № 935). Слайд 9
Например, отрезок 30 см. Можем ли мы его начертить в ученической тетради?
Уменьшим его длину в два раза и построим отрезок в 2 раза короче, то есть длиной 15 см.
В таком случае говорят, что отрезок изображен в масштабе один к двум.
Как мы это запишем, найдите в учебнике.
Задача. Слайд 10
Божья коровка за 10 мин проползла 10 см. Изобразите ее путь в тетради в масштабе 1 : 2.
Запомните:
Размеры на чертеже записывают независимо от масштаба изображения.
Учебник: с. 193, №936 (1, 3). Слайды 11, 12
Масштаб может быть разным: М 1:2, М 1:5, М 1:10, М 1:100.
Это значит, что размеры уменьшаются соответственно в 2, 5, 10, 100 раз. Слайд 13
1) Открыли учебник на с. 194, №937. Слайд 14
Решаем в тетради, потом решение проверяем на слайде:
20 см : 5 = 4 см
2) с. 194, №938. Слайд 15
Решение этой задачи завершаем построением двух отрезков:
20 см : 5 = 4 см
15 см : 5 = 3 см
3) с. 194, №939.
194, №939.
Решение и построение выполнить в тетради, а потом сравнить с экраном Слайд 16
4) с. 194, №940. Слайд 17
Решение:
- 4 м = 400 см;
- 3 м = 300 см;
- 400 : 100 = 4 см;
- 300 : 100 = 3 см.
Чертеж к задаче выполнить самостоятельно.
V. Итог урока
Выставление оценок.
VI. Домашнее задание
с. 194, №941 Слайд 18
VII. Список литературы
Приложение 2.
Масштабы чертежей » НПП «Фотограмметрия». Высокоточные обмеры архитектурных объектов.
Масштаб — отношение линейных размеров изображенного на чертеже предмета к его размерам в натуре. Масштаб может быть выражен числом (числовой масштаб) или изображен графически (линейный масштаб).
Числовой масштаб обозначают дробью, которая показывает кратность увеличения или уменьшения размеров изображения на чертеже. При выполнении чертежей в зависимости от их назначения, сложности форм предметов и сооружений, их размеров применяют следующие числовые масштабы (ГОСТ 2. 302—68) *:
302—68) *:
уменьшения: 1:2; 1 : 2,5; 1:4; 1:5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000;
увеличения: 2:1; 2,5: 1; 4:1; 5:1; 10 : I; 20 : 1; 40 : 1; 50 : 1; 100 : 1;
натуральная величина 1:1.
При проектировании генеральных планов крупных объектов используют масштабы 1 : 2000; 1 : 5000; 1 : 10 000; 1 : 20 000; 1 : 25 000; 1 : 50 000.
В том случае, если чертеж выполнен в одном масштабе, его значение указывают в предназначенной для этого графе основной надписи чертежей по типу 1:1; 1:2; 1 : 100 и т. д. Если же какое-либо изображение на чертеже выполнено в масштабе, отличающемся от указанного в основной надписи, то под соответствующим наименованием изображения указывают масштаб по типу М 1:1; М 1 : 2 и т. д.
Применяя числовой масштаб при выполнении чертежей, приходится делать вычисления, чтобы определить размеры отрезков линий, наносимых на чертеже. Например, чтобы определить длину отрезка на чертеже при длине изображаемого предмета 4000 мм и числовом масштабе 1 :50, нужно 4000 мм разделить на 50 (степень уменьшения) и полученную величину (80 мм) отложить на чертеже.
Для сокращения вычислений пользуются масштабной линейкой или строят соответствующий числовому линейный масштаб, как это показано на рисунке для числового масштаба 1 : 50.
Проводят прямую линию и на ней откладывают несколько раз основание масштаба — величину, которая получается в результате деления принятой единицы измерения (1 м = 1000 мм) на размер уменьшения 1000 : 50 = 20 мм. Первый отрезок с левой стороны делят на несколько равных частей так, чтобы каждое деление соответствовало целому числу. Если этот отрезок разделить на 10 частей, то каждое деление будет соответствовать 0,1 м; если на 5 частей — то 0,2 м. Над точками деления линии на отрезки, равные основанию масштаба, надписывают числовые значения, которые соответствуют натуральным размерам, при этом у первого деления справа всегда ставят нуль. Значение мелких делений от нуля влево также надписывают, как это изображено на рисунке.
Для того чтобы взять, пользуясь построенным линейным масштабом, например, размер 4,65 м (4650 мм), нужно одну ножку циркуля-измерителя поставить на 4 м, а другую — на шестое с половиной дробное деление слева от нуля. Если точность окажется недостаточной, применяют поперечный масштаб.
Если точность окажется недостаточной, применяют поперечный масштаб.
Поперечный масштаб дает возможность выразить или определить размер с погрешностью до сотых долей основной единицы измерения. Так, на рисунке ниже показано определение размера, равного 4,65 м.
Десятые доли берут на горизонтальном отрезке масштаба, а сотые — на вертикальном.
В тех случаях, когда требуется построить увеличенное или уменьшенное изображение, выполняемое по заданному чертежу, масштаб которого может быть произвольным, применяют угловой (пропорциональный) масштаб.
Угловой масштаб строят в виде прямоугольного треугольника, отношение катетов которого равно кратности изменения масштаба изображения (h:H). С помощью углового масштаба можно изменять масштаб изображения, пользуясь отвлеченными величинами и не вычисляя размеров изображаемого объекта.
Например, требуется изобразить заданный чертеж в увеличенном масштабе. Для этого строим прямоугольный треугольник АВС, у которого вертикальный катет ВС равен отрезку какой- либо прямой, взятой на заданном чертеже, а горизонтальный катет АВ равен длине соответствующего отрезка в масштабе увеличенного чертежа. Таким образом, чтобы увеличить какой-либо отрезок прямой заданного чертежа, например h, надо отложить его параллельно катету ВС углового масштаба (по вертикали) между катетом А В и гипотенузой АС, Тогда увеличенный размер отрезка будет равен размеру Н, взятому (по горизонтали) на стороне АВ углового масштаба.
Таким образом, чтобы увеличить какой-либо отрезок прямой заданного чертежа, например h, надо отложить его параллельно катету ВС углового масштаба (по вертикали) между катетом А В и гипотенузой АС, Тогда увеличенный размер отрезка будет равен размеру Н, взятому (по горизонтали) на стороне АВ углового масштаба.
Можно применить и другой способ. Как и в первом случае, отложим по вертикали какой-либо отрезок заданного чертежа h. Затем в этом же месте отложим длину отрезка h2 с соответствующим увеличением и через полученную точку проведем наклонную прямую AD. Искомые отрезки получим аналогичным образом. Удобно пользоваться измерителем, вычерчивая угловой масштаб на миллиметровой бумаге.
Угловой масштаб может быть использован также и для перевода величин из одного числового масштаба в другой.
На увеличенном чертеже, как и на заданном, необходимо указывать числами действительные размеры, которые имеет изображаемый предмет в натуре, а не на чертеже.
распечатать
Вконтакте
Одноклассники
Google+
Масштаб в Автокаде.
 Настройка и изменение масштаба в Автокаде
Настройка и изменение масштаба в Автокаде
В этой статье рассмотрим, как масштабировать в Автокаде не отдельный объект, а сразу весь чертеж. Если перед вами стоит вопрос изменения масштаба конкретного элемента, то ознакомьтесь со статьей «Команда AutoCAD — Масштаб».
Работая в Автокаде, следует придерживаться правила: в пространстве Модели построение чертежа всегда и при любых обстоятельствах выполняется в размере 1:1 (см. видео про концепцию работы с пространствами Модель и Лист). Убедитесь, что на вкладке «Модель» в Автокад масштаб 1:1 (см. рис.).
ПРИМЕЧАНИЕ: Бывает, что при построении объекта больших размеров он не вписывается в экран, а прокрутка мыши не выполняет масштабирование. Чтобы это исправить, достаточно дважды щелкнуть по колесику мыши. Автоматически выполнится команда «Показать до границ», и все объекты будут в поле видимости, а прокрутка будет работать корректно.
Как поменять масштаб в Автокаде
В AutoCAD масштаб чертежа задается в правом нижнем углу в строке состояния (см.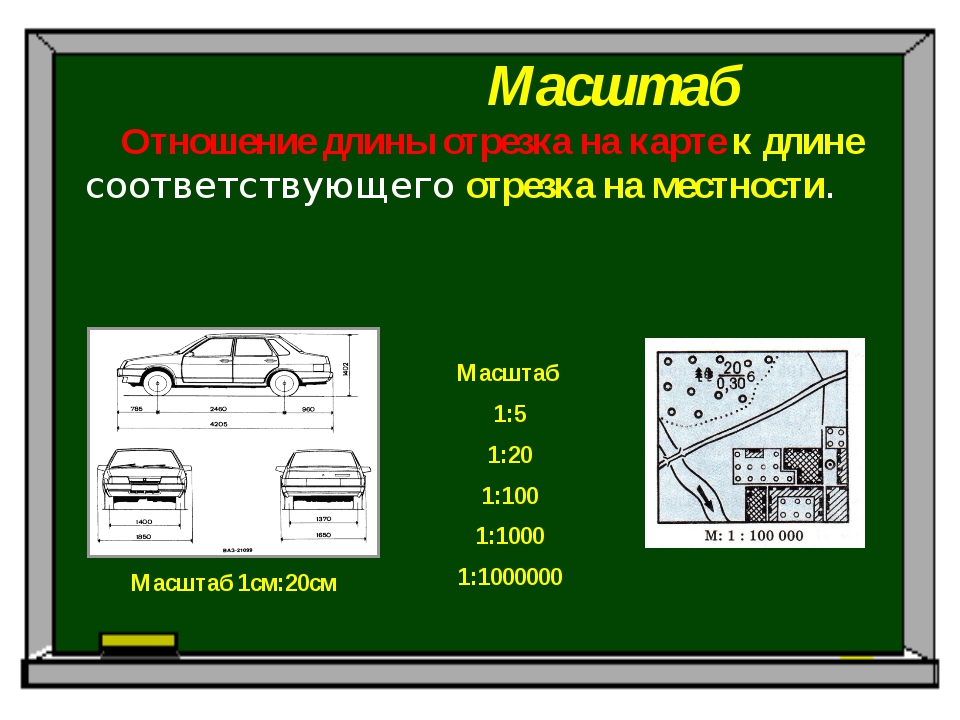 рис.). В Автокаде масштаб 1:100 или 2:1 выбирается из общего списка.
рис.). В Автокаде масштаб 1:100 или 2:1 выбирается из общего списка.
Рассмотрим, как изменять масштаб в Автокаде в пространстве Листа. Данная тема ранее была затронута ранее. Читайте, как в Автокаде сделать масштаб, отличный от стандартного, т.е. пользовательский, и как его применять к видовым экранам на Листах.
Масштаб Автокад видео и доп. материал
Предлагаю ознакомиться с бесплатным видеокурсом «Создание проекта от идеи до печати», в котором я затрагиваю тему, как настроить масштаб в Автокаде. Здесь речь идет про масштаб в Автокаде 2013, хотя существенной разницы с другими версиями нет.
Также можете посмотреть видеоролик про масштаб линии в Автокаде.
Особого внимания заслуживает масштаб размеров в Автокаде. В курсе «Оформление проектов по ГОСТ» про масштаб чертежа Автокад и простановку размеров при оформлении идет отдельная речь. В нём рассказывается, как пользоваться аннотативностью.
Как уменьшить масштаб в Автокаде отдельного объекта или, наоборот, увеличить с помощью нестандартного способа, смотрите в видеоуроке «Масштаб AutoCAD c помощью быстрого калькулятора».
Изучив данный материал, вы будете с легкостью настраивать как масштаб в Автокаде 2012, так и в 2015-2017 версиях.
cccp3d.ru | Изменение масштаба чертежа.
Что только АВТОГАДЧИКИ не придумают, чтобы делать «Как в автокаде»
Автокадчики главные враги….
Не надо всех под одну гребенку.. Я вот тоже с Автокада начинал.. И даже в нем все чертил точно по размерам в нужном масштабе, ибо сколько в нем работал, величину размера всегда можно было ввести арифметическим действием: реальный размер / масштаб..
И на SW перешел без всяких проблем.. Вот с Компасом так и не подружился, это да.. Ни с 2Д, ни с 3Д..
Я с ним дружу с 1989 года.
С версии 2.6.
А я с 1997.. И уже с 8 версии..
Потому что автокадчики стремятся загнать всю документацию предприятия, включая бухгалтерию, в один файл.
Не надо преувеличивать.. Весь комплект чертежей в одном файле Автокада — это удобно с точки зрения Ctrl+C/Ctrl+V и печати.. У нас плоттер позволяет портянки 15 метров печатать.. Правда, потом резать приходится.. Но для этого у нас теперь спец. машина есть..
Правда, некоторые перегибы были.. Были у нас любители в этих 15 метровых портянках весь текст Ариалом писать.. 10 лет назад компы, наиболее совремнные на тот момент, вешались при скроллинге. . Да и краски при печати много уходило..
. Да и краски при печати много уходило..
Как из квадроцикла сделать Газ-21
К сожалению авторы этого небольшого шедевра были очень скупы в описании процесса производства этого миниатюрной модели Газа 21 на платформе квадроцикла, потому здесь будут только фото процесса, однако они тоже очень интересные.
В качестве донора выступил детский квадроцикл на вариаторе. Чертежей не было изначально, как обычно всё по живому режется и лепится. Масштаб чуть более, чем 1 к 2. Копировать не цель. Хочется красивую волжанку с симпатичной мордашкой.
Строится на пространственной раме, кузов пластик, двс, электростартер+автозапуск с пду.
Паспортные данные:
Двигатель 0.5 бензиновый (6 л.с.)
Коробка передач — вариатор
Задний привод
Источник
Жми на кнопку, чтобы подписаться на «Как это сделано»!
Если у вас есть производство или сервис, о котором вы хотите рассказать нашим читателям, пишите Аслану (shauey@yandex. ru) и мы сделаем самый лучший репортаж, который увидят не только читатели сообщества, но и сайта Как это сделано
ru) и мы сделаем самый лучший репортаж, который увидят не только читатели сообщества, но и сайта Как это сделано
Подписывайтесь также на наши группы в фейсбуке, вконтакте, одноклассниках, в ютюбе и инстаграме, где будут выкладываться самое интересное из сообщества, плюс видео о том, как это сделано, устроено и работает.
Жми на иконку и подписывайся!
— http://kak_eto_sdelano.livejournal.com/
— https://www.facebook.com/kaketosdelano/
— https://www.youtube.com/kaketosdelano
— https://vk.com/kaketosdelano
— https://ok.ru/kaketosdelano
— https://twitter.com/kaketosdelano
— https://www.instagram.com/kaketosdelano/
Официальный сайт — http://ikaketosdelano.ru/
Мой блог — http://aslan.livejournal.com
Инстаграм — https://www.instagram.com/aslanfoto/
Facebook — https://www.facebook.com/aslanfoto/
Вконтакте — https://vk.com/aslanfoto
Геометрия
— Точка лежит на расширении коники с масштабным фактором $ k $, если ее полярность касается расширения этой коники с масштабным фактором $ 1 / k $
.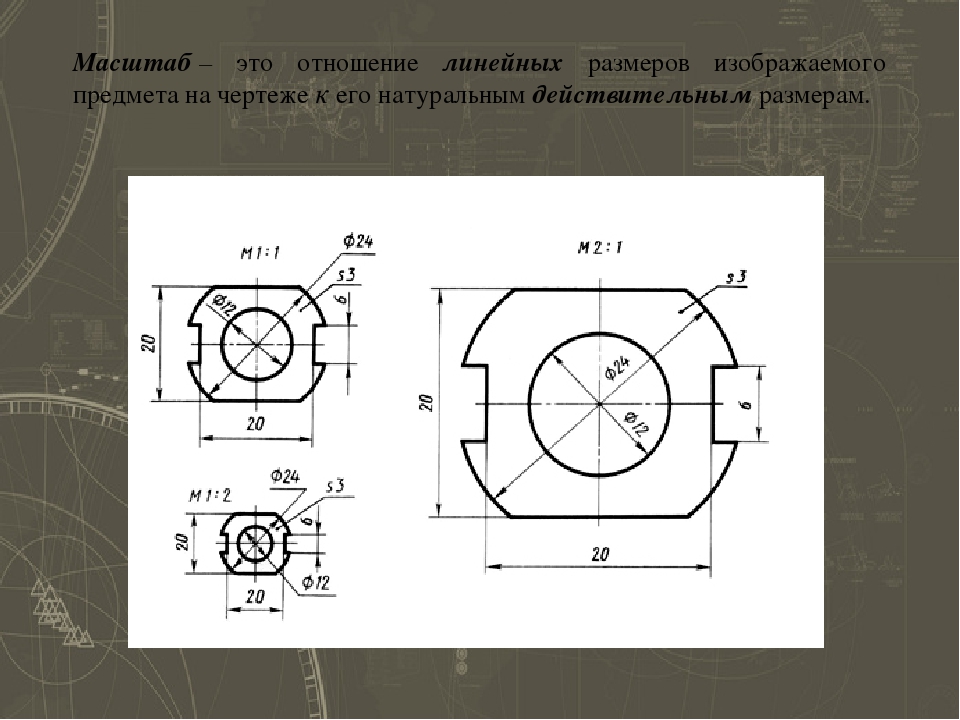
Кажется, что полярность точки относительно коники не зависит от выбора системы координат (см., Например, [VT, стр. 102]; к сожалению, мне не удалось найти точную формулировку этого факта. ни в моих (электронных) книгах, ни в поисках русских и английских ссылок), поэтому достаточно рассмотреть аффинные системы координат, в которых коника определяется каноническими уравнениями.2 = 2 (п / к) x. $$
Уравнение поляры точки $ (x_1, y_1) $ относительно коники $ C $ согласно [KK, 2.4-10]: $$ y_1y + p (x + x_1) = 0 $$ и уравнение прямой касательной к конике $ C_ {1 / k} $ в ее точке $ (x_2, y_2) $ согласно [KK, 2.4-10] имеет вид (1) $$ y_2y + p (x + x_2) /k=0.$$
Теперь мы можем доказать эквивалентность.
Точка $ P $ лежит на $ C_k $ ($ k \ neq 0 $) тогда и только тогда, когда полярность $ P $ относительно $ C $ касается $ C_ {1 / k} $.
Действительно, полярная точка $ \ ell $ в $ P $ относительно $ C $ касается $ C_ {1 / k} $ тогда и только тогда, когда существует точка $ P ‘(x_2, y_2) $ коники $ C_ { 1 / k} $ такая, что уравнение (1) определяет прямую $ \ ell $. 2 $, то есть тогда и только тогда, когда точка $ P (x_1, y_1) $ лежит на конике $ C_k $.
2 $, то есть тогда и только тогда, когда точка $ P (x_1, y_1) $ лежит на конике $ C_k $.
Список литературы
[KK] Гранино Корн, Тереза Корн Математический справочник для ученых и инженеров , 2-е издание, McGraw Hill, 1968 (русский перевод, Москва, «Наука», 1973).
[ВТ] Веселов А.П., Троицкий Е.В. Лекции по аналитической геометрии , Москва, Центр прикладных исследований механико-математического факультета МГУ, 2002 (на русском языке).
Определение композиционных структур социальной динамики с помощью глубокого обучения
1.Ромеро Д., Мидер Б., Кляйнберг Дж. (2011) Различия в механике распространения информации по темам: идиомы, политические хэштеги и комплексное заражение в Twitter. В: Proc. WWW.
3. Vieweg S, Hughes AL, Starbird K, Palen L (2010) Микроблоги во время двух стихийных бедствий: что Twitter может способствовать повышению осведомленности о ситуации. В: Proc. ОМС.
4.
Нааман М., Беккер Х, Гравано Л. (2011) Модный и модный: характеристика новых тенденций в твиттере. J Am Soc Inf Sci and Tech.DOI: 10.1002 / asi.21489
(2011) Модный и модный: характеристика новых тенденций в твиттере. J Am Soc Inf Sci and Tech.DOI: 10.1002 / asi.21489
[Google Scholar]
5. Ян Дж., Лесковец Дж. (2011) Паттерны временных изменений в онлайн-СМИ. Proc из WSDM.
6. Леманн Дж., Гонсалвес Б. (2012) Динамические классы коллективного внимания в твиттере. Proc из WWW.
7. Пэн Х. К., Маркулеску Р. (2014) ASH: Масштабируемый анализ коллективного поведения в социальных сетях с использованием римановой геометрии. В: Международная конференция ASE по социальным вычислениям.
8. Boureau Y, Cun Y (2008) Редкое изучение функций для сетей глубоких убеждений.Достижения в области обработки нейронной информации (NIPS): 1–8.
9. Hinton GE, Osindero S, Teh Y (2006) Алгоритм быстрого обучения для сетей с глубокими убеждениями. Алгоритм быстрого обучения для сетей глубоких убеждений. [PubMed]
10. Кавукчуоглу К., Серманет П. (2010) Изучение иерархий сверточных функций для визуального распознавания. Достижения в области обработки нейронной информации (NIPS): 1–9.
11. Taylor G, Fergus R, LeCun Y, Bregler C (2010) Сверточное обучение пространственно-временных характеристик. Компьютерное зрение ECCV 2010.
12. Ли Х., Гроссе Р., Ранганат Р., Нг А. (2009) Сверточные сети глубоких убеждений для масштабируемого неконтролируемого обучения иерархических представлений. Международная конференция по машинному обучению (ICML): 1–8.
13. Sochard R, Lin CCy, Ng AY, Manning CD (2011) Анализ естественных сцен и естественного языка. В: Международная конференция по машинному обучению (ICML).
14. Коллоберт Р. (2011) Глубокое обучение для эффективного дискриминантного анализа. В: Международная конференция по искусственному интеллекту и статистике.
15. Смит Г., Х. ДКЛ, Г. М., П. Р. (1998) Обнаружение правил из временных рядов. В: Proc. 3-го КДД.
16. Чен Дж. Р. (2007) Полезные результаты кластеризации от значимой кластеризации временных рядов. В: Proc. 6-й Австралазийской конференции по интеллектуальному анализу данных.
17. Rakthanmanon T (2011) Эпентеза временных рядов: кластеризация потоков временных рядов требует игнорирования некоторых данных. Международная конференция по интеллектуальному анализу данных (ICDM).
18. Mueen J, Keogh E (2012) Кластеризация временных рядов с использованием неконтролируемых шейплетов.В: Международная конференция по интеллектуальному анализу данных (ICDM).
19. Rakthanmanon T, Keogh E (2013) Быстрые шейплеты: масштабируемый алгоритм для обнаружения шейплетов временных рядов. Материалы тринадцатой конференции SIAM.
20.
Джеймс Д., Купман С.Дж. (2012) Анализ временных рядов методами пространства состояний. Издательство Оксфордского университета. [Google Scholar] 21. Ольсхаузен Б.А., Филд-ди-джей (1998). Появление свойств рецептивного поля простых ячеек путем изучения разреженного кода для естественного изображения. Природа. [PubMed]
22.Гроссе Р., Райна Р., Квонг Х., Нг А. (2007) Разреженное кодирование с инвариантным сдвигом для классификации аудио. Proc UAI.
Proc UAI.
23. Zeiler MD, Krishnan D, Taylor GW, Fergus R (2010) Деконволюционные сети. Proc of CVPR: 2528–2535.
24. Хинтон Г.Е., Салахутдинов Р.Р. (2006) Уменьшение размерности данных с помощью нейронных сетей. Наука. [PubMed]
25. Асур С., Хуберман Б.А., Сабо Г., Ван С. (2011) Тенденции в социальных сетях: стойкость и упадок. В: Proc. ICWSM.
26. Kleinberg J (2002) Неустойчивая и иерархическая структура в потоках.Proc of KDD.
27.
Бойд С.П., Ванденберге Л. (2004) Выпуклая оптимизация. Издательство Кембриджского университета. [Google Scholar]
28. Нестеров Ю. (2007). Градиентные методы минимизации составной целевой функции.
30. Лесковец Дж., Кляйнберг Дж., Фалаутсос С. (2005) Графики с течением времени: законы уплотнения, сужающиеся диаметры и возможные объяснения. В: Proc. КДД.
31. Lin Y, Chi Y, Zhu S (2008) Facetnet: структура для анализа сообществ и их эволюции в динамических сетях.Proc из WWW.
32. Пэн Х.К., Маркулеску Р. (2013) Определение динамики и коллективного поведения в следах микроблогов. В: Proc. АСОНАМ.
В: Proc. АСОНАМ.
34. Sumi R, Yasseri T, Rung A, Kornai A, Janos K (2011) Редактировать войны в Википедии. В: Международная конференция IEEE по социальным вычислениям (SocialCom).
Графическая параллельная крупномасштабная структура из Motion
1 Введение
В последние годы исследование SfM быстро продвинулось вперед. Он добился большого успеха в сценах малого и среднего масштаба.Однако восстановление крупномасштабных наборов данных остается большой проблемой с точки зрения как эффективности, так и надежности.
Начиная с [DBLP: conf / iccv / AgarwalSSSS09] добился большого успеха и стал важной вехой, инкрементальные подходы широко используются в современных приложениях SfM. [DBLP: conf / cvpr / SnavelySS08, DBLP: conf / 3dim / Wu13 , DBLP: conf / accv / MoulonMM12, DBLP: conf / mm / SweeneyHT15, DBLP: conf / cvpr / SchonbergerF16] . Геометрическая фильтрация в сочетании с процессом RANSAC [DBLP: journals / cacm / FischlerB81]
позволяет эффективно удалять выбросы. Начиная с надежной исходной реконструкции, добавочный SfM затем добавляет камеры одну за другой с помощью PnP
Начиная с надежной исходной реконструкции, добавочный SfM затем добавляет камеры одну за другой с помощью PnP
[DBLP: conf / cvpr / KneipSS11, DBLP: journals / ijcv / LepetitMF09] . После успешной регистрации камер используется дополнительный шаг настройки связки для оптимизации поз и трехмерных точек [DBLP: conf / iccvw / TriggsMHF99] , что делает инкрементный SfM надежным и точным, однако также делает инкрементный SfM затруднительным при работе с крупномасштабные наборы данных. Поскольку повторяющаяся оптимизация путем корректировки пакета [DBLP: conf / iccvw / TriggsMHF99] делает инкрементную SfM неэффективной, а требования к памяти также становятся узким местом.Кроме того, способ постепенного добавления новых представлений приводит к тому, что такие подходы легко страдают от дрейфа, хотя используется дополнительный этап повторной триангуляции [DBLP: conf / 3dim / Wu13] .
Global SfM приближается к [DBLP: conf / cvpr / Govindu01, DBLP: conf / eccv / WilsonS14, DBLP: journals / pami / CrandallOSh23, DBLP: conf / iccv / CuiT15, DBLP: conf / iccv / ChatterjeeG13 /, DBLP: conf / iccv / ChatterjeeG13 /, DBLP: conf / iccv / ChatterjeeG13 /, eccv / HavlenaTP10, DBLP: conf / eccv / WilsonBS16, Govindu2006Robustness, Govindu2004Lie, DBLP: conf / cvpr / OzyesilS15, Moulon2013Global] имеют преимущества перед инкрементными в эффективности. Когда все доступные относительные движения получены, глобальные подходы сначала получают глобальные вращения, эффективно и надежно решая задачу усреднения вращения [DBLP: conf / cvpr / Govindu01, DBLP: conf / cvpr / Govindu04, DBLP: journals / ijcv / HartleyTDL13, DBLP : conf / cvpr / HartleyAT11, DBLP: conf / iccv / ChatterjeeG13, DBLP: journals / pami / ChatterjeeG18, DBLP: conf / cvpr / ErikssonOKC18, DBLP: conf / eccv / WilsonBS16]
Когда все доступные относительные движения получены, глобальные подходы сначала получают глобальные вращения, эффективно и надежно решая задачу усреднения вращения [DBLP: conf / cvpr / Govindu01, DBLP: conf / cvpr / Govindu04, DBLP: journals / ijcv / HartleyTDL13, DBLP : conf / cvpr / HartleyAT11, DBLP: conf / iccv / ChatterjeeG13, DBLP: journals / pami / ChatterjeeG18, DBLP: conf / cvpr / ErikssonOKC18, DBLP: conf / eccv / WilsonBS16]
. Затем глобальные ориентации и относительные переводы используются для оценки перемещений камеры (или центров камеры) путем усреднения перевода
[DBLP: conf / eccv / WilsonS14, DBLP: conf / cvpr / OzyesilS15, DBLP: conf / eccv / GoldsteinHLVS16, DBLP: журналы / корр / абс-1901-00643] .С известными позами камеры можно выполнить триангуляцию (может потребоваться повторная триангуляция) для получения трехмерных точек, а затем только один раз, когда потребуется этап настройки связки. Хотя глобальные подходы являются эффективными, недостатки очевидны: усреднение перевода трудно решить, поскольку относительные переводы декодируют только направление перевода, а масштаб неизвестен; выбросы по-прежнему являются головной болью при усреднении перевода, что является основной причиной запрета на практическое использование глобальных подходов SfM.
Преодолеть проблему неэффективности в инкрементальных SfM и в то же время сохранить надежность реконструкции, естественная идея
заключается в проведении реконструкции по принципу «разделяй и властвуй». Пионерской работой, предложившей эту идею, является [DBLP: conf / accv / BhowmickPCGB14] , в котором изображения сначала разделяются путем вырезания графа, а каждая суб-реконструкция сшивается путем преобразования подобия. Затем следует [Zhu2017Parallel, DBLP: conf / cvpr / ZhuZZSFTQ18] , где в каждой суб-реконструкции используются как преимущества инкрементального, так и глобального подходов.Однако оба этих подхода «разделяй и властвуй» больше ориентированы на локальные реконструкции, а их трубопроводы не учитываются глобально, что может привести к провалу SfM.
Вдохновленный предыдущей выдающейся работой «разделяй и властвуй». [DBLP: conf / accv / BhowmickPCGB14, DBLP: conf / 3dim / SweeneyFHT16, Zhu2017Parallel, DBLP: conf / cvpr / ZhuZZSFTQ18] , мы решаем крупномасштабные SfM параллельно режим, в то время как весь конвейер спроектирован с использованием единой структуры, основанной на теории графов. Предлагаемая структура новизны начинается с глобальной точки зрения, где этап кластеризации изображений предназначен как для надежной локальной реконструкции, так и для этапа слияния окончательных суб-реконструкций, на котором каждый кластер рассматривается как узел внутри графа. И этап объединения суб-реконструкций может дополнительно использовать структуру кластерного графа для получения надежных результатов объединения. Более конкретно, сначала изображения делятся на кластеры без перекрытия, и каждый кластер является узлом графа. Во-вторых, потерянные ребра собираются и используются для построения максимального остовного дерева (MaxST).Затем эти потерянные края добавляются вдоль MaxST для создания перекрывающихся изображений и улучшения связей между кластерами. В-третьих, локальные решатели SfM выполняются в параллельном или распределенном режиме. Наконец, после завершения всех локальных заданий SfM предлагается новый алгоритм объединения суб-реконструкций для регистрации кластеров. Наиболее точные преобразования подобия N-1 выбираются в пределах минимального остовного дерева (MinST), и строится дерево минимальной высоты (MHT), чтобы найти подходящий опорный кадр и подавить накопленную ошибку.
Предлагаемая структура новизны начинается с глобальной точки зрения, где этап кластеризации изображений предназначен как для надежной локальной реконструкции, так и для этапа слияния окончательных суб-реконструкций, на котором каждый кластер рассматривается как узел внутри графа. И этап объединения суб-реконструкций может дополнительно использовать структуру кластерного графа для получения надежных результатов объединения. Более конкретно, сначала изображения делятся на кластеры без перекрытия, и каждый кластер является узлом графа. Во-вторых, потерянные ребра собираются и используются для построения максимального остовного дерева (MaxST).Затем эти потерянные края добавляются вдоль MaxST для создания перекрывающихся изображений и улучшения связей между кластерами. В-третьих, локальные решатели SfM выполняются в параллельном или распределенном режиме. Наконец, после завершения всех локальных заданий SfM предлагается новый алгоритм объединения суб-реконструкций для регистрации кластеров. Наиболее точные преобразования подобия N-1 выбираются в пределах минимального остовного дерева (MinST), и строится дерево минимальной высоты (MHT), чтобы найти подходящий опорный кадр и подавить накопленную ошибку.
Наши взносы в основном трехкратные:
Мы предложили надежный алгоритм кластеризации изображений, в котором изображения группируются в группы подходящего размера с перекрытием, а возможность подключения улучшается с помощью MaxST.
Мы предложили новый алгоритм слияния подмоделей, основанный на графах, в котором MinST создан для поиска точных преобразований подобия, а MHT создан для предотвращения накопления ошибок во время процесса слияния.
Временная сложность линейно связана с количеством изображений, в то время как большинство современных алгоритмов являются квадратичными.
2 Связанные работы
Интересной работой в области крупномасштабной реконструкции являются иерархические подходы к SfM [Farenzena2009Structure, Gherardi2010Improving, Toldo2015Hierarchical, DBLP: conf / 3dim / NiD12, DBLP: journals / cviu / ChenCLSW17] . Эти подходы принимают каждое изображение как листовой узел. Облака точек и позы камеры объединены снизу вверх.Для получения сбалансированной дендрограммы принят принцип «сначала наименьшее», что делает иерархические подходы нечувствительными к ошибкам инициализации и дрейфа. Однако из-за недостаточного соответствия функций [DBLP: journals / ijcv / Lowe04, DBLP: journals / pr / MaJJG19] восстановленные сцены имеют тенденцию терять детали сцены и становиться неполными. Кроме того, качество реконструкций может ухудшиться из-за выбора похожих пар изображений.
Облака точек и позы камеры объединены снизу вверх.Для получения сбалансированной дендрограммы принят принцип «сначала наименьшее», что делает иерархические подходы нечувствительными к ошибкам инициализации и дрейфа. Однако из-за недостаточного соответствия функций [DBLP: journals / ijcv / Lowe04, DBLP: journals / pr / MaJJG19] восстановленные сцены имеют тенденцию терять детали сцены и становиться неполными. Кроме того, качество реконструкций может ухудшиться из-за выбора похожих пар изображений.
В некоторых более ранних работах предпринимается попытка решить крупномасштабную SfM с помощью многоядерных процессоров [DBLP: conf / iccv / AgarwalSSSS09] или уменьшить бремя исчерпывающего попарного сопоставления путем построения скелетных графов [DBLP: conf / cvpr / SnavelySS08] .Bhowmick [DBLP: conf / accv / BhowmickPCGB14] попытался решить крупномасштабную SfM методом «разделяй и властвуй», и вырезал график [DBLP: journals / pami / DhillonGK07, DBLP: journals / pami / ShiM00] был принят сделать раздел данных.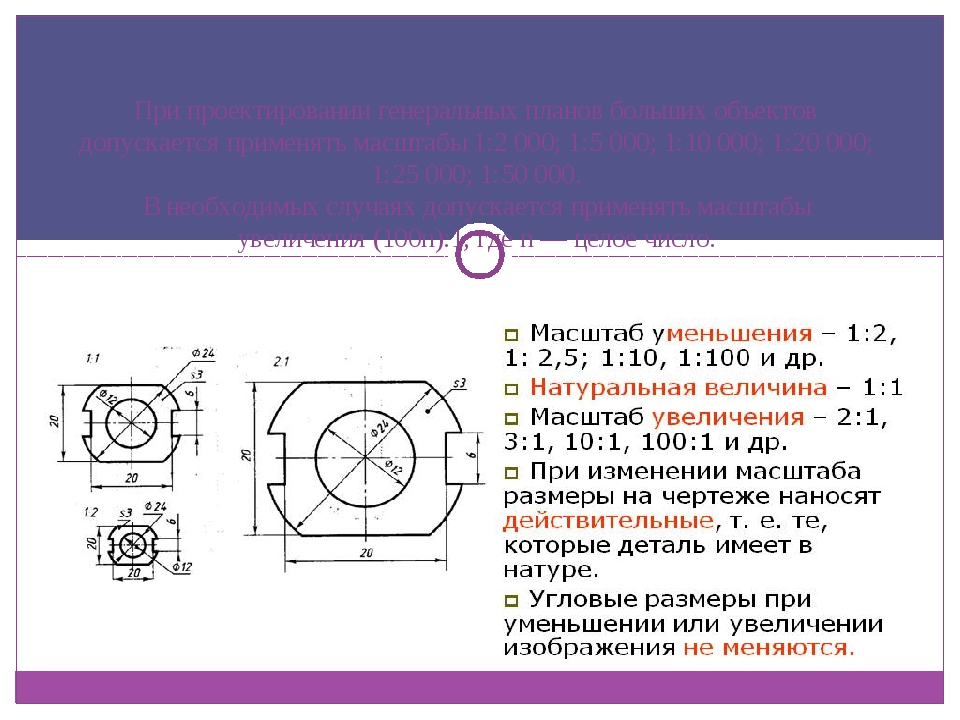 После завершения всех суб-реконструкций в каждой суб-реконструкции регистрируются дополнительные камеры для создания перекрывающихся областей, а затем для их объединения. Затем он был улучшен в [DBLP: conf / 3dim / SweeneyFHT16] для кластеризации набора данных и объединения каждого кластера с помощью модели распределенной камеры [DBLP: conf / eccv / SweeneyFHT14, DBLP: conf / 3dim / SweeneyFHT16] .Однако оба [DBLP: conf / 3dim / SweeneyFHT16, DBLP: conf / accv / BhowmickPCGB14] либо не принимали во внимание стратегию кластеризации графов, либо пренебрегали тщательной разработкой алгоритма кластеризации и слияния, что делает реконструкцию хрупкой и страдает от проблема дрейфа. Кроме того, потеря связи между различными компонентами делает реконструкцию хрупкой. Кроме того, оценка подобия, которая используется в качестве веса при разбиении графа, снижает надежность результата.Следует отметить один недостаток: процесс инкрементного слияния страдает от смещенных ошибок, а также от традиционных инкрементных подходов.
После завершения всех суб-реконструкций в каждой суб-реконструкции регистрируются дополнительные камеры для создания перекрывающихся областей, а затем для их объединения. Затем он был улучшен в [DBLP: conf / 3dim / SweeneyFHT16] для кластеризации набора данных и объединения каждого кластера с помощью модели распределенной камеры [DBLP: conf / eccv / SweeneyFHT14, DBLP: conf / 3dim / SweeneyFHT16] .Однако оба [DBLP: conf / 3dim / SweeneyFHT16, DBLP: conf / accv / BhowmickPCGB14] либо не принимали во внимание стратегию кластеризации графов, либо пренебрегали тщательной разработкой алгоритма кластеризации и слияния, что делает реконструкцию хрупкой и страдает от проблема дрейфа. Кроме того, потеря связи между различными компонентами делает реконструкцию хрупкой. Кроме того, оценка подобия, которая используется в качестве веса при разбиении графа, снижает надежность результата.Следует отметить один недостаток: процесс инкрементного слияния страдает от смещенных ошибок, а также от традиционных инкрементных подходов.
Следуйте за работой Bhowmick [DBLP: conf / accv / BhowmickPCGB14] , [Zhu2017Parallel, DBLP: conf / cvpr / ZhuZZSFTQ18] дополните процесс вырезания графа в [DBLP: conf / accv14, BhowLickPc / 3dim / SweeneyFHT16] в два этапа: разрезание двоичного графа и расширение графа. В их работе этап вырезания графа и этап расширения графа чередовались, а затем сходились, когда удовлетворяются как ограничение размера, так и ограничение полноты.Затем компоненты регистрируются путем усреднения глобального движения [Zhu2017Parallel] . Однако усреднение трансляции на уровне кластера по-прежнему страдает от выбросов и может привести к несвязанным моделям. Эта работа была дополнительно улучшена в [DBLP: conf / cvpr / ZhuZZSFTQ18] , где был принят подход к регистрации кластеров из [DBLP: conf / accv / BhowmickPCGB14] , а затем позы камеры были разделены на внутрикамерные и межкамерные. -камеры для усреднения движения, которые могут улучшить скорость сходимости окончательной настройки пакета [DBLP: conf / iccvw / TriggsMHF99, DBLP: conf / cvpr / ErikssonBCI16, DBLP: conf / iccvw / RamamurthyLAPV17, DBLP: conf / iccvQ17] .
3 Графическая структура из Motion
Для работы с крупномасштабными наборами данных мы применяем стратегию «разделяй и властвуй», аналогичную [DBLP: conf / accv / BhowmickPCGB14, Zhu2017Parallel] . Для полноты и эффективности реконструкции мы предлагаем использовать единый графовый каркас для решения задачи кластеризации изображений и слияния суб-реконструкций. Конвейер нашего алгоритма SfM показан на рисунке 1. Во-первых, мы извлекаем признаки и используем их для сопоставления.Предполагается, что эпиполярная геометрия отфильтровывает совпадающие выбросы. После сопоставления признаков мы используем предложенный нами алгоритм кластеризации изображений для разделения изображений на разные группы. Затем кластеры могут быть реконструированы локальным SfM параллельно. После слияния всех локальных реконструкций с помощью нашего алгоритма слияния на основе графов в качестве альтернативы можно выполнить следующий шаг повторной триангуляции и уравнивание связки. Мы опишем более подробную информацию о нашем алгоритме в следующих подразделах.
Мы опишем более подробную информацию о нашем алгоритме в следующих подразделах.
Рисунок 1: Предлагаемый нами трубопровод SfM.После сопоставления признаков мы используем предложенный нами алгоритм кластеризации изображений для разделения изображений на разные группы. Затем кластеры могут быть реконструированы локальным SfM параллельно. После слияния всех локальных реконструкций с помощью нашего алгоритма слияния на основе графов в качестве альтернативы можно выполнить следующий шаг повторной триангуляции и уравнивание связки.
3.1 Кластеризация изображений
Мы стремимся сгруппировать m изображений в k кластеров, каждый кластер находится под ограничением памяти компьютера. Кроме того, каждый кластер должен быть реконструирован как можно точнее, и на него не должно сильно влиять потеря геометрических ограничений.В этом разделе мы поделимся простым, но довольно эффективным подходом для двухэтапной кластеризации изображений: (1) вырезание графика. (2) Расширение изображений на основе максимального связующего дерева. Оба эти шага основаны на интуитивной теории графов. Кроме того, мы используем два условия, предложенные в [Zhu2017Parallel] , чтобы ограничить шаги кластеризации: ограничение размера и ограничение полноты. Ограничение размера дает верхнюю границу изображений в каждом кластере. Ограничение полноты определяется как η (i) = ∑j ≠ i∣∣Ci∩Cj∣∣Ci.В отличие от алгоритма кластеризации изображений, предложенного в [Zhu2017Parallel] , который чередуется между вырезанием и расширением графа, мы просто выполняем однократное вырезание графика и однократное расширение изображения. И мы утверждаем, что новинка нашего этапа расширения заключается в использовании MaxST для помощи на последнем этапе объединения.
Оба эти шага основаны на интуитивной теории графов. Кроме того, мы используем два условия, предложенные в [Zhu2017Parallel] , чтобы ограничить шаги кластеризации: ограничение размера и ограничение полноты. Ограничение размера дает верхнюю границу изображений в каждом кластере. Ограничение полноты определяется как η (i) = ∑j ≠ i∣∣Ci∩Cj∣∣Ci.В отличие от алгоритма кластеризации изображений, предложенного в [Zhu2017Parallel] , который чередуется между вырезанием и расширением графа, мы просто выполняем однократное вырезание графика и однократное расширение изображения. И мы утверждаем, что новинка нашего этапа расширения заключается в использовании MaxST для помощи на последнем этапе объединения.
3.1.1 Кластеризация изображений
На этапе вырезания графа каждое изображение считается узлом графа, а каждое ребро представляет связь между изображениями. В случае SfM это может быть представлено результатами двух геометрий обзора.Вес ребер — это количество совпадений после геометрической фильтрации.
Чтобы решить эту проблему, связь между изображениями можно рассматривать как ребра внутри графа. Предположим, что каждая камера является узлом графа, связь между двумя камерами можно рассматривать как взвешенное ребро (здесь мы называем ребра изображения). Учтите ограничение размера, каждый кластер должен иметь одинаковый размер. Проблема кластеризации изображений может быть решена разрезанием графа [DBLP: journals / pami / DhillonGK07, DBLP: journals / pami / ShiM00] .Чтобы улучшить соединение кластеров и выровнять их вместе, необходимо выполнить дополнительный шаг расширения. В нашем случае нам нужно расширить эти независимые кластеры некоторыми общими изображениями (мы называем их перекрывающейся областью), а затем вычислить преобразования подобия, чтобы объединить их вместе. Поскольку итерационный подход Zhu [Zhu2017Parallel] требует много времени, мы предложили наш одношаговый подход к процедуре расширения в следующем подразделе.
3.1.2 Расширение изображений
На этапе расширения изображения мы обобщаем график на уровень кластеров. Каждый кластер представляет собой узел, ребра между кластерами — это потерянные ребра после вырезания графа (здесь мы называем ребра кластера). Сначала мы собираем все потерянные ребра Elost = {Ek1k2, i | k1, k2∈ [K], i∈ | Ek1k2 |} для пар кластеров, где K — количество кластеров. Затем мы строим граф, вес края кластера — это количество краев потерянного изображения между двумя кластерами. Интуитивно понятно, что если внутри парных кластеров теряется больше краев изображения, мы предпочитаем создавать для них соединения, чтобы избежать потери информации.Имея это в виду, как только мы получаем граф кластера, создается MaxST, чтобы вызвать шаг расширения. Мы собираем края изображения из MaxST и сортируем их по убыванию. Затем мы добавляем края потерянного изображения в кластеры, где не выполняется ограничение полноты, и добавляются только верхние k краев. Наконец, мы проверяем все кластеры и собираем их вместе, если ограничение полноты любого из них не выполняется. Для краев кластера, которые не содержатся в MaxST, мы выбираем их случайным образом и аналогичным образом добавляем края изображения в эти кластеры.
Каждый кластер представляет собой узел, ребра между кластерами — это потерянные ребра после вырезания графа (здесь мы называем ребра кластера). Сначала мы собираем все потерянные ребра Elost = {Ek1k2, i | k1, k2∈ [K], i∈ | Ek1k2 |} для пар кластеров, где K — количество кластеров. Затем мы строим граф, вес края кластера — это количество краев потерянного изображения между двумя кластерами. Интуитивно понятно, что если внутри парных кластеров теряется больше краев изображения, мы предпочитаем создавать для них соединения, чтобы избежать потери информации.Имея это в виду, как только мы получаем граф кластера, создается MaxST, чтобы вызвать шаг расширения. Мы собираем края изображения из MaxST и сортируем их по убыванию. Затем мы добавляем края потерянного изображения в кластеры, где не выполняется ограничение полноты, и добавляются только верхние k краев. Наконец, мы проверяем все кластеры и собираем их вместе, если ограничение полноты любого из них не выполняется. Для краев кластера, которые не содержатся в MaxST, мы выбираем их случайным образом и аналогичным образом добавляем края изображения в эти кластеры.
Процедура нашего алгоритма кластеризации изображений показана на рисунке 2. На рис. 2 (а) граф изображений сначала группируется с использованием алгоритма вырезания графа, при котором ребра со слабыми связями обычно удаляются. На рис. 2 (b) граф кластеров после вырезания графа, где узлы — это кластеры, а ребра — это потерянные ребра в графе изображений, количество потерянных ребер — это веса ребер. На рис. 2 (c) сплошные линии представляют края построенного максимального остовного дерева. Пунктирная линия может быть добавлена для улучшения связи кластеров.На рис. 2 (d) показаны окончательные кластеры развернутого изображения. Полный алгоритм кластеризации изображений приведен в Alg. 1.
Рисунок 2: Процедура кластеризации изображений. (а). Граф изображений сгруппирован по NCut, где обычно удаляются ребра со слабыми связями. (б). Кластерный граф после вырезания графа, где узлы — это кластеры, а ребра — это потерянные ребра в графе изображений, количество потерянных ребер — это веса ребер. (c). Сплошные линии представляют собой края построенного максимального остовного дерева. Пунктирная линия может быть добавлена для улучшения связи кластеров.(d) Окончательные кластеры расширенных изображений.
(c). Сплошные линии представляют собой края построенного максимального остовного дерева. Пунктирная линия может быть добавлена для улучшения связи кластеров.(d) Окончательные кластеры расширенных изображений.
1: начальный граф изображения G: = {(V, E)}, максимальное количество кластеров Smax, коэффициент полноты C, количество перекрывающихся изображений между двумя кластерами Omax, количество изображений n.
2: кластеры изображений с пересечением Ginter = {Gk}
3: K: = ⌊n / Smax⌋
4: Gintra: = GraphPartition (G), Gintra, i∈Gintra, i∈ [K]
5. Соберите потерянные ребра Elost: = {Ek1k2 | k1, k2∈ [K]}
6: Построить кластерный граф Gcluster: = ∅ от Elost
7: Emst: = Kruskal (Gcluster), i: = 0, j: = 0, Ginter: = Gintra
8: пока i <| Emst | делать
9: край Ek1k2, i = Emst, i
10: Gk1inter, Gk2inter добавляют потерянные ребра в Ek1k2, i
11: я ← я + 1
12: пока не выполнено ограничение полноты, выполните
13: Выбрать край Ek1k2, r из Elost случайным образом
14: Gk1inter, Gk2inter добавляют потерянные ребра в Ek1k2, r
Алгоритм 1 Алгоритм кластеризации изображений
3.
 2 Объединение локальных реконструкций на основе графов
2 Объединение локальных реконструкций на основе графов
После кластеризации изображений каждый кластер может быть реконструирован с использованием локального подхода SfM. Из-за устойчивости к выбросам мы выбираем инкрементные SfM. Поскольку реконструированные изображения ограничены ниже порогового значения, проблема дрейфа устраняется. Когда все кластеры реконструированы, нам нужен последний шаг, чтобы сшить их, поскольку каждый кластер имеет свою локальную систему координат.
Чтобы построить надежный алгоритм слияния, мы рассматриваем три основные проблемы:
В качестве опорного кадра следует выбрать кластер, который мы назвали узлом привязки.
Шаг слияния других кластеров с узлом привязки должен быть максимально точным.
Поскольку может не существовать перекрытия между узлом привязки и некоторыми другими кластерами, мы должны найти путь, чтобы объединить их в узел привязки. Из-за накопленных ошибок путь каждого кластера к узлу привязки не должен быть слишком длинным.

Чтобы решить указанную выше проблему, мы построим граф на уровне кластера. Алгоритм состоит из трех основных шагов: (1) Инициализация кластерного графа.(2) Поиск узлов привязки. (3) Расчет пути и упрощение. Для инициализации кластерного графа мы сначала находим общие камеры между попарными кластерами и вычисляем преобразования подобия. Затем мы строим минимальное остовное дерево (MST), чтобы выбрать наиболее точные ребра. Мы нашли узел привязки, имея дело с деревом минимальной высоты (MHT) [DBLP: journals / dam / LaberN04] проблемой. Сначала мы покажем, как проблема может быть преобразована в проблему MinST.
3.2.1 Преобразование попарного подобия
Мы обсудили, как построить перекрывающиеся области в разд.3.1, мы дополнительно используем перекрывающуюся информацию для вычисления попарного преобразования подобия. Учитывая соответствие поз камеры, то есть {Pk1ik1} и {Pk2ik2}, сначала оценим относительный масштаб. При известной относительной шкале оценка сходства выродилась в евклидову оценку. sk1k2 = (Ck1ik1 − Ck1jk1) / (Ck2ik2 − Ck2jk2).sk1k2}.
sk1k2 = (Ck1ik1 − Ck1jk1) / (Ck2ik2 − Ck2jk2).sk1k2}.
Оценка евклидова преобразования
Когда относительный масштаб известен, преобразование подобия вырождается в евклидову оценку. То есть нам нужно только оценить относительное вращение и относительный перенос. Предположим, что трехмерная точка X расположена в глобальной системе координат, а X1, X2 расположены в локальной системе координат k1, k2 двумя евклидовыми преобразованиями (R1, t1), (R2, t2) соответственно. Тогда у нас
Дальше можем получить
| X2 = R2R − 11 (X1 − t1) + t2 = R2RT1X1 + (t2 − R2RT1t1). | (4) |
Тогда относительное преобразование равно
| R12 = R2RT1, t12 = t2 − R2RT1t1. | (5) |
Поскольку кластеры k1 и k2 имеют масштаб до sk1k2, мы должны переформулировать относительное преобразование как
| tk1k2 = tk2 − Rk2RTk1tk1 = −RTk2Ck2 + sk1k2Rk2RTk1Rk1Ck1 = sk1k2Ck1 − RTk2Ck2, | (6) |
, где Ck1 и Ck2 — центры камер в кластере k1, k2 соответственно. Чтобы справиться с наличием выбросов, мы объединили евклидову оценку с RANSAC.
Чтобы справиться с наличием выбросов, мы объединили евклидову оценку с RANSAC.
3.2.2 Инициализация кластерного графа
В нашем подходе каждый кластер рассматривается как узел графа, а ребра соединяют узлы, совместно использующие некоторые общие камеры. Предположим, что имеется k кластеров графа кластеров C
, и мы обозначим вероятность получения хорошего преобразования из пары кластеров
(i, j) как pij. Следовательно, вероятность того, что все k − 1 ребра в остовном дереве c могут быть восстановлены, аппроксимируется как
| P = ∏i = 1…k − 1pck1ck2, | (7) |
, где ck1 и ck2 — два кластера, связанные с k-м краем c. P можно рассматривать как вероятность того, что глобальная трехмерная реконструкция может быть достигнута при условии, что все остовные пары реконструированы правильно. Затем мы пытаемся максимизировать вероятность P, определенную в уравнении (7). Это эквивалентно минимизации функции стоимости
f = −log (∏i = 1 .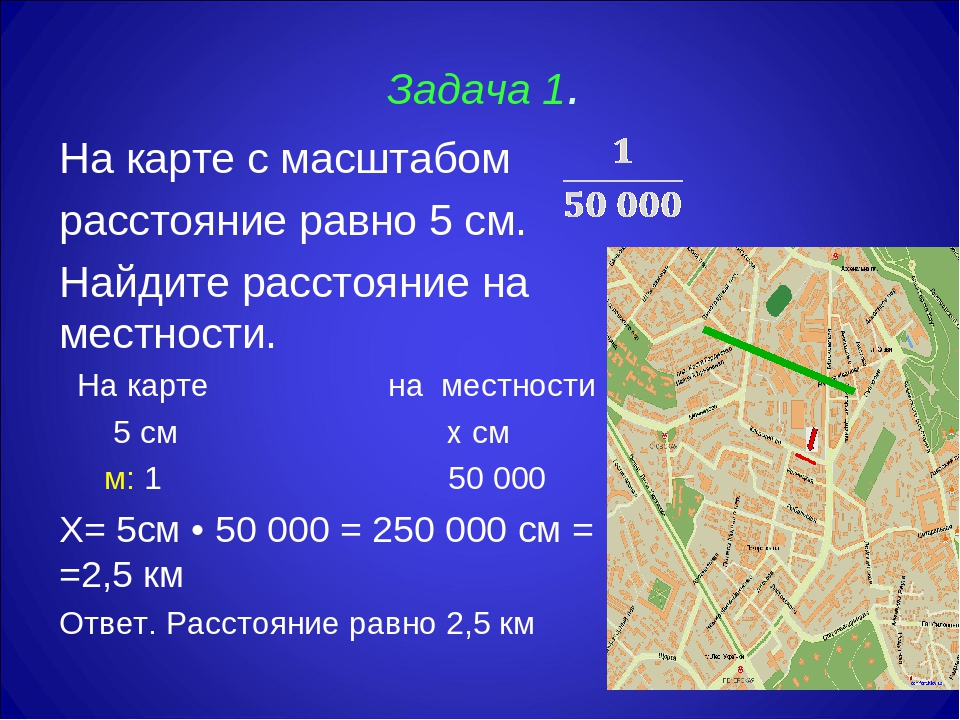 .. k − 1pck1ck2). .. k − 1pck1ck2). | (8) |
Чтобы найти оптимальное остовное дерево, мы определяем вес ребра, соединяющего кластеры i и j, как
Теперь задача максимизации совместной вероятности P преобразована в задачу поиска MinST в неориентированном графе.Обратите внимание, что в вычислениях MinST конкретное значение весов ребер не имеет значения, но их порядок имеет значение. То есть достаточно сопоставимой силы связей между кластерами вместо точной оценки P достаточно, чтобы помочь сгенерировать хорошее связующее дерево. Это наблюдение приводит нас к следующей схеме определения веса остаточной ошибки.
Остаточная ошибка
В качестве надежной меры качества слияния кластеров мы используем среднеквадратическое расстояние (MSD), которое помогает определить вес ребра.Среднеквадратичная ошибка (MSE) от кластера k1 к кластеру k2 определяется как:
| msek1k2 = 12n (n∑i = 1∥∥Tk1, k2Xk1i − Xk2i∥∥22) 12, | (10) |
, где Tk1, k2 — преобразование подобия из кластера k1 в кластер k2, Xki — это i-я общие точки в кластере k. Уравнение (10) описывает ошибку преобразования из кластера k1 в кластер k2. Чтобы преобразовать MSE в симметричную метрику, мы используем максимум mse для определения MSD:
Уравнение (10) описывает ошибку преобразования из кластера k1 в кластер k2. Чтобы преобразовать MSE в симметричную метрику, мы используем максимум mse для определения MSD:
| мсд (k1, k2) = макс (msek1k2, msek1k2). | (11) |
Тогда вес ребра между вершинами k1 и k2 в C определяется msd (k1, k2).
3.2.3 Конструкция дерева минимальной высоты
После вычисления всех весов процесс инициализации графа завершен. Затем мы можем построить алгоритм MinST по Крускалу, чтобы выбрать наиболее точные преобразования подобия N − 1. После нахождения MinST нам нужно найти базовый узел как эталон глобального выравнивания всех кластеров в MinST.Мы накладываем ограничения на выбор базового узла: (1) Базовый узел должен быть достаточно большим. (2) Путь от других узлов к базовому узлу не должен быть слишком длинным. Первое ограничение рассматривается для эффективности. Второе ограничение используется, чтобы избежать накопления ошибок.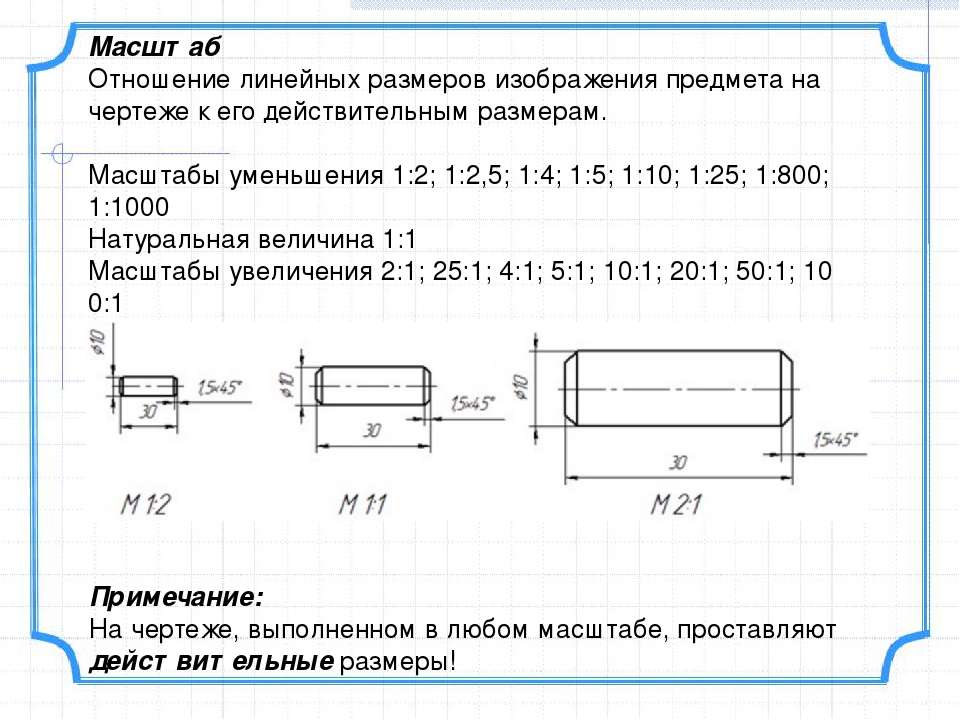 Взяв аналогичную идею дерева минимальной высоты (MHT) из [DBLP: journals / dam / LaberN04] , мы преобразовываем задачу поиска базового узла в задачу MHT. Сначала мы познакомим вас с концепцией MHT.
Взяв аналогичную идею дерева минимальной высоты (MHT) из [DBLP: journals / dam / LaberN04] , мы преобразовываем задачу поиска базового узла в задачу MHT. Сначала мы познакомим вас с концепцией MHT.
Определение 1.
Для неориентированного графа с древовидными характеристиками мы можем выбрать любой узел в качестве корня. Полученный граф является корневым деревом. Среди всех возможных корневых деревьев деревья с минимальной высотой называются деревьями минимальной высоты (MHT).
Мы решаем проблему MHT путем слияния листовых узлов слой за слоем. На каждом слое мы собираем все листовые узлы и объединяем их с соседями. Наконец, может остаться два или один узел. Если осталось два узла, то мы выбираем узел большего размера в качестве базового.Если остался только один узел, то он является базовым.
Процесс слияния изображен на рис.3. Преимущество использования алгоритма поиска базового узла показано на рисунке 4. Благодаря надежности нашего алгоритма, который может находить точные преобразования подобия, а края с большим msd фильтруются, мы можем точно объединить все суб-реконструкции. Полный алгоритм слияния подмоделей проиллюстрирован в Alg.2.
Полный алгоритм слияния подмоделей проиллюстрирован в Alg.2.
Рисунок 3: Процесс объединения суб-реконструкций.(a) показывает построенный MinST, где пунктирные линии представляют края с большим msd. В (b) листовые узлы (c0, c2, c4) обозначены зеленым цветом, c0 и c2 объединены в c1, c4 объединены в c3. В (c) объединенные узлы отмечены желтым цветом, c1 и c3 теперь являются листовыми узлами. В (d) листовые узлы, которые были объединены в первом слое, отмечены темно-желтым, а листовые узлы, объединенные во втором слое, отмечены желтым. Поскольку остался только листовой узел, мы выбираем узел большего размера (так как | c1 |> | c3 |, тогда c3 следует объединить с c1, а c1 является базовым узлом.) Рисунок 4: Результаты выравнивания с нашим алгоритмом объединения локальных реконструкций на основе графа и без него.
1: Кластеры C: = {Ck}, соответствующие трехмерные точки X: = {Xik | i∈ [n]}, X ′: = {X′ik | i∈ [n]}, где k∈ [m]
2: Окончательный объединенный кластер Cfinal
3: Инициализировать кластерный граф G: = {N, E}
4. Постройте MinST M с помощью алгоритма Крускала из кластерного графа G.
Постройте MinST M с помощью алгоритма Крускала из кластерного графа G.
5: я: = 0
6: пока | M |> 1 делать
7. Найдите все конечные узлы {Nileaf} и связанные с ними узлы {Nicon}
8. Замените {Nicon} на {Nileaf + Nicon}
9: Удалить узлы Nileaf
10. Если | M | = 2, то
11: выберите кластер большего размера в качестве базового узла.
12: Удалите другой узел
13: перерыв
14: я: = я + 1
Алгоритм 2 Алгоритм объединения локальных реконструкций на основе графов
4 эксперимента
В этом разделе мы оцениваем наш GraphSfM на различных типах наборов данных, включая неоднозначные наборы данных и крупномасштабные наборы данных аэрофотосъемки.
4.1 Экспериментальные среды
Наш алгоритм GraphSfM реализован на основе COLMAP [DBLP: conf / cvpr / SchonbergerF16] и протестирован на различных типах наборов данных. Все эксперименты проводятся на ПК с 4 ядрами процессора Intel 7700 и 32 ГБ оперативной памяти. Кроме того, мы используем SIFT [DBLP: journals / ijcv / Lowe04] для извлечения точек характеристик для всех оцененных подходов SfM.
Кроме того, мы используем SIFT [DBLP: journals / ijcv / Lowe04] для извлечения точек характеристик для всех оцененных подходов SfM.
4.2 Обзор наборов данных
Чтобы оценить надежность и эффективность нашего алгоритма, мы сначала построим и соберем несколько различных типов наборов данных.Наборы данных первого типа собираются из 9 сцен на открытом воздухе, которые включают мелкомасштабные и средние наборы данных, а количество изображений составляет от 60 до 2248. Наборы данных второго типа собираются из общедоступных наборов данных, которые включают сцены на улице (Джеррард Холл , Персональный зал, Южное здание) [DBLP: conf / cvpr / SchonbergerF16] и неоднозначные сцены (Стадион и Небесный храм) [DBLP: conf / eccv / ShenZFZQ16] . Последний вид наборов данных — это 3 крупномасштабных набора аэрофотоснимков, где требования к памяти и эффективность являются проблемами для традиционных подходов.
4.3 Оценка эффективности и надежности
Мы оценили эффективность нашего алгоритма с помощью двух современных инкрементальных подходов SfM (TheiaSfM [DBLP: conf / mm / SweeneyHT15] и COLMAP [DBLP: conf / cvpr / SchonbergerF16] ) и 2 современные глобальные подходы к SfM (1DSfM [DBLP: conf / eccv / WilsonS14] и LUD [DBLP: conf / cvpr / OzyesilS15] ). Ради справедливости, наш GraphSfM работает на одном компьютере, хотя может работать и в распределенном режиме.Результаты оценки показаны на рис. 5 и в таблице 1. Неудивительно, что поэтапные подходы требуют больше времени на реконструкцию, чем глобальные подходы. По мере увеличения масштаба набора данных время, которое занимает COLMAP [DBLP: conf / cvpr / SchonbergerF16] , быстро растет из-за повторяющейся и трудоемкой настройки пакета [DBLP: conf / iccvw / TriggsMHF99] step. Хотя наш подход является своего рода инкрементальным, масштаб изображений можно контролировать до постоянного размера в каждом кластере.Таким образом, время настройки пакета может быть значительно сокращено, и время растет линейно по мере увеличения количества изображений. Хотя TheiaSfM [DBLP: conf / mm / SweeneyHT15] также является инкрементным SfM, он выбирает несколько хороших треков [DBLP: journals / pr / CuiSh27] для выполнения настройки пакета, что экономит много времени, но может стать нестабильным в некоторых случаях. Кроме того, время, затрачиваемое TheiaSfM, превосходит наш GraphSfM, когда масштаб изображения превышает 2000. Таблица 1 дает более подробную информацию о результатах реконструкции.Очевидно, что наш GraphSfM так же надежен, как и COLMAP с точки зрения реконструированных камер, и более точен, чем другие подходы с точки зрения ошибок перепроецирования. Эти факты демонстрируют превосходную производительность нашего GraphSfM для обработки крупномасштабных наборов данных. Мы подчеркиваем, что наш алгоритм работает только на одном компьютере, и время реконструкции можно значительно сократить, если мы будем запускать его на нескольких компьютерах распределенным образом.
Ради справедливости, наш GraphSfM работает на одном компьютере, хотя может работать и в распределенном режиме.Результаты оценки показаны на рис. 5 и в таблице 1. Неудивительно, что поэтапные подходы требуют больше времени на реконструкцию, чем глобальные подходы. По мере увеличения масштаба набора данных время, которое занимает COLMAP [DBLP: conf / cvpr / SchonbergerF16] , быстро растет из-за повторяющейся и трудоемкой настройки пакета [DBLP: conf / iccvw / TriggsMHF99] step. Хотя наш подход является своего рода инкрементальным, масштаб изображений можно контролировать до постоянного размера в каждом кластере.Таким образом, время настройки пакета может быть значительно сокращено, и время растет линейно по мере увеличения количества изображений. Хотя TheiaSfM [DBLP: conf / mm / SweeneyHT15] также является инкрементным SfM, он выбирает несколько хороших треков [DBLP: journals / pr / CuiSh27] для выполнения настройки пакета, что экономит много времени, но может стать нестабильным в некоторых случаях. Кроме того, время, затрачиваемое TheiaSfM, превосходит наш GraphSfM, когда масштаб изображения превышает 2000. Таблица 1 дает более подробную информацию о результатах реконструкции.Очевидно, что наш GraphSfM так же надежен, как и COLMAP с точки зрения реконструированных камер, и более точен, чем другие подходы с точки зрения ошибок перепроецирования. Эти факты демонстрируют превосходную производительность нашего GraphSfM для обработки крупномасштабных наборов данных. Мы подчеркиваем, что наш алгоритм работает только на одном компьютере, и время реконструкции можно значительно сократить, если мы будем запускать его на нескольких компьютерах распределенным образом.
| набор данных | Изображения | COLMAP [DBLP: conf / cvpr / SchonbergerF16] | TheiaSfM [DBLP: conf / mm / SweeneyHT15] | 1DSfM [DBLP: conf / eccv / WilsonS14] | LUD [DBLP: conf / cvpr / OzyesilS15] | Наши | |||||||||||||||
| Nc | Np | Err | т | Nc | Np | Err | т | Nc | Np | Err | т | Nc | Np | Err | т | Nc | Np | Err | т | ||
| DS-60 | 60 | 60 | 16387 | 0.478 | 26,22 | 60 | 8956 | 1,915 | 10,934 | 60 | 8979 | 1,923 | 1,317 | 60 | 8979 | 1,923 | 1,360 | 60 | 13923 | 0,456 | 24,48 |
| DS-158 | 158 | 158 | 68989 | 0,420 | 170,34 | 158 | 39506 | 1.911 | 87,711 | 157 | 39527 | 1,918 | 7,758 | 158 | 39517 | 1,917 | 7,951 | 158 | 62020 | 0,438 | 168,48 |
| DS-214 | 214 | 214 | 71518 | 0,512 | 122,64 | 138 | 6459 | 1.704 | 45,888 | 187 | 7080 | 1.539 | 4,248 | 162 | 5099 | 1.454 | 1,691 | 214 | 68882 | 0,487 | 121,56 |
| DS-319 | 319 | 319 | 154702 | 0,498 | 529,14 | 204 | 11550 | 1,796 | 186.078 | 290 | 142967 | 1,821 | 17,525 | 270 | 13484 | 1.755 | 18,774 | 319 | 151437 | 0,473 | 482,4 |
| DS-401 | 401 | 370 | 166503 | 0,584 | 568,68 | 305 | 23742 | 1,967 | 241.609 | 348 | 23081 | 1.886 | 18,891 | 316 | 22160 | 1,848 | 17,931 | 370 | 164495 | 0.552 | 562,74 |
| DS-628 | 628 | 628 | 268616 | 0,394 | 562,74 | 628 | 133300 | 1,918 | 421,233 | 610 | 133146 | 1,908 | 34.803 | 628 | 133747 | 1,910 | 35,029 | 628 | 259333 | 0,388 | 605,58 |
| DS-704 | 704 | 703 | 345677 | 0.575 90 300 | 1918,86 | 449 | 35659 | 1,861 | 603,85 | 641 | 42716 | 1,934 | 108,154 | 547 | 34296 | 1,908 | 97,8192 | 703 | 346394 | 0,546 | 1839,9 |
| DS-999 | 999 | 980 | 419471 | 0,523 | 1918,86 | 733 | 40246 | 1.859 | 731,842 | 745 | 172864 | 1,769 | 77,798 | 611 | 31254 | 1,742 | 70,775 | 980 | 416512 | 0,504 | 2570,34 |
| DS-2248 | 2248 | 2248 | 1609026 | 0,634 | 71 736 90 300 | 2248 | 187392 | 2.474 | 7255.700 | 2247 | 188102 | 2.475 | 667,585 | 2248 | 188134 | 2.474 | 694,736 | 2242 | 1445227 | 0,650 | 6,108,06 |
Таблица 1: Оценка эффективности и точности с наборами данных, имеющими разные масштабы. Np, Nc, T представляют количество трехмерных точек, количество восстановленных камер и время восстановления соответственно. Err представляет ошибку перепроецирования, и лучшие результаты выделены жирным шрифтом.Рисунок 5: Оценка эффективности наборов данных с разными масштабами.
4.4 Оценка общедоступных наборов данных
Мы оценили наш алгоритм на нескольких общедоступных наборах данных [DBLP: conf / cvpr / SchonbergerF16, DBLP: conf / eccv / ShenZFZQ16] . Для этих небольших наборов данных мы запускаем GraphSfM только на одном компьютере. Некоторые визуальные результаты показаны на рис. 6, а статистика представлена в таблице 2. COLMAP снова является наиболее неэффективным подходом, и наш подход в 1,2 — 3 раза быстрее, чем COLMAP, хотя мы запускаем его только на одном компьютере.TheiaSfM выбирает хорошие треки [DBLP: journals / pr / CuiSh27] для оптимизации, и два глобальных подхода являются наиболее эффективными. Однако, как показано на рис. 6, мы можем видеть, что оба глобальных подхода потерпели неудачу в наборах данных Person Hall и Guangzhou Stadium, что показывает, что глобальные подходы легко нарушаются выбросами. В качестве инкрементального подхода TheiaSfM также потерпел неудачу в наборах данных Person Hall и Guangzhou Stadium. Наш подход так же надежен, как и COLMAP, но более эффективен, чем он сам.
Рисунок 6: Результаты реконструкции наборов данных для общедоступных храмов.Сверху вниз представлены наборы данных Gerrard Hall, Person Hall и Guangzhou Stadium соответственно.
Неоднозначные наборы данных
Это сложная работа для восстановления на неоднозначных наборах данных для подходов SfM. Хотя совпадения функций фильтруются по геометрическим ограничениям, есть еще много неправильных совпадений, которые проходят этап проверки. Как показано на рисунке 7, наш GraphSfM демонстрирует преимущества перед традиционными подходами SfM в таких наборах данных. Из-за этапа кластеризации изображений некоторые неправильные края отбрасываются в кластерах, поэтому на отдельные реконструкции не влияют неправильные совпадения.Однако трудно обнаружить неправильные совпадения в традиционных подходах SfM, особенно в самоподобных наборах данных или наборах данных с повторяющимися структурами, что является основной причиной сбоя в неоднозначных наборах данных.
| набор данных | Изображения | COLMAP [DBLP: conf / cvpr / SchonbergerF16] | TheiaSfM [DBLP: conf / mm / SweeneyHT15] | 1DSfM [DBLP: conf / eccv / WilsonS14] | LUD [DBLP: conf / cvpr / OzyesilS15] | Наши | |||||||||||||
| Nc | Np | T | Nc | Np | T | Nc | Np | T | Nc | Np | T | Nc | Np | ТГК | ТСфМ | TBA | T | ||
| Джеррард Холл | 100 | 100 | 42795 | 303.066 | 100 | 50232 | 93,346 | 99 | 49083 | 15,821 | 100 | 44844 | 13,816 | 100 | 42274 | 0,010 | 114 | 3,848 | 118,68 |
| Персонал | 330 | 330 | 141629 | 1725.798 | 113 | 39101 | 157,416 | 42 | 6239 | 768.752 | 325 | 93386 | 107,558 | 330 | 140859 | 0,040 | 713,94 | 25,128 | 742,92 |
| Южное здание | 128 | 128 | 61151 | 303,06 | 128 | 68812 | 155,844 | 128 | 436640 | 27,711 | 128 | 69110 | 34,695 | 128 | 58483 | 0.032 | 125,28 | 4,745 | 131,28 |
| Стадион | 157 | 157 | 85723 | 418,74 | 30 | 6345 | 18,729 | 65 | 6319 | 5,555 | 77 | 4549 | 4,736 | 157 | 71605 | 0,026 | 403,86 | 16,167 | 421,62 |
| Храм Неба | 341 | 341 | 185750 | 8678.76 | 336 | 1201 | 46039 | 339 | 13356 | 40,959 | 340 | 14019 | 44.089 | 341 | 181583 | 0,044 | 2784.378 | 46,737 | 2856.258 |
Таблица 2: Сравнение результатов реконструкции. Np, Nc представляют количество 3D-точек и количество восстановленных камер соответственно. TGC, TSfM, TPCA, T∑ соответственно обозначают временные затраты (в секундах) на шаг кластера графа, шаг локального SfM, шаг выравнивания облаков точек и общее время.Рисунок 7: Реконструкции по набору данных храмового неба. (a): Результат, реконструированный COLMAP [DBLP: conf / cvpr / SchonbergerF16] . (b): Результат, реконструированный LUD [DBLP: conf / cvpr / OzyesilS15] . (c): Результат, восстановленный нашим GraphSfM.
4.5 Оценка крупномасштабных наборов аэрофотоснимков
Наш подход также оценивается на крупномасштабных наборах аэрофотоснимков. Мы оценивали наш алгоритм как на одном компьютере последовательно (каждый кластер реконструируется один за другим), так и на трех компьютерах в параллельном режиме.Результаты реконструкции приведены в таблице 3. Наш алгоритм может восстанавливать такое же количество камер, как и COLMAP. Кроме того, при работе на одном компьютере наш подход примерно в 6 раз быстрее, чем COLMAP; при распределенной работе на трех компьютерах наш алгоритм примерно в 17 раз быстрее, чем COLMAP. Наш алгоритм можно еще больше ускорить, если у нас будет больше компьютерных ресурсов. TheiaSfM немного медленнее, чем наш подход, однако количество реконструированных трехмерных точек на одну величину меньше нашего подхода.Хотя 1DSfM и LUD по-прежнему являются наиболее эффективными, их надежность может решить проблему в крупномасштабных наборах аэрофотоснимков.
| набор данных | Изображения | COLMAP [DBLP: conf / cvpr / SchonbergerF16] | TheiaSfM [DBLP: conf / mm / SweeneyHT15] | 1DSfM [DBLP: conf / eccv / WilsonS14] | LUD [DBLP: conf / cvpr / OzyesilS15] | Наши | |||||||||||
| Nc | Np | т | Nc | Np | т | Nc | Np | т | Nc | Np | т | Nc | Np | т | Td | ||
| Антенна-5155 | 5155 | 5155 | 1798434 | 41823.27 | 4383 | 203942 | 3527,43 | 4591 | 243490 | 482,45 | 4723 | 278924 | 390,59 | 5155 | 1834875 | 2491,78 | 936,74 |
| Антенна-7500 | 7500 | 7455 | 5184368 | 95007,59 | 5327 | 432347 | 6237.91 | 6264 | 478234 | 931.84 | 5934 | 467230 | 832,40 | 7455 | 4968142 | 5834,37 | 2166,59 |
| Антенна-12306 | 12306 | 11259 | 3934391 | 146172 | 8347 | 478237 | 25783,12 | 8923 | 509543 | 4941,27 | 8534 | 489238 | 4589,73 | 11259 | 3 | 22663.86 | 8970.01 |
Таблица 3: Сравнение результатов реконструкции. Np, Nc представляют количество 3D-точек и количество восстановленных камер соответственно. T обозначает общее время, а Td обозначает общее время, которое оценивается в распределенной системе. Рисунок 8: Реконструкции на крупномасштабных наборах аэрофотоснимков.
5 Заключение
В этой статье мы предложили новый конвейер SfM под названием GraphSfM, который основан на теории графов, и разработали унифицированный каркас для решения крупномасштабных задач SfM.Наш двухэтапный алгоритм кластеризации графов улучшает связи кластеров с помощью MaxST. На последнем этапе объединения построение MinST и MHT позволяет нам выбрать наиболее точные преобразования подобия и уменьшить накопление ошибок. Таким образом, наш GraphSfM является высокоэффективным и надежным для крупномасштабных наборов данных, а также демонстрирует превосходство в неоднозначных наборах данных по сравнению с традиционными современными подходами SfM. Более того, GraphSfM может быть легко реализован в распределенной системе, поэтому реконструкция не ограничивается масштабом наборов данных.
Комплексное моделирование и компенсация термических ошибок для портальных станков с масштабной решеткой при обработке крупных конструкций
Xiang ST, Deng M, Li HM, Du ZC, Yang JG (2019) Моделирование, измерение и компенсация поперечной деформации для портального шлифовального станка с направляющими с учетом тепловых эффектов. Meas Sci Technol 30: 065007
Статья
Google Scholar
Gomez-Acedo E, Olarra A, Lopez LN (2012) Метод термических характеристик и моделирования больших станков портального типа.Int J Adv Manuf Technol 62: 875–886
Статья
Google Scholar
Feng WL, Li ZH, Gu QY, Yang JG (2015) Моделирование и компенсация тепловых ошибок позиционирования на основе анализа тепловых характеристик. Int J Mach Tools Manuf 93: 26–36
Артикул
Google Scholar
Duan M, Lu H, Zhang XB, Li ZJ, Zhang YQ, Liu Q (2019) Моделирование ошибок позиционирования на основе многомерных ортогональных полиномов и активная компенсация системы подачи с двойным приводом.Int J Adv Manuf Technol 104: 2593–2605
Статья
Google Scholar
Miao EM, Liu Y, Xu JG, Liu H (2015) Исследование влияния изменений в чувствительных к температуре точках на модель компенсации тепловой ошибки для станков с ЧПУ. Int J Mach Tools Manuf 97: 50–59
Артикул
Google Scholar
Feng WL, Yao XD, Azamat A, Yang JG (2015) Компенсация ошибки прямолинейности для больших портальных фрезерных центров с ЧПУ на основе моделирования B-шлицевых кривых.Int J Mach Tools Manuf 88: 165–174
Артикул
Google Scholar
Fan KG, Yang JG, Yang LY (2014) Компенсация пространственной ошибки на основе унифицированной модели ошибок для четырех типов обрабатывающих центров с ЧПУ: часть II — компенсация пространственной ошибки на основе унифицированной модели. Mech Syst Signal Pr 49: 63–76
Артикул
Google Scholar
Wu CW, Tang CH, Chang CF, Shiao YS (2012) Метод компенсации тепловой ошибки для центра станка.Int J Adv Manuf Technol 59: 681–689
Статья
Google Scholar
Li Y, Zhao J, Ji SJ (2018) Моделирование ошибок теплового позиционирования станков с использованием нейронной сети обратного распространения на основе алгоритма летучих мышей. Int J Adv Manuf Technol 97: 2575–2586
Статья
Google Scholar
Cheng Q, Qi Z, Zhang GJ, Zhao YS, Sun BW, Gu PH (2016) Надежное моделирование и прогнозирование термически индуцированной позиционной ошибки на основе теории грубых множеств Серого и нейронных сетей.Int J Adv Manuf Technol 86: 753–764
Статья
Google Scholar
Ким С.К., Чо Д.В. (1997) Оценка распределения температуры в шарико-винтовой системе в реальном времени. Int J Mach Tools Manuf 37: 451–464
Артикул
Google Scholar
Xu ZZ, Liu XJ, Choi CH, Lyu SK (2012) Исследование улучшения погрешности позиционирования шарико-винтовой системы с жидкостным охлаждением.Int J Precis Eng Man 13: 2173–2181
Статья
Google Scholar
Li JG, Wang SQ (2017) Деформация, вызванная остаточными напряжениями при механической обработке деталей из авиационных алюминиевых сплавов: последние достижения. Int J Adv Manuf Technol 89: 997
Артикул
Google Scholar
Цао Х.Дж., Чжу Л.Б., Ли XG, Чен П., Чен Ю.П. (2016) Компенсация тепловых ошибок зубофрезерного станка с учетом тепловой деформации заготовки.Int J Adv Manuf Technol 86: 1739–1751
Статья
Google Scholar
, где мы симметризовали с помощью k1 и k2
для представления k − k ′ и k ′ соответственно.п).
Мы можем построить угловой спектр мощности, рассматривая
⟨Al1m1a ∗ l2m2⟩.
В предположении, что температурное поле статистически
изотропный, корреляция не зависит от m, и мы можем записать
угловой спектр мощности как
| ⟨a ∗, kSZl1m1akSZl2m2⟩ = δDl1l2δDm1m2CkSZl1. | (250) |
Корреляцию можно записать с помощью
| ⟨a ∗, kSZl1m1akSZl2m2⟩ = (4π) 69∫dr1g˙GG∫dr2g˙GG | (251) | ||||
| × | ∫d3k1 (2π) 3d3k2 (2π) 3d3k′1 (2π) 3d3k′2 (2π) 3⟨δlinδ (k′1) δg (k′2) δ ∗ linδ (k1) δ ∗ g (k2)⟩ | ||||
| × | ∑l′1m′1l′′1m′′1m ′ ′ ′ 1l′2m′2l′′2m′′2m ′ ′ ′ 2 (−i) l′1 + l′′1 (i) l′2 + l′′2jl′2 (k′1r2) jl′′2 (k′2r2) k′2jl′1 (k1r1) k1jl′′1 (k2r1) | ||||
| × | ∫d ^ mYl2m2 (^ m) Y ∗ l′2m′2 (^ m) Y ∗ l′′2m′′2 (^ m) Y ∗ 1m ′ ′ ′ 2 (^ m) | ||||
| × | ∫d ^ nY ∗ l1m1 (^ n) Yl′1m′1 (^ n) Yl′′1m′′1 (^ n) Y1m ′ ′ ′ 1 (^ n) | ||||
| × | ∫d ^ k′1∫d ^ k′2Yl′2m′2 (^ k′1) Y1m ′ ′ ′ 2 (^ k′2) Yl′′2m′′2 (^ k′1) | ||||
| × | ∫d ^ k1∫d ^ k2Y ∗ l′1m′1 (^ k1) Y ∗ 1m ′ ′ ′ 1 (^ k1) Y ∗ l′′1m′′1 (^ k2). |
Мы можем разделить взносы так, чтобы общая сумма составляла
корреляции
следующие ⟨vgvg⟩⟨δgδg⟩
и ⟨vgδg⟩⟨vgδg⟩
в зависимости от
рассматриваем ли мы кумулянты, комбинируя k1 с k′1
или k′2 соответственно. После некоторого простого, но утомительного
алгебры, и отмечая, что
| ∑m′1m′2 (l′1l′2l1m′1m′2m1) (l′1l′2l2m′1m′2m2) = δm1m2δl1l22l1 + 1, | (252) |
мы можем написать
| CkSZl = 22π2∑l1l2 [(2l1 + 1) (2l2 + 1) 4π] (ll1l2000) 2 | ||||
| × | ∫dr1g˙GG∫dr2g˙GG∫k21dk1∫k22dk2 | |||
| × | [Plinδδ (k1) Pgg (k2) jl1 (k2r2) jl1 (k2r1) j′l2 (k1r1) k1j′l2 (k1r2) k1 | |||
| + | Pδb (k1) Pδb (k2) jl2 (k2r1) j′l1 (k1r1) k1jl1 (k1r2) j′l2 (k2r2) k2]. |
Здесь первый член представляет собой вклад от vgvg⟩⟨δgδg⟩, а второй член равен
⟨vgδg⟩⟨vgδg⟩
вклад соответственно.
При упрощении интегралов, содержащих сферические гармоники, имеем
использовали свойства коэффициентов Клебша-Гордона, в
в частности, с l = 1.
В интеграл входят два расстояния
и двух мод Фурье и суммируется по символу Вигнера-3j до
получить спектр мощности.
Поскольку нас в первую очередь интересует вклад при малых
угловых масштабов здесь можно пренебречь вкладом в эффект kSZ
с учетом корреляции между линейным полем плотности и барионами и
учитывайте только вклад, обусловленный барион-барионами и
плотность-плотность
корреляции.Фактически, согласно приведенному здесь описанию ореола, там
нет корреляции барионного поля внутри гало и скорости
поле, прослеживаемое отдельными ореолами (см. § 7).
Таким образом, вклад в
корреляция барионной скорости происходит только от члена с двумя гало
плотностное поле-барионная корреляция. Эта корреляция подавляется при
малых масштабов и не вносит значительного вклада в кинетическую СЗ
спектр мощности [119] .
Аналогично приближению Лимбера [168] ,
чтобы упростить вычисления, связанные с ⟨vgvg⟩⟨δgδg⟩, мы используем уравнение
включающая полноту сферических функций Бесселя
(уравнение 178) и примените
до интеграла по k2, чтобы получить
| CkSZl = 2π∑l1l2 [(2l1 + 1) (2l2 + 1) 4π] (ll1l2000) 2 | ||||
| × | ∫dr1 (g˙G) 2d2A∫k21dk1Plinδδ (k1) Pgg [l1dA; r1] (j′l2 (k1r1) k1) 2. |
Альтернативный подход, который использовался в качестве метода расчета в
многие из предыдущих статей [285, 72, 130, 68, 119] ,
это к
использовать приближение плоского неба
с кинетическим спектром мощности SZ, записанным как
| CkSZl = 18π2∫dr (g˙GG) 2d2APδδ (k) 2Iv (k = ldA), | (255) |
с интегралом связи мод, задаваемым
| Iv (k) = ∫dk1∫ + 1−1dμ (1 − μ2) (1−2μy1) y22Pδδ (ky1) Pδδ (k) Pδδ (ky2) Pδδ (k).k1, y1 = k1 / k и y2 = k2 / k = √1−2μy1 + y21. Это приближение плоского неба использует приближение Лимбера [168] для дальнейшего упрощать расчет с заменой k = l / dA. Спектры мощности здесь представляют собой спектр мощности барионного поля спектр мощности поля скорости; первый предполагал проследить поле плотности темной материи, в то время как последнее обычно связанных с линейным полем плотности темной материи за счет использования линейный теория аргументов. Соответствие между плоским небом и всем небом
Здесь v2rms — среднеквадратичное значение однородной объемной скорости.
1/3 возникает из-за того, что среднеквадратичное значение в каждом компоненте составляет 1/3 Рисунок 59: Температура На рисунке 55 мы показываем наш прогноз для кинетической Разница между двумя эффектами возникает из-за того, что Как показано на рисунке 55 (b), На рисунке 59 мы показываем несколько дополнительных прогнозов для В дополнение к вкладу из-за движения ореолов по линии прямой видимости, Для отдельного кластера на красном смещении z с угловым
где
Здесь θ — угол луча зрения относительно скопления. Фигура 60. Для описания вращения гало запишем безразмерный спин
, где вириальная концентрация для профиля NFW равна Чтобы связать угловую скорость ω со спином, мы сначала
Функции f (c), g (c) и
На рисунке 60 показаны колебания температуры. По порядку величины этот вращательный вклад может быть Рисунок 61: Колебания температуры из-за скоплений галактик: (a) кинетическая SZ На рисунке 61 мы показываем Интересная экспериментальная возможность здесь состоит в том, можно ли получить BangyBang Tubes Vintage Telefunken 1U4 / 1T4 / DF91 / W17 / 1K2 Миниатюрный экранированный пентодный клапан Промышленные электрические усилителиBangyBang Tubes Vintage Telefunken 1U4 / 1T4 / DF91 / W17 / 1K2 Миниатюрный экранированный пентодный клапан Промышленные электрические усилители
|
