Математика 5 класс задачи на проценты: Задачи репетитора по математике на проценты (5 класс)

alexxlab

Содержание

Проценты. Задачи на проценты: нахождение процента от величины и величины по её проценту. Математика, 5 класс: уроки, тесты, задания.






















1.
Проценты как несократимая дробь


Сложность:
среднее

2


2.
Проценты как десятичная дробь


Сложность:
лёгкое

1


3.
Проценты в виде десятичной дроби (сотни)


Сложность:
лёгкое

1


4.
Проценты в виде десятичной дроби (десятичная дробь)


Сложность:
лёгкое

1


5.
Десятичные дроби в виде процентов (тысячные)


Сложность:
лёгкое

1


6.
Десятичные дроби в виде процентов (сотые)


Сложность:
лёгкое

2


7.
Десятичная дробь как проценты


Сложность:
среднее

2


8.
Обыкновенная дробь в виде процентов


Сложность:
среднее

1


9.
Нахождение процентов от данного числа


Сложность:
среднее

2


10.
Нахождение числа по его процентам (десятичная дробь)


Сложность:
среднее

2


11.
Проценты и прямоугольник


Сложность:
среднее

2


12.
Проценты от величины, тысячи


Сложность:
среднее

2


13.
Сравнение процентов и дроби (переход к процентам)


Сложность:
среднее

2


14.
Покупка для засолки


Сложность:
среднее

2


15.
Себестоимость детали


Сложность:
среднее

2


16.
Количество страниц в книге


Сложность:
среднее

2


17.
Количество девочек в школе


Сложность:
среднее

2


18.
Мука из пшеницы


Сложность:
сложное

4


19.
Части прямого угла


Сложность:
сложное

3


20.
Участок прямоугольной формы


Сложность:
сложное

6

Открытый урок по теме Проценты» 5 класс

Открытый урок по теме Проценты» 5 класс.

Цели урока:

  • Переводить процент в десятичную дробь и обратно;

  • Учить ребят решать текстовые задачи;

  • Совершенствовать вычислительные навыки

  • Научить применять изученный материал в повседневной жизни.

Тип урока: закрепление учебного материала.

План урока:

1. Организационный момент. (2 мин)

2. Актуализация опорных знаний (5 мин)

3. Работа по теме урока (20 мин)

4. Физкультминутка (2 мин)

5. Самостоятельная работа (9 мин)

6. Заключение (5 мин)

7. Подведение итогов урока (2 мин)

ХОД УРОКА

  1. Организационный момент (2 мин.)

. — Здравствуйте ребята!

Урок математики я хочу начать словами «Гений состоит из 1% вдохновения и 99% потения» Эдисон Т.

Я предлагаю Вам рабочий лист. В углу этого рабочего листа изображен смайлик. Изобразите свое настроение и эмоциональное состояние, вначале данного на уроке.

Подпишите данный лист.

Я желаю вам сегодня удачи. Вы готовы к работе?

 II. Актуализация опорных знаний.

  1. Работают в рабочем листе.

Чтобы узнать тему нашего урока вы должны правильно выполнить задание и вписать в таблицу буквы, соответствующие найденным ответам. Расположите данные числа в порядке убывания.

0,1

Ответ: процент.

— Правильно «процент». Итак, ребята, тема сегодняшнего урока – “Проценты”. Мы наработали багаж знаний по данной теме. Сегодня наша главная задача закрепить эти знания, выявить затруднения и ликвидировать их.

Мы узнали на прошедших уроках, где в повседневной жизни встречаются проценты. Наши полученные знания на уроках математики вам помогут в дальнейшем при решении задач по физике, по химии. При сдаче ЕГЭ дают текстовые задачи на проценты. Поэтому наша цель, научиться решать уже сейчас, и в дальнейшем применять полученные знания.

Учитель делает сообщение «История возникновения процента».

Слово “процент” происходит от латинских слов рro centum,что буквально означает “со ста”. Широко начали использовать проценты в Древнем Риме, но идея процентов возникла много раньше- вавилонские ростовщики уже умели находить проценты . А знак % произошел, как предполагают, благодаря опечатке. В рукописях pro centum часто заменяли словом “cento”(сто) и писали его сокращенно — cto. В 1685 году в Париже была напечатана книга-руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %. После этой ошибки многие математики стали употреблять знак % для обозначения процентов. Были известны проценты и в Индии.

В Европе проценты появились на 1000 лет позже. Их ввел бельгийский ученый Симон Стевин, который в1584 году впервые опубликовал таблицы процентов.

2. Повторим необходимый нам теоретический материал. (работают в рабочих листах)

  1. Что называется процентом? ( Процент – сотая часть числа)

  2. Какой значок используется при написании процента? (Знак %)

  3. Как обратить десятичную дробь в проценты, а проценты в десятичную дробь? (Чтобы обратить десятичную дробь в проценты, надо её умножить на 100. Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100).

III. Закрепление материала

Задание 1. 

Переведите проценты в десятичную дробь?

  • 7%=0.07

  • 9%=0.09

  • 59%=0.59

  • 125%=1,25

  • 2,9%=0,029

  • 0,4%=0. 004

Задание 2. 

Запишите десятичную дробь в процентах?

  • 0,17=17%

  • 1, 67=167%

  • 0,803=80,3%

  • 2, 4169=241,69%

Учитель: Итак, мы повторили что нужно делать, чтобы десятичную дробь выразить в процентах или проценты представить в виде десятичной дроби?

  1. Решение примеров по учебнику

Сколько типов задач на проценты мы выучили?

Давайте еще раз отработаем их решения.

А) Решаем № 1569 (у доски)

500 : 100 • 60 = 300 (н)

Ответ: 300 насосов.

Б) № 1577 (у доски)

120 : 15 • 100 = 800 (кг)

Ответ: масса белого медведя 800 кг.

В) № 1580

357 : 700 = 0,51 = 51%

Ответ: мальчики составляют 51% учащихся школы.

IV. Физкультминутка 

Крепко зажмурить глаза (считать до 3), открыть, посмотреть вдаль (считая до 5). Повторить 4 раза.

V. Самостоятельная работа учеников

1. Заполнить таблицу

Десятичная дробь

2. Решить задачу.
У горного барана массой 150 кг масса рогов равна 30 кг. Сколько процентов составляет масса рогов от массы тела?

Решение 
30:150*100=20% — составляют рога
Ответ: 20%

Учащиеся обмениваются тетрадями, проверяют работы, выставляют оценки.

Критерий:

«5» — без ошибок

«4» — 1,2 ошибки

«3»- 3 ошибки

VI. Заключение. Рефлексия

Итак, ребята, сегодня мы с вами закрепили понятие процента. Повторили как выражать десятичную дробь в процентах и процент представлять в виде десятичной дроби, решали простейшие задачи на проценты.

Самостоятельная работа показала, как вы усвоили и закрепили этот материал.

VII. Подведение итогов урока 

— Что такое процент?

Выставляются оценки за активную работу на уроке, все получают оценку за тест.

Оцените свою работу. (в рабочих листах)

— у меня все получилось, я доволен своей работой.

— у меня не все получилось, но я доволен своей работой.

— я хорошо знаю теоретический материал, но в практической работе у меня не все

получилось

? — мне было сложно и мало понятно.

В углу рабочего листа изображен второй смайлик. Изобразите свое настроение и эмоциональное состояние в конце урока.

Сдайте свои рабочие листы. Большое спасибо за урок, успехов.

VIII. Домашнее задание.

Повторить п.40, решить № 1609, 1610, 1611.

3,5

1,5

0,36

0,9

3,2

0,25

Т

П

О

Е

Ц

Р

Н

0,5

0,15

0,03

0,6

1,35

Проценты

50%

15%

3%

60%

135%

Контрольная работа по теме «Проценты» (5 класс) — Математика 5 класс — Школьная математика — Каталог статей

(Ф. Хаусдорф.)

‘

quotes[1]='»Математика — это язык, на котором написана книга природы. «

(Г. Галилей)

‘

quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на­стойчивость и упорство в достижении цели.»

(А. Маркушевич)

‘

quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»

(А.Н. Крылов)

‘

quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»

(М.И. Калинин)

‘

quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»

(Платон)

‘

quotes[6]='»Математика есть лучшее и даже единственное введение в изу­чение природы.»

(Д.И. Писарев)

‘

quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии.»

(А.С. Пушкин)

‘

quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»

(В. Произволов)

‘

quotes[9]='»В математике есть своя красота, как в живописи и поэзии. «

(Н.Е. Жуковский)

‘

quotes[10]='»Химия – правая рука физики, математика – ее глаз.»

(М.В. Ломоносов)

‘

quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит.»

(М.В. Ломоносов)

‘

quotes[12]='»Математика — это язык, на котором говорят все точные науки.»

(Н.И. Лобачевский)

‘

quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»

(Л. Эйлер)

‘

quotes[14]='»Числа не управляют миром, но они показывают, как управляется мир.»

(И. Гете)

‘

quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»

(В.Ф. Каган)

‘

quotes[16]='»Счет и вычисления — основа порядка в голове.»

(Песталоцци)

‘

quotes[17]='»Величие человека — в его способности мыслить.»

(Б. Паскаль)

‘

quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. «

(Д.Пойа)

‘

quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»

(Б. Паскаль)

‘

quotes[20]='»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.»

(И. Ньютон)

‘

quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»

(Л. Карно)

‘

quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»

(М.В. Остроградский)

‘

quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»

(Н.К. Крупская)

‘

quotes[24]='»Математика уступает свои крепости лишь сильным и смелым.»

(А.П. Конфорович)

‘

quotes[25]='»Доказательство — это рассуждение, которое убеждает.»

(Ю.А. Шиханович)

‘

quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»

(И. Кант)

‘

var whichquote= Math.floor(Math.random()*(quotes.length))
document.write(quotes[whichquote])

Материалы для организации дистанционного обучения. Математика (5-6 классы)






























































































































































КлассНазвание урокаСсылка на учебные материалы
5Ряд натуральных чисел. Десятичная система записи натуральных чиселhttps://resh.edu.ru/subject/lesson/7719/main/234018/
5Сравнение натуральных чиселhttps://resh.edu.ru/subject/lesson/7718/main/235258/
5Сравнение именованных чиселhttps://interneturok.ru/lesson/matematika/5-klass/bnaturalnye-chislab/izmerenie-velichin-edinitsy-izmereniya?block=player
5Измерение отрезковhttps://resh.edu.ru/subject/lesson/7740/main/234855/
5Длина отрезкаhttps://resh. edu.ru/subject/lesson/6914/main/235937/
5Прямая, луч, отрезокhttps://resh.edu.ru/subject/lesson/7741/main/235227/
5Координатный лучhttps://resh.edu.ru/subject/lesson/7756/main/234421/
5Представление натуральных чисел на координатном лучеhttps://resh.edu.ru/subject/lesson/7738/main/233801/
5Сложение натуральных чисел. Законы сложенияhttps://resh.edu.ru/subject/lesson/7723/main/
5Арифметические действия с натуральными числамиhttps://mosobr.tv/release/7856
5Вычитаниеhttps://resh.edu.ru/subject/lesson/7717/main/235289/
5Правила вычитания суммы из числа и числа из суммыhttps://znaika.ru/catalog/5-klass/matematika/Svoystva-vychitaniya-naturalnykh-chisel. html
5Решение текстовых задач с помощью сложения и вычитанияhttps://resh.edu.ru/subject/lesson/7716/main/233832/
5Числовые выраженияhttps://resh.edu.ru/subject/lesson/7708/main/266123/
5Углы. Измерение угловhttps://resh.edu.ru/subject/lesson/589/
5Углы. Измерение угловhttps://resh.edu.ru/subject/lesson/7735/main/234886/
5Многоугольникиhttps://resh.edu.ru/subject/lesson/7727/main/267638/
5Треугольникиhttps://resh.edu.ru/subject/lesson/7734/main/234917/
5Четырёхугольникиhttps://resh.edu.ru/subject/lesson/7733/main/233522/
5Симметрия относительно точки, относительно прямой и относительно плоскостиhttps://resh. edu.ru/subject/lesson/983/
5Умножение. Законы умноженияhttps://resh.edu.ru/subject/lesson/7722/main/235069/
5Распределительный законhttps://resh.edu.ru/subject/lesson/7724/main/266247/
5Умножение. Законы умноженияhttps://resh.edu.ru/subject/lesson/7712/main/235041/
5Деление нацелоhttps://resh.edu.ru/subject/lesson/7712/main/235041/
5Деление с остаткомhttps://resh.edu.ru/subject/lesson/7709/main/235165/
5Степень с натуральным показателемhttps://resh.edu.ru/subject/lesson/7713/main/234793/
5Решение текстовых задач с помощью умножения и деленияhttps://resh.edu.ru/subject/lesson/7711/main/234760/
5Площадь прямоугольника. Единицы площадиhttps://resh.edu.ru/subject/lesson/7732/main/233181/
5Прямоугольный параллелепипедhttps://resh.edu.ru/subject/lesson/7731/main/234669/
5Объём прямоугольного параллелепипеда. Единицы объёмаhttps://resh.edu.ru/subject/lesson/7730/main/272356/
5Объём прямоугольного параллелепипедаhttps://resh.edu.ru/subject/lesson/7753/main/234824/
5Понятие дробиhttps://resh.edu.ru/subject/lesson/7782/main/233643/
5Сравнение обыкновенных дробейhttps://resh.edu.ru/subject/lesson/16/
5Задачи на дроби (нахождение части целого)https://resh.edu.ru/subject/lesson/7780/main/234203/
5Дроби и деление натуральных чиселhttps://znaika. ru/catalog/5-klass/matematika/Delenie-i-drobi.html
5Нахождение целого по его частиhttps://resh.edu.ru/subject/lesson/7779/main/233956/
5Задачи на дроби (нахождение части целого)https://resh.edu.ru/subject/lesson/7780/main/234203/
5Сложение дробей с одинаковым знаменателемhttps://resh.edu.ru/subject/lesson/7774/main/233212/
5Понятие смешанной дробиhttps://resh.edu.ru/subject/lesson/7761/main/233026/
5Сложение смешанных дробейhttps://resh.edu.ru/subject/lesson/7760/main/233336/
5Вычитание смешанных дробейhttps://resh.edu.ru/subject/lesson/7759/main/233615/
5Понятие положительной десятичной дробиhttps://resh.edu.ru/subject/lesson/6903/main/235413/
5Сравнение положительных десятичных дробейhttps://resh. edu.ru/subject/lesson/6902/main/236096/
5Округление натуральных чисел. Теоретическая частьhttps://resh.edu.ru/subject/lesson/23/
5Округление десятичных дробейhttps://resh.edu.ru/subject/lesson/27/
5Чтение и запись десятичных дробейhttps://video-ypoku.com/dlya-detej-i-roditelej/shkolnikam/1383-matematika-5-klass-desyatichnye-drobi
5Сложение положительных десятичных дробейhttps://resh.edu.ru/subject/lesson/6901/main/236064/
5Вычитание положительных десятичных дробейhttps://resh.edu.ru/subject/lesson/6900/main/236033/
5Сложение и вычитание десятичных дробейhttps://resh.edu.ru/subject/lesson/719/
5Умножение и деление десятичной дроби на 10, 100, 1000https://resh. edu.ru/subject/lesson/720/
5Умножение положительных десятичных дробей. Часть 1https://resh.edu.ru/subject/lesson/6898/main/235559/
5Умножение положительных десятичных дробей. Часть 2https://resh.edu.ru/subject/lesson/6897/main/236204/
5Деление натуральных чиселhttps://mosobr.tv/release/7932
5Деление десятичной дроби на целое числоhttps://resh.edu.ru/subject/lesson/722/
5Умножение и деление десятичной дроби на 10, 100, 1000https://resh.edu.ru/subject/lesson/720/
5Деление положительных десятичных дробей. Часть 1https://resh.edu.ru/subject/lesson/6896/main/236240/
5Деление положительных десятичных дробей. Часть 2https://resh.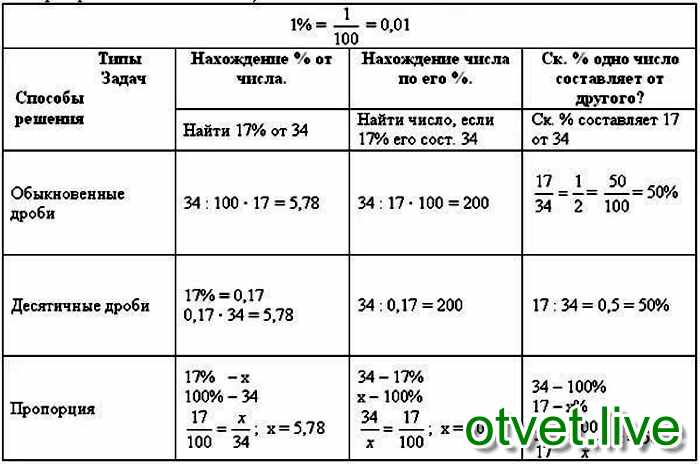 edu.ru/subject/lesson/6895/main/237500/
5Среднее арифметическоеhttps://resh.edu.ru/subject/lesson/715/
5Среднее арифметическое нескольких чиселhttps://resh.edu.ru/subject/lesson/22/
5Понятие о процентеhttps://resh.edu.ru/subject/lesson/6846/main/237181/
5Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентахhttps://resh.edu.ru/subject/lesson/1060/
5Задачи на проценты. Часть 1https://resh.edu.ru/subject/lesson/6848/main/237738/
5Задачи на проценты. Часть 2https://resh.edu.ru/subject/lesson/6839/main/237149/
5Занимательные задачи по теме «Смешанные дроби»https://resh.edu.ru/subject/lesson/7752/main/233553/
5Итоговое обобщение и систематизация знаний по темам «Делимость натуральных чисел»https://resh. edu.ru/subject/lesson/7790/main/234080/
5Итоговое обобщение и систематизация знаний по темам «Обыкновенные дроби и смешанные дроби»https://resh.edu.ru/subject/lesson/7789/main/266061/
5Единицы длиныhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/687915
5Шкала. Примеры шкалhttps://infourok.ru/videouroki/2947
5Буквенное выражение и его значениеhttps://infourok.ru/videouroki/2952
5Формулыhttps://infourok.ru/videouroki/2922
5Уравнениеhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4369029
5Биссектриса углаhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/2680471
5Равные фигурыhttps://uchebnik. mos.ru/catalogue/material_view/atomic_objects/4909803
5Прямоугольник. Периметр прямоугольникаhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/1299188
5Порядок действийhttps://infourok.ru/videouroki/2920
5Понятие площадиhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/856976
5Пирамидаhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3149941
5Ломаная. Длина ломанойhttps://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/4454434
5Развёртки геометрических фигурhttps://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/5795070
5Округление чисел. Прикидкиhttps://uchebnik. mos.ru/catalogue/material_view/atomic_objects/5206540
5Умножение десятичных дробей на 0,1, 0,01, 0,001 и т. д.https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/439985
5Деление десятичной дроби на 0,1, 0,01, 0,001 и т. д.https://znaika.ru/catalog/5-klass/matematika/Delenie-na-desyatichnuyu-drob.html
6Делители натурального числаhttps://resh.edu.ru/subject/lesson/694/
6Признаки делимостиhttps://resh.edu.ru/subject/lesson/7750/main/234576/
6Простые и составные числаhttps://resh.edu.ru/subject/lesson/7749/main/234979/
6Наибольший общий делитель (НОД)https://resh.edu.ru/subject/lesson/7747/main/233739/
6Наименьшее общее кратное (НОК)https://resh. edu.ru/subject/lesson/7746/main/234266/
6Равенство дробейhttps://resh.edu.ru/subject/lesson/7781/main/269492/
6Понятие дробиhttps://resh.edu.ru/subject/lesson/7782/main/233643/
6Приведение дробей к общему знаменателю. Сокращение дробейhttps://resh.edu.ru/subject/lesson/7777/main/233115/
6Приведение дробей к общему знаменателю. Сокращение дробейhttps://resh.edu.ru/subject/lesson/7778/main/233708/
6Сравнение дробейhttps://resh.edu.ru/subject/lesson/7776/main/233243/
6Сравнение дробей. Сравнение с единицей. Сравнение остатков до единицыhttps://resh.edu.ru/subject/lesson/7775/main/233398/
6Сложение дробей с одинаковым знаменателемhttps://resh. edu.ru/subject/lesson/7774/main/233212/
6Сложение дробей с разными знаменателямиhttps://resh.edu.ru/subject/lesson/7773/main/233057/
6Вычитание дробейhttps://resh.edu.ru/subject/lesson/7771/main/233150/
6Решение задач с использованием вычитания дробейhttps://resh.edu.ru/subject/lesson/7770/main/233925/
6Умножение натурального числа на дробьhttps://resh.edu.ru/subject/lesson/7769/main/234483/
6Законы умножения. Распределительный законhttps://resh.edu.ru/subject/lesson/7767/main/234545/
6Нахождение части целого и целого по его частиhttps://resh.edu.ru/subject/lesson/7764/main/233584/
6Решение задач на применение умножения дроби на натуральное число и умножение дробейhttps://resh. edu.ru/subject/lesson/7768/main/234142/
6Умножение и деление обыкновенной дроби на обыкновенную дробьhttps://resh.edu.ru/subject/lesson/710/
6Деление дробейhttps://resh.edu.ru/subject/lesson/7766/main/234948/
6Свойства деленияhttps://znaika.ru/catalog/5-klass/matematika/Delenie-naturalnykh-chisel-i-ego-svoystva.html
6Понятие положительной десятичной дробиhttps://resh.edu.ru/subject/lesson/6903/main/235413/
6Бесконечные периодические десятичные дробиhttps://resh.edu.ru/subject/lesson/6915/main/236435/
6Разложение положительной обыкновенной дроби в конечную десятичную дробьhttps://resh.edu.ru/subject/lesson/6919/main/237273/
6Отношение чисел и величинhttps://resh. edu.ru/subject/lesson/6844/main/235847/
6Пропорцииhttps://resh.edu.ru/subject/lesson/6841/main/237211/
6Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентахhttps://resh.edu.ru/subject/lesson/1060/
6Прямая и обратная пропорциональностьhttps://resh.edu.ru/subject/lesson/6849/main/237769/
6Деление числа в данном отношенииhttps://resh.edu.ru/subject/lesson/6842/main/235816/
6Окружность и круг. Сфера и шарhttps://resh.edu.ru/subject/lesson/588/
6Длина окружности. Площадь кругаhttps://resh.edu.ru/subject/lesson/6913/main/236498/
6Куб, шар, пирамида, цилиндр, конусhttps://resh.edu. ru/subject/lesson/557/
6Столбчатые и круговые диаграммыhttps://resh.edu.ru/subject/lesson/1228/
6Отрицательные целые числаhttps://resh.edu.ru/subject/lesson/6872/main/237087/
6Координатная ось. Часть 1https://resh.edu.ru/subject/lesson/6912/main/236158/
6Представление целых чисел на координатной осиhttps://resh.edu.ru/subject/lesson/6866/main/236343/
6Координатная ось. Часть 2https://resh.edu.ru/subject/lesson/6920/main/236020/
6Противоположные числа. Модуль числаhttps://resh.edu.ru/subject/lesson/6862/main/237056/
6Сравнение целых чиселhttps://resh.edu.ru/subject/lesson/6861/main/237025/
6Сложение целых чисел. Часть 1https://resh.edu.ru/subject/lesson/6863/main/236994/
6Сложение целых чисел. Часть 2https://resh.edu.ru/subject/lesson/6864/main/236963/
6Сложение целых чисел. Часть 3https://resh.edu.ru/subject/lesson/6865/main/236933/
6Законы сложения целых чиселhttps://resh.edu.ru/subject/lesson/6860/main/237335/
6Рациональное вычисление значений арифметических выражений с применением вычитания, как алгебраического сложения. Часть 1 (теория)https://resh.edu.ru/subject/lesson/1380/
6Разность целых чисел. Часть 1https://resh.edu.ru/subject/lesson/6859/main/237552/
6Разность целых чисел. Часть 2https://resh.edu.ru/subject/lesson/6858/main/236901/
6Произведение целых чисел. Часть 1https://resh.edu.ru/subject/lesson/6857/main/236870/
6Произведение целых чисел. Часть 2https://resh.edu.ru/subject/lesson/6856/main/237301/
6Произведение целых чисел. Часть 1https://resh.edu.ru/subject/lesson/6857/main/236870/
6Распределительный законhttps://resh.edu.ru/subject/lesson/6871/main/236746/
6Раскрытие скобок и заключение в скобкиhttps://resh.edu.ru/subject/lesson/6855/main/235382/
6Частное целых чисел. Часть 1https://resh.edu.ru/subject/lesson/6869/main/237521/
6Частное целых чисел. Часть 2https://resh.edu.ru/subject/lesson/6870/main/236808/
6План и этапы решения задачи. Анализ решения, Проверка решения, проверка обратным действиемhttps://resh. edu.ru/subject/lesson/608/
6Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимостьhttps://resh.edu.ru/subject/lesson/346/
6Использование таблиц, схем, чертежей, других средств представления данных при решении задачиhttps://resh.edu.ru/subject/lesson/340/
6Построение фигур, симметричных относительно заданной точки или прямой. Часть 1https://resh.edu.ru/subject/lesson/1392/
6Построение фигур, симметричных относительно заданной точки или прямой. Часть 2.https://resh.edu.ru/subject/lesson/1120/
6Декартова система координат на плоскостиhttps://resh.edu.ru/subject/lesson/6921/main/236560/
6Столбчатые диаграммы. Графикиhttps://resh. edu.ru/subject/lesson/6911/main/235706/
6Построение столбчатых диаграмм. Чтение графиковhttps://resh.edu.ru/subject/lesson/6922/main/236622/
6Обобщение и систематизация знаний по теме «Декартова система координат на плоскости»https://resh.edu.ru/subject/lesson/6917/main/236653/
6Занимательные задачи на процентыhttps://resh.edu.ru/subject/lesson/6918/main/235909/
6Сложные задачи на процентыhttps://resh.edu.ru/subject/lesson/6910/main/236839/
6Обобщение и систематизация знаний по темам «Десятичные дроби, проценты, решение задач на проценты»https://resh.edu.ru/subject/lesson/6923/main/236777/
6Случайные событияhttps://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost. html
6Вероятность случайного событияhttps://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost.html
6Арифметические действия с рациональными числамиhttps://clck.ru/MWVCo
6Свойства умножения рациональных чиселhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4033089
6Свойства вычитания рациональных чиселhttps://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4368360
6Коэффициентhttps://infourok.ru/videouroki/2988
6Перпендикулярные прямыеhttps://infourok.ru/videouroki/2991
6Параллельные прямыеhttps://infourok.ru/videouroki/2992

Конспект урока по математике 5 класс «Решение текстовых задач на проценты» Урок -обобщение.

Муниципальное общеобразовательное учреждение

Россоловская основная общеобразовательная школа

Галичского муниципального района Костромской области

Конспект урока

математики в 5 классе

по теме:

«Решение текстовых задач на проценты »

Разработала

учитель математики

Боброва Любовь Вячеславовна

2013 год, п.Россолово , Галичский район

Класс: 5

Тема урока: «Решение текстовых задач на проценты».

Вид урока: урок закрепления знаний и способов действий.

Используемый учебник: Н.Я.Виленкин «Математика 5 класс» — М.: Мнемозина, 2011.

Место урока в системе уроков по теме: 5 урок по теме «Проценты».

Цель: Повторение основных приемов и методов решения задач на проценты.

Задачи:

Образовательные: закрепить умения решать задачи на проценты; формировать умения и навыки определять тип задачи и метод её решения; отработка практических навыков в вычислении процентов.

Развивающие: развивать математическое мышление, владениями интеллектуальными умениями и мыслительными операциями; развивать навыки самоконтроля; развивать культуру устной и письменной речи.

Воспитательные: воспитывать эмоционально – положительную направленность на практическую деятельность.

Оборудование: компьютер, интерактивная доска, проектор, презентация по данной теме, карточки, опорная схема, раздаточный материал.

Структура урока:

1. Организационный этап (2 мин).

2. Актуализация опорных знаний и умений учащихся (8 мин).

3. Закрепление знаний и способов действий (10 мин).

4. Контроль и самопроверка (13 мин).

5. Подведение итогов урока Рефлексия (5 мин).

6. Постановка домашнего задания (2 мин).

Ход урока.

1. Организационный момент Проверка готовности класса к уроку

Мотивация урока

Слайд №2 Учитель: Здравствуйте, ребята! Сегодняшний урок я хочу начать  словами французского философа Ж.Ж. Руссо (1712–1778 гг.): «Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошего умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению. ..»

Я желаю вам уже сегодня на уроке убедиться в верности этих слов .

— Вы готовы к работе?

Актуализация опорных знаний 1. Проверка домашнего задания по карточкам – эталонам и самоанализ

2. Устный счет.

Учитель: Математическая разминка сегодня будет не простая, выполняя задания вам необходимо составить слова и прочесть тему сегодняшнего урока.

Слайд №3 1. задание

Выберите для каждого процента соответствующий рисунок и прочти слово. Учитель: Ребята, что такое проценты ?

Ученики: Сотая часть числа

(Ученики подбирают для обозначения процентов соответствующий рисунок с заштрихованной частью круга и составляют слово «задачи»)

Учитель: Запишите полученное слово с заглавной буквы в тетрадь. Ученики записывают в тетрадь слово «задачи»

2 задание. Выразите в процентах десятичные дроби Слайд №4

Учитель: Как выразить десятичную дробь в процентах

Ученики: Умножить десятичную дробь на 100%

Учитель: Выберите ответы больше 100% и прочтите слово

Ученики: 104% ,250% слово «на»

Учитель: запишите составленное слово

3 задание. Выразите проценты десятичными дробями

Учитель: Как выразить десятичную дробь в процентах

Ученики: Разделить проценты на 100%

Учитель: расставьте десятичные дроби в порядке убывания Прочтите слово и запишите его в тетрадь.

Учитель: Ребята, какова же тема сегодняшнего урока. Прочтите её в вашей тетради. (проверка по слайду № 5)

Тема урока

Задачи на проценты

Задачи урока

Определять…..Закрепить алгоритмы…Решать….

Сформулировать задачи на сегодняшний урок вам помогут начало предложений на слайде

Ученики 1. определять вид задач на проценты

2. закрепить алгоритмы решения задач

3. решать задачи на проценты различного типа

3. Закрепление знаний и способов действий

Учитель: Какие 3 вида задач на проценты вы знаете

1. Работа с опорной схемой. ( Слайд №6)

— Какие три задачи на проценты вы знаете?

Учитель

— Как найти количество процентов от числа?

Повторите алгоритм

— Сформулируйте алгоритм нахождения числа по его проценту.

— Как найти процентное отношение двух чисел?

(Во время работы все алгоритмы появляются на слайде)

Коллективная работа с классом слайд №7 . Устное решение задач

Учитель: — По предложенным схемам определите тип задачи (Проверяют тип задачи по слайду № 7 ), составьте и решите задачи к данным схемам:

Нахождение числа по процентам

Нахождение процентов от числа

Нахождение процентного отношения

100% – х р.7% – 21р.

100% – 500км56 % – х км

100% – 165 м .у % – 10м .

Контроль и самопроверка Учитель: Теперь я предлагаю проверить свои знания и выполнить самостоятельную работу. Каждый ученик получит карточку-задание, в которой содержатся шесть задач практического характера.

За правильно выполненное с 1-го по 5 –е задание ученик получает два балла, 6- е задание 3 балла

КАРТОЧКА №1

Клубника содержит в среднем 6% сахара. Сколько килограммов сахара в клубники?

В парке 150 деревьев. Липы составляют 8 % от числа всех деревьев. Сколько лип в парке?

За контрольную работу по математике отметку «5» получили 8 учеников, что составляет 40% всех учеников. Сколько учеников в классе?

На клумбе посадили 36 луковиц тюльпанов, это 48% всех купленных луковиц. Сколько всего луковиц купили?

Ученик решил 17 задач из 68 . Сколько процентов задач он решил?

Завод должен изготовить 360 стульев. В первую неделю он выполнил 70% задания, во вторую- 20%. За какую неделю изготовлено больше стульев и на сколько?

КАРТОЧКА №2

Найдите число, 40% которого равны 80?

Маша прочитала 14 страниц, что составляет 20 % книги. Сколько всего страниц в книге?

Молоко содержит 4% жира. Сколько килограммов жира содержится в молока?

В сплаве есть медь, содержание которой составляет 25 %. Сколько меди содержится в сплаве массой 68 кг

Туристу нужно пройти 80 км. К концу дня он прошёл 20 км. Сколько процентов пути прошёл турист?

Площадь сада . Яблони занимают 55 % этой площади, а вишни – 25 % . На сколько гектаров площадь, занятая вишнями, меньше площади, отведенной под яблони?

КАРТОЧКА №3

Найдите число, 12% которого равны 120?

Рыбак поймал 14 окуней, что составляет 28% всего улова. Сколько всего рыб поймал рыбак?      

При молотьбе пшеницы получается 28% мякины. Сколько мякины получиться из 45 ц пшеницы?

Ученик решил 17 задач из 68 . Сколько процентов задач он решил?

В музыкальной школе учатся 120 детей. Среди них 60 % девочки. Сколько мальчиков учится в музыкальной школе?

Турист прошел . Из них 66 % расстояния он шел лесом, 26% — полем. На сколько километров он прошел больше лесом, чем полем?

Оценки выставляются по следующим критериям:

13 баллов – оценка “;10- баллов – оценка “;6-8 баллов – оценка “;меньше 6 баллов – оценка “2”.

5. Подведение итогов урока.

После окончания работы, учащиеся сверяют полученные результаты с ответами на карточке и проставляют соответствующее количество баллов. Таким образом, учащиеся самостоятельно выставляют себе оценку за проверочную работу.

Рефлексия (5 мин).

Учитель: Обратимся к вашим результатам самостоятельной работы? Задачи каких видов вы хорошо умеете решать? Какие задачи на проценты вызвали у вас затруднения? Какие задания вам бы хотелось выполнить ещё раз?

Так как вам предстоит проверить ваши знания по теме «Проценты» дома я предлагаю вам выполнить задания на карточках разного уровня.

Белые карточки простые задачи, цветные карточки – задачи повышенного уровня.

Учащиеся самостоятельно выбирают уровень задач для домашней работы

Урок подошёл к концу. Вы хорошо сегодня поработали. Спасибо.

Приложение

КАРТОЧКА №1

Количество баллов

Задание

Отметка о выполнении

Клубника содержит в среднем 6% сахара. Сколько килограммов сахара в клубники?

В парке 150 деревьев. Липы составляют 8 % от числа всех деревьев. Сколько лип в парке?

Ученик решил 17 задач из 68 . Сколько процентов задач он решил?

За контрольную работу по математике отметку «5» получили 8 учеников, что составляет 40% всех учеников. Сколько учеников в классе?

5. На клумбе посадили 36 луковиц тюльпанов, это 48% всех купленных луковиц. Сколько всего луковиц купили?

6. Завод должен изготовить 360 стульев. В первую неделю он выполнил 70% задания, во вторую- 20%. За какую неделю изготовлено больше стульев и на сколько?

______________________________________________________________________________

КАРТОЧКА №2

Количество баллов

Задание

Отметка о выполнении

Найдите число, 40% которого равны 80?

Маша прочитала 14 страниц, что составляет 20 % книги. Сколько всего страниц в книге?

Молоко содержит 4% жира. Сколько килограммов жира содержится в молока?

В сплаве есть медь, содержание которой составляет 25 %. Сколько меди содержится в сплаве массой 68 кг ?

Туристу нужно пройти 80 км. К концу дня он прошёл 20 км. Сколько процентов пути прошёл турист?

6 . Площадь сада . Яблони занимают 55 % этой площади, а вишни – 25 % . На сколько гектаров площадь, зан. ..

Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.

Задачи на проценты (Сказочные герои в стране математики)

Автор(ы) проекта

Крислинг Ирина

Тема проекта

Задачи на проценты (Сказочные герои в стране математики)

Предмет, класс

Математика, 5 класс

Краткая аннотация проекта (образовательные стандарты, примерная продолжительность проекта и т.д.)

Проблема Показать, что тема «проценты» имеет практическое применение…

«Тот, кто не знает математики, не может узнать никакой другой науки
и даже не может обнаружить своего невежества»
Роджер Бэкон

Проценты — одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что, например, в выборах приняли участие 54,5% избирателей, рейтинг победителя хит-парада равен 85%, промышленное производство сократилось на 10,2% ,уровень инфляции составляет 8%в год, банк начисляет 12% годовых, молоко содержит 3,2% жира и т. д.

Проценты в мире появились из практической необходимости, при решении определенных задач. Первая потребность процентов была экономическая, но после проценты стали широко применяться в различных отраслях и науках (математика, химия, физика и т д.), и в наше время проценты приобрели широкое распространение. Поэтому надо отметить важность процентов в нашей жизни. Сейчас проценты проникли, практически, во все отрасли знаний. Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость, умение оперативно решать поставленные задачи – это динамическая характеристика практического интеллекта, проявляется в количестве времени, которое проходит с момента возникновения задачи до ее практического решения. Тема «Проценты» изучается в школьном курсе рано в 5 классе, изучается непродолжительно и, наконец, к задачам на части и проценты возвращаются в старших классах на ЕГЭ.

Из Стандартов Образования Проценты. Нахождение процента от величины, величины по ее проценту.
Отношение, выражение отношения в процентах.

Вопросы, направляющие проект

Основополагающий вопрос

«Мал золотник да дорог?»

Проблемные вопросы

Учебные вопросы

  • Что такое процент?

  • Как появились проценты?

  • Как находить процент от его величины и величину по его проценту?

  • Как находить отношение процентов чисел?

  • Где в повседневной жизни применяются проценты?

  • Что нужно сделать, чтобы перевести проценты в десятичную дробь?

План проведения проекта


Создайте свой собственный mind карты при MindMeister

Дидактические цели и ожидаемые результаты обучения

Цели:

  • Формирование навыков работы в группе

  • Умение осуществлять сотрудничество с учителем и сверстниками, договариваться и приходить к общему решению в совместной деятельности

  • Уметь организовывать свою деятельность, определять её цели и задачи.

  • Умение работать с различными источниками информации

  • Формирование знаний о процентах

  • Умение представить знания о процентах в повседневной жизни

  • Научить детей использовать эти знания не только в учебно-познавательном процессе, но и в повседневной жизни.

  • Научить детей находить процент от числа и число от процента.

  • Научить детей находить соотношение процентов.

Презентация учителя для выявления представлений и интересов учащихся

Пример продукта проектной деятельности учащихся

Материалы по формирующему и итоговому оцениванию

План оценивания

  • Чтобы оценить готовность учеников к работе над проектом была проведена проверочная работа в игровой форме, которая выявила первичные знания учащихся по данной теме.

  • Чтобы ученики могли показать свои знания, в данный проект были включены вопросы, ответами на которые служат ситуации из повседневной жизни

  • Чтобы привлечь внимание учеников и помочь понять им каковы ожидания от проекта и критерии оценивания, была создана презентация учителя.

  • Чтобы ученики узнали, что они добились цели и результата, поставленного в начале проекта, данный проект они будут защищать.

График оценивания

До работы над проектом Ученики работают над проектом и выполняют задания После завершения работы над проектом
Выявить первоначальные навыки с помощью вводной презентации, «мозговой штурм» Лист продвижения, таблица самооценивания Итоговая презентация, тест

Описание методов оценивания

«Мозговой штурм» В ходе презентации ребятам предлагается провести «мозговой штурм» Учащимся предлагается обсудить ответы на основополагающий вопрос («Мал золотник, да дорог?»), проблемные и учебные вопросы. Задача «мозгового штурма» пробудить интерес к работе, дать представление о новой форме проведения комплексов уроков и определить роль самостоятельной деятельности каждого.

Самооценки в группах Наблюдение за работой групп позволяет оценить навыки совместной деятельности. Ученики оценивают групповую работу, используя рефлексию и контрольные листы.

Таблица продвижения Используется для наблюдения за ходом выполнения заданий проекта и заполняется учениками.

Тест Тест служит прямым доказательством приобретения знаний и понимания.

Итоговая презентация Последний урок по данной теме, защита проекта. В ходе конференции участники демонстрируют и защищают свои работы.

Необходимые начальные знания, умения и навыки

Материалы для дифференцированного обучения

Ученик с проблемами освоения учебного материала

Одаренный ученик

  • Задание: Составить 3 задачи на нахождение процентов от числа.

  • Творчески оформить уже готовые задачи.

Ученик, для которого язык изучения не является родным

Материалы и ресурсы, необходимые для проекта

Оборудование:

Программное обеспечение:

Материалы на печатной основе:

  • Задачник по теме «Проценты» для 5 класса

  • Учебник по математике за 5 класс

  • Дидактические материалы по теме «проценты»

Интернет-ресурсы:

Проекты с аналогичной тематикой

Отзывы на проект

Тест по математике Понятие процента 5 класс

Тест по математике Понятие процента, Задачи на проценты для учащихся 5 класса. Тест состоит из 2 вариантов, в каждом варианте по 8 заданий.

1 вариант

1. Все ли равенства верны?

0,36 = 36%
0,8 = 80%
20% = 0,2
140% = 1,4

1) все
2) не все

2. Выразите в процентах число 0,09.

1) 0,9%
2) 90%
3) 9%
4) 3,5%

3. Представьте в виде десятичной дроби 250%.

1) 0,25
2) 2,5
3) 2,05
4) 20,5

4. Верно ли, что 12% числа 50 равны 6?

1) да
2) нет

5. Пять процентов неизвестного числа равны 100. Какое это число?

1) 20
2) 500
3) 200
4) 2000

6. От куска ткани отрезали 4 м. Это составило 20% длины всего куска. Сколько ткани было в куске?

1) 24 м
2) 40 м
3) 20 м
4) 80 м

7. Катя нашла в лесу 200 белых грибов; 75% всех грибов высушили. Сколько грибов высушили?

1) 100
2) 150
3) 50
4) 175

8. Плащ-дождевик стоил 300 р. Через некоторое время его цену снизили на 10%. Какова новая цена плаща?

1) 270 р.
2) 290 р.
3) 310 р.
4) 297 р.

2 вариант

1. Все ли равенства верны?

0,96 = 96%
0,7 = 70%
25% = 0,25
160% = 1,6

1) все
2) не все

2. Выразите в процентах число 0,02.

1) 20%
2) 0,2%
3) 2%
4) 4%

3. Представьте в виде десятичной дроби 135%.

1) 2,7
2) 0,135
3) 13,5
4) 1,35

2. Верно ли, что 45% числа 20 равны 9?

1) да
2) нет

5. Десять процентов неизвестного числа равны 500. Какое это число?

1) 50
2) 5000
3) 500
4) 2500

6. Из ящика взяли 3 кг яблок. Это составило 60% массы всех яблок, находящихся в ящике. Сколько килограм­мов яблок было в ящике?

1) 20 кг
2) 18 кг
3) 4 кг
4) 5 кг

7. Дети собрали в лесу 800 г земляники. Из 70% собран­ной земляники мама сварила варенье. Сколько граммов земляники она взяла для варенья?

1) 700 г
2) 750 г
3) 560 г
4) 650 г

8. Цена платья 900 р. Через некоторое время его цену снизили на 30%. Какова новая цена платья?

1) 270 р.
2) 630 р.
3) 870 р.
4) 730 р.

Ответы на тест по математике Понятие процента, Задачи на проценты
1 вариант
1-1
2-3
3-2
4-1
5-4
6-3
7-2
8-1
2 вариант
1-1
2-3
3-4
4-1
5-2
6-4
7-3
8-2

задач по интересам — GMAT Math

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Формула с примерами и практическими задачами. Как работает формула

Сложные проценты — отличная вещь, когда вы их зарабатываете! Сложные проценты — это когда банк выплачивает проценты как на основную сумму (первоначальную сумму денег), так и на проценты, уже заработанные на счете.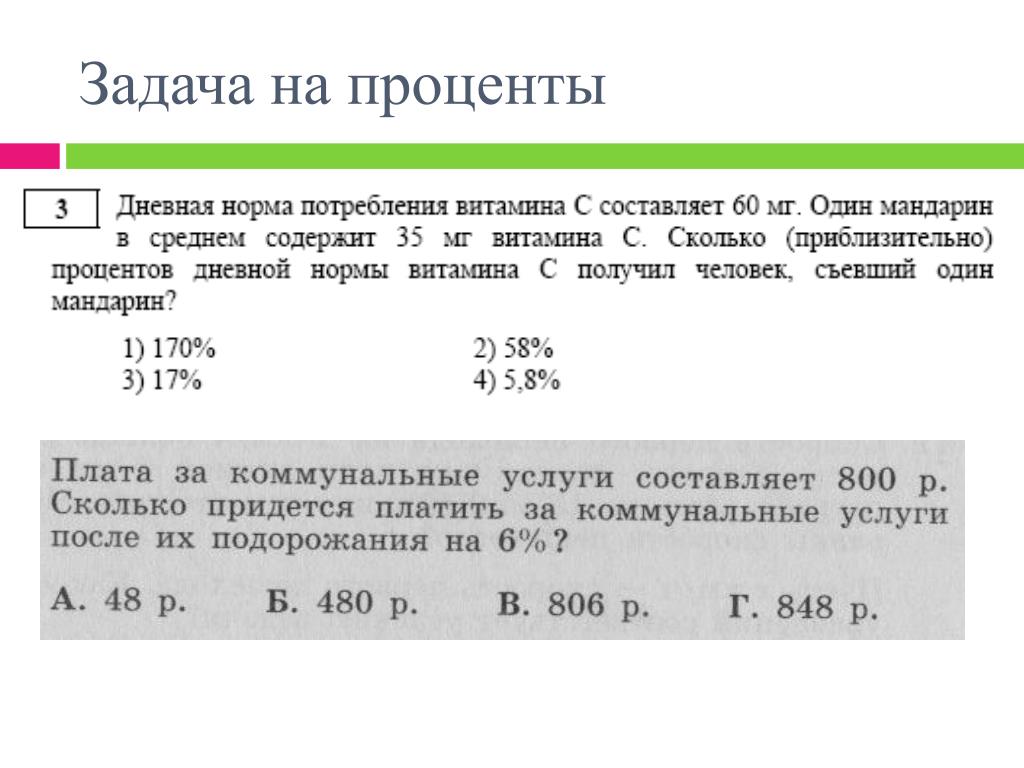

Для расчета сложных процентов используйте приведенную ниже формулу. В формуле A представляет собой окончательную сумму на счете после t лет, сложенную n раз по процентной ставке r с начальной суммой p.

Эта страница посвящена пониманию формулы сложных процентов; Если вы хотите глубже понять, как работают сложные проценты, и изучить некоторые примеры из реального мира, прочтите нашу статью здесь.

Проблема 1

Если у вас есть банковский счет с основной суммой в 1000 долларов, и ваш банк взимает проценты дважды в год по ставке 5%, сколько денег у вас будет на вашем счете в конце года?

Количество денег

Проблема 2

Если вы открываете банковский счет с 10 000 долларов, и ваш банк ежеквартально взимает проценты по ставке 8%, сколько денег у вас будет на конец года? (предположим, что вы не добавляете и не снимаете деньги со счета)

Количество денег

Проблема 3

С первой кредитной карты, которую вы получили, списания 12. 49% процентов своим клиентам и соединениям с ежемесячными процентами. В течение одного дня после получения первой кредитной карты вы максимально исчерпываете кредитный лимит, потратив 1200 долларов США. Если вы больше ничего не покупаете по карте и не производите никаких платежей, сколько денег вы должны компании через 6 месяцев?

Конечная сумма после смешивания

Примечание: , поскольку продолжительность составляет полгода, стоимость т. составляет ½.


6 месяцев — это половина года, а т в формуле сложных процентов измеряются годами.

Проблема 4

Вы выигрываете в лотерею и получаете 1 000 000 долларов. Вы решаете, что хотите вложить все деньги на сберегательный счет. {60}
\\
A = 1 348 850,15 $
$$

Я бы выбрал вариант №1

План 2

Банк дает вам процентную ставку 12% и начисляет проценты каждые 2 месяца .{30}
\\
A = 1 811 361,58 долл. США
$$

Я бы выбрал вариант №2

Вопрос: Какой тарифный план принесет вам больше денег через 5 лет.

Формула простого процента и примеры

Простые проценты — это когда проценты по ссуде или инвестиции рассчитываются только на первоначально вложенную или ссуду сумму. Это отличается от сложных процентов, где проценты начисляются на первоначальную сумму и на любые полученные проценты. Как вы увидите в примерах ниже, простую формулу процентов можно использовать для расчета заработанных процентов, общей суммы и других значений в зависимости от проблемы.

реклама

Примеры определения процентов, полученных по простой формуле процентов

Во многих простых задачах с процентами вы будете находить общий процент, заработанный за установленный период, который представлен как \ (I \).Формула для этого:

Рассмотрим на примере, как работает эта формула. Помните, что в формуле основная сумма \ (P \) — это начальная сумма инвестиций.

Пример

Двухлетняя ссуда в размере 500 долларов предоставляется с простой процентной ставкой 4%. Найдите заработанные проценты.

Решение

Всегда находите время, чтобы определить значения, указанные в проблеме. Здесь дано:

  • Время 2 года: \ (t = 2 \)
  • Начальная сумма $ 500: \ (P = 500 \)
  • Ставка 4%. Запишите это в виде десятичной дроби: \ (r = 0,04 \)

Теперь примените формулу:

\ (\ begin {align} I & = Prt \\ & = 500 (0,04) (2) \\ & = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {40} \ end {align} \)

Ответ : Полученные проценты составляют 40 долларов.

В этом примере время указано в годах, как и в формуле. Но что, если вам дается только несколько месяцев? Давайте рассмотрим другой пример, чтобы увидеть, как это может быть по-другому.

Пример

Общая сумма инвестиций составляет 1200 долларов США по простой процентной ставке 6% сроком на 4 месяца.Сколько процентов заработано на этих инвестициях?

Решение

Прежде чем мы сможем применить формулу, нам нужно будет записать время в 4 месяца в годах. Поскольку в году 12 месяцев:

\ (\ begin {align} t & = \ dfrac {4} {12} \\ & = \ dfrac {1} {3} \ end {align} \)

С поправкой на годы, теперь мы можем применить формулу с \ (P = 1200 \) и \ (r = 0,06 \).

\ (\ begin {align} I & = Prt \\ & = 1200 (0,06) \ left (\ dfrac {1} {3} \ right) \\ & = \ bbox [граница: 1 пиксель сплошной черный; отступ: 2 пикселя] {24} \ end {align} \)

Ответ : Полученные проценты составляют 24 доллара.

Если бы вы не обратились здесь, вы бы нашли проценты за 4 года, что было бы намного выше. Поэтому всегда проверяйте, что время исчисляется годами, прежде чем применять формулу.

Важно! Время должно быть в годах, чтобы применить формулу простого процента. Если вам даны месяцы, используйте дробь, чтобы представить их годами.

Другой тип проблем, с которыми вы можете столкнуться при работе с простыми процентами, — это определение общей суммы задолженности или общей стоимости инвестиций через заданный промежуток времени.Это называется будущей стоимостью, и ее можно рассчитать несколькими способами.

Определение будущей стоимости простых процентов

Один из способов рассчитать будущую стоимость — просто найти проценты, а затем добавить их к основной сумме. Однако более быстрый способ — использовать следующую формулу.

Вы знаете, как использовать эту формулу, когда вам задают такие вопросы, как «какова общая сумма, которая должна быть возвращена» или «какова стоимость инвестиций» — все, что кажется относящимся к общей сумме после учета процентов.

Пример

Бизнес берет простую ссуду под проценты в размере 10 000 долларов по ставке 7,5%. Какую общую сумму выплатит бизнес при выдаче кредита сроком на 8 лет?

Решение

Общая сумма, которую они выплатят, является будущей стоимостью \ (A \). Нам также сообщается, что:

  • \ (t = 8 \)
  • \ (г = 0,075 \)
  • \ (P = 10 \, 000 \)

Использование простой формулы процента для будущей стоимости:

\ (\ begin {align} A & = P (1 + rt) \\ & = 10 \, 000 (1 + 0.075 (8)) \\ & = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2px] {16 \, 000} \ end {align} \)

Ответ : Компания выплатит в общей сложности 16 000 долларов.

Это может показаться высоким, но помните, что в контексте ссуды проценты — это просто плата за взятие денег в долг. Чем больше процентная ставка и дольше срок, тем дороже ссуда.

Также обратите внимание, что вы можете рассчитать это, сначала найдя процент, I = Prt = 10000 (0,075 (8)) = 6000 долларов, и добавив его к основной сумме в 10000 долларов.Окончательный ответ одинаков при использовании любого метода.

объявление

Продолжить интересующее вас исследование

Теперь, когда вы изучили простую формулу процента, вы можете изучить более сложную идею сложных процентов. Большинство сберегательных счетов, кредитных карт и ссуд основаны на сложных процентах, а не на простых процентах. Вы можете просмотреть эту идею здесь:

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Повышение успеваемости и интереса к изучению математики с помощью Math-Island | Исследования и практика в области технологий расширенного обучения

  • Аль-Зуби, С. М., и Юнес, М. А. Б. (2015). Низкая успеваемость: причины и результаты. Теория и практика языковых исследований, 5 (11), 2262.

    Google Scholar

  • Артер, Дж. А., и Спандель, В. (2005). Использование портфолио студенческих работ в обучении и оценивании. Образовательные вопросы измерения и практика, 11 (1), 36–44.

    Google Scholar

  • Азеведо Р., Фейзи-Бенах Р., Даффи М., Харли Дж. И Треворс Г. (2012). Метапознание и саморегулируемое обучение в среде обучения, ориентированной на учащихся.В Д. Йонассен и С. Лэнд (ред.), Теоретические основы среды обучения, ориентированной на учащихся, (стр. 171–197). Нью-Йорк: Рутледж.

  • Барлетт, К. П., Андерсон, К. А., и Свинг, Э. Л. (2009). Подтвержденные, предполагаемые и спекулятивные эффекты видеоигр: обзор доказательств. Моделирование и игры, 40 (3), 377–403.

    Google Scholar

  • Барр Р. Б. и Тагг Дж. (1995).От преподавания к обучению — новая парадигма высшего образования. Change The Magazine of Higher Learning, 27 (6), 12–26.

    Google Scholar

  • Биргин О. и Баки А. (2007). Использование портфолио для оценки успеваемости студента. Журнал турецкого научного образования, 4 (2), 75–90.

    Google Scholar

  • Чан, Т. В., Рошель, Дж., Си, С., Киншук, Шарплс, М., Браун, Т. и др. (2006). Индивидуальное обучение с использованием технологий: возможность для глобального научного сотрудничества. Исследования и практика в области технологий расширенного обучения, 1 (01), 3–29.

    Google Scholar

  • Чейз К. и Абрахамсон Д. (2015). Алгебра обратных лесов: эмпирическая оценка проектной архитектуры. ZDM Mathematics Education, 47 (7), 1195–1209.

    Google Scholar

  • Чен, Ю. Х., Луи, К. К., Линь, К. П., Шао, Ю. Дж., И Чан, Т. В. (2012a). Использование совместной игры-головоломки с числами для развития вычислительных способностей сложения и вычитания. Образовательные технологии и общество, 15 (1), 354–366.

    Google Scholar

  • Чен, З. Х., Ляо, К. К., Ченг, Х. Н., Йе, С. Ю., и Чан, Т. В. (2012b). Влияние игровых заданий на удовольствие и целеустремленность учащихся при обучении математике. Журнал образовательных технологий и общества, 15 (2), 317–327.

    Google Scholar

  • Ченг, Х. Н. Х., Ян, Э. Ф. Й., Ляо, К. С. Я., Чанг, Б., Хуанг, Ю. С. Я., и Чан, Т. В. (2015). Поиск строительных лесов: обратный дизайн строительных лесов в компьютерном решении текстовых задач. Журнал образовательных компьютерных исследований, 53 (3), 409–435.

    Google Scholar

  • Чу, Х.К. , Ян, К. Х., и Чен, Дж. Х. (2015). Подход с концептуальной картой, ориентированный на временную последовательность, к разработке образовательных компьютерных игр для курсов истории. Интерактивные среды обучения, 23 (2), 212–229.

    Google Scholar

  • Давенпорт, Т. Х. и Прусак, Л. (2000). Практические знания: как организации управляют своими знаниями . Бостон: Издательство Гарвардской школы бизнеса.

  • Дакворт, А.Л., Гендлер Т. С. и Гросс Дж. Дж. (2014). Самоконтроль у детей школьного возраста. Психолог-педагог, 49 (3), 199–217.

    Google Scholar

  • Эбенер, С., Хан, А., Шадемани, Р., Компернолл, Л., Белтран, М., Лансанг, М. А., и Липпман, М. (2006). Отображение знаний как метод поддержки перевода знаний. Бюллетень Всемирной организации здравоохранения, 84 , 636–642.

    Google Scholar

  • Гонсалес-Калеро, Дж. А., Арнау, Д., Пуиг, Л., и Аревалилло-Эрраэс, М. (2014). Интенсивные строительные леса в интеллектуальной обучающей системе для обучения решению алгебраических словесных задач. Британский журнал образовательных технологий, 46 (6), 1189–1200.

    Google Scholar

  • Ханус, М. Д., Фокс, Дж. (2015). Оценка эффектов геймификации в классе: продольное исследование внутренней мотивации, социального сравнения, удовлетворенности, усилий и успеваемости. Компьютеры и образование, 80 , 152–161.

    Google Scholar

  • Хван, Г. Дж., Чиу, Л. Ю., и Чен, К. Х. (2015). Подход к обучению на основе контекстных игр для повышения успеваемости студентов на курсах социальных наук. Компьютеры и образование, 81 , 13–25.

    Google Scholar

  • Хван, Г. Дж., Су, Дж. М., и Чен, Н.С. (2012). Введение и практика электронного обучения . Тайвань: Дрмасте.

    Google Scholar

  • Kiili, K., & Ketamo, H. (2007). Изучение механизма обучения в обучающих играх. Журнал вычислительных и информационных технологий, 15 (4), 319–324.

    Google Scholar

  • Килпатрик Дж., Сваффорд Дж. И Финделл Б. (ред.). (2001). Сложим: помогаем детям изучать математику . Вашингтон, округ Колумбия: Национальная академия прессы.

    Google Scholar

  • Койвисто Дж. И Хамари Дж. (2014). Демографические различия в предполагаемых выгодах от геймификации. Компьютеры в поведении человека, 35 , 179–188.

    Google Scholar

  • Krapp, A. (1999). Интерес, мотивация и обучение: образовательно-психологическая перспектива. Европейский журнал психологии образования, 14 (1), 23–40.

    Google Scholar

  • Ку, О. , Чен, С. Ю., Ву, Д. Х., Лао, А. С., и Чан, Т. В. (2014). Влияние игрового обучения на математическую уверенность и успеваемость: высокие способности по сравнению с низкими. Журнал образовательных технологий и общества, 17 (3), 65–78.

    Google Scholar

  • Лао, А.К. К., Ченг, Х. Н., Хуанг, М. К., Ку, О., и Чан, Т. В. (2017). Изучение мотивационной ориентации и стратегий обучения в компьютерном самостоятельном обучении (CS-SDL) по математике: перспектива внутренних и внешних целей. Журнал образовательных компьютерных исследований, 54 (8), 1168–1188.

    Google Scholar

  • Ли Ю. М. (2012). Различение моделей мотивации низкой успеваемости по математике: сравнение учащихся из неблагополучных семей и других учащихся начальной и средней школы. Журнал исследований в области педагогических наук, 57 (4), 39–71. https://doi.org/10.3966/2073753X2012125704002.

    Google Scholar

  • Li, M.-C., & Tsai, C.-C. (2013). Игровое обучение в естественнонаучном образовании: обзор соответствующих исследований. Журнал естественно-научного образования и технологий, 22 (6), 877–898. https://doi.org/10.1007/s10956-013-9436-x.

    Google Scholar

  • Ляо, К.К., Ченг, Х. Н., Чанг, В. К., и Чан, Т. В. (2017). Поддержка участия родителей в школе BYOD (принеси свое собственное устройство). Журнал «Компьютеры в образовании», 4 (2), 107–125.

    Google Scholar

  • Линь Б.Г., Ли Р.П. и Хуанг Ю.З. (2009). Учебное пособие по тесту математических способностей для школьников . Тайбэй: Министерство образования.

    Google Scholar

  • Линь П.Дж. И Цай, В. Х. (2001). Использование основанных на исследованиях примеров для улучшения понимания будущими учителями преподавания математики и их размышлений. В Ф. Л. Лин (ред.), Здравый смысл в математическом образовании. Материалы конференции по здравому смыслу в математическом образовании 2001 г., Нидерланды и Тайвань, (стр. 231–272). Тайбэй, Тайвань.

    Google Scholar

  • Лю Т. Ю. и Чу Ю. Л. (2010). Повсеместное использование игр в курсах аудирования и говорения на английском языке: влияние на результаты обучения и мотивацию. Компьютеры и образование, 55 (2), 630–643. https://doi.org/10.1016/j.compedu.2010.02.023.

    Google Scholar

  • Макларен, Б. М., Адамс, Д. М., Майер, Р. Э. и Форлицци, Дж. (2017). Компьютерная игра, которая способствует изучению математики больше, чем традиционный подход. Международный журнал игрового обучения, 7 (1), 36–56.

    Google Scholar

  • Министерство образования.(2003). Методические указания по учебной программе 1-9 классов начальной и неполной средней школы . Получено с https://www.k12ea.gov.tw/92_sid17/%E6%96%B0%E7%B8%BD%E7%B6%B1%E8%8B%B1%E6%96%87%E7%89 % 88.pdf.

    Google Scholar

  • Маллис, И. В. С., Мартин, М. О., Фой, П., и Друкер, К. Т. (2012). Международные результаты PIRLS 2011 по чтению . Честнат-Хилл: Международный учебный центр TIMSS и PIRLS, Бостонский колледж.

    Google Scholar

  • Маллис, И. В. С., Мартин, М. О., Фой, П., и Хупер, М. (2016). Международные результаты TIMSS 2015 по математике. Получено с http://timssandpirls.bc.edu/timss2015/international-results/

    Google Scholar

  • Нильсон, Л. Б. (2014). Секрет саморегулируемого обучения. In Приглашенная статья для факультета Focus: Higher Ed Teaching Strategies из Magna Publications .

    Google Scholar

  • OECD. (2013). Результаты PISA 2012 в фокусе: что знают 15-летние и что они могут сделать с тем, что они знают: ключевых результатов PISA 2012.

    Google Scholar

  • OECD. (2016). В фокусе — результаты PISA 2015. Получено с: https://www.oecd.org/pisa/pisa-2015-results-in-focus.pdf.

    Google Scholar

  • Рулон И., Бейкер, Р. С. Дж. Д., Алевен, В., и Кёдингер, К. Р. (2014). О преимуществах поиска (и избегания) помощи в среде решения проблем в Интернете. Journal of the Learning Sciences, 23 (4), 537–560.

    Google Scholar

  • Шроу Г., Флауэрдей Т. и Леман С. (2001). Повышение ситуационного интереса в классе. Обзор педагогической психологии, 13 (3), 211–224.

    Google Scholar

  • Сингх К.(2011). Изучение мотивации достижения по отношению к академической успеваемости студентов. Международный журнал планирования и управления образованием, 1 (2), 161–171.

    Google Scholar

  • Тауб М., Азеведо Р., Буше Ф. и Хосравифар Б. (2014). Можно ли предсказать использование когнитивных и метакогнитивных стратегий саморегулируемого обучения на основе уровней предшествующих знаний учащихся в среде гипермедиа обучения? Компьютеры в поведении человека, 39 , 356–367.

    Google Scholar

  • Велес, Дж., Фабрегат, Р., Булл, С., и Уэва, Д. (2009). Возможности открытых моделей учащихся в адаптивных виртуальных обучающих средах. В С. Д. Крейг и Д. Дичева (ред.), AIED 2009: 14-я Международная конференция по искусственному интеллекту в образовательных семинарах, том 8 (стр. 11–20). Брайтон: Международное общество AIED.

    Google Scholar

  • Ян Э.Ф. Ю., Ченг, Х. Н. Х., Чинг, Э. и Чан, Т. У. (2012). Дизайн обучения открытию на основе вариаций в индивидуальном классе математики. В G. Biswas, L.-H. Вонг, Т. Хирасима и В. Чен (редакторы), Труды 20-й Международной конференции по компьютерам в образовании (стр. 811–815). Сингапур: Азиатско-Тихоокеанское общество компьютеров в образовании.

    Google Scholar

    • Начало года Опрос по интересам к математике

    Математика может быть весьма поляризующим предметом для многих учеников, когда они переходят в 4–5 классы.Некоторым ученикам это нравится и они уверены в себе, а некоторым нужна небольшая (или много) дополнительная поддержка и поощрение, чтобы заниматься математикой и получать от нее удовольствие. Это так важно, чтобы мы как можно скорее узнали наших учеников и их взгляды на математику. Эти бесплатные цифровые анкеты по математике помогут вам узнать своих учеников и их убеждения / мнения о математике, чтобы вы могли использовать их для обучения.

    Примечание. В этом посте можно найти распечатанный опрос по математике.

    Эти цифровые математические опросы доступны в формате Google Slides.Нажмите здесь, чтобы узнать больше о назначении Google Slides через Google Classroom.

    В этот цифровой ресурс включены несколько различных заданий по математике (к которым можно получить доступ, используя ссылку в PDF-файле в разделе «Загрузить БЕСПЛАТНЫЙ опрос и задания по математике здесь»).

    Вы можете использовать одно занятие в день в течение первой или около того недели в школе. Или вы можете выбрать занятия, которые лучше всего подходят вашим ученикам и вашим конкретным потребностям.Вы обнаружите, что в некоторых вопросах может быть небольшое совпадение с , если вы использовали все действия.

    Согласен или не согласен? Сортировка по интересам по математике

    Этот опрос по интересам к математике — один из моих любимых. Чтобы выполнить это задание, учащиеся сортируют утверждения по математике в зависимости от того, согласны они с ними или нет.

    Пример выписок:

    • Я хорошо изучаю математику.
    • Я предпочитаю заниматься математикой в ​​одиночку.
    • Мне нравится заниматься математикой на бумаге.
    • Мне нравится математика.

    Это или То? Деятельность с интересом к чтению

    Для выполнения этого задания по математике учащиеся используют цифровой «круг», чтобы обвести его в кружок, который они предпочитают из двух вариантов.

    Вот несколько примеров:

    Выполнение математики на бумаге ИЛИ Выполнение математики на компьютере

    Самостоятельная игра в математические игры ИЛИ игра в математические игры с другими людьми

    целей по математике

    Заставьте своих учеников задуматься о своих целях с помощью этого быстрого задания из 3 вопросов, которое заставит учеников задуматься о том, как они хотят улучшить свои знания по математике.

    Привычки к математике

    Узнайте больше о своих учениках, их отношении и привычках к математике с помощью этого быстрого слайда из 4 вопросов.

    Выбор по математике

    Этот математический опрос по интересам немного сложнее, потому что здесь нет вариантов. Помните об этом при назначении вашим ученикам. Он требует, чтобы учащиеся обдумали области математики, которые им нравятся и не нравятся, и почему. Некоторым учащимся может быть сложно создать области без доступных вариантов или вариантов.

    Быстрые ответы по математике

    Получите быстрые данные от своих учеников с помощью этого безопасного математического задания «Быстрые ответы». Учащиеся отвечают на простые и быстрые вопросы, чтобы вы могли узнать еще больше подробностей об их математических предпочтениях, таких как их любимая математическая тема, их любимый практический математический инструмент и т. Д.

    Закончите предложение… Занятие по математике

    Это упражнение по интересам математики похоже на быстрое письмо, но с математическим фокусом.Учащиеся заканчивают такие математические предложения, как «Самым интересным математическим заданием, которое я когда-либо делал по математике, было…» и «Хороший ученик по математике…». Это еще один отличный способ получить представление о математическом мышлении ваших учеников.

    Рейтинг навыков по математике

    Это задание по математике, безусловно, является наиболее продвинутым, но вашим ученикам, которые любят сложные задания, оно может понравиться. Чтобы завершить задание, студенты перемещают цифровые элементы, чтобы расположить их в порядке от наименее заинтересованного к наиболее заинтересованному.Это не та деятельность, которую я бы рекомендовал отправлять всем студентам самостоятельно, если вы не научите их, как ее выполнять.

    Загрузите БЕСПЛАТНЫЕ опросы и задания по цифровой математике здесь

    Щелкните здесь или на изображении, чтобы загрузить PDF-файл со ссылкой для копирования цифровых математических опросов и занятий на свой Google Диск.

    Оттуда вы можете назначить их своим ученикам (Нажмите здесь, чтобы получить пошаговое руководство по назначению в Google Classroom.)

    Опрос по интересам к чтению

    Щелкните здесь, чтобы загрузить упражнения с опросом по интересам к чтению, аналогичные математическим, показанным в этом посте.

    Нужно больше цифровых мероприятий для 4–5 классов?

    Google Slides — математические задания

    Сортировки по математике для 4-го класса

    Сортировки по математике для 5-х классов

    Упражнения по цифровой математике для 4-го класса для целого числа и разряда

    Упражнения по цифровой математике для 5-го класса для десятичных знаков

    5-й класс Снова в школу по математике

    Верные или ложные задания по математике для 4-го и 5-го классов

    Доски выбора по математике (доступны 3-5 классы)

    Плакаты по математике для 5-х классов

    Запросы в журнал по математике для 5-го класса

    Задачи по поиску ошибок (доступны 3-5 классы)

    Математические центры для 5-х классов — Независимые или партнерские — Цифровые и печатные

    Google Формы — упражнения для самостоятельной оценки

    Задания по обзору чтения — включают 13 форм, каждая из которых посвящена одному определенному навыку.

    Google Slides — мероприятия по обучению грамоте

    Обзор чтения для 4 и 5 классов

    Раскраска по упражнениям по чтению

    Текстовые свидетельства с цветовой кодировкой для печати

    Интервенционные отрывки при чтении со звуком чтения вслух

    Флипбук для чтения для 4 и 5 классов

    Тематические мероприятия — печатная и цифровая версии

    Действия по выводу — Версия для печати и цифровая

    Виды деятельности — Версия для печати и цифровая

    Действия с элементами истории — печатная и цифровая версии

    Урок седьмого класса Простой процент

    Я начну с основного вопроса: как можно рассчитать простой процент?

    Раздел примечаний начинается с простого абзаца о процентах.Либо ученик, либо класс, либо я прочитаю абзац. Мы будем заполнять пропуски по ходу дела. В окончательной версии должно быть указано:

    Деньги, которые вы откладываете на банковский счет, могут расти. Деньги, которые вы занимаете в банке, платные.

    «Проценты — это деньги, выплаченные или заработанные за использование денег. Принцип — это сумма денег, заимствованных или внесенных. Простые проценты — это деньги, выплаченные или заработанные только на основную сумму.

    Затем формула представляется в ее наиболее распространенной форме.

    Прежде чем переходить к примерам, вероятно, стоит обсудить случаи, когда может возникнуть интерес. Я спрошу и / или приведу примеры заимствования денег — с использованием кредитных карт, автокредитов, ссуд на обучение, ипотеки. По этим займам выплачиваются проценты (хотя часто и не простые проценты!). Я хочу, чтобы студенты понимали, что за получение денег в долг нужно платить. И наоборот, деньги, помещенные на сберегательный счет, паевые инвестиционные фонды, пенсионные счета и т. Д., Могут расти в зависимости от процентов. Так что на свои деньги можно зарабатывать деньги.Опять же, я могу сказать, что интерес студентов к этим типам счетов обычно не является простым интересом, но концепция простого интереса поможет нам понять другие типы, когда они их изучают.

    Затем я прочту первый пример. После первого чтения я перейду к значениям задачи и аннотирую их. Я обозначу 500 долларов как основную сумму, 3% как ставку (написано 0,03) и 3 года как время. Затем в части A я напишу p = 500, r = 0,03 и t = 3. Уравнение будет записано, значения будут подставлены и уравнение будет решено.

    В части B студентам необходимо знать, что «баланс» означает, сколько денег находится на счете. В данном случае это основная сумма плюс проценты.

    У студентов есть проверка на понимание проблемы. Я ожидаю увидеть аннотации и назначения переменных так же, как в примере.

    Простые рабочие листы с ответами

    Расчет простых процентов — важный навык для любого, кто ведет банковский счет, имеет баланс кредитной карты или подает заявку на получение ссуды.Бесплатные распечатанные рабочие листы в этом уроке улучшат ваши уроки математики на дому и помогут вашим ученикам стать лучше в расчетах.

    Этот набор рабочих листов также поможет студентам понять процесс, используя текстовые задачи. Для удобства выставления оценок даются ответы на каждый из пяти рабочих листов на второй странице.

    Введение в урок

    Перед тем, как ученики начнут работать с рабочими листами, объясните, что, занимая деньги, вы должны вернуть взятую сумму, а также любые дополнительные проценты, которые представляют собой стоимость займа.Таким же образом объясните студентам, что когда вы ссужаете деньги или вкладываете средства на процентные счета, вы обычно получаете процентный доход, делая свои деньги доступными для других людей.

    Рабочий лист простых процентов 1

    Д. Рассел

    Распечатайте PDF: Рабочий лист простых процентов № 1

    В этом упражнении учащиеся ответят на задачи из 10 слов о вычислении процентов. Эти упражнения помогут домашним школьникам научиться рассчитывать доходность инвестиций и проиллюстрировать, как проценты могут накапливаться с течением времени.

    Студенты ответят на такие вопросы, как,

    «Сколько процентов приносит инвестиция в 318 долларов при 9% в течение одного года?»

    Объясните учащимся, что ответ будет 28,62 доллара, потому что 318 долларов на 9 процентов — это то же самое, что 318 долларов на 0,09 доллара, что равняется 28,62 доллара. Объясните студентам, что они должны будут уплатить эту сумму процентов в дополнение к к погашению основной суммы, сумме первоначальной ссуды, 318 долларов.

    Рабочий лист простых процентов 2

    Д.Рассел

    Распечатайте PDF: Рабочий лист простого интереса № 2

    Эти 10 вопросов укрепят уроки из рабочего листа № 1. Домашние школьники и другие ученики узнают, как рассчитывать ставки и определять процентные платежи. В этом PDF-файле учащиеся ответят на такие вопросы, как:

    «Если остаток по истечении восьми лет по инвестиции в размере 630 долларов, вложенной по ставке 9 процентов, составляет 1 083,60 доллара, какова сумма процентов?»

    Если учащиеся испытывают затруднения, объясните, что для вычисления этого ответа требуется только простое вычитание, когда вы вычитаете начальные инвестиции в размере 630 долларов из конечного баланса в 1083 долларов.60. Студенты поставят задачу следующим образом:

    1083,60–630 долларов = 453,60 долларов

    Объясните, что некоторая информация в вопросе была посторонней и не нужна для решения проблемы.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *