Содержание
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Самостоятельная работа по математике Наибольший общий делитель 6 класс
Самостоятельная работа по математике Наибольший общий делитель. Взаимно простые числа 6 класс с ответами. Самостоятельная работа включает 2 варианта, в каждом по 6 заданий.
Вариант 1
1. Найдите все общие делители чисел:
а) 4 и 8
б) 18 и 48
в) 45 и 98
2. Найдите наибольший общий делитель чисел:
а) 425 и 625
б) 532 и 665
в) 36, 72 и 198
3. Являются ли взаимно простыми числа:
а) 28 и 36
б) 3; 5 и 26
4. В каждом из одинаковых наборов посуды имеются рюмки и бокалы. Всего 35 рюмок и 21 бокал. Сколько всего наборов? Сколько рюмок и бокалов в каждом наборе?
5. Запишите все правильные дроби со знаменателем 18, у которых числитель и знаменатель — взаимно простые числа.
6. Сколькими способами могут разместиться 5 пассажиров в 6-местной лодке?
Вариант 2
1. Найдите все общие делители чисел:
а) 5 и 15
б) 12 и 48
в) 51 и 65
2. Найдите наибольший общий делитель чисел:
а) 232 и 261
б) 124 и 148
в) 24; 48 и 54
3. Являются ли взаимно простыми числа:
Являются ли взаимно простыми числа:
а) 36 и 37
б) 2 и 14
4. В одинаковых новогодних подарках всего 26 шоколадок, 11 7 шоколадных конфет и 169 карамелек. Сколько всего подарков? Сколько шоколадок, шоколадных конфет и карамелек в каждом наборе?
5. Запишите все правильные дроби со знаменателем 22, у которых числитель и знаменатель не являются взаимно простыми числами.
6. Сколькими способами могут разместиться 4 пассажира в 6-местной лодке?
Ответы на самостоятельную работу по математике Наибольший общий делитель. Взаимно простые числа 6 класс
Вариант 1
1.
а) 1, 2, 4
б) 1, 2, 3, 6
в) 1.
2.
а) 25
б) 133
в) 18
3.
а) нет
б) да
4. 7 наборов, 5. рюмок и 3 бокала
5. 1/18, 5/18, 7/18, 11/18, 13/18, 17/18
6. 720 способами
Вариант 2
1.
а) 1, 5
б) 1, 2, 3, 4, 6, 12
в) 1.
2.
а) 29
б) 4
в) 6.
3.
а) да
б) нет
4. 13 подарков; 2 шоколадки; 9 шоколадных конфет и 13 карамелек
5. 2/22, 4/22, 6/22, 8/22, 10/22, 11/22, 12/22, 14/22, 16/22, 18/22, 20/22
6. 360 способами
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ, алгоритм как найти НОД
Наибольший общий делитель чисел – это наибольшее число, на которое делятся все заданные числа.
Алгоритм поиска НОД
Вычисление НОД похоже на поиск НОК. Чтобы найти наибольший общий делитель, нужно использовать следующий алгоритм:
- Разложить все числа на простые множители, используя признаки делимости чисел.
- Найти совпадающие множители во всех числах и выписать их.
- Перемножить совпадающие множители.
Если среди множителей чисел не были найдены одинаковые, числа являются взаимно простыми.
Примеры поиска наибольшего общего делителя
Рассмотрим, как найти НОД с помощью алгоритма на нескольких примерах.
Пример 1:
Найдите наибольший общий делитель чисел 420 и 990.
Решение:
Разложим оба числа на простые множители:
Получили, что:
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
990 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 11
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 3 ⋅ 5 = 30
Ответ: 30
Пример 2:
Найдите наибольший общий делитель чисел 588 и 1820.
Решение:
Разложим оба числа на простые множители:
Получили, что:
588 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 7
1820 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 13
Выпишем все совпадающие множители для обоих чисел и перемножим их:
НОД = 2 ⋅ 2 ⋅ 7 = 28
Ответ: 28
Пример 3:
Найдите наибольший общий делитель чисел 1000 и 3267.
Решение:
Разложим оба числа на простые множители:
Получили, что:
1000 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5
3267 = 3 ⋅ 3 ⋅ 3 ⋅ 11 ⋅ 11
Совпадающих множителей у этих 2 чисел нет, поэтому они являются взаимно простыми, то есть
Ответ: 1
Наибольший общий делитель
Просмотр содержимого документа
«Наибольший общий делитель»
Наибольший общий делитель
- Назовите все делители числа 28
1 ; 2 ; 4; 7 ; 14 ; 28
- Назовите все делители числа 42
1 ; 2 ; 3; 6; 7 ; 14 ; 21; 42
Красным цветом выделены числа 1; 2; 7; 14 – которые являются общими делителями чисел 28 и 42
Среди общих делителей число 14
является наибольшим
Наибольшее натуральное число, на которое делится нацело каждое из двух данных чисел, называют наибольшим общим делителем (НОД) этих чисел
НОД чисел a и b обозначают НОД (a;b )
НОД (28; 42) = 14
Легко установить, что НОД (10;25 )=5,
НОД (18;24 )=6, НОД (3;7)=1
НОД многозначных чисел удобно находить, предварительно разложив их на простые множители
Найдите НОД (455; 770)
455 5
770 2
91 7
385 5
13 13
77 7
1
11 11
1
НОД (455; 770) = 5 ∙ 7 = 35
Найдите НОД (180; 840)
840 2
180 2
420 2
90 2
210 2
45 3
105 3
15 3
35 5
5 5
7 7
1
1
180 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 840 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 5 ∙ 7
НОД (455; 770) = 2 ∙ 2 ∙ 3 ∙ 5 = 60
Найдите НОД (585; 616)
616 2
585 3
308 2
195 3
154 2
65 5
77 7
13 13
11 11
1
1
585 = 3 ∙ 3 ∙ 5 ∙ 13 616 = 2 ∙ 2 ∙ 2 ∙ 7 ∙ 11
НОД (585; 616) = 1
Если общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми
Найдите НОД (250; 3000)
Здесь нет необходимости раскладывать число на простые множители, так как число 250 – делитель 3000
НОД (250; 3000) = 250
Найдите НОД (132; 180; 144)
180 2
144 2
90 2
72 2
45 3
36 2
15 3
18 2
5 5
9 3
1
3 3
1
132 2
66 2
33 3
11 11
1
132 = 2 ∙ 2 ∙ 3 ∙ 11 180 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 144 = 2 ∙ 2 ∙ 2 ∙ 2∙ 3 ∙ 3
НОД (132; 180; 144) = 2 ∙ 2 ∙ 3 = 12
- Какое число называют НОД двух чисел?
- Какие числа называют взаимно простыми?
- Чему равен НОД (25; 1000)
найдите наибольший общий делитель чисел 12 18 и 24
Вы искали найдите наибольший общий делитель чисел 12 18 и 24? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найдите наибольший общий делитель чисел 12 и 18 24, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «найдите наибольший общий делитель чисел 12 18 и 24».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как найдите наибольший общий делитель чисел 12 18 и 24,найдите наибольший общий делитель чисел 12 и 18 24. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и найдите наибольший общий делитель чисел 12 18 и 24. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите наибольший общий делитель чисел 12 18 и 24).
Где можно решить любую задачу по математике, а так же найдите наибольший общий делитель чисел 12 18 и 24 Онлайн?
Решить задачу найдите наибольший общий делитель чисел 12 18 и 24 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Математика Мерзляк Контрольная 1 | Частная школа.
 6 класс
6 класс
Математика Мерзляк Контрольная 1 + ОТВЕТЫ. Контрольная работа № 1 по математике 6 класс с ответами (УМК Мерзляк) по теме «Делимость натуральных чисел». Цитаты из учебного пособия «Дидактические материалы по математике 6 класс» использованы в учебных целях. Ответы на контрольные работы адресованы родителям.
Контрольная работа № 1 по математике 6 класс
«Делимость натуральных чисел» (УМК Мерзляк)
КР-01. Вариант 1
- Из чисел 378, 576, 893, 4 139 выпишите те, которые делятся нацело: 1) на 2; 2) на 9.
- Разложите число 1 056 на простые множители.
- Найдите наибольший общий делитель чисел: 1) 24 и 42; 2) 280 и 588.
- Найдите наименьшее общее кратное чисел: 1) 3 и 6; 2) 28 и 9; 3) 15 и 20.
- Докажите, что числа 728 и 1 275 — взаимно простые.
- Вместо звёздочки в записи 1 73* поставьте такую цифру, чтобы полученное число было кратно 3 (рассмотрите все возможные случаи).
- Дима собирает модели самолётов.
 Их можно расставить поровну на 14 полках, а можно, тоже поровну, — на восьми полках. Сколько моделей у Димы, если известно, что их больше 100, но меньше 120?
Их можно расставить поровну на 14 полках, а можно, тоже поровну, — на восьми полках. Сколько моделей у Димы, если известно, что их больше 100, но меньше 120?
КР-01. Вариант 2
- Из чисел 135, 240, 594, 3 251 выпишите те, которые делятся нацело: 1) на 5; 2) на 9.
- Разложите число 1 584 на простые множители.
- Найдите наибольший общий делитель чисел: 1) 36 и 63; 2) 180 и 312.
- Найдите наименьшее общее кратное чисел: 1)15 и 30; 2) 8 и 35; 3) 10 и 16.
- Докажите, что числа 945 и 208 — взаимно простые.
- Вместо звёздочки в записи 2 38* поставьте такую цифру, чтобы полученное число было кратно 3 (рассмотрите все возможные случаи).
- Катя собирает фигурки лошадок. Их можно расставить поровну на 9 полках, а можно, тоже поровну, — на 15 полках. Сколько фигурок у Кати, если известно, что их больше 110, но меньше 140?
Ответы на контрольную работу
Вернуться к Списку контрольных работ по математике (УМК Мерзляк)
Вы смотрели: Математика Мерзляк Контрольная 1 + ОТВЕТЫ. Контрольная работа по математике 6 класс с ответами по УМК Мерзляк и др. Цитаты из учебного пособия «Дидактические материалы по математике» использованы в учебных целях. Ответы на контрольные работы адресованы родителям.
Контрольная работа по математике 6 класс с ответами по УМК Мерзляк и др. Цитаты из учебного пособия «Дидактические материалы по математике» использованы в учебных целях. Ответы на контрольные работы адресованы родителям.
Школа олимпийского резерва. Математика: занятие 15
Тема: Делимость и остатки
3. Алгоритм Евклида
На этой страничке вы можете найти определение НОД двух натуральных чисел и правило его нахождения. Но как быть, если требуется найти НОД двух больших чисел? Разложение на простые множители займет много времени. На помощь придет алгоритм Евклида.
При условии, что a > b выполняется равенство: НОД (a;b) = НОД (b;a — b).
Вот как работает алгоритм Евклида для конкретных чисел:
НОД (451; 287) = НОД (287; 451-284) = НОД (287; 164) = НОД (164; 287 — 164) = = НОД (164; 123) = НОД (123; 164 — 123) = НОД (123; 41) = НОД (41; 123 — 41) = = НОД (82; 41) = НОД (41; 41) = 41.
Применение алгоритма Евклида.
Задача 19. Найдите наибольший общий делитель чисел 2n + 13 и n + 7.
Решение: НОД (2n + 13; n + 7) = НОД (n + 7; n + 6) = НОД (n + 6; 1) = 1.
Задачи для самостоятельного решения
Учитывая, что для сокращения дробей необходим наибольший общий делитель, который находится с помощью НОД, решите:
Задача 20. Докажите, что дробь несократима ни при каком натуральном n.
Задача «не в тему №1». Отец вдвое старше сына. Сын родился, когда отцу было 28 лет. Сколько лет отцу сейчас?
Задача «не в тему №2». Как разрезать клетчатый квадрат 5 на 5 на 8 различных фигур, чтобы все клеточки остались целыми. Фигуры считаются различными, если их нельзя наложить друг на друга так, чтобы они совпали.
Задача «не в тему №3». На столе стоят 8 стаканов с водой. Разрешается взять любые два стакана и перелить часть воды из одного стакана в другой так, чтобы воды в них стало поровну. Как несколькими такими переливаниями добиться, чтобы воды во всех стаканах стало поровну?
Как несколькими такими переливаниями добиться, чтобы воды во всех стаканах стало поровну?
Решения и ответы
Задача 20. НОД (12n +1; 30n + 2) = НОД (12n +1; 18n +1) = НОД (12n + 1; 6n) = = НОД (6n; 6n + 1) = 1, что говорит о том, что числитель и знаменатель этой дроби не имеют общих делителей, кроме 1, то есть дробь несократима ни при каком натуральном n.
Задача «не в тему №1. Отец вдвое старше сына, то есть до рождения сына отец прожил столько же лет, сколько и после его рождения. 28 + 28 = 56.
Ответ: отцу 56 лет
Задача «не в тему №2». Вспоминаем про фигурки пентамино
С помощью этих фигурок можно замостить квадрат 5 на 5 различными способами и затем разрезать.
Задача «не в тему №3». Пронумеруем стаканы числами от 1 до 8. Сначала уравняем количество воды в первом и втором, третьем и четвёртом, пятом и шестом,, седьмом и восьмом. Затем уравняем первый стакан с третьим, а второй — с четвертым. Теперь во всех стаканах с первого по четвертый воды поровну. Добьёмся того же в стаканах с пятого по восьмой. Уффф!
Затем уравняем первый стакан с третьим, а второй — с четвертым. Теперь во всех стаканах с первого по четвертый воды поровну. Добьёмся того же в стаканах с пятого по восьмой. Уффф!
Теперь уравниваем первый с пятым, второй с шестым, третий с седьмым, четвертый — с восьмым.
Готово!
Наибольший общий множитель — Бесплатная справка по математике
Определение
Наибольший общий множитель, как это звучит, является наибольшим числом, которое делится на два или более больших числа поровну. Например, наибольший общий множитель (GCF) 15 и 25 равен 5, потому что 5 — это наибольшее число, которое делится на 15 и 25 равномерно.
Чтобы найти GCF малых чисел, таких как 12 или 16, может быть проще просто перечислить все факторы и найти наибольший общий множитель, но для больших чисел, таких как 490 и 819, вам нужен более быстрый метод.Первый шаг — выполнить факторизацию каждого числа на простые множители. Найдите любое число (2 будет работать), которое делит 490 равномерно, и вы получите 245. Продолжайте делить и отслеживать числа в таком формате:
Найдите любое число (2 будет работать), которое делит 490 равномерно, и вы получите 245. Продолжайте делить и отслеживать числа в таком формате:
Следовательно, 7 * 7 * 5 * 2 = 490. Эти четыре числа, обведенные красным, являются простыми и больше не могут быть разложены на множители, так что вы должны закончить. Это простое разложение 490. Теперь вы можете сделать то же самое со своим другим числом 819.
Простые множители 819: 3,3,7 и 13.Теперь мы должны сравнить простые множители обоих чисел:
$$ 819 = 3 * 3 * 7 * 13 $$
$$ 490 = 2 * 5 * 7 * 7 $$
Мы хотим взять все, что является общим для обоих чисел. Общим является только один множитель, и это 7, поэтому мы знаем, что 7 — это GCF для 490 и 819. Давайте попробуем другую пару чисел, 1012 и 10580. Разложение чисел на простые множители выявляет эту ситуацию:
$$ 1012 = 2 * 2 * 11 * 23 $$
$$ 10580 = 2 * 2 * 5 * 23 * 23 $$
У каждого числа есть две общие двойки и одна 23, поэтому мы будем использовать эти числа. Мы не можем использовать остальные 23, потому что у 1012 есть только один, и мы не можем использовать 11, потому что у 10580 их нет. Запишите общие числа и умножьте их, чтобы получить GCF:
Мы не можем использовать остальные 23, потому что у 1012 есть только один, и мы не можем использовать 11, потому что у 10580 их нет. Запишите общие числа и умножьте их, чтобы получить GCF:
.
$$ 2 * 2 * 23 = 92 $$
Вот и все, что нужно для определения наибольшего общего множителя (GCF) числа. Если вам нужна дополнительная помощь, посетите еще один урок, посвященный наиболее общим факторам, просмотрите наш сайт или воспользуйтесь поисковой системой, например Google, чтобы найти дополнительную информацию.
Как найти наибольший общий множитель двух чисел
Обновлено 22 декабря 2020 г.
Ли Джонсон
Нахождение наибольшего общего множителя, или GCF, двух чисел полезно во многих математических ситуациях, но особенно когда дело касается для упрощения дробей.Если вы боретесь с этим или находите общие знаменатели, изучение двух методов нахождения общих факторов поможет вам достичь того, что вы собираетесь делать. Тем не менее, во-первых, неплохо было бы узнать основы факторов; Затем вы можете рассмотреть два подхода к поиску общих факторов. Наконец, вы можете посмотреть, как применить свои знания, чтобы упростить дробь.
Наконец, вы можете посмотреть, как применить свои знания, чтобы упростить дробь.
Что такое фактор?
Факторы — это числа, которые вы умножаете, чтобы получить другое число.Например, 2 и 3 являются множителями 6, потому что 2 × 3 = 6. Точно так же 3 и 3 являются множителями 9, потому что 3 × 3 = 9. Как вы, возможно, знаете, простые числа — это числа, у которых нет других факторов, кроме сами и 1. Таким образом, 3 — простое число, потому что единственные два целых числа (целых числа), которые можно умножить вместе, чтобы дать 3 в качестве ответа, — это 3 и 1. Точно так же 7 — простое число, как и 13
Из-за этого часто бывает полезно разбить число на «простые множители». Это означает нахождение всех множителей простого числа другого числа.По сути, он разбивает число на его фундаментальные «строительные блоки», что является полезным шагом на пути к нахождению наибольшего общего делителя двух чисел, а также бесценным, когда дело доходит до упрощения квадратных корней.
Нахождение наибольшего общего множителя: первый метод
Самый простой способ найти наибольший общий множитель двух чисел — просто перечислить все множители каждого числа и найти наибольшее общее число. Представьте, что вы хотите найти наибольший общий множитель 45 и 60.Во-первых, посмотрите на разные числа, которые вы можете умножить, чтобы получить 45.
Самый простой способ начать — с двух, которые, как вы знаете, будут работать, даже для простого числа. В этом случае мы знаем, что 1 × 45 = 45, поэтому мы знаем, что 1 и 45 являются множителями 45. Это первый и последний множители 45, поэтому вы можете просто заполнить их оттуда. Затем выясните, является ли 2 фактором. Это легко, потому что любое четное число делится на 2, а любое нечетное — нет. Итак, мы знаем, что 2 не является фактором 45. А как насчет 3? Вы должны уметь определить, что 3 — это коэффициент 45, потому что 3 × 15 = 45 (вы всегда можете использовать свои знания, чтобы решить эту проблему, например, вы знаете, что 3 × 12 = 36, и добавив тройки к этому приводят вас к 45).
Далее, является ли 4 множителем 45? Нет, вы знаете, что 11 × 4 = 44, так что не может быть! А что насчет 5? Это еще один простой способ, потому что любое число, заканчивающееся на 0 или 5, делится на 5. И с этим вы можете легко определить, что 5 × 9 = 45. Но 6 не годится, потому что 7 × 6 = 42 и 8 × 6 = 48. Из этого вы также можете видеть, что 7 и 8 не являются множителями 45. Мы уже знаем, что 9 есть, и легко увидеть, что 10 и 11 не множители. Продолжайте этот процесс, и вы заметите, что 15 — это фактор, а все остальное — нет.
Итак, множители 45 следующие: 1, 3, 5, 9, 15 и 45.
Для 60 вы выполняете точно такой же процесс. На этот раз число четное (так что вы знаете, что 2 — это фактор) и делимое на 10 (так что 5 и 10 — оба фактора), что немного упрощает задачу. Пройдя этот процесс еще раз, вы должны увидеть, что множители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60.
Сравнение двух списков показывает, что 15 — это наибольший общий множитель 45 и 60. Этот метод может занять много времени, но он прост и всегда будет работать. Вы также можете начать с любого высокого общего множителя, который сразу заметите, а затем просто искать более высокие множители для каждого числа.
Вы также можете начать с любого высокого общего множителя, который сразу заметите, а затем просто искать более высокие множители для каждого числа.
Нахождение наибольшего общего множителя: второй метод
Второй метод определения общего коэффициента для двух чисел — использовать простые множители. Процесс простой факторизации немного проще и более структурирован, чем поиск каждого фактора. Давайте рассмотрим процесс для 42 и 63.
Процесс разложения на простые множители в основном включает разбиение числа на части до тех пор, пока у вас не останутся только простые числа.Лучше всего начать с наименьшего простого числа (двух) и работать оттуда. Итак, для 42 легко увидеть, что 2 × 21 = 42. Затем рассмотрим 21: является ли 2 фактором? Нет. 3? Да! 3 × 7 = 21, а 3 и 7 — простые числа. Это означает, что простыми множителями 42 являются 2, 3 и 7. Первый «разрыв» использовал 2, чтобы получить 21, а второй разбил это на 3 и 7. Вы можете проверить это, умножив все ваши множители вместе и проверив. вы получите исходное число: 2 × 3 × 7 = 42.
Вы можете проверить это, умножив все ваши множители вместе и проверив. вы получите исходное число: 2 × 3 × 7 = 42.
Для 63 2 — не фактор, а 3, потому что 3 × 21 = 63.Опять же, 21 делится на 3 и 7 — оба простые числа — так что вы знаете простые множители! Проверка показывает, что 3 × 3 × 7 = 63, что и требуется.
Вы найдете наивысший общий множитель, посмотрев, какие простые множители у этих двух чисел являются общими. В данном случае у 42 есть 2, 3 и 7, а у 63 — 3, 3 и 7. У них общие 3 и 7. Чтобы найти наибольший общий делитель, умножьте все общие простые множители вместе. В этом случае 3 × 7 = 21, поэтому 21 является наибольшим общим делителем 42 и 63.
Предыдущий пример также может быть решен быстрее таким образом.Поскольку 45 делится на три (3 × 15 = 45), а 15 также делится на три (3 × 5 = 15), простые делители 45 равны 3, 3 и 5. Для 60 оно делится на два (2 × 30 = 60), 30 также делится на два (2 × 15 = 30), а затем у вас остается 15, которое, как мы знаем, имеет три и пять в качестве простых множителей, оставляя 2, 2, 3 и 5. Сравнивая два списка, три и пять являются общими простыми множителями, поэтому наибольший общий множитель равен 3 × 5 = 15.
Сравнивая два списка, три и пять являются общими простыми множителями, поэтому наибольший общий множитель равен 3 × 5 = 15.
В случае, если есть три или более общих простых множителя, вы умножаете их все вместе таким же образом. найти наибольший общий фактор.5 × 3 = 2 × 2 × 2 × 2 × 2 × 3
Должно быть ясно, что 2 5 = 32 является наивысшим общим множителем. Разделив обе части дроби на 32, получим:
\ frac {32} {96} = \ frac {1} {3}
Нахождение общих знаменателей — аналогичный процесс. Представьте, что вам нужно сложить дроби 15/45 и 40/60. Из первого примера мы знаем, что 15 — это наибольший общий делитель 45 и 60, поэтому мы можем сразу выразить их как 5/15 и 10/15. Поскольку 3 × 5 = 15, и оба числителя также делятся на пять, мы можем разделить обе части обеих дробей на пять, чтобы получить 1/3 и 2/3.Теперь их намного проще добавить, и вы увидите, что
\ frac {15} {45} + \ frac {40} {60} = 1
Калькулятор GCD, который показывает шаги
Методы НОД
В этом калькуляторе используются четыре метода поиска GCD. Покажем их на примерах.
Покажем их на примерах.
Метод 1. Найдите НОД, используя метод разложения на простые множители
Пример: найти НОД 36 и 48
Шаг 1: найдите разложение на простые множители каждого числа:
42 = 2 * 3 * 7
70 = 2 * 5 * 7
Шаг 2: обведите все общие множители:
42 = ② * 3 *
70 = ② * 5 *
⑦
Мы видим, что НОД есть * ⑦ = 14
Метод 2: найти НОД с помощью повторного деления
Пример: найти НОД 84 и 140.
Шаг 1: Поместите числа внутри разделительной полосы:
Шаг 2. Разделите оба числа на 2:
.
Шаг 3: Продолжайте делить до тех пор, пока числа не перестанут иметь общий делитель.
| ② | 84 | 140 |
| ② | 42 | 70 |
| ⑦ | 21 | 35 |
| 3 | 7 |
Шаг 4: НОД для 84 и 140:
② * ② * ⑦ = 28
Метод 3: алгоритм Евклида
Пример: Найдите НОД 52 и 36, используя алгоритм Евклида.
Решение:
Разделите 52 на 36 и получите напоминание, затем разделите 36 с напоминанием из предыдущего шага.
Когда напоминание равно нулю, НОД является последним делителем.
| 52 | : | 36 | = | 1 | напоминание (16) | ||||
| 36 | : | 16 | = | 1 | напоминание (4) | ||||
| 16 | : | ④ | = | 4 | напоминание ( 0 ) | ||||
Делаем вывод, что НОД = 4.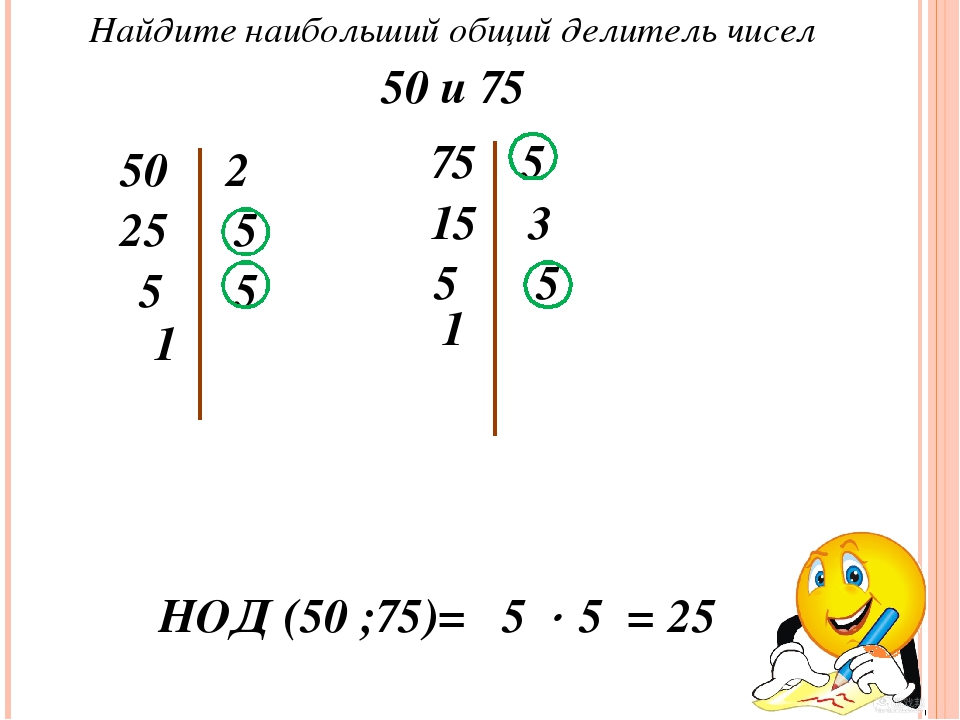
Метод 4: Перечисление факторов
Пример: найдите НОД 45 и 54, перечислив факторы.
Шаг 1: Найдите все делители заданных чисел:
Делители 45 равны 1, 3, 5, ⑨, 15 и 45
Делители 54 равны 1, 2, 3, 6, 18, 27 и 54
Шаг 2: Наибольший делитель = ⑨
GCF — наибольший общий коэффициент
Помните, что множители — это числа, которые мы умножаем вместе, чтобы получить другое число.
Пример: 2 x 9 = 18
2 и 9 — множители 18.
Когда у нас есть два или более заданных числа, мы можем найти наибольший множитель, который является общим для обоих чисел. Это называется GCF или наибольший общий коэффициент.
Есть несколько различных методов, которые можно использовать для поиска GCF. Давайте посмотрим на некоторые методы.
Метод 1: Перечислите факторы.
Пример: Найдите GCF 64 и 96.
Шаг 1: Составьте список множителей каждого числа.
64: 1, 2, 4, 8, 16, 32, 64
96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
Шаг 2: Посмотрите для факторов, которые есть в обоих списках.
Шаг 3: Выберите самый большой фактор, который есть в обоих списках, и назовите его GCF.
Следовательно, GCF для 64 и 96 равно 32.
Метод 2: Upside Down Division
Найдите GCF для 280 и 144.
Шаг 1. Поместите числа в перевернутую полосу деления.
Шаг 2: Теперь нам нужно разделить оба числа на общий множитель. Поскольку оба числа четные, мы могли бы начать с 2.Ответ находится под панелью.
Шаг 3. Мы продолжим делить, пока не получим два относительно простых числа. Помните, что относительно простое число означает два числа, у которых нет никаких общих делителей, кроме 1.
35 и 18 являются взаимно простыми числами.
Шаг 4: Теперь мы берем все множители и умножаем их вместе.
2 x 2 x 2 = 8
Это означает, что GCF 280 и 144 равняется 8.
Метод 3: Факторизация на простые множители
Мы также можем использовать факторизацию двух чисел на простые множители, чтобы получить GCF.
Пример: найдите GCF 150 и 225.
Шаг 1: Начните с построения факторных деревьев для каждого из чисел.
Шаг 2: Перечислите факторизацию на простые множители для каждого числа.
Шаг 3. Теперь обведите простые множители, общие для каждого числа.
Шаг 4: Затем умножьте числа в кружке.3 x 5 x 5 = 75
Это говорит нам, что GCF 150 и 225 равен 75.
Вы можете задаться вопросом, почему GCF важен. GCF не только чрезвычайно важен при работе с дробями, но также может использоваться при применении свойства распределения или при решении текстовых задач. Давайте посмотрим на пример задачи со словом, в которой используется GCF.
Пример: Мария имеет 160 кусочков шоколадных конфет и 144 фруктовых конфет. Она хочет дать каждому ребенку одинаковое количество конфет, чтобы никто не чувствовал себя обделенным.Какое максимальное количество детей она может дать конфетами?
Она хочет дать каждому ребенку одинаковое количество конфет, чтобы никто не чувствовал себя обделенным.Какое максимальное количество детей она может дать конфетами?
Шаг 1: Мы знаем, что это вопрос GCF, потому что Мария разбивает конфеты на группы и задачу, используя ключевое слово «величайший». Во-первых, мы должны выбрать метод. Воспользуемся перевернутым делением.
Шаг 2: Найдите GCF.
Шаг 3. Используйте GCF, чтобы ответить на вопрос.
Из перевернутого деления видно, что она могла раздать конфеты 16 детям. Нижняя часть перевернутого раздела дает нам еще больше информации.
Из перевернутого деления мы видим, что каждый ребенок получит 10 шоколадных конфет и 9 фруктовых конфет. Никаких конфет не останется, и каждый ребенок получит одинаковое количество.
Давайте рассмотрим:
GCF — это самый большой фактор, который является общим для двух или более чисел. Вы можете найти его, перечислив факторы, используя перевернутое деление или используя разложение на простые множители. GCF также помогает в решении проблем. Когда мы видим ключевые слова, такие как самый большой, самый большой и самый большой, в сочетании с вопросами о разбиении вещей на группы, мы знаем, что решаем вопрос GCF.
GCF также помогает в решении проблем. Когда мы видим ключевые слова, такие как самый большой, самый большой и самый большой, в сочетании с вопросами о разбиении вещей на группы, мы знаем, что решаем вопрос GCF.
Наибольший общий фактор (GCF) — Smartick
В этом посте мы узнаем, что такое наибольший общий фактор (GCF) и как его рассчитать.
Какой наибольший общий фактор (GCF)?
Это наибольшее число, которое делится точно на два или более числа.
Термины:
- Фактор: Фактор числа — это число, которое равномерно делится на исходное число, то есть остаток равен нулю.
Давайте посмотрим на пример:
Факторы 15: 1, 3, 5,15
Факторы 20: 1, 2, 4, 5,10, 20
Мы собираемся вычислить множители 15:
15/1 = 15, что означает, что 1 и 15 являются множителями 15.
15/2 имеет остаток 1, поэтому 2 не является множителем 15.
15/3 = 5, поэтому 3 и 5 являются множителями 15.
15/4 имеет остаток 3, поэтому 4 не является множителем 15.
Теперь мы разделим на 5, но поскольку мы уже знаем, что это множитель, мы закончили вычислять множители 15.
Теперь посчитаем множители 20.
20/1 = 20, поэтому 1 и 20 делятся на 20.
20/2 = 10, поэтому 2 и 10 являются множителями 20.
20/3 имеет остаток 2, поэтому 3 не является множителем 20.
20/4 = 5, поэтому 4 и 5 являются множителями 20.
Теперь мы разделим на 5, но поскольку мы уже знаем, что 5 — это множитель 20, мы закончили вычислять множители 20.
- Общий множитель: Число, которое одновременно является множителем для двух или более чисел, то есть является общим множителем для этих чисел.
Если мы продолжим предыдущий пример, в котором мы вычислили множители 15 и 20, теперь мы можем взглянуть на общие множители этих двух чисел.
В данном случае общие множители 15 и 20 равны 1 и 5.
- Наибольший общий множитель: Наибольшее количество общих множителей.
Продолжая предыдущий пример, наибольший общий множитель 15 и 20 равен 5.
Как найти наибольший общий фактор?
Давайте рассмотрим различные методы определения GCF.
- Метод 1: Записываем все множители каждого числа и на их основе отмечаем общие множители. Наибольший отмеченный фактор будет GCF этих чисел. Этот метод мы уже объясняли выше.
- Метод 2: Мы разбиваем каждое число на его простые множители. Затем мы отмечаем общие простые множители, включая повторы. Наконец, мы умножаем общие простые множители.
Давайте посмотрим на пример:
Мы вычисляем GCF 8 и 12.
Метод 1:
- Факторы 8: 1, 2, 4, 8
- Факторы 12: 1, 2, 3, 4, 6, 12
- Общие множители 8 и 12: 1, 2, 4
- Наибольший общий делитель 8 и 12: 4
Метод 2:
- Общие простые множители, включая повторы: 2, 2
- Наибольший общий делитель 8 и 12: 2 x 2 = 4
Мы рекомендуем вам выполнять упражнения в увлекательной игровой форме!
Попробуйте Smartick бесплатно.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Три способа найти наибольший общий фактор — доктора математики
В прошлый раз мы рассмотрели упрощение дроби, и появился GCF (наибольший общий коэффициент, также называемый GCD для наибольшего общего делителя или HCF для наибольшего общего множителя).В конце я сослался на источник информации об алгоритме Евклида для его вычисления, и здесь кажется уместным рассмотреть этот и несколько других методов.
Список всех факторов
Мы можем начать с этого вводного вопроса, начиная с 2005 г .:
Объяснение наибольшего общего фактора Я пытаюсь понять, что такое GCF, но не могу этого понять. Это так сложно понять. Я думаю, это как-то связано с умножением. Помогите, пожалуйста.
Доктор Ян ответил:
Часто, когда они составляют имя типа « наибольший общий множитель », вы можете понять, что оно означает, просто взглянув на отдельные слова.Например, давайте посмотрим на два числа, например, 12 и 20. Что такое , множители из 12? Это числа, которые его делят поровну:
12 = 1 * 12
= 2 * 6
= 3 * 4 Факторы: 1, 2, 3, 4, 6, 12
А как насчет множителей 20?
20 = 1 * 20
= 2 * 10
= 4 * 5 Факторы: 1, 2, 4, 5, 10, 20
Есть ли у них общие факторы? То есть, есть ли числа, которые являются множителями обоих, числа, которые появляются в обоих списках? На самом деле есть:
1, 2, 4
Итак, это « общих множителей » 12 и 20.Все идет нормально?
Итак, какой из этих трех общих факторов является наибольшим ? Было бы 4, не так ли? Итак, 4 - это «наибольший общий делитель» 12 и 20.
Имеет ли это смысл? Это самый простой способ найти GCF двух (или более) чисел, просто следуя определению. Мы перечисляем факторы каждого числа, находим те, которые у них общие, а затем выбираем самый большой из них.
Мы перечисляем факторы каждого числа, находим те, которые у них общие, а затем выбираем самый большой из них.
Вот еще один пример с большими числами. Предположим, наши числа 84 и 90.Чтобы перечислить множители 84, мы можем просто попробовать разделить по очереди на 1, 2, 3 и так далее. Мы находим, что $$ 84 = 1 \ times 84 = 2 \ times 42 = 3 \ times 28 = 4 \ times 21 = 6 \ times 14 = 7 \ times 12 $$ С опытом вы можете найти более быстрые способы сделать это; например, когда дело дошло до попытки 6, я увидел, что \ (6 = 2 \ times 3 \), и у меня уже было \ (3 \ times 28 \), поэтому я мог снять 2 с 28 и прикрепить его к 3, чтобы получилось \ (6 \ раз 14 \).
Аналогично, мы находим, что $$ 90 = 1 \ times 90 = 2 \ times 45 = 3 \ times 30 = 5 \ times 18 = 6 \ times 15 = 9 \ times 10 $$.
Итак, множители следующие: $$ 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 $$ 90: 1, 2, 3, 5, 6, 9, 10 , 15, 18, 30, 45, 90 $$
Общие множители: 1, 2, 3 и 6; так что GCF равен 6.
Этот метод отлично подходит для небольших чисел, а также для понимания того, что такое GCF. Но это не самый простой способ, когда цифры становятся больше. Даже этот пример был непростым.
Использование факторизации на простые множители
Чтобы продемонстрировать следующий метод, который полезен для чисел среднего размера, вот вопрос от 1998 года:
Нахождение наибольшего общего множителя двух разных чисел Помощь! Я понимаю, как найти множители целых чисел с помощью дерева факторинга .Есть ли способ найти наибольший общий делитель двух разных чисел после этого?
Факторное дерево — это один из методов факторизации числа как произведения простых чисел. Примеры и объяснения этого см. На этой странице (и по ссылке внизу внизу):
Запишите числа как произведение основных факторов
Ответила доктор Соня, взяв оттуда:
Дорогой Джаред, Вы говорите, что можете найти множители числа, используя деревья факторизации.Очень хороший.Это первое, что вам нужно уметь делать. Теперь мы хотим использовать деревья факторинга, чтобы найти GCF. Вы правы, есть ярлык. Я не собираюсь рассказывать вам, что это такое, но дам вам кое-что для размышления. Прежде чем приступить к каким-либо сложным математическим размышлениям (что мы собираемся сделать), мы должны быть абсолютно ясны в наших терминах. Так что же такое GCF? Наибольший общий делитель двух чисел - это наибольшее целое число, которое делится на оба числа поровну. Вы согласны с этим определением?
У нас есть определение, и мы предполагаем, что у нас есть простых фактора (а не список из всех факторов , как мы делали раньше).Что теперь?
Вы уже знаете, что определение GCF имеет какое-то отношение к деревьям факторизации, поэтому давайте подумаем о том, какое отношение GCF двух чисел имеет к их факторам. Я приведу пример, чтобы было понятнее. Допустим, у нас есть два числа 18 и 24, и мы хотим найти GCF. Из факторного дерева мы знаем, что:
18 = 2 х 3 х 3
24 = 2 х 2 х 2 х 3
Теперь каждый множитель 18 должен быть некоторой комбинацией до одной 2 и двух троек. Итак, у нас есть в качестве наших факторов:
2
3
2 х 3 = 6
3 x 3 = 9 и т. Д.Чтобы число было GCF 18 и 24, оно должно быть множителем 18, верно? Если это не так, то это никак не может быть наибольшим общим фактором 18 и чего-то еще.
Если наш GCF является множителем 18, то он должен состоять из некоторой комбинации двоек и троек (максимум одна двойка и максимум две тройки). Вы понимаете почему?
Итак, у нас есть в качестве наших факторов:
2
3
2 х 3 = 6
3 x 3 = 9 и т. Д.Чтобы число было GCF 18 и 24, оно должно быть множителем 18, верно? Если это не так, то это никак не может быть наибольшим общим фактором 18 и чего-то еще.
Если наш GCF является множителем 18, то он должен состоять из некоторой комбинации двоек и троек (максимум одна двойка и максимум две тройки). Вы понимаете почему? Вы можете подумать о том, чтобы поставить небольшой флажок над каждым штрихом в списке; каждый набор проверок (например, выбор 2 и одной из троек) дает множитель 18; но если вы вставите какие-либо простые числа, кроме указанных в списке (например,грамм. выберите 2, 3, и 17), вы не получите множитель.
Итак, наш GCF также должен быть множителем 24, так что это значит для чисел, из которых он состоит? Верно, это должна быть некоторая комбинация двоек и троек, но не более трех двоек и не более одной тройки (помните множители 24.) Подведем итоги того, что мы сделали на данный момент. Мы ищем GCF 18 и 24. Из нашего факторного дерева мы знаем, что: 18 = 2 х 3 х 3 24 = 2 х 2 х 2 х 3. Мы также кое-что знаем о факторах самого ЗКФ.Поскольку мы разложили на множители 18, мы знаем, что оно состоит из двоек и троек, и в нем может быть не более одной двойки и не более двух троек. Поскольку мы разложили на множители 24, мы знаем, что они состоят из двоек и троек, не более трех двоек и одной 3. Когда мы сложим все это вместе, что мы получим? Что ж, у нашего GCF должны быть только двойки и тройки в качестве факторов. Это начало. Мы также знаем, что в качестве множителя может быть не более единицы 2 (из 18). В нем может быть не более одной тройки (из 24). Таким образом, наш выбор для GCF ограничен: 2 (один 2, нет 3) 3 (№ 2, один 3) 2 x 3 = 6 (один 2, один 3) 6, самый большой, является самым большим общим фактором.1 & & & = 6 \ end {matrix} $$
Этот метод отлично подходит для чисел среднего размера, когда вам (а) нужно , чтобы посмотреть на простые множители, чтобы увидеть все сразу, и (б) может найти простые множители без особых проблем.

Что делать, если числа слишком велики, чтобы их легко разложить на множители? Вот где в игру вступает большой механизм.
Евклидов алгоритм: введение
Вот вопрос, который я упоминал в последний раз, от 1997 года:
Евклидов алгоритм У меня есть этот проект, в котором задействована теорема Евклида (на самом деле речь идет о наибольшем общем знаменателе).Не могли бы вы рассказать мне, что это такое, понятным языком, или попытаться упростить, пожалуйста?Доктор Эзра взял это:
У Евклида было несколько теорем, но я подозреваю, что интересующая вас также известна как алгоритм Евклида. Это алгоритм или процедура для поиска наибольшего общего делителя (или НОД) двух чисел, и он основан на том, с чем вы, вероятно, знакомы. Но сначала, что такое НОД двух чисел? Это просто самое большое число, которое точно делит оба числа, не оставляя остатка.Например, делители 6 равны 1, 2, 3 и 6, а делители 15 - 1, 3, 5 и 15, поэтому НОД 6 и 15 - это наибольшее число, которое может появиться в обоих списках: 3.В Таким же образом вы можете проверить, что НОД 36 и 210 равно 6, а НОД 15 и 8 равно 1.
И снова мы начнем с определения, которому должен удовлетворять этот метод.
Евклид знал, что если вы разделите одно число на другое, вы получите частное и остаток, а остаток меньше делителя.Например, если вы разделите 7 на 39, получится 5 раз (это частное) с остатком 4: 39 = 5 * 7 + 4. Кроме того, разделите 17 на 829: получится 48 раз, осталось 13: 829 = 816 + 13 = 48 * 17 + 13.Это также можно выразить так: Если мы разделим 829 на 17, получится 48, а остаток - 13.
Итак, сказал Евклид, чтобы найти НОД двух чисел, разделите одно из них на другое, и я гарантирую, что НОД также точно разделит остаток. Например, 210 = 5 * 36 + 30 НОД 210 и 36 равны 6, а 6 точно делит 30 (30 = 5 * 6).Почему это? Что ж, глядя на уравнение \ (210 = 5 \ умножить на 36 + 30 \), если и 210, и 36 кратны 6, то остаток \ (30 = 210 \ - 5 \ умноженный на 36 \) будет разностью двух кратных 6, поэтому мы можем вынести 6: \ (30 = 6 (35 \ - 5 \ times 6) \), чтобы показать, что остаток также кратен 6.
Это показывает, что любой делитель числа делимое и делитель (то есть любой общий делитель ) по-прежнему являются делителем остатка. Это, в частности, верно для наибольшего общего делителя .
Теперь разделите старый остаток на старый делитель, и НОД старого делителя и старого остатка точно разделят новый остаток. Продолжайте делать это, сказал Евклид, пока не получите остаток 0. Последний ненулевой остаток, который вы получите, будет НОД двух чисел, с которыми вы начали. Сделаем это с 210 и 36: 210 = 5 * 36 + 30 Делитель 36, остаток 30 36 = 1 * 30 + 6 Делитель 30, остаток 6 30 = 5 * 6 + 0 Делитель 6, остаток 0. Итак, 6 - это последний ненулевой остаток, и это НОД 210 и 36.Попробуйте это с 21 и 36, с 21 и 34 и с 288 и 178.Мне нравится помнить, что последний делитель является наибольшим общим делителем .
Евклидов алгоритм: пример
Для примера того, как мы делаем это на практике, вот вопрос от 1997 года:
Формула наибольшего общего делителя Есть ли формула для получения наибольшего общего множителя?Доктор Джерри ответил:
Я полагаю, вы имеете в виду наибольший общий делитель целых чисел a и b, наибольшее целое число, которое делит как a, так и b.Его можно рассчитать с помощью 2300-летнего метода, называемого алгоритмом Евклида. Я объясню алгоритм на примере. Давайте найдем gcd 210 и 990. Разделите 990 на 210: частное 4, остаток 150; игнорировать частное Разделить делитель от предыдущего шага на остаток от предыдущего шага разделить 210 на 150: частное 1, остаток 60; игнорировать частное Разделить делитель от предыдущего шага на остаток от предыдущего шага разделить 150 на 60: частное 2, остаток 30; игнорировать частное Разделить делитель от предыдущего шага на остаток от предыдущего шага разделите 60 на 30: частное 2, остаток 0.Когда остаток станет 0, как всегда, перейдите к предыдущему шагу и выберите остаток, в данном случае 30. Это gcd! Аккуратный! Шаг деления и игнорирования частного можно выполнить на многих калькуляторах с помощью операции MOD. Например, на моем калькуляторе (HP48G) я ввожу 990 и 210 и нажимаю MOD. У меня на экране 150.
Калькулятор Windows также имеет кнопку «mod» в научном режиме.
Используя это, нам просто нужно ввести это:
990 мод 210 = 150
210 мод 150 = 60
150 мод 60 = 30
60 мод 30 = 0
Таким образом, последний делитель 30 - это GCF.
Алгоритм Евклида: доказательство
Для более глубокого изучения рассмотрим этот вопрос из 1998 г .:
Объяснение алгоритма Евклида Существует алгоритм разложения на простые множители, называемый алгоритмом деления. Для целых чисел s и t, t> 0, существуют уникальные целые числа q и r такие, что s = t * q + r и 0 =Каково объяснение того, почему эти конкретные шаги дают вам GCF двух чисел? Доктор Роб объяснил:
На каждом шаге вы можете показать, что если d делит делитель t и делимое s, оно также делит остаток r. Если d делит t, напишите t = d * T. Если d делит s, напишите s = d * S. Затем используя уравнение: г = с - д * т г = д * S - д * д * Т г = д * (S - q * T) г = д * R и поэтому d тоже делит r.Это формальная версия того, что я продемонстрировал на простом примере выше.
Это показывает, что любой общий делитель первых двух чисел должен также делить последний делитель, работая по цепочке уравнений по одному. (Вы можете использовать принцип математической индукции для определения количества шагов, чтобы превратить это в доказательство.) Аналогично, если d делит делитель t и остаток r, он также делит делимое s. Напишите t = d * T, r = d * R. Потом: s = q * t + r s = q * d * T + d * R s = d * (q * T + R) s = d * S так что d тоже делит s.Это показывает, что любой множитель последнего делителя, включая сам последний делитель, также делит оба первых числа, обрабатывая цепочку уравнений по одному шагу за раз. (Вы также можете превратить это в доказательство, используя принцип математической индукции.) Соедините эти две части вместе, чтобы сделать вывод, что наибольший общий делитель двух чисел равен последнему делителю в алгоритме Евклида.
Необходимо было пойти обоими путями, чтобы показать, что каждый шаг не теряет общих факторов и не вводит новые общие факторы.В результате GCF сохраняется на протяжении всего процесса, и последний делитель (который, как выяснилось, делит предыдущий точно) должен быть наибольшим общим делителем исходной пары.
Немного об истории метода см .:
Официальный алгоритм ЕвклидаЕще один метод (Кнут) см .:
Наибольший общий факторИ если вы хотите пойти дальше, прочтите:
Использование алгоритма Евклида с тремя числамиОбъединив все, что мы видели, у нас есть три основных способа найти GCF:
- Для чисел, достаточно малых, чтобы легко перечислить все факторы каждого, просто сделайте это и выберите наибольшее из обоих списков.
 (Или просто посмотрите на числа и узнайте GCF, как в случае с 6 и 18, где «очевидно», что 6 само по себе является GCF.)
(Или просто посмотрите на числа и узнайте GCF, как в случае с 6 и 18, где «очевидно», что 6 само по себе является GCF.) - Для чисел, где это было бы сложно, но вы все равно можете составить факторное дерево и выписать разложение на простые множители, сделайте это и выберите наименьшую степень каждого простого числа в любом из чисел. Если в обоих числах нет простого числа, то его показатель степени равен 0, и вы можете игнорировать его.
- Для чисел, которые не нужно множить, используйте алгоритм Евклида.Это может быть больше работы, чем другие методы для некоторых небольших чисел, но отлично работает для больших.
Найдите наибольший общий множитель
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике ... Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, Equation from slopeLines Theotation, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторинг триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок
.
