Статика, условие равновесия твердого тела, давление жидкости

Основные понятия и законы кинематики

Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.

По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.

Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x₀ + V_xt, где x₀ — начальная координата тела, V_x — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с², не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:

Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:

Угловая скорость связана с линейной скоростью соотношением

где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν

Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.

Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).

Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде

где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле

где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения

Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.

Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.

Сила тяжести — это сила, с которой все тела притягиваются к Земле:

При неподвижной опоре вес тела равен по модулю силе тяжести:

Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес

Видно, что вес тела больше веса покоящегося тела.

При движении тела с ускорением, направленным вниз, его вес

В этом случае вес тела меньше веса покоящегося тела.

Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.

где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна

1.3. Основные понятия и законы статики и гидростатики

Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).

Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.

Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.

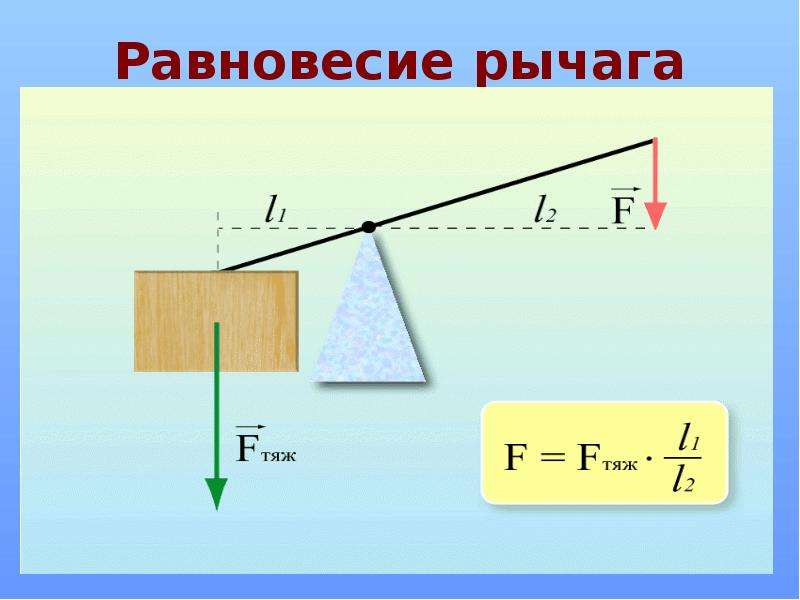
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:

Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей

где ρ — плотность жидкости, h — глубина проникновения в жидкость.

Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае

Высоты столбов жидкости обратно пропорциональны плотностям:

Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то

Тогда A1 = A2.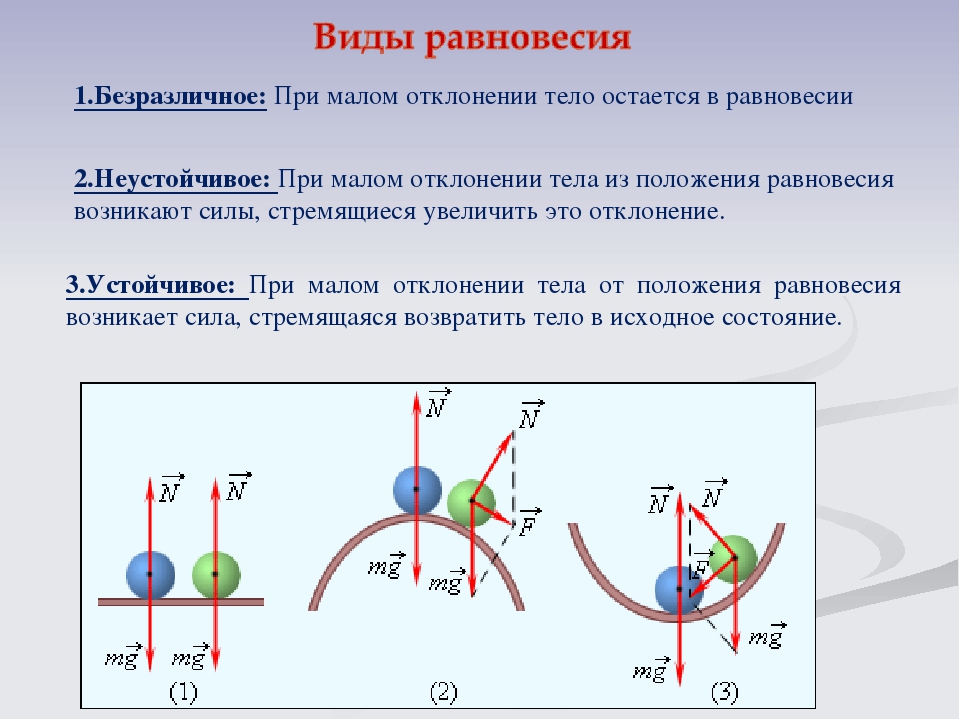
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:

где ρ_жидк — плотность жидкости, в которую погружено тело; V_погр — объём погружённой части тела.

Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.

1.4. Законы сохранения

Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:

Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:

Мощность — это работа, совершённая в единицу времени:

Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле

Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле

где h — высота подъёма

Энергия сжатой пружины:

где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.

Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.

1.5. Механические колебания и волны

Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.

Величина A, равная наибольшему абсолютному значению колеблющейся физической величины
x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое
колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:

Частота измеряется в с^-1. Эта единица называется герц (Гц).

Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.

Период колебаний математического маятника определяется по формуле

где l — длина маятника.

Период колебаний груза на пружине определяется по формуле

где k — жёсткость пружины, m — масса груза.

Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:

где v — скорость распространения волны.

Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.

Статика — Физика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Основы статики

К оглавлению…

Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:

• Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
• Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
• Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:

Момент силы. Правило моментов

К оглавлению…

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:

Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.

Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).

Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.

Алгоритм решения задач на правило моментов (задач по статике):

1. Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
2. Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
3. Записать правило моментов относительно данной оси, на забывая про правило знаков.
4. При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
5. Выразить искомую силу.

Рычаги и блоки

К оглавлению…

Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:

• Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
• Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
• Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
• Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
• Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.

Центр тяжести тела

К оглавлению…

Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).

Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:

1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.

2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:

где: l₁ – расстояние от центра масс до тела с массой m₁, а l₂ – до тела с массой m₂.

3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:

Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).

4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.

5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:

Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:

Равновесие • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Равновесием называется такое состояние системы, при котором силы, действующие на систему, уравновешены между собой. Равновесие может быть устойчивым, неустойчивым или безразличным.

Понятие равновесия — одно из самых универсальных в естественных науках. Оно применимо к любой системе, будь то система планет, движущихся по стационарным орбитам вокруг звезды, или популяция тропических рыбок в лагуне атолла. Но проще всего понять концепцию равновесного состояния системы на примере механических систем. В механике считается, что система находится в равновесии, если все действующие на нее силы полностью уравновешены между собой, то есть гасят друг друга. Если вы читаете эту книгу, например, сидя в кресле, то вы как раз и находитесь в состоянии равновесия, поскольку сила земного притяжения, тянущая вас вниз, полностью компенсирована силой давления кресла на ваше тело, действующей снизу вверх. Вы не проваливаетесь и не взлетаете именно потому, что пребываете в состоянии равновесия.

Различают три типа равновесия, соответствующие трем физическим ситуациям.

Устойчивое равновесие

Именно его большинство людей обычно и понимают под «равновесием». Представьте себе шар на дне сферической чаши. В состоянии покоя он находится строго в центре чаши, где действие силы гравитационного притяжения Земли уравновешено силой реакции опоры, направленной строго вверх, и шар покоится там подобно тому, как вы покоитесь в своем кресле. Если сместить шар в сторону от центра, откатив его вбок и вверх в направлении края чаши, то, стоит его отпустить, как он тут же устремится обратно к самой глубокой точке в центре чаши — в направлении положения устойчивого равновесия.

Вы, сидя в кресле, находитесь в состоянии покоя благодаря тому, что система, состоящая из вашего тела и кресла, находится в состоянии устойчивого равновесия. Поэтому при изменении каких-то параметров этой системы — например, при увеличении вашего веса, если, предположим, вам на колени сел ребенок, — кресло, будучи материальным объектом, изменит свою конфигурацию таким образом, что сила реакции опоры возрастет, — и вы останетесь в положении устойчивого равновесия (самое большее, что может произойти, — подушка под вами промнется чуть глубже).

В природе имеется множество примеров устойчивого равновесия в различных системах (и не только механических). Рассмотрим, например, отношения хищник—жертва в экосистеме. Соотношение численностей замкнутых популяций хищников и их жертв достаточно быстро приходит в равновесное состояние — столько-то зайцев в лесу из года в год стабильно приходится на столько-то лис, условно говоря. Если по каким-либо причинам численность популяции жертв резко изменяется (из-за всплеска рождаемости зайцев, например), экологическое равновесие будет очень скоро восстановлено за счет быстрого прироста поголовья хищников, которые начнут истреблять зайцев ускоренными темпами, пока не приведут поголовье зайцев в норму и не начнут сами вымирать от голода, приводя в норму и собственное поголовье, в результате чего численности популяций и зайцев, и лис придут к норме, которая наблюдалась до всплеска рождаемости у зайцев. То есть в устойчивой экосистеме также действуют внутренние силы (хотя и не в физическом понимании этого слова), стремящиеся вернуть систему в состояние устойчивого равновесия в случае отклонения системы от него.

Аналогичные эффекты можно наблюдать и в экономических системах. Резкое падение цены товара приводит к всплеску спроса со стороны охотников за дешевизной, последующему сокращению товарных запасов и, как следствие, росту цены и падению спроса на товар — и так до тех пор, пока система не вернется в состояние устойчивого ценового равновесия спроса и предложения. (Естественно, в реальных системах, и в экологических, и в экономических, могут действовать внешние факторы, отклоняющие систему от равновесного состояния — например, сезонный отстрел лис и/или зайцев или государственное ценовое регулирование и/или квотирование потребления. Такое вмешательство приводит к смещению равновесия, аналогом которого в механике будет, например, деформация или наклон чаши.)

Неустойчивое равновесие

Не всякое равновесие, однако, является устойчивым. Представьте себе шар, балансирующий на лезвии ножа. Направленная строго вниз сила земного притяжения в этом случае, очевидно, также полностью уравновешена направленной вверх силой реакции опоры. Но стоит отклонить центр шара в сторону от точки покоя, приходящейся на линию лезвия хоть на долю миллиметра (а для этого достаточно мизерного силового воздействия), как равновесие будет мгновенно нарушено и сила земного притяжения начнет увлекать шар всё дальше от него.

Примером неустойчивого природного равновесия служит тепловой баланс Земли при смене периодов глобального потепления новыми ледниковыми периодами и наоборот (см. Циклы Миланковича). Среднегодовая температура поверхности нашей планеты определяется энергетическим балансом между суммарным солнечным излучением, достигающим поверхности, и суммарным тепловым излучением Земли в космическое пространство. Неустойчивым этот тепловой баланс становится следующим образом. В какую-то зиму выпадает больше снега, чем обычно. На следующее лето тепла не хватает, чтобы растопить излишки снега, и лето оказывается также холоднее обычного вследствие того, что из-за переизбытка снега поверхность Земли отражает обратно в космос большую долю солнечных лучей, чем прежде. Из-за этого следующая зима оказывается еще более снежной и холодной, чем предыдущая, а следующим за ней летом на поверхности остается еще больше снега и льда, отражающего солнечную энергию в космос… Нетрудно увидеть, что чем больше такая глобальная климатическая система отклоняется от исходной точки теплового равновесия, тем быстрее нарастают процессы, уводящие климат еще дальше от нее. В конечном итоге, на поверхности Земли в приполярных областях за долгие годы глобального похолодания образуются многокилометровые напластования ледников, которые неумолимо продвигаются в направлении всё более низких широт, принося с собой на планету очередной ледниковый период. Так что трудно себе представить более шаткое равновесие, чем глобально-климатическое.

Особого упоминания заслуживает разновидность неустойчивого равновесия, называющаяся метастабильным, или квазиустойчивым равновесием. Представьте себе шар в узкой и неглубокой канавке — например, на повернутом острием вверх лезвии фигурного конька. Незначительное — на миллиметр-другой — отклонение от точки равновесия приведет к возникновению сил, которые вернут шар в равновесное состояние в центре канавки. Однако уже чуть большей силы хватит для того, чтобы вывести шар за пределы зоны метастабильного равновесия, и он свалится с лезвия конька. Метастабильные системы, как правило, обладают свойством пребывать какое-то время в состоянии равновесия, после чего «срываются» из него в результате какой-либо флуктуации внешних воздействий и «сваливаются» в необратимый процесс, характерный для нестабильных систем.

Типичный пример квазиустойчивого равновесия наблюдается в атомах рабочего вещества некоторых типов лазерных установок. Электроны в атомах рабочего тела лазера занимают метастабильные атомные орбиты и остаются на них до пролета первого же светового кванта, который «сбивает» их с метастабильной орбиты на более низкую стабильную, испуская при этом новый квант света, когерентный пролетающему, который, в свою очередь, сбивает с метастабильной орбиты электрон следующего атома и т. д. В результате запускается лавинообразная реакция излучения когерентных фотонов, образующих лазерный луч, которая, собственно, и лежит в основе действия любого лазера.

Безразличное равновесие

Промежуточный случай между устойчивым и неустойчивым равновесием — так называемое безразличное равновесие, при котором любая точка системы является точкой равновесия, и отклонение системы от исходной точки покоя ничего не изменяет в раскладе сил внутри нее. Представьте себе шар на абсолютно гладком горизонтальном столе — куда бы вы его ни сместили, он останется в состоянии равновесия.

Механическое равновесие и его устойчивость

    Известно, что любая механическая система стремится занять наиболее устойчивое равновесие с минимумом потенциальной энергии. Например, частицы сыпучего материала стремятся перемещаться либо в направлении силы тяжести, либо в направлении действия приложенных к ним нагрузок. Сопротивление частиц сдвигу обусловлено действием множества элементарных сил внутреннего трения в точках контакта, направленных в сторону, противоположную сдвигающей силе и определяемых коэффициентом (или углом) внутреннего трения, который характеризует границу подвижного и неподвижного состояния сыпучего мате-рпала. Трепне частиц на границе двух сред (зернистый слой — стенка емкости) характеризуется углом внешнего трения. Угол естественного откоса определяет свободную поверхность сыпучего материала. [c.26]

    Допустим, что на связь между атомами действует внешняя растягивающая сила меньшая, чем предел прочности Рт (рис. 249). Тогда окажутся возможными два положения механического равновесия устойчивое при деформации Аг] = [c.453]

    Это такое разрушение, при котором данному значению внешней силы соответствует определенная длина трещины. При достаточно медленном изменении величины внешней нагрузки трещина последовательно и непрерывно проходит через ряд устойчивых состояний, при этом каждый элемент объема тела находится в состоянии механического равновесия. При постоянных внешних силах длина трещины также постоянна. Так как скорость разрушения мала, процесс является изотермическим и может быть обратимым или необратимым. [c.191]

    Т и п II. Движущиеся неустойчивые трещины Это рост трещины, который происходит при постоянных внешних силах, в некоторых объемах тела механическое равновесие не сохраняется. Самопроизвольный рост трещины (при постоянных внешних силах) — результат отсутствия механического равновесия. Каждое из промежуточных состояний при росте трещины является термодинамически и механически неравновесным. Трещина растет до тех пор, пока система не придет к состоянию механического и термодинамического равновесия, т.е. к полному разрушению тела, или к достижению длины, соответствующей устойчивому механическому равновесию при данных значениях внешних сил. [c.194]

    Устойчивое равновесие означает равновесие термическое, механическое и химическое. При термическом и механическом равновесиях соответственно температуры и давления во всех точках системы одинаковы. При химическом равновесии отсутствует движущая сила для переноса вещества внутри фаз и от одной фазы системы к другим фазам. Это означает, что химический потенциал (х, (см. [c.194]

    При распространении наших исследований на другие проблемы помимо проблем, связанных с относительным расположением макроскопических тел, необходимо принимать во внимание изменения любого характера. Так, приходится учитывать, например, изменения давления, температуры, химического состава и физического состояния. Физико-химическое равновесие устанавливается тогда, когда произойдут все изменения, какие только могли совершиться, и будет достигнуто устойчивое состояние. Можно показать, что некоторые из этих изменений можно рассматривать отдельно друг от друга. Механическое равновесие определяется только тем условием, что механическая потенциальная энергия минимальна, в то время как тепловое равновесие достигается тогда, когда все части системы приобретут одну и ту же температуру. Отсюда ясно, что температура ведет себя как потенциал (термический потенциал) и определяет направление теплообмена. В этом предложении заключена основная идея так называемого нулевого закона термодинамики. [c.47]

    Известно, что в механических системах устойчивое равновесие соответствует минимуму потенциальной энергии системы. Так, шарик самопроизвольно скатывается из положения а на наклонной поверхности (рис. 69), причем его потенциальная энергия переходит сначала в кинетическую энергию движеиия шарика как целого, а затем в энергию теплового движения молекул. В положении б шарик находится в равновесии. [c.190]

    Системы разных рангов могут сосуществовать и каждая из них будет стремиться к устойчивому равновесию, характерному для ее ранга. Так, если нагретый маятник, постепенно охлаждаясь, одновременно приближается к механическому равновесию, то обе системы, и механическая и термодинамическая, независимо одна от другой приходят Б устойчивое состояние. Системы могут быть генетически связаны друг с другом и существование одной из них в этом случае представляет собой необходимое условие появления другой. Поток теплоты, т. е. система третьего ранга, возникает лишь при условии, что имеются надлежащие тепловые резервуары, т. е. имеется система второго ранга. Тогда тела, имеющие разные температуры и соединенные проводящим тепло стержнем, приходят. в термодинамическое равновесие, в то время как поток тепла в стержне стремится к стационарному состо- [c.26]

    Уменьшение устойчивости жидких пен может происходить и из-за нарушения механического равновесия в пеносистеме в результате действия внешних механических сил или внутренних (статистических) флуктуаций давления в газовой фазе. Вероятность статистических флуктуаций давления описывается выражением, аналогичным выражению (1.27) для температурных флуктуаций, и их влияние на процесс уменьшения толщины жидких пленок, а следовательно, и на устойчивость пены также незначительно. [c.34]

    Вследствие взаимодействия микрочастиц, образующих макротела, неоднородность в распределении между ними любой другой динамической характеристики ведет к перераспределению ее значений между микрочастицами до тех пор, пока не будет достигнута однородность в ее распределении между микрочастицами, которая будет далее сохраняться практически столь долго, сколько данное тело будет изолировано от внешних воздействий. Так, неоднородность в распределении импульса между микрочастицами, являющаяся причиной различия давления в разных частях макроскопического тела, ведет к перераспределению импульса между микрочастицами до тех пор, пока для подавляющего числа микрочастиц он не окажется заключенным в узких пределах около некоторого значения и во всем макротеле не установится определенное давление, постоянное во всех его частях, которое может быть изменено только в результате воздействия на тело извне. Такое состояние устойчивого равновесия называется состоянием механического равновесия макротела. Неоднородность в составе микрочастиц, образующих макротело, также вызывает самопроизвольный процесс, ведущий к ее ликвидации и установлению однородного состава микрочастиц, т. е. к установлению химического равновесия. [c.11]

    Сказанное иллюстрирует рис. 255, на котором нанесены две кривые, одна из которых отвечает механическому равновесию [см. формулу (VI,135)], а другая химической устойчивости [см. уравнение (VI,140)]. Точка пересечения этих кривых соответствует критическим параметрам пузырька. [c.660]

    Механическое равновесие жидкости в поле силы тяжести при отсутствии теплового равновесия возможно, если температура жидкости меняется только вдоль вертикальной оси Oz. Это равновесие устойчиво, если выполняется условие отсутствия конвекции [50] [c.90]

    Задачи о механическом равновесии жидкости возникают в различных областях науки и техники. Обычно они не просты и для решения требуют привлечения высшей математики и некоторых специальных методов. Еще более сложными, а потому и более интересными, являются задачи об устойчивости равновесия. Часто задачи о равновесии жидкостей и его устойчивости возникают или рассматриваются на стыке наук, и тогда неспециалисту в области физики трудно сориентироваться и понять проблему. Так, некоторые задачи, рассмотренные в книге, имеют прямое отношение к синергетике и теории катастроф, к космической технологии и метеорологии. Все это приводит к необходимости достаточно целостного и доступного изложения соответствующего материала, тем более что имеющиеся науч-но-популярные публикации по теме книги немногочисленны и к тому же разрознены. [c.5]

    Механическое равновесие и его устойчивость [c.9]

    Флокуляция особенно характерна для обратных эмульсий, в которых силы дальнего электростатического отталкивания обычно иеве-лики из-за малых значений заряда капель. — Однако и для заряженных капель в обратной эмульсии электростатическое отталкивание при достаточной их концентрации может не обеспечивать устойчивости к флокуляции это связано с тем, что 1из-за небольшого содержания электролитов в системе и низкого значения диэлектрической проницаемости среды толщина ионной атмосферы может быть очень велика (микроны и десятки микрон), что соизмеримо с расстоянием между каплями. Напомним, что положение энергетического барьера взаимодействия частиц, определяемого равновесием сил молекулярного притяжения и электростатического отталкивания (см. 4 гл. IX), отвечает толщине зазора, близкой к удвоенной толщине ионной атмосферы поэтому капли в достаточно концентрированных обратных эмульсиях как бы уже с самого начала расположены на расстояниях, соответствующих преодолению энергетического барьера. Устойчивость обратных эмульсий к флокуляции возможна при наличии структурно-механического барьера, обеспечивающего достаточно малую величину энергии взаимодействия капель при этом электростатическое отталкивание может содействовать уменьшению сил притяжения частиц. Проблема стабилизации обратных эмульсий против флокуляции капель приобрела в последнее время большое значение в связи с попытками использования подобных систем в виде водно-топливных эмульсий, содержащих до 30% воды. Введение эмульгированной воды в бензин и другие топлива, помимо более эффективного использования горючего, обеспечивают повышение его октанового числа и улучшение состава выхлопных газов при работе двигателя внутреннего сгорания. [c.290]

    Большинство задач, с которыми приходится сталкиваться физикам, сводятся к следующей схеме. В какой-то момент (принимаемый за начальный) известно состояние системы и характер ее взаимодействия. Следует определить состояние системы в последующие моменты времени. В этом плане состояние устойчивого равновесия системы уникально наравне с начальным состоянием становятся известны и все последующие состояния. Подобной значимостью для физики обладают законы сохранения. Значение сохраняющейся величины со временем не меняется. Отсюда понятна важность изучения и исследования равновесных состояний. Состояния равновесия системы могут быть различными термодинамическое равновесие, механическое равновесие и т. д. В этой книге мы будем рассматривать механическое равновесие, т. е. равновесие в смысле отсутствия макроскопического движения тела или его частей. [c.9]

    Следовательно, если свободная энергия имеет минимум, то система находится в состоянии устойчивого равновесия, так как если бы какое-нибудь превращение могло увеличить свободную энергию, то это противоречило бы (113). В случае механических систем устойчивое равновесие устанавливается при минимальной потенциальной энергии. Поскольку условием устойчивого равновесия термодинамической системы, заключенной в жесткий резервуар и имеющей температуру окружающей среды, является минимальность свободной энергии, то свободная энергия часто называется термодинамическим потенциалом при постоянном объеме. Строго говоря, условие обоснования неравенства (113) состоит не только в постоянстве объема сосуда, но и в невозможности совершить над системой внешнюю работу. Однако, если в системе давление однородно, то эти два условия эквивалентны. [c.86]

    Существуют устойчивые и неустойчивые состояния равновесия механических систем. Для решения вопрос а об устойчивости равновесия нужно установить каковы последствия возможного нарушения этого состояния. Если возмущения приводят к удалению от состояния равновесия (возрастание амплитуды колебаний, в частности), то состояние следует считать неустойчивым. В противном случае — состояние устойчивое. [c.39]

    В реальных системах энтропия характеризует неустойчивые степени свободы, и именно к ним применимо понятие энтропии. В этом случае говорят о термодинамическом равновесии по неустойчивым степеням свободы. Однако по строго детерминистическим (механическим) степеням свободы система не находится в состоянии термодинамического равновесия. Более того, само понятие энтропии можно применять лишь к тем степеням свободы, по которым за время наблюдения за системой развивается неустойчивость. Устойчивые степени свободы не вносят вклад в статистический вес системы и не учитываются в ее общей энтропии. С их позиций твердые стенки сосуда с газом — гигантская термодинамическая флуктуация, время релаксации которой соответствует времени существования сосуда, т.е. времени, намного большему времени наблюдения за системой. [c.397]

    Можно отметить следующие преимущества, обеспечивающие преобладающее использование привитых сорбентов на основе силикагеля механическая устойчивость к высоким давлениям отсутствие перехода привитой фазы в растворитель в процессе хроматографического разделения (если не протекают реакции, приводящие к химическому отщеплению привитой фазы) устойчивость к действию растворителей, температуры, воды, pH быстрота установления равновесия при смене элюента, что обеспечивает оперативность работы и возможность работы в градиентном режиме с быстрым возвратом к исходному режиму возможность варьировать в широких пределах селективность за счет изменения степени прививки, дополнительной химической обработки и замены растворителя. [c.91]

    Тело с трещиной находится в состоянии механического равновесия, когда в любом элементе объема тела (как и для всего тела в целом) соблюдаются условия равновесия. Это означает, что нагрузка постоянна, нет движения элементов объема, следовательно, нет распространения трещины (трещина неподвижна). Чтобы трещина начала распространяться, необходимо увеличить внешнюю нагрузку или (при постоянной нагрузке) уменьшить энергию разрушения. С медленным ростом нагрузки трещина медленно растет. Малому приращению нагрузки соответствует малое приращение длины трещины. Такое состояние тела с трещиной называют устойчивым (иногда квазистатиче-ским или докритическим) ростом трещины (или просто трещину называют устойчивой). Для устойчивой трещины соблюдается условие — >0, т.е. в предельном состоя- [c.189]

    Первый результат применения уравнения (4) состоял в получении коависимым методом [331 уравнения (2) теории Фрумкина — Дерягина, описывающего условия полного термодинамического равновесия пленки с объемной жидкостью. Далее оказалось, что решение уравнения (4) применительно к состояниям механического равновесия мениска позволяет определить также значения наступающего и отступающего краевых углов. На рис. 4 показаны критические профиля переходной зоны для этих случаев. При краевом угле большем 0л или меньшем 0/ происходит нарушение механического равновесия, профиль теряет устойчивость и начинается течение жидкости. Таким образом, уравнение (4) содержит информацию не только о равновесных, но также и о гистерезисных краевых углах. Заметим, что этот механизм гистерезиса не связан с шероховатостью поверхности и объясняет возможность гистерезисных явлений также и на гладких поверхностях. Так, Фишер [34] наблюдал гистерезис для капель на молекулярно [c.29]

    Рассматривая механическое равновесие плоской мицеллы, мы пришли к выводу, что ее натяжение отрицательно, а линейное натяжение на краю положительно, и обе величины уравновешивают друг друга в соответствии с двумерным уравнением Лапласа. Однако такое двумерное равновесие не. может быть абсолютно устойчивым в трехмерной системе (если бы мицелла была истинно двумерной, равновесие было бы просто неустойчивым относительная устойчивость обеспечивается толщиной мицеллы). При большом отношении диаметра плоской мицеллы к ее толщине становятся существенными флуктуации изгиба и, если в середине мицеллы образуется выпуклость, то стягивающее действие линейного натяжения на краях будет ее усиливать (рис, 26), так как оно направлено на уменьшение периметра мииеллы, В конце концов края мицеллы соединяются и образуется везикула (см, рис, 26), [c.219]

    Однако и структурно-механический фактор устойчивости, равно как и кинетический, не всегда позволяет объяснить причины стабильности пен. Исследования, проведенные авторами работы [23], навели на мысль о наличии термодинамического равновесия между капиллярным давлением и силами отталкивания, являюпщмися функцией толщины пленки, как причины стабилизации пен. [c.56]

    Необходимо более подробно изучить условия равновесия, образования н разрушения ассоциатов на участке АВ (см. рис. 4), влияние отношения ф/Кд, с иа кинетику выделения твердой фазы, форму и размеры надмолекулярных структур, структурно-механические свойства, а также на устойчивость различных нефтяных дисперсных систем и установить более обшие закономерности для управления этими сложными ироцессами, имеющими важное промышленное значение. [c.43]

    В книгу включены дополнения, в частности новые данные автора по линейному натяжению на контуре трехфазного контакта и его роли в зародышеобразовании. Одним из нас (Е. Д. Щ,укиным) с согласия автора написана новая глава о структурно-механических свойствах и реологии дисперсных систем. Другая дополнительная глава (Б. В. Дерягина и Н. В. Чураева) посвящена современному состоянию исследований смачивающих пленок — их равновесия и устойчивости, зависящих от молекулярной, электростатической и структурной составляющих расклинивающего давления. Эти исследования важны как для теории коллоидно-поверхностных явлений — смачивания, адсорбции и капиллярной конденсации, так и для приложений — флотации, нанесения покрытий, почвоведения и гидротехники. [c.6]

    Наряду с термодинамическими факторами устойчивости, к которым следует отнести двойной электричес1й1Й слой и сольватную оболочку вокруг коллоидной частицы, на устойчивость коллоидных систем может в иять и прочность структурно-механического барьера, возникающего по тем или иным причинам на поверхности частицы. Этот фактор, согласно П. А. Ребиндеру, нельзя назвать термодинамическим, поскольку при удалении или разрыве оболочки, представляющей структурно-механический барьер, она не обязательно должна восстанавливаться самопроизвольно. Кроме того, у этой оболочки отсутствует равновесие с окружающей средой. [c.283]

    Возникает вопрос в чем причина определенной направлен-Рис. 6.3. Шарик ности химических процессов, какие факторы обусловливают самопроизволь- хо или иное состояние Известно, что в механических си-но скатывается стемах устойчивое равновесие соответствует минимуму по-из положения а тенциальной энергии системы. Так, шарик самопроизволь-в положение 6. но скатывается нз положения о. на наклонной поверхности (рис. 6.3), причем его потенциальная энергия переходит сначала в кинетическую энергию движения шарика как целого, а затем в энергию теплового движения молекул, В положении б шарик находится в равновесии. [c.178]

    Теперь рассмотрим изотерму 0 = / (С), когда в равновесии с раствором находятся кристаллы данного вещестЕ.а (более тугоплавкого, чем другие), т. е. раствор насыщен им. В этом случае диаграмма будет иметь вид, изображенный на рис. 86. Так как при этой температуре для вещества А более устойчиво твердое состояние (точка а ), чем жидкое (точка а), то 0 кривой раствора, получим точку с. Ее абсцисса отвечает составу раствора, насыщенного (при данной температуре) компонентом А, а любая точка между [c.267]

    Из сказанного следует, что состояние системы будет устойчивым, если условие равновесия (механического) (I. 127) будет соответствовать наименьшему, а не наибольшему значению внутренней энергии системы. Аналогичным образом, из рассмотрения кривой L/(S) при К = onst можно показать, что условию термической устойчивости равновесия соответствует минимальное значение внутренней энергии при сохранении V = = onst. [c.57]

    Условиям устойчивости равновесия системы можно придать иные формы. Так, из уравнений (I. 124а), взяв вторую производную от i/ по I/ при til, S = onst, получим условия, так называемой, механической устойчивости систем  [c.59]

    Мы ограничимся здесь кратким рассмотрением наиболее важных свойств углеводородных пленок и характеристик, имеющих прямое отношение к устойчивости обратных эмульсий и черных пленок. Мы не будем рассматривать такие факторы стабилизации, как отталкивание двойных электрических слоев, имеющее первостепенное значение для равновесия и устойчивости водных пленок и дисперсий, структурно-механический барьер, часто возникающий в полимолекулярных слоях жидкостей, например в прямых эмульсиях, стабилизированных белками и другНми высокомолекулярными соединениями [c.155]

    Кривая / ц5 пересекает кривую Р,. слева снизу в одной точке М (рис. 4-8,а), т.е. при Ре = Рер с цб/с Ре>->йРс1йШ. Поскольку в требования Гурвица (4-42) не входят начальные условия, то характер движения частицы, вращающейся ранее по равновесной траектории, после нанесения ей бесконечно малого возмущения не зависит от направления действия этого возмущения (импульса силы). Поэтому будем рассматривать такой импульс, после действия которого частица в. новом положении имеет. скорость, равную скорости газа. в точке, соответствующей ее нов ому положению. Если под действием внешнего импульса частица сместилась к периферии на расстояние Лр, то в новом положении на нее действуег сила сопротивления Рс>Рцб, стремящаяся вернуть ее назад, к равновесной траектории. Аналогичный процесс происходит и при смещении частицы к центру вращения. Так, в этом случае равновесие пылинки устойчивое. На рис. 4-8 для этого и последующих случаев приведены простейшие механические аналогии. [c.137]

Уравнения равновесия [wiki.eduVdom.com]

Проекция силы на ось — характеризует действие этой силы вдоль этой оси.

То есть Проекция силы на ось Ох ($ P_x = \sum X_i $ ) характеризует действие этой силы вдоль оси Ох.

А проекция силы на ось Оу ($ P_y = \sum Y_i $ ) характеризует действие этой силы вдоль оси Оу.

И если сумма проекций всех сил на ось Ох равна нулю ($ \sum X_i = 0 $ )– значит действие этих сил вдоль этой оси Ох нет ,
силы вдоль этой оси друг друга уравновешивают.

И если сумма проекций всех сил на ось Оу равна нулю ($ \sum Y_i = 0 $ )- значит действие этих сил вдоль этой оси Оу нет , силы друг друга вдоль этой оси Оу уравновешивают.

Вращательное действие силы относительно точки О характеризует момент этой силы относительно этой точки О ($ M_0(P)=0 $) .

И если сумма моментов всех сил относительно точки О равно нулю ($ \sum M_O =0 $), то вращательного действия всех этих сил на тело относительно точки О нет, они его не производят, или их вращательные действия их взаимно уравновешены.

Теперь — если проекции всех сил на оси Ох и Оу равны нулю , и сумма моментов всех сил относительно любой — какой угодно — точки равны нулю, то тело находится в равновесии.

$$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$

Это и есть условия равновесия тела под действием произвольной плоской системы тел:

Система сил, действующих на тело, называется сходящейся, если линии действия этих сил пересекается в одной точке.

Условие равновесия системы сходящихся сил

Для того, чтобы система сходящихся сил была уравновешенной, то есть под действием ее тело будет находится в равновесии —
условие равновесия системы сходящихся сил,
может быть записано :
$$ \sum X_i = 0
\\ \sum Y_i = 0
$$

Или другими словами — для плоской системы сходящихся сил, лежащих в плоскости Oxy,
соответствующие уравнения равновесия примут вид:

$$ \sum X_i = 0
\\ \sum Y_i = 0
$$

Проекция силы на ось

Определение. Проекцией силы $\vec{Р}$ на ось Ox называется взятая с знаком $\pm$
длина отрезка этой оси, заключенная между проекциями на неё начала и конца
вектора силы.

Эту проекцию обычно обозначают как Р_x или X. В соответствии с
определением она равна:

$$ P_x = X = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{i}) = P \cdot \cos \alpha $$

$$ P_y = Y = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{j}) = P \cdot \sin \alpha $$

, где $\vec{i}$ – единичный вектор оси /Ox/, а $\alpha$ – угол между ним и силой $\vec{Р}$ (Рис.1).

Рис.1

Таким образом:

$$ P_x > 0\text{, если }0 \leq \alpha < \frac{\pi}{2} $$
$$ P_x = 0\text{, если } \alpha = \frac{\pi}{2} $$
$$ P_x < 0\text{, если } \frac{\pi}{2} < \alpha \leq \pi $$

Проекция силы на ось равна нулю, если сила перпендикулярно оси.

Аналогично находится проекция силы Р на ось Oy.2}
\\ \cos (\vec{Р}, \vec{i}) = \frac{X}{P}
\\ \cos (\vec{Р}, \vec{j}) = \frac{Y}{P}
$$

Момент силы относительно центра

Приложим в точке А силу P и выясним — чем определяется момент силы относительно точки О, который характеризует
вращательное действие этой силы относительно точки О(Рис.1).

Рис.1

Очевидно, что воздействие силы на тело будет зависеть не только от ее
величины, но и от того, как она направлена, и в конечном итоге будет
определяться ее моментом относительно центра О.

Рассмотренное определение момента силы подходит только для плоской
системы сил.

Определение 1. Моментом силы Р относительно центра О называется
взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть длину
перпендикуляра, опущенного из моментной точки на линию действия силы.

Правило знаков: момент силы считается положительным, если сила
стремится повернуть тело против хода часовой стрелки и отрицательным, если
она вращает тело по ходу часовой стрелки.

В соответствии с данным определением момент силы численно равен
удвоенной площади треугольника OAB, построенного на векторе силы P с
вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .

Отметим, что момент силы относительно точки О равен нулю, если линия
действия силы проходит через моментную точку.

Уравнения равновесия плоской системы сил

Уравнения равновесия плоской системы сил,
которые можно записать в трех различных формах:

1. Первая форма:
   $$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$

2. Вторая форма:
   $$ \sum M_A=0 \\ \sum M_B=0 \\ \sum Y=0 $$ , где ось Oy не перпендикулярна отрезку АВ

3. Третья форма:
   $$ \sum M_A=0 \\ \sum M_B=0 \\ \sum M_C=0 $$ , где точки А, В и С не лежат на одной прямой.

Таким образом, любая из этих трех форм эквивалентна условию равновесия плоской системы сил и наоборот.

Центр тяжести

Центр тяжести — точка, через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.

Если тело имеет ось или центр симметрии, то центр тяжести лежит там.

Центр тяжести квадрата и прямоугольника — точка пересечения его диагоналей.

Центр тяжести круга — в его центре.

Центр тяжести треугольника — в точке пересечения медиан.

Задачи и опыты

Задачи

Опыты с пояснением — физика 9 кл.

Рекомендуем

subjects/physics/уравнения_равновесия.txt · Последние изменения: 2020/12/18 18:40 — ¶

4.5. Условия равновесия фаз

%PDF-1.5
%
2 0 obj
>
/Metadata 4 0 R
/Pages 5 0 R
/StructTreeRoot 6 0 R
/Type /Catalog
>>
endobj
4 0 obj
>
stream

application/pdf

2020-03-29T18:35:42+03:00Microsoft® Office Word 20072020-03-30T16:38:12+03:00Microsoft® Office Word 2007uuid:e99d88fe-0bb2-4a5c-a80e-28bad046587duuid:18f3c385-4911-4497-a79c-914cad35dd79

endstream
endobj
14 0 obj
>
stream
x=َ7vQKܗ@10I3c;~%.åHmyl[VC_~w_.||ߗo?|||O~/?xy͇zU?}C/K/FnjSoߐˏ?}\>7n޾TmºEnDV_p,(a~_÷(߮&e RBu]y\> P??]h2vv3T

Вся статика — теоретическая механика

Определение и роль статики в теоретической механике

Статика

– это раздел теоретической механики, в котором изучаются условия равновесия материальных тел, находящихся под действием сил, а также методы преобразования сил в эквивалентные системы.

Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.

Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.

Понятие силы

Сила

, действующая на материальную точку с радиус-вектором со стороны других точек – это мера воздействия других точек на рассматриваемую точку, в результате которой она получает ускорение относительно инерциальной системы отсчета. Величина силы определяется по формуле:
,
где m – масса точки – величина, зависящая от свойств самой точки. Эта формула называется вторым законом Ньютона.

Подробнее, см. «Силы в теоретической механике».

Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.

Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.

Система сил,

действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.

Эквивалентные системы сил

Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.

Эквивалентное преобразование системы сил

– это переход от одной системы сил к эквивалентной ей системе.

Система взаимно уравновешивающихся сил

– это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.

Равнодействующая

– это одна сила, действие которой эквивалентно действию данной системы сил.

Закрепленные, скользящие и свободные векторы

Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.

Закрепленный вектор

– это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.

Скользящий вектор

– это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.

Свободный вектор

– это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.

Линия действия силы

– это прямая, проведенная через точку приложения силы параллельно ее направлению.

Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.

С математической точки зрения, статика – это алгебра скользящих векторов.

Проекции силы на оси координат

Сила в трехмерном пространстве

Вектор силы и ее проекции на оси пространственной системы координат.

Пусть у нас есть декартова система координат Oxyz. И пусть – единичные векторы, направленные вдоль ее осей , и , соответственно. Пусть – проекции вектора силы на оси координат. Тогда разложение силы на составляющие вдоль координатных осей имеет вид:
.
Абсолютное значение (модуль) силы:
.

Введем единичный вектор , направленный вдоль вектора силы . Тогда
.
Эта формула выражает тот факт, что вектор силы можно задать, указав ее модуль F и направление . Вектор имеет три проекции на оси координат: . Поскольку его длина равна единице: , то они связаны соотношением:
.
То есть единичный вектор имеет только две независимые компоненты. Таким образом, для задания вектора силы нужно знать три величины:
либо три проекции на оси координат ;
либо модуль F и направление , которое задается двумя независимыми величинами.

Введем углы между вектором силы и осями координат , и . Тогда проекции силы на оси координат определяются по формулам:
;
.
Косинусы углов называются направляющими косинусами.

Направляющие косинусы

вектора – это косинусы углов между вектором и осями координат. Они являются проекциями единичного вектора , сонаправленного с :
,
и связаны соотношением:
.

Сила на плоскости

Вектор силы и ее проекции на оси плоской системы координат.

Результаты, приведенные выше, можно применить и для плоской декартовой системы координат Oxy. В этом случае имеем:
;
;
;
;
;
;
.
Поскольку , то   . Последнее уравнение представляет собой известную тригонометрическую формулу:
.
Для задания вектора силы , необходимо знать две независимые величины:
либо проекции вектора на оси координат ;
либо модуль F и направление , которое задается одним углом .

Аксиомы статики

Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.

1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

То есть, если силы и приложены в одной точке, то их можно заменить равнодействующей , приложенной к той же точке. Сумму векторов можно найти двумя способами.
1) Можно вычислить проекции сил на оси прямоугольной системы координат:
.

Сложение сил по правилу параллелограмма

2) Можно сложить векторы по правилу параллелограмма (см. рисунок).
;
.
Здесь – угол между векторами и . Точкой обозначено скалярное произведение векторов.

5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.

То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Подробнее, см. «Аксиомы статики».

Система сходящихся сил

Сходящиеся силы

– это силы, линии действия которых пересекаются в одной точке.

Система сходящихся сил всегда имеет равнодействующую , равную векторной сумме этих сил:
,
и приложена в точке их пересечения.

Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.

Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.

Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.

Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.

Параллельные силы

Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.

Две силы одного направления

Две параллельные силы F₁ и F₂ имеют равнодействующую R.

Пусть мы имеем две однонаправленные параллельные силы и . Переместим точки их приложения вдоль линий их действия в точки A и B так, чтобы отрезок AB был перпендикулярен силам. Тогда система сил и имеют равнодействующую , приложенную в точке C. Направление равнодействующей совпадает с направлениями и . Абсолютная величина равна сумме сил:
.
Точка приложения C находится между A и B и делит отрезок AB обратно пропорционально модулям сил:
.

Две противоположно направленные силы

Две не равные противоположно направленные силы F₁ и F₂ имеют равнодействующую R.

Теперь рассмотрим противоположно направленные силы и , различающиеся по величине, . Пусть . Эта система также имеет равнодействующую , направление которой совпадает с направлением большей по модулю силы, а абсолютное значение равно абсолютному значению разности модулей сил:
.
Точка приложения C равнодействующей находится на продолжении отрезка AB, ближе к наибольшей по модулю силе . Расстояния до точек A и B также обратно пропорциональны и :
.

Момент силы относительно точки

Определение

Моментом силы

, приложенной к телу в точке A, относительно точки O, называется вектор , равный векторному произведению векторов и :
(2)   .

Плечом силы

относительно точки O, называется кратчайшее расстояние между линией действия этой силы и точкой O. Другими словами, плечо силы – это длина перпендикуляра, опущенного из точки O на линию действия силы.

Абсолютное значение момента силы относительно точки O равно произведению силы на плечо этой силы относительно выбранной точки O. Направление момента перпендикулярно плоскости, проходящей через точку O и линию действия силы.
Доказательство

Геометрическая интерпретация

Момент силы равен произведению силы F на плечо OH.

Пусть векторы  и  расположены в плоскости рисунка. Согласно свойству векторного произведения, вектор перпендикулярен векторам  и  , то есть перпендикулярен плоскости рисунка. Его направление определяется правилом правого винта. На рисунке вектор момента направлен на нас. Пусть α – угол между векторами и . Абсолютное значение момента:
.

Из точки O проведем перпендикуляр OH к линии действия силы . Из прямоугольника OAH имеем: . Тогда
.
То есть абсолютное значение момента силы относительно точки O равно произведению силы F на плечо |OH| этой силы относительно точки O.

Компоненты момента силы в декартовой системе координат

Выберем декартову систему координат Oxyz с началом в точке O. Найдем компоненты вектора момента силы в этой системе координат относительно ее начала.

.
Здесь – единичные векторы в направлении осей ; – координаты точки A в выбранной системе координат: .

Таким образом, момент силы имеет следующие компоненты:
(М.1)   ;
(М.2)   ;
(М.3)   .
Компоненты представляют собой значения момента силы относительно осей , соответственно.

Свойства момента силы относительно центра

Момент относительно центра O, от силы, проходящей через этот центр, равен нулю.
Доказательство

Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство

Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство

То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.

Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство

Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.

Пара сил

Из предыдущих формул ⇑ видно, что если противоположно направленные силы имеют равные модули: , то система сил не имеет равнодействующей. Действительно, в этом случае . Пытаясь использовать предыдущие формулы, мы получим деление на нуль. Такую систему сил называют парой сил.

Пара сил

– это система из двух сил , равных по абсолютной величине, имеющих противоположные направления, приложенных к разным точкам тела и не лежащих на одной прямой.

Плечо пары сил

– это кратчайшее расстояние h между линиями действия сил, входящих в пару.

Момент пары сил

– это векторная сумма моментов сил, входящих в пару, вычисленная относительно любой точки. Абсолютное значение момента пары равно произведению силы на плечо пары:
.

Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.

Момент силы относительно оси

Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.

Момент силы относительно оси,

проходящей через точку O – это проекция вектора момента силы относительно точки O, на направление оси.

Свойства момента силы относительно оси

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство

Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство

Вычисление момента силы относительно оси

Момент силы относительно оси.

Пусть на тело, в точке A действует сила . Найдем момент этой силы относительно оси O′O′′.

Построим прямоугольную систему координат. Направим ось z вдоль O′O′′. Из точки A опустим перпендикуляр AO на O′O′′. Через точки O и A проводим ось Ox. Перпендикулярно Ox и Oz проводим ось Oy. Разложим силу на составляющие вдоль осей системы координат:
.
Сила пересекает ось O′O′′. Поэтому ее момент равен нулю. Сила параллельна оси O′O′′. Поэтому ее момент также равен нулю. По формуле (М.3) находим:
.

Заметим, что компонента направлена по касательной к окружности, центром которой является точка O. Направление вектора определяется правилом правого винта.

Условия равновесия

Главный вектор и главный момент

Главный вектор

– это векторная сумма всех сил, приложенных к телу.

Главный момент

относительно данного центра – это векторная сумма моментов всех сил, приложенных к телу относительно выбранного центра.

Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.

Пространственная система сил

Основная форма условий равновесия

Условия равновесия системы сил
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор и главный момент, относительно произвольной точки C, равнялись нулю:
;
.
Здесь – точка приложения силы , .
Доказательство

Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.

Вторая форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
;
;
.
Доказательство

Третья форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
;
;
;
.
Доказательство

Плоская система сил

Плоская система сил

– это система сил, расположенных в одной плоскости. То есть точки приложения всех сил расположены в одной плоскости, а направления сил параллельны этой плоскости.

Все изложенное для пространственной системы сил является применимым и для плоской системы. Направим оси x и y декартовой системы координат в плоскости действия сил, а ось z – перпендикулярно. Тогда z компоненты координат точек и сил равны нулю: . Также равны нулю x, y компоненты моментов сил относительно произвольной точки C: . То есть момент может иметь отличное от нуля значение только для z компоненты. Поскольку z компонента не входит в плоскую систему координат xy, то, в двумерном пространстве, момент силы уже не является вектором, а является скаляром (точнее псевдоскаляром). Его называют алгебраическим моментом силы относительно центра C (или просто моментом силы относительно центра C), и обозначают символом с маленькой буквы без знака вектора:
.

Величина является моментом силы относительно оси, проходящей через точку C перпендикулярно плоскости действия сил. Момент вычисляют как произведение модуля силы на плечо со знаком плюс или минус:
.
Если, при неподвижном центре C, сила стремится повернуть систему против часовой стрелки, то момент положителен . В противном случае – отрицательный: .

Величину момента от силы , приложенной в точке A, относительно центра C, также можно выразить через компоненты векторов по формуле:
,
где и – координаты точек A и C, соответственно.

Условия равновесия плоского тела

Для плоской системы сил можно составить три уравнения, из которых можно определить три неизвестных величины. Считаем, что сила приложена в точке .

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Связи и их реакции

Определения и свойства

Свободное тело

Тело называется свободным, если его перемещения ничем не ограничены.

Несвободное тело

Тело, перемещение которого ограничено другими телами, называется несвободным.

Связи

Тела, ограничивающие перемещения данного тела, называются связями.

Реакции связей

Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей и их реакции

Плоские и пространственные задачи

Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.

Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.

Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.

Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.

Плоские задачи

Следующие связи применяют только в плоских задачах.

Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.

Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.

Пространственные задачи

Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.

Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.

Силы трения

Сила трения

Пусть два тела находятся в соприкосновении. Сила трения – это сила, параллельная плоскости соприкосновения тел, которая возникает между телами при попытке сместить одно тело относительно другого, препятствующая их относительному смещению.

Трение скольжения

Сила трения скольжения F_тр = f·N.

Рассмотрим тело, которое скользит по поверхности другого тела с отличной от нуля скоростью v под действием внешней силы . Если поверхности абсолютно гладкие, то в точках соприкосновения тел возникает только сила давления N, перпендикулярная плоскости соприкосновения тел. Для шероховатых поверхностей, возникает еще сила трения , параллельная плоскости соприкосновения, направленная в сторону, противоположную скорости движения. Величина силы трения пропорциональна силе давления и не зависит от площади соприкосновения поверхностей:
(Т1)   .
Здесь f – безразмерный коэффициент, который называется динамическим коэффициентом трения, или коэффициентом трения скольжения. Он зависит от материалов и обработки соприкасаемых поверхностей и почти не зависит от скорости относительного движения. При расчетах его считают постоянной.

Сила трения скольжения

– это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.

Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.

Трение сцепления

Сила трения сцепления. Движение возможно при tg φ > f₀.

Теперь рассмотрим статическую задачу. Пусть тело покоится, и на него действуют внешние силы с равнодействующей , приложенной под углом φ к нормали поверхности. Разложим ее на две составляющие: параллельную поверхности, и перпендикулярную . На тело также действуют сила реакции , перпендикулярная плоскости соприкосновения тел, и сила трения , которую при отсутствии скольжения называют силой сцепления. Сила сцепления направлена параллельно поверхности, препятствуя движению. Она может принимать значения от нуля до максимальной величины , определяемой аналогично (Т1):
(Т2)   .
Здесь – статический коэффициент трения, который еще называют коэффициентом сцепления. Он не может быть меньше динамического коэффициента трения: .

Если , тело покоится. При этом сила трения сцепления меньше максимальной величины: . При , возникает движение. Когда , сила трения достигает предельной величины, возникает состояние предельного равновесия. Дальнейшее увеличение приводит к потере равновесия.

Сила трения сцепления

– это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.

Предельная сила трения

– это максимальное значение силы трения сцепления.

Предельное равновесие

– это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.

Из условий равновесия имеем: . Подставим в (Т2):
.
Отсюда получаем, что система будет находиться в равновесии, если
.
Видно, что условие равновесия зависит от угла φ, под которым приложена равнодействующая внешних сил, и не зависит от ее величины. Введем предельный угол трения: . Эту величину также называют просто углом трения. Тогда, условие равновесия можно записать так:
.
Это неравенство определяет конус в пространстве, который называется предельным конусом трения, конусом трения, или конусом сцепления. Если направление силы выходит за пределы этого конуса, то система начинает движение. Если направление силы попадает в конус сцепления, то система остается в состоянии покоя. Такое явление называется заклиниванием механизма.

Заклинивание механизма

– это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.

Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.

Трение качения

Силы, возникающие при деформации, препятствуют качению тела круглой формы по плоской поверхности.

Рассмотрим случай, когда одно из тел круглой формы катится без проскальзывания по поверхности другого. С точки зрения механики, такие тела соприкасаются в одной точке A. Площадь их соприкосновения бесконечно мала, в результате чего возникает бесконечно большое давление, которое не могут выдержать реальные материалы. Поэтому вблизи точки соприкосновения тел возникает деформация, которая имеет место только в небольшом участке соприкасающихся тел. В основной части тел, удаленных от точек соприкосновения, деформация практически отсутствует, и их можно рассматривать как абсолютно твердые тела. Тогда систему сил, возникающую в результате соприкосновения, можно привести к некоторой равнодействующей силе . При этом оказывается, что точка ее приложения смещена относительно оси симметрии катящегося тела. Это приводит к появлению момента сил относительно точки A, расположенной на оси симметрии круглого тела. Изучение деформированного состояния выходит за рамки теоретической механики. Поэтому мы приводим лишь результаты, применяемые в расчетах.

Расчетная схема трения качения.

1. Поскольку деформации, для небольших значений внешних сил малы, то, считают, что они не влияют на геометрические характеристики тел. То есть считают, что тела округлой формы соприкасаются в одной точке.
2. В точке соприкосновения, на тело действуют:
сила давления , перпендикулярная соприкасающимся поверхностям;
сила сцепления , лежащая в касательной плоскости, проходящей через точку соприкосновения поверхностей;
момент силы трения , препятствующий движению.
Максимальное значение момента силы трения определяется по формуле:
,
где δ – коэффициент трения качения, который имеет размерность длины.
3. Коэффициент трения качения зависит от соприкасающихся материалов и состояния их поверхностей. Он не зависит от кривизны поверхностей и угловой скорости вращения тела. А при движении с проскальзыванием, не зависит от скорости скольжения.

Центр тяжести тела

Центр тяжести в пространстве

Пусть тело состоит из n материальных точек. И пусть на каждую точку B_i действует сила тяжести , . Все силы тяжести, действующие на точки, параллельны. Поэтому мы имеем дело с параллельной системой сил. Как и для системы из двух однонаправленных сил, такая система сил имеет равнодействующую. Найдем ее.

Пусть – главный вектор. Поскольку все силы имеют одинаковое направление, то введем единичный вектор , направленный вдоль сил:
. Отсюда .

Найдем момент сил тяжести относительно произвольно расположенного центра O.
,
где
(ЦТ1)   .

Отсюда видно, что формула вычисления момента имеет вид формулы момента от одной силы , приложенной в точке C. Точка C, положение которой определяется формулой (ЦТ1), называется центром тяжести тела. Таким образом, равнодействующая отдельных сил тяжести точек тела равна главному вектору силы тяжести, приложенному в центре тяжести. Модуль P равнодействующей называют весом тела.

Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.

Центр тяжести твердого тела

– это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.

Вес тела

– это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.

Координаты центра тяжести определяются по формулам:
(ЦТ2)   .
Здесь – абсолютное значение равнодействующей сил тяжести, или вес тела. – координаты точек тела. Эти формулы также можно записать в векторном виде.
.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.

В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.

Для сплошного однородного тела, мы от суммирования переходим к интегрированию. Элементарная сила тяжести выражается через плотность ρ_i элементарной частицы тела, массой , и занимающей объем :
.
Здесь g – ускорение свободного падения. Переходя от суммированию к интегрированию, имеем:
(ЦТ3)   .

Центр тяжести плоской фигуры

Рассмотрим плоскую фигуру. Выберем двумерную систему координат Oxy. Тогда положение центра тяжести определяется по тем же формулам (ЦТ2) и (ЦТ3), из которых нужно убрать переменную z.

Однородная фигура

Рассмотрим плоскую однородную фигуру. Для такой фигуры, плотность ρ является постоянной; сила тяжести Δp_i элементарной частицы пропорциональна площади ΔA_i этой частицы: Δp_i = ρΔA_ig. Вес P фигуры пропорционален площади A всей фигуры: P = ρAg.

Подставляя эти величины в формулы, определяющие положение центра тяжести находим:
.
Переходим от суммирования к интегрированию:
.
Мы видим, что сюда не входят плотность ρ и ускорение свободного падения g. Остались величины, зависящие только от геометрии сечения. Таким образом, для тела с постоянной плотностью, центр тяжести является геометрической характеристикой.

В этих формулах, y_C есть алгебраическое расстояние от центра тяжести до оси x; y_k или y – алгебраическое расстояние элементарного участка до той же оси. x_C, x_k и x – соответствующие алгебраические расстояния до оси y. В этой связи вводят новую геометрическую характеристику сечения, которую называют статическим моментом.

Статический момент относительно некоторой оси

– это сумма произведений элементарных площадей , входящих в состав фигуры, на алгебраические значения их расстояний до этой оси.

В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.

Центры тяжести простейших фигур

Параллелограмм, прямоугольник, квадрат: в точке пересечения диагоналей.
Треугольник: в точке пересечения медиан, которая делит каждую медиану в соотношении 1:2.
Дуга окружности с центральным углом 2α: .
Круговой сектор: .

Теоремы, применяемые при расчете центра тяжести

Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Центр тяжести фигуры, составленной из n более простых фигур, определяется по формуле:
(ЦТ4)   .
Здесь – площадь всей фигуры; – площадь и координаты центра тяжести простой фигуры, входящей в состав сложной.

Способ отрицательных площадей (объемов)
Если k — я фигура вырезана из объемлющей ее части, то, в формуле (ЦТ4), соответствующая ей площадь считается отрицательной: .

Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести: . Площадь поверхности вращения A, полученной вращением плоской кривой L вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой L на длину окружности, описанной ее центром тяжести: .

Распределенная нагрузка

Равномерно (А) и линейно (Б) распределенная нагрузка.

Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.

Равномерно распределенная нагрузка q (рисунок А). Ее можно заменить равнодействующей силой величины , приложенной в центре тяжести эпюры. Поскольку, на рисунке А, эпюра представляет собой прямоугольник, то ее центр тяжести находится в центре основания эпюры – в точке C: |AC| = |CB|.

Линейно распределенная нагрузка q (рисунок В). Ее также можно заменить равнодействующей. Величина равнодействующей равна площади эпюры:
.
Точка приложения находится в центре тяжести эпюры. Центр тяжести треугольника, высотой h, находится на расстоянии от основания. Поэтому .

Приведение системы сил к центру

Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Теорема о приведении системы сил к заданному центру
Любую систему сил, действующих на данное тело, можно привести к заданному центру O – то есть заменить одной силой, равной главному вектору, приложенной к точке приведения O, и парой сил с моментом M_O, равным главному моменту относительно центра O.

Статические инварианты

Статические инварианты

пространственной системы сил – это такие величины, которые не зависят от центра приведения.

Такими инвариантами являются:
1) главный вектор ;
2) скалярное произведение главного вектора на главный момент .
Главный вектор равен векторной сумме всех сил и поэтому не зависит от центра приведения O. Главный момент зависит от положения центра O, относительно которого вычисляются моменты. Но величина его скалярного произведения на главный вектор не зависит от того, относительно какой точки вычисляется главный момент.

Хотя главный вектор не зависит от положения центра O, но величины его проекций на оси координат зависят от выбора системы координат. Поэтому они также не являются инвариантами. По той же причине и направление главного вектора не является инвариантом. Единственной численной величиной, которая не зависит от выбора системы координат, является модуль главного вектора. Но, в математическом отношении, проще иметь дело с квадратом модуля. Поэтому мы выберем его в качестве основного инварианта.

Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.

Динама

Разложим главный момент на компоненту , параллельную главному вектору , и на компоненту , перпендикулярную :
(П1)   .
Тогда .
Отсюда получаем упомянутый выше результат, что инвариантом является алгебраическая величина проекции главного момента на направление главного вектора:
.

Динама – одна из простейших систем сил.

То есть, при изменении положения центра O, меняется вектор , в то время как вектор остается постоянным. Выбором центра приведения O, можно обратить в нуль. Тогда мы получим систему, состоящую из главного вектора и пары сил с моментом , лежащих в плоскости, перпендикулярной главному вектору. Такая система называется динамой или силовым винтом. Система приводится к динаме, если второй статический инвариант не равен нулю.

Динама

– это простейшая система сил, состоящая из силы , приложенной к некоторой точке C, и паре сил, перпендикулярных . При этом момент пары параллелен линии действия силы. Динаму также называют силовым винтом, динамическим винтом, или статическим винтом.

Ось винта

– это линия действия силы динамического винта.

Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.

Центральная ось системы сил

Пусть и – главный вектор и главный момент относительно некоторого центра O, который выберем за начало координат. И пусть второй инвариант отличен от нуля:
.
Найдем положение такой точки C, относительно которой система сил приводится к динаме. Для этого преобразуем главный момент от центра O к C:

.
Отсюда
(П2)   .
Для динамы, векторы и направлены вдоль одной прямой. Поэтому
, где λ – некоторое число. Отсюда получаем два уравнения:
(П3)   .
Пусть – компоненты вектора . Тогда подставив (П2) в (П3), имеем:
.
Это уравнение прямой в пространстве, которую называют центральной осью системы сил. Относительно точек этой прямой, система сил приводится к динаме, а главный момент имеет наименьшее по модулю значение.

Центральная ось системы сил

– это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.

Приведение системы сил к простейшему виду

Пара сил

Пусть .
Тогда . Второй инвариант также равен нулю: . В этом случае, вектор главного момента не зависит от положения центра O. Система сил приводится к паре с моментом .

Если и , то это уравновешенная система сил. Она эквивалентна отсутствию сил.

Равнодействующая сила

Пусть .
В этом случае существует прямая, относительно точек которой главный момент равен нулю:
.
То есть система приводится к одной силе – равнодействующей, равной главному вектору приложенному к любой из точек упомянутой выше прямой. Эта прямая является линией действия главного вектора. Примеры: система сходящихся сил, система параллельных сил. Это системы, которые имеют равнодействующую.

Динама

При , как показано выше, система сил приводится к динаме.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов.     Опубликовано: 03-10-2017   Изменено: 07-05-2020

Mechanical Equilibrium — обзор

4.1. Взаимодействие в бинарных жидких смесях

Для бинарной жидкости, где — j ₁ = j ₂ , при механическом равновесии с пренебрежимо малой объемной силой и для диффузии, основанной на средней массовой скорости, теперь мы можем установить набор феноменологических уравнений, представляющих связь между тепломассопереносом [Eqs. (4) и (5)]

−J ″ q = Lqq∇lnT + L1q1w2 (∂μ1∂w1) T, P∇w1 − j1 = Lq1∇lnT + L111w2 (∂μ1∂w1) T, P∇w1

Эти уравнения подчиняются соотношениям взаимности Онзагера, согласно которым феноменологическая матрица коэффициентов симметрична.Коэффициенты L _qq и L ₁₁ связаны с теплопроводностью k и взаимной диффузией D соответственно, а перекрестный коэффициент L _{1 q} или L _{q 1} определяет явления связи, а именно термодиффузию (эффект Соре) и тепловой поток из-за диффузии вещества i (эффект Дюфура). Эти эффекты называются силами, однако роли сил и потоков симметричны.

Теплота переноса Q1 * компонента 1 определяется уравнением. (52)

, и его можно использовать в феноменологических уравнениях для исключения коэффициентов L _q1 или L _{1 q} . Если мы выразим L _{1 q} через теплоту переноса Q1 * (L1q = Q1 * L11), уравнение (59) становится

(64) η = (Lqq / L11) 1 / 2λ + Q1 * (L11 / Lqq) 1 / 2Q1 * (L11 / Lqq) 1 / 2λ + (L11Lqq) 1/2

Степень сцепления q можно выразить через теплоту транспортировки

Степень сцепления может использоваться в качестве основы для сравнения систем с различными связанными силами.Феноменологические коэффициенты выражаются через коэффициенты переноса

, k, D и Q1 *

(66) L1q = Q1 * ρDM1M2w1w2 [MRT (1 + Γ11)]

(68) L11 = ρw2D (∂ μ∂w1) −1

, где Γ ₁₁ = (∂lnγ ₁ / ∂ln x ₁ ) _{T, P} известен как термодинамический фактор и может быть определен экспериментальным путем. данные или модель коэффициента активности, например NRTL или UNIFAC. Феноменологическая стехиометрия z определена в формуле.(61)

С определениями степени связи q и феноменологической стехиометрией z , уравнение. (64) можно записать как

(70) η = zλ + Q1 * / zQ1 * λ / z + 1 / z

Ур. (70) показывает, что, когда степень связи приближается к нулю, каждый поток становится независимым, и мы имеем отношение потоков, приближающееся к η → z ² λ. Если q приближается к ± 1, то два потока больше не связаны с силами, и отношение потоков приближается к фиксированному отношению λ → ± z. Этот корпус — комплектная муфта. Отрицательные значения η связаны с ситуациями, когда дифференциация химического потенциала по концентрации отрицательна из-за неидеальности смеси. Степень связи не является уникальной характеристикой системы, поскольку могут существовать различные способы описания потоков и сил, согласующиеся с заданной скоростью рассеяния. Для полной муфты q = ± 1 для любого выбора потоков и сил, а z имеет уникальное значение.

Степень связи q и коэффициент термодиффузии компонента 1 K _{T, 1} могут быть выражены через коэффициенты переноса и Γ с помощью уравнения. (65)

(71) q = Q1 * T (ρDM1M2w1w2kMR (1 + Γ11)) 1/2

(72) KT, 1 = q (kM1M2w1w2ρDMR (1 + Γ11)) 1/2

Ур. (71) показывает, что q прямо пропорционально теплоте переноса и обратно пропорционально температуре. Степень сцепления зависит от переносимого тепла, теплопроводности и коэффициента диффузии, тогда как L _{1 q} не зависит от теплопроводности.Поскольку тепловой и диффузионный потоки являются векторами, знак q связан с направлением потоков вещества. Если q > 0, поток вещества может увлекать другое вещество в том же направлении, однако он может толкать другое вещество в противоположном направлении, если q <0. Для тепловых и массовых потоков функция рассеяния по формуле. (64) определяет два предельных значения q как + l и −1.

На основе функции диссипации, приведенной в формуле. (1), мы можем определить отношение рассеивания из-за теплового и массового потоков с точки зрения приведенного отношения сил и степени сцепления q

Ур.(73) известна как эффективность преобразования энергии в физических и биологических системах, а j ₁ X ₁ показывает вход, а J ″ qXq — выходную мощность. Следовательно, диффузия управляет тепловым потоком, и член ( zλ / q ) изменяется между 0 и -1. Поскольку ηλ равно нулю, когда либо J ″, либо X _q равно нулю, тогда оно должно проходить через максимум при промежуточных значениях. Значения ηλ часто малы в областях, представляющих физический интерес, и максимум зависит только от степени связи

(74) (ηλ) max = q2 (1 + 1 − q2) 2

Вставка уравнений.(4) и (5) в функцию диссипации уравнения. (1) получаем три вклада за счет тепла, массы и связанного переноса, соответственно

(75) Ψ = Lqq (1T∇T) 2 + L11 [1w2 (∂μ1∂w1) ∇w1] 2 + 2L1q (1T∇T) [1w2 (∂μ1∂w1) ∇w1]

Мы также можем использовать коэффициенты переноса, указанные в уравнениях. (66) — (68) и степень связи в функции диссипации, и мы получаем

(76) Ψ = kT (1T∇T) 2 + ρD [1w2 (∂μ1∂w1) (∇w1) 2 ] + 2ρDQ1 * (1T∇T) [1w2 (∂μ1∂w1) ∇w1]

Путем дифференцирования химического потенциала в терминах Γ

(77) (∂μ1∂w1) = MRT (1 + Γ11) w1M1M2

и используя определение q [(Ур.71)], мы можем выразить функцию диссипации через степень связи q , термодинамический фактор Γ, а также коэффициенты переноса теплопроводности k и коэффициент диффузии D

(78) Ψ = kT (1T∇T) 2 + ρDMRT (1 + Γ11) w1w2M1M2 (∇w1) 2 + 2q (ρDMRT (1 + Γ11) w1w2M1M2) 1/2 (∇T) (∇w1)

Слагаемые в правой части сторона уравнения. (78) показывают, что рассеяние из-за теплового потока, массового расхода и связи между тепловым и массовым потоками, соответственно.

Rowley et al. [11, 12] измерили теплоту переноса, теплопроводность и коэффициенты взаимной диффузии при 30 ° C и атмосферном давлении для ряда бинарных систем. Данные имеют уровни погрешности 2% для коэффициентов диффузии и теплопроводности и около 4% для измерений тепла при переносе. Степень связи прямо пропорциональна произведению Q1 * (D / k) ½, и, следовательно, уровень ошибки прогнозов q в основном связан с сообщаемыми уровнями ошибок значений Q1 *.Полином соответствует теплопроводности, массовому коэффициенту диффузии и теплоте переноса алканов в хлороформе и четыреххлористом углероде, которые приведены в Приложении B, Таблицы B1 – B3. Теплопроводность смеси гексан-четыреххлористый углерод предсказывалась моделью локального состава [10]. Для расчета термодинамических факторов использовались модели NRTL и UNIFAC с данными, приведенными в серии DECHEMA [2]. Однако следует отметить, что термодинамические факторы, полученные из различных молекулярных моделей, а также из двух наборов параметров для одной и той же модели, могут быть разными.

Таблица 1. Степень связи q и максимальный коэффициент рассеяния (ηλ) _max : (а) для алканов в хлороформе

2

902 для углерода

Таблица 2.Коэффициент термодиффузии для растворенного вещества K _{T, 1} : (a) для алканов в хлороформе

Metane

9025

0,4

Таблица 3. Коэффициенты в уравнении сглаживания феноменологических коэффициентов для тройной смеси толуола (1) -хлорбензола (2) -бромбензола (3): Lik = ao + ao + ao + a2w12 + a3w2 + a4w1w2 + a5w22

−3,375255 104,986

шестиуглеродистая смесь из шести атомов углерода-9, состоящая из шести углеводородов, состоящих из шести углеродных смесей n-9 , н-гептан, н-октан, 3-метилпентан, 2,3-диметилпентан и 2,2,4-триметилпентан в хлороформе и четыреххлористом углероде.Эти системы представляют собой прямые и разветвленные цепи алканов в двух растворителях. Поскольку степень связи и коэффициент термодиффузии зависят от коэффициентов тепломассопереноса, графики q и K _{T , 1} в сравнении с составами алканов x ₁ показывают комбинированный эффект коэффициентов переноса на q и K _{T , 1} в различных растворителях, как показано на рисунках 1 и 2, соответственно.

Рис. 1. Изменение степени связывания q в зависимости от концентрации алканов x ₁ при 30 ° C и давлении окружающей среды: (а) и (в) алканы с прямой цепью; (-) н-гексан, (-), н-гептан, (-) н-октан; (б) и (г) алканы с разветвленной цепью; (-) 3-метилпентан, (-) 2,2-диметинентан, (-) 2,2,4-триметилпентан.

Перепечатано с разрешения Elsevier, Int. J. Heat Mass Transfer, 43 (2002) 75.

Рис. 2. Изменение коэффициента термодиффузии K _{T , 1} при концентрациях алканов x ₁ при 30 ° C и давлении окружающей среды : (а) алканы с прямой цепью; (-) н-гексан, (-), н-гептан, (-) н-октан; (б) алканы с разветвленной цепью; (-) 3-метилпентан, (-) 2,2-диметинентан, (-) 2,2,4-триметилпентан.

Перепечатано с разрешения Elsevier, Int. J. Heat Mass Transfer, 43 (2002) 75.

Степень связи q между тепловым и массовым потоками и коэффициент тепловой диффузии K _{T , 1} рассчитываются для всего диапазона составов по формулам. (71) и (72) и показаны на рис. 1 и 2; графики показывают четыре важных свойства сцепления. Во-первых, абсолютные значения q и K _{T , 1} достигают пиковых значений при определенной концентрации алкана, и эти пиковые значения уменьшаются с увеличением молекулярной массы.Во-вторых, концентрации растворенных веществ при максимальных значениях связывания постепенно уменьшаются по мере увеличения молекулярных масс. В-третьих, поведение алканов сходно до определенной концентрации растворенного вещества в зависимости от комбинированного воздействия разветвления и растворителя на q и K _{T, 1} (приблизительно через x ₁ = 0,2), но при более высоких концентрациях они ведут себя иначе. В-четвертых, абсолютная максимальная степень связывания мала, как и ожидалось, и разветвление алканов оказывает лишь незначительное влияние на явления связывания.

В таблицах 1 и 2 значения q и K _{T , 1} и концентрации, при которых возникают пики, показаны как для линейных, так и для разветвленных алканов по отдельности как в хлороформе, так и в растворителе. четыреххлористый углерод. Общая тенденция состоит в том, что разветвление молекулы растворенного вещества оказывает минимальное влияние на связывание рассматриваемых алканов. В таблицах также показано влияние растворителя на q и K _{T , 1} .Концентрации алканов, где встречаются пики q и K _{T , 1} , в хлороформе ниже, чем в четыреххлористом углероде. Как правило, пиковые значения q _max также меньше в четыреххлористом углероде, чем в хлороформе. Следовательно, оказывается, что концентрация важна для уровня сцепления в жидких смесях.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовать
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О MIT

Меню ↓

Поиск

Меню

Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!

Что вы ищете?

Увидеть больше результатов

Предложения или отзывы?

12.1 Условия статического равновесия — University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Определите физические условия статического равновесия.
• Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
• Объясните, как условия равновесия позволяют нам решать задачи статики.

Мы говорим, что твердое тело находится в состоянии равновесия , когда его линейное и угловое ускорение равны нулю относительно инерциальной системы отсчета.Это означает, что тело в состоянии равновесия может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в статическом равновесии , когда оно находится в состоянии покоя в нашей выбранной системе отсчета . Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы координат, тот же объект кажется, находится в равномерном движении с постоянной скоростью.Поскольку движение составляет относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.

Согласно второму закону движения Ньютона, линейное ускорение твердого тела вызывается действующей на него чистой силой, или

Здесь сумма всех внешних сил, действующих на тело, где м, — его масса, а

— это линейное ускорение его центра масс (концепция, которую мы обсуждали в статьях «Линейный импульс и столкновения по импульсу и столкновениям»).В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение на ноль на (Рисунок), мы получим следующее уравнение:

Первое условие равновесия

Первое условие равновесия для статического равновесия твердого тела выражает поступательное равновесие:

Первое условие равновесия (рисунок) — это условие равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.

Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов чистой силы:

Аналогично (рисунок) можно констатировать, что ускорение вращения

твердого тела вокруг фиксированной оси вращения вызывается чистым крутящим моментом, действующим на тело, или

Здесь

— это инерция вращения тела при вращении вокруг этой оси, и в сумме все крутящие моменты

внешних сил в (рисунок).В состоянии равновесия ускорение вращения равно нулю. Обнуляя правую часть (рисунок), мы получаем второе условие равновесия:

Второе состояние равновесия

Второе условие равновесия для статического равновесия твердого тела выражает вращательное равновесие:

Второе условие равновесия (рисунок) — это условие равновесия для крутящих моментов, с которым мы столкнулись при изучении динамики вращения.Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:

Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг любой оси.

Первое и второе условия равновесия указаны в конкретной системе отсчета.Первое условие включает только силы и поэтому не зависит от источника системы отсчета. Однако второе условие связано с крутящим моментом, который определяется как перекрестное произведение,

, где вектор положения

относительно оси вращения точки приложения силы входит в уравнение. Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, они также сохраняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент вокруг любой оси вращения по-прежнему равен нулю.Объяснение этому довольно простое.

Предположим вектор

— позиция начала новой инерциальной системы отсчета

в старой инерциальной системе отсчета S . Из нашего исследования относительного движения мы знаем, что в новой системе отсчета

вектор положения

точки, где действует сила

относится к

через уравнение

Теперь мы можем просуммировать все крутящие моменты

всех внешних сил в новой системе отсчета,

На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета, S , первый член исчезает из-за (Рисунок), а второй член исчезает из-за (Рисунок).Следовательно, мы видим, что чистый крутящий момент в любой инерциальной системе отсчета

равно нулю при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .

Практическое значение этого состоит в том, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала отсчета системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой проблемы. В одной системе координат математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе координат те же условия могут иметь более простую математическую форму, которую легко решить.Начало выбранной системы отсчета называется точкой поворота .

В самом общем случае условия равновесия выражаются шестью скалярными уравнениями ((Рисунок) и (Рисунок)). Для плоских задач равновесия с вращением вокруг фиксированной оси, которые мы рассматриваем в этой главе, мы можем сократить количество уравнений до трех. Стандартная процедура состоит в том, чтобы принять систему отсчета, в которой ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только компонент z , все силы, которые имеют ненулевые крутящие моменты, лежат в плоскости xy , и, следовательно, вклад в чистый крутящий момент поступает только от x — и y — составляющие внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия для сил и моментов:

, где суммирование ведется по всем внешним силам Н, , действующим на тело, и их крутящим моментам. На (Рисунок) мы упростили обозначения, опустив индекс z , но мы понимаем, что здесь суммирование ведется по всем вкладам вдоль оси z , которая является осью вращения.На (Рисунок) z — составляющая крутящего момента

от силы

это

где

— длина плеча рычага силы и

— это величина силы (как вы видели в разделе «Вращение с фиксированной осью»). Угол

— угол между векторами

и

измерение от вектора

в вектор

в направлении против часовой стрелки ((Рисунок)).При использовании (рисунок) мы часто вычисляем величину крутящего момента и присваиваем ее значение положительному значению

или отрицательно

в зависимости от направления вращения, вызванного только этим крутящим моментом. На (Рисунок) чистый крутящий момент представляет собой сумму членов, каждый член вычисляется из (Рисунок), и каждый член должен иметь правильный смысл . Аналогичным образом на (Рисунок) мы назначаем

Знак

для принудительного включения компонентов в

x — направление и

знак компонентов в

x — направление.Это же правило должно последовательно соблюдаться на (Рисунок) при вычислении составляющих силы по оси y .

Рисунок 12.2 Крутящий момент силы: (a) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.

Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес. На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из статей «Линейный импульс» и «Столкновения» о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс расположены в разных точках.Однако на практике даже такие большие объекты, как здания или круизные лайнеры, находятся в однородном гравитационном поле на поверхности Земли, где ускорение свободного падения имеет постоянную величину

.

В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.

Когда ЦМ расположен вне оси вращения, на объекте возникает чистый гравитационный момент . Гравитационный момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет опоры для его балансировки. Величина гравитационного момента зависит от того, как далеко от оси находится ЦМ. Например, в случае самосвала ((Рисунок)) ось поворота расположена на линии, где шины соприкасаются с поверхностью дороги.Если CM расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик. Легковые автомобили с низко расположенной КМ, близкой к тротуару, более устойчивы к опрокидыванию, чем грузовики.

Рисунок 12.3 Распределение массы влияет на положение центра масс (CM), где вектор веса

прилагается. Если центр тяжести находится в зоне опоры, погрузчик возвращается в исходное положение после опрокидывания [см. Левую панель в (b)].Но если центр тяжести находится за пределами зоны опоры, грузовик перевернется [см. Правую панель в (b)]. Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль на (а) находится в равновесии: низкое расположение центра тяжести затрудняет опрокидывание.

Пример

Центр тяжести автомобиля

Легковой автомобиль с колесной базой 2,5 м имеет 52% веса на передних колесах на ровной поверхности, как показано на (Рисунок). Где находится ЦМ этого автомобиля по отношению к задней оси?

Рисунок 12.4 Распределение веса между осями автомобиля. Где находится центр тяжести?

Стратегия

Вес автомобиля w нам неизвестен. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес, а 0,48 w толкает вниз на поверхность в точках контакта задних колес. Также точки соприкосновения отделены друг от друга расстоянием

В этих точках контакта автомобиль испытывает нормальные силы реакции с величиной

и

на передней и задней оси соответственно.Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес которого w действует на его ЦМ. ЦМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии x от точки, где

акта. Наша задача найти х . Таким образом, мы идентифицируем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для расширенного твердого тела, как показано на (Рисунок).

Рисунок 12.5 Диаграмма свободного тела для автомобиля четко указывает векторы сил, действующих на автомобиль, и расстояния до центра масс (CM). Когда CM выбран в качестве точки поворота, эти расстояния являются плечами рычагов нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.

Мы почти готовы записать условия равновесия (рисунок) — (рисунок) для автомобиля, но сначала мы должны определиться с системой отсчета.Предположим, мы выбрали ось x по длине кабины, ось y — вертикальную, а ось z — перпендикулярно этой плоскости xy . При таком выборе нам нужно только написать (рисунок) и (рисунок), потому что все компоненты y тождественно равны нулю. Теперь нам нужно определиться с расположением точки поворота. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы разместили ось вращения на CM, как показано на схеме свободного тела для автомобиля.На этом этапе мы готовы написать условия равновесия для автомобиля.

Решение

Каждое условие равновесия содержит только три члена, потому что их

силы, действующие на автомобиль. Первое условие равновесия (рисунок) читается как

.

Это условие тривиально выполняется, потому что, когда мы подставляем данные, (рисунок) становится

Второе условие равновесия (рисунок) читается как

.

где

— момент силы

— это гравитационный момент силы w и

— момент силы

Когда шарнир расположен в CM, гравитационный момент идентично нулю, потому что плечо рычага груза относительно оси, проходящей через CM, равно нулю.Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на (Рисунок) мы имеем

для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент

вызывает вращение вокруг оси CM по часовой стрелке, поэтому его направление отрицательное; и крутящий момент

вызывает вращение против часовой стрелки вокруг оси CM, поэтому его направление положительное. Имея эту информацию, запишем второе условие равновесия как

С помощью диаграммы свободного тела определяем величины силы

и

и соответствующие им рычаги

и

Теперь мы можем записать второе условие равновесия (рисунок) в явном виде в терминах неизвестного расстояния x :

Здесь вес w отменяется, и мы можем решить уравнение для неизвестного положения x CM.Ответ

Решение

Выбор шарнира в положении передней оси не меняет результата. Схема свободного тела для этого места поворота представлена ​​на (Рисунок). Для этого выбора точки поворота второе условие равновесия —

.

Когда мы подставляем величины, указанные на диаграмме, получаем

Ответ, полученный путем решения (рисунок), опять же:

Рисунок 12.6 Эквивалентная диаграмма свободного тела для автомобиля; точка поворота четко обозначена.

Значение

Этот пример показывает, что при решении задач статического равновесия мы можем выбрать точку поворота. Для различных вариантов выбора точки поворота у нас есть разные наборы условий равновесия, которые необходимо решить. Однако любой выбор приводит к одному и тому же решению проблемы.

Проверьте свое понимание

Решите (рисунок), выбрав шарнир в месте расположения задней оси.

[show-answer q = ”fs-id1163713143559 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163713143559 ″]

[/ hidden-answer]

Проверьте свое понимание

Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; (б) пеликан, который парит в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал двигателя припаркованного автомобиля.

[show-answer q = ”fs-id1163709667984 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163709667984 ″]

(б), (в)

[/ hidden-answer]

Особый случай статического равновесия возникает, когда все внешние силы на объект действуют на оси вращения или вдоль нее, или когда пространственное протяжение объекта можно не принимать во внимание. В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия (рисунок), потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться.Диаграмма свободного тела и стратегия решения задач для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона». В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.

Пример

Разрывное напряжение

Маленькая кастрюля массой 42,0 г поддерживается двумя струнами, как показано на (Рисунок). Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше, пока одна из струн не сломается.Какая это струна? Какую массу нужно добавить, чтобы это произошло?

Рисунок 12.7 Масса постепенно добавляется к кастрюле, пока одна из струн не лопнет.

Стратегия

Эта механическая система, состоящая из струн, масс и сковороды, находится в статическом равновесии. В частности, узел, который привязывает струны к кастрюле, находится в статическом равновесии. Узел можно рассматривать как точку; следовательно, нам нужно только первое условие равновесия. Три силы, тянущие к узлу, — это натяжение

.

в районе 5.Струна 0 см, натяжение

в тетиве 10,0 см, а гиря

чаши, удерживающей массы. Мы принимаем прямоугольную систему координат с осью y , направленной противоположно направлению силы тяжести, и рисуем диаграмму свободного тела для узла (см. (Рисунок)). Чтобы найти компоненты натяжения, необходимо определить направления углов

и

, что струны образуют горизонтальное направление оси x .Как вы можете видеть на (Рисунок), струны составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на (Рисунок), и найти синус и косинус углов

.

и

Затем мы можем разложить напряжения на их прямоугольные составляющие, подставить в первое условие равновесия ((Рисунок) и (Рисунок)) и решить для напряжений в струнах. Первой порвется струна с большим натяжением.

Рисунок 12.8 Схема свободного тела для узла на (Рисунок).

Решение

Вес w , тянущий за узел, связан с массой M чаши и массой m , добавленной к чаше, или

С помощью диаграммы свободного тела на (Рисунок), мы можем установить условия равновесия для узла:

Из диаграммы свободного тела, величины компонентов в этих уравнениях равны

Подставляем эти компоненты в условия равновесия и упрощаем.Затем мы получаем два уравнения равновесия для натяжений:

Уравнение равновесия для направления x говорит нам, что натяжение

в 5,0-сантиметровой тетиве вдвое превышает натяжение

в шнур длиной 10,0 см. Таким образом, более короткая струна порвется. Когда мы используем первое уравнение для исключения

из второго уравнения получаем соотношение между массами

на сковороде и натяжной

в более короткой строке:

Струна рвется, когда натяжение достигает критического значения

Предыдущее уравнение может быть решено для критической массы м , которая разрывает струну:

Значение

Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри лифта, поднимающегося вверх.Пока лифт движется вверх с постоянной скоростью, результат остается неизменным, потому что вес

не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес

становится больше на кажущуюся массу из-за ускорения лифта. Тем не менее, во всех случаях более короткая струна рвется первой.

Сводка

• Тело находится в равновесии, когда оно остается либо в равномерном движении (поступательном и вращательном), либо в состоянии покоя.Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.
• Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил была равна нулю (второе условие равновесия). Эти два условия должны одновременно выполняться в состоянии равновесия. Если один из них не удовлетворен, тело не находится в равновесии.
• Диаграмма свободного тела для тела — полезный инструмент, который позволяет нам правильно подсчитать все вклады от всех внешних сил и моментов, действующих на тело. Диаграммы свободного тела для равновесия вытянутого твердого тела должны указывать точку поворота и плечи рычага действующих сил по отношению к оси вращения.

Концептуальные вопросы

Что вы можете сказать о скорости движущегося тела, находящегося в динамическом равновесии?

[show-answer q = ”fs-id1163713268541 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163713268541 ″]

постоянная

[/ hidden-answer]

При каких условиях вращающееся тело может находиться в равновесии? Привести пример.

Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?

[show-answer q = ”fs-id1163713358733 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163713358733 ″]

Величина и направление силы, а ее плечо рычага

[/ hidden-answer]

Механики иногда кладут кусок трубы на рукоятку гаечного ключа, пытаясь открутить очень тугой болт. Как это помогает?

Для следующих четырех задач оцените утверждение как истинное или ложное и объясните свой ответ.

Если на объект действует только одна внешняя сила (или крутящий момент), он не может находиться в равновесии.

[показывать-ответ q = ”fs-id1163713282665 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713282665 ″]

Верно, поскольку в этом случае сумма сил не может быть равна нулю, если сама сила не равна нулю.

[/ hidden-answer]

Если объект находится в равновесии, на него должно действовать четное число сил.

Если на объект действует нечетное количество сил, объект не может находиться в равновесии.

[show-answer q = ”fs-id1163709692362 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163709692362 ″]

Ложь, если силы складываются в ноль как векторы, тогда может быть достигнуто равновесие.

[/ hidden-answer]

Тело, движущееся по окружности с постоянной скоростью, находится в равновесии вращения.

Для чего нужен длинный и гибкий шест, который переносят канатоходцы?

[show-answer q = ”fs-id1163713272740 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id1163713272740 ″]

Помогает канатоходцу сохранять равновесие.

[/ hidden-answer]

Проблемы

При затяжке болта вы нажимаете гаечный ключ перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прикладываете относительно центра болта?

При открытии двери вы нажимаете на нее перпендикулярно с усилием 55,0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете к петлям?

[показывать-ответ q = ”fs-id1163713470139 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713470139 ″]

[/ hidden-answer]

Найдите величину натяжения каждого поддерживающего троса, показанного ниже.В каждом случае вес подвешенного тела составляет 100,0 Н, а массой кабелей можно пренебречь.

Какая сила должна быть приложена в точке P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначительный.

[show-answer q = ”264812 ″] Показать ответ [/ show-answer]
[hidden-answer a =” 264812 ″] 153,4 ° [/ hidden-answer]

Можно ли приложить силу при P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначительный.

Двое детей толкают противоположные стороны двери во время игры. Оба толкаются горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.

[показывать-ответ q = ”fs-id1163713183876 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1163713183876 ″]

23.3 N

[/ hidden-answer]

Небольшой внедорожник массой 1000 кг имеет колесную базу 3,0 м. Если 60%, если его вес приходится на передние колеса, насколько далеко позади передних колес находится центр масс фургона?

Унифицированные качели сбалансированы в центре масс, как показано ниже. Маленький мальчик справа имеет массу 40,0 кг. Какая масса у его друга?

[show-answer q = ”

5 ″] Показать ответ [/ show-answer]
[hidden-answer a =”

5 ″] 80.0 кг [/ hidden-answer]

Глоссарий

центр тяжести

точка, к которой прикреплен вектор весов

равновесие

Тело находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета

первое условие равновесия

выражает поступательное равновесие; все внешние силы, действующие на тело, уравновешиваются и их векторная сумма равна нулю

гравитационный момент

крутящий момент на корпусе, вызванный его весом; это происходит, когда центр тяжести тела не расположен на оси вращения

второе условие равновесия

выражает вращательное равновесие; все моменты из-за внешних сил, действующих на тело, уравновешиваются, и их векторная сумма равна нулю

статическое равновесие

тело находится в статическом равновесии, когда оно покоится в выбранной нами инерциальной системе отсчета

12.2 примера статического равновесия — University Physics Volume 1

Силы в предплечье

Тяжелоатлет держит в предплечье гирю в 50,0 фунтов (эквивалент 222,4 Н), как показано на рисунке 12.11. Его предплечье расположено под углом β = 60 ° β = 60 ° по отношению к его плечу. Предплечье поддерживается сокращением двуглавой мышцы, которое вызывает крутящий момент вокруг локтя. Предполагая, что напряжение в двуглавой мышце действует в вертикальном направлении, определяемом силой тяжести, какое напряжение должна прикладывать мышца, чтобы удерживать предплечье в показанном положении? Какая сила действует на локтевой сустав? Предположим, что вес предплечья незначителен.Дайте окончательные ответы в единицах СИ.

Рисунок 12.11 Предплечье вращается вокруг локтя ( E ) за счет сокращения двуглавой мышцы, что вызывает напряжение T → M.T → M.

Стратегия

Мы выделяем три силы, действующие на предплечье: неизвестная сила F → F → в локте; неизвестное напряжение T → MT → M в мышце; и вес w → w → с величиной w = 50 фунтов. w = 50 фунтов. Мы принимаем систему отсчета с осью x вдоль предплечья и шарниром в локтевом суставе. Вертикальное направление — это направление веса, которое совпадает с направлением плеча.Ось x составляет угол β = 60 ° β = 60 ° с вертикалью. Ось y перпендикулярна оси x . Теперь создадим диаграмму свободного тела для предплечья. Сначала мы рисуем оси, точку поворота и три вектора, представляющие три идентифицированные силы. Затем мы определяем угол ββ и представляем каждую силу ее составляющими x и y , не забывая перечеркнуть исходный вектор силы, чтобы избежать двойного счета. Наконец, мы помечаем силы и их рычаги.Схема свободного тела для предплечья показана на рисунке 12.12. На этом этапе мы готовы создать условия равновесия для предплечья. Каждая сила имеет компоненты x и y ; следовательно, у нас есть два уравнения для первого условия равновесия, по одному уравнению для каждого компонента чистой силы, действующей на предплечье.

Рисунок 12.12 Схема свободного тела для предплечья: Ось находится в точке E (локоть).

Обратите внимание, что в нашей системе отсчета вклад во второе условие равновесия (для крутящих моментов) происходит только от y -компонент сил, потому что все x -компоненты сил параллельны плечам их рычагов, поэтому что для любого из них sinθ = 0 sinθ = 0 в уравнении 12.10. Для компонентов y мы имеем θ = ± 90 ° θ = ± 90 ° в уравнении 12.10. Также обратите внимание, что крутящий момент силы в локте равен нулю, потому что эта сила приложена к шарниру. Таким образом, вклад в чистый крутящий момент вносят только крутящие моменты TyTy и wy.wy.

Решение

Из диаграммы свободного тела видно, что составляющая x чистой силы удовлетворяет уравнению
+ Fx + Tx − wx = 0 + Fx + Tx − wx = 0

12,21

и y -компонент чистой силы удовлетворяет

+ Fy + Ty − wy = 0.+ Fy + Ty − wy = 0.

12,22

Уравнение 12.21 и уравнение 12.22 — это два уравнения первого условия равновесия (для сил). Затем мы читаем из диаграммы свободного тела, что чистый крутящий момент вдоль оси вращения составляет

+ rTTy − rwwy = 0. + rTTy − rwwy = 0.

12,23

Уравнение 12.23 является вторым условием равновесия (для крутящих моментов) для предплечья. На диаграмме свободного тела показано, что длина плеч рычага rT = 1,5 дюйма, rT = 1,5 дюйма. и rw = 13,0 дюйма. rw = 13,0 дюйма. На этом этапе нам не нужно переводить дюймы в единицы СИ, поскольку эти единицы согласованы в уравнении 12.23, они отменяются. Снова используя диаграмму свободного тела, находим величины составляющих сил:

Fx = Fcosβ = Fcos60 ° = F / 2Tx = Tcosβ = Tcos60 ° = T / 2wx = wcosβ = wcos60 ° = w / 2Fy = Fsinβ = Fsin60 ° = F3 / 2Ty = Tsinβ = Tsin60 ° = T3 / 2wy = wsinβ = wsin60 ° = w3 / 2.Fx = Fcosβ = Fcos60 ° = F / 2Tx = Tcosβ = Tcos60 ° = T / 2wx = wcosβ = wcos60 ° = w / 2Fy = Fsinβ = Fsin60 ° = F3 / 2Ty = Tsinβ = Tsin60 ° = T3 / 2wy = wsinβ = wsin60 ° = w3 / 2.

Мы подставляем эти величины в Уравнение 12.21, Уравнение 12.22 и Уравнение 12.23, чтобы получить, соответственно,

F / 2 + T / 2-w / 2 = 0F3 / 2 + T3 / 2-w3 / 2 = 0rTT3 / 2-rww3 / 2 = 0.F / 2 + T / 2-w / 2 = 0F3 / 2 + T3 / 2-w3 / 2 = 0rTT3 / 2-rww3 / 2 = 0.

Когда мы упрощаем эти уравнения, мы видим, что остались только два независимых уравнения для двух неизвестных величин силы, F и T , потому что уравнение 12.21 для компонента x эквивалентно уравнению 12.22 для у -компонент. Таким образом, мы получаем первое условие равновесия для сил

и второе условие равновесия моментов

rTT-rww = 0. rTT-rww = 0.

12,25

Величина напряжения мышцы определяется решением уравнения 12.25:

.
T = rwrTw = 13,01,5 (50 фунтов) = 43313 фунтов 433,3 фунта T = rwrTw = 13,01,5 (50 фунтов) = 43313 фунтов 433,3 фунта.

Сила в колене получается путем решения уравнения 12.24:

F = w-T = 50,0 фунта-433,3 фунта = -383,3 фунта F = w-T = 50,0 фунта-433,3 фунта = -383,3 фунта.

Отрицательный знак в уравнении говорит нам, что действительная сила в локте антипараллельна рабочему направлению, принятому для построения диаграммы свободного тела. В окончательном ответе мы конвертируем силы в единицы силы СИ.Ответ

F = 383,3 фунта = 383,3 (4,448N) = 1705N вниз T = 433,3 фунта = 433,3 (4,448N) = 1927N вверх. F = 383,3 фунта = 383,3 (4,448N) = 1705N вниз T = 433,3 фунта = 433,3 (4,448N) = 1927N вверх.

Значение

Здесь стоит отметить два важных момента. Первый касается преобразования в единицы СИ, который может быть выполнен в самом конце решения, если мы сохраняем согласованность в единицах измерения. Второй важный вопрос касается шарнирных соединений, например, локтевого. При первоначальном анализе проблемы следует всегда предполагать, что шарнирные соединения прикладывают силу в произвольном направлении , а затем вы должны решать для всех компонентов шарнирной силы независимо.В этом примере сила в локтевом суставе оказывается вертикальной, потому что задача предполагает, что напряжение бицепса также является вертикальным. Однако такое упрощение не является общим правилом.

Решение

Предположим, мы используем систему отсчета с направлением оси y вдоль 50-фунтового груза и шарнира, расположенного в колене. В этой системе отсчета все три силы имеют только y -компонент, поэтому у нас есть только одно уравнение для первого условия равновесия (для сил).Нарисуем диаграмму свободного тела для предплечья, как показано на рисунке 12.13, с указанием оси поворота, действующих сил и их плеч рычагов по отношению к оси поворота, а также углов θTθT и θwθw, по которым силы T → MT → M и w → w → (соответственно) сделать своими рычагами. В определении крутящего момента, приведенном в уравнении 12.10, угол θTθT — это угол направления вектора T → M, T → M, отсчитываемый против часовой стрелки на от радиального направления плеча рычага, который всегда направлен от оси вращения. По такому же соглашению угол θwθw измеряется против часовой стрелки на от радиального направления плеча рычага до вектора w →.w →. При таком подходе ненулевые крутящие моменты легче всего вычислить путем прямой подстановки в уравнение 12.10 следующим образом:
τT = rTTsinθT = rTTsinβ = rTTsin60 ° = + rTT3 / 2τw = rwwsinθw = rwwsin (β + 180 °) = — rwwsinβ = −rww3 / 2.τT = rTTsinθT = rTTsinβ = rTTsin60 ° = β + 180 °) = — rwwsinβ = −rww3 / 2.

Рисунок 12.13 Схема свободного тела для предплечья для эквивалентного решения. Ось находится в точке Е (колено).

Второе условие равновесия, τT + τw = 0, τT + τw = 0, теперь может быть записано как

rTT3 / 2-rww3 / 2 = 0.rTT3 / 2-rww3 / 2 = 0.

12,26

Из диаграммы свободного тела первое условие равновесия (для сил) —

−F + T − w = 0. −F + T − w = 0.

12,27

Уравнение 12.26 идентично уравнению 12.25 и дает результат T = 433,3 фунта T = 433,3 фунта. Уравнение 12.27 дает

F = T − w = 433,3 фунта − 50,0 фунта = 383,3 фунта F = T − w = 433,3 фунта − 50,0 фунта = 383,3 фунта.

Мы видим, что эти ответы идентичны нашим предыдущим ответам, но второй выбор системы отсчета приводит к эквивалентному решению, которое является более простым и быстрым, поскольку не требует разделения сил на их прямоугольные составляющие.

Равновесие сил

Очень простая концепция при работе с
силы
это идея равновесия или баланса .
В общем, на объект могут действовать несколько сил.
в то же время.
Сила — это
векторная величина
что значит
что он имеет как величину (размер), так и направление, связанное с ним.
Если размер и направление сил, действующих на объект, равны
точно сбалансировано, тогда на объект не действует чистая сила
и объект находится в состоянии равновесия .Поскольку нет никакой чистой силы, действующей на объект в равновесии,
затем из Ньютона
первый закон
движения, неподвижный объект останется в покое, а объект в движении
останется в движении.

Начнем с простейшего примера двух сил, действующих на объект.
Затем мы покажем примеры
три силы, действующие на планер, и
четыре силы, действующие на летательный аппарат с двигателем.

В примере 1 на слайде мы показываем синий шар, который толкает
две силы, обозначенные Force # 1 F1 и Force # 2 F2 .Помни это
силы — векторные величины, и направление важно.
Две силы одинаковой величины, но разные направления
не равны силы. По факту,

F1 = — F2

для показанной системы координат
с буквой X под мячом. Если сложить силы, действующие на мяч,
получаем силовое уравнение слева:

F1 + F2 = F сеть = 0

где F net — чистая сила, действующая на мяч.Поскольку результирующая сила равна нулю, силы в примере 1 равны
действует в равновесии.

В Примере 1 на мяч не действует чистая сила, так как мяч изначально находится в состоянии покоя.
(скорость равна нулю), мяч останется в покое согласно Ньютону.
первый закон
движения. Если бы мяч двигался с постоянной скоростью, он продолжал бы двигаться.
с той же скоростью.

В Примере 2 мы увеличили величину Силы №1, так что она намного больше.
чем Force # 2.Силы больше не находятся в равновесии.
Уравнение силы остается прежним, но результирующая сила не равна нулю.
Величина чистой силы определяется по формуле:

F1> — F2

F1 + F2 = F нетто

| F net | = | F1 | — | F2 |

где «| |» символы указывают величину количества, заключенного между концами.
Направление чистой силы будет в положительном направлении X , потому что F1
больше F2 .По мнению Ньютона
второй закон
движения мяч начинал ускоряться вправо. Потому что в
Пример 2, силы не находятся в равновесии.

Навигация ..

Руководство для начинающих Домашняя страница

Термодинамическая концепция равновесия

Интуитивно концепция равновесия передает сообщение о том, что что-то «уравновешивается».«Равновесие описывает состояние исчезающих движущих сил или градиентов, когда все остается как есть. Если система находится в равновесии, она сохраняет свое текущее состояние, потому что нет движущих сил, вызывающих какие-либо изменения.

Если два материала имеют одинаковую температуру, мы говорим, что они находятся в тепловом равновесии . Теплообмен не происходит, потому что нет температурных градиентов. Например, жидкая и паровая фаза находятся в тепловом равновесии , когда:

Tl = Tv Это уравнение не отображается должным образом из-за несовместимого браузера.См. Технические требования в Ориентации для получения списка совместимых браузеров.

(16,1)

Мы достигаем механического равновесия , если два вещества находятся под одинаковым давлением. Объемного движения жидкости не происходит, потому что нет градиентов давления . Механическое равновесие жидкая и паровая фаза происходит, когда:

Pl = Pv Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,2)

Для того чтобы термодинамическая система находилась в равновесии, все интенсивные (температура, давление) и экстенсивные термодинамические свойства (U, G, A, H, S и т. Д.) Должны быть постоянными. Следовательно, полное изменение любого из этих свойств (dℑЭто уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».
) в состоянии равновесия должен быть равен нулю.

Теперь мы хотели бы иметь понятие термодинамического равновесия для парожидкостного равновесия.Рассмотрим замкнутую гетерогенную парожидкостную систему. Любые изменения общего свойства системы будут результатом изменений этого свойства в жидкой фазе плюс изменения этого свойства в паровой фазе.

dℑ (всего) = dℑ (жидкость) + dℑ (пар) Это уравнение не отображается должным образом из-за несовместимости браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,3)

В этом случае жидкость и пар сами по себе не являются замкнутыми системами; они могут обмениваться материей между собой, но не с окружающей средой.Чтобы подробнее разобраться в концепции равновесия, давайте посмотрим на уравнение (15.26c). Поскольку он записывается в терминах изменений давления и температуры, двух измеряемых лабораторных величин, это самое «дружелюбное» из всех фундаментальных уравнений. Пишем для обеих фаз:

dℑ (жидкость) = (VdP − SdT) l + ∑iμildnil Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,4a)

dG (steam) = (VdP − SdT) v + ∑iμivdniv Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,4b)

В (16.3) для ℑ = GT это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».
, получаем:

dG (total) = dG (жидкость) + dG (пар) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16.5)

Следовательно,

dG (total) = (VdP − SdT) l + (VdP − SdT) v + ∑iμildnil + ∑iμivdniv Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,16)

Поскольку в состоянии равновесия все экстенсивные свойства, такие как G, должны оставаться постоянными, dG ^(total) должен быть равен нулю. Для этого и при проверке уравнения (16.6) условия термодинамического равновесия следующие:

dP = 0 [Механическое равновесие] Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,7)

EdT = 0 [Тепловое равновесие] Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,8)

∑iμildnil + ∑iμivdniv = 0 [μi критерий равновесия] Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,9)

Также можно доказать, что в состоянии равновесия полная свободная энергия системы (G ^(общая) ) должна принимать минимальное значение; это подтверждает тот факт, что dG ^(всего) = 0 в состоянии равновесия. Критерий минимальной энергии Гиббса для равновесия — это повторение второго закона термодинамики, из которого мы знаем, что энтропия системы в состоянии равновесия должна быть максимальной, учитывая все возможные состояния равновесия.

В некотором смысле разумно, что для условия истинного равновесия не должно быть ни давления, ни градиентов температуры (уравнения 16.7 и 16.8). Это потому, что равновесие — это, по крайней мере, состояние отсутствия градиентов. Но что пытается нам сказать уравнение (16.9)? Чтобы прояснить уравнение (16.9), напомним, что мы имеем дело с замкнутой системой, следовательно, общее количество молей на вид:

ni (total) = ni (l) + ni (v) Это уравнение не отображается должным образом из-за несовместимости браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,10)

должен быть постоянным (мы не допускаем химических реакций в системе).Таким образом мы пишем:

dni (total) = dni (l) + dni (v) = 0 Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,11)

Следовательно,

dni (v) = — dni (l) Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,12)

(16,12) в (16,11) дает:

∑i (μi (l) −μi (v)) dni (v) = 0 Это уравнение не отображается должным образом из-за несовместимого браузера.Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,13)

Чтобы уравнение (16.13) выполнялось,

μi (l) = μi (v) для всех i = 1,2, … nc Это уравнение не отображается должным образом из-за несовместимого браузера. Список совместимых браузеров см. В разделе «Технические требования в ориентации».

(16,14)

Затем мы пришли к критериям парожидкостного равновесия для системы при постоянном давлении и температуре: химический потенциал всех частиц должен быть одинаковым в обеих фазах. Мы можем обобщить это открытие на любое количество фаз, для которых химический потенциал каждого вида должен быть одинаковым во всех фазах. Поскольку химический потенциал является движущей силой, которая перемещает частицы из одной фазы в другую, уравнение (16.14) является физически разумным. Если химический потенциал веществ в одной фазе такой же, как и в другой, то движущая сила равна нулю и, следовательно, нетто-перенос частиц в равновесии.

12.2: Условия статического равновесия

Цели обучения

• Определите физические условия статического равновесия.
• Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
• Объясните, как условия равновесия позволяют нам решать задачи статики.

Мы говорим, что твердое тело находится в состоянии равновесия , когда его линейное и угловое ускорение равны нулю относительно инерциальной системы отсчета. Это означает, что тело в состоянии равновесия может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в статическом равновесии , когда оно находится в состоянии покоя в нашей выбранной системе отсчета .Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным, то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы координат, тот же объект кажется, находится в равномерном движении с постоянной скоростью. Поскольку движение составляет относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.

Согласно второму закону движения Ньютона, линейное ускорение твердого тела вызывается действующей на него чистой силой, или

\ [\ sum_ {k} \ vec {F} _ {k} = m \ vec {a} _ {CM} \ ldotp \ label {12.1} \]

Здесь сумма всех внешних сил, действующих на тело, где m — это его масса, а \ (\ vec {a} _ {CM} \) — линейное ускорение его центра масс (концепция, которую мы обсуждали в Linear Импульс и столкновения по импульсу и столкновениям). В состоянии равновесия линейное ускорение равно нулю.Если мы установим нулевое ускорение в уравнении \ ref {12.1}, мы получим следующее уравнение:

Первое условие равновесия

Первое условие равновесия для статического равновесия твердого тела выражает поступательное равновесие:

\ [\ sum_ {k} \ vec {F} _ {k} = \ vec {0} \ ldotp \ label {12.2} \]

Первое условие равновесия, Equation \ ref {12.2}, является условием равновесия для сил, с которым мы столкнулись при изучении приложений законов Ньютона.

Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов чистой силы:

\ [\ sum_ {k} F_ {kx} = 0, \; \ sum_ {k} F_ {ky} = 0, \; \ sum_ {k} F_ {kz} = 0 \ ldotp \ label {12.3} \]

Аналогично уравнению \ ref {12.1}, мы можем утверждать, что ускорение вращения \ (\ vec {\ alpha} \) твердого тела вокруг фиксированной оси вращения вызывается чистым крутящим моментом, действующим на тело, или

\ [\ sum_ {k} \ vec {\ tau} _ {k} = I \ vec {\ alpha} \ ldotp \ label {12.4} \]

Здесь I — инерция вращения тела при вращении вокруг этой оси, а сумма всех моментов \ (\ vec {\ tau} _ {k} \) внешних сил в уравнении \ ref {12.2} составляет более всех моментов. В состоянии равновесия ускорение вращения равно нулю. Обнуляя правую часть уравнения \ ref {12.4}, мы получаем второе условие равновесия:

Второе состояние равновесия

Второе условие равновесия для статического равновесия твердого тела выражает вращательное равновесие:

\ [\ sum_ {k} \ vec {\ tau} _ {k} = \ vec {0} \ ldotp \ label {12.5} \]

Второе условие равновесия, Equation \ ref {12.5}, является условием равновесия для крутящих моментов, с которым мы столкнулись при изучении динамики вращения. Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:

\ [\ sum_ {k} \ tau_ {kx} = 0, \; \ sum_ {k} \ tau_ {ky} = 0, \; \ sum_ {k} \ tau_ {kz} = 0 \ ldotp \ label {12.6} \]

Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг любой оси. Первое и второе условия равновесия указаны в конкретной системе отсчета. Первое условие включает только силы и поэтому не зависит от источника системы отсчета. Однако второе условие включает крутящий момент, который определяется как перекрестное произведение: \ (\ vec {\ tau} _ {k} = \ vec {r} _ {k} \ times \ vec {F} _ {k} \ ), где вектор положения \ (\ vec {r} _ {k} \) относительно оси вращения точки приложения силы входит в уравнение.Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, они также сохраняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент вокруг любой оси вращения по-прежнему равен нулю. Объяснение этому довольно простое.

Предположим, что вектор \ (\ vec {R} \) — это позиция начала координат новой инерциальной системы отсчета S ‘в старой инерциальной системе отсчета S.Из нашего исследования относительного движения мы знаем, что в новой системе отсчета S ′ вектор положения \ (\ vec {r} ′ _ {k} \) точки, в которой сила \ (\ vec {F} _ {k} \) связано с \ (\ vec {r} _ {k} \) через уравнение

\ [\ vec {r} ‘_ {k} = \ vec {r} _ {k} — \ vec {R} \ ldotp \]

Теперь мы можем просуммировать все моменты \ (\ vec {\ tau} ‘_ {k} = \ vec {r}’ _ {k} \ times \ vec {F} _ {k} \) всех внешних сил в новый опорный кадр, S ‘:

\ [\ sum_ {k} \ vec {\ tau} ‘_ {k} = \ sum_ {k} \ vec {r}’ _ {k} \ times \ vec {F} _ {k} = \ sum_ { k} (\ vec {r} _ {k} — \ vec {R}) \ times \ vec {F} _ {k} = \ sum_ {k} \ vec {r} _ {k} \ times \ vec { F} _ {k} — \ sum_ {k} \ vec {R} \ times \ vec {F} _ {k} = \ sum \ vec {\ tau} _ {k} — \ vec {R} \ times \ сумма_ {k} \ vec {F} _ {k} = \ vec {0} \ ldotp \]

На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета S первый член исчезает из-за Уравнения \ ref {12.5}, а второй член обращается в нуль из-за уравнения \ ref {12.2}. Следовательно, мы видим, что чистый крутящий момент в любой инерциальной системе отсчета S ‘равен нулю при условии, что оба условия равновесия выполняются в инерциальной системе отсчета \ ref {S}.

Практическое значение этого состоит в том, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала отсчета системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой проблемы.В одной системе координат математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе координат те же условия могут иметь более простую математическую форму, которую легко решить. Исходная точка выбранной системы отсчета называется точкой поворота.

В наиболее общем случае условия равновесия выражаются шестью скалярными уравнениями (Equations \ ref {12.3} и \ ref {12.6}). Для плоских задач равновесия с вращением вокруг фиксированной оси, которые мы рассматриваем в этой главе, мы можем сократить количество уравнений до трех.Стандартная процедура состоит в том, чтобы принять систему отсчета, в которой ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только z-компоненту, все силы, которые имеют ненулевые крутящие моменты, лежат в плоскости xy, и, следовательно, вклады в чистый крутящий момент происходят только от x- и y-компонентов внешних силы. Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy, мы имеем следующие три условия равновесия для сил и моментов:

\ [F_ {1x} + F_ {2x} + \ cdots + F_ {Nx} = 0 \ label {12.7} \]

\ [F_ {1y} + F_ {2y} + \ cdots + F_ {Ny} = 0 \ label {12.8} \]

\ [\ tau_ {1} + \ tau_ {2} + \ cdots + \ tau_ {N} = 0 \ label {12.9} \]

, где суммирование ведется по всем N внешним силам, действующим на тело, и по их моментам. В уравнении \ ref {12.9} мы упростили обозначения, опустив индекс z, но мы понимаем, что здесь суммирование ведется по всем вкладам вдоль оси z, которая является осью вращения. В уравнении \ ref {12.9} z-составляющая крутящего момента \ (\ vec {\ tau} _ {k} \) от силы \ (\ vec {F} _ {k} \) равна

\ [\ tau_ {k} = r_ {k} F_ {k} \ sin \ theta \ label {12.10} \]

, где r _k — длина плеча рычага силы, а F _k — величина силы (как вы видели в разделе «Вращение с фиксированной осью»). Угол \ (\ theta \) — это угол между векторами \ (\ vec {r} _ {k} \) и \ (\ vec {F} _ {k} \), измеряемый от вектора \ (\ vec {r} _ {k} \) в вектор \ (\ vec {F} _ {k} \) в направлении против часовой стрелки (рисунок \ (\ PageIndex {1} \)). При использовании уравнения \ ref {12.10} мы часто вычисляем величину крутящего момента и назначаем ее значение как положительное (+) или отрицательное (-), в зависимости от направления вращения, вызванного только этим крутящим моментом.В уравнении \ ref {12.9} чистый крутящий момент представляет собой сумму членов, каждый член вычисляется из уравнения \ ref {12.10}, и каждый член должен иметь правильное значение . Точно так же в уравнении \ ref {12.7} мы назначаем знак + компонентам силы в направлении + x и знак — компонентам в направлении — x. Это же правило должно последовательно соблюдаться в уравнении \ ref {12.8} при вычислении компонентов силы по оси y.

Рисунок \ (\ PageIndex {1} \): Крутящий момент силы: (а) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен ось вращения.(b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.

Примечание

Просмотрите эту демонстрацию, чтобы увидеть, как две силы действуют на твердый квадрат в двух измерениях. Всегда выполняются условия статического равновесия, задаваемые уравнениями \ ref {12.7} — уравнениями \ ref {12.9}. Вы можете изменять величину сил и их плеч рычагов и наблюдать за тем, как эти изменения влияют на квадрат.

Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес. На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из статей «Линейный импульс» и «Столкновения» о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс расположены в разных точках.Однако на практике даже такие большие объекты, как здания или круизные лайнеры, находятся в однородном гравитационном поле на поверхности Земли, где ускорение свободного падения имеет постоянную величину g = 9,8 м / с ² . В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей этой главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.

Когда ЦМ расположен вне оси вращения, на объекте возникает чистый гравитационный момент . Гравитационный момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет опоры для его балансировки. Величина гравитационного момента зависит от того, как далеко от оси находится ЦМ. Например, в случае с самосвалом (рис. \ (\ PageIndex {2} \)) точка поворота расположена на линии контакта шин с поверхностью дороги.Если CM расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик. Легковые автомобили с низко расположенной КМ, близкой к тротуару, более устойчивы к опрокидыванию, чем грузовики.

Рисунок \ (\ PageIndex {2} \): распределение массы влияет на положение центра масс (CM), к которому прикреплен вектор веса \ (\ vec {w} \). Если центр тяжести находится в зоне опоры, погрузчик возвращается в исходное положение после опрокидывания [см. Левую панель в (b)].Но если центр тяжести находится за пределами зоны опоры, грузовик перевернется [см. Правую панель в (b)]. Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль на (а) находится в равновесии: низкое расположение центра тяжести затрудняет опрокидывание.

Примечание

Если вы наклоните ящик так, чтобы один край оставался в контакте со столом под ним, тогда один край основания опоры станет шарниром. Пока центр тяжести коробки остается над основанием опоры, гравитационный момент вращает коробку обратно в исходное положение устойчивого равновесия.Когда центр тяжести перемещается за пределы основания опоры, гравитационный момент вращает коробку в противоположном направлении, и коробка опрокидывается. Просмотрите эту демонстрацию, чтобы поэкспериментировать со стабильным и нестабильным положением коробки.

Пример 12.1: Центр тяжести автомобиля

Легковой автомобиль с колесной базой 2,5 м имеет 52% веса на передних колесах на ровной поверхности, как показано на Рисунке 12.4. Где находится ЦМ этого автомобиля по отношению к задней оси?

Рисунок \ (\ PageIndex {3} \): Распределение веса между осями автомобиля.Где находится центр тяжести?

Стратегия

Вес автомобиля w неизвестен. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52w давит на поверхность в точках контакта передних колес, а 0,48w давит на поверхность в точках контакта задних колес. Также точки контакта удалены друг от друга на расстояние d = 2,5 м. В этих точках контакта автомобиль испытывает нормальные силы реакции с величиной F _F = 0.52w и F _R = 0,48w на передней и задней оси соответственно. Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес w которого действует на его ЦМ. КМ находится где-то между точками действия нормальных сил реакции, где-то на расстоянии x от точки, в которой действует F _R . Наша задача найти x. Таким образом, мы идентифицируем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для расширенного твердого тела, как показано на рисунке \ (\ PageIndex {4} \).

Рисунок \ (\ PageIndex {4} \): Диаграмма свободного тела для автомобиля четко указывает векторы сил, действующих на автомобиль, и расстояния до центра масс (CM). Когда CM выбран в качестве точки поворота, эти расстояния являются плечами рычагов нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.

Мы почти готовы записать условия равновесия Уравнение \ ref {12.7} — Уравнение \ ref {12.9} для автомобиля, но сначала мы должны определиться с системой отсчета. Предположим, мы выбрали ось x по длине автомобиля, ось y — вертикаль, а ось z — перпендикулярно этой плоскости xy. При таком выборе нам нужно только написать Equation \ ref {12.7} и Equation \ ref {12.9}, потому что все y-компоненты тождественно равны нулю. Теперь нам нужно определиться с расположением точки поворота. Мы можем выбрать любую точку в качестве местоположения оси вращения (ось z). Предположим, мы разместили ось вращения на CM, как показано на схеме свободного тела для автомобиля.На этом этапе мы готовы написать условия равновесия для автомобиля.

Решение

Каждое условие равновесия содержит только три члена, потому что на автомобиль действуют N = 3 силы. Первое условие равновесия, Уравнение \ ref {12.7}, читается как

.

\ [+ F_ {F} — w + F_ {R} = 0 \ ldotp \ label {12.11} \]

Это условие тривиально выполняется, потому что, когда мы подставляем данные, уравнение \ ref {12.11} становится + 0,52w — w + 0,48w = 0. Второе условие равновесия, уравнение \ ref {12.9}, читается как

.

\ [\ tau_ {F} + \ tau_ {w} + \ tau_ {R} = 0 \ label {12.12} \]

, где \ (\ tau_ {F} \) — момент силы F _F , \ (\ tau_ {w} \) — гравитационный момент силы w, а \ (\ tau_ {R} \) — момент силы F _R . Когда шарнир расположен в CM, гравитационный момент идентично нулю, потому что плечо рычага веса относительно оси, проходящей через CM, равно нулю. Линии действия обеих нормальных сил противодействия перпендикулярны плечам их рычагов, поэтому в уравнении \ ref {12.10} имеем | sin \ (\ theta \) | = 1 для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент \ (\ tau_ {F} \) вызывает вращение по часовой стрелке вокруг оси в CM, поэтому его направление отрицательное; и крутящий момент \ (\ tau_ {R} \) вызывает вращение против часовой стрелки вокруг оси CM, поэтому его направление положительное. Имея эту информацию, запишем второе условие равновесия как

\ [- r_ {F} F_ {F} + r_ {R} F_ {R} = 0 \ ldotp \ label {12.13} \]

С помощью диаграммы свободного тела идентифицируем величины силы F _R = 0.48w и F _F = 0,52w, и соответствующие им рычаги r _R = x и r _F = d — x. Теперь мы можем записать второе условие равновесия, Уравнение \ ref {12.13}, явно через неизвестное расстояние x:

\ [- 0,52 (d — x) w + 0,48xw = 0 \ ldotp \ label {12.14} \]

Здесь вес w сокращается, и мы можем решить уравнение для неизвестного положения x CM. Ответ: x = 0,52d = 0,52 (2,5 м) = 1,3 м. Решение Выбор шарнира в положении передней оси не меняет результата.Схема свободного тела для этой точки поворота представлена ​​на рисунке 12.6. Для этого выбора точки поворота второе условие равновесия —

.

\ [- r_ {w} w + r_ {R} F_ {R} = 0 \ ldotp \ label {12.15} \]

Когда мы подставляем величины, указанные на диаграмме, получаем

\ [- (d — x) w + 0,48dw = 0 \ ldotp \ label {12.16} \]

Ответ, полученный путем решения уравнения \ ref {12.13}, опять же, x = 0,52d = 1,3 м.

Рисунок \ (\ PageIndex {5} \): эквивалентная диаграмма свободного тела для автомобиля; точка поворота четко обозначена.

Значение

Этот пример показывает, что при решении задач статического равновесия мы можем выбрать точку поворота. Для различных вариантов выбора точки поворота у нас есть разные наборы условий равновесия, которые необходимо решить. Однако любой выбор приводит к одному и тому же решению проблемы.

Упражнение 12.1

Решите Пример 12.1, выбрав шарнир в месте расположения задней оси.

Упражнение 12.2

Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; (б) пеликан, который парит в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал двигателя припаркованного автомобиля.

Особый случай статического равновесия возникает, когда все внешние силы на объект действуют на оси вращения или вдоль нее, или когда пространственное протяжение объекта можно не принимать во внимание. В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, уравнении \ ref {12.9}, потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться.Диаграмма свободного тела и стратегия решения задач для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона». В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.

Просмотрите эту демонстрацию, чтобы увидеть три груза, которые связаны веревками на шкивах и связаны в узел. Вы можете поэкспериментировать с весами, чтобы увидеть, как они влияют на положение равновесия узла, и в то же время увидеть представление на векторной диаграмме первого условия равновесия в действии.

Пример 12.2: Разрывное напряжение

Маленькая кастрюля массой 42,0 г поддерживается двумя струнами, как показано на рисунке 12.7. Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше, пока одна из струн не сломается. Какая это струна? Какую массу нужно добавить, чтобы это произошло?

Рисунок \ (\ PageIndex {6} \): Масса постепенно добавляется к сковороде, пока одна из струн не сломается.

Стратегия

Эта механическая система, состоящая из струн, масс и сковороды, находится в статическом равновесии.В частности, узел, который привязывает струны к кастрюле, находится в статическом равновесии. Узел можно рассматривать как точку; следовательно, нам нужно только первое условие равновесия. Три силы, тянущие к узлу: натяжение \ (\ vec {T} _ {1} \) в 5,0-сантиметровой струне и натяжение \ (\ vec {T} _ {2} \) в 10,0-сантиметровой струне. струна и вес \ (\ vec {w} \) сковороды, удерживающей гири. Мы принимаем прямоугольную систему координат с осью Y, направленной противоположно направлению силы тяжести, и рисуем диаграмму свободного тела для узла (см. Рисунок 12.8). Чтобы найти компоненты натяжения, мы должны определить углы направления \ (\ alpha_ {1} \) и \ (\ alpha_ {2} \), которые струны образуют с горизонтальным направлением, которое является осью x. Как вы можете видеть на рис. 12.7, струны составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке 12.8, и найти синус и косинус углов \ (\ alpha_ {1} \) и \ (\ alpha_ {2} \). Затем мы можем разложить напряжения на их прямоугольные составляющие и подставить в первое условие равновесия (Уравнение \ ref {12.7} и уравнение \ ref {12.8}) и решите натяжение струн. Первой порвется струна с большим натяжением.

Рисунок \ (\ PageIndex {7} \): диаграмма свободного тела для узла в примере 12.2.

Решение

Вес w, натянутый на узел, возникает из-за массы M чашки и массы m, добавленной к ней, или w = (M + m) g. С помощью диаграммы свободного тела на рис. 12.8 мы можем установить условия равновесия для узла:

в направлении x, \ [- T_ {1x} + T_ {2x} = 0 \] в направлении y, \ [+ T_ {1y} + T_ {2y} — w = 0 \ ldotp \]

Из диаграммы свободного тела, величины компонентов в этих уравнениях равны

\ [\ begin {split} T_ {1x} & = T_ {1} \ cos \ alpha_ {1} = \ frac {T_ {1}} {\ sqrt {5}}, \ quad T_ {1y} = T_ {1} \ sin \ alpha_ {1} = \ frac {2T_ {1}} {\ sqrt {5}} \\ T_ {2x} & = T_ {2} \ cos \ alpha_ {2} = \ frac {2T_ {2}} {\ sqrt {5}}, \ quad T_ {2y} = T_ {2} \ sin \ alpha_ {2} = \ frac {T_ {2}} {\ sqrt {5}} \ ldotp \ end {split} \]

Подставляем эти компоненты в условия равновесия и упрощаем.Затем мы получаем два уравнения равновесия для натяжений:

по оси x, \ [T_ {1} = 2T_ {2} \]

в направлении y, \ [\ frac {2T_ {1}} {\ sqrt {5}} + \ frac {T_ {2}} {\ sqrt {5}} = (M + m) g \ ldotp \]

Уравнение равновесия для направления x говорит нам, что натяжение T ₁ в 5,0-сантиметровой струне вдвое превышает натяжение T ₂ в 10,0-сантиметровой струне. Таким образом, более короткая струна порвется. Когда мы используем первое уравнение для исключения T ₂ из второго уравнения, мы получаем соотношение между массой m на чаше и натяжением T ₁ в более короткой струне:

\ [\ frac {2.{2}} — 0,042 \; кг = 0,277 \; кг = 277,0 \; g \ ldotp \]

Значение

Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри лифта, поднимающегося вверх. Пока лифт движется вверх с постоянной скоростью, результат остается неизменным, поскольку вес w не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес M + m становится больше из-за кажущегося веса из-за ускорения лифта.Тем не менее, во всех случаях более короткая струна рвется первой.

Авторы и ссылки

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

.