Всего вопросов: 20
Вопрос 1. Изображен график скорости движения мотоцикла от времени. Чему равна скорость мотоцикла в момент времени t=5c?
Вопрос 2. На рисунке изображен график зависимости скорости прямолинейного движения тела от времени. Чему равно ускорение тела?
Вопрос 3. На рисунке изображен график зависимости скорости прямолинейного движения тела от времени. Чему равно ускорение тела?
Вопрос 4. На рисунке изображена зависимость скорости движения тела от времени. На каком из участков тело движется равноускоренно?
Вопрос 5. На рисунке представлен график зависимости скорости движения тела от времени. На каком из участков тело движется равноускоренно?
Вопрос 6. На рисунке представлен график зависимости скорости движения тела от времени. На каком из участков тело движется равноускоренно?
На каком из участков тело движется равноускоренно?
Вопрос 7. На рисунке изображен график зависимости скорости движения тела от времени. Используя данные графика, запишите уравнение зависимости скорости от времени движения тела.
Вопрос 8. Проекция скорости тела изменяется с течением времени так, как показано на рисунке. Какое из нижеприведенных уравнений соответствует зависимости координаты этого тела от времени? (В момент начала наблюдения тело находилось на расстоянии двух метров левее начала координат)
Вопрос 9. Проекция скорости тела изменяется с течением времени так, как показано на рисунке. Какое из нижеприведенных уравнений, соответствует зависимости координаты этого тела от времени? (Учитывая, что в момент начала наблюдения рассматриваемая точка находилась на расстоянии 5 м левее начала координат)
Вопрос 10. По графику зависимости модуля скорости от времени, представленному на рисунке, определите перемещение тела за 2 с.
Вопрос 11. Используя информацию, приведенную на рисунке, определить проекцию перемещения тела через 14 с после начала движения.
Вопрос 12. Используя информацию, приведенную на рисунке, определить путь пройденный телом за девять секунд.
Вопрос 13. Автомобиль начинает двигаться равноускоренно и вдруг тормозит. Какой вид графика соответствует зависимости ускорения автомобиля от времени?
Вопрос 14. На рисунке 1 изображен график зависимости ускорения от времени движения тела. Как зависит скорость движения этого тела от времени (рисунок 2), если начальная скорость равна нулю?
Вопрос 15. На рисунке приведен график зависимости проекции скорости тела от времени. Определить в какой момент времени тело остановилось.
Вопрос 16. На рисунке представлен график зависимости проекции скорости от проекции перемещения.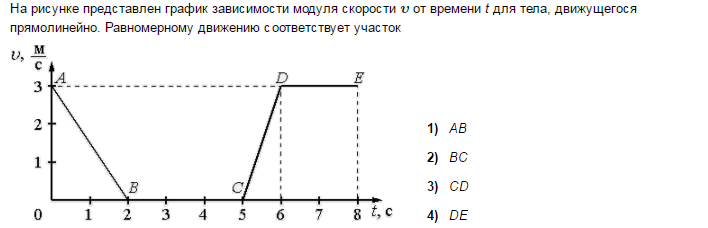 Определить ускорение этого тела.
Определить ускорение этого тела.
Вопрос 17. На рисунке представлен график зависимости проекции скорости двух тел от времени. Определите скорость первого тела через три секунды после начала движения.
Вопрос 18. Определить, в каком соотношении между собой находятся проекции перемещения тел, графики зависимости проекций скоростей от времени которых, показаны на рисунке, в момент времени, когда скорости тел одинаковы?
Вопрос 19. На рисунке приведен график зависимости проекции скорости трех тел от времени. В каком из нижеприведенных соотношений находятся значения модулей ускорений и перемещений этих тел в момент времени 10 с?
Вопрос 20. Тело, имеющее начальную скорость 2 м/с, направленную против выбранной оси координат, двигается с ускорением, график зависимости проекции которого от времени приведен на рисунке. Какой из нижеприведенных графиков соответствует зависимости проекции скорости этого тела от времени для промежутка времени (0, 8) с?
Содержание
Кинематика.
 Физика. 10 класс. — Графики прямолинейного равномерного движения.
Физика. 10 класс. — Графики прямолинейного равномерного движения.
Комментарии преподавателя
Графики прямолинейного движения
Для начала рассмотрим законы равномерного прямолинейного движения, полученные нами на прошлом уроке:
Если внимательно исследовать эти выражения, видно, что обе зависимости являются линейными. Из курса алгебры вы должны знать, что графиком любой линейной зависимости является прямая линия. Поскольку скорость тела при равномерном прямолинейном движении не меняется, графиком этой зависимости всегда будет прямая, параллельная оси времени.
Построим данные зависимости (Рис. 1):
Рис. 1. Графики равномерного прямолинейного движения при разных скоростях
На левом графике изображена зависимость координаты трех разных движущихся тел от времени.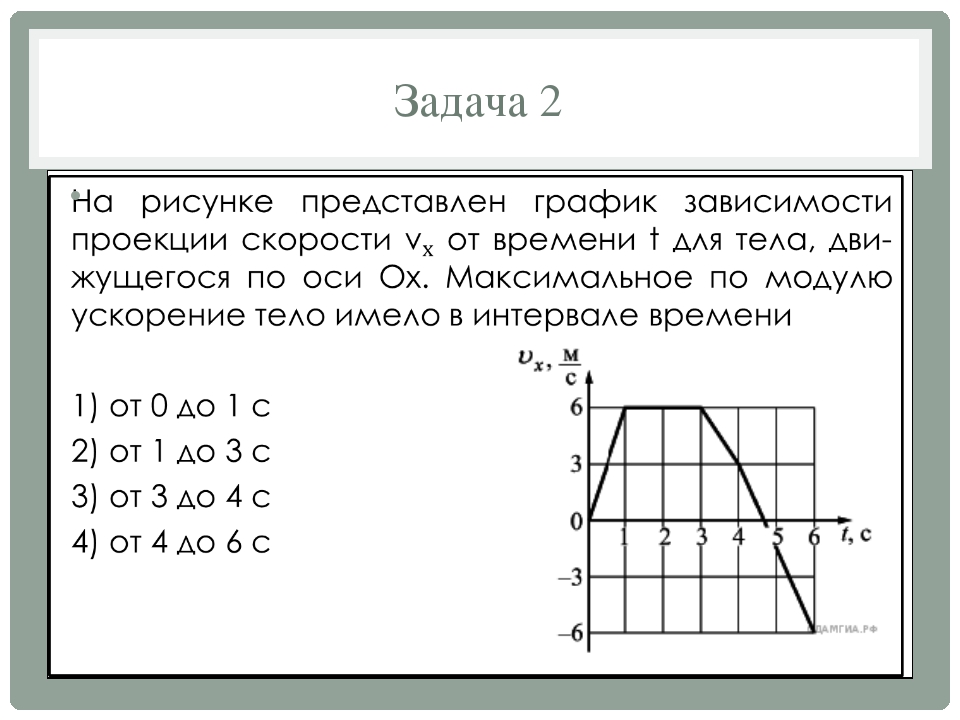 Красный график соответствует случаю, когда скорость тела направлена в ту же сторону, что и ось координат. Зеленый график соответствует случаю покоящегося тела. Синий – случаю, когда скорость противоположно направлена к оси координат. Точка , в которой каждый из трех графиков пересекает ось , – это начальная координата тела.
Красный график соответствует случаю, когда скорость тела направлена в ту же сторону, что и ось координат. Зеленый график соответствует случаю покоящегося тела. Синий – случаю, когда скорость противоположно направлена к оси координат. Точка , в которой каждый из трех графиков пересекает ось , – это начальная координата тела.
На правом графике изображены зависимости скоростей тела от времени. Поскольку при равномерном прямолинейном движении скорости тел не меняются, графики являются прямыми, параллельными оси времени. Красный график соответствует положительной скорости (скорость направлена в ту же сторону, что и ось координат), зеленый график соответствует покоящемуся телу (скорость постоянна и равна нулю), а синий – отрицательной скорости (скорость противоположно направлена оси координат).
Таким образом, мы можем восстановить законы движения по графикам:
Поговорим о начальной координате. Эту величину всегда можно определить как точку пересечения графика зависимости координаты от времени с осью координат (Рис. 2).
Эту величину всегда можно определить как точку пересечения графика зависимости координаты от времени с осью координат (Рис. 2).
Рис. 2. Графики равномерного прямолинейного движения тел с разными начальными положениями
Из графиков видно, что начальное положение тела, соответствующего красной кривой, положительно, зеленой кривой – равно нулю, а синей – отрицательно.
Обсудим теперь то, как можно получить из графика скорость тела при равномерном прямолинейном движении. Из курса алгебры вы должны знать, что линейная зависимость задается выражением
где коэффициент равен тангенсу угла наклона прямой на графике. Эта зависимость аналогична закону движения тела при равномерном прямолинейном движении. Таким образом, скорость – это тангенс угла наклона графика зависимости координаты тела от времени (Рис. 3).
3).
Рис. 3. Связь между тангенсом угла наклона графика координаты от времени и скоростью тела при равномерном прямолинейном движении
Рис. 4. Связь между путем, пройденным телом, и площадью под графиком зависимости скорости тела от времени
Осталось поговорить о том, как, зная график скорости тела от времени, определить пройденный путь за какой-либо промежуток времени. Оказывается, что путь равен площади фигуры, ограниченной осью времени, прямыми и , и графиком зависимости скорости от времени (Рис.4).
Итак, на этом уроке мы изучили, как, зная законы движения тел, движущихся равномерно и прямолинейно, нарисовать графики зависимости скорости тела от времени и координаты тела от времени. Корме того, мы научились определять по графикам зависимостей координаты и скорости от времени, определять начальное положение, скорость тела и пройденный телом путь.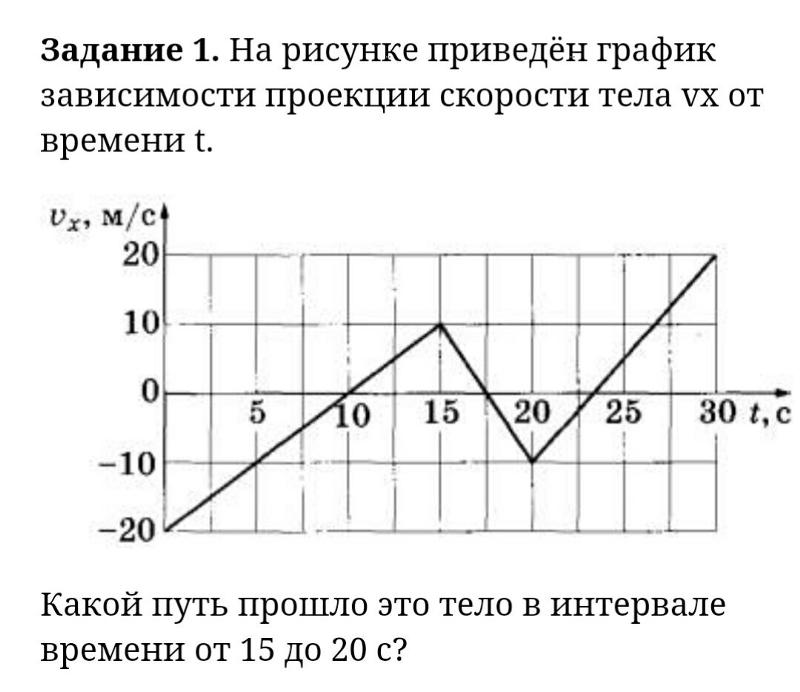
Домашнее задание
- Задача. Парашютист спускается со скоростью 18 км\ч. На высоте 1000 метров из его кармана падает шарик от настольного тенниса и падает равномерно со скоростью 54 км\ч. Определите графически, какое время пройдет между приземлением шарика и парашютиста.
- Рассмотрите следующие вопросы и ответы на них:
- Вопрос: Если измерить угол наклона графика транспортиром и вычислить его тангенс, будет ли это скоростью тела?
- Вопрос: Можно ли измерять площадь под графиком скорости палеткой?
- Вопрос: Как определить место и время встречи двух тел?
К занятию прикреплен файл «Ребусы по теме». Вы можете скачать файл в любое удобное для вас время.
Использованные источники:
- http://interneturok.
 ru/ru/school/physics/10-klass/
ru/ru/school/physics/10-klass/ - http://www.youtube.com/watch?v=QL-ktMb5Zx0
Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
Цели урока:
обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;
развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный (письменный) опрос, решение задач).
Связи:
межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные: равномерное и равноускоренное движение.
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
3. Объяснение нового материала.
Скачать этот видеоурок
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.
Если движение равномерное, то:
1. Скорость тела не меняется с течением времени;
2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;
3. Уравнение перемещения имеет вид:
4. И — кинематическое уравнение равномерного движения.
Для равноускоренного:
1. Ускорение тела не изменяется с течением времени;
2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло
3. Уравнение скорости для равноускоренного движения имеет вид:
4. — уравнение перемещения для равноускоренного движения;
5. — кинематическое уравнение равноускоренного движения.
Для большей наглядности движение можно описывать с помощью графиков.
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.
Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.
По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.
Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.
Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v0 + at, т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.
По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.
Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.
При этом проекция перемещения для первого тела будет положительной.
Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.
Проекция перемещения — отрицательна.
Теперь рассмотрим зависимость пройденного пути от времени.
Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.
При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
Теперь перейдем к рассмотрению зависимости перемещения от времени.
Рассмотрим равномерное движение.
Т.к. при равномерном движении перемещение линейно зависит от времени (sx = υxt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.
А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.
Для 2-го тела ускорение и начальная скорость тела больше нуля.
Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.
У 4-го тела начальная скорость и ускорение меньше нуля.
Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.
И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.
И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).
Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.
График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.
В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
С помощью графика движения можно определить:
1. координаты тела в любой момент времени;
2. путь, пройденный телом за некоторый промежуток времени;
3. время, за которое пройден какой-то путь;
4. кратчайшее расстояние м/у телами в любой момент времени;
5. момент и место встречи и т. д.
По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).
Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).
При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.
4. Этап обобщения и закрепления нового материала
И так, сделаем главный вывод.
Механическое движение для большей наглядности можно описывать с помощью графиков:
1) Зависимости скорости от времени;
2) Зависимости ускорения от времени;
3) Зависимость координаты тела от времени;
4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
6. Домашнее задание.
Карточки по физике
Муниципальное образовательное учреждение «Средняя общеобразовательная
школа № 8 города Новоузенска Саратовской области»
ФИЗИКА
Карточкизадания по теме «КИНЕМАТИКА»
9 класс
Выполнила: Купенова Г.М.
учитель физики
2017 Карточка 1
На рисунке приведён график зависимости скорости
Карточка 2
движения электропоезда метрополитена на
прямолинейном участке дороги от времени v = v(t).
На рисунке
приведён график зависимости пути,
Чему равна скорость электропоезда? Скорость
пройденного мопедом на прямолинейном участке дороги,
выразите в метрах в секунду.
от времени s = s (t). Чему равна скорость мопеда?
А. 5 м/с. Б. 18 м/с. В. 64,8 м/с. Г. 90 м/с.
А.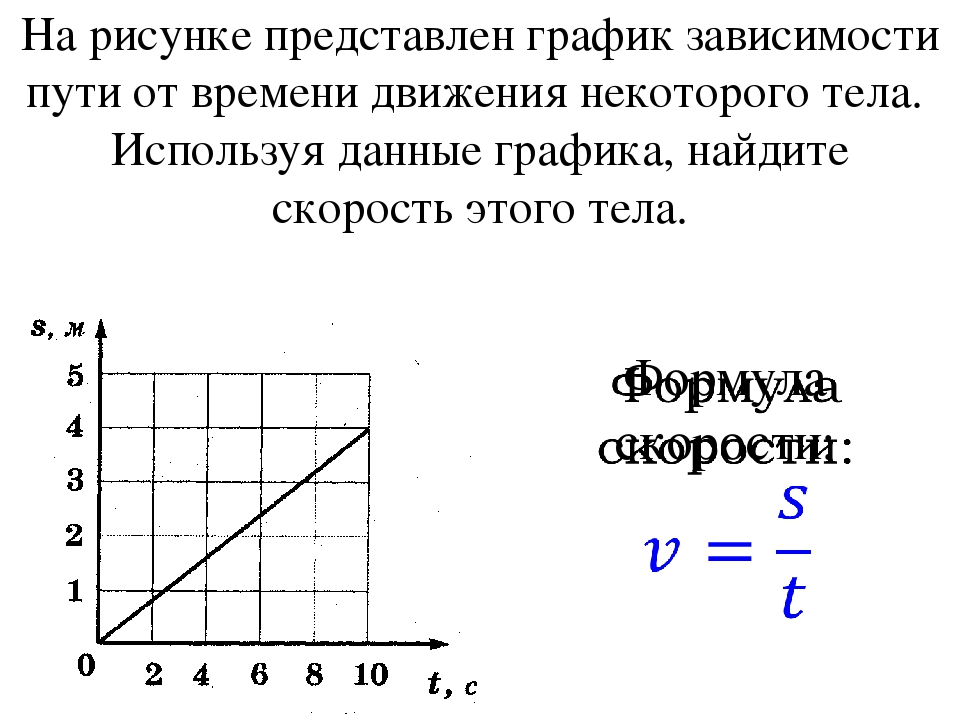 0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
Карточка 1
На рисунке приведён график зависимости скорости движения электропоезда
Карточка 2
метрополитена на прямолинейном участке дороги от времени v = v(t).
Чему равна скорость электропоезда? Скорость
приведён график зависимости пути,
На рисунке
выразите в метрах в секунду.
пройденного мопедом на прямолинейном участке дороги,
А. 5 м/с. Б. 18 м/с. В. 64,8 м/с. Г. 90 м/с.
от времени s = s (t). Чему равна скорость мопеда?
А. 0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
Карточка 1
На рисунке приведён график зависимости скорости
Карточка 2
движения электропоезда метрополитена на
прямолинейном участке дороги от времени v = v(t).
приведён график зависимости пути,
На рисунке
Чему равна скорость электропоезда? Скорость
пройденного мопедом на прямолинейном участке дороги,
выразите в метрах в секунду.
от времени s = s (t). Чему равна скорость мопеда?
А. 5 м/с. Б. 18 м/с. В. 64,8 м/с. Г. 90 м/с.
Г. 90 м/с.
А. 0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
Карточка 1
Карточка 2
На рисунке приведён график зависимости скорости
движения электропоезда метрополитена на
приведён график зависимости пути,
На рисунке
прямолинейном участке дороги от времени v = v(t).
пройденного мопедом на прямолинейном участке дороги,
Чему равна скорость электропоезда? Скорость
от времени s = s (t). Чему равна скорость мопеда?
выразите в метрах в секунду.
А. 0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
А. 5 м/с. Б. 18 м/с. В. 64,8 м/с. Г. 90 м/с.
Карточка 2
Карточка 1
На рисунке приведён график зависимости скорости
приведён график зависимости пути,
На рисунке
движения электропоезда метрополитена на
пройденного мопедом на прямолинейном участке дороги,
прямолинейном участке дороги от времени v = v(t).
от времени s = s (t). Чему равна скорость мопеда?
Чему равна скорость электропоезда? Скорость
А. 0,025 км/ч. Б. 40 км/ч. В. 40 км/с. Г. 22,5 км/ч.
22,5 км/ч.
выразите в метрах в секунду.
А. 5 м/с. Б. 18 м/с. В. 64,8 м/с. Г. 90 м/с. Карточка 3
На рисунке приведён график зависимости скорости
движения автобуса на прямолинейном участке дороги
от времени.
Чему равна скорость автобуса?
А. 20 м/с. Б. –20 м/с. В. 0. Г. 40 м/с.
Карточка 3
На рисунке приведён график зависимости скорости
движения автобуса на прямолинейном участке дороги
от времени.
Чему равна скорость автобуса?
А. 20 м/с. Б. –20 м/с. В. 0. Г. 40 м/с.
Карточка 3
На рисунке приведён график зависимости скорости
движения автобуса на прямолинейном участке дороги
от времени.
Чему равна скорость автобуса?
А. 20 м/с. Б. –20 м/с. В. 0. Г. 40 м/с.
Карточка 3
На рисунке приведён график зависимости скорости
движения автобуса на прямолинейном участке дороги
от времени.
Чему равна скорость автобуса?
А. 20 м/с. Б. –20 м/с. В. 0. Г. 40 м/с.
Карточка 3
На рисунке приведён график зависимости скорости
движения автобуса на прямолинейном участке дороги
от времени.
Чему равна скорость автобуса?
А. 20 м/с. Б. –20 м/с. В. 0. Г. 40 м/с. Карточка 4
На рисунке изображён график зависимости
координаты пригородного электропоезда от времени
движения х = х (t). . С помощью графика определите
начальную
тела.
А. 0. Б. 0,5 км. В. 1 км. Г. 1,5 км.
координату
Карточка 4
На рисунке изображён график зависимости
координаты пригородного электропоезда от времени
движения х = х (t). . С помощью графика определите
начальную
тела.
А. 0. Б. 0,5 км. В. 1 км. Г. 1,5 км.
координату
Карточка 4
На рисунке изображён график зависимости координаты
электропоезда
пригородного
времени
. С помощью графика определите
движения х = х (t).
начальную
тела.
А. 0. Б. 0,5 км. В. 1 км. Г. 1,5 км.
координату
от
Карточка 4
На рисунке изображён график зависимости
координаты пригородного электропоезда от времени
движения х = х (t). . С помощью графика определите
начальную
тела.
А. 0. Б. 0,5 км. В. 1 км. Г. 1,5 км.
координату
Карточка 4
На рисунке изображён график зависимости
координаты пригородного электропоезда от времени
движения х = х (t). . С помощью графика определите
начальную
тела.
А. 0. Б. 0,5 км. В. 1 км. Г. 1,5 км.
координату Карточка 5
На рисунке приведён график зависимости
скорости движения электропоезда метрополитена
Карточка 6
на прямолинейном участке дороги от
На рисунке приведён график зависимости
времени v = v(t).
скорости движения электропоезда
Чему равен путь, пройденный электропоездом за
метрополитена на прямолинейном участке
5 с движения? Путь выразите в метрах.
дороги от времени v = v(t).
А. 0,28 м. Б. 1 м. В. 25 м. Г. 90 м.
На каком из графиков — 1, 2, 3 или 4 —
правильно отражена зависимость пути от
времени
электропоезда
Карточка 5
метрополитена?
На рисунке приведён график зависимости скорости движения электропоезда метрополитена на
А. 1. Б. 2. В.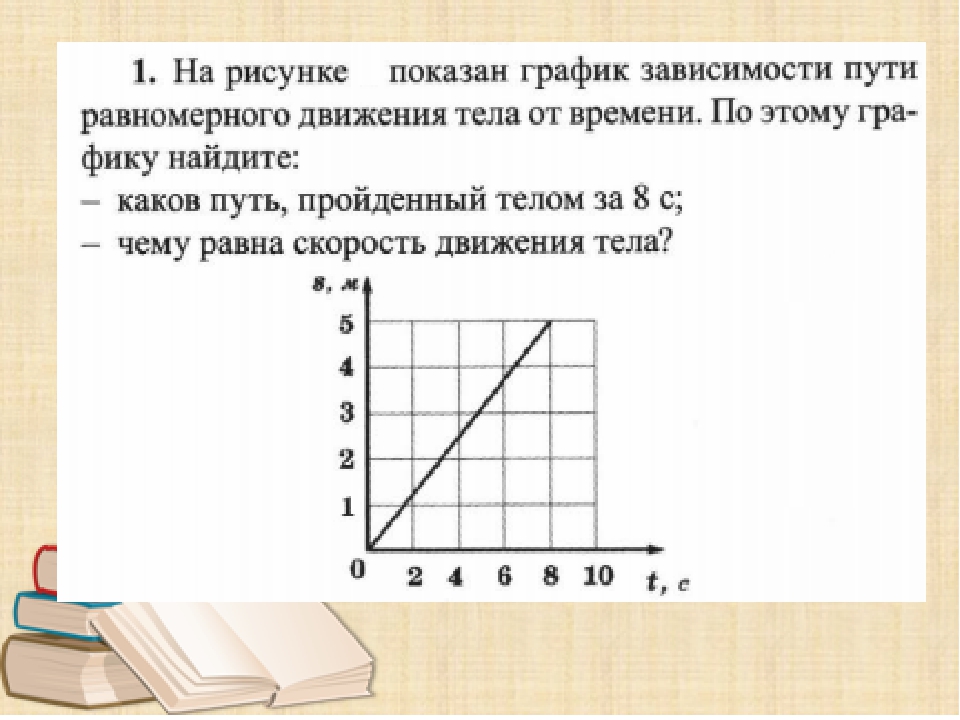 3. Г. 4.
3. Г. 4.
прямолинейном участке дороги от времени v = v(t).
Чему равен путь, пройденный электропоездом за 5 с движения? Путь выразите
в метрах.
А. 0,28 м. Б. 1 м. В. 25 м. Г. 90 м.
движения
Карточка 5
На рисунке приведён график зависимости скорости движения электропоезда метрополитена на
прямолинейном участке дороги от времени v = v(t).
Чему равен путь, пройденный электропоездом за 5 с движения? Путь выразите
в метрах.
А. 0,28 м. Б. 1 м. В. 25 м. Г. 90 м.
Карточка 6
На рисунке приведён график зависимости
скорости движения электропоезда
метрополитена на прямолинейном участке
Карточка 5
дороги от времени v = v(t).
На рисунке приведён график зависимости скорости движения электропоезда метрополитена на
На каком из графиков — 1, 2, 3 или 4 —
прямолинейном участке дороги от времени v = v(t).
правильно отражена зависимость пути от
Чему равен путь, пройденный электропоездом за 5 с движения? Путь выразите
электропоезда
времени
в метрах.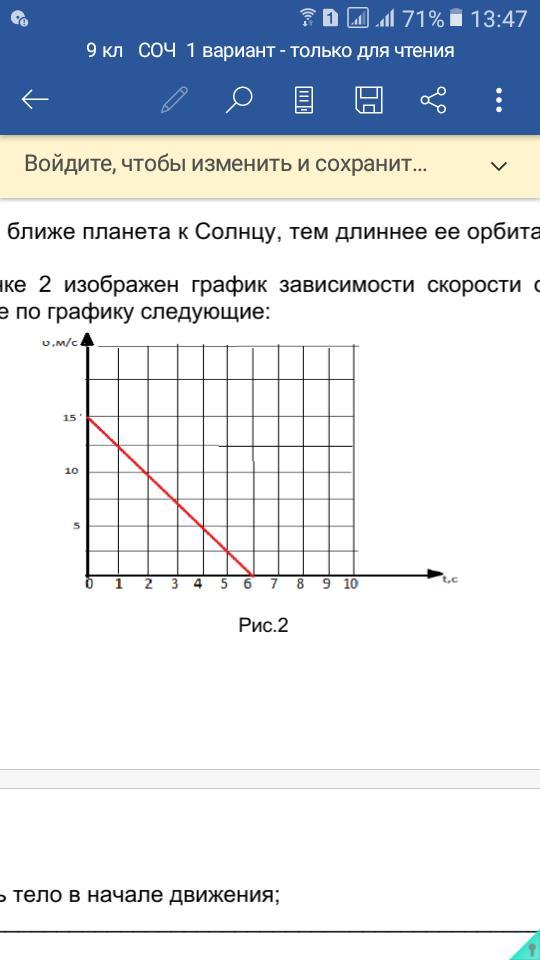
метрополитена?
А. 0,28 м. Б. 1 м. В. 25 м. Г. 90 м.
А. 1. Б. 2. В. 3. Г. 4.
движения
Карточка 5
На рисунке приведён график зависимости скорости движения электропоезда метрополитена на
прямолинейном участке дороги от времени v = v(t).
Чему равен путь, пройденный электропоездом за 5 с движения? Путь выразите
в метрах.
А. 0,28 м. Б. 1 м. В. 25 м. Г. 90 м. Карточка 7
приведён график
На рисунке
скорости движения автобуса на
прямолинейном участке дороги от
На каком из графиков — 1, 2, 3 или 4 (рис. 9) —
правильно отражена зависимость пути от времени
движения автобуса?
А. 1. Б. 2. В. 3. Г. 4.
зависимости
времени.
Карточка 7
На рисунке
приведён график
скорости движения автобуса на
прямолинейном участке дороги от
На каком из графиков — 1, 2, 3 или 4 (рис. 9) —
правильно отражена зависимость пути от времени
движения автобуса?
А. 1. Б. 2. В. 3. Г. 4.
3. Г. 4.
зависимости
времени. Карточка 8
На рисунке изображён график зависимости скорости
движения пешехода от времени v = v (t). На каком
участке пешеход движется равноускоренно?
А. Только на
участке АВ. В. Только на участке ВС.
Г. На участках ОА и ВС.
участке ОА. Б. Только на
Карточка 8
На рисунке изображён график зависимости скорости
движения пешехода от времени v = v (t). На каком
участке пешеход движется равноускоренно?
А. Только на
участке АВ. В. Только на участке ВС.
Г. На участках ОА и ВС.
участке ОА. Б. Только на
Карточка 8
На рисунке изображён график зависимости скорости
движения пешехода от времени v = v (t). На каком
участке пешеход движется равноускоренно?
А. Только на
участке АВ. В. Только на участке ВС.
Г. На участках ОА и ВС.
участке ОА. Б. Только на
Карточка 8
На рисунке изображён график зависимости скорости
движения пешехода от времени v = v (t). На каком
участке пешеход движется равноускоренно?
А. Только на
Только на
участке АВ. В. Только на участке ВС.
Г. На участках ОА и ВС.
участке ОА. Б. Только на
Карточка 8
На рисунке изображён график зависимости скорости
движения пешехода от времени v = v (t). На каком
участке пешеход движется равноускоренно?
А. Только на
участке АВ. В. Только на участке ВС.
Г. На участках ОА и ВС.
участке ОА. Б. Только на Карточка 9
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени v = v(t). На
каком участке лифт движется равноускоренно?
А. Только на участке ОА. Б. Только на участке АВ.
В. Только на участке ВС. Г. На участках ОА и ВС.
Карточка 9
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени v = v(t). На
каком участке лифт движется равноускоренно?
А. Только на участке ОА. Б. Только на участке АВ.
В. Только на участке ВС. Г. На участках ОА и ВС.
Карточка 9
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени v = v(t).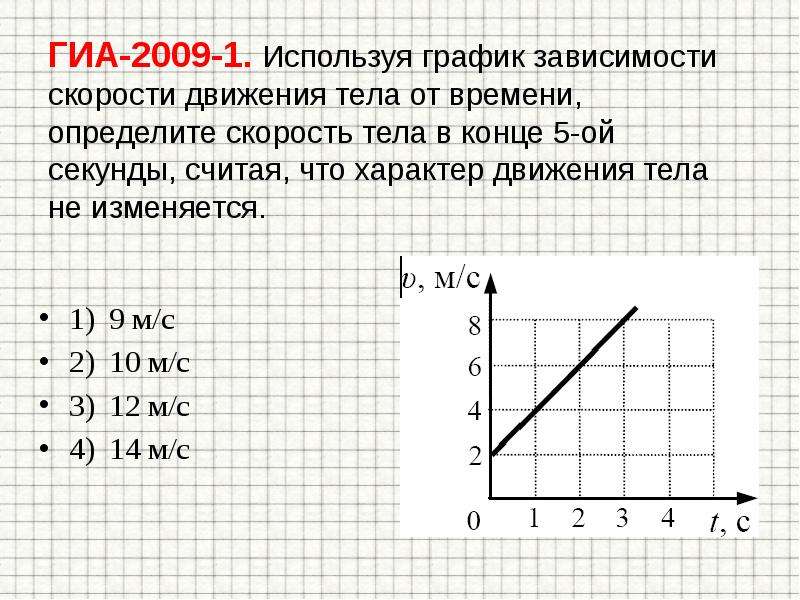 На
На
каком участке лифт движется равноускоренно?
А. Только на участке ОА. Б. Только на участке АВ.
В. Только на участке ВС. Г. На участках ОА и ВС.
Карточка 9
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени v = v(t). На
каком участке лифт движется равноускоренно?
А. Только на участке ОА. Б. Только на участке АВ.
В. Только на участке ВС. Г. На участках ОА и ВС. Карточка 10
Карточка 11
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости скорости
движения товарного поезда от времени v = v(t). На каком
движения трамвая на прямолинейном участке дороги от
участке поезд двигался равномерно?
времени v = v(t). На каком участке трамвай движется
А. Только на участке АВ. Б. Только на участке ВС.
равномерно?
В. Только на участке CD. Г. На участках АВ и CD.
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 10
Карточка 11
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости скорости
движения товарного поезда от времени v = v(t).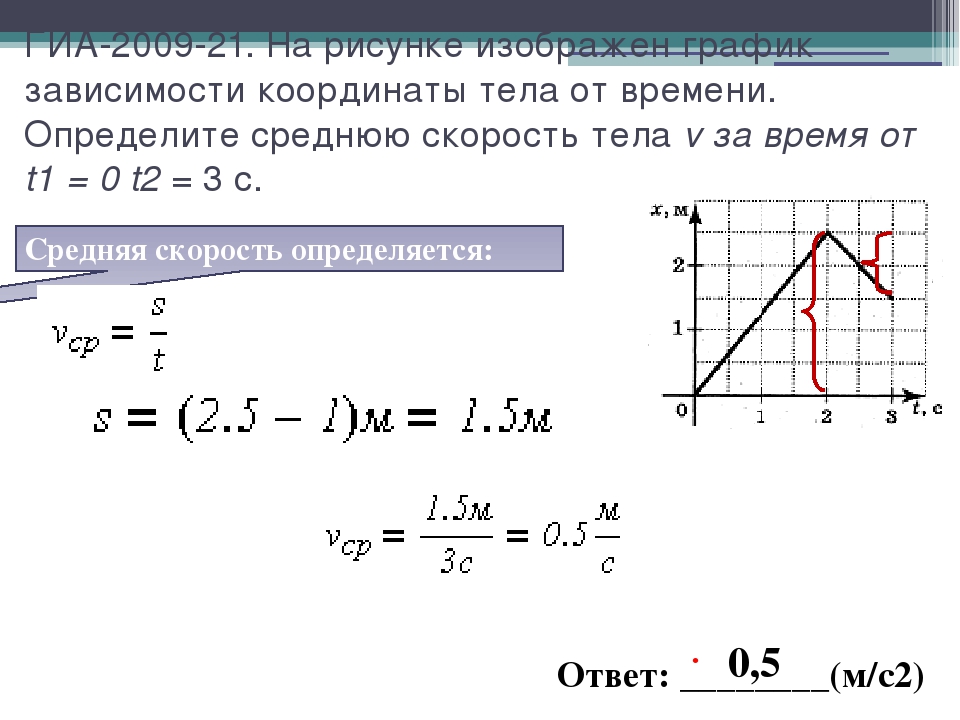 На каком
На каком
движения трамвая на прямолинейном участке дороги от
участке поезд двигался равномерно?
времени v = v(t). На каком участке трамвай движется
А. Только на участке АВ. Б. Только на участке ВС.
равномерно?
В. Только на участке CD. Г. На участках АВ и CD.
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 10
Карточка 11
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
движения товарного поезда от времени v = v(t). На каком
времени v = v(t). На каком участке трамвай движется
участке поезд двигался равномерно?
равномерно?
А. Только на участке АВ. Б. Только на участке ВС.
А. Только на участке АВ. В. Только на участке CD.
В. Только на участке CD. Г. На участках АВ и CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 10
Карточка 11
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
движения товарного поезда от времени v = v(t). На каком
На каком
времени v = v(t). На каком участке трамвай движется
участке поезд двигался равномерно?
равномерно?
А. Только на участке АВ. Б. Только на участке ВС.
А. Только на участке АВ. В. Только на участке CD.
В. Только на участке CD. Г. На участках АВ и CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 11
Карточка 10
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
На рисунке изображён график зависимости скорости
времени v = v(t). На каком участке трамвай движется
движения товарного поезда от времени v = v(t). На каком
равномерно?
участке поезд двигался равномерно?
А. Только на участке АВ. В. Только на участке CD.
А. Только на участке АВ. Б. Только на участке ВС.
Б. Только на участке ВС. Г. На участках АВ и CD.
В. Только на участке CD. Г. На участках АВ и CD. Карточка 12
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). На каком участке трамвай тормозит?
А.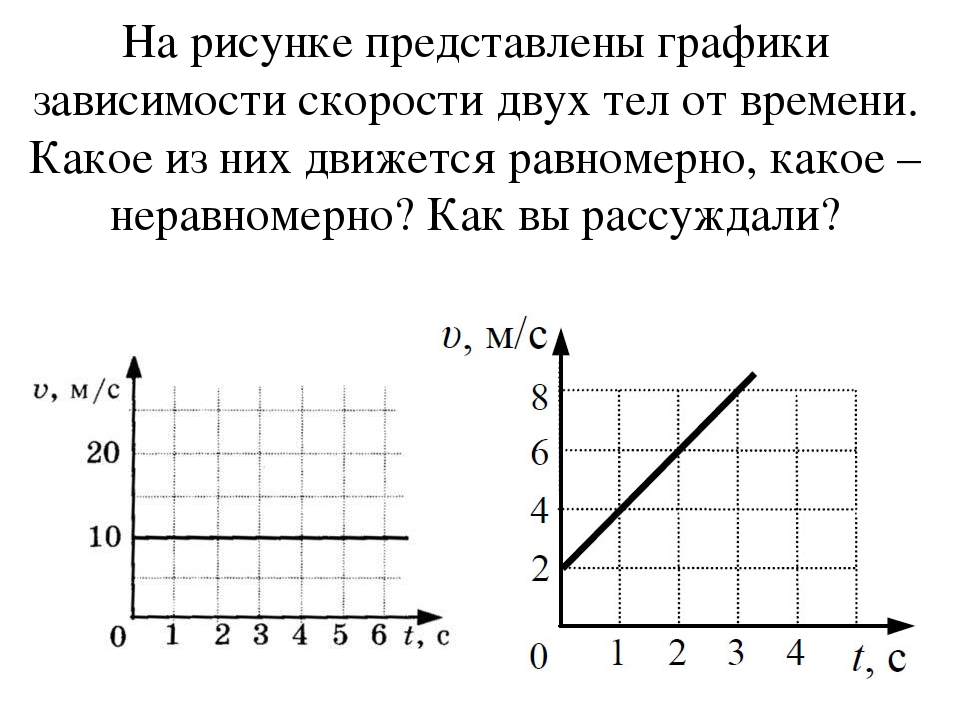 Только на участке АВ. В. Только на участке CD.
Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 12
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). На каком участке трамвай тормозит?
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 12
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). На каком участке трамвай тормозит?
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 12
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). На каком участке трамвай тормозит?
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD.
Карточка 12
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t).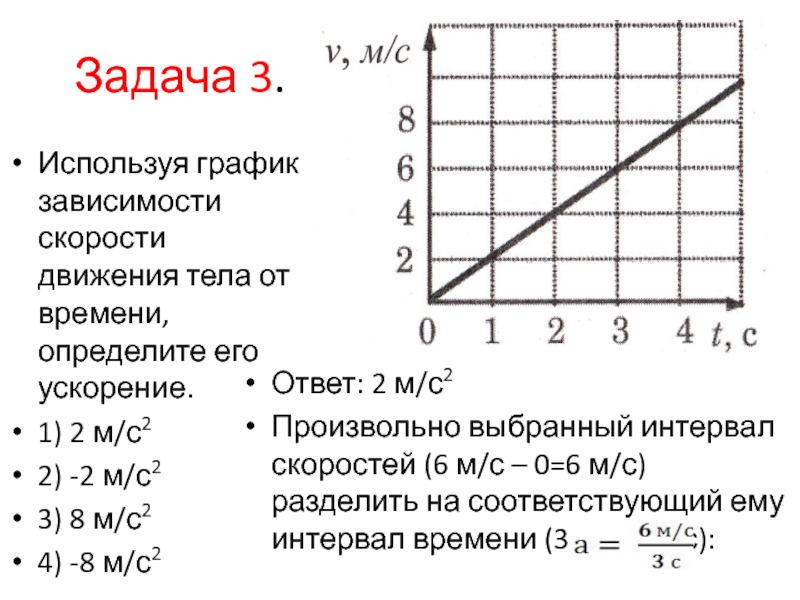 На каком участке трамвай тормозит?
На каком участке трамвай тормозит?
А. Только на участке АВ. В. Только на участке CD.
Б. Только на участке ВС. Г. На участках АВ и CD. Карточка 13
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). Чему равен модуль ускорения трамвая
участке CD?
А. 0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
Карточка 13
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). Чему равен модуль ускорения трамвая
участке CD?
А. 0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
Карточка 13
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). Чему равен модуль ускорения трамвая
на участке CD?
А. 0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
Карточка 13
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). Чему равен модуль ускорения трамвая
участке CD?
А.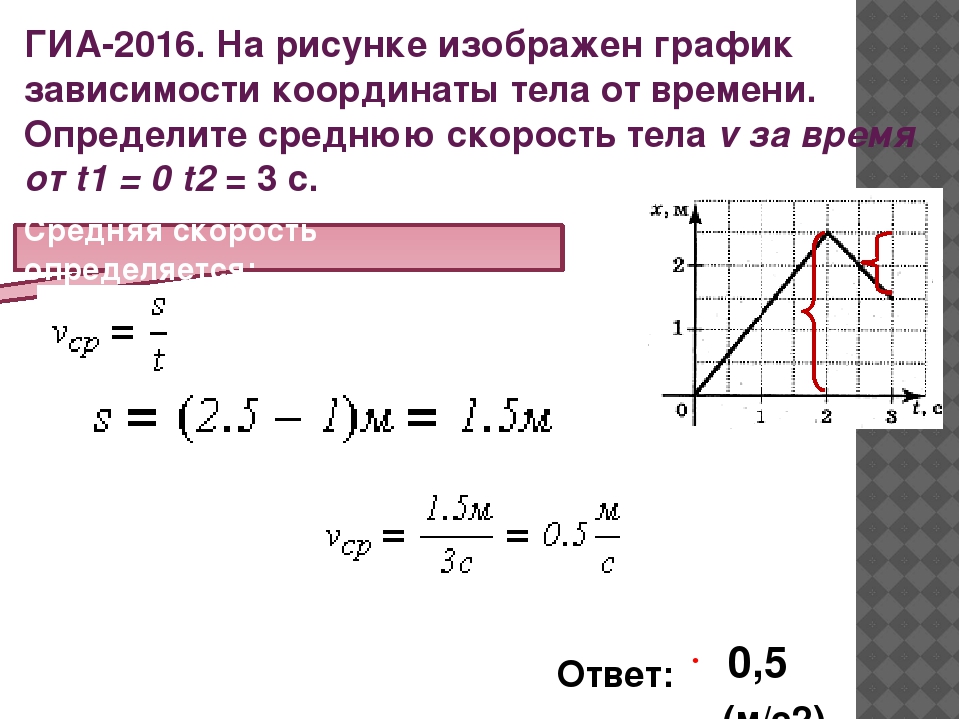 0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
Карточка 13
На рисунке изображён график зависимости скорости
движения трамвая на прямолинейном участке дороги от
времени v = v(t). Чему равен модуль ускорения трамвая
участке CD?
А. 0. Б. 0,5 м/с2. В. 1 м/с2. Г. 1,5 м/с2.
на
на
на
на Карточка 14
На рисунке изображён график зависимости скорости
Карточка 15
движения трамвая на прямолинейном участке дороги
На рисунке изображён график зависимости координаты
времени v = v(t). Используя данные графика (см.
пригородного электропоезда от времени движения х = х (t). .
рис. 14), запишите уравнение зависимости скорости
С помощью графика (см. рис. 13) определите модуль
движения трамвая на участке АВ от времени.
скорости тела. Скорость выразите в метрах в секунду.
A. v = 2,5 + 0,5t, м/с. В. v = 7,5, м/с.
А. ≈ 16,7 м/с. Б. ≈ 22,2 м/с. В. ≈ 11,1 м/с. Г. 180 000 м/с.
Б. v = 0,5t, м/с. Г. v = 7,5 – 1,5t, м/с.
Карточка 14
На рисунке изображён график зависимости скорости
Карточка 15
движения трамвая на прямолинейном участке дороги
На рисунке изображён график зависимости координаты
времени v = v(t). Используя данные графика (см.
Используя данные графика (см.
пригородного электропоезда от времени движения х = х (t). .
рис. 14), запишите уравнение зависимости скорости
С помощью графика (см. рис. 13) определите модуль
движения трамвая на участке АВ от времени.
скорости тела. Скорость выразите в метрах в секунду.
A. v = 2,5 + 0,5t, м/с. В. v = 7,5, м/с.
А. ≈ 16,7 м/с. Б. ≈ 22,2 м/с. В. ≈ 11,1 м/с. Г. 180 000 м/с.
Б. v = 0,5t, м/с. Г. v = 7,5 – 1,5t, м/с.
Карточка 14
Карточка 15
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости координаты
движения трамвая на прямолинейном участке дороги
пригородного электропоезда от времени движения х = х (t). .
времени v = v(t). Используя данные графика (см.
С помощью графика (см. рис. 13) определите модуль
рис. 14), запишите уравнение зависимости скорости
скорости тела. Скорость выразите в метрах в секунду.
движения трамвая на участке АВ от времени.
А. ≈ 16,7 м/с. Б. ≈ 22,2 м/с. В. ≈ 11,1 м/с.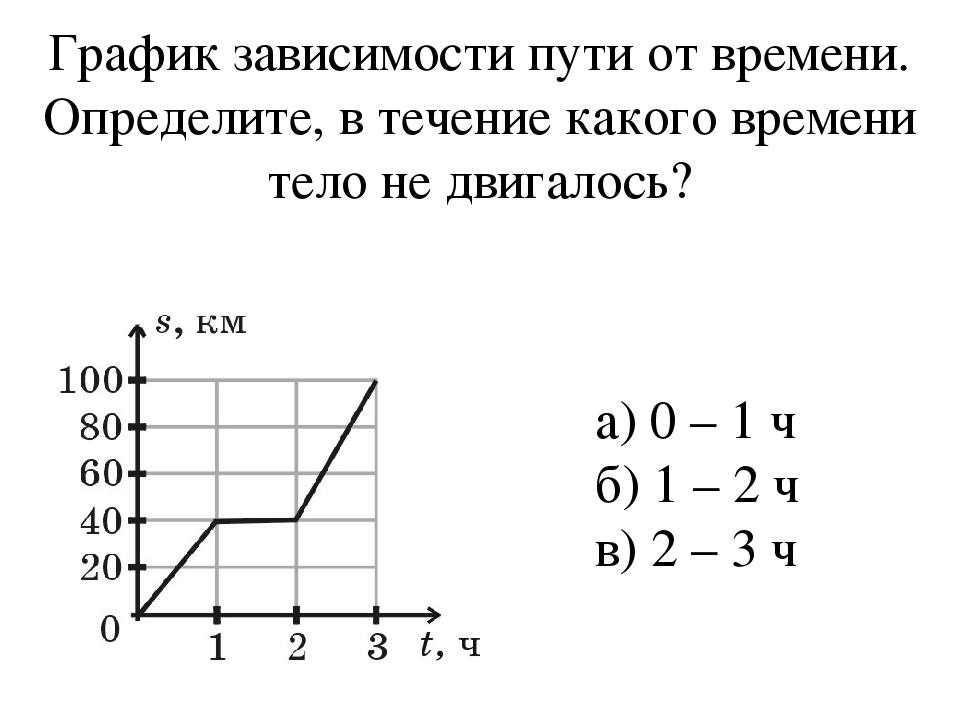 Г. 180 000 м/с.
Г. 180 000 м/с.
A. v = 2,5 + 0,5t, м/с. В. v = 7,5, м/с.
Б. v = 0,5t, м/с. Г. v = 7,5 – 1,5t, м/с.
Карточка 14
Карточка 15
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости координаты
движения трамвая на прямолинейном участке дороги
пригородного электропоезда от времени движения х = х (t). .
времени v = v(t). Используя данные графика (см.
С помощью графика (см. рис. 13) определите модуль
рис. 14), запишите уравнение зависимости скорости
скорости тела. Скорость выразите в метрах в секунду.
движения трамвая на участке АВ от времени.
А. ≈ 16,7 м/с. Б. ≈ 22,2 м/с. В. ≈ 11,1 м/с. Г. 180 000 м/с.
A. v = 2,5 + 0,5t, м/с. В. v = 7,5, м/с.
Б. v = 0,5t, м/с. Г. v = 7,5 – 1,5t, м/с.
Карточка 14
Карточка 15
На рисунке изображён график зависимости скорости
На рисунке изображён график зависимости координаты
движения трамвая на прямолинейном участке дороги
пригородного электропоезда от времени движения х = х (t). .
.
времени v = v(t). Используя данные графика (см.
С помощью графика (см. рис. 13) определите модуль
рис. 14), запишите уравнение зависимости скорости
скорости тела. Скорость выразите в метрах в секунду.
движения трамвая на участке АВ от времени.
А. ≈ 16,7 м/с. Б. ≈ 22,2 м/с. В. ≈ 11,1 м/с. Г. 180 000 м/с.
A. v = 2,5 + 0,5t, м/с. В. v = 7,5, м/с.
Б. v = 0,5t, м/с. Г. v = 7,5 – 1,5t, м/с.
от
от
от
от
от Карточка 16
На рисунке изображен график зависимости скорости
Карточка 17
движения пассажирского лифта от времени при его
пуске.
лифта?
На рисунке изображен график зависимости скорости
А. 10 м/с2. Б. 7,5 м/с2. В. 3,3 м/с2. Г. 0,3 м/с2.
движения парашютиста от времени при его приземлении.
Чему
парашютиста?
А. 0,2 м/с2. Б. 5 м/с2. В. 10 м/с2. Г. 180 м/с2.
ускорение
ускорение
Чему
равно
равно
.
Карточка 16
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени при его
Карточка 17
пуске.
лифта?
А. 10 м/с2. Б. 7,5 м/с2. В. 3,3 м/с2. Г. 0,3 м/с2.
На рисунке изображен график зависимости скорости
движения парашютиста от времени при его приземлении.
Чему
парашютиста?
А. 0,2 м/с2. Б. 5 м/с2. В. 10 м/с2. Г. 180 м/с2.
ускорение
ускорение
Чему
равно
равно
Чему
.
Карточка 16
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени при его
Карточка 17
пуске.
лифта?
А. 10 м/с2. Б. 7,5 м/с2. В. 3,3 м/с2. Г. 0,3 м/с2.
На рисунке изображен график зависимости скорости
движения парашютиста от времени при его приземлении.
Чему
парашютиста?
А. 0,2 м/с2. Б. 5 м/с2. В. 10 м/с2. Г. 180 м/с2.
ускорение
ускорение
равно
равно
равно
ускорение
.
Карточка 16
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени при его пуске.
Чему
лифта?
Карточка 17
А. 10 м/с2. Б. 7,5 м/с2. В. 3,3 м/с2. Г. 0,3 м/с2.
В. 3,3 м/с2. Г. 0,3 м/с2.
На рисунке изображен график зависимости скорости
движения парашютиста от времени при его приземлении.
парашютиста?
Чему
А. 0,2 м/с2. Б. 5 м/с2. В. 10 м/с2. Г. 180 м/с2.
Карточка 16
.
На рисунке изображен график зависимости скорости
движения пассажирского лифта от времени при его пуске.
Чему
лифта?
А. 10 м/с2. Б. 7,5 м/с2. В. 3,3 м/с2. Г. 0,3 м/с2.
Карточка 17
ускорение
ускорение
равно
равно
На рисунке изображен график зависимости скорости
движения парашютиста от времени при его приземлении.
Чему
парашютиста?
А. 0,2 м/с2. Б. 5 м/с2. В. 10 м/с2. Г. 180 м/с2.
ускорение
равно
. Карточка 18
Карточка 19
На рисунке изображены графики зависимости скорости
движения четырёх автомобилей от времени v = v(t). Какой
На рисунке изображены графики зависимости скорости
из автомобилей – 1,2,3 или 4 – прошел наибольший путь за
движения четырёх автомобилей от времени v = v(t).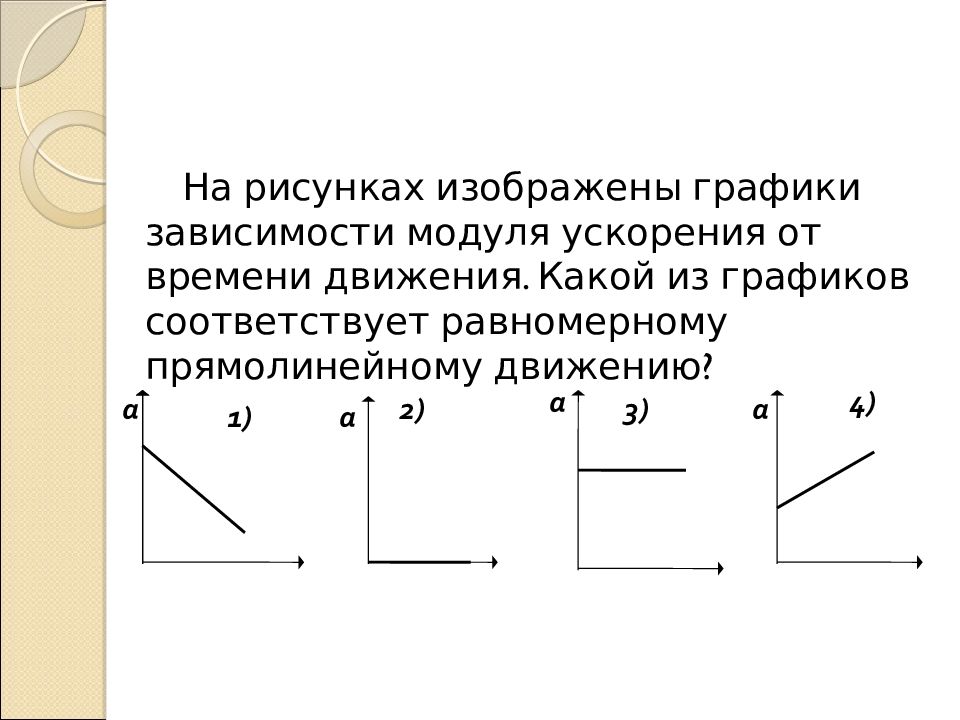 Чему
Чему
первые
движения?
равен путь, пройденный вторым автомобилем за 20 с
А. 1. Б. 2. В. 3. Г. 4.
движения?
А. 200 м. Б. 360 м. В. 400 м. Г. 720 м.
20
с
Карточка 18
Карточка 19
На рисунке изображены графики зависимости скорости
движения четырёх автомобилей от времени v = v(t).
На рисунке изображены графики зависимости скорости
Какой из автомобилей – 1,2,3 или 4 – прошел
движения четырёх автомобилей от времени v = v(t). Чему
наибольший путь за первые 20 с движения?
равен путь, пройденный вторым автомобилем за 20 с
А. 1. Б. 2. В. 3. Г. 4.
движения?
А. 200 м. Б. 360 м. В. 400 м. Г. 720 м.
Карточка 18
Карточка 19
На рисунке изображены графики зависимости скорости
движения четырёх автомобилей от времени v = v(t).
На рисунке изображены графики зависимости скорости
Какой из автомобилей – 1,2,3 или 4 – прошел
движения четырёх автомобилей от времени v = v(t). Чему
Чему
наибольший путь за первые 20 с движения?
равен путь, пройденный вторым автомобилем за 20 с
А. 1. Б. 2. В. 3. Г. 4.
движения?
А. 200 м. Б. 360 м. В. 400 м. Г. 720 м.
Карточка 18
Карточка 19
На рисунке изображены графики зависимости скорости
движения четырёх автомобилей от времени v = v(t).
На рисунке изображены графики зависимости скорости
Какой из автомобилей – 1,2,3 или 4 – прошел
движения четырёх автомобилей от времени v = v(t).
наибольший путь за первые 20 с движения?
Чему равен путь, пройденный вторым автомобилем за
А. 1. Б. 2. В. 3. Г. 4.
20 с
движения?
А. 200 м. Б. 360 м. В. 400 м. Г. 720 м.
Карточка 18
Карточка 19
На рисунке изображены графики зависимости скорости
движения четырёх автомобилей от времени v = v(t).
На рисунке изображены графики зависимости скорости
Какой из автомобилей – 1,2,3 или 4 – прошел
движения четырёх автомобилей от времени v = v(t).
наибольший путь за первые 20 с движения?
Чему равен путь, пройденный вторым автомобилем за
А. 1. Б. 2. В. 3. Г. 4.
20 с
движения?
А. 200 м. Б. 360 м. В. 400 м. Г. 720 м. Карточка 20
На рисунке приведён график зависимости скорости движения трамвая на прямолинейном участке
дороги от времени v = v(t). Используя график, рассчитайте путь, пройденный трамваем за 1,5 мин
движения.
Карточка 20
На рисунке приведён график зависимости скорости движения трамвая на прямолинейном участке
дороги от времени v = v(t). Используя график, рассчитайте путь, пройденный трамваем за 1,5 мин
движения.
Карточка 20
На рисунке приведён график зависимости скорости движения трамвая на прямолинейном участке
дороги от времени v = v(t). Используя график, рассчитайте путь, пройденный трамваем за 1,5 мин
движения. Карточка 21
На рисунке приведён график зависимости скорости
движения моторной лодки от времени v = v(t). Используя
график, рассчитайте путь, пройденный лодкой за 3 мин
движения.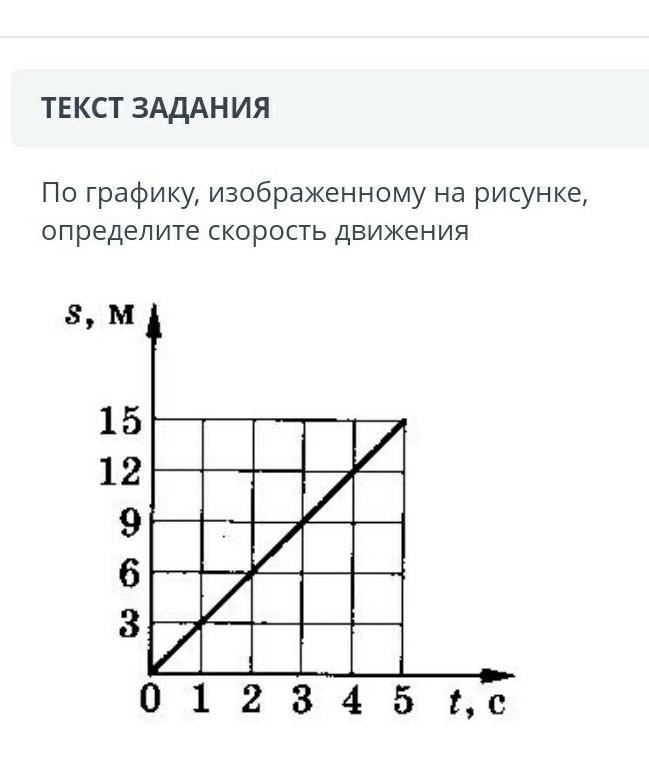
.
Карточка 21
На рисунке приведён график зависимости скорости
движения моторной лодки от времени v = v(t). Используя
график, рассчитайте путь, пройденный лодкой за 3 мин
движения.
.
Карточка 21
На рисунке приведён график зависимости скорости
движения моторной лодки от времени v = v(t). Используя
график, рассчитайте путь, пройденный лодкой за 3 мин
движения.
.
Карточка 21
На рисунке приведён график зависимости скорости
движения моторной лодки от времени v = v(t). Используя
график, рассчитайте путь, пройденный лодкой за 3 мин
движения.
.
Карточка 21
На рисунке приведён график зависимости скорости
движения моторной лодки от времени v = v(t). Используя
график, рассчитайте путь, пройденный лодкой за 3 мин
движения.
. Карточка 22
На рисунке приведён график зависимости пути,
Карточка 23
пройденного электропоездом на прямолинейном участке
дороги, от времени s = s (t).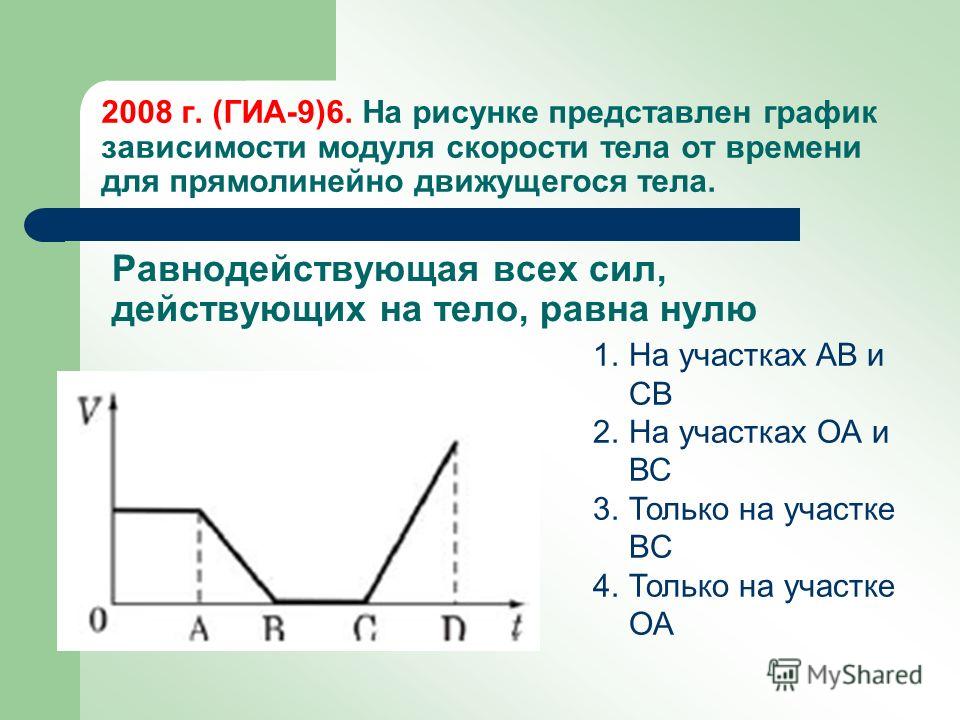 Чему равна скорость
Чему равна скорость
На рисунке приведен график зависимости скорости полёта
электропоезда? Скорость выразите в километрах в час.
пассажирского самолёта от времени v = v(t). С помощью
графика рассчитайте расстояние, которое пролетит самолёт
за 45 с полёта. Расстояние выразите в километрах.
Карточка 22
На рисунке приведён график зависимости пути,
Карточка 23
пройденного электропоездом на прямолинейном участке
дороги, от времени s = s (t). Чему равна скорость
На рисунке приведен график зависимости скорости полёта
электропоезда? Скорость выразите в километрах в час.
пассажирского самолёта от времени v = v(t). С помощью
графика рассчитайте расстояние, которое пролетит самолёт
за 45 с полёта. Расстояние выразите в километрах.
Карточка 22
На рисунке приведён график зависимости пути,
Карточка 23
пройденного электропоездом на прямолинейном участке
дороги, от времени s = s (t). Чему равна скорость
На рисунке приведен график зависимости скорости полёта
электропоезда? Скорость выразите в километрах в час.
пассажирского самолёта от времени v = v(t). С помощью
графика рассчитайте расстояние, которое пролетит самолёт
за 45 с полёта. Расстояние выразите в километрах.
Карточка 22
На рисунке приведён график зависимости пути,
Карточка 23
пройденного электропоездом на прямолинейном участке
дороги, от времени s = s (t). Чему равна скорость
На рисунке приведен график зависимости скорости полёта
электропоезда? Скорость выразите в километрах в час.
пассажирского самолёта от времени v = v(t). С помощью
графика рассчитайте расстояние, которое пролетит самолёт
за 45 с полёта. Расстояние выразите в километрах.
Карточка 22
На рисунке приведён график зависимости пути,
Карточка 23
пройденного электропоездом на прямолинейном участке
дороги, от времени s = s (t). Чему равна скорость
На рисунке приведен график зависимости скорости полёта
электропоезда? Скорость выразите в километрах в час.
пассажирского самолёта от времени v = v(t). С помощью
графика рассчитайте расстояние, которое пролетит самолёт
за 45 с полёта.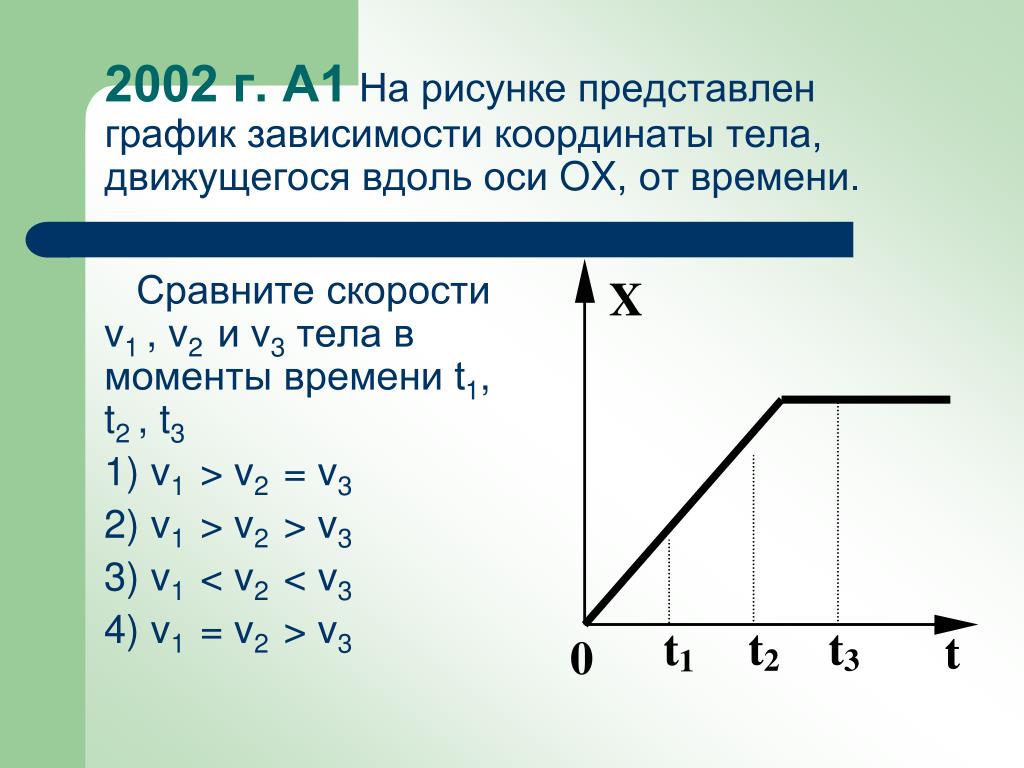 Расстояние выразите в километрах. Карточка 24
Расстояние выразите в километрах. Карточка 24
На рисунке приведён график зависимости скорости
движения пассажирского реактивного самолета Як40 от
времени v = v(t). Рассчитайте максимальное ускорение при
разбеге самолёта. Каков физический смысл знака («+» или
«–»)у значения
ускорения?
Карточка 24
На рисунке приведён график зависимости скорости
движения пассажирского реактивного самолета Як40 от
времени v = v(t). Рассчитайте максимальное ускорение при
разбеге самолёта. Каков физический смысл знака («+» или
«–»)у значения
ускорения?
Карточка 24
На рисунке приведён график зависимости скорости
движения пассажирского реактивного самолета Як40 от
времени v = v(t). Рассчитайте максимальное ускорение при
разбеге самолёта. Каков физический смысл знака («+» или
ускорения?
«–»)у значения
Карточка 24
На рисунке приведён график зависимости скорости
движения пассажирского реактивного самолета Як40 от
времени v = v(t). Рассчитайте максимальное ускорение при
разбеге самолёта.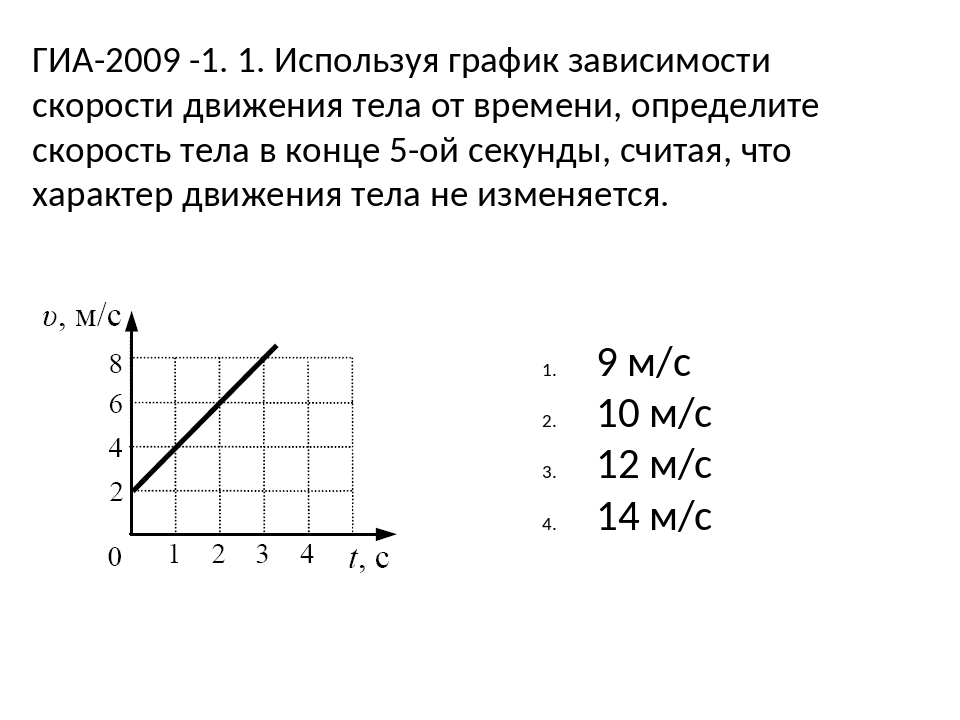 Каков физический смысл знака («+» или
Каков физический смысл знака («+» или
ускорения?
«–»)у значения
Карточка 24
На рисунке приведён график зависимости скорости
движения пассажирского реактивного самолета Як40 от
времени v = v(t). Рассчитайте максимальное ускорение при
разбеге самолёта. Каков физический смысл знака («+» или
«–»)у значения
ускорения? Карточка 25
На рисунке
приведён график зависимости скорости
движения автомобиля «Жигули» от времени v = v(t).
Рассчитайте максимальное ускорение автомобиля (в м/с2).
Каков физический смысл знака («+» или «–») у значения
ускорения?
Карточка 25
На рисунке
приведён график зависимости скорости
движения автомобиля «Жигули» от времени v = v(t).
Рассчитайте максимальное ускорение автомобиля (в м/с2).
Каков физический смысл знака («+» или «–») у значения
ускорения?
Карточка 25
На рисунке
приведён график зависимости скорости
движения автомобиля «Жигули» от времени v = v(t).
Рассчитайте максимальное ускорение автомобиля (в м/с2).
Каков физический смысл знака («+» или «–») у значения
ускорения?
Карточка 25
приведён график зависимости скорости
На рисунке
движения автомобиля «Жигули» от времени v = v(t).
Рассчитайте максимальное ускорение автомобиля (в м/с2).
Каков физический смысл знака («+» или «–») у значения
ускорения?
Карточка 25
На рисунке
приведён график зависимости скорости
движения автомобиля «Жигули» от времени v = v(t).
Рассчитайте максимальное ускорение автомобиля (в м/с2).
Каков физический смысл знака («+» или «–») у значения
ускорения? Карточка 26
На рисунке приведён график зависимости скорости движения
Карточка 27
электровоза на прямолинейном участке дороги от
времени v = v(t). Используя график, выполните задания.
На рисунке приведён график зависимости скорости движения
1.Опишите движение электровоза на участках АB, ВС и CD.
скоростного лифта Останкинской телебашни от
2. Рассчитайте ускорение электровоза на каждом участке.
времени v = v(t) при нажатии кнопки «Пуск». Рассчитайте
максимальное ускорение лифта. Каков физический смысл
знака («+» или «–») у значения ускорения?
Карточка 26
На рисунке приведён график зависимости скорости движения
Карточка 27
электровоза на прямолинейном участке дороги от
времени v = v(t). Используя график, выполните задания.
На рисунке приведён график зависимости скорости движения
скоростного лифта Останкинской телебашни от
1.Опишите движение электровоза на участках АB, ВС и CD.
2. Рассчитайте ускорение электровоза на каждом участке.
времени v = v(t) при нажатии кнопки «Пуск». Рассчитайте
максимальное ускорение лифта. Каков физический смысл
знака («+» или «–») у значения ускорения?
Карточка 26
Карточка 27
На рисунке приведён график зависимости скорости движения
электровоза на прямолинейном участке дороги от
На рисунке приведён график зависимости скорости движения
времени v = v(t). Используя график, выполните задания.
скоростного лифта Останкинской телебашни от
1.Опишите движение электровоза на участках АB, ВС и CD.
времени v = v(t) при нажатии кнопки «Пуск». Рассчитайте
2. Рассчитайте ускорение электровоза на каждом участке.
максимальное ускорение лифта. Каков физический смысл
знака («+» или «–») у значения ускорения?
Карточка 26
Карточка 27
На рисунке приведён график зависимости скорости движения
электровоза на прямолинейном участке дороги от
На рисунке приведён график зависимости скорости движения
времени v = v(t). Используя график, выполните задания.
скоростного лифта Останкинской телебашни от
1.Опишите движение электровоза на участках АB, ВС и CD.
времени v = v(t) при нажатии кнопки «Пуск». Рассчитайте
2. Рассчитайте ускорение электровоза на каждом участке.
максимальное ускорение лифта. Каков физический смысл
знака («+» или «–») у значения ускорения?
Карточка 27
Карточка 26
На рисунке приведён график зависимости скорости движения
На рисунке приведён график зависимости скорости движения
электровоза на прямолинейном участке дороги от
скоростного лифта Останкинской телебашни от
времени v = v(t). Используя график, выполните задания.
времени v = v(t) при нажатии кнопки «Пуск». Рассчитайте
1.Опишите движение электровоза на участках АB, ВС и CD.
максимальное ускорение лифта. Каков физический смысл
2. Рассчитайте ускорение электровоза на каждом участке.
знака («+» или «–») у значения ускорения? ОТВЕТЫ
«К И Н Е М А Т И К
А»
№
карточки
Ответ
№
карточки
Ответ
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
19
А Б Б Г В Б В Г Г Б Б В Г А В Г Б В В
20
21
22
23
24
25
26
27
405
м
1080
м
36
км/ч
7,5
км
2
м/с2
0,4
м/с2
аAB = 0,4 м/с2, аBC = 0,
аCD = –0,4 м/с2.
1,4
м/с2
Продолжение следует.
Литература:
1. Ф а д е е в а А. А. Физика: карточкизадания: 8 кл.: кн. для учащихся / А. А. Фадеева. — М.:
Просвещение, 2009.
2.3 Графики положения в зависимости от времени — физика
Графическое представление положения в зависимости от времени
График, как и картинка, стоит тысячи слов. Графики содержат не только числовую информацию, но и показывают взаимосвязь между физическими величинами. В этом разделе мы исследуем кинематику, анализируя графики положения во времени.
Графики в этом тексте имеют перпендикулярные оси, одна горизонтальная, а другая вертикальная. Когда две физические величины наносятся друг на друга, горизонтальная ось обычно считается независимой переменной, а вертикальная ось — зависимой переменной.В алгебре вы назвали бы горизонтальную ось осью x , а вертикальную ось — осью y . Как показано на рис. 2.10, прямолинейный граф имеет общий вид y = mx + by = mx + b.
Здесь м — уклон, определяемый как подъем, деленный на длину (как показано на рисунке) прямой линии. Буква b — это точка пересечения y , которая является точкой, в которой линия пересекает вертикальную ось y . С точки зрения физической ситуации в реальном мире эти величины будут иметь особое значение, как мы увидим ниже.(Рисунок 2.10.)
Рисунок 2.10 На диаграмме показан прямолинейный график. Уравнение для прямой линии: y равно mx + b .
В физике время обычно является независимой переменной. Говорят, что от него зависят и другие величины, такие как смещение. График положения в зависимости от времени, следовательно, будет иметь положение на вертикальной оси (зависимая переменная) и время на горизонтальной оси (независимая переменная). В этом случае, к чему будут относиться наклон и перехват y ? Давайте вернемся к нашему первоначальному примеру при изучении расстояния и смещения.
Дорога в школу находилась в 5 км от дома. Предположим, поездка заняла 10 минут, и ваш родитель все это время вел машину с постоянной скоростью. График зависимости положения от времени для этого участка пути будет выглядеть так, как показано на рисунке 2.11.
Рисунок 2.11 Показан график зависимости положения от времени на дорогу в школу. Как бы выглядел график, если бы мы добавили обратный путь?
Как мы уже говорили, d 0 = 0, потому что мы звоним домой по нашему O и начинаем вычисление оттуда.На рисунке 2.11 линия также начинается с d = 0. Это b в нашем уравнении для прямой. Нашей исходной позицией на графике зависимости положения от времени всегда является место, где график пересекает ось x при t = 0. Каков наклон? Подъем — это изменение положения (т. Е. Смещение), а пробег — это изменение во времени. Это отношение также можно записать
Это соотношение было тем, как мы определили среднюю скорость.Следовательно, наклон на графике d по сравнению с t — это средняя скорость.
Советы для успеха
Иногда, как в случае, когда мы строим график как поездки в школу, так и обратного пути, поведение графика выглядит по-разному в разные промежутки времени. Если график выглядит как серия прямых линий, то вы можете рассчитать среднюю скорость для каждого временного интервала, посмотрев на наклон. Если вы затем захотите рассчитать среднюю скорость за всю поездку, вы можете вычислить средневзвешенное значение.
Давайте посмотрим на другой пример. На рис. 2.12 показан график положения в зависимости от времени для реактивного автомобиля на очень плоском высохшем дне озера в Неваде.
Рис. 2.12 На диаграмме показан график положения в зависимости от времени для автомобиля с реактивным двигателем на солончаках Бонневиль.
Используя соотношение между зависимыми и независимыми переменными, мы видим, что наклон на графике на рисунке 2.12 — это средняя скорость, v avg , а точка пересечения — смещение в нулевой момент времени, то есть d 0 .Подставляя эти символы в y = mx + b , получаем
или
Таким образом, график положения в зависимости от времени дает общую взаимосвязь между перемещением, скоростью и временем, а также дает подробную числовую информацию о конкретной ситуации. Из рисунка видно, что автомобиль занимает позицию 400 м при т = 0 с, 650 м при т = 1,0 с и так далее. И мы также можем узнать о скорости объекта.
Поддержка учителей
Поддержка учителей
Демонстрация учителей
Помогите учащимся узнать, какие графики смещения отличаются от других.время похоже.
[Визуальный] Установите измерительную линейку.
- Если вы можете найти машину с дистанционным управлением, попросите одного ученика записать время, когда вы отправляете машину вперед вдоль ручки, затем назад, затем снова вперед с постоянной скоростью.
- Возьмите записанное время и изменение положения и сложите их вместе.
- Попросите студентов научить вас рисовать график зависимости положения от времени.
Каждый отрезок пути должен представлять собой прямую линию с разным уклоном.Участки, по которым машина двигалась вперед, должны иметь положительный наклон. Та часть, где он идет назад, будет иметь отрицательный наклон.
[OL] Спросите, влияет ли на график место, которое они принимают как ноль .
[AL] Реально ли нарисовать любой график положения, который начинается в состоянии покоя, без какой-либо кривой? Почему в некоторых сценариях можно пренебречь кривой?
[Все] Обсудите, что можно обнаружить на этом графике. Учащиеся должны уметь считывать чистое смещение, но они также могут использовать график для определения общего пройденного расстояния.Затем спросите, как скорость или скорость отражаются на этом графике. Посоветуйте учащимся увидеть, что крутизна линии (уклона) является мерой скорости, а направление уклона — направлением движения.
[AL] Некоторые студенты могут понять, что кривая на линии представляет собой своего рода наклон наклона, предварительный просмотр ускорения, о котором они узнают в следующей главе.
Snap Lab
Построение графика движения
В этом упражнении вы отпустите мяч по наклонной плоскости и построите график зависимости смещения мяча от смещения.время.
- Выберите открытое место с большим пространством, чтобы было меньше шансов споткнуться или упасть из-за катящихся шаров.
- 1 мяч
- 1 доска
- 2 или 3 книги
- 1 секундомер
- 1 рулетка
- 6 штук малярной ленты
- 1 миллиметровая бумага
- 1 карандаш
Процедура
- Постройте пандус, поместив один конец доски поверх стопки книг.При необходимости отрегулируйте местоположение так, чтобы не было препятствий на прямой линии от нижней части пандуса до следующих 3 м.
- Отметьте расстояния 0,5 м, 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса. Напишите расстояния на ленте.
- Пусть один человек возьмет на себя роль экспериментатора. Этот человек выпустит мяч с вершины рампы. Если мяч не достигает отметки 3,0 м, увеличьте наклон пандуса, добавив еще одну книгу.При необходимости повторите этот шаг.
- Попросите экспериментатора выпустить мяч. Попросите второго человека, таймера, начать отсчет времени попытки, когда мяч достигнет нижней части рампы, и остановить отсчет, когда мяч достигнет 0,5 м. Попросите третьего человека, записывающего устройства, записать время в таблицу данных.
- Повторите шаг 4, остановив раз на расстоянии 1,0 м, 1,5 м, 2,0 м, 2,5 м и 3,0 м от нижней части пандуса.
- Используйте свои измерения времени и смещения, чтобы составить позицию vs.временной график движения мяча.
- Повторите шаги с 4 по 6 с разными людьми, которые берут на себя роли экспериментатора, таймера и записывающего устройства. Получаете ли вы одинаковые значения измерений независимо от того, кто выпускает мяч, измеряет время или записывает результат? Обсудите возможные причины расхождений, если таковые имеются.
Контроль захвата
Верно или неверно: средняя скорость мяча будет меньше средней скорости мяча.
- Истинно
- Ложь
Поддержка учителя
Поддержка учителя
[BL] [OL] Подчеркните, что движение в этой лабораторной работе — это движение мяча, катящегося по полу.Спросите студентов, где должен быть ноль.
[AL] Спросите учащихся, как бы выглядел график, если бы они начали отсчет времени вверху по сравнению с основанием пандуса. Почему график должен выглядеть иначе? Чем может объясняться разница?
[BL] [OL] Попросите учащихся сравнить графики, построенные с разными людьми, выполняющими разные роли. Попросите их определить и сравнить среднюю скорость для каждого интервала. Каковы были абсолютные различия в скоростях и каковы были различия в процентах? Оказываются ли различия случайными или существуют систематические различия? Почему могут существовать систематические различия между двумя наборами измерений с разными людьми в каждой роли?
[BL] [OL] Попросите учащихся сравнить графики, построенные с разными людьми, выполняющими разные роли.Попросите их определить и сравнить среднюю скорость для каждого интервала. Каковы были абсолютные различия в скоростях и каковы были различия в процентах? Оказываются ли различия случайными или существуют систематические различия? Почему могут существовать систематические различия между двумя наборами измерений с разными людьми в каждой роли?
Решение задач с использованием графиков положения и времени
Итак, как мы можем использовать графики для решения таких задач, как скорость?
Рабочий пример
Использование графика положения и времени для расчета средней скорости: Jet Car
Найдите среднюю скорость автомобиля, положение которого показано на Рисунке 1.13.
Стратегия
Наклон графика d против t — это средняя скорость, поскольку наклон равен подъему за пробег.
наклон = ΔdΔt = vsсклон = ΔdΔt = v
2,7
Поскольку наклон здесь постоянный, любые две точки на графике могут использоваться для определения наклона.
Решение
- Выберите две точки на линии. В этом случае мы выбираем точки, помеченные на графике: (6,4 с, 2000 м) и (0,50 с, 525 м). (Обратите внимание, однако, что вы можете выбрать любые две точки.)
- Подставьте значения d и t выбранных точек в уравнение. Помните, что при вычислении изменения (Δ) мы всегда используем конечное значение минус начальное значение.
v = ΔdΔt = 2000 м − 525 м6,4 с − 0,50 с = 250 м / с, v = ΔdΔt = 2000 м − 525 м6,4 с − 0,50 с = 250 м / с,2,8
Обсуждение
Это впечатляюще высокая сухопутная скорость (900 км / ч или около 560 миль / ч): намного больше, чем типичное ограничение скорости на шоссе, равное 27 м / с или 96 км / ч, но значительно ниже рекордных 343 м. / с или 1234 км / ч, установленный в 1997 году.
Teacher Support
Teacher Support
Если график положения представляет собой прямую линию, то единственное, что ученикам нужно знать для расчета средней скорости, — это наклон линии, подъем / бег. Они могут использовать любые наиболее удобные точки на линии.
А что, если график позиции сложнее прямой? Что, если объект ускоряется или поворачивается и движется назад? Можем ли мы выяснить что-нибудь о его скорости из графика такого движения? Давайте еще раз посмотрим на реактивный автомобиль.График на рис. 2.13 показывает его движение по мере того, как он набирает скорость после запуска в состоянии покоя. Время для этого движения начинается с нуля (как если бы оно измерялось секундомером), а смещение и скорость изначально составляют 200 м и 15 м / с соответственно.
Рис. 2.13 На диаграмме показан график положения автомобиля с реактивным двигателем в течение периода времени, когда он набирает скорость. Наклон графика зависимости расстояния от времени — это скорость. Это показано в двух точках. Мгновенная скорость в любой точке — это наклон касательной в этой точке.
Рис. 2.14 Реактивный автомобиль ВВС США едет по рельсовому пути. (Мэтт Тростле, Flickr)
График положения в зависимости от времени на рис. 2.13 представляет собой кривую, а не прямую линию. Наклон кривой становится более крутым с течением времени, показывая, что скорость увеличивается с течением времени. Наклон в любой точке графика зависимости положения от времени — это мгновенная скорость в этой точке. Его можно найти, проведя прямую касательную к кривой в интересующей точке и взяв наклон этой прямой.Касательные линии показаны для двух точек на рисунке 2.13. Средняя скорость — это чистое смещение, деленное на пройденное время.
Рабочий пример
Использование графика положения и времени для расчета средней скорости: реактивный автомобиль, дубль
Рассчитайте мгновенную скорость реактивного автомобиля за время 25 с, найдя наклон касательной в точке Q на рисунке 2.13.
Стратегия
Наклон кривой в точке равен наклону прямой, касательной к кривой в этой точке.
Решение
- Найдите касательную к кривой при t = 25 st = 25 с.
- Определите конечные точки касательной. Они соответствуют положению 1300 м за 19 с и положению 3120 м за 32 с.
- Подставьте эти конечные точки в уравнение, чтобы найти наклон, v .
уклон = vQ = ΔdQΔtQ = (3120−1300) м (32−19) s = 1820 м13 s = 140 м / с уклон = vQ = ΔdQΔtQ = (3120−1300) м (32−19) s = 1820 м13 s = 140 м / с2.9
Обсуждение
Таким образом можно получить весь график v и t .
Поддержка учителя
Поддержка учителя
Изогнутая линия — более сложный пример. Определите касательную как линию, которая касается кривой только в одной точке. Покажите, что, когда прямая линия меняет свой угол рядом с кривой, она на самом деле несколько раз ударяет по кривой в основании, но только одна линия никогда не соприкасается. Эта линия образует прямой угол с радиусом кривизны, но на этом уровне они могут просто смотреть на нее.Наклон этой линии дает мгновенную скорость. Самая полезная часть этой строки состоит в том, что учащиеся могут определять, когда скорость увеличивается, уменьшается, положительная, отрицательная и нулевая.
[AL] Вы можете найти мгновенную скорость в каждой точке графика, и если вы изобразите каждую из этих точек, вы получите график скорости.
3.3 Среднее и мгновенное ускорение — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Рассчитайте среднее ускорение между двумя точками времени.
- Рассчитайте мгновенное ускорение с учетом функциональной формы скорости.
- Объясните векторную природу мгновенного ускорения и скорости.
- Объясните разницу между средним ускорением и мгновенным ускорением.
- Найдите мгновенное ускорение в заданное время на графике зависимости скорости от времени.
Важность понимания ускорения охватывает наш повседневный опыт, а также обширные просторы космического пространства и крошечный мир субатомной физики.В повседневном разговоре до разогнаться означает разогнаться; нажатие на педаль тормоза приводит к замедлению движения автомобиля. Мы, например, знакомы с ускорением нашей машины. Чем больше ускорение, тем больше изменение скорости за заданный промежуток времени. Ускорение широко наблюдается в экспериментальной физике. Например, в экспериментах с линейным ускорителем частиц субатомные частицы ускоряются до очень высоких скоростей в экспериментах по столкновению, которые сообщают нам информацию о структуре субатомного мира, а также о происхождении Вселенной.В космосе космические лучи — это субатомные частицы, которые были ускорены до очень высоких энергий в сверхновых (взрывающихся массивных звездах) и активных ядрах галактик. Важно понимать процессы, которые ускоряют космические лучи, потому что эти лучи содержат очень проникающее излучение, которое может, например, повредить электронику, установленную на космических кораблях.
Среднее ускорение
Формальное определение ускорения согласуется с этими только что описанными понятиями, но является более всеобъемлющим.
Среднее ускорение
Среднее ускорение — это скорость изменения скорости:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} — {v} _ { 0}} {{t} _ {\ text {f}} — {t} _ {0}}, [/ latex]
, где [latex] \ overset {\ text {-}} {a} [/ latex] — среднее ускорение, v — скорость, а t — время. (Полоса над на означает среднее ускорение .)
Поскольку ускорение — это скорость в метрах, разделенная на время в секундах, единицы измерения ускорения в системе СИ часто обозначаются сокращенно: м / с 2 , то есть метры в секунду в квадрате или метры в секунду в секунду.Это буквально означает, на сколько метров в секунду изменяется скорость каждую секунду. Напомним, что скорость — это вектор, он имеет как величину, так и направление, что означает, что изменение скорости может быть изменением величины (или скорости), но также может быть изменением направления. Например, если бегун, движущийся со скоростью 10 км / ч на восток, замедляется до остановки, меняет направление, продолжает свой бег со скоростью 10 км / ч на запад, его скорость изменилась в результате изменения направления, хотя величина скорости одинаковы в обоих направлениях.Таким образом, ускорение происходит, когда скорость изменяется по величине (увеличение или уменьшение скорости) или по направлению, или по обоим направлениям.
Ускорение как вектор
Ускорение — это вектор в том же направлении, что и , изменение скорости на , [latex] \ Delta v [/ latex]. Поскольку скорость является вектором, она может изменяться по величине или по направлению, или по обоим направлениям. Следовательно, ускорение — это изменение скорости или направления, или и того, и другого.
Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда в направлении движения.Когда объект замедляется, его ускорение противоположно направлению его движения. Хотя это обычно называется замедлением , фигура , мы говорим, что поезд ускоряется в направлении, противоположном его направлению движения.
Рисунок 3.10. Поезд метро в Сан-Паулу, Бразилия, замедляет ход, когда подъезжает к станции. Он ускоряется в направлении, противоположном направлению его движения. (Источник: Юсуке Кавасаки)
Термин замедление может вызвать путаницу в нашем анализе, поскольку он не является вектором и не указывает на конкретное направление относительно системы координат, поэтому мы его не используем.Ускорение — это вектор, поэтому мы должны выбрать для него соответствующий знак в выбранной нами системе координат. В случае поезда на рисунке ускорение составляет в отрицательном направлении в выбранной системе координат , поэтому мы говорим, что поезд испытывает отрицательное ускорение.
Если движущийся объект имеет скорость в положительном направлении по отношению к выбранной исходной точке и приобретает постоянное отрицательное ускорение, объект в конечном итоге останавливается и меняет направление на противоположное.Если мы подождем достаточно долго, объект пройдет через начало координат в противоположном направлении. Это показано на рисунке.
Рис. 3.11. Объект, движущийся с вектором скорости на восток при отрицательном ускорении, останавливается и меняет направление на противоположное. Через достаточно долгое время он проходит исходную точку в обратном направлении.
Пример
Расчет среднего ускорения: скакун покидает ворота
Скаковая лошадь, выходящая из ворот, набирает скорость до 15.0 м / с на запад за 1.80 с. Какое у него среднее ускорение?
Рис. 3.12. Скачки вылетают из ворот. (кредит: Джон Салливан)
Стратегия
Сначала мы рисуем эскиз и назначаем систему координат проблемной фигуре. Это простая проблема, но всегда помогает ее визуализировать. Обратите внимание, что мы назначаем восток как положительный, а запад как отрицательный. Таким образом, в этом случае мы имеем отрицательную скорость.
Рисунок 3.13 Определите систему координат, данную информацию и то, что вы хотите определить.
Мы можем решить эту проблему, определив [latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex] из заданной информации, а затем вычислив среднее ускорение непосредственно из уравнения [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} — {v} _ {0}} {{t } _ {\ text {f}} — {t} _ {0}} [/ latex].
Решение
Сначала определите известные: [latex] {v} _ {0} = 0, {v} _ {\ text {f}} = — 15.0 \, \ text {m / s} [/ latex] (отрицательный указывает направление на запад), Δ t = 1.80 с.
Во-вторых, найдите изменение скорости. Поскольку лошадь движется с нуля до –15,0 м / с, ее изменение скорости равно ее конечной скорости:
[латекс] \ Delta v = {v} _ {\ text {f}} — {v} _ {0} = {v} _ {\ text {f}} = — 15,0 \, \ text {м / с }. [/ латекс]
Наконец, подставьте известные значения ([latex] \ Delta v \, \ text {and} \, \ Delta t [/ latex]) и найдите неизвестное [latex] \ overset {\ text {-}} {a } [/ latex]:
[латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {-15.0 \, \ text {m / s}} {1.{2}. [/ Латекс]
Значение
Отрицательный знак ускорения указывает на то, что ускорение направлено на запад. Ускорение 8,33 м / с 2 на западе означает, что лошадь увеличивает свою скорость на 8,33 м / с на западе каждую секунду; то есть 8,33 метра в секунду в секунду, что мы записываем как 8,33 м / с 2 . Это действительно среднее ускорение, потому что поездка не гладкая. Позже мы увидим, что ускорение такой величины потребовало бы от всадника держаться с силой, почти равной его весу.{2}. [/ Латекс]
Мгновенное ускорение
Мгновенное ускорение Ускорение или в определенный момент времени получается с использованием того же процесса, что и для мгновенной скорости. То есть мы вычисляем среднюю скорость между двумя точками времени, разделенными [латексом] \ Delta t [/ latex], и позволяем [latex] \ Delta t [/ latex] приближаться к нулю. Результатом является производная функции скорости v ( t ), которая составляет мгновенное ускорение и математически выражается как
.
[латекс] a (t) = \ frac {d} {dt} v (t).[/ латекс]
Таким образом, подобно тому, как скорость является производной функции положения, мгновенное ускорение является производной функции скорости. Мы можем показать это графически так же, как мгновенную скорость. На рисунке мгновенное ускорение в момент времени t 0 — это наклон касательной к графику зависимости скорости от времени в момент времени t 0 . Мы видим, что среднее ускорение [latex] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} [/ latex] приближается к мгновенному ускорению, как [latex] \ Delta t [/ latex ] стремится к нулю.Также в части (а) рисунка мы видим, что скорость имеет максимум, когда ее наклон равен нулю. Это время соответствует нулю функции ускорения. В части (b) показано мгновенное ускорение при минимальной скорости, которая также равна нулю, поскольку наклон кривой там тоже равен нулю. Таким образом, для данной функции скорости нули функции ускорения дают либо минимальную, либо максимальную скорость.
Рис. 3.14. На графике зависимости скорости от времени мгновенное ускорение представляет собой наклон касательной.(a) Показано среднее ускорение [латекс] \ overset {\ text {-}} {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {\ text {f}} — {v} _ {i}} {{t} _ {\ text {f}} — {t} _ {i}} [/ latex] между временами [латекс] \ Delta t = {t} _ {6} — {t} _ {1}, \ Delta t = {t} _ {5} — {t} _ {2} [/ latex] и [latex] \ Delta t = {t} _ {4} — { t} _ {3} [/ latex]. Когда [latex] \ Delta t \ равняется 0 [/ latex], среднее ускорение приближается к мгновенному ускорению в момент времени t0. В виде (а) мгновенное ускорение показано для точки на кривой скорости при максимальной скорости. В этой точке мгновенное ускорение — это наклон касательной, равный нулю.В любое другое время наклон касательной — и, следовательно, мгновенное ускорение — не будет нулевым. (b) То же, что (a), но показано для мгновенного ускорения при минимальной скорости.
Чтобы проиллюстрировать эту концепцию, давайте рассмотрим два примера. Во-первых, простой пример показан с использованием рисунка (b), графика зависимости скорости от времени на рисунке, чтобы найти ускорение графически. Этот график изображен на рисунке (а), который представляет собой прямую линию. Соответствующий график ускорения в зависимости от времени находится по наклону скорости и показан на рисунке (b).В этом примере функция скорости представляет собой прямую линию с постоянным наклоном, поэтому ускорение является постоянным. В следующем примере функция скорости имеет более сложную функциональную зависимость от времени.
Рис. 3.15. (a, b) График зависимости скорости от времени является линейным и имеет постоянный отрицательный наклон (a), который равен ускорению, показанному на (b).
Если мы знаем функциональную форму скорости, v ( t ), мы можем вычислить мгновенное ускорение a ( t ) в любой момент времени в движении, используя рисунок.{2} \, \ text {m / s} [/ латекс].
- Найдите функциональную форму ускорения.
- Найдите мгновенную скорость при t = 1, 2, 3 и 5 с.
- Найдите мгновенное ускорение при t = 1, 2, 3 и 5 с.
- Интерпретируйте результаты (c) в терминах направлений векторов ускорения и скорости.
Стратегия
Мы находим функциональную форму ускорения, взяв производную от функции скорости.{2} [/ латекс]
При t = 2 с, скорость увеличилась до [latex] v (2 \, \ text {s)} = 20 \, \ text {m / s} [/ latex], где она максимальна, что соответствует моменту, когда ускорение равно нулю. Мы видим, что максимальная скорость достигается, когда наклон функции скорости равен нулю, что является просто нулем функции ускорения.
При t = 3 с, скорость равна [latex] v (3 \, \ text {s)} = 15 \, \ text {m / s} [/ latex], а ускорение отрицательное. Частица уменьшила свою скорость, и вектор ускорения отрицательный. Частица замедляется.
При t = 5 с, скорость равна [latex] v (5 \, \ text {s)} = — 25 \, \ text {m / s} [/ latex], а ускорение становится все более отрицательным. Между моментами времени t = 3 с и t = 5 с частица уменьшила свою скорость до нуля, а затем стала отрицательной, таким образом изменив свое направление.Теперь частица снова ускоряется, но в противоположном направлении.
Мы можем видеть эти результаты графически на рисунке.
Рис. 3.16. (а) Скорость в зависимости от времени. Касательные линии указаны в моменты времени 1, 2 и 3 с. Наклон касательных — это ускорение. При t = 3 с скорость положительная. При t = 5 с скорость отрицательна, что указывает на то, что частица изменила направление на противоположное. (б) Ускорение против времени. Сравнивая значения ускорений, представленные черными точками, с соответствующими наклонами касательных линий (наклон линий через черные точки) на (а), мы видим, что они идентичны.
Значение
Выполняя численный и графический анализ скорости и ускорения частицы, мы можем многое узнать о ее движении. Численный анализ дополняет графический анализ, давая полное представление о движении. Нуль функции ускорения соответствует максимуму скорости в этом примере. Также в этом примере, когда ускорение положительное и в том же направлении, что и скорость, скорость увеличивается. По мере того, как ускорение стремится к нулю и в конечном итоге становится отрицательным, скорость достигает максимума, после чего начинает уменьшаться.Если мы подождем достаточно долго, скорость также станет отрицательной, что указывает на изменение направления. Реальным примером такого движения является автомобиль, скорость которого увеличивается до максимума, после чего он начинает замедляться, останавливается, а затем меняет направление движения.
Проверьте свое понимание
Самолет приземляется на взлетно-посадочной полосе, летящей на восток. Опишите его ускорение.
Показать решение
Если мы возьмем восток за положительное значение, тогда самолет будет иметь отрицательное ускорение, потому что он ускоряется на запад.Он также замедляется; его ускорение противоположно направлению его скорости.
Ощущение ускорения
Вы, вероятно, привыкли испытывать ускорение, когда заходите в лифт или нажимаете на педаль газа в машине. Однако ускорение происходит со многими другими объектами в нашей Вселенной, с которыми мы не имеем прямого контакта. На рисунке представлены ускорения различных объектов. Мы можем видеть, что величины ускорений простираются на многие порядки.
| Разгон | Значение (м / с 2 ) |
|---|---|
| Скоростной поезд | 0,25 |
| Лифт | 2 |
| Гепард | 5 |
| Объект в свободном падении без сопротивления воздуха у поверхности Земли | 9,8 |
| Максимум космического челнока во время запуска | 29 |
| Пик парашютиста при нормальном раскрытии парашюта | 59 |
| Самолет F16 выходит из пикирования | 79 |
| Взрывной выброс сиденья с самолета | 147 |
| Ракета Sprint | 982 |
| Максимальное пиковое ускорение ракетных салазок | 1540 |
| Прыгающая блоха | 3200 |
| Бейсбольный удар битой | 30 000 |
| Смыкание губок муравья-ловушки | 1 000 000 |
| Протон в большом адронном коллайдере | [латекс] 1.{9} [/ латекс] |
В этой таблице мы видим, что типичные ускорения сильно различаются для разных объектов и не имеют никакого отношения к размеру объекта или его массивности. Ускорение также может сильно меняться со временем во время движения объекта. У дрэг-рейсинга большое ускорение сразу после старта, но затем оно уменьшается, когда транспортное средство достигает постоянной скорости. Его среднее ускорение может сильно отличаться от его мгновенного ускорения в определенный момент времени во время его движения.На рисунке показано графическое сравнение среднего ускорения с мгновенным ускорением для двух очень разных движений.
Рис. 3.17. Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений. (а) Ускорение меняется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (б) Ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается.В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением.
Сводка
- Ускорение — это скорость изменения скорости. Ускорение — это вектор; он имеет как величину, так и направление. Единица измерения ускорения в системе СИ — метр на секунду в квадрате.
- Ускорение может быть вызвано изменением величины или направления скорости, либо и тем, и другим.
- Мгновенное ускорение a ( t ) является непрерывной функцией времени и дает ускорение в любой конкретный момент во время движения.Он рассчитывается по производной функции скорости. Мгновенное ускорение — это наклон графика зависимости скорости от времени.
- Отрицательное ускорение (иногда называемое замедлением) — это ускорение в отрицательном направлении в выбранной системе координат.
Концептуальные вопросы
Возможно ли, чтобы скорость была постоянной, когда ускорение не равно нулю?
Показать решение
Нет, в одном измерении постоянная скорость требует нулевого ускорения.
Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять.
Приведите пример, в котором скорость равна нулю, а ускорение — нет.
Показать решение
Мяч подбрасывается в воздух, и его скорость равна нулю на вершине броска, но ускорение не равно нулю.
Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное?
Знаки плюс и минус используются в одномерном движении для обозначения направления.{2} [/ латекс]
Доктор Джон Пол Стапп был офицером ВВС США, изучавшим влияние экстремального ускорения на человеческое тело. 10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с и резко остановившись всего за 1,40 с. Вычислите его (а) ускорение в направлении его движения и (б) ускорение, противоположное его направлению движения. Выразите каждое значение кратным g (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения.
Нарисуйте график зависимости ускорения от времени из следующего графика зависимости скорости от времени.
Показать ответ
Пассажир выезжает на машине из гаража с ускорением 1,40 м / с 2 . а) Сколько времени ей нужно, чтобы набрать скорость 2,00 м / с? (b) Если она затем тормозит до остановки за 0,800 с, каково ее ускорение?
Предположим, межконтинентальная баллистическая ракета выходит из состояния покоя на суборбитальную скорость 6,50 км / с за 60 секунд.0 с (фактическая скорость и время классифицируются). Каково его среднее ускорение в метрах в секунду и кратное g (9,80 м / с 2 )?
Показать решение
[латекс] a = 11,1 г [/ латекс]
Самолет, стартуя из состояния покоя, движется по взлетно-посадочной полосе с постоянным ускорением в течение 18 с, а затем взлетает со скоростью 60 м / с. Какое среднее ускорение самолета?
Глоссарий
- среднее ускорение
- скорость изменения скорости; изменение скорости с течением времени
- мгновенное ускорение
- ускорение в определенный момент времени
звуковых волн | PASCO
Что такое звук
В физиологии звук возникает, когда вибрации объекта проходят через среду, пока не попадают в барабанную перепонку человека.В физике звук создается в виде волны давления. Когда объект вибрирует, он заставляет молекулы окружающего воздуха вибрировать, инициируя цепную реакцию колебаний звуковой волны во всей среде. В то время как физиологическое определение включает восприятие звука субъектом, физическое определение признает, что звук существует независимо от восприятия человеком.
Вы можете узнать этот раздел из нашего сообщения в блоге «Что такое звуковая волна в физике?» Продолжайте читать, чтобы подробнее узнать о звуковых волнах.
Типы звуков
Есть много разных типов звука, включая слышимый, неслышимый, неприятный, приятный, тихий, громкий, шум и музыку. Вы, вероятно, найдете звуки, издаваемые пианистом, мягкими, слышимыми и музыкальными. И хотя звук дорожных работ рано утром в субботу тоже слышен, он, конечно, не из приятных или мягких. Другие звуки, например свист собаки, не слышны человеческому уху. Это связано с тем, что собачий свист производит звуковые волны, которые находятся ниже диапазона человеческого слуха от 20 Гц до 20 000 Гц.Волны ниже 20 Гц называются инфразвуковыми волнами (инфразвук), а более высокие частоты выше 20 000 Гц известны как ультразвуковые волны (ультразвук).
Инфразвуковые волны (Инфразвук)
Инфразвуковые волны имеют частоты ниже 20 Гц, что делает их неслышными для человеческого уха. Ученые используют инфразвук для обнаружения землетрясений и извержений вулканов, для картирования подземных горных пород и нефтяных образований, а также для изучения активности человеческого сердца. Несмотря на нашу неспособность слышать инфразвук, многие животные используют инфразвуковые волны для общения в природе.Киты, бегемоты, носороги, жирафы, слоны и аллигаторы — все используют инфразвук для связи на впечатляющих расстояниях — иногда на сотни миль!
Ультразвуковые волны (ультразвук)
Звуковые волны с частотой выше 20,00 Гц производят ультразвук. Поскольку ультразвук происходит на частотах за пределами диапазона человеческого слуха, человеческое ухо не слышит его. Ультразвук чаще всего используется медицинскими специалистами, которые используют сонограммы для исследования внутренних органов своих пациентов.Некоторые менее известные применения ультразвука включают навигацию, визуализацию, смешивание образцов, обмен данными и тестирование. В природе летучие мыши излучают ультразвуковые волны, чтобы находить добычу и избегать препятствий.
Как производится звук?
Звук издается, когда объект вибрирует, создавая волну давления. Эта волна давления заставляет частицы в окружающей среде (воздух, вода или твердое тело) совершать колебательные движения. Когда частицы вибрируют, они перемещают соседние частицы, передавая звук дальше через среду.Человеческое ухо улавливает звуковые волны, когда вибрирующие частицы воздуха вызывают колебания мелких деталей внутри уха.
Во многом звуковые волны похожи на световые. Оба они происходят из определенного источника и могут распространяться или рассеиваться различными способами. В отличие от света, звуковые волны могут распространяться только через среду, такую как воздух, стекло или металл. Это значит, что в космосе нет звука!
Как распространяется звук?
Средние
Прежде чем мы обсудим, как распространяется звук, важно понять, что такое среда и как она влияет на звук.Мы знаем, что звук может распространяться через газы, жидкости и твердые тела. Но как они влияют на его движение? Звук наиболее быстро распространяется через твердые тела, потому что его молекулы плотно упакованы вместе. Это позволяет звуковым волнам быстро передавать колебания от одной молекулы к другой. Звук движется в воде аналогичным образом, но его скорость более чем в четыре раза выше, чем в воздухе. Скорость звуковых волн, движущихся в воздухе, может быть дополнительно снижена за счет высоких скоростей ветра, которые рассеивают энергию звуковой волны.
Среды и скорость звука
Скорость звука зависит от типа среды, через которую проходят звуковые волны. В сухом воздухе при 20 ° C скорость звука составляет 343 м / с! В морской воде комнатной температуры звуковые волны распространяются со скоростью около 1531 м / с! Когда физики наблюдают возмущение, которое распространяется быстрее, чем местная скорость звука, это называется ударной волной. Когда сверхзвуковой самолет пролетает над головой, может наблюдаться локальная ударная волна! Обычно звуковые волны распространяются быстрее в более теплых условиях.Как вы думаете, как это повлияет на скорость звуковых волн в океане, когда океан нагревается из-за глобального климата?
Распространение звуковых волн
Когда объект вибрирует, он создает кинетическую энергию, которая передается молекулами в среде. Когда вибрирующая звуковая волна входит в контакт с частицами воздуха, кинетическая энергия передается ближайшим молекулам. Когда эти возбужденные молекулы начинают двигаться, они активизируют другие молекулы, которые повторяют этот процесс. Представьте себе обтягивающего человека, спускающегося по лестнице.При падении с лестницы движение обтяжки начинается с расширения. Когда первое кольцо расширяется вперед, оно тянет вперед кольца позади себя, вызывая волну сжатия. Эта цепная реакция толкания и вытягивания заставляет каждое кольцо катушки обтягивания смещаться из своего исходного положения, постепенно передавая исходную энергию от первой катушки к последней. Сжатие и разрежение звуковых волн подобны толканию и вытягиванию спиралей обтекателя.
Сжатие и разрежение
Звуковые волны состоят из моделей сжатия и разрежения.Сжатие происходит, когда молекулы плотно упакованы вместе. Кроме того, разрежение происходит, когда молекулы удалены друг от друга. Когда звук проходит через среду, его энергия заставляет молекулы двигаться, создавая чередующиеся модели сжатия и разрежения. Важно понимать, что молекулы не движутся со звуковой волной. По мере прохождения волны молекулы получают энергию и перемещаются из своих исходных положений. После того, как молекула передает свою энергию соседним молекулам, движение молекулы уменьшается, пока на нее не воздействует другая проходящая волна.Передача энергии волной — это то, что вызывает сжатие и разрежение. При сжатии давление высокое, а при разрежении — низкое. Разные звуки создают разные модели изменений высокого и низкого давления, что позволяет их идентифицировать. Длина волны звуковой волны состоит из одного сжатия и одного разрежения.
Звуковые волны теряют энергию при прохождении через среду, что объясняет, почему вы не слышите людей, говорящих на большом расстоянии, но вы можете слышать их шепот поблизости.Когда звуковые волны движутся в пространстве, они отражаются такими средами, как стены, столбы и камни. Это звуковое отражение более известно как эхо. Если вы когда-нибудь были в пещере или каньоне, вы, вероятно, слышали, как ваше эхо распространяется намного дальше, чем обычно. Это связано с тем, что большие каменные стены отражают ваш звук друг от друга.
Типы волн
Итак, какой тип волны является звуковой? Звуковые волны делятся на три категории: продольные волны, механические волны и волны давления.Продолжайте читать, чтобы узнать, что их квалифицирует как таковые.
Продольные звуковые волны
Продольная волна — это волна, в которой движение частиц среды параллельно направлению переноса энергии. Звуковые волны в воздухе и жидкостях — это продольные волны, потому что частицы, переносящие звук, колеблются параллельно направлению распространения звуковой волны. Если вы толкаете обтяжку вперед и назад, катушки будут двигаться параллельно (вперед и назад). Точно так же при ударе по камертону направление звуковой волны параллельно движению частиц воздуха.
Механические звуковые волны
Механическая волна — это волна, которая зависит от колебаний вещества, что означает, что она передает энергию через среду для распространения. Эти волны требуют первоначального ввода энергии, которая затем проходит через среду до тех пор, пока не будет эффективно передана начальная энергия. Примеры механических волн в природе включают водные волны, звуковые волны, сейсмические волны и внутренние водные волны, которые возникают из-за разницы в плотности в водоеме. Есть три типа механических волн: поперечные волны, продольные волны и поверхностные волны.
Почему звук — это механическая волна? Звуковые волны движутся по воздуху, вытесняя частицы воздуха в цепной реакции. Когда одна частица смещается из положения равновесия, она толкает или притягивает соседние молекулы, заставляя их смещаться из положения равновесия. Поскольку частицы продолжают перемещать друг друга с помощью механических колебаний, возмущение распространяется по среде. Эти механические колебания звуковой проводимости между частицами квалифицируют звуковые волны как механические волны.Звуковая энергия или энергия, связанная с вибрациями, создаваемыми вибрирующим источником, требует перемещения среды, что превращает звуковую энергию в механическую волну.
Беспроводной датчик звука
Беспроводной датчик звука включает в себя два основных датчика в одном портативном корпусе: датчик звуковой волны для измерения относительных изменений звукового давления и датчик уровня звука со шкалой, взвешенной как в дБА, так и в дБВ.
Благодаря отчетности в реальном времени и широкому спектру дисплеев (БПФ, осциллограф, цифры) простой дизайн беспроводного датчика звука упрощает его использование для вводных звуковых исследований, а его встроенная память и надежные программные функции поддерживают исследования более высокого уровня в области науки. звука.
Звуковые волны давления
Волна давления или волна сжатия имеет регулярную структуру областей высокого и низкого давления. Поскольку звуковые волны состоят из сжатий и разрежений, их области колеблются между моделями низкого и высокого давления. По этой причине звуковые волны считаются волнами давления. Например, когда человеческое ухо принимает звуковые волны из окружающей среды, оно определяет разрежения как периоды низкого давления и сжатия как периоды высокого давления.
Поперечные волны
Поперечные волны движутся с колебаниями, перпендикулярными направлению волны. Звуковые волны не являются поперечными волнами, потому что их колебания параллельны направлению переноса энергии; однако звуковые волны могут становиться поперечными при очень определенных обстоятельствах. Поперечные волны или поперечные волны распространяются с меньшей скоростью, чем продольные волны, а поперечные звуковые волны могут быть созданы только в твердых телах. Океанские волны — самый распространенный пример поперечных волн в природе.Более наглядный пример может быть продемонстрирован путем покачивания одной стороны струны вверх и вниз, в то время как другой конец закреплен (см. Видео о стоячих волнах ниже). Все еще немного запутались? Посмотрите визуальное сравнение поперечных и продольных волн ниже.
Визуальное сравнение продольных и поперечных волн.
Как создать стоячие волны
С помощью струнного вибратора, генератора синусоидальных волн и стробоскопической системы PASCO учащиеся могут создавать, манипулировать и измерять стоячие волны в реальном времени.Генератор синусоидальной волны и струнный вибратор работают вместе для распространения синусоидальной волны по веревке, в то время как система стробоскопа может использоваться для «замораживания» волн во времени. Создавайте четко определенные узлы, освещайте стоячие волны и исследуйте квантовую природу волн в режиме реального времени с помощью этого современного исследовательского подхода. Вы можете ознакомиться с некоторыми из наших любимых волновых приложений в видео ниже.
4 Свойства звука
Что отличает музыку от шума? Птичий крик более мелодичен, чем автосигнализация.И, как правило, мы можем отличить сирену скорой помощи от полицейской сирены, но как это сделать? Мы используем четыре свойства звука: высоту, динамику (громкость или мягкость), тембр (цвет тона) и продолжительность.
Частота (высота)
Pitch — это качество, которое позволяет нам оценивать звуки как «выше» и «ниже». Он предоставляет метод организации звуков на основе частотной шкалы. Высота звука может быть интерпретирована как музыкальный термин для обозначения частоты, хотя это не совсем то же самое.Высокий звук заставляет молекулы быстро колебаться, а низкий звук вызывает более медленные колебания. Высота звука может быть определена только в том случае, если частота звука достаточно четкая и постоянная, чтобы отличить ее от шума. Поскольку высота звука в первую очередь основана на восприятии слушателя, это не объективное физическое свойство звука.
Амплитуда (динамика)
Амплитуда звуковой волны определяет ее относительную громкость. В музыке громкость ноты называется ее динамическим уровнем.В физике мы измеряем амплитуду звуковых волн в децибелах (дБ), которые не соответствуют динамическим уровням. Более высокие амплитуды соответствуют более громким звукам, а более короткие амплитуды соответствуют более тихим звукам. Несмотря на это, исследования показали, что люди воспринимают звуки на очень низких и очень высоких частотах как более мягкие, чем звуки на средних частотах, даже если они имеют одинаковую амплитуду.
Тембр (цвет тона)
Тембр относится к цвету тона или «ощущению» звука.Звуки с разным тембром создают разные формы волн, которые влияют на нашу интерпретацию звука. Звук фортепьяно имеет другой цвет тона, чем звук гитары. В физике мы называем это тембром звука. Это то, что позволяет людям быстро распознавать звуки (например, кошачье мяуканье, проточная вода, звук голоса друга).
Продолжительность (темп / ритм)
В музыке продолжительность — это время, в течение которого длится тон или тон. Их можно охарактеризовать как длинные, короткие или требующие некоторого времени.Продолжительность ноты или тона влияет на тембр и ритм звука. Классическая фортепианная пьеса будет иметь ноты большей продолжительности, чем ноты, сыгранные клавишником на поп-концерте. В физике продолжительность звука или тона начинается после того, как звук регистрируется, и заканчивается, когда он не может быть обнаружен.
Создание музыки с использованием 4 свойств звука
Музыканты манипулируют четырьмя свойствами звука, создавая повторяющиеся паттерны, образующие песню. Продолжительность — это время, в течение которого длится музыкальный звук.Когда вы играете на гитаре, звук прекращается, когда вы успокаиваете струны. Высота звука — это относительная высота или слабость звука, которая определяется частотой звуковых колебаний. Более быстрые колебания производят более высокую высоту звука, чем более медленные. Более толстые струны гитары производят более медленные вибрации, создавая более глубокую высоту тона, в то время как более тонкие струны производят более быстрые вибрации и более высокую высоту звука. Звук с определенной высотой или определенной частотой называется тоном.Тоны имеют определенные частоты, которые достигают уха через равные промежутки времени, например 320 циклов в секунду. Когда два тона имеют разные высоты, они звучат по-разному, и разница между их высотой звука называется интервалом. Музыканты часто используют интервал, называемый октавой, который позволяет двум тонам разной высоты звучать одинаково. Динамика относится к степени громкости или мягкости звука и связана с амплитудой вибрации, производящей звук. Чем сильнее натянута гитарная струна, тем громче будет звук.Цвет тона или тембр описывает общее ощущение звука, производимого инструментом. Если бы мы описали цвет тона трубы, мы могли бы назвать его ярким или блестящим. Когда мы рассматриваем виолончель, мы можем сказать, что у нее насыщенный цветовой тон. Каждый инструмент предлагает свой собственный цвет тона, и можно создавать новые цвета тона, совмещая инструменты друг с другом. Кроме того, современные музыкальные стили, такие как EDM, представили новые стили тона, которые были недоступны до создания цифровой музыки.
Что делает звук музыкой или шумом?
Акустики, или ученые, изучающие акустику звука, изучали, как различные типы звуков, в первую очередь шум и музыка, влияют на людей.Рандомизированные неприятные звуковые волны часто называют шумом. Кроме того, построенные модели звуковых волн известны как музыка. Исследования показали, что человеческое тело по-разному реагирует на шум и музыку, что может объяснить, почему строительство дороги субботним утром делает нас более напряженными, чем песня пианиста.
Акустика
Акустика — это междисциплинарная наука, изучающая механические волны, включая вибрацию, звук, инфразвук и ультразвук в различных средах, таких как твердые тела, жидкости и газы.Профессионалы в области акустики могут варьироваться от инженеров-акустиков, которые исследуют новые области применения звука в технологиях, до инженеров-звукорежиссеров, специализирующихся на записи и управлении звуком, до акустиков, которые являются учеными, занимающимися наукой о звуке.
Резонансная воздушная колонна
Независимо от того, нужен ли вам универсальный волновой демонстратор или доступное по цене устройство, которое позволяет студентам на практике экспериментировать с резонансом и гармониками, Resonance Air Column — ваш лучший инструмент.Резонансная воздушная колонна состоит из полой трубы с поршнем внутри.
Когда поршень перемещается через резонансную воздушную колонну, каждый раз, когда он сталкивается с узлом, издается громкий звуковой сигнал.
Используя измерители и кольца для крепления на ремне, учащиеся могут определять, измерять и отмечать расположение узлов и пучностей в резонансной воздушной колонне — и все это при просмотре данных в реальном времени с помощью дисплея БПФ Capstone.
После изучения резонансной частоты, узлов и пучностей учащиеся могут сравнить свои экспериментальные измерения с ожидаемыми измерениями, используя свои собственные графики и расчеты.
Характеристики звуковых волн
Есть пять основных характеристик звуковых волн: длина волны, амплитуда, частота, период времени и скорость. Длина звуковой волны указывает расстояние, которое проходит волна, прежде чем она повторится. Сама длина волны — это продольная волна, которая показывает сжатие и разрежение звуковой волны. Амплитуда волны определяет максимальное смещение частиц, возмущенных звуковой волной, когда она проходит через среду.Большая амплитуда указывает на большую звуковую волну. Частота звуковой волны указывает количество звуковых волн, производимых каждую секунду. Низкочастотные звуки производят звуковые волны реже, чем высокочастотные звуки. Временной период звуковой волны — это количество времени, необходимое для создания полного волнового цикла. Каждая вибрация от источника звука производит звук величиной с волну. Каждый полный волновой цикл начинается с впадины и заканчивается в начале следующей впадины. Наконец, скорость звуковой волны показывает, насколько быстро волна движется, и выражается в метрах в секунду.
Диаграмма звуковой волны. Между двумя впадинами возникает волновой цикл.
Единиц звука
Когда мы измеряем звук, нам доступны четыре различных единицы измерения. Первая единица называется децибелом (дБ). Децибел — это логарифмическое отношение звукового давления к эталонному давлению. Следующей наиболее часто используемой единицей измерения является герц (Гц). Герцы — это мера звуковой частоты. Герцы и децибелы широко используются для описания и измерения звуков, но также используются фон и звуковой сигнал.Сон — это воспринимаемая громкость звука, а фон — это единица громкости для чистых тонов. Кроме того, фон относится к субъективной громкости, а звук — к воспринимаемой громкости.
Пояснения к графам звуковых волн
Звуковые волны можно описать с помощью графика смещения или плотности. Графики смещения-времени показывают, насколько далеко частицы находятся от своих первоначальных мест, и показывают, в каком направлении они двигались. Частицы, которые появляются на нулевой линии на графике смещения частиц, вообще не двигались из своего нормального положения.Эти, казалось бы, неподвижные частицы испытывают большее сжатие и разрежение, чем другие частицы. Поскольку давление и плотность взаимосвязаны, график зависимости давления от времени будет отображать ту же информацию, что и график зависимости плотности от времени. Эти графики показывают, где частицы сжаты, а где сильно расширены. В отличие от графиков смещения, частицы вдоль нулевой линии на графике плотности никогда не сжимаются и не растягиваются. Напротив, это частицы, которые больше всего движутся вперед и назад.
Звуковое давление
Звуковое давление описывает локальное отклонение давления от окружающего атмосферного давления при распространении звуковой волны. Важно понимать, что звуковое давление и давление воздуха — разные понятия. В целом, на скорость звука не влияет давление воздуха. Когда звуковые волны проходят от источника звука через воздух, они изменяют давление, испытываемое соседними частицами воздуха.
Уровень звука
Уровень звука — это сравнение давления звуковой волны относительно контрольной точки.Уровень звука измеряется в децибелах, причем более высокие децибелы соответствуют более высоким уровням звука. Некоторые звуковые инструменты измеряют уровень звука в дБн, который представляет собой отношение мощности (децибел) сигнала к его несущему сигналу. Другие звуковые инструменты измеряют относительную громкость звуков, воспринимаемых человеческим ухом, с помощью децибел, взвешенных по шкале А, известной как дБа. Когда используется дБа, звуки на низких частотах уменьшаются в децибелах по сравнению с невзвешенными децибелами.
Уровень звука — это сравнение давления звуковой волны относительно контрольной точки.Измеритель дБн измеряет высокие и низкие частоты, а измеритель дБа измеряет частоты среднего уровня.
Интенсивность звука
Интенсивность звука — это мощность звуковой волны на единицу площади. Чем интенсивнее звук, тем больше будут колебания амплитуды. По мере увеличения интенсивности звука давление, оказываемое звуковыми волнами на близлежащие объекты, также увеличивается. Децибелы используются для измерения отношения заданной интенсивности (I) к порогу интенсивности слышимости, которая обычно имеет значение 1000 Гц для человеческого уха.
Интенсивность звука — это мощность звуковой волны на единицу площади. Чем интенсивнее звук, тем больше будут колебания амплитуды. По мере увеличения интенсивности звука давление, оказываемое звуковыми волнами на близлежащие объекты, также увеличивается.
Интенсивность звука в столбе воздуха
Воздушный столб — это большая полая труба, открытая с одной стороны и закрытая с другой. Условия, создаваемые воздушным столбом, особенно полезны для исследования звуковых характеристик, таких как интенсивность и резонанс.Посмотрите видео ниже, чтобы увидеть, как воздушные колонны можно использовать для исследования узлов, пучностей узлов и резонанса.
13.2 Свойства волн: скорость, амплитуда, частота и период
Геология: физика сейсмических волн
Рис. 13.9 Разрушительный эффект землетрясения — очевидное свидетельство энергии, переносимой землетрясением. Оценка землетрясений по шкале Рихтера зависит как от их амплитуды, так и от переносимой ими энергии. (Старшина 2-го класса Кэндис Вильярреал, U.S. Navy)
Геологи в значительной степени полагаются на физику при изучении землетрясений, поскольку землетрясения включают несколько типов волновых возмущений, включая возмущение поверхности Земли и возмущения давления под поверхностью. Поверхностные волны землетрясений похожи на поверхностные волны на воде. Волны под поверхностью Земли имеют как продольную, так и поперечную составляющие. Продольные волны при землетрясении называются волнами давления (P-волнами), а поперечные волны называются поперечными волнами (S-волнами).Эти два типа волн распространяются с разными скоростями, и скорость, с которой они распространяются, зависит от жесткости среды, в которой они движутся. Во время землетрясений скорость продольных волн в граните значительно превышает скорость поперечных волн. Оба компонента землетрясений распространяются медленнее в менее твердых материалах, таких как отложения. P-волны имеют скорость от 4 до 7 км / с, а S-волны имеют скорость от 2 до 5 км / с, но оба они быстрее в более жестких материалах. P-волна все больше опережает S-волну по мере прохождения через земную кору.По этой причине разница во времени между P- и S-волнами используется для определения расстояния до их источника, эпицентра землетрясения.
Мы знаем из сейсмических волн, вызванных землетрясениями, что части недр Земли жидкие. Сдвиговые или поперечные волны не могут проходить через жидкость и не передаются через ядро Земли. Напротив, сжатие или продольные волны могут проходить через жидкость и проходить через ядро.
Все волны несут энергию, а энергию землетрясений легко наблюдать, исходя из количества повреждений, оставшихся после того, как земля перестала двигаться.Землетрясения могут повергнуть в землю целые города, выполняя работу тысяч разрушительных шаров. Количество энергии в волне зависит от ее амплитуды. Землетрясения большой амплитуды вызывают большие смещения грунта и больший ущерб. По мере распространения землетрясений их амплитуда уменьшается, поэтому чем дальше они удаляются от источника, тем меньше повреждений.
Проверка захвата
Какая связь между скоростью распространения, частотой и длиной волны S-волн при землетрясении?
- Соотношение между скоростью распространения, частотой и длиной волны vw = fλ.vw = fλ.
- Соотношение между скоростью распространения, частотой и длиной волны: vw = fλ.vw = fλ.
- Соотношение между скоростью распространения, частотой и длиной волны: vw = λf.vw = λf.
- Соотношение между скоростью распространения, частотой и длиной волны: vw = fλ.vw = fλ.
Простое гармоническое движение — Концепции
Введение
Вы когда-нибудь задумывались, почему напольные часы показывают точное время? Движение маятника — это особый вид повторяющегося или периодического движения, называемого простым гармоническим движением или SHM.Положение колеблющегося объекта изменяется синусоидально со временем. Многие объекты колеблются взад и вперед. Движение ребенка на качелях можно представить себе как синусоидальное и, следовательно, можно рассматривать как простое гармоническое движение. Некоторые сложные движения, такие как турбулентные волны на воде, не считаются простым гармоническим движением.
Когда объект находится в простом гармоническом движении, можно легко определить скорость, с которой он колеблется взад и вперед, а также его положение относительно времени.В этой лабораторной работе вы проанализируете простой маятник и систему пружина-масса, которые демонстрируют простое гармоническое движение.
Обсуждение принципов
Частица, которая колеблется вертикально в простом гармоническом движении, перемещается вверх и вниз между двумя крайними точками y = ± A . Максимальное смещение A называется амплитудой . Это движение показано графически на графике зависимости положения от времени на рисунке 1.
Одно полное колебание или цикл или колебание — это движение, например, от
y = −A
до
y = + A
и обратно до
y = −A.
Временной интервал T , необходимый для завершения одного колебания, называется периодом . Связанная величина — частота f , которая представляет собой количество колебаний, которые система делает за единицу времени. Частота обратно пропорциональна периоду и измеряется в герцах, сокращенно Гц;
1 Гц = 1 с −1 .
Если частица колеблется вдоль оси y , ее положение на оси y в любой момент времени t , измеренное от начала колебания, определяется уравнением
Напомним, что скорость объекта — это первая производная, а ускорение — вторая производная функции смещения по времени.Скорость v и ускорение a частицы в момент времени t определяются следующим образом.
(3)
v = 2 π fA cos (2 π футов)
(4)
a = — (2 π f) 2 [A sin (2 π футов)]
Обратите внимание, что скорость и ускорение также синусоидальны. Однако функция скорости имеет разность фаз 90 ° или π /2, в то время как функция ускорения имеет разность фаз 180 ° или π относительно функции смещения.Например, когда смещение является положительным максимумом, скорость равна нулю, а ускорение — отрицательному максимуму.
Подстановка из уравнения 2 в уравнение 4 дает
Из уравнения 5 мы видим, что ускорение объекта в SHM пропорционально смещению и имеет противоположный знак. Это основное свойство любого объекта, совершающего простое гармоническое движение.
Рассмотрим несколько критических точек в цикле, как в случае колебательной системы пружина-масса. Система пружина-масса состоит из массы, прикрепленной к концу пружины, подвешенной к стойке.Масса слегка опускается и отпускается, чтобы заставить пружину и массу колебаться в вертикальной плоскости. На рисунке 2 показаны пять критических точек, когда нагрузка на пружину проходит полный цикл. Положение равновесия для системы пружина-масса — это положение массы, когда пружина не растягивается и не сжимается.
Масса завершает полный цикл, переходя из положения A в положение E. Описание каждой позиции приводится ниже.
Положение A: пружина сжата; масса выше точки равновесия при
y =
A и вот-вот будет выпущена.Положение B: Масса движется вниз, проходя через точку равновесия.
Положение C: Груз на мгновение находится в состоянии покоя в самой нижней точке перед тем, как начать движение вверх.
Положение D: Масса движется вверх, когда проходит через точку равновесия.
Положение E: гиря на мгновение находится в состоянии покоя в наивысшей точке, прежде чем снова двинуться вниз.
Отметив время, когда отрицательное максимальное, положительное максимальное и нулевое значения возникают для положения, скорости и ускорения колеблющегося объекта, вы можете построить график функции синуса (или косинуса).Это сделано для системы колеблющейся пружины и массы в таблице ниже, а три функции показаны на рисунке 3. Обратите внимание, что положительное направление обычно выбирается как направление, в котором пружина растягивается. Следовательно, положительное направление в этом случае — вниз, и начальное положение A на фиг. 2 фактически является отрицательным значением. Самый сложный параметр для анализа — это ускорение. Это помогает использовать второй закон Ньютона, который говорит нам, что отрицательное максимальное ускорение происходит, когда результирующая сила равна отрицательному максимуму, положительное максимальное ускорение происходит, когда результирующая сила равна положительному максимуму, и ускорение равно нулю, когда результирующая сила равна нулю.Для этого конкретного начального условия (начальное положение в точке A на рисунке 2) кривая положения является функцией косинуса (фактически отрицательной функцией косинуса), кривая скорости является функцией синуса, а кривая ускорения является просто отрицательной функцией кривой положения. .
Масса и пружина
Масса, подвешенная на конце пружины, растянет ее на некоторое расстояние y . Сила, с которой пружина тянет вверх груз, определяется формулой Hooke ‘ s law
где k — жесткость пружины, а y — растяжение пружины, когда к пружине прикладывается сила F .Константа пружины k является мерой жесткости пружины.
Жесткость пружины может быть определена экспериментально, позволяя грузу неподвижно висеть на пружине, а затем добавляя дополнительную массу и записывая дополнительное растяжение пружины, как показано ниже. На рисунке 4а подвеска груза подвешена к концу пружины. На рисунке 4b к подвеске была добавлена дополнительная масса, и теперь пружина выдвинута на величину
Δy.
Эта экспериментальная установка также показана на фотографии устройства на рисунке 5.Когда масса неподвижна, ее ускорение равно нулю. Следовательно, согласно второму закону Ньютона, результирующая сила должна быть равна нулю. На массу действуют две силы: сила тяжести, направленная вниз, и сила пружины, направленная вверх. См. Диаграмму свободного тела на Рисунке 6 ниже.
Итак, второй закон Ньютона дает нам
где
Δm
— изменение массы,
Δy
— изменение растяжения пружины, вызванное изменением массы, g — ускорение свободного падения, а k — жесткость пружины.Уравнение 7 также можно выразить как
Второй закон Ньютона, примененный к этой системе, равен
ma = F = −ky.
Подставим из уравнения 5
a = −4 π 2 f 2 y.
для разгона получить
(9)
м (−4 π 2 f 2 y) = −ky
откуда получаем выражение для частоты f и периода T .
(10)
f =
(11)
Т = 2 π
Используя уравнение 11, мы можем предсказать период, если мы знаем массу пружины и ее жесткость.В качестве альтернативы, зная массу на пружине и экспериментально измеряя период, мы можем определить жесткость пружины.
Обратите внимание, что в уравнении 11 связь между T и m не является линейной. График зависимости периода от массы не будет прямой линией. Если возвести в квадрат обе части уравнения 11, мы получим
Теперь график
T 2
по сравнению с м будет прямой линией, и жесткость пружины может быть определена по наклону.
Простой маятник
Другой пример простого гармонического движения, который вы исследуете, — это простой маятник . Простой маятник состоит из массы м , называемой бобом маятника, прикрепленной к концу веревки. Длина L простого маятника измеряется от точки подвешивания струны до центра боба, как показано на Рисунке 7 ниже.
Если боб перемещен из положения покоя на некоторый угол смещения θ , как на рисунке 8, возвращающая сила вернет боб обратно в положение равновесия.Силы, действующие на боб, — это сила тяжести и сила натяжения струны. Сила натяжения струны уравновешивается составляющей силы тяжести, которая соответствует струне (то есть перпендикулярна движению боба). Возвращающей силой здесь является тангенциальная составляющая гравитационной силы.
Когда мы применяем тригонометрию к меньшему треугольнику на рисунке 8, мы получаем величину возвращающей силы | F | = мг sin θ .Эта сила зависит от массы боба, ускорения свободного падения g и синуса угла, на который натянута струна. Снова должен применяться второй закон Ньютона, поэтому
(13)
ма = F = −mg sin θ
где отрицательный знак означает, что возвращающая сила действует противоположно направлению движения боба.
Поскольку боб движется по дуге окружности, угловое ускорение определяется как
α = a / L.
Из уравнения 13 получаем
На рисунке 9 синяя сплошная линия представляет собой график зависимости sin ( θ ) от θ , а прямая линия представляет собой график θ в градусах по сравнению с θ в радианах. Для малых углов эти две кривые практически неразличимы. Следовательно, пока смещение θ мало, мы можем использовать приближение sin θ ≈ θ .
В этом приближении уравнение 14 принимает вид
Уравнение 15 показывает, что (угловое) ускорение пропорционально отрицательному значению (углового) смещения, и, следовательно, движение боба является простым гармоническим, и мы можем применить уравнение 5
a = −4 π 2 f 2 г.
получить
Комбинируя уравнение 15 и уравнение 16 и упрощая, мы получаем
(17)
f =
а также
(18)
Т = 2 π
.
Обратите внимание, что частота и период простого маятника не зависят от массы.
Авторские права © 2013 Advanced Instructional Systems, Inc. и Государственный университет Северной Каролины | Кредиты
Кинематика — обзор | ScienceDirect Topics
Кинематика реконструированного коленного сустава передней крестообразной связки
Сообщалось также о кинематических изменениях коленного сустава у пациентов, перенесших реконструкцию ПКС во время ходьбы и других динамических действий. 42,52,53 В частности, большеберцовая кость имеет тенденцию быть более повернутой наружу в колене с реконструированной ACL, в отличие от сдвига в сторону внутренней ротации в колене с дефицитом ACL. В коленном суставе, реконструированном на ACL, большеберцовая кость сохраняет смещение внешней ротации (в среднем 2,3 градуса; 95% ДИ 1,0-3,7 градуса) относительно нормы на протяжении фазы опоры цикла ходьбы (рис. 6-9). 42 Эти наблюдения дополнительно подтверждают утверждение, что ACL играет критическую роль в управлении вторичными движениями колена и что обычная реконструкция ACL неэффективна при воспроизведении сложной анатомии и функции нативной связки.Это согласуется с ранее опубликованными биомеханическими исследованиями in vitro, которые продемонстрировали, что традиционные методы реконструкции ACL часто размещают трансплантаты в неанатомической ориентации, которая не может воспроизвести стабильность вращения, обеспечиваемую нативной ACL. 27,45
Интересно, что реконструкция ПКС не снижает частоту преждевременного ОА коленного сустава после травмы ПКС. 29,33 Основываясь на кинематических данных и естественной истории коленного сустава с недостаточностью ACL, многие исследователи также считают, что измененная кинематика большеберцовой кости является фактором, провоцирующим дегенеративный процесс в коленном суставе, реконструированном на ACL. 6,7,20,42,43 Аналогичным образом смещение вращательного выравнивания коленного сустава с реконструированной ПКС во время ходьбы также смещает нагрузку на области тибиофеморального хряща, которые не могут адаптироваться к испытываемым высоким нагрузкам. во время ходьбы. Хотя сдвиг в контакте, вызванный изменением положения вращения, на первый взгляд может показаться относительно небольшим, он представляет собой довольно существенное изменение при рассмотрении общего диапазона вращательного движения, которое обычно происходит во время ходьбы (~ 10 градусов). 42 Предполагается, что в сочетании с хроническим повторяющимся характером ходьбы кумулятивный эффект даже незначительного кинематического изменения во времени может в конечном итоге сыграть важную роль в раннем начале ОА в этой популяции. Взятые вместе, эти исследования дополнительно подтверждают важность оценки успеха новых методов реконструкции ПКС на основе их способности воспроизводить нормальную трехмерную анатомию сустава, восстанавливать амбулаторную механику и предотвращать долгосрочные дегенеративные изменения.
Общие сведения о независимых и зависимых переменных
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
