На рисунке показаны силы действующие на материальную точку модуль равнодействующей силы равен: На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Модуль — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Задачи по теме «Равнодействующая» с ответами

Равнодействующая

1. Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок).

Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)

2. На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)

3. Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)

1. Ответ: 500 2.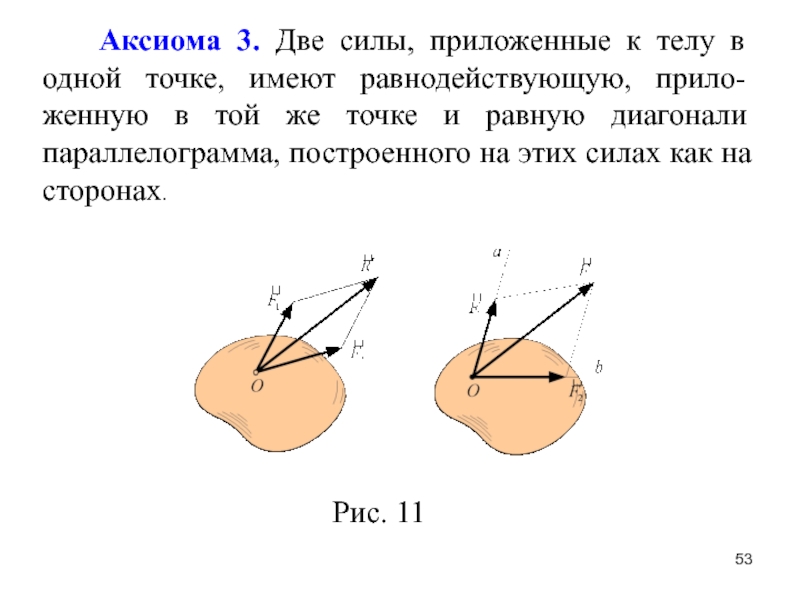 Ответ: 3,2 3. Ответ: 5

4. Под действием одной силы F₁ тело движется с ускорением 4 м/с². Под действием другой силы F₂, направленной противоположно силе F₁, ускорение тела равно 3 м/с². С каким ускорением тело будет двигаться при одновременном действии сил F₁ и F₂? (Ответ дайте в метрах в секундах в квадрате.)

5. Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)

6. На рисунке представлены три вектора сил, лежащих в одной плоскости и приложенных к одной точке.

Масштаб рисунка таков, что сторона одного квадрата сетки соответствует модулю силы 1 H. Определите модуль вектора равнодействующей трех векторов сил.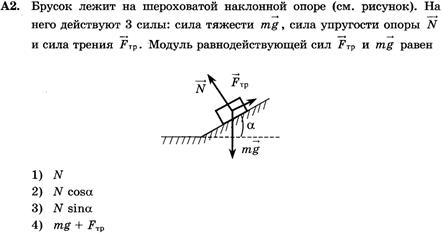 (Ответ дайте в ньютонах.)

7. На рисунке представлены четыре вектора сил. Модуль вектора силы равен 3 Н. Чему равен модуль равнодействующей векторов и ? (Ответ дайте в ньютонах.)

8. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.Модуль вектора силы F₁ равен 4 Н. Чему равен модуль равнодействующей векторов F₁, F₂ и F₃? (Ответ дайте в ньютонах.)

9. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости. Модуль вектора силы F₁ равен 3 Н. Чему равен модуль равнодействующей векторов F₁, F₂ и F₃? (Ответ дайте в ньютонах.)

10. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.

Модуль вектора силы F₁ равен 5 Н. Чему равен модуль равнодействующей векторов F₁, F₂ и F₃? (Ответ дайте в ньютонах.)

11. Тело массой 6 кг движется вдоль оси Ox. В таблицу приведена зависимость проекции скорости v_xэтого тела от времени t.

Считая равнодействующую всех сил, приложенных к телу, постоянной, определите, чему равна проекция этой равнодействующей на ось Ox. (Ответ дайте в ньютонах.)

12.

Тело массой 2 кг движется вдоль оси Ox. На рисунке представлен график зависимости проекции скорости v_x этого тела от времени t. Чему равен модуль проекции силы F_x, действующей на это тело в течение первой секунды движения? (Ответ дайте в ньютонах. )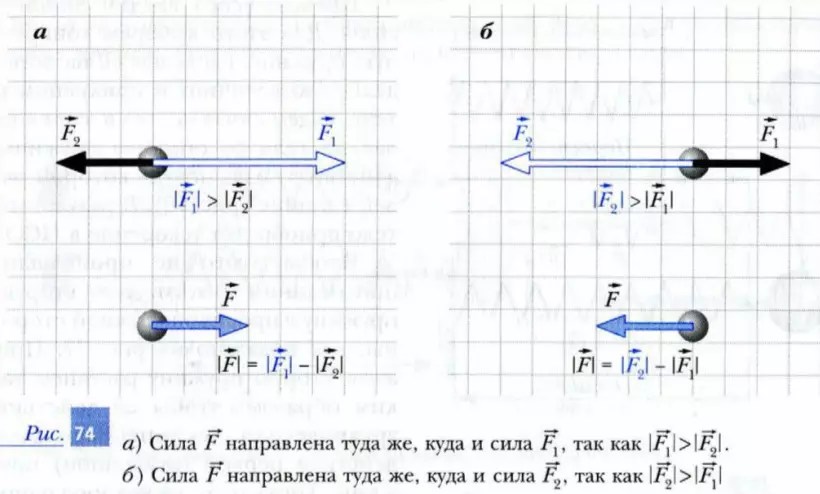

13. На рисунке показаны силы, действующие на материальную точку. Определите модуль равнодействующей силы (в заданном масштабе). (Ответ дайте в ньютонах и округлите до десятых.)

14. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку в инерциальной системе отсчёта. Чему равен модуль равнодействующей этих сил в данной системе отсчёта? (Ответ дайте в ньютонах и округлите до десятых.)

15. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Чему равен модуль равнодействующей силы? (Ответ дайте в ньютонах и округлите до десятых.)

Ответы:

1. Ответ: 500 2. Ответ: 3,2 4. Ответ: 1 5. Ответ: 5 6. Ответ: 10 7. Ответ: 3

8. Ответ: 5 9.Ответ: 0 10. Ответ: 5 11. Ответ: 12 12. Ответ: 4 13. Ответ: 3,6

14. Ответ: 1,4 15.Ответ: 4,5

Зависимость проекции на ось ох равнодействующих сил

Тело массой 6 кг движется вдоль оси Ox. В таблицу приведена зависимость проекции скорости v_x этого тела от времени t.

Согласно условию, равнодействующая всех сил, приложенных к телу, постоянна, а значит, по второму закону Ньютона она сообщает телу постоянное ускорение: Действительно, из таблицы видно, что за равные промежутки времени проекция скорости тела увеличивается на равные величины. Отсюда находим проекцию ускорения на ось :

Следовательно, проекция равнодействующей всех сил, приложенных к телу, равна:

Тестирование онлайн

Определение

Это векторная сумма всех сил, действующих на тело.

Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности

Взаимосвязь со вторым законом Ньютона

Вспомним закон Ньютона:

Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.

Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз.

Сила тяжести уравновешивается силой упругости. Книга покоится

Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.

Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.

Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее.

Нахождение равнодействующей силы

Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.

Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю.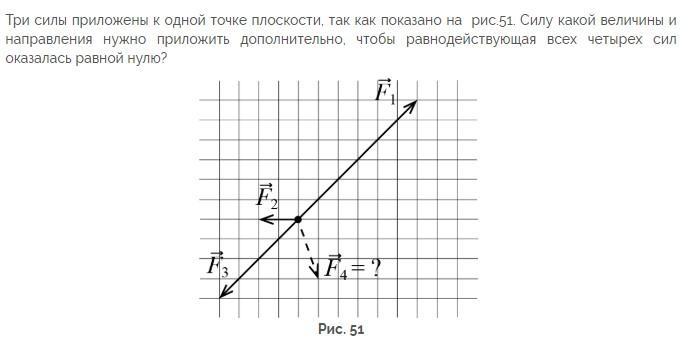 Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Примеры

На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.

Обозначим силы, выберем координатные оси

Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Системы и блоки*

Блок – механическое устройство, колесо, вращающееся вокруг своей оси. Блоки могут быть подвижными и неподвижными.

Неподвижный блок используется лишь для изменения направления силы.

Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.

Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.

Ускорение тела А в два раза меньше ускорения тела В.

Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии

Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

1. Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox , изменяется со временем в соответствии с графиком (см. рисунок).

1. Ответ: 500 2. Ответ: 3,2 3. Ответ: 5

4. Под действием одной силы F ₁ тело движется с ускорением 4 м/с 2 . Под действием другой силы F ₂ , направленной противоположно силе F ₁ , ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F ₁ и F ₂ ? (Ответ дайте в метрах в секундах в квадрате.)

6. На рисунке представлены три вектора сил, лежащих в одной плоскости и приложенных к одной точке.

8. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.Модуль вектора силы F ₁ равен 4 Н.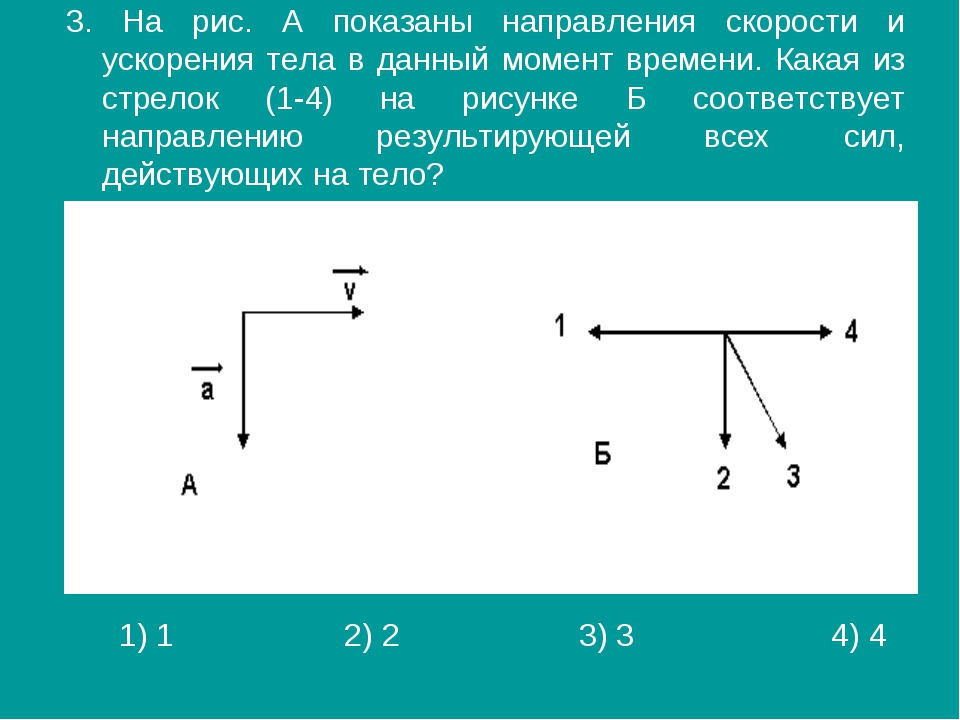 Чему равен модуль равнодействующей векторов F ₁ , F ₂ и F ₃ ? (Ответ дайте в ньютонах.)

9. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости. Модуль вектора силы F ₁ равен 3 Н. Чему равен модуль равнодействующей векторов F ₁ , F ₂ и F ₃ ? (Ответ дайте в ньютонах.)

10. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.

Модуль вектора силы F ₁ равен 5 Н. Чему равен модуль равнодействующей векторов F ₁ , F ₂ и F ₃ ? (Ответ дайте в ньютонах.)

11. Тело массой 6 кг движется вдоль оси Ox . В таблицу приведена зависимость проекции скорости v _x этого тела от времени t .

12.

Тело массой 2 кг движется вдоль оси Ox . На рисунке представлен график зависимости проекции скорости v _x этого тела от времени t . Чему равен модуль проекции силы F _x , действующей на это тело в течение первой секунды движения? (Ответ дайте в ньютонах.)

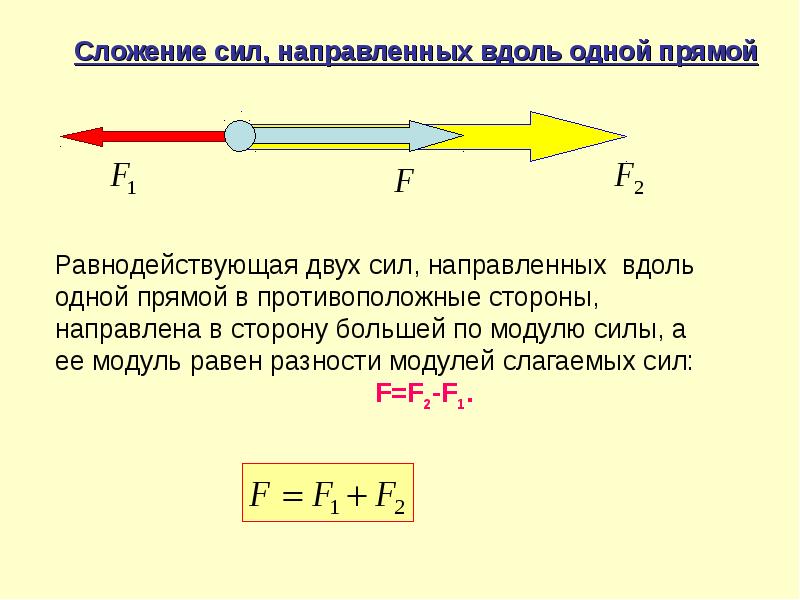1. Ответ: 500 2. Ответ: 3,2 4. Ответ: 1 5. Ответ: 5 6. Ответ: 10 7. Ответ: 3

8. Ответ: 5 9.Ответ: 0 10. Ответ: 5 11. Ответ: 12 12. Ответ: 4 13. Ответ: 3,6

На рисунке 50 представлены 4 вектора. Перечислите, от каких из приведенных ниже величин зависит момент инерции однородного тела

Равнодействующая

Скорость автомобиля массой 1000 кг, движущегося вдоль оси
Ox

, изменяется со временем в соответствии с графиком (см. рисунок).

На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если
(Ответ дайте в ньютонах и округлите до десятых.)

Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)

1. Ответ: 500 2. Ответ: 3,2 3. Ответ: 5

Под действием одной силы
F

тело движется с ускорением 4 м/с
2

. Под действием другой силы
F

, направленной противоположно силе
F

, ускорение тела равно 3 м/с
2

. С каким ускорением тело будет двигаться при одновременном действии сил
F

? (Ответ дайте в метрах в секундах в квадрате.)

Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)

На рисунке представлены три вектора сил, лежащих в одной плоскости и приложенных к одной точке.

На рисунке представлены четыре вектора сил. Модуль вектора силы
и

? (Ответ дайте в ньютонах. )

На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.Модуль вектора силы
F

равен 4 Н. Чему равен модуль равнодействующей векторов
F

? (Ответ дайте в ньютонах.)

равен 3 Н. Чему равен модуль равнодействующей векторов
F

? (Ответ дайте в ньютонах.)

10.

На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.

Модуль вектора силы
F

равен 5 Н. Чему равен модуль равнодействующей векторов
F

? (Ответ дайте в ньютонах.)

11.

Тело массой 6 кг движется вдоль оси
Ox

. В таблицу приведена зависимость проекции скорости
v

этого тела от времени
t

Считая равнодействующую всех сил, приложенных к телу, постоянной, определите, чему равна проекция этой равнодействующей на ось
Ox

. (Ответ дайте в ньютонах.)

12.

Тело массой 2 кг движется вдоль оси
Ox

. На рисунке представлен график зависимости проекции скорости
v

этого тела от времени
t

. Чему равен модуль проекции силы
F

, действующей на это тело в течение первой секунды движения? (Ответ дайте в ньютонах.)

13.

На рисунке показаны силы, действующие на материальную точку. Определите модуль равнодействующей силы (в заданном масштабе). (Ответ дайте в ньютонах и округлите до десятых.)

14.

На рисунке показаны силы (в заданном масштабе), действующие на материальную точку в инерциальной системе отсчёта. Чему равен модуль равнодействующей этих сил в данной системе отсчёта? (Ответ дайте в ньютонах и округлите до десятых.)

15.

На рисунке показаны силы (в заданном масштабе), действующие на материальную точку.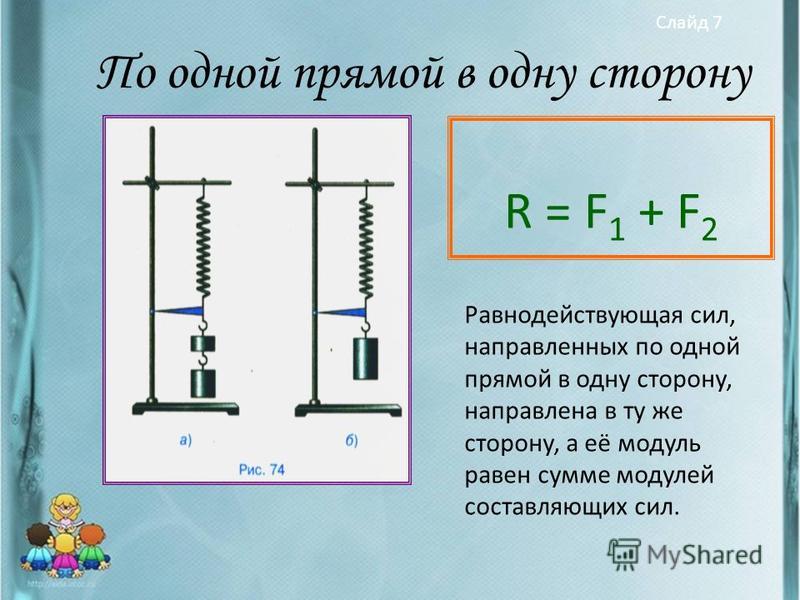 Чему равен модуль равнодействующей силы? (Ответ дайте в ньютонах и округлите до десятых.)

Ответы:

1. Ответ: 500 2. Ответ: 3,2 4. Ответ: 1

5. Ответ: 5

6. Ответ: 10

7. Ответ: 3

8. Ответ: 5

9.Ответ: 0

10. Ответ: 5

11. Ответ: 12 12. Ответ: 4 13. Ответ: 3,6

14. Ответ: 1,4

15.Ответ: 4,5

По графику на рисунке 4.1.1 определите путь, пройденный велосипедистом за интервал времени от до.

Рисунок 4.1.1

Согласно графику движение равномерное, V = 3м/с; S 1 = 3м; S 2 = 9м.

ДS = S 2 — S 1 = 6м

Ответ: 6 метров

Задача зачтена.

Автомобиль движется равномерно по выпуклому мосту (рисунок 4.2.1). Какое направление имеет вектор равнодействующей всех приложенных к автомобилю сил?

Рисунок 4.2.1

Варианты ответов

:

1) 1; 2) 2; 3) 3; 4) 4; 5).

Согласно рисунку, автомобиль, движущийся по закругленному мосту равномерно, испытывает центростримительное ускорение, так же, как и тело, движущееся по окружности.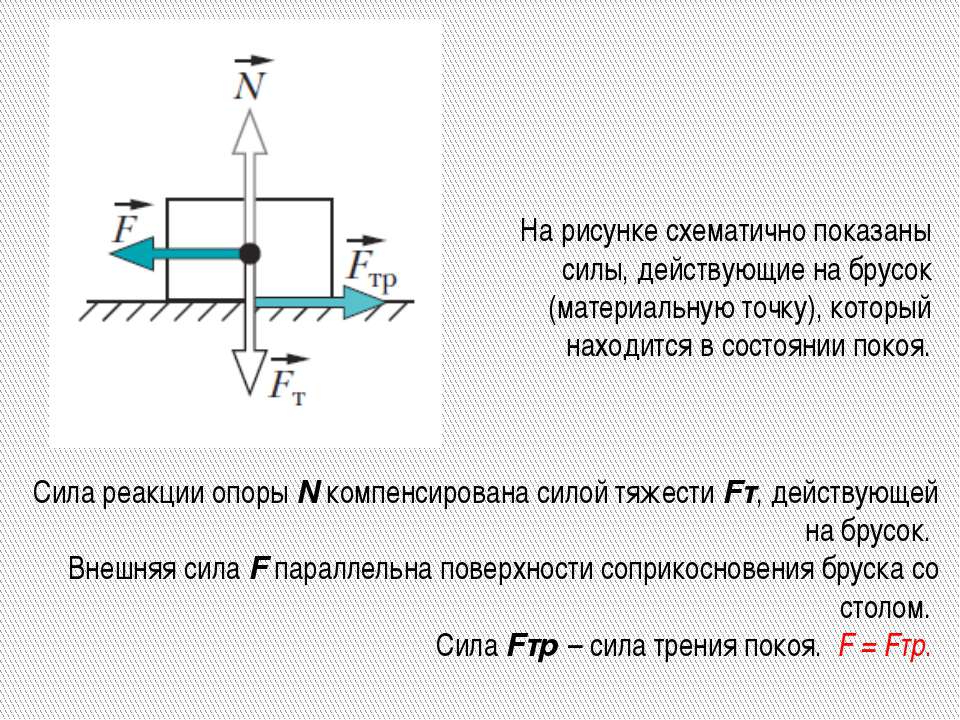 Следовательно, равнодействующая сил направлена по вектору 1. (F = ma)

Задача зачтена.

На рисунке 4.3.1 представлены четыре варианта взаимного расположения векторов силы, действующей на тело, и скорости тела.

Рисунок 4.3.1

В каком случае работа силы равна нулю на пути, отличном от нуля?

На пути отличном от нуля работа силы равна нулю, когда сила перпендикулярна скорости движения. Так как A = F*S*cosЬ.

Где: F — действующая сила

Ь — угол между F и V

Задача зачтена.

В пистолете длина пружины l, её упругость k. Пружина сжата на 0,2 своей длины. С какой скоростью вылетит из пистолета пуля массой m после выстрела?

При выстреле потенциальная энергия деформированной пружины приходит в кинетическую энергию, т.е.

Задача зачтена.

Перечислите, от каких из приведенных ниже величин зависит момент инерции однородного тела.

Варианты ответа:

а) от момента приложенных к телу сил при заданной оси; б) от выбора оси вращения; в) от формы тела; г) от массы тела; д) от углового ускорения.

Момент инерции однородного тела равен:

J = mr 2 , где:

m — масса тела

r — расстояние от оси вращения до края тела перпендикулярно оси.

Т.е. J — зависит от:

б) от выбора оси вращения;

в) от формы тела;

г) от массы тела.

И не зависит:

а) от момента сил приложенных к телу (M = z)

д) от углового ускорения в

Задача зачтена.

Два одинаковых заряженных маленьких шарика подвешены на изолирующих нитях одинаковой длины в общей точке и находятся в равновесии. Как изменится угол между нитями, если заряд и массу шариков удвоить при неизменных длинах нитей?

На шарик действуют силы:

1) Кулона;

2) натяжения нити;

3) тяжести.

Система находится в равновесии => силы уравновешивают друг друга.

тогда для начального положения системы:

для второго положения, после увеличения зарядов и массы, имеем.

Основные вопросы:

Инерциальные системы отсчета.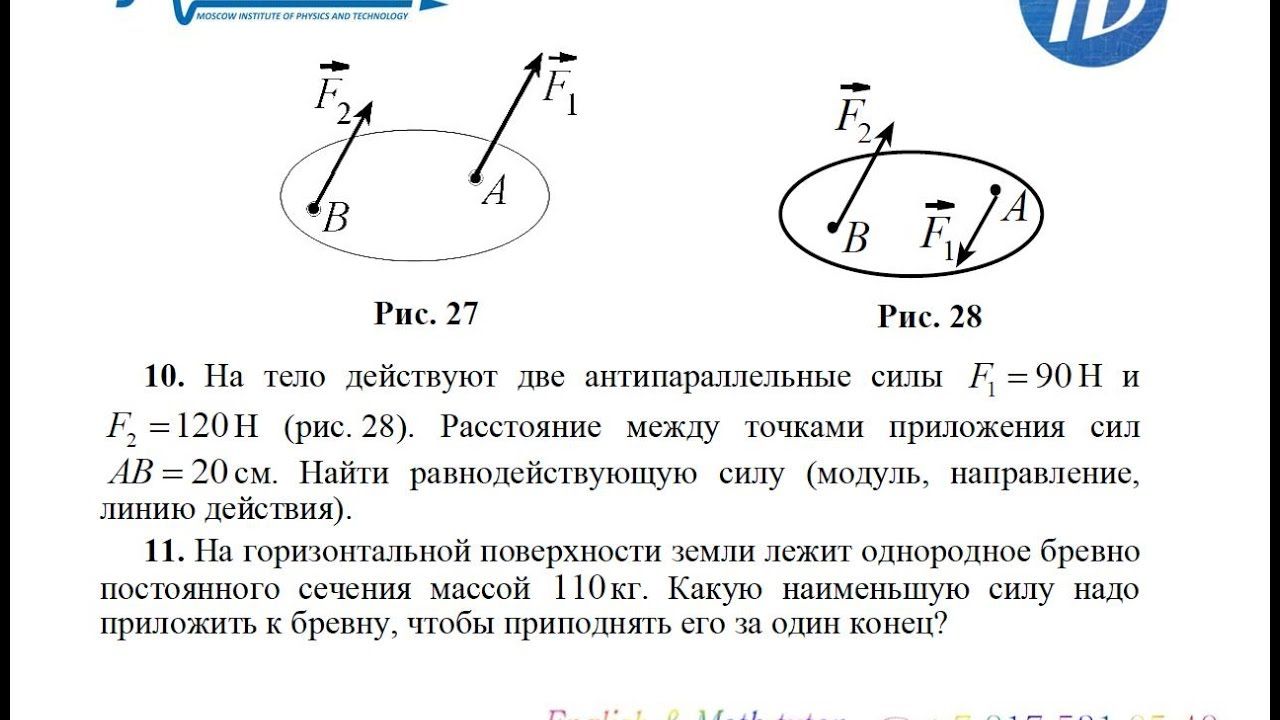 Первый закон Ньютона. Масса тела. Плотность вещества. Сила. Принцип суперпозиции сил. Второй закон Ньютона. Третий закон Ньютона.

Задачи:

1. Масса сплошного куба, сделанного из некоторого вещества 8 кг. Какую массу будет иметь этот куб, если длину его ребра уменьшить в 2 раза? (1 кг
)

2. При одинаковых объемах кусок железа имеет массу на 12,75 кг большую, чем кусок алюминия. Определите массу кусков железа и алюминия.(19,5 кг; 6,75 кг
)

3. Масса канистры, полностью заполненной бензином, 24 кг. Масса канистры, полностью заполненной водой, 29 кг. Какова масса пустой канистры? Плотность бензина 700 кг/м 3 , воды 1000 кг/м 3 . (12 кг
)

4. Имеются два кубика одинаковой массы. Один изготовлен из платины, другой из алюминия. Во сколько раз различаются объемы кубиков и длины ребер? Плотность платины 21,5 г/см 3 , плотность алюминия 2,7 г/см 3 .( 8; 2
)

5. В куске кварца содержится небольшой самородок золота. Масса куска 100 г, а его плотность 8 г/см 3 . Определите массу золота, содержащегося в куске. Плотность кварца 2,65 г/см 3 , плотность золота 19,36 г/см 3 .(77,5 г
)

6. Ученик измеряет плотность тела, не подозревая, что оно изготовлено из двух частей, массы, которых одинаковы. Плотности материалов этих частей 6 г/см 3 и 3 г/см 3 .(4 г/см 3
)

7. Деталь из латуни (сплав меди и цинка) при объеме 40 см 3 имеет массу 320 г. Определите массу цинка в этой детали. Считать, что объем детали равен сумме объемов меди и цинка. Плотность меди 9 г/см 3 , цинка-7 г/см 3 .(140 г
)

8. Система отсчета связана с лифтом. Эту систему можно считать инерциальной в случае, когда лифт движется

9. Мяч, неподвижно лежащий на полу вагона, движущегося относительно Земли, покатился вперед по ходу поезда. Это произошло в результате того, что скорость поезда относительно Земли

10. Мяч, неподвижно лежащий на полу вагона, движущегося относительно Земли, покатился влево, если смотреть по ходу поезда. Как изменилось движение поезда?

11. На тело действуют четыре силы: направленная на север равна 6Н, на восток равна 1Н, на юг равна 3Н, а на запад равна 4Н. Куда направлена равнодействующая сила?

1)на север 2) на северо-запад 3) на юг 4) на юго-восток

12. На рисунке представлены четыре вектора сил.

Модуль вектора силы F 1 равен 3 Н. Модуль равнодействующей всех сил

1)(8+ ) Н 2) Н 3) 3Н 4) 0 Н

13. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.

Модуль вектора силы F 1 равен 4 Н. Модуль равнодействующей всех сил

1) 9 Н 2) 7 Н 3) 5 Н 4) 1 Н

14. На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости.

Модуль вектора силы F 1 равен 5 Н. Модуль равнодействующей всех сил

1) 11 Н 2) 7 Н 3) 5 Н 4) 0 Н

15. В инерциальной системе отсчета сила 100 Н сообщает некоторому телу ускорение 10 м/с 2 . Какая сила сообщает этому телу ускорение 7 м/с 2

1) 35 Н 2) 70 Н 3)143 Н 4) 170 Н

16. Парашютист массой 70 кг падает с ускорением 8 м/с 2 . Равнодействующая всех сил, действующих на него равна

1) 70 Н 2) 1260 Н 3) 700 Н 4) 560 Н

17. Земля притягивает к себе подброшенный мяч силой 5Н. С какой силой этот мяч притягивает к себе Землю.

1) 0 Н 2) 5 Н 3) 10 Н 4) 50 Н

18. Полосовой магнит массой m поднесли к массивной стальной плите массой M. Сравните силу действия магнита на плиту F 1 с силой действия плиты на магнит F 2 .

1) F 1 = F 2 2)) F 1 > F 2 3)) F 1

19. Две пружинырастягиваются силами одной и той же величины F. Удлинение первой пружины в 1,5 раза больше, чем удлинение второй пружины. Определите жесткость первой пружины, если жесткость второй пружины к 2 .

1) 0,5 к 2 2) 2 к 2 3) 1,5 к 2 4) 0,67 к 2

20. Груз подвешен на пружине. Если массу груза уменьшить а два раза, то сила упругости…….

21. Если массу тела уменьшить в 5 раз, то сила трения скольжения, действующая на него при его движении по горизонтальной шероховатой поверхности

22. Под действием постоянной силы 10 Н тело движется прямолинейно и зависимость пройденного пути от времени имеет вид . Найдите массу тела.

1) 1 кг 2) 1,5 кг 3) 2 кг 4)2,5 кг

23. При торможении автомобиля на прямой горизонтальной дороге на него действует тормозящая сила 150 Н. Масса автомобиля равна 1500 кг. С каким по модулю ускорением движется автомобиль?

1)0,1 м/с 2 2)2,25 м/с 2 3) 0,25 м/с 2 4) 2,4 м/с 2

24. На горизонтальном полу стоит ящик массой 10 кг. Коэффициент трения скольжения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении прикладывают силу 20 Н. При этом ящик

1)	Останется в покое
2)	Будет двигаться равномерно
3)	Будет двигаться с ускорением 1,5 м/с 2
4)	Будет двигаться с ускорением 1 м/с 2

25. Каков будет вес космонавта на Луне, если в земных условиях его вес в скафандре равен 720Н. Ускорение свободного падения на Луне в 6 раз меньше, чем на Земле.

1) 720 Н 2) 120 Н 3) 4320 Н 4) 432Н

26. Тело соскальзывает с наклонной плоскости. Между телом и плоскостью заливают смазку. Как при этом изменятся сила тяжести, сила трения и ускорение тела?

27. В момент начала свободного падения первого тела второе тело стало скользить без трения с наклонной плоскости, имеющей угол наклона . Сравните скорости тел у основания наклонной плоскости и время их движения.( ; =sinα
)

28. Брусок скользит с наклонной плоскости, образующей угол 30 0 с горизонтом. Коэффициент трения бруска о наклонную плоскость 0,1. Найти ускорение бруска. (4 м/с 2
)

29. Тело соскальзывает с наклонной плоскости. На тело помещают дополнительный груз. Как при этом изменятся сила тяжести, сила трения и ускорение тела?

Для каждой величины подберите соответствующий характер изменения:

1)увеличится 2) уменьшится 3)не изменится

Запишите в таблицу выбранные цифры для каждой физической величины

30. Тело массой 5 кг соскальзывает без начальной скорости с наклонной плоскости длиной 50 см. Угол наклона плоскости к горизонту 30 0 , коэффициент трения равен 0,1. Какую скорость будет иметь тело у основания плоскости? (2 м/с
)

31. Жесткость пружины равна 50 Н/м. Если с помощью этой пружины равномерно тянуть по полу коробку массой 2 кг, то длина пружины увеличится с 10 до 15 см. какова сила упругости, возникающая в этом случае? Чему равен коэффициент трения между коробкой и полом? (2,5 Н; 0,125
)

32. Троллейбусмассой 10 т, трогаясь с места, приобрел на пути 50 м скорость 10 м/с. Найти коэффициент трения, если сила тяги равна 14 кН.(0,04
)

33. Брусок массой m движется с постоянной скоростью по шероховатой горизонтальной плоскости под действием постоянной силы F, направленной под углом к горизонту. Определите коэффициент трения между бруском и плоскостью. ()

34. При движении в лифте вес человека в одном случае оказался равным 630 Н. В другом – 770 Н. Какова масса человека? Каково значение модуля ускорения? (70 кг; 1 м/с 2
)

35. С какой силой давит на дно лифта человек массой 60 кг, если а)ускорение лифта направлено вверх и б) ускорение лифта направлено вниз? В обоих случаях ускорение равно 1 м/с 2 . (660 Н; 540 Н
)

36. Груз массой 200г подвешен на пружине к потолку лифта. Лифт в течение 2 с равноускоренно опускается вниз на расстояние 5 м. Каково удлинение пружины при опускании груза, если ее жесткость 100 Н/м, а начальная скорость груза равна нулю. (1,5 см
)

37. Какой массы состав может везти тепловоз, если уравнение его движения должно иметь вид х=0,05t 2 и он развивает силу тяги 300 кН при коэффициенте трения 0,01? (1,5∙10 6 кг
)

38. С какой горизонтальной силой надо действовать на брусок массой 2 кг, находящийся на наклонной плоскости с углом наклона 30 0 к горизонту, чтобы он: 1)оставался в покое; 2)двигался равномерно вверх по наклонной плоскости? Коэффициент трения бруска о наклонную плоскость равен 0,3. (4,72 Н; 21 Н
)

39. На наклонной плоскости длиной 5 м и высотой 3 м лежит груз массой 50 кг. Коэффициент трения равен 0,2. Какую силу, направленную вдоль плоскости, надо приложить к грузу, чтобы удержать груз? Какую силу надо приложить к грузу вдоль плоскости, чтобы втаскивать груз равномерно наверх? Какую силу надо приложить к грузу вдоль плоскости, чтобы втаскивать груз наверх с ускорением 1 м/с 2 ? (220 Н; 380Н; 430Н
)

40. Ледяная гора составляет с горизонтом угол 10 0 . По ней пускают вверх камень, который, поднявшись на некоторую высоту, затем соскальзывает по тому же пути вниз. Каков коэффициент трения, если время спуска в 2 раза больше времени подъёма?tg 10 0 = 0,1763. (0,1
)

41. Тело массой 0,8 кг движется вверх по плоскости, наклоненной под углом 30 0 к горизонту. К телу прикреплена пружина жесткостью 120Н/м, к которой приложена сила F. Коэффициент трения между телом и плоскостью 0,4. Ускорение тела равно 1,2 м/с 2 . Определите деформацию пружины. (6.4 см
)

ЕГЭ по физике онлайн — пройдите тест

Вопрос №3
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза больше, чем для второй. Каково отношение R1/R2 радиусов орбит первой и второй планет?

Вопрос №4
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счёт сопротивления воздуха составила 4 Дж?

Вопрос №7

После удара шайба массой m начала скользить со скоростью ῡ вверх по плоскости, установленной под углом α к горизонту (см. рисунок). Коэффициент трения шайбы о плоскость равен µ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) модуль ускорения при движении шайбы вверх

Б) модуль силы трения

ФОРМУЛЫ

1) g (sin α — µ cos α)

2) µmg cos α

3) µmg sin α

4) g ( µ cos α + sin α)

Вопрос №10
Тепловая машина с КПД 40% за цикл работы отдаёт холодильнику количество теплоты, равное 60 Дж. Какое количество теплоты машина получает за цикл от нагревателя?

Вопрос №19
Сравните состав ядер изотопов фосфора 33/15 Р и хлора 33/17 Cl. У этих изотопов одинакова(-о)

разность чисел нейтронов и протонов

число нейтронов

сумма чисел протонов и нейтронов

число протонов

Вопрос №20
В результате какой из серий радиоактивных распадов полоний Ро 214/84 превращается в висмут Bi 210/83

двух α-распадов и одного β-распада

одного α-распада и двух β-распадов

одного α-распада и одного β-распада

четырёх α-распадов и одного β-распада

Вопрос №21
Образец радиоактивного радия находится в закрытом сосуде. Ядра радия 224/88 Ra испытывают α-распад с периодом полураспада 3,6 суток. Определите количество гелия (в моль) в сосуде через 3,6 суток, если в начальный момент времени образец содержал 1,8 моль радия-224.

Вопрос №25
Мяч брошен вертикально вверх с начальной скоростью 20 м/с. Чему равно перемещение мяча за 3 с, считая от момента броска? Сопротивлением воздуха пренебречь.

Вопрос №27
На дифракционную решётку, имеющую 100 штрихов на 1 мм, перпендикулярно её поверхности падает луч света, длина волны которого 650 нм. Каков максимальный порядок дифракционного максимума, доступного для наблюдения?

Узнать результат

13. Задание 2 № 6039.

Тело
массой 2 кг движется вдоль
оси OX .
На рисунке представлен
график зависимости
проекции скорости v_x этого
тела от времени t.
В течение первой секунды
движения модуль проекции
силы F_x,
действующей на это тело, равен

1) 4 Н

2) 2 Н

3) 1 Н

4) 0 Н

Ответ:
1

14.
Задание 2 № 6332. Точечное
тело, на которое действуют
три постоянные силы, движется
равномерно вдоль горизонтальной
оси OX.
На каком из рисунков правильно
изображены силы, действующие
на это тело?

1) только
на рис. 1

2) только
на рис. 2

3) на
обоих рисунках

4) ни на
одном из рисунков

Ответ:
1

15.
Задание 2 № 6481. На
рисунке показаны силы,
действующие на материальную
точку. Определите модуль
равнодействующей силы (в
заданном масштабе).

1) 6 Н

Ответ:
2

16.
Задание 2 № 6721. На
рисунке показаны силы (в
заданном масштабе),
действующие на материальную
точку в инерциальной системе
отсчета. Чему равен модуль
равнодействующей этих
сил в данной системе отсчета?

Ответ:
2

17.
Задание 2 № 6754. На
рисунке представлены
векторы скорости и ускорения
материальной точки в
инерциальной системе
отсчёта. Определите направление
вектора равнодействующей
силы, действующей на материальную
точку в этой системе отсчета.

1)
→

2)
↑

3)
↗

4)
↓

Ответ:
2

18.
Задание 2 № 6810. На
небольшое тело массой 0,1 кг,
движущееся по инерции по
гладкой плоскости XOY,
начинает действовать
постоянная по модулю сила
0,2 Н, всегда направленная
вдоль оси OX.
Через 3 секунды после начала
действия силы модуль скорости
этого тела

1) меньше 6 м/с	2) равен 6 м/с
3) больше 6 м/с	4) может иметь любое значение

Ответ:
4

19.
Задание 2 № 6883. Брусок
лежит на шероховатой
наклонной опоре (см. рисунок).
На него действуют три силы: сила
тяжестисила
нормальной реакции опорыи
сила тренияЧему
равен модуль равнодействующей
силиесли
брусок движется равномерно
вниз по прямой?

1) F_тр + N

2) N cosα

3) F_трsin
α

4) mg

Ответ:
4

20.
Задание 2 № 7101. Брусок
лежит на шероховатой
наклонной опоре (см. рисунок).
На него действуют три силы: сила
тяжестиmg,
сила упругости опоры N
и сила трения F_тр.
Если брусок покоится, то
модуль равнодействующей
сил N
и F_тр равен

1) N + F_тр

2) mg sinα

3)
(N + F_тр)cos
α

4) mg

Ответ:
4

21.
Задание 2 № 7173. На
рисунке показаны силы (в
заданном масштабе),
действующие на материальную
точку. Модуль равнодействующей
силы равен

2) 6 Н

4) 2 H

Ответ:
1

Пояснения Ответы Ключ Источник Печать PDF-версия

Второй закон Ньютона

1.
Задание 3 № 318. Под
действием силы 8 Н первоначально
покоившееся тело массой
4 кг будет двигаться:

1)
равномерно со скоростью ;

2)
равноускоренно с ускорением ;

3)
равноускоренно с ускорением ;

4)
равномерно со скоростью .

Ответ:
2

2.
Задание 3 № 644. Тележка
массой 0,1 кг удерживается
на наклонной плоскости с
помощью нити (см. рисунок).

Сила
натяжения нити равна

1) 0,5 H

2) 1,0 H

3) 1,5 H

4) 2,0 H

Ответ:
1

3.
Задание 3 № 3869. Лифт
массой 800 кг, закрепленный
на тросе, поднимается
вертикально вверх. На рисунке
изображен график зависимости
модуля скорости лифта
от времени

На каких
из приведенных ниже рисунков
правильно изображена
зависимость модуля силы
натяжения троса
от времени?

1) 1

2) 2

3) 3

4) 4

Ответ:
2

4.
Задание 3 № 4339. Камень
брошен с поверхности земли
и летит в воздухе, поднимаясь
вверх. Со стороны воздуха на
камень действует сила трения,
направленная противоположно
вектору скоростикамня.
Скорость камня в некоторый
момент времени направлена
под углом к горизонту. На каком
рисунке правильно показано
направление вектора
ускорениякамня
в этот же момент?

1) 1

2) 2

3) 3

4) 4

Ответ:
3

5.
Задание 3 № 4374. Камень
брошен с поверхности земли
и летит в воздухе, опускаясь
вниз. Со стороны воздуха на
камень действует сила трения,
направленная противоположно
вектору скорости и камня.
Скорость камня в некоторый
момент времени направлена
под углом к горизонту. На каком
рисунке правильно показано
направление вектора
ускорения а камня в этот же момент?

1) 1

2) 2

3) 3

4) 4

Ответ:
3

6.
Задание 3 № 5715. Невесомость
можно наблюдать

1) на
борту космического корабля,
стартующего с космодрома

2) на
борту космической станции,
движущейся по околоземной
орбите

3) в
спускаемом аппарате,
совершающем посадку
на Землю при помощи парашюта

4) во
всех трёх перечисленных выше
случаях

Ответ:
2

7.
Задание 3 № 5750. Невесомость
можно наблюдать

1) в
лифте, ускоренно движущемся
вверх

2) в
свободно падающем лифте

3) в
лифте, равномерно движущемся
вниз

4) во
всех трёх перечисленных выше
случаях

Ответ:
2

8.
Задание 3 № 5954. Два
искусственных спутника
Земли массой 200 кг и 400 кг обращаются
по круговым орбитам
одинакового радиуса.
Модули скоростей этих
спутников

1)
одинаковы

2)
отличаются в 2 раза

3)
отличаются в 4 раза

4)
отличаются в раза

Ответ:
1

9.
Задание 3 № 5989. Два
искусственных спутника
обращаются по круговым
орбитам одинакового
радиуса: первый спутник
— вокруг Земли, второй — вокруг
Луны. Масса Луны в 81 раз меньше массы
Земли. Модули скоростей этих
спутников

1)
одинаковы

2)
отличаются в 81 раз

3)
отличаются в 3 раза

4)
отличаются в 9 раз

Ответ:
4

10.
Задание 3 № 6885. Под
действием постоянной силы
за 10 с импульс тела, движущегося
по прямой в одном направлении,
изменился на 50 кг · м/с. Чему
равен модуль силы?

Ответ:
5

11.
Задание 3 № 7135. Тело
движется по прямой под действием
постоянной силы, равной по
модулю 10 Н. Сколько времени
потребуется для того, чтобы
под действием этой силы импульс
тела изменился на 50 кг · м/с?

Ответ:
5

Задание 2 ЕГЭ по физике

Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения

В. З. Шапиро

Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.

Применение закона всемирного тяготения

Необходимая теория: Сила тяготения

1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?

Ответ: в _________________________ раз(а).

В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:

(1).

(2).

Разделив (2) на (1), получим:

Ответ: в 1,5 раза.

Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.

Применение II закона Ньютона

Необходимая теория: Второй и третий законы Ньютона

2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.

Равнодействующая сила равна геометрической сумме сил, приложенных к телу.

Следующий шаг – найти сумму проекций сил на оси OX и OY.

Сумма проекций сил на ось OX равна:

Сумма проекций сил на вертикальную ось равна:

По теореме Пифагора, модуль равнодействующей силы определяется:

Ответ: 2 Н.

Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.

Применение формулы силы упругости (закон Гука)

Необходимая теория: Сила упругости

3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?

Ответ: ___________________________ см.

Запишем формулу закона Гука для двух случаев:

(1)

(2)

Разделим (2) на (1).

(м).

Ответ: 16 см.

Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.

Применение формул для силы реакции опоры и силы трения

Необходимая теория: Сила трения

4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.

Ответ: ___________________________.

Общая формула для силы трения имеет вид:

где N — сила реакции опоры.

Отсюда коэффициент трения можно выразить

Проведем расчет:

Ответ: 0,25.

Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.

Результирующая сила — урок. Физика, 7 класс.

Если на тело одновременно действует несколько сил, тогда состояние тела или его движение определяет результирующая сила — сумма всех сил.

Если силы действуют в одном направлении, результирующая сила равна сумме сил.

F1→F2→

Fрез=F1+F2

Сила тяги обеих лошадей суммируется

Обрати внимание!

Если силы действуют в противоположных направлениях, результирующая сила равна разности сил — от большей силы отнимают меньшую, результирующая сила действует в направлении большей силы.

Например, при движении автомобиля на него действуют две силы: сила тяги \(Fт\), создаваемая двигателем и направленная в сторону движения, и сила трения \(Fтр\) с поверхностью дороги, которая направлена в противоположном направлении (силу сопротивления воздуха не учитываем).

Fрез=Fт−Fтр

Fтр→ Fт→

Fрез=Fтр−Fт

В этом случае движение автомобиля будет замедленным, так как сила трения больше, чем сила тяги.

Если сила тяги одинакова с силой трения, тогда автомобиль двигается с постоянной скоростью.

Эти силы компенсируют друг друга. Сумма всех сил равна нулю, и автомобиль двигается без ускорения.

Fрез=0

1-й закон Ньютона:

Если на тело не действуют силы или они уравновешены, тогда тело остаётся неподвижным или двигается равномерно и прямолинейно.

Когда автомобиль стоит на дороге, он находится в статическом равновесии. На него действуют две силы — сила притяжения (гравитации) и сила упругоcти опоры (дороги), которые компенсируют друг друга, их сумма равна нулю.

Каждое тело стремится оказывать сопротивление изменению скорости, оказывая сопротивление силе, вызывающей ускорение.

Стремление тела сопротивляться изменению скорости называют инерцией, или инертностью. Масса является мерой инертности (чем больше масса, тем больше инертность тела).

Обрати внимание!

Из-за инерции тормозной путь у автобуса длиннее, чем у легкового автомобиля!

12.3 Напряжение, деформация и модуль упругости — University Physics Volume 1

Учебные цели

К концу этого раздела вы сможете:

Объяснять концепции напряжения и деформации при описании упругих деформаций материалов
Описывать виды упругого деформирования предметов и материалов

Модель твердого тела — это идеализированный пример объекта, который не деформируется под действием внешних сил.Это очень полезно при анализе механических систем, а многие физические объекты действительно в значительной степени жесткие. Степень, в которой объект может восприниматься как жесткий, зависит от физических свойств материала, из которого он изготовлен. Например, мяч для пинг-понга, сделанный из пластика, является хрупким, а теннисный мяч, сделанный из резины, эластичен, когда на него воздействуют сжимающие силы. Однако при других обстоятельствах и мяч для пинг-понга, и теннисный мяч могут хорошо отскакивать как твердые тела.Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическая комбинация костей и тканей представляет собой эластичную среду.

В оставшейся части этой главы мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы называется деформацией. Известно, что даже очень небольшие силы вызывают некоторую деформацию.Деформация испытывается объектами или физическими средами под действием внешних сил — например, это может быть сжатие, сжатие, разрыв, скручивание, срезание или растяжение объектов. На языке физики два термина описывают силы, действующие на объекты, подвергающиеся деформации: напряжение и напряжение .

Напряжение — это величина, которая описывает величину сил, вызывающих деформацию. Напряжение обычно определяется как сил на единицу площади .Когда силы притягивают объект и вызывают его удлинение, например, при растяжении эластичной ленты, мы называем такое напряжение растягивающим напряжением. Когда силы вызывают сжатие объекта, мы называем это напряжением сжатия. Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением). В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, и все же вызывать заметную деформацию. Например, предположим, что вы держите книгу в ладонях, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой вы нажимаете и тянете заднюю обложку в направлении ты.В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «поперечными» силами, а вызываемое ими напряжение — поперечным напряжением.

Единицей измерения напряжения в системе СИ является паскаль (Па). Когда сила в один ньютон воздействует на единицу площади квадратного метра, результирующее напряжение составляет один паскаль:

один паскаль = 1.0Па = 1.0N1.0м2. один паскаль = 1.0Па = 1.0N1.0м2.

В британской системе единиц единицей измерения напряжения является «фунт / кв. Дюйм», что означает «фунт на квадратный дюйм» (фунт / дюйм2).(фунт / дюйм2). Другой единицей измерения объемного напряжения является атм (атмосфера). Коэффициенты пересчета:

1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв. Дюйм · атм = 1,013 × 105 Па = 14,7 фунт / кв. Дюйм. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10–4 фунт / кв.

Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформацией. Деформация задается как частичное изменение длины (при растягивающем напряжении), объема (при объемном напряжении) или геометрии (при напряжении сдвига). Следовательно, деформация — это безразмерное число.Деформация под действием растягивающего напряжения называется деформацией растяжения, деформация под действием объемного напряжения называется объемной деформацией (или объемной деформацией), а деформация, вызванная напряжением сдвига, называется деформацией сдвига.

Чем больше напряжение, тем больше напряжение; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, вызываемая им деформация прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости.В линейном пределе низких значений напряжения общее соотношение между напряжением и деформацией составляет

напряжение = (модуль упругости) × деформация. напряжение = (модуль упругости) × деформация.

12,33

Как видно из анализа размеров этого соотношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.

Из уравнения 12.33 также видно, что, когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико. С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию.Например, напряжение на резиновой ленте вызывает большую деформацию (деформацию), чем такое же напряжение на стальной ленте тех же размеров, потому что модуль упругости резины на два порядка меньше модуля упругости стали.

Модуль упругости при растяжении называется модулем Юнга; то, что для объемного напряжения называется объемным модулем упругости; а напряжение сдвига называется модулем сдвига. Обратите внимание, что соотношение между напряжением и деформацией — это соотношение , наблюдаемое и , измеренное в лаборатории.Модули упругости для различных материалов измеряются при различных физических условиях, таких как изменяющаяся температура, и собираются в таблицах технических данных для справки (таблица 12.1). Эти таблицы являются ценными справочными материалами для промышленности и для всех, кто занимается проектированием или строительством. В следующем разделе мы обсудим отношения между деформацией и напряжением за пределами линейного предела, представленного уравнением 12.33, в полном диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выражаемый уравнением 12.33.

Материал	Модуль Юнга × 1010 Па × 1010 Па	Объемный модуль × 1010 Па × 1010 Па	Модуль сдвига × 1010 Па × 1010 Па
Алюминий	7,0	7,5	2,5
Кость (напряжение)	1,6	0,8	8,0
Кость (компрессия)	0,9
Латунь	9.0	6,0	3,5
Кирпич	1,5
Бетон	2,0
Медь	11,0	14,0	4,4
Коронное стекло	6,0	5,0	2,5
Гранит	4,5	4,5	2,0
Волосы (человеческие)	1.0
Твердая древесина	1,5		1,0
Утюг	21,0	16,0	7,7
Свинец	1,6	4,1	0,6
Мрамор	6,0	7,0	2,0
Никель	21,0	17,0	7,8
полистирол	3.0
шелк	6,0
Крестовина с резьбой	3,0
Сталь	20,0	16,0	7,5
ацетон		0,07
этанол		0,09
Глицерин		0.45
Меркурий		2,5
Вода		0,22

Таблица 12.1 Приблизительные модули упругости для выбранных материалов

Напряжение при растяжении или сжатии, деформация и модуль Юнга

Напряжение или сжатие возникает, когда две антипараллельные силы равной величины действуют на объект только в одном из его измерений таким образом, что объект не перемещается.Один из способов представить себе такую ситуацию показан на рисунке 12.18. Сегмент стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно его поперечному сечению. Чистый эффект таких сил состоит в том, что стержень изменяет свою длину от исходной длины L0L0, которая была у него до появления сил, на новую длину L , которую он имеет под действием сил. Это изменение длины ΔL = L-L0ΔL = L-L0 может быть либо удлинением (когда L больше, чем исходная длина L0) L0), либо сжатием (когда L меньше исходной длины L0).L0). Напряжение растяжения и деформация возникают, когда силы растягивают объект, вызывая его удлинение, и изменение длины ΔLΔL является положительным. Напряжение сжатия и деформация возникают, когда силы сжимают объект, вызывая его сокращение, а изменение длины ΔLΔL отрицательно.

В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы F⊥F⊥ к площади A поперечного сечения деформируемого объекта. Символ F⊥F⊥, который мы оставляем для деформирующей силы, означает, что эта сила действует перпендикулярно поперечному сечению объекта.Силы, действующие параллельно поперечному сечению, не изменяют длину объекта. Определение растягивающего напряжения —

.
растягивающее напряжение = F⊥A. растягивающее напряжение = F⊥A.

12,34

Деформация растяжения — это мера деформации объекта при растягивающем напряжении и определяется как частичное изменение длины объекта, когда объект испытывает растягивающее напряжение.

деформация растяжения = ΔLL0. деформация растяжения = ΔLL0.

12,35

Напряжение сжатия и деформация определяются по той же формуле, уравнение 12.34 и уравнение 12.35 соответственно. Единственное отличие от ситуации с растяжением состоит в том, что для напряжения и деформации сжатия мы берем абсолютные значения правых частей в уравнениях 12.34 и 12.35.

Рис. 12.18. Когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою исходную длину L0.L0. (a) Натяжение: стержень удлинен на ΔL.ΔL. (b) Сжатие: стержень сжимается на ΔL.ΔL. В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению.В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.

Модуль Юнга Y — это модуль упругости, когда деформация вызвана либо растягивающим, либо сжимающим напряжением, и определяется уравнением 12.33. Разделив это уравнение на деформацию растяжения, мы получим выражение для модуля Юнга:

Y = растягивающая деформация растяжения = F⊥ / AΔL / L0 = F⊥AL0ΔL.Y = растягивающая деформация растяжения = F⊥ / AΔL / L0 = F⊥AL0ΔL.

12,36

Пример 12.7

Напряжение сжатия в опоре

Скульптура весом 10 000 Н стоит на горизонтальной поверхности на вершине 6.Вертикальный столб высотой 0 м Рис. 12.19. Площадь поперечного сечения столба 0,20 м 20,20 м 2, он выполнен из гранита с удельной массой 2700 кг / м3. 2700 кг / м3. Найдите сжимающее напряжение в поперечном сечении, расположенном на 3,0 м ниже вершины столба, и значение сжимающей деформации верхнего 3,0-метрового сегмента столба.

Рисунок 12.19 Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)

Стратегия

Сначала мы находим вес 3.Верхняя часть столба длиной 0 м. Нормальная сила, действующая на поперечное сечение, расположенное на 3,0 м ниже вершины, складывается из веса столба и веса скульптуры. Когда у нас есть нормальная сила, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице 12.1 и инвертируем уравнение 12.36.

Решение

Объем сегмента колонны высотой h = 3,0мh = 3,0м и площадью поперечного сечения A = 0,20м2A = 0,20м2 составляет
V = Ah = (0.20м2) (3,0м) = 0,60м3. V = Ah = (0,20м2) (3,0м) = 0,60м3.

При плотности гранита ρ = 2,7 × 103 кг / м3, ρ = 2,7 × 103 кг / м3 масса сегмента столба составляет

m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг. m = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг.

Вес сегмента стойки

wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н. wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н.

Вес скульптуры ws = 1,0 × 104 Н, ws = 1,0 × 104 Н, поэтому нормальная сила на поверхности поперечного сечения, расположенной на 3,0 м ниже скульптуры, составляет

F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N. F⊥ = wp + ws = (1.568 + 1.0) × 104N = 2.568 × 104N.

Следовательно, напряжение

напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа. напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа.

Модуль Юнга для гранита составляет Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Следовательно, деформация сжатия в этом положении равна

.
деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6.

Значение

Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения колонны, не постоянна по ее длине, а изменяется от наименьшего значения наверху до наибольшего значения внизу колонны.Таким образом, если опора имеет равномерную площадь поперечного сечения по всей длине, наибольшее напряжение у ее основания.

Проверьте свое понимание 12.9

Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.

Пример 12,8

Растяжка стержня

Стальной стержень длиной 2,0 м имеет площадь поперечного сечения 0,30 см2 0,30 см2. Штанга является частью вертикальной опоры, которая удерживает тяжелую платформу весом 550 кг, которая подвешена к нижнему концу штанги. Пренебрегая весом стержня, каково растягивающее напряжение стержня и удлинение стержня под действием напряжения?

Стратегия

Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.34. Затем мы инвертируем уравнение 12.36, чтобы найти удлинение стержня, используя L0 = 2,0 м. L0 = 2,0 м. Из таблицы 12.1 модуль Юнга для стали составляет Y = 2,0 × 1011 Па. Y = 2,0 × 1011 Па.

Решение

Подстановка числовых значений в уравнения дает нам
F⊥A = (550 кг) (9,8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 м2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.F⊥ A = (550 кг) (9,8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 м2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.

Значение

Как и в примере с колонной, растягивающее напряжение в этом примере неоднородно по длине стержня.Однако, в отличие от предыдущего примера, если принять во внимание вес штанги, напряжение в штанге будет наибольшим в верхней части и наименьшим в нижней части штанги, к которой прикреплено оборудование.

Проверьте свое понимание 12.10

Проволока длиной 2,0 м растягивается на 1,0 мм под действием нагрузки. Какова деформация растяжения в проволоке?

Объекты часто могут одновременно испытывать напряжение сжатия и растяжения. Рис. 12.20. Один из примеров — длинная полка, загруженная тяжелыми книгами, которая провисает между концевыми опорами под весом книг.Верхняя поверхность полки испытывает напряжение сжатия, а нижняя поверхность полки — растягивающее напряжение. Точно так же длинные и тяжелые балки провисают под собственным весом. В современном строительстве такие деформации изгиба можно практически исключить с помощью двутавровых балок. Рисунок 12.21.

Рис. 12.20 (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части. (б) Элитные тяжелоатлеты часто временно сгибают железные прутья во время подъема, как на Олимпийских играх 2012 года.(кредит б: модификация работы Александра Кочерженко)

Рисунок 12.21 Стальные двутавровые балки используются в строительстве для уменьшения деформаций изгиба. (Источник: модификация работы «Инженерный корпус армии США в Европе» / Flickr)

Объемное напряжение, деформация и модуль

Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс или, другими словами, давление. Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта.Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности. Рис. 12.22. Эффект этих сил заключается в уменьшении объема погруженного объекта на величину ΔVΔV по сравнению с объемом V0V0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема относительно исходного объема:

объемная деформация = ΔVV0. объемная деформация = ΔVV0.

12,37

Рис. 12.22 Объект при увеличении объемного напряжения всегда подвергается уменьшению своего объема.Равные силы, перпендикулярные поверхности, действуют со всех сторон. Эффект этих сил заключается в уменьшении объема на величину ΔVΔV по сравнению с исходным объемом V0.V0.

Объемная деформация является результатом объемного напряжения, которое представляет собой силу F⊥F⊥, нормальную к поверхности, которая давит на единицу площади поверхности A погруженного объекта. Такая физическая величина, или давление p , определяется как

.
давление = p≡F⊥A. давление = p≡F⊥A.

12,38

Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что это скалярная величина, не имеющая определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления ΔpΔp по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.Когда ваша рука не погружена в воду, вы чувствуете нормальное давление p0p0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение — это увеличение давления, или Δp, Δp, по сравнению с нормальным уровнем, p0.p0.

Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.33. Константа пропорциональности в этом соотношении называется объемным модулем, B или

.
B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV.

12,39

Знак минус, который появляется в уравнении 12.39, предназначен для согласованности, чтобы гарантировать, что B является положительной величиной. Обратите внимание, что знак минус (-) (-) необходим, потому что увеличение ΔpΔp давления (положительная величина) всегда вызывает уменьшение ΔVΔV в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемного сжатия, называется сжимаемостью k, k или

.
k = 1B = −ΔV / V0Δp.k = 1B = −ΔV / V0Δp.

12,40

Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей).Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 × 10–5 / атм. 4,64 × 10–5 / атм, а сжимаемость ацетона составляет 1,45 × 10–4 / атм. 1,45 × 10–4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.

Пример 12.9

Гидравлический пресс

В гидравлическом прессе Рисунок 12.23, 250-литровый объем масла подвергается увеличению давления на 2300 фунтов на квадратный дюйм. Если сжимаемость масла составляет 2,0 × 10–5 / атм, 2,0 × 10–5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.

Рис. 12.23 В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается через масло на большой поршень, заставляя большой поршень двигаться вверх. Небольшая сила, приложенная к маленькому поршню, вызывает большую прижимающую силу, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается.Устройство действует как механический рычаг.

Стратегия

Мы должны перевернуть уравнение 12.40, чтобы найти объемную деформацию. Во-первых, мы преобразуем увеличение давления из фунтов на квадратный дюйм в атм, Δp = 2300psi = 2300 / 14,7atm≈160atm, Δp = 2300psi = 2300 / 14.7atm≈160atm, и определяем V0 = 250L.V0 = 250L.

Решение

Подставляя значения в уравнение, имеем
объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160 атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250L) = 0,78L. объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0.0032V0 = 0,0032 (250 л) = 0,78 л.

Значение

Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем у масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.

Проверьте свое понимание 12.11

Если нормальная сила, действующая на каждую грань кубического стального куска 1,0 м31,0 м3, изменится на 1,0 × 107 Н, 1,0 × 107 Н, найдите результирующее изменение объема стального куска.

Напряжение сдвига, деформация и модуль

Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не относятся к жидкостям.

Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке 12.24. Сдвиговая деформация характеризуется постепенным смещением ΔxΔx слоев в направлении, касательном к действующим силам. Эта градация ΔxΔx происходит в поперечном направлении на некотором расстоянии L0.L0. Деформация сдвига определяется отношением наибольшего смещения ΔxΔx к поперечному расстоянию L0L0

деформация сдвига = ΔxL0. деформация сдвига = ΔxL0.

12,41

Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, действующих на параллельно поверхности. Для таких сил мы используем символ F∥F forces.Величина F∥F∥ на площадь поверхности A , где применяется сила сдвига, является мерой напряжения сдвига

.
напряжение сдвига = F∥A. напряжение сдвига = F∥A.

12,42

Модуль сдвига является константой пропорциональности в уравнении 12.33 и определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается как S :

.
S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.

12,43

Рис. 12.24. Объект, находящийся под напряжением сдвига: две антипараллельные силы равной величины действуют по касательной к противоположным параллельным поверхностям объекта.Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L0L0 не изменяется. Сдвиговая деформация характеризуется постепенным смещением ΔxΔx слоев в направлении, касательном к силам.

Пример 12.10

Старая книжная полка

Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, касаясь его поверхности самой верхней полки. Однако единственный заметный эффект от этих усилий аналогичен эффекту, показанному на рисунке 12.24, и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180 см и шириной 90 см с четырьмя полками глубиной 30 см, частично заполненными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая смещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.

Стратегия

Единственная важная информация — это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой.Мы определяем F∥ = 50.0N, Δx = 15.0cm, F∥ = 50.0N, Δx = 15.0cm, L0 = 180.0cm, L0 = 180.0cm и A = (30.0 cm) (90.0 cm) = 2700.0 cm2, A = (30,0 см) (90,0 см) = 2700,0 см2, и мы используем уравнение 12.43 для вычисления модуля сдвига.

Решение

Подставляя числа в уравнения, получаем для модуля сдвига
S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Nm2 = 209 × 103Pa = 2.222 кПа S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Нм2 = 209 × 103Па = 2,222 кПа.

Мы также можем найти напряжение сдвига и деформацию соответственно:

F∥A = 50.0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.F∥A = 50,0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.

Значение

Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.

Проверьте свое понимание 12.12

Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.

Равновесие и статика

Когда все силы, действующие на объект, уравновешены, считается, что объект находится в состоянии равновесия . Силы считаются уравновешенными , если правые силы уравновешиваются левыми, а восходящие силы уравновешиваются нисходящими. Однако это не обязательно означает, что все силы на равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже.Обратите внимание, что два объекта находятся в равновесии, потому что действующие на них силы уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.

Если объект находится в равновесии, силы уравновешены. Сбалансированный — ключевое слово, используемое для описания ситуаций равновесия. Таким образом, результирующая сила равна нулю, а ускорение равно 0 м / с / с. Объекты в состоянии равновесия должны иметь ускорение 0 м / с / с.Это происходит из первого закона движения Ньютона. Но наличие ускорения 0 м / с / с не означает, что объект находится в состоянии покоя. Объект в состоянии равновесия — это либо …

в состоянии покоя и в состоянии покоя, или
в движении и продолжает движение с той же скоростью и направлением.

Это тоже происходит от первого закона движения Ньютона.

Анализ ситуации статического равновесия

Если объект находится в состоянии покоя и находится в состоянии равновесия, то мы бы сказали, что объект находится в «статическом равновесии».«Статический» означает стационарный или в состоянии покоя . Обычная физическая лаборатория заключается в том, чтобы подвесить объект на двух или более веревках и измерить силы, которые действуют под углом на объект, чтобы выдержать его вес. объект анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на струне, на которую действуют три силы. См. диаграмму справа. Если объект находится в состоянии равновесия, то результирующая сила, действующая на объект должен быть 0 Ньютон.Таким образом, если все силы складываются вместе как векторы, то результирующая сила (векторная сумма) должна быть 0 Ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или результат сложения всех отдельных сил по направлению «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения результирующей. Ниже приведены примеры данных для такой лаборатории.

	Сила А	Force B	Сила C
Величина	3.4 с.ш.	9.2 с.ш.	9.8 с.ш.
Направление	161 град.	70 град.	270 град.

Для большинства студентов результат был 0 Ньютонов (или, по крайней мере, очень близок к 0 Н).Это то, что мы ожидали — поскольку объект находился в состоянии равновесия, результирующая сила (векторная сумма всех сил) должна быть 0 Н.

Другой способ определения чистой силы (векторной суммы всех сил) включает использование тригонометрических функций для разделения каждой силы на ее горизонтальную и вертикальную составляющие. Как только компоненты известны, их можно сравнить, чтобы увидеть, сбалансированы ли вертикальные силы и горизонтальные силы.На схеме ниже показаны векторы A, B и C и их соответствующие компоненты. Для векторов A и B вертикальные компоненты могут быть определены с использованием синуса угла, а горизонтальные компоненты могут быть проанализированы с помощью косинуса угла. Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.

Данные в таблице выше показывают, что силы почти уравновешивают.Анализ горизонтальных компонентов показывает, что левый компонент A почти уравновешивает правый компонент B. Анализ вертикальных компонентов показывает, что сумма восходящих компонентов A + B почти уравновешивает нисходящий компонент C. Векторная сумма всех сил ( почти ) равна 0 Ньютону. Но как насчет разницы в 0,1 Н между направленными вправо и влево силами и разницы в 0,2 Н между восходящими и нисходящими силами? Почему компоненты силы только почти уравновешивают? Данные образца, используемые в этом анализе, являются результатом данных измерений на реальной экспериментальной установке.Разница между фактическими результатами и ожидаемыми результатами связана с ошибкой, возникшей при измерении силы A и силы B. Мы должны сделать вывод, что этот низкий предел экспериментальной ошибки отражает эксперимент с превосходными результатами. Можно сказать, что это «достаточно близко для работы правительства».

Анализ висящего знака

Приведенный выше анализ сил, действующих на объект в состоянии равновесия, обычно используется для анализа ситуаций с объектами в состоянии статического равновесия.Наиболее распространенное применение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрите картину справа, висящую на стене. Картина находится в состоянии равновесия, и поэтому все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 Ньютонов, а все вертикальные компоненты должны составлять 0 Ньютонов. Натяжение троса А влево должно уравновешивать натяжение троса В вправо, а сумма натяжения троса А и троса В вверх должна уравновешивать вес знака.

Предположим, что измеренное натяжение обоих кабелей составляет 50 Н, а угол, который каждый кабель образует с горизонталью, составляет 30 градусов. Какой вес у знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих компонентов натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопроводительные работы показаны ниже.

Поскольку каждый трос тянет вверх с силой 25 Н, общее тяговое усилие знака вверх составляет 50 Н. Следовательно, сила тяжести (также известная как вес) равна 50 Н по направлению вниз. Знак весит 50 Н.

В вышеупомянутой задаче натяжение в тросе и угол , который трос образует с горизонталью, используются для определения веса знака .Идея в том, что натяжение, угол и вес связаны. Если известны любые два из этих трех, то третья величина может быть определена с помощью тригонометрических функций.

В качестве еще одного примера, иллюстрирующего эту идею, рассмотрим симметричное развешивание знака, как показано справа. Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в состоянии равновесия (хорошее предположение, если он остается в состоянии покоя), два троса должны обеспечивать достаточную восходящую силу, чтобы уравновесить нисходящую силу тяжести.Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m * g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями составляет 100 градусов, каждый кабель должен составлять 50 градусов с вертикалью и 40 градусов с горизонталью. Набросок этой ситуации (см. Диаграмму ниже) показывает, что натяжение кабеля можно определить с помощью синусоидальной функции. Треугольник ниже иллюстрирует эти отношения.

Концептуальное мышление

Есть важный принцип, который вытекает из некоторых из тригонометрических вычислений, выполненных выше.Принцип состоит в том, что по мере увеличения угла к горизонтали величина силы натяжения, необходимая для удержания знака в состоянии равновесия, уменьшается. Чтобы проиллюстрировать это, рассмотрим картинку с напряжением 10 Ньютон, удерживаемую тремя разными ориентациями проводов, как показано на схемах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол между проводами и горизонтом варьируется от 60 до 15 градусов. Используйте эту информацию и диаграмму ниже, чтобы определить натяжение проволоки для каждой ориентации.По завершении нажмите кнопку, чтобы просмотреть ответы.

В заключение, равновесие — это состояние объекта, в котором все силы, действующие на него, уравновешены. В таких случаях чистая сила равна 0 Ньютонам. Зная силы, действующие на объект, тригонометрические функции могут использоваться для определения горизонтальных и вертикальных компонентов каждой силы. В случае равновесия все вертикальные компоненты должны уравновешиваться, а все горизонтальные компоненты должны уравновешиваться.

Мы хотели бы предложить …

Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов».Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте и обеспечить интерактивный опыт с навыком добавления векторов.

Проверьте свое понимание

Следующие вопросы предназначены для проверки вашего понимания ситуаций равновесия. Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.

1.На стене висит следующая картина. Используйте тригонометрические функции, чтобы определить вес изображения.

2. Табличка внизу висит снаружи класса физики, рекламируя самую важную истину, которую можно найти внутри. Знак опирается на диагональный трос и жесткий турник. Если вывеска имеет массу 50 кг, определите натяжение диагонального троса, поддерживающего его вес.

3. Следующий знак можно найти в Гленвью. Знак имеет массу 50 кг. Определите натяжение тросов.

4. После самой последней доставки печально известный аист объявляет хорошие новости. Если знак имеет массу 10 кг, то какова сила натяжения в каждом тросе? Используйте тригонометрические функции и эскиз, чтобы помочь в решении.

5. Предположим, что ученик тянет с двумя большими силами (F ₁ и F ₂), чтобы поднять книгу весом 1 кг за два троса. Если кабели образуют угол в 1 градус с горизонталью, то каково натяжение кабеля?

Эластичность: напряжение и деформация | Физика

Цели обучения

К концу этого раздела вы сможете:

Закон штата Гука.
Объясните закон Гука, используя графическое представление между деформацией и приложенной силой.
Обсудите три типа деформаций, такие как изменение длины, сдвиг в сторону и изменение объема.
Опишите на примерах модуль Юнга, модуль сдвига и модуль объемной упругости.
Определите изменение длины с учетом массы, длины и радиуса.

Теперь мы переходим от рассмотрения сил, влияющих на движение объекта (таких как трение и сопротивление), к тем, которые влияют на форму объекта.Если бульдозер втолкнет машину в стену, машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы представляет собой деформацию . Известно, что даже очень небольшие силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей исходной форме, когда сила снимается, то есть деформация является упругой для небольших деформаций. Во-вторых, размер деформации пропорционален силе, то есть при малых деформациях соблюдается закон Гука.В форме уравнения Закон Гука определяется как

F = k Δ L ,

, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, которая зависит от формы и состава объекта и направления сила. Обратите внимание, что эта сила является функцией деформации Δ L — она не постоянна, как кинетическая сила трения.Переставляем это на

[латекс] \ displaystyle \ Delta {L} = \ frac {F} {k} [/ latex]

дает понять, что деформация пропорциональна приложенной силе. На рисунке 1 показано соотношение по закону Гука между удлинением Δ L пружины или человеческой кости. Для металлов или пружин область прямой линии, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область небольшая, а перелом резкий. В конце концов, достаточно большое напряжение материала приведет к его разрушению или разрушению.

Закон Гука

F = kΔL ,

[латекс] \ displaystyle \ Delta {L} = \ frac {F} {k} [/ latex]

Рисунок 1. График деформации ΔL в зависимости от приложенной силы F.Прямой отрезок — это линейная область, в которой соблюдается закон Гука. Наклон прямой области [латекс] \ frac {1} {k} [/ latex]. Для больших сил график изогнут, но деформация остается упругой — ΔL вернется к нулю, если сила будет устранена. Еще большие силы деформируют объект до тех пор, пока он не сломается. Форма кривой возле трещины зависит от нескольких факторов, в том числе от того, как прикладывается сила F . Обратите внимание, что на этом графике наклон увеличивается непосредственно перед трещиной, указывая на то, что небольшое увеличение F дает большое увеличение L рядом с трещиной.

Константа пропорциональности k зависит от ряда факторов материала. Например, гитарная струна из нейлона растягивается при затягивании, а удлинение Δ L пропорционально приложенной силе (по крайней мере, для небольших деформаций). Более толстые нейлоновые и стальные струны меньше растягиваются при одной и той же приложенной силе, что означает, что они имеют больший размер k (см. Рисунок 2). Наконец, все три струны возвращаются к своей нормальной длине, когда сила снимается, при условии, что деформация мала.Большинство материалов будут вести себя таким образом, если деформация будет меньше примерно 0,1% или примерно 1 часть на 10 ³.

Рис. 2. Одна и та же сила, в данном случае груз (w), приложенная к трем различным гитарным струнам одинаковой длины, вызывает три различных деформации, показанные заштрихованными сегментами. Левая нить из тонкого нейлона, посередине — из более толстого нейлона, а правая — из стали.

Растянись немного

Как бы вы измерили константу пропорциональности k резиновой ленты? Если резинка растянулась на 3 см, когда к ней была прикреплена 100-граммовая масса, то насколько она растянулась бы, если бы две одинаковые резинки были прикреплены к одной и той же массе — даже если соединить их параллельно или, наоборот, если связать вместе последовательно?

Теперь мы рассмотрим три конкретных типа деформаций: изменение длины (растяжение и сжатие), сдвиг в сторону (напряжение) и изменения объема.Все деформации считаются небольшими, если не указано иное.

Изменения длины — растяжение и сжатие: модуль упругости

Изменение длины Δ L происходит, когда к проволоке или стержню прилагается сила, параллельная ее длине L ₀, либо растягивая (натяжение), либо сжимая. (См. Рисунок 3.)

Рис. 3. (а) Напряжение. Стержень растягивается на длину ΔL при приложении силы, параллельной его длине. (б) Сжатие.Тот же стержень сжимается силами той же величины в противоположном направлении. Для очень малых деформаций и однородных материалов ΔL примерно одинаково для одинаковой величины растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.

Эксперименты показали, что изменение длины (Δ L ) зависит только от нескольких переменных. Как уже отмечалось, Δ L пропорциональна силе F и зависит от вещества, из которого сделан объект.Кроме того, изменение длины пропорционально исходной длине L ₀ и обратно пропорционально площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растягивается больше, чем короткая, а толстая струна растягивается меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для Δ L :

[латекс] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex],

, где Δ L — изменение длины, F — приложенная сила, Y — коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества, A — площадь поперечного сечения, и L ₀ — исходная длина.В таблице 1 перечислены значения Y для нескольких материалов — те, которые имеют большой Y , как говорят, имеют большую прочность на разрыв , потому что они деформируются меньше при заданном растяжении или сжатии.

Таблица 1. Модули упругости
Материал	Модуль Юнга (растяжение-сжатие) Y (10 ⁹ Н / м ²)	Модуль сдвига S (10 ⁹ Н / м ²)	Объемный модуль B (10 ⁹ Н / м ²)
Алюминий	70	25	75
Кость — напряжение	16	80	8
Кость — компрессия	9
Латунь	90	35	75
Кирпич	15
Бетон	20
Стекло	70	20	30
Гранит	45	20	45
Волосы (человеческие)	10
Твердая древесина	15	10
Чугун литой	100	40	90
Свинец	16	5	50
Мрамор	60	20	70
нейлон	5
Полистирол	3
шелк	6
Крестовина с резьбой	3
Сталь	210	80	130
Сухожилие	1
ацетон			0.7
Этанол			0,9
Глицерин			4,5
Меркурий			25
Вода			2,2

Модули Юнга не указаны для жидкостей и газов в таблице 1, потому что они не могут быть растянуты или сжаты только в одном направлении. Обратите внимание, что существует предположение, что объект не ускоряется, поэтому на самом деле существуют две приложенные силы величиной F , действующие в противоположных направлениях.Например, струны на Рисунке 3 тянут вниз силой величиной w и удерживаются потолком, который также оказывает силу величиной w .

Пример 1. Растяжение длинного кабеля

Подвесные тросы используются для перевозки гондол на горнолыжных курортах. (См. Рис. 4). Рассмотрим подвесной трос, длина которого без опоры составляет 3 км. Рассчитайте степень растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное натяжение, которое он может выдержать, равно 3.0 × 10 ⁶ Н.

Рис. 4. Гондолы перемещаются по подвесным тросам на горнолыжном курорте Гала Юдзава в Японии. (Источник: Руди Херман, Flickr)

Стратегия

Сила равна максимальному натяжению, или F = 3,0 × 10 ⁶ Н. Площадь поперечного сечения π r ² = 2,46 × 10 ^–3 м ². Уравнение [latex] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex] можно использовать для определения изменения длины.{2}} \ right) \ left (\ text {3020 m} \ right) \\ & = & \ text {18 m}. \ End {array} [/ latex]

Обсуждение

Это довольно большое натяжение, но только около 0,6% от длины без опоры. В этих условиях влияние температуры на длину может быть важным.

Кости в целом не ломаются от растяжения или сжатия. Скорее они обычно ломаются из-за бокового удара или изгиба, что приводит к срезанию или разрыву кости. Поведение костей при растяжении и сжатии важно, потому что оно определяет нагрузку, которую кости могут нести.Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревья. Несущие конструкции обладают особенностями; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости расположена в виде тонких листов, разделенных костным мозгом, в то время как в других местах кости могут быть цилиндрическими и заполненными костным мозгом или просто твердыми.Люди с избыточным весом имеют тенденцию к повреждению костей из-за длительного сжатия костных суставов и сухожилий.

Другой биологический пример закона Гука встречается в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу для большего напряжения. На рисунке 5 показана зависимость напряжения от деформации человеческого сухожилия. Некоторые сухожилия имеют высокое содержание коллагена, поэтому деформация или изменение длины относительно невелико; другие, например, опорные сухожилия (например, в ноге), могут изменять длину до 10%.Обратите внимание, что эта кривая напряжения-деформации является нелинейной, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальца, волокна сухожилия начинают выравниваться в направлении напряжения — это называется распаковка . В линейной области фибриллы будут растянуты, а в области разрушения отдельные волокна начнут разрываться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения.Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.

Рис. 5. Типичная кривая «напряжение-деформация» для сухожилия млекопитающих. Показаны три области: (1) область пальца ноги (2) линейная область и (3) область разрушения.

В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть легко растяжимыми. Эластичные свойства артерий важны для кровотока. Когда кровь выкачивается из сердца, давление в артериях увеличивается, и стенки артерий растягиваются.Когда аортальный клапан закрывается, давление в артериях падает, и артериальные стенки расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий, когда кровь хлынет через каждый насос сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластичными свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но расслабляемся свободно и эластично, когда мы выдыхаем. Наша кожа особенно эластична, особенно для молодых.Молодой человек может подняться от 100 кг до 60 кг без видимого провисания кожи. С возрастом снижается эластичность всех органов. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-х годов.

Пример 2. Расчет деформации: насколько укорачивается нога, когда вы стоите на ней?

Рассчитайте изменение длины кости верхней части ноги (бедренной кости), когда мужчина весом 70,0 кг поддерживает на ней 62,0 кг своей массы, считая, что кость эквивалентна стержню, равному 40.0 см в длину и 2,00 см в радиусе.

Стратегия

Сила равна поддерживаемому весу, или F = мг = (62,0 кг) (9,80 м / с ²) = 607,6 Н, а площадь поперечного сечения равна π r ² = 1,257 × 10 ^–3 м ². Уравнение [latex] \ displaystyle \ Delta {L} = \ frac {1} {Y} \ text {} \ frac {F} {A} L_0 [/ latex] можно использовать для определения изменения длины.

Решение

Все величины, кроме Δ L , известны.{-5} \ text {m.} \ End {array} [/ latex]

Обсуждение

Это небольшое изменение длины кажется разумным, поскольку мы знаем, что кости жесткие. Фактически, даже довольно большие силы, возникающие при напряженных физических нагрузках, не сжимают и не сгибают кости в значительной степени. Хотя кость более жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 1, имеют более высокие значения модуля Юнга Y . Другими словами, они более жесткие и обладают большей прочностью на разрыв.

Уравнение изменения длины традиционно переставляется и записывается в следующем виде:

[латекс] \ displaystyle \ frac {F} {A} = Y \ frac {\ Delta {L}} {L_0} [/ latex].

Отношение силы к площади, [латекс] \ frac {F} {A} [/ latex], определяется как напряжение (измеряется в Н / м ²), а отношение изменения длины к длина, [латекс] \ frac {\ Delta {L}} {L_0} [/ latex], определяется как деформация (безразмерная величина). Другими словами, напряжение = Y × деформация.

В этой форме уравнение аналогично закону Гука с напряжением, аналогичным силе, и деформацией, аналогичной деформации. Если снова переписать это уравнение к виду

[латекс] \ displaystyle {F} = YA \ frac {\ Delta {L}} {L_0} [/ latex],

мы видим, что он совпадает с законом Гука с константой пропорциональности

[латекс] \ displaystyle {k} = \ frac {YA} {L_0} [/ latex].

Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны небольшим деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.

Напряжение

Отношение силы к площади, [латекс] \ frac {F} {A} [/ латекс], определяется как напряжение, измеренное в Н / м ².

Штамм

Отношение изменения длины к длине, [латекс] \ frac {\ Delta {L}} {L_0} [/ latex], определяется как деформация (безразмерная величина). Другими словами, напряжение = Y × деформация.

Боковое напряжение: модуль сдвига

На рисунке 6 показано, что подразумевается под боковым напряжением или срезающей силой .Здесь деформация называется Δ x , и она перпендикулярна L ₀, а не параллельна, как при растяжении и сжатии. Деформация сдвига аналогична растяжению и сжатию и может быть описана аналогичными уравнениями. Выражение для деформации сдвига : [latex] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex], где S — модуль сдвига ( см. Таблицу 1) и F — сила, приложенная перпендикулярно к L ₀ и параллельно площади поперечного сечения A .Опять же, чтобы препятствовать ускорению объекта, на самом деле есть две равные и противоположные силы F , приложенные к противоположным граням, как показано на рисунке 6. Уравнение логично — например, легче согнуть длинный тонкий карандаш (маленький A ), чем короткие толстые, и оба гнуть легче, чем аналогичные стальные стержни (большие S ).

Рис. 6. Сила сдвига прилагается перпендикулярно длине L ₀ и параллельно области A , создавая деформацию Δx.Вертикальные силы не показаны, но следует иметь в виду, что в дополнение к двум силам сдвига, F , должны существовать поддерживающие силы, препятствующие вращению объекта. Искажающие эффекты этих поддерживающих сил игнорируются при этом лечении. Вес объекта также не показан, поскольку он обычно незначителен по сравнению с силами, достаточно большими, чтобы вызвать значительные деформации.

Деформация сдвига

[латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex],

, где S — модуль сдвига, а F — сила, приложенная перпендикулярно к L ₀ и параллельно площади поперечного сечения A .

Изучение модулей сдвига в таблице 1 выявляет некоторые характерные закономерности. Например, для большинства материалов модули сдвига меньше модулей Юнга. Кость — замечательное исключение. Его модуль сдвига не только больше, чем модуль Юнга, но и такой же, как у стали. Это одна из причин того, что кости могут быть длинными и относительно тонкими. Кости могут выдерживать нагрузки, сопоставимые с бетонными и стальными. Большинство переломов костей возникает не из-за сжатия, а из-за чрезмерного скручивания и изгиба.

Позвоночный столб (состоящий из 26 позвоночных сегментов, разделенных дисками) обеспечивает основную опору для головы и верхней части тела. Позвоночник имеет нормальную кривизну для стабильности, но это искривление может быть увеличено, что приведет к увеличению силы сдвига на нижних позвонках. Диски лучше выдерживают силы сжатия, чем силы сдвига. Поскольку позвоночник не является вертикальным, вес верхней части тела влияет на обе части. Беременным женщинам и людям с избыточным весом (с большим животом) необходимо отвести плечи назад, чтобы поддерживать равновесие, тем самым увеличивая искривление позвоночника и тем самым увеличивая сдвигающий компонент напряжения.Увеличенный угол из-за большей кривизны увеличивает поперечные силы вдоль плоскости. Эти более высокие усилия сдвига увеличивают риск травмы спины из-за разрыва дисков. Пояснично-крестцовый диск (клиновидный диск под последними позвонками) особенно подвержен риску из-за своего расположения.

Модули сдвига для бетона и кирпича очень малы; они слишком изменчивы, чтобы их можно было перечислить. Бетон, используемый в зданиях, может выдерживать сжатие, как в колоннах и арках, но очень плохо противостоит сдвигу, который может возникнуть в сильно нагруженных полах или во время землетрясений.Современные конструкции стали возможны благодаря использованию стали и железобетона. Почти по определению жидкости и газы имеют модуль сдвига, близкий к нулю, потому что они текут в ответ на сдвигающие силы.

Пример 3. Расчет силы, необходимой для деформации: гвоздь не сильно изгибается под нагрузкой

Найдите массу картины, висящей на стальном гвозде, как показано на рисунке 7, учитывая, что гвоздь изгибается только на 1,80 мкм. (Предположим, что модуль сдвига известен с двумя значащими цифрами.)

Рис. 7. Гвоздь, вид сбоку, на котором висит изображение. Гвоздь очень слабо прогибается (показан намного больше, чем на самом деле) из-за срезающего воздействия поддерживаемого веса. Также показано направленное вверх усилие стенки на гвоздь, иллюстрирующее равные и противоположные силы, приложенные к противоположным поперечным сечениям гвоздя. См. Пример 3 для расчета массы изображения.

Стратегия

Сила F на гвоздь (без учета собственного веса гвоздя) — это вес изображения w .Если мы сможем найти w , то масса изображения будет просто [latex] \ frac {w} {g} [/ latex]. Уравнение [латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex] может быть решено для F .

Решение

Решая уравнение [латекс] \ displaystyle \ Delta {x} = \ frac {1} {S} \ frac {F} {A} L_0 [/ latex] для F , мы видим, что все остальные величины могут быть найдены :

[латекс] \ displaystyle {F} = \ frac {SA} {L_0} \ Delta {x} [/ latex]

S находится в таблице 1 и составляет S = 80 × 10 ⁹ Н / м ².{-6} \ text {m} \ right) = 51 \ text {N} [/ latex]

Эта сила 51 Н составляет вес w изображения, поэтому масса изображения [латекс] m = \ frac {w} {g} = \ frac {F} {g} = 5.2 \ text {kg} [ /латекс].

Обсуждение

Это довольно массивное изображение, и впечатляет то, что гвоздь прогибается всего на 1,80 мкм — величину, невидимую невооруженным глазом.

Изменения объема: модуль объемной упругости

Объект будет сжиматься во всех направлениях, если внутренние силы приложены равномерно ко всем его поверхностям, как показано на рисунке 8.Относительно легко сжимать газы и чрезвычайно сложно сжимать жидкости и твердые тела. Например, воздух в винной бутылке сжимается, когда она закупорена. Но если вы попытаетесь закупорить бутылку с полными краями, вы не сможете сжать вино — некоторые из них необходимо удалить, если нужно вставить пробку. Причина такой разной сжимаемости заключается в том, что атомы и молекулы разделены большими пустыми пространствами в газах, но плотно упакованы в жидкостях и твердых телах. Чтобы сжать газ, вы должны сблизить его атомы и молекулы.Чтобы сжать жидкости и твердые тела, вы должны действительно сжать их атомы и молекулы, и очень сильные электромагнитные силы в них препятствуют этому сжатию.

Рис. 8. Внутренняя сила на всех поверхностях сжимает этот куб. Его изменение в объеме пропорционально силе на единицу площади и его первоначальному объему и связано со сжимаемостью вещества.

Мы можем описать сжатие или объемную деформацию объекта уравнением. Во-первых, отметим, что сила, «приложенная равномерно», определяется как имеющая одинаковое напряжение или отношение силы к площади [латекс] \ frac {F} {A} [/ латекс] на всех поверхностях.Произведенная деформация представляет собой изменение объема Δ V , которое, как было обнаружено, ведет себя очень аналогично сдвигу, растяжению и сжатию, обсуждавшимся ранее. (Это неудивительно, поскольку сжатие всего объекта эквивалентно сжатию каждого из его трех измерений.) Связь изменения объема с другими физическими величинами определяется выражением [latex] \ displaystyle \ Delta {V} = \ frac {1} {B} \ frac {F} {A} V_0 [/ latex], где B — модуль объемной упругости (см. Таблицу 1), V ₀ — исходный объем, а [латекс] \ frac {F} {A} [/ latex] — это сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.Обратите внимание, что объемные модули для газов не приводятся.

Какие есть примеры объемного сжатия твердых тел и жидкостей? Одним из практических примеров является производство алмазов промышленного качества путем сжатия углерода с чрезвычайно большой силой на единицу площади. Атомы углерода перестраивают свою кристаллическую структуру в более плотно упакованный узор алмазов. В природе аналогичный процесс происходит глубоко под землей, где чрезвычайно большие силы возникают из-за веса вышележащего материала. Еще один естественный источник больших сжимающих сил — давление, создаваемое весом воды, особенно в глубоких частях океанов.Вода воздействует на все поверхности погружаемого объекта и даже на саму воду. На больших глубинах вода ощутимо сжата, как показано в следующем примере.

Пример 4. Расчет изменения объема с деформацией: насколько вода сжимается на глубинах Великого океана?

Рассчитайте частичное уменьшение объема [латекс] \ left (\ frac {\ Delta {V}} {V_0} \ right) [/ latex] для морской воды на глубине 5,00 км, где сила на единицу площади составляет 5,00 × 10 ⁷ Н / м ².

Стратегия

Уравнение [латекс] \ displaystyle \ Delta {V} = \ frac {1} {B} \ frac {F} {A} V_0 [/ latex] является правильным физическим соотношением. Все величины в уравнении, кроме [latex] \ frac {\ Delta {V}} {V_0} [/ latex], известны.

Решение

Решение для неизвестного [латекса] \ frac {\ Delta {V}} {V_0} [/ latex] дает [latex] \ displaystyle \ frac {\ Delta {V}} {V_0} = \ frac {1} {B } \ frac {F} {A} [/ латекс].

Замена известных значений значением модуля объемной упругости B из таблицы 1,

[латекс] \ begin {array} {lll} \ frac {\ Delta {V}} {V_0} & = & \ frac {5.2} \\ & = & 0.023 = 2.3 \% \ end {array} [/ latex]

Обсуждение

Хотя это можно измерить, это незначительное уменьшение объема, учитывая, что сила на единицу площади составляет около 500 атмосфер (1 миллион фунтов на квадратный фут). Жидкости и твердые вещества чрезвычайно трудно сжимать.

И наоборот, очень большие силы создаются жидкостями и твердыми телами, когда они пытаются расшириться, но не могут этого сделать, что эквивалентно их сжатию до меньшего, чем их нормальный объем.Это часто происходит, когда содержащийся в нем материал нагревается, поскольку большинство материалов расширяются при повышении их температуры. Если материалы сильно стеснены, они деформируют или ломают свой контейнер. Другой очень распространенный пример — замерзание воды. Вода, в отличие от большинства материалов, при замерзании расширяется, и она может легко сломать валун, разорвать биологическую клетку или сломать блок двигателя, который встанет у нее на пути.

Другие типы деформаций, такие как кручение или скручивание, ведут себя аналогично рассмотренным здесь деформациям растяжения, сдвига и объемной деформации.

Сводка раздела

Закон Гука определяется выражением [латекс] F = k \ Delta {L} [/ latex], где [latex] \ Delta {L} [/ latex] — величина деформации (изменение длины), F — приложенная сила, а k — константа пропорциональности, которая зависит от формы и состава объекта, а также направления силы. Связь между деформацией и приложенной силой также может быть записана как [latex] \ displaystyle \ Delta L = \ frac {1} {Y} \ frac {F} {A} {L} _ {0} [/ latex] , где Y — это модуль Юнга , который зависит от вещества, A — площадь поперечного сечения, а [латекс] {L} _ {0} [/ latex] — исходная длина.
Отношение силы к площади, [латекс] \ frac {F} {A} [/ латекс], определяется как напряжение , измеренное в Н / м ².
Отношение изменения длины к длине, [латекс] \ frac {\ Delta L} {{L} _ {0}} [/ latex], определяется как деформация (безразмерная величина). Другими словами, [латекс] \ текст {напряжение} = Y \ times \ text {напряжение} [/ латекс].
Выражение деформации сдвига [латекс] \ displaystyle \ Delta x = \ frac {1} {S} \ frac {F} {A} {L} _ {0} [/ latex], где S — модуль сдвига и F — это сила, приложенная перпендикулярно [латексу] {L} _ {\ text {0}} [/ latex] и параллельно площади поперечного сечения A .
Связь изменения объема с другими физическими величинами определяется выражением [latex] \ displaystyle \ Delta V = \ frac {1} {B} \ frac {F} {A} {V} _ {0} [/ latex ], где B — объемный модуль, [latex] {V} _ {\ text {0}} [/ latex] — исходный объем, а [latex] \ frac {F} {A} [/ latex] — сила на единицу площади, равномерно приложенная внутрь ко всем поверхностям.

Концептуальные вопросы

Эластические свойства артерий важны для кровотока. Объясните важность этого с точки зрения характеристик кровотока (пульсирующий или непрерывный).
Что вы чувствуете, когда щупаете пульс? Измерьте частоту пульса в течение 10 секунд и 1 минуты. Есть ли разница в 6 раз?
Изучите различные типы обуви, включая спортивную обувь и шлепанцы. С точки зрения физики, почему нижние поверхности устроены именно так? Какие различия будут иметь для этих поверхностей сухие и влажные условия?
Ожидаете ли вы, что ваш рост будет разным в зависимости от времени суток? Почему или почему нет?
Почему белка может спрыгнуть с ветки дерева на землю и убежать целой, а человек может сломать кость при таком падении?
Объясните, почему беременные женщины часто страдают растяжением спины на поздних сроках беременности.
Уловка старого плотника, чтобы удерживать гвозди от сгибания, когда они забиваются в твердый материал, заключается в том, чтобы крепко удерживать центр гвоздя плоскогубцами. Почему это помогает?
Когда стеклянная бутылка, полная уксуса, нагревается, и уксус, и стекло расширяются, но уксус расширяется значительно больше с температурой, чем стекло. Бутылка разобьется, если наполнить ее до плотно закрытой крышки. Объясните, почему, а также объясните, как воздушный карман над уксусом предотвратит разрыв.(Это функция воздуха над жидкостями в стеклянных контейнерах.)

Задачи и упражнения

Во время циркового номера один артист качается вверх ногами, висит на трапеции, держа другого, также перевернутого, за ноги. Если восходящая сила, действующая на более низкую спортсменку, в три раза превышает ее вес, насколько растягиваются кости (бедра) в ее верхних конечностях? Вы можете предположить, что каждый из них эквивалентен одинаковому стержню длиной 35,0 см и радиусом 1,80 см. Ее масса 60.0 кг.
Во время схватки борец 150 кг ненадолго встает на одну руку во время маневра, призванного сбить с толку его и без того умирающего противника. Насколько укорачивается длина кости плеча? Кость может быть представлена однородным стержнем длиной 38,0 см и радиусом 2,10 см.
(a) «Грифель» в карандашах представляет собой состав графита с модулем Юнга примерно 1 × 10 ⁹ Н / м ². Вычислите изменение длины грифеля в автоматическом карандаше, если постучите им прямо по карандашу с силой 4.0 Н. Шнур диаметром 0,50 мм и длиной 60 мм. б) разумен ли ответ? То есть согласуется ли это с тем, что вы наблюдали при использовании карандашей?
антенн телевещания — самые высокие искусственные сооружения на Земле. В 1987 году физик весом 72,0 кг разместил себя и 400 кг оборудования на вершине одной антенны высотой 610 м для проведения гравитационных экспериментов. Насколько была сжата антенна, если считать ее эквивалентом стального цилиндра радиусом 0,150 м?
(a) На сколько стоит 65.Альпинист весом 0 кг натягивает нейлоновую веревку диаметром 0,800 см, когда она висит на 35,0 м ниже скалы? б) Соответствует ли ответ тому, что вы наблюдали для нейлоновых веревок? Имел бы смысл, если бы веревка была на самом деле эластичным шнуром?
Полый алюминиевый флагшток высотой 20,0 м по жесткости эквивалентен твердому цилиндру диаметром 4,00 см. Сильный ветер изгибает полюс так же, как горизонтальная сила в 900 Н. Насколько далеко в сторону прогибается верхняя часть шеста?
По мере бурения нефтяной скважины каждая новая секция бурильной трубы выдерживает собственный вес, а также вес трубы и бурового долота под ней.Рассчитайте растяжение новой стальной трубы длиной 6,00 м, которая поддерживает 3,00 км трубы, имеющей массу 20,0 кг / м, и буровое долото 100 кг. Труба эквивалентна по жесткости сплошному цилиндру диаметром 5 см.
Рассчитайте усилие, которое настройщик рояля применяет для растяжения стальной рояльной струны на 8,00 мм, если проволока изначально имеет диаметр 0,850 мм и длину 1,35 м.
Позвонок подвергается действию силы сдвига 500 Н. Найдите деформацию сдвига, принимая позвонок в виде цилиндра 3.00 см в высоту и 4,00 см в диаметре.
Диск между позвонками позвоночника подвергается действию силы сдвига 600 Н. Найдите его деформацию сдвига, приняв модуль сдвига 1 × 10 ⁹ Н / м ². Диск эквивалентен сплошному цилиндру высотой 0,700 см и диаметром 4,00 см.
При использовании ластика для карандашей вы прикладываете вертикальное усилие 6,00 Н на расстоянии 2,00 см от соединения ластика с твердой древесиной. Карандаш имеет диаметр 6,00 мм и держится под углом 20 °.0º к горизонтали. а) Насколько дерево прогибается перпендикулярно своей длине? б) Насколько он сжат в продольном направлении?
Чтобы рассмотреть влияние проводов, подвешенных на столбах, мы возьмем данные из рисунка 9, на котором были рассчитаны натяжения проводов, поддерживающих светофор. Левая проволока образовывала угол 30,0 ° ниже горизонтали с вершиной своего столба и выдерживала натяжение 108 Н. Полый алюминиевый столб высотой 12,0 м по жесткости эквивалентен твердому цилиндру диаметром 4,50 см.а) Насколько он наклонен в сторону? б) Насколько он сжат?
Рисунок 9. Светофор подвешен на двух тросах. (б) Некоторые из задействованных сил. (c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную ( y ) и горизонтальную ( x ) оси. Горизонтальные составляющие натяжения должны компенсироваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора.{-2} [/ латекс]). Какую силу на единицу площади вода может оказывать на емкость при замерзании? (В этой задаче допустимо использовать объемный модуль упругости воды.) (B) Удивительно ли, что такие силы могут разрушать блоки двигателя, валуны и тому подобное?
Эта проблема возвращается к канатоходцу, изученному на рисунке 10, который создал натяжение 3,94 × 10 ³ Н в тросе, образующем угол 5,0 ° ниже горизонтали с каждой опорной стойкой. Подсчитайте, насколько это натяжение растягивает стальную проволоку, если она изначально была длиной 15 м и равной 0.50 см в диаметре.
Рис. 10. Вес канатоходца вызывает провисание каната на 5,0 градуса. Интересующая здесь система — это точка на проволоке, на которой стоит канатоходец.
Полюс на Рисунке 11 находится под изгибом 90,0º в линии электропередачи и поэтому подвергается большей силе сдвига, чем полюса на прямых участках линии. Натяжение в каждой линии составляет 4,00 × 10 ⁴ Н при показанных углах. Шест 15,0 м в высоту, 18,0 см в диаметре и, как считается, имеет вдвое меньшую жесткость, чем древесина твердых пород.(а) Рассчитайте сжатие полюса. (б) Найдите, насколько он изгибается и в каком направлении. (c) Найдите натяжение троса, используемого для удержания вехи прямо, если она прикреплена к верхней части столба под углом 30,0 ° к вертикали. (Ясно, что растяжка должна быть в направлении, противоположном изгибу.)

Рис. 11. Этот телефонный столб находится под углом 90 ° к линии электропередачи. Оттяжка прикрепляется к вершине мачты под углом 30º к вертикали.

Глоссарий

Сила сопротивления: F _D, как оказалось, пропорционально квадрату скорости объекта; математически

[латекс] \ begin {array} \\ F _ {\ text {D}} \ propto {v} ^ 2 \\ F _ {\ text {D}} = \ frac {1} {2} C \ rho {Av } ^ 2 \ end {array} [/ latex],

, где C — коэффициент лобового сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости.

Закон Стокса: F _s = 6 πrη v , где r — радиус объекта, η — вязкость жидкости, а v — величина объекта. скорость.

Решения проблем и упражнения

1. 1.90 × 10 ⁻³ см

3. а) 1 мм; (б) Это кажется разумным, поскольку кажется, что поводок немного сжимается, когда вы на него нажимаете.

5. (а) 9 см; (б) Это кажется разумным для нейлоновой веревки для лазания, поскольку она не должна сильно растягиваться.

7. 8,59 мм

9. 1.49 × 10 ⁻⁷ м

11. (а) 3.99 × 10 ⁻⁷ м; (б) 9,67 × 10 ⁻⁸ м

13. 4 × 10 ⁶ Н / м ². Это примерно 36 атм, больше, чем может выдержать обычная банка.

15. 1,4 см

EM3SolSupp.dvi

% PDF-1.4
%
1 0 obj
>>>] / ON [1229 0 R] / Заказ [] / RBGroups [] >> / OCGs [1229 0 R] >> / Страницы 3 0 R / Тип / Каталог >>
эндобдж
1228 0 объект
> / Шрифт >>> / Поля 1233 0 R >>
эндобдж
1227 0 объект
> поток
GPL Ghostscript 8.702013-07-19T16: 07: 55 + 02: 002013-07-19T09: 14: 28 + 02: 00dvips (k) 5.98 Авторские права 2009 Radical Eye Software2013-07-19T16: 07: 55 + 02: 0066061264-285f-11ee -0000-a83325857ed1uuid: 157c1e4d-2bbf-473d-acd1-2b762ae690d5application / pdf

EM3SolSupp.dvi

конечный поток
эндобдж
3 0 obj
>
эндобдж
4 0 объект
> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
18 0 объект
> / XObject >>> / Тип / Страница >>
эндобдж
19 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
25 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
44 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
52 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
59 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
66 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
71 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
76 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
81 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
88 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
93 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
98 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
105 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
110 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
115 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
120 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
130 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
135 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
142 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
147 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
152 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
161 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
166 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
171 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
176 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
186 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
197 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
202 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
207 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
212 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
217 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
224 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
229 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
234 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
239 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
246 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
252 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
257 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
262 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
267 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
278 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
283 0 объект
> / XObject >>> / Тип / Страница >>
эндобдж
284 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
289 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
295 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
303 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
308 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
315 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
320 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
327 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
332 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
340 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
345 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
352 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
357 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
362 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
367 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
372 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
377 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
382 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
391 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
401 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
406 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
413 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
418 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
424 0 объект
> / XObject >>> / Тип / Страница >>
эндобдж
425 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
430 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
438 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
446 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
458 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
463 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
470 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
475 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
484 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
489 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
498 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
503 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
508 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
513 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
518 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
527 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
532 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
538 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
543 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
548 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
553 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
558 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
563 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
569 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
574 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
582 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
589 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
594 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
599 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
606 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
611 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
616 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
621 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
626 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
634 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
639 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
647 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
652 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
657 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
662 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
667 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
672 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
679 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
684 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
689 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
694 0 объект
> / XObject >>> / Тип / Страница >>
эндобдж
695 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
700 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
708 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
713 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
719 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
724 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
729 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
734 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
739 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
744 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
749 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
754 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
763 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
768 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
773 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
778 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
784 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
789 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
794 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
799 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
804 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
809 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
814 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
819 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
824 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
829 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
834 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
839 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
844 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
849 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
854 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
860 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
867 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
872 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
880 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
885 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
892 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
897 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
904 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
910 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
915 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
923 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
928 0 объект
> / ExtGState> / Font> / Pattern> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
936 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
941 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
946 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
952 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
957 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
968 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
977 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
985 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
990 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB / ImageC] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
997 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1002 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1011 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1016 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1021 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1026 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1032 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1037 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1043 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1048 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1053 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1062 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1067 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1074 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1080 0 объект
> / Font> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / Rotate 0 / Type / Page >>
эндобдж
1780 0 объект
> поток
HWnF3b% Р.dK (
i-e 꽾 # = j1KQH & c.n \] r `

Механика материалов: деформация» Механика тонких конструкций

Штамм

До сих пор мы сосредоточились на напряжении внутри структурных элементов. Когда вы прикладываете напряжение к объекту, он деформирует . Представьте себе резинку: вы тянете за нее, и она становится длиннее — она тянется на . Деформация — это мера того, насколько объект растянут, а деформация — это соотношение между деформацией и исходной длиной.Думайте о деформации как о -процентном удлинении — насколько больше (или меньше) объект при его нагрузке.

Как и напряжение, конструкция может испытывать два типа деформации: 1. Нормальная деформация и 2. Деформация сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она вызывает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим стержень при одноосном растяжении.Стержень удлиняется под этим натяжением до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к исходной длине стержня.

Деформация — это безразмерная мера того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация возникает, когда удлинение объекта происходит в ответ на нормальное напряжение (то есть перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует деформации при растяжении , отрицательное — при сжатии .Деформация сдвига возникает, когда деформация объекта является ответом на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой гамма .

Механическое поведение материалов

Ясно, что напряжение и напряжение связаны. Напряжение и деформация связаны основным законом , и мы можем определить их взаимосвязь экспериментально, измерив, сколько напряжения требуется для растяжения материала. Это измерение может быть выполнено с помощью теста на растяжение . В простейшем случае, чем больше вы тянете за объект, тем больше он деформируется, а для малых значений деформации эта зависимость является линейной. Эта линейная упругая связь между напряжением и деформацией известна как Закон Гука . Если вы построите график зависимости напряжения от деформации, для малых деформаций этот график будет линейным, а наклон линии будет свойством материала, известного как Модуль упругости . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали.Для большинства конструкционных материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые являются линейно-эластичными (т.е. они подчиняются закону Гука) и изотропными (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простое соотношение для деформации материала.

Интуитивно этот экзамен имеет некоторый смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или толстому материалу, получите меньшую деформацию.Если конструкция меняет форму или материал, или по-разному нагружается в разных точках, то мы можем разделить эти множественные нагрузки, используя принцип наложения .

Обобщенный закон Гука

На последнем уроке мы начали узнавать, как связаны стресс и напряжение — через закон Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили о напряжении или деформации только в одном направлении.В этом уроке мы собираемся рассмотреть обобщенный закон Гука для однородных, изотропных и упругих материалов, подвергающихся действию сил по более чем одной оси.

Перво-наперво, даже простое вытягивание (или толкание) большинства материалов в в одном направлении фактически вызывает деформацию в во всех трех ортогональных направлениях . Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что при натяжении объекта в осевом направлении он сжимает в поперечном направлении в поперечных направлениях:

Таким образом, если потянуть за него в направлении x , он сожмется в направлениях y и z .Это свойство материала известно как коэффициент Пуассона , и обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это в виде уравнения:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона — это свойство материала . Коэффициент Пуассона может находиться в диапазоне от -1 до 0.5. Для большинства конструкционных материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а у каучуков коэффициент Пуассона составляет около 0,5, и они называются «несжимаемыми». Несжимаемый просто означает, что любая сумма, которую вы сжимаете в одном направлении, будет расширяться на такую же величину в других направлениях — следовательно, его объем не изменится.

За последнее десятилетие было проведено несколько очень интересных исследований по созданию структурированных материалов , которые используют геометрию и упругую нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона.Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип может быть применен в 3D для создания расширяемых / складных оболочек:

Благодаря коэффициенту Пуассона теперь у нас есть уравнение, которое связывает деформацию в направлении y или z с деформацией в направлении z. Мы, в свою очередь, можем связать это со стрессом с помощью закона Гука.Это важное замечание: при натяжении объекта в в одном направлении возникает напряжение только в этом направлении , а вызывает деформацию во всех трех направлениях . Итак, сигма _y = сигма _z = 0. Давайте запишем деформации в направлении y и z через напряжение в направлении x .

Помните, что до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях.Полезный способ понять это — представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжений , которые на перпендикулярны каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях .Итак, теперь мы включили эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Что ж, если объект меняет форму во всех трех направлениях, это означает, что он изменит свой объем на .Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:

Теперь, когда у нас есть уравнение для изменения объема или расширения в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, вызывающий расширение, известен как гидростатический стресс. Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Итак, в случае гидростатического давления мы можем свести наше окончательное уравнение для расширения к следующему:

Это последнее соотношение важно, потому что оно является определяющим соотношением того, как объем материала изменяется под действием гидростатического давления.Префактор p может быть переписан как модуль объемной упругости материала , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой изменения объема материала при заданном давлении — если коэффициент Пуассона для материала равен 0,5?

Закон Гука при сдвиге

В предыдущем разделе мы разработали взаимосвязь между нормальным напряжением и нормальной деформацией.Теперь поговорим о сдвиге. Вернемся к этому воображаемому кубу материала. Помимо внешних сил, вызывающих напряжения, нормальные к каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба. А, как известно, напряжения, параллельные поперечному сечению, составляют касательных напряжений

Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж и плохо. На каждой поверхности есть два напряжения сдвига, а нижние индексы говорят вам, в каком направлении они указывают и какой поверхности параллельны.Например, возьмем правую грань куба. Напряжения, нормальные к этой грани, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно направлено в направлении y (обозначено tau _xy), а другое направлено в направлении z (обозначено tau _xz). Чтобы куб был в равновесии, tau _xy = tau _yx (в противном случае куб вращался бы). Таким образом, теперь существует шести напряжений (сигма _x, sigmay, sigmaz, tau _xy, tau _yz, tau _xz), которые характеризуют состояние напряжения в однородном, изотропном, упругом материале.

Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука для сдвига очень похож на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорциональность между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала . Это уравнение в его общей форме, но мы можем переписать его более явно в терминах его компонентов: x, y и z . Это даст нам обобщенный закон Гука для однородных, изотропных, эластичных материалов.

В нашем обобщенном законе Гука есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это соотношение задается следующим уравнением:

Сводка

В этой лекции мы представили концепцию напряжения. Деформация — это деформация материала под действием напряжения. Это просто отношение изменения длины к исходной длине.Деформации, приложенные перпендикулярно поперечному сечению, составляют нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, составляют деформаций сдвига . Для линейных упругих материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как модуль упругости материала . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под воздействием внешней нагрузки.

Кроме того, в этом разделе мы узнали о многоосной нагрузке .В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона — соотношение между поперечной и осевой деформациями. Деформации, возникающие в трех ортогональных направлениях, могут дать нам меру расширения материала в ответ на многоосную нагрузку. В частности, материал может обычно изменять объем в ответ на изменения внешнего давления или гидростатического напряжения .Это привело к определению сопротивления материала изменению объема под действием гидростатического напряжения — объемного модуля . Изучив воображаемый кубический элемент в произвольном материале, мы смогли представить себе напряжения, возникающие нормально и параллельно каждой грани куба. Это дало нам шесть напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы связали друг с другом, используя обобщенный закон Гука для гомогенных , изотропных и упругих материалов.Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости , модулем сдвига и коэффициентом Пуассона .

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.

Усилия в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа разработки LWBR) (Технический отчет)

Кресчиманно, П. Дж., И Келлер, К. Л. Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа развития LWBR) . США: Н. П., 1981. Интернет. DOI: 10,2172 / 6551356.

Крещиманно, П.Дж. И Келлер, К. Л. Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа разработки LWBR) . Соединенные Штаты. https://doi.org/10.2172/6551356

Crescimanno, P. J., and Keller, K. L. Sun. «Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа развития LWBR)».Соединенные Штаты. https://doi.org/10.2172/6551356. https://www.osti.gov/servlets/purl/6551356.

@article {osti_6551356, title = {Силы в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа разработки LWBR)}, author = {Crescimanno, P. J. and Keller, K. L.}, abstractNote = {Представлены аналитические методы и данные испытаний, использованные при проектировании стержней болтовых соединений для активной зоны LWBR.Эффекты внешних рабочих нагрузок, теплового расширения и релаксации напряжения материала учитываются в формулировке, разработанной для анализа характеристик соединений. Расширения этих методов также предусмотрены для болтовых соединений, обладающих как осевой, так и изгибной гибкостью, а также для влияния пластической деформации на внутренние силы, возникающие в болтовом соединении. Дизайн-приложения проиллюстрированы примерами.}, doi = {10.2172 / 6551356}, url = {https: // www.osti.gov/biblio/6551356}, журнал = {}, номер =, объем =, place = {United States}, год = {1981}, месяц = {3} }

Распределение усилий по схеме расположения болтов | MechaniCalc

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

Схема расположения болтов — это набор болтовых соединений, обычно четыре или более, которые соединяют два или более компонентов вместе.При разработке схемы расположения болтов важно иметь представление о нагрузках, которым она должна будет противостоять при работе, а также о том, каким образом эти приложенные нагрузки будут распределяться между отдельными болтами схемы. После того, как осевые и поперечные нагрузки были рассчитаны для отдельных болтовых соединений в массиве, отдельные соединения могут быть проанализированы, как описано здесь.

В следующих разделах подробно описывается методология разделения сил и моментов, приложенных к массиву болтов, на осевые и поперечные нагрузки, действующие на отдельные болтовые соединения в массиве.

Содержание

Обзор и обсуждение

Распределение сил и моментов по схеме расположения болтов аналогично анализу балки или вала. Приложенные нагрузки переводятся в центр тяжести шаблона (аналогично нейтральной оси балки или вала). Затем силы и моменты в центре тяжести разделяются на осевые и поперечные силы, действующие на отдельные болтовые соединения. Осевые силы распределяются по схеме расположения болтов в зависимости от площади схемы A и моментов инерции I _c.x и I _c.y. Аналогичным образом поперечные силы распределяются на основе площади шаблона A и полярного момента инерции I _c.p.

Обратите внимание, что мы сохраняем различие, заключающееся в том, что силы распределяются на отдельные болтовые соединения , а не на отдельные болты . Причина этого в том, что не вся нагрузка, приложенная к болтовому соединению, фактически воспринимается болтом, как обсуждается здесь.

В следующих двух разделах обсуждаются два общих условия нагружения, за которыми следует обсуждение обобщенного подхода к распределению приложенных нагрузок по схеме расположения болтов.

Эксцентриковая сдвигающая нагрузка в плоскости

На рисунке ниже показан шаблон с эксцентрической поперечной нагрузкой, приложенной в плоскости шаблона. Нагрузка является эксцентричной, потому что она не действует через центр тяжести узора. Следовательно, он вызывает крутящий момент вокруг оси Z (перпендикулярно плоскости рисунка), который будет стремиться повернуть рисунок вокруг его центра тяжести. В этом случае болты нагружены только сдвигом (без осевых нагрузок), а поперечные нагрузки возникают из-за сочетания прямой поперечной силы и индуцированного момента.Нагрузка этого типа аналогична валу при комбинированной сдвигающей и скручивающей нагрузке.

Эксцентрическая поперечная нагрузка вне плоскости

На рисунке ниже показан образец с эксцентрической поперечной нагрузкой, приложенной вне плоскости рисунка. В то время как эта приложенная нагрузка проходит через центроид в плоскости X-Y, ее линия действия смещена от центроида в Z-направлении. Поэтому приложенная поперечная нагрузка вызывает изгибающий момент вокруг оси X, что приводит к осевой нагрузке на болты.

Существует несколько стандартных подходов к распределению осевых нагрузок между болтами в подобном случае, каждый из которых включает вычисление момента инерции шаблона относительно некоторой оси изгиба и последующее использование (Mr / I) · A для распределения нагрузок. (Следует отметить, что если все болты в шаблоне имеют одинаковый размер, то (Mr / I) · A упрощается до Mr / Σ r ²). Ключевым отличием стандартных подходов является выбор точки, вокруг которой предполагается разворачиваться паттерн:

Один из подходов состоит в том, чтобы проверить геометрию компонента и предположить, что узор будет «крениться» вокруг некоторой разумной точки, скажем, основания кронштейна на рисунке выше.
Другой подход состоит в том, чтобы рассматривать эту проблему, как если бы шаблон был изгибающейся балкой, и рассчитывать подходящее положение нейтральной оси.
Методология, изложенная в «Руководстве по стальным конструкциям» AISC, признает, что на стороне сжатия балки сжатая область равна площади контакта компонентов ниже нейтральной оси. На стороне натяжения балки в напряжении находятся только болты. Расположение нейтральной оси определяется с помощью итерационной процедуры, с помощью которой предполагаемое положение нейтральной оси изменяется до тех пор, пока момент инерции болтов в напряжении выше нейтральной оси не станет равным моменту инерции сжатых пластин ниже нейтральная ось.
Более простой подход учитывает только области болтов и предполагает, что нейтральная ось балки лежит в центре тяжести массива болтов.

Важно понимать, что по мере того, как предполагаемое место поворота перемещается дальше от шаблона, осевые нагрузки на болты снижаются. Причина этого в том, что осевые нагрузки пропорциональны Mr / Σ r ², где r — расстояние между точкой поворота и интересующим болтом.По мере увеличения r влияние члена r ² в знаменателе превосходит влияние члена r в числителе. Поэтому наиболее консервативный подход состоит в том, чтобы считать, что узор вращается вокруг своего центра тяжести.

Общий подход

Если вы решите применить консервативный подход к переносу всей приложенной нагрузки в центр тяжести группы болтов, то становится легко обобщить анализ любой группы болтов с любой приложенной нагрузкой, как показано на рисунке ниже.

Шаги по распределению приложенных сил и моментов к отдельным болтовым соединениям в массиве:

Рассчитайте соответствующие свойства массива (площадь, центроид, моменты инерции).
Переведите все приложенные силы и моменты в центр тяжести массива.
Рассчитайте осевые и поперечные нагрузки, действующие на отдельные болтовые соединения в массиве.

Подробная информация о выполнении каждого из этих шагов представлена в следующих разделах.

Свойства массива болтов

Те же свойства, которые требуются при анализе балки или вала, также требуются при распределении усилий по схеме расположения болтов. Следует отметить, что уравнения, представленные в этом разделе для расчета свойств массива, не требуют, чтобы болты в массиве были одинакового размера.

Область расположения болтов

Суммарная площадь всех болтов в массиве должна быть рассчитана для распределения прямых усилий между болтами:

где A _i — площадь растягивающего напряжения отдельного болта.

Расположение болтов Центроид

Точно так же, как изгибающие напряжения в балке и скручивающие напряжения в валу сосредоточены вокруг нейтральной оси, моменты на болтовой диаграмме будут иметь тенденцию вращать конфигурацию вокруг ее центра тяжести. Расположение центроида шаблона рассчитывается как:

где A _i — площадь болта, а x _i и y _i — места расположения болтов x и y соответственно.

Следует отметить, что этот расчет прямо аналогичен расчету центра тяжести поперечного сечения.

Моменты инерции расположения болтов

Моменты инерции схемы болтов указывают на ее способность противостоять изгибающим моментам. Мы консервативно предполагаем, что моменты будут иметь тенденцию заставлять образец вращаться вокруг его центра тяжести, поэтому моменты инерции относительно центра тяжести образца представляют интерес. Центроидные моменты инерции рассчитываются как:

	Центроидный момент инерции относительно оси X
	Центроидный момент инерции относительно оси Y

где A _i — площадь болта, а r _{c.x, i} и r _{c.y, i} — это расстояния x и y болта от центра тяжести массива, соответственно.

Полярный момент инерции рисунка указывает на его способность сопротивляться крутящим моментам (то есть моментам относительно оси Z, перпендикулярной плоскости рисунка), и рассчитывается как:

где r _{c.xy, i} — кратчайшее расстояние между болтом и центром тяжести и рассчитывается как

Следует отметить, что эти расчеты прямо аналогичны расчету момента инерции поперечного сечения и полярного момента инерции поперечного сечения.

Силы и моменты на центроиде

Как обсуждалось ранее, все приложенные силы и моменты переводятся в центр тяжести схемы расположения болтов. Как показано на рисунке ниже, к группе болтов в любом месте можно приложить любое количество сил.

Силы в центре тяжести рассчитываются как сумма всех приложенных сил:

Моменты в центроиде рассчитываются как сумма всех приложенных моментов плюс сумма перекрестного произведения каждой приложенной силы с вектором от центроида до местоположения этой приложенной силы:

В приведенных выше уравнениях полосы над переменными указывают, что они являются векторами.Переменная F представляет собой вектор силы, состоящий из составляющих силы в каждом направлении: F _x, F _y и F _z. Точно так же M — это вектор момента, составленный из моментов относительно каждой оси. R — вектор местоположения, определяющий местоположение приложенной силы по отношению к центроиду рисунка. Вектор местоположения R указывает от центроида до местоположения приложенной силы.

Усилия на отдельные болтовые соединения

После того, как свойства массива известны и приложенные силы и моменты переведены в центр тяжести массива, можно рассчитать осевые и поперечные силы на отдельных болтовых соединениях.На рисунке ниже показано отдельное болтовое соединение с приложенной осевой нагрузкой и нагрузкой на сдвиг:

Осевые силы

Осевые силы являются результатом прямой силы в направлении Z, F _cz, центроидного момента вокруг оси X, M _cx, и центроидного момента вокруг оси Y, M _cy, как показано на рисунке ниже:

Прямое усилие в Z-направлении, F _c.z, распределяется между отдельными болтовыми соединениями в соответствии с их жесткостью.Поскольку предполагается, что все болты имеют одинаковый материал и длину, жесткость зависит только от площади. Осевое усилие, действующее на болтовое соединение, вызванное прямой силой по оси Z, рассчитывается как:

где A — площадь рассматриваемого болта. Если области болтов одинаковы, приведенное выше уравнение упрощается до P _z.FZ = F _c.z / n, где n — количество болтов в массиве.

Осевые силы на болт из-за моментов вокруг осей X и Y рассчитываются как:

	Осевое усилие на болт из-за MX около центра тяжести
	осевое усилие на болт из-за центра тяжести MY около

где M _c.x и M _cy — это центроидные моменты относительно осей X и Y, r _cx и r _cy — расстояния между болтами от центроида в направлениях X и Y, а I _cx и I _cy — моменты инерции схемы относительно осей X и Y.

Если области болтов совпадают, приведенные выше уравнения упрощаются до:

Общая осевая сила, действующая на болт, складывается из составляющих осевой силы:

P _осевой = P _z.FZ и плюс; P _z.MX и плюс; P _z.MY

Сила сдвига

Сдвиговые силы являются результатом прямой силы в направлении X, F _cx, прямой силы в направлении Y, F _cy, и центроидного момента вокруг оси Z, M _cz, как показано на рисунке ниже:

Прямые силы в направлениях X и Y, F _c.x и F _c.y, соответственно, распределяются между болтами в соответствии с их жесткостью.Поскольку предполагается, что все болты имеют одинаковый материал и длину, жесткость зависит только от площади. Сдвиговые реакции на болт из-за прямых сил по осям X и Y рассчитываются как:

	Х-реакция на болт из-за прямого усилия в X
	Y-образная реакция на болт из-за прямого усилия в Y

где A — площадь рассматриваемого болта. Если области болтов совпадают, приведенные выше уравнения упрощаются до P _x.FX = F _c.x / n и P _y.FY = F _c.y / n, где n — количество болтов в шаблоне.

Реакция на сдвиг на болте из-за момента относительно оси Z рассчитывается как:

где M _c.z — это центроидный момент относительно оси Z, а I _c.p — полярный момент инерции шаблона. Значение r _c.xy является кратчайшим расстоянием между болтом и центром тяжести и рассчитывается как

Затем реакция сдвига P _xy.MZ разделяется на компоненты X и Y на основе угла θ (см. Рисунок выше):

P _x.MZ = P _xy.MZ · sinθ	Х-реакция на болте из-за MZ около центра тяжести
P _y.MZ = −P _xy.MZ · cosθ	Y-образная реакция на болте из-за MZ около центра тяжести

Значение θ представляет собой угол между положением болта и положительной осью X и рассчитывается как θ = tan ^-1 (r _c.y / r _c.x).

Полная реакция на сдвиг на болте рассчитывается как векторная сумма X-компонентов плюс Y-компонентов:

Что дальше?

Теперь, когда осевые и поперечные силы на отдельных болтовых соединениях были рассчитаны, напряжения в болтовых соединениях можно проанализировать, как описано здесь.

Список литературы

Барретт, Ричард Т., «Руководство по проектированию крепежа», справочная публикация НАСА 1228, 1990 г.
Бикфорд, Джон, «Введение в конструкцию и поведение болтовых соединений», 4-е изд.
Брюн, Э. Ф., «Анализ и проектирование конструкций летательных аппаратов», июнь 1973 г.
Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.
Ниу, Майкл К., «Анализ напряжений и определение размеров планера», октябрь 2011 г.
«Руководство по стальным конструкциям», Американский институт стальных конструкций (AISC), 14-е изд.

Задачи по теме «Равнодействующая» с ответами

Зависимость проекции на ось ох равнодействующих сил

Тестирование онлайн

Определение

Взаимосвязь со вторым законом Ньютона

Нахождение равнодействующей силы

Примеры

Главное запомнить

Системы и блоки*

На рисунке 50 представлены 4 вектора. Перечислите, от каких из приведенных ниже величин зависит момент инерции однородного тела

По графику на рисунке 4.1.1 определите путь, пройденный велосипедистом за интервал времени от до.

Автомобиль движется равномерно по выпуклому мосту (рисунок 4.2.1). Какое направление имеет вектор равнодействующей всех приложенных к автомобилю сил?

На рисунке 4.3.1 представлены четыре варианта взаимного расположения векторов силы, действующей на тело, и скорости тела.

В пистолете длина пружины l, её упругость k. Пружина сжата на 0,2 своей длины. С какой скоростью вылетит из пистолета пуля массой m после выстрела?

Перечислите, от каких из приведенных ниже величин зависит момент инерции однородного тела.

ЕГЭ по физике онлайн — пройдите тест

13. За­да­ние 2 № 6039.

Второй закон Ньютона

Задание 2 ЕГЭ по физике

Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения

Результирующая сила — урок. Физика, 7 класс.

12.3 Напряжение, деформация и модуль упругости — University Physics Volume 1

Учебные цели

Напряжение при растяжении или сжатии, деформация и модуль Юнга

Пример 12.7

Напряжение сжатия в опоре

Стратегия

Решение

Значение

Пример 12,8

Растяжка стержня

Стратегия

Решение

Значение

Объемное напряжение, деформация и модуль

Пример 12.9

Гидравлический пресс

Стратегия

Решение

Значение

Напряжение сдвига, деформация и модуль

Пример 12.10

Старая книжная полка

Стратегия

Решение

Значение

Равновесие и статика

Эластичность: напряжение и деформация | Физика

Цели обучения

Закон Гука

Растянись немного

Изменения длины — растяжение и сжатие: модуль упругости

Пример 1. Растяжение длинного кабеля

Стратегия

Обсуждение

Пример 2. Расчет деформации: насколько укорачивается нога, когда вы стоите на ней?

Стратегия

Решение

Обсуждение

Напряжение

Штамм

Боковое напряжение: модуль сдвига

Деформация сдвига

Пример 3. Расчет силы, необходимой для деформации: гвоздь не сильно изгибается под нагрузкой

Стратегия

Решение

Обсуждение

Изменения объема: модуль объемной упругости

Пример 4. Расчет изменения объема с деформацией: насколько вода сжимается на глубинах Великого океана?

Стратегия

Решение

Обсуждение

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Решения проблем и упражнения

EM3SolSupp.dvi

Механика материалов: деформация» Механика тонких конструкций

Усилия в болтовых соединениях: методы анализа и результаты испытаний, используемые для ядерных приложений (Программа разработки LWBR) (Технический отчет)

13. Задание 2 № 6039.