Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители

Рассмотрим два основных метода нахождения НОД двумя основными способами: с использованием алгоритма Евклида и путем разложения на простые множители. Применим оба метода для двух, трех и большего количества чисел.

Алгоритм Евклида для нахождения НОД

Алгоритм Евклида позволяет с легкостью вычислить наибольший общий делитель для двух положительных чисел. Формулировки и доказательство алгоритма Евклида мы привели в разделе «Наибольший общий делитель: определитель, примеры».

Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком, в ходе которого получается ряд равенств вида:

a=b·q1+r1, 0<r1<bb=r1·q2+r2, 0<r2<r1r1=r2·q3+r3, 0<r3<r2r2=r3·q4+r4, 0<r4<r3⋮rk-2=rk-1·qk+rk, 0<rk<rk-1rk-1=rk·qk+1

Мы можем закончить деление тогда, когда rk+1=0, при этом rk=НОД(a, b).

Пример 1

Найдите наибольший общий делитель чисел 64 и 48.

Решение

Введем обозначения: a=64, b=48.

На основе алгоритма Евклида проведем деление 64 на 48.

Получим 1 и остаток 16. Получается, что q1=1, r1=16.

Вторым шагом разделим 48 на 16, получим 3. То есть q2=3, а r2=0. Таким образом число 16 – это наибольший общий делитель для чисел из условия.

Ответ: НОД(64, 48)=16.

Пример 2

Чему равен НОД чисел 111 и 432?

Решение

Делим 432 на 111. Согласно алгоритму Евклида получаем цепочку равенств 432=111·3+99, 111=99·1+12, 99=12·8+3, 12=3·4.

Таким образом, наибольший общий делитель чисел 111 и 432 – это 3.

Ответ: НОД(111, 432)=3.

Пример 3

Найдите наибольший общий делитель чисел 661 и 113.

Решение

Проведем последовательно деление чисел и получим НОД(661, 113)=1. Это значит, что 661 и 113 – это взаимно простые числа. Мы могли выяснить это до начала вычислений, если бы обратились к таблице простых чисел.

Ответ: НОД(661, 113)=1.

Нахождение НОД с помощью разложения чисел на простые множители

Для того, чтобы найти наибольший общий делитель двух чисел методом разложения на множители, необходимо перемножить все простые множители, которые получаются при разложении этих двух чисел и являются для них общими.

Пример 4

Если мы разложим числа 220 и 600 на простые множители, то получим два произведения: 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими в этих двух произведениях будут множители 2,2 и 5. Это значит, что НОД(220, 600)=2·2·5=20.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 5

Найдите наибольший общий делитель чисел 72 и 96.

Решение

Найдем все простые множители чисел 72 и 96:

72361893122233

96482412631222223

Общими для двух чисел простые множители: 2, 2, 2 и 3. Это значит, что НОД(72, 96)=2·2·2·3=24.

Ответ: НОД(72, 96)=24.

Правило нахождения наибольшего общего делителя двух чисел основано на свойствах наибольшего общего делителя, согласно которому НОД(m·a1, m·b1)=m·НОД(a1, b1), где m– любое целое положительное число.

Нахождение НОД трех и большего количества чисел

Независимо  от количества чисел, для которых нам нужно найти НОД, мы будем действовать по одному и тому же алгоритму, который заключается в последовательном нахождении НОД двух чисел. Основан этот алгоритм на применении следующей теоремы: НОД нескольких чисел a1, a2, …, ak равен числу dk, которое находится при последовательном вычислении НОД(a1, a2)=d2, НОД(d2, a3)=d3, НОД(d3, a4)=d4, …, НОД(dk-1, ak)=dk.

Пример 6

Найдите наибольший общий делитель четырех чисел 78, 294, 570 и 36.

Решение

Введем обозначения: a1=78, a2=294, a3=570, a4=36.

Начнем с того, что найдем НОД чисел 78 и 294: d2=НОД(78, 294)=6.

Теперь приступим к нахождению d3=НОД(d2, a3)=НОД(6, 570). Согласно алгоритму Евклида 570=6·95. Это значит, что d3=НОД(6, 570)=6.

Найдем d4=НОД(d3, a4)=НОД(6, 36). 36 делится на 6 без остатка. Это позволяет нам получить d4=НОД(6, 36)=6.

d4=6, то есть, НОД(78, 294, 570, 36)=6.

Ответ: НОД(78, 294, 570, 36)=6.

А теперь давайте рассмотрим еще один способ вычисления НОД для тех и большего количества чисел. Мы можем найти НОД, перемножив все общие простые множители чисел.

Пример 7

Вычислите НОД чисел 78, 294, 570 и 36.

Решение

Произведем разложение данных чисел на простые множители: 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.

Для всех четырех чисел общими простыми множителями будут числа 2 и 3.

Получается, что НОД(78, 294, 570, 36)=2·3=6.

Ответ: НОД(78, 294, 570, 36)=6.

Нахождение НОД отрицательных чисел

Если нам приходится иметь дело с отрицательными числами, то для нахождения наибольшего общего делителя мы можем воспользоваться модулями этих чисел. Мы можем так поступить, зная свойство чисел с противоположными знаками: числа n и -n имеют одинаковые делители.

Пример 8

Найдите НОД отрицательных целых чисел −231 и −140.

Решение

Для выполнения вычислений возьмем модули чисел, данных в условии. Это будут числа 231 и 140. Запишем это кратко: НОД(−231, −140)=НОД(231, 140). Теперь применим алгоритм Евклида для нахождения простых множителей двух чисел: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и 42=7·6. Получаем, что НОД(231, 140)=7.

А так как НОД(−231, −140)=НОД(231, 140), то НОД чисел −231 и −140 равен 7.

Ответ: НОД(−231, −140)=7.

Пример 9

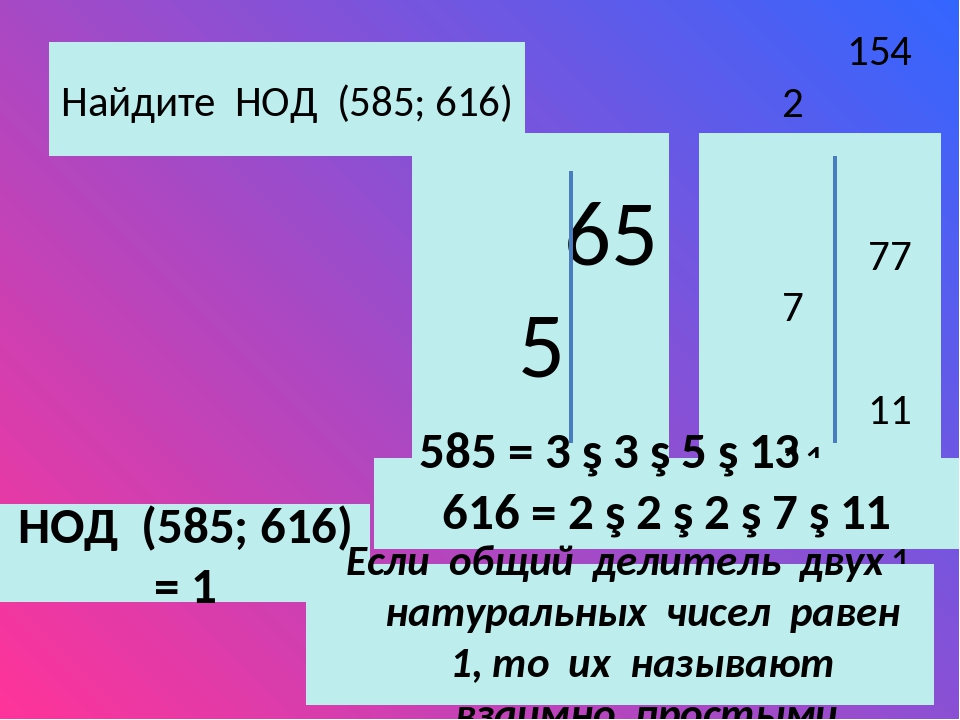
Определите НОД трех чисел −585, 81 и −189.

Решение

Заменим отрицательные числа в приведенном перечне на их абсолютные величины, получим  НОД(−585, 81, −189)=НОД(585, 81, 189). Затем разложим все данные числа на простые множители: 585=3·3·5·13, 81=3·3·3·3 и 189=3·3·3·7. Общими для трех чисел являются простые множители 3 и 3. Получается , что НОД(585, 81, 189)=НОД(−585, 81, −189)=9.

Ответ: НОД(−585, 81, −189)=9.

Как найти НОД и НОК

Чтобы найти наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) двух чисел воспользуйтесь нашим онлайн калькулятором:

Просто введите числа и получите результат.

Как найти НОК двух чисел

Наименьшее общее кратное (НОК) двух или нескольких чисел – это самое маленькое число, которое можно разделить на каждое из этих чисел без остатка.

Для того чтобы найти наименьшее общее кратное (НОК) двух чисел можно воспользоваться следующим алгоритмом (5 класс):

1. Оба числа разложим на простые множители (сначала наибольшее число).
2. Сравним множители большего числа с множителями меньшего. Выделим все множители меньшего числа, которых нет у большего.
3. Добавим выделенные множители меньшего числа к множителям большего.
4. Найдём НОК, перемножив ряд множителей, полученных в пункте 3.

Пример

Для примера определим НОК чисел 8 и 22.

1) Раскладываем на простые множители:

22 = 2⋅11

8 = 2⋅2⋅2

2) Выделим все множители 8-ми, которых нет у 22-х:

8 = 2⋅2⋅2

3) Добавим выделенные множители 8-ми к множителям 22-х:

НОК (8; 22) = 2 · 11 · 2 · 2

4) Вычисляем НОК:

НОК (8; 22) = 2 · 11 · 2 · 2 = 88

Как найти НОД двух чисел

Наибольший общий делитель (НОД) двух или нескольких чисел – это наибольшее натуральное целое число, на которое эти числа можно разделить без остатка.

Чтобы найти наибольший общий делитель (НОД) двух чисел, для начала необходимо разложить их на простые множители. Затем нужно выделить общие множители, которые имеются и у первого числа и у второго. Перемножаем их – это и будет НОД. Чтобы лучше понять алгоритм рассмотрим пример:

Пример

Для примера определим НОД чисел 20 и 30.

20 = 2⋅2⋅5

30 = 2⋅3⋅5

НОД(20,30) = 2⋅5 = 10

Если одно или несколько из рассматриваемых чисел являются простыми, то НОД этих чисел будет равен 1.

См. также

Нахождение НОД

Главная »
Простые числа, факторизация » Нахождение НОД
Разложение числа на множители,
Нахождение НОД,
Нахождение НОК,
Таблица простых чисел,
Признак делимости на 2,
Признак делимости на 3,
Признак делимости на 4,
Признак делимости на 5,
Признак делимости на 6,
Признак делимости на 9,
Признак делимости на 10,
Признак делимости на 12

Нахождение НОД

Делитель числа – это число, на которое нацело делится данное. Например, делители числа 100 – это числа 1, 2, 5, 10, 20, 25, 50, 100, т. к. число 100 делится нацело на каждое из них. (Кстати, 1 – делитель любого натурального числа).

НОД (наибольший общий делитель) двух и более чисел – это наибольшее число, на которое делится нацело каждое из заданных чисел.

Поясним на примере. Пусть даны два числа: 20 и 30. Каждое из этих чисел делится на следующие: 1, 2, 5, 10. То есть, 1, 2, 5 и 10 – общие делители чисел 20 и 30. Из чисел 1, 2, 5 и 10 наибольшее число 10 – это и есть НОД.

Записывают: НОД (20, 30) = 10.

Алгоритм нахождения НОД

Для того, чтобы найти НОД двух чисел, нужно:

1. Разложить оба числа на простые множители.
2. В обоих разложениях найти общие множители.
3. Перемножить их между собой.

Если в обоих разложениях на 2-м шаге не окажется общих множителей, то НОД обоих чисел будет равен 1. Такие числа называются взаимно простыми.

Если числа равны между собой, то их НОД равен им самим.

Пример нахождения НОД

Для того, чтобы просмотреть объяснение того, как находить НОД двух чисел, введите в форму выше два числа (например, 100 и 125), и нажмите кнопку «Объяснить, как найти НОД».

Нахождение НОД нескольких чисел

Часто спрашивают: как найти НОД трех чисел? Ответ прост: сперва нужно найти НОД двух чисел, а затем НОД третьего числа и уже найденного НОДа:

НОД (a, b, c) = НОД(НОД(a, b), c)

Аналогично дело обстоит с четырьмя и более числами.

Наибольший общий делитель (НОД)

Пример 2. Найти наибольший общий делитель чисел 120, 45, 150.

Выпишем разложения на простые множители для заданных чисел и подчеркнем те множители, которые входят в разложения всех чисел:

120 = 2*2*2*3*5,

45 = 3*3*5,

150 = 2*3*5*5.

Cледовательно, НОД(120, 45, 150) = 3*5=15.

Пример 3. Найти наибольший общий делитель чисел 324, 432.

Выпишем разложения на простые множители для заданных чисел и подчеркнем те множители, которые входят в разложения всех чисел:

324 = 2*2*3*3*3*3,

432 = 2*2*2*2*3*3*3.

Cледовательно, НОД(324, 432) = 2*2*3*3*3=108.

Пример 4. Найти наибольший общий делитель чисел 48, 60, 80.

Выпишем разложения на простые множители для заданных чисел и подчеркнем те множители, которые входят в разложения всех чисел:

48 = 2*2*2*2*3,

60 = 2*2*3*5,

80 = 2*2*2*2*5.

Cледовательно, НОД(48, 60, 80) = 2*2=4.

Алгоритм Евклида нахождения наибольшего общего делителя двух чисел

Кроме указанного способа нахождения НОД нескольких чисел, существует алгоритм Евклида нахождения наибольшего общего делителя двух чисел a и b (a >&n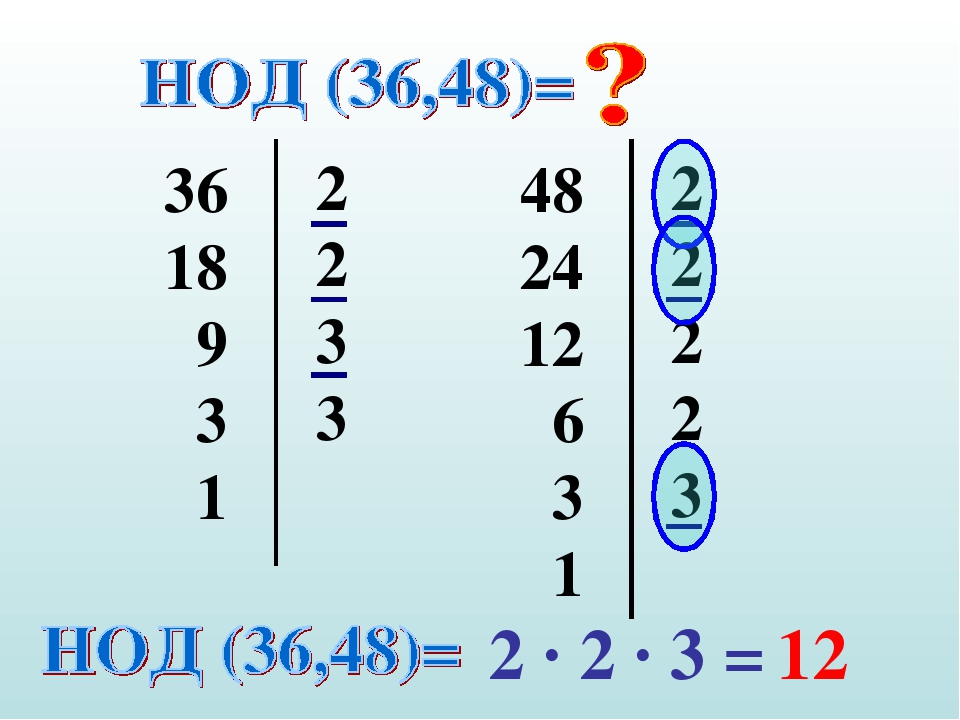bspb). Его можно описать так:

получаем цепочку чисел a > b > r₁ > r₂ > r₃ > … > r_n в соответствии с формулами

a = b*q₀ + r₁, где r₁ – остаток от деления a на b;

b = r₁*q₁ + r₂, где r₂ – остаток от деления b на r₁;

r₁ = r₂*q₂ + r₃, где r₃ — остаток от деления r₁ на r₂;

…

r_n-2 = r_n-1*q_n-1 + r_n, где r_n – остаток от деления r_n-2 на r_n-1;

r_n-1 = r_n*q_n;

НОД(a,b) = r_n.

Другими словами, нужно находить остатки от деления большего числа на меньшее в этой цепочке, пока не получим в остатке ноль. Последний делитель и будет НОД двух чисел.

Примеры.

Пример 1. С помощью алгорима Евклида найти наибольший общий делитель чисел 48 и 18.

48 = 18*2 + 12; (48 делим на 18, в остатке 12)

18 = 12*1 + 6; (18 делим на 12, в остатке 6)

12 = 6*2; (12 делим на 6, в остатке 0, последний делитель и есть НОД).

Cледовательно, НОД(48, 18) = 6.

Пример 2. С помощью алгорима Евклида найти наибольший общий делитель чисел 126 и 900.

900 = 126*7 + 18; (900 делим на 126, в остатке 18)

126 = 18*7; (126 делим на 18, в остатке 0, последний делитель и есть НОД)

Cледовательно, НОД(126, 900) = 18.

Пример 3. С помощью алгорима Евклида найти наибольший общий делитель чисел 495 и 270.

495 = 270*1 + 225; (495 делим на 270, в остатке 225)

270 = 225*1 + 45; (270 делим на 225, в остатке 45)

225 = 45*5; (225 делим на 45, в остатке 0, последний делитель и есть НОД)

Cледовательно, НОД(495, 270) = 45.

Алгоритм Евклида можно использовать и в том случае, если необходимо найти НОД нескольких чисел. Для этого нужно сначала найти НОД первых двух чисел, потом НОД полученного результата и третьего числа, затем НОД этого результата и четвертого числа и т. д. Последний полученный НОД и будет ответом.

Функция НОД — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции НОД в Microsoft Excel.

Описание

Возвращает наибольший общий делитель двух или более целых чисел. Наибольший общий делитель — это наибольшее целое число, на которое делятся число1 и число2 без остатка.

Синтаксис

НОД(число1;[число2];…)

Аргументы функции НОД описаны ниже.

• 
  Число1, число2,…    Число1 является обязательным, последующие числа — нет. От 1 до 255 значений. Если какое-либо из этих чисел не является целым, оно усекается.

Замечания

• Если какой-либо из аргументов не является числом, он возвращает #VALUE! значение ошибки #ЗНАЧ!.

• Если какой-либо из аргументов меньше нуля, он возвращает #NUM! значение ошибки #ЗНАЧ!.

• Единица является делителем любого числа.

• Простое число делится только само на себя и на единицу. 53, она возвращает #NUM! значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

5.

3.4. Нахождение наибольшего общего делителя (НОД) данных чисел.

Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 196 Опубликовано 28 мая 2012

• Наибольшим общим делителем данных натуральных чисел называют наибольшее натуральное число, на которое делится каждое из этих чисел.
•  Наибольший общий делитель данных чисел равен произведению общих простых множителей в разложениях этих чисел. Пример. НОД(24, 42)=2·3=6, т. к. 24=2·2·2·3, 42=2·3·7, их общие простые множители 2 и 3.
•  Если натуральные числа имеют только один общий делитель-единицу, то эти числа называют взаимно простыми.

Пример 1. Найти НОД(15; 35).

Решение.

Разложим данные числа на простые множители.

 15=3∙5,               35=5∙7

Общий делитель чисел 15 и 35 – это число 5.

Ответ: НОД(15; 35)=5.

Пример 2. Найти НОД(72; 64).

Решение.

 Разложим числа 72 и 64 на простые множители.

72=2∙2∙2∙3∙3 или 72=2³∙3²,          64=2∙2∙2∙2∙2∙2 или 64=2⁶

Нужно взять произведение общих множителей: 2∙2∙2=2³=8.

Ответ: НОД(72; 64)=2³=8.

Примечание: из разложений данных чисел нужно брать общие множители с наименьшими показателями. У нас в первом разложении было 2³, а во втором 2⁶, поэтому, взяли 2³.

Пример 3. Найдите наибольший общий делитель разности чисел 69 и 19 и суммы чисел 36 и 39.

Решение.

Требуется найти НОД(50; 75). Разложим эти числа на простые множители.

50=2∙5² ;              75=3∙5²

Общий делитель 5 берем во второй степени.

НОД(50; 75)=5²=5∙5=25.

Ответ: НОД(50; 75)=25.

Наименьшее общее кратное и наибольший общий делитель (ЕГЭ — 2021)

Как ты уже понял, это числа, противоположные натуральным, то есть:

\( \displaystyle  -1;\ -2;\ -3;\ -4\) и т.д.

Отрицательные числа можно складывать, вычитать, умножать и делить – все как в натуральных.

Казалось бы, что в них такого особенного?

А дело в том, что отрицательные числа «отвоевывали» себе законное место в математике аж до XIX века (до этого момента было огромное количество споров, существуют они или нет).

Само отрицательное число возникло из-за такой операции с натуральными числами, как «вычитание».

Действительно, из \( \displaystyle  3\) вычесть \( \displaystyle  11\) – вот и получается отрицательное число. Именно поэтому, множество отрицательных чисел часто называют «расширением множества натуральных чисел».

Отрицательные числа долго не признавались людьми.

Так, Древний Египет, Вавилон и Древняя Греция – светочи своего времени, не признавали отрицательных чисел, а в случае получения отрицательных корней в уравнении (например, как у нас \( \displaystyle  3-11\)), корни отвергались как невозможные.

Впервые отрицательные числа получили свое право на существование в Китае, а затем в VII веке в Индии.

Как ты думаешь, с чем связано это признание?

Правильно, отрицательными числами стали обозначать долги (иначе — недостачу).

Считалось, что отрицательные числа – это временное значение, которое в результате изменится на положительное (то есть, деньги кредитору все же вернут). Однако, индийский математик Брахмагупта уже тогда рассматривал отрицательные числа наравне с положительными.

В Европе к полезности отрицательных чисел, а также к тому, что они могут обозначать долги, пришли значительно позже, эдак, на тысячелетие.

Первое упоминание замечено в 1202 году в «Книге абака» Леонарда Пизанского (сразу говорю — к Пизанской башне автор книги отношения никакого не имеет, а вот числа Фибоначчи – это его рук дело (прозвище Леонардо Пизанского — Фибоначчи)).

Далее европейцы пришли к тому, что отрицательные числа могут обозначать не только долги, но и нехватку чего бы то ни было, правда, признавали это не все.

Так, в XVII веке Паскаль считал что \( \displaystyle  0-4=0\).

Как думаешь, чем он это обосновывал?

Верно, «ничто не может быть меньше НИЧЕГО».

Отголоском тех времен остается тот факт, что отрицательное число и операция вычитания обозначается одним и тем же символом – минусом «-». И правда: \( \displaystyle  6-8\). Число «\( \displaystyle  8\)» положительное, которое вычитается из \( \displaystyle  6\), или отрицательное, которое суммируется к \( \displaystyle  6\)?… Что-то из серии «что первое: курица или яйцо?» Вот такая вот, своеобразная эта математическая философия.

Поиск узла в двоичном дереве

class newNode:

def __init __ ( self data ) .data = data

self .left = Нет

self . правый = Нет

def ifNodeExists (узел, ключ):

if (узел = = = )

возврат False

if (node.data = = key):

res1 = ifNodeExists (node.слева, клавиша)

if res1:

return True

000 000

ifNodeExists (node.right, key)

возврат res2

if __name__ 0005 = 000 = __ корень = новый узел ( 0 )

корень. left = newNode ( 1 )

root.left.left = newNode ( 3 .left . слева = newNode ( 7 )

root.left.right = newNode ( 4 ) left.right.left = newNode ( 8 )

root.left. right. right = newNode ( 9 root.right = newNode ( 2 )

root.right.left = newNode ( 5 ) . .справа.право = newNode ( 6 )

ключ = 4

, если 9000Node, если корневой ключ, 9000ist (если 9000Node) :

печать ( «ДА» )

еще :

» (печать ) NO

Получение пути от корня к узлу в двоичном дереве

Мы открываем новую область компьютерных наук. Если у вас есть несколько лет опыта в области компьютерных наук или исследований, и вы заинтересованы в том, чтобы поделиться этим опытом с сообществом (и, конечно, получать деньги за свою работу), загляните на страницу «Напишите для нас».
Ура, Евгений

1. Обзор

В этом руководстве мы обсудим проблему поиска пути от корня до узла в двоичном дереве. У этой проблемы может быть много версий. Итак, поясним общую идею на примере.

Также мы представим две версии проблемы и опишем решения для каждой из них.

2. Определения

Прежде всего, нам нужно определить путь от корня до узла в двоичном дереве.

Возьмем следующий пример:

В этом примере корнем является узел. Если нам нужно получить путь от корня к узлу, то мы замечаем, что он идет от корня к узлам, а затем к узлу.

Точно так же, если нам нужно перейти от корня к узлу, мы пройдем через узел.

В общем, есть два способа получить путь к узлу в дереве. Либо мы начинаем с корня и переходим к дочернему элементу, который является предком целевого узла. Или мы начинаем с целевого узла и продолжаем двигаться вверх к его родительскому узлу, пока не достигнем корня .

Оба подхода прекрасны. Однако это зависит от информации, хранящейся внутри каждого узла дерева. Например, если каждый узел не содержит указателя на своего родителя, мы не можем использовать второй подход.

Важно отметить, что, начиная с корня, мы можем найти единственный путь, который соединяет корень с определенным узлом .Причина в том, что деревья — это неориентированные графы, не содержащие циклов. Следовательно, мы можем найти только одну последовательность на узлах, которая начинается с корня и заканчивается на каждом узле.

В зависимости от свойства пути проблема может иметь множество версий. В этом руководстве мы обсудим две версии этой проблемы.

3. Поиск пути к целевому узлу

В этой версии задачи нам дано двоичное дерево с корнем в каком-то узле. Нас просят вернуть список, содержащий все узлы, начиная с корня и заканчивая заданным целевым узлом .

Эту проблему можно решить двумя способами. Обсудим каждый из них отдельно.

3.1. Подход сверху вниз

Нисходящий подход выполняет операцию DFS (поиск в глубину), начиная с корня. На каждом шаге он рекурсивно ищет целевой узел, начиная с левого и правого потомков.

Давайте посмотрим на реализацию нисходящего подхода:

Во-первых, мы инициализируем список пустым.Этот список будет использоваться для хранения узлов в текущем пути, который исследует функция DFS.

Во-вторых, мы выполняем вызов DFS, начиная с текущего узла. Мы также передаем целевой узел, чтобы функция DFS могла остановиться, когда он достигнет целевого узла. Если функция DFS возвращается, значит, узел был найден, и мы возвращаем узлы, хранящиеся внутри списка.

В противном случае мы просто возвращаемся, указывая, что целевой узел не существует в этой ветви дерева.

Внутри функции DFS мы начинаем с проверки, достигли ли мы значения. Если да, мы просто возвращаемся, указывая, что целевой узел не найден в этой ветви. В противном случае мы добавляем текущий узел к пути .

Если мы достигли целевого узла, мы вернемся, что должно остановить функцию от углубления в дерево. В противном случае мы выполняем рекурсивный вызов для левого и правого потомков.

Если один из этих вызовов возвращается, мы немедленно останавливаемся и также возвращаем истину, чтобы функция не углубилась в дерево.

Если обе функции возвращаются, значит целевой узел не был найден внутри этой ветви дерева. В этом случае мы удаляем текущий узел из пути и возвращаем, указывая, что операция поиска должна продолжаться с других узлов .

Сложность нисходящего подхода составляет , где — количество узлов внутри двоичного дерева.

3.2. Подход снизу вверх

В этом подходе мы обращаем процесс вспять. Вместо того, чтобы начинать с корня, мы начинаем с целевого узла.

Давайте посмотрим на реализацию восходящего подхода:

Начинаем с целевого узла.На каждом шаге мы переходим к родительскому элементу текущего узла.

Этот процесс продолжается, пока мы не дойдем до корня. Достигнув корня, значит, мы нашли нужный путь. Следовательно, мы останавливаем цикл.

Однако есть на что обратить внимание. Поскольку цикл прерывается, когда мы достигаем корня, это означает, что корень не будет добавлен в список . Следовательно, мы добавляем корень в список после завершения цикла.

Предполагая, что каждая операция добавляет узел в конец списка, мы получим обратный путь, который начинается от целевого узла и заканчивается в корне.Таким образом, мы переворачиваем список перед его возвратом.

Сложность восходящего подхода составляет , где — высота дерева. Причина в том, что мы исследуем только нужный путь внутри дерева. Таким образом, мы можем закончить, не исследуя все узлы внутри дерева.

Конечно, худший случай — это когда. В этом случае сложность будет, но это верно только для почти линейных деревьев.

3.3. Сравнение

Подход снизу вверх лучше с точки зрения сложности и обычно рекомендуется для использования .

Однако к нему предъявляются два основных требования. Первое требование — мы должны иметь возможность быстро получить указатель на целевой узел. Таким образом, мы сможем начать с целевого узла, а не с корня.

С другой стороны, второе требование состоит в том, что мы должны хранить родительский элемент каждого узла внутри структуры узла. В противном случае мы не сможем переходить к родительскому на каждом этапе.

Если одно из этих двух требований невозможно выполнить, тогда нам следует рассмотреть возможность использования нисходящего подхода.

4. Поиск всех путей с целевой суммой

В этой задаче нас просят найти все пути внутри двоичного дерева, которые начинаются с корня, так что сумма значений внутри каждого узла пути равна целевой сумме.

Давайте посмотрим на подходы сверху вниз и снизу вверх в случае этой проблемы.

4.1. Подход сверху вниз

Нисходящий подход аналогичен представленному выше. Давайте посмотрим на реализацию нисходящего подхода:

Мы начинаем с инициализации списка, в котором будет храниться текущий путь, по которому мы идем.Также инициализируем список, в котором будет храниться ответ.

После этого вызываем функцию DFS и возвращаем ответ.

Переходя к функции DFS, она принимает текущий узел, текущую сумму и целевую сумму в качестве параметров.

В первую очередь проверяем, дошли ли мы, потом просто возвращаемся. В противном случае мы добавляем текущий узел к пути и увеличиваем сумму на . Если сумма достигает целевой суммы, мы сохраняем копию списка внутри ответа.

Обратите внимание, что, если мы достигли целевой суммы, мы не останавливаем функцию. Причина в том, что если некоторые узлы имеют нулевое значение, мы хотим позволить функции немного расширить путь.

Следующим шагом является выполнение рекурсивного вызова DFS для левого и правого потомков с обновленной суммой. После завершения этих вызовов мы удаляем текущий узел из пути, чтобы можно было исследовать другие узлы внутри дерева.

Сложность нисходящего подхода составляет , где — количество узлов, а — высота дерева.Причина в том, что всякий раз, когда мы достигаем узла, у нас может быть действительный ответ, и нам нужно сохранить его копию для ответа.

Следовательно, нам может потребоваться скопировать список в большинстве случаев. Кроме того, список может содержать не более узлов, поскольку любой путь, начинающийся от корня, может содержать не более узлов.

4.2. Подход снизу вверх

Обратите внимание, что в этой задаче нет смысла начинать с целевого узла и каждый раз двигаться вверх к родительскому, пока мы не достигнем корня. Причина в том, что у нас нет целевого узла.Вместо этого у нас есть целевая сумма, которую нам нужно достичь.

В этом случае нам нужно будет начинать с каждого узла внутри дерева и продолжать движение вверх к корню, накапливая сумму значений узлов. Если мы будем следовать этому подходу, мы получим подход, который имеет худшую сложность, чем подход сверху вниз.

Кроме того, нам потребуется прямой доступ к каждому узлу внутри дерева и возможность перемещаться от каждого узла к его родительскому.

Следовательно, нет смысла решать эту проблему восходящим подходом.

5. Сравнение

В этом руководстве мы обсудили проблему поиска путей внутри двоичного дерева, которое начинается с корня и имеет определенное свойство.

Во-первых, мы обсудили проблему поиска пути, который заканчивается в целевом узле. Мы представили два подхода к решению этой проблемы.

Во-вторых, мы объяснили проблему поиска всех путей, у которых есть заданная сумма. В этой версии мы объяснили только нисходящий подход.

алгоритмов — найти узел с максимальным расстоянием от узла запроса в дереве

Допустим, ваши $ k $ запросы находятся в следующем порядке $ \ {v_1, v_2, \ ldots v_k \} $.Для $ v_1 $ у нас не будет информации, поэтому мы просто выполняем DFS, определяем самый дальний узел $ u $ и возвращаем его. Считайте $ v_1 $ корнем этого дерева DFS. Для каждого дочернего элемента $ v_1 $ $ \ {u_1, u_2, \ ldots \} $ мы также будем отслеживать самый глубокий узел в поддереве с корнем $ u_i $. Назовем это $ d (v_1, u_i) $. Обратите внимание, что максимальное расстояние узла от $ v_1 $ составляет:

$$ d (v_1) = \ max_i d (v_1, u_i) $$

Здесь важно отметить, что для запроса $ v_2 $ мы можем сохранить много информации из $ d (v_1, u_i) $, если путь к самому дальнему узлу от $ v_2 $ включает $ v_1 $.Предположим, что w.l.o.g. что $ v_2 $ находится в поддереве с корнем $ u_j $ в дереве DFS $ v_1 $. Мы снова сделаем DFS для самого глубокого узла в дереве DFS $ v_2 $, однако, когда мы нажмем $ v_1 $, мы можем остановиться, и нам нужно только сохранить расстояние $ \ delta (v_2, v_1) $. Теперь мы вычисляем $ d (v_2) $ как:

$$ d (v_2) = \ max \ {\ max_i d (v_2, y_i), \ \ delta (v_2, v_1) + \ max_ {i \ neq j} d (v_1, u_i) \} $$

Эту идею можно повторить для остальных запросов, где $ v_i $ полагается на информацию из запросов $ \ {v_1, v_2, \ ldots v_ {i-1} \} $.В запросе $ v_i $ мы можем описать работу следующим образом. Рассмотрим дерево DFS с корнем в $ v_i $, работа по «поиску», выполняемая в любом поддереве с корнем в $ \ {v_1, v_2, \ ldots v_ {i-1} \} $, является постоянной на основе наших предварительно вычисленных значений. Нам нужно только позаботиться о проделанной работе, прежде чем мы достигнем этих узлов. Вот пример анализа, в котором мы считаем, что запрос $ v_ {i + 1} $ находится в «середине» самого большого оставшегося поддерева.

1. Первый запрос берет $ cn $ и разбивает дерево на деревья $ T_1 $ и $ T_2 $ размером $ n / 2 $ каждое.i} = O (\ ell \ cdot n) = O (n \ log k) $$

   ---

   В качестве примечания, большая часть работы будет зависеть от порядка запросов. Например, если у нас есть связанный список ребер: $ \ {(v_1, v_2), (v_2, v_3), \ ldots \} $ и мы предполагаем, что порядок запроса равен $ \ {v_1, v_2, \ ldots v_k \} $ тогда:

   1. Первый запрос берет cn и разбивает дерево на деревья $ T_1 $ и $ T_2 $ размером $ 1 $ и $ n-1 $ каждое.
   2. Второй запрос принимает c (n-1) и разбивает $ T_2 $ на деревья $ T_3 $ и $ T_4 $ размером $ 1 $ и $ n-2 $ каждое.k c (n-i) = O (nk) $$

      Однако, если мы упорядочим запросы как $ \ {v_k, v_ {k-1}, \ ldots v_1 \} $, тогда:

      1. Первый запрос берет cn и разбивает дерево на деревья $ T_1 $ и $ T_2 $ размером $ k-1 $ и $ n-k + 1 $ каждое.
      2. Второй запрос берет c (k-1) и разбивает $ T_1 $ на деревья $ T_3 $ и $ T_4 $ размером $ k-2 $ и $ 1 $ каждое. 2) $$

         Даже с порядком $ \ {v_k, v_ {k / 2}, v_ {k / 4}, v_ {3k / 4}, \ ldots \} $ мы могли бы получить сложность $ O (n + k \ журнал k) $.Таким образом, сложность во многом зависит от порядка запросов. Если мы предположим, что запросы являются случайными, то это все еще нормально, и мы можем получить $ O (n \ log k) $. Если мы сможем изменить порядок запросов, то мы сможем с жадностью выбрать узел, который разбивает дерево ближе всего к пополам, и продолжить. Это должно дать примерно $ O (n \ log k) $, хотя у меня нет доказательств, и я не буду работать с ним здесь.

         День 2 Найдите соответствующий узел двоичного дерева в клоне этого дерева

         Проблема
         

         Даны два двоичных дерева , исходный и , клонированный , и дана ссылка на узел , целевой в исходном дереве.

         Клонированное дерево — это копия исходного дерева .

         Вернуть ссылку на тот же узел в клонированном дереве.

         Обратите внимание, , что вам не разрешено изменять любое из двух деревьев или целевой узел, и ответ должен быть ссылкой на узел в клонированном дереве.

         Последующие действия: Решите проблему, если разрешены повторяющиеся значения в дереве.

         Пример:

           Ввод: дерево = [7,4,3, null, null, 6,19], target = 3
         Выход: 3
         Объяснение: Во всех примерах показаны исходные и клонированные деревья.Целевой узел - это зеленый узел из исходного дерева. Ответ - желтый узел из клонированного дерева.
           

         Войти в полноэкранный режимВыйти из полноэкранного режима

         Мои тесты
         

         Ссылка на код утилиты

           импортная копия
         из .util import TreeNode
         from.Day2 import Решение
         
         s = Решение ()
         
         
         def test_find_node ():
             tree = TreeNode (7)
             tree.left = TreeNode (4)
             tree.right = TreeNode (3)
             tree.right.left = TreeNode (6)
             tree.right.right = TreeNode (19)
         
             оригинал = дерево
             clone = копия.deepcopy (дерево)
         
             assert s.getTargetCopy (оригинал, клон, tree.right) .val == 3
           

         Войти в полноэкранный режимВыйти из полноэкранного режима

         Мое решение
         

           из .util import TreeNode
         
         
         def search (tree: TreeNode, val: int) -> TreeNode:
             если tree.val == val:
                 дерево возврата
         
             если tree.left не равно None:
                 l = поиск (tree.left, val)
                 если l не равно None:
                     вернуться л
             если tree.right не равно None:
                 r = поиск (tree.right, val)
                 если r не равно None:
                     вернуть г
             return None
         
         
         класс Решение:
             def getTargetCopy (
                 сам, исходный: TreeNode, клонированный: TreeNode, цель: TreeNode
             ) -> TreeNode:
                 возвратный поиск (клонированный, целевой.val)
           

         Войти в полноэкранный режимВыйти из полноэкранного режима

         Анализ
         

         Мой комментарий
         

         Сначала я подумал, что это слишком просто. Обычно я нахожу большинство проблем трудными. Даже «легкие». Меня немного смутил тот факт, что мы получили оригинальное дерево. Поиск, похоже, помог. Я думал, что нашел решение довольно быстро, и анализ выглядел хорошо, но потом я заметил память.Я, по-видимому, вообще не справляюсь с использованием памяти.

         В тот день у меня не было много времени, поэтому я не смог работать над лучшим решением или дополнительным вопросом.

         Могу только предположить, что мы можем каким-то образом использовать исходное дерево, чтобы ускорить его, или, может быть, меня просто подвело отсутствие знаний о Python. Я добавляю эту закладку, чтобы вернуться к ней позже.

         узлов | Узел GoJS API

         | GoJS API

         ---

         Иерархия

         Индекс

         Конструкторы

         Недвижимость

         Методы

         Константы

         Конструкторы

         конструктор
         

         Недвижимость

         можно избежать
         : логический

         можно избежать

         Маржа
         : MarginLike

         Только чтение
         

         Ссылка Метка
         : логический

         is

         Дерево Расширенное
         : логический

         is

         Дерево Лист
         : логический

         с надписью

         Ссылка
         : Ссылка

         ссылка

         Подключено
         : (thisNode: Node, newLink: Link, thisPort: GraphObject) => void

         ссылка

         отключена
         : (thisNode: Node, oldLink: Link, thisPort: GraphObject) => void

         ссылка

         Проверка
         : (fromNode: Node, fromPort: GraphObject, toNode: Node, toPort: GraphObject, link: Link) => boolean

         Только чтение
         ссылки

         Подключено
         : Итератор <Ссылка>

         Только чтение
         порт
         : GraphObject

         порт

         Распространение
         : EnumValue

         Только чтение
         порты
         : Итератор

         дерево

         Расширено Изменено
         : (thisNode: Node) => void

         было

         Дерево Расширенное
         : логический

         Методы

         свернуть

         Дерево
         

         • свернуть Дерево (уровень ?: номер): void

         развернуть

         Дерево
         

         • развернуть Дерево (уровень ?: номер): void

         найти

         Общий Дерево Родитель
         

         • Параметры

           Узел возврата

           может быть нулевым, если в разных деревьях,
           или может быть самим собой, если ДРУГОЙ аргумент является ЭТОМ узлом,
           или может быть самим собой, если ДРУГОЙ узел является потомком ЭТОГО узла,
           или может быть ДРУГИМ узлом, если ЭТО узел находится в дереве ДРУГОГО узла.

         найти

         Ссылки Между
         

         • find Links Between (othernode: Node, pid ?: string, otherpid ?: string): Iterator

         • Параметры

           • othernode: Узел

           • Необязательный pid: строка

           • Необязательный otherpid: строка

           Возвращает Итератор

           <Ссылка>

         Виртуальный
         найти

         Ссылки Подключено
         

         найти

         ссылки в
         

         найти

         ссылки из из
         

         найти

         Ссылки Кому
         

         • Параметры

           • othernode: Узел

           • Необязательный pid: строка

           • Необязательный otherpid: строка

           Возвращает Итератор

           <Ссылка>

         найти

         Узлы Подключено
         

         найти

         узлов в
         

         найти

         узлов из из
         

         найти порт

         
         

         найти

         Дерево Дети Ссылки
         

         найти

         Дерево Дети Узлы
         

         найти

         Дерево Уровень
         

         найти

         Дерево Родитель Цепочка
         

         найти

         Дерево Родитель Ссылка
         

         • найти Дерево Родитель Ссылка (): Ссылка

         найти

         Дерево Родительский узел
         

         • найти Дерево Родительский Узел (): Узел

         найти

         Дерево Детали
         

         • найти Дерево Детали (уровень ?: номер): Установить <Деталь>

         найти

         Дерево Корень
         

         это

         InTree Of
         

         • — это InTree Of (узел: узел): логическое

         • Параметры

           Возвращает логическое значение

           true, если данный узел является предком этого узла, и false в противном случае, включая false, если это тот же узел.

         Константы

         Статический
         Распространение

         Равномерно
         : EnumValue

         Статический
         Распространение

         Нет
         : EnumValue

         Статический
         Распространение

         Фасованное
         : EnumValue

         Авторские права © 1998-2021, Northwoods Software Corporation.

         Поиск узла в Babel AST

         В некоторых случаях может потребоваться поиск определенного узла
         в JSX AST, например, если вы хотите изменить свойство.

         Это операция, которую мы используем в блоках
         чтобы найти конкретный элемент, который нужно изменить при его редактировании.

         В этом случае мы хотим найти элемент JSX, в котором установлен id
         к привет . Итак, код, который выглядит так:
         

         Привет, мир!

         Мы можем начать с посещения всех JSXOpeningElement и извлечения
         атрибуты (реквизит).

           экспорт по умолчанию api => {
           const {типы: t} = api
         
           возвращаться {
             посетитель: {
               JSXOpeningElement (путь) {
                 const attrs = путь.node.attributes
                 console.log (attrs)
               }
             }
           }
         }
           

         Теперь, когда мы обращаемся к элементам, которые нам нужны для поиска конкретных
         имя пропуска, id .

           экспорт по умолчанию api => {
           const {типы: t} = api
         
           возвращаться {
             посетитель: {
               JSXOpeningElement (путь) {
                 const attrs = path.node.attributes
                 const attr = attrs.find (attr => attr.name.name === 'id')
         
                 console.log (attr)
               }
             }
           }
         }
           

         Затем мы можем увидеть, существует ли атрибут с правильным значением.

           экспорт по умолчанию api => {
           const {типы: t} = api
         
           возвращаться {
             посетитель: {
               JSXOpeningElement (путь) {
                 const attrs = path.node.attributes
                 const attr = attrs.find (attr => attr.name.name === 'id')
         
                 если (! attr) {
                   возвращаться
                 }
         
                 константное значение = attr.value.value
                 if (значение! == 'привет') {
                   возвращаться
                 }
         
                 console.log (attr)
               }
             }
           }
         }
           

         Когда мы добрались до console.log , мы успешно нашли узел.Здесь мы можем изменить его, если захотим.

           экспорт по умолчанию api => {
           const {типы: t} = api
         
           возвращаться {
             посетитель: {
               JSXOpeningElement (путь) {
                 const attrs = path.node.attributes
                 const attr = attrs.find (attr => attr.name.name === 'id')
         
                 если (! attr) {
                   возвращаться
                 }
         
                 константное значение = attr.value.value
                 if (значение! == 'привет') {
                   возвращаться
                 }
         
                 attr.value.value = t.stringLiteral ('привет-мир')
               }
             }
           }
         }
           

         Теперь мы получим

         Hello, world!

         .

         Однако есть еще одна вещь, которую нужно решить. Что будет, если мы узнаем
         что опора будет существовать только один раз? Мы хотим остановить обход дерева
         чтобы гарантировать, что мы не продолжим проходить весь AST.

         Итак, мы можем сделать это с помощью path.stop () . Это скажет Бабелю
         перестаньте смотреть на другие узлы.

         Все вместе

           экспорт по умолчанию api => {
           const {типы: t} = api
         
           возвращаться {
             посетитель: {
               JSXOpeningElement (путь) {
                 const attrs = путь.node.attributes
                 const attr = attrs.find (attr => attr.name.name === 'id')
         
                 если (! attr) {
                   возвращаться
                 }
         
                 константное значение = attr.value.value
                 if (значение! == 'привет') {
                   возвращаться
                 }
         
                 attr.value.value = t.stringLiteral ('привет-мир')
                 path.stop ()
               }
             }
           }
         }
           

         Линейный поиск связанного списка в Python

         Связанный список — это фундаментальная структура данных в информатике, часто встречающаяся при технических собеседованиях и задачах программирования.Одна из простейших задач и отличная отправная точка для изучения связанных списков — поиск связанного списка, чтобы узнать, содержит ли он заданное значение.

         Линейный поиск связанных списков

         В отличие от массивов, которые разрешают произвольный доступ к отдельным элементам, связанные списки представляют собой цепочку узлов, которые необходимо пройти один за другим, чтобы увидеть, содержит ли список заданное значение. Каждый узел обычно содержит значение и указатель на следующий узел. Поочередное обход узлов для нахождения значения называется линейным поиском , а производительность линейного поиска в наихудшем случае равна O (n).По мере увеличения количества узлов в связанном списке увеличивается и производительность в худшем случае. Как и следовало ожидать, связанные списки обычно не являются идеальной структурой данных для алгоритмов, которые постоянно ищут большое количество значений.

         Существуют разные способы реализации связанных списков, но в основном это сводится к классу или структуре, обычно называемой узлом , который содержит значение и указатель на другой узел. Для простоты вот образец класса Node в Python.

          Узел класса (объект):
             def __init __ (self, value: int, next_node: "Node" = None):
                 себя.значение = значение
                 self.next_node = next_node
         
             def __repr __ (сам):
                 вернуть "Node <{}>". format (self.value)
          

         Мы можем создать связанный список, объединив несколько узлов вместе. Вот связанный список в Python, содержащий целые числа от 1 до 5.

          связанный_лист = Узел (1, Узел (2, Узел (3, Узел (4, Узел (5))))) 

         Когда у нас есть связанный список, мы можем передать его функции, которая выполняет линейный поиск, чтобы увидеть, содержит ли он значение. Для простоты функция поиска вернет True, если связанный список содержит значение, или False, если его нет.Функция принимает заголовок (первый узел) связанного списка, а также целочисленное значение для поиска.

          def find (head: Node, value: int) -> bool:
             "" "Возвращает True, если значение в связанном списке, иначе False." ""
         
             current_node = голова
             в то время как current_node не равен None:
                 если current_node.value == значение:
                     вернуть True
         
                 current_node = current_node.next_node
         
             return False 

         Алгоритм линейного поиска для связанного списка посещает каждый узел один за другим, чтобы узнать, равно ли его значение значению поиска.Если значение найдено, возвращается True. Если алгоритм линейного поиска перебирает все экземпляры Node в связанном списке и оказывается пустым, он возвращает False.

         Полное решение в Python для поиска значения в связном списке с помощью линейного поиска выглядит следующим образом.

          Узел класса (объект):
          def __init __ (self, value: int, next_node: "Node" = None):
          self.value = значение
          self.next_node = next_node
          def __repr __ (сам):
          вернуть "Node <{}>". format (self.значение)
         def find (head: Node, value: int) -> bool:
          "" "Возвращает True, если значение в связанном списке, иначе False." ""
          current_node = голова
          в то время как current_node не равен None:
          если current_node.