Содержание
Расстояние между плоскостями. Онлайн калькулятор
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
1. Проверяем коллинеарность нормальных векторов n1=(A1, B1, C1) и n2=(A2, B2, C2).
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами. Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
Пусть A1≠0, A2≠0. Уравнение плоскости (2) не изменится, если умножим на A1/A2:
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
или
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
где
2. Найдем некоторую точку на плоскости (1).
Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2») вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2») (или (1) и (2)):
где
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
Подставим значения A, B, C, D1, D2 в (9):
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
и
Решение.
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
и
Решение.
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
Расстояние между двумя параллельными плоскостями: определение и примеры нахождения
Материал данной статьи позволяет получить навык определения расстояния между двумя параллельными плоскостями при помощи метода координат. Дадим определение расстояния между параллельными плоскостями, получим формулу для его расчета и рассмотрим теорию на практических примерах.
Расстояние между двумя параллельными плоскостями: определение
Определение 1
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из рассматриваемых параллельных плоскостей до другой плоскости.
Пусть заданы две параллельные плоскости ϒ1 и ϒ2. Из произвольной точки М1 плоскости ϒ1 опустим перпендикуляр М1Н1 на другую плоскость ϒ2. Длина перпендикуляра М1Н1 и будет являться расстоянием между заданными плоскостями.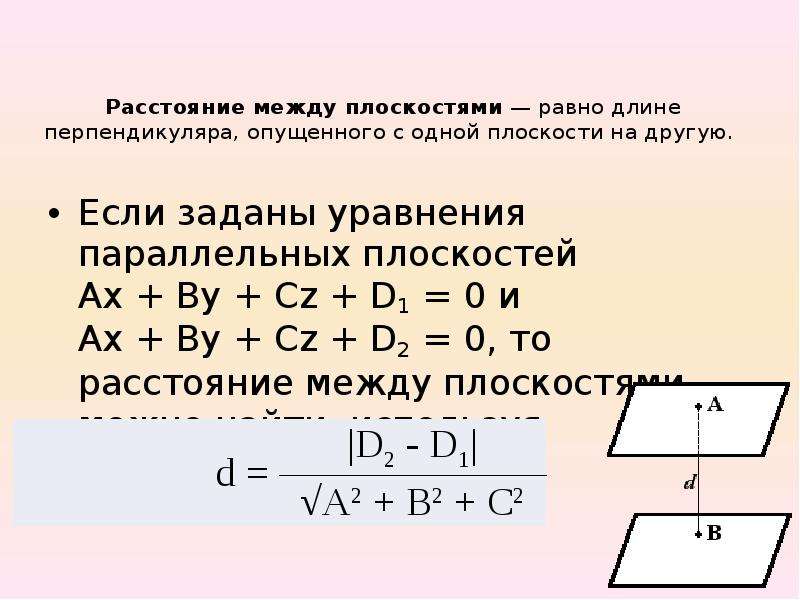
Указанное определение расстояния между параллельными плоскостями имеет взаимосвязь со следующей теоремой.
Теорема
Если две плоскости параллельны, то все точки одной из параллельных плоскостей находятся на одном и том же расстоянии от другой плоскости.
Доказательство
Допустим, заданы две параллельные плоскости ϒ1 и ϒ2. Для получения доказательства теоремы необходимо доказать, что перпендикуляры, опущенные из различных произвольных точек одной плоскости к другой плоскости, равны. Пусть будут заданы некоторые произвольные точки М1 и М2 на плоскости ϒ1, и из них опущены перпендикуляры М1Н1 и М2Н2 на плоскость ϒ2. Таким образом, нам предстоит доказать, что М1Н1 = М2Н2.
Прямые М1Н1 и М2Н2 параллельны, поскольку перпендикулярны одной плоскости. Опираясь на аксиому о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, можем утверждать, что через две параллельные прямые проходит единственная плоскость. Будем считать, что существует некоторая плоскость ϒ3, проходящая через две параллельные прямые М1Н1 и М2Н2.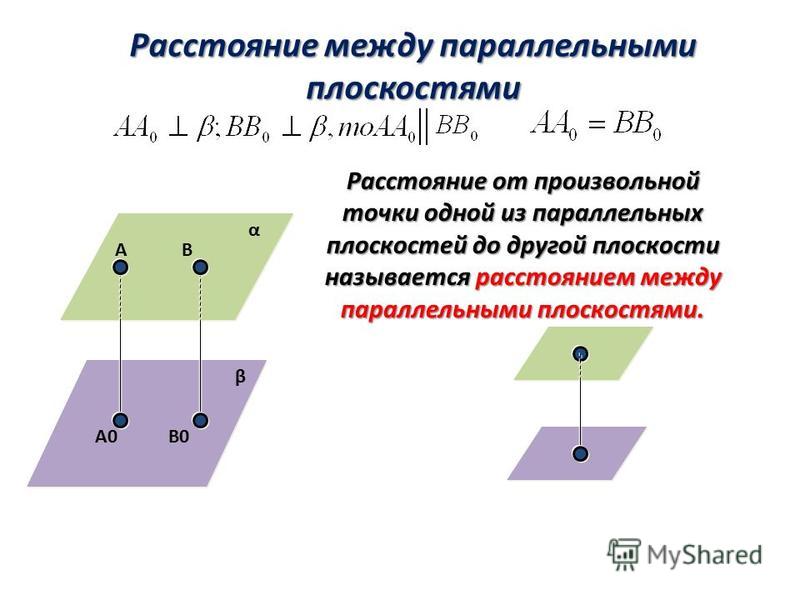 Очевидным фактом является то, что плоскость ϒ3 пересекает плоскости ϒ1 и ϒ2 по прямым М1M2 и Н1Н2, которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М1М2Н1Н2, у которого противоположные стороны являются попарно параллельными, т.е. М1М2Н1Н2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит |М1Н1| = |М2Н2|. Что и требовалось доказать.
Очевидным фактом является то, что плоскость ϒ3 пересекает плоскости ϒ1 и ϒ2 по прямым М1M2 и Н1Н2, которые не пересекаются, а значит – параллельны (в ином случае, заданные плоскости имели бы общую точку, что невозможно в силу их параллельности по условию задачи). Таким образом, мы наблюдаем четырехугольник М1М2Н1Н2, у которого противоположные стороны являются попарно параллельными, т.е. М1М2Н1Н2 – параллелограмм (в рассматриваемом случае – прямоугольник). Следовательно, противоположные стороны у этого параллелограмма равны, а значит |М1Н1| = |М2Н2|. Что и требовалось доказать.
Заметим также, что расстояние между параллельными плоскостями – наименьшее из расстояний между произвольными точками этих плоскостей.
Нахождение расстояния между параллельными плоскостями
По программе 10-11 классов расстояние между параллельными плоскостями определяется построением перпендикуляра из любой точки одной плоскости, опущенного к другой плоскости; после чего находится длина этого перпендикуляра (при помощи теоремы Пифагора, признаков равенства, или подобия треугольников, или определения синуса, косинуса, тангенса угла).
В случае, когда уже задана или есть возможность задать прямоугольную систему координат, то мы имеем возможность определить расстояние между параллельными плоскостями при помощи метода координат.
Пусть задано трехмерное пространство, а в нем — прямоугольная система координат и две параллельные плоскости ϒ1 и ϒ2. Найдем расстояние между этими плоскостями, опираясь, в том числе, на определение расстояния между плоскостями, данное выше.
В исходных данных — плоскости ϒ1 и ϒ2, и мы можем определить координаты (x1, y1, z1) некой точки M1, принадлежащей одной из заданных плоскостей: пусть это будет плоскость ϒ1. Также получим нормальное уравнение плоскости ϒ2: cos α·x+cos β·y+cos λ·z-p=0. В таком случае, искомое расстояние |М1Н1| будет равно расстоянию от точки М1(x1, y1, z1) до плоскости ϒ2 (ей соответствует нормальное уравнение cos α·x+cos β·y+cosγ·z-p=0). Тогда нужное расстояние вычислим по формуле: M1h2=cos α·x1+cos β·y1+cosγ·z1-p. Вывод данной формулы можно изучить в теме вычисления расстояния от точки до плоскости.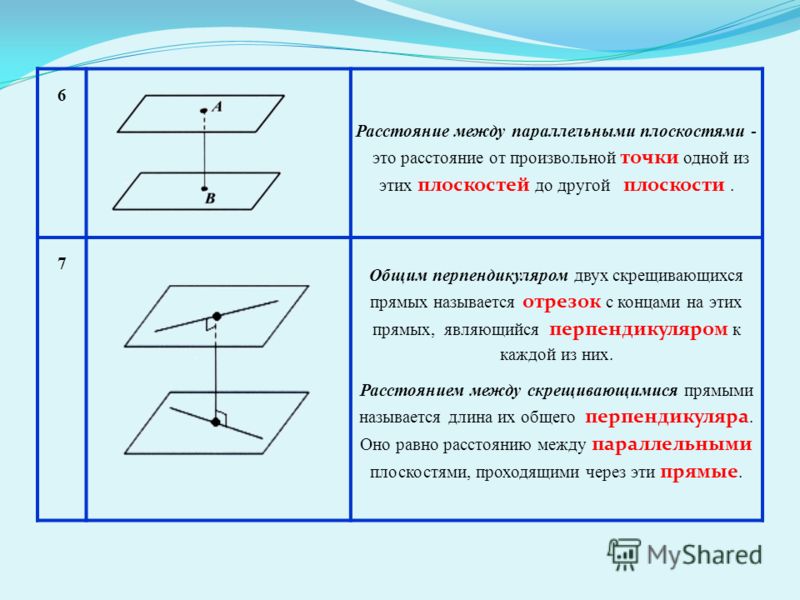
Резюмируем. Для того,чтобы определить расстояние между двумя параллельными плоскостями, необходимо:
Определение 2
— найти координаты (x1, y1, z1) некой точки М1, принадлежащей одной из исходных плоскостей;
— определить нормальное уравнение другой плоскости в виде cosα·x+cos β·y+cosγ·z-p=0;
— произвести расчет требуемого расстояние, используя формулу: M1h2=cos α·x1+cos β·y1+cosγ·z1-p.
Если в прямоугольной системе координат плоскость ϒ1 задается общим уравнением плоскости A·x+B·y+C·z+D1=0, а плоскость ϒ2 – общим уравнением A·x+B·y+C·z+D2=0, тогда расстояние между параллельными плоскостями необходимо вычислять по формуле:
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
M1h2=D2-D1A2+B2+C2
Покажем, как данная формула получена.
Пусть точка М1(x1, y1, z1) принадлежит плоскости ϒ1. В таком случае координаты этой точки будут отвечать уравнению плоскости A·x+B·y+C·z+D1=0, или верным будет равенство: A·x1+B·y1+C·z1+D1=0.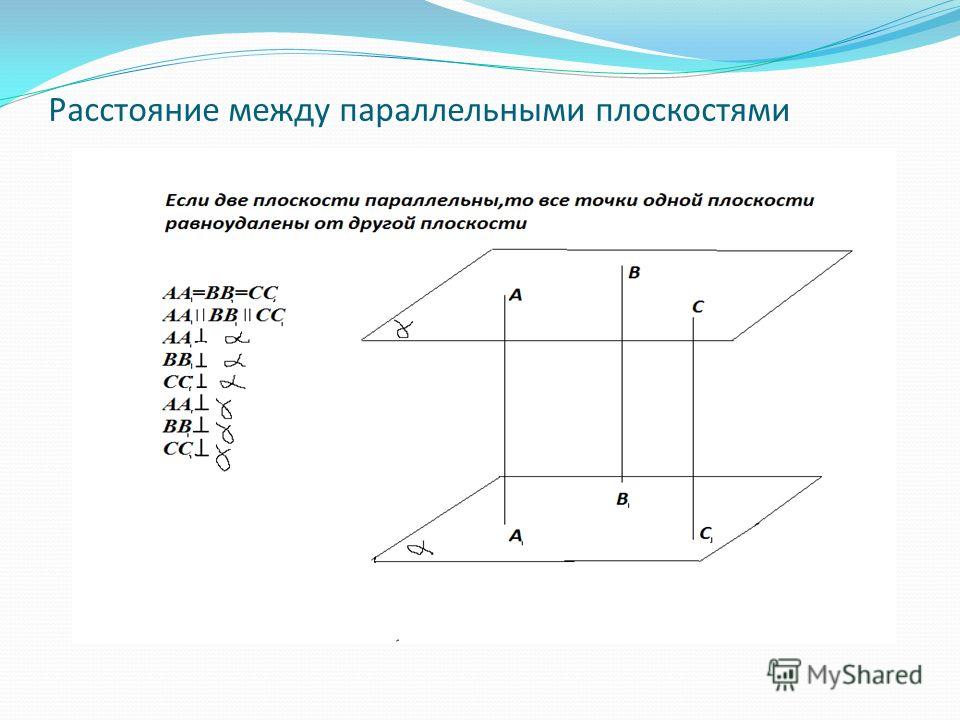 Отсюда получим: A·x1+B·y1+C·z1+D1=0. Полученное равенство нам еще пригодится.
Отсюда получим: A·x1+B·y1+C·z1+D1=0. Полученное равенство нам еще пригодится.
Плоскость ϒ2 будет описываться нормальным уравнением плоскости A·x+B·y+C·z+D2A2+B2+C2=0 или -A·x+B·y+C·z+D2A2+B2+C2=0 (в зависимости от знака числа D2). Однако при любом значение D2 расстояние |М1Н1| возможно рассчитать, используя формулу:
M1h2=A·x1+B·y1+C·z1+D2A2+B2+C2=A·x1+B·y1+C·z1+D2A2+B2+C2
Теперь задействуем полученное ранее равенство A·x1+B·y1+C·z1=-D1 и преобразуем формулу:
M1h2=-D1+D2A2+B2+C2=D2-D1A2+B2+C2
Пример 1
Даны две параллельные плоскости ϒ1 и ϒ2, описываемые уравнениями x16+y-14+z143=1 и 3x-2y+23z-20=0 соответственно. Необходимо определить расстояние между заданными плоскостями.
Решение
Решим задачу двумя способами.
- Уравнение плоскости в отрезках, которое задано в условии задачи, дает возможность определить координаты точки М1, принадлежащей плоскости, описываемой этим уравнением. Как точку М1 используем точку пересечения плоскости ϒ1 и оси Ox.
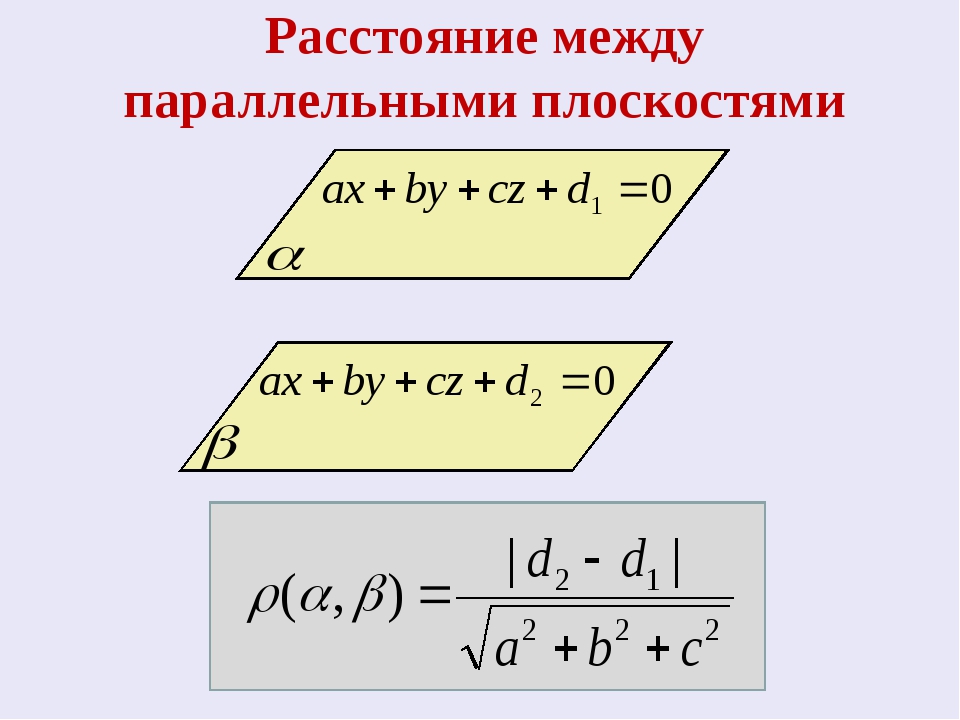 Таким образом, имеем: M116, 0, 0.
Таким образом, имеем: M116, 0, 0.
Преобразуем общее уравнение плоскости ϒ2 в нормальный вид:
3x-2y+23z-20=0⇔3x-2y+23z-2032+(-2)2+232=0⇔⇔35x-25y+235z-4=0
Вычислим расстояние |М1Н1| от точки M116, 0, 0 до плоскости 35x-25y+235z-4=0:
M1h2=35·16-25·0+235·0-4=110-4=3910
Так мы получили искомое расстояние между исходными параллельными плоскостями.
- Преобразуем уравнение плоскости в отрезках в общее уравнение плоскости:
x16+y-14+z143=1⇔6x-4y+43z-1=0
Приравняем коэффициенты при переменных x, y, z в общих уравнениях плоскостей; с этой целью умножим обе части крайнего равенства на 2:
3x-2y+23z-20=0⇔6x-4y+43z-40=0
Воспользуемся формулой для нахождения расстояния между параллельными плоскостями:
M1h2=D2-D1A2+B2+C2=-40-(-1)62+(-4)2+(43)2=39100=3910.
Ответ: 3910.
Пример 2
Даны две параллельные плоскости, описываемые уравнениями: 6x+4y-12z+3=0 и 3x+2y-6z-2=0. Необходимо найти расстояние между этими плоскостями.
Решение
Удобнее будет использовать второй способ решения подобных задач. Умножим обе части второго уравнения на 2, и коэффициенты в уравнениях плоскостей станут равны: 6x+4y-12z+3=0 и 6x+4y-12z-4=0. Теперь можно использовать формулу:
M1h2=-4-362+42+(-12)2=7196=12
Однако попробуем найти ответ и первым способом: допустим, точка M1(x1, y1, z1) принадлежит плоскости 6x+4y-12z+3=0. Соответственно, координаты этой точки отвечают уравнению плоскости, и верным будет равенство:
6×1+4y1-12z1+3=0
Пусть y1= 0, z1 = 0, тогда x1: 6×1+4·0-12·0+3=0⇔x1=-12
Таким образом, точка получает точные координаты: M1-12, 0, 0.
Преобразуем общее уравнение плоскости 3x+2y-6z-2=0 в нормальный вид:
3x+2y-6z-2=0⇔3x+2y-6z-2=032+22+-6=0⇔37x+27y-67z-27=0
В таком случае, требуемое расстояние между плоскостями равно: 37·-12+27·0-67·0-67·0-27=-12=12
Ответ: 12.
Автор:
Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Как найти расстояние между двумя параллельными плоскостями
В этой статье содержится ответ на вопрос: «Как найти расстояние между двумя параллельными плоскостями методом координат»? Сначала дано определение расстояния между параллельными плоскостями. Далее получена формула, позволяющая вычислять расстояние между параллельными плоскостями, которые заданы в прямоугольной системе координат. В заключении разобраны решения примеров и задач на нахождение расстояния между параллельными плоскостями.
Навигация по странице.
Расстояние между двумя параллельными плоскостями – определение.
Расстояние между двумя параллельными плоскостями определяется через расстояние от точки до плоскости. Покажем, как это делается.
Рассмотрим две параллельные плоскости и . Возьмем на любой из этих плоскостей точку М1 и опустим перпендикуляр М1H1 из этой точки на другую плоскость. Длина перпендикуляра M1H1 является расстоянием между параллельными плоскостями и .
Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
Такое определение расстояния между параллельными плоскостями не случайно. Оно тесно связано со следующей теоремой.
Все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости.
Пусть нам даны две параллельные плоскости и . Чтобы доказать эту теорему нам нужно доказать, что два перпендикуляра М1H1 и M2H2 , проведенные из различных точек М1 и М2 одной из заданных параллельных плоскостей к другой плоскости, имеют одинаковую длину.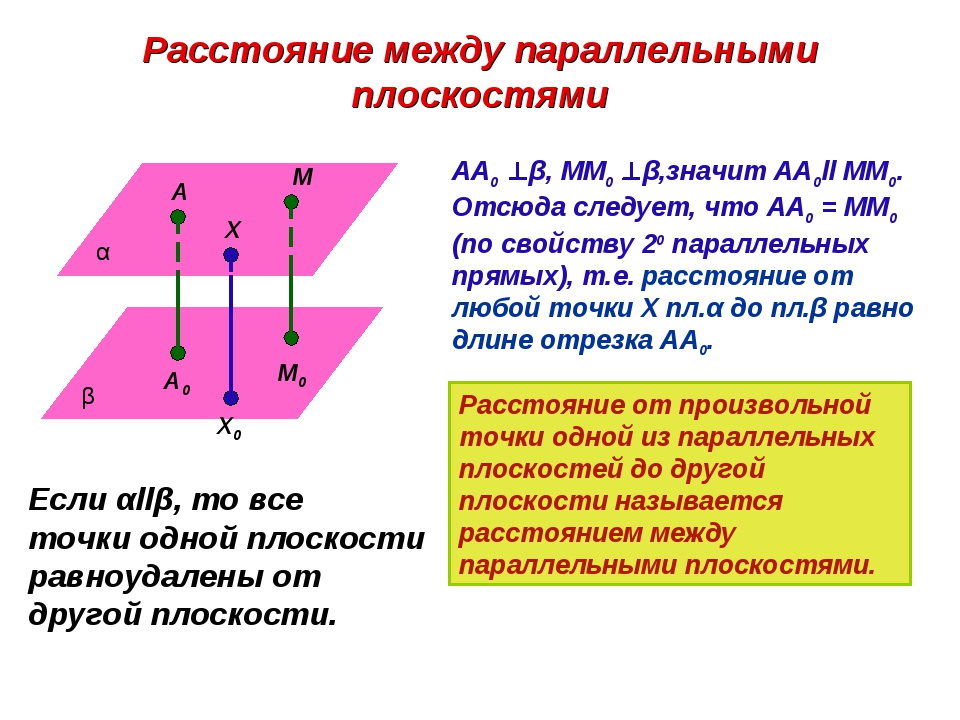
Прямые М1H1 и M2H2 параллельны, так как они перпендикулярны к одной плоскости. Из аксиомы о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, следует, что через две параллельные прямые проходит единственная плоскость (об этом мы упоминали в разделе способы задания плоскости). Тогда будем считать, что через параллельные прямые M1H1 и M2H2 проходит плоскость . Очевидно, плоскость пересекает плоскости и по прямым М1М2 и H1H2 . Эти прямые не пересекаются (в противном случае плоскости и имели бы общую точку, что невозможно, так как они параллельны по условию), значит, они параллельны. Таким образом, в четырехугольнике М1М2H2H1 противоположные стороны попарно параллельны, следовательно, М1М2H2H1 – параллелограмм (в нашем случае прямоугольник).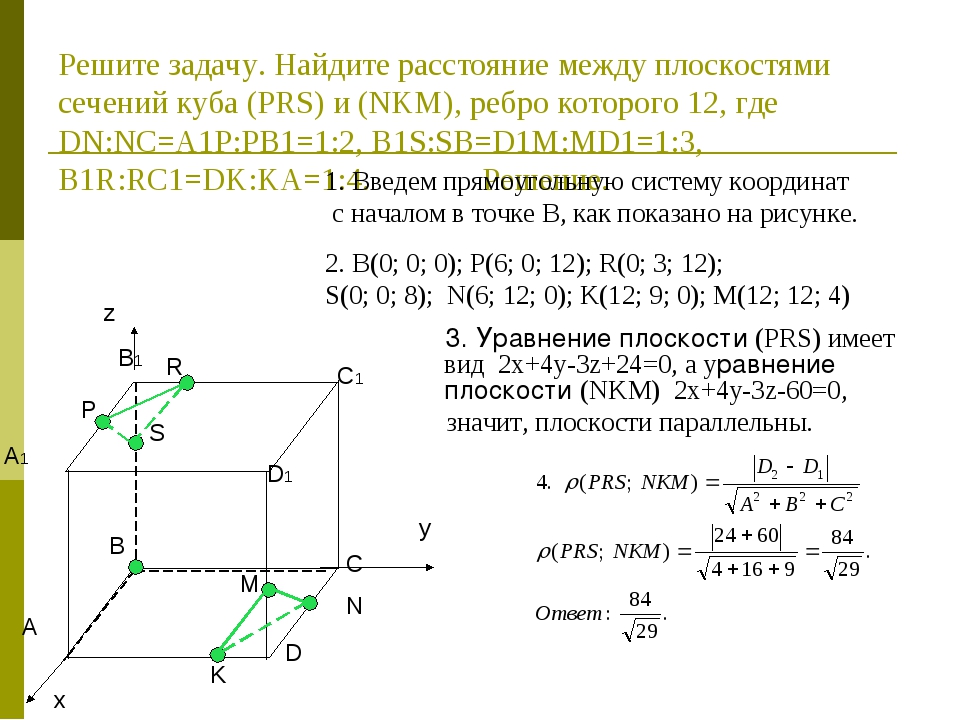 Следовательно, его противоположные стороны равны. То есть, , что и требовалось доказать.
Следовательно, его противоположные стороны равны. То есть, , что и требовалось доказать.
Следует отметить, что расстояние между параллельными плоскостями является наименьшим из расстояний между произвольными точками этих параллельных плоскостей.
Нахождение расстояния между параллельными плоскостями – теория, примеры, решения.
Переходим к вопросу нахождения расстояния между параллельными плоскостями.
На уроках геометрии в 10-11 классах расстояние между параллельными плоскостями находится примерно так: строится какой-нибудь перпендикуляр от некоторой точки одной плоскости к другой плоскости и определяется его длина. Для этого, в зависимости от условий задачи, применяется либо теорема Пифагора, либо признаки равенства или подобия соответствующих треугольников, либо определения синуса, косинуса, тангенса угла.
Если же есть возможность ввести прямоугольную систему координат и заданные параллельные плоскости описать с помощью уравнений, то расстояние между параллельными плоскостями можно отыскать методом координат. Давайте детально его разберем.
Давайте детально его разберем.
Сформулируем условие задачи.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и заданы две параллельные плоскости и . Требуется найти расстояние между этими параллельными плоскостями.
Решение будем строить на основе определения расстояния между параллельными плоскостями.
Так как в условии задачи определены плоскости и , то мы можем отыскать координаты некоторой точки М1 , лежащей на одной из заданных плоскостей (для определенности будем считать, что точка лежит в плоскости ). Также мы можем получить нормальное уравнение плоскости в виде . Тогда искомое расстояние между параллельными плоскостями равно расстоянию от точки до плоскости , которой соответствует нормальное уравнение вида . Это расстояние вычисляется по формуле (ее вывод смотрите в разделе вычисление расстояния от точки до плоскости).
Итак, чтобы найти расстояние между двумя параллельными плоскостями нужно:
- определить координаты точки М1 , лежащей в одной из заданных плоскостей;
- найти нормальное уравнение другой плоскости в виде ;
- вычислить искомое расстояние по формуле .

В частности, если в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости , а плоскости – общее уравнение плоскости вида , то расстояние между параллельными плоскостями и вычисляется по формуле .
Поясним, как была получена эта формула.
Пусть точка лежит в плоскости . Тогда координаты точки М1 удовлетворяют уравнению плоскости , то есть, справедливо равенство , откуда имеем . Это равенство мы используем позже.
Нормальное уравнение плоскости в зависимости от знака числа D2 имеет вид или . Но при любом значении числа D2 расстояние от точки до плоскости можно вычислить по формуле . Учитывая полученное выше равенство , последняя формула примет вид .
Осталось разобрать решения нескольких примеров.
Найдите расстояние между параллельными плоскостями и , которые в прямоугольной системе координат Oxyz определены уравнениями и соответственно.
Заданное уравнение плоскости в отрезках вида позволяет легко найти координаты точки М1 , лежащей в этой плоскости. В качестве точки М1 возьмем точку, в которой плоскость пересекает ось Ox , то есть, .
В качестве точки М1 возьмем точку, в которой плоскость пересекает ось Ox , то есть, .
Приведем общее уравнение плоскости к нормальному виду:
Теперь вычисляем расстояние от точки до плоскости :
.
Это и есть искомое расстояние между заданными параллельными плоскостями.
От уравнения плоскости в отрезках перейдем к общему уравнению плоскости: . Чтобы коэффициенты при переменных x , y и z в общих уравнениях плоскостей и стали равными, умножим обе части второго уравнения на два: . Теперь мы можем воспользоваться формулой для вычисления расстояния между параллельными плоскостями: .
.
Вычислите расстояние между параллельными плоскостями и .
Очевидно, при таком условии задачи удобно использовать второй способ для нахождения расстояния между параллельными плоскостями. Если умножить обе части второго уравнения плоскости на два, то коэффициенты при переменных x , y и z в уравнениях и станут равны и можно будет применить формулу: .
Несомненно, можно было использовать первый способ.
Пусть точка лежит в плоскости , тогда ее координаты удовлетворяют уравнению плоскости, то есть, справедливо равенство . Приняв , вычислим x1 : . Следовательно, .
Теперь приведем общее уравнение плоскости к нормальному виду: . Тогда искомое расстояние между параллельными плоскостями равно .
.
Формула для вычисления расстояния между плоскостями
Если заданы уравнения параллельных плоскостей A x + B y + C z + D1 = 0 и A x + B y + C z + D2 = 0, то расстояние между плоскостями можно найти, используя следующую формулу
| d = | |D2 – D1| |
| √ A 2 + B 2 + C 2 |
Примеры задач на вычисление расстояния между плоскостями
Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2
2 x + 4 y – 4 z + 18 = 0
Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:
| d = | |18 – (-6)| | = | |24| | = | 24 | = 4 |
| √ 2 2 + 4 2 + (-4) 2 | √ 36 | 6 |
Ответ: расстояние между плоскостями равно 4.
Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!
С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между плоскостями − теория
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.
Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:
- Проверка коллинеарности нормальных векторов плоскостей.
- Нахождение некоторой точки M0 на первой плоскости.
- Вычисление расстояния между точкой M0 и второй плоскостью.
Выведем формулу вычисления расстояния между плоскостями.
Запишем уравнения двух плоскостей:
Очевидно, что нормальные векторы n1 и n2 не могут быть нулевыми векторами.Если из пары коэффициентов (A1,A2),(B1,B2), (C1,C2) один нулевой а другой − нет, то нормальные векторы n1 и n2 неколлинеарны. Т.е. задача неразрешима.
| (2′) |
Нормальный вектор уравнения (2′) имеет следующий вид:
Для коллинеарности векторов n1 и n’2(или n1 и n2) необходимо и достаточно выполнение следующих равенств:
| (3) |
| (3′) |
Если удовлетворяется условие (3) (или (3′)), то векторы n1 и n’2(или n1 и n2) коллинеарны, т. е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:
| A1x+B1y+C1z+D’2=0 | (2”) |
2. Найдем некоторую точку на плоскости (1).
Легко убедится, что точка
| (4) |
принадлежит плоскости (1):
3. Расстояние от точки M0(x0, y0, z0) до плоскости (2”) вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):
| (5) |
Подставляя координаты точки M0 из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2”) (или (1) и (2)):
| (6) |
Расстояние между плоскостями − примеры и решения
Пример 1. Найти расстояние между плоскостями
Найти расстояние между плоскостями
| (7) |
| (8) |
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.
| (8′) |
Общее уравнение плоскости имеет вид:
где n=(A,B,C)− называется нормальным вектором плоскости.
Нормальный вектор плоскости (7) равен n1=(1, 2, −4), нормальный вектор плоскости (8′) равен n2=(1, 2, −4). n1=n2. Следовательно эти плоскости параллельны.
Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:
| (9) |
Упростим и решим:
Ответ. Расстояние между плоскостями равен:
Пример 2. Найти расстояние между плоскостями
| (10) |
| (11) |
Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет.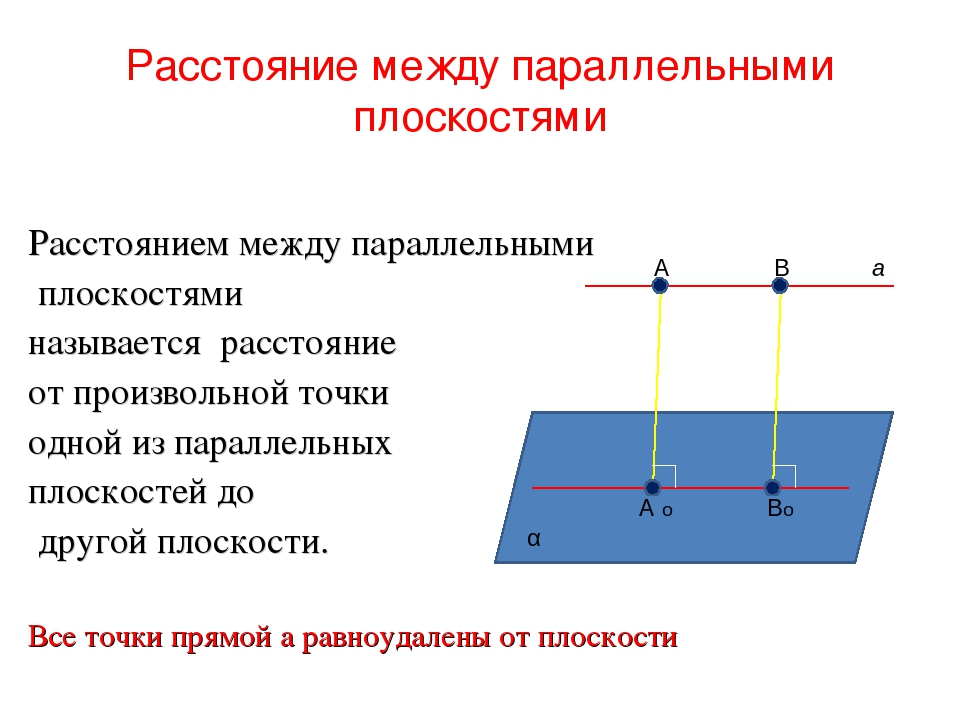 Невозможно найти расстояние между непараллельными плоскостями.
Невозможно найти расстояние между непараллельными плоскостями.
Пример 3. Найти расстояние между плоскостями
| (12) |
| (13) |
Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.
| (13′) |
Нормальный вектор плоскости (12) равен n1=(4, 2, 8), нормальный вектор плоскости (13′) равен n2=(4, 16/3, 64/3). n1≠n2. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.
Урок 16. многогранники. методы решения — Геометрия — 11 класс
1. Расстояние между двумя точками
Расстояние между точками А и В можно вычислить:
1) как длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон;
2) по формуле
p(A;B)=$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$ , где A( x1 ; y1 ; z1) , B (x2 ; y2 ; z2 );
3) по формуле $|\vec A \vec B |$ = $\sqrt{\vec A \vec B^2 }$
. 2. Расстояние от точки до прямой
2. Расстояние от точки до прямой
- Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
- Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
- Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
3. Расстояние от точки до плоскости
- Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
- Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
- Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
- Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
- Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

Методом объёмов мы называем приравнивание двух подходящих выражений для объёма, в результате чего удаётся вычислить искомую величину (расстояние или угол).
Метод объёмов можно использовать, вычисляя:
• расстояние от точки до плоскости;
• угол между плоскостями;
• расстояние между скрещивающимися прямыми.
Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми
\({\color{red}{\textbf{Факт 1. Про векторы}}}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), то вектор \(\overrightarrow{AB}\) имеет координаты \[\overrightarrow{AB} = \{x_2-x_1;y_2-y_1;z_2-z_1\}\]
\(\bullet\) Если в пространстве заданы два вектора \(\vec{a}
=\{x_1;y_1;z_1\}\) и \(\vec{b}=
\{x_2;y_2;z_2\}\), то:
\(\qquad \blacktriangleright\) сумма этих векторов \(\vec{a}+\vec{b}=\{x_1+x_2;y_1+y_2;z_1+z_2\}\)
\(\qquad \blacktriangleright\) разность этих векторов \(\vec{a}-\vec{b}=\{x_1-x_2;y_1-y_2;z_1-z_2\}\)
\(\qquad \blacktriangleright\) произведение вектора на число \(\lambda
\vec{a}=\{\lambda x_1;\lambda
y_1;\lambda z_1\}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), а точка \(O\) — середина отрезка \(AB\), то \(O\) имеет координаты \[O\left(\dfrac{x_1+x_2}2;\dfrac{y_1+y_2}2;\dfrac{z_1+z_2}2\right)\]
\(\bullet\) Длина вектора \(\vec{a}=\{x;y;z\}\) обозначается \(|\vec{a}|\) и вычисляется по формуле \[|\vec{a}|=\sqrt{x^2+y^2+z^2}\]
\(\bullet\) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.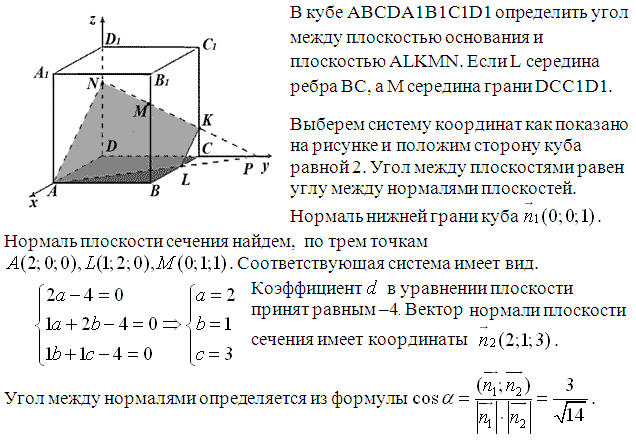
\({\color{red}{\textbf{Факт 2. Про скалярное произведение}}}\)
\(\bullet\) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: \[{\large{(\vec{a},
\vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos \angle (\vec{a},
\vec{b})}}\] На рисунке показано, что такое угол между векторами:
\(\bullet\) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: \[(\vec{a}, \vec{b})=0 \quad\Leftrightarrow\quad
\vec{a}\perp \vec{b}\]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: \[|\vec{a}|=\sqrt{(\vec{a},
\vec{a})}\]
III. Переместительный закон: \[(\vec{a}, \vec{b})=(\vec{b},
\vec{a})\]
IV. Распределительный закон: \[(\vec{a}+\vec{b},
\vec{c})=(\vec{a}, \vec{c})+(\vec{b}, \vec{c})\]
V. 2_2}}}}\]
2_2}}}}\]
\({\color{red}{\textbf{Факт 3. Про уравнение плоскости}}}\)
\(\bullet\) Если \(\vec{n}=\{a;b;c\}\) – нормаль к плоскости, то уравнение плоскости имеет вид \[ax+by+cz+d=0\] Для того, чтобы найти \(d\), нужно подставить в уравнение плоскости вместо \(x, y, z\) координаты любой точки, лежащей в этой плоскости.
Пример: если \(\vec{n}=\{1;2;3\}\) – нормаль к плоскости, \(O(4;5;6)\) – точка из плоскости, то справедливо: \(1\cdot 4+2\cdot 5+3\cdot
6+d=0\), откуда \(d=-32\), следовательно, уравнение плоскости имеет вид \(x+2y+3z-32=0\).
\(\bullet\) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть \(A(1;0;0), \
B(0;3;4), \ C(2;0;5)\) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: \[\begin{cases}
1\cdot a+0\cdot b+0\cdot c+d=0\\
0\cdot a+3\cdot b+4\cdot c+d=0\\
2\cdot a+0\cdot b+5\cdot c+d=0\end{cases} \quad\Rightarrow\quad
\begin{cases}
d=-a\\
3b+4c-a=0\\
a+5c=0\end{cases}\quad\Rightarrow\quad \begin{cases} d=-a\\
a=-5c\\
b=-3c\end{cases}\quad\Rightarrow\quad\begin{cases}a=-5c\\
b=-3c\\
d=5c\end{cases}\] Следовательно, уравнение плоскости имеет вид: \[-5c\cdot x-3c\cdot y+c\cdot z+5c=0\] Можно разделить обе части на \(c\), так как \(c\ne 0\) (иначе \(a=b=c=d=0\)), следовательно, уравнение плоскости имеет вид \[-5x-3y+z+5=0\]
\({\color{red}{\textbf{Факт 4. 2}}\]
2}}\]
\(\bullet\) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
| Две точки |
Определение расстояния: |
| Точка, лежащая на прямой |
Расстояние равно 0. |
| Точка, не лежащая на прямой |
Определение расстояния: |
| Две параллельные прямые параллельные прямые |
Определение расстояния: |
| Две пересекающиеся прямые пересекающиеся прямые |
Расстояние равно 0. |
| Две скрещивающиеся прямые скрещивающиеся прямые |
Определение расстояния: |
| Точка, лежащая на плоскости |
Расстояние равно 0. |
| Точка, не лежащая на плоскости |
Определение расстояния: |
Расстояние равно 0. |
Расстояние равно 0. |
Определение расстояния: |
| Две пересекающиеся плоскости |
Расстояние равно 0. |
| Две параллельные плоскости |
Определение расстояния: |
| Парабола y = a x2 + b x + c, не пересекающая ось абсцисс, и ось абсцисс |
Определение расстояния: |
| Окружность и не пересекающая ее прямая |
Определение расстояния: |
| Две непересекающиеся окружности, каждая из которых лежит вне другойДве непересекающиеся окружности, каждая из которых лежит вне другой |
Определение расстояния: |
Гипербола где k – любое, отличное от нуля, число, и ось абсцисс. |
Расстояние между гиперболой и осью абсцисс считается равным 0. поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой). |
Расстояние между прямыми и плоскостями
Под расстоянием между двумя любыми геометрическими фигурами понимается расстояние между их ближайшими точками (если такие существуют). Поэтому, чтобы определить расстояние между прямыми и плоскостями, надо знать их ближайшие точки.
1. Расстояние между параллельными плоскостями.
Определение. Расстоянием между параллельными плоскостями
называют длину перпендикуляра, опущенного из любой точки одной
плоскости на другую (рис. 43). В самом деле, все перпендикуляры между
двумя параллельными плоскостями равны, потому что отрезки
параллельных прямых, заключенные между параллельными
плоскостями, равны (теорема 10).
Примером расстояния между параллельными плоскостями может служить высота призмы, высота потолка в комнате и т. д.
д.
2. Расстояниемежду плоскостью и параллельной ей прямой.
Определение. Расстоянием между плоскостью и параллельной
ей прямой называется длина перпендикуляра, проведенного из любой точки прямой к плоскости (рис. 44).
. Расстояние между скрещивающимися прямыми.Сначала дадим понятие общего перпендикуляра скрещивающихся прямых.
Определение. Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых и перпендикулярный к каждой из них.
На рисунке 45 отрезок АВ — общий перпендикуляр скрещивающихся прямых оиЬ. Объясним это.
Скрещивающиеся прямые аи Ъ лежат в параллельных плоскостях. Обозначим их соответственно а, р. Пусть проекция а1 прямой а на плоскости р пересекает прямую Ъ в некоторой точке В. Точка В является проекцией на Р некоторой точки А е а. Отрезок АВ будет общим перпендикуляром плоскостей а и р, а поэтому и общим перпендикуляром прямых а и 6. Если теперь возьмем любой другой отрезок XY (Xea, Yeb), то |АВ|<|ХУ|.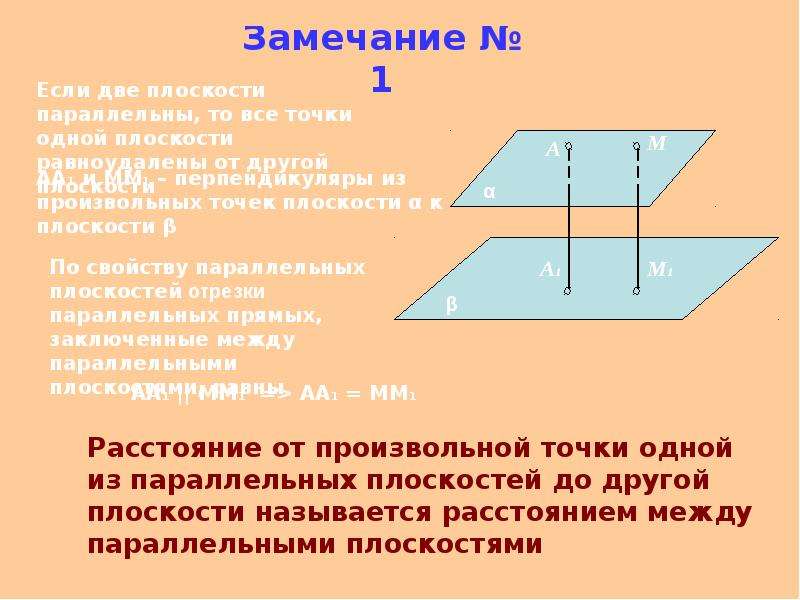 Поэтому расстояние между скрещивающимися прямыми связано с их общим перпендикуляром.
Поэтому расстояние между скрещивающимися прямыми связано с их общим перпендикуляром.
Определение. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Вопросы и задания
1.Как можно найти расстояние между параллельными плоскостями?
2. Что такое расстояние между плоскостью и параллельной ей прямой?
3. Что такое общий перпендикуляр скрещивающихся прямых?
4. Как можно найти расстояние между скрещивающимися прямыми?
Задачи
А
128. Расстояние между двумя параллельными плоскостями равно h. Отрезок длины а своими концами упирается в эти плоскости. Найдите проекцию отрезка на каждую из плоскостей.
129. Из концов отрезка АВ, не пересекающего плоскость, опущены
перпендикуляры. Их длины 7 и 10 см, а расстояние между их
основаниями равно 4 см. Найдите длину АВ.
130. Концы данного отрезка, не пересекающего плоскость, удалены
от нее на 3 и 5 см. Как удалена от плоскости точка: 1) делящая
данный отрезок пополам; 2) в отношении 3 : 7?
131. Ребро куба равно а. Найдите расстояние между скрещивающи
Ребро куба равно а. Найдите расстояние между скрещивающи
мися диагоналями его противоположных граней.
132. Два отрезка, длины которых 13 и 37 дм, упираются концами в
две параллельные плоскости. Проекция меньшего из них на
плоскость равна 5 дм. Найдите длину проекции большего отрезка.
В
133. Отрезок длиной 10 дм пересекает плоскость, концы его удалены
от плоскости на 5 и 3 дм. Найдите длину проекции отрезка на
плоскость.
134. Из точки к плоскости проведены две наклонные, равные 17 и
10 м. Разность проекций этих наклонных равна 9 м. Найдите
расстояние от точки до плоскости.
13 5. К плоскости треугольника из центра вписанной в него окружности радиусом 0,4дм восстановлен перпендикуляр длиной 0,3 дм. Найдите расстояние от конца этого перпендикуляра до сторон треугольника.
136. Из вершины квадрата опущен перпендикуляр к его плоскости. Расстояния от конца этого перпендикуляра до других вершин квадрата равны тип (т<п).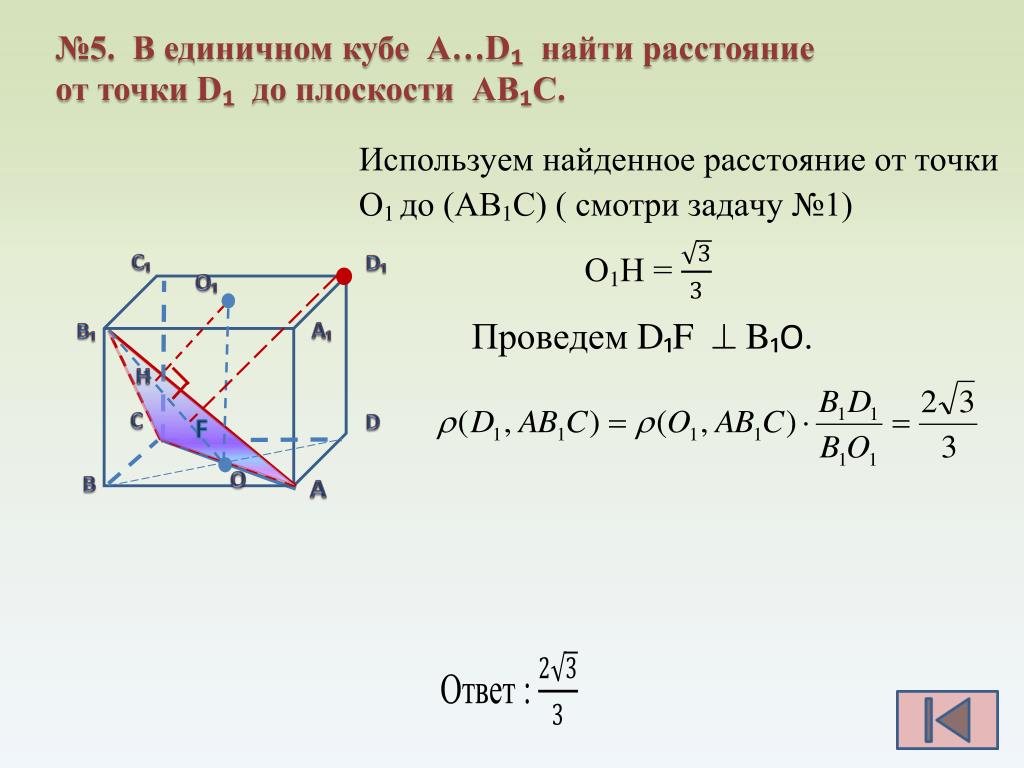 Найдите длину перпендикуляра и сторону квадрата.
Найдите длину перпендикуляра и сторону квадрата.
137. Стороны равностороннего треугольника равны 6 дм. Найдите
расстояние до плоскости треугольника от точки, которая нахо
дится на расстоянии 4 дм от каждой из его вершин.
138. Стороны треугольника равны 2, 6,5 и 7,5 дм. Из вершины
большего угла восстановлен перпендикуляр длиной 6 дм к его
плоскости. Найти расстояние от концов перпендикуляра до
большей стороны треугольника.
139. Ребро правильного тетраэдра а. Найдите расстояние между его
противоположными ребрами.
140. Из вершины А прямоугольника ABCD восстановлен перпенди
куляр АЕ к его плоскости. Найдите длину перпендикуляра АЕ,
если его конец Е удален от вершин В, С и D на расстояния 5,11 и
10 дм.
Как найти расстояние между двумя плоскостями (видео и примеры)
Стены вашего класса, школы или дома, вероятно, вертикальны полу и потолку. Это означает, что две стены в комнате, вероятно, параллельны друг другу. Если бы вы могли представить эти две стены, бесконечно расширяющиеся в двух направлениях (ширине и длине, а не высоте), у вас были бы две плоскости на заданном расстоянии друг от друга. Вы можете математически найти расстояние между этими двумя плоскостями.
Если бы вы могли представить эти две стены, бесконечно расширяющиеся в двух направлениях (ширине и длине, а не высоте), у вас были бы две плоскости на заданном расстоянии друг от друга. Вы можете математически найти расстояние между этими двумя плоскостями.
Содержание
- Расстояние между двумя параллельными плоскостями
- шагов для определения расстояния между двумя плоскостями
- Формула расстояния точка-плоскость
- Определение расстояния между двумя плоскостями
Расстояние между двумя параллельными плоскостями
Под расстоянием между двумя параллельными плоскостями понимается кратчайшее расстояние между их поверхностями.Подумай об этом; если плоскости не параллельны, в конечном итоге они должны пересекаться. Если они пересекаются, то на этой линии пересечения у них нет расстояния — 0 расстояния — между ними. Часть вашей детективной работы — выяснить, параллельны ли две плоскости.
шагов для определения расстояния между двумя плоскостями
Пять шагов следующие:
- Запишите уравнения в стандартном формате для обеих плоскостей
- Узнать, параллельны ли две плоскости
- Определите коэффициенты a, b, c и d из уравнения одной плоскости
- Найдите точку (x1, y1, z1) в другой плоскости
- Заменить a, b, c, d, x1, y1 и z1 в формуле расстояния
Предварительно просмотрев шаги, давайте пройдемся по ним.
Шаг 1: Напишите уравнения для плоскостей в стандартном формате, ax + by + cz + d = 0, с нижними индексами, обозначающими две плоскости, 1 и 2, в наших общих уравнениях:
a1x + b1y + c1z + d1 = 0
a2x + b2y + c2z + d2 = 0
Шаг 2: Они пересекаются или параллельны? Помните, если они параллельны, ваша работа сделана! Расстояние равно 0. Сравните отношения трех идентифицированных точек каждой плоскости (a1a2, b1b2, c1c2). Две плоскости параллельны, если их отношения равны:
a1a2 = b1b2 = c1c2
Шаг 3: Определите коэффициенты a, b, c и d в одном из уравнений плоскости.Просто посмотрите на одно уравнение и извлеките эти коэффициенты, понимая, что a1 — это a (если вы используете первую плоскость), b1 — это b, и так далее.
Шаг 4: Укажите точку (x1, y1, z1) на другой плоскости. В нашей общей задаче мы используем вторую плоскость. Использование точки с двумя значениями 0 упрощает вашу работу: x = 0 = y, что дает вам:
a20 + b20 + c2z1 + d2 = 0
Решить относительно z1 (неизвестная третья точка):
c2z1 + d2 — d22 = 0 — d2 (вычесть d2 с обеих сторон)
c2z1 = 0 — d2
c2z1c2 = -d2c2 (разделить обе стороны на c2)
z1 = -d2c2
Наши три точки теперь ясны:
х1 = 0
у1 = 0
z1 = -d2c2
Не зацикливайтесь на переменных в нашем общем примере. У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений.
У вас будут реальные числа в реальных уравнениях, что значительно упростит внешний вид этих уравнений.
Шаг 5: Подставьте и подставьте обнаруженные значения в формулу расстояния. Вы нашли a, b, c и d на шаге 3 выше. Это коэффициенты уравнения одной плоскости. Вы нашли x1, y1 и z1 на шаге 4 выше. Это координаты точки на другой плоскости. Подставьте найденные значения в формулу расстояния точка-плоскость.
Формула расстояния точка-плоскость
D = ax1 + by1 + cz1 + da2 + b2 + c2
Определение расстояния между двумя плоскостями
Вот два уравнения для самолетов:
3x + 4y + 5z + 9 = 0
9x + 12y + 15z — 27 = 0
Выполните пять шагов:
- Напишите уравнения в стандартном формате для обеих плоскостей — мы уже сделали это за вас!
- Узнать, параллельны ли две плоскости:
- Определите коэффициенты a, b, c и d из уравнения одной плоскости:
- Найдите точку (x1, y1, z1) в другой плоскости, которая в данном случае является первой плоскостью:
- Подставьте a, b, c, d, x1, y1 и z1 в формулу расстояния:
39 = 412 = 515 = 13
Две плоскости параллельны.
Вместо того, чтобы повторять варианты из нашего общего примера, мы будем использовать второе уравнение, давая нам следующие значения:
а = 9
б = 12
с = 15
д = -27
Попробуйте использовать x = y = 0 для двух координат точки и решите для z1:
3x + 4y + 5z + 9 = 0
3 (0) + 4 (0) + 5 (z1) + 9 = 0
5 (z1) + 9 = 0
5 (z1) + 9-9 = 0-9 (вычесть d1 с обеих сторон)
5 (z1) = -9
(5 (z1)) / 5 = -9/5 (разделите обе стороны на c1)
z1 = -9/5 = -1. 8
8
Наши три точки на первом плане:
х = 0
у = 0
г = -9/5 = -1,8
Расстояние между нашими двумя плоскостями примерно 2,54.
Следующий урок:
Формула расстояния
векторных пространств — Минимальное расстояние между 2 плоскостями
Вопрос (часть (ii)) выше ставит под сомнение мою способность мыслить векторами.Решение этого вопроса вызывает у меня некоторое замешательство, и я был бы признателен, если бы на него пролили свет. Вот каков был мой мыслительный процесс:
- Кратчайшее расстояние между двумя точками — прямая. Это должно означать, что для решения этой проблемы нормальная линия для плоскости 1 должна быть скаляром нормальной линии для плоскости 2. Если бы это было не так, я не знаю, как бы я мог это решить.
К счастью, это так, и когда я попытался решить проблему, я установил следующее:
$ 2 \ overline n_1 = \ overline n_2 $
Это верно при рассмотрении уравнений плоскости.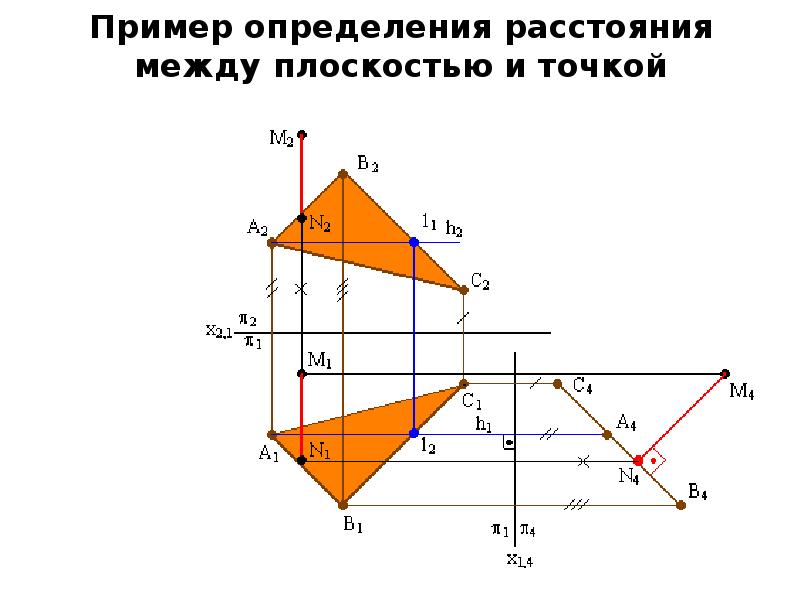 Теперь моя следующая мысль:
Теперь моя следующая мысль:
- Я могу создать векторное уравнение для прямой, чтобы найти точку на любой плоскости, используя любой $ n $ в качестве параллельного вектора.
- Я могу произвольно выбрать точку на одной из плоскостей и использовать ее как $ a $ в $$ r = a + t (n) $$
- Если я установлю $ t = 2 $, тогда я получу $ n_2 $, если решу $ r $ сейчас, и поэтому я, возможно, должен получить координаты для другой точки, которая мне понадобится на плоскости 2.
Я выбрал точку на плоскости 1 (1, 2, 1). Решение для $ r $ с $ t (n) = n_2 $ дает мне (3,6, -3).
Хорошо, это пункт 2. Если я возьму разницу между этими двумя точками, а именно $ — (1, 2, 1) + (3, 6, -3) $, у меня будет вектор, который мне нужен. Принимая во внимание его величину, я должен получить это расстояние.
Когда все было сказано и сделано, мое расстояние оказалось равным 6. Тем не менее, вот изображение решения, приложенное к этому рабочему листу:
Должен сказать, я запутался. 2 $.Они также использовали декартово уравнение своей линии для разных вещей. У меня следующие вопросы:
2 $.Они также использовали декартово уравнение своей линии для разных вещей. У меня следующие вопросы:
- Есть ли какие-нибудь ошибки в моей логике?
- Почему здесь подразумевается, что мы решаем на $ t $?
- Где расходятся мой ответ и мой ответ лектора? Я понимаю, что наша методология была явно другой, но я не совсем уверен в мыслительном процессе, который стоит за его ответом.
Как найти расстояние между двумя плоскостями — Видео и стенограмма урока
Определение расстояния между двумя плоскостями
Подумайте о стене.Стена — это ровная поверхность. Если бы стена продолжалась во всех направлениях до бесконечности, у нас была бы плоскость . Стена обычно имеет вертикальную ориентацию, но плоскость может иметь любую ориентацию. Расстояние между двумя плоскостями — это кратчайшее расстояние между поверхностями плоскостей.
Давайте найдем это расстояние!
Шаг 1: Напишите уравнения для каждой плоскости в стандартном формате.
Стандартный формат, который мы будем использовать: a x + b y + c z + d = 0.Для двух уравнений имеем:
Шаг 2: Определите, параллельны ли плоскости.
Если плоскости не параллельны, они в конечном итоге пересекутся, потому что каждая плоскость простирается до бесконечности во всех направлениях. Таким образом, если плоскости не параллельны, расстояние между плоскостями равно нулю, и мы можем остановить процесс определения расстояния. Чтобы узнать, параллельны ли плоскости, проверьте отношения a 1/ a 2, b 1/ b 2 и c 1/ c 2.
Плоскости параллельны, если эти отношения равны.
Если плоскости параллельны, мы переходим к следующему шагу.
Шаг 3: Из одного из уравнений плоскости определите коэффициенты
a , b , c и d .
Эта деталь очень проста. Допустим, мы выбрали первое плоское уравнение. Затем
Шаг 4. Найдите точку (
x 1, y 1, z 1) в другой плоскости.
Подойдет любая точка. Хороший выбор обычно — позволить любой из двух координат равняться нулю, а затем решить для третьей координаты. Например, если x = y = 0, это означает следующее:
и решение для z 1 означает:
Таким образом,
- x 1 = 0
- y 1 = 0
- z 1 = — d 2/ c 2
Примечание. Эта часть может показаться сложной из-за всех буквенных переменных.На практике у нас есть числа, и работа выглядит намного проще. Мы покажем это позже в разделе приложений.
Шаг 5: Подставьте в формулу расстояния и упростите.
Замените a , b , c , d , x 1, y 1 и z 1 в формуле для определения расстояния, D, между двумя плоскостями.
Видео с вопросом: Определение расстояния между двумя плоскостями
Стенограмма видео
Найдите расстояние между двумя плоскостями: отрицательное 𝑥 минус два 𝑦 минус два 𝑧 равно отрицательным двум, а отрицательное два 𝑥 минус четыре 𝑦 минус четыре 𝑧 равно трем.
В этом вопросе нас просят найти расстояние между двумя заданными самолетами. И чтобы сделать это, первый вопрос, который мы можем задать, заключается в том, что именно означает расстояние между двумя плоскостями. Когда нас просят найти расстояние между двумя плоскостями или двумя линиями, или точками, и плоскостями, и точками, и прямыми, это всегда означает перпендикулярное расстояние. Это потому, что перпендикулярное расстояние между двумя из этих объектов всегда будет кратчайшим расстоянием между этими двумя объектами. И очень полезно знать кратчайшее расстояние между двумя объектами.
И очень полезно знать кратчайшее расстояние между двумя объектами.
Но мы не знаем, как найти расстояние по перпендикуляру между двумя плоскостями. Поэтому вместо этого нам нужно получить представление о том, что происходит. На самом деле, есть три возможности. Первая возможность: нам дадут два совершенно одинаковых самолета. Конечно, если нам даны две совершенно одинаковые плоскости, то эти плоскости пересекаются в каждой отдельной точке, потому что это одна и та же плоскость. Так что расстояние будет просто нулем.
Второй вариант — две непараллельные плоскости. И точно так же, как с двумя непараллельными линиями, если две плоскости не параллельны, то они пересекутся. Фактически, они пересекаются по всей линии. Так что в этом случае расстояние также будет равно нулю. Один из способов показать это — решить эти уравнения как одновременные. Тогда мы могли бы найти уравнение линии пересечения.
Третий вариант: нам даны две параллельные плоскости.И здесь стоит указать, когда мы говорим, что они параллельны, мы также имеем в виду, что это не одна и та же плоскость, поскольку мы уже рассмотрели это в первом варианте.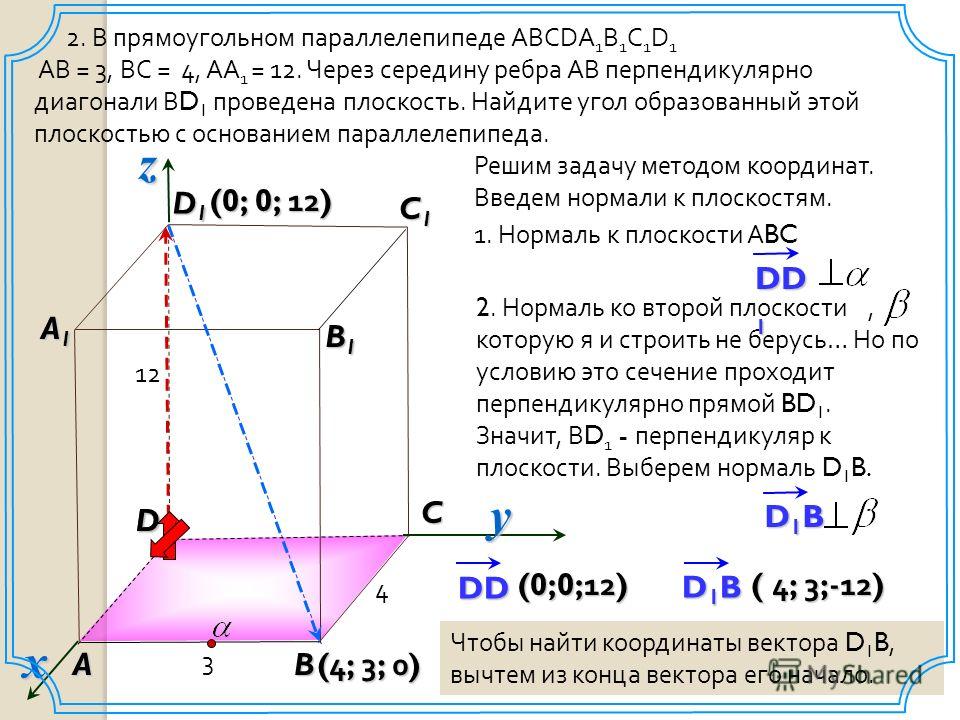 И этот вариант немного посложнее. Как мы собираемся найти расстояние между двумя параллельными плоскостями? Поскольку плоскости параллельны, мы, в частности, знаем, что они не пересекутся, поэтому расстояние между ними должно быть больше нуля. Если бы мы выбрали точку на любой из наших двух плоскостей, мы могли бы вычислить перпендикулярное расстояние между точкой и плоскостью, просто используя нашу формулу для вычисления расстояния между точкой и плоскостью.
И этот вариант немного посложнее. Как мы собираемся найти расстояние между двумя параллельными плоскостями? Поскольку плоскости параллельны, мы, в частности, знаем, что они не пересекутся, поэтому расстояние между ними должно быть больше нуля. Если бы мы выбрали точку на любой из наших двух плоскостей, мы могли бы вычислить перпендикулярное расстояние между точкой и плоскостью, просто используя нашу формулу для вычисления расстояния между точкой и плоскостью.
Но тогда возникает новый вопрос. Как мы узнаем, какую точку выбрать? Фактически, мы можем показать, что не имеет значения, какую точку мы выберем. Все они будут на одинаковом расстоянии. Представьте, что вместо этого мы выбрали другую точку на нашем самолете. И снова мы можем рассчитать перпендикулярное расстояние, используя нашу формулу. И мы знаем, что оба они образуют прямые углы с нашей плоскостью, потому что это перпендикулярное расстояние. Затем мы хотим подумать о четырехугольнике, который мы получили бы, соединив все четыре эти вершины вместе. Используя тот факт, что эти прямые параллельны, и тот факт, что они перпендикулярны, мы могли бы также показать, что они должны быть прямыми углами. Следовательно, это просто прямоугольник. И мы знаем, что противоположные стороны прямоугольника должны быть равны. Так что не имеет значения, какую точку мы можем выбрать. Мы можем выбрать любую точку.
Используя тот факт, что эти прямые параллельны, и тот факт, что они перпендикулярны, мы могли бы также показать, что они должны быть прямыми углами. Следовательно, это просто прямоугольник. И мы знаем, что противоположные стороны прямоугольника должны быть равны. Так что не имеет значения, какую точку мы можем выбрать. Мы можем выбрать любую точку.
Итак, чтобы ответить на этот вопрос, нам сначала нужно определить, в какой из трех ситуаций мы находимся. И для этого было бы проще записать обе наши плоскости в векторной форме.Начнем с первой плоскости отрицательной 𝑥 минус два 𝑦 минус два 𝑧 равно отрицательной двойке. Во-первых, мы можем найти вектор, нормальный к нашей плоскости, взяв коэффициенты при 𝑥, 𝑦 и. Таким образом, мы получаем вектор нормали отрицательный один, отрицательный два, отрицательный два. И это в точности то же самое, что сказать, что наш вектор 𝐫 — это вектор 𝑥, 𝑦, 𝑧. И теперь мы можем видеть из нашего уравнения, что скалярное произведение между этими двумя вещами должно быть равно отрицательным двум.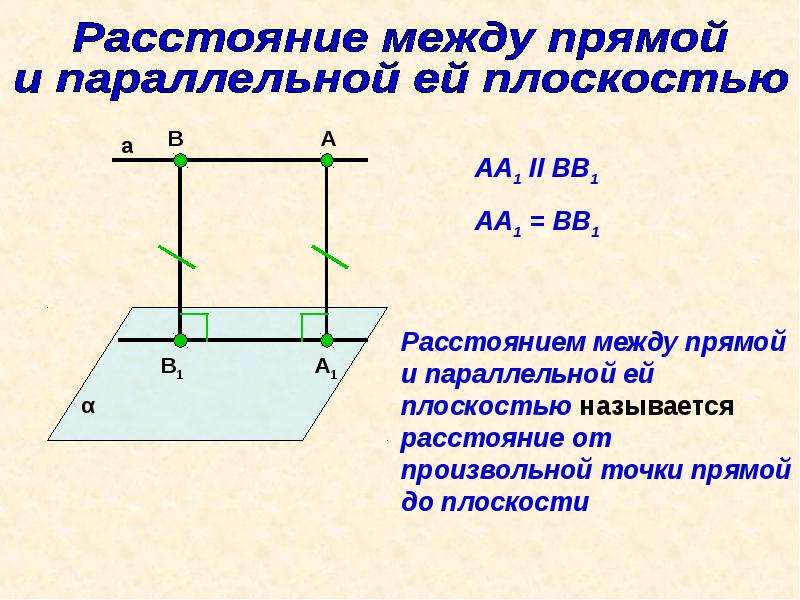 Таким образом, это дает нам векторную форму нашей первой плоскости, 𝐫 точка отрицательная одна, отрицательная два, отрицательная два должны быть равны отрицательным двум.
Таким образом, это дает нам векторную форму нашей первой плоскости, 𝐫 точка отрицательная одна, отрицательная два, отрицательная два должны быть равны отрицательным двум.
Затем мы можем проделать то же самое с другим нашим самолетом. Сделав то же самое, что и раньше, мы получим векторное уравнение этой плоскости: точка отрицательное два, отрицательное четыре, отрицательное четыре равно трем. Итак, мы хотим определить, в какой из трех ситуаций мы находимся. И самый простой способ сделать это — начать с проверки, параллельны ли наши две плоскости. И для этого нам нужно помнить, как проверять параллельность двух плоскостей по их векторным формам.
Напомним, что две плоскости будут параллельны, если их нормальные векторы ненулевые скалярные кратные друг другу.И мы видим, что в данном случае это действительно так. Мы можем увидеть, если мы установим наш скаляр равным половине, тогда половина, умноженная на вектор, отрицательный два, отрицательный четыре, отрицательный четыре, равняется векторному отрицательному единице, отрицательному двум, отрицательному двум. Таким образом, мы можем исключить наш второй вариант, потому что знаем, что плоскости указывают в одном направлении. Однако технически нам нужно быть осторожными. Нам все еще нужно убедиться, что это не совсем один и тот же самолет.
Таким образом, мы можем исключить наш второй вариант, потому что знаем, что плоскости указывают в одном направлении. Однако технически нам нужно быть осторожными. Нам все еще нужно убедиться, что это не совсем один и тот же самолет.
И самый простой способ сделать это — умножить второе уравнение на наш скаляр, равный половине.Если мы умножим обе части этого уравнения пополам, мы получим следующее уравнение для нашей плоскости. Теперь помните, половина, умноженная на наш вектор нормали, равна вектору нормали другой нашей плоскости. Но мы замечаем, что три, умноженные на половину, не равны двум отрицательным. Итак, эти уравнения не представляют одну и ту же плоскость. На самом деле они параллельны. Итак, все, что нам нужно сделать, это найти расстояние между любой точкой на любой из наших плоскостей и другой плоскостью. И для этого мы начнем с освобождения места.
Теперь нам нужно вспомнить, как мы находим расстояние по перпендикуляру между точкой и плоскостью. Напомним, расстояние по перпендикуляру между точкой 𝑥 один, 𝑦 один, 𝑧 один и плоскостью 𝑎𝑥 плюс 𝑏𝑦 плюс 𝑐𝑧 плюс 𝑑 равно нулю, определяется расстоянием, прописным 𝐷 равно абсолютному значению 𝑎𝑥 один плюс 𝑏𝑦 один. плюс 𝑐𝑧 один плюс 𝑑 все делится на квадратный корень из в квадрате плюс 𝑏 в квадрате плюс 𝑐 в квадрате. В нашем случае точка 𝑃 может быть любой точкой на любой из двух наших плоскостей.
плюс 𝑐𝑧 один плюс 𝑑 все делится на квадратный корень из в квадрате плюс 𝑏 в квадрате плюс 𝑐 в квадрате. В нашем случае точка 𝑃 может быть любой точкой на любой из двух наших плоскостей.
Итак, нам просто нужно найти точку на любой из наших двух плоскостей.Мы можем сделать это, решив любое из уравнений. Мы могли бы попробовать, что 𝑥 равно нулю, 𝑦 равно единице, а 𝑧 равно нулю в нашей первой плоскости. Подставляя эти значения в нашу плоскость, мы видим, что отрицательные два равны отрицательным двум. Итак, эта точка находится на нашем самолете. Итак, мы установим наше значение one равным нулю, наше значение 𝑦 one равным единице и наше значение 𝑧 one равным нулю. Теперь мы почти готовы использовать нашу формулу, чтобы найти это расстояние. Нам просто нужно найти значения 𝑎, 𝑏, 𝑐 и строчные.
И мы можем сделать это прямо из декартова уравнения нашей второй плоскости. Мы видим, что 𝑎 равно отрицательным двум, 𝑏 равно отрицательным четырем, а 𝑐 равно отрицательным четырем. Однако нам нужно быть немного осторожными, потому что наша константа указана в правой части нашего уравнения. Однако в нашей формуле он находится в левой части уравнения. Значит, нам нужно поменять знак этого. Наше значение 𝑑 будет равно трем отрицательным.
Однако в нашей формуле он находится в левой части уравнения. Значит, нам нужно поменять знак этого. Наше значение 𝑑 будет равно трем отрицательным.
Теперь все, что осталось сделать, это подставить наши значения 𝑎, 𝑏, 𝑐, строчные 𝑑 и 𝑥 one, 𝑦 one, 𝑧 one в нашу формулу.Мы получаем расстояние, заглавная буква, равняется абсолютному значению отрицательного двойного нуля плюс отрицательного четырех умноженного на единицу плюс отрицательное четыре, умноженного на ноль минус три, все деленное на квадратный корень из отрицательных двух в квадрате плюс отрицательные четыре в квадрате плюс отрицательные четыре в квадрате. . Вычисляя выражение в нашем числителе, мы получаем абсолютное значение минус семь. И вычисляя выражение в нашем знаменателе, мы получаем квадратный корень из 36.
И, конечно, абсолютная величина отрицательной семи равна семи, а квадратный корень 36 равен шести.Итак, мы просто получаем, что это семь на шесть. И помните, это расстояние, поэтому мы можем сказать, что это семь на шесть единиц длины. Таким образом, мы смогли показать, что расстояние между двумя плоскостями отрицательное 𝑥 минус два 𝑦 минус два 𝑧 равно отрицательным двум, а отрицательное два 𝑥 минус четыре 𝑦 минус четыре 𝑧 равно трем, равно семи на шесть единиц длины.
Таким образом, мы смогли показать, что расстояние между двумя плоскостями отрицательное 𝑥 минус два 𝑦 минус два 𝑧 равно отрицательным двум, а отрицательное два 𝑥 минус четыре 𝑦 минус четыре 𝑧 равно трем, равно семи на шесть единиц длины.
Расстояние между двумя плоскостями
Векторы: расстояние между двумя плоскостями
Напомним, что уравнение плоскости через точку A с положением
вектор {\ bf a}, перпендикулярный вектору {\ bf n}, равен
$$ {\ bf r} \ cdot {\ bf n} = {\ bf a} \ cdot {\ bf n}.$$
Сейчас,
$$ {\ bf a} \ cdot {\ bf n} = | {\ bf a} | \, | {\ bf n} | \ cos \ theta, $$
где \ theta — угол между {\ bf a} и {\ bf n}. Но, как
На рисунке показано, что расстояние между плоскостью и началом координат равно
$$ | {\ bf a} | \, \ cos \ theta. $$
Отсюда следует, что по уравнению плоскости мы можем получить расстояние между
это и начало координат путем деления на величину вектора направления:
расстояние между самолетами
$$ {\ bf r} \ cdot {\ bf n} = D $$
и происхождение
$$ \ frac {D} {| {\ bf n} |}. $$
$$
Обратите внимание, что если вектор нормали направлен от плоскости при размещении в
от начала координат, это расстояние будет отрицательным.
Обратите внимание, что если у нас есть две параллельные плоскости, мы можем вычислить расстояние
между ними путем вычитания их расстояний от начала координат.
И наконец, обратите внимание, что, имея плоскость и точку, легко вычислить расстояние.
между ними, найдя уравнение параллельной плоскости, проходящей через точку.
Например, чтобы найти расстояние между плоскостью \ Pi по уравнению
$$ {\ bf r} \ cdot (2 \, {\ bf i} +3 \, {\ bf j} — {\ bf k}) = 5 $$
и точку (-1,1,2), сначала отметим, что плоскость, параллельная \ Pi
но содержащий (-1,1,2) имеет уравнение
$$ {\ bf r} \ cdot (2 \, {\ bf i} +3 \, {\ bf j} — {\ bf k}) = (- {\ bf i} + {\ bf j} +2 \, {\ bf k}) \ cdot (2 \, {\ bf i} +3 \, {\ bf j} — {\ bf k}) = — 1.$$
Назовем этот самолет \ Pi ‘. Теперь расстояние между \ Pi и началом координат
равно 5 / \ sqrt {4 + 9 + 1} = 5 / \ sqrt {14}, а между \ Pi ‘и началом координат
-1 / \ sqrt {14}: то есть 1 / \ sqrt {14} в противоположном направлении. Расстояние
Расстояние
между плоскостями поэтому 6 \ sqrt {14}.
Рисунок 1. Расстояние между плоскостью и началом координат
Расстояние между точкой и плоскостью
Расстояние между точкой и плоскостью
В этом уроке мы увидим, как вычислить расстояние между точкой и плоскостью.Мы также увидим, как вычислить расстояние между двумя параллельными линиями и плоскостями.
«Кратчайшее расстояние от точки до плоскости равно длине перпендикуляра , который начинается от точки и соединяется с плоскостью»
Другими словами, мы можем сказать, что Кратчайшее расстояние между точкой и плоскостью — это длина перпендикулярной линии от точки до плоскости.
Лучшие доступные репетиторы по математике
Первый урок бесплатно
Формула для расчета расстояния между точкой и плоскостью
Предположим, что есть плоскость
и точка P, как показано ниже:
Расстояние между
и P будет перпендикулярной линией, проведенной от точки P к плоскости. Это расстояние можно рассчитать по следующей формуле:
Это расстояние можно рассчитать по следующей формуле:
Расстояние от точки P до плоскости π — это наименьшее расстояние от точки до одной из бесконечных точек на плоскости. Давайте воспользуемся этой формулой для вычисления расстояния между плоскостью и точкой в следующих примерах.
Пример
Рассчитайте расстояние от точки P = (3, 1, 2) и плоскостей
и
Решение
Деталь a
Используйте следующую формулу для вычисления расстояния между точкой и плоскостью.Сначала мы вычислим расстояние между
и P.
Подставим A = 3, b = 4, C = 1 и D = 3 в приведенную выше формулу:
Часть b
Теперь мы вычислим расстояние между
и точкой P. Используйте следующую формулу для вычисления расстояния между точкой и плоскостью.
Замените A = 1, B = 2, C = 3 и D = 1 в приведенной выше формуле:
Расстояние между параллельными линиями
Один из важных элементов в трех -мерная геометрия — прямая линия.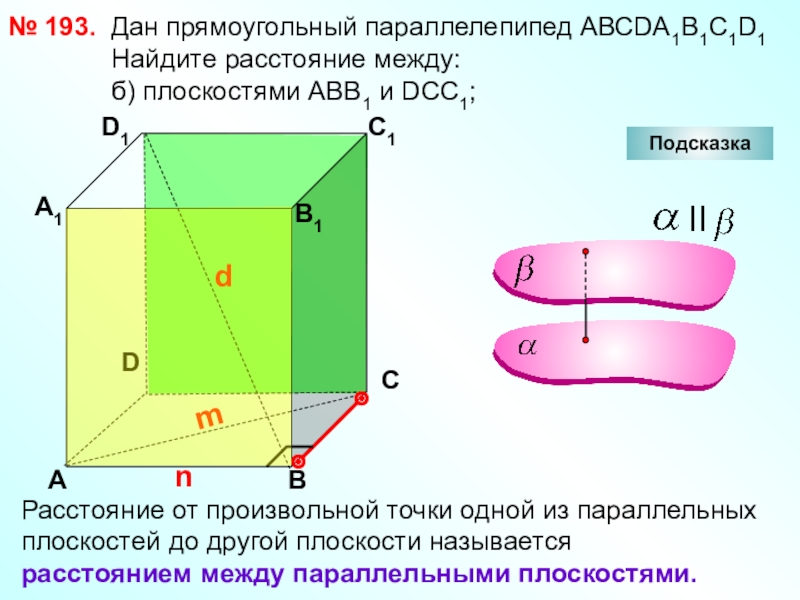 В декартовой плоскости отношения между двумя прямыми линиями различаются, потому что они могут просто пересекать друг друга, быть перпендикулярными друг другу или могут быть параллельными линиями. Когда две линии пересекаются на друг с другом, расстояние между ними составляет ноль . Расстояние между двумя параллельными линиями равно , всегда одинаково . Наклон параллельных прямых всегда одинаковый.
В декартовой плоскости отношения между двумя прямыми линиями различаются, потому что они могут просто пересекать друг друга, быть перпендикулярными друг другу или могут быть параллельными линиями. Когда две линии пересекаются на друг с другом, расстояние между ними составляет ноль . Расстояние между двумя параллельными линиями равно , всегда одинаково . Наклон параллельных прямых всегда одинаковый.
Вам может быть интересно, как вычислить расстояние между двумя параллельными линиями? Что ж, в этом разделе мы обсудим, как вычислить расстояние между двумя параллельными линиями.
Кратчайшее расстояние между двумя параллельными линиями равно длине перпендикуляра между ними. Расположение точек значения не имеет. Единственное, что имеет значение, это то, что две точки должны быть на линиях. Предположим, есть две параллельные прямые
и. Расстояние между этими двумя линиями можно рассчитать по следующей формуле:
Пример
Вычислите расстояние между следующими двумя параллельными линиями.
a) 2x + 2y + 3 = 0 и 2x + 2y + 5 = 0
b) x + 3y = — 6 и 3x + 9 y = -3
Решение
Часть a
Здесь
и . Подставьте эти значения в формулу ниже, чтобы получить расстояние:
Часть b
Сначала мы преобразуем указанные выше две строки в форму
.
Строка 1 =
Строка 2 =
Чтобы сделать коэффициенты равными, разделим уравнение строки 2 на константу 3.В результате получится следующее уравнение:
Замените
и в приведенной ниже формуле:
Расстояние между двумя параллельными плоскостями
Расстояние между двумя плоскостями, параллельными друг другу, можно определить, рассматривая кратчайшее расстояние между поверхностями двух плоскостей. Если плоскости не параллельны, то они будут пересекать друг друга. Если две плоскости пересекают друг друга, то расстояние между ними равно нулю.Прежде чем определять расстояние, сначала необходимо определить, параллельны ли две плоскости или нет.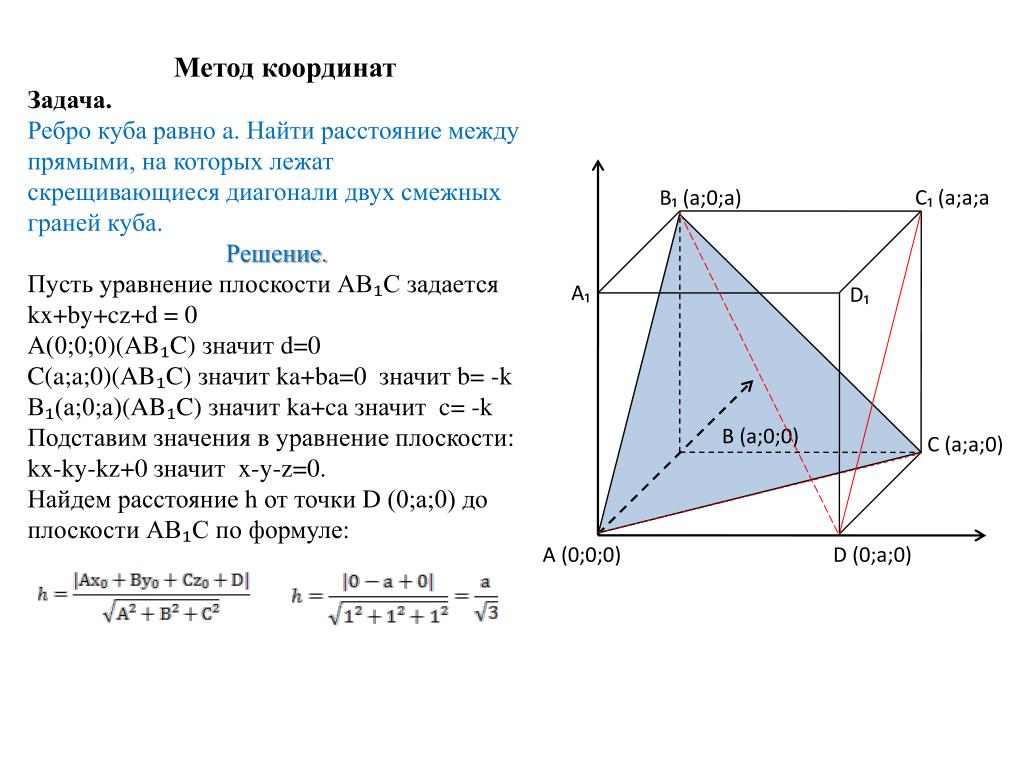
«Расстояние между двумя параллельными плоскостями — это расстояние от любой точки одной плоскости до другой точки другой плоскости»
Предположим, что две плоскости имеют следующие уравнения:
Формула для вычисления расстояния между этими двумя плоскостями приведено ниже:
Следующие пять шагов необходимо выполнить при вычислении расстояния между двумя параллельными плоскостями.
Шаги для вычисления расстояния между двумя параллельными плоскостями
Шаг 1
Убедитесь, что уравнения плоскостей записаны в стандартной форме. Уравнение плоскости в стандартной форме приведено ниже:
Шаг 2
На этом шаге вы определяете, параллельны ли две плоскости или нет. Это потому, что если плоскости не параллельны, то в какой-то момент они обязательно пересекутся друг с другом.Расстояние между перпендикулярными плоскостями равно нулю.
Чтобы определить, параллельны плоскости или нет, рассмотрите следующие отношения:
Если линии параллельны, то эти отношения равны. Математически мы запишем это как:
Шаг 3
Определите значения коэффициентов A, B и C. Если две строки не имеют одинаковых коэффициентов, то вы можете уравнять их, умножив или разделив любое уравнение на константу.
Шаг 4
На этом шаге вы получите значения
и из двух уравнений.
Шаг 5
Подставьте эти значения в формулу для вычисления расстояния между двумя параллельными плоскостями. Эта формула приведена выше в этой статье.
Пример
Вычислите расстояние между следующими двумя параллельными плоскостями:
Решение
Выполните следующие действия, чтобы вычислить расстояние между двумя указанными выше плоскостями.
Шаг 1
Во-первых, нам нужно преобразовать уравнения в стандартную форму. В этом примере уравнения плоскостей уже приведены в стандартной форме, поэтому на этом шаге мы ничего делать не будем и перейдем ко второму шагу.
В этом примере уравнения плоскостей уже приведены в стандартной форме, поэтому на этом шаге мы ничего делать не будем и перейдем ко второму шагу.
Шаг 2
На этом шаге мы увидим, параллельны ли две плоскости или нет. Чтобы определить это, нам нужно посмотреть на определенные соотношения.
Коэффициенты равны, что означает, что плоскости параллельны.
Шаг 3
Теперь мы найдем значения коэффициентов A, B и C. Два уравнения:
Мы разделим уравнение плоскости 2 на константу 2, чтобы получить те же коэффициенты. в обоих уравнениях:
Шаг 4
На этом шаге мы получим значения
и из двух уравнений.
В этом примере
и
Шаг 5
Подставьте все значения в формулу ниже, чтобы вычислить расстояние между двумя параллельными плоскостями:
Трехмерная координатная геометрия — расстояние
В трехмерном пространстве точки представлены их положениями вдоль осей xxx, yyy и zzz, каждая из которых перпендикулярна друг другу; это аналогично интерпретации 2-х координатной геометрии, в которой каждая точка представлена только двумя координатами (по осям xxx и yyy).