Содержание
Урок 50. тригонометрические неравенства — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №50. Тригонометрические неравенства.
Перечень вопросов, рассматриваемых в теме
- решение простейших тригонометрических неравенств с помощью тригонометрической окружности;
- решение тригонометрических неравенств, сводимых к квадратным;
- решение тригонометрических неравенств методом интервалов.
Глоссарий по теме
- Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Тангенсом угла называется отношение к
Угол может выражаться и в градусах и в радианах.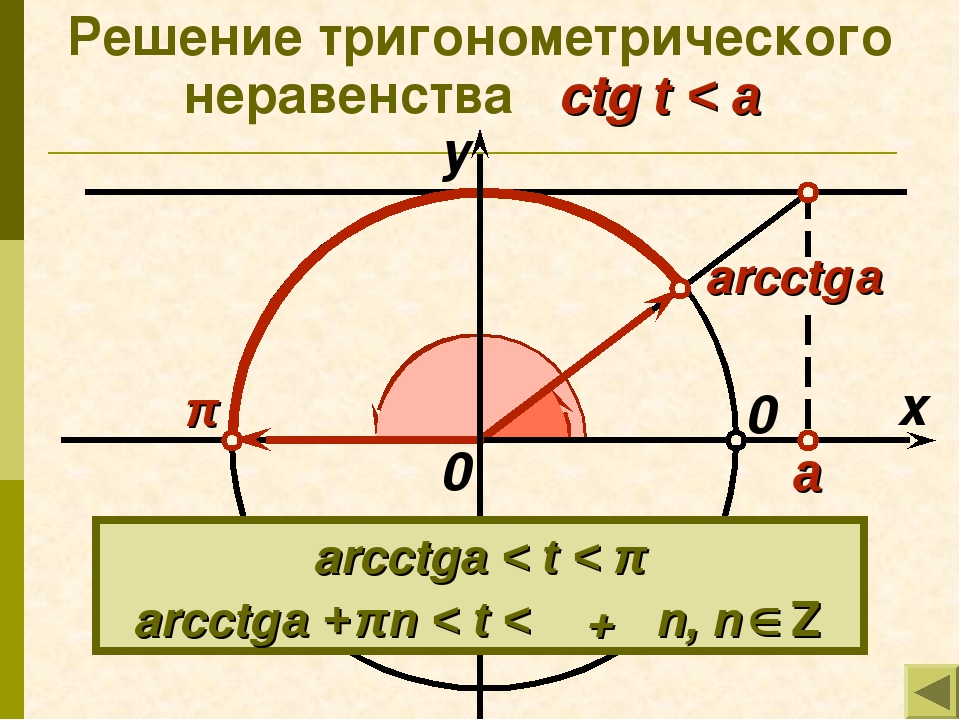
- Арккосинусом числа называется такое число α, что: . Арккосинус числа m обозначают: .
- Арксинусом числаназывается такое число α, что: и . Арксинус числа m обозначают:.
- Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни под ред. А.Б. Жижченко. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 334-337.
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. 353-367.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
1. Рассмотрим простейшие тригонометрические неравенства.
Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства .
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на (получим неравенство , то решением его будет множество точек, в которых . Это числа .
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
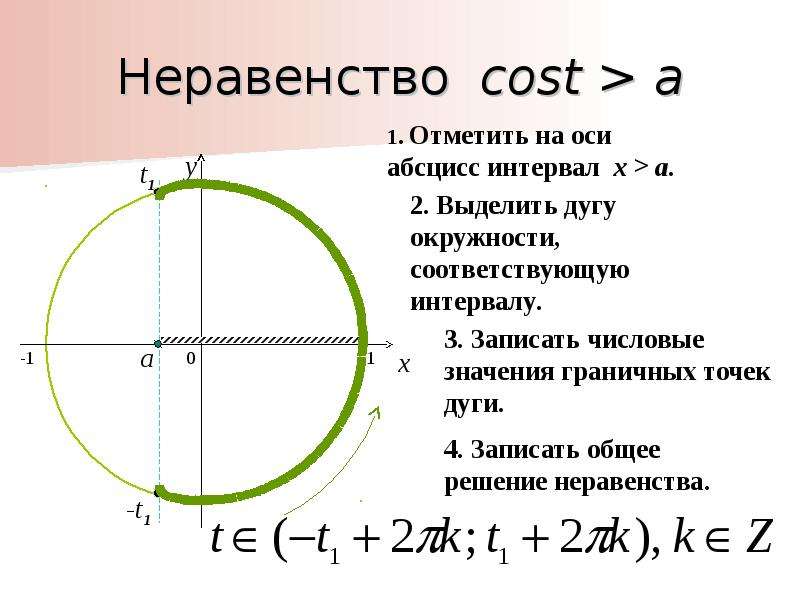
Рассмотрим теперь значение (рис.3).
Рисунок 3 – Решение неравенства
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1) , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением :
(для строгого неравенства) – множество интервалов;
(для нестрогого неравенства) – множество отрезков.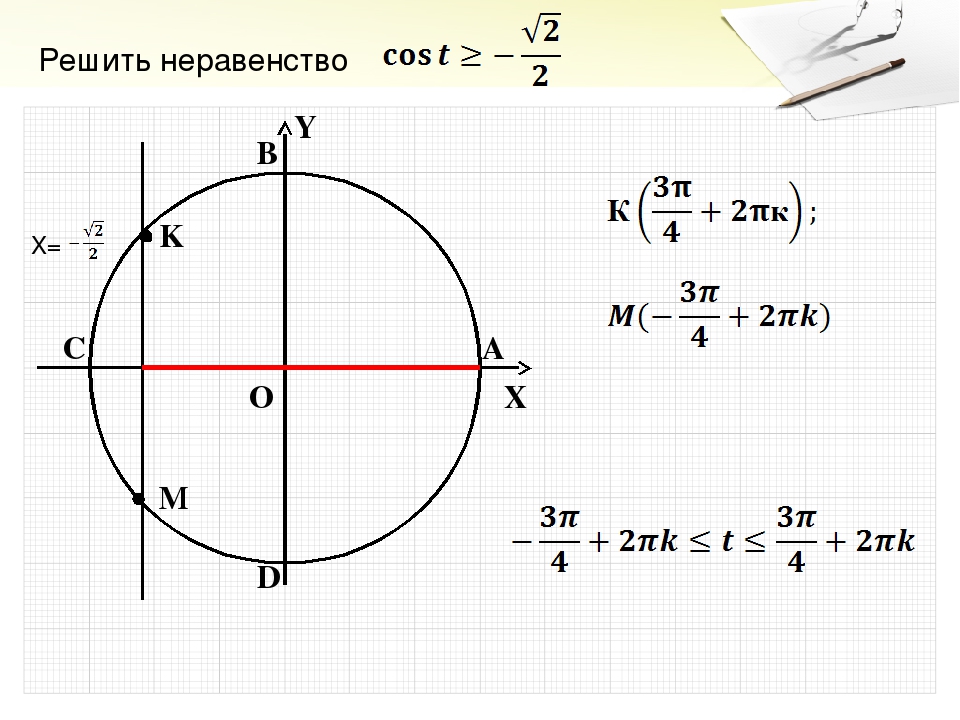
Если значение a= – 1,то получим следующую картинку (рис. 4):
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства является любое действительное число. Если неравенство строгое, то решением неравенства является любое действительное число, кроме чисел вида .
Наконец, если , то решением неравенства является любое действительное число.
Решение неравенства рассмотрим более коротко.
Очевидно, что если , то решением неравенства является любое действительное число.
Если , то решением неравенства является любое действительное число, а решением неравенства является любое действительное число, за исключением чисел вида .
Если , то решением неравенства являются числа вида , а неравенство решений не имеет. То же самое можно сказать о решении неравенств и в случае .
Случай рассмотрим более подробно (рис. 5).
Рисунок 5 – Решение неравенства
Решение неравенства для :
(для строгого неравенства) — множество интервалов;
(для нестрогого неравенства) — множество отрезков.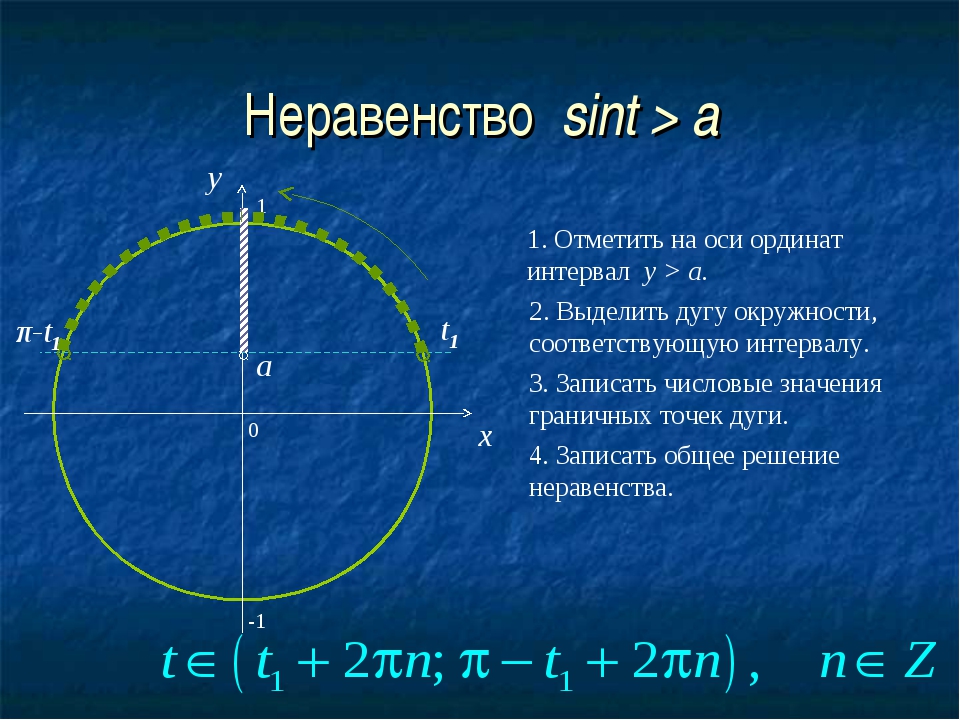
2. Теперь рассмотрим решение неравенств и .
Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для неравенство решений не имеет, а решением неравенства является любое действительное число.
Для неравенство решений не имеет, а решением неравенства является любое действительное число.
Рассмотрим случай более подробно.
Рассмотрим решение неравенства (рис. 6).
Рисунок 6 – Решение неравенства
Множество решений этого неравенства:
.
Теперь рассмотрим неравенство (рис. 7).
Рисунок 7 – Решение неравенства
Множество решений этого неравенства:
.
3. Теперь рассмотрим решение простейших неравенств и .
Сначала рассмотрим неравенство (рис. 8).
Рисунок 8 – Решение неравенства
Множество решений этого неравенства:
.
Соответственно, множество решений неравенства :
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.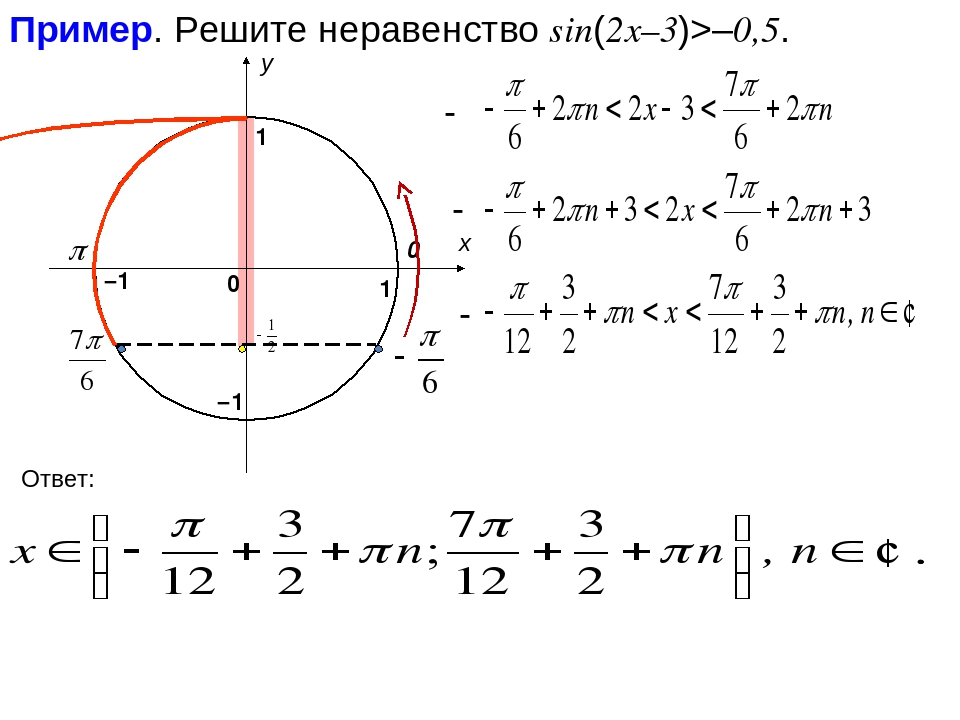
Решите неравенство. Заполните пропуски
Решение:
Ведем новую переменную: .
Вспомогательное неравенство имеет вид:
, .
Вернемся к исходной переменной: .
Второе неравенство решений не имеет. Решением первого неравенства является:
.
Ответ: .
Пример 2.
Решите неравенство. Найдите коэффициенты
Решение:
Выразим
Рисунок 9 – решение неравенства
Ответ:
Решение тригонометрических неравенств онлайн · Как пользоваться Контрольная Работа РУ
Рассмотрим пример решения тригонометрического неравенства онлайн на сайте Контрольная Работа РУ.
Этот сайт даёт полное решение тригонометрического неравенства.
Плюс для некоторых неравенств есть решение, изображённое на графике.
Итак, рассмотрим пример:
Требуется решить тригонометрическое неравенство cos(x/4-pi/3) > 1/2 и найти x, при которых выполняется это неравенство.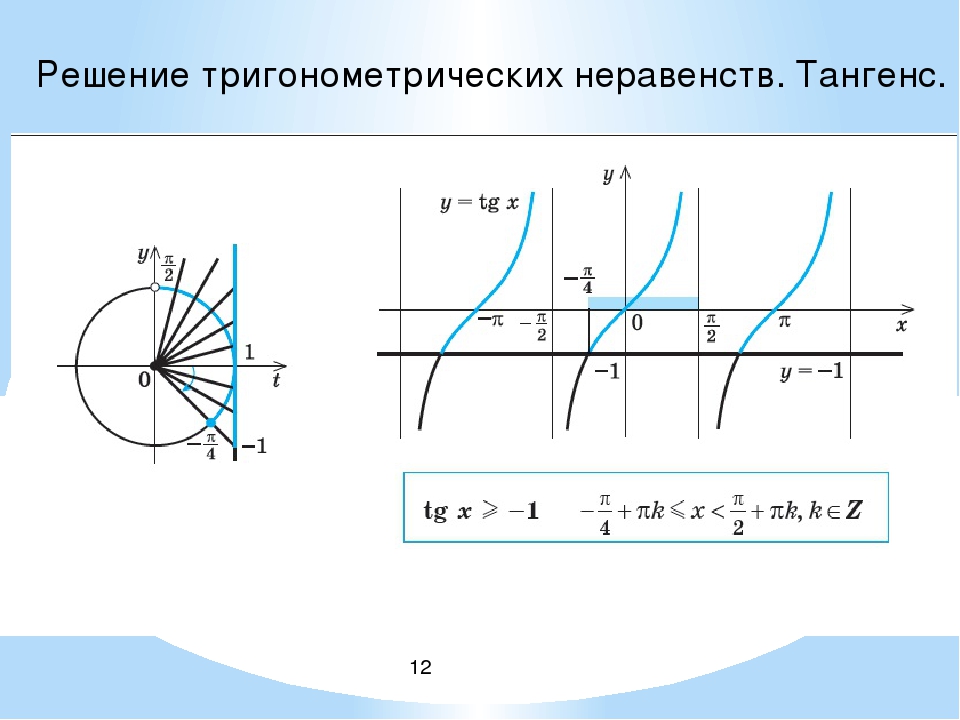
Для этого переходим на страницу
>>неравенства онлайн<<
и нажимаем Решить неравенство!
.
Получаем ответ 8*pi*n<x<1/3*(24*pi*n+8*pi), где n принадлежит N.
А также следующее подробное решение:
Дано неравенство: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ Решаем:
Дано уравнение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ — это простейшее тригонометрическое ур-ние.
Это ур-ние преобразуется в $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \operatorname{asin}{\left (\frac{1}{2} \right )}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n — \operatorname{asin}{\left (\frac{1}{2} \right )} + \pi$$ Или $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{\pi}{6}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{5 \pi}{6}$$ , где n — любое целое число.
Перенесём $$\frac{\pi}{6}$$ в правую часть ур-ния с противоположным знаком, итого: $$\frac{x}{4} = 2 \pi n$$ $$\frac{x}{4} = 2 \pi n + \frac{2 \pi}{3}$$ Разделим обе части полученного ур-ния на $$\frac{1}{4}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ Данные корни $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{1}$$ Возьмём например точку $$x_{0} = x_{1} — \frac{1}{10}$$ = $$8 \pi n + — \frac{1}{10}$$ = $$8 \pi n — \frac{1}{10}$$ подставляем в выражение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$
/8*pi*n - 1/10 pi\ cos|------------- - --| > 1/2 | 1 1| \ 4 3 / /1 pi \ cos|-- + -- - 2*pi*n| > 1/2 \40 3 /
Тогда $$x < 8 \pi n$$ не выполняется, значит одно из решений нашего неравенства будет при: $$x > 8 \pi n \wedge x < 8 \pi n + \frac{8 \pi}{3}$$
_____
/ \
-------ο-------ο-------
x1 x2
Тригонометрические уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1).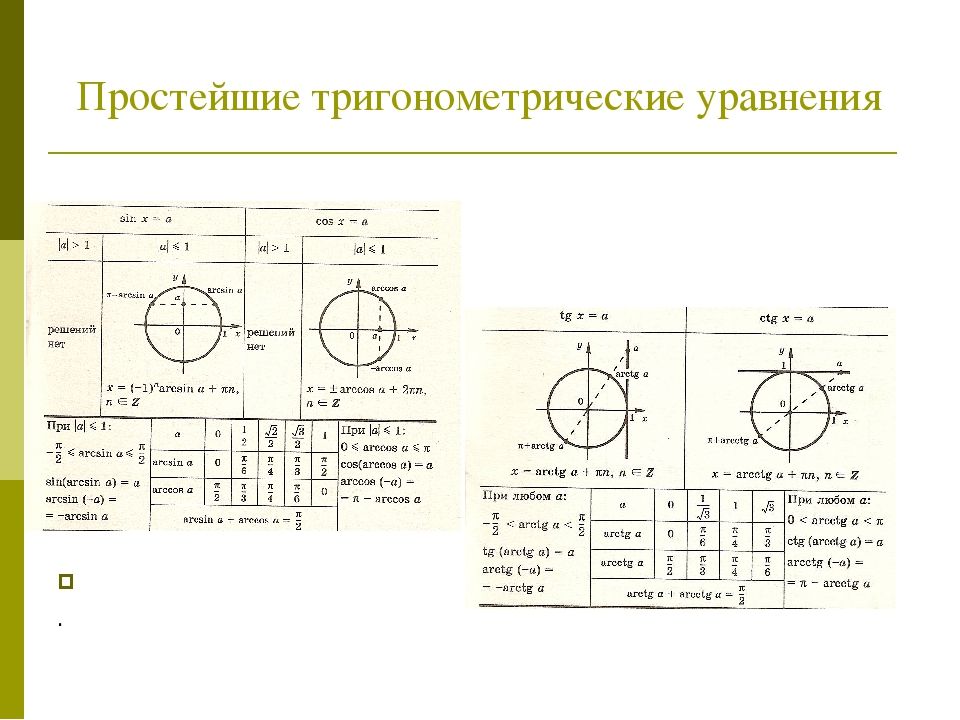 Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ:
3. Бывает, что перед разложением суммы или разности тригонометрических функций в произведение надо проделать обратную процедуру: превратить произведение в сумму (разность).
Решим уравнение:
Домножаем обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:
Ответ:
4. Ещё пример, где финальное разложение на множители поначалу замаскировано:
Здесь используем формулу понижения степени:
(которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
угла). Получаем:
и дальше ясно.
5. Многие оказываются в ступоре при виде следующего уравнения:
Переносим косинус влево и применяем формулу приведения
Дальше — дело техники.
6. А в этом примере нужны совсем другие манипуляции:
Раскладываем синус двойного угла, всё собираем в левой части и группируем:
Цель достигнута.
Рассмотрим уравнение:
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене
степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.
Предположим, что . Тогда в силу уравнения и , что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию , и мы можем поделить обе его части на .
В результате деления приходим к равносильному квадратному уравнению относительно тангенса:
и дальнейший ход решения трудностей не представляет
1. Рассмотрим уравнение
Рассмотрим уравнение
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение :
и дело сделано.
2. Неожиданным образом сводится к однородному следующее уравнение:
Казалось бы, где тут однородность? Переходим к половинному углу!
откуда
| (3) |
Мы не случайно довели это уравнение до ответа. В следующем разделе оно будет решено другим методом, и ответ окажется внешне непохожим на этот.
Введение дополнительного угла
Этот метод применяется для уравнений вида . Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
1. Рассмотрим уравнение
Делим обе части на 2:
Замечаем, что :
В левой части получили синус суммы:
,
откуда и
2. Другой пример:
Другой пример:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
3. Рассмотрим теперь общий случай — уравнение
Делим обе части на :
| (4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :
Соотношение (4) тогда приобретает вид:
,
или
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол .
4. Снова решим уравнение
Делим обе части на :
Существует угол такой, что . Например, . Получаем:
,
,
,
,
В предыдущем разделе мы решили это уравнение, сведя его к однородному, и получили в качестве ответа выражение (3). Сравните с полученным только что выражением. А ведь это одно и то же множество решений!
Сравните с полученным только что выражением. А ведь это одно и то же множество решений!
Универсальная подстановка
Запомним две важные формулы:
Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной подстановки. Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
1. Решим уравнение
Выражаем , используя универсальную подстановку:
Делаем замену :
Получаем кубическое уравнение:
Оно имеет единственный корень . Стало быть, , откуда .
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .
2. Рассмотрим уравнение
А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем в уравнение и убеждаемся, что это — решение.
Теперь обозначаем и применяем универсальную подстановку:
После простых алгебраических преобразований приходим к уравнению:
Следовательно, и .
Ответ: .
Метод оценок
В некоторых уравнениях на помощь приходят оценки .
3. Рассмотрим уравнение
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
том случае, когда они равны единице одновременно:
Таким образом, должны одновременно выполняться следующие равенства:
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:
Умножаем обе части на 90 и сокращаем на π:
Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Искать k, в принципе, уже не нужно. Сразу находим x:
Ответ: .
4. Рассмотрим уравнение
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
Имеем:
Ищем пересечение:
Умножаем на 21 и сокращаем на π:
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
5. Страшное с виду уравнение
также решается методом оценок. В самом деле, из неравенств следует, что . Следовательно, , причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.
Это не сложно.
Учёт тригонометрических неравенств
Рассмотрим уравнение:
Перепишем его в виде, пригодном для возведения в квадрат:
Тогда наше уравнение равносильно системе:
Решаем уравнение системы:
,
,
Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:
Теперь нужно произвести отбор решений в соответствии с неравенством . Серия не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .
Ответ: .
Специальные приёмы
В этом разделе рассматриваются некоторые типы уравнений, приёмы решения которых нужно знать обязательно.
1. Рассмотрим уравнение
Это сравнительно редкий случай, когда используется исходная формула косинуса двойного угла:
,
,
,
Каждое из уравнений полученной совокупности мы решать умеем.
2. Теперь рассмотрим такое уравнение:
Метод решения будет совсем другим. Сделаем замену . Как выразить через t? Имеем:
Сделаем замену . Как выразить через t? Имеем:
,
откуда . Получаем:
,
,
,
Как действовать дальше, мы знаем.
3. Надо обязательно помнить формулы косинуса и синуса тройного угла (чтобы не изобретать их на экзамене):
,
Вот, например, уравнение:
Оно сводится к уравнению относительно :
,
,
Дальше всё понятно.
4. Как бороться с суммой четвёртых степеней синуса и косинуса? Рассмотрим уравнение
Выделяем полный квадрат!
,
,
,
,
,
,
5. А как быть с суммой шестых степеней? Рассмотрим такое уравнение:
Раскладываем левую часть на множители как сумму кубов: .
Получим:
,
С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
Основное Тригонометрическое Тождество — Доказательство
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2α + 1 = 1/cos2α и равенство 1 + сtg2α + 1 = 1/sin2α выводят из основного тождества, разделив обе части на sin2α и cos2α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin2α + cos2α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.

- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.
Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = .
- Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
1 | sin2α + cos2α = 1 |
2 | |
3 | |
4 | tgα * ctgα = 1 |
5 | tg2α + 1 = |
6 | 1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.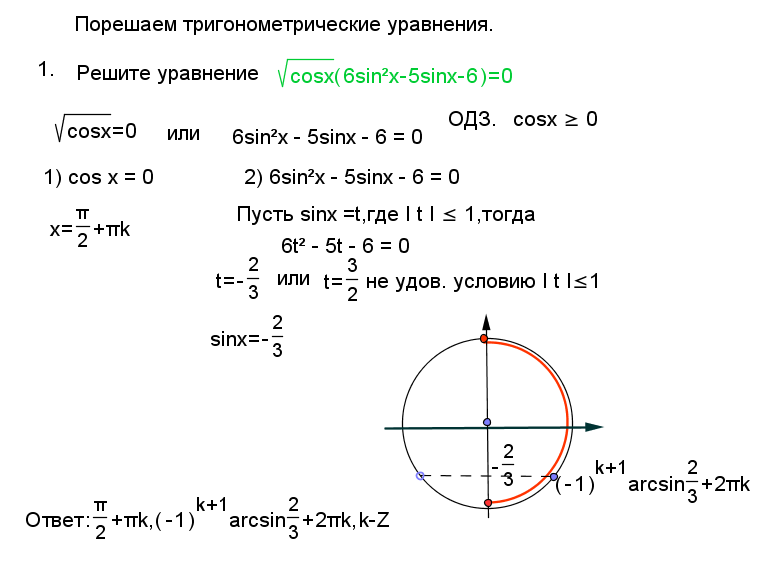
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
Задачка 2. Найдите значение cos α,
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Задача на нахождение корней тригонометрического уравнения — «Шпаргалка ЕГЭ»
Решите уравнение: .
Решение задачи
Данный урок показывает, как правильно решить тригонометрическое уравнение, представленное в виде дроби, у которой числитель представлен квадратным тригонометрическим выражением, а знаменатель – иррациональной тригонометрической функцией. Для решения подобного необходимо представить решение в виде системы, в которой первое выражение – это числитель дроби приравненный к нулю, а второе выражение – неравенство, полученное из условия положительности подкоренного выражения. В данном случае первое выражение – квадратное тригонометрическое уравнение, для решения которого используется замена с помощью основной тригонометрической формулы: . Последующая замена тригонометрической функции на неизвестную, позволяет получить стандартное квадратное уравнение, решение которого можно получить через нахождение дискриминанта или по теореме Виета. После получения корней квадратного уравнения, выполняем обратную замену и находим решения уже двух тригонометрических уравнений. Следует помнить, что при работе с синусами и косинусами, значения функции должны находится в границах [-1; 1], в противном случае такое тригонометрическое уравнение корней не имеет. Полученные корни тригонометрических уравнений наносим на тригонометрическую окружность, с помощью которой легко выбрать корни, которые входят в область определения функции – это значение мы получаем, решив тригонометрическое неравенство. В данном случае это просто значение синуса, а следовательно, нас в решении будут интересовать только первая и вторая четверти. Исключив лишние корни, получаем итоговый ответ.
Решение данной задачи рекомендовано для учащихся 10-х классов при изучении тем «Тригонометрические функции» («Синус и косинус»), «Тригонометрические уравнения» («Арккосинус», «Арккосинус и решение уравнения cost=a», «Арксинус», «Арксинус и решение уравнения sint=a»). При подготовке к ЕГЭ урок рекомендован при повторении тем «Тригонометрические функции», «Тригонометрические уравнения».
29. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость ортогональной системы функций
и
– неравенство
Бесселя
для
ортогональных систем
4)(?)
f(x)L2[a,
b] , f(x)~,
Ck=
T
Для того,
чтобы обобщенный ряд Фурье
– сходился в среднем к функцииf(x)
на отрезке [a,
b],
необходимо и достаточно, чтобы неравенство
Бесселя обращалось для f(x)
в равенство, т.е.
и
Доказательство:
Ряд
сходится в среднем на [a,
b],
если
,
–равенство
Парсеваля – Стеклова
.
Ортогональная
система функций (0,
1,
2,
…,
n)
в пространстве L2[a,
b]
называются полной, если для
выполняется равенство Парсеваля-Стеклова
E3
– Евклидово 3хмерное пространство, E3(– ортонормированный базис |ei
| = 1
,
,
–теорема Пифагора
для пространства E3.
В ортонормированном
базисе ||f||2=– теорема Пифагора в бесконечномерном
пространстве.
Вывод: Любая
функция f(x)
принадлежащая пространству L2[a,
b]
может быть разложена в сходящийся к ней
в среднем ряд Фурье по ортогональной
на отрезке [a,b]
системе функций, если эта система
является полной в пространстве L2[a,
b].
30. Тригонометрические ряды Фурье для периодических функций. Признак сходимости тригонометрического ряда Фурье (теорема Дирихле)
Пусть f(x) кусочно
непрерывная функция, периодичная с
периодом T=2l
, [-l,l]
Пример:
),
где ||1||=
f(x)~==
(солнышко)
О. Тригонометрический
ряд
,
коэффициенты которого определены по
формулам (солнышко) называется
тригонометрическим для периодичной
функции f(x).
Если f(x) четная, то
,
если нечетная, то
Если f(x) – четная,
то
Если f(x) — нечетная,
то
Уравнение Ляпунова
Т.
основная тригонометрическая система
функций является полной в пространстве
.
—
число ⇒
сходитcя
⇒ a→ 0, n→
,b→
0, n→
Признаки сходимости
тригонометрических рядов Фурье
кусочно-непрерывная
функция f(x) называется кусочно-гладкой
на [a,b], если её производная имеет
конечное число точек разрыва 1 рода и
существует правосторонняя производная
в точке A и левосторонняя в точке B.
T1
Если функция f(x)
т. е она кусочно-непрерывна на[-l,
l], то
тригонометрический ряд Фурье сходится
к f(x) в среднем.
Т2 (Дирихле)
Если f(x)
является кусочно гладкой на [-l,
l],
то её тригонометрический ряд Фурье
сходится в каждой точке этого отрезка
для суммы S(x) ряда Фурье :
S(x) = f(x), если x —
точка непрерывности функции f(x)S(,
еслиточка
разрыва 1 рода функции f(x)S(-l)
=
S(l)=
T3 Если функция
f(x)
яфляется кусочно гладкой и непрерывной
на [-l, l]
и f(l)=f(-l), то и тригонометрический ряд
Фурье сходится к f(x) на [-l,
l] равномерно.
Разложение в ряд
Фурье четных и нечетных ф-ций на интервале
.
Пусть функция
f(x)
– четная, т. е. f(-x)=f(x).
Значит:
;
Ряд Фурье для
четных функций – ряд только по косинусам:
Пусть функция
f(x)
– нечетная, т. е. f(-x)=-f(x).
Значит:
Ряд Фурье для
нечетных функций – ряд только по синусам.
31. Разложение непериодических функций в тригонометрический ряд Фурье. Ряд Фурье только по косинусам или только по синусам
f(x)
– непериодичная функция
Вместо функции
f(x)
рассматривают функцию f*(x)
с периодом 2l,
причем [a,
b][-l,
l]
и на [a,
b]
функция f*(x)
совпадает с функцией f(x).
Поскольку функция
f*(x)
–периодическая, то её разлагают в ряд
Фурье.
Рассмотрим один
важный случай, пусть функция f(x)
задана на интервале (0, l).
Её надо доопределить на интервале (-l,
0). Можно это сделать двумя способами:
четным и нечетным. В первом случае мы
получаем ряд Фурье только по косинусам,
во втором – только по синусам.
1) Пусть f(x)
задана на (0, l).
Доопределим её четным
образом.
Функция будет выглядеть так:
Пусть
f(x)
задана на (0, l).
Доопределим её четным образом. Функция
будет выглядеть так:
Как решать С1. Урок 5. ЕГЭ по математике 2014 — решения.егэцентр.рф
Поздравляю вас, дорогие читатели!
Наконец-то мы дошли до решения тригонометрических уравнений. Сейчас мы решим несколько уравнений, которые похожи на задания ЕГЭ. Конечно, в реальном экзамене, задачи будут немного сложнее, но суть останется та же.
Для начала рассмотрим легкое уравнение (подобные мы уже решали в прошлых уроках, но повторить всегда полезно).
$$(2\cos x + 1) (2\sin x — \sqrt{3}) = 0.$$
Думаю, объяснения, как решать, излишни.
$$2\cos x + 1 = 0 \text{ или } 2\sin x — \sqrt{3} =0,$$
$$\cos x = -\frac{1}{2} \text{ или } \sin x = \frac{\sqrt{3}}{2},$$
Горизонтальным пунктиром отмечено решение для уравнения с синусом, вертикальным — с косинусом.
Таким образом, итоговое решение можно записать, например, так:
$$\left[ \begin{array}{l}x= \pm \frac{2\pi}{3},\\x = \frac{\pi}{3}+2\pi k. \end{array}\right.$$
Тригонометрическое уравнение с ОДЗ
$$(1+\cos x)\left(\frac{1}{\sin x} — 1\right) = 0.$$
Важное отличие в этом примере, что в знаменателе появился синус. Хотя мы немного решали подобные уравнения в предыдущих уроках, стоит остановиться на ОДЗ поподробнее.
ОДЗ
`\sin x \neq 0 \Rightarrow x \neq \pi k`. Когда мы будем отмечать решение на круге, эту серию корней мы отметим специально проколотыми (открытыми) точками, чтобы показать, что `x` не может принимать такие значения.2 — 6t +5 =0, $$
$$t_1 = 5, t_2 = 1.$$
Обратная замена.
$$\tg x = 5, \tg x = 1.$$
$$\left[\begin{array}{l}2x = \arctan{5}+\pi k, \\ 2x = \frac{\pi}{4} + \pi k. \end{array} \right.$$
Теперь поделим обе серии на два, чтобы узнать, чему равен, собственно, `x`.
$$\left[\begin{array}{l}x = \frac{1}{2}\arctan{5}+\frac{\pi k}{2}, \\ 2x = \frac{\pi}{8} + \frac{\pi k}{2}. \end{array} \right.$$
Вот мы и получили ответ.
Последнее уравнение (произведение тангенса на синус)
$$\tg x \cdot \sin 2x = 0.$$
ОДЗ
Поскольку тангенс — это дробь, знаменателем которой является косинус, то в ОДЗ получим, что `\cos x \neq 0 \Rightarrow x \neq \frac{\pi}{2}+\pi k.`
Решение
$$\tg x =0 \text{ или } \sin 2x = 0.$$
Эти уравнения решаются легко. Получим:
$$x = \pi k \text{ или } 2x = \pi k,$$
$$x = \pi k \text{ или } x = \frac{\pi k}{2}.$$
Теперь самое интересное: поскольку у нас было ОДЗ, нужно выполнить отбор корней.2 \left(x-\frac{\pi}{3} \right) — 3 =0`.
На этом хватит. Будут вопросы — спрашивайте! Оставляйте лайки, если мой труд оказался полезен 🙂
Единичный круг — Алгебра и тригонометрия
Цели обучения
В этом разделе вы:
- Найдите значения функции для синуса и косинуса
- Определите область и диапазон функций синуса и косинуса.
- Найдите опорные углы.
- Используйте исходные углы для оценки тригонометрических функций.
Рисунок 1. Singapore Flyer — самое высокое колесо обозрения в мире. (кредит: ʺVibin JKʺ / Flickr)
Ищете острые ощущения? Тогда подумайте о поездке на Singapore Flyer, самом высоком колесе обозрения в мире.Колесо обозрения, расположенное в Сингапуре, взлетает на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя с земли на вершину и снова вниз по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Затем мы можем обсудить круговое движение в терминах пар координат.
Нахождение синусов и косинусов специальных углов
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы, и мы нашли их синусы и косинусы, используя прямоугольные треугольники. Мы также можем вычислить синусы и косинусы особых углов, используя тождество Пифагора.
Нахождение синусов и косинусов углов и
Затем мы найдем косинус и синус под углом или Сначала мы нарисуем треугольник внутри круга с одной стороной под углом, а другая под углом, как показано на (Рисунок).Если в результате два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут такими, как показано на (Рисунок).
Рис. 12.
Рисунок 13.
Поскольку все углы равны, стороны также равны. Вертикальная линия увеличилась, так как все стороны равны, мы также можем сделать вывод, что или с
А так как в нашем единичном круге
Используя тождество Пифагора, мы можем найти значение косинуса.
Координаты точки на окружности с радиусом под углом at Радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, как показано на (Рисунок).Угол имеет меру. В какой-то момент мы проводим угол с мерой. Мы знаем, что углы в треугольнике складываются из суммы углов. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13.
Угол составляет 30 °. Угол равен двойному углу, поэтому его размер составляет 60 °. Это серединный перпендикуляр к нему, поэтому он разрезает пополам. Это означает, что это радиус, или Обратите внимание, что это координата x точки, которая находится на пересечении угла 60 ° и единичной окружности.Это дает нам треугольник с гипотенузой 1 и длиной стороны
.
Из теоремы Пифагора получаем
Подставляя получаем
Решая для получения
Так как сторона вывода находится в квадранте I, где координата y- положительна, мы выбираем положительное значение.
В (60 °) координаты точки на окружности радиуса под углом a, таким образом, мы можем найти синус и косинус.
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности.(Рисунок) суммирует эти значения.
(рисунок) показывает общие углы в первом квадранте единичной окружности.
Рисунок 14.
Использование калькулятора для определения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов, мы обращаемся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы вычисляем на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Как записаться
Если задан угол в радианах, воспользуйтесь графическим калькулятором, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Попробуйте
Оценить
[show-answer q = ”fs-id2027699 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2027699 ″]
примерно 0.866025403
[/ hidden-answer]
Поиск опорных углов
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса — это координата y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на (Рисунок), угол имеет то же значение синуса, что и угол, значения косинуса противоположны.Угол имеет то же значение косинуса, что и угол, значения синуса противоположны.
Рисунок 16.
Напомним, что исходный угол угла — это острый угол, образованный конечной стороной угла и горизонтальной осью. Базовый угол — это всегда угол между идиандианами. Как видно из (Рисунок), для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
Рисунок 17.
Поиск опорного угла
Найдите опорный угол, как показано на (Рисунок).
Рисунок 17.
[show-answer q = ”fs-id1710670 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1710670 ″]
Поскольку он находится в третьем квадранте, опорный угол составляет
[/ скрытый-ответ]
Попробуйте
Найдите опорный угол
[show-answer q = ”fs-id1967998 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1967998 ″]
[/ hidden-answer]
Использование опорных углов
А теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела.Предположим, всадник делает снимок, остановившись на высоте двадцати футов над землей. Затем всадник совершает поворот на три четверти по кругу. Что такое новый рост райдера? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса под углами, превышающими 90 градусов, или под отрицательным углом. Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат этих углов.Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности. Они показаны на (Рисунок). Найдите время, чтобы узнать координаты всех основных углов в первом квадранте.
Ключевые уравнения
| Косинус | |
| Синус | |
| Пифагорейская идентичность |
Упражнения по разделам
Устный
Опишите единичный круг.
[show-answer q = ”fs-id2077250 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2077250 ″]
Единичный круг — это круг радиуса 1 с центром в начале координат.
[/ hidden-answer]
Что означают координаты x- и y- точек на единичной окружности?
Обсудите разницу между концевым углом и опорным углом.
[show-answer q = ”fs-id1827178 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1827178 ″]
Coterminal углы — это углы, которые имеют одну и ту же конечную сторону. Базовый угол — это размер наименьшего острого угла, образованного конечной стороной угла и горизонтальной осью.
[/ hidden-answer]
Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
[show-answer q = ”fs-id1801846 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1801846 ″]
Значения синуса равны.
[/ hidden-answer]
Алгебраические
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором находится определяемая конечная точка.
и
и
[show-answer q = ”fs-id2261414 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2261414 ″]
Я
[/ hidden-answer]
и
и
[show-answer q = ”fs-id2645567 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2645567 ″]
IV
[/ hidden-answer]
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
[show-answer q = ”fs-id2236023 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2236023 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2379850 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2379850 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2084847 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2084847 ″]
[/ hidden-answer]
[detect-answer q = ”fs-id2212611 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2212611 ″]
0
[/ hidden-answer]
[show-answer q = ”fs-id2387567 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2387567 ″]
–1
[/ hidden-answer]
[show-answer q = ”fs-id1760509 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1760509 ″]
[/ hidden-answer]
Числовой
Для следующих упражнений укажите исходный угол для данного угла.
[show-answer q = ”fs-id2523531 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2523531 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2227804 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2227804 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2369627 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2369627 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2266093 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2266093 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1535165 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1535165 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2077048 ″] Показать решение [/ show-answer]
[hidden-answer a = ”fs-id2077048 ″]
[/ hidden-answer]
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла.Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.
[show-answer q = ”fs-id2283059 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2283059 ″]
Квадрант IV,
[/ hidden-answer]
[show-answer q = ”fs-id1861830 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1861830 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2782866 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2782866 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2516883 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2516883 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id1577224 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1577224 ″]
Квадрант III,
[/ hidden-answer]
[show-answer q = ”fs-id2547413 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2547413 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2755206 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2755206 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2428233 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2428233 ″]
Квадрант IV,
[/ hidden-answer]
Найдите требуемое значение для следующих упражнений.
Ифанди в четвертом квадранте, найдите
Ифанди в первом квадранте, найдите
[show-answer q = ”fs-id2256400 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2256400 ″]
[/ hidden-answer]
Ифанди во втором квадранте, найдите
Ифанди в третьем квадранте, найдите
[show-answer q = ”fs-id2280210 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2280210 ″]
[/ hidden-answer]
Найдите координаты точки на окружности радиуса 15, соответствующей углу
.
Найдите координаты точки на окружности радиуса 20, соответствующей углу
.
[show-answer q = ”fs-id2800208 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2800208 ″]
[/ hidden-answer]
Найдите координаты точки на окружности радиуса 8, соответствующей углу
Найдите координаты точки на окружности радиуса 16, соответствующей углу
.
[show-answer q = ”fs-id2757988 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2757988 ″]
[/ hidden-answer]
Укажите область определения функций синуса и косинуса.
Укажите диапазон функций синуса и косинуса.
[show-answer q = ”fs-id1347973 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1347973 ″]
[/ hidden-answer]
Технологии
Для следующих упражнений используйте графический калькулятор.
[show-answer q = ”fs-id2428151 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2428151 ″]
-0,1736
[/ hidden-answer]
[show-answer q = ”fs-id2363394 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2363394 ″]
0.9511
[/ hidden-answer]
[show-answer q = ”fs-id17
″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id17
″]
-0,7071
[/ hidden-answer]
[show-answer q = ”fs-id1675635 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1675635 ″]
-0,1392
[/ hidden-answer]
[show-answer q = ”fs-id2497789 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2497789 ″]
−0.7660
[/ hidden-answer]
Расширения
Оцените следующие упражнения.
[show-answer q = ”fs-id2755303 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2755303 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2755134 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2755134 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2631652 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2631652 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2523205 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2523205 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2756010 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2756010 ″]
0
[/ hidden-answer]
Реальные приложения
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку, то есть в правильном положении на север. Предположим, карусель вращается против часовой стрелки.
Какие координаты ребенка через 45 секунд?
Какие координаты ребенка через 90 секунд?
[show-answer q = ”fs-id2245184 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2245184 ″]
[/ hidden-answer]
Какие координаты ребенка через 125 секунд?
Когда у ребенка будут координаты, если поездка длится 6 минут? (Есть несколько ответов.)
[show-answer q = ”fs-id2755933 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id2755933 ″]
37,5 секунды, 97,5 секунды, 157,5 секунды, 217,5 секунды, 277,5 секунды, 337,5 секунды
[/ hidden-answer]
Когда у ребенка будут координаты, если поездка длится 6 минут?
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- y -значение точки на единичной окружности, соответствующей заданному углу
[PDF] УСТРАНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ — Скачать бесплатно PDF
Скачать РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ…
УСТРАНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ (КОНЦЕПЦИЯ, МЕТОДЫ И ШАГИ) Нги Х. Нгуен ОПРЕДЕЛЕНИЕ. Тригонометрическое неравенство представляет собой неравенство в стандартной форме: R (x)> 0 (или
tan x + cot x> 2 cos 2x + 3sin x> 1,5
sin (2x + Pi / 3) 3
Пример множеств решений тригонометрических неравенств в виде интервалов: (Pi / 4, 2Pi / 3); [0, 2Pi]; [-Pi / 2, Pi / 2]; (20 град., 80 град.); (30 град., 120 град.) ТРИГОВАЯ ЕДИНИЦА КРУГ Это круг с радиусом R = 1 единица, с началом O.Переменная дуга AM, которая вращается против часовой стрелки на единичной окружности триггера, определяет 4 общие триггерные функции дуги x. Когда дуга AM изменяется на единичной окружности триггера: Горизонтальная ось OAx определяет триггерную функцию f (x) = cos x. Вертикальная ось OBy определяет триггерную функцию f (x) = sin x. Вертикальная ось At определяет триггерную функцию f (x) = tan x. Горизонтальная ось Bu определяет триггерную функцию f (x) = cot x. Круг триггерного блока будет использоваться в качестве доказательства при решении основных тригонометрических уравнений и основных тригонометрических неравенств.ОБЩИЙ ПЕРИОД ТРИГОВОГО НЕРАВЕНСТВА Общий период тригонометрического неравенства является наименьшим кратным из всех периодов триггерных функций, представленных в неравенстве. Примеры: Тригонометрическое неравенство: sin x + sin 2x + cos x / 2 2 имеет общий период 2Pi. Тригонометрическое неравенство: tan x + cos x / 2
Страница 1 из 8
ОСНОВНЫЕ ТРИГОВЫЕ НЕРАВЕНСТВА. Существует 4 основных распространенных типа базовых тригонометрических неравенств: sin xa) tan xa)
cos xa) cot xa)
a — заданное число
Решение базовых тригонометрических неравенств происходит с использованием таблиц преобразования триггеров (или калькуляторов), затем рассматривая различные положения переменной дуги x, которая вращается на триггерной окружности.Пример 1. Решите неравенство: sin x> 0,709 Решение. Набор решений представлен как таблицей триггеров, так и кругом триггерных единиц. На круге триггерного блока sin x> 0,709, когда дуга x изменяется от Pi / 4 до 3Pi / 4: Pi / 4
Ответ в течение периода 2Pi Расширенные ответы
tan x
Решение. Набор решений представлен единичным кругом и калькулятором. На круговой единице триггера tan x> 0,414, когда дуга x изменяется между значениями — Pi / 2 (или 3Pi / 2) и Pi / 8. -Pi / 2
cos (2x + Pi / 4)
Ответ в течение периода Pi Расширенные ответы в течение периода 2Pi
Решение.Набор решений, заданный единичным кругом и калькулятором: Pi / 3
Ответ
кроватка (2x — Pi / 6)
(в пределах периода Pi)
Решение. Набор решений, заданный тригонометрическим кругом и калькулятором: 2Pi / 3
Ответ Стр. 2 из 8
Чтобы полностью узнать, как решать основные тригонометрические неравенства и т.п., см. Книгу под названием «Тригонометрия: решение тригонометрических уравнений и неравенств» (Amazon e -book 2010) РЕШЕНИЕ КОНЦЕПЦИИ Чтобы решить тригонометрическое неравенство, преобразуйте его в одно или несколько тригонометрических неравенств.Решение тригонометрических неравенств в конечном итоге приводит к решению основных тригонометрических неравенств. Чтобы преобразовать тригонометрическое неравенство в базовое, учащиеся могут использовать общие алгебраические преобразования (общий фактор, полиномиальные тождества…), определения и свойства триггерных функций и триггерные тождества, что является наиболее необходимым. Существует около 31 триггерного тождества, среди них последние 14 тождеств (с № 19 по № 31) называются тождествами преобразования, поскольку они являются необходимыми инструментами для преобразования тригонометрических неравенств (или тригонометрических уравнений) в базовые.См. Книгу, упомянутую выше. Пример 5. Преобразуйте неравенство sin x + cos x
sin x + cos x = sin x + sin (Pi / 2 — x) = = 2sin Pi / 4.sin (a + Pi / 4)
Используйте Sum в Product Identity, # 28
Пример 6. Преобразуйте неравенство sin 2x — sin x> 0 в решение продукта.
sin 2x — грех x = 2sin x. cos x — sin x = sin x (2cos x — 1)> 0
Идентификация триггера и общий множитель
Пример 7. Преобразование (cos 2x
cos 2x — 1 — sin x
(Заменить cos 2x на 1 — 2sin ^ 2 x)
Важное примечание.Процесс преобразования неравенства R (x)> 0 (или 0 (или
Пример. Неравенство (sin x + sin 2x> — sin 3x) будет преобразовано в стандартную форму R (x) = sin x + sin 2x) + sin 3x> 0. Шаг 2. Найдите общий период. Общий период должен быть наименьшим кратным периодам всех триггерных функций, представленных в неравенстве. Полный набор решений должен, по крайней мере, охватывать один общий общий период. Пример • Тригонометрическое неравенство R (x) = cos 2x — 3sin x — 2 0 имеет общий период 4Pi.Пример. Тригонометрическое неравенство R (x) = tan x + 2 cos x + sin 2x
cos x + cos 2x> — cos 3x
(0
Решение. Шаг 1. Стандартная форма: R (x) = cos x + cos 2x + cos 3x> 0 Шаг 2. Общий период: 2Pi Шаг 3. Решите R (x) = 0. Преобразуйте его в продукт, используя Sum to Product Identity: R (x) = cos x + cos 2x + cos 3x = cos 2x (1 + 2cos x) = 0. Затем решите 2 основных триггерных уравнения f (x) = cos 2x = 0 и g (x) = (1 + 2cos x) = 0, чтобы получить все значения x в пределах период 2Pi.Эти значения x будут использоваться на шаге 4. Пример 9. Решите
sin x + sin 2x
(0
Решение. Шаг 1: sin x + sin 2x + sin 3x
b. МЕТОД 2. Этот метод преобразует тригонометрическое неравенство с двумя или более триггерами в тригонометрическое неравенство, имеющее только одну триггерную функцию (называемую t) в качестве переменной. Затем решите для t из этого тригонометрического уравнения в качестве основного тригонометрического уравнения. Затем найдите x из этих значений of t. В качестве функциональной переменной следует выбрать следующие триггерные функции: sin x = t; cos x = t, cos 2x = t; tan x = t; и tan x / 2 = t.2 — 1) = 0
Пусть tan x = t Умножьте обе части на t Выведите множитель (2t + 1)
Затем решите 3 основных тригонометрических уравнения: (2tan x +1) = 0; тангенс х = -1; tan x = 1. Шаг 4. Решите тригонометрическое неравенство R (x) 0). Затем выразите множество решений в виде интервалов. Основываясь на найденных значениях x из шага 3, решите алгебраически тригонометрическое неравенство R (x) 0), отдельно решая каждое базовое тригонометрическое неравенство f (x), g (x) .., а затем устанавливая знак соболь (знаковая карта). Пример 12. Решить:
sin x + sin 3x
Решение.Шаг 1. Стандартная форма:
R (x) = sin x + sin 2x + sin 3x
Шаг 2. Общий период 2Pi Шаг 3. Решите R (x) = 0. Преобразуйте R (x) в произведение, используя Идентификатор триггера № 28; R (x) = 2sin 2x (2cos x + 1) = 0
(0
Затем решите основное тригонометрическое уравнение: f (x) = sin 2x = 0. Дуги решения x равны: 0, Pi / 2 , Pi, 3Pi / 2, 2Pi. Используя круг триггерного блока в качестве доказательства, определите изменение f (x) от 0 до 2Pi со значениями (+) и (-): Страница 5 из 8
x 0 Pi / 2 Pi 3Pi / 2 2Pi ——————————————— ——————————————— f (x) 0 + 0 0 + 0 0 Решить g (x) = 2cos x + 1 = 0.Дуги решения: 2Pi / 3, 4Pi / 3. Определите изменение g (x) от 0 до 2Pi с помощью (+) и (-) значений: x 0 2Pi / 3 4Pi / 3 2Pi ——————- ————————————————— ——————— g (x) + 0 0 +
Шаг 4. Решите неравенство R (x)
. Вы также можете использовать графические калькуляторы, чтобы непосредственно решить тригонометрическое неравенство R (x) 0). Этот метод, если он разрешен, является быстрым, точным и удобным. Чтобы узнать, как действовать, прочитайте последнюю главу упомянутой выше книги (электронная книга Amazon, 2010 г.).ПРИМЕРЫ УСТРАНЕНИЯ НЕРАВЕНСТВА TRIG Пример 13. Решите:
(2cos x — 1) / (2cos x — 1)
(0
Решение. Шаг 1: Функция F (x) = f (x) / g ( x) = (2cos x + 1) / (2cos x — 1)
tan x + cot x
(0
Решение. Шаг 1. Преобразуйте неравенство в стандартную форму: sin x / cos x + cos x / sin x + 4 = 2 / sin 2x + 4
undefined, если x = kPi / 2 и x = kPi
Шаг 2. Общий период F (x) равен Pi, поскольку период sin 2x равен Pi.
Страница 7 из 8
Шаг 3. Сначала решите f (x) = 2sin 2x + 1 = 0 sin 2x = -1/2 x = 7Pi / 2; x = 11Pi / 12 Затем решаем g (x) = sin 2x = 0 sin 2x = 0 x = 0; x = Pi / 2 Шаг 4. Решите F (x)
Ответ или набор решений: (Pi / 2, 7Pi / 2); (11Pi / 12, Pi)
(Эта статья написана Нги Х. Нгуеном, соавтором нового метода диагональной суммы для решения квадратных уравнений)
Страница 8 из 8
| Ссылки: | Colignatus — это имя в науке Томаса Кула, эконометриста и учителя математики, Схевенинген, Голландия, http: // econpapers.repec.org/RAS/pco170.htm Ссылки в тексте на Википедию относятся к ней как к порталу, а не как к источнику. Балинкси, М. и Х.П. Янг (1976), «Критерии пропорционального представительства», Отчет об исследовании IIASA, декабрь, RR-76-020, http://pure.iiasa.ac.at/525/1/RR-76-020.pdf Балинкси, М. и Х.П. Янг (1980), «Метод распределения Вебстера», Proceedings of the National Academy of Sciences 77 (1): 1-4, February, https://www.researchgate.net/publication/7186641_The_Webster_method_of_apportionment Белов, Д.и Р.Д. Армстронг (2011), «Распределения дивергенции Кульбака-Лейблера с приложениями», J.Math. Стат. Psychol., Май, 64 (Pt 2): 291-309, https://www.ncbi.nlm.nih.gov/pubmed/214 , res. отчет: https://www.lsac.org/docs/default-source/research-(lsac-resources)/rr-09-02.pdf Beumer, M. (2010), «Распределение в теории и практике», диссертация на степень магистра логики, UvA, http://www.illc.uva.nl/Research/Publications/Reports/MoL-2010-07.text .pdf Borg, I. & P.J.F. Гроенен (2005), «Современное многомерное масштабирование», Springer, http: // www.springer.com/gp/book/9780387251509 Кэри, Дж. М., и Хикс, С. (2009), «Избирательная зона: пропорциональные избирательные системы малой величины», рабочий документ (черновик, цветные графики), http://www.lse.ac.uk/ правительство / исследования / resgroups / PSPE / pdf / PSPE_WP1_09.pdf Кэри, Дж. М., и Хикс, С. (2011), «Сладкое место для выборов: пропорциональные избирательные системы с низкой величиной», Американский журнал политических наук, 55 (2), 383-397, открытый источник http: // onlinelibrary.wiley.com/doi/10.1111 / j.1540-5907.2010.00495.x / full и http://personal.lse.ac.uk/hix/Working_Papers/Carey-Hix-AJPS2011.pdf Колфилд, MJ (2010), «Распределение представителей в Конгрессе США», Конвергенция MAA, https://www.maa.org/press/periodicals/convergence/apportioning-presentatives-in-the-united-states- съезд-введение Colignatus, Th. (2006), «О выборочном распределении скорректированного коэффициента детерминации (R2Adj) в OLS», http: //library.wolfram.ru / infocenter / MathSource / 6269 / Colignatus, Th. (2007), «Корреляция и регрессия в таблицах непредвиденных обстоятельств. Мера связи или корреляции в номинальных данных (таблицах непредвиденных обстоятельств) с использованием детерминант», https://mpra.ub.uni-muenchen.de/3660/ Colignatus, Th. (2009, 2015), «Элегантность с субстанцией», https://zenodo.org/record/2 Colignatus, Th. (2010), «Выборы с одним голосом и несколькими местами. Дидактика округа по сравнению с пропорциональным представительством, на примерах Соединенного Королевства и Нидерландов», https: // mpra.ub.uni-muenchen.de/22782/ Colignatus, Th. (2011), «Покорение мира», https://zenodo.org/record/2 Colignatus, Th. (2014), «Теория голосования за демократию», Thomas Cool Consultancy & Econometrics, https://zenodo.org/record/2 Colignatus, Th. (2017a), «Выполнение четырех возможных правил выбора премьер-министра после парламентских выборов в Нидерландах в марте 2017 года», https://mpra.ub.uni-muenchen.de/77616/ Colignatus, Th.(2017b), «Два условия применения кривой Лоренца и коэффициента Джини для голосования и распределения мест», https://mpra.ub.uni-muenchen.de/80297/ Colignatus, Th. (2017c), «Сравнение голосов и мест с диагональной (не) пропорциональной мерой, используя наклон-диагональное отклонение (SDD) с косинусом, синусом и знаком», первая версия этого документа, на MPRA, 17 августа, № 80833 ; 1-я редакция 24 августа № 80965; 2-я редакция, 16 сентября, № 81389. Эта четвертая редакция стала настоящим документом с заголовком: «Сравнение голосов и мест с косинусом, синусом и знаком, с учетом наклона и повышенной чувствительностью к неравенству / непропорциональности» Colignatus, Th.(2017d), «Одна женщина, один голос. Хотя не в США, Великобритании и Франции », https://mpra.ub.uni-muenchen.de/82513/ Colignatus, Th. (2017e), «Статистика, наклон, косинус, синус, знак, значение и R-квадрат», https://boycottholland.wordpress.com/2017/10/21/statistics-slope-cosine-sine-sign-significance- и-rsquared / Colignatus, Th. (2017f), «Aan de Staatscommissie parlementair stelsel», http://thomascool.eu/Thomas/Nederlands/Wetenschap/Advies/2017-12-21-Staatscie-parl-stelsel.pdf Colignatus, Th. (2018a), «Сравнение расстояния Эйчисона и углового расстояния для использования в качестве меры неравенства или диспропорциональности для голосов и мест», https://mpra.ub.uni-muenchen.de/84387 также на https://www.wolframcloud .com / objects / thomas-cool / Voting / 2018-01-18-Aitchison.nb. Colignatus, Th. (2018b), «Меры политической дистанции и неравенства / непропорциональности голосов и мест», https://mpra.ub.uni-muenchen.de/84324/, также на https: //www.wolframcloud.com / objects / thomas-cool / Voting / 2018-02-02-PolicyDistance.nb Донген, С. ван и А.Дж. Энрайт (2012), «Метрические расстояния, полученные из косинусного подобия и корреляций Пирсона и Спирмена», https://arxiv.org/abs/1208.3145 Dumont, P. & J.-F. Колье (2003), «Эффективное количество соответствующих партий»: Как сила голоса улучшает индекс Лааксо-Таагепера », http://centres.fusl.ac.be/CEREC/document/2003/cerec2003_7.pdf Draper, N.R. И Янг Янг (1997), «Обобщение функциональной зависимости среднего геометрического», Вычислительная статистика и анализ данных, том 23, выпуск 3, 9 января 1997 г., страницы 355-372; Препринт 1995 Технический отчет № 943, http: // www.stat.wisc.edu/node/1470 Эйзенхауэр, J.G. (2003), «Регрессия через происхождение», Статистика преподавания. Том 25, номер 3, осень 2003 г., стр. 76-80 Эрб, И. и К. Нотредэйм (2016), «Как мы должны измерять пропорциональность данных об относительной экспрессии генов?», Theory Biosci. (2016) 135: 21–36, https://link.springer.com/content/pdf/10.1007%2Fs12064-015-0220-8.pdf или https://link.springer.com/article/10.1007%2Fs12064 -015-0220-8 Галлахер, М. (1991), «Пропорциональность, непропорциональность и избирательные системы», Исследования по выборам, 10: 1, 33-51, https: // www.tcd.ie/Political_Science/draft/staff/michael_gallagher/ElectoralStudies1991.pdf Галлахер М. (1992), «Сравнение избирательных систем с пропорциональным представительством: квоты, пороги, парадоксы и большинство», B.J. Pol.S. 22, 469-496 Gallagher, M. (2007), Веб-сайт избирательных систем, Дублин, Тринити-колледж, http://www.tcd.ie/Political_Science/Staff/Michael.Gallagher/ElSystems/index.php Gallagher, M. (2017), «Набор данных индексов выборов», по состоянию на 31 июля 2017 г., http: // www.tcd.ie/Political_Science/staff/michael_gallagher/ElSystems/Docts/ElectionIndices.pdf Goldenberg, J. & S.D. Фишер (2017), «Индекс непропорциональности и Hill, I.D. (1997), «Измерение пропорциональности», Вопросы голосования, 8, стр. 7-8, http://www.mcdougall.org.uk/VM/VOL1/ISSUE01-23.pdf Джонстон, Дж. (1972), «Эконометрические методы», 2-е издание, McGraw-Hill Карпов, А.(2008), «Измерение диспропорциональности в системах пропорционального представления», Математическое и компьютерное моделирование, Том 48, выпуски 9–10, ноябрь 2008 г., страницы 1421-1438, http://www.sciencedirect.com/science/article/pii / S0895717708001933 Кестельман, П. (2005), «Распределение и пропорциональность: измеренное мнение», Вопросы голосования, 20, стр. 12-22, http://www.votingmatters.org.uk/ISSUE20/I20P4.PDF Коппель М. и Дискин А. (2009), «Измерение диспропорциональности, изменчивости и неправильного распределения: аксиоматизация и решения», Социальный выбор и благосостояние, Козак А. и Козак Р. А. (1995), «Заметки о регрессии через происхождение», Лесная хроника, май / июнь, Том 71 № 3, стр. 326-330 Лааксо, М. (1980), «Избирательная справедливость как критерий для различных систем пропорционального представительства», Скандинавские политические исследования, Bind 3 (New Series) (1980) 3, https://tidsskrift.dk/scandinavian_political_studies/article / view / 32355/30159 Лааксо, М., & R. Taagepera (2007), «Пропорциональное представительство в Скандинавии: последствия для Финляндии», Скандинавские политические исследования, https://www.researchgate.net/publication/230000636_Proportional_Representation_in_Scandinavia_Implications_for_Finland Лезник, М. и К. Тофаллис (2005), «Оценка инвариантных главных компонентов с использованием диагональной регрессии», http://researchprofiles.herts.ac.uk/portal/en/publications/estimating-invariant-principal-components- с использованием диагональной регрессии (d3379080-bda2-4d76-ab8d-b557c7fabea1).html Lovell, D. V. Pawlowsky-Glahn, J.J. Egozcue, S. Marguerat, J. Bähler (2015), «Пропорциональность: действительная альтернатива корреляции для относительных данных», PLOS Computational Biology, http://journals.plos.org/ploscompbiol/article?id=10.1371/journal. pcbi.1004075 Малькевич Дж. (2002), «Распределение», колонка характеристик AMS, http://www.ams.org/samplings/feature-column/fcarc-apportion1 Малькевич, Дж. (2017 г.), «Попарный капитал в пропорциональном распределении (2017 г.)», Статистическое программное обеспечение NCSS (без даты), «Коэффициент корреляции согласованности Лина», глава 301 документации, https://ncss-wpengine.netdna-ssl.com/wp-content/themes/ncss/pdf/Procedures/NCSS/ Lins_Concordance_Correlation_Coefficient.pdf Pawlowsky-Glahn, V., J.J. Egozcue, R. Meziat (2007), «Статистический анализ композиционных данных: геометрия Эйчисона», https: //laboratoriomatematicas.uniandes.edu.co/cursocoda/04-Vera-geometry.pdf Pukelsheim, F. (2014), «Пропорциональное представление. Методы распределения и их приложения», Springer, Ренвик А. (2015), «Электоральная диспропорциональность: что это такое и как мы должны ее измерять?», Http://blogs.reading.ac.uk/readingpolitics/2015/06/29/electoral-disproportionality- что-это-это-и-как-нам-это-измерить / Самуэльсон П. (1942), «Заметка об альтернативных регрессиях», Econometrica, Vol. 10, вып.1 (январь 1942 г.), стр. 80-83,: http://www.jstor.org/stable/1 4 Таагепера Р. и М.С. Шугарт (1989), «Места и голоса», Йельский университет Таагепера, Р. и М. Лааксо (2006), «Профили пропорциональности западноевропейских избирательных систем», Европейский журнал политических исследований 8 (4): 423 — 446 · май 2006 г., https://www.researchgate.net / Publication / 230041613_Proportionality_Profiles_of_West_European_Electoral_Systems Таагепера, Р. и Б. Грофман (2003), «Картирование индексов диспропорциональности голосов и количества голосов и нестабильности между выборами», Политика партии, 9 (6), p659-677, http: // escholarship.org / uc / item / 0m9912ff # page-1 Тейл, Х. (1969), «Желаемая политическая энтропия», Американский обзор политической науки, Тофаллис, К. (2000), «Множественная нейтральная регрессия», Рабочий исследовательский документ 14, UHBS 2000: 13, http://uhra.herts.ac.uk/bitstream/handle/2299/689/S7.pdf? последовательность = 1 Таллок, Г. (2008), «Public Choice», Новый экономический словарь Палгрейва, второе издание, http: //www.dictionaryofeconomics.ru / article? id = pde2008_P000240 & q = рациональный% 20choice & topicid = & result_number = 10 Куинн, Т. (2017), «Введение в соразмерность», https://cran.r-project.org/web/packages/propr/vignettes/a_introduction.html Янг, H.P. (2004), «Справедливость в распределении», Mimeo, подготовлено для симпозиума Бюро переписи США, http://www.census.gov/history/pdf/Fairness_in_Apportionment_Young.pdf Занд, М.С., Дж. Ван, С. Халчи (2015), «Графическое представление мер близости для многомерных данных.Классическое и метрическое многомерное масштабирование », The Mathematica Journal 17, http://www.mathematica-journal.com/2015/09/graphical-presentation-of-proximity-measures-for-multidimensional-data/ |
|---|
Разница между алгеброй II и тригонометрией
Длинные части школьной математики, алгебры II и тригонометрии часто являются необходимыми курсами для выпуска и поступления в колледж. Хотя и алгебра II, и тригонометрия включают решение математических задач, алгебра II фокусируется на решении уравнений и неравенств, в то время как тригонометрия — это изучение треугольников и того, как стороны связаны с углами.
Курсовая работа по алгебре II
В отличие от тригонометрии, которая имеет более геометрическую направленность, алгебра II делает упор на решении линейных уравнений и неравенств. Курсовая работа охватывает полиномиальные, обратные, экспоненциальные, логарифмические, квадратичные и рациональные функции. Другие темы, затронутые в курсе алгебры II, включают степени, корни и радикалы; построение графиков квадратных и кубических корней и рациональных функций; обратная и совместная вариация, дробные выражения, координатная геометрия, комплексные числа, матрицы и определители, комплексные числа, последовательности и ряды и вероятность.
Практическое применение алгебры II
Алгебра II находит практическое применение в науке и бизнесе. Функции и концепции алгебры II используются в статистике и вероятности. Другие области карьеры, в которых используется Алгебра II, включают программное обеспечение и компьютерную инженерию, медицину, фармацевт, банковское дело, финансы и страхование. Концепции алгебры II составляют основу страхового актуария и таблиц смертности. Полиция и следователи ДТП используют Алгебру II для определения скорости транспортного средства.Финансовые аналитики используют Алгебру II при расчете нормы прибыли на инвестиции. Метеорологи используют Алгебру II для определения погодных условий.
Курсовая работа по тригонометрии
Тригонометрия фокусируется на сторонах и углах. Основные термины включают синус, косинус и тангенс, прямой угол, прямоугольный треугольник, наклон, дугу и радиант. Курсы тригонометрии охватывают теорему Пифагора, измерение углов; отношения между синусами, хордами, косинусами и прямоугольными треугольниками; радианты и длина дуги, углы возвышения и понижения, определение касательных и наклонов, тригонометрия или прямоугольные и наклонные треугольники, закон синусов и косинусов и определение площади треугольника.Рассматриваются геометрические, а не числовые функции, такие как:
- синус
- косинус
- тангенс
- котангенс
- секанс
- косеканс
Тригонометрия также касается арксинус, инверсных функций и арктангенс.
Практическое применение тригонометрии
Тригонометрия считается чистой формой математики. В отличие от алгебры II, которая используется в основном в теории вероятностей и статистики, тригонометрия находит применение в науке.Некоторые из приложений тригонометрии включают астрономию, навигацию, инженерию, физику и географию. Тригонометрия считается предпосылкой для исчисления.
Важность алгебры II
Хотя тригонометрия легла в основу многих научных открытий, алгебра II приобретает все большее значение. Согласно исследованию, проведенному Энтони Карневейлом и Алисой Дерошер в Службе образовательного тестирования и опубликованному The Washington Post, из тех людей, которые занимали высшие должности, 84 процента изучали алгебру II или более высокий класс в качестве своего последнего школьного математика. курс.Вооруженные этим исследованием, многие школьные округа требуют для окончания учебы по алгебре II.
Функции синуса и косинуса · Precalculus
Единичный круг: функции синуса и косинуса · Precalculus
В этом разделе вы:
- Найдите значения функции для синуса и косинуса
30 ° или (π6), 45 ° или (π4)и
60 ° или (π3).
- Определите область и диапазон функций синуса и косинуса.
- Используйте исходные углы для оценки тригонометрических функций.
Ищете острые ощущения? Тогда подумайте о поездке на Singapore Flyer, самом высоком колесе обозрения в мире. Колесо обозрения, расположенное в Сингапуре, взлетает на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя с земли на вершину и снова вниз по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат.Затем мы можем обсудить круговое движение в терминах пар координат.
Поиск значений функции для синуса и косинуса
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичного круга, круга с центром в начале координат с радиусом 1, как показано в [ссылка]. Угол (в радианах), который t
точек пересечения образуют дугу длиной s.
По формуле s = rt,
и зная, что r = 1,
мы видим, что для единичной окружности s = t.
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление, в котором будет разворачиваться положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла t,
, мы можем обозначить пересечение конечной стороны и единичной окружности его координатами (x, y).
Координаты x
и
будут выходами тригонометрических функций f (t) = cos t
и f (t) = sin t,
соответственно.Это означает, что x = cos t
и y = sin t.
Единичный круг
Единичная окружность имеет центр в точке (0,0)
и радиус 1
. В единичном круге длина перехваченной дуги равна радианам центрального угла t.
Пусть (x, y)
— конечная точка единичной окружности дуги длиной s.
(х, у)
координаты этой точки можно описать как функции угла.
Определение функций синуса и косинуса
Теперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как (x, y)
Координаты
относятся к длине дуги и углу . Синусоидальная функция связывает действительное число t
до y -координаты точки, где соответствующий угол пересекает единичную окружность. Точнее синус угла t
равно значению y конечной точки единичной окружности дуги длины t.
В [ссылка] синус равен y.
Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — это координата y соответствующей точки на единичной окружности.
Функция косинуса угла t
равно x -значению конечной точки на единичной окружности дуги длины t.
В [ссылка] косинус равен x.
Поскольку понятно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: sin t
совпадает с sin (t)
и cos t
совпадает с cos (t).
Аналогично cos2t
— это обычно используемое сокращенное обозначение (cos (t)) 2.
Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Функции синуса и косинуса
Если t
— действительное число и точка (x, y)
на единичной окружности соответствует углу t,
, затем
cos t = x
грех т = у
* Дана точка * P (x, y)
на единичной окружности, соответствующей углу t,
найти синус и косинус.**
- Синус
tсовпадает с координатой y точки
P: грех t = y.
- Косинус
tсовпадает с координатой x точки
P: cos t = x.
Нахождение значений функций для синуса и косинуса
Пункт P
— точка на единичной окружности, соответствующая углу t,
, как показано в [ссылка]. Найти cos (t)
и sin (t).
Мы знаем, что cos t
— это координата x соответствующей точки на единичной окружности, а sin t
— это координата y соответствующей точки на единичной окружности. Итак:
x = cos t = 12y = sin t = 32
Определенный угол t
соответствует точке на единичной окружности (−22,22)
, как показано в [ссылка]. Найти cos t
и син т.
cos (t) = — 22, sin (t) = 22
Нахождение синусов и косинусов углов на оси
Для квадрантных углов соответствующая точка единичной окружности попадает на ось x- или y . В этом случае мы можем легко вычислить косинус и синус из значений x
.
и г.
Вычисление синусов и косинусов по оси
Найти cos (90 °)
и sin (90 °).
Перемещение на 90 °
против часовой стрелки вокруг единичной окружности от положительной оси x приводит нас к вершине круга, где (x, y)
координаты (0, 1), как показано в [ссылка].
Используя наши определения косинуса и синуса,
x = cos t = cos (90 °) = 0y = sin t = sin (90 °) = 1
Косинус 90 ° равен 0; синус 90 ° равен 1.
Найдите косинус и синус угла π.
cos (π) = — 1, sin (π) = 0
Пифагорейская идентичность
Теперь, когда мы можем определить синус и косинус, мы узнаем, как они соотносятся друг с другом и с единичной окружностью. Напомним, что уравнение единичной окружности: x2 + y2 = 1.
Поскольку x = cos t
и y = sin t,
можно заменить на x
и
, чтобы получить cos2t + sin2t = 1.
Это уравнение, cos2t + sin2t = 1,
известен как Пифагорейская идентичность .См. [Ссылка].
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам необходимо дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем, в каком квадранте находится угол, мы можем легко выбрать правильное решение.
Пифагорейская идентичность
Пифагорейская идентичность утверждает, что для любого действительного числа t
cos2 t + sin2 t = 1
Зная синус некоторого угла t и его положение в квадранте, найдите косинус t.
- Заменить известное значение
sin (t)в пифагорейскую идентичность.
- Решить для
Стоимость). - Выберите решение с соответствующим знаком для значений x в квадранте, где
тнаходится.
Нахождение косинуса из синуса или синуса из косинуса
Если sin (t) = 37
и т
находится во втором квадранте, найдите cos (t).
Если мы опустим вертикальную линию из точки на единичной окружности, соответствующей t,
мы создаем прямоугольный треугольник, из которого мы можем видеть, что тождество Пифагора — это просто один из случаев теоремы Пифагора. См. [Ссылка].
Подстановка известного значения синуса в тождество Пифагора,
cos2 (t) + sin2 (t) = 1 cos2 (t) + 949 = 1 cos2 (t) = 4049 cos (t) = ± 4049 = ± 407 = ± 2107
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицательный.Итак, cos (t) = — 2107
Если cos (t) = 2425
и т
находится в четвертом квадранте, найдите sin (t).
sin (t) = — 725
Нахождение синусов и косинусов специальных углов
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы особых углов, используя Пифагорова идентичность и наши знания о треугольниках.
Нахождение синусов и косинусов углов 45 °
Сначала посмотрим на углы 45 °
или π4,
, как показано в [ссылка]. A 45 ° –45 ° –90 °
Треугольник
— это равнобедренный треугольник, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
При t = π4
, что составляет 45 градусов, радиус единичной окружности делит пополам первый квадратный угол .Это означает, что радиус лежит вдоль линии y = x.
Единичный круг имеет радиус, равный 1. Итак, прямоугольный треугольник образовался ниже линии y = x
имеет стороны x
и y (y = x),
и радиус = 1. См. [ссылка].
Из теоремы Пифагора получаем
х2 + у2 = 1
Подставляя y = x,
получаем
х2 + х2 = 1
Комбинируя одинаковые термины, получаем
2×2 = 1
И решение относительно x,
получаем
х2 = 12 х = ± 12
В квадранте I x = 12.
При t = π4
или 45 градусов,
(x, y) = (x, x) = (12,12) x = 12, y = 12 cos t = 12, sin t = 12
Если мы затем рационализируем знаменатели, мы получим
cos t = 1222 = 22 sin t = 1222 = 22
Следовательно, (x, y)
координаты точки на окружности радиуса 1
под углом 45 °
являются (22,22).
Нахождение синусов и косинусов углов 30 ° и 60 °
Далее мы найдем косинус и синус под углом 30 °,
или π6
.Сначала нарисуем внутри круга треугольник с одной стороной под углом 30 °,
и еще один под углом −30 °,
, как показано в [ссылка]. Если полученные два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут равны 60 °,
, как показано в [ссылка].
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину 2y,
.
и поскольку все стороны равны, мы также можем заключить, что r = 2y
или у = 12р.
Так как sin t = y
,
грех (π6) = 12r
А так как r = 1
в нашем единичном круге ,
грех (π6) = 12 (1) = 12
Используя тождество Пифагора, мы можем найти значение косинуса.
cos2π6 + sin2 (π6) = 1 cos2 (π6) + (12) 2 = 1 cos2 (π6) = 34 Используйте свойство квадратного корня. cos (π6) = ± 3 ± 4 = 32 Поскольку y положительно, выбираем положительный корень.
(х, у)
координаты точки на окружности радиуса 1
под углом 30 °
являются (32,12).
При t = π3
(60 °), радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, BAD,
, как показано в [ссылка]. Угол А
имеет меру 60 °.
В точке B,
рисуем угол ABC
с размером 60 °.
Мы знаем углы в треугольнике в сумме 180 °,
так что мера угла C
тоже 60 °.
Теперь у нас есть равносторонний треугольник.Поскольку каждая сторона равностороннего треугольника ABC
— это та же длина, и мы знаем, что одна сторона — это радиус единичной окружности, все стороны должны иметь длину 1.
Мера угла ABD
составляет 30 °. Так, если двойной, угол ABC
— 60 °. BD
— биссектриса переменного тока,
, поэтому он режет AC
пополам. Это означает, что
г.
это 12
радиус, или 12.
Обратите внимание, что AD
— это координата x точки B,
, который находится на пересечении угла 60 ° и единичной окружности.Это дает нам треугольник BAD
с гипотенузой 1 и стороной x
длиной 12.
Из теоремы Пифагора получаем
х2 + у2 = 1
Подставляя x = 12,
получаем
(12) 2 + y2 = 1
Решение для y,
получаем
14 + y2 = 1 y2 = 1−14 y2 = 34 y = ± 32
Так как t = π3
имеет конечную сторону в квадранте I, где координата y- положительна, мы выбираем y = 32,
положительное значение.
При t = π3
(60 °), (x, y)
координаты точки на окружности радиуса 1
под углом 60 °
сот (12,32),
, поэтому мы можем найти синус и косинус.
(x, y) = (12,32) x = 12, y = 32 cos t = 12, sin t = 32
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. [ссылка] суммирует эти значения.
| Угол | 0 | π6, или 30 | π4, или 45 ° | π3, или 60 ° | π2, или 90 ° |
| Косинус | 1 | 32 | 22 | 12 | 0 |
| Синус | 0 | 12 | 22 | 32 | 1 |
[ссылка] показывает общие углы в первом квадранте единичной окружности.
Использование калькулятора для определения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы оцениваем cos (30)
на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Если задан угол в радианах, воспользуйтесь графическим калькулятором, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Использование графического калькулятора для поиска синуса и косинуса
Вычислить cos (5π3)
с помощью графического калькулятора или компьютера.
Введите следующие нажатия клавиш:
COS (5 × π ÷ 3) ВВЕДИТЕ
cos (5π3) = 0,5
Анализ
Мы можем найти косинус или синус угла в градусах прямо на калькуляторе в градусном режиме. Для калькуляторов или программного обеспечения, которые используют только радианный режим, мы можем найти знак 20 °,
, например, включив коэффициент преобразования в радианы как часть входных данных:
SIN (20 × π ÷ 180) ВВОД
примерно 0.866025403
Определение области и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны. Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут входить в функции? Поскольку углы меньше 0 и углы больше 2π
все еще можно изобразить на единичной окружности и иметь реальные значения x, y,
.
и р,
не существует нижнего или верхнего предела углов, которые могут входить в функции синуса и косинуса.Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичный круг , как показано в [ссылка]. Границы координаты x равны [−1,1].
Границы координаты y также равны [−1,1].
Следовательно, диапазон функций синуса и косинуса равен [-1,1].
Поиск опорных углов
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса — это координата y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано в [ссылка], угол α
имеет то же значение синуса, что и угол t;
значения косинуса противоположны.Угол β
имеет то же значение косинуса, что и угол t;
значения синуса противоположны.
sin (t) = sin (α) и cos (t) = — cos (α) sin (t) = — sin (β) и cos (t) = cos (β)
Напомним, что опорный угол угла — это острый угол, t,
.
образует оконечную сторону угла t
и горизонтальная ось. Базовый угол — это всегда угол между 0
.
и 90 °,
или 0
и π2
радиана.Как видно из [ссылка], для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.
** Дан угол между 0
и 2π,
найдите его опорный угол. **
- Угол в первом квадранте является его собственным опорным углом.
- Для угла во втором или третьем квадранте опорный угол равен
\ | π − t \ |или
\ | 180 ° −t \ |.
- Для угла в четвертом квадранте опорный угол равен
2π − tили
360 ° −т.
- Если угол меньше
0или больше
2π,
добавить или вычесть
2π
столько раз, сколько необходимо, чтобы найти эквивалентный угол между
0
и
2π.
Поиск опорного угла
Найдите опорный угол 225 °
, как показано в [ссылка].
Потому что 225 °
находится в третьем квадранте, опорный угол
\ | (180 ° −225 °) \ | = \ | −45 ° \ | = 45 °
Найдите опорный угол 5π3.
№3
Использование опорных углов
А теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись на высоте двадцати футов над землей. Затем всадник совершает поворот на три четверти по кругу. Что такое новый рост райдера? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов, или при отрицательном угле .Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения (x, y)
координат для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для оценки тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если мы знаем косинус или синус его опорного угла.Абсолютные значения косинуса и синуса угла такие же, как и у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и косинусы и синусы их опорных углов.Знак (положительный или отрицательный) можно определить по квадранту угла.
Для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и значения y в квадранте исходного угла.
Использование опорных углов для поиска синуса и косинуса
- Используя опорный угол, найдите точное значение
cos (150 °)и
грех (150 °).
- Используя опорный угол, найти
cos 5π4и
грех 5π4.
150 ° находится во втором квадранте.Угол, который он образует с осью x , составляет 180 ° — 150 ° = 30 °, поэтому опорный угол составляет 30 °.
Это говорит нам о том, что 150 ° имеет те же значения синуса и косинуса, что и 30 °, за исключением знака. Мы знаем, чтоcos (30 °) = 32 и sin (30 °) = 12.
Поскольку 150 ° находится во втором квадранте, координата x точки на окружности отрицательна, поэтому значение косинуса отрицательное. Координата y положительна, поэтому значение синуса положительное.
cos (150 °) = — 32 и sin (150 °) = 12
- 5π4
находится в третьем квадранте. Его опорный угол составляет
°.
5π4 − π = π4.Косинус и синус числа
π4
равны
22.
В третьем квадранте оба
х
и
y
отрицательны, поэтому:
cos 5π4 = −22 и sin 5π4 = −22
- Используйте опорный угол
315 °, чтобы найти
cos (315 °)
и
грех (315 °).
- Используйте опорный угол
−π6, чтобы найти
cos (−π6)
и
грех (−π6).
- cos (315 °) = 22, sin (315 °) = — 22
- cos (−π6) = 32, sin (−π6) = — 12
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности.Они показаны в [ссылка]. Найдите время, чтобы изучить (x, y)
координаты всех основных углов в первом квадранте.
В дополнение к изучению значений специальных углов, мы можем использовать опорные углы, чтобы найти (x, y)
координаты любой точки на единичной окружности, используя то, что мы знаем об углах отсчета вместе с идентификаторами
х = cos ty = sin t
Сначала мы находим опорный угол, соответствующий данному углу.Затем мы берем значения синуса и косинуса опорного угла и даем им знаки, соответствующие значениям квадранта y и x .
** Учитывая угол точки на окружности и радиус окружности, найдите (x, y)
координаты точки. **
- Найдите опорный угол, измерив наименьший угол к оси x .
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для
хи
y
в данном квадранте.
Использование единичного круга для поиска координат
Найдите координаты точки на единичной окружности под углом 7π6.
Мы знаем, что угол 7π6
находится в третьем квадранте.
Во-первых, давайте найдем опорный угол, измерив угол к оси x .Чтобы найти опорный угол угла, конечная сторона которого находится в квадранте III, мы находим разность угла и π.
7π6 − π = π6
Далее мы найдем косинус и синус опорного угла:
cos (π6) = 32 sin (π6) = 12
Мы должны определить соответствующие знаки для x и y в данном квадранте. Поскольку наш исходный угол находится в третьем квадранте, где оба x
и
отрицательны, косинус и синус отрицательны.
cos (7π6) = — 32 sin (7π6) = — 12
Теперь мы можем вычислить (x, y)
координат с использованием тождеств x = cos θ
и y = sin θ.
Координаты точки: (−32, −12)
на единичной окружности.
Найдите координаты точки на единичной окружности под углом 5π3.
(12, −32)
Ключевые уравнения
| Пифагорейская идентичность | cos2t + sin2t = 1 |
Ключевые понятия
- Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом 1 единица.
- Используя единичную окружность, синус угла
tравно y -значение конечной точки на единичной окружности дуги длиной
t
, тогда как косинус угла
t
равно x -значению конечной точки. См. [Ссылка].
- Значения синуса и косинуса наиболее точно определяются, когда соответствующая точка единичной окружности попадает на ось. См. [Ссылка].
- Когда синус или косинус известны, мы можем использовать пифагорову тождество, чтобы найти другое.Пифагорейская идентичность также полезна для определения синусов и косинусов особых углов. См. [Ссылка].
- Калькуляторы и программное обеспечение для построения графиков полезны для поиска синусов и косинусов, если известна правильная процедура ввода информации. См. [Ссылка].
- Все функции синуса и косинуса являются действительными числами.
- Диапазон функций синуса и косинуса равен
[-1,1]. - Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус его опорного угла.
- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла — это размерный угол,
t,образует оконечную сторону угла
t
и горизонтальная ось. См. [Ссылка].
- Опорные углы можно использовать для определения синуса и косинуса исходного угла. См. [Ссылка].
- Опорные углы также можно использовать для определения координат точки на окружности.См. [Ссылка].
Упражнения по разделам
Устный
Опишите единичный круг.
Единичный круг — это круг радиуса 1 с центром в начале координат.
Что означают координаты x- и y- точек на единичной окружности?
Обсудите разницу между концевым углом и опорным углом.
Coterminal углы — это углы, которые имеют одну и ту же конечную сторону.Базовый угол — это величина наименьшего острого угла, t,
образует оконечную сторону угла t
и горизонтальная ось.
Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
Значения синуса равны.
Алгебраические
Для следующих упражнений используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором конечная точка определяется t
лжи.
sin (t) <0
и cos (t) <0
sin (t)> 0
и cos (t)> 0
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
Числовой
Для следующих упражнений укажите исходный угол для данного угла.
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.
300 °
60 °,
Квадрант IV, sin (300 °) = — 32, cos (300 °) = 12
135 °
45 °,
Квадрант II, sin (135 °) = 22,
cos (135 °) = — 22
120 °
60 °,
Квадрант II, sin (120 °) = 32,
cos (120 °) = — 12
150 °
30 °,
квадрант II, sin (150 °) = 12,
cos (150 °) = — 32
7π6
π6,
Квадрант III, sin (7π6) = — 12,
cos (7π6) = — 32
3π4
π4,
Квадрант II, sin (3π4) = 22,
cos (4π3) = — 22
2π3
π3,
Квадрант II, sin (2π3) = 32,
cos (2π3) = — 12
7π4
π4,
Квадрант IV, sin (7π4) = — 22,
соз (7π4) = 22
Найдите требуемое значение для следующих упражнений.
Если cos (t) = 17
и т
находится в квадранте 4 , найдите sin (t).
Если cos (t) = 29
и т
находится в квадранте 1 -го , найдите sin (t).
779
Если sin (t) = 38
и т
находится в квадранте 2 и , найдите cos (t).
Если sin (t) = — 14
и т
находится в квадранте 3 rd , найдите cos (t).
−154
Найдите координаты точки на окружности радиуса 15, соответствующей углу 220 °.
Найдите координаты точки на окружности с радиусом 20, соответствующей углу 120 °.
(-10,103)
Найдите координаты точки на окружности радиуса 8, соответствующей углу 7π4.
Найдите координаты точки на окружности радиуса 16, соответствующей углу 5π9.
(–2,778,15,757)
Укажите область определения функций синуса и косинуса.
Укажите диапазон функций синуса и косинуса.
[–1,1]
Графический
Для следующих упражнений используйте данную точку на единичном круге, чтобы найти значение синуса и косинуса t.
! [График четверти круга с вписанными углами 0, 30, 45, 60 и 90 градусов. Показана эквивалентность углов в радианах.Отмечены точки вдоль круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_201.jpg)
! [График вписанной окружности с углом t. Точка (отрицательный квадратный корень из 3 на 2, 1/2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_202.jpg)
sint = 12, стоимость = −32
! [График вписанной окружности с углом t. Точка (1/2, отрицательный квадратный корень из 3 по 2) находится на пересечении конечной стороны угла и края круга.] (/ precalculus-book / resources / CNX_Precalc_Figure_05_02_203.jpg)
! [График вписанной окружности с углом t. Точка (отрицательный квадратный корень из 2 по 2, отрицательный квадратный корень из 2 по 2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_204.jpg)
sin t = −22, cos t = −22
! [График вписанной окружности с углом t. Точка (1/2, квадратный корень из 3 по 2) находится на пересечении конечной стороны угла и края круга.] (/ precalculus-book / resources / CNX_Precalc_Figure_05_02_205.jpg)
! [График вписанной окружности с углом t. Точка (-1/2, квадратный корень из 3 по 2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_206.jpg)
sin t = 32, cos t = −12
! [График вписанной окружности с углом t. Точка (-1/2, отрицательный квадратный корень из 3 по 2) находится на пересечении конечной стороны угла и края круга.] (/ precalculus-book / resources / CNX_Precalc_Figure_05_02_207.jpg)
! [График вписанной окружности с углом t. Точка (квадратный корень из 2 на 2, отрицательный квадратный корень из 2 на 2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_208.jpg)
sin t = −22, cos t = 22
! [График вписанной окружности с углом t. Точка (1,0) находится на пересечении конечной стороны угла и края окружности.] (/ precalculus-book / resources / CNX_Precalc_Figure_05_02_209.jpg)
! [График вписанной окружности с углом t. Точка (-1,0) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_210.jpg)
sin t = 0, cos t = −1
! [График вписанной окружности с углом t. Точка (0.111,0.994) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_211.jpg)
! [График вписанной окружности с углом t. Точка (0.803, -0.596 находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_212.jpg)
sin t = -0,596, cos t = 0,803
! [График вписанной окружности с углом t. Точка (отрицательный квадратный корень из 2 по 2, квадратный корень из 2 по 2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_213.jpg)
! [График вписанной окружности с углом t. Точка (квадратный корень из 3 на 2, 1/2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_214.jpg)
sin t = 12, cos t = 32
! [График вписанной окружности с углом t. Точка (отрицательный квадратный корень из 3 по 2, -1/2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_215.jpg)
! [График вписанной окружности с углом t. Точка (квадратный корень из 3 на 2, -1/2) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_216.jpg)
sin t = −12, cos t = 32
! [График вписанной окружности с углом t. Точка (0, -1) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_217.jpg)
! [График вписанной окружности с углом t.Точка (-0.649, 0.761) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_218.jpg)
sin t = 0,761, cos t = −0,649
! [График вписанной окружности с углом t. Точка (-0.948, -0.317) находится на пересечении конечной стороны угла и края круга.] (/ Precalculus-book / resources / CNX_Precalc_Figure_05_02_219.jpg)
! [График вписанной окружности с углом t. Точка (0, 1) находится на пересечении конечной стороны угла и края окружности.] (/ precalculus-book / resources / CNX_Precalc_Figure_05_02_220.jpg)
sin t = 1, cos t = 0
Технологии
Для следующих упражнений используйте графический калькулятор.
Расширения
Оцените следующие упражнения.
грех (−9π4) cos (−π6)
−64
Реальные приложения
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку (0,1),
, то есть на северной позиции. Предположим, карусель вращается против часовой стрелки.
Какие координаты ребенка через 45 секунд?
Какие координаты ребенка через 90 секунд?
(0, –1)
Какие координаты ребенка через 125 секунд?
Когда у ребенка будут координаты (0.707, –0.707)
если поездка длится 6 минут? (Есть несколько ответов.)
37,5 секунды, 97,5 секунды, 157,5 секунды, 217,5 секунды, 277,5 секунды, 337,5 секунды
Когда у ребенка будут координаты (−0,866, −0,5)
если ехать последние 6 минут?
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 1
- синусоидальная функция
- y -значение точки на единичной окружности, соответствующей заданному углу
- единичный круг
- круг с центром в
(0,0)и радиус 1.
Эта работа находится под международной лицензией Creative Commons Attribution 4.0.
Вы также можете бесплатно скачать по адресу http://cnx.org/contents/[email protected]
Атрибуция:
Как использовать линейные комбинации для решения тригонометрических уравнений?
Я отвечал на все эти старые математические вопросы. Трудно понять, читает ли кто-нибудь ответы.
Линейная комбинация косинуса и синуса одного и того же угла соответствует масштабированию и фазовому сдвигу.Давайте объясним, как это работает.
Линейная комбинация косинуса и синуса одного и того же угла является выражением формы:
# a cos x + b sin x #
Это очень похоже на формулу суммы углов для синуса или формулу разностного угла для косинуса:
# sin (alpha + beta) = sin alpha cos beta + cos alpha sin beta #
# cos (альфа — бета) = cos alpha cos beta + sin alpha sin beta #
Действительно, мы можем взять нашу линейную комбинацию и преобразовать ее в масштабированную версию любого из них.Совет профессионала: когда есть выбор, предпочитайте косинус синусу.
Умножим на коэффициент масштабирования # r # и установим #alpha = x, beta = theta. #
# r cos (x — тета) = r cos theta cos x + r sin theta sin x #
Соответствие нашей линейной комбинации приводит нас к желанию решить для # r # и # theta #:
#a = r cos theta #
#b = r sin theta #
Мы видели это раньше. Вот как мы превращаем полярные координаты #P (r, theta) # в прямоугольные координаты, здесь # (a, b).2} #
#sin theta = b / r #
#cos theta = a / r #
# тан тета = б / а #
#theta = текст {arctan2} (b //, a) #
Обычно это записывается как обычный арктангенс, но это не совсем так. Обычный арктангенс покрывает только два квадранта и не работает по оси y. Это двухпараметрический арктангенс с четырьмя квадрантами, который возвращает действительную тэту для всех реальных входных пар. # //, # преднамеренно, напоминая нам, что есть два отдельных параметра, и which is which.