Калькулятор онлайн — Решение тригонометрических неравенств

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.

Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Тригонометрические неравенства

Неравенства вида \( \sin x > a \) и \( \sin x

Пусть дано простейшее неравенство \( \sin x > a \).

1) При \(-1


Из данного рисунка видно, что в этом случае решение неравенства будет таким:

$$ x \in (\arcsin a + 2\pi k; \;\; \pi — \arcsin a + 2\pi k), k \in \mathbb{Z} $$

2) При \(а \geqslant 1 \) неравенство не имеет решений: \( x \in \emptyset \)

3) При \(а
4) При \(а = -1 \) решением неравенства является любое действительное число, отличное от \( -\frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)

Пусть дано простейшее неравенство \( \sin x

1) При \(-1


Из данного рисунка видно, что в этом случае решение неравенства будет таким:

$$ x \in (\pi — \arcsin a + 2\pi k; \;\; 2\pi + \arcsin a + 2\pi k), k \in \mathbb{Z} $$

2) При \(а > 1 \) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)

3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)

4) При \(а \leqslant -1 \) неравенство не имеет решений.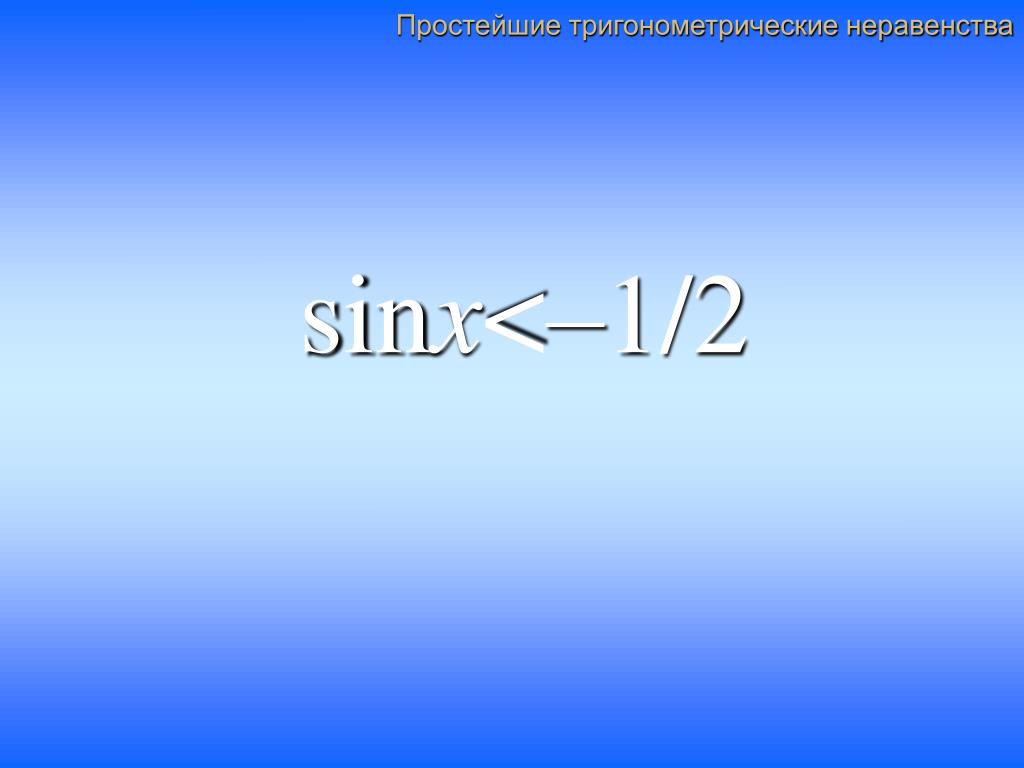

Неравенства вида \( \cos x > a \) и \( \cos x

Пусть дано простейшее неравенство \( \cos x > a \).

1) При \(-1


Из данного рисунка видно, что в этом случае решение неравенства будет таким:

$$ x \in (-\arccos(a) + 2\pi k; \;\; \arccos a + 2\pi k), \; k \in \mathbb{Z} $$

2) При \( a \geqslant 1\) неравенство не имеет решений.

3) При \(а
4) При \(а = -1\) решением неравенства является любое действительное число, отличное от \( \pi + 2\pi k, \; k \in \mathbb{Z} \)

Пусть дано простейшее неравенство \( \cos x

1) При \(-1


Из данного рисунка видно, что в этом случае решение неравенства будет таким:

$$ x \in (\arccos a + 2\pi k; \;\; 2\pi — \arccos a + 2\pi k), \; k \in \mathbb{Z} $$

2) При \(a > 1\) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)

3) При \(a \leqslant -1\) неравенство не имеет решений.

4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb{Z} \)

Неравенства вида \( tg \;x > a \) и \( tg \;x

Пусть дано простейшее неравенство \( tg \;x > a \).

Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:

$$ x \in \left(arctg \;a + \pi k; \;\; \frac{\pi}{2} + \pi k \right), \; k \in \mathbb{Z} $$

Пусть дано простейшее неравенство \( tg \;x

Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:

$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \;a + \pi k\right), \; k \in \mathbb{Z} $$

Неравенства вида \( ctg \;x > a \) и \( ctg \;x

Пусть дано простейшее неравенство \( ctg \;x > a \).

Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:

$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb{Z} $$

Пусть дано простейшее неравенство \( ctg \;x

Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:

$$ x \in ( arcctg \; a + \pi k; \;\; \pi + \pi k ), \; k \in \mathbb{Z} $$

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство \( \sin x > \frac{1}{2} \).

Так как \( -1
$$ x \in \left( \arcsin \frac{1}{2} + 2\pi k; \;\; \pi — \arcsin \frac{1}{2} + 2\pi k \right), \; k \in \mathbb{Z} $$

Так как \( \arcsin \frac{1}{2} = \frac{\pi}{6} \), то решение можно переписать в виде

$$ x \in \left(\frac{\pi}{6} + 2\pi k; \;\; \frac{5\pi}{6} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 2. Решим неравенство \( \sin \;x
Так как \( -1
$$ x \in \left(\pi — \arcsin \left( -\frac{2}{3} \right) + 2\pi k; \;\; 2\pi + \arcsin \left( -\frac{2}{3} \right) + 2\pi k \right), \; k \in \mathbb{Z} $$

Воспользовавшись равенством \( \arcsin(-a) = -\arcsin a \), перепишем решение в виде

$$ x \in \left(\pi + \arcsin \frac{2}{3} + 2\pi k; \;\; 2\pi — \arcsin \frac{2}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 3. Решим неравенство \( \cos x > \frac{1}{2} \).

Так как \( -1
$$ x \in \left(-\frac{\pi}{3} + 2\pi k; \;\; \frac{\pi}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 4. Решим неравенство \( \cos x
Так как \( -1
$$ x \in (\arccos(-0{,}3) + 2\pi k; \;\; 2\pi — \arccos(-0{,}3) + 2\pi k), k \in \mathbb{Z} $$

Воспользовавшись равенством \( \arccos(-a) = \pi — \arccos a \), перепишем решение в виде

$$ x \in (\pi-\arccos 0{,}3 + 2\pi k; \;\; \pi + \arccos 0{,}3 + 2\pi k), \; k \in \mathbb{Z} $$

ПРИМЕР 5. Решим неравенство \( tg \;x > 1 \).

Очевидно, что решение неравенства будет таким:

$$ x \in \left(\frac{\pi}{4} + \pi k; \;\; \frac{\pi}{2} + \pi k\right), \; k \in \mathbb{Z} $$

ПРИМЕР 6. Решим неравенство \( tg \;x
Очевидно, что решение неравенства будет таким:

$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \left( -\frac{1}{2} \right) + \pi k\right), \; k \in \mathbb{Z} $$

Воспользовавшись равенством \( arctg(-a) = -arctg \; a \), перепишем решение в виде

$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; -arctg \frac{1}{2} + \pi k\right), \; k \in \mathbb{Z} $$

ПРИМЕР 7. Решим неравенство \( ctg \;x > \frac{\sqrt{3}}{3} \).

Очевидно, что решение неравенства будет таким:

$$ x \in \left( \pi k; \;\; \frac{\pi}{3} + \pi k \right), \; k \in \mathbb{Z} $$

ПРИМЕР 8. Решим неравенство \( ctg \;x
Очевидно, что решение неравенства будет таким:

$$ x \in \left( arcctg \left( -\frac{5}{4} \right) + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$

Воспользовавшись равенством \( arcctg(-a) = \pi — arcctg \;a \), перепишем решение в виде

$$ x \in \left( \pi — arcctg \frac{5}{4} + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$

или в виде

$$ x \in \left( — arcctg \frac{5}{4} + \pi n; \;\; \pi n \right), \; n \in \mathbb{Z} $$

sinx>a

Простейшие тригонометрические неравенства вида sin x>a — основа для решения более сложных тригонометрических неравенств.

Рассмотрим решение простейших тригонометрических неравенств вида sin x>a  на единичной окружности.

1) при 0<a<1

С помощью ассоциации косинус-колобок (оба начинаются с ко-, оба «кругленькие»), вспоминаем, что косинус — это x, соответственно, синус — y. Отсюда строим график y=a — прямую, параллельную оси ox. Если неравенство строгое, точки пересечения единичной окружности и прямой y=a выколотые, если неравенство нестрогое — точки закрашиваем (как легко запомнить, когда точка выколотая, когда — закрашенная, смотрите здесь). Наибольшие затруднение при решении простейших тригонометрических неравенств вызывает правильное нахождение точек пересечения единичной окружности и прямой y=a.

 Первую из точек найти несложно — это arcsin a. Определяем путь, по которому из первой точки идем ко второй. На прямой y=a  sinx=a, сверху, над прямой, sin x>a, а ниже, под прямой, sin x<a. Поскольку мы решаем неравенство sinx>a, нам нужен верхний путь.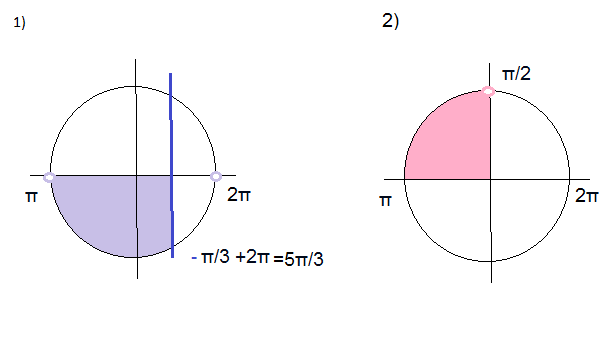 Таким образом, от первой точки, arcsin a, ко второй, мы идем против часовой стрелки, то есть в сторону увеличения угла. Мы не доходим до п. На сколько не доходим? На arcsin a. Раз не дошли до п, то вторая точка меньше п, значит, чтобы ее найти, надо из п вычесть arcsina. Решением неравенства sin x>a в этом случае является промежуток от arcsin a до п-arcsin a.   Поскольку период синуса равен 2п, чтобы учесть все решения неравенства (а таких промежутков — бесконечное множество), к каждому из концов интервала прибавляем 2пn, где n — целое число (n принадлежит Z).

2) a=0, то есть sin x>0

В этом случае первая точка промежутка — 0, вторая — п. К обоим концам промежутка с учетом периода синуса прибавляем 2пn.

3) при a=-1, то есть sinx>-1

В этом случае первая точка -п/2, а чтобы попасть во вторую, обходим всю окружность против часовой стрелки.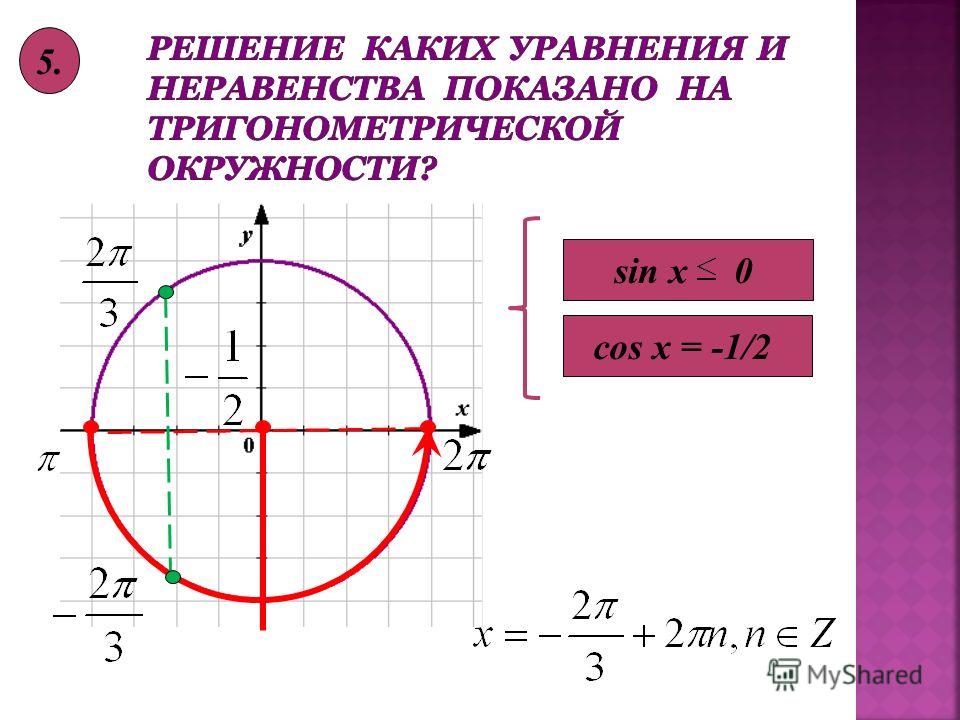 Попадаем в точку -п/2+2п=3п/2. Чтобы учесть все интервалы, являющиеся решением данного неравенства, к обоим концам прибавляем 2пn.

4) sinx>-a, при 0<a<1

Первая точка — как обычно, arcsin(-a)=-arcsina. Чтобы попасть во вторую точку, идем верхним путем, то есть в сторону увеличения угла.

 На этот раз мы за п переходим. На сколько переходим? На arcsin x. Значит, вторая точка — это п+arcsin x. Почему нет минуса? Потому что минус в записи -arcsin a  обозначает движение по часовой стрелки, а мы шли против. И в заключении, к каждому концу интервала прибавляем 2пn.

5) sinx>a, если а>1.

Единичная окружность лежит целиком под прямой y=a. Нет ни одной точки выше прямой. Значит, решений нет.

6) sinx>-a, где a>1.

В этом случае вся единичная окружность целиком лежит над прямой y=a. Поэтому любая точка удовлетворяет условию sinx>a. Значит, x — любое число.

И здесь x — любое число, поскольку точки -п/2+2пn входят в решение, в отличие от строгого неравенства sinx>-1. Ничего исключать не надо.

Единственной точкой на окружности, удовлетворяющей данному условию, является п/2. С учетом периода синуса, решением данного неравенства является множество точек x=п/2+2пn.

Например, решить неравенство sinx>-1/2:

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )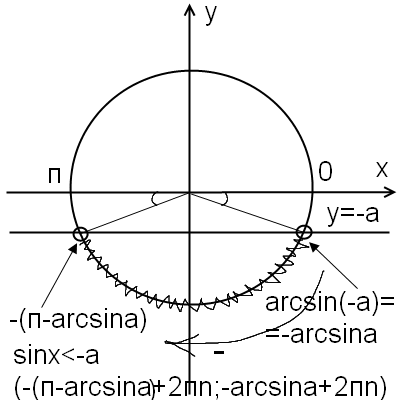
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )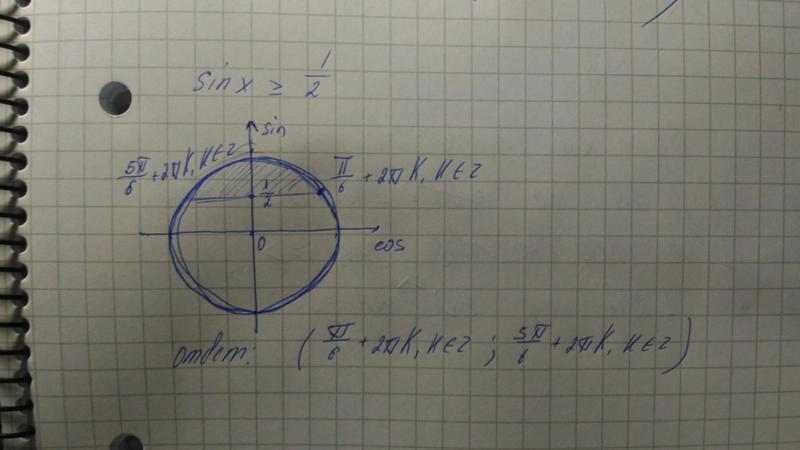
23	Найти точное значение	arctan(- квадратный корень 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )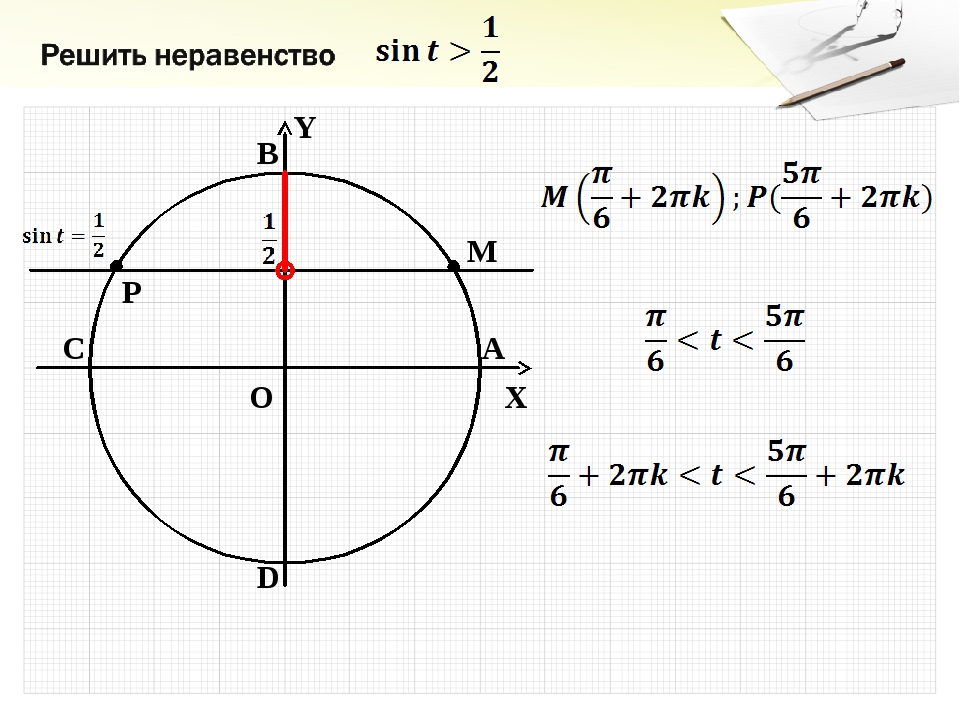
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )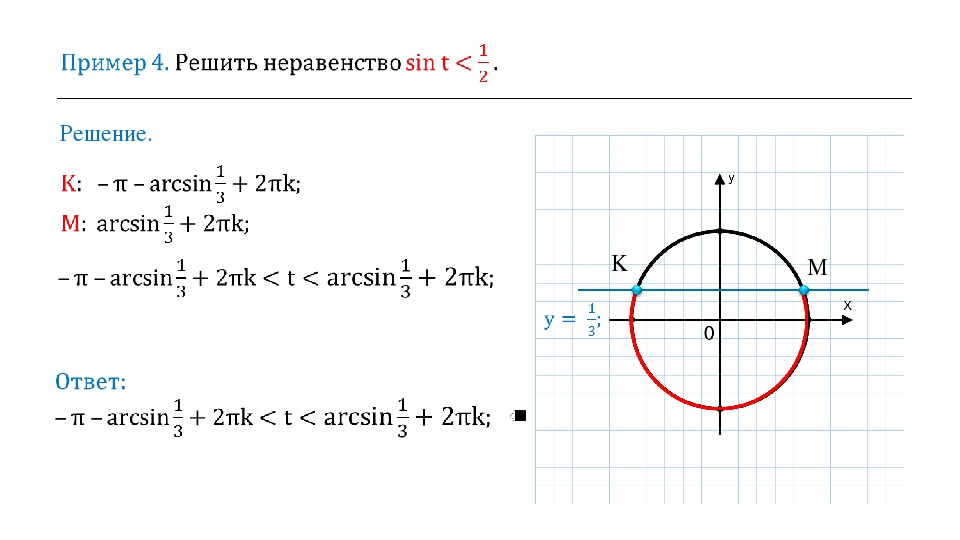
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Новосибирский государственный архитектурно-строительный университет — Сибстрин

Решение тригонометрических неравенств

Задача
1.

Решить
неравенство cos x > 1/2.

Решение.

По
определению косинуса cos x – это абсцисса
точки единичной окружности. Чтобы решить
неравенство cos x > 1/2, нужно выяснить,
какие точки единичной окружности имеют
абсциссу, большую 1/2.

Абсциссу,
равную 1/2, имеют две точки единичной
окружности М₁ и
М₂.

Точка
М₁ получается
поворотом точки Р (0; 1) на угол -π/3, а также
на углы -π/3 + 2πn, где n = +/-1, +/-2, …; точка
М₂ –
поворотом на угол π/3, а также на углы
π/3 + 2πn, где n = +/-1, +/-2, …

Абсциссу,
большую 1/2, имеют все точки М дуги
единичной окружности, лежащие правее
прямой М₁М₂.
Таким образом, решениями неравенства 
cos x > 1/2 являются все числа х из промежутка
-π/3 < х < π/3.

Ответ.
Все решения данного неравенства –
множество интервалов π/3 + 2πn < х < π/3
+ 2πn, n € Z.

Задача
2.

Решить
неравенство cos
x ≤ 1/2.

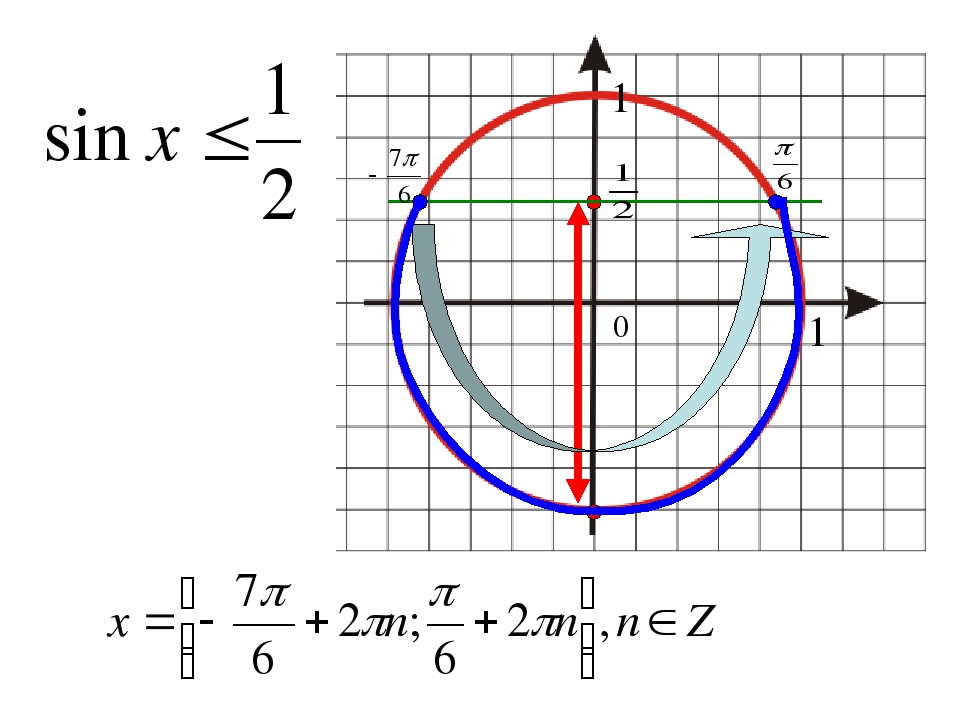
Решение.

Абсциссу,
не большую 1/2, имеют все точки дуги
М₁ММ₂ единичной
окружности. Поэтому решениями неравенства
cos x ≤ 1/2 являются числа х, которые
принадлежат промежутку π/3 ≤ х ≤ 5π/3.

Ответ.
Все решения данного неравенства –
множество отрезков π/3 + 2πn ≤ х ≤ 5π/3 +
2πn, n € Z.

Задача
3.

Решить
неравенство sin
x ≥ -1/2. 

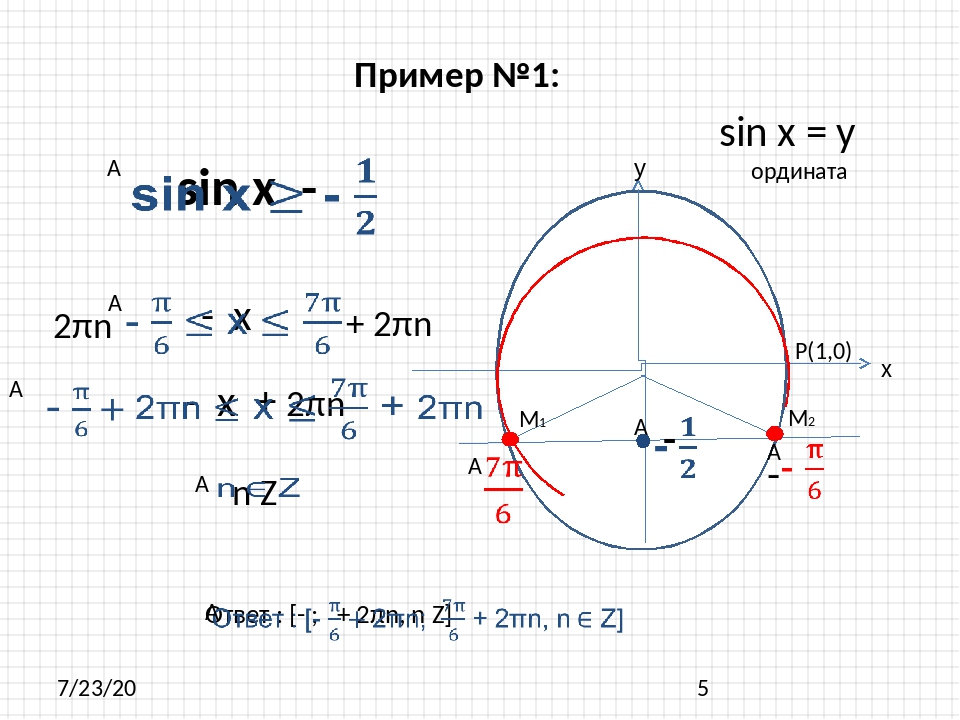
Решение.

Ординату,
не меньшую -1/2, имеют все точки дуги
М₁ММ₂  единичной
окружности. Поэтому решениями неравенства
sin x ≥ -1/2 являются числа х, принадлежащие
промежутку -π/6 ≤ х ≤ 7π/6. Все решения
данного неравенства – множество отрезков
-π/6 + 2πn ≤ х ≤ 7π/6 + 2πn, n € Z.

Отметим,
что все точки окружности, лежащие ниже
прямой М₁М₂,
имеют ординату, меньшую -1/2.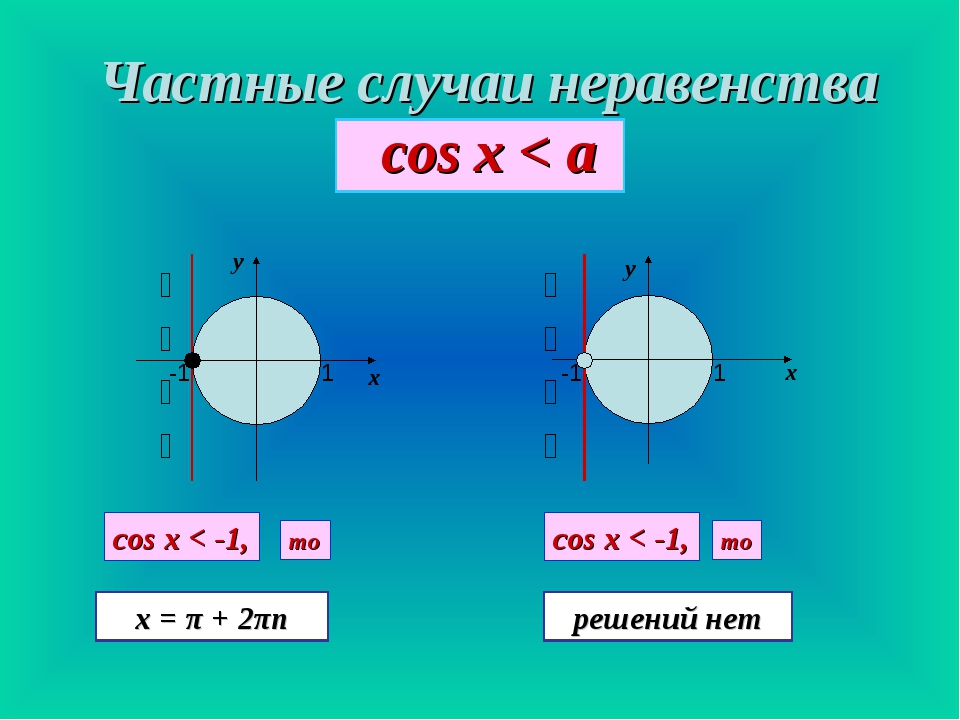 Поэтому все
числа х € (-5π/6; -π/6) являются решениями
неравенства sin x < -1/2.

Ответ.
Все решения этого неравенства – интервалы
(-5π/6 + 2πn; -π/6 + 2πn), n € Z.

Задача
4.

Решить
неравенство cos
(x/4 – 1) ≤ -(√2/2).

Решение.

Обозначим
x/4 – 1 = у. Решая неравенство cos у ≤ -(√2/2),
находим 
3π/4 + 2πn ≤ у ≤ 5π/4 + 2πn, n €
Z.

Заменяя
у = x/4 – 1, получаем 3π/4 + 2πn ≤ x/4 – 1 ≤ 5π/4
+ 2πn, откуда 
1 + 3π/4 + 2πn ≤ x/4 ≤ 1 + 5π/4
+ 2πn, 4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n € Z.

Ответ.
4 + 3π + 8 πn ≤ х ≤ 4 + 5π + 8 πn, n € Z.

Текст
задания:

1. Решите
   тригонометрические уравнения

2. Решите
   тригонометрические неравенства

НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА

уметь:

—
Вычислять производные и
первообразные
элементарных функций, используя
справочные материалы;

—
Исследовать в простейших случаях функции
на монотонность, находить наибольшие
и наименьшие значения функций, строить
графики многочленов и
простейших рациональных функций
с использованием аппарата математического
анализа;

—
Вычислять
в простейших случаях площади с
использованием первообразной;

использовать
приобретенные знания и умения в
практической деятельности и повседневной
жизни для:

— Решения
прикладных задач, в том числе
социально-экономических и физических,
на наибольшие и наименьшие значения,
на нахождение скорости и ускорения;

Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике

Часть 1.  

(Часть 2 см. здесь)

Примеры решения простейших тригонометрических неравенств

Простейшими тригонометрическими неравенствами называются неравенства вида

,

 ,

 ,

,

где – один из знаков , .

Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I,  часть II).

Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.

Пример 1.

Решить неравенство:

Решение: 

Отмечаем на оси  косинусов

Все значения , меньшие – левее точки на оси косинусов.

Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше

Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .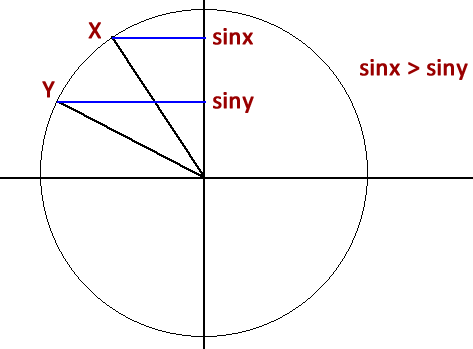

Обратите внимание, многие, назвав первую точку вместо второй точки    указывают точку , что неверно!

Становится видно, что неравенству удовлетворяют следующие значения

Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».

Не забываем «накидывать» счетчик 

Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:

Пример 2.

Решить неравенство:

Решение:

Отмечаем на оси  косинусов

Все значения , большие или равные – правее точки , включая саму точку.

Тогда выделенные красной дугой аргументы отвечают тому условию, что  .

Пример 3.

Решить неравенство:

Решение:

Отмечаем на оси синусов

Все значения , большие или равные – выше точки , включая саму точку.

«Транслируем» выделенные точки на тригонометрический круг:

Пример 4.

Решить неравенство:

Решение:

Кратко:

или все , кроме

Пример 5.

Решить неравенство:

Решение:

Неравенство равносильно уравнению , так как область значений функции –

Пример 6.

Решить неравенство:

Решение:

Действия  – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.

Здесь, конечно, нужно знать определение арксинуса.

Если не очень понятно, загляните сюда –>+ показать

Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен

А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.

Поэтому

Тренируемся в решении простейших тригонометрических неравенств

Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:

1. Решить неравенство:

Ответ: + показать

2. Решить неравенство:

Ответ: + показать

3. Решить неравенство:

Ответ: + показать

4. Решить неравенство:

Ответ: + показать

5. Решить неравенство:

Ответ: + показать

Часть 2
Если у вас  есть  вопросы, – пожалуйста, – спрашивайте!

Решение тригонометрических уравнений и неравенств (урок обобщения и систематизации знаний в 11-м классе вечерней школы)

Цели урока:

1. систематизация знаний, умений и навыков решения
   тригонометрических уравнений и неравенств;
2. развитие логического мышления, умений
   анализировать, сравнивать, обобщать; развитие
   математической речи учащихся;
3. воспитание уверенности в себе; воспитание
   культуры общения, умения работать в коллективе,
   группе.

Оборудование:

• карточки-задания для каждого участника;
• задания для капитанов команд — -
  «цветик-семицветик»;
• карточки-задания для консультантов;
• плакат “Решение простейших тригонометрических
  уравнений и неравенств”.

Форма проведения: урок – КВН

Ход урока

Класс разбит на 3 команды, выбраны капитаны, в
каждой команде есть консультант, который ведёт
контроль за правильностью решения примеров.

1. Разминка: (устно)

Найти значение выражения: (правильный
ответ – 1 балл)

Составить неравенство и указать его решение: (правильный ответ – 2 балла)

2. Конкурс-блиц: (1 задание – 1
балл)

Решить уравнения:

1. sin x = -1

cos x = 1

tg x = 0

arcsin 3x =

cos 2x = 2

2. sin x = 0

cos x = -1

tg x = 1

arccos 4х =

2sin x = 4

3. sin x = 1

cos x = 0

tg x = -1

arctg 2x =

sin 4x = 2

Решить неравенство:

1. sin x < -1 2. cos x > 1 3. sin x > 1

Самопроверка, с использованием плаката
“Решение простейших тригонометрических
уравнений и неравенств” (Приложение 1).

3. Конкурс команд:

Каждому учащемуся из команды предлагается
задание, состоящее из двух тригонометрических
уравнений и одного неравенства. Работа
выполняется по индивидуальным
карточкам-заданиям трёх уровней сложности.

(зелёная карточка – 4 балла; синяя – 5 баллов;
красная – 6 баллов)

Решить уравнение:

1. 2cos 3x + 1 = 0
2. 1 + 2sin 2x = 0
3. tg=1
4. tg = 1
5. 3tg
6. sin
7. 2cos
8. sin
9. ctg
10. cos x = —
11. sin =
12. sin 3x·cos x – cos 3x·sin x = 0
13. cos 3x·cos x — sin 3x·sin x = 0
14. sin 5x·cos x – cos 5x·sin x =
15. cos 5x·cos x + sin 5x·sin x =
16. cos 2x·cos x — sin 2x·sin x = 1
17. cos 3x·cos x — sin 3x·sin x =
18. coscos x + sin x·sin =
19. 2sin² x – 2cos x =
20. 2cos² x + 2 sin x = 2,5
21. 3cos² x + 7sin x – 5 = 0
22. cos² x + 6sin x – 6 = 0
23. 5sin² x + cos x – 1 = 0
24. 2sin² x + 5cos x = 4
25. 5sin² + 8cos (? +
    x) = 0
26. sin²— 3cos (4? +
    x) = 4
27. 4sin² x – 4sin x + 1 = 0
28. 2sin² x + 5cos x + 1 = 0
29. 2sin² x + 11cos x — 7 = 0
30. 5sin² x + cos x — 1 = 0
31. 2sin² x + 7cos x + 2 = 0
32. 3tg³ x – 3tg x = 0
33. 2 — cos² x + sin x = 0
34. sin x + cos x = 0
35. sin x + cos x = 0
36. sin x +cos x = 0
37. sin 2x + cos 2x = 0
38. sin 2x — cos 2x = 0
39. sin 2x = 2 sin² x
40. sin 2x — 2sin² x = 0
41. 2sin² (? — x) = cos 2x
42. sin 2x + cos 2x = 1
43. sin= sin x
44. sin= cos x
45. cos x = 2 cos
46. sin x +cos x = 2
47. sin x – cos x = 1
48. sin x +cos x = 1

Решить неравенство:

1. sin x ?
2. tg x ? —
3. cos x ?
4. tg x > -1
5. cos x >
6. sin x ?
7. 2sin x > -1
8. 2cos x < —
9. ctg x < 1
10. -2cos x > 1
11. tg 2x ?
12. 3tg 3x >
13. tg ? -1
14. cos 2x < -0,5
15. sin 2x < -0,5
16. sin 4x >
17. sin (x + ) >
18. cos<
19. tg (x + ) > 1
20. tg
21. 2cos
22. 2sin
23. 2cos
24. 3tg

4. Конкурс капитанов:

Капитаны работают у доски. Им предлагается
оторвать один лепесток «цветика-семицветика» (Приложение 2) с заданием (правильный
ответ – 3 балла)

Решить уравнение:

1. sin 2x = 2 sin² x
2. 3sin 2x + 7cos 2x = 0
3. (cos x + sin x)² = cos 2x
4. 1 – 2sin 2x = 6cos² x
5. sin x – cos x = 2
6. 7sin 2x + 2cos²x – 6 = 0
7. sin x + cos x =

5. Конкурс консультантов: (правильный
ответ – 4 балла)

Решите систему уравнений:

1. 2.
3.

6. Конкурс эрудитов:

Пока команды готовят вопросы друг для друга,
слушаем сообщение об истории развития учения о
тригонометрических функциях (Приложение 3).

Вопросы: (правильный ответ – 2
балла)

1. Кем и когда были составлены первые
   тригонометрические таблицы?
2. Что больше сos 35° или cos 50°?
3. Что больше sin 50° или sin 55°?

Итоги урока: Подсчитываем количество баллов,
набранных командами и каждым учащимся. Каждому
учащемуся команды-победительницы + 1 балл.
Ученикам, набравшим:

10 и более баллов – «5» (отлично);

7–9 баллов – «4» (хорошо);

4–6 баллов – «3»
(удовлетворительно).

Домашнее задание:

Решите систему уравнений:

1. 2.
3.

Рефлексия: вопрос классу: «Оцените своё
самочувствие на уроке, поставив какой-либо
значок на графике функции у = sin х, изображенной на
отвороте доски. Где вы себя ощущали: на гребне
волны синусоиды или во впадине?»

Основные тригонометрические неравенства

Неизвестная переменная (угол): \ (x \)
Набор целых чисел: \ (\ mathbb {Z} \)
Целое число: \ (n \)
Набор действительных чисел: \ (\ mathbb {R} \)
Действительное число номер: \ (a \)

Тригонометрические функции: \ (\ sin x, \) \ (\ cos x, \) \ (\ tan x, \) \ (\ cot x \)
Обратные тригонометрические функции: \ (\ arcsin a, \) \ (\ arccos a, \) \ (\ arctan a, \) \ (\ text {arccot} a \)

1. Неравенство, включающее тригонометрические функции от неизвестного угла, называется тригонометрическим неравенством.
2. Следующие \ (16 \) неравенства относятся к основным тригонометрическим неравенствам:
   \ (\ sin x \ gt a \), \ (\ sin x \ ge a \), \ (\ sin x \ lt a \), \ (\ sin x \ le a \),
   \ (\ cos x \ gt a \), \ (\ cos x \ ge a \), \ (\ cos x \ lt a \), \ (\ cos x \ ле а \),
   \ (\ тан х \ gt а \), \ (\ тан х \ ге а \), \ (\ тан х \ lt а \), \ (\ тан х \ ле а \),
   \ (\ cot x \ gt a \), \ (\ cot x \ ge a \), \ (\ cot x \ lt a \), \ (\ cot x \ le a \).
   Здесь \ (x \) — неизвестная переменная, \ (a \) может быть любым действительным числом.

Неравенства вида \ (\ sin x \ gt a, \) \ (\ sin x \ ge a, \) \ (\ sin x \ lt a, \) \ (\ sin x \ le a \)

Фигура 1.

Фигура 2.

Неравенство \ (\ sin x \ gt a \)

3. Если \ (\ left | a \ right | \ ge 1 \), неравенство \ (\ sin x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
4. Если \ (a \ lt -1 \), решением неравенства \ (\ sin x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
5. Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ sin x \ gt a \) выражается в виде
   \ (\ arcsin a + 2 \ pi n \ lt x \ ) \ (\ lt \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (1 \)).

Неравенство \ (\ sin x \ ge a \)

6. Если \ (a \ gt 1 \), неравенство \ (\ sin x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
7. Если \ (a \ le -1 \), решением неравенства \ (\ sin x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
8. Случай \ (a = 1 \)
   \ (x = \ pi / 2 +2 \ pi n, \) \ (n \ in \ mathbb {Z} \)
9. Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ ge a \) включает граничные углы и имеет вид
   \ (\ arcsin a + 2 \ pi n \ le x \) \ (\ le \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (1 \)).

Неравенство \ (\ sin x \ lt a \)

10. Если \ (a \ gt 1 \), решением неравенства \ (\ sin x \ lt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
11. Если \ (a \ le -1 \), неравенство \ (\ sin x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
12. Для \ (- 1 \ lt a \ le 1 \) решение неравенства \ (\ sin x \ lt a \) лежит в интервале
    \ (- \ pi — \ arcsin a + 2 \ pi n \ lt x \) \ (\ lt \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)).

Неравенство \ (\ sin x \ le a \)

13. Если \ (a \ ge 1 \), решением неравенства \ (\ sin x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
14. Если \ (a <-1 \), неравенство \ (\ sin x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
15. Случай \ (a = -1 \)
    \ (x = — \ pi / 2 + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \)
16. Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ le a \) находится в интервале
    \ (- \ pi — \ arcsin a + 2 \ pi n \ le x \) \ (\ le \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)).

Неравенства вида \ (\ cos x \ gt a, \) \ (\ cos x \ ge a, \) \ (\ cos x \ lt a, \) \ (\ cos x \ le a \)

Рисунок 3.

Рисунок 4.

Неравенство \ (\ cos x \ gt a \)

17. Если \ (a \ ge 1 \), неравенство \ (\ cos x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
18. Если \ (a \ lt -1 \), решением неравенства \ (\ cos x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
19. Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ cos x \ gt a \) имеет вид
    \ (- \ arccos a + 2 \ pi n \ lt x \) \ (\ lt \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)).

Неравенство \ (\ cos x \ ge a \)

20. Если \ (a \ gt 1 \), неравенство \ (\ cos x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
21. Если \ (a \ le -1 \), решением неравенства \ (\ cos x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
22. Случай \ (a = 1 \)
    \ (x = 2 \ pi n, \) \ (n \ in \ mathbb {Z} \)
23. Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ ge a \) выражается формулой
    \ (- \ arccos a + 2 \ pi n \ le x \) \ (\ le \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)).

Неравенство \ (\ cos x \ lt a \)

24. Если \ (a \ gt 1 \), неравенство \ (\ cos x \ lt a \) верно для любого действительного значения \ (x \): \ (x \ in \ mathbb {R} \)
25. Если \ (a \ le -1 \), неравенство \ (\ cos x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
26. Для \ (- 1

    Неравенство \ (\ cos x \ le a \)

27. Если \ (a \ ge 1 \), решением неравенства \ (\ cos x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
28. Если \ (a \ lt -1 \), неравенство \ (\ cos x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
29. Случай \ (a = -1 \)
    \ (x = \ pi + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \)
30. Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ le a \) записывается как
    \ (\ arccos a + 2 \ pi n \ le x \) \ (\ le 2 \ pi — \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (4 \)).

Неравенства вида \ (\ tan x \ gt a, \) \ (\ tan x \ ge a, \) \ (\ tan x \ lt a, \) \ (\ tan x \ le a \)

Рисунок 5.

Рисунок 6.

Неравенство \ (\ tan x \ gt a \)

31. Для любого действительного значения \ (a \) решение строгого неравенства \ (\ tan x \ gt a \) имеет вид
    \ (\ arctan a + \ pi n \ lt x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)).

Неравенство \ (\ tan x \ ge a \)

32. Для любого действительного значения \ (a \) решение неравенства \ (\ tan x \ ge a \) выражается в виде
    \ (\ arctan a + \ pi n \ le x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)).

Неравенство \ (\ tan x \ lt a \)

33. Для любого значения \ (a \) решение неравенства \ (\ tan x \ lt a \) записывается в виде
    \ (- \ pi / 2 + \ pi n \ lt x \) \ ( \ lt \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)).

Неравенство \ (\ tan x \ le a \)

34. Для любого значения \ (a \) неравенство \ (\ tan x \ le a \) имеет следующее решение:
    \ (- \ pi / 2 + \ pi n \ lt x \) \ (\ le \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)).

Неравенства вида \ (\ cot x \ gt a, \) \ (\ cot x \ ge a, \) \ (\ cot x \ lt a, \) \ (\ cot x \ le a \)

Рисунок 7.

Рисунок 8.

Неравенство \ (\ cot x \ gt a \)

35. Для любого значения \ (a \) решение неравенства \ (\ cot x \ gt a \) имеет вид
    \ (\ pi n \ lt x \ lt \ text {arccot} a + \ pi n , \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)).

Неравенство \ (\ cot x \ ge a \)

36. Нестрогое неравенство \ (\ cot x \ ge a \) имеет аналогичное решение:
    \ (\ pi n \ lt x \ le \ text {arccot} a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)).

Неравенство \ (\ cot x \ lt a \)

37. Для любого значения \ (a \) решение неравенства \ (\ cot x \ lt a \) лежит на открытом интервале
    \ (\ text {arccot} a + \ pi n \ lt x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)).

Неравенство \ (\ cot x \ le a \)

38. Для любого значения \ (a \) решение нестрогого неравенства \ (\ cot x \ le a \) находится в полуоткрытом интервале
    \ (\ text {arccot} a + \ pi n \ le x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)).

Тригонометрическое неравенство — Учебные материалы для IIT JEE

Тригонометрическое неравенство — важная тема в программе математики IIT JEE. Неравенство тригонометрии содержит одну или несколько тригонометрических функций функции x в виде R [f (x), g (x)…]> 0 (или <0), в котором f (x), g (x), ... - тригонометрические функции от x. Решение для x подразумевает поиск значений x, которые делают неравенство истинным. Все такие значения x составляют множество решений данного тригонометрического неравенства. Некоторые примеры тригонометрических неравенств:

sin x + sin 2x> -sin 3x

грех x + грех 3x <1

2тан x + загар 2x> 3 кроватки x

cos 2x -2> -3sin x

Вопросы о тригонометрическом неравенстве IIT JEE представляют собой смесь как средних, так и сложных вопросов.Мы перечисляем здесь некоторые иллюстрации, чтобы дать представление о типах вопросов, задаваемых по этой теме.

Иллюстрация:

Найти множество решений неравенства sinx> 1/2.

Решение:

Когда sinx = ½, два значения x между 0 и 2π равны π / 6 и 5π / 6.

у = грех х

Из графика y = sinx очевидно, что между 0 и 2π

sinx> 1/2 для π / 6

Следовательно, sinx 1/2 ⇒ 2nπ + π / 6

Требуемый набор решений — ∪ (2nπ + π / 6, 2nπ + 5π / 6).

Иллюстрация:

Найти множество решений неравенства cosx> –1/2.

Решение:

Сформируйте график y = cosx, очевидно, что cosx> –1/2

Если -2π / 3≤x≤2π / 3.

y = cos x

Отсюда общее значение для cosx> -1/2

⇒ 2nπ -2π / 3 ≤ x ≤2nπ + 2π / 3.

Требуемый набор решений — ∪ (2nπ -2π / 3,2nπ + 2π / 3).

Иллюстрация:

Решить :

sin4x = 1 + tan8x.

Решение: рассмотрение обеих сторон по очереди

L.H.S. = sin4x <1.

R.H.S. = 1 + tan8x> 1.

L.H.S. = R.H.S. только когда

sin4x = 1 и 1 + tan8x = 1 ⇒ sin2x = 1 и tan8x = 0.

, что невозможно, так как sinx и tanx исчезают одновременно.

Следовательно, данное уравнение не имеет решения.

Иллюстрация:

Решите sin2x + cos2y = 2sec2z.

Решение:

L.H.S. = sin2x + cos2y <2.

R.H.S. = 2 секунды2z> 2.

Следовательно, L.H.S. = R.H.S. только когда

sin2x = 1, cos2y = 1, sec2z = 1

⇒ | sin x | = 1, | cos y | = 1, | cos z | = 1

⇒ x = (2m + 1) π / 2, y = nπ и z = tπ, где m, n, t — целые числа.

Иллюстрация:

Решите неравенство cos 2x ½ на интервале 0

Решение:

Сначала решите уравнение cos 2x = ½.

Если мы выберем k = 0 и 1, мы получим решения / 6 и 7/6 (30 ° и 210 °).

Мы пытаемся узнать эти значения с помощью правила

.

cos x = cos (−x)

2х = — / 3 + к · 2

х = — / 6 + к ·

Если мы используем значения k = 1 и 2, мы получим решения 5/6 и 11/6 (150 ° og 330 °).

Теперь нарисуем диаграмму, чтобы увидеть решения неравенства

На диаграмме показаны графики y = cos 2x и y = ½. Заштрихованные интервалы над горизонтальной линией показывают решения неравенства. Таким образом, решениями являются следующие интервалы:

0 x / 6 или 5/6 x 7/6 или 11/6 x <2

Чтобы иметь четкое представление о вопросах тригонометрического неравенства, просмотрите образцы статей.

Посмотрите это видео, чтобы получить дополнительную информацию

Чтобы узнать больше, купите учебные материалы по номеру Тригонометрия , включая примечания к исследованию, примечания к изменениям, видеолекции, решенные вопросы за предыдущий год и т.Также просмотрите дополнительные учебные материалы по математике здесь .

Вся элементарная математика — Учебное пособие — Тригонометрия

Вся элементарная математика — Учебное пособие — Тригонометрия — Тригонометрические неравенства …

| Главная | О нас | Ссылки |
Свяжитесь с нами |

Авторское право 2002-2007 гг.Юрий Беренгард.
Все права защищены.

Решите неравенство sin x + sqrt3cos x0 математика класса 11 CBSE

Подсказка: в этом вопросе нам сначала нужно разделить обе стороны на 2. Затем запишите постоянные члены в терминах тригонометрических соотношений некоторых известных углов синуса и косинуса. Теперь используйте тригонометрические отношения формулы составных углов и преобразуйте ее в функцию синуса.Затем, используя неравенство, получаем значение x.
\ [\ sin \ left (A + B \ right) = \ sin A \ cos B + \ cos A \ sin B \]

Полный пошаговый ответ:
Теперь из данного неравенства в вопросе мы имеем ,
\ [\ Rightarrow \ sin x + \ sqrt {3} \ cos x> 0 \]
Давайте теперь разделим на 2 с обеих сторон
\ [\ Rightarrow \ dfrac {1} {2} \ sin x + \ dfrac {\ sqrt {3}} {2} \ cos x> 0 \]
Как мы уже знаем,
\ [\ cos \ dfrac {\ pi} {3} = \ dfrac {1} {2}, \ sin \ dfrac {\ pi} {3} = \ dfrac {\ sqrt {3}} {2} \]
Теперь давайте запишем постоянные значения в терминах стандартных значений, упомянутых выше
\ [\ Rightarrow \ sin x \ cos \ dfrac {\ pi} {3} + \ cos x \ sin \ dfrac {\ pi} {3}> 0 \]
Как мы уже знаем, из тригонометрических соотношений формулы составных углов
\ [\ sin \ left ( A + B \ right) = \ sin A \ cos B + \ cos A \ sin B \]
По этой формуле указанное выше неравенство может быть преобразовано как
\ [\ Rightarrow \ sin \ left (x + \ dfrac {\ pi } {3} \ right)> 0 \]
Как мы уже знаем, что функция синуса положительна в первом и втором квадрантах, мы можем получить значение e угла, на котором он лежит,
Теперь синусоидальная функция положительна для углов
\ [\ Rightarrow 0Теперь, используя это условие из вышеприведенного неравенства, мы получаем
Теперь при сравнении мы получаем, что
\ [\ theta = x + \ dfrac {\ pi} {3} \]
Теперь, применив вышеупомянутое условие, мы получим
\ [\ Rightarrow 0 Давайте теперь вычтем \ [\ dfrac {\ pi} {3} \] из каждого из термины
\ [\ Rightarrow 0- \ dfrac {\ pi} {3} Теперь, при дальнейшем упрощении, мы получаем
\ [\ следовательно — \ dfrac {\ pi} {3}

Примечание:
Вместо того, чтобы писать в терминах функции синуса, используя формулу составных углов, мы также можем преобразовать ее в функцию косинуса и еще больше упростить.Оба метода дают одинаковый результат.
Важно отметить, что нам необходимо рассмотреть все возможные квадранты, в которых выполняется данное неравенство, поскольку рассмотрение только одного из них полностью меняет результат.

Вы в одном шаге от ответа!

Подпишитесь бесплатно!

Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!

Использование теоремы о сжатии для определения пределов математических функций

Примеры с решениями

Пример 1

Найти предел lim _{x → 0} x ² cos (1 / x)

Решение примера 1:

Когда x приближается к 0, 1 / x становится очень большим по модулю, а cos (1 / x) становится сильно колеблющимся.Однако cos (1 / x) принимает значения в интервале [-1,1], который является диапазоном cos x, поэтому

-1 ≤ cos (1 / x) ≤ 1

Умножьте все члены приведенного выше неравенства на x ² (x не равно 0)

— x ² ≤ x ² cos (1 / x) ≤ x ²
Приведенное выше неравенство справедливо для любого значения x, кроме 0, где x ² cos (1 / x) не определено. Когда x приближается к 0, оба — x ² и x ² приближаются к 0, и согласно теореме сжатия мы получаем

lim _{x → 0} x ² cos (1 / x) = 0

Пример 2

Найти предел lim _{x → 0} sin x / x

Решение примера 2:

Предположим, что 0

Точка C — это точка на единичной окружности (радиус = 1), имеющая координаты (cos x, sin x). Найдем площади треугольника OAC, сектора OAC и треугольника
, площадь треугольника OAC = (1/2) * (основание) * (высота)

= (1/2) * (1) * (координата y точки C) = (1/2) (sin x)

Примечание: мы использовали base = radius = 1

площадь сектора OAC = (1/2) * (x) * (радиус) ²
= (1/2) (1) ² x = (1/2) x

площадь треугольника OAB = (1/2) * (основание) * (высота)

= (1/2) * (1) * (tan x) = (1/2) tan x

Сравнивая три области, мы можем записать неравенство
площадь треугольника OAC <площадь сектора OAC <площадь треугольника OAB
Замените площади в приведенном выше неравенстве их выражениями, полученными выше.
(1/2) (sin x) <(1/2) x <(1/2) tan x
Умножение всех членов на 2 / sin x дает
1 Возьмите обратную величину и переверните два символа неравенства в двойном неравенстве
1> sin x / x> cos x

Что то же самое, что
cos x Можно показать, что указанное выше неравенство имеет место для -Pi / 2 lim _{x → 0} cos x = 1

и
lim _{x → 0} 1 = 1,

мы можем применить теорему сжатия, чтобы получить
lim _{x → 0} sin x / x = 1

Этот результат очень важен и будет использован для нахождения других пределов тригонометрических функций и производных.
Подробнее о лимитах

Учебники и задачи по исчислению

(PDF) Некоторые неравенства, построенные с помощью интегрального неравенства Чебышева

10 F.QI, LI-HONG CUI, AND SEN-LIN XU

Ссылки

[1] У. Абель и Д. Качча, Обострение неравенства Иордании, Amer. Математика. Ежемесячно 93 (1986),

нет. 7, 568.

[2] Дж. Т. Чу, Об оценках нормального интеграла, Биометрика 42 (1955), 263–265.

[3] Дж. М. Конте, Решение задачи 5607, Revue Math. Спец. 74 (1963/64), 227–230.

[4] Дж. Х. Харди, Дж. Э. Литтлвуд и Г. П’оля, Неравенства, 2-е издание, Кембриджский университет

Press, 1952.

[5] А. А. Кришнасвами Айянгар, Задача 1800, Математика. Student 11 (1943), 63.

[6] Г. Кламбауэр, Математический анализ, китайское издание, The People’s Press of Hunan, Chang-

sha, China, 1981. (Перевод Ben-Wang Sun)

[ 7] Ji-Chang Kuang, Applied Inequalities, 2-е издание, Hunan Education Press, Changsha,

China, 1993. (китайский)

[8] Д.С. Митринович, Проблема 5555, Amer. Математика. Ежемесячно 75 (1968), 84 и 1129–1130.

[9] Д.С. Митринович, Аналитические неравенства, Springer-Verlag, Berlin, 1970.

[10] Д.С. Митринович, Дж. Э. Пекариц, А.М. Финк, Классические и новые неравенства в анализе,

Kluwer Academic Publishers, Dordrecht / Boston / London, 1993.

[11] A. Ostowski, Vorlesungen ¨uber Di ff erential-und Integralrechnung, Vol. 3, Basel-Stuttgart,

1954.

[12] Фэн Ци, Доказательства одного класса интегральных неравенств и их приложений, Сборник статей

Первого ежегодного молодежного академического собрания провинции Хэнань, 91–93 , Press of Science

and Technology of China, Пекин, Китай, 1995.(Китайский)

[13] Фэн Ци, Обобщенные средневзвешенные значения с двумя параметрами, Proc. Рой. Soc. Лондон

сер. А 454 (1998), нет. 1978, 2723–2732.

[14] Фэн Ци, О двухпараметрическом семействе неоднородных средних значений, Tamkang Journal of

Mathematics 29 (1998), вып. 2, 155–163.

[15] Ф. Ци, Монотонность результатов и неравенства для гамма- и неполных гамма-функций,

Math. Неравно. Прил. 5 (2002), нет. 1, 61–67. RGMIA Res. Rep.Coll. 2 (1999), нет. 7, ст. 7,

1027–1034. Доступно в Интернете по адресу http://rgmia.vu.edu.au/v2n7.html.

[16] Фэн Ци и Бай-Ни Го, Оценка снизу первого собственного значения для оператора Лапласа на компактном римановом многообразии

, Китайский квартальный журнал математики, 8 (1993), вып. 2,

40–49.

[17] Фэн Ци и Сен-Линь Гуо, Неравенства для неполной гаммы и связанных функций,

Math. Ineq. Прил. 2 (1999), нет. 1, 47–53.

[18] Фэн Ци и Цинь-Дао Хао, Уточнения и уточнения неравенства Джордана и Кобера,

Mathematics and Informatics Quarterly 8 (1998), no.3, 116–120.

[19] Фэн Ци и Чжэн Хуанг, Неравенства полных эллиптических интегралов, Tamkang Journal

of Mathematics 29 (1998), вып. 3, 165–169.

[20] Фэн Ци и Цзя-Цян Мэй, Некоторые неравенства неполной гаммы и связанных функций,

Zeitschrift f¨ur Analysis und ihre Anwendungen 18 (1999), № 3, 793–799.

[21] Фэн Ци и Сен-Линь Сюй, Функция (bx − ax) / x: Неравенства и свойства, Proc. Амер.

Math. Soc.126 (1998), нет. 11, 3355–3359.

[22] Фэн Ци и Сен-Линь Сюй, Уточнения и расширения неравенства, II, J. Math. Анальный.

Заявл. 211 (1997), 616–620.

[23] Фэн Ци и Ши-Цинь Чжан, Замечание о монотонности обобщенных взвешенных средних значений, Proc.

Рой. Soc. Лондон сер. А 455 (1999), нет. 1989, 3259–3260.

(F. Qi) Кафедра прикладной математики и информатики, Научно-исследовательский институт

Прикладная математика, Политехнический университет Хэнань, город Цзяоцзуо, Хэнань 454000, Китай

Адрес электронной почты: qifeng @ hpu.edu.cn, [email protected]

URL: http: //rgmia.vu.edu.au/qi.html, http://dami.hpu.edu.cn/staff/qifeng.html

Кафедра фундаментальных курсов, Зерновой колледж Чжэнчжоу, город Чжэнчжоу,

Хэнань 450052, Китайская Народная Республика

Кафедра математики, Университет науки и технологий Китая, Хэфэй

Город, Аньхой 230026, Китайская Народная Республика

Справка по математике

Примечание : Интервал такой же, как: ˗ π / 6 ≤
(х ˗ π / 6)
≤ π / 6

ф (х)
= грех х,
f (π / 6) = 1/2, f ‘(x)
= cos
Икс ,
f ‘(π / 6) = √3
/ 2

ф » (х)
= ˗ sin x, f
» (π / 6) = ˗ 1/2, f » ‘(x) =
˗ cos x, f
» ‘(π / 6) = ˗ √3 / 2

f » » (х)
= sin x, f
» » (π / 6) = 1/2,
f ^v (x) = cos x, f
^v (π / 6) = √3 / 2

T ₄ (x) = 1/2 + (√3
/ 2) (x ˗ π / 6) ˗ (1/2) (x ˗ π / 6) ²
/ (2!) ˗ (√3 / 2) (х ˗ π / 6) ³
/ (3!)

+ (1/2) (x ˗ π / 6) ⁴ /
(4!) (Результат по части а)

| R ₄ (x) | ≤
М / (4 + 1)! | x ˗ π / 6 | ^{4+ 1} =
М / (5!) | x ˗ π / 6 | ⁵ =

Выберите наибольшее значение для M,
f ^v (x), дюйм 0
≤ х ≤
π / 3, что равно cos (0) = 1

и | x ˗ π / 6 | знак равно
π / 6

|
R ₄ (x) | ≤ (1) | π / 6 | ⁵ /
(5!) = 0.