Содержание
Калькулятор корней. Решение корней онлайн. Извлечение корня из числа
Калькулятор корней — одна из многих функций, которой обладает бесплатный калькулятор онлайн, предлагаемый на нашем сайте. Извлечение корня из числа часто используется в различных расчётах, поэтому калькулятор, предлагающий решение корней онлайн, — это отличный инструмент для математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчёты, содержащие извлечение корня. Корень третьей степени калькулятор онлайн посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Мы, конечно, не станем использовать такое решение корня. Во-первых, придётся потратить массу времени на подобные расчёты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Решение корней в онлайн калькуляторе
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трёх клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления странице Функции калькулятора.
Более детальная информация о панели управления странице Функции калькулятора.
Калькулятор корней
И корень кубический калькулятор посчитает, и корень квадратный калькулятор найдёт!
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Решение квадратных корней в калькуляторе
Если под корнем отрицательное число, а степень корня чётная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Корень квадратный из отрицательного числа
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени
Точный корень n ой степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчёт получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом
Решение примеров с корнями
Вычислить корень калькулятор может из различных чисел и выражений. Рассмотрим на примерах дроби, корня и степени.
Корень из дроби
Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае всё рассчитает верно.
В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае всё рассчитает верно.
Пример, как извлечь корень из корня
Степень в корне
Выполняя извлечение корня степени, следует помнить, что по свойству корней степень самого корня и степень под корнем по возможности сокращаются на наибольший общий делитель (НОД). Кстати, функционал калькулятора включает также нахождение НОД, подробнее на странице Дополнительные функции.
Калькулятор корень степени позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени
Используйте этот бесплатный онлайн калькулятор всегда, когда нужно извлечь корень онлайн!
Калькулятор Инструкция — обзор всех функций калькулятора и общие сведения о том, как пользоваться калькулятором.
Мы продолжаем создавать калькуляторы – сегодня калькулятор, на кортом вы сможете посчитать квадратный корень из числа!
Скорее, правильнее будет сказать извлечёт квадратный корень
Вариант № 1 извлечь квадратный корень онлайн
Как посчитать квадратный корень онлайн!?
В поле ввода вставляем то число из которого нужно вывести квадратный корень! И нажимаем извлечь!
Справа от квадратного корня есть равно и после него будет показан результат извлечения квадратного корня из числа онлайн!
Вариант № 2 извлечь квадратный корень онлайн
Второй вариант извлечения корня квадратного онлайн вам потребуется наш калькулятор онлайн.
Вводите число, и нажимаете корень квадратный. Вот так быстро и просто… можно извлечь квадратный корень из числа онлайн.
Написать что-нибудь…
квадратный корень онлайн ,
корень квадратный онлайн калькулятор ,
найти квадратный корень онлайн ,
решение квадратных корней онлайн ,
вычислить корень квадратный онлайн ,
число из квадратного корня онлайн ,
извлечь квадратный корень онлайн ,
извлечь квадратный корень онлайн калькулятор ,
вычислить квадратный корень онлайн калькулятор ,
решить корень квадратный онлайн ,
нахождение квадратного корня онлайн ,
квадратные корни класс тест онлайн ,
вычисление квадратного корня онлайн ,
найти квадратный корень из числа онлайн ,
корень квадратный онлайн калькулятор с решением ,
корень квадратный из числа онлайн калькулятор ,
арифметический квадратный корень онлайн ,
найти квадратный корень онлайн калькулятор ,
извлечение квадратного корня онлайн ,
решение уравнений с квадратным корнем онлайн ,
степень квадратного корня онлайн ,
квадратный корень онлайн калькулятор дробей ,
формула корень квадратный онлайн ,
найти корень квадратный из числа онлайн калькулятор ,
посчитать квадратный корень онлайн ,
вычислить квадратный корень из числа онлайн ,
извлечь квадратный корень из числа онлайн ,
Калькулятор корней онлайн — особенности извлечения корней с подробным объяснением
Калькулятор
Заполните поля для вычисления корня из числа
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни. Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.
При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9.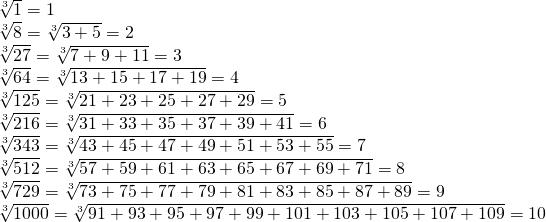 Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.
Внесение под знак корня
При решении задач и примеров возникает необходимость вносить под корень множитель. Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 22х3 и 32х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные. Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто.
Кубический корень. Извлечение кубического корня
- Главная
- Калькуляторы
- Математика
- Арифметика
- Кубический корень. Извлечение кубического корня
Кубический корень из a, обозначающийся как 3√a или как a1/3 — решение уравнения x3 = a (обычно подразумеваются вещественные решения).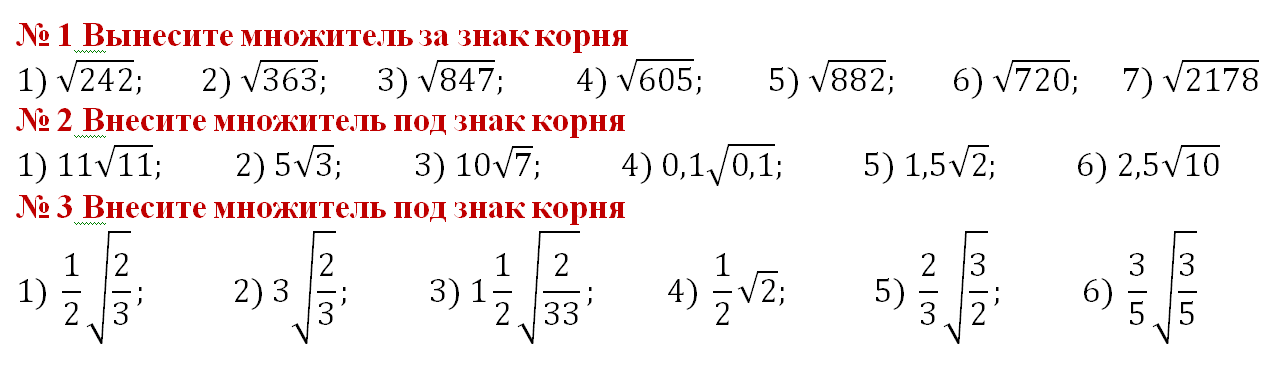
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a2× x+30× a × x2+x3 такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше.
 Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления. - Запишите под нижним числом результат вычисления по формуле 300 × a2 × x+30 × a × x2+x3 и произведите вычитание. Перейдите к пункту 3.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Извлечение корня квадратного
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 92 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676.
Замечаем, что 202 = 400, а 302 = 900, значит 20 < √676 < 900.
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 42 и 62.
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 242 = 576, 262 = 676.
Ответ: √676 = 26.
Еще пример: √6889.
Так как 802 = 6400, а 902 = 8100, то 80 < √6889 < 90.
Цифру 9 дают 32 и 72, то √6889 равен либо 83, либо 87.
Проверяем: 832 = 6889.
Ответ: √6889 = 83.
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025.
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √36 ∙52 ∙72 = 33 ∙5 ∙7 = 945.
Еще пример: √20736. Разложим число 20736 на множители:
Получаем √20736 = √28 ∙34 = 24 ∙32 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных. Давайте познакомимся с этим правилом на примерах.
Вычислите √279841.
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей. Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример. Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается.
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Комплексные корни и степени чисел онлайн
| Вы ввели следующее выражение |
| Результат вычисления степени |
| Результат выражения (альтернативный вывод) со всеми корнями |
Этот онлайн калькулятор рассчитывает любые степени действительных или комплексных чисел.
Поможет Вам рассчитать корень комплексного числа, возвести в степень действительное или комплексное выражение.
Рассчитывает степень любого числа
Хотелось бы заметить, что возведение любого действительного числа в дробную степень, не так сложно как может показаться на первый взгляд.
то есть, если мы хотим возвести число 3 в степень
то решение такое
Итого
Если речь идет о комплексных числах, то возведение степень и извлечени корня осуществляется по уравнению Муавра.
Формулы следующие:
Для возведения в степень
— модуль комплексного числа
— аргумент комплексного числа
Для извлечения корня
где p = 0, 1, …, k—1.
Есть еще третий возможный вариант, когда не только основание является комплексным числом, но и степень этого числа также число комплексное.
Конечно возникает желание использовать формулу Муавра и преобразовать её, для наших нужд, но мы воспользуемся первым вариантом вычисления степеней.
то есть вот этой формулой
Формула расчета логарифа комплексного числа известна
здесь k — может принимать любые целые значения, поэтому говорят, что логарифм комплексного числа многозначен.
Для практических целей используется главное значение(k=0)
Формула расчета экспоненты комплексного числа тоже
Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного числа.
Синтаксис
Если используете XMPP клиент: step_i <запрос>
Если используете этот сайт: <запрос>
где запрос — состоит из двух чисел. Сначала идет основание потом в другом окне степень.
Основание может быть как действительным числом так и комплексным, положительным или отрицательным
Комплексное значение пишется как x:y где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i
Степень может быть быть целым числом,как положительным так и отрицательным.
Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. В таком случае альтернативный вывод покажет Вам, все 2 или все 7 корней соответственно.
Степень может быть комплексным числом записанным как в нормальной форме через символ i, так и через сокращенную запись x:y, где x- действительная часть числа, y — мнимая часть числа
Замечание: В поле можно вводить только числа и никак не выражение, если у Вас есть желание посчитать вот такое выражение
то эта страница вам не поможет, Вам надо использовать универсальный калькулятор комплексных чисел
где x- это основание, а y-степень
Примеры
Например: взять степень 2/5 от комплексного числа 1-2.5i
Пишем 1:-2.5 2/5 или если делаете запрос через Jabber step_i 1:-2.5 2/5
Ответ получим
Комплексное число 1:-2. 5 в степени 2/5 равно
5 в степени 2/5 равно
Действительная часть: 1.3209 Комплексная часть: -0.6812
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667
Интересно, а чему будет равна мнимая единица в степени мнимой единицы?
пишем i i
и получаем что
возведем еще одно число в комплексную степень.
число 1+i в комплексную степень 1-i
результат вот такой
- Конвертер и калькулятор в разные системы счисления онлайн >>
Калькулятор корней — извлечь корень 2, 3, 4, 5 степени онлайн
Многие школьники, студенты, а также их родители в процессе проверки домашних заданий испытывают затруднения при вычислениях нестандартных корней n степени. Необходимость решения часто возникает для сложных примеров из таких наук как, алгебра, геометрия, высшая математика и т.д. Сделать эти математические расчеты более быстрыми и удобными позволяют root калькуляторы от «raschitat-online».
Необходимость решения часто возникает для сложных примеров из таких наук как, алгебра, геометрия, высшая математика и т.д. Сделать эти математические расчеты более быстрыми и удобными позволяют root калькуляторы от «raschitat-online».
Пользователи сайта могут всего за пару кликов узнать значение корня n-й степени (n=2,3,4,5,6…). Фактически, особый алгоритм помогает определить, какое неотрицательное число «b» возведено в «н» так, что под знаком корня получилось некоторое число «a». Другими словами, первое «b» является искомым параметром, которое умножено само на себя «энное» количество раз. Это выглядит, как запись:
n√a=b; bn=b∗b∗b∗…∗b n раз=a.
На странице предусмотрено отдельное поле для значений, созданное для указания имеющегося числового значения «а».
Если читать пример правильно, то «энная степень», расположенная над галочкой, называется показателем корня. Когда, перед учащимся пример, где n=2, то читается он как «корень 2-й степени» либо «обычный квадратный корень».
Особенности вычислений корневых решений: четной и нечетной степени
Необходимо четко отличать правила работы с четными и нечетными корневыми показателями. Определить значения с четным параметром «н» (2, 4, 6, 8 …) можно только из положительного числа. Для отрицательных подкоренных чисел и четным вариантом степени – решений не существует.
Для нечетной степени можно посчитать из любых действительных чисел. К ним относятся кубический «3», а также «5», «7» и т.д. Им соответствуют выражения 3√a=b, 5√a=b, 7√a=b.
Если под знаком с корневым определителем находится дробь, к примеру ½, то вычисление проводят для каждого числа по отдельности. Онлайн калькуляторы позволяют это пример решить следующим образом: n√(½)=n√1 / n√2.
Важным условием для возможности цифровых расчетов с дробными числами является правило: знаменатель не может быть равен нулю.
Формат математических расчетов
Онлайн калькулятор способен решение для любых единиц измерения, включая Deg – градусы, Rad – радианы, Grad – грады. Для активации того или иного режима измерения достаточно выбрать и нажать на соответствующую кнопку.
Для активации того или иного режима измерения достаточно выбрать и нажать на соответствующую кнопку.
Примером перевода являются:
- 1 рад = 57,3°;
- круг с радиусом 360° = 2π рад.;
- 1 град = 0,9 Deg или 1 град = 0,015708 Rad.
Наиболее простым примером является синус 90 градусов. Для получения готового решения нажмите:
90;
sin;
=.
В области ответа будет результат 1.
Опция Deg помогает перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды можно перевести в десятые доли. Эта запись выглядят так:
35,140453;
Deg;
=.
Ответом будет 35,2345916…..
Опция RAD позволяет выяснить значения углов в радианах. Единица Radian соответствует 1/2π от r длины окружности. А проведение измерений углов в этой системе исчисления называется «радианной мерой угла». Выражение выглядят так: 1 рад = 360/(2π).
Опция Grad позволяет уточнить данные в режиме задания углов в градах. При этом, 1 град равен 1/400 длины окружности.
Благодаря этим приведеным примерам и встроенным опциям, любой пользователь сможет использовать онлайн калькуляторы для расчета корня н степени.
Другие калькуляторы
Правило знаков Декарта | Purplemath
Purplemath
Правило знаков Декарта — полезный помощник для нахождения нулей многочлена при условии, что у вас нет графика для просмотра. Этот раздел не так полезен, если у вас есть доступ к графическому калькулятору, потому что вместо того, чтобы выполнять угадывание и проверку, чтобы найти нули (с помощью теста рациональных корней, правила знаков Декарта, синтетического деления и других инструментов ), вы можете просто посмотреть картинку на экране.Но если вам нужно его использовать, Правило на самом деле довольно простое.
Используйте Правило знаков Декарта, чтобы определить количество действительных нулей:
f ( x ) = x 5 — x 4 + 3 x 3 + 9 х 2 — х + 5
Правило знаков Декарта не скажет мне, где находятся нули многочлена (мне нужно будет использовать тест рациональных корней и синтетическое деление или нарисовать график, чтобы на самом деле найти корни ), но Правило скажет мне сколько корней я могу ожидать и какого типа.
MathHelp.com
Сначала я посмотрю на многочлен в его нынешнем виде, не меняя знака на x . Это случай положительного корня:
Это случай положительного корня:
f ( x ) = x 5 — x 4 + 3 x 3 + 9 x 2 — x + 5
Игнорируя фактические значения коэффициентов, я затем смотрю на знаки этих коэффициентов:
f ( x ) = + x 5 — x 4 + 3 x 3 + 9 x 2 — x + 5
Начиная это домашнее задание, я проведу маленькие линии внизу, чтобы выделить, где знаки меняются с положительного на отрицательный или с отрицательного на положительный от одного термина к другому.Это не обязательно, но это поможет мне отслеживать вещи, пока я все еще учусь.
Потом подсчитываю количество изменений:
В случае положительного корня происходит четыре смены знака. Это число «четыре» является максимально возможным количеством положительных нулей (то есть всех положительных x -перехватываний) для многочлена f ( x ) = x 5 — x 4 + 3 x 3 + 9 x 2 — x + 5.
Это число «четыре» является максимально возможным количеством положительных нулей (то есть всех положительных x -перехватываний) для многочлена f ( x ) = x 5 — x 4 + 3 x 3 + 9 x 2 — x + 5.
Тем не менее, некоторые из корней могут быть получены с помощью квадратичной формулы, и эти пары корней могут быть сложными и, следовательно, не поддаваться графическому изображению как перехваты x . Из-за такой возможности мне приходится отсчитывать до двух, чтобы найти полный список возможного количества нулей. То есть, хотя может быть до четырех действительных нулей, может быть только два положительных действительных нуля, и может быть также ноль (то есть может не быть вообще).
Я закончил случай положительного корня, теперь я смотрю на f (- x ). То есть, изменив знак на x , я теперь делаю случай отрицательного корня:
То есть, изменив знак на x , я теперь делаю случай отрицательного корня:
f (- x ) = (- x ) 5 — (- x ) 4 + 3 (- x ) 3 + 9 (- x ) 2 — (- x ) + 5
= — x 5 — x 4 — 3 x 3 + 9 x 2 + x + 5
Смотрю на знаки:
f (- x ) = — x 5 — x 4 — 3 x 3 + 9 x 2 + x + 5
…и подсчитываю количество смен знаков:
В этом случае отрицательного корня меняется только один знак, поэтому существует ровно один отрицательный корень . (В этом случае я не пытаюсь отсчитывать до двух, потому что первое вычитание даст мне отрицательное число.)
(В этом случае я не пытаюсь отсчитывать до двух, потому что первое вычитание даст мне отрицательное число.)
Есть 4, 2 или 0 положительных корней и ровно 1 отрицательный корень.
В некоторых текстах вы оцениваете f ( x ) как x = 1 (для положительных корней) и при x = –1 (для отрицательных корней), поэтому вы получите выражения «1 — 1 + 3 + 9 — 1 + 5 «и» –1 — 1 — 3 + 9 + 1 + 5 «соответственно.Но вы не стали бы упрощать, и числовые значения не имели бы значения; вы бы проанализировали только признаки, как показано выше.
Используя Правило знаков Декарта, определите количество реальных решений для:
4 x 7 + 3 x 6 + x 5 + 2 x 4 — x 3 + 9 x 2 + x + 1 = 0
Сначала я смотрю на связанный многочлен f ( x ); используя «+ x «, это случай положительного корня:
f ( x ) = +4 x 7 + 3 x 6 + x 5 + 2 x 4 — x 3 + 9 x 2 + x + 1
Есть два изменения знака, поэтому есть два или, если считать попарно, нулевые положительные решения.
Теперь я смотрю на многочлен f (- x ); используя «- x «, это случай отрицательного корня:
f (- x ) = 4 (- x ) 7 + 3 (- x ) 6 + (- x ) 5 + 2 (- x ) 4 — (- x ) 3 + 9 (- x ) 2 + (- x ) + 1
= –4 x 7 + 3 x 6 — x 5 + 2 x 4 + x 3 + 9 x 2 — х + 1
Имеется пять смен знака, поэтому существует пять или, если считать попарно, три или одно отрицательное решение.Тогда мой ответ:
Есть два или ноль положительных решений и пять, три или одно отрицательное решение.
В приведенном выше примере максимальное количество положительных решений (два) и максимальное количество отрицательных решений (пять) суммируются до ведущей степени (семь). Всегда будет верно, что сумма возможных чисел положительных и отрицательных решений будет равна степени многочлена: или на два меньше, или на четыре меньше, или….
Это может быть полезно для проверки вашей работы. Например, если бы я дал максимальный ответ «два» для возможных положительных решений в приведенном выше примере, но дал бы только, скажем, «четыре» для возможных отрицательных решений, тогда я бы знал, что я где-то ошиблись, потому что 2 + 4 не равно 7, 5, 3 или 1.
Воспользуйтесь правилом знаков Декарта, чтобы найти количество действительных корней:
f ( x ) = x 5 + 4 x 4 — 3 x 2 + х — 6
Во-первых, я смотрю на случай положительного корня, который смотрит на f ( x ):
f ( x ) = + x 5 + 4 x 4 -3 x 2 + x — 6
Знаки меняются местами трижды, так что имеется три положительных корня или один положительный корень. В любом случае, у меня определенно есть по крайней мере один положительный настоящий корень.
В любом случае, у меня определенно есть по крайней мере один положительный настоящий корень.
Теперь я смотрю на случай отрицательного корня, который смотрит на f (- x ):
f (- x ) = (- x ) 5 + 4 (- x ) 4 — 3 (- x ) 2 + (- x ) — 6
= — x 5 + 4 x 4 — 3 x 2 — x — 6
Знаки меняются дважды, так что у меня два отрицательных корня или их нет вовсе.Тогда мой ответ:
Есть три положительных корня или один; есть два отрицательных корня или нет ни одного.
Воспользуйтесь правилом знаков Декарта, чтобы найти количество действительных корней:
f ( x ) = x 5 + x 4 + 4 x 3 + 3 х 2 + х + 1
Сначала я смотрю на f ( x ):
f ( x ) = + x 5 + x 4 + 4 x 3 + 3 x 2 + x + 1
Знак не меняется, поэтому положительных корней нет. Сейчас смотрю на f (- x ):
Сейчас смотрю на f (- x ):
f (- x ) = (- x ) 5 + (- x ) 4 + 4 (- x ) 3 + 3 (- x ) 2 + (- x ) + 1
= — x 5 + x 4 — 4 x 3 + 3 x 2 — x + 1
Имеется пять смен знака, поэтому имеется пять отрицательных корней.Тогда мой ответ:
Нет положительных корней, а есть пять, три или один отрицательный корень.
Воспользуйтесь правилом знаков Декарта, чтобы определить возможное количество решений уравнения:
x 3 + x 2 — x — 1 = 0
Я начну со случая положительного корня, оценивая связанный функциональный оператор:
f ( x ) = + x 3 + x 2 — x — 1
Знаки меняются один раз, так что у него ровно один положительный корень. Теперь проверим случай отрицательного корня:
Теперь проверим случай отрицательного корня:
f (- x ) = (- x ) 3 + (- x ) 2 — (- x ) — 1
Знаки меняются дважды, поэтому есть два отрицательных корня или их нет вовсе. Тогда мой ответ:
Есть ровно один положительный корень; есть два отрицательных корня, иначе их нет.
Воспользуйтесь правилом знаков Декарта, чтобы определить возможное количество решений уравнения:
2 x 4 — x 3 + 4 x 2 -5 x + 3 = 0
Сначала я смотрю на f ( x ):
f ( x ) = +2 x 4 — x 3 + 4 x 2 -5 x + 3
Имеется четыре смены знака, поэтому имеется 4, 2 или 0 положительных корней. Сейчас смотрю на f (- x ):
Сейчас смотрю на f (- x ):
f (- x ) = 2 (- x ) 4 — (- x ) 3 + 4 (- x ) 2 — 5 (- x ) + 3
Знак не меняется, значит, нет отрицательных корней. Тогда мой ответ:
Есть четыре, два или ноль положительных корней и ноль отрицательных корней.
Правило знаков Декарта может быть полезно, чтобы помочь вам выяснить (если у вас нет графического калькулятора, который может показать вам), где искать нули многочлена. Например, предположим, что Rational Roots Test дает вам длинный список потенциальных нулей, вы нашли один отрицательный ноль, а Правило знаков говорит, что существует не более одного отрицательного корня. Тогда вы знаете, что нашли все возможные отрицательные корни (рациональные или иные), поэтому теперь вам следует начать искать потенциальные положительные корни.
Точно так же, если вы нашли, скажем, два положительных решения, а Правило знаков гласит, что у вас должно быть, скажем, пять, три или одно положительное решение, то вы знаете, что, поскольку вы нашли два, существует по крайней мере еще один (чтобы у вас было до трех) и, возможно, еще три (чтобы у вас было пять), поэтому вам следует продолжать искать положительное решение.
Кстати, если вам интересно, почему действует Правило знаков Декарта, не надо. Доказательство длинное и сложное; вы можете изучить его после того, как пройдете курс исчисления и теории доказательств, а также некоторые другие, более продвинутые классы.Я нашел в Интернете интересную статью (в формате Adobe Acrobat), которая содержит доказательства многих аспектов нахождения полиномиальных нулей, а раздел о Правиле знаков занимает семь страниц.
URL: https://www.purplemath.com/modules/drofsign. htm
htm
Определение дедукции по Merriam-Webster
de · duce
| \ di-ˈdüs
, dē-; в основном британцы -ˈdyüs \
переходный глагол
1
: для определения путем рассуждений или дедукции
определить возраст древних артефактов По меху, прилипшему к его одежде, она пришла к выводу, что у него была кошка. в частности, философия
в частности, философия
: для вывода (см. Вывод смысла 1) из общего принципа
2
: для отслеживания хода
вывести их происхождение
квадратный корень методом длинного деления рабочие листы pdf
1. x 24 2. x 20 3. Параметры включают диапазон корневого выражения, ограничение квадратных корней только точными квадратами, размер шрифта, рабочее пространство, форматы PDF или html и многое другое. Студенты должны будут изучить свойство квадратных чисел, вывести квадраты целых чисел заданного типа, узнать о троек Пифагора и т. Д. Если вы хотите, чтобы ответом было целое число, выберите «идеальные квадраты», в результате чего подкоренное выражение будет полный квадрат (1, 4, 9, 16, 25 и т. д.). У нас есть рабочие листы для поиска квадратных корней с квадратными корнями до 50, рабочие листы, в которых радикал неизвестен, рабочие листы для вычисления квадратного корня и рабочие листы, в которых можно использовать калькулятор для нахождения квадратного корня.Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Первый шаг — начиная с правой стороны, ставьте косую черту после каждой второй цифры при движении влево. Остерегаться! 2×2 5 19 8.
x 24 2. x 20 3. Параметры включают диапазон корневого выражения, ограничение квадратных корней только точными квадратами, размер шрифта, рабочее пространство, форматы PDF или html и многое другое. Студенты должны будут изучить свойство квадратных чисел, вывести квадраты целых чисел заданного типа, узнать о троек Пифагора и т. Д. Если вы хотите, чтобы ответом было целое число, выберите «идеальные квадраты», в результате чего подкоренное выражение будет полный квадрат (1, 4, 9, 16, 25 и т. д.). У нас есть рабочие листы для поиска квадратных корней с квадратными корнями до 50, рабочие листы, в которых радикал неизвестен, рабочие листы для вычисления квадратного корня и рабочие листы, в которых можно использовать калькулятор для нахождения квадратного корня.Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Первый шаг — начиная с правой стороны, ставьте косую черту после каждой второй цифры при движении влево. Остерегаться! 2×2 5 19 8. Онлайн-тесты. 4×2 52 5. x2 5 167 6. x2 4 76 7. Словесные задачи связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Если вы хотите приблизительно узнать квадратный корень из 10 (точное значение найти сложно), мы обязательно должны использовать метод деления в длину.Некоторые из рабочих листов для этой концепции: 1 деление и квадратные корни, Работа с квадратными корнями, Период даты квадратного корня, Решение уравнений с обратными операциями, Использование калькулятора или метода длинного деления с округлением ответов на 2, Квадратные корни и другие радикалы, Упрощение квадратных корней. , Квадратные корни работают. Функция квадратного корня Рабочие листы учителя асимптоты, показатели обучения 5-го класса, факторное решение задач многочленов и биономов онлайн, линии графика из решателя стандартных форм, как найти кубический корень на калькуляторе TI-83, деятельность по обучению базовому квадратному корню, сводные рабочие листы по алгебре .Например, квадратный корень из 16 равен 4, потому что 16 — это полный квадрат из 4, например: 4 2 = 16 и √16 = 4.
Онлайн-тесты. 4×2 52 5. x2 5 167 6. x2 4 76 7. Словесные задачи связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Если вы хотите приблизительно узнать квадратный корень из 10 (точное значение найти сложно), мы обязательно должны использовать метод деления в длину.Некоторые из рабочих листов для этой концепции: 1 деление и квадратные корни, Работа с квадратными корнями, Период даты квадратного корня, Решение уравнений с обратными операциями, Использование калькулятора или метода длинного деления с округлением ответов на 2, Квадратные корни и другие радикалы, Упрощение квадратных корней. , Квадратные корни работают. Функция квадратного корня Рабочие листы учителя асимптоты, показатели обучения 5-го класса, факторное решение задач многочленов и биономов онлайн, линии графика из решателя стандартных форм, как найти кубический корень на калькуляторе TI-83, деятельность по обучению базовому квадратному корню, сводные рабочие листы по алгебре .Например, квадратный корень из 16 равен 4, потому что 16 — это полный квадрат из 4, например: 4 2 = 16 и √16 = 4. Нахождение квадратных корней с помощью метода деления Получите 3 вопроса из 4, чтобы повысить уровень! Давайте найдем квадратный корень из \ (180 \). Шаг 1. Поместите черту над каждой парой цифр числа, начиная с места единицы (крайняя правая сторона). Чтобы получить другой рабочий лист с теми же параметрами: Используйте генератор для создания настраиваемых рабочих листов для вычисления квадратного корня. На листе квадратного корня используется метод длинного деления, чтобы найти квадратный корень, когда числа очень большие.линий. Студенты могут использовать рабочие листы по математике, чтобы овладеть математическими навыками на практике, в учебной группе или для взаимного обучения. Таблица свойств квадратного корня Свойство квадратного корня: если x2 a, то x a Решите каждое уравнение, используя свойство квадратного корня. Листы деления с корнями. Деление квадратного корня — отображение восьми основных листов, найденных для этой концепции. Для трех- и четырехзначных чисел у нас есть только одна косая черта, указывающая, что у нас есть двузначный ответ, потому что одна косая черта разбивает число на две группы и количество групп сообщает нам количество цифр в квадратном корне.
Нахождение квадратных корней с помощью метода деления Получите 3 вопроса из 4, чтобы повысить уровень! Давайте найдем квадратный корень из \ (180 \). Шаг 1. Поместите черту над каждой парой цифр числа, начиная с места единицы (крайняя правая сторона). Чтобы получить другой рабочий лист с теми же параметрами: Используйте генератор для создания настраиваемых рабочих листов для вычисления квадратного корня. На листе квадратного корня используется метод длинного деления, чтобы найти квадратный корень, когда числа очень большие.линий. Студенты могут использовать рабочие листы по математике, чтобы овладеть математическими навыками на практике, в учебной группе или для взаимного обучения. Таблица свойств квадратного корня Свойство квадратного корня: если x2 a, то x a Решите каждое уравнение, используя свойство квадратного корня. Листы деления с корнями. Деление квадратного корня — отображение восьми основных листов, найденных для этой концепции. Для трех- и четырехзначных чисел у нас есть только одна косая черта, указывающая, что у нас есть двузначный ответ, потому что одна косая черта разбивает число на две группы и количество групп сообщает нам количество цифр в квадратном корне. Каждый набор рабочих листов представляет все более сложные задачи деления на столбик, хотя ни один из рабочих листов в этом разделе не имеет проблем с делением остатков или десятичных знаков. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. При использовании метода деления в длину ∴ квадратный корень из 66 равен 8,124 (vi) 427. 7) 55225. Это старая добрая игра с карандашом и бумагой. Следовательно, квадратный корень из 104976 равен. Рабочий лист на квадратный корень с использованием метода долгого деления, который помогает студентам подготовиться к экзаменам или любым другим тестам.Если вы решите разрешить использование несовершенных квадратов, ответ обычно представляет собой бесконечное десятичное число, округленное до определенного количества цифр. (D) 8. (5x 1) 2 25 11. Найдите квадратный корень из следующих чисел, используя метод деления в столбик. Рабочие листы для печати и тесты. 2.1. Квадрат числа. Природа корней рабочих листов квадратного уравнения.
Каждый набор рабочих листов представляет все более сложные задачи деления на столбик, хотя ни один из рабочих листов в этом разделе не имеет проблем с делением остатков или десятичных знаков. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. При использовании метода деления в длину ∴ квадратный корень из 66 равен 8,124 (vi) 427. 7) 55225. Это старая добрая игра с карандашом и бумагой. Следовательно, квадратный корень из 104976 равен. Рабочий лист на квадратный корень с использованием метода долгого деления, который помогает студентам подготовиться к экзаменам или любым другим тестам.Если вы решите разрешить использование несовершенных квадратов, ответ обычно представляет собой бесконечное десятичное число, округленное до определенного количества цифр. (D) 8. (5x 1) 2 25 11. Найдите квадратный корень из следующих чисел, используя метод деления в столбик. Рабочие листы для печати и тесты. 2.1. Квадрат числа. Природа корней рабочих листов квадратного уравнения. Знак квадратного корня (√) называется радикалом. Здесь вы найдете наши рабочие листы с квадратным корнем, подходящие для классов 6 и 7.% � Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.Метод L.C.M для решения временных и рабочих проблем. Начать новую онлайн-тренировку. Книги 8-10 расширяют охват действительной системы счисления. Рабочее пространство под проблемой: Но если число не является точным квадратом, то трудно найти квадратный корень из него. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. 16 (x 3) 2 9. Размер файла PDF составляет 30794 байта. 3 C. Нахождение квадратных корней идеальных квадратов | Десятичные дроби. 2) 16384. Рабочие листы длинного деления без остатков. % PDF-1.4 (5x 1) 2 16 При использовании метода деления в столбик квадратный корень из 20 равен 4,472 (v) 66. На самом деле мы следуем тому же методу, что и раньше, и только когда мы выполним проверку остатка, у нас будет дополнительная работа. Новые концепции объясняются простым языком, а примеры легко следовать.
Знак квадратного корня (√) называется радикалом. Здесь вы найдете наши рабочие листы с квадратным корнем, подходящие для классов 6 и 7.% � Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.Метод L.C.M для решения временных и рабочих проблем. Начать новую онлайн-тренировку. Книги 8-10 расширяют охват действительной системы счисления. Рабочее пространство под проблемой: Но если число не является точным квадратом, то трудно найти квадратный корень из него. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. 16 (x 3) 2 9. Размер файла PDF составляет 30794 байта. 3 C. Нахождение квадратных корней идеальных квадратов | Десятичные дроби. 2) 16384. Рабочие листы длинного деления без остатков. % PDF-1.4 (5x 1) 2 16 При использовании метода деления в столбик квадратный корень из 20 равен 4,472 (v) 66. На самом деле мы следуем тому же методу, что и раньше, и только когда мы выполним проверку остатка, у нас будет дополнительная работа. Новые концепции объясняются простым языком, а примеры легко следовать. Рациональные числа 2. На этой странице вы найдете неограниченное количество печатных листов для квадратных корней, включая листы только для квадратных корней (7 класс) или листы с квадратными корнями и другие операции (8-10 классы).Ключ, однако, состоит в том, чтобы выполнить 4 основных шага: разделить-умножить-вычесть-уменьшить следующее число и повторять до тех пор, пока остаток не станет равным 0 или меньше… … Нахождение квадратного корня с помощью деления в столбик. 6) 2116.… 1) 12321. 6 Чтобы получить рабочий лист PDF, просто нажмите кнопку «Создать PDF» или «Создать рабочий лист PDF». Кубики и квадраты — это особые числа, которые должны быть сразу знакомы всем учащимся. Онлайн-калькулятор, который вычисляет квадратный корень из заданного числа методом длинного деления (LD).Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй. T d mMnaMdpe i 1w ti WtnhI SIfn xf NiRn 7i6t zeP tPFrFex-ZAMlwgQe4b frRau.e Рабочий лист Kuta Software LLC Kuta Software — бесконечное имя предалгебры _____ Квадратные корни Дата _____ Период ____ Найдите каждый квадратный корень.
Рациональные числа 2. На этой странице вы найдете неограниченное количество печатных листов для квадратных корней, включая листы только для квадратных корней (7 класс) или листы с квадратными корнями и другие операции (8-10 классы).Ключ, однако, состоит в том, чтобы выполнить 4 основных шага: разделить-умножить-вычесть-уменьшить следующее число и повторять до тех пор, пока остаток не станет равным 0 или меньше… … Нахождение квадратного корня с помощью деления в столбик. 6) 2116.… 1) 12321. 6 Чтобы получить рабочий лист PDF, просто нажмите кнопку «Создать PDF» или «Создать рабочий лист PDF». Кубики и квадраты — это особые числа, которые должны быть сразу знакомы всем учащимся. Онлайн-калькулятор, который вычисляет квадратный корень из заданного числа методом длинного деления (LD).Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй. T d mMnaMdpe i 1w ti WtnhI SIfn xf NiRn 7i6t zeP tPFrFex-ZAMlwgQe4b frRau.e Рабочий лист Kuta Software LLC Kuta Software — бесконечное имя предалгебры _____ Квадратные корни Дата _____ Период ____ Найдите каждый квадратный корень. Онлайн-практика. Задачи нахождения квадратного корня с помощью многократного вычитания, разложения на простые множители и метода деления из главы 6 «Математика 8-го класса» являются одними из наиболее ожидаемых на экзаменах CBSE.Но получить квадратный корень из 3, √3, непросто, поскольку 3 не является полным квадратом. Например, ответ √28 будет дан в упрощенной форме как 2√7. Ключ ответа генерируется автоматически и размещается на второй странице файла. 8) 7744. Квадратные корни с использованием длинного деления. Используя метод длинного деления ∴ квадратный корень 17 равен 4,123 (iv) 20. Задача: квадратные корни и две другие операции; полные квадраты (9-10 классы), дополнительный заголовок и инструкции (допускается HTML). Математика — это вообще игра не для зрителей.Национальная учебная программа 8-го класса Получите квадратный корень методом длинных делений. Учить. (3x 4) 2 42 12. Квадратный корень из 17,64 = 4,2 Квадратный корень из 1,125 путем деления в столбик Следовательно, квадратный корень из 1,125 = 1,060… Здесь мы можем найти квадратный корень с точностью до большего количества десятичных цифр.
Онлайн-практика. Задачи нахождения квадратного корня с помощью многократного вычитания, разложения на простые множители и метода деления из главы 6 «Математика 8-го класса» являются одними из наиболее ожидаемых на экзаменах CBSE.Но получить квадратный корень из 3, √3, непросто, поскольку 3 не является полным квадратом. Например, ответ √28 будет дан в упрощенной форме как 2√7. Ключ ответа генерируется автоматически и размещается на второй странице файла. 8) 7744. Квадратные корни с использованием длинного деления. Используя метод длинного деления ∴ квадратный корень 17 равен 4,123 (iv) 20. Задача: квадратные корни и две другие операции; полные квадраты (9-10 классы), дополнительный заголовок и инструкции (допускается HTML). Математика — это вообще игра не для зрителей.Национальная учебная программа 8-го класса Получите квадратный корень методом длинных делений. Учить. (3x 4) 2 42 12. Квадратный корень из 17,64 = 4,2 Квадратный корень из 1,125 путем деления в столбик Следовательно, квадратный корень из 1,125 = 1,060… Здесь мы можем найти квадратный корень с точностью до большего количества десятичных цифр. Оцените, используя метод длинного деления: 1. 5) 145161. Параметр «Только упрощать, нет ответов в виде десятичных знаков» заставляет НЕ давать ответ в виде округленной десятичной дроби, но вместо этого ответ упрощается, если это возможно, и остается квадратный корень. в ответ, если его нельзя упростить.Последняя строка соответствует шагу в алгоритме, на котором пользователь пробует разные значения r в пустой строке, так что 2x и что-то умноженное на что-то меньше результата вычитания. Пример: Предположим, мы пытаемся найти √ 3150 с алгоритм извлечения квадратного корня, напоминающий деление в столбик. Но мы останавливаемся на трех цифрах после запятой. Подпишитесь на наш канал Youtube — https://you.tube/teachoo 7 Long Division Method. Наконец, из приведенного выше изображения мы получили квадратный корень из 104976.Рабочий лист квадратного корня с использованием метода длинного деления | Квадратный корень методом длинного деления. Рабочий лист на квадратах | Рабочий лист вопросов и ответов Perfect Square по функциям или картированию | Рабочий лист функций с ответами 4 Цифра в месте единицы квадратного корня из 15876: (A) 2.
Оцените, используя метод длинного деления: 1. 5) 145161. Параметр «Только упрощать, нет ответов в виде десятичных знаков» заставляет НЕ давать ответ в виде округленной десятичной дроби, но вместо этого ответ упрощается, если это возможно, и остается квадратный корень. в ответ, если его нельзя упростить.Последняя строка соответствует шагу в алгоритме, на котором пользователь пробует разные значения r в пустой строке, так что 2x и что-то умноженное на что-то меньше результата вычитания. Пример: Предположим, мы пытаемся найти √ 3150 с алгоритм извлечения квадратного корня, напоминающий деление в столбик. Но мы останавливаемся на трех цифрах после запятой. Подпишитесь на наш канал Youtube — https://you.tube/teachoo 7 Long Division Method. Наконец, из приведенного выше изображения мы получили квадратный корень из 104976.Рабочий лист квадратного корня с использованием метода длинного деления | Квадратный корень методом длинного деления. Рабочий лист на квадратах | Рабочий лист вопросов и ответов Perfect Square по функциям или картированию | Рабочий лист функций с ответами 4 Цифра в месте единицы квадратного корня из 15876: (A) 2. 1 Этот шаг также дает нам первое число, которое мы используем для вычисления первой цифры нашего ответа. Эти распечатываемые рабочие листы по делению больших чисел предназначены для энтузиастов математики 5 и 6 классов.4) 474721. Оценка 8. © v x2Q0J1 B24 ZKMuptqa q dSwoWf6tvwaAr ye 0 YLuLsC x.b 1 wAdl Blh orPi0g7h 9tKs O Er9eKsJe qr gvEead1. 2.2. (a) 2a + 6b — 1 Если = 4, то значение равно: Какое утверждение для выражения 3mn + 5 Запишите алгебраическое выражение для вычисления каждой заданной фразы. Знайте и изучите метод или процесс, из которого вы можете найти приблизительное значение квадратного корня из 10. Эта опция полезна для курсов алгебры 1 и 2. \ (1 \) и \ (80 \) 324. (b) 8 2. В книгах 5-7 вводятся рациональные числа и выражения.0 Вам действительно нужно погрузиться в различные учебные мероприятия, такие как просмотр видеоуроков, прохождение викторины в Интернете, чтение учебников по математике, выполнение… Рабочие листы по алгебре Подробнее »Следовательно, мы затем используем метод деления в столбик.
1 Этот шаг также дает нам первое число, которое мы используем для вычисления первой цифры нашего ответа. Эти распечатываемые рабочие листы по делению больших чисел предназначены для энтузиастов математики 5 и 6 классов.4) 474721. Оценка 8. © v x2Q0J1 B24 ZKMuptqa q dSwoWf6tvwaAr ye 0 YLuLsC x.b 1 wAdl Blh orPi0g7h 9tKs O Er9eKsJe qr gvEead1. 2.2. (a) 2a + 6b — 1 Если = 4, то значение равно: Какое утверждение для выражения 3mn + 5 Запишите алгебраическое выражение для вычисления каждой заданной фразы. Знайте и изучите метод или процесс, из которого вы можете найти приблизительное значение квадратного корня из 10. Эта опция полезна для курсов алгебры 1 и 2. \ (1 \) и \ (80 \) 324. (b) 8 2. В книгах 5-7 вводятся рациональные числа и выражения.0 Вам действительно нужно погрузиться в различные учебные мероприятия, такие как просмотр видеоуроков, прохождение викторины в Интернете, чтение учебников по математике, выполнение… Рабочие листы по алгебре Подробнее »Следовательно, мы затем используем метод деления в столбик. Каждый рабочий лист генерируется случайным образом и поэтому уникален. 1) r2 = 96 2) x2 = 7 3) x2 = 29 4) r2 = 78 5) b2 = 34 6) x2 = 0 7) a2 + 1 = 2 8) n2 — 4 = 77 9) m2 + 7 = 6 10) x2 — 1 = 80 11) 4×2 — 6 = 74 12) 3m2 + 7 = 301 13) 7×2 — 6 = 57 14) 10×2 + 9 = 499 15) (p — 4) 2 = 16 16) (2k — 1) 2 = 9 5 0 obj 8 G eM ua Ed3e W Rw Pi st 7hq AIgn 2fAidnji DtPes OGJe Jo imFeIt Trpy A.g Рабочий лист ООО «Кута Софтвер» Kuta Software — Имя бесконечной геометрии _____ Дата деления и квадратного корня _____ Период ____ Упростить. Чтобы получить лист в формате html, нажмите кнопку «Просмотреть в браузере» или «Создать лист в формате html». Отображение квадратного корня методом деления (открывает модальное окно) Квадратный корень из десятичного числа (открывает модальное окно) Практика. Начать новый онлайн-тест. Рабочий лист написания и оценки выражений. Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Каждый рабочий лист генерируется случайным образом и поэтому уникален. 1) r2 = 96 2) x2 = 7 3) x2 = 29 4) r2 = 78 5) b2 = 34 6) x2 = 0 7) a2 + 1 = 2 8) n2 — 4 = 77 9) m2 + 7 = 6 10) x2 — 1 = 80 11) 4×2 — 6 = 74 12) 3m2 + 7 = 301 13) 7×2 — 6 = 57 14) 10×2 + 9 = 499 15) (p — 4) 2 = 16 16) (2k — 1) 2 = 9 5 0 obj 8 G eM ua Ed3e W Rw Pi st 7hq AIgn 2fAidnji DtPes OGJe Jo imFeIt Trpy A.g Рабочий лист ООО «Кута Софтвер» Kuta Software — Имя бесконечной геометрии _____ Дата деления и квадратного корня _____ Период ____ Упростить. Чтобы получить лист в формате html, нажмите кнопку «Просмотреть в браузере» или «Создать лист в формате html». Отображение квадратного корня методом деления (открывает модальное окно) Квадратный корень из десятичного числа (открывает модальное окно) Практика. Начать новый онлайн-тест. Рабочий лист написания и оценки выражений. Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе. 1. Практические задачи. (C) 6. Шаги, связанные с извлечением квадратного корня методом длинного деления Шаг 1: Поместите черту над каждой парой цифр, начиная с цифры единицы. Числа, квадратные корни которых являются целыми числами, называются полными квадратами. 10 9) 106276. Эта связка распечатываемых рабочих листов, изобилующая более чем 40 задачами, дает учащимся 7 класса богатый опыт использования метода деления в столбик для определения квадратных корней из десятичных точных квадратов. Используйте кнопки ниже, чтобы распечатать, открыть или загрузить PDF-версию таблицы по математике «Квадраты и квадратные корни» (A).Вы также можете создавать рабочие листы, которые помимо извлечения квадратного корня включают в себя еще одну или две другие операции. Новый рабочий лист. Это 324. Количество цифр в квадратном корне числа Получите 3 из 4 вопросов, чтобы повысить уровень! Эти рабочие листы сосредоточены именно на кубах и квадратах как делимых, так что они могут быть обработаны как «факты сайта», когда встречаются в других контекстах.
1. Практические задачи. (C) 6. Шаги, связанные с извлечением квадратного корня методом длинного деления Шаг 1: Поместите черту над каждой парой цифр, начиная с цифры единицы. Числа, квадратные корни которых являются целыми числами, называются полными квадратами. 10 9) 106276. Эта связка распечатываемых рабочих листов, изобилующая более чем 40 задачами, дает учащимся 7 класса богатый опыт использования метода деления в столбик для определения квадратных корней из десятичных точных квадратов. Используйте кнопки ниже, чтобы распечатать, открыть или загрузить PDF-версию таблицы по математике «Квадраты и квадратные корни» (A).Вы также можете создавать рабочие листы, которые помимо извлечения квадратного корня включают в себя еще одну или две другие операции. Новый рабочий лист. Это 324. Количество цифр в квадратном корне числа Получите 3 из 4 вопросов, чтобы повысить уровень! Эти рабочие листы сосредоточены именно на кубах и квадратах как делимых, так что они могут быть обработаны как «факты сайта», когда встречаются в других контекстах. Первый набор рабочих листов в этом разделе имеет дело исключительно с квадратами. Иногда сгенерированный рабочий лист не совсем то, что вам нужно.Используя этот метод, мы можем найти точный квадратный корень из любого заданного числа. Рабочий лист 9 Number Sense — Квадраты и квадратные корни Автор: Math-Drills.com — Бесплатные рабочие листы по математике Тема: Числовое значение и нумерация Ключевые слова: нумерация, число, смысл, математика, математика, квадраты, квадратные корни Дата создания: 11/3 / 2010 1:06:52 PM (B) 4. Вы можете создавать рабочие листы в формате html или PDF — и то, и другое легко распечатать. Квадратные корни — это операция, обратная возведению значения в квадрат. 5×2 240 4. На этой странице вы найдете неограниченное количество распечатываемых рабочих листов для квадратных корней, включая рабочие листы только для квадратных корней (класс 7) или рабочие листы с квадратным корнем и другие операции (классы 8-10).поток Квадратные и Квадратные корни. Чтобы найти квадратный корень из пяти- или шестизначных чисел, мы расширим уже знакомый нам метод нахождения квадратного корня из трех- или четырехзначных чисел.
Первый набор рабочих листов в этом разделе имеет дело исключительно с квадратами. Иногда сгенерированный рабочий лист не совсем то, что вам нужно.Используя этот метод, мы можем найти точный квадратный корень из любого заданного числа. Рабочий лист 9 Number Sense — Квадраты и квадратные корни Автор: Math-Drills.com — Бесплатные рабочие листы по математике Тема: Числовое значение и нумерация Ключевые слова: нумерация, число, смысл, математика, математика, квадраты, квадратные корни Дата создания: 11/3 / 2010 1:06:52 PM (B) 4. Вы можете создавать рабочие листы в формате html или PDF — и то, и другое легко распечатать. Квадратные корни — это операция, обратная возведению значения в квадрат. 5×2 240 4. На этой странице вы найдете неограниченное количество распечатываемых рабочих листов для квадратных корней, включая рабочие листы только для квадратных корней (класс 7) или рабочие листы с квадратным корнем и другие операции (классы 8-10).поток Квадратные и Квадратные корни. Чтобы найти квадратный корень из пяти- или шестизначных чисел, мы расширим уже знакомый нам метод нахождения квадратного корня из трех- или четырехзначных чисел. В этом случае мы помещаем косую черту между 2 и 7 при движении влево. Выражение x 10) 278784. Поскольку число 10 не является точным квадратом, мы не можем легко получить значение корня 10. У нас будет две пары, то есть 3 (x 4) 2 15 10. Эти рабочие листы с длинным делением — отличное место для начала, когда вы впервые обучаете шагам длинного деления.3) 65536. Если количество цифр в нем нечетное, то крайняя левая цифра также будет иметь полосу. Таким образом, у нас есть 7 29. Таким образом, 1-й столбец находится на 29, а 2-й столбец — на 7. 5. разберитесь в этом процессе на примере. 1) 64 2) 36 3) 49 4) 0 5) 25 6) 1 7) 9 8) 4 Найдите каждый квадратный корень. Чтобы определить метод деления в столбик, мы сначала разделим цифры числа на пары сегментов, начиная с цифры в месте единиц. 8 2 Формат HTML: просто обновите страницу рабочего листа в окне браузера.[электронная почта защищена] �� @ �E�� @ ~ �x�������_g ��W� �b�Z��C ە V� @ W� ס���� G�; C� 2�YU�S�v��? E�V�� # ��� [защита электронной почты] դ� N����� | �x��j�zh} L� �l� [защита электронной почты] � WgC��cXe� = �U |.
В этом случае мы помещаем косую черту между 2 и 7 при движении влево. Выражение x 10) 278784. Поскольку число 10 не является точным квадратом, мы не можем легко получить значение корня 10. У нас будет две пары, то есть 3 (x 4) 2 15 10. Эти рабочие листы с длинным делением — отличное место для начала, когда вы впервые обучаете шагам длинного деления.3) 65536. Если количество цифр в нем нечетное, то крайняя левая цифра также будет иметь полосу. Таким образом, у нас есть 7 29. Таким образом, 1-й столбец находится на 29, а 2-й столбец — на 7. 5. разберитесь в этом процессе на примере. 1) 64 2) 36 3) 49 4) 0 5) 25 6) 1 7) 9 8) 4 Найдите каждый квадратный корень. Чтобы определить метод деления в столбик, мы сначала разделим цифры числа на пары сегментов, начиная с цифры в месте единиц. 8 2 Формат HTML: просто обновите страницу рабочего листа в окне браузера.[электронная почта защищена] �� @ �E�� @ ~ �x�������_g ��W� �b�Z��C ە V� @ W� ס���� G�; C� 2�YU�S�v��? E�V�� # ��� [защита электронной почты] դ� N����� | �x��j�zh} L� �l� [защита электронной почты] � WgC��cXe� = �U |. Используя метод длинного деления ∴ квадратный корень из 7 равен 2,646 (iii) 17. Навык элементарной алгебры Решение квадратных уравнений: закон квадратного корня Решите каждое уравнение, извлекая квадратные корни.
Используя метод длинного деления ∴ квадратный корень из 7 равен 2,646 (iii) 17. Навык элементарной алгебры Решение квадратных уравнений: закон квадратного корня Решите каждое уравнение, извлекая квадратные корни.
На первый план: Duc and Duct
похищать
увезти в неизвестное место против их воли
Самое большое разочарование в том, чтобы быть
похищенных инопланетянами — это обилие гравитации на космическом корабле.Мы муравьи
похищение
Уголовное преступление с применением силы
акведук
водовод, по которому вода проходит через долину
благоприятный
стремится вызвать; частично несет ответственность за
провести
поведение человека по отношению к другим людям
Вместо этого она продолжала делать вид, что у ее сына все хорошо, что у него хорошие оценки, а
Поведение улучшалось.Крик
проводимость
свойство передачи тепла, электричества или звука
«Чугун не теряет температуру так сильно, как более тонкие сковороды с лучшими
, проводимость ”, как у алюминия и нержавеющей стали. New York Times (28 июня 2016 г.)
New York Times (28 июня 2016 г.)
дирижер
руководитель музыкальной группы
Как
дирижер замахал руками, он лепил воздух, как пригоршни мягкой глины, и музыканты внимательно следовали его указаниям.Призрачная будка
вычет
рассуждения от общего к частному
герцогский
, принадлежащие или подходящие для герцога
Верона очаровывает
герцогских итальянских городов: величие и интимность одновременно Форбс (5 апреля 2015 г.)
канал
закрытый канал для жидкости
пластичный
можно придавать форму, изгибать или вытягивать
обучать
дать знания, полученные в процессе обучения и инструктажа
Но после того, как у нее родились двое детей, мама и наш дядя Джим, она стала учителем, потому что никому не доверяла
воспитывают им.Стеклянный Замок
выявлять
выявить или развить, особенно из потенциального состояния
Латинский корень слова «просвещать» — «
educe », что означает« вытянуть то, что находится внутри ученика »Форбс (21 ноября 2012 г. )
)
побуждение
положительное мотивационное влияние
В то время как Северная Америка и Европа несколько лет назад запретили щедрые подарки врачам, финансовые
стимулов остаются обычным явлением во многих частях мира.Reuters (12 июля 2013 г.)
индукция
рассуждения от подробных фактов к общим принципам
Но есть разница между тем, чтобы поверить в это, имея причину — мой
индукция на основе знания фактов и сообщения об этом как о факте. Wall Street Journal (4 января 2017 г.)
представлять
привнесите что-то новое в окружающую среду
Астролябия была
ввел в Европу к одиннадцатому веку, где он широко использовался до эпохи Возрождения.Длина окружности
вступление
акт запуска чего-либо в первый раз
несводимый
невозможно сделать меньше или проще
производить
причина возникновения, возникновения или существования
Хорошая еда должна
дают хороших разговоров, которые я слышал.
продукт
Товар выставлен на продажу
производство
акт или процесс создания чего-либо
Опыт Лоуренса в качестве импресарио большой науки дал ему инстинктивное понимание того, как масштабировать процесс от прототипа до
производство .Большая наука
снижение
акт уменьшения чего-либо
Более высокие темпы экономического роста, чему способствовали периодические дозы либерализации, способствовали распространению бедности
сокращение .The World Is Flat
соблазнять
соблазнить или увести от обязанностей, принципов или надлежащего поведения
«Не будьте
соблазнил ложным гламуром; не уклоняйтесь от своих обязанностей; не блуждай ночью в лесу в одиночестве ».
Алгебра — Комплексные числа
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-7: Комплексные числа
Последняя тема в этом разделе на самом деле не связана с большей частью того, что мы сделали в этой главе, хотя, как мы увидим, она в некоторой степени связана с разделом радикалов.Кроме того, в оставшейся части этого курса материалы здесь не будут так часто понадобиться, но есть пара разделов, в которых они нам понадобятся, поэтому сейчас лучше не мешать.
В разделе радикалов мы отметили, что не получим действительное число из квадратного корня отрицательного числа.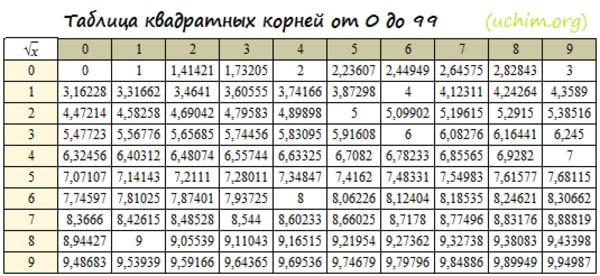 Например, \ (\ sqrt {- 9} \) не является действительным числом, поскольку нет действительного числа, которое мы могли бы возвести в квадрат и получить ОТРИЦАТЕЛЬНЫЙ 9.
Например, \ (\ sqrt {- 9} \) не является действительным числом, поскольку нет действительного числа, которое мы могли бы возвести в квадрат и получить ОТРИЦАТЕЛЬНЫЙ 9.
Теперь мы также увидели, что если \ (a \) и \ (b \) оба положительны, то \ (\ sqrt {ab} = \ sqrt a \, \ sqrt b \).На секунду забудем об этом ограничении и сделаем следующее.
\ [\ sqrt {- 9} = \ sqrt {\ left (9 \ right) \ left ({- 1} \ right)} = \ sqrt 9 \ sqrt {- 1} = 3 \ sqrt {- 1} \]
Итак, \ (\ sqrt {- 1} \) не является действительным числом, но если подумать, мы можем сделать это для любого квадратного корня отрицательного числа. Например,
\ [\ begin {align *} \ sqrt {- 100} & = \ sqrt {100} \ sqrt {- 1} = 10 \ sqrt {- 1} \\ \ sqrt {- 5} & = \ sqrt 5 \, \, \ sqrt {- 1} \\ \ sqrt {- 290} & = \ sqrt {290} \, \, \ sqrt {- 1} \ hspace {0.25 дюймов} и т. Д. \ End {align *} \]
Итак, даже если число не является точным квадратом, мы всегда можем уменьшить квадратный корень отрицательного числа до квадратного корня положительного числа (с которым мы или калькулятор можем справиться), умноженное на \ (\ sqrt { — 1} \).
Итак, если бы у нас был способ иметь дело с \ (\ sqrt {- 1} \), мы могли бы иметь дело с квадратными корнями из отрицательных чисел. Что ж, реальность такова, что на этом уровне просто нет никакого способа справиться с \ (\ sqrt {- 1} \), поэтому вместо того, чтобы иметь дело с ним, мы «заставим его уйти», так сказать, используя следующее определение.2} = — 1}} \]
Об этом будет важно помнить позже. Это показывает, что каким-то образом \ (i \) — единственное «число», которое мы можем возвести в квадрат и получить отрицательное значение.
Используя это определение, все квадратные корни выше становятся,
\ [\ begin {align *} \ sqrt {- 9} & = 3 \, i & \ hspace {0,5 дюйма} \ sqrt {- 100} & = 10 \, i \\ \ sqrt {- 5} & = \ sqrt 5 \, i & \ hspace {0,5 дюйма} \ sqrt {- 290} & = \ sqrt {290} \, i \ end {align *} \]
Это все примеры комплексных чисел .
Здесь, вероятно, возникает естественный вопрос: а почему нас это волнует? Ответ заключается в том, что, как мы увидим в следующей главе, иногда мы сталкиваемся с квадратными корнями из отрицательных чисел, и нам понадобится способ справиться с ними.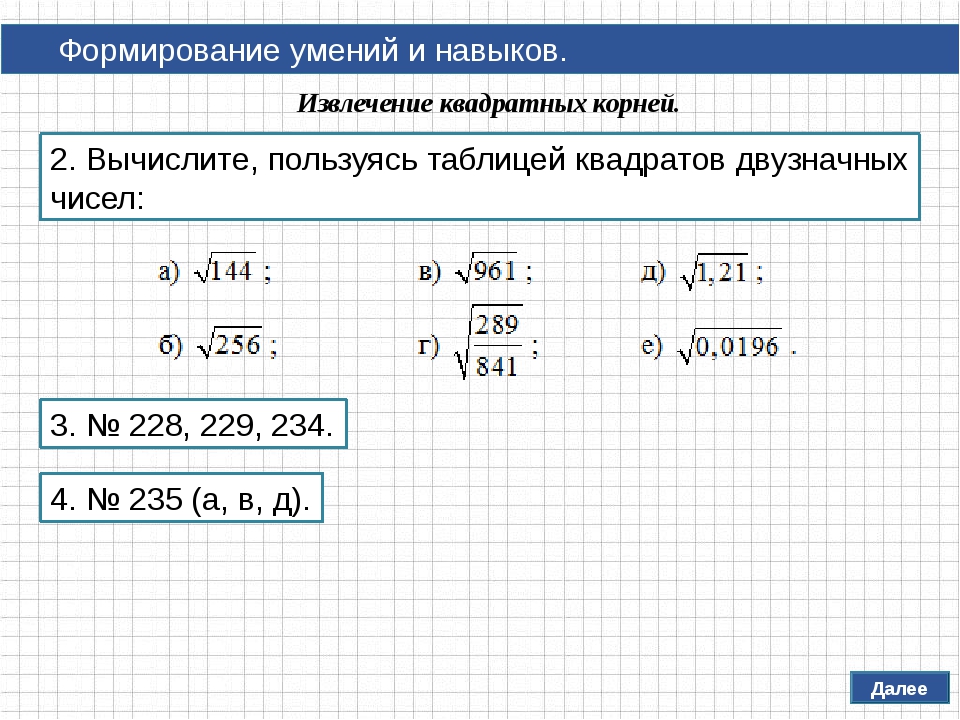 Итак, чтобы разобраться с ними, нам нужно будет обсудить комплексные числа.
Итак, чтобы разобраться с ними, нам нужно будет обсудить комплексные числа.
Итак, давайте начнем с некоторых основных определений и терминологии для комплексных чисел. Стандартная форма комплексного числа —
\ [а + би \]
, где \ (a \) и \ (b \) — действительные числа, и они могут быть любыми, положительными, отрицательными, нулями, целыми числами, дробями, десятичными знаками, это не имеет значения.Когда в стандартной форме \ (a \) называется действительной частью , комплексного числа, а \ (b \) называется мнимой частью, комплексного числа.
Вот несколько примеров комплексных чисел.
\ [3 + 5i \ hspace {0.25in} \, \, \, \, \ sqrt 6 — 10i \, \, \, \, \, \, \, \ frac {4} {5} + i \, \, \, \, \, \, \, 16i \, \, \, \, \, \, \, \, \, 113 \]
Последние два, вероятно, нуждаются в более подробном объяснении. Вполне возможно, что \ (a \) или \ (b \) могут быть равны нулю, и поэтому в 16 \ (i \) действительная часть равна нулю. Когда действительная часть равна нулю, мы часто будем называть комплексное число чисто мнимым числом . В последнем примере (113) мнимая часть равна нулю, и у нас фактически есть действительное число. Итак, размышляя о числах в этом свете, мы можем видеть, что действительные числа — это просто подмножество комплексных чисел.
Когда действительная часть равна нулю, мы часто будем называть комплексное число чисто мнимым числом . В последнем примере (113) мнимая часть равна нулю, и у нас фактически есть действительное число. Итак, размышляя о числах в этом свете, мы можем видеть, что действительные числа — это просто подмножество комплексных чисел.
Сопряжение комплексного числа \ (a + bi \) является комплексным числом \ (a — bi \). Другими словами, это исходное комплексное число с измененным знаком мнимой части.Вот несколько примеров комплексных чисел и их сопряженных.
\ [\ begin {array} {* {20} {c}} {{\ mbox {комплексное число}}} & {\ hspace {0,25in} {\ mbox {conugate}}} \\ {3 + \ frac { 1} {2} i} & {\ hspace {0,25 дюйма} 3 — \ frac {1} {2} i} \\ {12 — 5i} & {\ hspace {0,25 дюйма} 12 + 5i} \\ {1 — i} & {\ hspace {0,25 дюйма} 1 + i} \\ {45i} & {\ hspace {0,25 дюйма} — 45i} \\ {101} & {\ hspace {0,25 дюйма} 101} \ end {массив } \ hspace {0,25 дюйма} \]
Обратите внимание, что сопряжение действительного числа — это само себя без изменений.
Теперь нам нужно обсудить основные операции с комплексными числами. Начнем со сложения и вычитания. Самый простой способ думать о сложении и / или вычитании комплексных чисел — это думать о каждом комплексном числе как о многочлене и выполнять сложение и вычитание так же, как мы складываем или вычитаем многочлены.
Пример 1 Выполните указанную операцию и запишите ответы в стандартной форме.
- \ (\ left ({- 4 + 7i} \ right) + \ left ({5 — 10i} \ right) \)
- \ (\ left ({4 + 12i} \ right) — \ left ({3 — 15i} \ right) \)
- \ (5i — \ left ({- 9 + i} \ right) \)
Показать решение
Здесь действительно особо нечего делать, кроме как прибавлять или вычитать.Обратите внимание, что круглые скобки в первых числах служат только для обозначения того, что мы думаем об этом термине как о комплексном числе и в целом не используются.
a \ (\ left ({- 4 + 7i} \ right) + \ left ({5 — 10i} \ right) = 1 — 3i \)
b \ (\ left ({4 + 12i} \ right) — \ left ({3 — 15i} \ right) = 4 + 12i — 3 + 15i = 1 + 27i \)
c \ (5i — \ left ({- 9 + i} \ right) = 5i + 9 — i = 9 + 4i \)
Теперь давайте посмотрим на умножение. Опять же, с одним небольшим отличием, вероятно, проще всего думать о комплексных числах как о многочленах, поэтому перемножайте их, как о многочленах. Единственное отличие проявится на последнем этапе, как мы увидим.
Опять же, с одним небольшим отличием, вероятно, проще всего думать о комплексных числах как о многочленах, поэтому перемножайте их, как о многочленах. Единственное отличие проявится на последнем этапе, как мы увидим.
Пример 2 Умножьте каждый из следующих пунктов и запишите ответы в стандартной форме.
- \ (7i \ left ({- 5 + 2i} \ right) \)
- \ (\ left ({1 — 5i} \ right) \ left ({- 9 + 2i} \ right) \)
- \ (\ left ({4 + i} \ right) \ left ({2 + 3i} \ right) \)
- \ (\ left ({1 — 8i} \ right) \ left ({1 + 8i} \ right) \)
Показать все решения Скрыть все решения
a \ (7i \ left ({- 5 + 2i} \ right) \) Показать решение
Итак, все, что нам нужно сделать, это распределить 7 \ (i \) через круглые скобки.2}}} \]
Теперь мы дали эту формулу с комментарием, что она будет удобна, когда дело доходит до деления комплексных чисел, поэтому давайте рассмотрим пару примеров.
Пример 3 Запишите каждое из следующих утверждений в стандартной форме.
- \ (\ displaystyle \ frac {{3 — i}} {{2 + 7i}} \)
- \ (\ displaystyle \ frac {3} {{9 — i}} \)
- \ (\ displaystyle \ frac {{8i}} {{1 + 2i}} \)
- \ (\ displaystyle \ frac {{6–9i}} {{2i}} \)
Показать все решения Скрыть все решения
Показать обсуждение
Итак, в каждом случае мы действительно смотрим на деление двух комплексных чисел.Однако основная идея здесь заключается в том, что мы хотим записать их в стандартной форме. Стандартная форма не позволяет использовать \ (i \) в знаменателе. Итак, нам нужно вывести \ (i \) из знаменателя.
На самом деле это довольно просто, если вспомнить, что комплексное число, умноженное на его сопряжение, является действительным числом. Итак, если мы умножим числитель и знаменатель на сопряжение знаменателя, мы сможем исключить \ (i \) из знаменателя.
Теперь, когда мы выяснили, как это сделать, давайте продолжим и решим проблемы.2}}} = \ frac {{16 + 8i}} {5} = \ frac {{16}} {5} + \ frac {8} {5} i \]
d \ (\ displaystyle \ frac {{6 — 9i}} {{2i}} \) Показать решение
Это немного отличается от предыдущих, так как знаменатель — чисто мнимое число. Это можно сделать так же, как и предыдущие, но есть более простой способ решить проблему.
Сначала разделите дробь следующим образом.
\ [\ frac {{6 — 9i}} {{2i}} = \ frac {6} {{2i}} — \ frac {{9i}} {{2i}} = \ frac {3} {i} — \ frac {9} {2} \]
Теперь мы хотим, чтобы \ (i \) вне знаменателя, и, поскольку в знаменателе первого члена стоит только \ (i \), мы просто умножим числитель и знаменатель первого члена на \ (i \).8} & = 1 \ конец {выравнивание *} \]
Вы видите узор? Все степени if \ (i \) могут быть уменьшены до одного из четырех возможных ответов, и они повторяются каждые четыре степени. Об этом удобно помнить.
Об этом удобно помнить.
Теперь нам нужно решить проблему с квадратными корнями из отрицательных чисел. Из раздела о радикалах мы знаем, что можем сделать следующее.
\ [6 = \ sqrt {36} = \ sqrt {\ left (4 \ right) \ left (9 \ right)} = \ sqrt 4 \, \ sqrt 9 = \ left (2 \ right) \ left (3 \ справа) = 6 \]
Другими словами, мы можем разбить произведение квадратного корня на произведение квадратного корня, если оба числа положительны.
Оказывается, мы действительно можем сделать то же самое, если одно из чисел отрицательное. Например,
\ [6i = \ sqrt {- 36} = \ sqrt {\ left ({- 4} \ right) \ left (9 \ right)} = \ sqrt {- 4} \, \ sqrt 9 = \ left ({2i } \ right) \ left (3 \ right) = 6i \]
Однако, если ОБА числа отрицательны, это больше не будет работать, как показано ниже.
\ [6 = \ sqrt {36} = \ sqrt {\ left ({- 4} \ right) \ left ({- 9} \ right)} \ ne \ sqrt {- 4} \, \ sqrt {- 9} = \ left ({2i} \ right) \ left ({3i} \ right) = 6 {i ^ 2} = — 6 \]
Мы можем резюмировать это как набор правил. Если \ (a \) и \ (b \) оба положительные числа, тогда
Если \ (a \) и \ (b \) оба положительные числа, тогда
\ [\ begin {align *} \ sqrt a \, \ sqrt b & = \ sqrt {ab} \\ \ sqrt {- a} \, \ sqrt b & = \ sqrt {- ab} \\ \ sqrt a \ , \ sqrt {- b} & = \ sqrt {- ab} \\ & \\ \ sqrt {- a} \, \ sqrt {- b} & \ ne \ sqrt {\ left ({- a} \ right) \ left ({- b} \ right)} \ end {align *} \]
Почему это настолько важно, чтобы беспокоиться? Рассмотрим следующий пример.
Пример 4 Умножьте следующее и напишите ответ в стандартной форме.\ [\ left ({2 — \ sqrt {- 100}} \ right) \ left ({1 + \ sqrt {- 36}} \ right) \]
Показать решение
Если бы мы умножили это в его нынешнем виде, мы получили бы,
\ [\ left ({2 — \ sqrt {- 100}} \ right) \ left ({1 + \ sqrt {- 36}} \ right) = 2 + 2 \ sqrt {- 36} — \ sqrt {- 100 } — \ sqrt {- 36} \, \ sqrt {- 100} \]
Так вот, если бы мы не были осторожны, мы, вероятно, объединили бы два корня в последнем члене в один, что невозможно!
Итак, есть общее практическое правило работы с квадратными корнями из отрицательных чисел. 2} = 62 + 2i \]
2} = 62 + 2i \]
Эмпирическое правило, приведенное в предыдущем примере, достаточно важно, чтобы его повторить. Когда вы сталкиваетесь с квадратными корнями из отрицательных чисел, первое, что вам нужно сделать, это преобразовать их в комплексные числа.
Есть еще одна последняя тема, которую мы должны затронуть перед тем, как покинуть этот раздел. Как мы уже отмечали в разделе о радикалах, хотя \ (\ sqrt 9 = 3 \) на самом деле есть два числа, которые мы можем возвести в квадрат, чтобы получить 9. Мы можем возвести в квадрат и 3, и -3.2} = — 9 \]
и поэтому, если возвести в квадрат -3 \ (i \), мы также получим -9. Итак, извлекая квадратный корень из отрицательного числа, мы можем возвести в квадрат два числа, чтобы получить число под корнем. Однако мы ВСЕГДА будем принимать положительное число за значение квадратного корня, как мы это делаем с квадратным корнем из положительных чисел.
Как определить первопричину
Введение
Прежде чем мы перейдем к теме, позвольте мне рассказать небольшой рассказ.
Однажды, когда я был холостяком в новом городе, я пошел к врачу. У меня была высокая температура, и последние пару дней я чувствовал себя плохо. Осмотрев меня, он пришел к выводу, что это малярия. Он прописал мне лекарства и лечил меня. Через пару дней я снова встал на ноги и приступил к работе.
Я не очень часто болею и обычно хорошо о себе забочусь. Несмотря на это, он вернулся через месяц. Врач снова дал мне лекарства и вылечил.Когда мне стало лучше, я попросил совета, как остановить рецидив болезни. Ответ, который он дал, был прост — не допускайте попадания комаров в окружающую среду.
Вы могли бы подумать — это действительно просто, почему я не понял этого раньше. Что ж, бывает во многих ситуациях!
Я искал лекарство от симптомов раньше. Чтобы положить конец рецидиву, мне пришлось определить и устранить причину.
Для устранения или решения проблемы обязательно зайти в корень того же.Перейдите к «Первопричине» и устраните проблему.
Что такое анализ первопричин (RCA)?
Позвольте мне продолжить вышеупомянутую историю и связанную с ней аналогию.
Первопричиной проблемы в этой истории было нездоровое окружение возле моего дома. Как только я поддерживаю чистоту вокруг, я уничтожаю комаров. Я останавливаю или уменьшаю рецидив болезни.
Анализ первопричин — это способ найти основную причину проблемы.
Устраните основную причину проблемы, чтобы устранить или уменьшить вероятность повторения проблемы.Вот где полезны концепция анализа первопричин и связанные с ними инструменты.
Почему анализ первопричин?
Сегодняшняя быстро меняющаяся среда вынуждает организации постоянно вводить новшества. Внедряйте инновации как в продукты, так и в предложения услуг.
Пример
— ведущая организация, владеющая сетью пиццерий. Растет стабильными темпами, а также расширяется географический охват. Их забота — даже постоянные покупатели жалуются на качество их продукта.
Провели обзор проблемы. Им необходимо увеличить насыщенность начинки, используемой в их популярных предложениях для пиццы.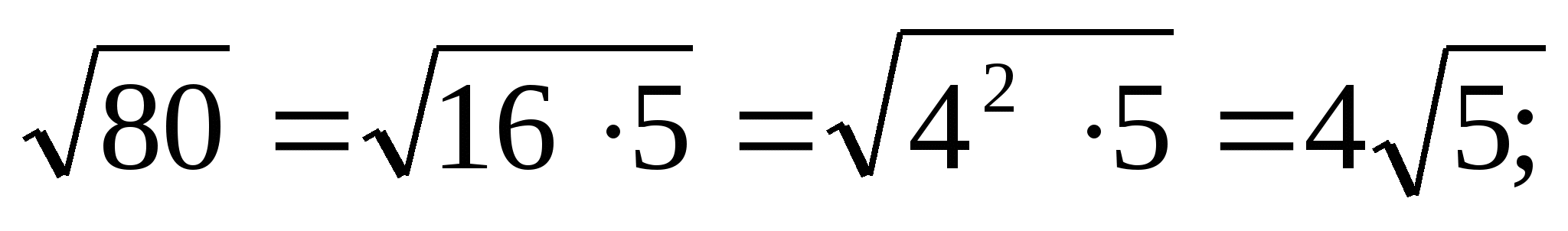 Я один из их постоянных клиентов. Побывав недавно в одной из их торговых точек, я удивился внешнему виду и вкусу обновленного продукта. Понравилось ли мне и моей семье новое предложение — держите пари!
Я один из их постоянных клиентов. Побывав недавно в одной из их торговых точек, я удивился внешнему виду и вкусу обновленного продукта. Понравилось ли мне и моей семье новое предложение — держите пари!
Недостаточно просто рассматривать проблемы и связанные с ними причины на высоком уровне. Копать, чтобы определить основную причину — тяжелая работа, но она необходима! Особенно для организаций, которые стремятся постоянно совершенствоваться.
Как провести анализ первопричин?
Существуют различные инструменты для проведения анализа первопричин; Подробнее об этом мы поговорим позже в этой статье.
Этапы анализа основной причины —
Определите проблему
Убедитесь, что вы определили проблему и согласовали с потребностями клиента
Если не существует, предвидеть проблему с точки зрения клиента
Какие конкретные проблемы вы наблюдаете
Что произойдет, если вы не решите проблему сейчас — каково влияние на бизнес
Сбор данных, относящихся к проблеме
Есть ли данные, подтверждающие конкретную проблему?
По возможности поговорите с клиентами или сотрудниками, узнайте их голос
Это повторяющаяся проблема, как часто в прошлом
Каково измеримое влияние проблемы на результаты ключевых клиентов
Определите причину проблемы
Определите основную причину
Каков фактор или их комбинация, приводящие к этому
Определите как можно больше причин, не думайте о решениях на этом этапе
Привлекайте свои команды и соответствующие заинтересованные стороны
Используйте анализ 5Y или Fishbone, подробнее об этом позже
Определите приоритетность причин
Не беритесь сразу, отдавайте предпочтение
- Матрица
PICK — хороший инструмент для достижения этой цели.
Помните о влиянии и усилиях, отдавая приоритет
Технологии могут стать ключевым отличием на данном этапе
Определите решения основной проблемы и внесите изменения
Главное внимание уделяется устранению проблемы, чтобы она больше не повторялась
Кто будет реализовывать изменения и когда
Кто отвечает за мониторинг и контроль нового процесса
Каков метод и периодичность представления отчетности
Монитор и сустейн
Недостаточно определить решение, ключ к успеху — исполнение
Встраивать новый процесс в существующие бизнес-процессы
Обеспечение мониторинга и поддержки воздействия улучшений
Приведенный выше процесс определяет на упрощенном уровне, как решение первопричин вписывается в культуру операционного превосходства.Приложение может отличаться в зависимости от критичности проблемы.
Методы анализа первопричин
Анализ первопричин — это простой метод, выполняемый с целью понять причину проблемы.
Используется несколько популярных инструментов. Давайте разберемся с каждым из них.
1. 5 Почему анализ
Очень просто описанный, этот метод заключается в том, чтобы спросить «Почему?» пять раз и более. Цель состоит в том, чтобы найти первопричину проблемы.
Рисунок 1
Источник изображения — http://www.educational-business-articles.com/5-whys/
Простая проблема превышения скорости решает заменой будильника. Или более дисциплинированно относиться к замене батареек.
А теперь замените это в бизнес-сценарии ресторана на вынос.
Задержка с доставкой еды может быть связана с пробками на дорогах. Основной причиной может быть неисправный прибор на кухне.
В любом случае этот инструмент важен, поскольку он фокусируется на основной причине проблемы. Он стремится устранить то же самое, чтобы проблема больше не повторялась.
2. Диаграмма Fishbone или Ishikawa
Диаграмма
Исикава названа в честь доктора Каору Исикава. Доктор Исикава разработал простой метод отображения причин проблемы. Эта диаграмма стала известна как диаграмма Исикавы, или «Рыбья кость», или «Причинно-следственная диаграмма».
Шаги для изображения причины и следствия на диаграмме Fishbone:
Определите свою проблему
Обсудите с командой возможные причины проблемы
Используйте при этом 6 Ms
Человек — люди, выполняющие процесс или участвующие в процессе
Станки — оборудование и инструменты, используемые в процессе
Метод — соблюдаемые процедуры
Материал — входные данные, необходимые в процессе
Измерение — данные о вводе или спецификации продукта
Мать-природа — среда, в которой работают люди и машины
Классифицируйте все причины в соответствии с 6M.
Окончательное изображение будет выглядеть, как на рисунке ниже.Как вы можете видеть на рисунке 2, он выглядит как Fishbone, и поэтому его название.
Рисунок 2Источник изображения — https://goleansixsigma.com/achieve-a-19-improvement-in-response-time-using-a-cause-and-effect-diagram/
Назначьте приоритет базовым данным и групповому обзору. На приведенной выше диаграмме команда считает, что выделенные причины являются основными способствующими факторами.
Проведите мозговой штурм по приоритетным причинам и внедрите
«Рыбья кость» или «Диаграмма причинно-следственных связей» — эффективный инструмент.Он представляет все возможные причины и побуждает команду думать с точки зрения 6М.
Есть и другие варианты 6M.
Некоторые компании-производители используют 4M (Человек, Машина, Материал, Метод). В то время как некоторые сервисные компании используют 8P (Вещественные доказательства, люди, место, услуги, цена, продвижение, процесс, производительность и качество).
3. Анализ Парето
Анализ Парето основан на принципе, что «80% последствий происходят от 20% причин».Другими словами, «20% работы создают 80% результата». Это также называется правилом «80/20».
Посмотрите на это с любой точки зрения — основное внимание уделяется «немногим жизненно важным», а не «банальному множеству».
Любая проблема, которую мы начнем рассматривать, может привести к очевидным причинам. Наша энергия должна быть сосредоточена на «немногих жизненно важных», будь то с точки зрения решения проблем или доставки.
Консультант по менеджменту Джозеф М. Джуран предложил принцип.Он назвал его в честь итальянского экономиста Вильфредо Парето. Находясь в Лозаннском университете, Парето отметил связь 80/20. Он показал, что 80% земли в Италии принадлежит 20% населения.
Шаги для проведения анализа Парето:
Определите категории или классификации причин
Сбор данных из исторических источников или сбор данных через журналы
Назначьте период времени, для которого данные относятся или должны быть собраны
Рассчитайте количество появлений или наблюдений для каждой из категорий
Преобразование чисел в проценты от общего числа
Сортировка данных по числам, от наибольшего к наименьшему
Вычислить совокупные проценты
Нарисуйте график с помощью Minitab или Microsoft Excel
Давайте возьмем пример процесса взыскания страховых премий.Проблема заключается в большом количестве запросов, отправленных клиентами по выставленным счетам. Воздействие отложено на сбор премий.
Таблица данных выглядит следующим образом —
ABC Insurance — Сборы премий | |||
Количество обращений клиентов по категориям | |||
Период — январь ’17 — декабрь ’17 | |||
Категория | Номер | % возраст | Совокупный возраст,% |
Недостаточно доказательств резервного копирования | 115 | 33% | 33% |
Несовпадение налоговых расчетов | 101 | 29% | 62% |
Неполная документация | 80 | 23% | 85% |
Несовпадение комиссии | 40 | 11% | 96% |
Прочие | 14 | 4% | 100% |
| 350 |
|
|
Диаграмма Парето, отображаемая на графике (с использованием Excel), выглядит, как на рисунке 3.
Рисунок 3
Согласно диаграмме Парето на Рисунке 3, 85% причин задержки сбора премий из-за запросов —
Недостаточно доказательств резервного копирования
Несовпадение налоговых расчетов
Неполная документация
Как команда, основное внимание будет уделяться устранению или сокращению этих запросов, тем самым положительно влияя на коллекции.
4. Мозговой штурм
Как инструмент RCA, это один из самых простых для понимания; труднее всего применить.
Мозговой штурм собирает всех заинтересованных членов команды в комнату. Цель — понять возможные причины проблемы. Сосредоточьтесь на решениях только после выявления основных причин.
Этапы процесса —
Начинает чемпион с участием руководителя процесса, проектной группы, малых и средних предприятий и группы «Шесть сигм»
Просмотрите определенную проблему
Найдите все возможные причины проблемы — раздайте плакаты участникам и запросите отдельные мнения (без обсуждений)
Используйте 6M для стимуляции возможных причин
Классифицирует причины с помощью диаграммы сходства (рисунок 4)
Определите приоритеты причин, обсудите и составьте краткий список возможных решений посредством голосования и группового консенсуса
Обзор решений Champion для бай-ина, включенных в окончательный список, с указанием следующих шагов для последующего исследования
Список дальнейших действий, распространен протокол собрания
Мозговой штурм может дать эффективные результаты.В последнее время мозгописание также превратилось в инструмент.
Это обновленная версия мозгового штурма. Первоначально основное внимание уделяется индивидуальным точкам зрения (как на стадии причинно-следственной связи, так и на стадии решения).
Рисунок 4
В двух словах
«Шесть сигм» обычно воспринимают как технически сложное пространство. Реальность такова: упрощенные инструменты, такие как анализ первопричин, эффективно вписываются в культуру операционного превосходства. Это подход к решению проблем, основанный на здравом смысле.
Надеюсь, вам понравилась эта статья. Обратная связь через ссылку на дискуссионный форум. Дайте мне знать, если вам понадобится дополнительная информация по любой из концепций, прокомментировав здесь.
Откройте для себя больше инструментов для повышения эффективности — пройдите сертификацию прямо сейчас!
Кладограмм | BioNinja
Навык:
• Анализ кладограмм для установления эволюционных взаимосвязей
Все построенные кладограммы обычно имеют определенные ключевые особенности:
- Корень — начальный предок, общий для всех организмов в пределах кладограммы (входящая линия показывает, что он происходит из более крупной клады)
- Узлы — Каждый узел соответствует гипотетический общий предок, который, по определению, дал начало двум (или более) дочерним таксонам
- Внешняя группа — наиболее отдаленно родственный вид на кладограмме, который функционирует как точка сравнения и контрольная группа
- Clades — Общий предок и все его потомки (т.е. узла и всех связанных с ним ветвей)
Основные характеристики кладограммы
Построение кладограмм
Кладограммы могут быть построены на основе сравнения морфологических (структурных) признаков или молекулярных свидетельств
- Исторически структурные особенности использовались для построения кладограмм, но теперь чаще используются молекулярные свидетельства
1. Использование структурных доказательств
Шаг 1: Организовать выбранные организмы в соответствии с определенными характеристиками
- Использовать характеристики, которые фиксируются в процессе развития (т. Е. Врожденные) и не подвержены влиянию окружающей среды
Шаг 2: Последовательный порядок организмов в соответствии с общими характеристиками для построения кладограммы
- Группирование организмов может быть облегчено путем построения диаграммы Венна до разработки кладограммы
- Каждая характеристика будет представлена узлом, с более общим характеристики, представляющие более ранние узлы
- Вид с наименьшим количеством общих характеристик будет представлять внешнюю группу (устанавливает базовые свойства)
2. Использование молекулярных доказательств
Шаг 1: Выберите ген или белок, общий для ряда выбранных организмов
- Примеры молекул, которые повсеместно встречаются у многих животных, включают гемоглобин и цитохром c
Шаг 2 : Скопируйте молекулярную последовательность (ДНК или аминокислоту) для каждого из выбранных организмов
- Используйте онлайн-базы данных, такие как Genbank или Ensembl, для идентификации соответствующих последовательностей ДНК или аминокислот
- Последовательности можно сопоставить в документе Word, а затем сохранить как документ в текстовом формате (.txt)
- Перед каждой последовательностью укажите название вида, которому предшествует стрелка вперед (например, «> Человек» или «> Шимпанзе»)
Шаг 3: Выполните множественное выравнивание для сравнения молекулярных последовательностей (ДНК или амино acid)
- Программное обеспечение для множественного выравнивания сравнивает последовательности ДНК или белков на предмет сходства и различий
- Ожидается, что близкородственные виды будут иметь более высокую степень сходства в их молекулярной последовательности
- Clustal Omega — это бесплатный онлайн-инструмент, который сравнивает несколько ДНК или аминокислотные последовательности для сравнения
Шаг 4: Создайте филогенетическое дерево (кладограмму) из данных множественного выравнивания
- Clustal Omega может генерировать разветвленные филограммы после завершения выравнивания последовательностей (выберите «Филогенетическое дерево»)
- ниже представляет собой простой текстовый файл, который можно загрузить для сравнения аминокислотных последовательностей разных видов:
- HBA — H Альфа-цепь гемоглобина (аминокислотная последовательность) разных видов
Множественное выравнивание последовательности белка разных видов
.
