Способ сложения способ подстановки и: Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Решение СЛАУ методами подстановки и сложения

Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

Например, уравнение

—

линейное, а уравнения

и

не являются линейными.

В общем виде система m линейных уравнений с n переменными записывается так:

. (1)

Числа

называются коэффициентами при переменных, а
—
свободными членами.

Совокупность чисел

называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений
с двумя переменными и два метода их решения — метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе
высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера —
основан на использовании определителей).

Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.

Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают
одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению
с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.

Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.

Пример 1. Решить систему линейных уравнений методом подстановки:

Выразим из первого уравнения
данной системы y через x (можно и наоборот) и получим:

Подставив во второе уравнение данной системы вместо y выражение , получим систему

Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную.
Решим это уравнение:

Соответствующее значение y найдём, подставив вместо x число -5 в выражение
, откуда

Пара (-5; 2) является решением системы линейных уравнений.

Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.

Пример 2. Решить систему линейных уравнений методом подстановки:

Из третьего уравнения системы выразим :

Подставим это выражение во второе уравнение данной системы:

Произведём преобразования и выразим из этого уравнения :

Полученные выражения для и подставим в первое уравнение системы и получим

Вместо можно вновь подставить его выражение, тогда получим
уравнение с одним неизвестным:

откуда

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

Пример 3. Решить систему линейных уравнений методом подстановки:

Из первого уравнения системы выразим :

Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:

Из третьего уравнения выразим :

Полученное выражение для подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:

Произведём преобразования и найдём :

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём
одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной
(равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.

Пример 4. Решить систему линейных уравнений методом сложения:

Решение. В уравнениях данной системы в этом примере системы коэффициенты при y — противоположные числа.
Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:

, или , .

Заменим одно из уравнений исходной системы, например, первое, уравнением . Получим систему

Решим полученную систему. Подставив значение
в уравнение , получим уравнение с одной переменной y:

Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением
исходной системы, так как эти две системы линейных уравнений равносильны.

Пример 5. Решить систему линейных уравнений методом сложения

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3,
а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:

Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной:
. Из этого уравнения находим, что . Получили

Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).

Пример 6. Решить систему линейных уравнений методом сложения:

Решение. Для упрощения решения произведём замену переменных:

, .

Приходим к системе линейных уравнений:

или

Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим
,
. Тогда .

Следовательно, имеем систему уравнений

или

Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим

Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования,
необходимые для решениях систем линейных уравнений в курсе высшей математики.

Продолжение темы «Системы уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

Системы уравнений. Способы решения систем уравнений

Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:

	x — 4y = 2
	3x — 2y = 16

Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.

Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.

Способ подстановки

Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.

Рассмотрим решение системы уравнений:

	x — 4y = 2
	3x — 2y = 16

Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:

x — 4y = 2;

x = 2 + 4y.

Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:

3x	— 2y = 16;
3(2 + 4y)	— 2y = 16.

Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.

3(2 + 4y) — 2y = 16;

6 + 12y — 2y = 16;

6 + 10y = 16;

10y = 16 — 6;

10y = 10;

y = 10 : 10;

y = 1.

Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:

x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.

Ответ: x = 6, y = 1.

Способ сравнения

Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу.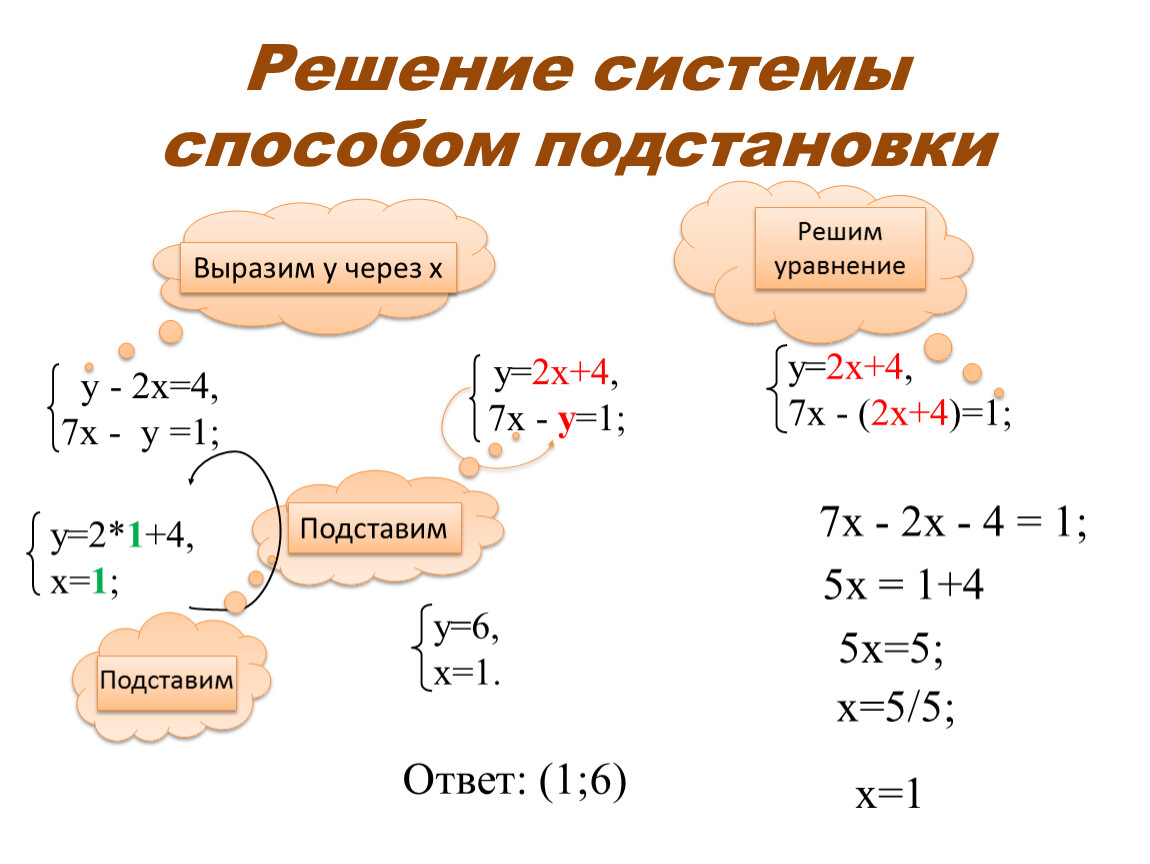 Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.

Например, для решение системы:

	x — 4y = 2
	3x — 2y = 16

найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):

x — 4y = 2	3x — 2y = 16
-4y = 2 — x	-2y = 16 — 3x
y = (2 — x) : — 4	y = (16 — 3x) : -2

Составляем из полученных выражений уравнение:

Решаем уравнение, чтобы узнать значение x:

2 — x	· (-4) =	16 — 3x	· (-4)
-4		-2

2 — x = 32 — 6x

—x + 6x = 32 — 2

5x = 30

x = 30 : 5

x = 6

Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:

x — 4y = 2	3x — 2y = 16
6 — 4y = 2	3 · 6 — 2y = 16
-4y = 2 — 6	-2y = 16 — 18
-4y = -4	-2y = -2
y = 1	y = 1

Ответ: x = 6, y = 1.

Способ сложения или вычитания

Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.

Рассмотрим систему:

	x — 4y = 2
	3x — 2y = 16

Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:

(3x — 2y) · -2 = 16 · -2

-6x + 4y = -32

Получим:

	x — 4y = 2
	-6x + 4y = -32

Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:

+	x — 4y = 2
+	-6x + 4y = -32
	-5x = -30

Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.

Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.

Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:

(x — 4y) · 3 = 2 · 3

3x — 12y = 6

Получим:

	3x — 12y = 6
	3x — 2y = 16

Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:

—	3x — 12y = 6
—	3x — 2y = 16
	-10y = -10

Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:

3x — 2y = 16

3x — 2 · 1 = 16

3x — 2 = 16

3x = 16 + 2

3x = 18

x = 18 : 3

x = 6

Ответ: x = 6, y = 1.

Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:

Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.

Решение системы линейных уравнений с двумя переменными способом сложения и способом

Метелик летів на луг, 10 бджіл летіло на луг ,а ще 5 ос летіли на луг і кожна оса їла пилок .Скільки комах летіло на луг.

17. На базаре продаются рыбки, большие и маленькие. Сегодня три
больших и одна маленькая стоят вместе столько же, сколько пять
больших вчера. А две бо
…

льшие и одна маленькая сегодня стоят вместе
столько же, сколько три больших и одна маленькая вчера. Можно ли
по этим данным выяснить, что дороже одна большая и две маленьких
сегодня, или пять маленьких вчера?
68, в классе учится меньше 50 школьников. За контрольную работу
седьмая часть учеников получила пятёрки, третья — четверки, половина
— тройки. Остальные работы были оценены как
неудовлетворительные. Сколько было таких работ?
P.S. Ребят можете ответить сразу на два, а можете на один

В птичком дворе находиться: гусей-3471,кур-5981,индюков-1679,уток-7398.завезли 2139 цисарки.Забили уток 2139,кур 3788,гусей 1843, индюков 782,цисарок
…

1893.Сколько птиц до за воза,после завоза,после забоя.На сколько птиц меньше каждого вида после забоя?

Артемон подарил Мальвине букет из аленьких цветочков и чёрных роз.
У каждой чёрной розы 4 пестика и 4 тычинки, а на стебле два листка. У
каждого алень
…

кого цветочка 8 пестиков и 10 тычинок, а на стебле три
листка. Листков в букете на 108 меньше, чем пестиков. Сколько
Тычинок в букете?

B трёх мешках лежат сникерсы. В первом мешке на 6 кг сникерсов
меньше, чем в двух других вместе. А во втором – на 10 кг меньше, чем
в двух других вмес
…

те. Сколько орехов в третьем мешке, если каждый
сникерс весит 50 г, а в каждом сникерсе 16 орехов?

Саше хочется купить семь разных книг. Книги стоят одинаково, а денег хватает
только на три книги. Сколькими способами Саша может выбрать три книги из
…

семи?

В птичком зборе находилось : 3471
кур-5981,индюков 1679, уток 7398 завезли 2152 цисарки.
забили уток 2139 кур3788
гусей 1843,индюков 782 цисарки 1893
…

.
сколько птиц было до за воза после завоза после збоя.
на сколько птиц стало меньше каждого из вида после забоя?

1) Начертите в тетради окружности с разными радиусами. 2) Начертите два радиуса окружности и назовите их. 3) Начертите три диаметра окружности и назов
…

ите их. 4) Начертите две хорды окружности и назовите их.

Решите уравнение: 784 : (x – 8) = 8 ∙ 8 – 8.

Решение систем уравнений: способ сложения + примеры

Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:

{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2

Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 – некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.

Алгоритм решения способом сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

5. Сделать проверку решения.

Пример решения способом сложения

Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:

{3*x + 2*y = 10;
{5*x + 3*y = 12;

Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.

{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2

Получим следующую систему уравнений:

{9*x+6*y = 30;
{10*x+6*y=24;

Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.

10*x+6*y – (9*x+6*y) = 24-30; x=-6;

Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.

{3*(-6) + 2*y =10;
{2*y=28; y =14;

Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.

{3*x + 2*y = 10;
{5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Как видите, получились два верных равенства, следовательно, мы нашли верное решение.

Ответ: (6, 14)

Нужна помощь в учебе?

Предыдущая тема: Решение систем уравнений: способ подстановки + примеры
Следующая тема:&nbsp&nbsp&nbspРешение задач с помощью систем уравнений: общая схема решения

Урок алгебры по теме: «Решение систем линейных уравнений способом сложения» (7 класс)

ПЛАН-КОНСПЕКТ УРОКА 1.

ФИО

ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет

Подробнее

Тема: «Сложение дробей с одинаковыми

Урок по математике. 4 класс. Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.

Подробнее

действия деятельности

Технологическая карта урока Предмет алгебра Класс 9 Автор УМК Алгебра 9 класс. Учебник для учащихся общеобразовательных учреждений / С.М.Никольский, М.Н. Потапов, Н.Н.Решетников, А.В. Шевкин Москва «Просвещение»

Подробнее

МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ

МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ Развёрнутый план урока по теме «Замена двузначного числа суммой разрядных слагаемых» ТЕМА: «Замена двузначного числа суммой разрядных слагаемых» (ч. 1: с. 15) ЦЕЛЕВЫЕ УСТАНОВКИ:

Подробнее

Конспект урока, 7 класс.

Конспект урока алгебры в 7 классе. Взаимное расположение графиков линейных функций Автор: Дмитриева Наталья Анатольевна, Московская область, город Подольск, МОУ «Лицей 26». Описание материала: Предлагаю

Подробнее

Технологическая карта урока

Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение

Подробнее

Сложение и вычитание смешанных чисел

Предмет: Математика Класс: 5 «Б» класс Сложение и вычитание смешанных чисел Учебник: Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А. Г. Мерзляк, В.Б. Полонский, М.С. Якир.

Подробнее

Урок математики в 3 «б» классе

Урок математики в 3 «б» классе Тема: Переменная. Запись выражений и предложений с помощью переменной Цели: 1. Дать понятие о переменной, как букве, обозначающей меняющиеся (переменные) значения элементов

Подробнее

y 12 = 2y 7,5 y 2y = 12 7,5 -y = 4,5 y = — 4,5

Муниципальное бюджетное общеобразовательное учреждениесредняя общеобразовательная школа 7г. Белгорода Разработка урока по теме «Решение уравнений» (6 класс) Подготовила учитель математики Гриценко Т.Г.

Подробнее

Занятие 1 (2 часа) Ход занятия.

Тема Целая и дробная части числа Занятие 1 ( часа) Цель занятия Дидактическая Познакомить учащихся с целой и дробной частью числа Установить их свойства и соотношения между ними Научить строить простейшие

Подробнее

«Числовые и буквенные выражения».

Муниципальное казѐнное общеобразовательное учреждение «Дуровская средняя общеобразовательная школа» Сафоновского района Смоленской области «Числовые и буквенные выражения». Учитель математики I категории

Подробнее

Тема урока: Системы счисления

Тема урока: Системы счисления Цели занятия: Дидактическая: познакомить правилами выполнения арифметических операций (сложение, умножение, вычитание) в двоичной системе счисления. Развивающая: развитие

Подробнее

Технологическая карта урока

Технологическая карта урока Учитель: Марахина Ольга Анатольевна Предмет: алгебра 7 класс УМК: А.Г. Мордкович, Алгебра 7 класс Тема урока: Взаимное расположение графиков линейных функций Тип урока: изучение

Подробнее

Оборудование: проектор, ноутбуки, рабочие листы, тетради, учебники, раздаточный материал

Достаточно часто в школах мы встречаем ситуацию, когда учитель прекрасно объясняет материал, учащиеся его внимательно слушают, но через несколько минут, выходя из кабинета, забывают, о чем шла речь на

Подробнее

Комментарий пояснение.

методическая разработка урока с использованием ИКТ Учебный предмет алгебра Тема урока Линейная функция 7 класс Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 10 г. Сочи

Подробнее

Конспект урока по алгебре «Решение систем уравнения способом подстановки и алгебраического сложения» 7 класс

Конспект коррекционно-развивающего урока алгебры в 7 классе.

Тип урока: закрепление знаний и умений.

Базовый учебник: Ш. А. Алимов Алгебра 7 класс.

Класс: коррекционный класс VII вида (12 обучающихся).

Тема урока: Решение систем уравнения способом подстановки и алгебраического сложения.

Цель урока: создание условий для обобщения знаний и закрепления навыков решения систем уравнений.

Задачи урока:

Образовательная – повторить алгоритм решения систем линейных уравнений методом подстановки и алгебраического сложения; закрепить умение решать системы линейных уравнений изученными способами.
Развивающая – продолжить развивать грамотность математического письма, внимание, память, логическое мышление, умение слушать и способность к рефлексии собственной деятельности.
Воспитательная – воспитывать умение доводить до конца начатую работу.
Коррекционная – коррекция устных вычислительных навыков, слухового восприятия и тренировка устойчивости внимания.

Ход урока

Организационный момент (создание условий для успешной совместной деятельности).

— Я сегодня пришла на урок с хорошим настроением. А у кого настроение плохое? Вы его умножьте на 0. Что получилось? Всё плохое исчезло. С этой «весёлой нотки» начинаем наш урок.

Сообщение темы и постановка учебной задачи урока.

— Знания, по какой теме вы получили на прошлых уроках?

— Какие способы решения систем линейных уравнений, вы знаете?

— Как вы думаете, какую цель поставим на этом уроке?

— Откройте тетради, запишите число и тему урока.

Устный счёт.

— Ребята, скажите, пожалуйста, какие устройства придумали люди для быстрого счёта?

— Представьте, что все электронно-вычислительные машины сломались, а нам надо срочно посчитать.

— Как мы будем считать, если нет ничего под рукой?

— Без устного счёта не сдвинется с места любая работа.

Дети по цепочки устно решают примеры.

— 3,2 – 5,8 = 1 — =

0,8 – 6 = — 2³ =

— 0,25 • 40 = 7,2 : 0,1 =

— 6 + 6 = =

Дима моет 4 тарелки за тоже время, что и 6 чашек. Что он моет быстрее – тарелку или чашку?

— Теперь я проверю, насколько внимательно вы изучаете математику.

— Я буду говорить слова, а вы должны определить, если это математическое понятие, вы показываете зелёную карточку, в остальных случаях красную.

Слова: медиана, уравнение, приставка, диффузия, пропорция, вулкан, род, хорда, молекула, ордината.

Закрепление изученного материала (на данном этапе урока используется технология дифференцированного обучения).

— Решите систему линейных уравнений способом подстановки и алгебраическим сложением.

Двое обучающихся с подробным комментированием решают на школьной доске, предложенную систему линейных уравнений. При решении используют опорную (печатную) схему с алгоритмом выполнения действий.

Трое учеников, которые нуждаются в направляющей помощи со стороны учителя, решают индивидуальное задание.

Карточка №1

Решить уравнение: 21 – 2(3 – 4х) = 3 – 2х

Карточка №2

Вычислить:

— 4,8 – 5,2 = — 8 : 0,2 =

3,4 – 9 = — 8 + 8 =

0 – (- 6) = — 1,7 + 0,7 =

Карточка №3

Вычислить:

5 • 0,3² + 1,7 = : =

— = ( — 0,3) • 5 – 3 =

Физкультминутка – комплекс упражнений на общее развитие организма.

— Представьте себе, прямоугольник, у которого длина 3 см, а ширина 2 см.

— Сожмите кисти рук столько раз, чему равна площадь этого прямоугольника.

— Присядьте столько раз, чему равен периметр этого прямоугольника.

— Сделайте столько наклонов вниз туловищем, чему равна площадь квадрата со стороной 2 см.

Самостоятельная работа по вариантам (самоконтроль).

Двое обучающихся решают систему линейных уравнений на обратной стороне школьной доски.

Вариант 1

Вариант 2

Коллективная проверка индивидуальной работы.

Подведение итогов урока. Рефлексия.

— Какими способами, можно решить систему линейных уравнений?

— Какой способ является более простым и рациональным?

— Теперь с помощью листа самооценки оцените свою учебную деятельность на уроке.

Обучающиеся по кругу в устной форме заканчивают, на выбор одну из предложенных фраз из листа самооценки.

Лист самооценки

Сегодня я узнал…
У меня получилось…
Мне было интересно…
Было трудно…
Теперь я умею…

Постановка домашнего задания (дифференцированный подход)

«3» — №635 (чётные)

«4» и «5» — самостоятельно составить систему линейных уравнений и решить её.

Методы замены и добавления

Результаты обучения

Используйте метод подстановки, чтобы найти решение (я) системы двух линейных уравнений.
Используйте метод сложения, чтобы найти решение (я) системы линейных уравнений.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод. Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как сделать: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример: решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]

Показать решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {align} -x + y & = — 5 \\ — \ left (8 \ right) + \ left (3 \ right) & = — 5 && \ text {True} \\ [3mm] 2x — 5y & = 1 \\ 2 \ left (8 \ right) -5 \ left (3 \ right) & = 1 && \ text {True} \ end {align} [/ latex]

Попробуйте

Вы можете использовать онлайн-инструмент построения графиков, который поможет вам решить систему уравнений путем подстановки.Мы будем использовать следующую систему, чтобы показать вам, как:

[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]

Сначала решите оба уравнения относительно y:

[латекс] \ begin {align} y & = x-3 \\ y & = \ frac {3} {2} x — 2 \ end {align} [/ latex]

Теперь введите [latex] x-3 = \ frac {3} {2} x — 2 [/ latex] в Desmos. Вы увидите, что Desmos предоставил вам [латекс] x = -2 [/ latex].

Теперь вы можете заменить [latex] x = -2 [/ latex] в оба уравнения. Если вы получите одинаковый результат для обоих, вы нашли решение для упорядоченной пары. Попробуйте.

Показать решение

[латекс] \ влево (-2, -5 \ вправо) [/ латекс]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.

Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений.Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю.Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений методом сложения.

Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
Запишите одно уравнение над другим, выровняв соответствующие переменные.Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и решите для второй переменной.
Проверьте решение, подставив значения в другое уравнение.

Пример: решение системы методом сложения

Решите данную систему уравнений сложением.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]

Показать решение

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент [латекс] x [/ латекс] во втором уравнении, –1, противоположен коэффициенту [латекс] x [/ латекс] в первом уравнении, 1.Мы можем сложить два уравнения, чтобы исключить [latex] x [/ latex] без умножения на константу.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]

Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].

[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]

Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]

Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].

Проверьте решение в первом уравнении.

[латекс] \ begin {align} x + 2y & = — 1 \\ \ left (- \ frac {7} {3} \ right) +2 \ left (\ frac {2} {3} \ right) & = \\ — \ frac {7} {3} + \ frac {4} {3} & = \\ — \ frac {3} {3} & = \\ -1 & = — 1 && \ text {True} \ end { align} [/ латекс]

Анализ решения

Мы получаем важное представление о системах уравнений, глядя на графическое представление.Посмотрите на график ниже, чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Пример: использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения .

[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]

Показать решение

Добавление этих уравнений в представленном виде не приведет к удалению переменной.Однако мы видим, что в первом уравнении есть [latex] 3x [/ latex], а во втором уравнении — [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], термины x прибавятся к нулю.

[латекс] \ begin {align} x — 2y & = 11 \\ -3 \ left (x — 2y \ right) & = — 3 \ left (11 \ right) && \ text {Умножаем обе стороны на} -3 \ \ -3x + 6y & = — 33 && \ text {Использовать свойство распределения}. \ end {align} [/ latex]

А теперь добавим их.

[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]

На последнем этапе мы подставляем [latex] y = -4 [/ latex] в одно из исходных уравнений и решаем относительно [latex] x [/ latex].

[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]

Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex]. Проверьте решение в исходном втором уравнении.

[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-6, -2 \ вправо) [/ латекс]

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]

Показать решение

Одно уравнение имеет [латекс] 2x [/ латекс], а другое — [латекс] 5x [/ латекс].Наименьшее общее кратное — [latex] 10x [/ latex], поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Давайте удалим [latex] x [/ latex], умножив первое уравнение на [latex] -5 [/ latex], а второе уравнение на [latex] 2 [/ latex].

[латекс] \ begin {align} -5 \ left (2x + 3y \ right) & = — 5 \ left (-16 \ right) \\ -10x — 15y & = 80 \\ [3 мм] 2 \ left (5x — 10y \ right) & = 2 \ left (30 \ right) \\ 10x — 20y & = 60 \ end {align} [/ latex]

Затем мы складываем два уравнения.

[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]

Подставьте [latex] y = -4 [/ latex] в исходное первое уравнение.

[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]

Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]

Пример: использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]

Показать решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

[латекс] \ begin {align} 6 \ left (\ frac {x} {3} + \ frac {y} {6} \ right) & = 6 \ left (3 \ right) \\ [1 мм] 2x + y & = 18 \\ [3 мм] 4 \ left (\ frac {x} {2} — \ frac {y} {4} \ right) & = 4 \ left (1 \ right) \\ [1 мм] 2x-y & = 4 \ end {align} [/ latex]

Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .

[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]

Добавьте два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .

[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]

Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.

[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]

Решение: [latex] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} \ frac {x} {2} — \ frac {y} {4} & = 1 \\ [1 мм] \ frac {\ frac {11} {2}} {2} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {11} {4} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {4} {4} & = 1 \ end {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (10, -4 \ вправо) [/ латекс]

В следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить страницуПодробнее

Методы замены и добавления

Результаты обучения

Используйте метод подстановки, чтобы найти решение (я) системы двух линейных уравнений.
Используйте метод сложения, чтобы найти решение (я) системы линейных уравнений.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как сделать: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример: решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]

Показать решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.

Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями. По мере того, как вы приобретете больший опыт в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.

совет к успеху

Поскольку концепции в этом модуле во многом основаны на концепциях из предыдущих модулей, не стесняйтесь возвращаться к просмотру информации, которую вы, возможно, не получили полностью с первого раза.Математика лучше всего усваивается с течением времени с повторением, которое приводит к более глубокому пониманию вовлеченных идей.

Дополнительная практика также поможет вам развить навыки, творчески используя усвоенные концепции, чтобы делать правильный выбор техники в различных ситуациях.

Попробуйте

Вы можете использовать онлайн-калькулятор для построения графиков, который поможет вам решить систему уравнений путем подстановки. Мы будем использовать следующую систему, чтобы показать вам, как:

[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]

Сначала решите оба уравнения относительно y:

[латекс] \ begin {align} y & = x-3 \\ y & = \ frac {3} {2} x — 2 \ end {align} [/ latex]

Теперь введите [латекс] x-3 = \ frac {3} {2} x — 2 [/ latex] в калькулятор. Вы увидите, что калькулятор предоставил вам [латекс] x = -2 [/ latex].

Показать решение

[латекс] \ влево (-2, -5 \ вправо) [/ латекс]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений. Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений методом сложения.

Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
Запишите одно уравнение над другим, выровняв соответствующие переменные. Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и решите для второй переменной.
Проверьте решение, подставив значения в другое уравнение.

Пример: решение системы методом сложения

Решите данную систему уравнений сложением.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]

Показать решение

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]

Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].

[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]

Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]

Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].

Проверьте решение в первом уравнении.

Анализ решения

В следующем видео вы увидите еще один пример того, как использовать метод исключения для решения системы линейных уравнений.

Пример: использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения .

[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]

Показать решение

Добавление этих уравнений в представленном виде не приведет к удалению переменной. Однако мы видим, что в первом уравнении есть [latex] 3x [/ latex], а во втором уравнении — [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], термины x прибавятся к нулю.

А теперь добавим их.

[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]

[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]

Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex].Проверьте решение в исходном втором уравнении.

[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]

Ниже приведен еще один видео-пример использования метода исключения для решения системы линейных уравнений, когда требуется умножение одного уравнения.

совет к успеху

Не забудьте проработать приведенные примеры и отработать задачи на бумаге и более одного раза, чтобы углубить свое понимание.

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-6, -2 \ вправо) [/ латекс]

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]

Показать решение

Затем мы складываем два уравнения.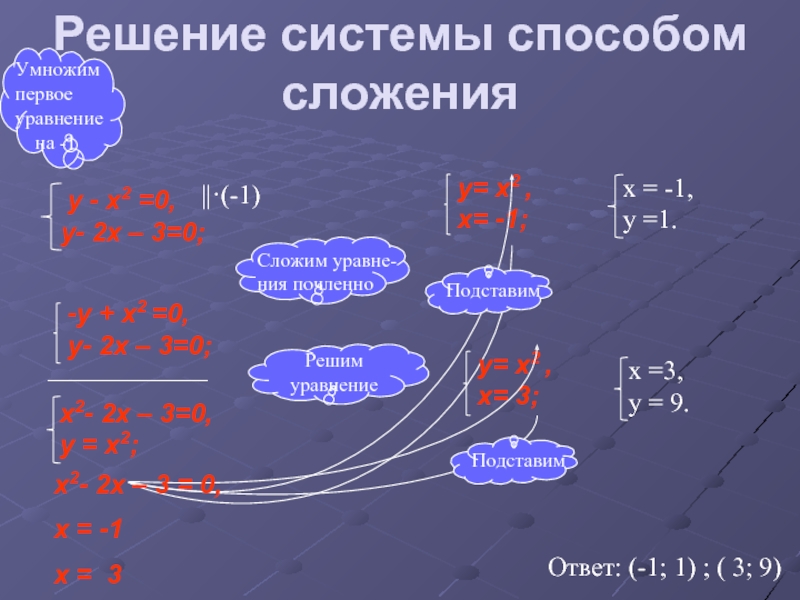

[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]

Подставьте [latex] y = -4 [/ latex] в исходное первое уравнение.

[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]

Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]

Пример: использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]

Показать решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .

[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]

Добавьте два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .

[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]

Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.

[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]

Решение: [latex] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.

В следующем видео вы найдете еще один пример использования метода исключения для решения системы; у этого есть коэффициенты, которые являются дробями.

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (10, -4 \ вправо) [/ латекс]

Метод сложения и замены для линейных систем уравнений с параметрами

Я думал, что решение линейной системы уравнений 2×2 с использованием метода подстановки или метода сложения (добавление двух уравнений для исключения переменной, а затем использование метода подстановки для получения значения другой переменной) приведет к тому же результату даже если уравнения содержат параметры (которые я рассматриваю как обычные числа).2 $

($ x $ и $ y $ — переменные, $ a $ и $ b $ — параметры)

Пытаясь решить эту систему, используя только метод подстановки, я, должно быть, допустил ошибку на этом пути, но это напомнило мне, что я должен (?) Быть в состоянии технически получить тот же ответ, даже при использовании добавления В данном конкретном случае метод требует меньше работы. Поэтому я создал два более простых уравнения, чтобы проверить это:

1) $ xa + yb = 3b $

2) $ xb + ya = 20a $

Когда я решаю эту предположительно более простую систему, используя метод сложения (умножаю (1) на $ a $ и (2) на $ -b $, чтобы исключить $ y $, добавить, изолировать $ x $ и упростить и т. Д.2 $ (часть этого упражнения заключалась в том, чтобы научиться определять значения параметров, для которых система не имеет решения).

Однако когда я пытаюсь решить эту проблему, используя только метод подстановки, я получаю совершенно разные ответы. Что я делаю неправильно? Ниже представлена моя подробная работа:

Способ замены:

Изолятор $ x $ в (2):

(2) $ xb + ya = 20a $

$ \ Rightarrow xb = 20a — ya $

$ \ Rightarrow x = {a (20-y) \ over b}

долларов США

Теперь подставьте $ x $ в (1) и выделите $ y $ (ОБНОВЛЕНО):

(1) $ xa + yb = 3b $

$ \ Rightarrow ({a (20-y) \ over b}) a + yb = 3b $

$ \ Rightarrow {a ^ 2 (20-y) \ over b} + yb = 3b $ (умножить на $ b $)

$ \ Rightarrow {a ^ 2 (20-y)} + yb ^ 2 = 3b ^ 2 $ (умножить скобки)

$ \ Rightarrow 20a ^ 2-ya ^ 2 + yb ^ 2 = 3b ^ 2 $ (вычесть $ 20a ^ 2 $)

$ \ Rightarrow -ya ^ 2 + yb ^ 2 = 3b ^ 2 — 20a ^ 2 $ (за вычетом $ y $)

$ \ Rightarrow y (-a ^ 2 + b ^ 2) = 3b ^ 2 — 20a ^ 2 $ (разделить на $ b ^ 2-a ^ 2 $)

$ \ Rightarrow y = {3b ^ 2 — 20a ^ 2 \ over b ^ 2-a ^ 2} $

Поскольку этот ответ для $ y $ в терминах $ a $ и $ b $ по-прежнему отличается от ответа выше (когда я использовал метод сложения), я запутался. 2} $

Любая помощь с этим будет очень признательна, заранее спасибо!

Предварительное вычисление алгебры — Нужна помощь в решении линейных уравнений методом исключения и замены

Вместо того, чтобы решать за вас домашнее задание, я покажу вам, как каждый из методов работает с немного более сложной системой линейных уравнений.

Вот система линейных уравнений, над которой я буду работать:

$$ \ begin {cases} x-3y + \ frac 43z = 2 \\ 2x- z = 1 \\ 3y-4z = 0 \ end {cases} $$

Что означает , решающий этой системы линейных уравнений? Если означает, что мы находим $ x $, $ y $ и $ z $, которые работают в всех $ 3 $ уравнениях .

Итак, давайте попробуем несколько разных подходов:

Метод замещения:

Для этого метода мы хотим найти переменную в терминах других переменных, а затем подставить это в другое уравнение. Это может помочь нам уменьшить количество переменных в данном уравнении. Посмотрим, как это работает:

Я заметил, что второе и третье уравнения имеют только $ 2 $ переменных, поэтому давайте начнем с одного из них. Я начну со второго уравнения и выделю одну переменную с одной стороны, а все остальное с другой стороны:

$$ 2x-z = 1 \ подразумевает z = 2x-1 $$

Теперь, когда у нас есть это, мы можем подключить его к двум другим уравнениям.Затем у нас есть новая и эквивалентная система:

$$ \ begin {case} x-3y + \ frac 43z = x-3y + \ frac 43 (2x-1) = \ frac {11} 3x -3y — \ frac 43 = 2 \\ z = 2x-1 \\ 3y-4z = 3y-4 (2x-1) = -8x + 3y + 4 = 0 \ end {cases} \\ \ iff \ begin {cases} \ frac {11} 3x -3y = \ frac {10} 3 \\ z = 2x-1 \\ -8x + 3y = -4 \ end {case} $$

Обратите внимание, что первое и третье уравнения имеют только две переменные — и, что важно, это те же и две переменные. Итак, давайте решим одну переменную в одной из них, а затем вставим это выражение в другую:

$$ — 8x + 3y = -4 \ подразумевает x = \ frac {3y + 4} {8} $$

Теперь давайте подставим это выражение в первое уравнение, чтобы получить новую систему уравнений:

$$ \ begin {cases} \ frac {11} 3x -3y = \ frac {11} 3 (\ frac {3y + 4} {8}) — 3y = \ frac {11} 8 y + \ frac {11 } 6 -3y = \ frac {10} 3 \\ z = 2x-1 \\ -8x + 3y = -4 \ end {cases} \\ \ iff \ begin {cases} y = — \ frac {12} { 13} \\ z = 2x-1 \\ -8x + 3y = -4 \ end {case} $$

Теперь, когда мы решили одну, мы почти закончили. Подставьте $ y = — \ frac {12} {13} $ в уравнение $ -8x + 3y = -4 $, чтобы получить $ x = \ frac 2 {13} $, а затем вставьте это в $ z = 2x-1 $. чтобы получить $ z = — \ frac 9 {13} $. И мы закончили!

Метод исключения:

В этом методе мы будем складывать / вычитать кратные одного уравнения из другого, чтобы избавиться от переменных. Посмотрим, как это работает:

Я заметил, что если бы я добавил третье уравнение к первому, член $ y $ уменьшился бы в каждом. Итак, давайте сделаем это:

$$ x-3y + \ frac 43z = 2 \\
\ underline {+ \ \ \ \ \ 3y-4z = 0} \\
\ \ \ \ \ \ \ x- \ frac 83z = 2 $$

Если мы заменим наше первое уравнение этим новым, мы получим новую систему уравнений:

$$ \ begin {cases} x- \ frac 83z = 2 \\ 2x- z = 1 \\ 3y-4z = 0 \ end {cases} $$

Теперь обратите внимание, что если мы вычтем $ 2 $, умноженное на первое уравнение, из второго, мы сможем избавиться от $ x $.Итак, давайте сделаем это:

$$ 2x- z = 1 \\
\ underline {- \ \ \ (2x- \ frac {16} 3z = 4)} \\
\ frac {13} 3z = -3 $$

Решая, что получаем $ z = — \ frac 9 {13} $. Подставляя это в первое уравнение, мы получаем $ x $, а в третьем уравнении получаем $ y $. Сделанный.

Метод матрицы коэффициентов:

Обратите внимание, что нам действительно нужны только $ x $, $ y $ и $ z $ в качестве заполнителей в наших вычислениях до самого конца — вся математика в конечном итоге просто влияет на коэффициенты.Итак, давайте перепишем нашу систему без , когда эти $ x $, $ y $ и $ z $ мешают. Запишем его как матрицу :

$$ \ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
2 & 0 & -1 & 1 \\
0 & 3 & -4 & 0
\ end {array} \ right] $$

Убедитесь, что вы понимаете, как я построил эту матрицу.

Теперь вспомните, что это просто более удобный способ написать систему линейных уравнений. Также помните, что есть несколько вещей, которые мы можем сделать с системой уравнений, не меняя решений.Мы можем

Умножьте обе части уравнения на ненулевую константу.
Измените порядок уравнений.
Складывать одно уравнение к другому, кратное одному.

Как мы выполняем эти три операции с нашими матрицами? Каждая из этих операций эквивалентна следующим операциям с нашей матрицей:

Умножьте любую строку на ненулевую константу.
Измените порядок строк нашей матрицы.
Добавить строку, кратную строке, в другую строку.

Теперь, когда у нас есть эти операции, какой должна быть наша цель? Было бы неплохо, если бы мы могли получить матрицу в виде

$$ \ left [\ begin {array} {ccc | c}
1 & 0 & 0 & а \\
0 & 1 & 0 & b \\
0 & 0 & 1 & c
\ end {array} \ right] $$

, потому что тогда, если бы мы преобразовали эту матрицу обратно в форму уравнения, у нас было бы просто

$$ \ begin {case} x + 0y + 0z = x = a \\
0х + у + 0z = у = Ь \\
0x + 0y + z = c \ end {case} $$

, и тогда мы могли просто зачитать наши ответы.Итак, теперь, когда у нас есть операции и есть цель, давайте посмотрим, сможем ли мы достичь этой цели:

$$ \ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
2 & 0 & -1 & 1 \\
0 & 3 & -4 & 0
\ end {array} \ right] _ {R_2 \ to R_2 — 2 \ cdot R_1} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
0 & 6 & — \ frac {11} 3 & -3 \\
0 & 3 & -4 & 0
\ end {array} \ right] _ {R_2 \ to \ frac 16R_2} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
0 & 1 & — \ frac {11} {18} & — \ frac 12 \\
0 & 3 & -4 & 0
\ end {array} \ right] _ {R_3 \ to R_3-3 \ cdot R_2} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
0 & 1 & — \ frac {11} {18} & — \ frac 12 \\
0 & 0 & — \ frac {13} 6 & \ frac 32
\ end {array} \ right] _ {R_3 \ to — \ frac 6 {13} \ cdot R_3} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
0 & 1 & — \ frac {11} {18} & — \ frac 12 \\
0 & 0 & 1 & — \ frac 9 {13}
\ end {array} \ right] _ {R_2 \ to R_2 + \ frac {11} {18} \ cdot R_3} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & -3 & \ frac 43 & 2 \\
0 & 1 & 0 & — \ frac {12} {13} \\
0 & 0 & 1 & — \ frac 9 {13}
\ end {array} \ right] _ {R_1 \ to R_1 +3 \ cdot R_2 — \ frac 43 \ cdot R_3} \\ \ sim
\ left [\ begin {array} {ccc | c}
1 & 0 & 0 & \ frac 2 {13} \\
0 & 1 & 0 & — \ frac {12} {13} \\
0 & 0 & 1 & — \ frac 9 {13}
\ end {array} \ right] $$

Что дает нам ответ $ x = \ frac 2 {13} $, $ y = — \ frac {12} {13} $, $ z = — \ frac 9 {13} $ — именно то, что мы нашли выше.

4.11: Решение одновременных уравнений — метод подстановки и метод сложения

Что такое одновременные уравнения и системы уравнений?

Термины систем уравнений и систем уравнений относятся к условиям, при которых две или более неизвестных переменных связаны друг с другом посредством равного числа уравнений.

Пример:

Для этой системы уравнений существует только одна комбинация значений для x и y, которая удовлетворяет обоим.Любое уравнение, рассматриваемое по отдельности, имеет бесконечное количество допустимых (x, y) решений, но вместе существует только одно. На графике это условие становится очевидным:

Каждая линия на самом деле представляет собой континуум точек, представляющих возможные пары решений x и y для каждого уравнения. Каждое уравнение в отдельности имеет бесконечное количество упорядоченных парных (x, y) решений. Есть только одна точка, где две линейные функции x + y = 24 и 2x — y = -6 пересекаются (где одно из многих их независимых решений работает для обоих уравнений), и это где x равно значению 6 и y равно значению 18.

Однако обычно построение графиков не является очень эффективным способом определения набора одновременных решений для двух или более уравнений. Это особенно непрактично для систем из трех и более переменных. В системе с тремя переменными, например, решение может быть найдено путем пересечения трех плоскостей в трехмерном координатном пространстве — сценарий, который нелегко представить.

Решение одновременных уравнений методом подстановки

Существует несколько алгебраических методов решения одновременных уравнений.Возможно, самый простой для понимания — это метод замены на .

Возьмем, к примеру, нашу задачу с двумя переменными:

В методе подстановки мы манипулируем одним из уравнений таким образом, чтобы одна переменная определялась в терминах другой:

Затем мы берем это новое определение одной переменной и заменяем его на ту же переменную в другом уравнении. В этом случае мы берем определение y, равное 24 — x, и подставляем его вместо члена y, найденного в другом уравнении:

Теперь, когда у нас есть уравнение с одной переменной (x), мы можем решить его, используя «обычные» алгебраические методы:

Теперь, когда x известен, мы можем подставить это значение в любое из исходных уравнений и получить значение для y. Или, чтобы сэкономить нам немного работы, мы можем вставить это значение (6) в уравнение, которое мы только что сгенерировали, чтобы определить y через x, поскольку оно уже находится в форме для решения для y:

Применение метода подстановки к системам из трех или более переменных включает аналогичный шаблон, только с дополнительным объемом работы. Обычно это верно для любого метода решения: количество шагов, необходимых для получения решения, быстро увеличивается с каждой дополнительной переменной в системе.

Чтобы решить для трех неизвестных переменных, нам нужно как минимум три уравнения.Рассмотрим этот пример:

Поскольку первое уравнение имеет простейшие коэффициенты (1, -1 и 1 для x, y и z соответственно), кажется логичным использовать его для разработки определения одной переменной в терминах двух других. В этом примере я решаю x через y и z:

Теперь мы можем заменить это определение x, где x появляется в двух других уравнениях:

Приведение этих двух уравнений к их простейшей форме:

До сих пор наши усилия привели к сокращению системы с трех переменных в трех уравнениях до двух переменных в двух уравнениях. Теперь мы можем снова применить технику подстановки к двум уравнениям 4y — z = 4 и -3y + 4z = 36, чтобы решить для y или z. Сначала я манипулирую первым уравнением, чтобы определить z через y:

Затем мы заменим это определение z на y, где мы видим z в другом уравнении:

Теперь, когда y — известное значение, мы можем подставить его в уравнение, определяющее z через y, и получить число для z:

Теперь, когда значения y и z известны, мы можем подставить их в уравнение, в котором мы определили x через y и z, чтобы получить значение x:

В заключение, мы нашли для x, y и z значения 2, 4 и 12 соответственно, которые удовлетворяют всем трем уравнениям.

Решение одновременных уравнений с использованием метода сложения

Хотя метод подстановки может быть самым простым для понимания на концептуальном уровне, нам доступны и другие методы решения. Одним из таких методов является так называемый метод сложения и , при котором уравнения складываются друг с другом с целью исключения переменных членов.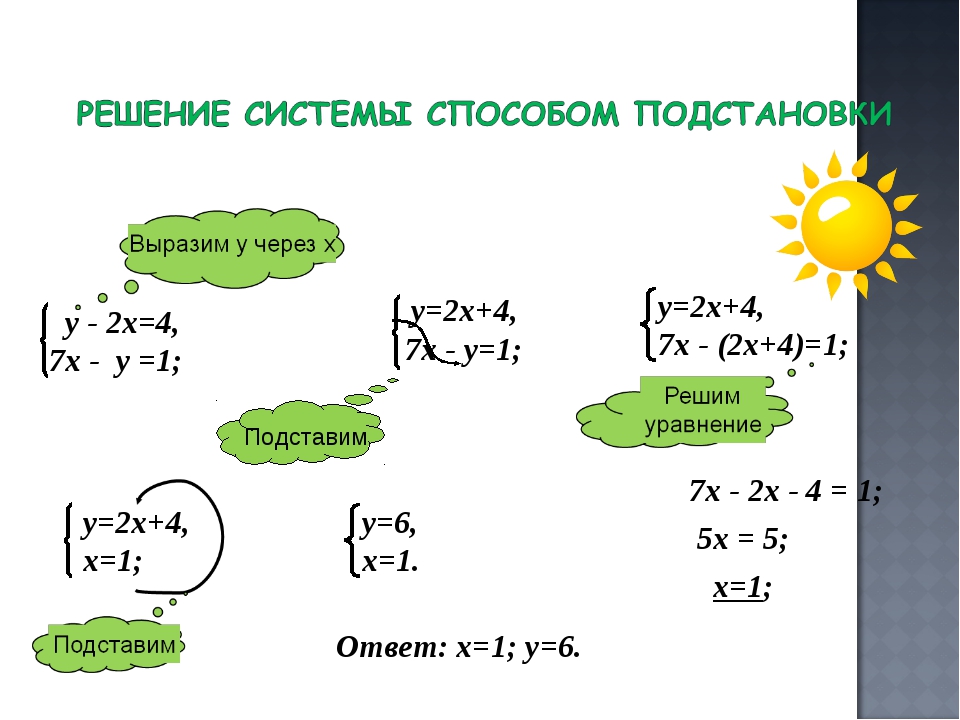

Давайте возьмем нашу систему с двумя переменными, использованную для демонстрации метода подстановки:

Одно из наиболее часто используемых правил алгебры состоит в том, что вы можете выполнять любую арифметическую операцию с уравнением, если вы делаете это одинаково для обеих сторон .Что касается сложения, это означает, что мы можем добавить любую величину, которую пожелаем, к обеим сторонам уравнения — при условии, что это то же самое количество — без изменения истинности уравнения.

У нас есть возможность сложить соответствующие части уравнений вместе, чтобы сформировать новое уравнение. Поскольку каждое уравнение является выражением равенства (одна и та же величина по обе стороны от знака =), добавление левой части одного уравнения к левой части другого уравнения действительно до тех пор, пока мы добавляем два уравнения ‘правые части тоже вместе.В нашем примере набора уравнений, например, мы можем добавить x + y к 2x — y, а также сложить 24 и -6 вместе, чтобы сформировать новое уравнение. Какая польза от этого для нас? Изучите, что произойдет, когда мы сделаем это с нашим примером набора уравнений:

Поскольку верхнее уравнение содержало положительный член y, а нижнее уравнение содержало отрицательный член y, эти два члена компенсировали друг друга в процессе сложения, не оставляя члена y в сумме. У нас осталось новое уравнение, но с единственной неизвестной переменной x! Это позволяет нам легко найти значение x:

Когда у нас есть известное значение x, конечно, определение значения y — это простой вопрос подстановки (замены x числом 6) в одно из исходных уравнений.В этом примере метод сложения уравнений хорошо сработал для создания уравнения с одной неизвестной переменной. А как насчет примера, где все не так просто? Рассмотрим следующий набор уравнений:

Мы могли бы сложить эти два уравнения вместе — это вполне допустимая алгебраическая операция — но это не принесет нам пользы для получения значений для x и y:

Полученное уравнение по-прежнему содержит две неизвестные переменные, как и исходные уравнения, поэтому мы не продвинемся дальше в поиске решения. Однако что, если бы мы могли манипулировать одним из уравнений, чтобы получить отрицательный член, который при добавлении аннулировал бы соответствующий член в другом уравнении? Затем система сведется к одному уравнению с единственной неизвестной переменной, как в последнем (случайном) примере.

Если бы мы могли только превратить член y в нижнем уравнении в член — 2y, так что, когда два уравнения складываются вместе, оба члена y в уравнениях сократятся, оставив нам только член x, это принесет нам ближе к решению.К счастью, сделать это несложно. Если мы умножим каждый член нижнего уравнения на -2, получится результат, который мы ищем:

Теперь мы можем добавить это новое уравнение к исходному, верхнему уравнению:

Решая относительно x, получаем значение 3:

Подставляя это новое найденное значение для x в одно из исходных уравнений, значение y легко определяется:

Использование этого метода решения в системе с тремя переменными немного сложнее. Как и в случае подстановки, вы должны использовать этот метод, чтобы уменьшить систему из трех уравнений с тремя переменными до двух уравнений с двумя переменными, а затем применить его снова, чтобы получить одно уравнение с одной неизвестной переменной. Для демонстрации я воспользуюсь системой уравнений с тремя переменными из раздела о заменах:

Поскольку верхнее уравнение имеет значения коэффициента, равные 1 для каждой переменной, это уравнение будет простым для манипулирования и использования в качестве инструмента отмены. Например, если мы хотим отменить член 3x из среднего уравнения, все, что нам нужно сделать, это взять верхнее уравнение, умножить каждый из его членов на -3, а затем добавить его в среднее уравнение следующим образом:

Мы можем избавить нижнее уравнение от члена -5x таким же образом: возьмите исходное верхнее уравнение, умножьте каждый из его членов на 5, затем добавьте это модифицированное уравнение к нижнему уравнению, оставив новое уравнение только с y и z сроки:

На данный момент у нас есть два уравнения с теми же двумя неизвестными переменными, y и z:

При осмотре должно быть очевидно, что член -z верхнего уравнения может быть использован для отмены члена 4z в нижнем уравнении, если только мы умножим каждый член верхнего уравнения на 4 и сложим два уравнения вместе:

Взяв новое уравнение 13y = 52 и решив относительно y (разделив обе части на 13), мы получим значение 4 для y. Подстановка этого значения 4 вместо y в любое из уравнений с двумя переменными позволяет нам решить относительно z. Подстановка обоих значений y и z в любое из исходных уравнений с тремя переменными позволяет нам решить относительно x. Конечный результат (я избавлю вас от алгебраических шагов, поскольку они уже должны быть вам знакомы!) Состоит в том, что x = 2, y = 4 и z = 12.

Метод сложения

— Джеймс Бреннан

Метод сложения

Вся проблема с решением системы уравнений состоит в том, что вы не можете решить уравнение, в котором есть два неизвестных.Вам нужно уравнение только с одной переменной, чтобы вы могли изолировать переменную с одной стороны уравнения. Оба метода, которые мы рассмотрим, представляют собой методы исключения одной из переменных, чтобы дать вам уравнение только с одним неизвестным, которое вы затем можете решить обычными методами.

Первый метод решения систем линейных уравнений — это метод сложения, в котором два уравнения складываются вместе, чтобы исключить одну из переменных.

Добавление уравнений означает, что мы складываем левые части двух уравнений вместе, а правые части складываем вместе.Это допустимо из-за принципа сложения, который гласит, что мы можем добавить одинаковую сумму к обеим сторонам уравнения
. Поскольку левая и правая части любого уравнения равны друг другу, мы действительно добавляем одинаковую сумму к обеим сторонам уравнения.

Рассмотрим этот простой пример:

Пример:

Если мы сложим эти уравнения вместе, члены, содержащие y , в сумме дадут ноль (2 y плюс –2 y ), и мы получим

или

5 x = 5
x = 1

Однако мы еще не закончили — мы знаем x , но мы еще не знаем y .Мы можем решить относительно y , подставив теперь известное значение x в любое из наших исходных уравнений. Это даст уравнение, которое можно решить относительно y :

Теперь, когда мы знаем и x , и y , мы можем сказать, что решением системы является пара (1, 1/2).

Этот последний пример было легко увидеть из-за удачного присутствия как положительного, так и отрицательного 2 y . Не всегда так везет.Рассмотрим

Пример:

Сейчас нет ничего более очевидного, но мы все еще можем кое-что сделать. Если мы умножим первое уравнение на –3, мы получим

(Не забудьте умножить каждый член уравнения на обе стороны от знака равенства). Теперь, если мы сложим их вместе, члены, содержащие x , отменит:

или

Как и в предыдущем примере, теперь, когда мы знаем y , мы можем найти x , подставив любое исходное уравнение.Первое уравнение выглядит наиболее простым для решения для x , поэтому мы будем использовать его:

Итак, точка решения (–4, 7/2).

Теперь посмотрим на еще менее очевидный пример:

Пример:

Здесь нет ничего особенно привлекательного в том, чтобы идти после x или y . В любом случае оба уравнения необходимо умножить на некоторый коэффициент, чтобы получить общий коэффициент.Это очень похоже на ситуацию, с которой вы сталкиваетесь, пытаясь найти наименьший общий знаменатель для сложения дробей, за исключением того, что здесь мы называем это наименьшим общим кратным (НОК). Как правило, проще всего исключить переменную с наименьшим НОК. В данном случае это будет y , потому что НОК 2 и 3 равно 6. Если бы мы хотели исключить x , нам пришлось бы использовать НОК 10 (5 умножить на 2). Итак, мы решили преобразовать коэффициенты y в плюс и минус 6.Для этого первое уравнение нужно умножить на 3, а второе уравнение на 2:

или

Теперь сложение этих двух вместе удалит термины, содержащие y :

или

x = 2

Нам все еще нужно подставить это значение в одно из исходных уравнений, чтобы найти y :

Таким образом, решение — это точка (2, 2).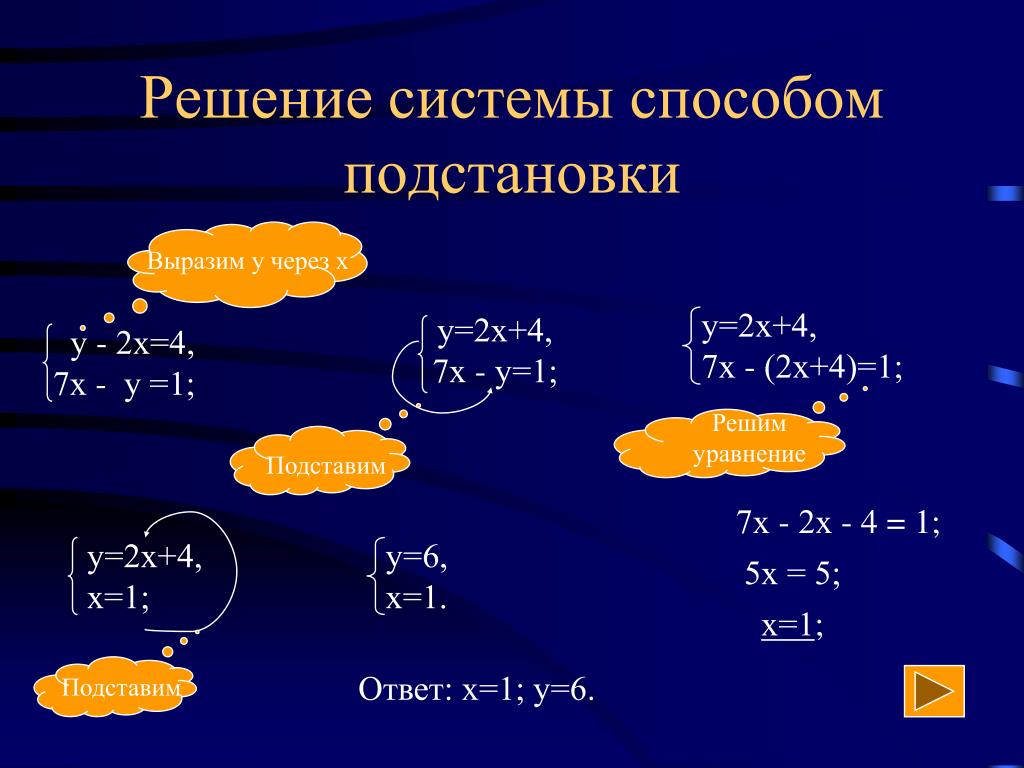

Одновременных уравнений: метод сложения и метод замены

В математике мы можем использовать два уравнения для решения вычислительной задачи. Если в уравнении есть два неизвестных числа, мы не можем найти ответ. Однако, если есть два уравнения, мы можем найти ответ, даже если в уравнении есть два неизвестных числа.

Комбинация двух или более уравнений называется одновременными уравнениями (или системой линейных уравнений). Используя систему линейных уравнений, мы можем получить ответ, даже если существует более одного неизвестного ответа.

Есть два способа решить одновременные уравнения. Кроме того, математика предназначена для повседневного использования, и очень важно уметь решать текстовые задачи для системы уравнений. Важно не только научиться определять и решать одновременные уравнения, но и самостоятельно создавать уравнения и решать проблемы.

Поэтому мы объясним не только, как решать одновременные уравнения, но и как составлять уравнения в текстовых задачах, включая упражнения.

Есть два способа решить систему линейных уравнений

Линейное уравнение, которое вы изучаете в математике, представляет собой следующее уравнение.

Однако это уравнение имеет бесконечное количество ответов. Это потому, что значения $ x $ и $ y $ могут быть изменены по желанию. Есть несколько шаблонов $ x $ и $ y $, которые дают ответ 8.

Итак, в системе уравнений мы комбинируем два или более выражений. Например, у нас есть следующее.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 2x + 3y = 8 \\ 2x + 5y = 12 \ end {array} \ right. \ End {eqnarray} $

Есть один $ x $ и один $ y $, удовлетворяющие обоим уравнениям.Даже если имеется несколько неизвестных чисел, вы можете получить конкретный ответ, используя одновременные уравнения. Важно отметить, что есть два способа решения одновременных уравнений. Это следующие два метода.

Метод сложения (или метод сложения / вычитания)
Метод замены

Мы объясним каждый из этих методов.

Метод сложения / вычитания: Удалить $ x $ или $ y $ сложением или вычитанием

Метод решения системы уравнений сложением или вычитанием называется методом сложения / вычитания.Добавляя или вычитая линейное уравнение, вы можете исключить $ x $ или $ y $.

Например, в случае описанных выше систем уравнений общая буква — $ 2x $. Затем можно выполнить вычитание, чтобы создать линейное уравнение, подобное приведенному ниже.

Если коэффициенты совпадают, буквы можно удалить методом сложения / вычитания. В этом расчете мы можем найти ответ $ y = 2 $, вычитая уравнения друг из друга.

-Замените и получите значение $ x $ или $ y $

Затем получите другой ответ.Теперь, когда мы знаем, что $ y = 2 $, мы можем найти значение $ x $. Замените $ y = 2 $ на любое из следующих выражений.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 2x + 3y = 8 \\ 2x + 5y = 12 \ end {array} \ right. \ End {eqnarray} $

Вы можете замените их на $ y = 2 $. Это потому, что они оба дают одинаковый ответ.

$ 2x + 3 × 2 = 8

$ 2x + 6 = 8

$ 2x = 2

$ x = 1

$ 2x + 5 × 2 = 12

$ 2x + 10 = 12 $

$ 2x = 2 $

$ x = 1 $

Это система линейных уравнений, которая дает нам $ x $ и $ y $, которые удовлетворяют двум уравнениям.Поэтому, естественно, окончательный ответ будет одним и тем же независимо от того, какое уравнение вы ему приписываете.

Различайте сложение и вычитание с помощью плюса и минуса

Чтобы определить, следует ли вам прибавлять или вычитать, проверьте знак. Даже если абсолютные значения коэффициентов одинаковы, метод расчета будет меняться в зависимости от того, положительный или отрицательный знак.

В предыдущей системе линейных уравнений абсолютные значения коэффициентов и знаки совпадают.Поэтому мы вычитали его. С другой стороны, что, если абсолютные значения коэффициентов одинаковы, а знаки разные? Например, у нас есть следующий случай.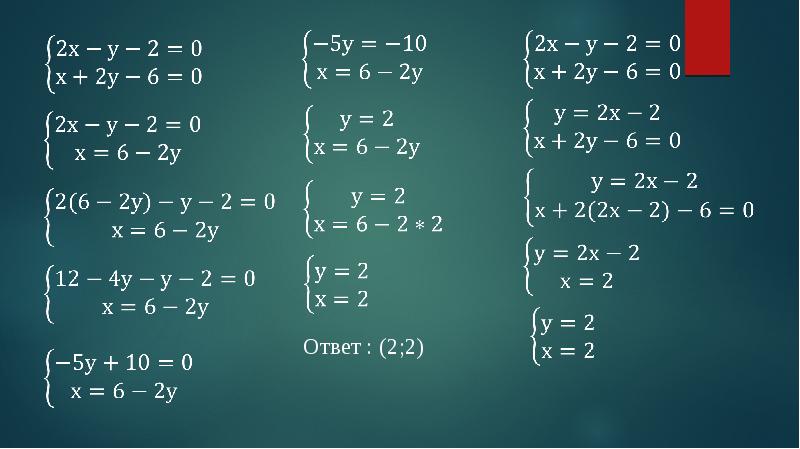

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 2x + 2y = 8 \\ 4x-2y = 10 \ end {array} \ right. \ End {eqnarray} $

В этом случай, сделайте добавление. Выглядит это примерно так.

Затем вы можете заменить $ x = 3 $, чтобы получить ответ $ y = 1 $.

Что касается того, прибавляете ли вы или вычитаете в методе сложения / вычитания, сделайте различие в зависимости от того, является ли буква, которую вы хотите стереть, положительной или отрицательной.

Выровняйте коэффициенты $ x $ или $ y $

Ранее мы использовали простые примеры с одновременными уравнениями, чтобы просто объяснить их. Однако в реальных расчетах абсолютные значения $ x $ и $ y $ в каждом уравнении часто различаются. Например, каков ответ на следующие одновременные уравнения?

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 2x + 3y = 16 \\ 3x-4y = 10 \ end {array} \ right. \ End {eqnarray} $

Оба $ x $ и $ y $ имеют разные абсолютные значения чисел. Поэтому попробуйте сопоставить абсолютные значения, умножив обе стороны. Это так.

Таким образом мы можем выровнять абсолютные значения чисел перед буквами. Затем мы можем сложить или вычесть уравнение, чтобы получить значения $ x $ и $ y $.

Вам решать, какое из абсолютных значений $ x $ и $ y $ вы хотите согласовать. Постарайтесь сопоставить абсолютные значения коэффициентов, чтобы упростить расчет.

-В дробных вычислениях исключение дробей является основным

Обратите внимание, что в системе уравнений в уравнении часто встречаются дроби.Сложение и вычитание дробей затруднено и часто приводит к просчетам.

Поэтому попробуйте исключить дроби, умножив обе части уравнения. Когда дроби входят в систему уравнений, хитрость состоит в том, чтобы исключить дроби, чтобы получить ответ.

Удалить буквы методом подстановки

В системе уравнений есть еще один способ решения одновременных уравнений. Это метод подстановки. Решая проблему, вы должны подставить конкретное число в $ x $ или $ y $, чтобы получить ответ.В математике можно назначать не только числа, но и буквы.

Итак, в системе линейных уравнений вы можете получить ответ, подставив. Например, давайте решим следующие одновременные уравнения методом подстановки.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} x + 3y = 11 \\ 2x-4y = -8 \ end {array} \ right. \ End {eqnarray} $

In метод подстановки, он должен быть выражением $ x = □ $ или $ y = □ $. Кроме того, коэффициент перед буквой должен быть равен 1.

В предыдущем одновременном уравнении измените форму $ x + 3y = 11 $. Мы можем преобразовать его в форму $ x = □ $, переставив $ 3y $, как показано ниже.

$ x + 3y = 11 $

$ x = -3y + 11 $

Изменив форму уравнения, мы получим $ x = -3y + 11 $. Поскольку $ x $ равно $ -3y + 11 $, мы можем подставить его в другое уравнение, $ 2x-4y = -8 $. Затем мы можем исключить $ x $ так же, как мы это сделали с методом сложения.

И, подставив в уравнение $ y = 3 $, мы получаем ответ $ x = 2 $.

$ x = -3y + 11

$ x = -3 × 3 + 11

$ x = 2

В методе замены установите коэффициент при $ x $ или $ y $ равным 1. После создания уравнения $ x = □ $ или $ y = □ $ ответ можно найти, подставив другое уравнение.

Можно использовать метод сложения или замены

Некоторые люди задаются вопросом, следует ли им использовать метод сложения или метод подстановки при решении системы уравнений. Для этого вы можете использовать любой метод.

В зависимости от проблемы может быть проще использовать метод сложения / вычитания.А иногда проще использовать метод подстановки для некоторых расчетов. В математике чем проще расчет, тем меньше будет ошибок. Следовательно, вы должны иметь возможность использовать как метод сложения / вычитания, так и метод подстановки.

Что важно, так это то, что есть два способа ответить на систему линейных уравнений.

Какой из них лучше всего решить проблему, зависит от вопроса. Итак, решите одновременные уравнения, определив, какое из них легче вычислить.

Как решать задачи со словами в системе уравнений

После того, как вы поймете, как решать одновременные уравнения, вы должны уметь отвечать на задачи со словами.

Прежде чем изучать систему линейных уравнений, мы всегда изучаем линейные уравнения. В линейных уравнениях мы также должны решать текстовые задачи. В математике есть определенный способ решения словесных задач, и вам нужно составить уравнение из проблемного предложения. Даже с одновременными уравнениями вы должны сначала создать уравнение.

В линейных уравнениях неизвестное число равно $ x $. С другой стороны, в системе уравнений есть два неизвестных числа. Поэтому установите неизвестные числа в $ x $ и $ y $ соответственно. Затем мы создаем систему линейных уравнений, чтобы найти ответ. Весь процесс выглядит следующим образом.

Сделайте неизвестные $ x $ и $ y $.
Создайте два уравнения.
Решите системы уравнений.

В алгебраических выражениях мы всегда превращаем неизвестные числа в алфавит.Поэтому используйте $ x $ и $ y $ для создания выражений.

Обязательно замените и просмотрите ответ

Кроме того, обязательно просмотрите свои ответы для одновременных уравнений после их решения. Анализ ваших ответов — ключ к сокращению просчетов при решении проблем.

Например, решите следующую систему уравнений.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 4x + 3y = 14 \\ 3x + 2y = 11 \ end {array} \ right. \ End {eqnarray} $

Например , предположим, что мы решили эту задачу и получили $ x = 3, y = 1 $.Но действительно ли это правильный ответ? Давайте применим его к обоим уравнениям, а не только к одному.

$ 4 × 3 + 3 × 1 = 15 $: неверно

$ 3 × 3 + 2 × 1 = 11 $: правильно

Таким образом, одно уравнение не соответствует ответу. Следовательно, мы знаем, что наши расчеты ошибочны, потому что ответ должен удовлетворять двум уравнениям.

Итак, мы пересчитываем и получаем $ x = 5, y = -2 $. В этом случае ответ удовлетворяет обоим уравнениям. Все делают просчеты. Однако мы можем предотвратить просчеты, просмотрев их.

Упражнения: как решать одновременные уравнения и задачи со словами

Q1: Решите следующие одновременные уравнения.

(a)

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 0,4x + 0,8y = 6 \\ 2x + 1,2y = 16 \ end {array} \ right. \ end {eqnarray} $

(b)

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} \ displaystyle \ frac {2} {3} x- \ displaystyle \ frac { 3} {4} y = -5 \\ — \ displaystyle \ frac {1} {6} x + \ displaystyle \ frac {4} {2} y = 23 \ end {array} \ right.\ end {eqnarray} $

A1: Ответы.

Если в уравнение включены дроби, исключите их, умножив обе части уравнения. При этом следует выровнять абсолютные значения.

(a)

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 0,4x + 0,8y = 6 \\ 2x + 1,2y = 16 \ end {array} \ right. \ end {eqnarray} $

Проверяя $ x $ и $ y $, кажется, легче подобрать коэффициенты $ x $. Итак, делаем следующее.

0,4x + 0,8y = 6

$ (0.4x + 0.8y) \ textcolor {red} {× 5} = 6 \ textcolor {red} {× 5} $

$ 2x + 4y = 30 $

Таким образом, мы можем исправить следующие одновременные уравнения.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} 2x + 4y = 30 \\ 2x + 1.2y = 16 \ end {array} \ right. \ End {eqnarray} $

Расчет это так.

$ \ begin {array} {r} 2x + 4y = 30 \\\ underline {-) \ phantom {0} 2x + 1.2y = 16} \\ 2.8y = 14 \ end {array} $

Расчет $ 2,8y = 14 $, получаем $ y = 5 $. Также, подставив $ y = 5 $ в систему уравнений, мы получим $ x = 5 $.Следовательно, $ x = 5, y = 5 $ — правильный ответ.

(b)

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} \ displaystyle \ frac {2} {3} x- \ displaystyle \ frac {3} {4} y = -5 \\ — \ displaystyle \ frac {1} {6} x + \ displaystyle \ frac {4} {2} y = 23 \ end {array} \ right. \ End {eqnarray} $

Мы можем решить проблема либо методом сложения, либо методом подстановки. Мы также можем исключить дроби, умножив обе части. Доли в каждом уравнении можно исключить с помощью следующих вычислений.

$ \ displaystyle \ frac {2} {3} x- \ displaystyle \ frac {3} {4} y = -5 $

$ \ left (\ displaystyle \ frac {2} {3} x- \ displaystyle \ frac {3} {4} y \ right) \ textcolor {red} {× 12} = — 5 \ textcolor {red} {× 12} $

$ 8x-9y = -60 $

$ — \ displaystyle \ frac {1} {6} x + \ displaystyle \ frac {4} {2} y = 23 $

$ \ left (- \ displaystyle \ frac {1} {6} x + \ displaystyle \ frac { 4} {2} y \ right) \ textcolor {red} {× (-6)} = 23 \ textcolor {red} {× (-6)} $

$ x-12y = -138 $

$ x = 12y-138 $

Затем подставьте $ x = 12y-138 $.В этом примере мы решаем проблему методом подстановки, а не методом сложения / вычитания.

$ 8 \ textcolor {red} {(12y-138)} — 9y = -60 $

$ 96y-1104-9y = -60 $

$ 87y = 1044 $

$ y = 12 $

Подстановка $ y = 12 $, чтобы получить ответ, получаем $ x = 6, y = 12 $.

Q2: Решите следующую проблему со словами.

Вы купили апельсины по 2 доллара за штуку и арбузы по 5 долларов за штуку. Итого 20 апельсинов и арбузов, итого 82 доллара. Сколько апельсинов и арбузов вы купили соответственно?

A2: Ответ.

В задачах о словах в системе уравнений неизвестными числами являются $ x $ и $ y $. Неизвестные числа — это количество купленных вами апельсинов и арбузов. Итак, делаем следующее.

Количество купленных апельсинов: $ x
Количество купленных арбузов: $ y $

Тогда мы можем составить следующие два выражения.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} x + y = 20 \\ 2x + 5y = 82 \ end {array} \ right. \ End {eqnarray} $

Итого количество апельсинов и арбузов — 20 штук.Следовательно, $ x + y = 20 $.

Также количество апельсинов составляет 2 × x $. Сумма арбуза — 5 $ x y $. Общая сумма составляет 82 доллара, поэтому она должна быть 2x + 5y = 82 доллара. Итак, решаем эту систему линейных уравнений. Если мы воспользуемся методом подстановки, то сделаем следующее.

$ x + y = 20 $

$ x = 20-y $

Далее мы подставляем $ x = 20-y $.

$ 2 \ textcolor {red} {(20-y)} + 5y = 82 $

$ 40-2y + 5y = 82 $

$ 3y = 42 $

$ y = 14 $

И, подставив $ y = 14 $, получаем $ x = 6 $.Итак, мы видим, что вы купили 6 апельсинов и 14 арбузов.

Q3: Решите следующую проблему со словами.

Выйдя из дома, вы направились в библиотеку, которая находится в 2400 метрах. Сначала вы бежали со скоростью 100 м / мин, но по дороге устали и шли со скоростью 40 м / мин. Вы добирались до библиотеки за 30 минут. Узнайте, сколько времени вам понадобилось на бег и ходьбу.

A3: Ответ.

Установите время бега равным $ x $ минут, а время ходьбы — $ y $ минут.Поскольку общее время бега и ходьбы составляет 30 минут, справедливо следующее уравнение.

Кроме того, пробег составляет 100 × x $. В отличие от этого пройденное расстояние составляет $ 40 × y $. Поскольку от дома до библиотеки 2400 метров, справедливо следующее уравнение.

Затем решите следующие одновременные уравнения.

$ \ begin {eqnarray} \ left \ {\ begin {array} {l} x + y = 30 \\ 100x + 40y = 2400 \ end {array} \ right. \ End {eqnarray} $

Решено с помощью сложения, результат будет следующим.

$ x + y = 30 $

$ (x + y) \ textcolor {red} {× 40} = 30 \ textcolor {red} {× 40} $

$ 40x + 40y = 1200 $

$ \ begin {array} {r} 40x + 40y = 1200 \\\ underline {-) \ phantom {0} 100x + 40y = 2400} \\ — 60x = -1200 \ end {array} $

Расчет $ -60x = -1200 $, получаем x = 20 $. Подстановка $ x = 20 $ дает $ y = 10 $. Таким образом, время бега составляет 20 минут, а время ходьбы — 10 минут.

Решение систематических уравнений методом сложения и метода подстановки

Используя систему линейных уравнений, мы можем получить ответ, даже если у нас есть два неизвестных числа.