Определение трапеции и свойства: Трапеция. Иллюстрированный гид (ЕГЭ — 2021) — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

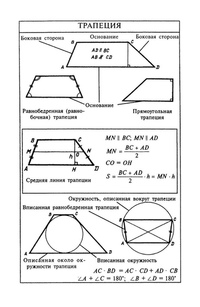
Трапеция. Формулы, признаки и свойства трапеции

Определение.

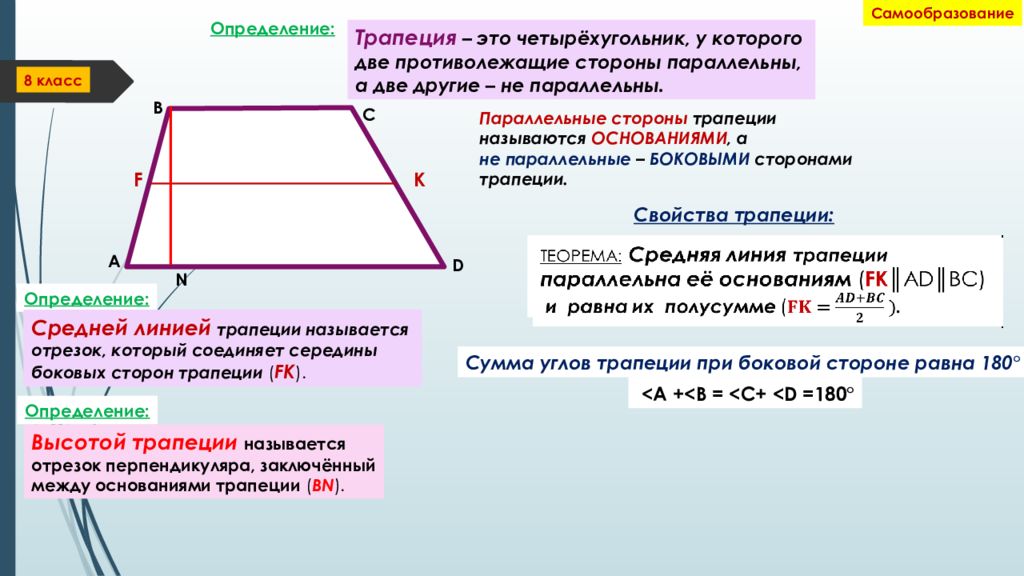
Трапеция — это четыреугольник у котрого две стороны паралельны, а две другие стороны не паралельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четыреугольник у которого одна пара противоположных сторон паралельна и стороны не равны между собой.

Элементы трапеции:

Основы трапеции — параллельные стороны
Боковые стороны — две другие строрны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция — трапеция у которой боковые стороны равны
Прямоугольная трапеция — трапеция у которой одна из боковых сторон перпендикулярна основам


Рис.1		Рис.2

Основные свойства трапеции

1. В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции паралельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины как сотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через середнюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁d₂	=	sin δ ·	d₁d₂
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁d₂	=	sin δ ·	d₁d₂
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos β

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab —	a(d ² — c²)	d₂ =	√	c² + ab —	a(c² — d ²)
			a — b				a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c² —	(	(a — b)² + c² — d ²	)	²
	2				2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
	\|a — b\|

где

p =	a + b + c + d	— полупериметр трапеции.
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
	4√p(p — a)(p — c)(p — d₁)

где
a — большее основание

Окружность вписанная в трапецию

В трапецию можна вписать окружность если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. \circ\).

2) Т.к. $AD\parallel BC$ и $BD$ – секущая, то $\angle DBC=\angle
BDA$ как накрест лежащие.
Также $\angle BOC=\angle AOD$ как вертикальные.
Следовательно, по двум углам $\triangle BOC \sim \triangle AOD$.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$. Пусть $h$ – высота трапеции. Тогда $S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}$. Тогда: \[S_{\triangle AOB}=S_{\triangle ABD}-S_{\triangle AOD}=S_{\triangle ACD}-S_{\triangle AOD}=S_{\triangle
COD}\]

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем параллельность.

Проведем через точку $M$ прямую $MN’\parallel AD$ ($N’\in CD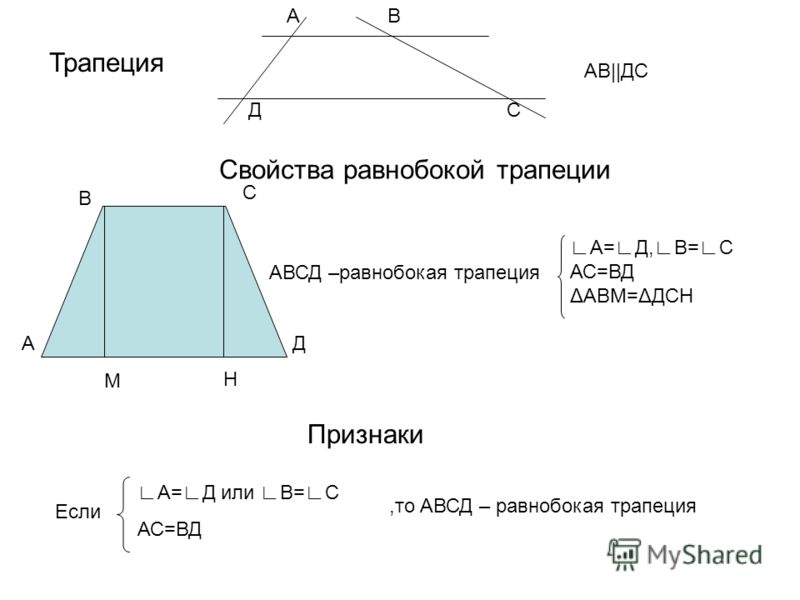$). Тогда по теореме Фалеса (т.к. $MN’\parallel AD\parallel BC, AM=MB$) точка $N’$ — середина отрезка $CD$. Значит, точки $N$ и $N’$ совпадут.

2) Докажем формулу.

Проведем $BB’\perp AD, CC’\perp AD$. Пусть $BB’\cap MN=M’, CC’\cap
MN=N’$.

Тогда по теореме Фалеса $M’$ и $N’$ — середины отрезков $BB’$ и $CC’$ соответственно. Значит, $MM’$ – средняя линия $\triangle
ABB’$, $NN’$ — средняя линия $\triangle DCC’$. Поэтому: \[MM’=\dfrac12 AB’, \quad NN’=\dfrac12 DC’\]

Т.к. $MN\parallel AD\parallel BC$ и $BB’, CC’\perp AD$, то $B’M’N’C’$ и $BM’N’C$ – прямоугольники. По теореме Фалеса из $MN\parallel AD$ и $AM=MB$ следует, что $B’M’=M’B$. Значит, $B’M’N’C’$ и $BM’N’C$ – равные прямоугольники, следовательно, $M’N’=B’C’=BC$.

Таким образом:

\[MN=MM’+M’N’+N’N=\dfrac12 AB’+B’C’+\dfrac12 C’D=\] \[=\dfrac12 \left(AB’+B’C’+BC+C’D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

1) Докажем, что точки $P$, $N$ и $M$ лежат на одной прямой.

Проведем прямую $PN$ ($P$ – точка пересечения продолжений боковых сторон, $N$ – середина $BC$). Пусть она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

Рассмотрим $\triangle BPN$ и $\triangle APM$. Они подобны по двум углам ($\angle APM$ – общий, $\angle PAM=\angle PBN$ как соответственные при $AD\parallel BC$ и $AB$ секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим $\triangle CPN$ и $\triangle DPM$. Они подобны по двум углам ($\angle DPM$ – общий, $\angle PDM=\angle PCN$ как соответственные при $AD\parallel BC$ и $CD$ секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$. Но $BN=NC$, следовательно, $AM=DM$.

2) Докажем, что точки $N, O, M$ лежат на одной прямой.

Пусть $N$ – середина $BC$, $O$ – точка пересечения диагоналей. Проведем прямую $NO$, она пересечет сторону $AD$ в точке $M$. Докажем, что $M$ – середина $AD$.

$\triangle BNO\sim \triangle DMO$ по двум углам ($\angle OBN=\angle
ODM$ как накрест лежащие при $BC\parallel AD$ и $BD$ секущей; $\angle BON=\angle DOM$ как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично $\triangle CON\sim \triangle AOM$. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$. Но $BN=CN$, следовательно, $AM=MD$.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

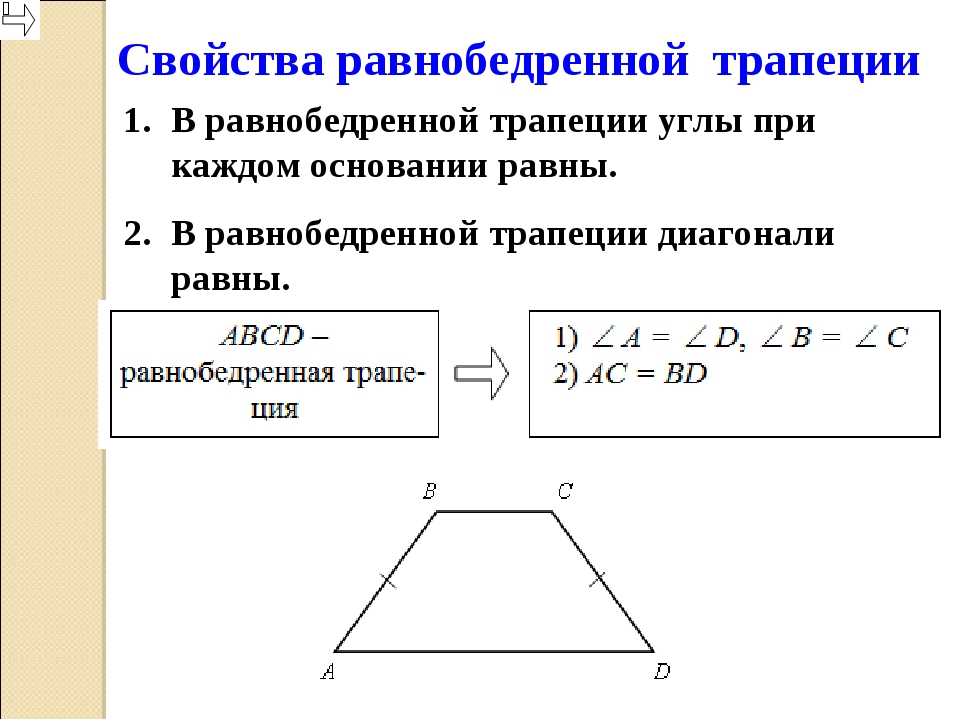
Теоремы: свойства равнобедренной трапеции

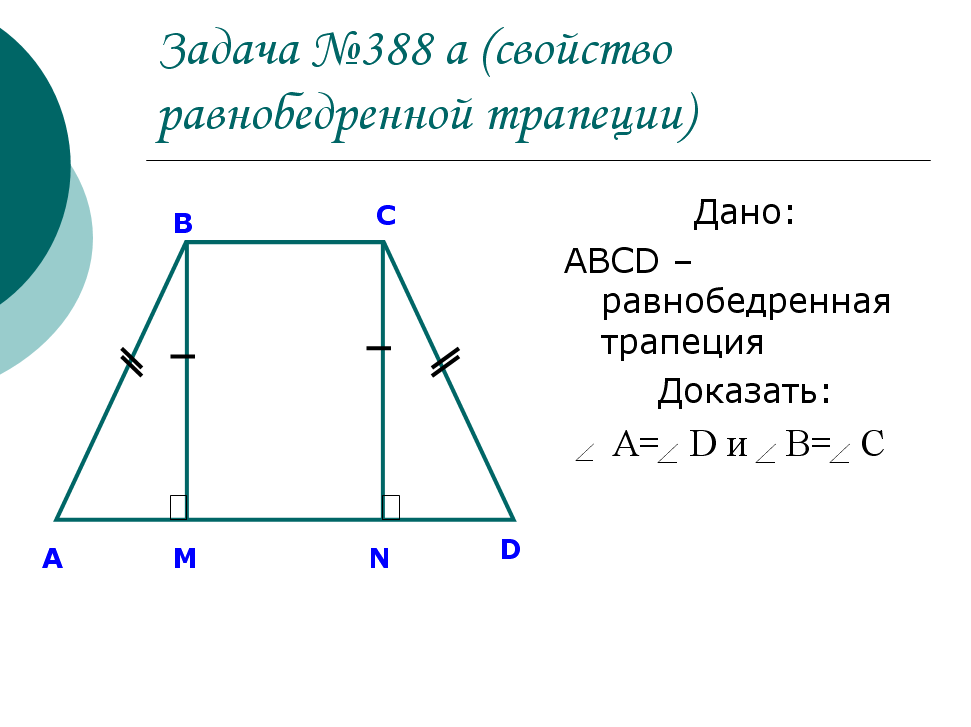
1) У равнобедренной трапеции углы при основании равны.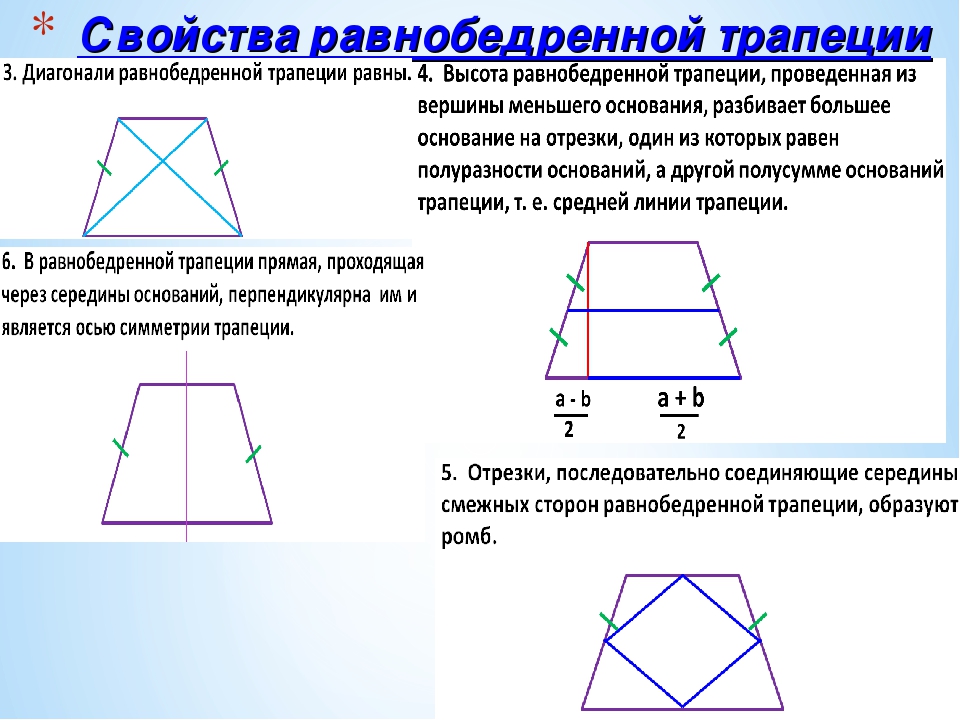

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию $ABCD$.

Из вершин $B$ и $C$ опустим на сторону $AD$ перпендикуляры $BM$ и $CN$ соответственно. Так как $BM\perp AD$ и $CN\perp AD$, то $BM\parallel CN$; $AD\parallel BC$, тогда $MBCN$ – параллелограмм, следовательно, $BM = CN$.

Рассмотрим прямоугольные треугольники $ABM$ и $CDN$. Так как у них равны гипотенузы и катет $BM$ равен катету $CN$, то эти треугольники равны, следовательно, $\angle DAB = \angle CDA$.

Т.к. $AB=CD, \angle A=\angle D, AD$ – общая, то по первому признаку $\triangle ABD=\triangle ACD$. Следовательно, $AC=BD$.

3) Т.к. $\triangle ABD=\triangle ACD$, то $\angle BDA=\angle CAD$. Следовательно, треугольник $\triangle AOD$ – равнобедренный.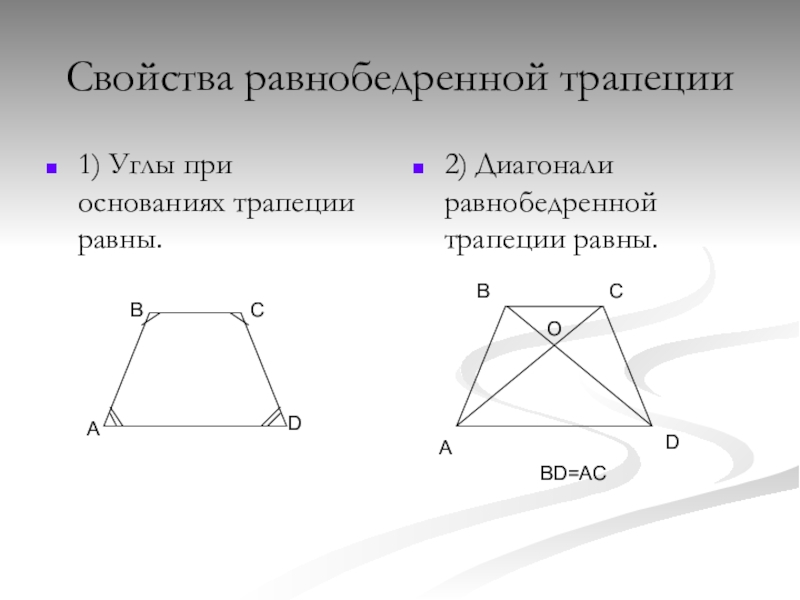 Аналогично доказывается, что и $\triangle BOC$ – равнобедренный.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию $ABCD$, такую что $\angle A = \angle D$.

Достроим трапецию до треугольника $AED$ как показано на рисунке. Так как $\angle 1 = \angle 2$, то треугольник $AED$ равнобедренный и $AE
= ED$. Углы $1$ и $3$ равны как соответственные при параллельных прямых $AD$ и $BC$ и секущей $AB$. Аналогично равны углы $2$ и $4$, но $\angle 1 = \angle 2$, тогда $\angle 3 = \angle 1 = \angle 2 =
\angle 4$, следовательно, треугольник $BEC$ тоже равнобедренный и $BE = EC$.

В итоге $AB = AE — BE = DE — CE = CD$, то есть $AB = CD$, что и требовалось доказать.

2) Пусть $AC=BD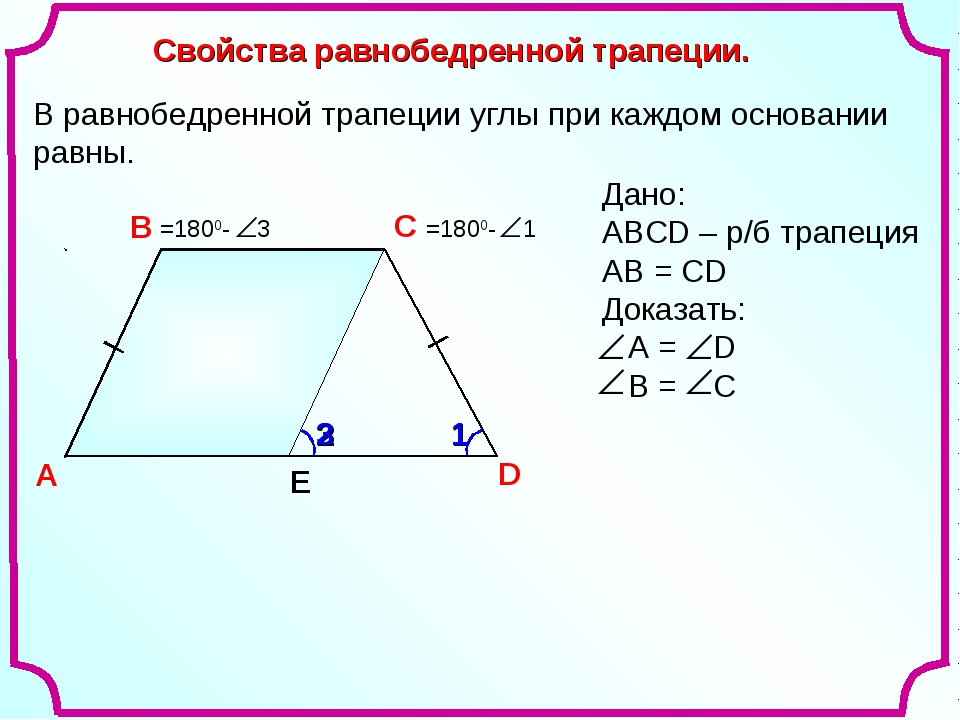$. Т.к. $\triangle AOD\sim \triangle BOC$, то обозначим их коэффициент подобия за $k$. Тогда если $BO=x$, то $OD=kx$. Аналогично $CO=y \Rightarrow AO=ky$.

Т.к. $AC=BD$, то $x+kx=y+ky \Rightarrow x=y$. Значит $\triangle AOD$ – равнобедренный и $\angle OAD=\angle ODA$.

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$ ($AC=BD, \angle OAD=\angle ODA, AD$ – общая). Значит, $AB=CD$, чтд.

Свойства трапеции, с примерами

Параллельные стороны называются основаниями трапеции. Две другие стороны называются ее боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

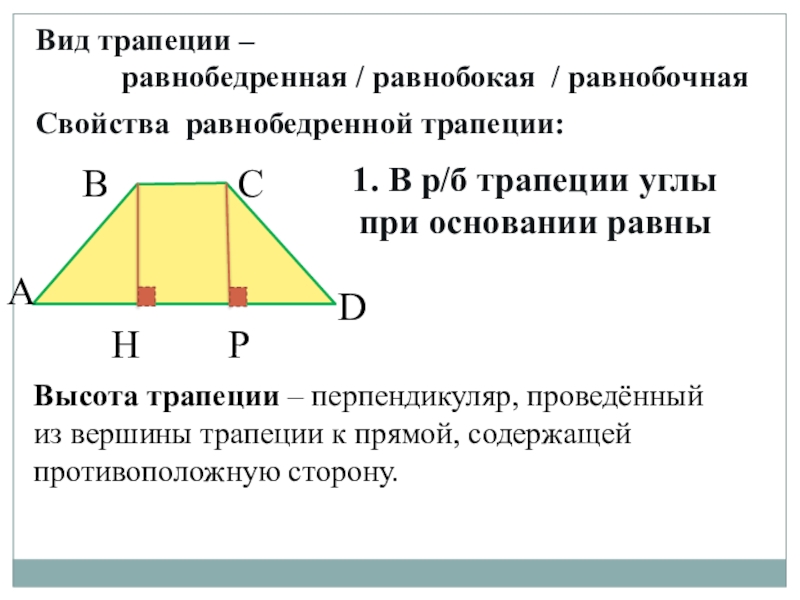
Трапеция, у которой боковые стороны равны, называется равнобокой (равнобедренной) трапецией. Трапеция, у которой при одной боковой стороне прямые углы называется прямоугольной.

Свойства трапеции

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.

Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

Треугольники, образованные при пересечении диагоналей и лежащие на основаниях трапеции, подобные:

Треугольники, образованные при пересечении диагоналей и лежащие на боковых сторонах трапеции, равновеликие:

Если трапеция равнобокая, то ее диагонали равны и углы при основании равны.

Если трапеция равнобокая, то около нее можно описать окружность.

Если сумма оснований трапеции равна сумме боковых сторон, то в нее можно вписать окружность.

Площадь трапеции вычисляется по формуле

где – основания трапеции, – высота трапеции.

Если в трапецию вписана окружность радиуса и она делит боковую сторону точкой касания на два отрезка длины и , то .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Параллелограмм и трапеция

Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.

Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.

Свойства параллелограмма

1. Противолежащие стороны равны.
На рис. 11 AB = CD; BC = AD.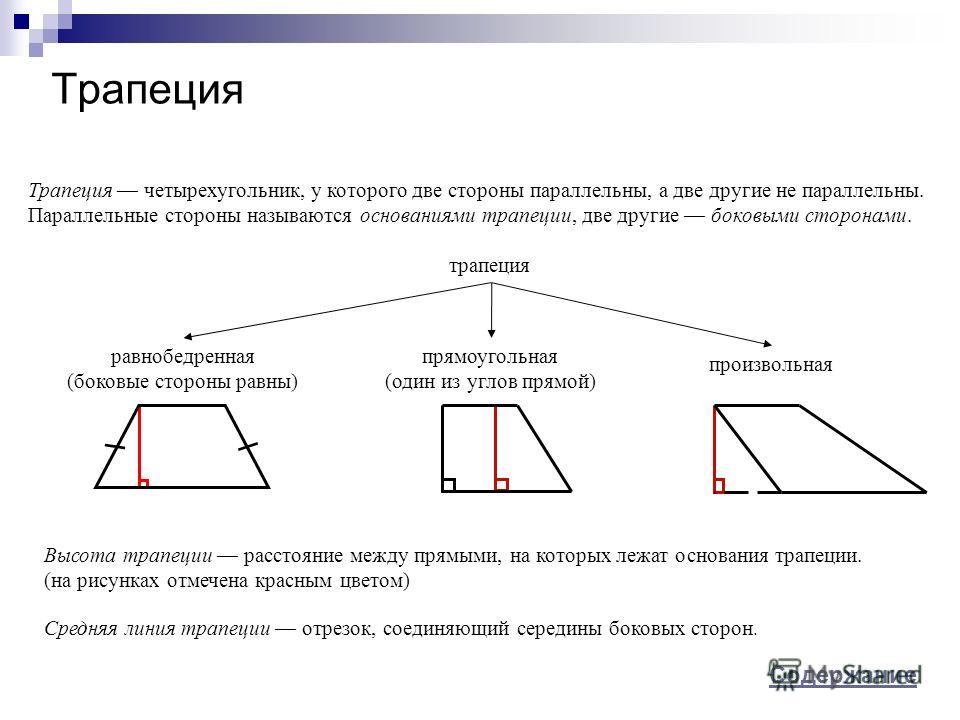

2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A = ∠C; ∠B = ∠D.

3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.

На рис. 11 отрезки AO = OC; BO = OD.

Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.

Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.

Виды трапеций

1. Трапеция, у которой боковые стороны не равны,
называется разносторонней (рис. 12).

2. Трапеция, у которой боковые стороны равны, называется равнобокой (рис. 13).

3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной (рис. 14).

Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).

Площадь параллелограмма и трапеции

Правило. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Правило. Площадь трапеции равна произведению полусуммы ее оснований на высоту (рис. 17).

У прямоугольной трапеции (рис. 14) высотой служит боковая сторона, перпендикулярная основаниям. Вместо полусуммы оснований трапеции можно взять длину средней линии трапеции (на рис. 15 отрезок MN).

Проектная работа «Трапеция и её свойства. Решение задач»

Слайд 1

Презентация по теме «Трапеция и её свойства. Решение задач». План Определение трапеции , ее элементы и виды. Общие свойства . Свойства равнобедренной трапеции . Вписанная и описанная окружность . Площадь . Возможные варианты задач в ГИА-9 про трапеции (часть 2). Подготовила ученица 9 класса «А» Петренко Ангелина

Слайд 2

Определение трапеции и ее виды. Трапе́ция — четырёхугольник, у которого только одна пара противолежащих сторон параллельна. Элементы трапеции Параллельные стороны называются основаниями трапеции. (BC и AD) Две другие стороны называются боковыми сторонами. (AB и CD) Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. (LM) Расстояние между основаниями называется высотой трапеции. (LH) В основание С L M А D основание

Слайд 3

Виды трапеций. Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной . Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной .

Слайд 4

Свойства трапеции. 1) Средняя линия трапеции параллельна основаниям и равна их полусумме. LM=(AB+DC)/2 2) Отрезок, соединяющий середины диагоналей, равен полуразности оснований. NK=(DC-AB)/2 3) Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен 2 *AB*DC /( AB + DC ) Формула Буракова ) А В E O F L M D C

Слайд 5

Свойства трапеции. 3) Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середины оснований лежат на одной линии .( O, G, W, V a) 4) Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности . VW=(AD-BC)/2, если ВА D + CAD=90° 5) В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон. ( AD+BC=AB+CD) G B V C A D

Слайд 6

Свойства трапеции. 6) Биссектрисы односторонних углов пересекаются под прямым углом. ( AFB= CED=90°) 8) Отрезок, соединяющий точки пересечения биссектрис односторонних углов параллелен основаниям. ( FE ΙΙ BC ΙΙ AD) B C F E A D

Слайд 7

Свойства равнобедренной трапеции.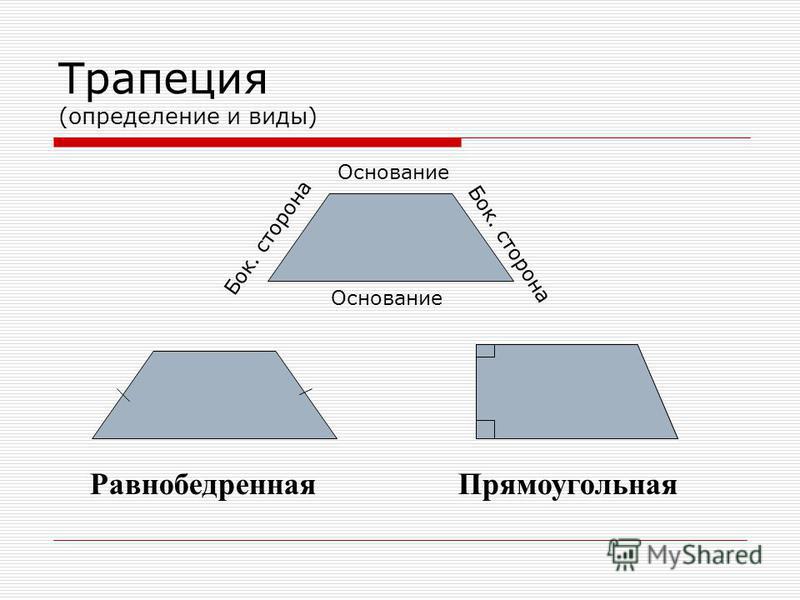 1) В равнобедренной трапеции углы при любом основании равны . 2) В равнобедренной трапеции длины диагоналей равны . АС=В D 3) Если трапецию можно вписать в окружность , то она равнобедренная. AB=CD B C A D

Слайд 8

Свойства равнобедренной трапеции. 4) Около равнобедренной трапеции можно описать окружность. (AB=CD) 5) Если в равнобедренной трапеции диагонали перпендикулярны , то высота равна полусумме оснований. BH=(AD+BC)/2 B C A D

Слайд 9

Свойства равнобедренной трапеции. 6) Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции. (NM) 7) Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. HD=(AD+BC)/2 ; AH=(AD-BC)/2 B C N A M D

Слайд 10

Вписанная и описанная окружность . 1) Если сумма оснований трапеции равна сумме боковых сторон , то в неё можно вписать окружность. (AB+CD=BC+AD) 2) Если трапеция равнобедренная , то около неё можно описать окружность.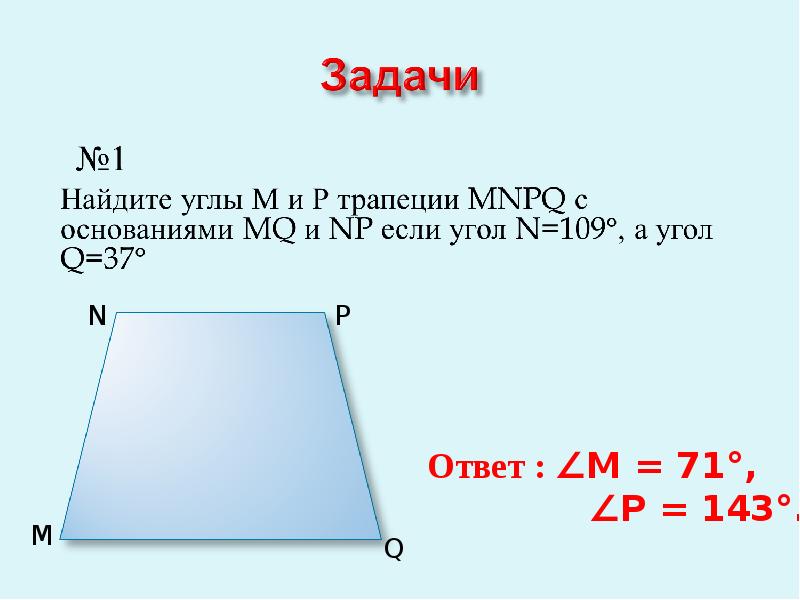 2 =АН*НВ=4 ( как средний пропорциональный) АН+НВ=5. Решив систему, получаем НВ=1=ВМ=МС(как касательные из одной точки и т.к. трапеция равнобедренная) 4)Т.к. в трапецию можно вписать окружность, то АВ+С D= ВС+ AD=5+5=10 S ABCD=1/2(BC+AD)*BH=20 Ответ:20

Слайд 20

Возможные варианты задач в ГИА-9 про трапеции (часть 2). 23. Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке P , Q – точка пересечения диагоналей этой трапеции. Найдите отношение площади треугольника ADQ к площади треугольника BCP , если известно, что AD=3BC . P B N C Q S A D

Слайд 21

APD подобен ВРС(т.к. ВС ΙΙ А D) K= AD/BC=3DC/DC=3 , значит, PN/PH=1/3 BCQ подобен AQD( т.к. ВС ΙΙ А D ) К1= BC/AD=1/3 , значит, NS/SH=1/3 3) Пусть PN=x , тогда PH=3x Пусть NS=y , тогда SH=3y PH=PN+NS+SH=x+y+3y=x+4y X+4y=3x 2y=x Значит , PN=2y 4) S ADQ/S BPC=(AD*HS*2)/(2*BC*PN)=3*3/2=4.5 Ответ:4,5

Трапеция. Свойства трапеции — презентация онлайн

Тема: ТРАПЕЦИЯ
Тема: ТРАПЕЦИЯ
B
A
C
ABCD –
трапеция
D
BC, AD – основания трапеции, ВС ║ АD
AB,CD – боковые стороны
Определение:
Четырехугольник, у которого две стороны
параллельны, а две другие не параллельны
называется трапецией.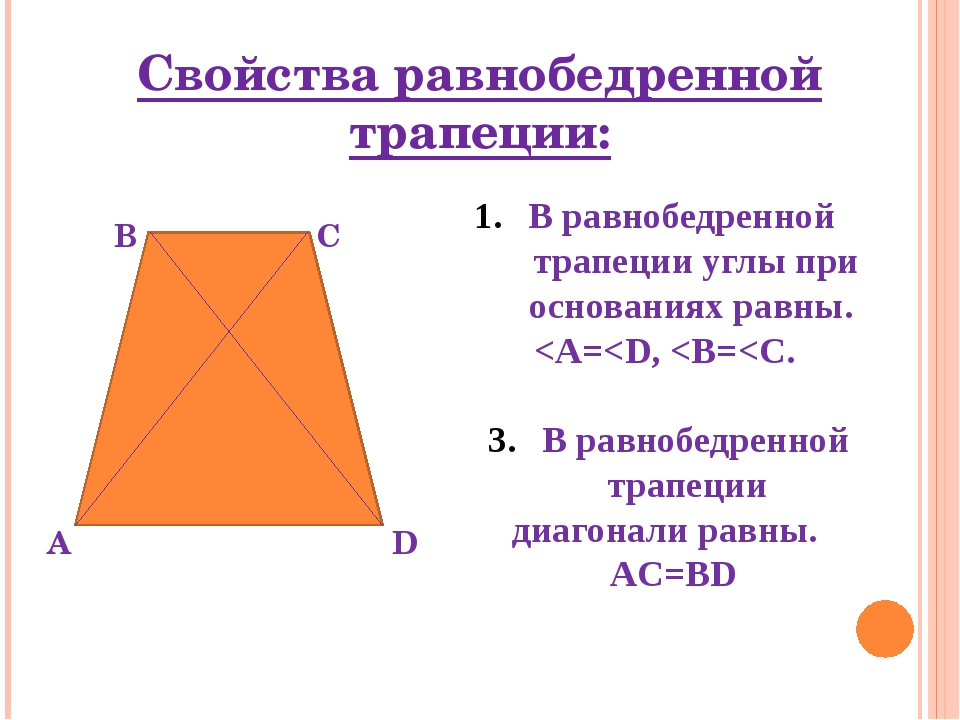
Равнобедренная трапеция
B
C
AB=CD
ABCD равнобедренная
трапеция
A
D
Определение:
Трапеция, у которой боковые стороны
равны, называется равнобедренной.
Свойства равнобедренной трапеции
1. В равнобедренной трапеции углы при
каждом основании равны.
2. В равнобедренной трапеции диагонали
равны.
Признаки равнобедренной трапеции
1. Если углы при основании трапеции
равны, то она равнобедренная.
2. Если диагонали трапеции равны, то
она равнобедренная.
Прямоугольная трапеция
B
C
A=
В = 900
ABCD прямоугольная
трапеция
A
D
Определение:
Трапеция, у которой один из углов
прямой, называется прямоугольной.
Средняя линия трапеции
B
MN — средняя линия
трапеции
C
N
M
D
A
Определение:
Отрезок, соединяющий середины боковых
сторон, называется средней линией трапеции.
Свойство средней линии трапеции
Средняя линия трапеции параллельна
основаниям и равна их полусумме
B
M
A
C
MN ║ ВС ║ АD
N
MN = ( BC + AD) / 2
D
Задача 1
B
C
Дано: ABCD – трапеция,
АВ = СD = ВС.
Найти: углы трапеции.
A
D
Задача 2
5
B
C
Дано: ABCD – трапеция,
АD = 7, ВС = 5, АВ = CD.
Найти: СD.
600
A
600
К
Р
D
Задача 3
C
B
AD = 30, угол С = 1350,
1350
СС1 ┴ AD, угол ВАС = 450
450
A
Дано: ABCD – трапеция,
Найти: ВС.
C1
D
В
М
Задача 4
С
Дано: ABCD – трапеция,
МК – средняя линия.
К
ВС =13, МК = 25.
Найти: АD.
А
D
Самое главное сегодня!
1. Какой четырёхугольник называется
трапецией?
2. Какая трапеция называется равнобедренной?
3. Какая трапеция называется прямоугольной?
4. Сформулируйте свойства и признаки
равнобедренной трапеции.
5. Что такое средняя линия трапеции?
Домашнее задание
П. 44, записи в тетрадях,
№ 387, № 390.
Всем спасибо!
Желаю успехов!

Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

18 января 2021

Определение
Происхождения слова
Стороны трапеции
Равнобедренная и прямоугольная
Свойства трапеций

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo. ru. В этой статье мы решили подробно рассказать о такой геометрической фигуре, как ТРАПЕЦИЯ.

Ее подробно изучают на уроках геометрии в 8-м классе. И эти уроки являются частью общего знакомства школьников с различными четырехугольниками.

Определение трапеции

Трапеция – геометрическая фигура, которая представляет собой четырехугольник, у которого две противоположные стороны располагаются на параллельных прямых. А две другие стороны должны, наоборот, быть не параллельными.

Вот так выглядит классическая трапеция:

У этой фигуры стороны АВ и CD являются параллельными. А вот AD и CB – нет.

Происхождения слова

Первое упоминание об этой фигуре встречается еще в трудах известного древнегреческого математика Евклида.

В его книге «Начала» этим термином описывается абсолютно любой четырехугольник, который не является параллелограммом.

Если кто не помнит, параллелограммом называют четырехугольник, у которого противоположные стороны параллельны.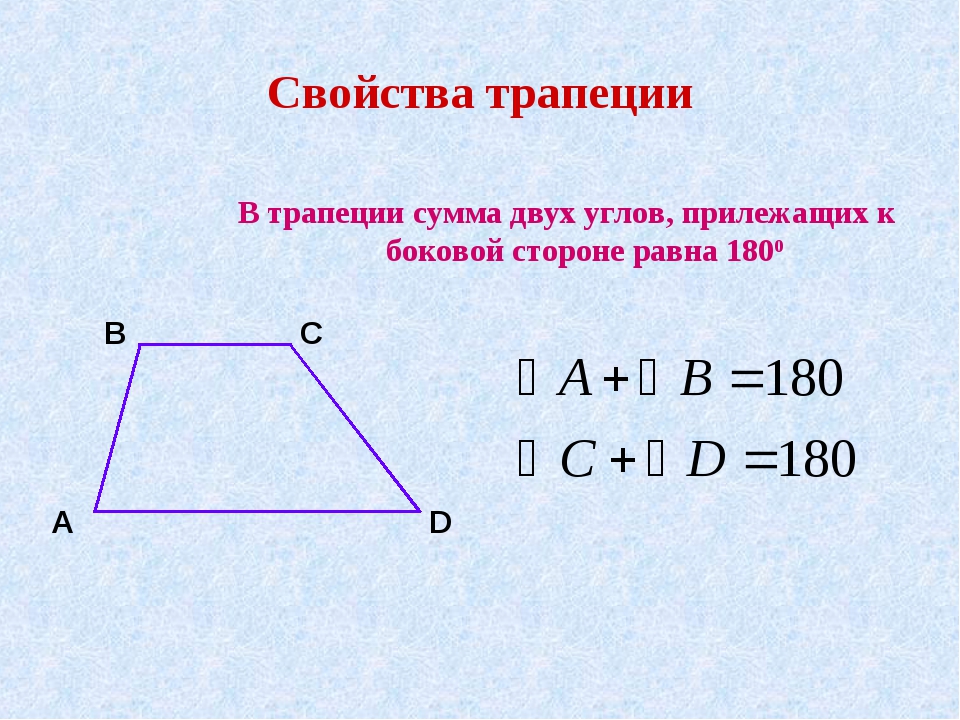 Выглядит эта фигура в классическом понимании вот так:

Интересно, что и всем известные фигуры – квадрат, прямоугольник (что это?) и ромб (это как?) – также являются частным случаем параллелограмма. Ведь действительно – у них противоположные стороны параллельны друг к другу.

И получается, что Евклид был в целом прав. Он просто поделил все четырехугольники на две большие категории – параллелограммы и трапеции.

Кстати, само слово ТРАПЕЦИЯ также имеет греческое происхождение. В древние времена оно звучало как «трапедзион». И в переводе это означает «обеденный стол». Поэтому слово «трапеза», которое у нас является синонимом любого приема пищи тоже родом оттуда.

Стороны трапеции

Парные стороны трапеций имеют свои названия:

Основания трапеции – стороны, которые располагаются на параллельных прямых.
Боковые – стороны, которые не находятся на параллельных прямых.

Закрепим это с помощью рисунка:

В данном случае стороны АВ и CD параллельны друг другу. А значит, именно они являются основаниями. А вот АС и BD – наоборот, явно не параллельны. И соответственно, это боковые стороны.

Кстати, расположение сторон не зависит от расположения самой фигуры. Даже вот в таких положениях

все равно параллельные стороны будут считаться основаниями, а непараллельные – боковыми.

Равнобедренная и прямоугольная трапеции

Вариант трапеции, который мы рассмотрели – это самые распространенные виды геометрической фигуры. Но есть и частные случаи:

Равнобедренная трапеция – та, у которой боковые (не параллельные) стороны равны. Ее еще называют равнобокой или равнобочной.

Выглядит она вот так:

В данном примере графически показано, что стороны AD и ВС равны между собой. Об этом свидетельствуют небольшие черточки.

Прямоугольная трапеция – та, у которой одна из боковых сторон и основания образовывают прямой угол.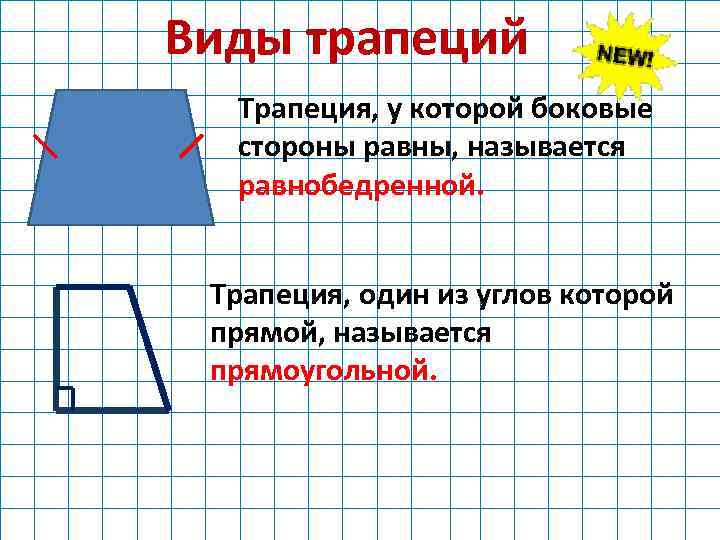

Выглядит она вот так:

В данном примере, углы DAB и ADC являются прямыми, то есть равны 90 градусам. А соответственно, трапеция называется прямоугольной.

Тут важно заметить, что под прямым углом к основанию должна идти только одна боковая сторона. Если будут обе, то трапеция автоматически превратится в квадрат.

Свойства трапеций

С трапециями связаны несколько понятий в геометрии, которые активно используются для решения различных теорем.

Средняя линия

Средняя линия трапеции – это отрезок, который идет параллельно основаниям и соединяет середины:

Со средней линией связана одна интересная теорема. Очень часто на уроках геометрии школьников просят определить ее длину. И сделать это весьма просто.

Длина средней линии трапеции равна половине суммы длин ее оснований.

Звучит может и несколько тяжеловато. Но на деле – это весьма просто. Так, чтобы посчитать в нашем примере длину отрезка MN, который является средней линией, надо применить формулу:

MN = (AD + ВС) / 2

И это правило распространяется на все виды трапеций.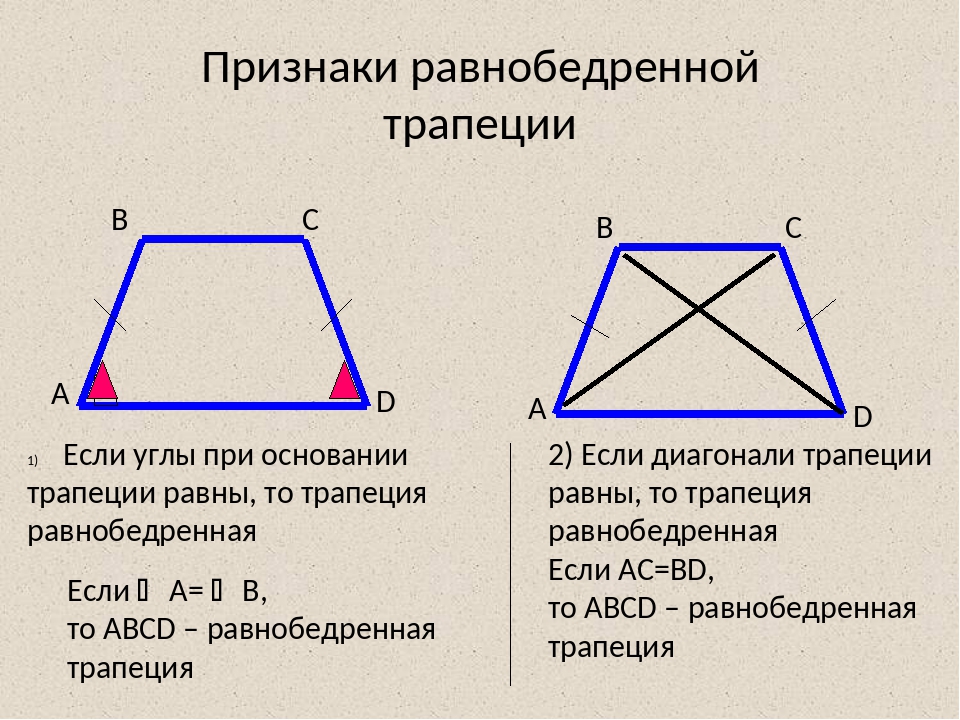

Биссектриса углов трапеции

Биссектриса – это линия (луч), которая делит угол пополам. Так вот

Любая биссектриса, выведенная из угла трапеции, отсекает на основании отрезок, равный по длине боковой стороне.

На данном рисунке отрезок АЕ является биссектрисой угла ABD. И исходя из этого, отрезки АВ и ВЕ равны между собой, о чем свидетельствуют небольшие черточки на них.
В то же время у биссектрис в трапеции есть еще одно свойство.

Две биссектрисы, выведенные из углов одной боковой стороны, пересекаются под прямым углом.

Все эти теоремы в процессе школьного обучения, ученикам еще необходимо доказывать. Ну а мы решили не приводить долгие математические и геометрические выкладки. Просто примите как данность!

Вот и все, что мы хотели рассказать вам о трапеции.

трапеций: определение и свойства — математический класс [видео 2021] </h2> <h3> Свойство </h3> Трапеции имеют одно свойство, которое необходимо соблюдать. Свойство в том, что у него должна быть одна пара параллельных сторон. Если вы посмотрите на трапецию, вы увидите, что у нее две плоские стороны. Эти плоские стороны параллельны друг другу. Если вы продлите эти линии, они никогда не встретятся. Попытайся. <h3> Словарь </h3> При работе с трапециями есть несколько слов, которые мы должны добавить в наш словарь. Первое слово — это оснований , которые являются сторонами, параллельными друг другу. Нарисуйте треугольник, нижняя сторона которого будет одной из ваших основ. Сторона, полученная путем срезания вершины треугольника, является другой основой.<img src='/800/600/https/sun1-14.userapi.com/IcSGlv6-tNM3Z9OGSJ365EhytlKkzYIA9J7dDg/H1fwXF1CRqU.jpg' /> Второе слово, которое следует рассмотреть, — это ножек . Это наклонные стороны, которые образуют левый и правый край трапеции, которая находится самой длинной стороной вниз. Возвращаясь к разрезанному треугольнику, ноги — это стороны, которые поднимаются и встречаются на вершине треугольника.Но поскольку вершина треугольника срезана, ноги заканчиваются там, где произошел срез. Третье слово — высота , что просто высота трапеции. Это то, насколько высока трапеция, когда вы сидите на плоской поверхности. Вы можете определить высоту, измерив расстояние от одной базы до другой. <h3> Специальные трапеции </h3> Когда ноги вашей трапеции имеют одинаковую длину и когда углы, которые каждая сторона образует с основанием, равны, тогда у вас есть так называемая равнобедренная трапеция .Это означает, что, если трапеция расположена ровно с самым длинным основанием вниз, два нижних угла будут равны, а два верхних угла также будут равны. Представьте себе эту трапецию как равнобедренный треугольник (треугольник с двумя равными сторонами и двумя равными углами) с отрезанной вершиной.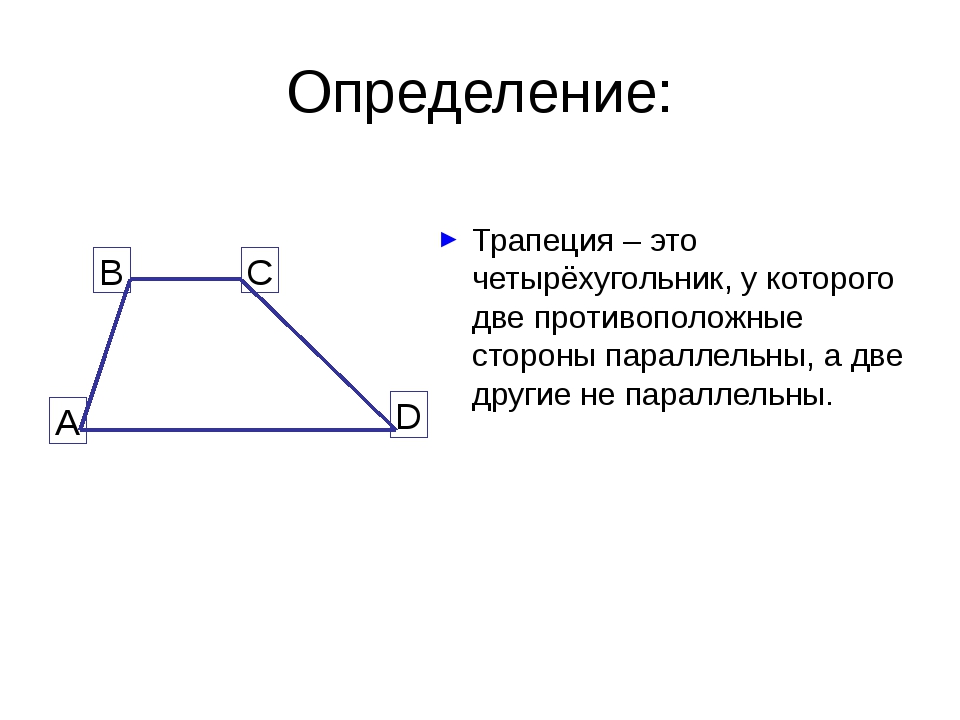<img src='/800/600/https/ds02.infourok.ru/uploads/ex/1343/0000c30a-a4ebc219/img2.jpg' /> Теперь представьте себе разносторонний треугольник (треугольник, все стороны которого имеют разную длину) и отрежьте его вершину. Когда вы это сделаете, вы получите разностороннюю трапецию , трапецию, ноги которой имеют разную длину. Третий вид специальной трапеции — это правая трапеция , трапеция, в которой одна ножка перпендикулярна основанию. Он будет выглядеть как прямоугольный треугольник (треугольник с одним прямым углом) с обрезанной вершиной. <h3> Краткое содержание урока </h3> Вау! Посмотрите, что мы узнали всего за несколько минут! Мы узнали, что трапеция представляет собой четырехстороннюю плоскую форму с одной парой параллельных сторон. Трапеции выглядят как треугольники со срезанной вершиной. Единственное свойство, которому должны соответствовать все трапеции, — это то, что у них должны быть две стороны, параллельные друг другу. Специальные слова, которые мы используем с трапециями, — это основания, ноги и высота. Основания относятся к двум сторонам, параллельным друг другу.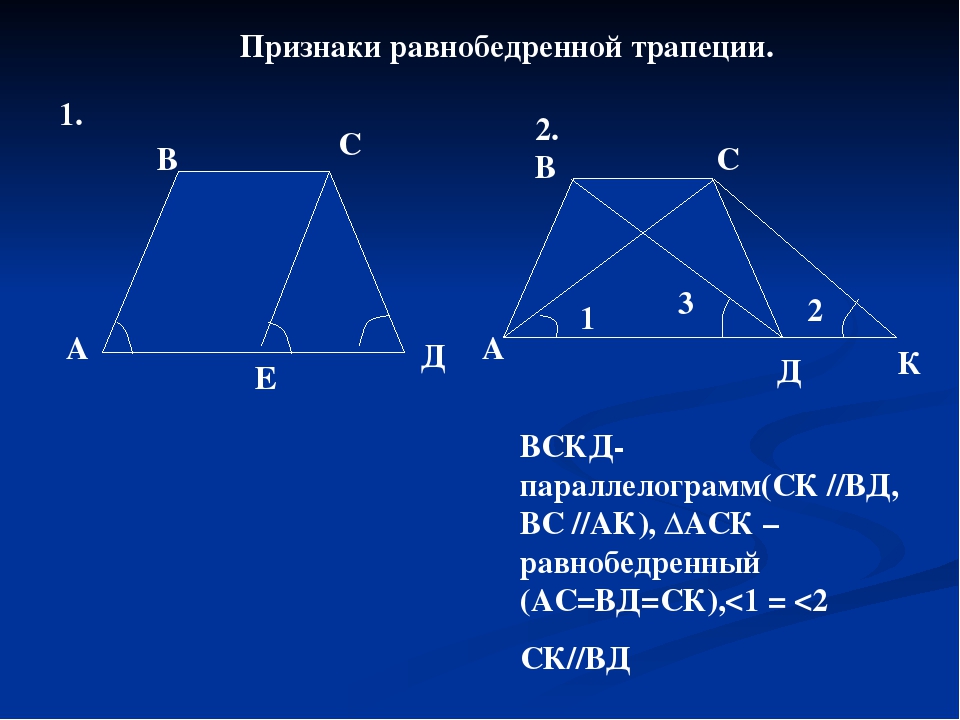<img src='/800/600/https/ds05.infourok.ru/uploads/ex/00fe/000a74c5-d08cd383/img6.jpg' /> Ножки , относятся к двум наклонным сторонам, а высота — это просто высота трапеции, когда она сидит ровно, ее самое длинное основание опущено. Особый случай равнобедренной трапеции возникает, когда у вас есть ноги, равные по длине друг другу, и углы, образованные ногами и основаниями, также равны друг другу.Итак, у равнобедренной трапеции два нижних и два верхних угла равны друг другу. Особый случай разносторонней трапеции возникает, когда обе ноги имеют разную длину, а правая трапеция возникает, когда одна нога перпендикулярна основанию. <h3> Результаты обучения </h3> Усвоение информации из этого урока может привести к вашей способности: <ul> <li> Распознавать свойство, связанное с трапециями </li> <li> Определяет основания, опоры и высоту относительно трапеций </li> <li> Характеризуйте особые трапеции: равнобедренную, разностороннюю и правую </li> </ul> <h2><span class="ez-toc-section" id="%D0%A4%D0%BE%D1%80%D0%BC%D0%B0_%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D1%8F_-_%D1%8D%D0%BB%D0%B5%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D1%80%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0"> Форма: трапеция — элементарная математика </h2> <h3> Значение </h3> Трапеция — четырехугольник, по крайней мере, с одной парой параллельных сторон.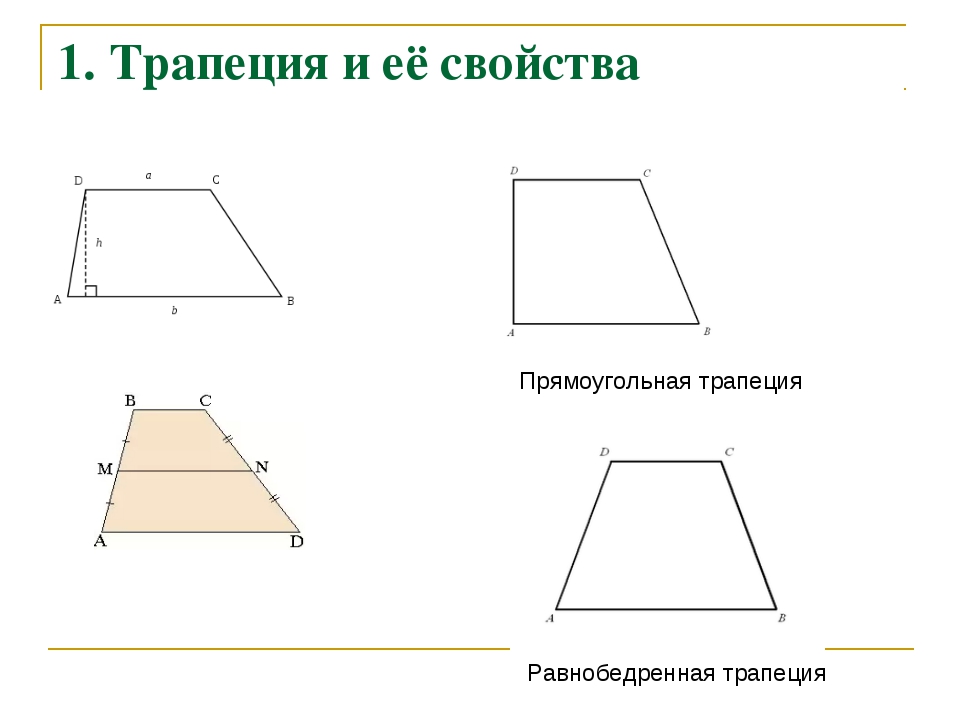<img src='/800/600/https/ds02.infourok.ru/uploads/ex/036f/00035ece-90406bcc/img2.jpg' /> Никакие другие особенности не имеют значения. (В англоязычных странах за пределами Северной Америки эквивалентным термином является трапеция.) Параллельные стороны могут быть вертикальными, горизонтальными или наклонными. Фактически, по определению, даже это трапеция, потому что у нее есть «по крайней мере одна пара параллельных сторон» (и никакие другие особенности не имеют значения) как есть. На этих фигурах две другие стороны также параллельны, и поэтому они удовлетворяют не только требованиям для того, чтобы быть трапецией (четырехугольник, по крайней мере, с одной парой параллельных сторон), но также и требованиям для того, чтобы быть параллелограммом. Приведенное выше определение принято в математическом сообществе и, все чаще, в образовательном сообществе. Многие источники, относящиеся к школьному образованию, исторически ограничивали определение трапеции, требуя ровно одной пары параллельных сторон. Этот более узкий вид исключает параллелограммы как подмножество трапеций и оставляет только такие фигуры, как, и.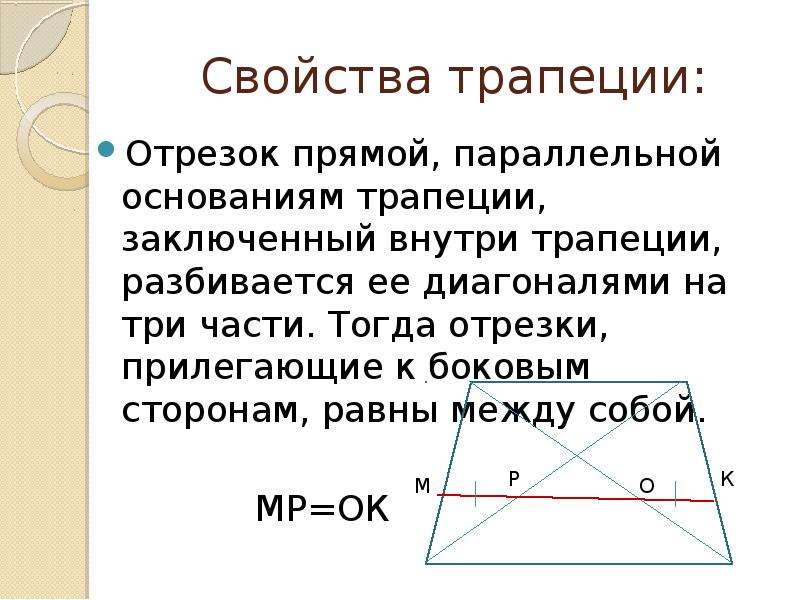<img src='/800/600/https/mypresentation.ru/documents_6/d276c634fab68306a55080f3cda95cd8/img4.jpg' /> Это более узкое определение трактует трапеции, как если бы они были треугольниками с «одной вершиной, отрезанной параллельно противоположной стороне.«Даже с ограниченным определением для учащихся важно видеть нестандартные примеры — асимметричные, как примеры зеленого и коричневого, и в нестандартных ориентациях, как красный пример, — чтобы создаваемое ими изображение фокусировалось на Существенная особенность: пара параллельных сторон. <h3> Классифицирующие трапеции </h3> Параллелограммам с особыми характеристиками, такими как прямые углы или все совпадающие стороны (или и то и другое), даны собственные отличительные имена: прямоугольник, ромб и квадрат.Единственная особенность трапеции , которой присвоено собственное отличительное имя, — это вторая пара параллельных сторон, которая превращает специальную трапецию в параллелограмм. Когда две стороны (кроме оснований) имеют одинаковую длину, трапеция называется равнобедренной («равнобедренная трапеция»), так же как треугольники с двумя сторонами равной длины (кроме основания) называются равнобедренными треугольниками.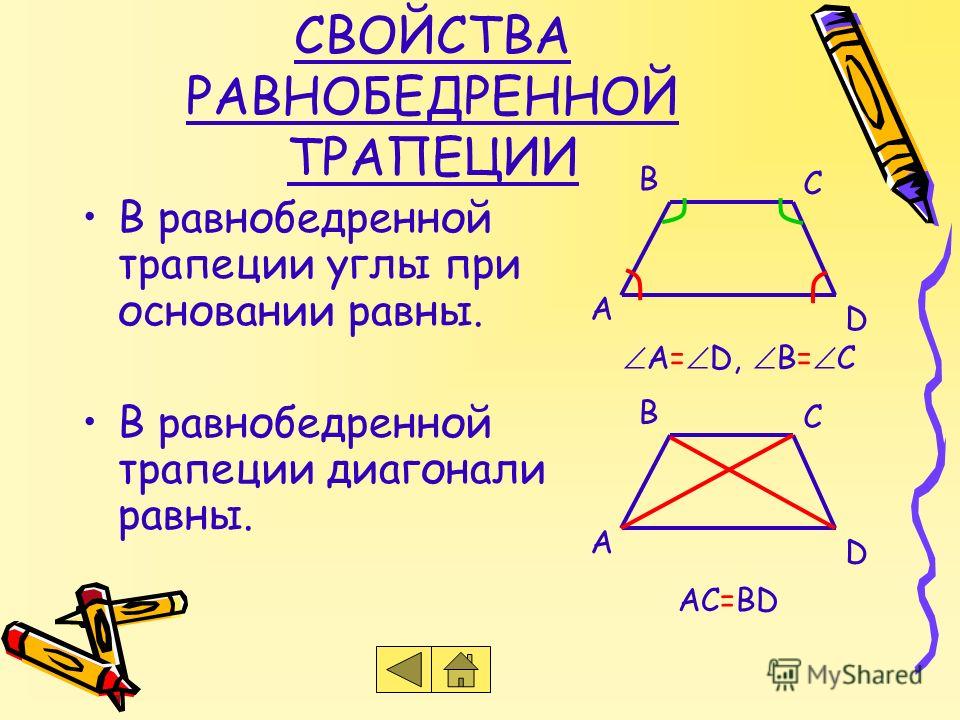<img src='/800/600/http/images.myshared.ru/6/550191/slide_13.jpg' /> Никакие другие отличительные названия не используются для трапеций с особыми характеристиками (например, прямые углы или три совпадающие стороны). <h3> Что одним словом? </h3> Суффикс -оид предполагает, что он «похож» на что-то, но не на то же самое: сфероид похож на сферу, но не обязательно на идеальную сферу; гуманоид похож на человека, но не на человека; и трапеция имеет форму трапеции, но не трапеция. Современное значение trapeze предполагает цирковые качели ( — это часто трапециевидная форма, сиденье должно быть параллельно перекладине, на которой свисает трапеция), но trapeze первоначально означало «стол», от tra ( «четыре», как в tetra- ) pez («нога» или «ступня», которые мы чаще видим как ped , как в pedal или pedestrian ). <h2><span class="ez-toc-section" id="%D0%A2%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D1%8F_-_%D0%BE%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%B8_%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%D1%8B"> Трапеция — определение, свойства, формулы и примеры </h2> <h3> Определение </h3> Трапеция — это плоская геометрическая форма с четырьмя прямыми сторонами, имеющая по крайней мере одну пару противоположных параллельных сторон.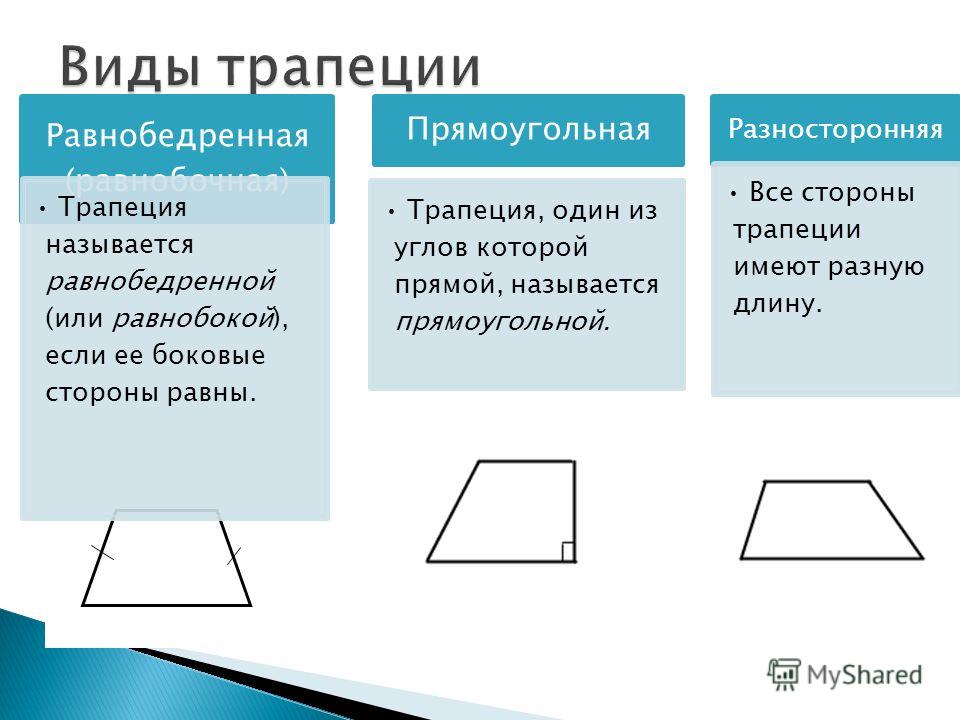<img src='/800/600/http/images.myshared.ru/6/685930/slide_5.jpg' /> Это похоже на треугольник, у которого срезана верхняя часть. Параллельные стороны являются основаниями, а две другие стороны называются ножками или боковыми сторонами. Его также называют трапецией в Великобритании и некоторых других частях света. Трапеция <h3> Недвижимость </h3> Свойства трапеции <ol type="1"> <li> Имеет четыре стороны и четыре угла; в трапеции ABCD, AB, BC, CD и DA — четыре стороны, составляющие углы ∠DAB, ∠ABC, ∠BCD, а ∠CDA </li> <li> Имеет одну пару параллельных сторон.Две параллельные стороны — это основания, а непараллельные стороны — ноги; здесь AD = короткое основание, BC = длинное основание, в то время как AB = отрезок 1 и CD = отрезок 2, и AD ∥ BC </li> <li> Смежные углы в сумме составляют 180 °; Итак, DAB + ∠ABC = 180 °, ∠ABC + ∠BCD = 180 °, ∠BCD + ∠CDA = 180 ° и ∠CDA + ∠DAB = 180 ° </li> <li> Медиана параллельна двум основаниям и разделяет непараллельные стороны на две равные части; Итак, EF ∥ AD и EF ∥ BC </li> </ol> <h3> Формулы </h3> <h4> Медиана </h4> Это отрезок посередине между двумя основаниями.<img src='/800/600/https/cf2.ppt-online.org/files2/slide/k/kOuiWxMaepcvY51tAdmRbNFsPgjDoSQJKTUrV6/slide-16.jpg' /> Его еще называют средней линией или средним сегментом. Формула приведена ниже: Медиана трапеции <dd> Найдите середину трапеции с основаниями размером 7 м и 9 м. </dd> Решение: Как известно, Медиана ( M ) = ½ ( a + b ) , здесь a = 9 м и b = 7 м = ½ (9 + 7) м = 16/2 м = 8 м <h4> Площадь </h4> Общее пространство, ограниченное трапецией.Формула приведена ниже: Площадь трапеции <dd> Найдите площадь трапеции, когда два основания составляют 8 см и 6 см, а высота — 10 см </dd> Решение: Как известно, Площадь ( A ) = ½ ( a + b ) × h , здесь a = 8 см, b = 6 см, и h = 10 см = 1/2 × (8 + 6) × 10 см 2 = ½ × 14 × 10 см 2 = 70 см 2 <dt> Задача: Нахождение площади трапеции, когда известны МЕДИАНА и ВЫСОТА </dt> <dd> Найдите площадь трапеции, у которой медиана 5 см и высота 11 см </dd> Решение: Здесь мы воспользуемся альтернативной формулой, A = м × h , здесь м = медиана и h = высота В этой трапеции м = 5 см и h = 11 см Так как, A = м × h = 5 × 11 см 2 = 55 см 2 <h4> Периметр </h4> Общее расстояние, пройденное по краю трапеции.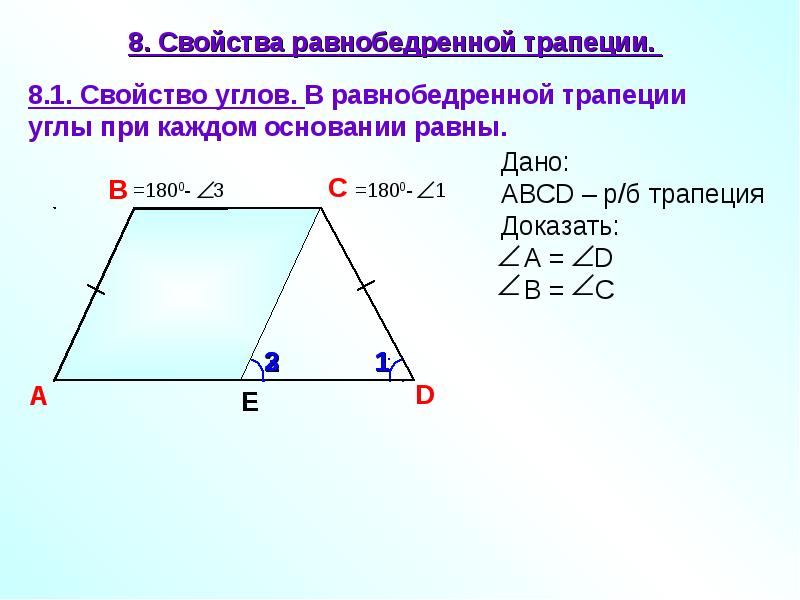<img src='/800/600/https/mypresentation.ru/documents_6/a21e9b80102c6abcb790cecd99cca41e/img16.jpg' /> Формула приведена ниже: Периметр трапеции <dd> Найдите периметр трапеции со сторонами размером 6 м, 8 м, 12 м и 15 м. </dd> Решение: Как известно, Периметр ( P ) = a + b + c + d , здесь a = 15 м, b = 12 м, c = 6 м и d = 8 м = 15 м + 12 м + 6 м + 8 м = 41 м <h3> Типы </h3> Трапеции делятся на две группы: по сторонам : 1) разносторонняя и 2) равнобедренная трапеция; на основе углов : 1) острый, 2) тупой и 3) правая трапеция. Различия между типами приведены ниже: Типы трапеции <h2><span class="ez-toc-section" id="%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%84%D0%BE%D1%80%D0%BC%D0%B0_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D1%82%D0%B8%D0%BF%D1%8B_%D0%B8_%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%D1%8B"> Определение, форма, свойства, типы и примеры </h2> Трапеция: Это выпуклая четырехугольная форма, состоящая из одной пары параллельных сторон с четырьмя ребрами и вершинами. Параллельные стороны трапеции называются основаниями, а другие стороны — ногами.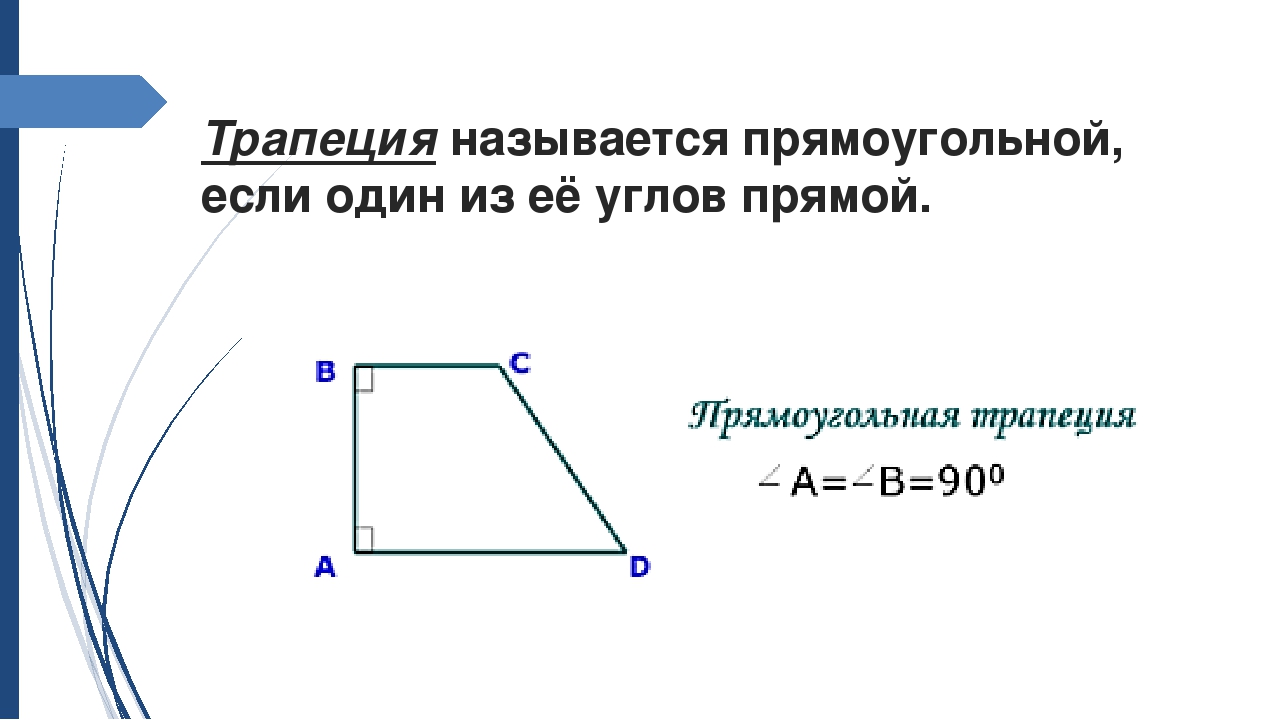<img src='/800/600/https/ds04.infourok.ru/uploads/ex/0ada/00091f11-d2a86abb/img3.jpg' /> Расстояние между параллельными сторонами называется высотой. В некоторых регионах трапецию также называют трапецией.Существуют разные типы трапеций, такие как правая, разносторонняя и равнобедренная. Можно сказать, что параллелограмм не трапеция, так как он состоит из двух противоположных параллельных сторон. Трапеция — это двумерная многоугольная фигура, имеющая площадь и периметр. Это одна из самых важных геометрических фигур в математике. Он также используется в области архитектуры, инженерии, науки и т. Д. Студенты изучают трапецию с раннего возраста, чтобы решать математические задачи за доли секунды.Вы можете проверить решение NCERT для класса 9 по математике, глава 8, на четырехугольниках. Мы предоставили подробную информацию о трапециях в этой статье. Прочтите, чтобы узнать о его определении, свойствах, типах и примерах. <h3> Определение трапеции </h3> Термин трапеция произошел от греческого слова Trapezoin, означающего «столик».<img src='/800/600/https/fsd.multiurok.ru/html/2017/05/05/s_590ce1525474d/img12.jpg' /> Трапеция — это выпуклый четырехугольник, состоящий из одной пары противоположных параллельных сторон. Это двухмерная фигура с ребрами и вершинами.Параллельные стороны трапеции называются основанием, а непараллельные стороны — ножками. Необязательно, чтобы параллельные стороны были прямой линией, так как она может быть как горизонтальной, так и наклонной. Расстояние между двумя параллельными сторонами называется высотой или высотой. Реальными примерами трапеции могут быть мост, стол, сумочка и т. Д. Трапеция могла быть параллелограммом, если бы обе пары имели параллельные стороны. И он мог бы назвать квадрат, если бы обе стороны были равной длины, и прямоугольник, если бы обе стороны были параллельны друг другу. Источник: Учебник NCERT. <h4> Свойства трапеции </h4> Некоторые свойства трапеции приведены ниже: <ol> <li> Это многоугольник </li> <li> Это двухмерная фигура, подобная прямоугольнику, квадрату и параллелограмму. </li> <li> Он состоит из четырех сторон </li> <li> Он состоит из четырех ребер и вершин </li> <li> Он имеет дополнительные смежные углы.<img src='/800/600/http/images.myshared.ru/6/598499/slide_9.jpg' /> </li> <li> Середины сторон лежат на одной прямой с пересечением диагоналей. </li> <li> Диагонали трапеции делятся в одинаковом соотношении.</li> </ol> <h4> Типы трапеции </h4> Различные типы трапеций упомянуты ниже: <ol> <li> Scalene Trapezoid: Имеет четыре неравные стороны и углы. Основания параллельны друг другу, но разной длины. </li> <li> Правая трапеция : У нее одна пара прямых углов между основанием и ножкой. </li> <li> Равнобедренная трапеция: Основания имеют неравную длину, тогда как ноги имеют одинаковую длину. </li> </ol> <h4> Площадь и периметр трапеции </h4> Площадь трапеции — это среднее значение пары оснований, умноженное на высоту.Его можно рассчитать по следующей формуле: <table> <tbody> <tr> <td> Площадь трапеции = 1/2 (a + b) h </td> </tr> </tbody> </table> Тогда как периметр — это сумма всех сторон. Его можно рассчитать по следующей формуле: <table> <tbody> <tr> <td> Периметр трапеции = a + b + c + d </td> </tr> </tbody> </table> <h4> Примеры трапеции </h4> Некоторые примеры трапеции приведены ниже: Пример 1: Найдите площадь трапеции с основанием 4 и 6 метров и высотой 8 метров.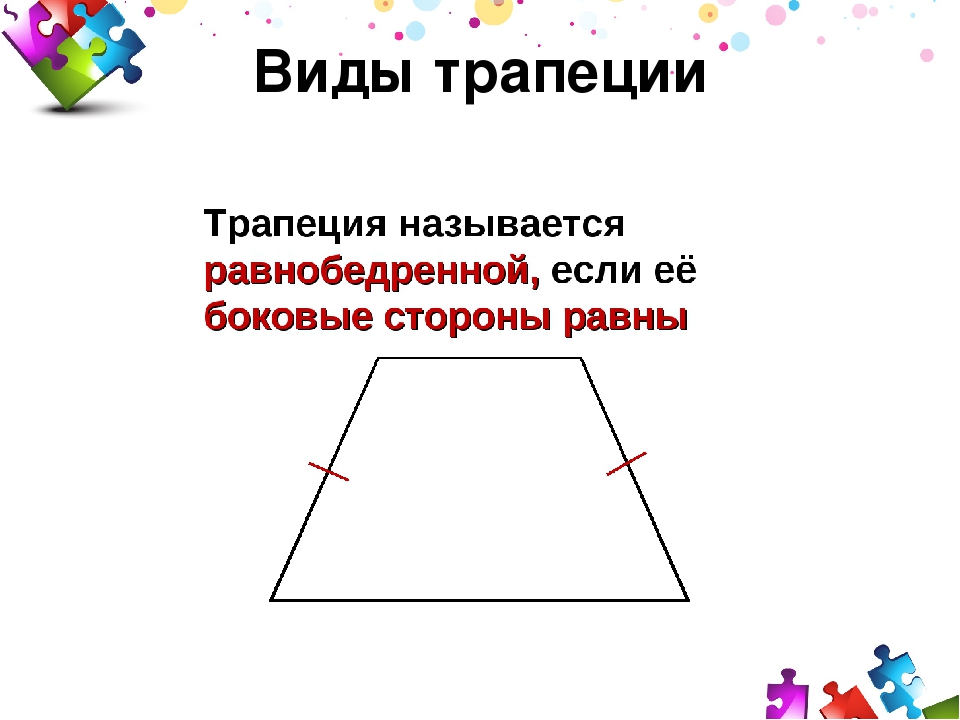<img src='/800/600/https/ds04.infourok.ru/uploads/ex/1177/001742f6-7bd27e12/img4.jpg' /> Решение: Мы знаем, что площадь трапеции составляет 1/2 (a + b) × h Площадь = 4 + 6/2 × 8м2 = Площадь = 10/2 × 8м2 = 40 м2 Пример 2: Трапеция имеет четыре стороны размером 2 м, 4 м, 6 м и 3 м. Найдите его периметр. Решение: Мы знаем, что Периметр задается суммой всех сторон. Следовательно, Периметр = 2 + 4 + 6 + 3 = 15 м Статьи по теме, <h3><span class="ez-toc-section" id="%D0%A7%D0%B0%D1%81%D1%82%D0%BE_%D0%B7%D0%B0%D0%B4%D0%B0%D0%B2%D0%B0%D0%B5%D0%BC%D1%8B%D0%B5_%D0%B2%D0%BE%D0%BF%D1%80%D0%BE%D1%81%D1%8B_%D0%BE_%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D0%B8"> Часто задаваемые вопросы о трапеции </h3> Часто задаваемые вопросы о трапеции приведены ниже: <table> <tbody> <tr> <td> Q.Что такое трапеция? A. Это выпуклый четырехугольник, состоящий из одной пары параллельных сторон с четырьмя ребрами и вершинами. </td> </tr> </tbody> </table> <table> <tbody> <tr> <td> В. Какие бывают типы трапеции? A. Типы трапеции — разносторонняя, правая и равнобедренная.<img src='/800/600/https/cf2.ppt-online.org/files2/slide/h/HYmDbdEKQMNAn0crpLy18af3slIk4gvetWJF56/slide-10.jpg' /> </td> </tr> </tbody> </table> <table> <tbody> <tr> <td> В. Является ли параллелограмм трапецией? A. Параллелограмм не является трапецией, поскольку он состоит из двух противоположных параллельных сторон.</td> </tr> </tbody> </table> <table> <tbody> <tr> <td> В. Какова площадь и периметр трапеции? A. Площадь трапеции — это среднее значение пары оснований, умноженное на высоту. Он рассчитывается по формуле 1/2 (a + b) h. Тогда как периметр — это сумма всех сторон. Он рассчитывается по формуле a + b + c + d. </td> </tr> </tbody> </table> Теперь, когда у вас есть подробная информация о трапеции, попрактикуйтесь со всеми вопросами в Embibe для лучшей подготовки.Мы надеемся, что эта статья о Trapezoid вам поможет. Если у вас есть какие-либо вопросы, не стесняйтесь размещать их здесь. Мы свяжемся с вами в ближайшее время. Следите за обновлениями на embibe.com . 394 Просмотры <h2> Иллюстративная математика </h2> <h3> Комментарий IM </h3> Цель этого задания — дать учащимся определение трапеции.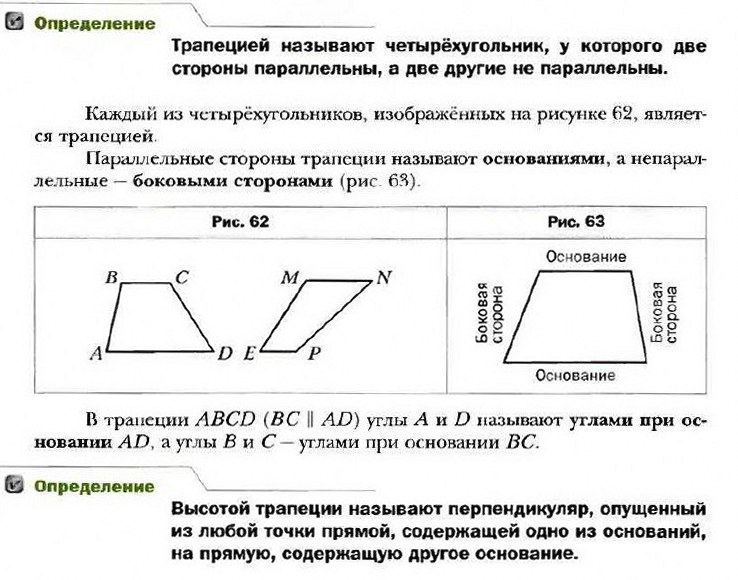<img src='/800/600/https/xn--b1agatbqgjneo2i.xn--p1ai/wp-content/uploads/2019/02/2019-02-07_17-03-35.jpg' /> Есть два конкурирующих определения слова «трапеция»: <ul> <li> Исключительное определение трапеции гласит, что трапеция имеет ровно одну пару параллельных противоположных сторон. </li> <li> Включенное определение гласит, что трапеция имеет по крайней мере одну пару параллельных противоположных сторон. </li> </ul> Иногда люди говорят, что у трапеций «одна пара противоположных сторон параллельна», поэтому остается неясным, может быть их больше одной или нет. Вторая часть задания подталкивает учащихся к четкому пониманию того, какую версию они намереваются. Из-за того, что учащиеся должны внимательно относиться к определениям, эта задача в значительной степени опирается на MP6, «Заботиться о точности». После того, как учащиеся сформулировали определения для себя или с партнером, класс должен обсудить определение вместе. Класс должен выбрать одно определение, с которым все согласны, поскольку смысл четко сформулированных определений состоит в том, что мы все знаем, что говорим об одном и том же.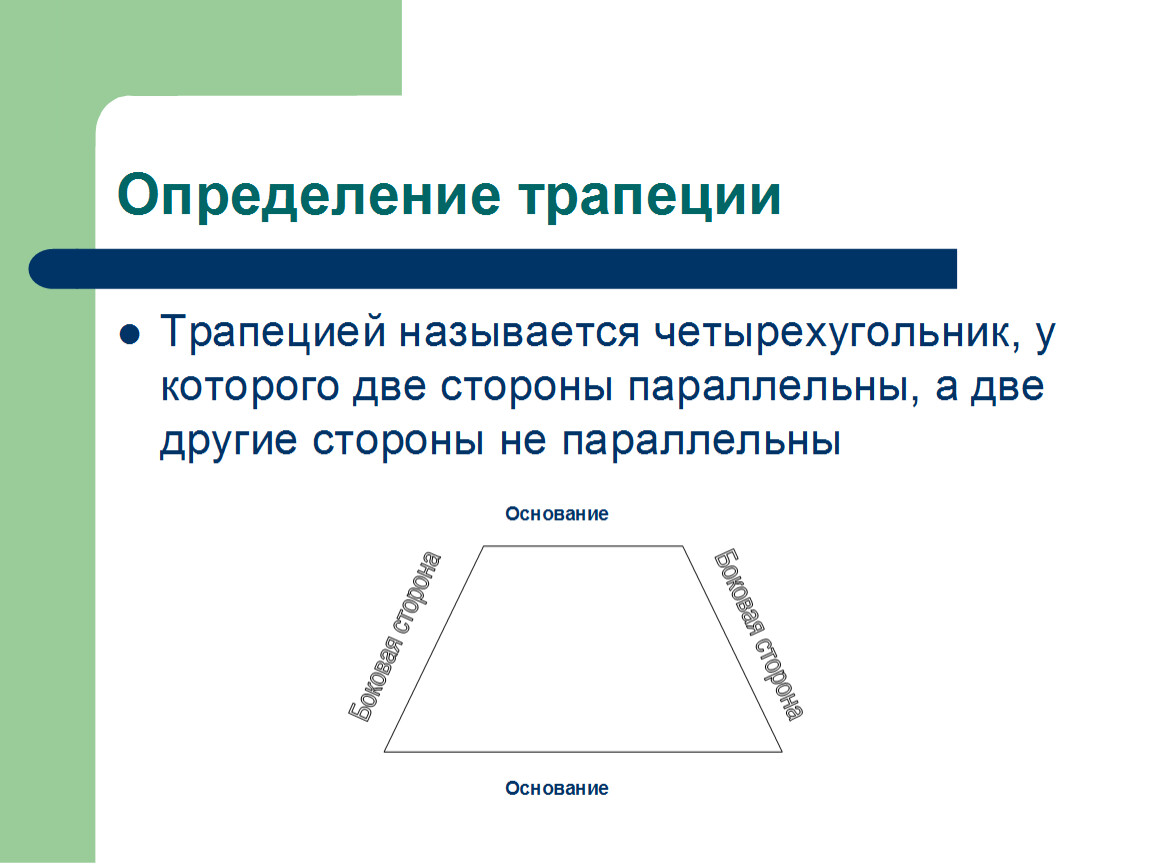<img src='/800/600/https/fs.znanio.ru/d5af0e/42/07/38cd6ad29cf659eb071b36b5d4cd794324.jpg' /> Хотя оба определения законны, преимущество инклюзивного определения состоит в том, что любая теорема, верная для трапеции, верна и для параллелограмма. Кроме того, в своем исследовании Классификация четырехугольников (Information Age Publishing, 2008) Usiskin et al.заключение, <blockquote> Преобладание преимуществ всеобъемлющего определения трапеции привело к тому, что все статьи, которые мы могли найти по этому предмету, и большинство выпускаемых колледжем книг по геометрии, отдали предпочтение всеобъемлющему определению. </blockquote> Инклюзивное определение устанавливает взаимосвязь между параллелограммами и трапециями, которая в точности аналогична взаимосвязи между квадратами и прямоугольниками; определение прямоугольников включает квадраты так же, как включающее определение трапеций включает параллелограммы. Дополнительную информацию об этих проблемах см. В документе K-6 Geometry Progressions: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.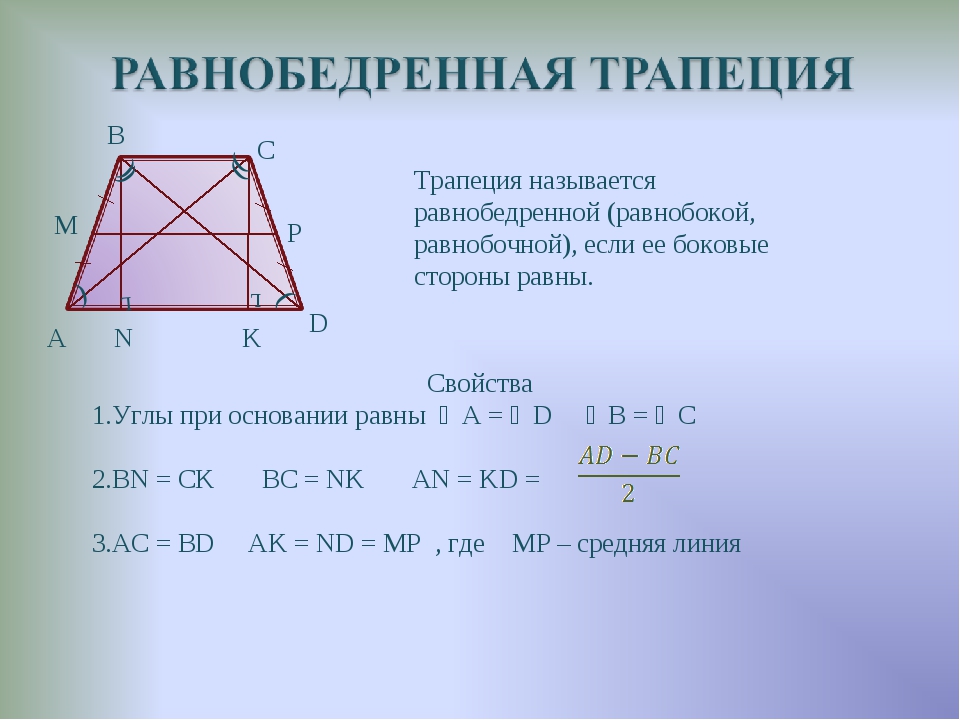<img src='/800/600/https/ds03.infourok.ru/uploads/ex/0477/00066d16-4d7a995b/img3.jpg' /> pdf. <h3> Решение </h3> <ol> <li> Трапеция — это четырехугольник, одна пара противоположных сторон которого параллельна. Он может иметь прямые углы (прямая трапеция) и равнобедренные стороны, но это не обязательно. </li> <li> Иногда люди определяют трапеции, чтобы иметь по крайней мере одну пару противоположных сторон, параллельных, а иногда говорят, что существует одна и только одна пара противоположных сторон, параллельных.Параллелограмм соответствует «по крайней мере одному» варианту определения, поскольку он имеет две пары противоположных сторон, параллельных друг другу, поэтому он попадает в категорию как трапеции, так и параллелограмма. Параллелограмм не подходит под «один-единственный» вариант определения. То, как студенты ответят на этот вопрос, зависит от их определения. </li> </ol> Примечание: если учащиеся дают разные определения, поначалу это нормально. Однако, чтобы иметь возможность обсуждать математические идеи в будущем, класс должен остановиться на одной из этих версий и двигаться дальше.<img src='/800/600/https/cf2.ppt-online.org/files2/slide/7/74xvET2IrhPgtCuKWl0sZOaH8YRAVi9ncz1pLj/slide-1.jpg' /> См. Примечание в комментарии, поощряющее версию определения, включающую параллелограммы. <h2> Иллюстративная математика </h2> <h3> Задача </h3> Нико и Карлос изучают параллелограммы и трапеции. Они согласны с тем, что параллелограмм — это четырехугольник с двумя парами параллельных сторон. Нико говорит: <blockquote> Трапеция имеет одну пару параллельных сторон, а параллелограмм — две пары параллельных сторон. Итак, параллелограмм — это тоже трапеция. </blockquote> Карлос говорит: <blockquote> Нет — у трапеции может быть только одна пара параллельных сторон.</blockquote> Нико говорит: <blockquote> Это неправда. Трапеция имеет по крайней мере одну пару параллельных сторон , но может иметь и другую. </blockquote> <ol> <li> Обсудите с партнером разницу между определением трапеции, данным Нико и Карлосом. </li> <li> Некоторые люди используют определение трапеции, данное Нико, а некоторые используют определение Карлоса.<img src='/800/600/https/ds02.infourok.ru/uploads/ex/0d21/0007fc60-5958be1c/hello_html_b716761.png' /> Какие утверждения ниже согласуются с определением Нико? Какие утверждения согласуются с определением Карлоса? <ol> <li> Все параллелограммы трапециевидные.</li> <li> Некоторые параллелограммы представляют собой трапеции. </li> <li> Никакие параллелограммы не являются трапециями. </li> <li> Все трапеции параллелограммы. </li> <li> Некоторые трапеции представляют собой параллелограммы. </li> <li> Нет трапеций — параллелограммов. </li> </ol> </li> <li> Какое изображение представляет отношения между трапециями и параллелограммами для каждого определения? <ol> <li> </li> <li> </li> <li> </li> </ol> </li> </ol> <h3> Комментарий IM </h3> Цель этого задания — сравнить разные определения трапеций.Некоторые люди определяют трапеции так, чтобы имели одну и только одну пару противоположных сторон, параллельных друг другу, в то время как некоторые люди определяют трапеции, чтобы иметь как минимум одну пару параллельных противоположных сторон.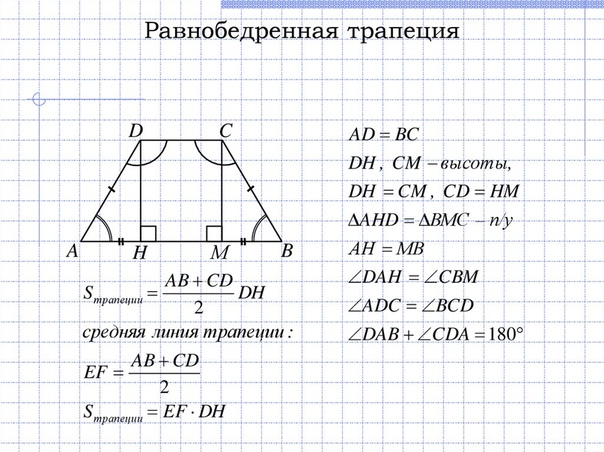<img src='/800/600/https/sun9-65.userapi.com/c858328/v858328737/1f1a0d/j-jHm99juJQ.jpg' /> Вопрос о том, являются ли параллелограммы трапециями, зависит от того, с каким из этих определений мы согласны. Из-за того, что учащиеся должны внимательно относиться к определениям, эта задача в значительной степени опирается на MP6, «Заботиться о точности». Наиболее распространенные четырехугольники имеют универсально согласованное определение: * Параллелограммы — это четырехугольники с двумя парами противоположных параллельных сторон.* Прямоугольники — это четырехугольники с четырьмя прямыми углами. * Ромбы — это четырехугольники с равной длиной сторон. * Квадраты — это четырехугольники с равными сторонами и четырьмя прямыми углами. Ситуация с трапециями несколько необычна, но она дает студентам возможность понять, что определения — это условности, и по этой причине нам нужно рассуждать на основе согласованных определений, а не только распознавать формы. Хотя оба определения законны, преимущество определения Нико (иногда называемого «включающим определением») состоит в том, что любая теорема, верная для трапеции, верна и для параллелограмма.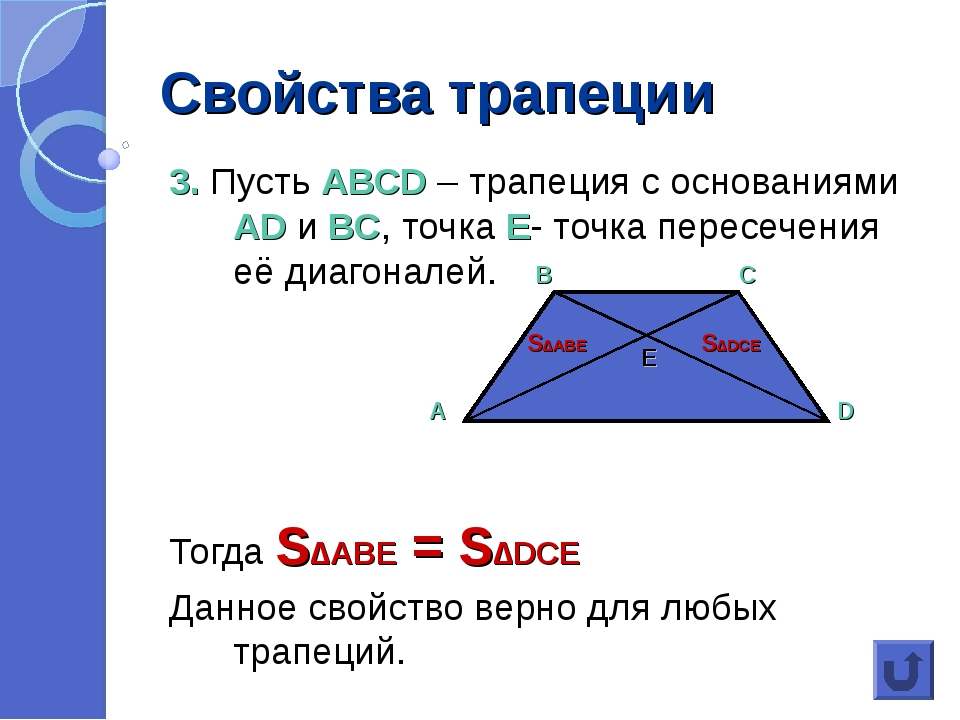<img src='/800/600/https/ds03.infourok.ru/uploads/ex/004c/0003bd53-49354d64/img12.jpg' /> Кроме того, в своем исследовании Классификация четырехугольников (Information Age Publishing, 2008) Usiskin et al. заключение, <blockquote> Преобладание преимуществ всеобъемлющего определения трапеции заставило все статьи, которые мы могли найти по этому предмету, и большинство книг по геометрии, выпускаемых колледжем, отдать предпочтение всеобъемлющему определению. </blockquote> Инклюзивное определение устанавливает взаимосвязь между параллелограммами и трапециями, которая в точности аналогична взаимосвязи между квадратами и прямоугольниками; определение прямоугольников включает квадраты так же, как включающее определение трапеций включает параллелограммы.Дополнительную информацию об этих проблемах см. В документе K-6 Geometry Progressions: http://commoncoretools.me/wp-content/uploads/2012/06/ccss_progression_g_k6_2012_06_27.pdf. <h2><span class="ez-toc-section" id="%D0%A1%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0_%D1%87%D0%B5%D1%82%D1%8B%D1%80%D0%B5%D1%85%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0_-_%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA_%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82_%D0%BF%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC_%D1%80%D0%BE%D0%BC%D0%B1_%D1%82%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D1%8F"> Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция </h2> В евклидовой геометрии четырехугольник — это четырехсторонняя двумерная фигура, сумма внутренних углов которой равна 360 °.<img src='/800/600/https/cf2.ppt-online.org/files2/slide/l/lTRPKINJd10seH95Yhqt3oMaVLxr7nZyE4CUvk/slide-33.jpg' /> Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно.Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Итак, каковы свойства четырехугольника? Четырехугольники имеют два свойства: <ul> <li> Четырехугольник должен быть замкнутой формы с 4-мя сторонами </li> <li> Сумма всех внутренних углов четырехугольника составляет 360 ° </li> </ul> В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь с их свойствами четырехугольников. Это то, что вы прочитаете в статье: Вот видео, объясняющее свойства четырехугольника: <iframe loading="lazy" src="https://www.youtube.com/embed/wx6LPIVyXK0" frameborder="0" allowfullscreen="allowfullscreen">

На приведенной ниже схеме показан четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов составляет 360 °.

Таким образом, A + ∠B + ∠C + ∠D = 360 °

Различные типы четырехугольников

Существует 5 типов четырехугольников в зависимости от их формы. Эти 5 четырехугольников:

Прямоугольник
Квадрат
Параллелограмм
Ромб
Трапеция

Давайте подробно обсудим каждый из этих пяти четырехугольников:

Вот вопросы, которые научат вас применять свойства всех пяти четырехугольников, которые вы узнаете в этой статье.

Прямоугольник

Прямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °). Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.

Свойства прямоугольников

Прямоугольник имеет три свойства:

Все углы прямоугольника равны 90 °
Противоположные стороны прямоугольника равны и параллельны
Диагонали прямоугольника делят друг друга пополам

Формула прямоугольника — Площадь и периметр прямоугольника

Если длина прямоугольника L, а ширина B, то

Площадь прямоугольника = длина × ширина или длина × ширина
Периметр прямоугольника = 2 × (L + B)

Эти практические вопросы помогут вам закрепить свойства прямоугольников

Планируете ли вы поступить в бизнес-школу США? Позвольте нам помочь вам пройти первый этап процесса i.е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.

Площадь

Квадрат — четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.

Недвижимость квадрата

Чтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:

Все углы квадрата равны 90 °
Все стороны квадрата равны и параллельны друг другу
Диагонали делят друг друга пополам перпендикулярно

Формула квадрата — Площадь и периметр квадрата

Если сторона квадрата — «а», тогда

Площадь квадрата = a × a = a²
Периметр квадрата = 2 × (a + a) = 4a

Эти практические вопросы помогут вам закрепить свойства квадратов

Если вы набрали Q50-51 за GMAT, вы сможете набрать 700+ баллов за GMAT.Почему бы вам не начать подготовку к GMAT с помощью наших бесплатных подготовительных ресурсов и не начать свой путь к получению Q50-51 на GMAT. Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.

Параллелограмм

Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Причем противоположные углы в параллелограмме равны, а его диагонали делят друг друга пополам.

Свойства параллелограмма

Четырехугольник, удовлетворяющий указанным ниже свойствам, будет классифицироваться как параллелограмм.Параллелограмм имеет четыре свойства:

Противоположные углы равны
Противоположные стороны равны и параллельны
Диагонали делят друг друга пополам
Сумма любых двух смежных углов равна 180 °

Формулы параллелограмма — Площадь и периметр параллелограмма

Если длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:

Периметр параллелограмма = 2 × (l + b)
Площадь параллелограмма = l × h

Эти практические вопросы помогут вам закрепить свойства параллелограмма

Ромб

Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу.Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», так как он похож на ромб в игральных картах.

Свойства ромба

Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:

Противоположные углы равны
Все стороны равны, а противоположные стороны параллельны друг другу
Диагонали делят друг друга перпендикулярно
Сумма любых двух смежных углов составляет 180 °

Формулы ромба — Площадь и периметр ромб

Если сторона ромба — это, то периметр ромба = 4a

Если длина двух диагоналей ромба равна d ₁ и d ₂, то площадь ромба = ½ × d ₁ × d ₂

Эти практические вопросы помогут вам закрепить свойства ромба

Трапеция

Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон.Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.

Свойства трапеции

Трапеция — это четырехугольник, в котором одно свойство:

Только одна пара противоположных сторон параллельна друг другу

Формулы трапеции — Площадь и периметр трапеции

Если высота трапеции « h» (как показано на диаграмме выше), то:

Периметр трапеции = Сумма длин всех сторон = AB + BC + CD + DA
Площадь трапеции = ½ × (Сумма длин параллельных сторон) × h = ½ × (AB + CD) × h

Эти практические вопросы помогут вам закрепить свойства трапеции

Свойства четырехугольника

В таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:

Важные формулы четырехугольника

В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:

Свойства четырехугольника

Прямоугольник

Квадрат

Параллелограмм

Ромб

Трапеция

Все стороны равны

✖

Стороны равны

✔

✖

Противоположные стороны параллельны

✔

9038 ✔

9038

✔

✖

Противоположные углы равны

✔

двух смежных углов

✖

✔

✖

Разделить пополам

✔ 9038 8

✔

✖

Перпендикулярно пополам

✖

✔

✖

✔

000 ✖

✔

000 ✖

Четырехсторонние формулы	Прямоугольник	Квадрат	Параллелограмм	Ромб		9038	b		l × h	½ × d1 × d2	½ × (Сумма параллельных сторон) × высота
Периметр	2 × (l + b)	4a	2 × (l + b)	4a	Сумма всех сторон

Дополнительная литература:

Четырехсторонние вопросы

Попрактикуемся в применении свойств четырехугольника на следующих типовых вопросах:

Вопрос 1

Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.Сколько метров забора нужно купить, чтобы ограждать весь сад?

20 метров
25 метров
30 метров
40 метров
50 метров

Решение

Шаг 1: Дано

У Адама прямоугольный сад.
- Он имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.

Шаг 2: найти

Длина, необходимая для ограждения всего сада.

Шаг 3: подход и разработка

Забор можно строить только вокруг внешней стороны сада.

Итак, общая необходимая длина забора = Сумма длин всех сторон сада.
- Поскольку сад прямоугольный, сумма длин всех сторон — это не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров

Следовательно, необходимая длина забора — 50 метров.

Следовательно, вариант E — правильный ответ.

Вопрос: 2

Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если стена 25 метров в длину и 18 метров в ширину, то какова общая стоимость покраски стены?

$ 300
$ 350
$ 450
$ 600
$ 675

Решение

Шаг 1: Дано

Стив хочет покрасить одну стену своей комнаты.
- Стена 25 метров в длину и 18 метров в ширину.
- Стоимость покраски стены составляет 1,5 доллара за квадратный метр.

Шаг 2: найти

Общая стоимость покраски стены.

Шаг 3: подход и разработка

Стена окрашена по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, мы сможем получить общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 $ = 675 $

Следовательно, правильный ответ — вариант E.

Мы надеемся, что к настоящему времени вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь.

Вот еще несколько статей по математике:

Повысьте точность в вопросах по математике по многоугольникам
Вопросы по геометрии — наиболее распространенные ошибки | GMAT Quant Prep

Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Мы — самая обсуждаемая компания по подготовке к GMAT на gmatclub: мы получили более 2060 отзывов.

Почему бы вам не воспользоваться бесплатным испытанием и не судить сами?

Напишите нам по адресу [email protected]

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

Свойства трапеции, с примерами

Свойства трапеции

Примеры решения задач

Параллелограмм и трапеция

Свойства параллелограмма

Виды трапеций

Площадь параллелограмма и трапеции

Проектная работа «Трапеция и её свойства. Решение задач»

Трапеция. Свойства трапеции — презентация онлайн

Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

Определение трапеции

Происхождения слова

Стороны трапеции

Равнобедренная и прямоугольная трапеции

Свойства трапеций

Средняя линия

Биссектриса углов трапеции

Различные типы четырехугольников

Прямоугольник

Свойства прямоугольников

Формула прямоугольника — Площадь и периметр прямоугольника

Площадь

Недвижимость квадрата

Формула квадрата — Площадь и периметр квадрата

Параллелограмм

Свойства параллелограмма

Формулы параллелограмма — Площадь и периметр параллелограмма

Ромб

Свойства ромба

Формулы ромба — Площадь и периметр ромб

Трапеция

Свойства трапеции

Формулы трапеции — Площадь и периметр трапеции

Свойства четырехугольника

Важные формулы четырехугольника

Четырехсторонние вопросы

Вопрос 1

Решение

Вопрос: 2

Решение

Добавить комментарий Отменить ответ