Основаниями усеченной пирамиды являются правильные треугольники 5 и 3: Найдите площадь боковой поверхности усеченной пирамиды. Вопросы и задачи 270, Геометрия, 10-11 класс, Атанасян Л.С. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Усеченная пирамида — Большая Энциклопедия Нефти и Газа, статья, страница 3

Усеченная пирамида

Cтраница 3

Основаниями усеченной пирамиды служат прямоугольники, причем точки пересечения диагоналей оснований находятся на одном перпендикуляре к плоскости основания. Стороны одного прямоугольника равны 54 см и 30 см периметр другого прямоугольника 112 см расстояние между их плоскостями равно 12 см. Определить боковую поверхность этой усеченной пирамиды.
[31]

Основаниями усеченной пирамиды служат правильные треугольники со сторонами а и Ъ одно из боковых ребер, равное с, перпендикулярно к плоскостям оснований.
[32]

Основаниями усеченной пирамиды служат прямоугольники, причем точки пересечения диагоналей оснований находятся на одном перпендикуляре к плоскостям оснований. Стороны одного прямоугольника равны 54 см и 30 см; периметр другого прямоугольника 112 см; расстояние между их плоскостями равно 12 см. Определить боковую поверхность этой усеченной пирамиды.
[33]

Изображение усеченной пирамиды в аксонометрической проекции выполняют в следующей последовательности ( рис. 25, б): строят основание пирамиды, затем фигуру сечения ( треугольник) и ребра.
[34]

Основание усеченной пирамиды — четырехугольник ABFD — помещено у боковой грани ASB. Фигура сечения — & DFE — присоединена к основанию пирамиды своей стороной DF, которая является общей для этих фигур.
[35]

Объем усеченной пирамиды равен одной трети произведения ее высоты на сумму площадей многоугольников, лежащих в ее основаниях, и среднего геометрического этих площадей.
[37]

Основаниями усеченной пирамиды служат правильные треугольники. Прямая, проходящая через середину одной стороны верхнего основания и середину параллельной ей стороны нижнего основания, перпендикулярна плоскостям оснований.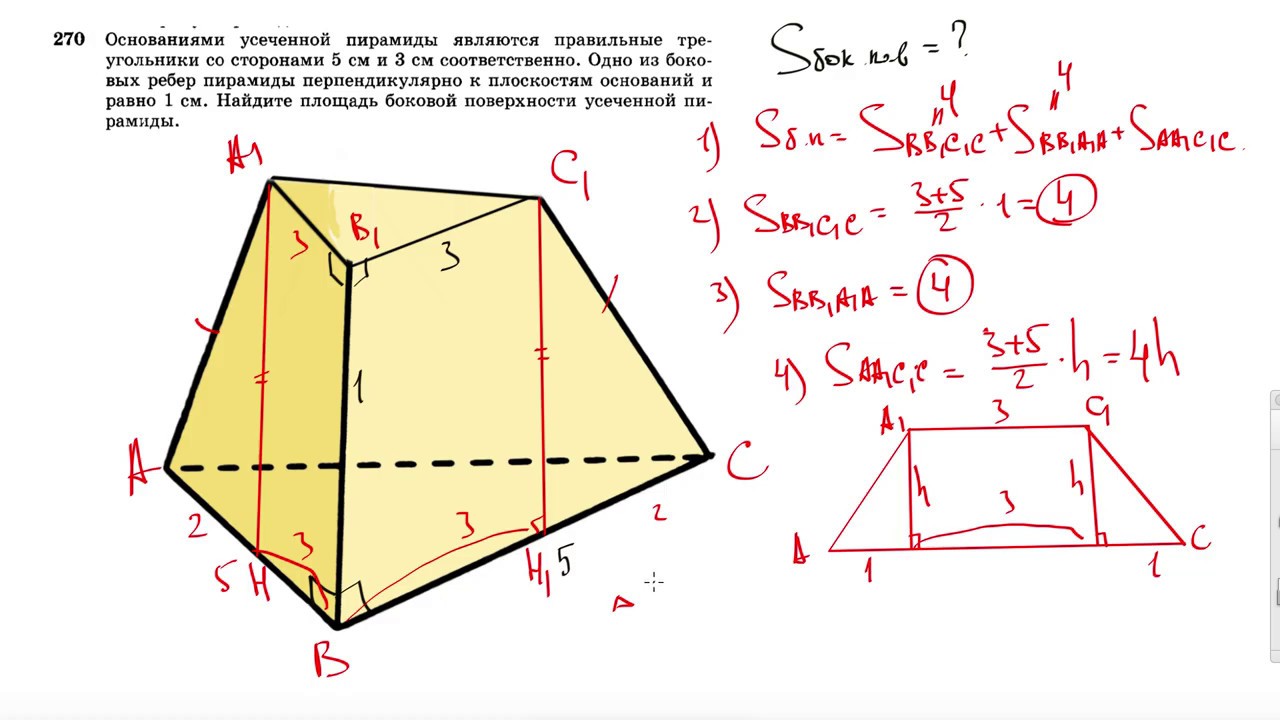 Большее боковое ребро равно / и составляет с плоскостью основания угол а.
[38]

Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.
[39]

Основаниями усеченной пирамиды служат два правильных восьмиугольника. Усеченная пирамида достроена до полной.
[40]

Основаниями усеченной пирамиды служат два правильных восьмиугольника. Усеченная пирамида достроена до полной.
[42]

Объемы усеченных пирамид с квадратным основанием вычисляются как объемы параллелепипедов, вместо площади основания которых берется средняя арифметическая площадей оснований усеченной пирамиды.
[44]

Основания усеченной пирамиды соответственно равны 27 и 12 см2, высота равна 5 см. Вычислить высоту соответствующей полной пирамиды.
[45]

Страницы:

1

2

3

4

Задания для устного счета по теме«Усеченная пирамида», геометрия 10 класс

Урок 1. Пирамида. Площадь полной поверхности пирамиды.

Цель: познакомить с новым видом многогранника

Задачи: образовательная – дать понятие пирамиды, её основных элементов, понятие полной поверхности пирамиды;

развивающая — развивать умение самостоятельно мыслить, делать выводы;

воспитательная – воспитывать дисциплинированность, аккуратность.

Вид урока: комбинированный: лекция и практикум по решению задач.

Средства обучения: презентация.

Оборудование: компьютер, экран, мультимедийный проектор, модели пирамид, интерактивная доска.

План урока:

1. Организационный момент (2 мин).

2. Объяснение нового материала (20-25 мин).

3. Закрепление материала (15 мин).

4. Подведение итогов. Домашняя работа (3 мин).

Ход урока:

1.Учитель организует учащихся к уроку.

2. Учитель: Тема нашего сегодняшнего урока «Пирамида», сегодня на уроке мы должны познакомиться с новыми видом многогранника, с его основными элементами, научиться решать простейшие задачи на пирамиду. (Демонстрируется слайд № 3) Начнем с истории. Слово пирамида нам знакомо с детства, это детская игрушка, а также при слове пирамида мы вспоминаем о египетских пирамидах — величайших архитектурных памятниках, которые историки относят к эпохе Древнего Египта, среди которых одно из «семи чудес света» — пирамида Хеопса. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы (оттуда и название), предположительно построенные в качестве гробниц для фараонов Древнего Египта. Всего в Египте было обнаружено 118 пирамид (на ноябрь 2008 года).

А теперь давайте познакомимся с пирамидой как с многогранником. (Демонстрируется слайд № 4). Рассмотрим многоугольник и точку, не лежащую в плоскости этого многоугольника, соединим отрезками точку и вершины многоугольника, получим треугольники. Многогранник, состоящий и многоугольника и треугольников, называется пирамидой.

Как же называются основные элементы пирамиды? (демонстрируется слайд №5).

В зависимости от вида многоугольника существуют разные виды пирамид (демонстрируется слайд № 6).

Как и призма, пирамида имеет поверхность. Из чего же состоит поверхность пирамиды? Как найти площадь полной поверхность пирамиды? (демонстрируется слайд № 7). Таким образом, говоря о полной поверхности пирамиды, мы подразумеваем площадь основания и площадь боковой поверхности, которая складывается из суммы площадей боковых граней. Так как в основании пирамиды лежит многоугольник, а боковыми гранями являются треугольники, то чтобы найти площадь основания или боковой грани, нужно знать формулы.

А какие формулы вы знаете для нахождения площади треугольника и многоугольника?

3. Учитель: А теперь, давайте, выполним математический диктант (демонстрируется слайд № 8). Ученики выполняют диктант в тетрадях самостоятельно, а затем проводится фронтальная проверка.

Учитель: А теперь решим устно задачи (демонстрируется слайд № 9).При решении задач необходимы дополнительные построения, поэтому можно из презентации вызвать интерактивный режим (если есть в наличии интерактивная доска) и проводить построения, параллельно решая задачу на слайде.

Задача 1.В основании пирамиды квадрат. Высота пирамиды равна стороне квадрата и проходит через одну из его вершин. Найти двугранные углы при основании.

Решение: боковые грани АЕО и СЕО перпендикулярны основанию, так как ЕО высота. Следовательно, двугранные углы при ребрах АЕ и СЕ прямые. Треугольники АЕО и СЕО равнобедренные, так как высота ЕО равна стороне квадрата. Значит углы ОСЕ и ЕАО равны 45º, следовательно, двугранные углы, линейными углами которых они являются, тоже равны 45º.

Задача 2. Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника и равна 12 см. Найти высоту пирамиды.

Решение: боковые ребра пирамиды равны и высота пирамиды общая, следовательно, и равны их проекции и они являются радиусами описанной около основания окружности. Центр окружности описанной около прямоугольного треугольника лежит на середине гипотенузы. Треугольник АВА2 равносторонний, его высота ВВ1 является медианой, а также и высотой пирамиды. По теореме Пифагора находим, что высота равна .

(набор задач не является обязательным, учитель вправе сам выбрать задачи в зависимости от уровня подготовленности класса)

Учитель: Решим задачи из учебника № 239.

Задача № 239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 7 см.

Решение: (чертеж к задаче выполняется на интерактивной доске). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Δ АВО прямоугольный с катетом 4 см и гипотенузой 5 см, отсюда по теореме Пифагора находим

АО ===3 см. Δ ASOпрямоугольный, так как SO- высота пирамиды. Отсюда по теореме Пифагора находим боковое ребро AS===см. Δ SOBпрямоугольный, следовательно, SB=== см. SC=AS, SD=SB.

Задача № 241. Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности.

Решение: (чертеж к задаче выполняется на интерактивной доске или можно подготовить шаблон заранее). Площадь полной поверхности равна сумме площадей основания и боковой поверхности. По теореме косинусов найдем косинус острого угла параллелограмма =,, отсюда S=4*5* м2. Площадь боковой поверхности равна сумме площадей боковых граней, так как у параллелограмма противоположные стороны равны, то и боковые грани, опирающиеся на эти стороны, тоже будут равны, поэтому достаточно найти площади только двух граней. Найдем высоту параллелограмма 12=5*h2, отсюда h2= м . Найдем высоту боковой грани по теореме Пифагора, она будет равна = м. Найдем другую высоту параллелограмма 12=4*h3, отсюда h3=3 м. Найдем высоту другой боковой грани, она будет равна м. Найдем теперь площадь боковой поверхности, она равна S= м2. Площадь полной поверхности равна S = 12+10+2м2.

4. Учитель: Давайте подведем итог.

Что такое пирамида?

Назовите основные элементы пирамиды (на модели).

Как найти площадь полной поверхности пирамиды?

Учитель оценивает работу учащихся. При оценивании учитывается полнота, логически правильный, сформулированный ответ.

Задает домашнее задание: п. 28, задача из учебника № 242.

Урок 2. Правильная пирамида.

Цель: познакомить учащихся с правильной пирамидой.

Задачи: образовательная – дать понятие правильной пирамиды, вывести формулу площади боковой поверхности правильной пирамиды;

развивающая — развивать логический стили мышления; умение самостоятельно мыслить, делать выводы;

воспитательная – дисциплинированность, аккуратность.

Вид урока: комбинированный: лекция и решение задач.

Средства обучения: презентация.

Оборудование: модели пирамид, компьютер, экран, мультимедийный проектор, интерактивная доска.

План урока:

1. Организационный момент (2 мин).

2. Теоретический опрос (5-7 мин).

3. Объяснение нового материала (15- 20 мин).

4. Закрепление материала (15 мин).

5. Подведение итогов. Домашняя работа (3 мин).

Ход урока:

1. Учитель организует учащихся к уроку.

2. Учитель: Что такое пирамида?

Назовите основные элементы пирамиды (на модели).

Какие виды пирамид вы знаете?

Как найти площадь полной поверхности пирамиды?

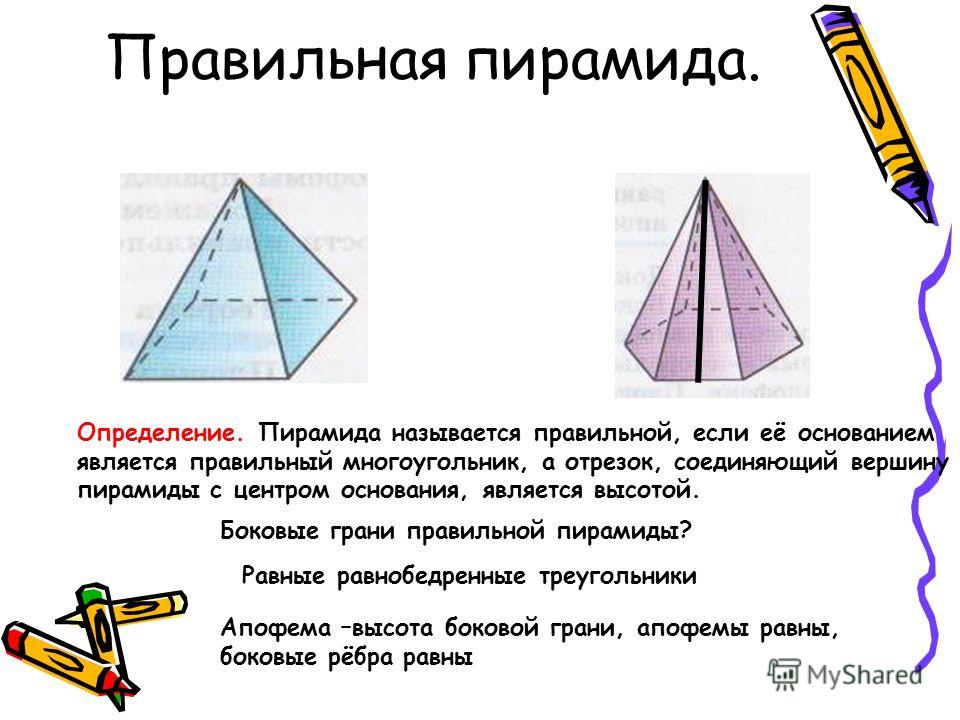
3. Учитель: Тема нашего сегодняшнего урока «Правильная пирамида», сегодня на уроке мы должны познакомиться с новым понятием (демонстрируется слайд № 10). Пирамида называется правильной, если в её основании лежит правильный многоугольник.

Какие правильные многоугольники вы знаете?

У правильной пирамиды боковые ребра равны, боковые грани равные равнобедренные треугольники. Высота боковой грани называется апофемой. Высотой правильной пирамиды называется отрезок, соединяющий вершину и центр основания. Центром основания правильного многоугольника является центр описанной около него окружности.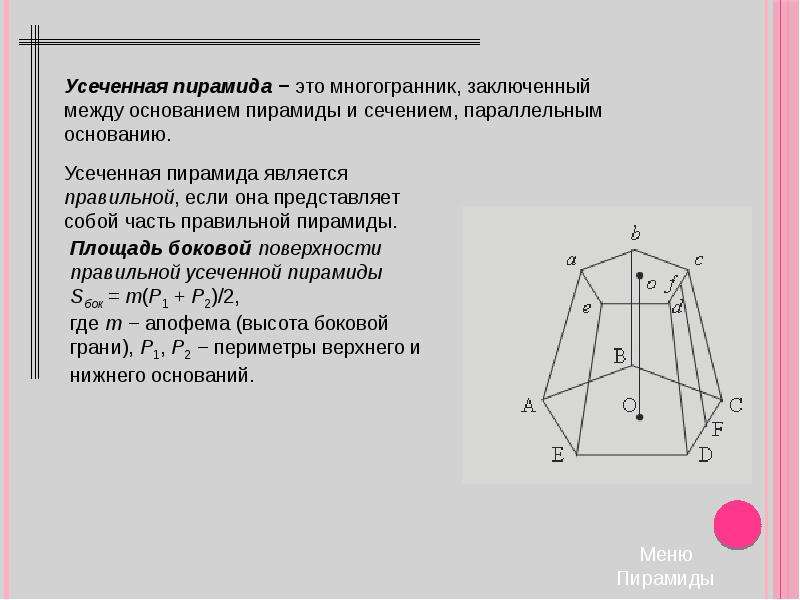

Можно легко доказать, что боковые ребра равны, так как они являются гипотенузами прямоугольных треугольников, в которых один катет (высота пирамиды) общий, а другие катеты равны как радиусы описанной окружности, отсюда по теореме Пифагора каждое боковое ребро равно .

4.Учитель: Вспомните формулы нахождения сторон правильных многоугольников и радиусов вписанной и описанной окружностей.

; ; где n – количество сторон в многоугольнике.

Учитель: решим задачи (демонстрируется слайд № 11)

Задача.Высота правильной четырехугольной пирамиды равна половине стороны основания. Найти двугранные углы при основании.

Решение: пусть сторона основания равна а, тогда высота АА5 = а/2. Радиус вписанной окружности А5 А6=а/2 . Треугольник АА5 А6 равнобедренный. Угол АА6 А5 =45º.

Учитель: А теперь выведем формулу боковой поверхности правильной пирамиды (демонстрируется слайд № 12).

Скажите, из чего складывается площадь боковой поверхности пирамиды?

Так как боковые грани правильной пирамиды равнобедренные треугольники, то у них равны высоты. Площадь каждой грани находиться по формуле где l – апофема. Боковых граней несколько, сумма длин сторон основания дает периметр. Таким образом, получаем формулу площади боковой поверхности правильной пирамиды.

Учитель: Решим задачи на нахождение площади боковой поверхности правильной пирамиды (демонстрируется слайд № 13).

Задача. Найти площадь боковой поверхности правильной

а) четырехугольной пирамиды со стороной основания 6, высотой 4.

б) треугольной пирамиды со стороной 6, высотой 1.

Решение: а) найдем апофему по теореме Пифагора, , , l= 5. А теперь найдем площадь боковой поверхности пирамиды S=0.5*(6*4)*5=60.

б) найдем апофему по теореме Пифагора , , l=2. А теперь найдем площадь боковой поверхности пирамиды S=0.5*(6*4)*2=24.

Учитель: Решим задачу № 255 из учебника.

Задача № 255. В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ. Найдите высоту этой пирамиды.

Решение: Найдем радиус вписанной окружности см.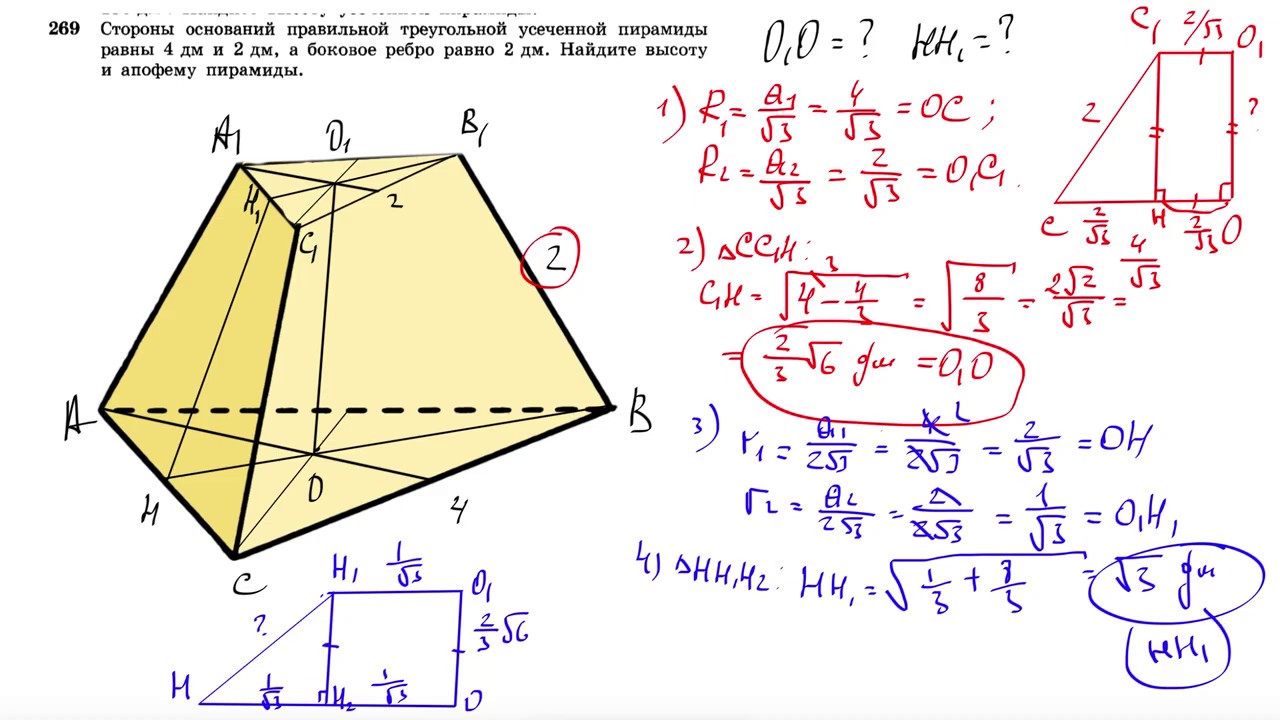 Высота боковой грани (апофема) является медианой и биссектрисой, найдем ее см. Найдем высоту пирамиды см.

5.Учитель: Давайте подведем итог.

Учитель оценивает учащихся (знание теории, активную работу на уроке).

Задает домашнее задание: п. 29, задача из учебника № 258.

Урок 3. Усеченная пирамида.

Цель: ознакомить учащихся с усеченной пирамидой.

Задачи: образовательная – познакомить с видами сечений, дать понятие усеченной пирамиды, познакомиться с её элементами, вывести формулу боковой поверхности усеченной пирамиды;

развивающая — развивать логический стили мышления; умение самостоятельно мыслить, делать выводы.

воспитательная – воспитывать дисциплинированность, аккуратность.

Вид урока: лекция и решение задач.

Средства обучения: презентация.

Оборудование: компьютер, экран, мультимедийный проектор, интерактивная доска.

План урока:

1. Организационный момент (2 мин).

2. Теоретический опрос (5 — 7 мин).

3. Объяснение нового материала (15 — 18 мин).

4. Закрепление материала (15 мин).

5. Подведение итогов. Домашняя работа (3 мин).

Ход урока:

1.Учитель организует учащихся к уроку.

2. Учитель: Какая пирамида называется правильной?

Докажите теорему о площади боковой поверхности правильной пирамиды.

3. Учитель:Рассмотрим сечения пирамиды (демонстрируются слайд № 14, 15). Сечение, проходящее через вершину пирамиды и диагональ основания, называются диагональными. Они имеют вид треугольников. Существуют сечения, которые параллельны основанию (демонстрируется слайд № 16). Они, как правило, имеют вид многоугольника подобного тому, который находится в основании. Решим задачу (демонстрируется слайд № 17):

Задача. В пирамиде проведено сечение параллельно основанию через середину высоты. Площадь основания равна Q. Найти площадь сечения.

Решение: так как сечение проходит через середины боковых ребер, то каждая сторона многоугольника (сечения) является средней линей боковой грани и равна половине стороны многоугольника, находящегося в основании. То есть можно сказать, что основание и сечение, подобные многоугольники, к=2. А площади подобных фигур относятся квадрат коэффициента подобия. Значит, площадь сечения равна Q/4.

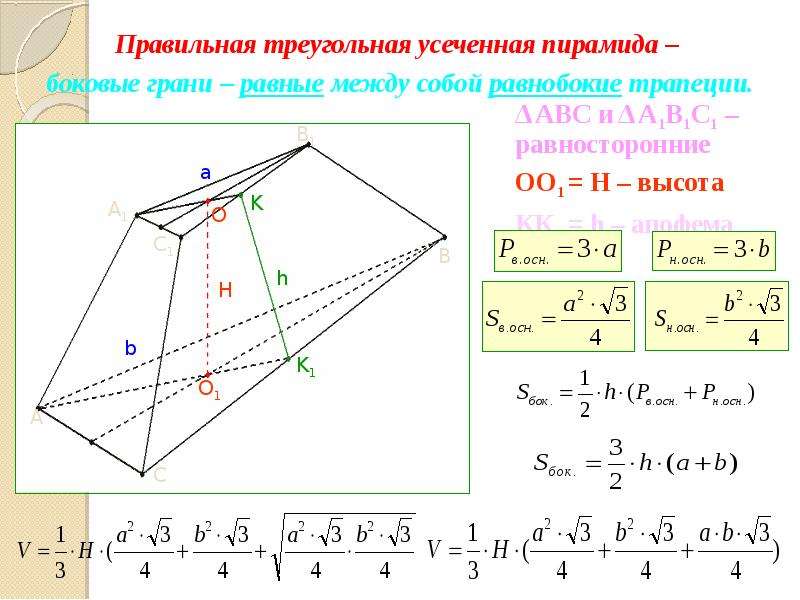
Дадим понятие усеченной пирамиды (демонстрируется слайд № 18). Пусть дана пирамида. Проведем плоскость параллельную основанию, которая пересечет боковые ребра. Наша секущая плоскость разделяет нашу пирамиду на два многогранника: один — пирамида, подобная данной, а второй многогранник, заключенный между сечением и основанием, называется усеченной пирамидой. Назовем основные элементы усеченной пирамиды (демонстрируется слайд № 19). Площадь боковой поверхности усеченной пирамиды равна сумме площадей боковых граней.

Если усеченная пирамида получена сечением правильной пирамиды, то она называется правильной усеченной пирамидой, у которой есть свои особенности в названии элементов (демонстрируется слайд № 20). Так как в правильной усеченной пирамиде, боковые грани являются равнобедренными трапециями и равны между собой, то площадь боковой поверхности усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

4. Учитель: проведем математическое исследование (демонстрируется слайд № 21). Учащиеся выполняют исследование самостоятельно, а затем сообщают о полученных результатах в классе (можно данное исследование дать на дом).

Учитель: Решим задачу № 269.

Задача № 269. Стороны основания правильной треугольной усеченной пирамиды равны 4 дм и 2 дм, а боковое ребро равно 2 дм. Найдите высоту и апофему пирамиды.

Решение: боковая грань правильной треугольной усеченной пирамиды является равнобедренной трапецией, её высота (апофема) равна дм. Найдем радиусы вписанных окружностей в нижнее и верхнее основания, дм, дм. Высота усеченной пирамиды является высотой прямоугольной трапеции, где основания радиусы вписанных окружностей, а боковая сторона апофема.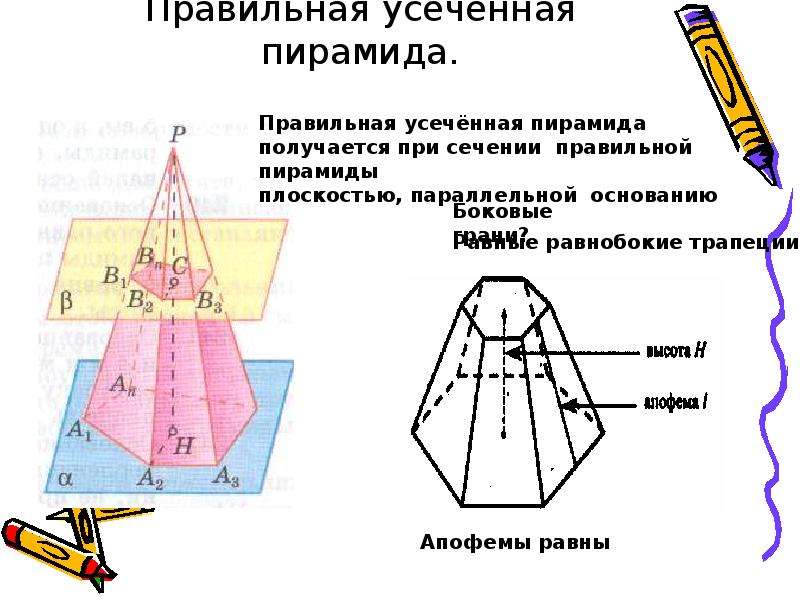 Отсюда высота усеченной пирамиды равна дм.

5. Учитель: Давайте подведем итог.

Что такое усеченная пирамида?

Какая усеченная пирамида называется правильной?

Учитель оценивает учащихся (знание теории, активную работу на уроке),задает домашнее задание: п. 30.задача из учебника № 268.

Урок 4. Решение задач.

Цель: повторить и закрепить изученный материал в ходе решения задач.

Задачи: образовательная – научить практическому применению знаний учащихся по теме к решению задач;

развивающая — развивать умение логически мыслить, делать выводы;

воспитательная – воспитывать дисциплинированность, аккуратность.

Вид урока: практикум по решению задач.

Оборудование: интерактивная доска.

План урока:

1. Организационный момент (2 мин).

2. Теоретический опрос (5 мин).

3. Практикум по решению задач (30 — 35 мин).

4. Подведение итогов. Домашняя работа (3 мин).

Ход урока:

1.Учитель организует учащихся к уроку.

2. Учитель: Ответьте на следующие вопросы:

Что называется высотой пирамиды?

Что такое апофема?

Какая пирамида называется правильной?

Учитель: Ответьте на вопросы, ответ обоснуйте:

Будет ли пирамида правильной, если её боковыми гранями являются правильные треугольники?

Существует ли четырехугольная пирамида, у которой противоположные боковые грани перпендикулярны к основанию?

Могут ли все грани треугольной пирамиды быть прямоугольными треугольниками?

3.Учитель: Сегодня мы будем решать задачи на нахождение длин элементов пирамиды (по своему усмотрению учитель может выбрать другие задачи).

Задача № 252. Основанием пирамиды DABC является равнобедренный треугольник АВС, в котором АВ=АС, ВС=6 см, высота АH=9 см. Известно также, что DA=DB=DC=13 см. Найдите высоту пирамиды.

Решение: найдем площадь основания см2. Найдем сторону равнобедренного треугольника АВ = см. Найдем радиус описанной окружности см. Найдем высоту пирамиды H=см.

Задача № 256. В правильной четырехугольной пирамиде сторона основания равна т. А плоский угол при вершине равен α. Найдите: а) высоту пирамиды; б) боковое ребро; в) угол между боковой гранью и плоскостью основания; г) двугранный угол при боковом ребре пирамиды.

Решение: апофема пирамиды является медианой и биссектрисой, найдем апофему, она равна . Найдем боковое ребро . Найдем радиус вписанной окружности, он равен . Найдем высоту пирамиды . Найдем угол между боковой гранью и основанием . Найдем площадь боковой грани S=, через площадь и сторону найдем другую высоту боковой грани h=m*cos. Половина диагонали равна . Две высота боковых граней будут образовывать двугранный угол при боковом ребре, найдем половину этого угла , отсюда весь угол равен 2arcsin(.

Задача № 267. Пирамида пересечена плоскостью, параллельной основанию. Докажите, что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Решение: рассмотрим треугольники: боковую грань и треугольник, отсекаемый сечением. Так как сечение параллельно основанию, то соответственные углы при параллельных прямых равны. Следовательно, треугольники подобны по первому признаку, отсюда следует, что боковое ребро делится на пропорциональные части. Аналогично доказывается, что треугольник, образованный высотой пирамиды, боковым ребром и радиусом вписанной в основание окружности подобен треугольнику, отсеченному от данного сечением.

4.Учитель: Давайте подведем итог.

Чему научились сегодня на уроке?

Учитель оценивает учащихся (знание теории, активную работу на уроке), задает домашнее задание: задача из учебника № 253, № 259.

Урок 5. Решение задач.

Цель: научить практическому применению знаний учащихся по теме к решению задач.

Задачи: образовательная – закрепить навыки в решении задач на нахождение площади поверхности пирамиды;

развивающая — развивать умение логически мыслить, делать выводы;

воспитательная – воспитывать дисциплинированность, аккуратность.

Вид урока: практикум по решению задач.

Оборудование: интерактивная доска.

План урока:

1. Организационный момент (2 мин).

2. Теоретический опрос (5 мин).

3. Практикум по решению задач (30 — 35 мин).

4. Подведение итогов. Домашняя работа (3 мин).

Ход урока:

1.Учитель организует учащихся к уроку.

2. Учитель: Ответь на следующие вопросы:

Из чего складывается поверхность пирамиды?

Как найти боковую поверхность правильной пирамиды?

Как найти боковую поверхность усеченной пирамиды?

3.Учитель: Сегодня мы будем решать задачи на нахождение площади поверхности пирамиды (по своему усмотрению учитель может выбрать другие задачи).

Задача № 243. Основанием пирамиды DABC является треугольник АВС, у которого АВ=АС=13 см, ВС=10 см; ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.

Решение: площадь боковой поверхности пирамиды складывается из суммы площадей боковых граней. Две грани будут равны и являются прямоугольными треугольниками, их площадь равна см2. Третья грань является равнобедренным треугольником. Найдем высоту основания, она равна см. Найдем высоту боковой грани, она равна см. Отсюда, площадь боковой грани равна см2. Площадь свей поверхности равна см2.

Задача № 264. Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона её основания равна а, а площадь боковой грани равна площади сечения, поведенного через вершину пирамиды и большую диагональ основания.

Решение: периметр основания равен 6а. Большая диагональ основания равна 2а, площадь сечения равна , а площадь боковой грани равна , отсюда . Следовательно, боковая грань наклонена к плоскости основания под углом 30º. Радиус вписанной в основание окружности равен , таким образом получаем, что площадь боковой поверхности правильной шестиугольной пирамиды равна см2.

Задача № 270. Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 см и 3 см. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности усеченной пирамиды.

Решение: две грани усеченной пирамиды будут являться прямоугольными трапециями и будут равны между собой, их площадь равна см2. Третья грань является равнобедренной трапецией, найдем высоту этой грани, а затем и площадь. Боковое ребро пирамиды равно см, высота боковой грани равна см, площадь боковой грани равна см2. Таким образом, площадь боковой поверхности усеченно пирамиды равна 16 см2.

4. Учитель: Давайте подведем итог.

Учитель оценивает учащихся (знание теории, активную работу на уроке), задает домашнее задание: задача из учебника № 257, № 266.

Урок 6. Самостоятельная работа.

Цель: проверить уровень освоенности материала по данной теме, умение решать различные учебные задачи

Задачи: образовательная – проконтролировать уровень ЗУНа у учащихся;;

развивающая — развивать умение самостоятельно мыслить, делать выводы.

воспитательная – дисциплинированность, аккуратность.

Методические рекомендации к уроку: учащимся предлагаются дифференцированные задания по вариантам.

При оценивании работы учитывается:

— самостоятельность;

— объём выполненной работы.

Вариант 1 .

1. В правильной четырехугольной пирамиде высота равна 4 см, а длина диагонали основания равна см. Найдите площадь полной поверхности пирамиды.

2. Основанием пирамиды МАВС служит прямоугольный треугольник АВС (ےС =90º), ВС = а, ےА=30º. Боковые ребра наклонены к основанию под углом 60º. Найдите высоту пирамиды.

3. В правильной треугольной пирамиде сторона основания равна а, а боковые грани наклонены к нему под углом 60º. Найдите площадь сечения, поведенного через среднюю линию основания параллельно боковой грани.

Вариант 2.

1. В пирамиде МАВС боковое ребро МА перпендикулярно плоскости основания АВС, а грань МВС составляет с ним угол 60º, АВ=АС=10, ВС=16.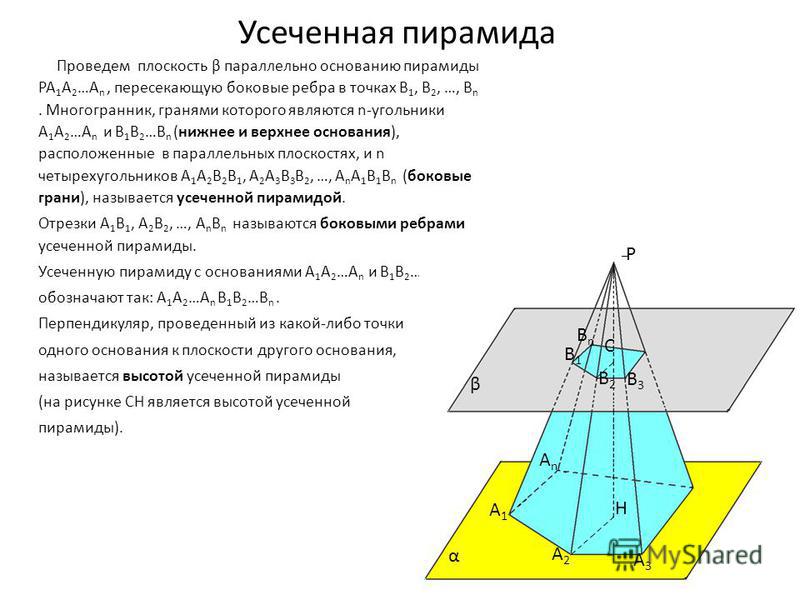 Найдите площадь боковой поверхности пирамиды.

2. В правильной треугольной пирамиде сторона основания равна а, а высота равна 2а. Найдите углы наклона боковых ребер и боковых граней к плоскости основания.

3. В правильной четырехугольной усеченной пирамиде стороны оснований равны 6 и 8 см, а боковые грани наклонены к плоскости основания под углом 45º. Найдите площадь боковой поверхности пирамиды.

Математика 11 Тематические тестовые задания по геометрии (физико-математическое направление)

Тригонометрические уравнения

Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие

Подробнее

Все прототипы задания В11 (2013)

Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного

Подробнее

Прямоугольный параллелепипед

ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.

Подробнее

Все прототипы заданий В года

1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13

Подробнее

7. Задачи по стереометрии

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии

Подробнее

ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ

ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ Инструкция. Решите задание. Дайте краткий ответ. 1. Апофема правильной треугольной пирамиды 4 см, а сторона основания 8 см. Найдите площадь боковой поверхности пирамиды.

Подробнее

Все прототипы заданий года

1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12

Подробнее

«Объёмы многогранников и тел вращения»

«Объёмы многогранников и тел вращения» Работа учащихся в группах по карточкам. Задачи по теме «Объёмы» подобраны из тестовых задач по математике Задачи для группы.. Образующая прямого конуса равна 4 см

Подробнее

Задание 16 Задачи по стереометрии

Задание 16 Задачи по стереометрии Куб 1.Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30

Подробнее

Все прототипы заданий В года

1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий

Подробнее

Задание 8 Стереометрия.

Задание 8 Стереометрия. Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Объем куба равен 8. Найдите площадь его поверхности. 3. Если каждое ребро куба увеличить на 1, то его площадь

Подробнее

Тест по теме «Задачи стереометрии»

Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л.С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют

Подробнее

Все прототипы задания В9 (2013)

Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,

Подробнее

Предмет «Математика» Вариант ХХХХ

Предмет «Математика» Вариант ХХХХ I часть При выполнении заданий 1-15 следует записать только ответ. 1. Найдите знаменатель дроби, которая равна дроби, если ее числитель равен. 2. Найдите точку пересечения

Подробнее

Все прототипы В года

1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние

Подробнее

Стартовая контрольная работа

Стартовая контрольная работа Контрольная работа 1(на 20 мин) 1. Найдите координаты вектора АВ, если А (5; 1; 3), В (2; 2; 4). 2. Даны векторы b (3; 1; 2) и c 2b c (1; 4; 3). Найдите. 3. Изобразите систему

Подробнее

Тест 250. Отрезок. Длина

Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол

Подробнее

Задачи по с т е р е о м е т р и и

Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета

Подробнее

Куб. Прямоугольный параллелепипед

Куб 1. Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3.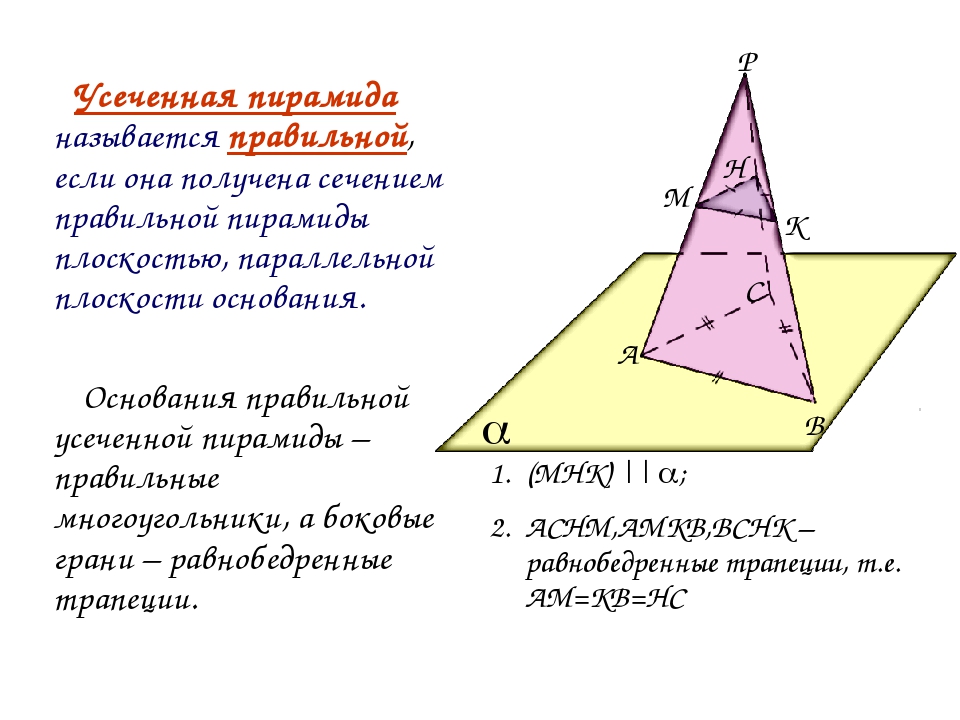 Задание

Подробнее

Задание 13. Задачи по стереометрии

Задание 13 Задачи по стереометрии 1.Диагональ куба равна Куб. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см

Подробнее

ПРЯМОЙ И НАКЛОННЫЙ КОНУС

ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг

Подробнее

ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС

ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС ПРОВЕРОЧНАЯ РАБОТА 1 1) Найти площадь равнобедренного треугольника с углом при основании, если а) боковая сторона равна с; б) основание равно р 2) Стороны параллелограмма

Подробнее

Многогранники.

Призма

Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,

Подробнее

Геометрия. Тренировочный вариант 1

Геометрия. Тренировочный вариант 1 1. Найдите площадь трапеции, изображённой на рисунке. 2. Около треугольника MNP описана окружность с центром О. Найдите угол РОМ, если угол PNM равен 17. Ответ дайте

Подробнее

Тест по теме 60 «Параллелепипед и куб»

Тест по теме 60 «Параллелепипед и куб» 1. Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?, если в основании квадрат 2. Существует ли параллелепипед, у которого

Подробнее

Основные определения, теоремы и формулы планиметрии.

Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне

Подробнее

Количество набранных баллов

Варианты заданий для проведения государственной итоговой аттестации по математике в 11 классах Задания для проведения государственной итоговой аттестации по математике в 11 классах академического уровня

Подробнее

Стереометрия: комбинации тел.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед

Подробнее

Задание 8, 14. Стереометрия

Задание 8, 4. Стереометрия Основные определения Аксиомы стереометрии Теорема. Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой

Подробнее

Сфера (шар), вписанная в призму

Сфера (шар), вписанная в призму Сфера (шар) называется вписанной в призму, если она касается каждой грани призмы В призму можно вписать сферу тогда и только тогда, когда в перпендикулярное сечение призмы

Подробнее

Geometrické útvary a tělesa

Geometrické útvary a tělesa Линии. Термин «линия» (или «кривая» в широком смысле слова) не имеет определения, хотя мысленно линию можно представить как след движущейся точки. Бесчисленные попытки определить

Подробнее

ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ)

И.М. Смирнова, В.А. Смирнов ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ) ОБЪЕМЫ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ ПРОСТРАНСТВЕННЫХ ФИГУР Москва 2008 1 ВВЕДЕНИЕ В настоящем пособии собраны задачи на нахождение объемов и площадей поверхностей

Подробнее

10 класс.

Интеллектуальные марафоны в школе. 5-11 классы

1 тур

ГРУППА А

1. Назовите страны, входящие в «Большую восьмерку».

2. Как газ бутан очистить от примеси бутена?

3. При охлаждении жидкости интенсивность ее испарения: а) не изменяется; б) повышается; в) уменьшается?

4. Решите следующее неравенство: sin х + 1 ? 0.

5. Перечислите правильные многогранники.

6. The first book was printed in: a) France; 6) Germany; в) England?

7. Что позволило предку человека выйти из-под контроля естественного отбора?

8. В каком виде спорта победа иногда присуждается после того, как судья досчитает до 10?

9. Что можно отнести к стихийным бедствиям: а) снежные заносы, сход лавин; б) землетрясения; в) разливы сильно действующих ядовитых веществ; г) авиационные катастрофы?

10. Сколько бит в байте?

11. Какое событие связано с датой 1 августа 1914 года: а) Россия объявила войну Германии; б) Австро-Венгрия объявила войну России; в) Германия объявила войну России?

12. Что такое менеджмент?

13. Каким русским критикам посвящены следующие фрагменты стихотворений Николая Алексеевича Некрасова:

1. «Был особенно любим,

Молясь твоей многострадальной тени,

Учитель! Перед именем твоим

Позволь смиренно преклонить колени».

2. «Его еще покамест не распяли,

Но час придет, он будет на кресте.

Его послал Бог гнева и печали

Рабом земли напомнить о Христе».

3. «Сознательно мирские наслажденья

Ты отвергал, ты чистоту хранил.

Ты жажде сердца не дал утоленья.

Как женщину, ты Родину любил».

ГРУППА Б

1. Ему не меньше 7 раз меняли форму носа, а кроме того укорачивали левое веко, делали насадку на верхнюю челюсть… О ком идет речь?

2. Каков был результат операции, проведенной профессором Преображенским и доктором Борменталем, по пересадке псу гипофиза?

3. У него 99 имен, а вот сотое имя, согласно Исламу, знать никому не дано. О ком идет речь?

4. Написав роман «Отверженные», Виктор Мари Гюго уехал из Парижа, но и на отдыхе забеспокоился, хорошо ли продается его книга. Чтобы не утомлять руки, Гюго написал издателю только: «?». Каким был столь же лаконичный ответ издателя?

5. Эти упругие волны недоступны слуху человека, зато их прекрасно «слышат» рыбы и летучие мыши.

6. Какой диэлектрик с очень высоким удельным сопротивлением буквально окружает нас?

7. Во Франции его называют «салатом по-русски», а в России он носит имя француза. Как называется этот замечательный салат?

2 тур

ГРУППА А

1. Каковы цели и механизмы проведения государственной демографической политики?

2. Указать, какие вещества получаются в превращениях:

Назовите эти вещества.

3. Какое условие из приведенных ниже выполняется при адиабатном сжатии газа: a) Q = – А; б) Q = А в) А = 0; г) А’ = 0; д) ?U = 0; е) Q = 0.

4. Решите следующую систему:

5. Найдите объем правильного тетраэдра с ребром а = 1 (объем пирамиды

6. Australia was discovered in: a) the 17 century; 6) the 16 century; в) the 18 century?

7. Результатом какого отбора является возникновение крестообразного клюва у клеста-еловика?

8. Каким видом спорта, по утверждению Владимира Высоцкого, нужно заняться, чтобы узнать своего друга?

9. Услышав дома сигнал опасности химического заражения в результате выброса ядовитых веществ, необходимо:

а) выйти из дома, предварительно захватив документы и деньги;

б) провести влажную уборку с последующим проветриванием;

в) надеть средства индивидуальной защиты, провести герметизацию помещения?

10. Что такое модем?

11. Какой город после смерти Юрия Владимировича Андропова был назван его именем: а) Набережные Челны; б) Рыбинск; в) Ульяновск; г) Ишимбай?

12. В творчестве какого писателя впервые прозвучала знаменитая формула: «Если нет Бога, то все позволено»:

а) Франца Кафки;

б) Максима Горького;

в) Федора Михайловича Достоевского.

13. Объясните выражение: «на честном слове держится». Составьте предложение с ним.

ГРУППА Б

1. За взятие Измаила генерал Александр Васильевич Суворов получил звание подполковника Преображенского полка, которым командовал полковник…?

2. Реклама какого товара дала шутливое название всем многосерийным кинофильмам?

3. Морская свинка – 2 месяца, овца – 5 месяцев, дельфин – 12 месяцев, носорог – 16 месяцев, человек —? месяцев.

4. Этим средством во времена Мольера лечили от всех болезней, в том числе и мнимого больного Аргона. Каким?

5. В какое из 4 времен года стада поднимаются на джайлоо, джай-ляу и различные яйлы?

6. Он умер в чине генерал-майора во время пятой Тянь-шаньской экспедиции. На берегу Иссык-Куля стоит памятник «первому исследователю Центральной Азии». Кто он?

7. У этого музыкального инструмента 45 струн и 7 педалей. Назовите его.

3 тур

ГРУППА А

1. Эту страну нередко сравнивают с веером: десятки дорог радиально расходятся от столицы. В районе, где находится столица, на почти идеально ровной низменности, проживает 3/4 населения и производится 90 % промышленной продукции страны. Это и главный сельскохозяйственный район. Помимо столицы, здесь располагается второй по числу жителей город страны – центр авто– и авиастроения, а третий город – главный порт по вывозу зерна.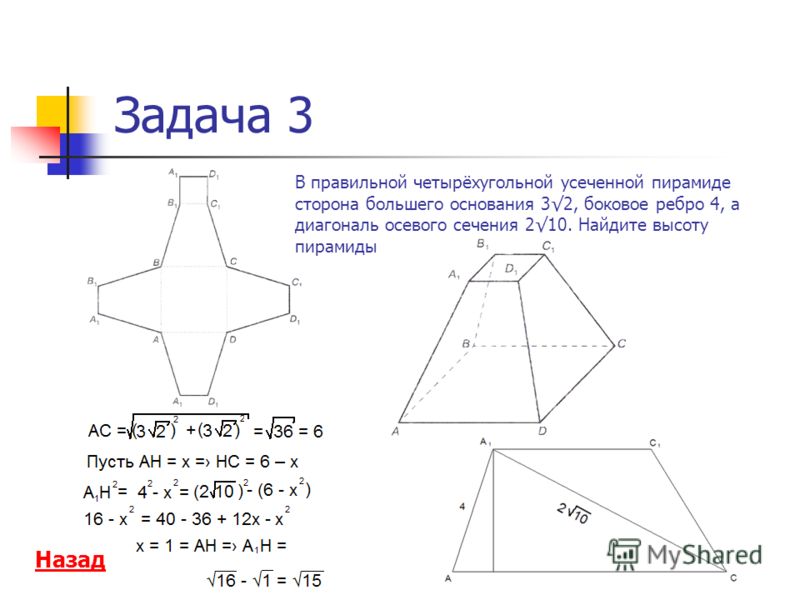 Как называются страна и три крупнейших города? О какой зерновой культуре идет речь?

2. Определите массу 40 %-ного раствора гидроксида натрия, необходимого для нейтрализации смеси, состоящей из уксусной кислоты, фенола и этилового спирта по 1 молю каждого.

3. Над идеальным газом совершили цикл 1-2-3, изображенный на диаграмме Р-Т (рис. 18). Найти отношение максимального и минимального объемов.

Рис. 18.

4. Найдите уравнения касательных, проведенных через точку М(0, 1) к параболе у = х2 + 2х + 2.

5. Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 и 3 см. Одно из боковых ребер перпендикулярно к плоскости основания и равно 1 см. Найдите площадь боковой поверхности усеченной пирамиды.

6. Find the mistake: I have been wearing it 3 years now.

7. Десять подвидов популяции hams argentatus – fuscus (серебристая чайка) образуют непрерывное кольцо, которое тянется от Британских островов через Скандинавию, Россию, Берингов пролив, Аляску и Канаду и возвращается к Британским островам с другой стороны. Если бы подвиды, обитающие в районе Берингова пролива и Аляски, исчезли, то какие это имело бы последствия для популяции?

8. Какой вид спорта появился благодаря открытию китайских химиков и последовавшему за этим изобретению?

9. Что можно отнести к средствам оповещения гражданской обороны: а) почта и телеграф; б) предсказания астрологов; в) местное телевидение и радио; г) международная телефонная сеть; д) местные газеты и журналы?

10. Назовите основные алгоритмические конструкции.

11. Целковый – это монета достоинством: а) 5 копеек; б) 25 копеек; в) 1 рубль?

12. В 1811 году посланник Сардинского королевства при русском дворе Жозеф Мари де Местр, сообщая в своем письме о новых законах, изданных Александром I, употребил выражение, ставшее широко известным, особенно в наши дни. Какое:

а) «Каждый народ имеет то правительство, которое он заслуживает»;

б) «Отсюда хоть 3 года скачи, ни до какого государства не доскачешь»;

в) «Народ безмолвствует»?

13. Кто из русских писателей XIX века совершил кругосветное путешествие? Назовите произведение, в котором отразились его впечатления.

ГРУППА Б

1. Так воины Дмитрия Донского называли то, что мы зовем сегодня арбалетом.

2. Этот новый этап в жизни шахмат начался партией между королем Англии Генрихом I и королем Франции Людовиком V в 1119 году. Сейчас подобным образом играют тысячи шахматистов. О каком виде соревнований идет речь?

3. Назовите имя легендарного комиссара Мегрэ.

4. Из-за нее в 1812 году русские солдаты убивали иногда своих же офицеров. Особенно ночью. Что это?

5. Столица этого государства, спроектированная в форме самолета с размахом крыльев по 12 км, была торжественно открыта 21 апреля 1960 года. О каком государстве идет речь?

6. Это самый низкий женский голос, хотя в его название входит итальянское слово «высокий».

7. Чай подразделяется на прессованный, гранулированный и…?

4 тур

ГРУППА А

1. На гербе какого государства изображен географический объект, расположенный в другом государстве? Что это за объект?

2. Неизвестный алкен массой 7 г присоединяет бромоводород, объем которого одинаков с объемом метана массой 2 г. Найдите молекулярную формулу алкена.

3. Две батарейки с одинаковой ЭДС (Ел = Е = Е), но разными внутренними сопротивлениями (r1 = 0,1 Ом; r2 = 1,1 Ом) включены в цепь, содержащую конденсатор, емкость которого С, и резистор К, сопротивления которых R1 = 2,8 Ом и R2 = 1,12 Ом. Сначала, когда цепь разомкнута, идеальный вольтметр, присоединенный к клеммам батареи Е1 показывает напряжение U0= 8 В; затем вольтметр присоединяют к клеммам батареи Е2 и замыкают ключ К (рис. 19). Найдите показания вольтметра непосредственно после замыкания ключа и после того, как токи в цепи установятся.

Рис. 19.

4. В шар радиуса R = 1 вписан конус наибольшего объема. В полученный конус вписан цилиндр наибольшего объема. Найдите площадь поверхности цилиндра.

5. Сколько существует плоскостей, каждая из которых равноудалена от 4 заданных точек, не лежащих в одной плоскости?

6. Translate: it is a small world.

7. Каковы результаты адаптивной радиации?

8. Какому спортивному достижению нельзя поставить приставку «экс»?

9. К сильно действующим ядовитым веществам можно отнести: а) хлор; б) ртуть; в) сероводород; г) аммиак; д) аргон; е) неон; ж) азот; з) бутан; и) криптон?

10. Напишите программу вычисления наименьшего общего кратного двух натуральных чисел.

11. Как в царской полиции записывали преступников, скрывавших свои анкетные данные?

12. Кем была высказана мысль: «Россия не может определить себя, как Восток, и противополагать себя Западу. Россия должна сознавать себя и Западом, и Востоком, Востоко-Западом, соединителем двух миров»?

13. Кто из великих писателей, похороненных на Новодевичьем кладбище, в 1886–1890 годах жил по адресу: Москва, ул. Садово-Кудринская, 6?

ГРУППА Б

1. Кто из наших соотечественников в XX веке стали лауреатами Нобелевской премии: 1) Вернадский и Циолковский; 2) Марков и Стеклов; 3) Павлов и Мечников?

2. Для создания телеграфной линии между Вашингтоном и Балтимором Сэмюэлю Морзе пришлось заняться сбором пустых бутылок. Зачем?

3. Почему в Иране кондуктор общественного транспорта располагается посредине салона? Какова его главная обязанность?

4. Изабелла Кастильская была замужем за Фердинандом II Арагонским, за Фердинандом III Неаполитанским, за Фердинандом V Кастильским… А сколько всего раз она выходила замуж?

5. Кому Константин Михайлович Симонов посвятил строки: «Жди меня, и я вернусь…»?

6. Эта птичка дала свое имя певице Эдит Гассион.

7. В середине прошлого века он написал «Проект о введении единомыслия в России».

Реферат по геометрии на тему:»Фигуры.Пирамида»(9 класс)

СОДЕРЖАНИЕ

Тема страница

1.Пирамиды в геометрии 2

2. Виды пирамид 3

3. Теоремы 5

4.Пирамиды в мире 6

Пирамиды в геометрии

Пирамида-многогранник,основание которого-многоугольник,а грани-треугольники,которые имеют общую вершину.По числу углов основания пирамиды различают на треугольные,четырехугольные и т.д.

Общая вершина боковых граней-вершина пирамиды.Высота пирамиды-перпендикуляр, который опущен из вершины пирамиды на плоскость основания.

Виды пирамид

1.Правильная пирамида— пирамида, у которой в основании лежит правильный многоугольник, а высота, которая опущена из вершины пирамиды на плоскость основания является отрезком, который соединяет вершину пирамиды с центром основания.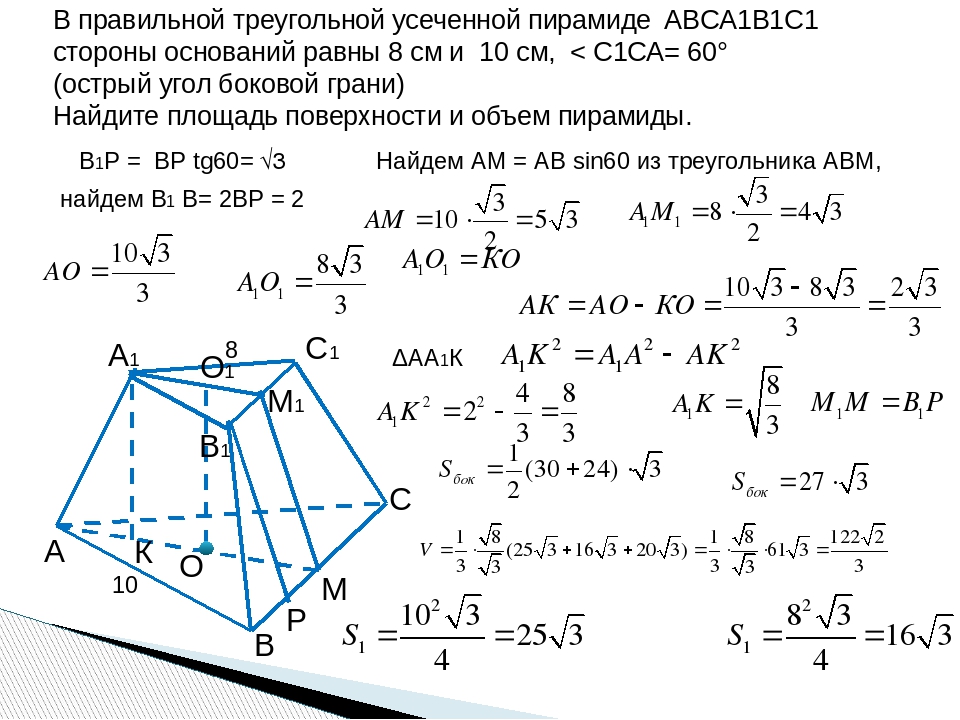

Свойства правильной пирамилы:

1.Все боковые рёбра правильной пирамиды равны между собой

2.Все боковые грани являются равными равнобедренными треугольниками

3.Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на высоту боковой грани, которая называется апофемой.

S=0,5*P*h

P-периметр основания

h-апофема

Объём любой пирамиды равен трети произведения площади основания на высоту:

V=1/3*S*H

S-площадь боковой поверхности

H-высота

2.Пирамида, вписанная в конус- пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершина пирамиды- вершина конуса. Боковые ребра пирамиды- стороны, образующие конус.

3.Пирамида,описанная около конуса- пирамида, основание которой есть многоугольник, описанный около основания конуса, а вершина пирамиды- вершина конуса. Плоскости боковых граней касательны плоскостям конуса.

4.Усечённая пирамида- пирамида, которая получается следующим способом: берётся произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: пирамида подобная исходной и многогранник, который называется усечённой пирамидой. Основаниями усечённой пирамиды служат подобные многоугольники.

Если усечённая пирамида получается из правильной пирамиды, то она называется правильной усечённой пирамидой. Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями. Высота боковой грани называется апофемой правильной усечённой пирамиды. Перпендикуляр, опущенный из точки верхнего основания на нижнее основание, называется высотой усечённой пирамиды.

Площадь полной поверхности усечённой пирамиды равна сумме площадей оснований и боковых граней.

Объём усечённой пирамиды вычисляется по формуле:

V=1/3*H(S1+S2+(S1+S2)^0,5

H-высота усечённой пирамиды

S1, S2-площади оснований усеченной пирамиды

Площадь боковой поверхности правильной усеченной пирамиды вычисляется по формуле:

S=0,5*(p+P)*h

P-периметр нижнего основания усеченной пирамиды

p-периметр верхнего основания усеченной пирамиды

h-апофема правильной усеченной пирамиды

Теоремы

1.Площадь боковой поверхности равна половине произведения периметра основания на апофему

Доказательство:

Боковые грани правильной пирамиды- равные равнобедренные треугольники , основания которых-стороны основания пирамиды , а высоты равны апофеме Площадь боковой поверхности пирамиды равна сумме произведений сторон основания на половину апофемы. Вынося множитель 0.5h за скобки, получаем в скобках сумму сторон основания пирамиды- периметр.

2. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полупериметра основания на апофему.

Доказательство:

Если сторона основания а, число сторон n, то боковая поверхность пирамиды равна: половине произведения периметра основания на апофему пирамиды.

Если пирамида неправильная, то ее боковая поверхность будет равна сумме площадей ее боковых граней

Пирамиды в мире

«…Отчего же пословицу древнюю повторяют феллахи и птицы, что боятся все люди времени, а время боится пирамид!»

Поэма «Монолог египетской пирамиды»

Чудеса света создавались на протяжении огромного промежутка времени с 30 до 2 века до н.э. Давным-давно были разрушены 6 чудес света. Осталось самое древнейшее — египетские пирамиды — само олицетворение незыблемости и вечности.

Суровые, скупые и строгие, они стоят на самом краю необозримой Ливийской пустыни к югу от Каира. Издалека они кажутся призрачными, почти прозрачными и голубыми. По мере приближения к пирамидам свет сгущается, переходя из пепельного цвета в более светлый. Они поражают туристов своей громадностью.

Что такое боковая поверхность пирамиды. Площадь боковой поверхности пирамиды. Соблюдение вашей конфиденциальности на уровне компании

Площадь боковой поверхности произвольной пирамиды равна сумме площадей её боковых граней. Специальную формулу для выражения этой площади имеет смысл дать в случае правильной пирамиды. Так, пусть дана правильная пирамида, в основании которой лежит правильный n-угольник со стороной, равной а. Пусть h — высота боковой грани, называется также апофемой
пирамиды. Площадь одной боковой грани равна 1/2ah, а вся боковая поверхность пирамиды имеет площадь, равную n/2ha.Так как na — периметр основания пирамиды, то можно написать найденную формулу в виде:

Площадь боковой поверхности
правильной пирамиды равна произведению её апофемы на половину периметра основания.

Что касается площади полной поверхности
, то просто к боковой прибавляем площадь основания.

Вписанные и описанные сфера и шар
. Нужно отметить, что центр вписанной в пирамиду сферы лежит на пересечении биссекторных плоскостей внутренних двугранных углов пирамиды. Центр описанной около пирамиды сферы лежит на пересечении плоскостей, проходящих через середины ребер пирамиды и перпендикулярных им.

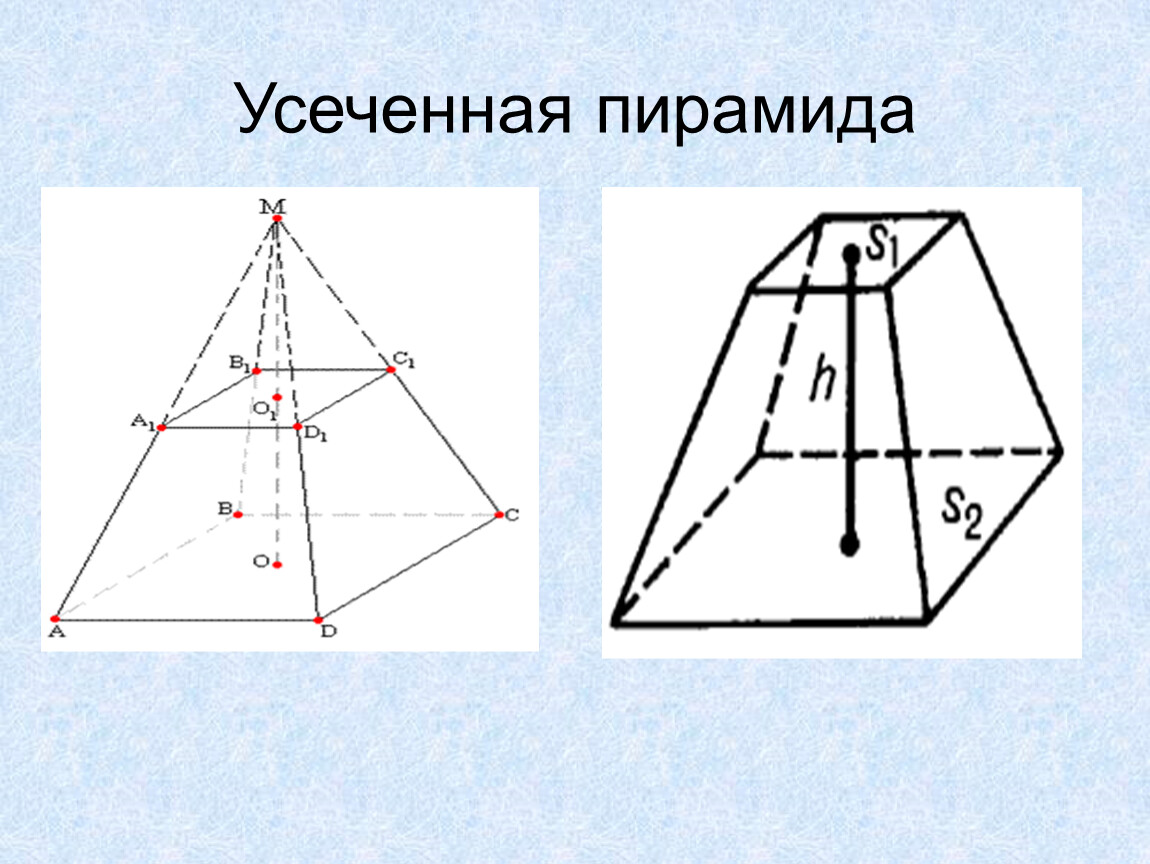
Усеченная пирамида.
Если пирамиду рассеч плоскостью, параллельной её основанию, то часть, заключенная между секущей плоскостью и основанием, называется усеченной пирамидой.
На рисунке показана пирамида, отбрасывая её часть, лежащую выше секущей плоскости, получаем усеченную пирамиду. Ясно, что малая отбрасываемая пирамида гомотетична большой пирамиде с центром гомотетии в вершине. Коэффициент подобия равен отношению высот: k=h 2 /h 1 , или боковых ребер, или других соответствующих линейных размеров обеих пирамид. Мы знаем, что площади подобных фигур относятся, как квадраты линейных размеров; так площади оснований обеих пирамид (т.е. пощади оснований усеченной пирамиды) относятся, как

Здесь S 1 — площадь нижнего основания, а S 2 — площадь верхнего основания усеченной пирамиды. В таком же отношении находятся и боковые поверхности пирамид. Сходное правило имеется и для объемов.

Объемы подобных тел
относятся, как кубы их линейных размеров; например, объемы пирамид относятся, как произведения их высот на площади оснований, откуда наше правило получается сразу. Оно имеет совершенно общий характер и прямо следует из того, что объем всегда имеет размерность третей степени длины. Пользуясь этим правилом, выведем формулу, выражающую объем усеченной пирамиды через высоту и площади оснований.

Пусть дана усеченная пирамида с высотой h и площадями оснований S 1 и S 2 . Если представить себе, что она продолжена до полной пирамиды, то коэффициент подобия полнорй пирамиды и малой пирамиды легко найти, как корень из отношения S 2 /S 1 . Высота усеченной пирамиды выражается как h = h 1 — h 2 = h 1 (1 — k). Теперь имеем для объема усеченной пирамиды (через V 1 и V 2 обозначены объемы полной и малой пирамид)

формула объема усеченной пирамиды

Выведем формулу площади S боковой поверхности правильной усеченной пирамиды через периметры Р 1 и Р 2 оснований и длину апофемы а. Рассуждаем точно так же, как и при выводе формулы для объема. Дополняем пирамиду верхней частью, имеем P 2 = kP 1 , S 2 =k 2 S 1 , где k — коэффициент подобия, P 1 и P 2 — периметры оснований, а S 1 и S 2 — лощади боковых поверхностей всей полученной пирамиды и её верхней части соответственно. Для боковой поверхности найдем (а 1 и а 2 — апофемы пирамид, а = а 1 — а 2 = а 1 (1-k))

формула площади боковой поверхности правильной усеченной пирамиды

В этом уроке:

Задача 1. Найти площадь полной поверхности пирамиды
Задача 2. Найти площадь боковой поверхности правильной треугольной пирамиды

См. также материалы по теме:
.

Примечание

. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√»
.

Задача 1
. Найти площадь полной поверхности правильной пирамиды

Высота основания правильной треугольной пирамиды равна 3 см. а угол между боковой гранью и основанием пирамиды равен 45 градусов.
Найти площадь полной поверхности пирамиды

Решение
.

В основании правильной треугольной пирамиды лежит равносторонний треугольник.
Поэтому для решения задачи воспользуемся свойствами правильного треугольника:

Нам известна высота треугольника, откуда можно найти его площадь.
h = √3/2 a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3

Откуда площадь основания будет равна:
S = √3/4 a 2
S = √3/4 (6 / √3) 2
S = 3√3

Для того, чтобы найти площадь боковой грани, вычислим высоту KM. Угол OKM по условию задачи равен 45 градусам.
Таким образом:
OK / MK = cos 45
Воспользуемся таблицей значений тригонометрических функций и подставим известные значения.

OK / MK = √2/2

Учтем, что OК равен радиусу вписанной окружности. Тогда
OK = √3/6 a
OK = √3/6 * 6/√3 = 1

Тогда
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2

Площадь боковой грани тогда равна половине произведения высоты на основание треугольника.
Sбок = 1/2 (6 / √3) (2/√2) = 6/√6

Таким образом, площадь полной поверхности пирамиды будет равна
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6

Ответ
: 3√3 + 18/√6

Задача 2
. Найти площадь боковой поверхности правильной пирамиды

В правильной треугольной пирамиде высота равна 10 см, а сторона основания 16 см. Найти площадь боковой поверхности

.

Решение
.

Поскольку основанием правильной треугольной пирамиды является равносторонний треугольник, то AO является радиусом описанной вокруг основания окружности.
(Это следует из )

Радиус окружности, описанной вокруг равностороннего треугольника найдем из его свойств

Откуда длина ребер правильной треугольной пирамиды будет равна:
AM 2 = MO 2 + AO 2
высота пирамиды известна по условию (10 см), AO = 16√3/3
AM 2 = 100 + 256/3
AM = √(556/3)

Каждая из сторон пирамиды представляет собой равнобедренный треугольник. Площадь равнобедренного треугольника найдем из первой формулы, представленной ниже

S = 1/2 * 16 sqrt((√(556/3) + 8) (√(556/3) — 8))
S = 8 sqrt((556/3) — 64)
S = 8 sqrt(364/3)
S = 16 sqrt(91/3)

Поскольку все три грани у правильной пирамиды равны, то площадь боковой поверхности будет равна
3S = 48 √(91/3)

Ответ:
48 √(91/3)

Задача 3. Найти площадь полной поверхности правильной пирамиды

Сторона правильной треугольной пирамиды равна 3 см а угол между боковой гранью и основанием пирамиды равен 45 градусов. Найдите площадь полной поверхности пирамиды
.

Решение
.
Поскольку пирамида правильная, в ее основании лежит равносторонний треугольник. Поэтому площадь основания равна

So = 9 * √3/4

Для того, чтобы найти площадь боковой грани, вычислим высоту KM. Угол OKM по условию задачи равен 45 градусам.
Таким образом:
OK / MK = cos 45
Воспользуемся

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.

Как быть при нахождении площади основания пирамиды?

Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.

Правильный треугольник

То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:

S = (а 2 * √3) / 4.

Квадрат

Формула для вычисления его площади самая простая, здесь «а» — снова сторона:

Произвольный правильный n-угольник

У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.

S = (n * а 2) / (4 * tg (180º/n)).

Как поступить при вычислении площади боковой и полной поверхности?

Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.

Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение — «А». Общая формула для площади боковой поверхности выглядит так:

S = ½ Р*А, где Р — периметр основания пирамиды.

Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:

S = n/2 * в 2 sin α.

Задача № 1

Условие.
Найти общую площадь пирамиды, если в его основании лежит со стороной 4 см, а апофема имеет значение √3 см.

Решение.
Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см 2 .

Для треугольника в основании получится такое значение площади: (4 2 *√3) / 4 = 4√3 см 2 .

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см 2 .

Ответ.
10√3 см 2 .

Задача № 2

Условие
. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение.
Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм 2 . Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 мм 2 . Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм 2 .

Ответ
. Искомое значение 267,576 мм 2 .

Задача № 3

Условие
. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение.
Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3 2 + 4 2) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+6 2 = 96 (см 2).

Ответ.
96 см 2 .

Задача № 4

Условие.
Дана правильная Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение.
Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см 2 .

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61) 2)=√435600=660 см 2 . Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см 2 . Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2 .

Ответ.
Основания — 726√3 см 2 , боковой поверхности — 3960 см 2 , вся площадь — 5217 см 2 .

Какую фигуру мы называем пирамидой? Во-первых, это многогранник. Во-вторых, в основании этого многогранника расположен произвольный многоугольник, а стороны пирамиды (боковые грани) обязательно имеют форму треугольников, сходящихся в одной общей вершине. Вот теперь, разобравшись с термином, выясним, как найти площадь поверхности пирамиды.

Понятно, что площадь поверхности такого геометрического тела составится из суммы площадей основания и всей его боковой поверхности.

Вычисление площади основания пирамиды

Выбор расчетной формулы зависит от формы лежащего в основании нашей пирамиды многоугольника. Он может быть правильным, то есть со сторонами одинаковой длины, или неправильным. Рассмотрим оба варианта.

В основании – правильный многоугольник

Из школьного курса известно:

площадь квадрата будет равна длине его стороны, возведенной в квадрат;
площадь равностороннего треугольника равна квадрату его стороны, деленному на 4 и умноженному на квадратный корень из трех.

Но существует и общая формула, для расчета площади любого правильного многоугольника (Sn): надо умножить значение периметра этого многоугольника (Р) на радиус вписанной в него окружности (r), а затем разделить полученный результат на два: Sn=1/2P*r.

В основании – неправильный многоугольник

Схема нахождения его площади заключается в том, чтобы сначала разбить весь многоугольник на треугольники, вычислить площадь каждого из них по формуле: 1/2a*h (где а – основание треугольника, h – опущенная на это основание высота), сложить все результаты.

Площадь боковой поверхности пирамиды

Теперь рассчитаем площадь боковой поверхности пирамиды, т.е. сумму площадей всех ее боковых сторон. Здесь также возможны 2 варианта.

Пусть у нас имеется произвольная пирамида, т.е. такая, в основании которой – неправильный многоугольник. Тогда следует вычислить отдельно площадь каждой грани и сложить результаты. Так как боковыми сторонами пирамиды по определению могут быть только треугольники, то расчет идет по упомянутой выше формуле: S=1/2a*h.
Пусть наша пирамида – правильная, т.е. в ее основании лежит правильный многоугольник, и проекция вершины пирамиды оказывается в его центре. Тогда для вычисления площади боковой поверхности (Sб) достаточно найти половину произведения периметра многоугольника-основания (Р) на высоту (h) боковой стороны (одинаковую для всех граней): Sб=1/2 Р*h. Периметр многоугольника определяется сложением длин всех его сторон.

Полная площадь поверхности правильной пирамиды найдется суммированием площади ее основания с площадью всей боковой поверхности.

Примеры

Для примера вычислим алгебраически площади поверхности нескольких пирамид.

Площадь поверхности треугольной пирамиды

В основании такой пирамиды – треугольник. По формуле Sо=1/2a*h находим площадь основания. Эту же формулу применяем для нахождения площади каждой грани пирамиды, также имеющей треугольную форму, и получаем 3 площади: S1, S2 и S3. Площадь боковой поверхности пирамиды является суммой всех площадей: Sб= S1+ S2+ S3. Сложив площади боковых сторон и основания, получим полную площадь поверхности искомой пирамиды: Sп= Sо+ Sб.

Площадь поверхности четырехугольной пирамиды

Площадь боковой поверхности — это сумма 4-ех слагаемых: Sб= S1+ S2+ S3+ S4, каждое из которых вычислено по формуле площади треугольника. А площадь основания придется искать, в зависимости от формы четырехугольника — правильного или неправильного. Площадь полной поверхности пирамиды снова получится путем сложения площади основания и полной площади поверхности заданной пирамиды.

Пирамида

— основание, пирамиды, треугольники и высота

Пирамида — это геометрическое тело, форма которого прославилась царскими гробницами Древнего Египта. Это твердое тело, основание которого представляет собой многоугольник, а боковые грани — треугольники с общей вершиной (вершиной пирамиды). В случае египетской пирамиды Хеопса основание представляет собой почти идеальный квадрат 755 футов (230 м) по краю и грани треугольников, которые приблизительно равносторонние.

Пирамиды в Гизе, Египет. Фотография Дилипа Мехиа / Свяжитесь с Гизой. Фондовый рынок. Воспроизведено с разрешения автора.

Основание пирамиды может быть любым многоугольником с тремя или более гранями, а имена пирамид соответствуют количеству ребер в основании. Когда основание представляет собой треугольник, пирамида представляет собой треугольную пирамиду. Он также известен как тетраэдр , поскольку он имеет четыре грани, включая основание. Когда эти грани представляют собой равносторонние треугольники, это квадратная пирамида, в основе которой лежит квадрат.

Наиболее часто встречающиеся пирамиды — это «правильные» пирамиды.Они имеют правильный многоугольник в качестве основания и равнобедренные треугольники для боковых сторон. Однако не все пирамиды правильные.

Высоту пирамиды можно измерить двумя способами: от вершины по линии , перпендикулярной к основанию, и от вершины по линии, перпендикулярной одному из краев основания. Последняя мера называется наклонной высотой. Однако, если боковые грани не являются конгруэнтными треугольниками, наклонная высота может варьироваться от грани к грани и не будет иметь большого значения для пирамиды в целом.Если слово наклон не включено, термин высота (или высота) относится к высоте.

Если помимо конгруэнтности боковые грани равнобедренные, пирамида будет правильной. В правильной пирамиде прямоугольных треугольников можно встретить в изобилии. Предположим, у нас есть правильная пирамида с высотой VC и наклонной высотой VD. Здесь треугольники VCD, VDE, VCE и CDE являются прямоугольными треугольниками. Если в любом из этих треугольников известны две стороны, можно использовать теорему Пифагора , чтобы вычислить третью.Это, в свою очередь, может быть использовано в других треугольниках для определения еще других неизвестных сторон. Например, если правильная квадратная пирамида имеет наклонную высоту в две единицы и основание из двух единиц на краю, боковые края должны быть √5 единиц, а высота √3 единиц.

Существуют формулы для вычисления боковой и общей площади некоторых специальных пирамид, но в большинстве случаев проще вычислить площади различных граней и сложить их.

Том — другое дело.Вычислить объем без формулы может быть очень сложно. К счастью, существует довольно примечательная формула, возраст которой насчитывает не менее 2300 лет.

В предложении 7 книги XII своих элементов, Евклид показал, что «Любая призма , имеющая треугольное основание, делится на три равные друг другу пирамиды с треугольными основаниями». Это означает, что каждая из трех пирамид, на которые была разделена призма, имеет треть объема призмы. Поскольку объем призмы равен площади, B, ее основания, умноженной на высоту, h: объем пирамиды составляет одну треть от этого, или Bh / 3.

Пирамиды, основания которых составляют многоугольников. с более чем тремя сторонами могут быть разделены на треугольные пирамиды, и к каждой из них применяется формула Евклида. Тогда, если B — это сумма площадей треугольников, на которые был разделен многоугольник, общий объем пирамиды снова будет Bh / 3.

Если срезать верхушку пирамиды, она обрезается. Если срез проходит на параллельно основанию, усеченная пирамида называется усеченной пирамидой. Объем пирамиды определяется любопытной формулой (B + B ‘+ √BB) h / 3, где B и B’ — площади верхнего и нижнего оснований, а h — расстояние по перпендикуляру между ними.

Правильная треугольная пирамида — Калькулятор геометрии

1D линия, круговая дуга, парабола, спираль, кривая Коха
2D
Правильных многоугольников:
Равносторонний треугольник, Квадрат, Пентагон, Шестиугольник, Семиугольник, Восьмиугольник, Нонагон, Десятиугольник, Хендекагон, Додекагон, Шестиугольник, N-угольник, Кольцо многоугольника

Другие многоугольники:
Треугольник, Прямой треугольник, Равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, воздушный змей, воздушный змей, правая трапеция, равнобедренная трапеция, треугольная равносторонняя трапеция, трапеция, циклический четырехугольник, тангенциальный четырехугольник, стрелка, вогнутый четырехугольник, крест Антипараллелограмм, Форма дома, Симметричный пятиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Параллелогон, Вытянутый шестиугольник, Вогнутый шестиугольник, Стрелка-шестиугольник, Прямоугольный шестиугольник, L-образная форма, Острый перегиб, T-образная форма, Усеченный квадрат, Рамка, Открытая рамка, сетка, крест, форма X, форма H, тройная звезда, четыре звезды, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, многоугольник с двойной звездой, многоугольник, многоугольник

90 003 Круглые формы:
Круг, Полукруг, Круговой сектор, Круговой сегмент, Круговой слой, Круговой центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Остроконечный овал, Ланцетная арка, Бугорок, Кольцо, Кольцевой сектор , Изогнутый прямоугольник, закругленный многоугольник, закругленный прямоугольник, эллипс, полуэллипс, эллиптический сегмент, эллиптический сектор, эллиптическое кольцо, стадион, спираль, бревно.Спираль, Треугольник Рило, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межрасовый треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник

3D
Платоновых тел:
тетраэдр, куб, октаэдр, додекаэдр, икосаэдр

архимедова Solids:
усеченный тетраэдр, кубооктаэдр, усеченный куб, усеченный октаэдр, ромбокубооктаэдр, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, Snub куб, ромбоикосододекаэдр , Усеченный икосододекаэдр, Snub Додекаэдр

Каталонских Сухой остаток:
триакистетраэдр, ромбический додекаэдр, триакисоктаэдр, тетракисгексаэдр, дельтоидальный икоситетраэдр, гексакис октаэдр, ромбический триаконтаэдр, триакисикосаэдр, пентакисдодекаэдр, Пятиугольные Icositetrahedron, дельтоидальный гексеконтаэдр, гексакис Икосаэдр, Пятиугольный гексеконтаэдр

Твердые тела Джонсона:
Пирамиды, купола, ротонда, удлиненные пирамиды, гиро-продолговатые пирамиды, бипирамиды, удлиненные бипирамиды, гиро-продолговатая квадратная дипирамида, гиробифастигениум, дисфагениум Sphenocorona, Disphenocingulum

Другие многогранники:
Кубоид, квадратный столб, треугольная пирамида, квадратная пирамида, правильная пирамида, пирамида, правильная пирамида, конус, правильная бипирамида, бипирамида, бифрустум, клин-фрустум, клин-фрустум Полутетраэдр, ромбоэдр, параллелепипед, правильная призма, призма, наклонная призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клин-кубоид, полукубоид, скошенный кубоид, слиток, скошенная трехгранная призма , Усеченный кубоид, кубоид с тупыми краями, удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый кубоид, полый кубоид, полая пирамида, полая пирамида, звездная пирамида, звездчатый октаэдр, малый звездчатый додекаэдр, большой звездчатый додекаэдр 000, Большой додекаэдр 000 Круглые формы:
сфера, полусфера, сферический угол, цилиндр, отрезной цилиндр, наклонный цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный Цилиндр, конус, усеченный конус, косой круговой конус, эллиптический конус, биконус, усеченный биконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калотт , Сферический клин, полуцилиндр, диагонально разрезанный пополам цилиндр, цилиндрический клин, цилиндрический сектор, цилиндрический сегмент, цилиндр с плоским концом, полуконус, конический сектор, конический клин, сферическая оболочка, полусферическая оболочка, цилиндрическая оболочка, цилиндрическая оболочка с вырезом, косо-цилиндрическая оболочка , Полый конус, усеченный полый конус, сферическое кольцо, тор, шпиндельный тор, тороид, сектор тора, сектор тороида, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, сферический цилиндр, линза, вогнутый Линза, ствол, форма яйца, параболоид, гиперболоид, олоид, твердые тела Штейнмеца, твердое тело вращения

4D
Тессеракт, Гиперсфера

Расчеты на правильной треугольной пирамиде.Это правильная пирамида с основанием 3, соответственно общий тетраэдр с равносторонним треугольником в качестве основания и тремя равными равнобедренными треугольниками с основанием a и сторонами b в качестве боковых граней. При a = b это правильный тетраэдр. Введите два значения длины основания, длины кромки и высоты. Выберите количество десятичных знаков, затем нажмите «Рассчитать».

Формулы:
b² = h² + a² / 3
s = √ (4 * b² — a²) / 4
A = √3 / 4 * a² + 3/2 * a * s
V = √3 / 12 * a² * h

Длина и высота указаны в одинаковых единицах измерения (например,грамм. метр), площадь имеет эту единицу в квадрате (например, квадратный метр), объем имеет эту единицу в степени, равной трем (например, кубический метр). A / V имеет этот блок ^-1.

Доля:

Объем пирамиды

пирамида

является многогранником с одним основанием, которое является произвольным

многоугольник

. Остальные его грани — треугольники.

В

объем

из

-размерное твердое тело — это объем занимаемого пространства.Объем измеряется в кубических единицах (

футов

см

и так далее). Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.

Громкость

пирамиды составляет одну треть площади основания

раз больше высоты

час

знак равно

час

Пример:

Найдите объем правильной квадратной пирамиды со сторонами основания

см и высота

см.

Решение

Нарисуйте фигуру.

Формула объема пирамиды:

знак равно

час

Поскольку основание пирамиды представляет собой квадрат, площадь основания равна

или же

100

см

Итак, заменим

100

для

а также

для

час

в формуле.

знак равно

(

100

)

(

)

знак равно

600

Следовательно, объем квадратной пирамиды равен

600

см

Калькулятор объема пирамиды

Определите объем любого пирамидального твердого тела с помощью нашего калькулятора объема пирамиды. Выберите один из двух вариантов: рассчитать объем пирамиды с обычным основанием, поэтому вам нужно указать только сторону, форму и высоту, или напрямую ввести площадь основания и высоту пирамиды. Калькулятор не имеет проблем с определением объема тетраэдра или объема квадратной пирамиды.Если вы все еще не знаете, как пользоваться инструментом и как рассчитать объем пирамиды — продолжайте читать!

Формула объема пирамиды

Пирамида — это многогранник, образованный соединением многоугольного основания и вершины. Основная формула для объема пирамиды такая же, как для конуса:

объем = (1/3) * base_area * height , где height — высота от основания до вершины.

Эта формула работает для любого типа базового многоугольника, а также для наклонных и прямых пирамид.Все, что вам нужно знать, это эти два значения — базовая площадь и высота.
Однако есть и другие полезные формулы, если вы не знаете базовую площадь. Для любой пирамиды с правильным основанием можно использовать уравнение:

объем = (n / 12) * высота * длина стороны² * кроватка (π / n) , где n — количество сторон основания правильного многоугольника

Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды

Мы знаем формулу, а что дальше? Как пользоваться калькулятором объема пирамиды? Лучший способ продемонстрировать, как это работает, — самая известная пирамида в мире — пирамида Хеопса:

Выберите базовую форму .Для пирамиды Хеопса, также называемой пирамидой Хуфу, это квадрат. Конечно, это не идеальный квадрат, но можно предположить, что это так — разница в длине ребер меньше 1.
Введите высоту пирамиды . Высота пирамиды Хуфу равна 146 м (вы можете изменить единицы измерения на метры, просто нажав на единицу измерения. Также вы можете ознакомиться с нашим конвертером объема).
Определите длину стороны . Длина ребра пирамиды Хеопса в среднем 230.36 мес.
Примерный объем квадратной пирамиды равен 2 582 532 м³.

Названия томов пирамид

Пирамида с n-сторонним основанием имеет:

n + 1 грань (n-треугольник + 1 n-угольник)
2n ребра
n + 1 вершина

Название пирамиды происходит от формы основания:

Грани	Ребра	Вершины	Форма основания	Имя пирамиды
4	6	4	треугольник	тетраэдр 2	9024 8 треугольник	5	квадрат	квадратная пирамида
6	10	6	пятиугольник	пятиугольная пирамида
7	12	7	шестиугольник 95	5	5 шестиугольник	8	14	8	семиугольник	семиугольная пирамида
9	16	9	восьмиугольник	восьмиугольная пирамида

Расчет объема тетраэдра

В качестве примера возьмем пирамиду с сыпучим чаем:

Выберите форму основания .В нашем случае это правильный треугольник.
Введите высоту пирамиды . Предположим, что для чайной пирамиды он равен 1,2 дюйма
Введите длину стороны . Например, 1,5 дюйма
Объем тетраэдра отображается ниже . Для нашей чайной пирамиды он равен 0,39 куб. Дюйма

Если вы хотите рассчитать объем правильного тетраэдра — тот, в котором все четыре грани представляют собой равносторонние треугольники, а не только основание — вы можете использовать формулу:

объем = a³ / 6√2 , где a — край твердого

Высота в этом случае может быть рассчитана как:
высота = a√3 / 6 ~ 0.2887 * , поэтому, если вы хотите вычислить, например объем правильного многогранника с ребром = 3 введите 3 * 0,2887 в поле «Высота» калькулятора объема пирамиды.

Что дальше?

Теперь вы специалист и точно знаете, как рассчитать объем пирамиды! Почему бы не проверить другие калькуляторы объема?

Калькулятор треугольной призмы

Если вы когда-нибудь задумывались, как определить объем треугольной призмы, этот калькулятор треугольной призмы — это то, что вам нужно.Он не только может рассчитать объем, но также может быть полезен, если вам нужно определить площадь поверхности треугольной призмы. Выберите вариант, соответствующий вашим потребностям, и поэкспериментируйте с инструментом! Если вас интересуют формулы треугольной призмы за калькулятором, прокрутите вниз, чтобы узнать больше.

Треугольная призма — что это?

Что такое призма? Это твердый объект с:

идентичные две базы
три прямоугольных грани (правая призма) или в форме параллелограмма (наклонная призма)
то же сечение по всей длине

Мы используем термин треугольная призма для описания правильной треугольной призмы , что является довольно распространенной практикой.Если вы ищете призму другого типа, воспользуйтесь нашим калькулятором прямоугольной призмы.

Формулы треугольной призмы

Обычно вам нужно рассчитать объем треугольной призмы и площадь ее поверхности. Два основных уравнения:

объем = 0,5 * b * h * длина , где b — длина основания треугольника, h — высота треугольника и длина — длина призмы
площадь = длина * (a + b + c) + (2 * base_area) , где a, b, c — стороны треугольника, а base_area — треугольная площадь основания

Но что, если у нас нет высоты и основания треугольника? А как найти площадь поверхности треугольной призмы без всех сторон треугольного основания? Ознакомьтесь с другими формулами треугольной призмы!

Треугольная призма объем

В калькуляторе треугольной призмы вы можете легко определить объем этого твердого тела.Общая формула: объем = длина * base_area ; один параметр, который вам всегда нужно указывать, — это длина призмы, и есть четыре способа рассчитать площадь основания треугольника. Все они реализованы в нашем калькуляторе с треугольной призмой, разве это не круто?

Конкретные формулы выглядят следующим образом:

Длина * Площадь основания треугольника с учетом основания и высоты треугольника
Это известная формула, о которой говорилось ранее:
объем = длина * 0.5 * ш * в
Длина * Треугольное основание с трех сторон (SSS)
Если вам известны длины всех сторон, используйте формулу Герона , чтобы найти площадь треугольного основания:
объем = длина * 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
Длина * Треугольное основание с учетом двух сторон и угла между ними (SAS)
Вы можете легко вычислить площадь треугольника по тригонометрии:
объем = длина * 0.5 * а * б * sin (γ)
Длина * Треугольное основание с двумя углами и стороной между ними (ASA)
Вы можете рассчитать это с помощью тригонометрии:
объем = = длина * a² * sin (β) * sin (γ) / (2 * sin (β + γ))

Площадь поверхности треугольной призмы

Если вы хотите вычислить площадь поверхности твердого тела, наиболее известная формула — это формула с учетом трех сторон треугольного основания:

площадь = длина * (a + b + c) + (2 * base_area) = длина * base_perimeter + (2 * base_area)

Однако у нас не всегда есть три стороны.Что тогда?

Треугольное основание: заданы две стороны и угол между ними (SAS)
Используя закон косинусов, мы можем найти третью сторону треугольника:
площадь = длина * (a + b + √ (b² + a² - (2 * b * a * cos (угол)))) + a * b * sin (угол)
Треугольное основание: заданы два угла и сторона между ними (ASA)
Используя закон синусов, мы можем найти две стороны основания треугольника:
площадь = (длина * (a + a * (sin (angle1) / sin (angle1 + angle2)) + a * (sin (angle2) / sin (angle1 + angle2)))) + a * ((a * sin (угол1)) / sin (угол1 + угол2)) * sin (угол2)

Единственный вариант, когда вы не можете рассчитать объем треугольной призмы, — это задать основание треугольника и его высоту (знаете почему? Задумайтесь на минутку).Все другие версии могут быть рассчитаны с помощью нашего калькулятора треугольной призмы.

Давайте проверим, каков объем и площадь поверхности палатки в виде треугольной призмы:

Узнайте, какова длина треугольной призмы . Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы.
Выберите вариант с заданными параметрами . Например, даны три стороны нашей базы.
Введите стороны основания .Наша палатка имеет a = 60 дюймов, b = 50 дюймов и c = 50 дюймов.
Площадь поверхности и объем треугольной призмы появляются мгновенно . Это 96 000 куб. Дюймов (55,56 куб. Футов) и 15 200 кв. Дюймов (105,56 кв. Футов).

Прямоугольная пирамида | Блог по математике ∞

Когда вы входите в мир трехмерных форм, математика приобретает совершенно новый уровень глубины. Некоторым может быть сложно найти объем простых, обычных форм, но когда вы начинаете строить их в направлении вверх и наружу, процесс становится еще более сложным.Пирамиды — одни из самых известных трехмерных фигур. Хотя вы найдете множество типов с любым количеством треугольных граней, мы пока сосредоточимся на прямоугольных пирамидах.

Определение объема прямоугольной пирамиды

Прямоугольные пирамиды имеют четырехсторонние основания и четыре треугольные стороны, соединяющиеся в вершине, или то, что мы называем более простым заостренным концом. Ваша общая формула для определения объема этих многогранных форм: V = (l x w x h) / 3.По сути, ваш первый шаг — найти площадь основания, умножив длину на ширину.

После определения площади основания умножьте ее на высоту. Высота — это расстояние от центральной точки основания до вершины. Умножив площадь основания на высоту, вы разделите свой ответ на три, чтобы получить объем. Вот пример прямоугольной пирамиды и некоторые примеры измерений:

Начните с основной формулы, введите данные измерения и действуйте осторожно.

V = (длина x ширина x высота) / 3

В = (9 х 7 х 15) / 3

В = (63 х 15) / 3

В = 945/3

V = 315 футов ³

Вы также можете увидеть формулу, записанную как: V = 1/3 Bh. Это просто означает, что вы умножаете основание на высоту и делите на три, что является одним и тем же процессом. Имейте в виду, что оба варианта работают и для квадратных пирамид, поскольку квадраты являются типами прямоугольников.

В некоторых случаях вам может потребоваться определить высоту пирамиды, прежде чем вы сможете рассчитать ее объем.Допустим, вам дана наклонная высота пирамиды, то есть расстояние от вершины до центра одной из треугольных граней. Это немного усложняет задачу, но отнюдь не делает невозможным. Вот пример:

Имейте в виду, что линия, представляющая высоту, проходит от вершины к центру основания и образует угол 90 градусов у основания пирамиды. Это делает треугольник, образованный высотой, наклонной высотой и основанием, правильным, поэтому вы можете использовать теорему Пифагора (a ² + b ² = c ²), чтобы найти недостающее число.Ваша гипотенуза, или сторона «c», самая длинная, она всегда находится прямо напротив угла 90 градусов в прямоугольном треугольнике.

Мы еще не знаем высоту или сторону «А». Поскольку базовое измерение, которое будет использоваться здесь, составляет три фута, высота от центра до наклона будет равна 1,5. Это будет твоя сторона «б». Вот процесс определения недостающей высоты:

a ² + b ² = c ²

а ² + 1,5 ² = 10 ²

а ² + 2.25 = 100

а ² + 2,25 — 2,25 = 100 — 2,25

а ² = 97,75

а ≈ 9,9

Зная, что высота вашей пирамиды почти равна 9,9, вы можете, как обычно, вычислить ее объем.

Учитывая размеры основания и высоту прямоугольной пирамиды, вы можете решить, чтобы найти ее объем. Если у вас есть наклонная высота, но не фактическая высота, позвольте Пифагору помочь вам, прежде чем вы попытаетесь решить для «V». Оттачиваете ли вы свои геометрические навыки или готовитесь к поездке в Гизу, вы будете готовы найти объем любой прямоугольной пирамиды на своем пути!

Как найти наклонную высоту квадратных пирамид

Обновлено 14 ноября 2020 г.

Джон Замбони

Наклонная высота квадратной пирамиды — это расстояние между ее вершиной, или вершиной , до земли вдоль одной из его сторон.Вы можете найти наклонную высоту, визуализировав ее как один элемент треугольника. При этом вы можете использовать теорему Пифагора для сравнения наклонной высоты с высотой пирамиды и длиной сторон

Определение наклонной высоты в виде треугольника

Чтобы найти наклонную высоту, вы можете понимать наклонную высоту как одну линию в прямоугольном треугольнике. внутри пирамиды. Две другие линии треугольника будут высотой от центра пирамиды до ее вершины и линией, равной половине длины одной из сторон пирамиды, которая соединяет центр с нижней частью наклона.2

«²» в формуле означает, что вы возводите в квадрат чисел. Возведение числа в квадрат означает, что вы умножаете его само на себя. Таким образом, c ² совпадает с c × c .

Определение высоты и основания

Если вы знаете высоту пирамиды и длину одной из сторон ее квадратного основания, вы можете использовать теорему Пифагора для определения наклонной высоты.2

Допустим, у вас есть пирамида высотой 4 дюйма и квадратным основанием со сторонами 6 дюймов. Чтобы найти половину длины стороны, разделите длину стороны на 2. Таким образом, эта пирамида будет иметь высоту 4 дюйма и половину длины 3 дюйма.

Возведение в квадрат высоты и основания

В теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон. Теперь возведите в квадрат высоту и половину длины и сложите числа в квадрате.2

Таким образом, квадрат высоты наклона равен 25.

Извлечение квадратного корня

Теперь вы знаете, что квадрат высоты наклона, возведенный в квадрат или умноженный сам на себя, равен 25.

Усеченная пирамида — Большая Энциклопедия Нефти и Газа, статья, страница 3

Усеченная пирамида

Задания для устного счета по теме«Усеченная пирамида», геометрия 10 класс

Математика 11 Тематические тестовые задания по геометрии (физико-математическое направление)

Тригонометрические уравнения

Все прототипы задания В11 (2013)

Прямоугольный параллелепипед

Все прототипы заданий В года

7. Задачи по стереометрии

ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ

Все прототипы заданий года

«Объёмы многогранников и тел вращения»

Задание 16 Задачи по стереометрии

Все прототипы заданий В года

Задание 8 Стереометрия.

Тест по теме «Задачи стереометрии»

Все прототипы задания В9 (2013)

Предмет «Математика» Вариант ХХХХ

Все прототипы В года

Стартовая контрольная работа

Тест 250. Отрезок. Длина

Задачи по с т е р е о м е т р и и

Куб. Прямоугольный параллелепипед

Задание 13. Задачи по стереометрии

ПРЯМОЙ И НАКЛОННЫЙ КОНУС

ПРОВЕРОЧНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ. 1 КУРС

Многогранники.

Геометрия. Тренировочный вариант 1

Тест по теме 60 «Параллелепипед и куб»

Основные определения, теоремы и формулы планиметрии.

Количество набранных баллов

Стереометрия: комбинации тел.

Задание 8, 14. Стереометрия

Сфера (шар), вписанная в призму

Geometrické útvary a tělesa

ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ)

10 класс.

Реферат по геометрии на тему:»Фигуры.Пирамида»(9 класс)

Что такое боковая поверхность пирамиды. Площадь боковой поверхности пирамиды. Соблюдение вашей конфиденциальности на уровне компании

Задача 3. Найти площадь полной поверхности правильной пирамиды

Сбор и использование персональной информации

Раскрытие информации третьим лицам

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Как быть при нахождении площади основания пирамиды?

Как поступить при вычислении площади боковой и полной поверхности?

Задача № 1

Задача № 2

Задача № 3

Задача № 4

Вычисление площади основания пирамиды

В основании – правильный многоугольник

В основании – неправильный многоугольник

Площадь боковой поверхности пирамиды

Примеры

Площадь поверхности треугольной пирамиды

Площадь поверхности четырехугольной пирамиды

— основание, пирамиды, треугольники и высота

Правильная треугольная пирамида — Калькулятор геометрии

Объем пирамиды

Калькулятор объема пирамиды

Формула объема пирамиды

Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды

Названия томов пирамид

Расчет объема тетраэдра

Что дальше?

Калькулятор треугольной призмы

Треугольная призма — что это?

Формулы треугольной призмы

Треугольная призма объем

Площадь поверхности треугольной призмы

Прямоугольная пирамида | Блог по математике ∞

Как найти наклонную высоту квадратных пирамид

Определение наклонной высоты в виде треугольника

Определение высоты и основания

Возведение в квадрат высоты и основания

Извлечение квадратного корня

Добавить комментарий Отменить ответ