Площадь фигуры заданной параметрически: Площадь фигуры ограниченной параметрическими кривыми — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически

Если фигура
ограничена кривой, заданной параметрическими
уравнениями
,
прямымии осью9рис. 5), то площадь ее вычисляется по
формулам:

(42)

а пределы
интегрирования находятся из уравнений
на отрезка.
Порядок вычисления аналогичен п. 2.9.1.

Пример. Найти
площадь фигуры, ограниченной линиями,
заданными уравнениями:.

Решение.
Построим кривую, заданную параметрическими
уравнениями (рис. 5). Для этого вычислим
значения
ии поместим их в табл. 5.

ОТРЕДАКТИРОВАТЬ

Таблица 5

Вспомогательная таблица для построения параметрически заданной кривой

Мы подставляли
значения
из верхней строки таблицы в параметрические
уравнения и последовательно получали
значенияи.
Построим также и прямую(см. рис. 6). Найдем пределы интегрирования.
Приравняем,
отсюда.
Посколькуизменяется отдо.
Так как фигура, площадь которой мы хотим
навйти, симметрична относительно оси,
то можно интегрировать отдо.
А результат затем удвоить. Подставляем
в формулу (42)::

Для вычисления
интеграла воспользуемся формулами
(22)-(27) из п. 1.7:

2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах

Пусть кривая задана
в полярных координатах уравнением
и двумя лучамии,
тогда ее площадь (рис. 7) вычисляется по
формуле:

(43)

Порядок вычислений
аналогичен п. 2.9.1.

Пример. Найти
площадь фигуры, ограниченной линией
,
перейдя предварительно к полярным
координатам.

Решение. Переход
от декартовых к полярным координатам
осуществляется по формулам:Подставив эти выражения в уравнение
кривой, получим:или.
Отсюда получаем уравнение кривой в
полярных координатах:.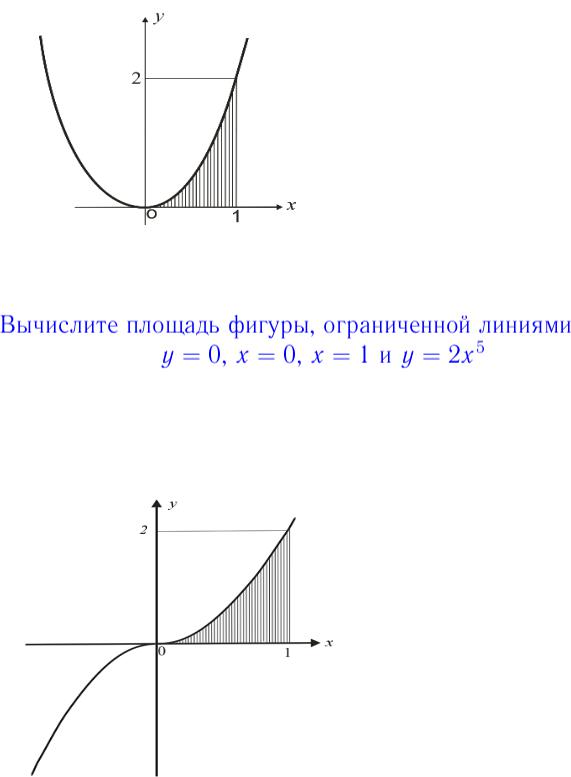

Поскольку в правой
части уравнения стоит неотрицательная
величина, то полярный угол может принимать
любые значения
.
В силу периодичности функциивычислим подробно таблицу значений для
аргументов в промежутке(табл. 6).

Таблица 6

Вспомогательная таблица для построения кривой, заданной в полярных координатах

Построим эту кривую
( четырехлепестковую розу). В силу
симметрии фигуры достаточно проинтегрировать
по
отдо,
а затем результат умножить на 8.

Применим формулу
(43):
.
Для вычисления интеграла воспользуемся
формулой понижения степени (15) из п. 1.7:.

Вычислить интеграл
непосредственно зачастую весьма
непросто. Поэтому создаются специальные
таблицы интегралов. При затруднениях
в вычислении того или иного интеграла,
полученного при решении конкретной
технической задачи, можно ими
воспользоваться. Есть класс так называемых
«неберущихся» интегралов, т.е. класс
функций, первообразные для которых не
являются элементарными. Тем не менее,
интегралы от таких функций часто
встречаются в математике и приложениях.
Так, в теории вероятностей мы встретимся
с функцией
,
выражающейся через такой «неберущийся»
интеграл. Такого рода интегралы
встречаются в электротехнике, оптике
и т.д.

Для вычисления
таких интегралов разработаны специальные
методы. Например, формулы прямоугольников,
трапеций, Симпсона или с помощью рядов.

Определенный
интеграл применяется в математике для
нахождения длин дуг кривых, объемов
различных тел, площади поверхности тел
вращения и др. Широко применяется
определенный интеграл в механике и
физике. Это вычисление статических
моментов, моментов инерции плоских дуг
кривых и фигур, координат центра тяжести,
а также вычисление работы, давления и
многого другого.

Приложение.

Вычисление
длины кривой, заданной явным уравнением.

Если кривая задана
явным уравнением в прямоугольных
декартовых координатах

то
.

(1)

Пример.

Вычислить
длину дуги куска графика логарифмической
функции
.

Решение. Подставляя
в формулу (1)
,
получим:

Вычисление
длины кривой, заданной параметрическим
уравнением.

Если кривая задана
параметрическим уравнением в прямоугольных
декартовых координатах

то.
(2)

Пример.
Найти длину
дуги четверти астроиды
между точкамии.

Решение. Найдем
вначале пределы интегрирования из
уравнений:
,.
Отсюда.
Вычислим также элементы подкоренного
выражения:.
Преобразуем подынтегральное выражение,
используя основное тригонометрическое
тождество:.
Подставив полученное выражение и пределы
интегрирования в формулу (2), окончательно
получаем выражение для длины дуги
четверти астроиды:

Вычисление
длины кривой, заданной уравнением в
полярных координатах.

Если кривая задана
уравнением в полярных координатах

то.

(3)

Пример.
Вычислить
длину дуги одного витка логарифмической
спирали
,
где.

Решение. Подставим
ив формулу (3), получим:

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2),

Математический анализ — 2 — тест 13

Главная / Математика /
Математический анализ — 2 / Тест 13

Упражнение 1:

Номер 1

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp9/2&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp1/6&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp9/2&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp32/3&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp4/3&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp32/3&nbsp

Упражнение 2:

Номер 1

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , ,

Ответ:

&nbsp3&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp44/3&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp7/ 3&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , , . Ответ введите в виде дроби.

Ответ:

&nbsp16/3&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , , . Ответ введите в виде дроби.

Ответ:

&nbsp4/3&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp44/3&nbsp

Упражнение 3:

Номер 1

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  ,

Ответ:

&nbsp9&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , , . Ответ введите в виде дроби.

Ответ:

&nbsp20/3&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp1/3&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp1/6&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp2/3&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp12/54&nbsp

Упражнение 4:

Номер 1

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp1/2&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp2&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp1/6&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp7/3&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp28/3&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp28/3&nbsp

Упражнение 5:

Номер 1

Найдите площадь фигуры, ограниченной кривой, заданной параметрически.  , . Ответ введите в виде дроби.

Ответ:

&nbsp8/15&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. , . Ответ введите в виде дроби.

Ответ:

&nbsp81/20&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. , . Ответ введите в виде дроби.

Ответ:

&nbsp1/60&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривой, заданной параметрически.  ,

Ответ:

&nbsp6&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. ,

Ответ:

&nbsp5&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. ,

Ответ:

&nbsp12&nbsp

Упражнение 6:

Номер 1

Найдите площадь фигуры, ограниченной кривой, заданной параметрически.  ,

Ответ:

&nbsp8&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. ,

Ответ:

&nbsp4&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. ,

Ответ:

&nbsp2&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривой, заданной параметрически.  , . Ответ введите в виде дроби.

Ответ:

&nbsp3/2&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. ,

Ответ:

&nbsp3&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривой, заданной параметрически. , , . Ответ введите в виде дроби.

Ответ:

&nbsp3/4&nbsp

Упражнение 7:

Номер 1

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp1/4&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. ,

Ответ:

&nbsp1&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp3/2&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах.  , . Ответ введите в виде дроби.

Ответ:

&nbsp3/2&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp3/2&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp9/2&nbsp

Упражнение 8:

Номер 1

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах.  ,

Ответ:

&nbsp3&nbsp

Номер 2

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. ,

Ответ:

&nbsp3&nbsp

Номер 3

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. ,

Ответ:

&nbsp3&nbsp

Номер 4

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах.  ,

Ответ:

&nbsp1&nbsp

Номер 5

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. ,

Ответ:

&nbsp1&nbsp

Номер 6

Найдите площадь фигуры, ограниченной кривой, заданной в полярных координатах. , . Ответ введите в виде дроби.

Ответ:

&nbsp1/3&nbsp

Вычисление площади фигуры с помощью определенного интеграла Геометрический смысл определенного интеграла

Если непрерывная кривая задана в
прямоугольных координатах уравнением

, то площадь криволинейной трапеции, ограниченной этой
кривой, двумя вертикалями в точках

и

, и отрезком оси абсцисс

определяется
формулой:

То есть определенному интегралу
(если он существует) геометрически соответствует площадь некоторой фигуры.

На основании геометрического смысла
определенного интеграла покоится целый класс задач на нахождение площадей
фигур, ограниченных линиями.

В более общем случае, если площадь

ограничена
непрерывными кривыми

и

и двумя
вертикалями

и

, где

при

, то будем иметь:

Если кривая задана уравнениями в
параметрической форме

,

, то площадь криволинейной трапеции, ограниченной этой
кривой, двумя вертикалями, соответствующими

и

, и отрезком оси

, выражается интегралом:

где

и

определяются из
уравнений:

на отрезке

Если непрерывная кривая задана в
полярных координатах уравнением

, то площадь сектора

, ограниченного дугой кривой и двумя полярными
радиусами

и

, соответствующими значениям

и

, выразится интегралом

Задача 1

Найти
площадь фигуры, ограниченной линиями;

Решение

Сделаем
чертеж:

Искомую
площадь можно найти по формуле:

В этом примере для вычисления неопределенного интеграла используется
непосредственное табличное интегрирование

Ответ:

Задача 2

Вычислить
площадь фигуры, ограниченной одной аркой циклоиды

и осью

Решение

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

Площадь
криволинейной трапеции, заданной параметрически, выражается интегралом:

Ответ:

Задача 3

Вычислить
площадь фигуры, ограниченной трехлепестковой розой

Решение

Сделаем
чертеж:

Площадь
фигуры, заданной в полярных координатах:

Найдем
площадь одного лепестка. В этом случае:

Искомая
площадь трехлепестковой розы:

Ответ:

Построение графика функции, заданной параметрически

Введите график функции

Важно
a должно быть меньше b,
иначе график не сможет построиться

Видео пример:

Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы. 2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7.3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание
15/7: — дробь

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi: Число «Пи», которое примерно равно ~3.14159..
e: Число e — основание натурального логарифма, примерно равно ~2,7183..
i: Комплексная единица
oo: Символ бесконечности — знак для бесконечности

Методические особенности темы «Вычисление площадей плоских фигур в случае параметрического задания функции и в полярных координатах» Текст научной статьи по специальности «Науки об образовании»

ISSN 2304-120X

ниепт

научно-методический электронный журнал

Вергазова О. Б. Методические особенности темы «Вычисление площадей плоских фигур в случае параметрического задания функции и в полярных координатах» // Научно-методический электронный журнал «Концепт». -2017. — № 5 (май). — 0,6 п. л. — URL http://e-koncept.ru/2017/170114.htm.

ДРТ 170114

УДК 372.851

Вергазова Ольга Бухтияровна,

кандидат философских наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва [email protected]

Методические особенности темы «Вычисление площадей плоских фигур в случае параметрического задания функции и в полярных координатах»

Аннотация. Работа предлагает методику изложения темы «(Решение задач на вычисление площадей плоских фигур» в курсе «(Интегральное исчисление». Статья написана на основе опыта преподавания математического анализа во втузе и будет полезна как преподавателям при проведении практических занятий, так и студентам для самостоятельной работы по указанной теме. Цель работы — помочь студентам приобрести и развить навыки применения методов интегрирования к решению различных задач. При решении задач на вычисление площадей студенты, как правило, испытывают затруднения при работе с полярными координатами и функциями, заданными параметрически. В этом случае полезно рассмотреть решение задачи разными способами. В работе кратко изложены основные теоретические сведения, рассмотрены примеры и типовые задачи, необходимые для совершенствования навыков интегрирования, а также приводятся сведения из истории математики с целью развития познавательного интереса к изучаемому вопросу.

Ключевые слова: геометрические приложения определенного интеграла, вычисление площади фигуры, методические особенности.

Раздел: (01) педагогика; история педагогики и образования; теория и методика обучения и воспитания (по предметным областям).

Площадь криволинейной трапеции, заданной условиями вида равна Б = / /»(х)^х (1) (рис.. Заметим, что из неравенства а < Ь не следует, что

U < t,

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Рассмотрим пример решения задачи на вычисление площади разными способами. В качестве такой фигуры рассмотрим эллипс. При этом отметим ряд исторических фактов, касающихся истории открытия и изучения свойств указанной кривой.

b \i

—j

j 1 «2

-а С 0 a

-b

Рис. 2

Эллипс — фигура (кривая), образованная точками, у которых сумма расстояний от двух заданных точек фиксирована (и больше расстояния между двумя указанными точками). Иными словами, если F1, F2 — данные точки, то эллипс образован точками М, для которых F1M + F2M = const > F1 F2. Свойство эллипса, выраженное условием F1М+ F2M = const, называют фокальным свойством эллипса (рис. 2). Благодаря фокальному свойству можно быстро и просто начертить эллипс: достаточно закрепить в фокусах эллипса на листе бумаги две булавки, прикрепить к ним нитку длиной в две большие полуоси, затем, оттягивая нить острием карандаша, обвести одну половину эллипса, потом — вторую (рис. 3 [1]).

Рис. 3

Знаменитый ученый древности Менехм (IV в. до н. э.), ученик Евдокса, прославился работами по астрономии и математике, и прежде всего решением делосской

ISSN 2304-120X

ниепт

научно-методический электронный журнал

задачи об удвоении куба. Изучение конуса привело Менехма к открытию конических сечений — кривых, полученных путем пересечения конуса секущей плоскостью. Менехм рассматривал исключительно конусы вращения. Конусы вращения в зависимости от величины угла при вершине (угла, составленного двумя образующими, расположенными в плоскости осевого сечения) Менехм делил на прямоугольные, тупоугольные и остроугольные. Для получения конических сечений рассматривалась плоскость, перпендикулярная образующей. Коническое сечение прямоугольного конуса дает параболу, тупоугольного конуса — гиперболу, остроугольного конуса — эллипс. Сами названия кривых, которые были введены Аполлонием Пергским (III в. до н. э.), связаны как раз с упомянутым выше углом при вершине конуса. Так, эллипс (¿AAeiyig — изъян, недостаток угла конуса до прямого), гипербола (unepßMÄq — преувеличение, преобладание угла конуса над прямым), парабола (napaßoAq — приближение, то есть равенство угла конуса прямому углу). Позже было установлено, что все данные кривые можно получить на одном конусе, изменяя наклон секущей плоскости, независимо от угла при вершине. При этом следует брать конус, состоящий из двух полостей, и полагать, что они простираются в бесконечность [2, 3] (см. рис. 4).

Рис. 4

Задача. Найти площадь, ограниченную эллипсом. Решение

Рассмотрим в данном случае два способа вычисления площади фигуры. 1. Пусть эллипс задан каноническим уравнением:

2 2 X2 у2

-+ — = 1. | = 4bar(arcsin1 — arcsinO) =

= 2ab n = nab. _ 2

Отметим, что интеграл J» Va2 — x2dx вычисляется методом интегрирования по частям.

Ответ: nab.

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

{X = V

Определим значения ti и ti. ti — решение системы {° =

X = acost, y = bsint. О = acost,

bsint.

ti — найдем, решив

fa = acost, систему {0 = bsint.

S = 4ab / sint(—sint)dt = 4ab Г2 sin2t dt = 4ab /

r- l-cos2t

‘0

dt = 2ab(t —sm2t) I 2 = nab. 2 0 Ответ: яаЬ.

Следует также рассмотреть решение задачи, в которой требуется найти площадь фигуры, которая не является криволинейной трапецией.

(х = v3cos3t у = 8sm3t.

Решение

Сделаем чертеж (рис.’

2 0

= 48V3 |

6 n

= 48V3 Г-si Я 4

dx =

2 9

sin4t • cos2tdt — — = 4

2-9 , 9

sin22t • sin2tdt — — = 4

Г1 1 — cos2t 9

= 12V3 I sin22t—-dt—г =

=3V3(/„2

24 ■dt — 1/7r2stn22t • d(sin2t))

к 1 rT

=3V3((J — J) — ±sm4t | £ — ±sm32t | £) — 9= W3..

Рис. 6

Если фигура не является криволинейным сектором, ее площадь находится как сумма или разность площадей криволинейных секторов.

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Например, площадь Si:

Вергазова О. Б. Методические особенности темы «Вычисление площадей плоских фигур в случае параметрического задания функции и в полярных координатах» // Научно-методический электронный журнал «Концепт».) = 0 соответственно, лучи ф = а, ф = Y — касательные лучи в полюсе (см. рис. 9).

ISSN 2304-120X

ниепт

научно-методический электронный журнал

Рис. 8 р=р: (ф)

Рис. 9

ниегп

issn 2304-i20x Вергазова О. Б. Методические особенности темы «Вычисление площадей плоских фигур в случае параметрического задания функции и в полярных координатах» // Научно-методический электронный журнал «Концепт».Зсояф.

Получим ф =—.

Проведем указанный луч. Получим фигуру, площадь которой надо найти (рис. 10).

Рис. 10

Составим интеграл для вычисления площади.

ISSN 2304-120X

ниепт

научно-методический электронный журнал

1 — — S = 1J03(V3COS<P)2) dq> + 1р(5т<р)2)ф = 3/0

_ 3 г— l+cos2^

Ф + l/J1-^ =

— . , V3

Ответ: —+—.

24 4

2 J-

HL) 24 4 .

В заключение следует добавить, что для самостоятельной работы по данной теме можно рекомендовать задачи из источников [4-8].

Ссылки на источники

1. Александров А. Д., Нецветаев Н. Ю. Геометрия. — М.: Наука, 1990. — 669 с.

2. Там же.

3. Чистяков В. Д. Три знаменитые задачи древности. — М., 1963. — 94 с.

4. Данко П. Е. и др. Высшая математика в упражнениях и задачах: в 2 ч. Ч. 1. — М.: Изд. дом «ОНИКС 21 век», 2003. — 304 с.

5. Данко П. Е. и др. Высшая математика в упражнениях и задачах: в 2 ч. Ч. 2. — М.: Изд. дом «ОНИКС 21 век». 2003. — 416 с.

6. Лунгу К. Н. Систематизация приемов учебной деятельности при обучении математике. — М.: Ком-Книга, 2007. — 424 с.

7. Малыгина О. А. Изучение математического анализа на основе системно-деятельностного подхода. -М.: Изд. ЛКИ, 2008. — 416 с.

8. Ляшко И. Я. и др. Математический анализ в примерах и задачах. — Киев, 1974. — 678 с.

Olga Vergazova,

Candidate of Philosophical Sciences, Associate Professor, Moscow State Technical Bauman University, Moscow [email protected]

Methodological features of the topic «Calculating of the plane figures area in case of functions para-metrization and in polar coordinates»

Abstract. This work suggests a methodology for the presentation of the topic «Solution of plane figures areas calculating problems » in the course «Integral calculus». The article is based on experience of mathematical analysis teaching in technical university and it will be useful both to teachers in conducting practical classes and to students in their independent work on the topic. The aim of this work is to help students to acquire and develop skills of integration methods application for various problems solving. When solving tasks on the areas calculation students have as a rule difficulties working with polar coordinates and functions defined parametri-cally. In this case, it is useful to consider the problem solution in different ways. The basic theoretical information is briefly stated in this article. The author gives examples and standard tasks that are necessary to improve integrating skills and provides information from the history of mathematics which helps to develop cognitive interest to the explored subject.

Key words: geometrical applications of definite integral, figures area calculation, the methodological features. References

1. Aleksandrov, A. D. & Necvetaev, N. Ju. (1990). Geometrija, Nauka, Moscow, 669 p. (in Russian).

2. Ibid.

3. Chistjakov, V. D. (1963). Tri znamenitye zadachi drevnosti, Moscow, 94 p. (in Russian).

4. Danko, P. E. et al. (2003). Vysshaja matematika v uprazhnenijah i zadachah: v 2 ch. Ch. 1, Izd. dom «ONIKS 21 vek», Moscow, 304 p. (in Russian).

5. Danko, P. E. et al. (2003). Vysshaja matematika v uprazhnenijah i zadachah: v 2 ch. Ch. 2, Izd. dom «ONIKS 21 vek», Moscow, 416 p. (in Russian).

6. Lungu, K. N. (2007). Sistematizacija priemov uchebnoj dejatel’nostipriobucheniimatematike, KomKniga, Moscow, 424 p. (in Russian).

7. Malygina, O. A. (2008). Izuchenie matematicheskogo analiza na osnove sistemno-dejatel’nostnogo pod-hoda, Izd. LKI, Moscow, 416 p. (in Russian).

8. Ljashko, I. Ja. et al. (1974). Matematicheskij analiz vprimerah i zadachah, Kiev, 678 p. (in Russian).

ISSN 2Э04-120Х

ниепт

научно-методический электронный журнал

Рекомендовано к публикации:

Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»

Поступила в редакцию Received 11.05.17 Получена положительная рецензия Received a positive review 12.05.17

Принята к публикации Accepted for publication 12.05.17 Опубликована Published 15.05.17

www.e-koncept.ru

Площадь плоской фигуры — Студопедия

1. Фигура ограничена кривой (или кривыми), заданной явной функцией :

, где

Рис. 1.

2. Фигура ограничена кривой, заданной параметрически где . Тогда её площадь равна .

3. Фигура ограничена кривой, заданной в полярной системе координат:

, где

Рис. 2.

Пример 1. Вычислим площадь фигуры, ограниченной линиями и .

Решение. Построим фигуру, площадь которой необходимо найти:

Найдем точки пересечения графиков заданных функций, решив систему уравнений:

Это будут точки и .

Т.к. для всех , то для вычисления площади используем формулу (рис.1). Определённый интеграл при этом вычислим двумя способами:

Замечание. Если абсциссы точек пересечения графиков функций определяются по рисунку, систему уравнений можно не решать.

Пример 2. Найдем площадь, ограниченную одной аркой циклоиды

Решение. Напомним, что одна арка циклоиды образуется при изменении .

Для вычисления площади нам потребуется производная от функции . Найдем ее отдельно и далее используем при вычислениях. Интеграл, как и в предыдущем случае, вычислим двумя способами.

Пример 3. Вычислим площадь фигуры, ограниченной окружностью и кардиоидой (вне кардиоиды).

Решение. Построим фигуру, площадь которой необходимо найти:

Значение j, при которых кривые пересекаются, можно определить, решив систему уравнений:

Этими значениями будут и .

Используя формулу (рис. 2) и учитывая, что для всех , вычисляем искомую площадь:

Замечание. Если фигура симметрична относительно какой-либо из осей, то в некоторых случаях при вычислении интеграла может получиться ноль. В этом случае следует вычислить площадь одной из симметричных частей, а для нахождения искомой площади умножить результат на число таких одинаковых частей.

10.2: Исчисление с параметрическими кривыми

Теперь, когда мы ввели концепцию параметризованной кривой, наш следующий шаг — научиться работать с этой концепцией в контексте исчисления. Например, если мы знаем параметризацию данной кривой, можно ли вычислить наклон касательной к кривой? Как насчет длины дуги кривой? Или площадь под кривой?

Другой сценарий. Предположим, мы хотим изобразить положение бейсбольного мяча после того, как мяч покидает руку питчера.Если положение бейсбольного мяча представлено плоской кривой \ ((x (t), y (t)) \), тогда мы должны иметь возможность использовать исчисление для определения скорости мяча в любой момент времени. Кроме того, мы должны иметь возможность вычислить, как далеко прошел этот шар, в зависимости от времени.

Производные параметрических уравнений

Мы начинаем с вопроса, как вычислить наклон прямой, касательной к параметрической кривой в точке. Рассмотрим плоскую кривую, заданную параметрическими уравнениями

\ [\ begin {align} x (t) & = 2t + 3 \ label {eq1} \\ y (t) & = 3t − 4 \ label {eq2} \ end {align} \]

в пределах \ (- 2≤t≤3 \).

График этой кривой показан на рисунке \ (\ PageIndex {1} \). Это отрезок, начинающийся в \ ((- 1, −10) \) и заканчивающийся в \ ((9,5). \)

Рисунок \ (\ PageIndex {1} \): График отрезка линии, описываемого заданными параметрическими уравнениями.

Мы можем исключить параметр, решив сначала уравнение \ ref {eq1} для \ (t \):

\ (х (t) = 2t + 3 \)

\ (х − 3 = 2t \)

\ (t = \ dfrac {x − 3} {2} \).

Подставляя это в \ (y (t) \) (Уравнение \ ref {eq2}), мы получаем

\ (у (t) = 3t − 4 \)

\ (y = 3 \ влево (\ dfrac {x − 3} {2} \ right) −4 \)

\ (y = \ dfrac {3x} {2} — \ dfrac {9} {2} −4 \)

\ (y = \ dfrac {3x} {2} — \ dfrac {17} {2} \).

Наклон этой прямой определяется выражением \ (\ dfrac {dy} {dx} = \ dfrac {3} {2} \). Затем мы вычисляем \ (x ′ (t) \) и \ (y ′ (t) \). Это дает \ (x ′ (t) = 2 \) и \ (y ′ (t) = 3 \). Обратите внимание, что

\ [\ dfrac {dy} {dx} = \ dfrac {dy / dt} {dx / dt} = \ dfrac {3} {2}. \ nonumber \]

Это не совпадение, как указано в следующей теореме.

Производная от параметрических уравнений

Рассмотрим плоскую кривую, заданную параметрическими уравнениями \ (x = x (t) \) и \ (y = y (t) \). Предположим, что \ (x ′ (t) \) и \ (y ′ (t) \) существуют, и предположим, что \ (x ′ (t) ≠ 0 \).Тогда производная \ (\ dfrac {dy} {dx} \) равна

\ [\ dfrac {dy} {dx} = \ dfrac {dy / dt} {dx / dt} = \ dfrac {y ′ (t)} {x ′ (t)}. \ label {paraD} \]

Проба

Эту теорему можно доказать с помощью цепного правила. В частности, предположим, что параметр \ (t \) можно исключить, получив дифференцируемую функцию \ (y = F (x) \). Тогда \ (y (t) = F (x (t)). \) Дифференцируя обе части этого уравнения с помощью цепного правила, получаем

\ [y ′ (t) = F ′ \ big (x (t) \ big) x ′ (t), \ nonumber \]

т.

\ [F ′ \ big (x (t) \ big) = \ dfrac {y ′ (t)} {x ′ (t)}.\ nonumber \]

Но \ (F ′ \ big (x (t) \ big) = \ dfrac {dy} {dx} \), что доказывает теорему.

□

Уравнение \ ref {paraD} можно использовать для вычисления производных плоских кривых, а также критических точек. Напомним, что критической точкой дифференцируемой функции \ (y = f (x) \) является любая точка \ (x = x_0 \) такая, что либо \ (f ′ (x_0) = 0 \), либо \ (f ′ (x_0 )\) не существует. Уравнение \ ref {paraD} дает формулу для наклона касательной к кривой, определенной параметрически, независимо от того, может ли кривая быть описана функцией \ (y = f (x) \) или нет.3−3t + 4, \ quad \ text {for} −2≤t≤2 \)

\ (x (t) = 5 \ cos t, \ quad y (t) = 5 \ sin t, \ quad \ text {for} 0≤t≤2π \)

Решение

а. Чтобы применить уравнение \ ref {paraD}, сначала вычислите \ (x ′ (t) \) и \ (y ′ (t) \):

\ (х ′ (t) = 2t \)

\ (у ′ (t) = 2 \).

Затем подставьте их в уравнение:

\ (\ dfrac {dy} {dx} = \ dfrac {dy / dt} {dx / dt} \)

\ (\ dfrac {dy} {dx} = \ dfrac {2} {2t} \)

\ (\ dfrac {dy} {dx} = \ dfrac {1} {t} \).3−3 (1) + 4 = 1−3 + 4 = 2, \)

, что соответствует точке \ ((3,2) \) на графике. Точка \ ((3,2) \) является относительным минимумом, а точка \ ((- 1,6) \) является относительным максимумом, как показано на следующем графике.

Рисунок \ (\ PageIndex {3} \): график кривой, описанной параметрическими уравнениями в части b.

г. Чтобы применить уравнение \ ref {paraD}, сначала вычислите \ (x ′ (t) \) и \ (y ′ (t) \):

\ (x ′ (t) = — 5 \ sin t \)

\ (y ′ (t) = 5 \ cos t. \)

Затем подставьте их в уравнение:

\ (\ dfrac {dy} {dx} = \ dfrac {dy / dt} {dx / dt} \)

\ (\ dfrac {dy} {dx} = \ dfrac {5 \ cos t} {- 5 \ sin t} \)

\ (\ dfrac {dy} {dx} = — \ cot t.\)

Эта производная равна нулю, когда \ (\ cos t = 0 \), и не определена, когда \ (\ sin t = 0. \) Это дает \ (t = 0, \ dfrac {π} {2}, π, \ dfrac {3π} {2}, \) и \ (2π \) как критические точки для t . Подставляя каждый из них в \ (x (t) \) и \ (y (t) \), получаем

\ (т \)	\ (х (т) \)	\ (у (т) \)
0	5	0
\ (\ dfrac {π} {2} \)	0	5
\ (π \)	−5	0
\ (\ dfrac {3π} {2} \)	0	−5
\ (2π \)	5	0

Эти точки соответствуют сторонам, верху и низу круга, представленного параметрическими уравнениями (рисунок \ (\ PageIndex {4} \)).2−3, \ quad y (t) = 2t − 1, \ quad \ text {for} −3≤t≤4 \]

, когда \ (t = 2 \).

Решение

Сначала найдите наклон касательной с помощью уравнения \ ref {paraD}, что означает вычисление \ (x ′ (t) \) и \ (y ′ (t) \):

\ (х ′ (t) = 2t \)

\ (у ′ (t) = 2 \).

Затем подставьте их в уравнение:

\ (\ dfrac {dy} {dx} = \ dfrac {dy / dt} {dx / dt} \)

\ (\ dfrac {dy} {dx} = \ dfrac {2} {2t} \)

\ (\ dfrac {dy} {dx} = \ dfrac {1} {t} \).2−3 = 1 \) и \ (y (2) = 2 (2) −1 = 3 \),

, что соответствует точке \ ((1,3) \) на графике (рисунок \ (\ PageIndex {5} \)). Теперь используйте форму точки наклона уравнения прямой, чтобы найти уравнение касательной:

\ (у-у_0 = м (х-х_0) \)

\ (y − 3 = \ dfrac {1} {2} (x − 1) \)

\ (y − 3 = \ dfrac {1} {2} x− \ dfrac {1} {2} \)

\ (y = \ dfrac {1} {2} x + \ dfrac {5} {2} \).

Рисунок \ (\ PageIndex {5} \): Касательная линия к параболе, описываемой заданными параметрическими уравнениями, когда \ (t = 2 \). 2} = \ dfrac {d} {dx} \ left [\ dfrac {dy} {dx} \ right].3} \). Критические точки \ ((5,4), \, (−3, −4) \) и \ ((- 4,6). \)

Интегралы, содержащие параметрические уравнения

Теперь, когда мы увидели, как вычислить производную плоской кривой, следующий вопрос: как найти площадь под кривой, заданной параметрически? Вспомните циклоиду, определяемую этими параметрическими уравнениями

\ [\ begin {align *} x (t) & = t− \ sin t \\ [4pt] y (t) & = 1− \ cos t. \ end {align *} \]

Предположим, мы хотим найти площадь заштрихованной области на следующем графике.

Рисунок \ (\ PageIndex {6} \): График циклоиды с выделенной аркой над \ ([0,2π] \).

Вывести формулу площади под кривой, определяемой функциями

\ [\ begin {align *} x & = x (t) \\ [4pt] y & = y (t) \ end {align *} \]

где \ (a≤t≤b \).

Мы предполагаем, что \ (x (t) \) дифференцируемо, и начинаем с равного разбиения интервала \ (a≤t≤b \). Предположим, \ (t_0 = a

Рисунок \ (\ PageIndex {7} \): аппроксимация площади под параметрически определенной кривой.2t = \ dfrac {1− \ cos (2t)} {2} \).

Ответ: \ (A = 3π \) (Обратите внимание, что интегральная формула фактически дает отрицательный ответ. Это связано с тем, что \ (x (t) \) является убывающей функцией на интервале \ ([0, π]; \) то есть кривая ведется справа налево.)

Длина дуги параметрической кривой

В дополнение к нахождению площади под параметрической кривой нам иногда необходимо найти длину дуги параметрической кривой.В случае линейного сегмента длина дуги равна расстоянию между конечными точками. Если частица перемещается из точки \ (A \) в точку \ (B \) по кривой, то расстояние, которое проходит частица, равно длине дуги. Чтобы разработать формулу для длины дуги, мы начнем с аппроксимации отрезками линии, как показано на следующем графике.

Рисунок \ (\ PageIndex {7} \): Аппроксимация кривой отрезками прямых. 2} Δt.2} \, dt. \ end {align *} \]

При переходе к пределу значения \ (\ hat {t_k} \) и \ (\ tilde {t_k} \) оба содержатся в одном и том же постоянно сокращающемся интервале ширины \ (Δt \), поэтому они должны сходиться к той же стоимости.

Мы можем резюмировать этот метод в следующей теореме.

Длина дуги параметрической кривой

Рассмотрим плоскую кривую, заданную параметрическими уравнениями

\ [x = x (t), \ quad y = y (t), \ quad \ text {для} t_1≤t≤t_2 \ nonumber \]

и предположим, что \ (x (t) \) и \ (y (t) \) — дифференцируемые функции от \ (t \).2} \, dx, \ nonumber \]

, который представляет собой формулу для длины дуги, полученную во Введении в приложения интеграции.

Пример \ (\ PageIndex {5} \): определение длины дуги параметрической кривой

Найдите длину дуги полукруга, определяемую уравнениями

\ [x (t) = 3 \ cos t, \ quad y (t) = 3 \ sin t, \ quad \ text {для} 0≤t≤π. \ nonumber \]

Решение

Значения от \ (t = 0 \) до \ (t = π \) очерчивают синюю кривую на рисунке \ (\ PageIndex {8} \). 3, \ quad \ text {для} 1≤t≤3.2} \, dt \ label {ParSurface} \]

при условии, что \ (y (t) \) не отрицательно на \ ([a, b] \).

Пример \ (\ PageIndex {6} \): поиск площади поверхности

Найдите площадь поверхности сферы радиуса \ (r \) с центром в начале координат.

Решение

Начнем с кривой, определяемой уравнениями

\ [x (t) = r \ cos t, \ quad y (t) = r \ sin t, \ quad \ text {для} 0≤t≤π. \ nonumber \]

Это создает верхний полукруг радиуса \ (r \) с центром в начале координат, как показано на следующем графике.{1} (x (t) y (t)) ‘\, dt = x (1) y (1) — x (0) y (0) = 0.∫xdy + ∫ydx = ∫01 [x (t ) y ′ (t) + y (t) x ′ (t)] dt = ∫01 (x (t) y (t)) ′ dt = x (1) y (1) −x (0) y ( 0) = 0. Таким образом, две формулы для площади равны до знака .

Это иллюстрирует идею о том, что эта формула фактически дает знаковую область , что означает, что значение интеграла ∫y dx \ int y \, dx∫ydx является положительным или отрицательным в зависимости от того, лежит ли ограниченная область слева или справа от Кривая. Например, обратите внимание, что области, ограниченные замкнутыми кривыми (x (t), y (t)) (x (t), y (t)) (x (t), y (t)) и (y (t) , x (t)) (y (t), x (t)) (y (t), x (t)) имеют одинаковую площадь без знака (которая равна абсолютному значению площади со знаком), поскольку одна кривая — это просто отражение другого по линии y = xy = xy = x; но сумма их подписанных областей равна нулю.

7.2 Расчет параметрических кривых — том 2

Цели обучения

7.2.1 Определение производных и уравнений касательных для параметрических кривых.
7.2.2 Найдите площадь под параметрической кривой.
7.2.3 Используйте уравнение для длины дуги параметрической кривой.
7.2.4 Примените формулу площади поверхности к объему, полученному с помощью параметрической кривой.

Теперь, когда мы ввели концепцию параметризованной кривой, наш следующий шаг — научиться работать с этой концепцией в контексте исчисления.Например, если мы знаем параметризацию данной кривой, можно ли вычислить наклон касательной к кривой? Как насчет длины дуги кривой? Или площадь под кривой?

Другой сценарий. Предположим, мы хотим изобразить положение бейсбольного мяча после того, как мяч покидает руку питчера. Если положение бейсбольного мяча представлено плоской кривой (x (t), y (t)), (x (t), y (t)), тогда мы сможем использовать математические вычисления для определения скорости движения мяча. мяч в любой момент времени.Кроме того, мы должны иметь возможность вычислить, как далеко прошел этот шар, в зависимости от времени.

Производные параметрических уравнений

x (t) = 2t + 3, y (t) = 3t − 4, −2≤t≤3.x (t) = 2t + 3, y (t) = 3t − 4, −2≤t≤3.

График этой кривой представлен на Рисунке 7.16. Это отрезок, начинающийся в (−1, −10) (- 1, −10) и заканчивающийся в (9,5).(9,5).

Рисунок 7.16 График отрезка прямой, описываемый заданными параметрическими уравнениями.

Мы можем исключить параметр, сначала решив уравнение x (t) = 2t + 3x (t) = 2t + 3 для t :

x (t) = 2t + 3x − 3 = 2tt = x − 32. x (t) = 2t + 3x − 3 = 2tt = x − 32.

Подставляя это в y (t), y (t), получаем

y (t) = 3t − 4y = 3 (x − 32) −4y = 3×2−92−4y = 3×2−172.y (t) = 3t − 4y = 3 (x − 32) −4y = 3×2−92− 4у = 3х2−172.

Наклон этой прямой равен dydx = 32.dydx = 32. Затем мы вычисляем x ′ (t) x ′ (t) и y ′ (t).y ′ (t). Это дает x ′ (t) = 2x ′ (t) = 2 и y ′ (t) = 3. y ′ (t) = 3. Обратите внимание, что dydx = dy / dtdx / dt = 32.dydx = dy / dtdx / dt = 32. Это не совпадение, как указано в следующей теореме.

Теорема 7.1

Производная параметрических уравнений

Рассмотрим плоскую кривую, заданную параметрическими уравнениями x = x (t) x = x (t) и y = y (t) .y = y (t). Предположим, что существуют x ′ (t) x ′ (t) и y ′ (t) y ′ (t), и предположим, что x ′ (t) ≠ 0.x ′ (t) ≠ 0. Тогда производная dydxdydx равна

dydx = dy / dtdx / dt = y ′ (t) x ′ (t).dydx = dy / dtdx / dt = y ′ (t) x ′ (t).

(7,1)

Проба

Эту теорему можно доказать с помощью цепного правила. В частности, предположим, что параметр t может быть исключен, давая дифференцируемую функцию y = F (x) .y = F (x). Тогда y (t) = F (x (t)). Y (t) = F (x (t)). Дифференцируя обе части этого уравнения с помощью правила цепочки, получаем

y ′ (t) = F ′ (x (t)) x ′ (t), y ′ (t) = F ′ (x (t)) x ′ (t),

т.

F ′ (x (t)) = y ′ (t) x ′ (t). F ′ (x (t)) = y ′ (t) x ′ (t).

Но F ′ (x (t)) = dydx, F ′ (x (t)) = dydx, что доказывает теорему.

□

Уравнение 7.1 можно использовать для вычисления производных плоских кривых, а также критических точек. Напомним, что критической точкой дифференцируемой функции y = f (x) y = f (x) является любая точка x = x0x = x0 такая, что либо f ′ (x0) = 0f ′ (x0) = 0, либо f ′ (x0 ) f ′ (x0) не существует. Уравнение 7.1 дает формулу для наклона касательной к кривой, заданной параметрически, независимо от того, может ли кривая быть описана функцией y = f (x) y = f (x) или нет.

Пример 7.4

Нахождение производной параметрической кривой

Рассчитайте производную dydxdydx для каждой из следующих параметрически определенных плоских кривых и найдите любые критические точки на соответствующих графиках.

x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4
x (t) = 2t + 1, y (t) = t3−3t + 4, −2≤t≤5x (t) = 2t + 1, y (t) = t3−3t + 4, −2≤t ≤5
x (t) = 5cost, y (t) = 5sint, 0≤t≤2πx (t) = 5cost, y (t) = 5sint, 0≤t≤2π

Решение

Чтобы применить уравнение 7.1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = 2ty ′ (t) = 2. x ′ (t) = 2ty ′ (t) = 2.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 22tdydx = 1t.dydx = dy / dtdx / dtdydx = 22tdydx = 1t.
Эта производная не определена при t = 0. t = 0. Вычисление x (0) x (0) и y (0) y (0) дает x (0) = (0) 2−3 = −3x (0) = (0) 2−3 = −3 и y (0 ) = 2 (0) −1 = −1, y (0) = 2 (0) −1 = −1, что соответствует точке (−3, −1) (- 3, −1) на графике. График этой кривой представляет собой параболу, раскрывающуюся вправо, а точка (−3, −1) (- 3, −1) является ее вершиной, как показано.
Рис. 7.17. График параболы, описываемый параметрическими уравнениями в части a.
Чтобы применить уравнение 7.1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = 2y ′ (t) = 3t2−3.x ′ (t) = 2y ′ (t) = 3t2−3.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 3t2-32.dydx = dy / dtdx / dtdydx = 3t2-32.
Эта производная равна нулю при t = ± 1. t = ± 1. Когда t = −1t = −1, мы имеем
x (−1) = 2 (−1) + 1 = −1andy (−1) = (- 1) 3−3 (−1) + 4 = −1 + 3 + 4 = 6, x (−1) = 2 (−1) + 1 = −1andy (−1) = (- 1) 3−3 (−1) + 4 = −1 + 3 + 4 = 6,
что соответствует точке (−1,6) (- 1,6) на графике. При t = 1t = 1 имеем
x (1) = 2 (1) + 1 = 3andy (1) = (1) 3−3 (1) + 4 = 1−3 + 4 = 2, x (1) = 2 (1) + 1 = 3andy (1) = (1) 3−3 (1) + 4 = 1−3 + 4 = 2,
что соответствует точке (3,2) (3,2) на графике.Точка (3,2) (3,2) является относительным минимумом, а точка (−1,6) (- 1,6) является относительным максимумом, как показано на следующем графике.
Рисунок 7.18 График кривой, описываемой параметрическими уравнениями в части b.
Чтобы применить уравнение 7.1, сначала вычислите x ′ (t) x ′ (t) и y ′ (t): y ′ (t):
x ′ (t) = — 5sinty ′ (t) = 5cost.x ′ (t) = — 5sinty ′ (t) = 5cost.
Затем подставьте их в уравнение:
dydx = dy / dtdx / dtdydx = 5cost − 5sintdydx = −cott.dydx = dy / dtdx / dtdydx = 5cost − 5sintdydx = −cott.
Эта производная равна нулю, когда cost = 0cost = 0, и не определена, когда sint = 0. sint = 0. Это дает t = 0, π2, π, 3π2 и 2πt = 0, π2, π, 3π2 и 2π в качестве критических точек для t. Подставляя каждое из них в x (t) x (t) и y (t), y (t), получаем
tt х (т) х (т) г (т) г (т)
0 5 0
π2π2 0 5
ππ −5 0
3π23π2 0 −5
2π2π 5 0
Эти точки соответствуют сторонам, верху и низу круга, представленного параметрическими уравнениями (рисунок 7.19). На левом и правом краях круга производная не определена, а сверху и снизу производная равна нулю.
Рисунок 7.19 График кривой, описываемой параметрическими уравнениями в части c.

КПП 7,4

Вычислить производную dy / dxdy / dx для плоской кривой, определяемой уравнениями

x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3

и найдите критические точки на его графике.

Пример 7.5

Поиск касательной

Найдите уравнение касательной к кривой, определяемой уравнениями

x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4whent = 2. x (t) = t2−3, y (t) = 2t − 1, −3≤t≤ 4whent = 2.

Решение

Сначала найдите наклон касательной с помощью уравнения 7.1, что означает вычисление x ′ (t) x ′ (t) и y ′ (t): y ′ (t):

x ′ (t) = 2ty ′ (t) = 2. x ′ (t) = 2ty ′ (t) = 2.

Затем подставьте их в уравнение:

dydx = dy / dtdx / dtdydx = 22tdydx = 1t.dydx = dy / dtdx / dtdydx = 22tdydx = 1t.

Когда t = 2, t = 2, dydx = 12, dydx = 12, значит, это наклон касательной. Вычисление x (2) x (2) и y (2) y (2) дает

x (2) = (2) 2−3 = 1andy (2) = 2 (2) −1 = 3, x (2) = (2) 2−3 = 1andy (2) = 2 (2) −1 = 3,

, что соответствует точке (1,3) (1,3) на графике (рисунок 7.20). Теперь используйте форму точки наклона уравнения прямой, чтобы найти уравнение касательной:

y − y0 = m (x − x0) y − 3 = 12 (x − 1) y − 3 = 12x − 12y = 12x + 52. y − y0 = m (x − x0) y − 3 = 12 (x− 1) y − 3 = 12x − 12y = 12x + 52.

Рис. 7.20. Касательная к параболе, описываемой данными параметрическими уравнениями при t = 2.т = 2.

КПП 7.5

Найдите уравнение касательной к кривой, определяемой уравнениями

x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤10whent = 5. x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤ 10whent = 5.

Деривативы второго порядка

Наша следующая цель — увидеть, как взять вторую производную функции, определенной параметрически. Вторая производная функции y = f (x) y = f (x) определяется как производная от первой производной; то есть

d2ydx2 = ddx [dydx] .d2ydx2 = ddx [dydx].

Поскольку dydx = dy / dtdx / dt, dydx = dy / dtdx / dt, мы можем заменить yy в обеих частях этого уравнения на dydx.dydx. Это дает нам

d2ydx2 = ddx (dydx) = (d / dt) (dy / dx) dx / dt. d2ydx2 = ddx (dydx) = (d / dt) (dy / dx) dx / dt.

(7,2)

Если мы знаем dy / dxdy / dx как функцию от t, , то эту формулу легко применить.

Пример 7.6

Поиск второй производной

Вычислите вторую производную d2y / dx2d2y / dx2 для плоской кривой, заданной параметрическими уравнениями x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4.x (t) = t2−3, y (t) = 2t − 1, −3≤t≤4.

Решение

Из примера 7.4 мы знаем, что dydx = 22t = 1t.dydx = 22t = 1t. Используя уравнение 7.2, получаем

d2ydx2 = (d / dt) (dy / dx) dx / dt = (d / dt) (1 / t) 2t = −t − 22t = −12t3.d2ydx2 = (d / dt) (dy / dx) dx / dt = (d / dt) (1 / t) 2t = −t − 22t = −12t3.

КПП 7,6

Вычислить вторую производную d2y / dx2d2y / dx2 для плоской кривой, определяемой уравнениями

x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3x (t) = t2−4t, y (t) = 2t3−6t, −2≤t≤3

и найдите критические точки на его графике.

Интегралы, включающие параметрические уравнения

Теперь, когда мы увидели, как вычислить производную плоской кривой, следующий вопрос: как найти площадь под кривой, заданной параметрически? Напомним циклоиду, определяемую уравнениями x (t) = t − sint, y (t) = 1 − cost.x (t) = t − sint, y (t) = 1 − cost. Предположим, мы хотим найти площадь заштрихованной области на следующем графике.

Рисунок 7.21 График циклоиды с выделенной аркой над [0,2π] [0,2π].

Вывести формулу площади под кривой, определяемой функциями

x = x (t), y = y (t), a≤t≤b, x = x (t), y = y (t), a≤t≤b,

мы предполагаем, что x (t) x (t) дифференцируема, и начинаем с равного разбиения интервала a≤t≤b.а≤t≤b. Предположим, что t0 = a

Рис. 7.22. Аппроксимация площади под параметрически заданной кривой.

Мы используем прямоугольники для аппроксимации площади под кривой. Высота типичного прямоугольника в этой параметризации равна y (x (t – i)) y (x (t – i)) для некоторого значения t – it – i в подынтервале i , а ширину можно вычислить как x (ti) −x (ti − 1) .x (ti) −x (ti − 1). Таким образом, площадь прямоугольника и равна

.
Ai = y (x (t – i)) (x (ti) −x (ti − 1)).Ai = y (x (t – i)) (x (ti) −x (ti − 1)).

Тогда сумма Римана для площади равна

.
An = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1)). An = ∑i = 1ny (x (t – i)) (x (ti) −x ( ti − 1)).

Умножение и деление каждой площади на ti − ti − 1ti − ti − 1 дает

An = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) ti − ti − 1) (ti − ti − 1) = ∑i = 1ny (x (t – i )) (x (ti) −x (ti − 1) Δt) Δt.An = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) ti − ti − 1) (ti − ti − 1) = ∑i = 1ny (x (t – i)) (x (ti) −x (ti − 1) Δt) Δt.

Если принять предел, когда nn стремится к бесконечности, получаем

A = limn → ∞An = ∫aby (t) x ′ (t) dt. A = limn → ∞An = ∫aby (t) x ′ (t) dt.

Это приводит к следующей теореме.

Теорема 7.2

Площадь под параметрической кривой

Рассмотрим несамопересекающуюся плоскую кривую, определяемую параметрическими уравнениями

x = x (t), y = y (t), a≤t≤bx = x (t), y = y (t), a≤t≤b

и предположим, что x (t) x (t) дифференцируема. Площадь под этой кривой равна

.
A = aby (t) x ′ (t) dt. A = aby (t) x ′ (t) dt.

(7,3)

Пример 7.7

Определение площади под параметрической кривой

Найдите площадь под кривой циклоиды, определяемой уравнениями

x (t) = t − sint, y (t) = 1 − стоимость, 0≤t≤2π.x (t) = t − sint, y (t) = 1 − стоимость, 0≤t≤2π.

Решение

Используя уравнение 7.3, получаем

A = ∫aby (t) x ′ (t) dt = ∫02π (1 − cost) (1 − cost) dt = ∫02π (1-2cost + cos2t) dt = ∫02π (1-2cost + 1 + cos2t2) dt = ∫02π (32−2cost + cos2t2) dt = 3t2−2sint + sin2t4 | 02π = 3π.A = ∫aby (t) x ′ (t) dt = ∫02π (1 − cost) (1 − cost) dt = ∫02π (1−2cost + cos2t) dt = ∫02π (1−2cost + 1 + cos2t2) dt = ∫02π (32−2cost + cos2t2) dt = 3t2−2sint + sin2t4 | 02π = 3π.

КПП 7,7

Найдите площадь под кривой гипоциклоиды, определяемой уравнениями

x (t) = 3cost + cos3t, y (t) = 3sint − sin3t, 0≤t≤π.x (t) = 3cost + cos3t, y (t) = 3sint − sin3t, 0≤t≤π.

Длина дуги параметрической кривой

В дополнение к нахождению площади под параметрической кривой нам иногда необходимо найти длину дуги параметрической кривой. В случае линейного сегмента длина дуги равна расстоянию между конечными точками. Если частица перемещается из точки A в точку B по кривой, то расстояние, которое проходит частица, является длиной дуги. Чтобы разработать формулу для длины дуги, мы начнем с аппроксимации отрезками линии, как показано на следующем графике.

Рисунок 7.23 Аппроксимация кривой отрезками прямых.

Для плоской кривой, определяемой функциями x = x (t), y = y (t), a≤t≤b, x = x (t), y = y (t), a≤t≤b, мы начните с разделения интервала [a, b] [a, b] на n равных подинтервалов: t0 = a

d1 = (x (t1) −x (t0)) 2+ (y (t1) −y (t0)) 2d2 = (x (t2) −x (t1)) 2+ (y (t2) −y (t1 )) 2etc.d1 = (x (t1) −x (t0)) 2+ (y (t1) −y (t0)) 2d2 = (x (t2) −x (t1)) 2+ (y (t2) −y (t1 )) 2etc.

Затем сложите их. Пусть s обозначает точную длину дуги, а snsn обозначает аппроксимацию n отрезками линии:

s≈∑k = 1nsk = ∑k = 1n (x (tk) −x (tk − 1)) 2+ (y (tk) −y (tk − 1)) 2. k) Δty (tk) −y (tk − 1) = y ′ (t ˜k) (tk − tk − 1) = y ′ (t˜k) Δt.k и t˜kt˜k содержатся в одном и том же постоянно сокращающемся интервале шириной Δt, Δt, поэтому они должны сходиться к одному и тому же значению.

Мы можем резюмировать этот метод в следующей теореме.

Теорема 7.3

Длина дуги параметрической кривой

Рассмотрим плоскую кривую, определяемую параметрическими уравнениями

x = x (t), y = y (t), t1≤t≤t2x = x (t), y = y (t), t1≤t≤t2

и предположим, что x (t) x (t) и y (t) y (t) — дифференцируемые функции от t. Тогда длина дуги этой кривой равна

.
s = ∫t1t2 (dxdt) 2+ (dydt) 2dt.s = ∫t1t2 (dxdt) 2+ (dydt) 2dt.

(7,5)

На этом этапе боковой вывод приводит к предыдущей формуле для длины дуги. В частности, предположим, что параметр можно исключить, что приведет к функции y = F (x) .y = F (x). Тогда y (t) = F (x (t)) y (t) = F (x (t)) и цепное правило дает y ′ (t) = F ′ (x (t)) x ′ (t). y ′ (t) = F ′ (x (t)) x ′ (t). Подставляя это в уравнение 7.5, получаем

s = ∫t1t2 (dxdt) 2+ (dydt) 2dt = ∫t1t2 (dxdt) 2+ (F ′ (x) dxdt) 2dt = ∫t1t2 (dxdt) 2 (1+ (F ′ (x)) 2) dt = ∫t1t2x ′ (t) 1+ (dydx) 2dt.s = ∫t1t2 (dxdt) 2+ (dydt) 2dt = ∫t1t2 (dxdt) 2+ (F ′ (x) dxdt) 2dt = ∫t1t2 (dxdt) 2 (1+ (F ′ (x)) 2) dt = ∫t1t2x ′ (t) 1+ (dydx) 2dt.

Здесь мы предположили, что x ′ (t)> 0, x ′ (t)> 0, что является разумным предположением. Цепное правило дает dx = x ′ (t) dt, dx = x ′ (t) dt, и, полагая a = x (t1) a = x (t1) и b = x (t2) b = x (t2), мы получить формулу

s = ab1 + (dydx) 2dx, s = ∫ab1 + (dydx) 2dx,

, который представляет собой формулу для длины дуги, полученную во Введении в приложения интеграции.

Пример 7.8

Определение длины дуги параметрической кривой

Найдите длину дуги полукруга, определяемую уравнениями

x (t) = 3cost, y (t) = 3sint, 0≤t≤π.x (t) = 3cost, y (t) = 3sint, 0≤t≤π.

Решение

Значения от t = 0t = 0 до t = πt = π очерчены красной кривой на рисунке 7.23. Чтобы определить его длину, используйте уравнение 7.5:

.
s = ∫t1t2 (dxdt) 2+ (dydt) 2dt = ∫0π (−3sint) 2+ (3cost) 2dt = ∫0π9sin2t + 9cos2tdt = ∫0π9 (sin2t + cos2t) dt = ∫0π3dt = 3t | 0π = 3π. s = ∫t1t2 (dxdt) 2+ (dydt) 2dt = ∫0π (−3sint) 2+ (3cost) 2dt = ∫0π9sin2t + 9cos2tdt = ∫0π9 (sin2t + cos2t) dt = ∫0π3dt = 3t | 0π = 3π.

Обратите внимание, что формула для длины дуги полукруга равна πrπr, а радиус этой окружности равен 3.Это отличный пример использования исчисления для вывода известной формулы геометрической величины.

Рис. 7.24. Длина дуги полукруга равна его радиусу, умноженному на π.π.

КПП 7,8

Найдите длину дуги кривой, определяемой уравнениями

x (t) = 3t2, y (t) = 2t3,1≤t≤3.x (t) = 3t2, y (t) = 2t3,1≤t≤3.

Теперь вернемся к задаче, поставленной в начале раздела, о том, что бейсбольный мяч выходит из руки питчера. Игнорируя эффект сопротивления воздуха (если это не криволинейный шар!), Мяч движется по параболической траектории.Предполагая, что рука питчера находится в начале координат, а мяч движется слева направо в направлении положительной оси x , параметрические уравнения для этой кривой можно записать как

x (t) = 140t, y (t) = — 16t2 + 2tx (t) = 140t, y (t) = — 16t2 + 2t

, где t представляет время. Сначала мы вычисляем расстояние, которое проходит мяч, как функцию времени. Это расстояние представлено длиной дуги. Мы можем немного изменить формулу длины дуги. Сначала перепишите функции x (t) x (t) и y (t) y (t), используя v в качестве независимой переменной, чтобы исключить путаницу с параметром t :

х (v) = 140v, y (v) = — 16v2 + 2v.х (v) = 140v, y (v) = — 16v2 + 2v.

Затем запишем формулу длины дуги следующим образом:

s (t) = ∫0t (dxdv) 2+ (dydv) 2dv = ∫0t1402 + (- 32v + 2) 2dv.s (t) = ∫0t (dxdv) 2+ (dydv) 2dv = ∫0t1402 + (- 32v + 2) 2дв.

Переменная v действует как фиктивная переменная, которая исчезает после интегрирования, оставляя длину дуги как функцию времени t. Чтобы интегрировать это выражение, мы можем использовать формулу из Приложения A,

A2 + u2du = u2a2 + u2 + a22ln | u + a2 + u2 | + C. a2 + u2du = u2a2 + u2 + a22ln | u + a2 + u2 | + C.

Положим a = 140a = 140 и u = −32v + 2.и = −32v + 2. Это дает du = −32dv, du = −32dv, поэтому dv = −132du.dv = −132du. Следовательно,

∫1402 + (- 32v + 2) 2dv = −132∫a2 + u2du = −132 [(- 32v + 2) 21402 + (- 32v + 2) 2 + 14022ln | (−32v + 2) +1402 + (- 32v + 2) 2 |] + C∫1402 + (- 32v + 2) 2dv = −132∫a2 + u2du = −132 [(- 32v + 2) 21402 + (- 32v + 2) 2 + 14022ln | (- 32v + 2) +1402 + (- 32v + 2) 2 |] + C

s (t) = — 132 [(- 32t + 2) 21402 + (- 32t + 2) 2 + 14022ln | (−32t + 2) +1402 + (- 32t + 2) 2 |] +132 [1402 + 22 + 14022ln | 2 + 1402 + 22 |] = (t2−132) 1024t2−128t + 19604−12254ln | (−32t + 2) + 1024t2−128t + 19604 | + 1960432 + 12254ln (2 + 19604) .s (t ) = — 132 [(- 32t + 2) 21402 + (- 32t + 2) 2 + 14022ln | (−32t + 2) +1402 + (- 32t + 2) 2 |] +132 [1402 + 22 + 14022ln | 2 + 1402 + 22 |] = (t2−132) 1024t2−128t + 19604−12254ln | (−32t + 2) + 1024t2−128t + 19604 | + 1960432 + 12254ln (2 + 19604).

Эта функция представляет расстояние, пройденное мячом, как функцию времени. Для расчета скорости возьмем производную этой функции по т. Хотя это может показаться сложной задачей, можно получить ответ непосредственно из Фундаментальной теоремы исчисления:

ddx∫axf (u) du = f (x). ddx∫axf (u) du = f (x).

Следовательно,

s ′ (t) = ddt [s (t)] = ddt [∫0t1402 + (- 32v + 2) 2dv] = 1402 + (- 32t + 2) 2 = 1024t2−128t + 19604 = 2256t2−32t + 4901.s ′ (T) = ddt [s (t)] = ddt [∫0t1402 + (- 32v + 2) 2dv] = 1402 + (- 32t + 2) 2 = 1024t2−128t + 19604 = 2256t2−32t + 4901.

Через треть секунды после того, как мяч покидает руку питчера, расстояние, которое он проходит, равно

.
s (13) = (1 / 32−132) 1024 (13) 2−128 (13) + 19604−12254ln | (−32 (13) +2) +1024 (13) 2−128 (13) +19604 | + 1960432 + 12254ln (2 + 19604) ≈46.69feet.s (13) = (1 / 32−132) 1024 (13) 2−128 (13) + 19604−12254ln | (−32 (13) +2) + 1024 (13) 2−128 (13) +19604 | + 1960432 + 12254ln (2 + 19604) ≈46.69 футов.

Это значение составляет чуть более трех четвертей пути к исходной тарелке. Скорость мяча

s ′ (13) = 2256 (13) 2−16 (13) + 4901≈140,34 фут / с.s ′ (13) = 2256 (13) 2−16 (13) + 4901≈140.34 фута / с.

Эта скорость соответствует примерно 95 милям в час — фастбол высшей лиги.

Площадь поверхности, созданная параметрической кривой

Вспомните задачу о нахождении площади поверхности объема вращения. В разделах Длина кривой и Площадь поверхности мы вывели формулу для определения площади поверхности объема, созданного функцией y = f (x) y = f (x) от x = ax = a до x = b, x = b, вращается вокруг оси x :

S = 2π∫abf (x) 1+ (f ′ (x)) 2dx. S = 2π∫abf (x) 1+ (f ′ (x)) 2dx.

Теперь рассмотрим объем вращения, создаваемый вращением параметрически определенной кривой x = x (t), y = y (t), a≤t≤bx = x (t), y = y (t), a≤t ≤b вокруг оси x , как показано на следующем рисунке.

Рис. 7.25 Поверхность вращения, образованная параметрически заданной кривой.

Аналогичная формула для параметрически определенной кривой:

S = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dtS = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dt

(7,6)

при условии, что y (t) y (t) не отрицательно на [a, b]. [A, b].

Пример 7.9

Поиск площади поверхности

Найдите площадь поверхности сферы радиуса r с центром в начале координат.

Решение

Начнем с кривой, определяемой уравнениями

x (t) = rcost, y (t) = rsint, 0≤t≤π.x (t) = rcost, y (t) = rsint, 0≤t≤π.

Это создает верхний полукруг радиусом r с центром в начале координат, как показано на следующем графике.

Рис. 7.26. Полукруг, созданный параметрическими уравнениями.

Когда эта кривая вращается вокруг оси x , она образует сферу радиусом r . Чтобы вычислить площадь поверхности сферы, мы используем уравнение 7.6:

S = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dt = 2π∫0πrsint (−rsint) 2+ (rcost) 2dt = 2π∫0πrsintr2sin2t + r2cos2tdt = 2π∫0πrsintr2 ( sin2t + cos2t) dt = 2π∫0πr2sintdt = 2πr2 (−cost | 0π) = 2πr2 (−cosπ + cos0) = 4πr2.S = 2π∫aby (t) (x ′ (t)) 2+ (y ′ (t)) 2dt = 2π∫0πrsint (−rsint) 2+ (rcost) 2dt = 2π∫0πrsintr2sin2t + r2cos2tdt = 2π∫0πrsintr2 ( sin2t + cos2t) dt = 2π∫0πr2sintdt = 2πr2 (−cost | 0π) = 2πr2 (−cosπ + cos0) = 4πr2.

Фактически, это формула площади поверхности сферы.

КПП 7.9

Найдите площадь поверхности, образованную плоской кривой, определяемой уравнениями

x (t) = t3, y (t) = t2,0≤t≤1x (t) = t3, y (t) = t2,0≤t≤1

вращается вокруг оси x .

Раздел 7.2. Упражнения

В следующих упражнениях каждый набор параметрических уравнений представляет собой линию.Не удаляя параметр, найдите наклон каждой линии.

62.

x = 3 + t, y = 1 − tx = 3 + t, y = 1 − t

64.

x = 4−3t, y = −2 + 6tx = 4−3t, y = −2 + 6t

65.

x = −5t + 7, y = 3t − 1x = −5t + 7, y = 3t − 1

Для следующих упражнений определите наклон касательной, затем найдите уравнение касательной при заданном значении параметра.

66.

x = 3sint, y = 3cost, t = π4x = 3sint, y = 3cost, t = π4

67.

x = стоимость, y = 8sint, t = π2x = стоимость, y = 8sint, t = π2

68.

x = 2t, y = t3, t = −1x = 2t, y = t3, t = −1

69.

x = t + 1t, y = t − 1t, t = 1x = t + 1t, y = t − 1t, t = 1

Для следующих упражнений найдите все точки кривой с заданным наклоном.

71.

x = 4cost, y = 4sint, x = 4cost, y = 4sint, slope = 0,5

72.

x = 2cost, y = 8sint, slope = −1x = 2cost, y = 8sint, slope = −1

73.

x = t + 1t, y = t − 1t, наклон = 1x = t + 1t, y = t − 1t, наклон = 1

74.

x = 2 + t, y = 2−4t, наклон = 0x = 2 + t, y = 2−4t, наклон = 0

Для следующих упражнений запишите уравнение касательной в декартовых координатах для данного параметра t .

75.

x = et, y = 1 − lnt2, t = 1x = et, y = 1 − lnt2, t = 1

76.

x = tlnt, y = sin2t, t = π4x = tlnt, y = sin2t, t = π4

77.

x = et, y = (t − 1) 2, при (1,1) x = et, y = (t − 1) 2, при (1,1)

78.

Для x = sin (2t), y = 2sintx = sin (2t), y = 2sint, где 0≤t <2π.0≤t <2π. Найдите все значения t , при которых существует горизонтальная касательная.

79.

Для x = sin (2t), y = 2sintx = sin (2t), y = 2sint, где 0≤t <2π.0≤t <2π. Найдите все значения t , при которых существует вертикальная касательная.

80.

Найдите все точки на кривой x = 4sin (t), y = 4cos (t) x = 4sin (t), y = 4cos (t), которые имеют наклон 0,50,5

81.

Найдите dydxdydx для x = sin (t), y = cos (t) .x = sin (t), y = cos (t).

82.

Найдите уравнение касательной к x = sin (t), y = cos (t) x = sin (t), y = cos (t) при t = π4.t = π4.

83.

Для кривой x = 4t, y = 3t − 2, x = 4t, y = 3t − 2 найдите наклон и вогнутость кривой при t = 3.t = 3.

84.

Для параметрической кривой, уравнение которой имеет вид x = 4cosθ, y = 4sinθ, x = 4cosθ, y = 4sinθ, найдите наклон и вогнутость кривой при θ = π4.θ = π4.

85.

Найдите наклон и вогнутость кривой, уравнение которой: x = 2 + secθ, y = 1 + 2tanθx = 2 + secθ, y = 1 + 2tanθ при θ = π6.θ = π6.

86.

Найдите все точки на кривой x = t + 4, y = t3−3tx = t + 4, y = t3−3t, в которых есть вертикальные и горизонтальные касательные.

87.

Найдите все точки на кривой x = secθ, y = tanθx = secθ, y = tanθ, в которых существуют горизонтальные и вертикальные касательные.

Для следующих упражнений найдите d2y / dx2.d2y / dx2.

88.

x = t4−1, y = t − t2x = t4−1, y = t − t2

89.

x = sin (πt), y = cos (πt) x = sin (πt), y = cos (πt)

90.

x = e − t, y = te2tx = e − t, y = te2t

Для следующих упражнений найдите точки на кривой, в которых касательная линия является горизонтальной или вертикальной.

91.

x = t (t2−3), y = 3 (t2−3) x = t (t2−3), y = 3 (t2−3)

92.

x = 3t1 + t3, y = 3t21 + t3x = 3t1 + t3, y = 3t21 + t3

Для следующих упражнений найдите dy / dxdy / dx в значении параметра.

93.

x = стоимость, y = синт, t = 3π4x = стоимость, y = синт, t = 3π4

94.

x = t, y = 2t + 4, t = 9x = t, y = 2t + 4, t = 9

95.

x = 4cos (2πs), y = 3sin (2πs), s = −14x = 4cos (2πs), y = 3sin (2πs), s = −14

Для следующих упражнений найдите d2y / dx2d2y / dx2 в заданной точке, не удаляя параметр.

96.

x = 12t2, y = 13t3, t = 2x = 12t2, y = 13t3, t = 2

97.

x = t, y = 2t + 4, t = 1x = t, y = 2t + 4, t = 1

98.

Найдите t интервалов, на которых кривая x = 3t2, y = t3 − tx = 3t2, y = t3 − t вогнута вверх и вниз.

99.

Определите вогнутость кривой x = 2t + lnt, y = 2t − lnt.x = 2t + lnt, y = 2t − lnt.

100.

Нарисуйте и найдите площадь под одной аркой циклоиды x = r (θ − sinθ), y = r (1 − cosθ) .x = r (θ − sinθ), y = r (1 − cosθ).

101.

Найдите площадь, ограниченную кривой x = cost, y = et, 0≤t≤π2x = cost, y = et, 0≤t≤π2 и линиями y = 1y = 1 и x = 0.x = 0.

102.

Найдите площадь, заключенную в эллипс x = acosθ, y = bsinθ, 0≤θ <2π.x = acosθ, y = bsinθ, 0≤θ <2π.

103.

Найдите площадь области, ограниченной x = 2sin2θ, y = 2sin2θtanθ, x = 2sin2θ, y = 2sin2θtanθ, для 0≤θ≤π2.0≤θ≤π2.

Для следующих упражнений найдите площадь областей, ограниченных параметрическими кривыми и указанными значениями параметра.

104.

x = 2cotθ, y = 2sin2θ, 0≤θ≤πx = 2cotθ, y = 2sin2θ, 0≤θ≤π

105.

[T] x = 2acost − acos (2t), y = 2asint − asin (2t), 0≤t <2πx = 2acost − acos (2t), y = 2asint − asin (2t), 0≤t < 2π

106.

[T] x = asin (2t), y = bsin (t), 0≤t <2πx = asin (2t), y = bsin (t), 0≤t <2π («песочные часы»)

107.

[T] x = 2acost − asin (2t), y = bsint, 0≤t <2πx = 2acost − asin (2t), y = bsint, 0≤t <2π («слеза»)

Для следующих упражнений найдите длину дуги кривой на указанном интервале параметра.

108.

x = 4t + 3, y = 3t − 2,0≤t≤2x = 4t + 3, y = 3t − 2,0≤t≤2

109.

x = 13t3, y = 12t2,0≤t≤1x = 13t3, y = 12t2,0≤t≤1

110.

x = cos (2t), y = sin (2t), 0≤t≤π2x = cos (2t), y = sin (2t), 0≤t≤π2

111.

х = 1 + t2, y = (1 + t) 3,0≤t≤1x = 1 + t2, y = (1 + t) 3,0≤t≤1

112.

x = etcost, y = etsint, 0≤t≤π2x = etcost, y = etsint, 0≤t≤π2 (выразите ответ в виде десятичной дроби с округлением до трех знаков)

113.

x = acos3θ, y = asin3θx = acos3θ, y = asin3θ на интервале [0,2π) [0,2π) (гипоциклоида)

114.

Найдите длину одной дуги циклоиды x = 4 (t − sint), y = 4 (1 − cost) .x = 4 (t − sint), y = 4 (1 − cost).

115.

Найдите расстояние, пройденное частицей с положением (x, y) (x, y), поскольку t изменяется в заданном временном интервале: x = sin2t, y = cos2t, 0≤t≤3π.x = sin2t, y = cos2t, 0≤t≤3π.

116.

Найдите длину одной дуги циклоиды x = θ − sinθ, y = 1 − cosθ.x = θ − sinθ, y = 1 − cosθ.

117.

Покажите, что общая длина эллипса x = 4sinθ, y = 3cosθx = 4sinθ, y = 3cosθ равна L = 16∫0π / 21 − e2sin2θdθ, L = 16∫0π / 21 − e2sin2θdθ, где e = cae = ca и с = a2 − b2.с = a2 − b2.

118.

Найдите длину кривой x = et − t, y = 4et / 2, −8≤t≤3.x = et − t, y = 4et / 2, −8≤t≤3.

Для следующих упражнений найдите площадь поверхности, полученную вращением данной кривой вокруг оси x .

119.

x = t3, y = t2,0≤t≤1x = t3, y = t2,0≤t≤1

120.

x = acos3θ, y = asin3θ, 0≤θ≤π2x = acos3θ, y = asin3θ, 0≤θ≤π2

121.

[T] Используйте CAS, чтобы найти площадь поверхности, созданную вращением x = t + t3, y = t − 1t2,1≤t≤2x = t + t3, y = t − 1t2,1≤t ≤2 около оси x .(Ответ с точностью до трех знаков после запятой.)

122.

Найдите площадь поверхности, полученную вращением x = 3t2, y = 2t3,0≤t≤5x = 3t2, y = 2t3,0≤t≤5 вокруг оси y .

123.

Найдите площадь поверхности, образованную вращением x = t2, y = 2t, 0≤t≤4x = t2, y = 2t, 0≤t≤4 относительно оси x .

124.

Найдите площадь поверхности, образованную вращением x = t2, y = 2t2,0≤t≤1x = t2, y = 2t2,0≤t≤1 относительно оси y .

Исчисление и параметрические уравнения

Раздел 10.3 Исчисление и параметрические уравнения

В предыдущем разделе определены кривые на основе параметрических уравнений. В этом разделе мы будем использовать методы исчисления для изучения этих кривых.

Нас по-прежнему интересуют прямые, касательные к точкам кривой. Они описывают, как \ (y \) — значения меняются относительно \ (x \) — значений, они полезны при приближении и указывают мгновенное направление движения.

Рисунок 10.3.1. Видео-введение в Раздел 10.3

Наклон касательной по-прежнему равен \ (\ frac {dy} {dx} \ text {,} \), и правило цепочки позволяет нам вычислить его в контексте параметрических уравнений. Если \ (x = f (t) \) и \ (y = g (t) \ text {,} \), правило цепочки утверждает, что

\ begin {уравнение *}
\ frac {dy} {dt} = \ frac {dy} {dx} \ cdot \ frac {dx} {dt} \ text {.}
\ end {уравнение *}

Решая для \ (\ frac {dy} {dx} \ text {,} \), получаем

\ begin {уравнение *}
\ frac {dy} {dx} = \ frac {dy} {dt} \ Bigg / \ frac {dx} {dt} = \ frac {g ‘(t)} {\ fp (t)} \ text {,}
\ end {уравнение *}

при условии, что \ (\ fp (t) \ neq 0 \ text {.} \) Это важно, поэтому мы называем это ключевой идеей.

Мы используем это для определения касательной.

Определение 10.3.3. Касательная и нормальная линии.

Пусть кривая \ (C \) параметризована как \ (x = f (t) \) и \ (y = g (t) \ text {,} \), где \ (f \) и \ (g \) являются дифференцируемыми функциями на некотором интервале \ (I \), содержащем \ (t = t_0 \ text {.} \) Касательная линия к \ (C \) в точке \ (t = t_0 \) — это прямая, проходящая через \ (\ big (f (t_0), g (t_0) \ big) \) с наклоном \ (m = g ‘(t_0) / \ fp (t_0) \ text {,} \) при условии \ (\ fp (t_0) \ neq 0 \ text {.} \)

Нормальная линия до \ (C \) в точке \ (t = t_0 \) — это линия, проходящая через \ (\ big (f (t_0), g (t_0) \ big) \) с наклоном \ (m = — \ fp (t_0) / g ‘(t_0) \ text {,} \) provided \ (g’ (t_0) \ neq 0 \ text {.} \)

Определение оставляет два особых случая для рассмотрения. Когда касательная линия горизонтальна, нормальная линия не определена приведенным выше определением как \ (g ‘(t_0) = 0 \ text {.} \) Аналогично, когда нормальная линия горизонтальна, касательная линия не определена. Кажется разумным, чтобы эти линии были определены (например, можно провести касательную линию к «правой стороне» круга), поэтому мы добавляем следующее к приведенному выше определению.2 + 6t-1 \ text {,} \) и пусть \ (C \) — кривая, определяемая этими уравнениями.

Найдите уравнения касательной и нормали к \ (C \) в точке \ (t = 3 \ text {.} \)
Найдите, где \ (C \) имеет вертикальные и горизонтальные касательные.

Решение

Начнем с вычисления \ (\ fp (t) = 10t-6 \) и \ (g ‘(t) = 2t + 6 \ text {.} \) Таким образом,
\ begin {уравнение *}
\ frac {dy} {dx} = \ frac {2t + 6} {10t-6} \ text {.}
\ end {уравнение *}
Обратите внимание на то, что может показаться необычным: \ (\ frac {dy} {dx} \) является функцией \ (t \ text {,} \), а не \ (x \ text {.} \) Точно так же, как точки на кривой находятся в терминах \ (t \ text {,} \), так же и наклоны касательных линий. Точка на \ (C \) в \ (t = 3 \) равна \ ((31,26) \ text {.} \) Наклон касательной линии равен \ (m = 1/2 \), а наклон нормальной строки \ (m = -2 \ text {.} \) Таким образом,
- уравнение касательной: \ (\ ds y = \ frac12 (x-31) +26 \ text {,} \) и
- уравнение нормальной линии: \ (\ ds y = -2 (x-31) +26 \ text {.} \)
Это показано на Рисунке 10.3.5.
Рисунок 10.3.5. Построение касательных и нормальных прямых в примере 10.3.4.
Чтобы найти, где \ (C \) имеет горизонтальную касательную, мы устанавливаем \ (\ frac {dy} {dx} = 0 \) и решаем для \ (t \ text {.} \). В этом случае это составляет установить \ (g ‘(t) = 0 \) и решить для \ (t \) (и убедившись, что \ (\ fp (t) \ neq 0 \)).
\ begin {уравнение *}
g ‘(t) = 0 \ Rightarrow 2t + 6 = 0 \ Rightarrow t = -3 \ text {.}
\ end {уравнение *}
Точка на \ (C \), соответствующая \ (t = -3 \), — это \ ((67, -10) \ text {;} \) касательная линия в этой точке горизонтальна (следовательно, с уравнением \ (y = -10 \)).Чтобы найти, где \ (C \) имеет вертикальную касательную, мы находим, где у него есть горизонтальная нормальная линия, и устанавливаем \ (- \ frac {\ fp (t)} {g ‘(t)} = 0 \ text { .} \) Это равносильно установке \ (\ fp (t) = 0 \) и решению для \ (t \) (и проверке того, что \ (g ‘(t) \ neq 0 \)).
\ begin {уравнение *}
\ fp (t) = 0 \ Rightarrow 10t-6 = 0 \ Rightarrow t = 0,6 \ text {.}
\ end {уравнение *}
Точка на \ (C \), соответствующая \ (t = 0.6 \), равна \ ((2.2,2.96) \ text {.} \) Касательная линия в этой точке равна \ (x = 2.2 \ text {.} \) Точки, в которых касательные являются вертикальными и горизонтальными, указаны на графике на рисунке 10.3.5.

Пример 10.3.6. Касательная и нормальная прямые к окружности.

Найдите единичную окружность, определяемую \ (x = \ cos (t) \) и \ (y = \ sin (t) \) на \ ([0,2 \ pi] \ text {,} \ ) имеет вертикальные и горизонтальные касательные.
Найдите уравнение нормальной линии в точке \ (t = t_0 \ text {.} \)

Решение

Мы вычисляем производную, следуя ключевой идее 10.3.2:
\ begin {уравнение *}
\ frac {dy} {dx} = \ frac {g ‘(t)} {\ fp (t)} = — \ frac {\ cos (t)} {\ sin (t)} \ text {.}
\ end {уравнение *}
Производная равна \ (0 \), когда \ (\ cos (t) = 0 \ text {;} \), то есть когда \ (t = \ pi / 2, \, 3 \ pi / 2 \ text {. } \) Это точки \ ((0,1) \) и \ ((0, -1) \) на окружности. Нормальная линия горизонтальна (и, следовательно, касательная вертикальна), когда \ (\ sin (t) = 0 \ text {;} \), то есть когда \ (t = 0, \, \ pi, \, 2 \ pi \ text {,} \), соответствующие точкам \ ((- 1,0) \) и \ ((0,1) \) на окружности. Эти результаты должны иметь интуитивный смысл.
Наклон нормальной линии в точке \ (t = t_0 \) равен \ (\ ds m = \ frac {\ sin (t_0)} {\ cos (t_0)} = \ tan (t_0) \ text {.} \) Эта нормальная линия проходит через точку \ ((\ cos (t_0), \ sin (t_0)) \ text {,} \), давая строку
\ begin {align *}
y \ amp = \ frac {\ sin (t_0)} {\ cos (t_0)} (x- \ cos (t_0)) + \ sin (t_0) \\
\ amp = (\ tan (t_0)) x \ text {,}
\ end {выровнять *}
до тех пор, пока \ (\ cos (t_0) \ neq 0 \ text {.} \) Важно понимать, что нормальные линии к окружности проходят через его центр, как показано на рис. 10.3.7. Другими словами, любая линия, проходящая через центр круга, пересекает круг под прямым углом.2 (t)} \ text {(Мы можем сократить как \ (t \ neq 0 \).)} \\
\ amp = \ lim_ {t \ to0} — \ frac {\ sin (t)} {\ cos (t)} \\
\ amp = 0 \ текст {.}
\ end {выровнять *}
Мы достигли чего-то значительного. Когда производная \ (\ frac {dy} {dx} \) возвращает неопределенную форму в \ (t = t_0 \ text {,} \), мы можем определить ее значение, установив его равным \ (\ lim \ limits_ {t \ to t_0} \) \ (\ frac {dy} {dx} \ text {,} \), если этот предел существует. Это позволяет нам находить наклоны касательных на выступах, что может быть очень полезным.
Рисунок 10.2} = \ frac {d} {dx} \ left [\ frac {dy} {dx} \ right] \ text {,}
\ end {уравнение *}
, но помните, что \ (\ frac {dy} {dx} \) является функцией \ (t \ text {,} \), а не \ (x \ text {,} \), что делает это вычисление непростым.
Чтобы упростить последующие обозначения, пусть \ (h (t) = \ frac {dy} {dx} \ text {.} \) Мы хотим \ (\ frac {d} {dx} [h (t) ] \ text {;} \) то есть мы хотим \ (\ frac {dh} {dx} \ text {.} \) Мы снова обращаемся к правилу цепочки. Примечание:
\ begin {уравнение *}
\ frac {dh} {dt} = \ frac {dh} {dx} \ cdot \ frac {dx} {dt} \ Rightarrow \ frac {dh} {dx} = \ frac {dh} {dt} \ Bigg / \ гидроразрыв {dx} {dt} \ text {.2} \ neq 0 \) для всех \ (t \ text {.} \) Не определено, когда \ (5t-3 = 0 \ text {;} \), то есть когда \ (t = 3/5 \ text {.} \) Следуя работе, изложенной в разделе 3.4, мы смотрим на значения \ (t \) больше / меньше \ (3/5 \) на числовой прямой:
Просматривая пример 10.3.4, мы видим, что когда \ (t = 3/5 = 0,6 \ text {,} \) график параметрических уравнений имеет вертикальную касательную. Эта точка также является точкой перегиба графика, показанного на рис. 10.3.12.
Видео на рис. 10.3.13 показывает, как эту информацию можно использовать для рисования кривой вручную.2} = 0 \ text {.} \) Это нетривиально, поскольку уравнения, которые смешивают полиномы и тригонометрические функции, обычно не имеют «хороших» решений.
На рисунке 10.3.15. (А) мы видим график второй производной. Он показывает, что он имеет нули примерно на \ (t = 0,5, \, 3,5, \, 6,5, \, 9,5, \, 12,5 \) и \ (16 \ text {.} \). Эти приближения не очень хорошие, сделанные только взглянув на график. Метод Ньютона обеспечивает более точные приближения. С точностью до 2 знаков после запятой имеем:
\ begin {уравнение *}
т = 0.2} \ text {,} \), где оно примерно равно 0. В (b) график параметрических уравнений из примера 10.3.14 вместе с точками перегиба.
Подраздел 10. 2} \, dt \ text {.}
\ end {уравнение *}

Примечание: Теорема 10.3.17 использует дифференцируемость на отрезках, как это было сделано в разделе 7.4.
Как и раньше, эти интегралы часто нелегко вычислить. Мы начнем с простого примера, а затем дадим еще один пример, в котором мы приближаем решение.
Пример 10.3.18. Длина дуги окружности.

Найдите длину дуги окружности, параметризованной как \ (x = 3 \ cos (t) \ text {,} \) \ (y = 3 \ sin (t) \) на \ ([0,3 \ pi / 2 ] \ text {.} \)
Решение
Путем прямого применения теоремы 10.2 + 1} \, dt \ text {.}
\ end {выровнять *}
К сожалению, подынтегральное выражение не имеет первообразной, выражаемой элементарными функциями. Мы обращаемся к численному интегрированию, чтобы приблизить его значение. Используя 4 подинтервала, правило Симпсона приближает значение интеграла как \ (2.65051 \ text {.} \). С помощью компьютера легко использовать больше подынтервалов, а \ (n = 20 \) дает значение \ (2.71559 \) text {.} \) Увеличение \ (n \) показывает, что это значение стабильно и хорошо приближается к фактическому значению.
Рисунок 10.3.20. График параметрических уравнений в Примере 10.3.19, где вычислена длина дуги капли.
Подраздел 10.3.3 Площадь поверхности твердого тела вращения

С формулой для определения длины дуги связана формула для определения площади поверхности. Мы можем адаптировать формулу, найденную в теореме 7.4.13 из раздела 7.4, аналогично тому, как это было сделано для получения формулы для длины дуги, сделанной ранее.
Теорема 10.3.21. Площадь поверхности твердого тела вращения.2-1 \), как показано в Примере 10.3.19. Найдите площадь поверхности, если эта форма вращается вокруг оси \ (x \), как показано на рисунке 10.3.23.
Решение
Форма капли образуется между \ (t = -1 \) и \ (t = 1 \ text {.} \). Используя теорему 10.3.21, мы видим, что нам нужно \ (g (t) \ geq 0 \) на \ ([- 1,1] \ text {,} \), а это не так. Чтобы исправить это, мы упрощаем замену \ (g (t) \) на \ (- g (t) \ text {,} \), которая переворачивает весь график вокруг оси \ (x \) (и не меняет площадь поверхности полученного твердого тела).2 + 1} \, dt \ text {.}
\ end {выровнять *}
Мы снова приходим к интегралу, который мы не можем вычислить в терминах элементарных функций. Используя правило Симпсона с \ (n = 20 \ text {,} \), мы находим, что площадь равна \ (S = 9,44 \ text {.} \). Использование больших значений \ (n \) показывает, что это верно с точностью до 2 мест. после десятичной дроби.
Рисунок 10.3.23. Вращение формы капли вокруг оси \ (x \) — в примере 10.3.22.
После определения нового способа создания кривых на плоскости, в этом разделе мы применили методы вычисления к параметрическому уравнению, определяющему эти кривые, чтобы изучить их свойства.В следующем разделе мы определим другой способ формирования кривых на плоскости. Для этого мы создаем новую систему координат, называемую полярными координатами , которая идентифицирует точки на плоскости иначе, чем при измерении расстояний от осей \ (y \) — и \ (x \) -.
Упражнения 10.3.4 Упражнения

1.
Верно или неверно? Даны параметрические уравнения \ (x = f (t) \) и \ (y = g (t) \ text {,} \) \ (\ lz {y} {x} = \ fp (t) / g ‘(t ) \ text {,} \) до тех пор, пока \ (g ‘(t) \ neq 0 \ text {.} \)
2.
Даны параметрические уравнения \ (x = f (t) \) и \ (y = g (t) \ text {,} \) производная \ (\ frac {dy} {dx} \), как указано в ключевой идее 10.3. .2 является функцией?
3.
Верно или неверно? Даны параметрические уравнения \ (x = f (t) \) и \ (y = g (t) \ text {,} \), чтобы найти \ (\ lzn {2} {y} {x} \ text {,} \ ) просто вычисляется \ (\ lzoo {t} {\ lz {y} {x}} \ text {.} \)
4.
Верно или неверно? Если \ (\ lz {y} {x} = 0 \) в \ (t = t_0 \ text {,} \), то нормальная линия к кривой в \ (t = t_0 \) является вертикальной линией.2 \ text {;} \) \ (t = 1 \)
Решение
1. \ (\ displaystyle \ frac {dy} {dx} = 2t \)
2. Касательная линия: \ (y = 2 (x-1) +1 \ text {;} \) нормальная линия: \ (y = -1/2 (x-1) +1 \)
6.
\ (x = \ sqrt {t} \ text {,} \) \ (y = 5t + 2 \ text {;} \) \ (t = 4 \)
Решение
1. \ (\ displaystyle \ frac {dy} {dx} = 10 \ sqrt {t} \)
2. Касательная линия: \ (y = 20 (x-2) +22 \ text {;} \) нормальная линия: \ (y = -1/20 (x-2) +22 \)
7.2} {2 т} \)
\ (t = 0 \ text {:} \) Касательная линия: \ (x = -1 \ text {;} \) нормальная линия: \ (y = 0 \) \ (t = 1 \ text {:} \) Касательная линия: \ (y = x \ text {;} \) нормальная линия: \ (y = -x \)

9.

\ (x = \ sec (t) \ text {,} \) \ (y = \ tan (t) \) на \ ((- \ pi / 2, \ pi / 2) \ text {;} \) \ (т = \ пи / 4 \)

Решение

\ (\ displaystyle \ frac {dy} {dx} = \ csc (t) \)
\ (t = \ pi / 4 \ text {:} \) Касательная линия: \ (y = \ sqrt {2} (x- \ sqrt {2}) + 1 \ text {;} \) нормальная линия: \ (y = -1 / \ sqrt {2} (x- \ sqrt {2}) + 1 \)

10.

\ (x = \ cos (t) \ text {,} \) \ (y = \ sin (2t) \) на \ ([0,2 \ pi] \ text {;} \) \ (t = \ пи / 4 \)

Решение

\ (\ displaystyle \ frac {dy} {dx} = -2 \ cos (2t) \ csc (t) \)
\ (t = \ pi / 4 \ text {:} \) Касательная линия: \ (y = 1 \ text {;} \) нормальная линия: \ (x = \ sqrt {2} / 2 \)

11.

\ (x = \ cos (t) \ sin (2t) \ text {,} \) \ (y = \ sin (t) \ sin (2t) \) на \ ([0,2 \ pi] \ text {;} \) \ (t = 3 \ pi / 4 \)

Решение

\ (\ Displaystyle \ frac {dy} {dx} = \ frac {\ cos (t) \ sin (2t) +2 \ sin (t) \ cos (2t)} {- \ sin (t) \ sin (2t) +2 \ cos (t) \ cos (2t)} \)
Касательная линия: \ (y = x- \ sqrt {2} \ text {;} \) нормальная линия: \ (y = -x \)

12.3-т \)

17.

\ (x = \ sec (t) \ text {,} \) \ (y = \ tan (t) \) на \ ((- \ pi / 2, \ pi / 2) \)

Решение

На графике нет горизонтальной касательной.

18.

Найдите значения \ (t \) в \ ([0,2 \ pi) \), где кривая определяется как \ (x = \ cos (t) \ text {,} \) \ (y = \ sin ( 2t) \) имеет горизонтальную касательную. (Если их несколько, разделяйте их запятыми.)

\ (т \ ин \ большой \ {\) \ (\ большой \} \)

В каких точках на плоскости проходят горизонтальные касательные? (Если их несколько, разделяйте их запятыми. 2 (t)) \ text {.3 (t) \ text {;} \) вогнуть вверх на \ ((- \ pi / 2,0) \ text {;} \) вогнуть вниз на \ ((0, \ pi / 2) \ text {.} \)

30.

Для кривой, определенной как \ (x = \ cos (t) \ text {,} \) \ (y = \ sin (2t) \ text {,} \), найдите \ (\ lzn {2} {y} { x} \) (как функция от \ (t \)). Затем определите интервалы (в пределах \ ([0,2 \ pi) \)), на которых график кривой вогнут вверх / вниз.

\ (\ lzn {2} {y} {x} = \)

Кривая вогнута вверх для \ (t \) в интервале (ах). (Если интервалов несколько, разделяйте их запятыми.{3/2} \ text {,} \) \ (y = 3t \) на \ ([0,1] \)

В следующих упражнениях приблизительно определите заданную длину дуги.

37.

Приблизительно длина дуги одного лепестка кривой розы \ (x = \ cos (t) \ cos (2t) \ text {,} \) \ (y = \ sin (t) \ cos (2t) \), используя Правило Симпсона и \ (n = 4 \ text {.} \)

Решение

\ (L \ приблизительно 2,4416 \) (фактическое значение: \ (L = 2,42211 \))

38.

Приблизительно длина дуги «кривой галстука-бабочки» \ (x = \ cos (t) \ text {,} \) \ (y = \ sin (2t) \), используя правило Симпсона и \ (n = 6 \ text {.2} 2} \ text {.} \) Используйте эту формулу для аппроксимации окружности \ (x = 5 \ cos (t) \ text {,} \) \ (y = 3 \ sin (t) \) и сравните это приближение, данное Правилом Симпсона и \ (n = 6 \ text {.} \)

Решение

Формула: \ (C \ приблизительно 25.9062 \ text {;} \) Правило Симпсона: \ (C \ приблизительно 25.4786 \) (фактическое значение: \ (C = 25.527 \))

В следующих упражнениях описывается твердое тело вращения. Найдите или приблизительно определите его площадь поверхности, как указано.

41.

Найдите площадь поверхности сферы, образованной вращением окружности \ (x = 2 \ cos (t) \ text {,} \) \ (y = 2 \ sin (t) \) примерно:

ось \ (x \) и
ось \ (y \).

Решение

Ответ — \ (16 \ pi \) для обоих (конечно), но интегралы разные.

42.

Найдите площадь поверхности тора (или «бублика»), образованного вращением окружности \ (x = \ cos (t) +2 \ text {,} \) \ (y = \ sin (t) \) относительно \ (y \) — ось.

43.

Приблизительно площадь поверхности твердого тела, образованного вращением «верхней правой половины» кривой галстука-бабочки \ (x = \ cos (t) \ text {,} \) \ (y = \ sin (2t) \) на \ ([0, \ pi / 2] \) вокруг оси \ (x \), используя правило Симпсона и \ (n = 4 \ text {.} \)

Решение

\ (SA \ приблизительно 8,50101 \) (фактическое значение \ (SA = 8.02851 \)

44.

Приблизительно площадь поверхности твердого тела, образованного вращением одного лепестка кривой розы \ (x = \ cos (t) \ cos (2t) \ text {,} \) \ (y = \ sin (t) \ cos (2t) \) на \ ([0, \ pi / 4] \) вокруг оси \ (x \), используя правило Симпсона и \ (n = 4 \ text {.} \)

Решение

\ (SA \ приблизительно 1.36751 \) (фактическое значение \ (SA = 1.36707 \))

Параметрических уравнений и полярных координат

Параметрические уравнения

Параметрические уравнения — это набор уравнений, в которых координаты (например,g., [latex] x [/ latex] и [latex] y [/ latex]) выражаются через один третий параметр.

Цели обучения

Выразите две переменные через третью переменную с помощью параметрических уравнений

Основные выводы

Ключевые моменты

Параметрические уравнения полезны для рисования кривых, так как уравнение можно интегрировать и дифференцировать по членам.
Типичный пример — кинематика, где траектория точки обычно представлена параметрическим уравнением со временем в качестве параметра.
Уравнения можно преобразовать между параметрическими уравнениями и одним уравнением.

Ключевые термины

координата : число, представляющее положение точки на линии, дуге или аналогичной одномерной фигуре

В математике параметрическое уравнение кривой — это представление кривой через уравнения, выражающие координаты точек кривой как функции переменной, называемой параметром. Например,

[латекс] x = \ cos (t) \\ y = \ sin (t) [/ латекс]

— параметрическое уравнение для единичной окружности, где [латекс] t [/ латекс] — параметр.2 [/ латекс].

Этот способ изображения кривых практичен и эффективен; например, такие кривые можно интегрировать и дифференцировать по срокам. Таким образом, можно описать скорость частицы, следующей по такому параметризованному пути, следующим образом:

[латекс] v (t) = (x ‘(t), y’ (t)) [/ латекс]

Это функция производных [latex] x [/ latex] и [latex] y [/ latex] по параметру [latex] t [/ latex].

Преобразование набора параметрических уравнений в одно уравнение включает удаление переменной из одновременных уравнений.Если одно из этих уравнений может быть решено относительно [латекс] t [/ латекс], полученное выражение можно подставить в другое уравнение, чтобы получить уравнение, включающее [латекс] x [/ латекс] и [латекс] y [/ латекс] Только. Если есть рациональные функции, то методы теории уравнений, такие как результирующие, могут быть использованы для исключения [латекс] т [/ латекс]. В некоторых случаях нет единого уравнения в замкнутой форме, эквивалентного параметрическим уравнениям.

Параметрический пример : Один пример эскиза, определяемого параметрическими уравнениями.Обратите внимание, что он нанесен на параметрические оси.

Исчисление с параметрическими кривыми

Исчисление можно также применять к параметрическим уравнениям.

Цели обучения

Используйте дифференциацию для описания вертикальной и горизонтальной скорости изменения [латекс] t [/ латекс]

Основные выводы

Ключевые моменты

Параметрические уравнения — это уравнения, которые зависят от одного параметра.
Типичный пример из физики.Траектория объекта хорошо представлена параметрическими уравнениями.
Запись горизонтального и вертикального смещения через параметр времени делает определение скорости простым делением дифференцирования по параметру time. Параметризация упрощает такой анализ.

Ключевые термины

ускорение : изменение скорости во времени (может включать замедление или изменение направления)
смещение : векторная величина, которая обозначает расстояние с направленным компонентом
траектория : путь тела в пространстве

Параметрические уравнения — это уравнения, которые зависят от одного параметра.Вы можете переписать [latex] y = x [/ latex] так, чтобы [latex] x = t [/ latex] и [latex] y = t [/ latex], где [latex] t [/ latex] — параметр.

Типичный пример встречается в физике, где необходимо проследить траекторию движущегося объекта. Положение объекта определяется как [latex] x [/ latex] и [latex] y [/ latex], что означает горизонтальное и вертикальное смещение соответственно. Со временем объект летит по своему пути, и [latex] x [/ latex] и [latex] y [/ latex] меняются. Следовательно, мы можем сказать, что и [latex] x [/ latex], и [latex] y [/ latex] зависят от параметра [latex] t [/ latex], которым является время.

Траектории : Траектория — полезное место для использования параметрических уравнений, поскольку она связывает горизонтальное и вертикальное расстояние со временем.

Этот способ изображения кривых практичен и эффективен; например, такие кривые можно интегрировать и дифференцировать по срокам. Таким образом, можно описать скорость частицы, следующей параметризованной траектории, как:

[латекс] v (t) = r ‘(t) \\ \, \ quad = (x’ (t), y ‘(t), z’ (t)) \\ \, \ quad = (- a \ sin (t), a \ cos (t), b) [/ латекс]

где [латекс] v [/ латекс] — скорость, [латекс] r [/ латекс] — расстояние, а [латекс] x [/ латекс], [латекс] y [/ латекс] и [латекс] z [/ latex] — координаты.Апостроф представляет собой производную по параметру.

Ускорение можно записать следующим образом с двойным апострофом, обозначающим вторую производную:

[латекс] a (t) = r » (t) \\ \, \ quad = (x » (t), y » (t), z » (t)) \\ \, \ quad = (- a \ cos (t), — a \ sin (t), b) [/ latex]

Запись этих уравнений в параметрической форме дает общий параметр, от которого зависят оба уравнения. Это упрощает интеграцию и дифференциацию, поскольку они полагаются на одну и ту же переменную.Запись [latex] x [/ latex] и [latex] y [/ latex] явно в терминах [latex] t [/ latex] позволяет дифференцировать и интегрировать по отношению к [latex] t [/ latex]. Горизонтальная скорость — это скорость изменения значения [latex] x [/ latex] во времени, а вертикальная скорость — это скорость изменения значения [latex] y [/ latex] во времени. Запись в параметрической форме упрощает это.

Полярные координаты

Полярные координаты определяют положение объекта на плоскости с помощью расстояния и угла от опорной точки и оси.

Цели обучения

Используйте полярные координаты для определения точки с помощью [latex] r [/ latex] (расстояние от полюса) и [latex] \ theta [/ latex] (угол между осью и лучом)

Основные выводы

Ключевые моменты

Полярные координаты используют расстояние от центральной точки, называемое радиальным расстоянием, обычно указываемое как [латекс] r [/ латекс].
Полярные координаты используют измерение угла от полярной оси, которая обычно располагается горизонтально и указывает вправо.Против часовой стрелки обычно положительный.
Чтобы преобразовать полярные координаты в декартовы координаты, нарисуйте треугольник от горизонтальной оси к точке. Координата [latex] r [/ latex] — это [latex] r \ cos \ theta [/ latex], а координата y — [latex] r \ sin \ theta [/ latex].

Ключевые термины

полярный : системы координат, определяющей положение точки на плоскости с помощью радиуса и угла

Мы используем системы координат каждый день, даже если не осознаем этого.Например, если вы пройдете 20 метров вправо от парковки, чтобы найти машину, вы используете систему координат. Системы координат — это способ определения местоположения интересующей точки или объекта по отношению к чему-то еще. Система координат, с которой вы, скорее всего, знакомы, — это система координат [latex] xy [/ latex], где местоположения описываются как горизонтальные ([latex] x [/ latex]) и вертикальные ([latex] y [/ latex] ) расстояния от произвольной точки. Это называется декартовой системой координат.

[latex] xy [/ latex] или декартова система координат не всегда является самой простой системой для решения каждой задачи. В некоторых задачах, например, связанных с кругами, легче определить местоположение точки с помощью расстояния и угла. Такие определения называются полярными координатами.

В полярных координатах каждая точка на плоскости определяется расстоянием от фиксированной точки и углом от фиксированного направления.

Расстояние называется радиальным расстоянием и обычно обозначается как [латекс] r [/ латекс].

Угол известен как полярный угол или радиальный угол и обычно обозначается как [латекс] \ тета [/ латекс].

Положительный угол обычно измеряется против часовой стрелки от полярной оси, а положительный радиус — в том же направлении, что и угол. Отрицательный радиус будет противоположным направлению угла, а отрицательный угол будет измеряться по часовой стрелке от полярной оси. Полярная ось обычно проводится горизонтально и направлена вправо.

Полярные координаты : Набор полярных координат.Обратите внимание, что полярный угол увеличивается, когда вы идете по кругу против часовой стрелки, при этом 0 градусов указывает горизонтально вправо.

Связь между декартовыми и полярными координатами : Декартова координата [latex] x [/ latex] задается как [latex] r \ cos \ theta [/ latex], а декартова координата [latex] y [/ latex] задается автор: [latex] r \ sin \ theta [/ latex].

Полярные координаты в [latex] r [/ latex] и [latex] \ theta [/ latex] могут быть преобразованы в декартовы координаты [latex] x [/ latex] и [latex] y [/ latex].Это можно сделать, отметив, что радиальное расстояние [латекс] r [/ латекс] и полярный угол [латекс] \ тета [/ латекс] могут определять треугольник с горизонтальной длиной [латекс] x [/ латекс] и вертикальной длиной. [латекс] и [/ латекс]. Таким образом, используя тригонометрию, можно показать, что координата [latex] x [/ latex] равна [latex] r \ cos \ theta [/ latex], а координата [latex] y [/ latex] — [latex] r \ грех \ тета [/ латекс].

Площадь и длина дуги в полярных координатах

Площадь и длина дуги вычисляются в полярных координатах путем интегрирования.

Цели обучения

Оценить площадь сегмента дуги и длину дуги с использованием полярных координат и интегрирования

Основные выводы

Ключевые моменты

Длина дуги — это линейная длина кривой, если она была выпрямлена.
Площадь — это размер области, определяемой радиусом кривой, а также углом и длиной соединительных линий, охватывающих эту область.
Чтобы вычислить эти размеры, используйте интегрирование по углу.

Ключевые термины

полярный : системы координат, определяющей положение точки на плоскости с помощью радиуса и угла

Длина дуги

Если бы вы выпрямили изогнутую линию, измеренная длина была бы длиной дуги. Поскольку линейное измерение длины дуги может быть очень трудным, решение состоит в использовании полярных координат. 2} d \ theta} [/ latex]

Решение этого интеграла даст длину дуги.

Длина дуги : Изогнутые линии, ограничивающие область [латекс] R [/ латекс], являются дугами. Их длину можно рассчитать с помощью исчисления. Площадь области [латекс] R [/ латекс] также может быть вычислена интегрированием.

Площадь сегмента дуги

Чтобы найти площадь, ограниченную дугами, радиусом и полярными углами, вы снова используете интегрирование.

Пусть [латекс] R [/ латекс] обозначает область, ограниченную кривой [латекс] r (\ theta) [/ latex] и лучи [латекс] \ theta = a [/ latex] и [латекс] \ theta = b [/ latex], где [latex] 0

Этот результат можно найти следующим образом.

Сначала интервал [latex] [a, b] [/ latex] делится на подинтервалы [latex] n [/ latex], где [latex] n [/ latex] — произвольное положительное целое число. Таким образом, [latex] \ Delta \ theta [/ latex], длина каждого подинтервала, равна [latex] ba [/ latex] (общая длина интервала), деленному на [latex] n [/ latex], количество подынтервалов. Для каждого подынтервала [latex] i = 1, 2, \ cdots, n [/ latex] пусть [latex] \ theta_i [/ latex] будет серединой подынтервала, и постройте сектор с центром на полюсе, радиус [латекс] r (\ theta_i) [/ latex], центральный угол [латекс] \ Delta \ theta [/ latex] и длина дуги [латекс] r (\ theta_i) \ Delta \ theta [/ latex].2 \ Delta \ theta} [/ latex]

И общая площадь складывается из этих секторов. Бесконечная сумма этих секторов — это то же самое, что и интегрирование.

Конические секции

Конические сечения определяются пересечением конусов с плоскостями.

Цели обучения

Обозначить конические сечения как кривые, полученные от пересечения конуса с плоскостью

Основные выводы

Ключевые моменты

Конические сечения — это кривые, полученные от пересечения конуса с плоскостью.
Графики квадратных уравнений от двух переменных представляют собой конические сечения.
Конические сечения важны в астрономии: орбиты двух массивных объектов, которые взаимодействуют в соответствии с законом всемирного тяготения Ньютона, являются коническими сечениями, если их общий центр масс считается покоящимся.

Ключевые термины

конус : поверхность вращения, образованная вращением сегмента линии вокруг другой линии, пересекающей первую линию

В математике коническое сечение (или просто «коническое») — это кривая, полученная из пересечения конуса (точнее, правильной круговой конической поверхности) с плоскостью.В аналитической геометрии конику можно определить как плоскую алгебраическую кривую степени 2. Возможен ряд других геометрических определений, одно из наиболее полезных состоит в том, что коника состоит из тех точек, расстояние от которых до некоторой другой точки (называемой фокус) и некоторые другие линии (называемые директрисой) находятся в фиксированном соотношении, называемом эксцентриситетом.

Традиционно тремя типами конического сечения являются гипербола, парабола и эллипс. Круг является частным случаем эллипса и сам по себе представляет такой интерес, что его иногда называют четвертым типом конического сечения.Тип конуса соответствует его эксцентриситету: те, у которых эксцентриситет меньше 1, являются эллипсами, те, у которых эксцентриситет равен 1, являются параболами, а те, у которых эксцентриситет больше 1, являются гиперболами. В определении коники фокус-директрисой круг является предельным случаем с эксцентриситетом 0. В современной геометрии некоторые вырожденные случаи, такие как объединение двух прямых, также включаются как коники.

В декартовой системе координат график квадратного уравнения с двумя переменными всегда является коническим сечением, хотя он может быть вырожденным, и все конические сечения возникают таким образом.

Конические сечения важны в астрономии: орбиты двух массивных объектов, которые взаимодействуют согласно закону всемирного тяготения Ньютона, являются коническими сечениями, если их общий центр масс считается покоящимся. Если они связаны вместе, они оба начертят эллипсы; если они расходятся, они оба будут следовать параболам или гиперболам. В проективной геометрии конические сечения на проективной плоскости эквивалентны друг другу с точностью до проективных преобразований.

Типы конических сечений : Существует три типа конических сечений: 1.Парабола; 2. Эллипс; 3. Гипербола.

Длина дуги и скорость

Длина и скорость дуги в параметрических уравнениях могут быть рассчитаны с помощью интегрирования и теоремы Пифагора.

Цели обучения

Вычислить длину дуги путем интегрирования скорости движущегося объекта по времени

Основные выводы

Ключевые моменты

Длина дуги — это длина кривой.Чтобы вычислить его в параметрических уравнениях, воспользуйтесь теоремой Пифагора.
Длину дуги можно рассчитать, сложив серию бесконечно малых длин вдоль дуги. Для этого установите интеграл по параметру.
Скорость — это скорость изменения длины дуги во времени. Производные [latex] x [/ latex] и [latex] y [/ latex] по времени включены в теорему Пифагора, чтобы определить скорость объекта, движущегося по дуге.

Ключевые термины

Теорема Пифагора : Теорема, утверждающая, что гипотенуза прямоугольного треугольника равна квадратному корню из суммы квадратов двух других сторон
кривая : простая фигура без прямых участков и углов

Иногда бывает трудно измерить длину кривой.Кривую можно представить себе как бесконечное количество бесконечно малых отрезков прямой, каждый из которых указывает немного в другом направлении, составляя кривую. Сложить все эти длины вместе было бы равносильно вытягиванию кривой прямо и измерению ее длины. Длина кривой называется длиной дуги.

Чтобы вычислить длину дуги, мы используем интегрирование, потому что это эффективный способ сложить серии бесконечно малых длин.

Длину дуги можно использовать для определения расстояния, пройденного объектом, имеющим путь дуги.Рассмотрим случай, когда объект движется по траектории в декартовой плоскости ([latex] xy [/ latex] -плоскость). Его положение по горизонтали определяется как [latex] x = f (t) [/ latex], а его положение по вертикали определяется как [latex] y = g (t) [/ latex], где [latex] f [/ latex] и [latex] g [/ latex] — это функции, которые зависят от параметра, [latex] t [/ latex]. Поскольку есть две функции для положения, и обе они зависят от одного параметра — времени, — мы называем эти уравнения параметрическими уравнениями . 2} dt} [/ latex]

Это уравнение получено с помощью теоремы Пифагора.2} [/ латекс]. Складывая каждую крошечную гипотенузу, получаем длину дуги.

Приблизительная длина дуги с гипотенузами : Длину кривой можно аппроксимировать с помощью серии прямоугольных треугольников с гипотенузами, лежащими вдоль кривой. Чем меньше треугольники, тем точнее будет приближение.

Однако, поскольку [latex] x [/ latex] и [latex] y [/ latex] зависят от параметра [latex] t [/ latex], мы захотим интегрировать по [latex] t [/ latex], а не поверх [латекса] х [/ латекса] и [латекса] у [/ латекса].2}} [/ latex]

, где скорость изменения длины гипотенузы зависит от скорости изменения [латекса] x [/ латекса] и [латекса] y [/ латекса]. Интегрирование скорости по времени дает расстояние, как показано выше.

Конические сечения в полярных координатах

Конические сечения — это сечения конусов, которые могут быть представлены в полярных координатах.

Цели обучения

Определить типы конических сечений по полярным координатам

Основные выводы

Ключевые моменты

Конические сечения — это точки пересечения конусов с плоскостью.
Три типа конических сечений: гипербола, парабола и эллипс.
Полярные координаты предлагают нам удобный способ представления конических сечений.

Ключевые термины

конус : поверхность вращения, образованная вращением сегмента линии вокруг другой линии, пересекающей первую линию
гипербола : коническое сечение, образованное пересечением конуса с плоскостью, которая пересекает основание конуса и не касается конуса

В математике коническое сечение (или просто коническое) — это кривая, полученная как пересечение конуса (точнее, правильной круговой конической поверхности) с плоскостью.Возможен ряд других геометрических определений. Одно из наиболее полезных определений, поскольку оно включает только плоскость, состоит в том, что коника состоит из тех точек, расстояние которых до некоторой точки, называемой фокусом, и некоторой линии, называемой директрисой, находится в фиксированном соотношении, называемом эксцентриситетом. .

Традиционно тремя типами конического сечения являются гипербола, парабола и эллипс. Круг является частным случаем эллипса и сам по себе настолько интересен, что его иногда называют четвертым типом конического сечения.Тип конуса соответствует его эксцентриситету: те, у которых эксцентриситет меньше 1, являются эллипсами, те, у которых эксцентриситет равен 1, являются параболами, а те, у которых эксцентриситет больше 1, являются гиперболами. В определении коники фокус-директрисой круг является предельным случаем с эксцентриситетом 0. В современной геометрии некоторые вырожденные случаи, такие как объединение двух прямых, также включаются как коники.

В полярных координатах коническое сечение с одним фокусом в начале координат определяется следующим уравнением:

[латекс] \ displaystyle {r = \ frac {l} {1 + ecos (\ theta)}} [/ латекс]

, где е — эксцентриситет, а l — половина прямой кишки.Как на рисунке, для [latex] e = 0 [/ latex] у нас есть круг, для [latex] 0 1 [/ латекс] гипербола. b {f \ left (x \ right) dx} = F \ left (b \ right) — F \ left (a \ right), \]

, где \ (F \ left (x \ right) \) — любая первообразная от \ (f \ left (x \ right).b {\ left [{f \ left (x \ right) — g \ left (x \ right)} \ right] dx}} = {F \ left (b \ right) — G \ left (b \ right) — F \ left (a \ right) + G \ left (a \ right),} \]

, где \ (F \ left (x \ right) \) и \ (G \ left (x \ right) \) — первообразные функций \ (f \ left (x \ right) \) и \ (g \ left (x \ right), \) соответственно.

Обратите внимание, что эта область всегда будет неотрицательной как \ (f \ left (x \ right) — g \ left (x \ right) \ ge 0 \) для всех \ (x \ in \ left [{a, b } \ right]. \)

Если есть точки пересечения, мы должны разбить интервал на несколько подинтервалов и определить, какая кривая больше на каждом подынтервале.\ prime \ left (t \ right), \) \ (y \ left (t \ right) \) здесь предполагается непрерывными на интервале \ (\ left [{a, b} \ right]. \) Кроме того то есть функция \ (x \ left (t \ right), \) должна быть монотонной на этом интервале. \ prime \ left (t \ right) y \ left (t \ right)} \ right] dt}.2} \) на интервале \ (\ left [{1, b} \ right] \) равно \ (1? \)

Пример 3

Найдите координату точки \ (a \), которая разделяет область под корневой функцией \ (y = \ sqrt {x} \) на интервале \ (\ left [{0,4} \ right] \) на равные части.

Пример 4

Область ограничена вертикальными линиями \ (x = t \), \ (x = t + \ large {\ frac {\ pi} {2}} \ normalsize \), осью \ (x — \) и кривая \ (y = a + \ cos x, \), где \ (a \ ge 1. \). Определите значение \ (t \), при котором область имеет наибольшую площадь.{t + \ frac {\ pi} {2}}} = {a \ left ({t + \ frac {\ pi} {2}} \ right) + \ sin \ left ({t + \ frac {\ pi } {2}} \ right)} — {at — \ sin t} = {\ cancel {at} + \ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi} {2}} \ right)} — {\ cancel {at} — \ sin t} = {\ frac {{a \ pi}} {2} + \ sin \ left ({t + \ frac {\ pi } {2}} \ right) — \ sin t.} \]

Использование тождества разницы синусов

\ [{\ sin \ alpha — \ sin \ beta} = {2 \ cos \ frac {{\ alpha + \ beta}} {2} \ sin \ frac {{\ alpha — \ beta}} {2}, } \]

получаем

\ [{A = \ frac {{a \ pi}} {2}} + {2 \ cos \ frac {{t + \ frac {\ pi} {2} + t}} {2} \ sin \ frac {{\ cancel {t} + \ frac {\ pi} {2} — \ cancel {t}}} {2}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ( {t + \ frac {\ pi} {4}} \ right) \ sin \ frac {\ pi} {4}} = {\ frac {{a \ pi}} {2} + 2 \ cos \ left ({ t + \ frac {\ pi} {4}} \ right) \ cdot \ frac {{\ sqrt 2}} {2}} = {\ frac {{a \ pi}} {2} + \ sqrt 2 \ cos \ left ({t + \ frac {\ pi} {4}} \ right).} \]

Область имеет наибольшую площадь, когда \ (\ cos \ left ({t + \ large {\ frac {\ pi} {4}} \ normalsize} \ right) = -1. \)

Решая это уравнение, находим

\ [{\ cos \ left ({t + \ frac {\ pi} {4}} \ right) = — 1,} \; \; \ Rightarrow {t + \ frac {\ pi} {4} = \ pi + 2 \ pi n,} \; \; \ Rightarrow {t = \ frac {{3 \ pi}} {4} + 2 \ pi n, \, n \ in \ mathbb {Z}.} \]

Пример 5.

Найдите площадь области, заключенной между кривой \ (y = \ sqrt {x + 1} \) и прямой \ (y = x + 1. \)

Решение.0} = {\ left ({\ frac {2} {3} — 0 — 0} \ right) — \ left ({0 — \ frac {1} {2} + 1} \ right)} = {\ frac {2} {3} — \ frac {1} {2}} = {\ frac {1} {6}.} \]

Пример 6.

Найдите площадь области, заключенной между корневой кривой \ (y = \ sqrt {x} \) и прямой \ (y = kx, \), где \ (k \ gt 0. \)

Решение.

Сначала находим точки пересечения обеих кривых:

\ [{\ sqrt x = kx,} \; \; \ Rightarrow {\ sqrt x — kx = 0,} \; \; \ Rightarrow {\ sqrt x \ left ({1 — k \ sqrt x} \ right) = 0,} \; \; \ Rightarrow {{x_1} = 0, \;} \ kern0pt {{x_2} = \ frac {1} {{{k ^ 2}}}.

2.9.2. Площадь фигуры, ограниченной кривой, заданной параметрически

Вспомогательная таблица для построения параметрически заданной кривой

2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах

Вспомогательная таблица для построения кривой, заданной в полярных координатах

Страница не найдена — ПриМат

Математический анализ — 2 — тест 13

Вычисление площади фигуры с помощью определенного интеграла Геометрический смысл определенного интеграла

Задача 1

Задача 2

Задача 3

Построение графика функции, заданной параметрически

Введите график функции

Видео пример:

Площадь плоской фигуры — Студопедия

10.2: Исчисление с параметрическими кривыми

Производные параметрических уравнений

Интегралы, содержащие параметрические уравнения

Длина дуги параметрической кривой

7.2 Расчет параметрических кривых — том 2

Цели обучения

Производные параметрических уравнений

Производная параметрических уравнений

Проба

Пример 7.4

Нахождение производной параметрической кривой

Решение

КПП 7,4

Пример 7.5

Поиск касательной

Решение

КПП 7.5

Деривативы второго порядка

Пример 7.6

Поиск второй производной

Решение

Интегралы, включающие параметрические уравнения

Площадь под параметрической кривой

Пример 7.7

Определение площади под параметрической кривой

Решение

Длина дуги параметрической кривой

Длина дуги параметрической кривой

Пример 7.8

Определение длины дуги параметрической кривой

Решение

Площадь поверхности, созданная параметрической кривой

Пример 7.9

Поиск площади поверхности

Решение

Раздел 7.2. Упражнения

Исчисление и параметрические уравнения

Раздел 10.3 Исчисление и параметрические уравнения

Определение 10.3.3. Касательная и нормальная линии.

Пример 10.3.6. Касательная и нормальная прямые к окружности.

Подраздел 10. 2} \, dt \ text {.} \ end {уравнение *}

Пример 10.3.18. Длина дуги окружности.

Подраздел 10.3.3 Площадь поверхности твердого тела вращения

Упражнения 10.3.4 Упражнения

1.

2.

3.

4.

6.

7.2} {2 т} \)

9.

10.

11.

12.3-т \)

17.

18.

30.

37.

38.

41.

42.

43.

44.

Параметрических уравнений и полярных координат

Параметрические уравнения

Цели обучения

Подраздел 10. 2} \, dt \ text {.}
\ end {уравнение *}