для нахождения площади треугольника, как пользоваться

Формула Герона

Формула Герона носит такое название в честь греческого математика и инженера Герона Александрийского. Он жил в I веке нашей эры. Герон занимался механикой, оптикой, геометрией и гидростатикой. Учёный интересовался треугольниками с целочисленными сторонами и целочисленными площадями. Такие фигуры получили название Героновых треугольников.

Формулировка теоремы Герона

Формула Герона – это арифметическая формула для вычисления площади треугольника по длинам его сторон. В таком случае площадь равна корню из произведения разностей полупериметра и каждой из его сторон.

Формула и доказательство

Формула Герона выглядит следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). 2}\)

А так как \(S=\frac12ch\), то теорема доказана.

Для каких треугольников действует теорема

Применение формулы Герона допустимо для треугольников, у которых известны длины всех их сторон.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

\(p=\frac{6+8+6}2=10\)

Тогда площадь треугольника равна:

\(S=10\sqrt{\left(10-6\right)\left(10-8\right)\left(10-6\right)}=320\)

Ответ: 320 см².

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD  пересекаются в точке O.

Если  AD = 51,  AC = 40  и  BD = 74,  то  AO = 20,  OD = 37.

По формуле Герона:

\(S_{ABCD} = 4S_{AOD} = \sqrt{54\left(54-51\right)\left(54-37\right)\left(54-20\right)}=1224\)

Ответ: 1224 см². 2}=\sqrt{2\times50}=10\)

Следовательно,  \(PQ = AQ – AP = 13 – 10 = 3\)

\(S_{BPQ} = ½ PQ·BP = \frac{3\times24}2=36\)

Ответ: 36 см².

Урок 14. формула герона — Геометрия — 8 класс

Выведем формулу, которая связывает площадь треугольника и длины его сторон. Рассмотрим треугольник ABC в котором известны его стороны. Обозначим их a, b, c.

Для доказательства воспользуемся формулой для вычисления площади треугольника. Проведем высоту BH к стороне AC треугольника ABC и обозначим ее h. Точка h разделила сторону АС на два отрезка, обозначим их х и у.

Треугольник АBН – прямоугольный. По теореме Пифагора получим: h² = c² − x².
Треугольник CBH тоже прямоугольный. По теореме Пифагора получим: h² = a² − y²
Приравняем правые части полученных равенств.
c² − x² = a² − y² или y² − x² = a² − c²
Воспользуемся формулой разности квадратов, получим:
(y − x)(y + x) = a² − c²
Из условия известно, что отрезки х и у в сумме составляют отрезок b, поэтому верны равенства:
y + x = b и y − x = (a² − c²) : b (2)
Преобразуем:
2y = b + (a² − c²) : b
2y = b + (a² — c²)/b = (b² + a² — c²)/b или y = (b² + a² — c²)/2b
Вернемся к треугольнику СВН, подставим в формулу для нахождения высоты треугольника АВС выражение для отрезка у, получим:
h² = a² − y² = (a − y)(a + y) = (a − (b² + a² — c²)/2b)(a + (b² + a² — c²)/2b)
h² = ((2ab — b² — a² + c²)/2b)((2ab + b² + a² — c²)/2b)
Проведем преобразования, получим:
h² = (((a + b + c) — 2a)((a + b + c) — 2b)((a + b + c) — 2c)(a + b + c))/4b²
a + b + c = 2p, поэтому
h² = ((2p — 2a)(2p — 2b)(2p — 2c)2p)/4b² = (16(p — a)(p — b)(p — c)p)/4b²
S_∆ = 1/2AC ∙ h = 1/b ∙ √(16(p — a)(p — b)(p — c)p)/4b² = √(p(p — a)(p — b)(p — c))
S_ABC = √p(p — a)(p — b)(p — c), где p = (a + b + c)/2
Эта формула названа в честь древнегреческого ученого Герона.
Формулой Герона удобно пользоваться не только при вычислении площади треугольника, в котором известны три стороны, но и при вычислении площади параллелограмма, в котором известны стороны и одна из диагоналей.
В параллелограмме стороны равны 10 и 20, а одна из диагоналей равна 24. Найдите площадь параллелограмма.
Решение:
Диагональ разбивает параллелограмм на два равных треугольника. Вычислив площадь одного из них, найдем площадь всего параллелограмма
P = (10 + 20 + 24)/2 = 27
S_∆ = √(27∙(27 — 10)∙(27 — 20)(27 — 24) ) = 9√119
S_{параллелограмма} = 18√119

Формула Герона — геометрия и искусство

Герон Александрийский — греческий математик и механик.

Он первым изобрёл автоматические двери, автоматический театр кукол, автомат для продаж, скорострельный самозаряжающийся арбалет, паровую турбину, автоматические декорации, прибор для измерения протяжённости дорог (древний одометр) и др. Первым начал создавать программируемые устройства (вал со штырьками с намотанной на него верёвкой).

Занимался геометрией, механикой, гидростатикой, оптикой. Основные произведения: Метрика, Пневматика, Автоматопоэтика, Механика (произведение сохранилось целиком в арабском переводе), Катоптрика (наука о зеркалах; сохранилась только в латинском переводе) и др. В 1814 году было найдено сочинение Герона «О диоптре», в котором изложены правила земельной съёмки, фактически основанные на использовании прямоугольных координат. Герон использовал достижения своих предшественников: Евклида, Архимеда, Стратона из Лампсака. Многие из его книг безвозвратно утеряны (свитки содержались в Александрийской библиотеке).

В трактате «Механика»  Герон описал пять типов простейших машин: рычаг, ворот, клин, винт и блок.

В трактате «Пневматика» Герон описал различные сифоны, хитроумно устроенные сосуды, автоматы, приводимые в движение сжатым воздухом или паром. Это эолипил, представлявший собой первую паровую турбину — шар, вращаемый силой струй водяного пара; автомат для открывания дверей, автомат для продажи «святой» воды, пожарный насос, водяной орган, механический театр марионеток.

В книге «О диоптре» описан диоптр — простейший прибор, применявшийся для геодезических работ. Герон излагает в своём трактате правила земельной съёмки, основанные на использовании прямоугольных координат.

В «Катоптрике» Герон обосновывает прямолинейность световых лучей бесконечно большой скоростью их распространения.  Герон рассматривает различные типы зеркал, особое внимание уделяя цилиндрическим зеркалам.

«Метрика» Герона и извлечённые из неё «Геометрика» и «Стереометрика» представляют собой справочники по прикладной математике. Среди содержащихся в «Метрике» сведений:

• Формулы для площадей правильных многоугольников.

• Объёмы правильных многогранников, пирамиды, конуса, усечённого конуса, тора, шарового сегмента.

• Формула Герона для расчёта площади треугольника по длинам его сторон (открытая Архимедом).

• Правила численного решения квадратных уравнений.

• Алгоритмы извлечения квадратных и кубических корней.

Книга Герона «Определения» представляет собой обширный свод геометрических определений, по большей части совпадающих с определениями «Начал» Евклида.

площадь треугольника по формуле Герона

Следующий калькулятор делает расчет площади треугольника по известной формуле Герона.

Если кому то интересно больше узнать о формуле Герона, то вы без проблем можете это сделать на странице:

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 . . %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1.
Value: ‘%2’.
Error:
%3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v. d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

Формула Герона — ГЕОМЕТРИЯ — Уроки для 9 классов — конспекты уроков — План урока — Конспект урока — Планы уроков

УРОК № 13

Тема. Формула Герона

Цель урока: вывод формулы Герона для площади треугольника. Формирование умений учащихся применять выведенную формулу к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Площади треугольников и четырехугольников» [13].

Требования к уровню подготовки учащихся: используют формулу Герона во время решения задач.

Ход урока

И. Проверка домашнего задания

Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учащихся при их выполнении.

Задача 1. Решение

Поскольку квадрат и ромб имеют одинаковые периметры, то их стороны равны. Пусть длина стороны равна а, тогда площадь квадрата равна а2, а площадь ромба a2sinα, где α — угол ромба.

Поскольку sinα 1, то a2sinα а2. Следовательно, площадь ромба меньше площадь квадрата.

Ответ. Квадрат.

Задача 2. Решение

Поскольку в треугольнике ABC (рис. 45) АВ = а, CAB = 45°, то АС = АВ ∙ cos CAB = a ∙ cos45° = a ∙ = .

SΔAВC = AC2 == .

Ответ. .

Задача 3. Решение

Пусть в треугольнике ABC (рис. 46) АС = ВС = 1 м, С = 70°, тогда S = ∙ AC ∙ BC ∙ sinC = ∙ 1 ∙ 1 ∙ sin70° = ∙ sin70° ∙ 0,94 = 0,47 (м2).

Ответ. 0,47 м2.

Математический диктант

1. 1) Найдите площадь прямоугольника со сторонами 2 см и 3 см.
2. 2) Найдите площадь прямоугольного треугольника с катетами 3 см и 2 см.
3. 3) Найдите площадь правильного треугольника со стороной 2 см.
4. 4) Найдите площадь параллелограмма со сторонами 2 см и см, если угол между сторонами составляет 60°.
5. 5) Найдите площадь ромба, диагонали которого равны 3 см и 4 см.
6. 6) Найдите площадь треугольника, стороны которого равны см и 3 см, а угол между ними составляет 135°.

Ответы. 1) 6 см2; 2) 3 см2; 3) см2; 4) 3 см2; 5) 6 см2; 6) 1,5 см2.

II. Восприятие и осознание нового материала

Вы научились находить площадь произвольного треугольника с известными:

1. 1) стороной и высотой, проведенной к этой стороне;
2. 2) сторонами и углом между ними.

Сегодня мы ознакомимся с тем, как можно найти площадь треугольника, если известны три его стороны. Эту формулу получил Герон Александрийский древнегреческий ученый, живший в Александрии в i в. н. есть. Известно, что он был ученым-инженером, занимался геодезией и прикладной математикой.

Проведем высоту к наибольшей стороны треугольника ABC (рис. 47). Пусть АС = b — наибольшая сторона этого треугольника, АВ = с, ВС = а, BDAC. Пусть AD = х, тогда DC = b — х. Из прямоугольного треугольника ABD имеем: BD2 = c2 — x2. Из прямоугольного треугольника BCD имеем: BD2 = а2 — (b — x)2. Тогда имеем уравнение с2 — х2 = a2 — (b — х)2, из которого найдем х.

с2 — х2 = а2 — b2 + 2bx — x2; 2bx = c2 + b2 — a2; .

Тогда BD = = = .

Следовательно, S = b ∙ ВD = = = = =

= = = .

Учитывая, что , имеем:

S = =.

Что и требовалось доказать.

Коллективное решение задач

Найдите площадь треугольника по трем сторонам:

а) 17, 65, 80; б) , , 6; в) 15, 37, 47; г) 2, 3, 1,83.

Решение

а) S = = = = 288.

б) .

S = = = 10.

в) .

S = = = 42= = = 193.

г) .

S=== = = = 1,4.

III. Закрепление и осмысление нового материала

Коллективное решение задач

Стороны треугольника равны а, b, с. Найдите высоту треугольника, опущенную на сторону с.

Решение

, .

Поскольку S = chc, то hc = = .

Ответ. .

Самостоятельное решение задач

Боковые стороны треугольника равны 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равна: а) 25 см; б) 11 см.

Решение

а) ,

 (см2).

S = ∙ 25 ∙ h, 300 = ∙ 25 h, h = = 24 (см).

Ответ. 24 см.

б) ,

(см2).

S = ∙ 11 ∙ h, 132 = ∙ 11 ∙ h, h = = 24 (см).

Ответ. 24 см.

Коллективное решение задачи

Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания. Найдите высоту треугольника, опущенную на боковую сторону.

Решение

Пусть треугольник ABC (рис. 48) равнобедренный, АВ = ВС. Пусть АС = х см, тогда АВ = ВС = (х + 11) см. Поскольку периметр равен 64 см, то имеем:

x + 11 + x + 11 + x = 64; 3х + 22 = 64; 3х = 42; х = 14. Следовательно, АС = 14 см, АВ = ВС = 25 см.

Поскольку == 7 ∙ 4 ∙ 6 = 168 (см2), S = ∙ АВ ∙ h, то h = = = 13,44 (см).

Ответ. 13,44 см.

IV. Самостоятельная работа

Вариант 1

1. 1. Найдите наименьшую высоту треугольника со сторонами 5, 5, 6.
2. 2. Найдите наибольшую высоту треугольника со сторонами , , 6.

Вариант 2

1. 1. Найдите наименьшую высоту треугольника со сторонами 17, 65, 80.
2. 2. Найдите наибольшую высоту треугольника со сторонами 13, 37, 47-.

Решение задач самостоятельной работы

Вариант 1

1. = 8, = 12(см2).

S = ∙ 6 h, h = — = = = 4 (см).

Ответ. 4 см.

2. S = 10 см 2. S = ∙ ∙ h, h = = = = 4,8 (см).

Ответ. 4,8 см.

Вариант 2

1. = 81, = 288(см2).

S = ∙ 80 ∙ h, h = = = 7,2 (см).

Ответ. 7,2 см.

2. S = 2 см. S = ∙ 13 ∙ h, h = = = = 29 (см).

Ответ. 29 см.

V. Домашнее задание

Решить задачи.

1. 1. Найдите площадь треугольника по трем сторонам, равны:

а) 13, 14, 15; б) 5, 5, 6.

1. 2. Найдите высоты треугольника, у которого стороны равны 13 см, 14 см, 15 см.
2. 3. Найдите высоту треугольника со сторонами 2, 3, 1,83, проведенная на основание 2.

VI. Подведение итогов урока Задача класса

1. 1. Запишите известные вам формулы для нахождения площади треугольника.
2. 2. Найдите площадь треугольника, если его стороны равны 3 см, 3 см и 2 см.

✅ Формула герона объяснение. — sundaria.su

Формула герона объяснение.

Эта формула позволяет вычислить площадь S треугольника по его сторонам a, b и с:

где р — полупериметр треугольника, т.е. р = (а + b + c)/2. Формула названа в честь древнегреческого математика Герона Александрийского (около I в.). Герон рассматривал треугольники с целочисленными сторонами, площади которых также являются целыми числами. Такие треугольники называют героновыми. Например, это треугольники со сторонами 13, 14, 15 или 51, 52, 53.

Вывод формулы Герона для площади треугольника

Одним из способов позволяющим вывести формулу Герона является использование свойств вписанной в треугольник окружности. Это свойство позволяет вычислить радиус вписанной в треугольник окружности через длины сторон треугольника и полупериметр треугольника.

Предположим у нас есть произвольный треугольник с вершинами А,В и С сторонами длины которых равны а, b и с.

Впишем в этот треугольник окружность.

Из центра этой окружности опустим перпендикуляры к каждой из сторон треугольника и обозначим длину каждого из перпендикуляров буквой r.

Теперь из каждой вершины треугольника проведем к центру окружности три отрезка.

В результате мы видим, что наш треугольник АВС состоит из трех малых треугольников: АОС, АОВ, ВОС

Следовательно, площадь треугольника АВС мы можем вычислить суммированием площадей малых треугольников, т.е.

Далее, площадь треугольника можно найти, также используя формулу S = а*h/2 (2), где а – длина основания треугольника; h – высота треугольника (в нашем случае она равно r).

Теперь запишем формулу (1) выразив площади малых треугольников через формулу (2), т.е.

Давайте упрости формулу (3) вынеся высоту треугольника r и знаменатель каждого из слагаемых за скобки. В итоге мы получим следующую формулу

Часть выражения справа, а именно (а + b + c)/2 есть не что иное, как периметр треугольника, деленный пополам или говоря просто полупериметр треугольника. Обозначим полупериметр треугольника малой буквой р.

В результате формулу (4) мы можем записать в виде

Как уже говорилось выше, радиус вписанной в треугольник окружности можно выразить через длины сторон треугольника и его полупериметр. Формула для радиуса вписанной в треугольник окружности будет выглядеть следующим образом:

Теперь давайте запишем формулу (5) выразив радиус через длины сторон треугольника и его полупериметр,

И после того как перед коренное значение мы заведем под корень, мы получим окончательную формулу

Как мы видим формула (8) есть не что иное, как хорошо известная с античных времен формула Герона.

Формула Герона для площади четырехугольников

Существуют аналоги формулы Герона для четырехугольников. В связи с тем что задача на построение четырехугольника по его сторонам а, b, с и d имеет не единственное решение, для вычисления в общем случае площади четырехугольника недостаточно только знания длин сторон. Приходится вводить дополнительные параметры или накладывать ограничения. Например, площадь вписанного четырехугольника находится по формуле:

Если же четырехугольник и вписанный, и описанный одновременно, его площадь находится по более простой формуле:



Формула Герона для площади треугольника

Треугольник – это фигура, которая образуется после соединения трех точек, не лежащих на одной прямой отрезками.

Точки называются вершинами, а отрезки сторонами. Для расчета треугольника существует множество формул, которые помогают найти как длины сторон, радиусы углов и прочие составляющие фигуры, так и площадь треугольника.

Самой распространенной формулой для расчета площади треугольника по трем сторонам является формула Герона

. Если известны длины всех сторон, то можно вычислить площадь фигуры, применив формулу Герона для площади треугольника.

где a , b , c – длины сторон, а p – полупериметр.
Полупериметр – это сумма длин всех сторон поделенная на два.

Три окружности с радиусами 6, 7, 8 внешне попарно касаются друг друга. Найти площадь треугольника, образованного центрами этих окружностей. Посмотреть решение

училась в школе шесть десятков лет назад, геометрию забыла, но в связи с тем, что мебель из ДСП смешно ставить в сантехническую кабину (недолговечна), а из дерева и красивая пока недоступна. На сайтах гостиниц Бахрейна очень понравилась, примерно в похожем стиле хочу сделать сама угловой шкаф в ванную, но чтобы закупить материалы, надо начертить детали и посчитать объем и без геометрии здесь не обойтись. Поэтому я благодарна Вам за теорему Пифагора, за древнеиндийских математиков, за тригонометрические формулы и за калькуляторы расчетов. С искренним уважением Нина Ивановна!

#мыэтонепроходили
Что это за точка на гипотенузе С, которая делит ее на два отрезка С1 и С2 ? Причем произведение С1 на С2 численно равно площади треугольника.

Вбиваем стороны 2,3,5 и вуаля:

Ответ: Площадь треугольника = 0.000

Каждая сторона должна быть меньше суммы двух других. 5>2+3?!

Это не треугольник, это 3 точки на одной прямой

Стороны: 3,4,7 и оппа!
Ответ: Площадь треугольника = 0. 000

Потому что у треугольника со сторонами 3, 4 и 7 площадь таки будет 0. 3+4=7. Треугольник вырождается в отрезок.

Нет, по теории, любой треугольник можно назвать таковым, если сумма двух сторон его больше или равна оставшейся стороны.

Например:
стороны 10 25 30, следует что это треугольник так как
(10+25)>30
(10+30)>25
(30+25)>10

Пытался воспользоваться Вашим калькулятором…бесполезно. говорит : такого треугольника нет ……а именно : 3.354 +3.54+12.40.
Может кто-то поможет ?

Ответ: сумма любых 2-х сторон треугольника > 3-й стороны. А у Вас получается 3,…+3,…

Господа, неравенство треугольника ещё никто не отменял. Поэтому, прежде чем вычислять площадь треугольника, проверяют его существование, используя неравенство треугольника.

Формула Герона.

Формула Герона позволяет определить площадь треугольника (S) из его сторон a, b, c.

Чтобы вычислить площадь треугольника ∆ABC, если известны длины его сторон a, b и c, используют формулу Герона:

где p — полупериметр треугольника:

.

Рассмотрим нахождение площади треугольника с помощью формулы Герона:

Есть треугольник со сторонами a = 5, b = 6, c = 7. Вычислим полупериметр:

Далее подставляем данные в формулу для определения площади:

Площадь треугольника, определенная при помощи формулы Герона равняется 14,7 см 2 .

Формула Герона, доказательство.

В нем: CH — высота треугольника ABC, которая проведена из вершины C, |CH|=h, |AH|=x, |BH|=y.

Тогда c=x+y, и из теоремы Пифагора из треугольников ACH и BCH имеем:

Учитывая, что x+y=c, получаем

и .

Складываем последнее равенство с равенством y+x=c, получаем:

Далее находим высоту h треугольника:

Подставляем эти выражения в определенное выражение для h 2 :

Учитываем то, что

, получаем требуемое.

Источники:

http://www.maths.yfa1.ru/ensiklopedija.php?id=geron
http://2mb. ru/matematika/geometriya/formula-gerona-dlya-ploshhadi-treugolnika/
http://www.calc.ru/Formula-Gerona.html

Площадь треугольника

Площадь треугольника, формулы для вычисления площади различных видов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей треугольников.

Таблица с формулами площади треугольника (в конце страницы)

Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)

— Вычисления   (показано)
  (скрыто)

— примечания   (показано)
  (скрыто)

Для всех треугольников

1

Площадь треугольника по основанию и высоте

Сторона a

Высота h

Основанием треугольника может быть выбрана любая из сторон треугольника.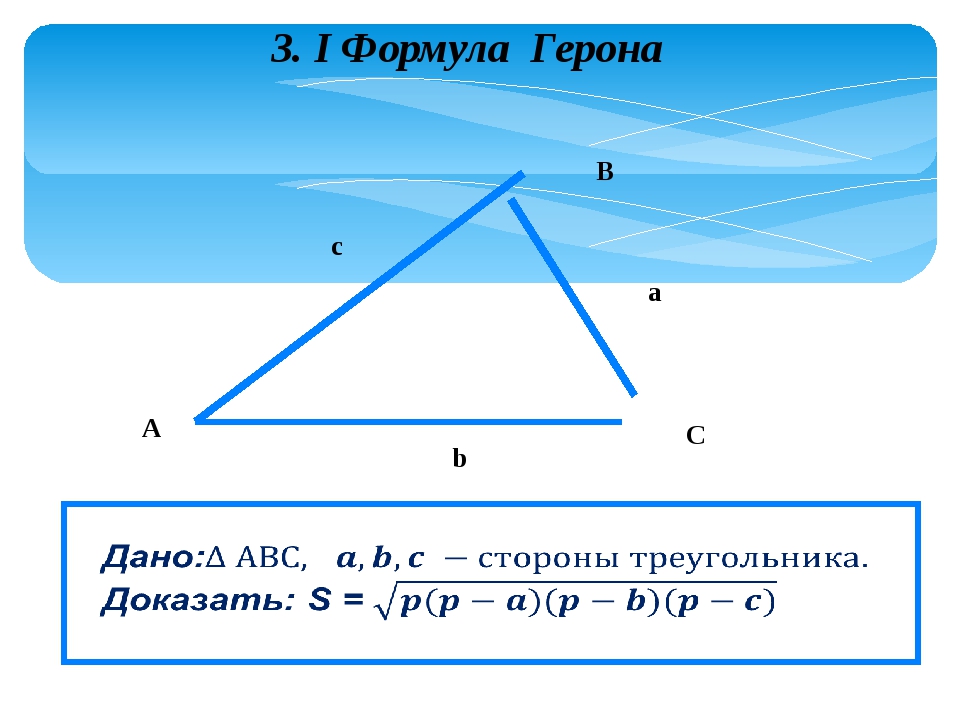

2

Площадь треугольника по двум сторонам и углу между ними

Сторона a

Сторона b

Угол α° между сторонами a и b

Угол α между сторонами может быть любым: тупым, острым, прямым.

3

Площадь треугольника по радиусу вписанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус r вписанной окружности

4

Площадь треугольника по радиусу описанной окружности и трем сторонам

Сторона a

Сторона b

Сторона c

Радиус R описанной окружности

5

Площадь треугольника по формуле Герона

Полупериметр: 

Сторона a

Сторона b

Сторона c

6

Площадь произвольного треугольника по стороне и двум прилежащим углам

Сторона a

Угол β°

Угол α°

Для равнобедренных треугольников

7

Площадь равнобедренного треугольника по боковым сторонам и основанию

Сторона a (a = b)

Сторона c

8

Площадь равнобедренного треугольника по боковым сторонам и углу между ними

Боковая сторона a (a = b)

Угол α° между боковыми сторонами

9

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними

Боковая сторона a (a = b)

Основание треугольника c

Угол β° между основанием и стороной

10

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами

Основание треугольника c

Угол α° между боковыми сторонами

Для равносторонних треугольников

11

Площадь равнобедренного треугольника по высоте и основанию

Основание треугольника c

Высота h

12

Площадь равностороннего треугольника по стороне

Сторона a (a = b = c)

13

Площадь равностороннего треугольника по высоте

Высота h

14

Площадь равностороннего треугольника по радиусу вписанной окружности

Радиус r вписанной окружности

15

Площадь равностороннего треугольника по радиусу описанной окружности

Радиус R описанной окружности

Для прямоугольных треугольников

16

Площадь прямоугольного треугольника по двум катетам

Катет a

Катет b

17

Площадь прямоугольного треугольника через гипотенузу и угол

Сторона c

Угол α

18

Площадь прямоугольного треугольника через катет и угол

Сторона b

Угол α

19

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность

Отрезок d

Отрезок e

20

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность

Сторона с

Радиус r

21

Площадь прямоугольного треугольника по формуле Герона

Полупериметр: 

Сторона a

Сторона b

Сторона c

Для вычисления площади треугольника применяются различные формулы, в зависимости от известных исходных данных.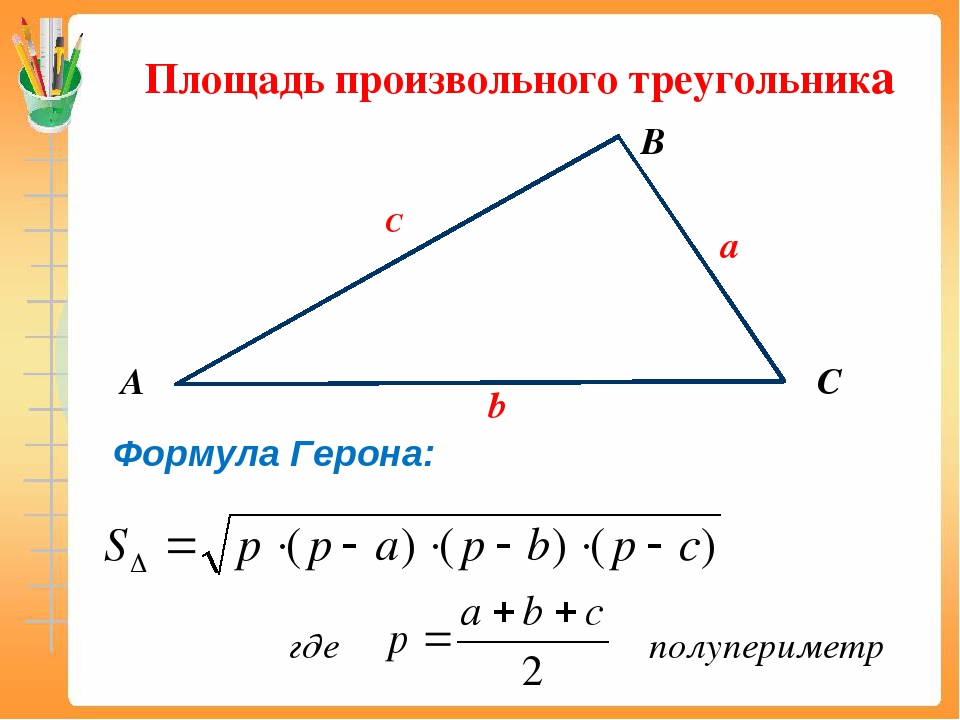 Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные вычисления. Приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.

Наш калькулятор для вычисления площади поможет вам вычислить площадь разных видов треугольников или проверить уже выполненные вычисления.

В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.

Таблица с формулами площади треугольника

Определения

Площадь треугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Отрезки называют сторонами треугольника, а точки – вершинами треугольника.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Скачать формулы площади треугольника в виде картинки

Расчет площади треугольника Херона

Это также может быть хорошим упражнением, чтобы задать вопросы о
выполнимость определенных сторон треугольника. Файл Excel
может не дать правильных расчетов до определенного момента. Некоторый
расчеты тоже могут не иметь смысла. Это может привести к
исследование теоремы о неравенстве треугольника. Ты можешь
установить диапазон, в котором должна находиться третья сторона треугольника.
упади, если тебе даны две другие стороны и ты сможешь протестировать
это через файл Excel и файл Java. Проверить это
и попытайтесь выяснить, почему правила, установленные
Теорема о неравенстве треугольника верна.

СУММА ДВУХ СТОРОН ДОЛЖНА ДОБАВИТЬСЯ, ЧТОБЫ БЫТЬ БОЛЬШЕ, ЧЕМ
ДЛИНА ОСТАВШЕЙСЯ ТРЕТЬЕЙ СТОРОНЫ.

ИЛИ (со сторонами A, B, C):

• A + B> C,
• В + С> А,
• и A + C> B

Итак, можно ли получить треугольник со сторонами 5, 12, 16?

А как насчет 5, 12, 13? Как это выглядит?

Интересно, что формула цапли тоже приводит нас к результату
где мы можем вычислить высоту треугольника.С участием
основание c и высота h высота составляет,

Еще темы для размышлений….

1. Представьте себе треугольник, основание и вершина которого не
на основании, но на линии, параллельной этому основанию. Что бы
произойдет с периметром и площадью этого треугольника, если
база осталась прежней, но вершина все время перетаскивалась
линия параллельна основанию?

Вот занятие для
пытаться…

2. Можете ли вы начать доказательство формулы цапли? это
довольно приятно пройти и очень провокационно.Я призываю вас изучить его хотя бы в этом
текст, который я отсканировал.

Формула и калькулятор площади треугольника Цапли

Решенный пример

Приведенный ниже пример решенной задачи может быть полезен для понимания того, как значения используются в математических формулах для определения площади треугольника цапли.

Пример задачи:
Найти площадь треугольника со сторонами a = 18 см, b = 12 см и c = 10 см?

Решение:
Приведенные значения
длина a = 18 см
длина b = 12 см
длина c = 10 см

Пошаговый расчет
формула для определения полупериметра s = ( a + b + c) / 2
замените значения
= (18 + 12 + 10) / 2
= 20 см

формула цапли, чтобы найти площадь = √s (s — a) (s — b) ( s — c)
подставляем значения
= √20 x (20-18) x (20-12) x (20-10)
= √20 x 2 x 8 x 10
= 56.56 см

Площадь треугольника может потребоваться для расчета в системе СИ, метрической или стандартной системе единиц США, поэтому калькулятор площади треугольника цапли снабжен функцией преобразования основных единиц измерения для нахождения выходных значений в различных обычных единицах, таких как дюймы (дюймы), футы (футы), метры (м), сантиметры (см) и миллиметры (мм), используя приведенную ниже таблицу преобразования.

В области вычислений площади и объема определение площади треугольника очень важно для понимания элементов базовой математики. Приведенные выше формулы, пошаговый расчет и решенный пример могут помочь пользователям понять, как вычислить площадь треугольника вручную, однако, когда дело доходит до онлайн для выполнения быстрых вычислений, калькулятор треугольника Герона может быть полезен для поиска результатов .

Формула Герона — математический путь

Выберите свой язык EnglishSpanish

Формула Херона дает площадь треугольника, когда мы знаем все три стороны.

Площадь вычисляется из полупериметра треугольника, s и длины сторон ( a , b и c ).

Упражнение 1

Найдите площадь данного треугольника.

Решение:

В этом треугольнике мы знаем три стороны: a = 4 см, b = 5 см и c = 3 см. Мы собираемся найти его площадь по формуле Герона.

Сначала вычисляем полупериметр s .

Теперь применим формулу Герона:

Площадь треугольника 6 см ² .

Упражнение 2

Найдите высоту на стороне b данного треугольника.

Решение:

Применяя формулу Герона, мы видим, что его площадь составляет 6 см ² .

Мы также знаем, что площадь треугольника равна:

С помощью этой формулы мы можем вычислить высоту:

То есть х = 2,4 см.

Описанный круг в треугольнике

У нас есть еще одна процедура для вычисления площади треугольника, если мы знаем его три стороны и радиус R описанной окружности или описанной окружности , без необходимости прибегать к формуле Герона.

Начертанный круг в треугольнике

Аналогично, без формулы Герона у нас есть еще одна процедура для вычисления площади треугольника, но теперь по радиусу вписанной окружности, или вписанной окружности .

Таблица формул площади треугольника

Вы можете увидеть таблицу формул площади треугольника . В зависимости от типа треугольника вам может понадобиться один элемент, как в равностороннем треугольнике, два (основание и высота) или три.В последнем случае, если это не три угла.

Формула Герона (видео и примеры) // Tutors.com

Содержание

1. Что такое формула Герона?
2. Формула Герона
3. Полупериметр
4. Квадратные корни
5. Когда использовать формулу площади Герона
6. Доказательство формулы Герона

Что такое формула Герона?

Подумайте, каким великим мыслителем вы должны были бы быть, чтобы люди запомнили ваше имя спустя более 19 веков после вашей жизни.Герон Александрийский был жителем Александрии в то время, когда римляне правили городом.

Его имя связано с формулой для определения площади любого треугольника, если вы знаете только длины их сторон. Формула, которая все еще носит его имя все эти столетия спустя, известна как Формула Герона или Формула Героя.

Формула Герона

Чтобы увидеть формулу Герона в действии, вам понадобится треугольник. Постройте один, нарисовав любые три пересекающихся отрезка линии.Каждая сторона будет помечена буквами a, b и c.

Расстояние вокруг треугольника — его периметра — складывается из a + b + c. Полупериметр треугольника составляет половину периметра. Обозначим полупериметр s.

Не нужно беспокоиться об углах; не нужно знать высоту! Используя формулу Герона, нам нужны только длины сторон.

А теперь, сквозь пески времени, вот формула Герона для определения площади (A) любого треугольника, если вы знаете длины сторон a, b и c и полупериметр s:

A = s (s — a) (s — b) (s — c)

Сначала решите математические задачи в круглых скобках, чтобы вычесть длину каждой стороны из полупериметра

Затем умножьте все три ответа, а затем умножьте на полупериметр.

После этого вы извлекаете квадратный корень из этого ответа.

Полупериметр

Некоторые люди находят понятие половины периметра многоугольника немного… ну, странным. Но полупериметр — половина периметра — очень полезен, а для формулы Герона он вам нужен!

Нахождение полупериметра s — это двухэтапный процесс: сначала складывают длину трех сторон, а затем делят на 2 .

Давай попробуем. У вас есть треугольник со сторонами 3, 4 и 5 футов.

с = 3 + 4 + 52

с = 122

с = 6 футов

Другой пример

Попробуйте сами. У треугольника стороны 36, 48 и 60 сантиметров. Какой у него полупериметр?

с = 36 + 48 +602

с = 1442 = 72 см

Несколько слов о квадратных корнях

Возможно, вы раньше не встречали квадратные корни на уроках математики. Квадратный корень — это число, которое дает вам конкретный ответ при умножении на само.

Предположим, вы хотите узнать квадратный корень из 49; какое число, умноженное на само, даст вам 49?

? ×? = 49

Ответ 7. Итак, sqrt 49 = 7.

Обычно квадратный корень из числа не получается так точно. Просто переход к соседнему числу из нашего примера, 49, показывает это. Квадратный корень из 50 равен 7,07106781187.

Иногда ваш ответ с использованием формулы Герона дает ответ со многими десятичными знаками. Обычно вы округляете свой ответ до определенного числа десятичных знаков, чтобы достичь определенного уровня точности.

Ответ, который вы получите, используя формулу Герона, конечно же, выражается в квадратных единицах любых линейных единиц.

Когда использовать формулу площади Герона

В большинстве случаев площадь треугольника рассчитывается путем умножения основания на высоту, равную ½ основания. Однако вы не всегда знаете высоту треугольника. Основание — это одна из сторон треугольника, поэтому, если вы знаете длины двух других сторон, у вас будет достаточно информации, чтобы подставить три длины в формулу Герона:

Попробуйте

Вернемся к нашему примеру треугольника со сторонами 3, 4 и 5 футов (стороны a, b и c).Мы уже вычислили полупериметр выше, где s = 6.

Подставьте все эти числа в формулу Герона:

A = s (s — a) (s — b) (s — c)

А = 6 (6 — 3) (6 — 4) (6 — 5)

А = 6 (3) (2) (1)

А = 6 (6)

А = 36

A = 6 футов2

Доказательство формулы Герона

Для вашей первой самостоятельной попытки мы будем использовать маленькие значения, чтобы облегчить умножение. Представьте треугольник со сторонами 15, 20 и 25 ( a , b и c ) дюймов в длину.Начнем с вычисления полупериметра треугольника:

с = 15 + 20 + 252

с = 602 = 30 дюймов

Теперь поместите стороны a, b и c вместе с полупериметром s , 30 дюймов в формулу Герона:

А = 30 (30-15) (30-20) (30-25)

А = 30 (15) (10) (5)

А = 30 (750)

А = 22 500

A = 150 дюйм2

Готовы к более тяжелому примеру?

Используйте другой треугольник из нашего примера со сторонами 36, 48 и 60 сантиметров (a, b, c).Сначала посчитаем полупериметр:

с = 36 + 48 + 602

с = 1442 = 72 см

Подставьте все эти числа в формулу Герона:

А = 72 (72 — 36) (72 — 48) (72 — 60)

А = 72 (36) (24) (12)

А = 746 496

A = 864 см2

Резюме урока

Посмотрев видео и прочитав этот урок, вы теперь можете рассчитать площадь треугольника, если знаете длины сторон треугольника, узнаете причины использования формулы Герона, примените знания о квадратных корнях для решения задачи и примените формулу Герона для вычислить площадь треугольника.

A = s (s — a) (s — b) (s — c)

Следующий урок:

Справка по геометрии

Заключительный проект

Заключительный проект

MATH 7200: Основы геометрии
Я

Университет Джорджии, осень
2000

Доктор МакКрори, инструктор

Финальный проект: Формула Герона

Шеннон Амбергер

Содержание

I. Краткая история Heron
Александрии

II. Heron’s Formula , включая
эскиз GSP для проверки

III. Три доказательства Герона
Формула: одна алгебраическая, одна геометрическая и одна тригонометрическая

IV. Связанные темы:

A. Обобщение Брахмагупты ,
включая эскиз GSP для тестирования и доказательство

B. Расширение Брахмагупты
Обобщение, включая эскиз GSP для проверки

C. Теорема Пифагора ,
включая доказательство с использованием формулы Херона

В. ресурсов

Цапля Александрийская

Немногое известно о человеке по имени Герон Александрийский.
Даже его имя не определено; его звали Герон и Герой.
Никто точно не знает, когда он жил, хотя принято считать, что
что он жил где-то между 150 г. до н. э. и 250 г. н.э. Герон сделал
живут в великом ученом городе Александрия, Египет, где многие
Учились греческие математики и ученые. Пока не известно
был ли он греком или на самом деле египтянином с греческим образованием.Однако можно сказать наверняка, что Герон Александрийский был блестящим
человек, который дал современному миру глубокое понимание математических
и физические науки.

Херон написал так много работ по математическим и физическим предметам.
что «его принято называть энциклопедическим
писатель в этих областях »(Eves, p. 178). Большинство этих работ
можно разделить на две категории: геометрические и механические.
Хотя были обнаружены примерно четырнадцать его трактатов,
есть ссылки на другие утраченные произведения.

Один из трактатов Герона, названный Pneumatica , описывает
почти сотня машин и игрушек, в том числе пожарная машина,
духовой орган и устройство для открывания храмовых дверей огнем
на алтаре. Его Dioptra состоит из инженерных приложений
старинного типа маркшейдерского проезда. Работа Catoptrica
занимается свойствами и конструкциями зеркал.

Возможно, величайший вклад Герона в математический мир
была его работа под названием Metrica , которая была написана тремя
книги.Он имел в основном геометрический характер, касался площади и
измерение объема различных полигонов и твердых тел. Он исследовал
свойства правильных многоугольников, окружностей и конических сечений. В
в этой работе Герон также дал метод нахождения приближения
из квадратного корня неквадратного целого числа; этот метод используется
сегодня на многих компьютерах.

Наконец, Metrica содержит доказательство Герона формулы
используется для определения площади треугольника по длинам трех
стороны. Большинство ученых считают, что это предположение действительно должно быть
приписывается Архимеду.Но формула получила имя Герона,
и именно с помощью термина Формула Герона высказывается
теперь широко известен.

Вернуться к началу

Формула Герона

Большинству школьников известна традиционная формула, по которой
площадь треугольника: A = (1/2) * b * h. Очевидно, чтобы найти
площадь треугольника по этой формуле, необходимо знать длину
стороны треугольника (основание, b) и длину
высота в ту сторону (высота, h).

С другой стороны, Формула Герона может быть использована для нахождения
площадь треугольника, когда известны длины трех сторон.
Обратите внимание, что не обязательно знать высоту, чтобы использовать
эта формула.

Формула Герона утверждает:

Учитывая длины a, b и c трех сторон треугольника …

… и после нахождения полупериметра треугольника …

… площадь треугольника можно найти по следующей формуле:

Нажмите здесь для
файл SketchPad от Geometer для управления традиционными
формула площади к формуле Герона.

Вернуться к началу

Доказательства формулы Герона

Существует множество доказательств формулы Герона. Большинство можно разделить на категории
как алгебраический, геометрический или тригонометрический. Следующий список
включает в себя представление по одному доказательству каждого из этих типов.

Нажмите здесь
чтобы увидеть алгебраическое доказательство формулы Герона.

Нажмите здесь
чтобы увидеть геометрическое доказательство формулы Герона. Это доказательство основано
на доказательстве Герона формулы в Metrica .

Нажмите здесь
чтобы увидеть тригонометрическое доказательство формулы Герона.

Вернуться к началу

Связанная тема: Брахмагупта
Обобщение

Брахмагупта был индуистским математиком, жившим в Индии во времена
в седьмом веке нашей эры.Он написал Брахма-спхута-сидд’ханта ,
который был в основном трудом по астрономии, но две его главы
занимался математикой. В эту работу была включена формула, которая
можно использовать, чтобы найти площадь вписанного четырехугольника, когда задано
длины четырех сторон.Формулу часто называют формулой Брахмагупты.
Обобщение, в отличие от формулы Брахмагупты, потому что позже
комментаторы предположили, что это формула, которая будет использоваться для определения области
из любой четырехугольник. Потому что они не увидели ограничения
формулы, критики обнаружили, что она не работает во всех
случаи.

Обобщение Брахмагупты утверждает:

Дан четырехугольник, вписанный в круг, со сторонами
длина a, b, c и d, …

… и после нахождения полупериметра s четырехугольника…

… площадь четырехугольника можно найти по этой формуле:

*** Обратите внимание, что когда расстояние d равно 0, вписанный четырехугольник
становится треугольником. Затем обобщение Брахмагупты сокращает
к формуле Герона.

Нажмите здесь для
файл SketchPad от Geometer для проверки обобщения Брахмагупты.

Нажмите здесь
чтобы увидеть доказательство обобщения Брахмагупты.

Вернуться к началу

Связанные
Тема: Расширение обобщения Брахмагупты

Поскольку обобщение Брахмагупты работает только для циклических
четырехугольника, интересно отметить, что продолжение
по его формуле можно найти площадь любого четырехугольника.

Это расширение обобщения Брахмагупты
состояния:

Дан четырехугольник со сторонами длиной a, b, c и d, …

… пусть угол между сторонами a и d равен A,
а угол между сторонами b и c должен быть B.

После определения полупериметра s четырехугольника …

… площадь четырехугольника можно найти по этой формуле:

*** Обратите внимание, что когда расстояние d равно 0, четырехугольник
становится треугольником.Это расширение обобщения Брахмагупты
затем сводится к формуле Герона.

Нажмите здесь для
файл SketchPad от Geometer для тестирования этого расширения Брахмагупты
Обобщение.

Вернуться к началу

Связанная тема: The
Теорема Пифагора

Есть много-много способов доказать теорему Пифагора.
Один из способов — использовать формулу Герона.

Теорема Пифагора утверждает:

Дан прямоугольный треугольник с катетами длины a и b и гипотенузой.
длины c ,…

… можно констатировать следующее соотношение:

Нажмите здесь , чтобы
см. доказательство теоремы Пифагора с использованием формулы Герона.

Вернуться к началу

ресурсов

Книги

Coxeter, H.S.M. и С.Л. Грейтцер. Новый взгляд на геометрию .
Random House, Inc., Нью-Йорк, 1967.

Евс, Ховард. Введение в историю математики ,
6-е изд.Издательство Saunders College Publishing, Орландо, 1990.

Сайты

Математические страницы Кевина Брауна: http://www.seanet.com/~ksbrown/kmath296.htm

Cut-the-Knot: http://www.cut-the-knot.com/pythagoras/herons.html

Курс доктора Джима Уилсона по решению проблем: http://jwilson.coe.uga.edu/emt725/Heron/Trig.Heron.html

Вернуться к началу

Вернуться к Шеннон
домашняя страница

Объяснение формулы Герона

Периметр треугольника складывается из трех его сторон.Площадь треугольника довольно интересна. Обычно это выражается как площадь = (1/2) x основание x высота, A = (1/2) b * h , где высота измеряется как вертикальная линия от основания до противоположной вершины. Эта формула позволяет относительно легко вычислить площадь треугольника, но довольно сложно естественным образом найти треугольник, у которого есть хотя бы одна известная сторона (основание) и известная высота. Получить длину всех трех сторон треугольника зачастую намного проще. К счастью, существует формула для вычисления площади треугольника, когда известны все три стороны.

Формула

Герона позволяет нам найти площадь треугольника, зная длины всех трех сторон этого треугольника. Оказывается, мы можем вычислить его площадь, не доказывая никаких дополнительных теорем или используя тригонометрию. Следующее уравнение является формулой Герона.

A = sqrt (s (s-a) (s-b) (s-c))

Где s = (a + b + c) / 2 или 1/2 периметра, а A обозначает площадь

Вывод формулы Геррона

Треугольник DeltaABC имеет стороны a , b и c .Мы можем создать формулу для площади треугольника ABC, используя эти три стороны.

Во-первых, мы вспомним стандартное уравнение для определения площади треугольника — это основание, умноженное на высоту треугольника, деленное на два (1/2) bh . Нам известны все три длины сторон, поэтому мы можем использовать любую из них в качестве основы — в данном случае мы выбираем сторону b . Поскольку у нас нет высоты треугольника, мы рисуем линию высоты h под прямым углом к ​​стороне b до вершины a и c .Линия h создает два прямоугольных треугольника — один справа и один слева от h .

Обозначив сечение стороны b от h до вершины b и c как x , теперь у нас есть два прямоугольных треугольника. Левый треугольник имеет стороны h , (b-x) и a , а правый треугольник имеет стороны h , x и c .

Используя теорему Пифагора, мы можем получить выражения для x и h , просто используя a , b и c .2)) ((b + c) + a) ((b + c) -a) (a + (b-c)) (a- (b-c))

Отсюда следует, что h = (1 / (2b)) sqrt ((b + c + a) (b + c-a) (a + b-c) (a + c-b) .

Поскольку площадь треугольника равна (1/2) bh , мы можем просто умножить их вместе, чтобы получить

A = (1/4) sqrt ((b + c + a) (b + c-a) (a + b-c) (a + c-b) .

Упрощение формулы Херона до окончательной формы

Итак, давайте поиграем с длинами, чтобы получить более простую формулу и интересный результат.

Поскольку a , b и c — стороны треугольника, a + b + c — его периметр.Определив s как половину периметра, мы получим s = (a + b + c) / 2 , или 2s = b + c + a .

Отсюда получаем, что b + c-a = 2 (s-a) ; a + b-c = 2 (s-c) и a + c-b = 2 (s-b) . Подставляя их в уравнение для площади DeltaABC выше, мы получаем

A = (1/4) sqrt ((2s) (2 (s-a)) (2 (s-b)) (2 (s-c)) .

Затем, с некоторым упрощением и небольшой перестановкой, получаем

A = sqrt (s (s-a) (s-b) (s-c)) .

Теперь мы достигли окончательного состояния формулы Герона и можем использовать ее, чтобы найти площадь треугольника, если высота неизвестна, но известны все три стороны.

Примеры использования формулы Герона

Хотя формула Герона используется для определения площади треугольника по длинам трех сторон, ее также можно использовать для определения высоты треугольника.

Использование формулы Герона для определения площади

Если у вас есть все три стороны, используйте формулу Геррона.Формула Херрона состоит из двух частей. Сначала вы должны найти переменную s , которая равна половине периметра треугольника. Эта формула: s = (a + b + c) / 2 .

Для треугольника с длинами сторон a = 3 , b = 4 и c = 5 ,

с = (3 + 4 + 5) / 2

с = (12) / 2

с = 6

Затем используйте вторую часть уравнения Герона, A = sqrt (s (s-a) (s-b) (s-c)) . A = sqrt (6 (6-3) (6-4) (6-5))

A = sqrt (6 (3) (2) (1)) = 6

Площадь треугольника составляет 6 квадратных единиц.

Использование формулы Герона для определения высоты

Помимо определения площади треугольника, когда известны только три стороны, эта формула также позволяет нам вычислить высоту треугольника. Для этого задайте для области значение 1 / 2bh , а затем вычислите высоту. Это дает нам уравнение 1 / 2bh = sqrt (s (s-a) (s-b) (s-c)) или h = (2sqrt (s (s-a) (s-b) (s-c))) / b

Для нашего примера треугольник с длинами сторон 3, 4 и 5 решается следующим образом.

(1/2) (4) h = sqrt (6 (6-3) (6-4) (6-5)

2 часа = 6

ч = 3

Итак, со стороной b в качестве основания, высота равна 3.

Оставьте первый комментарий ниже.

Площади треугольников

Наиболее распространенная формула для определения площади треугольника: K = ½ bh , где K — площадь треугольника, b — основание треугольника и h это высота.(Буква K используется для обозначения площади треугольника, чтобы избежать путаницы при использовании буквы A для обозначения угла треугольника.) Полезны три дополнительные категории формул площади.

Две стороны и включенный угол (SAS): Учитывая Δ ABC (рисунок), высота определяется как h = c sinA. Следовательно,

Рис. 1
Справочные треугольники для формул площади.

Два угла и сторона (AAS) или (ASA): Использование закона синусов и замена в предыдущих трех формулах приводит к следующим формулам:

Аналогично

Три стороны (SSS): Известный греческий философ и математик Герон (или Герой) разработал формулу, которая вычисляет площадь треугольников, учитывая только длины трех сторон. Это известно как формула Герона .Если a, b и c — длины трех сторон треугольника, а s — это полупериметр , то

и

Одно из многих доказательств формулы Герона начинается с Закона косинусов:

Пример 1: (SAS) Как показано на Рисунке 2, две стороны треугольника имеют размеры 25 и 12. Измерение включенного угла составляет 51 °. Найдите площадь треугольника.

Рисунок 2
Чертеж для примера 1.

Используйте формулу SAS:

Пример 2: (AAS и ASA) Найдите площадь треугольника, показанного на рисунке 3.

Рисунок 3
Чертеж для примера 2.

Сначала найдите размер третьего угла треугольника, так как все три угла используются в формуле площади.

Пример 3: (AAS или ASA) Найдите площадь равностороннего треугольника с периметром 78.