Содержание
Калькулятор онлайн расчета площади боковой поверхности правильной усеченной пирамиды трапеции с отображением формулы и подробным решением.
Калькулятора онлайн рассчитывает площадь боковой и полной поверхности правильной усеченной пирамиды и выводит формулы с подробным решением.
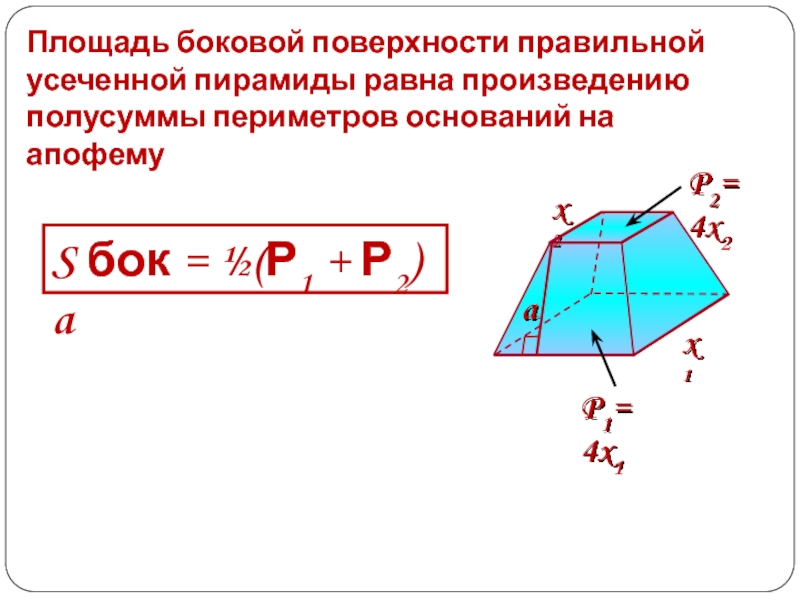
Использование онлайн калькулятора позволяет рассчитать площадь боковой Sside и полной Sfull поверхности правильной треугольной пирамиды: боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
II. Для справки:
1. Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. Пирамида называется треугольной, четырехугольной, и т. д., если основанием пирамиды является треугольник, четырехугольник и т.д. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и т.д.
д., если основанием пирамиды является треугольник, четырехугольник и т.д. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и т.д.
2. Усеченная пирамида — часть пирамиды между ее основанием и этим сечением. Сечение параллельное основанию пирамиды делит пирамиду на две части. Это сечение для усеченной пирамиды является одним из её оснований. Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды. Усеченная пирамида называется правильной, если пирамида, из которой она была получена, была правильной. Все боковые грани правильной усеченной пирамиды — это равные равнобокие трапеции. Высота трапеции боковой грани правильной усеченной пирамиды называется — апофема правильной усеченной пирамиды.
3. Правильная усеченная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный многоугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
4. Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
5. Площадь поверхности — аддитивная числовая характеристика поверхности.
Площадь боковой поверхности усеченной пирамиды
Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна.
 Также они наклонены к основанию под одним углом.
Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Площадь усеченной. Онлайн-калькулятор для расчета площади поверхности усеченной пирамиды
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями
, а оставшийся многоугольник – основанием
пирамиды.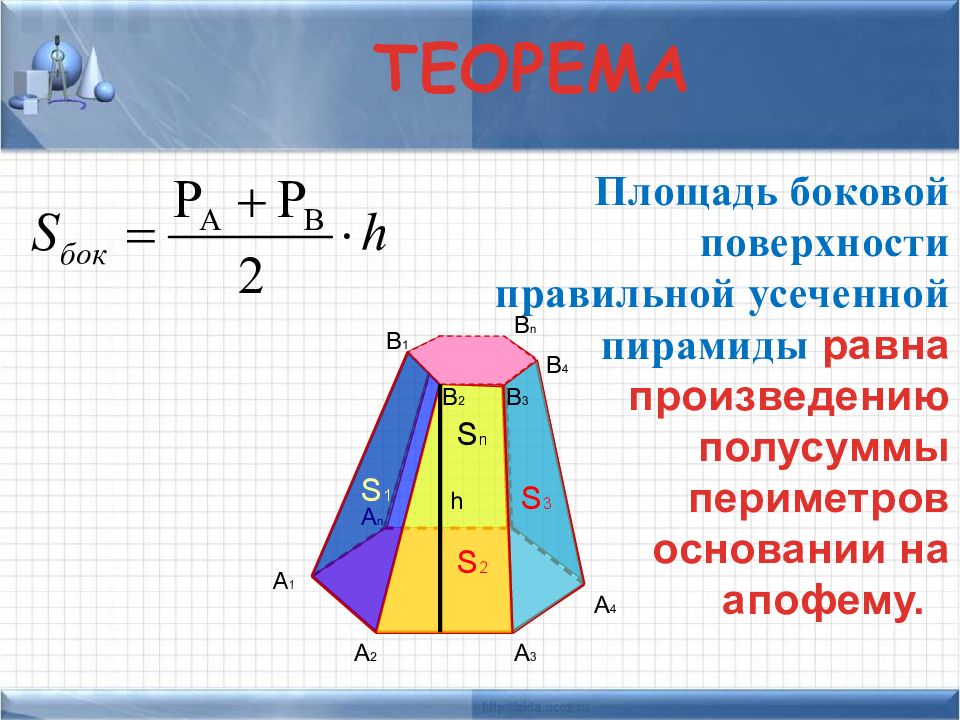
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной
.
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми
, а их общая точка – это вершина
пирамиды. Другие ребра пирамиды обычно называют сторонами основания
.
Пирамиду называют правильной
, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой
пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды
имеют место следующие формулы:
1) S полн = S бок + S осн
, где
S полн – площадь полной поверхности пирамиды;
S бок – площадь боковой поверхности, т.е.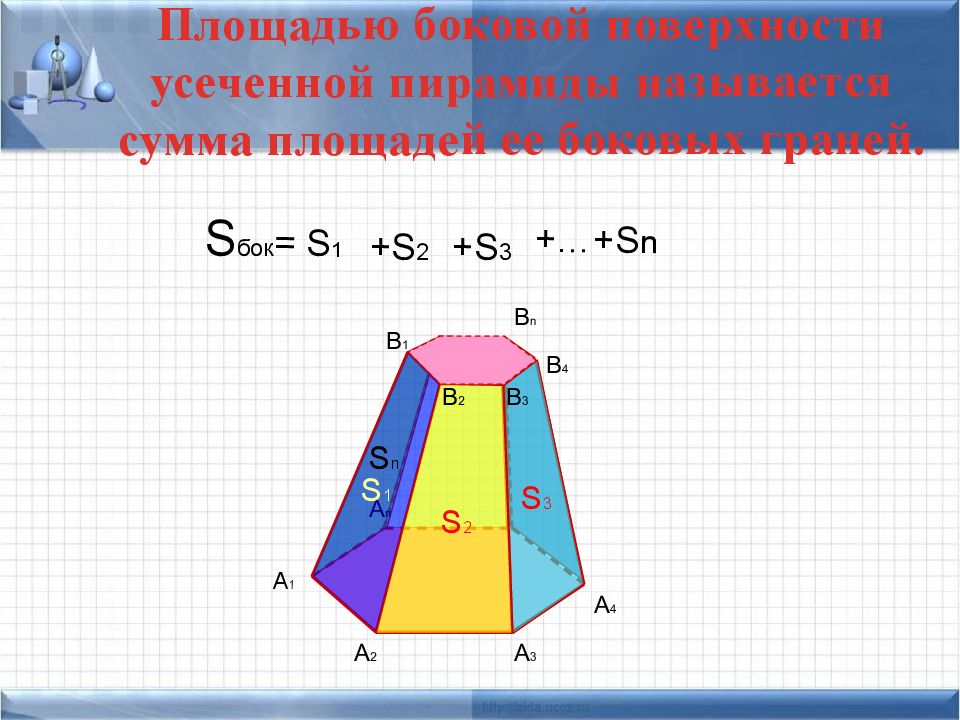 сумма площадей всех боковых граней пирамиды;
сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 S осн · Н
, где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды
имеет место:
S бок = 1/2 P осн h
, где
P осн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой
.
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями
усеченной пирамиды. Остальные грани называют боковыми
. Расстояние между плоскостями оснований называют высотой
усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми
.
Кроме того, основания усеченной пирамиды подобные n-угольники
. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной
.
Для произвольной усеченной пирамиды
имеют место следующие формулы:
1) S полн = S бок + S 1 + S 2
, где
S полн – площадь полной поверхности;
S бок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S 1 , S 2 – площади оснований;
2) V = 1/3(S 1 + S 2 + √(S 1 · S 2))H
, где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды
также имеем:
S бок = 1/2(P 1 + P 2) · h,
где
P 1 , P 2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА 1 В 1 С 1 , изображенную на рисунке1.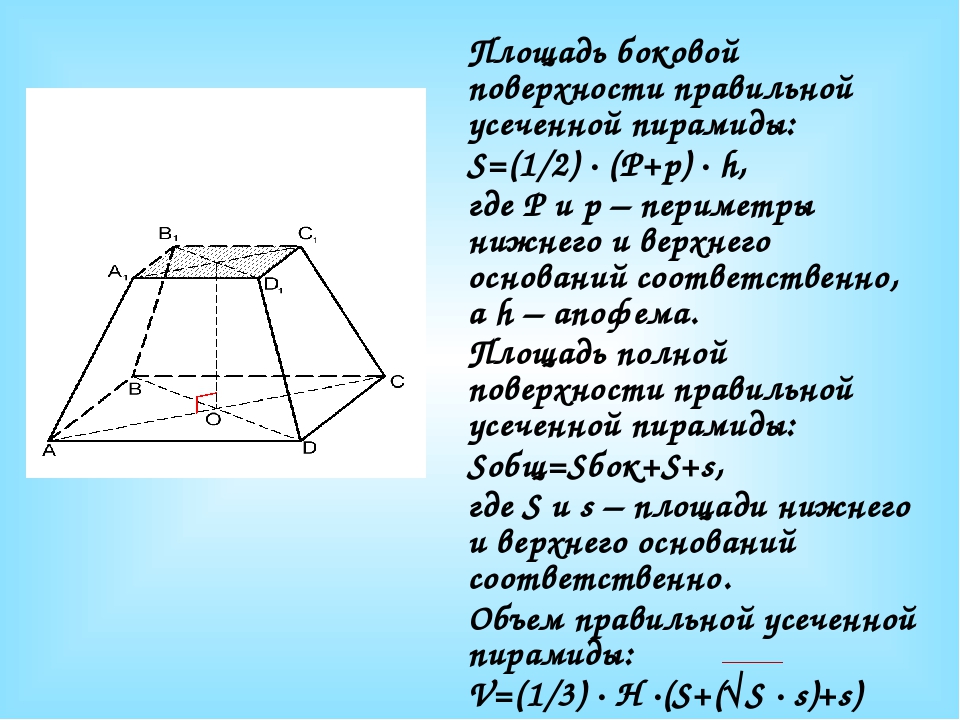
1.
Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S 1 + S 2 + √(S 1 · S 2)), где S 1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p 1 = (27 + 29 + 52)/2 = 54.
S 1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2.
Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А 1 В 1 С 1 . Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S 1 /S 2 = (P 1) 2 /(P 2) 2 = 108 2 /72 2 = 9/4. Отсюда S 2 = 4S 1 /9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1: 2?
В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1: 2?
Решение.
Рассмотрим АВСА 1 В 1 С 1 – усеченную пирамиду, изображенную на рис. 2.
Так как в основаниях стороны относятся как 1: 2, то площади оснований относятся как 1: 4 (треугольник АВС подобен треугольнику А 1 В 1 С 1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S 1 + S 2 + √(S 1 · S 2)) = 1/3h · (4S 2 + S 2 + 2S 2) = 7/3 · h · S 2 , где S 2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA 1 B 1 C 1 составляет V 1 = S 2 · h и, значит,
V 2 = V – V 1 = 7/3 · h · S 2 — h · S 2 = 4/3 · h · S 2 .
Итак, V 2: V 1 = 3: 4.
Ответ: 3: 4.
Задача 3.
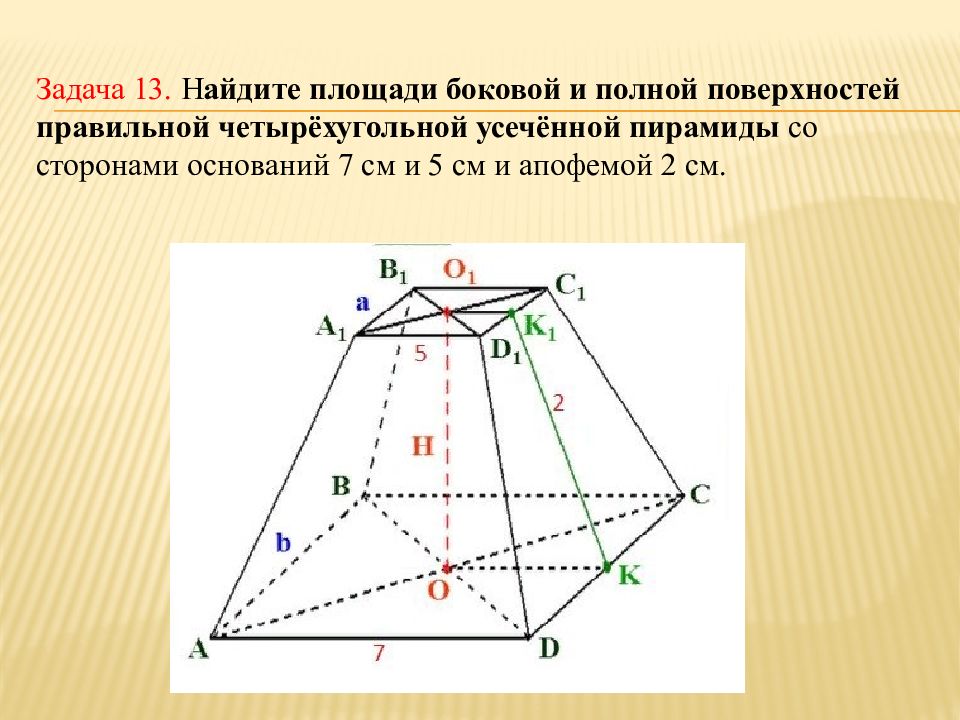
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части.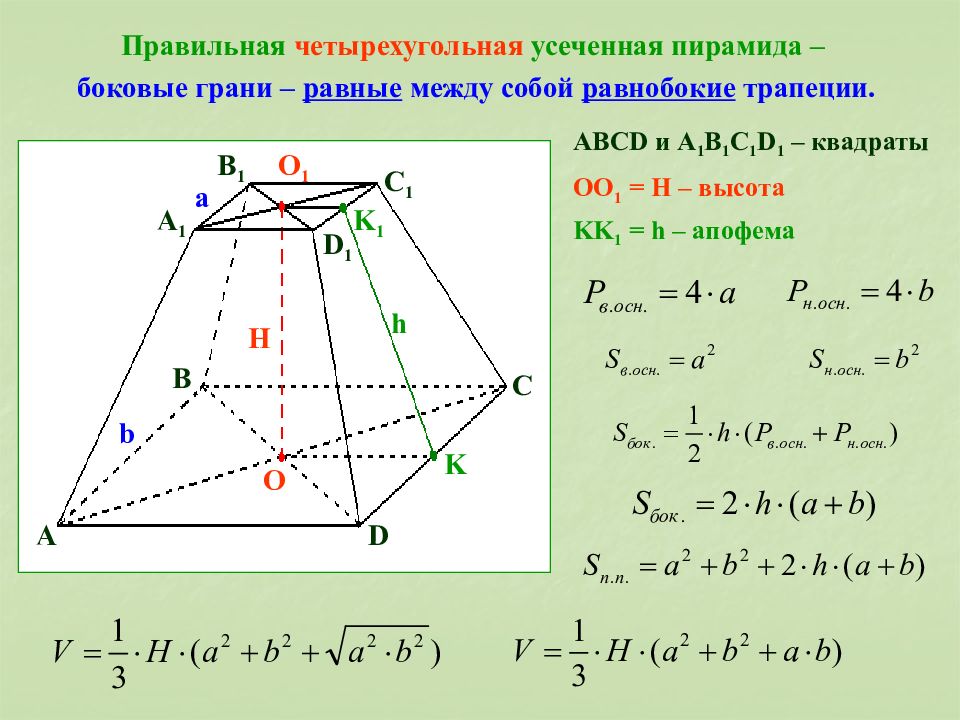 Найти объем каждой из них.
Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА 1 В 1 С 1 D 1 , изображенную на рис. 3.
Обозначим О 1 О 2 = х, тогда ОО₂ = О 1 О – О 1 О 2 = 3 – х.
Рассмотрим треугольник В 1 О 2 D 1 и треугольник ВО 2 D:
угол В 1 О 2 D 1 равен углу ВО 2 D как вертикальные;
угол ВDO 2 равен углу D 1 B 1 O 2 и угол O 2 ВD равен углу B 1 D 1 O 2 как накрест лежащие при B 1 D 1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В 1 О 2 D 1 подобен треугольнику ВО 2 D и имеет место отношение сторон:
В1D 1 /ВD = О 1 О 2 /ОО 2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В 1 D 1 В и треугольник LО 2 B: угол В – общий, а так же имеется пара односторонних углов при B 1 D 1 || LM, значит, треугольник В 1 D 1 В подобен треугольнику LО 2 B, откуда В 1 D: LO 2 = OO 1: OO 2 = 3: 2, т.е.
LO 2 = 2/3 · B 1 D 1 , LN = 4/3 · B 1 D 1 .
Тогда S KLMN = 16/9 · S A 1 B 1 C 1 D 1 = 16/9.
Итак, V 1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V 2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
– это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:
- Боковые грани пирамиды являются трапециями;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания являются подобными многоугольниками;
- В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции
. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l
= 5 см, длина грани в большом основании равна a
= 6 см, а грань в меньшем основании b
= 4 см. Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Подставляем данные в формулу:
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований
.
Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата
. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
- 29.05.2016
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания. Резонансная частота контура определяется так называемой формулой Томсона: ƒ = 1/(2π√(LC)) Для …
- 20.09.2014
Приемник предназначен для приема сигналов в диапазоне ДВ(150кГц…300кГц). Главная особенность приемника в антенне, которая имеет большую индуктивность чем обычная магнитная антенна. Что позволяет применить емкость подстроечного конденсатора в пределах 4…20пФ, а так же такой приемник обладает приемлемой чувствительностью и небольшом усилении тракта РЧ.
 Работает приемник на головные телефоны (наушники), питается …
Работает приемник на головные телефоны (наушники), питается … - 24.09.2014
Это уст-во предназначено для контроля уровня жидкости в резервуарах, как только жидкость поднимется до установленного уровня уст-во начнет подавать непрерывный звуковой сигнал, когда уровень жидкости достигнет критического уровня уст-во начнет подавать прерывистый сигнал. Индикатор состоит из 2-х генераторов ими управляет сенсорный элемент E. Его размещают в резервуаре на уровне до …
- 22.09.2014
КР1016ВИ1 — цифровой многопрограммный таймер, предназначенный для работы с индикатором ИЛЦ3-5\7. Она обеспечивает отсчет и отображение на индикаторе текущего времени в часах и минутах, день недели и номер канала управления(9 будильников). Схема будильника показана на рисунке. Тактируется микросхема кв. резонатором Q1 на 32768Гц. питание — отрицательное, общий плюс поступает на …
Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.
Пирамида как объемная фигура
Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:
2*n = (n+1) + (n+1) — 2.
Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.
Набор пирамид с разными основаниями приведен на фото ниже.
Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.
Формула объема пирамиды
Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.
Площадь каждого такого слоя можно вычислить по формуле:
A(z) = A 0 *(h-z) 2 /h 2 .
Здесь A 0 — площадь основания, z — значение вертикальной координаты.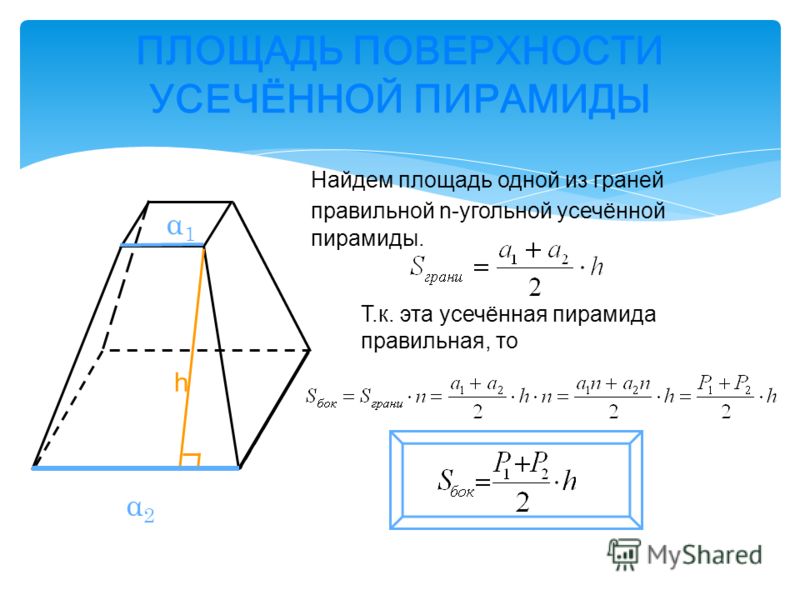 Видно, что если z = 0, то формула дает значение A 0 .
Видно, что если z = 0, то формула дает значение A 0 .
Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:
V = ∫ h 0 (A(z)*dz).
Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:
V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.
Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.
Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.
и ее объем
Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:
A 0 = n/4*L 2 *ctg(pi/n).
Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.
Символ pi — это число пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.
Для правильной четырехугольной пирамиды формула объема приобретает вид:
V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Пирамида усеченная
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.
Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.
Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:
V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.
В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.
Основание пирамиды с высокой точностью является квадратным.
Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:
Подставляем цифры, получаем:
V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .
Объем пирамиды Хеопса равен практически 2,6 млн м 3 . Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!
Урок- лекция на тему «Площадь поверхности пирамиды». 11 класс
Урок- лекция на тему «Площадь поверхности пирамиды». 11 класс
Цель: формировать понятие площади боковой и полной поверхности пирамиды; «открыть» формулы для нахождения площади боковой и полной поверхности правильной и усеченной пирамиды.
Образовательная задача: ввести определения понятий площади боковой и полной поверхности пирамиды и формулы для нахождения площади боковой и полной поверхностей пирамиды; «открыть» формулы для нахождения для площади боковой поверхности правильной пирамиды, площади боковой и полной поверхностей усеченной пирамиды; формировать понятие «усеченная пирамида».
Развивающая задача: развивать самостоятельность, умение работать в парах.
Воспитательная задача: повышать интерес к предмету, формировать логическое мышление.
Предполагаемые результаты: свободно оперировать понятием площади боковой и полной поверхности пирамиды; знание формул для нахождения площади боковой и полной поверхности правильной и усеченной пирамиды; осознание того, что площадь боковой и полной поверхности пирамиды можно вычислять по-разному: в зависимости от вида пирамиды и их особенностей.
План урока (45 мин.):
1. Организационный момент и ознакомление с планом мастерской – 2 мин.
2. Фронтальная работа с классом– 10 мин.
3. Индивидуальная работа – 5 мин.
4.Фронтальная работа с классом (выработка общего мнения) – 2 мин.
5. Работа в группах – 18 мин
6. Комментарии учителя – 3 мин.
Комментарии учителя – 3 мин.
7. Обсуждение мастерской – 3 мин.
8. Задание на дом – 2 мин.
Ход урока
1. Организационный момент и ознакомление с планом мастерской – 2 мин.
Учащимся перед этим уроком было дано домашнее задание:
«Сделайте развертку правильной пирамиды из бумаги по вариантам: 1 вариант — треугольной пирамиды; 2 вариант – четырехугольной пирамиды; 3 вариант – пятиугольной пирамиды. Подумайте и ответьте письменно в тетради на вопросы:
1. Как найти площадь боковой поверхности пирамиды?
2. Как найти площадь полной поверхности пирамиды?
3. Очевидно, что площадь боковой поверхности правильной пирамиды можно вычислить проще. Назовите вершины пирамиды, запишите формулу для нахождения площади боковой поверхности произвольной пирамиды, преобразуйте формулу. Что получили?» (Приложение 1)
Что получили?» (Приложение 1)
В результате выполнения домашней работы предполагаются получить такие ответы учащихся:
1. Площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней.
2. Площадь полной поверхности пирамиды равна сумме площадей ее боковых граней и площади основания.
3. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на высоту боковой грани (апофему): , где периметр, высота боковой грани (апофема).
2. Фронтальная работа с классом (выработка общего мнения) – 5 мин.
Обсуждение выполненного домашнего задания.
Учитель задает вопросы учащимся (актуализация знаний).
1. Сформулируйте теорему о трех перпендикулярах.
2. Какими свойствами обладает вписанная и описанная окружность в треугольнике?
3. Сформулируйте теорему о площади ортогональной проекции многоугольника.
Сформулируйте теорему о площади ортогональной проекции многоугольника.
В результате устного опроса предполагаются получить такие ответы:
1. Если на плоскости проведена прямая перпендикулярно проекции наклонной, то эта прямая перпендикулярна и самой наклонной.
2. а) центром вписанной окружности является точка пересечения биссектрис треугольника;
б) центр описанной окружности является точка пересечения серединных перпендикуляров к сторонам треугольника;
в) у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.
3. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскости проекций. .
Учитель: мы находили с вами площадь боковой поверхности произвольной пирамиды, также правильной пирамиды.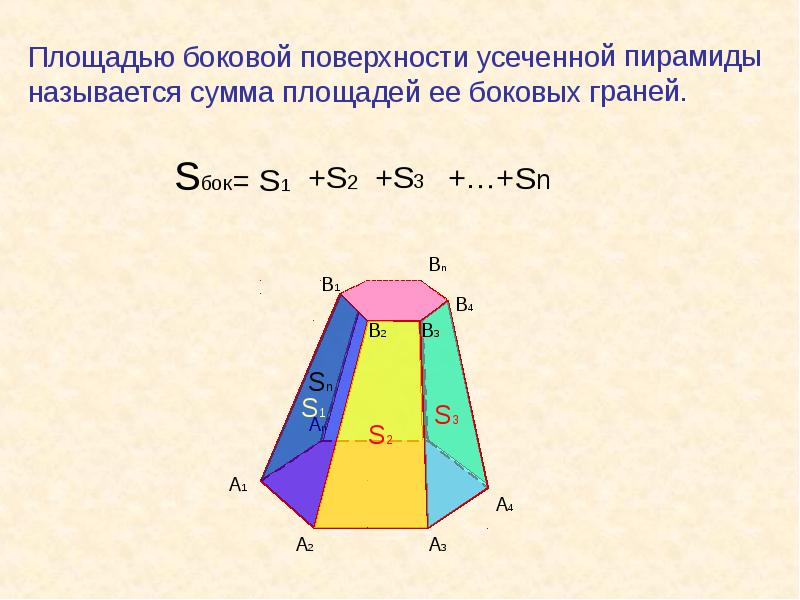
Допустим, что все боковые грани пирамиды наклонены к плоскости основания под углом , и высота пересекает основание.
Возникает вопрос: чему будет равна площадь ее боковой поверхности.
3. Индивидуальная работа (на базе имеющихся знаний) — 10 мин.:
Задание 1 (каждому учащемуся раздается карточка с заданиями).
1. Запишите в тетради тему мастерской «Площадь поверхности пирамиды».
2. В учебнике Е.В. Потоскуева, Л.И. Звавича на стр. 118 изучите теорему 18 и разберите её доказательство.
Если все боковые грани пирамиды наклонены к плоскости основания под углом , и высота пересекает основание, то .
3. Решите задачу №2.251 из задачника, применив теорему 18.
2.251. Найдите площадь боковой поверхности правильной треугольной пирамиды, если сторона основания и боковое ребро образует с плоскостью основания угол в .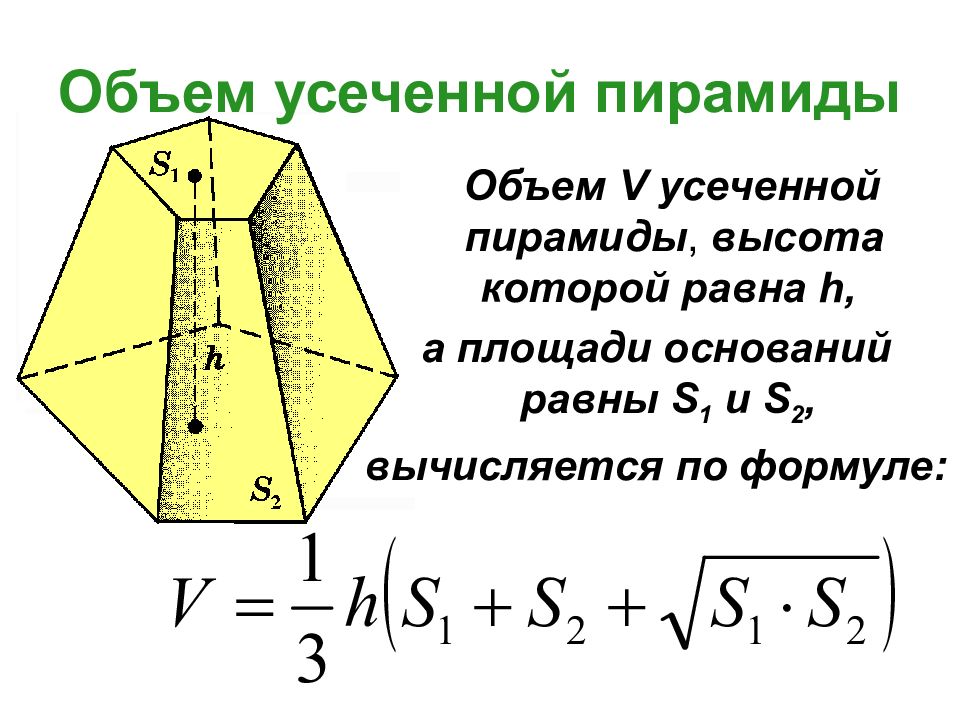
Решение задачи получится следующее:
Применяем формулу .
По формуле площади равностороннего треугольника находим , тогда .
Ответ: .
Зафиксируйте ответы в тетради. Выполните корректировку записей после обсуждения в паре.
4. Фронтальная работа с классом (выработка общего мнения) – 2 мин.
После обсуждения с учащимися класса выполненных заданий, учитель обобщает полученные результаты: если все боковые грани пирамиды наклонены к плоскости основания под углом , и высота пересекает основание, то площадь ее боковой поверхности будет вычисляться по формуле: .
Учитель: предположим, что пирамида пересечена плоскостью, параллельной основанию. Возникает вопрос: о какой пирамиде идет речь и как вычислить площадь ее боковой и полной поверхности.
5. Работа в группах – 18 мин
Задание 2 (выдается каждой группе).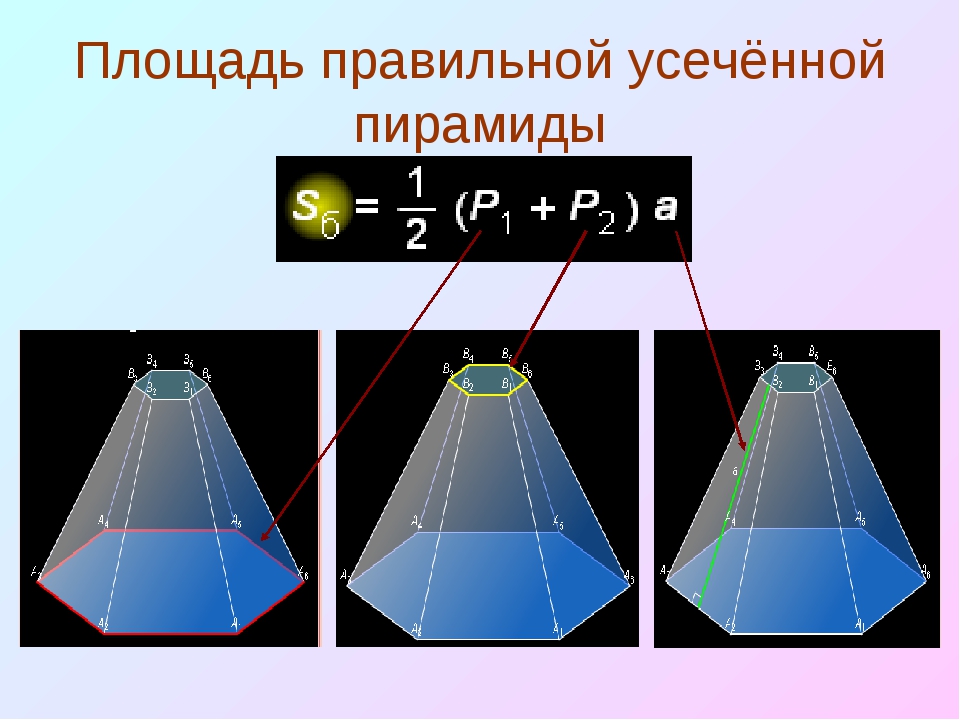 Обсудите в группе ответы на предложенные вопросы и запишите ответы в тетрадь. Если возникнут затруднения, воспользуйтесь учебником.
Обсудите в группе ответы на предложенные вопросы и запишите ответы в тетрадь. Если возникнут затруднения, воспользуйтесь учебником.
1. На какие два многогранника поделилась пирамида на Рис.3?
2. Что за фигура лежит в плоскости ?
3. Что за фигура лежит в плоскости ?
4. Назовите основания усеченной пирамиды.
5. Что лежит в боковых гранях усеченной пирамиды?
6. Что является высотой усеченной пирамиды?
7. Что является апофемой усеченной пирамиды?
В результате выполнения задания 2 предполагается получить такие ответы:
1. Пирамида и многогранник.
2. Пирамида .
3. Многогранник .
Учитель: «Говорят, что многогранник называется усеченной пирамидой».
4. Нижнее основание, верхнее основание.
5. Равнобедренные трапеции.
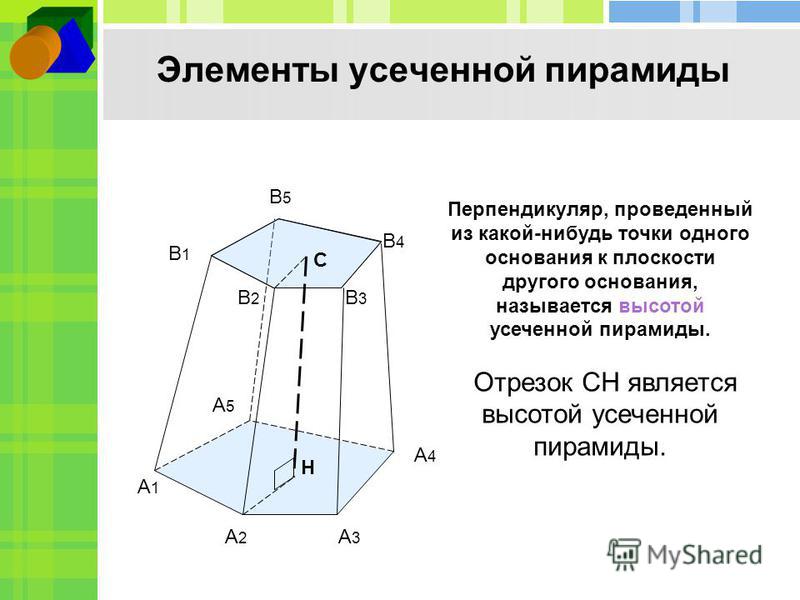
6. Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого» [11, C. 121].
7. Высота трапеций, лежащих в боковых гранях, соединяющие середины их оснований.
Задание 3 (выдается каждой группе).
Группа 1. На стр. 132 учебника прочитайте теорему 20 и приведите доказательства данной теоремы.
Группа 2. Докажите формулу для нахождения площади боковой поверхности усеченной пирамиды . На стр. 132 учебника воспользуйтесь подсказкой.
6. Комментарии учителя (акцентирование внимания на ключевых моментах, выделение находок, ошибок) – 5 мин.
7. Обсуждение мастерской (подведение общих итогов, формулирование нерешенных проблем) – 5 мин.
1. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему: , где периметр, высота апофема.
2. Если все боковые грани пирамиды наклонены к плоскости основания под углом , и высота пересекает основание, то .
3. Усеченная пирамида – это часть полной пирамиды, заключенная между ее основанием и параллельным ему сечением.
4. Для нахождения правильной усеченной пирамиды существует 2 формулы:
1) , где периметры нижнего и верхнего оснований усеченной пирамиды, ее апофема;
2) , где , площади большего и меньшего оснований пирамиды, угол наклона бокового ребра к плоскости основания.
8. Задание на дом – 2 мин. (§14.4-14.6; подготовить сообщение об истории развития понятия площади фигур в математи)
Список рекомендованной литературы:
Глейзер Г.И. История математики в школе 7-8 кл. Пособие для учителей. – М.: Просвещение, 1982. – 240 с.
Малых А.
 Е., Данилова В.И. Влияние геометрической алгебры Древней Греции на развитие математики // Вестник Пермского Университета. Серия: Математика. Механика. Информатика. – 2012. — №2. – С. 76-85. URL: http://elibrary.ru/download/51343972.pdf
Е., Данилова В.И. Влияние геометрической алгебры Древней Греции на развитие математики // Вестник Пермского Университета. Серия: Математика. Механика. Информатика. – 2012. — №2. – С. 76-85. URL: http://elibrary.ru/download/51343972.pdfМалых А.Е. Площади геометрических фигур: учеб. пособие / А.Е. Малых, М.И. Глухова: Перм. гос. пед. ун-т. – Пермь, 2011. – 108 с.
Приложение 1
В результате выполнения домашней работы предполагаются получить следующие развертки пирамиды:
1 вариант:
Развертка правильной треугольной пирамиды Модель пирамиды
2 вариант:
Развертка правильной четырехугольной Модель пирамиды
пирамиды
3 вариант:
Развертка правильной пятиугольной Модель пирамиды
пирамиды
100 ballov.
 kz образовательный портал для подготовки к ЕНТ и КТА
kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Задачи на усеченную пирамиду
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.
Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) Sполн = S бок + Sосн, где
Sполн – площадь полной поверхности пирамиды;
Sбок – площадь боковой поверхности, т.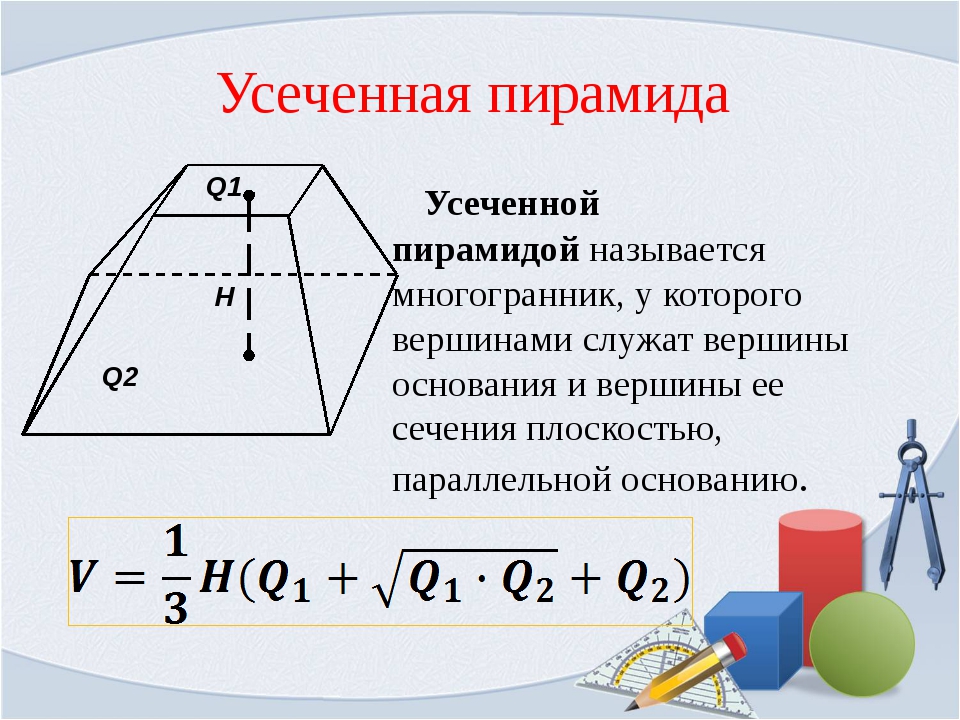 е. сумма площадей всех боковых граней пирамиды;
е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 Sосн · Н, где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
Sбок = 1/2 Pосн h, где
Pосн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.
Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) Sполн = Sбок + S1 + S2, где
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S1, S2 – площади оснований;
2) V = 1/3( S1 + S2 + √(S1 · S2 ))H, где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
Sбок = 1/2(P1 + P2) · h, где
P1 , P2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).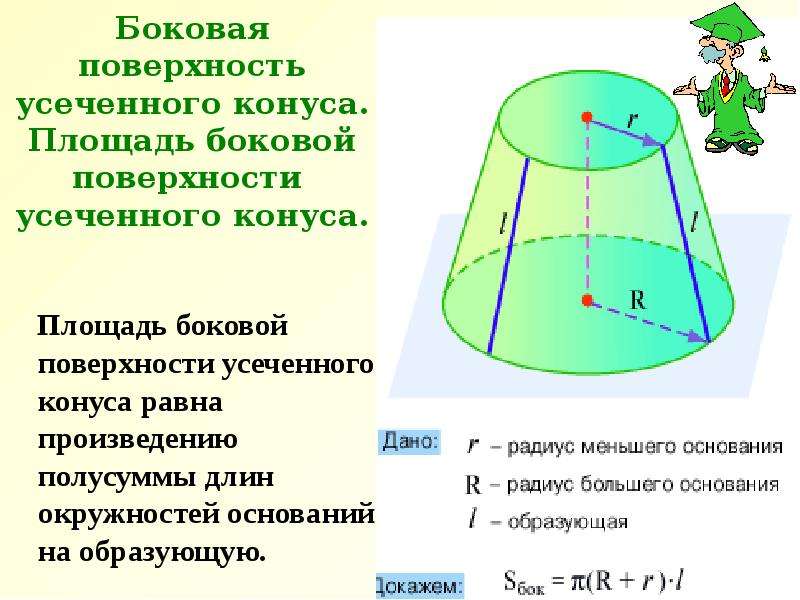
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА1В1С1, изображенную на рисунке1.
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S1 + S2 + √(S1 · S2)), где S1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p1 = (27 + 29 + 52)/2 = 54.
S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Отсюда S2 = 4S1/9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?
Решение.
Рассмотрим АВСА1В1С1 – усеченную пирамиду, изображенную на рис. 2.
2.
Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А1В1С1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S1 + S2 + √(S1 · S2)) = 1/3h · (4S2 + S2 + 2S2) = 7/3 · h · S2, где S2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA1B1C1 составляет V1 = S2 · h и, значит,
V2 = V – V1 = 7/3 · h · S2 — h · S2 = 4/3 · h · S2.
Итак, V2 : V1 = 3 : 4.
Ответ: 3 : 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА1В1С1D1, изображенную на рис. 3.
Обозначим О1О2 = х, тогда ОО₂ = О1О – О1О2 = 3 – х.
Рассмотрим треугольник В1О2D1 и треугольник ВО2D:
угол В1О2D1 равен углу ВО2D как вертикальные;
угол ВDO2 равен углу D1B1O2 и угол O2ВD равен углу B1D1O2 как накрест лежащие при B1D1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В1О2D1 подобен треугольнику ВО2D и имеет место отношение сторон:
В1D1/ВD = О1О2/ОО2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В1D1В и треугольник LО2B: угол В – общий, а так же имеется пара односторонних углов при B1D1 || LM, значит, треугольник В1D1В подобен треугольнику LО2B, откуда В1D : LO2 = OO1 : OO2 = 3 : 2, т.е.
LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.
Тогда SKLMN = 16/9 · SA1B1C1D1 = 16/9.
Итак, V1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Добро пожаловать!10 «А»
Материалы и задания на период с 13 по 18 апреля
Информатика
Обратная связь: gruzd.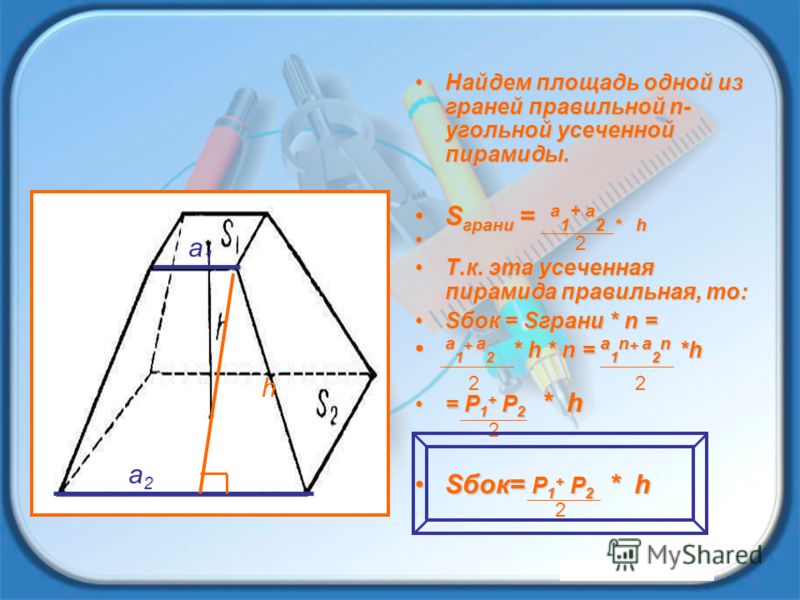 [email protected]
[email protected]
Дата | Тема | Ресурс | Домашнее задание |
13.04 – 18.04 | Проверочная работа | Якласс | Выполнить задания в разделе «Проверочные работы» |
Математика 10 класс
13 апреля (понедельник)
Понятие многогранника. Выпуклые многогранники.
Призма. Прямая, правильная и наклонная призмы. Площадь полной поверхности призмы.
П.27,30,№221
13 апреля (понедельник)
Площадь боковой поверхности прямой призмы. Решение задач на нахождение площади поверхности призмы
П. 30,№229(б,в),231
30,№229(б,в),231
14 апреля (вторник)
Пирамида. Площадь полной поверхности пирамиды
П.32,№239,241
15 апреля (среда)
Площадь боковой поверхности правильной пирамиды
П.33,№258
16 апреля (четверг)
Усечённая пирамида. Площадь боковой поверхности правильной усечённой пирамиды
П.34,№266
Основы математической логики
сайт Решу ЕГЭ апрельские варианты №1,2(база, профиль по выбору учащихся)
Выполненные домашние работы (с заданиями именно на этот урок) отправлять в день урока с 8.30 до 15.00 на электронную почту [email protected] ,подписать фамилию, класс, дату.
Необходимо сделать фото работы и прикрепить файлы.
Убедительная просьба фото переворачивать.
Желаю успехов!
Литература
Обратная связь: [email protected], Тел. 8 909 2805938
Дата | Тема | Ресурсы | Задание |
16. | Анализ эпизода «Аустерлицкое сражение» | Том I, часть III, главы XI-XIX https://yadi.sk/i/hHENQuv46_2j7Q | Сделайте презентацию «Роль эпизода в романе. «Аустерлицкое сражение», используя план. Фото в помощь прилагаю. 1.Сцена военного совета (Как ведут себя генералы? Сравните их поведение с поведением Кутузова. Зачем эта сцена введена в роман? Какую роль в его идейном содержании она играет?) 2. Что чувствует и что думает князь Андрей перед Аустерлицским сражением? Как эти мысли и чувства характеризуют героя? 3.Подвиг Андрея Болконского в битве при Аустерлице(Зачем он его совершил, ведь исход битвы был уже предрешён?) 4.Описание «высокого неба» Аустерлица (Что же понял князь Андрей, глядя на высокое небо?) 5. О чём после Аустерлица мечтает князь Андрей? |
17. |
История России
Обратная связь: [email protected], региональный интернет-дневник, 89807439979 (Viber, WhatsApp)
Дата | Тема | Электронный ресурс | Задание |
15.04 | Изменения в политической системе в послевоенные годы | П 28 | Составить таблицу из 2 столбиков
|
16.04 | Смена политического Курса | П 31 https://yandex. | Стр 119 вопрос 1 ( вопросы и задания для работы с текстом параграфа) письменно |
Обществознание
Обратная связь: [email protected]
1) Практическая работа (эссе) : «Легитимация власти. Легитимная власть школьного самоуправления». Дать определение термина «легитимность», представить свое видение школьного самоуправления и его значение для ученика и учителя» (письменно).
2) Практическая работа (эссе): «Имидж лидера. Значение харизматичности политического лидера».
Общество (электив)
Обратная связь: [email protected]
Выполнение ранее заявленных практических работ.
Право
Обратная связь: [email protected]
1) Практическая работа (глава 2 Конституции): «Судебная система РФ. Гражданские права и обязанности ученика школы по Конституции Российской Федерации».
2) Практическая работа (эссе): «А судьи кто?» (анализ факта (на 2-х примерах) безусловного исполнения решений суда и причины оспаривания судебных решений).
Дополнительный Интернет-ресурс: interneturok.ru. Сайт имеет разработанные конспекты, видео запись по урокам «Обществознание», «Право».
Английский язык (Шеремет А. В.)
Обратная связь: [email protected]
Дата | Тема урока | Ресурс | Домашнее задание |
13.04 – 18.04 | Мир возможностей. Путешествие как способ расширить свой кругозор. Известные программы обмена для школьников за рубежом. | Учебник | Стр 128 № 1,2. №8, №9 выписать в тетрадь с примерами. № 10 |
Английский язык (Вельс А. Е.)
Обратная связь: [email protected]
Дата | Тема | Ресурс | Домашнее задание |
13.04 – 18.04 | «Роботизация в современном мире» | Учебник | Упр16,стр 132 читать вслух, перевод письменно. |
«Хобби» | Учебник | Упр 22,23 стр 133, письменно | |
«Хобби» | Учебник | Упр 30, стр 135, письменно |
Технология
Обратная связь: zhirnov. [email protected]
[email protected]
Дата | Тема урока | Домашнее задание |
13.04 – 18.04 | Творческий проект | Начать разработку проекта садовой мебели для дачи |
Технология (Ширнина Г. Н.)
Обратная связь: [email protected]
Дата | Тема. | Задание |
17.04.20 | Виды творческой деятельности. Ее влияние на развитие качеств личности.
Информацию найти в интернете
| Подготовить Письменное сообщение по теме |
Химия (Ширнина Г. Н.)
Обратная связь: [email protected]
Дата | Тема. | Задание |
13.04.20 | Сложные эфиры. Жиры. Углеводы. | П.16 Стр. 86 зад. 1-5 П.17 Стр. 92 зад. 1-7 |
Биология
Обратная связь: 89622083433, [email protected]
География
Обратная связь: [email protected]
Дата | Тема | Электронный ресурс | Домашнее задание |
13.04 – 18.04 | География отраслей мирового хозяйства. | https://yandex.ru/video/preview/?filmId=426646546480452653 | Тема 5 Пар.1 Стр.183 задание 10, 12,13. |
ОБЖ
Обратная связь: [email protected]
Дата | Тема | Электронный ресурс | Домашнее задание |
13.04 – 18.04 | Виды кровотечений. Правила остановки артериального и венозного кровотечения. Виды повязок. Первая помощь при переломах и кровотечениях. | https://yandex.ru/video/preview/?filmId=1075333292587986648 | Составить таблицу «Виды кровотечений и правила остановки кровотечений» |
Астрономия
Обратная связь: региональный интернет-дневник
Наша Галактика. | Размеры и строение Галактики. Расположение и движение Солнца. Плоская и сферическая подсистемы Галактики. Ядро и спиральные рукава Галактики. Вращение Галактики и проблема «скрытой массы» | 13-18 апреля |
Физика
Обратная связь: региональный интернет-дневник
Электрическое поле. Напряженность электрического поля. | §59, стр.318 | 13-18 апреля |
Графическое изображение электрических полей | §60, стр.324 | 13-18 апреля |
Объем усеченной квадратной пирамиды Калькулятор
- Цель использования
- Поиск объема
- Комментарий / Запрос
- Расскажите, пожалуйста, формула объема усеченной прямоугольной пирамиды
[1] 2020/07/10 20:40 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- help проверка уравнений для домашнего задания по математике
[2] 2020/02/11 05:52 Мужчина / До 20 лет / Начальная школа / Младший школьник / Очень /
- Цель использования
- Рассчитать объем запасов для хранения выкопанного грунта на строительной площадке
[3] 2020/01/16 05:00 Мужчина / 20-летний уровень / Инженер / Очень /
- Цель использования
- Проектирование акустической системы метронома.
[4] 2020/01/04 23:24 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- Двойная проверка расчетов объема
- Комментарий / запрос
- Для проверки использовалось это уравнение расчеты объема и расхода, полученные из уравнения сохранения массы. Это оказался отличный ресурс.
[5] 2019/10/21 21:53 Мужчина / 30-летний уровень / Инженер / Очень /
- Цель использования
- Расчет объема бетона, необходимого для заполнения формы
[6] 2019/07/02 22:44 Мужчина / 50 лет / Инженер / Очень /
- Цель использования
- Расчет объема стального слитка, произведенного на заводе по переработке расплава радиоактивных металлов в Швеции.
[7] 2019 / 06/25 01:17 Мужчина / Уровень 30 лет / Инженер / Очень /
- Цель использования
- Расчетный проект
[8] 17.06.2019 17:54 Женщина / Уровень 20 лет / Инженер / Очень /
- Цель использования
- Назначение
- Комментарий / запрос
- Я не совсем понимаю формулу площади
[9] 22.05.2019 17: 11 Мужчина / До 20 лет / Средняя школа / Университет / аспирант / Немного /
- Цель использования
- оценка
[10] 2019 / 05/17 17:38 Мужчина / Уровень 20 лет / Офисный работник / Государственный служащий / Полезно /
Площадь поверхности пирамиды — объяснение и примеры
Прежде чем мы начнем, давайте рассмотрим, что такое пирамида.В геометрии пирамида — это трехмерное твердое тело, основание которого — любой многоугольник, а боковые грани — треугольники.
В пирамиде боковые грани (которые представляют собой треугольники) встречаются в общей точке, известной как вершина. Название пирамиды происходит от названия многоугольника, образующего ее основу. Например, квадратная пирамида, прямоугольная пирамида, треугольная пирамида, пятиугольная пирамида и т. Д.
Площадь поверхности пирамиды — это сумма площадей боковых граней.
В этой статье будет обсуждаться, как найти общую площадь поверхности и площадь боковой поверхности пирамиды .
Как найти площадь поверхности пирамиды?
Чтобы найти площадь поверхности пирамиды, вам нужно получить площадь основания, а затем добавить площадь боковых сторон, которая равна одной грани, умноженной на количество сторон.
Поверхность пирамиды, формула
Общая формула для площади поверхности любой пирамиды (правильной или неправильной) дается как:
Площадь поверхности = Площадь основания + Боковая площадь
Площадь поверхности = B + LSA
Где TSA = общая площадь поверхности
B = площадь основания
LSA = площадь боковой поверхности.
Для правильной пирамиды формула имеет следующий вид:
Общая площадь поверхности правильной пирамиды = B + 1/2 ps
, где p = периметр основания и s = наклонная высота.
Примечание. Никогда не путайте наклонную высоту (ы) и высоту (h) пирамиды. Расстояние по перпендикуляру от вершины до основания пирамиды называется высотой (h), а расстояние по диагонали от вершины пирамиды до края основания называется наклонной высотой (ями).
Площадь поверхности квадратной пирамиды
Для квадратной пирамиды общая площадь поверхности = b (b + 2s)
Где b = длина основания и s = наклонная высота
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды = ½ b (a + 3s)
Где a = длина апофемы пирамиды
b = длина основания
s = наклонная высота
Площадь поверхности пятиугольной пирамиды
Общая площадь правильной пятиугольной пирамиды равна;
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
Где a = апофема длина основания
и b = длина стороны основания, s = наклонная высота пирамиды
Площадь поверхности шестиугольной пирамиды
Гексагональная пирамида — это пирамида с шестиугольником в основании.
Общая площадь поверхности шестиугольной пирамиды = 3b (a + s)
Площадь боковой поверхности пирамиды
Как говорилось ранее, площадь боковой поверхности пирамиды — это площадь боковых граней пирамиды. Поскольку все боковые грани пирамиды представляют собой треугольники, площадь боковой поверхности пирамиды равна половине произведения периметра основания пирамиды и высоты наклона.
Площадь боковой поверхности (LSA = 1/2 ps)
Где p = периметр основания и s = наклонная высота.
Давайте разберемся с площадью поверхности формулы пирамиды, решив несколько примеров задач.
Пример 1
Какова площадь поверхности квадратной пирамиды с длиной основания 4 см и высотой наклона 5 см?
Решение
Дано:
Длина основания, b = 4 см
Наклонная высота, s = 5 см
По формуле
Общая площадь квадратной пирамиды = b (b + 2s)
TSA = 4 (4 + 2 x 5)
= 4 (4 + 10)
= 4 x 14
= 56 см 2
Пример 2
Какова площадь поверхности квадратная пирамида с перпендикулярной высотой 8 м и длиной основания 12 м?
Решение
Дано;
Высота по перпендикуляру, h = 8 м
Длина основания, b = 12
Чтобы получить наклонную высоту s, применим теорему Пифагора.
с = √ [8 2 + (12/2) 2 ]
с = √ [8 2 + 6 2 ]
с = √ (64 + 36)
с = √100
= 10
Следовательно, наклонная высота пирамиды составляет 10 м
Теперь вычислите площадь поверхности пирамиды.
SA = b (b + 2s)
= 12 (12 + 2 x 10)
= 12 (12 + 20)
= 12 x 32
= 384 м 2 .
Пример 3
Вычислите площадь поверхности пирамиды, наклонная высота которой составляет 10 футов, а ее основание представляет собой равносторонний треугольник с длиной стороны 8 футов.
Решение
Дано:
Базовая длина = 8 футов
Наклонная высота = 10 футов
Примените теорему Пифагора, чтобы получить длину апофемы пирамиды.
a = √ [8 2 — (8/2) 2 ]
= √ (64 — 16)
= √48
a = 6,93 фута
Таким образом, длина апофемы пирамиды составляет 6,93 фута
Но площадь поверхности треугольной пирамиды = ½ b (a + 3s)
TSA = ½ x 8 (6.93 + 3 x 10)
= 4 (6,93 + 30)
= 4 x 36,93
= 147,72 футов 2
Пример 4
Найдите площадь поверхности пятиугольной пирамиды, длина апофемы которой составляет 8 м, длина основания 6 м, высота уклона 20 м.
Решение
Дано;
Длина апофемы, a = 8 м
Длина основания, b = 6 м
Наклонная высота, s = 20 м
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
TSA = 5 / 2 x 6 (8 + 20)
= 15 x 28
= 420 м 2 .
Пример 5
Рассчитайте общую площадь поверхности и площадь боковой поверхности шестиугольной пирамиды с апофемой 20 м, длиной основания 18 м и наклонной высотой 35 м.
Решение
Дано;
апофема, a = 20 м
Длина основания, b = 18 м
Наклонная высота, s = 35 м
Площадь поверхности шестиугольной пирамиды = 3b (a + s)
= 3 x 18 ( 20 + 35)
= 54 x 55
= 2970 м 2 .
Площадь боковой поверхности пирамиды = 1/2 пс
Периметр, p = 6 x 18
= 108 м
LSA = ½ x 108 x 35
= 1890 м 2
Предыдущий урок | Главная страница | Следующий урок
Площадь пирамиды
В
боковой
площадь поверхности
регулярного
пирамида
— сумма площадей его боковых граней.
В
общая площадь правильной пирамиды
— сумма площадей его боковых граней и основания.
Общая формула для
площадь боковой поверхности
правильной пирамиды
L
.
S
.
А
.
знак равно
1
2
п
л
где
п
представляет периметр основания и
л
наклонная высота.
Пример 1:
Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждое ребро основания имеет размер
8
дюймов и наклонная высота
5
дюймы.
Периметр основания равен сумме сторон.
п
знак равно
3
(
8
)
знак равно
24
дюймы
L
.S
.
А
.
знак равно
1
2
(
24
)
(
5
)
знак равно
60
дюймы
2
Общая формула для
общая площадь поверхности
правильной пирамиды
Т
.S
.
А
.
знак равно
1
2
п
л
+
B
где
п
представляет периметр основания,
л
наклонная высота и
B
площадь основания.
Пример 2:
Найдите общую площадь поверхности правильной пирамиды с квадратным основанием, если каждое ребро основания имеет размер
16
дюймов, наклонная высота стороны составляет
17
дюймов и высота
15
дюймы.
Периметр основания равен
4
s
так как это квадрат.
п
знак равно
4
(
16
)
знак равно
64
дюймы
Площадь базы составляет
s
2
.
B
знак равно
16
2
знак равно
256
дюймы
2
Т
.
S
.
А
.знак равно
1
2
(
64
)
(
17
)
+
256
знак равно
544
+
256
знак равно
800
дюймы
2
Не существует формулы для площади поверхности неправильной пирамиды, поскольку не определена наклонная высота.Чтобы найти
области, найдите площадь каждой грани и площадь основания и сложите их.
Калькулятор площади
| Определение
Этот калькулятор площади поверхности поможет вам найти площадь наиболее распространенных трехмерных тел. Если вы когда-нибудь задумывались, как найти площадь поверхности или площадь боковой поверхности, этот калькулятор здесь, чтобы вам помочь. В этой статье вы можете найти формулы для площади поверхности сферы, куба, цилиндра, конуса, пирамиды и прямоугольной / треугольной призмы.Мы также объясним, как вычислить площадь поверхности сферы в качестве примера.
Что такое площадь поверхности? Определение площади поверхности
Площадь поверхности — это общая площадь, которую занимает поверхность объекта . Другими словами, это общая площадь поверхности 3D-объекта.
Иногда площадь поверхности может быть разделена на сумму базовой площади (ов) и площади боковой поверхности . Боковая поверхность — это площадь всех сторон объекта, за исключением его основания и вершины.Это разделение используется для форм, где существует очевидное различие между основанием и другой частью — например, для цилиндра, конуса, пирамиды или треугольной призмы. Он редко применяется к твердым телам, для которых мы не уверены, какие грани следует рассматривать как основы (например, в кубе или коробке), и мы не используем его для гладких поверхностей, таких как сфера.
Формула площади поверхности …
Наш калькулятор площади поверхности может найти площадь поверхности семи различных твердых тел. Формула зависит от типа твердого тела.
- Площадь поверхности сферы:
A = 4πr², где r обозначает радиус сферы. - Площадь поверхности куба:
A = 6a², где a — длина стороны. - Площадь цилиндра:
A = 2πr² + 2πrh, где r — радиус, а h — высота цилиндра. - Площадь конуса:
A = πr² + πr√ (r² + h²), где r — радиус, а h — высота конуса. - Площадь поверхности прямоугольной призмы (прямоугольник):
A = 2 (ab + bc + ac), где a , b и c — длины трех сторон кубоида. - Площадь поверхности треугольной призмы:
A = 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) + h * (a + b + c), где a , b и c — это длины трех сторон основания треугольной призмы, а h — высота (длина) призмы. - Площадь поверхности пирамиды:
A = l * √ (l² + 4 * h²) + l², где l — длина стороны квадратного основания, а h — высота пирамиды.
Но откуда берутся эти формулы? Как найти площадь поверхности основных трехмерных фигур? Продолжайте читать, и вы узнаете!
Площадь поверхности сферы
Чтобы рассчитать площадь поверхности сферы, все, что вам нужно знать, — это радиус сферы или ее диаметр.
-
A = 4 * π * r², гдеr— радиус.
Поскольку мы знаем, что диаметр сферы равен двум радиусам d = 2r , мы можем преобразовать уравнение в другую форму:
-
A = 4 * π * (d / 2) ² = π * d², гдеd— диаметр сферы.
Для вывода этой формулы площади поверхности требуется интегрирование. Если вам интересно, посмотрите это доказательство.
Площадь цилиндра
Чтобы узнать площадь поверхности цилиндра, у вас должно быть два значения: радиус (или диаметр) основания и высота цилиндра.Общее уравнение обычное — площадь основания умножить на высоту . В нашем случае круг — это основа.
Откуда взялась эта формула? Вы можете записать уравнение для площади поверхности цилиндра как:
-
A = A (сбоку) + 2 * A (основание)
Найти площадь основания несложно — запомним известную формулу площади круга: A (основание) = π * r² . Но какова форма боковой поверхности? Попробуйте представить, что мы его «разворачиваем».Вы узнаете это? Это прямоугольник ! Длина одной стороны равна высоте цилиндра, а вторая — окружности развернутого круга.
-
A (база) = π * r² -
A (сбоку) = h * (2 * π * r)
Площадь конуса
Мы можем разделить поверхность конуса на две части:
-
A = A (боковой) + A (основание), так как у нас только одно основание, в отличие от цилиндра.
Основание — это снова площадь круга A (основание) = π * r² , но происхождение площади боковой поверхности может быть не так очевидно:
-
A (боковой) = π * r * √ (r² + h²)
Давайте посмотрим на этот вывод шаг за шагом:
- Раскатайте боковую поверхность. Это круговой сектор, который является частью окружности с радиусом s ( s — наклонная высота конуса).
- Для окружности с радиусом s, длина окружности равна
2 * π * s. Длина дуги сектора равна2 * π * r. - Площадь сектора , который является нашей боковой поверхностью конуса, определяется по формуле:
-
A (сбоку) = (s * (длина дуги)) / 2 = (s * 2 * π * r) / 2 = π * r * s
Формула может быть получена из пропорции: отношение площадей фигур такое же, как отношение длины дуги к окружности:
(площадь сектора) / (площадь большого круга) = (длина дуги) / (окружность большого круга) так:
(площадь сектора) / (π * s²) = (2 * π * r) / (2 * π * s)
(площадь сектора) = (π * s²) * (2 * π * r) / (2 * π * s)
- Обычно нам задают не значение
s, аh, что составляет высоту конуса. Но это совсем не проблема! Мы можем легко преобразовать формулу, используя теорему Пифагора:
Таким образом, формула площади боковой поверхности выглядит следующим образом:
-
A (боковой) = π * r * √ (r² + h²)
- Наконец, сложите площади основания и боковой части, чтобы найти окончательную формулу для площади поверхности конуса :
-
A = A (сбоку) + A (основание) = π * r * s + π * r²дляrиsили -
A = π * r * √ (r² + h²) + π * r²дляrиh.
Площадь куба
Площадь поверхности куба — это самое простое, что вы можете себе представить: каждая из сторон представляет собой квадрат! Поскольку каждый куб имеет шесть одинаковых квадратных граней, площадь поверхности равна:
Поскольку площадь квадрата является произведением длины его сторон, окончательная формула для определения площади поверхности куба будет:
-
A = 6 * l², гдеl— сторона квадрата
Площадь пирамиды
Пирамида — это трехмерное тело с многоугольным основанием и треугольными боковыми гранями.Когда вы слышите пирамида , обычно предполагается, что это правильная квадратная пирамида . Обычный означает, что он имеет правильное основание многоугольника и представляет собой правую пирамиду (вершина прямо над центром тяжести его основания) и квадрат — что он имеет эту форму в качестве основания. Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности.
Формула площади поверхности пирамиды:
-
A = l * √ (l² + 4 * h²) + l², гдеl— сторона основания, аh— высота пирамиды
Опять же, мы можем разделить уравнение на:
-
A = A (основание) + A (сбоку) = A (основание) + 4 * A (боковая поверхность)
Основание имеет форму квадрата, поэтому A (основание) = l² .Чтобы рассчитать площадь боковой поверхности, начнем с площади одной треугольной грани:
- Чтобы найти высоту треугольника, нам снова понадобится формула гипотенузы:
- Вычислите гипотенузу треугольника ABC (которая одновременно является высотой треугольной грани):
-
c = √ (h² + (l / 2) ²) = √ (h² + l² / 4)
- Площадь треугольника (в нашем случае это равнобедренный треугольник) можно рассчитать как:
-
A = высота * основание / 2так -
A (боковая сторона) = √ (h² + l² / 4) * l / 2
- Итак, окончательная формула площади поверхности пирамиды:
-
A = l² + 4 * √ (h² + l² / 4) * l / 2 = l² + 2 * l * √ (h² + l² / 4) -
A = l² + l * √ (4 * h² + l²)
Площадь прямоугольной призмы
Чтобы вычислить площадь поверхности прямоугольной призмы, все, что вам нужно сделать, это вычислить площади сторон прямоугольника:
где:
-
A1 = длина * ширина -
A2 = ш * в -
A3 = длина * высота
Таким образом, окончательная формула:
-
A = 2 * (д * ш + ш * в + д * в)
Площадь поверхности треугольной призмы
Чтобы понять, откуда взялась формула для площади поверхности треугольной призмы, давайте взглянем на этот вывод:
- Часть площади боковой поверхности в этом случае легко вычислить.Как видно из рисунка, он состоит из трех прямоугольников с общей длиной одной стороны:
-
A (сбоку) = a * h + b * h + c * h = h * (a + b + c)
, который мы также можем записать сокращенно:
-
A (боковой) = h * P, гдеP— периметр базового треугольника
- Затем найдите площадь треугольного основания. Вы можете сделать это разными способами, в зависимости от того, что вам дают. В нашем калькуляторе мы реализовали расчет на основе формулы Герона — она используется, когда у вас есть три стороны треугольника (SSS).
A (основание) = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)))
- Окончательная формула площади поверхности треугольной призмы:
-
A = A (сбоку) + 2 * A (основание) -
A = h * (a + b + c) + 0,5 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c ))
Площадь поверхности тела
Вы можете рассчитать поверхность любого твердого тела, например, вашего тела — это не обязательно должна быть простая геометрическая форма! Если вам интересно, какова площадь внешней поверхности человеческого тела, воспользуйтесь этим калькулятором площади поверхности тела.
Как рассчитать площадь поверхности шара?
Если вы хотите найти площадь поверхности сферы, вам необходимо выполнить следующие действия:
- Определите радиус сферы. Можно принять радиус 10 см.
- Введите это значение в формулу
A = 4πr². - Рассчитайте результат:
A = 4π * 10² = 1256 см². - Вы также можете использовать этот калькулятор площади поверхности, чтобы найти радиус сферы, если вы знаете ее площадь.
Прочие соображения
Единицами площади поверхности всегда являются квадратные единицы длины. Например, вы можете выразить это в см², дюймах, фут², м², а также в акрах и гектарах.
Если вы хотите определить объем любого из этих твердых веществ, воспользуйтесь нашим калькулятором объема.
Объем усеченной призмы прямоугольный. Площадь боковой поверхности усеченной пирамиды
- 22.09.2014
Принцип действия. Когда вы нажимаете кнопку первой цифры кода SA1, DD1.1 триггер переключится и на входе D высокого уровня триггера DD1.2 появится напряжение … Следовательно, при нажатии следующей кнопки кода SA2 триггер DD1.2 меняет свое состояние и готовит следующий триггер для переключение. При дальнейшем правильном наборе триггер DD2.2 сработает последним, и …
- 03.10.2014
Предлагаемое устройство стабилизирует напряжение до 24В и ток до 2А с защитой от короткого замыкания. В случае нестабильного запуска стабилизатора следует применять синхронизацию от автономного генератора импульсов Рис.2. Схема стабилизатора представлена на рис. 1. На VT1 VT2 собран триггер Шмитта, управляющий мощным регулирующим транзистором VT3. Детали: VT3 оснащен радиатором …
- 20.09.2014
Усилитель (см. Фото) выполнен по традиционной схеме с автоподзаводом на лампах: выходные — AL5, драйверы — 6G7, кенотрон — AZ1. Схема одного из двух каналов стереоусилителя представлена на рис. 1. С регулятора громкости сигнал поступает на сетку лампы 6Г7, усиливается и с анода этой лампы через разделительный конденсатор С4 поступает. к …
- 15.11.2017
NE555 — универсальный таймер — устройство для формирования (генерации) одиночных и повторяющихся импульсов со стабильными временными характеристиками. Это асинхронный RS-триггер с определенными входными порогами, точно определяемыми аналоговыми компараторами и встроенным делителем напряжения (прецизионный триггер Шмитта с RS-триггером). Из него строят различные генераторы, модуляторы, реле времени, пороговые устройства и др. …
— Это многогранник, который образован основанием пирамиды и параллельным ему участком.Можно сказать, что усеченная пирамида — это пирамида с усеченной вершиной. Эта форма обладает множеством уникальных свойств:
- Боковые грани пирамиды — трапеции;
- Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
- Основания похожи на многоугольники;
- В правильной усеченной пирамиде грани идентичны равнобедренной трапеции, площадь которой равна. Они также наклонены к основанию под таким же углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:
Поскольку стороны усеченной пирамиды являются трапециями, вам нужно будет использовать формулу для вычисления параметров площадь трапеции … Для правильной усеченной пирамиды вы можете применить другую формулу площади. Поскольку все его стороны, грани и углы у основания равны, можно применить периметры основания и апофемы, а также вывести площадь через угол у основания.
Если в соответствии с условиями в правильной усеченной пирамиде заданы апофема (высота боковой стороны) и длины сторон основания, то площадь может быть вычислена через полупродукт суммы периметры оснований и апофемы:
Рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании а = 6 см, а края в меньшем основании b = 4 см.Вычислить площадь усеченной пирамиды.
Сначала определим периметры баз. Поскольку нам дана пятиугольная пирамида, мы понимаем, что основания — это пятиугольники. Это означает, что в основании лежит фигура с пятью одинаковыми сторонами. Находим периметр большего основания:
Таким же образом находим периметр меньшего основания:
Теперь мы можем вычислить площадь правильной усеченной пирамиды. Подставляем данные в формулу:
Таким образом, мы вычислили площадь правильной усеченной пирамиды по периметрам и апофемой.
Еще один способ вычисления площади боковой поверхности правильной пирамиды — формула через углы у основания и площадь этих самых оснований .
Давайте посмотрим на пример расчета. Помните, что эта формула применима только к обычной усеченной пирамиде.
Пусть дана правильная четырехугольная пирамида. Фаска нижнего основания — a = 6 см, а фаска верхнего основания — b = 4 см.Двугранный угол у основания β = 60 °. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Поскольку пирамида правильная, все грани оснований равны друг другу. Учитывая, что в основании есть четырехугольник, мы понимаем, что нужно будет вычислить квадратов площадью … Это произведение ширины и длины, но эти значения в квадрате совпадают.Найдите площадь большего основания:
Теперь используем найденные значения для расчета площади боковой поверхности.
Зная несколько простых формул, мы легко вычислили площадь боковой трапеции усеченной пирамиды через различные значения.
Пирамида называется многогранником, одна из граней которого представляет собой многоугольник ( основание
), а все остальные грани — треугольники с общей вершиной ( боковые грани
) (рис.15). Пирамида называется правильная
, если ее основание представляет собой правильный многоугольник, а вершина пирамиды проецируется на центр основания (рис. 16). Треугольная пирамида, в которой все стороны равны, называется тетраэдром .
.
Боковое ребро пирамида — это сторона боковой грани, не относящаяся к основанию Высота
Пирамидой называется расстояние от ее вершины до плоскости основания.Все боковые грани правильной пирамиды равны между собой, все боковые грани представляют собой равнобедренные треугольники. Высота боковой грани правильной пирамиды, нарисованной сверху, называется апофемой .
. Диагональное сечение
разрез пирамиды называется плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадь боковой поверхности пирамиды называется суммой площадей всех боковых граней. Полная площадь
называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые грани одинаково наклонены к плоскости основания, то вершина пирамиды проецируется в центр окружности, описанной вокруг основания.
2. Если в пирамиде все боковые грани имеют одинаковую длину, то вершина пирамиды проецируется в центр окружности, описанной вокруг основания.
3. Если в пирамиде все грани одинаково наклонены к плоскости основания, то вершина пирамиды проецируется в центр круга, вписанного в основание.
Для расчета объема произвольной пирамиды верна формула:
где V — объем;
S main — базовая площадь;
H — высота пирамиды.
Для правильной пирамиды формулы верны:
где p — периметр основания;
h — апофема;
H — высота;
S полный
Сторона S
S main — базовая площадь;
V — объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельная основанию пирамиды (рис. 17). Правильная усеченная пирамида
называется частью правильной пирамиды, заключенной между основанием и секущей плоскостью, параллельной основанию пирамиды.
Фундаменты усеченных пирамид — аналогичные многоугольники. Боковые поверхности
— трапеция. Высота
усеченная пирамида — это расстояние между ее основаниями. Диагональ
усеченной пирамидой называется отрезок, соединяющий ее вершины, не лежащие на одной грани. Диагональное сечение
разрез усеченной пирамиды называется плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Для усеченной пирамиды действительны следующие формулы:
(4)
, где S 1, S 2 — площади верхнего и нижнего оснований;
S полная — площадь общая;
S сторона — площадь боковой поверхности;
H — высота;
V — объем усеченной пирамиды.
Для правильной усеченной пирамиды формула верна:
где p 1, p 2 — периметры основания;
h a — апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол у основания равен 60º. Найдите тангенс угла наклона боковой кромки к плоскости основания.
Решение. Сделаем чертеж (рис.18).
Пирамида правильная. Это означает, что у основания есть равносторонний треугольник, а все боковые грани представляют собой равнобедренные треугольники. Двугранный угол у основания — это угол наклона боковой грани пирамиды к плоскости основания. Линейный угол — это угол a между двумя перпендикулярами: и т. Е. Вершина пирамиды проецируется в центр треугольника (центр описанной окружности и вписанной окружности в треугольник ABC ).Угол наклона бокового ребра (например, SB ) — это угол между самой кромкой и ее выступом на базовую плоскость. Для ребра SB этим углом будет угол SBD … Чтобы найти касательную, вам нужно знать отрезки SO и OB … Пусть длина отрезка BD равна 3 и … точка О сегмент линии BD делится на части: и Из находим SO : Из находим:
Ответ:
Пример 2. Найдите объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота равна 4 см.
Решение. Чтобы найти объем усеченной пирамиды, воспользуемся формулой (4). Чтобы найти площадь оснований, нужно найти стороны квадратов оснований, зная их диагонали. Стороны оснований 2 см и 8 см соответственно. Итак площади оснований и Подставив все данные в формулу, вычисляем объем усеченной пирамиды:
Ответ: 112 см 3.
Пример 3. Найдите площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем чертеж (рис. 19).
Боковая грань пирамиды представляет собой равнобедренную трапецию. Чтобы рассчитать площадь трапеции, нужно знать основание и высоту. Базы даны по условию, неизвестна только высота.Мы найдем его откуда И 1 E перпендикуляр от точки И 1 на плоскости нижнего основания, A 1 D — перпендикуляр от И 1 на AS . И 1 E = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительный чертеж, на котором изобразим вид сверху (рис. 20). Точка ПРО — проекция центров верхнего и нижнего оснований.поскольку (см. рис. 20) и С другой стороны OK — это радиус вписанной окружности и OM — радиус вписанной окружности:
МК = DE .
По теореме Пифагора из
Площадь боковой грани:
Ответ:
Пример 4. В основании пирамиды лежит равнобедренная трапеция, основания которой и и b ( a > b ).Каждая боковая грань образует угол с базовой плоскостью пирамиды, равный j … Найдите общую площадь поверхности пирамиды.
Решение. Сделаем чертеж (рис. 21). Общая площадь поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .
Воспользуемся утверждением, что если все грани пирамиды одинаково наклонены к плоскости основания, то вершина проецируется на центр окружности, вписанной в основание.Точка ПРО — проекция вершины S на основание пирамиды. Треугольник SOD представляет собой ортогональную проекцию треугольника CSD на плоскость основания. По теореме об ортогональной площади проекции плоская фигура получаем:
Аналогично это означает Таким образом, задача свелась к нахождению площади трапеции ABCD … Нарисуйте отдельно трапецию ABCD (рис. 22). Точка ПРО — центр окружности, вписанной в трапецию.
Так как круг может быть вписан в трапецию, либо From, по теореме Пифагора, имеем
Умение рассчитывать объем пространственных фигур важно при решении ряда практических задач по геометрии. Одна из самых распространенных форм — пирамида. В этой статье мы рассмотрим как полные, так и усеченные пирамиды.
Пирамида как трехмерная фигура
Все знают о египетских пирамидах, поэтому имеют хорошее представление о том, о какой фигуре пойдет речь.Тем не менее, египетские каменные сооружения — лишь частный случай огромного класса пирамид.
Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой пространства, не принадлежащей плоскости основания. Это определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.
Любая пирамида состоит из n + 1 граней, 2 * n ребер и n + 1 вершины. Поскольку рассматриваемая фигура представляет собой совершенный многогранник, номера отмеченных элементов подчиняются равенству Эйлера:
2 * n = (n + 1) + (n + 1) — 2.
Многоугольник в основании дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями показан на фото ниже.
Точка, в которой соединяются n треугольников фигуры, называется вершиной пирамиды. Если от него к основанию опустить перпендикуляр и он пересекает его в геометрическом центре, то такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.
Прямая фигура, основание которой образовано равносторонним (конформным) n-угольником, называется правильной.
Формула объема пирамиды
Мы будем использовать интегральное исчисление для вычисления объема пирамиды. Для этого разделим фигуру плоскостями сечения, параллельными основанию, на бесконечное количество тонких слоев. На рисунке ниже показана четырехугольная пирамида с высотой h и длиной стороны L, в которой слой тонкого сечения отмечен четырехугольником.
Площадь каждого такого слоя можно рассчитать по формуле:
A (z) = A 0 * (h-z) 2 / h 2.
Здесь A 0 — базовая площадь, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0.
Для получения формулы объема пирамиды следует вычислить интеграл по всей высоте фигуры, то есть:
В = ∫ h 0 (A (z) * dz).
Подставляя зависимость A (z) и вычисляя первообразную, приходим к выражению:
V = -A 0 * (h-z) 3 / (3 * h 2) | h 0 = 1/3 * A 0 * h.
Получили формулу объема пирамиды. Чтобы найти значение V, достаточно высоту фигуры умножить на площадь основания, а затем результат разделить на три.
Обратите внимание, что полученное выражение действительно для вычисления объема пирамиды произвольного типа.То есть он может быть наклонным, а его основание может быть произвольным n-угольником.
и его объем
Общая формула для объема, полученная в предыдущем абзаце, может быть уточнена в случае пирамиды с правильным основанием … Площадь такого основания рассчитывается по следующей формуле:
A 0 = n / 4 * L 2 * ctg (пи / п).
Здесь L — длина стороны правильного многоугольника с n вершинами. Символ пи — это пи.
Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:
V n = 1/3 * n / 4 * L 2 * h * ctg (pi / n) = п / 12 * L 2 * h * ctg (пи / п).
Например, для треугольной пирамиды эта формула приводит к следующему выражению:
V 3 = 3/12 * L 2 * h * ctg (60 o) = √3 / 12 * L 2 * h .
Для правильной четырехугольной пирамиды формула объема принимает вид:
V 4 = 4/12 * L 2 * h * ctg (45 o) = 1/3 * L 2 * h.
Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.
Усеченная пирамида
Предположим, мы взяли произвольную пирамиду и отрезали от нее часть боковой поверхности, содержащую вершину. Оставшаяся форма называется усеченной пирамидой. Он уже состоит из двух n-угольных оснований и n соединяющих их трапеций. Если секущая плоскость была параллельна основанию фигуры, то образуется усеченная пирамида с параллельными аналогичными основаниями. То есть длины сторон одного из них можно получить, умножив длины другого на некоторый коэффициент k.
На картинке выше изображен усеченный правильный, видно, что его верхнее основание, как и нижнее, образовано правильным шестиугольником.
Формула, которую можно вывести с помощью аналогичного интегрального исчисления:
V = 1/3 * h * (A 0 + A 1 + √ (A 0 * A 1)).
Где A 0 и A 1 — площади нижнего (большого) и верхнего (малого) оснований соответственно. Переменная h обозначает высоту усеченной пирамиды.
Объем пирамиды Хеопса
Любопытно решить задачу определения объема, который самая большая египетская пирамида содержит внутри себя.
В 1984 году британские египтологи Марк Ленер и Джон Гудман установили точные размеры пирамиды Хеопса. Его первоначальная высота составляла 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составляла 230,363 метра. Основание пирамиды квадратное с высокой точностью.
Мы будем использовать приведенные выше цифры, чтобы определить объем этого каменного гиганта. Поскольку пирамида правильная четырехугольная, то для нее справедлива формула:
Подставляем числа, получаем:
V 4 = 1/3 * (230.363) 2 * 146,5 ≈ 25
м 3.
Объем пирамиды Хеопса составляет почти 2,6 млн м3. Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. М3. То есть, чтобы заполнить всю пирамиду Хеопса, таких бассейнов будет больше 1000. нужный!
Frustum | Math Wiki | Фэндом
- Информацию о графической технике, известной как отсечение усеченной поверхности, см. В разделе «Определение скрытой поверхности». или пирамида, лежащая между двумя параллельными плоскостями, разрезающими твердое тело.Этот термин обычно используется в компьютерной графике для описания трехмерной области, видимой на экране (которая образована обрезанной пирамидой).
Элементы, особые случаи и связанные концепции
Каждая плоская секция представляет собой пол пирамиды. Ось усеченного конуса, если таковая имеется, совпадает с осью исходного конуса или пирамиды. Усеченная пирамида — это круглая , если у нее круглые основания; это правый , если ось перпендикулярна обоим основаниям, и наклонный в противном случае.
Конусы и пирамиды можно рассматривать как вырожденные случаи усеченных пирамид, когда одна из секущих плоскостей проходит через вершину (так что соответствующее основание сводится к точке). Пирамидальные усики являются подклассом призматоидов.
Две фруста, соединенные в основании, образуют двустворчатый ствол.
Формулы
Том
Формула объема усеченной пирамиды была введена древнеегипетскими математиками в так называемом Московском математическом папирусе, написанном ок.1850 г. до н.э .:
, где a и b — длина основания и верхней стороны усеченной пирамиды, а h — высота.
Египтяне знали правильную формулу для получения объема усеченной квадратной пирамиды, но никаких доказательств этого уравнения в московском папирусе не приводится.Объем конической или пирамидальной усеченной части — это объем твердого тела до отсечения вершины за вычетом объема вершины:
где B 1 — площадь одного основания, B 2 — площадь другого основания и h 1 , h 2 — перпендикуляр высоты от вершины до плоскостей двух оснований.
Учитывая, что
- α
формулу для объема можно выразить как произведение этой пропорциональности α / 3 и разности кубов высот h 1 и h 2 только.
Путем факторинга ( h 2 — h 1 ) = h , высота усеченной вершины и α ( h 1 2 + h 6 1 h 2 + h 2 2 ) / 3, и, распределяя α и подставляя из его определения, получается среднее Герона площадей B 1 и B 2 .Альтернативная формула поэтому
Герон Александрийский известен тем, что вывел эту формулу и встретил мнимое число, квадратный корень из отрицательного числа. [2]
В частности, объем усеченного кругового конуса равен
, где π равно 3,14159265 …, а R 1 , R 2 — радиусы двух оснований.
Объем пирамидальной усеченной кости, основания которой составляют n правильных многоугольников со сторонами , равен
, где a 1 и a 2 — стороны двух оснований.
Площадь
Для правой круговой усеченной конуса [3]
и
, где R 1 и R 2 — это базовый и верхний радиусы соответственно, а s — наклонная высота усеченного конуса.
Площадь поверхности правой усеченной пирамиды, основания которой аналогичны правильным n -сторонним многоугольникам, равна
, где a 1 и a 2 — стороны двух оснований.
Примеры
Примечание
Внешние ссылки
Шаблон: Wiktionarypar
Шаблон: Commonscatcs: Komolý jehlan
da: Кеглестуб
eo: Trunko (геометрический)
это: Tronco (геометрия)
nl: Afgeknotte пирамид
pt: Tronco de base paralelas
th: ฟ รัส ตั ม
sv: Avstympat partiЗадачи оптимизации в 3D-геометрии
Пример 8.
Китайская чайная чаша имеет форму сферической крышки с радиусом \ (r \) и высотой \ (h \) (рисунок \ (8a \)).2}} = {\ frac {S} {\ pi} — \ frac {S} {{2 \ pi}}} = {\ frac {S} {{2 \ pi}};} \]
Затем
\ [r = \ sqrt {\ frac {S} {{2 \ pi}}}, \]
, поэтому соотношение \ (\ large {\ frac {h} {r}} \ normalsize \) равно
\ [\ frac {h} {r} = \ frac {{\ sqrt {\ frac {S} {{2 \ pi}}}}} {{\ sqrt {\ frac {S} {{2 \ pi} }}}} = 1. \]
Пример 9.
Тело имеет форму цилиндра, основания которого увенчаны полусферами (рис. \ (9а \)). Определите высоту цилиндра \ (H \) и радиус полусфер \ (R, \), при которых площадь поверхности при фиксированном объеме \ (V \) является наименьшей. 2} + 2 \ pi RH.2}}} — \ frac {2} {3} \ sqrt [3] {{\ frac {{3V}} {{5 \ pi}}}}} = {\ frac {5} {3} \ sqrt [ 3] {{\ frac {{3V}} {{5 \ pi}}}} — \ frac {2} {3} \ sqrt [3] {{\ frac {{3V}} {{5 \ pi}}) }}} = {\ sqrt [3] {{\ frac {{3V}} {{5 \ pi}}}}.} \]
Следовательно, ответ
\ [R = H = \ sqrt [3] {{\ frac {{3V}} {{5 \ pi}}}}. \]
Пример 11.
Цилиндр вписан в сферу радиуса \ (a \) (рисунок \ (11a \)). Найдите радиус основания \ (R \) и высоту \ (H \) цилиндра с максимально возможным объемом.
Решение.{\ prime \ prime} \ left (a \ right)} = {- \ frac {{54a}} {4}} = {- \ frac {{27a}} {2}.} \]
Это отрицательное значение для \ (a \ gt 0, \), поэтому точка \ (a = \ large {\ frac {{\ sqrt S}} {{3 \ sqrt [4] {3}}}} \ normalsize \ ) является точкой локального максимума по тесту второй производной.
Теперь мы можем рассчитать максимальный объем призмы:
\ [{{V _ {\ max}} = V \ left ({a = \ frac {{\ sqrt S}}} {{3 \ sqrt [4] {3}}}} \ right)} = {\ frac {{\ sqrt 3 \ cdot \ frac {{\ sqrt S}} {{3 \ sqrt [4] {3}}} \ cdot S — 9 {{\ left ({\ frac {{\ sqrt S}} { {3 \ sqrt [4] {3}}}} \ right)} ^ 3}}} {4}} = {\ frac {{{3 ^ {\ frac {1} {2}}} \ cdot {S ^ {\ frac {3} {2}}}}} {{3 \ cdot {3 ^ {\ frac {1} {4}}}}} — \ frac {{{3 ^ 2} \ cdot {S ^ {\ frac {3} {2}}}}} {{{3 ^ 3} \ cdot {3 ^ {\ frac {3} {4}}}}}} = {\ frac {{{S ^ {\ frac {3} {2}}}}} {{{3 ^ {\ frac {3} {4}}}}} — \ frac {{{S ^ {\ frac {3} {2}}}}} {{{3 ^ {\ frac {7} {4}}}}}} = {\ frac {{{S ^ {\ frac {3} {2}}}}} {{{3 ^ {\ frac { 3} {4}}}}} \ left ({1 — \ frac {1} {3}} \ right)} = {\ frac {2} {3} \ cdot \ frac {{{S ^ {\ frac {3} {2}}}}} {{{3 ^ {\ frac {3} {4}}}}}} = {\ frac {{2 \ sqrt {{S ^ 3}}}}} {{3 \ sqrt [4] {3}}}.3}}} {{3 \ sqrt 3}}.} \]
Пример 14.
Предположим, что у нас есть журнал длины \ (H \) в виде усеченного конуса с радиусами \ (R \) и \ (r \) (\ (R \ gt r \)). Из этого бревна требуется вырезать брус максимально большого объема. Балка имеет форму прямоугольного параллелепипеда с квадратным поперечным сечением и той же оси, что и бревно (рисунок \ (14a \)).
Решение.
Усеченный конус и вписанный параллелепипед схематично показаны в поперечном сечении на рисунке \ (14a.2} y, \]
где \ (x \) — сторона квадратного основания, \ (y \) — высота параллелепипеда.
Рассматривая аналогичные треугольники \ (CBR \) и \ (CKM, \), мы можем записать следующую пропорцию:
\ [
{\ frac {{MK}} {{AB}} = \ frac {{MC}} {{AC}}, \; \;} \ Rightarrow
{\ frac {y} {H} = \ frac {{R — \ frac {x} {2}}} {{R — r}}.}
\]Следовательно, высота \ (y \) равна
\ [y = \ frac {{H \ left ({R — \ frac {x} {2}} \ right)}} {{R — r}}. 3}}) } {2}} \ right).2}}} {2}} \ right)}
= {\ frac {{Hx}} {{R — r}} \ left ({2R — \ frac {{3x}} {2}} \ right). }
\]Найдите стационарную точку:
\ [
{V ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{\ frac {{Hx}} {{R — r}} \ left ({2R — \ frac {{ 3x}} {2}} \ right) = 0, \; \;} \ Rightarrow
{2R — \ frac {{3x}} {2} = 0, \; \;} \ Rightarrow
{x = \ frac {{4R}} {3}.}
\]Производная положительна слева от этой точки и отрицательна справа. Следовательно, это точка максимума функции \ (V \ left (x \ right).\) Тогда высота параллелепипеда
\ [
{y = \ frac {{H \ left ({R — \ frac {x} {2}} \ right)}} {{R — r}}}
= {\ frac {{H \ left] ({R — \ frac {{4R}} {6}} \ right)}} {{R — r}}}
= {\ frac {{HR \ left ({1 — \ frac {2} {3} } \ right)}} {{R — r}}}
= {\ frac {{HR}} {{3 \ left ({R — r} \ right)}}.}
\]Итак, параллелепипед, вписанный в усеченный конус, имеет наибольший объем, когда его стороны равны
\ [{x = \ frac {{4R}} {3},} \; \; \; \ kern-0.3pt {y = \ frac {{HR}} {{3 \ left ({R — r} \верно)}}.2}}}}} {{\ sqrt [3] {4}}}} = {\ frac {{\ sqrt 5 \ sqrt [3] {{3V}}}} {{\ sqrt [6] {2} }}.} \]
Пример 16.
Конус имеет объем \ (V. \). Какой радиус основания \ (R \) и высота \ (H \) минимизируют площадь боковой поверхности конуса (рисунок \ (16a \))?
Решение.
Обозначим наклонную высоту конуса через \ (m \) (рисунок \ (16a \)).
Рисунок 16а.
Площадь боковой поверхности выражается формулой
\ [{S _ {\ text {L}}} = \ pi Rm. \]
Далее будем обозначать площадь боковой поверхности конуса просто буквой \ (S.{\ large \ frac {1} {2} \ normalsize}} = \ sqrt 2.}
\]Таким образом, высота конуса с наименьшей площадью боковой поверхности должна быть примерно в \ (1,4 \) раз больше, чем радиус основания.
Интересно, каково отношение высоты к радиусу основания у такого конусообразного мегапроекта, как Развлекательный центр «Хан Шатыр» (рисунок \ (16b \))? Если площадь боковой поверхности была одним из критических факторов при проектировании, вполне вероятно, что ее форма должна быть близка к нашему решению.

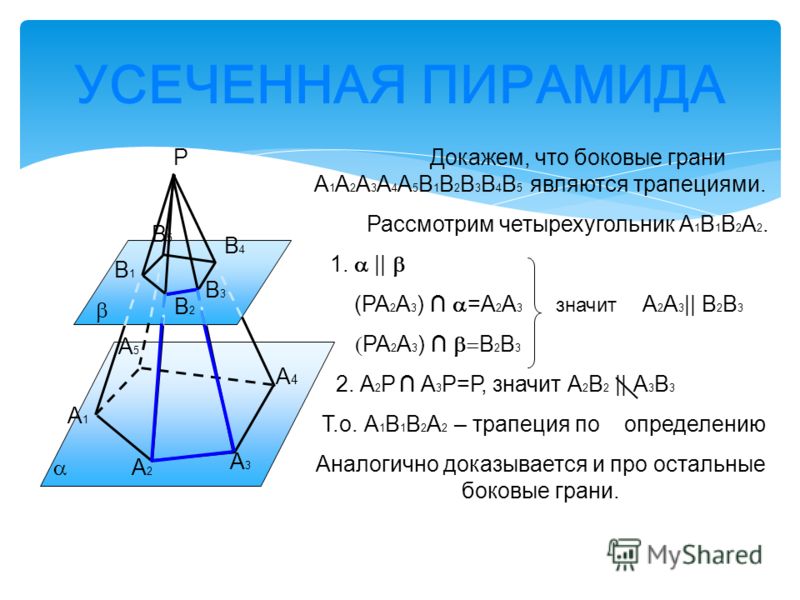 04
04 04
04 ru/video/preview?filmId=10071685978824333342
ru/video/preview?filmId=10071685978824333342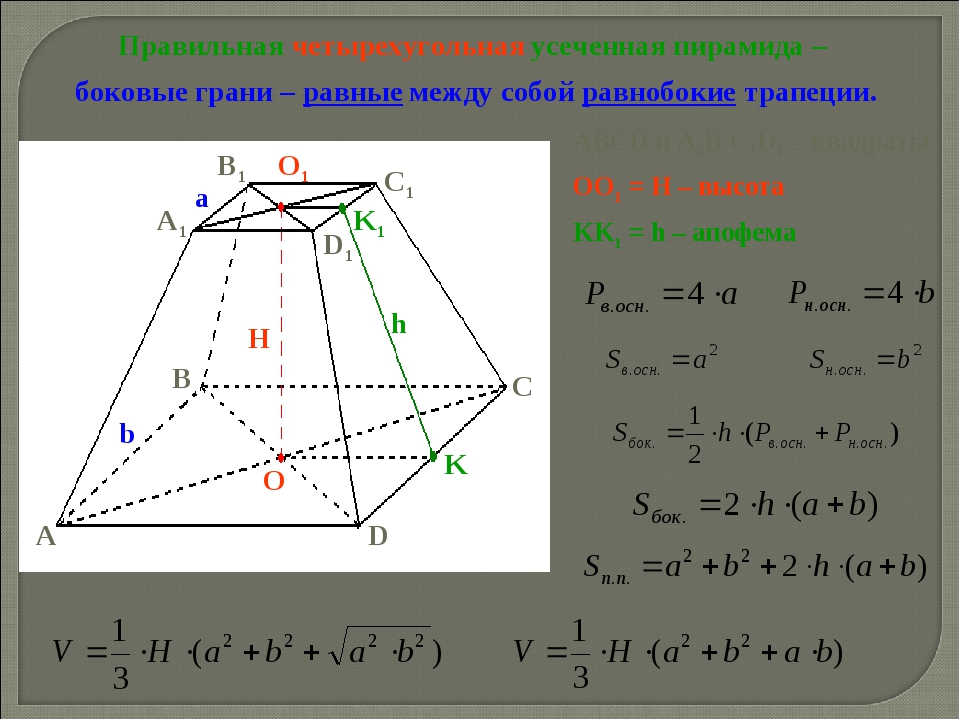 №3-выписать понятия в тетрадь, № 7 разобрать правило, выписать примеры с переводом.
№3-выписать понятия в тетрадь, № 7 разобрать правило, выписать примеры с переводом.