Содержание
Площадь ромба
Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.
Таблица с формулами площади ромба (в конце страницы)
— Вычисления (показано)
(скрыто)
— примечания (показано)
(скрыто)
1
Площадь ромба по стороне и высоте
… подготовка …
a — сторона
h — высота
2
Площадь ромба по двум диагоналям
… подготовка …
d1 — диагональ
d2 — диагональ
3
Площадь ромба по углу и противолежащей диагонали
. .. подготовка …
.. подготовка …
d — диагональ
α° — угол между сторонами
4
Площадь ромба по углу и диагонали проведенной из этого угла
… подготовка …
d — диагональ
α° — угол между сторонами
5
Площадь ромба по стороне и углу между сторонами
… подготовка …
a — сторона
α° — угол между сторонами
6
Площадь ромба по радиусу вписанной окружности и углу между сторонами
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
7
Площадь ромба по радиусу вписанной окружности и стороне
. .. подготовка …
.. подготовка …
a — сторона
r — радиус вписанной окружности
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
Определения
Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Ромб – это частный случай параллелограмма.
Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.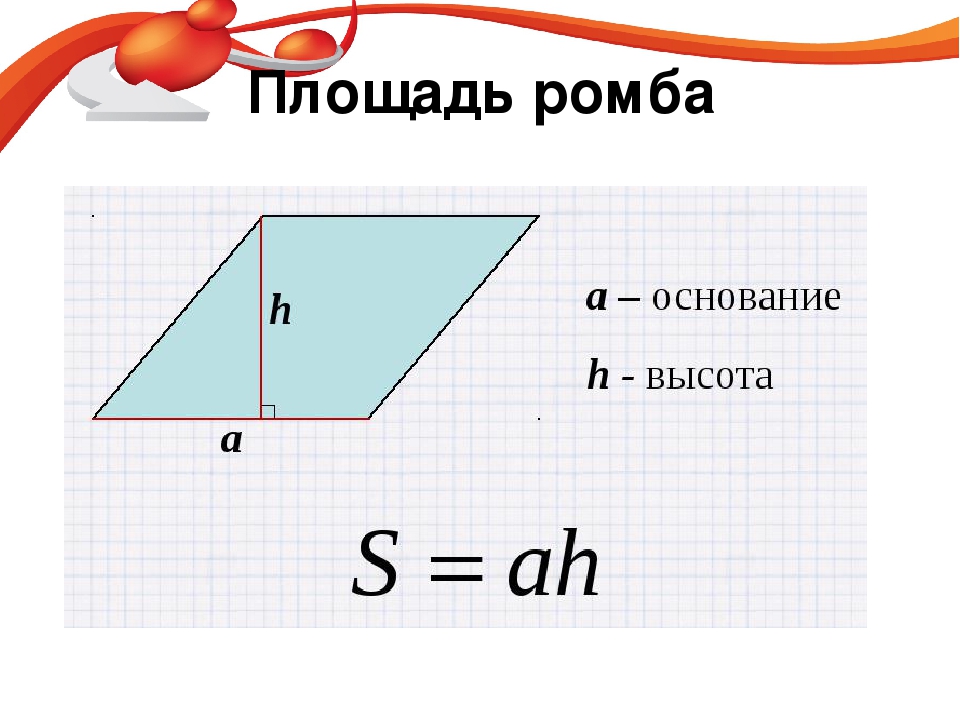
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.
Площадь ромба | Мозган калькулятор онлайн
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
Формула для нахождения площади ромба через сторону и высоту:
a — сторона ромба; h — высота ромба.
Через диагонали
Формула для нахождения площади ромба через диагонали:
d1, d2 — диагонали ромба.
Через сторону и угол
Формула для нахождения площади ромба через сторону и угол:
a — сторона ромба; α — угол между сторонами. 2}{sin(\alpha)}»/>
2}{sin(\alpha)}»/>
r — радиус окружности; α — угол между сторонами.
Через сторону и радиус вписанной окружности
Формула для нахождения площади ромба через сторону и радиус вписанной окружности:
a — сторона ромба; r — радиус вписанной окружности.
© Все права защищены
Ромб. Площадь, периметр, радиус
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD. Ниже приведен рисунок на котором изображен ромб.
Ниже приведен рисунок на котором изображен ромб.
Свойства ромба
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.

- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
P=4a.
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
r=h/2.
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S) ромба и величина острого угла (alpha) то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Периметр ромба
Периметр ромба равен сумме всех его сторон. Учитывая то что они все равны периметр принимает значение
P=4a.
И в завершение запомните что периметр измеряется в единицах длины, а площадь в квадратных единицах. Теперь Вы знаете как найти площадь и периметр ромба, поэтому пользуйтесь приведенным формулам при решении задач.
Посмотреть материалы:
Формула площади ромба
Что такое Ромб? Ромб — это параллелограмм, у которого все стороны равны.
РОМБ, фигура на плоскости, четырехугольник с равными сторонами.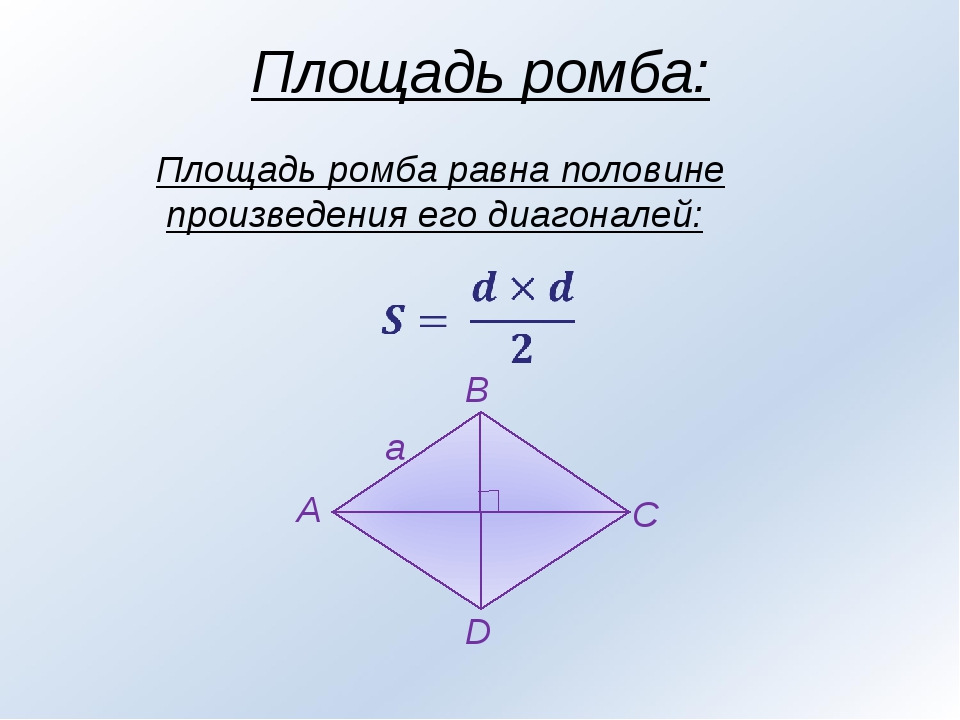 {2} \cdot sin(\alpha) \]
{2} \cdot sin(\alpha) \]
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]
4. Если известен радиус r окружности, вписанной в ромб , и сторона ромба a, то его площадь вычисляется по формуле:
\[ S = 2 \cdot a \cdot R \]
Свойства ромба
На рисунке выше \( ABCD \) — ромб, \( AC = DB = CD = AD \) . Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
\[ r = \frac{ AH }{2} \]
Свойства ромба
Диагонали ромба перпендикулярны;
Диагонали ромба являются биссектрисами его углов.
Признаки ромба
Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
Калькулятор площади ромба
Расчитать площадь фигуры онлайн
Калькулятор: Площадь ромба
Входные данные
Результат
Площадь геометрической фигуры, или площадь фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади фигуры выражается числом заключающихся в него квадратных единиц.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Простые формулы площади ромба!
В статье рассмотрим формулу площади ромба и не одну! На картинках покажем, как легко находиться площадь ромба по простым формулам.
Существует большое количество заданий на нахождение той или иной величины в ромбе и в этом нам помогут формулы, о которых и пойдет речь.
Ромб относится к отдельному виду четырехугольников, так как у него все стороны равны. Так же представляет частный случай параллелограмма в котором стороны АВ=ВС=СD=АD равны.
Заметка: Если Вам нужна курсовая, контрольная или дипломная работа, тогда вам на webmath.ru. или просто перейдите по ссылке заказать курсовую работу (http://www.webmath.ru/zakaz_kursovye.php).
Ромб обладает следующими свойствами:
— у ромба параллельные углы равные,
— сложение двух соседних углов равно 180 градусам,
— Пересечение диагоналей под углом в 90 градусов,
— Биссектрисами ромба, приходятся его же диагонали,
— Диагональ при пересечении делится на равные части.
Ромб обладает следующими признаками:
— Если у параллелограмма в котором диагонали встречаются под углом 90 градусов, то он называется ромбом.
— Если у параллелограмма в котором биссектриса это диагональ, то он называется ромбом.
— Если у параллелограмма равные стороны — это ромб.
— Если у четырехугольника равные стороны — это ромб.
— Если у четырехугольника в котором биссектриса это диагональ и диагонали встречаются под углом 90 градусов, то это ромб.
— Если у параллелограмма одинаковые высоты — это ромб.
Из вышеперечисленных признаков можно сделать вывод, что они нужны для того чтобы научиться отделять ромб от других схожих с ним фигур.
Так как в ромбе все стороны одинаковы периметр находится по следующей формуле:
Р=4а
Площадь ромба формула
Данных формул несколько. Самая простая решается как сложение площадь 2 треугольников, которые получились в результате деления диагоналей.
С помощью второй формулы можно решать задачи с известными диагоналями ромба. В этом случае площадью ромба будет: сумма диагоналей деленная на два.
Очень просто в решении и не забудется.
Третью формулу можно использовать когда знаешь угол между сторон. Зная его можно найти площадь ромба, она будет равна квадрату сторон на синус угла.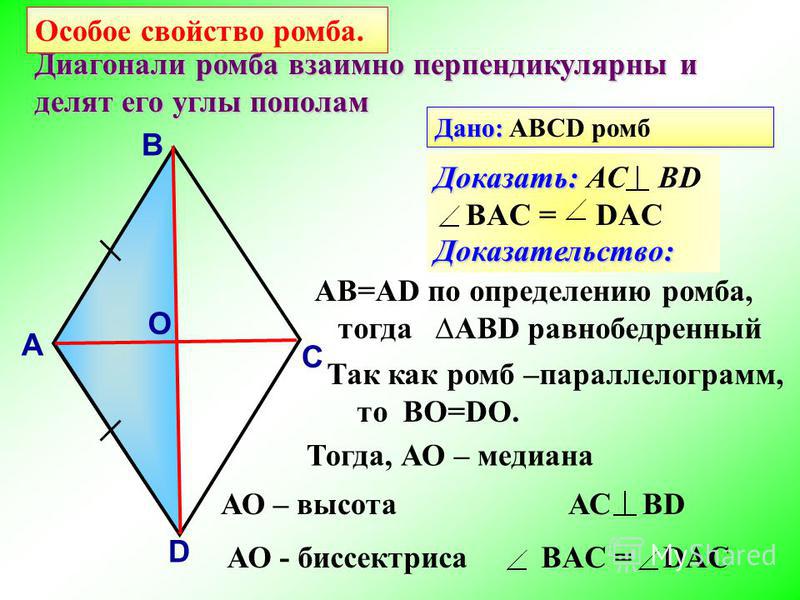 При чем нет разницы какой угол. так как синус угла имеет единое значение.
При чем нет разницы какой угол. так как синус угла имеет единое значение.
Важно помнить что измерение площади происходит в квадратах, а периметра в единицах. Данные формулы очень легко применяются на практике.
Так же могут встретиться задачи на поиск радиуса по вписанной в ромб окружности.
Для этого так же существует несколько формул:
В помощью первой формулы радиус находится как произведение диагоналей поделенное на число полученное от сложения всех сторон. либо равняется половине высоты ( r=h/2).
Во второй формуле взят принцип из первой, применяется мы знаем диагонали и стороны ромба.
В третьей формуле радиус выходит из высоты меньшего из треугольников, получившегося в результате пересечения.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Площадь ромба: онлайн калькулятор, формулы, примеры решений
Ромб — это четырехугольник, все стороны которого одинаковы.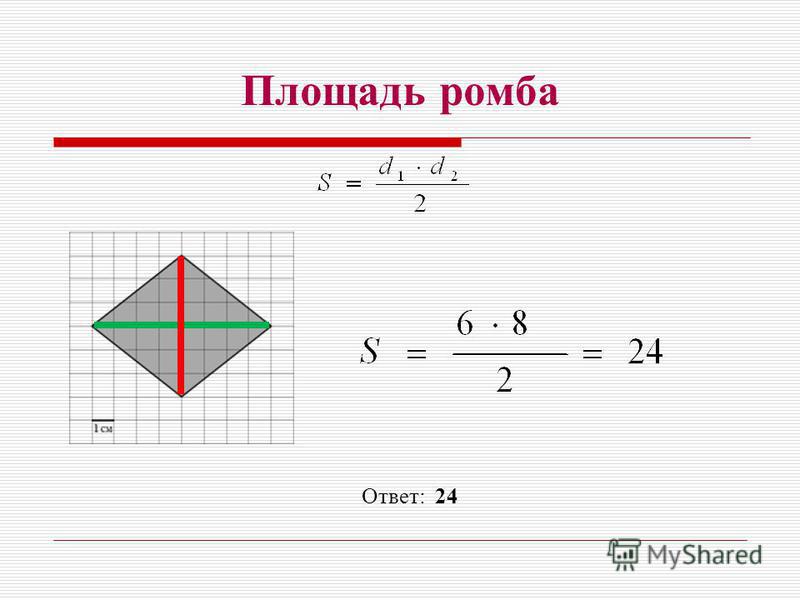 Ромб представляет собой частный случай параллелограмма, а квадрат — частный случай ромба. Следовательно, каждый квадрат — это ромб, а каждый ромб — параллелограмм.
Ромб представляет собой частный случай параллелограмма, а квадрат — частный случай ромба. Следовательно, каждый квадрат — это ромб, а каждый ромб — параллелограмм.
Геометрия ромба
Термин «ромб» с греческого языка означает «бубен», который в древности выполняли в виде четырехугольника, а не круга. Ромб — равносторонний параллелограмм с неравными углами. Любой равносторонний четырехугольник, который имеет два острых и два тупых угла может называться ромбом. Таким образом, ромб в отличие от квадрата является косоугольником. Параллелограмм будет считаться ромбом, если фигура соответствует хотя бы одному из условий:
- две смежные стороны равны, соответственно, равны все стороны;
- диагонали фигуры пересекаются под прямым углом;
- все высоты косоугольника равны;
- диагонали делят четырехугольник на 4 одинаковых прямоугольных треугольника;
- одна из диагоналей является биссектрисой для внутренних треугольников.
Данная фигура в своей классической форме не часто встречается в реальной жизни. Чаще всего ромбы можно найти в металлообработке: пластины резцов различных инструментов имеют именно ромбовидную форму. Кроме того, ромбические элементы встречаются в архитектуре и строительстве, а наиболее очевидным примером реального ромба является тротуарная плитка. Встречая ромбы в реальности, вам может понадобиться определить площадь данной фигуры для решения практических задач.
Чаще всего ромбы можно найти в металлообработке: пластины резцов различных инструментов имеют именно ромбовидную форму. Кроме того, ромбические элементы встречаются в архитектуре и строительстве, а наиболее очевидным примером реального ромба является тротуарная плитка. Встречая ромбы в реальности, вам может понадобиться определить площадь данной фигуры для решения практических задач.
Площадь ромба
Площадь ромба — это плоскость, ограниченная периметром фигуры. Площадь такого четырехугольника можно найти шестью способами, используя для расчетов такие параметры как величины углов, длины сторон или диагоналей. Наиболее простая формула для определения площади ромбовидной фигуры оперирует диагоналями. Диагональ ромба — это отрезок, который соединяет вершины противоположных углов косоугольника. Зная длину диагоналей ромба, вы можете вычислить площадь по следующей формуле:
S = 0,5 d1 × d2
Для определения площади ромба вы можете использовать наш онлайн-сервис, который позволяет найти не только площадь или периметр фигуры, но и определяет ее углы, длину сторон и высоту.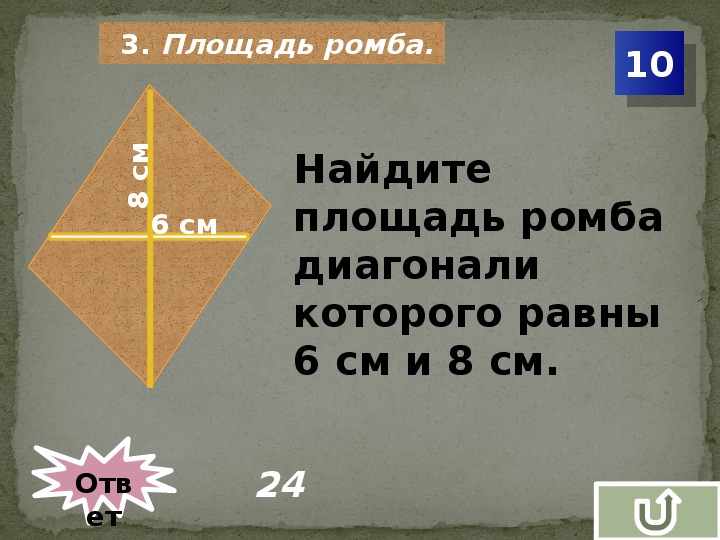 Для вычислений вам потребуется ввести в форму два параметра на выбор:
Для вычислений вам потребуется ввести в форму два параметра на выбор:
- две диагонали;
- высоту и сторону.
Зная эти два значения, программа рассчитает все остальные свойства ромба, которые могут вам понадобиться при решении практических задач. Рассмотрим пару примеров.
Примеры из реальной жизни
Плитка
Ранее мы выяснили, что тротуарная плитка — это самый банальный пример ромбических фигур в реальной жизни. Допустим, есть участок, который вы хотите замостить такой плиткой. Для определения необходимого количества плитки, которое нужно закупить, вам потребуется узнать два параметра: площадь участка и площадь одного элемента тротуарного покрытия. Пусть площадь участка составляет 20 квадратных метров, а диагонали плитки равны 20 см и 10 см. Для правильного расчета необходимо выразить длину диагоналей в метрах (0,2 и 0,1 м) и ввести их в поля «Диагонали». Вы получите результат в виде:
S = 0,01
Следовательно, площадь одного элемента составляет 0,01 квадратных метров, и вам понадобится 2 000 маленьких ромбов для обустройства участка.
Геральдика
Большая часть гербов исполняется на ромбовидных геральдических щитах. Если вы захотите сделать собственный ромбовидный герб для фестиваля исторической реконструкции, то вам понадобится узнать, сколько ткани нужно для его создания. Вы можете прикинуть только длину стороны и высоту ромба. Пусть высота фигуры составляет 0,3 м, а сторона — 0,5 м. Тогда площадь герба будет равна:
S = 0,15
Таким образом, для создания герба вам понадобится 0,15 квадратных метров ткани.
Заключение
Ромб не занимает в реальной жизни человека значимое место: фигура встречается нечасто, в основном в машиностроении, архитектуре и дизайне. Для решения практических задач или школьных заданий вы можете воспользоваться онлайн-калькулятором, который мгновенно выдаст вам не только правильный результат, но и вычислит углы, стороны и высоту ромба.
Площадь ромба по диагоналям формула. Площадь ромба: формулы и факты
– это параллелограмм, у которого все стороны равны.
Ромб с прямыми углами называется квадратом и считается частным случаем ромба. Найти площадь ромба можно различными способами, используя все его элементы – стороны, диагонали, высоту. Классической формулой площади ромба считается расчет значения через высоту.
Пример расчета площади ромба по этой формуле очень прост. Необходимо только подставить данные и высчитать площадь.
Площадь ромба через диагонали
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2.
Рассмотрим пример расчета площади ромба через диагонали. Пусть дан ромб с диагоналями
d1
=5 см и d2
=4. Найдем площадь.
Формула площади ромба через стороны подразумевает и применение других элементов. Если в ромб вписана окружность, то площадь фигуры можно просчитать по сторонам и ее радиусу:
Пример расчета площади ромба через стороны также весьма прост. Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Требуется только просчитать радиус вписанной окружности. Его можно вывести из теоремы Пифагора и по формуле .
Площади ромба через сторону и угол
Формула площади ромба через сторону и угол используется очень часто.
Рассмотрим пример расчета площади ромба через сторону и угол.
Задача:
Дан ромб, диагонали которого равны d1
=4 см,d2
=6 см. Острый угол равен α
= 30°. Найдите площадь фигуры через сторону и угол.
Для начала найдем сторону ромба. Используем для этого теорему Пифагора. Мы знаем, что в точке пересечения диагонали делятся пополам и образуют прямой угол. Следовательно:
Подставим значения:
Теперь мы знаем сторону и угол. Найдем площадь:
– это параллелограмм , у которого все стороны равны, то для него действуют все те же формулы, как и для параллелограмма, включая формулу нахождения площади через произведение высоты и стороны .
Площадь ромба можно найти, также зная его диагонали . Диагонали делят ромб на четыре абсолютно одинаковых прямоугольных треугольника . Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если мы их рассортируем, так чтобы получить прямоугольник , то его длина и ширина будут равны одной целой диагонали и половине второй диагонали. Поэтому площадь ромба находится умножением диагоналей ромба, сокращенных на два (как площади получившегося прямоугольника).
Если в распоряжении только угол и сторона , то можно вооружиться диагональю в качестве помощника и начертить ее напротив известного угла. Тогда она разделит ромб на два конгруэнтных треугольника, площади которых в сумме дадут нам площадь ромба. Площадь каждого из треугольников будет равна половине произведения квадрата стороны на синус известного угла, как площадь равнобедренного треугольника . Поскольку таких треугольников два, то коэффициенты сокращаются, оставив только сторону во второй степени и синус:
Если внутри ромба вписать окружность , то его радиус будет относиться к стороне под углом 90°
, что значит, что удвоенный радиус будет равен высоте ромба . Подставив вместо высоты h=2r
в предыдущую формулу, получим площадь S=ha=2ra
Если же вместе с радиусом вписанной окружности, дана не сторона, а угол, то следует сначала найти сторону, проведя высоту таким образом, чтобы получить прямоугольный треугольник с заданным углом.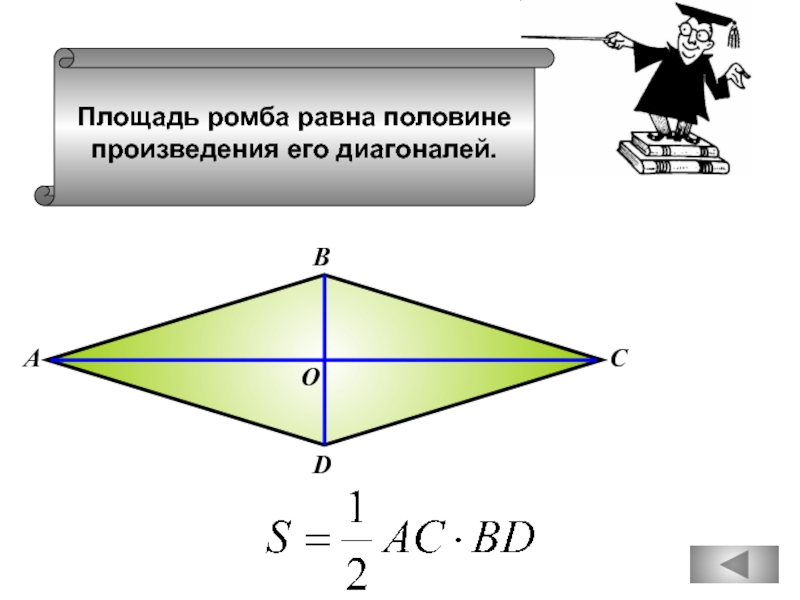 Тогда сторона a
Тогда сторона a
может быть найдена из тригонометрических отношений по формуле . Подставляя это выражение в ту же стандартную формулу площади ромба, выходит
Ромб — это частный случай параллелограмма. Он представляет собой плоскую четырехугольную фигуру, в которой все стороны равны. Данное свойство определяет то, что у ромбов параллельны противоположные стороны и равны противолежащие углы. Диагонали ромба пресекаются под прямым углом, точке их пересечения приходится на середину каждой диагонали, а углы из который они выходят делятся пополам. То есть они диагонали ромба являются биссектрисами углов. Исходя из приведенных определений и перечисленных свойств ромбов их площадь может быть определена различными способами.
1. Если известны обе диагонали ромба AC и BD, то площадь ромба может быть определена как половина произведения диагоналей.
S = ½ ∙
AC ∙
BD
где AC, BD — длина диагоналей ромба.
Чтобы понять почему это так, можно мысленно вписать в ромб прямоугольник таким образом, чтобы стороны последнего были перпендикулярны диагоналям ромба.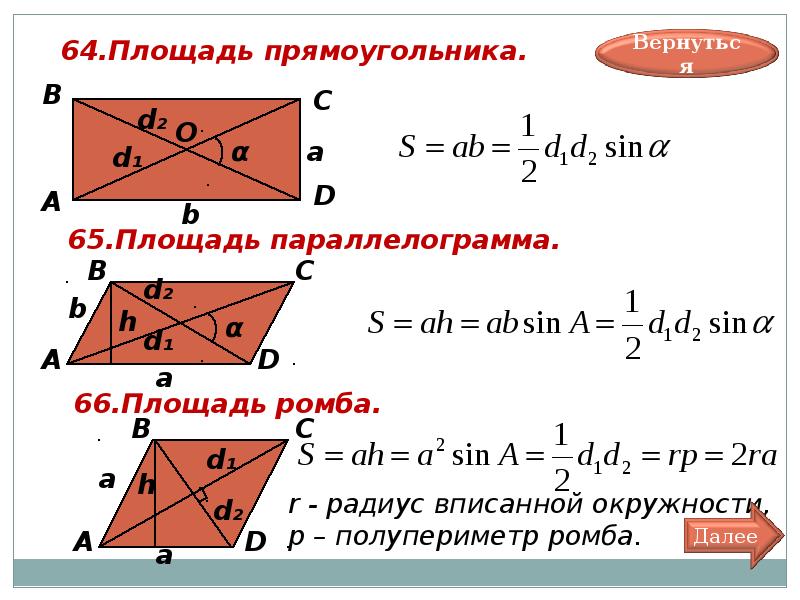 Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
Становится очевидным, что площадь ромба будет равна половине площади вписанного данным образом в ромб прямоугольника, длина и ширина которого будут соответствовать величине диагоналей ромба.
2. По аналогии с параллелепипедом площадь ромба может быть на найдена как произведение его стороны, на высоту перпендикуляра с опущенного к данной стороне с противолежащей стороны.
S = а ∙
h
где а — сторона ромба;
h — высота перпендикуляра, опущенного на данную сторону.
3. Площадь ромба также равна квадрату его стороны, умноженному на синус угла α
.
S = a 2 ∙
sinα
где, a — сторона ромба;
α
— угол между сторонами.
4. Также площадь ромба может быть найдена через его сторону и радиус вписанной в него окружности.
S = 2 ∙
a ∙
r
где, a — сторона ромба;
r — радиус вписанной в ромб окружности.
Интересные факты
Слово ромб произошло от древнегреческого rombus, что в переводе означает «бубен». В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
В те времена бубны действительно имели ромбовидную форму, а не круглую, как мы привыкли видеть их в настоящее время. С тех же времен произошло и название карточной масти «бубны». Очень широко ромбы различных видов используются в геральдике.
Математика — школьный предмет, который изучается всеми, независимо от профиля класса. Однако она не всеми любима. Порой незаслуженно. Эта наука постоянно подбрасывает ученикам задачи, которые позволяют их мозгу развиваться. Математика отлично справляется с тем, чтобы не дать мыслительным возможностям детей угаснуть. Особенно хорошо с этим справляется один из ее разделов — геометрия.
Любая из тем, которые в ней изучаются, достойна внимания и уважения. Геометрия — это способ развить пространственное воображение. Примером может служить тема о площадях фигур, в частности ромбов. Эти задачки могут завести в тупик, если не разобраться в деталях. Потому что возможны разные подходы к поиску ответа. Кому-то проще запомнить разные варианты формул, которые написаны ниже, а кто-то способен сам их получить из ранее усвоенного материала. В любом случае безвыходных ситуаций не бывает. Если немного подумать, то решение обязательно найдется.
В любом случае безвыходных ситуаций не бывает. Если немного подумать, то решение обязательно найдется.
Ответить на этот вопрос нужно, чтобы понять принципы получения формул и ход рассуждения в задачах. Ведь чтобы разобраться в том, как найти площадь ромба, нужно отчетливо понимать, что это за фигура и каковы ее свойства.
Для удобства рассмотрения параллелограмм, который является четырехугольником с попарно параллельными сторонами, примем за «родителя». У него есть двое «детей»: прямоугольник и ромб. Оба они являются параллелограммами. Если продолжать параллели, то это — «фамилия». Значит, для того чтобы найти площадь ромба, можно воспользоваться уже изученной формулой для параллелограмма.
Но, как и все дети, ромб имеет и нечто свое. Это немного отличает его от «родителя» и позволяет рассматривать как отдельную фигуру. Ведь прямоугольник не ромб. Возвращаясь к параллелям — они как брат и сестра. В них много общего, но они все же различаются. Эти отличия — их особенные свойства, которыми нужно пользоваться. Было бы странно знать о них и не применять в решении задач.
Было бы странно знать о них и не применять в решении задач.
Если продолжить аналогии и вспомнить еще одну фигуру — квадрат, то она будет продолжением ромба и прямоугольника. В этой фигуре объединены все свойства и одного, и другого.
Свойства ромба
Их пять и они перечислены ниже. Причем некоторые из них повторяют свойства параллелограмма, а какие-то присущи только рассматриваемой фигуре.
- Ромб — это параллелограмм, который принял особую форму. Из этого следует, что его стороны являются попарно параллельными и равными. Причем равны они непросто попарно, а все. Как это было бы у квадрата.
- Диагонали этого четырехугольника пересекаются под углом, который равен 90º. Это удобно и во многом упрощает ход рассуждений при решении задач.
- Другое свойство диагоналей: каждая из них делится точкой пересечения на равные отрезки.
- Лежащие друг напротив друга углы у этой фигуры равны.
- И последнее свойство: диагонали ромба совпадают с биссектрисами углов.

Обозначения, которые приняты в рассмотренных формулах
В математике полагается решать задачи с использованием общих буквенных выражений, которые называются формулами. Тема про площади не является исключением.
Для того чтобы перейти к записям, которые расскажут, как найти площадь ромба, нужно договориться о буквах, которыми заменены все числовые значения элементов фигуры.
Теперь пришла пора написания формул.
Среди данных задачи — только диагонали ромба
Правило утверждает, что для нахождения неизвестной величины нужно перемножить длины диагоналей, а потом произведение разделить пополам. Результат деления — это и есть площадь ромба через диагонали.
Формула для этого случая будет выглядеть так:
Пусть эта формула будет идти под номером 1.
В задаче даны сторона ромба и его высота
Чтобы вычислить площадь, потребуется найти произведение этих двух величин. Пожалуй, это самая простая формула. Причем она известна еще из темы про площадь параллелограмма. Там такая формула уже изучалась.
Там такая формула уже изучалась.
Математическая запись:
Номер этой формулы — 2.
Известны сторона и острый угол
В этом случае нужно возвести в квадрат величину стороны ромба. Потом найти синус угла. И третьим действием вычислить произведение двух образовавшихся величин. Ответом будет площадь ромба.
Буквенное выражение:
Его порядковый номер — 3.
Данные величины: радиус вписанной окружности и острый угол
Для вычисления площади ромба нужно найти квадрат радиуса и умножить его на 4. Определить значение синуса угла. Потом разделить произведение на вторую величину.
Формула принимает такой вид:
Она будет пронумерована цифрой 4.
В задаче фигурируют сторона и радиус вписанной окружности
Чтобы определить, как найти площадь ромба, потребуется вычислить произведение данных величин и числа 2.
Формула для этой задачи будет выглядеть так:
Ее номер по порядку — 5.
Примеры возможных заданий
Задача 1
Одна из диагоналей ромба равна 8, а другая — 14 см. Требуется найти площадь фигуры и длину ее стороны.
Решение
Для нахождения первой величины потребуется формула 1, в которой Д 1 = 8, Д 2 = 14. Тогда площадь вычисляется так: (8 * 14) / 2 = 56 (см 2).
Диагонали делят ромб на 4 треугольника. Каждый из них обязательно будет прямоугольным. Этим нужно воспользоваться, чтобы определить значение второй неизвестной. Сторона ромба станет гипотенузой треугольника, а катетами будут половины диагоналей.
Тогда а 2 = (Д 1 /2) 2 + (Д 2 /2) 2 . После подстановки всех значений получается: а 2 = (8 / 2) 2 + (14 / 2) 2 = 16 + 49 = 65. Но это квадрат стороны. Значит, нужно извлечь квадратный корень из 65. Тогда длина стороны будет приблизительно равна 8,06 см.
Ответ: площадь 56 см 2 , а сторона 8,06 см.
Задача 2
Сторона ромба имеет значение, равное 5,5 дм, а его высота — 3,5 дм. Найти площадь фигуры.
Решение
Для того чтобы найти ответ нужна будет формула 2. В ней а = 5,5, Н = 3,5. Тогда, заменив в формуле буквы на числа, получим, что искомая величина равна 5,5 * 3,5 = 19,25 (дм 2).
Ответ: площадь ромба равна 19,25 дм 2 .
Задача 3
Острый угол у некоторого ромба равен 60º, а его меньшая диагональ — 12 см. Требуется вычислить его площадь.
Решение
Чтобы получить результат, нужна будет формула под номером 3. В ней вместо А
будет 60, а значение а
неизвестно.
Для нахождения стороны ромба потребуется вспомнить теорему синусов. В прямоугольном треугольнике а
будет гипотенузой, меньший катет равен половине диагонали, а угол делится пополам (известно из свойства, где упоминается биссектриса).
Тогда сторона а
будет равна произведению катета на синус угла.
Катет нужно вычислить как Д/2 = 12/2 = 6 (см). Синус(А/2) будет равен его значению для угла 30º, то есть 1/2.
Выполнив несложные вычисления, получим такое значение стороны ромба: а = 3 (см).
Теперь площадь — это произведение 3 2 и синуса 60º, то есть 9 * (√3)/2 = (9√3)/2 (см 2).
Ответ: искомая величина равна (9√3)/2 см 2 .
Итоги: все возможно
Здесь были рассмотрены некоторые варианты того, как найти площадь ромба. Если в задаче напрямую непонятно, какую формулу использовать, то нужно немного подумать и попробовать связать ранее изученные темы. В других темах обязательно найдется подсказка, которая поможет связать известные величины с теми, что есть в формулах. И задача решится. Главное — помнить, что все раньше изученное можно и нужно использовать.
Кроме предложенных заданий, возможны и обратные задачи, когда по площади фигуры нужно вычислить значение какого-либо элемента ромба. Тогда нужно воспользоваться тем уравнением, которое ближе всего к условию. А потом преобразовать формулу, оставив в левой части равенства неизвестную величину.
Что такое Ромб? Ромб — это параллелограмм, у которого все стороны равны.
РОМБ, фигура на плоскости, четырехугольник с равными сторонами. Ромб — частный случай ПАРАЛЛЕЛОГРАММА, у которого или две смежные стороны равны, или диагонали пересекаются под прямым углом, или диагональ делит угол пополам.{2} \cdot sin(\alpha) \]
3. Площадь ромба также равна полупроизведению диагоналей, то есть:
\[ S = \dfrac{d_{1} \cdot d_{2} }{2} \]
4. Если известен радиус r
окружности, вписанной в ромб, и сторона ромба a
, то его площадь вычисляется по формуле:
\[ S = 2 \cdot a \cdot R \]
Свойства ромба
На рисунке выше \(ABCD \)
— ромб, \(AC = DB = CD = AD \)
. Так как ромб — это параллелограмм, то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности
равен половине высоты ромба:
\[ r = \frac{ AH }{2} \]
Свойства ромба
Диагонали ромба перпендикулярны;
Диагонали ромба являются биссектрисами его углов.
Признаки ромба
Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Как найти площадь ромба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Ромб
(Перейти к области ромба или периметру ромба)
Ромб — плоская форма с 4 равными прямыми сторонами.
Ромб похож на бриллиант
| Все стороны имеют одинаковую длину | |
| Противоположные стороны параллельны, а противоположные углы равны (это параллелограмм). | |
| Высота — это расстояние под прямым углом к двум сторонам | |
| И диагонали «p» и «q» ромба. разделите друг друга пополам под прямым углом. |
Играть ромбом:
Площадь ромба
Площадь можно рассчитать по:
- высота, умноженная на длину стороны:
Площадь = высота × с
- квадрат длины стороны (s 2 ), умноженный на синус угла A (или угла B):
Площадь = с 2 sin (A)
Площадь = с 2 sin (B)
- , умножив длины диагоналей и разделив на 2:
Площадь = (p × q) / 2
Пример: ромб имеет диагонали 6 м и 8 м. Какова его площадь?
Площадь = (6 м × 8 м) / 2 = 24 м 2
Если вы можете нарисовать свой ромб, попробуйте инструмент «Площадь многоугольника путем рисования».
Периметр ромба
Периметр — это расстояние по краям.
Периметр равен , в 4 раза умноженным на s (длина стороны) Периметр = 4s |
Пример: длина стороны ромба 12 см. Каков его периметр?
Периметр = 4 × 12 см = 48 см
Квадрат — это ромб?
Да, потому что квадрат — это просто ромб, в котором все углы прямые.
Другие названия
Эту форму чаще называют ромбом , но некоторые люди называют ее ромбом или даже ромбом .
Множественное число — это ромбов или ромбов и, реже, ромбов или ромбов (с двойным b).
Название «ромб» происходит от греческого слова rhombos : кусок дерева, вращающийся на веревке, издает рев!
Как найти площадь ромба (формула и видео) // Репетиторы.com
Содержание
- Что такое ромб?
- Площадь Формулы ромба
- Как найти площадь ромба
Ромб — плоская фигура, поэтому она двумерна. Это замкнутая фигура с прямыми (линейными) сторонами, один из множества четырехугольников (четырехугольников). Это частный случай параллелограмма. Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны.Это оно!
Ромб можно также назвать ромбом, ромбом или ромбом. Квадрат — это ромб с четырьмя равными (прямыми) углами.
Иногда вы видите ромб с двумя горизонтальными сторонами, как если бы квадрат врезался автобусом и перевернулся (это удобная мнемоника, чтобы запомнить его название: беги, автобус; ромб). На этой презентации можно очень легко увидеть высоту (высоту) ромба.
Иногда ромб рисуется так, чтобы одна из двух его диагоналей (линий, соединяющих противоположные вершины) была горизонтальной, что делает форму ромба более очевидной.
Необычным качеством ромба является то, что его диагонали всегда перпендикулярны друг другу, независимо от углов четырех вершин ромба.
Эти диагонали также делят друг друга пополам, что означает, что они делят ромб на четыре прямоугольных треугольника. Квадраты длин двух диагоналей всегда в четыре раза больше квадрата стороны.
Ромб такой простой формы имеет множество частей и размеров. Знание того, как использовать эти измерения, может помочь вам найти площадь, периметр и другие сведения о ромбе.
Площадь Формулы ромба
Есть три разные формулы для определения площади ромба. Один использует высоту и сторону, другой — сторону и угол, а третий — диагонали. Три формулы для определения площади зависят от информации, которую вы знаете о ромбе.
- Если вы знаете высоту (высоту) и сторону s, формула будет следующей:
площадь = высота × s - Если вам известна длина одной стороны s и размер одного угла, формула будет иметь следующий вид:
площадь = s2 sin∠A = s2 sin∠B - Если вам известны длины диагоналей, формула будет следующей:
площадь = (d1 × d2) 2
Как найти площадь ромба
Построим ромб со сторонами s и четырьмя вершинами с внутренними углами A, B, C и D.Мы можем соединить противоположные углы диагоналями d1 и d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. В нашем ромбе:
- Четыре стороны равной длины: AB, BC, CD и DA
- Четыре внутренних угла с равными противоположными углами: ∠a = ∠c и ∠b = ∠d
- Две диагонали: d1 и d2; только в квадрате это будут диагонали одинаковой длины
- Высота или высота — Когда ромб сидит с двумя сторонами горизонтально (плоско), высота h — это расстояние от одной стороны до противоположной стороны; отрезок прямой, перпендикулярный одной стороне, соединяющийся с противоположной стороной
Поскольку четыре стороны равны, если вы знаете длину любой стороны s, вы знаете длину всех четырех сторон.
Поскольку противоположные углы равны, а четыре угла складываются в 360 °, если вы знаете один угол, вы можете найти все углы. Поскольку противоположные стороны параллельны, смежные углы в ромбе складываются в 180 °.
Для определения площади необходимо знать высоту или высоту h ромба.
Помните, что высота не равна длине стороны.
Формула с использованием высоты и стороны
Если у вас есть мысленное представление о ромбе как о наклонном квадрате, этот первый метод будет иметь большой смысл.
Если бы ромб был квадратом, его площадь в квадратных единицах была бы сторона x сторона, верно? Что ж, когда ромб наклонен, вы можете представить, как отрезать треугольную часть на одной стороне ромба и сдвинуть ее к соответствующей другой стороне, восстанавливая форму до ее прямоугольности.
На самом деле вы не можете разрезать каждый встреченный ромб, поэтому подумайте, что это за перпендикулярная сторона на самом деле: высота или высота ромба.
Итак, первый и, возможно, самый простой способ определить площадь ромба — это определить длину одной стороны и высоту ромба.Умножьте их, и вы получите площадь в квадратных единицах:
.
площадь = высота × сторона
Пример:
Итак, если у вас есть ромб высотой 3 дюйма со сторонами 5 дюймов, то площадь этого ромба составляет:
3 дюйма × 5 дюймов = 15 дюймов2
Другой пример: сторона s составляет 15 футов, а высота — 11 футов. Площадь этого ромба:
15 × 11 = 165 квадратных футов
Формула с использованием стороны и угла
Второй способ найти площадь ромба — это знать длину стороны s и величину одного угла (∠A или ∠B).Здесь нужно найти синус угла, но формула все еще проста:
площадь = s2 sin∠A
площадь = s2 sin∠B
Как видите, эти две формулы дают одинаковый результат, поэтому
площадь = s2 sin∠A = s2 sin∠B
Пример:
В ромбе со стороной 10 ярдов и внутренними прилегающими углами 60 ° и 120 °, чтобы найти площадь этого ромба, мы должны включить это в нашу формулу для площади, используя сторону и угол.
площадь = 102 sin60 °
, что также совпадает с
площадь = 102 sin120 °
Затем мы умножаем эти два числа вместе:
площадь = 100 × 0,866
Тогда получаем ответ:
площадь = 86,6 квадратных ярда
Помните, что для этого метода угол, который вы выбираете, не имеет значения. Формула одинакова для обоих углов; вам просто нужно выбрать один.
Синус 60 ° и 120 ° одинаков, 0,866
Формула с использованием диагоналей
Помните, что диагонали ромба всегда пересекаются под прямым углом и делят друг друга пополам.Это означает, что две диагонали образуют две стороны квадрата, который в два раза больше ромба.
Вы можете найти площадь ромба в квадратных единицах, умножив длины двух диагоналей (d1 и d2) и разделив на два.
Если у нашего ромба есть только размеры диагоналей, мы бы использовали эту формулу.
Пример:
Если бы наш ромб имел диагонали 24 и 18 метров в длину, то, чтобы найти площадь этого ромба, мы бы подставили числа в нашу формулу.
площадь = (24 × 18) 2
Умножаем две диагонали:
площадь = (432) 2
Тогда получаем ответ:
площадь = 216 квадратных метров
Краткое содержание урока
Вы рассмотрели, что такое ромб, как он вписывается в семейство четырехугольников, каковы его различные части и как найти его площадь.
Следующий урок:
Воздушные змеи в геометрии
Калькулятор площади ромба
Калькулятор площади ромба — отличный инструмент для определения площади ромба, а также его периметра и других характеристик: диагоналей, углов, длины стороны и высоты.Взгляните на множество способов найти область ромба: по диагоналям ромба, используя основание и высоту, сторону и любой выбранный угол … Вы все еще не знаете, как найти площадь ромба или периметра ромба? Проверьте формулы площади ромба ниже или просто поэкспериментируйте с инструментом.
Ромб и его свойства
Ромб — это простой четырехугольник, у которого все стороны равны. Другие названия — равносторонний четырехугольник или ромб (как на игральных картах ♢).
Основные свойства ромба:
- Две диагонали ромба перпендикулярны и делят друг друга пополам,
- Его диагонали делят пополам противоположные углы,
- Противоположные углы имеют одинаковую меру.
Каждый ромб представляет собой параллелограмм и воздушный змей.
Формула площади ромба
Есть три полезные формулы для вычисления площади ромба:
- Зная основание и высоту
площадь = основание * высота
- Зная диагонали ромба
площадь = (e * f) / 2
- Знающая сторона и любой (!) Угол
площадь = s² * sin (угол)
Почему мы можем использовать и любой угол в последней формуле площади ромба? Потому что мы знаем, что два соседних угла являются дополнительными, и sin (угол) = sin (180 ° — угол) .
Существуют и другие варианты этих уравнений (например, вычисление площади с учетом высоты и угла), но они представляют собой всего лишь простые тригонометрические преобразования этих трех самых популярных формул площади ромба.
Ромб по периметру
Найти периметр ромба тривиально, если мы знаем длину стороны — это 4 * . Но что, если мы знаем только диагонали ромба? Проверим:
- Мы знаем, что диагонали перпендикулярны и делят друг друга пополам.Итак, ромб — это не что иное, как четыре равных треугольника с катетами, равными e / 2 и f / 2.
- Все, что нам нужно сделать, это найти гипотенузу треугольника. Вы можете использовать здесь калькулятор прямоугольного треугольника или калькулятор теорем Пифагора.
- Умножьте полученное значение гипотенузы на 4. Это ваш ромбовидный периметр!
Также вы можете использовать эту формулу:
-
периметр = 4 * √ (e / 2) ²- (f / 2) ²)
Или просто введите длину диагоналей в калькулятор площади ромба !
Как найти площадь ромба?
Вы все еще не знаете, как пользоваться калькулятором? Покажем его потенциал на простом примере:
- Введите первое полученное значение .Предположим, это сторона = 10 дюймов.
- Введите второе значение . Например, угол, равный 30 °.
- Вау! Калькулятор площади ромба отображает все остальные значения — площадь, высоту, периметр, угол и диагонали . Впечатляет, правда?
Наш инструмент действительно гибкий — если есть возможность посчитать, он это сделает. Обычно двух заданных значений достаточно, попробуйте!
Квадрат — это ромб? Или ромб — это параллелограмм?
Ответ: да на оба вопроса. Каждый квадрат представляет собой ромб , так как для ромба единственное необходимое условие — это то, что все стороны должны быть одинаковой длины. Как вы прекрасно знаете, у квадрата должны быть равны все стороны и все четыре равных угла, поэтому он удовлетворяет условиям, чтобы быть ромбом.
Точно так же, ромб — это параллелограмм , так как любая форма должна иметь две пары параллельных сторон, чтобы быть параллелограммом, а у ромба они есть. Таким образом, ромб всегда является параллелограммом, но параллелограмм является ромбом только в частном случае — для параллелограмма с четырьмя сторонами одинаковой длины.
Площадь ромба — объяснения и примеры
В статье «Многоугольник» мы видели, что ромб — это четырехугольник с четырьмя параллельными сторонами равной длины . Противоположные углы ромба также равны.
Аналогично, диагонали ромба пересекаются под прямым углом, и их длины всегда равны . Квадрат — это разновидность ромба, у которого все четыре угла являются прямыми углами. Иногда ромб называют ромбом, ромбом или ромбом.
Из этой статьи вы узнаете, как рассчитать площадь ромба, используя формулы трех площадей ромба.
Как рассчитать площадь ромба?
Площадь ромба — это область, ограниченная четырьмя сторонами ромба .
Есть три способа найти площадь ромба.
Односторонний — это использование высоты и стороны ромба. Второй метод влечет за собой использование стороны и угла, а последний метод влечет за собой использование диагоналей.
Эти формулы для вычисления площади ромба известны как формулы площади ромба. Давайте взглянем.
Формула площади ромба
Площадь ромба можно определить разными способами. Мы увидим каждого из них по очереди ниже.
Площадь ромба с использованием высоты и основания
Если высота или высота и длина сторон ромба известны, площадь определяется по формуле;
Площадь ромба = основание × высота
A = b × h
Давайте посмотрим, чтобы понять это на примере:
Пример 1
Найдите площадь ромба, сторона которого 30 см и высота 15 см.
Раствор
A = b × h
= (30 x 15) см 2
= 450 см 2
Следовательно, площадь ромба 450 см 2 .
Пример 2
Рассчитайте площадь ромба, показанного ниже.
Раствор
A = b × h
= (18 x 24) мм 2
Пример 3
Если высота и площадь ромба 8 см и 72 см 2, соответственно, найти размеры ромба.
Раствор
A = b × h
72 см 2 = 8 см x b
Разделите обе стороны на 8.
72 см 2 /8 см = b
b = 9 см.
Следовательно, размеры ромба 9 см на 9 см.
Пример 4
Основание ромба в 3 раза плюс 1 больше высоты. Если площадь ромба 10 м 2 , найдите основание и высоту ромба.
Решение
Пусть высота ромба = x
и основание = 3x + 1
A = b × h
10 м 2 = x (3x + 1)
10 = 3x 2 + x
3x 2 + x — 10 = 0
Решите квадратное уравнение.
⟹ 3x 2 + x — 10 = 3x 2 + 6x — 5x — 10
⟹ 3x (x + 2) — 5 (x + 2)
⟹ (3x — 5) (x + 2 ) = 0
⟹ 3x — 5 = 0
⟹ x = 5/3
⟹ x + 2 = 0
x = -2
Теперь подставьте значение x.
Высота = x = 5/3 м
База = 3x + 1 = 3 (5/3) + 1 = 6 м
Итак, основание ромба 6 м, а высота 5/3 м .
Площадь ромба по диагоналям
Учитывая длину диагоналей, площадь ромба равна половине произведения диагоналей.
A = ½ × d 1 × d 2
Где d 1 и d 2 — диагонали ромба.
Пример 5
Две диагонали ромба составляют 12 см и 8 см. Рассчитайте площадь ромба.
Решение:
Пусть d 1 = 12 см и d 2 = 8 см.
A = ½ × d 1 × d 2
= (½ × 12 × 8) см 2 .
= 48 см 2 .
Пример 6
Рассчитайте длину стороны, если ее площадь составляет 24 см. 2 , диагональ 8 см, а высота 3 см.
Решение
Пусть d 1 = 8 см.
д 2 =?
A = ½ × d 1 × d 2
24 см 2 = ½ × 8 × d 2
24 см 2 = 4d 2
Разделить обе стороны на 4 чтобы получить,
6 = d 2
Следовательно, другая диагональ 6 см.
Теперь посчитайте длины сторон ромба.
A = b × h
24 см 2 = 3 см x b
Разделите обе стороны на 3.
8 см = b.
Следовательно, длина сторон ромба равна 8 см.
Пример 7
Найдите диагонали ромба, показанного ниже, если его площадь составляет 3458 см 2 .
Решение
A = ½ × d 1 × d 2
3,458 см 2 = ½ * 6x * 8x
3,458 см 2 = 24x
Divide с обеих сторон на 24.
3,458 / 24 = x 2
144 = x 2
Найдите квадратный корень из обеих частей.
x = -12 или 12.
Длина не может быть отрицательным числом; поэтому подставляем только x = 12 в уравнения диагоналей.
6x = 6 * 12 = 72 см
8x = 8 * 12 = 96 см
Следовательно, длины диагоналей равны 72 см и 96 см.
Пример 8
Предположим, стоимость полировки пола составляет 4 доллара за квадратный метр.Найдите стоимость полировки пола в форме ромба, каждая из диагоналей которого составляет 20 м и 12 м.
Раствор
Чтобы узнать стоимость полировки пола, умножьте коэффициент полировки на площадь пола в форме ромба.
A = ½ × 20 м × 12 м
= 120 м 2
Стоимость покраски = 120 м 2 x 4 доллара за м.
= 480 $
Площадь ромба с использованием длины сторон и включенного угла.
Площадь ромба равна квадрату длины стороны продукта и синусу угла между двумя сторонами.
Площадь ромба = b 2 × синус (A)
Где A = угол, образованный между двумя сторонами ромба.
Пример 9
Найдите площадь ромба со сторонами 8 см и углом между двумя сторонами 60 градусов.
Решение
A = b 2 × синус (A)
= 8 2 x синус (60)
= 55,43 см 2 .
Практические вопросы
- Найдите длину диагонали ромба, если длина другой диагонали составляет 5 единиц, а площадь ромба составляет 30 квадратных единиц.
- Воздушный змей имеет более короткую диагональ длиной 16 единиц, более короткую сторону длиной 10 единиц и более длинную сторону длиной 17 см. Какова длина другой диагонали?
- Какая площадь у ромба с длиной стороны 18 см и одной диагональю 20 см?
Предыдущий урок | Главная страница | Следующий урок
Площадь ромба
Площадь ромба — это пространство внутри его периметра. Ромб — это параллелограмм, у которого все стороны равны.Серое пространство — это область ромба на диаграмме ниже.
Формула площади
Есть несколько формул, по которым можно найти площадь ромба в зависимости от известных параметров.
Использование диагоналей
Площадь A ромба равна половине произведения двух его диагоналей.
, где d 1 и d 2 — длины двух диагоналей.
Ссылка на ромб ABCD выше, Пусть AC = d 1 и BD = d 2 .Диагонали ромба перпендикулярны друг другу, поэтому AC⟂ DB. Ромб ABCD можно разложить на треугольники ABC и ADC.
Площадь ABC =, где BE — высота ABC. Площадь ADC = где DE — высота △ ADC. Площадь ромба ABCD равна сумме площадей △ ABC и △ ADC.
Пример:
Если площадь ромба равна 230, а одна из его диагоналей равна 10, какова длина другой диагонали?
Пусть d 1 = 10. Поскольку A = 230, мы можем найти d 2 следующим образом:
230 = 5 × d 2
д 2 = 46
Использование стороны и высоты
Поскольку ромб также является параллелограммом, мы можем использовать формулу площади параллелограмма:
A = b × h
, где b — основание или длина стороны ромба, а h — соответствующая высота.
Использование стороны и угла
Если даны длина стороны и один из углов ромба, то площадь равна:
A = a 2 × sin (θ)
, где a — длина стороны, а θ — один из углов.
Нахождение области по сетке
Другой способ найти площадь ромба — определить, сколько единичных квадратов нужно, чтобы покрыть его поверхность. Ниже представлен единичный квадрат размером 1 см.
При определении площади ромба можно использовать сетку из единичных квадратов.
Сетка выше содержит единичные квадраты площадью 1 см 2 каждый. Ромб слева содержит 8 полных квадратов и 12 частичных квадратов, поэтому его площадь составляет примерно
.
Ромб справа содержит 25 полных квадратов, поэтому его площадь составляет примерно 25 см. 2 .
С помощью этого метода можно найти площадь любой формы; ромбами он не ограничивается. Однако это лишь приблизительная стоимость площади. Чем меньше используемый единичный квадрат, тем выше точность приближения.Использование сетки из квадратов размером 1 мм в 10 раз точнее, чем использование сетки из квадратов размером 1 см.
Площадь ромба — объяснение и примеры
Что происходит, когда вы толкаете квадрат, сохраняя его основание фиксированным?
Если вы думаете, что думаем мы, вы правы. Квадрат наклоняется.
Теперь, хотя его стороны те же самые, его углы больше не прямые, что делает квадрат ромбом.
Теперь, когда мы познакомились с ромбом, мы можем узнать площадь ромба.Мы можем определить площадь ромба с помощью калькулятора и даже определить площадь ромба, зная его стороны.
План урока
Что такое площадь ромба?
Площадь ромба можно определить как объем пространства, заключенного ромбом в двумерном пространстве.
- Ромб — это равносторонний четырехугольник, потому что все стороны имеют одинаковую длину.
- Ромб — это параллелограмм, у которого противоположные стороны параллельны, противоположные углы равны, а соседние углы дополняют друг друга.
- В ромбе диагонали пересекают друг друга под прямым углом.
- Диагонали — это биссектрисы.
- Площадь ромба можно определить разными способами: используя основание и высоту, используя диагонали и используя тригонометрию.
Площадь ромба равна половине произведения длин диагоналей.
Где \ (d_1 \) и \ (d_2 \) — диагонали ромба.
Четыре стороны совпадают.
\ (а = b = c = d \)
Диагонали пересекают друг друга пополам.
\ (BD = BE + ED \) и \ (AC = AE + EC \)
Четыре внутренних угла с равными противоположными углами.
, где \ (\ angle \) A = \ (\ angle \) C и \ (\ angle \) B = \ (\ angle \) D
Две диагонали — это AC и BD.
Площадь ромба = \ (\ dfrac {1} {2} \ times \) (AC \ (\ times \) BD) кв. Единиц
Площадь вывода формулы ромба
Рассмотрим ромб ABCD.
Пусть E — точка пересечения двух диагоналей.
Площадь ромба ABCD = Площадь ∆ ADC + Площадь ∆ ABC
Площадь ромба = 2 \ (\ times \) Площадь ∆ ABC — (1) (\ (\ потому что \) ∆ ABC конгруэнтно ∆ ADC)
Площадь ∆ ABC
\ [\ begin {align} & = \ dfrac {1} {2} \ times \ text {Base} \ times \ text {Height} \\ & = \ dfrac {1} {2} \ times \ text {AC} \ times \ text {BE} \\ & = \ dfrac {1} {2} \ times \ text {AC} \ times \ dfrac {1} {2} \ times \ text {BD} (\ потому что \ text {BE } = \ dfrac {\ text {BD}} {2}) \\ & = \ dfrac {1} {4} (\ text {AC} \ times \ text {BD}) — (2) \ end { align} \]
Площадь ромба ABCD
\ [\ begin {align} & = 2 \ times \ dfrac {1} {4} \ times \ text {AC} \ times \ text {BD} \\ & = \ dfrac {1} {2} \ times \ text {AC} \ times \ text {BD} \ text {(Из (1) и (2))} \\ & = \ dfrac {1} {2} \ times \ text {diagonal 1} \ times \ text {diagonal 2} \ end {align} \]
| Площадь ромба = \ (\ dfrac {1} {2} \ times \) диагональ 1 \ (\ times \) диагональ 2 единицы \ (^ 2 \) |
Площадь ромба с заданными сторонами
Ромб — параллелограмм.2 \ times \ dfrac {1} {2} \\ & = 16 \ times \ dfrac {1} {2} \\\ text {Area} & = 8 \ text {квадратных ярдов} \ end {align} \]
Как рассчитать площадь ромба
Пояснение
Рассмотрим ромб ABCD.
AB, BC, CD, DA — равные (равные) стороны.
AC и BD — диагонали, они встречаются в E.
.
Учитывая CD = 17 футов и AE = 8 футов.
Теперь мы знаем диагональ 1, AC = \ (16 \) футов.2 & = 289-64 \\ & = 225 \\ \ text {BE} & = 15 \ text {ft} \\\ text {BD} & = 30 \ text {ft} \ end {align} \]
Пора подставить все значения в формулу калькулятора ромба.
Площадь ромба \ [\ begin {align} & = \ dfrac {1} {2} \ times \ text {d 1} \ times \ text {d 2} \ text {sq units} \\ & = \ dfrac {1} {2} \ times \ text {BD} \ times \ text {AC} \ text {квадратных футов} \\ & = \ dfrac {1} {2} \ times 16 \ times 30 \ text {квадратных футов} \\ \ text {Площадь} & = 240 \ text {кв. футов} \ end {align} \]
Решенные примеры
Для ромба, показанного на рисунке, Сиа знает длину диагоналей, но не может определить его площадь.2 \)
Марк может не знать длины обеих диагоналей ромба, но он знает, что сторона = \ (5 \) дюймов, а одна диагональ = \ (8 \) дюймов. Как он может найти площадь?
Решение
Учитывая сторону и диагональ, мы поможем Марку найти вторую диагональ.
\ [\ begin {align} \ text {Area} & = (\ text {AC} \ times \ text {BD}) \ div 2 \ text {sq inch} \\\ text {AC} & = 8 \ text {in} \\ \ text {AO} & = 4 \ text {in} (\ потому что \ text {AO} = \ dfrac {1} {2} AC) \ end {align} \]
Чтобы найти другую диагональ BD, рассмотрите AOD.2 & = 9 \\\ text {OD} & = 3 \ text {in} \\ \ text {BD} & = 6 \ text {in} (\ потому что \ text {BD} = 2 \ times \ text {OD }) \\\ text {Площадь} & = (8 \ times 6) \ div 2 \ text {квадратных дюймов} \\\ text {Area} & = 24 \ text {sq inch} \ end {align} \]
\ (\ следовательно \) Площадь ромба = \ (24 \) кв. 2 \\ 84 & = \ dfrac {14 \ times \ text {QS}} {2} \\ 84 \ times 2 & = 14 \ times \ text {QS} \\ 168 & = 14 \ times \ text {QS} \\\ dfrac {168} {14} & = \ text {QS} \\ & = 12 \ text {ярд} \ end {align} \]
Интерактивные вопросы Вот несколько упражнений для практики. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. Подведем итоги Мы надеемся, что вам понравилось изучать область ромба с помощью моделирования и практических вопросов.Теперь вы сможете легко решать задачи на вычислитель площади ромба, площади ромба со сторонами, площади примеров ромба и площади ромба, если указаны стороны и угол. О компании Cuemath В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим. Часто задаваемые вопросы (FAQ) 1. Равны ли площади ромба и квадрата? Нет, площади ромба и квадрата не равны. Квадрат — это ромб, потому что у него четыре стороны, и каждая сторона имеет одинаковую длину. Однако квадрат имеет дополнительное определение как форма, имеющая четыре равных угла по 90 градусов. 2. Какова формула периметра ромба? Поскольку у ромба 4 равные стороны, периметр ромба равен \ (4 \ times \) единицам сторон. . |