Содержание
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Формулы для площади треугольника
Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула площади | Обозначения |
| Произвольный треугольник | Посмотреть вывод формулы | a – любая сторона, | |
Посмотреть вывод формулы | a и b – две любые стороны, | ||
. Посмотреть вывод формулы Герона | a, b, c – стороны, Формулу называют «Формула Герона» | ||
Посмотреть вывод формулы | a – любая сторона, | ||
Посмотреть вывод формулы | a, b, c – стороны, | ||
Посмотреть вывод формулы | a, b, c – стороны, | ||
S = 2R2 sin A sin B sin C Посмотреть вывод формулы | A, B, С – углы, | ||
| Равносторонний (правильный) треугольник | Посмотреть вывод формулы | a – сторона | |
Посмотреть вывод формулы | h – высота | ||
Посмотреть вывод формулы | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | R – радиус описанной окружности | ||
| Прямоугольный треугольник | Посмотреть вывод формулы | a и b – катеты | |
Посмотреть вывод формулы | a – катет, | ||
Посмотреть вывод формулы | a – катет, | ||
Посмотреть вывод формулы | c – гипотенуза, |
| Произвольный треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
. где Формулу называют «Формула Герона» Посмотреть вывод формулы Герона | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2R2 sin A sin B sin C где Посмотреть вывод формулы | |
| Равносторонний (правильный) треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Прямоугольный треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
. где Формулу называют «Формула Герона» Посмотреть вывод формулы Герона |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2R2 sin A sin B sin C где Посмотреть вывод формулы |
| Равносторонний (правильный) треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
Вывод формул для площади произвольного треугольника
Утверждение 1. Площадь треугольника можно найти по формуле
Площадь треугольника можно найти по формуле
где a – любая сторона треугольника, а ha – высота, опущенная на эту сторону.
Доказательство.
Рис. 1
Достроив треугольник ABC до параллелограммапараллелограмма ABDC (рис. 1), получим
что и требовалось доказать.
Утверждение 2. Площадь треугольника можно найти по формуле
где a и b – две любые стороны треугольника, а С – угол между ними.
Доказательство.
Рис. 2
Поскольку
ha = b sin C ,
то, в силу утверждения 1, справедлива формула
что и требовалось доказать.
Утверждение 3. Площадь треугольника можно найти по формуле
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.
Замечание. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.
Доказательство.
Рис. 3
Поскольку (рис.3)
x = hactg C , y = hactg B ,
то
a = x + y =
= hactg C + hactg B =
= ha( ctg C + ctg B) .
Следовательно,
Поэтому
что и требовалось доказать.
Утверждение 4. Площадь треугольника можно найти по формуле
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.
Доказательство.
Рис. 4
Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим
что и требовалось доказать.
Утверждение 5. Площадь треугольника можно найти по формуле
где a, b, c – стороны треугольника, а R – радиус описанной окружности.
Доказательство.
Рис. 5
В силу теоремы синусов справедливо равенство
.
Следовательно,
Поэтому
что и требовалось доказать.
Утверждение 6. Площадь треугольника можно найти по формуле:
S = 2R2 sin A sin B sin C ,
где A, B, С – углы треугольника, а R – радиус описанной окружности.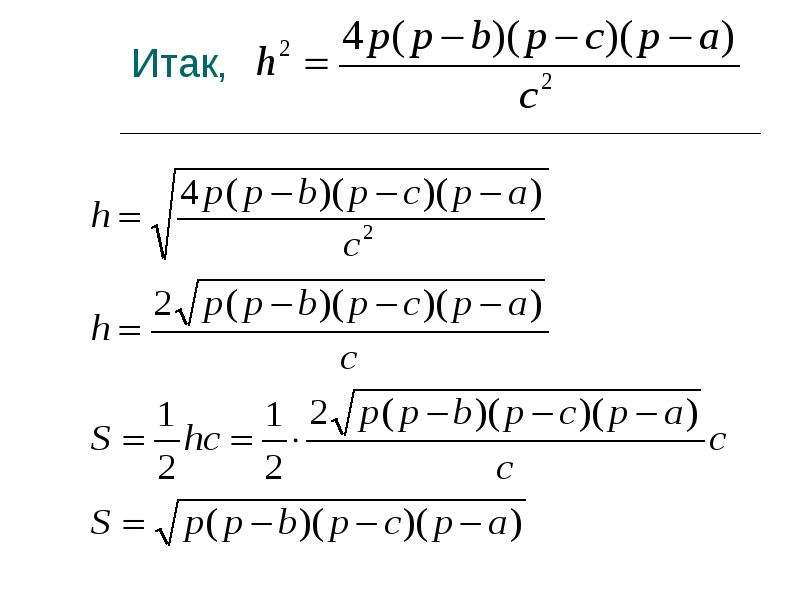
Доказательство.
Рис. 6
В силу теоремы синусов справедливо равенство
.
Поэтому
a = 2R sin A ,
b = 2R sin B ,
c = 2R sin C ,
В силу утверждения 5
что и требовалось доказать.
Вывод формул для площади равностороннего треугольника
Утверждение 7.
- Если h – высота равностороннего треугольника, то его площадь
Доказательство.
Рассмотрим рисунок 7.
Рассмотрим рисунок 8.

Рассмотрим рисунок 9.
Рассмотрим рисунок 10.
Рис. 7
В силу утверждения 2
Рис. 8
Поскольку
то
Рис. 9
Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство h = 3r. Следовательно,
Рис. 10
Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,
Доказательство утверждения 7 завершено.
Вывод формул для площади прямоугольного треугольника
Утверждение 8.
Доказательство.
Рассмотрим рисунок 11.
Рассмотрим рисунок 12.
Рассмотрим рисунок 13.
Рассмотрим рисунок 14.
Рис. 11
В силу утверждения 2
Рис. 12
Поскольку
b = a tg φ ,
то
Рис. 13
Поскольку
b = a ctg φ ,
то
Рис. 14
Поскольку
a = c cos φ ,
b = c sin φ ,
то
Доказательство утверждения 8 завершено.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Вычисление площади треугольника по формуле Герона на Питоне
На языке программирования Питон можно решить много разных задач, в том числе и по математике. Для начинающих изучать этот язык будет полезно решить задание на вычисление площади треугольника. Одним из способов вычисления этой величины является применение формулы Герона.
Для начинающих изучать этот язык будет полезно решить задание на вычисление площади треугольника. Одним из способов вычисления этой величины является применение формулы Герона.
Математическая часть задачи
Из школьного курса математики вы знаете, что площадь треугольника можно вычислить по данным длинам трёх его сторон по формуле Герона:
где
p – полупериметр треугольника.
Решение задачи на Питоне
На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.
Для ввода целых чисел используем функцию int().
Для решения задачи нам необходимо подключить библиотеку с математическими функциями. Делаем это с помощью строки импорта:
import math
Функция для извлечения квадратного корня в этой библиотеке записывается так:
math.sqrt()
Код программы для вычисления площади треугольника
import math #подключаем библиотеку математических функций
a=int(input("Введите сторону a="))
b=int(input(Введите сторону b=))
c=int(input(Введите сторону c=))
p=(a+b+c)/2
s=math.sqrt(p*(p-a)*(p-b)*(p-c))
print(s)
Результат выполнения кода программы
Python 3.5.2 (default, Dec 2015, 13:05:11)
[GCC 4.8.2] on Linux
12
13
14
72.30793524918272
Второй вариант решения задачи
Также можно воспользоваться стандартной функцией возведения числа в степень. Дело в том, что квадратный корень — это возведение в степень 1/2.
Синтаксис функции такой:
pow(x,y)
где x — число, возводимое в степень, а y — сама степень.
Вот так это запишется по формуле:
s=pow((p*(p-a)*(p-b)*(p-c)),1/2)
Результат выполнения кода:
Python 3.5.2 (default, Dec 2015, 13:05:11)
[GCC 4.8.2] on linux
12
13
14
72.30793524918272
Третий вариант решения задачи
Вместо извлечения корня можно возвести в степень 1/2 или 0,5. При этому функцию использовать не нужно.
При этому функцию использовать не нужно.
s=(p*(p-a)*(p-b)*(p-c))**0.5
Как видим, результат выполнения программы точно такой же.
Python 3.5.2 (default, Dec 2015, 13:05:11)
[GCC 4.8.2] on linux
12
13
14
72.30793524918272
Нахождение натуральных чисел с условием Вычисление площади фигур
Задача: Вычислить площадь треугольника по формуле Герона. Формула Герона для вычисления площади любого треугольника имеет вид:
Условный переход. Урок 9.
Условный переход Урок 9. Препятствие в виде возвышенности нет Умный? да Восхождение Обход Условие В условии 2 числа, или 2 строки, или 2 переменных, или 2 арифметических или строковых выражения сравниваются
Препятствие в виде возвышенности нет Умный? да Восхождение Обход Условие В условии 2 числа, или 2 строки, или 2 переменных, или 2 арифметических или строковых выражения сравниваются
Подробнее
Логический калькулятор
Краевая научно-практическая конференция учебно-исследовательских работ учащихся 9-11 классов «Прикладные и фундаментальные вопросы математики» Прикладные вопросы математики Логический калькулятор Захаров
Подробнее
Логические величины и выражения
Логические величины и выражения Логика это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений. Алгебра логики (другое название — Булева алгебра) это область
Подробнее
Изучение условного оператора IF.
Изучение условного оператора IF. Данная тема является одним из трех китов, на которых стоит программирование на языке Pascal. Без ее изучения невозможно дальнейшее программирование. Она помогает при решении
Данная тема является одним из трех китов, на которых стоит программирование на языке Pascal. Без ее изучения невозможно дальнейшее программирование. Она помогает при решении
Подробнее
Visual Basic (повторение).
Visual Basic (повторение). Visual Basic является системой объектноориентированного программирования и позволяет создавать графический интерфейс проекта. Интерфейс VB 2010 Основой графического интерфейса
Подробнее
Операции и выражения
Глава 5 Операции и выражения В этой главе Выражения в языке VBA Совместимость типов данных Оператор присваивания Арифметические операторы Логические операторы Операторы сравнения Строковые операторы Приоритеты
Подробнее
Программа: Число π и метод Монте Карло
Программа: Число π и метод Монте Карло Курс «Основы программирования в среде Visual Basic» Преподаватель: Тюкавина Татьяна Михайловна. МБОУ ДО Гатчинский Центр Непрерывного Образования «Центр Информационных
МБОУ ДО Гатчинский Центр Непрерывного Образования «Центр Информационных
Подробнее
Тема урока Условный оператор. Цель урока:
стр. 1 из 15 Тема урока Условный оператор Цель урока: 1. Образовательные: Познакомиться с новым типом оператора языка Turbo Pascal условный оператор, его особенностями исполнения. Обеспечить усвоение учащимися
Подробнее
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОР. МОСКВЫ
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОР. МОСКВЫ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ «МИСиС»
Подробнее
Программный блок логики
Программный блок логики Этот блок выполняет логическую операцию с входящими сигналами и посылает ответные сигналы истина/ложь через шину данных. Входящие сигналы (которые также должны иметь значения «истина»
Входящие сигналы (которые также должны иметь значения «истина»
Подробнее
ТРЕНИРОВОЧНАЯ РАБОТА 6А
ТРЕНИРОВОЧНАЯ РАБОТА 6А Создание приложения с пользовательской формой и элементами управления ТРЕНИРОВОЧНОЕ ЗАДАНИЕ Создать приложение для вычисления общей поверхности и объёма конуса по заданному радиусу
Подробнее
Лабораторная работа 1
1 Лабораторная работа 1 Использование элементов управления Button, Label и Text Box. Цель работы: ознакомиться с общим интерфейсом среды разработки Microsoft Visual Studio и языком программирования Microsoft
Подробнее
Программирование на языке QuickBASIC
Кубинская МОУ СОШ 2 имени Героя Советского Союза Безбородова В. П. Презентация на тему: Программирование на языке QuickBASIC Подготовила учитель информатики Жанкевич Т. А. : Определение Основные сведения
А. : Определение Основные сведения
Подробнее
Основы программирования на языке Python
Основы программирования на языке Python Основные типы данных 2 Основные числовые операции 3 Основные логические операции 4 Основные функции 5 Инструкция ветвления 7 Циклы 8 Функции 10 Списки 11 Основные
Подробнее
Информатика и ИКТ Лекция 7 1 курс
Информатика и ИКТ Лекция 7 курс ГБОУ СПО «УМТК» Кондаратцева Т.П. Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера ГБОУ СПО «УМТК» Кондаратцева Т.П. 2 Принципы
Подробнее
Информатика и ИКТ Лекция 6 1 курс
Информатика и ИКТ Лекция 6 1 курс ФГОУ СПО «УМТК» Кондаратцева Т.П. 1 Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера ФГОУ СПО «УМТК» Кондаратцева Т. П. 2
П. 2
Подробнее
Лабораторная работа 4
OpenOffice.org Base 31 Тема: «Запросы к базе данных» Лабораторная работа 4 Цель работы: ознакомиться со средствами поиска и выборки данных в Open Office.org Base, изучить основные принципы конструирования
Подробнее
Урок 10. Электронные таблицы
Урок 10. Электронные таблицы Основные параметры электронных таблиц (ЭТ). ЭТ позволяют обрабатывать большие массивы числовых данных. В отличии таблиц на бумаге, электронные таблицы обеспечивают проведение
Подробнее
Бинарный урок (9 класс)
Цели: Бинарный урок (9 класс) Завтур Г.А., учитель математики Клевакина О.А., учитель информатики Тема: «Решение квадратны уравнений в среде программирования QBasic» закрепить умение решать квадратные
Подробнее
Основы программирования на языке Pascal
Основы программирования на языке Pascal Структура программы 2 Основные типы данных 3 Основные операторы 4 Основные логические операторы 5 Структура условного оператора 6 Циклические операторы 7 Массивы
Подробнее
Тема 9.
 Логические основы ЭВМ.
Логические основы ЭВМ.
Тема 9. Логические основы ЭВМ. 1. Логика. Информация, обрабатываемая в ЭВМ, представляется с помощью физических величин, которые могут принимать только два устойчивых состояния и называются «двоичные переменные».
Подробнее
3.4. Работа с электронными таблицами
3.4. Работа с электронными таблицами 3.4.1. Пользовательский интерфейс программы Microsoft Excel. Создание и редактирование таблиц Документ в программе Microsoft Excel (MS Excel) называется рабочей книгой,
Подробнее
Основные понятия формальной логики
Основные понятия формальной логики Элементы логики Умение правильно рассуждать необходимо в любой области человеческой деятельности. Логика, как наука о том какие формы рассуждений правильны возникла немногим
Подробнее
Лабораторная работа 3.

Лабораторная работа 3. Тема. Создание интерфейса программы. Логические элементы управления. Цель: Научиться применять логические элементы для управления вводом и выводом данных, интерфейсом программы.
Подробнее
Алгоритмы с ветвящейся структурой
Алгоритмы с ветвящейся структурой Рассмотрим несколько задач, решение которых на компьютере получается с помощью ветвящихся алгоритмов. Первая задача: даны два числа, выбрать наибольшее из них. Пусть исходными
Подробнее
Информатика Открытый билет 10 класс
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ»
Подробнее
Основные элементы языка
Основные элементы языка Язык Pascal (Паскаль), изобретенный в начале 70-х годов 20-го века Н. Виртом и названный в честь французского математика и философа Блеза Паскаля, является одним из наиболее распространенных
Подробнее
ЭКОНОМИЧЕСКАЯ ИНФОРМАТИКА (ЧАСТЬ 2)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Курганский государственный университет» Кафедра
Подробнее
Лекция Автоматизация проектов VBA
Лекция 6 1. Автоматизация проектов VBA Реализации алгоритмов решения задачи табулирования функций с использованием средств VBA, рассмотренные в предыдущих лекциях, мало отличаются от реализаций этих же
Подробнее
1 Практическое занятие 1. Массивы данных
1 Практическое занятие 1 Массивы данных Цель работы: ознакомиться с понятием массива данных и методами его обработки. 1. Массивы данных Массив данных совокупность значений, объединенная общим названием.
1. Массивы данных Массив данных совокупность значений, объединенная общим названием.
Подробнее
Основные понятия алгебры логики.
Основные понятия алгебры логики. Для математического описания работы вычислительных устройств и их программного проектирования широко используется алгебра логики (булевская алгебра). Алгебра логики — часть
Подробнее
Площадь треугольника
Ниже приведены формулы нахождения площади произвольного треугольника которые подойдут для нахождения площади любого треугольника, независимо от его свойств, углов или размеров. Формулы представлены в виде картинки, здесь же приведены пояснения по применению или обоснованию их правильности. Также на отдельном рисунке указаны соответствия буквенных обозначений в формулах и графических обозначений на чертеже.
Примечание. Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
Если же треугольник обладает особыми свойствами (равнобедренный, прямоугольный, равносторонний), можно использовать формулы, приведенные ниже, а также дополнительно специальные, верные только для треугольников с данными свойствами, формулы:
Формулы площади треугольника
Пояснения к формулам:
a, b, c — длины сторон треугольника, площадь которого мы хотим найти
r — радиус вписанной в треугольник окружности
R — радиус описанной вокруг треугольника окружности
h — высота треугольника, опущенная на сторону
p — полупериметр треугольника, 1/2 суммы его сторон (периметра)
α — угол, противолежащий стороне a треугольника
β — угол, противолежащий стороне b треугольника
γ — угол, противолежащий стороне c треугольника
ha, hb, hc — высота треугольника, опущенная на сторону a, b, c
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.
- Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
- Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
- Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
- Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)
- Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
- Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
- Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов.
 (Формула 8)
(Формула 8) - Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
- Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
- Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин. Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений
См. также площадь равнобедренного треугольника.
Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √
В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √
Задача. Найти площадь по двум сторонам и углу между ними
Стороны треугольника равны 5 и 6 см. Угол между ними составляет 60 градусов. Найдите площадь треугольника.
Решение.
Для решения этой задачи используем формулу номер два из теоретической части урока.
Площадь треугольника может быть найдена через длины двух сторон и синус угла межу ними и будет равна
S=1/2 ab sin γ
Поскольку все необходимые данные для решения (согласно формуле) у нас имеются, нам остается только подставить значения из условия задачи в формулу:
S = 1/2 * 5 * 6 * sin 60
В таблице значений тригонометрических функций найдем и подставим в выражение значение синуса 60 градусов. Он будет равен корню из трех на два.
Он будет равен корню из трех на два.
S = 15 √3 / 2
Ответ: 7,5 √3 (в зависимости от требований преподавателя, вероятно, можно оставить и 15 √3/2)
Задача. Найти площадь равностороннего треугольника
Найти площадь равностороннего треугольника со стороной 3см.
Решение.
Площадь треугольника можно найти по формуле Герона:
S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
Поскольку a = b = c формула площади равностороннего треугольника примет вид:
S = √3 / 4 * a2
S = √3 / 4 * 32
S = 9 √3 / 4
Ответ: 9 √3 / 4.
Задача. Изменение площади при изменении длины сторон
Во сколько раз увеличится площадь треугольника, если стороны увеличить в 4 раза?
Решение.
Поскольку размеры сторон треугольника нам неизвестны, то для решения задачи будем считать, что длины сторон соответственно равны произвольным числам a, b, c. Тогда для того, чтобы ответить на вопрос задачи, найдем площадь данного треугольника, а потом найдем площадь треугольника, стороны которого в четыре раза больше. Соотношение площадей этих треугольников и даст нам ответ на задачу.
Далее приведем текстовое пояснение решения задачи по шагам. Однако, в самом конце, это же самое решение приведено в более удобном для восприятия графическом виде. Желающие могут сразу опуститься вниз решения.
Для решения используем формулу Герона (см. выше в теоретической части урока). Выглядит она следующим образом:
S = 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. первую строку рисунка внизу)
Длины сторон произвольного треугольника заданы переменными a, b, c.
Если стороны увеличить в 4 раза, то площадь нового треугольника с составит:
S2 = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c — 4a)(4a + 4c — 4b)(4a + 4b -4c) )
(см. вторую строку на рисунке внизу)
Как видно, 4 — общий множитель, который можно вынести за скобки из всех четырех выражений по общим правилам математики.
Тогда
S2 = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — на третьей строке рисунка
S2 = 1/4 sqrt( 256 ( a + b + c)(b + c — a)(a + c — b)(a + b -c) ) — четвертая строка
Из числа 256 прекрасно извлекается квадратный корень, поэтому вынесем его из-под корня
S2 = 16 * 1/4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
S2 = 4 sqrt( ( a + b + c)(b + c — a)(a + c — b)(a + b -c) )
(см. пятую строку рисунка внизу)
Чтобы ответить на вопрос, заданный в задаче, нам достаточно разделить площадь получившегося треугольника, на площадь первоначального.
Определим соотношения площадей, разделив выражения друг на друга и сократив получившуюся дробь.
S2 / S = 16
(см. внизу подробнее запись в виде дроби и ее сокращения — в последней строке)
На рисунке логика вычисления решения, описанного выше, приведена уже в виде формул (одна за другой)
Ответ: Площадь треугольника увеличится в 16 раз
Сумма углов треугольника |
Описание курса
| Медиана треугольника
Как найти площадь треугольника по формуле Герона
Вы можете использовать Формулу Герона для площади теугольника, чтобы найти область треугольника, даже если вы знаете только стороны треугольника, а не какие-либо из углов (которые называются SSS или боковые стороны в терминах тригонометрии). Формула Герона удобна, например, если вам нужно найти максимальную возможную площадь, учитывая сумму сторон треугольника.
Например, предположим, что у вас есть 240 ярдов для работы, и вы решили построить треугольный загон для своей ламы. Почему треугольная? Конечно, вы слышали, что ламы предпочитают форму. Вы хотите, чтобы у ламы было достаточно места для бега, поэтому вам нужно знать этот район. Какими должны быть длины сторон треугольника? Вы можете решить эту небольшую проблему, используя Формулу Герона для области треугольника.
Поиск площади треугольника используя формулу Герона
Формула Герона гласит, что если треугольник ABC имеет стороны длин a , b и c, противоположные соответствующим углам, и вы позволяете полупериметру, s, представлять половину периметра треугольника, тогда площадь треугольника равна:
В проблеме фехтования и ламы у вас есть много способов сделать треугольный загон с 240 ярдов фехтования. На следующем рисунке показаны некоторые из возможностей. Обратите внимание, что в каждом случае длины сторон составляют до 240. Ради этой проблемы не беспокойтесь о воротах.
Ради этой проблемы не беспокойтесь о воротах.
Треугольные загоны сделаны из 240 ярдов ограждения.
Какой треугольник имеет наибольшую площадь? Очевидно, один из них немного на тощей стороне, хотя он использует 240 ярдов фехтования, как и другие. Вот как вычислить области для трех треугольников.
Найдите полупериметр, s , для каждого треугольника.
Обратившись к предыдущему рисунку:
Неудивительно, что все полупериметры одинаковы, потому что все периметры равны 240.
Используйте Формулу Герона, чтобы найти каждую область.
Опять же, ссылаясь на предыдущий рисунок:
Наибольшая площадь имеет треугольник справа. Из фигур на рисунке этот треугольник является лучшим. Но вам может быть интересно, добавляет ли другая фигура больше площади, чем эта. Ответ: нет. С помощью исчисления вы можете доказать, что равносторонний треугольник дает вам максимально возможную площадь с любым количеством фехтования. Без исчисления вам просто нужно попробовать кучу фигур, чтобы убедить себя.
Без исчисления вам просто нужно попробовать кучу фигур, чтобы убедить себя.
Площадь треугольника. Онлайн-калькулятор
Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.
Выберите способ расчета площади:
через основание и высотучерез две стороны и уголпо трем сторонам (формула Герона)через радиус вписанной окружностичерез радиус описанной окружности
Рассчитать
Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).
Как найти площадь треугольника?
Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:
1) через основание и высоту
a – основание треугольника,
h – высота треугольника.
2) через две стороны и угол
a, b – стороны треугольника,
α – угол между сторонами.
3) По трем сторонам. Формула Герона.
a, b, с – стороны треугольника,
p – полупериметр треугольника.
4) Через радиус вписанной окружности.
a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.
5) Через радиус описанной окружности.
a, b, с – стороны треугольника,
R – радиус описанной окружности.
Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.
Площадь треугольника. Формулы
Формул для вычисления площади треугольника в интернете можно найти свыше 10. Немало из них применяется в задачах с известными сторонами и углами треугольника. Однако есть ряд сложных примеров где по условию задания известны только одна сторона и углы треугольника, или радиус описанной или вписанной окружности и еще одна характеристика. В таких случаях простую формулу применить не удастся.
В таких случаях простую формулу применить не удастся.
Приведенные ниже формулы позволят решить 95 процентов задач в которых требуется найти площадь треугольника.
Перейдем к рассмотрению распространенных формул площади.
Рассмотрим треугольник изображен на рисунке ниже
На рисунке и далее в формулах введены классические обозначения всех его характеристик
a,b,c – стороны треугольника,
R– радиус описанной окружности,
r – радиус вписанной окружности,
h[b],h[a],h[c] – высоты , проведенные в соответствии со сторонами a,b,c.
alpha, beta,hamma – углы возле вершин.
Основные формулы площади треугольника
1. Площадь равна половине произведения стороны треугольника на высоту опущенной к этой стороне. На языке формул это определение можно записать так
Таким образом, если известна сторона и высота — то площадь найдет каждый школьник.
Кстати, из этой формулы можно вывести одну полезную зависимость между высотами
2. Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
Если учесть, что высота треугольника через соседнюю сторону выражается зависимостью
то с первой формулы площади следуют однотипные вторые
Внимательно посмотрите на формулы — их легко запомнить, поскольку в произведении фигурирует две стороны и угол между ними. Если правильно обозначить стороны и углы треугольника (как на рисунке выше) то получим две стороны a,b и угол связан с третьей С (hamma).
3. Для углов треугольника справедливо соотношение
Зависимость позволяет применять в вычислениях следующие формулы площади треугольника
Примеры на эту зависимость встречаются крайне редко, но помнить что есть такая формула Вы должны.
4. Если известна сторона и два прилегающих угла то площадь находится по формуле
5. Формула площади через сторону и котангенс прилегающих углов следующая
Перестановкой индексов можете получить зависимости для других сторон.
6. Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами . В этом случае площадь равна половине определителя взятого по модулю.
В этом случае площадь равна половине определителя взятого по модулю.
7. Формула Герона применяют в примерах с известными сторонами треугольника.
Сначала находят полупериметр треугольника
а затем определяют площадь по формуле
или
Ее довольно часто используют в коде программ калькуляторов.
8. Если известны все высоты треугольника то площадь определяют по формуле
Она сложна для вычисления на калькуляторе, однако в пакетах MathCad, Mathematica, Maple площадь находится на «раз два ».
9. Следующие формулы используют известны радиусы вписанных и описанных окружностей.
В частности, если известно радиус и стороны треугольника, или его периметр то площадь вычисляется согласно формуле
10. В примерах где задано стороны и радиус или диаметр описанной окружности площадь находят по формуле
11. Следующая формула определяет площадь треугольника через сторону и углы треугольника.
Ну и напоследок — частные случаи :
Площадь прямоугольного треугольника с катетами a и b равна половине их произведения
Формула площади равностороннего ( правильного ) треугольника=
= одной четвертой произведения квадрату стороны на корень из тройки.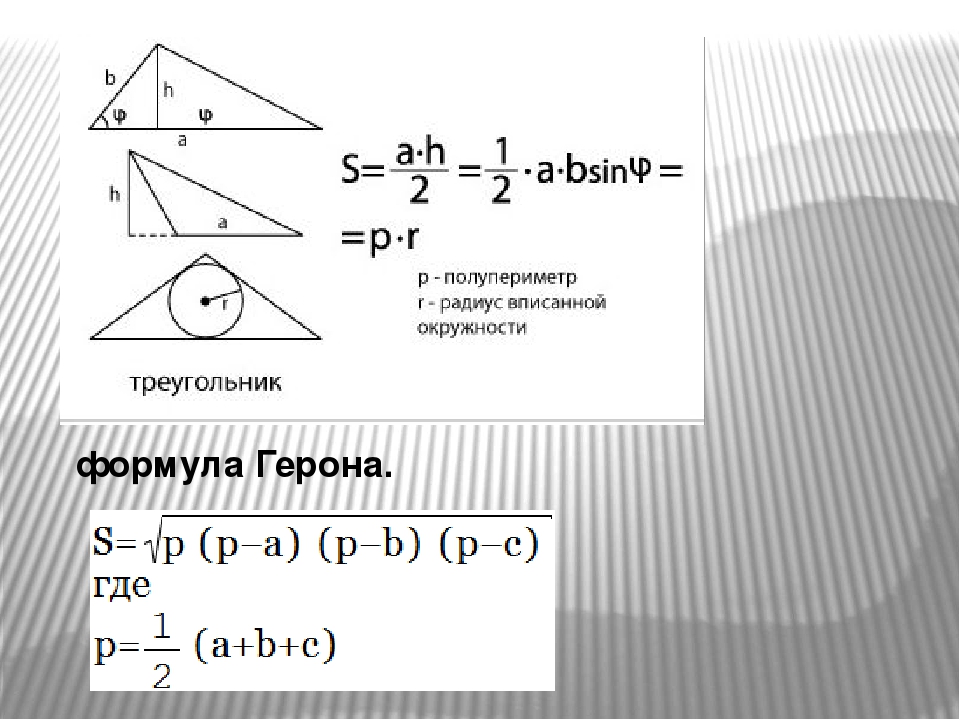
Пример. Стороны треугольника равны 3, 5, 6 см. Найти площадь треугольника.
Решение: Применим формулу Герона, для этого сначала найдем полупериметр
Подставляем в формулу площади
Ответ:Площадь треугольника равна 7.48 сантиметров квадратных.
————————————
Скачать все приведенные формулы площади треугольника Вы можете по следующей ссылке. Распечатывайте их и используйте в обучении.
{jd_file file==19}
Если материал был полезен Вам — поделитесь ссылкой с друзьями.
Посмотреть материалы:
{jcomments on}
Как найти площадь масштабного треугольника
Обновлено 3 ноября 2020 г.
Крис Дезиел
В отличие от равностороннего треугольника с тремя равными сторонами и углами, равнобедренного треугольника с двумя равными сторонами или прямоугольного треугольника с равномерный треугольник с углом в 90 градусов имеет три стороны случайной длины и три случайных угла. Если вы хотите узнать его площадь, вам нужно сделать пару замеров. Если вы можете измерить длину одной стороны и перпендикулярное расстояние от этой стороны до противоположного угла, у вас будет достаточно информации для расчета площади.Также можно рассчитать площадь, если вам известны длины всех трех сторон. Определение значения одного из углов, а также длины двух сторон, образующих его, также позволяет рассчитать площадь.
Если вы хотите узнать его площадь, вам нужно сделать пару замеров. Если вы можете измерить длину одной стороны и перпендикулярное расстояние от этой стороны до противоположного угла, у вас будет достаточно информации для расчета площади.Также можно рассчитать площадь, если вам известны длины всех трех сторон. Определение значения одного из углов, а также длины двух сторон, образующих его, также позволяет рассчитать площадь.
TL; DR (слишком длинный; не читал)
Площадь разностороннего треугольника с основанием b и высотой h равна 1/2 bh. Если вам известны длины всех трех сторон, вы можете рассчитать площадь с помощью формулы Герона, не вычисляя высоту. Если вы знаете значение угла и длины двух сторон, которые его образуют, вы можете найти длину третьей стороны, используя закон косинусов, а затем использовать формулу Герона для вычисления площади.
Общая формула поиска области
Рассмотрим случайный треугольник. Можно начертить вокруг него прямоугольник, который использует одну из сторон в качестве своей основы (не имеет значения, какой именно) и просто касается вершины третьего угла. Длина этого прямоугольника равна длине стороны треугольника, которая его формирует, которая называется основанием ( b ). Его ширина равна расстоянию по перпендикуляру от основания до вершины, которое называется высотой ( х ) треугольника.
Можно начертить вокруг него прямоугольник, который использует одну из сторон в качестве своей основы (не имеет значения, какой именно) и просто касается вершины третьего угла. Длина этого прямоугольника равна длине стороны треугольника, которая его формирует, которая называется основанием ( b ). Его ширина равна расстоянию по перпендикуляру от основания до вершины, которое называется высотой ( х ) треугольника.
Площадь только что начерченного прямоугольника равна b × h . Однако, если вы изучите линии треугольника, вы увидите, что они делят пару прямоугольников, образованных перпендикулярной линией от основания до вершины, ровно пополам. Таким образом, площадь внутри треугольника составляет ровно половину площади вне его, или 1/2 bh . Для любого треугольника:
\ text {Area} = \ frac {1} {2} \ text {base} × \ text {height}
Формула Герона
Математики знают, как вычислить площадь треугольника с тремя известными за тысячелетия сторонами сторонами. Они используют формулу Герона, названную в честь Герона Александрийского. Чтобы использовать эту формулу, вам сначала нужно найти полупериметр ( s ) треугольника, что вы делаете, складывая все три стороны и деля результат на два. Для треугольника со сторонами a , b и c полупериметр
Они используют формулу Герона, названную в честь Герона Александрийского. Чтобы использовать эту формулу, вам сначала нужно найти полупериметр ( s ) треугольника, что вы делаете, складывая все три стороны и деля результат на два. Для треугольника со сторонами a , b и c полупериметр
s = \ frac {1} {2} (a + b + c)
Как только вы зная s , вы вычисляете площадь по следующей формуле:
\ text {Area} = \ sqrt {s (s — a) (s — b) (s — c)}
Используя закон косинусов
Рассмотрим треугольник с тремя углами A , B и C .Длина трех сторон: a , b и c . Сторона a находится под противоположным углом A , сторона b находится под противоположным углом B , а сторона c находится под противоположным углом C . Если вам известен один из углов — например, угол C — и две стороны, которые его образуют — в данном случае a и b — вы можете рассчитать длину третьего сторона, используя эту формулу:
c ^ 2 = a ^ 2 + b ^ 2 — 2ab \ cos (C)
После того, как вы узнаете значение c , вы можете рассчитать площадь с помощью формулы Герона.
Площадь треугольника — JavaTpoint
В этом разделе мы подробно изучим определение треугольника , типы треугольников, формулу площади треугольника , производные и , как найти площадь обучаемого , а также подробно рассмотрим примеры.
Треугольник
Треугольник — это многоугольник, имеющий три вершины и три ребра. Сумма трех внутренних углов составляет 180 градусов. Следующая диаграмма представляет собой треугольник.
Виды треугольника
Существует трех типов треугольников :
- Равносторонний треугольник
- Равнобедренный треугольник
- Чешуйчатый треугольник
Равносторонний треугольник
Равносторонний треугольник имеет три стороны равной длины и три равных угла. Каждый угол составляет 60 градусов. Он имеет три линии симметрии.
Равнобедренный треугольник
Равнобедренный треугольник имеет две стороны равной длины и два равных угла. У него одна линия симметрии.
У него одна линия симметрии.
Чешуйчатый треугольник
Разносторонний треугольник не имеет равных по длине сторон и равных углов. У него нет линии симметрии.
Площадь треугольника
Площадь треугольника — это область, покрытая треугольником. Площадь треугольника равна половине основания, умноженной на высоту перпендикуляра треугольника.
Если данный треугольник прямоугольный, перемножьте две стороны, которые примыкают к прямому углу.
Если данный треугольник не является прямоугольным, сначала найдите перпендикулярную высоту треугольника, опуская вертикальную линию вниз от наивысшей точки треугольника к основанию, как показано на следующем рисунке.
Формула площади треугольника
Две формулы используются для определения площади треугольника.
Это половина основания, умноженная на высоту. Приведенная ниже формула работает для всех треугольников.
Площадь треугольника (A) = bh
Где b обозначает основание , и h обозначают высоту данного треугольника.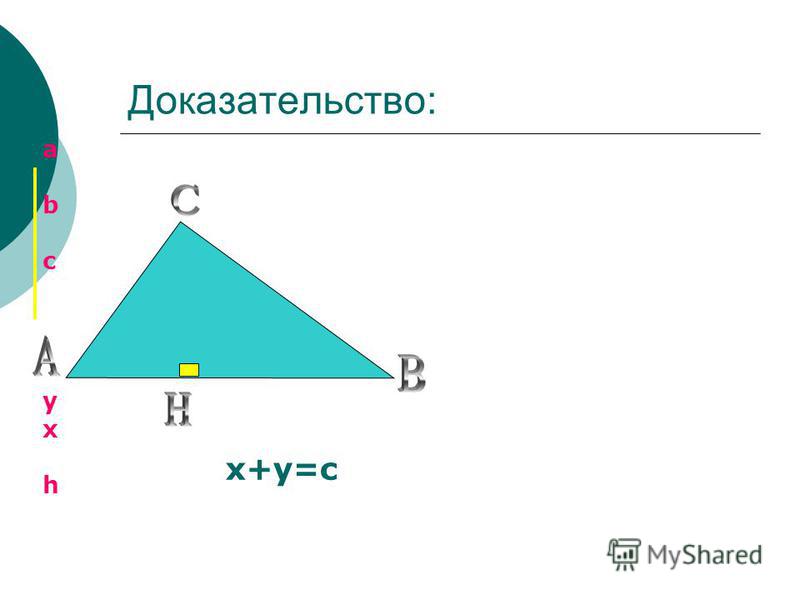
Примечание: мы можем выбрать любую сторону треугольника в качестве основы, но убедитесь, что высота измеряется под прямым углом к основанию.
Формула Герона
Формула Герона применяется, когда все три стороны треугольника заданы или три стороны не равны.
Он включает два важных шага:
Шаг 1: Сначала вычислите полупериметра (ов) , сложив длину трех сторон треугольника и разделив полученную сумму на 2.
полупериметр (ы) = (a + b + c) / 2
Где a, b, c — длина сторон.
Шаг 2: Примените полупериметр и три стороны a, b, c треугольника в формуле, чтобы найти площадь треугольника.
Площадь треугольника (A) = √ (s (s-a) (s-b) (s-c))
Мы также можем найти площадь треугольника, когда известны две стороны и угол. Но формула Герона там не работает.Формула зависит от того, какие стороны и углы указаны. Посмотрим формулы для разных сторон и углов.
- Когда даны стороны a, b и угол C , тогда формула для площади треугольника будет:
Площадь треугольника (A) = ½ ab sin C
- Когда даны сторон b, c, и угол A , тогда формула для площади треугольника будет:
Площадь треугольника (A) = ½ bc sin A
- Точно так же, когда даны сторон c, a, и угол B , тогда формула для площади треугольника будет:
Площадь треугольника (A) = ½ ca sin B
Площадь равностороннего треугольника
Равносторонний треугольник имеет три стороны равной длины.
Площадь равностороннего треугольника (A) = a 2
Где а — длина треугольника.
Площадь равнобедренного треугольника
Площадь равнобедренного треугольника (A) = ½ (основание × высота)
Вывод
Давайте разберемся, почему площадь треугольника составляет половину b * h.
- Нарисуйте треугольник с основанием b и высотой h, как показано ниже.
- Во вновь созданном треугольнике нарисуйте перпендикуляр.
- Вырежьте треугольник (желтую часть) и переместите его вправо, как показано на следующем изображении.
Мы видим, что треугольник теперь преобразован в прямоугольник. Мы знаем формулу площади прямоугольника:
Площадь прямоугольника (A) = длина * ширина
т.е. есть (b * h).
Основание, умноженное на высоту, в два раза больше площади треугольника (выделено синим цветом). Но нам нужно найти площадь треугольника i.е.
A = bh
Следовательно, площадь треугольника равна половине высоты основания *.
Следовательно, площадь треугольника равна половине высоты основания *.
Как найти площадь треугольника
Если указаны основание и высота
Пример 1. Найдите площадь треугольника высотой 20 см и основанием 15 см.
Решение:
Дано, база (b) = 15 см, высота (h) = 20 см.
Мы знаем,
Площадь треугольника (A) = ½ bh
Подставляя значения, получаем:
A = ½ 15 * 20
А = 150 кв.см.
Площадь треугольника 150 кв. См.
Пример 2: Найдите площадь треугольника, указанного ниже.
Решение:
Дано, основание (b) = 9 м, высота (h) = 13 м
Мы знаем,
Площадь треугольника (A) = ½ bh
Подставляя значения, получаем:
A = ½ 9 * 13
A = 58,5 м 2
Площадь треугольника 58.5 м 2 .
Пример 3: основание тупого треугольника составляет 6,6 дюйма, а высота — 14,7 дюйма. Найдите площадь треугольника.
Решение:
Учитывая, основание (b) = 6,6 дюйма, высота (h) = 14,7 дюйма
Мы знаем,
Площадь треугольника (A) = ½ bh
Подставляя значения, получаем:
A = ½ 6,6 * 14,7
A = 48,51 дюйма 2
Площадь треугольника 48. 51 дюйм 2 .
51 дюйм 2 .
Пример 4: Найдите площадь треугольника, указанного ниже.
Решение:
Из рисунка выше, база (b) = 177 см.
Примечание. Мы будем учитывать высоту, составляющую прямой угол основания, равную 100 см. Мы не будем считать 130 высотой, потому что это не прямой угол.
Мы знаем,
Площадь треугольника (A) = ½ bh
Подставляя значения, получаем:
A = ½ 177 * 100
A = 8850 кв.см
Площадь треугольника 8850 кв. См.
Если задана длина трех сторон
Пример 5: Найдите площадь треугольника, все стороны которого равны 7 см.
Решение:
Дано, a = 7 см, b = 9 см, c = 11 см
В этом вопросе дается длина всех трех сторон. Итак, применим формулу Герона.
Площадь треугольника (A) = √ (s (s-a) (s-b) (s-c))
Сначала мы рассчитаем полупериметр (ы).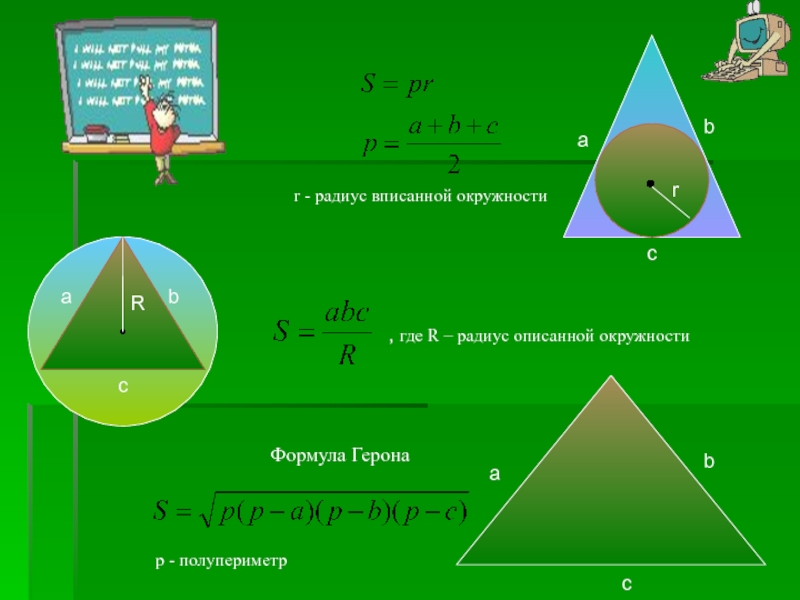
с = (7 + 9 + 11) / 2
s = 13,5 см
Подставляя значения в приведенную выше формулу, получаем:
A = √ (13,5 (13,5-7) (13,5-9) (13,5-11))
A = √ (13,5 (6,5) (4,5) (2,5))
А = √987.1875
A = 31,41 кв. См.
Площадь треугольника 31,41 кв. См.
Если задан SAS (боковой угол-сторона)
Пример 6: Найдите площадь треугольной площадки со стороной AB 125 м и стороной BC 220 м.Угол между AB и BC составляет .
Решение:
Сначала нарисуйте треугольник согласно заданной информации:
Дано, BC = a = 220 м, AB = c = 125 м и угол B = 123 °
Мы знаем,
Площадь треугольника (A) = ½ ac sin B
A = ½ (220 * 125) * (sin)
A = ½ (27500) * (0,83867)
A = ½ (23063.4407)
A = 11532 м 2
Площадь треугольника 11532 м 2 .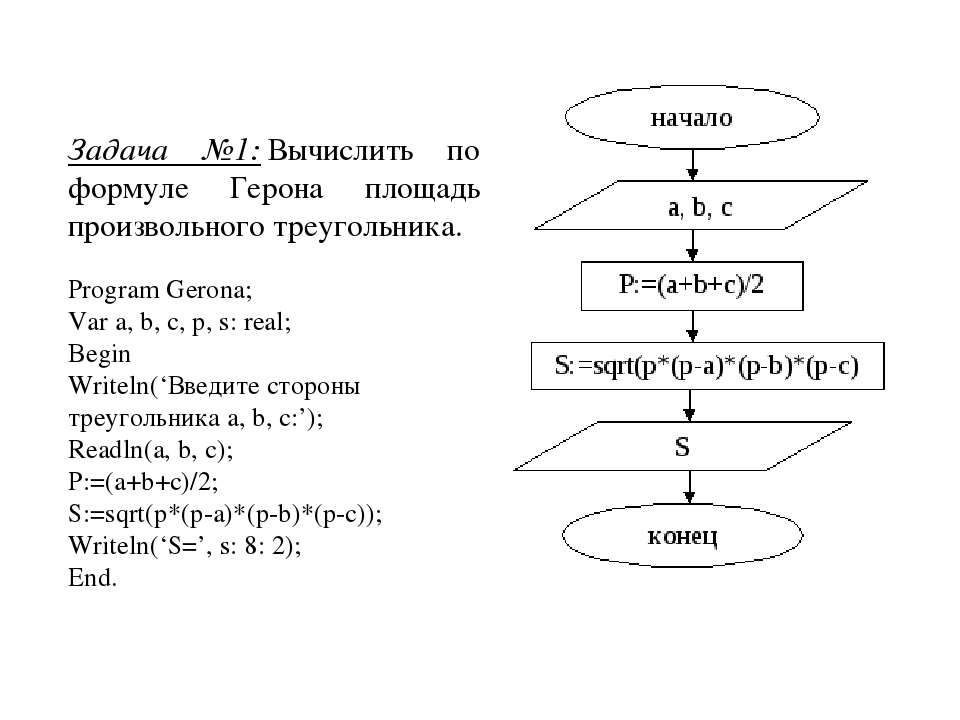
Пример 7: Найдите площадь треугольника, указанного ниже.
Решение:
Дано, CB = a = 9 см, AC = b = 14 см, а угол C равен 25 °
Мы знаем,
Площадь треугольника (A) = ½ ab sin C
A = ½ (9 * 14) * (sin 25 °)
A = ½ (126) * (0,42261)
A = ½ (53,24886)
A = 27 см 2
Площадь треугольника 27 см 2 .
Площадь равностороннего треугольника
Пример 8: В равностороннем треугольнике длина стороны десять см. Найдите площадь треугольника.
Решение:
Учитывая, a = 10 см
Нам известна формула площади равностороннего треугольника:
Формула Херона, решенные примеры и практические вопросы
Площадь треугольника : Треугольник — это правильный многоугольник с тремя сторонами. Это важная геометрическая форма, которая находит применение в различных областях науки и математики. Наряду с свойствами треугольников учащиеся должны знать формулу площади треугольника. Для вычисления площади треугольника существуют предопределенные формулы, которые меняются в зависимости от формы треугольника — его сторон и углов. Студентам полезно изучать и запоминать формулы треугольников в различных областях. Однако, обладая надлежащими знаниями о выводе формул, студенты могут легко запоминать и применять формулы.
Это важная геометрическая форма, которая находит применение в различных областях науки и математики. Наряду с свойствами треугольников учащиеся должны знать формулу площади треугольника. Для вычисления площади треугольника существуют предопределенные формулы, которые меняются в зависимости от формы треугольника — его сторон и углов. Студентам полезно изучать и запоминать формулы треугольников в различных областях. Однако, обладая надлежащими знаниями о выводе формул, студенты могут легко запоминать и применять формулы.
Как рассчитать площадь треугольника и какую формулу использовать — это наиболее распространенные вопросы, с которыми сталкиваются студенты при работе с треугольниками. Мы ответим на эти вопросы подробно.
Площадь треугольника: определение и типы
Треугольник — это замкнутая геометрическая фигура, имеющая три угла, три стороны и три вершины. Сумма трех углов треугольника составляет 180 °.
Существуют разные типы треугольников в зависимости от углов и сторон. По длине сторон треугольники бывают трех типов:
По длине сторон треугольники бывают трех типов:
- Масштабный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Исходя из внутренних углов, существует три типа треугольников:
- Острый треугольник
- Прямоугольный треугольник
- Тупоугольный треугольник
Давайте теперь посмотрим на формулы площади треугольника.
Формула площади треугольника: когда известны основание и высота
Треугольник можно представить как половину параллелограмма.Площадь треугольника определяется путем умножения основания треугольника и высоты треугольника, деленной на 2. Мы делим на 2, потому что треугольник является частью параллелограмма, который можно разделить на 2 треугольника.
Площадь треугольника = ½ x b x h
Давайте разберемся с площадью треугольника на примере:
Пример : Найдите площадь треугольника с основанием 10 см и высотой 15 см.
Решение : У нас есть площадь треугольника = ½ x основание x высота
Итак, подставив значения основания и высоты в приведенную выше формулу, мы получаем:
Площадь = ½ x 10 x 15
= 75
Следовательно, площадь треугольника 75 см 2 .
Формула для площади треугольника с тремя сторонами: Формула Герона
Когда мы знаем все три стороны треугольника, мы используем формулу Герона для вычисления площади. Для вычисления площади треугольника без высоты очень полезна формула Герона. Это двухэтапный процесс, который объясняется ниже:
Шаг 1 : Вычислите «s» — периметр треугольника, разделенный на 2.
$$ s = {{a + b + c} \ over 2} $$
Шаг 2: Затем вычислите площадь по формуле, приведенной ниже:
$$ Площадь = \ sqrt {s (s — a) (s — b) (s — c)} $$
Давайте разберемся с формулой Герона на примере:
Пример : Найдите площадь этого треугольника:
Решение: В этом примере у нас есть три стороны треугольника:
a = 7 см
b = 13 см
c = 14 см
Сначала мы вычисляем s, которое по формуле:
$$ s = {{a + b + c} \ over 2} = {{7 + 13 + 14} \ over 2} = {{34} \ over 2} = 17 $$
Теперь, используя формулу Герона, мы можем вычислить площадь этого треугольника.
$$ Площадь = \ sqrt {s (s — a) (s — b) (s — c)} $$
Подставляя значения s, a, b и c в приведенное выше уравнение, мы получаем:
$$ = \ sqrt {17 (17–7) (17–13) (17–4)} = \ sqrt {8840} = 94,021 $$
Следовательно, площадь треугольника 94,02 см 2 .
Формула площади треугольника, когда известны две стороны и входящий угол
Когда мы знаем две стороны и включенный угол (SAS) треугольника, есть другая формула (фактически три эквивалентные формулы) для вычисления площади.В зависимости от того, какие стороны и углы нам известны, площадь треугольника с использованием формулы синуса можно записать тремя способами:
$$ \ eqalign {
& Площадь = {1 \ более 2} ab \ sin C \ cr
& Площадь = {1 \ более 2} bc \ sin A \ cr
& Area = {1 \ over 2} ac \ sin B \ cr} $$
Давайте разберемся с этой формулой на примере:
Пример : В ∆ABC, A = 30 ° и b = 5, c = 4 в единицах. Какова площадь этого треугольника?
Решение : Площадь (∆ABC) = ½ bc sin A
= ½ (5) (4) sin 30
= 10 x ½ (поскольку sin 30 = ½)
= 5 кв. 2} — 2ab \ cos C $$
2} — 2ab \ cos C $$
Решенные примеры для области O f Формула треугольника
Здесь мы предоставили некоторые вопросы о площади треугольника вместе с решениями:
| Q1: Найдите площадь равнобедренного треугольника при b = 10 см и h = 15 см? A: Основание треугольника (b) = 10 см Высота треугольника (h) = 15 см Площадь равнобедренного треугольника = (1/2) × b × h = (1/2) × 10 × 15 = 5 × 15 = 75 см 2 |
| Q2: Найдите площадь разностороннего треугольника ABC со сторонами 8 см, 6 см и 4 см. A: a = 8 см b = 6 см c = 4 см Если указаны все стороны треугольника, используйте формулу Герона. Площадь треугольника = $$ \ sqrt {s (s — a) (s — b) (s — c)} $$ Теперь найдите значение полупериметра s = (a + b + c) / 2 = (8 + 6 + 4) / 2 = 18/2 s = 9 Теперь подставьте значение s в формулу площади, Area = $$ \ sqrt {9 (9-8) (9-6) (9–4)} = \ sqrt {9 (1) (3) (5)} = \ sqrt {135} $$ = 11,6 Следовательно, площадь разностороннего треугольника = 11.6 см 2 . |
| Q3: Найдите площадь равностороннего треугольника с периметром 12 см. A: Периметр равностороннего треугольника = 12 см По формуле: Периметр равностороннего треугольника = 3a, где «a» — сторона равностороннего треугольника. Шаг 1: Найдите сторону равностороннего треугольника по периметру. 3a = 12 a = 4 Таким образом, длина стороны 4 см. Шаг 2: Найдите площадь равностороннего треугольника по формуле: Площадь, A = √3 a 2 /4 квадратных единицы = √3 (4) 2 /4 см 2 = 4√3 см 2 Следовательно, площадь данного равностороннего треугольника равна 4√3 см 2 |
Практические вопросы по площади треугольника
Вот несколько важных вопросов о площади треугольника для вашей практики:
Вопрос 1 : Найдите площадь остроугольного треугольника с основанием 10 дюймов и высотой 8 дюймов.
Вопрос 2 : Найдите площадь прямоугольного треугольника с основанием 5 см и высотой 6 см.
Вопрос 3 : Найдите площадь тупоугольного треугольника с основанием 6 см и высотой 8 см.
Вопрос 4 : Найдите площадь равностороннего треугольника со стороной 9 см.
Вопрос 5 : Найдите площадь, высоту и периметр равнобедренного треугольника при a = 4 см (длина двух равных сторон), b = 10 см (основание).
Часто задаваемые вопросы
Вот некоторые из часто задаваемых вопросов о формуле для площади треугольников:
Q1: Какова формула площади треугольника?
A: Площадь треугольника определяется как область, занимаемая внутри границы этого треугольника.Формула для вычисления площади треугольника определяется следующим образом: 1/2 x b x h, где b — основание, а h — высота.
Q2: Как определить площадь неправильного треугольника?
A: Площадь неправильного треугольника определяется по формуле Герона, если известны все стороны. Если мы знаем основание и высоту неправильного треугольника, формула будет 1 / 2bh.
Q3: Что означает «s» в треугольнике?
A: s — это не что иное, как половина периметра.Когда мы делим периметр треугольника на 2, мы получаем значение s.
Q4: Как определить площадь тупого треугольника?
A: Тупой треугольник — это треугольник, угол одного угла которого превышает 90 градусов. Формула для вычисления площади такого треугольника такая же, как 1 / 2bh.
Q5: Как с помощью Герона найти площадь треугольника?
A: Формула Герона используется для вычисления площади треугольника, все три стороны которого известны.Подробное объяснение того, как использовать формулу Герона, представлено на этой странице.
Q6: Какова площадь прямоугольного треугольника?
A: Площадь прямоугольного треугольника определяется по формуле: 1/2 x b x h, где b — основание, а h — высота треугольника. Если мы не знаем ни одного из этих параметров, мы можем использовать для расчета теорему Пифагора.
Связанные понятия :
Мы надеемся, что эта подробная статья о формуле площади треугольника вам поможет.0,5
, где s — половина периметра (эмпериметр s ).
Формула
Герона — одно из самых элегантных решений для определения площади треугольника, не содержащего прямого угла.
(Для треугольников с прямым углом или известной высотой можно использовать более простой калькулятор по теореме Пифагора.)
Формула Герона работает с любым треугольником, длина каждой стороны которого известна. В формуле Герона и многих других стороны треугольника обычно обозначаются буквами a, b, c.Все остальные переменные в формуле рассчитываются на основе этих трех измерений.
Как вычислить «s»
Для решения формулы Герона требуется один вычисляемый член, это половина периметра или полупериметр , обычно обозначаемый как « s ». Не волнуйтесь, для расчета полупериметра требуются только три длины стороны. Как следует из названия, расчет включает уменьшение вдвое суммы длин трех сторон.
В этом примере полупериметр рассчитывается для образца треугольника с длинами сторон 3, 4, 5.0,5
Что означает ответ «0»?
Если калькулятор дает ответ ноль (0), это означает, что результирующая область слишком мала, чтобы ее можно было сообщить на уровне точности ввода. Регулировка точности в раскрывающемся меню позволит отображать больше десятичных знаков, и вы можете получить ответ. Однако, если бы вы визуализировали этот треугольник, он бы выглядел очень тонким, а область незаметно мала или, возможно, даже не существовала. Попробуйте вычислить треугольник со стороной 1, 2, 3.Результат равен нулю, потому что полученный треугольник не имеет площади, это просто набор перекрывающихся линий!
Что означает ответ «NaN»?
Ответ «NaN», вероятно, означает, что длина вашей входной стороны не может образовывать треугольник. Если одна сторона слишком велика по сравнению с длиной двух других сторон, замкнутый многоугольник не будет сформирован, и расчет не удастся. Ни одна сторона не может быть больше суммы двух других сторон (это не будет треугольник, многоугольник не будет замкнутым)!
Площадь треугольника
Площадь треугольника , формулы для расчета площади различных типов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и таблица с формулами площадей для треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисление (показано)
(скрыта)
— примечания (показаны)
(скрыта)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона а
Высота h
Основание треугольника можно выбрать с любой стороны треугольника.
2
Площадь двух сторон треугольника и угол между ними
Сторона а
Сторона b
Угол α ° между сторонами а и б
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трех сторон
Сторона а
Сторона b
Сторона c
Радиус r вписанный круг
4
Площадь треугольника по радиусу описанной окружности и трех сторонам
Сторона а
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона b
Сторона c
6
Площадь произвольного треугольника сбоку и двух смежных углов
Сторона а
Угол β °
Угол α °
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по сторонам и основанию
Сторона а (а = б)
Сторона c
8
Площадь равнобедренного треугольника по сторонам и угол между ними
Сторона а (а = б)
Угол α ° между сторонами
9
Площадь равнобедренного треугольника сбоку, в основании и угол между ними
Сторона а (а = б)
Основание треугольника c
Угол β ° между основанием и стороной
10
Площадь равнобедренного треугольника в основании и угол между сторонами
Основание треугольника c
Угол α ° между сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника сбоку
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанный круг
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Квадрат прямоугольного треугольника с двумя ножками
Катет а
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника, образованного катетом и углом
Сторона b
Угол α
19
Площадь прямоугольного треугольника вдоль отрезков, делящих гипотенузу на вписанную окружность
Отрезок линии d
Сегмент линии e
20
Площадь прямоугольного треугольника, проходящего через гипотенузу и вписанную окружность
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона b
Сторона c
Наш калькулятор для расчета площади поможет вам рассчитать площади треугольников разного типа или проверить уже выполненные расчеты.
В зависимости от известных входных данных для вычисления площади треугольника используются различные формулы. Выше приведены формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные расчеты. Общие формулы даны для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
В зависимости от типа треугольника и известных исходных данных площадь треугольника может быть вычислена с использованием различных формул.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это числовая характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя сегментами (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой.
Треугольник — это геометрическая фигура, образованная тремя сегментами, соединяющими три точки, не лежащие на одной прямой.Отрезки называются сторонами треугольника, а точки — вершинами треугольника.
Площадь — числовая характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т. Д.
Скачать формулы площади треугольника как картинку
Формула Херона: формула цапли
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Формула Геронов (Формула Героя):
Герон дал знаменитую формулу для определения площади треугольника через его три стороны. Формула Геронов названа в честь Героя Александрии. Используется, когда указаны все три стороны и нет высоты или высоты. Формула Героя приведена ниже:
Где
— это полупериметр ΔABC. Примечание: Это применимо ко всем типам треугольников, будь то прямоугольный, равносторонний или равнобедренный треугольник. Некоторые решенные примеры:
1) Найдите площадь треугольника со сторонами 13 см, 14 см и 15 см.
Решение:
a = 13 см, b = 14 см и c = 15 см.
∴ s = (a + b + c) / 2
s = (13 + 14 + 15) / 2 = 21 см.
По формуле Герона
Площадь = √ (21 x 8 x 7 x 6)
Площадь = √ (7 x 3 x 4 x 2 x 7 x 2 x 3)
Площадь = √ (7
2 x 2 2 x 2 2 x 3 2 )
Площадь = 7 x 2 x 2 x 3
Площадь = 84 см
2
_________________________________________________________________
2) Периметр треугольного поля составляет 450 м, а его стороны находятся в соотношении 13: 12: 5.Найдите площадь треугольника.
Решение:
Дано, что стороны a, b, c треугольника находятся в соотношении 13: 12: 5
⇒ a: b: c = 13: 12: 5 ⇒ a = 13x, b = 12x и c = 5x
Периметр треугольного поля = 450 м
⇒ 13 x + 12x + 5x = 450
⇒ 30x = 450
∴ x = 15
∴ с каждой стороны, a = 13 x 15 = 195 м; b = 12 x 15 = 180 м
и c = 15 x 5 = 75 см.
По формуле Герона
Площадь = √ (225 x 30 x 45 x 150)
Площадь = √ (45 562 500)
Площадь = 6750 м 2
_________________________________________________________________
3) Табло светофора с надписью равносторонний треугольник со сторонами «а».Найдите площадь сигнального табло по формуле Герона. Если его периметр 180 см. Какой будет площадь сигнального табло?
Решение:
Периметр = 180
a + a + a = 180
3a = 180
a = 60 см
s = полупериметр = Периметр / 2
s = 180/2 = 90 см
По формуле Херона
Площадь = √ (90 x 30 x 30 x 30)
Площадь = √ (2,430,000)
Площадь = 1558,85 см 2
_________________________________________________________________
Некоторые приложения формулы Герона
Формула Герона может использоваться для найти площадь неправильного четырехугольника, если заданы все его стороны.Для этого мы можем преобразовать этот четырехугольник в треугольники, а затем применить формулу Герона.
Решенные примеры:
1) Найдите площадь четырехугольника ABCD, в котором AB = 7 см, BC = 6 см,
CD = 12 см, DA = 15 см и AC = 9 см.
Решение:
Для ΔABC
s = (a + b + c) / 2 = (6 + 7 + 9) / 2 = 22/2 = 11 см
По формуле Герона
Площадь ΔABC = √ (11 x 5 x 4 x 2)
⇒ Площадь ΔABC = √ (440)
⇒ Площадь ΔABC = 20.98 см 2
Для ΔACD,
s = (9 + 12 + 15) / 2 = 36/2 = 18 см
По формуле Цапля
∴ Площадь ΔACD = √ (18 x 9 x 6 x 3)
⇒ Площадь ΔACD = √ (2916)
⇒ Площадь ΔACD = 54 см 2
Следовательно, площадь четырехугольника ABCD = Площадь ΔABC + Площадь ΔACD
= 20,98 + 54
∴ Площадь четырехугольника = 74,98 см 2
_________________________________________________________________
2) Зонт изготавливается путем сшивания 10 треугольных кусков ткани двух разных цветов: красного и синего.Каждая деталь имеет размер 20 см, 50 см и 50 см. Сколько ткани каждого цвета потребуется для зонта?
Решение:
Стороны треугольной ткани: a = 20 см, b = 50 см и c = 50 см
s = (20 + 50 + 50) / 2 = 60 см
По формуле Герона,
∴ Площадь треугольника = √ (60 x 40 x 10 x 10)
⇒ Площадь = √ (240,000)
⇒ Площадь = 489,89 ком 2
∴ Площадь каждого цвета = 5 x 489,89 = 2,449,48 см 2
Измерение: площадь и периметр
• Периметр и площадь неправильной формы
• Площадь и периметр прямоугольника
• Площадь квадрата (периметр квадрата)
• Периметр параллелограмма (площадь параллелограмма)
• Площадь Ромб (периметр ромба)
• Площадь трапеции (трапеция)
• Площадь треугольника (периметр треугольника)
• Формула Цапли
От формулы Херона до страницы измерения
От формулы Херона на главную страницу
Covid-19 повлиял на физический взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Площадь треугольника — координатная геометрия | Класс 10 по математике
Координатная геометрия определяется как изучение геометрии с использованием координатных точек на плоскости с любым размером. Используя координатную геометрию, можно найти расстояние между двумя точками, разделить линии в соотношении, найти среднюю точку линии, вычислить площадь треугольника в декартовой плоскости и т. Д.
Существуют различные методы для Найдите площадь треугольника в соответствии с заданными параметрами, такими как основание и высота треугольника, координаты вершин, длина сторон и т. д.Ниже приведены 3 таких метода определения площади треугольника.
Метод 1: Использование основания и высоты треугольника
Когда заданы основание и высота треугольника, мы будем использовать этот метод, и этот метод является самым простым из всех методов. Для данного треугольника, если высота треугольника составляет « h », а основание треугольника — « b », то площадь треугольника задается как:
Вывод формулы
Шаг 1: Рассмотрим прямоугольный треугольник ABC.
Шаг 2: Теперь проведите горизонтальную линию из точки A и вертикальную линию из точки C. Пусть точка будет D, где обе линии пересекаются.
Шаг 3: Фигура будет выглядеть примерно как прямоугольник, т.е. если мы добавим 2 одинаковых треугольника, то будет сгенерирован прямоугольник.
Шаг 4: Поскольку нам нужна площадь треугольника ABC, мы можем записать ее как (площадь прямоугольника ABCD / 2).
Шаг 5: Продолжение 4-го шага:
=> Площадь ABC = (площадь прямоугольника ABCD / 2)
=> Площадь ABC = (b × h) / 2
Следовательно, доказано эта площадь треугольника равна (1/2) × b × h
Примеры задач по формуле
Пример 1: Найдите площадь треугольника, высота и основание которого равны 6 см и 5 см?
Решение: В вопросе четко указано, что высота и основание равны:
Учитывая, h = 6 и b = 5
Площадь треугольника задается как = (1/2) × b × h
=> (1/2) × 6 × 5
=> 3 × 5 = 15
Следовательно, площадь данного треугольника равна 15 см 2
Пример 2: Найти высота треугольника, площадь которого 12 см 2 , а основание 6 см?
Решение:
Дано, площадь = 12 и b = 6
Площадь треугольника = (1/2) × b × h
=> 12 = (1/2) × 6 × h
=> h = 12/3 = 4
Следовательно, высота данного треугольника равна 4 см.
Метод 2: Использование формулы Герона
Когда не указаны ни основание, ни высота треугольника, мы можем использовать формулу Герона, если стороны треугольника заданы.
Если a, b, c — стороны треугольника, то площадь треугольника определяется как:
Вывод формулы
Шаг 1: Как известно, полупериметр s = (a + b + c) / 2
=> 2s = a + b + c
=> 2s — 2a = a + b + c — 2a [вычитая обе части 2a]
=> 2 (s — a) = b + c — a ————— 1
Аналогично,
=> 2 (s — b) = c + a — b ————— 2
=> 2 (s — c) = a + b — c ————— 3
Мы будем использовать эти соотношения позже при выводе.
Шаг 2: Теперь давайте возьмем разносторонний треугольник со сторонами a, b, c
Шаг 3: Поскольку у нас нет высоты или высоты треугольника, нарисуйте перпендикуляр из A на BC в D, и основание будет ‘a’.
Шаг 4: Теперь, если мы ясно заметим, образовались два треугольника: ∆ ABD и ∆ ADC . И если длина BD равна d, то длина DC будет a — d.
Шаг 5: Теперь в треугольнике ABD, по теореме Пифагора
=> h 2 = c 2 — d 2 ——————– 4
Аналогично в ∆ADC
=> h 2 = b 2 — (a — d) 2
Из уравнения 4 подставьте значение h 2
=> c 2 — d 2 = b 2 — (a — d) 2
=> c 2 — d 2 = b 2 — (a 2 + d 2 — 2ad)
После упрощения уравнения мы получим,
d = (c 2 + a 2 + b 2 ) / 2a
Теперь подставим указанное выше значение в уравнение 4
=> h 2 = c 2 — [(c 2 + a 2 + b 2 ) / 2a] 2
=> h 2 = (c — {(c 2 + a 2 + b 2) ) / 2a}) (c + {(c 2 + a 2 + b 2 ) / 2a}), потому что [a 2 — b 2 = (a + b) (a — b )]
=> h 2 = (1 / 4a 2 ) [b 2 — (a — c) 2 ] [(a + c) 2 — b 2 ]
=> h 2 = (1 / 4a 2 ) [(b — a + c) (b + a — c) (a + c — b) (a + b + c)], потому что [a 2 — b 2 = (a + b) (a — b)]
Из уравнений 1, 2 и 3 заменяется в уравнение выше
=> h 2 = (1 / 4a 2 ) [ 2 (s — a) × 2 (s — b) × 2 (s — c) × 2s]
=> h 2 = (4 / a 2 ) [s (s — a) (s — b) (s — c)]
=> h = (2 / a) √ [s (s — a) (s — b) (s — c)] ————– 5
Шаг 6 : Из метода 1 мы знаем, что если даны основание и высота треугольника, то площадь треугольника равна (основание × высота) / 2.Теперь подставьте высоту в эту формулу
=> площадь ABC = (1/2) × a × (2 / a) √ [s (s — a) (s — b) (s — c)]
После упрощение
=> площадь ABC = √ [s (s — a) (s — b) (s — c)]
Таким образом, формула цапли для площади треугольника доказана.
Примеры задач по формуле Герона
Пример 1: Если стороны треугольника равны 3 см, 4 см и 5 см, найдите площадь треугольника.
Решение:
Пусть a = 3, b = 4 и c = 5
Сначала мы должны найти полупериметр
=> s = (a + b + c) / 2
= > s = (3 + 4 + 5) / 2
=> s = 12/2 = 6
Как мы знаем, формула цапли √ [s (s — a) (s — b) (s — c)] , подставляя в него значения
=> √ [s (s — a) (s — b) (s — c)]
=> √ [6 (6 — 3) (6 — 4) (6 — 5 )]
=> √ [6 × 3 × 2 × 1]
=> √36 = 6
Площадь треугольника составляет 6 см 2
Пример 2: Использование формулы Герона выведите формулу, чтобы найти площадь равностороннего треугольника со стороной
Решение:
Чтобы найти полупериметр
=> s = (a + b + c) / 2
=> s = (a + a + a) / 2
=> s = 3a / 2
Теперь используя формулу цапли
=> √ [s (s — a) (s — b) (s — c)]
=> √ [( 3a / 2) ((3a / 2) — a) ((3a / 2) — a) ((3a / 2) — a)]
=> √ [(3a / 2) (a / 2) (a / 2) (a / 2)]
=> √ (3a 4 /16)
=> √3 (a 2 ) / 4
Следовательно, площадь равностороннего треугольника составляет √3 (a 2 ) / 4
Метод 3: Использование координат вершины
В предыдущих методах мы видели разные условия, в методе 3, если заданы координаты треугольника, мы увидим, как найти площадь треугольника.
Если координаты треугольника (x1, y1), (x2, y2) и (x3, y3), то площадь треугольника определяется как
Вывод формулы
Шаг 1: Нарисуйте перпендикуляры от координат P, Q и R к оси X в точках A, B и C соответственно.
Шаг 2: Теперь, если мы внимательно посмотрим на рисунок, в координатной плоскости формируются три разные трапеции, такие как PQAB, PBCR и QACR.
Шаг 3: Таким образом, площадь ∆QPR рассчитывается как
Площадь ∆PQR = [Площадь трапеции PQAB + Площадь трапеции PBCR] — [Площадь трапеции QACR] —- (1 )
Шаг 4: Теперь вычисляем площади всех 3 трапеций.
Т.к. Площадь трапеции = (1/2) (сумма параллельных сторон) × (расстояние между сторонами)
Нахождение области трапеции PQAB
=> Площадь трапеции PQAB = (1/2) (QA + PB) × AB
=> QA = y2
=> PB = y1
=> AB = OB — OA = x1 — x2
=> Площадь трапеции PQAB = (1 / 2) (y1 + y2) (x1 — x2) —- (2)
Нахождение области трапеции PBCR
=> Площадь трапеции PBCR = (1/2) (PB + CR) × BC
=> PB = y1
=> CR = y3
=> BC = OC — OB = x3 — x1
=> Площадь трапеции PBCR = (1/2) (y1 + y3) (x3 — x1) —- (3)
Нахождение области трапеции QACR
=> Площадь трапеции QACR = (1/2) (QA + CR) × AC
=> QA = y2
= > CR = y3
=> AC = OC — OA = x3 — x2
=> Площадь трапеции QACR = (1/2) (y2 + y3) (x3 — x2) —- (4)
Шаг 5: Подставляя (2), (3) и (4) в (1),
=> Площадь ∆PQR = (1/2) [( y1 + y2) (x1 — x2) + (y1 + y3) (x3 — x1) — (y2 + y3) (x3 — x2)]
=> Площадь ∆PQR = (1/2) | [x1 (y2 — y3) + x2 (y3 — y1) + x3 (y1 — y2)] |
Следовательно, это формула для определения площади треугольника, если указаны координаты.
Примечание: Обратите внимание, что есть модификация, которая указывает, что если мы получили отрицательное значение, мы должны рассматривать только числовое значение, так как площадь не может быть отрицательной.
Примеры задач по формуле
Пример 1: Какова площадь ∆ABC, вершинами которой являются A (1, 2), B (4, 2) и C (3, 5)?
Решение:
Во-первых, давайте нарисуем диаграмму для лучшего понимания.
Теперь сравниваем заданные координаты с (x1, y1), (x2, y2) и (x3, y3).
Пусть, (x1, y1) = (1, 2)
=> (x2, y2) = (4, 2)
=> (x3, y3) = (3, 5)
Сейчас мы должны подставить значения в (1/2) [x1 (y2 — y3) + x2 (y3 — y1) + x3 (y1 — y2)]
=> (1/2) [1 (2 — 5) + 4 (5 — 2) + 3 (2 — 2)]
=> (1/2) [(- 3) + 12 + 0]
=> (1/2) [9] = 4,5
Следовательно, площадь треугольника составляет 4,5 кв. Единиц
Пример 2: Каково значение x1, площадь треугольника которого равна единице координат (x1, 1), (2, 3), и (4, 5)?
Решение:
Во-первых, давайте нарисуем диаграмму для лучшего понимания.
В этой задаче мы должны найти значение ‘x1’, которое является координатой X точки A.
Дано, что площадь треугольника равна 1.
Теперь сравнивая заданные координаты с ( x1, y1), (x2, y2) и (x3, y3).
Пусть, (x1, y1) = (x1, 1)
=> (x2, y2) = (2, 3)
=> (x3, y3) = (4, 5)
Сейчас мы должны подставить значения в (1/2) [x1 (y2 — y3) + x2 (y3 — y1) + x3 (y1 — y2)]
=> (1/2) [x1 (3 — 5) + 2 (5 — 1) + 4 (1-3)] = 1
=> (1/2) [x1 (- 2) + 8 + -8] = 1
=> -x1 = 1
=> x1 = ± 1 квадратная единица.
Следовательно, значение x1 может быть как -1 , так и 1
Внимание, читатель! Не прекращайте учиться сейчас.


